Preprint
Article
Integration of Land-Use Potential in Energy System Optimization Models at Regional Scale: The Pantelleria Island Case Study
Altmetrics
Downloads
116
Views
58
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
03 January 2024
Posted:
04 January 2024
You are already at the latest version
Alerts
Abstract
In the context of the energy transition, the integration of land use considerations into energy planning is increasingly vital, especially in scenarios where land availability is a constraint. This study addresses the challenge of incorporating land-use aspects into Energy System Optimization Models (ESOMs), with a focus on the unique context of Pantelleria Island. It aims to bridge the gap in methodologies for renewable energy potential assessment and model integration, considering the critical role of land pricing and availability. It combines geospatial data aggregation with model adaptation to include detailed land use aspects. Findings highlight the substantial impact of land costs on renewable energy planning, with land pricing significantly altering model outcomes. This research offers key insights for sustainable energy planning and underscores the importance of considering land use in energy transition strategies.
Keywords:
Subject: Environmental and Earth Sciences - Sustainable Science and Technology
1. Introduction
The sharp rise in temperatures from pre-industrial levels caused by climate change is leading to a paradigm shift in the use of energy all sectors of the economy[1]. The typical mitigation strategy applied by most international authorities is represented by the reduction of the greenhouse gas emission footprint for all the energy intensive sectors [2]. Typically, the decarbonization practice in any sectors requires the replacement of its primary inputs with carbon-free alternatives, changing both production processes and involved technologies [3]. Among all the others, the power sector is found to be the major decarbonization player in the next decades [4]. Indeed, to further decarbonize the electricity sector and reach a net-zero energy system by 2050. a mix of increasingly affordable and mature VRE technologies, mainly solar photovoltaic (PV) and onshore wind turbines, will need to be deployed [5].
In this context, the importance of informed energy models play a crucial role. Several tools are available to evaluate the possible energy system evolution considering the expected energy transition with different sectorial coverage, time horizon and time steps, spatial scales and modeling methods [6]. For instance, Energy System Optimization Models (ESOMs) are characterized by a detailed techno-economic description of the main technologies (or processes) belonging to the most energy-intensive sectors of the system. For this reason, they are typically used to suggest possible optimal future evolution of the energy and technology mix over the long run, according to alternative socio-economic and policy scenarios [7]. They are optimization models evaluating the minimum-cost configuration of the system [8], according to the studied scenario and to the technology modules included in the model. Because of such features, ESOMs have been widely used to assess the effects of decarbonization strategies or innovative technologies on several sectors of the economy, focusing on several sectors (i.e., transport [9], industry [10], hydrogen [11]) and regions (e.g., Belgium [12], US [13], EU [14], World [15,16]) .
In the transition from a fossil-based to a renewable-based energy system there are, however, new challenges that traditional ESOMs are not yet able to address [17]. Among the others, Variable Renewable Energy Sources (VRES) are mainly characterized by intensive land-use and variable production [18]. In existing ESOMs, location-specific VRES production profiles are often used to estimate VRES potential, but land-use and land cover aspects have been largely ignored [19], with a consequent lack in the optimization result. In fact, the location of suitable sites to place a renewable energy plant (considering the physical and atmospheric parameters that determine its performance) may not coincide with the availability of electrical infrastructure [20]. Then, the land use of a specific site may be constrained by many factors (e.g., administrative, technical, economic) that limits the possibility of plants in a specific region [21]. Technical constraints encompass existing renewable energy facilities and areas with limited natural wind or solar resources [21]. Regulatory and environmental restrictions, considering local community concerns regarding land usage, can also curtail the available land for renewable energy projects [21]. All these limitations must be accounted for when assessing trade-offs and obstacles regarding land availability. Last but not least, the optimal land allocation should consider all the different multi-sectoral use options for that specific site, including not only its energy use, but also the agricultural use [22]. To illustrate better the above-mentioned points, at European level the land requirements to meet wind and photovoltaic solar capacity targets are substantial. In France, Germany, and Italy, where approximately 50% of the EU's renewable energy installations are anticipated, achieving the renewable capacity objectives for 2040 would necessitate an additional 23,000 to 35,000 square kilometers of additional land, equivalent in size to Belgium [23]. All these factors give rise to two primary challenges in the current energy models: the accessibility of information concerning renewable resource potential and land availability (assessment phase) [20], and the incorporation of such information into ESOMs to facilitate the decision-making process (integration phase)[20].
In the assessment phase, the Land Eligibility (LE) analysis comes before the VRES potential estimation [24]. The former refers to the identification of sites available for renewable capacity installations, while the latter provides energy potential estimation. Examples of LE analyses in the literature are common (as analyzed in the review of Ryberg et.al [21], covering more than 50 works). Although the examples therein operate in differing geographical scopes, the LE has been used in all cases to determine the locations available for either onshore wind turbines or open-field PV parks. A major attempt in unifying the way LE is evaluated is performed in GLAES tool (Geospatial Land Availability for Energy Systems) [21]. For the VRES potential assessment, several raw data sources are available and have been listed in a rigorous analysis in [25]. In this study, a repository of all the well-established sources classified by temporal and spatial resolution is proposed, encompassing all the existing renewable energy sources. Maclaurin et.al [26] developed The Renewable Energy Potential (reV) model, a platform for the detailed assessment of renewable energy resources and their geospatial intersection with grid infrastructure and land use characteristics. Moreover, there exist a recent attempt to incorporate all these VRES potential estimation in a unique versatile tool [27]. Such framework, called “at-lite”, retrieves global historical weather data, and converts it into power generation potentials and time series for VRES technologies like wind and solar power.
Diving in the integration phase of land availability and VRES potential into ESOMs, Stolten et al. in [24] have already demonstrated the benefits of spatial explicitness in energy planning. In their work, they used region clustering based on energy potential characteristics and find that increasing spatial resolution improves model accuracy. However, they also note a saturation effect of this benefit at higher resolutions and emphasize the importance of considering both time and spatial resolution to increase accuracy. A remarkable limitation of the study is the spatial scope given the focus on the whole European area. Indeed, as confirmed by Frysztacki et.al. ([28,29]), modelling a fully renewable European electricity system, even at a resolution of one node per country is insufficient to retrieve reliable capacity expansion suggestions. Other attempts at a lower spatial scale have been conducted. A comprehensive review on the topic of spatial resolution in ESOMs is performed in [30] by analyzing 36 multi-sectoral ESOMs from 22 countries, with varying levels of spatial and temporal resolution. The analysis demonstrate to what extent higher spatial resolution impacts the outcomes of energy system analysis. They observed that: (1) Fine-grained spatial resolution in ESOMs provides significant added value for regions with heterogeneous renewable potential or higher variability in energy services. (2) Spatially resolved models can significantly alter the scenario outcomes, particularly in scenarios with high shares of variable renewable energy sources. (3) Disaggregating renewable resources tends to reduce costs. Exploring smaller spatial scales, however, a lack of relevant works is highlighted.
Up to this point, the purpose of the integration phase for the selected studies is to provide better planning solution, generally reflected in minor system cost. But there is another area where land specific consideration may help. Notably, together with the cost, also the problem of optimal siting of renewable energy must be addressed [31]. There are two main reasons behind this need. First, trade-offs exist between the land use for energy and other land uses (e.g., agriculture, afforestation) [25] that must be evaluated as a function of the site where plants are installed. Second, the role of ESOM should not be limited to quantify the necessary capacity, but also to inform about where to install it, exploiting the potential of a region. Indeed, the optimal siting of energy plants can be viewed as a consequential aspect of the broader economic optimization process within the ESOM. In the pursuit of cost minimization, pinpointing the most suitable locations for these plants emerges as a pivotal sub-product.
In the depicted context, this study addresses three key questions:
1) Is it possible/easy to integrate spatially explicit considerations in ESOMs, and how much open-source available packages help in this practice?
2) Does explicitly spatial energy planning provide added value, when performed at a small spatial scale?
3) How is it possible to quantify the added value introduced by an explicitly spatial planning approach?
Our analysis aims to test and quantify how many and which characteristics of the land and land use can improve planning solutions within an ESOM, with reference to a test case corresponding to a small spatial scale. This study particularly focuses on small remote islands, which are often not connected to national power grids, as they offer an appropriate case study for the above issues, considering their significant landscape heritage and limited land availability [26].
2. Materials and Methods
This section details the methodology and the materials employed to answer the research questions formulated in the introduction. The description of the steps follows a chronological order that led to the achievement of the research objectives. It begins by defining the case study and introducing the energy model used to address the case, namely TEMOA (Tool for Energy Model Optimization and Analysis, Section 2.1). Next, the Geospatial Information Systems (GIS) and sources used in the analysis are briefly described (Section 2.2 and 2.3). As highlighted above, the coupling of land use data in energy models is divided into two main steps: the data gathering of renewable resource potential and land availability (assessment phase, Section 2.4 and 2.5), and the incorporation of such information into the selected modelling instance (integration phase, Section 2.6 and 2.7).
2.1. Modelling framework
In this paper, the TEMOA [32] ESOM has been selected, motivated by several key points:
- Open Source: TEMOA is open source, providing the transparency and customization needed for research. TEMOA's code is written in Python and optimized in Pyomo, a Python library for optimization, so it has no accessibility constraints.
- Similarity to other Models: The TEMOA model formulation is similar to the model generators MARKAL/TIMES [8,33], MESSAGE [34,35], and OSeMOSYS [36], Such tools, already commonly used in energy planning (e.g., MESSAGE in Syria [35], OSeMOSYS in Colombia [37] , TEMOA-US [38]. Moreover, TEMOA is a validated tool which convergence with the well-established TIMES framework has already been demonstrated in an Italian modeling instance [39].
The central component of the TEMOA framework is a technology-explicit description of the energy system model [40]. The goal of the model is to minimize the current cost of energy supply by distributing and utilizing energy processes and feedstocks over time to meet a set of exogenously specified end-use demands. The energy system is described algebraically as a network of linked processes that convert energy feedstocks (e.g., coal, oil, biomass, uranium, sunlight) into end-use demands (e.g., lighting, transportation, water heating) through a series of one or more intermediate energy forms (e.g., electricity, gasoline, ethanol). The system consists of three demand-side sectors (buildings, transportation, industry…)) and supply-side sectors (as the upstream and the energy sector) [40]. While the demand sectors consume energy to meet the final demand for energy services, the supply sectors produce the energy products consumed by the demand side (i.e.: fossil fuels, primary renewable potential, electricity, and heat) [40].
For the correct description and optimization of the energy system, a complete energy system modeling framework should be structured to include the techno-economic description of the technologies (or processes), the drivers for the demand projection and a set of constraints. Each process is defined by a set of engineering, economic, and environmental characteristics (e.g., capital cost, efficiency, capacity factor, emissions rate) associated with converting an energy commodity from one form to another. Processes are linked together in a network via model constraints representing the allowable flow of energy commodities [40].
2.2. Case study: The Pantelleria Island
Selecting a case study in energy modeling is a crucial step in conducting an accurate and meaningful analysis. In this regard, the following criteria were considered for the selection of the case study:
- Consistency with research objectives: As stated in Section 1, the focus of the analysis is to test the effectiveness of a spatially explicit model on a small scale. This defines the size of the area to be studied. In addition, it was specified that the suitability phase of the land can be an important factor in reducing soil availability. Therefore, the selection of a critical context from this point of view is necessary.
- Territorial and technological diversity: According to Stolten et.al [24], the benefit of the spatially explicit planning is higher if the territory under analysis presents geographical differences from the point of view of distribution of energy resources and possible land uses. For this reason, the choice of a small area but with characteristics of diversity, is a fundamental element.
- Data availability: The analysis is more significant if the data (both for the phase of suitability of the land and for the estimation of the energy potential) are present and at high resolution.
- Availability of modeling instances: The presence of existing and validated models on the chosen platform represents a strong added value in terms of reproducibility of the study.
Considering the four selection criteria described the Island of Pantelleria was selected as a case study, thanks to its properties of territorial diversity [41], the numerous data sources at regional [42], Italian [43], and European level, [CLC]), the existence of other studies with the same focus ([44,45]) and the presence of an established model instance (TEMOA-Pantelleria) [46]. Below, the main features of the island of Pantelleria and the TEMOA-Pantelleria model used for the analysis are described.
In Figure 1, the island of Pantelleria is shown, centrally positioned within the Strait of Sicily. Specifically, Pantelleria is situated at 36.785° latitude and 11.992° longitude, a geographical coordinate that underscores its pivotal location within the Strait of Sicily. This geographical circumstance yields meteorological conditions of paramount significance, rendering Pantelleria an exceptionally auspicious site for the harnessing of Variable Renewable Energy Sources (VRES). Pantelleria presents a consistently elevated level of solar radiation throughout the year, amounting to approximately 2000 kWh/m2. This abundance of solar irradiance is instrumental in the island's clean energy transition agenda, affording substantial potential for solar energy generation. Additionally, the island experiences a substantial and dependable prevalence of wind, predominantly originating from the northwest, with wind speeds averaging around 7 meters per second at an elevation of 25 meters above sea level. All these climatic factors, in conjunction with the strategic location, pose Pantelleria at the forefront of sustainable energy exploration and underscores its critical role in advancing clean energy initiatives [41], making it as a compelling case study in the pursuit of land and energy sustainability.
The Pantelleria energy system is subdivided into five sectors (three demand-side sectors and two supply-side sectors) [47]. The demand-side sectors are buildings (including the agriculture, commercial and residential sectors), transport and commercial. The supply-side sectors are the power sector and the upstream sector. Each sector includes a set of technologies, characterized by several techno-economic parameters, used to produce all the commodities necessary to ensure the production of the required final energy service demands. The upstream sector includes fossil fuel import and internal production of biomass, as well as a fictitious commodity representing renewable energy. The output commodities of the upstream sector (along with fuel imports) are inputs for the power sector and the demand-side sectors.
In order to perform future projections in the different sectors, the model relies on a database of existing and innovative technologies (both at commercial and research and development stage), while future service demands in each sector of the economy (e.g. driven distance by car or truck, residential/commercial space heating, industrial production of steel or paper, etc.) are projected according to a set of drivers and demand elasticities and must be satisfied by the model at each time step. Future projections are articulated over several time steps, some of which used for the model calibration and some others (set at the years 2025, 2030, 2040 and 2050) for the scenario analysis.
While the annual value of each final service demand of the model is known at the base year and projected along the time with exogenous drivers and elasticities, the intra-annual distribution of the demand is also important to consider seasonal and daily variations of environmental conditions that affect the energy demands. The division of the milestone year into more refined time-slices is performed in TEMOA-Pantelleria with 4 seasons (spring, summer, fall and winter) and 3 times of day (day, night, and peak), leading to 12 time slices per year.
2.3. Geospatial data and tools for land elegibility and energy potential analysis
In this paper, two macro categories of data are being used, and namely simple spatial data and spatiotemporal time series. Spatial data are represented as a list of numbers using a particular coordinate system. For example, the objects of an electronic map are represented using spatial data (roads, buildings, windspeed by location), represented as points and shapes with a specified position. In this analysis, spatial data are both the constraints used to perform the land eligibility analysis and, in general, all the spatial properties that are fixed during time (e.g., cost of land rent). The superimposition of the different thematic layer (e.g., administrative, or physical constrains) allow to draw the final land eligibility map. These kinds of data are fixed among all the scenario periods; therefore, they are applied once and does not change during time. On the contrary, spatiotemporal time series, related to the resource potential for both photovoltaic and wind, is time dependent. A geo-referenced time series keeps the whole history of the evolving object over a period [48]. Typical examples include the monitoring of crop health over years [49], and meteorological time-series [50].
For the manipulation of both types of data, the use of Geographic Information System(s) (GIS) is mandatory. GIS is a specialized tool designed for the organization and management of diverse datasets associated with geographic or spatial coordinates, utilizing a specific map projection system [23]. In our research, we employ the QGIS software [24] for handling, analyzing, and visualizing spatial information. GIS technology plays a pivotal role in spatial energy planning, as it enables the amalgamation of data pertaining to renewable energy resources, regulatory guidelines, and natural constraints.
2.4. Land eligibility analysis
Existing literature extensively discusses eligibility criteria, and although specific aspects may vary, there is a consensus on its broad scope. Thanks to a review of the main analysis about this topic (as summarized in Table 1), it becomes evident that several consistent exclusion components are commonly considered. These include economic factors, administrative and technical considerations, and social aspects. Thus, it is expected that a study aligned with the existing body of knowledge should incorporate these elements as essential components when assessing the eligibility of land for renewable installations.
It is evident from Table 1 that all the pertinent research concurs on the existence of two primary clusters, pertaining to administrative and technical constraints. Administrative limitations typically encompass regions where the establishment of new facilities is prohibited for various reasons, including natural protected areas [57], proximity to historical sites [58], and residential agglomerations [59]. On the other hand, technical constraints are predominantly linked to challenges in constructing or operating new facilities due to factors such as terrain and soil conditions [60], or adverse weather patterns (e.g., low wind speeds, shadowing effects from hills and mountains). Additionally, these factors may also exert an influence on economic constraints, as there are overlaps between technical and economic characteristics, including criteria such as wind speed thresholds and slope thresholds. As underscored by McKenna et al. [55], there is a pressing need within the literature for the validation of studies related to land eligibility. Furthermore, there appears to be a notable absence of social and political considerations in the existing analyses. Consequently, the adopted criteria and their associated clusters are reported in Table 2.
In accordance with Table 2, land availability is constrained by environmental/technical criteria, thereby rendering the construction phase of the plant unfeasible due to adverse soil conditions and distance from the grid. Similarly, operational convenience for the plant is compromised due to low resource availability. Data pertaining to resource availability are distinctly derived for wind and photovoltaic sources and are more comprehensively discussed in the resource assessment phase (Section 2.N). Information concerning crop types and soil conditions is obtained from the Corine Land Cover source [60], a widely recognized reference in the literature, corroborated by GLAES [21]. Data not accessible through extensive, open-access databases are sourced from localized Italian studies. The sole exception pertains to the grid distance, which is unavailable in both large databases and local studies.
Administrative and habitat constraints, predominantly driven by natural preservation objectives, are derived from Natura 2000 [64] and the World Database of Protected Areas (WDPA) [58]. Natura 2000 serves as the principal instrument of European Union policy for biodiversity conservation, while WDPA stands as the most exhaustive global database encompassing marine and terrestrial protected areas.
Lastly, for anthropic limitations, data are extracted from OpenStreetMap (OSM) [59], an open-access global database characterized by public participation during data collection. In Figure 2 the different limitation categories, for both wind and photovoltaic technologies, are reported. For the solar resource, its land availability is mainly eroded by anthropic and environmental limitations (~15% and ~31% of unavailable land respectively), while there is no specific constraint due to natural habitat and historical heritage. Considering overlapping of categories, the final available area results in ~35%. Differently, for wind, the main limitations are the habitat one (~51% of land made unavailable due to Natura 2000 [64]) and again, the anthropic one. This result in an overall ~10% of available land.
2.5. Potential Assessment
The way solar and wind resource are assessed should be in line with the most recent and well-established existing literature. As highlighted by McKenna et.al [55] in the above-mentioned review, the technical potential assessment requires a standardization of the analysis and the tools. This is justified by the need of reproducibility and data availability. To accomplish these requirements solar and wind technical potentials are estimated using the calculation methodology of Elkameen et. al [65]. Technical potential is estimated starting from solar irradiance and wind speed data and, after some passages, obtaining capacity factor for the different sites. The detailed steps are described in the specific photovoltaic and wind assessment sections, respectively.
The starting point in this paper is the choice of the data sources for the potential assessment. This practice must be in line with the needs of the analysis (e.g., extension of the area under study, temporal horizon, model resolution) [24]. Therefore, after having fixed the methodological steps, a detailed analysis of all the possible data sources for both wind and photovoltaic has been conducted.
Solar radiation and wind speed can be estimated in two different ways [55], trough database already providing the energy potential at a certain resolution, or trough detailed model considering slope, aspects, shadowing effects and roughness of the terrain that calculate the potential. Concerning the former, the analysis is conducted both considering large global databases and national specific ones.
The results are summarized in Table 3, presenting a classification of the main database for solar and wind technical potential assessment. Sources are characterized according to data typology, cover and resolution. For these last two items, data are differentiated also by temporal and spatial attributes. Sources belong to the following classes:
- Reanalysis: The reanalysis methodology integrates numerical weather prediction models with observed datasets, yielding comprehensive datasets encompassing various meteorological parameters [55]. Examples include ERA5 [69] and MERRA2 [68], which serve as reputable sources for historical climate data assessment in wind resource studies, while similar data sources exist for solar energy assessments [74].
- Climate models: Climate models from initiatives like the Climate Model Intercomparison Project (CMIP) and CORDEX simulate future climate conditions, facilitating the assessment of wind and solar resource variability in response to long-term climate changes ([70], [71]). These models are instrumental in understanding the potential impacts of climate change on renewable energy resources.
- Atlas: Wind and solar atlases, exemplified by the New European Wind Atlas (NEWA) and the Global Wind Atlas (GWA), offer high-resolution spatial information regarding energy potentials in specified regions ([75], [78]). These atlases play a crucial role in renewable energy planning and development by providing detailed assessments of wind and solar resources.
Most of the database are made available at a Global level, even if one exception is found for New European Wind Atlas (NEWA) with a European focus. In terms of temporal coverage, Atlas are the most limited since they only provide historical average or single year data. For both Observation and Reanalysis, the timeframe is wider (from the 10 to the 70 past years). Finally, Climate models are the only ones capable of providing future projections, even if there are non-negligible errors in models forecasts [55]. The limitation inherent to databases, whether they are global or local in scope, is their inherent inability to accommodate site-specific factors that exert a discernible influence on energy potential. In regions characterized by intricate topographical features, such as fluctuations in elevation, surface orientation (including slope and aspect), and the presence of shadows, pronounced local gradients in energy distribution become manifest ([81], [82]). Consequently, it becomes imperative to employ models capable of incorporating local considerations into energy estimations. In this context, the availability of hourly time series at a microscale resolution (~1.5 km) made available by RSE represent a pivotal step, and this has motivated the selection of it as source for wind potential of this analysis. It is worth noting, however, that the sources of solar data under examination do not inherently furnish specific microscale considerations. Consequently, the utilization of comprehensive models becomes indispensable for accounting for these intricacies. Existing literature offers a variety of potential approaches. Notably, the “r.sun” algorithm, a development within the GRASS-GIS framework [83], stands out as a robust contender, as it calculates solar radiation at an hourly resolution when supplied with a Digital Elevation Model (DEM) corresponding to the target region. Additionally, ArcGIS [84] provides a Solar Radiation Toolbox [85], which operates in a similar fashion to r.sun and has undergone calibration and validation through international research endeavors [86]. The advantage of r.sun is the number of users it has already reached, and so, the number of calibration and validations this tool has undergone [87]. Therefore, for solar potential assessment, r.sun was selected, applying the methodology described in the work of Gasparovic et.al. [88].
2.5.1. Photovoltaic Potential Assessment
To assess the yearly potential conversion capacity of a photovoltaic (PV) power facility, denoted as , within a specific grid cell denoted as 'i' we employed Equation (1) [65]. This calculation hinges on both the available solar resources and the specifications of the solar modules in use. Additionally, we determined the capacity factor, , for PV systems within grid cell 'i' using Equation (2) [65]. This factor signifies the actual electrical output that a PV power plant could generate at its designated location over a given time frame when compared to its theoretical maximum potential output, assuming uninterrupted operation. This capacity factor calculation considers technology-specific parameters and the accessibility of location-specific resources, thus enabling performance comparisons across different sites before the installation of PV systems.
In equations (1) and (2):
- represents the average global horizontal irradiation (kWh/m2/time).
- indicates the area within grid cell 'i' suitable for PV implementation (km2).
- represents the efficiency of the PV module in converting sunlight to electricity, with an assumed value of 21% [65].
- denotes the performance ratio for the solar module, set at 0.85 [65]. This ratio accounts for the disparity between performance under standard test conditions and the actual system output, factoring in losses due to conduction and thermal effects.
- signifies the total number of hours in a year, equivalent to 8760.
- represents the power density or of the solar PV system. For this study, we employed a value of 32 MW/km2 for a fixed-tilt utility-scale solar system using mono-crystalline silicon cells, which is the most common in actual market [89].
The GHI is derived from r.sun starting from a Digital Elevation Model (DEM) with a 10 m resolution. Subsequently, the original irradiance has been corrected for atmospheric attenuation based on the clear sky coefficient () as in Equation (3) [65].
TEMOA time slices are categorized into seasons, each comprising day, night and peak periods. As there is no sunlight during the night, the capacity factor (CF) is uniformly assumed to be zero for all seasons. Consequently, our focus narrows down to determining the seasonal CF values for two distinct periods: day and peak. This entails computing eight capacity values. For each of these, we have applied Equations (1) and (2), substituting the term "GHI" with the solar radiation received during the validity period of the capacity factor and the term "T" with the hours specific to that period. Aggregated solar radiation for the specific “T” period is obtain starting from the hourly irradiance (W/m2) and integrating all along the period T. A detailed explanation of this phase is provided in Appendix NN. Moreover, r.sun requires specifying a reference year on which the calculation is performed. Since the aim is to compare different lands under the same atmospheric conditions, yearly variability of solar irradiance is neglected, and 2020 values are assumed constant. Another remarkable hypothesis is related to the division between day and peak production. As specified above, within a season, a day might have various times of interest. For instance, the peak electrical load might occur midday in the summer, and a secondary peak might happen in the evening. This division should be accounted when evaluating the photovoltaic potential, since the mismatch between producibility potential and demand is one of the main problems with VRES [90]. Seasonal daily and peak capacity factors under the assumption before described are reported in Figure 3.
The presented box plots reveal that Spring and Summer exhibit higher median capacity factors compared to Autumn and Winter, indicative of a stronger solar potential during these warmer seasons (36% and 52% with respect to 31% and 17%). These periods also display broader capacity factor ranges, likely influenced by intermittent cloud cover or variations in solar incidence angles. Notably, Summer stands out with occasional exceptionally high-capacity factors, attributed to optimal sun angles and longer daylight hours. In contrast, the Winter season demonstrates a compact interquartile range (IQR) and lower median, reflective of shorter days and lower sun angles. Lower-end outliers in Winter may indicate days with minimal solar irradiance due to adverse weather conditions. The "Peak" period capacity factors also follow a seasonal trend, with Spring and Summer consistently outperforming Autumn and Winter. However, "Peak" distributions are narrower across all seasons compared to "Day" distributions, highlighting the reduced susceptibility of peak sunlight hours to diurnal and weather-induced fluctuations. Overall, these insights emphasize the critical importance of understanding the temporal variability in PV capacity factors for optimizing solar energy system planning and performance.
2.5.2. Wind Potential Assessment
The RSE AEOLIAN Platform provides wind speed data at heights of 50. 75, 100. 125, and 150 meters above sea level [77]. These values correspond to the most representative hub heights for both onshore currently installed wind turbines and future potential installations on both land and at sea. As was done for solar potential calculation, the goal is to obtain capacity factor values for each time-slice of the model. This primarily involves translating hourly wind speed data into site-specific energy production.
The site-specific energy production calculation is achieved by combining the historical time series (or probability density function) of wind speeds at the hub height of the wind turbine with the power curve of the specific wind turbine of interest, also expressed as a function of wind speed at the hub height. Theoretically, to calculate site-specific energy production, one should use many power curves and compute a representative average. However, due to difficulties in obtaining a representative set for data availability issues, the site-specific energy production analysis was conducted using a single wind turbine model for each hub height. We considered the three lower hub heights: 50. 75, and 100 meters asl, along with three commercially available wind turbine models accessible online. Table 4 provides the main characteristics of the three wind turbines used for the calculation at the considered hub heights:
Table 4 presents key specifications of WTG models at varying hub heights, ranging from 50 to 125 meters. Notably, it reveals the increasing nominal power and rotor diameter as hub height elevates, which is essential information for optimizing wind energy production at different altitudes. It also must be noticed that wind reference and hub heights differ. Therefore, there is an error introduced by the wind speed at the data level with respect to the real height at which the wind turbine is installed. Nevertheless, considering the power law at which wind speed variation is subjected [92], it has been checked (not shown) that the producibility errors is always below 5%.
After obtaining hourly site-specific energy production at different heights, in line with TEMOA-Pantelleria time-slices, the capacity factor for time-slice 'i' for turbine 't' was calculated as in Equation (4):
where the term [MWh] represent the integral of the hourly production function during the time-slice temporal horizon [h] of the turbine “t”, characterized by [MW].
The results of this process are shown in Figure 4. In this figure, two different kinds of pattern are observable. The analysis reveals distinct seasonal and daily patterns in wind turbine capacity factors. Across all turbine heights, winter consistently displays approximately 20-25% higher capacity factors compared to summer, notably pronounced during nighttime slices. In comparison to summer, autumn showcases marginally elevated capacity factors, approximately 10-15% higher, especially evident during day and night periods. The impact of turbine height is observable with a consistent increase in capacity factors across all seasons, with higher heights indicating approximately 15-20% better performance. Moreover, the variability within each season and time slice remains relatively consistent, with night periods displaying notably wider ranges than day. Outliers, though sporadic, suggest instances of extreme deviations in capacity factors.
2.5.3. Cost Assessment
The potential assessment phase determines the operational yield of the plant. Nevertheless, when seeking to differentiate various land types for capacity expansion plans, technical potential is not the only influencing parameter. According to International Renewable Energy Agency (IRENA) 2021 report [93], renewable installations levelized costs of electricity (LCOE) is mainly determined by: capacity factors, investments costs, operations & maintenance (O&M) and auxiliary costs. Since the purpose of spatially explicit energy planning is to consider geographic aspects capable of influencing ESOM outcomes [20], is necessary to identify which of the above-mentioned voices are spatial-dependent.
For capacity factors, this aspect has already been addressed. Coming to costs, when faced with the decision between lands of equal potential, the cost of the land (by rent or acquisition) and the expenses associated with its connection to grid infrastructure become pivotal factors [93].
The cost of land is assumed to be equal to the agricultural land price. Agricultural land rents refer to the price of renting one hectare of agricultural land without buildings or plantations for one year. This data is derived from a Eurostat analysis [94] dated 2021 with a spatial scope of the whole European territory and a spatial resolution of country regions. The arable land prices for the Italian regions span from 0.0216 to 0.1714 M€/km2. A significant variation is observed between the maximum and the minimum value, being the former around 10 times the latter. This is justified by the great diversity of the Italian territory.
While the focus of this analysis is limited to Pantelleria Island, situated in Sicily, the decision to employ Italian maximum and minimum land price values in both the above discussion and future utilization (as outlined in Section 3) serves as a deliberate methodological choice. This choice is driven by the overarching methodological and demonstrative objectives of this analysis, which aims to illustrate the implications of the new land use module component. To achieve this, we have opted to utilize this range of land price values for the purpose of conducting a sensitivity analysis within the model. This approach is designed to assess, specifically within the context of our case study, the extent to which the additional components influence the outcomes of the model.
For the cost of connection, there are some concerns that comes with its accounting. First, according to Italian Energy Transmission Authority (TERNA) [95], the specific point of connection (that determines the distance) is not known a priori, and strongly depend on design specific considerations. According to plant size and desired output voltage, the connection can be performed at a grid-level or at the primary cabin [95]. This introduces the first uncertainty in this cost estimation. Then, ESOMs generally do provide aggregated capacity for all the plants belonging to the same category [96], therefore it in not known how the aggregated capacity is discretized, with uncertainties also in the size term. Lastly, the detailed IRENA cost analysis of wind power technology [97] do not specify the distance from grid as a pivotal factor in determining the connection cost.
Given the design-specific nature of grid connection costs and the challenges in estimating them accurately, we have chosen not to include them as a factor in our analysis.
2.6. Data aggregation
At this stage of the analysis, the data pertaining to wind potential, solar potential, and the costs are presented as rasters with varying spatial resolutions, rendering them incompatible with the structure of ESOMs [32]. Notably, the TEMOA model requires a data format that is not geospatially explicit. As any other traditional energy system optimization model, TEMOA present an aggregated description of the system, where the spatial features of technology (e.g., land occupied) and costs (land rent according to soil occupancy) is not present. Therefore, it is necessary to pass the information of having geographically dependent technological and terrain features, in such a way that it do not to make the model computationally intractable. The aggregation of data based on spatial attributes (e.g., location and location-dependent costs) and technological attributes (notably, spatially explicit capacity factors) [24] has been then addressed through a spatial and technological aggregation scheme, to transform the numerous rasters into interpretable inputs for the model. Spatial aggregation entails the amalgamation of contiguous regions with similar characteristics, thus reducing the spatial resolution and intricacy of the ESOM data. Simultaneously, technological aggregation involves the grouping of similar technologies, such as the consolidation of wind turbines with comparable time series data [24]. Within this framework, an established methodology, as presented by Stolten et al. [24], offers a structured workflow for transitioning from multiple variable renewable energy sources (VRES) data to a limited number of aggregated technologies, each associated with a respective land cluster, representing the total available land area suitable for the installation of the corresponding technology. This framework, adapted to our work, is shown in Figure 5.
As depicted in Figure 5, aim of this phase is to translate raw data (rasters or shapefile at different resolution) into model interpretable amount. This step can be further divided in two sub operations: The data aggregation and the model adaptation.
In the technological aggregation phase, photovoltaic and wind technologies are categorized based on their capacity factors (CF) and cost characteristics. This categorization results in aggregated technology clusters, such as Agg_PV_X and Agg_WIND_Y, each with its own distinct capacity factor and associated cost. Spatial aggregation, on the other hand, condenses geographical information into discrete land clusters. Each cluster, represented by a land type such as Land X or Land Y, is defined by its area and the cost of land use. These spatial clusters form the basis for the physical constraints within the model, dictating the potential for technology deployment across different geographical areas. Finally, in the model adaptation phase, TEMOA original code is modified to account for land availability and for linking specific technologies at their belonging cluster
In the aggregation of data into clusters characterized by analogous attributes [24] (in this case, costs, and renewable energy potential) a rigorous data handling approach, as well as the application of advanced statistical techniques, becomes imperative. Data aggregation necessitates meticulous data preparation. Notably, one significant challenge in data preparation arises from the divergence in spatial resolutions among the various datasets. Additionally, a critical issue emerges when attempting to overlay the different layers involved in the analysis – is the lack of correct intersection of boundaries between them. This issue, also named the partition problem [98], is created by the mismatched spatial resolutions and boundaries and presents a formidable hurdle in the aggregation process. To solve this issue, a uniform mesh is created, in which data at different resolution and intersection should be aggregated. To preserve the smallest amount of information, the resolution of the mesh is the one of the layers with the highest definition, thus the solar radiation dataset, derived form a 10m10m DEM. Inside each mesh cell, data pertaining the solar and wind time slice specific capacity factors and costs are stored. The resulting geospatial object is an attribute table with as many rows as the 100 m2 cell necessary to cover the Pantelleria island, and with all the techno-economic attributes as columns.
Energy potential for cells excluded by the land eligibility analysis (Figure 2) is set equal to zero, and cells with both wind and photovoltaic null potential are deleted. This results in a final attribute table of approximately 250.000 elements. However, the sheer volume of data presents computational challenges for direct insertion into the TEMOA model. Implementing over 250.000 technologies and land area constraints renders the model computationally very demanding. To mitigate this computational complexity, the dataset is aggregated based on three independent geospatial features—land price, wind, and solar capacity factors. It is crucial to note that each particle originally contains 12 capacity factors (comprising 4 seasonal variations, 3 time slices, and 2 VRES technologies). However, in the clustering process, only the average yearly capacity factor is considered to condense the dataset and facilitate computational feasibility.
The clustering of the geospatial cells among the selected attributes is performed with multiple algorithms, to determine which one show the best performance according to data structure The three tested algorithms are the HDBSCAN [99], The Kmeans [100] and the DBSCAN [101]. HDBSCAN, a hierarchical density-based algorithm, is adept at identifying clusters of varied density without the need for pre-specifying the number of clusters. Its approach is particularly suitable for geospatial data, which often exhibits heterogeneous density distributions due to the irregular spatial distribution of renewable energy resources. In contrast, Kmeans—simple and efficient—a centroid-based algorithm, meaning that objects in the data are clustered by being assigned to the nearest centroid. However, a major pitfall of K-Means is its lack of detecting outliers, or noisy data points, which leads them to be classified incorrectly. Furthermore, K-Means has an intrinsic preference for globular clusters and does not work very well on data comprised of arbitrarily shaped clusters. DBSCAN stands as a middle ground between the rigidity of Kmeans and the flexibility of HDBSCAN. By designating core points within high-density regions and expanding clusters from these cores, DBSCAN excels in discovering clusters with arbitrary shapes, an attribute of high value when dealing with spatially complex landscapes. Moreover, its ability to treat outliers as noise renders it less sensitive to anomalies, thereby enhancing the robustness of the clustering process.
For the clustering algorithms requiring the computation of the distance matrix, a spatial sampling procedure is performed [102], clustering only the smallest subset of data. Then, nearest neighbor [103] method is used to predict the cluster affiliation for the non-sampled particles. The performance of these algorithms is tested both by their clustering acumen and by their computational demands, as reported in Table 5. The silhouette score [104]—ranging from -1 to 1— has been used as a quantitative measure of cluster cohesion and separation. A high silhouette score indicates a clustering configuration where inter-cluster distances are maximized and intra-cluster distances are minimized, reflecting distinct and well-separated clusters that are integral for spatial analysis. Complementarily, computational time and memory usage are critical metrics for assessing the scalability of these methods. They provide insight into the algorithms' operational efficiency and practicality for large-scale applications, where rapid processing and memory management are essential. Results of the clustering procedure for the three different algorithms are reported in Figure 7.
As appreciable in Table 5, Kmeans and DBSCAN outperform HDBSCAN in terms of silhouette score and memory usage, with Kmeans standing out as the best one in all the three metrics under analysis. The outstanding performance of k-means can be justified by the absence of outliers. Indeed, for both cost and renewable energy potential, the minimum value is zero where no installation is possible, and maximum values are constrained in a very similar range for all the data. (There is no drastic resource variability along the Pantelleria Island). Therefore, also considering the possibility of selecting clusters a-priori, Kmeans is selected for this analysis. Moreover, the underlying hypothesis of the Kmeans, that data must be globular and isotropic, is verified considering the high value of the silhouette score. Considering Figure 7 is appreciable how HDBSCAN and DBSCAN are more flexible in terms of cluster shapes, which is evident from the varied shapes and sizes of clusters. KMeans, on the other hand, assumes the clusters are spherical, leading to more uniform and rounded clusters. In term of noise, HDBSCAN and DBSCAN can identify outliers inserting them in the (-1) cluster, even if very few elements are present in this category (checked, not shown). The final number of clusters is another pivotal parameter in this analysis. In Kmeans it is imposed at 5, while the other methods reach 11 (HDBSCAN) and 17 (DBSCAN) clusters. In this case, especially for DBSCAN, the clusters are very fragmented and some of them appear to contain few elements. In conclusion, since the aim is to identify macro-areas characterized by similar energy properties and to have a method as scalable as possible, the Kmeans still guarantee the best outcome.
The refinement of geospatial data through clustering algorithms has yielded a comprehensive set of land and technological clusters, each distinctly characterized by both spatial and technological attributes. These clusters are delineated not only by their physical geography—encapsulated by land area and associated rental costs—but also by technological potential, specified through capacity factors for feasible renewable technologies like wind and photovoltaic systems.
2.7. Model Integration
After the data aggregation procedure, a reduced set of land and technological items is made available for model integration. Each cluster (or item) is characterized by land attributes (the area of the cluster and the land rent cost) and technological attributes (the capacity factors for the different technologies installable on that land). Therefore, for each cluster, a corresponding land item (characterized by an area) exists, as well as a set of wind and PV technologies with specific capacity factors and costs, that can be installed only on that cluster. In this context, there are two optimization goals. The first is to install the renewable energy technologies on the “best” cluster, where "best" denotes the cluster identified by the ESOM following the least cost optimization. The second is to have a renewable energy installation development compatible with land limitations of the Pantelleria island. Therefore, the ESOM must be capable of using the inputs of the clustering phase (technological parameters for renewables, land price and area for land clusters) to determine the optimal deployment of technologies across different land clusters. To achieve this goal, is necessary to bring some modification to the TEMOA code:
- 1)
- Insert in TEMOA a new set that describe the land resource. Traditional ESOM elements (mainly process and commodities) do not allow for a proper land representation. Indeed, it would be wrong to model the land consumed by plants installation as a commodity or a technology, for two main reasons. First, a commodity is something that is exchanged between processes as input or output. Here, the role of land is to host its associated technology (at certain conditions of capacity factor and cost) for the lifetime of this last. Second, the commodity consumption is related to the activity of a plant, passing through its efficiency (e.g., natural gas consumption proportional to combined cycle plant activity). In this case, land is consumed when new capacity is installed and becomes available as soon as the installed technology on that land dies. As depicted in Equation(5) and (6), the new TEMOA set is called for which a value is associated, describing the available area for the land cluster “l”.
- 2)
- Insert in the model a new parameter and new constraint, linking the capacity installation to land consumption. Indeed, as shown in Equation (7), the Land Use Intensity (LUI) parameter acts as a critical bridge linking the land clusters “ ” with the applicable technologies “j”. It quantifies the amount of land required for the installation of a unit of technology (e.g., megawatt of wind or solar power). The LUI parameter ensures that the model's solutions are not just economically optimized but also spatially feasible. If an LUI is not defined for a specific technology within a given land cluster, it implies that the technology cannot be installed in that cluster, thereby introducing a direct spatial constraint into the optimization process.
According to the TEMOA optimization module, thanks to Equation (7) the model has several opportunities to consume land area to install photovoltaic or wind plants, but the convenience is determined by the capacity factor of the process. Therefore, TEMOA will first select the best technology, and then consume the area of the cluster associated to that technology, and this is made possible by the introduction of the LUI parameter. In this way, the useful output will be both the capacity installed and the geographical location of the plant, at least in terms of land cluster. The number of clusters determines the precision of that information.
3. Results
This section presents a comparative analysis of energy scenarios derived from two modeling approaches: one integrating the advanced land feature considerations previously described, and a conventional one. The objective is to test the hypotheses stated before about the advantages of spatially explicit energy planning.
Section 3.1 introduces the initial findings, highlighting the advanced technological and spatial characterization introduced by the previous analysis. Activation of the land use constraint and land price components, as discussed in Section 3.2, leads to different final ESOM scenarios configuration.
The Discussion section (Section 4) elucidates the role of spatially explicit planning in optimizing the siting of energy facilities and efficient land use. These findings highlight the importance of spatial consideration in improving the efficacy of energy planning.
3.1. TEMOA-Pantelleria input differences
The two configurations of the model here analyzed are the traditional one (no land use module activation) and the new one (land use module activated). In both the model configurations the wind and photovoltaic capacity factors result from the technological discretization previously explained (resulting from Section 2.6).
In Figure 8 those cluster discretized capacity factors are reported and compared with the average ones, to highlight the improvements brought by the cluster analysis carried out. In the land cluster description, the available area and the installable technologies on the cluster are highlighted (Table 6). As mentioned above, the limitations introduced by Table 6 for the installation of specific technologies on certain clusters and the land price accounting in the objective function are present only in the TEMOA-Pantelleria land explicit configuration. Discretizing technologies based on their spatio-temporal attributes brings non-negligible advantages in terms of technological options for the model, which may cause a lower total cost of the system. Considering the relative difference between the old and the new technologies, is possible to observe values around 10% (Summer and Spring wind peak). Therefore, according to the sign of the difference, the model overestimate/underestimate the installed capacity of the same amount. Strongly influencing the cost. This consideration is further explained in the following graphs. Still related to the cost, is possible to see the impact of the spatial aggregation on the land side, when the rent cost is added, as shown in Table 6.
Table 6 reports the resulting land clusters from the K-means (Figure 7b) and their associated technologies. The only difference with Figure 7 (b) and Table 6 is that the fourth cluster has been deleted, since it presents zero potential for both photovoltaic and wind. Moreover, it is important to highlight the fact that not all the technologies can be installed on all the clusters. The low amount of land that can be allocated for wind turbines, totally reaching 1.54 km2 is also significant. In this context, further literature review highlighted that for social and administrative reasons, the total area that can be exploited for wind resources is even lower.
3.2. TEMOA-Pantelleria energy scenario analysis
Energy scenarios, referring to optimized technological mix in terms of activity and capacity, then generating emissions and costs, are here discussed. Since objective is to test how the land use module change model outcome, the results are proposed for the two different model configurations. The land explicit one is tested with a parametric analysis on the land price, making this last vary between the minimum and the maximum possible values. Due to the power sector focused approach of this work, the main outcomes presented are the electricity generation (capacity and activity, Figure 9 ), the relative energy system cost differences and the land consumption for the land explicit modelling instance. Starting from the power sector configuration, in Figure 9 the capacity (MW) and the electricity generation (GWh) are presented. In all the configurations, differences in the outcomes are appreciable both in terms of absolute and relative amounts. Indeed, the scenarios differs for the total installed capacity and the generated electricity, but also in the way these amounts are obtained. First, it can be easily noticed (and confirmed by subsequent data analysis, not shown) that the traditional model and the low land price configuration do not present any differences, as expected, while the high land price instance has significative differences with respect to the previous two. This is symptom of a threshold phenomenon that change model outcomes under a certain land price value.
Going into detail, the traditional TEMOA-Pantelleria and the low land price instances present a higher installed capacity with respect to the high land price configuration. In the first two cases, the capacity of energy technologies starts at just under 2 MW in 2020 and shows a more than threefold increase to approximately 7 MW by 2050. The technology mix remains relatively stable, with wind technologies dominating the share, followed by solar and biomass, this last mostly covering the base-load needs. Considering the activity, its level starts at around 15 GWh in 2020. increasing to nearly 23 GWh by 2050. This increase is justified by the increased electrification (mainly in the transport sector) caused by the decarbonization constraints at which the Island is subjected. The proportions of each technology within the activity profile change slightly over time, with "WIN1_N" gaining a larger share, indicative of not only increased capacity but also high utilization rates. The most valuable outcomes visible from Figure 9 are related to the differences in the photovoltaic installations and the overall power production between the two previously described configurations.
In both the zero (or low) and in the high land price configurations, there is a growth in capacity over time, but the technology preferences differ. In the low/null land price case (a)/(c), there is a major reliance on solar technology (PV_1, the highest performing one), which suggests that larger, more land-intensive solar projects are feasible and economically viable due to lower land costs. Conversely, with a higher land price (e), there is a marked preference for wind systems, indicative of a strategy to maximize energy yield per unit of land area. In particular, the total difference in 2050 is of 1,2 MW of installed capacity and around 2.2 GWh of electricity produced. With this consumption gap mainly driven by commercial and residential sectors.
It must be specified that, in all the cases, the limitation caused by the land use constraint of Equation (7) is not influencing the model outcome. This happens because the necessary capacity for the Pantelleria power sector is not occupying any land cluster at its maximum. Indeed, the model select the highest performing technologies (WIN1_N, PV1_N) considering area the limitation of the cluster these are installed in. This consideration is supported by Figure 10FigureFigure 10- , which highlights the land cluster occupation, and the land price costs in the two-model configuration.
In Figure 10 (a) the difference in land occupation by cluster in the two model configurations are shown. In both cases, the land cluster “LC_3” is the most consumed due to the installation of the solar technology “PV1_N”, reaching a maximum occupation of ~10% in low price and ~6% in low price in 2040. Even if the LC_3 is the one with the highest absolute occupation, the LC_2, due to its limited extension, is the one reaching the highest percentage of occupation. Indeed at 2040. due to the installation of WIN1_N, the LC_2 is occupied at 26% in both the configurations. These considerations are reflected in the cost, that notably show higher values for the high price configuration. In this configuration, land rent price start from 0.026 M€ at 2025, increasing and stabilizing around 0.07 M€ from 2040 to the last year. In the low-price instance, these costs are much lower, reaching a maximum of 0.014 M€ at 2040.
4. Discussion
The initial goal of this research was to quantify how much spatial information or consideration of spatial characteristics, when integrated within an energy system optimization modeling framework, can improve planning solutions. One of these improvements was to obtain a modeling instance able to optimally allocate the new installation of renewable energy plants, accounting for local conditions and being able to suggest siting considerations. In this context, the analysis has been divided in the assessment phase and in the integration phase. In general, this research effectively demonstrates the feasibility and benefits of incorporating spatially explicit considerations into ESOMs using open-source packages, highlighting the practicality and value of this approach. This integration not only enhances the realism and applicability of these models but also aligns with the pressing global shift toward sustainable and renewable energy sources. Also, by comparing traditional and spatially enhanced models, the study quantifies the added value brought by spatial planning and the influence of the new variable introduced in the model. While this approach does not represent a groundbreaking milestone in the field, it introduces an innovative methodology accompanied by certain limitations. As such, a critical discussion of the work is imperative.
Concerning the assessment phase, referring to the practice of gathering data about renewable energy potential of a region (both in terms of physical and administrative availability), this can be further divided in two subtopics: data gathering and elaboration. In terms of data gathering, it is evident the need for a unified tool to perform this kind of analysis. Actual literature still relies on many incompatible packages for this analysis, even if some exceptions are arising. For example, the GLAES framework for LE analysis [21] has found recent application in different studies [105]. In terms of renewable energy potential assessment phase, there exists many valuable attempts ([24] ,[27]), but a uniformly adopted methodology across studies is missing. In general, an interface to integrate spatial and temporal explicit data about VRES is needed. Even if, as confirmed by Aryanpur et.al. [106], the optimal choice of resolution is still dependent on model scope. The uncertainties inherent in the assessment phase predominantly stem from the analysis of land eligibility, complicated by ambiguous energy legislation. Notably, our approach did not consider buffer zones around any protected areas, a decision that potentially leads to an overestimation of available land. Further analysis (not detailed here) reveals that implementing buffer zones ranging from 25 to 200 meters around these areas drastically affects land availability. In some clusters, the analysis results in the complete unavailability of land, while in the most favorable scenarios it causes a reduction of approximately 25%. Specifically, in the context of wind technology, the application of buffer zones rendered certain land clusters unsuitable, significantly altering the potential energy mix. This outcome underscores the necessity for more transparent and comprehensible landscape regulations. The challenge in setting fixed buffer values, as indicated by [61] , further complicates this issue, necessitating a nuanced approach to landscape management in the context of renewable energy development.
Diving in the integration phase, the first and primary challenge in implementing the land-use in an ESOM is the proliferation of energy technologies. This challenge arises due to the necessity of introducing, for each implemented technology, a multitude of technologies equivalent to the number of clusters employed. For example, to effectively model each photovoltaic technology, the model must encompass an N number of PV technologies, where N corresponds to the number of clusters identified where the technology can be installed. While this approach may find some applicability in constrained environments like the island of Pantelleria, its feasibility diminishes significantly in more expansive scenarios, such as national or European contexts. In this context, there is the need to find a trade-off between model accuracy and computational effort. Stolten et.al [24] highlight how this practice is strongly dependent on both spatial and temporal resolution and should be faced case-by-case. Despite the methodological issues, there is general knowledge that can be extracted from results. Results clearly indicate how the cost of land has a strong influence in limiting the land use intensive renewable energy sources, such as photovoltaic. The sensitivity analysis conducted according to Eurostat [94] suggests that economic factors, such as land prices, significantly influence technology selection and deployment strategies, leading to regional differentiation in the energy mix. According to this point, another remarkable limitation of this study is not considering the trade-offs and synergies with respect to other land-use intensive sectors. For example, Agri voltaic is an innovative solution and further research is required estimate the actual benefits and their significance especially in relation to land type and soil conditions [25].
5. Conclusions
This study introduces a novel methodological framework for integrating spatial considerations within ESOMs. Focusing on the case of Pantelleria Island, the research emphasizes the importance of including land use aspects in energy planning, particularly in small, diverse geographical areas. The methodology starts with a comprehensive collection of geospatial data, followed by spatial and technological aggregation to derive model interpretable attributes. This approach addresses the lack of established methodologies and open-source tools for renewable energy potential screening. The study contributes to the advancement of such methodologies by combining open-access resources to facilitate broader VRES potential analysis. Results highlight the benefits of such analysis in model configuration, particularly due to the technological diversity revealed. Furthermore, the paper proposes a method to incorporate land use considerations directly into energy models, a technique applicable across various bottom-up energy models. The findings underscore the crucial role of detailed territorial descriptions in the modeling phase, considering technological discretization, land pricing, and area availability. A conducted sensitivity analysis on land pricing reveals threshold phenomena within models that could significantly alter scenario outcomes. This research underscores the need for precision in the modeling phase and consideration of trade-offs with the land use sector, offering valuable insights for future energy planning and policy development.
Author Contributions
Conceptualization, D.M. and L.S.; methodology, D.M. and L.R.; software, D.M. and L.R.; validation, D.M.; formal analysis, D.M. and L.R.; investigation, D.M. and L.R.; resources, L.S.; data curation, D.M.; writing—original draft preparation, D.M.; writing—review and editing, L.S. and L.R.; visualization, D.M.; supervision, L.S.; project administration, L.S.; funding acquisition, L.S. All authors have read and agreed to the published version of the manuscript.
Funding
The PhD activity opf D.M. is fully funded by Eni S.p.A.
Acknowledgments
The authors acknowledge the support given by the MAHTEP Group at PoliTo.
Conflicts of Interest
The authors declare no conflict of interest.
References
- S. Fawzy, A. I. S. Fawzy, A. I. Osman, J. Doran, and D. W. Rooney, “Strategies for mitigation of climate change: a review,” Environmental Chemistry Letters 2020 18:6, vol. 18, no. 6, pp. 2069–2094, Jul. 2020. [CrossRef]
- S. Vijayavenkataraman, S. S. Vijayavenkataraman, S. Iniyan, and R. Goic, “A review of climate change, mitigation and adaptation,” Renewable and Sustainable Energy Reviews, vol. 16, no. 1, pp. 878–897, Jan. 2012. [CrossRef]
- P. Gabrielli et al., “Net-zero emissions chemical industry in a world of limited resources,” One Earth, vol. 6, no. 6, pp. 682–704, Jun. 2023. [CrossRef]
- F. Martins, P. F. Martins, P. Moura, and A. T. de Almeida, “The Role of Electrification in the Decarbonization of the Energy Sector in Portugal,” Energies 2022, Vol. 15, Page 1759, vol. 15, no. 5, p. 1759, Feb. 2022. [CrossRef]
- International Renewable Energy Agency (IRENA), “Electricity storage and renewables: Costs and markets to 2030.” International Renewable Energy Agency, no. October, p. 132, 2017, Accessed: Jun. 26, 2023. [Online]. Available: https://www.irena.org/-/media/Files/IRENA/Agency/Publication/2017/Oct/IRENA_Electricity_Storage_Costs_2017.
- M. Chang et al., “Trends in tools and approaches for modelling the energy transition,” Appl Energy, vol. 290. p. 116731, 21. 20 May. [CrossRef]
- M. G. Prina, G. M. G. Prina, G. Manzolini, D. Moser, B. Nastasi, and W. Sparber, “Classification and challenges of bottom-up energy system models - A review,” Renewable and Sustainable Energy Reviews, vol. 129, p. 109917, Sep. 2020. [CrossRef]
- Loulou R, Goldstein G, Kanudia A, Lettila A, and Remme U, “Documentation for the TIMES Model: Part I,” 2016. Accessed: Oct. 17, 2022. [Online]. Available: http://www.iea-etsap.org/web/Documentation.
- D. Lerede, C. D. Lerede, C. Bustreo, F. Gracceva, Y. Lechón, and L. Savoldi, “Analysis of the Effects of Electrification of the Road Transport Sector on the Possible Penetration of Nuclear Fusion in the Long-Term European Energy Mix,” Energies (Basel), vol. 13, no. 14, p. 3634, Jul. 2020. [CrossRef]
- D. Lerede, C. D. Lerede, C. Bustreo, F. Gracceva, M. Saccone, and L. Savoldi, “Techno-economic and environmental characterization of industrial technologies for transparent bottom-up energy modeling,” Renewable and Sustainable Energy Reviews, vol. 140. p. 110742, Apr. 2021. [CrossRef]
- A. Balbo, G. A. Balbo, G. Colucci, M. Nicoli, and L. Savoldi, “Exploring the Role of Hydrogen to Achieve the Italian Decarbonization Targets Using an Open-Source Energy System Optimization Model,” in International Journal of Energy and Power Engineering, E. and T. World Academy of Science, Ed., Mar. 2023, pp. 89–100. Accessed: Apr. 25, 2023. [Online]. Available: https://publications.waset.org/10013040/exploring-the-role-of-hydrogen-to-achieve-the-italian-decarbonization-targets-using-an-open-source-energy-system-optimization-model.
- G. Limpens, H. G. Limpens, H. Jeanmart, and F. Maréchal, “Belgian Energy Transition: What Are the Options?,” Energies 2020. Vol. 13, Page 261, vol. 13, no. 1, p. 261, Jan. 2020. [CrossRef]
- H. Eshraghi, A. H. Eshraghi, A. Rodrigo De Queiroz, and J. F. Decarolis, “US Energy-Related Greenhouse Gas Emissions in the Absence of Federal Climate Policy,” 2018. [CrossRef]
- T. Barnes, A. T. Barnes, A. Shivakumar, M. Brinkerink, and T. Niet, “OSeMOSYS Global, an open-source, open data global electricity system model generator,” Sci Data, vol. 9, no. 1, Dec. 2022. [CrossRef]
- Sofia. Simoes et al., “The JRC-EU-TIMES model - Assessing the long-term role of the SET Plan Energy technologies,” p. 376, 2013. [CrossRef]
- D. Lerede, M. D. Lerede, M. Nicoli, L. Savoldi, and A. Trotta, “Analysis of the possible contribution of different nuclear fusion technologies to the global energy transition,” Energy Strategy Reviews, vol. 49, no. 101144, Sep. 2023. [CrossRef]
- V. Aryanpur, B. V. Aryanpur, B. O’Gallachoir, H. Dai, W. Chen, and J. Glynn, “A review of spatial resolution and regionalisation in national-scale energy systems optimisation models,” Energy Strategy Reviews, vol. 37, p. 100702, Sep. 2021. [CrossRef]
- J. Lovering, M. J. Lovering, M. Swain, L. Blomqvist, and R. R. Hernandez, “Land-use intensity of electricity production and tomorrow’s energy landscape,” PLoS One, vol. 17, no. 7, p. e0270155, Jul. 2022. [CrossRef]
- N. Wang, R. A. N. Wang, R. A. Verzijlbergh, P. W. Heijnen, and P. M. Herder, “A spatially explicit planning approach for power systems with a high share of renewable energy sources,” Appl Energy, vol. 260. Feb. 2020. [CrossRef]
- B. Resch et al., “GIS-Based Planning and Modeling for Renewable Energy: Challenges and Future Research Avenues,” ISPRS International Journal of Geo-Information 2014, Vol. 3, Pages 662-692, vol. 3, no. 2, pp. 662–692, 14. 20 May. [CrossRef]
- D. S. Ryberg, M. D. S. Ryberg, M. Robinius, and D. Stolten, “Evaluating land eligibility constraints of renewable energy sources in Europe,” Energies (Basel), vol. 11, no. 5, 2018. [CrossRef]
- E. P. Ramos et al., “Climate, Land, Energy and Water systems interactions – From key concepts to model implementation with OSeMOSYS,” Environ Sci Policy, vol. 136, pp. 696–716, Oct. 2022. [CrossRef]
- “Land: A crucial resource for Europe’s energy transition | McKinsey.” Accessed: Nov. 08, 2023. [Online]. Available: https://www.mckinsey.
- J. Krzywanski et al., “Advanced Spatial and Technological Aggregation Scheme for Energy System Models,” Energies 2022, Vol. 15, Page 9517, vol. 15, no. 24, p. 9517, Dec. 2022. [CrossRef]
- L. Stucchi, M. L. Stucchi, M. Aiello, A. Gargiulo, and M. A. Brovelli, “COPERNICUS AND THE ENERGY CHALLENGE,” The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, vol. XLVI-4-W2-2021, no. 4/W2-2021, pp. 189–196, Aug. 2021. [CrossRef]
- G. Maclaurin et al., “The Renewable Energy Potential (reV) Model: A Geospatial Platform for Technical Potential and Supply Curve Modeling,” 2021, Accessed: Feb. 01, 2023. [Online]. Available: https://www.nrel.gov/docs/fy19osti/73067.pdf.
- F. Hofmann, J. F. Hofmann, J. Hampp, F. Neumann, T. Brown, and J. Hörsch, “atlite: A Lightweight Python Package for Calculating Renewable Power Potentials and Time Series,” J Open Source Softw, vol. 6, no. 62, p. 3294, Jun. 2021. [CrossRef]
- M. M. Frysztacki, J. M. M. Frysztacki, J. Hörsch, V. Hagenmeyer, and T. Brown, “The strong effect of network resolution on electricity system models with high shares of wind and solar,” 2021. [CrossRef]
- M. M. Frysztacki, V. M. M. Frysztacki, V. Hagenmeyer, and T. Brown, “Inverse methods: How feasible are spatially low-resolved capacity expansion modelling results when disaggregated at high spatial resolution? ✩,” Energy, vol. 281, p. 128133, 2023. [CrossRef]
- V. Aryanpur, B. V. Aryanpur, B. O’Gallachoir, H. Dai, W. Chen, and J. Glynn, “A review of spatial resolution and regionalisation in national-scale energy systems optimisation models,” Energy Strategy Reviews, vol. 37, p. 100702, Sep. 2021. [CrossRef]
- D. Melgar Dominguez et al., “Optimal siting and sizing of renewable energy sources, storage devices, and reactive support devices to obtain a sustainable electrical distribution systems,” Energy Syst, vol. 9, pp. 529–550. 2018. [CrossRef]
- TemoaProject, “Temoa Project Documentation.” Accessed: Jul. 12, 2023. [Online]. Available: https://temoacloud.com/temoaproject/index.
- R. Loulou, A. R. Loulou, A. Lehtilä, A. Kanudia, U. Remme, and G. Goldstein, “Documentation for the TIMES Model: Part II,” 2016. [Online]. Available: http://www.iea-etsap.org/web/Documentation.
- “MESSAGEix-GLOBIOM documentation — message_doc 2020 documentation.” Accessed: Nov. 06, 2023. [Online]. Available: https://docs.messageix.
- A. Hainoun, M. A. Hainoun, M. Seif Aldin, and S. Almoustafa, “Formulating an optimal long-term energy supply strategy for Syria using MESSAGE model,” Energy Policy, vol. 38, no. 4, 2010. [CrossRef]
- M. Howells et al., “OSeMOSYS: The Open Source Energy Modeling System: An introduction to its ethos, structure and development,” Energy Policy, vol. 39, no. 10. pp. 5850–5870. Oct. 2011. [CrossRef]
- F. A. Plazas-Niño, R. F. A. Plazas-Niño, R. Yeganyan, C. Cannone, M. Howells, and J. Quirós-Tortós, “Informing sustainable energy policy in developing countries: An assessment of decarbonization pathways in Colombia using open energy system optimization modelling,” Energy Strategy Reviews, vol. 50. pp. 2211–467, 2023. [CrossRef]
- H. Eshraghi, A. H. Eshraghi, A. Rodrigo De Queiroz, and J. F. Decarolis, “US Energy-Related Greenhouse Gas Emissions in the Absence of Federal Climate Policy,” 2018. [CrossRef]
- M. Nicoli, F. M. Nicoli, F. Gracceva, D. Lerede, and L. Savoldi, “Can We Rely on Open-Source Energy System Optimization Models? The TEMOA-Italy Case Study,” Energies (Basel), vol. 15, no. 18, p. 6505, Sep. 2022. [CrossRef]
- TemoaProject, “GitHub - TemoaProject/temoa,” GitHub. Accessed: Feb. 11, 2023. [Online]. Available: https://github.
- “Pantelleria | Clean energy for EU islands.” Accessed: Jun. 14, 2023. [Online]. Available: https://energy.ec.europa.
- “Comune di Pantelleria.” Accessed: Feb. 01, 2023. [Online]. Available: https://www.comunepantelleria.
- “Aeolian.” Accessed: Nov. 08, 2023. [Online]. Available: https://atlanteeolico.rse-web.
- C. Moscoloni et al., “Wind Turbines and Rooftop Photovoltaic Technical Potential Assessment: Application to Sicilian Minor Islands,” Energies 2022, Vol. 15, Page 5548, vol. 15, no. 15, p. 5548, Jul. 2022. [CrossRef]
- R. Novo, F. D. R. Novo, F. D. Minuto, G. Bracco, G. Mattiazzo, R. Borchiellini, and A. Lanzini, “Supporting Decarbonization Strategies of Local Energy Systems by De-Risking Investments in Renewables: A Case Study on Pantelleria Island,” Energies 2022, Vol. 15, Page 1103, vol. 15, no. 3, p. 1103, Feb. 2022. [CrossRef]
- M. E. Alfano, “Modeling the Energy and the Water Systems in an open-access Energy System Optimization Model: the Pantelleria case study,” Politecnico di Torino, 2022. Accessed: Jan. 19, 2023. [Online]. Available: https://webthesis.biblio.polito. 2498.
- “ISOLA DI PANTELLERIA VERSO 100% RINNOVABILE - SCENARI PER NUOVI PAESAGGI DELL’ENERGIA.” Accessed: Nov. 18, 2023. [Online]. Available: https://it.readkong. 5867.
- M. Yousuf Ansari, A. M. Yousuf Ansari, A. Ahmad, S. S. Khan, and G. Bhushan, “Spatiotemporal clustering: a review,” Artif Intell Rev, vol. 53, pp. 2381–2423, 2020. [CrossRef]
- J. Balkovič et al., “Pan-European crop modelling with EPIC: Implementation, up-scaling and regional crop yield validation,” Agric Syst, vol. 120. pp. 61–75, Sep. 2013. [CrossRef]
- Joint Research Center (JRC), “European Meteorological derived High Resolution RES generation time series for present and future scenarios (EMHIRES),” 2021. Accessed: Jul. 12, 2023. [Online]. Available: https://data.jrc.ec.europa.eu/collection/id-0055#:~:text=EMHIRES is the first publically available European solar power generation,up to NUTS-2 level.
- R. Mckenna, S. R. Mckenna, S. Hollnaicher, and W. Fichtner, “Cost-potential curves for onshore wind energy: A high-resolution analysis for Germany,” 2013. [CrossRef]
- N. Wang, R. A. N. Wang, R. A. Verzijlbergh, P. W. Heijnen, and P. M. Herder, “A spatially explicit planning approach for power systems with a high share of renewable energy sources,” 2019. [CrossRef]
- D. S. Ryberg, Z. D. S. Ryberg, Z. Tulemat, D. Stolten, and M. Robinius, “Uniformly constrained land eligibility for onshore European wind power,” Renew Energy, vol. 146, pp. 921–931, Feb. 2020. [CrossRef]
- C. Moscoloni et al., “Wind Turbines and Rooftop Photovoltaic Technical Potential Assessment: Application to Sicilian Minor Islands,” Energies 2022, Vol. 15, Page 5548, vol. 15, no. 15, p. 5548, Jul. 2022. [CrossRef]
- R. Mckenna et al., “High-resolution large-scale onshore wind energy assessments: A review of potential definitions, methodologies and future research needs-NC-ND license (http://creativecommons.org/licenses/by-nc-nd/4.0/),” 2021. [CrossRef]
- C. W. Klok, A. F. C. W. Klok, A. F. Kirkels, and F. Alkemade, “Impacts, procedural processes, and local context: Rethinking the social acceptance of wind energy projects in the Netherlands A R T I C L E I N F O,” Energy Res Soc Sci, vol. 99, pp. 2214–6296, 2023. [CrossRef]
- “Rete Natura 2000 –, S.I.T. R – Sistema Informativo Territoriale Regionale.” Accessed: Feb. 01, 2023. [Online]. Available: https://www.sitr.regione.sicilia. 2000. [Google Scholar]
- “Explore the World’s Protected Areas.” Accessed: Nov. 09, 2023. [Online]. Available: https://www.protectedplanet.net/en/thematic-areas/wdpa?
- “OpenStreetMap.” Accessed: Nov. 09, 2023. [Online]. Available: https://www.openstreetmap.org/#map=7/42.727/12.
- A. Sousa, “The thematic accuracy of Corine land cover 2000 Assessment using LUCAS (land use/cover area frame statistical survey)”.
- “Comune di Pantelleria PIANO D’AZIONE PER L’ENERGIA SOSTENIBILE,” 2015, Accessed: Oct. 30. 2023. [Online]. Available: www.ambienteitalia.
- F. Lindberg et al., “Urban Multi-scale Environmental Predictor (UMEP): An integrated tool for city-based climate services,” Environmental Modelling & Software, vol. 99, pp. 70–87, Jan. 2018. [CrossRef]
- S. Tarquini, S. S. Tarquini, S. Vinci, M. Favalli, F. Doumaz, A. Fornaciai, and L. Nannipieri, “Release of a 10-m-resolution DEM for the Italian territory: Comparison with global-coverage DEMs and anaglyph-mode exploration via the web,” Comput Geosci, vol. 38, no. 1, pp. 168–170. Jan. 2012. [CrossRef]
- “Rete Natura 2000 | Ministero dell’Ambiente e della Sicurezza Energetica.” Accessed: Nov. 09, 2023. [Online]. Available: https://www.mase.gov. 2000.
- M. R. Elkadeem et al., “Geospatial-assisted multi-criterion analysis of solar and wind power geographical-technical-economic potential assessment,” 2022. [CrossRef]
- R. J. H. Dunn et al., “HadISD: A quality-controlled global synoptic report database for selected variables at long-term stations from 1973-2011,” Climate of the Past, vol. 8, no. 5, pp. 1649–1679, 2012. [CrossRef]
- J. Ramon, L. J. Ramon, L. Lledó, N. Pérez-Zanón, A. Soret, and F. J. Doblas-Reyes, “The tall tower dataset: A unique initiative to boost wind energy research,” Earth Syst Sci Data, vol. 12, no. 1, pp. 429–439, Feb. 2020. [CrossRef]
- “MERRA-2.” Accessed: Nov. 09, 2023. [Online]. Available: https://gmao.gsfc.nasa.
- B. Bell et al., “The ERA5 global reanalysis: Preliminary extension to 1950.” Quarterly Journal of the Royal Meteorological Society, vol. 147, no. 741, pp. 4186–4227, Oct. 2021. [CrossRef]
- “CMIP5 - Home | ESGF-CoG.” Accessed: Nov. 09, 2023. [Online]. Available: https://esgf-node.llnl.
- “EURO-CORDEX.” Accessed: Nov. 09, 2023. [Online]. Available: https://www.euro-cordex.
- “Global Solar Atlas.” Accessed: Nov. 09, 2023. [Online]. Available: https://globalsolaratlas.
- “Solar irradiance data | Solargis.” Accessed: Nov. 09, 2023. [Online]. Available: https://solargis.
- “HelioClim-3 Monthly Irradiation GHI - Data Europa EU.” Accessed: Nov. 09, 2023. [Online]. Available: https://data.europa.eu/data/datasets/7237e78b-b12b-4fdb-85fb-33e9fe0c6994?
- “NEW EUROPEAN WIND ATLAS -.” Accessed: Nov. 09, 2023. [Online]. Available: https://www.neweuropeanwindatlas.
- “Home | Dutch Offshore Wind Atlas.” Accessed: Nov. 09, 2023. [Online]. Available: https://www.dutchoffshorewindatlas.
- “Aeolian.” Accessed: Nov. 09, 2023. [Online]. Available: https://atlanteeolico.rse-web.
- “Global Wind Atlas.” Accessed: Nov. 09, 2023. [Online]. Available: https://globalwindatlas.
- “Windographer | Wind Data Analytics and Visualization Solution | UL Solutions.” Accessed: Nov. 09, 2023. [Online]. Available: https://www.ul.
- “Home | Mesonet.” Accessed: Nov. 09, 2023. [Online]. Available: https://mesonet.
- M. H. McCutchan, D. G. M. H. McCutchan, D. G. Fox, M. H. McCutchan, and D. G. Fox, “Effect of Elevation and Aspect on Wind, Temperatme and Humidity.,” JApMe, vol. 25, no. 12, pp. 1996–2013, 1986. [CrossRef]
- N. Chen, “Scale problem: Influence of grid spacing of digital elevation model on computed slope and shielded extra-terrestrial solar radiation”. [CrossRef]
- M. Ŝúri and J. Hofierka, “A New GIS-based Solar Radiation Model and Its Application to Photovoltaic Assessments,” Transactions in GIS, vol. 8, no. 2, pp. 175–190. Apr. 2004. [CrossRef]
- “Accesso di accesso - ArcGIS Online.” Accessed: Nov. 09, 2023. [Online]. Available: https://www.arcgis.com/index.
- “An overview of the Solar Radiation toolset—ArcGIS Pro | Documentation.” Accessed: Nov. 09, 2023. [Online]. Available: https://pro.arcgis.com/en/pro-app/latest/tool-reference/spatial-analyst/an-overview-of-the-solar-radiation-tools.
- B. B. Kausika and W. G. J. H. M. van Sark, “Calibration and Validation of ArcGIS Solar Radiation Tool for Photovoltaic Potential Determination in the Netherlands,” Energies 2021, Vol. 14, Page 1865, vol. 14, no. 7, p. 1865, Mar. 2021. [CrossRef]
- B. Hur Pintor et al., “Solar Energy Resource Assessment Using R.SUN In GRASS GIS And Site Suitability Analysis Using AHP For Groundmounted Solar Photovoltaic (PV) Farm In The Central Luzon Region (Region 3), Philippines,” Free and Open Source Software for Geospatial (FOSS4G) Conference Proceedings, vol. 15, no. 1, p. 3, Feb. 2018. [CrossRef]
- Gašparović, M. Gašparović, and D. Medak, “Determining and analysing solar irradiation based on freely available data: A case study from Croatia,” Environ Dev, vol. 26, pp. 55–67, Jun. 2018. [CrossRef]
- L. El Chaar, L. A. L. El Chaar, L. A. Lamont, and N. El Zein, “Review of photovoltaic technologies,” Renewable and Sustainable Energy Reviews, vol. 15, pp. 2165–2175, 2011. [CrossRef]
- “(PDF) Analysis of utility scale wind and solar plant performance in South Africa relative to daily electricity demand.” Accessed: Nov. 09, 2023. [Online]. Available: https://www.researchgate. 3211.
- “Benvenuti a wind-turbine-models.com.” Accessed: Nov. 10. 2023. [Online]. Available: https://it.wind-turbine-models.
- E. W. Peterson, J. P., Jr. E. W. Peterson, J. P., Jr. Hennessey, E. W. Peterson, and J. P., Jr. Hennessey, “On the Use of Power Laws for Estimates of Wind Power Potential.,” JApMe, vol. 17, no. 3, pp. 390–394, 1978. [CrossRef]
- IRNEA, “IRENA (2022), Renewable Power Generation Costs in 2021, International Renewable Energy Agency, Abu Dhabi. ISBN 978-92-9260-452-3,” International Renewable Energy Agency, p. 160. 2022, Accessed: Nov. 10. 2023. [Online]. Available: https://www.irena.org/-/media/Files/IRENA/Agency/Publication/2018/Jan/IRENA_2017_Power_Costs_2018.
- Eurostat data browser, “Yearly Land rent price for a year.” Accessed: Nov. 30. 2023. [Online]. Available: https://ec.europa.eu/eurostat/databrowser/view/APRI_LRNT__custom_5264437/bookmark/table? 5713.
- “Econnextion: la mappa delle connessioni rinnovabili - Terna spa.” Accessed: Nov. 10. 2023. [Online]. Available: https://www.terna.
- TemoaProject, “Temoa Project Documentation - Objective Function.” Accessed: Mar. 22, 2023. [Online]. Available: https://temoacloud.com/temoaproject/Documentation.
- “Wind Costs.” Accessed: Nov. 10. 2023. [Online]. Available: https://www.irena.
- M. Hughes et al., “System Integration with Multiscale Networks (Simon): A Modular Framework for Resource Management Models,” Proceedings - Winter Simulation Conference, vol. 2020-December, pp. 656–667, Dec. 2020. [CrossRef]
- R. J. G. B. Campello, D. R. J. G. B. Campello, D. Moulavi, and J. Sander, “Density-based clustering based on hierarchical density estimates,” Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics), vol. 7819 LNAI, no. PART 2, pp. 160–172, 2013. [CrossRef]
- S. Mannor et al., “K-Means Clustering,” Encyclopedia of Machine Learning, pp. 563–564, 2011. [CrossRef]
- M. Ester, H.-P. M. Ester, H.-P. Kriegel, J. Sander, and X. Xu, “A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise,” 1996, Accessed: Nov. 13, 2023. [Online]. Available: www.aaai.
- J.-F. Wang, A. J.-F. Wang, A. Stein, B.-B. Gao, and Y. Ge, “A review of spatial sampling,” Spat Stat, 2012. [CrossRef]
- G. Guo, H. G. Guo, H. Wang, D. Bell, Y. Bi, and K. Greer, “KNN model-based approach in classification,” Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics), vol. 2888, pp. 986–996, 2003. [CrossRef]
- P. J. Rousseeuw, “Silhouettes: a graphical aid to the interpretation and validation of cluster analysis,” J Comput Appl Math, vol. 20. pp. 53–65, 1987.
- D. S. Ryberg, Z. D. S. Ryberg, Z. Tulemat, D. Stolten, and M. Robinius, “Uniformly constrained land eligibility for onshore European wind power,” Renew Energy, vol. 146, pp. 921–931, Feb. 2020. [CrossRef]
- V. Aryanpur, B. V. Aryanpur, B. O’Gallachoir, H. Dai, W. Chen, and J. Glynn, “A review of spatial resolution and regionalisation in national-scale energy systems optimisation models,” Energy Strategy Reviews, vol. 37, p. 100702, Sep. 2021. [CrossRef]
Figure 1.
Visualization of the Pantelleria island and its placement in the Strait of Sicily.
Figure 2.
Land Eligibility analysis for the Pantelleria Island. (a),(b) and (c) represent the constraint for photovoltaic installations while (d) ,(e) and (f) are the ones for wind. (a),(d) are anthropic exclusions. (b) and (e) are constraint due to natural habitat and landscape heritage laws. (c) and (f) represent limitation associated to environmental reasons.
Figure 2.
Land Eligibility analysis for the Pantelleria Island. (a),(b) and (c) represent the constraint for photovoltaic installations while (d) ,(e) and (f) are the ones for wind. (a),(d) are anthropic exclusions. (b) and (e) are constraint due to natural habitat and landscape heritage laws. (c) and (f) represent limitation associated to environmental reasons.
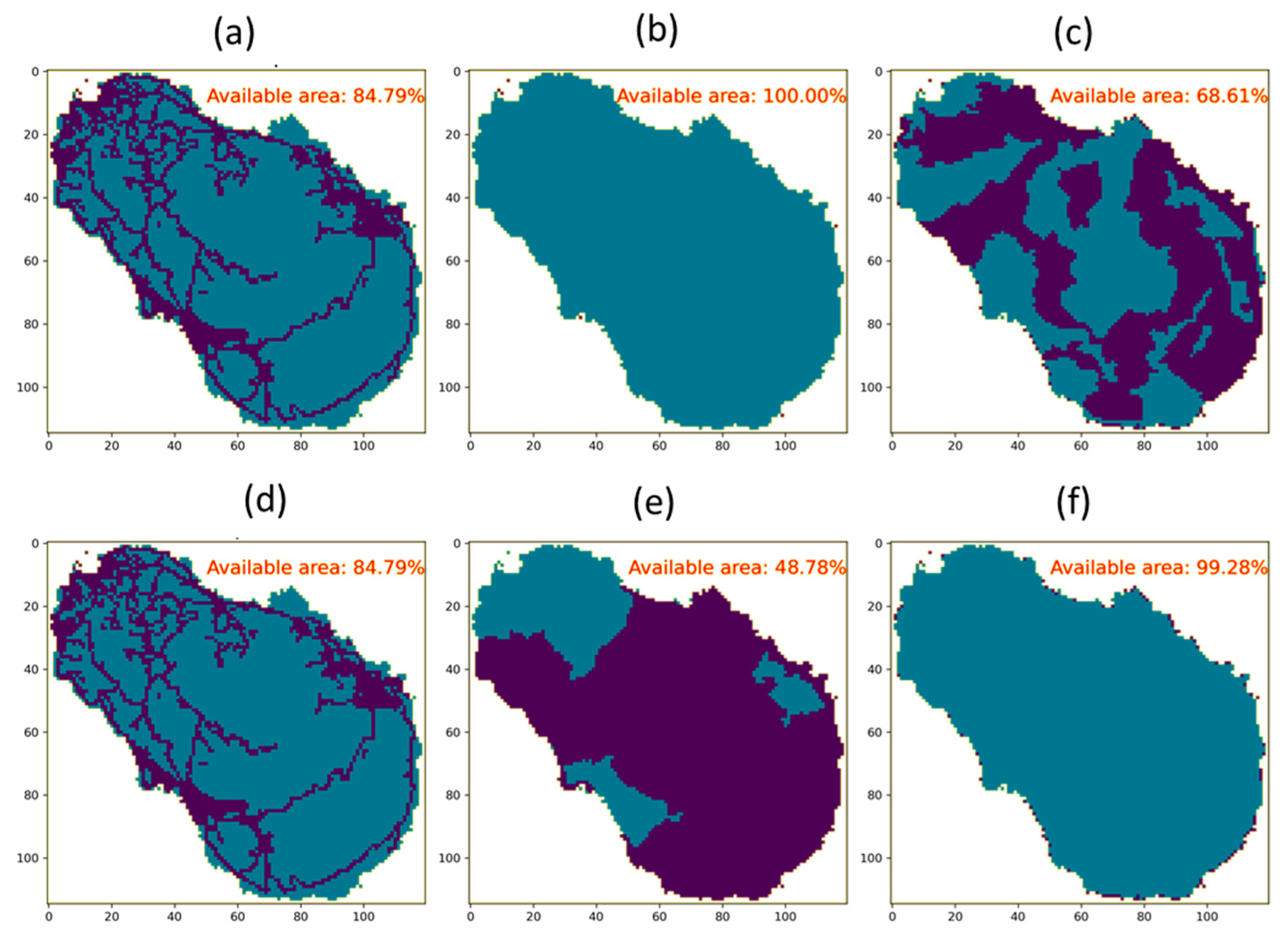
Figure 3.
Photovoltaic Capacity factor by season, Day and Peak time slices.
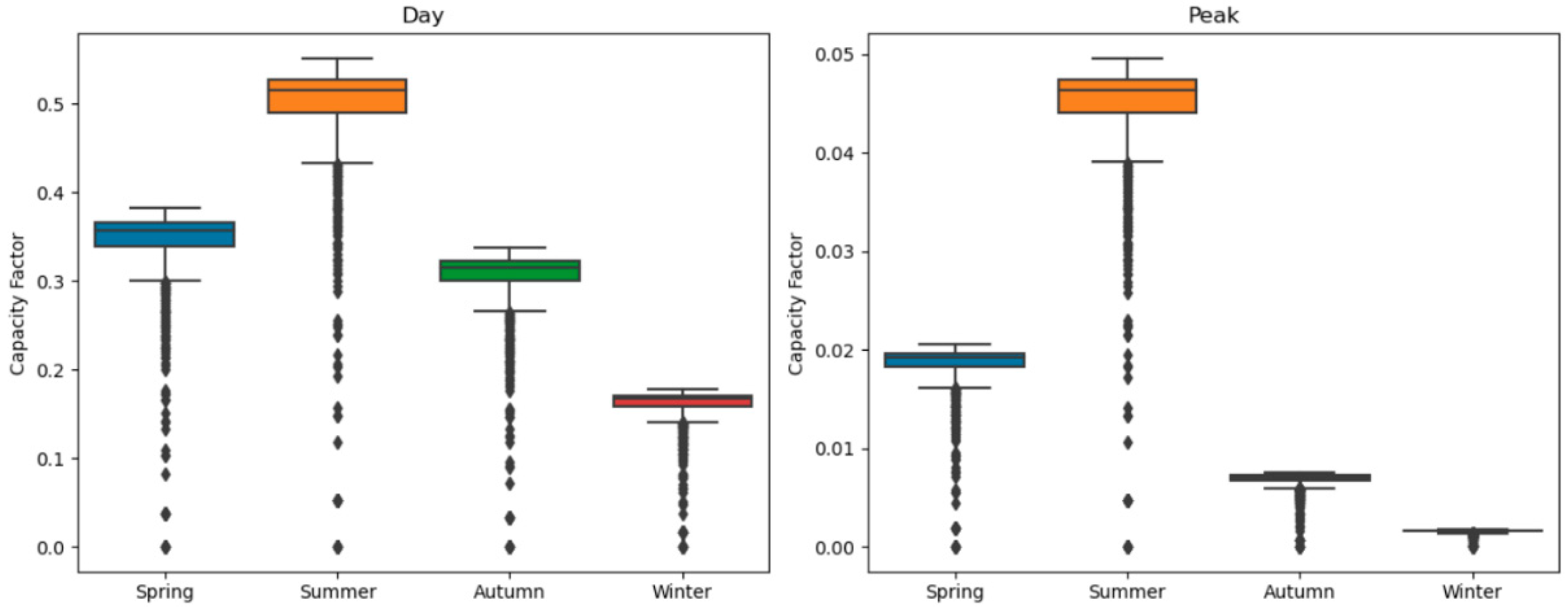
Figure 4.
Wind capacity factor by timeslice and height. Average value, standard deviation, minimun and maximum values.
Figure 4.
Wind capacity factor by timeslice and height. Average value, standard deviation, minimun and maximum values.
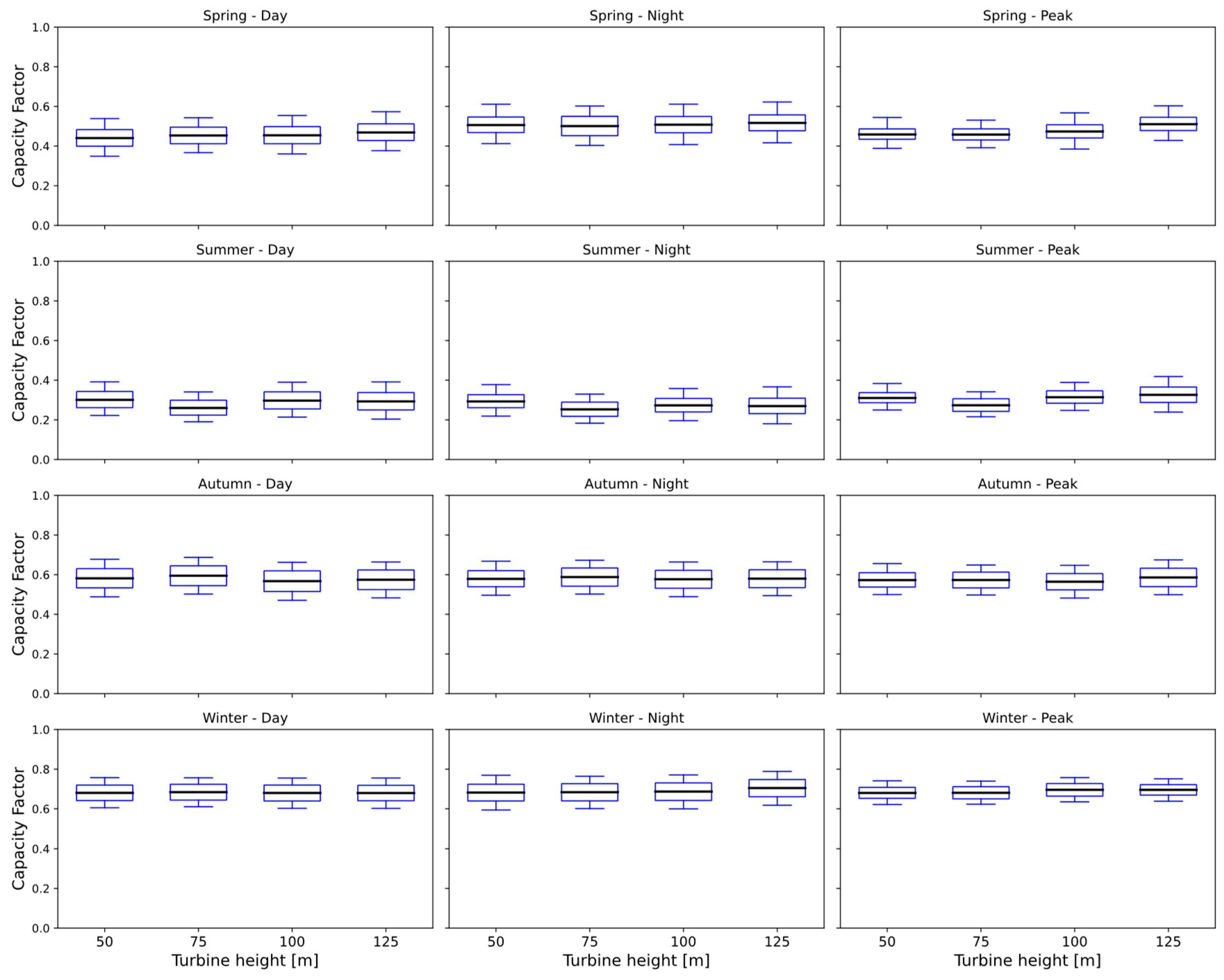
Figure 5.
Workflow of the data aggregation phase, from raw data to TEMOA-Pantelleria characterization.
Figure 5.
Workflow of the data aggregation phase, from raw data to TEMOA-Pantelleria characterization.
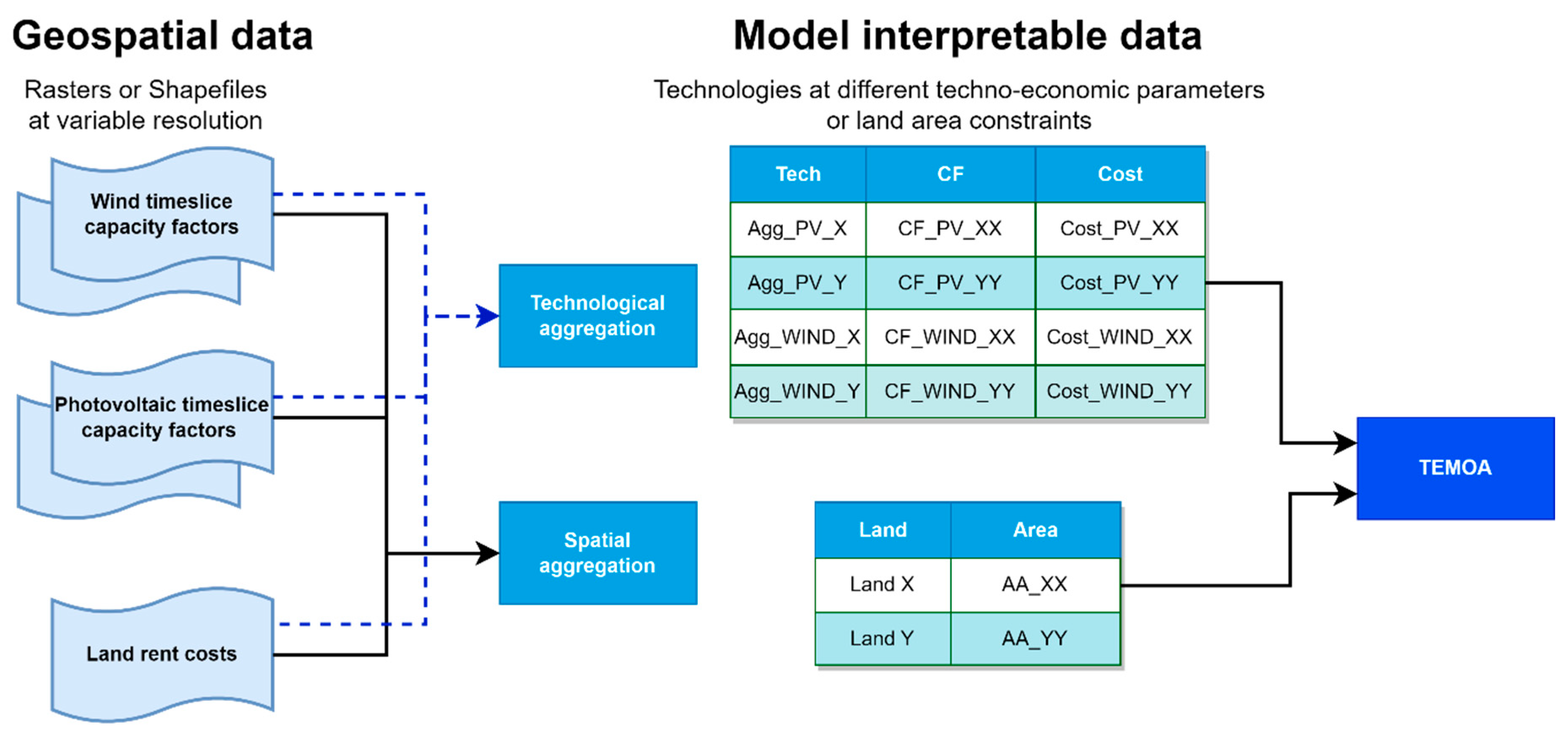
Figure 6.
Data partitioning before applying the clustering method.
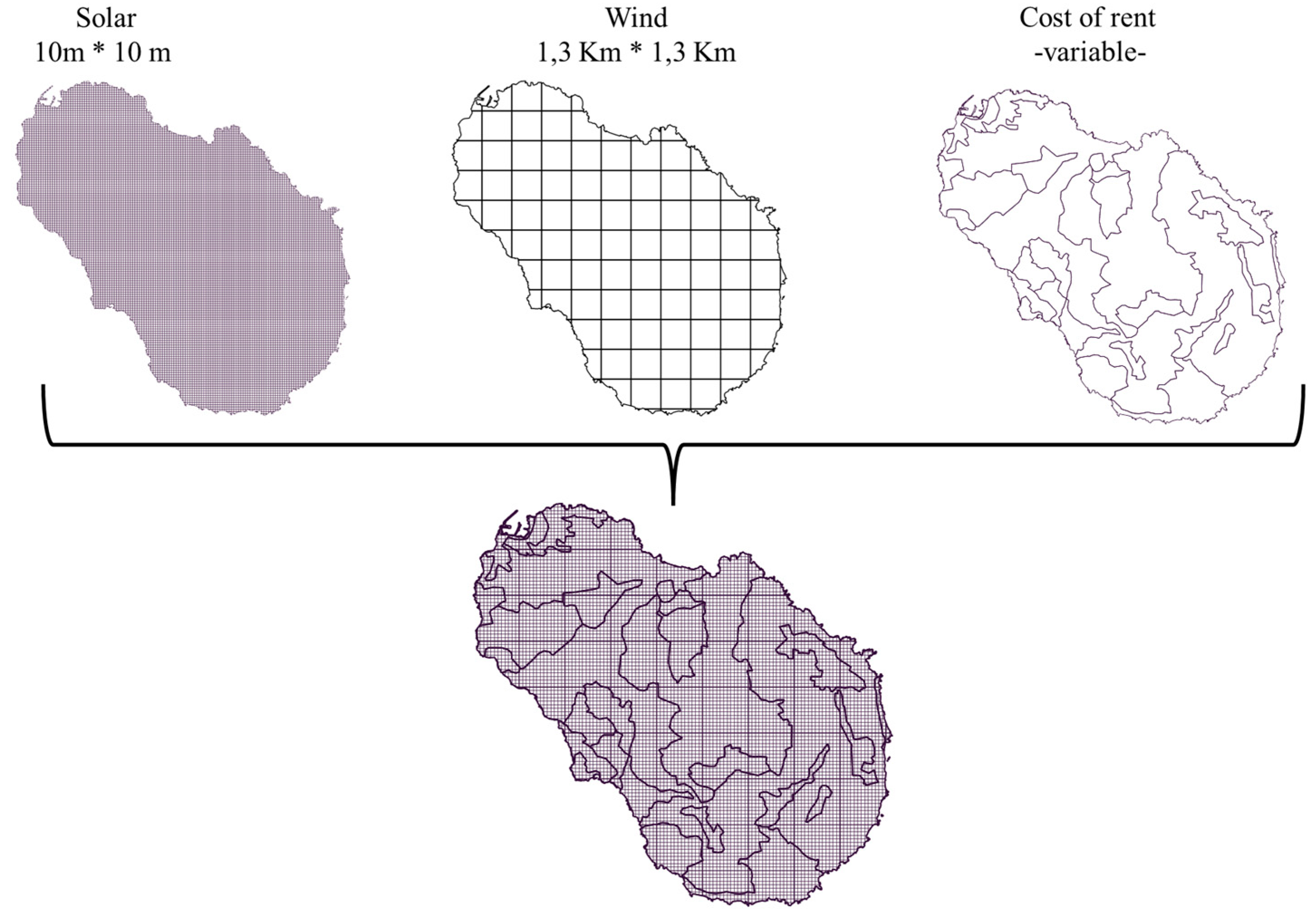
Figure 7.
Results of clustering with different algorithms. (a) HDBSCAN (b) K-Means and (c) DBSCAN.
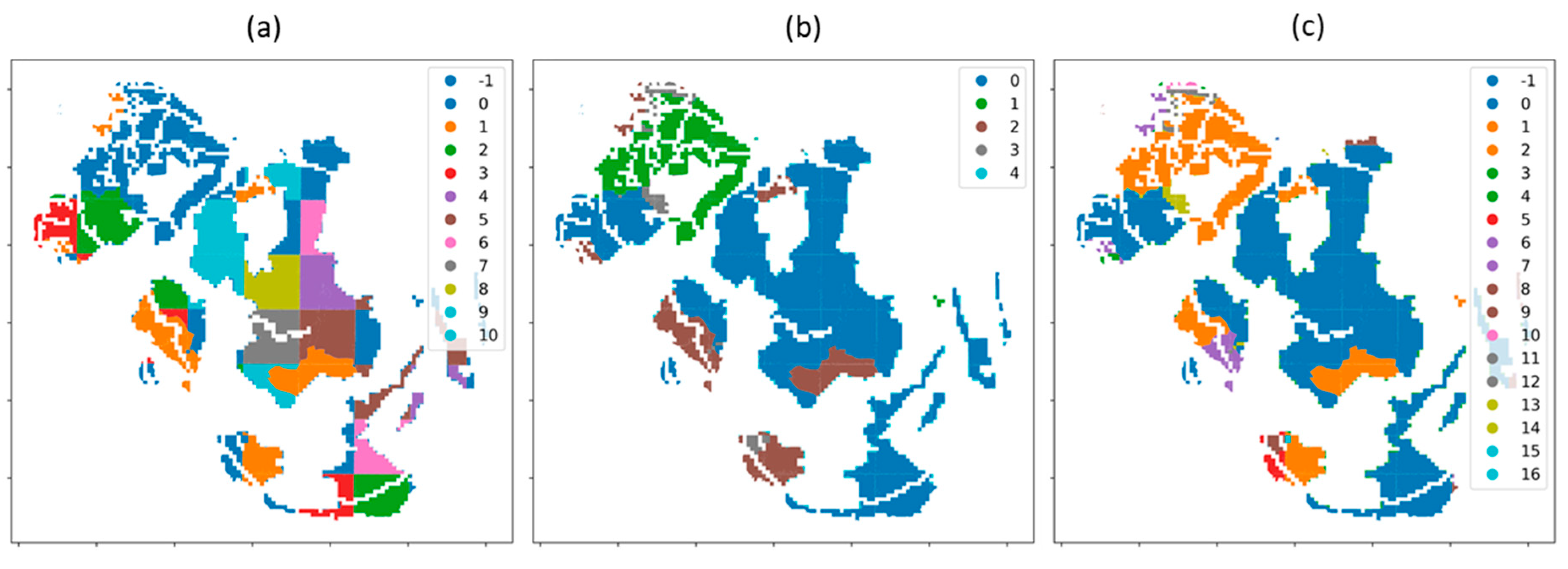
Figure 8.
TEMOA Pantelleria VRES characterization according to a traditional average (a) and cluster aggregation.
Figure 8.
TEMOA Pantelleria VRES characterization according to a traditional average (a) and cluster aggregation.
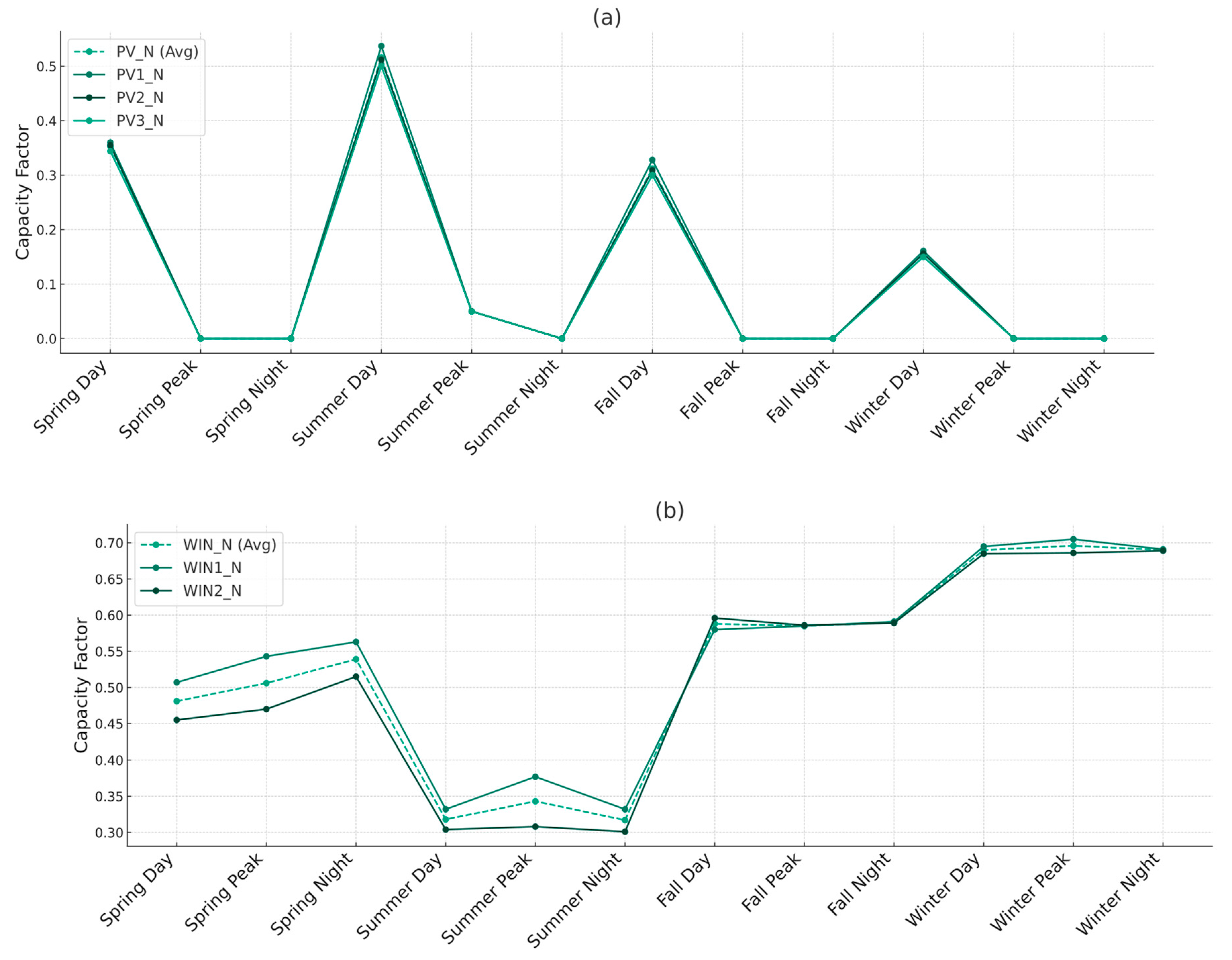
Figure 9.
Power sector capacity and activity for traditional modelling instance and land specific modeling instance . . Subplot (a) - (b) represents the traditional TEMOA modeling instance, while (c)-(d) the land explicit one in the low land price case, (e)-(f) the intermediate price case and (g)-(h) the highest price case.
Figure 9.
Power sector capacity and activity for traditional modelling instance and land specific modeling instance . . Subplot (a) - (b) represents the traditional TEMOA modeling instance, while (c)-(d) the land explicit one in the low land price case, (e)-(f) the intermediate price case and (g)-(h) the highest price case.
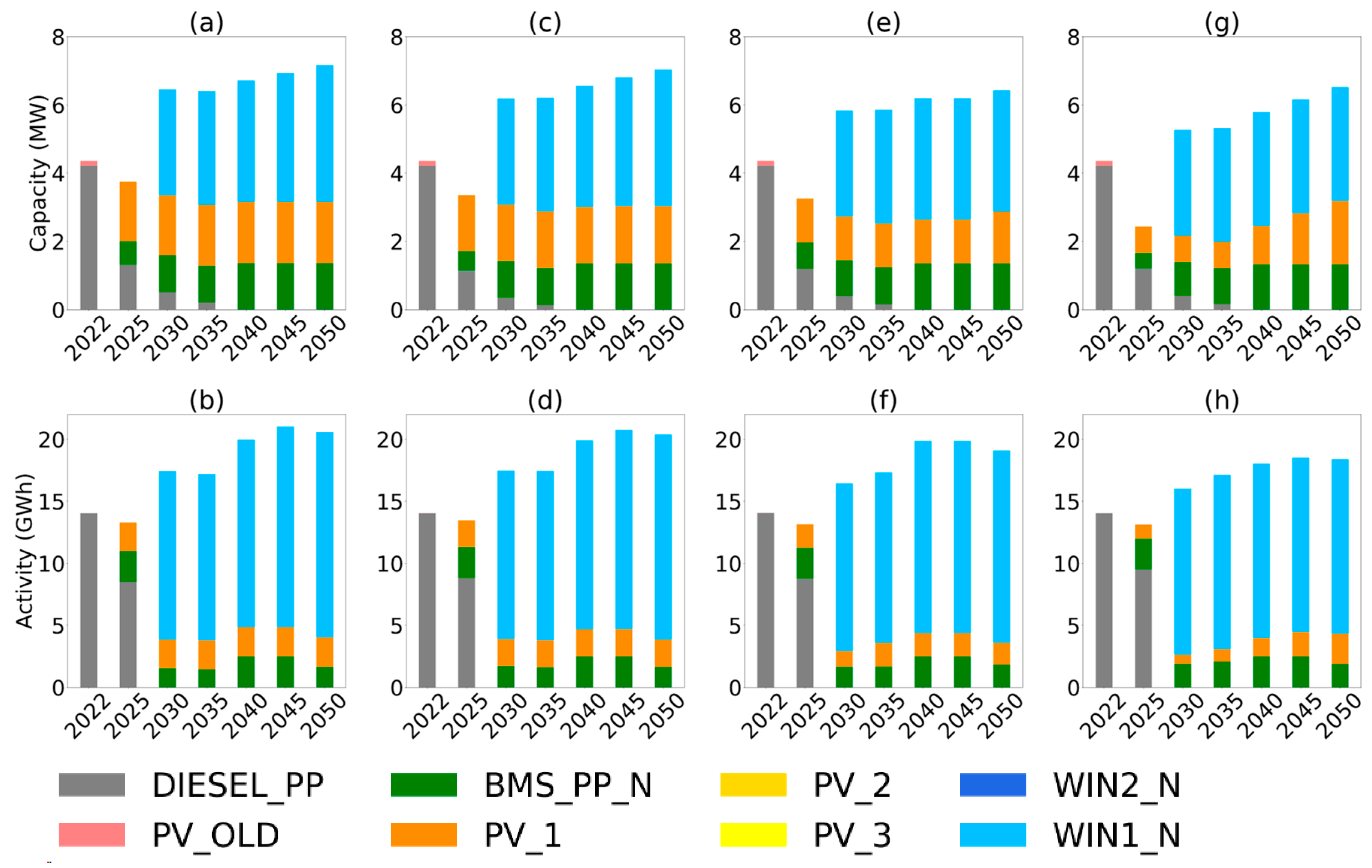
Figure 10.
Land occupation by cluster (a) and Total Cost of land rent (b) in Low Price and High price land rent configurations.
Figure 10.
Land occupation by cluster (a) and Total Cost of land rent (b) in Low Price and High price land rent configurations.
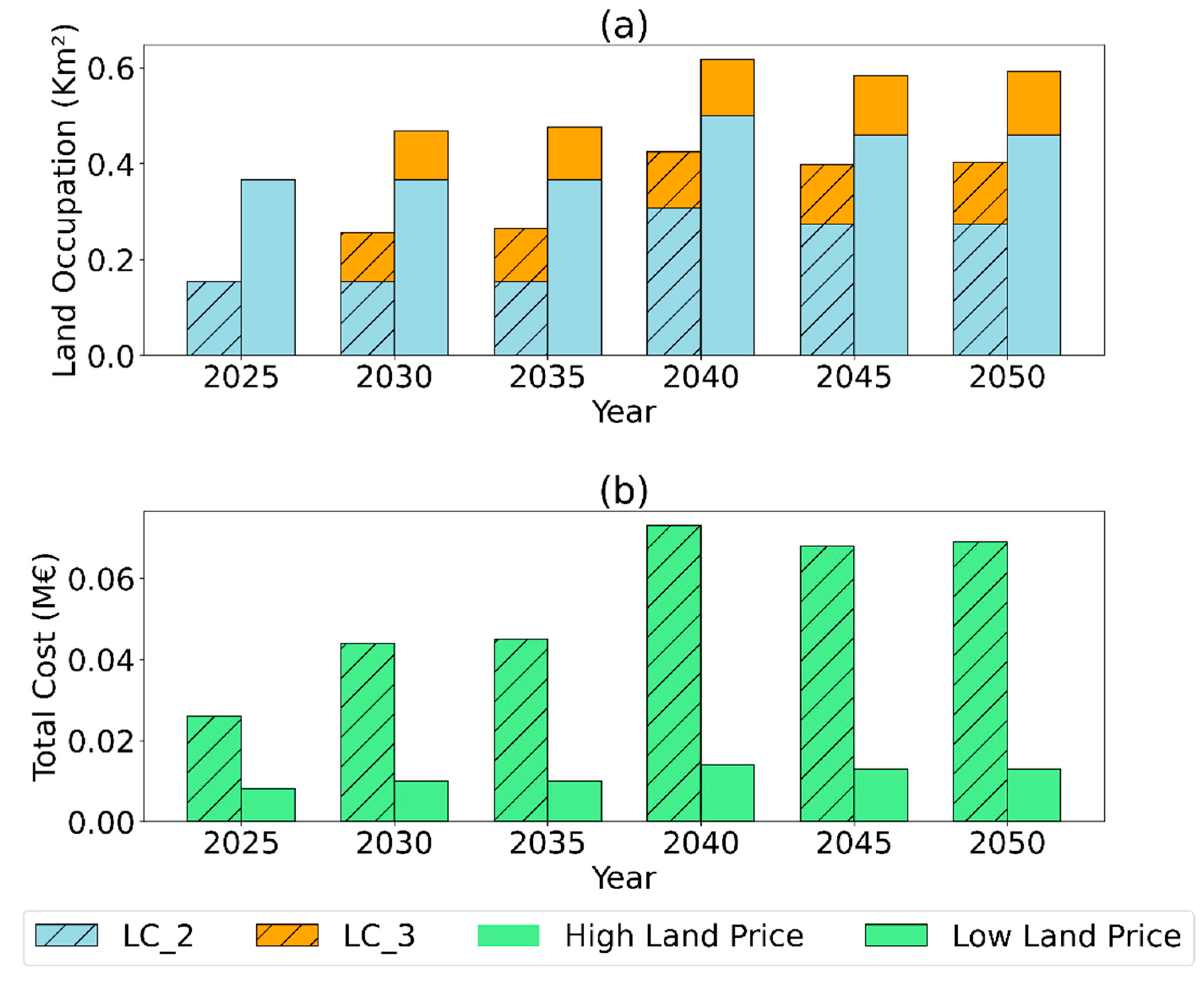
Table 1.
Review of the main land eligibility analysis found in literature.
| Administrative | Technical | Economic | Social | Year | Source |
|---|---|---|---|---|---|
| v | v | 2014 | [51] | ||
| v | v | v | v | 2018 | [21] |
| v | v | v | 2020 | [52] | |
| v | v | v | v | 2020 | [53] |
| v | v | v | v | 2021 | [27] |
| v | v | 2022 | [54] | ||
| v | v | v | v | 2022 | [55] |
| v | v | v | v | 2023 | [56] |
Table 2.
Constraint expression for Land Eligibility analysis. Exclusion rule for distance are derived from Italian regulation summarized in the Pantelleria Energy Plan [61.]
Table 2.
Constraint expression for Land Eligibility analysis. Exclusion rule for distance are derived from Italian regulation summarized in the Pantelleria Energy Plan [61.]
| Area | Constraint | Exlcusion rule | Source |
|---|---|---|---|
| Environmental/Technical | Wind Speed | below 4.5 m/s | RSE [43] |
| Irradiance | below 3.0 kWh/m2 day | UMEP ERA 5 [62] | |
| Slope | ≥15% | TinItaly [63] | |
| Permanent crops | Inside | CLC [60] | |
| Water bodies | Inside | - | |
| Rocks | Inside | - | |
| Coast | Inside | - | |
| Administrative/Habitat | Natural Habitats | Inside | Natura 2000 [64] |
| Bird Areas | Inside | - | |
| Biospheres | Inside | WDPA [58] | |
| Protected Landscape | <1000 m | - | |
| Reserves | Inside | - | |
| Parks | Inside | - | |
| Monuments | 1000 m | - | |
| Hydrological risk | Inside | GeoPortale [] | |
| Anthropic | Road distance | 100 m | OpenStreetMap [59] |
| Urban settlement | 200 m | - | |
| Industrial sites | 200 m | - | |
| Airport | 1500 m (Wind Only) | - | |
| Recreational Areas | 200 m | - |
Table 3.
Data sources for general and technology specific resource assessment. Characterization by spatial and temporal coverage and resolution.
Table 3.
Data sources for general and technology specific resource assessment. Characterization by spatial and temporal coverage and resolution.
| Technology | Data typology | Database names | Coverage | Resolution | |||
|---|---|---|---|---|---|---|---|
| Spatial | Temporal | Spatial | Temporal | ||||
| General | Observation | HadISD [66], Tall Tower Database [67] | Global | Historical, 20-50 years | Site specific | 5 min - 1 hr | |
| Reanalysis | MERRA-2 [68], ERA5 [69] | Global | Historical, 40-70 years | 30-60 km | 1-6 hr | ||
| Climate models | CMIP5 [70],EUROCORDEX [71] | Global | Historical and future, 80-250 years | 10-300 km | Hr- Montly | ||
| Solar | Atlas | GSA [72], SolarGIS [73] | Global | Historical | 90 m | 0.5-1 hr | |
| Reanalysis | HelioClim-3 [74] | Global | Historical and real time | 3 km | 15 min - 1 hr | ||
| Wind | Reanalysis | NEWA [75], DOWA [76], RSE[77] | Regional (EU) | Historical, 11-30 years | 1,5-3 km | 0.5-1 hr | |
| Atlas | GWA [78] | Global | Historical average | 50-200 m | N/A | ||
| Reanalysis | WINDographer [79], Mesonet [80] | USA | Historical | 3 km | Hourly | ||
Table 4.
Main characteristics of the wind turbine models used for the producibility calculation. For each turbine, data are obtained by the online wind-turbine-model repository [91.]
Table 4.
Main characteristics of the wind turbine models used for the producibility calculation. For each turbine, data are obtained by the online wind-turbine-model repository [91.]
| Reference Height [m] | WTG model | Nominal Power [MW] | Rotor Diameter [m] | Hub Height [m] |
|---|---|---|---|---|
| 50 m | Riva Calzoni 500.54 | 0.5 | 54 | 50 |
| 75 m | Leitwind LTW90- 950 | 0.95 | 90 | 80 |
| 100 m | Vestas V117 3450 | 3,45 | 117 | 91 |
| 125m | NREL_6MW_RTW | 6 | 128 | 119 |
Table 5.
Performance of the three different clustering algorithms.
| Method | Silhouette Score | Time (seconds) | Memory (MB) |
|---|---|---|---|
| HDBSCAN | 0.527 | 1,729 | 2,246 |
| Kmeans | 0.827 | 0.369 | 0.224 |
| DBSCAN | 0.807 | 2,940 | 0.810 |
Table 6.
Cluster characterization.
| Land Cluster | Available area [km2] | Installable technologies |
|---|---|---|
| LC_1 | 2,850 | PV2_N |
| LC_2 | 0.457 | WIN1_N, PV_1 |
| LC_3 | 4,909 | PV_1 |
| LC_4 | 1,947 | PV_ 3, WIN2_N |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated







