Prerpints.org logo
Preprint
Article

Unmanned Airborne Bistatic InSAR Data Processing Method Using Bi-Directional Synchronization Chain Signals

Altmetrics

Downloads

91

Views

27

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

03 January 2024

Posted:

04 January 2024

You are already at the latest version

Alerts
Abstract
The dual-station Interferometric Synthetic Aperture Radar (InSAR) system can overcome the physical limitations imposed by the baseline of single-station dual-antenna InSAR. It provides greater flexibility and can enhance elevation measurement accuracy through a well-designed baseline configuration.Unmanned aerial vehicles (UAV) equipped with dual-station InSAR, with relatively low cost and high flexibility, are useful for mapping and land resource exploration. However, due to challenges including spatiotemporal synchronization and motion errors, there are limited reports on UAV-borne dual-station InSAR. This paper proposes a comprehensive method for processing data from small UAV-borne dual-station InSAR by integrating two-way synchronization chain signals. The proposed method includes compensation for time and phase synchronization errors, trajectory refinement with synchronized chain and Position and Orientation System (POS) data, high-precision dual-station InSAR imaging and interferometric processing. Height inversion results based on the proposed method is also provided, demonstrating the effectiveness of the proposed method and improving interferometric accuracy at calibration points from 0.66 meters to 0.42 meters.
Keywords: 
Subject: Environmental and Earth Sciences  -   Remote Sensing

1. Introduction

Interferometric Synthetic Aperture Radar (InSAR) [1] technology generally refers to cross-track SAR interferometry, which is a remote sensing method that obtains the elevation of the target through interferometric processing. Applications of InSAR include terrain mapping, surface deformation monitoring, and urban planning. Interferometric SAR can be formed through various methods, including single-station re-tracking or repeated flight interferometry, single-station dual-antenna interferometry, and bistatic interferometry. Among them, the baseline length of the bistatic interferometric SAR [2] system can break through the physical limitations imposed on the baseline length of the single-station dual-antenna and has a greater degree of freedom, which is important for measuring elevation accurately, and has a great application prospect.
However, the clocks of the bistatic SAR transceiver system use different frequency sources, resulting in an inevitable synchronization error between the master and the slave. These errors in time and phase will degrade the SAR imaging quality and phase accuracy. In addition, there is no physical connection between the master and slave antennas of bistatic interferometric SAR, which is a purely flexible baseline. The maintenance of baseline configuration and high-accuracy measurement are also challenges for bistatic interferometric SAR.
Dual-station interferometric SAR can be categorized explicitly into airborne, spaceborne, and other types based on the carrying platforms. Specifically, space-borne SARs are unaffected by air currents, making it easier for space-borne SARs to form a relatively stable baseline configuration and maintain the synchronization chain. TerraSAR-X/TanDEM-X is the first international spaceborne bistatic interferometric SAR system, which has acquired a large amount of data and completed the production of global high-precision DEM data products, expanding the scientific and commercial applications of spaceborne bistatic interferometric SAR [3,4]. The Lutan-1(LT-1) mission is China's first civilian bistatic spaceborne synthetic aperture radar mission, consisting of two fully polarized L-band SAR satellites successfully launched on 26 January and 28 February 2022, respectively. LT-1 continuously provides high-quality observation data and interferometric data products for land monitoring and other purposes [5,6].
The success of the above bistatic interferometric SAR constellation shows that the current problems of time and phase synchronization, as well as baseline measurement of spaceborne InSAR, have been well resolved. The technical approaches mainly include using ultra-high stability optical clocks, setting ground calibration points, GNSS clock-based synchronization, continuous wave signal pair transmission, pulse signal pair transmission, etc. The TanDEM-X SAR system solves the phase synchronization problem by adopting the synchronization scheme of two-way transmission of alternating pulses, which ensures that the time synchronization error is less than 5 μs within 600 s [7]. LT-1 constellation adopts an advanced uninterrupted phase synchronization scheme. The synchronization pulses are exchanged immediately after the end time of the radar echo reception window and before the start time of the next pulse repetition interval without interrupting the normal operation of the SAR. The uninterrupted synchronization scheme has a high synchronization accuracy with a residual phase standard deviation (STD) of less than 0.3° [8].
However, on the one hand, the stability of the crystals used in airborne SAR is not as high as that of spaceborne SAR due to cost considerations. This leads to more prominent time and phase synchronization problems in airborne bistatic interferometric SAR. On the other hand, the baseline configuration of airborne bistatic InSAR is not easy to maintain, and the accuracy of the baseline measurements is also often limited due to the influence of the airflow. Therefore, the implementation of airborne bistatic interferometric SAR is challenging, and few related results have been reported. To the best of the authors' knowledge, only ESA has carried out the BelSAR bistatic interferometric experiment [9]. The BelSAR radar sensors were mounted on two Cessna 208 aircraft and synchronized by means of a technique based on a dedicated high-precision GPSDO system with a 10 MHz reference clock and a pulse-per-second output to synchronize the receivers with the transmitters [10]. However, no interferometric results and accuracy verification obtained from this experiment have been seen, indicating that this technique is far from reliable. Although there is few reports on airborne bistatic InSAR data processing methods, relevant research exists in bistatic SAR imaging, airborne SAR motion compensation, and interferometric processing.
As for the bistatic SAR imaging algorithm, in order to solve the frequency domain form in bistatic SAR imaging, Loffeld, Ding et al. convert the bistatic SAR echo data into single-station SAR data. This method is clear and simple, but the accuracy of the approximation is relatively low in the case of a larger scene [11]. Loffeld et al. use algebraic or geometrical methods to directly introduce the approximation in the frequency domain to get the approximate analytical expression of the 2D spectrum and then derive the bistatic SAR imaging algorithm on this basis. This method results in a relatively high accuracy but is very complicated [12]. Ender and Giroux et al. obtained an exact implicit expression for the 2D spectrum based on numerical calculations and a wave number domain algorithm by phase decomposition [13,14]. Qiu et al. proposed a bistatic SAR imaging algorithm based on a modified hyperbolic equivalent model [15] that can be used in the case of short bistatic baselines and a nonlinear CS algorithm [16] that can be used in the case of long baselines.
In terms of motion compensation, the separation of the transmitter and the receiver further complicates the motion error. On the one hand, step-by-step compensation is needed because of the two-dimensional space-variant motion error. Generally, motion errors are divided into the following categories and are compensated for separately: space-invariant motion error, distance-variant motion error, and azimuth-variant motion error. In particular, the step-by-step compensation of range space-invariant and range-variant errors is usually called a two-step motion compensation algorithm [17]. The one-step motion compensation algorithm is an improved version of the two-step motion compensation algorithm, which can compensate for the space-invariant motion error and the distance space-variant motion error before the imaging process, and effectively reduce the residual error before imaging [18,19]. The azimuth space-variant motion error is generally compensated on coarsely focused SAR images, and the Precise terrain and aperture-dependent motion compensation (PTA) algorithm can effectively compensate for the residual azimuth space-variant motion error in the SAR images, but the envelope of SAR image is required to be completely corrected in this method. In airborne SAR imaging processing, the Range Migration Algorithm (RMA) or Omega-K algorithm is a commonly used imaging algorithm in engineering, but the residual error will be coupled with the RMA algorithm, thus causing a large envelope error, which will seriously reduce the compensation effect of PTA [20,21]. Therefore, when higher accuracy is required, the BP algorithm is often used, sacrificing efficiency for processing accuracy [22].
In terms of airborne interferometric processing, the majority of research has been conducted on airborne single-station dual-antenna InSAR. For example, Fangfang Li et al. experimented with airborne dual-antenna InSAR for flight data and proposed a motion compensation method based on height iteration [23]. Mao et al. addressed multipath effects in airborne dual-antenna InSAR systems by proposing a theoretical model for calculating multipath errors [24]. Erxue Chen et al. used X-band single-polarization dual-antenna airborne InSAR data to estimate forest tree height [25]. However, methods for processing airborne dual-station InSAR are rarely reported.
In recent years, the rapid development of SAR miniaturization technology and UAV technology has brought more possibilities to realize bistatic interferometry using a small UAV platform. Small UAV-based bistatic InSAR is one of the directions for the development of low-cost and efficient airborne interferometric SAR technology. However, small UAV-borne SAR often requires higher cost control and is more susceptible to airflow, further increasing the difficulty of bistatic InSAR processing. To the best of the authors' knowledge, there has been no systematic international research on small UAV-borne bistatic InSAR imaging and interferometric processing methods.
The Aerospace Information Research Institute, Chinese Academy of Sciences led the design and development of the first international unmanned airborne bistatic interferometric SAR system [26], and flight experiments were carried out at the Bailing Airport in Inner Mongolia. Literature [26] describes the program design, basic composition, and main performance of the system, as well as the program and implementation of the first flight experiment.
This paper focuses on the small UAV-borne dual-station InSAR system and establishes a comprehensive method for high-precision synchronization error compensation, imaging processing, and interferometric processing. Firstly, a phase and time error compensation method based on the bistatic synchronization chain is derived, and the synchronization chain is used to compensate for the time and phase errors of the slave stations. Then, combining the synchronization chain information and POS data, Kalman filtering is used to refine the slave station trajectory and improve the trajectory accuracy of the slave station POS. In terms of imaging, a high-precision motion compensation using Doppler bandwidth segmentation and sub-aperture image synthesis combined with the RMA algorithm is used for motion compensation and imaging of echo data. On this basis, interferometric error calibration and interferometric processing are carried out, and high-precision elevation measurement results are obtained.
The chapters of this paper are organized as follows. Chapter 2 introduces the key synchronization chain scheme of the small UAV-borne dual-station InSAR system. Chapter 3 provides an overview of the data processing method for dual-station InSAR, including the synchronization error compensation method, the POS trajectory refinement method, the high-precision dual-station InSAR imaging processing method, and the interferometric processing method. Chapter 4 presents the experimental results, validating the effectiveness of the proposed methods. Chapter 5 concludes the paper.

2. Bidirectional Synchronization Chain Scheme

To ensure the coherence during flight between the master and slave station images of the small UAV-borne dual-station InSAR system, strict requirements are placed on time synchronization and phase (frequency) synchronization. Time synchronization refers to the clock alignment between two independent SAR channels or clock error measurement and compensation. The bistatic interferometric SAR system adopts a one-transmitter-two-receiver operating mode, and the transmitter-receiver timing between the two channels is required to be accurate to the microsecond or even nanosecond level. Establishing the correlation between the complex image pairs becomes impossible when the system timing is disrupted. As a result, the clock alignment of the two channels or the measurement and the compensation of the error is one of the synchronization problems that need to be solved. Existing time synchronization methods for bistatic SAR include the carrying clock method, one-way timing method, and two-way clock comparison method [27]. The time synchronization scheme of this system adopts the direct one-way timing method. The timing reference module of the synchronized clock reference signal provides a time synchronization reference for each radar extension. The system uses the respective crystals in the triggering of the echo recording window, which is triggered according to a fixed pulse repetition frequency, and presets a periodic compensation mechanism to ensure the validity of the echo recording. The compensation mechanism is counteracted by appropriate post-processing methods to bring the echo data back to its normal state.
Phase synchronization is the core problem and technical difficulty of the UAV dual-station InSAR system. This challenge arises due to the independent frequency sources used for receiving echo signals in InSAR systems, directly impacting the coherence of the complex image pairs and the interferometric phase accuracy [28]. Generally, the phase synchronization method of frequency sources can be divided into four types: independent frequency source synchronization method, data-based synchronization method, direct synchronization method, and indirect synchronization method. Based on the form of the transmitted synchronization signal and the use of the synchronization signal, the direct synchronization method can be further divided into the synchronization chain method and the reference signal transmission chain method. This system adopts a two-way synchronization chain to realize phase synchronization. In a two-way synchronization chain, the transmitted synchronization signals contain synchronization error information between frequency sources. Each unit records this information and uses it for synchronization error compensation during imaging processing, ultimately realizing phase synchronization between units. The synchronization chain in this system adopts a scheme of signal pair transmission between bistatic stations, i.e., after the master station sends the synchronization signal to the slave station, the slave station sends the synchronization signal from the slave station to the master station after a certain delay, so as to realize the transmission of two-way synchronization signals. The master and slave stations each record the synchronization signal for subsequent imaging processing. Figure 1 shows the schematic diagram of the two-way synchronization chain of the dual-station InSAR system.
The timing of the synchronization chain is designed to first handshake through 100 pulses and then perform the normal operating timing. In each Pulse Repetition Time (PRT), synchronization pulses are first transmitted and received, followed by radar pulse transmission and echo reception. Once the master and slave establish connection and synchronization, the master station controls the PRT according to the master's crystal oscillator and the slave station controls the PRT using its own crystal oscillator frequency source. Each station opens the echo acceptance window and starts the working time sequence according to a certain time delay.
Because the time synchronization error in the dual-station InSAR system can couple into the phase synchronization, the phase synchronization technique is combined with the time synchronization scheme to establish a direct wave communication link between the dual-station InSAR system. The synchronization signals received by the master and slave stations through two-way synchronization are compensated for the periodic position jumps caused by time synchronization. After that, the phase synchronization information of the echo is obtained by extracting the peak phase of the synchronized signal after pulse compression. Based on this phase synchronization information, the length of the time-varying baseline can be calculated and used to refine the POS data of the slave station.

3. Overall Processing Flow for Small UAV Bistatic InSAR

The overall processing flow and methodology of dual-station InSAR is as follows. Firstly, the synchronization data obtained from the two-way synchronization chain is used to compensate for the time and phase errors of the slave echoes, followed by master-slave radar data imaging. The data processing of bistatic SAR is carried out using the equivalent processing method of converting dual-site data to single-site data, combining the dual-site synchronization chain and POS data to improve the track accuracy of the slave POS. Then an imaging method based on a Doppler bandwidth segmentation and sub-aperture image synthesis with high precision motion compensation combined with RMA algorithm is used for transporting and imaging the echo data. Finally, the interferometric processing and elevation inversion of bistatic SAR are realized through the steps of complex image alignment, calibration of interferometric system parameters such as baseline, interferometric phase filtering and de-entanglement, and DEM generation. In this chapter, each part of the processing method will be introduced in turn.

3.1. Time and Phase Synchronization Error Compensation Methods

Firstly, based on the assumption that the fast and slow time are not coupled, let the slow time be η and the fast time be t. Located at the jth timing, the emitted synchronization signal is as follows:
f T T η j , t = rect ⁡ t T exp ⁡ j 2 π f T 0 η j − t + j φ T η j − t
where T is the pulse width of the transmitted signal (0.5 µs in this system), fT0 is the central frequency of the master station, and φT(·) is the time-varying phase of the master station.
Let the distance between the transmitter and receiver platforms at this point be
R B η j = X T η j − X R η j 2 + Y T η j − Y R η j 2 + Z T η j − Z R η j 2
where X T η j , Y T η j , Z T η j T and X R η j , Y R η j , Z R η j T are positions of the transmitter and receiver at time η j .
The demodulated signal received by the receiver is then
f R R η j , t = f T T η j , t ⋅ e x p ⁡ − j 2 π f R 0 η j − t − R B η j c − j φ R η j − t − R B η j c = r e c t t T exp ⁡ j 2 π f T 0 − f R 0 η j − t ⋅ exp ⁡ j 2 π f R 0 R B η j c ⋅ exp ⁡ j φ T η j − t − j φ R η j − t − R B η j c
where fR0 is the central frequency of the slave station and φR(·) is the time-varying phase of the slave station. Taking the peak phase after compression of the direct wave pulse is equivalent to taking the phase at t = 0, with
φ R R η j , 0 = 2 π f T 0 − f R 0 η j + 2 π f R 0 R B η j c + φ T η j − φ R η j − R B η j c
After receiving the direct wave signal, the receiver will transmit the direct wave signal at a small interval, and the start delay of the current sequence is Δt0 = 2us. In other words, the direct wave signal is produced by the receiver itself. The signal is as follows
f R T η j , t = rect ⁡ t T exp ⁡ j 2 π f R 0 η j − t − Δ t 0 + j φ R η j − t − Δ t 0
The transmitter receives, demodulates this signal and gets
f T R η j , t = r e c t t T exp ⁡ j 2 π f R 0 − f T 0 η j − t − Δ t 0 ⋅ exp ⁡ j 2 π f T 0 R B η j − Δ t 0 c exp ⁡ j φ R η j − t − Δ t 0 − j φ T η j − t − Δ t 0 − R B η j − Δ t 0 c
Pulse compression of this direct wave signal to take the peak phase is equivalent to taking the phase of the t = 0 moment
φ T R η j , 0 = 2 π f R 0 − f T 0 η j − Δ t 0 + 2 π f T 0 R B η j − Δ t 0 c + φ R η j − Δ t 0 − φ T η j − Δ t 0 − R B η j − Δ t 0 c
By comparing φ T R η j , 0 and φ R R η j , 0 and averaging both phases, we have
φ T R η j , 0 + φ R R η j , 0 / 2 = π f T 0 − f R 0 Δ t 0 … … … … … … … … … … … … … … … … … … … … … … … … … … . . ① + 1 2 2 π f R 0 R B η j c + 2 π f T 0 R B η j − Δ t 0 c … … … … … … … … … … … … … … … … . … . . ② + 1 2 φ T η j − φ R η j − R B η j c + 1 2 φ R η j − Δ t 0 − φ T η j − Δ t 0 − R B η j − Δ t 0 c . . ③
For the first term ①, because Δt0 = 2μs, a crystal oscillator frequency error of 100 MHz can reach 10-8. Because the system operates at a central frequency of 1.5 GHz, this term is 0.0054 degrees and can be neglected. The second term ② represents the phase introduced by the baseline, and the baseline can be calculated based on this term. The third term ③ is the synchronous phase error term, which can be neglected as long as the phase remains stable at the microsecond level. Based on previous test data, this error term is less than 0.1 degrees. Through theoretical and experimental data analysis, both terms ① and ③ in the above equation can be ignored. Consequently, based on the second term, the calibration method for the baseline is given by
R B η j ≈ c 2 π f 0 φ R R η j , t + φ T R η j , t
The subtraction of φ T R η j , 0 and φ R R η j , 0 yields the result in the following equation
φ T R η j , 0 − φ R R η j , 0 / 2 = 2 π f T 0 − f R 0 η j − Δ t 0 2 … … … … … … … … … … … … … … … … … … … … … … . . ① + 1 2 2 π f R 0 R B η j c − 2 π f T 0 R B η j − Δ t 0 c … … … … … … … … … … … … … … … … . … . . ② + 1 2 φ T η j − φ R η j − R B η j c + 1 2 φ T η j − Δ t 0 − R B η j − Δ t 0 c − φ R η j − Δ t 0 . . ③
where the first term ① is the phase error caused by the inconsistency of frequency sources, which changes linearly with azimuth time η j . The second term ② is approximately zero and can be ignored due to . And the third term ③ is the synchronous phase error excluding the linear phase. Further neglecting the variation of the above phase with fast time, we have:
φ R R η j , 0 − φ T R η j , 0 2 ≈ 2 π f T 0 − f R 0 η j + φ T η j − φ R η j
Assuming the SAR signal transmitted by the master station is
s T s η j , t = rect ⁡ t T s exp ⁡ j π K r t 2 + j 2 π f T 0 η j − Δ t 1 − t + j φ T η j − Δ t 1 − t
where Δt1 is the time difference between the transmission of the SAR signal and the synchronization signal, K r is the linear frequency modulation rate, and T s is the pulse width of the SAR signal. After reflection from the ground target, the signal received by the slave station is given by
s T R s η j , t = r e c t ⁡ t − R b i c T s exp ⁡ j π K r t − R b i c 2 ⋅ exp ⁡ j 2 π f T 0 η j − Δ t 1 − t − R b i c + j φ T η j − Δ t 1 − t − R b i c ⋅ exp ⁡ − j 2 π f R 0 η j − Δ t 1 − t − j φ R η j − Δ t 1 − t
and the synchronous phase error is given by
φ e r r η j , t = 2 π f T 0 − f R 0 η j − Δ t 1 − t + φ T η j − Δ t 1 − t − R b i c − φ R η j − Δ t 1 − t
Neglecting the variation of the phase error with fast time, we have
φ e r r η j , 0 ≈ 2 π f T 0 − f R 0 η j + φ T η j − φ R η j
As a result, the term φ R R η j , 0 − φ T R η j , 0 / 2 in Equation (11) represents the synchronous phase error that needs to be compensated in the slave station SAR echo.
During the above analysis on phase synchronization, it is assumed that the reference time η j at the beginning of each PRT is the same, and both master and slave stations are based on the same η j . However, due to the existence of time synchronization errors, this assumption does not hold and the effect of time synchronization needs to be further considered. In this paper, the UAV dual-station SAR system adopts relatively low crystal stabilization of 10-7 order of magnitude for the master and slave stations for cost consideration. In order to avoid the impact of the time drift of the slave station relative to the master station on the integrity of the echo acquisition, an echo recording window compensation mechanism with a period of 6.3s and an offset of 1us is pre-set in the actual system, which makes the echo data appear jagged. By analyzing the phase composition of the echo signal from the slave, it can be observed that the samples in the range direction are not aligned, and there is a term related to the azimuthal moment j, j 1 P R F f 0 T − f 0 R f 0 R , which is exactly the time offset that needs to be compensated by means of envelope alignment. This is compensated by performing an FFT along the distance direction, multiplying the distance direction frequency domain by e x p ⁡ − j 2 π f j 1 P R F f 0 T − f 0 R f 0 R , and then changing back to the time domain.
From the above analysis, the overall processing steps are:
  • Pulse compression and peak phase extraction are performed on the direct wave signal received by the receiver at each   η j moment to obtain φ R R η j , 0 ;
  • Pulse compression and peak phase extraction are performed on the direct wave signal received at the transmitter at each η j   moment to obtain φ T R η j , 0 ;
  • Calculate the baseline length inversion result φ R R η j , t + φ T R η j , t / 2 for subsequent interferometric processing;
  • Calculate the synchronization phase compensation term φ R R η j , t − φ T R η j , t / 2 and compensate the received echo signals at each η j   moment;
  • Envelope alignment, in which the echo is transformed by FFT along the range direction, multiplied by e x p ⁡ − j 2 π f j 1 P R F f 0 T − f 0 R f 0 R in the range direction in the frequency domain, and then transformed back to the time domain to obtain the envelope aligned slave echo for subsequent imaging.

3.2. Trajectory Refinement Method Combining Synchronization Chain and POS Data

Due to the limitation of the carrying capacity of the UAV platform, it is difficult to use traditional inertial measurement devices with large size, heavy weight, high power consumption and high accuracy, and the carrier POS accuracy is limited to a certain extent. Because the time-varying baseline can be extracted from the synchronous signal chain, the slave station's trajectory can be optimized using this baseline, contributing to trajectory refinement and improved accuracy of interference inversion. We propose the following optimization method for refining the trajectory at each azimuth moment of the slave station:
m i n R B − X 1 − X 2 + Δ x 2 + Y 1 − Y 2 + Δ y 2 + Z 1 − Z 2 + Δ z 2 2 + p * B → ⋅ B → ' | B → | 2 − 1 2
where RB is the baseline length according to the two-way synchronization chain (Equation (9)), (X1,Y1,Z1) and (X2,Y2,Z2) are the positions of the master and slave station according to POS data, respectively. B → = X 1 − X 2 , Y 1 − Y 2 , Z 1 − Z 2 T is the baseline vector from POS data, B → ' = X 1 − X 2 + Δ x , Y 1 − Y 2 + Δ y , Z 1 − Z 2 + Δ z T is the optimized baseline vector, and (Δx,Δy,Δz) is the amount to be optimized. In the above equation, the first term is the baseline length constraint term, aiming to make the optimized trajectory's baseline length as close as possible to the baseline length obtained from the two-way synchronous chain. The second term is the baseline direction constraint term, aligning the optimized baseline with the original baseline direction, where p is the weight (chosen as 0.2 in this study).
Through these constraints, the trajectory of the slave station is optimized and solved for each azimuth moment. The slave station trajectory is refined through smoothing and filtering the offset, and removing outliers.

3.3. High-precision Dual-site InSAR Imaging Processing Methods

Because the UAV platform is relatively light and small, the motion state of the carrier is disturbed by the airflow relatively seriously, leading to large position and attitude errors. The trajectory measurement error will bring baseline error. At the same time, the deviation of the trajectory after airflow and the trajectory measurement error together lead to the residual error after motion compensation, which cannot be canceled out in the case of the master-slave station carrier flying independently. This error makes the SAR image geometrically distorted and increases the difficulty of registration. The error also results in phase fluctuation, which affects the accuracy of the unmanned aircraft-carried bistatic SAR inversion DEM. Effectively compensating the motion error with distance and azimuthal null variability using high-precision imaging algorithms is an important task in imaging processing.
Figure 3 shows the UAV bistatic SAR imaging processing flow. For the slave station, when the baseline is short, the center of the master and slave positions can be used as the equivalent center position of the bistatic SAR. The hyperbolic equivalent approximation model of the bistatic SAR is used for the derivation of the ω-k algorithm, and the transport and imaging methods consistent with the single-site SAR are used for processing.
The raw SAR echoes are first range-compressed, and a one-step motion compensation is performed using the filtered and refined trajectory to remove the space-variance of the motion error with range direction. After that, azimuthal resampling is performed to homogenize the pulse sending and receiving intervals. Then azimuthal FFT is performed to divide the sub-aperture in the azimuthal frequency domain, and each sub-aperture data is imaged separately using the ω-k algorithm, and the PTA method is used to compensate for the motion error within the aperture. Finally, all the sub-aperture images are coherently synthesized to obtain high-precision imaging processing results.
This imaging processing flow is common for both master and slave stations, but there are two differences. First, the reference trajectories for the master and the slaves are different. For the master, the reference track is a straight line fitted by the master; for the slave, the motion compensation is based on the transmitting and receiving reference tracks. Secondly, the orientation resampling method is different. For the master station, the azimuth resampling is directly based on the master inertial guidance data and the master echo pulse timestamps. While for the slave station, the azimuth resampling method of bistatic SAR is used to obtain accurate azimuth resampling results. The method is described in more detail in Section 3.3.2.

3.3.1. One-step Motion Compensation Algorithm Based on High-precision Inertial Guidance

By recording the precise position of the master station at each sampling moment through high-precision inertial guidance, the motion error can be calculated through airborne geometry. The one-step motion compensation algorithm processes the time-domain echo signal after range compression before imaging, corrects the envelope error along the range direction by interpolation, and compensates for the phase error. The one-step motion compensation algorithm has higher accuracy when compared to the classical two-step motion compensation algorithm. It can compensate for more motion errors before imaging, and can compensate the envelope error of distance nulling with a higher accuracy.
Figure 4 shows the flight geometry of the carrier aircraft considering the trajectory offset, where P r e a l is the actual position of the target at a certain orientation moment, and R r e a l and R i d e a l are the slant range from the target to the actual position of the aircraft and the slant range from the target to the ideal position of the aircraft, respectively. While applying the one-step motion compensation algorithm, based on the approximation of the center of the beam, it is assumed that the target is located at the center of the beam, i.e., P M o C o , and the slant ranges from that point to the ideal and the actual position of the aircraft, R i d e a l M o C o and R r e a l M o C o , are used to calculate the motion error, so the compensated error is
R c o m p e n = R r e a l M o C o − R i d e a l M o C o
The residual error is
R r e s = R r e a l − R i d e a l − R r e a l M o C o − R i d e a l M o C o
In general, the residual error R r e s is much smaller than one distance unit.

3.3.2. Bistatic SAR Echo Azimuth Resampling

As the carrier aircraft cannot maintain an ideal uniform linear motion during flight, and there is acceleration along the flight direction, i.e., there is a change in velocity, which in turn causes the spatial spacing between pulses to be non-uniform. For single-station SAR systems, azimuthal resampling is often used to compensate for this, but in dual-station SAR, due to the existence of two platforms, the spatial intervals between transmit and receive are non-uniform, and resampling becomes difficult.
We propose to compensate for heading motion errors by using a bistatic SAR echo azimuthal resampling method with an equivalent average adopted moment, which is as follows.
Let the distance history of the nth pulse transmitting/receiving moment when the receiving/transmitting antenna is moving at a uniform linear speed be
R Y n ; x , y = X T − x 2 + Y T + V T n Δ η − y 2 + H T 2 + X R − x 2 + Y R + V R n Δ η − y 2 + H R 2
Where Δη = 1/PRF . Similarly, in the presence of heading motion error, the distance history at the nth pulse transmit/receive moment is
R ~ Y ( n ; x , y ) = X T − x 2 + Y T + V T n Δ η + Δ Y T ( n Δ η ) / V T − y 2 + H T 2 + X R − x 2 + Y R + V R n Δ η + Δ Y R n Δ η V R − y 2 + H R 2
Therefore, the transmitting antenna and receiving antenna can be regarded as moving at a uniform speed at   V T and V R , respectively. The nth pulse is transmitted and received at n Δ η + Δ Y T ( n Δ η ) / V T and n Δ η + Δ Y R ( n Δ η ) / V R , respectively. Since the transmitting and receiving should be regarded as simultaneous under the stop-go assumption, it is assumed that the n pulse under the heading motion error is transmitted and received respectively at this moment.
η ~ n = n Δ η + 1 2 Δ Y T n Δ η V T + Δ Y R n Δ η V R
Based on the above equivalent moments, azimuthal resampling (e.g., using Lagrange interpolation) can be performed on the bistatic SAR echoes to obtain the echo signal under uniform motion.

3.3.3. Highly Accurate Motion Compensation Method Based on Doppler Bandwidth Segmentation and Sub-Aperture Image Synthesis

From the above discussion, it can be seen that there is still a residual error in the signal processed by one-step motion compensation, although the residual error is generally much smaller than one range unit. But after the processing of frequency domain algorithms such as the distance migration algorithm, the residual error will be enlarged and cause serious envelope disorder, which can easily be more than one range unit, in which case the processing using only one-step motion compensation is not enough to obtain a well-focused image.
In order to deal with the problem of envelope disorder caused by the residual motion error after the distance migration algorithm, we propose a high-precision motion compensation method based on Doppler bandwidth segmentation and subaperture image synthesis. The echo data after one-step motion compensation is divided into multiple sub-apertures along the Doppler bandwidth in the 2D frequency domain, and each sub-aperture is zeroed to the original length and transformed to the 2D time domain. According to the time-frequency relationship, the corresponding squint angle of view of each sub-aperture is computed, and the residual error caused by the one-step mapping algorithm adopting the center-beam approximation is compensated. The sub-images are obtained by using a distance migration algorithm for imaging each sub-aperture echo. For each sub-image, the residual error is further reduced, which is not enough to cause envelope disorder for more than one distance unit, and then the PTA algorithm is used to compensate for all the intra-aperture motion errors for each sub-image. Finally, the error-free image is coherently summed to obtain the high-resolution big picture.

3.4. Interferometric Processing and Elevation Inversion

3.4.1. Interferometric calibration

Interferometric calibration mainly contains slant distance, baseline length, baseline angle, and interference phase calibration.
  • Slant range calibration
Here, only the slant range error ΔR of the main graph needs to be calibrated, and the slant range error calibration is obtained by optimizing the following objective function.
m i n ∑ i = 1 n   R i + Δ R − R G i 2
ere R i ,   R G _ i are the main station map up-slope and the measured slant distance from the main station antenna phase center position to the target point, respectively.
2.
Baseline length and baseline angle calibration
The master station data is selected as the reference map for the calibration of baseline length and baseline angle. In order to circumvent the influence of the channel phase error, the measurement position of the calibrator is used as the true value, and its distance to the reference straight-line trajectory of each channel imaging is calculated, so as to carry out the calibration of the baseline and baseline angle. The calibration formula is as follows:
m i n ∑ i = 1 n   cos ⁡ π 2 − θ + α − B 2 + R 1 i 2 − R 2 i 2 2 B R 1 i 2
where the baseline length B and the baseline angle α are the quantities to be calibrated, θ is the lower viewing angle of the reference figure. R 1 i and   R 2 i are the slant ranges of the ith calibrator in the reference and auxiliary figures, respectively.

3.4.2. Interferometric processing

The interferometric processing mainly includes master-slave complex data alignment, flat-earth phase removal, phase filtering, phase untangling, elevation inversion and accuracy analysis.
  • Complex image alignment and generation of interference phase
By using the coordinate relationship of homonymous points in the two complex images, the slave complex image is resampled so that it corresponds to the master image pixels. Generally, coherence is used as a quality evaluation index for complex image alignment. The interferometric phase map is obtained by multiplying the conjugate of the aligned complex images and calculating the phase.
2.
Flat-earth phase removal
Since the phase history grows with increasing transmit time, interference fringes are also present on flat terrain and vary linearly with the slant range, called the flat-earth phase. Due to the long baseline of the dual station, the fringes are very dense, and the terrain undulations cause large phase variations; removing the flat-earth phase is an important step in order to facilitate the subsequent phase de-entanglement. Using the calibrated baseline length, baseline angle, and interferometric phase error, the flat earth phase can be removed using the following expression.
φ flat   R 1 = − 2 π Q λ R 1 − R 1 2 + B 2 + 2 B R 1 sin ⁡ α − θ
3.
Phase Filtering
There are still a large number of noisy phases in the phase map after flat phase removing, which come from thermal noise decoherence, baseline decoherence, alignment error decoherence and other factors. In order to obtain high-quality interferometric phase maps and reduce the influence of phase noise, it is necessary to choose a better filtering method as well as a suitable filtering window. In this paper, the classical Goldstein phase filtering method is used. In view of the fact that some regions are relatively noisy, which affects the overall de-entanglement, the low-coherent regions are first screened and their neighboring phases are used for fitting and interpolation to obtain the estimated phases of the low-coherent regions, which results in the phases after the filtering process.
4.
Phase untangling
Due to the undulating terrain, the interferometric phase variation beyond 2π will be entangled in (-π, π] and is not the complete interferometric phase corresponding to the elevation, so phase untangling is required. We use the classical minimum cost flow method for phase untangling. The phase after de-entanglement is still relative and differs from the absolute phase value by a constant which can be calculated from any ground control point.
5.
Elevation inversion
The following height inversion formula was used to perform the elevation inversion using the phases from the untangling.
h = Z 1 − R 1 c o s ⁡ α + arcsin ⁡ B 2 R 1 − λ φ c + φ r 2 π Q B − λ 2 φ c + φ r 2 8 π 2 Q 2 R 1 B
where Z 1 is the height of the phase center of the master antenna, and φ r , φ c are the constant values of the post-decentering phase and its difference from the absolute phase, respectively.

4. Experiment

In order to verify the effectiveness of the established unmanned airborne dual-station InSAR synchronization compensation as well as the high-precision imaging processing flow and the elevation inversion capability of the system, we carried out the first integrated calibration flight experiment on August 17-29, 2022, at Bailing Airport, Dalhanmao Ming'an Union Banner, Inner Mongolia. Figure 5 shows the optical image of the experiment site and the deployment of the calibrator. Table 1 lists the basic parameters of the dual-station flight experiment as well as the SAR load parameters. Loads for the master and slave stations were the same.
Preprints 95394 g004
Figure 5. Optical image and corner reflector distribution.
Figure 5. Optical image and corner reflector distribution.
Preprints 95394 g004

4.1. Synchronization error compensation

Figure 5 shows the image after range compression before and after echo envelope alignment of the slave station, which shows that the time synchronization error is well compensated, and the compensation term is shown in Figure 6.
Preprints 95394 g005
Figure 5. Slave envelope alignment before (left) and after (right).
Figure 5. Slave envelope alignment before (left) and after (right).
Preprints 95394 g005
Figure 7 and Figure 8 show the slave phase synchronization compensation phases calculated according to the procedure in Section 3.1, and the error after removing the linear term.
Figure 9 shows both baselines as extracted from the synchronization signal and as calculated using GPS. Differences can be observed in the lower subplot.

4.2. Results of Slave Trajectory Refinement

The POS data of the slave station is refined using the baseline constraint based on the synchronization signal, as described in Section 3.2. Figure 10 shows the correction values for the slave station's trajectory in the x, y, and z directions for each sampling point. From Figure 11, it can be observed that, with the corrected slave station trajectory, the calculated baseline length (in green) closely matches the baseline extracted from the synchronization signal (in red). Figure 12 illustrates that the difference between these two baseline lengths is mainly within 1mm, which will be advantageous for interferometric inversion.

4.3. Bistatic InSAR Imaging Results

Now we applying the synchronization phase compensation shown in Figure 6 and Figure 7 to the imaging processing flow as described in Section 3.3. Figure 13 presents images of the slave station without synchronous phase compensation and with synchronous phase compensation. It can be observed that uncompensated phase errors lead to defocusing, highlighting the necessity and effectiveness of compensating for phase synchronization errors.
Figure 14 shows the imaging results of the slave station before and after trajectory refinement, indicating that the images has been well focused. Imaging quality tests on calibration points are shown in Figure 15, demonstrating that both the master and slave stations have been well focused.

4.4. Interference processing and elevation inversion results

Interferometric processing and elevation inversion are carried out according to the results of interferometric calibration. Firstly, the airport area in the master data and slave data (as in Figure 16) is selected for interferometric co-registration. The interferometric phase map (Figure 17), and inversion height (Figure 18) are calculated using a 5×5 window after co-registration. The elevation and elevation error statistics of the 14 calibration points are shown in Table 2 and Figure 19. It can be seen that the elevation error RMS of all 14 calibration points improved greatly from 0.66 m to 0.42 m after trajectory refinement.

5. Conclusions

This paper presents the overall processing workflow and methods for UAV-borne dual-station InSAR using the two-way synchronization chain and POS data. The methods include error compensation for time and phase synchronization, trajectory refinement combining synchronization chain and POS data, high-precision dual-station InSAR imaging processing, and interferometric processing. Experimental results indicate that the proposed processing methods effectively process data from UAV-borne dual-station InSAR and improve interferometric elevation accuracy through trajectory refinement.

References

  1. Rosen, P.A.; Hensley, S.; Joughin, I.R.; Li, F.K.; Madsen, S.N.; Rodriguez, E.; Goldstein, R.M. Synthetic aperture radar interferometry. Proceedings of the IEEE 2000, 88, 333–382. [Google Scholar] [CrossRef]
  2. Qiu, X.; Ding, C.; Hu, D. Dual-Site SAR Imaging Processing; Science Press: 2010.
  3. Yafei, S.; Liming, J.; Lin, L.; Yongling, S.; Hansheng, W. TanDEM-X bistatic SAR interferometry and its research progress. REMOTE SENSING FOR LAND & RESOURCES 2015, 27, 16–22. [Google Scholar]
  4. Zhang, W.; Yue, C.; Yan, P. TanDEM-X polarization interferometry SAR forest canopy height inversion. Journal of Northeast Forestry University 2017, 45, 47–54. [Google Scholar]
  5. Liang, D.; Liu, K.; Zhang, H.; Chen, Y.; Yue, H.; Liu, D.; Deng, Y.; Lin, H.; Fang, T.; Li, C. The processing framework and experimental verification for the noninterrupted synchronization scheme of LuTan-1. IEEE Transactions on Geoscience and Remote Sensing 2020, 59, 5740–5750. [Google Scholar] [CrossRef]
  6. Lin, H.; Deng, Y.; Zhang, H.; Liu, D.; Liang, D.; Fang, T.; Wang, R. On the Processing of Dual-Channel Receiving Signals of the LuTan-1 SAR System. Remote Sensing 2022, 14, 515. [Google Scholar] [CrossRef]
  7. Krieger, G.; Moreira, A.; Fiedler, H.; Hajnsek, I.; Werner, M.; Younis, M.; Zink, M. TanDEM-X: A satellite formation for high-resolution SAR interferometry. IEEE Transactions on Geoscience and Remote Sensing 2007, 45, 3317–3341. [Google Scholar] [CrossRef]
  8. Jin, G.; Liu, K.; Liu, D.; Liang, D.; Zhang, H.; Ou, N.; Zhang, Y.; Deng, Y.; Li, C.; Wang, R. An advanced phase synchronization scheme for LT-1. IEEE Transactions on Geoscience and Remote Sensing 2019, 58, 1735–1746. [Google Scholar] [CrossRef]
  9. Hendriks, I.; Meta, A.; Trampuz, C.; Coccia, A.; Placidi, S.; Davidson, M.; Schuettemeyer, D. MetaSensing's Novel L-Band Airborne SAR Sensors for the BelSAR Project: First Bistatic Results; 2017.
  10. Meta, A.; Trampuz, C.; Coccia, A.; Ortolani, M.; Turtolo, R. First results of the BelSAR L band airborne bistatic fully polarimetric Synthetic aperture radar campaign. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS); 2017; pp. 1040–1042. [Google Scholar]
  11. Ding, J.; Zhang, Z.; Xing, M.; Bao, Z. A new look at the bistatic-to-monostatic conversion for tandem SAR image formation. IEEE Geoscience and Remote Sensing Letters 2008, 5, 392–395. [Google Scholar] [CrossRef]
  12. Loffeld, O.; Nies, H.; Peters, V.; Knedlik, S. Models and useful relations for bistatic SAR processing. IEEE Transactions on Geoscience and Remote Sensing 2004, 42, 2031–2038. [Google Scholar] [CrossRef]
  13. Ender, J. A step to bistatic SAR processing. European conference on synthetic aperture radar (EUSAR’04), 2004, pp.359-364.
  14. Giroux, V.; Cantalloube, H.; Daout, F. An Omega-K algorithm for SAR bistatic systems. In Proceedings of the Proceedings. 2005 IEEE International Geoscience and Remote Sensing Symposium, 2005. IGARSS'05., 2005; pp. 1060-1063.
  15. Qiu, X.; Hu, D.; Ding, C. Focusing bistaitc images use RDA based on hyperbolic approximating. In Proceedings of the 2006 CIE International Conference on Radar; 2006; pp. 1–4. [Google Scholar]
  16. Qiu, X.; Hu, D.; Ding, C. An improved NLCS algorithm with capability analysis for one-stationary BiSAR. IEEE Transactions on Geoscience and Remote Sensing 2008, 46, 3179–3186. [Google Scholar] [CrossRef]
  17. Ren, Y.; Tang, S.; Guo, P.; Zhang, L.; So, H.C. 2-D spatially variant motion error compensation for high-resolution airborne SAR based on range-Doppler expansion approach. IEEE Transactions on Geoscience and Remote Sensing 2021, 60, 1–13. [Google Scholar] [CrossRef]
  18. Tao, L.; Yaowen, F.; Jianfeng, Z.; Wenpeng, Z.; Wei, Y. A Method of Line-of-sight Motion Error Compensation for Multi-rotor UAV SAR. Journal of Signal Processing 2022, 38. [Google Scholar]
  19. Xue, M.; Tan, W.; Xu, W.; Zhang, Z.; Huang, P. Motion Error Compensation Method for Airborne SAR Imaging Based on Moving Least Squares Method. Journal of Telemetry, Tracking and Command 2021, 42, 54–60. [Google Scholar]
  20. Jiang, Y.; Du, K.; Yang, Q.; Li, Z.; Wu, J.; Yang, J. Bistatic SAR Spatial-variant Motion Error Compensation Method via Joint-refocusing of Multi-subimages. In Proceedings of the 2023 6th International Conference on Electronics Technology (ICET); 2023; pp. 190–195. [Google Scholar]
  21. Zhang, T. Research on SAR Fast Time Domain Imaging and Motion Compensation Methods. Doctor, Xidian University, 2022.
  22. Yang, Q.; Guo, D.; Li, Z.; Wu, J.; Huang, Y.; Yang, H.; Yang, J. Bistatic forward-looking SAR motion error compensation method based on keystone transform and modified autofocus back-projection. In Proceedings of the IGARSS 2019-2019 IEEE International Geoscience and Remote Sensing Symposium, 2019; pp. 827-830.
  23. Li, F.; Hu, D.; Ding, C.; Qiu, X. Antiparallel Aspects of Airborne Dual-antenna InSAR Data Processing and Analysis. Journal of Radars 2015, 4, 38–48. [Google Scholar]
  24. Mao, Y.; Xiang, M.; Wei, L.; Han, S. The mathematic model of multipath error in airborne interferometric SAR system. In Proceedings of the 2010 IEEE International Geoscience and Remote Sensing Symposium; 2010; pp. 2904–2907. [Google Scholar]
  25. Qi, F.; Erxue, C.; Zengyuan, L.; Lan, L.; Lei, Z. Forest Height Estimation from Airborne X-band Single pass InSAR Data. Remote Sensing Technology and Application 2016, 31, 551–557. [Google Scholar]
  26. Jinbiao, Z.; Jie, P.; Xiaolan, Q.; Wen, J.; Yuquan, L.; Yongwei, D.; Wei, L.; Bei, L.; Fan, N.; Songtao, S.; et al. Analysis and Experimental Validation of Key Technologies for Unmanned Aerial Vehicle-borne Bistatic Interferometric Synthetic Aperture Radar. Journal of Radars 2023, 12, 832. [Google Scholar] [CrossRef]
  27. Zhou, L.; Liang, X.; Ding, C. A Dual Station SAR Synchronization Method and Synchronization System Design. Journal of Data Acquisition and Processing 2009, 24, 305–309. [Google Scholar]
  28. Zhou, L.; Liang, X.; Ding, C. Analysis of the Influence of Frequency Source Phase Noise on the Performance of Bistatic SAR. Journal of Network New Media 2009, 30, 7–12. [Google Scholar]
Preprints 95394 g001
Figure 1. Schematic of the two-way synchronization chain for a bistatic InSAR system.
Figure 1. Schematic of the two-way synchronization chain for a bistatic InSAR system.
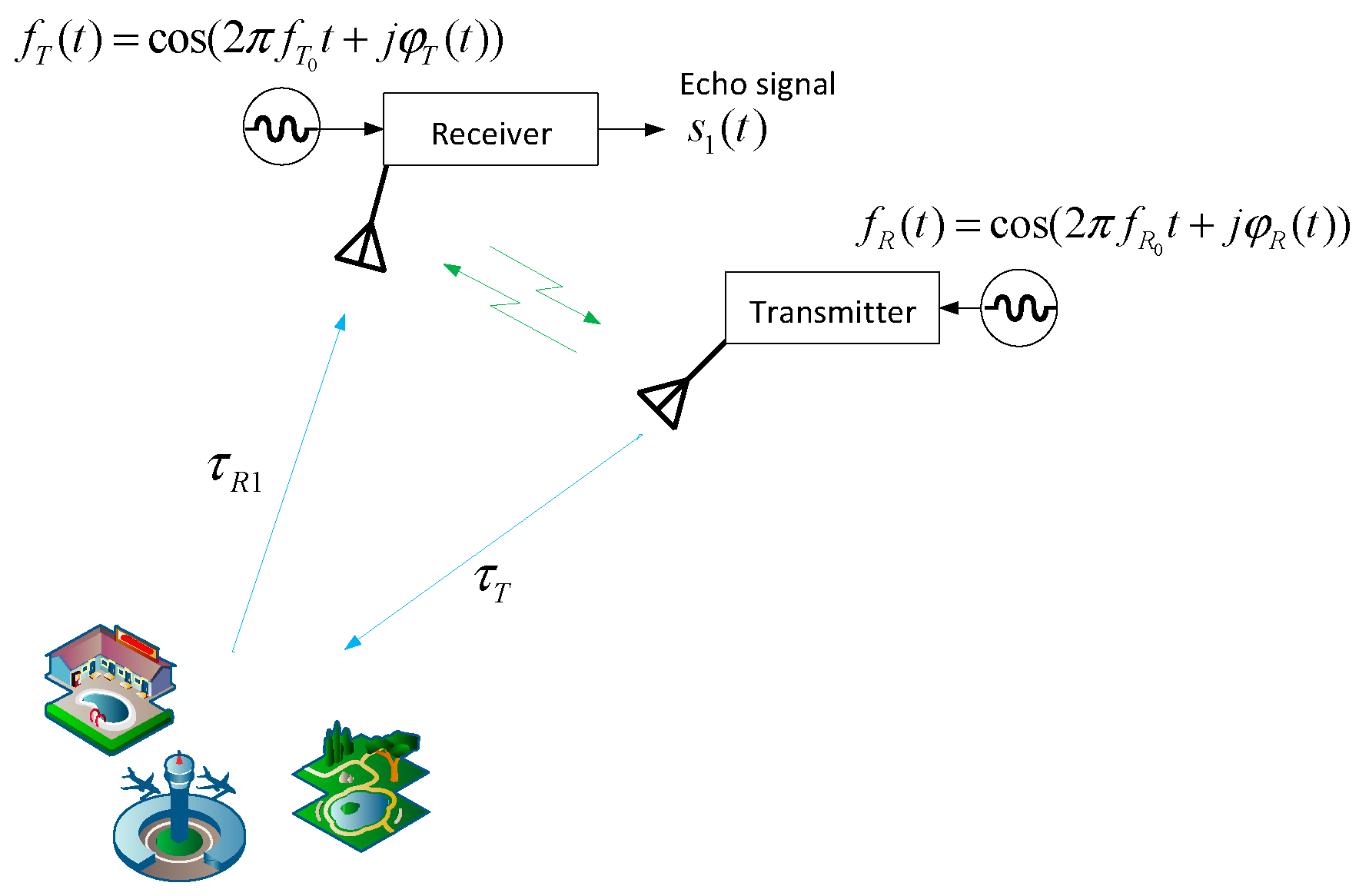
Preprints 95394 g001
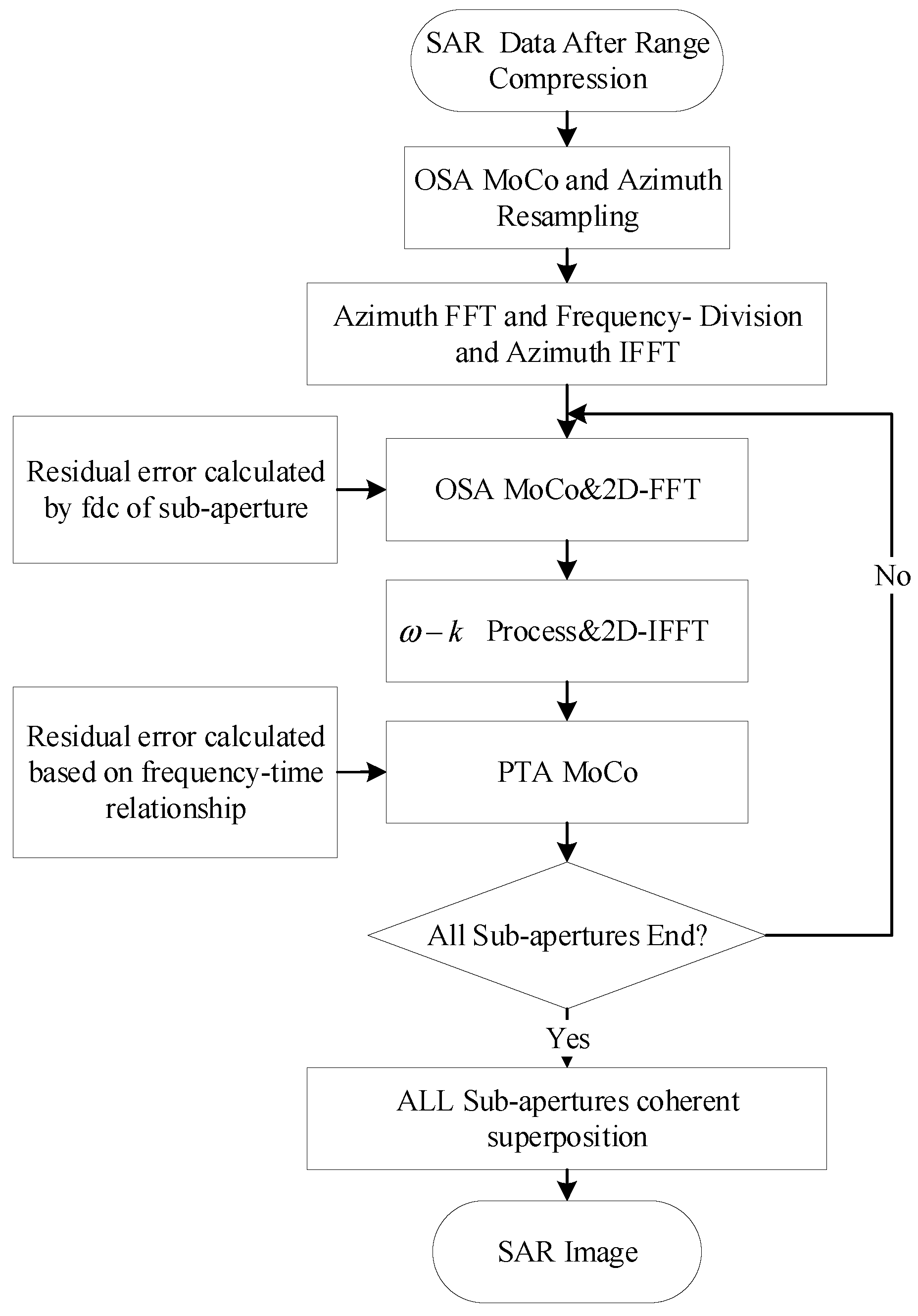
Preprints 95394 g002
Figure 3. Flowchart of unmanned airborne dual-station InSAR imaging processing.
Figure 3. Flowchart of unmanned airborne dual-station InSAR imaging processing.
Preprints 95394 g002
Preprints 95394 g003
Figure 4. Schematic diagram of geometric relationship.
Figure 4. Schematic diagram of geometric relationship.
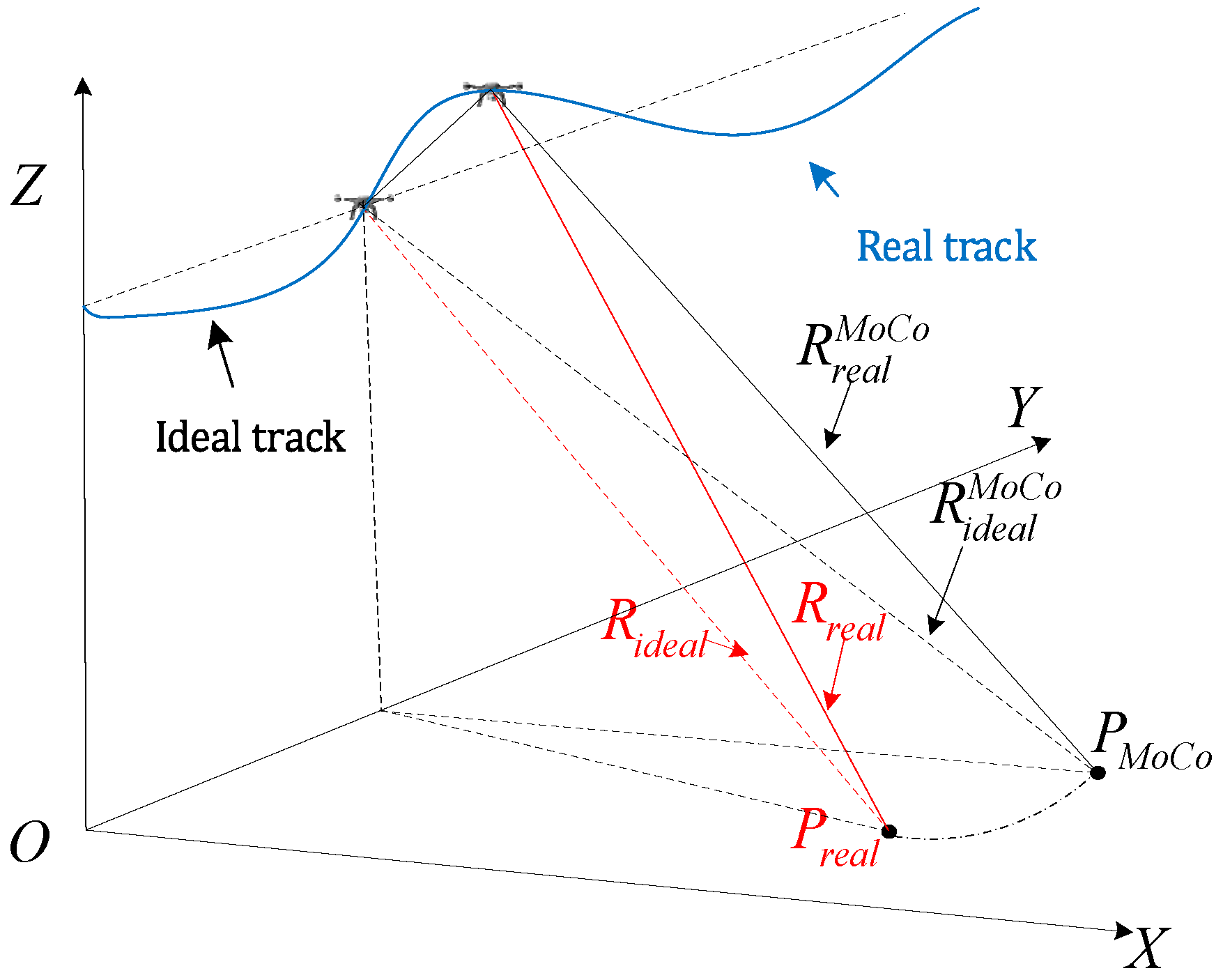
Preprints 95394 g003
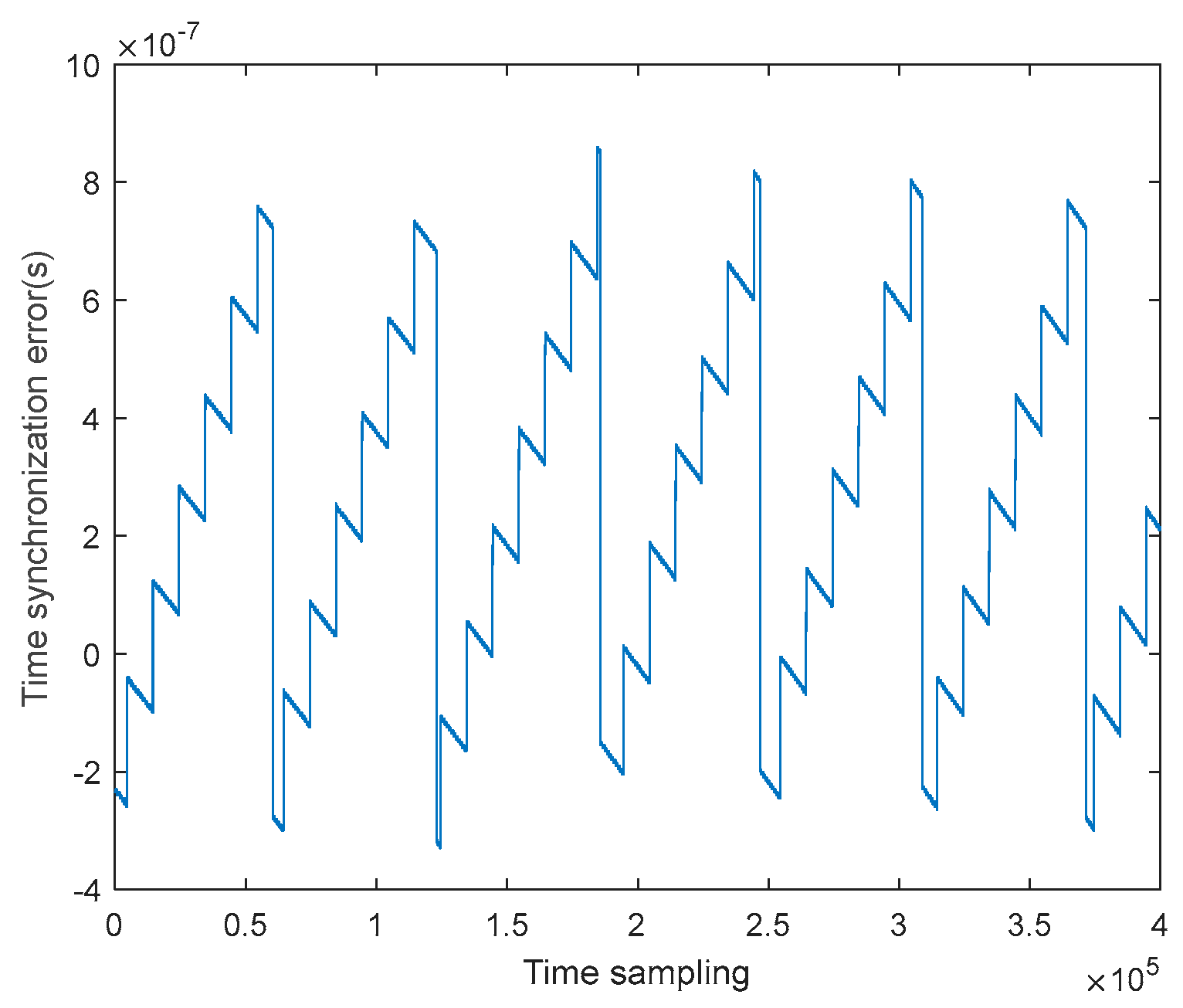
Preprints 95394 g006
Figure 6. Time synchronization error compensation.
Figure 6. Time synchronization error compensation.
Preprints 95394 g006
Preprints 95394 g007
Figure 7. Phase synchronization compensation term.
Figure 7. Phase synchronization compensation term.
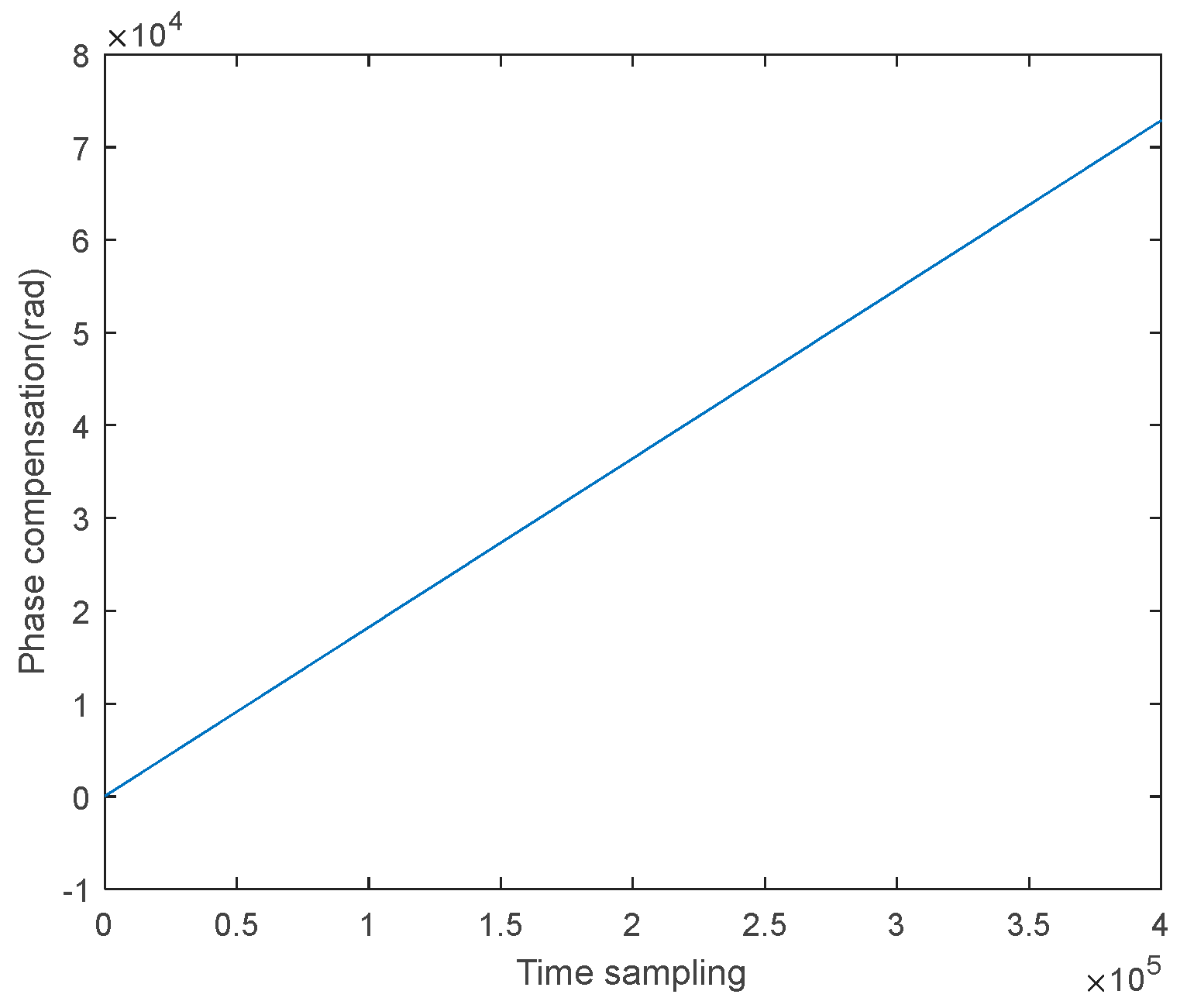
Preprints 95394 g007
Preprints 95394 g008
Figure 8. Residual term after removing the linear term for phase synchronization.
Figure 8. Residual term after removing the linear term for phase synchronization.
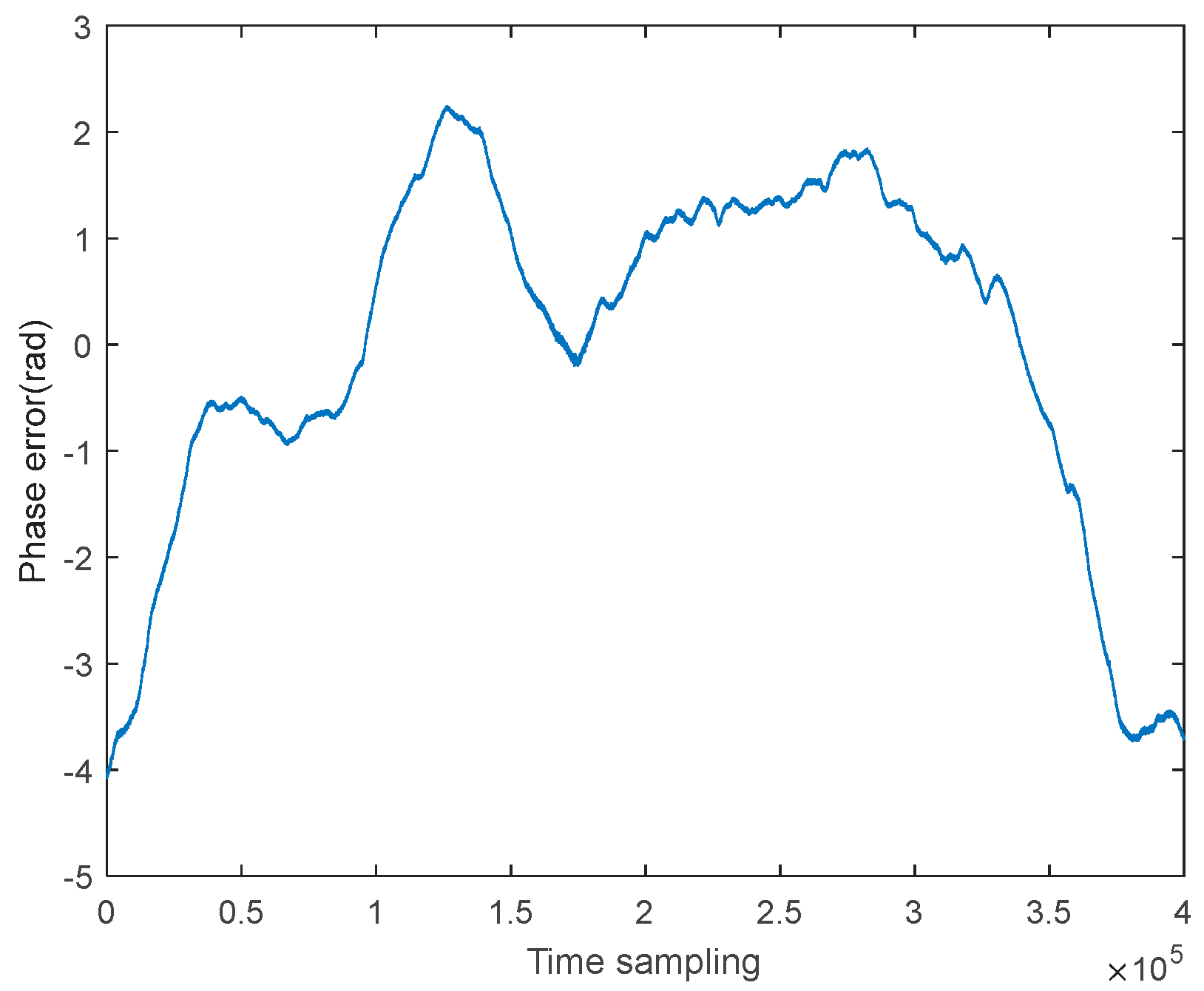
Preprints 95394 g008
Preprints 95394 g009
Figure 9. (Top) Baseline as extracted from the synchronization signal and as calculated using GPS (Bottom) Difference between the two baselines.
Figure 9. (Top) Baseline as extracted from the synchronization signal and as calculated using GPS (Bottom) Difference between the two baselines.
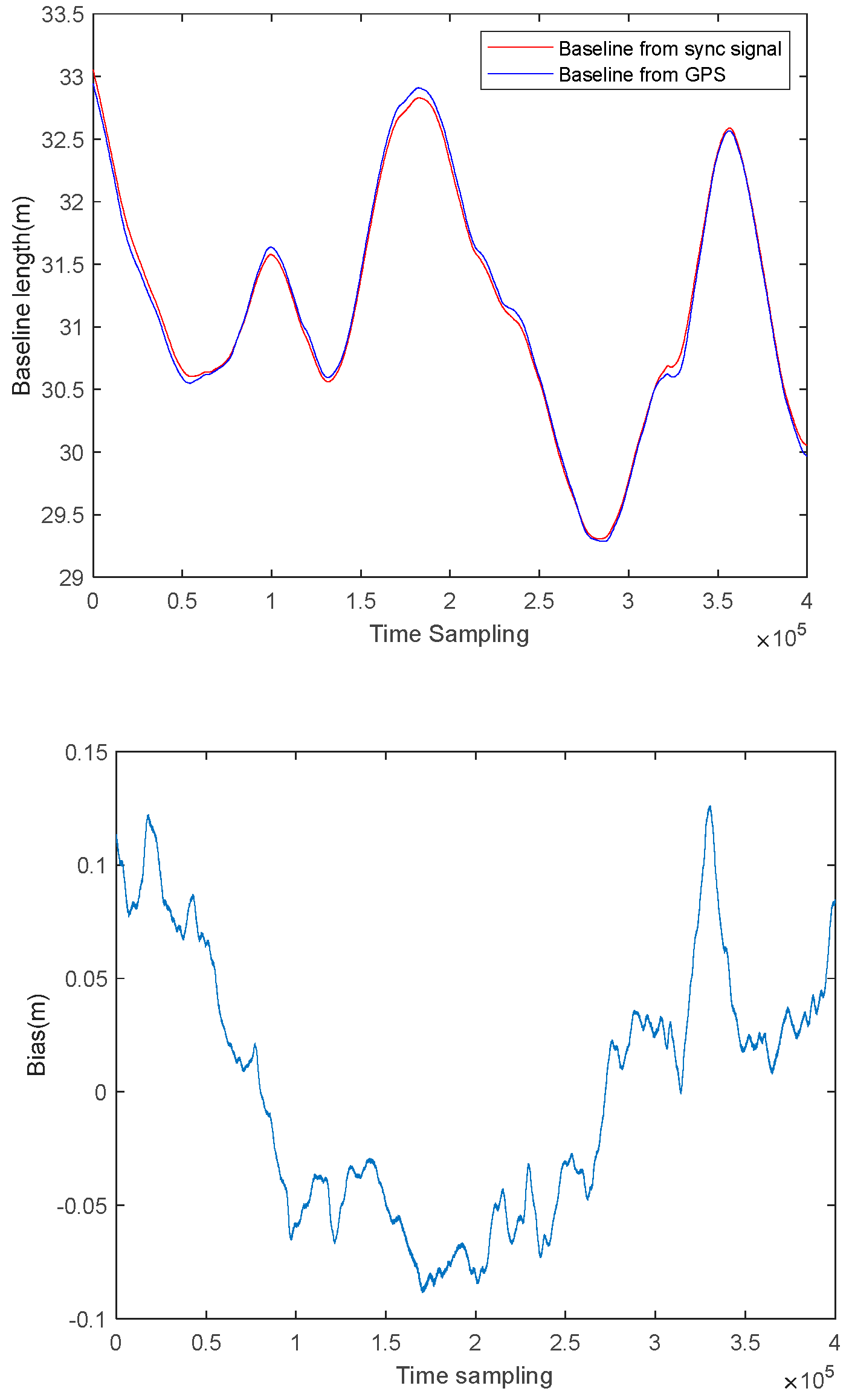
Preprints 95394 g009
Preprints 95394 g010
Figure 10. The correction values for the slave station’s trajectory.
Figure 10. The correction values for the slave station’s trajectory.
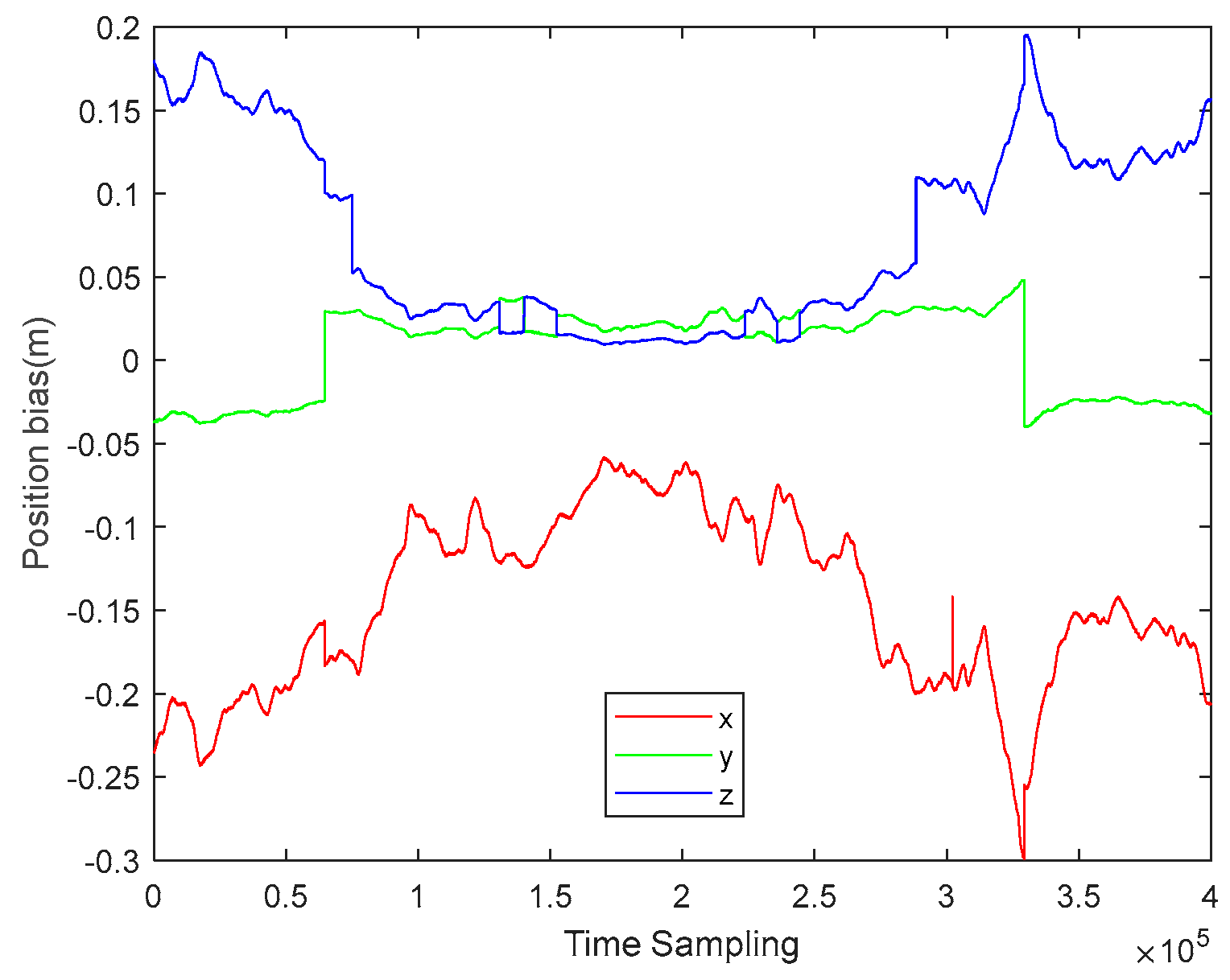
Preprints 95394 g010
Preprints 95394 g011
Figure 11. Baseline as extracted from the synchronization signal and as calculated using GPS.
Figure 11. Baseline as extracted from the synchronization signal and as calculated using GPS.
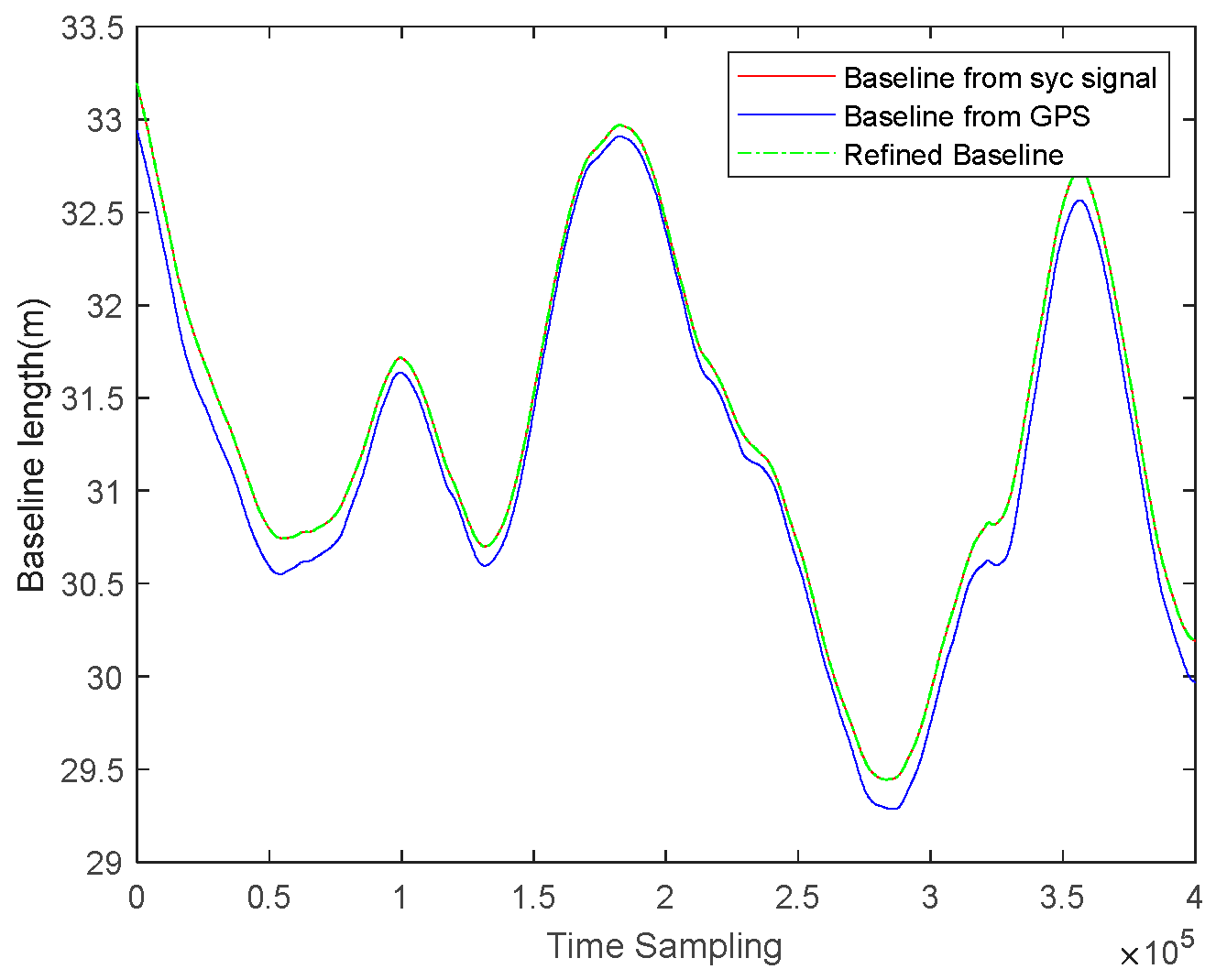
Preprints 95394 g011
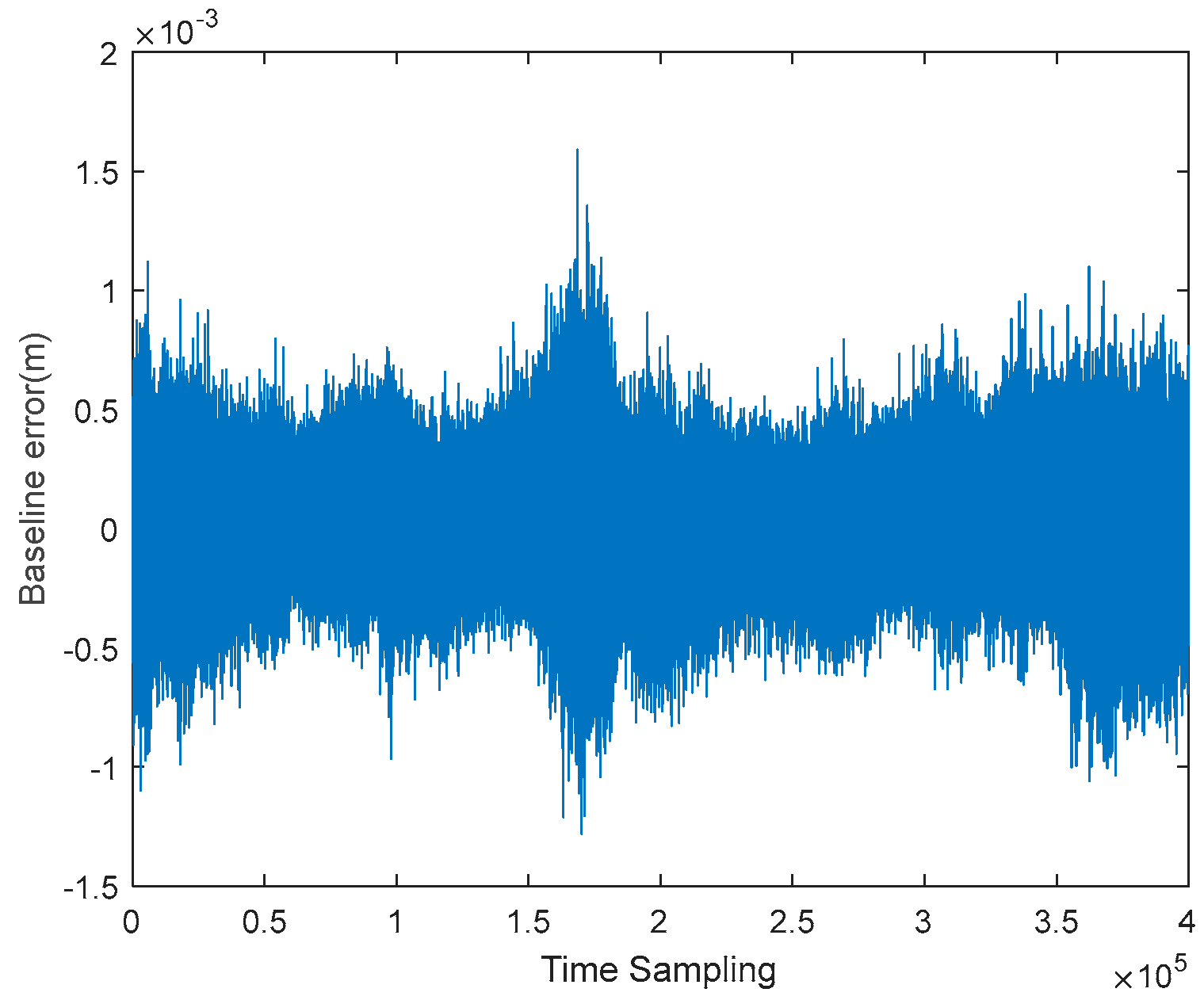
Preprints 95394 g012
Figure 12. The difference between the refined baseline and the baseline extracted from the synchronization signal.
Figure 12. The difference between the refined baseline and the baseline extracted from the synchronization signal.
Preprints 95394 g012
Preprints 95394 g013
Figure 13. Imaging results (top) before and (bottom) after synchronization phase compensation.
Figure 13. Imaging results (top) before and (bottom) after synchronization phase compensation.
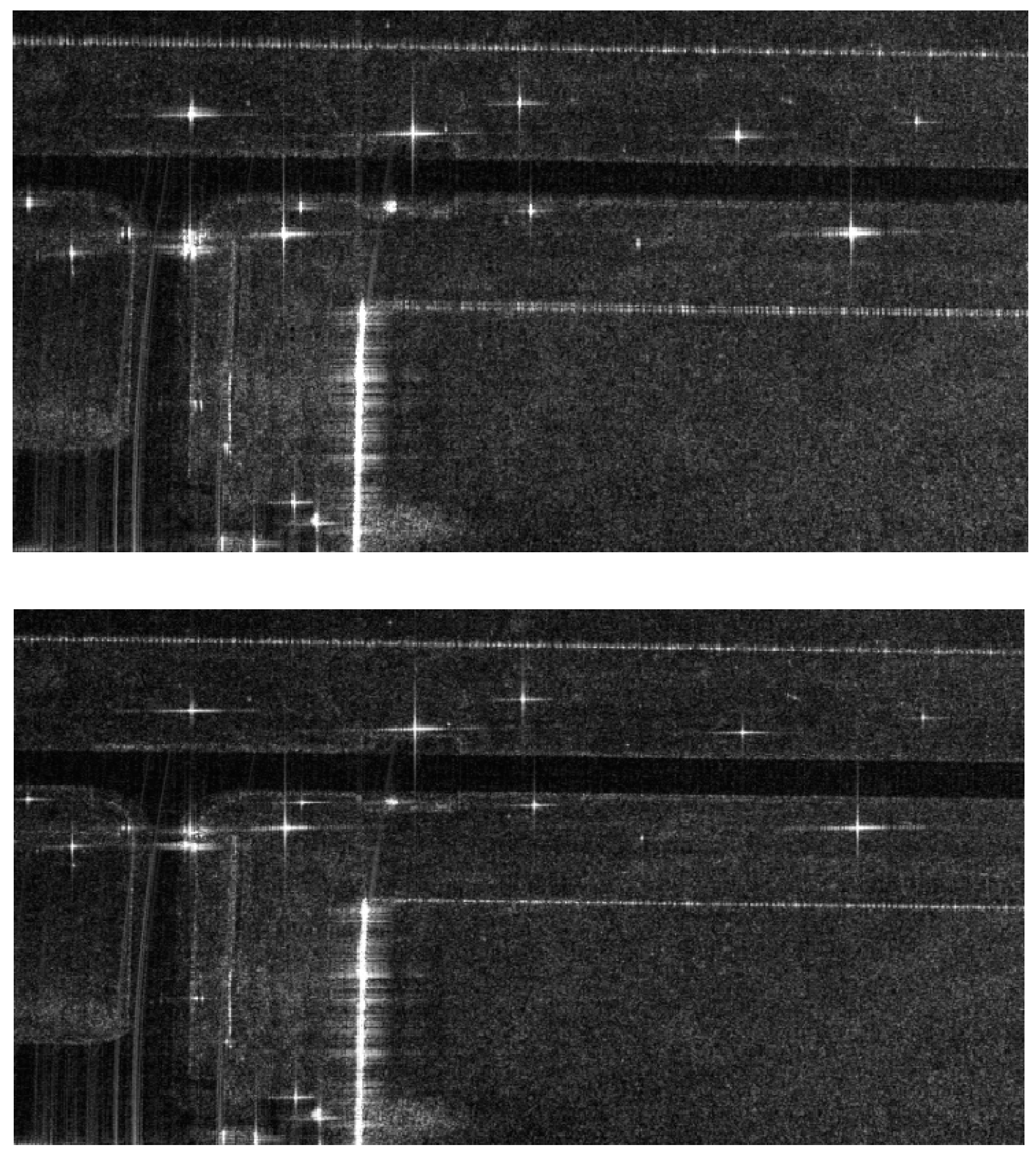
Preprints 95394 g013
Preprints 95394 g014
Figure 14. Imaging results (top) before and (bottom) after trajectory refinement.
Figure 14. Imaging results (top) before and (bottom) after trajectory refinement.
Preprints 95394 g014
Preprints 95394 g015
Figure 15. Azimuthal imaging quality test on calibration points.
Figure 15. Azimuthal imaging quality test on calibration points.
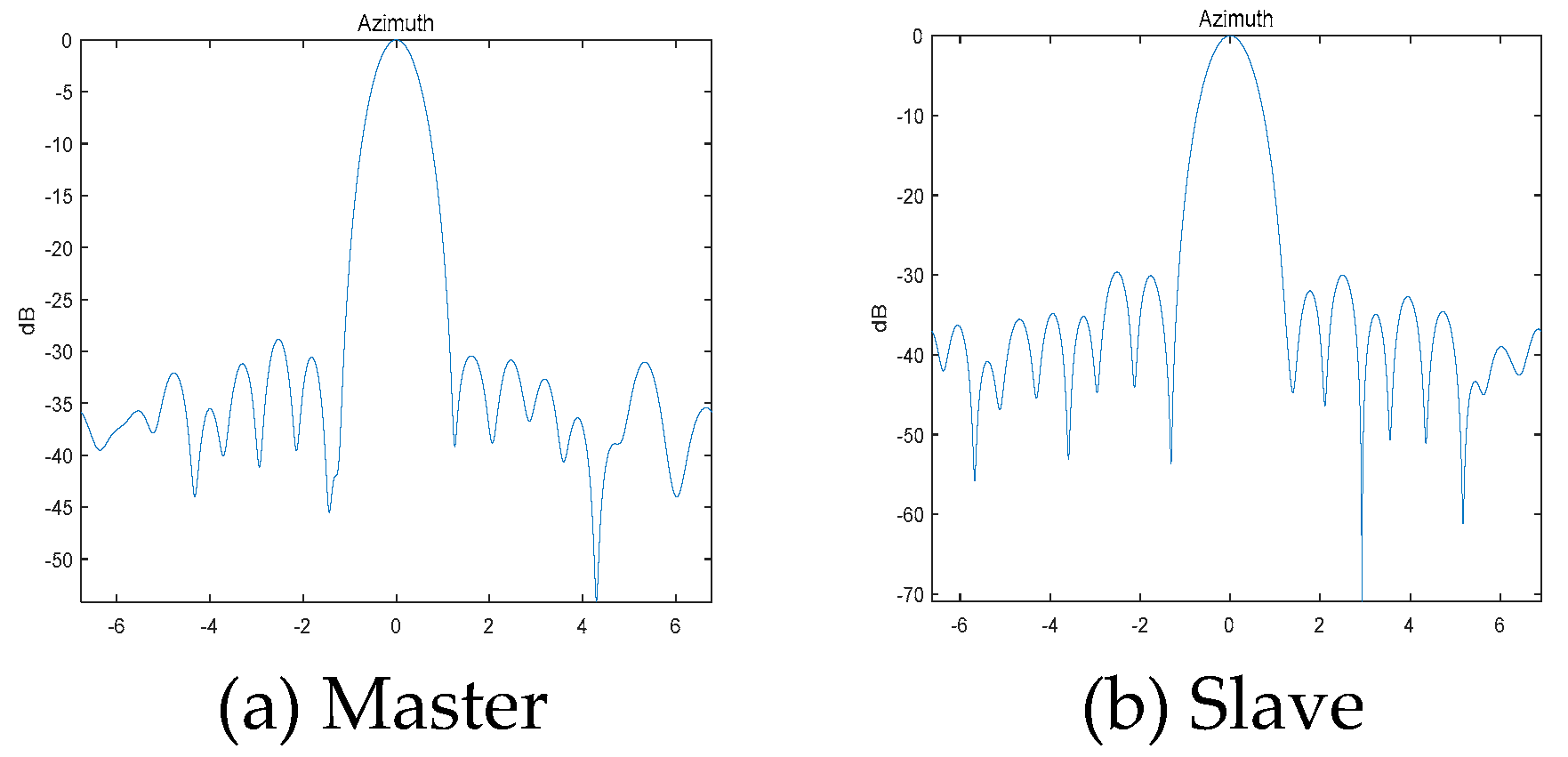
Preprints 95394 g015
Preprints 95394 g016
Figure 16. SAR images of localized areas of the airport.
Figure 16. SAR images of localized areas of the airport.
Preprints 95394 g016
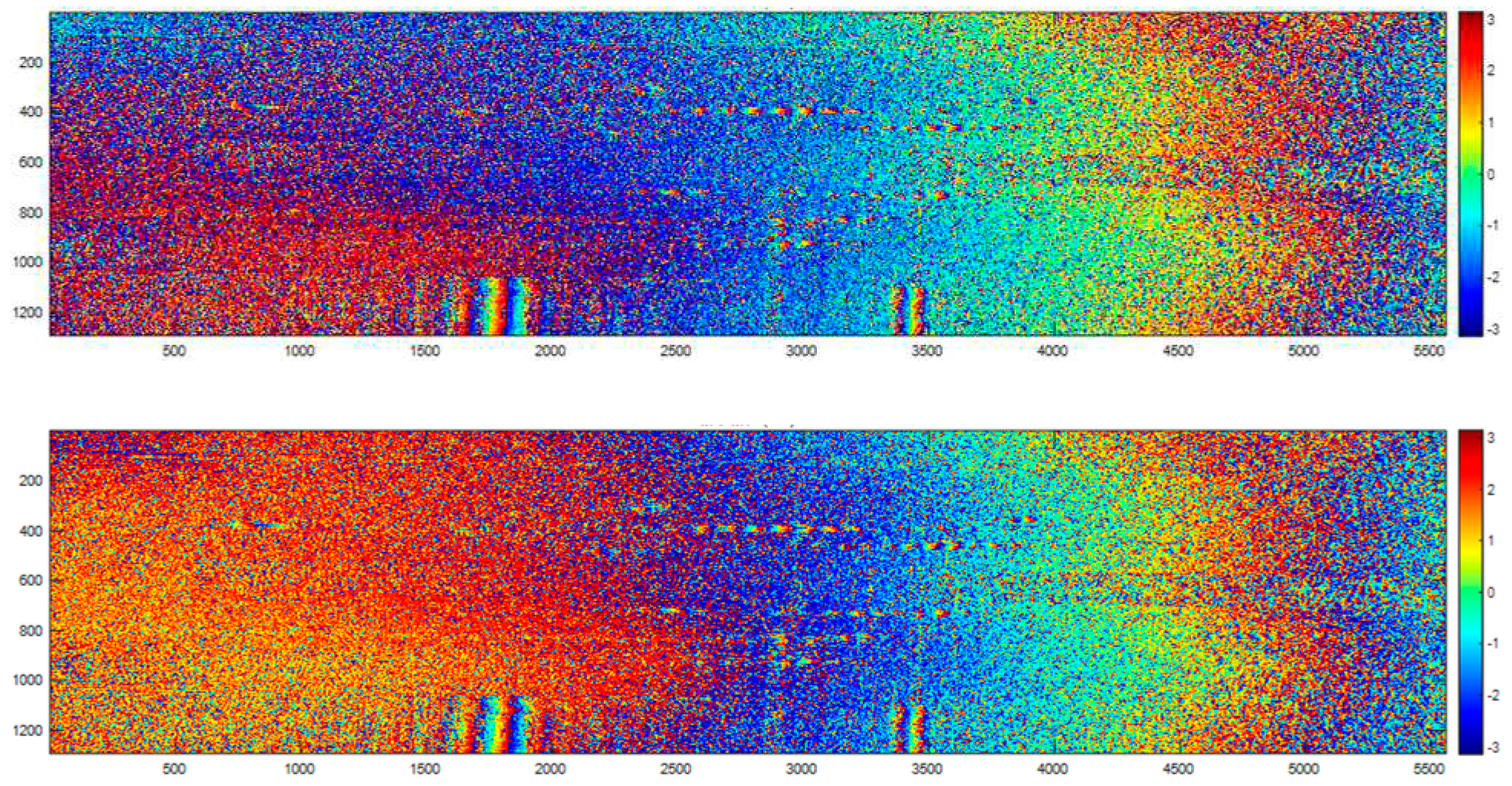
Preprints 95394 g017
Figure 17. Coherent phase (top) before and (bottom) after phase compensation.
Figure 17. Coherent phase (top) before and (bottom) after phase compensation.
Preprints 95394 g017
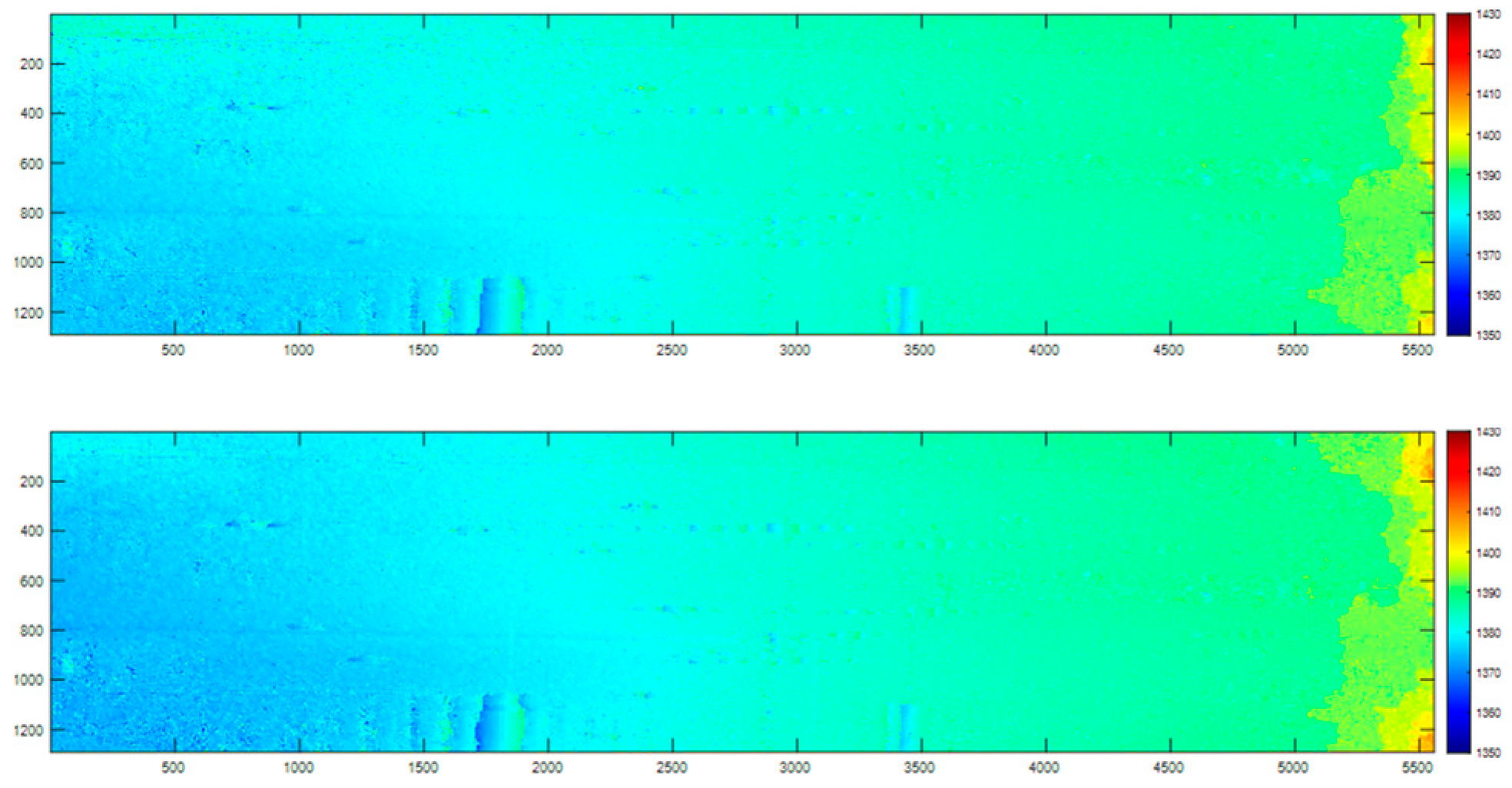
Preprints 95394 g018
Figure 18. Inversion height (top) before and (bottom) after phase compensation.
Figure 18. Inversion height (top) before and (bottom) after phase compensation.
Preprints 95394 g018
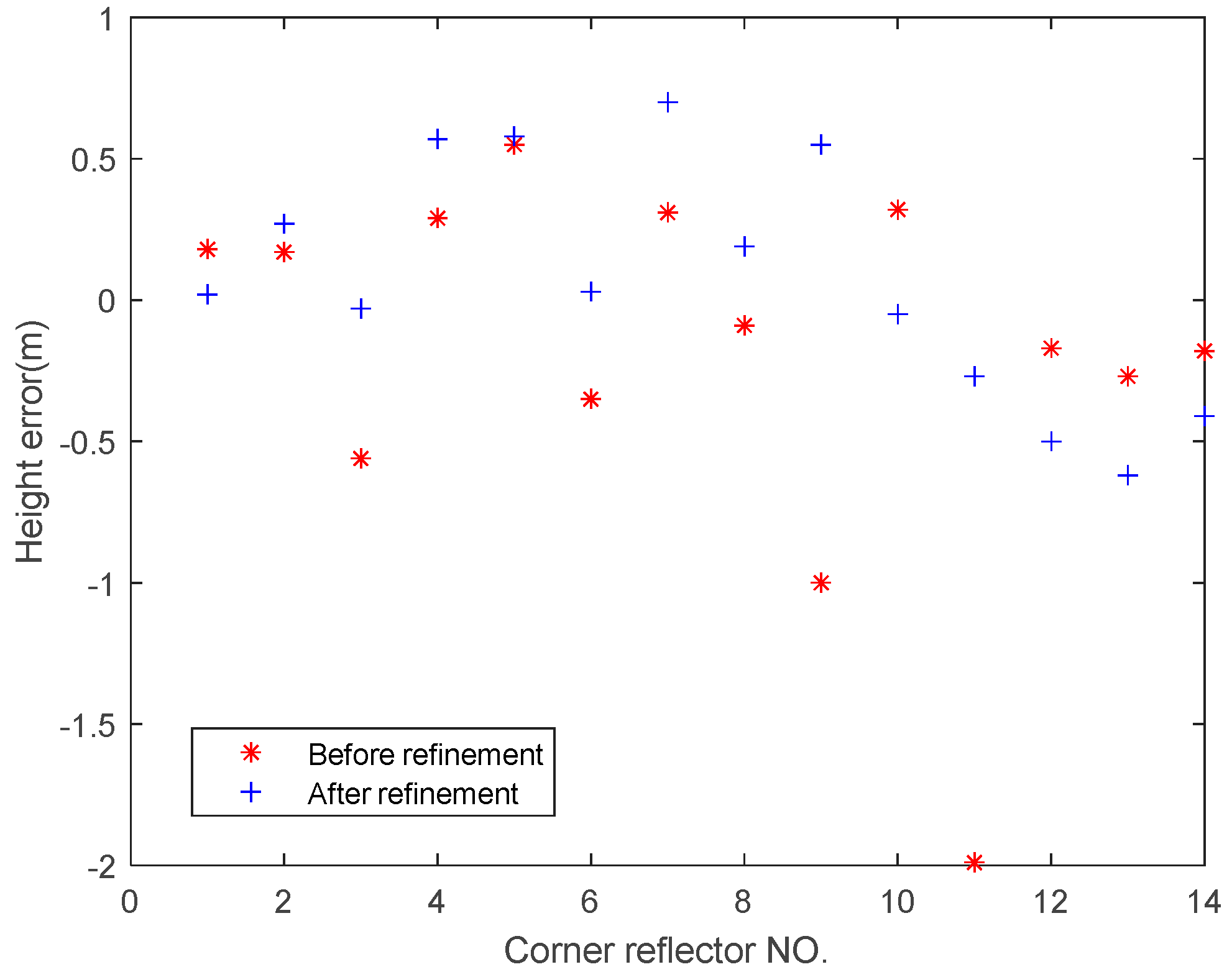
Preprints 95394 g019
Figure 19. Inversion height error before and after refinement.
Figure 19. Inversion height error before and after refinement.
Preprints 95394 g019
Table 1. Flight experiment parameters.
Table 1. Flight experiment parameters.
Parameter value
Flight altitude (relative to ground) 2 km
incident angle 45°
baseline angle 0°
Effective baseline length 30 m
Horizontal baseline length 42.43 m
frequency of carrier wave 1.5GHz
bandwidths 400MHz
sampling rate 625MHz
Azimuthal beamwidth 10°
Table 2. Table of height errors before and after trajectory refinement.
Table 2. Table of height errors before and after trajectory refinement.
Corner reflector Measured height
（m）		 Height error before refinement
（m）		 Height error after refinement
（m）
C1 1385.71 0.18 0.02
C2 1383.23 0.17 0.27
C3 1384.38 -0.56 -0.03
C4 1382.11 0.29 0.57
C5 1387.05 0.55 0.58
C6 1383.61 -0.35 0.03
C7 1382.98 0.31 0.70
C8 1386.03 -0.09 0.19
C9 1387.79 -1 0.55
C10 1387.68 0.32 -0.05
C11 1387.25 -1.99 -0.27
C12 1386.65 -0.17 -0.50
C13 1386.09 -0.27 -0.62
C14 1385.57 -0.18 -0.41
RMS 0.66 0.42
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated