1. Introduction

2. Materials and Methods

2.1. Study Area

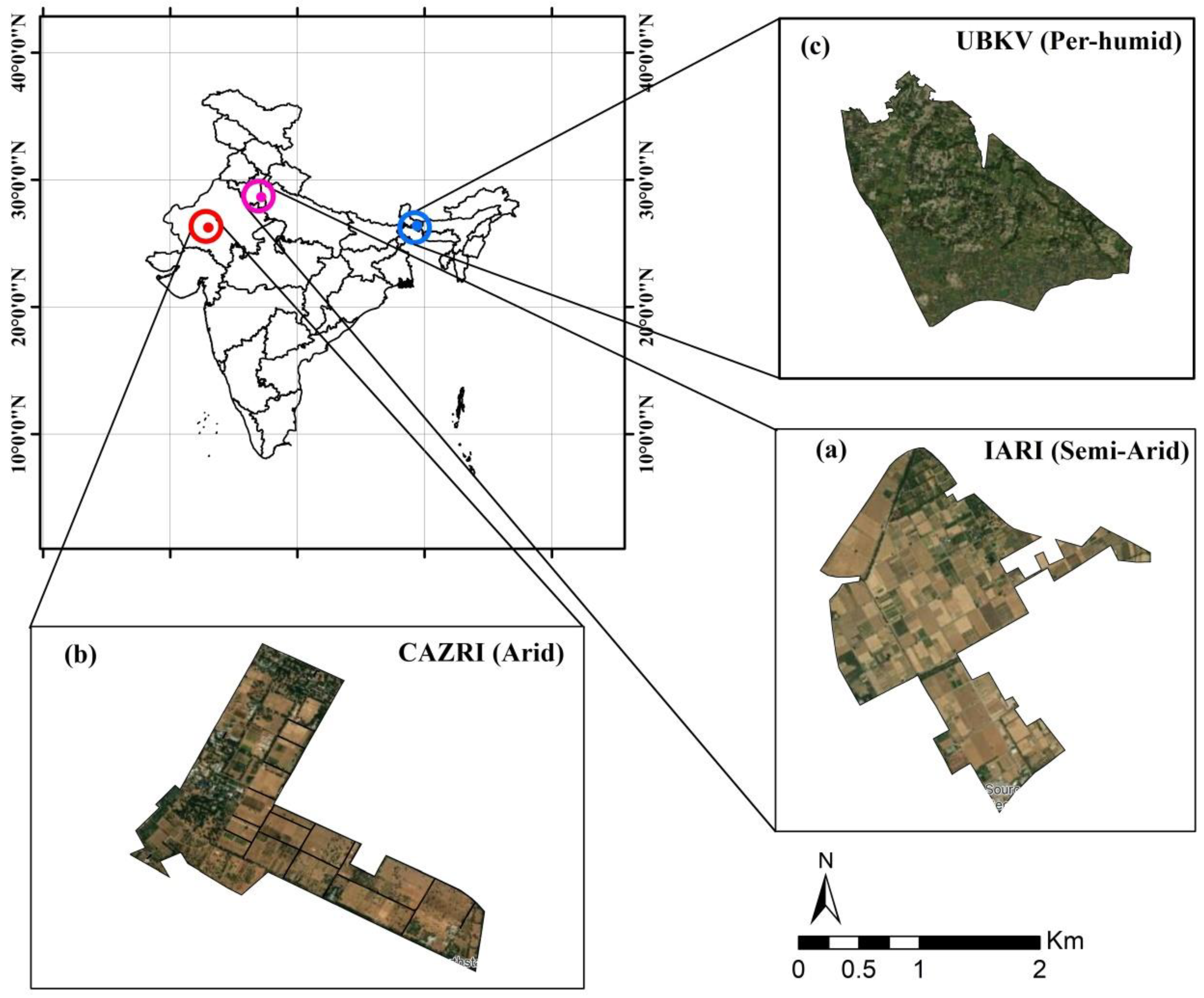
The proposed study was conducted over three experimental sites - 1) ICAR-Indian Agricultural Research Institute (IARI), New Delhi; 2) Central Arid Zone Research Institute (CAZRI), Rajasthan, and 3) Uttar Banga Krishi Viswavidyalaya, West Bengal located at semi-arid, arid, and per-humid agro-climatic regions respectively (Figure 1).

2.1.1. Semi-Arid, New Delhi (IARI)

The agricultural farm of the IARI, is situated at New Delhi between 28° 37′ 22.8″ N to 28° 38′ 58.92″ N and 77° 8′ 42.36″ to 77° 10′ 27.84″ E. The farm's total cropped area is 242 ha. The soil of the IARI farm is coarse loamy to fine loamy in texture. The farm has a semi-arid climate with an annual average rainfall of 765 mm, out of which 82.5% (632 mm) is received from June to September through the southwest monsoon. The rest of the rainfall comes during the post-monsoon period through western disturbances characterized by cloudy and foggy conditions over a few days. Wheat crop is dominant during the winter period followed by mustard, gram, and lentil.

2.1.2. Arid, Jodhpur (CAZRI)

The CAZRI agricultural farm is located at Jodhpur city in western Rajasthan extending from 26° 15′ 48.38″N to 26°14′ 26.08″N and 73° 0′ 38.90″ E to 72° 59′ 9.99″ E. The farm is spread across 241 ha which is dominated by agroforestry followed by crops and barren land. The climate is classified as arid with an annual mean temperature is 26.5 °C, mean annual rainfall is 500 mm, and potential evapotranspiration (PET) is 1400-2000 mm.

2.1.3. Per-Humid, Coochbehar (UBKV)

The study was also conducted at UBKV, Coochbehar district of West Bengal, India. It is extended from 26o 23' to 26o 2 N and 89o 23' E. The bio-climate of the area is humid to per-humid (Bhattacharyya et al., 2008). The area receives 2400 - 3700 mm of rainfall per year, with 70% of that falling between May and September. The average annual maximum and minimum temperature range from 37° to 5° Celsius (Coochbehar district Website, 2020).

Figure 1. Spatial extent of study area- a) IARI, New Delhi; b) CAZRI, Jodhpur and c) UBKV, coochbehar.

Figure 1. Spatial extent of study area- a) IARI, New Delhi; b) CAZRI, Jodhpur and c) UBKV, coochbehar.

2.2. Satellite Data

Optical-Thermal-SAR Data

The NASA Landsat-8 (L8) products were acquired from the United States of Geological Survey (USGS) Earth Explorer (https://ers.cr.usgs.gov) and ESA Level-1 Ground Range Detected (GRD) C-band synthetic aperture radar (SAR) Sentinel-1 data products in the Interferometric Wide (IW) swath was acquired from the ESA’s Sentinel scientific data hub (https://scihub.copernicus.eu/dhus/#/home). Sentinel-2 Level-2 products which provide bottom-of-atmosphere (BOA) reflectance images at 10 m, 20 m and ~10 days temporal resolution was acquired from the same platform. Landsat-8 has 11 spectral bands in the optical and thermal regions with 30 to 100 m spatial and 16 days temporal resolution. For the study, we used red, NIR, from Operational Land Imager (OLI), and thermal bands (Band 10; Thermal Infrared Sensor, TIRS, 10.6-11.19 μm). For IARI, New Delhi, the data were acquired from July 2020 to April 2022 spanning over both kharif and rabi seasons whereas for CAZRI, Jodhpur and UBKV, Coochbehar only the rabi season was covered. A set of total 75 level-1C S2 and Level-1 L8 cloud-free images were selected for this study. The detail on satellite sensors, data products, and dates of acquisition is listed in Table 1.

Table 1. Details of satellite data used in the study.

Table 1. Details of satellite data used in the study.

Test sites	Satellite	Sensor specifications	Data products (Resolution)	Date of acquisition
IARI, New Delhi	Sentinel-1	IW beam (VV, VH)	Backscatter coefficient (10 m)	3 July, 13 Sep, 25 Sep (Kharif, 2020); 31 Oct, 24 Nov, 18 Dec, 27 Jan, 20 Feb, 24 Mar (Rabi, 2020-2021); 04 June, 02 July (Kharif, 2021); 19 Nov, 13 Dec, 29 Dec, 15 Feb, 19 Mar, 04 April (Rabi, 2021-2022)
	Sentinel-2	Red band (0.665 µm); NIR band (0.842 µm)	NDVI (10 m)	3 July, 11 Sep, 01 Oct (Kharif-2020); 31 Oct, 20 Nov, 20 Dec; 29 Jan, 18 Feb, and 25 Mar (Rabi, 2020-2021); 08 June, 08 July (2021); 15 Nov, 15 Dec, 25 Dec, 13 Feb, 15 Mar, 04 April (2021-2022)
	Landsat-8	TIRS1 (10.895µm)	LST (100 m)	03 July,12 Sep, 28 Sep, (Kharif, 2020); 30 Oct, 24 Nov, 17 Dec, 27 Jan, 19 Feb, and 23 Mar (Rabi, 2020-2021); 04 June, 06 July (Kharif, 2021); 18 Nov, 13 Dec, 29 Dec, 15 Feb, 19 Mar, 04 April (Rabi, 2021-2022)
CAZRI, Jodhpur	Sentinel-1	IW beam (VV, VH)	Backscatter coefficient (10 m)	05 Mar, 22 Mar, 18 Dec (2021), 20 Feb (2022)
	Sentinel-2	Red band (0.665 µm); NIR band (0.842 µm)	NDVI (10 m)	03 Mar, 23 Mar, 18 Dec (2021), 20 Feb (2022)
	Landsat-8	TIRS1 (10.895 µm)	LST (100 m)	03 Mar, 23 Mar, 18 Dec (2021), 20 Feb (2022)
UBKV, Cooch Behar	Sentinel-1	IW beam (VV, VH)	Backscatter coefficient (10 m)	08 Mar, 24 Mar, 05 Dec, 21 Dec (2021)
	Sentinel-2	Red band (0.665 µm); NIR band (0.842 µm)	NDVI (10 m)	05 Mar, 25 Mar, 5 Dec, 20 Dec (2021)
	Landsat-8	TIRS1 (10.895 µm)	LST (100 m)	08 Mar, 24 Mar, 5 Dec, 21 Dec (2021)

2.4. LST Downscaling

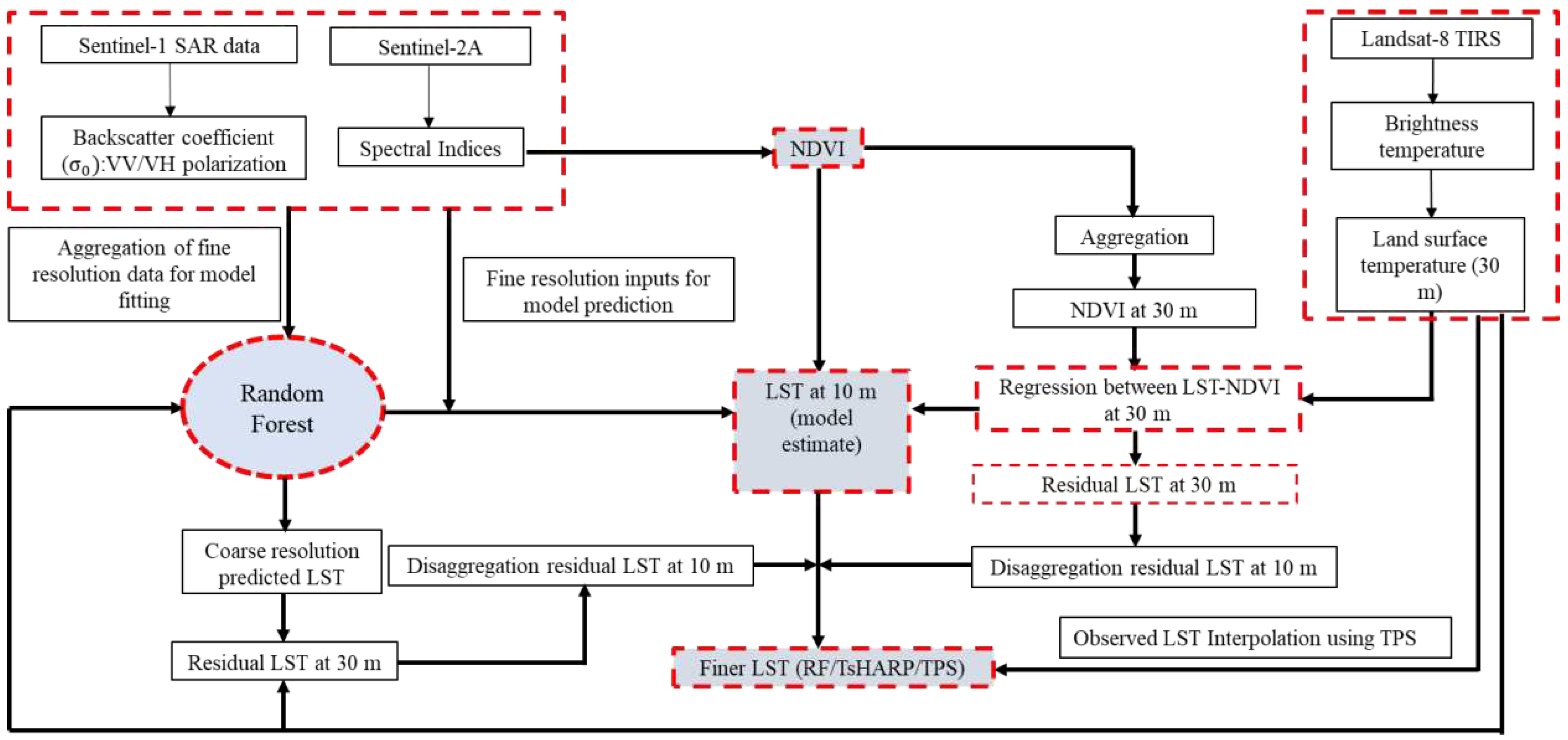
2.4.1. Thermal Sharpening (TsHARP)

In the present study, TsHARP model was used to downscale Landsat-8 thermal data at 100 m spatial resolution to 10 m using red (10 m) and NIR (10 m) reflectance bands obtained from sentinel-2A (Figure 2). TsHARP implies that the exclusive relationship exists between LST and VI using RS data at multiple spatial resolutions (Rawat, Sehgal and Ray, 2019; Pu, 2021). In the first step, TsHARP establish an empirical relationship between coarse resolution NDVI and LST-

$$\begin{array}{c}LS{T}_{coarse}=f_{reg}\left(VI\right)+{\delta }_{reg}\\ =a\ast NDV{I}_{coarse}+b+{\delta }_{reg}\end{array}$$

(1)

where f_reg is the regression function, VI is NDVI, coarse suffix represents poor resolution image (here, coarse = 30 m SR), a and b are regression parameters, ${\mathsf{\delta }}_{\mathrm{reg}}$is the residual field at poor resolution image pixel (30 m). The regression equation was applied over high-resolution NDVI images (10 m) and high-resolution LST (10 m) was calculated -

$$LS{T}_{fine\_reg}=a\ast NDV{I}_{fine}+b$$

(2)

Finally, high-resolution LST from TsHARP was obtained by adding residual field (δreg) behind of regression estimate -

$$\begin{array}{ll}LS{T}_{TsHARP}& =LS{T}_{fin{e}_{reg}}+{\delta }_{reg}\\ & =LS{T}_{fin{e}_{reg}}+LS{T}_{coarse}-LS{T}_{high=reg}\\ & =LS{T}_{coarse}+a\left[NDV{I}_{low}-NDV{I}_{high}\right]\end{array}$$

(3)

2.4.2. Thin Plate Spline (TPS)

TPS is a deterministic non-geostatistical surface fitting process or in simple terms, it is an interpolation method for known point data sets, used for downscaling of geo-data in raster format. The fundamental principle of the TPS technique is based on the spatial dependence of geo-data (Bindu et al., 2013). A general form of the TPS model is given by (Rawat, Sehgal and Ray, 2019)as -

$$f_{TPS}=a_0+a_{1}x+a_{2}y+\frac{1}{2}{\displaystyle \sum }_i^n{b}_i{r}_i^{2}log{r}_i^2$$

(4)

$${\displaystyle \sum }_{i=1}^n{b}_i={\displaystyle \sum }_{i=1}^n{b}_i{x}_i={\displaystyle \sum }_{i=1}^n{b}_i{y}_i=0$$

(5)

where, $r_i^2={\left(x-x_i\right)}^2$ +${\left(y-y_i\right)}^2$ and parameters are obtained by satisfying the following conditions-

$$f_{low\_TPS}=LS{T}_{coarse}$$

(6)

$$LS{T}_{TPS\_high}=f_{high\_TPS}$$

(7)

2.4.3. Random Forest (RF)

RF is an ensemble approach that assimilates decision trees and bagging models (Breiman, 2001). Based on the interpretation of the study region, the 35 foremost drivers of LST were considered for the RF model (Supplementary Table. S1). The models were adjusted in command to select the grouping of the hyperparameters that would give the highest precision. The hyperparameters of the ML models were optimized through 10-fold cross-validation with 5 repetitions using “caret” (Kuhn, 2008), “ranger” (Wright and Ziegler, 2015), “randomForest” (https://cran.rproject.org web/packages\\randomForest/index.html) packages in R version 4.0.2. Feature selection was performed to eliminate unsuitable variables. It ensures that model training is faster and less complicated, with a higher likelihood (Yan et al., 2019). The variable importance for the RF model was tested by the “varImp” function using the “caret” package in RStudio. For downscaling, the input predictors at fine resolution were first aggregated to match the coarse resolution LST data (equivalent to the ~100 m LST of Landsat-8 OLI/TIRS). The statistical relationship between the LST and predictor variables were developed using random forest algorithm as -

$$LS{T}_{100m}=f\left(S_i,{\delta }_{VV},{\delta }_{VH}\right)$$

(8)

where, $S_i$ is an i^th variable derived from optical data (Sentinel-2A) and ${\delta }_{VV},{\delta }_{VH}$ variable derived from SAR data (Sentinel-1), f is a non-linear function fitted by the random forest.

$$\mathsf{\Delta }LS{T}_{100m}=LS{T}_{100m}-PLS{T}_{100m}$$

(9)

$$PLS{T}_{10m}=PLS{T}_{10m}+\mathsf{\Delta }LS{T}_{100m}$$

(10)

The details in the description of the linear regression model were successively applied with a finer scale to calculate LST at a high resolution (Hutengs and Vohland, 2016).

Figure 2. Downscaling methodology of Landsat-8 LST data at 10 m resolution using TsHARP, TPS and RF.

Figure 2. Downscaling methodology of Landsat-8 LST data at 10 m resolution using TsHARP, TPS and RF.

2.4.4. Accuracy Evaluation

Three standard matrices were used to evaluate the model performance coefficient of determination (R²) (Eq. 11), root means square error (RMSE) (Eq. 12) and Mean Bias Error (MBE) (Eq. 13) given as -

$$R^2=\left(\frac{\frac{1}{n}{{\displaystyle \sum }}_{i=1}^n\left(LS{T}_P-\overline{LS{T}_P}\right)\left(LS{T}_O-\overline{LS{T}_O}\right)}{{\sigma }_P{\sigma }_O}\right)$$

(11)

$$RMSE=\sqrt{\frac{1}{n}{\displaystyle \sum }_{i=1}^n{\left(LS{T}_O-LS{T}_P\right)}^2}$$

(12)

$$MBE=\frac{{{\displaystyle \sum }}_i^n\left(LS{T}_O-LS{T}_P\right)}{n}$$

(13)

$LS{T}_P$ is model output; $\overline{LS{T}_P}$ and ${\sigma }_P$ are the mean and standard deviation of model outputs respectively, $LS{T}_O$ is observations; $\overline{LS{T}_O}$and ${\sigma }_O$ are the mean and standard deviation of observations, respectively. R² values close to 1 and RMSE close to 0 indicate better model performance.

3. Results

3.2. Variable Importance and Sensitivity Analysis

The sensitivity analysis performed in the study investigated the impact of selected variables on LST downscaling (Supplementary Figure S1). The variable importance and ALE plot sensitivity of predictor variables included in the process at each experiment site are demonstrated in Fig 3. The trends in variable importance were consistent between the semi-arid zone (IARI) and the arid zone (CAZRI). B11 (SWIR-1) was found to be the most important variable in LST downscaling at both these sites followed by B5, B1 and MNDWI (Figure 3a&b). These variables have a strong effect on LST prediction. The prediction tends to increase with increase in B11 until band value reaches 0.3 and 0.42 at IARI and CAZRI respectively. The relationship between prediction and B1 was discovered to be highly varied, with both being positively and negatively associated (0.05- 0.06 and 0.08- 0.1 at IARI; 0.06 - 0.8 and 0.16 onwards at CAZRI). MNDWI has a negative effect overall i.e. higher the MNDWI, the lower the prediction (Supplementary Figure S1 b).

However, the degree of different parameter’s sensitivity and importance varied significantly at per- humid area (UBKV) highlighting the difference in crop types, soil moisture availability and land use patterns. The coastal aerosol band (B1) was found to be most critical driver variable in LST downscaling at UBKV (Figure 3c) (Supplementary Figure S1c). B3, B9, B6, and B2 are among the other top variables that significantly affected the overall LST estimations at UBKV. B3 and B9 (peaked at 0.2), with their gradual and sharp changes, respectively, have mixed (positive and negative) effects. Between 0.175 and 0.19 band levels, B6 exhibited a significant negative impact on LST prediction.

Figure 3. ALE plots for sensitivity analysis of random forest downscaled LST over a ) IARI site at pre-monsoon to the post-monsoon period covering both inter and intra-seasonal time scale b) CAZRI and c) UBKV farm scale.

Figure 3. ALE plots for sensitivity analysis of random forest downscaled LST over a ) IARI site at pre-monsoon to the post-monsoon period covering both inter and intra-seasonal time scale b) CAZRI and c) UBKV farm scale.

3.3. Downscaled LST Validation with MODIS Data

Due to the unavailability of ground-observed LST data (use of a thermal camera in the field mounted on a pole could not be used for satellite LST validation; LST of the pixel of the camera and the corresponding pixel of the satellite showed large variations and disagreement), LST downscaled to 10 m was aggregated to 1000 m to match with MODIS LST (MOD11A1 and MYD11A1) of the same resolution, and was compared for all the sites. The statistical parameters -coefficient of determination, R2; Root Mean Square Error, RMSE’, and normalized RMSE for evaluating the accuracy of the models used for downscaling of LST are presented in Table 2 and Supplementary Figure S2. Overall, the RF provided the best predictability in terms of RMSE and nRMSE, compared to the TPS and TsHARP, while R2 values were nearly similar among the three approaches. It is interesting to note that, the machine learning approach (RF) and the TPS and TsHARP methods in the downscaled LST on different dates have quite varied RMSE and nRMSE values.

The downscaled and aggregated LST followed the trends with the MOD11A1 and MYD11A1 LST, although the values were underestimated in relation to both MODIS Aqua and MODIS Terra satellites. The regression line had R2= 0.82 (Aqua) and R2= 0.94 (Terra), but it showed a large deviation from the 1:1 line. At the semi-arid site (IARI) the machine learning based RF performed the best in terms of R2, RMSE, and nRMSE. The RF model had R2 values ranging between 0.44 and 0.93, RMSE between 0.80 and 11.47 K, and nRMSE between 0.27 and 3.84 across all dates of observation (Table 3). R2, RMSE and nRMSE for TsHARP model ranged between 0.39 to 0.93, 0.90 to 11.41 K, and 0.30 to 3.82 respectively, while for TPS the R2, RMSE and nRMSE varied between 0.38 to 0.92, 0.90 to 11.41 K, and 0.30 to 3.82 respectively. It could be noted that the RMSE values on September 12, 2020 at the IARI (semi-arid) location were significantly higher (11.41-11.47 K) for all three downscaling approaches.

At CAZRI, all three models showed a greater agreement (mean R2 >0.84) between the downscaled and reference LST (Table 3). RF method validation had R2 values between 0.75 and 0.91, RMSE between 1.15 and 12.80 K, and nRMSE between 0.36 and 4.30. On the other hand, the TPS method had R2 ranging from 0.75 to 0.92, RMSE 1.10-12.76 K, and the nRMSE 0.35-4.29, whereas the TsHARP method showed R2, RMSE, and nRMSE ranging between 0.75 and 0.89, 1.15 K and 12.94 K, and 0.49 and 4.56, respectively. The RMSE for all three methods were found to be high (12.76 - 12.94) on 20th February 2022 at the CAZRI site. For the UBKV site, the validation R2 in the case of the RF method ranged from 0.57-0.70, RMSE as 0.31- 3.13 K, and nRMSE as 0.11 -1.05. Similarly, in the case of TsHARP, the R2, RMSE, and nRMSE were varying between 0.62 and 0.72, 0.48 K and 3.06 K, and 0.16 and 1.03. The validation R2 for the TPS method ranged between 0.59 and 0.72, RMSE between 0.47 K and 3.10 K, and nRMSE between 0.16 and 1.04.

Table 2. Validation of downscaled aggregated LST with observed LST at 1000 m scale using MODIS terra product.

Table 2. Validation of downscaled aggregated LST with observed LST at 1000 m scale using MODIS terra product.

	RF			TsHARP			TPS
Date	R2	RMSE	nRMSE	R2	RMSE	nRMSE	R2	RMSE	nRMSE
	IARI
12.09.2020	0.68	11.47	3.84	0.66	11.41	3.82	0.66	11.41	3.82
28.09.2020	0.59	6.66	2.18	0.39	6.61	2.17	0.38	6.69	2.16
30.10.2021	0.83	4.38	1.45	0.77	4.36	1.45	0.78	4.33	1.44
24.11.2020	0.63	3.23	1.09	0.43	3.29	1.11	0.43	3.30	1.11
19.02.2021	0.55	1.59	0.53	0.57	1.71	0.57	0.56	1.71	0.57
23.03.2021	0.56	5.35	1.75	0.52	5.60	1.83	0.51	5.60	1.83
18.11.2021	0.44	1.27	0.43	0.44	1.26	0.42	0.43	1.24	0.42
15.02.2022	0.53	0.80	0.27	0.57	0.90	0.30	0.55	0.90	0.30
11.03.2022	0.58	1.25	0.57	0.52	2.03	0.68	0.48	2.02	0.68
19.03.2022	0.70	2.04	0.66	0.47	2.16	0.70	0.61	2.08	0.68
04.04.2022	0.93	6.77	2.26	0.93	6.72	2.20	0.92	6.71	2.19
Mean	0.64	4.07	1.37	0.57	4.18	1.39	0.57	4.18	1.38
SD	4.52	1.24	1.26	3.54	1.31	1.31	3.56	1.31	1.30
SE	1.36	0.37	0.38	1.07	0.40	0.39	1.07	0.39	0.39
	CAZRI
05.03.2021	0.88	2.82	0.90	0.88	2.77	0.89	0.88	2.75	0.88
21.03.2021	0.75	1.15	0.36	0.75	1.15	0.36	0.75	1.10	0.35
18.12.2021	0.91	1.56	0.52	0.89	1.54	0.52	0.92	1.53	0.52
20.02.2022	0.85	12.80	4.30	0.85	12.80	4.30	0.84	12.76	4.29
Mean	0.85	4.58	1.52	0.84	4.56	1.52	0.85	4.54	1.51
SD	11.90	0.83	0.82	12.81	0.82	0.81	11.43	0.82	0.81
SE	5.95	0.41	0.41	6.41	0.41	0.41	5.71	0.41	0.40
	UBKV
08.03.2021	0.70	0.31	0.11	0.72	0.48	0.16	0.72	0.47	0.16
24.03.2021	0.57	3.13	1.05	0.62	3.06	1.03	0.59	3.10	1.04
Mean	0.64	1.72	0.58	0.67	1.77	0.59	0.66	1.78	0.60
SD	7.04	0.86	0.86	9.48	0.97	0.97	6.91	0.96	0.96
SE	4.98	0.61	0.61	6.70	0.69	0.69	4.89	0.68	0.68

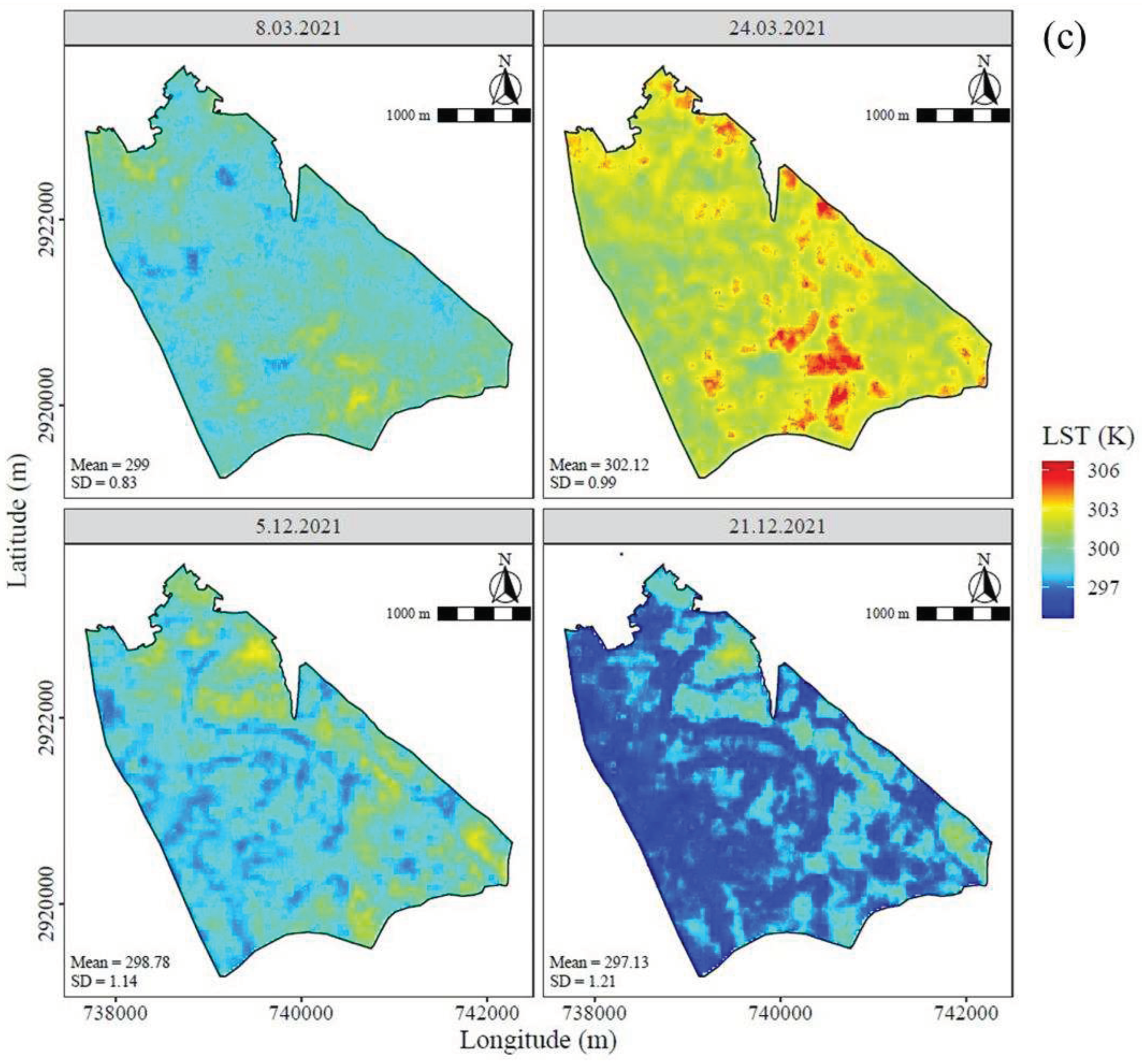
3.4. LST Maps at 30 and 10 m Resolutions

A simultaneous display of downscaled LST maps at 10 m and the Landsat-8 LST (the ‘reference’) at 30 m scales showed similar patterns and spatial distributions (Figure 4; Supplementary Figure S3, Figure S4, Figure S5, Figure S6 and Figure S7). The LST values could effectively pick up the temperature trends over the season and were evident at both resolutions. At the IARI farm, the image captured LST values as low as 16°C (December 17, 2020) and as high as 41°C (July 3, 2020) (Figure 4a; Supplementary Figure S3, Figure S4 and Figure S5). However, the reference LST had a fuzzy appearance and was homogeneous in distribution. Although the RF and TsHARP-generated 10 m maps appeared similar, the RF had more information, indicating the possibility of analysing plot-scale variations in temperature and identifying between crops and adjacent areas. The performance of TPS was compromised, and there was little improvement in image clarity (Supplementary Figure S4). For instance, the reference map and TPS maps both have hazy appearances in the north and west parts of the IARI farm on March 23, 2021, however RF exhibits higher distinction and clarity. It should be noted here that indistinctiveness was inevitable in RF and TsHARP methods which required residual correction procedures. In kharif, when the LST variations across space and time were perceptible, RF produced a better resolution in maps compared to the other two methods.

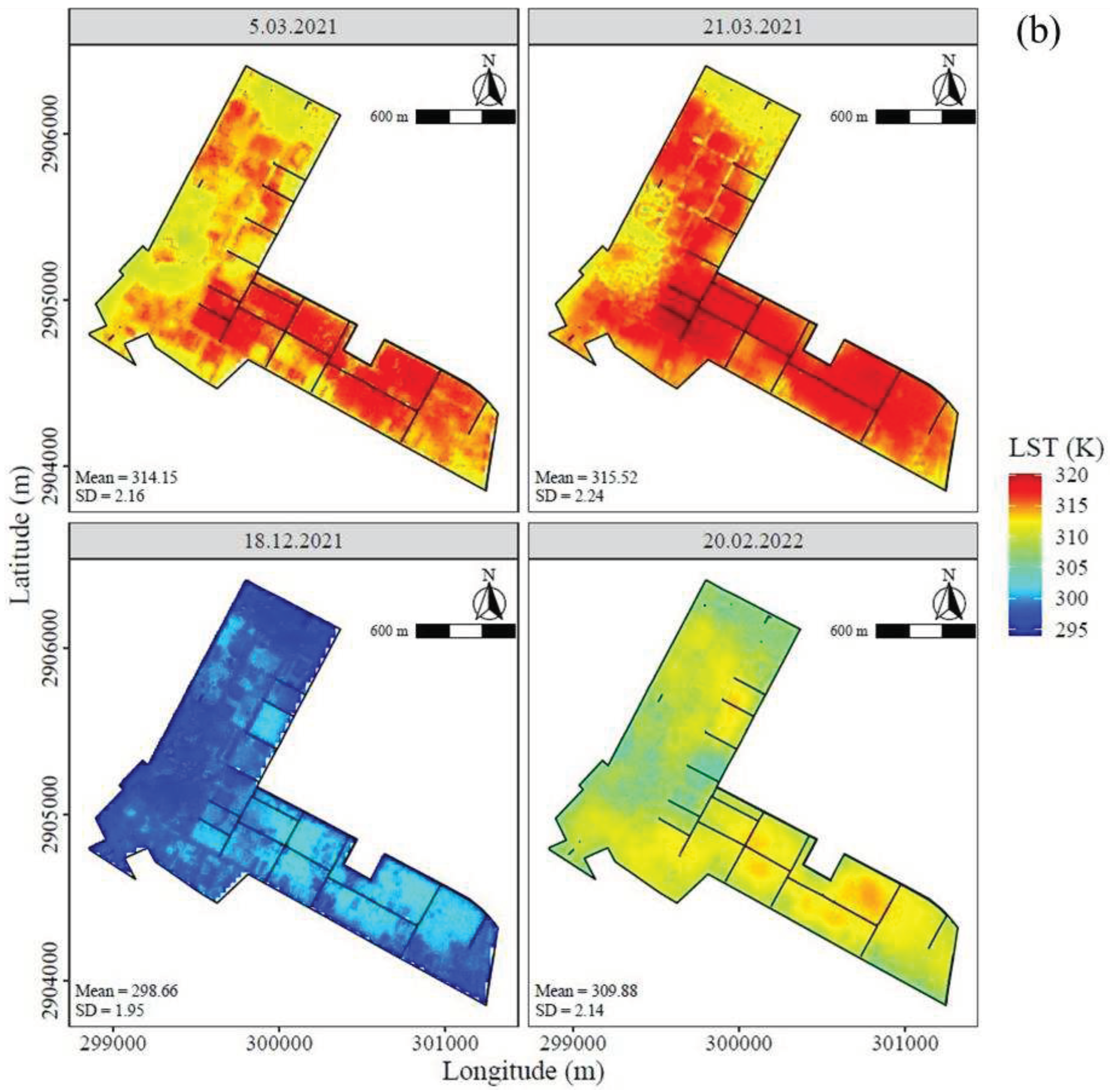
Similarly, over CAZRI, the mean LST values of images were similar over a specific date, irrespective of the methods, and were also similar to the reference map (Figure 4b; Supplementary Figure S6, Figure S7 and Figure S8). The CAZRI farm is diverse in land use and represents a mixed agricultural farm comprising cropland agroforestry, pasture, and bare land. The pixels appearing in red showed high values while blue pixels referred to low LST. Here also, LST maps derived from RF and TsHARP methods were similar as compared to the TPS and could distinguish the heterogeneity of land use. The reference image had a smoothing effect and was relatively uniform in appearance. It occurred that the centre and south-eastern blocks of CAZRI have greater LST values than the north-western area, which is where crops were grown. For the per-humid region (UBKV), the downscaled LST maps had a homogenous appearance in all the approaches (Figure 4c; Supplementary Figure S9, Figure S10 and Figure S11). The UBKV farm, is predominantly a lowland area with rice crops where the mean LST varied over a narrow range (24 - 29°C). However, the south-eastern block of the farm area had a considerably higher LST value (27°C; March 8, 2021) as it featured orchards, horticultural crops, rubber plantations, etc. intermingled with the rice fields. The north-western block was low-lying paddy areas showing comparatively lower values (~21°C) and was more distinguishable in RF maps.

Figure 4. Spatial extent of random forest downscaled LST (10 m) over (a) IARI site at pre-monsoon to the post-monsoon period covering both inter and intra-seasonal time scale (b) CAZRI and (c) UBKV farm scale.

Figure 4. Spatial extent of random forest downscaled LST (10 m) over (a) IARI site at pre-monsoon to the post-monsoon period covering both inter and intra-seasonal time scale (b) CAZRI and (c) UBKV farm scale.

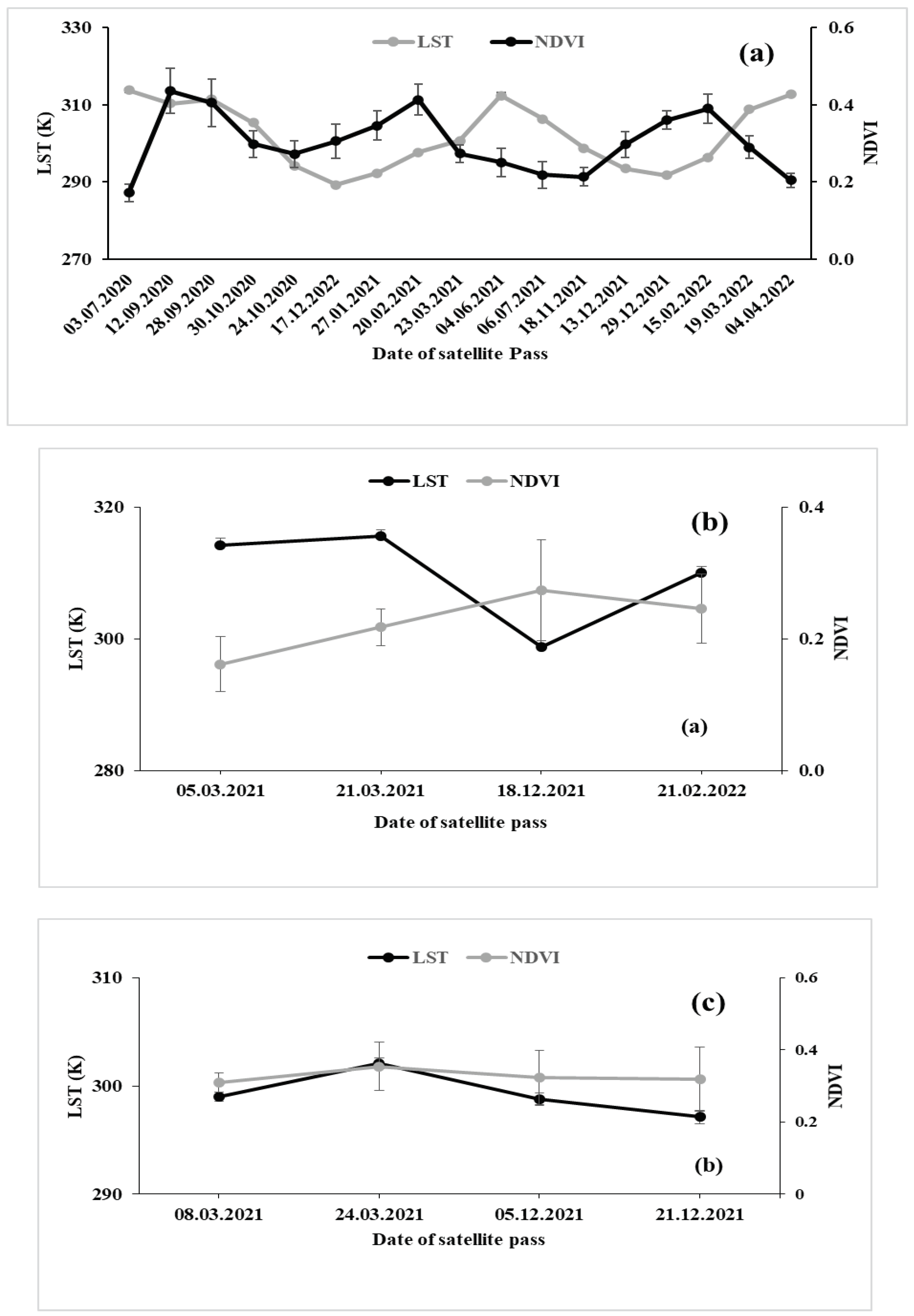
3.5. LST-NDVI Profile Distribution

The LST and NDVI profile distribution of IARI (averaged over the farm area) for multi date satellite passes demonstrated the inter- and intra-seasonal variations of these parameters for two consecutive years: rabi 2020-21 and 2021-22, and kharif 2020 and 2021 (Figure 5). The NDVI images of all three sites are also presented to understand the spatiotemporal changes in vegetation growth and vigour in the respective farms (Supplementary Supplementary Figure S12, Figure S13 and Figure S14). The trends are typically reversed to the LST values. At the IARI site, blue colours represent cropland with high values of NDVI (>0.5), indicating high levels of green biomass. The red tone, on the contrary, represents the lower values of NDVI corresponding to lesser biomass vigour or in the extreme case, bare land with no or sparse vegetation.

Figure 5. Mean LST-NDVI distribution over a) IARI site at pre-monsoon to the post-monsoon period covering both inter and intra-seasonal time scale b) CAZRI and c) UBKV.

Figure 5. Mean LST-NDVI distribution over a) IARI site at pre-monsoon to the post-monsoon period covering both inter and intra-seasonal time scale b) CAZRI and c) UBKV.

For IARI farm, on July 3, 2020, during the pre-monsoon season, the image displayed the mean maximum LST (313.7 K), while on October 30, 2020, during the post-monsoon season, it displayed 305.3 K (Figure 5a). The LST was lowered by 3.4 and 2.3 K on September 12 and 28, 2020 respectively in monsoon compared to the pre-monsoon period. During winters, the LST decreased sharply and was recorded 24.4 and 21.5 K lower on December 17, 2020 and January 27, 2021 respectively. The mean LST of the farm did not vary significantly across dates, regardless of the downscaling techniques used. Since there were only two dates available for the monsoon 2021, the LST may not have been adequately reflected over the study area, but the mean LST (June 4, 2021) followed a pattern that was comparable to that of the monsoon 2020. In the case of NDVI, the mean value was 0.17 in the pre-monsoon period (July 3, 2020) which increased to 0.44 during end of monsoon season (September 12, 2020) and decreased again (0.30) during the post-monsoon season (October 30, 2020). An increasing NDVI followed by a decreasing trend was the typical characteristic of crop growth both in the kharif and rabi seasons owing to phenological changes. This was more explicit in the rabi (winter) season owing to a large number of available images.

The mean value of LST over CAZRI was higher on March 21, 2021 (315.6 K) but lower on December 18, 2021 (298.5 K) (Figure 5b). The mean NDVI value was lower on March 5, 2021 (0.16) and higher on December 18, 2021 (0.27) at CAZRI. The lower values of NDVI at the central and south-eastern blocks in the CAZRI farm are dominated by bare soil and pasture land with low biomass vigour (Supplementary Figure S13). However, the north-western part has higher NDVI due to crops and agroforestry. The CAZRI farm had a variety of crops, grasslands, agroforestry, and under different soil moisture (adequately irrigated, limited irrigated, and non-irrigated plots) and followed heterogeneous cropping patterns as compared to semi-arid and per-humid regions. At UBKV site also, LST was higher on March 24, 2021 (302.1 K), while a lower value was recorded on December 5 and 21, 2021 (298.7 and 297.1 K, respectively) (Figure 5c). At UBKV farm, higher NDVI (deep blue patches) at the north-western block indicates to boro (winter) rice cultivation (November-May). The red-marked areas at the south-eastern block with low NDVI can be linked to limited biomass or fallow conditions. The NDVI at the UBKV site remained consistent over the dates, likely due to the presence of rice crops in the field.

4. Discussion

5. Conclusions

References

1. Atkinson, P.M. (2013) ‘Downscaling in remote sensing’, International Journal of Applied Earth Observation and Geoinformation, 22, pp. 106–114.
2. Becker, F. and Li, Z.-L. (1990) ‘Towards a local split window method over land surfaces’, Remote Sensing, 11(3), pp. 369–393.
3. Becker, F. and Li, Z. (1995) ‘Surface temperature and emissivity at various scales: Definition, measurement and related problems’, Remote sensing reviews, 12(3–4), pp. 225–253.
4. Bhattacharyya, T., Pal, D. K., Chandran, P., Ray, S. K., Mandal, C., & Telpande, B. (2008). Soil carbon storage capacity as a tool to prioritize areas for carbon sequestration. Current science, 482-494.
5. Bindhu, V.M., Narasimhan, B. and Sudheer, K.P. (2013) ‘Development and verification of a non-linear disaggregation method (NL-DisTrad) to downscale MODIS land surface temperature to the spatial scale of Landsat thermal data to estimate evapotranspiration’, Remote Sensing of Environment, 135, pp. 118–129.
6. Bindu, S. et al. (2013) ‘Development of transfer function model and analysis of the peaking capacitor and switch’, IEEE Transactions on Plasma Science, 41(8), pp. 2415–2420. [CrossRef]
7. Breiman, L. (2001) ‘Random forests’, Machine learning, 45(1), pp. 5–32.
8. Brodu, N. (2017) ‘Super-resolving multiresolution images with band-independent geometry of multispectral pixels’, IEEE Transactions on Geoscience and Remote Sensing, 55(8), pp. 4610–4617. [CrossRef]
9. Cao, B. et al. (2019) ‘A review of earth surface thermal radiation directionality observing and modeling: Historical development, current status and perspectives’, Remote Sensing of Environment, 232, p. 111304.
10. Casper, M.C. and Vohland, M. (2008) ‘Validation of a large scale hydrological model with data fields retrieved from reflective and thermal optical remote sensing data–A case study for the Upper Rhine Valley’, Physics and Chemistry of the Earth, Parts A/B/C, 33(17–18), pp. 1061–1067. [CrossRef]
11. Chen, C. and Li, Y. (2012) ‘A robust method of thin plate spline and its application to DEM construction’, Computers & Geosciences, 48, pp. 9–16. [CrossRef]
12. Colliander, A. et al. (2017) ‘Spatial downscaling of SMAP soil moisture using MODIS land surface temperature and NDVI during SMAPVEX15’, IEEE Geoscience and Remote Sensing Letters, 14(11), pp. 2107–2111. [CrossRef]
13. Coolbaugh, M.F. et al. (2007) ‘Detection of geothermal anomalies using advanced spaceborne thermal emission and reflection radiometer (ASTER) thermal infrared images at Bradys Hot Springs, Nevada, USA’, Remote Sensing of Environment, 106(3), pp. 350–359. [CrossRef]
14. Das, B. et al. (2021) ‘LST: Land Surface Temperature Retrieval for Landsat 8’.
15. Dash, P. et al. (2001) ‘Retrieval of land surface temperature and emissivity from satellite data: physics, theoretical limitations and current methods’, Journal of the Indian Society of Remote Sensing, 29, pp. 23–30.
16. Ebrahimy, H. and Azadbakht, M. (2019) ‘Downscaling MODIS land surface temperature over a heterogeneous area: An investigation of machine learning techniques, feature selection, and impacts of mixed pixels’, Computers & geosciences, 124, pp. 93–102.
17. Eskandari, A., De Rosa, R. and Amini, S. (2015) ‘Remote sensing of Damavand volcano (Iran) using Landsat imagery: Implications for the volcano dynamics’, Journal of Volcanology and Geothermal Research, 306, pp. 41–57. [CrossRef]
18. Fensholt, R. and Sandholt, I. (2003) ‘Derivation of a shortwave infrared water stress index from MODIS near-and shortwave infrared data in a semiarid environment’, Remote Sensing of Environment, 87(1), pp. 111–121. [CrossRef]
19. Gao, C. et al. (2013) ‘A generalized split-window algorithm for land surface temperature estimation from MSG-2/SEVIRI data’, International journal of remote sensing, 34(12), pp. 4182–4199.
20. Gao, Z. et al. (2021) ‘A two-step integrated MLP-GTWR method to estimate 1 Km land surface temperature with complete spatial coverage in humid, cloudy regions’, Remote Sensing, 13(5), p. 971. [CrossRef]
21. Ghent, D. et al. (2019) ‘A new approach to defining uncertainties for MODIS land surface temperature’, Remote Sensing, 11(9), p. 1021. [CrossRef]
22. Gillespie, A. et al. (1998) ‘A temperature and emissivity separation algorithm for Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) images’, IEEE transactions on geoscience and remote sensing, 36(4), pp. 1113–1126. [CrossRef]
23. Guo, F., Hu, D. and Schlink, U. (2022) ‘A new nonlinear method for downscaling land surface temperature by integrating guided and Gaussian filtering’, Remote Sensing of Environment, 271, p. 112915. [CrossRef]
24. Hale, R.C. et al. (2011) ‘Characterization of variability at in situ locations for calibration/validation of satellite-derived land surface temperature data’, Remote Sensing Letters, 2(1), pp. 41–50.
25. Huang, X. and Wang, Y. (2019) ‘Investigating the effects of 3D urban morphology on the surface urban heat island effect in urban functional zones by using high-resolution remote sensing data: A case study of Wuhan, Central China’, ISPRS Journal of Photogrammetry and Remote Sensing, 152, pp. 119–131. [CrossRef]
26. Hulley, G.C., Hook, S.J. and Baldridge, A.M. (2010) ‘Investigating the effects of soil moisture on thermal infrared land surface temperature and emissivity using satellite retrievals and laboratory measurements’, Remote Sensing of Environment, 114(7), pp. 1480–1493. [CrossRef]
27. Hurtado, E., Vidal, A. and Caselles, V. (1996) ‘Comparison of two atmospheric correction methods for Landsat TM thermal band’, International Journal of Remote Sensing, 17(2), pp. 237–247. [CrossRef]
28. Hutengs, C. and Vohland, M. (2016) ‘Downscaling land surface temperatures at regional scales with random forest regression’, Remote Sensing of Environment, 178, pp. 127–141. [CrossRef]
29. Jiménez-Muñoz, J.C. and Sobrino, J.A. (2009) ‘A single-channel algorithm for land-surface temperature retrieval from ASTER data’, IEEE Geoscience and Remote Sensing Letters, 7(1), pp. 176–179. [CrossRef]
30. Jiménez-Muñoz, J.C. and Sobrino, J.A. (2003) ‘A generalized single-channel method for retrieving land surface temperature from remote sensing data’, Journal of geophysical research: atmospheres, 108(D22).
31. Julien, Y. and Sobrino, J.A. (2009) ‘The Yearly Land Cover Dynamics (YLCD) method: An analysis of global vegetation from NDVI and LST parameters’, Remote sensing of environment, 113(2), pp. 329–334. [CrossRef]
32. Kamaraj, N.P. et al. (2021) ‘Detecting heat-inducing urban built-up surface material with multi remote sensing datasets using reflectance and emission spectroscopy’, Remote Sensing of Environment, 264, p. 112591. [CrossRef]
33. Karnieli, A. et al. (2010) ‘Use of NDVI and land surface temperature for drought assessment: Merits and limitations’, Journal of climate, 23(3), pp. 618–633. [CrossRef]
34. Khanal, S., Fulton, J. and Shearer, S. (2017) ‘An overview of current and potential applications of thermal remote sensing in precision agriculture’, Computers and Electronics in Agriculture, 139, pp. 22–32. [CrossRef]
35. Kuhn, M. (2008) ‘Building Predictive Models in R Using the caret Package’, Journal of Statistical Software, 28(5). [CrossRef]
36. Li, L. et al. (2021) ‘A novel surface water index using local background information for long term and large-scale Landsat images’, ISPRS Journal of Photogrammetry and Remote Sensing, 172, pp. 59–78. [CrossRef]
37. Li, Z.-L., Wu, H., et al. (2013) ‘Land surface emissivity retrieval from satellite data’, International Journal of Remote Sensing, 34(9–10), pp. 3084–3127.
38. Li, Z.-L., Tang, B.-H., et al. (2013) ‘Satellite-derived land surface temperature: Current status and perspectives’, Remote sensing of environment, 131, pp. 14–37. [CrossRef]
39. Liu, Y. et al. (2019) ‘Enterprise LST algorithm development and its evaluation with NOAA 20 data’, Remote Sensing, 11(17), p. 2003. [CrossRef]
40. Liu, Y., Qian, J. and Yue, H. (2021) ‘Comprehensive Evaluation of Sentinel-2 Red Edge and Shortwave-Infrared Bands to Estimate Soil Moisture’, IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 14, pp. 7448–7465. [CrossRef]
41. Maffei, C., Alfieri, S.M. and Menenti, M. (2018) ‘Relating spatiotemporal patterns of forest fires burned area and duration to diurnal land surface temperature anomalies’, Remote Sensing, 10(11), p. 1777. [CrossRef]
42. Mallick, K. et al. (2009) ‘Latent heat flux estimation in clear sky days over Indian agroecosystems using noontime satellite remote sensing data’, Agricultural and Forest Meteorology, 149(10), pp. 1646–1665. [CrossRef]
43. Meng, X. et al. (2023) ‘Estimating hourly Land Surface Temperature from FY-4A AGRI using an Explicitly Emissivity Dependent Split-Window Algorithm’, IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing [Preprint]. [CrossRef]
44. Merlin, O. et al. (2010) ‘An improved algorithm for disaggregating microwave-derived soil moisture based on red, near-infrared and thermal-infrared data’, Remote Sensing of Environment, 114(10), pp. 2305–2316.
45. Mia, M.B., Fujimitsu, Y. and Nishijima, J. (2018) ‘Monitoring of thermal activity at the Hatchobaru–Otake geothermal area in Japan using multi-source satellite images—With comparisons of methods, and solar and seasonal effects’, Remote Sensing, 10(9), p. 1430.
46. Neinavaz, E., Skidmore, A.K. and Darvishzadeh, R. (2020) ‘Effects of prediction accuracy of the proportion of vegetation cover on land surface emissivity and temperature using the NDVI threshold method’, International Journal of Applied Earth Observation and Geoinformation, 85, p. 101984. [CrossRef]
47. Nichol, J. (2005) ‘Remote sensing of urban heat islands by day and night’, Photogrammetric engineering and remote sensing, 71(5), pp. 613–621.
48. Petropoulos, G.P. et al. (2020) ‘Evaluating the capabilities of optical/TIR imaging sensing systems for quantifying soil water content’, Geocarto International, 35(5), pp. 494–511. [CrossRef]
49. Poursanidis, D. et al. (2019) ‘On the use of Sentinel-2 for coastal habitat mapping and satellite-derived bathymetry estimation using downscaled coastal aerosol band’, International Journal of Applied Earth Observation and Geoinformation, 80, pp. 58–70. [CrossRef]
50. Pu, R. (2021) ‘Assessing scaling effect in downscaling land surface temperature in a heterogenous urban environment’, International Journal of Applied Earth Observation and Geoinformation, 96, p. 102256. [CrossRef]
51. Pu, R. and Bonafoni, S. (2023) ‘Thermal infrared remote sensing data downscaling investigations: An overview on current status and perspectives’, Remote Sensing Applications: Society and Environment, p. 100921. [CrossRef]
52. Qin, Z. et al. (2004) ‘Comparison of split window algorithms for land surface temperature retrieval from NOAA-AVHRR data’, in IGARSS 2004. 2004 IEEE International Geoscience and Remote Sensing Symposium. IEEE, pp. 3740–3743.
53. Qin, Zhihao, Karnieli, A. and Berliner, P. (2001) ‘A mono-window algorithm for retrieving land surface temperature from Landsat TM data and its application to the Israel-Egypt border region’, International journal of remote sensing, 22(18), pp. 3719–3746. [CrossRef]
54. Qin, Z., Karnieli, A. and Berliner, P. (2001) ‘A mono-window algorithm for retrieving land surface temperature from Landsat TM data and its application to the Israel-Egypt border region’, International Journal of Remote Sensing, 22(18), pp. 3719–3746. Available at. [CrossRef]
55. R Core Team (2020) ‘R: A Language and Environment for Statistical Computing’. Vienna, Austria.
56. Rawat, K.S., Sehgal, V.K. and Ray, S.S. (2019) ‘Downscaling of MODIS thermal imagery’, The Egyptian Journal of Remote Sensing and Space Science, 22(1), pp. 49–58.
57. Sandholt, I., Rasmussen, K. and Andersen, J. (2002) ‘A simple interpretation of the surface temperature/vegetation index space for assessment of surface moisture status’, Remote Sensing of environment, 79(2–3), pp. 213–224. [CrossRef]
58. Santi, E. et al. (2018) ‘On the synergy of SMAP, AMSR2 AND SENTINEL-1 for retrieving soil moisture’, International journal of applied earth observation and geoinformation, 65, pp. 114–123.
59. Sekertekin, A. (2019) ‘Validation of physical radiative transfer equation-based land surface temperature using Landsat 8 satellite imagery and SURFRAD in-situ measurements’, Journal of Atmospheric and Solar-Terrestrial Physics, 196, p. 105161. [CrossRef]
60. Sekertekin, A. and Arslan, N. (2019) ‘Monitoring thermal anomaly and radiative heat flux using thermal infrared satellite imagery–A case study at Tuzla geothermal region’, Geothermics, 78, pp. 243–254. [CrossRef]
61. Sekertekin, A. and Bonafoni, S. (2020) ‘Land surface temperature retrieval from Landsat 5, 7, and 8 over rural areas: Assessment of different retrieval algorithms and emissivity models and toolbox implementation’, Remote sensing, 12(2), p. 294.
62. Sobrino, J.A. and Romaguera, M. (2004) ‘Land surface temperature retrieval from MSG1-SEVIRI data’, Remote sensing of environment, 92(2), pp. 247–254.
63. Subhanil, G. and Govil, H. (2021) ‘Relationship between land surface temperature and normalized difference water index on various land surfaces: A seasonal analysis’, International journal of engineering and geosciences, 6(3), pp. 165–173.
64. Trigo, I.F. et al. (2008) ‘An assessment of remotely sensed land surface temperature’, Journal of Geophysical Research: Atmospheres, 113(D17).
65. Wan, Z., Wang, P. and Li, X. (2004) ‘Using MODIS land surface temperature and normalized difference vegetation index products for monitoring drought in the southern Great Plains, USA’, International journal of remote sensing, 25(1), pp. 61–72. [CrossRef]
66. Wright, M.N. and Ziegler, A. (2015) ‘ranger: A fast implementation of random forests for high dimensional data in C++ and R’, arXiv preprint arXiv:1508.04409 [Preprint].
67. Xu, J. et al. (2020) ‘Downscaling ASTER land surface temperature over urban areas with machine learning-based area-to-point regression Kriging’, Remote Sensing, 12(7), p. 1082. [CrossRef]
68. Xu, N. et al. (2021) ‘Changes in the urban surface thermal environment of a Chinese coastal city revealed by downscaling MODIS LST with random forest algorithm’, Journal of Meteorological Research, 35(5), pp. 759–774. [CrossRef]
69. Yan, H., Song, X., Tian, K., Gao, J., Li, Q., Xiong, Y., & Min, S. (2019). A modification of the bootstrapping soft shrinkage approach for spectral variable selection in the issue of over-fitting, model accuracy and variable selection credibility. Spectrochimica Acta Part A: Molecular and Biomolecular Spectroscopy, 210, 362-371. [CrossRef]
70. Yang, J. et al. (2017) ‘Assessing the impacts of urbanization-associated green space on urban land surface temperature: A case study of Dalian, China’, Urban Forestry & Urban Greening, 22, pp. 1–10. [CrossRef]
71. Yu, X., Guo, X. and Wu, Z. (2014) ‘Land surface temperature retrieval from Landsat 8 TIRS—Comparison between radiative transfer equation-based method, split window algorithm and single channel method’, Remote sensing, 6(10), pp. 9829–9852.
72. Zhan, W. et al. (2013) ‘Disaggregation of remotely sensed land surface temperature: Literature survey, taxonomy, issues, and caveats’, Remote Sensing of Environment, 131, pp. 119–139.
73. Zhao, W. and Li, Z.-L. (2013) ‘Sensitivity study of soil moisture on the temporal evolution of surface temperature over bare surfaces’, International Journal of Remote Sensing, 34(9–10), pp. 3314–3331. [CrossRef]
74. Zhou, J. et al. (2015) ‘Developing a temporally land cover-based look-up table (TL-LUT) method for estimating land surface temperature based on AMSR-E data over the Chinese landmass’, International Journal of Applied Earth Observation and Geoinformation, 34, pp. 35–50. [CrossRef]