Induction Motor Improved Vector Control Using Predictive and Model Free Algorithms Together with Homotopy-based Feedback Linearization

Preprint

Article

Induction Motor Improved Vector Control Using Predictive and Model Free Algorithms Together with Homotopy-based Feedback Linearization

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

04 January 2024

Posted:

05 January 2024

You are already at the latest version

Alerts

Abstract

Usually, the vector control of the induction machine (IM) is done by using cascade control structures with conventional linear PI controllers, the inner loop being designed for current control, and the outer loop for rotor flux and speed control. In this paper, starting from the dq model of the IM with the rotor magnetic flux space vector aligned along the d axis, advanced control algorithms are proposed for the two control loops of the cascade structure. For the current inner loop, after the decoupling control of the two dq currents, predictive algorithms with constraints are used to control and limit the currents. Since the outer loop has a nonlinear affine multivariable plant model, a homotopy-based variant of feedback linearization is used to obtain a non-singular decoupling matrix of the feedback transformation even when the rotor flux is zero at the start-up of the motor. During the continuous variation of the homotopy parameter, the model of the plant is variable, in which case the model free algorithms are properly used to control the flux and speed of the IM. The comparative analysis obtained for the cascade structure with conventional PI controllers and advanced algorithms, respectively, shows that the last lead to improve the dynamical performance of the IM.

Keywords:

Subject: Engineering - Control and Systems Engineering

1. Introduction

The actual technological advancements in material science and digital computation structures lead to develop the induction machine (IM) with high close loop performances and minimal costs. Thus, in the last decades two main problems were successfully solved: a substantial increasing of efficiency, and developing of modern concepts in light weight, small costs, modularity, fault redundancies. Therefore, the applications of IM become more attractive for different sectors: electric traction, robotics, electrical vehicles, aerodynamics etc.

The classical advanced control structure of IM is traditionally designed in cascade topology, where the vector control, also called field orientated control (FOC), principle is used [1,2,3].

The vector control strategy is based on the dynamic dq model of the IM defined in the synchronously rotating reference frame. Usually, the inner loop is intended for the dq stator currents control, and the outer one for the rotor flux and the rotor mechanical speed control. Due to the nonlinear, multivariable coupled models of the two loop plants, various control techniques have been developed to solve the problems generated by the complex models.

For the inner loop, model linearization and its decoupling through feedforward components are generally used. Based on the resulting decoupled linear models, the dq stator currents are usually controlled with two PI controllers [3,4]. Due to the physics-based constraints generated by the limits imposed on the stator voltages and currents, PI control has been replaced with advanced techniques to solve this problem. In general, among the advanced techniques for the inner loop, the model predictive current control (MPCC) algorithms are preferred because the constraints due to the physics limitations of the stator voltages and currents can be imposed in the design phase. However, in most cases, MPCC is based on the multivariable coupled nonlinear model of the dq currents, resulting in the two currents not being separately controlled, according to the FOC requirement. Thus, in [5] two MPC cascade structures based on continuous control set and finite control set without PI controllers are analyzed, studying the advantages and difficulties. The inner loop generates the output control voltage considering the constraints of stator voltages and currents and the outer loop the torque reference, having in view the constraints of torque/speed characteristics of IM. A full predictive cascaded speed and current control of an IM is presented in [6]. The currents from the inner loop are controlled using a finite control-set MPC algorithm, while for the speed control, a continuous control-set MPC, based on the explicit inversion of the mechanical model is suggested. Considering the importance of constraints handling for induction machines, in [7] a cascade speed control structure with MPC controllers able of incorporating the constraints in the objective function is proposed. The inner loop uses an MPCC controller and the outer one an explicit MPC controller for speed control. The common limitations of stator voltages and currents described as quadratic inequality in dq-frame, are reformulated based on the fact that quadratic inequalities of current and voltage can be represented by the linear one of the torque. The linear inequality is parameter-varying because the limited torque depends nonlinearly on the rotor speed and for solving this problem a mp-QP (multiparametric quadratic programming) algorithm is utilized. To replace the inner PI current controllers and PWM (Pulse Width Modulation) block, and thus faster dynamics to obtain, in [8] a finite control set predictive current control approach is proposed to control the IM. For the rotor speed control, in the outer loop a PI controller is used and for the IM stator windings protection, the electromagnetic torque current command is limited. By including the magnetic saturation and the rotor speed-dependent iron-loss resistance in the IM model, in [9] an MPCC strategy is developed based on this model for IM control considering saturation and iron core losses, to which is added a control effort penalty to reduce the average switching frequency. The proposed strategy is based on replacing the PI current controllers in the inner loop with the proposed predictive control algorithm, while in the outer loop a classical PI controller is used to control the mechanical speed of the rotor. But there are also IM control structures that keep PI controllers in the inner loop. Thus, for a cascade control structure in [10], a multivariable generalized predictive control (GPC) controller is proposed for the rotor speed and flux control, while the inner loop currents are controlled with conventional PI controllers. The stator is protected against over electrical signals by the current constraints imposed to GPC controllers in the design phase and by restricting the module of the phase stator voltage through a limiting block attached to the PI controllers.

For the outer loop, the two controlled currents of the inner loop are used as inputs so that the d component keeps the rotor flux constant and the q one to control the rotor speed. The main problem of the outer loop control derives from the nonlinear coupled multivariable model of the plant. In the vector control approach, with the assumption that the rotor flux is constant after reaching its reference, the speed dynamics becomes linear and can be controlled with PI controllers [11]. A method to decouple the flux dynamics from the speed dynamics is to use the input-output feedback linearization method, which leads to separate flux and speed control. But the input-output feedback linearization method cannot be applied to the IM model, due to the singularity of the decoupling matrix of the feedback transformation when the flux is zero at start-up of the motor [4,12]. To solve this problem, in [11] based on an IM model which includes both electrical and mechanical dynamics, it is proposed to control the square of the rotor flux and the speed using the input-output linearization technique in conjunction with the use of an open loop controller at the start-up of the motor. As soon as the flux becomes greater than zero, the control input is switched from the open loop controller to the nonlinear state feedback control. Starting from the same reduced fourth-order state-space model of IM and control objectives from [11], in [13] a switching strategy based on the homotopy continuation is presented that allows the application of the input-output feedback linearization approach. The strategy is based on the construction of a homotopy that combines the output of the nonlinear model of the IM with the output of an attached linear model, which is then linearized by feedback. When the conventional feedback linearization cannot be applied, the control is switched to the parameter continuation method. In the continuation of the paper [13], the authors presented in [4] a new control approach for driving the output to zero using the combining the state feedback linearization and the homotopy numerical continuation, which does not require the switching between two computationally complex controllers. Both methods from [13] and [4] use a cascade control structure with a PI current control inner loop, and the outer loop controls the square of the flux and the speed in [13], while in [4] the deviation from the flux and speed references. Another method to dynamic feedback linearization control of an IM is presented in [14], where to avoid the impossibility of applying linearization through feedback, an integrator on the d axis is additionally added to the IM dq model and thus, the decoupling matrix of the feedback transformation is no longer singular at the start-up of the motor. The dq currents are controlled in an inner loop using conventional PI controllers. The introduction of an integrator on the q-axis instead of the d-axis is also analyzed, resulting the feedback linearization of the IM model, but with the disadvantage that the feedback controller is singular when the quadrature current is zero and implicitly the motor torque is zero. A speed/position control strategy for IM based on exact feedback linearization with state and state derivative feedback is presented in [15]. This control strategy also uses PI controllers for the current loop. IM speed sensorless feedback linearization control based on a current/flux and speed tracking controller is proposed in [16]. Using a cascade control structure, the feedback linearization controller is designed to control the inner current loop and, respectively, the speed and flux in the outer loop. To obtain the speed tracking throughout the operating range, a PI controller is added. Also using an input–output feedback linearization technique, in [17] a sliding-mode speed controller for the IM is proposed instead of the classical PI.

This paper presents a cascade control structure for the speed and flux control of an IM. For dq currents control, in the inner loop MPCC algorithms are used, while the outer loop plant is firstly linearized by feedback based on the homotopy continuation and then, model free iP algorithms are employed so that the two controlled outputs to track the related references. In the inner loop, the cross coupling of the dq currents and the back EMF (electromotive force) are considered disturbances that are compensated by a decoupling algorithm based on feedforward components. After decoupling, two linear single-input single-output (SISO) models result, which are used to design the MPCC algorithms, taking into account the physics constraints introduced by the limitations imposed on stator currents and voltages. To reduce the computational effort of the constraint optimization, a boxed linear constraint [3] was used. In the outer loop, in order to decouple the flux from the rotor speed and thus control them independently, the homotopy-based variant of feedback linearization from [4] was utilized. The linear plants obtained after the feedback linearization are controlled with model free iP algorithms to obtain the tracking of the references imposed on the flux and the rotor speed. This employment of constrained MPCC algorithms, together with the homotopy-based variant of feedback linearization and model free iP algorithms led to IM improved vector control compared to the use of conventional PI controllers instead of advanced algorithms, as shown by a case study.

The following are the major contributions of this paper:

By incorporating MPCC and model free advanced algorithms together with the homotopy-based feedback linearization to IM improved vector control.

To reduce the computational effort of the constrained optimization, our method uses a boxed linear constraint for considering the physics limitations of stator currents and voltages.

In order to solve the limitation related to the stator voltages, we developed a method by which the limitations were correlated with the outputs of the MPCC controllers and with the feedforward components of the decoupling algorithm.

To solve the reference tracking problem in conjunction with the feedback linearization, we used a model free algorithm due to the modeling uncertainty during the variation of the homotopy parameter from zero to one.

In order to demonstrate the ability to improve the vector control of IM with the proposed cascade control structure that includes advanced algorithms, a case study was performed.

The paper is organized as follows. Section II presents the dq IM model for the vector control strategy. Section III is dedicated to cascade control structure design of IM, considering a constrained predictive current control algorithm for the inner loop, and a homotopy-based variant of feedback linearization for the outer loop plant together with the model free control algorithms for the rotor flux and speed control. An illustrative case study is given in Section IV that presents a comparative analysis of the results obtained for both conventional controllers, and advanced ones. At last, in Section V the main features arisen from the study developed in the paper were summarized.

2. Nonlinear IM Model for Vector Control

The IM control is typically done by using the vector control strategy which has the ability to separate the stator current components that produce the rotor flux and electromagnetic torque, respectively. Thus, the well-known vector control strategy of IM is usually performed in the reference frame dq attached to the rotor flux space vector whose direct axis d is aligned with the rotor flux space vector. This alignment of the rotor flux space vector with the d-axis causes the q-axis component to be zero [11,18], resulting:

\begin{array}{l} ϕ_{r d} = ϕ_{d} \\ ϕ_{r q} = 0, \frac{d ϕ_{r q}}{d t} = 0 \end{array} .

(1)

The IM model represented in dq coordinates is composed by stator current equations, rotor flux and motion equations [11], respectively:

\begin{array}{l} \frac{d i_{s d}}{d t} = - \frac{1}{τ_{1}} i_{s d} + ω_{s} i_{s q} + \frac{β}{τ_{r}} ϕ_{r} + \frac{1}{L_{1}} u_{s d} \\ \frac{d i_{s q}}{d t} = - ω_{s} i_{s d} - \frac{1}{τ_{1}} i_{s q} - β ω_{e} ϕ_{r} + \frac{1}{L_{1}} u_{s q} \end{array},

(2)

\frac{d ϕ_{r}}{d t} = - \frac{1}{τ_{r}} ϕ_{r} + \frac{L_{m}}{τ_{r}} i_{s d},

(3)

\frac{d ω_{m}}{d t} = (T_{e} - T_{r}) / J,

(4)

where:

(u_{s d}, u_{s q})

and

(i_{s d}, i_{s q})

represent the components of the stator voltages and currents in the dq reference frame,

ϕ_{r}

is the rotor flux,

ω_{s}

denotes the synchronous angular speed,

(ω_{e}, ω_{m})

are the electrical and mechanical rotor angular speeds correlated by

ω_{m} = ω_{e} / p

, where

p

is the number of pole pairs,

T_{e}

and

T_{r}

are electromagnetic and load torques and

J

is the motor inertia. The parameters and the time constants related to the model described by the equations (2)-(4) are given by:

\begin{matrix} R_{1} = R_{s} + R_{r} (L_{m} / L_{r}); L_{1} = L_{s} - L_{m}^{2} / L_{r}; β = L_{m} / (L_{r} L_{1}); \\ τ_{1} = L_{1} / R_{1}; τ_{r} = L_{r} / R_{r}, \end{matrix}

(5)

where

(R_{s}, R_{r})

represent the stator and rotor resistances,

(L_{s}, L_{r})

are the stator and rotor self-inductances,

L_{m}

is the mutual inductance,

R_{1}

is the equivalent resistance and

L_{1}

the equivalent inductance,

τ_{1}

is the equivalent time constant,

τ_{r}

is the rotor time constant and

β

is a constant.

The synchronous angular speed

ω_{s}

from (2) is estimated using:

ω_{s} = ω_{e} + \frac{L_{m}}{τ_{r}} \frac{i_{s q}}{ϕ_{r}},

(6)

and the electromagnetic torque

T_{e}

from (4) is calculated with:

T_{e} = p \frac{L_{m}}{L_{r}} ϕ_{r} i_{s q} .

(7)

Analysing the IM model from equations (2)-(7), it turns out that it is a strongly nonlinear coupled multivariable system.

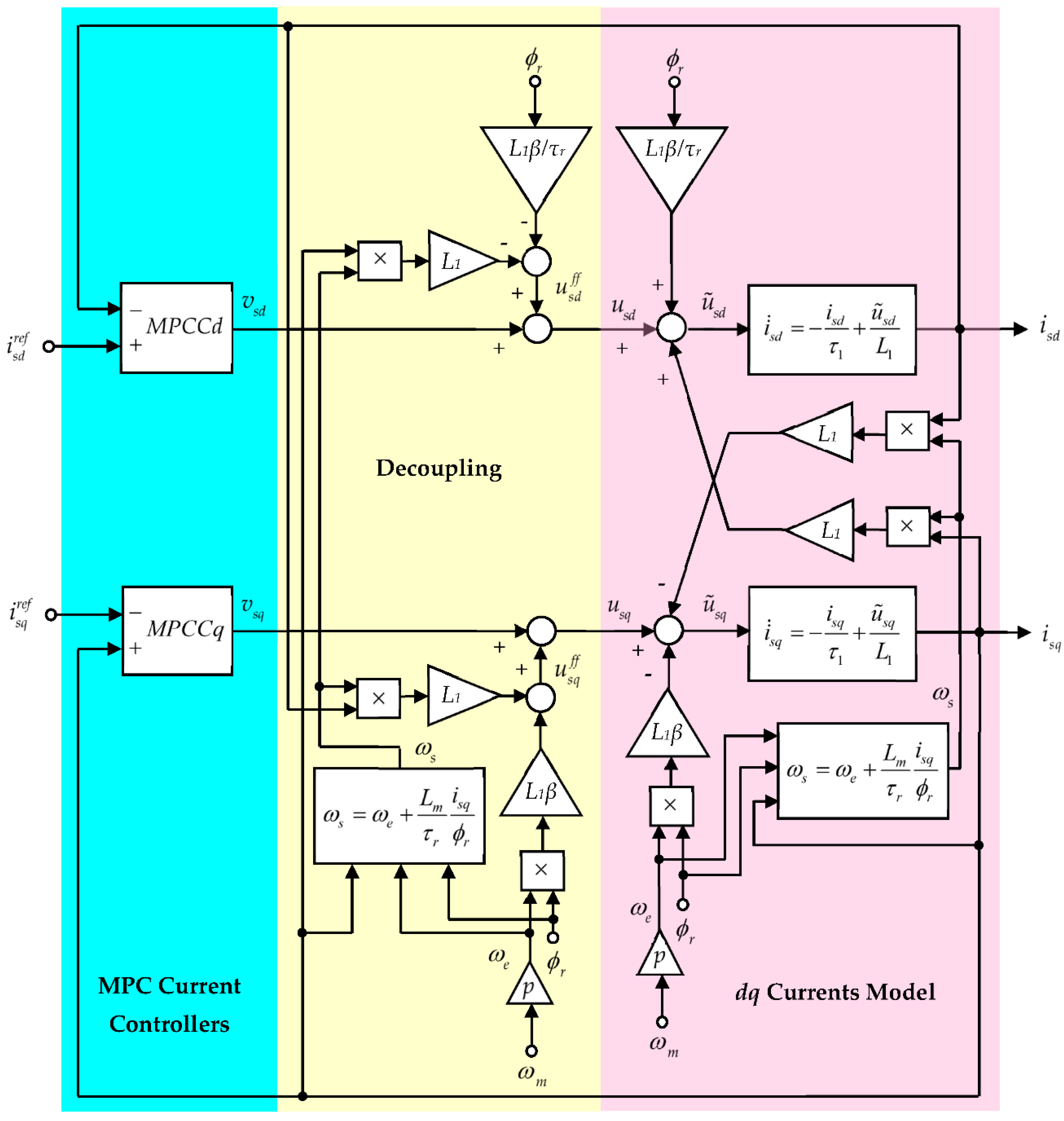
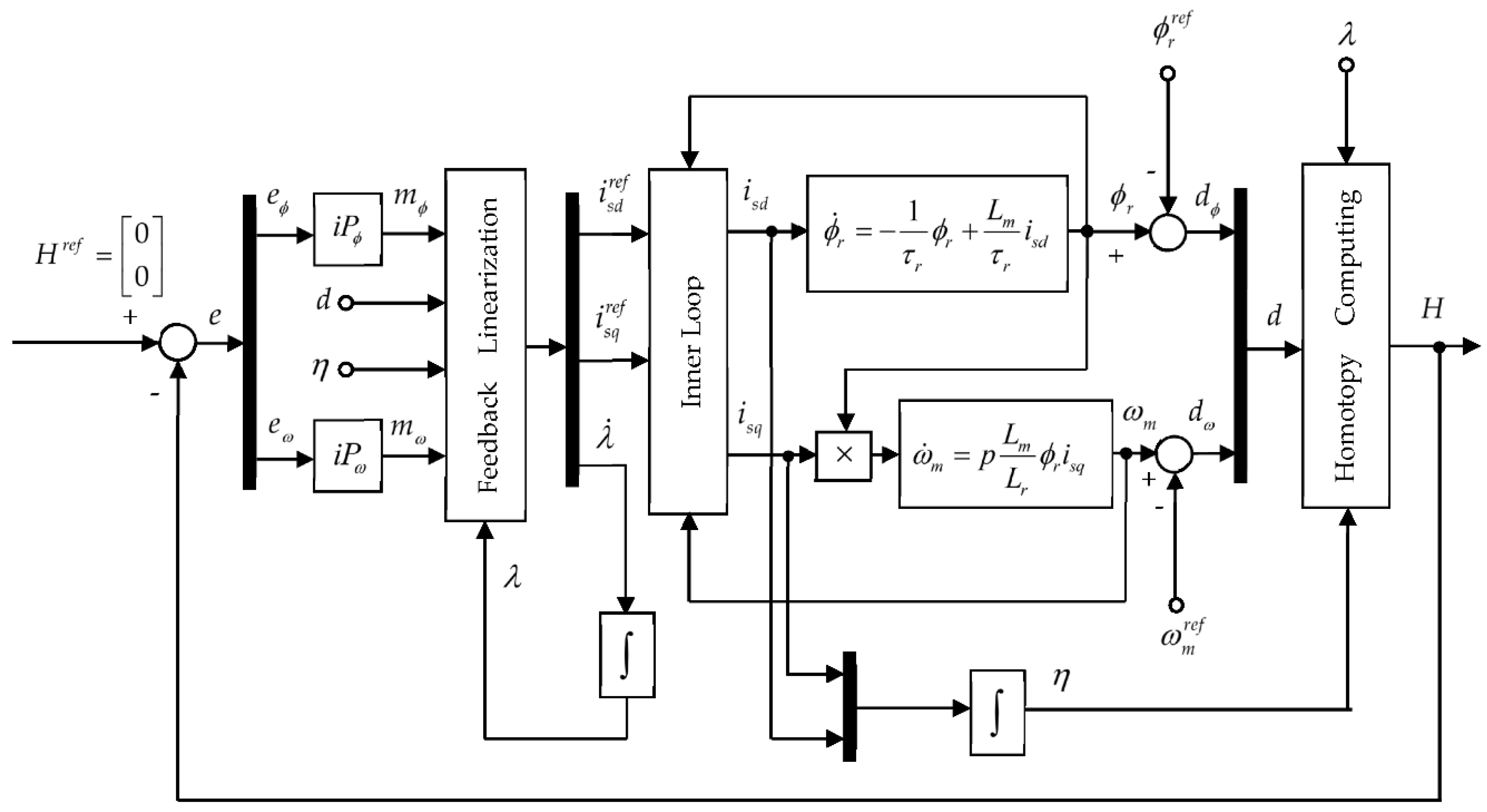
The rotor flux-oriented vector control strategy requires the independent control of the two currents,

i_{s d}

which produces the rotor flux and

i_{s q}

which generates the electromagnetic torque, respectively. The control of the two currents is realized by the stator voltages

u_{s d}

and

u_{s q}

which are not decoupled control variables, as can be seen from (2). In order to be decoupled and independently controlled the two stator currents

i_{s d / q}

, the stator voltage equations must be decoupled. The interactions between the stator currents and the nonlinearity of the current system are eliminated commonly using feedforward components. The control and decoupling of the stator currents is usually carried out in an inner loop of a cascade control structure. In the outer loop, the rotor flux

ϕ_{r}

and the mechanical rotor angular speed

ω_{m}

are controlled based on the affine nonlinear multivariable system generated by the equations (3) and (4) and using as control variables the current references

i_{s d}^{r e f}

and

i_{s q}^{r e f}

. To obtain a linear behavior between the inputs and outputs of the outer plant model, a feedback linearization strategy can be used.

3. Cascade control structure design of IM

The cascade control structure proposed for the vector control of an IM consists of an inner loop designed to control the dq currents with predictive control algorithms and an outer loop which, after applying a homotopy-based variant feedback linearization for nonlinear loop plant, the rotor flux and speed are controlled with model free algorithms.

In what follows, the design of the two control loops of the cascade control structure is presented.

3.1. Inner loop design

The current model (2) has a multivariable structure, being non-linear with a strong coupling between dq axes.

3.1.1. Decoupling algorithm

Since the stator currents

i_{s d / q}

must be controlled independently, according to the vector control requirements, it is necessary to decouple them. In this context, the current model (2) is rewritten as follows considering:

\begin{array}{l} u_{s d} = & L_{1} \frac{d i_{s d}}{d t} + R_{1} i_{s d} - L_{1} ω_{s} i_{s q} - L_{1} \frac{β}{τ_{r}} ϕ_{r} = v_{s d} + u_{s d}^{p}, \\ u_{s q} = & L_{1} \frac{d i_{s q}}{d t} + R_{1} i_{s d} + L_{1} ω_{s} i_{s d} + L_{1} β ω_{e} ϕ_{r} = v_{s q} + u_{s q}^{p} . \\ \underset{R L eqv . circuit}{\leftrightarrow} \underset{coupling and back EMF}{\leftrightarrow} \end{array}

(7)

Thus, two components of the stator voltages

u_{s d / q}

are highlighted, one linear

v_{d / q}

correlated with an RL equivalent circuit and another

u_{s d / q}^{p}

which is generated by cross-coupling and back EMF. The linear voltage components

v_{s d / q}

represent the controller outputs that control the currents

i_{s d / q}

and the voltage components

u_{s d / q}^{p}

are considered disturbances that must be compensated by a decoupling algorithm based on feedforward components. To decouple the stator voltage equation (7), the feedforward components

u_{d / q}^{f f}

are used, resulting in:

\begin{array}{l} u_{s d} = v_{s d} + u_{s d}^{f f} \\ u_{s q} = v_{s q} + u_{s q}^{f f} \end{array},

(8)

where the feedforward components are:

u_{s d}^{f f} = - L_{1} ω_{s} i_{s q} - L_{1} \frac{β}{τ_{r}} ϕ_{r},

(9)

u_{s q}^{f f} = L_{1} ω_{s} i_{s d} + L_{1} β ω_{e} ϕ_{r} .

(10)

Using the above decoupling procedure based on feedforward, the coupled multivariable nonlinear model of the currents (7) is transformed into two identical SISO linear models for the two currents:

L_{1} \frac{d i_{s d / q}}{d t} + R_{1} i_{s d / q} = v_{s d / q} .

(11)

3.1.2. Constraint formulation

In addition, for the stator currents control, the physics limitations imposed on the currents

i_{s d / q}

and voltages

u_{s d / q}

must be considered to prevent the IM damage. Thus, the two components of the dq currents and voltages must satisfy the limitations:

\begin{array}{l} \sqrt{i_{s d}^{2} + i_{s q}^{2}} \leq I_{s \max} \\ \sqrt{u_{s d}^{2} + u_{s q}^{2}} \leq U_{s \max} \end{array},

(12)

where the maximum value of the stator current

I_{s \max}

is chosen correlated with the nominal value

I_{s N}

of the stator current, and considering the DC-bus voltage

V_{D C}

, the maximum value of the stator voltages will be

U_{s \max} = V_{D C} / \sqrt{3}

. Since the constraint equations (12) are quadratic functions, to simplify the computation of the constrained optimization, a boxed linear constraint which approximated the circular area with a rectangular one can be used [3]. The box constraints for the

i_{s d / q}

stator currents are defined by finding a parameter

0 \leq γ_{c} \leq 1

so that:

i_{s d}^{\max} = γ_{c} I_{s \max},

(13)

and from here:

i_{s q}^{\max} = \sqrt{1 - γ_{c}^{2}} I_{s \max} .

(14)

The stator current

i_{s d}

, which generates the rotor flux

ϕ_{r}

, varies in the interval

i_{s d} \in [0, i_{s d N}]

, where the nominal value

i_{s d N}

is obtained from (3) in steady state, resulting:

i_{s d N} = \frac{ϕ_{r N}}{L_{m}} .

(15)

Since the maximum value

i_{s d}^{\max}

is the nominal value

i_{s d N}

, from (13) and (15) results the expression of the

γ_{c}

parameter:

γ_{c} = \frac{ϕ_{r N}}{L_{m} I_{s \max}} .

(16)

With the maximum values given by (14) and (15), the currents box constraints become:

\begin{array}{l} 0 \leq i_{s d} \leq i_{s d}^{\max} = i_{s d N} \\ - i_{s q}^{\max} \leq i_{s q} \leq i_{s q}^{\max} \end{array} .

(17)

Similarly, for the

u_{s d / q}

stator voltages, a parameter

0 \leq γ_{v} \leq 1

is chosen to calculate the maximum values:

\begin{array}{l} u_{s d}^{\max} = γ_{v} V_{D C} / \sqrt{3} \\ u_{s q}^{\max} = \sqrt{1 - γ_{v}^{2}} V_{D C} / \sqrt{3} \end{array},

(18)

and then the voltage box constraints are obtained:

\begin{array}{l} - u_{s d}^{\max} \leq u_{s d} \leq u_{s d}^{\max} \\ - u_{s q}^{\max} \leq u_{s q} \leq u_{s q}^{\max} \end{array} .

(19)

Limiting the stator voltages

u_{s d / q}

can be done by limiting the outputs

v_{s d / q}

of the current controllers using (8) as follows:

\begin{array}{l} v_{s d}^{\max} = u_{s d}^{\max} - u_{s d}^{f f - \max} \\ v_{s q}^{\max} = u_{s q}^{\max} - u_{s q}^{f f - \max} \end{array} .

(20)

The maximum value

u_{s d / q}^{f f - \max}

of the feedforward components is determined using (9)-(10) and considering the maximum values of the stator voltages

u_{s d / q}^{\max}

specified by (16), the nominal values of the angular velocities

ω_{s N}

and

ω_{e N}

, the nominal value of the rotor flux

ϕ_{r N}

and the maximum values

i_{s d / q}^{\max}

for the currents given by (13) and (14). With these assumptions, the maximum values of the current controller outputs will be:

\begin{array}{l} v_{s d}^{\max} = γ_{v} V_{D C} / \sqrt{3} - L_{1} ω_{s N} \sqrt{1 - γ_{c}^{2}} I_{s \max} - L_{1} \frac{β}{τ_{r}} ϕ_{r N} \\ v_{s q}^{\max} = \sqrt{1 - γ_{v}^{2}} V_{D C} / \sqrt{3} + γ_{c} I_{s \max} + L_{1} β ω_{e N} ϕ_{r N} \end{array},

(21)

and thus, the box constraints for the voltages

v_{s d / q}

are obtained:

\begin{array}{l} - v_{s d}^{\max} \leq v_{s d} \leq v_{s d}^{\max} \\ - v_{s q}^{\max} \leq v_{s q} \leq v_{s q}^{\max} \end{array},

(22)

Considering the above constraints imposed to the stator currents and voltages in the dq frame, MPCC controllers were chosen to control the currents

i_{s d / q}

based on the model (11).

3.1.3. MPCC controller design

The design of the MPCC controller is done using the discrete model of the two currents obtained from (11) by discretization with the sample period T_s. Considering that the parameters of the model (11) are identical for the two currents, the following discrete model was obtained:

i_{s j} (k + 1) = a i_{s j} (k) + b v_{s j} (k), j = d, q .

(23)

For reference tracking, a new state

x_{c} (k) = v_{s j} (k - 1)

is introduced in (23) to have as input the increment

Δ v_{s j} (k) = v_{s j} (k) - v_{s j} (k - 1)

, resulting the augmented current discrete model which incorporates integral action:

\underset{x_{j} (k + 1)}{\underset{︸}{[\begin{matrix} i_{s j} (k + 1) \\ x_{c} (k + 1) \end{matrix}]}} = \underset{Φ}{\underset{︸}{[\begin{matrix} a & b \\ 0 & 1 \end{matrix}]}} \underset{x_{j} (k)}{\underset{︸}{[\begin{matrix} i_{s j} (k) \\ x_{c} (k) \end{matrix}]}} + \underset{γ}{\underset{︸}{[\begin{matrix} b \\ 1 \end{matrix}]}} Δ v_{s j} (k) \Rightarrow x_{j} (k + 1) = Φ x_{j} (k) + γ Δ v_{s j} (k) .

(24)

Based on the one step ahead prediction given by (24), the predictions for the augmented model are recursively found, resulting:

x_{j} (k + n | k) = Φ^{n} x_{j} (k) + \sum_{s = 0}^{n - 1} Φ^{s} γ Δ v_{j} (k - 1 - s),

(25)

where

x_{j} (k + n | k)

denotes the value predicted at the discrete time k.

To design the MPCC controller based on the model (24) and considering the bounded outputs and inputs, the following quadratic cost function from [19] is used:

\begin{array}{l} J_{j} (V_{j}) = \sum_{n = 1}^{h p} {(δ_{j n} (i_{s j} (k + n | k) - i_{s j}^{r e f} (k)))}^{2} + \sum_{p = 0}^{h c} {(μ_{j p} Δ v_{s j} (k + p | k))}^{2} + ρ_{j ε} ε_{j} \\ s . t . \{\begin{matrix} j = d \Rightarrow \{\begin{matrix} 0 - ε_{d} W_{d}^{i_{s d} \min} \leq i_{s d} (k + n | k) \leq i_{s d}^{\max} + ε_{d} W_{d}^{i_{s d} \max}, n = 1, .., h p \\ - v_{s d}^{\max} - ε_{d} W_{d}^{v_{s d} \min} \leq v_{s d} (k + p | k) \leq v_{s d}^{\max} + ε_{d} W_{d}^{v_{s d} \max}, p = 0, .., h c - 1 \end{matrix} \\ j = q \Rightarrow \{\begin{matrix} - i_{s q}^{\max} - ε_{q} W_{q}^{i_{s q} \min} \leq i_{s q} (k + n | k) \leq i_{s q}^{\max} + ε_{q} W_{q}^{i_{s q} \max}, n = 1, .., h p \\ - v_{s q}^{\max} - ε_{q} W_{q}^{v_{s q} \min} \leq v_{s q} (k + p | k) \leq v_{s q}^{\max} + ε_{q} W_{q}^{v_{s q} \max}, p = 0, .., h c - 1 \end{matrix} \end{matrix} \end{array}

(26)

where hp and hc are prediction and control horizons,

δ_{j n}

and

μ_{j p}

are the output and control weights, is

V_{j} = \{Δ v_{s j} (k | k), Δ v_{s j} (k + 1 | k), ..., Δ v_{s j} (k + h c - 1 | k), ε_{j}\}

the future control sequence,

ε_{j}

is the slake variable introduced for obtaining soft constraints and

ρ_{j ε}

is the weight of the slake variable. The violation multipliers

W_{j}^{*}

vary continuously between 0 and 1, for

W_{j}^{*} = 0

hard constraints are obtained, otherwise soft constraints.

The output prediction can be obtained from (25):

i_{s j} (k + n | k) = [\begin{matrix} 1 & 0 \end{matrix}] x_{j} (k + n | k) .

(27)

Substituting the output prediction (27) in (26), the cost function minimization is formulated as a quadratic programming (QP) problem:

\begin{array}{l} V_{j}^{*} = \arg \min_{V_{j}} (\frac{1}{2} V^{T} M V + [\begin{matrix} i_{s j} (k) & i_{s j}^{r e f} (k) & v_{s j} (k - 1) \end{matrix}] N^{T} V) \\ s . t . : G V \leq W + S [\begin{matrix} i_{s j} (k) \\ i_{s j}^{r e f} (k) \\ v_{s j} (k - 1) \end{matrix}] \end{array},

(28)

where the optimal solution is:

V_{j}^{*} = {[Δ v_{s j}^{*} (k | k) Δ v_{s j}^{*} (k + 1 | k), ..., Δ v_{s j}^{*} (k + h c - 1 | k), ε_{j}^{*}]}^{T},

(29)

and the matrices of appropriate dimensions M, N, G, W and S have the expressions from [20,21].

Applying the receding horizon principle, only the first element of

V_{j}^{*}

is further used to obtain the MPCC control law:

v_{j} (k) = v_{j} (k - 1) + Δ v_{j}^{*} (k) .

(30)

The predictive currents control structure from the inner loop is represented in Figure 1.

3.2. Outer loop design

The inner loop intended to regulate the dq currents has a very fast dynamic compared to the rotor flux and the mechanical angular speed described by (3) and (4). In this context, the currents reach the imposed references extremely quickly, and it can be considered

i_{s d / q} \approx i_{s d / q}^{r e f}

and thus, the related outer loop plant is described only by (3) and (4), which generates the following coupled nonlinear affine system:

\underset{\dot{x}}{\underset{︸}{[\begin{matrix} {\dot{ϕ}}_{r} \\ {\dot{ω}}_{m} \end{matrix}]}} = \underset{f (x)}{\underset{︸}{[\begin{matrix} \frac{- 1}{τ_{r}} ϕ_{r} \\ 0 \end{matrix}]}} + \underset{g (x)}{\underset{︸}{[\begin{matrix} \frac{L_{m}}{τ_{r}} & 0 \\ 0 & \frac{p L_{m}}{J L_{r}} ϕ_{r} \end{matrix}]}} \underset{i_{s d / q}}{\underset{︸}{[\begin{matrix} i_{s d} \\ i_{s q} \end{matrix}]}} \Rightarrow \{\begin{matrix} \dot{x} = f (x) + g (x) i_{s d / q} \\ y = x \end{matrix} .

(31)

To achieve the decoupling of the rotor flux and angular speed dynamics, a common method is the use of input-output feedback linearization.

The nonlinear affine model (31) cannot be linearized by feedback because the input-output decoupling matrix is singular at the motor start-up when the rotor flux

ϕ_{r}

is zero.

To use the feedback linearization method, an open loop controller at start-up can be employed [11] or a homotopy-based variant of feedback linearization as in [4], the last approach being employed in this paper.

3.2.1. Homotopy-based feedback linearization

To apply the feedback linearization method based on homotopy continuation to the irregular affine system (31) with ill-define relative degree, first the controlled outputs are considered the deviations of the system (31) outputs from their references:

[\begin{matrix} d_{ϕ} \\ d_{ω} \end{matrix}] = [\begin{matrix} ϕ_{r} - ϕ_{r}^{r e f} \\ ω_{m} - ω_{m}^{r e f} \end{matrix}] .

(32)

Applying the first differentiation to the output

d = {[\begin{matrix} d_{ϕ} & d_{ω} \end{matrix}]}^{T}

, the same model (31) is obtained:

\{\begin{matrix} \dot{d} = f (x) + g (x) i_{s d / q} \\ y = d \end{matrix},

(33)

with

{[\begin{matrix} {\dot{d}}_{ϕ} & {\dot{d}}_{ω} \end{matrix}]}^{T} = {[\begin{matrix} {\dot{ϕ}}_{r} & {\dot{ω}}_{m} \end{matrix}]}^{T}

. The new model with outputs

d_{φ}

and

d_{ω}

cannot be linearized by feedback due to its ill-define relative degree generated by

ϕ_{r} = 0

. To solve the problem, the following linear dynamic system is associated with the outer loop plant model (33):

[\begin{matrix} {\dot{η}}_{d} \\ {\dot{η}}_{q} \end{matrix}] = [\begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix}] [\begin{matrix} i_{s d} \\ i_{s q} \end{matrix}] with η (0) = [\begin{matrix} 0 \\ 0 \end{matrix}] .

(34)

Using the outputs

d

and

η

of the two associated systems, a new output is constructed:

H = (1 - λ) η + λ d,

(35)

where the influence of the outputs

d

and

η

to the new output H is determined by the continuous time–dependent parameter

λ \in [0, 1]

. For

λ = 0

, the output of the linear model is obtained, which is continuously deformed into the output of the nonlinear model when

λ = 1

For the new augmented system, a controller will be determined through feedback linearization to ensure a linear dynamic. Applying the first differentiation to the output

H = {[\begin{matrix} h_{ϕ} & h_{ω} \end{matrix}]}^{T}

, we get:

[\begin{matrix} {\dot{h}}_{ϕ} \\ {\dot{h}}_{ω} \end{matrix}] = λ [\begin{matrix} {\dot{d}}_{ϕ} \\ {\dot{d}}_{ω} \end{matrix}] + (1 - λ) [\begin{matrix} i_{s d} \\ i_{s q} \end{matrix}] + \dot{λ} [\begin{matrix} d_{ϕ} - η_{d} \\ d_{ω} - η_{q} \end{matrix}] .

(36)

Since

{[\begin{matrix} {\dot{d}}_{ϕ} & {\dot{d}}_{ω} \end{matrix}]}^{T} = {[\begin{matrix} {\dot{ϕ}}_{r} & {\dot{ω}}_{m} \end{matrix}]}^{T}

, substituting in (36), the expressions of

{\dot{ϕ}}_{r}

and

{\dot{ω}}_{m}

from (31), we get:

[\begin{matrix} {\dot{h}}_{ϕ} \\ {\dot{h}}_{ω} \end{matrix}] = λ [\begin{matrix} - ϕ_{r} / τ_{r} + L_{m} i_{s d} / τ_{r} \\ p L_{m} ϕ_{r} i_{s q} / J L_{r} \end{matrix}] + (1 - λ) [\begin{matrix} i_{s d} \\ i_{s q} \end{matrix}] + \dot{λ} [\begin{matrix} d_{ϕ} - η_{d} \\ d_{ω} - η_{q} \end{matrix}] .

(37)

Grouping in a vector the currents

i_{s d}

and

i_{s q}

together with

\dot{λ}

, equation (37) becomes:

[\begin{matrix} {\dot{h}}_{ϕ} \\ {\dot{h}}_{ω} \end{matrix}] = \underset{A}{\underset{︸}{[\begin{matrix} λ L_{m} / τ_{r} + 1 - λ & 0 & d_{ϕ} - η_{d} \\ 0 & λ p L_{m} ϕ_{r} / J L_{r} + 1 - λ & d_{ω} - η_{q} \end{matrix}]}} [\begin{array}{l} \begin{matrix} i_{s d} \\ i_{s q} \end{matrix} \\ \dot{λ} \end{array}] + \underset{B}{\underset{︸}{[\begin{matrix} - λ ϕ_{r} / τ_{r} \\ 0 \end{matrix}]}} .

(38)

For the augmented system (38), in [4] it is proved that the state feedback equation:

[\begin{array}{l} \begin{matrix} i_{s d} \\ i_{s q} \end{matrix} \\ \dot{λ} \end{array}] = α τ + A^{+} (m - B) .

(39)

exists and the nonlinear feedback (39) transforms the nonlinear system (38) into the linear system:

[\begin{matrix} {\dot{h}}_{ϕ} \\ {\dot{h}}_{ω} \end{matrix}] = [\begin{matrix} m_{d} \\ m_{q} \end{matrix}],

(40)

which can be controlled with algorithms related to linear systems. In (39),

α \in R_{+}

is a constant,

A^{+}

is the Moore–Penrose inverse matrix of A and the vector

τ

is chosen to fulfill the constraints [4]:

A τ = 0, {‖τ‖}_{2} = 1, \det (\begin{matrix} A \\ τ^{T} \end{matrix}) > 0 .

(41)

Thus, the outer loop consists of two control loops, one for feedback linearization with (39) and the other for the resulting linear system control. For the second loop, we chose a model free iP algorithm to control the linear system due to the augmented model parametric uncertainty.

3.2.2. Model free iP controller design

After the feedback linearization, two integrator-type linear systems were obtained that will be controlled with two model free iP controllers [22,23] so that H tracks its zero reference. The controllers being of model free type, the models (40) of the linear systems are not used to tune the parameters, but the discrete time ultralocal model:

{\hat{\dot{h}}}_{ρ} (k) = F_{ρ} (k) + ψ_{ρ} m_{ρ} (k), ρ = ϕ, ω .

(42)

where

{\hat{\dot{h}}}_{ρ} (k)

notes the discrete approximation of the derivative of

{\dot{h}}_{ρ} (t)

F_{ρ} (k)

is a time-varying parameter which depends on the measurement of I/O without information of the plant dynamic model and

ψ_{ρ}

is a parameter chosen by the user. Employing I/O measurement,

F_{ρ} (k)

can be estimated with:

{\hat{F}}_{ρ} (k) = {\hat{\dot{h}}}_{ρ} (k) - ψ_{ρ} m_{ρ} (k - 1) .

(43)

The discrete time model free iP control law is defined by [24]:

m_{ρ} (k) = \frac{1}{ψ_{ρ}} ({\hat{\dot{h}}}_{ρ}^{r e f} (k) - {\hat{F}}_{ρ} (k) + K_{p ρ} (h_{ρ}^{r e f} (k) - h_{ρ} (k))),

(44)

where

K_{p ρ}

is the proportional gain. Substituting

{\hat{F}}_{ρ} (k)

from (43) in (44) and taking into account the control error

e_{ρ} (k) = h_{ρ}^{r e f} (k) - h_{ρ} (k)

, the model free iP algorithm becomes:

m_{r} (k) = m_{r} (k - 1) + \frac{1}{ψ_{r}} ({\hat{\dot{e}}}_{r} (k) + K_{p r} e_{r} (k)) .

(45)

From (45), the term

m_{ρ} (k - 1)

shows that the algorithm has an integral component. The tuning parameters of iP controllers,

ψ_{ρ}

and

K_{p ρ}

, can be designed using a pole placement method as in [25] or the Iterative Feedback Tuning approach from [24].

The outer loop structure with homotopy-based feedback linearization together with the flux and speed control with model free iP algorithms is represented in Figure 2.

4. Case Study

The improvement of the IM vector control by using the proposed cascade control structure with the block diagrams of the inner and outer loops from Figure 1 and Figure 2 implemented using MATLAB/Simulink software tools was tested and evaluated by simulation.

The IM specification data were taken from [4,11] and are given in Table 1.

The nominal voltage and current,

U_{N}

and

I_{N}

, from Table 1 are related on RMS (root mean square) values, which in practice have a physical meaning. For the vector control, considering the power invariant dq transformation, the nominal values of the space vector magnitude of the voltage and the current are defined as

I_{s N} = \sqrt{3} I_{N} = 16.21 A

and

U_{s N} = \sqrt{3} U_{p N} = 400 V

The performance evaluation was done in comparison with the use of conventional discrete time PI controllers instead of the MPCC controllers in the inner loop, respectively instead of the model free iP controllers in the outer loop. The design of PI controllers was done with the pole placement method from [26,27] and it is briefly presented in the following.

The PI controllers from the inner loop described by the transfer function:

C^{j} (z) = k_{p}^{j} + k_{i}^{j} \frac{T_{s}}{z - 1}, j = d, q

(46)

are designed based on the same plant described by the transfer function obtained from (23):

N^{j} (z) = \frac{b}{z - a} .

(47)

Using the two transfer functions (46) si (47), the following characteristic polynomial of the closed loop control system is obtained:

P_{c l}^{j} (z) = z^{2} + (b k_{p}^{j} - a - 1) z + k_{i}^{j} b T_{s} - k_{p}^{j} b + a .

(48)

Based on the required performances, the percent overshoot

σ %

and the settling time

t_{s}

, the desired characteristic polynomial is constructed:

P_{c d}^{j} (z) = z^{2} + ξ_{1}^{j} z + ξ_{2}^{j},

(49)

whose parameters are computed with:

ξ_{1}^{j} = - 2 e^{- ζ ω_{n} T_{s}} \cos (ω_{n} T_{s} \sqrt{1 - ζ^{2}}); ξ_{2}^{j} = e^{- 2 ζ ω_{n} T_{s}},

(50)

where the damping ratio

ζ

and natural frequency

ω_{n}

are calculated based on the desired performances, and

T_{s}

is the sampling period. The PI tuning parameters are computed solving the Diophantine equation:

P_{c l}^{j} (z) = P_{c d}^{j} \Rightarrow k_{p}^{j} = (ξ_{1}^{j} + a + 1) / b; k_{i}^{j} = (ξ_{2}^{j} + ξ_{1}^{j} + 1) / b .

(51)

In a similar way, the tuning parameters of the PI controllers from the outer loop:

C^{ρ} (z) = k_{p}^{ρ} + k_{i}^{ρ} \frac{T_{s}}{z - 1}, ρ = ϕ, ω

(52)

are obtained considering that now the plant is the integrator

N^{ρ} (z) = T_{s} / (z - 1)

obtained after the homotopy-based feedback linearization. In this case, the characteristic polynomial of the closed loop control system is:

P_{c l}^{ρ} (z) = z^{2} + (T_{s} k_{p}^{ρ} - 2) z + k_{i}^{ρ} T_{s}^{2} - k_{p}^{ρ} T_{s} + 1 .

(53)

Using a similar desired characteristic polynomial developed based on performances and solving a Diophantine equation, the following tuning parameters are found:

P_{c l}^{ρ} (z) = P_{c d}^{ρ} \Rightarrow k_{p}^{ρ} = (ξ_{1}^{ρ} + 2) / T_{s}; k_{i}^{ρ} = (ξ_{2}^{ρ} + ξ_{1}^{ρ} + 1) / T_{s}^{2} .

(54)

Employing the IM motor parameters and the desired performances for the inner loop

σ % = 4.3 %, t_{s}^{j} = 0 . 0399 \sec

, the following tuning parameters of the inner loop PI controllers are obtained for

T_{s} = 4 \cdot 10^{- 4} \sec

k_{p}^{j} = 5.71, k_{i}^{j} = 763 . 75 .

(55)

Similarly for the outer loop, by imposing the performances

σ % = 4.3 %, t_{s}^{ϕ} = 0.04 \sec, t_{s}^{ω} = 0.1 \sec

, the tuning parameters of the PI controllers resulted:

\begin{array}{l} k_{p}^{ϕ} = 179, k_{i}^{ϕ} = 1 . 5475 \cdot 10^{4}, \\ k_{p}^{ω} = 80, k_{i}^{ω} = 3 . 1502 \cdot 10^{3} . \end{array} .

(56)

The MPCC_j controllers from the inner loop are implemented using MPC controller block from the MPC Simulink library which is based on the SISO model (24). Employing the IM parameters from Table 1, the model becomes:

\begin{array}{l} \{\begin{matrix} x_{j} (k + 1) = Φ x_{j} (k) + γ Δ v_{s j} (k) \\ i_{j} (k) = [\begin{matrix} 1 & 0 \end{matrix}] x_{j} (k) \end{matrix}, \\ Φ = [\begin{matrix} 0.98 & 0.10 \\ 0 & 1 \end{matrix}]; γ = [\begin{matrix} 0.10 \\ 1 \end{matrix}], \end{array} .

(57)

The constraints formulations for the MPCC_d controller are based on the first inequalities from (17) and (22):

\begin{array}{l} 0 \leq i_{s d} \leq i_{s d}^{\max} = i_{s d N} \\ - v_{s d}^{\max} \leq v_{s d} \leq v_{s d}^{\max} \end{array} .

(58)

and for the MPCC_q controller the second inequalities:

\begin{array}{l} - i_{s q}^{\max} \leq i_{s q} \leq i_{s q}^{\max} \\ - v_{s q}^{\max} \leq v_{s q} \leq v_{s q}^{\max} \end{array} .

(59)

The maximum values of the stator current and voltage of IM are

I_{s \max} = 1.1 \cdot I_{s N} = 17.83 A

and

U_{s \max} = V_{D C} / \sqrt{3} = 433 . 01 V

, where IM is supplied by a power inverter with the DC-bus voltage

V_{D C} = 750 V

. Knowing the nominal rotor flux from Table 1, the nominal d-axis current results:

i_{s d N} = ϕ_{r N} / L_{m} = 5.43 A

, and its maximum value

i_{s d}^{\max} = i_{d N}

. Using (13) the parameter

γ_{c} = i_{s d}^{\max} / I_{s \max} = 0.3

is computed, and finally with (14) the q-axis current maximum value

i_{s q}^{\max} = 16.98 A

resulted.

In order to obtain the maximum values of the voltages

v_{s d / q}^{\max}

from (56) and (57), the parameter

γ_{v} = 0.42

is first chosen and then the maximum values of the voltages

u_{s d / q}^{\max}

are calculated using (18), resulting:

u_{s d}^{\max} = 181 . 86 V

and

u_{s q}^{\max} = 392 . 96 V

. Finally, with (21) the maximum values of the voltages

v_{s d / q}^{\max}

are determined:

v_{s d}^{\max} = 427 . 01 V

and

v_{s q}^{\max} = 64 . 08 V

The operation of the IM is done by imposing the nominal value of the rotor flux as its reference:

ϕ_{r}^{r e f} = ϕ_{r N}

For the inner loop, the designed MPCC controllers have the parameters depicted in Table 2.

The outer loop plant (33) having as outputs the deviations of the rotor flux and speed from their references, with the IM parameters from Table 1 becomes:

\begin{array}{l} \{\begin{matrix} \dot{d} = f (x) + g (x) i_{s d / q} \\ y = d \end{matrix}, \\ f (x) = [\begin{matrix} - 4.48 ϕ_{r} \\ 0 \end{matrix}]; g (x) = [\begin{matrix} 0.78 & 0 \\ 0 & 138.07 ϕ_{r} \end{matrix}] . \end{array}

(60)

Since the model (60) is not feedback linearizable for

ϕ_{r} = 0

when the decoupling matrix g(x) is singular, the linear dynamic system (34) is associated with the outer loop plant model (60). Using the outputs d and

η

of the two associated systems, a new output H is constructed based on the continuous time–dependent parameter

λ \in [0, 1]

, utilizing (35). For the augmented system H with the dynamics (36) is designed the state feedback controller (39) having the parameter

α = 12.26

, resulting a homotopy-based variant of feedback linearization which transformed the nonlinear system (38) into the linear one (40). The purpose of the state feedback controller (39) is to maintain

H = 0

[4] and thus for

λ = 1

the deviations defined by (32) will be zero and thus, the rotor flux and speed track their imposed references. For this reason,

H^{r e f} = {[\begin{matrix} 0 & 0 \end{matrix}]}^{T}

is chosen. For the integrator type linear system (40) obtained after homotopy-based feedback linearization, two additional control loops are built with the model free iP controllers to maintain the reference imposed to H and, respectively, d when

λ = 1

. Usually, PI controllers are used for these additional control loops [4], [13]. In this paper, model free iP controllers capable of dealing with the modeling uncertainty, especially during the variation of the

λ

parameter from 0 to 1, are proposed. The design of these controllers is made considering the connections between iP controllers and the conventional PI given in [22] and [24]. Thus, using (24) the following tuning parameters of the iP controller were obtained, based on the parameters (56) of the PI controllers:

\begin{array}{l} ψ_{ϕ} = 1 / (k_{P ϕ} T_{s}) = 13.97, K_{P ϕ} = k_{I ϕ} ψ_{ϕ} T_{s} = 86.45, \\ ψ_{ω} = 1 / (k_{P ω} T_{s}) = 31.25, K_{P ω} = k_{I ω} ψ_{ω} T_{s} = 39.38. \end{array}

(61)

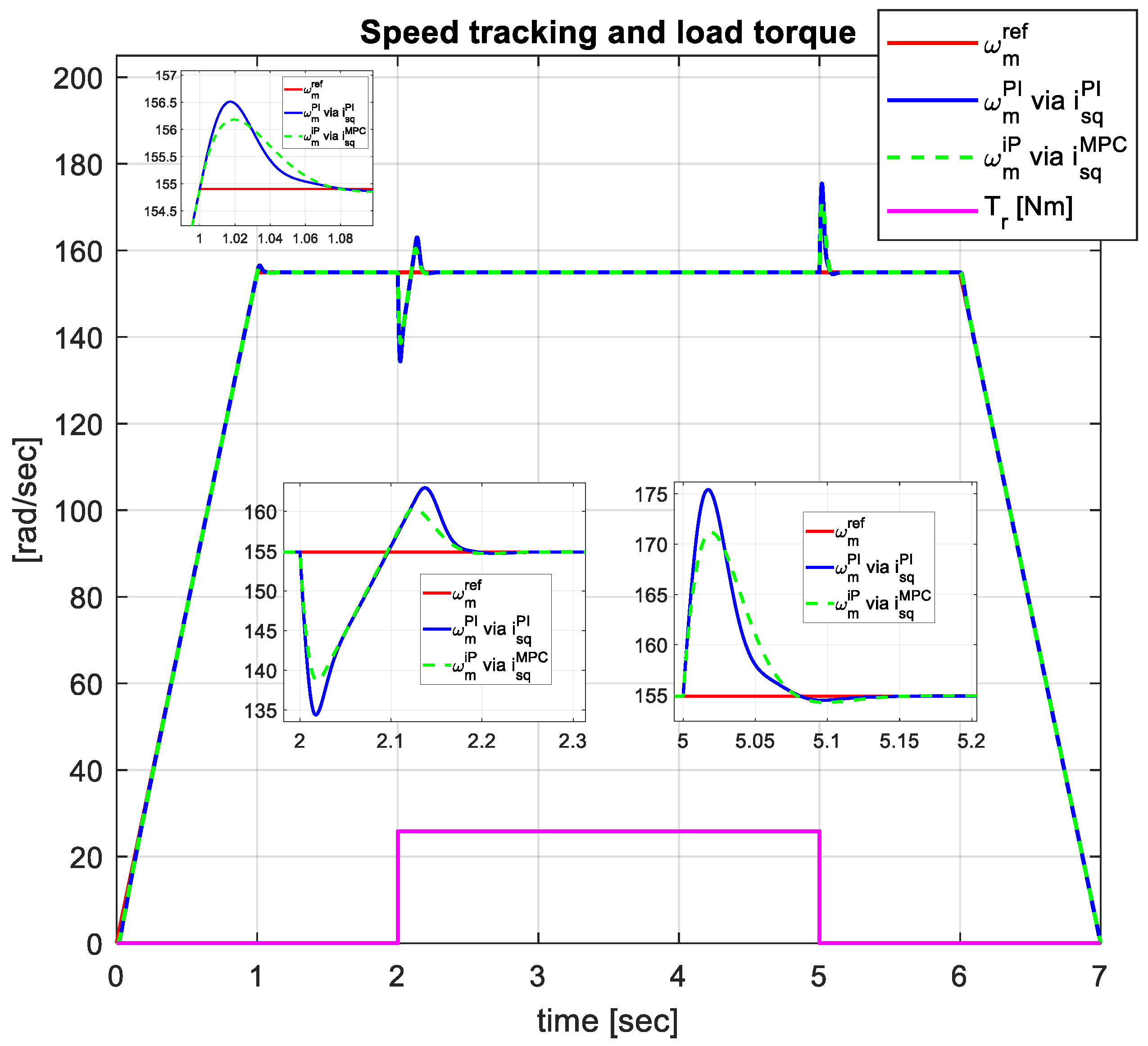
The simulation test consists of an acceleration of the angular speed to 154.9 rad/sec within 1 second, keeping this value 5 seconds and then deceleration to 0 in 1 second, while the rotor flux is maintained at its nominal value

ϕ_{r N} = 0.94 Wb

. A load torque

T_{r} = T_{e N} = 25.08 N m

is also applied starting with t = 2 sec for 3 seconds. The performances obtained with the proposed cascade vector control structure having MPCC controllers in the inner loop and homotopy based feedback linearization of the outer loop plant and the control of the resulting linear system with model free iP controllers are compared with those obtained with the conventional PI controllers in the two control loops.

The evolution of the rotor angular speed in relation to its reference during the test is represented in Figure 3 for both cascade control structures, with advanced control algorithms MPCC and iP and, respectively, with conventional PI controllers.

Reaching the nominal value of the rotor speed is done with a slightly lower overshoot of 0.8% in the case of the cascade with iP and MPCC algorithms compared to the cascade with PI controllers which has 1%. As well, a better rejection of the load torque is obtained for the case of advanced algorithms compared to PI.

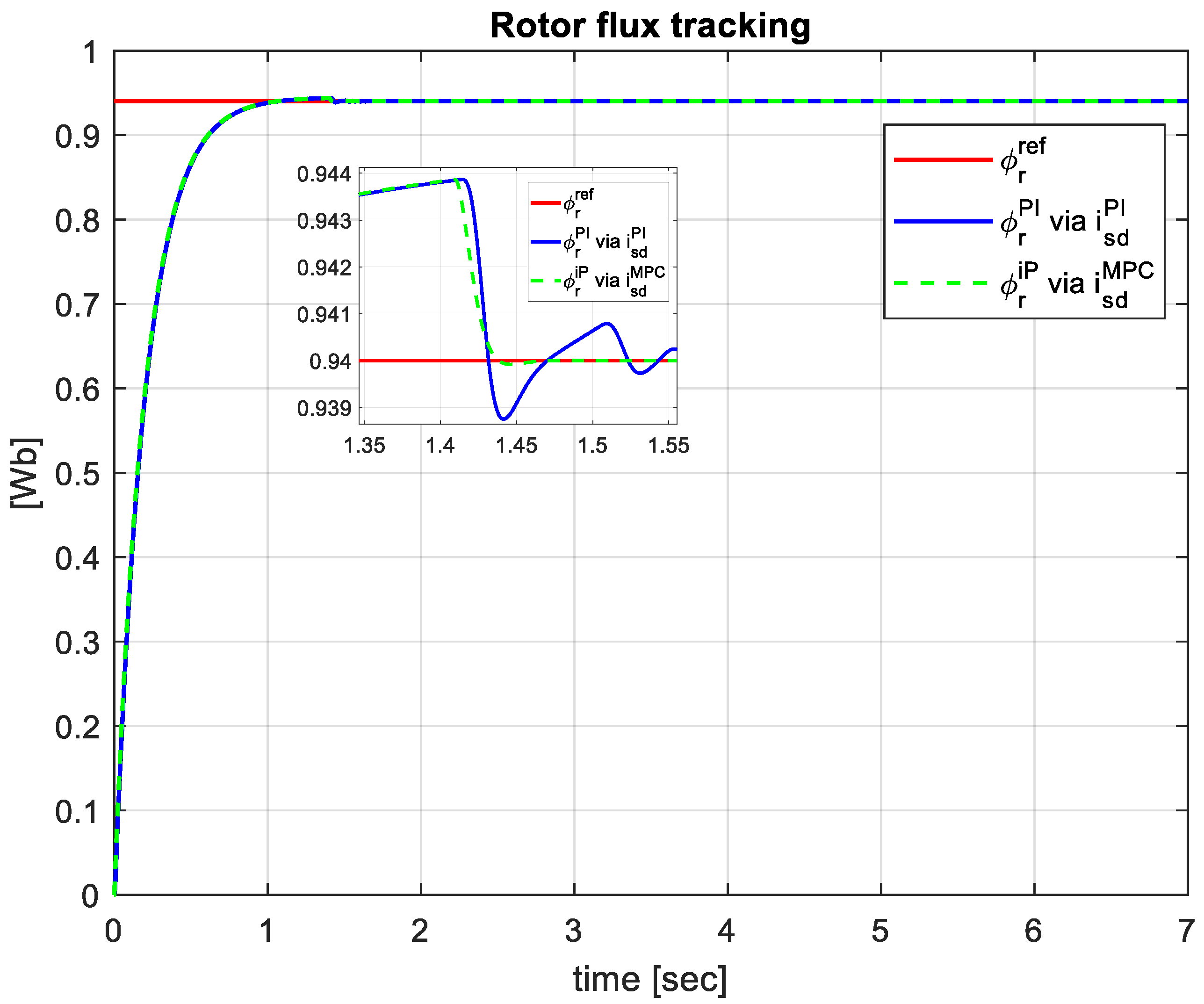
From the responses to the rotor flux reference represented in Figure 4, it can be seen that the performances obtained with the advanced algorithms MPCC and iP are very similar to those of PI controllers, with a slightly better behaviour of the MPCC-iP tandem.

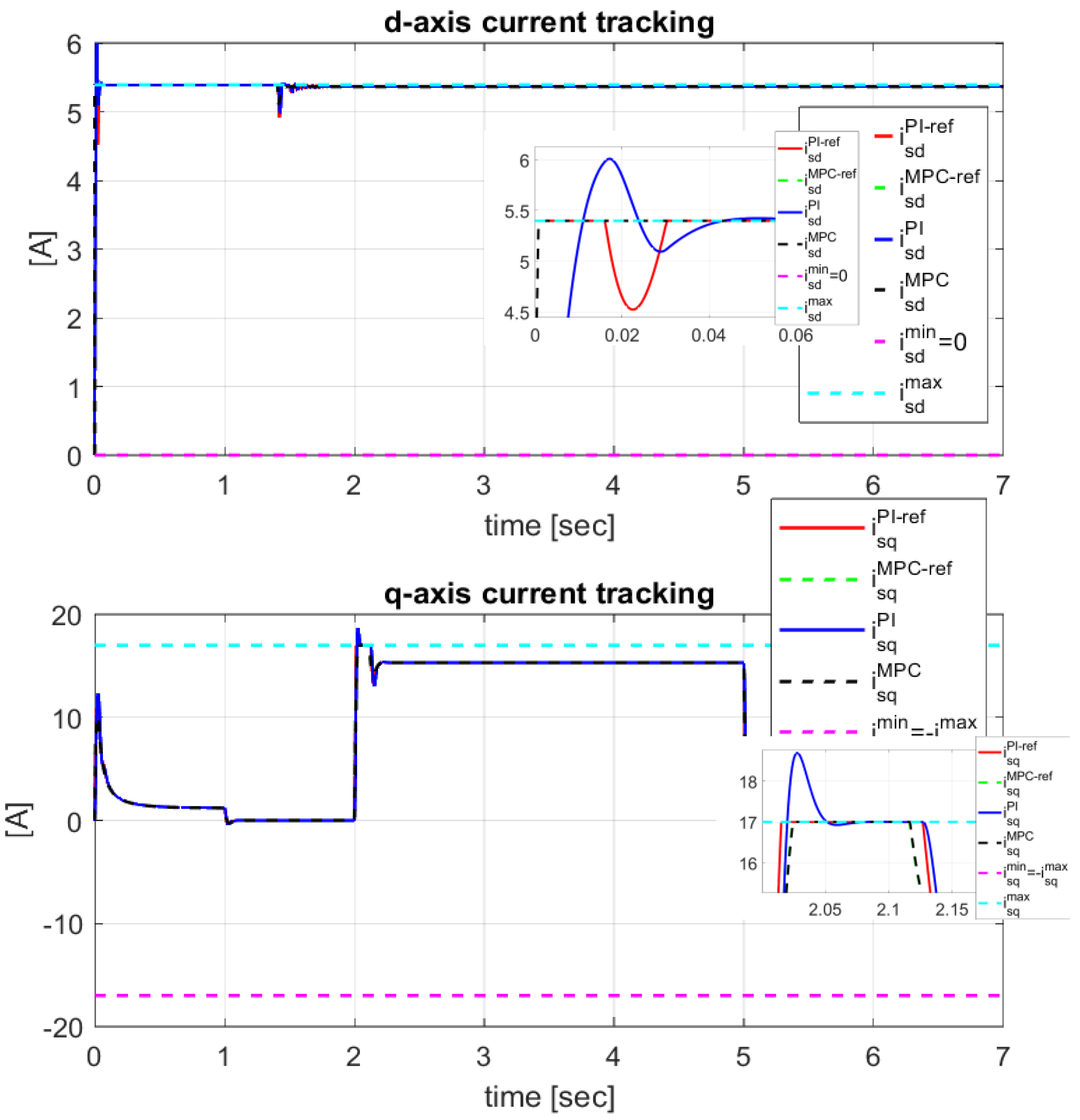
The

i_{s d / q}

currents tracking their references developed by the feedback linearization block is represented in Figure 5 for the two structures with MPCC controller and PI, respectively. The limits imposed to the two currents are also represented in the figure. Current limiting is done in a different way for the two types of controllers. Thus, for the MPCC controller, by imposing constraints (58) and (59) in the design phase, the

i_{s d / q}

currents do not violate the limits. For the case of the PI controller, the limitation of the currents was done by limiting the references developed by the feedback linearization block. But, because in transient state the currents can have overshoot, by exceeding the reference, the imposed limit is violated. For this reason, the current

i_{s q}^{P I}

when the load torque is applied exceeds in transient state the imposed limit value, as can be seen in Figure 5. Except for the flux transient state duration at motor start-up, the

i_{s d}

current is constant and equal to its reference, which demonstrates the efficiency of the decoupling algorithm.

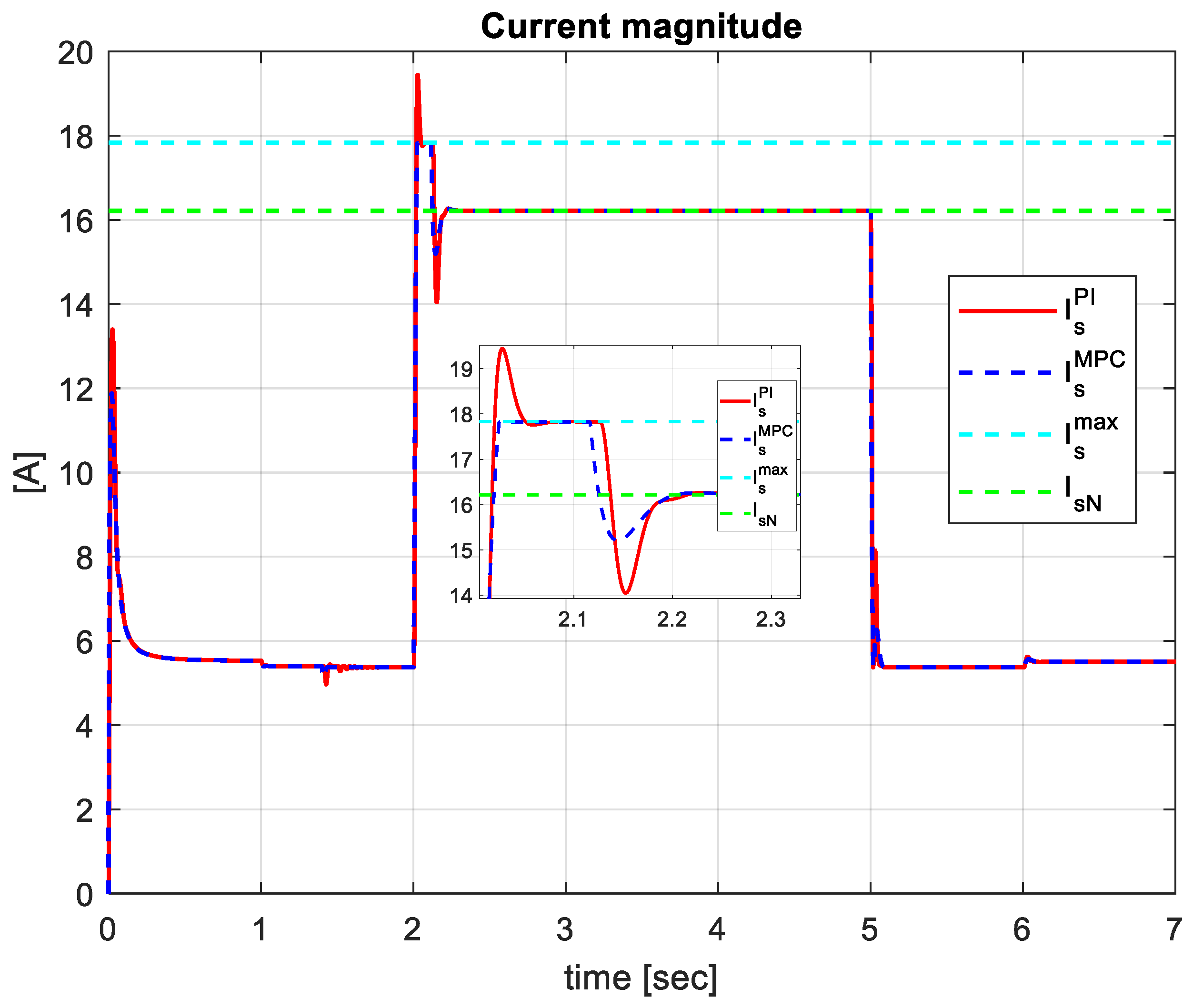
To better illustrate the satisfaction of the constraint (12) regarding the currents, Figure 6 shows the maximum value of the stator current

I_{s}^{\max}

, together with the maximum values obtained with MPCC,

I_{s}^{M P C} = \sqrt{i_{s d M P C}^{2} + i_{s q M P C}^{2}}

, respectively with PI,

I_{s}^{P I} = \sqrt{i_{s d P I}^{2} + i_{s q P I}^{2}}

. From the figure, when the load torque is applied only

I_{s}^{P I} > I_{s}^{\max}

, while in steady state both stator currents are equal to the nominal current:

I_{s}^{P I} = I_{s}^{M P C} = I_{s N}

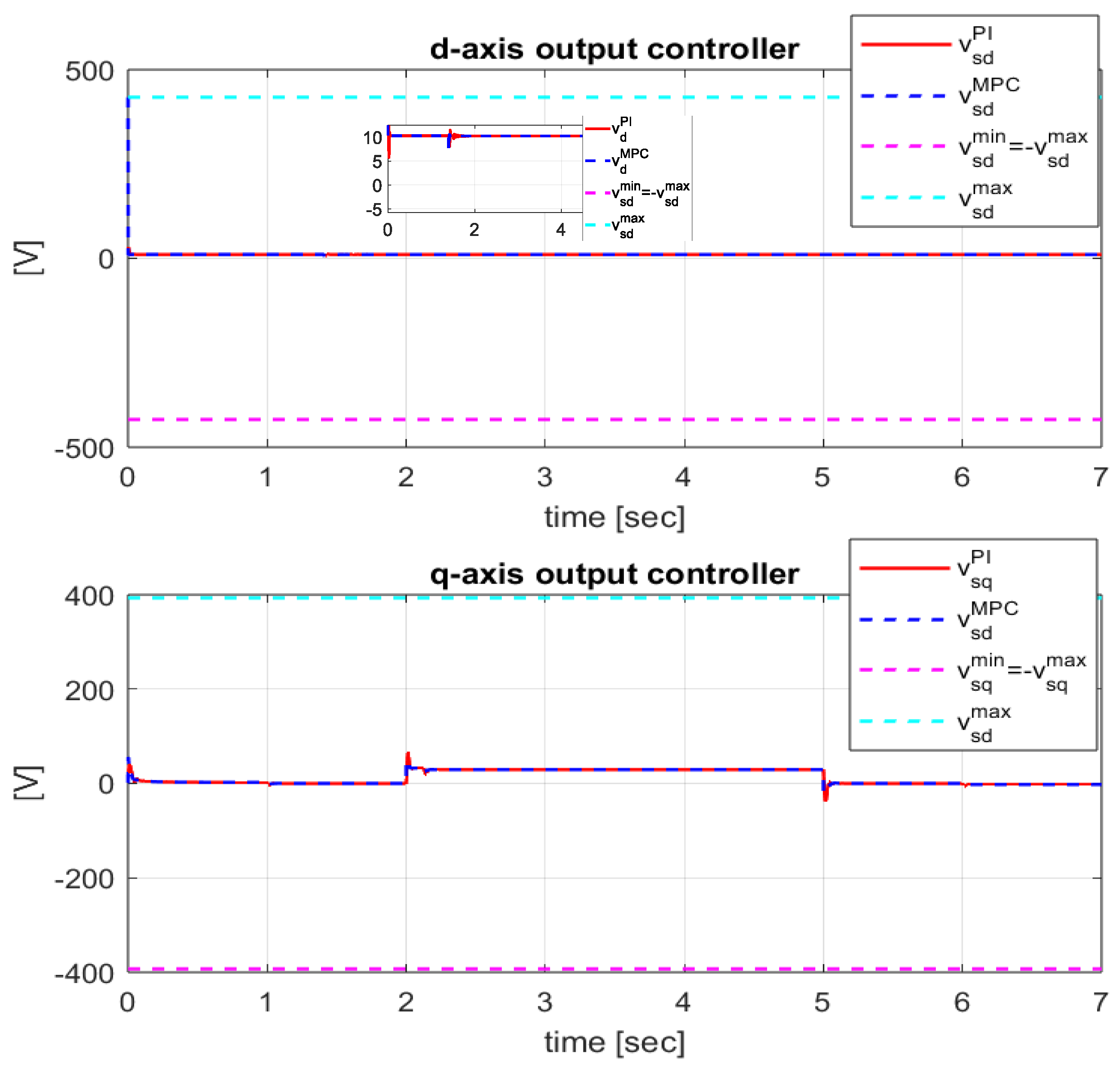
The MPCC and PI current controller outputs,

v_{s d / q}^{M P C}

and

v_{s d / q}^{P I}

together with their limits generated by the constraints are depicted in Figure 7. Due to the anticipative action of the MPCC controllers, especially on the d-axis, the dynamics of the current on this axis and implicitly of the flux is a little bit faster compared to PI.

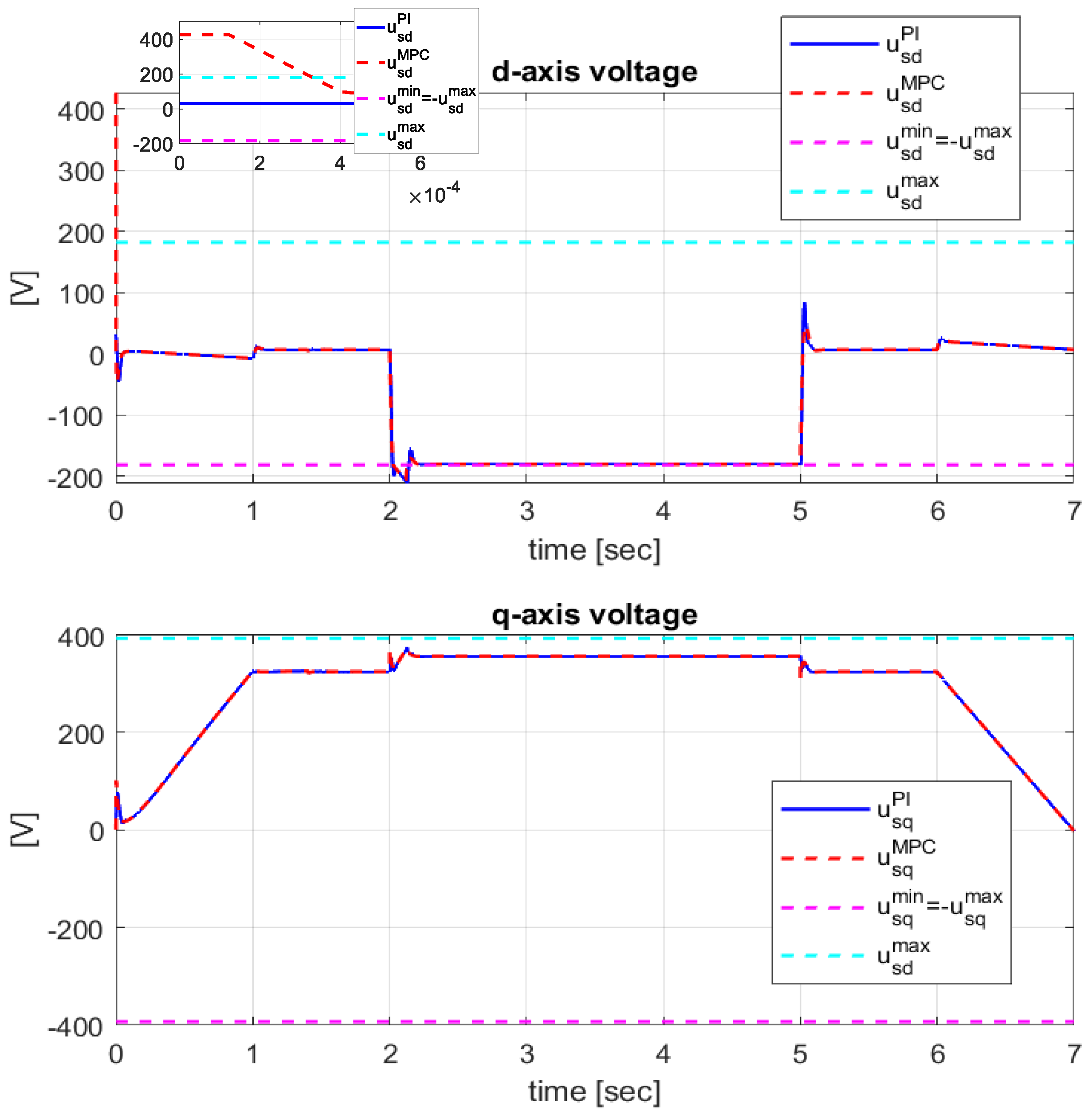
At the same time, due to MPCC controller constraints and the anti-windup mechanism of PI controllers, the imposed limits are not violated. For IM safety, it is important to respect the limits imposed on the input voltages

u_{s d / q}^{M P C}

and

u_{s d / q}^{P I}

whose dynamics are represented in Figure 8. From (8), it follows that the maximum values

u_{s d / q}^{\max}

are calculated based on the maximum values of the voltages

v_{s d / q}^{\max}

and, respectively, of the feedforward components

u_{s d / q}^{f f - \max}

. As presented in paragraph 3.1.2, the maximum values of the feedforward components are dependent on the nominal rotor flux

ϕ_{r N}

. For this reason, during the transitory state of the flux, when it is lower than the nominal value used as reference, the voltage

u_{s d}^{M P C}

is higher than the maximum value calculated with

ϕ_{r N}

. After the flux transitory state,

u_{s d}^{M P C}

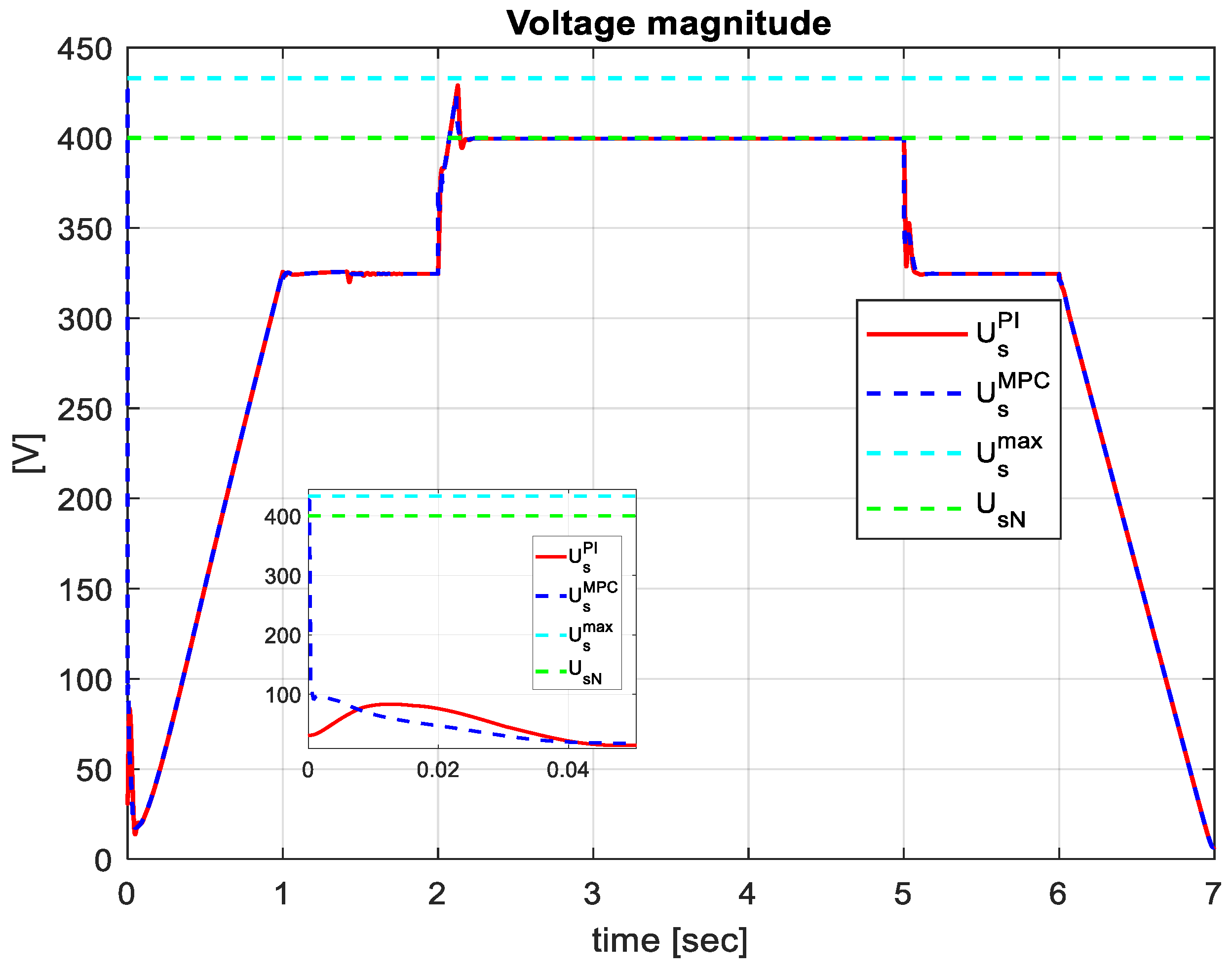
falls within the imposed limits. However, even in the transitory state generated at start-up, the voltage limit (12) is also respected for the MPCC regulator, as seen in Figure 9, where the stator voltages obtained with MPCC,

U_{s}^{M P C} = \sqrt{u_{s d M P C}^{2} + u_{s q M P C}^{2}}

, and PI,

U_{s}^{P I} = \sqrt{u_{s d P I}^{2} + u_{s q P I}^{2}}

are represented in relation to the maximum value

U_{s}^{\max}

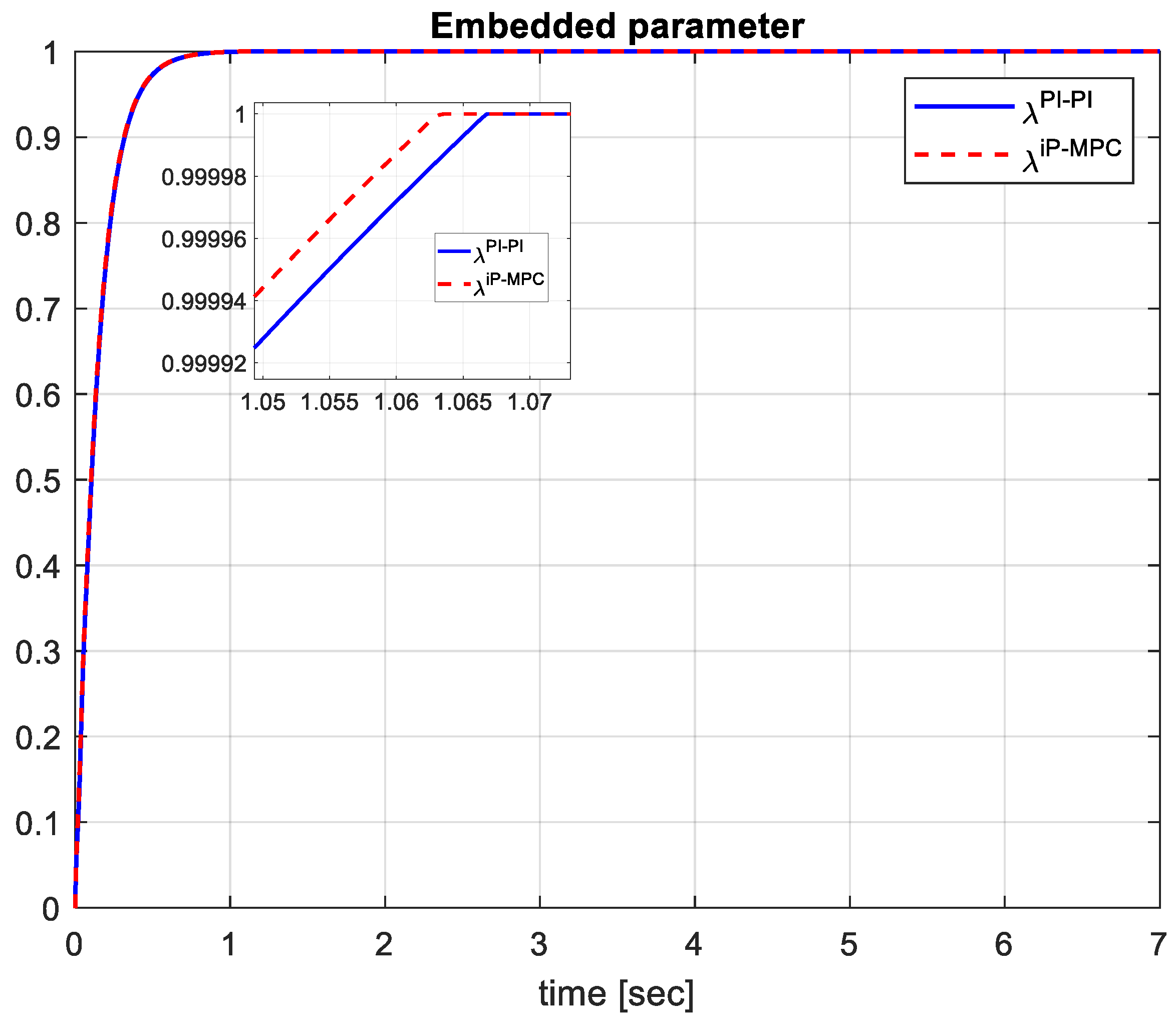
In Figure 10, the smooth transition of the homotopy continuous time–dependant parameter from

λ = 0

λ = 1

is represented, with faster dynamics in the case of the cascade control structure with advanced MPCC and iP algorithms, compared to the result obtained with conventional PI controllers.

In order to evaluate the reference tracking performance by the controlled outputs of the two cascade control structures with advanced MPCC and model free iP algorithms, respectively with conventional PI controllers, and using a homotopy-variant of feedback linearization for decoupling the flux and speed rotor, the following performance indices are used:

\begin{array}{l} J_{d} = \frac{1}{N_{s i m}} \sum_{k = 1}^{N_{s i m}} {(i_{d}^{r e f} (k) - i_{d} (k))}^{2}, \\ J_{q} = \frac{1}{N_{s i m}} \sum_{k = 1}^{N_{s i m}} {(i_{q}^{r e f} (k) - i_{q} (k))}^{2}, \\ J_{ϕ} = \frac{1}{N_{s i m}} \sum_{k = 1}^{N_{s i m}} {(ϕ_{r}^{r e f} (k) - ϕ_{r} (k))}^{2}, \\ J_{ω} = \frac{1}{N_{s i m}} \sum_{k = 1}^{N_{s i m}} {(ω_{m}^{r e f} (k) - ω_{m} (k))}^{2}, \end{array}

(62)

In (53),

T_{s t a r t} = 0

is the is the beginning of the evaluation time,

T_{e n d} = 7

is the simulation time and

N_{s i m} = (T_{e n d} - T_{s t a r t}) / T_{s}

is the total number of samples. The performances indices

J_{d}

and

J_{q}

are used to evaluate the current tracking results, while the next two indices,

J_{ϕ}

and

J_{ω}

, provide the performances evaluation of the flux and speed responses.

The evaluation results regarding the controlled outputs tracking of their references considering performance indices (62) are presented in Table 3.

The numerical values of the performance indices from Table 3 show that with advanced algorithms in the inner and outer loops lower values are obtained compared to those got with conventional PI controllers and thus, the improvement of the vectorial control of IM with the proposed control strategy is pointed out.

5. Conclusions

To improve the vector control of the IM, this paper proposes a cascade control structure that uses advanced control algorithms in the inner loop and the outer one instead of the classic PI controllers and a homotopy-variant of feedback linearization for decoupling the flux and speed rotor. For solving the dq current control problem, a current decoupling algorithm is used in the inner loop, followed by MPCC controllers capable of efficiently and independently controlling the currents, taking into account the constraints imposed by the electrical signal physics limitations. After decoupling the flux and rotor speed using a homotopy-variant of feedback linearization, the resulting integrator-type linear systems are controlled with additional loops with model free iP controllers to ensure the tracking of the references imposed on the flux and rotor speed. Model free control algorithms are used, due to their capabilities to manage complex dynamics from data, without requiring knowledge of the plant model, especially during the variation of the homotopy parameter from zero to one. The proposed cascade control strategy with advanced control algorithms in the two loops have been tested and evaluated by simulation in Matlab-Simulink environment. The performance evaluation is done in comparison with the use of conventional discrete time PI controllers instead of the MPCC controllers in the inner loop, respectively the model free iP controllers in the outer loop. With the advanced control algorithms, better performances are obtained in comparison with PI control in terms of tracking the references by the controlled outputs as well as the rejection of the load torque.

Author Contributions

Conceptualization, M.C. and C.L.; methodology, C.L. (Corneliu Lazar); software, M.C. (Madalin Costin); validation C.L.; formal analysis, C.L.; investigation, C.L.; resources, M.C.; writing—original draft preparation, M.C.; writing—review and editing, C.L.; visualization, M.C.; supervision, C.L. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

Data availability is not applicable to this article as the study did not report any data.

Conflicts of Interest

The authors declare no conflicts of interest.

References

Leonhard, W. Control of electrical drives, 2nd ed.; Springer-Verlag: Berlin, Germany, 1996. [Google Scholar]
Bose, B. K. Power electronics and motor drives advances and trends. Elsevier - Academic Press: California, USA, 2006.
Wang, L.; Chai, S.; Yoo, D.; Gan, L.; Ng, K. PID and predictive control of electrical drives and power converters, Wiley: New York, USA, 2015.
Borisevich, A.; Schullerus, G. Parameter homotopy continuation for feedback linearization of non-regular control-affine nonlinear systems. Int. J. Appl. Math. 2015, 28, 253–273. [Google Scholar] [CrossRef]
Ahmed, A. A.; Koh, B. K.; Lee, Y. I. I. A Comparison of finite control set and continuous control set model predictive control schemes for speed control of induction motors. IEEE Trans Ind. Informat. 2018, 14, 1334–1346. [Google Scholar] [CrossRef]
Garcia, C.; Rodriguez, J.; Silva, C.; Rojas, C.; Zanchetta, P.; Abu-Rub, H. Full predictive cascaded speed and current control of an induction machine. IEEE Trans. Power Electron. 2016; 31, 1059–1067. [Google Scholar]
Hu, Z.; Hameyer, K. A method of constraint handling for speed-controlled induction machines. IEEE Trans. Ind. Electron. 2016, 63, 4061–4072. [Google Scholar] [CrossRef]
Shiravani, F.; Alkorta, P.; Cortajarena, J. A.; Barambones, O. An improved predictive current control for IM drives. Ain Shams Eng. J. 2023, 14, 102037. [Google Scholar] [CrossRef]
Bašic, M.; Vukadinovic, D.; Grgic, I. Model predictive current control of an induction motor considering iron core losses and saturation. Processes 2023, 11, 2917. [Google Scholar] [CrossRef]
Alkorta, P.; Cortajarena, J. A.; Barambones, O.; Maseda F., J. Effective generalized predictive control of induction motor, ISA Trans. 2020, 103, 295–305.
Fekih, A.; Chowdhury, N. On Nonlinear Control of Induction Motors: Comparison of Two Approaches. In Proceedings of the 2004 American Control Conference, Boston, MA, USA, 30 June 02 July 2004; pp. 1135–1140. [Google Scholar]
Bodson, M.; Chiasson, J. Differential-geometric methods for control of electric motors. Int. Journal of Robust and Nonlinear Control 1998, 8, 923–954. [Google Scholar] [CrossRef]
Borisevich, A.; Schullerus, G. Switching strategy based on homotopy continuation for non-regular affine systems with application in induction motor control, 2012, arXiv preprint.
Chiasson, J. A new approach to dynamic feedback linearization control of an induction motor. IEEE Trans. Autom. Control 1998, 43, 391–397. [Google Scholar] [CrossRef]
Boukas, T. K.; Habetler, T. G. High performance induction motor speed control using exact feedback linearization with state and state derivative feedback. IEEE Trans. Power Electron, 2004; 19, 1022–1028. [Google Scholar]
Gastaldini, C.C.; Grundling, H.A. Speed-Sensorless Induction Motor Control with Torque Compensation. In Proceedings of the 2009 13th European Conference on Power Electronics and Applications, Barcelona, Spain, 8-10 September 2009; pp. 1–8. [Google Scholar]
Dendouga, A. Feedback linearization associated to a sliding mode controller for an operating with unity power factor of induction motor fed by matrix converter. SN Appl. Sci. 2020, 2, 879. [Google Scholar] [CrossRef]
Lepka, J.; Stekl, P. 3-Phase AC induction motor vector control using a 56F80x, 56F8100 or 56F8300 device. Design of motor control application. Freescale Semiconductor Application Note, 2005.
Bemporad, A. Model Predictive Control Design: New Trends and Tools. In Proceedings of the 45th IEEE Conference on Decision & Control, San Diego,USA, 13-15 December 2006; pp. 6678–6683. [Google Scholar]
Bemporad, A.; Morari, M.; Dua, V.; Pistikopoulos, E. The explicit linear quadratic regulator for constrained systems. Automatica 2002, 38, 3–20. [Google Scholar] [CrossRef]
Bemporad, A.; Morari, M.; Ricker, N.L. Model predictive control toolbox for Matlab – user’s guide. The Mathworks, Inc., 2023. Available online: https://www.mathworks.com/help/pdf_doc/mpc/mpc_ug.pdf (accessed on 28 November 2023).
Fliess, M.; Join, C. Model free control. Int. J. Control 2013, 86, 2228–2252. [Google Scholar] [CrossRef]
Join, C.; Fliess, M.; Chaxel, F. Model-Free Control as a Service in the Industrial Internet of Things: Packet loss and latency issues via preliminary experiments. In Proceedings of the 28th Mediterranean Conference on Control and Automation (MED2020), Saint-Raphaël, France, 16–18 September 2020; pp. 299–306. [Google Scholar]
Baciu, A.; Lazar, C. Iterative feedback tuning of model-free intelligent PID controllers. Actuators 2022, 12, 56. [Google Scholar] [CrossRef]
Baciu, A.; Lazar, C. Model Free Speed Control of Spark Ignition Engines. In Proceedings of the 23rd International Conference on System Theory, Control and Computing (ICSTCC), Sinaia, Romania, 9–11 October 2019; pp. 480–485. [Google Scholar]
Astrom, K. J.; Wittenmark, B. Computer-controlled systems: theory and design, 3rd ed.; Prentice Hall: New Jersey, USA, 1997. [Google Scholar]
Wittenmark, B. ; Årzén, K-E.; Åström, K. J. Computer Control: An Overview. IFAC Professional Brief 2002, International Federation of Automatic Control.

Figure 1. Inner loop – predictive currents control.

Figure 2. Outer loop – homotopy-based feedback linearization and model free iP control.

Figure 3. Dynamics of the rotor angular speed.

Figure 4. Dynamics of the rotor flux.

Figure 5. Dynamics of the dq currents.

Figure 6. The MPCC and PI stator currents in relation with the maximum value of stator current.

Figure 7. The outputs of the current inner loop controllers.

Figure 8. The plant inputs of the inner loop.

Figure 9. The MPCC and PI stator voltages in relation with the maximum value of stator voltage.

Figure 10. The homotopy parameter variation.

Table 1. IM specification data.

Symbol	Description	Value [unit]
$P_{N}$	Nominal power	4000 [W]
$ω_{m N}$	Nominal speed	154.9 [rad/sec]
$U_{N} / U_{p N}$	Nominal voltage (phase to phase/phase)	400/230 [V]
$I_{N}$	Nominal current	9.36 [A]
$ϕ_{r N}$	Nominal rotor flux	0.94 [Wb]
$T_{e N}$	Nominal electromagnetic torque	25.08 [Nm]
$R_{s}$	Stator resistence	1.2 [Ω]
$R_{r}$	Rotor resistence	0.873[Ω]
$L_{s}$	Stator self-inductance	0.195 [H]
$L_{r}$	Rotor self-inductance	0.195 [H]
$L_{m}$	Mutual inductance	0.175 [H]
$J$	Rotor inertia	0.013 [kg∙m²]
$p$	Number of pole pairs	2

Table 2. The MPCC controllers design parameters.

Weights		Horizons		Violation multipliers
Symbol	Value	Symbol	Value	Symbol	Value
$δ_{j n} / μ_{j p}$	$2 \cdot 10^{- 5}$ /0.5	$h p$	$40$	$W_{d / q}^{i_{s d / q} \min / \max}$	$1 A$
$ρ_{j ε}$	$10^{5}$	$h c$	$2$	$W_{d / q}^{v_{s d / q} \min / \max}$	$0 V$

Table 3. The evaluation of the IM control performance.

Control law		Performance
Inner Loop	Outer Loop	$J_{d}$	$J_{q}$	$J_{ϕ}$	$J_{ω}$
PI	PI	0.0376	0.1381	0.0138	3.5768
MPCC	iP	0.0103	0.0009	0.0129	2.7723

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Induction Motor Improved Vector Control Using Predictive and Model Free Algorithms Together with Homotopy-based Feedback Linearization

Abstract

1. Introduction

2. Nonlinear IM Model for Vector Control

3. Cascade control structure design of IM

3.1. Inner loop design

3.1.1. Decoupling algorithm

3.1.2. Constraint formulation

3.1.3. MPCC controller design

3.2. Outer loop design

3.2.1. Homotopy-based feedback linearization

3.2.2. Model free iP controller design

4. Case Study

5. Conclusions

Author Contributions

Funding

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe