Theoretical Derivation and Calculation of Electron Charge

Preprint

Article

Theoretical Derivation and Calculation of Electron Charge

Altmetrics

Downloads

224

Views

Comments

This version is not peer-reviewed

Submitted:

27 February 2024

Posted:

05 March 2024

You are already at the latest version

Alerts

Abstract

In this paper, we propose an assumption of which the relation between electron and phonon is discussed and investigated based on the experiment of γ photon and electric interconverting with each other. We calculated the charge of a particular standing wave topology with Maxwell’s equation rotated in accordance space with the SO3 transformation. The derived charge value is 1.6035 × 10E−19C around 0.0826% different from the experimental data, indicating the proposal is a promising theory to explain the origin of charge and spin of electron particle. Electron spin angular momentum comes from the orbital angular momentum of photon rotation (electromagnetic field rotation), and electron charge comes from photon, that is, the space-time rotation effect of electromagnetic wave.

Keywords:

Subject: Physical Sciences - Theoretical Physics

1. Introduction

In July 2020, Brookhaven National Laboratory reported an experiment result showing that two gamma photons with high energy can produce a pair of positron and negative electron, and the pair of positron and negative electron meeting to annihilate can produce gamma photons [1]. Therefore, from this point of view, it is reasonable to assume that there is some direct correlation between the two particles, and even further that the two particles are of the same origin and are the same substance. We can propose a theory that electrons and photons are just different in space-time structures and electron can be described as some kind of light topology. Based on this assumption, a theory that reveals the underlying properties of the charge can be developed without the need for a re-normalization scheme. It is well known that Maxwell’s equations (and any other system of linear equations) are equally valid in any suitable, conformal, orthogonal coordinate system. If there is a solution in any such space, there is a corresponding solution in any other such space. Here, we assume that electrons are vortices of photons localized in some way. Starting from Maxwell’s equation and Pauli’s matrix, single photon (electromagnetic wave) can be rotated in space in accordance with the SO3 group to evolve electron with charge. Based on this premise, the electron magnetic moment and electron charge are calculated. The electron magnetic moment equals to

ℏ / 2

, and the electron charge is

1.6299 \times 10^{- 19}

C, which is around 1.73% different from the experimental data, indicating the assumption that the electron is a special photon topology is a promising proposal.

2. Discussion

Arguing that electrons may be some kind of localized photonic topology, there are four differences in physical properties that need to be explained:

I: Electrons can be stationary, while photons move at the speed of light forever and cannot be stationary;
II: Electrons have static mass, while photons don’t have one;
III: The electron spin is 1/2 and the photon spin is 1;
IV: Electrons are charged while photons are not charged.

2.1. Localized Photon

For a single photon, there are two forms. One is a traveling wave photon, which is a common kind. The other is standing wave photons, which can only exist in special spaces such as two metal plates, wireless communication antennas. In linear Maxwell equations, local solutions have been proved to exist [2,3,4]. In the nonlinear field, it is also reported that there are spatial and temporal local states such as optical solitons in vacuum [5]. (It is reasonable because of the high energy density of electrons. The energy density is only available close to the neutron star even assuming that the electron radius is its Compton radius.) If the electron is a standing wave photon, the first difference can be logically explained: a standing wave is a wave of which energy remains basically stationary in a particular space. So electrons can exhibit energy that remains stationary in space, and standing wave photons themselves are still moving at the speed of light. Of course, there are many kinds of standing wave modes of photons, and electrons should be a special standing wave in three-dimensional space topology to meet the other three main differences between electrons and photons.

2.2. Mass and Spin

As for electronic quality, the Higgs mechanism has an explanation and we won’t discuss here. The spin difference: From the quantum field theory, it is known that spin 1/2 represents two loops of rotation can return to initial state, and spin 1 represents one loop of rotation, and a special standing wave, such as the standing wave of Mobius ring structure, is two loops of rotation to return to the initial state. The spin is 1/2, which can be understood as the structure of a standing wave photon, the electromagnetic field of a photon within a wavelength rotates two loops. (Of course, it can be proved that electrons are not standing wave photons in the Mobius ring structure).

2.3. Electron Charge

If the electron is a kind of localized standing wave photon, it means that the uncharged photon (electromagnetic wave) can show a charged state through the change of the space-time structure. The amount of electricity is equal to the amount of electron charge, that is, the origin of electron charge needs to be explained, which is not explained in nowadays physical theory. The following part of this paper focuses on the inference, calculation and discussion of the charge problem, which shows that the uncharged photon can create charge through space-time rotation. The essence of charge is an effect of electromagnetic field rotation in four-dimensional time and space.

3. Calculation

we use (x, y, z) for the fixed Cartesian spatial coordinate system, (r,

θ

, y) for the cylinder, and (r,

θ

ϕ

) for the sphere; ( $x^{'}$ , $y^{'}$ , $z^{'}$ ) for the Cartesian coordinate system of photon motion. Assuming that the photons that make up the electrons are single-photon plane waves, according to Maxwell’s equation, the wave equation for electromagnetic waves in a vacuum is:

\frac{\partial^{2} {\vec{E}}_{(r, t)}}{\partial t^{2}} - c^{2} \nabla^{2} {\vec{E}}_{(r, t)} = 0 \dots \dots (1)

The photon travel coordinate system is selected as the cylindrical coordinate, and the expression of the wave equation is as follows:

\frac{1}{r} \frac{\partial}{\partial r} (r \frac{\partial \vec{E}}{\partial r}) + \frac{1}{r^{2}} \frac{\partial^{2} \vec{E}}{\partial θ^{2}} + \frac{\partial^{2} \vec{E}}{\partial y^{2}} + k^{2} \vec{E} = 0 \dots \dots (2)

Here, the photon motion direction is selected as a cylindrical coordinate cylindrical vector y, r is a radial direction of the cylindrical coordinate, $θ$ is an angular coordinate of the cylindrical coordinate, according to the right hand rule, in a plane represented by the electric field direction r, may be decomposed into x and z components, and E is the electric field strength. k is the wave vector of the electromagnetic wave. The general solution of electromagnetic wave (plane wave) in cylindrical coordinates obtained by separating variables from Formulas (1) and (2) is:

{\vec{E}}_{(r, t)} = A * [C l n r + D + \sum (A_{l} r^{- l} + B_{l} r^{l})] * e^{i l θ} e^{i k y - i ω t} \dots \dots (3)

The coefficient of the electric field distribution function is l/C/D/ $A_{l}$ /A/ $B_{l}$ . Depending on the boundary conditions and initial conditions, the electron-based electrostatic field distribution must meet the Coulomb Formula:

E = \frac{Q q}{4 π ϵ_{0} r^{2}}

, lead to C=D=

B_{l}

=0, l=2, It is possible to produce electric field distributions satisfying the Coulomb Formula by rotation while keeping the space-time metric unchanged. Meanwhile, based on the assumption of single photon standing wave, there is only one coefficient that is not zero and standing wave is a single wave node. Therefore, n=0, m=1.

θ

is the rotation angle of the electromagnetic component around the y axis. Both

k \cdot y

and

ω t

are sine (without affecting the result). Formula (3) can be simplified as follows:

{\vec{E}}_{(r, t)} = A r^{- 2} e^{i 2 θ} e^{i k y - i ω t} \dots \dots (4)

The single photon standing wave hypothesis means that the Pauli matrix of electrons is the rotation matrix of photons in real space. In quantum computing, the Bloch ball model conforms to the Pauli matrix model, that is, the motion trajectory of photons forming electrons conforms to the Bloch ball trajectory. The surface of the sphere is an eigenstate, or standing wave state, and the circumference of the Bloch sphere is half the wavelength of the photon, so that the photon travels twice along the circumference to complete a wavelength length. (Two loops to return to the initial state, meeting the 1/2 spin requirement specified in Pauli matrix). Therefore, the radius of the Bloch sphere is

R_{0} = \frac{λ}{4 π}

, and the orbital angular momentum L of the photon is:

L = R_{0} \times P = \frac{λ}{4 π} ℏ k = \frac{λ}{4 π} ℏ / 2 π / λ = ℏ / 2

. P is the photon momentum, ℏ is the reduced Planck constant, k is the photon loss, and

λ

is the wavelength. In this case, the orbital angular momentum of the photon is exactly equal to the spin angular momentum of the electron, which accords with the experimental self-consistent solution.

The motion of photons along the Bloch sphere is a common and suitable space rotation motion corresponding to the Pauli matrix. The Pauli matrix multiplied by -i/2 as a generator of a Lie group is the SU2 group, which is the rotation group of complex space. There is a correspondence between SU2 group and SO3 group in real space–coverage from two to one. Considering the calculation of real space, it is assumed that the photons forming electrons should be rotated in accordance with the SO3 group on the Bloch sphere to ensure that they meet the requirements of Pauli matrix. In the coordinate system of the photon ( $x^{'}$ , $y^{'}$ , $z^{'}$ ), the photon moves in a straight line along $y^{'}$ . However, in the fixed coordinate system of the observer (x, y, z), the photon moves along the spherical surface, and the motion conforms to the following coordinate transformation:

(\begin{matrix} x \\ y \\ z \end{matrix}) =

(\begin{matrix} c o s ϕ & - s i n ϕ & 0 \\ s i n ϕ & c o s ϕ & 0 \\ 0 & 0 & 1 \end{matrix}) (\begin{matrix} 1 & 0 & 0 \\ 0 & c o s θ & - s i n θ \\ 0 & s i n θ & c o s θ \end{matrix}) [(\begin{matrix} - R \\ - R \\ - R \end{matrix}) + (\begin{matrix} c o s θ & 0 & s i n θ \\ 0 & 1 & 0 \\ - s i n θ & 0 & c o s θ \end{matrix}) (\begin{matrix} x^{'} \\ y^{'} \\ z^{'} \end{matrix})]

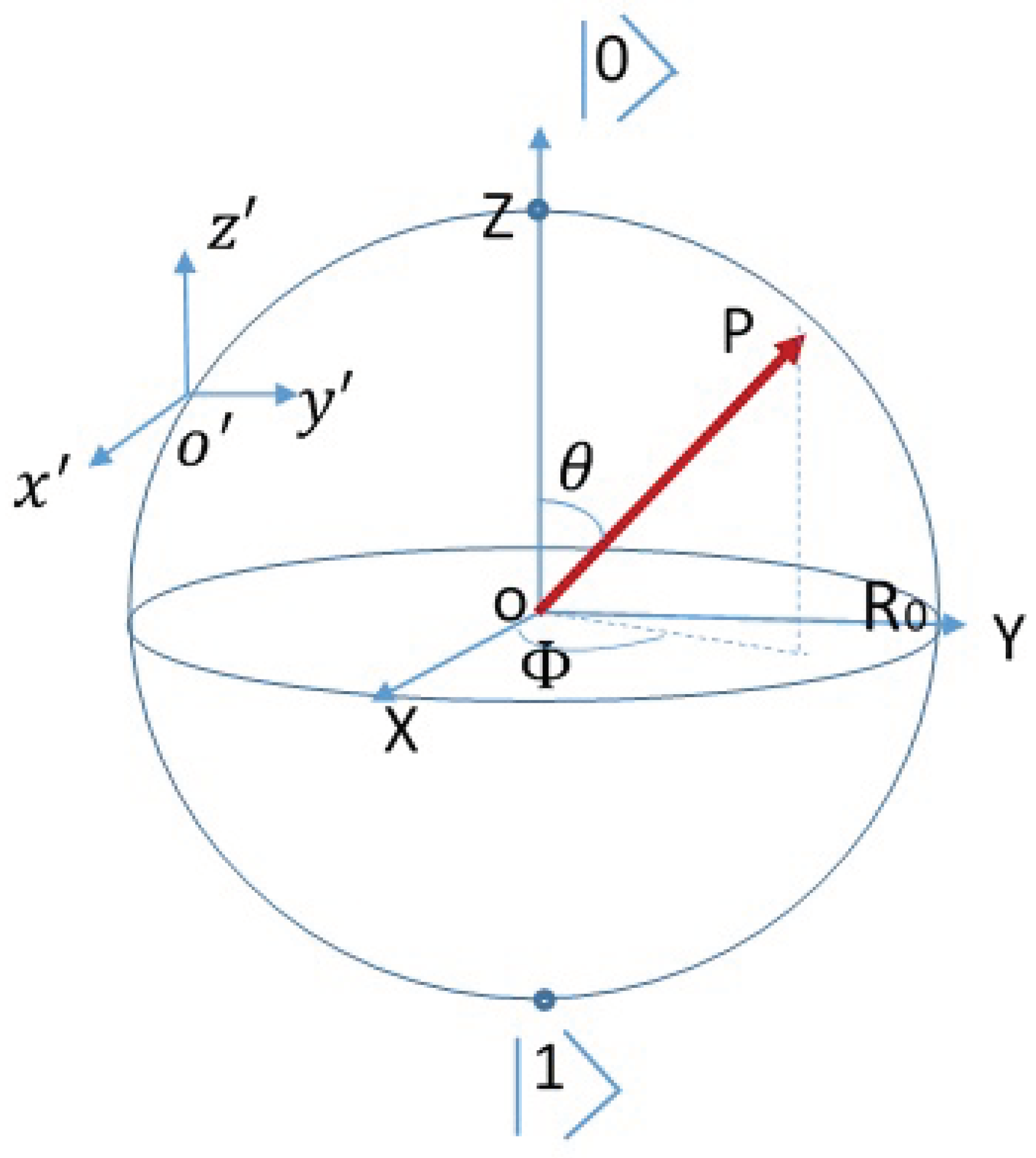
For the above three rotation matrices, the first one is a rotation matrix around the z axis, the second is a rotation matrix around the x axis, and the third is a rotation matrix around the y axis. The rotation angle around the x and y axes is theta, and the motion angle around the z axis is $ϕ$ to meet the requirements of the Bloch sphere model. These three rotation matrices are group elements of the SO3 group, and a translation is added because the fixed coordinate system is the one with the center of the Bloch sphere as its origin, and the photons rotate on the sphere. (corresponding to the photon coordinate system, the coordinate origin is on the sphere, and R is the initial offset from the origin of the photon coordinate system to the sphere center,as shown in Figure 1.) Because $y^{'}$ is the direction of the photon’s motion along the sphere, $y^{'}$ is always tangential to the sphere. The direction of the electric field is located in a plane perpendicular to the $y^{'}$ direction. Assuming that the radius of the sphere is

R_{0}

, then

R = R_{0} / \sqrt{3}

The above coordinate changes and deformations are as follows:

(\begin{matrix} x^{'} \\ y^{'} \\ z^{'} \end{matrix})

= (\begin{matrix} c o s θ (x c o s ϕ + y s i n ϕ + R) - s i n θ (x s i n ϕ s i n θ - y s i n θ c o s ϕ + z c o s θ + R) \\ - x s i n ϕ c o s θ + y c o s ϕ c o s θ + z s i n θ + R \\ s i n θ ((x c o s ϕ + y s i n ϕ + R) + c o s θ (x s i n ϕ s i n θ - y s i n θ c o s ϕ + z c o s θ + R) \end{matrix}) \dots \dots (5)

x = r s i n θ c o s ϕ, y = r s i n θ s i n ϕ, z = r c o s θ

, substitute into Formula (5):

\begin{matrix} x^{'} = & c o s θ (r s i n θ c o s^{2} ϕ + r s i n θ s i n^{2} ϕ + R) - s i n θ (r s i n^{2} θ c o s ϕ s i n ϕ - r s i n^{2} θ s i n ϕ c o s ϕ \\ + r {c o s}^{2} θ + R) = r (s i n θ c o s θ - s i n θ {cos}^{2} θ) + R (c o s θ - s i n θ) \end{matrix}

\begin{matrix} z^{'} = & s i n θ (r s i n θ c o s ϕ c o s ϕ + r s i n θ s i n ϕ s i n ϕ + R) + c o s θ (r s i n θ cos ϕ s i n ϕ s i n θ - \\ r s i n θ s i n ϕ s i n θ c o s ϕ + r c o s^{2} θ + R) = r ({s i n}^{2} θ + {c o s}^{3} θ) + R (s i n θ + c o s θ) \end{matrix}

$x^{'}$ , $y^{'}$ , $z^{'}$ corresponding to column coordinates $y^{'}$ , $r^{'}$ , `:

\begin{matrix} r^{' 2} = & x^{' 2} + z^{' 2} \\ = & [r (s i n θ c o s θ - s i n θ c o s 2 θ) + R (c o s θ - s i n θ)] 2 + {[r (s i n 2 θ + c o s 3 θ) + R (s i n θ + c o s θ)]}^{2} \\ = & r^{2} [{s i n}^{2} θ {c o s}^{2} θ {(1 - c o s θ)}^{2} + {({s i n}^{2} θ + {c o s}^{3} θ)}^{2}] + 2 R^{2} + 2 R r (s i n θ {c o s}^{2} θ + {s i n}^{2} θ {c o s}^{2} θ \\ + {s i n}^{3} θ + {c o s}^{4} θ) \end{matrix}

K = \frac{R}{r}

, get:

\begin{matrix} {r^{'}}^{2} = & r^{2} [{s i n}^{2} θ {c o s}^{2} θ {(1 - c o s θ)}^{2} + {({s i n}^{2} θ + {c o s}^{3} θ)}^{2} + 2 K (s i n θ {c o s}^{2} θ + s i n^{2} θ {c o s}^{2} θ + {s i n}^{3} θ + \\ {c o s}^{4} θ) + 2 K^{2}] \end{matrix}

Let:

\begin{matrix} f_{1} = & {s i n}^{2} θ {c o s}^{2} θ {(1 - c o s θ)}^{2} + {({s i n}^{2} θ + {c o s}^{3} θ)}^{2} + 2 K (s i n θ {c o s}^{2} θ + {s i n}^{2} θ {c o s}^{2} θ + {s i n}^{3} θ + \\ {c o s}^{4} θ) + 2 K^{2} \dots \dots (6) \end{matrix}

⟹ {r^{'}}^{2} = r^{2} f_{1}

The energy of the electromagnetic field is:

\int \frac{1}{2} ε_{0} E^{2} d v + \int \frac{1}{2} μ_{0} H^{2} d v = ℏ ω

Supposing the energy of Electric field and Magnetic field are same:

ε_{0} \int E^{2} d v = ℏ ω

Substitute into Formula (4), and simultaneously transform the photon motion coordinate system into a corresponding cylindrical coordinate system, where A is the amplitude of the electric field:

ε_{0} A^{2} \int {(\frac{1}{{r'}^{2}} e^{i 2 θ} e^{i k y - i ω})}^{2} d v = ℏ ω

Substitute into Formula (6):

ε_{0} A^{2} \int (\frac{s i n θ}{r^{2} f_{1}^{2}}) d θ d ϕ d r = ℏ ω \dots \dots (7)

d r = - \frac{R}{K^{2}} d k ⟹

ε_{0} A^{2} \int (\frac{s i n θ}{R f_{1}^{2}}) d θ d ϕ d k = ℏ ω \dots \dots (8)

There are two points that need to be discussed:

(1): Function integrable: in photon coordinate system, $\int {(\frac{1}{{r^{'}}^{2}})}^{2} d v$ is non-integrable. There is a second order singularity of infinity at $r = 0$ . After the rotation transformation, the function becomes integrable because of the addition of the trigonometric function term( $f_{1}$ ). (Only the rotation matrix that meets the requirements of the SO3 group has no singularity to integrate, which also indicates that it has a special requirements for the rotation mode when electrons are generated by photons rotating through space.)
(2): $e^{i k y}, e^{i ω t}, e^{2 i θ}$ : Phase changes of photon space and time changes respectively corresponding to photon motion coordinate systems. In the motion coordinate system, the photon moves along $y^{'}$ . $y^{'}$ is always tangent to the Bloch sphere surface. The trajectory of $y^{'}$ over time is the arc length of the Bloch sphere, and the angle of that corresponds to the phase of the photon. Supposing that $k y$ corresponds to $θ$ , therefore, in the above integral, since the quadratic integral is supposed to take the complex conjugate, the exponent is actually equal to 1.
(3): Integral limits of the angles: The range of the integral of $ϕ$ is from 0 to $2 π$ , and the upper and lower limits of the integral of $θ$ range from 0 to $2 π$ divided by 2. (From the formula, we find that the period of the integralled function is $2 π$ about $θ$ . The spin rotation is restored to the initial state for two loops and the two coverage requirements of SU2 for SO3 are consistent, which complies with the characteristics of Pauli matrix. Meanwhile, the integrand is exactly $2 π$ periodic for theta.)

Based on the above three points, Formula (8) can be deduced as follows:

{\frac{1}{2} ε}_{0} A^{2} \int_{0}^{2 π} d θ \int_{0}^{2 π} d Œ \int_{0}^{\infty} d k \frac{s i n θ}{R {f_{1}}^{2}} = ℏ ω \dots \dots (9)

Utilizing with Mathematical tool leads to:

A = \sqrt{\frac{2 h ω R}{\in_{0} * 17.6209}}

According to

λ = 4 π R_{0}, R_{0} = \sqrt{3} R \Rightarrow A = \sqrt{\frac{h c}{{2 \sqrt{3} π . \in}_{0} * 17.6209}}

And the charge of this model:

Q_{e} = \int ε_{0} \vec{E} \cdot d \vec{s} = \int ε_{0} \vec{E} \cdot \vec{n} d s

in which

\vec{n} = (s i n θ c o s ϕ, s i n θ s i n ϕ, c o s θ)

The direction of

\vec{E}

\hat{r^{'}}

\frac{x^{'}}{|r^{'}|} + \frac{z^{'}}{|r^{'}|}

—-unit vector of fixed coordinate system.

Which is obtained from Formula (5) (

\hat{\vec{E}}

is unit vector):

\frac{r^{'}}{|r^{'}|} ⟹ (\begin{matrix} x (c o s θ c o s ϕ - s i n 2 θ s i n ϕ + s i n θ c o s ϕ + c o s θ s i n ϕ s i n θ) / | r^{'} | \\ y (c o s θ s i n ϕ + s i n 2 θ c o s ϕ + s i n θ s i n ϕ - c o s θ s i n θ c o s ϕ) / | r^{'} | \\ z (c o s 2 θ - s i n θ c o s θ) / | r^{'} | \end{matrix})

Q_{e =} ε_{0} \int A r^{' 2} e^{i 2 θ} e^{i k y - i ω t} (\hat{\vec{E}} \cdot \hat{n}) d s

Here,

|r^{'}| = r * f_{1}^{\frac{1}{2}}

, and

\begin{matrix} \hat{\vec{E}} . \hat{n} = & [{s i n}^{3} θ {c o s}^{2} Œ (c o s θ c o s ϕ - {s i n}^{2} θ s i n ϕ + s i n θ c o s ϕ + c o s θ s i n ϕ s i n θ) + {s i n}^{3} θ {s i n}^{2} ϕ \\ * (c o s θ s i n ϕ + {s i n}^{2} θ c o s ϕ + s i n θ s i n ϕ - c o s θ c o s ϕ s i n θ) + c o s 2 θ s i n θ (c o s 2 θ - s i n θ c o s θ)] / f^{1 / 2} \end{matrix}

Substitute into Formula (10), since the electron charge is independent of time, we can ignore the term of time

e^{i ω t}

e^{2 i θ} e^{i k . y} = e^{2 i θ} e^{i θ}

. For complex integral, one exponent index need to be taken as complex conjugate, so

e^{2 i θ} e^{i θ}

should be

e^{2 i θ} e^{- i θ}

\begin{matrix} Q_{e} & = \sqrt{\frac{h c ε_{0}}{2 \sqrt{3} π * 17.6209}} * \int_{0}^{2 π} d θ \int_{0}^{2 π} d Œ \frac{e^{i 2 θ} e^{- i θ}}{{f_{1}}^{\frac{3}{2}} e^{i 2 θ} e^{- i θ}} f_{2} \\ = \sqrt{\frac{h c ε_{0}}{2 \sqrt{3} π * 17.6209}} * (1.7019 + i 1.7019) \end{matrix}

taking the Real Part as Q:

Q_{e} = R e (\sqrt{\frac{h c ε_{0}}{2 \sqrt{3} π * 17.6209}} * (1.7019 + i 1.7019)) = 1.6299 \times 10^{- 19} C

(

h = 6.62607015 \times 10^{- 34} J s, c = 2.99792458 \times 10^{8} m / s, ε_{0} = 8.854187817 \times 10^{- 12} f / m

) [6]

Physical measurement value of electric charge e is different [7,8,9,10,11,12,13]. Therefore, the error of the calculated electronic charge amount is

1.73 %

based on the e value published by the International Scientific and Technical Data Commission [6].

where the causes of the error are as follows: (1) The plane wave hypothesis can be adjusted to spherical wave, which is sticks to the natural law; (2) According to the literature reports, the fine structure constant also shows anisotropy in vacuum[14], which means the asymmetry of space. Here the reasoning and calculation assumes that the vacuum dielectric constant is unchanged, and the vacuum dielectric constant is different from the ordinary vacuum dielectric constant due to the large electron energy density. So the dielectric constant around electric could be adjust to meet the real value.

4. Conclusion

Based on the assumption that electrons are standing wave photons, we present the conclusions derived from the Pauli matrix of electrons and the corresponding Bloch sphere model as followed: Electron spin angular momentum comes from the orbital angular momentum of photon rotation (electromagnetic field rotation), and electron charge roots from photon,that is the space-time rotation effect of electromagnetic wave. The wave-particle duality of electrons is the embodiment of the fluctuation and standing wave characteristics of photons, which is the existence of standing wave photons. Therefore, this theory can make up for some defects of quantum mechanics and quantum field theory, such as the interpretation of electron spin, which is also consistent with the existing experimental results.

Acknowledgments

We wish to thank Prof. Jiaxin Zheng in Peking University and Mr. Ming Xu for for their expert advice on analyzing assumption details.

References

Jaroslav Adam et al. “Measurement of e+ e- momentum and angular distributions from linearly polarized photon collisions”. In: Physical review letters 127.5 (2021), p. 052302. [CrossRef]
Erik Bäcklin. “The X-Ray Crystal Scale, the Absolute Scale and the Electronic Charge”. In: Nature 135.3401 (1935), pp. 32–33. [CrossRef]
AO Barut and Aaron Grant. “Quantum particle-like configurations of the electromagnetic field”. In: Foundations of Physics Letters 3 (1990), pp. 303–309. [CrossRef]
Raymond T Birge. “Interrelationships of e, h/e and e/m”. In: Nature 137.3457 (1936), pp. 187–187. [CrossRef]
Raymond T Birge. “Probable values of the general physical constants”. In: Reviews of Modern Physics 1.1 (1929), p. 1. [CrossRef]
SV Bulanov et al. “Electromagnetic solitons in quantum vacuum”. In: Physical Review D 101.1 (2020), p. 016016. [CrossRef]
Arthur Stanley Eddington. “The charge of an electron”. In: Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character 122.789 (1929), pp. 358–369. [CrossRef]
Robert Andrews Millikan. “I. A new determination of e, N, and related constants”. In: The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science 34.199 (1917), pp. 1–30. [CrossRef]
Robert Andrews Millikan. “On the elementary electrical charge and the Avogadro constant”. In: Physical Review 2.2 (1913), p. 109. [CrossRef]
Antonio F Ranada. “A topological theory of the electromagnetic field”. In: Letters in Mathematical Physics 18 (1989), pp. 97–106. [CrossRef]
Antonio F Ranada. “Topological electromagnetism”. In: Journal of Physics A: Mathematical and General 25.6 (1992), p. 1621. [CrossRef]
Eite Tiesinga et al. “CODATA recommended values of the fundamental physical constants: 2018”. In: Journal of Physical and Chemical Reference Data 50.3 (2021). [CrossRef]
Arthur Pehr Robert Wadlund. “Absolute X-Ray Wave-Length Measurements”. In: Physical Review 32.6 (1928), p. 841. [CrossRef]
Michael R Wilczynska et al. “Four direct measurements of the fine-structure constant 13 billion years ago”. In: Science advances 6.17 (2020), eaay9672. [CrossRef]

Figure 1. scheme of fixed coordination and phonon moving coordination.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Theoretical Derivation and Calculation of Electron Charge

Abstract

1. Introduction

2. Discussion

2.1. Localized Photon

2.2. Mass and Spin

2.3. Electron Charge

3. Calculation

4. Conclusion

Acknowledgments

References

MDPI Initiatives

Important Links

Subscribe