Axial Vibration Control Technique for Crystal Growth from the Melt: Analysis of Vibrational Flows’ Behavior

A problem of efficacy of crystal growth methods for crystallization from solution or melt has been investigated. Axial vibrational control (AVC) technique was considered as a perspective method to manage both heat-mass transfer and chemical component composition of the melts in the case of crystallization of complex chemical compounds. Numerical modeling and the search for generalized dependencies made it possible to predict the AVC parameters that provide optimal heat and mass transfer modes for creating flat liquid-solid interfaces, as well as the component composition of dissociated melts of various chemical compounds – Ge, NaNO3, CdTe.

Keywords:

Subject: Chemistry and Materials Science - Chemical Engineering

1. Introduction

Over the past 20 years, in the field of functional materials, there has been a market shift towards thin-film and nano-sized structures [1]. Nevertheless, the market for single crystals still continues to grow [2]. In spite of the progress in polycrystal technology many properties which are found in single crystals cannot be replicated in polycrystals. In many practical applications only single crystal materials are able to provide the required and record-breaking functional characteristics [3,4].

To date single crystal of semiconducting materials are one of the most widely researched and used materials. Besides Si and Ge single crystals the single crystals of III–V semiconductors due to their outstanding optical and electronic properties, are an integral part of devices for application in fiber-optic communication, wireless and satellite communication, solid-state lighting, etc. [5,6].

In this regard, the tasks of both improving quality, primarily structural, and reducing the cost of crystals are fundamental. Taking into account the fact that more than 90% of all mass-production single crystals are grown from the liquid phase (solution or melt growth methods), the issue of improving these methods is extremely relevant.

Numerous studies on improving of crystals growth methods by various types of mixing (ultrasonic [7,8], ACRT – accelerated crucible rotation technique [9], CVS – coupled vibrational stirring [10], rotating baffle [11], HFR - heat field rotation [12], TMF – travelling magnetic field [13], AHP – axial heat flux technique [14]) were mainly aimed at effective control of heat and mass transfer, creating conditions for obtaining a flat interface in the case of directional crystallization methods.

At the same time, the issue of control of chemical thermodynamics states in growth systems has been considered extremely rarely. [15,16,18].

A study of the influence of low-frequency vibrations on the equilibrium of chemical reactions [19] showed that a clear effect of chemical equilibrium control was possible. In Ref. [16,17], when analyzing the crystals growth processes of chemical compounds, an explanation for this effect was given. It has been established that when an AVC is introduced into a liquid through harmonic vibrations of a solid chemically inert flat cylindrical disk, which has a sharp edge on a cylindrical generatrix, such high-energy flows are generated in the region of the sharp edge that the energy of viscous dissipation of liquid layers becomes comparable to the chemical interaction energy of clusters in the melt. And the transformation of the mechanical energy of a moving liquid into chemical energy leads to a change in the chemical nature of the liquid phase, in particular, to a change in the component composition and destruction of associates in the melt. From this point of view, the AVC technique can be considered not only as an effective tool for organizing the required heat and mass transfer, but also as a tool for controlling the thermodynamic properties of the liquid phase.

The efficacy of the AVC technique application for growth of both dielectric [20,21], and semiconductor crystals [22] has been demonstrated. The application of the AVC technique made it possible to both improve the structural perfection of the grown crystals and increase the volumetric growth rate in several times. However, for each specific crystal and each method, the authors were forced to experimentally optimize the AVC modes to achieve the desired result.

To determine a direct relationship between the parameters of vibration effects and the characteristics of vibration flows in a liquid, in the present research we excluded all factors, such as free surface, thermal convection and crystallization front, which are always present in the real growth process and interfere with an objective assessment of the characteristics of vibration flows.

2. Numerical model

To understand the nature of the vibratory flow formation and properties we have excluded from consideration the thermal convection, which always accompanies the melt crystal growth process, by conducting the system analysis in ideal isothermal conditions. Numerical simulation was made using ANSYS Fluent package and germanium, cadmium telluride and sodium nitrate melt were considered as model substances. The AVC technique was realized by low-frequency harmonic oscillations of a cylindrical disk submerged into the melt. The disk is specified by three critical parameters: 1) diameter - D, 2) thickness - d, and 3) radius of the edge curvature between a cylindrical generatrix and a faceplate - R. It had been demonstrated that the R-value sufficiently influenced on average flows’ generation [20].

2.1. Model of fluid motion under the AVC action

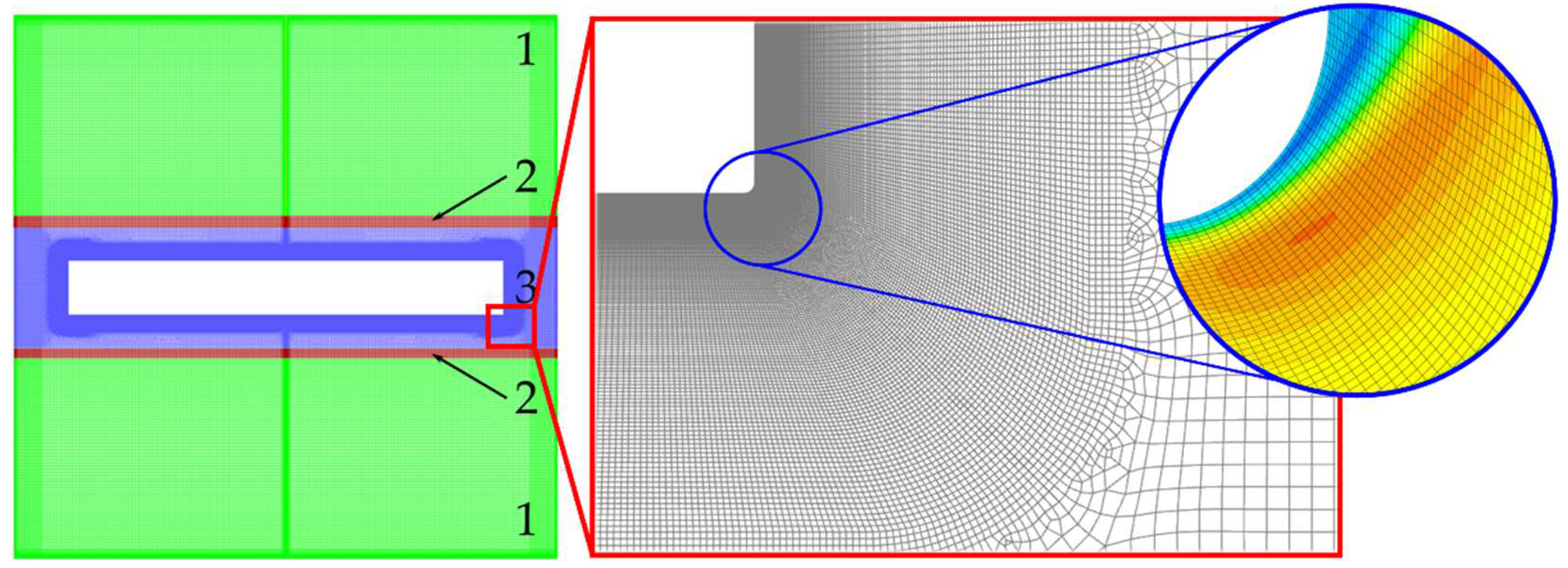
The analysis of the AVC technique was carried out by numerical modeling in a two-dimensional axisymmetric approximation using the geometric model shown in Figure 1. The grid model (see Figure 1 right) contains 187 000 cells for modeling half of the axially symmetric model with an average size of 0.5 mm in the region of the liquid phase with compaction of cell layers at the boundaries. The minimum cell size on the disk rounding is 3.3 μm with a gradual expansion into the main design volume. The dimensions of the geometric model are presented in Table 1.

The simulating area was divided into five zones (Figure 1 center). In a zone surrounding the vibrator – disk zone – grid was moving with the vibrator as well. In the two zones belonging to the upper and lower ends of the crucible – stationary zones – grids were non-moving. There were two zones between the moving disk zone and the non-moving stationary zones at the crucible ends. In these zones the grid was stretched and compressed.

The velocity and pressure fields were calculated using the Navier-Stokes equation, supplemented by the continuity equation, at constant density and viscosity:

ρ (\frac{\partial \vec{v}}{\partial t} + (\vec{v} \cdot \nabla) \vec{v}) = - \nabla p + μ ∆ \vec{v};

(1)

\nabla \cdot \vec{v} = 0;

(2)

The model was calculated under isothermal conditions:

T = c o n s t .

(3)

Boundary conditions for a stationary wall were specified using no-slip boundary condition:

{\vec{v}}_{n} = 0 .

(4)

The oscillation of the disk along the X-axis was specified using the boundary condition for changing the speed

\{\begin{matrix} v_{x} = A ω \cdot c o s (ω t); \\ v_{y} = 0, \end{matrix}

(5)

ω = 2 π f .

(6)

The numerical integration of the system of differential equations was carried out using the finite volume method. The search for a solution was carried out using the iterative Gauss-Seidel method using the pressure-velocity separated SIMPLE scheme. The gradients were discretized using the least squares method. Spatial discretization of velocity and pressure was carried out according to a second-order scheme. Time discretization was carried out according to a first-order scheme. The disk movement was accompanied by the use of a dynamic mesh.

2.2. Material properties

NaNO₃, Ge and CdTe melts were used as model liquid phases. Their physicochemical properties are presented in Table 2.

3. Results

3.1. AVC flows velocities

For the selected materials, non-stationary calculations were carried out with a time step equal to 1/400 of the oscillation period until a stationary regime of melt flow was established, that is, until the velocity values averaged over the oscillation period reached a constant value. Distributions of the flow velocity of melts of Ge, CdTe, and NaNO₃ were obtained at various values of the amplitude (A) and frequency (f) of disk oscillation, as well as at various radii of the disk edge (R) (Table 3).

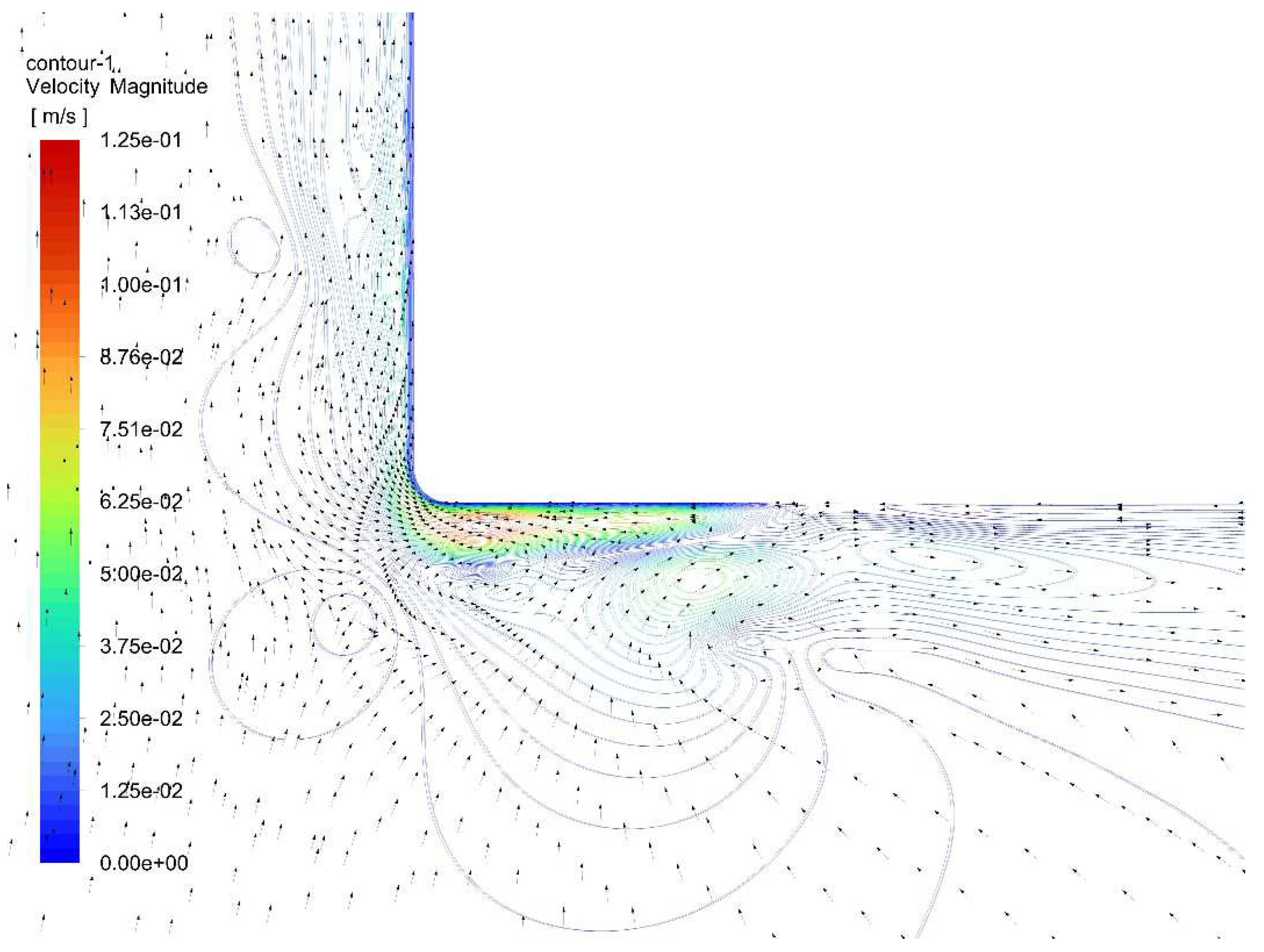
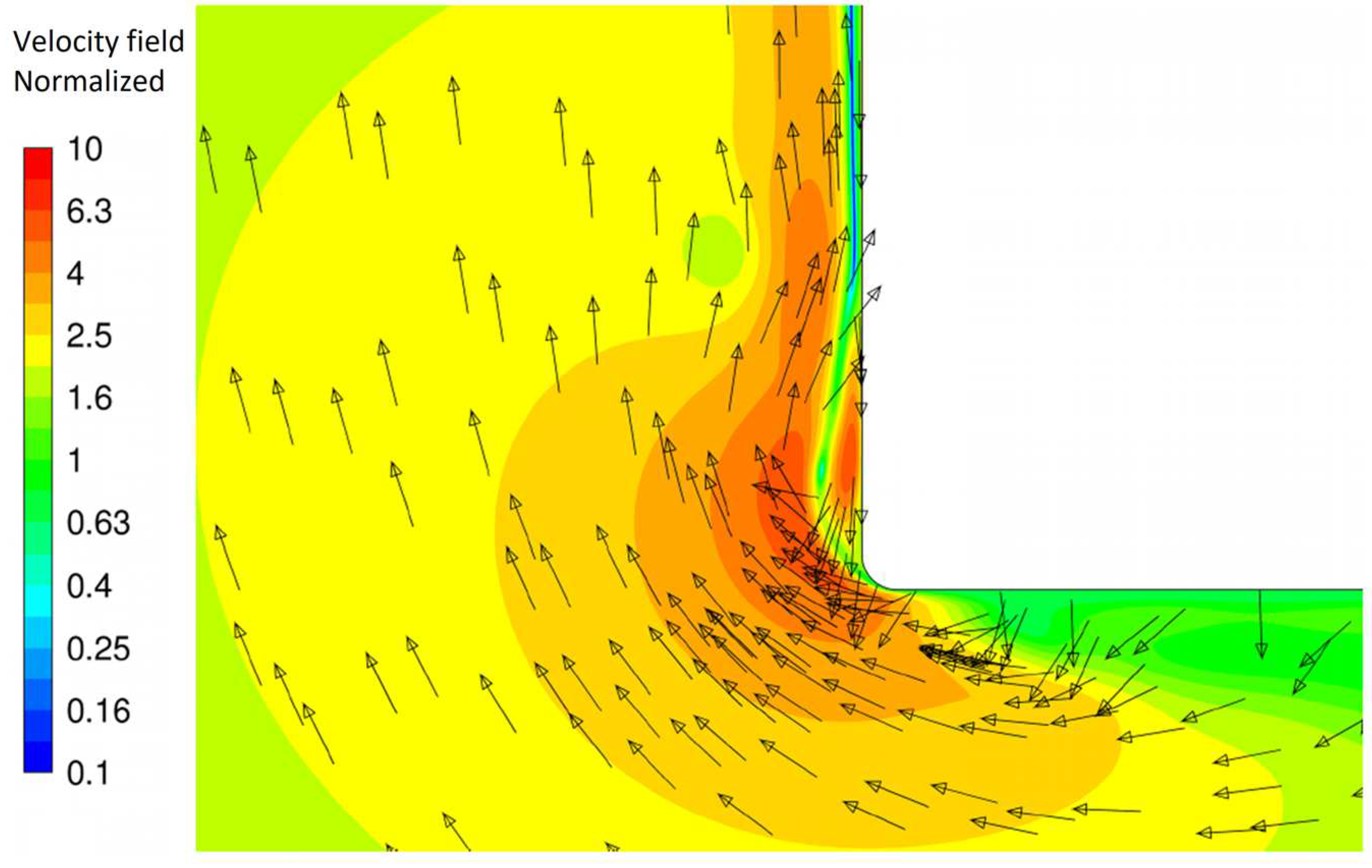
When a solid body oscillates in the melt near its edge, two types of vortices are generated (Figure 2): primary (wall) and secondary (external). The primary vortex occurs when the fluid adjacent to the disk moves when the disk oscillates. At the edge of the disk, the flow is divided: one part continues to flow around the disk, and the other forms the primary vortex. The speeds achieved in this vortex exceed the speed of body oscillation by 10-20 times, and it is in the primary vortex that the maximum energy of viscous dissipation occurs.

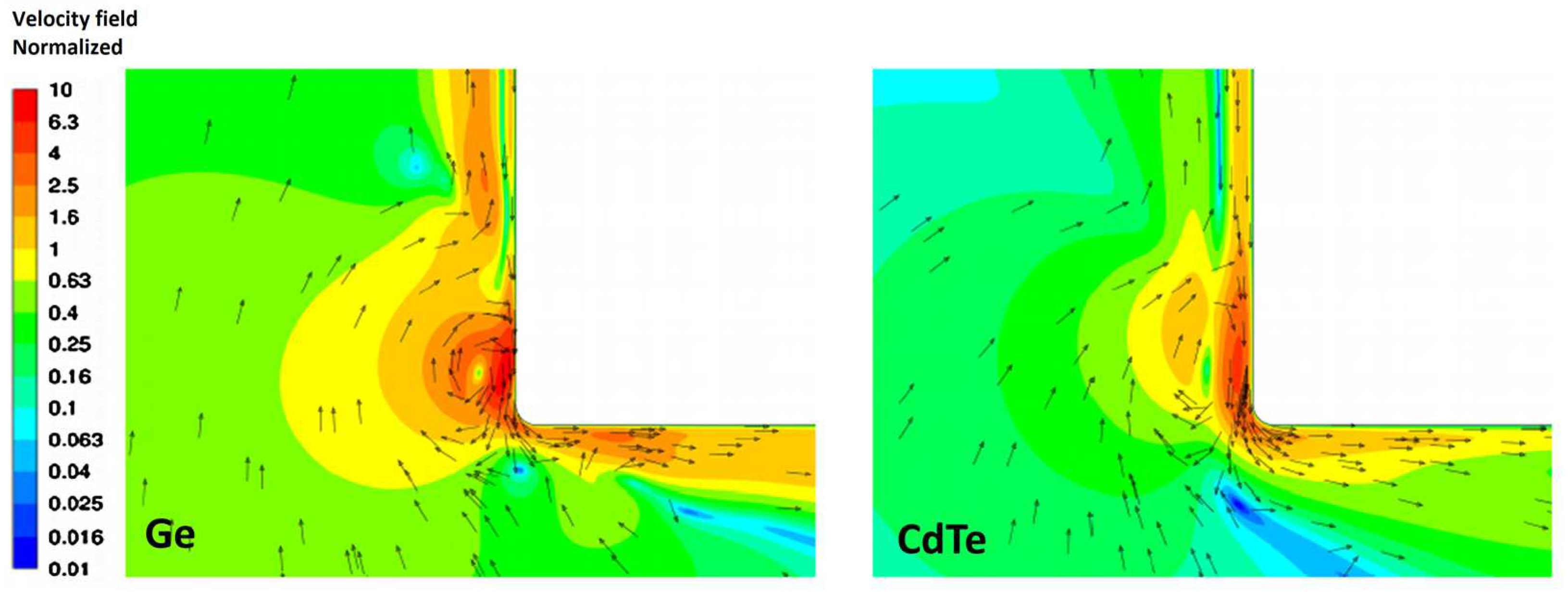
Analysis of fluid flows in normalized scale v/(Aω) at the edge of the disk showed that in the case of more viscous CdTe the thickness of the boundary layer on the side surface of the disk is significantly greater comparing to Ge melt (Figure 3). However, the scale of the edge vortex is almost the same in both cases.

It is also clear that for less viscous germanium, inertial effects are much stronger. Hence the higher speeds of jet flows from the corner, which create circulation in the main volume of the melt.

The mechanism of vortex generation is the tear off of flows when flowing around an edge of large curvature (small radius of curvature). Due to the tear off of flows during the forward and reverse disk motion, the liquid in the edge region moves along different trajectories, resulting in the formation of an edge vortex. The scale of the vortex is determined by the region of separated flow at the disk edge.

Analysis of separated flows in Ge melt at time point 7/8 of the period (after the disk passes the midpoint, but before stopping in the lower position) showed that during this separation it manifests itself most clearly.

The secondary vortex arises under the influence of a pressure gradient that is formed from the primary vortex. In general, depending on the geometry of the oscillating body and the space around the body, several secondary vortices can arise, but they arise together with the primary one due to the continuity equation. It is the secondary vortex, formed from the edge of the disk and propagating further into the liquid (Figure 5), that will reach the crystallization front of the crystal. Therefore, we are most interested in connecting the flow rate of the secondary vortex with the vibrational parameters and physical properties of the melt.

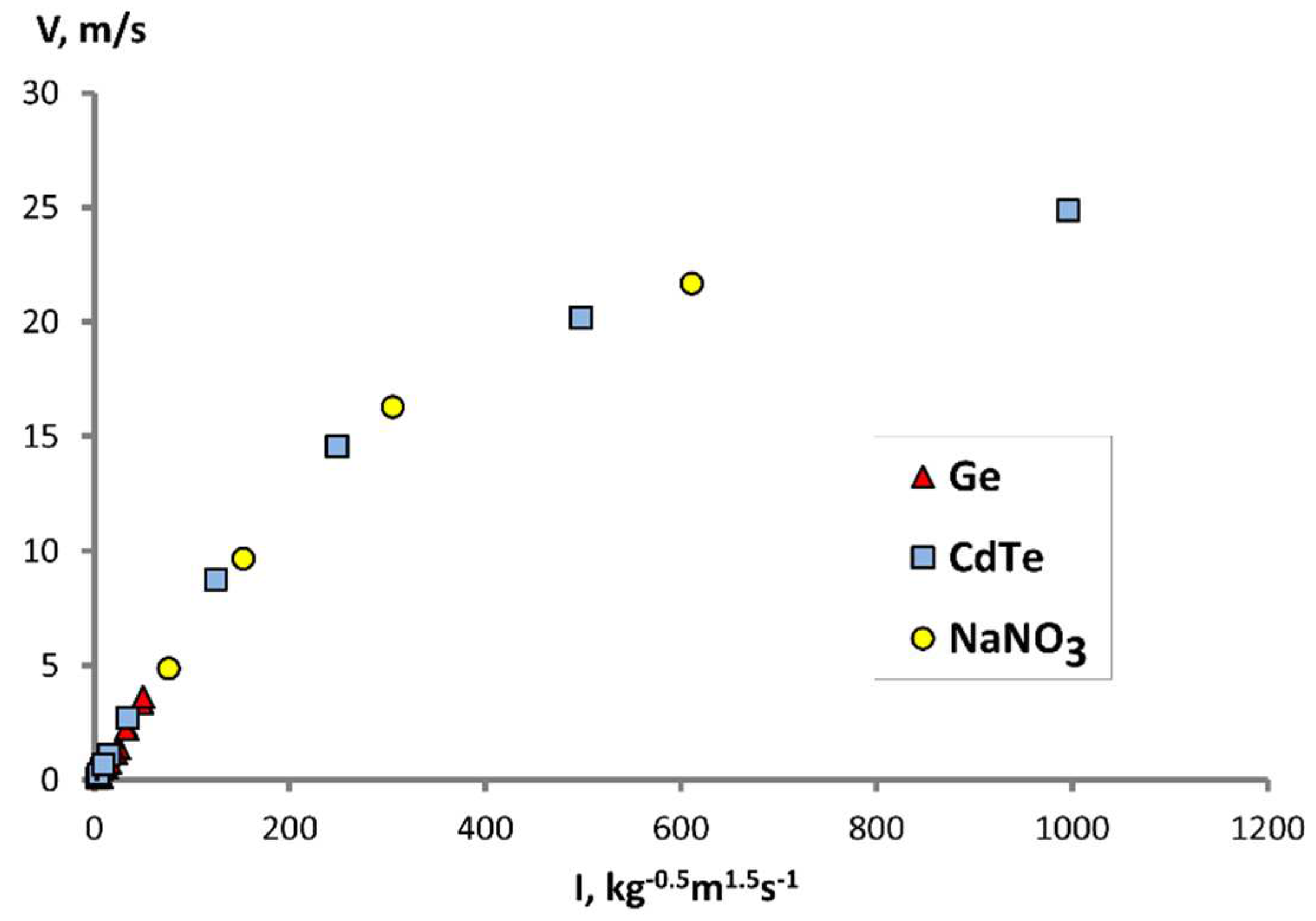
To analyze the influence of oscillatory parameters and physical properties of the substance on the nature of the flow, the modulus of the maximum flow velocity along the central axis was taken as a flow characteristic. We tried to find a power-law relationship (n_i) between the speed, amplitude A, angular frequency ω, disk edge radius R, melt density ρ and dynamic viscosity µ:

v ~ A^{n_{1}} ω^{n_{2}} R^{n_{3}} ρ^{n_{4}} μ^{n_{5}} .

(7)

In the case of laminar stationary motion, the data must fit into a linear relationship. As a result of selecting the degrees of n_i, we revealed (Figure 6) that the speed of the melt motion should be proportional to the expression, which for brevity we will denote as I and will call the intensity of oscillations:

v ~ \frac{ρ^{0.5} A^{3} ω^{2}}{R μ} ~ I .

(8)

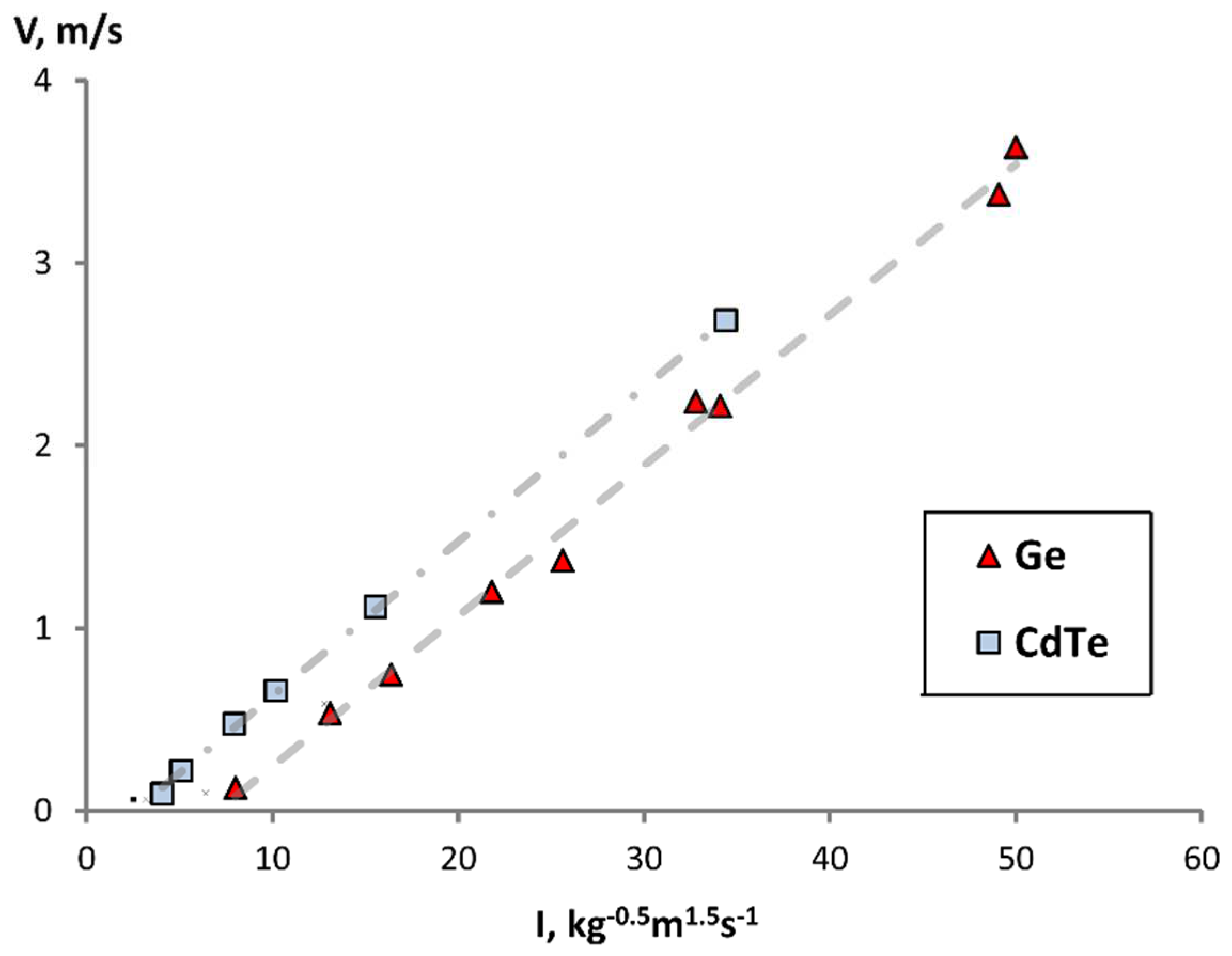
In the region of low frequencies and vibrations (Figure 7), in which the points of Ge and CdTe fall, a linear dependence is observed with a general slope of the straight line. The role of the shift of lines will be discussed in Section 4 when analyzing the obtained dependence. We observe that the linear dependence, hence the laminar flow regime, remains in the range of oscillation intensity from 10 to 50 kg^-0.5m^1.5s^-1.

At high frequencies and amplitudes of oscillations (Figure 6), which included points of CdTe and NaNO₃ at f = 25 Hz and A = 500 μm when R changed from 0.1 mm to 0.8 mm, it is clear that the mode of the melt flows is turbulent (Figure 8 and Figure 9). Separation vortices begin to form here, which are transferred from the edge of the disk to the region of the secondary vortex, leading to a change in the speed of the secondary vortex. 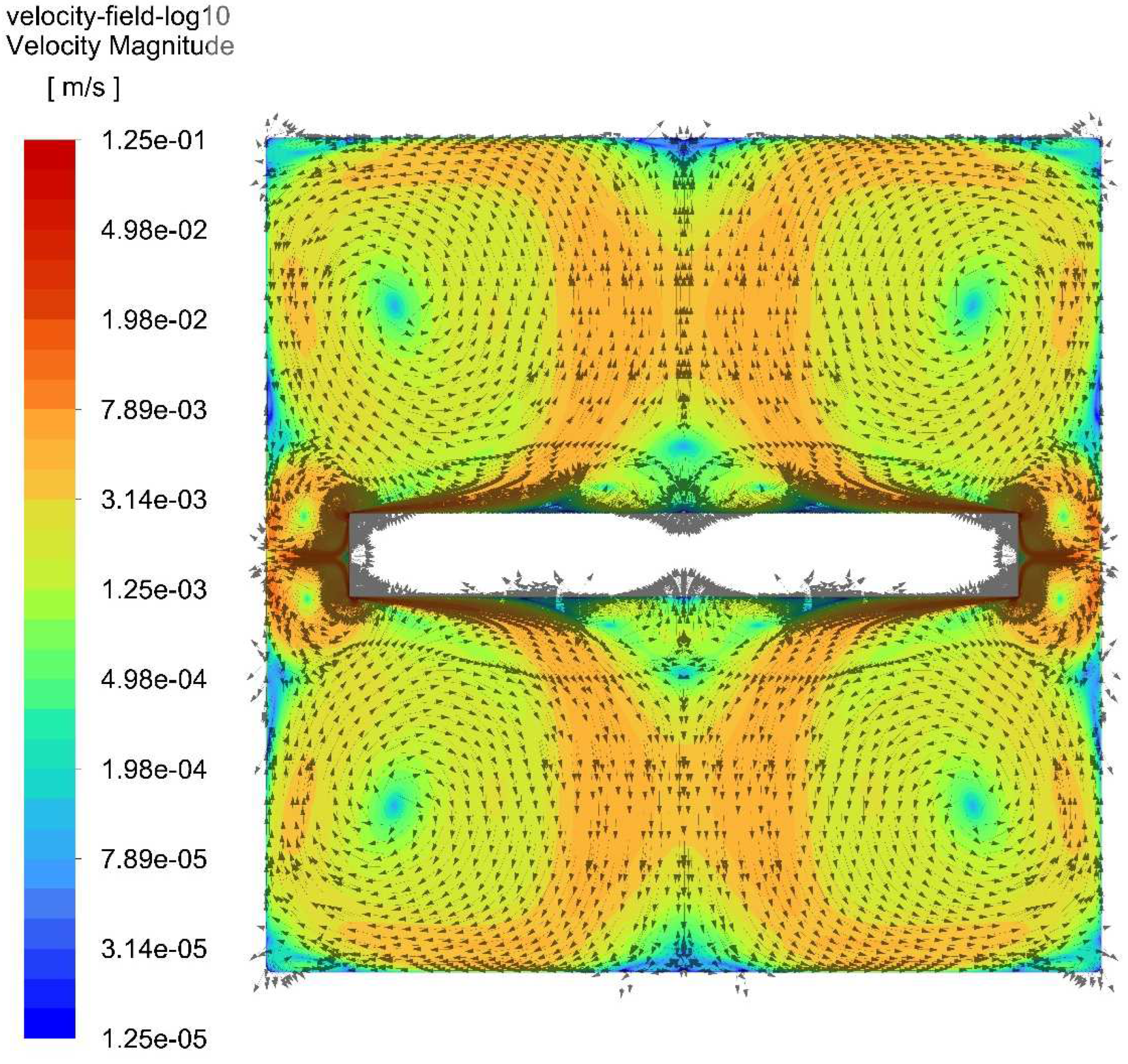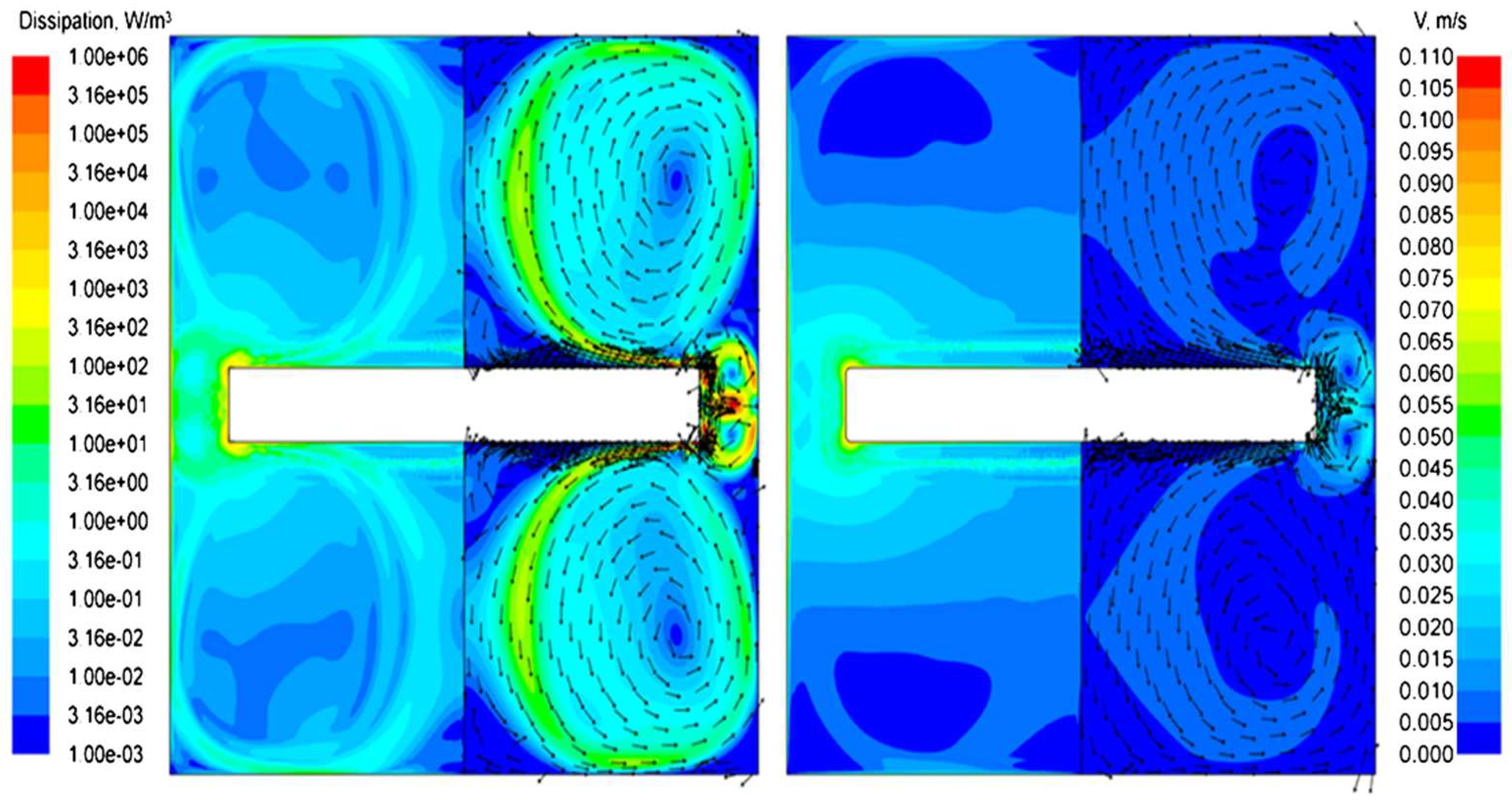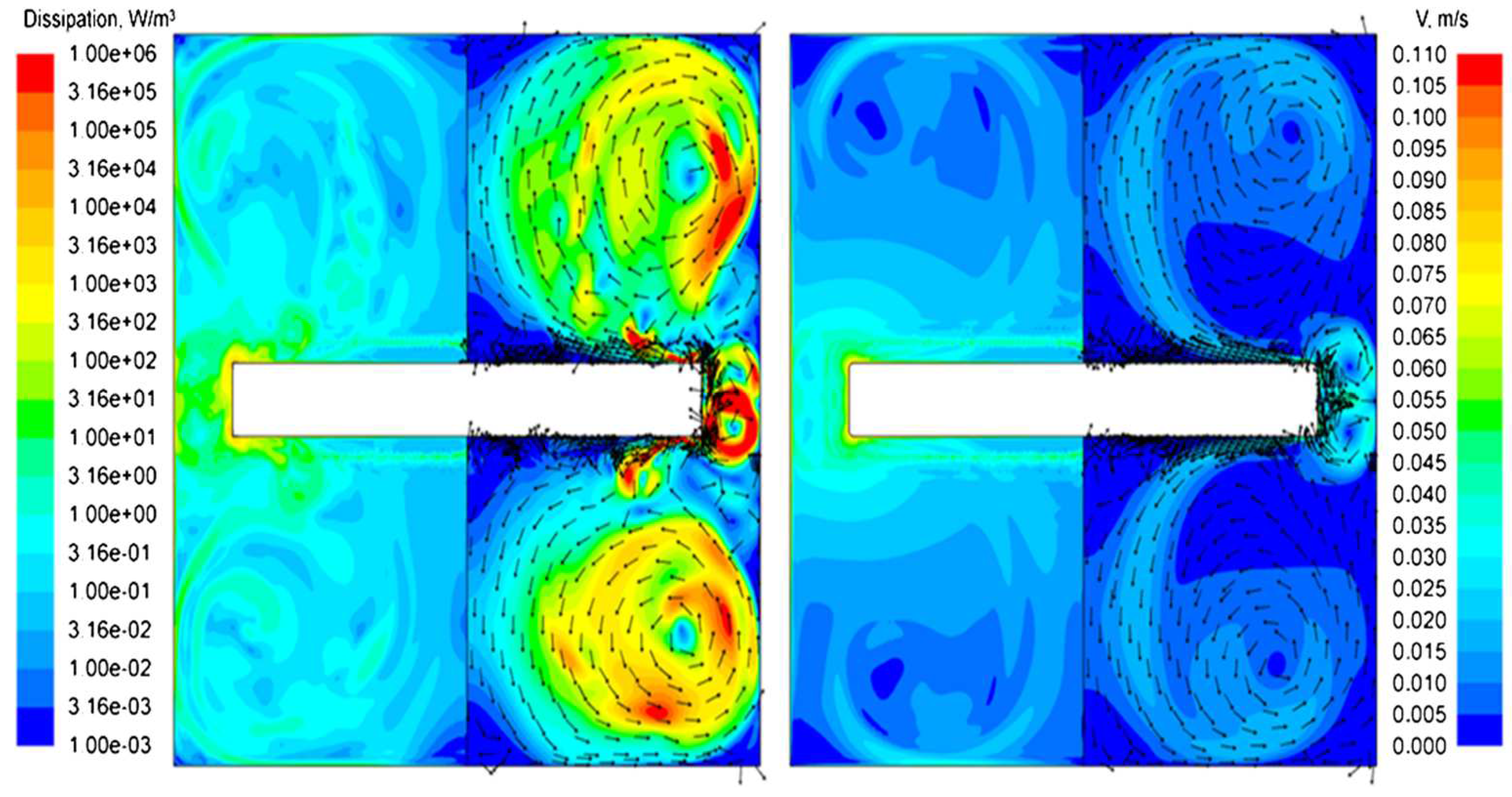This is most clearly visible in the velocity field of CdTe melt at R = 0.1 mm, where several small vortices can be seen that leave the disk edge and propagate into the central flow. Also, in the central region under the disk, a reverse flow occurs more actively, which also leads to a redistribution of velocity on the axis. It can be seen that with a decrease in the radius of the disk edge, this regime stabilizes, gradually reducing to a laminar flow regime.

3.2. AVC thermodynamic control

We carried out a detail analysis of R influence on generation and on parameters of steady vibrational flows as well as on viscous dissipation energy (P_w), determined by the expression

P_{w} = μ \cdot {(2 σ_{i j})}^{2},

(9)

σ_{i j} = \frac{1}{2} (\frac{\partial v_{i}}{\partial x_{j}} + \frac{\partial v_{j}}{\partial x_{i}}) .

(10)

During crystal growth process the average vibrational flows are responsible for heat-mass-transfer, while P_w determines structure characteristics of the melt of a complex chemical composition [16]. Numerical simulation showed that the mean velocity of vibrational flows was inversely to R and demonstrated a non-linear increase with AVC amplitude (A). Integral viscous dissipation energy for the whole melt volume, which can be processed by integrating equation (9) over the volume, demonstrated the cubic dependence vs the oscillating velocity and inverse proportionality to edge radius: P_w ~ A³ω³R^-1. The maximum viscous dissipation (Figure 10) near the disc edge is also proportional to oscillating velocity and inverse proportionality to edge radius A³ω³R^-1, but it increases faster with 3.8 number exponents.

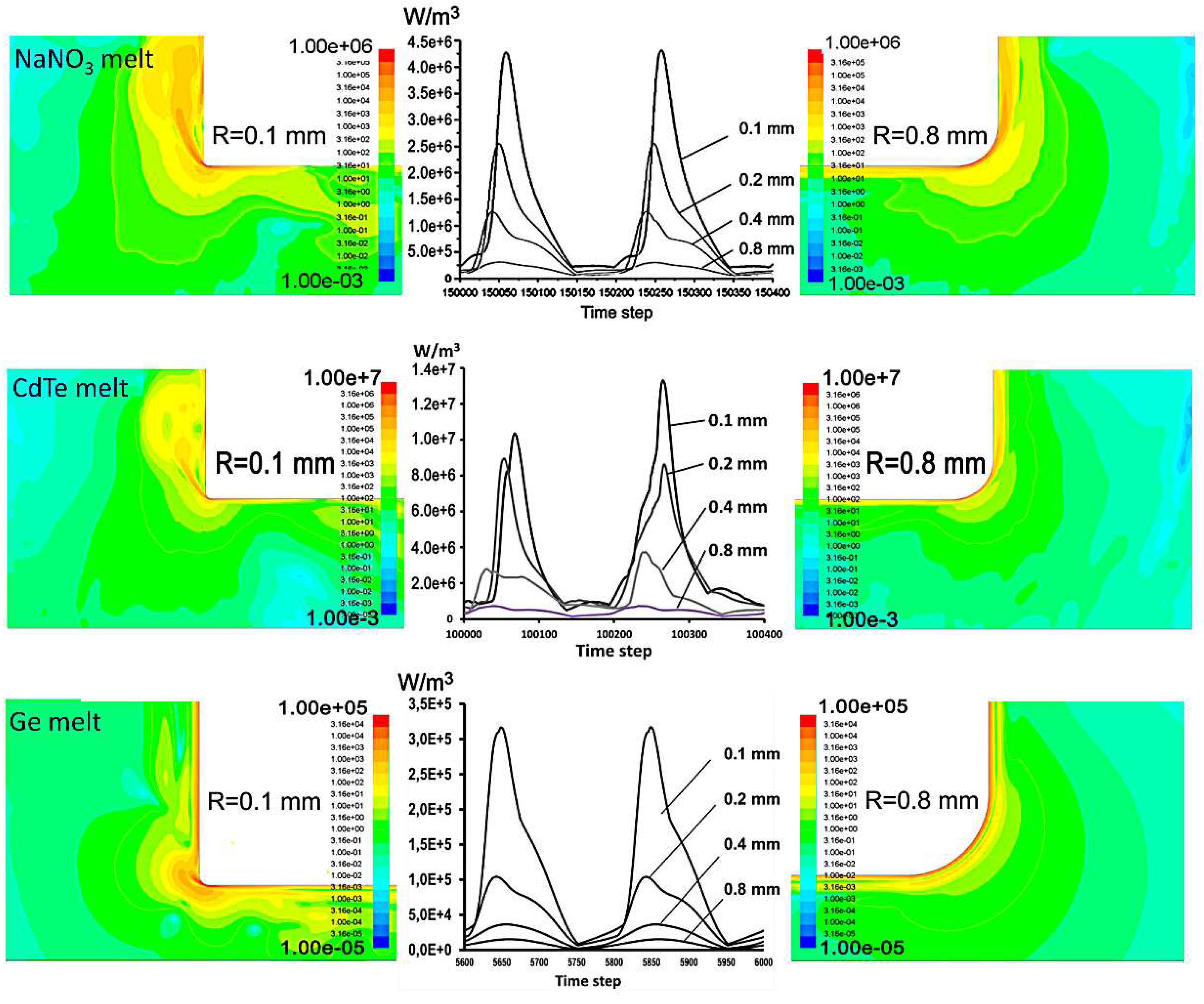
In the case of NaNO₃ melt, the most stable values of viscous dissipation energy were obtained, since at f = 25 Hz, A = 500 μm its flow, despite the formation of separation vortices, is still stable. Under these conditions, CdTe melt is in a stronger turbulent regime, which is expressed in variable values of the maximum dissipation energy. In the case of Ge-melt at f = 25 Hz, A = 500 μm, an extremely unstable turbulent regime of oscillatory flow is achieved, so we calculated the dissipation energy for the parameters f = 25 Hz, A = 100 μm.

Recalculation of an instant maximum dissipation rate for 0.1 mm edge radius, results in ~220 Joule/mole per second in the case of NaNO₃ melt; and ~330 Joule/mole per second for CdTe melt in one cubic nanometer near the disk edge. These values match the approximation for energy of cluster formation in a liquid phase [23]. For Ge at R = 0.1 mm we are able to introduce only ~2-3 Joule/mole per second in one cubic nanometer near the disc edge. This energy is enough to organize the laminar flow motion in the melt for desired heat-mass transfer, but it is insufficient to change the Ge melt thermodynamic state with respect to components' composition.

4. Discussion

The resulting dependence of the velocity v on the intensity I (eq. 8) is primarily a mathematical correlation, but it is also possible to speculate on its physical interpretation. The equation (8) could be transformed to the form:

ρ {(v - v_{0})}^{2} = b^{2} \frac{A^{6} ω^{4}}{R^{2} ν^{2}} = {(\frac{A^{2} ω}{ν} \cdot \frac{A}{R} \cdot b ω)}^{2},

(11)

where b is the proportionality coefficient,

ν = μ / ρ

is the kinematic viscosity. We see that the left side of the equation is reduced to the form of dynamic pressure of the melt. On the right side of the equation, the factor

{R e}_{s} = A^{2} ω / ν

) represents the Reynolds number for a stationary melt flow during oscillatory motion of the disk, and the factor

ε = A / R

is the ratio of the oscillation amplitude to the characteristic size of the body. Also, the factor

ε

can be interpreted as the ratio of the oscillatory velocity to the flow velocity, and this hints to us that this ratio must contain some other characteristic size, which is a function of R, since the flow velocity near the edge of the disk is 10 times greater than the oscillatory flow velocity 20 times, as stated earlier. In the case of direct proportionality, the missing parameter is included in b.

Both quantities are dimensionless, therefore, in the expression

ρ {(v - v_{0})}^{2} = {R e}_{s}^{2} \cdot ε^{2} \cdot {(b ω)}^{2},

(12)

Figure 10. Numerical simulation of momentum viscous dissipation in NaNO₃, CdTe (f = 25 Hz, A = 500 μm) and Ge (f = 25 Hz, A = 100 μm) melts activated by oscillation of cylindrical disc with different curvature of a sharp edge (R).

The factor

{(b ω)}^{2}

, obviously, must also be equal in dimension to pressure. Then you can evaluate:

[b^{2}] = [m / l] = [k g \cdot m^{- 1}],

(13)

and get that

\frac{ρ {(v - v_{0})}^{2} l}{m ω^{2}} = \frac{ρ {(v - v_{0})}^{2}}{∆ p} = {R e}_{s}^{2} \cdot ε^{2},

(14)

ρ {(v - v_{0})}^{2} = {R e}_{s}^{2} \cdot ε^{2} \cdot ∆ p .

(15)

The resulting expression is very similar in appearance to Bernoulli’s law for an ideal fluid with corrections for viscous dissipation. From the obtained dependence we can assume that

v_{0}

is the limiting speed at which the speed of the secondary vortex along the axis is determined only by the speed of oscillation of the disk. At low frequency and amplitude of oscillations,

{R e}_{s}^{2}

will decrease quite quickly, and then the right side will tend to zero. Also, an increase in the radius of the disk edge will lead to a decrease in the parameter

ε^{2}

, which in the limiting case will also lead to zeroing of the right side. At small values of

{R e}_{s}^{2}

and

ε^{2}

, a regime of complete flow around the disk should occur when it oscillates in a liquid, where the maximum velocity is concentrated in a thin layer near the disk. However, to confirm this hypothesis, it is necessary to conduct a study of fluid flow in the region of small amplitudes and vibration frequencies, as well as expand the nomenclature of materials.

To correctly identify the value of

b^{2}

and determine what pressure gradient ∆p is implied in the resulting recording, as well as to ensure the reliability of the calculation obtained, it is necessary to conduct additional studies of the velocity values for sodium nitrate in the laminar region, as well as for germanium in the turbulent region, and to consider the relationship of parameters with other speeds - for example, the maximum speed at the edge of the disk, as well as in the space between the disk and the crucible. These questions are of interest for further development of the study.

The obtained proportional dependence is useful in that it allows estimating the order of the speed of movement of the melt in the region near the crystallization front, since the flow motion speed along the axis and along the bottom wall are approximately equal for laminar stationary oscillatory motion. From the correlation (Figure 6) we obtain that the slope of the curve is 8.3∙10^-5 kg^0.5m^-0.5. This value, together with the oscillation intensity I, can be used when estimating the oscillatory contribution of melt motion in real crystal growth processes, where the main driving force of the process is thermal convection or diffusion.

5. Conclusions

The effects of AVC can be divided into two parts: 1) it is possible to control the oscillatory movement of the liquid in the melt and create vibration flows controlled in speed and configuration; 2) creation of average fast stable flows that provide a given heat and mass transfer and dominate over thermoconvective flows.

We were able to determine the linear dependence of the maximum melt velocity along the central axis on such system parameters as amplitude, frequency, radius of the disk edge, density and viscosity of the melt when the disk oscillates in a closed crucible. An assessment was made of the intensity of oscillations I, at which a stable mode of oscillatory flow is maintained, which ranges from 10 to 50 kg^-0.5m^1.5s^-1. An analysis of the obtained dependence was also carried out and a possible relationship between the parameters was identified, however, to confirm the obtained result it is necessary to collect a large sample of data.

Author Contributions

Conceptualization, O.N. and A.D.; methodology, V.K.; software, O.N., A.D. and V.K.; validation, I.A. and B.L..; formal analysis, B.L.; investigation, O.N., A.D., V.K. and B.L.; resources, I.A.; data curation, B.L.; writing—original draft preparation, I.A. and A.D.; writing—review and editing, O.N. and A.D.; visualization, B.L.; supervision, V.K.; project administration, I.A.; funding acquisition, A.D. All authors have read and agreed to the published version of the manuscript

Funding

This research was funded by the Ministry of Science and Higher Education of Russia through the project FSSM-2022-0005.

Data Availability Statement

Not applicable.

Acknowledgments

The authors are grateful to the Mendeleev Center for the Collective Use of Scientific Equipment for computational resources.

Conflicts of Interest

The authors declare no conflict of interest.

References

Progress in Nanoscale and Low-Dimensional Materials and Devices; Ünlü, H.; Horing, N. J. M. (Eds.) Topics in Applied Physics; Springer International Publishing: Cham, 2022; Volume 144. [Google Scholar] [CrossRef]
Available online: https://www.simco-groups.com/market_segment/crystal-growth (accessed on 17 December 2023).
Rudolph, P. Contributions to the Development of Crystal Growth Technologies. J. Cryst. Growth 2024, 625, 127456. [Google Scholar] [CrossRef]
Milisavljevic, I.; Wu, Y. Current Status of Solid-State Single Crystal Growth. BMC Mater. 2020, 2, 2. [Google Scholar] [CrossRef]
Frank-Rotsch C, Dropka N, Rotsch P. III Arsenide . In Single crystals of electronic materials: growth and properties; Fornari, R. (Ed.) Woodhead Publishing: Cambridge, 2018; pp. 181–240. [Google Scholar]
Kearns, JK. Kearns JK. Silicon single crystals. In Single crystals of electronic ma-terials: growth and properties; Fornari, R, Ed.; Elsevier Ltd: Amsterdam, 2019; pp. 5–56. [Google Scholar]
Kozhemyakin, G. N. Imaging of Convection in a Czochralski Crucible under Ultrasound Waves. J. Cryst. Growth 2003, 257, 237–244. [Google Scholar] [CrossRef]
Kozhemyakin, G. N.; Nemets, L. V.; Bulankina, a. a. Simulation of Ultrasound Influence on Melt Convection for the Growth of GaxIn1−xSb and Si Single Crystals by the Czochralski Method. Ultrasonics 2014, 54, 2165–2168. [Google Scholar] [CrossRef] [PubMed]
Scheel, H. J.; Schulz-Dubois, E. O. Flux Growth of Large Crystals by Accelerated Crucible-Rotation Technique. J. Cryst. Growth 1971, 8, 304–306. [Google Scholar] [CrossRef]
Zawilski, K. T.; Custodio, M. C. C.; Demattei, R. C.; Feigelson, R. S. Control of Growth Interface Shape Using Vibroconvective Stirring Applied to Vertical Bridgman Growth. J. Cryst. Growth 2005, 282, 236–250. [Google Scholar] [CrossRef]
Ostrogorsky, A. G.; Riabov, V.; Dropka, N. Interface Control by Rotating Submerged Heater/Baffle in Vertical Bridgman Configuration. J. Cryst. Growth 2018, 498, 269–276. [Google Scholar] [CrossRef]
Kokh, A. E.; Kononova, N. G. Crystal Growth under Heat Field Rotation Conditions. Solid. State. Electron. 2000, 44, 819–824. [Google Scholar] [CrossRef]
Miller, W.; Frank-Rotsch, C.; Czupalla, M.; Rudolph, P. Numerical Modelling of Czochralski Growth of Quadratic Silicon Crystals by Means of a Travelling Magnetic Field. Cryst. Res. Technol. 2012, 47, 285–292. [Google Scholar] [CrossRef]
Golyshev, V. .; Gonik, M..; Tsvetovsky, V.. Problems of Bi4Ge3O12 and Li2B4O7 Single Crystal Growth by Crusibleless Variant of AHP Method. J. Cryst. Growth 1999, 198–199, 501–506. [Google Scholar] [CrossRef]
Uda, S.; Koizumi, H.; Nozawa, J.; Fujiwara, K. Crystal Growth under External Electric Fields; 2014; pp. 261–264. [Google Scholar] [CrossRef]
Sadovskiy, A.; Sukhanova, E.; Belov, S.; Kostikov, V.; Zykova, M.; Artyushenko, M.; Zharikov, E.; Avetissov, I. Axial Vibration Control of Melt Structure of Sodium Nitrate in Crystal Growth Process. J. Cryst. Growth 2015, 417, 16–24. [Google Scholar] [CrossRef]
Avetissov, I.; Sadovskiy, A.; Belov, S.; Khomyakov, A.; Rekunov, K.; Kostikov, V.; Sukhanova, E. Thermodynamic Features of Axial Vibrational Control Technique for Crystal Growth from the Melt. CrystEngComm 2013, 15, 2213–2219. [Google Scholar] [CrossRef]
O. Barinova, A.Sadovskiy, I.Ermochenkov, S.Kirsanova, E.Sukhanova, V.Kostikov, S.Belov, E.Mozhevitina, A.Khomyakov, Z.Kuchuk, E.Zharikov, I. A. Li2MoO4 Crystal Growth from Solution Activated by Low-Frequency Vibrations. J. Cryst. Growth 2016. [CrossRef]
Fadeev, G. N.; Boldyrev, V. S.; Bogatov, N. A.; Nikolaev, A. L. Inhibition of Redox Reactions in a Low-Frequency Field. Dokl. Phys. Chem. 2019, 487, 91–93. [CrossRef]
Avetissov, I. C.; Sadovskiy, A. P.; Sukhanova, E. A.; Orlova, G. Y.; Belogorokhov, I. A.; Zharikov, E. V. Perfection of NaNO 3 Single Crystals Grown by Axial Vibrational Control Technique in Czochralski Configuration. J. Cryst. Growth 2012, 360, 167–171. [CrossRef]
Sadovsky, A.; Ermochenkov, I.; Dubovenko, E.; Sukhanova, E.; Bebyakin, M.; Dubov, V.; Avetissov, I. Potassium-Cobalt Sulphate Crystal Growth Assisted by Low Frequency Vibrations. J. Cryst. Growth 2018, 483, 31–38. [CrossRef]
Avetissov, I. C.; Sukhanova, E. A.; Khomyakov, A. V.; Zinovjev, A. Y.; Kostikov, V. A.; Zharikov, E. V. Simulation and Crystal Growth of CdTe by Axial Vibration Control Technique in Bridgman Configuration. J. Cryst. Growth 2011, 318, 528–532. [CrossRef]
Doye, J. P. K. The Structure, Thermodynamics and Dynamics of Atomic Clusters, Gonville & Caius College. 1996. Available online: http://doye.chem.ox.ac.uk/jon/PhD2/PhD.html .

Figure 1. Grid of calculation area (left) with grid extension near vibrating disk (right): 1— stationary zones, 2— stress– strained zone, 3—rigid zones.

Figure 2. Velocity field near the edge of the disk at the highest top position of the disk (f = 25 Hz, A = 100 μm) for Ge melt.

Figure 3. Normalized instantaneous velocity at the edge of the disk (f = 25 Hz, A = 100 μm, R= 0.1 mm) for Ge and CdTe melts with residual fluid movement when the oscillating disk stops at bottom dead center.

Figure 4. The separated flow in Ge melt when the disk moves downward (f = 25 Hz, A = 100 μm, R= 0.1 mm).

Figure 5. The velocity field of flows in Ge melt at the lowest bottom position of the oscillating disk (f = 25 Hz, A = 100 μm).

Figure 6. Dependence of the modulus of the maximum speed of melts along the central axis on the of oscillation intensity (I).

Figure 7. Dependence of the modulus of the maximum velocity of melts along the central axis on the intensity of oscillations I on the scale of laminar stationary oscillatory flow of the melt.

Figure 8. Numerical simulation of momentum viscous dissipation rate (left half of the simulated volume, see section 3.2) and velocity contours colored by velocity magnitude and supported by velocity vectors for NaNO₃ melt activated by oscillation (f = 25 Hz, A = 500 μm) of cylindrical disc with an edge radius 0.1 mm (left) and 0.8 mm (right).

Figure 9. Numerical simulation of momentum viscous dissipation rate (left half of the simulated volume, see section 3.2) and velocity contours colored by velocity magnitude and supported by velocity vectors for CdTe melt activated by oscillation (f = 25 Hz, A = 500 μm) of cylindrical disc with an edge radius 0.1 mm (left) and 0.8 mm (right).

Table 1. Geometrical parameters of the numerical model.

Parameter	Value, mm
Simulating area length	100
Simulating area height	100
Disk diameter, D	80
Disk thickness, d	10
Edge radius, R	0.1; 0.2; 0.4; 0.8
Distance from the disk to the bottom and top walls	45
Disk oscillation amplitude, A	0.080 – 0.500
Frequency oscillation, f	10 – 30 Hz

Table 2. Properties of the melts under study at T=T_m+5 K.

Property	Value
Property	NaNO₃	Ge	CdTe
Melting temperature, T_m (K)	579.95	1211.4	1369
Density, ρ (kg/m³)	1903	5490	5661.8
Dynamic viscosity, μ (Pa s)	2.2×10^-3	7.14×10^-4	2.33×10^-3

Table 3. Modules of the maximum melt velocity along the central axis at various values of amplitude, frequency, disk edge radius and intensity.

f, Hz	A, μm	R, mm	I, kg^0.5m^1.5s^-1	v, mm∙s^-1
Ge
10	125	0.1	8.00	0.126
10	200	0.1	32.77	2.240
20	100	0.1	16.39	0.744
20	110	0.1	21.81	1.199
25	80	0.1	13.11	0.535
25	100	0.1	25.61	1.370
25	110	0.1	34.08	2.217
25	125	0.1	50.01	3.635
30	110	0.1	49.08	3.376
25	100	0.2	12.80	0.587
25	100	0.4	6.40	0.096
25	100	0.8	3.20	0.060
25	50	0.05	6.40	0.096
CdTe
10	125	0.1	2.49	0.064
10	200	0.1	10.20	0.657
10	300	0.1	34.42	2.683
20	100	0.1	5.10	0.217
25	80	0.1	4.08	0.091
25	100	0.1	7.97	0.474
25	125	0.1	15.56	1.114
25	500	0.1	996.03	24.86
25	500	0.2	498.01	20.18
25	500	0.4	249.01	14.55
25	500	0.8	124.50	8.757
NaNO₃
25	500	0.1	611.57	21.67
25	500	0.2	305.79	16.27
25	500	0.4	152.89	9.655
25	500	0.8	76.45	4.857

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer