Tensile and Compressive Properties of woven fabric CFRP Laminates Containing Three-Dimensional Microvascular Channels

Preprint

Article

Tensile and Compressive Properties of woven fabric CFRP Laminates Containing Three-Dimensional Microvascular Channels

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

Ziqian An

Xiaoquan Cheng^*

,Dafang Zhao,Yihao Ma,Xin Guo,Yujia Cheng

Ziqian An

Xiaoquan Cheng^*

,Dafang Zhao,Yihao Ma,Xin Guo,Yujia Cheng

This version is not peer-reviewed

Submitted:

06 January 2024

Posted:

08 January 2024

You are already at the latest version

Alerts

Abstract

Microvascular self-healing composite materials have significant potential for application and their mechanical properties need in-depth investigation. In this paper, tensile and compressive properties of woven fabric carbon fiber reinforced polymers (CFRP) laminates containing three-dimensional microvascular channels were investigated experimentally. Several detailed finite element (FE) models were established to simulate the mechanical behavior of the laminate and the effectiveness of different models were examined. The damage propagation process of the microvascular laminates and the influence of microvascular parameters were studied by the validated models. The results show that microvascular channels arranged along the thickness direction (z-direction) of the laminates are critical locations under the loads. The channels have minimal effect on the stiffness of the laminates but causing a certain reduction in strength, which varies approximately linearly with the z-direction channel diameter within its common design range of 0.1~1mm. It is necessary to consider the resin-rich region formed around microvascular channels in the warp and weft fiber yarns of the woven fabric composite when establishing the FE model. And the layers in model should be assigned with equivalent unidirectional ply material in order to calculate the mechanical properties of laminates correctly.

Keywords:

Subject: Engineering - Aerospace Engineering

1. Introduction

Due to the poor interlaminar performance of fiber-reinforced polymer composite laminates and the shortcomings of existing non-destructive testing and repair methods for composite structures [1], the microvascular self-healing structural polymers and fiber-reinforced composites have been proposed and developed [2,3,4,5,6]. Inspired by the self-healing characteristics of organisms after injury, these materials use micro channels to transport healing agents to promptly repair delamination damage or matrix cracks [7]. This approach can effectively reduce maintenance costs, improve safety, and extend structures’ service life if implemented.

However, the microvascular channels can also be regarded as initial damage that affect the mechanical properties of the structure. Therefore, it is necessary to thoroughly study the mechanical performance of laminates containing microvascular channels so that to determine appropriate design parameters in actual structures.

Kousourakis et al. [8] tested the tensile and compressive properties of laminates containing micro channels located in mid-plane of the laminate. As the diameter of the microvascular increased from 0.3 mm to 3 mm, the strength and stiffness of the specimens with longitudinally oriented channels decreased by less than 10%. While the performance of the specimens with transversely oriented channels decreased significantly, with a maximum reduction in tensile strength of 50%. The main reason for the significant performance loss was the bending of fibers around the channels which resulting in a change of the stress state. Devi et al. [9] also reached similar conclusions. Saeed et al. [10] conducted three-point bending and short beam strength tests on laminates containing in-plane microvascular channels and found that both the bending strength and short beam strength of the specimens linearly decreased as the diameter of the channels increased. With a channel diameter of 1.5 mm, the short beam strength decreased by about 33%, and the bending strength decreased by about 15%. Coppola et al. [11] investigated tensile properties and damage propagation of 3D orthogonally woven glass fiber composites containing straight and undulating wave-shaped micro channels and found that reductions in strength and modulus only occurred when channels distorted the fiber architecture. Norris et al. [12] found that cutting the fibers around the channel can prevent the formation of resin-rich region, but this will lead to a more significant decrease in the mechanical performance of the laminate.

Some researchers have also attempted to conduct studies using finite element methods. Nguyen and Orifici [13] first conducted experiments on laminates containing micro channels with a diameter of 0.68 mm. They found that the tensile stiffness of the laminate perpendicular to the microvascular could decrease by up to 7.5%, and the compressive strength could decrease by 4.9%, while the performance decrease along the direction of the channel was not significant. They further established a representative volume element (RVE) model of the microvascular channel. The composite plies were modeled using continuous shell elements, and the two-dimensional Hashin criterion was used to determine the damage of the composite material. The resin-rich region was considered and the numerical results of mechanical performance and failure modes were in good agreement with the experimental results. Huang et al. [14] established a plane strain model, while Shawk et al, [15], Demiral et al. [16] and Zhao et al. [17] established three-dimensional models to study the influence of in-plane microvascular on different mechanical properties of laminates. Ran et al. [18] also considered the variation in fiber volume fraction in the area around the microvascular where fibers are bent in FE model. Compared to models that do not consider this factor, the calculated results of laminate strength and stiffness were more accurate.

It is evident that current researchers primarily focus on laminates with one-dimensional microvascular arranged between composite layers. A few studies have conducted research on three-dimensional microvascular but lacked simulation analysis. As delamination damage can occur at any position within the laminate during the structures’ manufacturing and service period [19]. In-plane micro channels can only repair damage between specific layers. And arranging channels in multiple layers would lead to a significant decline in the laminate's mechanical performance. Therefore, utilizing in-plane microvascular to transport healing agents, and z-direction microvascular to repair delamination damage at different position is more practical. It is essential to study the mechanical performance of laminates with such three-dimensional microvascular configuration.

In this paper, the tensile and compressive properties of woven fabric CFRP laminates containing three-dimensional microvascular were investigated experimentally. Detailed finite element models with resin-rich region and variations in fiber volume fraction around the microvascular were established, which were employed to study the damage propagation of laminates under tensile and compressive loads. And the effects of microvascular parameters, including diameter, spacing and volume fraction, on the tensile and compressive properties of the laminates were discussed. The study aims to provide reference and basis for the design of microvascular composite structures.

2. Experiment

2.1. Specimen manufacture

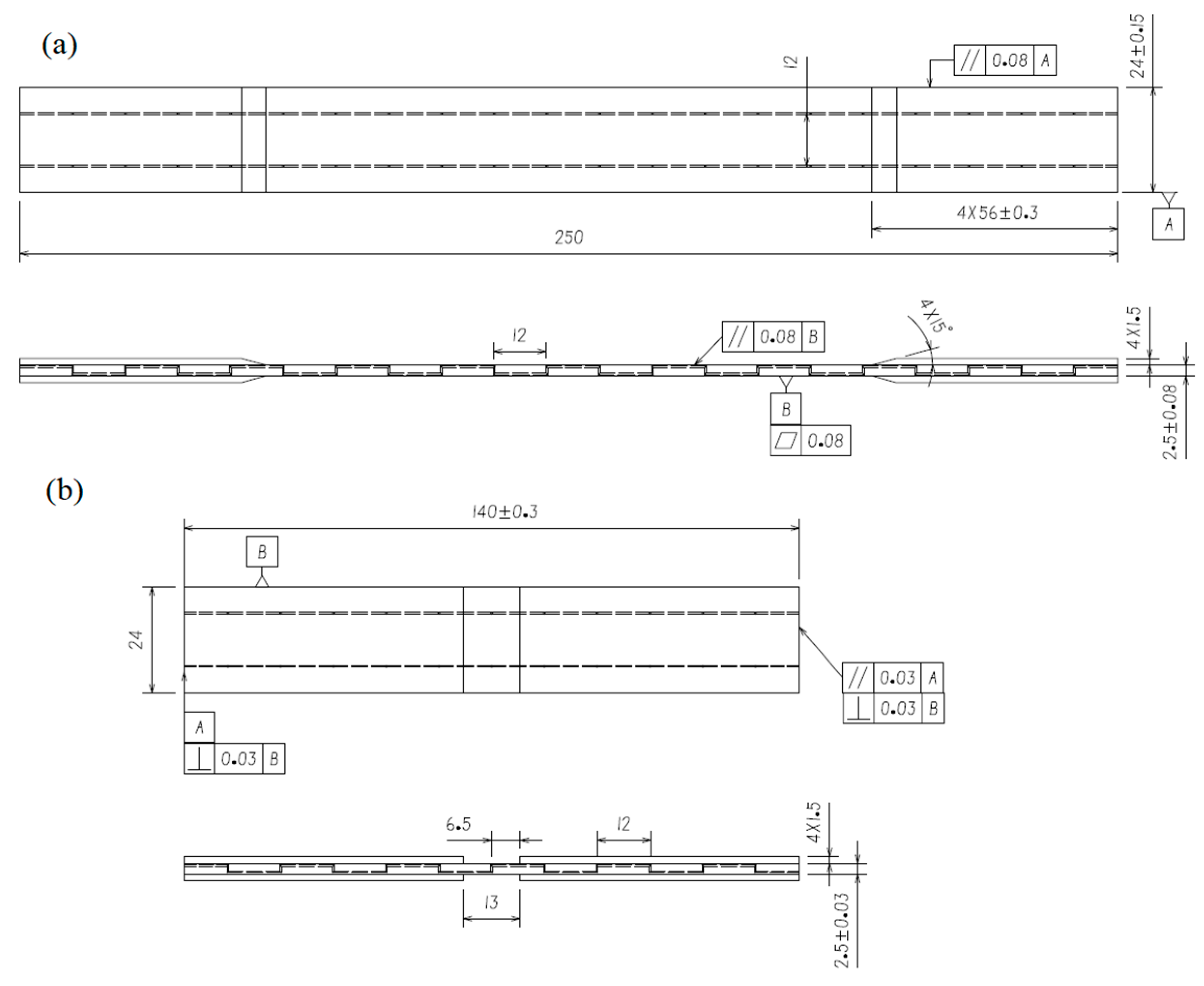
The tensile and compression specimens containing microvascular were designed according to the ASTM D3039 and D6641 standards. The specimens contain two parallel, three-dimensional microvascular channels, as illustrated in Figure 1. The laminates are made of CF3031 carbon fiber fabric and 5284 epoxy resin, with the mechanical properties listed in Table 1. The layup of the specimens is [(0,90)/±45/(0,90)/±45/(0,90)]s, with a nominal thickness of 0.25mm per layer. The width of the specimens is 24mm, and the spacing of the z-direction channels is 12mm. The diameter of the channel is 0.5mm, with the in-plane channels located two layers beneath the surface of the specimen, as illustrated in Figure 2. For compression specimens, care was taken during preparation to ensure the presence of z-direction channel within the gage section. Blank specimens were also prepared as controls.

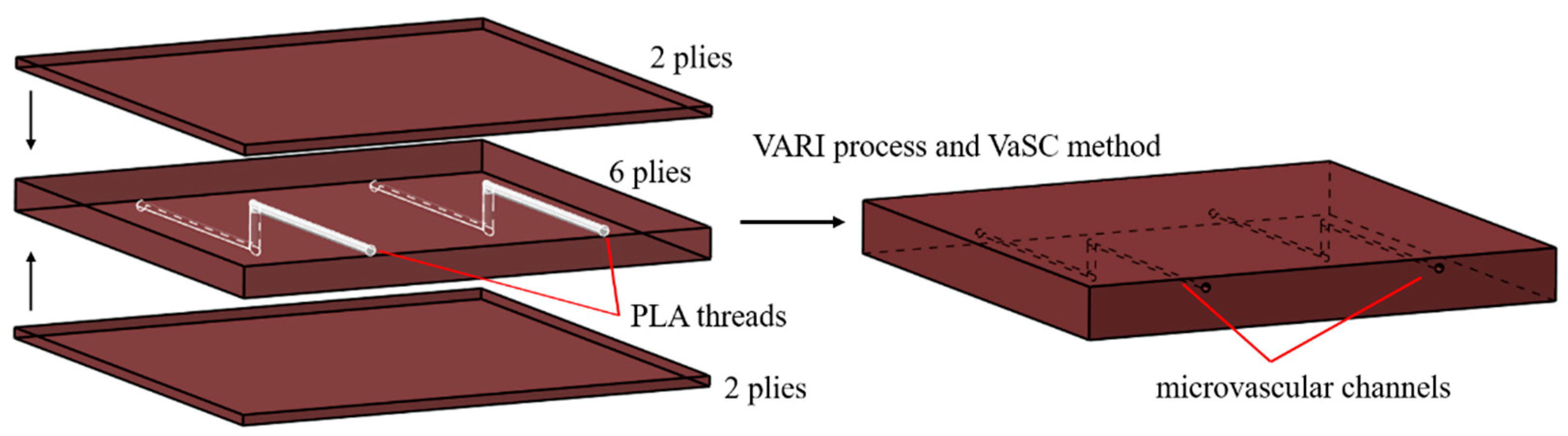
The specimens were manufactured using the vacuum assisted resin infusion (VARI) process. The microvascular channels were created using a vaporization of sacrificial component (VaSC) method. First, the carbon fiber woven fabric was manually laid to form a preform. Then, polylactic acid (PLA) threads were sewn into the preform at predetermined intervals. This process caused local bending of fibers adjacent to the sacrificial threads but did not cut the fibers. After this, the VARI process was used for resin impregnation and curing. Finally, the PLA threads were evaporated in an oven, leaving hollow channels. Catalyst was added into the PLA threads to lower its decomposition temperature below the glass transition temperature of the matrix resin.

2.2. Mechanical testing

Tensile and compression tests were conducted on an INSTRON-8801 testing machine in a standard laboratory environment (23±2°C, 50%±10% relative humidity), using displacement control loading at a rate of 2mm/min. The width and thickness of the gage section of each specimen were measured three times before testing, and the average values were taken.

The tensile test was conducted according to ASTM D3039, strain in the longitudinal and transverse directions of the specimen was measured using two extensometers. The stiffness of the specimen was calculated using data from the longitudinal extensometer within the range of 1000με to 3000με. Extensometers were removed when the longitudinal strain was 5000με, then the specimen was stretched to failure. The failure load and mode were recorded. The setup of the test is shown in Figure 3.

The compression test was conducted according to ASTM D6641. Four strain gauges were used on the gage section to measure the strain of the specimen. The stiffness of the specimen was calculated using the gauges’ data within the range of 1000με to 3000με. The specimen was loaded until failure, and the failure load and mode were recorded. The location of the strain gauges and the setup of the test are shown in Figure 3.

2.3. Result and analysis

Test results are shown in Table 2. The tensile stiffness and strength of the specimens with microvascular reduced by 6.1% and 11.9% compared with control group. While the compressive strength reduced by 10.3% but the stiffness increased by 2.1%. It can be observed that the microvascular has an evident effect on the strength of the laminates, but a relatively smaller effect on stiffness. The increased stiffness of the compression specimens with microvascular may be due to the dispersion of the material properties, which has a greater effect than that of the microvascular.

The failure modes of the tensile and compression specimens are shown in Figure 4. For tensile specimens, two failed at the top of the gage section where stress concentration existed, but the strength results were not significantly lower than others. In the rest of the specimens, the z-direction channels were visible at the fracture section, suggesting that z-direction microvascular are key sections in these specimen when bearing tensile load.

For compression specimens, the primary failure mode was brooming fracture in the middle of gage section, where z-direction microvascular channel located. But it was difficult to figure out the z-direction channel due to the extensive damage in the matrix of the compression specimens.

When bearing loads, the z-direction microvascular causes stress concentration around it, thereby reducing the strength. However, since the microvascular only causes a slight bending of fibers in local areas which is also the feature of woven fabric material itself. The fibers are not cut and the total fiber volume does not change, so that the stiffness of laminates is barely affected.

3. Finite element model

To further investigate the failure mechanism of laminates containing microvascular and to conduct parametric studies, it's necessary to establish a detailed finite element model. But modeling the whole structure is too hard to achieve. It's advisable to consider microvascular in two parts: in-plane microvascular and z-direction microvascular. The mechanical properties of laminates containing in-plane microvascular have been studied in some researches. And it's observed that the mechanical properties of the laminates along the direction of the in-plane channel are less affected. [8,9,11,13] Also, the experimental results in section 2 indicate that the z-direction microvascular is critical position. Therefore, the model will focus on the z-direction microvascular and its influence on the mechanical properties of the laminate.

3.1. Model generation

3.1.1. Resin-rich region

In laminates, the resin-rich region around microvascular can cause stress concentration or fiber bending, which are key factors affecting the mechanical performance of the laminate. It's important to consider the resin-rich region in the FE model. Ma et al. [20] developed a numerical method to predict the shape of resin-rich region around microvascular, and this paper refers to this method to determine the length of resin-rich region.

The z-direction microvascular in woven fabric composite will lead to formation of two perpendicular resin-rich regions within the warp and weft fiber yarns in one ply. Since the forming process involves stitching sacrificial lines into the preform before resin impregnation, the fibers are still continuous. Typical intralaminar resin-rich region in the current specimens are shown in Figure 5.

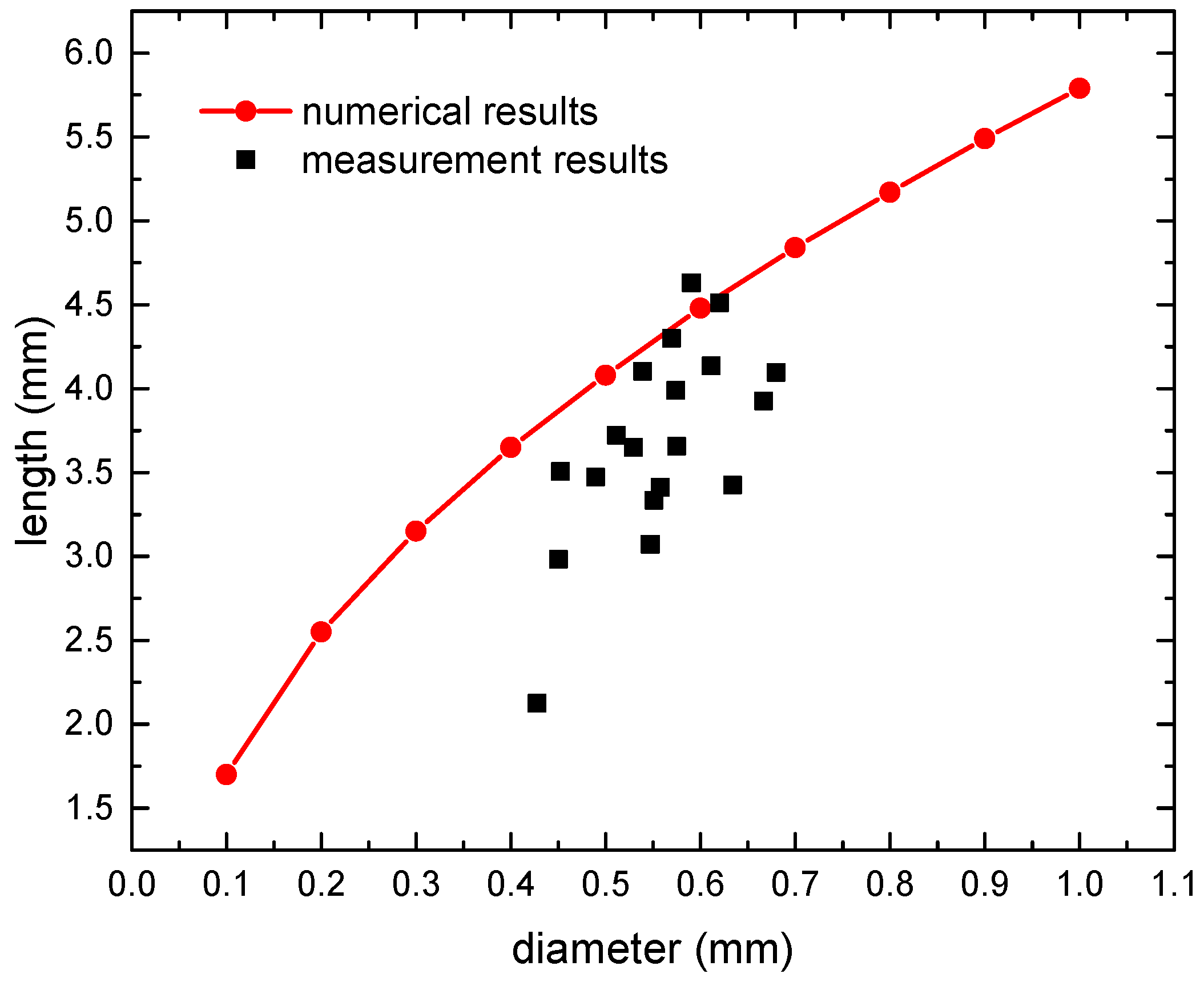
Some specimens were cut to measure the lengths of the resin-rich region. The measurement results were compared with the numerical results as illustrated in Figure 6. The measurement results show obvious dispersion, which is primarily due to the bending of fiber in the fabric material so that complete resin-rich region might not be observable on certain thickness sections. By adjusting the parameter values in the numerical methods, the calculated results exceed 95% of the measured values. The lengths of the resin-rich region used in the FE models are presented in Table 3.

3.1.2. Variation of fiber volume fraction

The fiber volume fraction around the microvascular will change as the fibers are pushed away, and the mechanical properties of the local material will be affected. literature [18] illustrated the necessity of considering this factor in in-plane microvascular model. This paper also considers this factor in the model of z-direction microvascular first, and then compares different modeling approaches without it.

Since there are two resin-rich regions in the warp and weft yarns in one layer, it is necessary to model them separately. This paper plans to divide the fabric layer into warp and weft sublayers in the model, treating each sublayer as an equivalent unidirectional ply. By assigning appropriate material properties, the mechanical performances of the combination of two sublayers will still be same with those of the original fabric material. And the properties of the sublayers and fabric layers satisfy the following relationships:

E_{L} = E_{T} = \frac{1}{2} (E_{11} + E_{22})

(1)

ν_{L} = ν_{T} = \frac{ν_{21} E_{11} + ν_{12} E_{22}}{E_{11} + E_{22}}

(2)

G_{LT} = G_{12}

(3)

X_{Lt} = X_{Tt} = \frac{1}{2} (X_{t} + \frac{X_{t}}{E_{11}} E_{22})

(4)

X_{Lc} = X_{Tc} = \frac{1}{2} (X_{C} + \frac{X_{c}}{E_{11}} E_{22})

(5)

where the subscripts L and T represent the longitudinal and transverse direction of the fabric. E_L, E_T, ν_L, ν_T, G_LT, X_Lt, X_Tt, X_Lc, X_Tc are elastic modulus, poison’s ratio, shear modulus, tensile strength and compression strength of the woven fabric. E₁₁, E₂₂, ν₁₂, ν₂₁, G₁₂, X_t, X_c are elastic modulus, poison’s ratio, shear modulus, tensile strength and compression strength of the unidirectional ply. The out-of-plane properties of the two materials are considered the same.

In order to ensure that the simulation results of the fabric material are consistent with the nominal values, it is necessary to apply correction factors when calculating the modulus and strength parameters of the unidirectional ply based on the properties of the fibers and resin. Referring to the Chamis [21] model, the calculation formulas are as follows:

E_{11} = α_{1} (V^{f} E_{11}^{f} + V^{m} E^{m})

(6)

E_{22} = α_{2} \frac{E_{22}^{f} E^{m}}{E_{22}^{f} - \sqrt{V^{f}} (E_{22}^{f} - E^{m})}

(7)

ν_{12} = α_{3} (V^{f} ν_{11}^{f} + V^{m} ν^{m})

(8)

G_{12} = α_{4} \frac{G_{12}^{f} G^{m}}{G_{12}^{f} - \sqrt{V^{f}} (G_{12}^{f} - G^{m})}

(9)

G_{23} = α_{5} \frac{G_{23}^{f} G^{m}}{G_{23}^{f} - \sqrt{V^{f}} (G_{23}^{f} - G^{m})}

(10)

X_{t} = β_{t} (V^{f} σ_{f} + V^{m} \frac{σ_{f}}{E_{11}^{f}} E^{m})

(11)

X_{c} = β_{c} (V^{f} σ_{f} + V^{m} \frac{σ_{f}}{E_{11}^{f}} E^{m})

(12)

where the subscripts f and m represent fiber and resin. V^f, V^m are fiber and resin’s volume fraction. E^m, G^m, ν^m are elastic modulus, poison’s ratio and shear modulus of the resin.

E_{11}^{f}

E_{22}^{f}

are elastic modulus in longitudinal and transverse direction of fiber.

ν_{12}^{f}

G_{12}^{f}

G_{23}^{f}

are poison’s ratio and shear modulus of the fiber. σ_f is the fiber’s strength. α and β are correction factors.

The properties of the fibers and resin used in the research are shown in Table 4, and the fiber volume fraction is 55%. The correction factors must be adjusted to ensure that the failure strain in the fiber direction of the unidirectional ply matches that of the actual fabric material, as indicated in Table 5. The calculated properties of the equivalent unidirectional ply are presented in Table 6. It is assumed that the transverse tensile and compressive strengths of the unidirectional ply are same as the strengths of the matrix. The material properties of the unidirectional ply used in following models are all calculated using the method described in this section.

3.2. Failure criteria and material property degradation

3.2.1. CFRP material

Three dimensional Hashin failure criteria[22], Chang fiber-shear failure criteria[23] and Ye delamination failure criteria[24] were employed to predict the different damage modes in the laminate, which are explained in detail as follows:

Fiber failure:

{(\frac{σ_{11}}{X_{T}})}^{2} + {(\frac{τ_{12}}{S_{12}})}^{2} + {(\frac{τ_{13}}{S_{13}})}^{2} \geq 1 (σ_{11} \geq 0)

(13)

{(\frac{σ_{11}}{X_{C}})}^{2} \geq 1 (σ_{11} < 0)

(14)

Matrix failure:

{(\frac{σ_{22}}{Y_{T}})}^{2} + {(\frac{τ_{12}}{S_{12}})}^{2} + {(\frac{τ_{23}}{S_{23}})}^{2} \geq 1 (σ_{22} \geq 0)

(15)

{(\frac{σ_{22}}{Y_{C}})}^{2} + {(\frac{τ_{12}}{S_{12}})}^{2} + {(\frac{τ_{23}}{S_{23}})}^{2} \geq 1 (σ_{22} < 0)

(16)

Fiber-matrix shear failure:

{(\frac{σ_{11}}{X_{C}})}^{2} + {(\frac{τ_{12}}{S_{12}})}^{2} + {(\frac{τ_{13}}{S_{13}})}^{2} \geq 1 (σ_{11} < 0)

(17)

Delamination:

{(\frac{σ_{33}}{Z_{T}})}^{2} + {(\frac{τ_{13}}{S_{13}})}^{2} + {(\frac{τ_{23}}{S_{23}})}^{2} \geq 1 (σ_{33} \geq 0)

(18)

{(\frac{σ_{33}}{Z_{C}})}^{2} + {(\frac{τ_{13}}{S_{13}})}^{2} + {(\frac{τ_{23}}{S_{23}})}^{2} \geq 1 (σ_{33} < 0)

(19)

where σ₁₁, σ₂₂, σ₃₃ are normal stress components along longitudinal, transvers and thickness directions, respectively. τ₁₂, τ₁₃, τ₂₃ are shear stress components. X_T, X_C are tensile and compressive strengths along longitudinal direction. Y_T, Y_C are tensile and compressive strength along transverse direction. Z_T, Z_C are tensile and compressive strength along thickness direction. S_12, S₁₃, S₂₃ are shear strengths.

Once the stress state of an element satisfies any of the above failure criteria, stiffness parameters of the element will be degraded to a certain value according to the degradation rules proposed by Camanho and Matthews[25] as listed in Table 7.

3.2.2. Resin

For the resin-rich region, the parabolic criterion [26] is used to determine the initiation of resin damage:

\frac{3 J + I (S_{mc} - S_{mt})}{S_{mc} S_{mt}} = 1 (I \geq 1)

(20)

- \frac{3 J = I (S_{mc} - S_{mt})}{S_{mc} S_{mt}} = 1 (I < 1)

(21)

where S_mt and S_mc are unidirectional tensile and compressive strength of resin as listed in Table 4. I and J are defined as follows:

I = {\tilde{σ}}_{m 1} + {\tilde{σ}}_{m 2} + {\tilde{σ}}_{m 3}

(22)

J = \frac{1}{6} [{({\tilde{σ}}_{m 1} - {\tilde{σ}}_{m 2})}^{2} + {({\tilde{σ}}_{m 1} - {\tilde{σ}}_{m 3})}^{2} + {({\tilde{σ}}_{m 2} - {\tilde{σ}}_{m 3})}^{2}]

(23)

where

{\tilde{σ}}_{m 1}

{\tilde{σ}}_{m 2}

{\tilde{σ}}_{m 3}

are principle stress components. The stiffness parameters of failure elements will be degraded according to the relation of

E^{m} = 0.2 E^{m}, μ^{m} = 0.2 μ^{m}

3.3. Model details

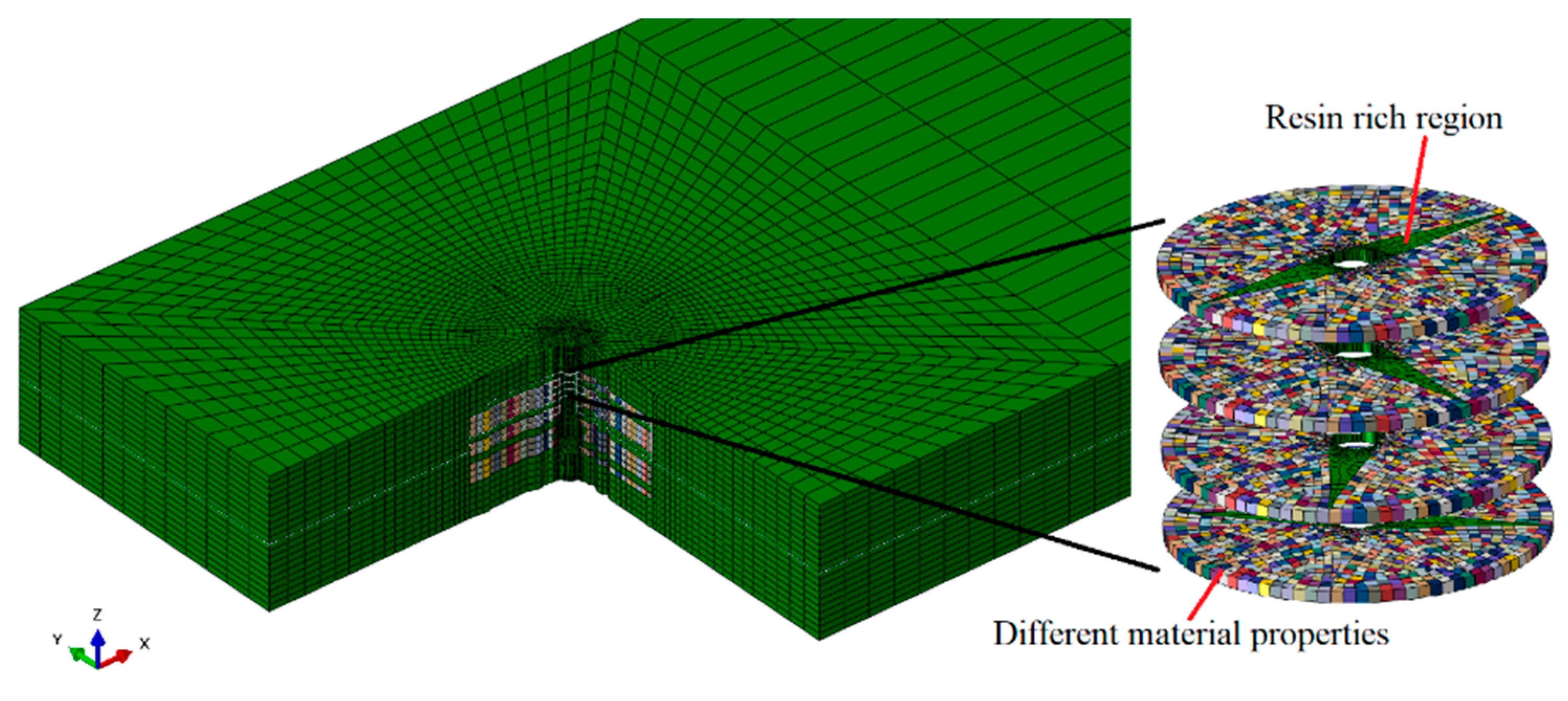
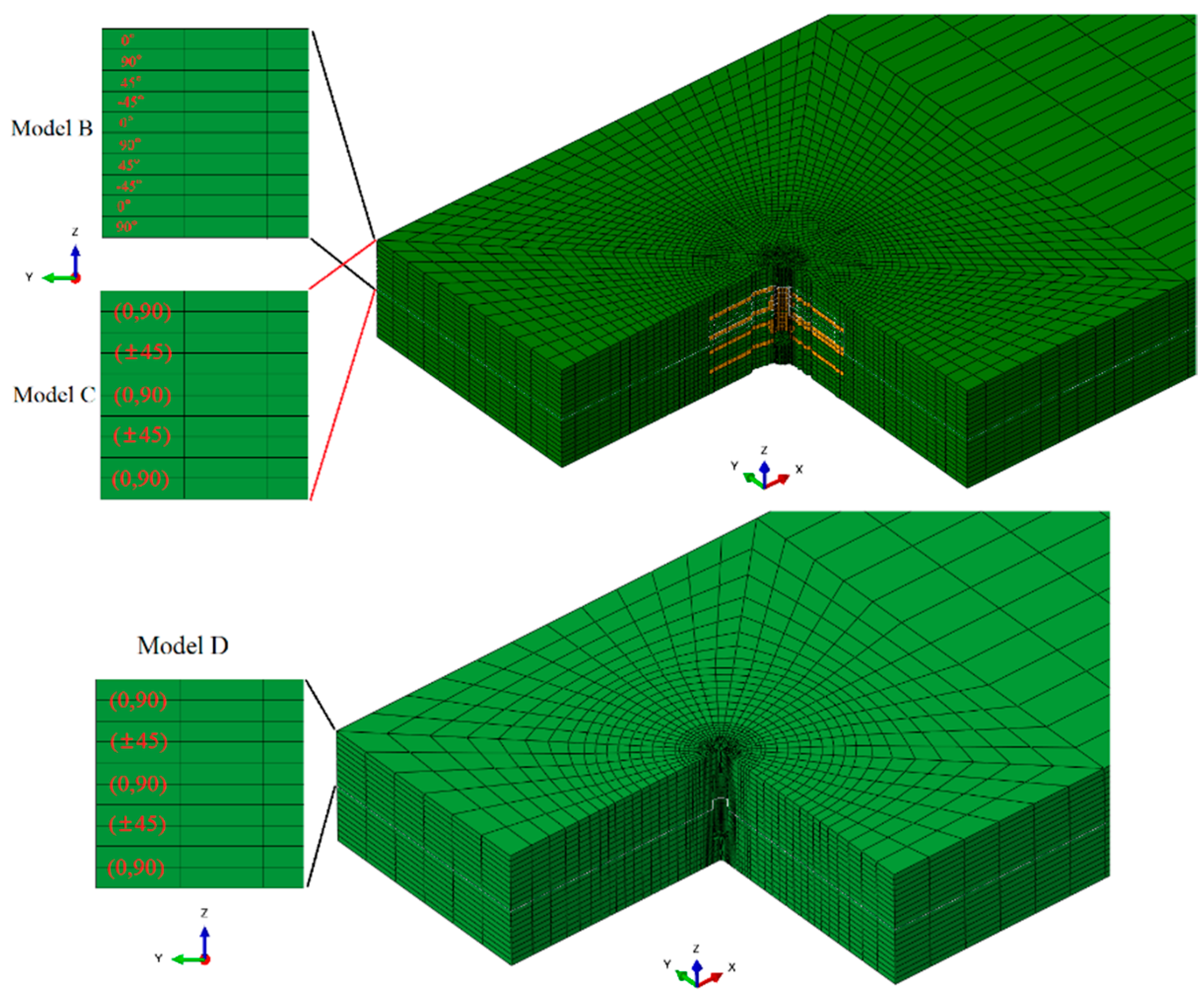
Finite element analysis was performed on ABAQUS software. The model with z-direction microvascular that considers resin-rich region, fiber bending, and variations in material properties is shown in Figure 7, referred to as model A. In this model, it is assumed that the fiber volume fraction linearly decreases from the edge of the channel to the surrounding area, while ensuring the conservation of the total fiber volume. Different colors in the elements represent different material properties. This was accomplished by python script. The coordinates of each node are read, and the fiber volume fraction is calculated based on the distance from the center of the element to the center of the channel. Then, the material parameters are calculated according to formulas (6) ~ (12) and assigned to the corresponding elements.

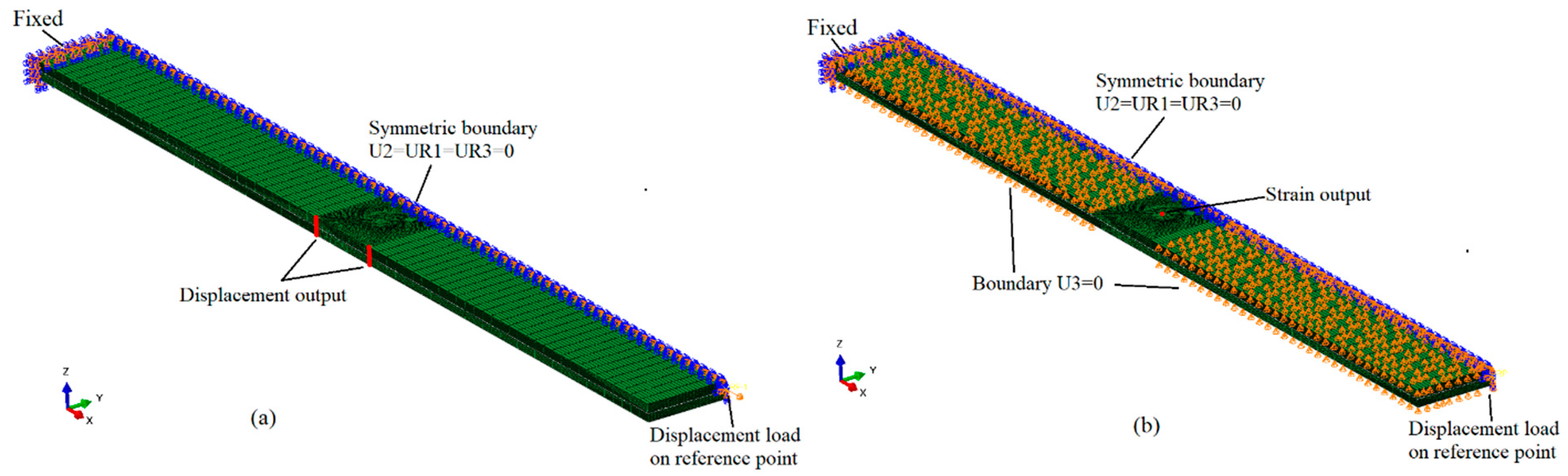
Symmetric models are established to save computational time. The tensile model only includes the gage section, while the compression model does not include reinforcement tabs. The z-direction microvascular structure is tied to overall structure. One end of the model is fixed, and the other is coupled with a reference point where the displacement load is applied, and the reaction force is extracted. In the tensile model, the displacements of the side nodes are extracted to calculate the stiffness, while in the compression model, the strain at the center of the surface is extracted for the same purpose, consistent with the experimental measurement method. The tensile and compression models of the laminates and boundary conditions, loading condition, and nodes for result output are shown in Figure 8. The element type in the model is C3D8R, with a few C3D6 elements in the resin-rich region.

To investigate the necessity of this modeling approach, several other z-direction microvascular models were also established for comparison. Model B does not consider the variation in fiber volume fraction compared to model A. Model C does not divide the fabric layer into two unidirectional ply and applied fabric material directly compared to model B. Model D does not consider the resin-rich regions, bending of fibers near the channel, and variation in fiber volume fraction. And also applied fabric material properties. This modeling process is simple but equivalent to cutting the fibers and reducing the total fiber volume. The control models are shown in Figure 9.

3.4. Validation and comparison of the FE models

The tensile and compressive performances of the microvascular laminates calculated by each model, along with their comparison to experimental results, are listed in Table 8. It shows that since model A considers the variation in the fiber volume fraction around the microvascular which resulting in higher material strength near the channel, the strengths of the laminate are slightly greater than those of model B. However, the results of model B are still very close to the experimental data. The strength results of model C and D are significantly lower than the experimental results, indicating that these modeling approaches do not accurately reflect the actual performances of the structure. In FE models, the element layers with longitudinal resin-rich region bear greater load because of higher stiffness and the total load reaches peak value when they fail. So the strengths of whole model mainly depend on the properties of these layers, which explains why model C has lager error with fabric material assigned. In model D, the fibers are cut and stress concentration is severer, which is inconsistent with reality. And the details are discussed in the following section. As for the stiffness performances of the laminates, since the impact of the microvascular is minimal, the simulation results of all models are relatively close.

Based on above results, it can be concluded that when modeling the z-direction microvascular in woven fabric material, the resin-rich regions formed within the warp and weft fibers and the bending of fibers should be considered. Furthermore, the fabric layer should be equivalently modeled as two unidirectional ply. It is not necessary to consider the variation in the fiber volume fraction around the microvascular, which simplifies modeling process appropriately.

3.5. Damage mechanism

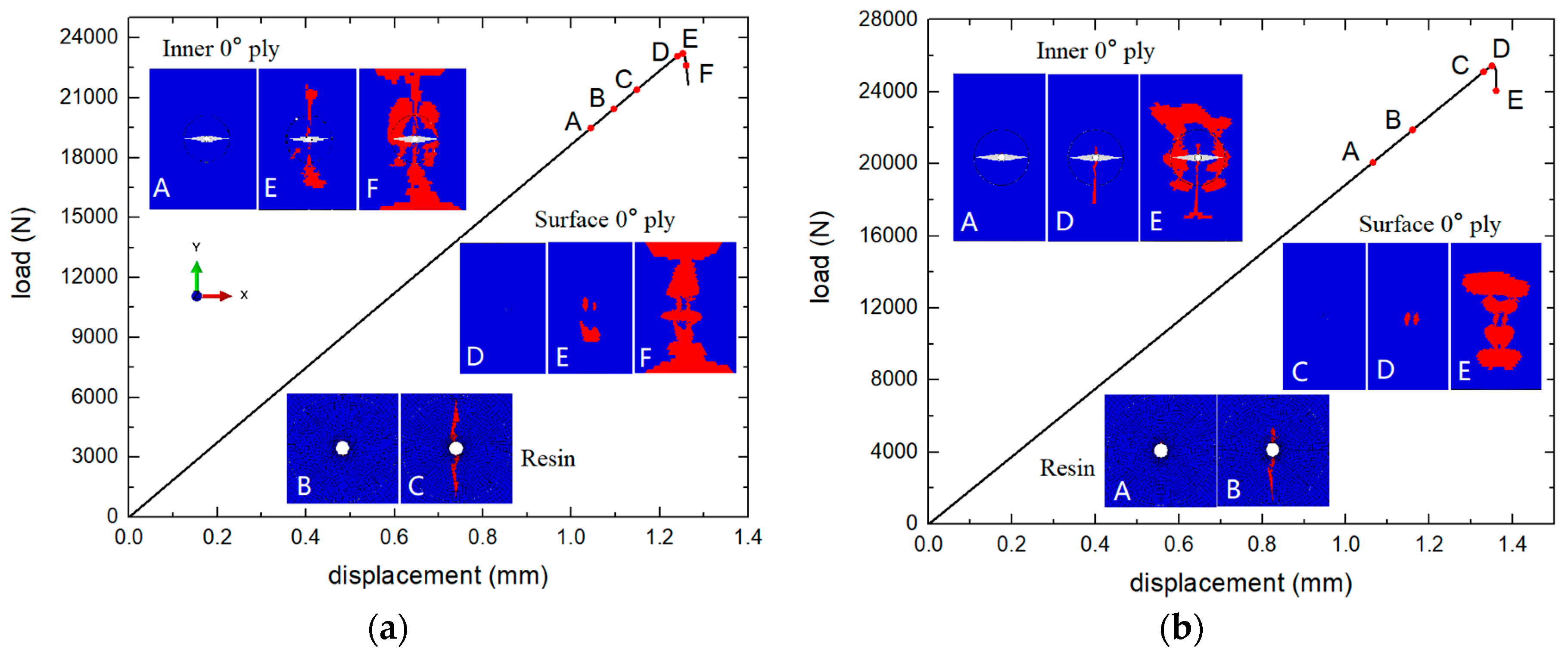
Figure 10 presents the load-displacement curves of the microvascular laminates simulated by model A, as well as the damage propagation process in different layers of the laminate.

During the tensile process, fiber damage first appeared around the microvascular in the internal 0° layers of the laminate at point A (19.5kN). At point B (20.4kN), resin damage appeared around the microvascular in the internal 90° layers, and extended to the entire resin-rich region at point C (21.4kN). Before reaching the peak load, the fiber damage in the internal 0° layers continued to extend towards the edges of the laminate, while the surface layers showed no significant damage. After reaching the peak load at point E (23.2kN), extensive fiber damage rapidly occurred in all layers until the specimen ultimately failed.

During the compression process, fiber damage first appeared around the microvascular in the internal 0° layers at point A (20.1kN), and damage in the resin-rich region around in the 90° layers also occurred. The damage had almost completely penetrated the resin-rich region by point B (21.9kN). Before reaching the peak load, the fiber damage in the internal layers continued to extend from the edge of channel towards the laminate edges, with no significant damage in the surface layers. After reaching the peak load at point D (25.4kN), extensive fiber damage occurred near the channel and at the tips of the resin-rich region in the internal 0° layers, while significant damage also appeared in the surface layers, leading to the final failure of the specimen.

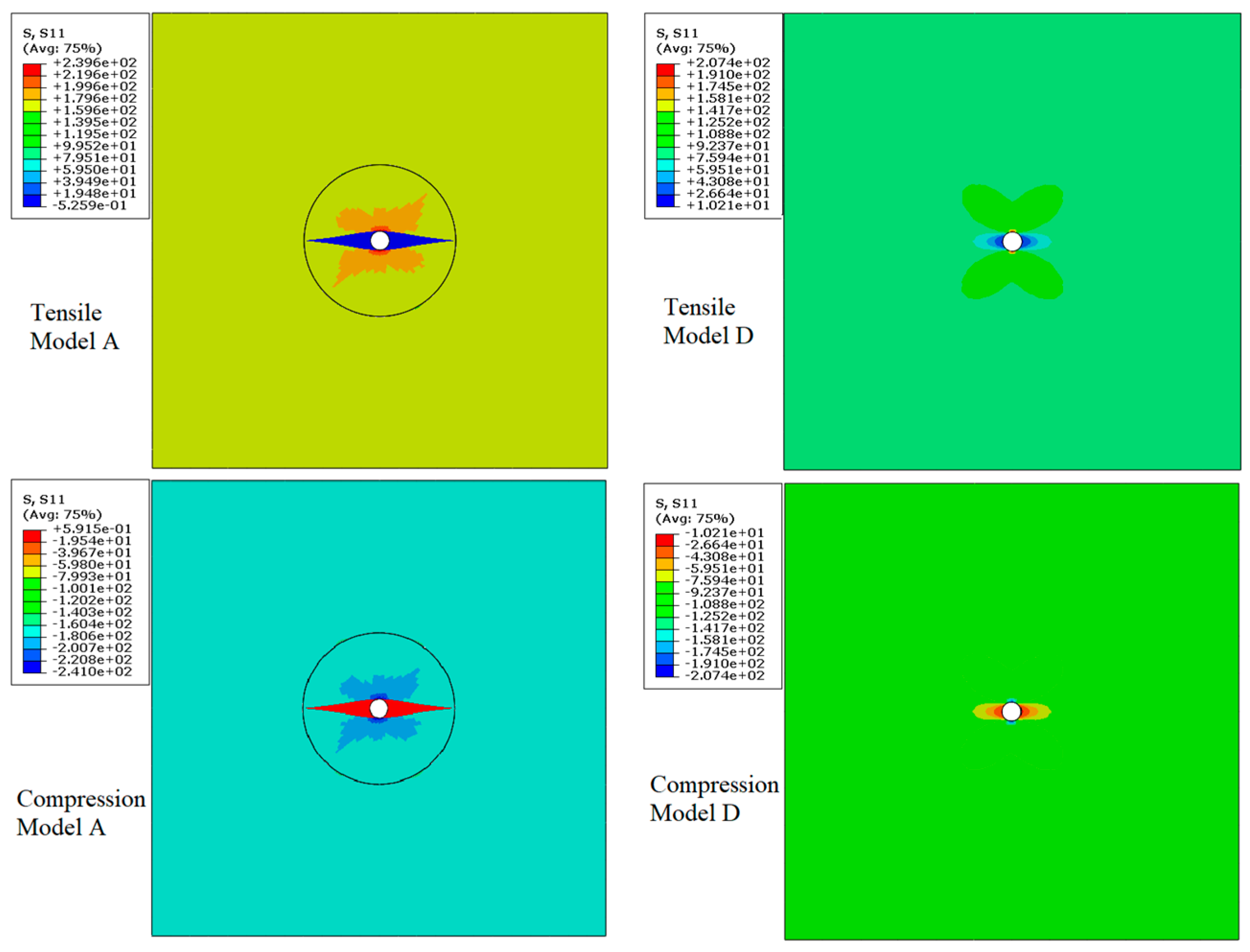
Figure 11 presents the S₁₁ stress maps around the microvascular in the 0° layers during the loading process, with the laminate under tensile or compression load of 70MPa and showing no damage. For comparison, the stress maps calculated by model D without resin-rich regions are also presented under the same load conditions. When the resin-rich regions are present, the stress concentration factor around the microvascular channel is approximately 1.44, whereas it is about 2.3 when not considering the resin-rich region. It can be seen that although the presence of resin-rich region leads to stress concentration, their impact is significantly less than directly drilling holes in the laminate, resulting in a relatively smaller loss in the strength of the laminate.

4. Parameter study

From section 3 it is known that model B can calculate the mechanical properties of the laminates accurately and the modeling approach is easier than model A. Therefore, this modeling method is utilized to investigate the influence of microvascular parameters on the mechanical properties of the laminates.

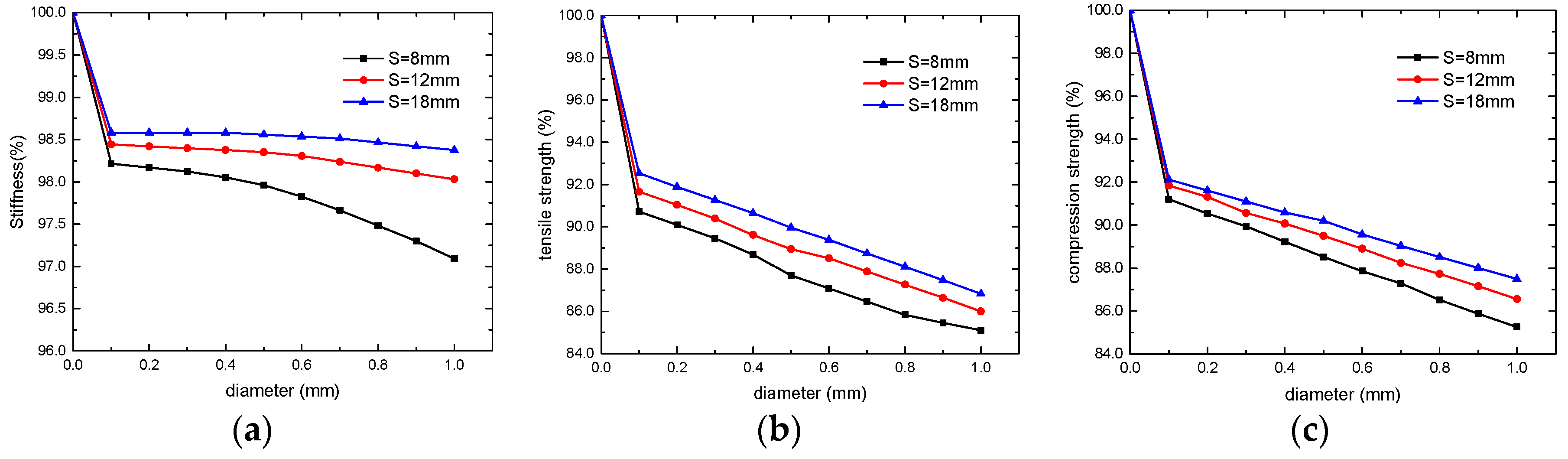
4.1. Diameter

The materials and layup sequence are the same as those in Section 3, with channel diameters ranging from 0.1mm to 1mm. This range is commonly used in current research, for smaller diameters are not conducive to the flow of the repair agent while larger diameters affect the laminate’s mechanical performances too much, which is impractical. The spacing of channels, S, is set to 8, 12, and 18mm. The changes in the stiffness and tensile/compressive strengths of the laminates with varying channel diameters are shown in Figure 12. All calculation results presented as a percentage relative to the results of control model.

It can be observed that the mechanical properties of the microvascular laminates are generally lower than those of the control laminates. However, within the diameter range of 0.1~1mm, the decrease in laminate stiffness is less than 3%, with a slightly increasing rate of decrease, while the strength of the laminates decreases approximately linearly with channel diameters. Microvascular with a spacing of 8mm and a diameter of 1mm can reduce the tensile and compressive strength of the laminates by about 15%.

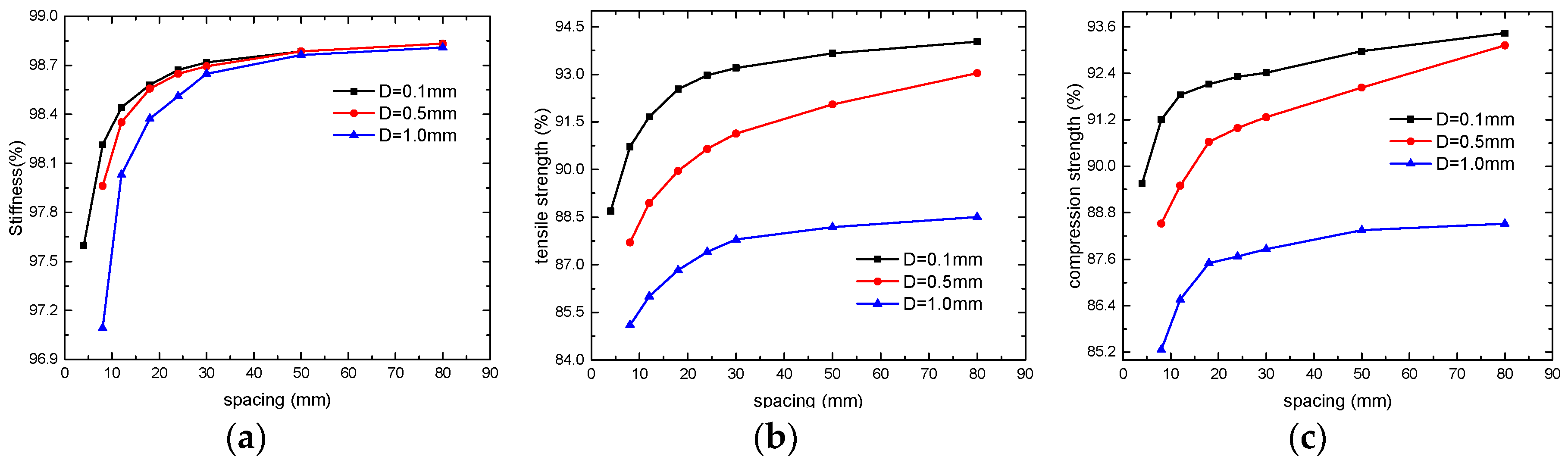
4.2. Spacing

With microvascular channel diameters D set to 0.1, 0.5, and 1mm, the changes in the stiffness and tensile/compressive strengths of the laminates with varying spacing of channel are shown in Figure 13. It can also be seen that within the current range of design parameters, the stiffness of the laminates is minimally affected by the microvascular. When the spacing between channels exceeds 30mm, there is almost no change in laminate stiffness, and the variations in tensile and compressive strengths are also relatively minor. However, when the spacing is less than 30mm, the decrease in the mechanical properties of the laminates becomes significantly more pronounced.

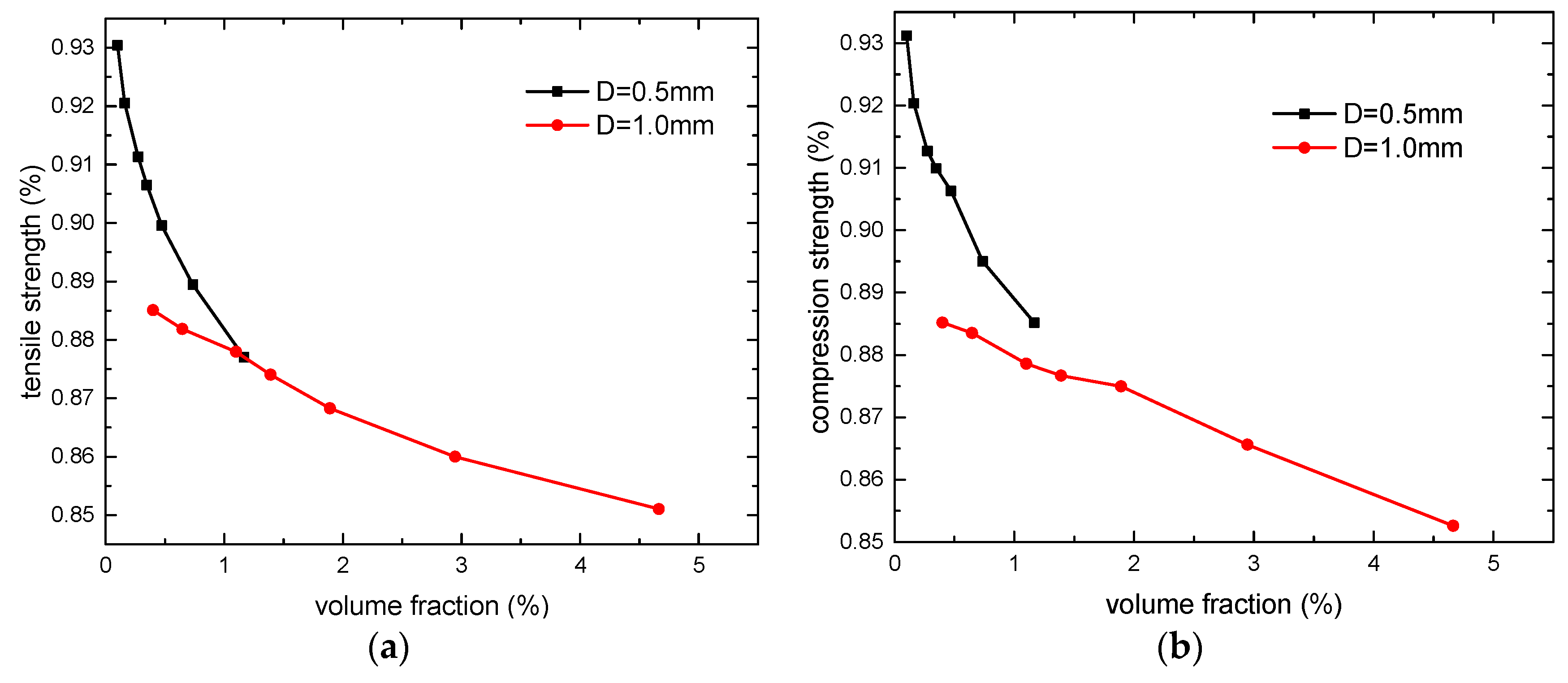
4.3. Volume fraction

The volume fraction of microvascular in the laminate is also an important design parameter in practical application. Based on the microvascular configuration in this paper, the volume fraction of microvascular corresponding to various channel diameters and spacing is calculated. Figure 14 presents the variation of the mechanical properties of the laminates under specified channel diameter. Since the volume fraction of microvascular with a 0.1mm diameter is extremely small, making the curve difficult to observe, only the curves with 0.5mm and 1mm diameters are presented. Furthermore, as the stiffness of the laminates is minimally affected, the focus is primarily on the variation of strength. It can be observed that the laminate with larger channel diameter has the lower slope of the strength curve. As the volume fraction of the microvascular increases, the slope of the strength curves decreases gradually.

4.4. Parameter design criteria

When designing microvascular self-healing composite structures, it is necessary to consider both the mechanical properties of the laminate and the damage repair capability of the microvascular. Generally, to ensure that self-healing is triggered in time before the damage propagation significantly affects the overall performances of the structure, the spacing of the microvascular must be less than a certain value. At the same time, there may also be requirements that the mechanical properties of the laminate should not fall below a certain level, or the volume fraction of the microvascular should not exceed a certain level when designing structures. So the variation of the mechanical properties of the microvascular composites can be determined through experiments or finite element methods first. And then the range of microvascular design parameters can be determined based on these limitations. Larger diameter and spacing are better within the allowable design range.

5. Conclusions

Tensile and compressive performances of woven fabric CFRP laminates containing three-dimensional microvascular channels were investigated experimentally. Different finite element models with z-direction microvascular were established and verified by experimental results. The validated models were used to investigate the damage propagation process and failure mechanism of the laminates under tensile and compressive loads. Then parameter study was conducted. The following conclusions can be obtained:

(1) Z-direction microvascular is critical position, which is prone to damage under tensile and compressive loads.

(2) Z-direction microvascular has minimal effect on the stiffness of laminates, but a certain effect on the strength. With a channel diameter of 0.5mm and a spacing of 12mm, the tensile and compressive strengths decrease by approximately 10% to 12% compared with blank laminates.

(3) For woven fabric CFRP composites, the different orientations of resin-rich region formed in the warp and weft fiber yarns should be considered when establishing FE model with z-direction microvascular. Equivalent unidirectional ply material properties should be assigned separately for more accurate calculation of the mechanical performances. The effect of variations in the fiber volume fraction around microvascular can be disregarded.

(4) Within the common microvascular diameter ranging from 0.1mm to 1mm, stiffness variation of the laminates is small, while the laminate strength varies approximately linearly with the channel diameter.

Author Contributions

Conceptualization, Ziqian An and Xiaoquan Cheng; Data curation, Xin Guo and Yujia Cheng; Investigation, Ziqian An; Methodology, Ziqian An and Yihao Ma; Project administration, Xiaoquan Cheng; Resources, Dafang Zhao; Supervision, Xiaoquan Cheng; Writing – original draft, Ziqian An; Writing – review & editing, Xiaoquan Cheng.

Funding

This research received no external funding.

Data Availability Statement

Data are contained within the article.

Conflicts of Interest

The authors declare no conflict of interest.

References

Liang, F.F.; Jin, D.; He, Y. Research on the maintenance of composite material structure. China adhesives 2019, 28, 57–61. [Google Scholar] [CrossRef]
Pang, J.W.C.; Bond, I.P. A Hollow Fibre Reinforced Polymer Composite Encompassing Self-Healing and Enhanced Damage Visibility. Composites Science and Technology 2005, 65, 1791–1799. [Google Scholar] [CrossRef]
Williams, G.; Trask, R.; Bond, I. A Self-Healing Carbon Fibre Reinforced Polymer for Aerospace Applications. Composites Part A: Applied Science and Manufacturing 2007, 38, 1525–1532. [Google Scholar] [CrossRef]
Patrick, J.F.; Krull, B.P.; Garg, M.; Mangun, C.L.; Moore, J.S.; Sottos, N.R.; White, S.R. Robust Sacrificial Polymer Templates for 3D Interconnected Microvasculature in Fiber-Reinforced Composites. Composites Part A: Applied Science and Manufacturing 2017, 100, 361–370. [Google Scholar] [CrossRef]
Norris, C.J.; White, J.A.P.; McCombe, G.; Chatterjee, P.; Bond, I.P.; Trask, R.S. Autonomous Stimulus Triggered Self-Healing in Smart Structural Composites. Smart Mater. Struct. 2012, 21, 094027. [Google Scholar] [CrossRef]
Patrick, J.F.; Hart, K.R.; Krull, B.P.; Diesendruck, C.E.; Moore, J.S.; White, S.R.; Sottos, N.R. Continuous Self-Healing Life Cycle in Vascularized Structural Composites. Advanced Materials 2014, 26, 4302–4308. [Google Scholar] [CrossRef] [PubMed]
Ma, Y.H.; Du, X.Y.; Hu, R.W; Zhao, D.F.; Li, B.T; Cheng, X.Q. Development of Self-Healing Composite Materials with Microvascular Networks. Polymer Materials Science and Engineering 2018, 34, 166–172. [Google Scholar] [CrossRef]
Kousourakis, A.; Bannister, M.K.; Mouritz, A.P. Tensile and Compressive Properties of Polymer Laminates Containing Internal Sensor Cavities. Composites Part A: Applied Science and Manufacturing 2008, 39, 1394–1403. [Google Scholar] [CrossRef]
Devi, U.; Pejman, R.; Phillips, Z.J.; Zhang, P.; Soghrati, S.; Nakshatrala, K.B.; Najafi, A.R.; Schab, K.R.; Patrick, J.F. A Microvascular-Based Multifunctional and Reconfigurable Metamaterial. Adv Materials Technologies 2021, 6, 2100433. [Google Scholar] [CrossRef]
Saeed, M.U.; Li, B.; Chen, Z.; Cui, S. Fabrication of Microchanneled Composites by Novel Selective Polymer Degradation. Materials and Manufacturing Processes 2016, 31, 2057–2063. [Google Scholar] [CrossRef]
Coppola, A.M.; Thakre, P.R.; Sottos, N.R.; White, S.R. Tensile Properties and Damage Evolution in Vascular 3D Woven Glass/Epoxy Composites. Composites Part A: Applied Science and Manufacturing 2014, 59, 9–17. [Google Scholar] [CrossRef]
Norris, C.J.; Bond, I.P.; Trask, R.S. The Role of Embedded Bioinspired Vasculature on Damage Formation in Self-Healing Carbon Fibre Reinforced Composites. Composites Part A: Applied Science and Manufacturing 2011, 42, 639–648. [Google Scholar] [CrossRef]
Nguyen, A.T.T.; Orifici, A.C. Structural Assessment of Microvascular Self-Healing Laminates Using Progressive Damage Finite Element Analysis. Composites Part A: Applied Science and Manufacturing 2012, 43, 1886–1894. [Google Scholar] [CrossRef]
Huang, C.Y.; Trask, R.S.; Bond, I.P. Characterization and Analysis of Carbon Fibre-Reinforced Polymer Composite Laminates with Embedded Circular Vasculature. J. R. Soc. Interface. 2010, 7, 1229–1241. [Google Scholar] [CrossRef] [PubMed]
Al-Shawk, A.; Tanabi, H.; Sabuncuoglu, B. Investigation of Stress Distributions in the Resin Rich Region and Failure Behavior in Glass Fiber Composites with Microvascular Channels under Tensile Loading. Composite Structures 2018, 192, 101–114. [Google Scholar] [CrossRef]
Demiral, M.; Tanabi, H.; Sabuncuoglu, B. Experimental and Numerical Investigation of Transverse Shear Behavior of Glass-Fibre Composites with Embedded Vascular Channel. Composite Structures 2020, 252, 112697. [Google Scholar] [CrossRef]
Zhao, Y.; Wang, Z.Q.; Jiang, P.; Wang, A.Y.; Chang, Z.P.; Kang, Y.G. Numerical Simulation on Mechanical Properties and Damage Behavior of CFRP with Self-Healing Microvascular Channels. Mechanics of Advanced Materials and Structures 2022, 1–17. [Google Scholar] [CrossRef]
Ran, G.L.; Ma, Y.H; An, Z.Q.; Zhao, D.F.; Guo, X.; Cheng, X.Q. Study of tensile properties of laminates containing microvascular channels with different diameters. Journal of Beijing University of Aeronautics and Astronautics 1–15. [CrossRef]
Fu, H.M.; Zhang, Y.B. On the Distribution of Delamination in Composite Structures and Compressive Strength Prediction for Laminates with Embedded Delaminations. Appl Compos Mater 2011, 18, 253–269. [Google Scholar] [CrossRef]
Ma, Y.H.; Cheng, X.Q.; Zhang, J.K.; Zhao, D.F.; Huang, W.J. Prediction of Resin Pocket Geometry around Rigid Fiber Inclusion in Composite Laminate by Hot-Pressing of Prepregs. Journal of Composite Materials 2020, 54, 1987–1999. [Google Scholar] [CrossRef]
Chamis, C.C. Mechanics of Composite Materials: Past, Present, and Future. Journal of Composites Technology & Research 1989, 11, 3–14. [Google Scholar] [CrossRef]
Hashin, Z. Failure Criteria for Unidirectional Fiber Composites. Journal of Applied Mechanics 1980, 47, 329–334. [Google Scholar] [CrossRef]
Chang, F.K.; Chang, K.Y. A Progressive Damage Model for Laminated Composites Containing Stress Concentrations. Journal of Composite Materials 1987, 21, 834–855. [Google Scholar] [CrossRef]
Ye, L. Role of Matrix Resin in Delamination Onset and Growth in Composite Laminates. Composites science and technology 1988, 4, 257–277. [Google Scholar] [CrossRef]
Camanho, P.P.; Matthews, F.L. A Progressive Damage Model for Mechanically Fastened Joints in Composite Laminates. Journal of Composite Materials 1999, 33, 2248–2280. [Google Scholar] [CrossRef]
Fiedler, B.; Hojo, M.; Ochiai, S.; Schulte, K.; Ando, M. Failure Behavior of an Epoxy Matrix under Different Kinds of Static Loading. Composites Science and Technology 2001, 61, 1615–1624. [Google Scholar] [CrossRef]

Figure 1. Configuration and geometric parameters of specimens, tensile specimen (a) and compression specimen (b).

Figure 2. Specimen structure and manufacturing process schematic.

Figure 3. Test set-up and extensometer installation in tensile test (a). Strain gauges on compression specimen (b). Test set-up in compression test (c).

Figure 4. Failure modes of the specimens, tensile failure (a), enlarged view of the tensile fracture section (b) and compression failure.

Figure 5. Intralaminar resin-rich region around the microvascular.

Figure 6. Comparison of numerical and measurement results of resin-rich region length.

Figure 7. Z-direction microvascular in model A.

Figure 8. Boundary conditions, loading condition and nodes for result output, tensile model (a) and Compression model (b).

Figure 9. Schematic of the comparison model.

Figure 10. Load-displacement curves and damage propagation of specimen, tensile(a) and Compression (b).

Figure 11. Stress distribution around the microvascular.

Figure 12. Variation of mechanical properties with diameter of microvascular, stiffness (a), tensile strength (b) and compression strength (c).

Figure 13. Variation of mechanical properties with spacing of microvascular, stiffness (a), tensile strength (b) and compression strength (c).

Figure 14. Variation of mechanical properties with volume fraction of microvascular, tensile strength (a) and compression strength (b).

Table 1. Mechanical properties of CF3031/5284 ply.

Property	Value	Property	Value
E₁, E₂/GPa	55.0	X_t, Y_t/MPa	550
E₃/GPa	8.4	X_c, Y_c/MPa	593
G₁₂/GPa	3.64	Z_t/MPa	80
G₁₃, G₂₃/GPa	3.0	Z_t/MPa	180
ν₁₂	0.051	S₁₂/MPa	84
ν₁₃, ν₂₃	0.15	S₁₃, S₂₃/MPa	80

Table 2. Test results.

Properties	Control group	Vascular specimens	Variation/%
Tensile stiffness/GPa	43.98	41.30	-6.1
Tensile strength/MPa	441.5	388.8	-11.9
Compression stiffness/GPa	40.90	41.75	2.1
Compression strength/MPa	462.9	415.1	-10.3

Table 3. Resin-rich region length in FE model.

Microvascular diameter /mm	Resin-rich region length /mm	Microvascular diameter /mm	Resin-rich region length /mm
0.1	1.70	0.6	4.48
0.2	2.55	0.7	4.84
0.3	3.15	0.8	5.17
0.4	3.65	0.9	5.49
0.5	4.04	1.0	5.79

Table 4. Mechanical properties of the fiber and resin.

$E_{11}^{f}$ /GPa	$E_{22}^{f}$ /GPa	$G_{12}^{f}$ /GPa	$G_{23}^{f}$ /GPa	$ν_{12}^{f}$	σf/MPa	Em/GPa	Gm/GPa	νm	$S_{t}^{m}$ /MPa	$S_{c}^{m}$ /MPa
230	13.8	9	4.8	0.2	3530	3.2	1.13	0.42	80	180

Table 5. Correction factor value.

α₁	α₂	α₃	α₄	α₅	β_t	β_c
0.8118	0.8257	1.5279	1.1322	1.1538	0.5321	0.5735

Table 6. Equivalent unidirectional ply properties calculated by modified Chamis model.

E₁₁/GPa	E₂₂/GPa	ν₁₂	G₁₂/GPa	G₁₂/GPa	X_t/MPa	X_c/MPa
103.86	6.14	0.46	3.64	3.00	1038.6	1119.8

Table 7. Stiffness degradation rules of composite.

Failure mode	Stiffness degradation rule
Fiber failure	0.07×all parameters
Matrix failure	0.2×E₂₂, G₁₂, G₂₃, μ₁₂, μ₂₃
Fiber-matrix shear failure	0.2×G₁₂, μ₁₂
Delamination	0.2×E₃₃, G₁₃, G₂₃, μ₁₃, μ₂₃

Table 8. Comparison of experiment and simulation results.

Properties	Experiment		Control model		Model A		Model B				Model C		Model D
Properties	Control	Vascular	FEM	error/%	FEM	error/%	FEM		error/%		FEM	error/%	FEM	error/%
Tensile stiffness/GPa	43.98	41.30	43.67	-0.7	42.95	4.0		42.98		4.1	43.05	4.2	43.29	4.8
Tensile strength/MPa	441.5	388.8	434.7	-1.5	386.6	-0.6		379.1		-2.5	315.1	-19.0	337.7	-13.1
Compression stiffness/GPa	40.90	41.75	43.49	6.3	41.69	-0.1		41.37		-0.9	42.87	2.7	42.86	2.7
Compression strength /MPa	462.9	415.1	469.5	1.4	424.2	2.2		413.1		-0.5	350.5	-15.6	360.4	-13.2

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Tensile and Compressive Properties of woven fabric CFRP Laminates Containing Three-Dimensional Microvascular Channels

Abstract

1. Introduction

2. Experiment

2.1. Specimen manufacture

2.2. Mechanical testing

2.3. Result and analysis

3. Finite element model

3.1. Model generation

3.1.1. Resin-rich region

3.1.2. Variation of fiber volume fraction

3.2. Failure criteria and material property degradation

3.2.1. CFRP material

3.2.2. Resin

3.3. Model details

3.4. Validation and comparison of the FE models

3.5. Damage mechanism

4. Parameter study

4.1. Diameter

4.2. Spacing

4.3. Volume fraction

4.4. Parameter design criteria

5. Conclusions

Author Contributions

Funding

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe