Prerpints.org logo
Preprint
Article

Damage Evaluation in Plain-Woven CFRP Plate with Circular Hole under Cyclic Tensile Loading Using Electrical Impedance Tomography

Altmetrics

Downloads

133

Views

67

Comments

0

Submitted:

05 January 2024

Posted:

08 January 2024

You are already at the latest version

Alerts
Abstract
Understanding and predicting damage progression within thin plain-woven CFRP components is an essential issue for scheduling maintenance intervals and structural inspections, and typically require extensive test series. However, uncertainties always remain and result in conservative design and unnecessary downtimes due to the repeated inspections of a healthy structure. SHM can be used to reduce these uncertainties, as it allows to evaluate the condition of a mechanical structure during operation. Numerous SHM methods are developed , that achieve different levels of damage identification but are often investigated at small coupons with non-realistic structural damages and loading conditions on both, structure and sensor. The present research investigates the electrical impedance tomography (EIT) featuring an elastoresistive thin-film sensor to evaluate damage that propagates from a circular hole in a large plate under cyclic tensile-tensile multi-block loading. Applied fatigue loads were increased multiple times up to a total number of two million cycles. During the loading damage initiated at the hole and continuously propagated into the plate. Repeated EIT evaluations of the applied sensor and validating evaluations by means of digital image correlation clearly revealed the robustness of the hardware and the potential of the SHM method for damage evaluation of plain-woven CFRP components.
Keywords: 
Subject: Engineering  -   Mechanical Engineering

1. Introduction

Carbon fiber-reinforced polymers (CFRPs) have become an established part of aviation and space industry. Their advantages over metallic materials, particularly in terms of fatigue behavior, cause them to be frequently preferred in recent developments. However, in contrast to metallic materials, fiber-reinforced composites exhibit very complex failure behavior, involving a wide range of damage modes that are dependent on a large number of factors [1,2,3,4].
In aerospace, safety is of highest importance. As a consequence, components made from fiber-reinforced composites are often designed with a higher material input than necessary, to include unknown design variables and unforeseen damage mechanisms. This more conservative layout results in more fail-safe components, but is in conflict with traditional lightweight design concepts, as the increased use of material adds additional weight [5]. This additional material input increases the fuel consumption or decreases the payload [6,7]. As stated by Flower and Soutis [8] a reduction of 1% mass could save nearly 3000 liters of fuel per year (analyzed for single aisle aircrafts).
Especially in commercial aviation, very high standards for safety and reliability are established, which have to be warranted and guaranteed throughout the service life of an aircraft. For this purpose, the manufacturers specify appropriate maintenance and service schedules, which have to be fulfilled by the operators. These rules also specify relevant inspection methods as well as the location for these inspections. In the case of CFRPs, ultrasonic testing is a well-established and commonly used method for a more in-depth inspection for potential damage locations. However, ultrasonic testing is time consuming, and thus, the aircrafts experience long and often unnecessary downtimes [2,9,10,11].
A comparatively novel and widely discussed approach to reduce these downtimes is structural health monitoring (SHM), which monitors the condition of a structural component continuously while an aircraft remains in operational service [2,11,12,13,14]. Numerous SHM methods are developed so far and can be classified into methods that actively excite a structural response or methods that use other sources of excitation, like e.g., mechanical loading. Different methods use, e.g., ultrasonic wave propagation or mechanical strains, for damage evaluation [14,15,16,17,18,19,20,21]. Another method is the EIT-based reconstruction of the spatial conductivity of an area of interest. This method may be of particular interest for large thin-walled and shell-shaped components, as it uses the mechanical structure itself (if conductive in the right magnitude, e.g., CFRP [22,23]) or a thin conductive coating applied onto the structure as a sensor. However, to overcome the challenges associated with direct contacting CFRP laminates and the underlying anisotropic electrical behavior, a conductive coating used as thin-film sensor is often preferred. These thin-film sensors are equipped with electrodes that are placed at their boundaries. The EIT method evaluates the sensor’s spatial conductivity by the electrical potential at the boundary electrodes due to systematic excitation by a defined current pattern. Thus, EIT featuring thin-film sensors can be used to evaluate damages [22,24,25,26], that change the conductivity of the covering thin-film.
Besides these damages that result in very large conductivity drops, recent investigations demonstrated that EIT can also be used to approximate mechanical strains. Tallman et al.[27] performed an inverse determination of strains. They applied an analytical piezoresistivity model with which the displacement field and the strains were derived, while the difference between experimentally determined conductivity and the conductivity of the analytical piezoresistivity model was minimized. A similar investigation was carried out by Lynch et al.[28], where carbon nanotube-based sensing skins applied on metallic specimens were utilized to identify spatial strain and impact damage. Another research was conducted by Hassan [29], where a generic algorithm and EIT analysis was used to evaluate conductivity changes induced by stress concentrations. The samples used in their research were weakened by a circular hole and subjected to static tensile loads. Validation through digital image correlation (DIC) and numerical simulations demonstrated accuracy of this proposed model. However previous research has typically used small specimens and has not investigated their sensor networks or evaluation methods under realistic operational loading conditions, nor for the corresponding damaging behavior.
The present paper investigates the potential of the EIT method featuring conductive thin-film sensors for damage initiation and propagation in CFRP components under fatigue loading. Therefore, a thin-walled plate-shaped plain-woven CFRP specimen with a centrally placed circular hole is considered and damage induced and propagated by sinusoidal tension-tension loading is examined. During experimental testing, load amplitude adjustments are done to investigate the effect on the damage propagation, as well as on the applied thin-film sensor and the EIT damage evaluation results. Accompanying 3D-DIC evaluations of the plate surface provide validation for the EIT results. The novelty of this investigation lies on the operational loading conditions and the consequently required compensation of fatigue loading induced changes to the sensor (e.g. “Set-In” effect [30] and potential environmental influences). On the basis of the EIT measurements collected throughout the fatigue loading, two damage evaluation approaches are proposed, with which changes to the sensor can be compensated.
The article is structured as follows. First the preparation of the specimen, the experimental procedure, and the damage evaluation approaches (3D-DIC and EIT) are described. The damage evaluation results by the 3D-DIC and the EIT reconstructions are presented afterwards. Finally the results are discussed and conclusions are made.

2. Material and methods

The manufacturing process of the specimen along with the experimental setup and procedure for damage evaluation are described in this Section.

2.1. Specimen

The experimental investigations are performed on the plate-shaped specimen containing a circular hole in its center presented in Figure 1. Therefore, four plain-woven CFRP plies were stacked 45 f / 0 f s , vacuum bagged and cured in an autoclave at 120 °C and 0.9 MPa to produce a composite blank with a thickness of 0.816mm. The individual plies contain 3k-T650 fibers and a Solvay CYCOM® 970 resin matrix, with a fiber volume fraction of 0.6. The final specimen geometry and the hole were cut by water jet cutting.
To obtain the configuration, depicted in Figure 1 the areas that are equipped with the clamping tabs are temporarily taped off and the frontside of the specimen is coated. This coating process, which comprises two steps, begins with the application of a two-component DeSoto 512X310 Epoxy Primer. After drying, a layer of a three-component Desothane HS CA8800 Topcoat is applied. Once the frontside of the specimen is prepared, the SunChemical C2130819D1 Carbon Paste is deposited on it by screen printing to generate the used elastoresistive thin-film sensor. For this deposition, an aluminium frame with a fine screen (mesh 120 T) is placed on the specimen and the SunChemical C2130819D1 Carbon Paste is applied with a silicone squeegee by a single, quick swipe. By masking the screen beforehand, the sensor size and shape is specified. The chosen SunChemical C2130819D1 Carbon Paste has been used by the authors in a previous study, were it was successfully used as EIT sensor material on a high cycle loaded aluminum specimen [31].
In a subsequent preparation step, glass fiber reinforced plastic (GFRP) clamping tabs are bonded in place with 3M™ Scotch-Weld™ DP490 and the backside of the specimen is prepared. On the backside a white primer is applied, on which small black dots are sprayed by airbrush to create a speckle pattern for the 3D-DIC evaluation. In the final step, wiring of the elastoresistive thin-film sensor on the frontside of the specimen is applied. The contacting of the 16 electrodes is provided by ELECTROLUBE Silver Conductive Paint, which is painted on by a brush and contacted with a high-conductive, two-component EPO-TEK H20E silver epoxy with which the stripped ends of the wires are fixed onto the ELECTROLUBE Silver Conductive Paint. Each of the 16 brushed-on lines starts slightly inside the elastoresistive thin-film sensor and ends 10 mm outside, where the stripped ends are positioned. Contacting electrodes are uniformly distributed along the boundary of the sensor. Subsequently the wiring is fixed to the specimen with LOCTITE EA9466™ so that the single wires are kept in position during the experimental investigation. The electrodes are numbered in clockwise order, number 1 is the electrode on the lower right edge of the elastoresistive thin-film sensor (see Figure 1).
The prepared specimen is placed in an oven multiple times to complete the different preparation steps, as this ensures optimum properties of the individual components. In Table 1, the curing parameters of the individual components used in the preparation steps in the order of application are listed. Those components cured at room temperature are indicated with RT (22°C). The applied temperatures to complete the individual preparation steps are considered to cause no damages to the test specimen.

2.2. Experimental procedure

The specimen prepared according to Section 2.1 is mounted on a test rig for mechanical loading. The test rig is placed in a laboratory environment where the ambient conditions are stable (typical moderate room temperature and humidity variations are present) to minimize their influence on the thin-film sensor. In Figure 2 the experimental setup, including the investigated CFRP plate with centrally placed circular hole and the used clamping fixture and hydraulic cylinder, the 3D-DIC system and the EIT measurement system are illustrated. For the EIT reconstructions, an experimental framework, developed by the authors[31], is applied consisting of all components with which the EIT measurements and evaluations are performed. In this arrangement, the wiring of the elastoresistive thin-film sensor (frontside) is routed into a multiplexer, driven by an Arduino® Mega 2560. This allows a defined current injection pattern in accordance with [31]. As current source the Keithley® 6620 is used. Measuring the resulting electrode voltages is performed with two HBM® QuantumX MX840B which are operated simultaneously. In a computer, which is connected to the HBM® QuantumX, the data acquisition and evaluation is carried out. These components are also depicted in Figure 2. The principle of the framework is described in Section 2.4, whereas a more detailed description is given in [31,32,33].
As illustrated in Figure 2, the plate is positioned in the center of the clamping fixture and held in place by tightening the clamping screws to avoid slipping out. The base part of the clamping fixture is attached to the test bed and the upper part of the clamping fixture is attached to a load cell which is then loaded by a servo-hydraulic cylinder (Zwick Roell®; nominal force 100kN). Lateral to the clamping fixture, guiding bars are provided on both ends to prevent the upper clamping fixture from rotating. The signals of the load cell are transmitted to a CUBUS controller (Zwick Roell®) and used as control variable for the cylinder loading.
The plate is alternatingly subjected to a single quasi-static loading and a fatigue loading block of sinusoidal tension-tension loads. Within the repeated quasi-static loadings the measurements for the damage evaluation from 3D-DIC and EIT are carried out. During the fatigue loading no measurements are done, the cyclic loading is only used to induce realistic damage to the considered specimen and stress the sensor system. The repeated quasi-static loading is always the same for comparability of the measurements. The load levels of the fatigue loading blocks vary and are chosen to be comparable to previous results of the authors[34]. The associated strains are between 3000 μ m / m and 12000 μ m / m , thus, well represent a realistic operational loading of CFRP components, leading to realistic damage. In Figure 3, a schematic representation of a mechanical loading sequence i, composed of a single quasi-static loading and a cyclic loading, with a tabular list of the cyclic loading details, are given.
For every quasi-static loading sequence the load is raised to S base , i =0.5 kN where an EIT measurement is carried out and 3D-DIC images are taken. Here, the load remains constant for 45 s, providing adequate sampling time and allowing a data acquisition at constant loading conditions. To change the load to the other levels it is changed with a rate of 0.5 kN/s. At ( S base , i , S mean , i , S max , i , S min , i ) the load remains constant for 45s and EIT measurements and 3D-DIC images are taken to preserve comparability. Within the quasi-static loading, 3D-DIC images are taken at intervals of 500ms each time when the load is held constant (see Figure 3). The two cameras of the 3D-DIC system (also indicated in Figure 2; provided by Correlated Solutions) are focused on the speckled area of the specimen with circular hole (backside).
After the quasi-static loading the cyclic loading starts. Cyclic loading is implemented with a frequency of 4Hz and a stress ratio of R = 0.1 . To introduce and end the cyclic loading between C max , i and C min , i with less intensity, five Fade-In cycles and five Fade-Out cycles at the beginning and at the end of the cyclic loadings are added. After completing the defined number of cycles (Ni), the load is reduced to S base , i + 1 and the next quasi-static and cyclic loading (i+1) is performed. The loading sequences are carried out until the specified number of repetitions are completed. After every 500k fatigue load cycles, the cyclic loading is raised by 10%. Following 2000k cycles, a final quasi-static loading is done (i=35), with which damage at the test end is evaluated.

2.3. Damage evaluation by digital image correlation (3D-DIC)

The speckled area on the backside of the specimen with centrally placed circular hole is utilized to evaluate occurring damage due to the cyclic loading. These evaluations are used to validate the EIT reconstructions. Basically, the 3D-DIC evaluation is done by selecting a reference image on which an evaluation area is specified. This evaluation area is discretized into subsets (tracked by image gray value) which are a fundamental quantity in the evaluation. Referring images to the defined reference image provides information (e.g. displacements, strains). During the evaluations, the spatial 1-standard deviation confidence in the correlation (correlation confidence) is also computed, which can be utilized to determine the quality of the match of the individual subsets [35,36]. To the extent that the subsets (gray values) are changed (e.g. noise, changes in lighting, spatial changes to the speckled area or displacements of the specimen) the correlation confidence is reduced [37,38]. Other changes, like e.g. cracks, also cause a reduction in the correlation confidence. Thus, this quantity is frequently considered as an indicator for damage [34,39,40].
To evaluate potential damage the spatial surface strains are evaluated from the acquired images taken at the quasi-static loading. In this process images of the base load S base , i are correlated to that of the peak load S max , i . An evaluation of the individual single quasi-static loadings reveal any changes inside the spatial strain field and might be an indicator for cyclically induced damage. The first image at the corresponding base load S base , i is taken as reference image. In Figure 4, the evaluated area, the selected subset size and the associated settings are shown.
Additional 3D-DIC evaluations are carried out in which the correlation confidence is utilized as an indicator for damage, as this allows an approximation of the area of damage. In this case, it is necessary to be aware that the correlation confidence is load dependent. Thus, to avoid the effect of loading on the correlation coefficient, evaluations of 3D-DIC images taken at the same load level ( S max , i ) are conducted. As reference image, the first image (i=1) at peak load S max , i is taken and subsequently all images at different cycles are correlated to this. For the reference image, the same evaluated area and associated setting as for the strain evaluation (see Figure 4) are used. The continuous acquisition of images (45s) at each quasi-static loading allows an averaging to reduce noise. Due to the evaluations of 3D-DIC images taken at the same load level ( S max , i ), changes to the correlation confidence are attributed to damage, since it is assumed that any other influences on the correlation confidence are negligible with the selected evaluation. In order to identify the shape and size of the damage, the spatial correlation coefficient of the subsets are evaluated by a threshold, a method that was demonstrated in [34].

2.4. Damage evaluation by electrical impedance tomography (EIT)

Contrary to the 3D-DIC damage evaluations, where an evaluation is performed on the entire evaluation area, the EIT reconstructions are performed only from data collected at the boundaries (measurements at electrodes). As a result, the EIT can only provide an estimation of the spatial conductivity changes. Therefore, the elastoresistive thin-film sensor is used to carry out differential EIT reconstructions of the conductivity. In this way, systematic voltage measurements on the placed electrodes are performed throughout the experiment (see Section 2.2) and give the boundary potential to solve the inverse solution. The EIT evaluation framework for measurement data collection, preprocessing and conductivity reconstruction was developed in a previous work[31]. In this process, the Gauss-Newton one-step algorithm is utilized to solve the differential inverse EIT reconstruction using a maximum a p o s t e r i o r i regularization approach [41,42,43]. In Equation 1 the resulting linearized inverse EIT approach is given.
Δ σ ^ = H ⊺ W H + λ 2 Q − 1 H ⊺ W Δ v
This approach involves the Noser prior for regularization. The estimated change of the spatial conductivity Δ σ ^ is obtained via the change of voltage potentials at the boundaries Δ v (electrodes). Additional variables in Equation 1 are the sensitivity matrix H , the weight matrix W , the regularization matrix Q and the hyperparameter λ , which help to solve the differential inverse linearized problem. The hyperparameter is defined as λ = 1.8307 × 10 6 , which is defined according to the method proposed in [32]. A detailed description of the underlying experimental framework and evaluation process can be found in [31].
However, the EIT-based damage reconstruction of realistic operational fatigue loading faces challenges due to the thin-film sensor material’s “Set-In” effect and other sensor related environmental influences (e.g. temperature or moisture). To overcome these issue, two evaluation approaches are investigated to demonstrate the EIT method for SHM application under fatigue and operational loading, respectively.

2.4.1. Fatigue damage evaluation using mean value adjustment

In line with the 3D-DIC evaluation of damage the EIT measurements at the same load level but at different numbers of cycles are taken for the systematic differential EIT reconstructions. As reference the EIT measurements of the first quasi-static loading are taken (i.e., the measurements at S base , 1 , S mean , 1 , S max , 1 ). Due to the fact that each differential EIT reconstruction refers to the first measurement, the cycle and strain dependent initial conductivity change of the sensor material affects the damage evaluation and needs to be considered. The associated effect is better known as the “Set-In” effect [30] and strongly influences the reconstruction results. However, assuming the “Set-In” effect to be homogeneous over the sensor area, and furthermore, assuming the influence of the damage on the mean conductivity to be small and not affecting the elastoresistivity, allows to compensate its influence by Δ σ ^ comp , i = Δ σ i ^ − ( mean ( σ ^ i ) − mean ( σ ^ 1 ) ) .
Thereby, the “Set-In” compensated conductivity change of the sensor Δ σ ^ comp , i is obtained by subtracting the difference of the ith mean conductivity of the sensor mean ( σ ^ i ) and the initial mean conductivity of the sensor mean ( σ ^ 1 ) from the ith conductivity change of the sensor Δ σ ^ i .
This mean value adjustment could also compensate for other environmental influences on the sensor’s conductivity, like e.g., temperature and humidity, as long as the sensor area is homogeneously affected and the elastoresistivity remains unaffected. Resulting spatial conductivity changes can be related to potential damage. Identification of this spatial conductivity change is performed with a conductivity change threshold.

2.4.2. Fatigue Damage evaluation using continuous reference measurement adjustment

Alternative of using a single reference EIT measurement, several EIT measurements as references can be used in order to evaluate potential damage. In this way, the “Set-In” effect and also potential other environmental influences on the sensors conductivity can be compensated. Compared to the mean value adaption method, the adaption of the reference measurement can also compensate inhomogeneous conductivity changes. However, also this method requires the assumption of an unaffected elastoresistivity. To investigate this proposed approach EIT measurements at base load S base , i are related to measurements at subsequent peak load S max , i , and EIT measurements at base load S base , i are related to measurements at subsequent mean load S mean , i . As the reconstructions are based on measurements at different load levels, the spatial conductivity changes are a combination of mechanical loading and potential damage. For damage evaluation solely the negative component of the spatial conductivity changes are utilized, as it is assumed that only a reduction in conductivity changes reflect potential damage.

3. Results

This Section presents the results of the validating 3D-DIC-based shape and size evaluation and the EIT-based evaluation of the initiating and propagating damage.
As part of the experimental investigation of the plate with a circular hole, validating 3D-DIC evaluations are performed on the backside and EIT reconstructions on the frontside. Since no fracture of the specimen, or measurement error due to a chipped electrode have been encountered damage evaluation could be carried out throughout the entire test duration. In addition, the electrical contacts did not show any visible deterioration after the test.
During the test free-edge delaminations were visually observed at the two highly stressed hole sides. First observation of the delaminations was approximately after 1500 cycles at the left side of the highly stressed hole. Shortly afterwards after 2000 cycles delaminations were also observed at the opposite side of the hole. Both delamination sites could be visually observed to continuously grow in size and number of delaminated plies. These results perfectly correlate with the findings presented for the same plate and loading in a previous work [34]. Furthermore, a post-test analysis of the specimen’s speckled surface around the hole using an optical microscope also revealed surface cracks. These cracks are aligned with the fiber bundles and most probably intralaminar matrix cracks that evolved from the propagating delaminations. However, a more detailed investigation of the damage behavior is not part of the present study.

3.1. 3D-DIC damage evaluation results

Evaluated changes inside the spatial surface strain field are considered as indicator for cyclically induced damage. Performed evaluations ( S base , i to S max , i ) yield to strain fields like those exemplarily illustrated in Figure 5. Thereby, the spatial distribution of the major principal strain ε 1 is plotted for chosen cycles. The selected colorbar remains unchanged to highlight the strain field alteration in the vicinity of the circular hole.
As cyclic fatigue loading continues, the 3D-DIC evaluated strain field also changes, although the considered static load level does not. In particular, the areas with high strains become larger in those regions that are exposed to the stress concentrations at the hole. This can be interpreted as an indicator of existing damage, which becomes apparent by selecting the upper scale level at 10000 μ m / m (maximum strain allowable for used plies), and observing how the red area (all strain values above 10000 μ m / m ) evolves over the increasing number of cycles. However, the used threshold is very high, and thus, according to the strength properties of the laminate, material degradation must be present in the plies at these regions. This is also supported by the surface cracks found in the post-test analysis, as these were only found in the regions strained above 10000 μ m / m at the test end. Thus, the increase of the highly strained area represents the propagating damage, although it may not reflect its true size and shape.
In order to demonstrate changes in the spatial surface strain field throughout the entire test, a summation of all spatial strains at which the upper scale level ( 10000 μ m / m ) is exceeded is performed. The resulting damage affected changes in the spatial surface strains are normalized with respect to the last evaluation and are shown in Figure 6.
From Figure 6 it is obvious that the damage already initiates before 2k cycles. This is supported by the fact that the predefined threshold value is exceeded at 2k cycles, which means that damage has occurred. Since only an evaluation at 2k cycles is performed, a more accurate evaluation of damage initiation and early damage propagation (within the first 2k cycles) is not possible. In Figure 6, this unknown propagation is represented by a dotted line, which, however, only serves as a qualitative indication. Thereafter the damage affected changes in the spatial surface strains become larger, as the number of cycles increases. This increase continues continuously throughout the fatigue loading. Within the different fatigue load levels, a systematic behavior is observed, with an initially more pronounced increase followed by a decelerating behavior as cyclic loading continues. Irrespective of the fact that this evaluation does not provide an actual damage size, it can be considered to qualitatively represent the changes, and thus the damage, resulting from fatigue loading.
A good and readily demonstrated approximation of the size and shape of the damage is provided by the spatial correlation confidence [34]. Comparing measurements acquired during the experimental investigation under the same load, but after an increasing numbers of fatigue cycles, provides information on damage initiation and damage propagation. All images obtained at peak load S max , i are evaluated independently with respect to S max , 1 . In Figure 7, exemplarily 3D-DIC evaluation results after different numbers of cycles are depicted. The color shading represents the evaluation’s spatial correlation confidence and is fixed. As threshold level for damage a correlation coefficient of 0.01 is selected, as this value was validated on identical specimens subjected to identical loads in a previous work [34].
The 3D-DIC evaluations depicted in Figure 7 indicate, that damage initiation already occurs before 2k cycles and that damage propagation takes place throughout the length of the experiment. Observing the vicinity of the hole reveals that the threshold surpassing area (red region) becomes larger. The red regions away from the hole do not correspond to any damage, but are attributable to a local overexposure, and thus, do not change throughout the experiment.
Summing up all portions where the defined threshold value (0.01) is exceeded yields to the area of damage for discrete cycles. The obtained path of damage progression based on the area of damage is normalized with respect to the found maximal area of damage (37.89 mm2, evaluated by the same method) and is presented in Figure 8.
Within the first 2k cycles (see detail in Figure 8) damage initiation is observed, as at this cycle count an initial increase in the area of damage is present. However, the exact cycle number of damage initiation can not be identified. Again the unclear cycle number of damage initiation and unclear propagation (up to 2k cycles) is indicated as dotted line. Thereafter damage propagation takes place and continues over 500k cycles. At 500k cycles the identified damage size is in agreement with the findings of a previous work [34]. Afterwards the load dependence of the correlation confidence is present, since the static load S max , i and the cyclic load C max , i are not identical (load increase by 10% after every 500k cycles) and thus the identified damage no longer corresponds to the actual damage. This means that the damage caused by C max , i is slightly larger than that evaluated at S max , i . Nevertheless, a qualitative evaluation of the damage growth is possible based upon the correlation confidence.

3.2. EIT-based fatigue damage evaluation results

Within this Section the results of the two approaches are presented, with which sensor conductivity changes due to fatigue loading and other potential environmental influences can be compensated.

3.2.1. Damage reconstruction using mean value adjustment

All EIT measurements carried out at the quasi-static loadings (mean load S mean , i and at peak load S max , i ) are evaluated individually with respect to the measurements at the initial static loading ( S mean , 1 , S max , 1 ). For the given laboratory setup with constant temperature and humidity, these differential EIT reconstructions provide the sole electrical conductivity change of the elastoresistive thin-film sensor. The resulting conductivity changes of the sensor are accounted by two phenomena, whereby the initially dominant “Set-In” effect is compensated at this proposed approach (see Section 2.4.1). Remaining portions of the negative component of the spatial conductivity changes are attributable to potential damage. In Figure 9 exemplarily the EIT reconstructions of the “Set-In” compensated spatial conductivity changes for selected cycles (index i allows a cycle assignment) at peak load S max , i are depicted. The used scaling remained unchanged, to visualize spatial conductivity changes that are attributable to potential damage.
In the evaluations of these EIT reconstructions partial increases in conductivity (attributable to compressive strains) and local decreases in conductivity (due to tensile strain and potential damage) are present. Besides these observations, a conductivity decrease at the sensor electrodes can be observed. However, this is due to the numerically linearized EIT reconstruction algorithm and measurement noise, and therefore, can be neglected. Nevertheless, Figure 9 reveals clear changes in the spatial conductivity throughout cyclic fatigue loading.
Based on an initial EIT reconstruction of the unloaded thin-film sensor (before the first quasi-static loading), the conductivity change threshold to identify potential damage is ascertained by − 53 S / m . The conductivity change threshold is chosen to represent 10% of the initial conductivity of the unloaded sensor. A summation of all spatial conductivity changes below this threshold provide information on the damage propagation over the number of cycles. In Figure 10 the summarized threshold exceeding spatial conductivity changes are plotted over the number of cycles.
Due to the mean value adaption of the EIT reconstructions the “Set-In” effect is compensated. Potential further environmental influences (e.g. temperature and moisture) stay constant at the institute’s test rig, and thus, can be excluded. Consequently, as the EIT measurements are taken at the same load levels, resulting decrease within the spatial conductivity is predominantly the result of an increasing damage. Both the spatial conductivity changes at mean load S mean , i and peak load S max , i show, that as the test duration advances, the spatial conductivity decreases. Spatial conductivity changes evaluated at mean load S mean , i follow an identical trend to that at peak load S max , i , also indicating an increasing damage. From both paths, a first drop of the conductivity is observed after 10k to 12k cycles. The spatial conductivity changes rapidly but slows down with an increasing number of cycles at the first cyclic load level. The same behavior can also be observed for every load increase (by 10% every 500k cycles), where the spatial conductivity change is more pronounced, before it slows down again. Conversely, when the load is adjusted to 100% (at 1500k cycles), there is no pronounced spatial conductivity change. Due to the definition of the conductivity change threshold (10% of the initial conductivity of the unloaded sensor), only spatial conductivity changes which cause a more significant drop are accounted, so that no spatial conductivity changes are determined up to 12k cycles (see detail Figure 10). Consequently, the detection of damage initiation by the proposed EIT-based method is less sensitive than the 3D-DIC system. Additionally, the absence of the measurement at 0k cycles is apparent, which is attributable to the differential EIT reconstruction.

3.2.2. Damage reconstruction using continuous reference measurement adjustment

The damage evaluation by continuously updated EIT reference measurements also allows the compensation of the “Set-In” effect and other possible environmental influences on the sensor material conductivity. As stated in Section 2.4.2 the resulting spatial conductivity change reconstructions reflect a combination of potential damage and strain due to the mechanical loading, as measurements at S base , i are used as reference and the immediately following measurements at S max , i or S mean , i are used to calculate the differential potential at the boundaries. In Figure 11, the EIT reconstructions of the spatial conductivity changes after different numbers of cycles are exemplarily depicted for three isolated cases, where S base , i to S max , i are evaluated.
In the areas of higher stresses, where also the delaminations and surface cracks were observed (at the hole, perpendicular to the loading direction), the EIT reconstructions reveal a decrease in spatial conductivity. In the initial evaluation before fatigue loading, this decrease in spatial conductivity can be assigned to the pure mechanical strain due to the loading, however, it becomes more pronounced with increasing number of cycles, which can only be explained by formation and growth of damage. In contrast, the spatial conductivity increases in the areas exposed to compressive stresses (at the hole, in loading direction, see Figure 5). This local increase in spatial conductivity is accounted to the compressive strains, and mainly to artifacts during the reconstructions. Similarly, boundary effects at the electrodes are present, but they are not considered.
In order to indicate the alterations in spatial conductivity changes over the cyclic fatigue loading, threshold values are specified that allow a summation of the damage affected sensor area for the individual reconstructions. The threshold values are defined as the minimum of the negative component of the spatial conductivity change at the first EIT reconstructions. Accordingly, the threshold values to describe spatial conductivity changes from S base , i to S max , i is − 341.80 S / m and for S base , i to S mean , i it is − 153.82 S / m . In Figure 12 the assumed damage affected area (sum of all elements that exceed the defined threshold) are plotted over the number of applied fatigue cycles for both evaluations.
Here, consistent with Figure 11, where selected reconstructions are given, the negative component of the spatial conductivity changes are found to grow throughout the cyclic fatigue loading. Reflecting an increase in the damage affected area as indicated in Figure 12. This outcome is obtained from both evaluations that have been carried out. The results derived from the evaluations at S base , i to S mean , i provides a more pronounced increase than that at S base , i to S max , i . Each time the cyclic load is increased, significant changes in the development of the EIT-evaluated damage affected area take place. After these temporary more pronounced changes, the EIT-evaluated damage affected area subsides thereafter, but indicate a continuous increase. As a consequence of the thresholds being defined, no alteration in the EIT-evaluated damage affected area are found in the first 10k cycles (see detail Figure 12), thus, the potential damage initiation was detected later that observed by the 3D-DIC system.

4. Discussion

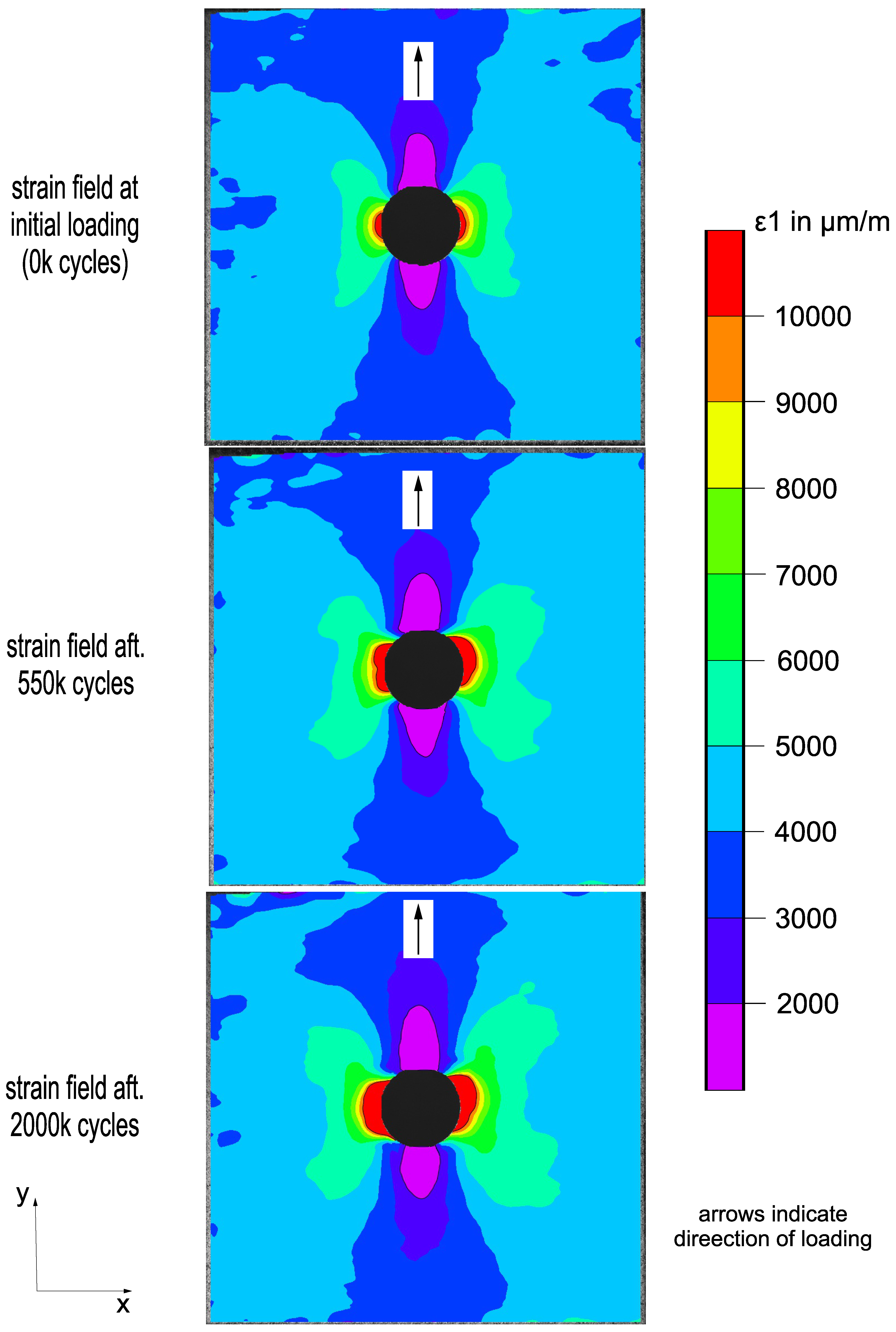
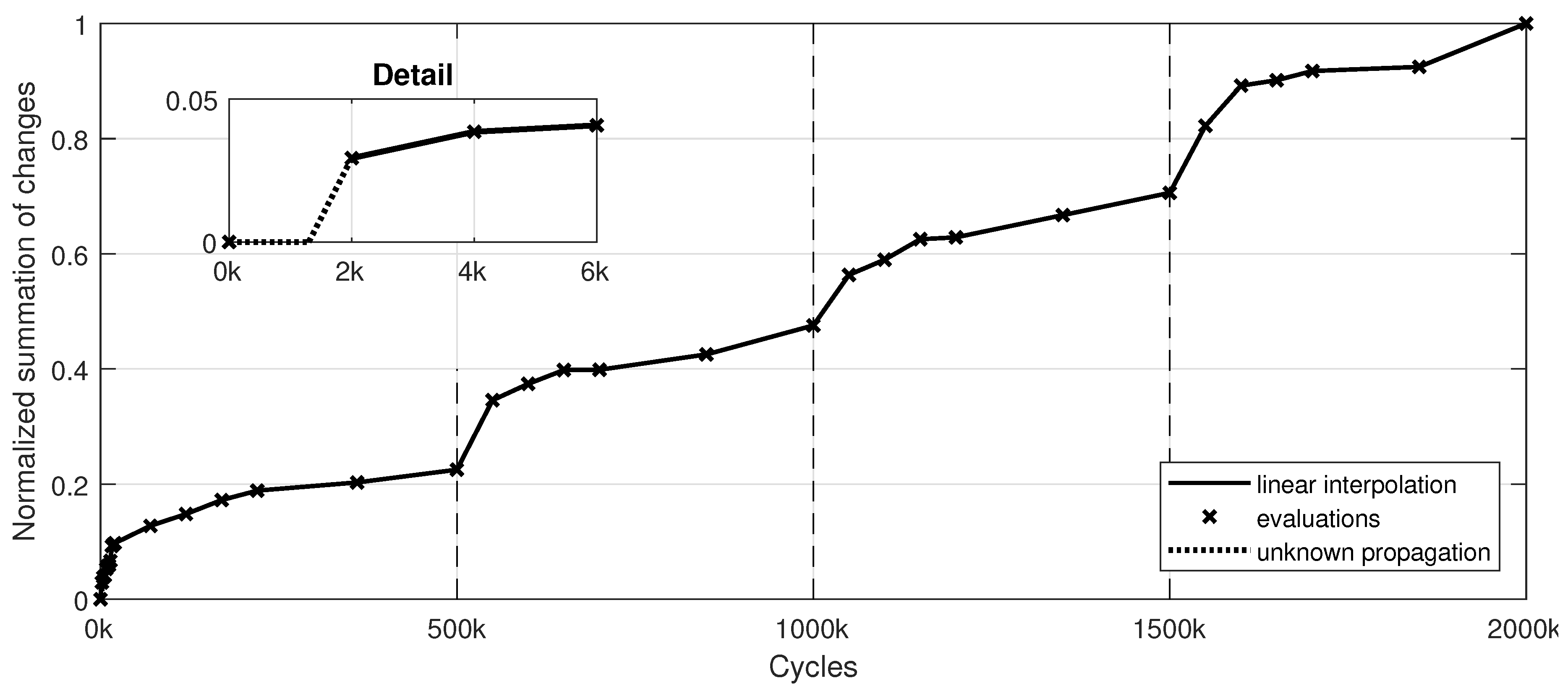
The damage induced by the cyclic fatigue loading is evaluated by measurements taken in the quasi-static loadings. As evaluations of the spatial surface strain field by 3D-DIC reveal, degradation in the vicinity of the hole occurs, providing an indication of existing damage. 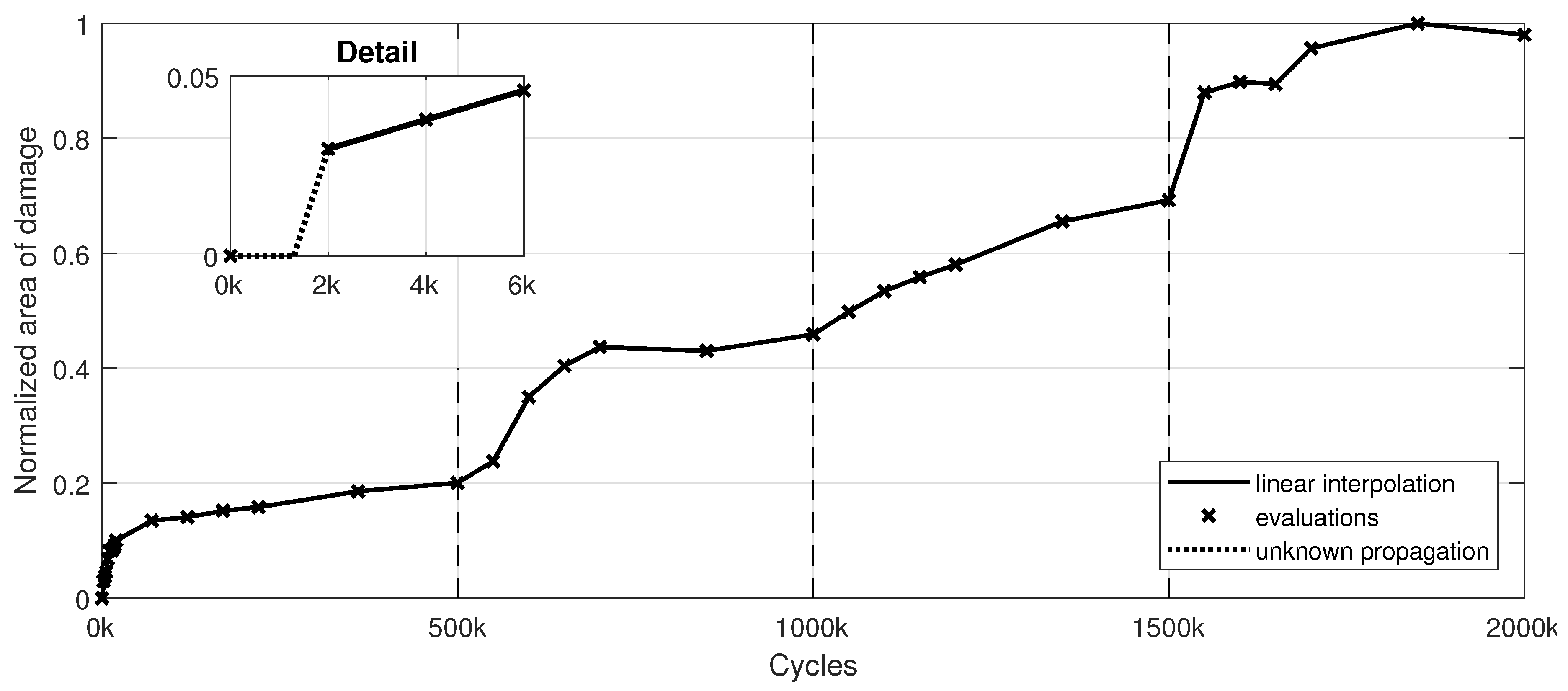While Figure 5 show this degradation for isolated cases, visualization of the degradation throughout the entire cyclic fatigue loading is achieved with a threshold value (see Figure 6). To identify the shape and size of the underlying damage with 3D-DIC, the correlation coefficient is used. The resulting path (determined with a threshold value), given in Figure 8 serves as a qualitative comparative quantity for the EIT evaluations.
This path, obtained by the 3D-DIC correlation coefficient, reveal damage initiation at the edge of the circular hole within the first 2k cycles (see detail Figure 8). This observation is in agreement with previous findings of the authors [34], where detailed focus was placed on damage initiation and propagation of similar specimens subjected to a single cyclic loading amplitude. The adopted threshold value also shows a comparative damage size at 500k cycles. Thereafter, the load dependency of the correlation confidence is present. Meaning that the arising delaminations and micro-cracks induced by higher cyclic loadings are not fully opened within the quasi-static loading, where the evaluation takes place. Thus, implying that the actual size of the damage is larger than that obtained from 3D-DIC evaluation. Nevertheless, the tendency of damage progression is still present throughout the cyclic fatigue loading.
Before the results of the 3D-DIC evaluations and the EIT reconstructions are compared, the results of the EIT reconstructions are verified to ensure that they are not due to degradation of the sensor itself. Therefore the baseline measurements S base , i are examined individually to obtain the mean spatial conductivity of the sensor. In Figure 13 the mean spatial conductivity of the sensor is plotted over the number of cycles.
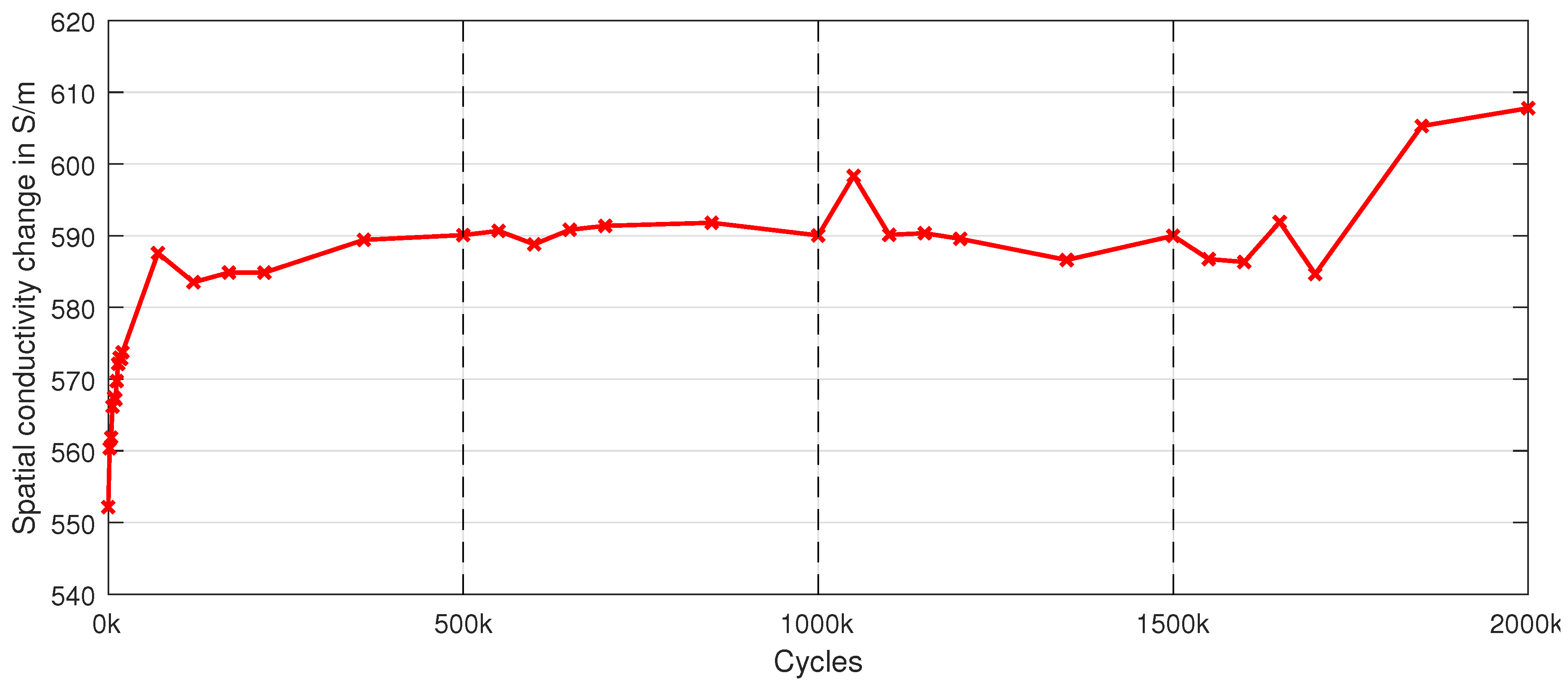
At the initial 70k cycles the “Set-In” effect is evident. Owing to this strong initial conductivity change, there is also no precise identification of the damage initiation, since it occurs within the first 2k cycles as indicated by the 3D-DIC evaluation. Likely the small extent of the damage at initiation may also influence the detectability, meaning that an evaluation by means of EIT may be possible only for damage above a certain size. After the “Set-In” effect, it appears that the conductivity of the sensor remains relatively stable and allows the evaluation of damage progression. Additionally, this indicates the suitability of the used thin-film sensor material for this application and that the obtained results are primarily attributable to spatial conductivity changes, caused by e.g. potential damage. After 1750k cycles the spatial conductivity of the sensor starts to increase, indicating a possible degradation of the sensor. However, further investigations are required to obtain more detailed information about the service life of the used sensor.
The first proposed approach, given in Section 2.4.1 deals with the compensation of the strong initial conductivity change (“Set-In” effect). Results given in Figure 9 and Figure 10 are obtained by referring EIT measurements taken at the same load level but at different cycles to an initial measurement (i=1). Consequently, environmental influences (e.g. humidity and temperature) which may occur are not accounted within this approach. Nevertheless, as these environmental influences remained stable throughout the experiment, they are not influencing the results.
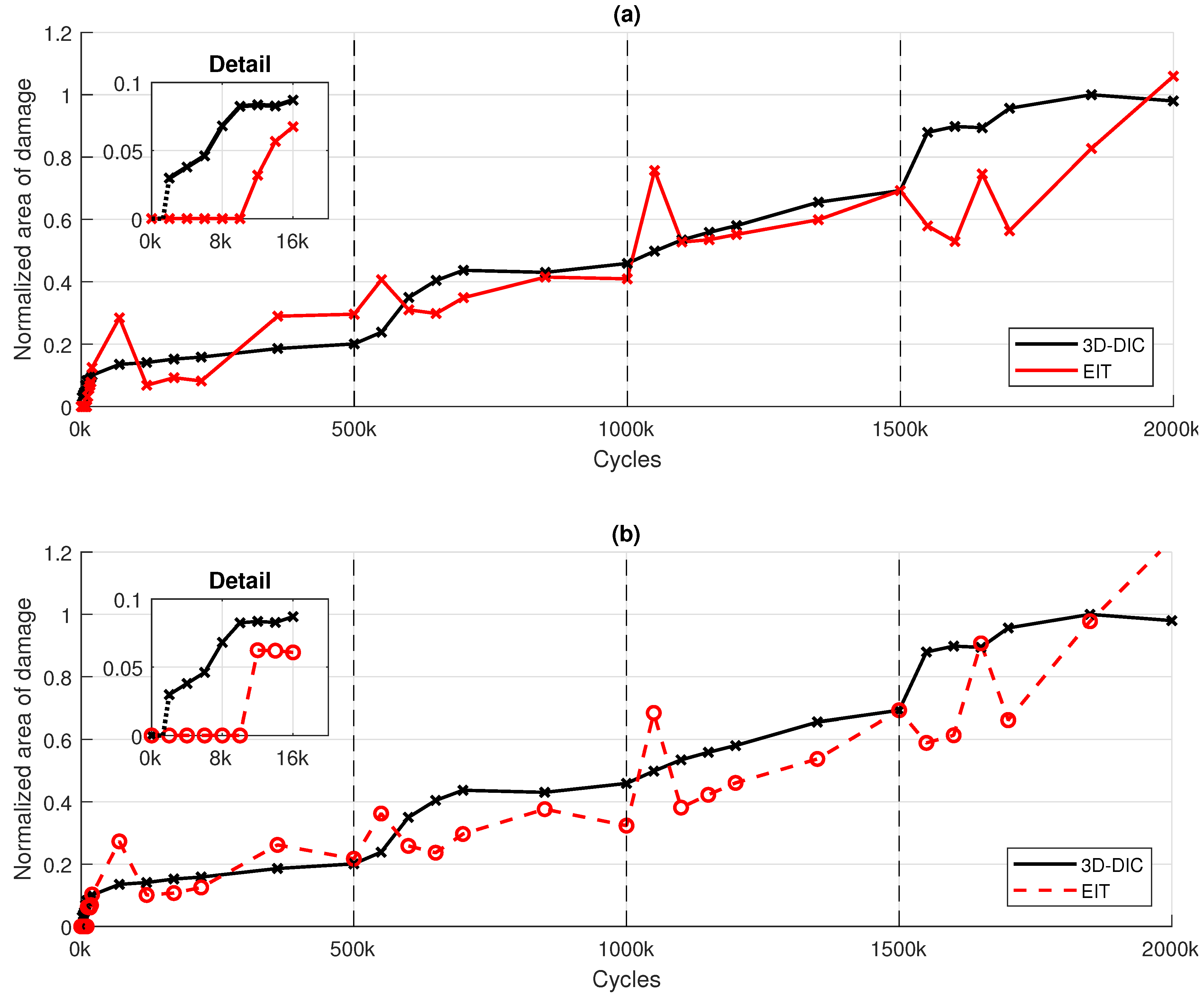
Using the area of spatial conductivity changes from Figure 10 and scale them to reflect the normalized damage size from the 3D-DIC evaluation at 1500k cycles allows a common representation. In Figure 14 the EIT reconstructions (also presented in Figure 10) and the 3D-DIC evaluation (also presented in Figure 8) are given, to validate the outcome of the EIT reconstructions.
This common representation reveals that the spatial conductivity changes correlate very well with the 3D-DIC outcomes. Comparing the 3D-DIC results with those of the EIT reconstructions at peak load S max , i yields a significantly stronger agreement than with those at mean load S mean , i . Up to 1500k cycles both EIT reconstructions show satisfactory agreement, beyond this cycle number the differences between 3D-DIC and EIT become larger. This may indicate a deterioration of the thin-film sensor, which is also supported by the mean spatial conductivity change given in Figure 13. This also explains the scaling of the EIT reconstructions at 1500k cycles. Nevertheless, both comparisons emphasize that EIT reconstructions can also be used to evaluate the damage progression, to the extent that the initial strong conductivity change is taken into account, as shown in the proposed approach.
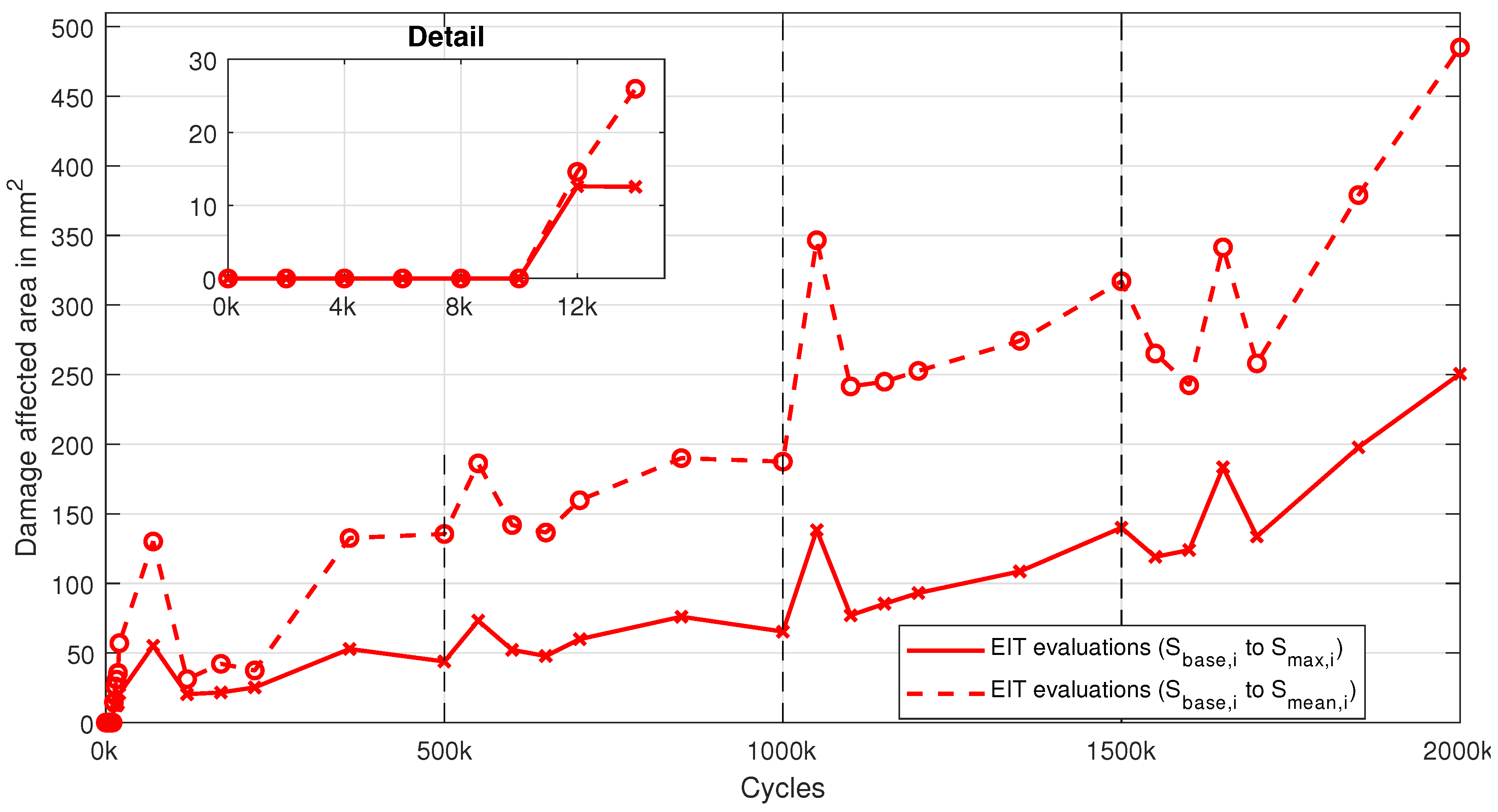
The second approach to enable EIT-based fatigue damage monitoring by compensation of the “Set-In” effect and further potential environmental influences uses a continuous reference measurement adjustment. Here, the baseline measurement S base , i is updated and subsequent measurements at peak load S max , i and mean load S mean , i are referred to these. Thereby, evaluated spatial conductivity changes are the result of a superposition of mechanical loading and potential damage. Results presented in Figure 12 reveal an increase of the damage affected area over the number of fatigue cycles. 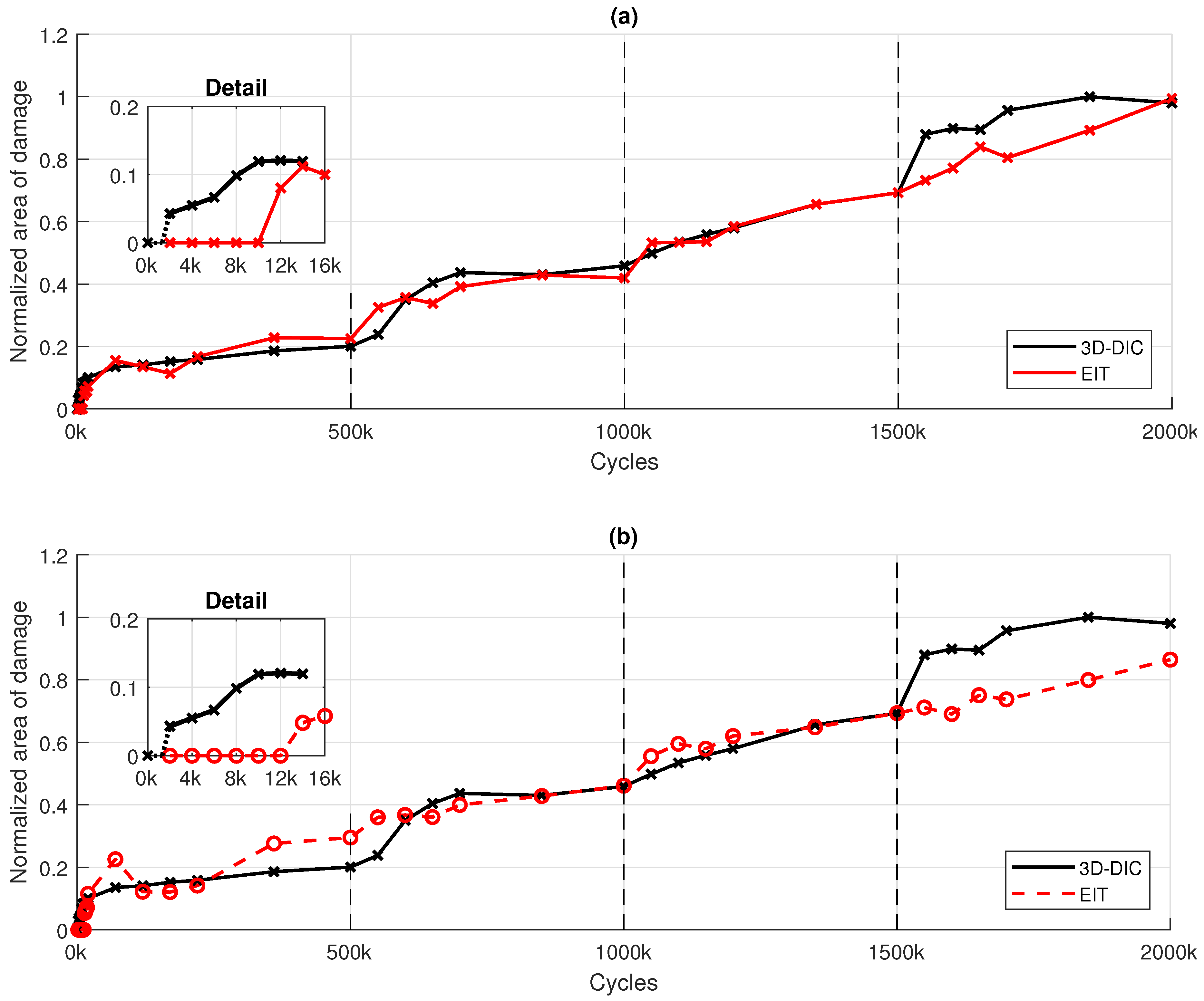Using these results and scale them in accordance with the normalized 3D-DIC results from Figure 8 provides a combined representation, as given in Figure 15. Again the 3D-DIC result at 1500k cycles is used for scaling of the EIT results. In Figure 15 (a), the 3D-DIC evaluations are plotted besides the EIT reconstructions of the S base , i to S max , i evaluations. In Figure 15 (b), the 3D-DIC evaluations are plotted besides the EIT reconstructions of the S base , i to S mean , i evaluations.
It can be seen that the propagation of the damage affected area evaluated by EIT qualitatively correlate with the results from the 3D-DIC. However, some noticeable differences are apparent. Existing differences as given in Figure 15 are attributable to certain aspects. Particular, the discrepancies may be explained by the fact that the spatial conductivity changes are derived from measurements at different load levels, which gives a combination of mechanical loading and potential damage. Likewise, the applied primer, on which the thin-film sensor has been deposited, may additionally blur the strains and local changes within the spatial strain field, which are not detected by the EIT reconstruction might also induce such differences. A further aspect is the choice of the conductivity change thresholds for damage detection. Although a reduction of these threshold values improved the sensitivity, it also led to a significantly higher noise detection. Therefore, the choice provided the best trade-off between accuracy and robustness.
All these aspects are also reflected in the first proposed approach, except the evaluation at different load levels. However, as shown in Figure 14, the differences between 3D-DIC and EIT reconstructions are considerably smaller, indicating that these aspects may have a minor contribution to the observed differences as can be seen in Figure 15. Consequently, the evaluation at different loads levels and the use of an updated baseline measurement S base , i is likely to have a more significant contribution to the differences.
Compared to the first proposed approach, the agreement of the second proposed approach with the results of the 3D-DIC is weaker. However, the second approach could compensate a potential inhomogeneous “Set-In” effect (or inhomogeneous temperature and moisture distributions). This is particularly advantageous for significantly enlarged sensors (e.g. for application on complete shell-shaped structures) in the case that inhomogeneity is present. In the absence of any inhomogeneity related to the “Set-In” effect, the first proposed approach could also be used for significantly larger sensors.
Nevertheless, both proposed approaches demonstrate that progressive damage can be evaluated. While the 3D-DIC evaluates the entire evaluation area, the EIT uses voltage measurements at the boundary to reconstruct the electrical conductivity within the thin-film sensor. Consequently, the resulting resolution of the EIT reconstructions is smaller. Both methods rely on local changes within the evaluated area. It is likely that strain changes due to delaminations and micro-cracks caused by cyclic loading are responsible for the detected local changes. Using 3D-DIC, the delaminations and micro-cracks result in changes to the subsets (change of the gray value) and hence allow an evaluation, as the correlation coefficient passes the defined threshold value. Within the EIT reconstructions, delaminations and micro-cracks deteriorate the local conductivity, allowing an evaluation. Despite the fact that opposite sides (3D-DIC on backside, EIT on frontside) are evaluated, it is assumed that the occurring damage is reflected identically on both sides.
In common, to enhance the findings through EIT reconstructions and to obtain better agreement between EIT and 3D-DIC the following considerations can be included. During the experiment, a single EIT measurement was performed at each load level. Several EIT measurements offer a possibility to identify potential outliers and the possibility of averaging the reconstructed spatial conductivity changes. In addition, a reduction in the size of the thin-film sensor or additional electrodes could be considered for improved spatial resolution. Both of these aspects would ensure that more information for the spatial reconstruction is available and, as a result, a more accurate evaluation could be carried out. Furthermore, a higher order reconstruction approach could be used like e.g., the generic algorithm according to Hassan[29]. Additionally, for the second proposed approach, a load independent analysis may be possible to compensate the mechanical loading component in the spatial conductivity change, so that only potential damage remains as a quantity. This may be achieved by a profound analysis of the elastoresistive properties and its dependency on fatigue loading. However, this is left for future research.

4.1. Conclusions

The present study demonstrates the potential of the EIT method featuring a spatial elastoresistive thin-film sensor for the monitoring of damage initiation and propagation in a cyclic fatigue loaded thin plain-woven CFRP component. As a case study, a CFRP plate with a centrally placed circular hole, that is subjected to high cyclic tensile-tensile loading, is used. The applied strains were between 3000 μ m / m and 12000 μ m / m , thus, well represent a realistic operational loading of CFRP components, leading to realistic damage. The observed damage is a multiple delamination in combination with micro-cracks that initiates and propagates at both sides of the hole. For validation of the EIT results a 3D-DIC system is used, to monitor the shape and size of the damage. The electrical contacts at the used thin-film sensor did not show any visible deterioration. However, the thin-film sensor material showed a strong “Set-In” effect, followed by very constant electrical properties until it seemed to in increasingly deteriorate over 1500k cycles. Consequently, the sensor network is concluded to be applicable for the monitoring of operational fatigue loading. Nevertheless, it is required to compensate this “Set-In” effect for fatigue, and therefore, realistic operational loading regimes. Two compensation approaches are proposed in the present article. The first, uses a conductivity mean value adaptation and provides a very good correlation with the damage propagation identified by the 3D-DIC system. The second approach also demonstrates potential to monitor damage propagation by EIT, however, the superimposition of mechanical loads and potential damage corrupts the correlation.
Due to the nature of the used EIT reconstruction algorithm, the true shape of the damage cannot be identified, and thus, also not directly correlated to the 3D-DIC results. For the evaluation if a damage at a location is present or not, a threshold is used. The damage propagation is observed by summation of these damage affected local areas. The damage locations identified by the EIT approaches perfectly match the 3D-DIC results. Furthermore, it is highly expected that more advanced reconstruction algorithms also enable the evaluation of the damage shape.
Future research shall address the characterization of the influence of the fatigue loading on the sensor material’s elastoresistivity, and furthermore, the identification of the true damage shape and the full spatial strain state by more advance EIT reconstruction algorithms to enable a better evaluation of the damage within the composite layup and its effect on the integrity of the structural component.
Nevertheless, it has been demonstrated within this paper that both proposed EIT approaches, which compensates EIT related issues, can be used to describe damage progression originating from a circular hole due to cyclic fatigue loading at multiple loading levels. Consequently, the use of thin-film sensors offers a complementary method, with which damage propagation of thin plain-woven CFRP laminates with a circular hole could be evaluated.

Acknowledgments

The authors are grateful to Alexander Schöfer for his technical support during the experimental investigations.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. K. Diamanti, C. Soutis, Structural health monitoring techniques for aircraft composite structures, Progress in Aerospace Sciences, Volume 46, Issue 8, 2010, Pages 342-352.
  2. V. Giurgiutiu, Structural Health Monitoring of Aerospace Composites, Academic Press, 2016, ISBN: 9780124096059. [CrossRef]
  3. C. Niu, M.C.Y. Niu, Composite Airframe Structures: Practical Design Information and Data, Adaso Adastra Engineering Center, 1992, ISBN: 9789627128069.
  4. A.P. Vassilopoulos, T. Keller, Fatigue of Fiber-reinforced Composites, Engineering Materials and Processes, Springer London, 2013, ISBN: 9781849961806. [CrossRef]
  5. S. Nonn, Effects of defects and damage localization in carbon fiber reinforced polymer lightweight structures, PhD thesis, Johannes Kepler University Linz, 2018.
  6. Australian Transport Safety Bureau, Fibre composite aircraft – capability and safety, Aviation Research and Analysis Report, AR-2007-21, 2008.
  7. A.C. Long, Design and Manufacture of Textile Composites, Elsevier Science, Woodhead Publishing Series in Textiles, 2005, ISBN: 9781845690823.
  8. H. Flower, C. Soutis, Materials for airframes, The Aeronautical Journal, Volume 107, Issue 1072, 2003, Pages 331-341. [CrossRef]
  9. W. J. Staszewski, C. Boller, G.R. Tomlinson, Health Monitoring of Aerospace Structures: Smart Sensor Technologies and Signal Processing, John Wiley & Sons, 2004, ISBN: 9780470843406. [CrossRef]
  10. S. Dalkilic, Improving aircraft safety and reliability by aircraft maintenance technician training, Engineering Failure Analysis, Volume 82, 2017, Pages 687-694. [CrossRef]
  11. H. Speckmann, R. Henrich, STRUCTURAL HEALTH MONITORING (SHM) – OVERVIEW ON TECHNOLOGIES UNDER DEVELOPMENT, Proceedings of the 16th World Conference on NDT, Volume 1, 2004.
  12. C.P. Dienel, H. Meyer, M. Werwer, C. Willberg, Estimation of airframe weight reduction by integration of piezoelectric and guided wave–based structural health monitoring, Structural Health Monitoring, Volume 18, Issue 5-6, 2019, Pages 1778-1788. [CrossRef]
  13. T. Dong, N.H. Kim, Cost-Effectiveness of Structural Health Monitoring in Fuselage Maintenance of the Civil Aviation Industry †, Aerospace, Volume 5, 2018, Number 3, Article No. 87. [CrossRef]
  14. X. Zhao, H. Gao, G. Zhang, B. Ayhan, F. Yan, C. Kwan, J.L. Rose, Active health monitoring of an aircraft wing with embedded piezoelectric sensor/actuator, Smart Materials and Structures, Volume 16, Issue 4, 2007. [CrossRef]
  15. R. Soleimanpour, C.-T. Ng, C.H. Wang, Higher harmonic generation of guided waves at delaminations in laminated composite beams, Structural Health Monitoring, Volume 16, Issue 4, 2017. [CrossRef]
  16. R. Di Sante, Fibre Optic Sensors for Structural Health Monitoring of Aircraft Composite Structures: Recent Advances and Applications, Sensors, Volume 15, 2015. [CrossRef]
  17. Ch.E. Katsikeros, G.N. Labeas, Development and validation of a strain-based Structural Health Monitoring system, Mechanical Systems and Signal Processing, Volume 23, Issue 2, 2009, Pages 372-383. [CrossRef]
  18. L.B. Andraju, G. Raju, Damage characterization of CFRP laminates using acoustic emission and digital image correlation: Clustering, damage identification and classification, Engineering Fracture Mechanics, Volume 277, Issue 4, 2023. [CrossRef]
  19. J. Cai, L. Qiu, S. Yuan, L. Shi, P.P. Liu, D. Liang Structural Health Monitoring for Composite Materials, 2012. [CrossRef]
  20. N. Makoond, L. Pelà, C. Molins, P. Roca, D. Alarcón, Automated data analysis for static structural health monitoring of masonry heritage structures, Structural Control Health Monitoring, Volume 27:e2581, 2020. [CrossRef]
  21. D. Feng, M.Q. Feng, Computer vision for SHM of civil infrastructure: From dynamic response measurement to damage detection - A review, Engineering Structures, Volume 156, 2018, Pages 105-117. [CrossRef]
  22. S. Nonn, M. Schagerl, Y. Zhao, S. Gschoßmann, C. Kralovec, Application of electrical impedance tomography to an anisotropic carbon fiber-reinforced polymer composite laminate for damage localization, Composites Science and Technology, Volume 160, 2018, Pages 231-236. [CrossRef]
  23. J. Cagáñ, J. Pelant, M. Kyncl, M. Kadlec, L. Michalcová, Damage detection in carbon fiber–reinforced polymer compo,site via electrical resistance tomography with Gaussian anisotropic regularization, Structural Health Monitoring, Volume 18, 2019, Pages 1698-1710. [CrossRef]
  24. B. R. Loyola, V. L. Saponara, K. J. Loh, T. M. Briggs, G. O’Bryan and J. L. Skinner, Spatial Sensing Using Electrical Impedance Tomography, IEEE Sensors Journal, Volume 13, 2013, Pages 2357-2367. [CrossRef]
  25. H. Rocha, C. Fernandes, N. Ferreira, U. Lafont, J.P. Nunes, Damage localization on CFRP composites by electrical impedance tomography, Materials Today Communications, Volume 32, 2022. [CrossRef]
  26. A. Baltopoulos, N. Polydorides, L. Pambaguian, A. Vavouliotis, V. Kostopoulos, Damage identification in carbon fiber reinforced polymer plates using electrical resistance tomography mapping, Journal of Composite Materials, Volume 47, 2013, Pages 285-3301. [CrossRef]
  27. T. Tallman, S. Gungor, G. Koo, C. Bakis, On the inverse determination of displacements, strains, and stresses in a carbon nanofiber/polyurethane nanocomposite from conductivity data obtained via electrical impedance tomography, Journal of Intelligent Material Systems and Structures, Volume 28, 2017, Pages 2617-2629. [CrossRef]
  28. K.J. Loh, T.C. Hou, J.P. Lynch, Carbon Nanotube Sensing Skins for Spatial Strain and Impact Damage Identification, Journal of Nondestructive Evaluation, Volume 28, 2009, Pages 9-25. [CrossRef]
  29. H. Hassan, T. Tallman, Failure prediction in self-sensing nanocomposites via genetic algorithm-enabled piezoresistive inversion, Structural Health Monitoring, Volume 19, 2020, Pages 765-780. [CrossRef]
  30. H. Enser, J.K. Sell, W. Hilber, B. Jakoby, Printed strain sensors in organic coatings: In depth analysis of sensor signal effects, Sensors and Actuators A: Physical, Volume 2, 2018, Pages 258-263. [CrossRef]
  31. J. Wagner, C. Kralovec, D. Kimpfbeck, L. Heinzlmeier, M. Schagerl, Framework for Strain Measurements at Cyclic Loaded Structures with Planar Elastoresistive Sensors Applying Electrical Impedance Tomography, European Workshop on Structural Health Monitoring - EWSHM 2022, Springer International Publishing, Pages 805-815. [CrossRef]
  32. J. Wagner, S. Gschoßmann, M. Schagerl, On the Capability of Measuring Actual Strain Values With Electrical Impedance Tomography Using Planar Silkscreen Printed Elastoresistive Sensors, IEEE Sensors Journal, Volume 21, 2021, Pages 5798-5808. [CrossRef]
  33. S. Gschoßmann, Y. Zhao, M. Schagerl, Development of Data Acquisition Devices for Electrical Impedance Tomography of Composite Materials, Proceedings of the 17th European Conference on Composite Materials (ECCM17), 2016.
  34. L. Heinzlmeier, S. Sieberer, C. Kralovec, M. Schagerl, Fatigue and Progressive Damage of Thin Woven CFRP Plates Weakened by Circular Holes, Experimental Mechanics, Volume 63, 2023, Pages 871–883. [CrossRef]
  35. VIC-2D Reference Manual, Correlated Solutions Inc., Knowledgebase - Manuals and Guides, Available online: https://correlated.kayako.com/section/9-manuals-and-guides (accessed 9 August 2023).
  36. VIC-3D Manual and Testing Guide, Correlated Solutions Inc., Knowledgebase - Manuals and Guides, Available online: https://correlated.kayako.com/article/57-vic-3d-8-manual-and-testing-guide (accessed 9 August 2023).
  37. M.A. Sutton, J.-J. Orteu, H. Schreier, Image Correlation for Shape, Motion and Deformation Measurements, Springer New York, NY 2009 ISBN: 9780387787466.
  38. S.H. Daly, Digital Image Correlation in Experimental Mechanics for Aerospace Materials and Structures, Encyclopedia of Aerospace Engineering, 2010. [CrossRef]
  39. B.R. Murray, K.A. Kalteremidou, D. Carrella-Payan, A. Cernescu, D. Van Hemelrijck, L. Pyl, Failure characterisation of CF/epoxy V-shape components using digital image correlation and acoustic emission analyses, Composite Structures, Volume 236, 2020. [CrossRef]
  40. A. Rogani, P. Navarro, S. Marguet, J-F. Ferrero, Study of post-impact behaviour of thin carbon/epoxy laminates subject to fatigue tensile loading, International Journal of Fatigue, Volume 148, 2021. [CrossRef]
  41. A. Adler, R. Guardo, Electrical impedance tomography: regularized imaging and contrast detection, IEEE Transactions on Medical Imaging, Volume 15, 1996, Pages 170-179. [CrossRef]
  42. A. Adler, T. Dai, W.R.B Lionheart, Temporal image reconstruction in electrical impedance tomography, Physiological Measurement, Volume 28, 2007, Pages S1-S11. [CrossRef]
  43. M. Cheney, D. Isaacson, J.C. Newell, S. Simske, J. Goble, Noser: An algorithm for solving the inverse conductivity problem, International Journal of Imaging Systems and Technology, Volume 2, 1990, Pages 66-75. [CrossRef]
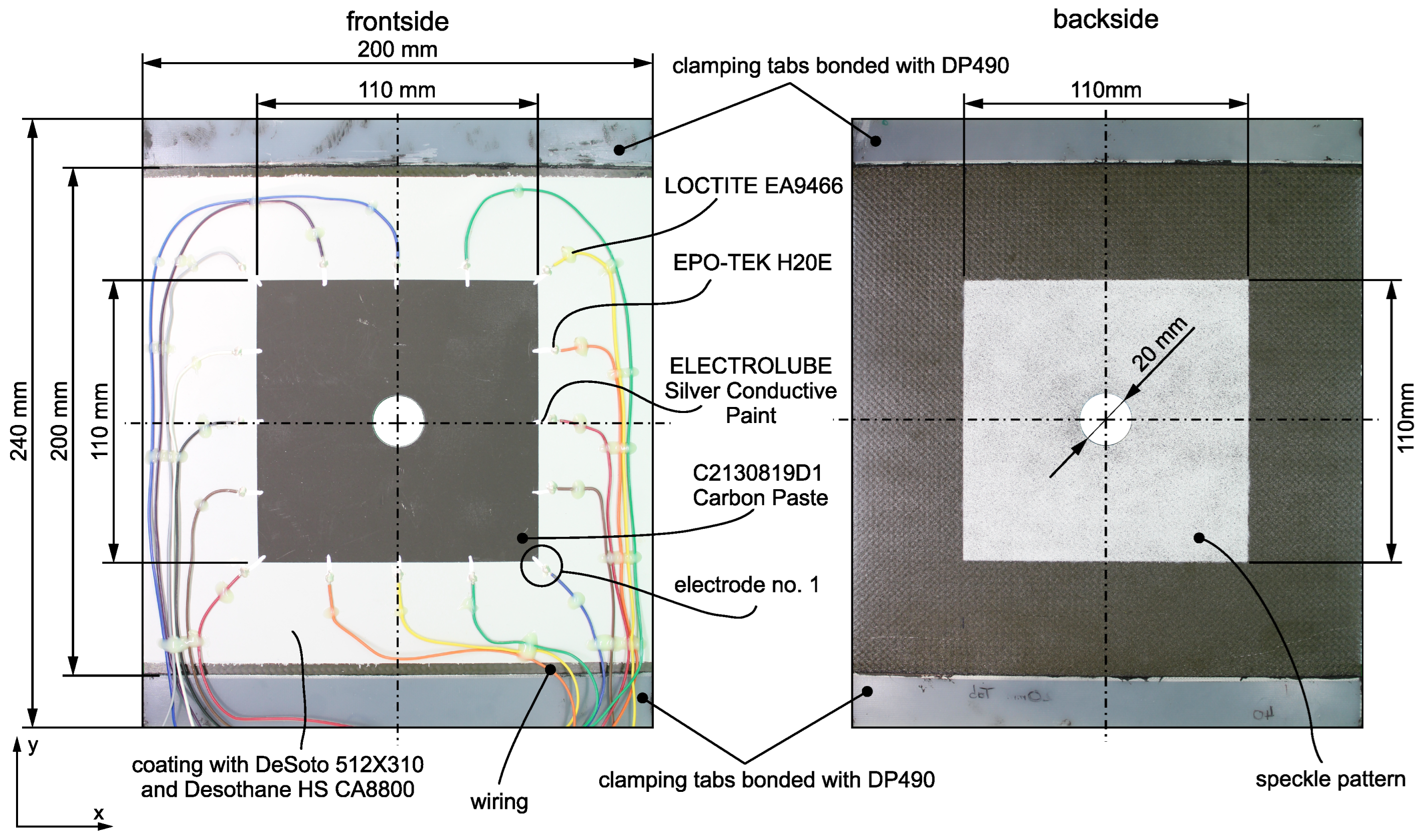
Preprints 95647 g001
Figure 1. Geometry and dimensions of the plate with hole, location of the GFRP tabs, thin-film sensor with electrodes and cabling, and speckle pattern for 3D-DIC evaluation.
Figure 1. Geometry and dimensions of the plate with hole, location of the GFRP tabs, thin-film sensor with electrodes and cabling, and speckle pattern for 3D-DIC evaluation.
Preprints 95647 g001
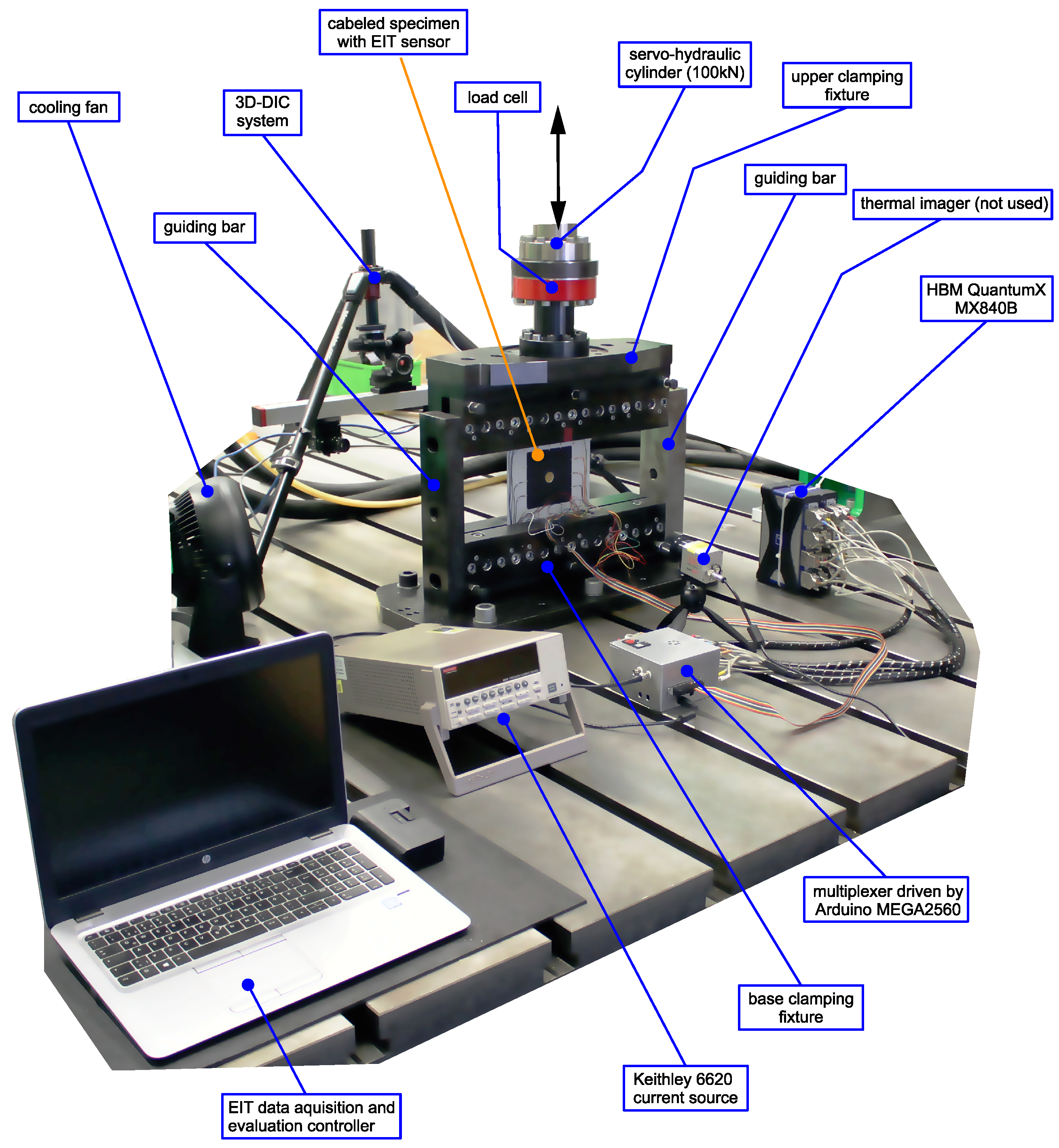
Preprints 95647 g002
Figure 2. Experimental setup.
Figure 2. Experimental setup.
Preprints 95647 g002
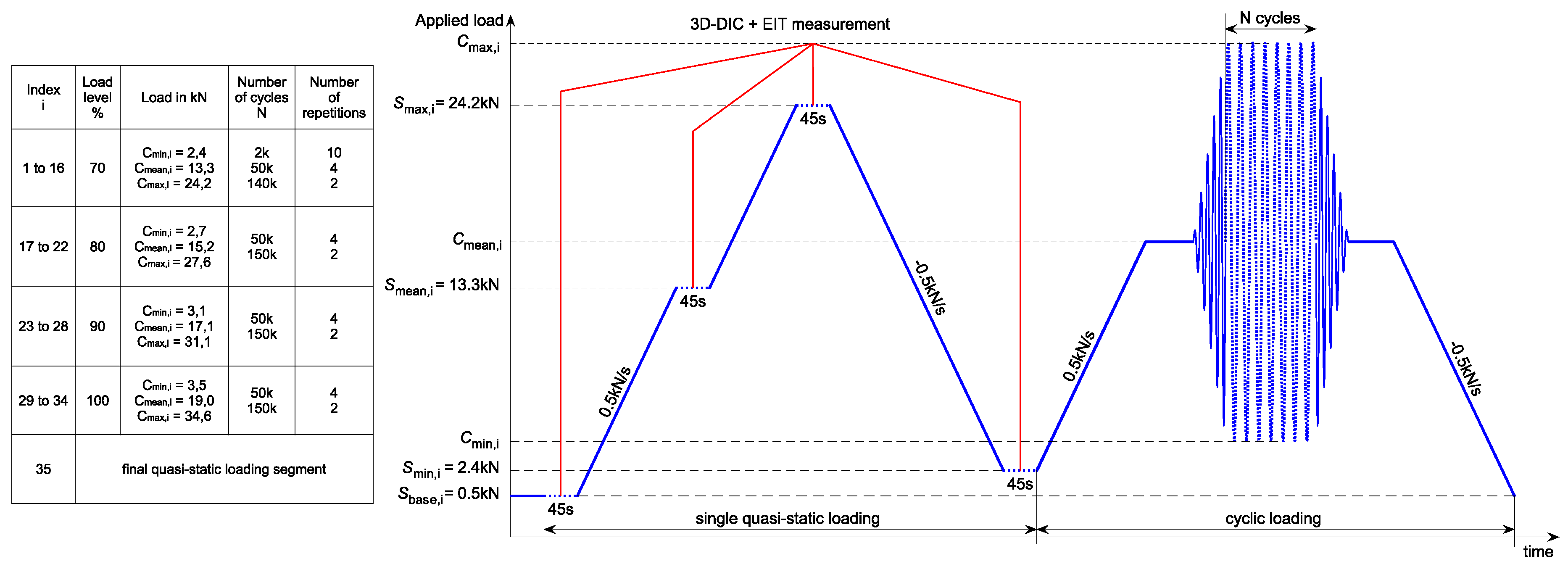
Preprints 95647 g003
Figure 3. Tabular list of the loading details along with a schematic representation of a loading sequence i consisting of a single quasi-static loading for EIT and 3D-DIC damage evaluation and cyclic fatigue loading to provoke damage initiation and propagation.
Figure 3. Tabular list of the loading details along with a schematic representation of a loading sequence i consisting of a single quasi-static loading for EIT and 3D-DIC damage evaluation and cyclic fatigue loading to provoke damage initiation and propagation.
Preprints 95647 g003
Preprints 95647 g004
Figure 4. Positioned evaluated area, magnified detail to visualize the subset size and associated settings.
Figure 4. Positioned evaluated area, magnified detail to visualize the subset size and associated settings.
Preprints 95647 g004
Preprints 95647 g005
Figure 5. 3D-DIC evaluated major principal strain ε 1 at different cycles (evaluated from S base , i to S max , i ).
Figure 5. 3D-DIC evaluated major principal strain ε 1 at different cycles (evaluated from S base , i to S max , i ).
Preprints 95647 g005
Preprints 95647 g006
Figure 6. Normalized changes in the spatial surface strains (major principal strain ε 1 ) versus the test length for S base , i to S max , i from 3D-DIC evaluations.
Figure 6. Normalized changes in the spatial surface strains (major principal strain ε 1 ) versus the test length for S base , i to S max , i from 3D-DIC evaluations.
Preprints 95647 g006
Preprints 95647 g007
Figure 7. 3D-DIC evaluation results for S max , i with respect to S max , 1 . The defined correlation confidence threshold reveals the damage shape and size (red region).
Figure 7. 3D-DIC evaluation results for S max , i with respect to S max , 1 . The defined correlation confidence threshold reveals the damage shape and size (red region).
Preprints 95647 g007
Preprints 95647 g008
Figure 8. Normalized 3D-DIC evaluated damage size for quasi-static load level S max , i with respect to S max , 1 over the number of cycles.
Figure 8. Normalized 3D-DIC evaluated damage size for quasi-static load level S max , i with respect to S max , 1 over the number of cycles.
Preprints 95647 g008
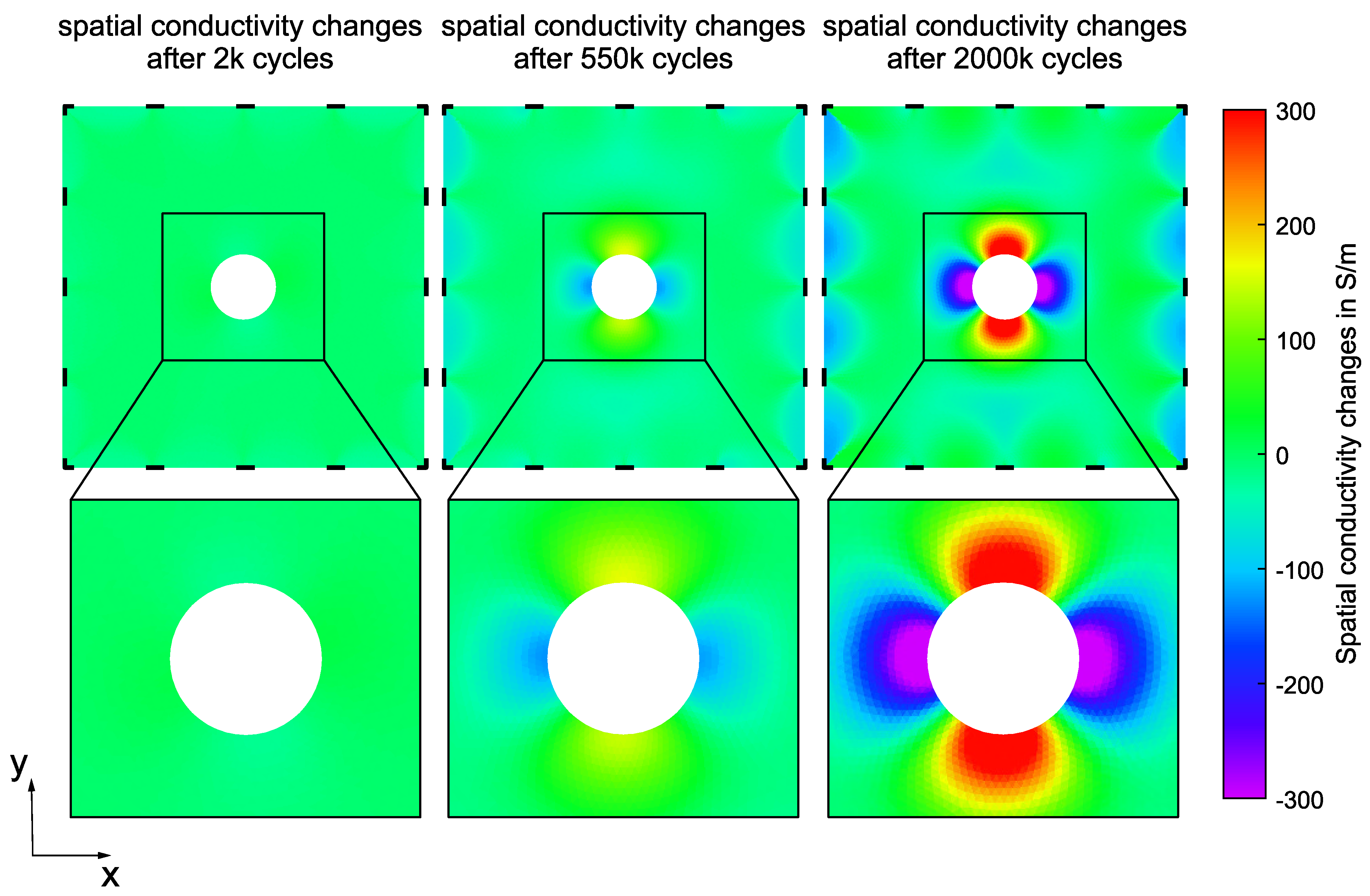
Preprints 95647 g009
Figure 9. Spatial conductivity changes at peak load S max , i for selected cycles.
Figure 9. Spatial conductivity changes at peak load S max , i for selected cycles.
Preprints 95647 g009
Preprints 95647 g010
Figure 10. Area of conductivity changes below threshold value over the number of cycles for S mean , 1 to S mean , i and S max , 1 to S max , i .
Figure 10. Area of conductivity changes below threshold value over the number of cycles for S mean , 1 to S mean , i and S max , 1 to S max , i .
Preprints 95647 g010
Preprints 95647 g011
Figure 11. EIT reconstructions of the spatial conductivity changes at different cycles (evaluated from S base , i to S max , i ).
Figure 11. EIT reconstructions of the spatial conductivity changes at different cycles (evaluated from S base , i to S max , i ).
Preprints 95647 g011
Preprints 95647 g012
Figure 12. Damage affected area over the number of cycles for S base , i to S max , i and S base , i to S mean , i EIT reconstructions.
Figure 12. Damage affected area over the number of cycles for S base , i to S max , i and S base , i to S mean , i EIT reconstructions.
Preprints 95647 g012
Preprints 95647 g013
Figure 13. Mean spatial conductivity of the thin-film sensor for S base , i evaluations, indicating the “Set-In” effect at the beginning and a stable sensor conductivity up to 1750k cycles.
Figure 13. Mean spatial conductivity of the thin-film sensor for S base , i evaluations, indicating the “Set-In” effect at the beginning and a stable sensor conductivity up to 1750k cycles.
Preprints 95647 g013
Preprints 95647 g014
Figure 14. 3D-DIC-based validation of EIT-based damage evaluation results using mean value adjustment for, (a) S max , 1 to S max , i , and (b) S mean , 1 to S mean , i .
Figure 14. 3D-DIC-based validation of EIT-based damage evaluation results using mean value adjustment for, (a) S max , 1 to S max , i , and (b) S mean , 1 to S mean , i .
Preprints 95647 g014
Preprints 95647 g015
Figure 15. 3D-DIC-based validation of EIT-based damage evaluation using continuous reference adjustment for, (a) S base , i to S max , i , and (b) S base , i to S mean , i .
Figure 15. 3D-DIC-based validation of EIT-based damage evaluation using continuous reference adjustment for, (a) S base , i to S max , i , and (b) S base , i to S mean , i .
Preprints 95647 g015
Table 1. Curing properties of the individual components in the order of application.
Table 1. Curing properties of the individual components in the order of application.
Designation Temperature in °C Time in h
DeSoto 512X310 Epoxy Primer RT 2.5
Desothane HS CA8800 Topcoat RT 90
SunChemical C2130819D1 Carbon Paste 60 0.5
3M™ Scotch-Weld™ DP490 60 2
ELECTROLUBE Silver Conductive Paint RT 0.2
EPO-TEK H20E 80 3
LOCTITE EA9466™ 80 0.5
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated