Preprint
Article
SNOWTRAN: A Fast UV-VNIR-SWIR Radiative Transfer Model for Polar Hyperspectral Remote Sensing Applications
Altmetrics
Downloads
123
Views
36
Comments
0
This version is not peer-reviewed
Submitted:
05 January 2024
Posted:
08 January 2024
You are already at the latest version
Alerts
Abstract
In this work, we develop a software suite for studies of atmosphere – underlying SNOW- spaceborne optical receiver light TRANsmission calculations (SNOWTRAN) with applications for the solution of forward and inverse radiative transfer problems in polar regions. Assuming that aerosol load is extremely low, the proposed theory does not require the numerical procedures for the solution of the radiative transfer equation and is based on analytical equations for the spectral nadir reflectance and simple approximations for local optical properties of atmosphere and snow. The model developed is validated using EnMAP and PRISMA spaceborne imaging spectroscopy data close to the Concordia research station in Antarctica. A new fast technique for the determination of the snow grain size and assessment of the snowpack vertical inhomogeneity is then proposed and further demonstrated on EnMAP imagery over the Aviator Glacier and in the vicinity of the Concordia research station in Antarctica. The results revealed a large increase in precipitable water vapor at the Concordia research station in February 2023 linked to warming event, and a 4 times larger grain size at Aviator Glacier compared to Dome C.
Keywords:
Subject: Environmental and Earth Sciences - Remote Sensing
1. Introduction
Radiative transfer modelling is an important tool for simulating and studying the interaction of radiation with different underlying surfaces and the atmosphere in order to make better use of remote sensing data. Multiple radiative transfer codes exist for the simulation of satellite signals at the top-of-atmosphere (TOA) (see, e.g., [1,2,3,4,5,6,7,8]). Papers [2,3,4,5,6,7,8]) are aimed at the solution of the general radiative transfer in various turbid media. In contrast, [1] has a special target - the spectral TOA reflectance over snow. The authors of [1] rely on the numerical solution of the radiative transfer equation (RTE), which slows down the calculation procedure considerably.
A new generation of spaceborne imaging spectroscopy sensors have been appearing in the recent years (e.g., EnMAP, PRISMA[9,10]) that have observational capacities to observe on demand polar areas with high spatial and spectral resolution covering the broad spectral range 400-2500nm. Furthermore, the next generation is in preparation for the operational, regularly repeating satellite measurements including polar areas such as CHIME[11] and SBG[12], which will significantly increase the amount of observation data. In this frame, the task of this paper is to develop a fast and accurate radiative transfer code for the simulation of hyperspectral satellite measurements over Antarctica and other polar regions with underlying snow surfaces based on the approximate analytical solutions of the RTE, that will be applicable to current and future nadir looking imaging spectroscopy missions. The Sobolev approximation [13] is used to simulate the radiative transfer in the atmosphere. This approximation is valid at small values of the average cosine of scattering angle g, which is a valid approximation, e.g., over Antarctica, where the aerosol load is extremely low and, therefore, the light scattering is mostly due to molecules. It is known that g=0 for molecular scattering. The spherical albedo of semi–infinite homogeneous snow surfaces is considered in the framework of the van de Hulst approximation valid at any level of light absorption in snow [14,15] We have extended the van Hulst approximation to the case of the nadir reflectance as observed by hyperspectral instruments orbiting our planet at present (see, e.g., [9,10]. Furthermore, we have used the analytical representation of both aerosol phase function and aerosol spectral extinction coefficient, which makes it possible to avoid time-consuming Mie calculations or the usage of respective look-up-tables. We have found that the shortwave infrared (SWIR) TOA reflectance spectra closely coincide with the spectra of the underlying surface modulated by the atmospheric gaseous absorption processes in this case. This is due to the weak aerosol load in polar regions.
The first version of a software suite for studies of atmosphere – underlying SNOW- spaceborne optical receiver light TRANsmission calculations (SNOWTRAN) has been proposed in [16] In this paper, we extend the range of the applicability of the SNOWTRAN to the spectral region 320-2500 nm using the extended databases of absorption cross sections of atmospheric molecules such as . The local (single scattering albedo, asymmetry parameter) and global (reflectance, albedo) snow optical properties are also calculated at any level of light absorption, making it possible to extend the range of the applicability of the respective equations and software to the shortwave infrared (SWIR) region. The main advantage of SNOWTRAN is the possibility to perform fast and accurate radiative transfer calculations for atmosphere – underlying snow system both for clean and polluted snow cases.
2. The Analytical Representation of the Top-of-Atmosphere Reflectance over Snow
2.1. The Radiative Transfer in a Snow Layer
The top-of-atmosphere (TOA) reflectance over snow as used in version 1.1 of the SNOWTRAN software, is given by the following analytical expression [16]:
where is the gaseous transmittance, R is the TOA reflectance of the gaseous absorption free atmosphere - underlying snow surface derived as
is atmospheric reflectance for the case of a black underlying surface, is the two-way atmospheric transmittance, is the snow reflectance (bottom of atmosphere (BOA) reflectance). The parameter accounts for the atmosphere–snow retro-reflections. The value of can be calculated using the following approximation strictly valid for the Lambertian underlying surfaces [16]:
where is the atmospheric albedo, is the snow spherical albedo.
It is assumed that the snow can be represented as a semi-infinite layer with irregularly shaped ice crystals. The spherical albedo of such a layer with the single scattering albedo and the asymmetry parameter can be estimated using the following approximation [14]:
where a=0.139, b=1.17 and
is the similarity parameter. It follows from Eq. (4) that various turbid media with close values of the similarity parameter s have similar values of spherical albedo. The approximation given by Eq. (4) is very accurate and can be used at any level of light absorption in snow, which is relevant for the modelling of visible-near infrared (VNIR) and SWIR snow spectra.
In this paper we derive the relevant approximation for the value of the nadir snow reflectance In principle, can be found solving the respective integro-differential radiative transfer equation [13,15]. It is assumed in the framework of SNOWTRAN that the nadir snow reflectance can be calculated using the following approximation derived from the parameterization of the simultaneous radiative transfer calculations of the snow reflectance and spherical albedo as presented in [15]:
where the parameters depend on the cosine of the solar zenith angle (see Appendix A). The accuracy of Eqs. (4), (6) is demonstrated in Figure 1 for the case of the Henyey - Greenstein phase function [13,15] with the asymmetry parameters g equal to 0.75 and 0.875 (typical for snow [17]) and several values of the single scattering albedo .
Eqs. (6) and (4) make it possible to calculate the global radiative transfer characteristics of snow layers for a given value of the similarity parameter s. It follows from Eq. (5) that the similarity parameter s depends on just two local optical characteristics of snow ( and ). Therefore, an important point is to find analytical relationships of these parameters with the size of ice grains. This also makes it possible to reduce the number of input parameters for the model proposed in this paper. Under assumption of clean snow, we shall use the following approximate equations for the relevant parameters [17,18]:
derived using the geometrical optics approximation for the fractal ice grains [17,19]. Here, is the probability of photon absorption (PPA) by pure snow at the wavelength , is the bulk ice absorption coefficient, is the imaginary part of the ice refractive index, is the effective diameter of ice grains and parameters depend on the assumed type/shape of ice crystals in snow. The effective grain diameter is defined as[17,20,21]:
where V is the average volume of the ice grains and is their average cross section perpendicular to the incident beam. It is assumed that particles are randomly oriented.
We have found that the volume of fractal grains used in simulations (Koch fractals of second generation [19]) is related to the side length by the following formula:
where Then it follows: , where . The numerical calculations show that the value of is close to /2.
We use the following equations for the parameters derived for the real part of the refractive index n in the range 1.25-1.35, which is the case for ice in the spectral region 0.3-2.5 μm [17,22]:
In addition, when fitting the numerical Monte–Carlo geometrical optical calculations with the use of Eqs. (7), we found that σ=0.9045, ε=0.8571. These parameters depend on the assumed shapes of ice crystals in snow.
The extinction cross section of large nonspherical randomly oriented particles can be calculated as follows [20,21]:
Therefore, it follows for the extinction coefficient [17]:
where c is the volumetric concentration of particles. Taking into account that c is close to 1/3 for natural snow [17], it is concluded that the extinction length in snow is close to the effective diameter of ice grains.
The intercomparison of results derived using simple Eqs. (7) and time consuming geometrical optical Monte - Carlo calculations [18] is shown in Figure 2 a,b for the case of large nonspherical particles (Koch fractals of the second generation [18] with the side length of the initial tetrahedron equal to 50, 100 and 300 μm ( or =0.027, 0.054, and 0.162 mm, respectively). The ice spectral refractive index proposed in [22] has been used. The high accuracy of Eqs. (7) is clearly demonstrated. Some deviations could be actually due to the statistical error of Monte – Carlo calculations and not due to the errors of Eqs. (7). Figure 2c shows the results of calculation of the similarity parameter s using Eqs. (5), (7) and Monte – Carlo geometrical optics calculations. Both results almost coincide, which makes it possible to derive analytical relationship between the value of the nadir reflectance (see Eqs. (6), (4)) and the effective diameter of ice grains, which is of importance for the solution of the inverse snow optics problems.
Figure 2.
a. The spectral dependence of the probability of photon absorption derived using the geometrical optics Monte Carlo code (lines) and simple Eq. (7) (symbols) for the length of the side of the initial ice tetrahedron for the Koch fractal of the second generation [17] equal to 50, 100 and 300µm.
Figure 2.
a. The spectral dependence of the probability of photon absorption derived using the geometrical optics Monte Carlo code (lines) and simple Eq. (7) (symbols) for the length of the side of the initial ice tetrahedron for the Koch fractal of the second generation [17] equal to 50, 100 and 300µm.
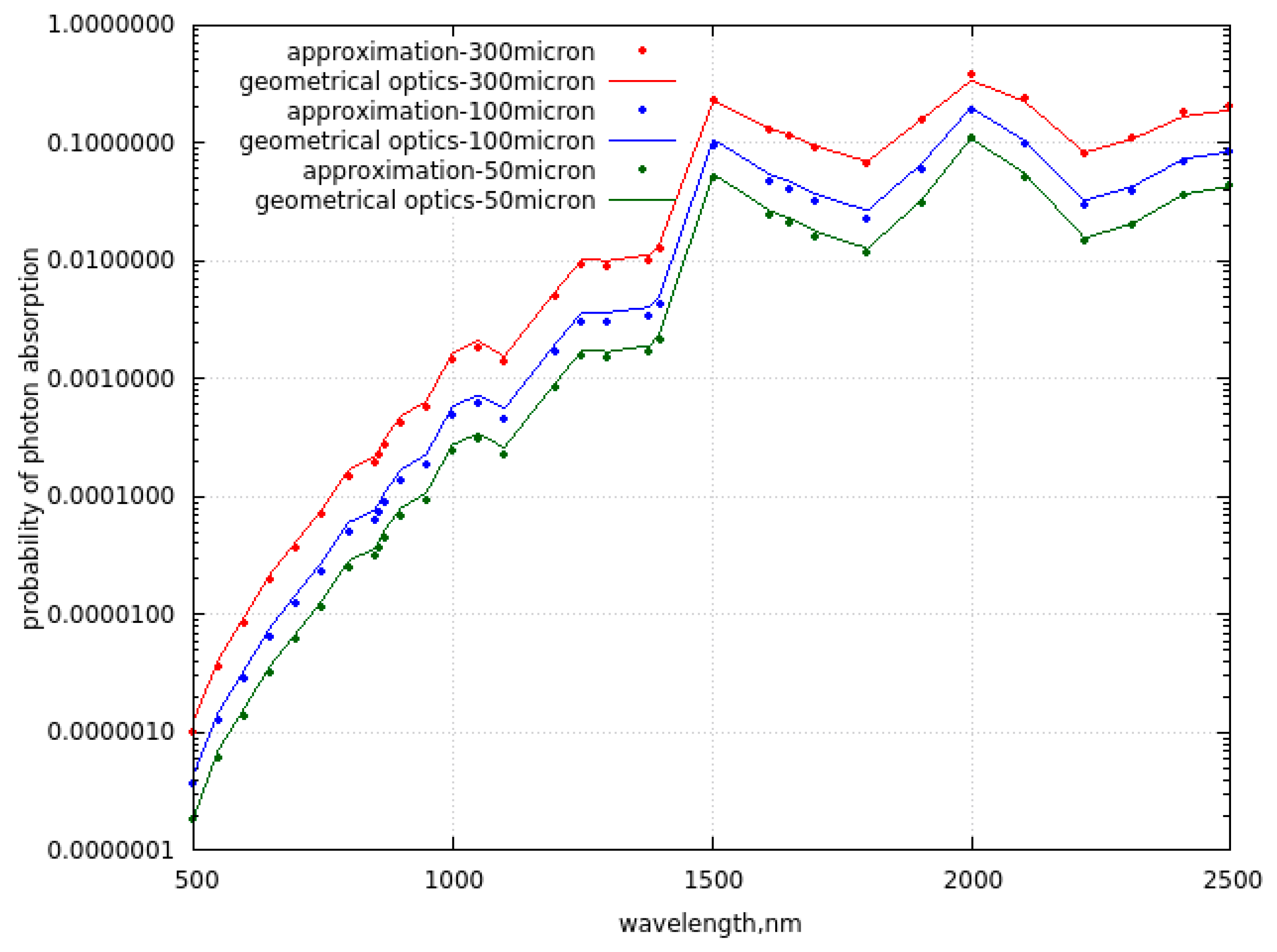
Figure 2.
b. The same as in Figure 2a except the asymmetry parameter is considered. The lower and upper lines give the spectral dependencies of the parameters and (upper line).
Figure 2.
b. The same as in Figure 2a except the asymmetry parameter is considered. The lower and upper lines give the spectral dependencies of the parameters and (upper line).
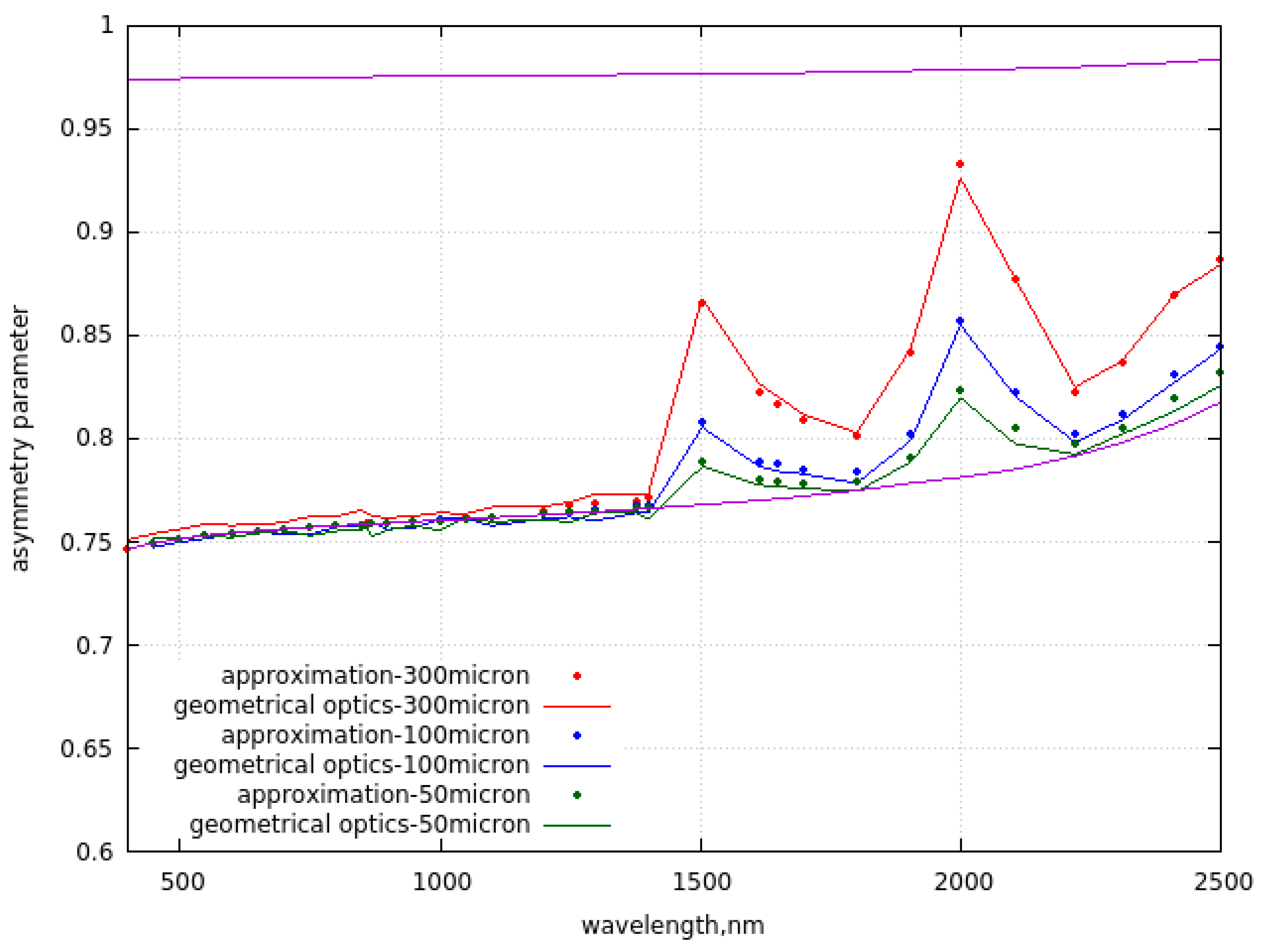
Figure 2.
c. The same as in Figure 2a except for the similarity parameter.
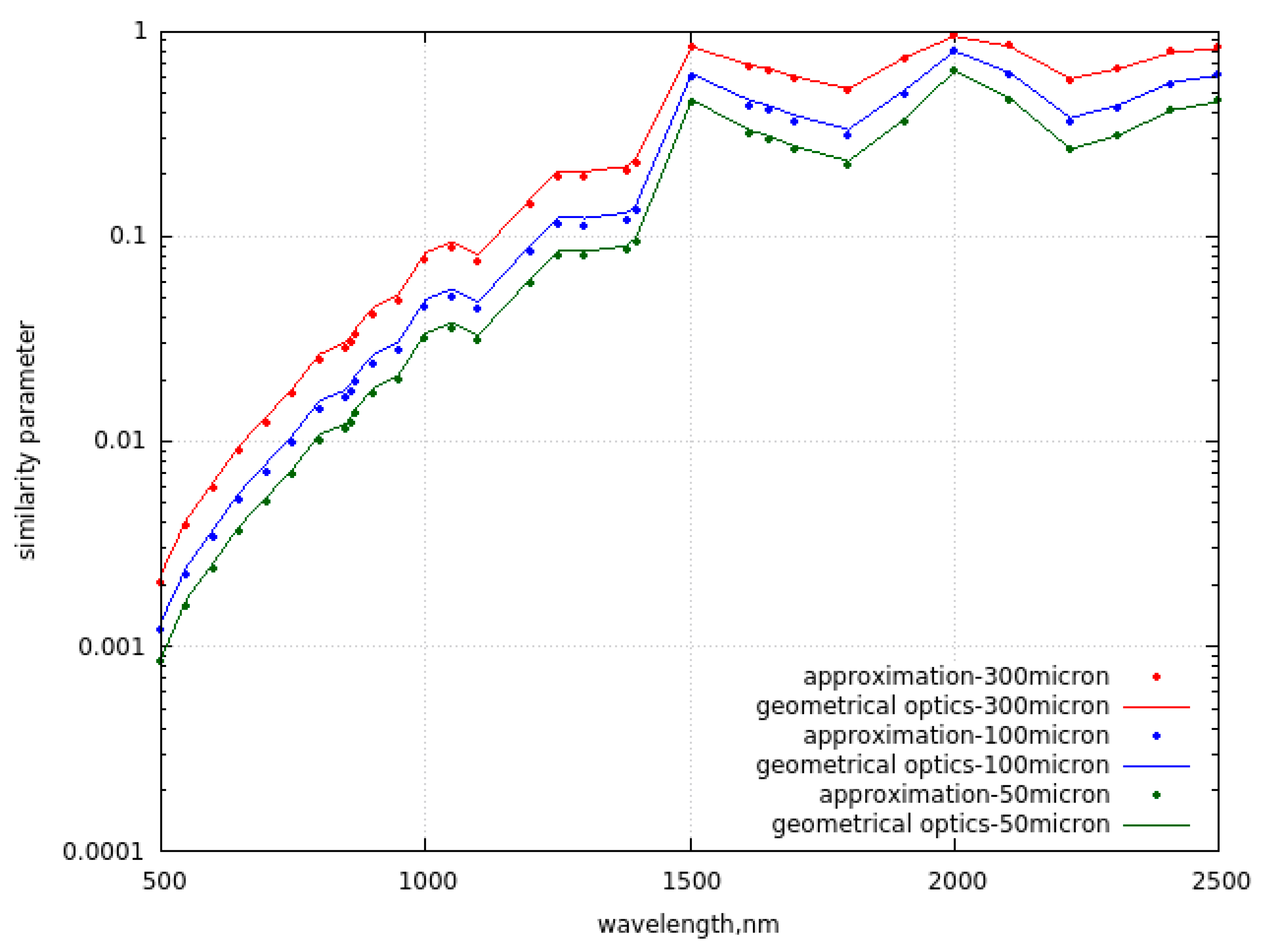
We have studied the case of type 1 snow (clean snow) in the discussion given above. Let us consider now the case of type 2 snow (snow with impurities). The level of snow pollution is usually low and, therefore, in a good approximation, we can assume that the light scattering and extinction processes in snow are dominated by ice grains. The absorption coefficient of snow with impurities can be presented as:
where is the volumetric concentration of ice grains and is the volumetric concentration of impurities. We assume that just one type of impurity is present in the snow, although the technique can easily take into account multiple types of impurities by adding additional terms in Eq. (13). The values of are volumetric absorption coefficients of ice grains and impurities, respectively. They can be calculated as follows:
where is the average absorption cross section of ice grains, is the average volume of ice grains, is the average absorption cross section of impurities, is the average volume of impurities. It follows for the probability of photon absorption:
where is the PPA for snow without impurities (see Eq. (7)), and thus (see Eqs. (15), (12)):
where =. One can see that the probability of photon absorption for the snow with impurities depend not only on the value of but also on the relative volumetric concentration of impurities c and their spectral volumetric absorption coefficient . We shall parameterize the spectrum in the following way:
where and m are the input parameters of the discussed analytical model. We shall assume that = 550 nm.
2.2. The Atmospheric Radiative Transfer
Let us consider the atmospheric radiative transfer processes now. It is assumed that the polar atmosphere is clean and the main contribution to light scattering and extinction in atmosphere is due to molecular scattering. Therefore, we use the same approach for the calculation of the atmospheric characteristics () as described in [16] The input for the atmospheric model is the spectral aerosol optical thickness presented as , where is the aerosol optical thickness at the wavelength = 550 nm[16] and B is the Angström parameter. The molecular optical thickness is calculated as suggested in [16]. The gaseous transmittance in Eq. (1) is found using the following approximation[16]:
where gaseous transmittances for water vapor, oxygen and ozone are given by the following expressions:
Here M is the airmass factor, , . The pair represents normal temperature (273.16K) and pressure (1013.25hPa) and the values give the average values of temperature and pressure over vertical for a given location. The parameters ( ) depend on the absorption band. The optical thicknesses for various gaseous absorbers are calculated as follows:
where is the absorption coefficient of water vapor, is the precipitable water vapor (PWV) measured in cm, is the molecular oxygen absorption coefficient , is the total molecular oxygen column (TMOC) (cm), is the total ozone column (in Dobson Units (DU)), is the absorption cross section of ozone molecule in the inverse DU (the multiplier 2.69 should be applied to transfer (usually provided in the units to the Dobson Units).
The vertical profile of molecular oxygen concentration could be considered as a constant one as compared to highly variable profiles of ozone and water vapor concentrations. Let us introduce the effective oxygen vertical column: =. Then it follows: . Therefore, for the calculation of the oxygen transmittance we use the value of , which reduces the number of parameters needed for the calculations. More precisely, the Normalized effective OXygen amount (NOX) is used as input in SNOWTRAN. It is defined as follows: =/, where is the molecular oxygen vertical column fo the standard atmosphere. The value of is equal to the ratio /at
We use the spectra , , and also parameters provided in at the spectral resolution of 7 nm (the triangular slit function has been used) in steps of 1 nm. In addition, we have calculated the oxygen absorption coefficient using the approximation provided in [23] for the oxygen absorption band located at the wavelength 1.27 μm, which is not provided in .
The geometrical approximation for the airmass factor has been used:
Here (ξ, η) are the cosines of the solar and observation zenith angles, respectively.
3. The Comparison of Theoretical Calculations with Satellite Measurements
Let us compare SNOWTRAN calculations with spaceborne hyperspectral measurements over Antarctica. We will use data of the German spaceborne imaging spectrometer mission EnMAP[10,24] and also the Italian Space Agency imaging spectrometer mission PRISMA [29].
The EnMAP performs the spectral radiance measurements with the spatial resolution 30m in the spectral range 418-2450 nm with the average spectral sampling distance 6.5nm in VNIR and 10 nm in SWIR (https://www.enmap.org/). The measurements are performed using two separate spectrometers (VNIR and SWIR). PRISMA (https://www.eoportal.org/satellite-missions/prisma-hyperspectral) has the same spatial resolution and the spectral range 407 – 2469 nm is covered with a spectral sampling interval ≤ 12 nm in both the VNIR and SWIR (https://www.prisma.asi/). The conversion of the spectral radiance I provided in L1C EnMAP data and also PRISMA top-of-atmosphere radiance data to the spectral reflectance R has been performed using the following equation:
where the parameter accounts for the Sun-Earth distance and is the solar irradiance at the top-of-atmosphere, which was also considered for the radiometric calibration of the sensor. The latter is important because TOA reflectance should be independent of the solar model, which is not the case if two different models were used. Therefore, we have applied the solar irradiance model given in [25] in case of EnMAP and the model provided in [26] in case of PRISMA.
Figures 4 and 5 show SNOWTRAN results compared with respectively EnMAP and PRISMA at different spectral resolutions, and Table 2 resumes the simulation parameters for both cases. The spectral reflectance derived from the EnMAP measurements for a single pixel located at (75.119S, 123.902E) is given in Figure 4a together with the calculations of the top-of atmosphere and bottom-of-atmosphere (BOA) snow reflectance. The EnMAP measurements have been performed on February 15, 2023, 00:36 UTC. We have used the values of surface pressure 651hPa, surface height of 3233m and average values of pressure and temperature along vertical equal to 491 hPA and 229 K as in our previous publication[27]. The values of TOC (250DU) and PWV (0.175cm) were taken coincident with those measured at the closely located Concordia research station ( Dome C, 75S, 123.3E). Other parameters used in SNOWTRAN simulations are given in Table 2. They have been selected by fitting SNOWTRAN and satellite measurements at several spectral points. It follows from Figure 4a that SNOWTRAN is indeed capable to describe efficiently the EnMAP hyperspectral satellite measurements.
Figure 4.
a. The intercomparison of SNOWTRAN spectra with the EnMAP measured spectra (75.119S,123.902E, February 15, 2023, 00:36UTC). The EnMAP data in the spectral range with strong water vapor absorption (e.g., around 1800nm) are not provided by the satellite ground system.
Figure 4.
a. The intercomparison of SNOWTRAN spectra with the EnMAP measured spectra (75.119S,123.902E, February 15, 2023, 00:36UTC). The EnMAP data in the spectral range with strong water vapor absorption (e.g., around 1800nm) are not provided by the satellite ground system.
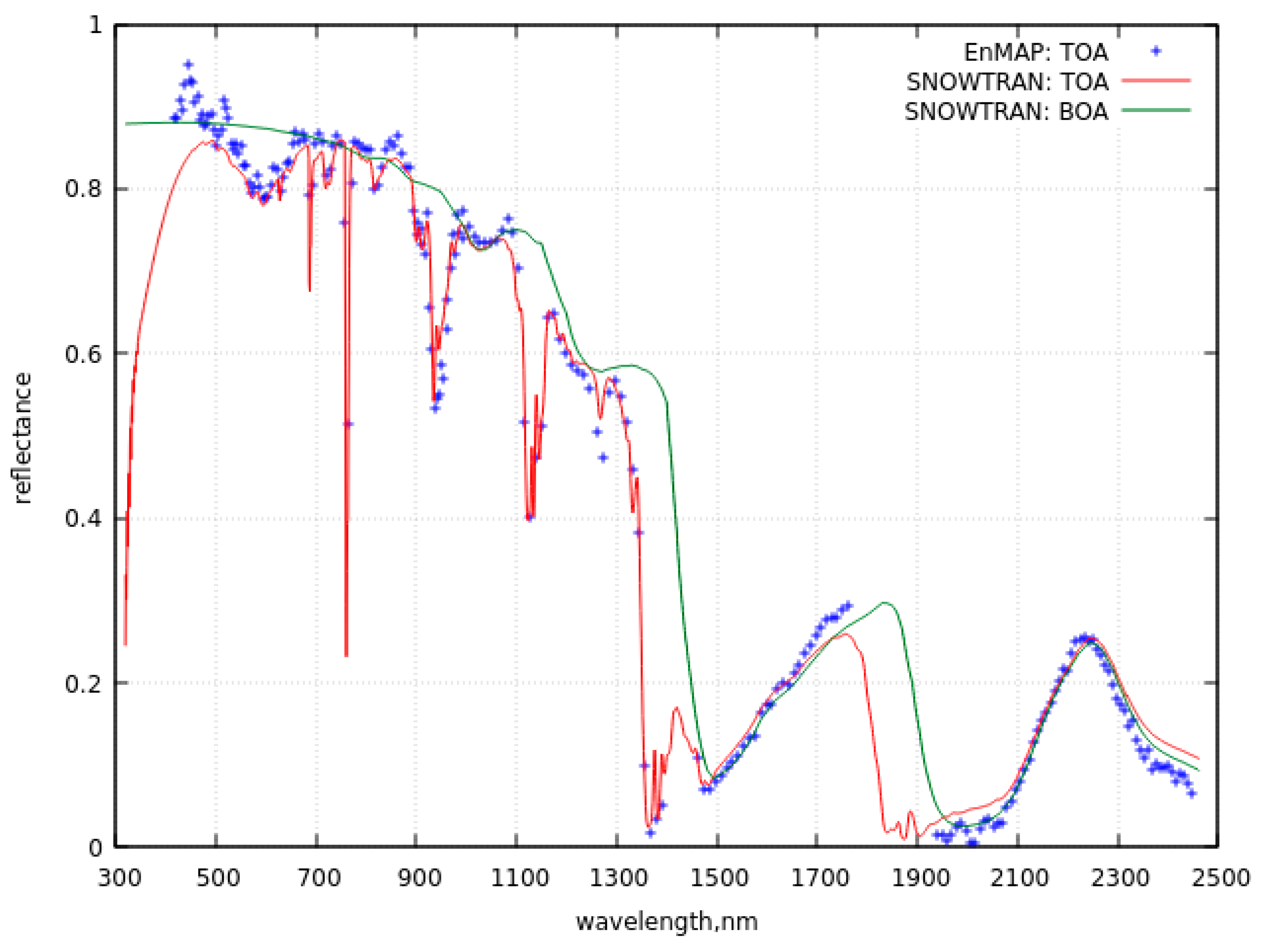
Figure 4.
b. The relative difference (in percent) between theoretical calculations and experimental data in the VNIR region.
Figure 4.
b. The relative difference (in percent) between theoretical calculations and experimental data in the VNIR region.
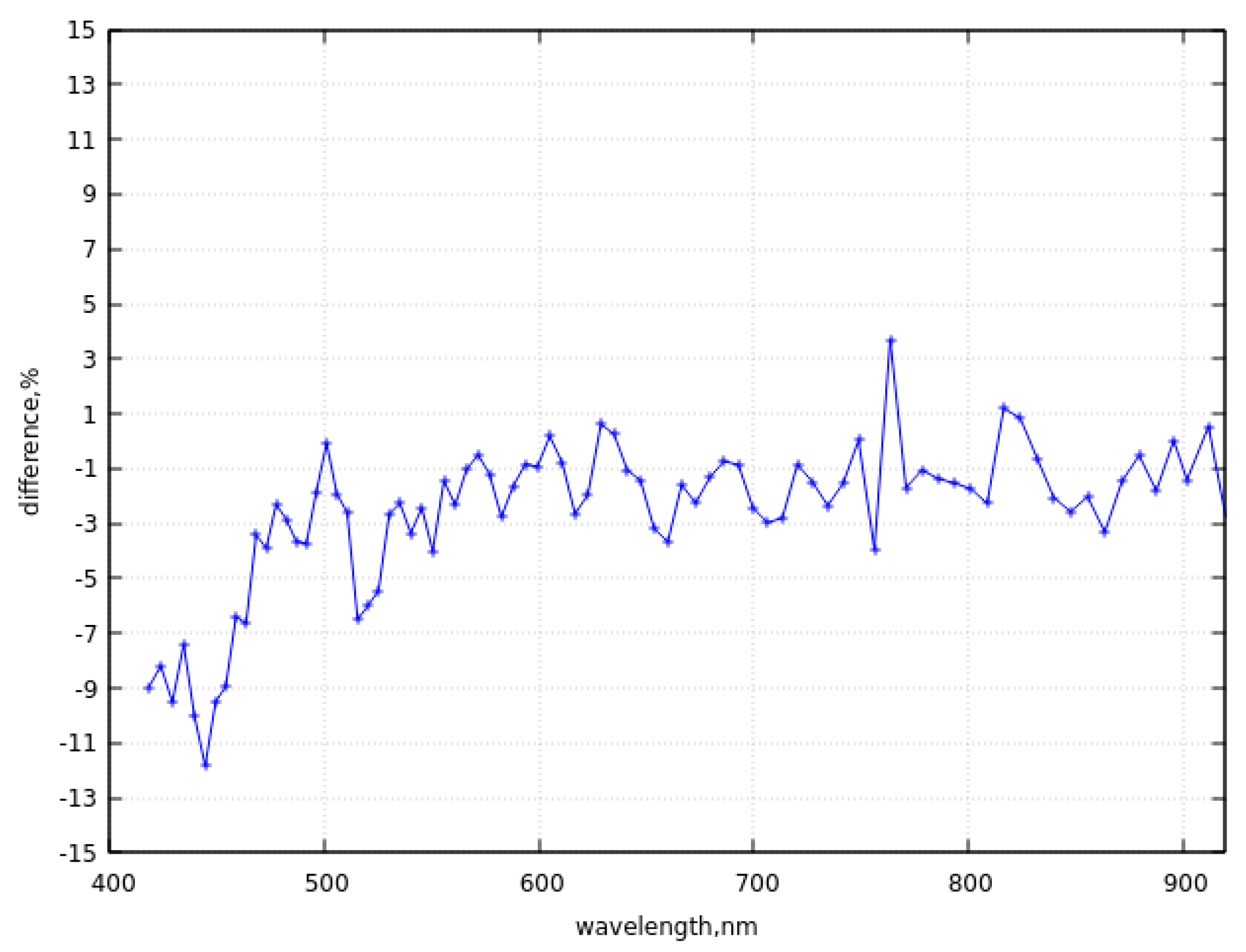
Figure 4.
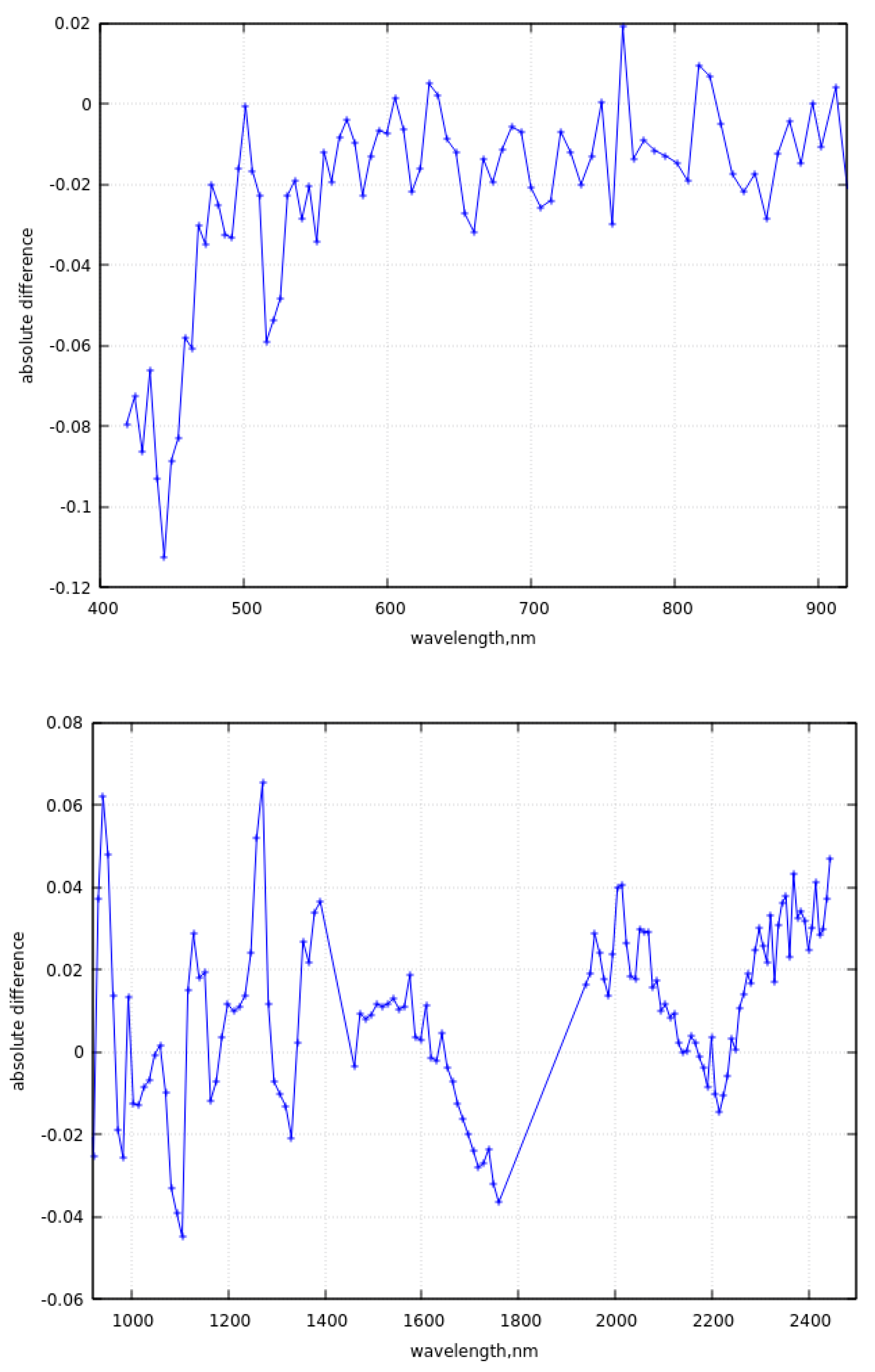
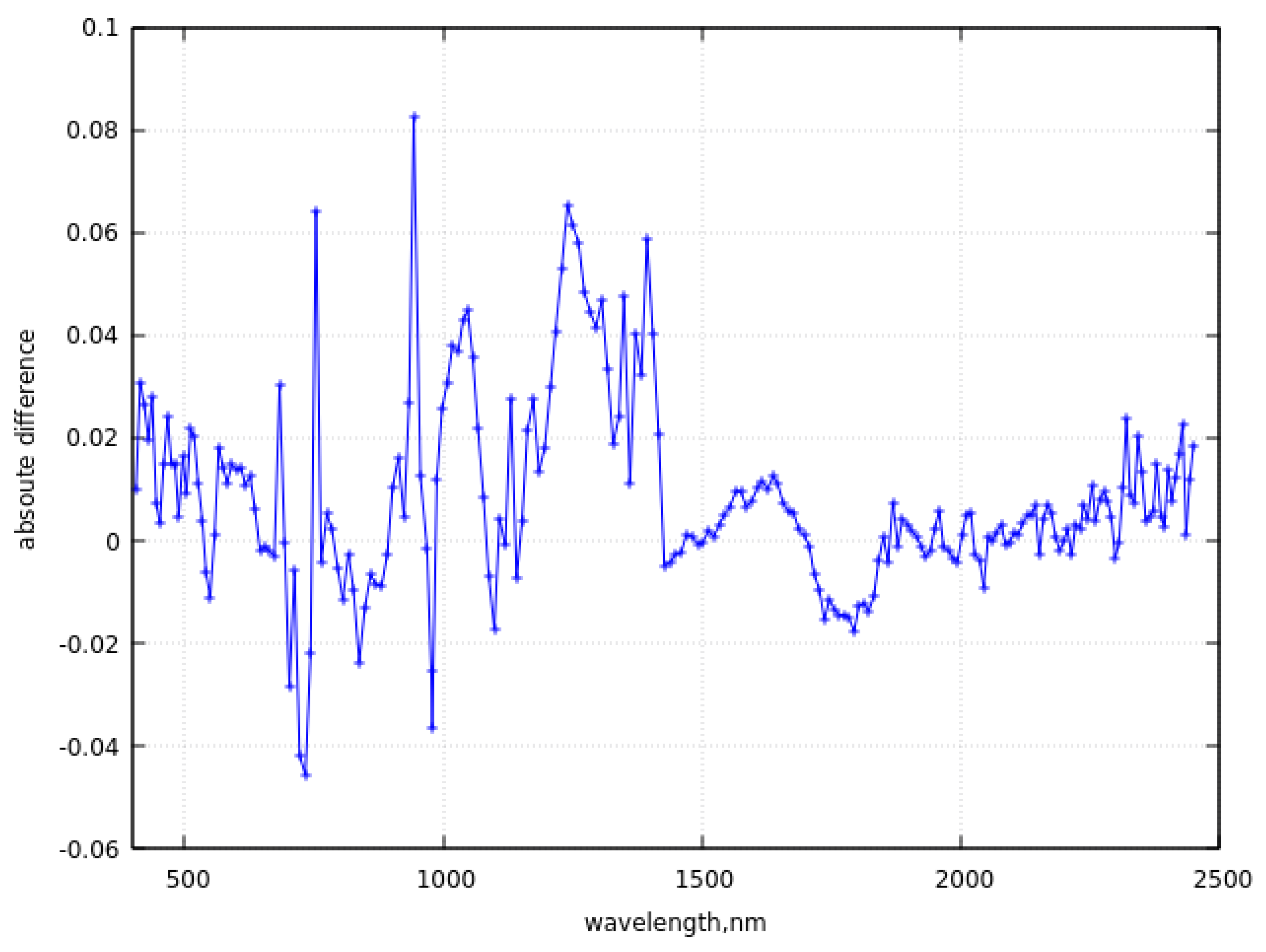
c. The absolute difference between theoretical calculations and experimental data in the VNIR (upper panel) and SWIR (lower panel).
Figure 4.
c. The absolute difference between theoretical calculations and experimental data in the VNIR (upper panel) and SWIR (lower panel).
The reason for the deviations of the theoretical calculations and EnMAP measurements in the range 418-500 nm for bright snow surfaces must be further investigated. It is unlikely that they are related to the inaccuracy of the SNOWTRAN model. Some deviations of theoretical calculations in gaseous absorption bands are due to different spectral sampling of SNOWTRAN (1 nm) and EnMAP (6.4- 10 nm) measurements.
We have re-sampled the SNOWTRAN data derived with 1nm spectral resolution to match the spectral sampling and spectral instrument response function of EnMAP. The difference between the re-sampled SNOWTRAN data and EnMAP spectra in the spectral range 418-920nm and 920-2500nm is given in Figure 4b,c. One can see that the difference is smaller than 2% for most of points not contaminated by gaseous absorption, which is an excellent result both with respect to the SNOWTRAN and EnMAP performance. The differences are somewhat larger in SWIR (see Figure 4c), which is explained by the influence gaseous absorption bands, especially water vapor. The difference in gaseous absorption bands needs more thorough analysis with possible account for other gaseous absorbers and change in the assumed abundance of atmospheric gaseous components in the SNOWTRAN run. The errors related to the integration of the oscillating spectral radiance in the gaseous absorption bands with account for the EnMAP spectral response function could be also of importance.
The fit of PRISMA measurements at the location (76.14S, 129.93E) situated at somewhat larger distance from the ground validation site located at Dome C is given in Figure 5a. The measurements have been taken on 21.12.2022, 00:14:07UTC. We also see that the SNOWTRAN can be successfully used to simulate the TOA PRISMA spectral reflectance. The ground observations at DOME C give TOC=269 DU and PWV=0.045 cm at the same date and time. These parameters are somewhat smaller than the parameters used in the simulations (289 DU and 0.055 cm, respectively). The parameters used in simulations have been selected to provide the best fit of experimental and theoretical curves in the ozone and water vapor absorption bands. Therefore, they can be considered as retrieved characteristics. The possible explanation for the differences between ground and satellite - derived parameters could be due to not exact collocation of ground and satellite measurements and also due to corresponding experimental errors of related retrieval techniques. The spectral relative and absolute difference of PRISMA data and re-sampled SNOWTRAN calculations are given in Figure 5b,c. The resampling has been performed to match the spectral sampling and spectra instrument response function for PRISMA. One can see that the relative difference is not larger than 5% in the deep blue region in contrast to the difference with EnMAP data shown in Figure 4b.
Figure 5.
a. The intercomparison of SNOWTRAN spectra with the PRISMA measured spectra (76.14S,129.93E, December 21, 2022, 00:14UTC).
Figure 5.
a. The intercomparison of SNOWTRAN spectra with the PRISMA measured spectra (76.14S,129.93E, December 21, 2022, 00:14UTC).
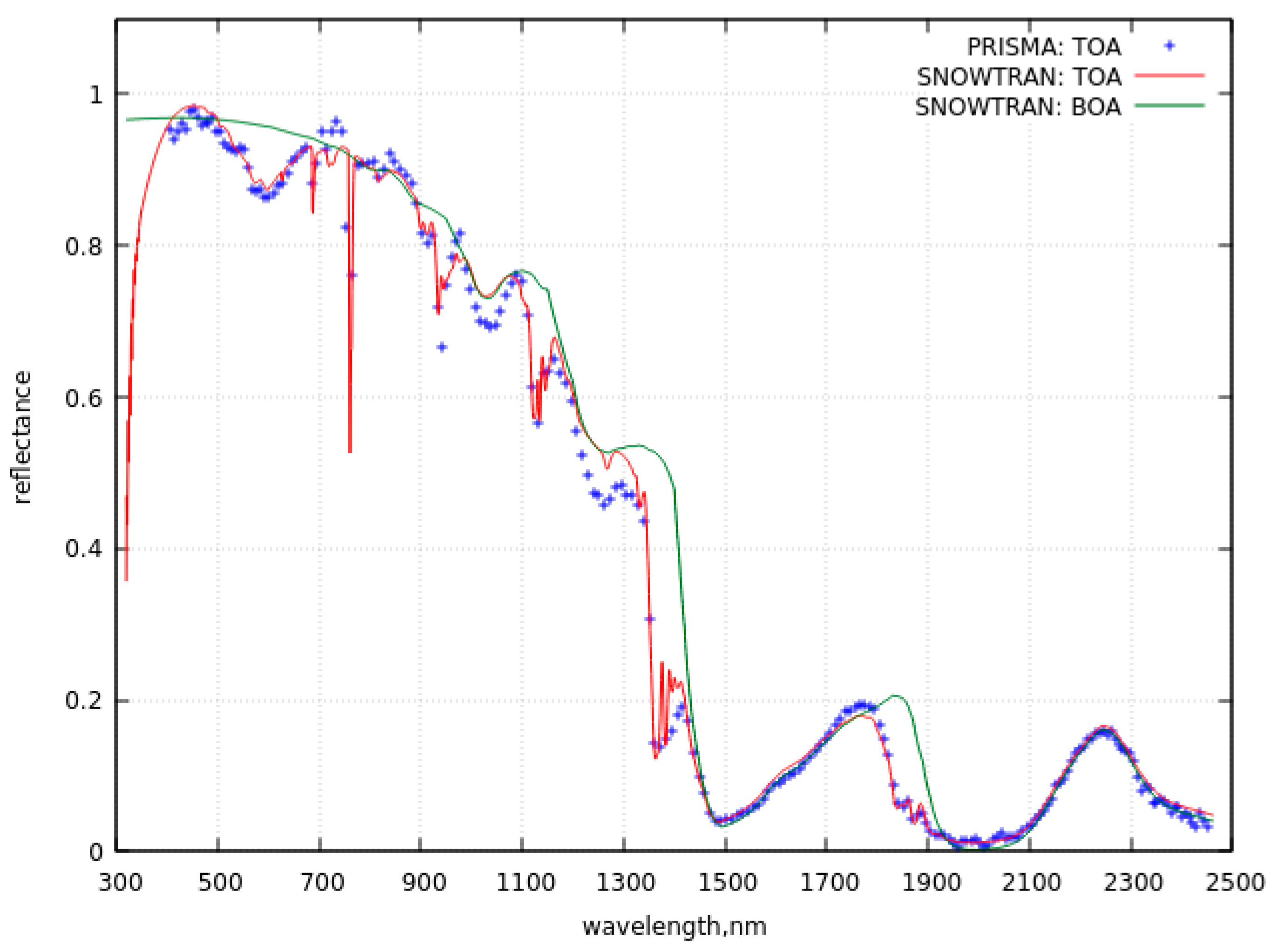
Figure 5.
b. The spectral relative difference (in percent) between theoretical calculations and PRISMA data in the VNIR region.
Figure 5.
b. The spectral relative difference (in percent) between theoretical calculations and PRISMA data in the VNIR region.
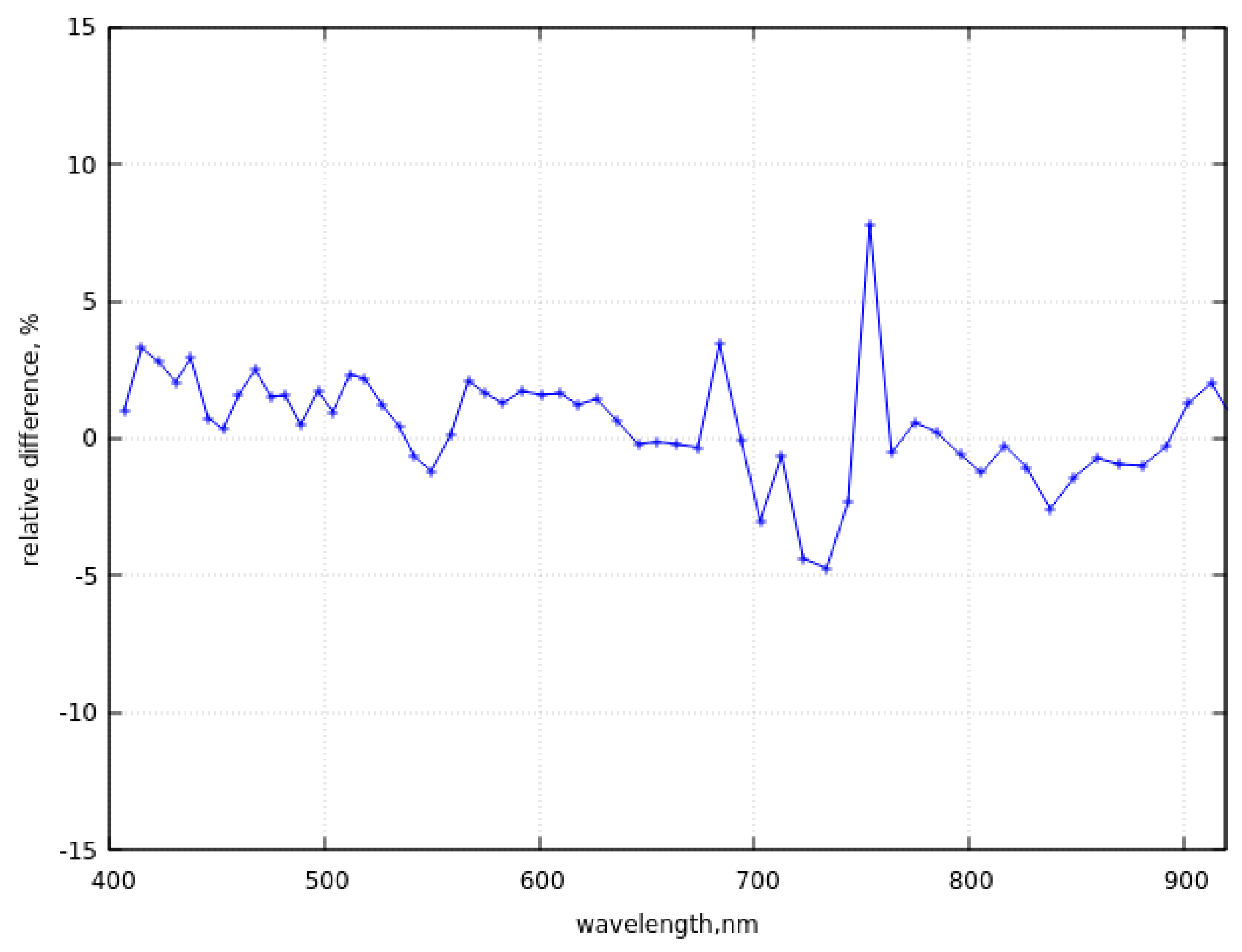
Figure 5.
c. The spectral absolute difference between theoretical calculations and PRISMA data.
It follows from Figure 4a that EnMAP measurements can be well fitted using SNOWTRAN both at 1030 nm and 2200 nm bands almost free of gaseous absorption and atmospheric scattering effects. This is not the case for the PRISMA measurements (see Figure 5a). This points to the fact that at the time and location of PRISMA measurements, the snow vertical inhomogeneity cannot be ignored. This brings us to the conclusion that snow vertical inhomogeneity could be potentially assessed using hyperspectral top-of-atmosphere reflectance measurements [27,28,29]. Also we can see that SNOWTRAN calculations and PRISMA measurements at 1500-2500 nm (and also for EnMAP, see Figure 4a) matches very well. This points out that this spectral range can be used to derive the snow grain size in upper snow layer due to the small penetration depth of the SWIR radiation in snow. This subject is considered in the next section.
One concludes from Figures 4a and 5a that the TOA reflectance is smaller than BOA reflectance in the gaseous absorption bands. At some channels the BOA reflectances are a little bit smaller than TOA reflectances. This is related to the uncertainties of the SNOWTRAN model. However, it should be underlined that the respective errors are smaller as compared to the calibration errors of the hyperspectral measurements.
Currently investigations are on-going for the differences in the spectral range 418-464nm (see Figure 4a) between SNOWTRAN and EnMAP data. Such differences and small – scale oscillations as seen in Figure 4b have been found for water surfaces as well. They might be related to the calibration of EnMAP data, which is indirectly supported by data shown in Figure 5a for PRISMA, where respective differences in the deep blue region of the electromagnetic spectrum are much smaller.
Table 2.
The parameters of the model used in simulations for the case of nadir observations shown in in Figs.4a, 5a. The ground-observed TOC and PWV at Dome C (75S, 123.3E) are given in the brackets. It has been assumed that snow is free of impurities. The small difference of satellite measurements ( up to 5 degrees) from the exact nadir direction is ignored.
Table 2.
The parameters of the model used in simulations for the case of nadir observations shown in in Figs.4a, 5a. The ground-observed TOC and PWV at Dome C (75S, 123.3E) are given in the brackets. It has been assumed that snow is free of impurities. The small difference of satellite measurements ( up to 5 degrees) from the exact nadir direction is ignored.
| Parameter | EnMAP 15.02.2023 |
PRISMA 21.12.2022 |
|---|---|---|
| , mm | 0.11 | 0.2 |
| TOC, DU | 250 | 289 (269) |
| PWV, cm | 0.175 | 0.055 (0.045) |
| TOX | 0.45 | 0.13 |
| 0.14 | 0.05 | |
| B | 1.0 | 1.35 |
| 68.0 | 57.6 | |
| Latitude, degrees | 75.119S | 76.140S |
| Longitude, degrees | 123.902E | 129.930E |
| Date/time (UTC) | 15.02.2023/ 00:36UTC |
21.12.2022/ 00:14UTC |
4. The Determination of the Snow Grain Size
In this section we consider the application of the proposed theoretical framework (forward model) for the determination of the snow grain size from EnMAP measurements. It is an important fact that both albedo and nadir reflectance primarily depend just on one parameter characterizing the snow microstructure (the similarity parameter s). Therefore, the inverse problem is reduced to the determination of snow microstructure from the value of the similarity parameter s. This parameter can be directly retrieved from the measurements of , i.e., it follows from Eq. (4):
where . One can see that s=0 at =1 and s=1 at =0 as it should be (see Figure 1 and Eq. (4)). The value of can be measured directly or derived from the nadir reflectance (see Eq. (6)):
Eqs. (5), (7) can be used to determine the value of the effective grain size from the value of the similarity parameter s analytically. Namely, it follows:
where is the bulk ice absorption coefficient at the wavelength λ, . The derivation of Eq. (25) has been performed at the assumption (see Eq. (7)), which is a valid approximation for the case at the study.
One can see that the value of can be derived analytically from the values of or (see Eqs. (23) - (25)). It is of importance that the values of s, and depend on the wavelength and is not (for vertically homogeneous snow layers). Therefore, the spectral dependence of is an indication of the snow vertical inhomogeneity. We select the measured reflectance at the wavelengths of 1030 nm, 1235 nm and 2200 nm, which are least affected by atmospheric scattering and absorption processes (see Figure 4a) and also sensitive to the snow grain size. Then it follows: ( see Eqs. (1), (2) and Figure 3).
Due to the different penetration of radiation in vertically inhomogeneous snow at different wavelengths, the values of derived at different wavelengths may differ. Let us introduce the ratio of effective diametersretrieved at 1235nm () and 2200nm () to that at 1030nm ():
It should be noted that it can generally be assumed that because the SWIR radiation with longer wavelengths generally penetrates to the smaller distances from the snow top, where new fresh fallen snow with smaller crystals are located. The radiation with the wavelength 1235 nm can penetrate into somewhat deeper snow layers as compared to that at the wavelength 2200nm.
We have derived the values of , and also for the EnMAP 30 km x 30 km scene located at the Aviator Glacier in Antarctica (16.02.2023, 22:11UTC). A glacier is a mass of ice with sufficient thickness to flow away from the source area in lobes, tongues or masses. The results are given in Figure 6a-c.
The valid results are given in the central part of the picture (Aviator Glacier Tonque) between two mountainous areas, where the ice flow to the ocean occurs. One can see that the value of and as one may expect. In particular, we have found that 0.52mm, 0.58mm, 0.21mm, and for the area A (73.75S-73.85S, 165-165.1E). Hence, the sizes of ice crystals at the top () are more than two times smaller compared to the sizes inside the snow layer () as one might expect due to the snow metamorphism processes. The spatial distribution of the parameter is given in Figure 7. It should be pointed out that although the parameters are affected by the assumed shape of light scattering particles, this is less the case for the ratios due to the cancellation of a common multiplier.
The retrievals for the case of vertically inhomogeneous snow requires the change of the forward model, which is out of scope of this paper. Because the value of is close to one, one may expect that the snow observed using the couple of wavelengths 1030 and 1235 nm can be considered as a homogeneous one. Therefore, the algorithm proposed in [27] is valid for the case considered here. Indeed, we have derived the value of 0.53mm from the algorithm described in [27] for the area A (see above), which is close to the value of derived in the framework of the algorithm discussed in this paper. It should be pointed out that the presented algorithm and the one described in [27] are based on different system of equations. Therefore, our conclusions confirm the consistency of both algorithms even though the current algorithm is able to determine the grain sizes at the very top of the snow surface, which is not the case for the algorithm described in [27]. Although we do not have grain sizes measured in situ and collocated with satellite measurements, our results are consistent with those presented in [31], where the most frequent grain size diameters in the range 0.2-0.4 mm at another coastal Antarctic site (67.7S, 139.72E, Adelie Land). More validation work is needed to relate the satellite - measured snow grain size with in situ derived values of the same parameter.
The snow grain size derived from EnMAP measurements at another location (closer to DOME C) using band 1030 nm is shown in Figure 8. It is obvious that the spatial distribution of the retrieved snow grain size is not so pronounced as in the case of the Aviator Glacier due to the reduced number of factors influencing the snow metamorphism processes (e.g., precipitation, surface inclination, proximity to the ocean and mountains). The average grain diameter derived from 1030 nm EnMAP measurements is 0.13 mm, which is close to the range of diameters (0.15-0.3 mm) measured at the site close to Dome C [31]. The spatial distribution of the ice grain diameter derived from the EnMAP measurements at 2200 nm is somewhat smaller (0.1 mm) with the spatial distribution similar to that shown in Figure 8. Basically, we can conclude that the vertical inhomogeneity of the snow is less pronounced as compared to the Aviator Glacier case shown in Figure 6, where the sizes at the top and inside the snow differ by more than two times, being larger at larger depths inside the snow. The small vertical variability of snow grain size around Dome C has been found using ground measurements as well [31].
It should be pointed out that the application of the channel 2200nm to the snow grain size retrieval must be performed only for the case of small ice crystals. With the increase of the crystal size, the reflectance at this channel saturates and the information on the snow grain size is lost (see Figure 9). The same applies to the channel 1640nm.
The EnMAP data can be used not only for the determination of snow parameters but also for the characterization of atmospheric state over the snow field as discussed in [27]. In particular, we have found a significant difference in the value of the Precipitable Water Vapor at Dome C on February 15, 2023 as compared to December 21, 2022 (see Table 2). This peculiarity is explained by the advective warming event at Dome C on February 15, 2023 reported in [32].
5. Conclusions
We have proposed a fast and simple fully analytical model for the calculation of the TOA reflectance over snow surfaces. The derived equations have been also used to derive the snow grain size, which can be used to estimate other snow parameters such as snow spectral and broadband albedo, bottom of atmosphere reflectance and snow specific surface area. It has been assumed that the snow is an ideally horizontal semi-infinite homogeneous surface without sastrugi and any inclination. The model can be easily extended considering Mie scattering by atmospheric particles and inclined surfaces. The case of nadir observations common for current and future hyperspectral missions is considered. The technique can be easily extended to the case off-nadir observations, if needed. The simplicity of the model makes it possible to apply the developed software for the solution of inverse problem, i.e. the determination of atmosphere and underlying snow properties from hyperspectral satellite observations as demonstrated here for EnMAP measurements. In particular, we have found a significant difference in the value of the Precipitable Water Vapor (PWV) at Dome C on February 15, 2023 as compared to December 21, 2022 (see Table 2).
Although the derived expression for the nadir snow reflectance as the function of the effective grain size is only approximation to the exact radiative transfer solution for the case of clean Antarctic atmosphere [33], the radiative transfer in natural snow is such a complicated process that exact solution can not be derived in principle taking into account irregular shape of particles and layered nature of snow layers with possible areas covered by frost and sastrugi. Therefore, we believe that our approach for modelling of radiative transfer in snow – underlying surface system will be useful for the various applied problems including the snow grain size and new fallen snow detection in polar regions using hyperspectral SWIR measurements. The technique can be also applied to other regions and surfaces (e.g., deserts). In this case the atmospheric correction procedure and respective expression for the similarity parameter as the function of the particle size must be modified taking into account spectral refractive index of light scattering particles and updates of several constants used in Eq. (7).
We have found that the snow grain sizes around Aviator Glacier are about 4 times larger as compared to those at Dome C. This leads to the increased light absorption by snow at this coastal site, which contributes to the increased rate of snow melting and formation of glacier rivers and lakes at favourable temperatures of surrounding air [34].
The SNOWTRAN can be coupled with the fast infrared radiative transfer codes (see, e.g., [35]) to provide users with a tool, which can be used to study various applied problems related to hyperspectral remote sensing observations in a broad spectral range from ultraviolet to the far infrared. The software is distributed upon request.
Acknowledgments
The authors are grateful to A. Macke for providing the Monte – Carlo ray tracing code, V. E. Cachorro for providing the database of gaseous absorption coefficients and B. Di Mauro for discussions related to the PRISMA data. The authors are thankful to A. Pellegrino for providing the solar spectrum adapted to the PRISMA specifications. The authors also acknowledge the support of the Antarctic Meteo - Climatological Observatory for providing data used in this work (https://www.climantartide.it), DLR for providing EnMAP data and also Italian Space Agency for providing PRISMA data. The ground total ozone and PWV data have been derived as explained in [27] and provided to us by B. Petkov and G. Bianchini, respectively. This research has been funded by the EnMAP science program under the Space Agency at DLR with resources from the German Federal Ministry of Economic Affairs and Climate Action (grant number 50EE1923).
Appendix A
In this Appendix A the simple approximate analytical equation for the snow nadir reflectance as the function of spherical albedo is proposed. In particular, we have studied the correlation between the nadir snow reflectance and spherical albedo for snow layers. It has been found using the radiative transfer calculations of both parameters for the same turbid layer at g=075 and the Heynye-Greenstein phase function that the following polynomial expression can be used;
where the coefficients can be represented by the cubic polynomial of the cosine of the solar zenith angle:
The parameters are given in Table A1. An important point is that the dependence of these parameters on snow microstructure can be neglected. It follows for a nonabsorbing snow layer from Eq. (A1):
which represents the semi - infinite nonabsorbing snow reflectance. Indeed, the variability of this parameter for the dry clean snow is low due to long paths of photons in snow in this case, which leads to the randomization of photon directions and similar values of nadir reflectance independently on single light scattering angular characteristics of a given snow layer. We note that the TOA reflectance in the SWIR is close to the value of snow reflectance outside gaseous absorption bands in the SWIR region due to negligible atmospheric scattering effects in this region over Antarctica.
Table A1.
The parameters in Eq. (A2).
| j/n | 0 | 1 | 2 |
| 0 | 0.01388 | 0.45760 | -0.02527 |
| 1 | -0.07413 | 1.65240 | 0.16899 |
| 2 | 0.05855 | -2.78192 | 0.89927 |
| 3 | -0.01099 | 1.18977 | -0.41984 |
References
- Stamnes, K.; Hamre, B.; Stamnes, S.; Chen, N.; Fan, Y.; Li, W.; Lin, Z.; Stamnes, J. Progress in forward-inverse modeling based on radiative transfer tools for coupled atmosphere-snow/ice-ocean systems: a review and description of the AccuRT model. Applied Sciences 2018, 8, 2682. [Google Scholar] [CrossRef]
- Mei, L.; Rozanov, V.; Rozanov, A.; Burrows, J.P. SCIATRAN software package (V4.6): update and further development of aerosol, clouds, surface reflectance databases and models. Geosci. Model Dev. 2023, 16, 1511–1536. [Google Scholar] [CrossRef]
- Nakajima, T.Y.; Murakami, H.; Hori, M.; Nakajima, T.; Aoki, T.; Oishi, T.; Tanaka, A. Efficient use of an improved radiative transfer code to simulate near-global distributions of satellite-measured radiances. Appl. Opt. 2003, 42, 3460–3471. [Google Scholar] [CrossRef]
- Mayer, B.; Kylling, A. Technical note: The libRadtran software package for radiative transfer calculations - description and examples of use. Atmospheric Chemistry and Physics 2005, 5, 1855–1877. [Google Scholar] [CrossRef]
- Berk, A.; Bernstein, L.S.; Anderson, G.P.; Acharya, P.K.; Robertson, D.C.; Chetwynd, J.H.; Adler-Golden, S.M. MODTRAN cloud and multiple scattering upgrades with application to AVIRIS. Remote Sensing of Environment 1998, 65, 367–375. [Google Scholar] [CrossRef]
- Spurr, R.; Christi, M. The LIDORT and VLIDORT linearized scalar and vector discrete ordinate radiative transfer models. Springer Series in Light Scattering (ed. by A. Kokhanovsky) 2019, 1–62.
- Ricchiazzi, P.; Yang, S.; Gautier, C.; Sowle, D. SBDART: A research and teaching software tool for plane-parallel radiative transfer in the Earth's atmosphere. Bull. Am. Meteorol. Soc. 1998, 79, 2101–2114. [Google Scholar] [CrossRef]
- Cachorro, V.E.; Antuña-Sanchez, J.C.; de Frutos, A.M. SSolar-GOA v1.0: A simple, fast, and accurate Spectral solar radiative transfer for clear skies. Geosci. Model Dev. 2022, 15, 1689–1712. [Google Scholar] [CrossRef]
- Cogliati, S.; Sarti, F.; Chiarantini, L.; Cosi, M.; Lorusso, R.; Lopinto, E.; Miglietta, F.; Genesio, L.; Guanter, L.; Damm, A.; et al. The PRISMA imaging spectroscopy mission: Overview and first performance analysis. Remote Sens. Environ. 2021, 262, 112499. [Google Scholar] [CrossRef]
- Storch, T.; Honold, H.-P.; Chabrillat, S.; et al. The EnMAP imaging spectroscopy mission towards operations, Rem. Sens. Env., 2023, 294, 113632.
- Rast, M.; J. Nieke; J. Adams; C. Isola; F. Gascon. Copernicus Hyperspectral Imaging Mission for the Environment (Chime). 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 2021, 108-111. [CrossRef]
- National Academies of Sciences, Engineering, and Medicine. Thriving on Our Changing Planet: A Decadal Strategy for Earth Observation from Space; The National Academies Press: Washington, DC, 2018. [Google Scholar] [CrossRef]
- Rast, M.; J. Nieke; J. Adams; C. Isola; F. Gascon. Copernicus Hyperspectral Imaging Mission for the Environment (Chime). 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 2021, 108-111. [CrossRef]
- Sobolev, V.V. Light Scattering in Planetary Atmospheres; Nauka: Moscow, 1975. [Google Scholar]
- van de Hulst, H.C. The spherical albedo of a planet covered with a homogeneous cloud layer. Astron. and Astrophysics 1974, 35, 209–214. [Google Scholar]
- van de Hulst, H.C. Multiple Light Scattering, v.1, 2; Academic Press: New York, NY, USA, 1980. [Google Scholar]
- Kokhanovsky, A. The approximate analytical solution for the top-of-atmosphere spectral reflectance of atmosphere—underlying snow system over Antarctica. Remote Sens. 2022, 14, 4778. [Google Scholar] [CrossRef]
- Kokhanovsky, A.A. Snow Optics; Springer Nature: Cham, Switzerland, 2021. [Google Scholar]
- Kokhanovsky, A.; Macke, A. Integral light-scattering and absorption characteristics of large nonspherical particles. Appl. Opt. 1997, 36, 8785–8790. [Google Scholar] [CrossRef] [PubMed]
- Macke, A.; Müller, J.; Raschke, E. Single scattering properties of atmospheric ice crystals. Journal of Atmospheric Sciences 1996, 53, 2813–2825. [Google Scholar] [CrossRef]
- Shifrin, K.S. Light scattering in a turbid medium; Nauka: Gostekhteorizdat, Leningrad, 1951. [Google Scholar]
- van de Hulst, H.C. Light scattering by small particles; Wiley: NY, 1958. [Google Scholar]
- Warren, S.; Brand, R.E. Optical constants of ice from the ultraviolet to the microwave: A revised compilation. J. Geophysical Research 2008, 113, D14. [Google Scholar] [CrossRef]
- Green, A.E.; Wagner, J.C.; Mann, A. Analytic spectral functions for atmospheric transmittance calculations. Appl. Opt. 1988, 27, 2266–2272. [Google Scholar] [CrossRef] [PubMed]
- Guanter, L.; Kaufmann, H.; Segl, K.; et al. The EnMAP spaceborne imaging spectroscopy mission for Earth Observation. Remote Sensing 2015, 7, 8830–8857. [Google Scholar] [CrossRef]
- Fontenla, J.N.; Harder, J.; Livingston, W.; Snow, M.; Woods, T. High-resolution solar spectral irradiance from extreme ultraviolet to far infrared. J. Geophys. Res. Atmos. 2011, 116, D20. [Google Scholar] [CrossRef]
- Kurucz, R.L. New atlases for solar flux, irradiance, central intensity, and limb intensity. Memorie della Società Astronomica Italiana Supplement 2005, 8, 189. [Google Scholar]
- Kokhanovsky, A.A.; Brell, M.; Segl, K.; Bianchini, G.; Lanconelli, C.; Lupi, A.; Petkov, B.; Picard, G.; Arnaud, L.; Stone, R.S.; et al. First retrievals of surface and atmospheric properties using EnMAP measurements over Antarctica. Remote Sens. 2023, 15, 3042. [Google Scholar] [CrossRef]
- Zhou, X.; Li, S.; Stamnes, K. Effects of vertical inhomogeneity on snow spectral albedo and its implication for optical remote sensing of snow. J. Geophys. Res. 2003, 108, 4738. [Google Scholar] [CrossRef]
- Saito, M.; Yang, P.; Loeb, N.G.; Kato, S. A novel parameterization of snow albedo based on a two-layer snow model with a mixture of grain habits. J. Atmos. Sci. 2019, 76, 1419–1436. [Google Scholar] [CrossRef]
- Gay, M.; Fily, M.; Genthon, C.; Frezzotti, M.; Oerter, H.; Winther, J.-G. Snow grain size measurements in Antarctica. J. Glaciol. 2002, 48, 527–535. [Google Scholar] [CrossRef]
- Bianchini, G.; C. Belotti; G. Di Natale, L. Palchetti. Exploiting a decadal time-series of spectrally resolved downwelling infrared radiances at Dome C, Antarctica to assess the occurrence of advective warming events. In Proceedings of the EGU General Assembly 2023, Vienna, Austria, 24–28 April 2023. [CrossRef]
- Six, D.; Fily, M.; Blarel, L.; Goloub, P. First aerosol optical thickness measurements at Dome C (East Antarctica), summer season 2003–2004. Atmos. Environ. 2005, 39, 5041–5050. [Google Scholar] [CrossRef]
- Dombrovsky, L.A.; Kokhanovsky, A.A. Deep heating of a snowpack by solar radiation. Frontiers in Thermal Engineering 2022, 2. [Google Scholar] [CrossRef]
- Zhang, Z.; Ping Yang, P.; George Kattawar, G.; et al. A fast infrared radiative transfer model based on the adding–doubling method for hyperspectral remote-sensing applications. Journal of Quantitative Spectroscopy and Radiative Transfer 2007, 105, 243–263. [Google Scholar] [CrossRef]
Figure 1.
The accuracy of the approximation for the spherical albedo (blue line) and nadir reflectance (red line) at the solar zenith angle 60 degrees.
Figure 1.
The accuracy of the approximation for the spherical albedo (blue line) and nadir reflectance (red line) at the solar zenith angle 60 degrees.
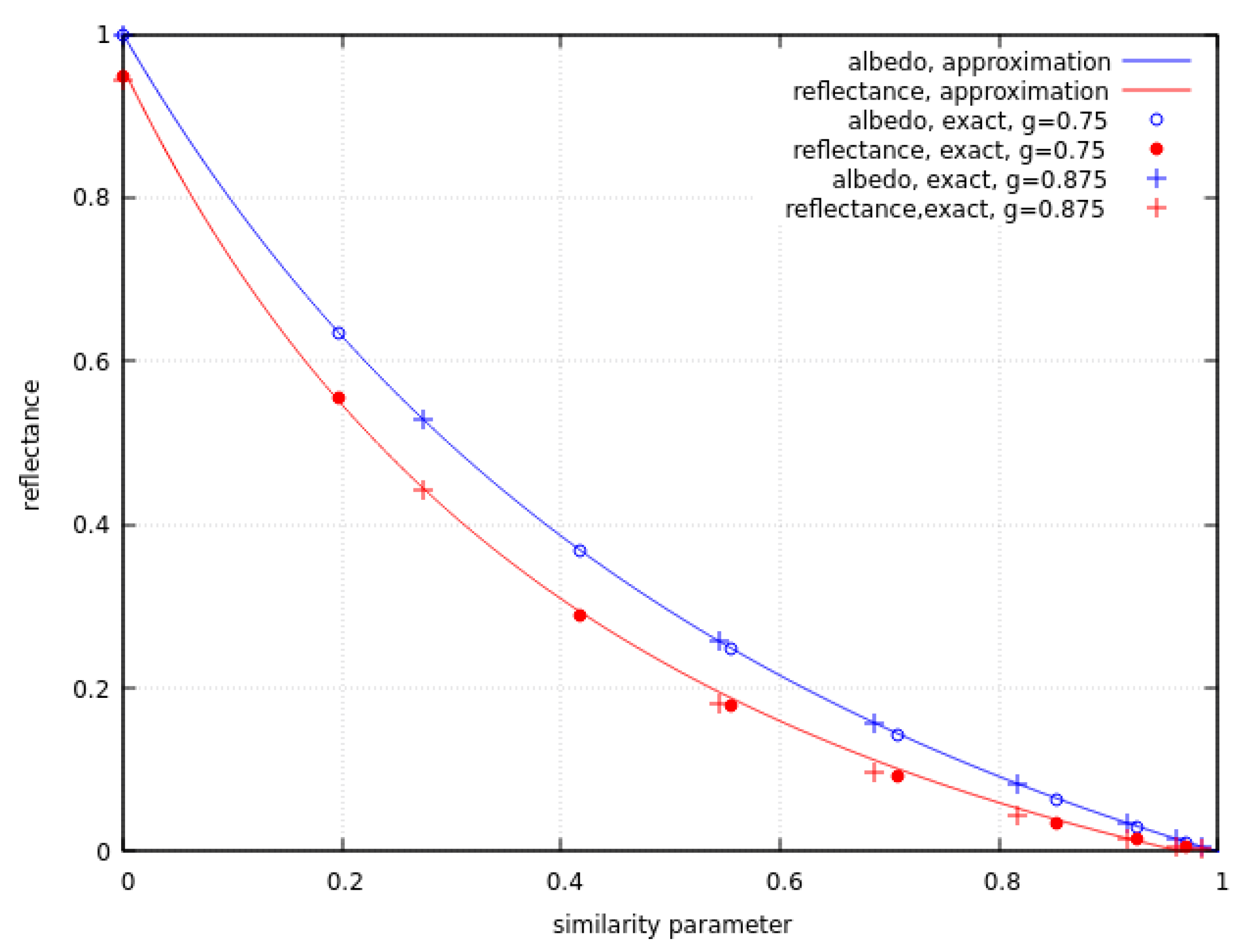
Figure 3.
The spectral dependence of BOA and TOA spectral reflectance of atmosphere – underlying dust - polluted snow system simulated using SNOWTRAN at the nadir observation and the solar zenith angle equal to 60 degrees.
Figure 3.
The spectral dependence of BOA and TOA spectral reflectance of atmosphere – underlying dust - polluted snow system simulated using SNOWTRAN at the nadir observation and the solar zenith angle equal to 60 degrees.
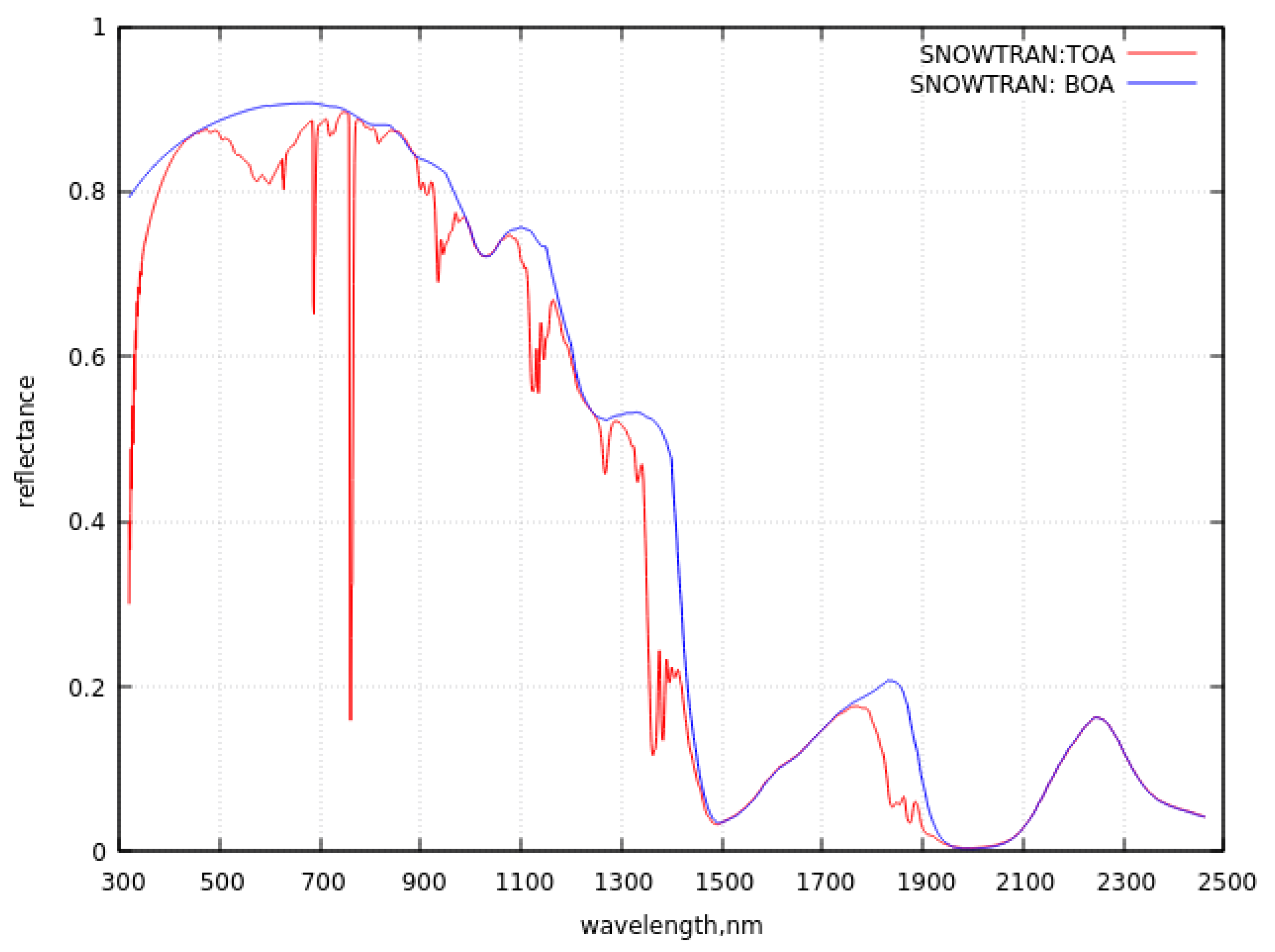
Figure 6.
The retrieved spatial distribution of snow grain diameter (mm) based on values (upper panel), (middle panel), and (lower panel) over the Aviator glacier based on EnMAP reflectance measurements.
Figure 6.
The retrieved spatial distribution of snow grain diameter (mm) based on values (upper panel), (middle panel), and (lower panel) over the Aviator glacier based on EnMAP reflectance measurements.
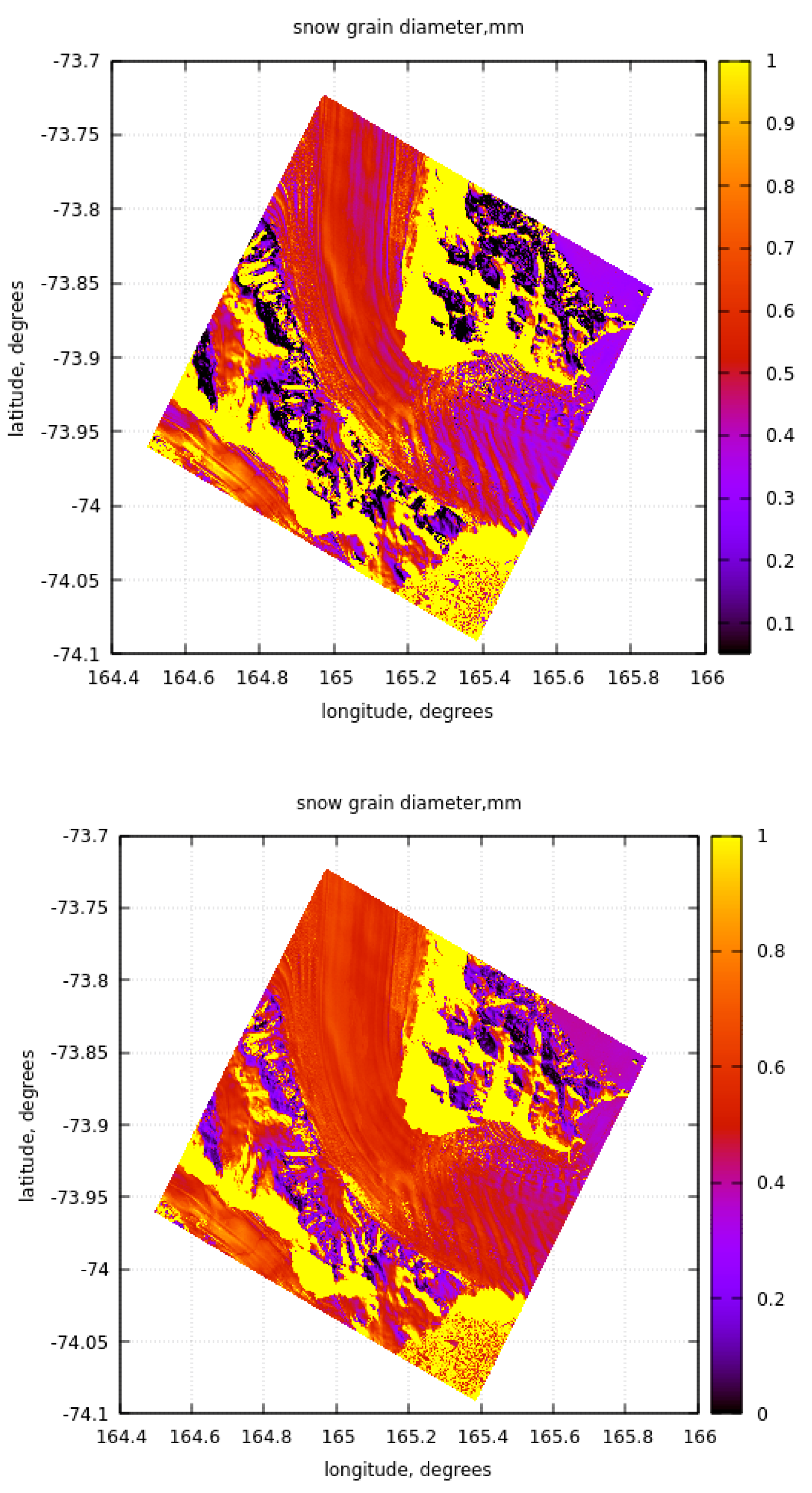
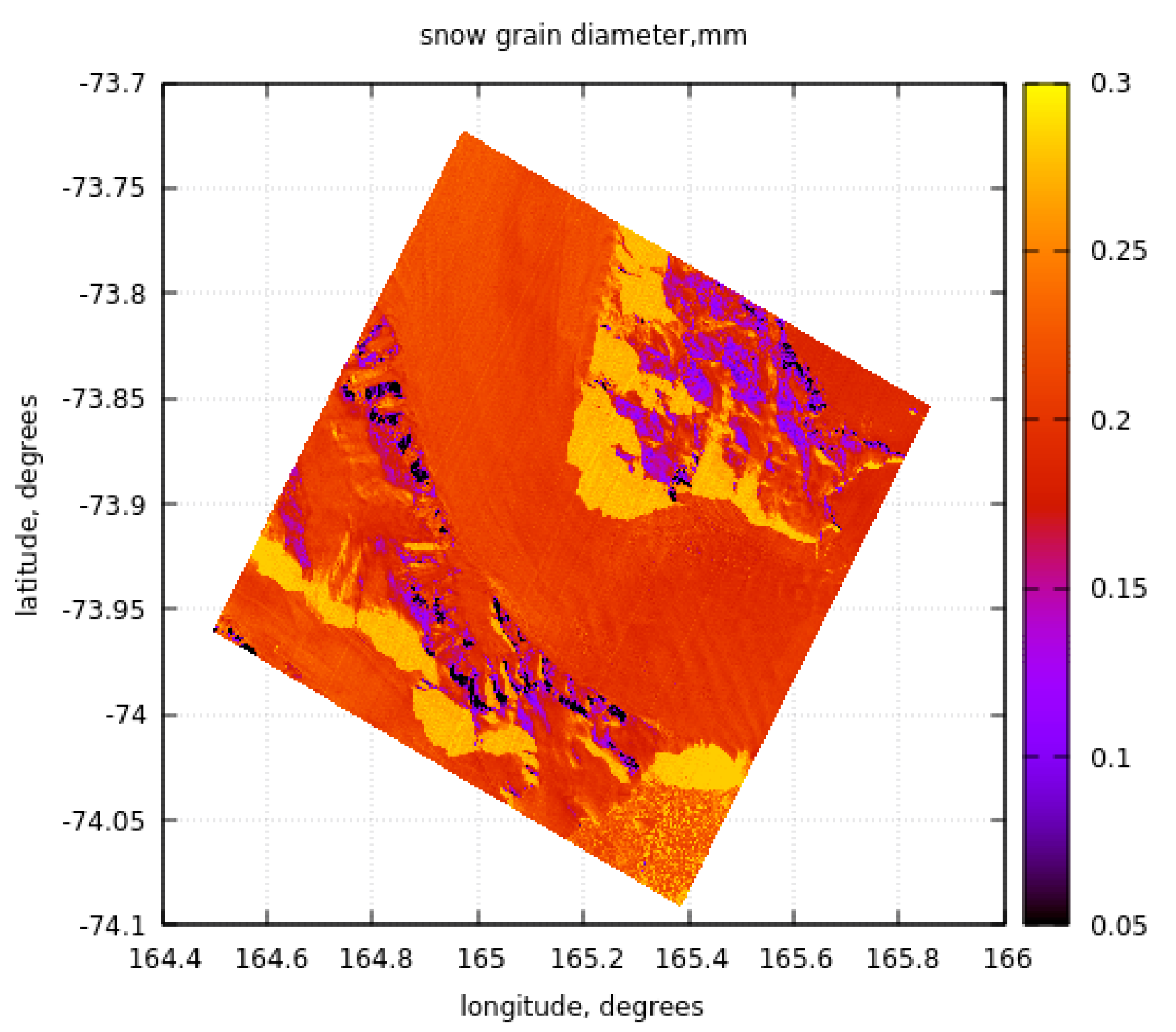
Figure 7.
The spatial distribution of the parameter over the Aviator Glacier.
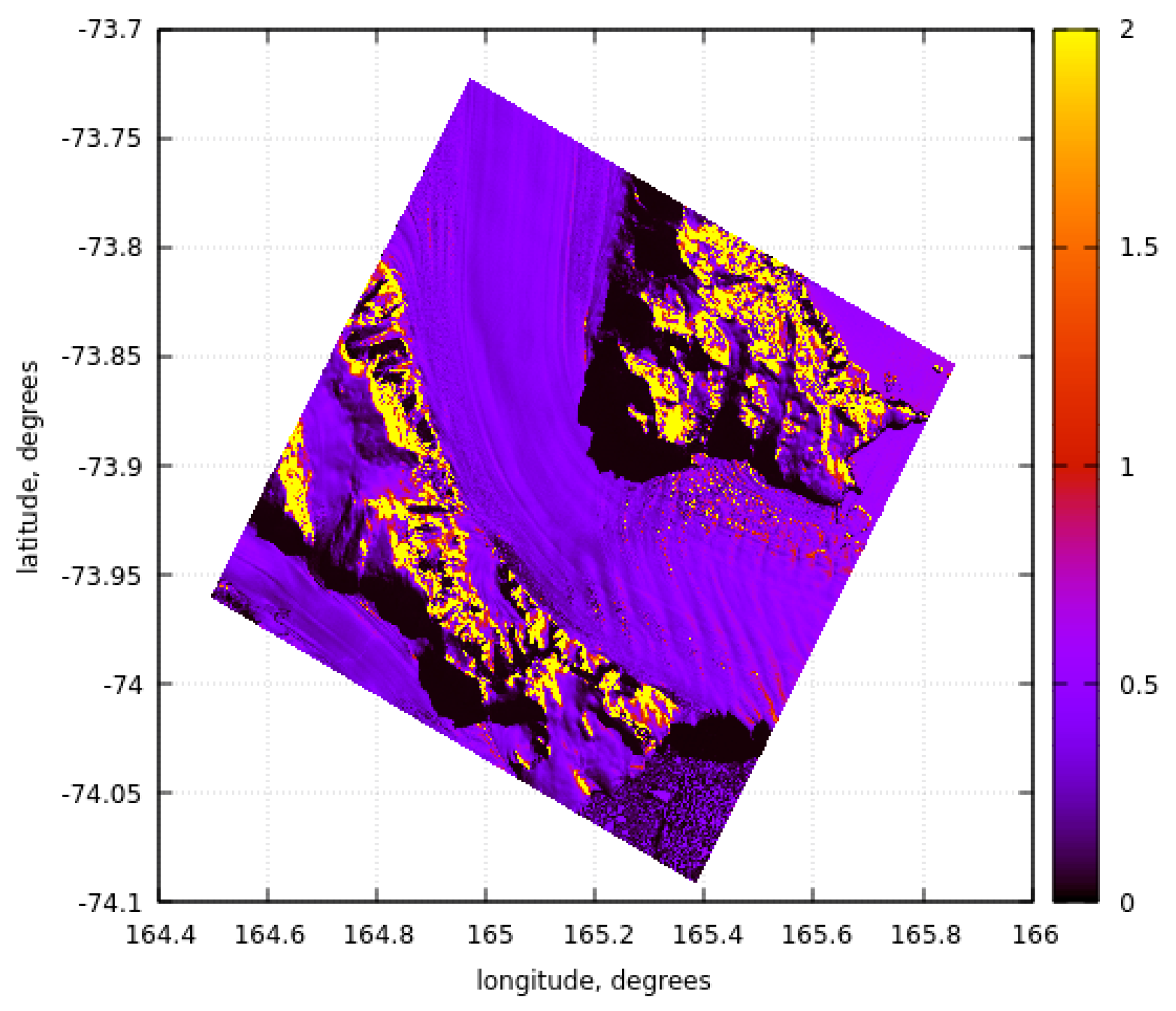
Figure 8.
The snow grain size spatial distribution in the vicinity of DOME C (75S, 123.3E, 26.10.2022, 00:33UTC), Concordia research station.
Figure 8.
The snow grain size spatial distribution in the vicinity of DOME C (75S, 123.3E, 26.10.2022, 00:33UTC), Concordia research station.
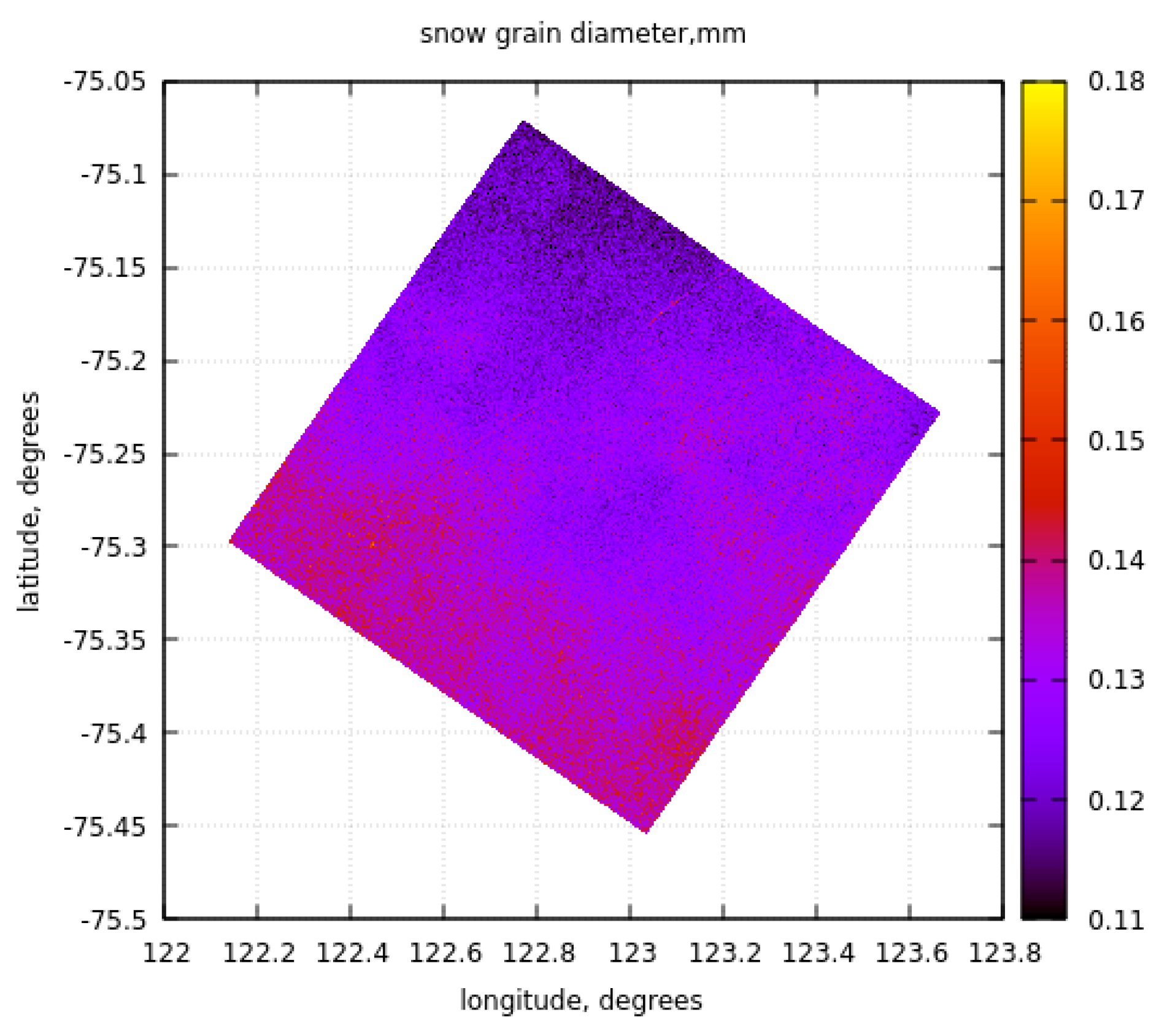
Figure 9.
The dependence of the nadir snow reflectance on the diameter of grains in snow at the solar zenith angle equal to 60 degrees.
Figure 9.
The dependence of the nadir snow reflectance on the diameter of grains in snow at the solar zenith angle equal to 60 degrees.
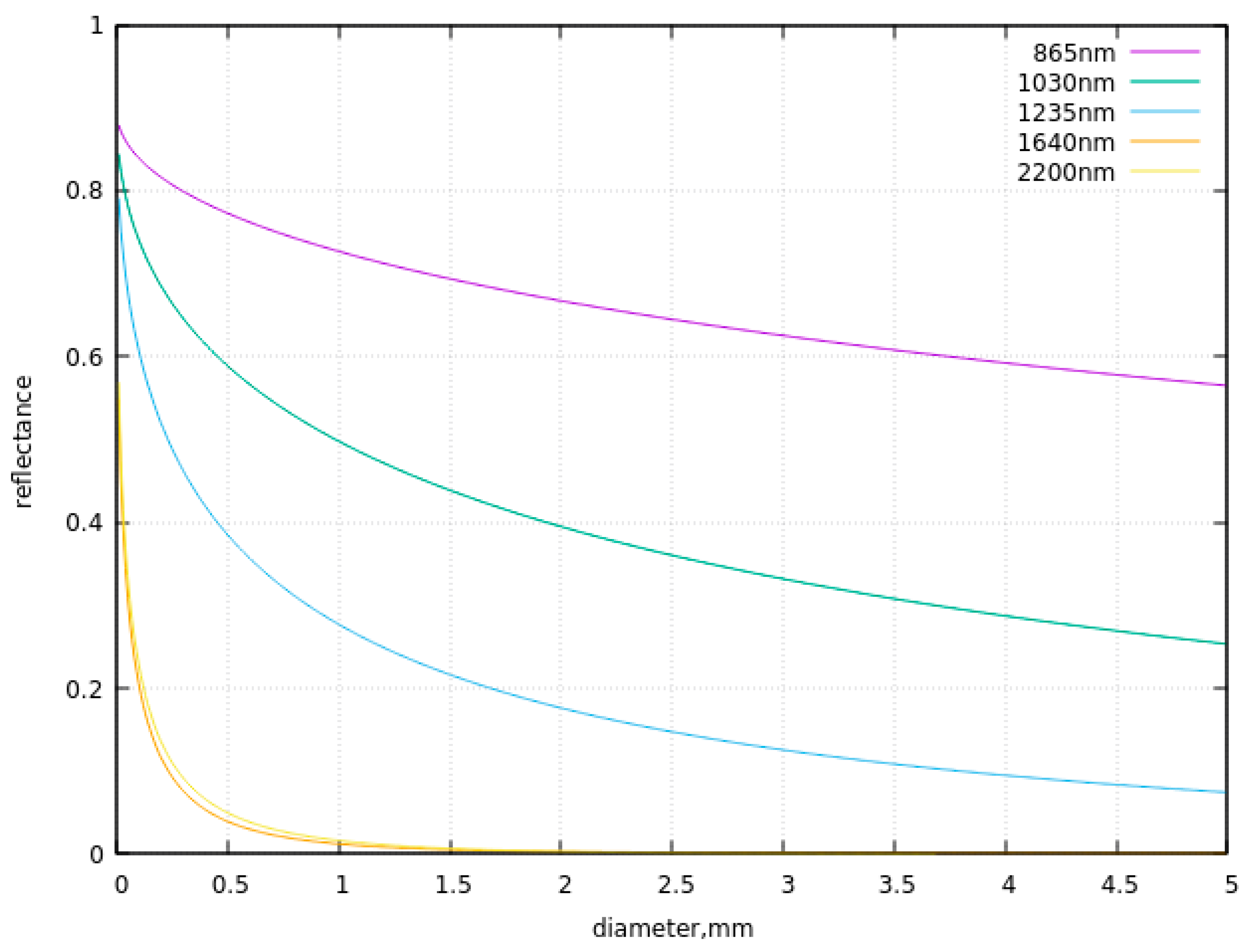
Table 1.
The parameters used in simulations shown in Figure 3.
Table 1.
The parameters used in simulations shown in Figure 3.
| Parameter | Physical meaning | Value |
|---|---|---|
| , mm | Effective grain diameter | 0.2 |
| TOC, DU | Total ozone column (TOC) | 289 |
| PWV, cm | Precipitable Water Vapor (PWV) | 0.055 |
| Normalized effective OXygen column (NOX) | 0.9 | |
| Aerosol optical thickness (AOT) at 550nm | 0.02 | |
| B | Aerosol Angström parameter | 1.8 |
| c, ppm | Relative impurity concentration | 50.0 |
| ,1/μm | Volumetric impurity absorption coefficient | 0.04 |
| m | Impurity absorption Angström parameter | 4.0 |
| H, m | Surface height | 3233 |
| , hPa | Surface pressure | 651 |
| T, K | Average temperature along vertical | 229 |
| P,hPa | Average pressure along vertical | 491 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated







