Hybrid-electric Vehicle Powertrain Mounting System Optimization Based on Cross-industry Standard Process for Data Mining

Preprint

Article

Hybrid-electric Vehicle Powertrain Mounting System Optimization Based on Cross-industry Standard Process for Data Mining

Altmetrics

Downloads

108

Views

Comments

A peer-reviewed article of this preprint also exists.

Yudong Wu^*

,Dandan Zhao,Jingyuan Peng,

Xingyu Xiang,

Haibo Huang^*

Yudong Wu^*

,Dandan Zhao,Jingyuan Peng,

Xingyu Xiang,

Haibo Huang^*

This version is not peer-reviewed

Submitted:

08 January 2024

Posted:

08 January 2024

You are already at the latest version

Alerts

Abstract

The meticulously engineered powertrain mounting system of hybrid-electric vehicles plays a critical role in minimizing vehicle vibrations and noise, thereby enhancing the longevity of vital powertrain components. However, developing and designing such a system demands substantial time and financial investments due to intricate analysis and modeling requirements. To tackle this challenge, this study integrates data-mining technology into the design and optimization processes of the powertrain mount system. The research focuses on the powertrain mounting system of a transverse four-cylinder hybrid-electric vehicle, employing the CRISP-DM (Cross-Industry Standard Process for Data Mining) methodology to establish a data-mining prediction model for mounting stiffness. This model utilizes three data mining algorithms—Multi-SVR, MRTs, and MLPR—assessing their predictive accuracy concerning mounting system stiffness estimation. A comparative analysis reveals that the MRTs algorithm outperforms others as the most effective prediction model. The proposed predictive model elucidates the quantifiable correlation between vibration isolation performance and installation stiffness, overcoming complexities associated with traditional modeling approaches. Applying this model in powertrain mounting system design showcases the efficacy of the CRISP-DM-based approach, significantly enhancing design efficiency without compromising prediction accuracy.

Keywords:

Subject: Engineering - Automotive Engineering

1. Introduction

The optimization of powertrain mounting systems constitutes a crucial technological aspect dedicated to enhancing the ride comfort and safety attributes of vehicles. A meticulously designed powertrain mounting system not only significantly reduces vehicular vibrations and noise but also extends the durability of pivotal powertrain components [1,2,3]. The design of the mounting system requires the isolation of frame vibrations induced by the engine and the mitigation of reverse shocks resulting from road excitation. This dual-pronged approach is imperative for prolonging powertrain component service life and improving vehicle Noise, Vibration, and Harshness (NVH) performance [4,5]. However, the procedural trajectory, spanning from the acquisition of powertrain parameter information to the analysis and optimization of mounting system performance, demands a foundation rooted in profound theoretical research coupled with experimental design and multi-body dynamics analysis [6,7,8,9].

Traditional mounting system design and optimization processes grapple with challenges, including exorbitant experimentation costs, protracted temporal commitments, stringent technical requisites for designers, and suboptimal data utilization. The realm of mounting system research is typically delineated into three hierarchical levels: mounting parts level, mounting system level, and vehicle level. Within the purview of mounting system level studies, variables such as stiffness, position, and angle are manipulated, with natural frequency, decoupling rate, and vibration isolation rate constituting the focal objectives for optimization analyses [10,11,12,13]. When both vehicle and powertrain parameters are substantively established, the optimization design of the mounting system predominantly centers on the modulation of mounting stiffness. This iterative process entails recurrent adjustments to the multibody dynamics model and mathematical theoretical model. However, this iterative approach proves inadequate for achieving the objectives of expeditious analysis and falls short of meeting the accuracy requisites intrinsic to multi-objective optimization designs for multiple mounts within the powertrain mounting system [14,15,16].

Consequently, there exists an imperative to explore innovative methodologies capable of aligning with the exigencies of mounting system development. In recent years, data mining technology is constantly being innovated and developed [17,18,19]. As data mining focuses on the correlations between data, while the correlation does not always indicate causation, the numerical computation in data mining is more concise than traditional design methods [20,21,22]. Since 2010, data mining technology is gradually introduced and applied to the vehicle powertrain mounting design, such as identifying the forward and inverse models of magnetorheological hydraulic mounting [23], predicting the noise quality of electric vehicle powertrain [24], predicting the dynamic parameters of hydraulic mounting [25], etc. These studies show that it is feasible to apply data mining technologies in powertrain mounting system design. However, most of the current research focuses on a single performance or a single dynamic characteristic, and the proposed methods cannot fully satisfy the requirements of multi-objective optimization design for multiple mounts in the powertrain mounting system.

Within this study, a comprehensive approach is pursued to align with the multi-objective design imperatives of the powertrain mounting system. In pursuit of this objective, data-mining technology is systematically integrated into the intricate processes governing the design and optimization of the powertrain mount system. A methodical data-mining design framework is consequently formulated, anchored in the well-established CRISP-DM (Cross-Industry Standard Process for Data Mining) paradigm. This design methodology undergoes meticulous evaluation of its predictive accuracy, employing three distinct data-mining algorithms. The efficacy of the method is further substantiated through empirical application within the context of a transverse four-cylinder hybrid-electric vehicle powertrain mounting system. This endeavor not only scrutinizes the method's efficiency but also underscores its fidelity in delivering precise outcomes, thus validating its utility within the specified application domain.

In this paper, the rest is organized as follows. Section 2 presents the CRISP-DM methodology of hybrid-electric vehicle powertrain mounting design and the optimization design algorithms used in CRISP-DM. In Section 3, the basic data sets and data preprocessing are described, and the prediction accuracy of mounting system design stiffness is discussed with three different data-mining algorithms, Multi-SVR, MRTs, and MLPR. Section 4 shows the application for a hybrid-electric vehicle powertrain mounting system design based on CRISP-DM. Finally, the paper concludes with a summary presented in Section 5.

2. Methods

2.1. CRISP-DM Methodology

Due to the disparate structural configurations of departments across various enterprises, the execution of data mining processes is often characterized by a pronounced lack of uniformity, resulting in substantial resource and labor inefficiencies. Consequently, the establishment of a cross-industry standard, transcending the constraints imposed by industry-specific nuances, tools, and applications, becomes imperative. This realization prompted the development of the Cross-Industry Standard Process for Data Mining (CRISP-DM). 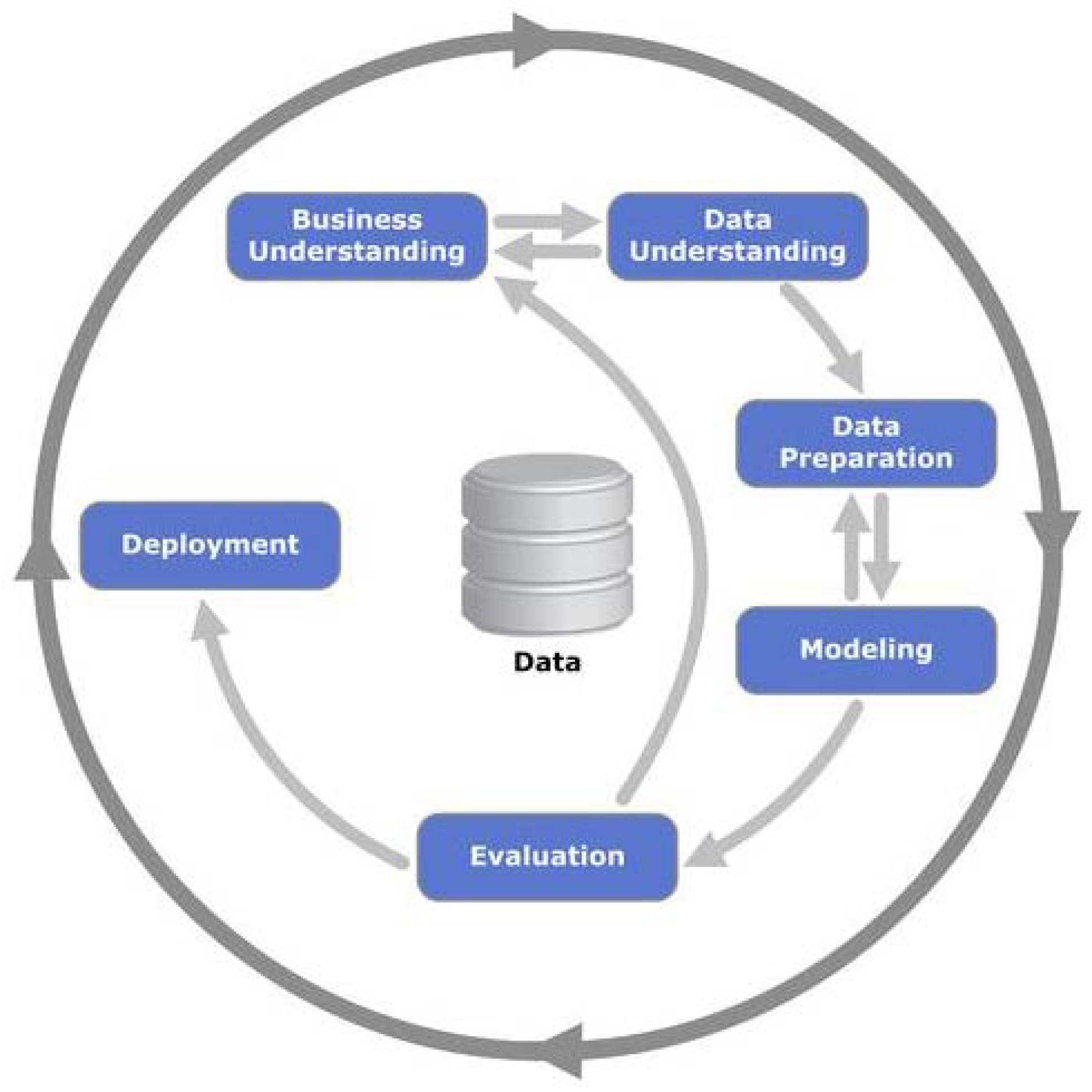CRISP-DM represents a freely accessible, open, and standardized framework for data mining, rendering it applicable to both business and research domains [26]. In accordance with CRISP-DM, a data mining project unfolds through six distinct phases: business understanding, data understanding, data preparation, modeling, evaluation, and deployment, as illustrated in Figure 1. The sequencing of these phases is adaptable, signifying those later stages are contingent upon the outcomes derived from antecedent phases. The interdependence between phases is visually represented by arrows, with the progression from one phase to the next influenced by the results of the preceding stages. For instance, if a data mining project is currently situated in the modeling phase, considerations regarding the behavior and characteristics of the model may necessitate a return to the data preparation phase for refinement before proceeding to subsequent stages.

In the project for the powertrain mounting design based on data mining, firstly, business understanding refers to determining data mining objectives according to the requirements of hybrid-electric vehicle powertrain mounting system. The data sets of interest are obtained based on the mounting design requirements in data understanding, and the original data is cleaned or transformed during data preparation. Modeling refers to the selection and application of the most suitable modeling methods for mounting design. Then, the quality and effectiveness of the model are evaluated, and the final data mining model is decided. Finally, the mining model is deployed and applied in engineering.

2.2. Optimization Design Algorithm

Compared with the prediction models built separately for each single target, multi-objective regression offers several advantages. Firstly, the scale of the multi-objective regression model is consistently smaller than that of multiple single-objective models. Secondly, the multi-objective model excels in accurately identifying the relationships between different target variables [27]. Therefore, the multi-objective regression algorithm is selected as the prediction algorithm in the CRISP-DM-based model. The three most commonly used multi-objective regression algorithms, namely, Multiple Output Regression Decision Tree (MRTs), Multi-Layer Perception Regression (MLPR), and Multiple Output Support Vector Machine Regression (Multi-SVR), are considered.

The multi-output regression decision tree algorithm demonstrates superior capability in handling the interaction between the input features of the mounting stiffness prediction model. Its calculations are simple, and the algorithm is easy to understand, with strong interpretability. Multi-output neural networks are adept at learning nonlinear models, allowing them to adapt to the nonlinear characteristics of mounting stiffness. The Multi-Output Support Vector Machine (MSVR) regression algorithm is well-suited for managing small samples of suspended data sets, and it exhibits excellent generalization performance.

(1) Multiple output regression decision tree

Suppose that data set

D

contains

N

data samples, and each variable can be expressed as

X_{1} \dots X_{m}

and

Y_{1} \dots Y_{m}

, that is, data set

D

D = \{{(x}^{(l)}, y^{(i)}), \dots, (x^{(N)}, y^{(N)}))

. The feature set has

m

dimensions, denoted by

x^{l} = (x_{1}^{l}, \dots, x_{j}^{l}, \dots, x_{m}^{l})

. The target set has

d

dimensions denoted by

y^{(i)} = (y_{1}^{(l)}, \dots, y_{i}^{(l)}, \dots, y_{d}^{(l)})

, where

i \in (1, d)

，

j \in (1, m)

and

l \in (1, N)

. For input variables and corresponding output variables, when the jth feature vector and the corresponding value

s

are selected as the partition variable and partition point, the training set is divided into two subsets, which are defined as

R_{1} (j, s) = \{x| x^{(j)} \leq s\}

(1.)

R_{2} (j, s) = \{x| x^{(j)} > s\}

(2.)

In the above formula,

R_{1} (j, s)

is the set whose characteristic value is less than or equal to

s

;

R_{2} (j, s)

is the set whose eigenvalue is greater than

s

. The optimal partition variables and the optimal partition points are required, shown as (3).

\min_{j, s} [\min_{R_{1}} \sum_{x_{i} \in R_{1} (j, s)} \sum_{i = 1}^{d} {(y_{i} - \bar{y_{1}})}^{2} + \min_{R_{2}} \sum_{x_{i} \in R_{2} (j, s)} \sum_{i = 1}^{d} {(y_{i} - \bar{y_{2}})}^{2}]

(3.)

\bar{y_{1}} = a v e (y_{i}| x_{i} \in R_{1} (j, s))

(4.)

\bar{y_{2}} = a v e (y_{i}| x_{i} \in R_{2} (j, s))

(5.)

where:

y_{i}

is the true value of input variable

x_{i}

; Traverse the variable

j

and find the values of

j

and

s

that make the minimum value, namely, the optimal sub-variable and the optimal partition point.

Divide the region with the selected optimal partition variable and the optimal partition point, and obtain the output value

\hat{c_{m}} = \frac{1}{N_{m}} \sum_{x \in R_{m} (j, s)} y_{i}, m = 1,2

(6.)

The process is repeated, dividing the input set into two subsets at a time, until the stop condition is met. Finally, the input set is divided into

M

regions

R_{1}, R_{2}, \dots, R_{M}

,generate decision tree

f (x) = \sum_{m = 1}^{M} \hat{c_{m}} I (x \in R_{m})

(7.)

Multi-output regression decision trees inherit the characteristics of univariate regression trees: easy to construct, and the results generated are highly interpretable. In addition, in the process of multi-output regression tree construction, when noise data or feature changes are added, the algorithm has good robustness, can automatically detect the interaction between variables, and deal with missing values in factor variables with minimum information loss [28].

(2) Multi-Layer Perception Regression (MLPR)

Multi-layer neural network Perception Regression (MLPR) is composed of three parts: input layer, hidden layer and output layer [29]. All nodes in the hidden and output layers are neurons using nonlinear activation functions. In addition, the hidden layer can be composed of multiple layers of neurons. The units of each layer are fully connected with each other, and the output of the previous layer is converted into the input value of the next layer through the activation function. The operation continues until the output layer is reached. The output value of the unit of the hidden layer is

y_{p j} = f_{j} \sum_{i} w_{i j} x_{p j} - ϴ_{j}

(8.)

In the type:

w_{i j}

is the first

i

nodes in the input layer and hidden layer first

j

connection weights of nodes;

x_{p j}

is the value of the jth input unit of the pth sample;

ϴ_{j}

is the threshold of the jth node,

f_{j}

is the activation function, which can usually be Tanh function, Sigmoid function

S i g m o i d (x) = \frac{1}{1 + e^{- x}}

(9.)

T a n h (x) = \frac{e^{x} - e^{- x}}{e^{x} + e^{- x}}

(10.)

R e l u (x) = \{\begin{matrix} x, x > 0 \\ 0, x \leq 0 \end{matrix}

(11.)

In this thesis, the MLP network by nonlinear activation patterns of three layers (input, a hidden layer and one output layer) composed of input layer has 18 nodes (corresponding to the 19 input parameters of powertrain), set up 17 neurons of hidden layers, there are 9 neurons in output layer (corresponding to the three-mounting stiffness on the direction of a total of 9 values). When network parameters are learned based on training data, the weights and biases of the connection between powertrain input parameters and stiffness are updated. When new data is applied, the predicted values are calculated based on the learned weights and biases.

(3) Multiple output support vector machine regression

The current support vector machine regression algorithm is specifically designed for single-output systems. However, when confronted with the task of predicting mounting stiffness, a methodology involving the construction of a series of single-output support vector machine models is employed to establish the multi-SVR [30,31]. SVR represents a typical least square regression model, extending the Support Vector Machine algorithm to address regression problems. In traditional regression algorithms, the loss value is computed as the difference between the model's output value and the actual value. Conversely, the SVM regression algorithm permits a certain deviation between the model's output values and the actual values. It initiates the calculation of loss only when the difference between the output value and the actual value falls below a predefined threshold ε.

Therefore, the support vector machine regression problem can be formalized as

\min_{w, b} \frac{1}{2} {ǁ w ǁ}^{2} + C \sum_{i = 1}^{m} l_{ε} (f (x_{i}) - y_{i})

(12.)

In the type:

w

as normal vector;

b

displacement vector;

C

regularization parameter;

ε

said deviation;

l_{ε} (z)

is the insensitive loss function, and its form is

l_{ε} (z) = \{\begin{matrix} 0, i f |z| \leq ε; \\ |z| - ε, o t h e r w i s e . \end{matrix}

(13.)

For the support vector machine model, the parameter range of kernel function is set as linear kernel, polynomial kernel, Gaussian kernel and Sigmoid kernel. The parameter range of kernel coefficient (

γ

) is (

10^{- 4}

10^{3}

). The penalty factor reflects the penalty degree of the algorithm on sample data (if

C

is too small, the training error will be large; if

C

is too large, the generalization ability of the model will be poor). Therefore, the parameter range of the penalty factor (

C

) is (

10^{- 4}

10^{3}

). The optimal parameter combination of the model was determined by grid search method, that is, the kernel function was Gaussian kernel, the gamma value was 0.05, and the penalty factor was 0.1.

3. Model Evaluation

3.1. Basic Data Sets and Data Preprocessing

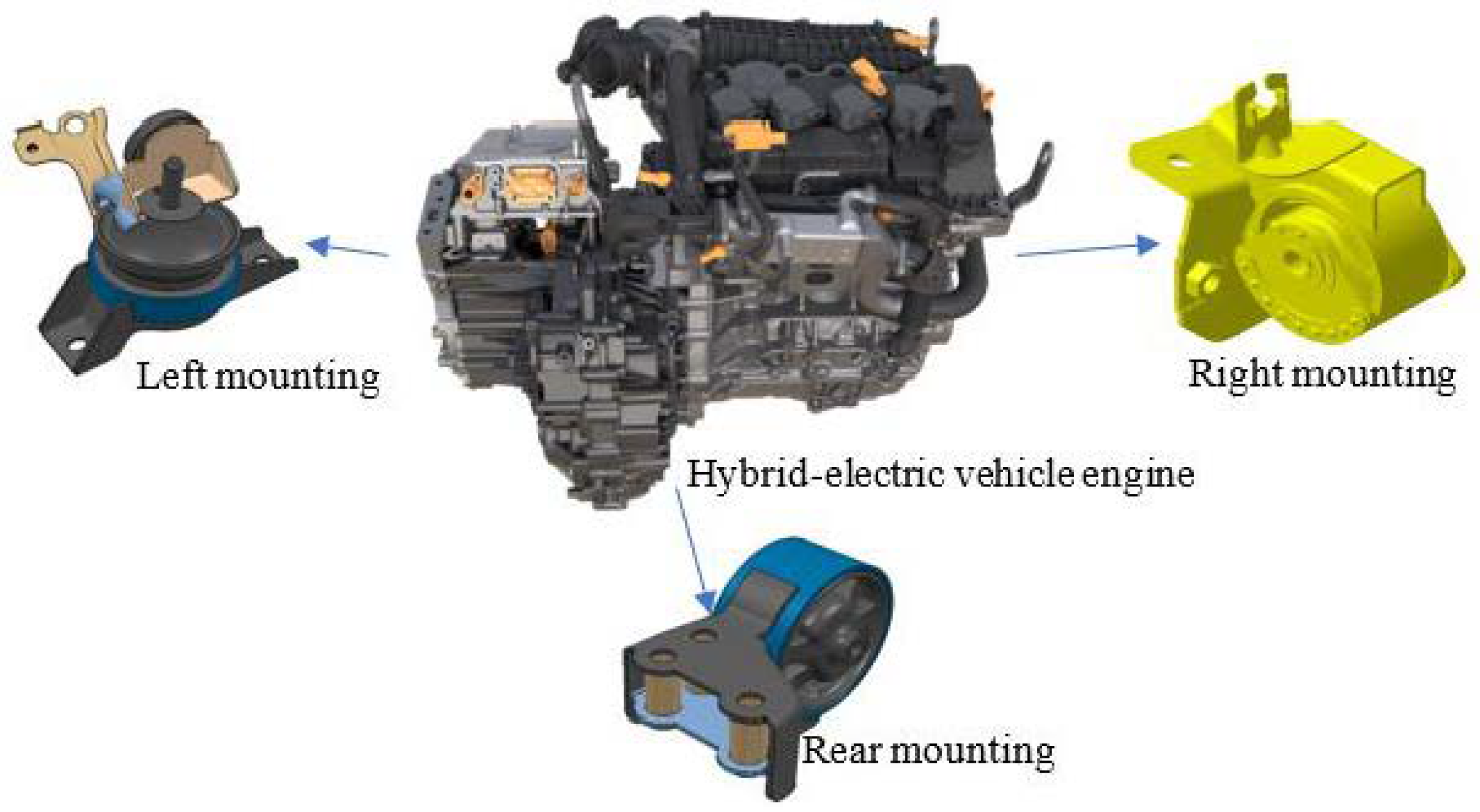
The research focuses on the mounting system of a transverse four-cylinder hybrid-electric vehicle, specifically examining the rear, left, and right mountings. Each mounting is arranged in a flat form, with the three perpendicular stiffness axes of each elastic support corresponding to the coordinate system parallel to the powertrain centroid. Figure 2 illustrates the positions of these mountings. Several influencing factors impact the engine powertrain mounting system, encompassing the inertia parameters of the powertrain, the centroid coordinates of the powertrain, the mounting coordinates of each individual mounting, the mounting angle, and the stiffness of each elastic spindle.

Therefore, in the multi-output regression model of the mounting system, the input parameters are the rotational inertia and inertia product

I_{i j}

(i, j = x, y, z)

, the centroid position coordinates

C_{m}

(m = x, y, z)

and the mounting stiffnesses

K_{n l} (n = 1, 2, 3; l = x, y, z)

, where

x

y

and

z

represent three directions respectively, and 1, 2 and 3 represent different mountings. Shown in Table 1 is one set of input parameter samples. The model has a total of 60 sets of data, with 80% data as the training set and 20% data as the test set. Since the selected object is flat mounted, the mounting angle is not used as a feature parameter.

To establish a robust mining model, stringent criteria must be applied to ensure data quality, encompassing accuracy, interpretability, consistency, timeliness, and credibility. A prerequisite for this involves thorough data preprocessing. For instances where mount position coordinates are missing, calculations are conducted based on the torque axis decoupling theory. Additionally, data sets are refined by reducing those with higher correlation coefficients, following Pearson's theory of correlation coefficient calculation. Lastly, the principal component analysis method is employed to reduce data dimensionality, resulting in a feature set condensed to 10 dimensions. This serves the dual purpose of model simplification and mitigating the risk of overfitting.

3.2. Prediction Results Evaluation

Machine learning regression models are typically assessed using performance metrics such as mean absolute error (MAE), root mean square error (RMSE), and R-squared (R²). The R² value, within the interval (0, 1), gauges the model's performance. A higher R² value, approaching 1, signifies superior model performance, while a value closer to 0 indicates weaker performance. In some instances, R² may take a negative value, suggesting the model perceives no regression relationship among predictor variables and deems them randomly distributed. For the evaluation of stiffness prediction regression models, RMSE and R² were chosen as the key metrics. RMSE serves to amplify values with significant prediction deviations, facilitating the comparison of different models' stability. On the other hand, R², akin to a standardized version of MSE, captures a portion of the response variance function, providing a nuanced performance assessment of the regression model. The commonly used metrics of RMSE and R² are calculated as follows:

R M S E = \sqrt{\frac{1}{N} Σ_{ⅈ = 1}^{N} {(y_{i} - {\hat{y}}_{i})}^{2}}

(14.)

R^{2} = 1 - \frac{\sum_{i = 1}^{N} {({\hat{y}}_{i} - y_{i})}^{2}}{\sum_{i = 1}^{N} {({\bar{y}}_{i} - y_{i})}^{2}}

(15.)

where

N

is the number of samples;

y_{i}

is the actual value;

{\bar{y}}_{i}

is the average and

{\hat{y}}_{i}

is the predicted value.

The model was trained according to the algorithm in Section 2.2, and a total of 9 stiffness of the three-point mount was predicted. Some samples were taken, and the prediction results of each model were compared with the input sample value. The comparison results are shown in Figure 3. RMSE and R² were used to evaluate the model, and the RMSE and R² results of different model training sets were obtained, as shown in Table 2.

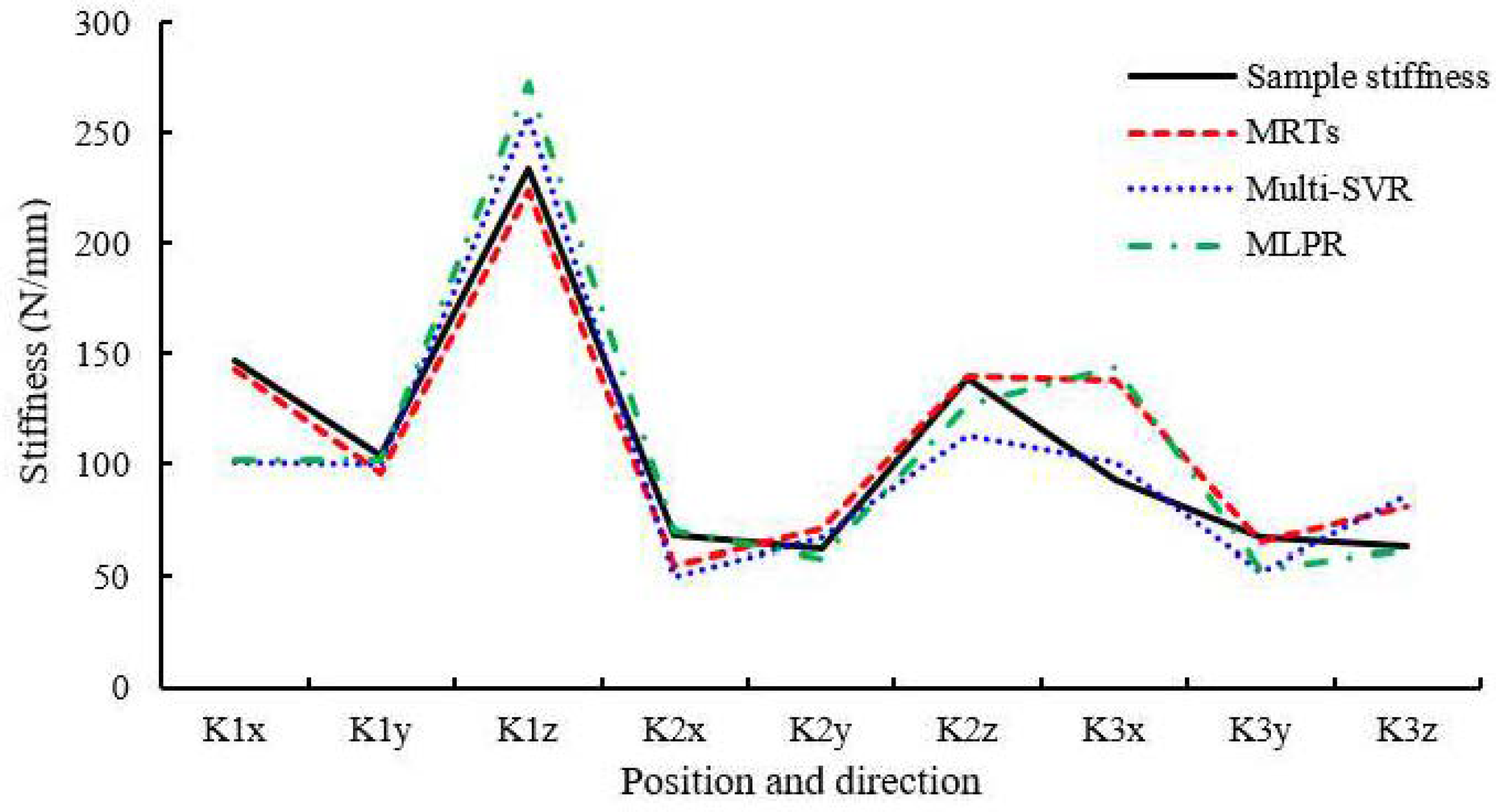
Multi-SVR represents an amalgamation of several regression models with a single output, depicted in Figure 3. The RMSE for Multi-SVR is the most extensive, indicating the largest prediction error, while its R² is the smallest, signifying the poorest fitting precision. In contrast, MRTs exhibit the smallest RMSE and the largest R², attesting to its superior prediction accuracy. The performance of MLPR falls between that of Multi-SVR and MRTs. Consequently, among the three models, MRTs demonstrate the most favorable prediction performance.

4. Application

The model undergoes evaluation through the metrics of RMSE and R², assessing the numerical proximity between predicted and actual values. Optimal vibration isolation performance in a powertrain system necessitates a balanced stiffness in the three directions of three mounts. This implies that closer proximity between predicted and actual values in the regression model does not inherently denote better performance. During the practical adjustment of the mounting system, each mounting stiffness is adjusted for overall optimal performance. Consequently, the mounting stiffness is considered not as a fixed value but as a value interval meeting specified requirements, where strict adherence to proximity between predicted and actual values is not obligatory.

The model evaluation extends beyond numerical metrics to consider engineering application-level indicators. This evaluation involves analyzing the natural frequency, decoupling rate, powertrain limit, and system vibration isolation rate. These factors provide a comprehensive assessment of the engineering significance and rationality of the data mining model. Upon establishing the vehicle and powertrain parameters, spatial constraints limit the mounting position and angle of the mount. The damping of the rubber mount has minimal influence on the dynamic performance of the mount system. Consequently, the optimization focuses shifts towards the stiffness of the mounting system. The optimization targets encompass the natural frequency, decoupling rate, and vibration isolation rate of the system.

When predicting the mounting stiffness for the data mining model, constructing separate output models for each direction would increase the model count. However, the anisotropic stiffness of each mounting exhibits a certain correlation, impacting other models when one is tuned. Hence, considering the correlation between objects becomes essential in establishing the multi-output model of mounting stiffness. Additionally, the application of the powertrain mounting system in engineering must adhere to engineering requirements related to natural frequency, decoupling rate, limit, and vibration isolation rate.

(1) Analysis of powertrain centroid displacement

The operational conditions of a vehicle are inherently intricate. Excessive displacement of the powertrain during vehicular motion poses a significant risk to surrounding components. Consequently, strict control over the ultimate displacement and rotation angle of the powertrain is imperative. The load conditions outlined in GM specification GMW14116 [32], applicable in North America, are employed for the meticulous calculation and analysis. Predicted stiffness values derived from various models are incorporated into the powertrain centroid displacement calculation results within the mathematical model. The ensuing comparison focuses on determining the maximum centroid displacement for each model, as detailed in Table 3.

The powertrain centroid displacement under the predicted values of Multi-SVR, MRTs and MLPR models basically meets the requirements in all directions, so it can be proved that the data mining model is reasonable to meet the limit.

(2) Natural frequency and decoupling rate analysis

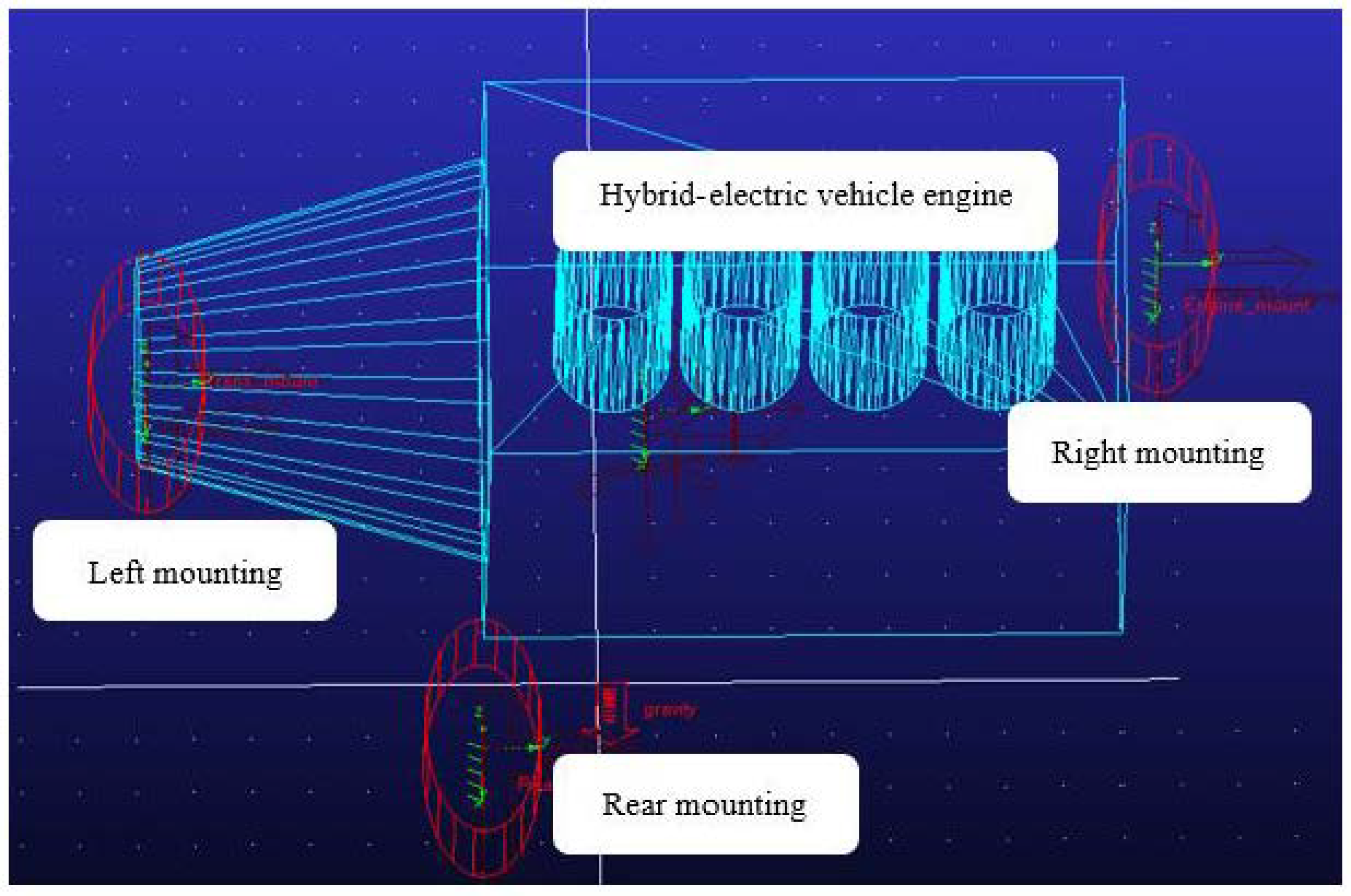
Employing the energy decoupling theory, a MATLAB program was scripted to formulate the mounting system model utilizing the specified parameters. Additionally, a 6-DOF (Degree of Freedom) model was instantiated through Adams View, illustrated in Figure 4. The powertrain was effectively represented by a square mass block, while the mounting element was modeled using the bushing unit. The inherent characteristics of this model were meticulously compared with the simulation results derived from the numerical model. The results indicate that the maximum error in the decoupling rate is confined to 5%, with an average error registering below 1.5%. These findings affirm a substantial concordance between the numerical model and the Adams model. Consequently, the numerical model is deemed reliable for the in-depth analysis of the mounting system's natural frequency, decoupling rate, and the rationality assessment of applying the data mining model in engineering.

The predicted stiffness values generated by the three multi-output regression models were incorporated into the numerical model, facilitating the subsequent calculation and comparison of the natural frequency and decoupling rate within the mounting system. A comprehensive analysis of various indices pertaining to the natural frequency and decoupling rate of distinct prediction models is presented:

a) Index 1 necessitates the first modal frequency to exceed the road excitation frequency.

b) Index 2 stipulates that the frequency interval for each order surpasses 1Hz.

c) Index 3 mandates that the ratio of the engine's excitation frequency to the highest engine modal frequency exceeds a specified threshold

\sqrt{2}

d) Index 4 calls for a decoupling rate exceeding 80% across all Degrees of Freedom (DOF).

The outcomes, detailed in Table 4, indicate that only the results derived from the MRTs model successfully satisfy all specified indices.

(3) Analysis of vibration isolation rate

The vibration isolation rate is formally defined as the ratio of the output amplitude to the input amplitude. In engineering applications, amplitude can manifest in various forms, such as force, velocity, acceleration, and other related parameters. The quantification of the vibration isolation rate is expressed through the following formula:

T_{i j} = \frac{A}{A_{0}}

(16)

Where

T_{i j}

is the vibration isolation rate of an engine mounting,

A

is the vibration amplitude at the passive end and

A_{0}

is the vibration amplitude at the active end.

The mountings, manufactured based on distinct optimization designs derived from the three models, are systematically installed onto the automobile. Subsequent vibration tests yield the vibration isolation rates for each mounting. The spatial arrangement of vibration accelerometers during the test is depicted in Figure 5, with the test conducted under vehicle acceleration conditions.

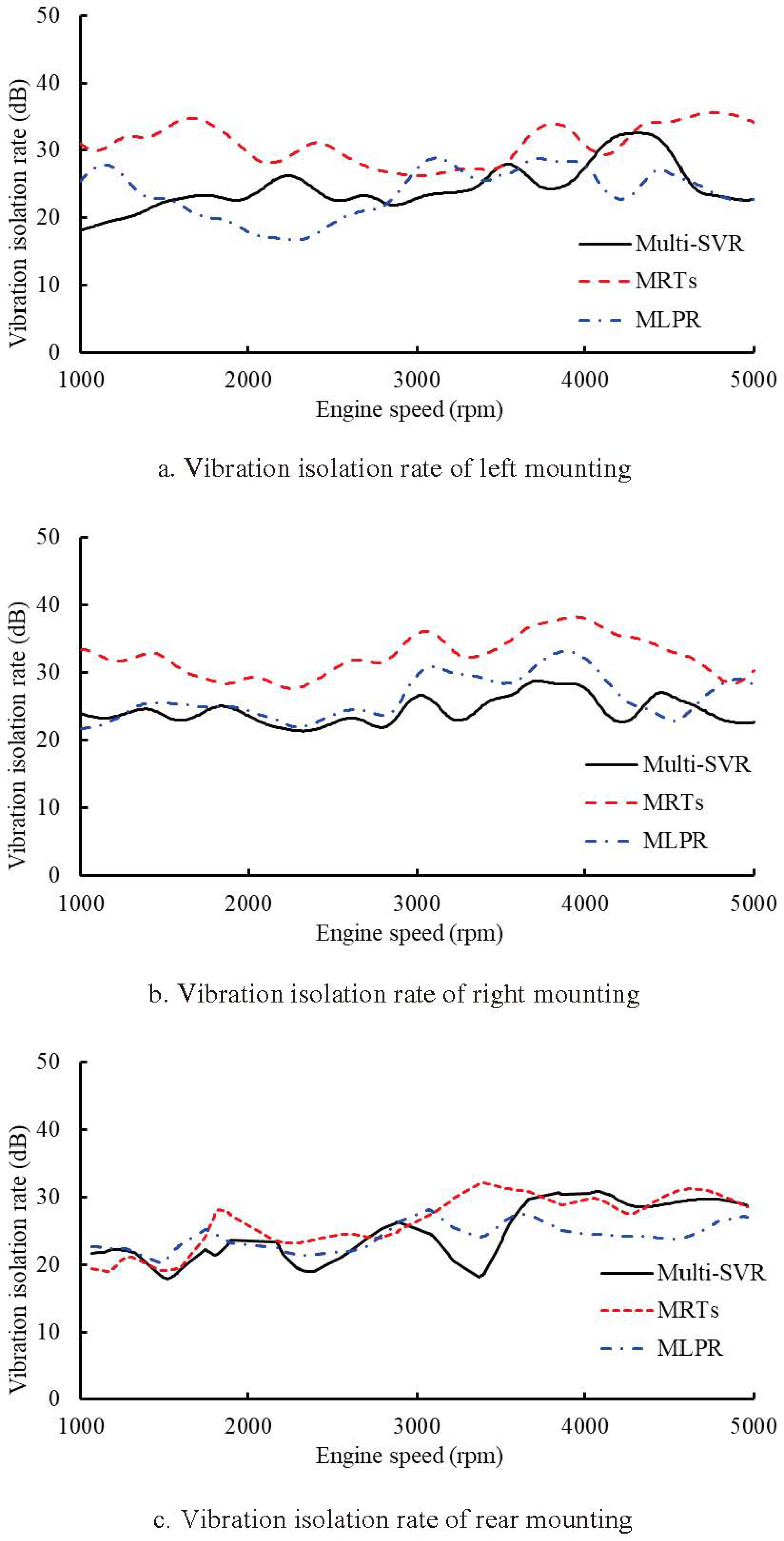
The vibration isolation rates of the mountings are presented in Figure 6. The results indicate that the vibration isolation rates of the mountings designed by all three models meet the specified target requirement of 20 dB. Regarding the left and right mountings, the design based on the MRTs model achieves the highest vibration isolation rate, surpassing the rates observed with the Multi-SVR and MLPR designs, which demonstrate relatively lower values. Conversely, for the rear mounting, the vibration isolation rates among mountings designed by the three models are approximately equivalent. In summary, the mountings designed by the MRTs model exhibit the most favorable performance in terms of vibration isolation rate.

(4) Validation of accuracy and efficiency of multiple output regression algorithm

The Genetic Algorithm (GA) is a computational method that simulates the process of natural evolution to efficiently search for optimal solutions, finding applications in parameter optimization and adaptive control of mounting systems.

To ascertain the accuracy and efficiency of the MRTs model in powertrain mounting optimization, a comparison is made between the decoupling rate of mountings optimized by the MRTs model and those designed using GA, with simultaneous recording of solution times. The decoupling rate results are presented in Table 5, and the time consumption for different models is outlined in Table 6. The tabulated data in Table 5 and Table 6 demonstrate that the MRTs algorithm not only satisfies the decoupling requirements (>90%) but also enhances the efficiency of mounting system optimization.

5. Conclusions

In this paper, to fulfill the multi-objective design requirements of hybrid-electric vehicle powertrain mounting systems, data-mining technology is introduced into the design and optimization of the powertrain mount system. A data-mining design method is established based on CRISP-DM and applied to the design of a transverse four-cylinder hybrid-electric vehicle engine mounting system. The following conclusions can be drawn from the results of this study:

a) Multi-objective regression algorithm is select as the prediction algorithm in the CRISP-DM based model. And in the three most commonly used multi-objective regression algorithms, Multi-SVR is a combination of multiple regression models with a single output, so its RMSE and R² indexes are lower than those of MRTs model and MLPR model. The performance of MRTs model is slightly higher than that of MLPR model. From the perspective of RMSE and R², the prediction performance of the MRTs is the best in the three algorithms.

b) The proposed predictive model elucidates the quantifiable correlation between vibration isolation performance and installation stiffness, thereby circumventing the intricacies associated with traditional modeling approaches. It is illustrated in the application for a transverse four-cylinder hybrid-electric vehicle engine mounting system design that the mountings designed by MRTs model performs best in the natural frequency, decoupling rate and vibration isolation rate requirements.

c) The MRTs model can achieve better results and enhance the efficiency in mounting system optimization. Therefore, the design method based on CRISP-DM could be applied in engineering practice to meet the multi-objective design requirement of the hybrid-electric vehicle mounting system.

Author Contributions

Conceptualization, Dandan Zhao; Funding acquisition, yudong wu; Investigation, Haibo Huang; Methodology, yudong wu; Software, Jingyuan Peng; Validation, Xingyu Xiang.

Funding

Please add: This study was funded by the Natural Science Foundation of Sichuan Province (2022NSFSC1892), the Fundamental Research Funds for the Central Universities (XJ2021KJZK054) and Liuzhou Science and Technology Program (2022DAA0102).

Data Availability Statement

The data used to support the findings of this study are available from the corresponding author upon request.

Acknowledgments

The authors thank the China Automotive Technology & Research Center for supporting the completion of this work.

Conflicts of Interest

The authors declare that there is no conflict of interests regarding the publication of this paper.

References

Igami, H.; Thompson, M.; Osodo, K. Automotive Powertrain Mounting System Design Optimization; SAE Technical Paper, 2008.
Shangguan, W. Engine mounts and powertrain mounting systems: a review. Int. J. Veh. Des. 2009, 49, 237–258. [Google Scholar] [CrossRef]
Sui, J.S.; Hoppe, C.; Hirshey, J. Powertrain mounting design principles to achieve optimum vibration isolation with demonstration tools; SAE Technical Paper, 2003.
Shangguan, W.; Zhao, Y. Dynamic analysis and design calculation methods for powertrain mounting systems. Int. J. Automot. Technol. 2007, 8, 731–744. [Google Scholar]
Huang, H.; Huang, X.; Ding, W.; Yang, M.; Fan, D.; Pang, J. Uncertainty optimization of pure electric vehicle interior tire/road noise comfort based on data-driven. Mech. Syst. Signal Proc. 2022, 165, 108300. [Google Scholar] [CrossRef]
Santhoshkumar, D.; Jayakumar, V.; Reddy, M.; Muniappan, A. Finite Element Modelling and Analysis of Novel Engine Mount: Technical Note. Int. J. Vehicle Structures & Systems 2018, 10, 415–416. [Google Scholar] [CrossRef]
Guo, R.; Wei, X.; Zhou, S.; Gao, J. Parametric identification study of an active engine mount: Combination of finite element analysis and experiment. Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering 2019, 233, 427–439. [Google Scholar] [CrossRef]
Tan, B.; Chen, Y.; Liao, Q.; Zhang, B.; Zhang, N.; Xie, Q. A condensed dynamic model of a heavy-duty truck for optimization of the powertrain mounting system considering the chassis frame flexibility. Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering 2020, 234, 2602–2617. [Google Scholar] [CrossRef]
Fan, D., Dai, P., Yang, M., Jia, W., Jia, X., Huang, H. Research on Maglev Vibration Isolation Technology for Vehicle Road Noise Control. SAE International Journal of Vehicle Dynamics, Stability, and NVH, 6(10-06-03-0016), 2022, 233-245. [CrossRef]
Hu, J.; Singh, R. Improved torque roll axis decoupling axiom for a powertrain mounting system in the presence of a compliant base. J. Sound Vibr. 2012, 331, 1498–1518. [Google Scholar] [CrossRef]
Erdelyi, H.E.; Roesems, D.; Toso, A.; Donders, S. Powertrain mounting system layout for decoupling rigid-body modes in the vehicle concept design stage; SAE Technical Paper, 2013.
Shangguan, W.; Liu, X.; Lv, Z.; Rakheja, S. Design method of automotive powertrain mounting system based on vibration and noise limitations of vehicle level. Mech. Syst. Signal Proc. 2016, 76, 677–695. [Google Scholar] [CrossRef]
Xu, X.; Su, C.; Dong, P.; Liu, Y.; Wang, S. Optimization design of powertrain mounting system considering vibration analysis of multi-excitation. Adv. Mech. Eng. 2018, 10, 754357354. [Google Scholar] [CrossRef]
Shui, Y.; Wen, H.; Zhao, J.; Wu, Y.; Huang, H. Optimization of Vehicle Powertrain Mounting System Based on Generalized Inverse Cascade Method under Uncertainty. Applied Sciences 2023, 13, 7615. [Google Scholar] [CrossRef]
Shangguan, W.; Liu, X.; Rakheja, S.; Hou, Q. Effective utilizing axial nonlinear characteristics of diaphragm spring and waveform plate to enhance breakaway performances of a clutch. Mech. Syst. Signal Proc. 2019, 125, 123–141. [Google Scholar] [CrossRef]
Cai, B.; Shangguan, W.; Lü, H. An efficient analysis and optimization method for the powertrain mounting system with hybrid random and interval uncertainties. Eng. Optimiz. 2020, 52, 1522–1541. [Google Scholar] [CrossRef]
Jun Lee, S.; Siau, K. A review of data mining techniques. Ind. Manage. Data Syst. 2001, 101, 41–46. [Google Scholar] [CrossRef]
Figueiredo, V.; Rodrigues, F.; Vale, Z.; Gouveia, J.B. An electric energy consumer characterization framework based on data mining techniques. IEEE Trans. Power Syst. 2005, 20, 596–602. [Google Scholar] [CrossRef]
Huang, H.; Lim, T.C.; Wu, J.; Ding, W.; Pang, J. Multitarget prediction and optimization of pure electric vehicle tire/road airborne noise sound quality based on a knowledge-and data-driven method. Mech. Syst. Signal Proc. 2023, 197, 110361. [Google Scholar] [CrossRef]
Ngai, E.W.; Xiu, L.; Chau, D.C. Application of data mining techniques in customer relationship management: A literature review and classification. Expert Syst. Appl. 2009, 36, 2592–2602. [Google Scholar] [CrossRef]
Mughal, M.J.H. Data mining: Web data mining techniques, tools and algorithms: An overview. Int. J. Adv. Comput. Sci. Appl. 2018, 9. [Google Scholar] [CrossRef]
Huang, H.; Huang, X.; Ding, W.; Yang, M.; Yu, X.; Pang, J. Vehicle vibro-acoustical comfort optimization using a multi-objective interval analysis method. Expert Syst. Appl. 2023, 213, 119001. [Google Scholar] [CrossRef]
Deng, Z.; Zheng, L.; Guo, M.; Zhang, Z. Model identification of magneto-rheological mount based on genetic algorithms and BP neural network. J. Univ. Electron. Sci. Technol. China 2014, 43, 955–960. [Google Scholar]
Fang, Y.; Zhang, T.; Chen, F.; Guo, R. Sound quality prediction of electric power train noise based on particle swarm optimization and support vector machine. J. Xian Jiaotong Univ 2016, 50, 41–46. [Google Scholar]
Jiang, M.; Liao, S.; Guo, Y.; Wu, J. The improvement on vibration isolation performance of hydraulic excavators based on the optimization of powertrain mounting system. Adv. Mech. Eng. 2019, 11, 753295612. [Google Scholar] [CrossRef]
Wirth, R.; Hipp, J. CRISP-DM: Towards a standard process model for data mining, Proceedings of the 4th international conference on the practical applications of knowledge discovery and data mining, 2000; Manchester, 2000.
Bandaru, S.; Ng, A.H.; Deb, K. Data mining methods for knowledge discovery in multi-objective optimization: Part A-Survey. Expert Syst. Appl. 2017, 70, 139–159. [Google Scholar] [CrossRef]
Spyromitros-Xioufis, E.; Tsoumakas, G.; Groves, W.; Vlahavas, I. Multi-target regression via input space expansion: treating targets as inputs. Mach. Learn. 2016, 104, 55–98. [Google Scholar] [CrossRef]
Huang, X.; Gao, L.; Crosbie, R.S.; Zhang, N.; Fu, G.; Doble, R. Groundwater recharge prediction using linear regression, multi-layer perception network, and deep learning. Water 2019, 11, 1879. [Google Scholar] [CrossRef]
Torres-Valencia, C.A.; álvarez, M.A.; Orozco-Gutiérrez, Á.A. Multiple-output support vector machine regression with feature selection for arousal/valence space emotion assessment, 2014 36th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, 2014; IEEE, 2014.
Saleh, A.A., & Weigang, L. Deep Self-Organizing Cube: A Novel Multi-Dimensional Classifier For Multiple Output Learning. Expert Systems with Applications, 2023, 120627. [CrossRef]
Lin, Z.; Zhao, J.; Wu, M. Design and analysis of semiactive mount for multi-flow path MR fluid. International Journal of Vehicle Noise and Vibration 2021, 17, 30–50. [Google Scholar] [CrossRef]

Figure 1. Cross-industry data mining process sketch.

Figure 2. Hybrid-electric vehicle powertrain mounting system.

Figure 3. The predicted results and the actual stiffness of the mountings.

Figure 4. Six degrees of freedom model in Adams.

Figure 5. Positions of vibration accelerometers in test.

Figure 6. Vibration isolation rates of the mountings.

Table 1. Input parameter sample.

Parameters	$I_{x y}$ $(k g ∙ m^{2})$	$I_{x y}$ $(k g ∙ m^{2})$	$I_{x y}$ $(k g ∙ m^{2})$	$I_{x y}$ $(k g ∙ m^{2})$	$I_{x y}$ $(k g ∙ m^{2})$	$I_{x y}$ $(k g ∙ m^{2})$
Value (Sample 1)	18.84	8.33	17.06	-0.73	3.04	0.19
Parameters	$C_{x} (m m)$	$C_{y} (m m)$	$C_{z} (m m)$	$K_{1 x}$ $(N / m m)$	$K_{1 y}$ $(N / m m)$	$K_{1 z}$ $(N / m m)$
Value (Sample 1)	-225	16	236	107	54	161
Parameters	$K_{2 x}$ $(N / m m)$	$K_{2 y}$ $(N / m m)$	$K_{2 z}$ $(N / m m)$	$K_{3 x}$ $(N / m m)$	$K_{3 y}$ $(N / m m)$	$K_{3 z}$ $(N / m m)$
Value (Sample 1)	100	100	200	164	15	15

Table 2. RMSE and R² results for different model training sets (RMSE/R²).

Model	Original Data	Dimensionality Reduction Data	Optimized Data
Multi-SVR	36.5/0.19	43.6/0.39	26.7/0.53
MRTs	12.8/0.93	10.3/0.94	10.6/0.96
MLPR	23.9/0.31	29.8/0.45	19.8/0.65

Table 3. Maximum displacement of powertrain under limit conditions (Limit/Actual).

angle	Tx(mm)	Ty(mm)	Tz(mm)	Rx(°)	Ry(°)	Rz(°)
Multi-SVR	10/6.38	10/8.17	15/12.8	1.0/0.35	3.5/3.63	1.0/0.57
MRTs	10/6.98	10/8.83	15/14.15	1.0/0.33	3.5/3.27	1.0/0.75
MLPR	10/5.44	10/7.13	15/10.39	1.0/0.21	3.5/2.85	1.0/0.53

Table 4. Comparison of natural frequency and decoupling rate of each model.

Model	Index 1	Index 2	Index 3	Index 4
Multi-SVR	Satisfy	Dissatisfy	Satisfy	Dissatisfy
MRTs	Satisfy	Satisfy	Satisfy	Satisfy
MLPR	Satisfy	Dissatisfy	Dissatisfy	Dissatisfy

Table 5. Comparison of the optimized decoupling rates (GA/MTRs).

Modal Number		1	2	3	4	5	6
Modal Frequency		5.9/5.72	7.85/8.09	8.83/8.91	12.06/11.27	13.02/12.34	16.37/15.98
Decoupling Rate%	X	0.61/0.09	91.17/93.55	0.30/1.54	0.96/0.56	6.88/4.21	0.09/0.04
	Y	97.28/97.09	1.12/0.27	0.21/1.09	0.05/0.35	0.68/0.01	0.67/1.19
	Z	0.16/0.77	0.17/1.33	98.63/94.60	0.25/0.07	0.14/0.00	0.66/3.23
	RX	1.10/1.63	0.07/-0.02	0.74/2.80	0.94/0.14	3.36/0.05	93.79/95.41
	RY	0.72/0.00	5.34/3.83	0.00/-0.04	3.57/0.28	87.77/95.64	2.61/0.28
	RZ	0.14/0.43	2.14/1.04	0.13/0.00	94.23/98.60	1.17/0.08	2.19/-0.15

Table 6. Time consumption of the operation with different models.

Algorithm	Iterations	Consumption of Time (s)	Decoupling Rate (%)
GA	460	120	>85
MRTs	1	2	>90

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Hybrid-electric Vehicle Powertrain Mounting System Optimization Based on Cross-industry Standard Process for Data Mining

Abstract

1. Introduction

2. Methods

2.1. CRISP-DM Methodology

2.2. Optimization Design Algorithm

3. Model Evaluation

3.1. Basic Data Sets and Data Preprocessing

3.2. Prediction Results Evaluation

4. Application

5. Conclusions

Author Contributions

Funding

Data Availability Statement

Acknowledgments

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe