Prerpints.org logo
Preprint
Article

Plato’s Allegory of the ‘Cave’ and Hyperspaces: Sonic Representation of the ‘Cave’ as a Four-Dimensional Acoustic Space via an Interactive Art Application

Altmetrics

Downloads

113

Views

61

Comments

0

A peer-reviewed article of this preprint also exists.

supplementary.mp4 (138.08MB )

Submitted:

07 January 2024

Posted:

08 January 2024

You are already at the latest version

Alerts
Abstract
Mathematician and philosopher, Charles Howard Hinton, posited a plausible correlation between of higher-dimensional spaces, also referred to as ‘hyperspaces’, and the allegorical concept artic-ulated by the Ancient Greek philosopher Plato in his work, Republic, known as the 'Cave.' In Plato's allegory, individuals find themselves situated in an underground 'Cave,' constrained by chains on their legs and neck, perceiving shadows and sound reflections from the ‘real’ world cast on the ‘Cave’ wall as their immediate reality. Hinton extended the interpretation of these 'shadows' through the induction method, asserting that, akin to a 3D object casting a 2D shadow, the 'shadow' of a 4D hyper-object would exhibit one dimension less, manifesting as a 3D object. Building upon this conceptual framework, the authors posit a correlation between the perceived acoustic space of the chained individuals within the 'Cave' and the characteristics of a 4D acoustic space, a proposition substantiated mathematically by scientific inquiry. Furthermore, the authors introduce an interactive art application developed as a methodical approach to exploring the hypothetical 4D acoustic space within Plato's 'Cave,' as perceived by the chained individuals and someone liberated from his constraints navigating through the 'Cave.'
Keywords: 
Subject: Arts and Humanities  -   Other

1. Introduction

1.1. Brief History of Hyperspaces

The initial exploration of higher dimensions finds its roots in ancient Greece, notably with Plato's allegory of the 'Cave' [1]. Pioneering philosophers and scientists such as Riemann raised fundamental questions about the dimensionality of the 'real' space and the geometry that defines it [2]. Although new spaces and dimensions were postulated, definitive proof of their existence is still elusive.
The scientific discipline of Mathematics, particularly Topology, underwent significant development from the nineteenth century onward. During this period, Henri Poincaré, Charles Hinton, and Claude Bragdon delved into the examination of hyper-solids and the interaction of hyperspace with our familiar 3D space [2]. By 1920, artists began grappling with the concept of the fourth spatial dimension, marking a common feature in the movements of modernity throughout the first three decades of the twentieth century [2].
Literature, influenced by Edwin Abbott's Flatland and H. G. Wells' works, and painting, particularly through the Cubists and Russian artists, actively sought to visualize the fourth spatial dimension [2]. Physics, however, brought both evolution and setbacks to the concept of higher dimensions, with significant shifts occurring since the late nineteenth century. The emergence of new phenomena, such as electrons, X-rays, and electromagnetic waves, sparked interpretations of an invisible world, complemented by the Theory of Ether. Notably, Einstein's Theories of Relativity in the early twentieth century challenged the existence of higher spatial dimensions, dampening general interest [2]. The resurgence of hyperspaces at the end of the century came with String Theory, proposing a 'Theory of Everything' explaining our Universe as vibrations of strings in eleven dimensions [3].
Advancements in computer graphics capabilities by the end of the twentieth century facilitated the simulation of hyper-solids' projections into 3D space. Collaboration between artists and scientists, fueled by computer and Virtual Reality technology, rekindled interest in the subject [2].

1.2. An Abbreviated Mathematical Examination of the Fourth Spatial Dimension

The predominant mathematical definition of spatial dimensionality posits that the number of coordinates distinguishing one point from another within a given space is equivalent to the dimensions of that space. Consequently, in 4D hyperspace, each point can be uniquely identified by four coordinates relative to others [4].

1.2.1. Generating the ‘Shadow’ of a Hypercube

A comprehensible four-step approach to conceptualizing the fourth spatial dimension involves progressing from the zeroth dimension to the fourth spatial dimension. The initial step entails beginning with a point (zeroth dimension) and transitioning it into a line segment, thereby entering the first dimension (Figure 1a). Subsequently, in the second step, the line segment is shifted in a perpendicular direction, giving rise to a square within the second dimension (Figure 1b). The third step involves further shifting the square perpendicularly to its two axes, resulting in the formation of a cube within the third dimension (Figure 1c). Finally, the cube undergoes a perpendicular shift relative to its three axes, producing the hypercube, a 4D object characterized by a hyper-surface comprising eight cubes. This directionality, however, is beyond our familiar comprehension, limited as we are to perceiving only 3D space. Consequently, what is observed in Figure 1d is the projection (shadow) of the hypercube onto 3D space [5].
The projection, as an interaction of a 3D solid with a 2D plane, may be employed, when applying the inductive method to understand the interaction of a 4D hyper-solid, e.g., the hypercube, with 3D space [5].
By holding a semitransparent 3D cube so that the light casts its shadow on a flat surface, it is possible, while turning it, to project different 2D shadow patterns on this flat surface. If the light comes at a vertical angle from a point near the cube, as shown in Figure 2a then a 2D shadow is formed. Correspondingly, Figure 2b shows the ‘shadow’ of a specific 3D projection of a hypercube, the hypersurface of which consists of eight cubes [5].

1.3. Hinton’s Inductive Approach to Plato’s Allegory of the ‘Cave’

Charles Howard Hinton, a mathematician and philosopher specializing in hyperspaces, expounded on the potential connection between higher-dimensional spaces and our perceived world in Chapter IV of his book The Fourth Dimension (1904). He asserted that ancient thinkers like Greek philosopher Parmenides and Asiatic scholars had initially conceived of such a relationship. Moreover, Hinton proposed a plausible link between Plato's renowned allegory of the 'Cave' and hyperspaces [1].
Plato introduced his 'Cave' allegory in the seventh book of Republic. Within sections 514a-515c, Socrates, engaging in a dialogue with Glaucon, envisions humans confined in an underground dark cave, tethered with chains on their legs and necks. Restricted from turning their heads, these individuals can only perceive the cave wall before them. A fire positioned at a distance and at a higher-level casts light behind them, projecting the shadows of humans, statues, and animal figures onto the cave wall in front of the chained observers. These shadows constitute the sole images accessible to the captives, leading them to construct their perceived reality based on these fleeting impressions [6].
Hinton expanded the meaning of the ‘shadows’ via the induction method: as the shadow of a 3D object is a 2D shape, similarly, the ‘shadow’ of a 4D hyper-object is one dimension less; that is, a 3D object and posited that Plato described a hyperspatial 'real' world, the shadows of which give rise to our perceptual environment [1].

2. Materials and Methods

Within the section 515b in the seventh book of Republic, Socrates, while elucidating the allegory of the 'Cave,' includes a reference to the auditory perception of sounds from the 'real' world by the individuals constrained within the ‘Cave’: “What if the prison had an echo from the wall in front of them? Every time one of the people passing by spoke, do you suppose they’d believe the source of the sound to be anything other than the passing shadow?” [6].
We advance further along the line of Hinton’s thought and propose that the manner in which sound reflects off the walls of the 'Cave', and is perceived as a 3D acoustic space by chained individuals, shares numerous similarities with the properties of 4D acoustic space.

2.1. Propagation of Sound Waves in 4D Space

When a wave is propagated in the familiar 3D space, we observe that if a source, a lamp for example, is lit for exactly three seconds, an observer standing at some distance from the source shall see the lamp’s light lasting for three seconds. The same goes for waves of any other type, as in our case a sound wave. This is a property of waves that features are valid only in spaces with an odd number of dimensions. A wave in these dimensions is propagated in a steady velocity and brings about the aforementioned result.
In the second spatial dimension, if a wave is generated, let’s say by a pebble thrown on the surface of a still pond, one would expect for a radial wave to be created which would move away from the source, from the point where the pebble fell, without any distortion on the surface before or after the wave. Our experience, however, suggests that the water surface will not be still within the circle. That is the surface of the pond enclosed by the radial main wave will be distorted by waves of smaller amplitude that follow the main wave and attenuate some time later. In terms of 4D space we expect that, just as in the case of the second dimension of space, some initial stimulation may cause a distortion which will be propagated in the form of a main wave followed by secondary waves of lower intensity (Figure 3). Accordingly, in 4D space, sound distortions manifest as primary soundwaves, followed by secondary waves of reduced intensity—a phenomenon reminiscent of the echoes resonating within a cave [7,8].

2.2. Sonic Representation of the ‘Cave’ as a 4D Acoustic Space via an Interactive Art Application

In order to facilitate a clearer comprehension of the aforementioned concept, we have developed an interactive art application that provides a representation of Plato’s 'Cave' as a 4D acoustic space. In this space, individuals who are chained experience an echoing effect when hearing authentic voices due to the propagation of sound waves through 4D space.
An additional characteristic of hyperspatial sound that we must encompass in our application is the heightened decay of intensity with distance from the source.
In an acoustic space, the sound intensity received by the surface of our eardrum depends on the amplitude of the oscillation of the sound wave and the distance from the source. Specifically, if a spherical wave propagates in a N-dimensional space, sound intensity is inversely proportional to the surface area of the N-dimensional spherical surface that anticipates a decrease following the inverse proportionality of RN-1, where R denotes the distance from the source and the radius of the N-dimensional sphere. In our conventional 3D environment, with a point source, sound intensity is inversely proportional to the square of the distance from the source. In a 4D space, we expect that sound intensity, that is generated from the same source, follows an inverse proportionality to the exponent three of this distance. It is proved, however, that for spaces with dimensionality higher than three the decrease is even greater. This heightened reduction is attributed to the amplitude containing terms inversely proportional to higher exponents of the distance from the source [9].

2.2.1. Description of the interactive art application

The depiction of the ‘Cave’ space and the design of user interaction were composed using ‘Processing’ open-source programming language and development environment. Adhering to Plato's depiction, a fire was positioned at the bottom of the screen. In proximity to the fire, three spheres are positioned, symbolizing 4D entities: Socrates, a musician and a man accompanied by two dogs. These entities, illuminated by the fire, cast their shadows on the ‘Cave’ wall positioned at the top of the screen. The user, portrayed as a sphere in its chained 4D nature, is approximately placed in the center of the screen.
Successively appearing on the screen based on the user's choice, Socrates, the musician, and the two dogs each generate their own sound disturbance in the space. Socrates recites a portion of Plato’s ‘Apology of Socrates’, the musician performs Seikilos song called Epitaph with the Lyre of Apollo, and the barking of dogs that resonates to the animal as described by Plato in his allegory of the ‘Cave’ (Figure 4) [10,11].
What would be the outcome if one of the individuals bound by constraints were to break free and move through the cave? This concept is also alluded to by Socrates in the seventh book of Plato's Republic.
“[…] ’Think what their release from their chains and the cure for their ignorance would be like. When one of them was untied, and compelled suddenly to stand up, turn his head, start walking, and look towards the light, he’d find all these things painful. Because of the glare he’d be unable to see the things whose shadows he used to see before. […] “ [6].
Our interactive art application enables the unrestricted movement of the unchained humans, allowing them to traverse in 4D ‘Cave’ space at variable speeds. This movement results in an auditory experience where sounds are echoed and shifted towards higher playback speeds as the humans approaches the source, and towards lower up to negative playback speeds as they move away from the source. These functions align with a theoretical 4D auditory system.
Specifically, in our familiar space the 3D waveforms of sound actuate our 2D membranes, namely our eardrums. Subsequent to processing primarily within the cerebral framework, this information culminates in the cognitive apprehension of the 3D acoustic environment. Employing the inductive approach, we posit the possibility of detecting 4D sound through 3D auditory sensory organs. The sound confined within a 3D eardrum could potentially processed by the brain in any direction and velocity. This replaces the accustomed one-dimensional linearity of a sonic stimulus with the two-dimensional nature of writing. In this context, navigating the sonic stimulus becomes akin to reading the pages of a book [12].
Within our interactive art installation, the user exercises control over his/her on-screen positioning through the utilization of an input device, such as a computer mouse. This control enables him/her to navigate the acoustic space generated by the three virtual sound sources: Socrates, the musician and the barking dogs, that create individualized acoustic spaces. Consequently, each point within the 'Cave' space corresponds to a specific point on the sound waveform contingent upon the temporal progression. As the user traverses the 'Cave' space, has the ability to perceive the sound emitted by each source at a standard, decelerated, or accelerated pace, aligning with the velocity, movement direction, and proximity to the source. Concurrently interacting with the acoustic environments of other sources, as well as considering the user's relative speed, movement direction, and distance from them, engenders a distinctive amalgamation of auditory experiences.

3. Results

The intersection of Plato’s work and hyperspaces gains prominence through the work of mathematician and hyperspace philosopher Charles Howard Hinton. In employing the induction method, Hinton extended the interpretation of the 'shadows' in Plato's allegory of the 'Cave.' Specifically, he characterized these shadows as projections of 4D entities onto 3D space.
This article builds upon this established connection and proposes an additional link between Plato’s ‘Cave’ and hyperspatial sound: the manner in which sound reflects off the walls of a cave creating a 3D acoustic experience for individuals, shares numerous similarities with the properties of a 4D acoustic space as supported in mathematical evidence. Within the fourth spatial dimension, certain initial stimuli can give rise to a distortion that propagates in the form of a main wave, succeeded by secondary waves of diminished intensity. Consequently, distortions in sound manifest as primary soundwaves, followed by secondary waves with reduced intensity—an occurrence reminiscent of echoes resonating within a cave.
To enhance comprehension of this connection, we have devised an interactive art installation that simulates a human with a hypothetical 4D auditory system that stands still or traverses through the Cave's acoustic space. The 4D sound entrapped in a hypothetical 3D eardrum could be traversed in any direction. This innovative technique introduces a wholly novel acoustic encounter, positing its potential utility as a tool for training the brain to potentially discern 4D sound.

4. Discussion

Can the human brain apprehend images and sounds of a 4D hyperspace, or are we confined within our familiar 3D spatial realm?
The human brain engages in the processing of incomplete information from visual, auditory, and tactile stimuli emanating from 3D objects to construct a comprehensive 3D model of the surrounding space. This developmental process initiates in early childhood and persists into adulthood [13]. Neuroscientific investigations into the evolution of our 3D perceptual and sensorimotor capacities, utilizing functional magnetic resonance imaging (fMRI), indicate that activations in various brain regions, including the entorhinal cortex and the visual system hierarchy, contribute to the extraction of 3D information [14]. According to neuroscientists, these areas might also play a role in the representation and integration of 4D information. In a separate study, neuroscientists contend that the human brain possesses the capability to compute positions, distances, and devise spatial routes within a simulated 4D environment [15]. This suggests a potential evolutionary trajectory for our cognitive abilities towards the perception of hyperspaces.
Numerous researchers have been undertaken to comprehend hyperspace through visual means [16,17,18,19]. However, the auditory 'visualization' of hyperspace emerges as a potentially more fruitful avenue. This could be attributed to parallels between the characteristics of sound and hyperspatial gravitational waves.
Specifically, in a parallel manner to an accelerating charge radiating electromagnetic waves, including light and radio waves, Albert Einstein, through his General Theory of Relativity, postulated that impactful events involving large masses or, more precisely, distributions of matter and energy undergoing acceleration, generate wave distortions akin to a pulse in the fabric of spacetime. These distortions are referred to as gravitational radiations or gravitational waves. A distinctive feature of gravitational waves is their ability to traverse space without significant interaction, in stark contrast to electromagnetic radiation like light, radio waves, X-rays, and Gamma rays, which can be influenced by other masses, charges, as well as magnetic or electric fields [20,21]. Furthermore, according to String Theory, gravitational waves possess the capability to travel in higher dimensions [22,23]. Consequently, if there were waves detectable by a hyperspatial sensory organ, gravitational waves would be prime candidates. Intelligent hyperspatial beings could potentially perceive their surrounding space based on these gravitational waves. Although human sensory organs are incapable of directly detecting gravitational waves, evidence suggests that they exhibit behavior reminiscent of sound waves [24]. Therefore, the auditory centers in our brain are better equipped for the perception of hyperspace, prompting a more effective outcome through an audio-centric approach.
Augmented Reality technology now enables the projection of virtual environments directly onto our 3D environment. This prompts a direct comparison of the aesthetic quality between virtual and real environments, challenging our cognitive perception. The integration of scientific, technocratic, and artistic knowledge gives rise to a new professional, the 'Technartist', capable of developing advanced audiovisual applications, including 3D interactive graphics. Technartists may further lead the way in creating interactive audiovisual 4D representations of exceptional aesthetic value, allowing us to perceive a 4D hyper-environment [25].

Supplementary Materials

The following supporting information can be downloaded at the website of this paper posted on Preprints.org.

Funding

This research received no external funding.

Author Contributions:

All authors have read and agreed to the published version of the manuscript.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Hinton, C.H. The Fourth Dimension; Swan Sonnenschein & Co: London, U.K.; John Lane: New York, N.Y., 1904; pp. 23-35.
  2. Henderson, L. D. The Fourth Dimension and Non – Euclidean Geometry in Modern Art; MIT Press: Cambridge, MA, 2013; pp. 5-7, 9, 15-20, 97, 105, 127-147, 315-316, 422, 505-508. [Google Scholar]
  3. Witten, E. String theory dynamics in various dimensions. Nuclear Physics 1995, 443, 85–126. [Google Scholar] [CrossRef]
  4. Matthews, B. Statics and Analytical Geometry; Ed-Tech Press: Essex, UK, 2019; p. 64. [Google Scholar]
  5. Bragdon, C. A Primer of Higher Space (The Fourth Dimension); Manas Press: Rochester, N.Y, 1913; PL: 1, 4, 5. [Google Scholar]
  6. Ferrari, G.R.F. (Ed.) Plato: The Republic; Tom, Griffith, Translator; Cambridge University Press: Cambridge, UK, 2000; pp. 220–221. [Google Scholar]
  7. Math Pages. Huygens’ Principle. Available online: www.mathpages.com/home/kmath242/kmath242.htm (accessed on 9 December 2023).
  8. Morley, T. A Simple Proof that the World is Three-Dimensional. SIAM review 1985, 27, 69–71. [Google Scholar] [CrossRef]
  9. Math Pages. Spherical Waves in Higher Dimensions. Available online: www.mathpages.com/home/kmath614/kmath614.htm (accessed on 9 December 2023).
  10. AncientGreek.eu. Plato: The Apology of Socrates. Available online: https://ancientgreek.eu/audiobooks/apology-p.html (accessed on 11 December 2023).
  11. FMA. Palera.L, Seikilos Epitaph with the Lyre of Apollo. Available online: https://freemusicarchive.org/music/Lina_Palera_Lyre_20_Project_player/An_Appreciation/01_Seikilos_Epitaph_with_the_Lyre_of_Apollo) (accessed on 11 December 2023).
  12. Traperas, D.; Floros, A.; Kanellopoulos, N. Sonic Representations in Hyper-spaces: A Creative Approach. Technoetic Arts: A Journal of Speculative Research 2017, 15, 221–228. [Google Scholar] [CrossRef] [PubMed]
  13. Dallos, P. The Auditory Periphery Biophysics and Physiology; Academic Press: New York, NY, 1973. [Google Scholar]
  14. Ogmen, H.; Shibata, K.; Yazdanbakhsh, A. Perception, Cognition, and Action in Hyperspaces: Implications on Brain Plasticity. Learning and, Cognition. Frontiers of Psychology 2020, 10, 3000. [Google Scholar] [CrossRef] [PubMed]
  15. Aflalo, T.N.; Graziano, M.S.A. Four-Dimensional Spatial Reasoning in Humans. Journal of Experimental Psychology: Human Perception and Performance 2008, 34, 1066–1077. [Google Scholar] [CrossRef] [PubMed]
  16. Ambinder, M. S.; Wang, R. F.; Crowell, J. A.; Francis, G. K. Human Fourdimensional Spatial Intuition in Virtual Reality. Psychon. Bull. 2009, Rev. 16, 818–823. [Google Scholar] [CrossRef]
  17. Wang, R.F. Human Four-Dimensional Spatial Judgments of Hyper-Volume. Spatial Cognition & Computation 2014, 14, 91–113. [Google Scholar] [CrossRef]
  18. Wang, R.F. Stronger Evidence for Four-Dimensional Spatial Representations: A Response to Frank. Spatial Cognition & Computation 2014, 14, 121–123. [Google Scholar] [CrossRef]
  19. Miwa, T.; Sakai, Y.; Hashimoto, S. Learning 4-D Spatial Representations Through Perceptual Experience with Hypercubes. IEEE Transactions on Cognitive and Developmental Systems 2018, 10, 250–266. [Google Scholar] [CrossRef]
  20. Einstein, A. Näherungsweise Integration der Feldgleichungen der Gravitation. Königlich Preußische Akademie der Wissenschaften (Berlin). Sitzungsberichte 1916, 688–696. [Google Scholar]
  21. Einstein, A. Über Gravitationswellen. Königlich Preußische Akademie der Wissenschaften (Berlin). Sitzungsberichte 1918, 154–167.
  22. Randall, L.; Sundrum, R. Large Mass Hierarchy from a Small Extra Dimension. Physical Review Letters 1999, 83, 3370. [Google Scholar] [CrossRef]
  23. Randall, L. and Sundrum, R. An Alternative to Compactification. Physical Review Letters 1999, 83, 4690. [CrossRef]
  24. Physics Today. Sounding off on Gravitational Waves: Grand, A.: Extra Dimensions. Available online: https://pubs.aip.org/physicstoday/Online/9795/Sounding-off-on-gravitational-waves (acessed on 9 December 2023). [CrossRef]
  25. Kanellopoulos, N. From Antikythera Analogue Computer to Quantum Computer. In Proceedings of the Audiovisual Arts Conference, Athens Concert Hall, Athens, Greece, 20–21 May 2017. [Google Scholar]
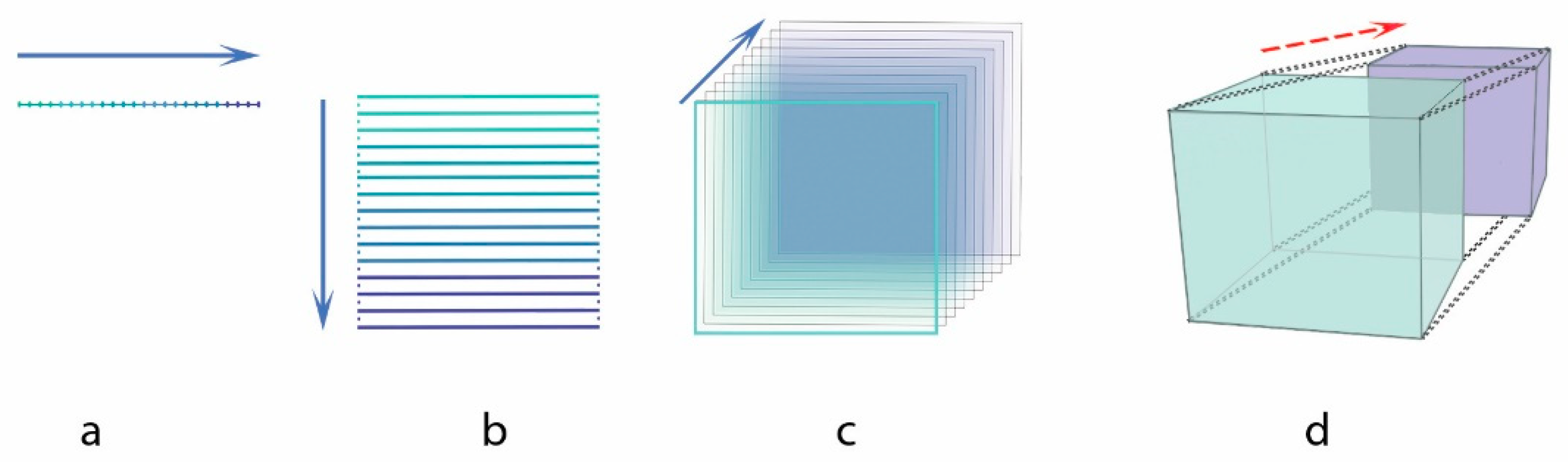
Preprints 95723 g001
Figure 1. (a–d) Generating a hypercube. (© 2020 Traperas, Gounaropoulos and Kanellopoulos).
Figure 1. (a–d) Generating a hypercube. (© 2020 Traperas, Gounaropoulos and Kanellopoulos).
Preprints 95723 g001
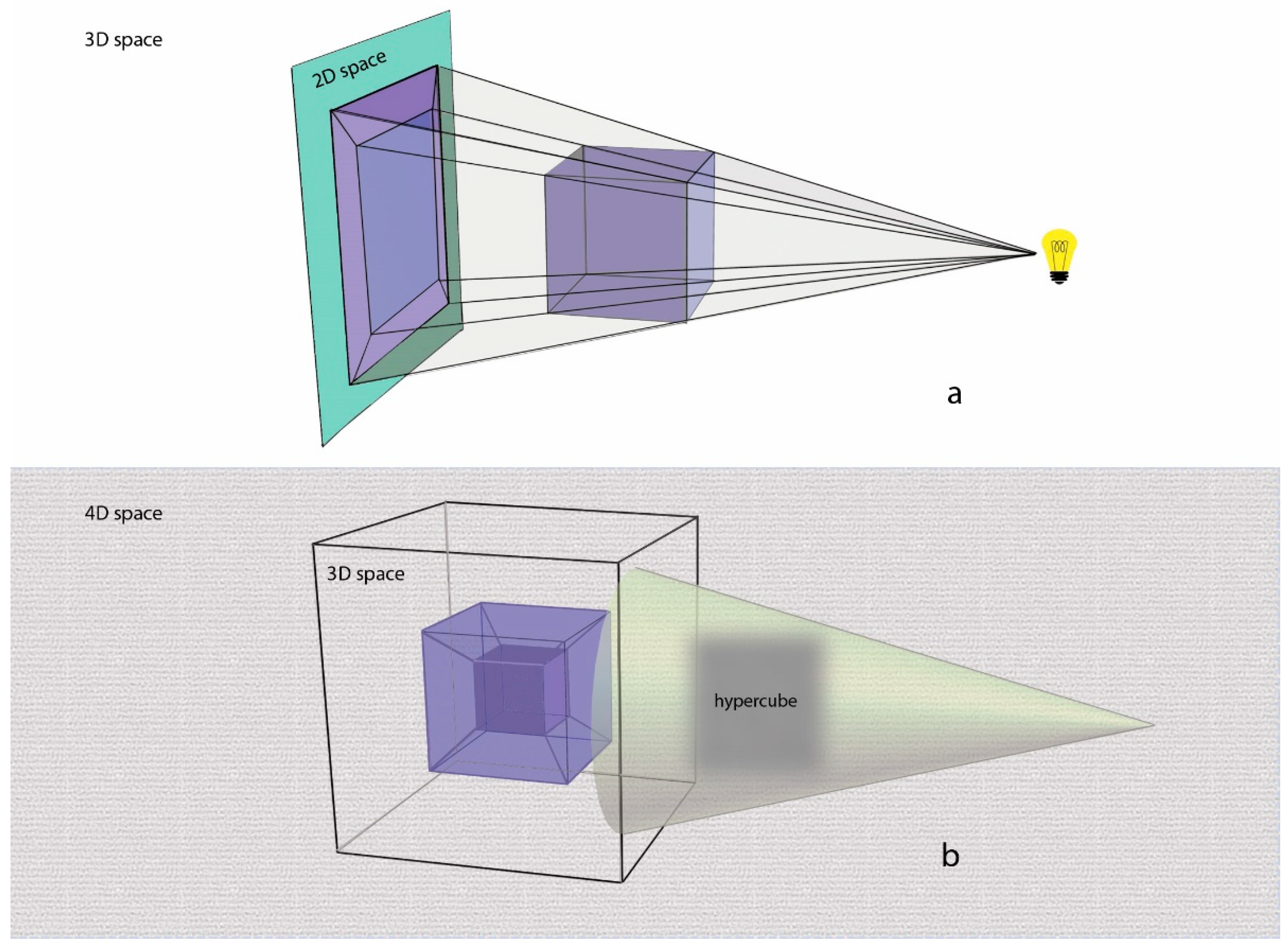
Preprints 95723 g002
Figure 2. (a) 2D projection - shadow of a 3D cube onto 2D space, (b) 3D projection - ‘shadow’ of a hypercube onto 3D space. (2022. © Traperas, Gounaropoulos and Kanellopoulos).
Figure 2. (a) 2D projection - shadow of a 3D cube onto 2D space, (b) 3D projection - ‘shadow’ of a hypercube onto 3D space. (2022. © Traperas, Gounaropoulos and Kanellopoulos).
Preprints 95723 g002
Preprints 95723 g003
Figure 3. Propagation of sound waves in 3D (left) and 4D (right) space (© 2023 Traperas, Floros and Kanellopoulos).
Figure 3. Propagation of sound waves in 3D (left) and 4D (right) space (© 2023 Traperas, Floros and Kanellopoulos).
Preprints 95723 g003
Preprints 95723 g004
Figure 4. Capture of the interactive art application emulating Plato’s ‘Cave’. (© 2023 Traperas, Floros and Kanellopoulos).
Figure 4. Capture of the interactive art application emulating Plato’s ‘Cave’. (© 2023 Traperas, Floros and Kanellopoulos).
Preprints 95723 g004
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated