Prerpints.org logo
Preprint
Article

Seismic Resilience of Emergency Departments: A Case Study

Altmetrics

Downloads

107

Views

37

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

05 January 2024

Posted:

08 January 2024

You are already at the latest version

Alerts
Abstract
In this work the seismic resilience of the Emergency Department of a real Hospital complex, located in Tuscany (Italy), has been quantified, with special reference to its nonstructural components and organizational features. Special attention has been paid to the ceilings, whose importance stood out in past earthquakes. A comprehensive meta-model has been set, able to relate all the considered parameters to the assumed response quantity, i.e. the waiting time of the red-code patients arriving to the Emergency Department in the hours immediately after the seismic event. The seismic resilience of the Emergency Department has been measured with reference to earthquakes compatible to the seismic hazard of the area.
Keywords: 
Subject: Engineering  -   Civil Engineering

1. Introduction

The analysis of the communities’ resilience has been widely investigated in the last years [1-6]. The resilience, indeed, despite including the contents proper of the risk mitigation analysis, extends its investigation to the capacity of a system to recover its properties and its functionality after the occurring of a catastrophic event. The resilience analysis, therefore, represents a comprehensive approach to measure the reliability of a system with reference to different possible risks and to recover its functionality.
The healthcare facilities are typical systems to represent through a resilience analysis, for their strategic role in the communities’ functionality, especially in case of emergency. Their capacity to recover a satisfactory functionality after a catastrophic event depends of many factors, such as the interruption of utility systems (e.g. power and communication), damaged facilities (e.g. collapse of ambulance bay), fluctuating staff, and even the patients’ perception regarding the building safety. A resilience analysis of a care facility, therefore, must include many different problems [7], which can involve the organizational asset of the health system at the regional scale [8-12].
Most part of analysis, however, are focused on specific aspects. The most part of contributions is limited to the structure [13-14], including eventually the nonstructural components [15-21]. Also the “human” issues, in turn, have been object of specific studies. In particular, the Institute of Medicine [22], such as the office of Assistant Secretary for Preparedness and Response [23], found out some of the vulnerability-keys which can affect the Hospital functionality, also in case of emergency. A social network analysis focused on the coordination between the Emergency Departments of different hospitals was used by Hossain & Kit [24] to examine the effect of group interaction on patients’ treatment. Fawcett & Oliveira [25] studied the impact of the emergency organization on the patients’ response.
The most recent contributions combine information coming from different areas [26-31], involving reliability analysis [32-35], Leontief model input-output analysis [36-37], network flow modelling [38], and dynamic simulations [39]. The Hugo framework [15], includes strategies and guidelines for mitigating the impact of disasters. It has achieved interesting results involving structural, nonstructural and administrative vulnerability of hospitals by using the health facility vulnerability evaluation (HVE). Yavari et al. [40] proposed a metric for assessing post-disaster functionality on the base of four major interacting systems of hospitals: structural, non-structural, lifelines and personnel. Due to the lack of available data, however, the Authors did not include the personnel system in their case study.
The analysis proposed by Miniati & Iasio [18] accounts for damage to structural and non-structural systems, as well as organizational factors (i.e. staffing levels, emergency plans, redundancies in equipment, etc.); the interdependencies among the involved subsystems, however, are based on experts’ opinions, and not validated by real earthquakes yet. McCabe et al. [41] describe the “ready, willing and able” framework, which however does not take into account physical damage. The first integration of “organizational resources” was introduced at the Multidisciplinary Centre for Earthquake Engineering Research [8].
The first “quantitative” evaluation of the hospitals’ functionality was proposed by Cimellaro et al. [42], who described the quality of service (QS) as the sum of all the partial functionalities within the facility. The functionality is described as a function of the waiting time of patients, on the basis of the outcome of the patients’ treatments. This approach has been further developed in 2010 [3], with the development of a performed-based meta-model, including both physical and organizational aspects. The correlation between these two “fields” is obtained by introducing proper “penalty factors” (Fs), defined after the conditional probabilities to have certain levels of damage. The total penalty factor affecting the organizational parameters results from a linear combination of the individual PFs, whose weight depends on the ratio between the cost of each component and the overall cost of the building.
Another approach to relate empirical data and functionality loss was suggested by Jacques et al. [28], which proposes a fault tree analysis based on three main contributing factors: staff, structure and stuff and three different kinds of event (top, basic and intermediate ones). Each branch is associated with a sub-system, representing a part of the total loss. The branches associated with staff include the availability of medical staff, support staff, and backup plans for staffing during an emergency. The branches associated with structure account for damage to all physical spaces and support infrastructures associated with critical hospital services (such as power, water, inpatients wards, means of egress, etc.). Finally, the branches associated with stuff account for loss of supplies and damage to equipment.
The recovery process is oversimplified by using recovery functions that can fit the more accurate results obtained with the model by Miles & Chang [43]. The result is a complicated multidimensional performance limit state function (MPLT) that aims at providing a quantitative definition of resilience in a rational way on the base of an analytical function that may fit both technical and organizational aspects.
This study is based on the resilience definition proposed by the most challenging issues of this research, where the functionality of the system is represented through one response parameter only, which must be time-variable, and representative of the quality of the whole system. The representative response quantity should be related to all the factors affecting the system. Therefore, the first step to face a resilience analysis of a complex system is defining all its parts, and relating their functionality to the one of the whole system. It is possible that each sub-system requires a different response quantity; in these cases, a common property to measure must be found or, at least, a correlation among all the response quantities must be defined, in order to control the system functionality through one parameter only.
In this framework, this work proposes the resilience analysis of the Emergence Department of the Sansepolcro Hospital (EDSH). The approach proposed by Bruneau et al. [8], has been selected, which describes the resilience as the ability of the system to reduce the chances of a shock, to absorb a shock if it occurs (like the abrupt reduction of a performance) and to recover quickly after a shock (to re-establish its normal performance). Special attention has been paid to some nonstructural components, such as the ceilings and the cabinets, and to the organizational properties of EDSH. A former work made by the Authors [44] provides a description of the main systems introduced for the EDSH representation, together with the tools adopted for their quantification. In this paper, instead, the resilience of the EDSH has been quantified with reference to various seismic scenarios compatible to the site hazard. In Section 2 the case study is presented, and the adopted meta-model is described, together with a brief resume of the adopted EDSH descriptors and response quantities. In Section 3 the considered seismic scenarios have been presented, and the effects of a possible earthquake have been assessed for both the physical systems (structure and nonstructural components) and the organizational one. consequent. Finally, Section 4 presents the metric assumed for the resilience assessment, and shows the results obtained in the current analysis. The functionality of the EDSH at the occurring of a catastrophic – seismic – event has been checked by performing a Monte Carlo numerical simulation, and the recovery of the functionality has been related to the assumed response parameter, i.e. the Waiting Time (WT).

2. EDSH Functionality and Proposed Metamodel

2.1. Case-Study: Emergency Department of the Sansepolcro Hospital (EMDH)

The Sansepolcro Hospital, shown in Figure 1, is placed in the area of Arezzo, in Tuscany (Italy), and it has been constructed between 1962 and 1979, i.e. before the introduction of the modern Technical Codes, even if various restorations have been made successively. It is made of 18 independent structural units, whose connections consist of structural joints with a thickness of about 10 cm.
Most part of the units, such as the one hosting the Emergency Department of the Sansepolcro Hospital (EDSH), are made of reinforced concrete. The building hosting the EDSH consists of a 2-storeys RC framed structure. Further details are available in [44].

2.2. The EMDH Functioning and the Assumed Response Parameter

The annual volume of work of the EDSH is about 13.000 patients. The rescue service is provided to the patients on the basis of the “triage” practice, which combines the arrival time to the severity of their needs. At the arrival to the EDSH, patients receive a “color code”, indicating their urgency level, and they must follow a specific protocol accordingly.
The most severe cases, called “Major Codes”, can be red (emergencies) and yellow (urgencies), whilst the “Minor Codes” consist of green (deferrable urgency), and white (no-urgency). Tuscany adopted a further code, the blue one, whose priority level is between the green and the white.
Depending on their code classification, the patients receive specific care procedures, which involve different rooms and medical personnel (see Figure 2) The rooms involved in the care rescue are:
-
Reception (REC), where the patients arrive;
-
Waiting Room (WR), where patients classified as “Minor Codes” wait for the assistance.
-
Minor Codes Ambulatory (ACM) where patients classified as “Minor Codes” the patients are visited.
-
Short Intensive Observation (OBI), where the patients are left to check their response to the treatment.
-
Emergency Room (ER), where patients classified as “Major Codes” receive the first rescue.
-
Recovery, patients classified as “Major Codes” are recovered.
In this study the EMDH functionality is measured in terms of waiting time (WT), defined as the time spent by the patients into the emergency department, before receiving the first medical treatment, i.e. not including the time spent for the triage.
Indeed, WT represents one of the most comprehensive factors describing the functionality of Emergency Departments, since it results to be suitable in both normal and emergency conditions [45]. In normal condition, it allows to measure the patients’ satisfaction [46,47] including those housed in the hospital [48]. Even at the occurring of emergencies, WT is a consistent parameter [3], since the Emergency service is directly correlated to the number of treated outpatients. This work is focused on the WT of the yellow-codes patients, i.e. the time from their arrival to the EDSH and the beginning of their treatment.

2.3. Systems Affecting the EMDH Functioning

2.3.1. The Structure

The plan of the EMDH, shown in Figure 3, has a rectangular shape with a small jetty in the longitudinal side. The structure is very irregular, since the columns at the ground level have different spacing and features form the ones at the first storey. The big columns at the ground level have been represented through equivalent rectangular sections, whose measures can be found in Figure 3, together with those of the other squared columns.
Even the beams are different at the two levels: those of the ground level have a variable height, whilst those at the first storey have an ordinary rectangular section. At the ground level, the deeper longitudinal beams have a base of 40 cm and a variable height ranging between 60 cm and 130 cm, whilst the other beams have a base of 35 cm and a height of 60 cm. The longitudinal beams at the first level have a rectangular 30cm x 60 cm sections. All the beams along the transverse direction have the same height of the slab floor, equal to 20 cm. The transverse reinforcement for the beam and column members varies in size from 6 mm to 10 mm, with a spacing of 20 cm. Concrete cover to longitudinal bars is 40 mm for the columns and 30 mm for the beams [49]. The structure features a hollow-brick slab on the first floor and roof level. The slabs were constructed in situ with the beam elements.
The concrete has a mean strength equal to 35.7 MPa. Concrete compressive stress has been determined through both destructive (crushing cylindrical core samples) and non-destructive (ultra-sonic) tests. Steel yield stress has been assumed equal to 412 MPa, on the basis of tensile tests made on bar samples. Testing procedures have been done according to the Italian standard [50]. Further information can be found in Przelazloski (2014) [49].

2.3.2. The Nonstructural Components

Health systems incudes a large number of nonstructural components, both architectural, such as partitions and ceilings, and related to utility systems, such as technological equipment. Furthermore, even the building content, such as cabinet and furniture, should be considered for assessing their functionality. In Figure 4 the main nonstructural components of the EMDH are shown. In this study, only the suspended ceilings and the cabinet are taken into account.
Suspended ceilings. Suspended ceilings typically consist of a grid system (see Figure 5), hanger or bracing wires, perimeter supports and lay-in tiles. In this case the grid system consists of hot-dipped galvanized inverted T-sections that form square or rectangular shaped frames for supporting the tiles.
They are divided in two main categories: main tees (MT) and cross tees (CT). Main tees come in higher capacity and bigger length, while cross tees provide the transverse restraint for the main tees. Figure 6 shows the measures of the rooms constituting the EMDH, together with the direction of suspended ceiling elements.
Cabinets. The cabinets have been included in the analysis since, at the occurring of earthquakes, their overturning can obstruct the rooms of the EMDH, preventing their access.

2.3.3. The Organizational System

The assessment of the WT requires to consider the number of steps involved by the rescue process, and the time needed for executing each of them. Furthermore, the total time required to complete the process is affected by the transfer through the various involved rooms. Therefore, even the mutual distances between each of the room plays a role in the assessment of WT, as much as the availability of the required personnel. All this information has been found through a 100-days observation made by the Hospital staff [51]. Table 1 shows the main information regarding the staying time of the patients in the various rooms and the mutual distances between the involved rooms. In the same table, the percentage of patients belonging to each color code during the observation period has been shown. Further information, such as the personnel involved in each step and its respective working time can be found in Pianigiani and Viti [44].
Figure 7 shows the patients’ arrival in the 100 days-time of observation, and the average arrival within a single day. As can be noticed, the rate of arrival is not regular, achieving its maximum intensity between 8:00 am and 1:00 pm and strongly reducing in the night time.

2.4. The Metamodel

2.4.1. Assessment of the WT in Standard Conditions

The numerical analysis has been performed by the software Promodel [52], which simulates the EDSH functioning on the basis of its effective plan. All the collected information regarding the patients’ arrival and treatment and the personnel working has been used to set the metamodel. The medical staff (nurses and doctors) is considered to be fully operational even at night, whilst the help operators are operative in the day-time only (8 hours). The Brief Intensive Observation (OBI) rooms is assumed to contain a maximum of 5 beds, whilst the Emergency room can accommodate one bed for the red-codes and two for the yellow-codes and the Waiting Room is considered to have an unlimited capability.
In the simulation, if two or more patients attempt to enter the same unit, a FIFO (First In - First Out) rule is used. In case a unit is full, patients who need to be treated in that unit experience a waiting time. The transportation time is reproduced on the basis of the assumed walking speed and mutual distances of the rooms. The simulation has been performed through a Monte Carlo approach, by considering 100 different cases for each set of data.
Thanks to the data provided by the 100-days observation, the results provided by the Monte Carlo analysis could be compared to the “experimental” ones, i.e. the effective average WT experienced by the patients. Figure 8 shows the results provided by the metamodel validation. Further detail on the analysis can be found in Pianigiani and Viti [44].

2.4.2. Assessment of the WT in Emergency Conditions

The emergency scenarios have been introduced as a function of the site hazard. At the occurring of an earthquake, most data change, both in the physical system and in organizational one. The physical systems (structure and nonstructural components) can – partially or completely – become condemned, preventing the use of some of the rooms and consequently increasing the WT. The gravity of the damages has been assumed on the basis of the fragility curve found for the structure and the structural components, respectively. In order to assess the serviceability of the EDSH, a comprehensive fragility curve has been found, as the envelope of the ones referred to structural and nonstructural components (see Figure 9). When the expected seismic intensity is known, the probability of failure can be easily estimated through the enveloped fragility curve, and used to assess the percentage of rooms to assume as out-of-service.
Figure 9 illustrates two different damage scenarios: a low-intensity seismic event, which intersects the comprehensive fragility curve for a probability of failure around 17%, and a higher intensity event, corresponding to a probability failure of 50%. Assuming a total number of rooms used for the rescue equal to 6, in the first the number of rooms considered as out-of-service is equal to 1, whilst in the second case is equal to 3.
It should be underlined that when the envelope coincides with the nonstructural fragility curve, the loss of serviceability is related to damages occurred to the nonstructural components. In this case, therefore, the room are assumed to be out-of-service only temporary, since the damage can likely be fixed in a short time. Instead, when the envelope coincides with the structural fragility curve, the percentage of failure is related to the structure and the consequent loss of service of the room must be considered as permanent, i.e. longer than the 30-days duration of the analytical simulation.
Even the organizational system would certainly change due to the emergency condition, experiencing an increase of demand, together with a strengthening of some aspects, such as the working schedule and the number of the personnel and the number of rooms dedicated to the rescue.
In the next Section the changes occurring in the system in emergency conditions are presented in detail.

3. The Seismic Response of the EDSH

3.1. Seismic Hazard of the Area

The seismic intensity of the area can be quantified according to the Italian Technical Code [53], which indicates a PGA equal to 0.227g for Return Period (RP) equal to 475 years (rock outcrop). The foundation soil of the EDSH has been object of a careful geological investigation (see [54]), which included a seismic refraction test (SRT), a downhole test (DHT), a multichannel analysis of surface waves (MASW), combined to an extended spatial autocorrelation (ESAC), and various H/V lectures. Figure 10a shows the map of the performed tests within the Hospital area.
The position where the tests have been performed is very important, since the soil has a slope, important excavation activities have been done for the buildings’ constructions. Each test provided an average value of the shear velocity of the uppermost 30 meters (vs,30), shown in Figure 10b. As can be seen, the various tests provided results different from each other. The investigation closest to the EDSH is the MASW/ESAC one, which provided a vs,30 equal 478 m/s. As a result of such investigation, therefore, the soil has been classified as belonging to the B-class, which is the most conservative assumption consistent to the experimental results according to the current Italian Technical Code [53]. The elastic spectrum of the area for the soil-class B is shown in Figure 10c.

3.2. The Seismic Input

In this work the seismic performance of the building has been represented in term of fragility curves. In order to find a fragility curves, an Incremental Dynamic Analysis (IDA) has been performed, considering many different intensities of the seismic input. For this reason, a wide range of seismic intensities have been considered, beyond of the PGA proper of the building site. Namely, PGAs ranging between 0.025g and 0.625g, with steps of 0.025g have been included in the analysis.
This analytical approach requires a special attention to the selection of the ground motions to represent the seismic input. If natural ground motions are adopted, indeed, they must be scaled in order to cover the entire range of considered ground motions; as a consequence, high values of the scale factors must be used. For this reason, in this work two different sets of ground motions have been considered to represent the seismic input, respectively provided by FEMA P695 [55], (set A) and selected among the local records (set B). The first set consists of 22 pairs of ground motions (listed in Table 2), with a total of 44 time histories. At the fundamental period of the structure (T = 0.816 sec), the median spectral acceleration is 0.445g. 24 different scale factors (SF), ranging between 0.112 and 1.404, have been adopted to obtain as many intensities of the ensemble.
The second record set, specifically developed for the site, consists of four subsets of 22 pairs of records each. The time histories in each of the subsets, listed in Table 3, correspond to a different probability of exceedance in 50 years, equal to 22%, 10%, 5%, and 2% respectively.
Each of the considered subsets was matched to the conditional mean spectra of the site at a fundamental period of 1 second, according to their deaggregated data, such as magnitude and distance to the source (see [49,56]). The assumed reference period is larger than the actual fundamental period of the case-study, to account for a fundamental period shift (lengthening) due to the inelastic involvement of the structure.
Details on the performed process for the ground motions setting can be found in [49], Appendix B. To fully cover the range of spectral acceleration for the IDAs, each subset needs to only be slightly scaled up or down. The advantage of this procedure is to reduce the uncertainties associated with the use of large scale factors (SF) on the time histories. Figure 11 shows the median spectra of the two records’ sets.

3.3. Effect of the Earthquake on the Physical Systems

3.3.1. Fragility Curves of the Structure

The functionality of the structure with reference to the seismic hazard can be easily evaluated by comparing its seismic response to the expected site earthquakes to the performance limits provided by the Codes. In this work the structural response of the building has been represented through a 3-D Ruaumouko model, developed in cooperation with the Istituto Universitario di Studi Superiori (IUSS) of Pavia, Italy [49,56]. The inelastic behavior of beams and columns has been described through concentrated plastic hinges at their ends, and neglecting the confinement effects of the transverse reinforcement, which does not comply the current standard, resulting almost ineffective. The effects of the shear mechanism on the joints behavior has been taken into account.
The seismic response of the structure has been checked by performing a preliminary modal analysis, followed by an incremental dynamic analysis for two sets of records of ground motions presented in § 3.2. The limit condition assumed in the IDA is the achievement of the assumed limit deformation of each structural element.
The response quantity selected to represent the seismic response of the structure is the interstorey drift (ID), read as the mean value of the response domain provided by IDA. The response domains have been compared to the limit values provided by FEMA P695 [55], and the cumulative conditional probability of exceeding the limit values has been determined. The obtained fragility curves have been shown in Figure 12.

3.3.2. Fragility Curves of the Nonstructural Components

The functionality of the building at the occurring of a seismic emergency has been checked by means of fragility curves referred to both the structure and the nonstructural components.
Suspended ceiling. Figure 13 shows the fragility curves [56] found for the two most strategic rooms of the EDSH, i.e. the Emergency Room (ER), where severely injured patients are located, and the Short Intensive Observation Room (OBI), which holds the patients needing in-depth examination. In Figure 15 the fragility curves referred to the structure and the considered nonstructural components (ceiling system and cabinet) have been superposed. The “final” fragility curves expressing the physical adequacy of the checked rooms are indicated by the red lines, which represent the most conservative conditions provided by the fragility analysis.
Cabinet. The cabinet non-structural component is considered for the overturning limit, due to the lack of data in other damage limit states, and because the change of position does not cause big problems into the emergency room. Other damage limit states could be considered for example in the pharmacy, where medicine faults can cause greater consequences. Figure 14 illustrates the fragility curve derived by Cosenza et al. [57] which for the present work have been assumed as reliable data.

3.3.3. Damages Scenarios at the Occurring of Seismic Excitation

As a consequence of seismic events, the building can experience eventual damages, occurring to the structure or to the structural components. As explained in Section 2.4, the safety status of the EDSH can be assessed comparing the expected PGA to the fragility curves of both structural and nonstructural components.
In this case-study, the nonstructural components result to be much stronger than the structure of the building. Therefore, the fragility envelope coincides with the structural fragility curves, and the eventual loss of service of the rooms must be considered as permanent. In the analysis, the number of rooms assumed as possibly “out-of-service” has been assumed ranging from 0 to three (half of the total), as shown in Figure 15, since a higher level of structural damage has been assumed to completely invalidate the EDSH functionality.

3.4. Effects of the Earthquake on the Organizational System

The EDSH activity is largely affected by the occurring of emergencies. Namely, at the occurring of an earthquake, the main changes involve the amount and type (color code) of care demand and the EDSH organization (personnel amount, schedule and number of used rooms).

3.4.1. Changes in the Rescue Demand

In case of earthquakes, due to the buildings’ damages, there is an abrupt increase of flow to the Emergency Departments. Such increase, despite being related to the intensity of the ground motion, is largely affected by the community peculiarity, such as the density of the population and the type of infrastructures.
Unfortunately, there are no available data regarding the possible increase in the arrivals to the EDSH in case of earthquake; therefore, the arrival increase has been determined on the basis of the functioning of the Northridge Hospital after the earthquake occurred in Los Angeles (CA) in 1994 [4], whose PGA was equal to 0.8 g. Since the expected ground motion has a much smaller intensity than the Northridge one, the arrival increase has been scaled consequently. In the investigation, two scaling criteria have been considered, basing respectively on the PGA of the two seismic events, and on their Modified Mercalli Intensity (MMI) scale. Finally, a value of 1.13 has been found as scale factor [51], and the arrival rate in the first three days after the occurring of the earthquake has been assumed as shown in Figure 16.
Another important change in the EDSH functioning concerns the type of rescue required by the patients. Even in this case, the available data are limited to two seismic event, both occurred in California, respectively in Northridge (January 1994) and in Loma Prieta (October 1989) [58-63]. Neither of such cases can be considered to be similar to the assumed case-study, so that a further adjustment has been required: the rescue provided in the Northridge Hospital has been classified according to the color-code approach used in the Italian health system (see [51]), in order to set the Metamodel. The percentage of required color codes’ rescue found as a result of such analysis is shown in Figure 17.

3.4.2. Changes in the EDSH Organization

The organization procedures are very sensitive to the occurring emergencies. In Italy, a special protocol has been set, called PEMAF (PEMAF (from the Italian: “Piano di Emergenza Massiccio Afflusso di Feriti”), which implies an immediate change in the personnel working, in the use of the available rooms of the Emergency Departments and in the criteria of providing the rescue.
Namely, a larger amount of personnel is engaged, with a 24-hours working time (see Table 4). Furthermore, some extra rooms, usually used for visits or surgeries, are assigned to the rescue. The entire ER building is used for the Major Codes, which are assumed to arrive only by ambulance, i.e. through the vehicular path. To resume, at the activation of PEMAC, the rescue involves the following areas:
- RED zone, used by Red and Yellow Codes, with 2 doctors, 2 nurses and 1 help operator; it can host 2 patients.
- YELLOW zone, with a number of doctors ranging between 1 and 3, 3 nurses and 2 help operators; it can host four patients.
- GREEN zone, with 2 doctors, 3 nurses and 1 help operators, hosting until 12 patients without alterations of vital parameters.
- OPERATING ROOMS are dedicated to the surgery and can host three patients. The involve personnel do not belong to the Emergency Unit, and therefore are not included in the information provided in Table 4.
Only the red and the yellow zones are located within the Emergency Department, whilst the green zone is placed in the rehabilitation-gymnasium area, in the adjacent building, and the operating rooms are located at the second floor. Therefore, they can be achieved only through the elevator, and the only one available elevator can host one patient only (accompanied by a nurse). In this study, the green zone is not included, since the analysis is focused on the major codes only. The flow chart of the major codes is shown in Figure 18.
Red Codes
Yellow Codes

3.5. The EDSH Functionality at the Occurring of a Seismic Emergency

The analysis of the EDSH functionality in emergency conditions has been performed on a period of 30 days (see Figure 19), by considering the occurring of a seismic emergency after two days of normal service of the hospital, three days of increased patient arrival and the remaining 24 days of a normal rate arrival.
In the analysis, different assumptions, compatible with the described seismic emergency, have been made regarding the increase of the patient arrival rate and the number of out-of-service number. Indeed, the seismic event described in the Section 3.2, has been assumed as the strongest expectable ground motion. The seismic scenario, therefore, is described through an increase (α) of rate of arrival ranging between 1.0 (no increase) and 1.6, and a loss of service of rooms (n) ranging between 0 (normal integrity of the EDSH) and 3 (three rooms out-of-service). For each of the 28 combinations of parameters, a Monte Carlo analysis consisting of 100 different cases have been run.
For sake of simplicity, only the yellow-code patients have been checked in this paper. Indeed, the increase of the waiting time affects the yellow-code patients much more than the red-code ones, since the number of the yellow-code patients is much larger, and the red-code ones can take advantage of the priority in the care.
Figure 20 and Figure 21 show the results of the analysis as a function of n and α, respectively. As can be noticed, the closure of one room does not affect very much the functionality of the system, whilst when the closure involves three rooms, the WT increases of almost 10 times.

4. EDSH Resilience

4.1. Resilience Modeling

In this work, the resilience has been quantified according to the approach provided by Bruneau & Reinhorn [2] who defined it as a non-stationary stochastic process, measured by the size of the expected degradation in functionality (probability of failure) over time (time to recovery), as shown in Figure 22.
The functionality of a system is assumed to vary with time, and it is defined as representative of the quality of an essential system in the community. The performance can change in a range from 0 to 100, where 100% represents no degradation in service and 0% means no service available. If an earthquake strikes at the time t0, the functionality of the system abruptly reduces; the restoration of the system is expected to occur over time, until time t1, when the functionality achieves 100% again.
R = ∫ t 0 t 1 100 − q ( t ) d t
The trend of R within the recovery time, TRE, defined as the range of time between t0 and t1, is not easy to assess, since the recovery process depends on multiple factors, such as: time dimensions, spatial dimensions (e.g. different neighborhoods may have different recovery paths), and interdependencies between different economic sectors involved [3], [43]. In this work, the simplified approach proposed by Cimellaro et al. [3] has been assumed; it leads to choose among three possible recovery functions depending on the system and the social response: (i) a linear equation, (ii) an exponential equation [64], and (iii) a trigonometric equation [65], shown in Figure 23 and described by the following relationships:
linear            f r e c t , T R E = 1 − t − t 0 T R E
exponential       f r e c ( t ) = e x p − ( t − t 0 ) ( l n 200 ) T R E
trigonometric       f r e c t = 0.5 1 + c o s t − t 0 T R E
where t is the time, t0 is the initial time of the extreme event E, and TRE is the recovery time. The simplest form is the linear recovery function that is generally used when there is no available information about the organization of the community. According to Cimellaro et al. [3], the linear model is suitable for average-prepared communities, (when no information is provided regarding preparedness and available sources), the trigonometric model is suitable for not well-prepared communities, whilst the exponential model is suitable for well prepared communities, with a good organization and organized support by surrounding areas.
In this work the linear model is assumed, since there is not any specific information about the preparedness of the Emergency Department to catastrophic events. As stated in the Introduction, the functionality of the system has been measured through the WT of yellow-code patients arriving to the EDSH.
In Figure 24a a generic WT function, representing the increase induced by an emergency, i.e. at the occurring of a ground motion, is shown. The loss of functionality corresponds to the area enveloped by the curve of the WT expressed in the time domain. In order to quantify the resilience of the system, such area needs to be quantified, by assuming an equivalent, simplified, distribution, as the one shown in Figure 24b. With reference to this simplified curve, the loss of functionality consists of the area inscribed under the poly-line B-C-D. It’s worth noting that point C becomes the representative point of the loss of functionality of the system, while point D represents the restoring point, i.e. the time the system reverts to its functionality.
The loss of functionality is determined on the base of the worst case calculated through the simulations, corresponding to the maximum value of WT registered in the analysis. By assuming a case of total loss of functionality it is possible to assess the other resilience curves, following the general equation exemplified below:
𝑓𝑢𝑙𝑙 𝑓𝑢𝑛𝑐𝑡𝑖𝑜𝑛𝑎𝑙𝑖𝑡𝑦 −𝑓𝑢𝑛𝑐𝑡𝑖𝑜𝑛𝑎𝑙𝑖𝑡𝑦 𝑙𝑜𝑠𝑠 (𝑝1=𝑖, 𝑝2=𝑘) = 𝑟𝑒𝑠𝑖𝑑𝑢𝑎𝑙 𝑓𝑢𝑛𝑐𝑡𝑖𝑜𝑛𝑎𝑙𝑖𝑡𝑦 (𝑝1=𝑖, 𝑝2=𝑘)
where 𝑝1 and 𝑝2 respectively represents the condition 1 and the condition 2 which vary during the scenario, and the functionality loss is represented by the maximum waiting time (point C).
100 − 𝑌𝑐𝑜𝑜𝑟𝑑𝑖𝑛𝑎𝑡𝑒𝐶 𝑝𝑜𝑖𝑛𝑡 (𝑝1=𝑖, 𝑝2=𝑘) = 𝑟𝑒𝑠𝑖𝑑𝑢𝑎𝑙 𝑓𝑢𝑛𝑐𝑡𝑖𝑜𝑛𝑎𝑙𝑖𝑡𝑦
In order to assess the Y-coordinate of point C in the resilience curve, it is necessary to equalize the results of the maximum waiting time (by representing point C on the WT-curve and the 0% of functionality in the system) for each simulation, through the following proportion:
𝑀𝑎𝑥𝑊(𝑝1=𝑚𝑎𝑥 , 𝑝2=𝑚𝑎𝑥) : 100 = 𝑀𝑎𝑥𝑊𝑇(𝑝1=𝑖 , 𝑝2=𝑘) : 𝑥
where 𝑝1 = 𝑚𝑎𝑥 and 𝑝2 = 𝑚𝑎𝑥 are the extreme conditions corresponding to the maximum WT. By assuming the maximum loss of functionality of the system and occurring at the maximum waiting time (Equation 8), all the other simulations due to the variation of the parameters involved are scaled on the base of the maximum value of C.
𝑀𝑎𝑥𝑊(𝑝1=𝑚𝑎𝑥 , 𝑝2=𝑚𝑎𝑥) = 𝑀𝑎𝑥𝐿𝑂𝑆𝑆(𝑝1=𝑚𝑎𝑥 , 𝑝2=𝑚𝑎𝑥) = 𝑀𝑖𝑛𝐹𝑈𝑁𝐶𝑇𝐼𝑂𝑁𝐴𝐿𝐼𝑇𝑌(𝑝1=𝑚𝑎𝑥 , 𝑝2=𝑚𝑎𝑥)

4.2. Resilience of the EDSH

The resilience of the EDSH has been assessed on a range of time equal to five times the emergency phase’s duration, assumed – in turn – as three days long. Therefore, the assessment of the EDSH functionality has been checked for 15 days from the earthquake occurrence, even though the system has not been completely restored yet. According to this assumption, the “perfect” resilience (R = 100%) corresponds to no lack of functionality (see Figure 25a), whilst the worst possible scenario (see Figure 25b) corresponds to the total lack of functionality due to the maximum increase of WT assumed in the catastrophic event. In Figure 25 is underlighted the considered “resilience area” (light grey) assumed to scale every eventual loss of functionality.
All the possible cases can be assessed by calibrating these opposite outcomes, on the basis of their damage level, i.e. the WT increase due to the seismic event, through the ratio of the area bounded by the curve.
In this work, the total loss of functionality (100%) is calculated by assuming the equivalence of the waiting time and the functionality curves. Table 5 shows the main coordinates of the WT and the functionality curves. The numerical values refer to none increase of rate (α =1.0) and maximum structural damage (three rooms permanently out of service, i.e. n=3), assuming a seismic shock (PGA= 0.27g) occurring at a t0 = 2 days.
The global behavior of the hospital system is summarized in Figure 26, where four percentages of damaged areas related to the corresponding n parameter are additionally plotted. The derivation of damages equal to 0%, 25%, 50%, 75% and 100% for the areas involved are calculated in order to understand the varying response of the system.
Point D of the resilience curves never changes within the same range (same n value) since the variation of the damaging is applied, without affecting the BD segment of the resilience curve, which is a function of the n parameter. By the contrary, the area of the resilience curve and, consequently, the peaks and the recovery segment (segments BC and CD, respectively), are influenced by the extension of the damaged area. By applying the equations (5-8) all the points needed for the construction of the resilience curve are assessed, for the simplified cases of n variable, 100% of functionality of the rooms available, and α =1.0.
The resilience is calculated within the range of 18 days, which cover the emergency-phase (3 days) plus further 15 days after the shock, i.e. five times the emergency phase length. This area is rudely scaled on the base of a “fully” operational curve, corresponding to resilience equal to 100%, and is associated with no occurred damages.
Figure 27 shows the functionality curves found for the different n-values, together with the corresponding value found for the resilience.

5. Conclusive Remarks

In this work the functionality of the Emergency Department of the Sansepolcro Hospital (EDSH), placed in Tuscan (Italy), has been analyzed with reference to both physical (structural and non-structural) and organizational factors. The assessment has been pursued by performing an analytical simulation through the software PROMODEL, by setting a metamodel, appositely calibrated and validated, where the waiting time (WT) of the patients has been assumed as response parameter.
The resilience of the EDSH has been checked with reference to an earthquake compatible to the seismic hazard of the area, defined according to the current Technical Code NTC 2018.
The response of structure has been checked by performing an Incremental Dynamic Analysis on the basis of two spectrum-compatible sets of ground motions. The comparison between the structural response and the Code requirements lead to determine the fragility curves of the structure. Two nonstructural components, i.e. ceilings and cabinets, have been considered in the analysis; their seismic response has been described through fragility curves, which have been found on the basis of experimental data. The organization of the Department at the occurring of the emergency has been described on the basis of the emergency protocol prepared by the Italian Civil Protection for the Hospitals. Furthermore, the increase of the care demand due to the earthquake has been considered in the simulation.
A Monte Carlo analysis has been performed to assess the variation in WT due to the assumed emergency, and the recovery time needed to restore the “normal” functioning of the EDSH. The analysis lead to determine the resilience curves of the EDSH related to the various assumptions.
The work provided relevant information on the functioning of the case-study, pointing out its strong points and its potential weaknesses, and achieving a realistic assessment of its resilience. Furthermore, the analysis highlighted some lack of data, which would be important to manage the EDSH functionality at the occurring of emergencies.

Author Contributions

Conceptualization, M.P., S.V.; methodology, M.P., S.V.; software, M.P.; validation, M.P., S.V.; formal analysis, M.P. S.V.; investigation, M.P.; data curation, M.P., M.T.; writing—original draft preparation, S.V.; writing—review and editing, S.V.; visualization, M.P., S.V.; supervision, M.P, M.T, S.V.

Funding

This research received no external funding.

Data Availability Statement

The data obtained through the survey will be provided on request from the corresponding author when compatible with the data policy of Institutions.

Acknowledgments

The authors thank AUSL 8 (Azienda Sanitaria Locale di Arezzo) for providing the data used in the analysis, and the Department of Architecture of the University of Florence for the support.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Bruneau M & Reinhorn AM, 2006. Overview of the Resilience Concept. Proceedings of the 8th US National Conference on Earthquake Engineering, (2040).
  2. Bruneau M. & Reinhorn AM, 2007. Exploring the Concept of Seismic Resilience for Acute Care Facilities. Earthquake Spectra, 23(1), pp.41–62. Available online: http://earthquakespectra.org/doi/abs/10.1193/1.2431396 (accessed on 1 July 2014).
  3. Cimellaro GP, Reinhorn AM & Bruneau M, 2010. Framework for analytical quantification of disaster resilience. Engineering Structures, 32, pp.3639–3649. [CrossRef]
  4. Cimellaro GP, Reinhorn AM & Bruneau M, 2011. Performed-based metamodel for healthcare facilities. Earthquake Engineering & Structural Dynamics, 40(December 2010), pp.1197–1217. Available at: http://onlinelibrary.wiley.com/doi/10.1002/eqe.2230/full. December.
  5. Liu J, Zhai C, Yu P (2022). A probabilistic framework to evaluate seismic resilience of hospital buildings using baysian networks. Reliability Engineering and System Safety 226, 1086444.
  6. Chang S & Shinozuka M, 2004. Measuring improvements in the disaster resilience of communities. Earthquake Spectra, 20(3), pp.739–755. [CrossRef]
  7. Ardagh MW, Richardson SK, Robinson V, Than M, Gee P, Henderson S, Khodaverdi L, McKie J, Robertson G, Schroeder PP, Deely JM, 2012. The initial health-system response to the earthquake in Christchurch, New Zealand, in February 2011. The Lancet, 379, pp.2109–2115. 20 February. [CrossRef]
  8. Bruneau M, Chang, Eguchi RT, Lee GC, O’Rourke TD, Reinhorn AM, Masanobu Shinozuka M, Tierney K, Wallace WA, Winterfeldt D, 2003. A Framework to Quantitatively Assess and Enhance the Seismic Resilience of Communities. Earthquake Spectra, 19(4), pp.733–752.
  9. Ceferino L, Mitrani-Reiser J, Kiremidjian A, Deierlein G & Bambarén C, 2020. Effective plans for hospital system response to earthquake emergencies. Nature Communications volume 11, Article number: 4325 (2020). [CrossRef]
  10. Tariverdi M, Miller-Hooks E, Kirsch T, 2018. Strategies for improved hospital response to mass casualty incidents, Disaster Med. Public Health Prep. 12 (6) (2018) 778–790. [CrossRef]
  11. Cimellaro GP, Piquet M, 2016. Resilience of a hospital emergency department under seismic event, Advances in Structural Engineering 19 (5) (2016) 825–836.
  12. Hassan EM, Mahmoud H, 2020. An integrated socio-technical approach for postearthquake recovery of interdependent healthcare system, Reliab. Eng. Syst. Saf. 201 (2020) 106953. [CrossRef]
  13. Viti S, Cimellaro GP & Reinhorn AM, 2006. Retrofit of hospital through strength reduction and enhanced damping. Smart Structures and Systems, 2(4), pp.339–335. [CrossRef]
  14. Nuti C & Vanzi I, 1998. Assessment of post-earthquake availability of hospital system and upgrading strategies. Earthquake Engineering & Structural Dynamics, 27(12), pp.1403– 423.
  15. WHO, 2006. Health facility seismic Health facility seismic vulnerability evaluation. World Health.
  16. Badillo-Almarez H, Reinhorn AM & Whittaker A, 2007. Seismic Fragility of Suspended Ceiling Systems. Earthquake Spectra, 23. [CrossRef]
  17. Myrtle RC, Masri SF, Nigbor RL, Caffrey JP, 2005. Classification and prioritization of essential systems in hospitals under extreme events. Earthquake Spectra, 21, pp.779–802. [CrossRef]
  18. Miniati R & Iasio C, 2012. Methodology for rapid seismic risk assessment of health structures: Case study of the hospital system in Florence, Italy. International Journal of Disaster Risk Reduction, 2, pp.16–24. [CrossRef]
  19. Masi A, Santarsiero G & Chiauzzi L, 2012. Vulnerability Assessment and Seismic Risk Reduction Strategies of Hospitals in Basilicata Region (Italy). In Proceedings of the 15th World Conference on Earthquake Engineering - WCEE, pp.1–10.
  20. Uma SR & Beattie GJ, 2010. Seismic Assessment of Engineering Systems in Hospitals – A Challenge for Operational Continuity. In New Zealand Society for Earthquake Engineering Annual Meeting.
  21. Davenport PN, 2004. Review of seismic provisions of historic New Zealand loading codes. In New Zealand Society for Earthquake Engineering Annual Meeting.
  22. IoM, 2006. 2Hospital-Based Emergency Care: At the Breaking Point, IPDED, I.P.D. and E.D., 2010. Project retrofitting Studies.
  23. ASPR, 2013. Hospital Preparedness Program. Available at: available at http://www.phe.gov/preparedness/plann.
  24. Hossain L & Kit DC, 2012. Modeling coordination in hospital emergency departments through social network analysis. Disasters, 36(2), pp. 338–364.
  25. Fawcett W & Oliveira CS, 2000. Casualty treatment after earthquake disasters: Development of a regional simulation model. Disasters, 24(3), pp.271–287. [CrossRef]
  26. Porter K & Ramer K, 2012. Estimating earthquake-induced failure probability and downtime of critical facilities. Journal of Business Continuity and Emergency Planning, 5, pp.352– 364.
  27. Unanwa CO, McDonald JR, Mehta KC, Smith DA, 2000. The development of wind damage bands for buildings. Journal of Wind Engineering and Industrial Aerodynamics, 84, pp.119–149.
  28. Jacques CC, McIntosh J, Giovinazzi S, Kirsch TD, Wilson T, Mitrani-Reiser J, 2014. Resilience of the Canterbury Hospital System to the 2011 Christchurch Earthquake. Earthquake Spectra, 30(1), pp.533–554. [CrossRef]
  29. Alowad A, Samaranayake P, Ahshan KB, Karim A, 2020. Enhancing patient flow in emergency department (ED) using lean strategies–an integrated voice of customer and voice of process perspective, Business Process Management Journal. [CrossRef]
  30. Sabir SM, Mustafa FA (2023). Performance-based building design: Impact of emergency department layout on its functional performance efficiency – the case of Erbil hospitals. Open House International.
  31. Ali AA, Azharul KA, Hisham AH, Kazi AK, Premaratne S (2020). Enhancing patient flow in emergency department (ED) using lean strategies–an integrated voice of customer and voice of process perspective. Business Process Management Journal.
  32. Setola R, 2007. Availability of healthcare services in a networkbased scenario. International Journal Networking Visual Organization, 4(2). [CrossRef]
  33. Kuwata Y & Takada S, 2007. Seismic risk assessment of lifeline considering hospital functions. Asian Journal of Civil Engineering, 21(3), pp.315–28.
  34. Yao G, 2000. Identification of earthquake damaged operational and functional components in hospital buildings. Journal of the Chinese Institute of Engineers, 23(4). [CrossRef]
  35. Lupoi G, Franchin P, Lupoi A, Pinto PE & Calvi GM, 2008. Probabilistic seismic assessment for hospitals and complex-social systems IUSS Press., Pavia.
  36. Leontief WW, 1986. Input-Output Economics, 2nd ed. Oxford University Press.
  37. Haimes YY, Horovitz BM, Lambert JH, Santos JR, Lian C, Crowther KG, 2005. Inoperability input–output model for interdependent infrastructures sectors. I: Theory and methodology. Journal of Infrastructure System, 11(2), pp.67–79.
  38. Lee EE, Mitchell JE, and Wallace WA, 2003. Restoration of services in interdependent infrastructure systems: a network flows approach, Troy, N.Y. [CrossRef]
  39. Arboleda CA, Abraham DM & Lubitz RM, 2007. Simulation as a tool to assess the vulnerability of the operation of a health care facility. Journal of Performance of Construction Facility, 21(4), pp.302–312. [CrossRef]
  40. Yavari S, Chang SE & Elwood KJ, 2010. Modeling post-earthquake functionality of regional health care facilities. Earthquake Spectra, 26, pp.869–892. [CrossRef]
  41. McCabe OL, Barnett DJ, Taylor HG, Links JM, 2010. Ready, willing, and able: A framework for improving the public health emergency preparedness system. Disaster medicine and public health preparedness,4, pp.161–168. [CrossRef]
  42. Cimellaro GP, Fumo C, Reinhorn AM and Bruneau M, 2008. Seismic resilience of health care facilities. 14th World Conference on Earthquake Engineering (14WCEE), Beijing, China, 12-17 October, 2008.
  43. Miles SB & Chang SE, 2006. Modeling community recovery from earthquakes. Earthquake Spectra, 22(2), pp.439–458. [CrossRef]
  44. Pianigiani M & Viti S, (2021). Functionality analysis of emergency departments: A case study. JOURNAL OF BUILDING ENGINEERING, vol. 40, pp. 1-13, ISSN:2352-7102.
  45. McCarthy K, McGee HM & O’Boyle CA, 2000. Outpatient clinic waiting times and nonattendance as indicators of quality. Psychology, Health and Medicine, 5, p.287. [CrossRef]
  46. Thompson DA & Yarnold PR, 1995. Relating patient satisfaction to waiting time perceptions and expectations: the disconfirmation paradigm. Academic emergency medicine: official journal of the Society for Academic Emergency Medicine, 2(12), pp.1057–1062. [CrossRef]
  47. Thompson DA Paul R Yarnold PR, Williams DR, Adams SL, 1996. Effects of actual waiting time, perceived waiting time, information delivery, and expressive quality on patient satisfaction in the emergency department. Annals of Emergency Medicine, 28(6), p.657. [CrossRef]
  48. Richards ME, Crandall CS & Hubble MW, 2006. Influence of ambulance arrival on emergency department time to be seen. Prehospital Emergency Care, 12(1-7), pp.440–446. [CrossRef]
  49. Przelazloski K, 2014. Collapse Fragility Analysis on Sansepolcro Hospital Structure. Master Degree Dissertation, Università degli Studi di Pavia.
  50. NTC 2008. Norme tecniche per le costruzioni. Decreto Ministeriale 14 gennaio 2008, Ministero Infrastrutture e Trasporti G.U.R.I. 4 Febbraio 2008, Roma, Italy (in Italian).
  51. Pianigiani M, 2016. Seismic Resilience of Hospital Systems. PhD Dissertation, Università degliu Studi di Firenze.
  52. Price RN, 1999. ProModel Manufacturing Simulation Software: Reference Guide, Version 4.2, ProModel Corporation, Orem, UT.
  53. NTC 2018. Aggiornamento delle Norme Tecniche per le Costruzioni; Decreto Ministeriale 17 gennaio 2018, Ministero delle Infrastrutture e dei Trasporti, G.U.R.I. n. 42 del 20 febbraio 2018. Roma, Italy (In Italian).
  54. Viti S, Tanganelli M, D’Intinosante V & Baglione M (2017): Effects of Soil Characterization on the Seismic Input, Journal of Earthquake Engineering. [CrossRef]
  55. FEMA, 2009, Quantification of Building Seismic Performance Factors, FEMA P-695, prepared by Applied Technology Council for the Federal Emergency Management Agency, Washington, D.C.
  56. Pianigiani M, Przelazloski K, Christovasilis IP, Cimellaro GP, De Stefani M, Filiatrault A, Sullivan TJ, Tanganelli M, 2014. A comprehensive methodology for evaluating the seismic resilience of health care facilities considering nonstructural components and organizational models. In Second European Conference on Earthquake andn seismology. Istanbul, Turkey, pp. 1–4.
  57. Cosenza E, Di Sarno L, Maddaloni G, Maddaloni, Magliulo G, Petrone C, Prota A, 2014. Shake table tests for the seismic fragility evaluation of hospital rooms. Earthquake Engineering & Structural Dynamics. Available at: http://onlinelibrary.wiley.com/doi/10.1002/eqe.2230/full.
  58. Aroni S & Durkin M, 1987. Injuries and occupant behavior in earthquakes. Samuel Aroni and Romulus Constantinescu. Washington D.C.
  59. Cheu DH, 1994. Northridge earthquake, January 17, 1994: the hospital response. 17 January.
  60. Durkin ME, 1995. Fatalities, non-fatal injuries and medical aspects of a Northridge earthquake. EEFIT, 2009. The L’Aquila, Italy, Earthquake of 6 April 2009. pp.1–54. 6 April.
  61. Mahue M, 1996. Methodologies for Comparing Injury Data: Impact of Northridge Injuries on Emergency Department in Los Angeles County.
  62. Olson RA & Alexander DE, 1996. Summary of Proceedings. In Jesuit Retreat House, Los Altos, California. Second National Workshop on Modelling Earthquake Casualties for Planning and Response.
  63. Salinas C, Salinas C. & Kurata J, 1998. The effects of Northridge Earthquake on the Pattern of Emergency Department Care. American Journal of Emergency Medicine, 16(3), pp.254–256.
  64. Kafali C & Grigoriu M, 2005. Rehabilitation decision analysis. In: ICOSSAR’05. In Proceedings of the 9th international conference on structural safety and reliability.
  65. Chang S, Svekla WD & Shinouza M, 2002. Linking infrastructure and urban economy – Simulation of water disruption impacts in Earthquakes. Environment and Planning B: Planning and Design, 29(2), pp.281–301.
Preprints 95573 g001
Figure 1. Sansepolcro Hospital. b. Air view (from https://www.ttv.it/) b. Structural units in the 3D model.
Figure 1. Sansepolcro Hospital. b. Air view (from https://www.ttv.it/) b. Structural units in the 3D model.
Preprints 95573 g001
Preprints 95573 g002
Figure 2. Flow chart of major and minor codes.
Figure 2. Flow chart of major and minor codes.
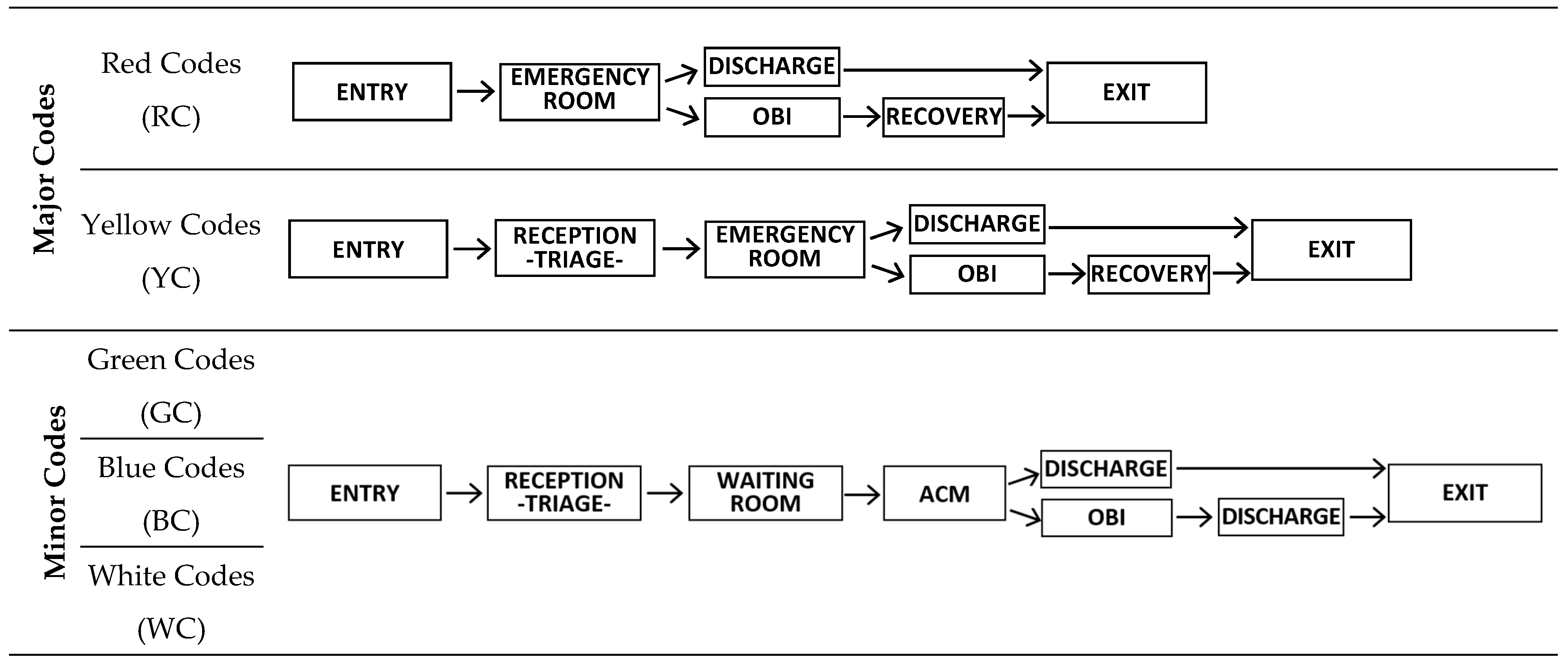
Preprints 95573 g002
Preprints 95573 g003
Figure 3. Plans and vertical sections of the structure.
Figure 3. Plans and vertical sections of the structure.
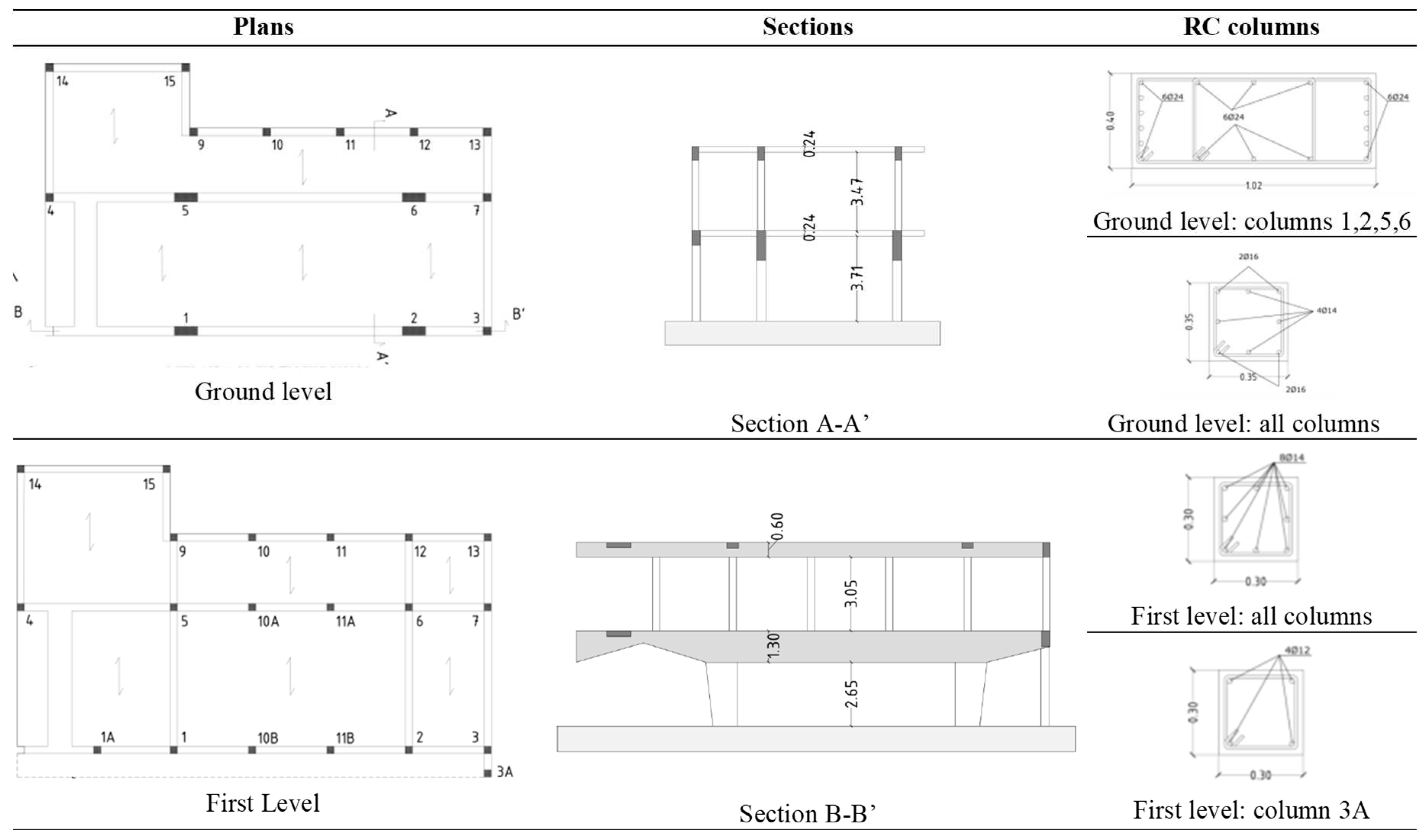
Preprints 95573 g003
Preprints 95573 g004
Figure 4. Nonstructural components within the EMDH.
Figure 4. Nonstructural components within the EMDH.
Preprints 95573 g004
Preprints 95573 g005
Figure 5. Scheme of the suspended ceiling in the EMDH.
Figure 5. Scheme of the suspended ceiling in the EMDH.
Preprints 95573 g005
Preprints 95573 g006
Figure 6. Dimensions of the rooms constituting the EMDH and direction of the suspended ceiling tees.
Figure 6. Dimensions of the rooms constituting the EMDH and direction of the suspended ceiling tees.
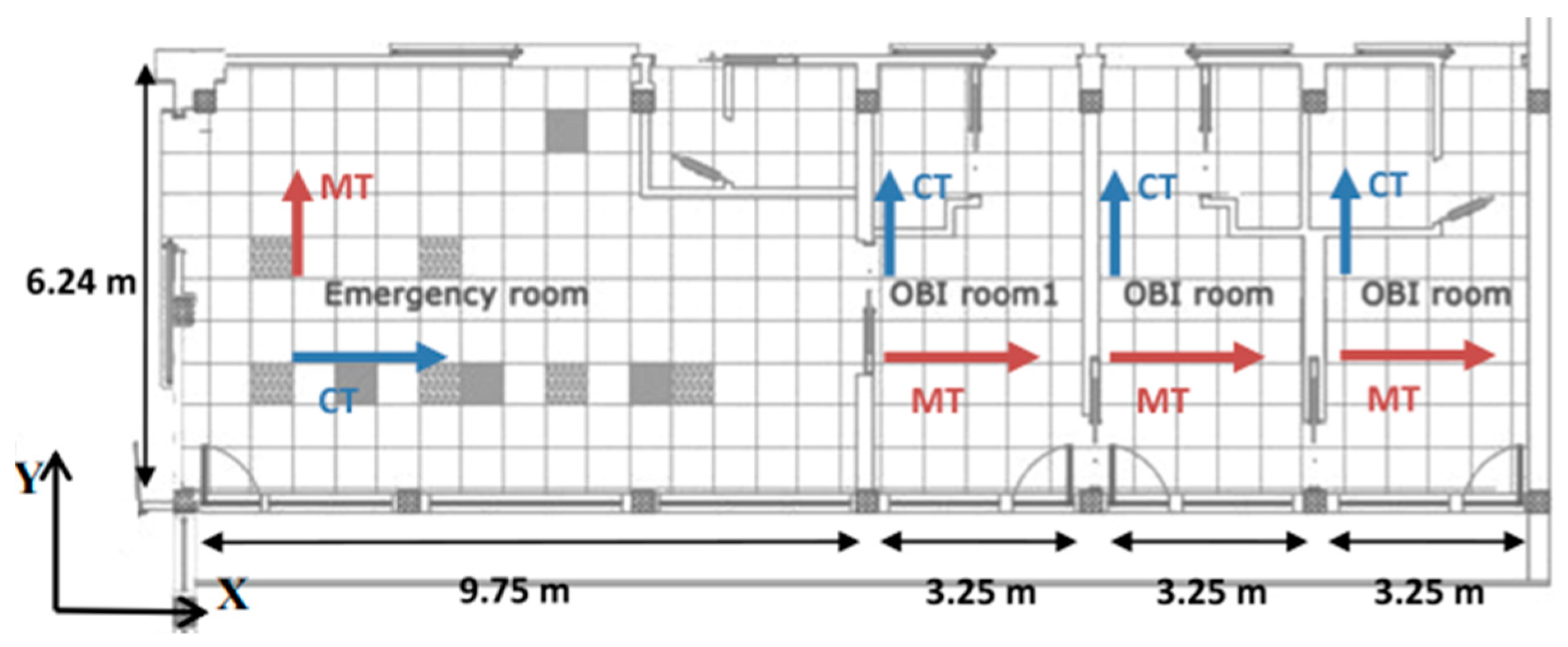
Preprints 95573 g006
Preprints 95573 g007
Figure 7. Patients arrival within the day and the year (one month).
Figure 7. Patients arrival within the day and the year (one month).
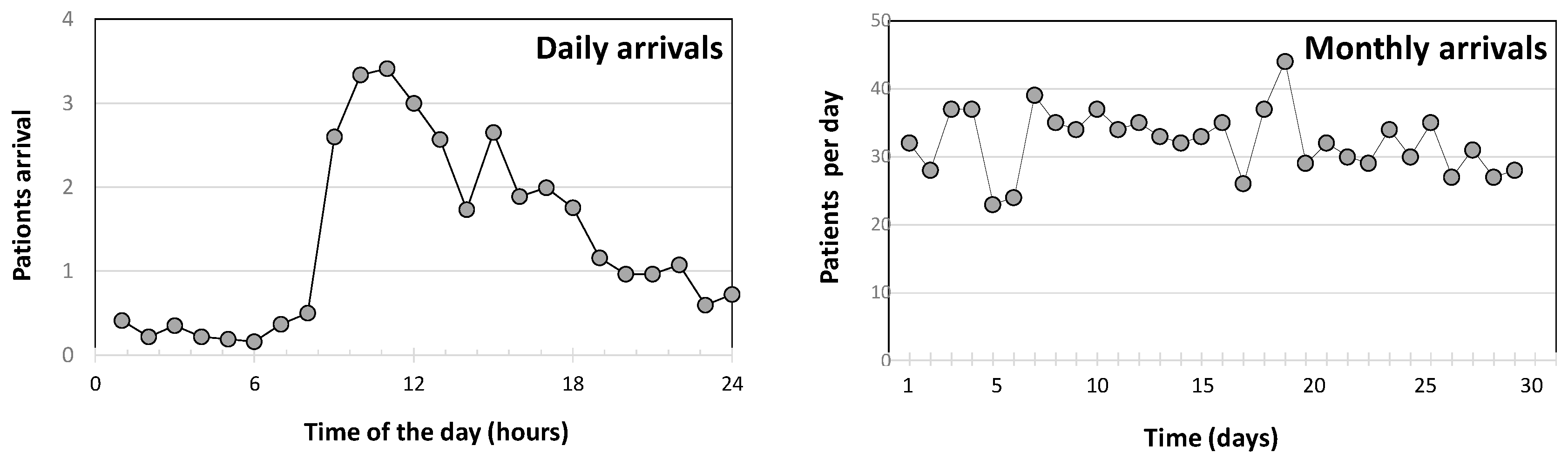
Preprints 95573 g007
Preprints 95573 g008
Figure 8. Comparison between the numerical results and the measured WT.
Figure 8. Comparison between the numerical results and the measured WT.
Preprints 95573 g008
Preprints 95573 g009
Figure 9. Envelope of fragility curves and possible damage scenarios.
Figure 9. Envelope of fragility curves and possible damage scenarios.
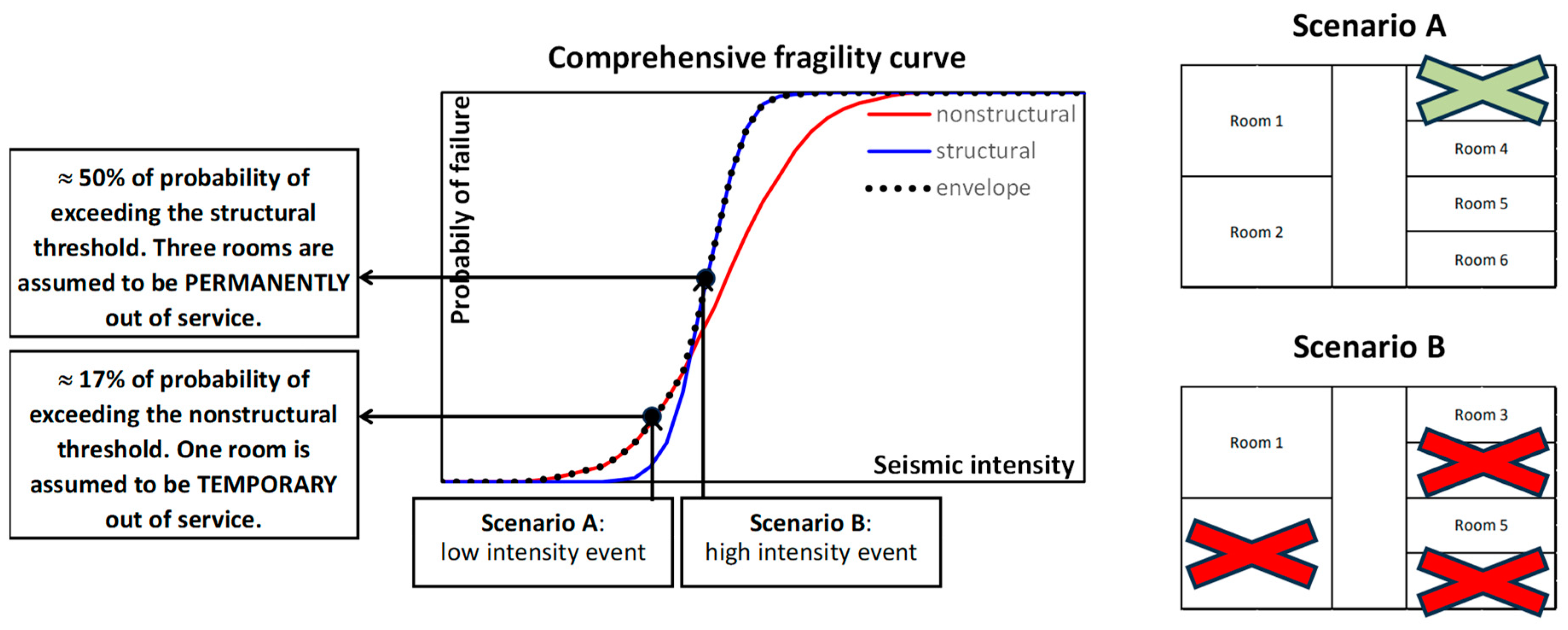
Preprints 95573 g009
Preprints 95573 g010
Figure 10. Experimental campaign for the soil characterization. a. Map of the performed tests; b. Average shear velocities provided by the experimental tests; c. Elastic B-soil spectram provided by the NTC 2018 [53].
Figure 10. Experimental campaign for the soil characterization. a. Map of the performed tests; b. Average shear velocities provided by the experimental tests; c. Elastic B-soil spectram provided by the NTC 2018 [53].
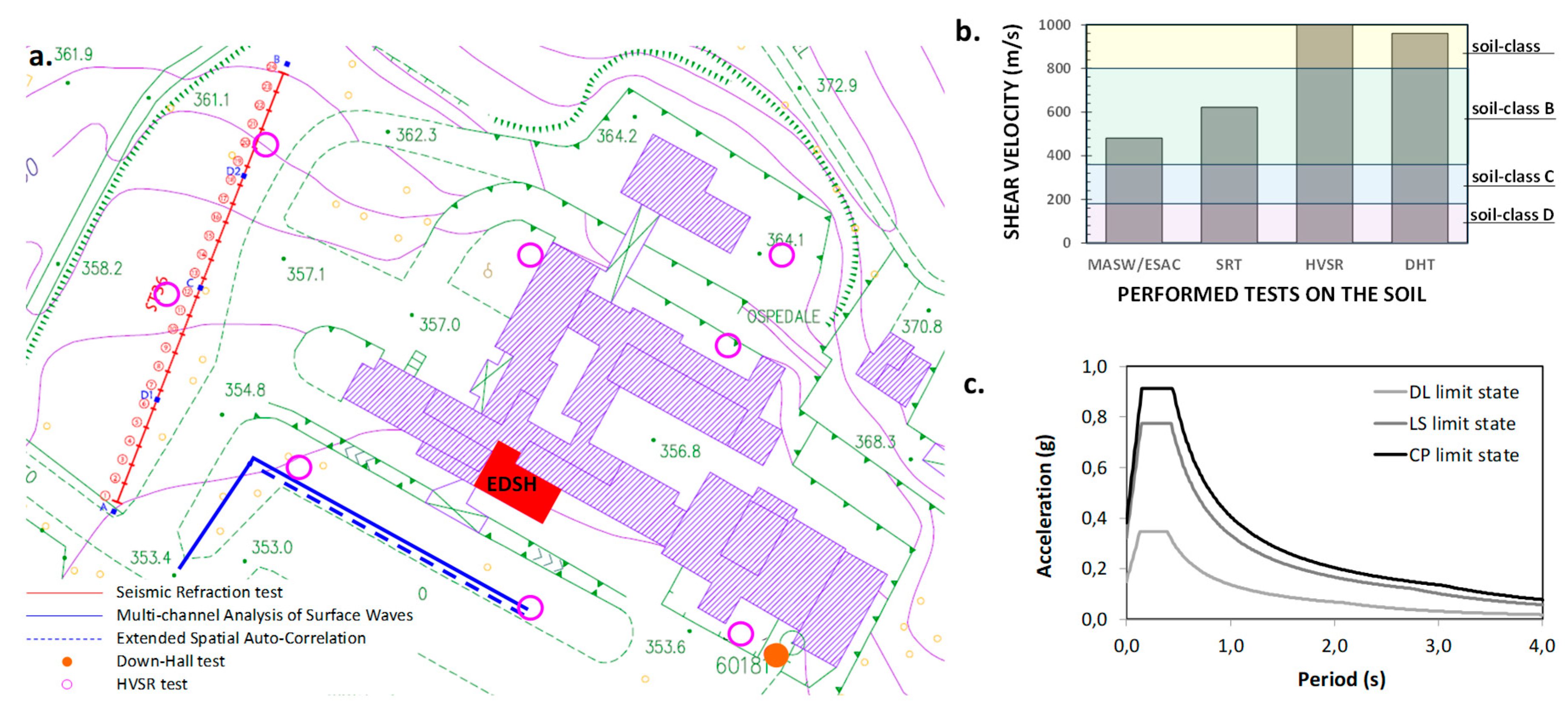
Preprints 95573 g010
Preprints 95573 g011
Figure 11. Median spectra of the assumed sets of ground motions.
Figure 11. Median spectra of the assumed sets of ground motions.
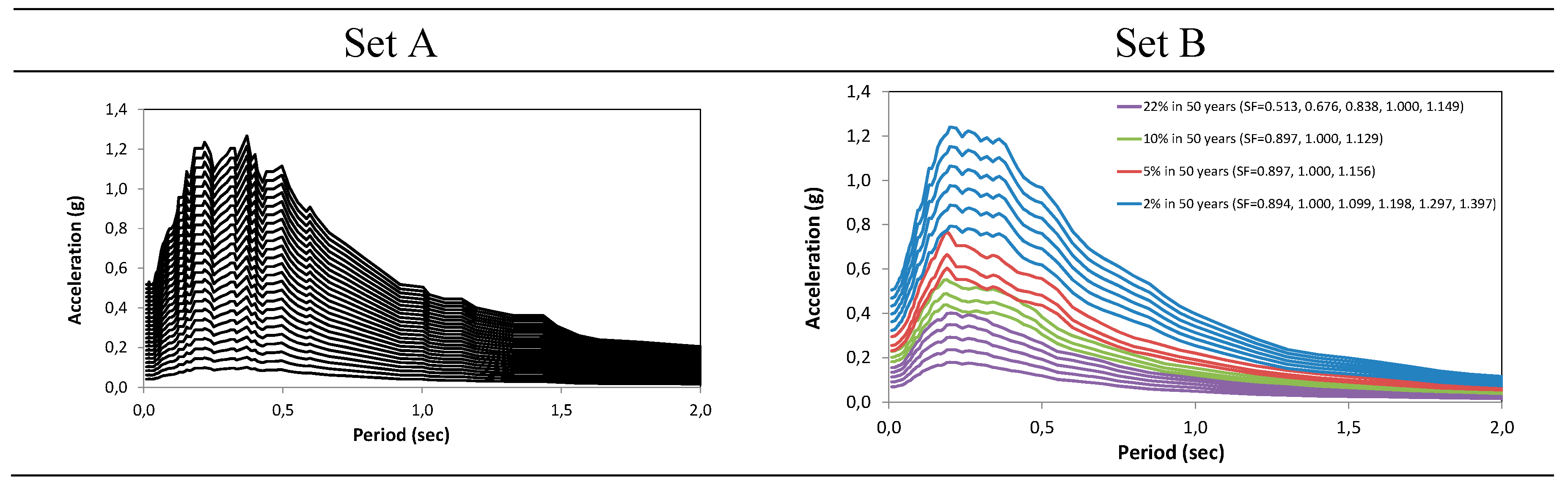
Preprints 95573 g011
Preprints 95573 g012
Figure 12. Fragility curves obtained for the considered limit states.
Figure 12. Fragility curves obtained for the considered limit states.
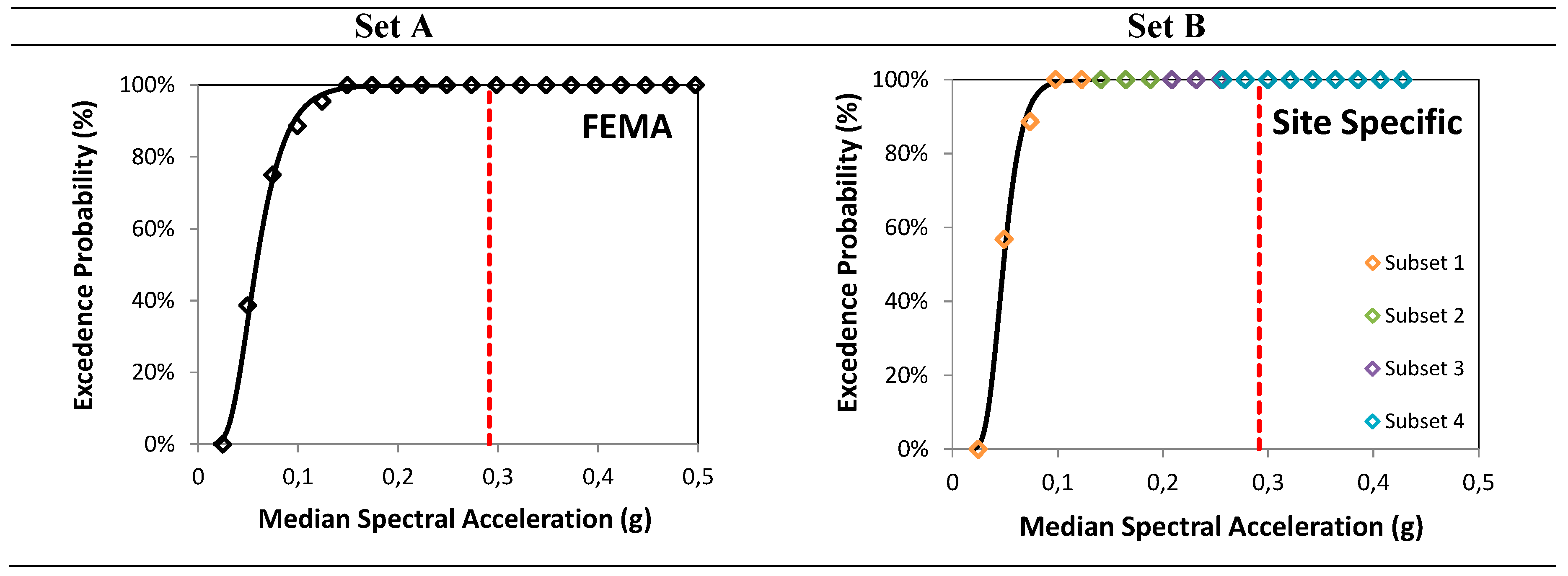
Preprints 95573 g012
Preprints 95573 g013
Figure 13. Structural and nonstructural fragility curves in the two most strategic rooms of EDSH.
Figure 13. Structural and nonstructural fragility curves in the two most strategic rooms of EDSH.
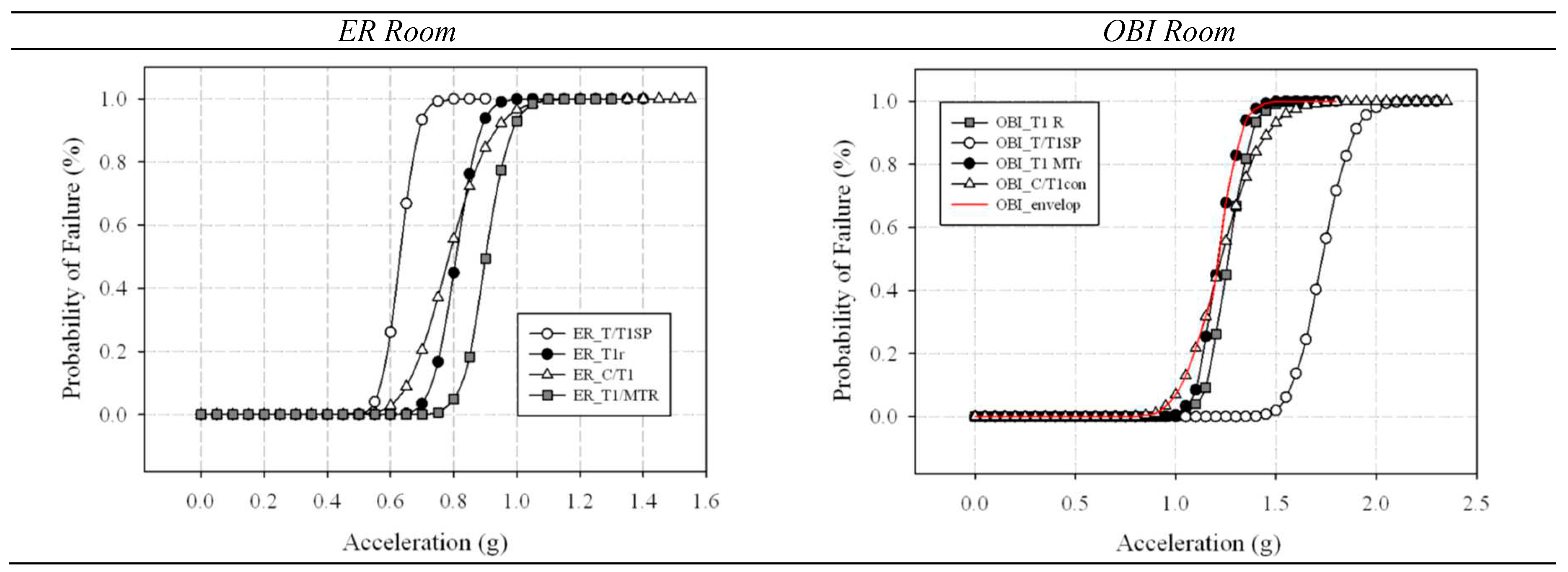
Preprints 95573 g013
Preprints 95573 g014
Figure 14. Fragility curves of cabinets, derived by the lab tests at the University of Naples (from [57]).
Figure 14. Fragility curves of cabinets, derived by the lab tests at the University of Naples (from [57]).
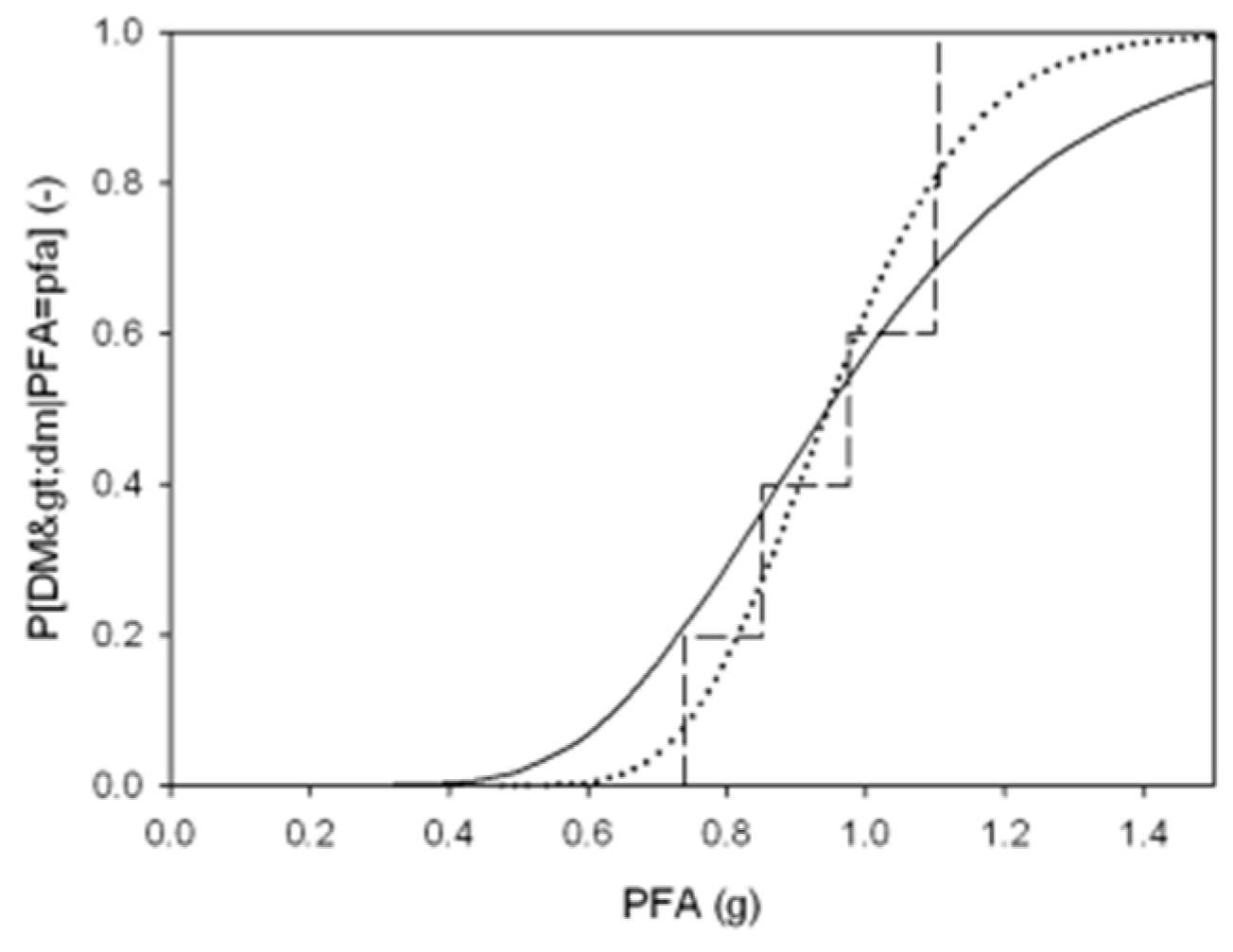
Preprints 95573 g014
Preprints 95573 g015
Figure 15. Three potential scenarios of loss of service of the EDSH rooms.
Figure 15. Three potential scenarios of loss of service of the EDSH rooms.
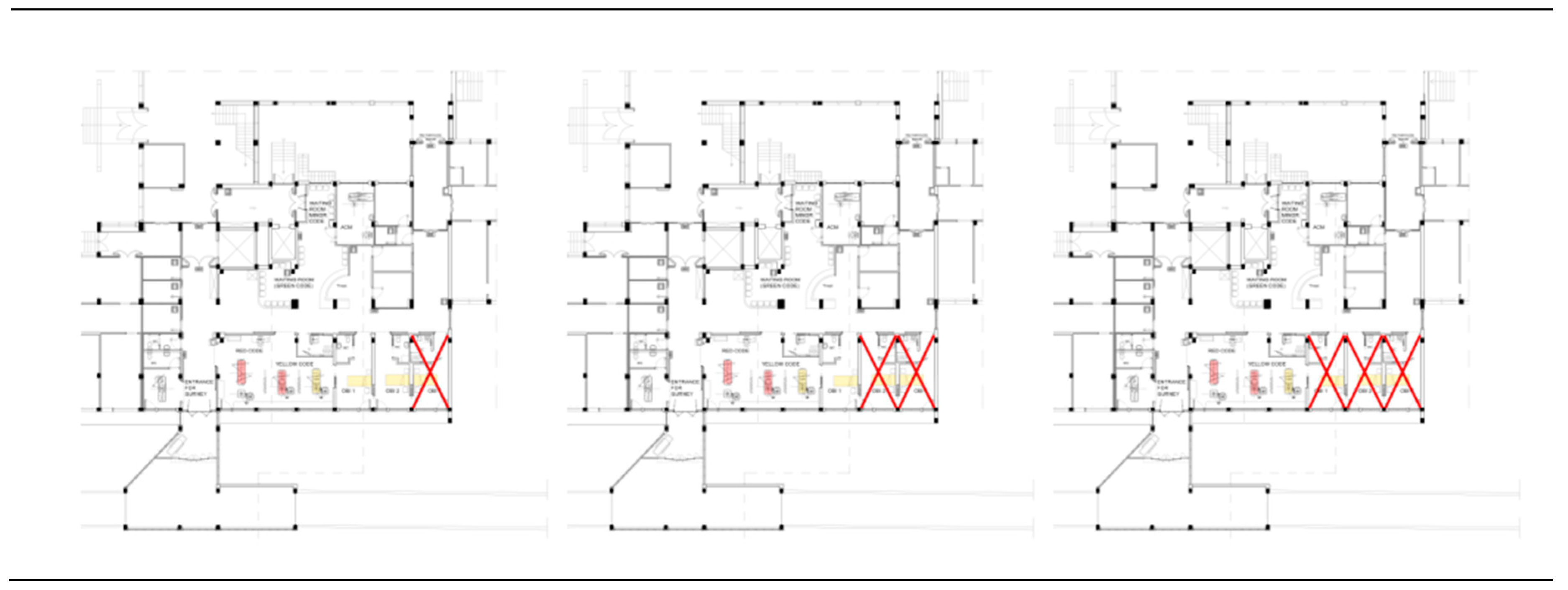
Preprints 95573 g015
Preprints 95573 g016
Figure 16. Patients’ arrival in the three days after the earthquake occurring.
Figure 16. Patients’ arrival in the three days after the earthquake occurring.
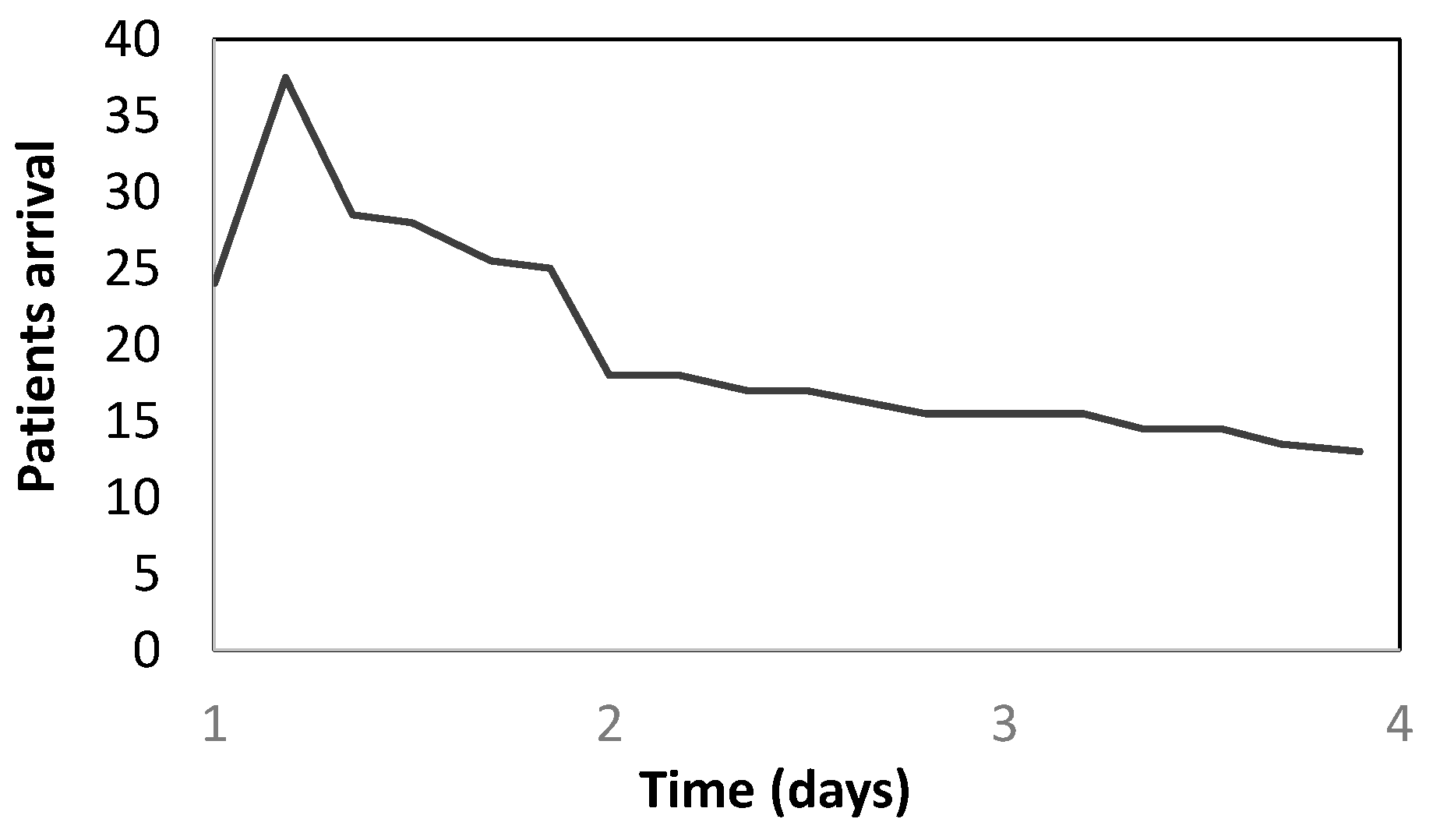
Preprints 95573 g016
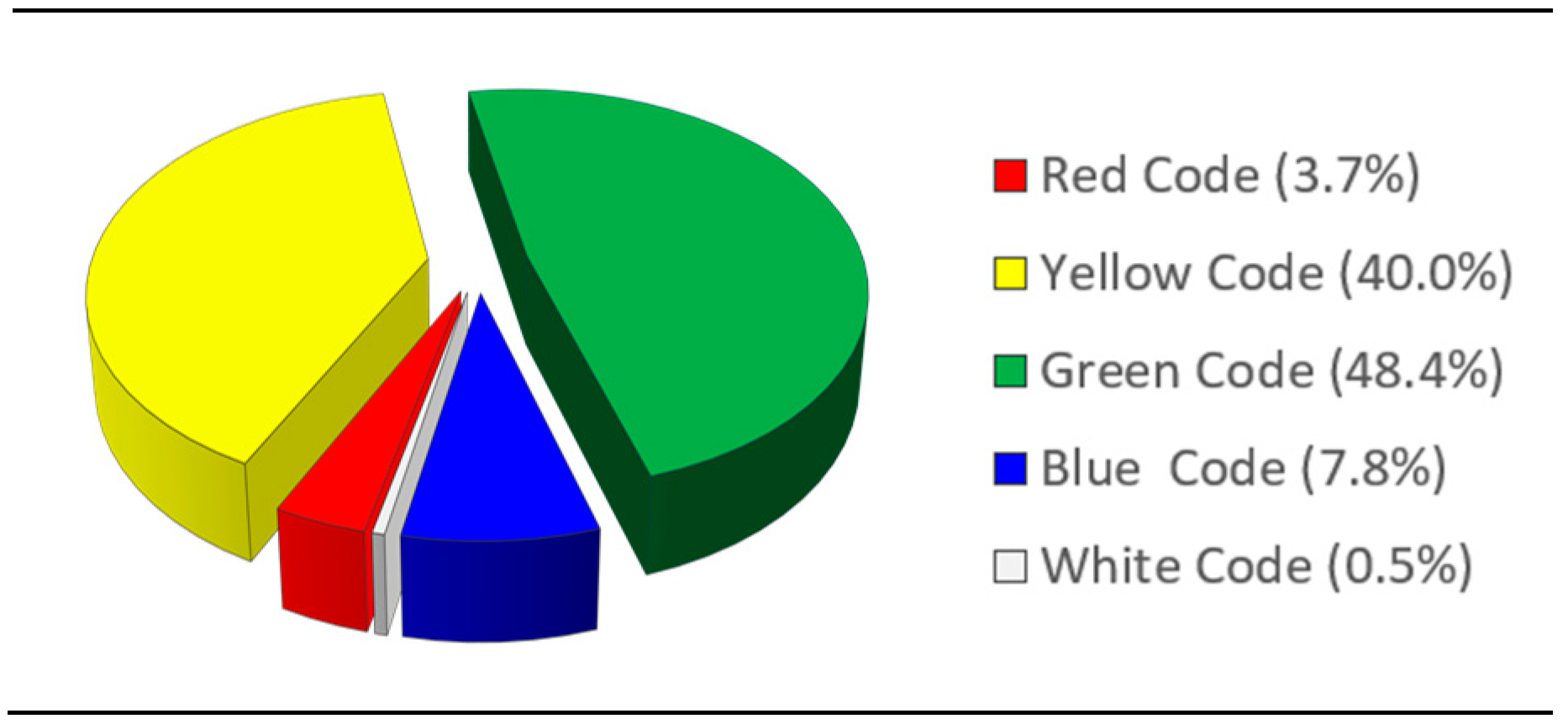
Preprints 95573 g017
Figure 17. Color-code of patients in emergency conditions.
Figure 17. Color-code of patients in emergency conditions.
Preprints 95573 g017
Preprints 95573 g018
Figure 18. Flow chart of major codes in case of emergency.
Figure 18. Flow chart of major codes in case of emergency.
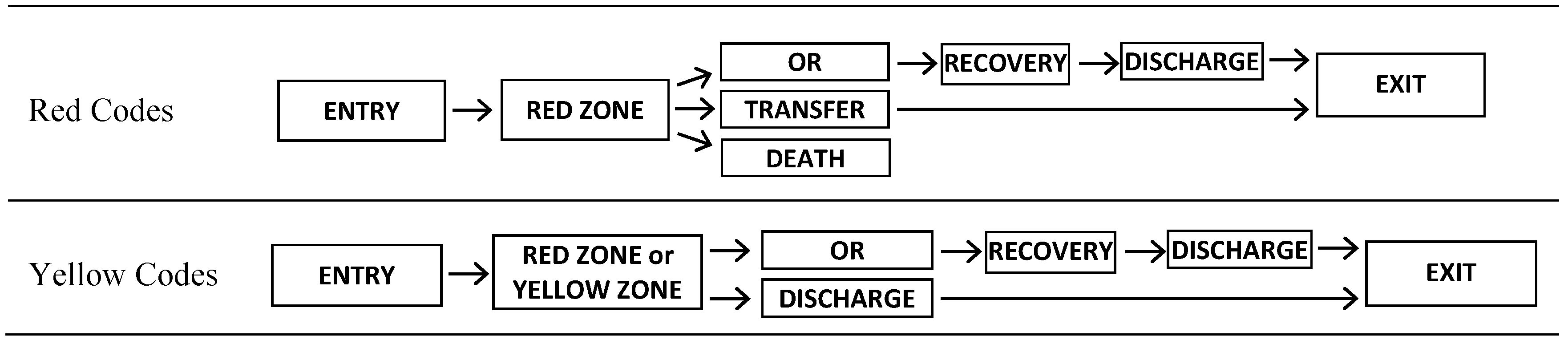
Preprints 95573 g018
Preprints 95573 g019
Figure 19. Scheme of the analysis represented the EDSH functionality in emergency conditions.
Figure 19. Scheme of the analysis represented the EDSH functionality in emergency conditions.
Preprints 95573 g019
Preprints 95573 g020
Figure 20. Results of the analysis as a function of the number of out-of-service rooms.
Figure 20. Results of the analysis as a function of the number of out-of-service rooms.
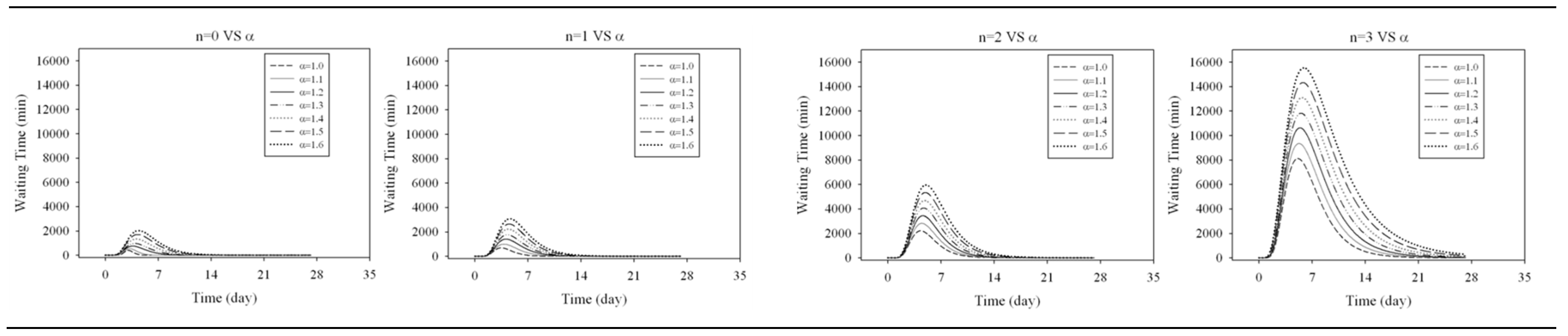
Preprints 95573 g020
Preprints 95573 g021
Figure 21. Results of the analysis as a function of the increase of the arrival day.
Figure 21. Results of the analysis as a function of the increase of the arrival day.
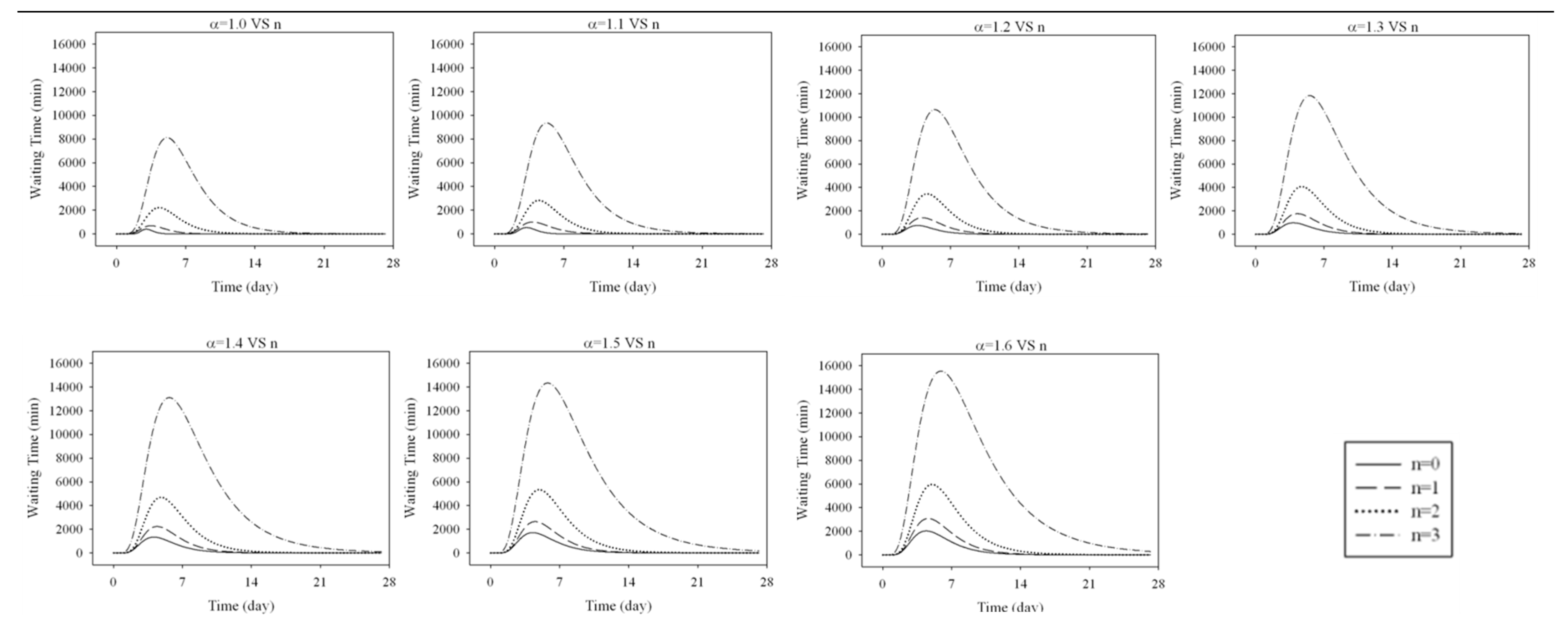
Preprints 95573 g021
Preprints 95573 g022
Figure 22. Resilience function according to Bruneau and Reinhorn [3].
Figure 22. Resilience function according to Bruneau and Reinhorn [3].
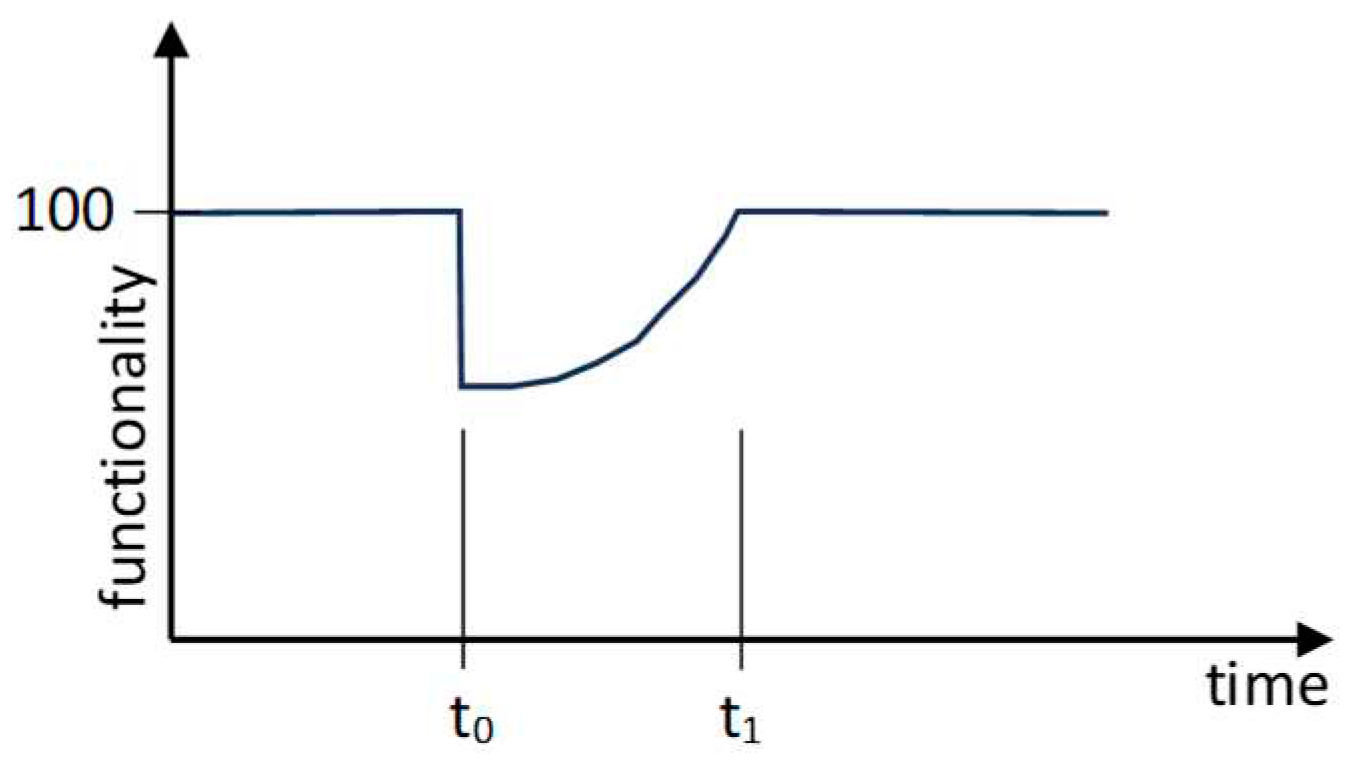
Preprints 95573 g022
Preprints 95573 g023
Figure 23. Recovery functions.
Figure 23. Recovery functions.
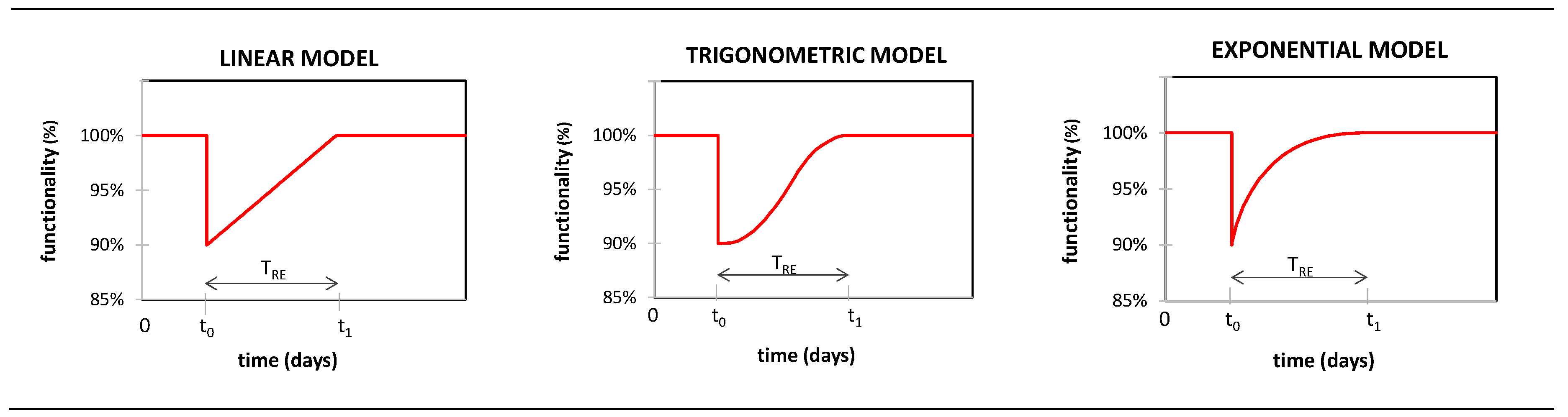
Preprints 95573 g023
Preprints 95573 g024
Figure 24. WT function as loss of functionality.
Figure 24. WT function as loss of functionality.
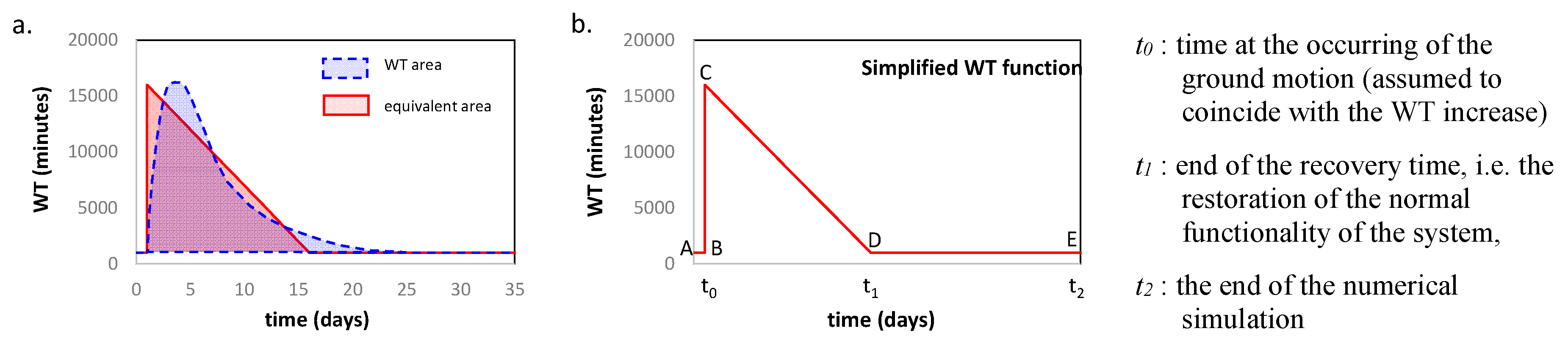
Preprints 95573 g024
Preprints 95573 g025
Figure 25. Resilience assessment by using the area method.
Figure 25. Resilience assessment by using the area method.
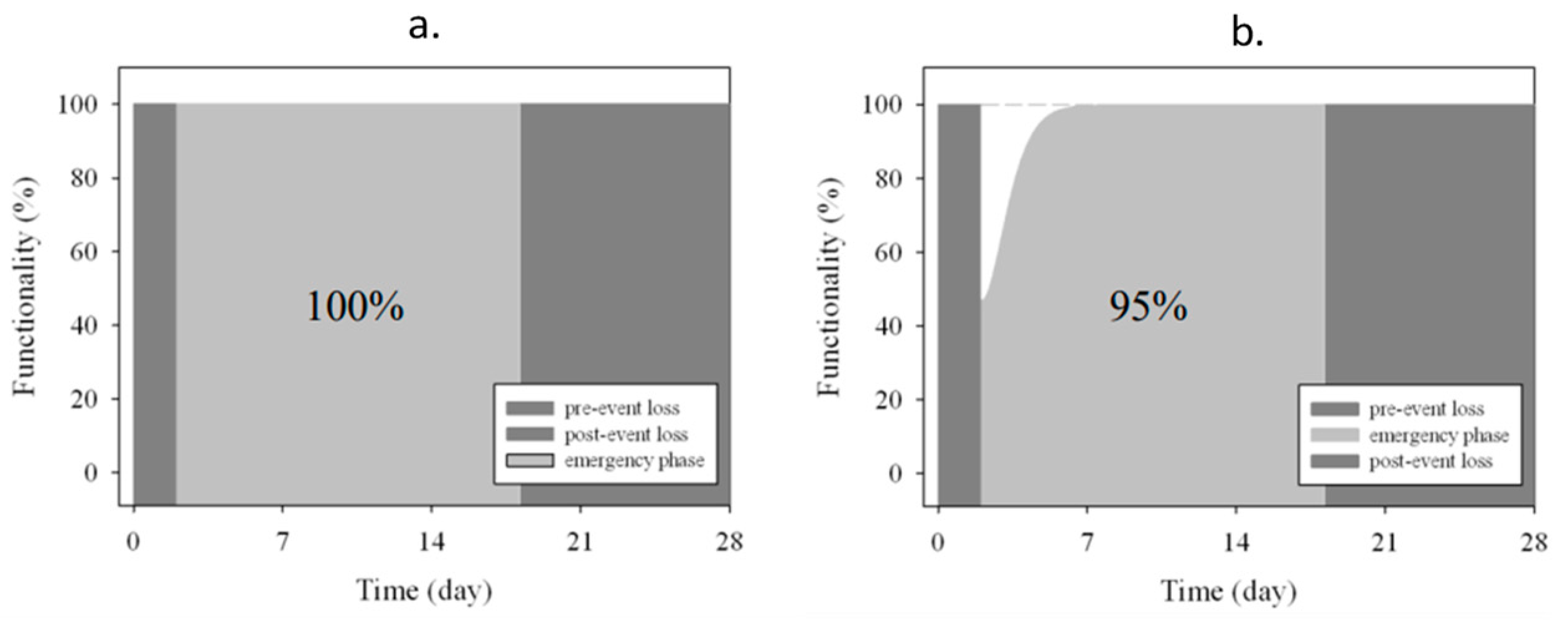
Preprints 95573 g025
Preprints 95573 g026
Figure 26. Functionality curves as a function of n (α =1.0).
Figure 26. Functionality curves as a function of n (α =1.0).
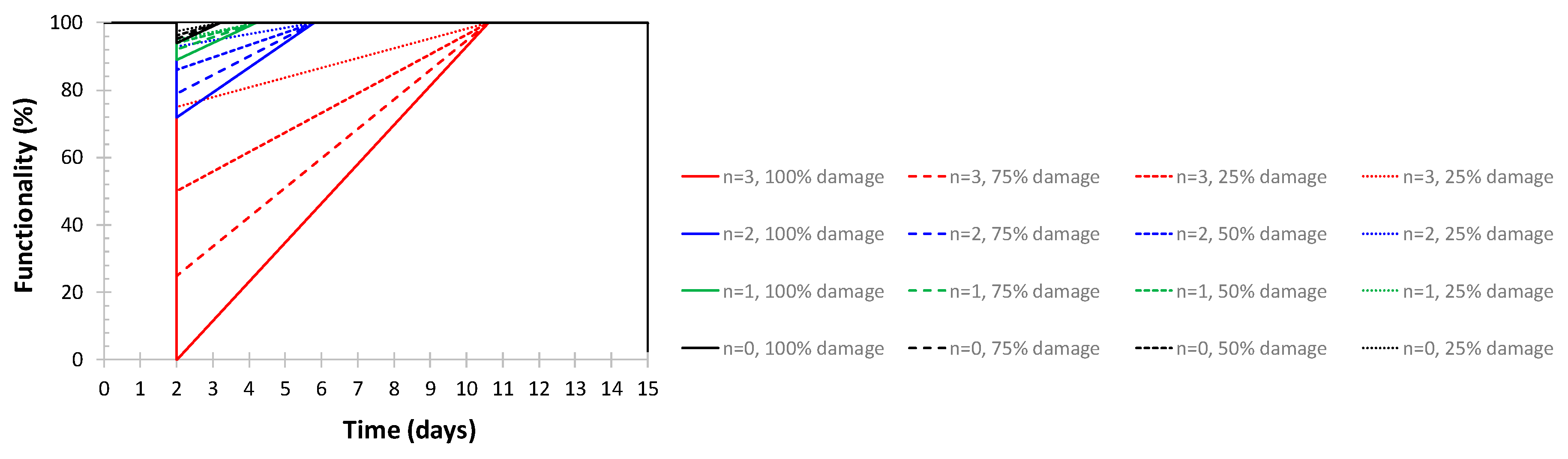
Preprints 95573 g026
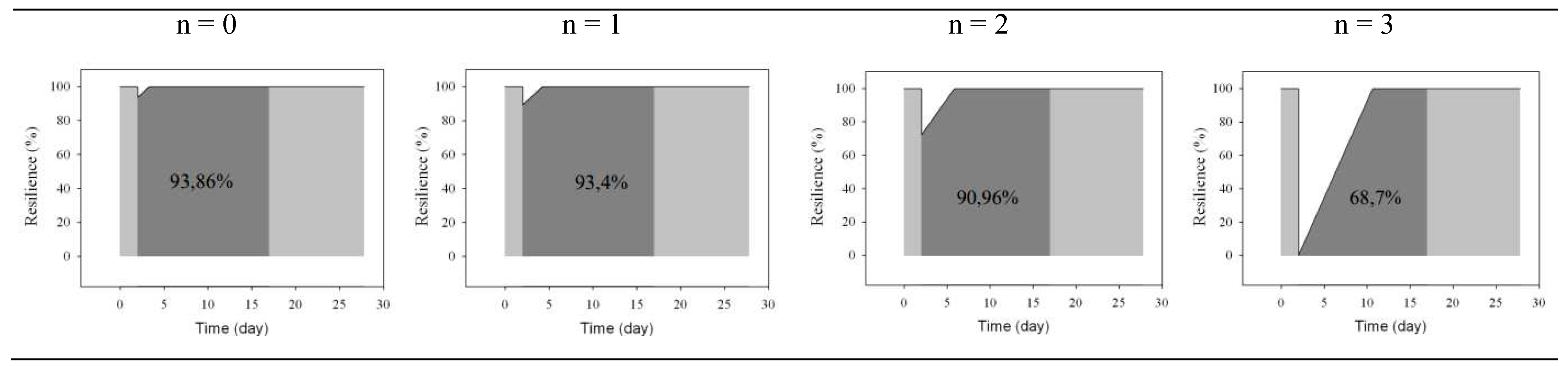
Preprints 95573 g027
Figure 27. Resilience curves (α =1.0).
Figure 27. Resilience curves (α =1.0).
Preprints 95573 g027
Table 1. Estimated time (in minutes) and time involved rooms for each color code.
Table 1. Estimated time (in minutes) and time involved rooms for each color code.
Estimate time (in minutes) of staying for each color code Mutual distances (in meters)
Red Yellow Green Blue White Entry REC ER WR ACM OBI
(0.5%) (10.6%) (45.1%) (1.72%) (41.8%) Entry 0 20 9 25 25 25
Entry REC 0 10 3 10 10
REC 2-5 2-5 5-10 5-10 5-10 ER 0 12.5 17.5 13
ER 15-30 15-30 WR 0 12 12
ACM 10-20 10-15 5-10 ACM 0 18
OBI 240-2880 OBI 0
Table 2. FEMA P695 record set (set A).
Table 2. FEMA P695 record set (set A).
ID Event Name Recording Station PGA ID Event Name Recording Station PGA
1 Northridge, CA Beverly Hills - 14145 Mulhol 0.52 12 Lander, CA Coolwater 0.42
2 Northridge, CA Canyon Country - W Lost Cany 0.48 13 Loma Prieta, CA Capitola 0.53
3 Duzce, Turkey Bolu 0.82 14 Loma Prieta, CA Gilroy Array #3 0.56
4 Hector Mine, CA Hector 0.34 15 Manjil, Iran Abbar 0.51
5 Imperial Valley, CA Delta 0.35 16 Superstition Hills, CA El Centro Imp. Co. Cent 0.36
6 Imperial Valley, CA El Centro Array #11 0.38 17 Superstition Hills, CA Poe Road (temp) 0.45
7 Kobe, Japan Nishi-Akashi 0.51 18 Cape Mendocino, CA Rio Dell Overpass - FF 0.55
8 Kobe, Japan Shin-Osaka 0.24 19 Chi-Chi, Taiwan CHY101 0.44
9 Kocaelia, Turkey Duzce 0.36 20 Chi-Chi, Taiwan TCU045 0.51
10 Kocaelia, Turkey Arcelik 0.22 21 San Fernando, CA LA - Hollywood Stor FF 0.21
11 Lander, CA Yermo Fire Station 0.24 22 Friuli, Italy Tolmezzo 0.35
Table 3. Site Specific Record Sets (set B).
Table 3. Site Specific Record Sets (set B).
22% in 50 years 10% in 50 years
No Event name Recording Station PGA No Event name Recording Station PGA
1 Northridge, CA LA - N Figueroa St 0.29 1 Coalinga, CA Palmer Ave 0.29
2 Whittier Narrows, CA LA - Baldwin Hills 0.18 2 Chi-Chi, Taiwan CHY032 0.18
3 Northridge, CA Burbank - Howard Rd. 0.20 3 Northridge, CA Manhattan Beach - Manhattan 0.20
4 Northwest China Jiashi 0.37 4 Coalinga, CA Skunk Hollow 0.37
5 Northridge, CA Newhall - Fire Station 0.45 5 Sierra Madre, CA Altadena - Eaton Canyon 0.45
6 Northridge, CA Santa Barbara - UCSB Goleta 0.23 6 Northridge, CA Downey - Co Maint Bldg 0.23
7 Hector Mine, CA Fun Valley 0.22 7 Chi-Chi, Taiwan TCU075 0.22
8 Chi-Chi, Taiwan CHY088 0.34 8 Chi-Chi, Taiwan TCU079 0.34
9 Landers, CA Fort Irwin 0.28 9 Sierra Madre, CA Pasadena - USGS/NSMP Office 0.28
10 Chi-Chi, Taiwan CHY015 0.49 10 Northridge, CA LA - Univ. Hospital 0.49
11 Taiwan SMART1 SMART1 M07 0.18 11 Mammoth Lakes, CA Convict Creek 0.18
12 Chi-Chi, Taiwan TCU129 0.14 12 Taiwan SMART1 SMART1 E02 0.14
13 Irpinia, Italy Rionero In Vulture 0.20 13 Hollister, CA Hollister City Hall 0.20
14 Northridge, CA Compton - Castlegate St 0.14 14 Northridge, CA Lakewood - Del Amo Blvd 0.14
15 Imperial Valley, CA Niland Fire Station 0.27 15 Prarkfield, CA Cholame - Shandon Array #8 0.27
16 Whittier Narrows, CA La Habra - Briarcliff 0.21 16 Northridge, CA LA - 116th St School 0.21
17 Chi-Chi, Taiwan HWA058 0.26 17 Northridge, CA San Gabriel - E Grand Ave 0.26
18 Whittier Narrows, CA San Marino - SW Academy 0.27 18 Kalamata, Greece Kalamata 0.27
19 Mammoth Lakes, CA Mammoth Lakes H. S. 0.19 19 Loma Prieta, CA Fremont - Emerson Court 0.19
20 Sierra Madre, CA Cogswell Dam - Right Abutment 0.23 20 Whittier Narrows, CA El Monte - Fairview Av 0.23
21 Northridge, CA Northridge - 17645 Saticoy St 0.61 21 Coalinga, CA Coalinga-14th & Elm (Old CHP) 0.61
22 Northwest China Jiashi 0.18 22 Northridge, CA Moorpark - Fire Station 0.18
5% in 50 years 2% in 50 years
No Event name Recording Station PGA No Event name Recording Station PGA
1 Prarkfield, CA Cholame - Shandon Array #5 0.44 1 Tabas, Iran Dayhook 0.41
2 Northridge, CA Pacific Palisades - Sunset 0.47 2 North Palm Springs, CA Desert Hot Springs 0.33
3 Northridge, CA LA - N Westmoreland 0.40 3 Northridge, CA Beverly Hills - 12520 Mulhol 0.62
4 Whittier Narrows, CA Downey - Birchdale 0.30 4 Northridge, CA LA 00 0.39
5 Kern County, CA Taft Lincoln School 0.18 5 Chi-Chi, Taiwan TCU080 0.54
6 Chi-Chi, Taiwan TCU075 0.22 6 Coalinga, CA Cantua Creek School 0.28
7 Chi-Chi, Taiwan CHY088 0.26 7 Coyote Lake, CA Gilroy Array #6 0.43
8 San Fernando, CA LA - Hollywood Stor FF 0.21 8 Northwest China Jiashi 0.30
9 Chi-Chi, Taiwan CHY010 0.23 9 Northridge, CA Stone Canyon 0.39
10 Chi-Chi, Taiwan CHY047 0.14 10 Chalfant Valley, CA Bishop - LADWP South St 0.25
11 San Fernando, CA Castaic - Old Ridge Route 0.32 11 Chi-Chi, Taiwan TCU078 0.47
12 Chalfant Valley, CA Bishop - LADWP South St 0.25 12 Managua, Nicaragua Managua, ESSO 0.42
13 Imperial Valley, CA Calexico Fire Station 0.27 13 Chi-Chi, Taiwan TCU078 0.39
14 Northridge, CA LA - Fletcher Dr 0.24 14 Northridge, CA LA - Chalon Rd 0.23
15 Kobe, Japan Tadoka 0.29 15 Corinth, Greece Corinth 0.30
16 Chi-Chi, Taiwan ILA067 0.20 16 Imperial Valley, CA SAHOP Casa Flores 0.51
17 Whittier Narrows, CA LA - Fletcher Dr 0.21 17 Friuli, Italy Tolmezzo 0.35
18 Whittier Narrows, CA Garvey Res. - Control Bldg 0.46 18 North Palm Springs, CA Whitewater Trout Farm 0.61
19 Loma Prieta, CA Gilroy - Gavilan Coll. 0.36 19 Coalinga, CA Oil City 0.87
20 Chi-Chi, Taiwan TCU129 0.95 20 Chi-Chi, Taiwan TCU095 0.71
21 Prarkfield, CA Cholame - Shandon Array #5 0.29 21 Northridge, CA Pacoima Dam (downstr) 0.43
22 Northridge, CA Pacific Palisades - Sunset 0.39 22 Yountville, CA Napa Fire Station #3 0.51
Table 4. Data to set the Metamodel with the PEMAC activation.
Table 4. Data to set the Metamodel with the PEMAC activation.
Staff functioning Mutual distances (in meters) between the zones
Staff Role Number Working time ENTRY R-zone Y-zone OR
Nurse 9 H24 ENTRY 0 7.5 30 60
Help Operator 4 H24 R-zone - 0 10 60
Doctors 7 H24 Y-zone - - 0 70
Other 2 H24 OR - - - 0
Table 5. Coordinates of normalized WT and functionality curves in the worst case.
Table 5. Coordinates of normalized WT and functionality curves in the worst case.
WT curve Functionality curve
Point X-coordinate (days) Y-coordinate (minutes) Point X-coordinate (days) Y-coordinate (%)
general α=1, n=3 general α=1, n=3 general α=1, n=3 general α=1, n=3
A 0 0 0 0 A 0 0 100 100
B t0 2 0 0 B t0 2 100 100
C t0 2 WT peak 8195.8 C t0 2 Residual functionality 0
D t0 + normalized recovery time 10.636 0 0 D t0 + equivalent recovery time 10.636 100 100
E Simulation end 27,77 0 0 E Simulation end 27,77 0 100
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated