Quantum mechanics can be considered one of the most successful physical theories. It describes the behavior of particles at the microscopic scale, where classical mechanics ceases to be an adequate description. The development of quantum mechanics has been a fascinating journey. Schrödinger formulated the wave equation, providing a mathematical description of quantum systems in terms of wave functions. Concurrently, Born introduced the probabilistic interpretation, the so-called Born rule, suggesting that the square of the wave function modulus represents the probability density of finding a particle in a particular state and emphasizing the statistical nature of quantum outcomes. Heisenberg, on the other hand, developed the dynamics based on the notion of commutation relations. Heisenberg’s uncertainty principle establishes the inherent limitations in simultaneously measuring certain pairs of physical properties. From a distinctive perspective, Feynman further expanded the quantum narrative by introducing the path integral formulation. This formulation underscored phase factors (actions) associated with different paths. Despite their differing starting points, they all arrived at the same conclusions consistent with experimental observations. However, counterintuitive concepts in quantum mechanics have been profoundly disturbing to physicists and philosophers alike. One may wonder whether it is a fact of nature, or a defect in the theory.

In 1964, Bell introduced an inequality to test the limits of classical correlations in quantum systems [1]. Bell’s inequality plays a crucial role in addressing the EPR paradox [2] and provide a criterion for testing the validity of local realism. For now, numerous experiments have tested and confirmed the violation of Bell’s inequality [3,4,5]. This implies that no local hidden variables can determine the outcome of quantum measurements and restore determinism. These results reaffirm the non-local nature of quantum entanglement, the orthodox interpretation and the fundamental principles of quantum mechanics. An investigation into the non-locality in quantum mechanics may help us understand the nature of space-time.

The history of physics tells us that no matter how perplexing a phenomenon in nature may be, its underlying mechanism is based on the simplest principles, such as symmetry, increasing entropy, least action, and so on. In this paper, we propose a novel scenario to reinterpret the indeterminacy in quantum mechanics. In this scenario, we consider particles together with the surrounding space as an indivisible whole due to the non-local nature of quantum mechanics, and then investigate the maximum symmetry of this system at the quantum level. From this perspective, we define a new quantity to describe the change of the symmetry of this system before and after measurement.

This paper is organized as follow. In Sec.2 we intrduced a new quantity related to symmetry. Sec.3 is dedicated to the relationship between symmetry and mass (or spin) of a particle. In Sec.4 we calculated the effective mass of gravity. Finally, in Sec.5 we summarize the main results obtained. For convenience, we set c=1.

In the classical world, a physical system consisting of a particle localized at a point and the surrounding space is evidently not in the most natural state, as it remains invariant under rotation but lacks uniformity in energy distribution in space. It’s important to note that here we are referring to the entire system rather than talking about the symmetry of this particle while treating the space as a background. In quantum mechanics, before we make any measurement, this particle can find a more natural state, namely, being evenly spread throughout the entire space. In other words, the particle does not have a precise position prior to measurement and is in a superposition state of positions. However, once we measure the particle’s position, we find it to be at a specific point. The measurement causes the collapse of the wave function and breaks the symmetry. On the other hand, according to the uncertainty principle, a particle at a specific position have possibilities of being in a state with higher energy, and it is still not a stable and natural state.

Here, from another perspective, let us introduce a new quantity S to describe the evolution of a system from a state of minimum symmetry or broken symmetry to a state of maximum symmetry (the most natural state of the system). In other words, S can tell us about how much symmetry a system possesses. Let us call it “degrees of symmetry” (DS). The DS is defined by where $\Omega$ is the number of states (or relative number of states) and we have introduced logarithms to make S additive. In some cases, the DS is somewhat similar to “entropy” but essentially different from the thermodynamic entropy and the quantum entanglement entropy. Let us start with a simple case. Consider the system of a particle confined in a box of volume V. Before measurement, the particle is in the superposition state of positions. The number of the position eigenstates is proportional to the volume of this box. The walls of the box will experience an “osmotic pressure” generated by this particle. By using dimensional analysis, the DS is where $V_p$ is the Planck volume. After measurement, the particle is in an specific position eigenstate, let us define the DS of this state as 0. In the case of the free particle, we have $V\to \infty$ and $S\to \infty$ and the system is in a natural state with maximum symmetry due to the uniform spreading of energy in space. However, the plane wave solutions does not represent physically realizable states; or, to put it another way, there is no such thing as a free particle with a definite energy. On the other hand, when considering relativistic effects, the limit of precision in locating a particle’s position is its Compton wavelength. A physically realizable state is a wave packet and the number of the states should be replaced by the wave packet width l. For the one-dimensional case, the corresponding DS is where $l_p$ is the Planck length.

Let us study the evolution of the DS of a particle with mass $\mu$ over time. Suppose that the initial wave function of the particle is given by a gaussian wave packet: where a is a constant. The uncertainty principle holds at all times, and at $t=0$, the system reaches the uncertainty limit: $\Delta x\Delta p=\hslash /2$. The square of the wave function at time t is where Then, the DS at time t is The DS increases over time and in the long time limit, we find The free Schrödinger equation is formally similar to the particle diffusion equation if one substitutes $i\hslash /2m$ with the diffusion coefficient. From this perspective, the uneven distribution of probability density in space leads to its diffusion.

We now turn to the intrinsic DS of quantum particles. Mass can be regarded as the energy confined in a point particle and a massive particle with mass $\mu$ should have intrinsic DS. A simple way to understand this is to recall that a quantum particle with uncertain position transitions into a classical object as the mass increases and a heavy classical object located in a specific point has minimum DS. In the opposite limit $\mu \to 0$, the Compton wavelength of the particle approaches infinity. The DS of a massive particle is given by where $m_p$ is the Planck mass. In fact, Eq. (8) already includes the contribution of mass to DS. For a massless particle, such as the quantized electromagnetic field (photons), $\mu$ is replaced by $h\nu$ with $\nu$ being the frequency of a photon.

A particle carrying spin s should also have intrinsic DS. The classical angular momentum with a specific spatial orientation, or equivalently the vector, has a broken symmetry. In quantum mechanics, the three spatial component of spin $s_x$, $s_y$ and $s_z$ are incompatible observables and we cannot know all three components simultaneously. An uncertain orientation can restore symmetry. Let’s say we start out with a particle of spin s in the spin up state along the z direction. After a measurement of $s_z$, the z-component of this particle’s spin angular momentum, we get the value $+m\hslash$. But we don’t know the values of $s_x$ and $s_y$. The DS is defined as the logarithm of the circumference of a circle satisfying the relation Before measurement, its DS is where Thus, the relative m-dependent DS after measurement is In the case of the orbital angular momentum, s is replaced by the quantum number l.

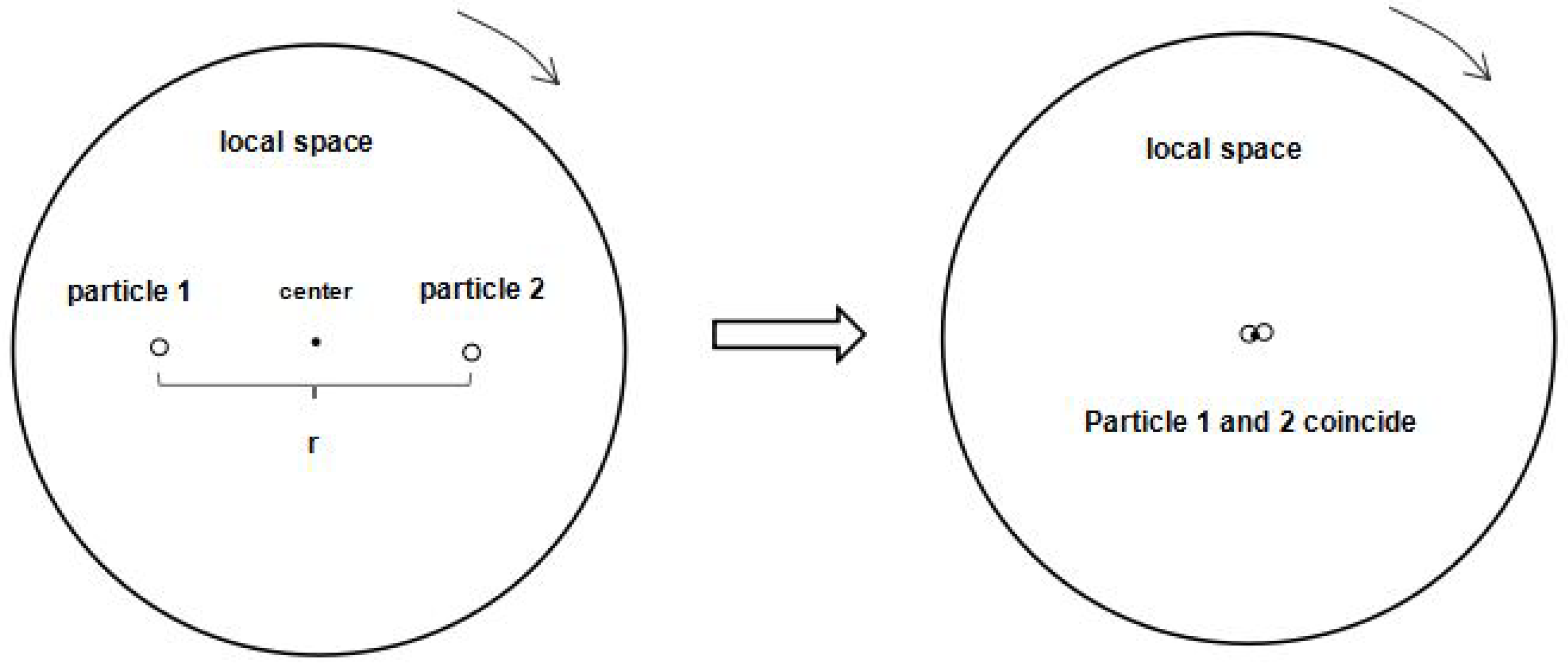
So far, we have only applied the DS to some simple cases. Let us consider a two-particle system containing particle 1 and particle 2. The wave packet sizes of these two particles are $w_1$ and $w_2$, respectively, and the distance between the centers of the wave packets is r. We add up the DS for these two particles and obtain where ${\rho }_p$ is the Planck density, and ${\mu }_1$ and ${\mu }_2$ are average masses, respectively. If particle 1 becomes very heavy and turns into a classical object, the system will lose the uniformity caused by quantum effects and only retain rotational invariance. However, once we add particle 2 to this system, it will break the rotational symmetry. All we can expect is that these two particles tend to be somewhat closer together to make the entire system invariant under rotation, see Figure 1. Since the most natural state is when particle 1 and particle 2 coincide, the system behaves as though there were a “force of attraction” between the two particles.

This produces an additional DS that depends on r. That is where $f\left(r\right)$ is a function of r. The total DS is The classical gravitational potential energy U of two pairwise point particles is given by Then, Eq. (16) becomes If we choose $f\left(r\right)\propto r$, the potential energy can be given by However, due to the non-locality of quantum mechanics, we assume that the distance is a classical notion that can be derived from quantum gravity theory in the classical limit. When discussing this global symmetry, we should try to avoid using classical notions such as coordinates and distances. Here, we cannot present more details about $f\left(r\right)$. We now define the effective masses of particle 1 and particle 2 as Thus, Eq. (16) can be written as If these two particles are free particles, we have $w_1\to \infty$ and $w_2\to \infty$, thus the effective masses drop to zero. It implies that before measurement, a truly free quantum particle as the source of energy and momentum does not produce gravity. On the other hand, a free particle can be regarded as a massive particle whose Compton wavelength approaches infinity in the limit $\mu \to 0$. Obviously, as the mass decreases, gravity weakens.

In this paper, all considerations are based on treating the object together with the surrounding space as an indivisible whole, and then analyzing the maximum symmetry of this system at the quantum level. We don’t need to be perplexed by the indeterminacy of quantum mechanics since it is actually a more natural state. We introduce a new quantity DS to measure the symmetry present in a system. We show that a massive particle carrying spin has intrinsic DS. In the case of a quantum particle trapped in a box, the walls of the box will experience an “osmotic pressure” generated by this particle since the system tends to be in a state with maximum symmetry. We might imagine that this particle is in a thermal bath and the walls of the box act as “semi-permeable membranes.” Here, for simplicity, we only consider the uniform spreading of energy in space. However, the procedure outline here may be used to include the spreading of energy in space-time. Similarly, the quantum spin tends to have an uncertain orientation to restore symmetry. More generally, any classical quantity with a definite spatial orientation has a broken symmetry and an uncertain orientation can restore symmetry at the quantum level. Thus, the linear momentum should also have uncertain direction at the quantum level.

According to the gauge field theory, a system containing a gauge field can maintain local symmetry. Hence, it is reasonable to investigate the symmetry of the system including objects along with their surrounding space-time as general relativity states that the gravitational field is the space-time itself. General relativity tells us that anything with energy or mass curves space-time. But general relativity does not tell us how gravity behaves with a quantum wave function. As a consequence, we cannot locate the curvature until the moment we measure it since this quantum particle is described by a wave function and could be anywhere prior to a measurement. Here, we define a gravitational effective mass. It is shown that before measurement, a free particle as the source of energy and momentum does not produce gravity. Furthermore, the vacuum energy of zero point fluctuations stems from purely quantum effects and is uniformly distributed throughout space. We may expect that it does not generate gravitational effects to avoid the humongous discrepancy between theoretical expectation and astrophysical observations. However, this guess needs a further exploration. Since little was known about quantum gravity, our intention was only to test the feasibility of this approach in the simplest possible framework and results are only adequate in the semi-classical case. We only focus on the mass source of gravity without showing other details. A deeper investigation into symmetry including space-time may shed more light on quantum gravity. I believe that a convincing theory of quantum gravity should be able to describe the gravitational properties of the vacuum fluctuations and to regulate the ultra-violet infinities that appear in the calculation of vacuum energy.