Preprint
Article
Application and Parameter Optimization of EKG Electrodes Based on the Wild Horse Optimizer in Horizontal Electric-Field Sludge Dewatering
Altmetrics
Downloads
102
Views
42
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
08 January 2024
Posted:
09 January 2024
You are already at the latest version
Alerts
Abstract
This study conducted experiments to optimize the electro-dewatering of sludge using a dynamic model calculation method and the Wild Horse optimizer. Specifically, we explored two factors that might influence dewatering: the composition of the electrode materials and the strength of the electrical field. Compared to other electrodes commonly used in electro-dewatering—such as RuO2/Ir2O3-Ti, graphite, Ir2O3/Ta2O5-Ti, and Ti—the Electro-kinetic Geosynthetics (EKG) electrode exhibited superior performance. This was determined by considering both energy consumption and model establishment. Our findings also identified electric-field strength as a crucial factor determining the final moisture content. As the electrical intensity increased, the dewatering effect improved, aligning with our model calculations. However, we observed a steep increase in energy consumption per kilogram of filtrate when the electric-field strength exceeded a certain threshold. To optimize the energy consumption of the dehydration process, we constructed a multi-factor model. The simulation results from this model confirmed that electric-field intensity is the primary factor affecting dehydration. It was established that 10 V/cm is a critical threshold for the process.
Keywords:
Subject: Environmental and Earth Sciences - Water Science and Technology
1. Introduction
The potential health risks associated with large amounts of dredged sludge have become a critical global issue. This sludge, which accumulates and concentrates various contaminants from communal/industrial wastewater, agriculture, shipping, and atmospheric deposition [1], poses significant challenges for disposal. And with ever more stringent legislation, the cost of sludge disposal is increasing [2], making the search for effective treatment methods imperative [3].
Sludge is a highly compressible, hydrophilic fluid, containing four types of water: free water (about 70%), interstitial water (about 20%), adsorbed water (about 7%), and binding water (about 3%) [4]. The complex structure and water distribution of sludge makes it challenging to dewater using conventional mechanical methods, which can only reduce the sludge water content to about 75% [5].
Currently, sludge dehydration treatment approaches mainly include physical dehydration, geotextile bag and ultrasonic treatment, chemical dehydration, coagulation sedimentation, and biological methods [6]. Interestingly, recent studies have shown electro-dewatering to be an effective method for improving sludge dewatering efficiency [7]. These studies typically apply a vertical electric field for sludge electro-dewatering, using pressure on the anode plate to perform a pressurized electro-dewatering process [8,9,10].
The mechanical-electrical dewatering process of sludge can be partitioned into five stages [11]. However, employing a vertical electric field introduces two issues: continuous moisture content reduction in the anode-attached sludge during dewatering; and gas concentration between the sludge and anode, generated from the electrode reaction. These phenomena markedly increase the system's resistance, consuming most of the facility’s voltage drop [12]. Although alternating electric fields have been explored to address these problems, results have been not satisfactory [13].
Recently, researchers have investigated electro-dewatering in a horizontal electric field, which, compared to the widely-used vertical field methods, offers advantages such as straightforward construction, efficiency, and ease of operation [14,15,16].
It has been hypothesized that the electrode plate material used, and the electric-field strength applied, could significantly influence electro-dewatering efficiency [17,18]. Some studies have found that inert electrode materials, such as titanium, exhibit better corrosion resistance and thus provide superior sludge dewatering performance compared to activated metal electrodes [19].
More recently, a novel material—Electro-kinetic Geosynthetics (EKG)—has been proposed for use in electro-dewatering [20]. EKG, similar in appearance to ordinary plastic drainage boards, is composed of electrode polyethylene (PE), polypropylene (PP), and other polymers, with added graphite and carbon black for electrical conductivity. It has been compared with other widely used electrode materials in this field, aiming to find a more practical electrode material for dewatering.
Additionally, the electric-field strength has a significant influence on the electro-dewatering process of sludge. Previous studies have shown that as the electric-field strength increases, the moisture content of the sludge decreases, and the dewatering effect improves. However, it is also important to note that when the electric-field strength exceeds a certain threshold, the energy consumption per kilogram of filtrate correspondingly increases sharply [21].
Previous studies have also aimed to improve electric power dehydration efficiency and reduce energy consumption [3,22,23]. To optimize the energy consumption of the dehydration process, we have constructed a multi-factor model using the Wild Horse optimizer. Through simulations, we confirmed that electric-field intensity is the primary factor affecting dehydration. This model also established that 10 V/cm is a critical threshold for the process. This value serves as a balance point, where any increase in the electric-field strength beyond this point results in a disproportionate increase in energy consumption.
The results of this study and the constructed model can contribute to the practical application of electro-dewatering in horizontal electric fields. By providing a more energy-efficient method of sludge dehydration, we hope to help resolve the issue of sludge disposal.
2. Materials and methods
2.1. Sample collection and pretreatment
The sludge samples used in this study were sourced from Tanghe Sewage Reservoir, located in Hebei, China. Four distinct locations were identified for sample collection: #1 (E115.666760°, N38.796865°), #2 (E115.666791°, N38.796857°), #3 (E115.666959°, N38.796930°), and #4 (E115.66777°, N38.796939°). The primary characteristics of the original sludge samples are detailed in Table 1.
Before initiating the experiments, we undertook a thorough preparation process for the sediment samples. First, the samples were filtered using a 10-mesh sieve to remove larger particles, such as stones and plant fibers. Following this, we air-dried the samples for several hours until no additional water could be drained. This step was crucial to ensure the smooth operation of the subsequent electro-dewatering process.
Once dried, the sludge samples were mixed proportionally, to maintain consistency throughout our experiments. As the final step in our sample preparation, the samples were stored at a temperature of 4 °C until the time of testing.
2.2. Experimental procedures
Previous research has investigated the use of a horizontal electric field with external pressure for dewatering, such as the study conducted by Citeau et al. [24]. Another approach, developed by Zhou et al. [25], used a relatively simple device that operates without external pressure.
In this study, we adopted the latter approach, utilizing a horizontal electric field dewatering facility without external pressure. The schematic of this setup is shown in Figure 1(a), and the structure of the sludge tank is depicted in Figure 1(b). The tank was 20 cm long, 10 cm wide, and 10 cm high. It had 28 round holes, each with a 5-cm radius, located under the cathode area. A water-receiving funnel was positioned at the bottom of the opening, and electrode plate slots were arranged every 4 cm along the length of the tank.
To intercept soil particles, a 300-mesh filter cloth was placed at the cathode. An electronic balance recorded the mass of the water removed, which was collected in a water storage bottle. Due to the high rate of electrodynamic dewatering, we recorded the water removal quality, sediment temperature, and current intensity at various intervals: every 1 min during the first 30 min, every 5 min from 30 to 60 min, every 10 min from 60 to 120 min, and every 20 min from 120 to 240 min.
To maintain a consistent contact area between the sample and the electrode plate across the different electrode plate spacing experiments, we added a consistent amount of sample—37.5 g per cm of electrode plate spacing.
For the part of the study investigating electrode materials, we set the electrode space at 4 cm and the voltage at 30 V. We selected the EKG electrode for the studies based on the influence of electric-field strength (which we will discuss in detail in Section 3.2). The electrode plate spacing was fixed at 2 cm, and the voltage gradient was set to four different values: 20 V, 30 V, 40 V, and 50 V, corresponding to electric-field strengths of 10 V/cm, 15 V/cm, 20 V/cm, and 25 V/cm, respectively.
Upon completion of the dewatering process, we calculated the water content of the sludge based on the mass of the water removed. We also calculated the energy consumption of the electric dewatering of the sludge, based on the change in current.
2.3. Analysis method for experimental results
The dependent variables in our study—final dry solid content, energy consumption, and dehydration yield of electro-dynamic dewatering—are expressed as functions of independent variables (referred to as response functions) and are described by Eq. (1). The variance evaluation of each dependent variable is segmented into linear, quadratic, and interactive parts. Furthermore, the responses of all experimental regions were anticipated using a binary nonlinear fitting function [26,27]:
In Eq. (1), z represents the predicted response (dry solids content, energy consumption, and dehydration yield); a is the intercept; b and c are the linear term coefficients; d, e, and f are the quadratic term coefficients; and x and y represent the voltage and plate spacing variables, respectively.
Determining the coefficient is essentially a process of solving an optimization problem—that is, identifying a suitable set of coefficients to minimize the mean square error (MSE) between the predicted response and the actual value.
This is where the Wild Horse optimizer [28] plays a pivotal role. Introduced in 2021, the Wild Horse Optimizer is a novel swarm intelligence algorithm known for its outstanding simplicity, optimization capability, and search accuracy. Its advantages over earlier particle swarm optimization algorithms and simulated annealing algorithms underscore its innovative contribution to this field.
In our study, we used the MSE [29] as the fitness function (described by Eq. (2)), and employed the Wild Horse optimizer to fine-tune the parameters, thereby enhancing the model's fitting accuracy.
In Eq. (2), MSE represents the Mean Square Error, n is the number of samples, is the sum of the errors of all the samples, Yi is the actual value, and is the predicted value.
3. Results and discussion
3.1. Effect of different electrode materials on dewatering efficiency
The changes in dehydration mass over time during the electroosmotic dewatering process with different electrode materials are shown in Figure 2(a). Based on previous research [30], the electroosmotic dewatering process can be divided into three stages: rapid dehydration, slow dehydration, and minimal dehydration. As can be seen from Fig. (a), in this experiment, Stage I (0-30 min) corresponds to the rapid dehydration phase, Stage II (30-140min) represents the slow dehydration phase, and Stage III (140-240 min) indicates the minimal dehydration phase, except for the Ti electrode.
This anomaly with the Ti electrode can be attributed to the characteristic nature of Ti as a threshold metal. When an electrical field is present, a dense metal oxide film rapidly forms on its anode, hindering further corrosion of the inner metal layer. Simultaneously, its resistance quickly increases, resulting in a rapid rise in the anode voltage drop. Consequently, the voltage drop used for the sludge cake decreases rapidly—an occurrence not conducive to dehydration.
After a comprehensive comparison of the dehydration effects of the five electrode materials, the final water removal quality was ranked as follows: EKG > Ir2O3/Ta2O5-Ti > RuO2/Ir2O3-Ti > Graphite > Ti. Compared to metal oxide-coated electrodes, the EKG electrode demonstrates a comparable, and slightly superior, dehydration performance. The Graphite electrode ranks next in efficiency, while the Ti electrode exhibits the least effective dehydration results.
Figure 2(b) illustrates the time-dependent changes in sludge temperature during the dehydration process with different anode materials. Irrespective of the material type, the sludge temperature saw a rapid rise within the initial 30 minutes after power activation, peaking between 15 and 25 minutes—a phase that aligns with earlier studies [30].
Following this initial phase, a consistent decrease in temperature was observed. This can be attributed to the low resistance of the sediment at the onset, leading to high heat production rates and a rapid temperature rise. As dehydration proceeded, the sediment's moisture content dropped, resistance increased, and the rate of heat production slowed, causing a consequent decrease in sludge temperature.
Interestingly, the peak temperature for the electrode with the Ti-based coating occurred earlier and was higher than for the other materials. Conversely, the graphite electrode displayed the lowest peak temperature, accompanied by significant fluctuations around the peak. The EKG electrode's peak temperature was slightly delayed compared to those observed for the other electrodes, with the highest temperature lower than that of the Ti-coated electrode.
Prior research suggests that even though a temperature rise in the sediment can lead to greater energy consumption, it facilitates water removal [31]. The increased temperature reduces soil viscosity to a certain extent, accelerating water molecule movement.
During the slow dehydration phase following the initial 30 minutes, the sludge temperature under the EKG electrode was consistently higher than that under the other electrodes. Upon examining Figure 2(a), it can be seen that the EKG electrode also maintained a higher dehydration rate than the other electrodes during this stage, and it achieved the greatest volume of water removal by the end of the slow dehydration stage. These findings not only reaffirm that an increase in temperature facilitates water removal; they also demonstrate the superior effectiveness of the EKG electrode in electroosmotic dewatering.
Figure 2(c) presents the variation in current during the dewatering process for the four types of electrodes. Notably, barring the Ti anode, an initial brief increase in current was observed in the process, followed by a swift decline after peaking.
This initial surge in current can be primarily attributed to the fact that the voltage was predominantly applied to the sludge cake at the process's inception. At this stage, polar water molecules and electrolyte ions were moving rapidly. Concurrently, moisture was accumulating on the cathode, while it had not yet dissipated at the anode.
Such conditions led to a decrease in the resistance between the electrode plate and the soil. Consequently, the sludge cake's temperature skyrocketed, and the thermal motion of water molecules and other ions accelerated. This, in turn, reduced the sludge cake's resistance, causing a short-term increase in the current [32,33].
As the process continued, the moisture content of the mud cake decreased. This led to a drastic increase in resistance near the anode within the sludge, and the current consequently dropped significantly.
Figure 2(d) illustrates the energy consumption per unit mass of water removed after electroosmotic dewatering using the different electrode materials. The energy consumption for Ti, RuO2/Ir2O3-Ti, EKG, Ir2O3/Ta2O5-Ti, and Graphite electrodes per unit mass of water removed were 0.299 kWh/kgH2O, 0.359 kWh/kgH2O, 0.346 kWh/kgH2O, 0.359kWh/kgH2O, and 0.379 kWh/kgH2O, respectively. Lower energy consumption indicates higher energy utilization efficiency.
Therefore, the relative energy utilization efficiencies of the five types of electrodes during the electroosmotic dewatering process is as follows: Ti > RuO2/Ir2O3-Ti > EKG > Ta2O5-Ti > Graphite. Excluding the Ti electrode, the RuO2/Ir2O3-Ti and EKG electrodes demonstrated superior performance, followed by the Ir2O3/Ta2O5-Ti electrode, with the Graphite electrode performing the worst.
In the present study, we conducted a fitting of the energy consumption and water removal quantity during the dehydration process for the different electrode materials. This resulted in obtaining both actual change curves and fitting curves for dehydration energy consumption and dehydration quality for each electrode material.
Figure 3 presents these findings. Impressively, the curves for all five test groups demonstrated linear relationships, which can be expressed by (Eq. 3):
where ‘a’ and ‘b’ are fitting coefficients. These coefficients are influenced by the electrode material and the physicochemical properties of the underlying mud.
y = ax + b
In the context of this study, the voltage applied directly to the two sides of the soil for electrical dehydration is defined as the effective voltage (Ve). Given the existence of an interface resistance between the polar plate and the soil, the expression for the effective voltage is given by (Eq. 4):
Ve = V0-Vc-Vd
Here, V0, Vc, and Vd represent the power supply output voltage, the anode potential drop, and the cathode potential drop, respectively.
During the electrical dehydration process, the slope of the fitted curve is inversely proportional to the energy consumption utilization rate [33]. According to Eq. (2), if the effective voltage (Ve) increases while the power supply output voltage (V0) remains unchanged, a smaller anode potential drop (Vc) would indicate a more stable electrode.
Interestingly, the fitting results shown in Figure 3 reveal that the order of the slopes of the curve is RuO2/Ir2O3-Ti < EKG < Ir2O3/Ta2O5-Ti < Graphite < Ti. Therefore, the RuO2 / Ir2O3-Ti and EKG electrodes exhibited the greatest stability.
Figure 4 provides a visual representation of the corrosion observed in several anode anti-corrosion electrodes after being energized for 240 minutes. Notably, the Ti electrode underwent a considerable color change on its surface. This alteration was attributed to the formation of an oxide film [33], which effectively prevented internal corrosion. In contrast, the RuO2 / Ir2O3-Ti– and Ir2O3 / Ta2O5-Ti–coated electrodes demonstrated negligible corrosion. This observation underscores the superior anti-corrosion properties of these electrodes, a characteristic that has earned them frequent use in the field of electrochemistry. However, the graphite electrodes displayed a significantly higher degree of corrosion. Evidence of extensive pitting was apparent, likely due to fluctuating current during the dehydration process. Last but not least, the EKG materials showed no discernible corrosion on the electrode. This result is comparable to that of the precious metal titanium-based coated electrode, further emphasizing the robustness of EKG materials in resisting corrosion.
3.2. Influence of electric-field strength on EDW
Analysis of Figure 5 suggests a tripartite division of the dewatering process into distinct stages of rapid dehydration, slow dehydration, and minimal dehydration. The rate of dehydration, denoted by the curve's slope, progressively diminishes, culminating in a plateau of water removal and a stabilization of the final dehydration effect. Concurrently, the electric current exhibits a transient initial increase followed by a swift decrease, eventually tapering off to zero. The temperature profile is characterized by a rapid ascendancy, subsequent decline, and ultimate stabilization around ambient conditions.
A close examination of the trend across these three parameters reveals a noteworthy alignment between the rapid dehydration stage and the periods of swift temperature surge and current decline in the sludge. The transition to the slow dehydration phase coincides with the temperature peaking, mirrored by a slower decrement in the electric current. As dehydration enters the negligible stage, both the temperature and the current approach a state of stability. This is attributed to an escalated resistance in the sludge cake, consequent to water removal and sludge cracking, leading to a reduction in current and deceleration of heat generation.
We can see from Figure 6(a) that with an increase in voltage, the initial rate of the electrodynamic dehydration stage also rose. When the voltages were 20 V, 30 V, 40 V, and 50 V, the times required to reach the basic non-dehydration stage were 100 min, 80 min, 55 min, and 100 min, respectively. The final moisture contents of the four groups of experimental samples were 60.3%, 50.16%, 48.05%, and 47.12%. It can be seen that as the voltage increased, the final moisture content of the sediment decreased, indicating that larger electric-field strength contributed to the final electrodynamic dehydration and curing effect. As the voltage increased from 20 V to 30 V, the rate of dewatering increased by 10.14%. However, when the voltage increased from 30 V to 40 V and from 40 V to 50 V, the rate of dehydration increased by 2.11% and 0.93% respectively. According to the experimental results depicted in Figure 6(a), during the dewatering process, if the voltage continued to increase at the higher voltages, the improvement in dehydration rate gradually decreased, perhaps because the sludge layer near the anode dried and cracked under the large electric-field strength. One possible explanation for this result is that high voltage could lead to excessive current, which might cause a large amount of gas near the anode drying electrode to increase the resistance. Another possibility is that the cracking of the sludge near the anode led to a reduction in the contact area between the sludge cake and the electrode plate [23].
Figure 6(b) shows the temperature variation curve for the sediment in the electric dehydration process. The times required to reach the highest temperature, for the four groups of experimental samples, were 17 min, 14 min, 10 min, and 7 min. The highest temperatures reached were 84.3℃, 93.9℃, 99.1℃, and 99.5℃. It can be seen that it took more time to reach the peak temperature when the voltage was higher. The peak temperature itself also rose with the voltage. When the voltage increased from 20 V to 30 V, the peak temperature increased by 9.6℃, while when the voltage increased from 30 V to 40 V and from 40 V to 50 V, the peak temperatures increased by 5.2℃ and 0.4℃, respectively. It can be concluded, then, that "40 V" was the extreme point in this experiment. After this point, the temperature increased less as the voltage rose. As mentioned above, dewatering occurred mainly in the rapid dehydration stage, as expected for the rapid temperature rise. The increase in temperature was beneficial to the removal of water. The experiment also showed that as the voltage increases, the temperature drops more sharply from its peak value, and the improvement in the dehydration rate decreases. The higher voltage improves the dehydration effect as the water content decreases, but the drying out of the anode then causes the soil to crack, increasing the resistance (Ma et al., 2020; Jing et al., 2014; Glendinning et al., 2010).
Figure 6(c) outlines the variation in the loop current over time under different voltage settings. The initial currents for the voltages of 20 V, 30 V, 40 V, and 50 V were 1.34 A, 2.50 A, 3.35 A, and 3.38 A, respectively. This indicates a direct relationship between voltage and initial current, with the latter escalating as the voltage increases. In the first 60 minutes of the experiment, a rapid decrease in the current was observed across all groups, particularly in the first half hour. Beyond the 60-minute mark, the currents for all four groups stabilized, gravitating toward 0.01 A. However, a deviation was observed during the initial 60-minute period at different voltages. The initial current values were higher at 40 V and 50 V, but these also experienced a sharper decline. This rapid decrease was especially pronounced at 50 V, where the accelerated dewatering process caused the sediments around the anode to dry out quickly, leading to significant soil cracking. This soil cracking increased the sediment resistance, which subsequently resulted in a decrease in the loop current. Thus, it can be concluded that as the voltage increased, the current decayed more quickly.
We employed MATLAB software and incorporated the Wild Horse algorithm to fit the curve representing the change in sediment moisture content over time in the electrodynamic sediment dewatering test. After several iterations, an effective fit was achieved using both exponential and Gaussian functions. The results of this fitting process are shown in Table 2.
Upon analysis, it was evident that the degree of fit (R²) for the 2-dimensional Gaussian function was higher than the exponential function across all groups in the dewatering experiment tests conducted at various voltages. This observation suggests that the relationship between water content and time during the process of electrodynamic dehydration of sediment better aligns with the 2-dimensional Gaussian function. The empirical model for this relationship is presented in Eq. (5), where a1, b1, a2, and b2 are empirical constants.
Leveraging this equation, we were able to obtain real-time predictions of the sediment's water content. These findings not only highlight the effectiveness of our approach but also provide useful insights for future investigations in this area.
Several previous studies have found a linear relationship between the dehydration rate and the current [34,35]. Consistent with this, [36] discovered that the electrodynamic dehydration effect was more pronounced at higher applied current densities.
In our study, the observation of Figure 7 reveals an obvious trend: the degree of curve fitting increases with the voltage. A closer look at the four fitting curves demonstrates that the actual flow rate near the current 0.5 A exceeds the midpoint of the fitting curve. When we juxtapose this with Figure 5, it becomes apparent that a current of 0.5 A corresponds to the peak temperature of the sediment.
Based on these observations, we conjectured that the dehydration rate is influenced not just by the current density, but also by the temperature of the sediment [34].
As depicted in Figure 8(a), the total energy consumption and unit water energy consumption for 240 minutes of dehydration vary with different voltages. The overall energy consumption during dehydration is significantly influenced by the voltage, indicating that the electric-field strength is a critical factor in the energy consumption of electric-power dehydration.
Given a constant plate spacing, an increase in voltage benefits the dehydration process. However, it also results in elevated energy consumption. Thus, in line with the findings of [35], the selection of an appropriate voltage requires a careful balance between energy consumption and the effectiveness of dehydration.
Further analysis of Figure 8(b) reveals that the least energy per kilogram of water was consumed at a voltage of 30 V.
3.3. Construction of prediction model
In the field of sludge dewatering, controlling and optimizing operational conditions is essential, to enhance efficiency and achieve desirable results. In this context, we established a response model that accounts for two key variables: electric-field strength and plate spacing.
The electric-field strength, in our model, ranges from 0 to 25 V/cm, and the plate spacing varies from 2 to 8 cm. These ranges were determined based on our experimental setup and the constraints of our equipment.
We implemented the Wild Horse algorithm in our model to predict the response interval. This algorithm, known for its robustness and accuracy, helps us understand the impact of changing operational conditions on the final solid content capacity and dewatering yield.
To ensure the validity of our model, we conducted a model verification process. This involved comparing the model's predictions against actual experimental results, in order to ascertain the model's predictive capability.
We also carried out a significance analysis to ascertain the statistical significance of our findings, to help us ensure that the observed effects were not merely due to chance.
Drawing on insights from the response model, we can optimize the operational conditions for electrodynamic sediment dewatering. By adjusting the electric-field strength and plate spacing according to the model's predictions, we can maximize the final solid content capacity and dewatering yield.
This approach not only improves the efficiency of the dewatering process but also provides a methodological framework that other researchers can use to optimize similar systems. Beyond its immediate application, this model serves as a valuable contribution to the broader field of sediment management and environmental engineering.
Figure 9(a) illustrates the variation curve of the final solid content and the electric-field intensity at different plate spacings. It becomes evident that with specific plate spacing, the final solid content of the sediments undergoing electrical dewatering increases with the electric-field intensity. This relationship, however, is not linear.
In the initial stages, substantial increases in final solid content are observed with increments in electric-field intensity. For instance, when the electric-field intensity is increased from 10 V/cm to 15 V/cm, the dry solid content is boosted from 39.7% to 49.84%, marking an increase of 25.54%.
However, beyond an electric-field intensity of 10 V/cm, further increases in field intensity result in relatively smaller increments in the final solid content. As an example, a rise in electric-field strength to 20V leads to a mere 4.23% increase in dry solid content (49.84% to 51.95%).
This indicates, as supported by [15], that the impact of increasing electric-field strength on the final solid content is significant at low electric-field strength but diminishes as the field strength increases beyond a certain point. It reaffirms the necessity of optimizing electric-field intensity to achieve efficient sediment dewatering.
Figure 9(b) shows the response model of the final solid content affected by the electric-field intensity and plate spacing, and its functional relationship is shown in Eq. (6):
Z=36.4273017-1.9873478x+0.80859633y+0.03050157x2-0.01622y2+0.2038898xy
(R2=0.9286947, MSE=3.7321915)
where x and y represent plate spacing and electric-field strength, respectively, and Z represents the final solid content. From Eq. (6), it can be found that without considering the expression of quadratic and interaction terms, Z is negatively correlated with x and positively correlated with X, indicating that the final solid content is negatively correlated with plate spacing and positively correlated with electric-field intensity. Therefore, increasing plate spacing is not conducive to improving the final solid content, but increasing electric-field intensity is.
As depicted in Figure 9(c), the relationship between energy consumption per unit mass of water and electric-field intensity is demonstrated at different plate spacings. For a given plate spacing, the energy consumption of electro-dynamic dehydration for sediment escalates with increasing electric-field intensity. Similarly, at a constant electric-field intensity, the energy consumption of electro-dynamic dehydration rises with an increase in plate spacing.
The practicality of electro-dynamic dehydration predominantly hinges on the cost of power. When energy consumption becomes too high, the technology loses its practicality, rendering it an inefficient solution. Consequently, the application of a low electric-field intensity holds practical significance for enhancing the cost efficiency of electrodynamic dehydration.
This observation aligns with the findings of [37], who established that the appropriate application of electric fields can result in significant energy savings. Therefore, by optimizing the electric-field intensity and plate spacing, we can strike a balance between operational efficiency and energy consumption, thereby improving the overall cost efficiency of sediment dewatering processes.
Figure 9(d) shows the response model of dehydration energy consumption affected by electric-field intensity and plate spacing, and its functional relationship is shown in Eq. (7):
Z=0.00102+0.07226473x+0.0098334y-0.0045783x2+8.1675∗10-5y2+0.0016057xy
(R2=0.7174657, MSE=0.0012978)
where x and y represent plate spacing and electric-field intensity respectively, and Z represents the energy consumption per unit mass of water removed. From Eq. (7), it can be found that without considering the expression of quadratic and interaction terms, Z and x are positively correlated, indicating that the final solid content is positively correlated with plate spacing and electric-field intensity. Therefore, increasing plate spacing and electric-field intensity will increase energy consumption, which is not conducive to energy saving or consumption reduction.
The rate of water yield is defined as the mass unit of filtrate (kgH2O/(kg·h) per kilogram of solid content per hour. The relationship between water yield and electric-field strength under different plate spacings is shown in Figure 9(e), which is similar to Figure 9(a). It can be seen that the higher the electric-field strength, the higher the rate of dehydration. After the electric-field strength rose above 10 V/cm, the dehydration yield grew more slowly with the increase of electric-field strength. Therefore, increasing the electric-field strength at low electric-field intensity (< 10 V/cm) was more effective for improving the dehydration yield.
Figure 9(f) shows the response model of water loss rate affected by electric-field intensity and plate spacing, and its function relationship is shown in Eq. (8):
Z= 0.5 -0.0763388x -0.0042212y+ 0.0023774 x2-3.361∗10-5 y2 +0.0066174xy
(R2=0.9304939, MSE=0.0009287)
where x and y represent plate spacing and electric-field intensity respectively, and Z is the dehydration rate. It can be found from Eq. (8) that when quadratic and interactive expressions are not considered, Z is negatively correlated with x and positively correlated with y, which indicates that the water removal rate is negatively correlated with plate spacing and positively correlated with electric-field intensity. Therefore, neither increasing plate spacing nor reducing electric-field intensity is conducive to improving the water removal rate.
4. Conclusion
The application of electro-dewatering on river sediment was investigated using a cake thickness of 4 cm and a voltage of 30 V. This procedure involved five types of electrode materials: EKG, Ti, RuO2/Ir2O3-Ti, Graphite, and Ir2O3/Ta2O5-Ti, all tested over a period of 4 hours. Experimental findings revealed that the EKG electrode exhibited superior stability during the dewatering process. Importantly, the EKG electrode also demonstrated excellent performance in terms of energy consumption.
An evaluation of electrode corrosion after the experiment showed that the EKG electrode possessed corrosion resistance comparable to the most expensive Ti-coated electrode. Furthermore, the EKG electrode displayed both merits and drawbacks in model simulation. In summary, the EKG electrode presents clear advantages in electro-dewatering.
To further explore the influence of electric-field intensity on the parameters of sludge dewatering and construct a prediction model using an EKG electrode, a detailed study was conducted. It was found that the relationship between water content and time in the process of electrodynamic dehydration of sediment conformed to a two-dimensional Gaussian function. Notably, when the electric-field intensity exceeded 10 V/cm, the water removal rate increased only minimally with increased electric-field intensity.
This result suggests that boosting the electric-field intensity is more effective for improving the dehydration yield at low electric-field intensities (< 10 V/cm), but that beyond this point, the dehydration effect did not significantly improve, while energy consumption increased substantially.
A multi-factor model of dewatering was constructed using mud cake samples with thicknesses of 2 cm, 4 cm, 6 cm, and 8 cm, treated at 20 V, 30 V, 40 V, and 50 V. This model was used to optimize the energy consumption of the dehydration process. The findings confirmed that 10 V/cm represents a critical point in the electro-dewatering process.
Acknowledgments
This work is supported by the National Natural Science Foundation of China (52170097), Beijing Natural Science Foundation (9222017), the Project of Construction and Support for high-level Innovative Teams of Beijing Municipal Institutions (BPHR20220108), the Open Research Fund of State Environmental Protection Key Laboratory for Lake Pollution Control (2022HPYB-06) and the Fundamental Research Funds for the Central Public-interest Scientific Institution (2022YSKY-02).
Disclosure statement
The authors declare no competing interests.
References
- Li, Y.; Yang, F.; Miao, S.; Wang, D.; Li, Z.; Yuan, X.; Yuan, L.; Liu, Q. Achieved deep-dewatering of dredged sediments by Fe(II) activating persulfate pretreatment: Filtrating performance and mechanistic insights. Chemical Engineering Journal 2021, 405. [Google Scholar] [CrossRef]
- Chu, X.; Ni, Y.; Wang, X.; Chu, Z. A win-win situation for environment and economy: Analysis of maximizing benefits in municipal sludge treatment plants. Journal of Cleaner Production 2023, 419. [Google Scholar] [CrossRef]
- Sun, X.; Ma, D.; Lin, S.; Wang, Y.; Liu, Q. Research on push-type sludge electro-dewatering equipment with fixed-plate electrodes. Separation and Purification Technology 2021, 267. [Google Scholar] [CrossRef]
- Yuan, H.; Zhu, N. Progress of improving waste activated sludge dewaterability: Influence factors, conditioning technologies and implications and perspectives. Science of The Total Environment 2023. [Google Scholar] [CrossRef] [PubMed]
- Vorobiev, E. Predictive model of constant rate expression for dewatering of semi-solid materials. Chemical Engineering Science 2023, 272. [Google Scholar] [CrossRef]
- Wei, Q.; Liu, X.; Zhang, Y.; Zhang, K.; Li, Z.; Shen, Z.; Chow, C.W.K. Effect of tannic acid on the dewaterability of dredged sediment and the conditioning mechanism. Journal of Environmental Chemical Engineering 2021, 9. [Google Scholar] [CrossRef]
- Sun, X.; Ma, D.; Lin, S.; Wang, Y.; Liu, Q. Research on push-type sludge electro-dewatering equipment with fixed-plate electrodes. Separation and Purification Technology 2021, 267, 118612. [Google Scholar] [CrossRef]
- Zhang, Y.; Lian, G.; Dong, C.; Cai, M.; Song, Z.; Shi, Y.; Wu, L.; Jin, M.; Wei, Z. Optimizing and understanding the pressurized vertical electro-osmotic dewatering of activated sludge. Process Safety and Environmental Protection 2020, 140, 392–402. [Google Scholar] [CrossRef]
- Sha, L.; Wu, Z.; Ling, Z.; Liu, X.; Yu, X.; Zhang, S. Dewaterability and energy consumption of electro-dewatered sludge near the anode and the cathode during electro-dewatering process. Journal of Environmental Chemical Engineering 2021, 9. [Google Scholar] [CrossRef]
- Li, C.; Zhao, M.; Ma, D.; Jia, X.; Zhang, F. Optimization of electro-dewatering performance of oily sludge by voltage control and coal-powdered activated carbon (CPAC) addition. Journal of Cleaner Production 2023, 426. [Google Scholar] [CrossRef]
- Liu, W.-H.; Zhang, H.; Zhang, Y.-L.; Sun, P.; Zeng, Y.-P.; Gao, Y.-Y.; Wang, H.-F.; Zeng, R.J. Beyond filterability: Understanding the complexities of sludge dewatering through typical coagulation and advanced oxidation. Journal of Cleaner Production 2023, 429. [Google Scholar] [CrossRef]
- Li, Y.; Liu, L.; Li, X.; Xie, J.; Guan, M.; Wang, E.; Lu, D.; Dong, T.; Zhang, X. Influence of alternating electric field on deep dewatering of municipal sludge and changes of extracellular polymeric substance during dewatering. Science of The Total Environment 2022, 842. [Google Scholar] [CrossRef] [PubMed]
- Yoshida, H.; Kitajyo, K.; Nakayama, M. ELECTROOSMOT1C DEWATERING UNDER A. C. ELECTRIC FIELD WITH PERIODIC REVERSALS OF ELECTRODE POLARITY. Drying Technology 1999, 17, 539–554. [Google Scholar] [CrossRef]
- Guo, X.; Wang, Y.; Wang, D. Permanganate/bisulfite (PM/BS) conditioning–horizontal electro-dewatering (HED) of activated sludge: Effect of reactive Mn(III) species. Water Research 2017, 124, 584–594. [Google Scholar] [CrossRef] [PubMed]
- Wu, P.; Shi, Y.; Wang, Z.; Xiong, Z.; Liu, D.; Gerson, A.R.; Pi, K. Effect of electric field strength on electro-dewatering efficiency for river sediments by horizontal electric field. Science of The Total Environment 2019, 647, 1333–1343. [Google Scholar] [CrossRef]
- Rao, B.; Pang, H.; Fan, F.; Zhang, J.; Xu, P.; Qiu, S.; Wu, X.; Lu, X.; Zhu, J.; Wang, G.; et al. Pore-scale model and dewatering performance of municipal sludge by ultrahigh pressurized electro-dewatering with constant voltage gradient. Water Research 2021, 189. [Google Scholar] [CrossRef]
- Xue, Z.; Tang, X.; Yang, Q. Influence of voltage and temperature on electro-osmosis experiments applied on marine clay. Applied Clay Science 2017, 141, 13–22. [Google Scholar] [CrossRef]
- Guo, X.; Qian, X.; Wang, Y.; Zheng, H. Magnetic micro-particle conditioning–pressurized vertical electro-osmotic dewatering (MPEOD) of activated sludge: Role and behavior of moisture and organics. Journal of Environmental Sciences 2018, 74, 147–158. [Google Scholar] [CrossRef]
- Zhang, Y.; Cao, M.; Lv, H.; Wei, J.; Gu, Y.; Liu, D.; Zhang, W.; Ryan, M.P.; Wu, X. Electrodeposited nanometer-size IrO2/Ti electrodes with 0.3 mg IrO2 cm−2 for sludge dewatering electrolysers. Electrochimica Acta 2018, 265, 507–513. [Google Scholar] [CrossRef]
- Martin, L.; Alizadeh, V.; Meegoda, J. Electro-osmosis treatment techniques and their effect on dewatering of soils, sediments, and sludge: A review. Soils and Foundations 2019, 59, 407–418. [Google Scholar] [CrossRef]
- Zhang, Q.; Cui, G.; He, X.; Wang, Z.; Tang, T.; Zhao, Q.; Liu, Y.-s. Effects of voltage and pressure on sludge electro-dewatering process and the dewatering mechanisms investigation. Environmental research 2022, 113490. [Google Scholar] [CrossRef] [PubMed]
- Deng, W.; Lai, Z.; Hu, M.; Han, X.; Su, Y. Effects of frequency and duty cycle of pulsating direct current on the electro-dewatering performance of sewage sludge. Chemosphere 2020, 243, 125372. [Google Scholar] [CrossRef] [PubMed]
- Ma, D.; Su, M.; Qian, J.; Wang, Q.; Meng, F.; Ge, X.; Ye, Y.; Song, C. Heavy metal removal from sewage sludge under citric acid and electroosmotic leaching processes. Separation and Purification Technology 2020, 242, 116822. [Google Scholar] [CrossRef]
- Citeau, M.; Larue, O.; Vorobiev, E. Influence of salt, pH and polyelectrolyte on the pressure electro-dewatering of sewage sludge. Water Research 2011, 45, 2167–2180. [Google Scholar] [CrossRef] [PubMed]
- Zhou, J.; Liu, Z.; She, P.; Ding, F. WATER REMOVAL FROM SLUDGE IN A HORIZONTAL ELECTRIC FIELD. Drying Technology 2001, 19, 627–638. [Google Scholar] [CrossRef]
- Shoesmith, E.; Box, G.E.P.; Draper, N.R. Empirical Model-Building and Response Surfaces. The Statistician 1988, 37, 82–82. [Google Scholar] [CrossRef]
- Mahmoud, A.; Olivier, J.; Vaxelaire, J.F.; Hoadley, A. Electro-dewatering of wastewater sludge: influence of the operating conditions and their interactions effects. Water research 2011, 45 9, 2795–2810. [Google Scholar] [CrossRef]
- Naruei, I.; Keynia, F. Wild horse optimizer: a new meta-heuristic algorithm for solving engineering optimization problems. Engineering with Computers 2021, 38, 3025–3056. [Google Scholar] [CrossRef]
- Hodson, T.O. Root-mean-square error (RMSE) or mean absolute error (MAE): when to use them or not. Geoscientific Model Development 2022. [Google Scholar] [CrossRef]
- Wu, P.; Shi, Y.; Wang, Z.; Xiong, Z.; Liu, D.; Gerson, A.R.; Pi, K.W. Effect of electric field strength on electro-dewatering efficiency for river sediments by horizontal electric field. The Science of the total environment 2019, 647, 1333–1343. [Google Scholar] [CrossRef]
- Weber, K.; Stahl, W.P.D. Improvement of filtration kinetics by pressure electrofiltration. Separation and Purification Technology 2002, 26, 69–80. [Google Scholar] [CrossRef]
- Reddy, K.R.; Urbanek, A.; Khodadoust, A. Electroosmotic dewatering of dredged sediments: bench-scale investigation. Journal of environmental management 2006, 78 2, 200–208. [Google Scholar] [CrossRef]
- Glendinning, S.; Mok, C.K.; Kalumba, D.; Rogers, C.D.F.; Hunt, D.V.L. Design Framework for Electrokinetically Enhanced Dewatering of Sludge. Journal of Environmental Engineering 2010, 136, 417–426. [Google Scholar] [CrossRef]
- Olivier, J.; Conrardy, J.-B.; Mahmoud, A.; Vaxelaire, J.F. Electro-dewatering of wastewater sludge: An investigation of the relationship between filtrate flow rate and electric current. Water research 2015, 82, 66–77. [Google Scholar] [CrossRef] [PubMed]
- Yu, W.; Yang, J.; Wu, X.; Gu, Y.; Xiao, J.; Yu, J.; Shi, Y.; Wang, J.; Liang, S.; Liu, B.; et al. Study on dewaterability limit and energy consumption in sewage sludge electro-dewatering by in-situ linear sweep voltammetry analysis. Chemical Engineering Journal 2017, 317, 980–987. [Google Scholar] [CrossRef]
- Mahmoud, A.; Hoadley, A.; Citeau, M.; Sorbet, J.M.; Olivier, G.; Vaxelaire, J.F.; Olivier, J. A comparative study of electro-dewatering process performance for activated and digested wastewater sludge. Water research 2018, 129, 66–82. [Google Scholar] [CrossRef] [PubMed]
- Mahmoud, A.; Hoadley, A.; Conrardy, J.-B.; Olivier, J.; Vaxelaire, J.F. Influence of process operating parameters on dryness level and energy saving during wastewater sludge electro-dewatering. Water research 2016, 103, 109–123. [Google Scholar] [CrossRef]
Figure 1.
(a) Schematic diagram of the experimental device; (b) Structure of the dehydration tank.
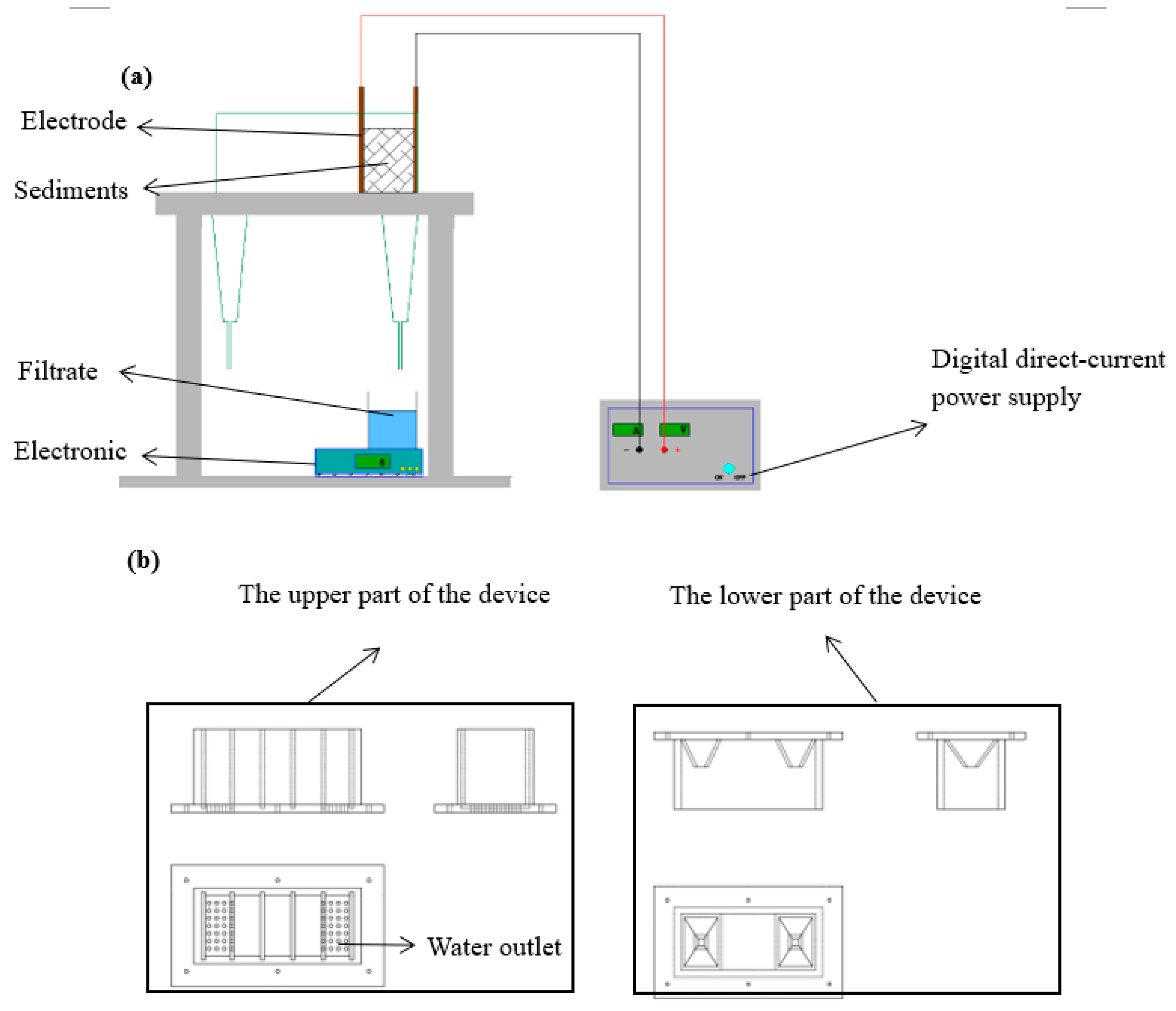
Figure 2.
(a) Change of water mass with time during the dewatering of the different electrode materials; (b) Variation of sediment temperature with time during the electro-dewatering of the different electrode materials; (c) Current over time, for the different electrode materials; (d) Energy consumption per unit mass of water removed for electro-dewatering of the different electrode materials.
Figure 2.
(a) Change of water mass with time during the dewatering of the different electrode materials; (b) Variation of sediment temperature with time during the electro-dewatering of the different electrode materials; (c) Current over time, for the different electrode materials; (d) Energy consumption per unit mass of water removed for electro-dewatering of the different electrode materials.
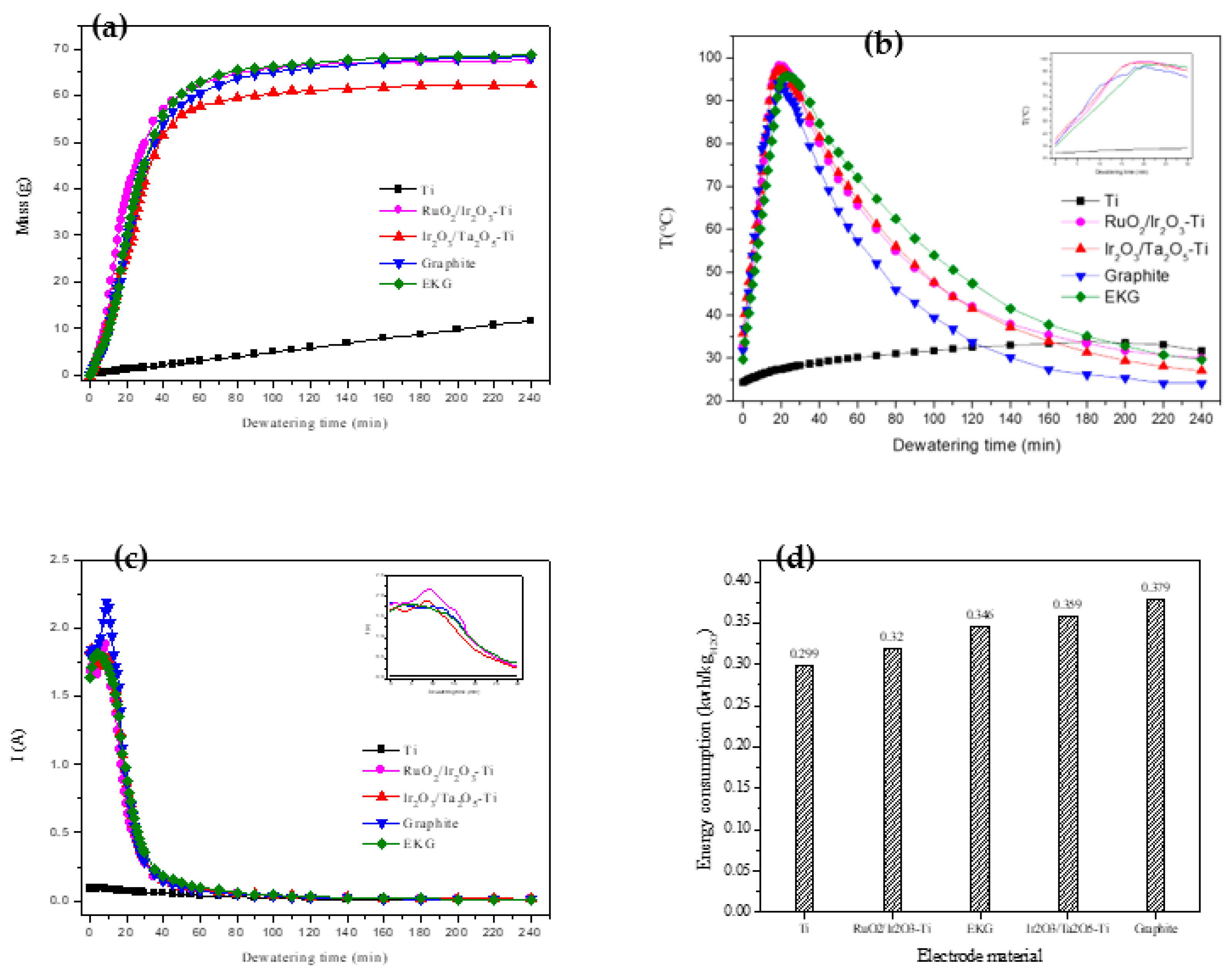
Figure 3.
Curves and fitting curves of energy consumption and dewatering water mass of different electrode materials.
Figure 3.
Curves and fitting curves of energy consumption and dewatering water mass of different electrode materials.
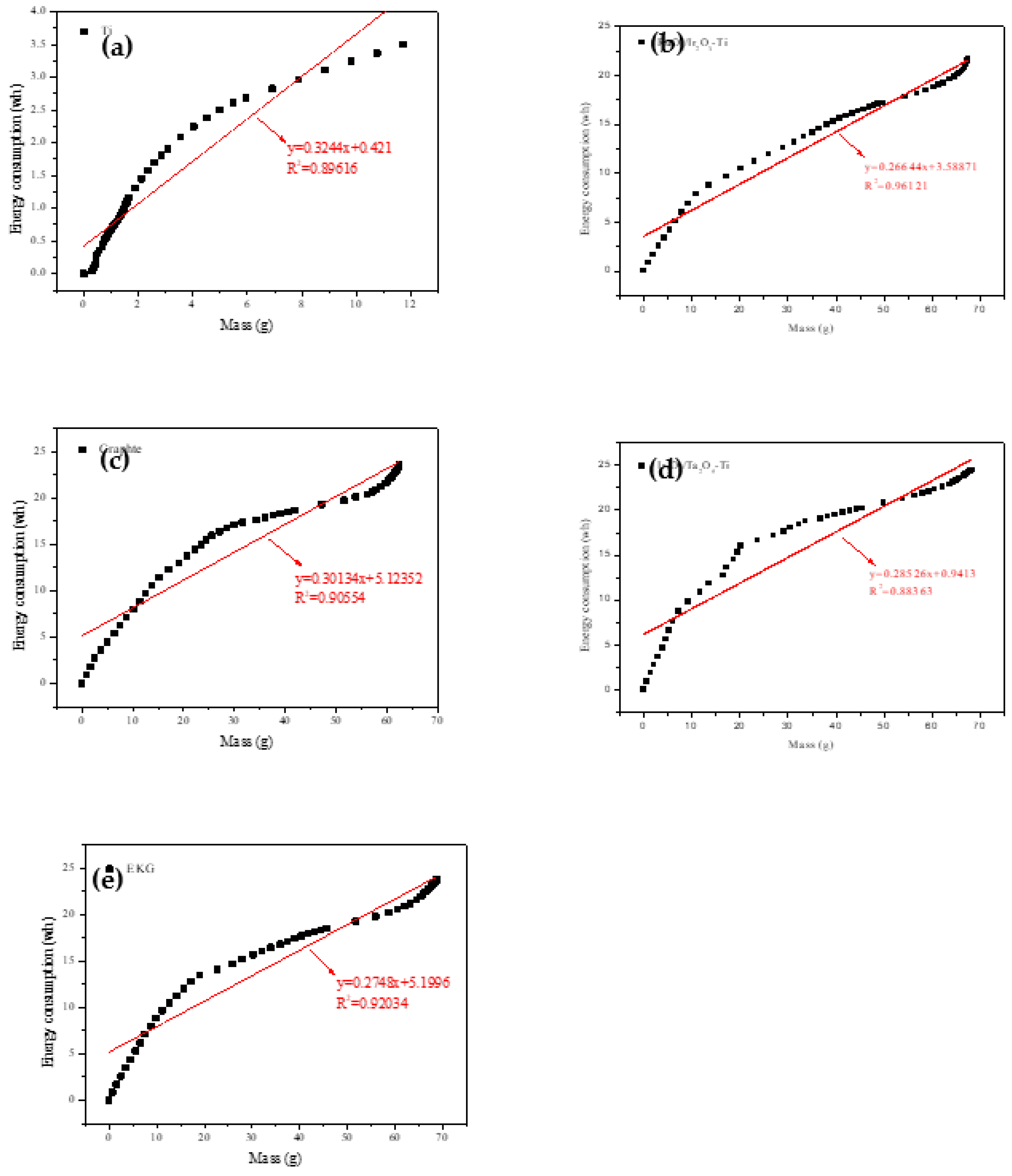
Figure 4.
Corrosion of the different electrode materials: (a) Ti electrode, (b) RuO2 / Ir2O3-Ti electrode, (c) Ir2O3 / Ta2O5-Ti electrode, (d) Graphite electrode, (e) EKG electrode.
Figure 4.
Corrosion of the different electrode materials: (a) Ti electrode, (b) RuO2 / Ir2O3-Ti electrode, (c) Ir2O3 / Ta2O5-Ti electrode, (d) Graphite electrode, (e) EKG electrode.

Figure 5.
Curves of water quality, current and temperature over time under different voltages.
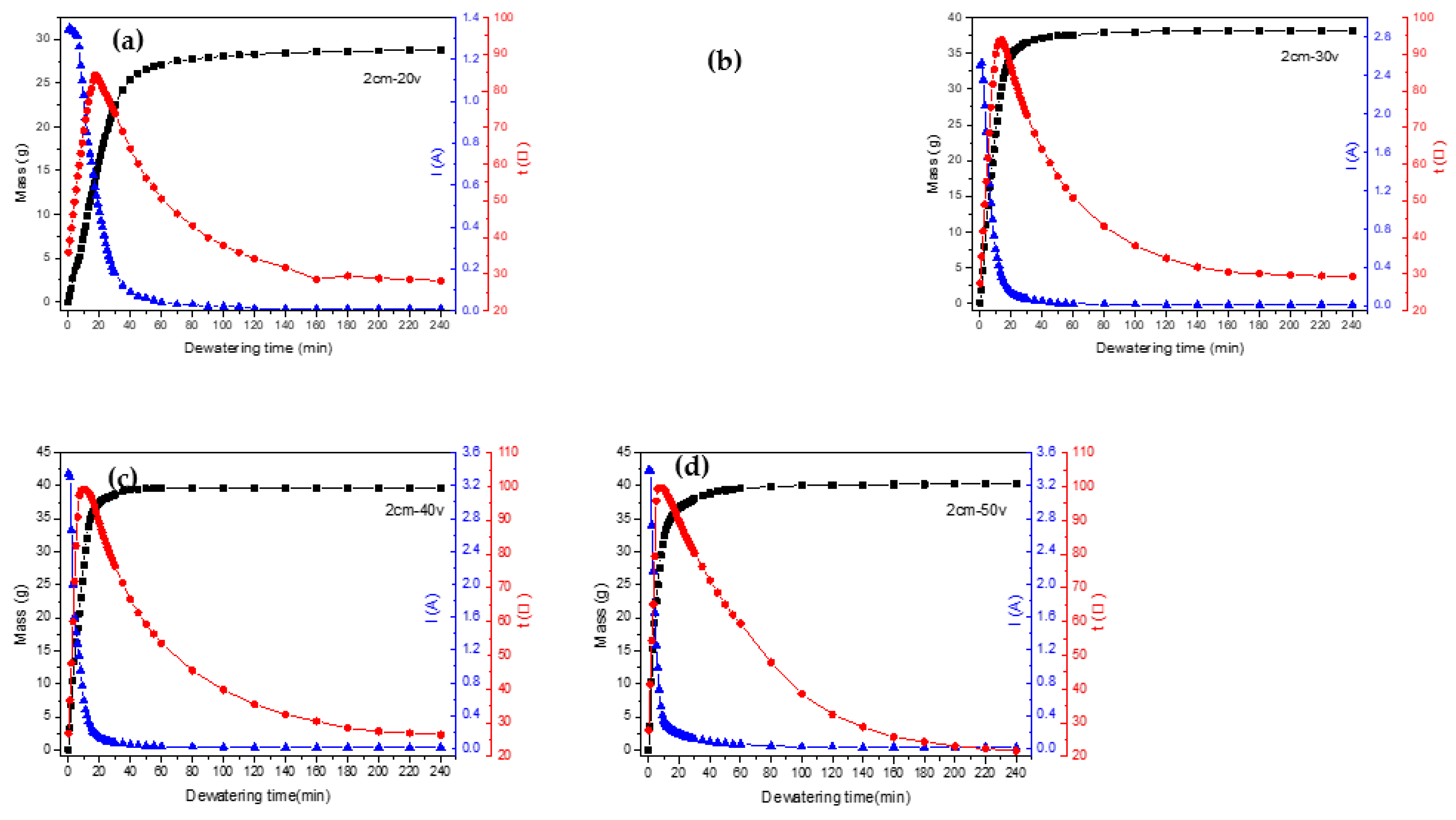
Figure 6.
(a) Change of water content with time during dewatering at different voltages; (b) Change of sediment temperature with time during dewatering at different voltages; (c) Change of current with time during dewatering at different voltages.
Figure 6.
(a) Change of water content with time during dewatering at different voltages; (b) Change of sediment temperature with time during dewatering at different voltages; (c) Change of current with time during dewatering at different voltages.
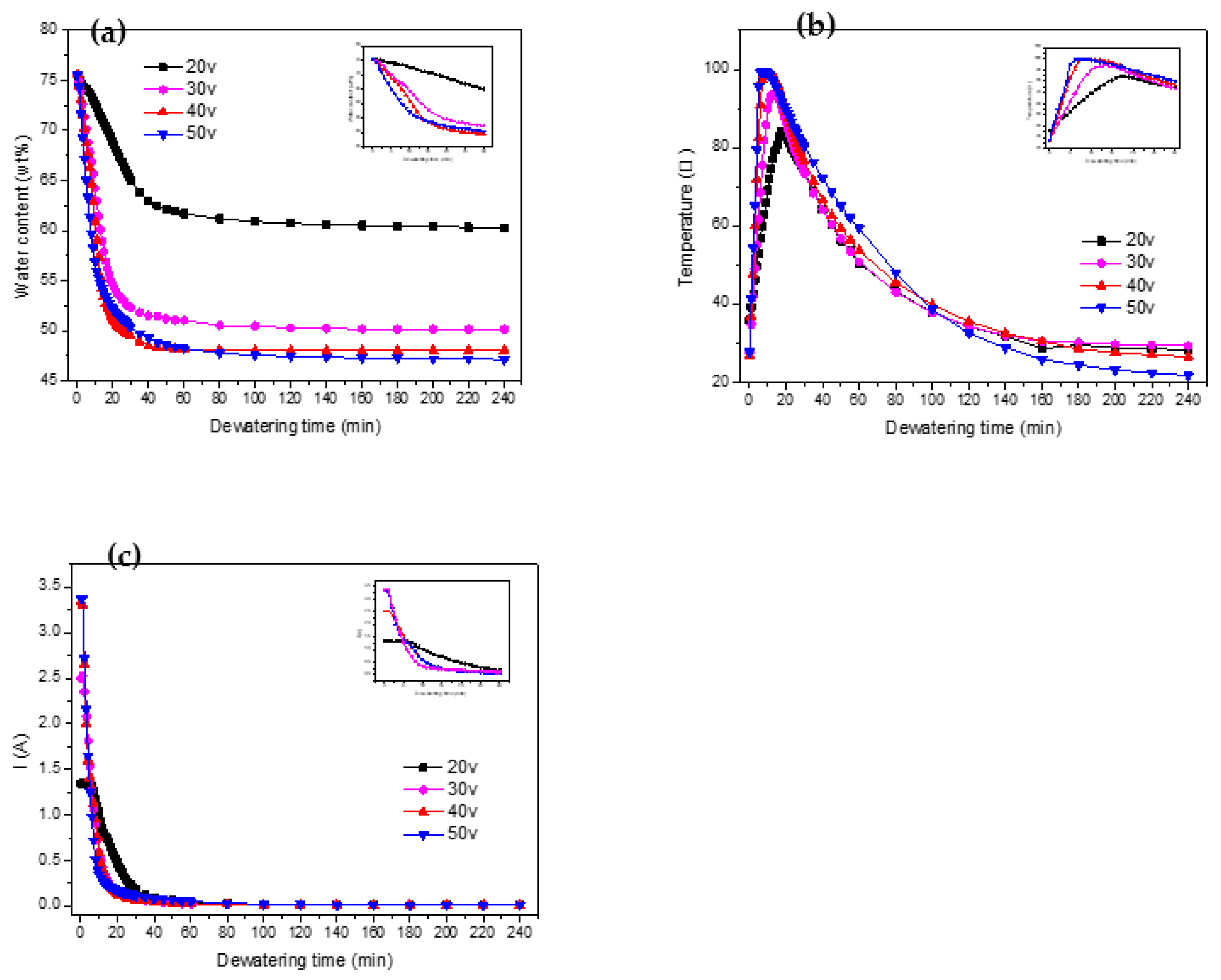
Figure 7.
Fitting curve of filtrate flow rate and loop current during dewatering at different voltages.
Figure 7.
Fitting curve of filtrate flow rate and loop current during dewatering at different voltages.
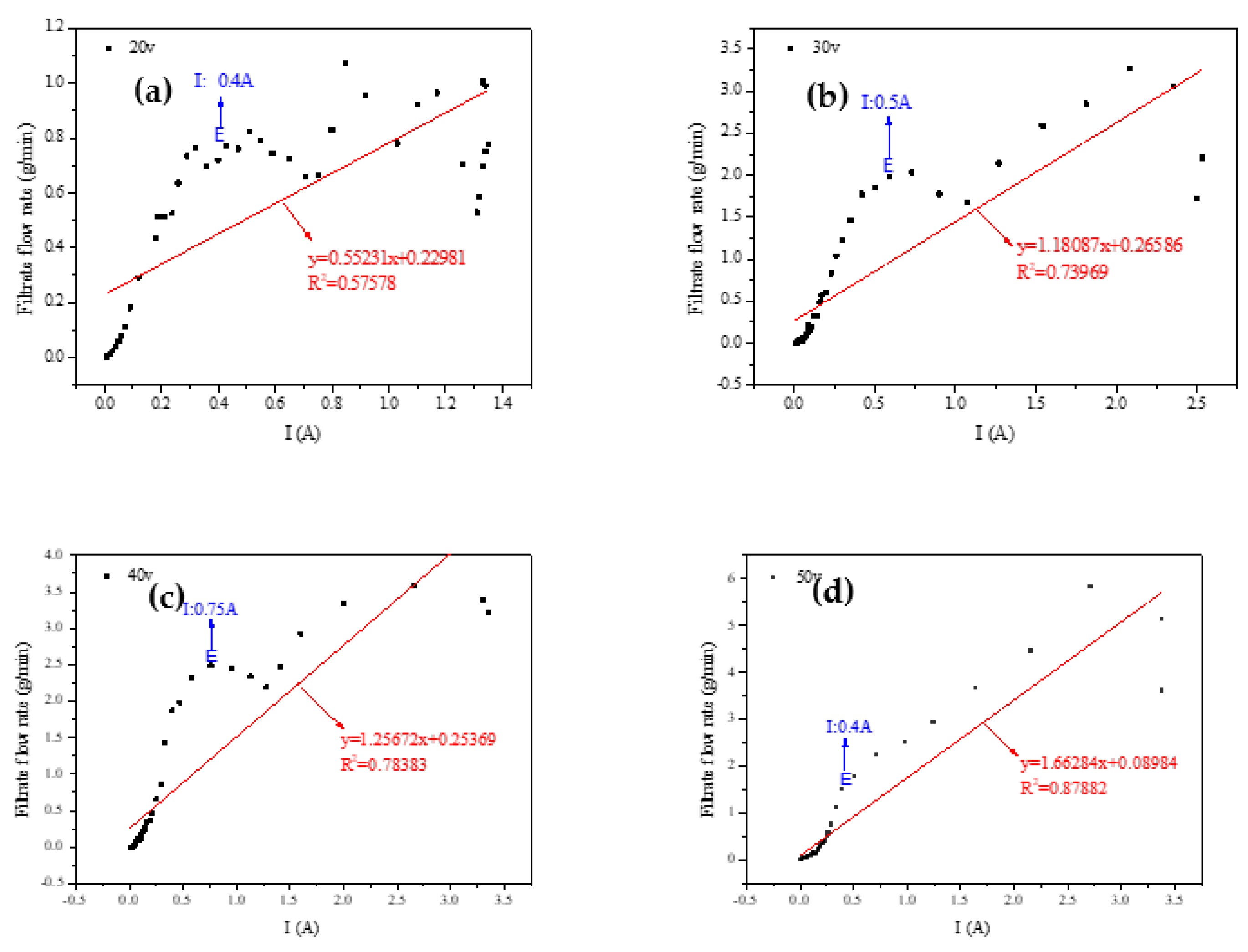
Figure 8.
(a) Change of energy consumption over time during dewatering at different voltages, (b) Energy consumption for electro-dewatering (EDW).
Figure 8.
(a) Change of energy consumption over time during dewatering at different voltages, (b) Energy consumption for electro-dewatering (EDW).
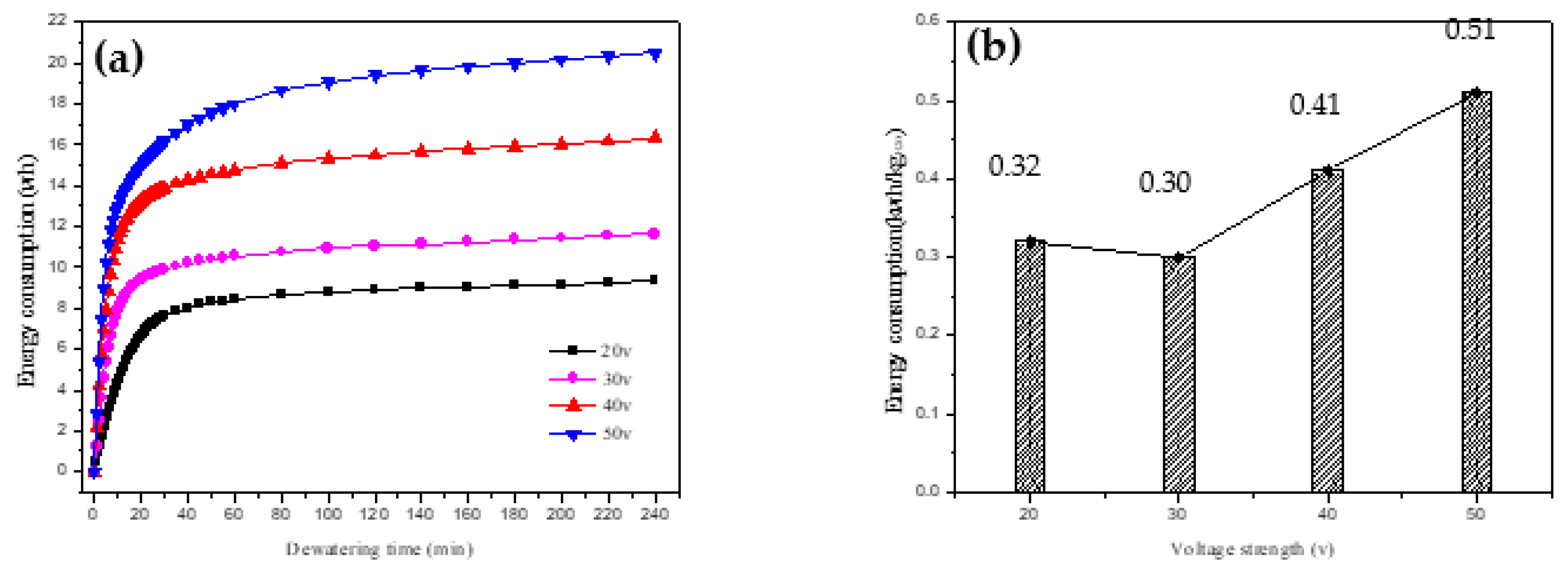
Figure 9.
Construction of multi-factor response model.
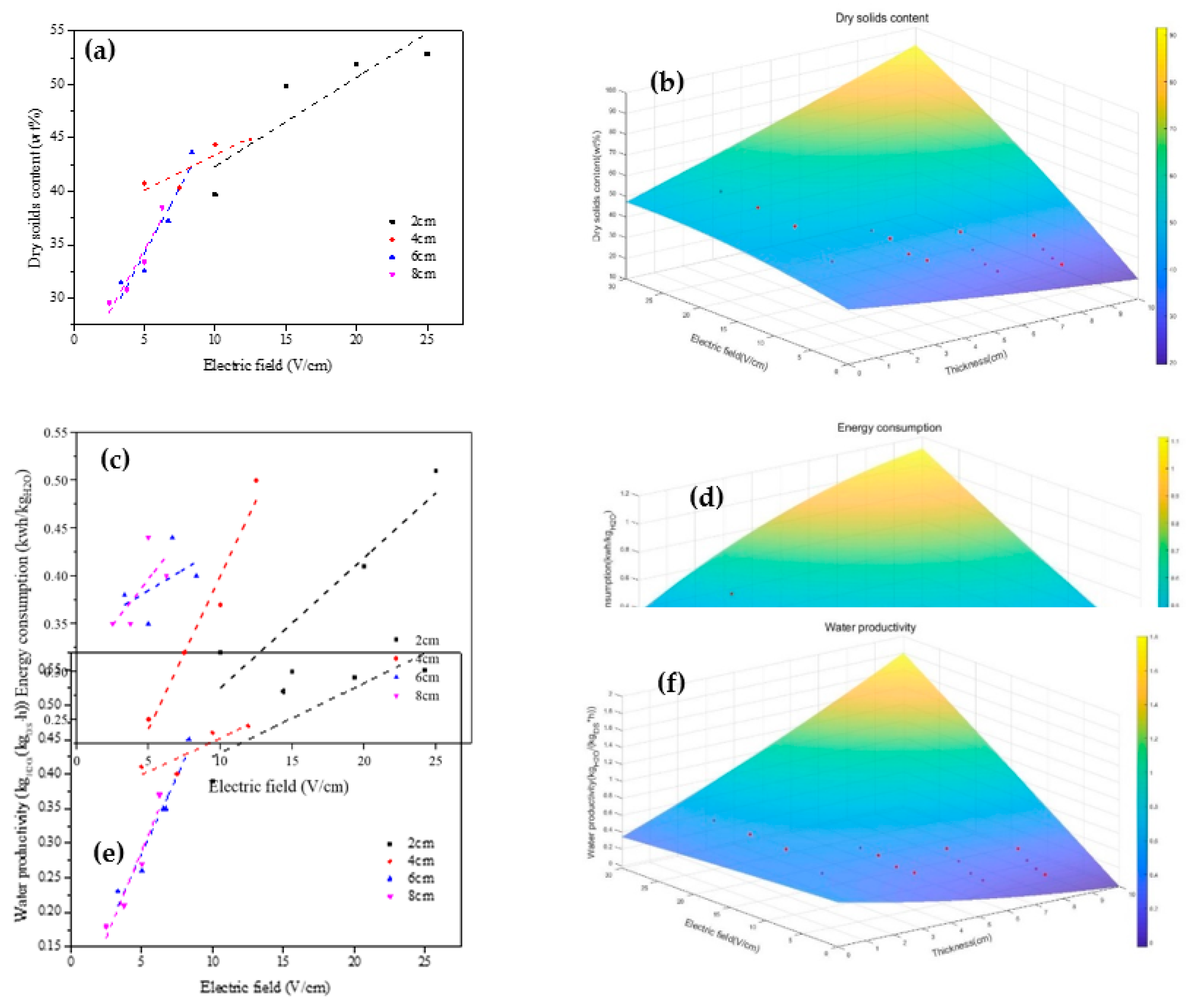
Table 1.
Main characteristics of the original sludge.
| Parameters | Value |
|---|---|
| Water content (wt%) | 75.55 |
| Organic content (wt%) | 31.07 |
| pH | 7.27 |
| Conductivity (ms/cm) | 9.07 |
| Particle size (D50/μm) | 21.9 |
| Permeability coefficient (cm/s) | 1.07×10-8 |
Table 2.
Fitting curve of moisture content and time under different voltages.
| Voltage strength(v) | Exponential | Guassian | ||
|---|---|---|---|---|
| R2 | R2 | |||
| 20 | 0.9857 | 0.9912 | ||
| 30 | 0.9860 | 0.9983 | ||
| 40 | 0.9815 | 0.9966 | ||
| 50 | 0.9952 | 0.9925 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated





