Preprint
Article
Development of a Consistent Understanding of Energy, Energy Conservation, and Derivation of a Systematic Set of Energy Forms
Altmetrics
Downloads
184
Views
228
Comments
0
This version is not peer-reviewed
Education for Sustainable Development and Science Teaching
Submitted:
08 January 2024
Posted:
09 January 2024
You are already at the latest version
Alerts
Abstract
“Energy” is probably the most important term in science and technology. The reason is energy can be converted while it is overall conserved, and thereby correlates changes of a wide variety. Despite its successful use in many areas over more than a century, an analysis of current literature shows that definitions of what energy is and explanations why it is conserved are inconsistent. With regard to energy forms not even a definition was found, and examples given are often wrong. Looking at two interacting objects in the most simple situations, with energy conservation but without conversion, a consistent understanding of energy and its conservation can be derived. Based on it, the systematic set of energy forms with a clear definition of each is then presented.
Keywords:
Subject: Physical Sciences - Theoretical Physics
1. Introduction
1.1. Importance of the basics of energy
“Energy” is probably the most important term in science and technology. The reason is energy can be converted while it is overall conserved, and thereby correlates changes of a wide variety. For example, if a pendulum swings gravitational energy is converted to kinetic energy and back. Gravitational energy and kinetic energy are called energy forms. For them a correlation between the change of observed height, respectively velocity, and the associated energy change is known. To know that energy is conserved thus allows to correlate change of height and change of velocity. In the energy system the fuel used is associated with chemical or with nuclear energy, correlated to the change of the amount of fuel, and the electricity generated is associated with electric energy, correlated to the number of electric charges. Using an electro-chemical reaction for electrolysis, to convert aluminium oxide to aluminium, it is correlated to the amount of aluminium produced.
1.2. What is an energy form? And which energy forms exist?
The term energy is used successfully, in a wide range of applications, for far more than a century. To use energy in calculations the energy forms are crucial as they are what conversion refers to. Thus, there must be a precise definition what an energy form is, and then of each energy form. Energy conservation was discovered by looking at the conversion between pairs of energy forms. Besides a clear definition of each energy form, for energy to be overall conserved in calculations, not counting things double or missing some, requires a complete, systematic set of energy forms. But no definition what an energy form is was found in literature. Many physics and chemistry textbooks do not treat energy forms at all (Halliday et al. 1993, Atkins 1990, Brown et al. 2015). One thermodynamics textbook (Çengel and Boles 2002) says energy can exist in numerous forms, splits up energy forms into macroscopic and microscopic energy forms, and also lists examples, but still does not give a definition of energy form nor the systematics behind the examples listed. Not surprising therefore, often definitions of energy forms are inconsistent, or even clearly wrong. Cleveland and Morris 2009 write that „thermal energy“ is (thermodynamics) “the kinetic energy associated with the motion of atoms or molecules in a substance; i.e. heat”. But heat is wrong, and not only atoms and molecules but also ions or free electrons must be included. And it also misses potential energy, e.g. in the vibration of molecules. But if simply included, kinetic and potential energy together would comprise all internal energy, thus also deformation energy etc. Halliday et al. 1993 specify the difference by adding randomness, writing “This energy is internal energy (or thermal energy), which is the collective kinetic and potential energies associated with the random motions of the atoms, molecules, and other microscopic bodies within an object.” But if thermal energy is the kinetic and potential energy of random motion it is a state function. Because changes of internal energy forms depend on conditions they are however path functions, e.g. the energy change in a chemical reaction is different for different process temperatures. Somewhat similar, chemical energy and nuclear energy are sometimes defined as the energy associated with a corresponding reaction, and sometimes as the energy associated with the bonds. The latter would even set a zero point of energy to the state of having no bonds between particles. Thus, the state of knowledge on energy forms is far from satisfactory.
1.3. What is energy? And why is energy conserved?
The starting point is obviously the definition of “energy”; it is the basis to derive anything else. Because of its importance, to understand “energy” is fundamental in understanding physics at all. Quite surprising, it is very common that textbooks don’t give any definition of what energy is, but instead simply use the term, without explaining it; examples are Reif 1985 and Çengel 1998. However, what is even more striking are the inconsistencies in definitions given in other sources. A common definition in scientific literature is that energy is the ability or the capacity to do work, or somewhat more detailed that energy is the capacity of a system to do work (e.g. Atkins 1990). It is also used in many dictionaries, official websites, and also widespread on websites for teaching (e.g. Encyclopaedia Britannica 2020, EIA 2019). This definition is wrong for several reasons. First, if energy is the ability to do work while energy is conserved then the ability to do work would be conserved. This is obviously wrong if there is friction. Actually, it would mean that perpetual motion is possible (Garver 1916), so it is in contradiction to the conservation of energy. To fix the definition it is sometimes modified to energy is the ability / capacity to do work and to supply heat (Brown et al. 2015). This makes it fit to the 1st law of thermodynamics “the change of the internal energy of a system is equal to the amount of heat supplied to the system, and less the work done by the system”, which results from energy conservation when looking at a system exchanging energy with its surrounding as work or as heat. But is energy an ability or capacity? Energy has a unit and value. Even more, in the 1st law of thermodynamics work and heat denote energy that is exchanged by a system, so they are “energy” themselves; consequently, they cannot be used to define what energy is. Çengel and Boles 2002 state “energy can be viewed as the ability to cause changes”, and similarly, Quaschning 2005 states “energy is the ability of a system to cause exterior impacts, for instance a force across a distance”. Energy is related to changes, but it is an imbalance of forces that causes changes (or a temperature difference etc.), and not energy. Walker et al. 2014 consequently state “Energy is a number that we associate with a system of one or more objects” and “After countless experiments, scientists and engineers realized that if the scheme by which we assign energy numbers is planned carefully, the numbers can be used to predict the outcomes of experiments …”, relating energy again to observed changes. They go on “This success is based on a wonderful property of our universe: energy can be transformed from one type to another and transferred from one object to another, but the total amount is always the same (energy is conserved).” Feynman put it in a similar way. Feynman, in his lectures called “The Feynman Lectures on Physics” (Feynman 1961 - 1963 a), emphasized that one of the most basic laws of physics is the law of the conservation of energy. He explains “It states that there is a certain quantity, which we call energy, that does not change in the manifold changes which nature undergoes.” This relates energy to changes seen in nature. He then added on its nature “That is a most abstract idea, because it is a mathematical principle; it says that there is a numerical quantity which does not change when something happens.” And he also emphasized what we miss: “It is not a description of a mechanism, or anything concrete; it is just a strange fact that we can calculate some number and when we finish watching nature go through her tricks and calculate the number again, it is the same.” He finally emphasizes then that “It is important to realize that in physics today, we have no knowledge of what energy is”. Looking back at the historical development, Lehrman (Lehrman 1973) described how from observations formulas were set up that showed something is conserved, and that only much later the term “energy” was introduced for it. He therefore concludes that “Energy has been defined because it is conserved. Any definition of energy that is not rooted in its conservation property is false at its core.” This is a crucial conclusion. Regarding an explanation he also adds “We assume that the reason we have always been able to find such terms is that they describe a general property of natural systems.”
Early observations were made by Huygens on collisions of balls, regarding changes of velocity, and by Galilei on free fall and swing of a pendulum, regarding changes of velocity and height. Huygens’s laws of collision state that some values regarding change of velocity remain constant, so “conserved”, and Galilei’s observations added changes of height to it, so some “conversion”. Bernoulli made similar observations on fluids instead bodies. Thus, for bodies as well as fluids, changes of velocity and changes of height during motion are correlated, something very useful. Leibnitz introduced terms which already corresponded to kinetic and gravitational energy, but used the term “vis viva”. That “energy cannot be created or destroyed, it can only be transformed from one form to another”, thus energy conservation and conversion, attributed to Mayer, Joule, and Helmholtz, was initially stated using terms like “living force” and “fall force”. Only later, Kelvin and Rankine introduced the term “energy” to replace the different terms “living force” and “fall force” and arrive at a set of common terms that today are called the energy forms. Originally the term “energy” was introduced by Aristotle, meaning “origin” or “source” of work. Today, “energy is the ability or the capacity to do work” is still quite often used as a definition of energy. But this is just about the initial meaning, not a definition or an explanation. Moreover, it is wrong: initially energy referred only to work, which is not conserved; today, comprising also heat, it is. Feynman, in his lectures called “The Feynman Lectures on Physics” (Feynman 1961 - 1963 a), also stated that we don’t know what energy is, and miss a mechanism for energy conservation. But we use it successfully: adding up energy forms correctly it is possible e.g. to correlate changes in so different things as the amount of fossil coal used as fuel for a power plant and the amount of electric energy produced, which in turn can be used to calculate how much light lamps deliver. So why bother? Is it necessary to know what “energy” is and why it is conserved? “Energy” has been defined because it is conserved, as the previous historic background shows. So, if we do not know why “energy” is conserved we also do not know what “energy” itself is! And if we do not know what “energy” is, we also don’t know what an energy form is and so not which ones exist. It happened already several times in history that observations indicated energy is not conserved. Later it was found that an energy form was missing in calculations, and that when integrating it energy is conserved again. This way, starting with kinetic and gravitational energy, later thermal, electric, magnetic, chemical, or nuclear energy were added. Thus, we know how to use “energy”. But we need to understand energy conservation. Surprisingly, literature has several explanations. A common explanation for energy conservation is from observations, as a “law of experience”; Lehrman (Lehrman 1973) in his historical review on energy explains that from observations formulas were set up that showed that something is conserved. He concludes that “energy has been defined because it is conserved” and that “with new discoveries (the neutrino, for instance) it became necessary to invent new terms in order to make the energy equation balance”. To say that energy conservation is a law of experience, based on the observations made, is thus correct. But it is not a real explanation. Specifically, an explanation requires a natural cause / mechanism. Feynman (Feynman 1961 – 1963 b) states “In the situations in which we cannot follow details, we need to know some general properties, that is, general theorems or principles which are consequences of Newton’s laws.” And “one of these is the principle of conservation of energy” as well as “another is the principle of conservation of momentum”. Contrary to the citation above, here in his lectures Feynman gave a mechanism: conservation is a consequence of Newton’s laws. The explanation for conservation of momentum was given already by Newton (Newton 1687) in Corollary III “For action and its opposite re-action are equal, by Law III, and therefore, by Law II, they produce in the motions equal changes towards opposite parts. Therefore if the motions are directed towards the same parts, whatever is added to the motion of the preceding body will be subducted from the motion of that which follows; so that the sum will be the same as before.” Feynman (Feynman 1961 – 1963 b) discusses it; he even mentions that in the elastic collision of two bodies also kinetic energy is conserved. Feynman also noted that energy conservation applies to levers. But the discussion that conservation of energy can be traced back to Newton’s 3rd and 2nd law (Feynman 1961 – 1963 c) he did with the free fall, suggesting it as most simple example. But free fall includes besides conservation also conversion of energy, while elastic collisions of bodies and levers don’t. Thus, the latter are the simplest examples, and promising more insight. The common scientific explanation is however different, by a symmetry of a physical system. Feynman (Feynman 1961 – 1963 a) states that “As independence in space has to do with the conservation of momentum, independence of time has to do with the conservation of energy”. More precise, if there is a translation symmetry regarding time, called homogeneity of time, then the energy of the physical system is conserved. If there is a translation symmetry regarding space, called homogeneity of space, linear momentum is conserved, and alike for a rotational symmetry angular momentum is conserved. The approach by a symmetry is generalized in what is known as Noether’s theorem “a symmetry of a physical system has a corresponding conservation law”. So, it is not that there is no explanation for energy conservation in literature, there are even two. However, both, Newton’s laws as well as symmetry of time, both are not really good explanations. As Newton’s laws are not generally applicable, e.g. in quantum mechanics, symmetry of space and time has become the common way of explaining the conservation of momentum and energy. The correspondence however means that symmetry is not a physical explanation of conservation. This is a misconception often found in literature. Feynman correctly said “… has to do with …”. Thus, Newton’s laws are a start to find the correct explanation, symmetry only has to do with it. For momentum conservation the explanation from Newton’s laws is even quite widely accepted. It is striking that Feynman discusses both approaches, by Newton’s laws and by symmetry, however then does not discuss the oddness of having two different approaches for conservation. The question arises if both approaches are related, and can then be traced back to a single one. This is not all yet. Physics has several correlations between kinetic energy Ekin and momentum p, e.g. for non-relativistic systems holds Ekin = p2/2m. Thus, if Ekin is conserved, e.g. in an ideal gas, then p must be conserved too. As a consequence, we must expect to have a single physical cause, common for conservation of energy and for momentum. Following Newton’s laws this is the case. From symmetries we have for energy the symmetry of time, for momentum symmetry of space. Besides the correlation between kinetic energy and momentum another thing points to a single, common explanation. If everything is described by particles and their interactions, energy and its conservation as well as momentum and its conservation must be a consequence, not independent.
1.4. Previous publication and goal of this work
Several of the previous questions have already been answered in the past, by desktop research, based on the fundamental concept in physics that everything that happens in nature can be described by particles and their interactions. The results are published in a book (Mehling 2019), however they have not been discussed by the scientific community yet. Specifically, a consistent definition of energy and energy form was found, the systematic set of energy forms was derived, the individual energy forms were defined, and energy and momentum conservation were shown to be both consequences of Newton’s 3rd law. As Newton’s 3rd law is not generally applicable it was concluded that a property of interactions is the natural cause, described by Newton’s 3rd law. Other questions, also mentioned before, were however not treated. The reason is these questions came up during further desktop research afterwards. For example, despite the connection between energy and momentum conservation was already clear, it was not discussed. It is however crucial to fully understand the connection between energy, momentum, and forces. Also, the property of interactions underlying Newton’s 3rd law was not discussed in any detail, nor how symmetry of space and time, when used to explain momentum and energy conservation, fit into the picture.
The goal of this paper is therefore specifically to investigate in more detail the real natural cause of the conservation laws, what the conservation laws have to do with symmetry of time or space, why by looking at interactions instead forces the explanation holds also in quantum mechanics, electrodynamics, etc., and how it leads to the general correlation between energy and momentum.
2. Methods
Like in the previous publication, Mehling 2019, all work presented here is from desktop research, analysing what is already available in published literature; no experimental work was performed. The crucial approach is to start looking at mutual interactions in the most simple situations with energy conservation but without conversion. Afterwards conversion can be included. Then more complex situations including also cases where Newton’s laws are not applicable are discussed. While literature specifically on materials usually discusses particles and their interactions, here the term “objects” is used as far as possible to refer to any arbitrary size, from atoms to planets.
3. Results and discussion
3.1. What is energy? And why is energy conserved?
The following derivation of momentum and energy conservation from Newton’s laws is for the conservation of momentum similar to what is found in literature, while for energy conservation it follows an approach different e.g. from Feynman’s approach. Further on the steps are rearranged, to build the basis for the following synthesis of conservation of momentum, energy, and forces. The synthesis then in turn leads to a consistent understanding of forces, momentum, and energy. These issues, treated here in sections 3.1.1 to 3.1.3, have already been treated in Mehling 2019. They are here refined as then required to answer the new questions stated in the goal of this work.
3.1.1. Momentum and energy conservation as consequences of Newton’s laws
As basis, Newton’s laws of motion are briefly repeated and discussed regarding their meaning. The formulas here correspond to the original statements which were in text form (Newton 1687), where “quantity of matter” corresponds to mass and “quantity of motion” is mass times velocity. For constant mass the “quantity of motion” corresponds to the more general term momentum p
Newton’s 1st law, also called law of inertia, states that if the net force F acting on a body is zero then its product of mass m and velocity v (incl. direction) does not change with time t, and reverse, no change in motion means that no force is acting. It can then be written as
Newton’s 1st law is a special case of his 2nd law, which goes significantly further in its statement. Newton’s 2nd law, also called principle of action, gives a quantitative correlation between the net force F acting on a body and the change of its motion
Newton’s 3rd law, also called principle of reaction, then states that the force on body 1 by body 2, F(2→)1, is equal in magnitude but opposite in direction to that on 2 by 1
Thus, in a mutual interaction the sum of the forces (called action and reaction forces) is zero.
Newton’s laws of motion describe nature by forces, in the framework called classical mechanics. But Newton’s laws cannot be used in all situations, so e.g. quantum mechanics was developed. Still, Newton’s laws have a meaning that holds beyond their applicability in classical mechanics. A basic model to describe nature is by particles that interact, and are affected by the interaction. It is crucial that forces and their laws are a concept developed for a mathematical description. Newton’s 1st law says that if the net force F acting on a body is zero, then its motion is unchanged, and reverse. A net zero force F means there is no interaction with another body. Therefore, Newton’s 1st law means without interaction motion does not change, and with interaction it does. Newton’s 2nd law means there is proportionality between the interaction on a body and the magnitude of the change of its motion. And Newton’s 3rd law means that in a mutual interaction between two bodies the effect on the bodies is always such that it affects them symmetrically.
Despite the drawback that forces and Newton’s laws cannot be used in all situations, they are still a good starting point as they are easy to comprehend, keeping in mind what they actually mean. Besides, none of the other concepts developed by physics is useful in all situations; all of them have their limits.
Forces and Newton’s laws can be used to derive conservation of linear momentum by looking at two objects that are interacting in a collision. This was as already done by Newton (Newton 1687), and in a similar way later repeated by Feynman (Feynman 1961 – 1963 b) as well as many others. Starting with Newton’s 3rd law (Eq. 4), inserting Newton’s 2nd law (Eq. 3) on both sides gives
Eliminating the forces (which describe the mutual interaction) from the equation gives
This is mathematically equivalent to saying that the individual changes of momentum cancel out
that the sum of the momentum does not change
or that the sum of the momentum is “conserved”
Feynman (Feynman 1961 – 1963 b) already stated that conservation of momentum is a consequence of Newton’s laws. Essentially it is conserved as a consequence of Newton’s 3rd law. Symmetry of space is not required, or more precise, symmetry of space is not obvious this way. The derivation holds for any pair of objects that are in mutual interaction, and consequently momentum is also conserved for any number of objects as long as the interactions are only mutual. It is noteworthy that conservation here does not imply that “momentum” is a real part of nature, in addition to the objects and their interactions.
That energy conservation is also a consequence of Newton’s laws was also stated by Feynman (Feynman 1961 – 1963 b). He showed that it can be traced back to Newton’s 3rd and 2nd law using the example of free fall, and suggested this as the most simple example (Feynman 1961 – 1963 c). However, free fall combines kinetic and gravitational energy, therefore conversion of energy, precisely conversion between motion and position, as observed by Galilei, Leibnitz, and others. But the collision of two objects, observed by Huygens, is much simpler as it is without conversion (for this it is assumed that the collision is elastic, an assumption investigated then in section 3.1.4.) The conservation of energy can then be derived by a slight modification of the derivation of the conservation of linear momentum (Mehling 2019). For this the terms in Eq. 5 are rearranged to
That changes of momentum cancel out is a consequence of Newton’s 3rd law, now multiplied by the time dt the forces act, which is the same in a mutual interaction (the same dt on both sides). The change of linear momentum is due to what is called impulse (force times the time it acts), also called impulse - linear momentum theorem. The “transfer” or “exchange” of momentum between both objects in Eq. 10 is by impulse. Linear momentum is conserved because the impulse on both objects in a mutual interaction cancels out; the explanation for this is Newton’s 3rd law. Newton’s 3rd law holds however not just at any time t of a mutual interaction, as used in Eq. 10, but also anywhere on the path s of the interaction. Then, with the same ds on both sides, follows
This is the basis of energy conservation. Using Newton’s 2nd law (Eq. 2) gives for constant mass
The change of the kinetic energy is by what is called work, the force times the distance it acts. Eq. 12 is also called the work - kinetic energy theorem. Using it on both sides of Eq. 11 gives
It can be understood as “transfer” or “exchange” of energy between both objects, here by work. Eq. 13 shows that kinetic energy is conserved because work in mutual interactions cancels out. Except for a factor ½ the result was already described by Huygens in his “laws of collision”. Another most simple example hides in Eq. 11. It is the “golden rule of mechanics”, stated by Galilei as "the driving force times the driving distance is equal to the load times the load distance". It was used in the Middle Ages to correlate forces and distances. If using a lever to lift a stone the force on one side of Eq. 11 is the force exerted by gravitation on the mass of the lifted stone
The corresponding term is called a potential energy, being energy related to a change of position. An easy way to get a more general description is now looking again at a collision of two objects, however now not horizontal but instead vertical, such that gravitational energy is included
Huygens laws of collision as well as the golden rule of mechanics are rarely used as examples of an energy balance as they just combine changes of motion respectively just changes of position. But it is exactly the focus on conservation, without conversion, which reveals the natural cause. At the same time, this focus is the reason for their use being limited to only few special situations. The range of situations increased dramatically with the later integration of conversion between motion and position, then allowing to describe e.g. the flow of fluids or the swing of a pendulum.
Despite that using Newton’s laws is widely accepted to explain the conservation of momentum, to do the same to explain the conservation of energy is surprisingly not commonly accepted at all. Of course, Newton’s laws are only applicable in classical mechanics, thus Newton’s 3rd law is not yet the natural cause of conservation of energy and momentum, and that holds equally for both.
3.1.2. Common basis for conservation of momentum and energy
The derivation using Newton’s laws, despite that it is only applicable in classical mechanics, can be the starting point for further conclusions. Thus, it is summarized in Figure 1 in a suitable way.
Crucial is that the derivation from Newton’s laws simplifies many things, and is comprehensible. The previous discussion has shown that force, momentum, and energy, are related. Specifically, the conservation of linear momentum is a consequence of Newton’s 3rd law, resulting if it is multiplied by the time an interaction acts (Eq. 10), and conservation of energy too, resulting if it is multiplied by the distance an interaction acts (Eq. 11, and Eq. 13 for the case of kinetic energy). Newton’s 3rd law is therefore at the core of the conservation of both, momentum as well as energy. Moreover, forces, momentum, and energy, all are not independent but instead are tightly related.
3.1.3. Common nature of forces, momentum, and energy, and their conservation
Force, momentum, particularly energy, are often comprehended as independent physical realities. The previous discussion shows that, in the same way as a force is not an own physical reality, momentum and energy are also no own physical realities. Instead, all are just different concepts to describe the effect of interactions between objects resulting in changes of motion and position. And it has to be that way. If we assume that everything can be described by objects and the interactions between them, then force, momentum, and energy cannot be independent of them. What should be considered “real” is the minimum set of things that is needed to describe nature, which is objects and their interactions, while force, momentum, and energy, are mathematical concepts to describe what happens, used to “explain” why it happens. The most intuitive concept, closest to common experience (so well known to everybody) and as a result also investigated first, is that of forces. The “origin” of forces are interactions; forces describe the effect of interactions. In simple situations, e.g. two objects, forces describe the effect of interactions between objects on motion and position of the objects. Newton’s laws of motion describe mathematically the most basic features of interactions: if there is no interaction nothing changes (and the same reverse), the effect of an interaction, and that interactions always act such that effects overall cancel out. The latter can also be understood as law of conservation of forces for only mutual interactions. The effect of interactions between objects on objects can however also be expressed by the concept of momentum or energy, being developed later. Each has advantages, and limitations. Momentum and energy allow a description of interactions also when things change dynamically in space and time, also when objects do not have a precise location as in quantum mechanics, even in situations when objects have no mass like photons in electrodynamics, actually even in situations where objects after an interaction are completely different ones like in an electron-positron annihilation resulting in photon creation. This is a consequence of eliminating forces, distances and locations, and times, by multiplication of Newton’s 3rd law (Eq. 10, Eq. 11, Eq. 13) and eliminating the terms, with just the conservation laws remaining. Similarly, Newton’s 3rd law multiplied by specific ds enforced by certain constraints leads to the principle of d’Alembert, which is the basis for the Langrange function and formalism (see Goldstein 1987).
Based on the previous results and synthesis a consistent and clear definition of energy is possible. Energy is one of several concepts in physics to describe nature, specifically to mathematically describe the effect of interactions between objects on the objects. Energy can be converted while it is overall conserved, thereby correlating changes of a wide variety, e.g. change of motion and position of individual objects, for many objects bulk deformation, and lots more. That energy connects changes is widely accepted (Lehrman 1973, Feynman 1961 - 1963 a, Walker et al. 2014). The investigation here showed what energy is, a mathematical concept, and its root in interactions.
3.1.4. Natural cause of conservation of forces, momentum, and energy
The issues investigated and discussed in sections 3.1.1 to 3.1.3, that conservation of momentum and energy are consequences of Newton’s 3rd law, that they have thus a common basis, and that momentum and energy are even of the same nature as forces being mathematical concepts to describe how interactions between objects affect them, was already presented in Mehling 2019. The previous derivation of conservation of momentum and energy in mutual interactions holds where Newton's laws are applicable, and then conservation is a consequence of Newton's 3rd law. That Newton's 3rd law is the correct “origin” can be concluded as this way also results in a single, common explanation for conservation of momentum and energy as e.g. required for an ideal gas. But the limited validity of Newton’s laws also makes clear it is the origin only within some limits. Newton originally wrote “To every action there is always opposed an equal reaction: or the mutual interactions of two bodies upon each other are always equal, and directed to contrary parts.” Thus, Eq. 4 is a mathematical way to express a general property of mutual interactions regarding action and reaction using forces; that it expresses something that has general validity is widely accepted. The question that is still unanswered, what exactly that general property is, is now investigated.
The easiest application of Newton’s 3rd law is in static situations. A simple example is a spring that pulls on the walls of a box (Figure 2, right). The force by the spring on the right wall by its support on the left is equal in magnitude and opposite in direction to the force on the left wall by its support on the right. It must be that way, simply because the situation is mirror symmetric. Also, if gravitation acts between two equal masses (Figure 2, centre) it acts mirror symmetric. Generally, however, to include things like the spin of a particle, forces must be of same magnitude and opposite direction but not necessarily on the same line (Goldstein 1987). This is compatible with Newton’s 3rd law. Consequently, the general case that interactions act symmetric with the same magnitude and opposite direction describes a point symmetry to the centre of the interaction (Figure 2, right).
That interactions act symmetric does however not cover all issues yet. In the previous derivation the requirement of having “elastic” collisions was used. What happens if collisions are not elastic? In a completely inelastic collision of two objects of the same mass and velocity their motion stops, consequently the kinetic energy as well as the momentum of each object after the collision is zero. The sum of the kinetic energy is zero too, however the total momentum as vector is still conserved. To analyse what happens it helps to imagine a direct collision, and interaction to be by a spring. In an elastic collision the objects approach each other, when the spring acts they slow down as energy of their motion is converted to energy in the interaction (deformation energy of the spring), and then converted back to energy of motion; no energy is lost by conversion to something else. If not elastic then during the interaction energy is at least partly converted, e.g. to thermal energy, and not back. If described by a force this means that the force on the back conversion way is less. That an interaction is elastic can be expressed saying all energy is converted in the desired way; the reason is the interaction is the same forward and backward, so it does not change with time. If two masses interact by gravitation, and only by it, then there is obviously no way for conversion.
Physics knows 4 fundamental interactions: besides gravitation the electromagnetic interaction, and the strong and the weak nuclear interaction. The electromagnetic interaction can be split up into electrostatic and magnetic interaction, where the latter is just a relativistic effect of the first. That the fundamental interactions fulfil the requirements, meaning acting symmetric in space and acting independent of time, is thus the natural cause for conservation of energy and momentum. Because everything can be described by fundamental particles and fundamental interactions, consequently follows that energy and momentum must be conserved in general.
For an arbitrary interaction the previous derivation of the conservation laws holds too if the interaction fulfils the same requirements of acting symmetric in space and independent of time. This was inherently included before: the symmetric effect is what is stated by Newton’s 3rd law, and that the interaction does not change with time was included by assuming an elastic collision. The natural cause for conservation of energy and momentum is thus that mutual interactions between objects act symmetric with respect to the effect, and that their effect is time independent. It is the natural cause, generally valid. It removes all inconsistencies identified in the introduction. The cause are the mutual interactions and their symmetries with respect to space and also to time. A general symmetry of space and of time is nowhere required. Before investigating what these symmetries “have to do” with the conservation laws it is helpful to investigate first another issue, which then explains what it means if a situation is not symmetric with respect to space or time.
3.1.5. Conditions for conservation of forces, momentum, and energy in systems
As shown, the cause of the conservation laws is that mutual interactions have a symmetry in space and are independent of time; both is the case for the fundamental interactions known in physics. This became clear looking at the simplest situation, two interacting objects in mutual interaction. Knowing that complex situations are then simply composed of many simple situations it is clear that the conservation laws hold in general, precisely if comprising complete mutual interactions.
Looking at the interior of a system (Figure 3, left), the energy associated with the motion of the objects and mutual interactions is called the internal energy. As there are only mutual interactions, the sum of all internal forces in the system cancels out; their sum is conserved (it is always zero), also momentum is conserved, as well as energy. They are always conserved together, never alone (energy conservation is only “violated” if conversion, e.g. by friction, is not correctly included). Only mutual interactions means no interaction with the surrounding.
If there are not only mutual interactions but also interactions with the surrounding of the system, so another system, the momentum as well as the energy of the system is not generally conserved. For linear momentum this case was discussed in detail by Feynman (Feynman 1961 – 1963 b). For energy this is discussed in detail in Mehling 2019, distinguishing two cases. The first case is an external interaction acts on the interior of the system, affects motion and position of its objects, therefore the energy related to the motion and position, thus changes the system’s internal energy. This case is reflected in the first law of thermodynamics, saying the change of the internal energy of a system is equal to the energy exchanged by work and heat. Work and heat denote energy exchanged between a system and its surrounding by interaction without respectively with entropy. The second case is the external interaction acts on the whole system, leading to external energy. For example, an electric field acting on a system of charges, e.g. a salt, changes the internal energy by dragging charges of opposite sign into different directions, and if the salt sample has some net charge the external field also changes its external energy by attracting or repelling the salt sample. Another example is the interaction between earth and moon: the gravitational field of the moon attracts the earth, but because of its inhomogeneity at the location of the earth it also pulls different parts of the earth differently and thereby causes a change of the internal energy, e.g. by the tides.
Strictly speaking there is a second condition for the conservation laws, besides that the system comprises all mutual interactions. The condition is that the system is in an inertial reference frame. An accelerated reference frame will cause motion in the system, thus change the momentum as well as the kinetic energy of objects in the system, even if they have only mutual interactions. The motion of the objects in the system is then not due to a real force, but by the reference frame. This connects to the principle of relativity, as stated first by Newton in Corollary V to the laws of motion (Newton 1687) as “The motions of bodies included in a given space are the same among themselves, whether that space is at rest or moves uniformly forward in a straight line.”
3.1.6. Connection between conservation laws and symmetry of space and time
The connection between conservation laws and symmetry of space and time is investigated next. It is crucial that in this context symmetry of space and time refers to a system, and that the previous discussion of systems without / with an interaction with their surrounding showed differences.
For systems which are not interacting with their surrounding all conservation laws hold, always. For systems that are interacting with their surrounding this is not the case. Thus, it is the interaction with the surrounding that seems to determine if a system has a symmetry or not. Fließbach 2020 states that external influences on a system lead in general to a system not being invariant under certain transformations; thus, the conclusion here is already accepted in literature. It is important to remember that the formulas used in physics to describe the behaviour of systems are merely a mathematical tool to describe the observations of the behaviour of systems in nature. If a system has a symmetry in space or time the symmetry is reflected in the system’s behaviour, and consequently it must be reflected then also in the formulas that are used to describe the system.
If a system behaves the same no matter where it is located then there is no effect of the location. This means that the formulas used to describe the behaviour of the system need to show the same independence of location, mathematically this requires a translation symmetry regarding space. Thus, no absolute space coordinates can be involved, just differentials or just relative coordinates. It is common in discussions of this topic to use T for kinetic energy, and V for potential energy. Looking at internal energy of a system comprising more than one objects in mutual interactions, it is possible to derive under which conditions energy and momentum conservation would hold. Goldstein 1987 looks at energy of a system of objects as the sum of kinetic and potential energy, the potential energy causing changes of the kinetic energy by work, via the forces that it causes. He derives that for energy to be conserved the forces of a mutual interaction must be caused by a potential energy that is a function of the relative distances only, so the resulting forces are then of the same size and have opposite direction; this is exactly the same as stated by Newton’s 3rd law. The result derived by Goldstein is the same as derived here, just with a different starting point. Mutual interactions are symmetric with respect to translations of space or time, so in agreement. The reason to be not symmetric must be, as derived before, an interaction with the surrounding. For simplicity only one space dimension is used. The kinetic energy T of the system is then
and the potential energy V, derived from a force acting on it, e.g.
The kinetic energy T, being a function of dx/dt, is not changed by a translation of space or time. The potential energy V, being a function of x, is changed by translation of space unless V = const. Since F = dV/dx, follows that symmetry with respect to translation in x means that no force acts, and consequently the momentum of the system is conserved; it is not if there is an external force. The force represents an interaction between the system and its surrounding, as discussed before. Regarding energy conservation, as discussed before it must be the same way, an interaction with the surrounding, thus an external force, has to be the cause if energy conservation does not hold. A force acting on the system will change the system’s energy, which must show up in the potential energy being dependent on time thus that V = V(x, t) is then not symmetric with respect to time. Thus, for momentum as well as energy, if there is no interaction with the surrounding there is a conservation law and for each a corresponding symmetry exists. They are not independent causes.
The correct natural cause of the conservation laws, and what symmetry of space and time of a system have to do with the conservation laws is now clarified. Finally, left is to investigate why symmetry of space and time are commonly believed to be the real cause of the conservation laws. As the symmetries correspond to a conservation law with regard to all isolated systems, there seems to be the belief that therefore the symmetries must be a general property of space and time. However, as shown before, this neglects that the natural cause is not the symmetry of the system but what is behind it: the presence of only mutual interactions in a system and no interaction with the system’s surrounding; the latter is not mutual as the surrounding is not a part of the system. Since the universe has no surrounding, by its definition, all interactions in it are mutual; therefore, momentum and energy are conserved. This does not require a general symmetry of space or time.
3.1.7. Correlation between energy and momentum
The approach chosen here, to start looking at mutual interactions being the most simple situation, and using Newton’s laws as they are easy to comprehend, has already helped to answer several questions and remove initial inconsistencies. One issue left to investigate is that in an ideal gas there is a correlation between kinetic energy and momentum by Ekin = p2/(2∙m), thus that the conservation of momentum and of energy cannot be independent. The conditions for energy and momentum to be conserved together or not have been discussed before in sections 3.1.4 and 3.1.5. For mutual interactions the condition is that no conversion with another energy form takes place, which would result in energy gains or losses. Consequently, the work exchanged as well as the impulse exchanged in a mutual interaction cancel out, which then results in the conservation laws. This is fulfilled in an ideal gas, as example, because elastic collisions are one assumption for it. The specific case is now understood, but the question arises if there is a general correlation.
The summary in Section 3.1.2, specifically in Figure 1, allows to derive a more general correlation. For this, the focus is now only on one side of an interaction. If a force acts on an object, the work done is the product of the force times the distance it acts, and equal to the change of its energy
The impulse is the product of the force and the time it acts, and equal to the change of momentum
Division of both correlations, and eliminating the force that represents the interaction, results in
Thus, an object, by an interaction, changes its energy in a relation to the momentum equal to ds/dt.
Interesting is the case where the origin of the interaction, in other words the centre of the mutual interaction, is at rest (Figure 4). The ratio of the distance ds and time interval dt the interaction acts on the object is then equal to the velocity of the object. The meaning of Eq. 20 is then clear. The equation can easily be checked looking at objects in free motion, having only kinetic energy. In classical mechanics Eq. 20 is fulfilled; Ekin = ½∙m∙v2 and p = m∙v, so Ekin = p2/2∙m and the right side of Eq. 20 is then equal to the velocity v on the left. This is not a surprise as the derivation in section 3.1.1, summarized in section 3.1.2, was withing the framework of classical mechanics. The correlation in Eq. 20 is also fulfilled beyond classical mechanics however. For photons holds E = h∙c/λ and p = h/λ, thus that E = p∙c, so the right side is again equal to the velocity c on the left.
3.2. What is an energy form? Which energy forms exist?
3.2.1. External and internal energy, and fundamental interactions
The previous discussion now allows a bottom-up derivation of the energy of systems of objects. Starting from 2 objects which mutually interact, going to many objects is now straight forward.
It was already discussed in Section 3.1.5, specifically Figure 3, that a system of interacting objects has energy within, called internal energy, due to the motion and mutual interaction of the objects. Additionally, if the system interacts with its surrounding (actually another system), it has energy as a whole from its motion and interaction with respect to the surrounding, called external energy. The interaction with the surrounding acts on the individual objects within the system, thus affects motion and position of them, consequently an external interaction can change the internal energy.
The motion and position and related interaction of all objects completely describes a system state. Physics knows 4 fundamental interactions: gravitation, the electromagnetic interaction, and the strong and weak nuclear interaction. Taking kinetic energy associated with motion in addition, this altogether gives 5 “fundamental energy contributions” that cover all energy (Mehling 2019). If the interactions are not treated by the interacting particles and their positions, they can also be treated by the corresponding field energies, e.g. for wave propagation, or by exchange particles. No energy is counted twice, or is missed, unless a new fundamental interaction is discovered.
3.2.2. Systematic derivation of the energy forms
To use fundamental energy contributions to describe systems has however several weaknesses, specifically if looking at materials with many small objects, commonly called particles: treating many particles is difficult, often there is not even interest in the individual motion and position, and most important, in everyday life we do not see particles and thus not their motion and position. Historically energy as a concept was derived from visual observations, thus that a different way of description, not following fundamental energy contributions, was established: energy forms. Energy forms are energy contributions associated with changes that are macroscopic, in many cases directly visible, but with regard to the internal energy of materials have microscopic origin. The fundamental energy contributions now allow a systematic treatment of the energy forms too.
External energy forms are energy forms related to a macroscopic system, due to its macroscopic visible motion, or its position by a fundamental interaction with the surrounding. The energies can be given absolute values as we see the position and motion. The energy forms are
- Kinetic energy: energy associated with motion of a mass, e.g. of a pendulum, a car, etc.
- Gravitational energy: energy associated with gravitation and relative position, e.g. the mass of a pendulum or a stone by interaction with the earth. The latter is crucial but often forgotten: gravitational energy is not “due to” the height of an object or its position.
- Electric energy: energy associated with the electric interaction and relative position, e.g. fluff sticks to a charged plastic slab, or relative orientation, e.g. for electric dipoles from coils.
- Magnetic energy; energy associated with the magnetic interaction and relative orientation, e.g. a compass interacting with the magnetic field of the earth.
Kinetic energy and gravitational energy are well known, e.g. from the historic observations on the collisions of balls or the swing of a pendulum. Electric and magnetic energy are often missed, here uncovered by the systematic approach following fundamental interactions. Despite that both originate from a single fundamental interaction, it is practical for the description of observations to split both; this is also the reason why initially they were discovered separately. Regarding nuclear interactions there is no associated energy form; their range is too short, so they are not acting between macroscopic bodies, and the nuclear particles where they act are also not visible.
Internal energy forms are energy forms related to a macroscopic system of microscopic particles due to their motion or position by fundamental interactions, associated to macroscopic changes. As a start, the well-known function in thermodynamics for the change of the internal energy U
can be used. It leads to several energy forms, but is not complete as the systematic analysis shows.
- Thermal energy: energy change (T∙dS) associated with undirected, random changes of the motion and position of all particles, described by the temperature T and entropy change dS.
- Deformation energy: energy change (p∙dV) associated with a directed deformation, thus changing the motion (e.g. in an ideal gas) and position of all particles, causing a macroscopic volume change dV.
It is crucial to note that thermal and deformation energy refer to all particles in a macroscopic system, and split up energy to that associated with random and respectively directed change. Therefore, all options with regard to all particles and no specific type of interaction are covered. Next are energy forms which are due to a specific interaction, usually acting on specific particles.
- Electric energy: energy change (E∙dP) associated with a directed effect by an external electric field E acting on electric charges and dipoles and leading to a shift of their position or orientation such that an overall macroscopic polarization change dP results.
- Magnetic energy: energy change (B∙dM) associated with a directed effect by an external magnetic field B acting on magnetic dipoles and leading to a shift of their orientation such that an overall magnetization change dM results.
For gravitation there is no corresponding term as the effect on microscopic particles is negligible. And for nuclear interactions there is also no corresponding term as nuclear interactions are too short range to affect a macroscopic system from outside. Nuclear interactions only act in particles. The final group of energy forms refers to changes within particles, incl. leading to new particles.
- Chemically energy: energy change (μ∙dN) associated with a change of chemical composition, specifically expressed as being proportional to the change of amount of substance dN of the initial substance or the new one after a chemical process between atoms and molecules.
- Nuclear energy: energy change associated with a change of composition of nuclei. It can also be expressed as being proportional to the change of amount of substance dN of the initial substance or the new one, similar as chemical energy. It is crucial to note that nuclear energy as energy form is not the energy of nuclear interactions; in nuclei also the electromagnetic interaction is relevant, e.g. in nuclear decay.
- Ionization energy: energy change associated with the ionization of atoms or molecules.
- Excitation energy: energy change associated with the excitation of atoms, molecules, or ions.
Ionization and excitation energy need to be added to make the set of energy forms associated with changes within particles complete. They complete the systematic set of internal energy forms. Again, the complete, systematic set of energy forms assures that no energy contribution is counted twice, and none is missed. For more details and an in-depth discussion, see Mehling 2019.
Finally, it is necessary to discuss crucial differences between internal and external energy forms. The motion and position and related interaction of all objects completely describes a system state, therefore also its energy. This works if a system is described by fundamental energy contributions, and in the same way for the external energy forms, however not for all the internal energy forms. For example, the internal electric energy of a system of charges has an absolute value, calculated from the position of all charges and their electric interaction. Regarding the internal energy form, associated with the change of macroscopic polarization P due to an external electric field E, there is however only the change of electric energy observable. This holds for all internal energy forms. Internal energy forms refer to macroscopic changes, e.g. of entropy, volume, polarization etc., and thus are only associated with energy changes. But this is not all as thermodynamics shows. Deformation energy p∙dV has no fixed value because even for the same dV it depends also on p. The pressure p can be changed between compression and expansion by changing the temperature. Therefore, the energy change associated with a deformation is not a function of state of the system. The same applies to all internal energy forms. The difference to external energy forms is crucial. In engineering, in a closed thermodynamic cycle it allows conversion between heat exchange, changing the thermal energy of the system, and change of work, changing the deformation energy. The reason is that the integral over the closed cycle of the changes of thermal energy is not zero, and the same holds for deformation energy. The same is not possible with external energy; here, in a closed cycle, the change of the energy form is always zero. Currently definitions of energy forms in literature almost never take into account these differences. This is not really surprising; only the systematic overview on energy forms allows a comprehensive and detailed analysis.
4. Conclusions
“Energy” is probably the most important term in science and technology. The reason is that energy can be converted while it is overall conserved, and thereby correlates changes of a wide variety. Despite its successful use in many areas over more than a century, an analysis of current literature shows that definitions of what energy is and explanations why it is conserved are inconsistent. With regard to energy forms not even a definition was found, and examples given are often wrong.
The crucial approach is to start looking at mutual interactions in the most simple situations with energy conservation but without conversion. Afterwards, conversion can be included, and more complex situations including also cases where Newton’s laws are not applicable can be discussed.
In a first step, an analysis of the simplest case, two mutually interacting objects that are interacting by a single interaction and therefore excluding conversion, was performed. The interaction was described using Newton’s laws. It was shown that the conservation of energy can be derived multiplying Newton’s 3rd law by the distance the interaction acts, in the same way as conservation of momentum can be derived multiplying it by the time the interaction acts (already well known). This means both conservation laws have their basis in mutual interaction, as should be expected by the general concept in physics of describing matter by particles and interactions between them. The real cause of energy and momentum conservation is what is expressed by Newton’s 3rd law: that mutual interactions act symmetric. Specifically, this holds for the fundamental interactions which describe everything in nature: gravitational, electromagnetic, strong, and weak interaction. The cause identified here is valid in general, not only within the validity of Newton’s laws. Knowing that energy has been defined because it is conserved then allowed to define energy: "Energy is one of several concepts in physics to describe nature, specifically to mathematically describe the effect of interactions between objects on the objects. Energy can be converted while it is overall conserved, thereby correlates changes of a wide variety like changes of motion and position of individual objects, bulk deformation, and many more." It was also shown that the common explanations for conservation of momentum and energy of a system, a symmetry of space and time, actually refer to the symmetry of the potential energy of a system that derives from interaction with the surrounding.
Regarding energy forms, based on their common use they can be defined as "Energy forms are energy contributions associated with changes that are macroscopic, in many cases directly visible, but with regard to the internal energy of materials have microscopic origin." Finally, in a bottom-up approach from simple to complex systems, the systematic set of all energy forms was derived and the individual energy forms defined. The results show that common lists of energy forms are often inconsistent, even incomplete, and that individual definitions are often incorrect.
References
- [Atkins 1990] Atkins P.W.: Physical chemistry. Oxford University Press, 4th ed., 1990, ISBN 0-19-855293-1.
- [Brown et al. 2015] Theodore E. Brown, H. Eugene LeMay, Bruce E. Bursten, Catherine Murphy, Patrick M. Woodward, Matthew E. Stoltzfus: Chemistry - The Central Science. Pearson, 13th ed. 2015. ISBN 978-1-292-05771-2.
- [Çengel 1998] Çengel Y.A.: Heat transfer – A practical approach. Mc Graw Hill, 1998, ISBN 0-07-115223-7.
- [Çengel and Boles 2002] Çengel Y.A., Boles M.A.: Thermodynamics – An engineering approach. Mc Graw Hill, 4th ed., 2002, ISBN 0-07-112177-3.
- [Cleveland and Morris 2009] C.J. Cleveland and C. Morris (eds.): Dictionary of energy. Elsevier, 2009, ISBN 978-0-08-096491-1.
- [EIA 2019] U.S. Energy Information Administration (EIA): What is energy? https://www.eia.gov/energyexplained/what-is-energy/, last update 2019, accessed April 28th 2020.
- [Encyclopaedia Britannica 2020] Encyclopaedia Britannica: Energy – physics. https://www.britannica.com/science/energy, last update 2020, accessed April 28th 2020.
- [Feynman 1961 – 1963 a] R.P. Feynman: The Feynman Lectures on Physics. Held from 1961 to 1963. Published in bookform Vol. I Ch. 4 “Conservation of energy”, content available at https://www.feynmanlectures.caltech.edu/I_04.html, accessed April 28th 2020.
- [Feynman 1961 – 1963 b] R.P. Feynman: The Feynman Lectures on Physics. Held from 1961 to 1963. Published in bookform Vol. I Ch. 10 “Conservation of momentum”, content available at https://www.feynmanlectures.caltech.edu/I_10.html, accessed May 2nd 2020.
- [Feynman 1961 – 1963 c] R.P. Feynman: The Feynman Lectures on Physics. Held from 1961 to 1963. Published in bookform Vol. I Ch. 13 “Work and Potential Energy (A), content available at https://www.feynmanlectures.caltech.edu/I_13.html, accessed May 4th 2020.
- [Fließbach 2020] Fließbach T.: Mechanik - Lehrbuch zur Theoretischen Physik I. 8th ed. 2020, Springer Spektrum, ISBN 978-3-662-61602-4.
- [Garver 1916] M. M. Garver: An Engineer's Idea of Energy. Science, New Series, Vol. 44, No. 1126 (Jul. 28, 1916), pp. 132-134. Published by: American Association for the Advancement of Science at https://www.jstor.org/stable/1644152?Search=yes&resultItemClick=true&searchText=garver&searchUri=%2Faction%2FdoBasicSearch%3FsearchType%3DfacetSearch%26amp%3Bsd%3D1916%26amp%3Bed%3D1916%26amp%3BQuery%3Dgarver&ab_segments=0%2Fbasic_SYC-5152%2Fcontrol&seq=1#metadata_info_tab_contents, accessed April 28th 2020.
- [Goldstein 1987] Herbert Goldstein: Klassische Mechanik. AULA Verlag 9th ed. 1987, ISBN: 3-89104-132-2. Translation of the original: Classical mechanics (English), 6th ed.
- [Halliday et al. 1993] David Halliday, Robert Resnick, Jearl Walker: Fundamentals of Physics. John Wiley & Sons, 4th ed. 1993. ISBN 0-471-59986-7.
- [Lehrman 1973] R.L. Lehrman: Energy is not the ability to do work. Phys. Teach. 11, 15 (1973). [CrossRef]
- [Mehling 2019] H. Mehling: Understanding the basics of energy - An introduction from simple to complex situations. Tredition, 2019, ISBN-13: 978-3748208969.
- [Newton 1687] Isaac Newton: The mathematical principles of natural philosophy. Original publication 1687, in Latin. Translated to English by Andrew Motte, published by Daniel Adee 1846. downloaded Aug. 16th 2021, from https://archive.org/details/newtonspmathema00newtrich/page/n43/mode/2up.
- [Quaschning 2005] Quaschning V.: Understanding renewable energy systems. Earthscan, 2005, ISBN 1-84407-128-6.
- [Reif 1985] Reif F.; Fundamentals of statistical and thermal physics. McGraw-Hill International editions, 1985, ISBN 0-07-085615-X, 1985.
- [Walker et al. 2014] Walker J., Halliday D., and Resnick R.: Principles of physics. 10th ed., international student version, Wiley, 2014, ISBN: 978-1-118-23074-9.
Figure 1.
Consequences of action and reaction in mutual interactions (source: Mehling 2019).

Figure 2.
Meaning of Newton’s 3rd law looking at a spring between two walls (left), gravitation acting between two masses (centre), and schematic (right).
Figure 2.
Meaning of Newton’s 3rd law looking at a spring between two walls (left), gravitation acting between two masses (centre), and schematic (right).

Figure 3.
System of interacting objects including motion: left without, and right with an interaction to the system’s surrounding (source: Mehling 2019).
Figure 3.
System of interacting objects including motion: left without, and right with an interaction to the system’s surrounding (source: Mehling 2019).
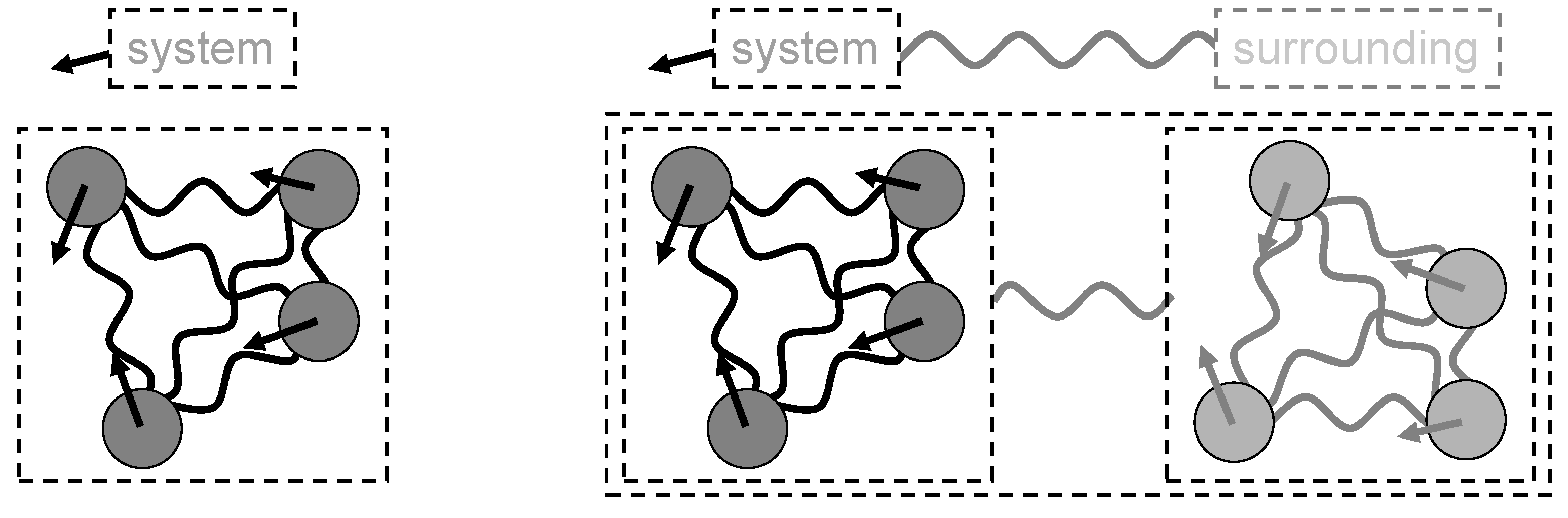
Figure 4.
Correlation between change of energy, momentum, and the velocity of an affected object.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated





