Hybrid Multi-Infeed Receiver Line Longitudinal Protection Scheme Based on Voltage Waveform Comprehensive Distance Similarity

1. Introduction

With the continuous development of China's socio-economic landscape, the electrical demand is rapidly increasing. In order to balance the rising demand for electricity and resource allocation, China is accelerating the development of the strategies of "west to east power transmission " and " north to south power transmission ". High voltage direct current (HVDC) transmission technology is being utilized in grid development to meet the inevitable requirements of long distances, high capacity, and high voltage levels. [1,2].

Line commutated converter (LCC) is suitable for long-distance and high-capacity scenarios. However, due to its semiconductor control, it suffers from the drawback of commutation failure and is generally used at the rectifier end. Conversely, voltage source converter (VSC), employing fully controlled devices, can resist commutation failure on the inverter side and flexibly control the active and reactive power of the system. Its application in multi-feed systems can enhance operational flexibility at the receiving end and expand transmission capacity [3,4]. However, the application of VSC as a fully controlled device means a higher economic investment Therefore, the combination of LCC and VSC in multi-infeed DC transmission harnesses the advantages of both to compensate for their respective shortcomings. This becomes especially advantageous in aspects such as multi-AC grid interconnection, multiple power supply, and multiple load connection, fully leveraging the economic and flexible nature of DC transmission. However, the introduction of multi-DC lines for feed-in complicates the system and makes protection prone to false operations [5]. Hence, research is necessary for the relay protection of the receiving end AC system.

Currently, the protection methods for AC transmission lines primarily rely on traditional relay protection principles, including directional protection, distance protection, and differential protection [6]. In comparison to traditional AC transmission, the fault characteristics for AC lines in hybrid multi-infeed DC systems change, prompting scholars to research the applicability of traditional relay protection [7,8,9,10,11,12,13,14]. For instance, Hao et al. [7] discovered that due to the fact that the protection unit near the inverter side can only identify continuous commutation failures occurring after a fault, it is ineffective at identifying faults where there is no commutation failure after the fault or when there is only one commutation failure. Therefore, when a single transmission corridor structure is used on the AC output side of the inverter side, traditional directional protection is not suitable for AC/DC hybrid interconnected networks. Additionally, continuous commutation failures might lead to severe faults on the AC side of multi-infeed DC systems, causing a sharp increase in the reactive power demand for system fault recovery [8,9,10,11]. This can lead to transient power reversals in neighboring multiple AC lines and the DC system [12,13], while the reverse power flow can lead to potential misoperation of the longitudinal directional protection [14]. Meanwhile, Huang et al. [15] proposed improvements to the protection setting principles of the second zone of distance protection based on fault characteristics, but were unable to address errors caused by high-order harmonics. Additionally, Huang et al. [16] presented a rapid fault detection method based on instantaneous active power and fault transient components to alleviate the effects of commutation failures and reactive power compensation. Ma et al. [17] used time-domain differential equations to calculate fault point location, enhancing the protective performance of fault distance measurement, but with poor anti-interference capabilities that are unable to protect the entire length of the line. Moreover, Zheng et al. [18] analyzed the impact of non-periodic components and harmonic components caused by DC feeding on the accuracy of algorithms, resulting in decreased protective operation performance. In summary, the multi-DC system feeding complicates the research for AC line protection at the receiving end of hybrid AC/DC systems, currently highlighting the following limitations: (1) Traditional directional and distance protection strategies are challenging to ensure the reliability of AC protection, and existing protection schemes still have shortcomings. (2) Higher harmonics on the DC side can also affect the reliability of AC protection operations. (3) Currently, there is limited research and analysis on the protection at the AC receiving end, with most of it being qualitative analysis.

This article introduces a new protection principle based on comprehensive voltage waveform analysis for multi-infeed AC/DC hybrid interconnected systems. The key contributions are as follows:

(1)

A novel protection method is proposed that relies on the similarity of voltage waveforms between measuring and reference points. It addresses the issue of unreliable operation of AC protection in AC/DC hybrid systems.

(2)

The Euclidean distance and dynamic time warping (DTW) distance are investigated to assess waveform similarity, thus avoiding the impact of data asynchrony or protection misoperation caused by a single distance metric.

(3)

The least squares method (LSM) is employed to fit the voltage waveform, effectively mitigating interference from high-order harmonics.

The article is structured as follows: Section 2 introduces the measurement method for voltage waveform distance similarity. Section 3 proposes the topology of the hybrid AC/DC multi-infeed interconnected system and analyzes the system's fault characteristics, then describes the protection scheme steps and processes. In Section 4, a model is established in PSCAD, and MATLAB is used to simulate and verify the feasibility of the protection scheme. The conclusion is presented in Section 5.

2. Comprehensive Voltage Waveform Similarity Calculation

2.1. Waveform Processing

In the event of an AC fault in the AC/DC hybrid network, the fault phase voltage amplitude rapidly decreases. Additionally, due to the introduction of high-order harmonics from DC injections, waveform preprocessing is necessary before comparing the similarity of the measured and reference voltage waveforms, in order to more intuitively reflect the trend of change. As for the high-order harmonic interference, common engineering solutions currently include wavelet transform, which suffers from drawbacks such as high computational complexity, poor speed, and low accuracy [19]. Filtering methods like amplitude limiting and median filtering perform poorly in handling periodic disturbances in AC/DC power systems and are prone to eliminating crucial waveform information [20]. Therefore, waveform signal processing must ensure both rapid response and the retention of waveform information that reflects trends. In this study, the use of the LSM to fit voltage waveforms meets both of these requirements.

LSM is a mathematical fitting technique that connects discrete points on a plane through a curve. It generally assumes that the curve can be represented by:

$$f\left(x\right)=a_0+a_{1}x+a_2{x}^2+a_3{x}^3+\cdots +a_N{x}^b$$

(1)

he unknown coefficients are denoted as a₀, a₁, a₂…a_N, and b in x_b represents the power to which we want to fit.

Assuming the voltage waveform is$\left(x_i,y_i\right)$,$i=\left(1,2,3,\cdots ,m\right)$, where m denotes the number of voltage values, the fitted curve is then given by:

$$f^{\prime }\left(x\right)=\min {\displaystyle \sum _i^m{\left[f^{\prime }\left(x_i\right)-y_i\right]}^2}$$

(2)

By fitting the measured voltage and reference voltage waveforms, high-order harmonic interference can be eliminated while retaining the variation trend.

2.2. Euclidean Distance Calculation

Euclidean distance, also known as Euclidean metric, is commonly used to measure the true distance between two points in a space, reflecting the overall distribution characteristics of waveform similarity [21]. The instantaneous values of measured voltages at the protection installation points M and N are extracted. Corresponding reference voltages are calculated using Equation (12), defining the sample time sequences of the measured voltages and the reference voltages as d_M, d_N, d_rM, and d_rN, respectively. Here, $d_M=\left(x_1,x_2,x_3,\cdots ,x_n\right)$、$d_N=\left(y_1,y_2,y_3,\cdots ,y_n\right)$、$d_{rM}=\left(z_1,z_2,z_3,\cdots ,z_n\right)$、$d_{rN}=\left(q_1,q_2,q_3,\cdots ,q_n\right)$, n represents the number of sample points, chosen based on the precision requirements of the protection method. The Euclidean distance of the voltage waveforms between the measured voltages and the corresponding reference voltages at the protection installation points on both sides is given by:

$$D_{WM}\left(d_M,d_{rM}\right)=\sqrt{{\displaystyle \sum _{i=1}^n{\left(x_i-z_i\right)}^2}}$$

(3)

$$D_{WN}\left(d_N,d_{rN}\right)=\sqrt{{\displaystyle \sum _{i=1}^n{\left(y_i-q_i\right)}^2}}$$

(4)

where D_WM and D_WN represent the Euclidean distance between the measured voltage and reference voltage waveforms at the installation points on sides M and N, respectively.

2.3. DTW Distance

The DTW method employs the concept of dynamic programming, adjusting the different sample points of sequences through compression and expansion, thus enabling a point in one sequence to match multiple points in another, optimizing the warped path. Therefore, when the DTW algorithm computes distance, it doesn't require a one-to-one correspondence of values based on the same sample points, unlike the calculation method for Euclidean distance. The DTW algorithm can address issues of sequence asynchrony, better capturing the overall dynamic characteristics of curves, and measuring the overall similarity of shapes between sequences [22]. For the sampled sequences d_M and d_rM, an n×m distance matrix D_M is constructed, where the elements are D_M(i, j) as per Equation (5). Similarly, for the sampled sequences d_N and d_rN, an n×m distance matrix D_N is built, with elements being D_N(i, j) as per Equation (4).

$$D_M\left(i,j\right)=\sqrt{{\left(x_i-z_j\right)}^2}\cdots 1\le i\le n,1\le j\le m$$

(5)

$$D_N\left(i,j\right)=\sqrt{{\left(y_i-q_j\right)}^2}\cdots 1\le i\le n,1\le j\le m$$

(6)

where Equation (5) represents the Euclidean distance between the sequences (d_M) and (d_rM) at the sequence points (x_i) and (z_j), while Equation (6) represents the Euclidean distance between the sequences (d_N) and (d_rN) at the sequence points (y_i) and (q_j).

The set composed of each pair of adjacent elements from D_M(i, j) and D_N(i, j) is defined as the bent path of the adopted waveform, denoted by L. Taking path L as an example, the element l_s refers to the coordinates of the s-th point on the path, i.e., l_s = (i, j). Path L must satisfy the following two-part constraints:

(I)The selected path must include all sampling points.

(II)Each sample point needs to be matched with the adjacent sample point, such that if l_s=(i, j), l_s+1=(a, b)satisfies $\{\begin{array}{c}0\le a-i\le 1\\ 0\le b-j\le 1\end{array}$.

This yields the DTW distance between the sequences d_M and d_rM, and the DTW distance between the sequences d_N and d_rN:

$$D_{Mdtw}\left(d_M,d_{rM}\right)=\underset{L}{\min }{\displaystyle \sum _{s=1}^{k}D\left(L_s\right)}$$

(7)

$$D_{Ndtw}\left(d_N,d_{rN}\right)=\underset{R}{\min }{\displaystyle \sum _{s=1}^{k}D\left(R_s\right)}$$

(8)

where D(L_s) and D(R_s) represent the cumulative distance of the bent path L and R, while D_Mdtw and D_Ndtw respectively denote the waveform DTW distance between the measured voltage and the reference voltage at the installation locations of the protections on both sides.

2.4. Local Dynamic Mapping

In order to better describe the local dynamic characteristics of the voltage waveform, reflecting its trend information at each sampling interval and fully considering the accuracy of the algorithm, the discrete sampling sequences$d_M$、$d_N$、$d_{rM}$and$d_{rN}$are transformed into shape sequences of length ${d^{\prime }}_M$、${d^{\prime }}_N$、${d^{\prime }}_{rM}$与${d^{\prime }}_{rN}$。Taking the element xʹ_i as an example, as shown in Equation (9), where Δt represents the time interval:

$${x_i}^{\prime }=\frac{x_{i+1}-x_i}{\Delta t}\cdots \cdots i=1,2,\cdots ,n-1$$

(9)

2.5. Comprehensive Voltage Waveform Similarity Description

This chapter combines the Euclidean distance with the DTWdistance to propose a measurement method for the comprehensive voltage waveform similarity that encompasses overall, local, and dynamic characteristics.

$$D_{M\phi }=\alpha D_{WM}\left(d_M,d_{rM}\right)+\beta D_{Mdtw}\left(d_M,d_{rM}\right)+\gamma D_{Mdtw}\left({d^{\prime }}_M,{d^{\prime }}_{rM}\right)$$

(10)

$$D_{N\phi }=\alpha D_{WN}\left(d_N,d_{rN}\right)+\beta D_{Ndtw}\left(d_N,d_{rN}\right)+\gamma D_{Ndtw}\left({d^{\prime }}_N,{d^{\prime }}_{rN}\right)$$

(11)

where D_M𝜙 and D_N𝜙 represent the comprehensive distance similarity of the measured voltage and reference voltage waveforms at the protection installation points on M and N sides, where φ = A, B, C represents the phase sequence index. The smaller the values of D_Mφ and D_Nφ, the higher the similarity of the voltage waveforms. D_WM(d_M, d_rM) and D_WN(d_N, d_rN) reflect the overall distribution characteristics of the voltage waveforms, while D_Mdtw(d_M, d_rM) and D_Ndtw(d_N, d_rN) reflect the overall dynamic characteristics of the voltage waveforms. Additionally, D_Mdtw(dʹ_M, dʹ_rM) and D_Ndtw(dʹ_N, dʹ_rN) reflect the local dynamic characteristics of the voltage waveforms. α, β, and γ are the weights assigned to each distance measure, and based on the actual sampling accuracy requirements and the principle of entropy weighting, their respective values are set to 0.4, 0.3, and 0.3 [22].

3. System Fault Characteristics and Protection Process

3.1. Hybrid DC Multi-Infeed AC/DC Interconnected System Topology Structure

The constructed hybrid AC/DC interconnected system with multiple DC inputs, as shown in Fig. 1, features the transmitting end's DC section consisting of two distinct ±500kV hybrid DC transmission lines: a bipolar double-end line commutated converter-modular multilevel converter (LCC-MMC) transmission system and a pseudo-bipolar double-end LCC-VSC transmission system. The receiving end's AC section comprises a 230kV dual-source system, with M and N denoting the positions of the protection units on both sides of the line. r_M represents the calculation reference point at end M, and r_N represents the calculation reference point at end N, defining the protection scope from the protection installation point to the reference point on that side. The overlap of the protection scopes at both ends indicates the range for determining internal faults, denoted by the green area in Fig. 1. This study focuses primarily on the central section, MN, where f₁ and f₅ represent faults occurring outside the protection scope, f₂ represents a fault occurring solely within the protection scope at end N but outside the reverse area, f₃ represents a fault occurring within the protection scope at both ends M and N, and f₄ represents a fault occurring solely within the protection scope at end M but outside the forward area.

In an LCC-VSC system, the rectifier side comprises two sets of twelve-pulse LCC converters connected in series. The rectifier side direct current is input into the constant current control circuit, which controls the α angle to regulate the rectifier-side converters. On the inverter side, low-cost and highly stable two-level VSC modules are employed. Through vector control, the modulated waves are input into the pulse width modulation (PWM) controller, which then produces the control signals.

In an LCC-MMC system, the rectifier side is similar to that of the LCC-VSC system, whereas the inverter side consists of two MMC modules connected in series. Input signals related to inverter-side power and current are sent to the inner and outer loop control circuits, and the output signals are directed to the bridge arms to control the inverter-side converters.

Figure 1. Topology diagram of the hybrid DC multi-feed system.

Figure 1. Topology diagram of the hybrid DC multi-feed system.

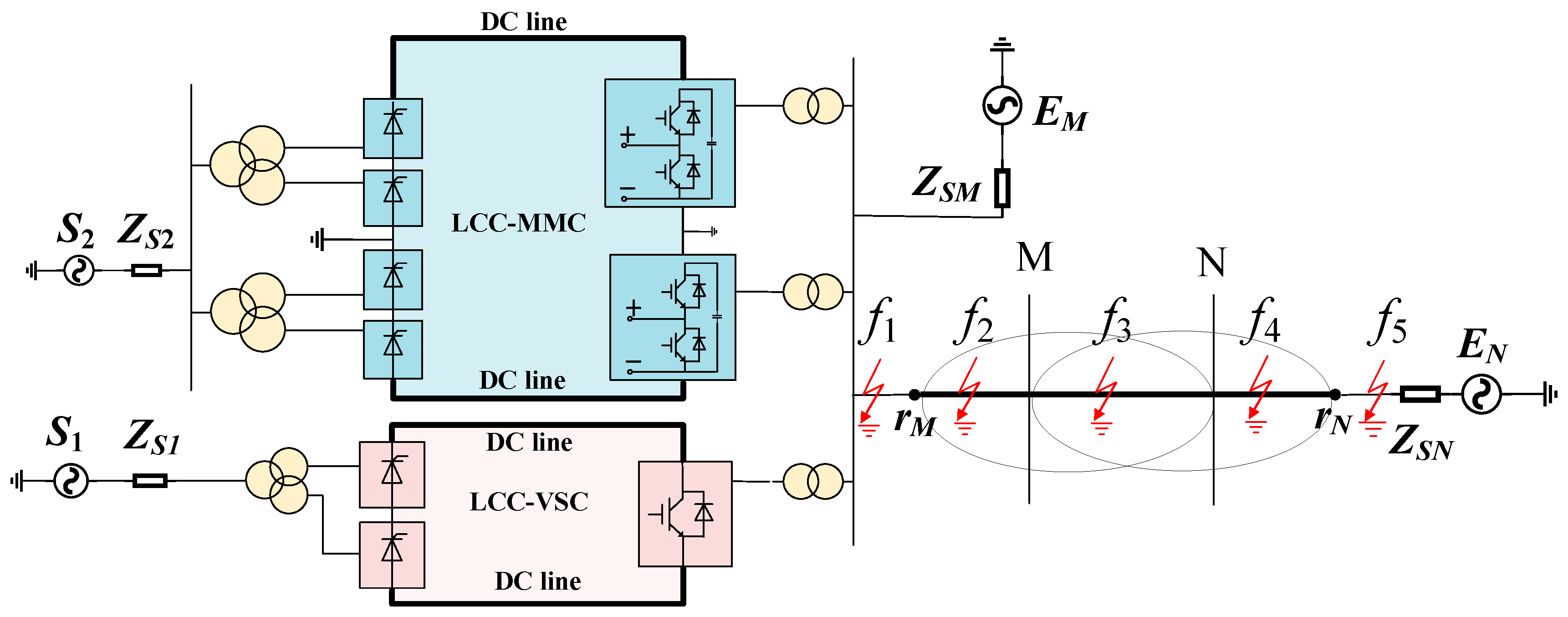
3.2. Reference Voltage Calculation and System Fault Characteristics

The similarity of the voltage waveforms between the measuring point and the reference point is calculated to determine if a fault has occurred, and the position of the reference point needs to be determined. The reference point is usually located outside the protection line to ensure sufficient sensitivity. Additionally, to reduce errors, the reference point should not be too far away; scholars both domestically and abroad typically position it within the range of 1.2 to 2.0 times the length of the protected line [23]. After extensive simulation experiments, it has been found that placing the reference point at 1.3 times the length of the line can meet the experimental requirements outlined in this paper, while allowing for flexible adjustments within the range based on specific protection needs and interference considerations.

Compared to traditional purely AC lines, in a multi-infeed interconnected grid, significant non-periodic components are introduced into the DC system after a fault occurs. This results in a more complex variation of electrical quantities in the AC lines. Obtaining accurate voltage phasors through traditional Fourier algorithms no longer guarantees accuracy. Instead, this paper proposes using instantaneous measurement methods to calculate the reference voltage, taking the M-side as an example.

In Fig. 2 (a), Z_SM and Z_SN represent the equivalent system impedances on both sides of the AC line, I_m and U_m represent the instantaneous measured currents and voltages, and I_r and U_r represent the instantaneous reference currents and voltages. Due to the rectifying sides of the hybrid multi-infeed DC system using constant current control, and the inverting side voltage being determined by the receiving-end AC bus, both can be considered equivalent to a voltage-controlled current source controlled by the receiving end. ΔI_dc.MMC and ΔI_dc.VSC represent the equivalent fault component currents for the LCC-MMC and LCC-VSC hybrid DC systems, respectively.

Based on the situation of the completed and ongoing multi-infeed AC/DC hybrid power grid projects, this paper sets a total line length of 160 km, using an equivalent π-type line model considering the electric shunt, as depicted in Fig. 2(b). After measuring the instantaneous current value I_m and the instantaneous voltage U_m, the reference voltage U_r can be obtained through the differential equation in Equation (12).

$$U_r=U_{\mathrm{m}}-[R\left(I_m-\frac{C}{2}\frac{d{U}_{\mathrm{m}}}{dt}\right)+L\frac{d\left(I_m-\frac{C}{2}\frac{d{U}_{\mathrm{m}}}{dt}\right)}{dt}]$$

(12)

Figure 2. Schematic diagram of system and line model (a) Simplify the system model; (b) Schematic diagram of system and line model.

Figure 2. Schematic diagram of system and line model (a) Simplify the system model; (b) Schematic diagram of system and line model.

Under normal operation, the voltage waveforms at the measurement point and reference point are similar. To analyze the fault characteristics of the system at different locations, we take the occurrence of a ground fault as an example and analyze the measured voltage U_m and the reference voltage U_r. Assuming the fault occurs at location k₁ as illustrated in Fig. 2(a), which represents an external fault in the opposite direction of M_rM, as shown in Fig. 3:

Figure 3. Schematic diagram of out-of-reverse fault system.

Figure 3. Schematic diagram of out-of-reverse fault system.

At this point in time, the actual current direction is opposite to the measured current direction during normal operation, hence Equation (12) can be rewritten as:

$${U^{\prime }}_{\mathrm{m}}=-\left[{R^{\prime }}_f\left({I^{\prime }}_m-\frac{{C^{\prime }}_f}{2}\frac{d{U^{\prime }}_{\mathrm{m}}}{dt}\right)+{L^{\prime }}_f\frac{d\left({I^{\prime }}_m-\frac{{C^{\prime }}_f}{2}\frac{d{U^{\prime }}_{\mathrm{m}}}{dt}\right)}{dt}\right]$$

(13)

$${U^{\prime }}_r=-\left[\begin{array}{l}{I^{\prime }}_m\left({R^{\prime }}_f-{R^{\prime }}_r\right)-\frac{d{U^{\prime }}_{\mathrm{m}}}{dt}\left(R_f\frac{{C^{\prime }}_f}{2}-R_r\frac{{C^{\prime }}_r}{2}\right)+\\ {L^{\prime }}_f\frac{d\left({I^{\prime }}_m-\frac{{C^{\prime }}_f}{2}\frac{d{U^{\prime }}_{\mathrm{m}}}{dt}\right)}{dt}-{L^{\prime }}_r\frac{d\left({I^{\prime }}_m-\frac{{C^{\prime }}_r}{2}\frac{d{U^{\prime }}_{\mathrm{m}}}{dt}\right)}{dt}\end{array}\right]$$

(14)

where Rʹ_f, Lʹ_f, and Cʹ_frepresent the resistance, inductance, and capacitance values from measurement point M to fault point k₁, respectively. Rʹ_r, Lʹ_r, and Cʹ_r represent the resistance, inductance, and capacitance values from measurement point M to reference point r_M, respectively. By comparing the two equations, it can be concluded that although there are differences in the amplitude of the measured voltage Uʹ_m and the reference voltage Uʹ_r, their variation trends are consistent. The computational relationship deduced from Equation (14) is identical to that of Equation (12), indicating that when an external fault occurs in the reverse direction area, the measured voltage and the reference voltage waveforms are similar.

Assuming that the fault occurs at position k₃ as shown in Fig. 2 (a), i.e., an external fault in the positive direction of M_rM, as illustrated in Fig. 4:

Figure 4. Schematic diagram of out-of-zone fault system.

Figure 4. Schematic diagram of out-of-zone fault system.

At this time, the actual current direction is the same as the measured current direction under normal operation, rewriting Equation (1) as follows:

$${U^{″}}_{\mathrm{m}}={R^{″}}_f\left({I^{″}}_m-\frac{{C^{″}}_f}{2}\frac{d{U^{″}}_{\mathrm{m}}}{dt}\right)+{L^{″}}_f\frac{d\left({I^{″}}_m-\frac{{C^{″}}_f}{2}\frac{d{U^{″}}_{\mathrm{m}}}{dt}\right)}{dt}$$

(15)

$${U^{″}}_r={I^{″}}_m\left({R^{″}}_f-{R^{″}}_r\right)-\frac{d{U^{″}}_{\mathrm{m}}}{dt}\left({R^{″}}_f\frac{{C^{″}}_f}{2}-{R^{″}}_r\frac{{C^{″}}_r}{2}\right)+{L^{″}}_f\frac{d\left({I^{″}}_m-\frac{{C^{″}}_f}{2}\frac{d{U^{″}}_{\mathrm{m}}}{dt}\right)}{dt}-{L^{″}}_r\frac{d\left({I^{″}}_m-\frac{{C^{″}}_r}{2}\frac{d{U^{″}}_{\mathrm{m}}}{dt}\right)}{dt}$$

(16)

where Rʺ_f, Lʺ_f, and Cʺ_frepresent the resistance, inductance, and capacitance values from measurement point M to fault point k₃, respectively. Rʺ_r, Lʺ_r, and Cʺ_r respectively represent the resistance, inductance, and capacitance values from measurement point M to reference point r_M. By comparing Equations (15) and (16), it can be observed that although there is a difference in the magnitude of the measured voltage Uʺ_m and the reference voltage Uʺ_r, their variation follows a consistent pattern. The computational relationship derived from Equation (16) is the same as Equation (12), indicating that when an external fault occurs, the measured voltage and the reference voltage waveforms are similar.

Suppose that the fault has occurred at k₂ in the area of M_rM, as shown in Fig. 2(a), depicting an internal fault in the M_rM area, as illustrated in Fig. 5:

Figure 5. Schematic diagram of fault system in the area.

Figure 5. Schematic diagram of fault system in the area.

At this time, the fault branch between Mr and M is increased, and the line structure is disrupted. Based on the characteristic that the distance from measuring point M to reference point r_M is greater than to the fault point during an internal fault, Equation (1) is modified as follows:

$${U^{‴}}_{\mathrm{m}}={R^{‴}}_f\left({I^{‴}}_m-\frac{{C^{‴}}_f}{2}\frac{d{U^{‴}}_{\mathrm{m}}}{dt}\right)+{L^{‴}}_f\frac{d\left({I^{‴}}_m-\frac{{C^{‴}}_f}{2}\frac{d{U^{‴}}_{\mathrm{m}}}{dt}\right)}{dt}$$

(17)

$$\begin{array}{c}{U^{‴}}_r=\left[{R^{‴}}_r\left({I^{‴}}_m-\frac{{C^{‴}}_r}{2}\frac{d{U^{‴}}_{\mathrm{m}}}{dt}\right)+L\frac{d\left({I^{‴}}_m-\frac{{C^{‴}}_r}{2}\frac{d{U^{‴}}_{\mathrm{m}}}{dt}\right)}{dt}\right]-{U^{‴}}_{\mathrm{m}}\\ =\frac{d{U^{‴}}_{\mathrm{m}}}{dt}\left({R^{‴}}_f\frac{{C^{‴}}_f}{2}-{R^{‴}}_r\frac{{C^{‴}}_r}{2}\right)-{I^{‴}}_m\left({R^{‴}}_f-{R^{‴}}_r\right)+\\ {L^{‴}}_f\frac{d\left(\frac{{C^{‴}}_f}{2}\frac{d{U^{‴}}_{\mathrm{m}}}{dt}-{I^{‴}}_m\right)}{dt}-{L^{‴}}_r\frac{d\left(\frac{{C^{‴}}_f}{2}\frac{d{U^{‴}}_{\mathrm{m}}}{dt}-{I^{‴}}_m\right)}{dt}\end{array}$$

(18)

where Rʺʹ_f, Lʺʹ_f, and Cʺʹ_frespectively represent the resistance value, inductance value, and capacitance value from measuring point M to fault point k₂. Rʺʹ_r, Lʺʹ_r, and Cʺʹ_r represent the resistance value, inductance value, and capacitance value from measuring point M to reference point r_M. By comparing Equations (17) and (18), it can be inferred that although there are differences in the amplitude of the measured voltage Uʺʹ_m and the reference voltage Uʺʹ_r, their variation trends remain consistent. Equation (18) deduces an operational relationship opposite to that of Equation (12), indicating that when an internal fault occurs, the measured voltage and the reference voltage waveforms are dissimilar.

In summary, it can be concluded that during an internal fault, the measured voltage and the reference voltage waveforms are dissimilar, whereas during normal operation and external fault occurrence, the voltage waveforms are similar. This provides a theoretical basis for the subsequent use of voltage comprehensive waveform similarity.

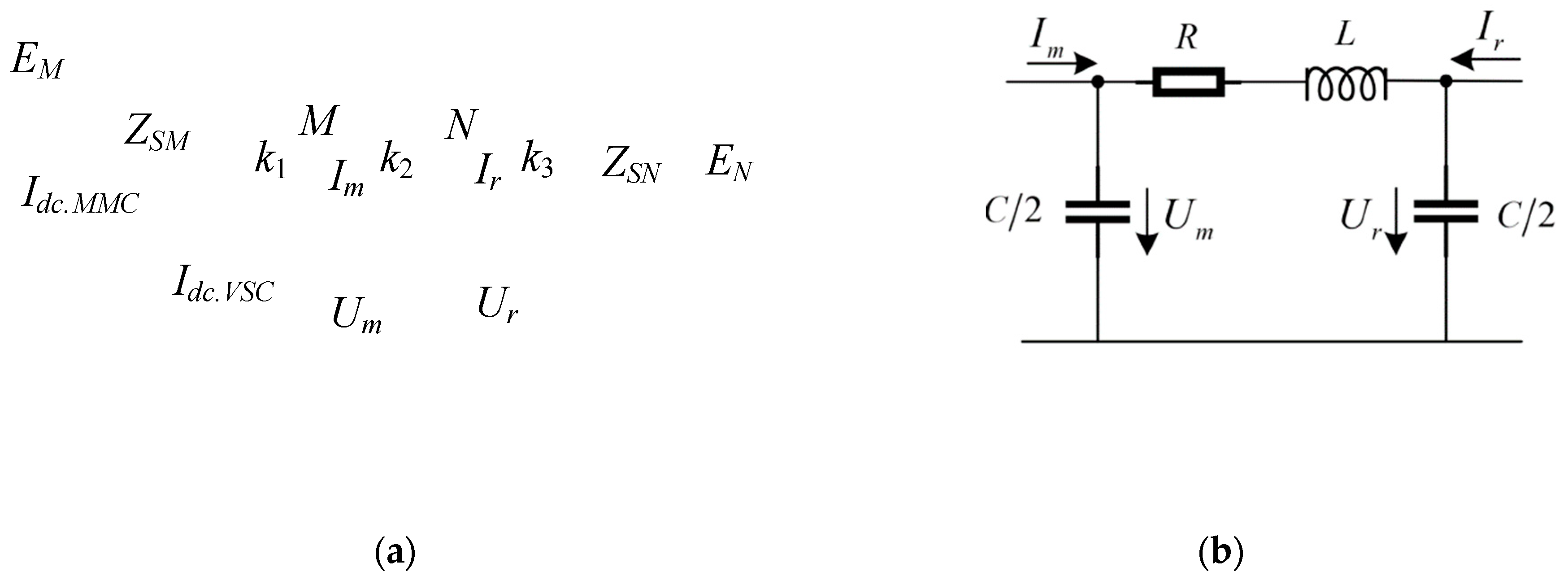
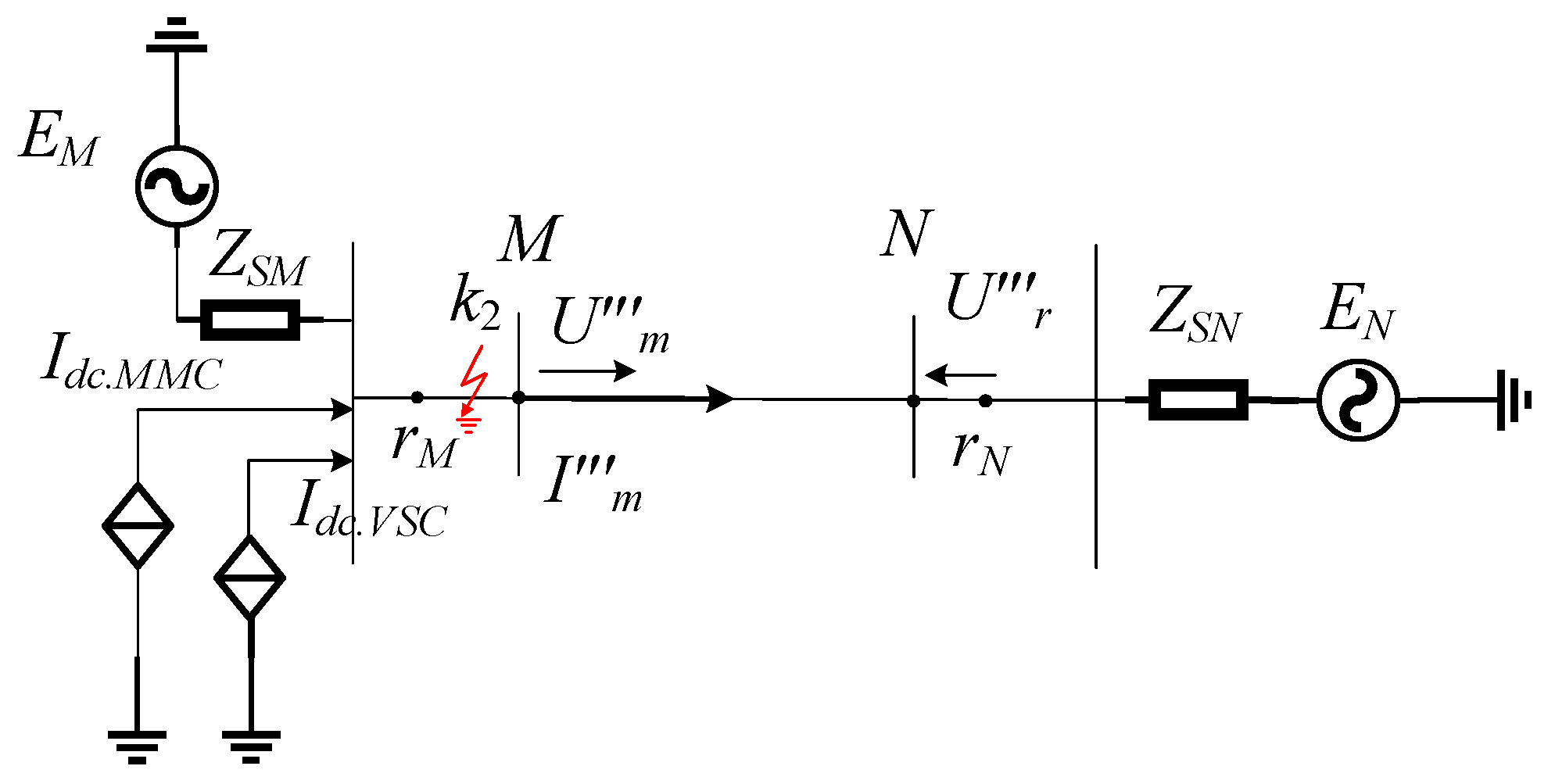
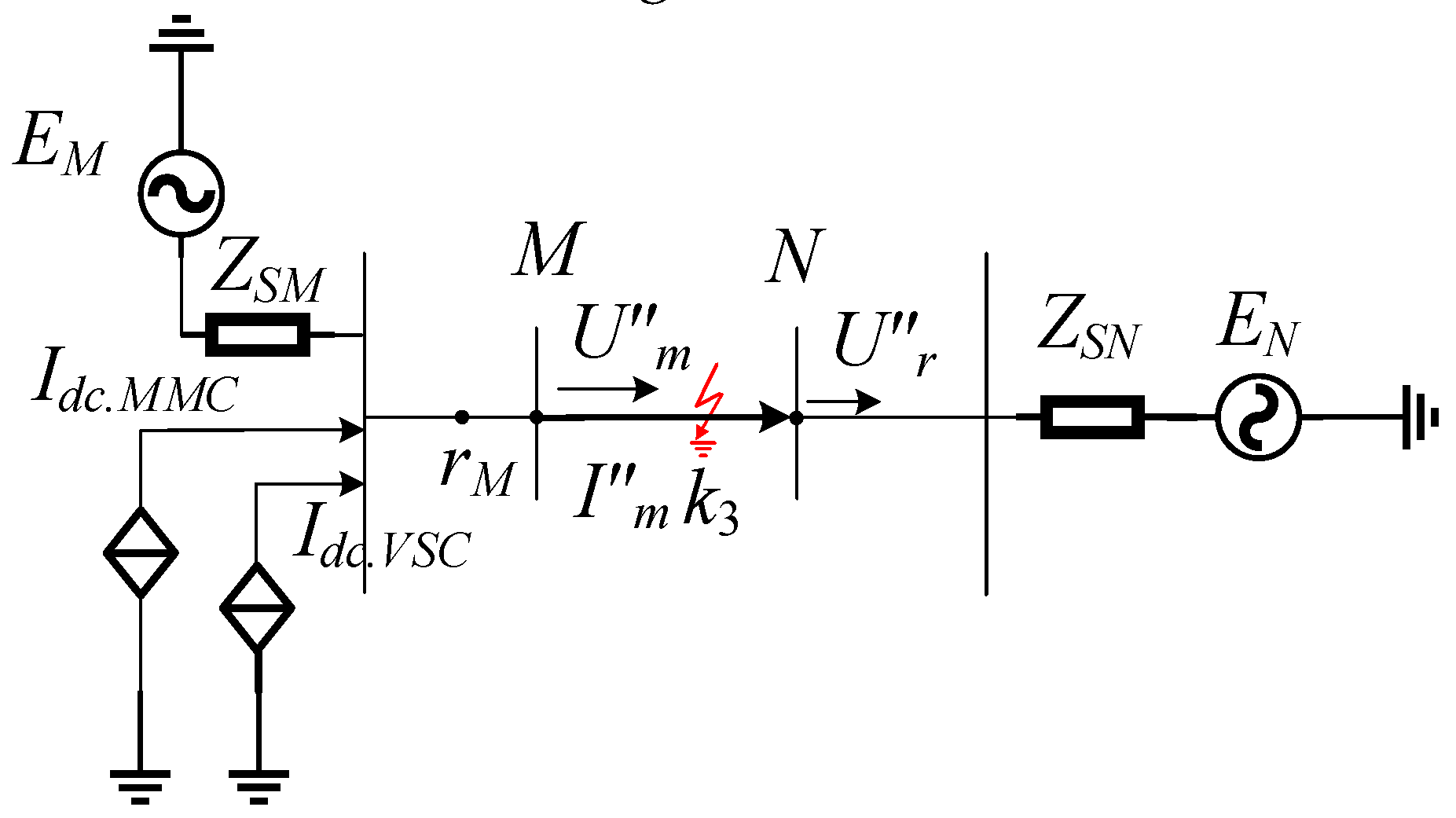
3.3. Protection Action Criteria

By employing the calculation method in Section 2.5, the comprehensive waveform similarity at both ends is obtained. From the computed results for the three phases, the maximum values are denoted as MAX(D_Mφ) and MAX(D_Nφ), and a threshold value D_set is established. When the voltage comprehensive waveform similarity exceeds the threshold value, it indicates dissimilarity between the two voltage waveforms. Considering the topological structure and operational conditions of the AC/DC hybrid system, along with practical engineering requirements and a large volume of simulation data, the threshold value D_set is chosen as 1.2. By comparing the relationship between MAX(D_Mφ), MAX(D_Nφ), and the protection threshold value D_set, fault locations can be further determined.

When MAX(D_Mφ) < D_set and MAX(D_Nφ) > D_set, the fault occurs between protection device M and reference point r_M, that is, the position f₂ in Fig. 1 represents an external fault.

When MAX(D_Mφ) > D_set and MAX(D_Nφ) < D_set, the fault occurs between protection device N and the reference point r_N, indicating that the fault location is external, as illustrated in position f₄ in Fig. 1.

When MAX(D_Mφ) < D_set and MAX(D_Nφ) < D_set, the fault occurs in areas outside protection devices M and N, i.e., positions f₁ and f₅ in Fig. 1 indicate an external fault zone.

When MAX(D_Mφ) > D_set and MAX(D_Nφ) > D_set, the fault is determined to have occurred between the two protective devices, i.e., the location f₃ in Fig. 1 indicates an internal fault, triggering the protective action.

When a fault occurs, the fault component of the current will increase or decrease. Based on the magnitude of this sudden change, protection initiation criteria can be established, and the fault component of the current can be extracted using the superposition theorem.

$$\Delta I_s(t)=I_s(t)-I_s(t-T)$$

(19)

where t denotes the sampling instant. I_s(t) represents the actual current value at location s at instant t. ΔI_s(t) stands for the fault component of the current extracted at location s at instant t for protection measurement. T represents the selected pre-fault sampling instant. Considering the system's operational stability, typically the two sampling cycles before the fault are chosen. Based on the variation in the fault component of the current obtained from Equation (19), the initiation criterion can be obtained as follows:.

$$\Delta I_{sM\phi }>0.01k{I}_n$$

(20)

$$\Delta I_{sN\phi }>0.01k{I}_n$$

(21)

where ΔI_sMφ and ΔI_sNφ respectively denote the change in current fault components at the protection installation points on sides M and N. Here, φ=A, B, C represents the phase sequence index, k is the reliability factor, and I_n stands for the rated line current. As long as any of the judgment conditions in Equations (20) and (21) are satisfied, the calculation of the comprehensive voltage waveform distance similarity can be initiated to further determine the fault area.

Based on the above fault analysis process and the introduction of the protection scheme, the overall protection process can be illustrated as shown in Fig. 6, with the specific steps outlined below:

(1) Run the system model, debug the protection measurement devices, collect electrical signal data, and extract the sampled values of voltage and current for the M and N ends of the AC transmission line using preset sensors.

(2) Extract transient changes in fault component from the sampled current values at ends M and N, and determine if a fault has occurred using a protection initiation criterion. When the criterion is met, it indicates a fault in the system.

(3) Calculate the reference voltages at both ends based on the sampled voltage and current values, and use the method of least squares to fit the waveform trend of the sampled and calculated values, thereby filtering out high-order harmonic interference.

(4) Derive the comprehensive waveform distance similarity metrics D_Mφ and D_Nφ between the measured voltage and the reference voltage at both ends of the line. Compare the maximum values of D_Mφ and D_Nφ with the protection set value D_set to determine the fault occurrence region.

When D_Mφ > D_set and D_Nφ > D_set, the fault is determined to occur between the two protective devices, indicating an internal fault, located at position f₃ in Fig. 1; otherwise, it is determined to be an external fault.

4. Experimental Verification

4.1. Introduction to the Experimental Platform

To verify the theoretical analysis and the feasibility of the protection scheme mentioned above, the PSCAD/EMTDC simulation platform is utilized to construct the hybrid DC multi-infeed system, as depicted in Fig. 1, for power system simulation. The electrical parameters are adjusted, and various fault occurrences are simulated under different conditions by controlling the fault area, line positions, and other interfering factors. Subsequently, the validation of the protection algorithm is carried out in MATLAB.

Figure 6. Schematic diagram of fault system in the area.

Figure 6. Schematic diagram of fault system in the area.

The sampling window for calculating the comprehensive voltage distance similarity in this paper is 1ms, and the sampling frequency for line protection is 10 kHz. Therefore, fault detection requires only 10 sampling points. In practical engineering applications, the synchronization error of the commonly used global positioning system (GPS) synchronization method is less than 2 μs. The protection algorithm investigated in this paper calculates the similarity value within the sampling interval and compares to find the maximum value, making it possible to accurately identify the fault position within a 1ms delay, without strict bi-directional timing and communication synchronization.

In conclusion, the simulated duration in this paper is set as 3s, and the fault occurs at 2.25s and lasts for 0.05s. Due to the rapid change in the current fault component, the protection can be activated in about 0.5ms, while the simulation data collection and the calculation of comprehensive voltage distance similarity can be completed within 2ms. Considering a certain margin, the proposed method can operate quickly and reliably within 3ms.

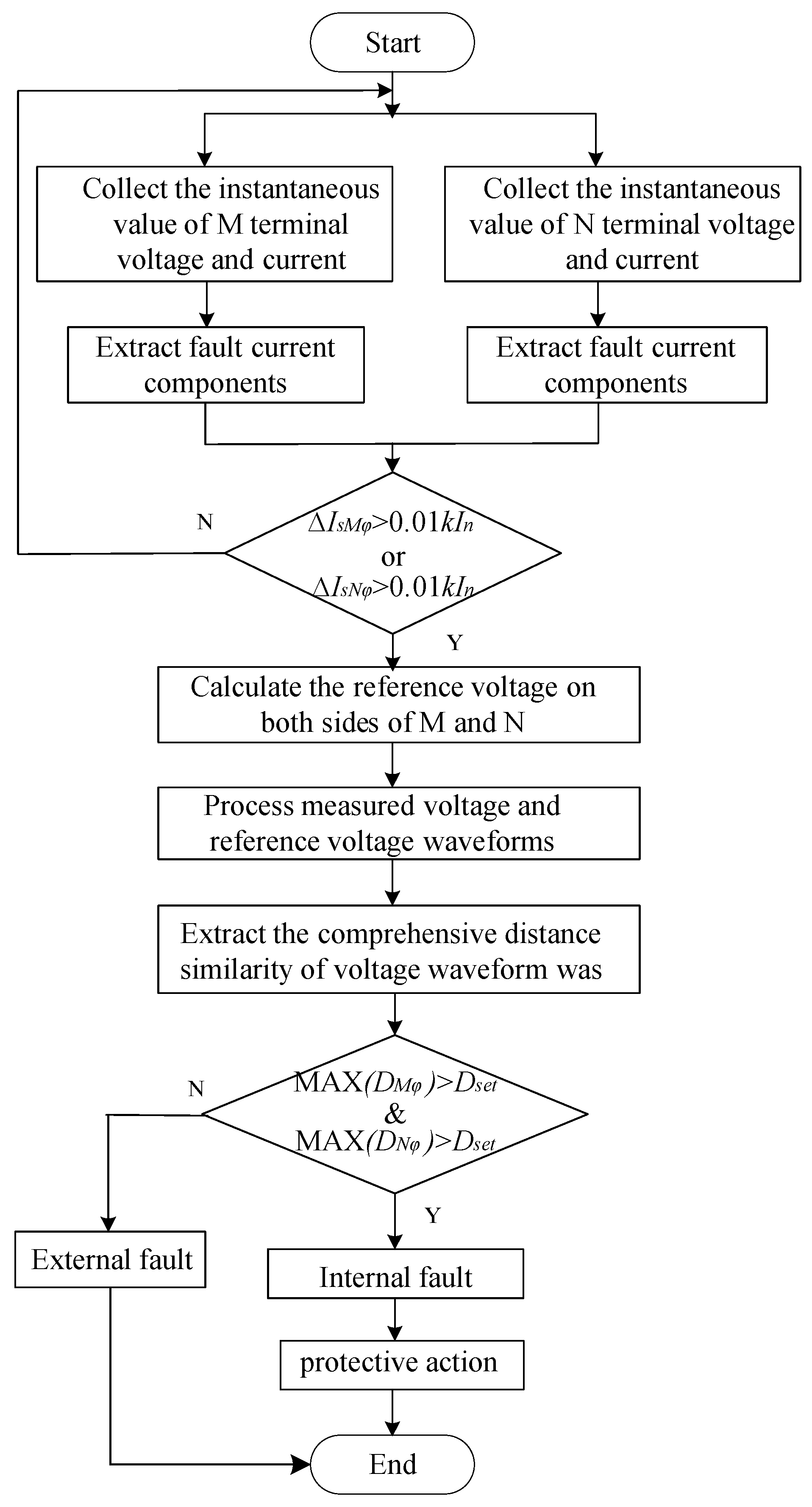
4.2. In-Zone Fault Simulation Result

In the positive direction of the AC line, a phase A-to-ground fault is set at a distance of 50 km. To stabilize the feed-in of the hybrid DC system, the fault is initiated at 2.25s and lasts for 0.05s. Taking the data at the M-end as an example, the simulation compares the waveform differences between the normal and fault states of both a pure AC system and a hybrid multi-feed-in system. The simulation window length is 0.025s, and the simulation results are shown in Fig. 4.

Figure 7. Comparison of measured voltage waveforms between pure AC system and hybrid multi-feed system (a) Comparison of measured voltage waveforms under normal operation; (b) Comparison of measured voltage waveforms under faults in the area.

Figure 7. Comparison of measured voltage waveforms between pure AC system and hybrid multi-feed system (a) Comparison of measured voltage waveforms under normal operation; (b) Comparison of measured voltage waveforms under faults in the area.

In Fig. 7, it is evident that after the introduction of multi-feed-in, both the voltage amplitude and phase undergo changes. Additionally, the system, besides experiencing voltage reduction after the fault, is also influenced by higher harmonics, leading to irregular oscillations in the fault waveform. By extracting data from the N-end and computing the reference voltage at both ends, Figure 8 compares the measured voltage and reference voltage waveforms.

Figure 8. Comparison of measured voltage waveforms between pure AC system and hybrid multi-feed system (a) Comparison of measured voltage waveforms under normal operation; (b) Comparison of measured voltage waveforms under faults in area.

Figure 8. Comparison of measured voltage waveforms between pure AC system and hybrid multi-feed system (a) Comparison of measured voltage waveforms under normal operation; (b) Comparison of measured voltage waveforms under faults in area.

In Figs 8(a) and 8(b), the measured voltage and reference voltage waveforms at terminals M and N both exhibit an upward trend before the fault occurs, with high waveform similarity. After the fault occurs, the measured voltage continues to rise, while the reference voltage decreases. The magnitudes of voltage fluctuations in both waveforms are quite similar, exhibiting an almost symmetrical relationship around 0kV, albeit with opposite directions. This aligns with the conclusion drawn in Section 1.2.

For irregular variations in fault waveforms in mixed multi-feed systems, directly applying a similarity algorithm focusing on detailed levels can lead to significant errors. However, after applying the waveform processing method in Section 2.1, waveform optimization can be achieved while retaining trend information, as illustrated in Fig. 9.

Figure 9. Comparison of voltage waveforms after treatment (a) Comparison of M-terminal voltage waveforms after optimization; (b) Comparison of N-terminal voltage waveforms after optimization.

Figure 9. Comparison of voltage waveforms after treatment (a) Comparison of M-terminal voltage waveforms after optimization; (b) Comparison of N-terminal voltage waveforms after optimization.

As shown in Fig. 9, the processed waveform is smoother and largely retains the trend information of the waveform changes, reducing errors in the subsequent calculation of the comprehensive distance similarity of voltage waveforms.

To study the changes in the comprehensive distance similarity of internal fault waveforms under various operating conditions, faults were set at 50km in the positive direction of lines M and N, with controlled transition resistance size. This involved simulating single-phase-to-ground faults (A-G), two-phase-to-ground faults (BC-G), three-phase-to-ground faults (ABC-G), and phase-to-phase short-circuit faults (BC). The fault initiation time was set at 2.25s, with a duration of 0.05s. Simulation data were tabulated in Table 1.

In Table 1, bolded data indicates values greater than the set value, and data marked in red, such as D_MA=4.4298 and D_NA=4.6376, represent the maximum values in this dataset. As Table 1 demonstrates, during the occurrence of faults, the comprehensive distance similarity of the faulted phase consistently exceeds the set value D_set, enabling correct action and non-operation for non-faulted phases. All of these are in line with the simulation results and theoretical analysis, meeting the protection requirements.

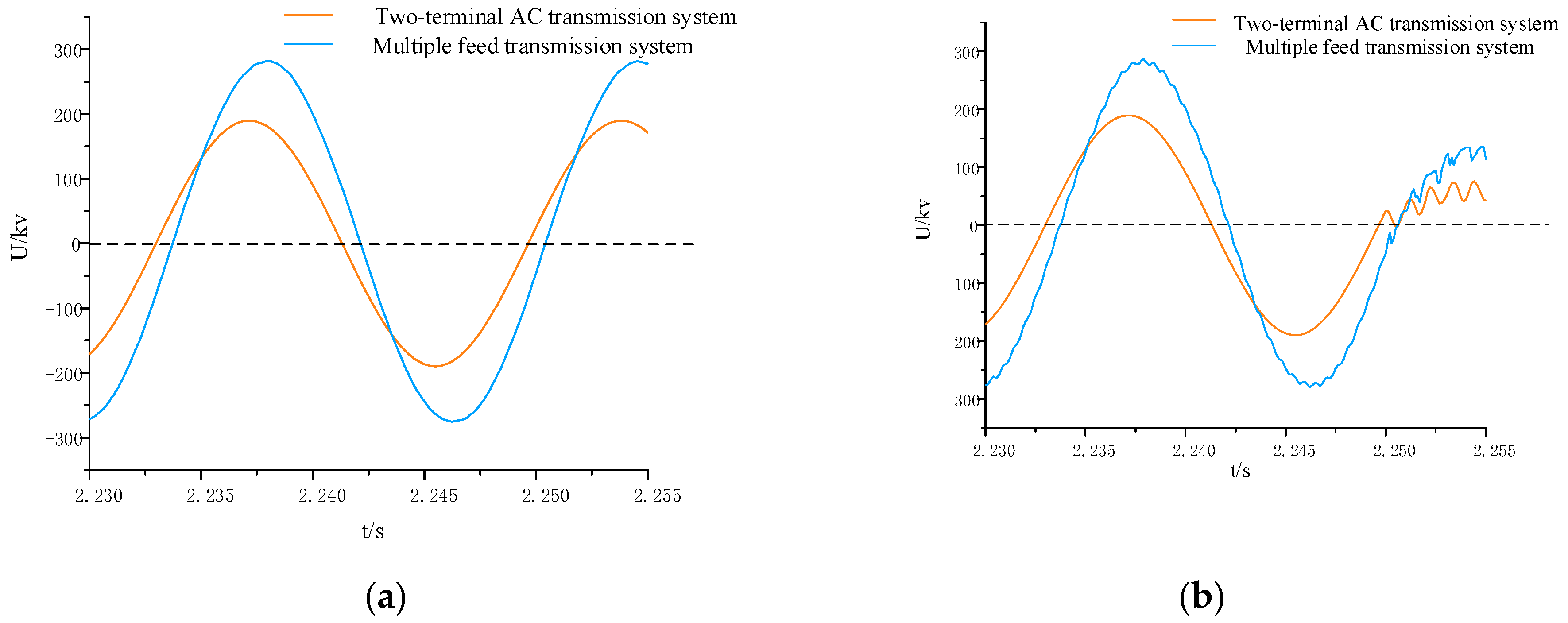
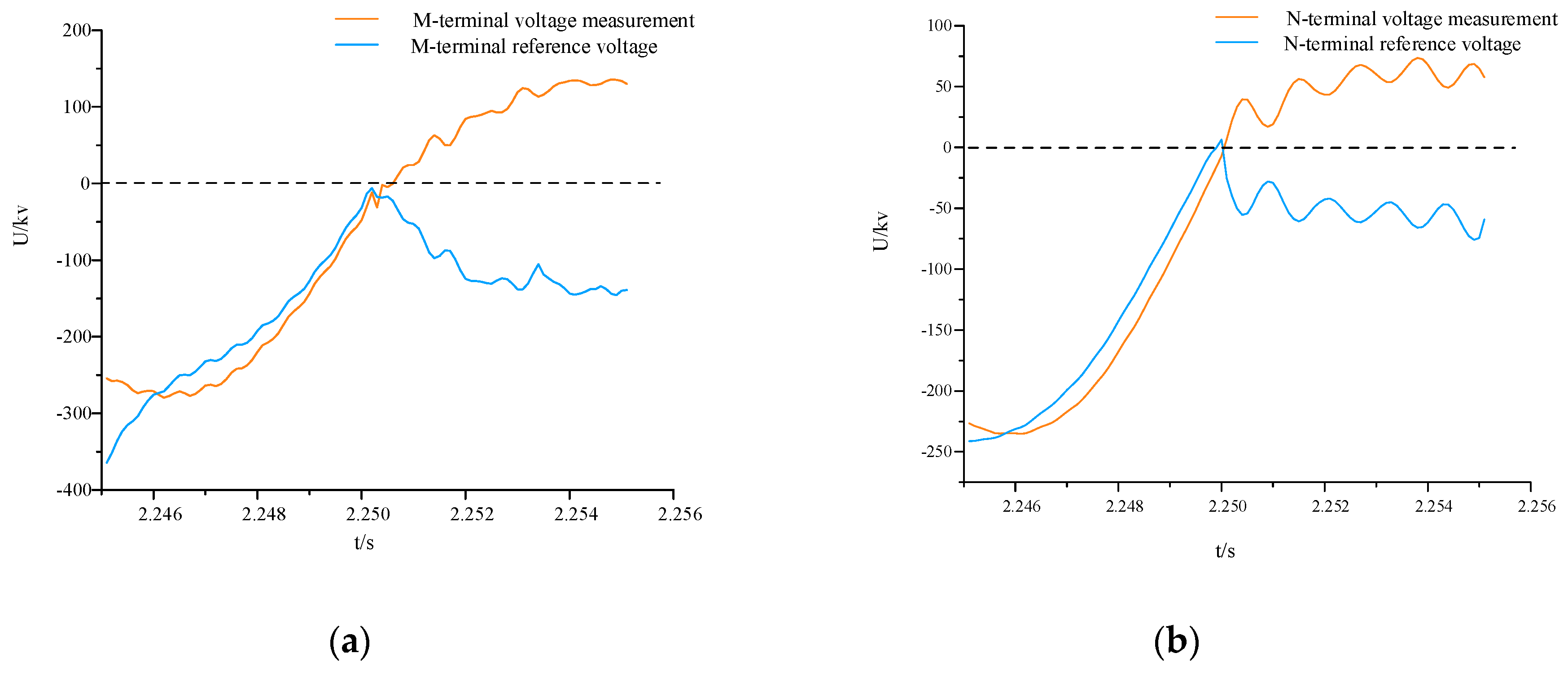
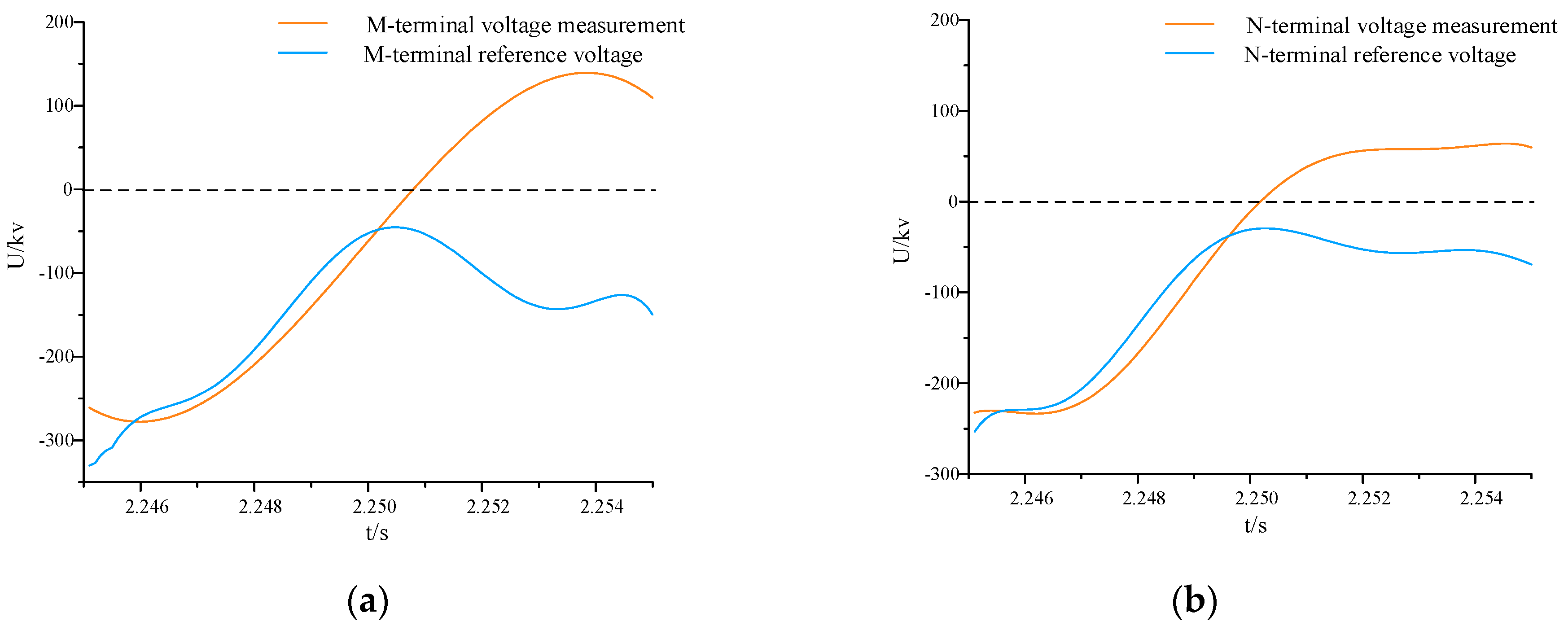
4.3. Out-of-Zone Fault Simulation Result

Referring to Fig. 1, a single-phase bolted fault (f₁) is established 40 km outside the M and N line in the opposite direction. Voltage and current data from both ends of M and N are extracted, the reference voltage is computed, and waveforms are processed. A comparison of the measured voltages at both ends and the reference voltage waveform is shown in Fig. 10.

In Fig. 10, the trends in the measured voltage and the reference voltage waveform are consistent, aligning with the conclusion derived from theoretical analysis concerning the similarity of the two voltage waveforms during an external fault. To further investigate the comprehensive distance similarity characteristics of the voltage waveform during external faults under various operating conditions, with reference to Fig. 1, f₁ and f₂ are faults set respectively 30 km and 10 km outside the opposite direction of the M, N line, and f₄ and f₅ are faults set respectively 10 km and 30 km outside the forward direction of the M, N line.

These faults simulate single-phase earth faults, two-phase earth faults, and three-phase earth faults. The fault initiation time is set at 2.25s, with a duration of 0.05s. The simulated data is summarized in Table 2.

Figure 10. Comparison of measured voltage and reference voltage waveform during out-of-zone fault (a) Comparison of M-terminal voltage waveforms; (b) Comparison of N-terminal voltage waveforms.

Figure 10. Comparison of measured voltage and reference voltage waveform during out-of-zone fault (a) Comparison of M-terminal voltage waveforms; (b) Comparison of N-terminal voltage waveforms.

Based on theoretical analysis, when an external fault occurs, the measured voltage and the reference voltage waveform are similar. In Table 2, bold data indicates values greater than the set value, while red data represents the maximum value within the dataset. For external faults occurring at f₁ and f₅, the data in Table 2 are all less than the set value (D_set), thus neither end of the protection devices act falsely. In the case of an f₂ external fault, as MAX(D_Mφ) remains consistently less than the set value D_set, both ends of the protection devices remain unaffected. Similarly, when an f₄ external fault occurs, as MAX(D_Nφ) consistently remains less than the set value D_set, both ends of the protection devices remain unaffected. In conclusion, the simulation results for external faults meet the protection requirements.

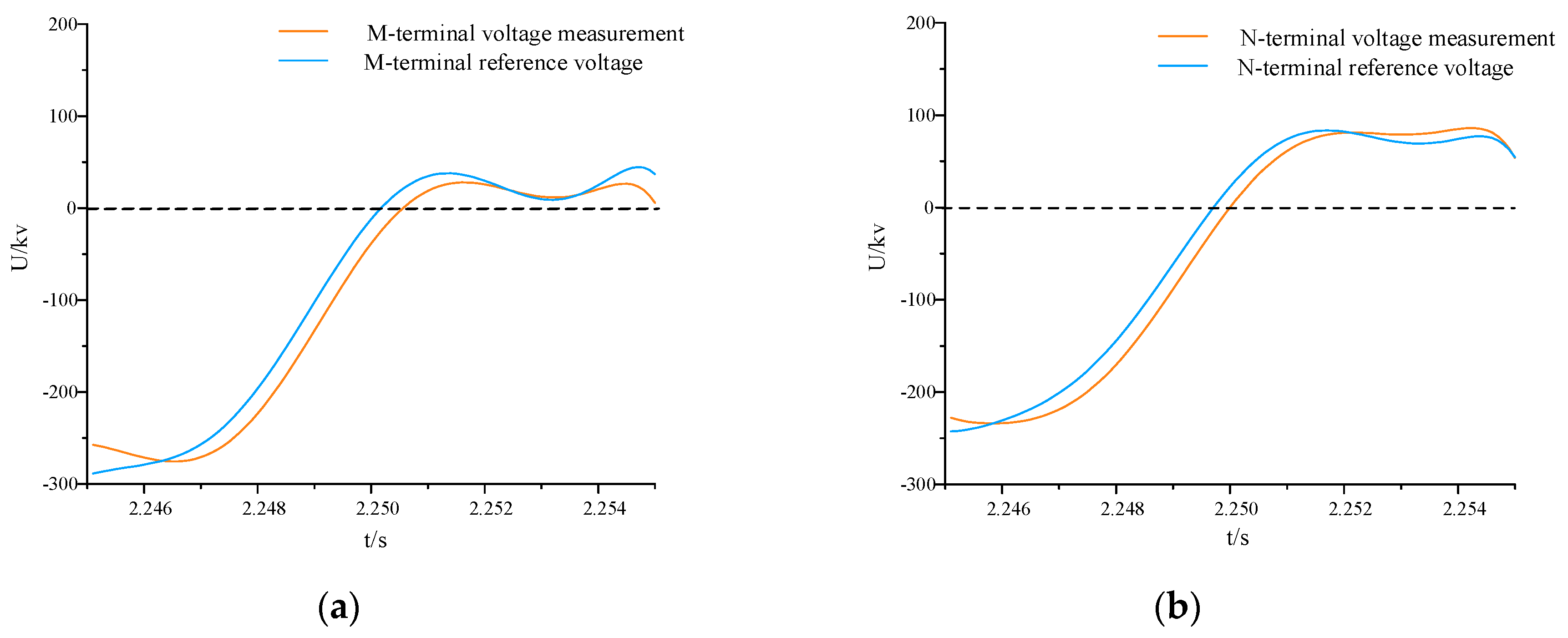
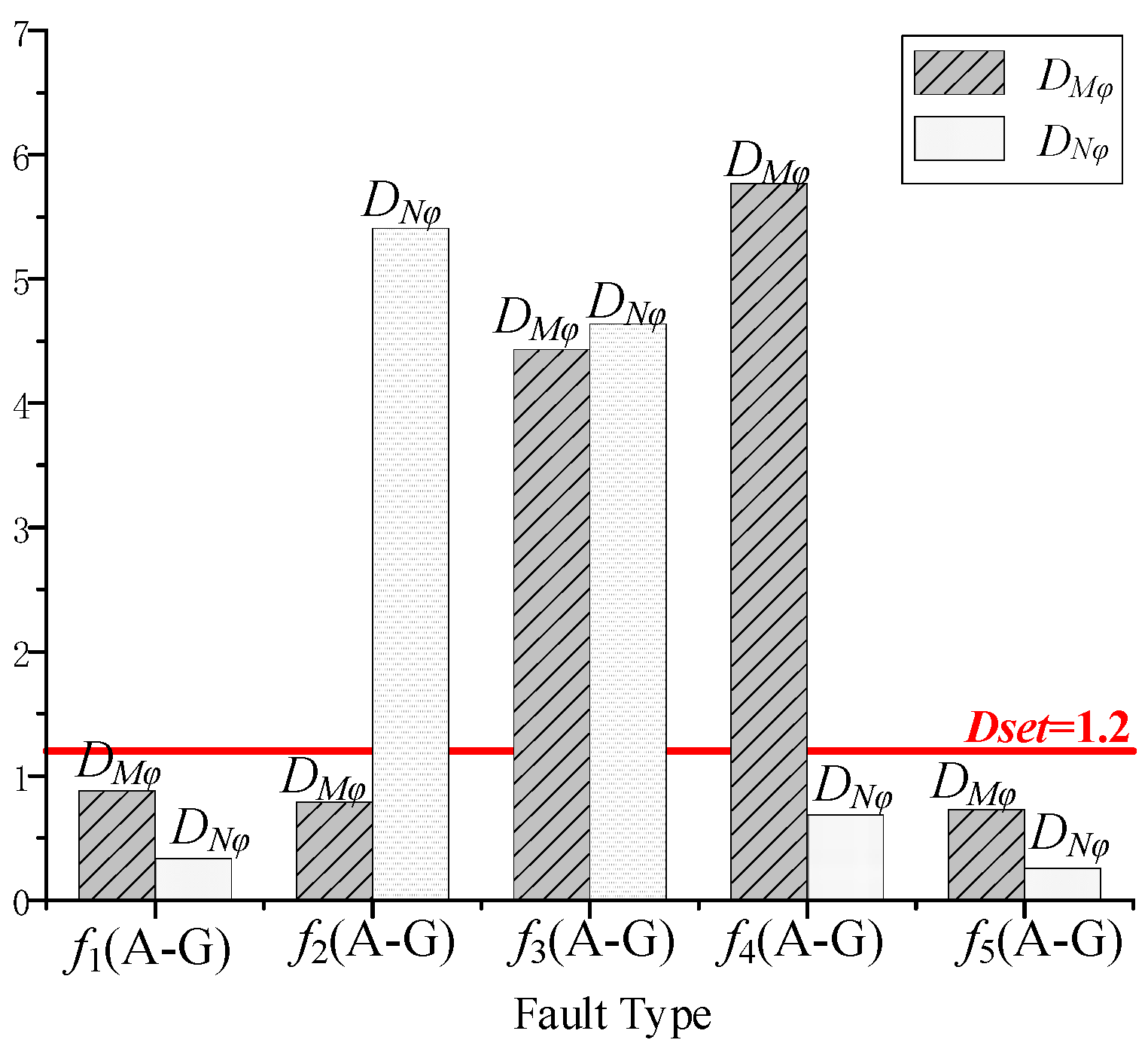
4.4. Protection Action Status

Currently, in practical engineering of AC transmission lines, the highest proportion of faults is single-phase-to-ground faults. Taking the occurrence of single-phase high-impedance ground faults as an example, simulated protection data is illustrated in Fig. 11.

Figure 11. Simulation results for internal and external faults identification.

Figure 11. Simulation results for internal and external faults identification.

From Fig. 11, it can be visually observed that the operating condition of D_Mφ > D_set and D_Nφ > D_set is satisfied only when an internal fault f₃ occurs. Selecting the setting value D_set = 1.2 provides a certain margin for the calculation results when the waveforms are similar. The proposed method can identify internal and external faults reliably and can meet the protection requirements.

4.5. Anti-Interference Analysis

In actual engineering scenarios, there exist numerous interferences. To test the method's resistance to interference, this paper introduced a 10dB noise ratio interference under a 100Ω grounding fault and simulated different positions within the zone. These positions were at 10%, 50%, and 90% of the total line length. The simulation data is summarized in Table 3:

In Table 3, bold data indicates values greater than the setting value, and red data represents the maximum value within the dataset. When comparing the interference-added comprehensive distance similarity calculation results at the 50% total line length with the data in Table 2, it is observed that there are varying degrees of increase or decrease in results after the addition of noise interference. For the 10% and 90% total length positions, the comprehensive distance similarity of the fault phase is greater than the setting value D_set, indicating non-rejection of misoperation. Conversely, the comprehensive distance similarity of the non-fault phase is lower than the setting value D_set, demonstrating non-operation. This shows that the proposed method can correctly operate even in the presence of noise interference, meeting the requirements for protection.

4.6. Comparison and Discussion

To demonstrate the superiority of the proposed method, it is compared with [24] and the longitudinal differential protection scheme. [24] uses the conclusion that reference voltage and measured voltage waveforms have different characteristics during faults inside and outside the area to roughly determine the fault location through the Pearson correlation coefficient. Then, adopting the longitudinal protection logic, it provides a more accurate judgment result. However, [24] lacks an analysis of the protection scheme's ability to withstand transition resistance. The longitudinal current differential protection scheme utilizes the assigned values and phases of both sides of the protected line to determine whether a fault has occurred. The criterion is shown in Equation (22).

$$\dot{I_d}>\dot{{KI}_r}$$

(22)

where the differential current $\dot{I_d}=\left|{\dot{I}}_M+{\dot{I}}_N\right|$ and the braking current $\dot{I_r}=\left|{\dot{I}}_M{\dot{I}}_N\right|$ are defined. ${\dot{I}}_M{、\dot{I}}_N$ represent the measured currents at both ends of M and N, respectively. K is the braking coefficient, and the operating threshold is set as the maximum unbalanced current.

To investigate the operational capabilities of various protection schemes for high-impedance grounding faults, three methods are applied to a self-built experimental model. A phase high-impedance grounding fault is set at 50km away from M end. The fault occurs at 2.25s and lasts for 0.05s. The transition resistors are set to 100Ω, 200Ω, and 1000Ω, [25] respectively. The comparison results of the three methods are shown in Table 5.

Since [24]'s sampling frequency is 4kHz, it requires 25 sampling points with a data window of 6.25ms, while the proposed method uses 10 sampling points with a data window of 1ms. Therefore, [24] has a larger computational burden and slower speed. The current-based differential protection scheme acts at 4.6ms under a 100Ω transition resistor, while the proposed method acts at 3ms. Therefore, the proposed method has faster speed. By simulating and recording the extreme nodes where the three methods show significant errors under different transition resistors, it is found that the proposed method only experiences computational errors at 1000Ω, indicating stronger tolerance to transition resistors. In conclusion, the proposed method has faster speed and stronger tolerance to transition resistors compared to the other two methods.

5. Conclusions

Based on the analysis of the voltage fault characteristics of mixed AC-DC multi-feed-in receiving-end AC lines, this paper proposes a series-connected protection scheme based on voltage waveform similarity. This proposal has practical significance for the reliable operation of hybrid AC/DC grids. Through simulation verification, it is evident that the proposed protection scheme can operate correctly under different fault distances, fault types, transition resistances, and noise interferences. Compared to other protection schemes, proposed method operates more rapidly within 3ms, exhibiting improved reliability, speed, and adaptability, while remaining unaffected by data asynchrony, thus meeting protective requirements. The proposed method is based on the analysis of multi-fed AC-DC system fault characteristics, theoretically applicable to fault protection in all types of mixed AC-DC interconnected systems under various fault conditions. Future research may further investigate the applicability of the protection scheme.