Fibonacci-Like Sequences Reveal the Genetic Code Symmetries, also When the Amino Acids Are in a Physiological Environment

Preprint

Article

Fibonacci-Like Sequences Reveal the Genetic Code Symmetries, also When the Amino Acids Are in a Physiological Environment

Altmetrics

Downloads

Views

370

Comments

A peer-reviewed article of this preprint also exists.

Tidjani Négadi^*

This version is not peer-reviewed

Submitted:

09 January 2024

Posted:

10 January 2024

You are already at the latest version

Alerts

Abstract

In this study, we once again use a set of Fibonacci-like sequences to examine the symmetries within the genetic code. This time, our focus is on the physiological state of the amino acids, considering them as charged, in contrast to our previous work where they were seen as neutral. In a pH environment around 7.4, there are four charged amino acids. We utilize the properties of our sequences to accurately describe the symmetries in the genetic code table. These include Rumer’s symmetry, the third-base symmetry and the "ideal" symmetry, along with the "supersymmetry" classification schemes. We also explore the special chemical structure of the amino acid proline, presenting two perspectives—shCherbak’s view and the Downes-Richardson view, which perspectives are included in the description of the above-mentioned symmetries. Our investigation employs also elementary modular arithmetic to precisely describe the chemical structure of proline, connecting the two views seamlessly. Finally, our Fibonacci-like sequences prove instrumental in quickly establishing the multiplet structure of non-standard versions of the genetic code. We illustrate this with an example, showcasing the efficiency of our method in unraveling the complex relationships within the genetic code.

Keywords:

Subject: Biology and Life Sciences - Life Sciences

1. Introduction

This paper is a continuation of a previous one, devoted to the study of the genetic code, using a novel mathematical technique based on a small set of Fibonacci-like sequences [1]. In this reference, we used these sequences, as well as some tools from elementary number theory, to derive the detailed chemical content of the amino acids encoded by the 61 sense codons, including their degeneracies and structured by three symmetries. In the above work, the 20 amino acids were considered in their neutral (uncharged) state. In the present work, we consider an extension where four amino acids are now considered in a physiological state (neutral pH), that is, charged. As in [1], we use our Fibonacci-like sequences to derive several hydrogen atom and atom patterns corresponding to the symmetries of the genetic code 64-codons table, mentioned above. In doing so, we consider also two possible views linked to the special structure of the amino acid proline, which is known to be the only amino acid whose side chain is bound to its backbone twice. Below, in this introduction, to give the paper a self-contained structure, we first give a summary of the (standard) genetic code (Section 1.1) and, next, the elemental (atomic) composition of the twenty amino acids (Section 1.2).

1.1. The genetic code

The genetic code is a set of rules used by the living organisms on Earth to translate the information contained in the genetic material (the genes) into proteins. Its experimental deciphering was beautifully realized in the 1960s, [2]. Out of a total of 64 possible codons, each being a combination of one of the three bases U (uracil), C (cytosine, A (adenine and G (guanine), there are in the standard genetic code 61 sense codons and each one of them is translated, by the biochemical machinery of the ribosome, into a given amino acid; the remaining three (non-sense) codons serve as termination signals or stop codons. The genetic code is also said degenerate, meaning that specific groups of codons correspond to an amino acid, we call them here “multiplets”. The sextets are coded by 6 codons, the quartets by four codons, the triplet by 3 codons, the doublets by 2 codons and finally the singlets by only 1 codon. These multiplets are gathered in Table 1 where the one-letter and the three-letter codes for the amino acids are given in parenthesis. In Table 2, the genetic code table, i.e., the codon-amino acid correspondence, is shown.

In this table, there are 16 family boxes and each one of them is a set of four codons sharing the same first and second base. An important peculiarity of the (standard) genetic code is the existence of the three sextets serine: {UCN, AGY}, arginine {CGN, AGR} and leucine {CUN, UUR} (N for any base, Y for pyrimidine U or C and R for purine A or G.) These three sextets have, each, their codons distributed over separate family boxes, that is, each 6-fold codon set is composed of separate 4-fold and 2-fold parts. There are also important symmetries of the genetic code and these will play a prominent role in this paper, as in [1], see Sections. 4, 5 and 6.

1.2. The elemental composition of the 20 amino acids

Below, in Table 3, we give the elemental composition of the twenty amino acids where four of them are in their charged (physiological) state. They are arginine (charge +1), Lysine (charge +1), glutamic acid (charge -1) and aspartic acid (charge -1). These charges are indicated in colors in the table (red for +1 and blue for -1). H in the third column is for hydrogen, C in the fourth column is for carbon, N, O and S, in the fifth column, correspond respectively to nitrogen, oxygen and sulfur. Atom numbers are given in the sixth column and the integer molecular mass (nucleon number) is shown in the seventh column. All the given numbers correspond to the side chains of the amino acids. The number of codons, or multiplicity M, encoding each amino acid and its name together with its three-letter symbol are given in column 1 and 2, respectively. To ease the calculations in the next sections, one can use, as we indeed do, the following pre-calculated sums for the hydrogen, atom and also nucleon contents (in the uncharged amino acids side chains). Hydrogen atoms: 21 in the 5 quartets, 22 in the 3 sextets, 50 in the 9 doublets, 9 in the 1 triplet,

15 (7 + 8)

in the 2 singlets (see Table 3). For the atom number: 31 in the 5 quartets, 35 in the 3 sextets, 96 in the 9 doublets, 13 in the 1 triplet,

29 (11 + 18)

in the 2 singlets (see Table 3). For the nucleon numbers: 145 in the 5 quartets, 188 in the 3 sextets, 660 in the 9 doublets, 57 in the 1 triplet,

205 (75 + 130)

in the 2 singlets (see Table 3). Now, in the computations below, in the next sections, the charges for some amino acids are to be included, when needed, and without forgetting, of course, the multiplicities or the degeneracies. Recall that, for an amino acid of multiplicity M, that is the number of codons coding it, the degeneracy is simply equal to

M - 1 .

(In the last five rows of Table 3, several hydrogen atom, atom and nucleon numbers have been calculated to ease the reading. Several of them, but not all, are involved in Section 4, Section 5 and Section 6.)

The general chemical structure of an amino acid is

R - C H (N H_{2}) - C O O H

where R is the side chain (or radical) and the remaining part constitutes the backbone. The side chain is bound to the α-carbon, once. Proline is the only amino acid where its side chain is connected to its backbone twice (forming a pyrrolidine loop). There is, therefore, no “clear cut” between the side chain and the backbone as it is the case for all the other 19 amino acids. In this work, we are going, in our applications, view the special amino acid proline in two equivalent ways. shCherbak, [3], to “standardize” the common backbone of the amino acids, with 74 nucleons, proposed an imaginary “borrowing” of one nucleon (one hydrogen atom) from the side chain of proline, which has only 73 nucleons in its backbone, to the benefit of this latter, to reach 74, as it is the case for the 19 other amino acids. In his next work with Makukov, [4], the above “borrowing” process, or (imaginary) transfer of one nucleon from its side chain to its backbone, has been termed “activation key”. Activating the key, i.e., standardizing, leads to an innumerable number of remarkable and beautiful arithmetical patterns with the 20 amino acids considered in their neutral (uncharged) state. On the other hand, Downes and Richardson, [5], have chosen the other way, that is, to not make such a “borrowing”, leaving proline’s side chain with its 42 nucleons, contrary to shCherbak’s choice of 41 nucleons. These authors derived also a no less remarkable nucleon (or integer molecular mass) balance with this choice together with considering the case where four amino acids are in their charged state (see above in this section). In the following sections, we are going to consider both cases concerning proline, termed here “activation key” on (shCherbak’s view) and “activation key” off (Downes and Richardson view) with the four amino acids, mentioned above, in their charged state. The data for proline, in this context, are shown in Table 3, noted respectively “on/off” (second row). In the computations below, concerning the situation where the “activation key” is on or off for proline, a factor “

+ 1

” is added to hydrogen number, atom number and nucleon number in the case “off”, and, nothing, in the case “on”.

1.3. The structure of the paper

In Section 2, we present our set of Fibonacci-like sequences. In Section 3, we present, as a first application of our Fibonacci-like sequences, the hydrogen atom content in the side chains of the amino acids coded by 61 codons, in the two views described above (“activation key” on and off) and fitting the degeneracy structure. As we said earlier, four amino acids are in their charged state. Next, we consider the three following symmetries of the genetic code, as we did in [1]: (i) Rumer’s symmetry, [6], (ii) the Findley-Findley-McGlynn third-base symmetry, [7] (see also [8]), and (iii) the Rosandić-Paar “ideal” symmetry and “supersymmetry”, [9,10]. For each one of these symmetries, we use our Fibonacci-like sequences and their properties to fit their hydrogen atom and atom patterns. This is done in Section 4, Section 5 and Section 6, respectively, also in the two views mentioned above. In Section 7, we return to the special amino acid proline and derive, from a few elements from modular arithmetic, its virtual “double” structure. In Section 8, we use again our sequences to show that they could also be applied to describe, not only the multiplet structure of the standard genetic code, but also the one of the non-standard genetic codes as well. An illustration example is given.

2. Fibonacci-like sequences

These sequences, see [1], could be defined in terms of the usual Fibonacci sequence by the recurrence relation (

n ≥ 2)

s_{n} ≔ p F_{n - 1} + q F_{n - 2}

(1)

where

s_{n}

denotes collectively the five sequences

a_{n}, a_{n}^{'}, b_{n}, c_{n}

and

g_{n}

. Their “seeds” or “initial conditions” are chosen as follows

a_{n} (p = 1, q = 6)

a_{n}^{'} (p = 6, q = 1), b_{n} (p = 9, q = 13)

c_{n} (p = 5, q = 30)

and

g_{n} (= - 3, q = 23)

. We show below, in Table 4, the first few terms

The “seeds” described above, which were initially chosen by a trial and error thought process, have proven to be extremely appropriate and useful in their consequences, not only concerning the “ideal” classification scheme, mentioned above but also to derive a large number of interesting results. Specifically, the “seed” for the Fibonacci-like sequences

b_{n}

and

c_{n}

are in the detail as follows. For

b_{n}

, 13

(= a_{1})

is the number of hydrogen atoms in serine (3) and arginine (10) while 9

(= a_{2})

is the number of hydrogen atoms in leucine, with a total of 22 (

{= a}_{3}

). For

c_{n}

, 30

(= c_{1})

is the number of atoms in leucine (13) and arginine (17) while 5

(= c_{2})

is the number of atoms in serine, with a total of 35 (

{= c}_{3}

). Note, importantly, that when we say atoms (not hydrogen atoms), we mean the whole set comprising hydrogen, carbon, oxygen, nitrogen and sulfur. We have devoted an entire section in [1] (Section 4.2.5) to explain the usefulness of not only the choice of the “seeds” of the above sequences

b_{n}

and

c_{n}

but also the one of the other three

a_{n} a_{n}^{'}

and

g_{n} .

It is worth noting that the sequences

a_{n}

and

a_{n}^{'}

can give, as a secondary product, both the Fibonacci and the Lucas sequences. The difference

a_{n} - a_{n - 1}^{'},

(2)

gives the (slightly modified) Fibonacci sequence noted

F_{n}^{'}

F_{n}^{'} : 1, 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, \dots; n = 1, 2, 3, \dots

(3)

in an unusual but interesting form: its “seeds” here are inverted with respect to the usual Fibonacci sequence. Also, the sum of any of its first members until a certain index gives a Fibonacci number, exactly, contrary to the usual Fibonacci sequence with seeds 0, 1 which always gives one unit less than a Fibonacci number. For example, in our case, for

n = 9

, we get

\sum_{1}^{9} F_{n}^{'} = 34

. The relation

L_{n} = F_{n}^{'} + F_{n + 2}^{'}

(4)

gives the Lucas sequence:

L_{n} : 2, 1, 3, 4, 7, 11, 18, 29, 47, 76

(5)

It is important to note that the sequences in Table 4 are highly intertwined by a (large) number of identities connecting them (see Equ.(2) in [1]). The reader could consult Appendix C, in [1], to see how it is possible to check them for any large or very large values of the index n by using a computer with a mathematical software containing a built-in Fibonacci function. For low values of the index n in Table 4, the verification could be easily done by hand or using a pocket calculator. We will also use some of these identities in our applications in this paper, as we successfully did in our recent paper, mentioned above. The identities, we need, will be presented as we go along, in the appropriate place, where we use them for the first time.

3. Hydrogen atom content

In this section, we use the Fibonacci-like sequences defined in the preceding section to derive the hydrogen atom content in the side chains of the amino acids encoded by 61 codons. Also, as explained in the introduction, we consider that four amino acids are charged and the side chain of proline can have, for the calculations in this section, either 5 hydrogen atoms in its side chain, in the situation “on”or

6 (= 5 + 1)

in the situation “off” (see the introduction)..

3.1. Hydrogen atom content: “activation key” on

In this case, we count, from Table 3, the number of hydrogen atoms

21 \times 4 + (22 + 1) \times 6 + (50 + 1 - 1 - 1) \times 2 + 9 \times 3 + 7 + 8 = 362

(6)

(We have used the pre-calculated sums mentioned above Table 3 and included the charges where they are necessary.) This number could be computed from our Fibonacci-like sequence

a_{n}^{'}

and using the identity

\sum_{1}^{k} a_{n}^{'} = a_{k + 2}^{'} - 6

(7)

For

k = 9

, we have, isolating the last term

a_{9}^{'}

\sum_{1}^{8} a_{k}^{'} = 219 + a_{9}^{'} = 219 + 139 = 364 - 6

(8)

As 6 is a perfect number (equal to the sum of its proper divisors), we have 6=1+2+3. By leaving the even number 2 at the right, transfering the odd numbers 1 and 3 to the left and arranging, we get

(219 + 3) + (139 + 1) = 222 + 140 = 362

(9)

We have here the correct distribution of the hydrogen atom pattern in the “

23 + 38

” codons pattern, to be compared with what the data of Table 3 give (see the last rows in the table):

21 + (22 + 1) \times 2 + (50 + 1 - 1 - 1) + 9 + 7 + 8 = 140,

in the “23” part (the sextets counted twice) and

21 \times 3 + (22 + 1) \times 4 + (50 + 1 - 1 - 1) + 9 \times 2 = 222

in the “38” degeneracy part. (see more about this pattern in [1]).

3.2. Hydrogen atom content: “activation key” off

In this case, proline has one more hydrogen atom in its side chain and we have from Table 3

(21 + 1) \times 4 + (22 + 1) \times 6 + (50 + 1 - 1 - 1) \times 2 + 9 \times 3 + 7 + 8 = 366

(10)

Here, we use the identity connecting the sequences

a_{n}

and

b_{n}

a_{n} + b_{n + 1} = a_{n + 4}

(11)

For

n = 4

, we have

8 + 53 = 61

. Multiplying both sides by 6, we have

6 \times 8 + 6 \times 53 = 6 \times 61 = 366

(12)

It suffices now to use the recurrence relation of

b_{n}

twice (

53 = 31 + 22, 31 = 22 + 9)

and arrange, to get finally

(6 \times 22 + 1 \times 9) + (5 \times 9 + 6 \times 22 + 6 \times 8) = 141 + 225 = 366

(13)

which is the desired result (see Table 3 and its last rows):

(21 + 1) + (22 + 1) \times 2 + (50 + 1 - 1 - 1) + 9 + 7 + 8 = 141,

in the “23” part (the sextets counted twice) and

(21 + 1) \times 3 + (22 + 1) \times 4 + (50 + 1 - 1 - 1) + 9 \times 2 = 225

in the “38” degeneracy part.

We can also compute the hydrogen atom content of the amino acids side chains in the different groups of multiplets (those in Table 1). Consider, first, the case “activation key” on. From Table 3, we have

21 \times 4 + (22 + 1) \times 6 + (50 + 1 - 1 - 1) \times 2 + 9 \times 3 + 7 + 8 = 84 + 138 + 98 + 27 + 7 + 8 = 362

(14)

These numbers are, respectively, the number of hydrogen atoms in the side chains of the quartets, the sextets, the doublets, the triplet, methionine and tryptophane. To compute these numbers by using our Fibonacci-sequences, let us rewrite the sum in Equs.(8-9) above as (see Table 4)

(1 + 6 + 7 + 13 + 20 + 33 + 53 + 86) + 3 + (139 + 1) = 362

(15)

and use the following identity

a_{n}^{'} - b_{n - 2} = 2 F_{n - 5}^{'} .

(16)

which, for n=7 and 8, gives respectively,

86 - 84 = 2

and

139 - 137 = 2

. By inserting the numbers

86

and

139

in the above relation, we have, by grouping

(13 + 33 + 53 + 7) + (20 + 6 + 1) + 84 + 2 + 3 + 2 + (137 + 1) = 362

(17)

It just remains to write the number

7

, in the first parenthesis, as

8 - 1

from the recurrence relation of the sequence

a_{n},

that is,

a_{2} + a_{3} = a_{4}

(

1 + 7 = 8

), to get finally

98 + 27 + 84 + 7 + 8 + 138 = 362

(18)

which are the numbers of hydrogen atoms in the five multiplets described above in Equ.(14). In the second case, “activation key” off, we start from the identity

{6 (a}_{n} + b_{n + 1}) = {6 a}_{n + 4}

, see Equ.(11); the multiplication by the factor 6 does not change it. We have

6 \times 61 = 6 \times (23 + 38) = 6 \times 23 + (6 \times 23 + 6 \times 7 + 6 \times 8) = 366

(19)

where we have used the recurrence relation for the sequence

a_{n}

thrice (

61 = 23 + 38, 38 = 23 + 15, 15 = 7 + 8)

. Arranging, we get, using also

8 = 7 + 1

(

a_{4} = a_{3} + a_{2})

6 \times 23 + (2 \times 23 + 6 \times 7) + (4 \times 23 + 1 \times 6) + 6 \times 7 = 366

(20)

The last term, 6×7, a bit whimsical, could be handled as follows. The Fibonacci -like sequences, we have defined, could be continued to negative values of their indices, as it is the case for the usual Fibonacci/Lucas sequences and for any other sequence of the same kind; this is well known. Now, here, we make only appeal to the first term of this continuation, here, the value

a_{0} = - 5

(see Table 4). It is not shown in this table but one could easily see it and understand that

a_{0} + a_{1} = {- 5 + 6 = a}_{2} = 1

6 = 5 + 1

; well. We therefore write the said term, 6×7, as

5 \times 7 + 7 = 5 \times 4 + 5 \times 3 + 7

, because 7 is a Lucas number (

7 = 4 + 3

). Finally,

5 \times 3 = 15 = 7 + 8

by virtue of the recurrence relation

a_{5} = a_{3} + a_{4}

. Ultimately, we end up with (

5 \times 4 + 7 = 27)

138 + 88 + 98 + 7 + 8 + 27 = 366

(21)

which could be compared with the result obtained from the Table 3

(21 + 1) \times 4 + (22 + 1) \times 6 + (50 + 1 - 1 - 1) \times 2 + 9 \times 3 + 7 + 8 = 88 + 138 + 98 + 27 + 7 + 8 = 366

(22)

4. Rumer’s symmetry

Rumer’s symmetry, [6], is defined by the transformation

U \leftrightarrow G, A \leftrightarrow C

. It divides the genetic code

8 \times 8

table into two equal halves of 32 codons each, we call them here

M_{1}

and

M_{2}

. In Table 5, below, we show such a division. The set

M_{1}

, shown in grey background and framed by thick lines, comprises 8 quartets of codons (8 family boxes, see Section 1.1), each, having the same two first bases and coding for the same amino acid, the third base being irrelevant. In this set, among the 8 quartets, 3 correspond to the quartet part of the 3 sextets serine, arginine and leucine. The set

M_{2}

comprises group-I amino acids (2 singlets), group-II amino acids (9 doublets), group-III amino acid (1 triplet) and also 3 stops or termination codons. The point here, concerning symmetry, is that under Rumer’s transformation, performed on all three bases, the sets

M_{1}

and

M_{2}

are exchanged:

M_{1}

↔

M_{2}

4.1. The hydrogen atom content

In this section, we compute the hydrogen atom content in the two Rumer’s sets

M_{1}

and

M_{2}

, using our Fibonacci-like sequences, and compare with what is counted from Table 3.

4.1.1. “Activation key” on

We have, from Table 3 (see the last row in the table)

M_{1} : 21 \times 4 + (22 + 1) \times 4 = 176 M_{2} : (22 + 1) \times 2 + (50 + 1 - 1 - 1) \times 2 + 9 \times 3 + 7 + 8 = 186

(23)

with total of 362. Now, we use again Equ.(8) of Section 3.1 and write it in the form

\sum_{1}^{7} a_{n}^{'} + a_{8}^{'} + a_{9}^{'} = (133 + 53) + 2 \times 86 = 186 + 2 \times 86 = 364 - 6

(24)

As we did before, we use the fact that 6 is a perfect number (

6 = 1 + 2 + 3

) to bring the above relation to the final form, to be compared with Equ.(23) above

186 + (2 \times 86 + 1 + 3) = 186 + 176 = 364 - 2 = 362

(25)

4.1.2. “Activation key” off

Table 3 gives, in this case

M_{1} : (21 + 1) \times 4 + (22 + 1) \times 4 = 180 M_{2} : (22 + 1) \times 2 + (50 + 1 - 1 - 1) \times 2 + 9 \times 3 + 7 + 8 = 186

(26)

With a total of

366

hydrogen atoms. Here, we use again Equ.(12) of Section 3.2

6 \times 8 + 6 \times 53 = 6 \times 61 = 366

(27)

and simply introduce the recurrence relation

53 = 31 + 22

of the sequence

b_{n}

, see Table 4, to get

6 \times (8 + 22) + 6 \times 31 = 180 + 186 = 366

(28)

which describes the two hydrogen atom values in Equ.(26) above.

4.2. The atom content (CHNOS)

4.2.1. “Activation key” on

From Table 3, we have

M_{1} : 31 \times 4 + (35 + 1) \times 4 = 268 M_{2} : (35 + 1) \times 2 + (96 + 1 - 1 - 1) \times 2 + 13 \times 3 + 11 + 18 = 330

(29)

With a total of

598

atoms. To describe this atom pattern, we use three ingredients: (i) elements of the sequence

g_{n}

, (ii) the relation

358 + 4 = 362

, from Equ.(7) in Section 3.1. and (iii) the identity

b_{n} + g_{n} = 6 a_{n}

(30)

This latter identity, for

n = 9

, gives

358 + 236 = 594

. Inserting the number

358

from the relation above Equ.(30), gives

362 - 4 + 236 = 594

362 + 236 = 598 .

Finally, by adding and subtracting the quantity

\sum_{1}^{5} g_{n} = 94

, computed from Table 4, in the left hand, we get

(362 - 94) + (236 + 94) = 268 + 330 = 598

(31)

This is the desired result.

4.2.2. “Activation key” off

In this case, we have from Table 3 (see also the last rows in the table)

M_{1} : (31 + 1) \times 4 + (35 + 1) \times 4 = 272 M_{2} : (35 + 1) \times 2 + (96 + 1 - 1 - 1) \times 2 + 13 \times 3 + 11 + 18 = 330

(32)

with a total of

602

atoms. This case could be handled by using the following identity

4 a_{n} + b_{n + 1} - 2 F_{n - 6}^{'} = 7 a_{n}^{'}

(33)

where

F_{n}^{'}

is the Fibonacci sequence defined in Equs.(2-3). For

n = 8

, we have

4 \times 61 + 358 - 2 \times 0 = 7 \times 86 = 602

(34)

By using the recurrence relation of the sequence

b_{n}

twice,

358 = 84 + 2 \times 137

and, next, replacing

84

86 - 2

from the identity in Equ.(16) of section 3.2 for

n = 7

, we get

(4 \times 61 + 86) + (2 \times 137 - 2) = 330 + 272 = 602

(35)

The numbers on the right hand side are therefore seen to describes correctly the pattern above for

M_{2}

and

M_{2}

, respectively.

5. The 3^rd base symmetry classification

In 1982, Findley et al., [7], by viewing the genetic code as an f-mapping, extracted a fundamental symmetry for the doubly degenerate codons (group-II). Below, to ease the reading, we reproduce, a few elements from the above reference to help the reader understand what is the f-mapping. The authors consider the 64-codons set,

C,

and define

C_{k} = \{C_{i j k} \in C | i, j \in B\}, k \in B

where i, j, k designate the 1^st, 2^nd and 3^rd base in the codon

C_{i j k}

(B is for base, U, C, A, G).

C_{k}

, k

\in B,

partitions

C

into four disjoints subsets where each subset contains only codons having the same third base. Each of these subsets may be mapped by f into members of the amino acids set A, with the image being denoted

f (C_{k});

this is shown in Table 6, below.

One has therefore

f (C_{U}) = f (C_{C})

and

f (C_{A}) \neq f (C_{G})

. With this f-mapping, the authors establish also relations that define a one-to-one correspondence between one member of a doubly degenerate codon pair and the other member (see the reference above for details). These relations could be stated, in words, as follows: (i) if a codon for an amino acid has 3^rd base U, then there is a codon for the same amino acid having 3^rd base C and vice versa OR (ii) if a codon for an amino acid has 3^rd base A, then there is a codon for the same amino acid having 3^rd base G and vice versa. For a doubly degenerate codon pair (i) and (ii) are mutually exclusive. For order-4, or quartets, (i) and (ii) hold simultaneously. For order-6, the sextets, the quartet part obeys (i) AND (ii) and, for the doublet part one has (i) OR (ii). For the odd-order degenerate codons (Ile, Met and Trp), however, there is a slight deviation from symmetry. In Table 6, we show this classification. In the last two rows of this table, we have calculated, from Table 3, the hydrogen atom content and the atom content in the side chains of the amino acids in the four columns, in the two views “on” and “off” (see Section 1.2.). Note the hydrogen atom balances (

2 \times 84, 2 \times 85

) and atom number balances (

2 \times 144, 2 \times 145

) in the last two rows in Table 6. These express the exact one-to-one correspondence mentioned above (here the two codons of isoleucine AUU and AUC constitute an order-2 doublet). These balances will be established from our Fibonacci-like sequences below in this section.

5.1. The hydrogen atom content

5.1.1. “Activation key” on

In the U/C third-base set, there are

2 \times 84

hydrogen atoms. In the A/G third-base set there are, respectively,

94

and

100

hydrogen atoms (grand total of

362

, see Table 6 above). To describe this pattern, using our Fibonacci-like sequences, let us start again from Equ.(24) of Section 4.1.1 and write it in the following form, by expliciting the sum

(1 + 6 + 7 + 13 + 20 + 53) + (33 + 53 + 2 \times 2 + 4) + 2 \times 84 = (100 + 94) + 2 \times 84 = 362

(36)

Note that we have included the sixth term of the sequence

a_{6}^{'} = 33

, in the sum

\sum_{1}^{7} a_{n}^{'}

, in the second parenthesis. In this way, we reach the correct hydrogen atom pattern.

5.1.2. “Activation key” off

In this case, let us recall Equ.(27) of Section 4.1.2 (or Equ.(12) of Section 3.2 which is the same)

6 \times (8 + 22) + 6 \times 31 = 180 + 186 = 366

(37)

and use the following identity linking the sequences

a_{n}

and

b_{n}

a_{n} + a_{n + 2} = b_{n}

(38)

which, for

n = 4

, writes

8 + 23 = 31

. By inserting this last number, 31, in the above equation and arranging, in a first step, we have

6 \times (8 + 22) + 2 \times 8 + (4 \times 8 + 6 \times 23) = 180 + 186 = 366

(39)

The second parenthesis in the left hand side can be written as

2 \times (2 \times 8 + 3 \times 23) = 2 \times 85

. This is the correct pattern for U/C third-base set but it remains to handle the other part in the above equation. A quick way consists in writing the factor

2 \times 8

above as

8 + 8 = 8 + 3 + 5

as 8 is a Fibonacci number. All this lets us to put the above equation in the following form

[3 \times (8 + 22) + (8 + 3)] + [3 \times (8 + 22) + 5] + 2 \times 85 = 101 + 95 + 2 \times 85 = 366

(40)

which could be compared with the data in Table 6 (case “off”).

5.2. The atom content

5.2.1. “Activation key” on

Let us, here, start from Equ.(30) in Section 4.2.1, written as

6 a_{9} + 4 = 6 \times 99 + 4 = 598

(41)

and use, first, in cascade the recurrence relation of the sequence

a_{n}

6 \times (38 + 23 + 23 + 15) + 4 = 598

(42)

Now, we arrange this relation as follows

2 \times (3 \times 38 + 2 \times 15) + 6 \times 23 + 2 \times 15 + 6 \times 23 + 4 = 2 \times 144 + 6 \times 23 + 2 \times 15 + 6 \times 23 + 4

(43)

To get the correct atom number pattern, we note that because of the following identity of the sequence

a_{n}

\sum_{1}^{k} a_{n} = a_{n + 2} - 1

(44)

we can, for

k = 4

, write

6 + 1 + 7 + 8 = 22 = 23 - 1

23 = 22 + 1

. By inserting this latter value in Equ.(43) above, we obtain

2 \times 144 + (6 \times 22 + 15) + (6 + 15 + 6 \times 23 + 4) = 2 \times 144 + 147 + 163 = 598

(45)

We recognize here the correct atom number pattern (see Table 6)

5.2.2. “Activation key” off

This case is easily handled by starting from Equ.(34) of Section 4.2.2. Using the recurrence relation of the sequence

b_{n}

(

137 = 84 + 53

), we write it as

4 \times 61 + 84 + 2 \times (84 + 53) = 602

(46)

Next, we use, again, the identity,

a_{n} + a_{n + 2} = b_{n}

, already considered in Section 5.2.1, but now for

n = 6

23 + 61 = 84

. By inserting this relation in the equation above, we have

2 \times (2 \times 61 + 23) + (2 \times 53 + 2 \times 61 + 84) = 602

(47)

As the first term is already correct, we examine the second. Using the recurrence relations of both sequence

b_{n}

and

a_{n}

, we can write

53 = 22 + 31 = 2 \times 22 + 9

and

61 = 38 + 23 = 23 + 2 \times 15 + 8

. By inserting these values in the equation above, we end up with

2 \times (2 \times 61 + 23) + (4 \times 22 + 4 \times 15) + (2 \times 9 + 2 \times 23 + 2 \times 8 + 84) = 2 \times 145 + 148 + 164 = 602

(48)

which us the correct answer.

6. The “ideal” symmetry and the “supersymmetry” classification schemes

The main idea behind the “Ideal” symmetry classification scheme, [9], is the use of the three sextets serine, arginine and leucine, each encoded by six codons, as “generators”, with serine playing the central role. This scheme divides the 64 codons matrix in two groups of 32 codons each, the “leading” group and the “nonleading” group and each one of them consists of A+U rich and G+C rich (equal) parts. The “ideal” classification scheme is generated by combining the six codons of serine, arginine and leucine, as mentioned above, in the following manner. Serine, the initial generator with its six codons, arginine also with its six codons and leucine with only the quartet part of its six codons part define the whole “leading” group (with 32 codons). The remaining doublet part of leucine, on the other hand, constitutes a “seed” for the construction of the “nonleading” group (with 32 codons). In this scheme, the genetic code table is created by codons sextets based on exact purine/pyrimidine symmetries, A+U rich/C+G rich symmetries and Direct/Complement symmetries (see [9]. The Table 7 below, shows these groups.

In this table, the “leading” group is shown in yellow (A+U rich) and orange (G+C rich) while the “nonleading” group is shown in light grey (A+U rich) and light blue (C+G rich).

Soon after the publication of their paper, [9], the authors postulated, in [10], the existence of what they call a “supersymmetric” genetic code table, derived from the “ideal” symmetry genetic code table, and having now five symmetries between bases, codons and amino acids. These are purine-pyrimidine between bases and codons, direct-complement symmetry of codons between boxes, A+U rich and C+G rich symmetry of codons between two columns, mirror symmetry between all purines and pyrimidines of the whole code and between second and third base of codons (see [10]. This “supersymmetry” genetic code table is shown in Table 8. It has been reproduced from [10] except, for colors. Importantly, the two “mirror” symmetry axes (vertical and horizontal) are shown in dotted lines. In columns 4 and 5, the authors took (purine: 0, pyrimidine: 1). The first column in Table 8 indicates the boxes: direct box (DB) and complement box (CB).

6.1. Hydrogen atom content

6.1.1. “Activation key” on

The hydrogen atom count is as follows, from Table 3 and Table 8, leading group (in yellow and orange, as in Table 7): 192; nonleading group (in light grey and light blue, as in Table 7): 170. To derive this hydrogen atom pattern, let us start from Equ.(25) of Section 4.1.1 and use again the equality

86 = 84 + 2

(from the identity in Equ.(16) of Section 3.2 for

n = 7

) to get, after arranging

(186 + 4 + 2) + (2 \times 84 + 2) = 192 + 170 = 362

(49)

which is the correct result.

6.1.2. “Activation key” off

In this case, the hydrogen atom count is as follows leading group: 192, nonleading group: 174. Here, we start from Equ.(27) of section 4.1.2

6 \times 8 + 6 \times 53 = 6 \times 61 = 366

(50)

In this case, we consider, first, the number 8 and use the recurrence relation of the sequence

a_{n}

, to write it as

8 = 7 + 1

and, next, use the recurrence relation of

b_{n} 53 = 22 + 31

. With these elements, we could write Equ.(50) as follows

6 \times (1 + 31) + 6 \times (22 + 7) = 192 + 174 = 366

(51)

This is the correct result.

6.2. Atom content

6.2.1. “Activation key” on

From Table 3 and Table 8, we have 316 atoms in the leading group and 282 atoms in the nonleading group. Here, we start from the relation

362 + 236 = 598

, which led to Equ.(31) of Section 4.2.1 but, this time, we add and subtract the quantity

\sum_{1}^{6} a_{n}^{'} = 80

, see Table 4, to get the correct result

(362 - 80) + (236 + 80) = 282 + 316 = 598

(52)

6.2.2. “Activation key” off

In this case, the atom number in the leading group is the same as before (316) but the atom number in the nonleading group is now equal to 286. This case could be handled by making appeal to the identity in Equ.(33) of Section 4.2.2, which writes again for

n = 8

4 \times 61 + 358 - 2 \times 0 = 7 \times 86 = 602

(53)

We first write

358

84 + 2 \times 137

, as in Section 4.2.2, but we now (i) select one copy of the number 61 in the above relation and write it as

23 + 38

, by virtue of the recurrence relation of the sequence

a_{n}

, and (ii) use the identity in Equ.(16) (

a_{n}^{'} - b_{n - 2} = 2 F_{n - 5}^{'}

) for

n = 8

, that is,

139 - 137 = 2

. This allows us to put Equ.(53) above in the form

(2 \times 139 + 38) + (84 + 3 \times 61 + 23 - 2 \times 2) = 316 + 286 = 602

(53)

which is the correct result.

6.3. The “supersymmetry” genetic code table

As the case of the “supersymmetry” genetic code table, [10], has not been considered in [1], where the 20 amino acids were all taken in the their uncharged state and proline’s side chain considered in shCherbak’s view (5 hydrogen atoms, 8 atoms and 41 nucleons), we give, here, the corresponding results and, next, consider the case where the four amino acids mentioned earlier are charged and proline with its two views, on and off.

6.3.1. Uncharged amino acids case and “activation key” on only

Consider, first, the identity

g_{n} + a_{n + 2} + 2 b_{n - 1} = c_{n} + 2 b_{n - 1}

(54)

where we have added to both sides the same quantity

2 b_{n - 1}

. For

n = 7

, we have from Table 4

91 + 99 + 2 \times 84 = 190 + 2 \times 84 = 358

(55)

The sum

190 + 2 \times 84 = 358

, describing the leading group/nonleading group hydrogen atom pattern has already been obtained in [1] but the (new) quantity

91 + 99 + 2 \times 84

, will be useful in what follows. Using again the identity in Equ.(16) for

n = 7

(

84 = 86 - 2

) and next the identity in Equ.(7) of Section 3.1 for

n = 6

, which gives

80 = 86 - 6

, we can put the left hand side of Equ.(55) in the form

91 + 99 + (80 + 88)

(56)

If we take the number 91, the 7th term of the sequence

g_{n}

91 = 37 + 54

and write it as

54 + 2 \times 17 + 3 = 88 + 3

, because

17 = 20 - 3

in the same sequence, we then have, from Equ.(56)

2 \times 88 + (99 + 3 + 80) = 176 + 182

(57)

This is the Direct Boxes/Complement Boxes hydrogen atom pattern, respectively (see Table 8). (The calculations from this table go along the same lines as in the above sections. For the Direct Boxes, for example, take all the amino acids inside all of them and, taking into account the number of their codons, compute the number of hydrogen atoms, and same for the Complement Boxes.) To derive the hydrogen atom pattern for the mirror symmetry, a more elegant and quick way is as follows. Consider the identity

g_{n} + b_{n - 3} = 2 a_{n + 1}

(58)

For

n = 7

, we have

91 + 31 = 2 \times 61

(see Table 4). By inserting this last relation in Equ.(56) above, we get

(2 \times 61 + 88) + (99 + 80 - 31) = 210 + 148

(59)

This is the hydrogen atom pattern for the “mirror” symmetry (see Table 8 above. See also Figure 2 in [10] and the detailed explanations therein about this beautiful symmetry).

6.3.2. Charged amino acids case, “activation key” on and off

Now, we consider the case where (four) amino acids are in their (physiological) charged state which is the main subject in this paper.

6.3.2.1. Hydrogen atom content

In the case “activation key” on, there are

174

hydrogen atoms in the Direct Boxes and

188

hydrogen atoms in the Complement Boxes (from Table 3 and Table 8). Here, we recall Equ.(25) of Section 4.1.1

186 + (2 \times 86 + 4) = 364 - 2 = 362

(60)

By using again the identity in Equ.(16) for

n = 7

84 = 86 - 2

, once, and arranging, we get

(186 + 2) + (86 + 84 + 4) = 188 + 174 = 362

(61)

which is the correct result. In the case “activation key” off, there are

178

hydrogen atoms in the Direct Boxes and

188

hydrogen atoms in the Complement Boxes. Here, we start from Equ.(12) of Section 3.2 and write it as

6 \times 8 + 6 \times (22 + 31) = 6 \times 61 = 366

(62)

where

53 = 22 + 31

from the recurrence relation of the sequence

b_{n}

. Next, we use the same identity in Equ.(38) of Section 5.1.2, again for

n = 4

(

31 = 23 + 8

), to rewrite (one copy) of the number

31

above

(6 \times 8 + 6 \times 22 + 8) + (5 \times 31 + 23) = 188 + 178 = 366

(63)

These are the correct hydrogen atom numbers mentioned above. Now, we look at the “mirror” symmetry. In the case “activation key” on, there are

208

hydrogen atoms in Column 1 and

154

hydrogen atoms in Column 2 of Table 8, using the data of Table 4. Here, we start from Equ.(60) above and put it in the following correct form

(186 + 22) + (31 + 33 + 86 + 4) = 208 + 154 = 362

(64)

where we have used the recurrence relation

86 = 53 + 33

of the sequence

a_{n}^{'}

and, next, replaced the number 53 of the latter sequence by the same number 53 of the sequence

b_{n}

which is equal to

22 + 31

. (Recall that, from Equ.(16), one has

a_{7}^{'} - b_{5} = 53 - 53 = 2 F_{2}^{'} = 2 \times 0 = 0 .

)

In the case “activation key” off, there are

208

hydrogen atoms in Column 1 and

158

hydrogen atoms in Column 2 (see Table 8, data from Table 4). Consider again Equ.(60) above

6 \times 8 + 6 \times (22 + 31) = 366

(65)

By using, repetitively, the recurrence relation of the sequence

b_{n}

and also the following relation

22 = 15 + 7

, from the identity

a_{n} + a_{n + 2} = b_{n}

for

n = 3

, we can put the equation above into the form

(11 \times 13 + 15) + (17 \times 9 + 7 + 6 \times 8) = 158 + 208 = 366

(66)

which is the correct answer.

6.3.2.2. Atom content

In the case “activation key” on, there are

300

atoms in the Direct boxes and

298

atoms in the Complement boxes with a total of 598 (see Table 8 and data from Table 4). In this case, we start from the relation

6 a_{n} + 4 = 6 \times 99 + 4 = 598

(67)

(see Equ.(30 and below,

n = 9

). It is now enough to write

4 = 3 + 1

, as a Lucas number, for example, and rewrite the above equation in the form

(3 \times 99 + 1) + (3 \times 99 + 3) = 298 + 300 = 598

(68)

which describes correctly the above atom content numbers. In the case “activation key” on, there are

348

atoms in Column 1 and

250

atoms in Column 2 (see Table 8, data from Table 4). Here, we start from Equ.(66) above and use the identity in Equ.(11),

a_{n} + b_{n + 1} = a_{n + 4}

with

n = 5

(

99 = 15 + 84)

. We have

6 \times (84 + 15) + 4 = 598

(69)

By introducing the identity in Equ.(16) with

n = 7

84 = 86 - 2,

and arranging, we get finally the above correct atom numbers

(4 \times 86 + 4) + (6 \times 15 + 2 \times 84 - 4 \times 2) = 348 + 250 = 598

(70)

In the case “activation key” off, there are

304

atoms in the Direct boxes and

298

atoms in the Complement boxes, with a total of 602 atoms (see Table 8, data from Table 4). To describe this case, we start by writing Equ.(34) of Section 4.2.2 as follows

4 \times 61 + (137 + 221) = 7 \times 86 = 602

(71)

Now we, first, take one copy of the number 61 and write it as

53 + 8

, using the identity

a_{n} + b_{n + 1} = a_{n + 4}

with

n = 4

(

61 = 8 + 53)

. Second, we write each of the other three copies of 61 using the recurrence relation

61 = 38 + 23

. Inserting these values in Equ.(71), we obtain

(3 \times 38 + 53 + 137) + (8 + 3 \times 23 + 221) = 304 + 298 = 602

(72)

which is what we are looking for.

In the case “activation key” off there are

348

atoms in Column 1 and

254

atoms in Column 2 (see Table 8, data from Table 4). It is possible to show that this case follows from the preceding one by noticing, as we did in the derivation of Equ.(64) above, that the number

53 = a_{7}^{'}

is equal to

b_{5} = 53

(these sequences are linked, see Equ.(16). By using the recurrence relation

a_{7}^{'} = 53 = a_{6}^{'} + a_{5}^{'} = 33 + 20

and arranging, we have finally the following right answer

(3 \times 38 + 20 + 137 + 8 + 3 \times 23) + (33 + 221) = 348 + 254 = 602

(73)

7. More on shCherbak’s Theory

In [1], we derived the relation

115 = 41 + 74 = 42 + 73

(74)

Her which describes proline’s singularity (see [3,4]). Here, in this section, we go far further, by presenting com completely new results. First, consider, once again, the sequence

a_{n}

, more exactly

a_{7} = 38

. We have, by s by squaring

a_{7}^{2} = 1444

(75)

It is not difficult to see, from Table 3, that this number corresponds to the number of nucleons (or integer molecular mass) in the side chains of the amino acids coded by 23 codons, where the sextets are counted twice, and proline has 42 nucleons in its side chain and only 73 nucleons in its backbone, contrary to the other 19 amino acids having 74 nucleons in their backbones (see Equ.(74) above). Second, from the identity

\sum_{1}^{k} a_{n} = a_{n + 2} - 1

, already considered in the sections above, we can write Equ.(75) as follows, using

n = 5

twice

a_{7}^{2} = 38^{2} = 38 \times (37 + 1) = (38 \times 37 + 37) + 1 = 1443 + 1

(76)

We recognize here the unit corresponding to the “singular” nucleon and the 1443 nucleons where proline, now, has 41 nucleons in its side chain and 74 nucleons in its backbone as the 19 other amino acids. Third, we can indeed derive the very molecular mass of proline from the above numbers of nucleons

1443

and

1444

. To see this, we make appeal to another tool from number theory, i.e., modular arithmetic which has many applications in mathematics (group theory, knot theory, ring theory) and computer science (computer algebra, coding theory, cryptography, and so on), see for example [11]. Also, several kinds of moduli are used in applications, as for example modulo 11 in the International Standard Book Number (ISBN) or mod 37 and mod 97 arithmetic in error detection in bank account numbers. We will, here, take as moduli, the integers

99

and

999

. (This is equivalent to summing the “digits” in base-100 and base-1000, respectively.) We have

(1443 m o d 99) + (1444 m o d 99) = 57 + 58 = 115

(77)

The reader could use, if desired, quick online calculators for the modulo function, for example here [12]. Using the trick of the digits summation, mentioned above (

57 = 14 + 43

and

58 = 14 + 44)

, we can arrange the above relation as

115 = 43 + 72

. In what follows, we will use two functions from elementary number theory, Euler’s ϕ-function of an integer n which counts the number of positive integers less than or equal to n which are relatively prime to n, [13], and also the φ-function which gives the sum of the divisors of an integer n, [14]. In the case where the integer is a prime number p, these function simplify greatly and one has simply

φ (p) = p - 1

and

σ (p) = p + 1

. Noting that 43 above is the only odd number out of three (14, 14 and 44) and, what’s more, a prime “digit” (remember we are in base-100), we get by calling its φ-function

115 = 42 + (72 + 1) = 42 + 73

, as

φ (43) = 43 - 1 = 42

. We have also

41 + (73 + 1)

if we use

σ (41) = 41 + 1 = 42

. These are the same relations as in Equ.(74) above. The numbers

1443

and

1444

are useful, as explained above but there is also a third number which will play, not only a role together with the other two, but it has also a meaningful interpretation. It is given by the following relation

1444 + (1444 m o d 1443) = 1444 + 1 = 1445

(78)

This number corresponds to the number of nucleons in the side chains of the amino acids encoded by 23 codons (the sextets counted twice) with proline’s side chain having 42 nucleons and four amino acids are in their charged state (see Section 1.2, Table 3 and above it):

(145 + 1) + (188 + 1) \times 2 + (660 + 1 - 1 - 1) + 57 + 130 + 75 = 1445

(79)

In the first parenthesis, 1 corresponds to the supplementary nucleon in proline’s side chain. In the second parenthesis, 1 corresponds to the charged arginine. In the third parenthesis, the units correspond respectively to lysine (charge +1), aspartic acid (charge -1) and glutamic acid (charge -1). We have therefore three meaningful numbers:

1443

1444

and

1445

. From these, we consider the following expression

(1443 m o d 999) + (1444 m o d 999) + (1445 m o d 999) = 444 + 445 + 446 = 1335

(80)

and take its

a_{0}

-function, the sum of its prime factors (

1335 = 3 \times 5 \times 89

), see below about this function.

a_{0} (1335) = 3 + 5 + 89 = 97

(81)

This number is equal to the number of nucleons (or molecular mass) of the residue of proline (see [5], Table 1). When two amino acids (or more) combine to form a peptide, a water molecule (two hydrogen atoms and one oxygen atom) is released and what remains of each amino acid is called a residue. Here, we have

115 - 97 = 18 (= 115 m o d 97)

, which is the molecular mass of the water molecule. Note that we have also, using two of the above numbers, 444 and 445

(444 m o d 99) + (445 m o d 99) = 48 + 49 = 97

(82)

Both relations give the same result, 97. From Equs.(81-82), we have the two-fold result

[(444 m o d 99) + (445 m o d 99)] + (115 m o d 97) = 97 + 18 = 115 a_{0} (1335) + (115 m o d 97) = 97 + 18 = 115

(83)

Finally, it is also possible to derive the detailed atomic composition of the (whole) molecule of proline:

C_{5} H_{9} O_{2} N

. Start from Equ.(81) and then add the quantity

115 m o d 97 = 18 = 2 \times 9

a_{0} (1335) + (115 m o d 97) = 3 + 5 + 89 + 18 = 115

(84)

Now,

89

, as a Fibonacci number, it could be decomposed successively as

55 + 34

and, next, as

55 + 21 + 13 = 55 + 13 + 13 + 8 = 55 + 13 + 5 + 8 + 8

. By inserting this decomposition in the above equation and arranging, we have

(5 + 55) + (5 + 9) + (3 + 13 + 8 + 8) + 9 = 60 + 14 + 32 + 9 = 115

(85)

This is the correct result. The number 60 has the prime factorization

2^{2} \times 3 \times 5 = (2 \times 6) \times 5

and gives 5 carbon atoms (carbon nucleus: 6 protons, 6 neutrons). The number 14 has the prime factorization

2 \times 7

and corresponds to one nitrogen atom (nitrogen nucleus: 7 protons, 7 neutrons). The number 32 has the prime factorization

2^{5} = 2 \times 2 \times 2^{3} = 2 \times (2 \times 8)

and corresponds to two oxygen atoms (oxygen nucleus: 8 protons, 8 neutrons). The last number, 9, corresponds to 9 hydrogen atoms.

In order to fully understand the reasoning presented below, it is important for the reader to keep in mind that, when looking at Equations 77 and 80, 1443 represents the number of nucleons in the side chains of the amino acids coded by 23 codons with the sextets counted twice and proline having 41 nucleons in its side chain, while 1444 represents the number of nucleons in the side chains of the amino acids coded by 23 codons with the sextets counted twice and proline now having 42 nucleons in its side chain. In fact, it appears that there is compelling evidence that the calculations performed here are "locked" technically. Below, we will show why but, before doing that, let us recall, briefly, a few elements of our so helpful arithmetic function

A_{0}

(see Appendix B in [1]). From the Fundamental Theorem of Arithmetic, an integer n can be represented, uniquely, as a product of prime numbers irrespective of their order:

n = p_{1}^{n_{1}} \times p_{2}^{n_{2}} \times \dots \times p_{k}^{n_{k}}

. The function

A_{0}

is defined by the formula

A_{0} (n) = a_{0} (n) + S P I (n) + Ω (n)

where

a_{0} (n)

is the sum of the prime factors (including the multiplicities)

p_{1} \times n_{1} + p_{2} \times n_{2} + \dots + p_{k} \times n_{k}

S P I (n)

is the sum of the Prime Indices of the prime factors (including the multiplicities)

P I (p_{1}) \times n_{1} + {P I (p}_{2}) \times n_{2} + \dots + P I (p_{k}) \times n_{k}

and

Ω (n)

, so-called Big Omega function, is the number of the prime factors

n_{1} + n_{2} + \dots + n_{k}

. The portion

a_{0} (n)

of this function was already involved above in the derivation of Equ.(81).

Now, let us look at the moduli

99

and

999

which were, together with the numbers

1443

and

1444

, critical in the derivation of Equs. (77), (80) and (82). Their prime factorization is given by

99 = 3^{2} \times 11

and

999 = 3^{3} \times 37

. We have

A_{0} (99) = 29

and

A_{0} (999) = 68

and, therefore,

A_{0} (99) + A_{0} (999) = 29 + 68 = 97

. This is nothing but, again, the integer molecular mass of proline’s residue, see Equs.(81)-(82). Also, by isolating the two terms

P I (37) = 12

and

Ω (37) = 1

, in

A_{0} (999)

, and including them in

A_{0} (99)

, we get

(29 + 12 + 1) + (3 \times 3 + 3 \times 2 + 37) = 42 + 55

. This is a more accurate description of proline’s residue (see [5], Table 1), which could also be seen from Equ.(81) above, remembering that 89 is a Fibonacci number,

3 + 5 + 89 = (3 + 5 + 34) + 55 = 42 + 55 .

By pushing the precision to the extreme, we can arrange the side chain part as follows

42 = (29 + 12 + 1) = (6 + 6) + (11 + 1) + 12 + (5 + 1) = 3 \times 12 + (5 + 1)

, where we have made explicit the portions of

A_{0} (99)

. We have 3 carbon atoms (atomic mass 12) and 6 hydrogen atoms, see the side chain in Figure 1 below. Observe the last term, interpreted as 6 hydrogen atoms in the side chain, (

5 + 1

), with one hydrogen atom being susceptible to be “transferred” from the side chain to the backbone (shCherbak’s “borrowing”, see above and Table 3). Of course, one has to add

18

, from Equ.(83), the water molecule, to get the whole molecule of proline. Below, in Figure 1, we show it with the side chain boxed.

The unique charm and covert attraction of proline's structure are concealed inside the integer molecule masses, just waiting to be gently revealed through the use of modular arithmetic.

8. Multiplet structures

This section deals with another application of our Fibonacci-lke sequences, more precisely, the sequence

a_{n}

and

a_{n}^{'}

. In [15], we have derived the exact multiplet structure of the genetic code, starting from the total number of codons, 64, expressed from the beginning, as

8 \times 8

and using Fibonacci/Lucas decompositions. We subsequently used either a property of “superperfect” numbers or the relation between Fibonacci and Lucas numbers to write one factor 8 as

7 + 1

and next 7 as 3+4 to derive the above-mentioned multiplet structure. Here, we show that all the ingredients of this derivation are, in fact, already ostensibly embedded in our Fibonacci-like sequences. Take

a_{4} = 8

(see Table 4). First, there is the recurrence relation

a_{3} + a_{2} = 7 + 1 = a_{4} = 8

. This is the decomposition of the number 8 mentioned above, obtained here without recourse to “superperfect” numbers, for example . Next, from the Lucas sequence in Equ.(4),

L_{n} = F_{n}^{'} + F_{n + 2}^{'}

, which is derived from the Fibonacci sequence

F_{n}^{'}

in Equ.(3), itself derived from the sequences

a_{n}

and

a_{n}^{'}

in Equ.(2), we have

7 = 4 + 3

. This is all we need to write

a_{4} \times (a_{3} + a_{2}) = 8 \times (4 + 3 + 1)

(86)

which leads, after writing the Fibonacci number 8 as

5 + 3

, to the following multiplet structure of the (standard) genetic code which could be expressed in two equivalent forms, Equ.(87) and Equ.(88)

(5 \times 4 + 3 \times 4) + (9 \times 2 + 3 \times 2 + 3 + 2 + 3) = 64

(87)

5 \times 4 + 3 \times (4 + 2) + 9 \times 2 + 3 + 2 + 3 = 64

(88)

The form in Equ.(87) describes Rumer’s division (see Section 4): 5 quartets (4 codons each) and 3 quartet-parts of the 3 sextets (4 codons each, in the first parenthesis (set

M_{1}

), and 9 doublets (2 codons each), 3 doublet-parts of the 3 sextets (2 codons each), 1 triplet (3 codons), 2 singlets (1 codon each) and 3 stops (3 codons), in the second parenthesis (set

M_{2}

). The form in Equ.(88) describes as for it the usual multiplet structure: 5 quartets, 3 sextets (6 codons each,

6 = 4 + 2

), 9 doublets, 1 triplet, 2 singlets and 3 stops. The vertebrate mitochondrial genetic code could also be easily derived from Equ.(88), see [1]. In fact, in unpublished notes, we have also derived from Equ.(86), with some little work, several other multiplet structures of the (non-standard) genetic codes. Let us give, here, only one example: the Alternative Yeast Nuclear Code (#12 in the database [16]. In this code, shown in Table 9 below, the only change concerns the reassignment of the codon CUG of leucine which now codes for serine. We have therefore 5 quartets (V, A, T, P, G), 1 sextet (R), 1 quintet (L, UUR, CUY, CUA), 1 septet (S, UCN, AGY, CUG), 9 doublets (F, Y, C, H, Q, D, E, N, K), 1 triplet (I), 2 singlets (M, W) and 3 stops. To describe this code, let us start from Equ.(88) and rewrite it in the form

5 \times 4 + 1 \times (4 + 2) + 8 + 4 + 9 \times 2 + 3 + 2 + 3 = 64

(89)

by selecting a factor

2 \times (4 + 2)

and developing it as

8 + 4

. Now, we write the Fibonacci number 8 as

8 = 5 + 3 = (3 + 2) + (2 + 1)

and insert it in Equ.(88). We have, writing again

3 = 2 + 1

5 \times 4 + 1 \times (4 + 2) + (1 + 2 + 2) + (4 + 2 + 1) + 9 \times 2 + 3 + 2 + 3 = 64

(90)

This relation describes this code. Arginine, the term

1 \times (4 + 2)

, is now the only sextet left. The term

(1 + 2 + 2)

is suitable for the quintet leucine coded now by five codons CUA (1 codon), CUY (2 codons), UUR (2 codons). The term

(4 + 2 + 1)

describes the septet serine coded now by seven codons UCN (4 codons), AGY (2 codons) and CUG (1 codon). The remaining terms are the usual ones (see above). The case of the other non-standard genetic codes could be handled along the same lines with, of course, some additional work.

9. Conclusion

We have once again studied the genetic code symmetries by taking an unexplored route. As previously mentioned, we recently used a small set of Fibonacci-like sequences that we designed to describe the symmetries of the genetic code [1]. However, this time, we thought of the amino acids as if they were submerged in a physiological environment (neutral pH), where four of them pick up a charge, either -1 (for aspartic acid and glutamic acid) or +1 (for arginine and lysine). The option examined in [5] and [4] is the same as this one. Additionally—and this is just as novel—we have examined two potential viewpoints for the unique amino acid proline, whose side chain is connected to its backbone twice: sCherbak's view and the Downes-Richardson view, see Section 1.2. We have outlined the patterns for the hydrogen atom content and the atom content for Rumer's symmetry, as well as this for the two viewpoints indicated above (referred to as "on" and "off" in the text), in Sections 4.1 and 4.2 with these two newly considered components. The same work has been done for the third-base symmetry in Sections 5.1 and 5.2 and the "ideal" symmetry as well as the more complex "supersymmetry" genetic code table in Sections 6.1–6.3. In Section 7, we have uncovered the remarkably unique chemical structure of proline along with its corresponding "activation" key, all with a basic application of modular arithmetic. Finally, we used our Fibonacci-like sequence

a_{n}

once more in Section 8 to demonstrate, via an example, how the multiplet structure of the non-standard variants of the genetic code can be determined.

References

Négadi, T. Revealing the genetic code symmetries through computations involving Fibonacci-like sequences and their properties. Computation 2023, 11, 154. [Google Scholar] [CrossRef]
Nirenberg, M.; Leder, P.; Bernfield, M.; Brimacombe, R.; Trupin, J.; Rottman, F.; O’Neal, C.N.A. Codewords and Protein Synthesis, VII. On the General Nature of the RNA Code. Proc. Natl. Acad. Sci. USA 1965, 53. [Google Scholar] [CrossRef] [PubMed]
shCherbak, V. The Arithmetical origin of the genetic code. In The Codes of Life: The Rules of Macroevolution; Barbieri, M., Ed.; Springer Publishers: New York, NY, USA, 2008; pp. 153–185. [Google Scholar]
shCherbak, V.; Makukov, M. The “wow! Signal” of the terrestrial genetic code. Icarus 2013, 224, 228–242. [Google Scholar] [CrossRef]
Downes, A.M.; Richardson, B.J. Relationships between genomic base content and distribution of mass in coded proteins. J. Mol. Evol. 2002, 55, 476–490. [Google Scholar] [CrossRef] [PubMed]
Rumer, Y. About systematization of the genetic code. Dok. Akad. Nauk SSSR 1966, 167, 1393–1394. [Google Scholar]
Findley, G.I.; Findley, A.M.; McGlynn, S.P. Symmetry characteristics of the genetic code. Proc. Natl. Acad. Sci. USA 1982, 79, 7061–7065. [Google Scholar] [CrossRef] [PubMed]
Shu, J.J. A new integrated symmetrical table for genetic codes. Biosystems 2017, 151, 21–26. [Google Scholar] [CrossRef] [PubMed]
Rosandić, M.; Paar, V. Codons sextets with leading role of serine create “ideal” symmetry classification scheme of the genetic code. Gene 2014, 543, 45–52. [Google Scholar] [CrossRef] [PubMed]
Rosandić, M.; Paar, V. , 2022. Standard Genetic Code vs. Supersymmetry Genetic code – Alphabetical table vs. physicochemical table. BioSystems, 2022, 218, 104695. [Google Scholar] [CrossRef] [PubMed]
Berggren, J.L. "modular arithmetic." Encyclopedia Britannica, November 17, 2023.
Available online: https://www.calculatorsoup.com/calculators/math/modulo-calculator.php (accessed on 23December2023).
Available online:. Available online: https://t5k.org/glossary/page.php?sort=EulersTheorem (accessed on 23 December 2023).
Available online: https://www.dcode.fr/divisors-list-number (accessed on 23 December 2023).
Négadi, T. Is the genetic code better described by elementary number theory? Academia Letters, 1004. [Google Scholar]
Available online:. Available online: https://www.ncbi.nlm.nih.gov/Taxonomy/Utils/wprintgc.cgi?chapter=tgencodes#SG2 (accessed on 23 December 2023).

Figure 1. Proline (the molecule).

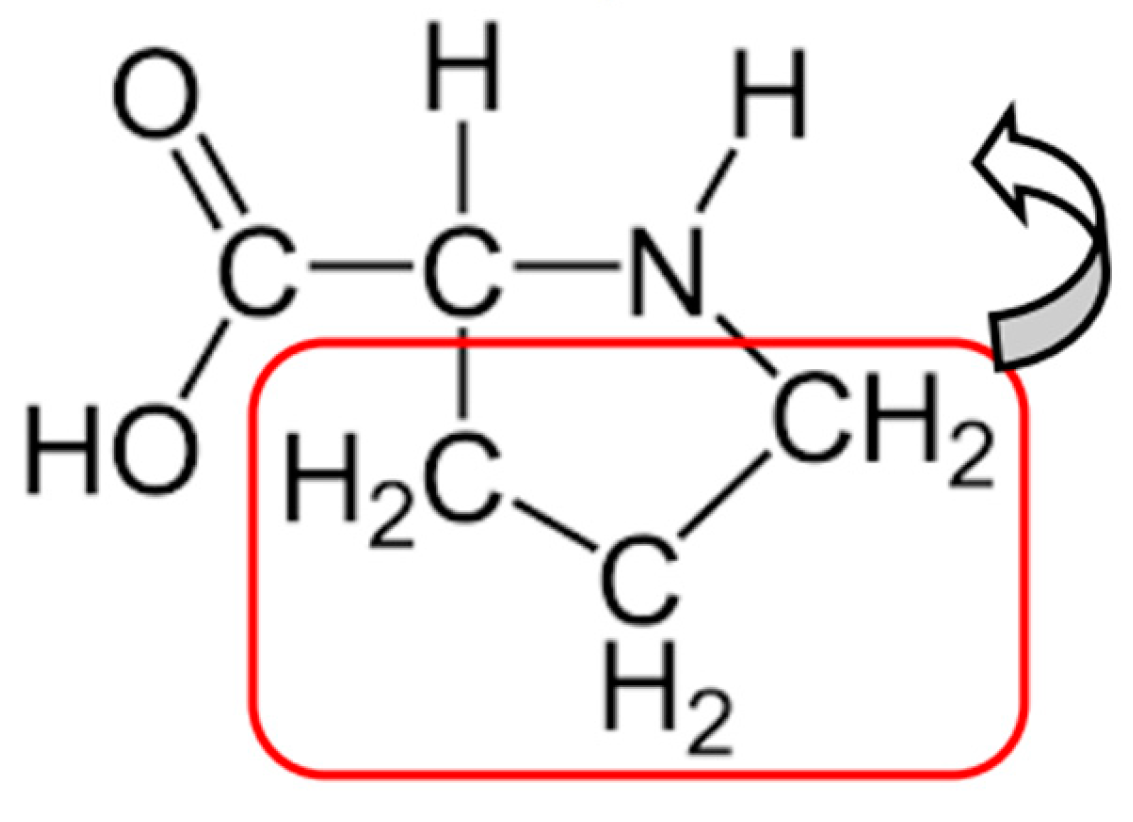
Table 1. the five multiplets of the standard genetic code.

Multiplets	Amino acids
3 sextets	serine (Ser, S), arginine (Arg R), leucine (Leu, L)
5 quartets	proline (Pro, P), alanine (Ala, A), threonine (Thr, T), valine (Val, V), glycine Gly, G)
1 triplet	isoleucine (Ile, I),
9 doublets	phenylalanine (Phe, F), tyrosine (Tyr, Y), cysteine (Cys, C), histidine (His, H), glutamine (Gln, Q), glutamic acid (Glu, E), aspartic acid (Asp, D), asparagine (Asn, N), lysine (Lys, K)
2 singlets	Methionine (Met, M), tryptophane (Trp, W)

Table 2. The genetic code table.

Table 3. The elemental composition of the 20 amino acids (see text for explanations).

M	amino acid	# H	# C	# N/O/S	# atoms	# nucleons
4	Proline (Pro) on/off	5 (+1)	3	0	8 (+1)	41 (+1)
	Alanine (Ala)	3	1	0	4	15
	Threonine (Thr)	5	2	0/1/0	8	45
	Valine (Val)	7	3	0	10	43
	Glycine (Gly)	1	0	0	1	1
6	Serine (Ser)	3	1	0/1/0	5	31
	Leucine (Leu)	9	4	0	13	57
	Arginine (Arg)	10 (+1)	4	3/0/0	17 (+1)	100 (+1)
2	Phenylalanine (Phe)	7	7	0	14	91
	Tyrosine (Tyr)	7	7	0/1/0	15	107
	Cysteine (Cys)	3	1	0/0/1	5	47
	Histidine (His)	5	4	2/0/0	11	81
	Glutamine (Gln)	6	3	1/1/0	11	72
	Asparagine (Asn)	4	2	1/1/0	8	58
	Lysine (Lys)	10 (+1)	4	1/0/0	15 (+1)	72 (+1)
	Aspartic Acid (Asp)	3 (-1)	2	0/2/0	7 (-1)	59 (-1)
	Glutamic Acid (Glu)	5 (-1)	3	0/2/0	10 (-1)	73 (-1)
3	Isoleucine (Ile)	9	4	0	13	57
1	Methionine (Met)	7	3	0/0/1	11	75
1	Tryptophane (Trp)	8	9	1/0/0	18	130
Total (20) on/off		117/118	67	20	204/205	1255/1256
Total (23) on/off		140/141	76	24	240/241	1444/1445
Total (38) on/off		222/225	104	32	358/361	1964/1967
Total (61) on/off		362/366	180	56	598/602	3408/3412
$M_{1} / M_{2}$ $\frac{o n}{o f f}$		176/186180/186			268/330272/330	1336/20721340/2072

Table 4. The first few terms of the sequences

a_{n}, {a_{n}^{'}, b}_{n}, c_{n} a n d g_{n} .

Table 4. The first few terms of the sequences

a_{n}, {a_{n}^{'}, b}_{n}, c_{n} a n d g_{n} .

Table 5. Rumer’s division of the genetic code table.

Table 6. The 3^rd base classification of the 64 codons, [7].

$C_{U}$	$f (C_{U})$	$C_{C}$	$f (C_{C})$	$C_{A}$	$f (C_{A})$	$C_{G}$	$f (C_{G})$
UCU	Ser	UCC	Ser	UCA	Ser	UCG	Ser
AGU	Ser	AGC	Ser	AGA	Arg	AGG	Arg
CGU	Arg	CGC	Arg	CGA	Arg	CGG	Arg
CUU	Leu	CUC	Leu	CUA	Leu	CUG	Leu
GCU	Ala	GCC	Ala	UUA	Leu	UUG	Leu
GUU	Val	GUC	Val	GCA	Ala	GCG	Ala
CCU	Pro	CCC	Pro	GUA	Val	GUG	Val
GGU	Gly	GGC	Gly	CCA	Pro	CCG	Pro
ACU	Thr	ACC	Thr	GGA	Gly	GGG	Gly
UUU	Phe	UUC	Phe	ACA	Thr	ACG	Thr
UAU	Tyr	UAC	Tyr	CAA	Gln	CAG	Gln
UGU	Cys	UGC	Cys	AAA	Lys	AAG	Lys
CAU	His	CAC	His	GAA	Glu	GAG	Glu
GAU	Asp	GAC	Asp	UAAUGA	StopSS	UAG	Stop
AAU	Asn	AAC	Asn	UAAUGA	StopSS	UGG	Trp
AUU	Ile	AUC	Ile	AUA	Ile	AUG	Met
H on/off	84/85		84/85		94/95		100/101
At. on/off	144/145		144/145		147/148		163/164

Table 7. The Rosandić-Parr”ideal” symmetry classification scheme [9]).

Table 8. The “supersymmetry” genetic code table (from [10]).

Boxes	aa	codons	Pu/Py	Pu/Py	codons	aa
DB	Start I I I	AUG AUA AUC AUU	010 010 011 011	010 010 011 011	GCA GCG GCU GCC	A A A A
CB	Y Y Stop Stop	UAC UAU UAG UAA	101 101 100 100	101 101 100 100	CGU CGC CGA CGG	R R R R
DB	E E D D	GAG GAA GAC GAU	000 000 001 001	000 000 001 001	AGA AGG AGU AGC	R R S S
CB	L L L L	CUC CUU CUG CUA	111 111 110 110	111 111 110 110	UCU UCC UCA UCG	S S S S
DB	L L F F	UUA UUG UUU UUC	110 110 111 111	110 110 111 111	CCG CCA CCC CCU	P P P P
CB	N N K K	AAU AAC AAA AAG	001 001 000 000	001 001 000 000	GGC GGU GGG GGA	G G G G
DB	Q Q H H	CAA CAG CAU CAC	100 100 101 101	100 100 101 101	UGG UGA UGC UGU	W Stop C C
CB	V V V V	GUU GUC GUA GUG	011 011 010 010	011 011 010 010	ACC ACU ACG ACA	T T T T
	Column 1			Column 2

Table 9. The Alternative Yeast Nuclear Code (#12 in [16]).

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Fibonacci-Like Sequences Reveal the Genetic Code Symmetries, also When the Amino Acids Are in a Physiological Environment

Abstract

1. Introduction

1.1. The genetic code

1.2. The elemental composition of the 20 amino acids

1.3. The structure of the paper

2. Fibonacci-like sequences

3. Hydrogen atom content

3.1. Hydrogen atom content: “activation key” on

3.2. Hydrogen atom content: “activation key” off

4. Rumer’s symmetry

4.1. The hydrogen atom content

4.2. The atom content (CHNOS)

4.2.1. “Activation key” on

4.2.2. “Activation key” off

5. The 3rd base symmetry classification

5.1. The hydrogen atom content

5.1.1. “Activation key” on

5.1.2. “Activation key” off

5.2. The atom content

5.2.1. “Activation key” on

5.2.2. “Activation key” off

6. The “ideal” symmetry and the “supersymmetry” classification schemes

6.1. Hydrogen atom content

6.1.1. “Activation key” on

6.1.2. “Activation key” off

6.2. Atom content

6.2.1. “Activation key” on

6.2.2. “Activation key” off

6.3. The “supersymmetry” genetic code table

6.3.1. Uncharged amino acids case and “activation key” on only

6.3.2. Charged amino acids case, “activation key” on and off

6.3.2.1. Hydrogen atom content

6.3.2.2. Atom content

7. More on shCherbak’s Theory

8. Multiplet structures

9. Conclusion

References

MDPI Initiatives

Important Links

Subscribe

5. The 3^rd base symmetry classification