Application of Surface-Stress Driven Model for Higher Vibrations Modes of Functionally Graded Nanobeams

Preprint

Article

Application of Surface-Stress Driven Model for Higher Vibrations Modes of Functionally Graded Nanobeams

Altmetrics

Downloads

158

Views

Comments

A peer-reviewed article of this preprint also exists.

Giuseppe Lovisi^*

Luciano Feo

Annavirginia Lambiase

Rosa Penna

Giuseppe Lovisi^*

Luciano Feo

Annavirginia Lambiase

Rosa Penna

This version is not peer-reviewed

Submitted:

11 January 2024

Posted:

11 January 2024

You are already at the latest version

Alerts

Abstract

This manuscript employs a surface stress-driven nonlocal model to explore the combined effects of long-range interaction and surface energy on higher vibration modes of functionally graded nanobeams. The nanobeam theory, based on Bernoulli-Euler kinematics, incorporates surface effects such as surface elasticity, surface residual stresses, surface density, and rotary inertia. Hamilton's principle is applied to derive the governing equation with size-dependent considerations. The main outcomes of a parametric investigation, considering four different kinematic boundary conditions (Cantilever, Simply-Supported, Clamped-Pinned, and Doubly-Clamped) while varying the nonlocal parameter and material gradient index, are presented and discussed. Additionally, the normalized natural frequencies for the second, third, fourth and fifth modes of vibrations are provided and analyzed for each case under study. The results underscore the model's effectiveness in capturing surface energy effects on the overall dynamic behavior of functionally graded Bernoulli-Euler nanobeams, offering a cost-effective approach for designing and optimizing nano-scaled structures.

Keywords:

Subject: Chemistry and Materials Science - Nanotechnology

1. Introduction

The last decades have seen significant progress in the field of nanoscience and nanotechnology, leading the scientific community to focus extensively on the analysis, modelling and development of nanostructures [1,2,3]. Nanostructures are now employed in various fields and it is crucial to have accurate models for their reliable and efficient design. Further progress has been made with the introduction of Functionally Graded Materials (FG) in the field of nanostructures, allowing them to maintain high performance even under conditions of high thermal and mechanical stress [4,5,6].

Hence, understanding the size-dependent behavior of these nanostructures is essential, considering their broad application in nanomechanical devices such as nanoelectromechanical actuators and nanomechanical resonators [7,8].

As commonly recognized, when the size of a structure reduces to the nanoscale, small-scale phenomena, negligible at the macro-scale, become predominant. In particular, atomic interaction and surface effects play a crucial role that cannot be neglected at the nanoscale.

Various approaches exist for the study of nanostructures, including experimental investigations and molecular dynamics simulations [9,10]. Both are characterized by high computational costs and long analysis times.

In recent years, researchers have explored the introduction of non-classical continuum models for the study of nanostructures, appropriately modified to capture long-range interactions and surface effects.

One of the earliest non-classical continuum models is the Eringen [11] one, which differs from the classical continuum formulation by assuming that the stress at a point also depends on the deformation of the surrounding points. Eringen proposed a theory to capture this effect, where the stress field is obtained through an integral convolution, driven by strain, between the elastic strain field and an averaging kernel. To overcome the mathematical difficulties of integral resolution, Eringen later proposed the equivalent differential formulation (EDM) [12]. Additional nonlocal models have been developed from this formulation, including the nonlocal Eringen mixture model [13] and the nonlocal Lim gradient strain model [14], obtained by coupling the EDM model with the Mindlin gradient model [15].

In addition, Gurtin and Murdoch [16,17] introduced Surface Elasticity Theory (SET) to address the effects of surface energy. In this theory the surface layer is considered as a membrane of negligible thickness, perfectly adhering to the mass continuum, and characterized by unique properties and constitutive laws distinct from those that govern the volume. This theory has often been coupled with the Eringen model to capture not only nonlocal effects but also surface effects.

Although these models have been widely used to study the static and dynamic aspect of nanostructures, the scientific community considers these models inapplicable for the study of nanostructures whose results are known as nanomechanics paradoxes [18,19,20,21].

To overcome the mathematical inconsistencies of the aforementioned models, Romano and Barretta proposed a new Stress-Driven Model (SDM) of nonlocal elasticity [22], in which the integral convolution is a function of the stress field instead of the strain one. It has been extensively used in recent years to study both the static and the dynamic response of functionally graded nanobeams subjected to thermo-mechanical stresses [23,24,25,26,27,28,29,30,31,32,33,34]. Furthermore, Penna [35] recently extended the SDM model by coupling it with the SET theory to create the Surface Stress-Driven Model (SSDM). This model, well-posed mathematically, not only captures long-range interactions but also addresses surface effects. This new model has been recently used to investigate the free vibrations of functionally graded nanobeams [36], analyze static response in the presence of discontinuous loads [37], and investigate the effects of cracks in FG nanobeams [38].

The main innovation of this manuscript lies in the pioneering use of the SSDM model to determine the frequencies of higher vibration modes. Specifically, it explores the effects of the nonlocal parameter, surface energy, and material gradient index on the natural frequency of the FG nanobeam, focusing on higher vibration modes for both square and circular cross-sectional shapes.

The document's structure is the following: in Section 2, the problem formulation is provided, including kinematics, geometry, material, and the governing equations of free oscillations derived from the use of the Hamilton's Principle. A brief description of the SSDM model and the size-dependent governing equations of transverse free oscillations are presented in Section 3. In the parametric analysis outlined in Section 4, we investigate and discuss the combined influences of the nonlocal parameter, surface effects, and gradient index on the higher-order vibration modes of the four considered static schemes. Finally, in Section 5, some concluding remarks are provided.

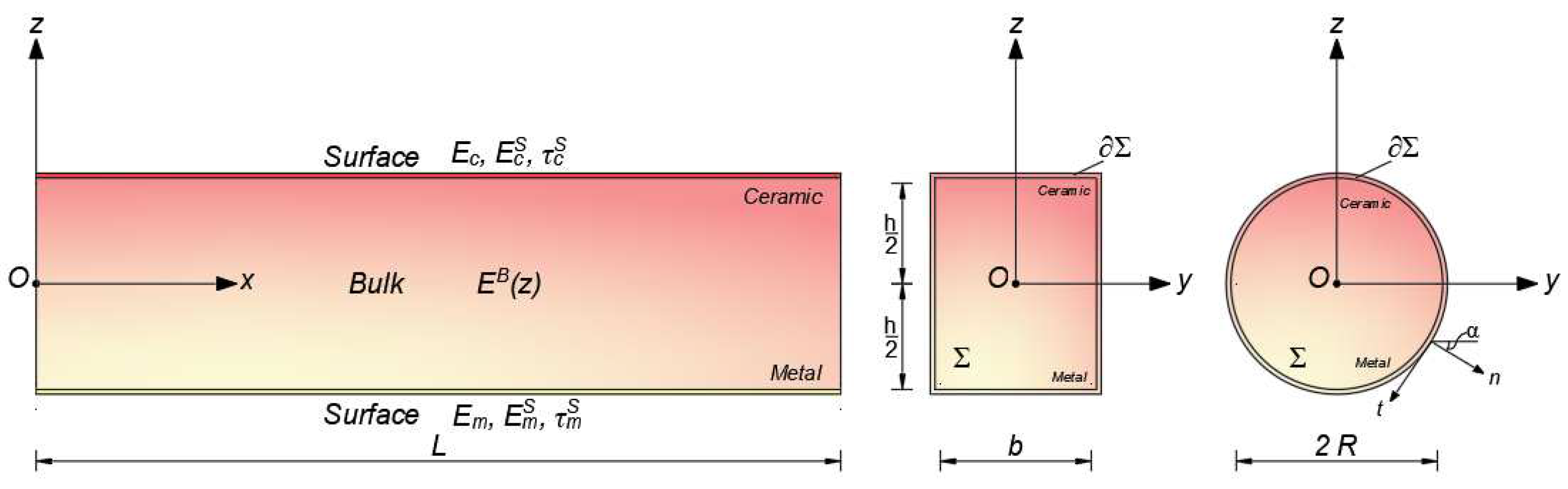
2. Problem formulation

Figure 1 shows the coordinate system and configuration of the FG nanobeam under investigation, composed of a bulk volume (B), made of a mixture of metal (m) and ceramic (c), and a thin surface layer (S), perfectly adhered to the bulk continuum (refer to Figure 1) with two distinct cross-sectional shapes.

As it is well-known, for a Bernoulli-Euler FG nanobeam whose mechanical and physical properties vary along the thickness (z), it can be assumed that the bulk elastic modulus of elasticity,

E^{B} = E^{B} (z)

, the surface modulus of elasticity,

E^{S} = E^{S} (z)

, the residual surface stress,

τ^{S} = τ^{S} (z)

, the bulk mass density,

ρ^{B} = ρ^{B} (z)

, and the surface mass density,

ρ^{S} = ρ^{S} (z)

, follow a power-law functions as given below [39]

E^{B} (z) = E_{m} + (E_{c} - E_{m}) {(\frac{1}{2} + \frac{z}{ζ})}^{n}

(1)

E^{S} (z) = E_{m}^{S} + (E_{c}^{S} - E_{m}^{S}) {(\frac{1}{2} + \frac{z}{ζ})}^{n}

(2)

τ^{S} (z) = τ_{m}^{S} + (τ_{c}^{S} - τ_{m}^{S}) {(\frac{1}{2} + \frac{z}{ζ})}^{n}

(3)

ρ^{B} (z) = ρ_{m} + (ρ_{c} - ρ_{m}) {(\frac{1}{2} + \frac{z}{ζ})}^{n}

(4)

ρ^{S} (z) = ρ_{m}^{S} + (ρ_{c}^{S} - ρ_{m}^{S}) {(\frac{1}{2} + \frac{z}{ζ})}^{n}

(5)

being

n

the material gradient index

(n \geq 0)

;

ζ

h,

in the case of square or rectangular cross-section and

ζ

2 R

, for a circular one. Poisson’s ratio is here assumed to be constant (

ν^{B} = ν^{S} = ν

2.1. Kinematic

The Bernoulli-Euler beam theory considers the following displacement field

u (x, t) = u_{x} (x, z, t) {\hat{e}}_{x} + u_{z} (x, z, t) {\hat{e}}_{z}

(6)

where

{\hat{e}}_{x}

and

{\hat{e}}_{z}

are, respectively, the unit vectors along x- and z-axes;

u_{x} (x, z, t) a n d

u_{z} (x, z, t)

indicate the Cartesian components of the displacement field along

x

and

z

axes at time t, expressed as follows

u_{x} (x, z, t) = - z \frac{\partial w (x, t)}{\partial x}

(7)

u_{z} (x, z, t) = w (x, t)

(8)

being

w (x, t) = w

the transverse displacement of the geometric center O (at time t). Within the assumptions of the small strain and displacement theory, the simplified Green-Lagrange strain tensor is

E \approx ε = ε_{x x} {\hat{e}}_{x} {\hat{e}}_{x}

(9)

where

ε_{x x} = ε_{x x} (x, z, t) = - z \frac{\partial^{2} w (x, t)}{\partial x^{2}}

(10)

being

\frac{\partial^{2} w (x, t)}{\partial x^{2}}

the geometric bending curvature

χ

2.2. Governing equations

The use of Hamilton's principle allows us to obtain the governing equation of the free vibrations problem [36]

\frac{\partial^{2} M}{\partial x^{2}} + T^{S} \frac{\partial^{2} w}{\partial x^{2}} = (A_{ρ}^{B} + A_{ρ}^{S}) \frac{\partial^{2} w}{\partial t^{2}} - (I_{ρ}^{B} + I_{ρ}^{S}) \frac{\partial^{4} w}{\partial x^{2} \partial t^{2}}

(11)

where

\{A_{ρ}^{B}, I_{ρ}^{B}\} = \int_{Σ} ρ^{B} \{1, z^{2}\} d Σ

(12)

\{A_{ρ}^{S}, I_{ρ}^{S}\} = \oint_{\partial Σ} ρ^{S} \{1, z^{2}\} d σ

(13)

Τ^{S} = \{\begin{matrix} \oint_{\partial Σ} τ^{S} d σ (r e c t a n g u l a r c r o s s - s e c t i o n) \\ \oint_{\partial Σ} τ^{S} n_{z} d σ (c i r c u l a r c r o s s - s e c t i o n) \end{matrix}

(14)

being

n_{z}

the z-component of the unit normal vector

n

, which is the outward normal to the cross-section lateral surface [35].

The appropriate boundary conditions of the FG nanobeam (

a t t h e n a n o b e a m e n d s x = 0

L

) can be determined by selecting a single condition from each of the two pairs of Standard Boundary Conditions (SBCs) [36]

(15)

(16)

being

M

the bending moment of FG nanobeam.

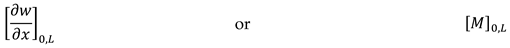
3. Surface stress-driven model for free vibrations analysis

3.1. A brief outline of the surface stress-driven nonlocal model

In this section, we provide a brief review of the surface stress-driven nonlocal model (SSDM) as outlined in [35]. Assuming a purely elastic constitutive behavior, the formulation of the surface stress-driven nonlocal model involves defining the bending curvature, χ, through the integral convolution, as detailed in the same reference [35]

χ = \int_{0}^{L} Φ_{L_{c}} (x - ξ, L_{c}) (- \frac{M^{*}}{I_{E}^{*}}) d ξ

(17)

where

x

and

ξ

are the positions of points of the domain of the Euclidean space occupied by the FG nanobeam at time t;

Φ_{L_{c}}

is an averaging kernel depending on the characteristic length of material,

L_{c} = λ_{c} L

;

I_{E}^{*}

and

M^{*}

are, respectively, the equivalent bending stiffness and the applied bending moment, defined as

I_{E}^{*} = \int_{Σ} [E^{B} + ν C] z^{2} d Σ + \oint_{\partial Σ} E^{S} z^{2} d σ

(18)

M^{*} = M^{*} (x, t) = M - M^{τ} - Λ \frac{\partial^{2} w}{\partial t^{2}}

(19)

being

C = \frac{2}{h} [{(\frac{z}{h})}^{2} - \frac{3}{4}] (τ_{c}^{S} + τ_{m}^{S}) - \frac{1}{2 z} (τ_{c}^{S} - τ_{m}^{S})

(20)

M^{τ} = \oint_{\partial Σ} τ^{S} z d σ

(21)

Λ = \int_{Σ} ν D z d Σ

(22)

and

D = 2 \frac{z}{h} [{(\frac{z}{h})}^{2} - \frac{3}{4}] (ρ_{c}^{S} + ρ_{m}^{S}) - \frac{1}{2} (ρ_{c}^{S} + ρ_{m}^{S})

(23)

As widely recognized, a specific function kernel, denoted as

Φ_{L_{c}}

, is chosen to be

Φ_{L_{c}} (x, L_{c}) = \frac{1}{2 L_{c}} \exp (- \frac{|x|}{L_{c}})

(24)

for smooth source fields

(- \frac{M^{*}}{I_{E}^{*}})

in the domain

[0, L]

, the elastic curvature χ, as expressed in Eq.17, is equivalent to the following second-order differential equations, as outlined in [35]

(1 - L_{c}^{2} \frac{\partial^{2}}{\partial x^{2}}) χ = - \frac{M^{*}}{I_{E}^{*}}

(25)

This equivalence is true if and only if the conventional Constitutive Boundary Conditions (CBCs) of the stress-driven nonlocal theory are satisfied at the ends of the FG nanobeam

\frac{\partial χ (0)}{\partial x} - \frac{1}{L_{c}} χ (0) = 0

(26)

\frac{\partial χ (L)}{\partial x} + \frac{1}{L_{c}} χ (L) = 0

(27)

By manipulating Eq. 25, we can derive the expression for the resultant bending moment in the surface stress-driven nonlocal model

M = M (x, t) = - (I_{E}^{B} + I_{E}^{S}) \frac{\partial^{2} w}{\partial x^{2}} + (I_{E}^{B} + I_{E}^{S}) L_{c}^{2} \frac{\partial^{4} w}{\partial x^{4}} + M^{τ} + Λ \frac{\partial^{2} w}{\partial t^{2}}

(28)

3.2. Size-dependent governing equation

By inserting Eq.28 into Eq.11, we obtain the equation that governs the dynamic problem of the FG nanobeam, incorporating both nonlocal and surface energy effects

(I_{E}^{B} + I_{E}^{S}) L_{c}^{2} \frac{\partial^{6} w}{\partial x^{6}} - (I_{E}^{B} + I_{E}^{S}) \frac{\partial^{4} w}{\partial x^{4}} + T^{S} \frac{\partial^{2} w}{\partial x^{2}} = (A_{ρ}^{B} + A_{ρ}^{S}) \frac{\partial^{2} w}{\partial t^{2}} - Λ \frac{\partial^{4} w}{\partial x^{2} \partial t^{2}} - (I_{ρ}^{B} + I_{ρ}^{S}) \frac{\partial^{4} w}{\partial x^{2} \partial t^{2}}

(29)

with the corresponding standard (Eqs. 15 and 16) and constitutive (Eqs. 26 and 27) boundary conditions at the FG nanobeam ends (

x = 0

L

Conclusively, by introducing the following dimensionless quantities

(30)

and by using the classical method of separation variables, in which ω indicates the natural nonlocal frequency of transverse vibrations

\tilde{w} (\tilde{x}, t) = \tilde{W} (\tilde{x}) e^{i ω t}

(31)

the dimensionless equation governing the linear transverse free vibrations based on SSDM can be expressed in terms of the non-dimensional spatial shape

\tilde{W} = \tilde{W} (\tilde{x})

, as follows

λ_{c}^{2} \frac{\partial^{6} \tilde{W}}{\partial {\tilde{x}}^{6}} - \frac{\partial^{4} \tilde{W}}{\partial {\tilde{x}}^{4}} + {\tilde{T}}^{S} \frac{\partial^{2} \tilde{W}}{\partial {\tilde{x}}^{2}} = {\tilde{ω}}^{2} ((\tilde{Λ} + {\tilde{g}}^{B} + {\tilde{g}}^{S}) \frac{\partial^{2} \tilde{W}}{\partial {\tilde{x}}^{2}} - (1 + \tilde{r}) \tilde{W})

(32)

being

{\tilde{ω}}^{2} = {\tilde{A}}_{ρ}^{B} ω^{2}

(33)

with the corresponding dimensionless standard and constitutive boundary conditions

(34)

(35)

- \frac{\partial^{3} \tilde{W} (0)}{\partial {\tilde{x}}^{3}} + \frac{1}{λ_{c}} \frac{\partial^{2} \tilde{W} (0)}{\partial {\tilde{x}}^{2}} = 0

(36)

- \frac{\partial^{3} \tilde{W} (1)}{\partial {\tilde{x}}^{3}} - \frac{1}{λ_{c}} \frac{\partial^{2} \tilde{W} (1)}{\partial {\tilde{x}}^{2}} = 0

(37)

being

\tilde{M}

the dimensionless surface stress-driven nonlocal resultant moment expressed as follows

\tilde{M} = \tilde{M} (\tilde{x}) = λ_{c}^{2} \frac{\partial^{4} \tilde{W}}{\partial {\tilde{x}}^{4}} - \frac{\partial^{2} \tilde{W}}{\partial {\tilde{x}}^{2}} + {\tilde{M}}^{τ} - {\tilde{ω}}^{2} \tilde{Λ} \tilde{W}

(38)

Eq.32 admits the following solution

\tilde{W} = \sum_{k = 1}^{6} q_{k} ⅇ^{\tilde{x} β_{k}}

(39)

It is essential to underline that the determination of the six unknown constants, indicated as

q_{k}

, depends on the satisfaction of the boundary conditions specified in Eqs. 34-37. The linear fundamental natural frequencies of the FG nanobeam are established by addressing the eigenvalue problem articulated in a six-dimensional array

q = {q_{1}, . ., q_{6}}

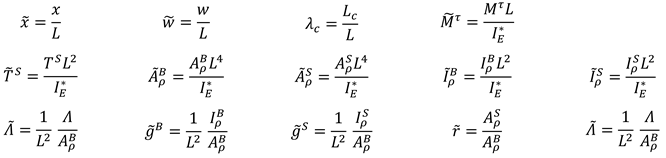
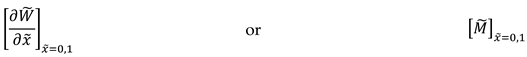
4. Results and discussion

In this paragraph, a higher order free vibration analysis of Bernoulli-Euler FG nanobeam with length L = 10 nm is developed by considering Cantilever (C-F), Simply-Supported (S-S), Clamped-Pinned (C-P) and Doubly-Clamped (C-C) static configurations.

The analysis has been conducted using both surface stress-driven model (SSDM) and stress-driven model (SDM) without considering the surface energy effects. In addition, the present study encompasses two distinct cross-sectional shapes having the same second moment of area about their principal axis of geometric inertia y: a square cross-section (b=h = 0.1L = 1nm) and a circular one of radius R=0.571nm.

The characteristic value of physical and elastic properties of the two constituent materials, in terms of bulk Young’s modulus,

E_{c}^{B}

and

E_{m}^{B}

, surface Young’s modulus,

E_{c}^{S}

and

E_{m}^{S}

, residual surface stress,

τ_{c}^{S}

and

τ_{m}^{S}

, bulk mass density,

ρ_{c}^{B}

and

ρ_{m}^{B}

, and surface mass density,

ρ_{c}^{S}

and

ρ_{m}^{S}

, are summarized in the following Table 1 [35].

The following results are expressed in terms of dimensionless nonlocal frequency, obtained as the ratio between the nonlocal dimensionless frequency (Eq. 31) and the dimensionless local frequency

{\tilde{ω}}_{l o c}^{2}

. The dimensionless local frequency,

{\tilde{ω}}_{l o c}^{2}

, is the natural frequency of the first order (obtained by setting

λ_{c} = {\tilde{g}}^{B} = {\tilde{g}}^{S} = \tilde{Λ} = \tilde{r} = {\tilde{T}}^{S} = n = 0)

and is assumed to be equal to 3.5160 for Cantilever FG nanobeam, 9.8696 for Simply-Supported, 15.4182 for Clamped-Pinned and 22.3733 for Doubly-Clamped.

Firstly, in Table 2, Table 3, Table 4 and Table 5 the present approach has been validated by comparing the corresponding results, in terms of dimensionless nonlocal frequencies, to those obtained by Raimondo et al. in Ref. [34] for homogenous nanobeams by neglecting both the surface energy effects and the gyration radius

{(\tilde{g}}^{B} = 0)

Table 2, Table 3, Table 4 and Table 5 provide a summary of the results of the free vibration analysis in terms of normalized nonlocal high frequencies, corresponding to

λ_{c} ∊

{0.00⁺, 0.01, 0.02, 0.03, 0.04, 0.05, 0.06, 0.07, 0.08, 0.09, 0.10} and to n

∊ {0,1, 3\}

for the first five vibrations modes.

Looking at the results, it is evident that an increase in the material gradient index consistently leads to higher normalized nonlocal frequencies for the square cross-section, regardless of the boundary constraints considered. However, for the circular cross-section the trend is conditioned by the specific static scheme considered.

Furthermore, from Table 2, Table 3, Table 4 and Table 5 and Figure 2, Figure 3, Figure 4 and Figure 5, it is easy to observe that the dimensionless nonlocal frequencies increase with increasing the order of the vibration modes for all the static schemes here considered. In addition, by fixing the values of nonlocal parameter and the material gradient index, it is observed that the dimensionless nonlocal frequencies reach their maximum value in the case of the Cantilever FG nanobeam and the minimum one in the case of Doubly-Clamped FG nanobeam for each vibration mode, regardless of the cross-sectional shapes chosen.

Therefore, it may be concluded that nonlocality strongly influences the normalized nonlocal frequencies, and its effects are stronger for higher vibrations modes. In fact, increasing the nonlocal parameter always shows an increase in the dimensionless nonlocal frequencies.

Moreover, in the case of a square cross-section, the presence of surface effects results in additional stiffness, leading to an increase in the normalized nonlocal frequencies for the first three vibration modes compared to the model without surface effects in Ref. [34]; however, the surface energy causes a reduction in normalized nonlocal frequencies for the fourth and fifth vibration modes. On the contrary, FG nanobeams characterized by a circular cross-section show a more general dynamic response. In fact, it depends on the intertwined effects of the nonlocal parameter and the material gradient index, together with the boundary conditions at the nanobeam ends.

Finally, in Figure 2, Figure 3, Figure 4 and Figure 5, a comparison between the normalized nonlocal frequency curves for the surface stress-driven model (SSDM) and the stress-driven model (SDM) without surface effects is presented. The comparison spans all static configurations and the two types of cross sections considered. For these illustrations the parameters λ

λ_{c} = 0.05

and

n = 1

are set. As it can be observed, the SSDM consistently provides a stiffening behavior as the number of vibration modes increases.

5. Conclusions

This study presents the main results of an application of the surface-stress driven model developed to investigate the coupled influences of the nonlocal parameter and the material gradient index on the higher order free vibrations analysis of the functionally graded nanobeams. The analysis is conducted using a Wolfram language code developed in Mathematica by the authors.

The results have been successfully compared to those presented by Raimondo et al. in Ref. [34], where the surface energy effects have been neglected, confirming the accuracy and reliability of the proposed approach.

The main conclusions are the following:

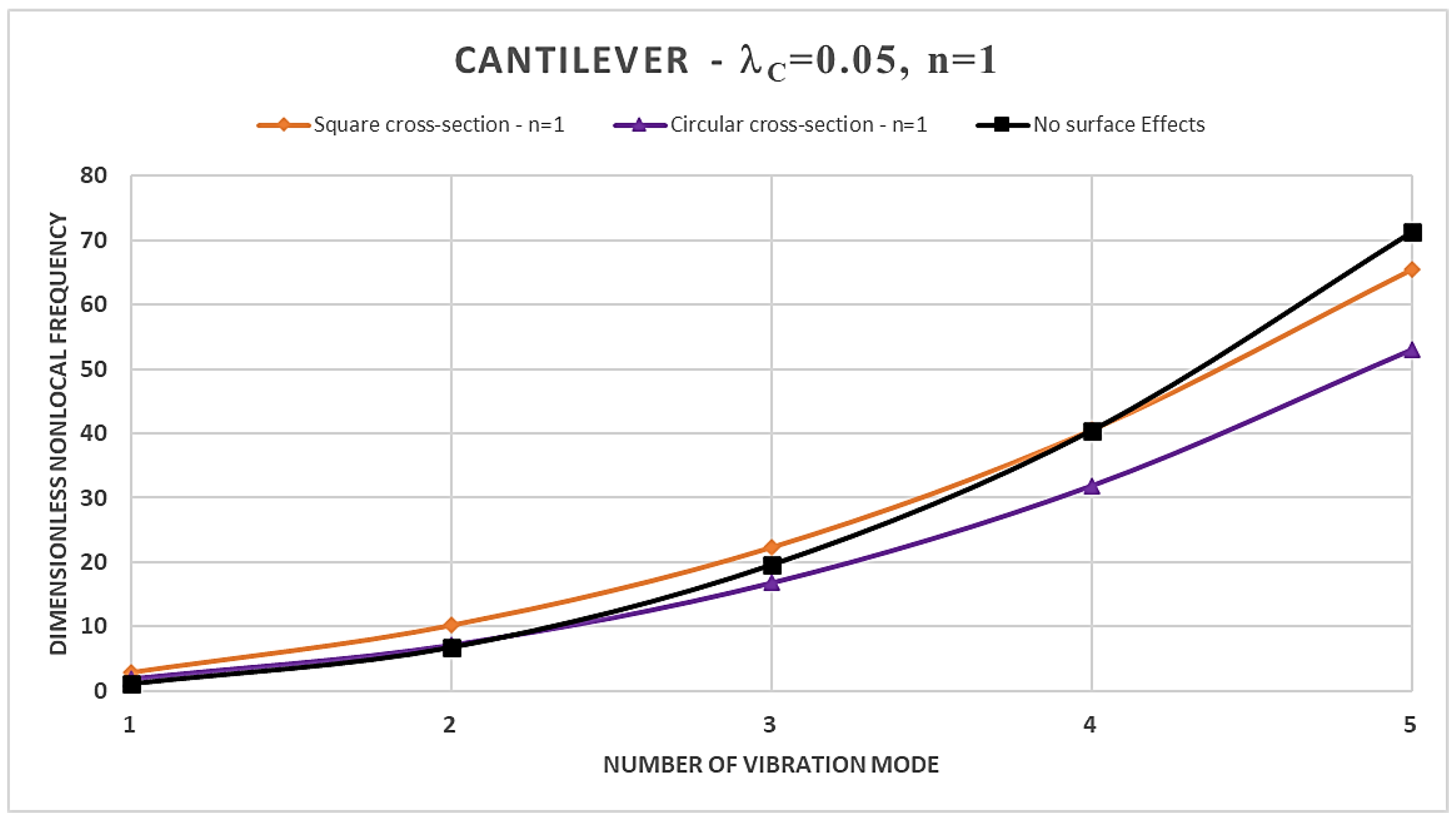
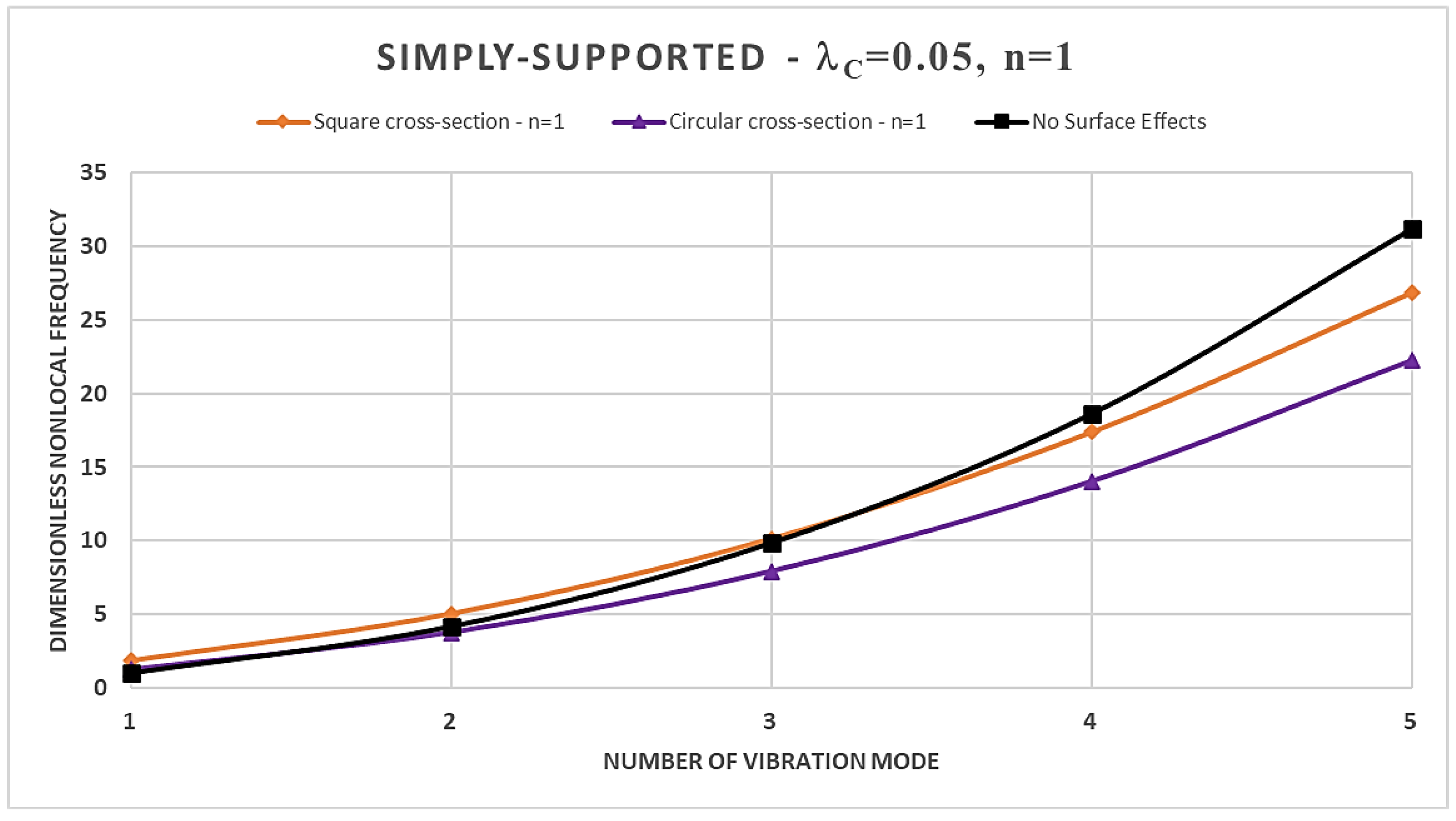
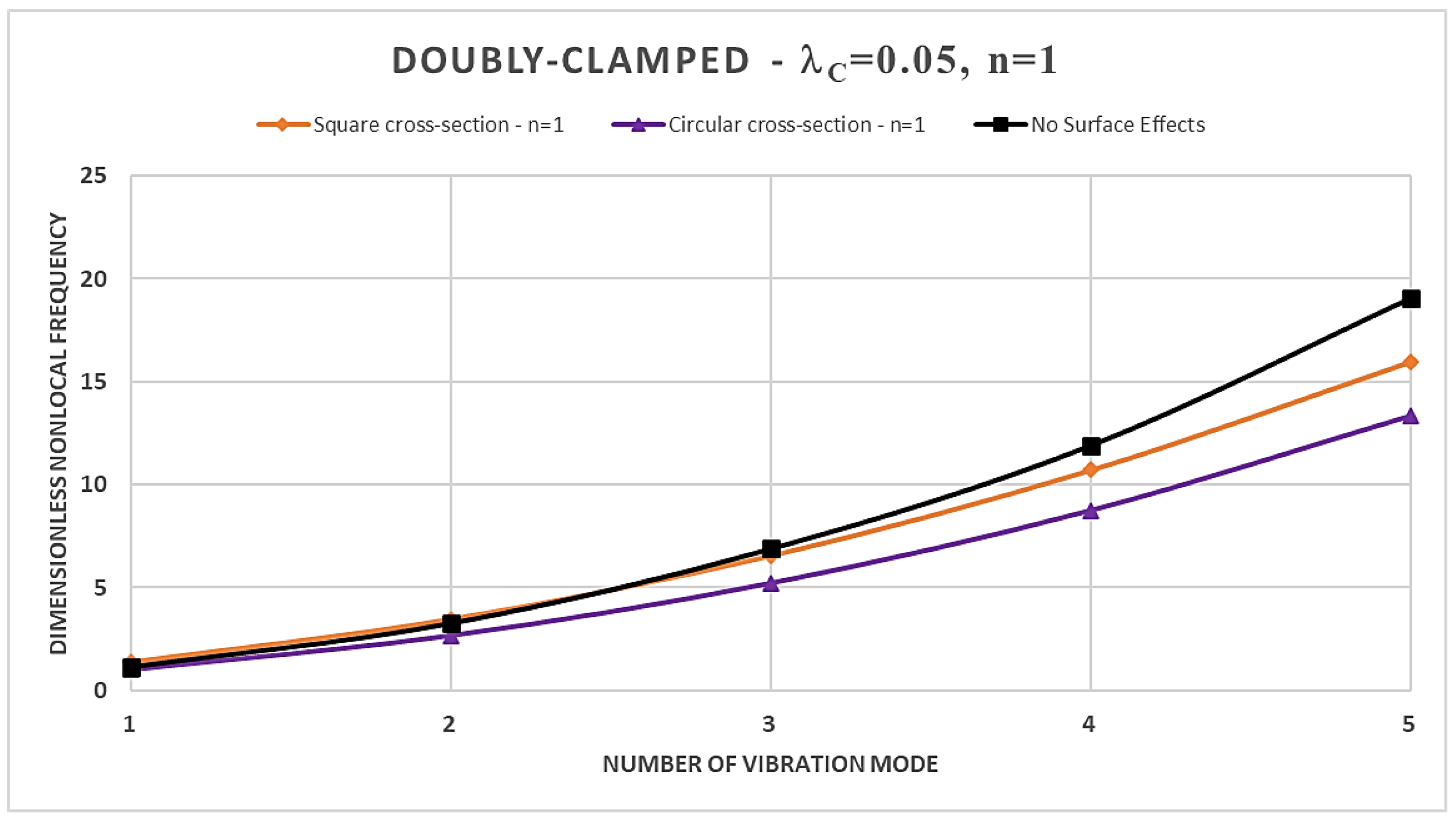
-: an increase in the material gradient index consistently results in an increase in the normalized nonlocal frequencies in the case of square cross-section, regardless of the boundary constrains are considered; while, for the case of the circular cross-section the trend is conditioned by the specific static scheme considered;
-: the normalized nonlocal frequencies increase by increasing the order of the vibration modes for each static schemes considered;
-: the dimensionless nonlocal frequencies reach their maximum value in the case of the C-F nanobeam and the minimum one in the case of C-C nanobeam for each vibration mode, regardless of the cross-sectional shapes chosen;
-: the nonlocality strongly influences the dimensionless frequencies, and its effects are stronger for higher vibration modes;
-: by increasing the nonlocal parameter, the SSDM formulation always shows an increase in the normalized nonlocal frequencies;
-: as the number of vibration modes increases the SSDM model always provides a stiffening behavior;
-: in the case of a square cross-section, the presence of surface effects results in additional stiffness, leading to an increase in the dimensionless normalized nonlocal frequencies for the first three vibration modes compared to the model without surface effects; however, the surface energy causes a reduction in dimensionless nonlocal frequencies for the fourth and fifth vibration modes;
-: finally, the dynamic behavior of circular FG nanobeams is influenced by the coupled effects of the material gradient index and the nonlocal parameter, as well as by the boundary conditions at the nanobeams ends, and, therefore, it is not possible to define a specific trend.

In summary, the results achieved in the present study demonstrate the capability of the proposed approach to capture both nonlocal and surface energy effects in the higher order dynamic response of functionally graded Bernoulli-Euler nanobeams. This approach offers a cost-effective method for designing and optimizing nano-scaled structures, including nanoelectromechanical systems (NEMS).

Author Contributions

For research articles with several authors, a short paragraph specifying their individual contributions must be provided. The following statements should be used “Conceptualization, L.F. and R.P.; methodology, L.F., G.L. and R.P.; software, L.F., G.L. and R.P.; validation, L.F., G.L. and R.P.; formal analysis, L.F., A.L., G.L. and R.P.; Investigation, L.F., A.L., G.L. and R.P.; resources, L.F. and R.P.; data curation, L.F., A.L., G.L. and R.P.; writing—original draft preparation, L.F., A.L., G.L. and R.P.; writing—review and editing, L.F., A.L., G.L. and R.P.; visualization, A.L. and G.L.; supervision, L.F. and R.P.; project administration, L.F. and R.P.; funding acquisition, L.F. and R.P. All authors have read and agreed to the published version of the manuscript.”.

Funding

This research was funded by the Italian Ministry of University and Research (MUR), Research Grant PRIN 2020 No. 2020EBLPLS on “Opportunities and challenges of nanotechnology in advanced and green construction materials” and Research Grant PRIN 2022 “ISIDE: Intelligent Systems for Infrastructural Diagnosis in smart-concretE”, N. 2022S88WAY - CUP B53D2301318.

Data Availability Statement

Not applicable.

Acknowledgments

The authors gratefully acknowledge the financial support of the Italian Ministry of University and Research (MUR), Research Grant PRIN 2020 No. 2020EBLPLS on “Opportunities and challenges of nanotechnology in advanced and green construction materials” and Research Grant PRIN 2022 “ISIDE: Intelligent Systems for Infrastructural Diagnosis in smart-concretE”, N. 2022S88WAY - CUP B53D2301318.

Conflicts of Interest

The authors declare no conflict of interest.

Nomenclature

		λ_c	Nonlocal parameter
		v^B, v^S	Poisson’s ratios of the bulk and surface layer
E	Euclidean space	n	material gradient index
L	Length of FG nanobeam	E_c	Young’s modulus ceramic
Σ	Generic cross-section	E_m	Young’s modulus metal
∂Σ	Perimeter of Σ	ρ_c	Mass density of ceramic
{O, X, Y, Z}	Cartesian coordinate system	ρ_m	Mass density of metal
O	Geometric center of Σ	$E_{c}^{S}$	Surface Young modulus of ceramic
x	Axis of FG nanobeam	$E_{m}^{S}$	Surface Young modulus of metal
y, z	Principal axes of geometric inertia of Σ	$ρ_{c}^{S}$	Surface mass density of ceramic
b, h	Width and thickness Σ	$ρ_{m}^{S}$	Surface mass density of metal
R	Radius of Σ	$τ_{c}^{S}$	Residual surface stress of ceramic
B, S	Bulk and surface layers of FG material	$τ_{m}^{S}$	Residual surface stress of metal

References

Ö. Civalek, B. Uzun, M. Ö. Yaylı, “On nonlinear stability analysis of saturated embedded porous nanobeams”, International Journal of Engineering Science, vol. 190, no. 103898, May 2023. [CrossRef]
F. Cornacchia, F. Fabbrocino, N. Fantuzzi, R. Luciano, R. Penna, “Analytical solution of cross- and angle-ply nano plates with strain gradient theory for linear vibrations and buckling”, Mech. Adv. Mater. Struct, vol. 28, no. 12, pp. 1201-1215, September 2019. [CrossRef]
X. Xu, D. Shahsavari, B. Karami, “On the forced mechanics of doubly-curved nanoshells”, International Journal of Engineering Science,vol. 168, no. 103538, November 2021. [CrossRef]
A. Gholipour, M. H. Ghayesh, “Nonlinear coupled mechanics of functionally graded nanobeams”, International Journal of Engineering Science, vol. 150, no. 103221, May 2020. [CrossRef]
B. Karami, M. Janghorban, “On the mechanics of functionally graded nanoshells”, International Journal of Engineering Science, vol. 153, no. 103309, August 2020. [CrossRef]
M. H. Ghayesh, A. Farajpour, “A review on the mechanics of functionally graded nanoscale and microscale structures”, International Journal of Engineering Science, vol. 137, pp. 8-36, April 2019. [CrossRef]
A. Farajpour, M. H. Ghayesh, H. Farokhi, ”A review on the mechanics of nanostructures”, International Journal of Engineering Science, vol. 133, pp. 231-263, December 2018. [CrossRef]
H. Akhavan, M. Ghadiri, A. Zajkani, “A new model for the cantilever MEMS actuator in magnetorheological elastomer cored sandwich form considering the fringing field and casimir effects”, Mechanical Systems and Signal Processing, vol. 121, pp. 551-561, April 2019. [CrossRef]
D.C.C. Lam, F. Yang, A.C.M. Chong, J. Wang, P. Tong, “Experiments and theory in strain gradient elasticity”, Journal of the Mechanics and Physics of Solids, vol. 51, no. 8, pp. 1477-1508, August 2003). [CrossRef]
S. J. L. Billinge, I. Levin, “The Problem with Determining Atomic Structure at the Nanoscale”, Science, vol. 316, no. 5824, pp. 561-565, April 2007. [CrossRef]
A. Eringen, “Linear theory of nonlocal elasticity and dispersion of plane waves”, Int J. Eng Sci, vol. 10, no. 5, pp. 425–435, May 1972. [CrossRef]
A. Eringen, “On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves”, J. Appl. Phys., vol. 54, pp. 4703-4710, September 1983. [CrossRef]
Eringen A.C., 1987. Theory of nonlocal elasticity and some applications, Res Mechanica 21, 313-342.
C. Lim, G. Zhang, J.N. Reddy, “A higher-order nonlocal elasticity and strain gradient theory and its applications in wave propagation”, J. Mech. Phys. Solids, vol. 78, pp. 298-313, May 2015. [CrossRef]
R. Mindlin, “Micro-structure in linear elasticity”, Archive for Rational Mechanics and Analysis, vol.16, no. 1, pp. 51–78, January 1964.
M. Gurtin, A. Murdoch, “A continuum theory of elastic material surfaces”, Archive for Rational Mechanics and Analysis, vol. 57, no. 4, pp.291–323, December 1975. [CrossRef]
M. Gurtin, A. Murdoch, “Surface stress in solids”, International Journal of Solids and Structures, vol. 14, no. 6, pp. 431–440, November 1977. 19 November. [CrossRef]
J. Fernández-Sáez, R. Zaera, J. Loya, J. Reddy, “Bending of Euler–Bernoulli beams using Eringen’s integral formulation: A paradox resolved”, International Journal of Engineering Science, vol. 99, pp. 107-116, February 2016. [CrossRef]
C. Li, L. Yao, W. Chen, S. Li, “Comments on nonlocal effects in nano-cantilever beams”, International Journal of Engineering Science, vol. 87, pp. 47-57, February 2015. [CrossRef]
G. Romano, R. Barretta, R, “Comment on the paper ‘‘Exact solution of Eringen’s nonlocal integral model for bending of Euler–Bernoulli and Timoshenko beams by Meral Tuna & Mesut Kirca’’, International Journal of Engineering Science, vol. 109, pp. 240–242, December 2016. [CrossRef]
G. Romano, R. Barretta, M. Diaco, F. Marotti de Sciarra, “Constitutive boundary conditions and paradoxes in nonlocal elastic nano-beams”, International Journal of Mechanical Sciences, vol. 121, pp. 151–156, August 2017. [CrossRef]
G. Romano and R. Barretta R., “Nonlocal elasticity in nanobeams: The stress-driven integral model”, Int. J. Eng. Sci., vol. 115, pp. 14-27, June 2017. [CrossRef]
R. Penna, L. Feo, G. Lovisi, “Hygro-thermal bending behavior of porous FG nano-beams via local/nonlocal strain and stress gradient theories of elasticity”, Composite Structures, vol. 263, no. 113627, May 2021. [CrossRef]
R. Penna, L. Feo, G. Lovisi, F. Fabbrocino, “Hygro-Thermal Vibrations of Porous FG Nano-Beams Based on Local/Nonlocal Stress Gradient Theory of Elasticity”, Nanomaterials, vol. 11, no. 910, March 2021. [CrossRef]
R. Penna, A. Lambiase, G. Lovisi and L. Feo, “Investigating hygrothermal bending behavior of FG nanobeams via local/nonlocal stress gradient theory of elasticity with general boundary conditions”, Mech. Adv. Mater. Struct, October 2023. [CrossRef]
H. Darban, F. Fabbrocino, L. Feo, R. Luciano, “Size-dependent buckling analysis of nanobeams resting on two-parameter elastic foundation through stress-driven nonlocal elasticity model”, Mech. Adv. Mater. Struct, vol. 28, March 2020. [CrossRef]
A. Apuzzo, R. Barretta, R. Luciano, F. Marotti de Sciarra, R. Penna, “Free vibrations of Bernoulli-Euler nano-beams by the stress-driven nonlocal integral model”, Composites Part B: Engineering, vol. 123, pp. 105-111, August 2017. [CrossRef]
Caporale, H. Darban, and R. Luciano, Exact closed-form solutions for nonlocal beams with loading discontinuities, Mech. Adv. Mater. Struct., vol. 29, no. 5, pp. 694–704, 2022. [CrossRef]
Y. Tang, and H. Qing, Bi-Helmholtz kernel based stress-driven nonlocal integral model with discontinuity for size-dependent fracture analysis of edge-cracked nanobeam, Mech. Adv. Mater. Struct., pp. 1–11, 2023. [CrossRef]
R. Barretta, L. Feo, L., R. Luciano, F. Marotti de Sciarra, R. Penna, "Nano-beams under torsion: a stress-driven nonlocal approach", PSU Research Review, vol. 1, no. 2, pp. 164-169, May 2017. [CrossRef]
R. Penna, G. Lovisi, L. Feo, “Dynamic Response of Multilayered Polymer Functionally Graded Carbon Nanotube Reinforced Composite (FG-CNTRC) Nano-Beams in Hygro-Thermal Environment”, Polymers, vol. 13, no. 2340, July 2021. [CrossRef]
Francesco Fabbrocino, Marco Francesco Funari, Fabrizio Greco, Paolo Lonetti, Raimondo Luciano, Rosa Penna, Dynamic crack growth based on moving mesh method,Composites Part B: Engineering, Volume 174, 2019, 107053. [CrossRef]
Andrea Apuzzo, Chiara Bartolomeo, Raimondo Luciano, Daniela Scorza, Novel local/nonlocal formulation of the stress-driven model through closed form solution for higher vibrations modes, Composite Structures, Volume 252, 2020, 112688. [CrossRef]
Raimondo Luciano, Hossein Darban, Chiara Bartolomeo, Francesco Fabbrocino, Daniela Scorza, Free flexural vibrations of nanobeams with non-classical boundary conditions using stress-driven nonlocal model, Mechanics Research Communications, Volume 107, 2020, 103536. [CrossRef]
R. Penna, “Bending analysis of functionally graded nanobeams based on stress-driven nonlocal model incorporating surface energy effects”, International Journal of Engineering Science, vol. 189, no. 103887, August 2023. [CrossRef]
L. Feo, G. Lovisi and R. Penna, “Free vibration analysis of functionally graded nanobeams based on surface stress-driven nonlocal model”, Mech. Adv. Mater. Struct, December 2023. [CrossRef]
Rosa Penna, Luciano Feo, Giuseppe Lovisi, Arturo Pascuzzo, A stress-driven model incorporating surface energy effects for the bending analysis of functionally graded nanobeams with loading discontinuities, Procedia Structural Integrity, Volume 47, 2023, Pages 789-799, ISSN 2452-3216. [CrossRef]
G. Lovisi, “Application of the surface stress-driven nonlocal theory of elasticity for the study of the bending response of FG cracked nanobeams”, Composite Structures, vol. 324, no. 117549, November 2023. [CrossRef]
S. Saffari, M. Hashemian, D. Toghraie, “Dynamic stability of functionally graded nanobeam based on nonlocal Timoshenko theory considering surface effects”, Physica B: Condensed Matter, vol. 520, pp. 97–105, September 2017. [CrossRef]

Figure 1. Coordinate system and configuration of the FG nanobeam: bulk continuum and surface layer.

Figure 2. Dimensionless nonlocal frequencies of FG nanobeams vs. number of vibration modes evaluated for FG Cantilever (C-F) condition, with

λ_{c} = 0.05

Figure 2. Dimensionless nonlocal frequencies of FG nanobeams vs. number of vibration modes evaluated for FG Cantilever (C-F) condition, with

λ_{c} = 0.05

Figure 3. Dimensionless nonlocal frequencies of FG nanobeams vs. number of vibration modes evaluated for FG Simply-Supported (S-S) condition, with

λ_{c} = 0.05

Figure 3. Dimensionless nonlocal frequencies of FG nanobeams vs. number of vibration modes evaluated for FG Simply-Supported (S-S) condition, with

λ_{c} = 0.05

Figure 4. Dimensionless nonlocal frequencies of FG nanobeams vs. number of vibration modes evaluated for FG Clamped-Pinned (C-P) condition, with

λ_{c} = 0.05

Figure 4. Dimensionless nonlocal frequencies of FG nanobeams vs. number of vibration modes evaluated for FG Clamped-Pinned (C-P) condition, with

λ_{c} = 0.05

Figure 5. Dimensionless nonlocal frequencies of FG nanobeams vs. number of vibration modes evaluated for FG Doubly-Clamped (C-C) condition, with

λ_{c} = 0.05

Figure 5. Dimensionless nonlocal frequencies of FG nanobeams vs. number of vibration modes evaluated for FG Doubly-Clamped (C-C) condition, with

λ_{c} = 0.05

Table 1. Physical and elastic properties of the two constituent materials of FG nanobeam.

Material	Parameters	Values	Unit
Ceramic (Si)	$E_{c}^{B}$	210	[GPa]
	$E_{c}^{S}$	-10.6543	[N/m]
	$τ_{c}^{S}$	0.6048	[N/m]
	$ρ_{c}^{B}$	2370	[kg/m³]
	$ρ_{c}^{S}$	3.1688 10^-7	[kg/m²]
Metal (Al)	$E_{m}^{B}$	70	[GPa]
	$E_{m}^{S}$	5.1882	[N/m]
	$ρ_{m}^{B}$	2700	[kg/m³]
	$τ_{m}^{S}$	0.9108	[N/m]
	$ρ_{m}^{S}$	5.4610 10^-7	[kg/m²]

Table 2. Dimensionless nonlocal frequencies of Cantilever (C-F) FG nanobeam for higher modes of vibrations.

$λ_{c}$	Mode	No Surface Effects		Square Cross-Section			Circular Cross-Section
$λ_{c}$	Mode	Present	Ref. [34]	$n = 0$	$n = 1$	$n = 3$	$n = 0$	$n = 1$	$n = 3$
0.00⁺	$1^{s t}$	1.0000	1.0000	2.2799	2.7626	3.0027	1.4981	1.7904	1.8865
	$2^{n d}$	6.2669	6.2669	8.5112	9.7142	10.3436	5.9107	6.7299	6.9369
	$3^{t h}$	17.5475	17.5475	19.1051	20.4685	21.2408	13.9919	15.2841	15.4319
	$4^{t h}$	34.3860	-	33.8579	35.1898	35.9955	25.6689	27.4754	27.5037
	$5^{t h}$	56.8427	-	51.8652	53.0981	53.9124	40.5012	42.7677	42.6559
0.01	$1^{s t}$	1.0101	-	2.2946	2.7797	3.0209	1.5081	1.8020	1.8985
	$2^{n d}$	6.3357	-	8.5816	9.7884	10.4201	5.9625	6.7859	6.9931
	$3^{t h}$	17.7713	-	19.3130	20.6764	21.4494	14.1515	15.4522	15.5981
	$4^{t h}$	34.9207	-	34.3280	35.6554	36.4594	26.0392	27.8616	27.8852
	$5^{t h}$	57.9402	-	52.7813	54.0042	54.8148	41.2392	43.5319	43.4113
0.03	$1^{s t}$	1.0309	-	2.3244	2.8137	3.0569	1.5284	1.8254	1.9228
	$2^{n d}$	6.5093	-	8.7539	9.9674	10.6034	6.0897	6.9227	7.1298
	$3^{t h}$	18.5002	-	19.9871	21.3409	22.1109	14.6669	15.9929	16.1306
	$4^{t h}$	37.0797	-	36.2703	37.5626	38.3510	27.5482	29.4378	29.4370
	$5^{t h}$	63.0858	-	57.2474	58.4058	59.1879	44.7714	47.2065	45.1013
0.05	$1^{s t}$	1.0524	1.0524	2.3545	2.8477	3.0926	1.5490	1.8491	1.9471
	$2^{n d}$	6.7278	6.7278	8.9646	10.1836	10.8232	6.2460	7.0897	7.2959
	$3^{t h}$	19.5634	19.5634	20.9672	22.2996	23.0608	15.4154	16.7767	16.9002
	$4^{t h}$	40.4580	-	39.3323	40.5640	41.3229	29.9179	31.9145	31.8738
	$5^{t h}$	71.3062	-	64.4541	65.5116	66.2479	50.4474	53.1200	52.8692
0.10	$1^{s t}$	1.1087	1.1087	2.4306	2.9331	3.1817	1.6011	1.9090	2.0088
	$2^{n d}$	7.4325	7.4325	9.6210	10.8467	11.4935	6.7369	7.6095	7.8101
	$3^{t h}$	23.2560	23.2560	24.3703	25.6113	26.3313	18.0146	19.4950	19.5662
	$4^{t h}$	52.1914	-	50.0444	51.0811	51.7429	38.1909	40.5729	40.3977
	$5^{t h}$	99.0703	-	88.9574	89.7452	90.3647	69.7106	73.2203	72.7155

Table 3. Dimensionless nonlocal frequencies of Simply-Supported (S-S) FG nanobeam for higher modes of vibrations.

$λ_{c}$	Mode	No Surface Effects		Square Cross-Section			Circular Cross-Section
$λ_{c}$	Mode	Present	Ref. [34]	$n = 0$	$n = 1$	$n = 3$	$n = 0$	$n = 1$	$n = 3$
0.00⁺	$1^{s t}$	1.0000	1.0000	1.5375	1.8218	1.9718	1.0416	1.2124	1.2649
	$2^{n d}$	4.0000	4.0000	4.4988	4.8850	5.1033	3.2633	3.5906	3.6395
	$3^{t h}$	9.0000	9.0000	9.0110	9.4167	9.6589	6.7903	7.2932	7.3111
	$4^{t h}$	16.0000	-	14.7940	15.1850	15.4386	11.4929	12.1644	12.1399
	$5^{t h}$	24.9999	-	21.5186	21.8782	22.1411	17.1945	17.9903	17.9198
0.01	$1^{s t}$	1.0005	-	1.5379	1.8221	1.9721	1.0419	1.2127	1.2651
	$2^{n d}$	4.0077	-	4.5052	4.8909	5.1090	3.2684	3.5953	3.6445
	$3^{t h}$	9.0391	-	9.0449	9.4485	9.6905	6.8170	7.3206	7.3380
	$4^{t h}$	16.1233	-	14.8988	15.2869	15.5391	11.5764	12.2508	12.2248
	$5^{t h}$	25.3003	-	21.7635	22.1185	22.3792	17.3934	18.2228	18.1220
0.03	$1^{s t}$	1.0042	-	1.5402	1.8240	1.9739	1.0438	1.2146	1.2669
	$2^{n d}$	4.0662	-	4.5541	4.9359	5.1521	3.3068	3.6349	3.6824
	$3^{t h}$	9.3321	-	9.2994	9.6921	9.9285	7.0167	7.5272	7.5399
	$4^{t h}$	17.0355	-	15.6762	16.0440	16.2860	12.1951	12.8912	12.8545
	$5^{t h}$	27.4868	-	23.5495	23.8728	24.1196	18.8430	19.6904	19.5969
0.05	$1^{s t}$	1.0110	1.0110	1.5446	1.8278	1.9774	1.0474	1.2181	1.2702
	$2^{n d}$	4.1740	4.1740	4.6445	5.0194	5.2322	3.3779	3.7440	3.7525
	$3^{t h}$	9.8598	9.8598	9.7601	10.1345	10.3614	7.3780	7.9012	7.9060
	$4^{t h}$	18.6338	-	17.0446	17.3809	17.6073	13.2832	14.0186	13.9640
	$5^{t h}$	31.2018	-	26.5951	26.8736	27.1016	21.3127	22.2403	22.1147
0.10	$1^{s t}$	1.0389	1.0389	1.5628	1.8431	1.9916	1.0623	1.2326	1.2838
	$2^{n d}$	4.5952	4.5952	5.0033	5.3532	5.5536	3.6588	3.9955	4.0315
	$3^{t h}$	11.8266	11.8266	11.4990	11.8171	12.0146	8.7368	9.3128	9.2904
	$4^{t h}$	24.3000	-	21.9395	22.1933	22.3809	17.1639	18.0516	17.9408
	$5^{t h}$	43.7693	-	36.9613	37.1361	37.3285	29.7045	30.9210	30.6978

Table 4. Dimensionless nonlocal frequencies of Clamped-Pinned (C-P) FG nanobeam for higher modes of vibrations.

$λ_{c}$	Mode	No Surface Effects		Square Cross-Section			Circular Cross-Section
$λ_{c}$	Mode	Present	Ref. [34]	$n = 0$	$n = 1$	$n = 3$	$n = 0$	$n = 1$	$n = 3$
0.00⁺	$1^{s t}$	1.0000	1.0000	1.2776	1.4411	1.5296	0.8955	1.0101	1.0362
	$2^{n d}$	3.2406	3.2406	3.4794	3.7020	3.8302	2.5552	2.7816	2.8020
	$3^{t h}$	6.7614	6.7614	6.6373	6.8740	7.0185	5.0325	5.3803	5.3797
	$4^{t h}$	11.5623	-	10.5625	10.7930	10.9466	8.2399	8.6987	8.6705
	$5^{t h}$	17.6435	-	15.0470	15.2594	15.4214	12.0630	12.5991	12.5415
0.01	$1^{s t}$	1.0108	-	1.2883	1.4520	1.5407	0.9035	1.0186	1.0447
	$2^{n d}$	3.2813	-	3.5167	3.7389	3.8670	2.5840	2.8118	2.8318
	$3^{t h}$	6.8644	-	6.7266	6.9619	7.1059	5.1033	5.4539	5.4523
	$4^{t h}$	11.7807	-	10.7415	10.9692	11.1219	8.3852	8.8487	8.8187
	$5^{t h}$	18.0579	-	15.3677	15.5760	15.7366	12.3295	12.8723	12.8117
0.03	$1^{s t}$	1.0375	-	1.3129	1.4763	1.5651	0.9221	1.0381	1.0639
	$2^{n d}$	3.4104	-	3.6320	3.8504	3.9766	2.6734	2.9048	2.9230
	$3^{t h}$	7.2715	-	7.0827	7.3084	7.4476	5.3834	5.7448	5.7382
	$4^{t h}$	12.7887	-	11.5928	11.8040	11.9489	9.0666	9.5542	9.5140
	$5^{t h}$	20.1774	-	17.0764	17.2602	17.4109	13.8938	14.3097	14.2316
0.05	$1^{s t}$	1.0703	1.0703	1.3416	1.5041	1.5925	0.9442	1.0611	1.0864
	$2^{n d}$	3.5967	3.5967	3.7972	4.0084	4.1311	2.8017	3.0378	3.0528
	$3^{t h}$	7.9066	7.9066	7.6426	7.8527	7.9839	5.8222	6.2008	6.1861
	$4^{t h}$	14.4028	-	12.9725	13.1593	13.2927	10.1653	10.6941	10.6379
	$5^{t h}$	23.5687	-	19.8429	19.9935	20.1319	15.9729	16.6313	16.5260
0.10	$1^{s t}$	1.1749	1.1749	1.4304	1.5875	1.6737	1.0131	1.1318	1.1418
	$2^{n d}$	4.2468	4.2468	4.3784	4.5650	4.6750	3.2517	3.5049	3.5094
	$3^{t h}$	10.1365	10.1365	9.6348	9.8008	9.9094	7.3762	7.8211	7.7804
	$4^{t h}$	19.9215	-	17.7410	17.8691	17.9770	13.9492	14.6302	14.5244
	$5^{t h}$	34.7602	-	29.0444	29.1236	29.2425	23.4328	24.3488	24.1620

Table 5. Dimensionless nonlocal frequencies of Doubly-Clamped (C-C) FG nanobeam for higher modes of vibrations.

$λ_{c}$	Mode	No Surface Effects		Square Cross-Section			Circular Cross-Section
$λ_{c}$	Mode	Present	Ref. [34]	$n = 0$	$n = 1$	$n = 3$	$n = 0$	$n = 1$	$n = 3$
0.00⁺	$1^{s t}$	1.0000	1.0000	1.1448	1.2397	1.2927	0.8225	0.9067	0.9181
	$2^{n d}$	2.7565	2.7565	2.8670	3.0045	3.0849	2.1245	2.2952	2.3016
	$3^{t h}$	5.4039	5.4039	5.2236	5.3724	5.4652	3.9804	4.2402	4.2136
	$4^{t h}$	8.9329	-	8.0769	8.2231	8.3237	6.3237	6.6614	6.6334
	$5^{t h}$	13.3443	-	11.2860	11.4210	11.5289	9.0751	9.4637	9.4155
0.01	$1^{s t}$	1.0214	-	1.1656	1.2606	1.3137	0.8382	0.9233	0.9345
	$2^{n d}$	2.8211	-	2.9263	3.0633	3.1436	2.1703	2.3433	2.3491
	$3^{t h}$	5.5464	-	5.3466	5.4941	5.5864	4.0783	4.3420	4.3320
	$4^{t h}$	9.2036	-	8.2957	8.4395	8.5393	6.5027	6.8459	6.8158
	$5^{t h}$	13.8141	-	11.6416	11.7729	11.8798	9.3734	9.7689	9.7176
0.03	$1^{s t}$	1.0726	-	1.2135	1.3075	1.3603	0.8745	0.9615	0.9720
	$2^{n d}$	3.0062	-	3.0942	3.2271	3.3054	2.3001	2.4789	2.4823
	$3^{t h}$	6.0329	-	5.7732	5.9120	6.0001	4.4141	4.6914	4.6761
	$4^{t h}$	10.2718	-	9.1936	9.3233	9.4169	7.2234	7.5923	7.5524
	$5^{t h}$	15.8833	-	13.2967	13.4079	13.5077	10.5476	11.1652	11.0979
0.05	$1^{s t}$	1.1349	1.1349	1.2701	1.3620	1.4138	0.9178	1.0066	1.0161
	$2^{n d}$	3.2614	3.2614	3.3252	3.4508	3.5253	2.4786	2.6649	2.6648
	$3^{t h}$	6.8814	6.8814	6.4143	6.5396	6.6208	4.9160	5.2143	5.1908
	$4^{t h}$	11.9129	-	10.5959	10.7059	10.7909	8.3411	8.7528	8.6978
	$5^{t h}$	19.0851	-	15.9012	15.9867	16.0780	12.8489	13.3540	13.2626
0.10	$1^{s t}$	1.1766	1.1766	1.4485	1.5316	1.5790	1.0549	1.1487	1.1546
	$2^{n d}$	4.1322	4.1322	4.1225	4.2251	4.2875	3.0922	3.3059	3.2939
	$3^{t h}$	9.2325	9.2325	8.6431	8.7337	8.7977	6.6519	7.0286	6.9793
	$4^{t h}$	17.4074	-	15.3466	15.4132	15.4815	12.1120	12.6785	12.5778
	$5^{t h}$	29.4704	-	24.4213	24.4545	24.5363	19.7635	20.5082	20.3449

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Application of Surface-Stress Driven Model for Higher Vibrations Modes of Functionally Graded Nanobeams

Abstract

1. Introduction

2. Problem formulation

2.1. Kinematic

2.2. Governing equations

3. Surface stress-driven model for free vibrations analysis

3.1. A brief outline of the surface stress-driven nonlocal model

3.2. Size-dependent governing equation

4. Results and discussion

5. Conclusions

Author Contributions

Funding

Data Availability Statement

Acknowledgments

Conflicts of Interest

Nomenclature

References

MDPI Initiatives

Important Links

Subscribe