Preprint
Article
A Thermal Regime and a Water Circulation in a Very Deep Lake: Lake Tazawa, Japan
Altmetrics
Downloads
65
Views
19
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
09 January 2024
Posted:
09 January 2024
You are already at the latest version
Alerts
Abstract
A thermal system in very deep Lake Tazawa (maximum depth, 423 m) was investigated by estimating the heat budget. In the heat budget estimate, the net heat input at lake surface and the heat input by river inflow and groundwater inflow were considered. Then, the heat loss by snowfall onto lake surface was taken into account. Meanwhile, lake water temperature was monitored at 0.2 m to the bottom by mooring temperature loggers for more than two years. The heat storage change of the lake from the loggers was calibrated by frequent vertical measurements of water temperature at every 0.1 m pitch by a profiler with high accuracy (± 0.01 °C). The heat storage change (W/m2) obtained by the temperature loggers reasonably accords to that from the heat budget estimate. In the heat budget, the net heat input at lake surface dominates the heat storage change, but the significant heat loss by river inflow sporadically occurred, which is caused by the relatively large discharge from a reservoir in the upper region. How deep the vertical water circulation in the lake occurs in winter was judged by the differences between water temperatures at 0.2 m depth and bottom and between vertical profiles of dissolved oxygen over winter. It is strongly suggested that the whole water circulation does not occur every winter, if any, very weak.
Keywords:
Subject: Environmental and Earth Sciences - Environmental Science
1. Introduction
In consideration of the ecosystem in a lake, it is quite important to know how the water temperature (WT) and dissolved oxygen (DO) change seasonally. Especially, in an acid deep lake such as Lake Tazawa (pH= 5.1 – 6.0), Akita Prefecture, Japan, the temporal and spatial changes of WT, DO and pH are very serious, because the lake water is utilized as irrigation water for the rice crop in the downstream region [1,2]. In lakes of the world, the mixing regime has been changing by an increase in surface water temperature by the climatic change; an increase in air temperature makes the lakes dimictic to monomictic and monomictic to oligomictic or meromictic [3,4]. Such less frequency in vertical whole mixing or a decrease in the downward degree of mixing could weaken the DO supply to the deeper zone, which results in a decline in water clarity by the decomposition of organic matters [5].
In Lake Biwa, one of monomictic lakes in Japan, the bottom water temperature consistently increased year by year after 1985, probably by global warming [3]. At present, the lake is becoming oligomictic from holomictic. In monomicic lakes such as Lake Biwa and Lake Tazawa undergoing the warming effect, it is very important to explore how thermal conditions change in the transition from monomictic to oligomictic lakes [6]. Hence, an accurate estimate of the present heat budget in such a lake should be done to understand how the lake responds to the climate change for the future and thereby how the ecosystem changes.
In Lake Tazawa, surface water temperature sometimes becomes nearly 4 °C or less in winter, being smaller than the bottom temperature at ca. 4.2 °C [7]. Under such a thermal condition, wind-driven convection in the upper layer and gravitational instability beneath could activate the vertical water circulation by the conditional instability [8]. Then, the downward degree of the vertical circulation depends on both how long surface water temperature keeps nearly 4.0 °C or less and how strong the wind-driven mixing is. Meanwhile, the DO in the lake keeps ca. 80 % or more in the whole layer even in the thermally stratified season [2]. This is probably due to the decomposition of less organic matters in the acid lake. Thus, the vertical water circulation in winter could control the spatial distribution of DO throughout the year. In this study, in addition to the volcanic effect on water quality of the lake [2], the thermal regime and associated water circulation were investigated by calculating every factor in the heat budget equation and scrutinizing vertical distributions of WT and DO on the base of data of more than two years.
2. Study Area
Lake Tazawa (39°43′30″ N, 140°39′41″ E), the deepest lake (maximum depth, 423 m) in Japan, is known as an acid lake, since the Tama River water including the Tamagawa hot spring of very high acidity at pH=1.1–1.3 was drawn into the lake in 1940 [1,2] (Figure 1). The intake of the acid river water drastically decreased the lake water’ pH from 6.5–6.7 before 1940 to 4.2–5.3 in 1948. Thereby, a land-locked type of sockeye salmon (alive at pH = 6.5–7.5), Oncorhynchus nerka kawamurae (local name, Kunimasu trout) was exterminated. The pH increased up to 5.3–6.0 in 2019–2021 by starting a neutralization facility in the downstream of the Tamagawa hot spring site in April 1991. However, Kunimasu trout cannot yet habitat the lake. At present, conduit B and conduit A are connected to the acid Tama River (pH=5.1 – 5.8) and the neutral Sendachi River (pH=6.7 – 7.1), respectively, and power plants at the downstream end of conduit B and conduit C generate the electric power of 7,300 kW and 31,500 kW at maximum, respectively. The outflow at conduit D (previous natural outlet) is regulated to occur only in the irrigation season of May – August.
Meanwhile, Hayashi et al. [9] reported that lake water temperature at a depth of 400 m of site MD increased at a rate of 0.05 °C per 10 yr in August 1937– July 2017. The authors also indicated that the increasing rate increased to 0.013 °C/yr in May 2015 – July 2017. Such an abrupt increase in the hypolimnion’s temperature could not occur, if the vertical water circulation in winter is strong enough to produce an isothermal condition by the continuous cooling at lake surface. Hence, the increase in the increasing rate suggests that, as the cooling was weakened by global warming, the vertical water circulation in the lake did not occur in the whole layer. Actually, the annual lowest water temperature at lake surface was recorded at ca. 2 °C in 1910’s [10], but at 4 °C or around in 2018 [2]. This suggests that vertical mixing in the lake changed in a dimictic to monomictic or oligomictic state.
3. Methods
In order to investigate a thermal system in Lake Tazawa, the heat budget of the lake was estimated. Then, the heat budget at lake surface and the heat flux by river inflow and groundwater inflow were evaluated by estimating the hydrological budget of the lake [2].
3.1. Heat Budget of an Open Lake
The heat budget equation for an open lake (with an outflow river or an outlet) such as Lake Tazawa is given as follows:
where ΔG/Δt is the total heat storage change (W or J/s) of the lake, is the net radiative heat flux (W/m2) at lake surface, and is the sensible and latent heat fluxes (W/m2) at the surface, respectively (negative for heat output), is the heat flux by precipitation over the lake, is the heat flux by river, HG is the heat flux by groundwater, HS is the geothermal heat flux at the lake bottom, and A0 is the lake water surface (m2).
The net radiative heat flux is composed of downward shortwave radiation K, downward longwave radiation L and upward longwave radiation in the following:
where is the albedo of shortwave radiation for water surface (here, assumed to be constant at 0.05). The upward longwave radiation L is calculated by following the Stefan-Bolzman law for surface water temperature (K), where the emissivity ε of water is constant at 0.97. The downward longwave radiation was evaluated by considering total effective water vapor content in the Stefan-Bolzman law for air temperature Ta [11].
Sensible heat flux QH and latent heat flux QE were acquired by the following bulk transfer method:
where is the isobaric specific heat of air (J/kg/K), is the air density (kg/m3), λ is the latent heat of evaporation (J/kg), u is the wind speed (m/s), Ts and Ta are the surface water temperature and air temperature, respectively (°C), qs is the saturated specific humidity at surface water temperature, qa is the specific humidity of air, and CH and CE are dimensionless bulk transfer coefficients for sensible and latent heat fluxes, respectively (here, CH=CE=0.0014 for the meteorology at 2 m above lake surface).
The heat flux QP by rainfall over the lake is given in the following:
where ρw is the water density (kg/m3) at Tw, Pr is the rainfall (m/s), cpw is the specific heat of water (J/kg/K) and Tw is the wet bulb temperature (°C). The Tw values were obtained by the dichotomy for the following psychrometer formula [11]:
where p is the air pressure (hPa) (p0=1013.2 hPa), ea and ew are the water vapor pressure (hPa) at Ta and the saturated water vapor pressure (hPa) at Tw, respectively, and B is the psychrometer constant (here, 0.667 hPa/K for the Assman ventilation psychrometer).
Tw = Ta + (ea – ew)(p0/p)/B
The heat flux by snowfall is as follows:
where ρi is the ice density (kg/m3) at Ta, Pi is the snowfall (m/s) as ice at Ta, cpi is the specific heat of ice (J/kg/K), Tmelt is the melting temperature of ice (here, 273 K or 0 °C) and L is the latent heat of fusion (333.6 kJ/kg for ice at 0 °C). The precipitation during snowfall is generally evaluated by melting the snow over a tipping bucket raingauge. Hence, the snowfall at Ta was obtained by multiplying the precipitation at 0 °C during snowfall by the ratio of water density (999.868 kg/m3 at 0 °C) to ice density at Ta. Here, the snow temperature was assumed to be equal to the air temperature Ta. The precipitation at Ta ≤0.5°C was supposed as snowfall [11] on the assumption that, at 0.5 ≥ Ta > 0 °C, the snow temperature is 0 °C. Then, the first term of the right side in equation (7) is zero.
The heat flux HR by river inflow and outflow and the heat flux HG by groundwater inflow and outflow are given as follows:
where Rin and Rout are the river inflow and outflow (m3/s), respectively, TRin and TRout are the water temperature of inflowing and outflowing rivers, respectively, To is the water temperature averaged in the surface layer of the lake, TL is the representative lake water temperature, Gin and Gout are the groundwater inflow and outflow (m3/s), respectively, TGin and TGout are the temperature of inflowing groundwater and that of outflowing groundwater, respectively, and Ao is the lake surface area (m2). Here, the volume-averaged water temperature at depths of 0.2 – 10 m, considering each area from the bathymetric map (Figure 1), was calculated as T0. Then, the water temperature at 0.2 m depth was assumed to be equal to that at lake surface. In equation (8), for the heat flux by river inflow, the inflowing water was assumed to intrude only into the surface layer at depths of 0 – 10 m as density overflow [12].
For the representative temperature TL, similarly, the volume averaged water temperature of the whole lake was given by the following equation:
where H is the water depth at the deepest point, Tz and Az are the water temperature and the area at a depth, z, respectively, and V is the lake volume. Here, H and V also vary temporally according to the temporal change of lake level. Equation (10) is based on the assumption that the water temperature at a certain depth is horizontally equal, i.e., exhibiting the thermal structure of a horizontal multi-layer in the lake. The supposition of TL for the groundwater outflow is due to the point that it is unknown at which depth the groundwater outflow prevails. With respect to the heat flux by groundwater inflow, the volume-averaged water temperature T0 between 0.2 m and 10 m in depth was chosen as the temperature on the lake side, assuming that the groundwater inflow into the lake occurs within 100 m offshore. According to spatial distributions of the confined aquifer exposed on lake bottom, Kabayashi [13] indicated that, in Lake Biwa, the seepage flux into the lake occurs mainly within 200 m offshore. Hence, considering the bathymetry of Lake Tazawa (Figure 1), the seepage flux into the lake was assumed to occur mainly at depths of 0 – 10 m within 100 m offshore. In equation (8) and (9), the second term of the right side was regarded to be almost zero, because TRout and TGout are likely to be equal to To and TL, respectively.
The geothermal heat flux Hs was estimated by the temporal change of vertical water temperature profiles at the deepest point during the thermal stratification [14].
Finally, the total heat storage change ΔG/Δt is numerically obtained by calculating each term of the right side in equation (1). Meanwhile, ΔG/Δt can be evaluated directly by monitoring water temperature at some depths between the lake surface and the bottom. Hence, it is possible to judge if the heat budget estimate is reasonable or not by a comparison with the heat storage change from the direct measurement.
3.2. Field Observations
In order to evaluate each term of the heat budget equation (1), the meteorology (solar radiation, air temperature Ta, relative humidity, rainfall, air pressure and wind velocity), and lake water temperature at 0.2 m depth were measured at 1 h intervals at site M on the lake shore and at site L for 1 August 2020 – 9 May 2023, respectively (Figure 1). Temperature loggers, TidbiT v2 (Onset Computer, Incorp., USA; accuracy of ±0.2 °C) were used for the monitoring of the surface water temperature. Rainfall at site M was recorded in April to October, and rainfall or snowfall in November to March was supposed using the high correlation (r2=0.869, p<0.001) with the rainfall data of a weather station at Senboku City, 6.5 km southeast of Lake Tazawa. At Ta ≤ 0.5 °C at site M, precipitation was assumed to be snowfall, and at Ta > 0.5 °C, to be rainfall. Here, the existence of sleet, i.e., the mixture of snow flakes and raindrops was neglected. The climatological effect on the lake was explored by using the 1977 – 2023 data from the weather station of Senboku City.
At site L, water temperature at 0.2 m depth were measured as lake surface temperature to calculate the sensible and latent heat fluxes QH and QE by the coupling with the meteorology, and the difference between air pressure at site M and water pressure at the bottom of site L allowed us to calculate the water depth to get the temporal variations of lake level. The lake surface area changed by the lake level was obtained by the bathymetry with 1 m depth contours (Figure 1) [2]. Inflow data at the conduits A and B, connected to the Tama River and the Sendachi River, respectively, were supplied by the Tohoku Electric Power Co., Ltd. (Figure 1). The data supply was done every fiscal year of 1 April 2020 – 31 March 2023. Temperature loggers, recorded at 1 h intervals, were fixed on the riverbank at sites T and S at 0.66 km and 0.2 km upstream of the entrances of the conduits A and B, respectively.
Meanwhile, lake water temperature was recorded every 1 h at depths of 0.2 m, 5 m, 10 m, 20 m, 50 m, 70 m, 100 m and 200 m and at the bottom of site MD by setting a mooring system of temperature loggers (Figure 2). At 0.2 m depth and the lake bottom, temperature loggers with the high accuracy of ±0.01 °C and the resolution of 0.001 °C (model DEFI2-T, JFE-Advantech, Co., Ltd., Japan: URL https://www.jfe-advantech.co.jp/products/ocean-defi2.html accessed on 12 October 2023) were fixed to judge the downward degree of vertical water circulation in water depth. At the other depths, the temperature loggers, TidbiT v2, were fixed.
Water temperature, electric conductivity at 25 °C (EC25) and dissolved oxygen (DO) were vertically measured at 0.1 m pitch by lowing a profiler on a boat (accuracies of ±0.01 °C, ±0.5 mS/m and ±0.4 mg/L, respectively; model ASTD, JFE-Advantech, Co., Ltd., Japan: URL https://www.jfe-advantech.co.jp/products/ocean-rinko.html, accessed on 13 October 2023). The measurement by the ASTD profiler was spent about 40 min at a point. Using the bathymetric map of the lake (Figure 1), the hourly heat storage Ghl (J) of the lake was calculated from the hourly temperature of the loggers. The Ghl values were calibrated by the correspondent heat storage Gp from the profiler, since there is a linear relationship between Ghl and Gp with a high correlation of r2=0.978 (p<0.01). Using the calibrated Ghl, the heat storage change (W) of the lake was calculated as daily mean, which was compared with the ΔG/Δt values from the heat budget estimate by equation (1).
4. Results
4.1. Heat budget at Lake Surface
Temporal variations of daily mean air temperature, diurnal precipitation and daily mean heat flux at lake surface by precipitation are shown in Figure 3. The precipitation was separated at Ta = 0.5 °C into rainfall and snowfall. In the rainfalls, the heat flux by precipitation varied at a range of -20 – 20 W/m2, but in the snowfalls, the heat flux reached to -171 W/m2 on 2 February 2021, when the precipitation was recorded at 45 mm/d. Thus, the cooling at the surface by snowfall is likely considerable.
In order to clarify the contribution of Q*, QH, QE and QP on the right side of equation (1) to heating or cooling at lake surface, their values calculated by equation (2)–(6) were compared with their sum, i.e., the net heat flux (Figure 4). In the rainfall season, the net heat flux is comparable in magnitude to the net radiation Q*, but in the snowfall season (December – March), the net heat flux consisted of 50 % Q* and 50 % (QH + QE). In particular, the heavy snowfall on 2 February 2021 produced the heat flux in magnitude at 58.4 % of the net heat flux (– 293.1 W/m2). The Q*, QH and QE values were then –89.2, –17.4 and –15.6 W/m2, respectively, thus occupying 30.4, 5.9 and 5.3 % of the neat heat flux in magnitude, respectively.
The Q*, QH, QE and QP values and their percentage in magnitude were averaged for the snowfall periods of December 2020 – February 2021 (Table 1). The Q* values were negative at any time in the snowfall periods, which reflects the magnitude of upward longwave radiation larger than the downward longwave radiation plus the net solar radiation in equation (2). As averages over the snowfalls, the QP value and its percentage in magnitude were –30.9 W/m2 and 19.2 %, respectively. This clearly indicates that the heat loss by snowfalls is effective for the cooling at lake surface.
Compared with the QP value (–0.6 W/m2) averaged over the rainfall periods and that (–1.2 W/m2) over rainfall days in February – December 2021, the mean QP value (–3.8 W/m2) on the rainfall days in the snowfall period is more effective for the cooling at lake surface (Table 1). It is seen that, on the non-rainfall days in the rainfall period, the net radiation dominates the heating at lake surface.
4.2. Heat Flux by River and Groundwater
Temporal variations of daily mean river inflow at conduits A and B and daily mean river water temperature at sites T and S are shown in Figure 5. For the period of 1 February 2021 – 31 March 2023, the water temperature varied seasonally, while the inflow at the conduits varied under the artificial control, following the snowmelt in March – April and the relatively large water demand for the paddy fields in the irrigation season of May – August. For the maintenance of the power plants at the conduits A and B, zero inflow occurred off the irrigation season (Figure 5a). The inflow averaged for the two years of 1 February 2021 – 31 January 2023 was 20.1 m3/s at conduit A and 3.0 m3/s at conduit B. Thus, as the heat flux by river inflow, that by the Tama River could be dominant because of the similar magnitude in water temperature of the two rivers (Figure 5b).
In order to calculate the heat flux by river inflow in equation (8), the volume-averaged water temperature To at depths of 0 – 10 m was numerically obtained by applying water temperature at depths of 0.2 m, 5 m and 10 m (Figure 6b) and the lake basin shape (Figure 1) to equation (10). Then, the temporal variation of lake level, surface area or each area at 5 m depth and 10 m depth from the basin shape was taken into account (Figure 6a). Here, the water temperature at 0.2 m depth was supposed to be equal to that at lake surface. Following the total river inflow in Figure 5a, the lake level varied with the maximum amplitude of 3.06 m in 2021, when the surface area ranged between 2.527×107 and 2.583×107 m2.
All the data of the water temperature and area in Figure 6 were utilized to calculate the volume-averaged lake temperature TL in equation (10). Then, the area at the bottom was regarded as a constant at 1.007×106 m2. Also, the volume-averaged water temperature from the time series of water temperature in Figure 6b was calibrated by that from the corresponding profiles at 0.1 m pitch (Figure 7). In the calculation of TL from the profiles, considering the large seasonal variation in water temperature at depths of 100 m or less and the basin shape in Figure 1, the heat storage of the lake was calculated every 5 m depth at depths of 100 m or less. At depths of more than 100 m, the area was obtained every 100 m depth at depths of 100 – 300 m, every 10 m depth at depths of 380 – 410 m and at the bottom (412.2 – 422.6 m in depth). The area at a certain depth of 100 m or less was then obtained by partitioning each 10 m contour into two equal parts on the bathymetric map of 10 m depth interval.
Meanwhile, also at depths of 100 m or more, water temperature increased gradually (see that inserted diagrams in Figure 7), especially before and after the winters as shown by the 22-Oct-20 and 19-Apr-21 profiles, the 10-Sep-21 and 21-Apr-22 profiles, and 29-Sep-22 and 11-May-23 profiles. During the thermal stratification in summer to autumn, such an increase was slight. Hence, the vertical circulation in winter is likely to be not strong enough to make the water temperature vertically uniform in the whole layer.
The 1977–2023 air temperature data at the weather station of Senboku City indicated that there exists a very significant trend (confidence level, 99.88 %) with an increasing rate of 0.039 °C/yr for air temperature averaged over February – March. The increasing rate of annual mean air temperature was then 0.028 °C/yr, exhibiting a very significant trend with a confidence level of 99.99 %. Thus, the increase of bottom temperature in winter appears to reflect one aspect of global warming, because the vertical water circulation from the pycnal instability is weak, inducing no contact or, if any, a short contact between the surface and bottom waters.
Consequently, there was a linear relationship with the high correlation of R2=0.977 (p<0.01) between the volume-averaged temperature from the loggers and that from the profiles (Figure 8). Of the eight plots in Figure 8, the two nearest plots on the right were produced from two measurements on 17 August 2022 (Figure 7). In Figure 8, it is clear that the TL values from the loggers is overestimated by 0.1 – 0.8 °C.
The groundwater inflow was supposed to be constant at 6.01 m3/s, according to the water budget estimate for Lake Tazawa by Chikita et al. [2]. According to Kobayashi [13], the groundwater temperature was assumed to be constant at 10.5 °C which is equal to the annual mean air temperature at site M for 1 February 2021 – 31 January 2023. Hence, the heat flux by groundwater inflow exhibited annual cycles with maximum (6.5 W/m2) in early March as the heating and minimun (–11.2 W/m2) in August or September as the cooling, since the temperature at depths of 0 – 10m varies seasonally (Figure 9a).
The heat fluxes by the inflow of the Tama River (conduit A) and the Sendachi River (conduit B) are also shown in Figure 9a. The heat flux by river inflow acts as the cooling to the lake in most of the period, sporadically exhibiting the negative sharp peaks smaller than the minimum heat fux by groundwater inflow.The sharp peaks are due to relatively large discharge with decreased water temperature in the Tama River, which was supplied by the upstream Yoroibata Reservoir (Figure 5). Compared with the QH, QE and QP values, the heat flux by river inflow make a minor contribution to the cooling or heating to the lake in the rainfall periods of March – November, but its contribution is more negligible in the snowfall periods of December – February (Figure 4 and 9b).
4.3. Geothermal Heat Flux
The geothermal heat flux HS in equation (1) has been estimated by calculating an increasing rate of water temperature in the bottom layer [14]. Actually, for the vertical profiles in Figure 7, the bottom layer of 0 – 118.4 m and 0 – 101.5m above the bottom consistently increased water temperature in the thermal stratification periods of 8 July – 10 September 2021 and 17 August – 29 September 2022, respectively (Figure 10). Here, considering the lake basin shape in Figure 1, the total heat storage was calculated for each layer of 0 – 118.4 m in 2021 and 0 – 101.5 m in 2022, and then the heat storage change in each of 2021 and 2022 was obtained as Hs in equation (1). As a result, Hs = 0.23 W/m2 and 0.25 W/m2 were acquired for 2021 and 2022, respectively, which are near to 0.27 W/m2 by Boehrer et al. [14]. Thus, the geothermal heat flux is negligibly small, compared with the heat flux by groundwater inflow at 4.5 – 6.0 W/m2 and the other heat fluxes (Figure 4 and 9). There exists little volcanic effect on the heat budget of the lake, although an active volcano, Mt. Komagatake, is located at 12.3 km east-northeast of the lake.
5. Discussion
5.1. Comparison of Heat Storage Change
For equation (1), each of the left side and the right side can be evaluated and compared by the heat storage change from the temperature monitoring and the heat budget estimate, respectively. Then, the heat storage G (J) from the temperature loggers at depths of 0.2 m, 5 m, 10 m, 20 m, 50 m, 70 m and 100 m and at the bottom of site MD was calibrated by that from the corresponding vertical temperature profiles in Figure 7, by using the high correlation (R2=0.978, p<0.01) between the two heat storages (Figure 11). Then, the lake basin shape in Figure 1 was considered as in the calculation of volume-averaged water temperature TL. In contrast to the TL values (Figure 8), the heat storage from the loggers tends to be underestimated. This is because the lake basin volume in the calculation from the profiles is larger than that in the calculation from the loggers. Here, the former volume is nearer to the actual lake volume.
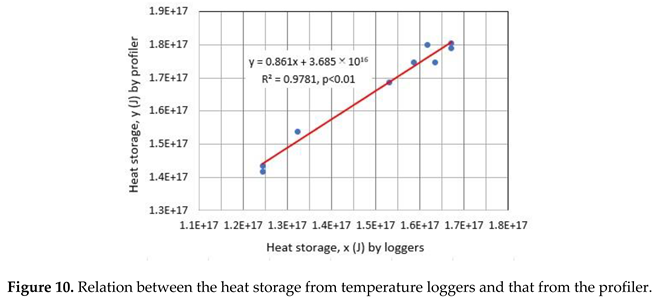
Figure 11.
(a) Time series of the heat storage change from the heat budget estimate (daily mean and 10-day moving average) and (b) a comparison between the heat storage change from the heat budget estimate and that from the loggers and profiler.
Figure 11.
(a) Time series of the heat storage change from the heat budget estimate (daily mean and 10-day moving average) and (b) a comparison between the heat storage change from the heat budget estimate and that from the loggers and profiler.
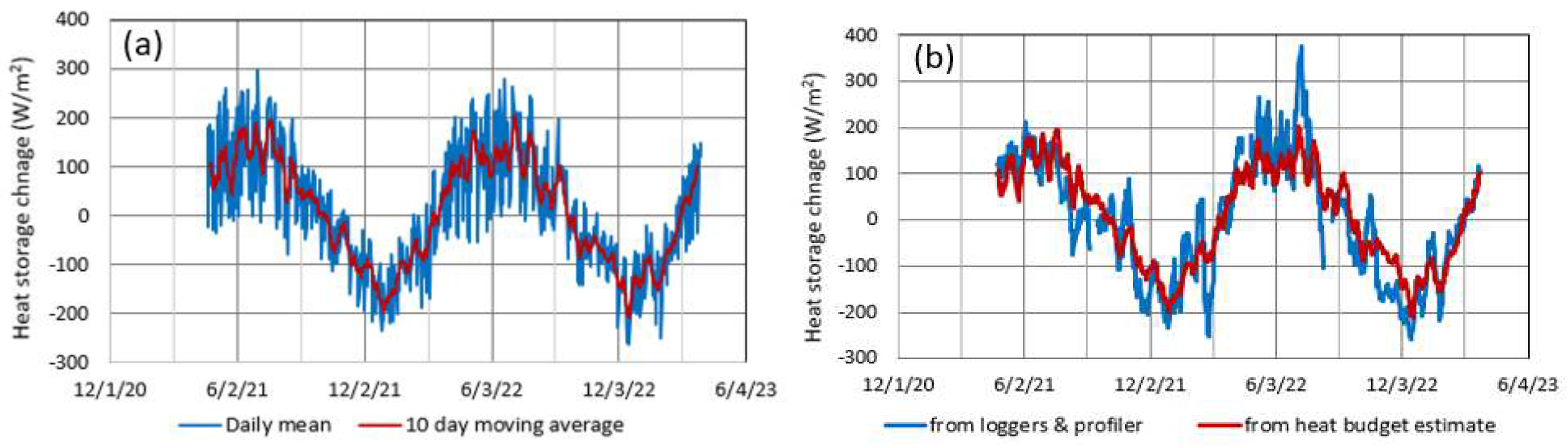
The heat storage change from the heat budget estimate is shown as daily mean time series of 20 April 2021 – 31 March 2023 and their 10-day moving average (Figure 11a). Focusing on the 10-day moving average, the heat storage change annually varies between 197 W/m2 in July 2021 and –196 W/m2 in December 2021 and between 205 W/m2 in July 2022 and –210 W/m2 in December 2022. The 10-day moving average time series allow us to separate the calculation periods into the heating stage of January – June and the cooling stage of July – December.
The 10-day moving heat storage change can be compared between the two ways, i.e., from the loggers’ data calibrated by the profiler and from the heat budget estimate (Figure 11b). Except for the periods of May – July 2022 (Figure 6b), when the heat storage change from the heat budget estimate is likely underestimated, the two heat storage changes are likely reasonable to each other. The root mean square error (RMSE) between the two was 57.5 W/m2 over the periods of 24 April 2021 – 26 March 2023. In the periods of May – July 2022, there probably does not hold the assumption that water temperature is horizontally equal at a certain depth (i.e., the thermal structure of a horizontal multi-layer). One of reasons for this is probably that the consistently large inflow from the Tama River (Figure 5a) produced the thermal heterogeneity in the surface layer as the cooling agent offshore from the outlet of conduit A (Figure 1). Actually, on 13 August 2022, the heat storage change from the loggers’ data greatly decreased (Figure 11b). This can be caused by the relatively large negative heat flux from the Tama River for 9 – 18 August (Figure 9a).
The correlation between the two heat storage changes in Figure 11b is shown in Figure 12. The heating and cooling stages separated by boundaries of December – January and June – July exhibit the high correlations at R2=0.859 and 0.794 as shown by the red and black regression lines, respectively. At a range of –200 to +200 W/m2, the mean difference between the two regression lines was 36.3 W/m2. The heat storage change from the heat budget estimate causes the difference by providing the underestimated values in the early cooling stage and the overestimated ones in the late heating stage (Figure 11b). Considering the mean difference and the RMSE value, in the winters of December – February, all the terms, at lake surface in equation (1) should be taken into account to estimate the heat storage change. In the cooling stage, in addition to , the heat flux by the Tama River could sporadically affect the heat storage change.
5.2. How Deep Vertical Water Circulation Occur?
As shown in Figure 6b, the water temperature at 0.2 m depth was very close to the bottom temperature at 4.21 – 4.27 °C for the periods of mid-February – early March. Hence, based on a comparison between vertical change of dissolved oxygen (DO) and 0.2 m-depth and bottom water temperatures for lake water, it was judged how deep the vertical circulation of lake water occurred.
Vertical distributions of DO in % and mg/L corresponding to those of water temperature in Figure 7 are shown in Figure 13. As shown in Figure 7, the water temperature in the thermally stratified season little changed temporally at depths of more than 100 m. The DO at depths of more than 100 m could thus be supplied only by the vertical water circulation in winter when the water temperature is vertically almost uniform at 4.2 °C or around.
In July – October with the clear thermocline in Figure 7, DO peaks with oversaturation near the depth of thermocline probably by the photosythesis of phytoplankton, but then maintains more than 80 % even at depths of more than 100 m. The latter suggests that the DO loss is small by the decomposition of less organic matter in the acid lake (pH, 5.3 –6.0) [2]. The DO at more than 100 m in depth could thus be redistributed only by vertical water circulation into the deeper zone. As an average over depths of more than 100 m, the DO increased at a rate of 0.0026 mg/L/day for 22 October 2020 – 19 April 2021 (179 days), but decreased at a rate of 0.0033 mg/L/day for 10 September 2021 – 21 April 2022 (223 days) and at a rate of 0.00071 mg/L/day 29 September 2022 – 11 May 2023 (224 days).
Meanwhile, in spring to autumn with no vertical water circulation at depths of more than 100 m, the DO increased at a rate of 0.0011 mg/L/d as averages for 19 April – 10 September 2021 (144 days) and for 21 April – 29 September 2022 (161 days). Hence, the increasing rate of 0.0011 mg/L/d was regarded as a threshold, when, at the less value, the vertical water circulation does not occur at more than 100 m in depth. The increasing rate of 0.0026 mg/L/day averaged over 22 October 2020 – 19 April 2021 thus suggests that the vertical water circulation reached to the bottom in February – March 2021 (Figure 6b). On the contrary, the rate of –0.0033 mg/L/day for 10 September 2021 – 21 April 2022 and the rate of –0.00071 mg/L/day for 29 September 2022 – 11 May 2023 suggest that the vertical circulation did not reach to the bottom. Especially, the large DO loss in September 2021 – April 2022 implies the occurrence of vertical circulation limited to the surface layer above the thermocline (see the 10-Sep-21 and 21-Apr-22 profiles in Figure 7 and Figure 13b). In September 2022 – May 2023 with the decreasing rate of 0.00071 mg/L/day, the vertical circulation did not probably occur in the deeper zone, since the rate is close to 0.0011 mg/L/day in spring to autumn. Actually, a comparison between the 29-Sep-22 and the 11-May-23 profiles in Figure 13b allows us to find that, at depths of more than 200 m, the DO decreased probably by no occurrence of the vertical circulation in the deeper zone.
Here, in order to investigate the vertical water circulation between the surface and bottom in the lake, the potential temperature was calculated for the bottom water. It is because the water density is a function of water temperature, pressure and salinity. The profiling at site MD in the lake showed the salinity at 0.040 – 0.054 ‰, corresponding to the EC25 (electric conductivity at 25 °C) at 10.0 – 13.4 mS/m (Figure 14). Here, a relation between EC25 (x) in mS/m and salinity (y) in ‰ was given by y=0.00428x–0.00293 (R2=0.999, p<0.001) for the profiler. Hence, the potential temperature for the bottom water at 4.20 – 4.30 °C (Figure 7) and 412 – 413 dbar was evaluated at 4.194 – 4.293 °C on water surface [15]. The water temperature recorded at the bottom can thus be compared directly with the 0.2-m depth temperature because of the slight difference (0.006 – 0.007 °C )within the accuracy of ±0.01 °C (resolution, 0.001 °C)for the loggers used.
Here, relations between 0.2-m depth and bottom water temperatures and wind speed in the three winters of 2021 – 2023 are detailed by using Figure 15. The addition of the wind speed data is caused by its large effect on the vertical mixing under condition of no thermal stratification [7,8]. In Figure 15, the hourly or 24-h moving average variations of surface and bottom water temperatures and wind speed are drawn only for the periods when 0.2-m depth temperature was less than the bottom temperature. Below the bottom water temperature, the surface water could sink into the deeper layer by producing relatively heavy water from the mixture with the below water. The data failure for bottom temperature occurred for the period of 1100h, 13 March – 1000h, 23 March 2021 (Figure 15a), when the values were extrapolated at 4.125 °C (green dotted line).
Of all the three periods in 2021 – 2023, including the hours when the 0.2-m depth temperature was less than the bottom temperature, the period in 2021 was longest for 0200h, 18 February – 0700h, 23 March (totally, 118 hrs for 33.21 days) (Figure 15a), while the periods in 2022 and 2023 were 0000h, 23 February – 0800h, 9 March (totally, 96 hrs for 14.33 days) (Figure 15b) and 0300h, 9 February – 0500h, 7 March (totally, 110 hrs for 26.08 days) (Figure 15c), respectively. The temporal variation of bottom temperature above the accuracy of the logger then occurred only for the three time periods of (1) 0300h – 2200h, 20 February, (2) 2100h, 2 March – 1900h, 4 March and (3) 0400h, 11 March – 0600h, 13 March (Figure 15a) in 2021. Compared with the hourly 0.2-m temperature and wind speed, these variations appear to coincide with decreasing surface temperature and strong winds. Especially, for the time period of 2300h, 2 March – 0800h, 3 March 2021 in the period of (2), the surface temperature decreased to 3.45 °C, accompanied by the high wind velocity with wind speed of 2.3 – 3.0 m/s and north to north-northwest wind direction. Then, any precipitation was not recorded. Hence, the connection of the decreasing surface temperature and strong winds produced the forced vertical convection accompanied by the pycnal instability from the production of 4 °C water, which likely caused the vertical circulation to reach to the bottom. Its arrival at the bottom probably increased the bottom temperature from 4.213 to 4.230 °C for 0900h, 3 March – 0500h, 4 March (see the inserted diagrams in Figure 7 and Figure 15a). Such a complete vertical circulation appears to have increased DO in the whole layer as shown by the 22-Oct-20 and 19-Apr-21 profiles in Figure 13a, even if the whole circulation happened for the short time.
Under fine weather condition, there exist daily cycles in 0.2-m depth temperature and wind speed, indicating a daily maximum temperature at a daily maximum wind speed. Thus, the connection between decreasing 0.2-m temperature and strong winds is produced only by the winter monsoon passing over the lake. In the periods of 2022 and 2023, the bottom temperature fluctuated within the accuracy of the logger except the unknown instantaneous increase up to 4.279 °C at 0400h, 13 February 2023. This suggests that the vertical circulation did not reach to the bottom in both 2022 and 2023. This is probably due to no existence of the connection between a decreasing surface temperature and a strong wind. Actually, the DO decreased in the whole layer over the winters of 2022 and 2023 (Figure 13b). The relatively large DO loss in the winter of 2022 could be caused partly by the relative short period (14.33 days) and less frequency (96 hours) for the 0.2-m depth temperature below the bottom temperature (Figure 14b).
Meanwhile, the basal temperature on the bottom temperature time series increased gradually from 4.210 °C in 2021 and 4.271 °C in 2023 (Figure 15). As shown by the inserted diagrams in Figure 7, this increase probably reflects the global warming effect under condition of the incomplete vertical water circulation in the lake [3]. The increasing rate of bottom temperature calculated from Figure 15 was 0.025 °C/yr for 24 February 2021–23 February 2022 and 0.036 °C/yr for 23 February 2022 – 22 February 2023. These values are comparable in magnitude to the increasing rates at 0.039 °C/yr and 0.028 °C/yr for the Feb-Mar averaged and annual mean air temperature of 1977 – 2023 at the Senboku City weather station, respectively. This clearly indicates that there exists the effect of global warming on water temperature in Lake Tazawa.
6. Conclusions
The temporal change of heat storage in very deep Lake Tazawa was evaluated by estimating the heat budget of the lake. Then, the heat fluxes by snowfall, river inflow and groundwater inflow and the geothermal heat flux from lake bottom were taken into account. Meanwhile, the monitoring of water temperature was performed at 1 h intervals at depths of 0.2 – 100 m and at the bottom of a deepest point of the lake. Consequently, the heat storage change from the heat budget estimate was reasonable in magnitude to that from the temperature monitoring with RMSE of 57.5 W/m2. This relatively large difference is probably caused by a horizontal bias of water temperature in the surface layer of 0 – 10 m depth, where the heat flux by river inflow is effective in offshore regions from the inlets of the two conduits.
It was explored how deep the vertical water circulation occur in the lake in the season of no thermal stratification. According to a difference between vertical DO profiles before and after the winter, in the winter of 2021, DO increased in the whole layer probably by the vertical circulation reaching to the bottom. On the other hand, in the winters of 2022 and 2023, DO rather decreased in the almost whole layer. This suggests that the vertical circulation was incomplete to the point of not reaching to the bottom. Also, the relatively large DO loss in the winter of 2022 appears to have result from the vertical circulation limited to the surface layer above the thermocline.
In the periods of 2021 – 2023, including the hours with 0.2-m depth water temperature below the bottom temperature in February – March, hourly data of 0.2-m depth temperature and wind speed were compared with those of hourly bottom temperature. The bottom temperature significantly increased only in the period of 2021, when the coupling of strong winds with decreasing 0.2-m temperature below the bottom temperature worked. This suggests that the vertical water circulation reached to the bottom with relatively warm water coming down. This is likely reflected by the DO increase in the whole layer. Meanwhile, in the periods of 2022 and 2023, the bottom temperature fluctuated within the logger’s accuracy. The vertical circulation then occurred probably in the upper layer away from the bottom, which resulted in the DO loss in the whole layer. Thus, how deep the vertical circulation occurs could be judged by the DO change over the winter in the whole layer and by investigating how the bottom temperature responds to temporal changes of the surface temperature and wind speed. The increase of bottom water temperature from winter to winter probably reflects an aspect of the global warming because of incomplete vertical water circulation.
Author Contributions
Conceptualization, K.A.C.; methodology, K.A.C., H.O. and K.A.; software, K.A.C.; validation, K.A.C. and H.O.; investigation, K.A.C. ; resources, H.O. and K.A.; data curation, H.O.; formal analysis, K.A.C.; writing—original draft preparation, K.A.C.; writing—review and editing, H.O. and K.A.; visualization, K.A.C.; supervision, K.A.C.; project administration, K.A.C.; funding acquisition, K.A.C., H.O. and K.A.
Funding
This research was funded by Earthquake Research Institute, the University of Tokyo, Joint Research programs 2021-KOBO22 and 2022-KOBO22 and Nanzan University Pache Research Subsidy I-A-2 for the 2021 and 2022 academic years.
Data Availability Statement
The data presented in this study are available on request to the corresponding author.
Acknowledgments
The authors express deep gratitude to A. Ohtake, T. Chiba and the other staff of the Lake Tazawa Kunimasu Trout Museum on the shore of Lake Tazawa for their great help in the field observations. The authors are also indebted to Tohoku Electric Power Co., Ltd., Japan for the welcome data supply of the discharge in Lake Tazawa.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Semboku City (Ed.). In Kunimasu; Akita Sakigake Simpo Co., Ltd.: Akita, Japan, 2017; 32p.
- Chikita, K.A.; Amita, K.; Oyagi, H.; Okada, J. Effects of a Volcanic-Fluid Cycle System on Water Chemistry of a Deep Caldera Lake: Lake Tazawa, Akita Prefecture, Japan. Water 2022, 14, 3186. [Google Scholar] [CrossRef]
- Endoh, S.; Yamashita, S.; Kawakami, M.; Okumura, Y. Recent Warming of Lake Biwa Water. Jpn. J. Limnol. 1999, 60, 223–228. Available online: https://www.jstage.jst.go.jp/article/rikusui1931/60/2/60_2_223/_pdf/-char/ja (accessed on 02 March 2021).
- Woolway, R.I.; Merchant, C.J. Worldwide Alteration of Lake Mixing Regimes in Response to Climate Change. Nat. Geosci. 2019, 12, 271–276. [Google Scholar] [CrossRef]
- Jane, S.F.; Hansen, G.J.A.; Kraemer, B.M.; Leavitt, P.R.; Mincer, J.L.; North, R.L.; Pilla, R.M.; Stetler, J.T.; Williamson, C.E.; Woolway, R.I.; et al. Widespread Deoxygenation of Temperate Lakes. Nature 2021, 594, 66–70. [Google Scholar] [CrossRef] [PubMed]
- Nakada, S.; Imai, A.; Shimotori, K.; Yamada, K.; Yamamoto, H.; Okamoto, T. What interrupted monomictic mixing in Lake Biwa? Heat Budget Analysis Using a Circulation Model. Hydrol. Sci. Jour. 2023, 68, 2298–2316. [Google Scholar] [CrossRef]
- Katamura, A.; Hayashi, T.; Ishiyama, D.; Oygawa, Y.; Ishiyama, Y. A Study of Water Circulation Mechanism Based on Data of Water Quality and Wind in Lake Tazawa. In Proceedings of the 2021 Annual Conference, Japan Society of Hydrology and Water Resources/Japanese Association of HydrologicalSciences, Online, 15–18 September 2021. Session ID: OP-6-04. [Google Scholar] [CrossRef]
- Farmer, D.M.; Carmack, E. Wind Mixing and Restratification in a Lake near the Temperature of Maximum Density. J. Phys. Oceanogr. 1982, 11, 1516–1533. [Google Scholar] [CrossRef]
- Hayashi, T.; Ishiyama, D.; Ogawa, Y.; Pham Minh, Q. Secular Change of Water Temperature in Hypolimnion of Lake Tazawa. In Proceedings of the Japan Geoscience Union Meeting 2018, Chiba, Japan, 20–24 May 2018; Available online: https://confit.atlas.jp/guide/event-img/jpgu2018/AHW22 (accessed on 02 March 2021).
- Tanaka, A. Lake Studies as a Hobby; Shueisha, Co., Ltd.: Tokyo, Japan, 1922. [Google Scholar]
- Kondo, J. Meteorology in Aquatic Environments; Asakura Publishing Ltd.: Tokyo, Japan, 1994; 350p. [Google Scholar]
- Knobauch, H. Overview of Density Flows and Turbidity Currents; Water Resources Research Laboratory, 1999, PAP-0816, 27p. Available online: https://usbr.gov/tsc/techreferences/hydraulics_lab/pubs/PAP/PAP-0816.pdf.
- Kobayashi, M. Interaction between Lake Water and Groundwater. J. Groundw. Hydrol. 2001, 43, 101–112. [Google Scholar] [CrossRef]
- Boehrer, B.; Fukuyama, R.; Chikita, K.A. Geothermal Heat Flux into Deep Caldera Lakes Shikotsu, Kuttara, Tazawa and Towada. Limnology 2013, 14, 129–134. [Google Scholar] [CrossRef]
- Jackett, D.R.; McDougall, T.J.; Freistel, R.; Wright, D.G.; Griffies, S.M. Algorithms for Density, Potential Temperature, Conservative Temperature, and the Freezing Temperature of Seawater. J. Atmos. Ocean. Technol. 2006, 23, 1709–1728. [Google Scholar] [CrossRef]
Figure 1.
Location of Lake Tazawa in Akita Prefecture, Japan, observation sites and four conduits A, B, C and D (thick dotted lines) on the bathymetric (thin dotted lines) and surrounding topographic (thin solid lines) maps with 100 m contours. MD: Deepest point, M: Meteorological station, L: Monitoring point of lake level, MD: Observation point of the ASTD102 profiler and monitoring point of water temperature, T and S: monitoring point of water temperature in the Tama River and the Sendachi River, respectively.
Figure 1.
Location of Lake Tazawa in Akita Prefecture, Japan, observation sites and four conduits A, B, C and D (thick dotted lines) on the bathymetric (thin dotted lines) and surrounding topographic (thin solid lines) maps with 100 m contours. MD: Deepest point, M: Meteorological station, L: Monitoring point of lake level, MD: Observation point of the ASTD102 profiler and monitoring point of water temperature, T and S: monitoring point of water temperature in the Tama River and the Sendachi River, respectively.
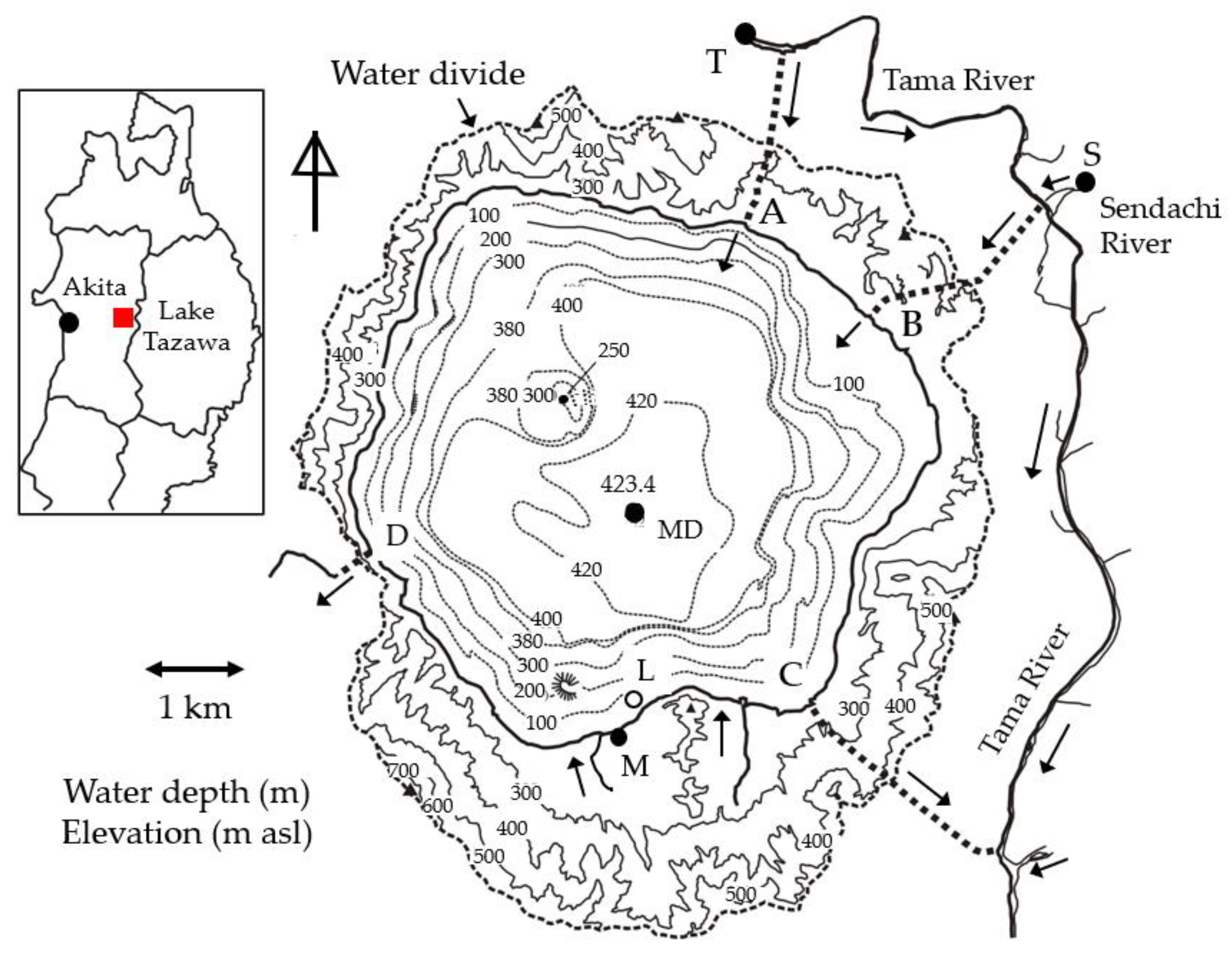
Figure 3.
Daily variations of air temperature, precipitation and heat flux QP by rainfall or snowfall for 1 August 2020 – 9 May 2023.
Figure 3.
Daily variations of air temperature, precipitation and heat flux QP by rainfall or snowfall for 1 August 2020 – 9 May 2023.
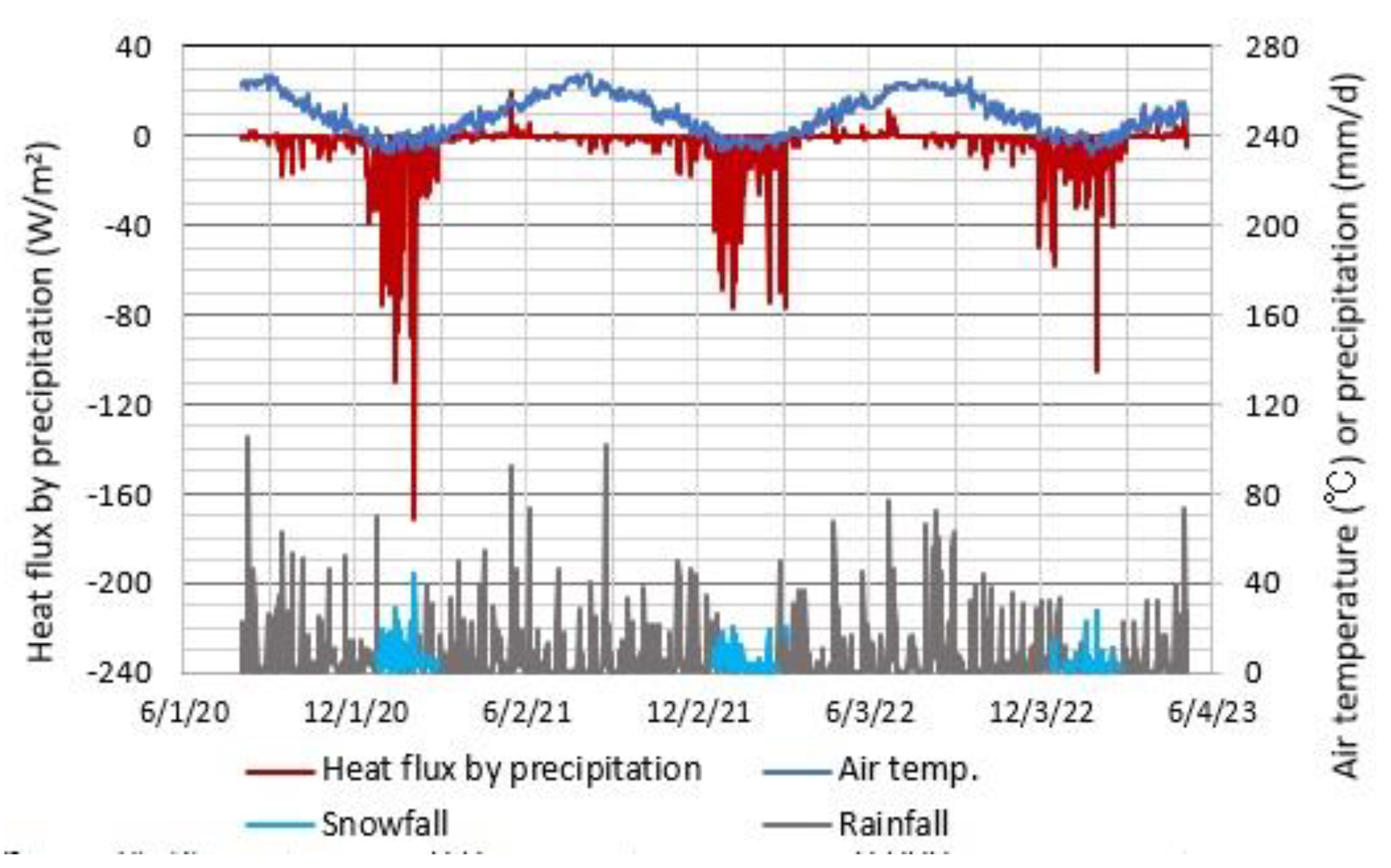
Figure 4.
Daily mean time series of (a) net heat flux and net radiation Q*, (b) the sensible heat flux QH and (c) the latent heat flux QE at lake surface for 1 August 2020 – 9 May 2023.
Figure 4.
Daily mean time series of (a) net heat flux and net radiation Q*, (b) the sensible heat flux QH and (c) the latent heat flux QE at lake surface for 1 August 2020 – 9 May 2023.
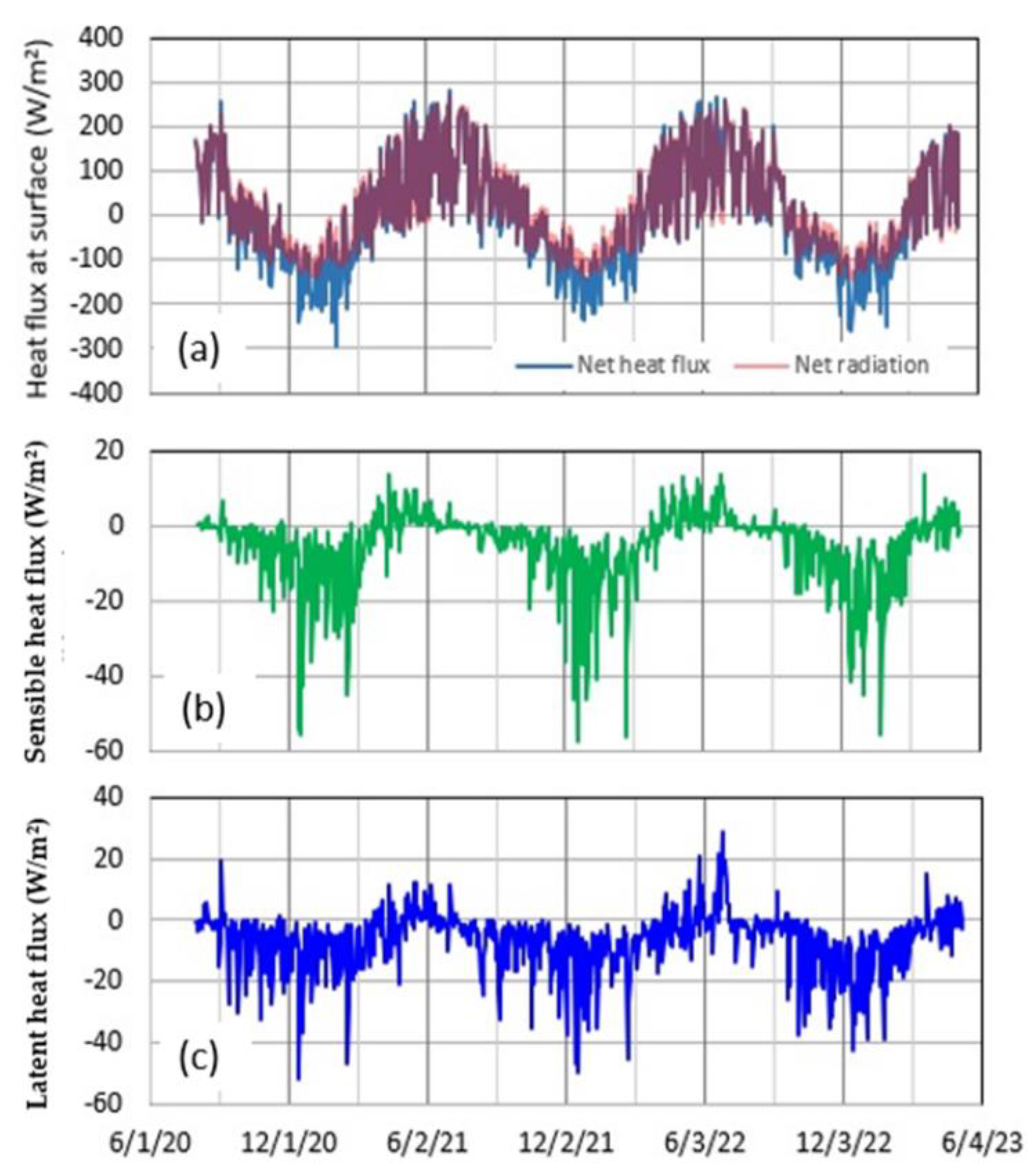
Figure 5.
Temporal variations of (a) daily mean river inflow at conduits A and B and (b) daily mean water temperature at sites T and S for 1 February 2021 – 31 March 2023 (Figure 1).
Figure 5.
Temporal variations of (a) daily mean river inflow at conduits A and B and (b) daily mean water temperature at sites T and S for 1 February 2021 – 31 March 2023 (Figure 1).
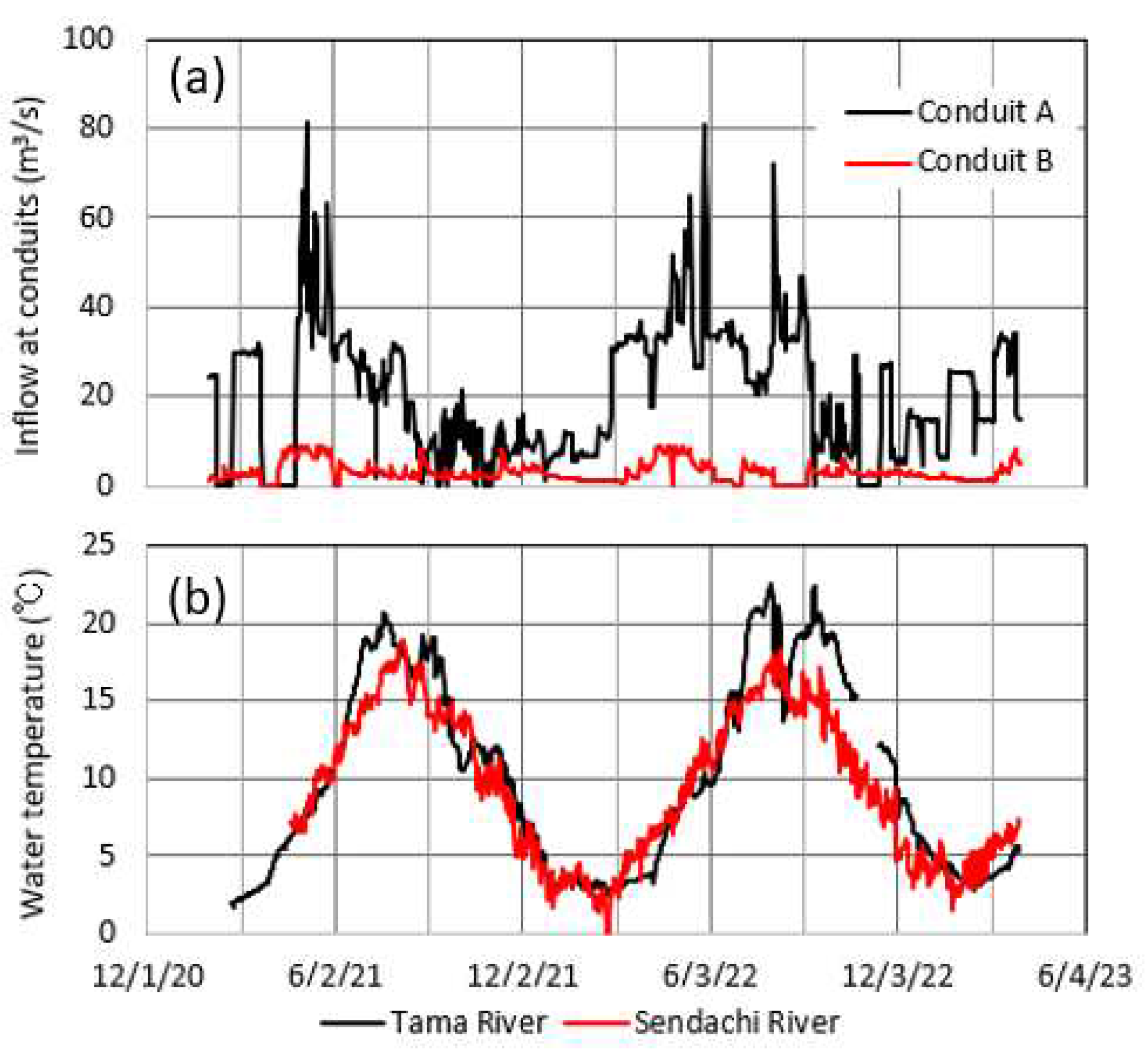
Figure 6.
Temporal variations of (a) daily mean lake level (m above sea level) and the area at the depths of monitoring water temperature and (b) daily mean water temperature at 0.2 m depth – bottom for 1 February 2021–10 May 2023.
Figure 6.
Temporal variations of (a) daily mean lake level (m above sea level) and the area at the depths of monitoring water temperature and (b) daily mean water temperature at 0.2 m depth – bottom for 1 February 2021–10 May 2023.
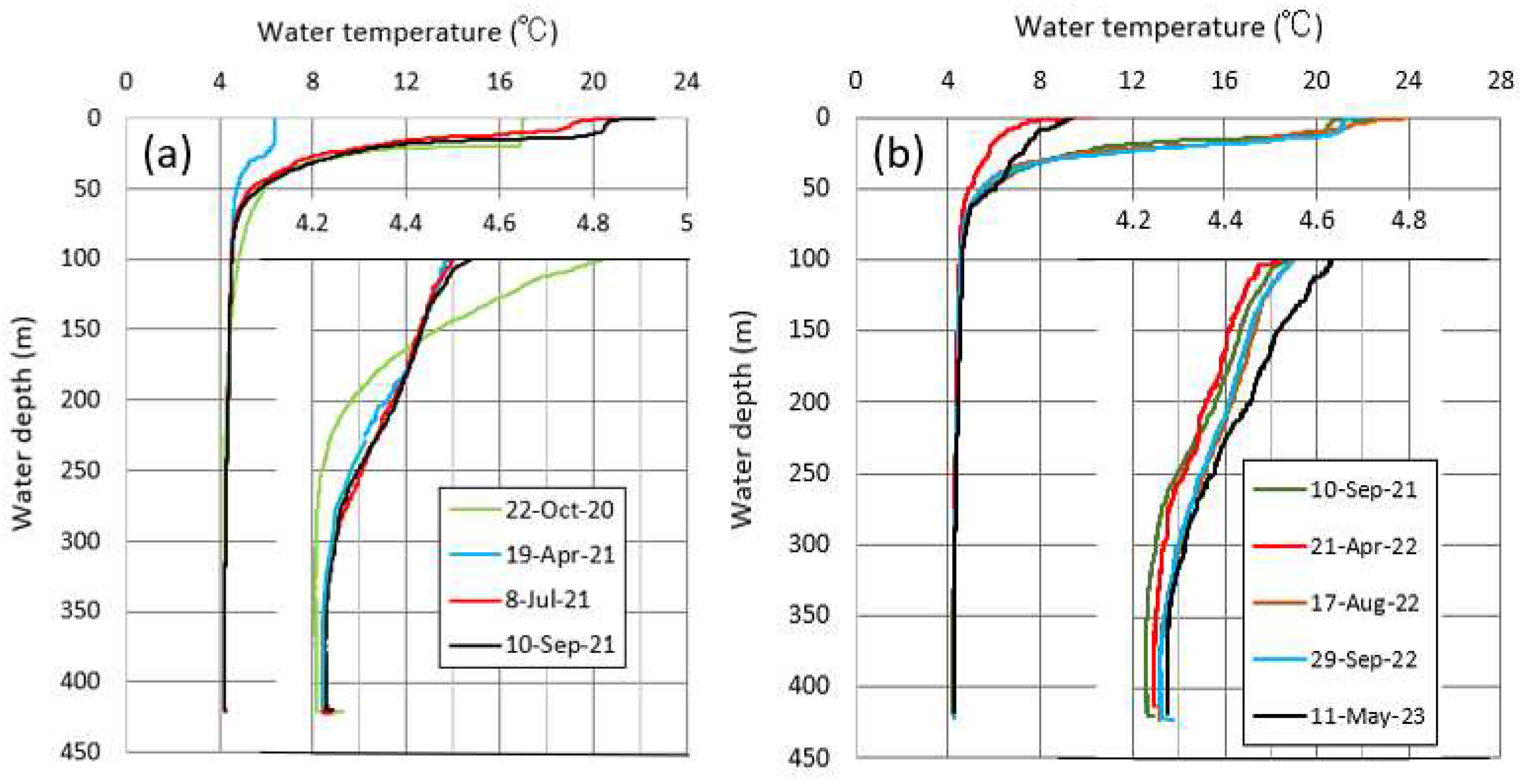
Figure 7.
Vertical distributions of water temperature at site MD in (a) October 2020 – September 2021 and (b) September 2021– May 2023 by the ASTD profiler. Water temperature at depths of more than 100 m are enlarged as in the inserted diagrams. For a comparison, the 10-Sep-21 profile is drawn together with the 2022–2023 profiles.
Figure 7.
Vertical distributions of water temperature at site MD in (a) October 2020 – September 2021 and (b) September 2021– May 2023 by the ASTD profiler. Water temperature at depths of more than 100 m are enlarged as in the inserted diagrams. For a comparison, the 10-Sep-21 profile is drawn together with the 2022–2023 profiles.
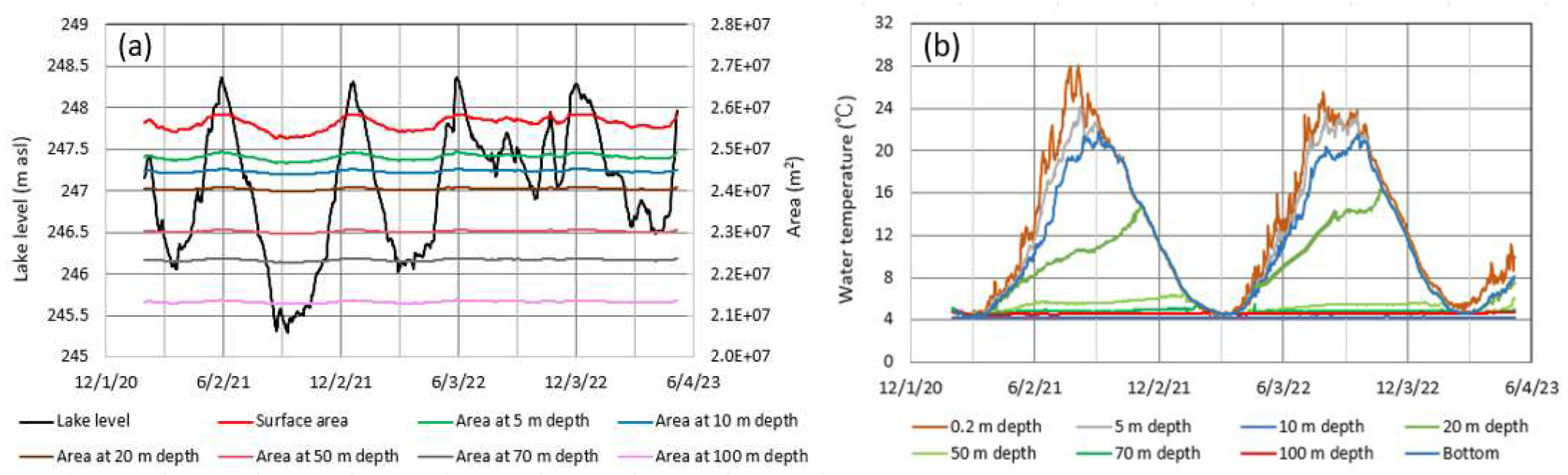
Figure 8.
Relation between volume-averaged water temperature (WT) from loggers and that from the profiles in Figure 7.
Figure 8.
Relation between volume-averaged water temperature (WT) from loggers and that from the profiles in Figure 7.
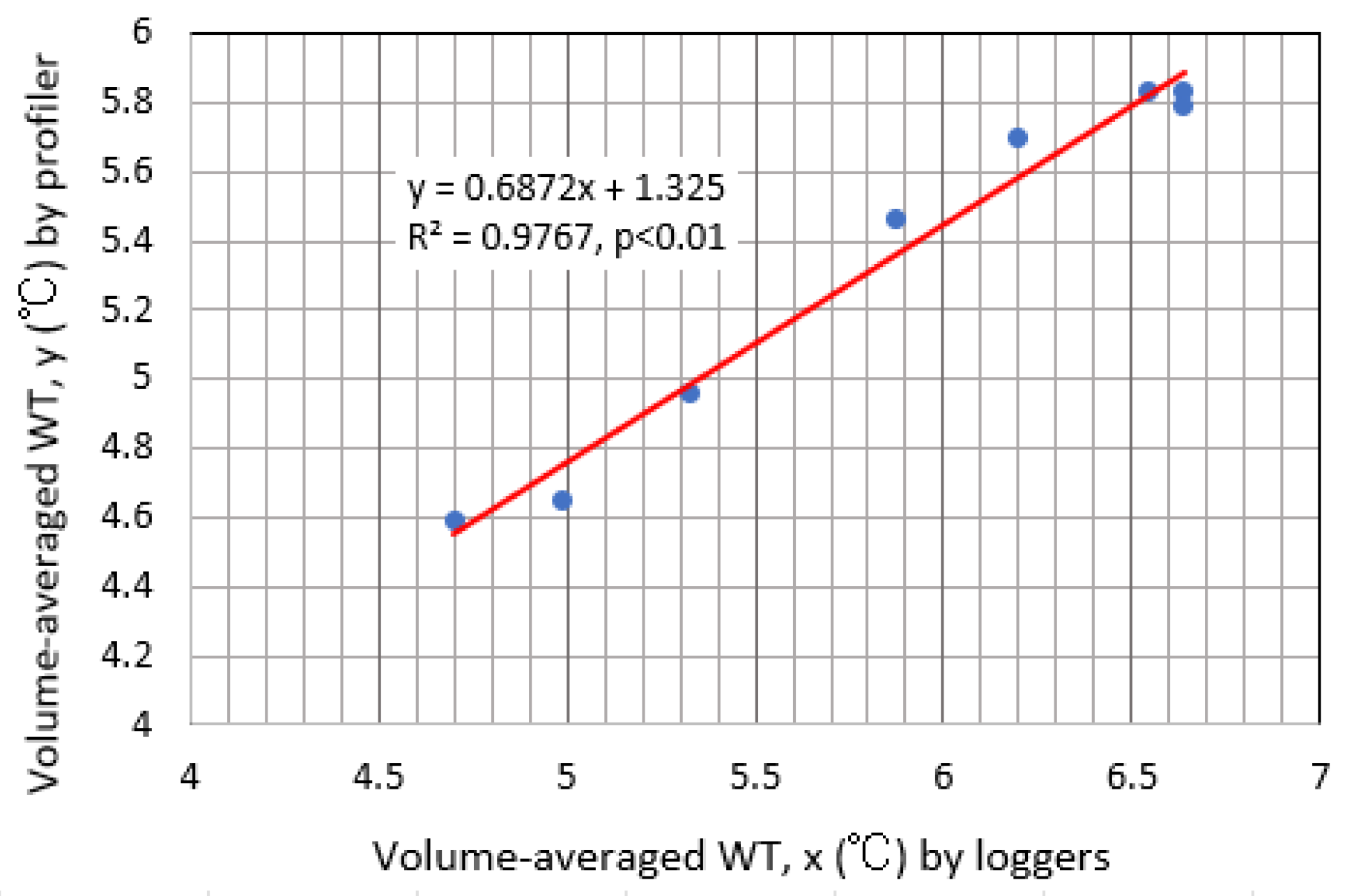
Figure 9.
(a) Daily mean time series of heat flux by river inflow and groundwater inflow and (b) total heat flux by river inflow, latent heat flux QE, sensible heat flux QH and heat flux by precipitation QP for 1 February 2021 – 31 March 2023.
Figure 9.
(a) Daily mean time series of heat flux by river inflow and groundwater inflow and (b) total heat flux by river inflow, latent heat flux QE, sensible heat flux QH and heat flux by precipitation QP for 1 February 2021 – 31 March 2023.
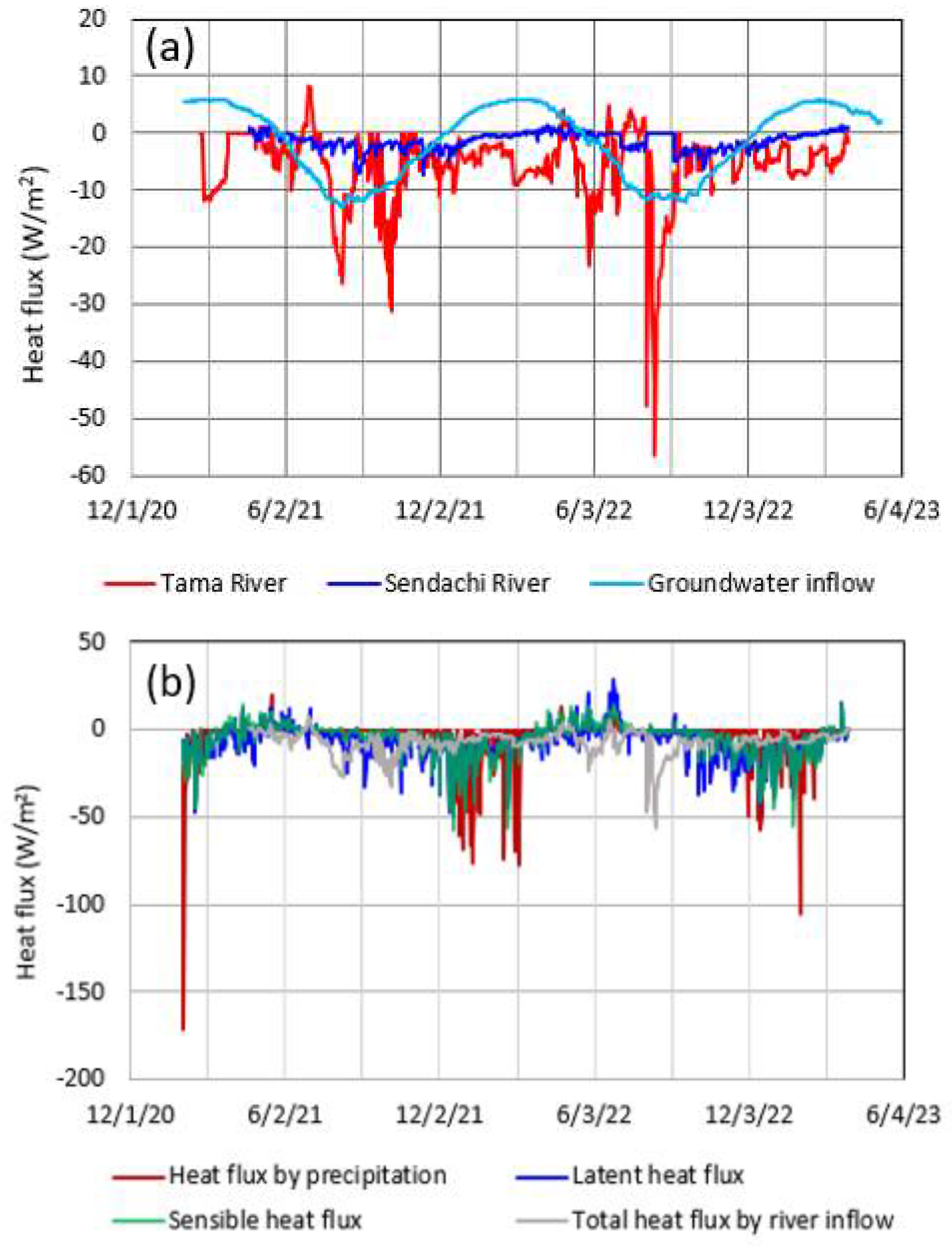
Figure 10.
Vertical distributions of water temperature at 200 m or less above the bottom of site MD in the stratification periods of 2021 and 2022 (Figure 7).
Figure 10.
Vertical distributions of water temperature at 200 m or less above the bottom of site MD in the stratification periods of 2021 and 2022 (Figure 7).
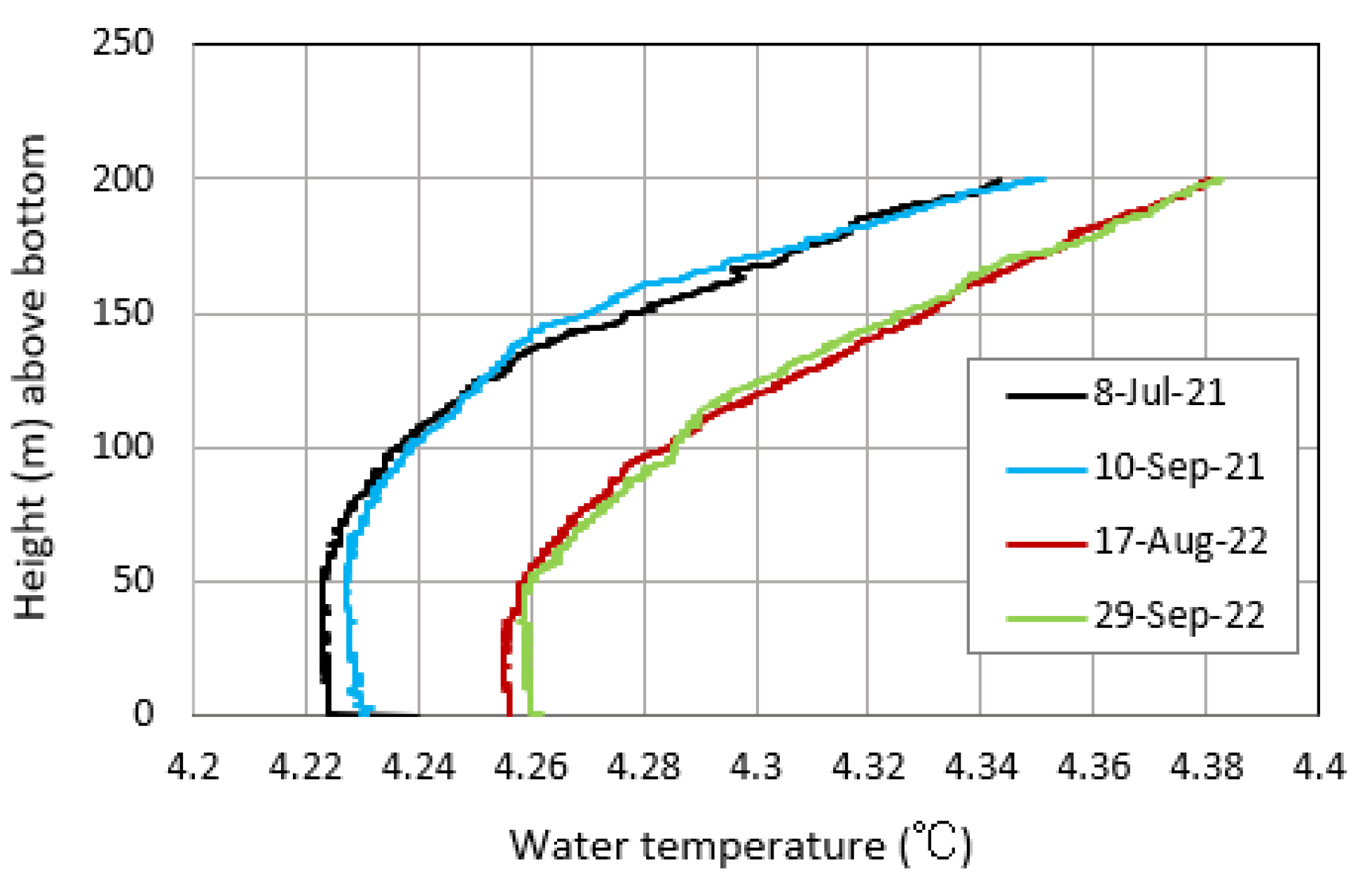
Figure 12.
Relations between the heat storage change (x) from the loggers and profiler and that (y) from the heat budget estimate. The calculated periods are separated into the heating and cooling stages.
Figure 12.
Relations between the heat storage change (x) from the loggers and profiler and that (y) from the heat budget estimate. The calculated periods are separated into the heating and cooling stages.
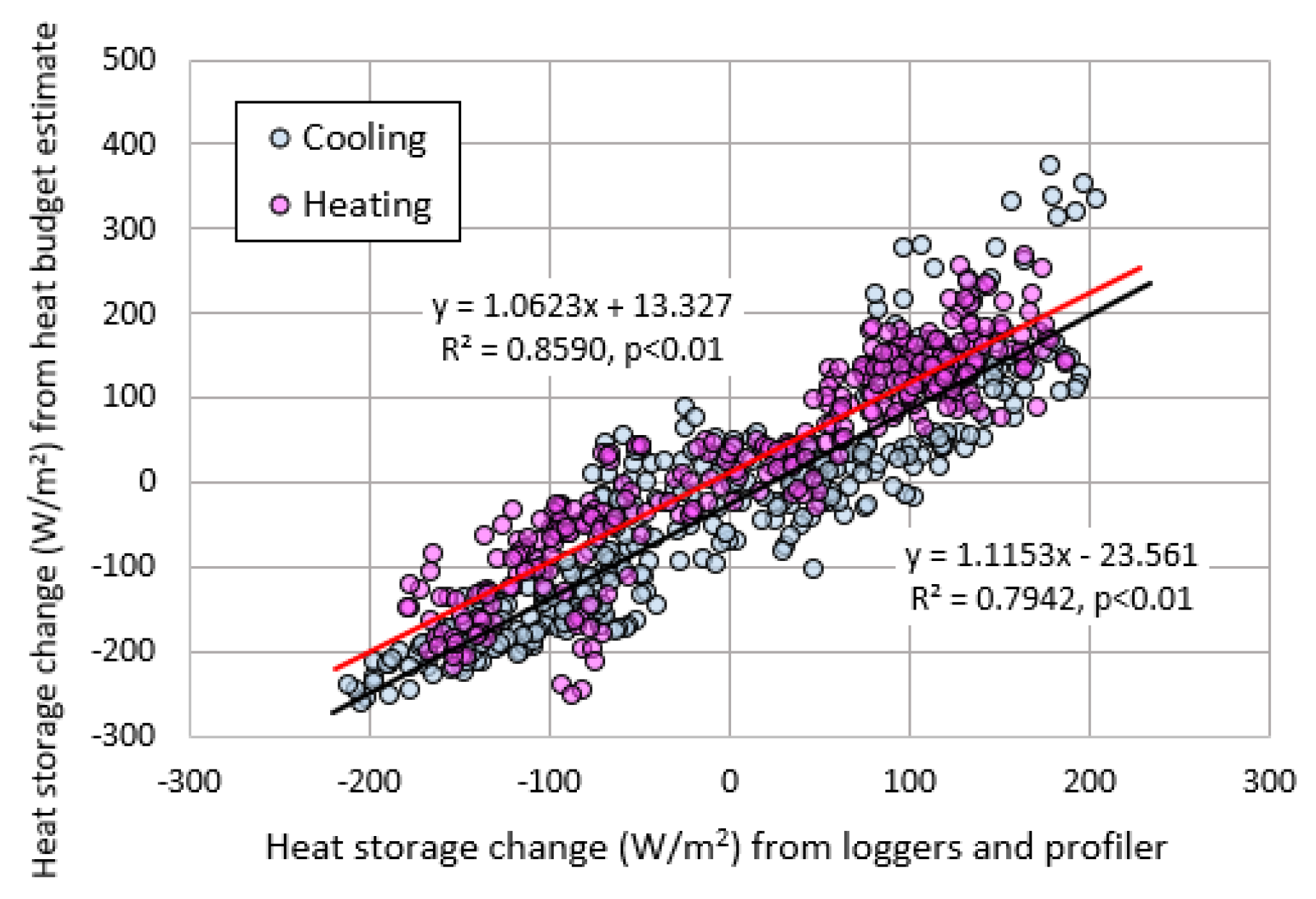
Figure 13.
Vertical profiles of dissolved oxygen (DO) in % or mg/L obtained for (a) 22 October 2020 – 10 September 2021 and (b) 10 September 2021 – 11 May 2023. For a comparison, the 10-Sep-21 profile is drawn together with the 2022–2023 profiles.
Figure 13.
Vertical profiles of dissolved oxygen (DO) in % or mg/L obtained for (a) 22 October 2020 – 10 September 2021 and (b) 10 September 2021 – 11 May 2023. For a comparison, the 10-Sep-21 profile is drawn together with the 2022–2023 profiles.
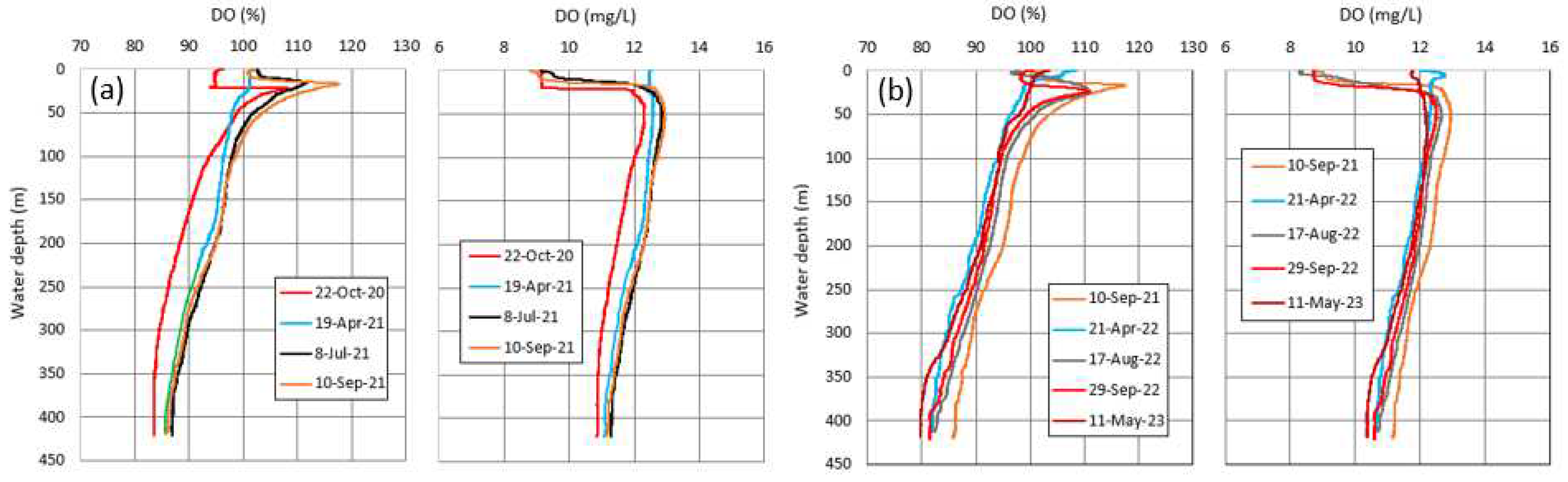
Figure 14.
Vertical distributions of EC25 (electric conductivity at 25 °C) at site MD in (a) October 2020 – September 2021 and (b) April 2022 – May 2023, corresponding to the temperature profiles in Figure 7.
Figure 14.
Vertical distributions of EC25 (electric conductivity at 25 °C) at site MD in (a) October 2020 – September 2021 and (b) April 2022 – May 2023, corresponding to the temperature profiles in Figure 7.
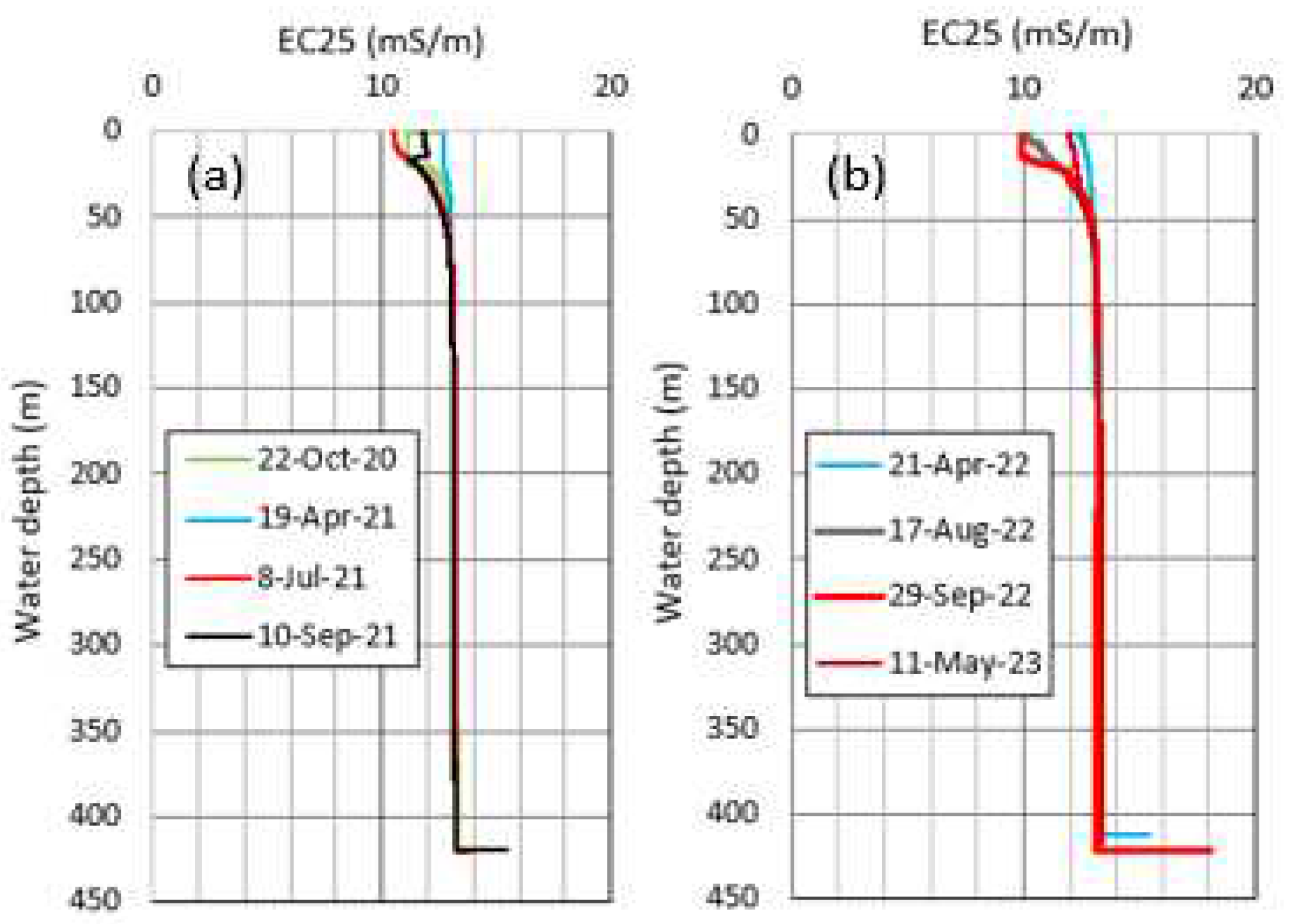
Figure 15.
Hourly variations of 0.2-m depth and bottom water temperatures and wind speed (upper) and bottom water temperature (lower) for the periods including the times with the 0.2-m temperature below the bottom temperature in (a) 2021, (b) 2022 and (c) 2023. For the wind speed and bottom temperature, 24-h moving averages are also shown. The legends in (a) are common to (b) and (c).
Figure 15.
Hourly variations of 0.2-m depth and bottom water temperatures and wind speed (upper) and bottom water temperature (lower) for the periods including the times with the 0.2-m temperature below the bottom temperature in (a) 2021, (b) 2022 and (c) 2023. For the wind speed and bottom temperature, 24-h moving averages are also shown. The legends in (a) are common to (b) and (c).
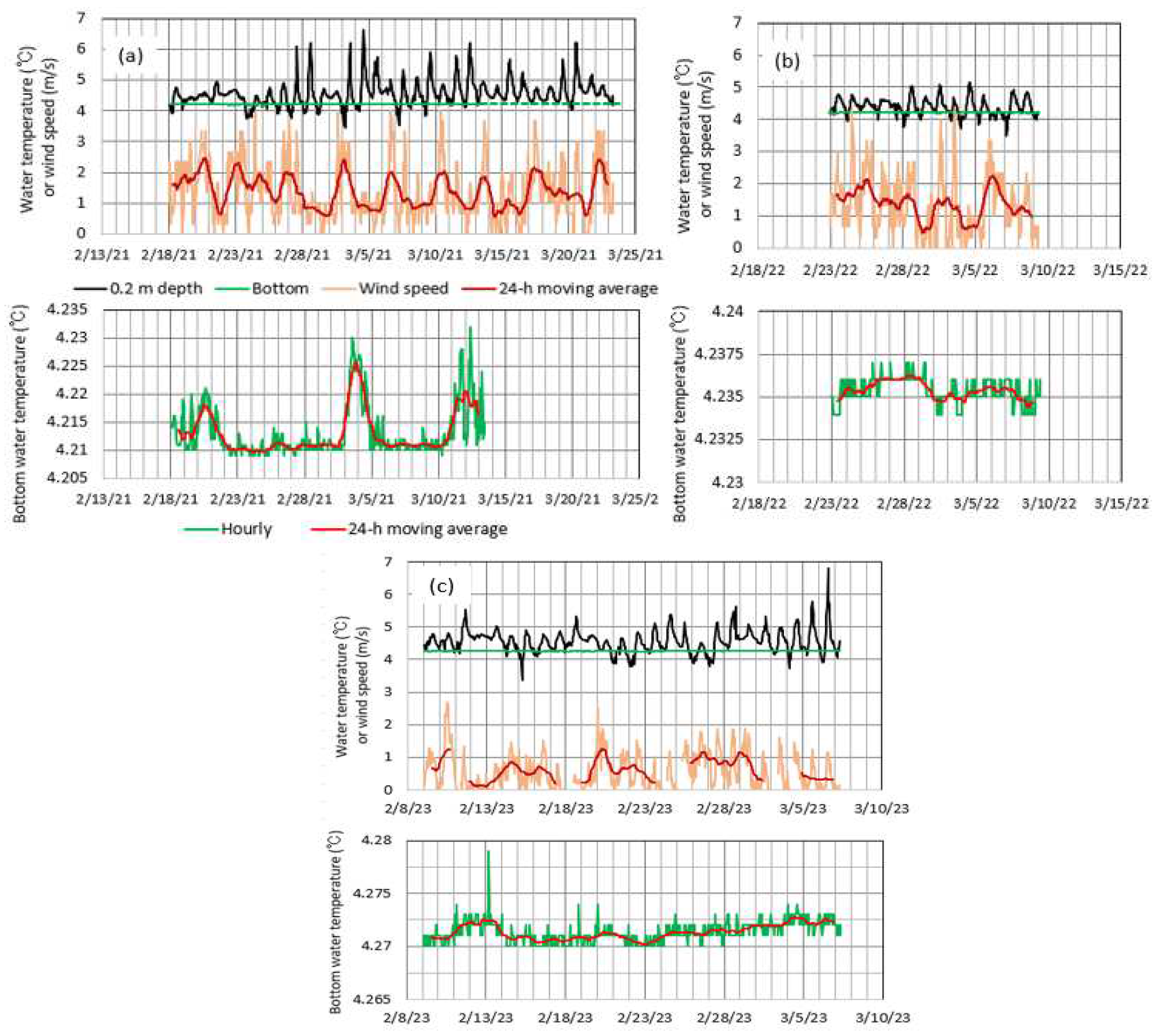
Table 1.
Total precipitation, snowfall and rainfall for the snowfall period of December 2020 – February 2021 and for the rainfall period of February 2021 – December 2021, and Q*, QH, QE and QP values and their percentage in magnitude averaged over each period.
Table 1.
Total precipitation, snowfall and rainfall for the snowfall period of December 2020 – February 2021 and for the rainfall period of February 2021 – December 2021, and Q*, QH, QE and QP values and their percentage in magnitude averaged over each period.
| Snowfall period | Days | Total (mm) | QP (W/m2) | Q* (W/m2) | QH (W/m2) | QE (W/m2) | |
|---|---|---|---|---|---|---|---|
| 13 Dec. 2020 – 26 Feb. 2021 | 76 | 600.8 | –21.5 (16.1%) | –82.4 (62.0%) | –15.8 (11.9%) | –13.3 (10.0%) | |
| Snowfall | 52 | 412.3 | –30.9 (19.2%) | –94.9 (58.9%) | –19.3 (12.0%) | –15.9 (9.9%) | |
| Rainfall | 8 | 188.5 | –3.8 (3.9%) | –83.8 (84.1%) | –5.1 (5.1%) | –6.9 (6.9%) | |
| No precipitation | 16 | – | – | –41.1 (70.0%) | –8.8 (16.5%) | –7.9 (13.5%) | |
| Rainfall period | Days | Total (mm) | QP (W/m2) | Q* (W/m2) | QH (W/m2) | QE (W/m2) | |
| 27 Feb. 2021 – 1 Dec. 2021 | 278 | 2041.2 | –0.6 | 58.6 | –1.7 | –4.9 | |
| rainfall | 140 | 2041.2 | –1.2 | 18.0 | –2.0 | –5.2 | |
| No precipitation | 138 | – | – | 104.6 | –0.7 | –4.1 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






