Preprint
Article
An Agent-Based Model for Disease Epidemics in Greece
Altmetrics
Downloads
168
Views
85
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Preprints on COVID-19 and SARS-CoV-2
Submitted:
09 January 2024
Posted:
10 January 2024
You are already at the latest version
Alerts
Abstract
In this research, we present the first steps taken towards a data-driven agent-based model (ABM) specifically designed for simulating infectious disease dynamics in Greece. Amidst the ongoing COVID-19 pandemic caused by SARS-CoV-2, this research holds significant importance as it can offer valuable insights into disease transmission patterns and assist in devising effective intervention strategies. To the best of our knowledge, no similar study has been conducted in Greece. We constructed a prototype ABM that utilizes publicly accessible data to accurately represent the complex interactions and dynamics of disease spread in the Greek population. By incorporating demographic information and behavioral patterns, our model captures the specific characteristics of Greece, enabling accurate and context-specific simulations. By using our proposed ABM, we aim to assist policymakers in making informed decisions regarding disease control and prevention. Through the use of simulations, policymakers have the opportunity to explore different scenarios and predict the possible results of various intervention measures. These may include strategies like testing approaches, contact tracing, vaccination campaigns, and social distancing measures. Through these simulations, policymakers can assess the effectiveness and feasibility of these interventions, leading to the development of well-informed strategies aimed at reducing the impact of infectious diseases on the Greek population. This study is an initial exploration toward understanding disease transmission patterns and a first step towards formulating effective intervention strategies for Greece.
Keywords:
Subject: Computer Science and Mathematics - Other
1. Introduction
During the COVID-19 pandemic peaks in Greece, there was a daily update by a scientific committee regarding the number of infections and other related statistical information. Based on this information, they were arguing in favor of specific interventions that would help mitigate the large wave of infections. Their prime argument related to the proposed interventions were the predictions based on models about the progress of the pandemic, if left unchecked. The question was raised about what models they were using to come to such decisions. It turns out, and to the best of our knowledge, that the models used by the scientific committee in Greece were based on an ODE approach. It’s worth noting that while the ABM approach has been utilized in other countries, there hasn’t been a study applying this approach specifically to Greece. Generally and in the case of epidemiologouty particularly, scientists use various tools, among which are predictive models, in order to promptly react to outbreaks as well as to understand the disease dynamics.
Simulation is a major tool for studying disease spread and it may be based either on an ordinary differential equations approach (ODE) (a descriptive approach) or on an Agent-Based Modeling (ABM) approach (mechanistic approach). In the ODE approach, the population is divided into compartments (groups) and the aggregate number of individuals that have a particular state (e.g., infected) is a function of time. These equations essentially describe the volume of people that move between different states (compartments) as a function of time. They can also be used to compute various characteristics of the population with respect to the epidemic, like the basic reproductive number. On the other hand, agent-based models simulate the population by entities (of different granularities depending on the application), corresponding to agents with specific traits and behaviors. In the case of epidemiology, each agent corresponds to a human within the population. These agents interact at a local level, and a global behavior emerges (e.g., an outbreak) as a result of these local interactions. While ODE (aggregated) and ABM (disaggregated) methods have their strengths and weaknesses, one notable strength of ABM is the fine-grained opportunities it offers to change agent traits, behaviors, interactions, and disease parameters while looking at their effects on global behavior. Interventions and sensitivity analyses are two examples that make use of such refinements. See [1] for a starting point on discussing such models. Indeed, one of the most important practical results and major impact of ABM in epidemiology is policy recommendation. There are quite a few studies related to how interventions affect the progress of an outbreak [2] as well as the economic impact of such interventions [3].
In this paper, we present the first steps towards developing an ABM tailored to the unique characteristics of the Greek territory. Our long-term goal is to assist policymakers in implementing effective intervention measures through the exploration of various what-if scenarios. The model will provide a fine-grained understanding of disease spread, giving access to valuable insights for decision-makers. Our contribution towards this goal is along two axes:
- We present a framework for creating synthetic populations in the Greek territory, utilizing statistical distributions derived from census data from various public sources. These synthetic populations serve as the foundation for a data-driven, multi-layer agent-based model specifically designed to simulate the dynamics of infectious diseases in Greece.
- We apply an SEIR virus propagation model to simulate the dynamics of the virus on the synthetic population.
In Section 2 we discuss basic notions used throughout the paper and also provide an overview of the relevant literature. In Section 3 we describe the methodology used throughout the paper. In particular, we analyze our approach for creating the synthetic population and we also discuss the virus propagatiom model. The experimental results and related discussion are given in Section 4, and we conclude in Section 5.
2. Preliminaries
Agent-based models (ABM) are microscale models that simulate multiple agents’ simultaneous operations and interactions in an attempt to re-create and predict the appearance of complex phenomena. In ABMs, higher-level system properties arise from the lower-level subsystem interactions, a phenomenon known as emergence. ABMs have been used extensively for modeling purposes in non-computing related scientific domains like biology, ecology, and social sciences [4].
Traditional epidemiological research focuses on rate-based differential equation modeling on perfectly mixed populations, in the sense that each agent can interact with any other in the population. This approach allows obtaining analytical expressions for certain quantities like the number of infected people in a population [5]. However, this is true for simple models only, in the sense that the number of population groups is small. In addition, such an approach completely disregards one of the critical factors in disease evolution: human interactions. To this end, Agent-Based Modeling (ABM) can be used as an implementation approach for complex disease models as well as rich human interactions. ABM provides the modeler with an extensive toolkit with respect to checking policy planning and making detailed predictions. The main hurdles related to this approach are the need for high-quality data, the difficulty in parameterization and tuning of the model as well as efficiency issues that come into play when the population is large.
Applying the agent-based modeling paradigm to epidemics requires two major components: the population and the disease model. Epidemiological Agent-Based Modeling relies critically on the definition of a population that is usually synthetic. The former entails statistical summaries or distributions of various population characteristics, often represented in the form of statistical tables, such as the count of individuals within specific age groups or income brackets. On the other hand, disaggregated data consists of individual-level records for persons or households, encompassing diverse attributes like age, income, gender, and more.
The first major challenge of an epidemiological ABM is the generation of the synthetic population and all its characteristics and properties. In particular, a synthetic population requires the definition of the agents and their properties that define the populations, their spatial placement, and finally their relations. In fact, this is usually the order in which the complete synthetic population is generated. Traditionally, population synthesis can be achieved through three approaches [6]: 1) Synthetic Reconstruction (SR) (e.g., [7]), 2) Combinatorial Optimization (e.g., [8]) (CO) and 3) Statistical Learning (SL) (e.g., [9,10]). Recently, there has been a very small number of studies that adopt machine learning (ML) approaches (e.g., [11]) that fall under the umbrella of SL but support efficiently the generation of synthetic populations with a high number of characteristics/traits, which is certainly not the focus of this paper. In principle, both SR and SL are based on samples of the population although SR methods have been devised that are sample-free. Sample-free methods try to rebuild disaggregated population data from the aggregated real population data while sample-based methods try to generate the entire population by replicating the available disaggregated data, which is a sample of the real population. Indeed, in [12] a comparison is made between a sample-free method and a similar sample-based method leading to the conclusion that the sample-free method is superior regarding the population fitting although it requires more preprocessing. In [6] a comparison is given between these approaches for generating a two-layered population (individuals and households) while at the same time they propose a decision-making procedure as to the best approach available based on the characteristics of the data that describe the real population.
Initially, the synthetic agents and their properties need to be defined, resembling the target population with respect to various statistical measures (e.g., age distribution among agents). The key objective is to reduce the disparity between the synthetic population and the actual population concerning these statistical measures.
The social interactions between the agents in the population are usually represented by networks. Usually, multilayer networks are used that are able to characterize numerous types of interactions that a typical monolayer network approach cannot. Edges (or links) in monolayer networks describe undirected or directed connections between nodes. Networks might, for example, describe social relationships (undirected edges) among wild animals (each individual being a node) or movement (directed edge) from one farm to another (each farm being a node). Multilayer networks likewise have nodes and edges, but the nodes are separated into layers, each indicating a particular type of interaction that connects to form an aspect. Aspects, or layers stacked together, can be used to represent many sorts of contacts, physical locations, subsystems, or temporal points. Intralayer connections are made between nodes in the same layer of an aspect, whereas interlayer connections are made between nodes in different layers [13,14]. Each layer can be a different type of a random network depending on the degree distribution, and as such, the appropriate generation process must be adopted. Non-random networks are rarely used and only in cases where the full network can be reconstructed from the available data. The type of the random network depends on the relation type. For example, modeling households corresponds to a network that consists of a set of small cliques (the size of the family) whose distribution is a power law. On the other hand, modeling random interactions in a geographical area can be simulated by random network that correponds to homogenous mixing.
2.1. Related Work
Before discussing ABM-based systems for virus propagation that contain a population synthesis module, we briefly discuss open-source approaches (we do not consider approaches that have not published their code) for population synthesis in general. Creation of synthetic populations (or ecosystems to be more precise) start all the way from 1996 with the Transportation Analysis Simulation System (TRANSIMS) [15], which simulates traffic patterns on synthetic individuals. In a rather outdated survey on population synthesizers [16], the goal was set to create a general software solution. Indeed, in 2017 a general framework for generating Synthetic Populations and Ecosystems of the World (SPEW) was implemented [17]. SPEW supports various sampling methods for constructing the synthetic population and their location within a geographic region. Given that appropriate data exists, SPEW can create a synthetic ecosystem for different agents. They also claim to have generated a synthetic population for over 70 countries worldwide (among which is Greece) based on the data taken from Integrated Public Use Microdata Series International (IPUMS-I) [18]. However, the web domain is deactivated and this synthesized data cannot be found anywhere.
Understanding the current state of medical knowledge about COVID-19 and considering demographic factors are crucial when developing strategies to mitigate its spread. Simulation models can aid policymakers in making informed decisions by taking into account the prevailing situation. Agent-based modeling (ABM), which incorporates human behavior and interactions, has proven particularly useful in studying the spread of COVID-19. A comprehensive literature search yielded several papers that focus on agent-based modeling of COVID-19 transmission pathways (a representative small subset is shown in Table 1 and discussed further below). These models vary in their objectives, the number of simulated individuals (agents), the geographical areas they represent, and their approaches to modeling transmission patterns, illness states, human behavior, and treatments. However, a gap exists between policymakers’ requirements and the capabilities of simulation models in accurately reflecting real-world factors that influence human decision-making and transmission dynamics [19].
[20] reports on the results of agent-based modeling of the COVID-19 outbreak in Australia using a fine-grained computational simulation. This model has been calibrated to meet important COVID-19 transmission parameters. The age-dependent fraction of symptomatic instances is a key calibration outcome, with this fraction for children being one-fifth of that for adults. The model is used to compare a variety of intervention techniques, including international flight restrictions, case isolation, home quarantine, social separation with varied levels of compliance, and school closures. School closures do not appear to provide significant benefits unless they are accompanied with a high level of social distancing compliance.
In [21], a stochastic agent-based microsimulation model of the COVID-19 epidemic in France is presented. The model also assesses the possible effects of post-quarantine interventions, such as social isolation, mask usage, and population shielding of those most susceptible to severe COVID-19 infection on the disease’s overall incidence and death, as well as on the utilization of ICU beds. The model was accurately calibrated, and changes in model parameter values had no effect on the estimations of the results. The authors concluded that even while quarantine is efficient in stopping viral transmission, no matter how long it lasts, it is unlikely to stop the epidemic from spreading again.
In [22], an agent-based model for towns in Ireland was created. A data-driven agent-based model to mimic the development of an airborne infectious illness in an Irish town using publicly accessible data was built. By recreating a measles outbreak that happened in Schull, Ireland in 2012, the model was put to the test. The same outbreak in 33 different towns was replicated, and then the relationships between the model’s output and the attributes of each town (such as population, area, vaccination rates, and age distribution) were examined, to see if these attributes have an impact on the model’s output.
In [23] a multilayer network with an extended SIR disease model taking into account homes, transport, workplaces, schools, religious activities, and random encounters was considered for the COVID-19 virus in Brazil. Due to efficiency issues, they considered only a population of agents that matches census data of Brazil and then scaled up their results. By explicitly calculating the demand for hospital ICUs in the case where the schools and universities are closed, social isolation of individuals over sixty is imposed and home quarantine is proposed in a voluntary basis, they show that the brazilian health system cannot cope with the demand.
EnerPol is another agent-based simulation framework used in disease spread in [24] for influenza and COVID-19 epidemics in Switzerland. They offer a stochastic model for daily activities as well as a mobility model and they also take into account mesoscopically the weather. All this information is extracted from publicly available data. The daily activities model, generate the contacts when agents are in the same place (workplace, school, etc.) while the mobility model allows for taking into account public/private transportation. For the mobility model, the road network and the train network as well as any public transportation method have been taken into account (e.g., buses or airports). For approximately 9 million agents over a 3-month period with sub-hourly time steps, a single scenario requires a few hours to run on a GPU.
A less sophisticated model called REINA (2020) (Realistic Epidemic Interaction Network Agent) [25] maintains 1.6 million agents in the region of Helsinki University Hospital, Finland. The implementation is open-source and one instance runs within a few seconds on their online platform. The agents are individuals with certain properties while the epidemic model is basically an SEIR with additional states related to hospitalization or ICU. The contact network is rather simple: each day an agent according to some age-dependent distribution has certain random contacts. Thus, the contacts are basically random (homogenous population mixing) and there is no consideration to model real social networks (e.g., working environments).
FRED (Framework for Reconstructing Epidemic Dynamics) is tailored for epidemic diseases in the USA. FRED is an open-source agent-based modeling system that is free to use and closely based on models used in earlier studies of the pandemic flu. FRED makes use of open-access census-based synthetic populations that accurately reflect the demographic and geographic diversity of the population, as well as social networks in the workplace, in homes, and in schools. Every state and county in the United States as well as a few other countries presently have access to FRED epidemic models [26].
In [27], the authors use an SEIR model for case importation and an individual-based model (IBM) for modeling the spread of pandemic influenza in Italy. The impact of various control strategies were assessed. Travel destinations that matched the information from the 2001 census for the 57 million Italians were used. Several values (, , and 2) to assess the effect of control methods (vaccination, antiviral prophylaxis, international air travel restrictions, and increased social distancing) were used.
In [28], an age-structured agent-based model of the Canadian population to simulate how public health actions at present and anticipated levels may affect the spread of SARS-CoV-2 was created. Case identification and isolation, contact tracing and quarantine, physical seclusion, and community closures were among the interventions that were tested separately and in combination.
In [29] they simulate the spread of COVID-19 Omicron by using an innovative three-dimensional agent-based model that takes into account Hong Kong’s vertically extended hyperdense urban environment. The model evaluated the efficacy of the "zero-COVID" initiatives, such as citywide lockdown and mandatory universal testing (CUT), that were under discussion during the Omicron wave in Hong Kong. It was discovered that even quicker and tougher execution was required for such rigorous interventions to be successful. They conclude that adaptable long-term methods for controlling and preventing future epidemics should also be taken into consideration.
In [30], the COVID-19 spread among the 11.2 million residents of Shenzhen City, China, using a spatially explicit agent-based model was replicated. It was achieved by integrating huge mobile phone tracking records, census data, and building features. The model was used to determine the likelihood of a COVID-19 comeback if sporadic cases appeared in a city that had been entirely restored after it had been validated by local epidemiological evidence. At different degrees of public compliance, combined scenarios of three crucial non-pharmaceutical treatments (contact tracking, mask-wearing, and quick testing) were evaluated.
In [31], an agent-based model is presented that replicates the spatiotemporal patterns of COVID-19 epidemic. The effects of various COVID-19 outbreak control tactics, including office closures, social exclusion, and closing of schools and educational facilities, in Urmia City, Iran are examined. All control methods used in Urmia city together with the accompanying actions of each control strategy were incorporated into the ABM. The transmission of COVID-19 between human agents was replicated using the SEIRD propagation model.
In [32], an agent-based model named INFEKTA is proposed for modeling the spread of infectious diseases subject to social distance regulations. INFEKTA combines demographic data (population density, age, and different types of people) from geographical regions of the actual town or city under investigation with the transmission dynamics of a particular disease (according to parameters discovered in the literature). Agents (virtual people) can roam through a complicated network of accessible venues defined on a Euclidean space that represents a town or city in accordance with their mobility patterns and the imposed social separation policy. With one million virtual people, INFEKTA simulates the COVID-19 transmission dynamics in Bogotá, the capital of Colombia, under various social exclusion policies. Based on the sensitivity study of the effects of social distance policies, they concluded that the implementation of "medium" strength social distance policies (i.e., closure of of the sites) significantly reduces the spread of the disease.
In [33], COVID-19 propagation modeling results for several mitigation and confinement scenarios are presented for the Madrid, Spain metropolitan region. Utilizing EpiGraph, an epidemic model that has been enhanced to replicate COVID-19 spread, these scenarios were put into practice and tested. In order to create a social interaction model that accurately reflects a variety of individual and group traits as well as their unique linkages, EpiGraph analyzes connection patterns in social networks. Along with the epidemiological and social interaction components, a transportation model is used to simulate how individuals move across short and large distances. These characteristics provide EpiGraph the ability to replicate the COVID-19 development and identify the medium-term consequences of the virus when using mitigation techniques, in addition to the ability to model scenarios with millions of people and apply various contention and mitigation mechanisms. In the Madrid metropolitan region, EpiGraph achieves closely linked infection and death curves associated with the first wave, attaining comparable seroprevalence levels. The authors demonstrate the reduction of the mortality toll when a selective lockdown policy for elderly (over 60) is imposed. Additionally, the impact of mask-wearing after the initial wave was considered, demonstrating that a key element in limiting the spread of the virus is the proportion of people who wear masks as instructed.
In [34], a method for calculating the level of immunization in the Austrian population and a discussion about possible repercussions on the effects of herd immunity were discussed. A calibrated agent-based simulation model that accurately simulates the COVID-19 epidemic in Austria is used to determine vaccination rates. The number of vaccinated individuals may be determined from the generated synthetic individual-based statistics. Then, by altering the acquired degree of vaccination in simulations of an imagined uncontrolled epidemic wave, the pandemic’s course to show potential implications on the effective reproduction rate was extrapolated.
In [35], an iterative process based on data from land use, questionnaire surveys, and population censuses was used to create a synthetic population for American Samoa. The population serves as the foundation for an agent-based model created primarily to close knowledge gaps regarding the transmission and eradication of lymphatic filariasis while also being easily adaptable to mimic other infectious diseases. The statistically realistic population and household structure, as well as the high-resolution geographic placements of households, were characteristics of the synthetic population. From 2010 to 2050, the population was simulated over a 40-year period. The projected and estimated populations from the U.S. Census Bureau were contrasted with those from the simulation. The findings suggested that contrary to the huge number of emigrants that were seen, the total population would continue to decline. The study indicated that the population was ageing, consistent with the estimates from the Bureau and the two latest population censuses. The examination of sex ratios across various age groups indicated a rise in the percentage of males in both the 0–14 and 15–64 age brackets. Concerning household size, the simulation consistently followed a Gaussian distribution, with an average size close to . Interestingly, this average size was slightly lower than the initial average size of .
In [36], a population-based prospective study on mixing patterns in eight European countries using a conventional paper-diary method was conducted. It was found that across many European countries, mixing patterns and contact features were remarkably similar. Strongly assortative age-related interaction patterns were seen, with young adults and schoolchildren in particular being more likely to associate with people of similar ages. Preliminary modeling predicts that during this measurement’s initial epidemic phase, when the population is most vulnerable, children aged 5 to 19 will have the highest prevalence of a new virus disseminated by social contacts.
In [37], the researchers focus on developing a high-resolution, data-driven agent-based model to analyze the spread of COVID-19 in five Spanish cities: Barcelona, Valencia, Seville, Zaragoza, and Murcia. Utilizing synthetic populations based on multiple data sources, the model incorporates detailed interaction environments through multilayer networks, considering home, nursing homes, school, work, university, and community layers. The research aims to simulate and assess the impact of various non-pharmaceutical interventions on COVID-19 transmission. The work addresses the need for quantitatine approaches to characterize intervention impacts, which can vary based on cultural, regional, and population-specific circumstances. By presenting a detailed framework, the study offers a tool for simulating different intervention scenarios, contributing to evidence-based decision-making in managing the pandemic. The model’s effectiveness is demonstrated through a case study, illustrating the impact of key interventions in the studied cities.
In [38], the limitations of existing models at capturing COVID-19’s impact on human mobility at a neighborhood level are addressed. Employing an agent-based model (VIABLE), the study simulates individual mobility choices based on social activities in neighborhoods, focusing on Porto Alegre, Brazil. The model considers agents’ adaptation to exposure risks and their impact on well-being, revealing temporal variations and segregation in mobility patterns among agents with different vulnerability levels. It highlights the shift in mobility choices during the pandemic, influenced by socio-demographic factors like age, car ownership, and economic status. While previous studies explored mobility tendencies at larger scales, this model aims to bridge the gap, providing insights into individual-level adaptations and neighborhood-specific mobility patterns under COVID-19, offering a nuanced perspective for urban planning and public health interventions.
In [39], the spread of a viral infection was modeled using agents representing citizens of the Moscow Oblast, Russia. In [40], an agent-based model framework was created to predict the Liberian Ebola epidemic in 2014–2015 and then used for Ebola forecasting. GSAM [41] is a global scale (billion agents) ABM Java framework. Its efficiency is critically based on the spatial homogeneity of the population at a specific granularity level. The GSAM is an agent-based epidemic modeling high-performance distributed platform that can simulate a disease outbreak in a population of several billion agents.
There are numerous other relevant research works. In [42], the applications of three simulation approaches (System Dynamics Model - SDM, Agent-Based Model - ABM, and Discrete Event Simulation - DES) and their hybrids in COVID-19 research are systematically reviewed. Out of 372 eligible papers, 72 focused on COVID-19 transmission dynamics, 204 evaluated interventions, 29 predicted the pandemic, and 67 investigated the impacts of COVID-19. ABM was the most widely used simulation method (275 papers), followed by SDM (54 papers), DES (32 papers), and hybrid models (11 papers). The primary focus was on evaluating and designing intervention scenarios, accounting for of the papers.
Table 1.
Indicative Agent-Based Models comparison per country
| Country | Population Creation | Number of Agents | Model type | Infection Model | Year | Reference |
|---|---|---|---|---|---|---|
| Australia | census, national data sources | 0.5m | several mixing groups | SEIR | 2020 | [20] |
| France | previous work, papers | 0.5m extrapolated to 67m | stochastic microsimulation ABM | not defined | 2020 | [21] |
| Ireland | census mainly | 0.1m | NetLogo User Community Models | SEIR | 2018 | [22] |
| Brazil | census | 10m | multi-layer network | SIRD | 2020 | [23] |
| Switzerland | synthetic population from census | 9m | ABM and a stochastic model that simulates, on a sub-hourly timescale, the different daily activities of all individuals | not defined | 2020 | [24] |
| Finland | census statistics | 1.6m | random interactions | SEIR | 2020 | [25] |
| USA | synthetic population from census | 30m | mixing patterns | SEIRS | 2013 | [26] |
| Italy | census | 57m | multi-layer network | SEIR | 2008 | [27] |
| Canada | projections | not defined | multi-layer network | SEIR | 2020 | [28] |
| Hong Kong | synthetic population from census | 0.73m | three-dimensional vertically expanded | not defined | 2022 | [29] |
| Shenzen, China | mobile phone records, census | 11.2m | spatially explicit ABM | SLIR | 2021 | [30] |
| Urmia, Iran | census and spatial data | 0.75m | mobile & static agents | SEIRD | 2020 | [31] |
| Bogotá, Colombia | synthetic population from census | 9m | random network | SEIRMD | 2021 | [32] |
| Madrid, Spain | census and social network data | 5m | multi-layer network | SEIR | 2021 | [33] |
| Austria | census | 9m | multi-layer network | not defined | 2022 | [34] |
| Moscow oblast, Russia | census | 10m | multi-layer network | SLIR | 2022 | [39] |
| American Samoa | census, questionnaires and land usage | 0.055m | age and household distribution, population evolution | not defined | 2017 | [35] |
3. Methodology
There are many challenges in developing ABM systems. First, an appropriate theoretical framework must be in place in order to describe and reason about this system. We choose to use graph dynamical systems [43] that model discrete dynamical processes on networks. This choice suits perfectly our case due to our intended use of multilayer networks as the environment of the ABM. Second, the construction of the synthetic population requires the extensive use of data that come from multiple sources. These data may be incomplete, at different levels of granularity (e.g., large or small age groups), and may be contradictory. Data fusion under these conditions is quite challenging. Third, the number of agents, the number of scenarios, the number of total interactions, and the time granularity make unavoidable the use of parallelism. In addition, the storage of all these networks requires special care, since naive storage may be space-consuming and time inefficient with respect to retrieval. In this paper, we do not consider this challenge since we focus on a small area of Greece. Fourth, the sophistication of the disease propagation model drives the functionality of the system. Simple models like SIR are easy to apply and have only a few parameters failing, however, to express many important states for epidemiology (like Asymptomatic). At the same time, they do not support sophisticated propagation models based on the characteristics of the particular virus (air-borne or contact-based). The propagation model must allow for building different scenarios based on interventions (e.g., obligatory masks in public spaces) or behavior modification (e.g., stay home when sick). In this paper we employ the rather simple SEIR model.
Our approach is similar to that of [44]. The intended method for generating the synthetic population and its representation is depicted in Figure 1 (inspired by [45]). We discuss all these steps, although our results do not contain spatial information.
- Create Agents - Individuals: Create individuals and their characteristics based on census data using an SR approach [46]. We adopt the SR approach since only aggregate data is available for Greece.
- Create Living Space: This is the spatial information injected into the model. We create space for representing relations within homes, work locations and schools. We do not consider geographical information.
The characteristics of the population real data are used to generate multilayer networks that define contacts or relations between agents. These layers have been constructed independently. This independence assumption is quite strong since there are statistical dependencies that should be taken into account. For example, we first generate individuals and then we place them in households. There are approaches that generate households with individuals in a single step, aiming at getting more realistic populations. We have defined the following layers:
- Household: A set of cliques for the members of a family. This is the easiest task considering that families have already been formed from the first step. This network represents relations and as such, it is static within a limited time horizon.
- Work: A set of small-world networks between agents in the same workplace. This is a contact network. An open-source method for creating home/work/school networks that follow this methodology can be found in [50].
- Schools: A set of small-world networks corresponding to the interactions between students.
- Random contact networks: They correspond to random interactions between agents within the world. Small-world networks are used and they changes between successive steps.
- Friendship Networks: Strong ties in the form of friendships are represented by a static network that could further give rise to more regular contacts. This network is formed by a social mixing matrix that measures the frequency of relationships between agents in the same or different age groups. We have adopted the social mixing matrix approach that is inferred by publicly available data of physical contacts and interactions for a country with a similar socio-economic structure and mentality like Italy [51].
Concerning the propagation model, we adopt a simple SEIR (Susceptible-Exposed-Infected-Recovered) model with a small set of parameters. The disease propagation model is executed in multiple scenarios. A scenario specifies the behavior of individuals as well as the applied public policies. Such scenarios are implemented by changing accordingly the layered networks while affecting the probabilities of the disease model.
3.1. The Synthetic Population
Synthetic populations, generated using computer simulation techniques, are statistical representations of actual populations. They have a vital role in research and policy analysis. They provide valuable insights into the behavior and characteristics of populations, while also allowing for the evaluation of different policies and interventions on population outcomes. To create a synthetic population, various attributes like age, gender, race, education, occupation, income, and location are carefully specified. Statistical models and algorithms are then used to simulate these attributes, either by utilizing real-world data or by making assumptions about their distribution within the population.
We obtain data from publicly accessible sources. Demographics and census data are otained from the Hellenic Statistical Authority 1, other open data from the Ministry of Digital Governance 2, geographical data from open geodata 3 and workforce data from Greek Manpower Employment Organization 4. We create a synthetic population mimicking the real attributes of the center of a major Greek city (Patras). We used real data (e.g., age and gender distribution) for the city of Patras from the Greek Statistic Service (ELSTAT) 5. We assume that all agents younger than 18 are students and we assign them an educational level per age (e.g. elementary school for ages between 6 and 12). For agents older than 18, we assume that either all work or that they are unemployed. We use unemployment data from the Greek Manpower Employment Organization (DYPA). We assume that all agents above 65 are retired. Then, we calculate family size from the Greek Statistic Service (ELSTAT) 6. Agent’s attributes are shown in Table 2.
The creation of the synthetic population is based on real data from the city of Patras and consists of the following steps:
- Collection and preprocessing of the data: We collected the real data on the demographics, education, employment, and other characteristics of the population from the Greek Statistic Service (ELSTAT) and the Greek Manpower Employment Organization (DYPA). This data is cleaned by removing missing and irrelevant values, in order to ensure that it is accurate and consistent.
- Definition of agent attributes: Based on the data collected in the previous step and the assumptions about the characteristics of the population, we defined the attributes of the agents in the synthetic population, as shown in Table 2. We use a Python dictionary to store the attributes of each agent.
- Generation of the synthetic data: We used statistical model distributions to generate synthetic data. This data represents the characteristics of the individual members of the population. These are based on the real aggregated data and the assumptions about the distribution of these characteristics.
- Assignment of the attributes to the agents: We iterate over the agents, and assign the generated attributes to each agent, based on the synthetic data from the previous step. In other words, we "expanded" the aggregated data to agents representing members of the population by simulating the real distributions.
- Calculation and initialization of additional attributes: Calculation of any additional attributes that are not included in the real data, such as the infection status of each agent. This is done by randomly initializing a small number of the agents as "Infected" and the rest as "Susceptible".
The synthetic population is modeling the population of the center of Patras city, based on the latest census by the Greek Statistical Service. We chose to model only the center of the city because of the homogeneity and statistical similarities in the population/agents. The population is organized in a multilayer network. The layers of the network correspond to families, schools, workplaces, age-based random interactions and we create at each step of the execution of the model a single layer that contains the random interactions.
We hypothesize family sizes from 1 to 10 members and distribute according to the distribution of the Greek population. All agents are assigned a family. If they are students, they are assigned a school and if they work, they are assigned a workplace. We assume that workplaces have 1 to 25 employees. This models the mean number of contacts in the workplace and not its total size. We distribute the employees to each workplace (Work_ID) with a Poisson distribution [52,53], since we couldn’t find statistical data from public sources.
As for students, we place them based on their age to nursery, kindergarten, elementary, and high school. All eligible students attend school. Ministry of Education’s data provide the number of existing schools per every level of education. The number of students for every school is produced by dividing the total number of available students by the number of schools. Then, we allocate the students to schools.
3.2. Propagation Model
We implement an SEIR infection model (Susceptible - Exposed - Infected - Recovered), which is an extension of the classic textbook SIR model [54]. SEIR models are extensively used in epidemiological research [55]. A population of size N is partitioned into compartments that contain individuals who are Susceptible (S), Exposed (E - infected but not yet infectious), Infectious (I), and Recovered (R) [56,57]. This is a simple model that assumes no changes in the population (deaths or births), no immunity or vaccination, and no measures (e.g. obligatory usage of masks, lock-downs, etc.). In addition, due to the limited time horizon of the simulation (a small number of months), we assume that once an agent becomes recovered, she will never become infected again. There is a nice comparison of epidemiological models for transmission of SARS-CoV-2 in [58] and [59]. The parameters beta (), sigma (), and gamma (), are key factors in the SEIR model [55]:
- : This is the transmission rate or contact rate, representing the probability of transmitting the disease from an infectious individual to a susceptible. A higher generally leads to a faster spread of the disease.
- : This parameter represents the rate at which exposed individuals become infectious. The reciprocal of is the mean incubation period. It accounts for the time between exposure to the virus and the individual becoming infectious.
- : This is the recovery rate, indicating the fraction of infected individuals recovering per unit of time. The reciprocal of is the average infectious period. A shorter infectious period corresponds to a higher recovery rate.
We have set these parameters in our experiments based on [60,61,62], as shown in Table 4. Finding transmission and recovery statistical data for the Greek epidemic was proven difficult, and thus we used values from the literature.
The propagation model executes as follows: we assume that in the beginning, a small number (e.g., 5) of agents (seeders) are infected. Then, at each "tick" of the clock, which corresponds to a day, they can infect one of their neighbors in their networks (family, work, school). The probability of infection varies in each network (e.g., it is much easier to infect a member of your family due to proximity and many interactions). There are also two "random" layers of interactions. An infected agent can infect a random agent with a very small probability. Additionally, agents with similar ages (based on the daily number of contacts from [36]) also infect one another with a small probability. The number of contacts for the age-based random layer was created by taking these probabilities from the Italian network [36]. This is because, there aren’t any such data for Greece and there are many similarities between Greeks and Italians concerning their social relations. Finally, a recovered agent cannot become susceptible again, due to the small time of the simulation; that is, we assume temporary immunity.
4. Experimental Results
We run a series of experiments to verify and validate our model. Our experiments focused on some interventional measures. These scenarios are presented in Table 3 and the comparative results in Figure 2 and Figure 3:
Table 3.
Interventional Scenarios
| Scenario | Description | |
|---|---|---|
| 1 | Base Case | The model runs without any interventional measures |
| 2 | School Closure | All schools are closed, all other layers remain |
| 3 | Workplace Closure | All workplaces are closed, all other layers remain |
| 4 | Targeted Age Group Interventions | All agents above 60 years old now get infected randomly with a tenth of the original possibility |
| 5 | Social Distancing & Mask usage | Possibility of Infection becomes a third of the original in all social interactions except inside families |
| 6 | Mild lock-down with (mostly) remote work | All schools are closed (tele-education), Workplace and random infection possibilities become a fourth of the original |
| 7 | Moderate lock-down with (mostly) remote work | All schools are closed (tele-education), Workplace and random infection possibilities become a sixth of the original |
| 8 | Strict lock-down with (mostly) remote work | All schools are closed (tele-education), Workplace and random infection possibilities become an eighth of the original |
Table 4.
Parameters used in various scenarios
| _FMLY | _WORK | _SCH | _RNDM | _SAME_AGE | |||
|---|---|---|---|---|---|---|---|
| 1 | 0.8 | 0.1 | 0.04 | 0.01 | 0.005 | 0.1 | 0.2 |
| 2 | 0.8 | 0.1 | 0 | 0.01 | 0.005 | 0.1 | 0.2 |
| 3 | 0.8 | 0 | 0.04 | 0.01 | 0.005 | 0.1 | 0.2 |
| 4 | 0.8 | 0.1 | 0.04 | 0.01 (<60y) | 0.005 | 0.1 | 0.2 |
| 0.8 | 0.1 | 0.04 | 0.01/10 (>60y) | 0.005/10 | 0.1 | 0.2 | |
| 5 | 0.8 | 0.1/3 | 0.04/3 | 0.01/3 | 0.005/3 | 0.1 | 0.2 |
| 6 | 0.8 | 0.1/4 | 0 | 0.01/4 | 0.005/4 | 0.1 | 0.2 |
| 7 | 0.8 | 0.1/6 | 0 | 0.01/6 | 0.005/6 | 0.1 | 0.2 |
| 8 | 0.8 | 0.1/8 | 0 | 0.01/8 | 0.005/8 | 0.1 | 0.2 |
The multi-layer agent-based model was built using python/mesa [63] framework.
4.1. Discussion
Our study provides insights into the behavior and characteristics of the synthetic population we created, highlighting its implications for policy analysis and decision-making. Through meticulous adherence to the steps of collecting and preprocessing real data, defining agent attributes, generating synthetic data, assigning attributes to agents, and calculating additional attributes, we successfully developed a synthetic population that carries the most basic characteristics of the population of the greek city of Patras, Greece.
The simulation studies aimed to assess how different intervention scenarios impact the spread of COVID-19 among the Greek population. Each scenario represents a unique set of measures designed to slow down the transmission of the virus. Over the course of 100 time steps, these experiments provide insights into the effectiveness of each intervention approach. In the absence of any intervention (Scenario 1), the model depicts a rapid increase in infections, acting as a baseline for comparison. Closing all schools (Scenario 2) results in a small but noticeable decrease in infections and a delay in the peak, especially for younger students. Similarly, closing all workplaces (Scenario 3) leads to a drop in infections, highlighting the impact of workplace interactions on transmission dynamics. Tailoring interventions for individuals over 60 (Scenario 4) shows a marginal effect in flattening the curve. All these scenarios emphasize the rather small impact that these policies have when applied separately. The combination of social distancing and mask usage (Scenario 5) results in a substantial decline in infections, showcasing the effectiveness of these measures in lowering the overall transmission rate. The most aggressive response, a strict lockdown with remote work (Scenarios 6-8), leads to the greatest reduction in infections, highlighting the significance of a multifaceted strategy that includes restricting social interactions, implementing remote work, and educational initiatives.
Comparatively, scenarios involving school and workplace closures, along with targeted interventions for specific age groups, prove effective in controlling the virus. The combined use of masks and social distancing emerges as a potent tactic, underscoring the role of individual behaviors in limiting transmission. While the strict lockdown scenario is highly effective, policymakers must carefully consider its societal and economic implications, emphasizing the need for a balanced approach.
It is crucial to note that the model’s accuracy relies on precise parameterization and assumptions, and thus real-world variations may occur. Individual compliance with interventions may vary, and the simulations assume homogeneous agent behavior. Changes in the impact of interventions may occur with new variations or shifts in human behavior over time. These simulation results provide policymakers with valuable insights for evidence-based decision-making. Tailored interventions that consider societal norms and demographic variables could offer a more focused and sustainable strategy.
5. Conclusions
Our study demonstrates the value of synthetic populations in understanding population behavior and evaluating policy interventions. The findings from our analysis provide valuable insights for policy analysis and decision-making processes. However, it is crucial to interpret the results cautiously and consider the limitations of the ABM approach. By addressing these considerations and continuously advancing synthetic population modeling, we can contribute to evidence-based policy-making and enhance the well-being of communities and societies.
The results presented in this paper are preliminary and constitute a first step. Our next steps are the following:
- Generalize our model to the whole Greek territory. In addition, we want to add more behaviors/traits in the population based on census and other publicly available data.
- Extend the propagation model to take into account various states for the agents. This will make the model more realistic but at the same time will make it harder to tune since the number of parameters will increase.
- Contact epidemiological research teams within Greece in order to further advance and tune the model and the system based on experts’ opinions.
- Extend the generator of the synthetic population towards other goals (e.g., transportation studies).
- Extend the model to look at social implications of interventions, like economic implications, e.g., what is the economic cost of imposing an upper bound on the number of customers as a function of the area of a shop?
We also intend to use methods for data-driven parameter calibration (e.g., based on machine learning methods [64]) and rudimentary sensitivity/parameter analysis. Finally, efficiency issues will have to be considered and mitigated. In particular, to accomplish the aforementioned goals, we require the execution of multiple scenarios on large populations with complicated propagation models. Parallelism or distributed computing can greatly enhance the efficiency of the ABM approach and we intend to use ABM libraries that offer these computational modes.
Author Contributions
Conceptualization, K.T. and V.T.; methodology, K.T.; software, V.T.; validation, K.T., V.T.; formal analysis, V.T.; investigation, K.T.; resources, V.T.; data curation, V.T.; writing—original draft preparation, V.T.; writing—review and editing, K.T.; visualization, V.T.; supervision, K.T.; project administration, V.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable
Informed Consent Statement
Not applicable
Data Availability Statement
Source code and reported data can be found here: https://github.com/vorlon83/abm-patras-greece.git
Acknowledgments
We would like to thank Prof. Dr. Spyros Sioutas and Theodoros Petrakis for their valuable support.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bjørnstad, O.N.; Shea, K.; Krzywinski, M.; Altman, N. Modeling infectious epidemics. Nature Methods 2020, 17, 455–456. [Google Scholar] [CrossRef] [PubMed]
- Barrett, C.; Bisset, K.; Leidig, J.; Marathe, A.; Marathe, M.V. An Integrated Modeling Environment to Study the Co-evolution of Networks, Individual Behavior and Epidemics. AI Magazine 2010, 31, 75–87. [Google Scholar] [CrossRef]
- Barrett, C.; Bisset, K.; Leidig, J.; Marathe, A.; Marathe, M. Economic and social impact of influenza mitigation strategies by demographic class. Epidemics 2011, 3, 19–31. [Google Scholar] [CrossRef]
- Bonabeau, E. Agent-based modeling: Methods and techniques for simulating human systems. Proceedings of the National Academy of Sciences 2002, 99, 7280–7287. [Google Scholar] [CrossRef] [PubMed]
- Rapti, A.; Tsichlas, K.; Sioutas, S.; Tzimas, G. Virus propagation: threshold conditions for multiple profile networks. Knowledge and Information Systems 2018, 60, 807–836. [Google Scholar] [CrossRef]
- Yaméogo, B.F.; Gastineau, P.; Hankach, P.; Vandanjon, P.O. Comparing Methods for Generating a Two-Layered Synthetic Population. Transportation Research Record 2021, 2675, 136–147. [Google Scholar] [CrossRef]
- Barthelemy, J.; Toint, P.L. Synthetic Population Generation Without a Sample. Transportation Science 2013, 47, 266–279. [Google Scholar] [CrossRef]
- Ma, L.; Srinivasan, S. Synthetic Population Generation with Multilevel Controls: A Fitness-Based Synthesis Approach and Validations. Computer-Aided Civil and Infrastructure Engineering 2015, 30, 135–150. [Google Scholar] [CrossRef]
- Sun, L.; Erath, A. A Bayesian network approach for population synthesis. Transportation Research Part C: Emerging Technologies 2015, 61, 49–62. [Google Scholar] [CrossRef]
- Wu, H.; Ning, Y.; Chakraborty, P.; Vreeken, J.; Tatti, N.; Ramakrishnan, N. Generating Realistic Synthetic Population Datasets. ACM Trans. Knowl. Discov. Data 2018, 12. [Google Scholar] [CrossRef]
- Borysov, S.S.; Rich, J.; Pereira, F.C. How to generate micro-agents? A deep generative modeling approach to population synthesis. Transportation Research Part C: Emerging Technologies 2019, 106, 73–97. [Google Scholar] [CrossRef]
- Lenormand, M.; Deffuant, G. Generating a Synthetic Population of Individuals in Households: Sample-Free Vs Sample-Based Methods. Journal of Artificial Societies and Social Simulation 2013, 16, 12. [Google Scholar] [CrossRef]
- Fichera, A.; Pluchino, A.; Volpe, R. A multi-layer agent-based model for the analysis of energy distribution networks in urban areas. Physica A: Statistical Mechanics and its Applications 2018, 508, 710–725. [Google Scholar] [CrossRef]
- Interdonato, R.; Magnani, M.; Perna, D.; Tagarelli, A.; Vega, D. Multilayer network simplification: Approaches, models and methods. Computer Science Review 2020, 36, 100246. [Google Scholar] [CrossRef]
- Beckman, R.J.; Baggerly, K.A.; McKay, M.D. Creating synthetic baseline populations. Transportation Research Part A: Policy and Practice 1996, 30, 415–429. [Google Scholar] [CrossRef]
- Müller, K.; Axhausen, K.W. Population Synthesis for Microsimulation: State of the Art. Transportation Research Board 90th Annual Meeting, 2010.
- Gallagher, S.; Richardson, L.; Ventura, S.; Eddy, W. SPEW: Synthetic Populations and Ecosystems of the World. Journal of Computational and Graphical Statistics 2017, 27. [Google Scholar] [CrossRef]
- Center, M.P. Integrated Public Use Microdata Series, International: Version 7.2 [dataset]. Minneapolis, MN: IPUMS, 2019. [CrossRef]
- Lorig, F.; Johansson, E.; Davidsson, P. Agent-Based Social Simulation of the Covid-19 Pandemic: A Systematic Review. Journal of Artificial Societies and Social Simulation 2021, 24, 5. [Google Scholar] [CrossRef]
- Chang, S.L.; Harding, N.; Zachreson, C.; Cliff, O.M.; Prokopenko, M. Modelling transmission and control of the COVID-19 pandemic in Australia 2020. [CrossRef]
- Hoertel, N.; Blachier, M.; Blanco, C.; Olfson, M.; Massetti, M.; Rico, M.S.; Limosin, F.; Leleu, H. Lockdown exit strategies and risk of a second epidemic peak: a stochastic agent-based model of SARS-CoV-2 epidemic in France 2020. [CrossRef]
- Hunter, E.; Namee, B.M.; Kelleher, J. An open-data-driven agent-based model to simulate infectious disease outbreaks. PLOS ONE 2018, 13, e0208775. [Google Scholar] [CrossRef] [PubMed]
- Canabarro, A.; Tenório, E.; Martins, R.; Martins, L.; Brito, S.; Chaves, R. Data-driven study of the COVID-19 pandemic via age-structured modelling and prediction of the health system failure in Brazil amid diverse intervention strategies. PLoS One 2020, 15, e0236310. [Google Scholar] [CrossRef]
- Marini, M.; Chokani, N.; Abhari, R.S. COVID-19 Epidemic in Switzerland: Growth Prediction and Containment Strategy Using Artificial Intelligence and Big Data 2020. [CrossRef]
- Tuomisto, J.T.; Yrjölä, J.; Kolehmainen, M.; Bonsdorff, J.; Pekkanen, J.; Tikkanen, T. An agent-based epidemic model REINA for COVID-19 to identify destructive policies 2020. [CrossRef]
- Grefenstette, J.J.; Brown, S.T.; Rosenfeld, R.; DePasse, J.; Stone, N.T.; Cooley, P.C.; Wheaton, W.D.; Fyshe, A.; Galloway, D.D.; Sriram, A.; Guclu, H.; Abraham, T.; Burke, D.S. FRED (A Framework for Reconstructing Epidemic Dynamics): an open-source software system for modeling infectious diseases and control strategies using census-based populations. BMC Public Health 2013, 13. [Google Scholar] [CrossRef]
- degli Atti, M.L.C.; Merler, S.; Rizzo, C.; Ajelli, M.; Massari, M.; Manfredi, P.; Furlanello, C.; Tomba, G.S.; Iannelli, M. Mitigation Measures for Pandemic Influenza in Italy: An Individual Based Model Considering Different Scenarios. PLoS ONE 2008, 3, e1790. [Google Scholar] [CrossRef] [PubMed]
- Ng, V.; Fazil, A.; Waddell, L.A.; Bancej, C.; Turgeon, P.; Otten, A.; Atchessi, N.; Ogden, N.H. Projected effects of nonpharmaceutical public health interventions to prevent resurgence of SARS-CoV-2 transmission in Canada. Canadian Medical Association Journal 2020, 192, E1053–E1064. [Google Scholar] [CrossRef] [PubMed]
- Koh, K.; Tang, K.C.; Axhausen, K.; Loo, B.P. A metropolitan-scale, three-dimensional agent-based model to assess the effectiveness of the COVID-19 Omicron wave interventions in a hyperdense city: a case study of Hong Kong. International Journal of Infectious Diseases 2022, 122, 534–536. [Google Scholar] [CrossRef] [PubMed]
- Yin, L.; Zhang, H.; Li, Y.; Liu, K.; Chen, T.; Luo, W.; Lai, S.; Li, Y.; Tang, X.; Ning, L.; Feng, S.; Wei, Y.; Zhao, Z.; Wen, Y.; Mao, L.; Mei, S. A data driven agent-based model that recommends non-pharmaceutical interventions to suppress Coronavirus disease 2019 resurgence in megacities. Journal of The Royal Society Interface 2021, 18, 20210112. [Google Scholar] [CrossRef] [PubMed]
- Gharakhanlou, N.M.; Hooshangi, N. Spatio-temporal simulation of the novel coronavirus (COVID-19) outbreak using the agent-based modeling approach (case study: Urmia, Iran). Informatics in Medicine Unlocked 2020, 20, 100403. [Google Scholar] [CrossRef] [PubMed]
- Gomez, J.; Prieto, J.; Leon, E.; Rodríguez, A. INFEKTA—An agent-based model for transmission of infectious diseases: The COVID-19 case in Bogotá, Colombia. PLOS ONE 2021, 16, e0245787. [Google Scholar] [CrossRef] [PubMed]
- Singh, D.E.; Marinescu, M.C.; Guzmán-Merino, M.; Durán, C.; Delgado-Sanz, C.; Gomez-Barroso, D.; Carretero, J. Simulation of COVID-19 Propagation Scenarios in the Madrid Metropolitan Area. Frontiers in Public Health 2021, 9. [Google Scholar] [CrossRef] [PubMed]
- Bicher, M.; Rippinger, C.; Schneckenreither, G.; Weibrecht, N.; Urach, C.; Zechmeister, M.; Brunmeir, D.; Huf, W.; Popper, N. Model based estimation of the SARS-CoV-2 immunization level in austria and consequences for herd immunity effects. Scientific Reports 2022, 12. [Google Scholar] [CrossRef]
- Xu, Z.; Glass, K.; Lau, C.L.; Geard, N.; Graves, P.; Clements, A. A Synthetic Population for Modelling the Dynamics of Infectious Disease Transmission in American Samoa. Scientific Reports 2017, 7. [Google Scholar] [CrossRef]
- Mossong, J.; Hens, N.; Jit, M.; Beutels, P.; Auranen, K.; Mikolajczyk, R.; Massari, M.; Salmaso, S.; Tomba, G.S.; Wallinga, J.; Heijne, J.; Sadkowska-Todys, M.; Rosinska, M.; Edmunds, W.J. Social Contacts and Mixing Patterns Relevant to the Spread of Infectious Diseases. PLoS Medicine 2008, 5, e74. [Google Scholar] [CrossRef]
- Rodríguez, J.P.; Aleta, A.; Moreno, Y. Digital cities and the spread of COVID-19: Characterizing the impact of non-pharmaceutical interventions in five cities in Spain. Frontiers in Public Health 2023, 11. [Google Scholar] [CrossRef]
- Peng, Y.; Rodriguez Lopez, J.M.; Santos, A.P.; Mobeen, M.; Scheffran, J. Simulating exposure-related human mobility behavior at the neighborhood-level under COVID-19 in Porto Alegre, Brazil. Cities 2023, 134, 104161. [Google Scholar] [CrossRef] [PubMed]
- Rykovanov, G.N.; Lebedev, S.N.; Zatsepin, O.V.; Kaminskii, G.D.; Karamov, E.V.; Romanyukha, A.A.; Feigin, A.M.; Chetverushkin, B.N. Agent-Based Simulation of the COVID-19 Epidemic in Russia. Herald of the Russian Academy of Sciences 2022, 92, 479–487. [Google Scholar] [CrossRef] [PubMed]
- Venkatramanan, S.; Lewis, B.; Chen, J.; Higdon, D.; Vullikanti, A.; Marathe, M. Using data-driven agent-based models for forecasting emerging infectious diseases. Epidemics 2018, 22, 43–49. [Google Scholar] [CrossRef]
- Parker, J.; Epstein, J.M. A Distributed Platform for Global-Scale Agent-Based Models of Disease Transmission. ACM Transactions on Modeling and Computer Simulation 2011, 22, 1–25. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Liu, S.; Osgood, N.; Zhu, H.; Qian, Y.; Jia, P. Using simulation modelling and systems science to help contain COVID-19: A systematic review. Systems Research and Behavioral Science 2022, 40, 207–234. [Google Scholar] [CrossRef] [PubMed]
- Morveit, H.; Reidys, C. An Introduction to Sequential Dynamical Systems; Springer International Publishing, 2007.
- Bissett, K.; Cadena, J.; Khan, M.; Kuhlman, C. Agent-Based Computational Epidemiological Modeling. Journal of the Indian Institute of Science 2021, 101. [Google Scholar] [CrossRef] [PubMed]
- Jiang, N.; Crooks, A.T.; Kavak, H.; Burger, A.; Kennedy, W.G. A method to create a synthetic population with social networks for geographically-explicit agent-based models. Computational Urban Science 2022. [Google Scholar] [CrossRef]
- Chapuis, K.; Taillandier, P.; Drogoul, A. Generation of Synthetic Populations in Social Simulations: A Review of Methods and Practices. Journal of Artificial Societies and Social Simulation 2022, 25, 6. [Google Scholar] [CrossRef]
- Watthanasutthi, N.; Muangsin, V. Generating synthetic population at individual and household levels with aggregate data. 2016 13th International Joint Conference on Computer Science and Software Engineering (JCSSE), 2016, pp. 1–6. [CrossRef]
- Wickramasinghe, B.N.; Singh, D.; Padgham, L. Building a large synthetic population from Australian census data. CoRR 2020, abs/2008.11660, [2008.11660].
- Murata, T.; Harada, T. Nation-wide synthetic reconstruction method. 2017 IEEE Symposium Series on Computational Intelligence (SSCI), 2017, pp. 1–6. [CrossRef]
- Burger, A.; Oz, T.; Crooks, A.; Kennedy, W.G. Generation of Realistic Mega-City Populations and Social Networks for Agent-Based Modeling. Proceedings of the 2017 International Conference of The Computational Social Science Society of the Americas; Association for Computing Machinery: New York, NY, USA, 2017; CSS 2017. [Google Scholar] [CrossRef]
- Guarino, S.; Mastrostefano, E.; Bernaschi, M.; Celestini, A.; Cianfriglia, M.; Torre, D.; Zastrow, L.R. Inferring Urban Social Networks from Publicly Available Data. Future Internet 2021, 13. [Google Scholar] [CrossRef]
- McGlashan, N. Uses of the Poisson Probability Model with Human Populations. Pacific Viewpoint 1976, 17, 167–174. [Google Scholar] [CrossRef]
- Kawakami, S.; Iwata, T.; Matsuda, K.; Sekimoto, Y. Workplace Assignment to Workers in Synthetic Populations in Japan. IEEE Transactions on Computational Social Systems 2022, pp. 1–10. [CrossRef]
- Kermack, W.O.; McKendrick, A.G. A contribution to the mathematical theory of epidemics. Proceedings of the royal society of london. Series A, Containing papers of a mathematical and physical character 1927, 115, 700–721. [Google Scholar]
- Heng, K.; Althaus, C.L. The approximately universal shapes of epidemic curves in the Susceptible-Exposed-Infectious-Recovered (SEIR) model. Scientific Reports 2020, 10. [Google Scholar] [CrossRef]
- Li, M.Y.; Graef, J.R.; Wang, L.; Karsai, J. Global dynamics of a SEIR model with varying total population size. Mathematical Biosciences 1999, 160, 191–213. [Google Scholar] [CrossRef]
- Berger, D.; Herkenhoff, K.; Mongey, S. An SEIR Infectious Disease Model with Testing and Conditional Quarantine. Technical report, 2020. [CrossRef]
- Purkayastha, S.; Bhattacharyya, R.; Bhaduri, R.; Kundu, R.; Gu, X.; Salvatore, M.; Ray, D.; Mishra, S.; Mukherjee, B. A comparison of five epidemiological models for transmission of SARS-CoV-2 in India. BMC Infectious Diseases 2021, 21. [Google Scholar] [CrossRef] [PubMed]
- Iranzo, V.; Pérez-González, S. Epidemiological models and COVID-19: a comparative view. History and Philosophy of the Life Sciences 2021, 43. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.; Hu, B.; Hu, C.; Zhu, F.; Liu, X.; Zhang, J.; Wang, B.; Xiang, H.; Cheng, Z.; Xiong, Y.; Zhao, Y.; Li, Y.; Wang, X.; Peng, Z. Clinical Characteristics of 138 Hospitalized Patients With 2019 Novel Coronavirus–Infected Pneumonia in Wuhan, China. JAMA 2020, 323, 1061. [Google Scholar] [CrossRef]
- Lauer, S.A.; Grantz, K.H.; Bi, Q.; Jones, F.K.; Zheng, Q.; Meredith, H.R.; Azman, A.S.; Reich, N.G.; Lessler, J. The Incubation Period of Coronavirus Disease 2019 (COVID-19) From Publicly Reported Confirmed Cases: Estimation and Application. Annals of Internal Medicine 2020, 172, 577–582. [Google Scholar] [CrossRef] [PubMed]
- Jayatilaka, R.; Patel, R.; Brar, M.; Tang, Y.; Jisrawi, N.; Chishtie, F.; Drozd, J.; Valluri, S. A mathematical model of COVID-19 transmission. Materials Today: Proceedings 2022, 54, 101–112. [Google Scholar] [CrossRef]
- Kazil, J.; Masad, D.; Crooks, A. Utilizing Python for Agent-Based Modeling: The Mesa Framework. In Social, Cultural, and Behavioral Modeling; Springer International Publishing, 2020; pp. 308–317. [Google Scholar] [CrossRef]
- Platas-López, A.; Guerra-Hernández, A.; Quiroz-Castellanos, M.; Cruz-Ramírez, N. Agent-Based Models Assisted by Supervised Learning: A Proposal for Model Specification. Electronics 2023, 12, 495. [Google Scholar] [CrossRef]
| 1 | https://www.statistics.gr |
| 2 | http://www.data.gov.gr |
| 3 | https://geodata.gov.gr |
| 4 | https://www.dypa.gov.gr/statistika |
| 5 | https://www.statistics.gr/el/statistics/-/publication/SAM03/2011 |
| 6 |
https://www.statistics.gr/documents/20181/1210503/A1602_SAM01_DT_DC_00_2011_03_F_GR.pdf/e1ac0b1c-8372-4886-acb8-d00a5a68aabe
|
Figure 1.
A high-level description of the generation process for the synthetic population.
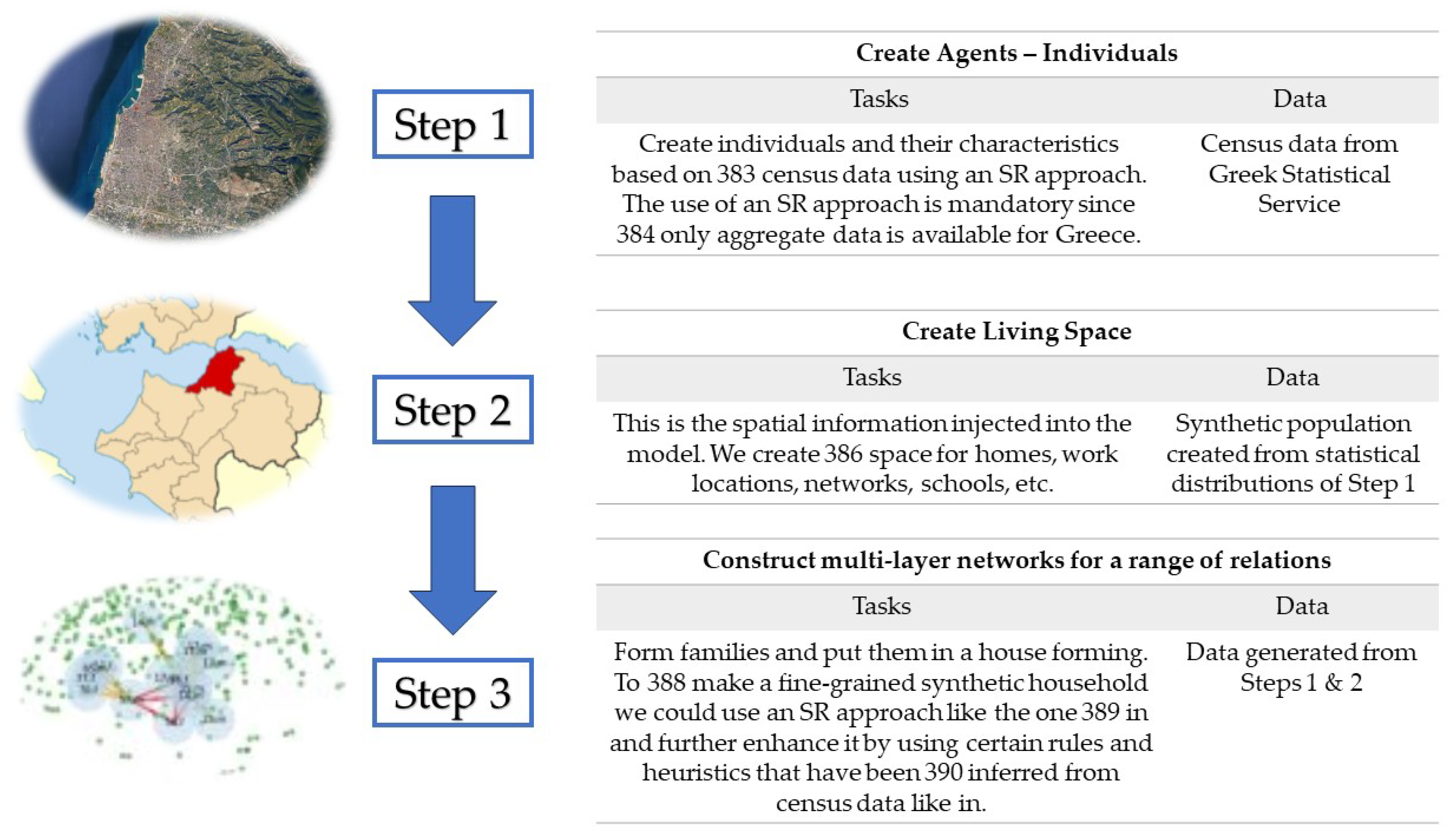
Figure 2.
Comparison of virus spread (infections per step) in different scenarios (180 steps).
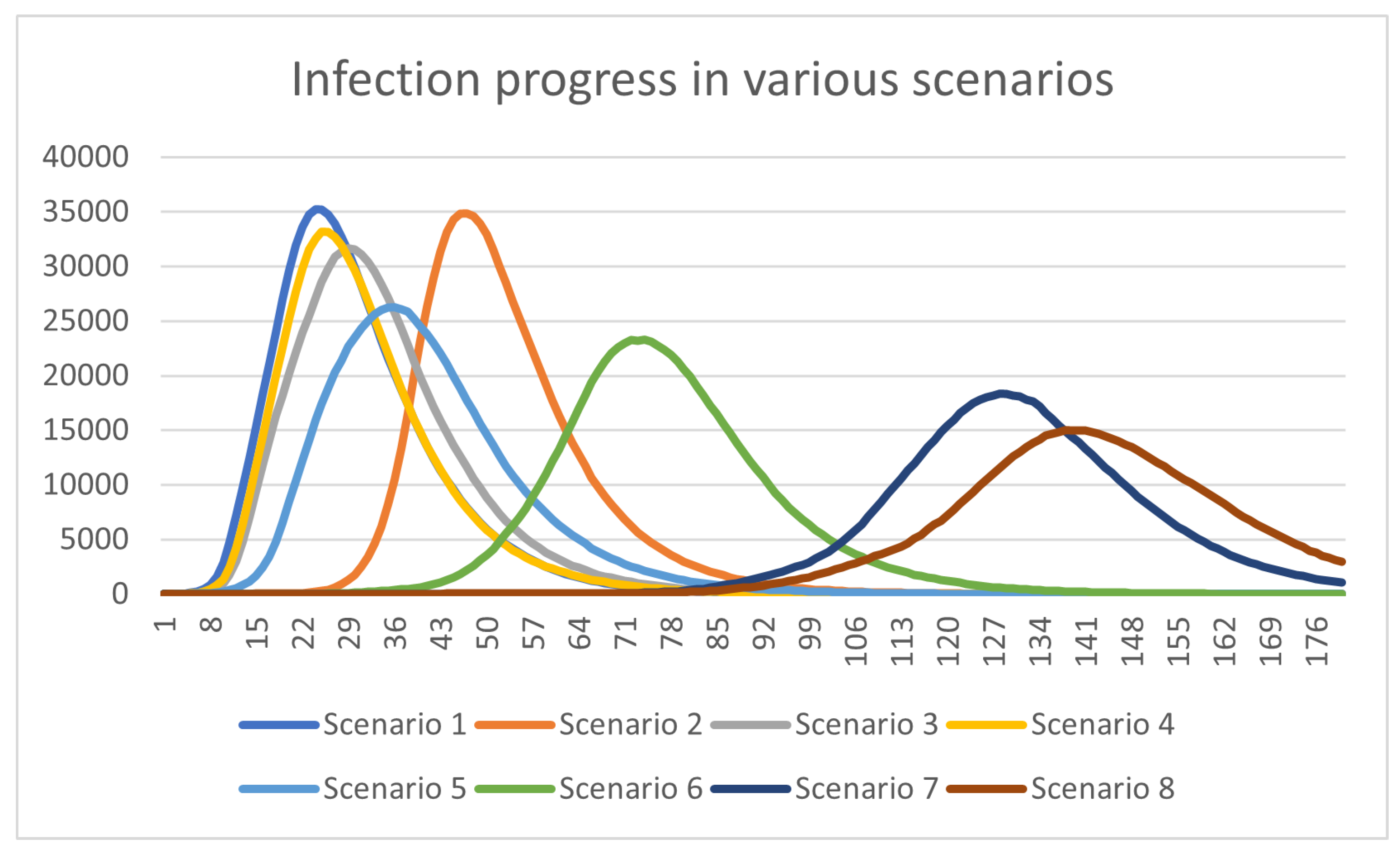
Figure 3.
The progress in 60 steps/days of virus propagation in various scenarios
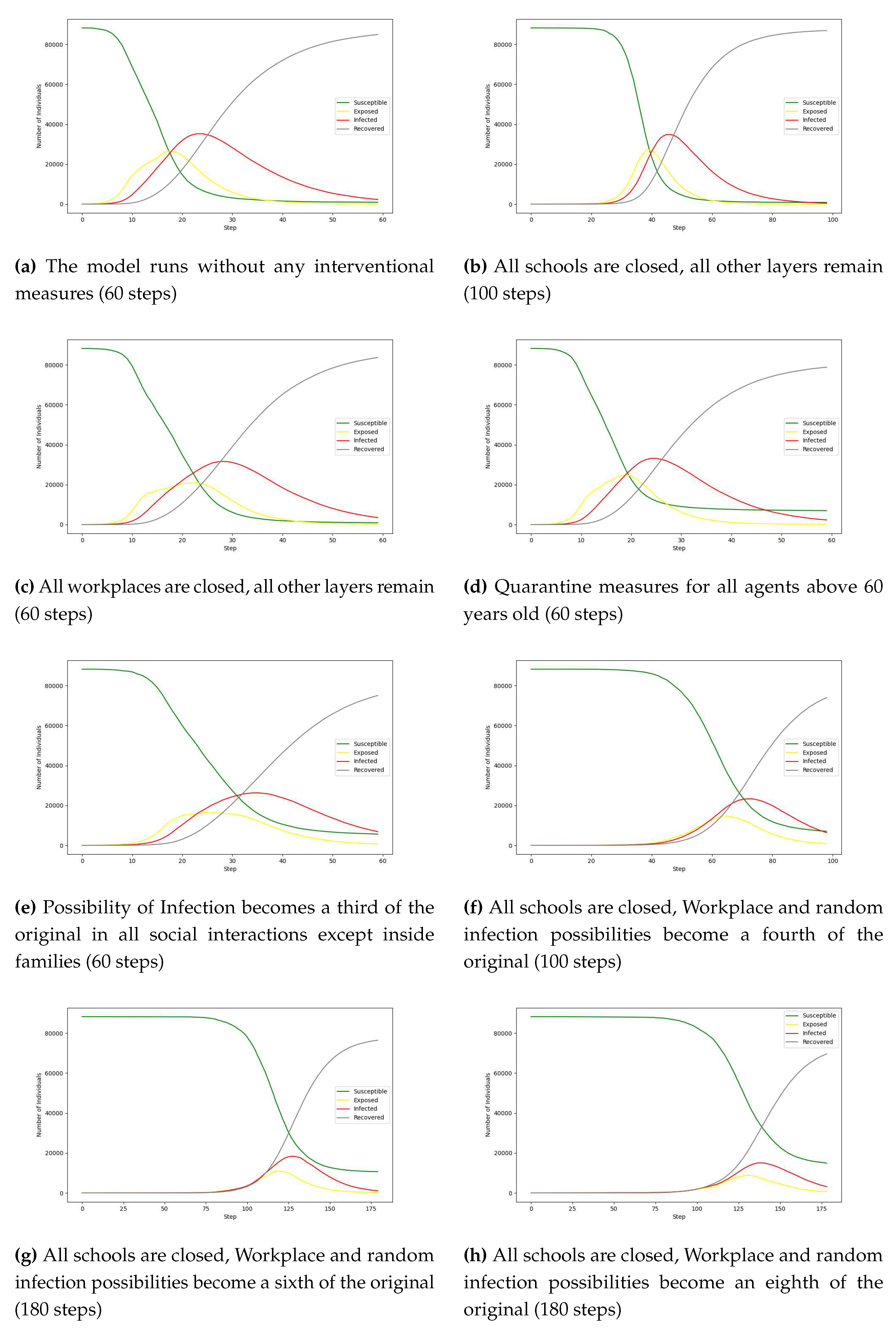
Table 2.
Agents attributes
| Attribute | Description |
|---|---|
| Agent_ID | Agent’s ID |
| Gender | Agent’s gender (Male/Female) |
| Age | Agent’s age from 0-100 |
| Family_size | Members of agent’s family |
| Family_ID | Determines families |
| Work_ID | Determines workplaces, if applicable |
| School_ID | Determines schools, if applicable |
| Infection Status | Suspectible/Exposed/Infected/Recovered |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






