Prerpints.org logo
Preprint
Article

Temporary Structural Health Monitoring of Historical Széchenyi Chain Bridge

Altmetrics

Downloads

108

Views

33

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

09 January 2024

Posted:

10 January 2024

You are already at the latest version

Alerts
Abstract
A temporary monitoring system was installed on the 175-years-old historical Széchenyi chain bridge under its reconstruction process. The bridge is in the downtown area of the capital city of Hungary and plays a significant role in city life of Budapest. Six-month-long measurements were conducted during the reconstruction process of the bridge, yielding crucial insights into the structural behaviour of the historical structure. Measurement results were evaluated; the findings encompass the rotation capacity of pins between chain elements, and structural response to temperature changes. This information helped the decision-making of designers and construction company during the reconstruction made between 2021 and 2023. For instance, daily temperature fluctuations result in increased bending moments in the chain elements, rising up to 158% compared to the values observed during a proof load test in 2018. Furthermore, the measurements reveal an approximate 42% increase in normal forces compared to the proof load test, which highlights the high sensitivity of chain bridges to temperature fluctuations, where geometric stiffness plays a crucial role. Reconstruction, reducing self-weight, notably intensifies the impact on normal forces and bending moments. These outcomes strongly emphasize the dominance of dead load and self-weight in the case of chain bridges.
Keywords: 
Subject: Engineering  -   Civil Engineering

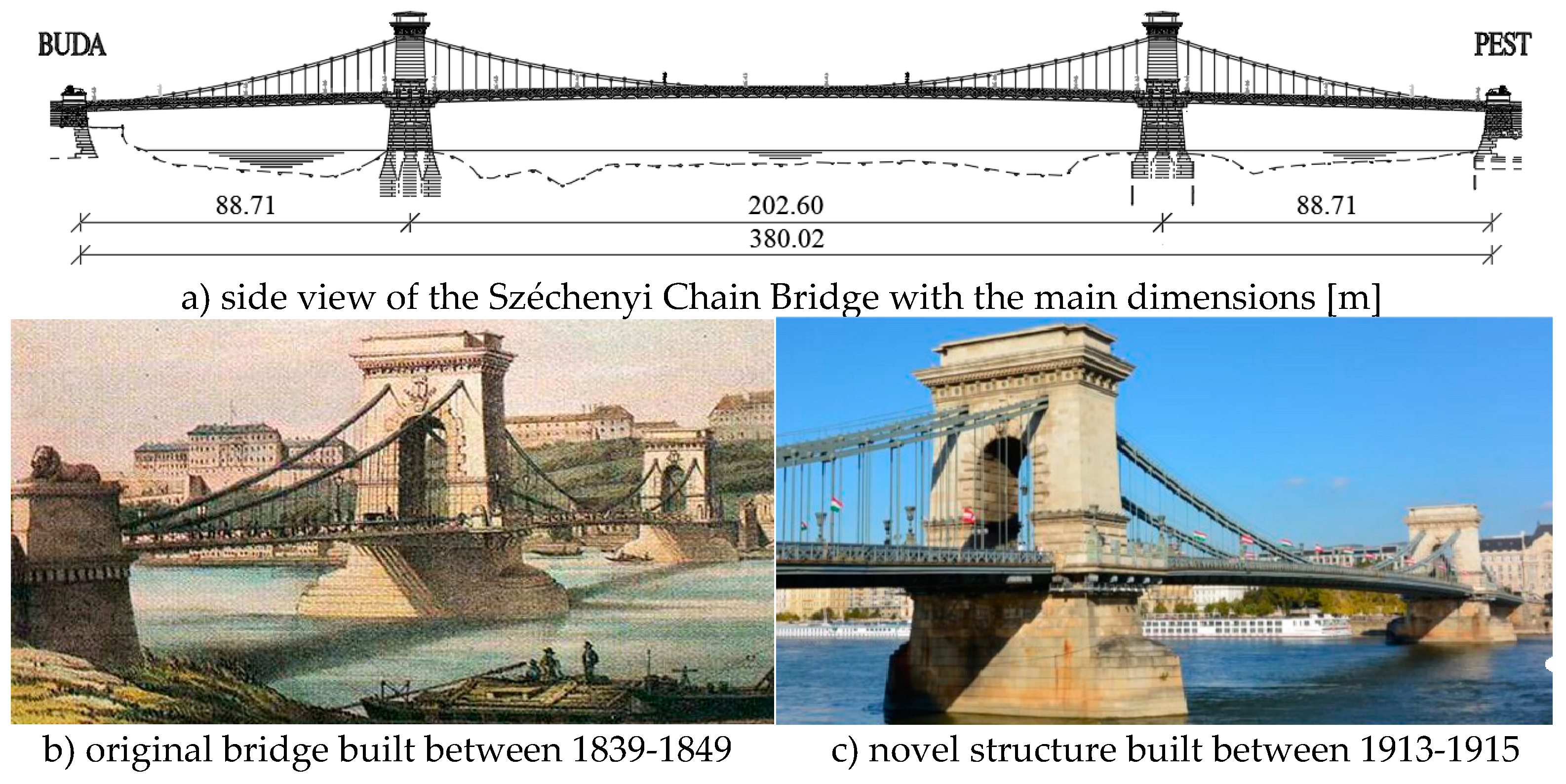
1. Introduction

The historical Széchenyi chain bridge is a 175-year-old structure in Budapest, Hungary, which has a vital role in the city life. The road bridge spanning the Danube River sees substantial daily vehicular traffic, serving as a major link between Buda and Pest. Its construction began in 1839 and finished in 1849. It was renowned as the most extensive chain bridge of its era, featuring a maximum mid-span of 202.60 meters (Figure 1). Currently, only the Hercílio Luz Bridge in Brazil (339 m) and Clifton Bridge in England (214 m) surpass its largest span.
Subsequently, the bridge has undergone several renovations. The original bridge was the first permanent bridge in the capital city of Hungary; it operated until 1913. The original structure lacked a stiffening girder, and a lightweight timber deck system was used, resulting in noticeable bridge deck vibrations. Therefore, a new supporting structure was designed incorporating twenty-five carbon steel chain bars between each node. It resulted in doubled length of chain bars and increased load-bearing capacity compared to the previous structure; thus, distance between pins and suspension bars increased from 1.8 m to 3.6 m. Total mass of the ironwork increased to 5200 tons following the introduction of the new truss stiffening girder using carbon steel with ultimate strength ranging between 480-560 MPa. Additionally, a reinforced concrete deck was also installed on the superstructure (Figure 2a). The bridge was destroyed in 1945 during World War II. Nevertheless, it was rebuilt without any significant changes of the structural system, and it was re-opened for traffic in 1949.
The Budapest University of Technology and Economics, Department of Structural Engineering conducted extensive investigations focusing on the Széchenyi chain bridge. Proof load tests of the bridge were performed in 2002 and 2018 to analyse the rotational capacity of the pins of chain elements. Fixed or partly stuck pins due to corrosion cause bending moments within the chain system and thus alter the structural behaviour of the bridge. From 1949 until 2021, no significant maintenance or reconstruction work were made on the structure (except small corrosion protections), while chain elements reached a lifetime of 100 years, and the deck system was more than 70 years old. Historical failures of similar bridges underscored the need for comprehensive assessment. A significant chain bridge failure occurred in the USA in 1967, claiming the lives of 46 individuals [1]. The collapse of the Silver Bridge stemmed from the failure of a single chain element, due to stress-corrosion crack resulting in fatigue and eventually fracture, leading to the complete breakdown of the entire chain system. Consequently, assessing the structural condition of structural elements became a crucial aspect of the historical bridge, since it is essential for determining load-bearing capacity and remaining lifetime. In 2019, noticeable corrosion problems were detected within the deck system, prompting the execution of an in-depth reliability analysis [2] to evaluate the risk of failure of the deck system until reconstruction commenced. On-site corrosion measurements were conducted, leading to the development of a Monte Carlo simulation-based stochastic reliability assessment method with a confidence level corresponding to 1-year lifetime. The approach employed an advanced finite element model-based resistance calculation (GMNI analysis) alongside state-of-the-art corrosion model. Based on the numerical simulation results, the bridge deck could have been verified only by the reduction of loading to keep the bridge in operation for one additional year. It was also concluded that the renovation of the historical structure could not be avoided and delayed any longer. During the latest reconstruction phase between 2021 and 2023, the bridge underwent substantial renewal. The aging deck system was substituted with an orthotropic steel deck (Figure 2b). However, chain elements, steel stiffening girder, and cross-girder system remained unaltered, solely receiving corrosion protection enhancements. Simultaneously, material loss of the chain bars due to corrosion was estimated by measurements during the reconstruction, since it can cause reduced tensile resistance leading to inappropriate ultimate resistance. Coupled with decreased pin rotational capability, deteriorating chain bars can reduce structural integrity.
The current paper primarily showcases findings from six-month-long temporary monitoring measurements conducted during the reconstruction process. The evaluated data provides pivotal understanding of the structural behaviour of the historical structure, including pin rotational capacity, and structural response due to temperature differences. These insights significantly influenced decisions made by designers and the construction company during the bridge reconstruction. On the other hand, importance of temporary Structural Health Monitoring is highlighted in the paper as well.

2. Literature review

The literature review introduces previously published results regarding Structural Health Monitoring (SHM) systems related to bridges. Therefore, findings presented in this paper can be readily introduced and differentiated.
SHM has been extensively applied across engineering sectors and remains a focal point in structural engineering research. Processing of periodically sampled real-time data in SHM facilitates early defect detection, to support decision-making on repairs, retrofitting, maintenance strategies and accurate remaining life predictions, by integrating diverse sensing technologies. In total, operational safety of the monitored structures could be upheld. The cost of monitoring and repairs typically outweighs the expenses of new construction, pressuring authorities to prolong structure lifespan while ensuring public safety. SHM potentially reduces costs by replacing scheduled maintenance with as-needed maintenance. Integrating SHM even during the design phase of new structures offers opportunities for reduced life-cycle expenses [3,4].
Long-term monitoring systems are currently in operation on bridges; Structural Health Monitoring of bridges has developed since the early 1990s. Utilizing in-situ field experimental techniques aids in comprehending the behaviour and performance of actual, full-scale bridges subject to real loading and environmental conditions. It serves to verify safety, serviceability, durability, and sustainability of bridges. For instance, Li and Ou [5] and Hovhanessian [6] have already recommended design approaches of SHM systems for bridges.
The characteristic of structures (e.g., modal parameters) are influenced by the natural environment (wind, temperature, etc.). Wind is one of the critical loads for long-span cable stayed bridges and can cause vortex-induced vibration of decks and cables, and rain-wind-induced vibration of cables. Anemoscopes are widely applied to measure wind velocity. Thermocouples or optical fibre Bragg grating (FBG) temperature sensors are frequently used to measure temperature of bridges. Degrauwe et al. [7] examined the influence of temperature and its measurement error on natural vibration frequency. Furthermore, Li et al. [8] applied a nonlinear principle component analysis (NPCA) to remove the influence of temperature and wind. Strain is one of the most important variables for the safety evaluation, fatigue assessment, and validation of models. Strain can be measured using e.g., a traditional strain gauge, a vibrating-wire strain gauge or FBG strain sensors. Okasha and Frangopol [9] presented a performance-based life-cycle bridge management framework with the integration of SHM, which can be used for the safety evaluation of different type of bridges. Li et al. [10,11,12,13] presented a framework of safety evaluation of bridges based on load-induced or environment-induced strains and deformations. Various new sensing technologies have been developed in the last two decades. Optical fibre and wireless sensing technologies have shown great potential and have been widely used in many SHM systems for bridges [14]. Nevertheless, application of artificial intelligence is also emerging in evaluating measurement results [3,15].
SHM systems are not only installed on relatively new structures; historical aging bridges are also involved [16,17]. However, the application of SHM system during reconstruction of a historical bridge has not been published yet according to the authors’ knowledge. It is a new application for evaluating the structural behaviour using a temporary system and assessing continuous six-month-long measurement data.

3. Analysis strategy

The strategy for analysing the structural behaviour of the Széchenyi chain bridge, and predicting structural integrity and performance of chain elements, is the following:
  • evaluating the measurement results of a proof load test, which was carried out in 2018, to conclude whether fixed or partly fixed pins would start rotating due to live load on the bridge,
  • assessing the temporary measurement results during reconstruction to conclude whether pins would start rotating due to reducing self-weight (dead load), which is mostly dominant for chain bridges.

4. Proof load test

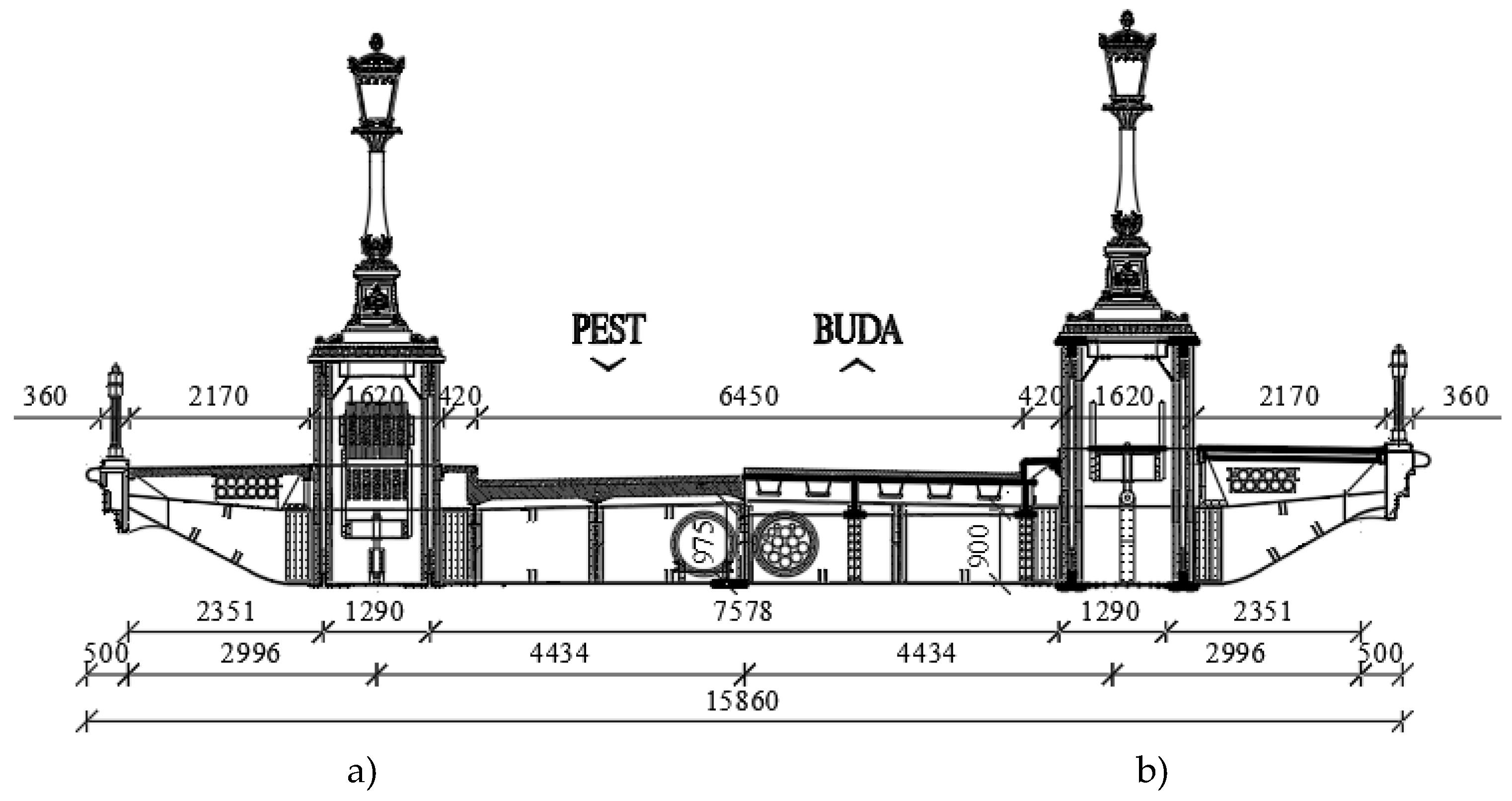
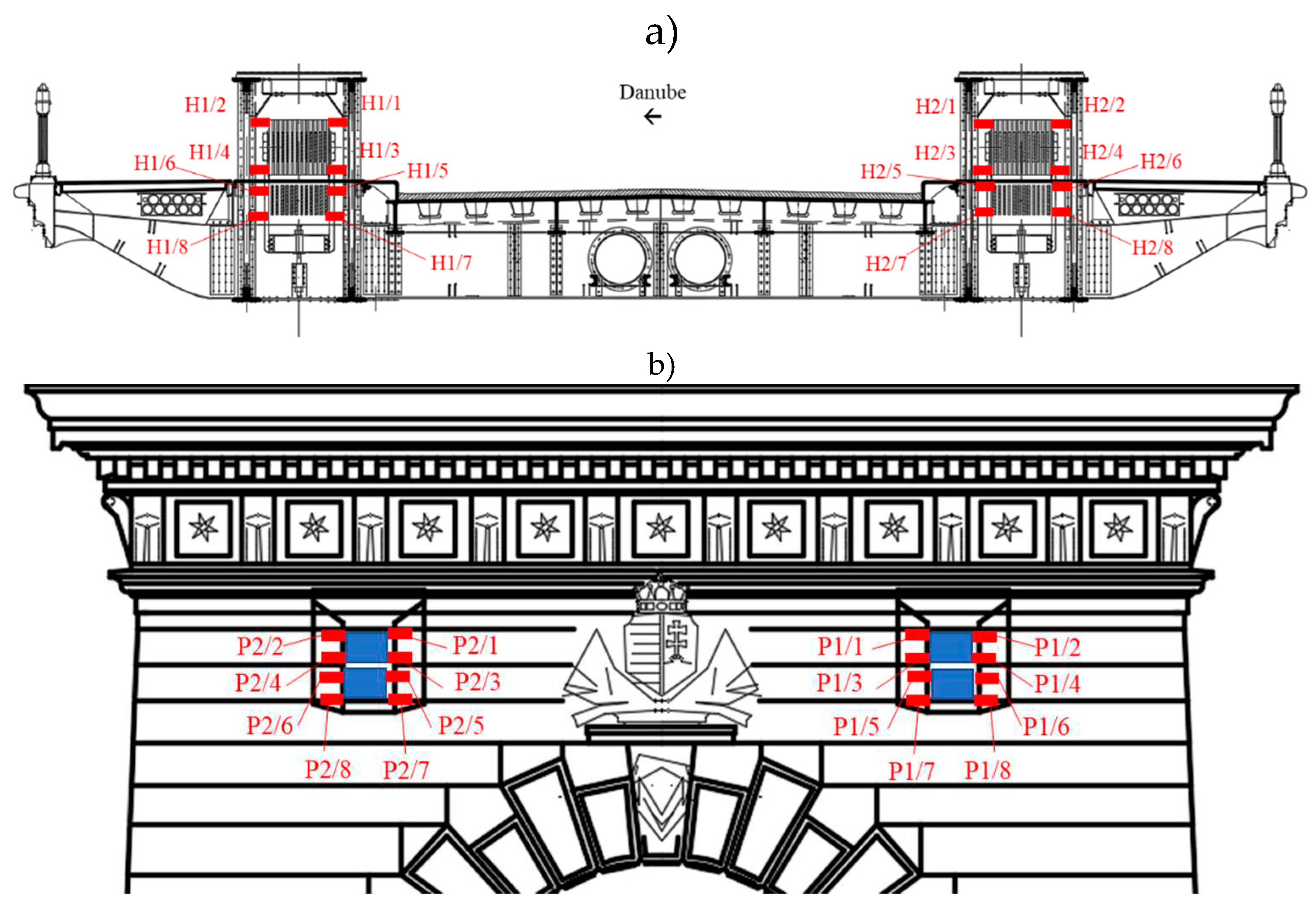
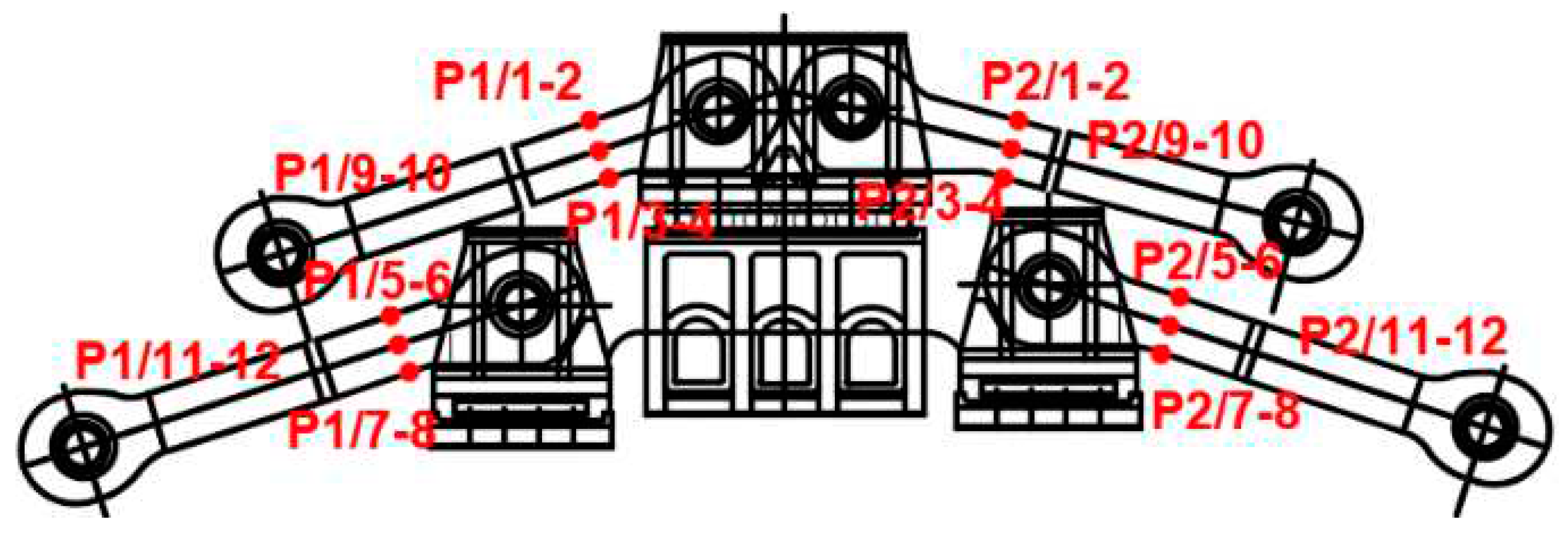
4.1. Configuration and measurement locations

The purpose of the proof load test is to determine the rotation capacity of the pins connecting the chain links, based on the determination of the normal stresses, by using strain gauges, resulting from the normal force and bending moment in the chains. Based on static calculations using finite element method, significant bending in the chain elements can only be generated in the first elements near the pylons and structural bearings at the abutments; therefore, these areas near the directional changes of the chain system are in the focus of the current measurements. A total of 8 different measurement locations are selected, the global layout is shown in Figure 3. A total of 8 strain gauges are placed on a chain element at each measuring point (notations are shown in Figure 4). Four strain gauges at each measurement locations are placed at the extreme fibres of the chain elements. The strain gauges denoted by Hx/1 – Hx/8 are placed at the eyebars around the abutment, where the chains have knickpoints. Strain gauges marked by Px/1 – Px/8 are placed on the eyebars around the pylons near to the breaking point of the chain system (x = 1…4 for the pylon and abutment as well). In each analysed cross-section, two strain gauges are placed at the upper and two at the lower extreme fibres to be able to determine the normal force and the in-plane bending moment changes during loading.
The strain measurement is carried out with a laptop-controlled HBM MGCplus data acquisition system and HBM CANhead amplifiers. The CANhead amplifiers are connected with CanBus high performance cables, which transmit the measurement signals to a laptop via the data acquisition system. Uniaxial strain gauges, with nominal resistance of 350 Ω, are applied for the short-term measurements. During the static proof load test, continuous measurements are taken for each load case with a sampling rate of 2 Hz.

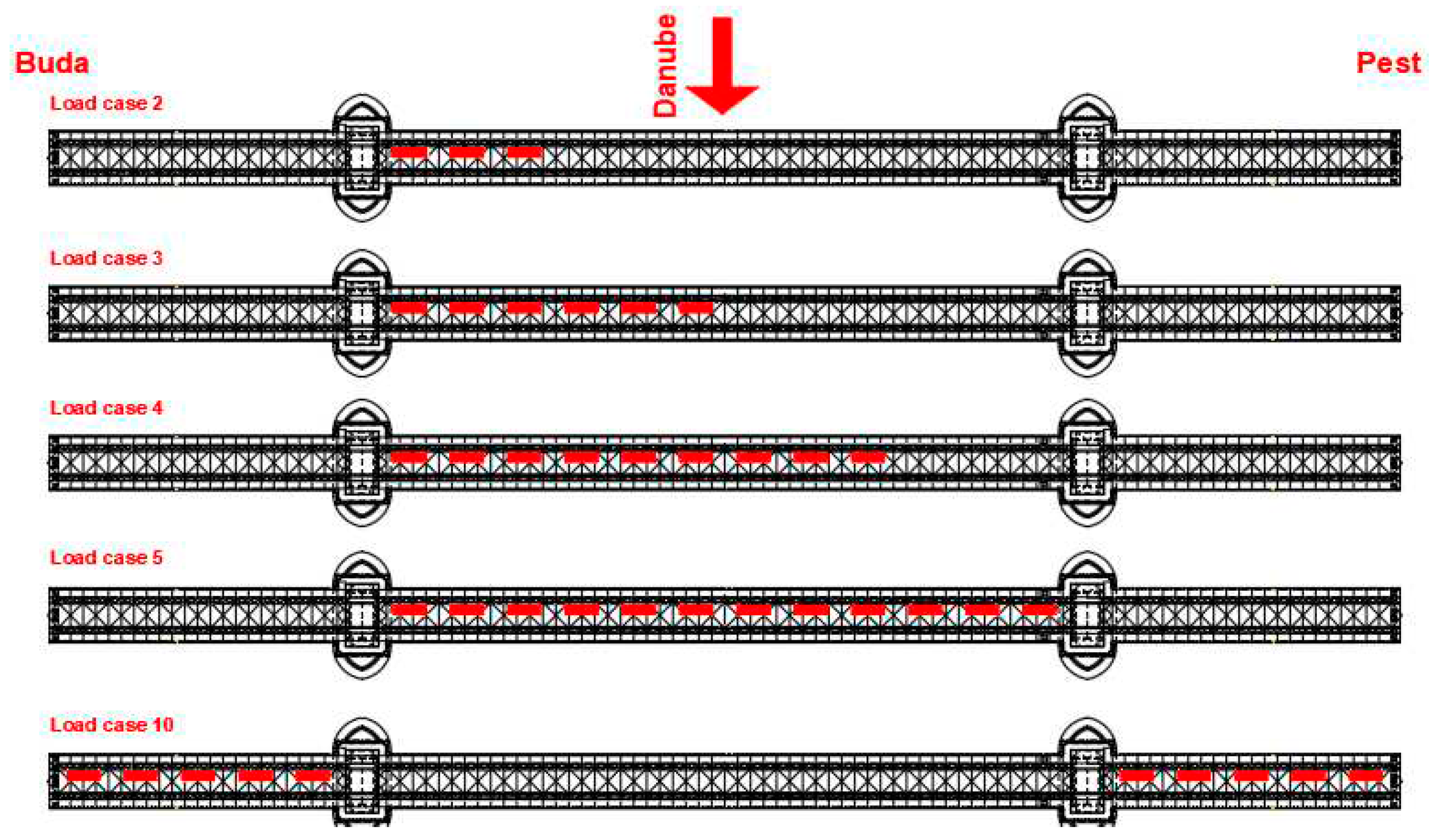
4.2. Load cases

The bridge is loaded with 12 four-axle trucks with an average weight of ~20 t. A total of 13 load cases are examined (load cases with lorries at the inflow side are demonstrated in Figure 5), including unloaded load cases to determine the effect of temperature and possible deterioration of the structure between different loading situations. The applied load cases where the followings:
1. unloaded bridge,
2. 3 trucks in one lane in the middle span of the bridge - inflow side,
3. 6 trucks in one lane in the middle span of the bridge - inflow side,
4. 9 trucks in one lane in the middle span of the bridge - inflow side,
5. 12 trucks in one lane in the middle span of the bridge - inflow side,
6. unloaded bridge,
7. 6 trucks in the middle span of the bridge - outflow side,
8. 12 trucks in the middle span of the bridge - outflow side,
9. unloaded bridge,
10. 5+5 trucks in the side spans - inflow side,
11. unloaded bridge,
12. 5+5 trucks in the side spans - outflow side,
13. unloaded bridge.

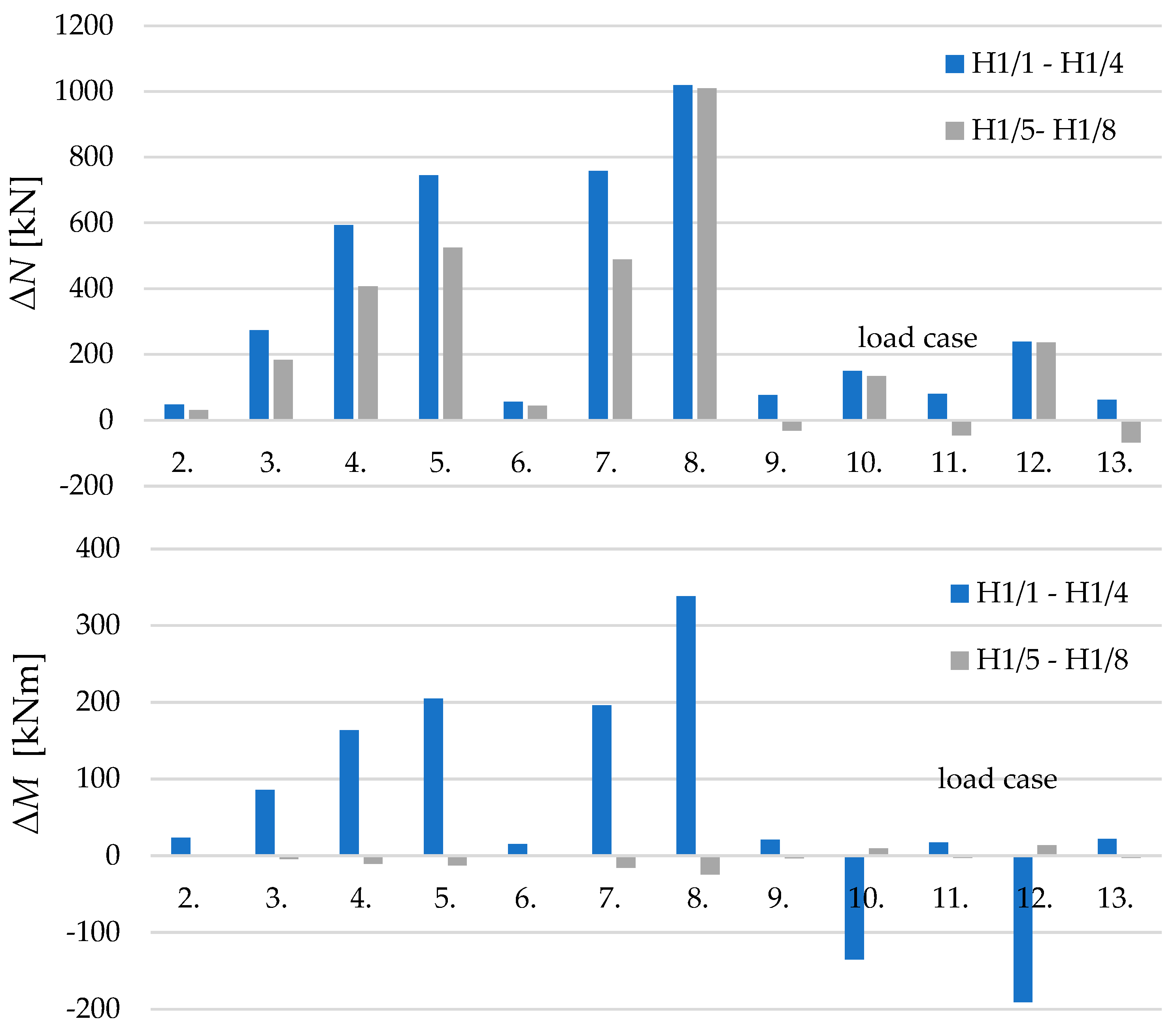
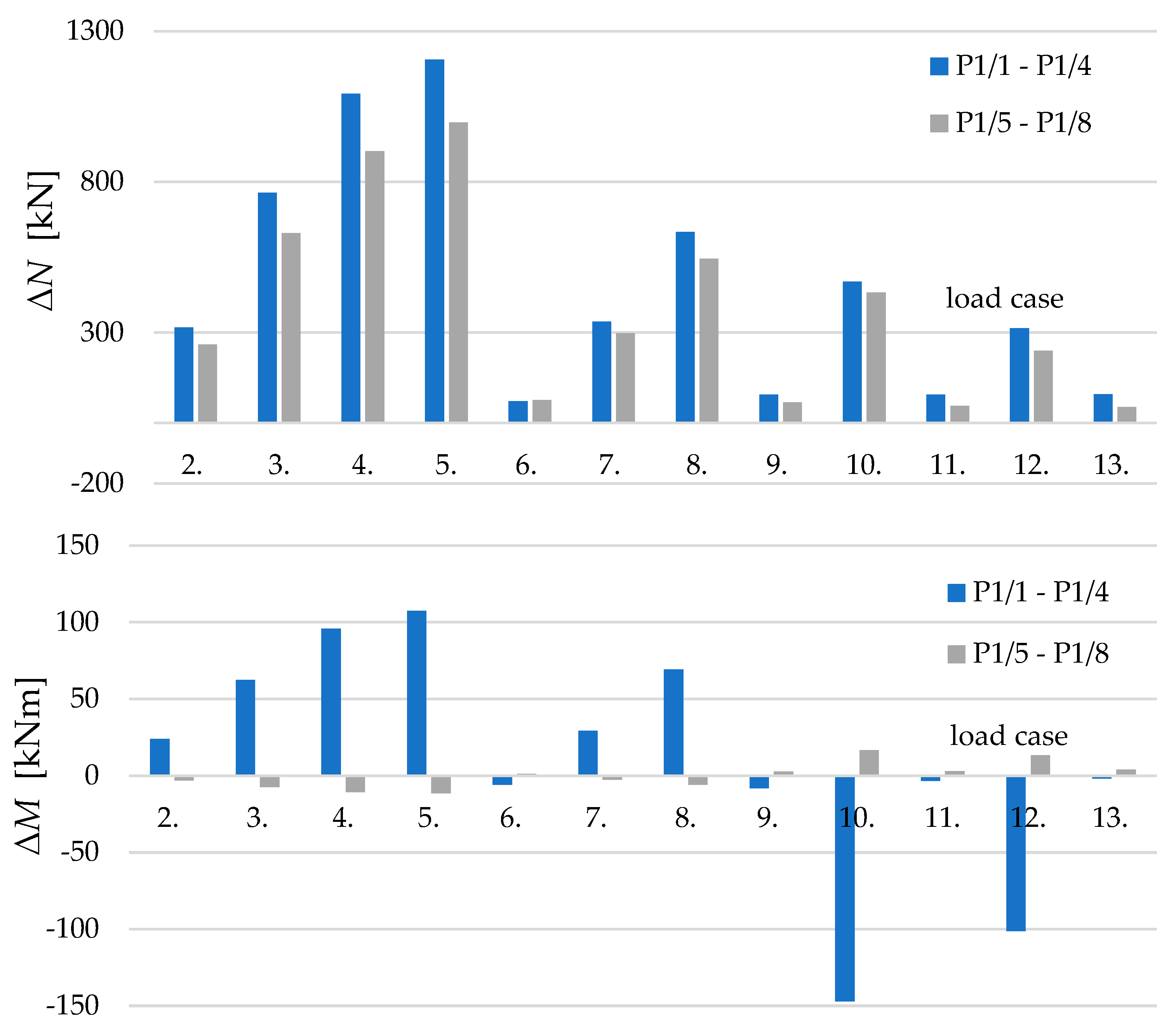
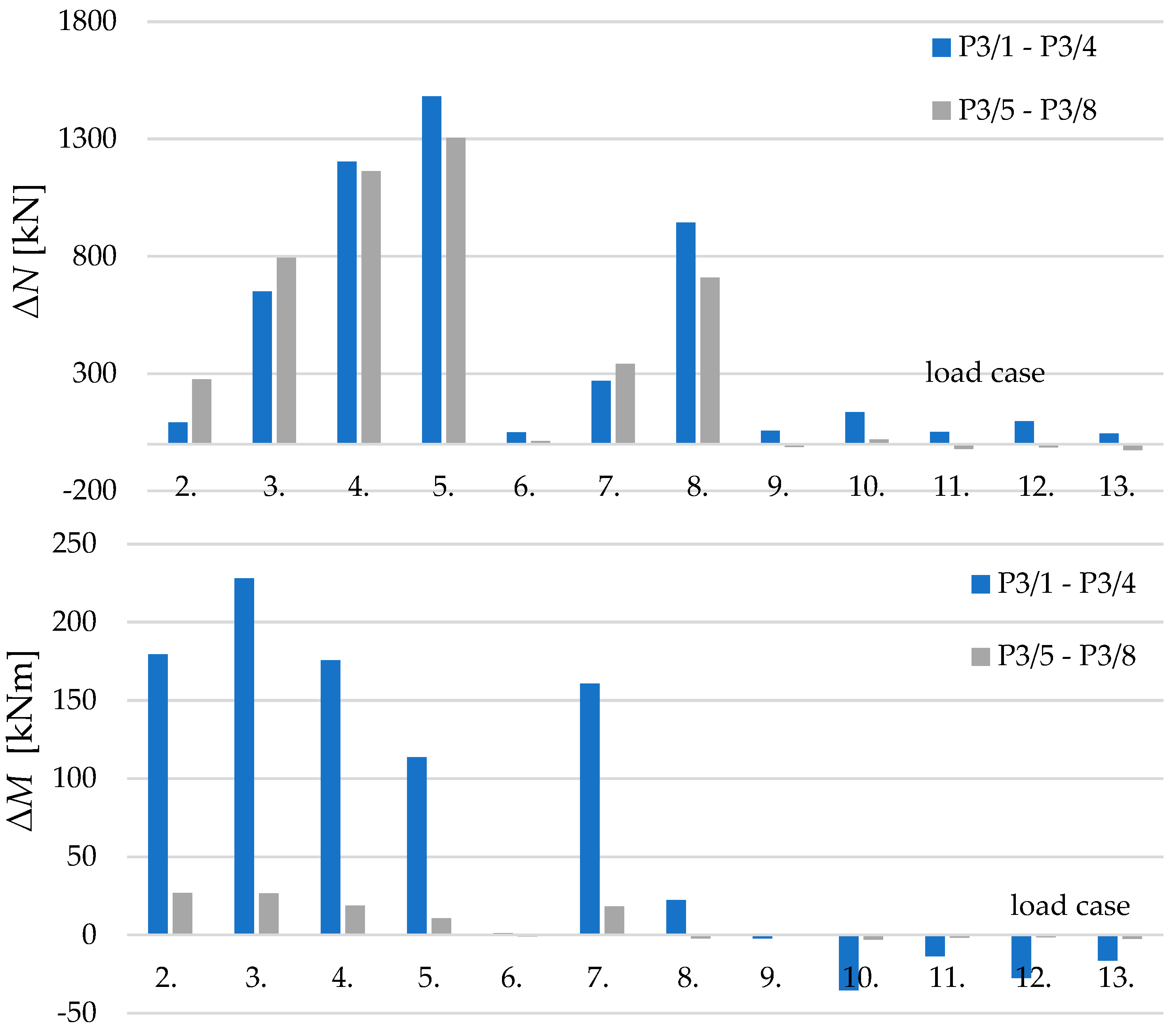
4.3. Measurement results

Axial strains due to the vehicle load are determined for all load cases. Since strain gauges are installed on the extreme fibres, normal forces and bending moments could be determined and separated by averaging and by deriving the average difference between top and bottom fibres, respectively. Then, average strains εmean are multiplied by EA, where E = 210 MPa is Young’s modulus and A = 1274 cm2 is cross sectional area to determine normal forces. In the case of bending moment, Δε is multiplied by 0.5EW, where the W = 7749 cm3 is elastic cross-sectional modulus. Derived changes in normal forces ΔN and bending moments ΔM are plotted in Figure 6 and Figure 7 for measurement location at the abutment and pylon, respectively.
The peak normal forces at the Pest abutment ranged between 907 to 972 kN, while on the Buda side, they varied between 927 to 1019 kN. In the side span, the normal force in the chain elements at the pylons fluctuated from 1040 to 1200 kN, with a maximum of 1482 kN in the mid-span (for comparison purposes the maximum normal force in the chain elements coming from self-weight is ~11300 kN). Measurements reveal a significant disparity between the variation in normal forces recorded in the side spans and mid-span, surpassing the variation expected solely from the change in chain element direction. Consequently, these findings suggest that the structural bearings at the top of pylons can withstand a portion of horizontal forces exerted by the applied load.
Measurements reveal significant variations in maximum bending moment at the abutments, ranging between 248 and 320 kNm for load cases 5 and 8, respectively, and -142 to -198 kNm for load cases 10 and 12. Similarly, the maximum bending moment variation in the chain elements near the pylon, specifically at measuring points P1, P2, and P4, oscillated between 107 and 141 kNm for load cases 5 and 8, and -141 to -147 kNm for load positions 10 and 12. Notably, at measurement location P3, the pin connection shifted following an approximate 230 kNm bending moment change, resulting in decreased bending. Hence, the measurements indicate that among the 8 tested pins, only one displayed the capacity to rotate under the applied live load. This observation suggests that the live load applied was insufficient to surpass the friction between chain elements for the remaining pins, which might be notably increased due to corrosion.
Consequently, further measurements were planned to be made during the reconstruction process of the bridge, anticipating larger internal force changes attributed to the alteration in the self-weight of the bridge. These measurements are executed by using a temporary monitoring system.

5. Temporary monitoring system

5.1. Configuration and measurement locations

The temporary measurement system consists of 80 strain gauges, which were installed on chain elements on both inflow and outflow side, in order to measure elongation variation, and track the structural behaviour during reconstruction. Data obtained from the measurement system also provides information on the changes in elongation of the structure due to non-reconstruction loads (e.g., due to temperature changes, or other meteorological effects), which can be used to better understand the behaviour of the structure. In addition, the temperature of the air and the steel structure are recorded as well. Continuously processed data made it possible to determine intraday, weekly and monthly measurement trends and changes between individual reconstruction stages.
The purpose of the measurement is to assess the stress induced in the chain elements under varying loads to infer the rotational capacity of pins. Eight distinct locations along the chains are measured. Four measurement sites (H1 - H4) are positioned at the bridge abutments on both the inflow and outflow sides, while four other sites (P1 - P4) are established at the pylon on the Buda side, similarly to the proof load test as shown in Figure 3 and Figure 4. Each location undergoes measurements on both the lower and upper chain elements. At the abutments (measurement sites H1 - H4), strain gauges are placed on the end of the parallel part of the chain elements (located at 100 mm from the rounding of the pin head in the axial direction, near the directional change at the structural bearing). Strain gauges are installed on both sides of the chain bars, 20 mm from the lower and upper edges. Accordingly, a total of four strain gauges per measurement location are used at the abutments. This approach allows for the independent determination and comparison of changes in bending moment and normal force within the chains. The same considerations are done for strain gauges at the pylon (measurement sites P1 - P4), except additional sensors are installed at the neutral axis of the chain elements. Thus, six sensors per measurement location are used at the pylon, which are illustrated in Figure 9.
HBM PMX data acquisition systems are used for accurate, reliable, and flexible measurement, which are ideally suited to process high data volumes for long-term multi-channel applications. Biaxial strain gauges, with nominal resistance of 350 Ω, are installed with temperature compensation. Measurement and data logging are controlled using CatmanEasy, the software of HBM. A sampling rate of 1 Hz is applied during data acquisition.

5.2. Reconstruction stages

A detailed organisation plan for the current reconstruction was drawn up. This paper does not describe the entire construction process, only those stages that are relevant for measurement evaluations, which are the followings:
1. crane track is built on the superstructure (15.07.2021),
2. suspended scaffolding is installed, while reinforced concrete slab is demolished in the main span (01.08.2021),
3. old steel stingers are dismantled in the main span, new orthotropic deck is installed in half of the main span, suspended scaffolding is installed in the side spans (03.11.2021),
4. the old concrete slab and steel stringers are dismantled on the entire bridge, the new orthotropic deck is installed between pylons, sidewalks in the main span are dismantled, suspended scaffolding is dismantled (03.01.2022).
For illustration purposes, Figure 10 shows the superstructure of the bridge between phases 3 and 4. The suspended scaffolding was installed in the side spans, and the old deck system (concrete slab and steel stringers) was already demolished. This erection phase gave a dominant loading situation from static point of view; thus, the maximum load was applied in the middle span, and the minimum in the side spans. It was expected that this erection phase could make the hinges rotate.

5.3. Measurement results

The strain gauge measurement outcomes are presented in a segmented way. First, longer time data series are presented, which aims to offer an overview of the daily cyclical elongation variations triggered by temperature changes and significant construction phases. Initially, observations from measurement site P1, at the pylon, are synthesized. Figure 11a,b showcase the findings of strain gauges P1/1-P1/4 (upper chain) and P1/5-P1/8 (lower chain). These graphs highlight substantial intraday temperature-induced fluctuations, recording a disparity of 100-120 μm/m (21-25.2 MPa) between the lower and upper extreme fibres due to temperature shifts, resulting in additional stress on the structure. Meanwhile, Figure 11c illustrates the strain changes of sensors P1/9-P1/12 along the neutral axis. A more notable alteration is noted from late November to early December 2021, primarily attributable to construction activities involving the construction stages of the deck plate between the pylons, and the demolition of the reinforced concrete deck plate and steel stringers in the side spans. Strain gauges positioned close to the upper extreme fibres (P1/1-P1/2 and P1/5-P1/6) experience increased tension, whereas those near the lower extreme fibres (P1/3-P1/4 and P1/7-P1/8) endure higher compression. Across the neutral axis (Figure 11c), all sensors indicate a marginally heightened tension starting from early December 2021.
Through averaging and subtracting the measured values from the respective strain gauges, the strain change curves depicting the impact of normal force ΔεN and bending moment alterations ΔεM are derived (Figure 12). It is evident that normal forces undergo minimal change, while bending moment notably increases in both the upper and lower chains. The measurement charts display continuity, apart from minor fluctuations within the day, suggesting no movement in the chain links during this timeframe.
The assessment of measurement results at test sites also includes separate Sundays (Figure 13), when no construction work occurred, enabling analysis of solely meteorological influences, primarily temperature changes. On 27th June 2021, variations of 110-125 μm/m are observed in daily strain near the upper extreme fibre of P1/1 and P1/2 (inflow side, upper chain, Buda side). Correspondingly, lower values, spanning 80-100 μm/m and 60-65 μm/m, are recorded on 4th July and 11th July 2021, respectively, mainly at P1/2 (south side of the chain). The recorded air temperatures in Budapest ranged from 19-31 °C across these days, with a temperature variation of 11-12 °C, although no significant changes occurred in the structural behaviour during this period. The impact of daily temperature fluctuations (warming and cooling) is distinctly evident in the measurement results. The variations caused by daily temperature changes are comparable with strains observed during the proof load test. Maximum measured daily strain, normal force and bending moment variations for the pylon sites are shown in Table 1. In the upper chain elements, the maximum change is 125 μm/m, while it is 140 μm/m for the lower ones in the extreme fibres. In the neutral fibre, the magnitude of maximum strain variation is 80 μm/m. Results show quasi linear strain pattern within the sections. Notably, for sensor sets P1 and P3, larger strains (tension) are observed in the top fibres compared to the bottom ones. Conversely, for sensor sets P2 and P4, an inverse pattern emerges. This trend illustrates a linear increase towards the top extreme fibres, influenced by additional moments in the chain links.
Maximum normal force and bending moment variations at the pylons (P1-P4) due to proof load test, reconstruction and daily temperature fluctuation are derived according to the methodology described in Section 4.3; results are summarized in Table 2. The analysis of the data suggests that daily temperature shifts could lead to additional bending moments up to 158% (P1, upper chain) compared to the values observed during the proof load test (~80% of the design live load of the bridge). Furthermore, normal force measurements even show a 42% higher value (P2, lower chain) than those registered during the load testing. This highlights the high sensitivity of chain bridges to temperature fluctuations, where geometric stiffness plays an important role. It also shows, if the bending moment applied by the live load of the bridge would make the pins rotate, the daily temperature change would also make it on the daily bases. However, most of the pins did not rotate during the load test, even under the internal forces caused by the temperature change. Both proves, that pins of this historical bridge are stuck, and the static skeleton of the structure can be assumed as fixed within the static calculations under the live load and meteorological loads.
Furthermore, reconstruction, due to reduced self-weight, notably intensifies the impact on normal forces and bending moments. For instance, the bending moment variation increased by approximately 380% in the upper chain at location P1. Although lower chains had relatively small bending moments (<30 kNm) during the proof load test, normal forces experienced a significant increase, measuring 208% higher at location P3. These results emphatically underscore the dominance of dead load and self-weight in the case of chain bridges. The measurement results also showed, that even the most significant bending moment change during the construction could not initiate the rotation of the pins, they are strongly corroded and fully stuck.
For easier interpretation and presentation of results, cross-sectional resistances of chains with nominal geometrical dimensions are also evaluated for comparison purposes to the measured internal forces. In 2015, statistical evaluation of previous tensile tests, from 1913 and 1948, was carried out at the BME Department of Structural Engineering and the characteristic yield strength fyk was determined. Based on the measured values the design resistances are calculated by Eurocode 3 formulae, as follows: the pure tensile resistance of a chain using nominal cross-section properties is NRd = A × fyk / γM0 = 1274 cm2 × 28.1 kN/cm2/ 1.0 = 35799 kN and bending moment resistance of a cross-section is MRd = W × fyk / γM0 = 7749 cm3 × 28.1 kN/cm2/ 1.0 = 2177.5 kNm. It can be seen that the largest normal force and bending moment change within the chain system coming from the proof load test, reconstruction or temperature change reaches only 13% of the tensile resistance and 33% of the bending resistance, respectively.
It is crucial to highlight that chains with fixed pins are subjected to a combination of axial tension and bending moments, compounded by the effects of corrosion on their cross-sectional properties, thereby diminishing their overall resistance.

6. Summary and conclusions

The paper presents the results of two temporary measurements made on the 175-years-old historical Széchenyi chain bridge under its reconstruction process. The major aim of the measurements was the investigation of the rotation capacity of the pins between the chain elements (eyebars). It can significantly affect the structural health of the bridge in accordance with the corrosion state of the chains and has clear impact on the further lifetime of the structure which had to be assessed by the designers.
The first measurement was a proof load test, which had the aim to check if the live load (traffic load) could make the pins of the bridge rotate or not. The second measurement was the six-month-long temporary monitoring system operating during the reconstruction process aiming to check the structural behaviour of the bridge under a longer period checking the rotation of the pins under temperature changes and during the removal of the old concrete deck, which has been replaced by a new orthotropic steel deck system. Based on the on-site measurements, the following conclusions could be drawn regarding the bridge behaviour:
-
all the measured pines are stuck, no rotations are expected coming from the live load (proof test load) or temperature change or removing the concrete deck during the reconstruction of the bridge;
-
internal forces coming from the daily and/or seasonal temperature change can reach or even overcome of the magnitude of the internal forces coming from the design traffic load, the effect of temperature change is significant on the bridge;
-
normal stresses coming from bending within the chain elements are significant; therefore, the bending component should always be considered in the static verification of the chain elements.

Acknowledgments

The presented research program has been partly financially supported by the Grant MTA-BME Lendület LP2021-06 / 2021 “Theory of new generation steel bridges” program of the Hungarian Academy of Sciences, which is gratefully acknowledged. The authors would like to express special thanks to the Designers (Főmterv Co and MSC Ltd. design offices) of the bridge reconstruction for their cooperation within the expertizing tasks and evaluation of the on-site measurements. Special thanks are given also to the Hídépítő Co who executed the reconstruction work of the bridge and provided the opportunity to execute the on-site measurements and gave always strong technical supports.

References

  1. Åesson, B. Understanding Bridge Collapses, 1st ed.; CRC Press: London, UK, 2008. [Google Scholar] [CrossRef]
  2. Kövesdi, B.; Kollár, D.; Dunai, L.; Horváth, A. Reliability analysis-based investigation of the historical Széchenyi Chain Bridge deck system. Results Eng. 2022, 15, 100555. [Google Scholar] [CrossRef]
  3. Neves, A.C.; González, I.; Leander, J.; Karoumi, R. Structural health monitoring of bridges: A model-free ANN-based approach to damage detection. J. Civ. Struct. Health Monit. 2017, 7, 689–702. [Google Scholar] [CrossRef]
  4. Neves, A.C.; Leander, J.; González, I.; Karoumi, R. An approach to decision-making analysis for implementation of structural health monitoring in bridges. Struct. Control Health Monit. 2019, 26, e2352. [Google Scholar] [CrossRef]
  5. Li, H.; Ou, J. Design approach of health monitoring system for cable-stayed bridges. In Proceedings of the 2nd International Conference of Structural Health Monitoring for Intelligent Infrastructure, Shenzhen, China, 16–18 November 2005. [Google Scholar]
  6. Hovhanessian, G. Health monitoring of cable stayed structures experience and implementation. In Conference Proceedings of the Society for Experimental Mechanics Series; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
  7. Degrauwe, D.; De Roeck, G.; Lombaert, G. Uncertainty quantification in the damage assessment of a cable-stayed bridge by means of fuzzy numbers. Comput. Struct. 2009, 87, 1077–1084. [Google Scholar] [CrossRef]
  8. Li, H.; Li, S.; Ou, J.; Li, H. Modal identification of bridges under varying environmental conditions: Temperature and wind effects. Struct. Control Health Monit. 2010, 17, 495–512. [Google Scholar] [CrossRef]
  9. Okasha, N.M.; Frangopol, D.M. Integration of structural health monitoring in a system performance based life-cycle bridge management framework. Struct. Infrastruct. Eng. 2012, 8, 999–1016. [Google Scholar] [CrossRef]
  10. Li, D.; Hu, Q.; Ou, J. Fatigue Damage Evolution and Monitoring of Carbon Fiber Reinforced Polymer Bridge Cable by Acoustic Emission Technique. Int. J. Distrib. Sens. Networks 2012, 8, 282139. [Google Scholar] [CrossRef]
  11. Li, D.; Ou, J.; Lan, C.; Li, H. Monitoring and Failure Analysis of Corroded Bridge Cables under Fatigue Loading Using Acoustic Emission Sensors. Sensors 2012, 12, 3901–3915. [Google Scholar] [CrossRef] [PubMed]
  12. Li, H.; Lan, C.M.; Ju, Y.; Li, D.S. Experimental and Numerical Study of the Fatigue Properties of Corroded Parallel Wire Cables. J. Bridg. Eng. 2011, 17, 211–220. [Google Scholar] [CrossRef]
  13. Li, H.; Li, S.; Ou, J.; Li, H. Reliability assessment of cable-stayed bridges based on structural health monitoring techniques. Struct. Infrastruct. Eng. 2012, 8, 829–845. [Google Scholar] [CrossRef]
  14. Li, H.; Ou, J. The state of the art in structural health monitoring of cable-stayed bridges. J. Civ. Struct. Health Monit. 2016, 6, 43–67. [Google Scholar] [CrossRef]
  15. Al-Hijazeen, A.Z.O.; Fawad, M.; Gerges, M.; Koris, K.; Salamak, M. Implementation of digital twin and support vector machine in structural health monitoring of bridges. Arch. Civ. Eng. 2023, 69, 31–47. [Google Scholar] [CrossRef]
  16. Barros, B.; Conde, B.; Cabaleiro, M.; Riveiro, B. Deterministic and probabilistic-based model updating of aging steel bridges. Structures 2023, 54, 89–105. [Google Scholar] [CrossRef]
  17. Borlenghi, P.; Gentile, C.; Pirrò, M. Vibration-based structural health monitoring of a historic arch bridge. Experimental Vibration Analysis for Civil Engineering Structures. EVACES 2023, Limongelli, M.P., Giordano, P.F., Quqa, S., Gentile, C., Cigada, A., Eds.; Lecture Notes in Civil Engineering, Springer: Berlin/Heidelberg, Germany, 2023; Volume 432. [Google Scholar] [CrossRef]
Preprints 95882 g001
Figure 1. The Széchenyi chain bridge located in Budapest, Hungary.
Figure 1. The Széchenyi chain bridge located in Budapest, Hungary.
Preprints 95882 g001
Preprints 95882 g002
Figure 2. Cross-section of the bridge a) before and b) after renewal in 2021-2023 with the main dimensions [mm].
Figure 2. Cross-section of the bridge a) before and b) after renewal in 2021-2023 with the main dimensions [mm].
Preprints 95882 g002
Preprints 95882 g003
Figure 3. Measurement locations, proof load test executed in 2018.
Figure 3. Measurement locations, proof load test executed in 2018.
Preprints 95882 g003
Preprints 95882 g004
Figure 4. Notation of strain gauges (i = 1…8), proof load test in 2018: a) Hx/i: strain gauges at abutment and b) Px/i: strain gauges at pylon (x = 1…4).
Figure 4. Notation of strain gauges (i = 1…8), proof load test in 2018: a) Hx/i: strain gauges at abutment and b) Px/i: strain gauges at pylon (x = 1…4).
Preprints 95882 g004
Preprints 95882 g005
Figure 5. Examples of analysed load cases, proof load test in 2018.
Figure 5. Examples of analysed load cases, proof load test in 2018.
Preprints 95882 g005
Preprints 95882 g006
Figure 6. Derived measurement results at the abutment, proof load test in 2018.
Figure 6. Derived measurement results at the abutment, proof load test in 2018.
Preprints 95882 g006
Preprints 95882 g007
Figure 7. Derived measurement results at the pylon (side span), proof load test in 2018.
Figure 7. Derived measurement results at the pylon (side span), proof load test in 2018.
Preprints 95882 g007
Preprints 95882 g008
Figure 8. Derived measurement results at the pylon (main span), proof load test in 2018.
Figure 8. Derived measurement results at the pylon (main span), proof load test in 2018.
Preprints 95882 g008
Preprints 95882 g009
Figure 9. Position of strain gauges at the pylon – temporary monitoring system.
Figure 9. Position of strain gauges at the pylon – temporary monitoring system.
Preprints 95882 g009
Preprints 95882 g010
Figure 10. Superstructure with suspended scaffolding after demolishing old concrete deck.
Figure 10. Superstructure with suspended scaffolding after demolishing old concrete deck.
Preprints 95882 g010
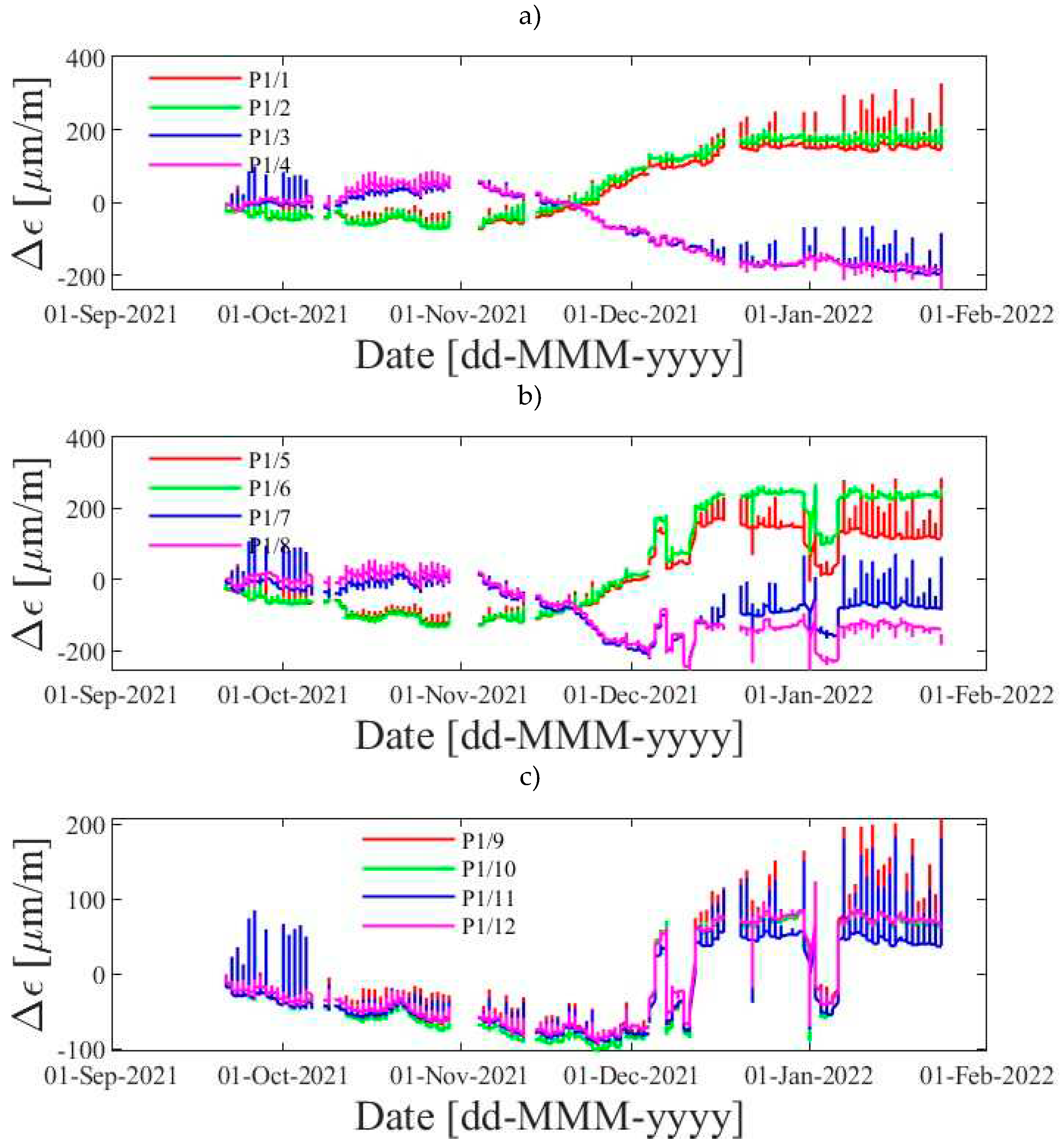
Preprints 95882 g011
Figure 11. Changes in strains in the pylon: a) upper chain, b) lower chain and c) neutral axis.
Figure 11. Changes in strains in the pylon: a) upper chain, b) lower chain and c) neutral axis.
Preprints 95882 g011
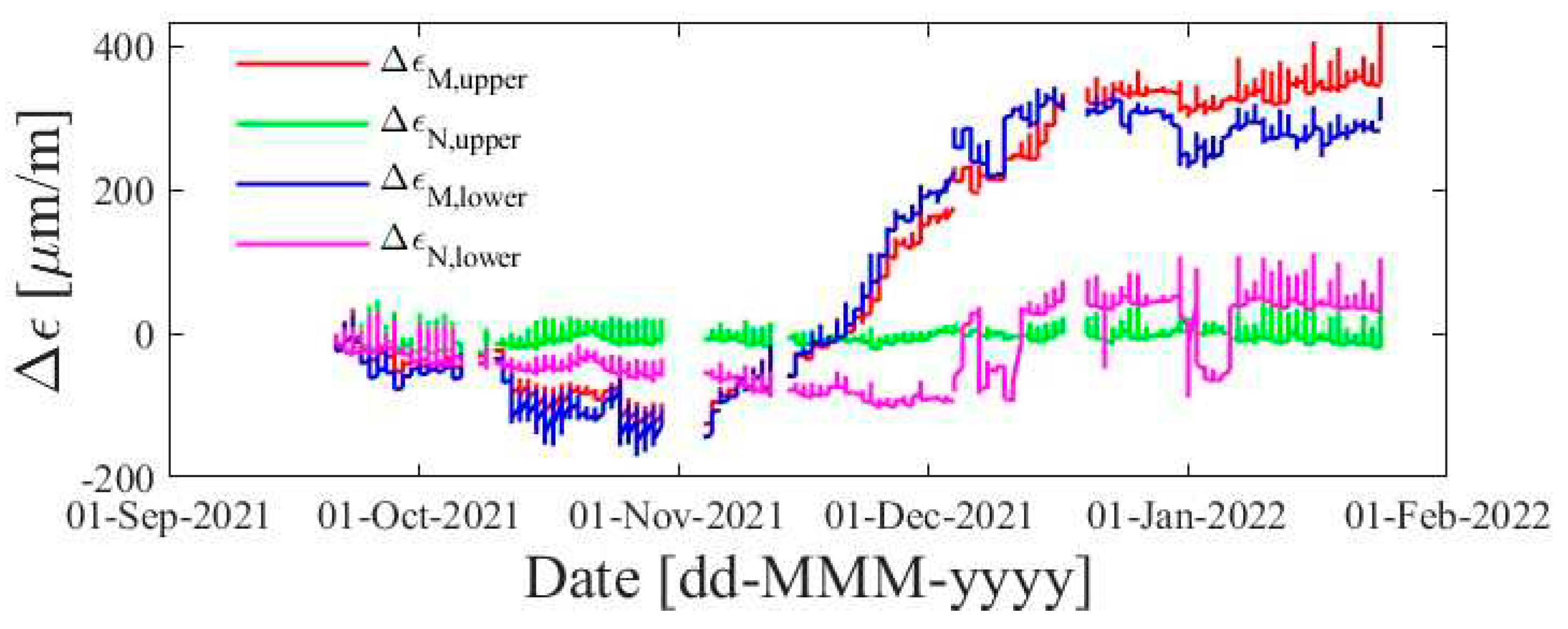
Preprints 95882 g012
Figure 12. Derived strain changes concerning normal force (ΔεN) and bending moment (ΔεM) on the upper and lower chains at measurement location P1.
Figure 12. Derived strain changes concerning normal force (ΔεN) and bending moment (ΔεM) on the upper and lower chains at measurement location P1.
Preprints 95882 g012
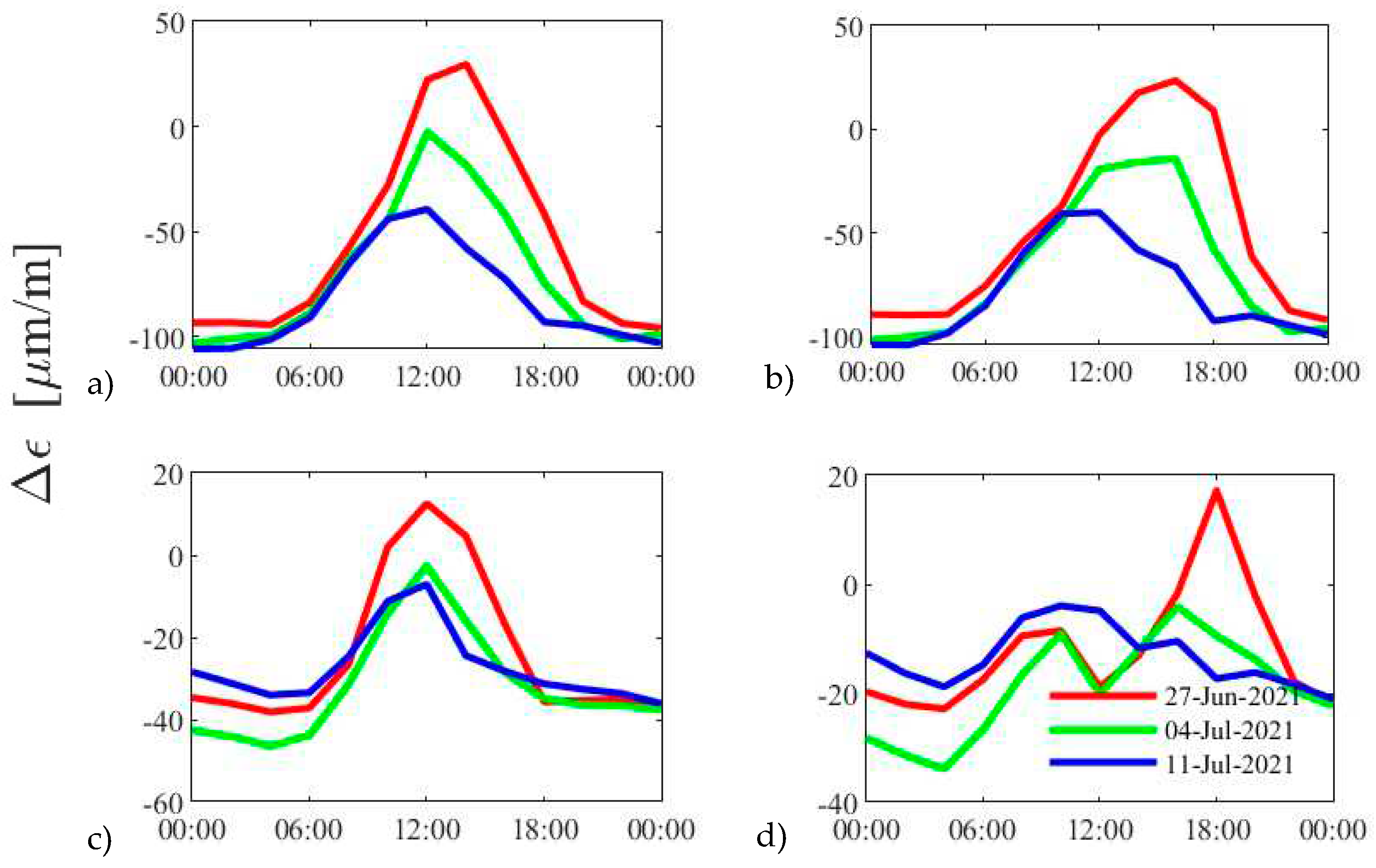
Preprints 95882 g013
Figure 13. Strain changes within a day without construction works on the bridge: a-d) P1/1-P1/4.
Figure 13. Strain changes within a day without construction works on the bridge: a-d) P1/1-P1/4.
Preprints 95882 g013
Table 1. Measured maximum daily strain variations [μm/m].
Table 1. Measured maximum daily strain variations [μm/m].
Fibre Chain P1 P2 P3 P4
Top Upper 110-125 85-110 105-120 80-105
Lower 100-125 110-135 100-140 95-140
Neutral Upper 60-80 35-80 60-80 40-80
Lower 55-70 35-80 65-85 25-80
Bottom Upper 40-50 85-120 45-50 115-125
Lower 40-110 115-115 45-110 95-140
Table 2. Derived maximum normal force (ΔN) and bending moment (ΔM) variations due to proof load test (PLT), reconstruction (REC) and daily temperature fluctuation (ΔT).
Table 2. Derived maximum normal force (ΔN) and bending moment (ΔM) variations due to proof load test (PLT), reconstruction (REC) and daily temperature fluctuation (ΔT).
Chain Quantity P1 P2 P3 P4
PLT REC ΔT PLT REC ΔT PLT REC ΔT PLT REC ΔT
Upper ΔN [kN] 1206 1517 1904 1036 1682 1439 1482 4568 1768 1042 2379 1426
ΔM [kNm] 147 702 151 146 359 268 228 457 142 141 366 285
Lower ΔN [kN] 998 2996 1215 801 2943 1134 1305 - 1316 959 2565 1132
ΔM [kNm] 17 560 197 23 263 270 27 - 220 21 347 326
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated