Prerpints.org logo
Preprint
Article

Experimental Study of Cavitation Control Around a Circular Cylinder Using a Passive Control Method

Altmetrics

Downloads

156

Views

81

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

09 January 2024

Posted:

10 January 2024

You are already at the latest version

Alerts
Abstract
Experimental investigations were conducted to uncover the impact of cavitation control - through the use of riblets (mesoscale surface structuring) - on cavitating flows around a circular cylinder. First, the dynamics of cavitation in the flow behind a finite cylinder (without riblets) was unveiled by visualizing the cavitation clouds and measuring the lift force fluctuations acting on the cylinder. Second, as a significant step forward, a comprehensive explanation was provided for the mechanism of cavitation control using two bio-inspired riblet morphologies positioned in different orientations and locations on the cylinder. For the first time, the effects of these tiny structures on the flow dynamics and the associated cavitation process were scrutinized. This showed that scalloped riblets, with their curved design, induced secondary vortices near their tips and distorted primary streamwise vortices, and that high velocity gradients near the jagged pattern peaks of sawtooth riblets delayed flow separation, which affected cavitation.
Keywords: 
Subject: Engineering  -   Marine Engineering

1. Introduction

Cavitation appears as an undesirable phenomenon in diverse industrial applications. To elaborate, cavitation lead to erosion on surface of propellers/rudders of ships, or it generate unwelcome vibration/noise within components of hydraulic systems; see, e.g., Reisman et al. [1], Dular et al. [2], Haosheng [3], Patella et al. [4], Kadivar et al. [5], and Lin et al. [6]. Franc and Micheal [7] noted that, at a constant temperature, cavitation may occur around immersed objects when the local pressure falls below the vapor pressure of the liquid. Additional factors, including turbulent flow characteristics, surface roughness [8,9], temperature and viscosity of the liquid [10], and density and radius of the nuclei [11], may affect cavitation or contribute to its initiation and on immersed bodies. Different types of the cavitation which commonly encountered on ship rudders, and the components of the hydraulic systems manifests itself as sheet-like cavitation, partial cavitation, or cloud cavitation. Among these, cloud cavitation is the most hazardous because it tends to induce severe erosion damage, thereby provoking surface vibrations on the immersed bodies as highlighted by Kadivar [12]. Prior investigations dealt with diverse cavitation dynamics that occur on hydrofoils. For instance, Li et al. [13] examined the partial cavitation dynamics in various regimes of cavitations on a hydrofoil surface. Callenaere et al. [14] investigated the partial cavitation occurring on a hydrofoil, along with the formation of a re-entrant jet that may arise within this specific cavitation regime. Their findings revealed that a re-entrant jet generates and progresses towards the leading edge of the hydrofoil in a regime of partial cavitation. This observation led them to conclude that this phenomenon is the predominant mechanism responsible for the shedding of cavities from the surface of the hydrofoil. Meanwhile, Stutz and Reboud [15] conducted experimental analyses to dissect the sheet cavitation formations on a geometry like venturi. They scrutinized the behavior of attached cavitation, including the length patterns of cavities and the phenomenon of reversed flow.
Leroux et al. [16,17] showed that two primary mechanisms contribute to the shedding of cavities on a hydrofoil surface in the partial cavitation regime. These mechanisms include the formation of a re-entrant jet and the formation of a shockwave subsequently causing the cavity’s collapse. The shockwave alters the cavitation dynamics. Over recent decades, numerous investigations focused on comprehending the dynamics of cloud cavitation, specifically aiming to elucidate the mechanisms of the cavity shedding and cavitation fluctuations. For instance, Ganesh et al. [18] explored the intricacies of unsteady cavitation emerging on an apex geometry through the use of a X-ray densitometer method. Their observations showed that a distinct shockwave contributes to the oscillation of unsteady cavitation at the aft part. Kadivar et al. [19,20] investigated the unsteady cavitation dynamics and surge cavitation occurring over both a hydrofoil and a semicircular flat plate. They concluded that the evolution of the sheet cavity to a cloud cavity diverges from the cavity structure dynamics within the cloud cavitating regime. Their findings pointed out that within the surge cavitation regime, the cavity fluctuations dynamics are driven by pressure waves generated within the cavity due to the collapsing of the cavity. In other words, the mechanism of the cavity shedding was not directly generated by a re-entrant jet in the cavitation surge regime. Pelz et al. [21] examined the influence of a re-entrant jet on unsteady cloud cavitation. Their research also presented insights into how the nucleation rate affects the cavity length and how the Reynolds number influences the formation of the re-entrant jet on the hydrofoil.
Circular cylinders or the similar geometries are commonly employed in marine contexts. Extensive prior studies have addressed cavitation around circular cylinders and the mechanism of cavitation shedding. For instance, Matsudaira et al. [22] examined the flow characteristics within the vortex cavitation. They discovered that the vortices’ shedding frequency aligns closely with the pressure pulsations caused by the collapse of cavity. Saito and Sato [23] examined the formation of Karman vortex-like cavity structures behind a cylinder. They analyzed the cavitation pulsations and the erosion induced by the cavity collapses on a plate made of aluminum mounted to the test section’s wall. Their hypothesis suggested that the erosion on the plate is caused by strong impulsive forces resulting from collapsing of cavities. Kumar et al. [24] studied experimentally the cavitation behind a cylinder at a Reynolds number of around 64000. They revealed that reducing the cavitation number leads to a decrease in the frequency of cavity shedding. Moreover, they identified that lower cavitation numbers correlate with higher pressure pulsations. Gnanaskandan and Mahesh [25], by numerically analyzing the pressure waves induced by the cavitation collapses, illustrated the significant impact of cavitation on the pressure distribution, and the resultant forces.
Dobroselsky [26] performed an experimental study of cavitating flows around a cylinder at critical Reynolds numbers. He found the quasi-periodic nature of the cavity shedding mechanism from the surface of the cylinder. Additionally, he indicated the dependence of cavitation onset on the Reynolds number. Brandao et al. [27] performed a numerical simulation of the cavitation behind a cylinder at various cavitating regimes and low Reynolds numbers from the laminar to turbulent flows. Their findings revealed a significant alteration in cavitation within the Karman vortices caused by the initiation of the propagation of condensation front. Gu et al. [28] employed the Large Eddy Simulation (LES) technique to explore cavitation dynamics behind a cylinder at Reynolds number of around 9500. Their findings highlighted that vortex cavitation plays an important role in influencing the shedding frequency of the cylinder’s wake. Sadri and Kadivar [29] investigated the behavior of unsteady cavitation and the noise generated by the cavity collapses around one and two cylinders. They specifically analyzed the cavitation in scenarios where two cylinders were positioned side by side with varying gaps between them. Their study indicated that, by gap reduction, the wake patterns formed behind these cylinders coalesce, giving rise to a singular vortex street.
Regarding cavitation control, extensive studies were conducted to explore various passive methods aimed at mitigating cavitation effects around immersible bodies. Custodio et al. [30] examined the impact of protuberances on cavitation. Their findings indicated that medium to large protuberance amplitudes hinder cavitation development at the aft part of the protuberance troughs. Hao et al. [31] analyzed the dynamics of cavitation around hydrofoils with different surfaces and they emphasized that the presence of a roughness across the hydrofoil’s surface may affect the cloud cavitation. They deduced that hydrofoils with a rough surface pattern experience heightened intensity of cloud cavitation. Zhao and Wang [32] investigated unsteady cloud cavitation control by implementing a bio-inspired structure situated on the suction side of the hydrofoil, showing that the bio-inspired structure possesses the capability to control the levels of turbulent kinetic energy. Furthermore, they demonstrated that hydrodynamic efficiency improves due to the presence of the bio-inspired structure. Zhang et al. [33] conducted both experimental and numerical studies focused on controlling the cavitation by incorporating an obstacle on the hydrofoil. They showed that the obstacle restricts the cavity fluctuations. Che et al. [34,35] examined the control of partial cavitation on a hydrofoil by employing micro vortex generators. They showed that these micro vortex generators effectively manipulate the location of cavitation inception near to the location of the flow separation within the unsteady cavitating regime of the hydrofoil. Kadivar et al. [36,37] showed that utilizing bubble generators effectively mitigate cavitation. Simanto et al. [38] showed that leading-edge protuberances mitigate the cavitation, and these protuberances reduce the noise, particularly at higher Reynolds numbers when the cavitation plays as the primary source of noise. Yu et al. [39] experimentally and numerically studied controlling cavitation using a porous pattern on a cylinder, demonstrating that a porous layer mitigated the generated vortices and the inception of cavities.
To the authors’ knowledge, the current work presents a unique and deeper experimental analysis to effectively reveal the detailed mechanism of cavitation control using riblets. The aim was to substantially improve our current understanding of cavitation dynamics and cavitation control. The paper was organized as follows. Section 2 describes the experimental setup, the experimental conditions, and the test cases considered. Section 3 portrays the main results, including the dynamics of cavitation in the flow region behind a cylinder, the morphological analysis of riblets, and the effects of flow conditions on cavitation control. Finally, Section 4 summarizes the conclusions.

2. Experimental Setup

The investigations were performed in the cavitation tunnel K23 at the Institute of Ship Technology of the Duisburg-Essen University. This tunnel functioned as a closed cavitation tunnel, comprising an electric motor-driven impeller, a vacuum pump, and an array of the pressure transducers and temperature sensors. The tunnel reached inlet velocities of up to 9.0 m/s, with fluctuations typically less than 0.1 m/s. The tunnel’s test section (with 1.1 m length) encompasses a square inlet section 0.3 by 0.3 m2. This test section, consisting of four Plexiglas walls, offered optimal observation from various perspectives. A high-speed camera, positioned at one side of the test section, monitored the flow. During the experiments, cylinders were vertically installed on the test section wall. Figure 1 illustrates the experimental setup, and the top view of two different configurations of riblet placement, with an arrow pointing in the flow direction.
A high-speed camera was used to capture the cavitation around a cylinder with and without riblet structures. A six DOF freedom load sensor, located on one side of the tunnel’s test section between the tunnel wall and the cylinder, measured the lift and drag forces acting on the circular cylinder. A pressure transducer, mounted at the outlet of the tunnel, measured the pressure fluctuations behind the cylinder and in the cylinder’s wake.
The experiments were conducted at different Reynolds numbers R e = 1.0 × 10 5 , 1.25 × 10 5 , and 1.5 × 10 5 and three cavitation numbers of σ = 1.0, 1.5, and 2.0. The cavitation number σ and the Reynolds number Re were here defined as follows:
σ = p r e f − p v 1 / 2 ρ r e f V r e f 2
R e = V r e f l r e f ν
where p r e f and p v are the reference static pressures at the middle of inlet section and the saturation vapor pressure of the operating liquid, respectively, V r e f is the inlet flow velocity, and ρ r e f and ν are the reference density and kinematic viscosity of the water, respectively.
The experimental conditions were constantly adjusted during the tests to assess the cavitation dynamics between comparative cases. To reduce the effect of varying air content, the air inside the cavitation tunnel was kept within the range of 1.2 mg/L and the water temperature of about 16 ◦C with a tolerance of 0.1◦C. Consequently, the uncertainty of the vapor pressure was almost 24 Pa, the uncertainty of the inlet pressure ranged between of 100 to 200 Pa; the uncertainty of the cavitation number, between 0.05 and 0.10, the uncertainty of the Reynolds number was between 1 and 2%. The high-speed imaging was captured at a frequency of 1000 Hz with an exposure time of 30 μs. The resolution of the captured images was 1632 x 1200 pixel counts.
A sampling rate of about 5 Hz was specified for the acquisition system that measures the force. Employing a measuring amplifier MX1601B, the six DoF force sensor relied on an HBM data acquisition system to capture the force fluctuations on the cylinder. A LaVision high-speed control system enabled the acquisition and post-processing of the captured images. A 5V trigger signal from this control system to the HBM measuring amplifiers synchronized the captured images with the data acquisition system.
Figure 2 shows the cylinders with horizontal/vertical scalloped/sawtooth riblets. The 13.0 cm long cylinders had a diameter of 2.5 cm. The riblets on the manufactured cylinders were 1.5 mm height and the spacing between riblets measured 3.0 mm. The top width of the scalloped riblets was 0.5 mm, and the groove radius between these riblets was 1.0 mm. The section of the manufactured riblets on the cylinder was 8.0 cm; that is, the riblets extended over only one part of the cylinders’ circumference and not over the rest of the cylinder.

3. Results and Discussion

3.1. Cavitation dynamics

Figure 3 presents cavity dynamics behind the cylinders caused by the flow at R e = 1.25 × 10 5 and σ = 1.0 . Figure 3a refers to the cylinder without riblets; Figure 3b,c, to the cylinder equipped with horizontal and vertical sawtooth riblets, respectively; Figure 3d,e, to the cylinder with horizontal and vertical scalloped riblets, respectively. As seen, the flow interacted with the cylinder, and miniature riblets induced the creation of small vortex structures nearby, where they significantly affected the instabilities in the absence of the riblets.
In the scenario where a smooth cylinder (without riblets) of finite length and with a free-end (tip) was exposed to an incident flow, a pair of counter-rotating trailing vortices emerged near the cylinder’s tip, as shown by the purple-colored vectors in Figure 3a. The formation of these vortices arose due to a phenomenon termed as upwash, caused by a weak upward-directed local velocity field at the cylinder’s tip [44]. As the flow proceeded over the tip, a downwash occurred, whereby the flow descended into the low-pressure region immediately behind the cylinder. The combination of an upwash flow on the sides and the downwash at the center triggered the formation of two counter rotating trailing vortices [45]. Additionally, segment of the incident flow close to the base moved downward as it approached the cylinder [46], and it subsequently circulated upstream of the junction between the cylinder and the wall. In this region, the horseshoe vortex took on its shape, wrapped around the cylinder, as shown by the yellow vectors in Figure 3a, and then progressed downstream [47]. The combined presence of upwash and downwash vortices led to shedding patterns of varying frequency and amplitude and generated unstable Karman vortices, as shown by the white vectors in Figure 3a, and this intricately dancing vortex trio added another layer of complexity to the formation of cavitation.
Cavitation on the cylinder occurred akin to hydrofoil cavitation, particularly in the proximity of the laminar separation bubble (LSB) and close to the flow reattachment point [20]. It started with the generation of linear instability-driven Tollmien–Schlichting (T–S) waves, i.e., constant-frequency traveling waves within the boundary layer. Especially these T-S waves contributed to laminar separation bubble formation. Subsequently, nonlinear three-dimensional (3D) instabilities arose from these linear waves that led to turbulence. Turbulent spots formed and expanded in both streamwise and spanwise directions. This T-S wave development within the stable laminar boundary layer crucially triggered the transition to turbulent flow. Pressure fluctuations, caused by flow instabilities on the cylinder surface, induced cavitation when the local water pressure dropped below the vapor pressure [40]. We focused our cavitation control strategy on managing flow instabilities, as well as pressure fluctuations, and mitigating LSB formation using miniature riblets.

3.2. Morphology of riblets

Riblets come in a range of shapes, often inspired from biological forms, and they are commonly employed to manage both flow separation and reduce drag [41,42,43]. The most common riblets include sawtooth and scalloped riblets. The usefulness of riblets is based on their capacity to generate vortices behind them, enabling the control of the boundary layer. As seen in Figure 3b–e, the geometric configuration of riblets and the method of their implementation on the cylinder’s surface significantly influenced flow control and, thus, the inception of cavitation. When considering flow control, the choice of riblet type plays a significant role. Optimal selection involves selecting riblets capable of directing fluid with higher momentum to the boundary layer, where momentum is comparatively low. This strategic selection aids in enhanced control of the boundary layer, a critical factor for effective flow management.
The mechanism behind controlling cavitation achieved through the utilization of riblets has been elucidated in our prior published research [34,35]. As the flow interacts with the cylinder, the presence of miniature riblets gives rise to the formation of small vortex structures in their vicinity. These compact vortices play a pivotal role in influencing the instabilities present within the boundary layer, which would otherwise emerge on the cylinder’s surface in the absence of riblets. This mechanism operates through the generation of streamwise vortices by the riblets, facilitating the transfer of fluid with higher momentum from the upper layer into the boundary layer. One significant result of riblet implementation is the increasing the velocities of boundary layer near the surface of the cylinder, which reduces the velocity pulsations inside boundary layer. Thus, employing riblets enabled us to manage the large-scale cavity pulsations generated behind the cylinder. This was achieved by decreasing the instabilities in the upstream boundary layer on the cylinder surface.
Figure 4 presents flow patterns developed near the scalloped riblet’s tip. As seen, scalloped riblets altered the roll-up and breakdown of streamwise vortices in different ways, leading to decisive changes in behavior and interaction with the surrounding flow. Thus, their effects varied, based on their ability to generate vortices influencing the boundary layer. The presence of scalloped riblets resulted in the generation of secondary vortices [49], inside the valleys near the tip of the riblets; see Figure 4a. In certain instances, both the primary large-scale streamwise vortices and these secondary vortices, induced by the riblet tips, underwent distortion, as seen in Figure 4b, and acquired an elongated shape. This altered vortex morphology significantly affected the flow dynamics and cavitation inception. These alterations in vortex structure hold substantial implications for flow dynamics.
In the case of sawtooth riblets, Goldstein et al. [50] observed a distinctive flow behavior. Close to the peaks of sawtooth riblets, the velocity gradient increased notably, suggesting a region of high velocity gradients. Conversely, within the valleys between the riblets, the velocity gradient is notably reduced. Recall that, occasionally, vorticities do extend into these valleys, it they are usually concentrated near the tips of the riblets. However, as seen in Figure 3b,c, while the jagged pattern of sawtooth riblets actively controlled the near wall flow by delaying flow separation, the curved pattern of scalloped riblets depicted in Figure 3d,e delayed the transition to turbulence.
Horizontal riblets modified the near wall flow, predominantly affecting turbulence levels, while vertical riblets smoothed the flow. As seen in Figure 3b,d, horizontal riblets led to a more stable and predictable flow. Conversely, as seen in Figure 3c,e, vertical riblets changed the intensity and the behavior of turbulence structures. Thus, riblets with different patterns, i.e., scalloped or sawtooth mounted horizontally or vertically, offered unique ways to alter flow dynamics [48] as well as the associated turbulence and separation characteristics of the Karman vortices. consequently, it is crucial to select riblets capable of redirecting the fluid with higher momentum into the boundary layer, even when the flow’s momentum is relatively low.
Figure 5 and Figure 6 present five sequential images at five time intervals (periodic) depicting cavitation process behind the cylinder with horizontal scalloped (SC-H) riblets and vertical scalloped (SC-V) riblets, both caused by the flow at R e = 1.25 × 10 5 and σ = 1.0 . These specific images were chosen from half of a standard period T (cyclic) that characterized the dynamics of cavity shedding. The red areas indicate regions where the riblets exerted their most significant influence on cavitation. Notably, the pressure increasing behind the riblets led to a reduction in the cavity volume behind the plain cylinder.
As expected, in the case with SC-H riblets, an effective vortex interaction with the boundary layer is seen (Figure 5). This occurred because flow moved through the tips and valley curves of the horizontal (SC-H) riblets [49], generating strong longitudinal vortices that affected the boundary layer. In comparison, the flow over the vertical scalloped riblets (SC-V) primarily engaged with the riblets’ sharp edges (Figure 6), promoting the merging of vortices further downstream.
For the cylinder with SC-V riblets, depicted in Figure 3e, the flow around these riblets mostly interacted with the sharpness of the riblets [50]. Instead of longitudinal vortices, this resulted in a vortex sheet forming behind the riblets. SC-H riblets facilitate better interaction as flow moves through valleys at both sides of the riblet instead of merely passing over them as with SC-V riblets. This increased interaction along the top and bottom surfaces of each riblet led to the merging of vortices downstream, thereby creating stronger vortices. Consequently, the horizontal (SC-H) riblets effectively directed higher-momentum fluid into the boundary layer due to their enhanced interaction with the flow.
We also conducted a more comprehensive analysis of how riblet shape and orientation impacted cavitation dynamics in flows at constant Reynolds and cavitation numbers. Riblets modified large-scale cavity structures into smaller ones. Consequently, the cylinder with riblets anticipated lower pressure fluctuations, resulting from detachment and also collapse of these smaller cavities. In essence, riblets mitigated lift force fluctuations and cavitation-induced vibrations on the cylinder surface. The reduced amplitude and shedding frequency of these vibrations represented a significant benefit of riblets. Note that the cavity shedding frequency was slightly higher for cylinder with riblets because the new small-scale cavities generated by these riblets had a higher frequency of the cavity shedding compared to the large-scale cavities.
Figure 7 presents comparative distributions of lift force Fy versus frequency f for the cylinder without and with riblets, caused by the flow at R = 1.25 × 10 5 and σ = 1.0 . Figure 7a plots these distributions for the cylinder with SC-H and SA-H riblets; Figure 7b, for the cylinder with SC-H and SC-V riblets. The frequencies with highest amplitudes corresponded to the shedding frequency of large-scale cavity structures.
As seen in Figure 7a, for the case with riblets mounted horizontally, the amplitude of the lift force was substantially reduced: specifically, by 41 % (from 1.44 to 0.84 N) for SA-H and by 43 % (from 1.44 to 0.82 N) for SC-H. Furthermore, the shedding frequency of cavities increased for SA-H and SC-H cases compared to the plain cylinder: specifically, from 31.6 Hz to 43.8 Hz. In Figure 7b, for SC-H cylinder, the lift force was also reduced by 43 % (from 1.44 to 0.82 N), and by 30 % (from 1.44 to 1.01 N) for SC-V. Here too, the shedding increased for the cylinder with scalloped riblets (SC-H and SC-V) compared to the smooth cylinder: specifically, from 31.6 to 44.4 Hz. Remarkably, horizontal scalloped riblets (SC-H) reduced the amplitude of lift fluctuations more effectively than vertical scalloped riblets (SC-V).
Figure 8 illustrates a comparison between the lift force amplitude and cavitation shedding frequency for plain cylinders and those with riblets mounted horizontally and vertically. The findings indicate that in the case of scallop riblets, horizontal installation results in a smaller lift force range. Conversely, for sawtooth riblets, vertical implementation has a more pronounced impact on reducing the amplitude of lift forces. Nonetheless, the shedding frequency is higher for cylinders with horizontal scalloped/sawtooth riblets compared to their vertical counterparts, with the case without riblets having the lowest shedding frequency. One reason for this increase in shedding frequency is the reduced time required for cavities to detach from the surface of the cylinder due to the presence of riblets. Consequently, riblet structures can be inferred to reduce amplitude of lift fluctuations while slightly increasing the shedding frequency.
Although placing riblets on the upstream face of the cylinder mostly altered the attached flow and the flow’s stability, rear riblets influenced the shedding of vortices in the wake region, thereby also mitigating cavitation. To explore the effects of placing riblets on the cylinder’s rear side, the cylinder with SC-H riblets was rotated 150 deg clockwise. Figure 9 shows the riblets situated on the upstream/downstream face of the cylinder, caused by the flow at R = 1.25 × 10 5 and σ = 1.0 . As seen, the riblets affected the attached flow and the flow’s stability, whereas rear riblets impacted vortex shedding in the wake region, potentially mitigating cavitation. The red surrounded area in Figure 9a shows the extensive cavitation cloud generated behind the plain cylinder as this cloud was transformed into smaller and less dense clouds for the cylinder with horizontal scalloped riblets (SC-H) facing upstream. The green surrounded areas in Figure 9b,c represent these cavitation clouds for the cylinder with unrotated and rotated SC-H riblets. While upstream-faced SC-H riblets promoted a smoother flow over the cylinder’s surface and delayed the transition to turbulence, the rotated SC-H riblets generated unstable and unpredictable flow patterns. These flow patterns reduced the shedding frequency of cloud cavitation.
Figure 10 presents five sequential images, captured at regular intervals, showing the progression of cavities around a cylinder with SC-H riblets rotated 150 deg clockwise, caused by the flow at R e = 1.25 × 10 5 and σ = 1.0 . While the upstream-oriented SC-H riblets resulted in a smoother flow and delayed the transition to turbulence, the rotated SC-H riblets induced unstable and unpredictable flow patterns. Although the rotated riblets had a lesser effect on modifying the wake behavior, they caused unstable and unpredictable flow patterns.
Figure 11 presents comparative plots of lift force amplitude (columns) versus cavitation shedding frequency (squares for 0 deg rotation, dots for 150 deg clockwise rotation) for the plain cylinder and for the cylinders equipped with horizontal and vertical riblets, caused by the flow at R e = 1.25 × 10 5 and σ = 1.0 . Shown is the morphological variation for the 0 and 150 deg cylinder rotation, displaying lift force amplitude (columns) and vortex shedding frequency (squares and dots) for the plain cylinder, SC-H, SC-V, SA-H, and SA-V riblets. Only the SC-H riblets caused a significant reduction of lift force amplitudes when rotated. In contrast, the other riblet configurations hardly affected the lift force amplitudes compared to those of the plain cylinder. Furthermore, the shedding frequency for the cylinders with the rotated riblets was similar to plain cylinder.

3.3. Effect of Reynolds number

Cavitation effects may be more intense at higher Reynolds numbers, where the Tollmien-Schlichting (T-S) waves grow in magnitude and become more prominent. However, the impacts of riblets on cavitation are influenced by the specific flow conditions. Although they may still be effective in controlling cavitation at different Reynolds numbers, their effectiveness may be limited by stronger turbulence and pressure fluctuations associated with turbulent flows.
Figure 12 shows cavitation structures behind the plain cylinder, SA-H, SA-V, SC-H, and SC-V riblets, caused by the flow at the lower R e = 1.0 × 10 5 . As seen, the transition occurred further downstream, where flow separation from the cylinder’s surface was less effective. Comparing Figure 12a with Figure 12b–e one can see that, at this lower R e = 1.0 × 10 5 , both the SA-H and the SA-V riblets reduced cavitation by improving flow stability although the SA-V riblets were more effective in mitigating cavitation. The SC-H and the SC-V riblets also effectively inhibited cavitation although the SC-H riblets had a greater effect on mitigating cavitation. All riblets stabilized the flow, reduced pressure fluctuations, and led to more stable and smaller cavitation structures; however, their effect on cavitation patterns differed slightly.
Figure 13 shows five sequential images captured at regular intervals of the progression of cavitation around the cylinder with SC-H. This series of images, caused by the flow at the lower R e = 1.0 × 10 5 , visualized the flow passing between riblet tips and valleys, thereby generating longitudinal vortices and facilitating effective vortex interaction within the boundary layer.
Figure 14 shows cavitation dynamics around the plain cylinder, SA-H, with SA-V, SC-H, and SC-V riblets, caused by the flow at the higher R e = 1.5 × 10 5 . As seen, now separation and flow reattachment occurred more readily due to the stronger turbulence generated by the T-S waves. Thus, the Reynolds number did influence the cavitation patterns. Comparative flow patterns shown in Figure 12a and Figure 14a demonstrated that, for the cylinder without riblets caused by the flow at the lower Reynolds number, the cavitation patterns became less structured and less dense. While riblets were still effective to mitigate cavitation at higher Reynolds numbers, their effectiveness was diminished due to the increased flow energy. Figure 14b–e show that, at this Reynolds number, SA-H, SA-V, and SC-V riblets provided only slight benefits although their effectiveness differed compared to the cases at lower Reynolds numbers. Notably, the SC-H riblets remained the most effective at mitigating the onset of cavitation. Furthermore, at R e = 1.5 × 10 5 , cavitation occurred further upstream, and the cavitation patterns were more pronounced and elongated.
Figure 15 pesents five sequential images captured at regular intervals, showing the progression of cavitation dynamics behind a cylinder with SC-H riblets at higher Reynolds number R e = 1.5 × 10 5 . Red surrounded areas indicate regions where the riblets exerted their most significant influence on cavitation. As seen, the SC-H riblets influenced the generation and distribution of the cavitation cloud, and they remained effective at delaying the onset of cavitation at this higher Reynolds number.
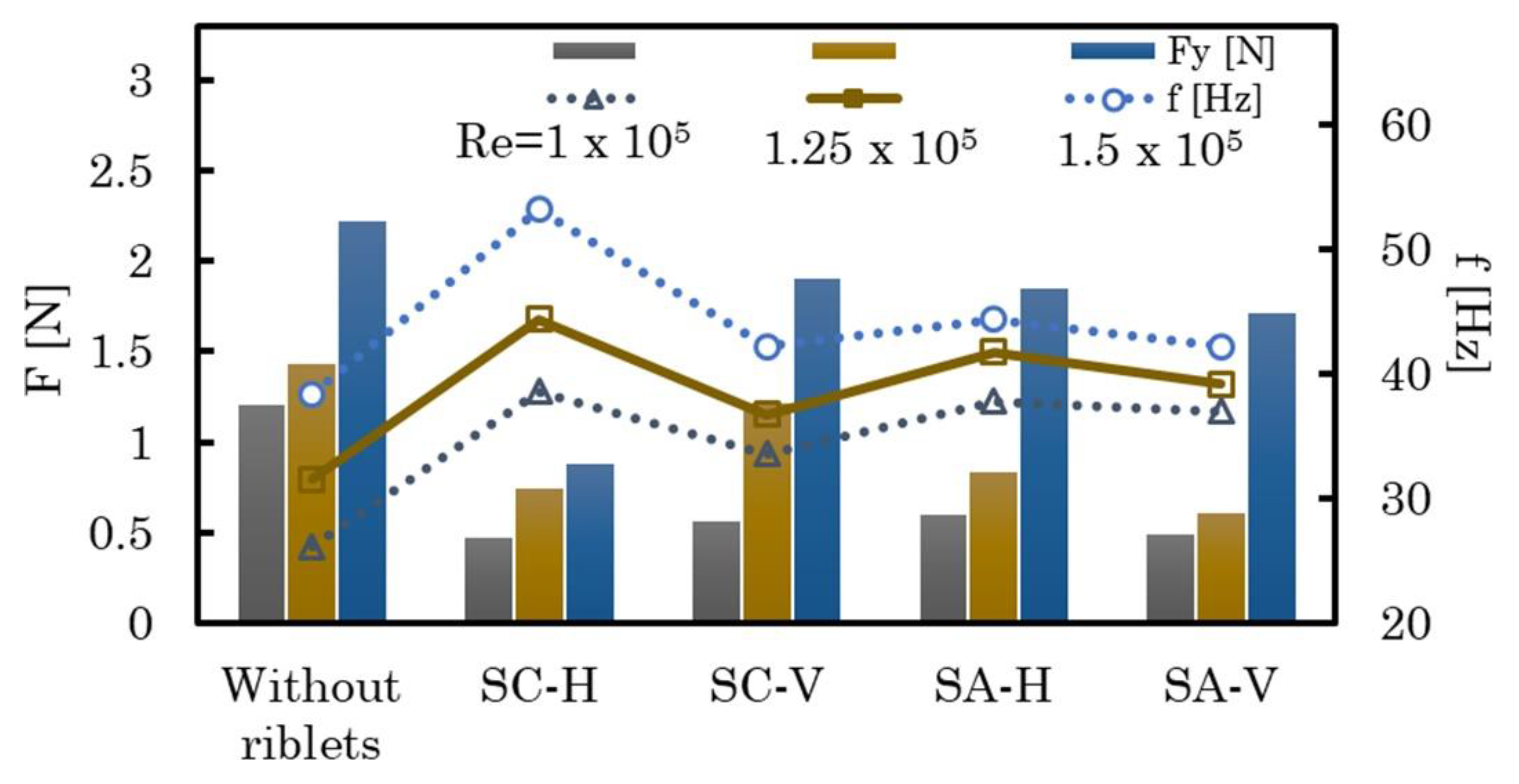
Figure 16 plots comparative lift force amplitudes and cavitation shedding frequencies for cylinder with the different kinds of riblets, caused by the flow at three different Reynolds numbers. Notably, at all Reynolds numbers, the SC-H riblets consistently reduced lift force amplitudes significantly. At R e = 1.0 × 10 5 and 1.25 × 10 5 , the other kinds of riblets also had a notable effect on lift force amplitudes. It was important to highlight that the introduction of riblets consistently led to an increase in shedding frequency at all Reynolds numbers. Interestingly, the shedding frequency of the cylinder with the SC-H riblets surpassed all other cases. This was due to the significantly reduced time required for cavities to detach themselves from the surface of the cylinder with SC-H riblets.

4. Conclusions

This experimental investigation first focused on the dynamics of cavitation occurring behind a smooth cylinder (without riblets) by obtaining high-speed cavitation images and measuring lift force fluctuations and cavitation shedding frequencies. Then the mechanism of cavitation control was comprehensively examined by employing various kinds of mesoscale riblets, positioned in different orientations and locations on the cylinder. The use of riblets, inspired from biological structures, has been widely applied to control both flow separation, as well as drag reduction. In our present work, two kinds of riblets were considered to control cavitation, namely, sawtooth and scalloped riblets. Our results demonstrated that riblets generated streamwise vortices by transferring the fluid with higher momentum to the low-momentum boundary layer, thereby effectively controlling the formation of large-scale cavity structures behind the cylinder. The effectiveness of these riblets was based on their capability to generate vortices behind them, which enabled controlling the boundary layer.
Scalloped riblets induced secondary vortices near their tips, causing the distortion of primary streamwise vortices. With sawtooth riblets, high velocity gradients appeared near riblet peaks; however, in the valleys between riblets, velocity gradients decreased, and the vorticity occasionally extended into the riblet valleys and tended to concentrate near riblet tips. With their curved design, scalloped riblets often delayed the transition to turbulence, while sawtooth riblets, with their jagged pattern, mostly delayed flow separation. Horizontal riblets modified the near-wall flow and affected turbulence; in contrast, vertical riblets created a smoother flow.
The considered riblets enabled distinct ways to influence flow dynamics and von Karman vortex characteristics. In summary, riblets effectively reduced cavitation-induced vibrations of the cylinder. For the cylinder with horizontal sawtooth (SA-H) and horizontal scalloped (SC-H) riblets, lift force fluctuations were significantly decreased. Specifically, amplitudes of cavitation-induced vibration were reduced by about 41% for the SA-H and 43% for the SC-H cylinders. Furthermore, the cavitation shedding frequencies increased to 43.8 Hz for the SA-H cylinder and to 44.4 Hz for SC-H cylinder compared to the smooth cylinder with a shedding frequency of 31.6 Hz. Riblets on the cylinder’s upstream side mostly affected flow attachment and flow stability, while rear riblets influenced wake vortex shedding. Upstream SC-H riblets provided a smoother flow and delayed the onset of turbulence, whereas rotated SC-H riblets induced an unstable flow. The shedding frequency of rotated riblets was similar to that of the smooth cylinder, as cavities detached at the same rate.
Our results also revealed that riblets controlled cavitation at differing Reynolds numbers; however, turbulent flows with higher pressure fluctuations limited their effectiveness. At the lower Reynolds number of 1.0 × 10 5 , the transition point occurred farther downstream, making flow separation less efficient, while, at the higher Reynolds number of 1.5 × 10 5 , turbulence caused separation and reattachment that affected cavitation patterns. At the lower Reynolds number of R e = 1.0 × 10 5 , the SA-H and SA-V riblets improved flow stability and reduced cavitation, whereby the effect of the SA-V riblets was more pronounced. Overall, at the Reynolds number of R e = 1.0 × 10 5 , riblets stabilized the flow, reduced pressure fluctuations, and caused more stable and smaller cavitation structures. At this lower Reynolds number, the SA-H, SA-V, and SC-V riblets were beneficial although their effectiveness varied compared to the cases at the higher Reynolds numbers. However, the SC-H riblets were the most effective in delaying the onset of cavitation and reducing pressure fluctuations. Furthermore, at this lower Reynolds number, cavitation with more pronounced and extended patterns occurred further upstream.

Data Availability Statement

The data supporting these findings were documented in this paper.

Acknowledgments

This work was supported by the German Research Foundation with a Project Number of 469042952. The design of the test cases was performed with the help of students Ms. Ataei and Mr. Ardalan.

References

  1. Reisman, G., Wang, Y. & Brennen, C. Observations of shock waves in cloud cavitation. J. Fluid Mech. 355 pp. 255-283 (1998). [CrossRef]
  2. Dular, M., Bachert, B., Stoffel, B. & Sirok, B. Relationship between cavitation structures and cavitation damage. Wear. 257 pp. 1176-1184 (2004). [CrossRef]
  3. Haosheng, C., Yongjian, L., Darong, C. & Jiadao, W. Experimental and numerical investigations on development of cavitation erosion pits on solid surface. Tribology Lett. 26 pp. 153159 (2007). [CrossRef]
  4. Patella, R., Choffat, T., Reboud, J. & Archer, A. Mass loss simulation in cavitation erosion: Fatigue criterion approach. Wear. 300 pp. 205-215 (2013). [CrossRef]
  5. Kadivar, E., el Moctar, O., Sagar, H. Experimental study of the influence of mesoscale surface structuring on single bubble dynamics. Ocean Engineering. 260 pp. 111892 (2022). [CrossRef]
  6. Lin, Y., Kadivar, E., el Moctar, O., Neugebauer, J. & Schellin, T.E. Experimental investigation on the effect of fluid–structure interaction on unsteady cavitating flows around flexible and stiff hydrofoils. J. Physics of Fluids. 34, pp. 083308 (2022). [CrossRef]
  7. Franc, J. & Micheal, J. Fundamentals of Cavitation. Kluwer Academic Publishers. (2005).
  8. Kadivar, E., el Moctar, O., Skoda, R., Lo¨schner, U. Experimental study of the control of cavitation-induced erosion created by collapse of single bubbles using a micro structured riblet. Wear 486-487, pp. 204087 (2021). [CrossRef]
  9. Arndt, Roger E., and Arthur T. Ippen. Cavitation near surfaces of distributed roughness. Massachusetts Institute of Technology Cambridge 1967.
  10. Phan, T.-H., Kadivar, E., Nguyen, V.-T., el Moctar, O., Park, W.-G. Thermodynamic effects on single cavitation bubble dynamics under various ambient temperature conditions. Physics of Fluids 34, pp. 023318 (2022). [CrossRef]
  11. Venning, James A., Bryce W. Pearce, and Paul A. Brandner. Nucleation effects on cloud cavitation about a hydrofoil. Journal of Fluid Mechanics A1, 947. [CrossRef]
  12. Kadivar, E. Experimental and Numerical Investigations of Cavitation Control Using Cavitating-bubble Generators. PhD Thesis, University Of Duisburg-Essen. (2020).
  13. Li, Q., Franc, J. & Michel, J. Partial Cavities: Global Behavior and Mean Pressure. Journal Of Fluids Engineering. 115 pp. 243-248 (1993). [CrossRef]
  14. Callenaere, M., Franc, J., Michel, J. & Rionde, M. The cavitation instability induced by the development of a re-entrant jet. Journal Of Fluid Mechanics. 444 pp. 223-256 (2001). [CrossRef]
  15. Stutz, B., and J-L. Reboud. Two-phase flow structure of sheet cavitation. Physics of fluids 9.12 pp. 3678-3686 (1997). [CrossRef]
  16. Leroux, J., Coutier-Delgosha, O. & A. Astolfi. A joint experimental and numerical study of mechanism associated to instability of partial cavitation on two-dimensional hydrofoil. Physics Of Fluids. 17 pp. 1-20 (2005). [CrossRef]
  17. Leroux, J., Astolfi, J. & Billard, J. An Experimental Study of Unsteady Partial Cavitation. Journal Of Fluids Engineering. 126 pp. 94-101 (2004). [CrossRef]
  18. Ganesh, H., Ma¨kiharju, S. & Ceccio, S. Bubbly shock propagation as a mechanism for sheet-to-cloud transition of partial cavities. Journal of Fluid Mechanics. 802 pp. 37-78 (2016). [CrossRef]
  19. Kadivar, E., Ochiai, T., Iga, Y., el Moctar, O. An experimental investigation of transient cavitation control on a hydrofoil using hemispherical vortex generators. Journal of Hydrodynamics. 33 pp. 1139-1147 (2020). [CrossRef]
  20. Kadivar, E., Timoshevskiy, M., Nichik, M., el Moctar, O., Schellin, T., Pervunin, K. Control of unsteady partial cavitation and cloud cavitation in marine engineering and hydraulic systems. Physics of Fluids. 32 pp. 052108 (2020). [CrossRef]
  21. Pelz, P., Keil, T. & T. F. Groß, The transition from sheet to cloud cavitation. Journal of Fluid Mechanics. 817 pp. 439-454 (2017). [CrossRef]
  22. Matsudaira, Y., Gomi, Y. & Oba, R. Characteristics of bubble-collapse pressures in a karman-vortex cavity. JSME International Journal. 35, 179-185 (1992). [CrossRef]
  23. Saito, Y. & Sato, K. Cavitation bubble collapse and impact in the wake of a circular cylinder. Fifth Int. Symp. Cavitation. pp. 3-8 (2003).
  24. Kumar, P., Chatterjee, D. & Bakshi, S. Experimental investigation of cavitating structures in the near wake of a cylinder. International Journal of Multiphase Flow. 89 pp. 207-217 (2017). [CrossRef]
  25. Gnanaskandan, A. & Mahesh, K. Numerical investigation of near-wake characteristics of cavitating flow over a circular cylinder. Journal of Fluid Mechanics. 790 pp. 453-491 (2016). [CrossRef]
  26. Dobroselsky, K. Cavitation streamlining of a round cylinder in the critical range. J. Phys. Conf. Ser. pp. 1-7 (2020). [CrossRef]
  27. Brandao, F., Bhatt, M. & Mahesh, K. Numerical study of cavitation regimes in flow over a circular cylinder. Journal of Fluid Mechanics. 885 pp. A19 (2019). [CrossRef]
  28. Gu, F., Huang, Y. & Zhang, D. Cavitation of multiscale vortices in circular cylinder wake at Re = 9500. Journal of Mar. Sci. Eng. 9, 1-7 (2021). [CrossRef]
  29. Sadri, M., Kadivar, E. Numerical investigation of the cavitating flow and the cavitation-induced noise around one and two circular cylinders. Ocean Engineering. 277 pp. 114178 (2023). [CrossRef]
  30. Custodio, D., Henoch, C. & Johari, H. Cavitation on hydrofoils with leading edge protuberances. Ocean Eng. 162 pp. 196-208 (2018). [CrossRef]
  31. Hao, J., Zhang, M. & Huang, X. The influence of surface roughness on cloud cavitation flow around hydrofoils. Acta Mech. Sin. 34 pp. 10-21 (2018). [CrossRef]
  32. Zhao, W. & Wang, G. Research on passive control of cloud cavitation based on a bionic fin-fin structure. Eng. Comput. 37 pp. 863-880 (2020). [CrossRef]
  33. Zhang, L., Chen, M. & Shao, X. Inhibition of cloud cavitation on a flat hydrofoil through the placement of an obstacle. Ocean Eng. 155 pp. 1-9 (2018). [CrossRef]
  34. Che, B., Chu, N., Schmidt, S., L. Cao, Likhachev, D. & Wu, D. Control effect of micro vortex generators on leading edge of attached cavitation. Physics of Fluids. 31 pp. 044102-1-044102-12 (2019). [CrossRef]
  35. Che, B., Chu, N., Cao, L., Schmidt, S., Likhachev, D. & Wu, D. Control effect of micro vortex generators on attached cavitation instability. Physics of Fluids. 31 pp. 064102-1-064102-11 (2019). [CrossRef]
  36. Kadivar, E., Timoshevskiy, M., Pervunin, K., el Moctar, O. Cavitation control using cylindrical cavitating-bubble generators (CCGS): experiments on a benchmark cav2003 hydrofoil. International Journal of Multiphase Flow. 125 pp. 103186 (2020). [CrossRef]
  37. Kadivar, E., el Moctar, O. Investigation of cloud cavitation passive control method for hydrofoils using Cavitating-bubble Generators (CGs). In: Proceedings of the 10th International Symposium on Cavitation, Baltimore, USA. [CrossRef]
  38. Simanto, R., Hong, J., Kim, K., Ahn, B. & Shin, S. Experimental investigation on cavitation and induced noise of two-dimensional hydrofoils with leading-edge protuberances. Physics of Fluids. 34 pp. 124115 (2022). [CrossRef]
  39. Yu, F., Zhang, Y., Liu, H., Zhou, Q. Experimental and numerical investigation of cavitation control with porous material on the hemisphere cylinder. J. Ocean Engineering. 266 pp. 112984 (2022). [CrossRef]
  40. van Rijsbergen, M. A review of sheet cavitation inception mechanisms. IS-ROMAC2016–International Symposium on Transport Phenomena and Dynamics of Rotating Machinery, Honolulu, HI, (2016).
  41. Bixler, G.D., Bhushan, B. Fluid drag reduction with shark-Skin riblet inspired microstructured surfaces. J. Advanced Functional Materials. 23 pp. 4507–4528 (2013). [CrossRef]
  42. Lulekar, S.S., Ghassemi, P., Alsalih, H., Chowdhury, S. Adaptive-fidelity design automation framework to explore bioinspired surface riblets for drag reduction. J. AIAA. 59 pp. 880-892 (2021). [CrossRef]
  43. Wang, Y., Huang, Y., Fu, S. On the tip sharpness of riblets for turbulent drag reduction. J. Acta Mech. Sin. 38 pp. 321389 (2022). [CrossRef]
  44. Kawamura, T., Hiwada, M., Hibino, T., Mabuchi, I., Kumada, M. Flow around a Finite Circular Cylinder on a Flat Plate: Cylinder height greater than turbulent boundary layer thickness. Bull. JSME. 27 pp. 2142-2151 (1984). [CrossRef]
  45. Kitagawa, T. Fujino, Y. Kimura, K. Mizuno, Y. Wind pressures measurement on end-cell-induced vibration of a cantilevered circular cylinder. J. Wind. Eng. Ind. Aerodyn. 90 pp. 395-405 (2002). [CrossRef]
  46. Graf, W.H. Yulistiyanto, B. Experiments on Flow around a cylinder; the velocity and vorticity fields. J. Hydraul. Res. 36 pp. 637-653 (1998). [CrossRef]
  47. Park, C.W. Lee, S.J. Free end effects on the near wake flow structure behind a finite circular cylinder. J. Wind. Eng. Ind. Aerodyn. 88 pp. 231-246 (2000). [CrossRef]
  48. Dean, B. Bharat, B. Shark-skin surfaces for fluid-drag reduction in turbulent flow: a review. Phil. Trans. R. Soc. A. 368 pp. 4775-4806 (2010). [CrossRef]
  49. Lee, S.J. Lee, S.H. Flow field analysis of a turbulent boundary layer over a riblet surface. Experiments in Fluids. 30 pp. 153-166 (2001). [CrossRef]
  50. Goldstein, D. Handler, R. Sirovich, L. Direct numerical simulation of turbulent flow over a modelled riblet covered surface. J. Fluid Mech. 302 pp. 333-376 (1995). [CrossRef]
Preprints 95953 g001
Figure 1. Schematic plan view of the test section with instrument. The top view presents two different configurations of riblet placement, with an arrow pointing in the flow direction.
Figure 1. Schematic plan view of the test section with instrument. The top view presents two different configurations of riblet placement, with an arrow pointing in the flow direction.
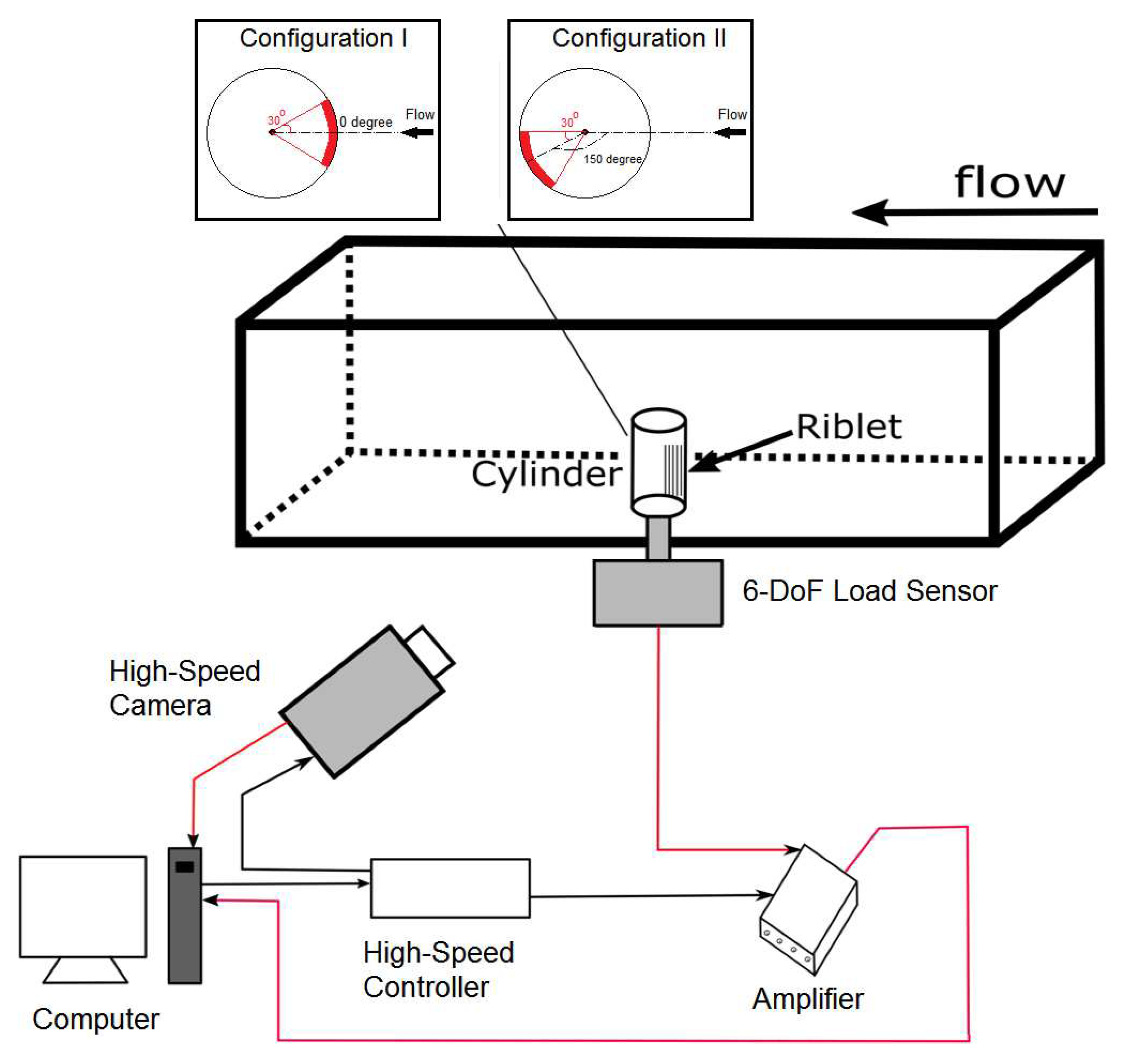
Preprints 95953 g001
Preprints 95953 g002
Figure 2. (a) Schematic view of the cylinder with vertical and horizontal sawtooth riblets and photos of the manufactured sawtooth riblets on the cylinders. (b) Schematic view of the cylinder with vertical and horizontal scalloped riblets and photos of the manufactured scalloped riblets on the cylinders.
Figure 2. (a) Schematic view of the cylinder with vertical and horizontal sawtooth riblets and photos of the manufactured sawtooth riblets on the cylinders. (b) Schematic view of the cylinder with vertical and horizontal scalloped riblets and photos of the manufactured scalloped riblets on the cylinders.
Preprints 95953 g002
Preprints 95953 g003
Figure 3. At R e = 1.25 × 10 5 and σ = 1.0 , cavitation patterns behind the circular cylinder without riblets (a), with horizontal sawtooth riblets SA-H (b), with vertical sawtooth riblets SA-V (c), with horizontal scalloped riblets SC-H (d), and with vertical scalloped riblets SC-V (e). As the flow interacted with the cylinder, miniature riblets induced the creation of small vortex structures nearby, and these small vortices significantly impacted the instabilities that typically formed on the plain cylinder’s surfactre.
Figure 3. At R e = 1.25 × 10 5 and σ = 1.0 , cavitation patterns behind the circular cylinder without riblets (a), with horizontal sawtooth riblets SA-H (b), with vertical sawtooth riblets SA-V (c), with horizontal scalloped riblets SC-H (d), and with vertical scalloped riblets SC-V (e). As the flow interacted with the cylinder, miniature riblets induced the creation of small vortex structures nearby, and these small vortices significantly impacted the instabilities that typically formed on the plain cylinder’s surfactre.
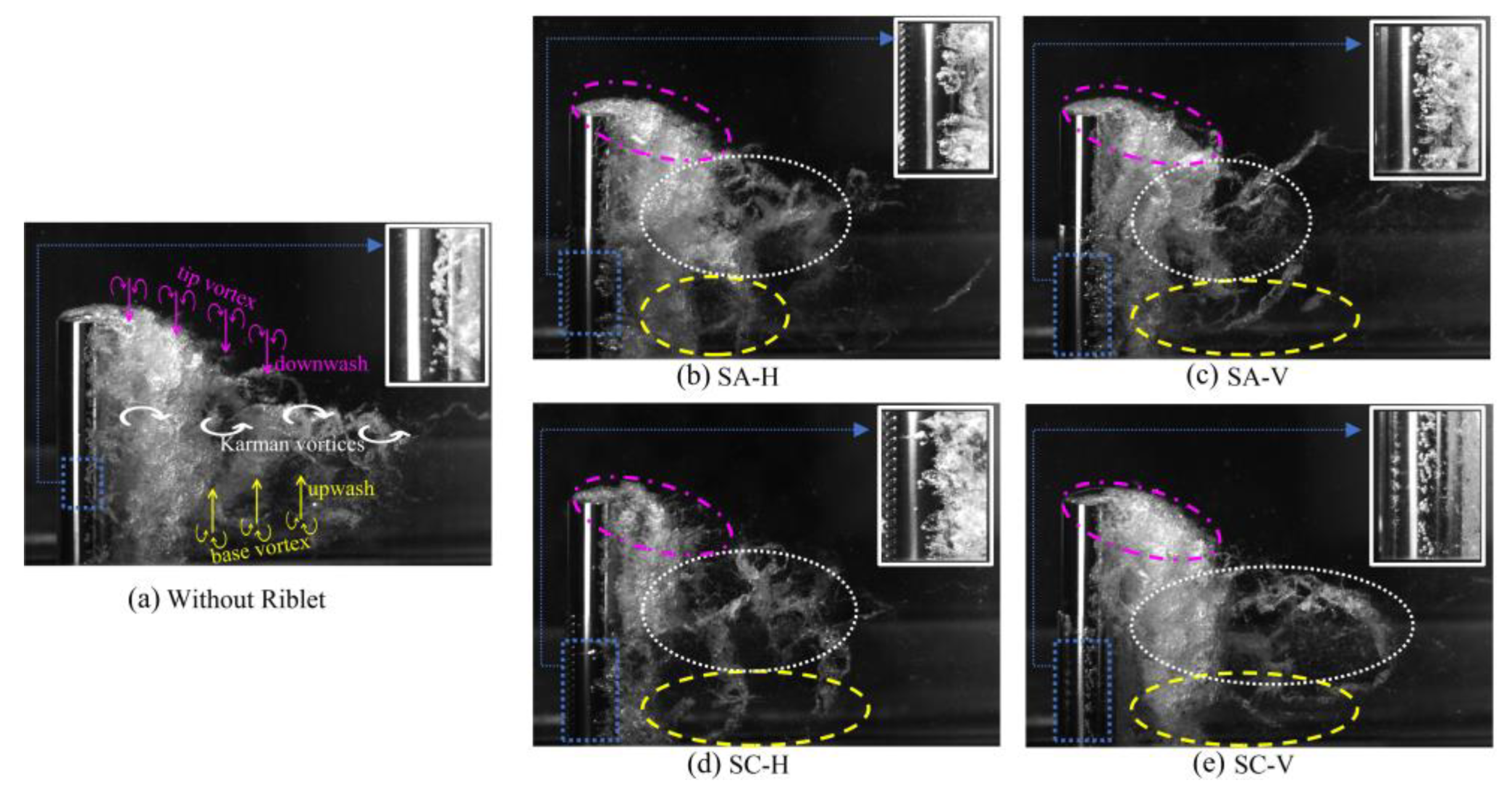
Preprints 95953 g003
Preprints 95953 g004
Figure 4. Scalloped riblets induced secondary vortices(a). In certain instances, both the primary large-scale streamwise vortices and these secondary vortices underwent distortion and became elongated (b). (adopted from [49]).
Figure 4. Scalloped riblets induced secondary vortices(a). In certain instances, both the primary large-scale streamwise vortices and these secondary vortices underwent distortion and became elongated (b). (adopted from [49]).
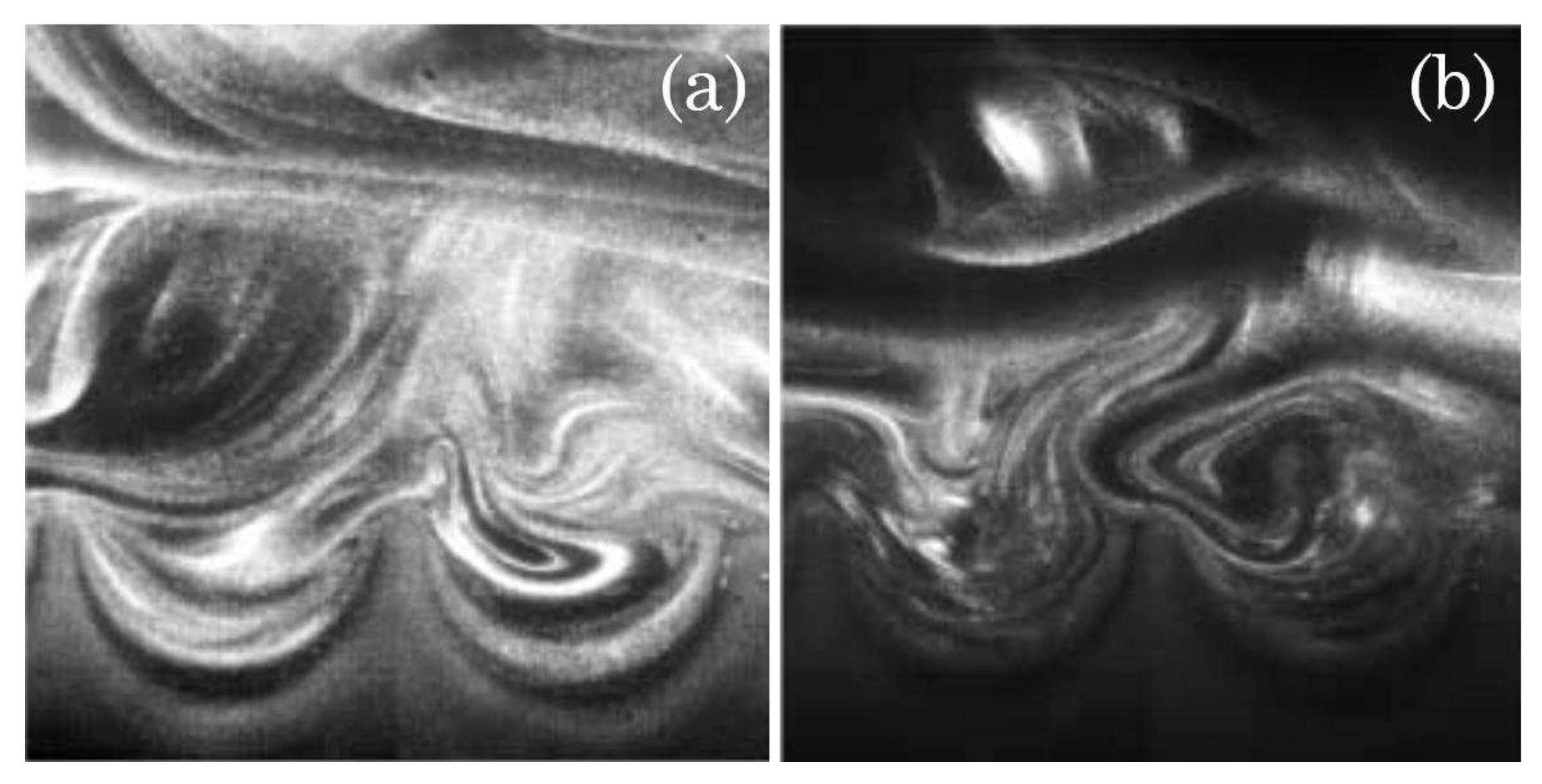
Preprints 95953 g004
Preprints 95953 g005
Figure 5. At R e = 1.25 × 10 5 and σ = 1.0 , five sequential images captured at regular intervals, showing the progression of cavitation behind the cylinder with SC-H riblets. These specific images were chosen from half of a standard cyclic period T that characterized shedding of cavitation. Red surrounded areas indicate regions where the riblets exerted their most significant influence on cavitation. The pressure increasing behind the SC-H riblets, reduced the cavity volume when compared to this volume behind the plain cylinder.
Figure 5. At R e = 1.25 × 10 5 and σ = 1.0 , five sequential images captured at regular intervals, showing the progression of cavitation behind the cylinder with SC-H riblets. These specific images were chosen from half of a standard cyclic period T that characterized shedding of cavitation. Red surrounded areas indicate regions where the riblets exerted their most significant influence on cavitation. The pressure increasing behind the SC-H riblets, reduced the cavity volume when compared to this volume behind the plain cylinder.
Preprints 95953 g005
Preprints 95953 g006
Figure 6. At R e = 1.25 × 10 5 and σ = 1.0 , five sequential images captured at regular intervals, showing the progression of cavitation behind the cylinder with SC-V riblets. These images were chosen from half of a standard cyclic period T that characterized shedding of cavitation. Red surrounded areas indicate regions where the riblets exerted their most significant influence on cavitation. The flow over SC-V riblets primarily engaged with the sharp edges of the riblets, promoting the merging of vortices further downstream.
Figure 6. At R e = 1.25 × 10 5 and σ = 1.0 , five sequential images captured at regular intervals, showing the progression of cavitation behind the cylinder with SC-V riblets. These images were chosen from half of a standard cyclic period T that characterized shedding of cavitation. Red surrounded areas indicate regions where the riblets exerted their most significant influence on cavitation. The flow over SC-V riblets primarily engaged with the sharp edges of the riblets, promoting the merging of vortices further downstream.
Preprints 95953 g006
Preprints 95953 g007
Figure 7. At R e = 1.25 × 10 5 and σ = 1.0 , (a) distributions of the frequency based on the lift force measurement for the plain cylinder, SC-H, and SA-H cylinders, (b) for the plain cylinder, and SC-H and SC-V cylinders. Frequencies with highest amplitudes corresponded to the shedding frequency of large-scale cavity structures. For cylinders with riblets, lift force amplitudes were reduced by 41 and 43 % for SA-H and SC-H cylinders, respectively, and by 43 and 30 % for the SC-H and SC-V cylinders, respectively.
Figure 7. At R e = 1.25 × 10 5 and σ = 1.0 , (a) distributions of the frequency based on the lift force measurement for the plain cylinder, SC-H, and SA-H cylinders, (b) for the plain cylinder, and SC-H and SC-V cylinders. Frequencies with highest amplitudes corresponded to the shedding frequency of large-scale cavity structures. For cylinders with riblets, lift force amplitudes were reduced by 41 and 43 % for SA-H and SC-H cylinders, respectively, and by 43 and 30 % for the SC-H and SC-V cylinders, respectively.
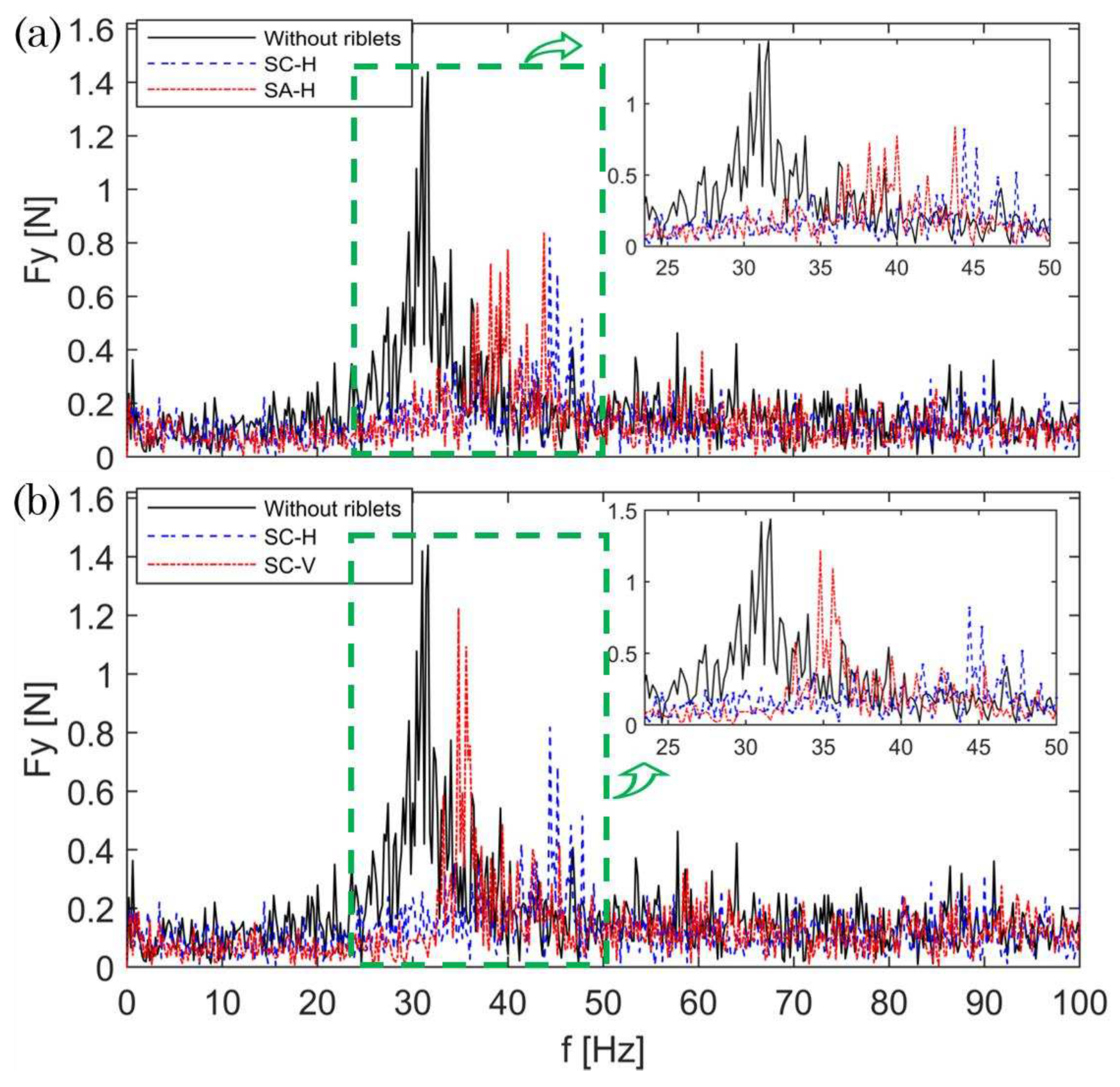
Preprints 95953 g007
Preprints 95953 g008
Figure 8. At R e = 1.25 × 10 5 and σ = 1.0 , lift force (blue columns, left scale) and vortex shedding frequency (coral dots, right scale) for the plain cylinder, SC-H, SC-V, SA-H, and SA-V cylinders. Horizontal scalloped riblets and vertical sawtooth riblets led to smaller lift force amplitudes. The shedding frequency of the cavity for SC-H and SA-H cylinders was higher compared to the frequency of the cavity shedding for the cylinders with vertical riblets, whereby the shedding frequency was lowest for the plain cylinder.
Figure 8. At R e = 1.25 × 10 5 and σ = 1.0 , lift force (blue columns, left scale) and vortex shedding frequency (coral dots, right scale) for the plain cylinder, SC-H, SC-V, SA-H, and SA-V cylinders. Horizontal scalloped riblets and vertical sawtooth riblets led to smaller lift force amplitudes. The shedding frequency of the cavity for SC-H and SA-H cylinders was higher compared to the frequency of the cavity shedding for the cylinders with vertical riblets, whereby the shedding frequency was lowest for the plain cylinder.
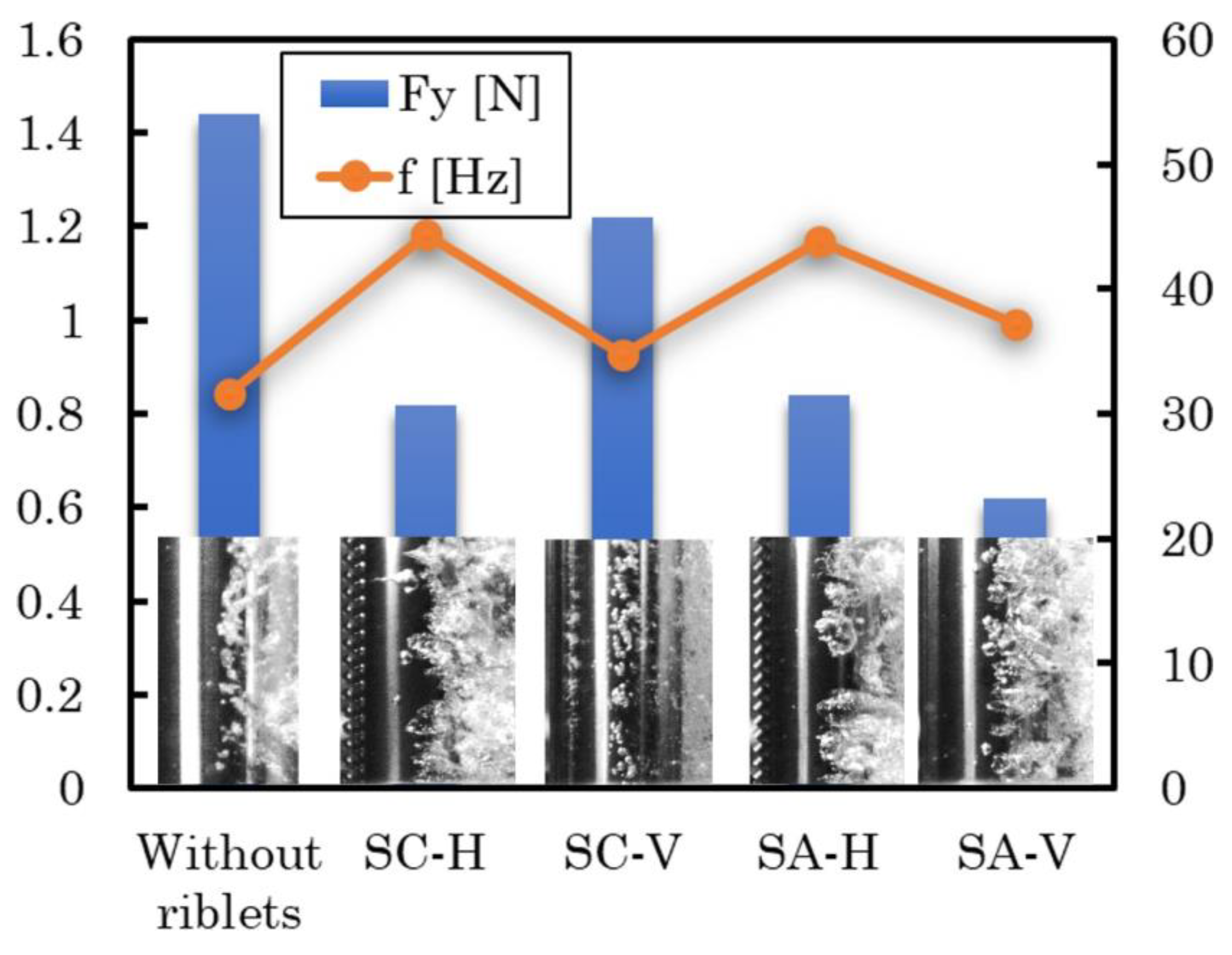
Preprints 95953 g008
Preprints 95953 g009
Figure 9. At R e = 1.25 × 10 5 and σ = 1.0 , placing riblets on the upstream face of the cylinder affected the attached flow and the flow’s stability, whereas rear riblets impacted vortex shedding in the wake region, thereby mitigating cavitation. The extensive cavitation cloud observed behind the smooth cylinder (a), indicated by the red surrounded area, was transformed into smaller and less dense clouds for the cylinder with upstream-faced SC-H riblets (b) and for the cylinder with rotated SC-H riblets (c), as indicated by the green surrounded areas. Although upstream-faced SC-H riblets promoted a smoother flow over the cylinder’s surface and delayed the transition to turbulence, rotated SC-H riblets generated unstable and unpredictable flow patterns.
Figure 9. At R e = 1.25 × 10 5 and σ = 1.0 , placing riblets on the upstream face of the cylinder affected the attached flow and the flow’s stability, whereas rear riblets impacted vortex shedding in the wake region, thereby mitigating cavitation. The extensive cavitation cloud observed behind the smooth cylinder (a), indicated by the red surrounded area, was transformed into smaller and less dense clouds for the cylinder with upstream-faced SC-H riblets (b) and for the cylinder with rotated SC-H riblets (c), as indicated by the green surrounded areas. Although upstream-faced SC-H riblets promoted a smoother flow over the cylinder’s surface and delayed the transition to turbulence, rotated SC-H riblets generated unstable and unpredictable flow patterns.
Preprints 95953 g009
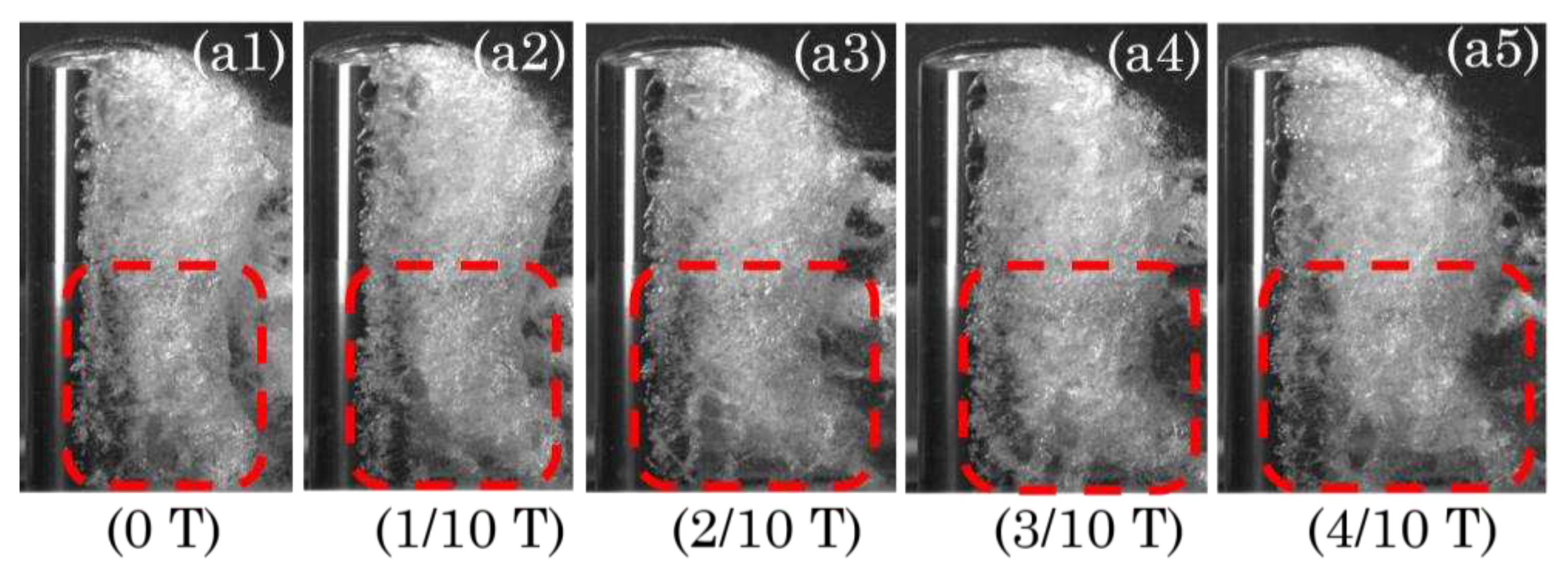
Preprints 95953 g010
Figure 10. At R e = 1.25 × 10 5 and σ = 1.0 , five sequential images captured at regular intervals, showing the progression of cavitation dynamics around a cylinder with rotated (150 degree clockwise) SC-H riblets. These images were chosen from half of a standard cyclic period T that characterized cavitation shedding dynamics. Red surrounded areas indicate regions where the riblets exerted their most significant influence on cavitation. While the upstream-oriented SC-H riblets resulted in a smoother flow and delayed the transition to turbulence, the rotated SC-H riblets induced an unstable and unpredictable flow pattern.
Figure 10. At R e = 1.25 × 10 5 and σ = 1.0 , five sequential images captured at regular intervals, showing the progression of cavitation dynamics around a cylinder with rotated (150 degree clockwise) SC-H riblets. These images were chosen from half of a standard cyclic period T that characterized cavitation shedding dynamics. Red surrounded areas indicate regions where the riblets exerted their most significant influence on cavitation. While the upstream-oriented SC-H riblets resulted in a smoother flow and delayed the transition to turbulence, the rotated SC-H riblets induced an unstable and unpredictable flow pattern.
Preprints 95953 g010
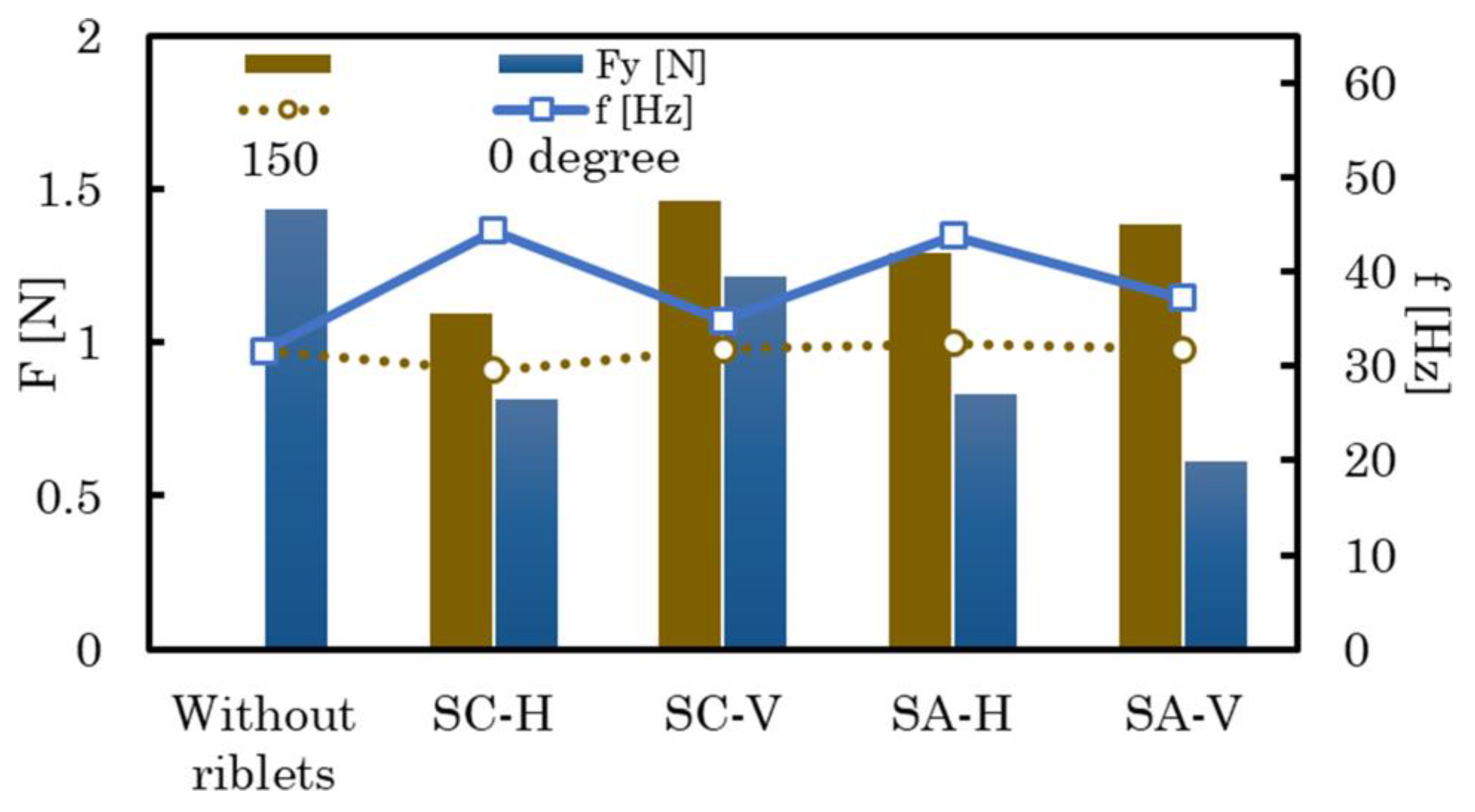
Preprints 95953 g011
Figure 11. At R e = 1.25 × 10 5 and σ = 1.0 , the morphological variations for the cylinder rotated 150 deg clockwise, displaying lift force amplitude (columns) and vortex shedding frequency (squares and dots) for the cylinder without riblets, with horizontal scalloped riblets (SC-H), with vertical scalloped riblets (SC-V), with horizontal sawtooth riblets (SA-H), and with vertical sawtooth riblets (SA-V). Only the SC-H riblets caused a significant reduction of lift force amplitudes when rotated. In contrast, the other riblet kinds hardly affected the lift force amplitudes compared to those for the smooth cylinder. Furthermore, rotating the riblets also hardly affected the shedding frequency, resembling the shedding frequency for the cylinder without riblets.
Figure 11. At R e = 1.25 × 10 5 and σ = 1.0 , the morphological variations for the cylinder rotated 150 deg clockwise, displaying lift force amplitude (columns) and vortex shedding frequency (squares and dots) for the cylinder without riblets, with horizontal scalloped riblets (SC-H), with vertical scalloped riblets (SC-V), with horizontal sawtooth riblets (SA-H), and with vertical sawtooth riblets (SA-V). Only the SC-H riblets caused a significant reduction of lift force amplitudes when rotated. In contrast, the other riblet kinds hardly affected the lift force amplitudes compared to those for the smooth cylinder. Furthermore, rotating the riblets also hardly affected the shedding frequency, resembling the shedding frequency for the cylinder without riblets.
Preprints 95953 g011
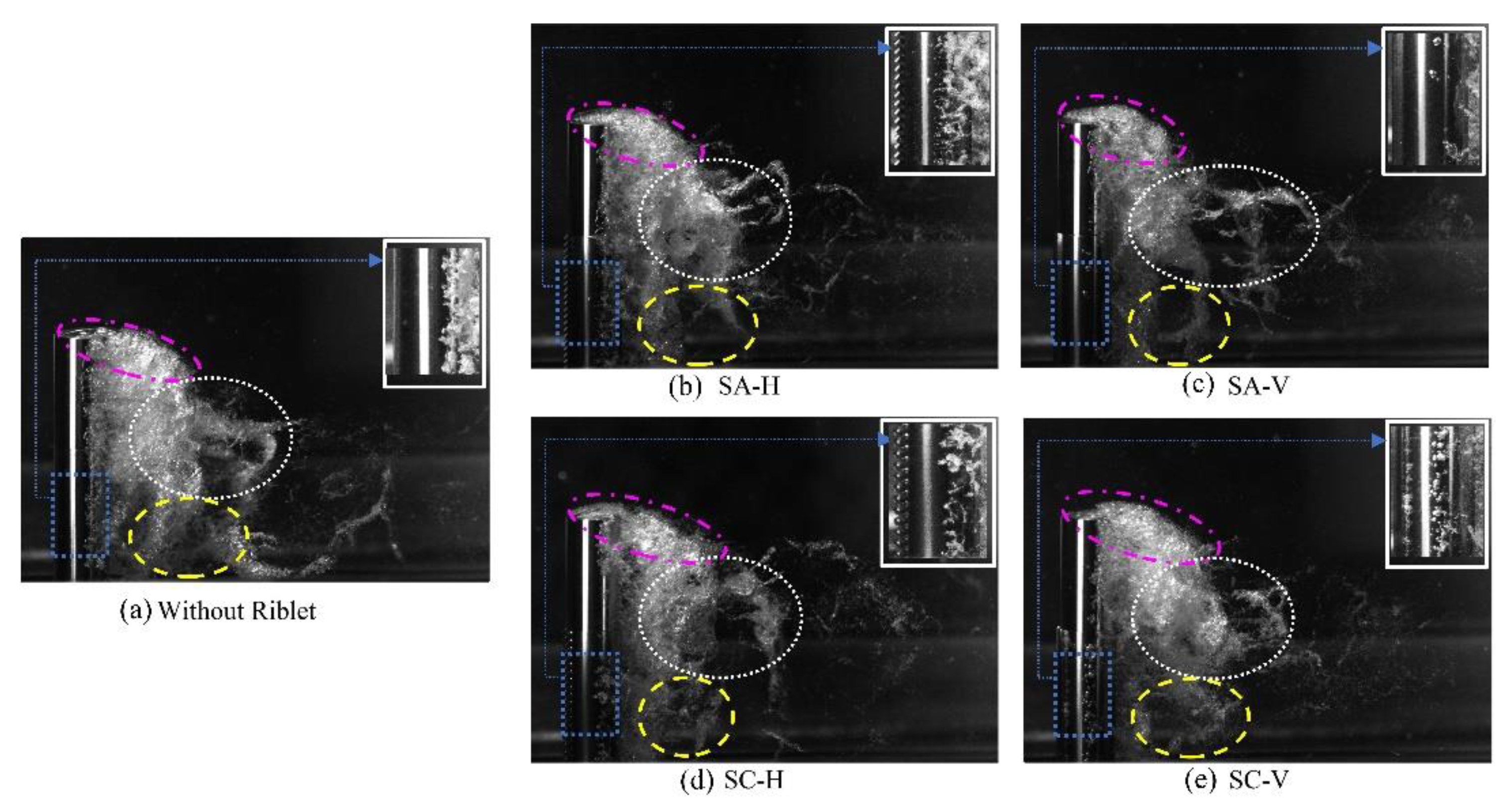
Preprints 95953 g012
Figure 12. At the lower R e = 1.0 × 10 5 and σ = 1.0 , cavity structures behind the plain cylinder (a), SA-H (b), SA-V (c), SC-H (d), and SC-V (e) cylinders.
Figure 12. At the lower R e = 1.0 × 10 5 and σ = 1.0 , cavity structures behind the plain cylinder (a), SA-H (b), SA-V (c), SC-H (d), and SC-V (e) cylinders.
Preprints 95953 g012
Preprints 95953 g013
Figure 13. At the lower R e = 1.0 × 10 5 and σ = 1.0 , five sequential images captured at regular intervals, showing the progression of cavitation behind a cylinder with SC-H riblets. These images were chosen from half of a standard cyclic period T that characterized cavitation shedding dynamics. Red surrounded areas indicate regions where the riblets exerted their most significant influence on cavitation.
Figure 13. At the lower R e = 1.0 × 10 5 and σ = 1.0 , five sequential images captured at regular intervals, showing the progression of cavitation behind a cylinder with SC-H riblets. These images were chosen from half of a standard cyclic period T that characterized cavitation shedding dynamics. Red surrounded areas indicate regions where the riblets exerted their most significant influence on cavitation.
Preprints 95953 g013
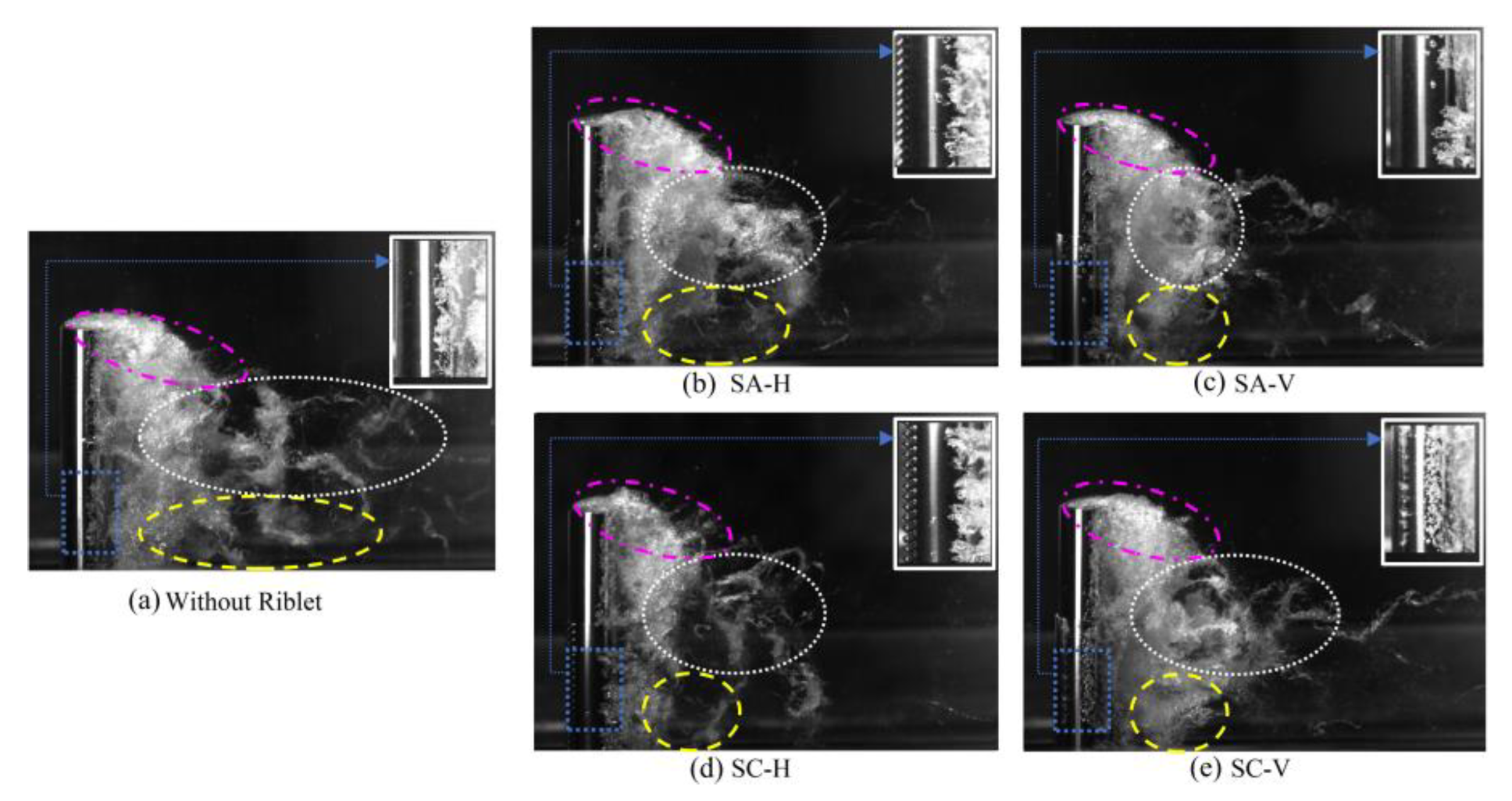
Preprints 95953 g014
Figure 14. At the higher R e = 1.5 × 10 5 and σ = 1.0 , cavity dynamics behind the plain cylinder (a), with SA-H (b), SA-V (c), SC-H (d), and SC-V (e) riblets.
Figure 14. At the higher R e = 1.5 × 10 5 and σ = 1.0 , cavity dynamics behind the plain cylinder (a), with SA-H (b), SA-V (c), SC-H (d), and SC-V (e) riblets.
Preprints 95953 g014
Preprints 95953 g015
Figure 15. At the higher R e = 1.5 × 10 5 and σ = 1.0 , five sequential images captured at regular intervals, showing the progression of cavitation behind a cylinder with SC-H riblets. These images were chosen from half of a standard cyclic period T that characterized cavity shedding dynamics. Red surrounded areas indicate regions where the riblets exerted their most significant influence on cavitation.
Figure 15. At the higher R e = 1.5 × 10 5 and σ = 1.0 , five sequential images captured at regular intervals, showing the progression of cavitation behind a cylinder with SC-H riblets. These images were chosen from half of a standard cyclic period T that characterized cavity shedding dynamics. Red surrounded areas indicate regions where the riblets exerted their most significant influence on cavitation.
Preprints 95953 g015
Preprints 95953 g016
Figure 16. At σ = 1.0 , lift force amplitude F and vortex shedding frequency f at R e = 1.0 × 10 5 , 1.25 × 10 5 , and 1.5 × 10 5 for the plain cylinder and cylinders with SC-H, SC-V, SA-H, and SA-V riblets.
Figure 16. At σ = 1.0 , lift force amplitude F and vortex shedding frequency f at R e = 1.0 × 10 5 , 1.25 × 10 5 , and 1.5 × 10 5 for the plain cylinder and cylinders with SC-H, SC-V, SA-H, and SA-V riblets.
Preprints 95953 g016
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated