Special Relativity in Terms of Hyperbolic Functions with Coupled Parameters in 3+1 Dimensions

Preprint

Article

Special Relativity in Terms of Hyperbolic Functions with Coupled Parameters in 3+1 Dimensions

Altmetrics

Downloads

106

Views

Comments

A peer-reviewed article of this preprint also exists.

Nikolai S. Akintsov^*

,Artem P. Nevecheria,Gennadii F. Kopytov,

Yongjie Yang

Nikolai S. Akintsov^*

,Artem P. Nevecheria,Gennadii F. Kopytov,

Yongjie Yang

This version is not peer-reviewed

Submitted:

10 January 2024

Posted:

10 January 2024

You are already at the latest version

Alerts

Abstract

This paper presents a new method for parameterizing the Lorentz group based on coupled parameters. From the Euler–Hamilton equations, an additional angular rapidity and perpendicular rapidity are obtained, and the Hamiltonian and Lagrangian of a relativistic particle are expanded into rapidity spectra. A so-called passage to the limit is introduced that makes it possible to decompose physical quantities into spectra in terms of elementary functions when explicit decomposition is difficult. New rapidity-dependent Lorentz-invariant coordinates are obtained, and the descriptions of particle motion using the old and new Lorentz-invariant forms as applied to plane waves are compared. Based on a classical model of particle motion in the field of a plane monochromatic electromagnetic wave and in that of a plane laser pulse, the rapidity-dependent spectral decompositions into elementary functions are presented, and the Euler–Hamilton equations are derived as rapidity functions in 3+1 dimensions.

Keywords:

Subject: Physical Sciences - Theoretical Physics

1. Introduction

Since the first work by Lorentz, Poincaré, and Einstein on the special theory of relativity (hereinafter referred to as special relativity), many researchers have developed various of its aspects. Most did so by shunning hyperbolic functions and instead adopting the orthogonal form of space–time relations based on local coordinates and local time [1,2,3,4,5]. However, unlike in hyperbolic form, the final formulas in orthogonal form are cumbersome, difficult to interpret, and hamper the derivation of new results.

The first representations of hyperbolic functions in special relativity were due to Minkowski [6] and Poincaré [7], who expressed the longitudinal velocity of a particle in terms of its rapidity

θ

, i.e.,

n β = \frac{n V}{c} = \tanh θ .

(1)

where

V

is the speed of the particle, c is the speed of light, and

n

is the gyrovector in Lobachevsky space, characterizing the direction of motion of the particle. In Refs. [6] and [7], the transition from Lobachevsky geometry to Euclidean geometry was introduced via the transformation

θ \to i θ^{'},

(2)

where

θ^{'}

is the rapidity in Euclidean geometry. Robb and Borel [8,9] also understood this fundamental connection, and Varicak [10] continued to develop the application of hyperbolic functions in special relativity. Furthermore, Karapetoff made a significant contribution to special relativity with hyperbolic functions, showing their advantages for describing various physical processes [11,12].

The main feature of Refs. [11] and [12] is that the Lorentz-invariant connection between coordinates in different inertial systems was presented via the Lorentz boost, whose argument is

θ

. However, the proper coordinates and proper time in inertial system K were considered as dynamic quantities independent of

θ

, and only in a special case was the connection

q / t = \tanh θ

introduced.

An attempt to introduce proper time via hyperbolic functions was made in Refs. [13], where the author assumed that proper time and rapidity are approximately equal, but that work did not introduce an invariant form to describe the dynamics of a particle. Rapidity itself is not invariant, and its value depends on the position of the coordinate axes. Rapidity is an additive quantity, and the sum (or difference) of two rapidities is also not invariant. The convenience of the hyperbolic representation of special relativity is that the sums (or differences) of particle velocities, momentums, and energies can be represented as those of arguments from the rapidities of hyperbolic functions. Therefore, some physical experiments and phenomena can be interpreted quite simply via hyperbolic functions [14,15]. As an example, because of the compactness of the notation, the hyperbolic approach is taken in relativistic hydrodynamics in the Landau [16], Khalatnikov [17], and Bjorken [18] models and in the Milekhin model [19], a relativistic hydrodynamic model with coupled parameters. In the Milekhin model, all physical quantities depend on one physical parameter, i.e., temperature.

In Ref. [20], special relativity in 2+1 dimensions was considered with many specifics of its reconciliation. However, the literature to date appears to lack any work in which (i) correct coordinates were introduced for local coordinates with respect to the Lorentz transformation and (ii) an invariant form was established when differentiating with respect to

θ

Herein, the method of coupled parameters is applied directly to special relativity, and all physical quantities are considered to depend on

θ

in different inertial frames of reference. The main goal is to introduce a new method for parameterizing the Lorentz group based on coupled parameters in 1+1 and 3+1 dimensions, showing the advantage of using hyperbolic functions for coupled parameters expressed in terms of

θ

in special relativity.

2. Generalization of existing results and problem statements

In Refs. [21] and [22], the trajectory of a relativistic particle in 1+1 dimensions was obtained in the representation of Lobachevsky geometry along the normal gyrovector

n,

where for the Lorentz-invariant coordinate

ξ

and depending on

θ

, the following correct coordinates pertain:

ξ = t - f q, t = 1 - \coth θ, q = \frac{n r}{c} = \frac{1}{2} \ln (\tanh^{2} θ) .

(3)

The longitudinal momentum, energy, and longitudinal velocity of a particle in dimensionless form in 1+1 dimensions are determined by the following expressions [22]:

n P = \frac{n p}{m c} = \sinh θ, H \equiv E = \frac{ε}{m c^{2}} = \cosh θ, n β = \tanh θ,

(4)

where m is the particle mass and H is the Hamiltonian of a free relativistic particle.

In 3+1 dimensions [23], curvilinear basis vectors were introduced into the Lobachevsky spaces

n

s

, and

k

, where the connection between the gyrovectors is determined from geometric relations via

θ

, i.e.,

n = s \cosh θ

k = s \sinh θ

, and

k = n \tanh θ

. Based on calculus of variations method, the correct coordinates along the basis vectors

s

and

k

are obtained, in addition to the coordinates from (3), i.e.,

ξ_{θ} = t - f q_{θ}, ξ_{⊥} = t - f q_{⊥}, q_{θ} = \frac{s r}{c} = \frac{1}{2} \ln (- \sinh^{2} θ), q_{⊥} = \frac{k r}{c} = θ .

(5)

In Ref. [23], the components (of phase and perpendicular) momentum and particle velocity were also obtained in addition to (4), where for real and positive particle momentum the following forms hold:

k β_{k} = \tanh^{2} θ, k P = \sinh θ \tanh θ, s β = sech θ \tanh θ, s P = \tanh θ .

(6)

To obtain a more general approach to describing the dynamics of a particle in terms of hyperbolic functions with coupled parameters, it is necessary to solve the following four problems.

Problem 1. In 1+1 dimensions for local coordinates

t^{'}

and

q^{'}

in inertial system

K^{'}

, parametrize the Lorentz group according to

θ

using the proper coordinates

t

and

q

from (3). The main goal here is to generalize the available results from special relativity for coupled parameters found in the inertial frame using

θ

Problem 2. As is known, from the Hamiltonian of a free relativistic particle as in (4), by taking the derivatives with respect to the angular rapidity

θ_{s}

and the perpendicular rapidity

θ_{⊥}

, the components of the particle’s momentum are determined as in (6). Knowing the Hamiltonian of a free particle as in (4) and the angular and perpendicular projections of the particle’s momentum as in (6), problem 2 involves determining

θ_{⊥}

and

θ_{s}

depending on

θ

and then establishing a dynamic relationship between them. From the projections of particle momenta as in (4) and (6), compose the Euler–Hamilton equations on the world line, and determine the proper coordinates of a free relativistic particle in 3+1 dimensions describing its dynamics on the world line.

Problem 3. Because the physical quantities under consideration are all related to

θ

, it seems possible to decompose them into rapidity spectra in terms of elementary functions.

Problem 4. In inertial frame K in 3+1 dimensions, the dynamics of a particle are determined by (3)–(6) via

θ

. Because of the first postulate of special relativity (i.e., physical processes proceed in the same way in all inertial systems), in inertial system

K^{'}

it is also possible to describe the dynamics of a particle by (3)–(6) via only

θ^{'}

. Problem 4 involves searching for a dynamic relationship for

θ^{'} = θ^{'} (θ)

in different inertial systems.

3. Action of Lorentz-invariant transformation with respect to rapidity $θ$

in 1+1 dimensions

For the proper coordinates and in 1+1 dimensions [21], the Lorentz transformation is applied with respect to

θ

[14], which yields the following representation in inertial system

K^{'}

for local coordinates

q^{'}

and

t^{'}

t^{'} = t \cosh θ - q \sinh θ, q^{'} = q \cosh θ - t \sinh θ .

(7)

For the Lorentz-invariant space–time coordinate

ξ^{'}

in inertial frame

K^{'}

, the representation

{ξ^{+}}^{'} = t^{'} - q^{'} = (t - q) γ^{+}, {ξ^{-}}^{'} = t^{'} + q^{'} = (t - q) γ^{-}

(8)

holds, whereupon the action s has the classical invariant form of

s^{2} = {ξ^{'}}^{+} {ξ^{'}}^{-} = ξ^{+} ξ^{-} = t^{2} - q^{2} = i n v .

(9)

Differentiating (9) with respect to

θ

gives

s \frac{d s}{d θ} = t \frac{d t}{d θ} - q \frac{d q}{d θ},

(10)

and differentiating the local coordinates

t^{'}

and

q^{'}

from (7) with respect to

θ

gives

\frac{d t^{'}}{d θ} = - q^{'} + \frac{d s}{d θ}, \frac{d q^{'}}{d θ} = - t^{'} .

(11)

The derivative of s with respect to

θ

has the form

\frac{d s}{d θ} = \frac{1}{\cosh θ \sinh^{2} θ}, s = \frac{3}{2} - gd (θ) - \frac{1}{\sinh θ},

(12)

where s is the action along the world line and

gd (θ)

is the Gudermann function [24]. The differential action ds for related parameters expresses a similar action from Ref. [25], i.e.,

d s = d t \sqrt{1 - β^{2}}

. Substituting the derivative of the action from (12) into (10) gives that in this case, the action is chosen along the direction of local time, i.e.,

s \equiv t^{'}

Eq. (12) for s in the direction of local time

t^{'}

is also easy to obtain from the geometric relations for

θ

in inertial frame K and

θ^{'}

in inertial frame

K^{'}

(e.g., see Ref. [11]), i.e.,

\frac{d t}{\cosh θ} = \frac{d t^{'}}{\cosh θ^{'}},

(13)

taking the proper coordinate t from (3) and assuming that the observer in inertial frame

K^{'}

chose

θ^{'}

equal to zero.

Just as for the relation of s in local time

t^{'}

, it is possible to introduce a perpendicular action

s_{⊥}

with respect to the relation in the coordinate

q^{'}

, where in Ref. [11] the following formula was obtained for the connection of coordinates

q

and

q^{'}

from geometric considerations, where substituting the proper coordinate from (3) gives

d q = d q^{'} / \cosh θ, s_{⊥} = q^{'} = \ln (\tanh (\frac{θ}{2})) .

(14)

The derivatives of the Lorentz-invariant coordinates from (8) with respect to s are given by

\frac{d {ξ^{'}}^{+}}{d s} = 1 + {ξ^{'}}^{+} \frac{d θ}{d s}, \frac{d {ξ^{'}}^{-}}{d s} = 1 - {ξ^{'}}^{-} \frac{d θ}{d s},

(15)

and for

ξ^{+}

and

ξ^{-}

along the world line, the following relations hold:

\frac{d ξ^{+}}{d s} = γ^{+} = \exp (- θ), \frac{d ξ^{-}}{d s} = γ^{-} = \exp (θ),

(16)

where

γ^{+}

and

γ^{-}

are the integrals of motion; see Ref. [22].

For

θ \geq 0

, taking the double derivative with respect to s from (7) and assuming that the action is

s \equiv t^{'}

gives

q^{'} \frac{d θ}{d s} = 0 .

(17)

From (15)–(17), it is possible to represent the following local coordinates on the world line:

t^{'} = ξ^{+} \exp (θ) = ξ^{+} γ^{-} = {ξ^{'}}^{+},

(18)

t^{'} = ξ^{-} \exp (- θ) = ξ^{-} γ^{+} = {ξ^{'}}^{-},

(19)

i.e., the rotation operation is carried out and the Lorentz-invariant coordinate

ξ^{'}

becomes purely a coordinate of local time

t^{'}

for the observer in inertial frame

K^{'}

, while

t^{'}

still contains components of space q and time t for the observer in inertial frame K.

Adding (18) and (19) gives the local time coordinate

t^{'}

from (7), and subtracting (18) from (19) gives

\frac{q}{t} = \tanh θ .

(20)

A similar case can be imagined when the observer in inertial system has one spatial coordinate

q^{'}

, while the observer in inertial system K has coordinates t and q, i.e.,

q^{'} = ξ^{-} \exp (- θ) = ξ^{-} γ^{+},

(21)

- q^{'} = ξ^{+} \exp (θ) = ξ^{+} γ^{-},

(22)

where adding (21) and (22) gives the relation for the particle velocity (20). Subtracting (21) from (22) gives the coordinate

q^{'}

via (7).

Differentiating (18) and (19) with respect to

θ

gives

\frac{d t^{'}}{d θ} = \frac{d s}{d θ} + {ξ^{'}}^{+}, \frac{d t^{'}}{d θ} = \frac{d s}{d θ} - {ξ^{'}}^{-},

(23)

where on the world line s for

θ \geq 0

, the following hold:

t^{'} \frac{d θ}{d s} = 0,

(24)

\frac{d t^{'}}{d s} = 1 + {ξ^{'}}^{+} \frac{d θ}{d s} = 1 - {ξ^{'}}^{-} \frac{d θ}{d s} = 1 .

(25)

In the present case, inertial frame

K^{'}

is chosen relative to the position of the particle in such a way that

\frac{d q^{'}}{d s} \equiv \frac{d q^{'}}{d t^{'}} = 0

for

θ \geq 0

4. Relationship between perpendicular rapidity and angular rapidity of free relativistic particle

Having projected the motion of a relativistic particle along the direction of one of the gyrovectors

s

k

, for the Hamiltonian H, the following equations of motion hold, which describe the components of the particle momentum from (6):

\frac{\partial H}{\partial θ_{s}} = s P = \tanh θ, \frac{\partial H}{\partial θ_{⊥}} = k P = \sinh θ \tanh θ .

(26)

where the angular rapidity

θ_{s}

and the perpendicular rapidity

θ_{⊥}

have the forms

θ_{s} = gd (θ), θ_{⊥} = \ln (\sinh θ) .

(27)

The relationship between

θ_{s}

and

θ_{⊥}

is defined as

d θ_{s} = \frac{1}{2} \frac{d θ_{⊥}}{\cosh θ_{⊥}}, \tan (θ_{s}) = \tanh (\frac{θ_{⊥}}{2}) .

(28)

5. Expansion into rapidity spectra for lagrangian, hamiltonian, and momentum of free relativistic particle

The spectral–angular characteristics of a relativistic particle offer understanding of the indefinite integrals of an arbitrary function

g = g (θ)

with respect to

θ

θ_{s}

, and

θ_{⊥},

i.e.,

G = \int g (θ) d θ, G_{s} = \int g (θ) d θ_{s}, G_{⊥} = \int g (θ) d θ_{⊥},

(29)

where the integrations allow

g = g (θ)

to be decomposed into spectra in terms of elementary functions. The integration constant is usually determined from the Cauchy problem.

For the Hamiltonian of a free relativistic particle, the expansions into rapidity spectra in terms of elementary functions have the following forms:

\int H d θ = n P, \int H d θ_{s} = θ, \int H d θ_{⊥} = E + s_{⊥} .

(30)

For the Lagrangian

L = \frac{L^{'}}{m c} = - sech θ

of a free relativistic particle, expanding into rapidity spectra gives

\int L d θ = - θ_{s}, \int L d θ_{s} = - n β, \int L d θ_{⊥} = - s_{⊥} .

(31)

Decomposing the longitudinal impulse (4) into spectral components

θ_{s}

and

θ_{⊥}

gives

\int n P d θ_{s} = \ln (\cosh θ) = q_{E}, \int n P d θ_{⊥} = θ .

(32)

Also, decomposing the transverse momentum !-- MathType@Translator@5@5@MathML2 (no namespace).tdl@MathML 2.0 (no namespace)@ --

of the particle from (6) into spectral components gives

\int k P d θ = n P - 2 \arctan (\tanh (\frac{θ}{2})), \int k P d θ_{s} = θ - \tanh θ, \int k P d θ_{⊥} = q_{E} .

(35)

Similarly, for the particle momentum

s P

from (6), the following hold:

\int s P d θ = q_{E}, \int s P d θ_{⊥} = θ_{s}, \int s P d θ_{s} = 1 - sech (θ) .

(34)

6. Euler–Hamilton equations in 3+1 dimensions

For

θ

θ_{s}

, and

θ_{⊥}

with respect to the invariant of action ds from (12), it is possible to introduce the following Euler–Hamilton equations describing the motion of a relativistic particle along the gyrovectors

n

s

, and

k

\frac{d}{d s} (\frac{\partial H}{\partial θ}) - \frac{\partial H}{\partial q^{'}} = 0, \frac{d}{d s} (\frac{\partial H}{\partial θ_{s}}) - \frac{\partial H}{\partial θ_{⊥}} = 0, \frac{d}{d s} (\frac{\partial H}{\partial θ_{⊥}}) - \frac{\partial H}{\partial \hat{q}} = 0 .

(35)

where

q^{'}

θ_{⊥}

, and

\hat{q}

are the coordinates describing the movement of the particle in the direction of the world line s:

q^{'} = sech θ + \ln (\tanh (\frac{θ}{2})), \hat{q} = - \frac{csch θ}{2} - \frac{\arctan (\frac{\sinh θ}{\sqrt{2}})}{2 \sqrt{2}} .

(36)

Regarding the “perpendicular” action

s_{⊥}

from (14), the Euler–Hamilton equations for

θ

θ_{s}

, and

θ_{⊥}

have the forms

\frac{d}{d s_{⊥}} (\frac{\partial H}{\partial θ}) - \frac{\partial H}{\partial θ_{s}} = 0, \frac{d}{d s_{⊥}} (\frac{\partial H}{\partial θ_{s}}) - \frac{\partial H}{\partial {θ^{'}}_{s}} = 0, \frac{d}{d s_{⊥}} (\frac{\partial H}{\partial θ_{⊥}}) - \frac{\partial H}{\partial {θ^{'}}_{⊥}} = 0 .

(37)

where

{θ^{'}}_{s} = \frac{1}{2} (θ + \sinh θ \cosh θ), {θ^{'}}_{⊥} = \frac{1}{2} (\arctan (\cosh θ) + s_{⊥}) .

(38)

7. Decomposition of local coordinates into rapidity spectra

Some spectral decompositions have complex forms, such as

\int q d θ = \frac{1}{2} \int \ln (\tanh^{2} θ) d θ,

(39)

so then it is convenient to introduce a so-called passage to the limit by analogy with relativistic hydrodynamics with related parameters [19].

The simplest way to expand a coordinate q into a spectrum in terms of

θ

without taking integral (39) in explicit form is to multiply and divide by t in the integrand and then adopt the following transition therein:

\frac{q}{t} \to n β = \tanh θ .

(40)

The passage to the limit is introduced by the arrow, this being because the relation for the coordinates

q / t

from (3) goes into (20) only for particle oscillations in a high-intensity field with

a \geq 20

(see Figure 1). As is known, the dimensionless field amplitude a is expressed in terms of the dimensionless

θ

in the following way [22]:

a \equiv P^{2} = \sinh^{2} θ,

(41)

and adopting the passage to the limit for local coordinates (7) gives

t^{'} = \frac{t}{\cosh θ}, q^{'} = 0 .

(42)

Expanding the local coordinate

t^{'}

into rapidity spectra gives

\int t^{'} d θ = θ_{s} - s_{⊥}, \int t^{'} d θ_{s} = n β - θ_{⊥} + q_{E}, \int t^{'} d θ_{⊥} = csch θ + s_{⊥},

(43)

and here the integration constant is taken to be zero. Next, the obtained elementary functions

θ

θ_{s}

θ_{⊥}

, and

s_{⊥}

form the basis for composing the Euler–Lagrange equations in 3+1 dimensions.

8. Spectral characteristics of relativistic particle in field of circularly polarized electromagnetic wave in 3+1 dimensions

Considered here is the movement of a relativistic charge in the field of a circularly polarized monochromatic electromagnetic wave. It is assumed that the plane wave and the relativistic particle are collinear to the direction of propagation of the normal gyrovector

n

. Then the four-vector potential of the wave has the form [25]

[φ, A] = [0, \frac{c E}{ω} \cos (ω ξ) e_{x}, \frac{c E}{ω} \sin (ω ξ) e_{y}],

(44)

where E (a constant) is the wave amplitude, ω (also a constant) is the oscillation frequency, and

e_{x}

and

e_{y}

are the orthogonal basis vectors relative to the normal gyrovector

n

The square of the vector potential

A

and the polarization gyrovector

k

are determined via the dimensionless field amplitude as [22]

\frac{e^{2} A^{2}}{m^{2} c^{4}} = \frac{e^{2} E^{2}}{m^{2} c^{2} ω^{2}} = a and k A = \frac{m c}{e} \sqrt{a},

(45)

where e is the electron charge and

E / ω \geq 0

The Lagrangian describing the dynamics of a relativistic particle in the field of a plane monochromatic wave depending on the rapidity has the form [22]

L_{c i r} = - sech θ + \sqrt{a} \tanh^{2} (θ),

(46)

and here the dimensionless field amplitude for a plane wave is a constant (

a = c o n s t

The connection between the Lagrangian and the Hamiltonian is found from the relationship between the integrals of motion that determine the longitudinal momentum of a particle, which is valid for both a free relativistic particle and a relativistic particle in an external electromagnetic field.

The limited longitudinal component of the particle velocity in the interval

n β \in [0; 1]

leads to the assumption that the rapidity of a free particle and that of a particle in an external electromagnetic field are approximately equal, i.e.,

θ \approx θ_{E M}

[22], then the following equation is also valid for an external electromagnetic field:

\frac{\partial H}{\partial θ} = \frac{\partial L}{\partial Q_{t}^{-}} = n P,

(47)

where

Q_{t}^{-}

is the integral of motion (see Ref. [22]).

Substituting the Lagrangian (46) into (47) gives the Hamiltonian of a particle in the external field of a plane monochromatic circularly polarized electromagnetic wave, i.e.,

H_{c i r} = \cosh θ + 2 \sqrt{a} q_{E},

(48)

where if the particle has no velocity at the initial moment of time (i.e.,

θ = 0

), then the Hamiltonian of (48) has the form

H_{c i r} (0) = 1

Expanding the Lagrangian (46) into spectra in terms of

θ

θ_{⊥}

, and

θ_{s}

gives

\int L_{c i r} d θ = - g d (θ) + \sqrt{a} (θ - \tanh θ), \int L_{c i r} d θ_{⊥} = - s_{⊥} + \sqrt{a} q_{E},

(49)

\int L_{c i r} d θ_{s} = - n β + \frac{\sqrt{a}}{2} (θ_{s} - \tanh θ sech θ),

(50)

where to the existing spectral components from (31) are added the components of oscillation of a particle in a plane wave, which contain the dimensionless field amplitude a.

Adopting the passage to the limit

q_{E} / θ \to \tanh θ

for the Hamiltonian of (48) and expanding into spectra in terms of

θ

θ_{⊥}

, and

θ_{s}

gives

\int H_{c i r} d θ = n P + \sqrt{a} (θ (θ + 2 \ln (\exp (- 2 θ))) - {Li}_{2} (- \exp (2 θ))),

(51)

\int H_{c i r} d θ_{s} = θ + 2 \sqrt{a} (gd (θ) - θ sech θ),

(52)

\int H_{c i r} d θ_{⊥} = \cosh θ + s_{⊥} + \sqrt{a} θ^{2},

(53)

where

{Li}_{2}

is a polylogarithmic function [26].

From the given solutions (49)–(53), the expansions of the Hamiltonian and Lagrangian of a particle in the field of a plane wave are non-trivial solutions for the related parameters, which allow estimation of the rapidity-dependent spectral components of the motion of a relativistic particle for a constant field amplitude a. Shown next is that spectral decomposition of the motion of a relativistic particle in the field of a plane wave with a constant field amplitude is more complex than that in the case of a plane laser pulse with a rapidity-dependent dynamically varying amplitude.

9. Spectral characteristics of relativistic charge in field of plane laser pulse in 3+1 dimensions

To describe the dynamics of a relativistic particle in the field of a plane laser pulse, it is assumed that the dimensionless field amplitude in the Lagrangian (46) is not constant and the value of the field amplitude changes in accordance with (41). Then the Lagrangian describing the dynamics of a charged particle in the field of a plane laser pulse with right-handed circular polarization, depending on

θ

, has the form

L_{S M}^{+} = \cosh θ - 2 sech θ .

(54)

Substituting the Lagrangian (54) into (47) gives the Hamiltonian of a particle in the field of a right-handed circularly polarized electromagnetic wave, i.e.,

H_{S M}^{+} = \frac{1}{3} \cosh θ (\cosh^{2} θ + 6) - \frac{4}{3} .

(55)

Expanding the Lagrangian (54) of a particle with right-handed circular polarization into spectra in terms of

θ

θ_{⊥}

, and

θ_{s}

gives the following spectral representations:

\int L_{S M}^{+} d θ = \sinh θ - 2 θ_{s}, \int L_{S M}^{+} d θ_{s} = θ - \tanh θ, \int L_{S M}^{+} d θ_{⊥} = \cosh θ - s_{⊥} .

(56)

Similarly, for the Hamiltonian of (55), expanding into rapidity spectra gives

\int H_{S M}^{+} d θ = \frac{1}{36} (- 48 θ + 81 \sinh θ + \sinh (3 θ)),

(57)

\int H_{S M}^{+} d θ_{s} = \frac{1}{6} (- 8 θ_{s} + 13 θ + \sinh θ \cosh θ),

(58)

\int H_{S M}^{+} d θ_{⊥} = \frac{1}{36} (87 \cosh θ + \cosh (3 θ) - 48 θ_{⊥} + 84 s_{⊥}) .

(59)

For a particle in the field of a plane laser pulse with left-handed circular polarization, the Lagrangian representation is

L_{S M}^{-} = - \cosh θ,

(60)

and from (60) and (47), the Hamiltonian of the system in the field of a plane circularly polarized laser pulse is

H_{S M}^{-} = \frac{4}{3} - \frac{1}{3} \cosh^{3} θ .

(61)

Expanding (60) and (61) into rapidity spectra gives

\int L_{S M}^{-} d θ = - \sinh θ, \int L_{S M}^{-} d θ_{s} = - θ, \int L_{S M}^{-} d θ_{s} = - \cosh θ - s_{⊥},

(62)

\int H_{S M}^{-} d θ = \frac{1}{36} (48 θ - 9 \sinh θ - \sinh (3 θ)),

(63)

\int H_{S M}^{-} d θ_{s} = \frac{1}{6} (8 θ_{s} - θ - \sinh θ \cosh θ),

(64)

\int H_{S M}^{-} d θ_{⊥} = \frac{1}{36} (- 15 \cosh θ - \cosh (3 θ) + 48 θ_{⊥} - 12 s_{⊥}),

(65)

where adding the spectral characteristics of the radiation of a relativistic charge in the field of a plane laser pulse with right and left circular polarizations and considering the normalization factor gives the spectral characteristics of the radiation for a free relativistic particle as in (30) and (31). As can be seen from the presented solutions, the spectral components of a relativistic particle in the field of a plane wave and a laser pulse using transformation (2) in the Euclidean phase plane are described well by the expansion by rapidity

θ_{⊥}

in the direction of the polarization gyrovector

k

, because in all cases it has a real oscillatory part.

10. Dynamics of relativistic particle in field of plane laser pulse with left-handed circular polarization in 3+1 dimensions

To describe the dynamics of a relativistic particle in the field of a plane circularly polarized laser pulse along the world line s, it is convenient to use

\frac{d}{d s} (\frac{\partial L_{S M}^{-}}{\partial θ}) - \frac{\partial L_{S M}^{-}}{\partial s} = 0,

(66)

and replacing the Lagrangian of a particle in the field of a left-handed circularly polarized laser pulse with that for a right-handed one gives the following oscillating parameter:

\frac{d}{d s} (\frac{\partial L_{S M}^{+}}{\partial θ}) - \frac{\partial L_{S M}^{+}}{\partial s} = 4 \tanh^{2} θ .

(67)

Because the action s from (12) contains the Gudermann function

θ_{s}

and the derivative of the action

s_{⊥}

with respect to

θ

, it is further of interest to introduce the Euler–Lagrange equation, which depends on only the Gudermann function

θ_{s}

or the functional action

s_{⊥}

Regarding the angular rapidity

θ_{s}

, it is also convenient to introduce the following Euler–Lagrange equation for a left-handed circularly polarized wave:

\frac{d}{d θ_{s}} (\frac{\partial L_{S M}^{-}}{\partial θ}) - \frac{\partial L_{S M}^{-}}{\partial L} = 0,

(68)

where L is the Lagrangian of a free relativistic particle. Similarly, substituting

L_{S M}^{-} \to L_{S M}^{+}

in (68) gives the following oscillatory parameter:

\frac{d}{d θ_{s}} (\frac{\partial L_{S M}^{+}}{\partial θ}) - \frac{\partial L_{S M}^{+}}{\partial L} = 4 {sech}^{2} (θ) .

(69)

Regarding the perpendicular rapidity

θ_{⊥}

, for a particle in the field of a plane left-handed circularly polarized laser pulse, the following equation holds:

\frac{d}{d θ_{⊥}} (\frac{\partial L_{S M}^{-}}{\partial θ}) - \frac{\partial L_{S M}^{-}}{\partial θ} = 0,

(70)

where substituting

L_{S M}^{-} \to L_{S M}^{+}

gives the following oscillatory parameter:

\frac{d}{d θ_{⊥}} (\frac{\partial L_{S M}^{+}}{\partial θ}) - \frac{\partial L_{S M}^{+}}{\partial θ} = - 4 sech θ \tanh^{3} θ .

(71)

Regarding the action

s_{⊥}

and the rapidities

θ

θ_{⊥}

, and

θ_{s}

, the following Euler–Lagrange equations of motion hold in the field of a plane laser pulse with left-handed circular polarization:

\frac{d}{d s_{⊥}} (\frac{\partial L_{S M}^{-}}{\partial θ}) - \frac{\partial L_{S M}^{-}}{\partial θ_{s}} = 0, \frac{d}{d s_{⊥}} (\frac{\partial L_{S M}^{-}}{\partial θ_{s}}) - \frac{\partial L_{S M}^{-}}{\partial {\tilde{θ}}_{s}} = 0, \frac{d}{d s_{⊥}} (\frac{\partial L_{S M}^{-}}{\partial θ_{⊥}}) - \frac{\partial L_{S M}^{-}}{\partial {\hat{θ}}_{⊥}} = 0,

(72)

where

{\tilde{θ}}_{s} = \arctan (\tanh θ)

and

{\hat{θ}}_{⊥} = (s_{⊥} + \arctan (\cosh θ)) / 2

Thus, in 3+1 dimensions, the dynamics of a relativistic particle are described well by the Euler–Lagrange equations using

θ

θ_{⊥}

, and

θ_{s}

both in the direction of motion

θ_{s}

and

s_{⊥}

in the field of a circularly polarized laser pulse. As can be seen, from the actions

θ_{⊥}

θ_{s}

, and

s_{⊥}

given here instead of the “global” action

s

, the resulting solutions are compact, and for a particle in the field of a left-handed circularly polarized wave, they allow coordinates to be obtained that describe the dynamics of the particle in 3+1 dimensions. The introduced coordinates relative to the dynamics of a particle in the field of a left-handed circularly polarized laser pulse are also valid for a right-handed circularly polarized pulse, but the equations have a dissipative oscillation parameter depending on the selected speeds and actions.

11. New Lorentz-invariant transformations in 1+1 and 3+1 dimensions

The coordinates q,

q_{θ}

, and

q_{⊥}

from (3) and (5) form a Lorentz-invariant form in 3+1 dimensions relative to

θ

, i.e.,

Q_{t}^{+} = \frac{d q_{⊥}}{d θ} - (\frac{d q_{θ}}{d θ} - \frac{d q}{d θ}) = 1 - \tanh θ, Q_{t}^{-} = \frac{d q_{⊥}}{d θ} + \frac{d q_{θ}}{d θ} - \frac{d q}{d θ} = 1 + \tanh θ .

(73)

Spectral decomposition of the longitudinal component of the particle’s momentum

n P

in terms of

θ_{s}

and

θ_{⊥}

gives the coordinate

q_{E}

and rapidity

θ

[see (32)] along the normal gyrovector

n

Eqs. (32) and (73) lead easily to a new representation of the Lorentz-invariant coordinate

ξ_{E}

ξ_{E} = θ - f q_{E} = θ - f \ln (\cosh θ),

(74)

where

f = \pm 1

(see Ref. [22]). Differentiating (74) with respect to

θ

gives a connection between the Lorentz-invariant coordinates

ξ_{E}

ξ

and the integral of motion

Q_{t}

from Ref. [22], i.e.,

\frac{d ξ_{E}}{d θ} = Q_{t} = \frac{d ξ}{d t} .

(75)

As can be seen from (75), when describing the dynamics of a particle using the new Lorentz-invariant coordinate

ξ_{E}

, when passing from

ξ

ξ_{E}

it is necessary to make the following replacement of coordinates and operators:

t \to θ, q \to q_{E}, \frac{d}{d t} \to \frac{d}{d θ}, \frac{d}{d q} \to \frac{d}{d q_{E}} .

(76)

For example, from (76), the classical equation of particle motion in an electromagnetic field can be represented in the form

\frac{d P_{E M}}{d θ} = \frac{e}{m c} (E + [β, H]),

(77)

where

P_{E M}

is the momentum of the particle in the electromagnetic field,

β

is the speed of movement of the particle in the electromagnetic field, and

E = E (ξ_{E})

and

H = H (ξ_{E})

are the intensities of the electric and magnetic fields, respectively, depending on the new Lorentz-invariant coordinate.

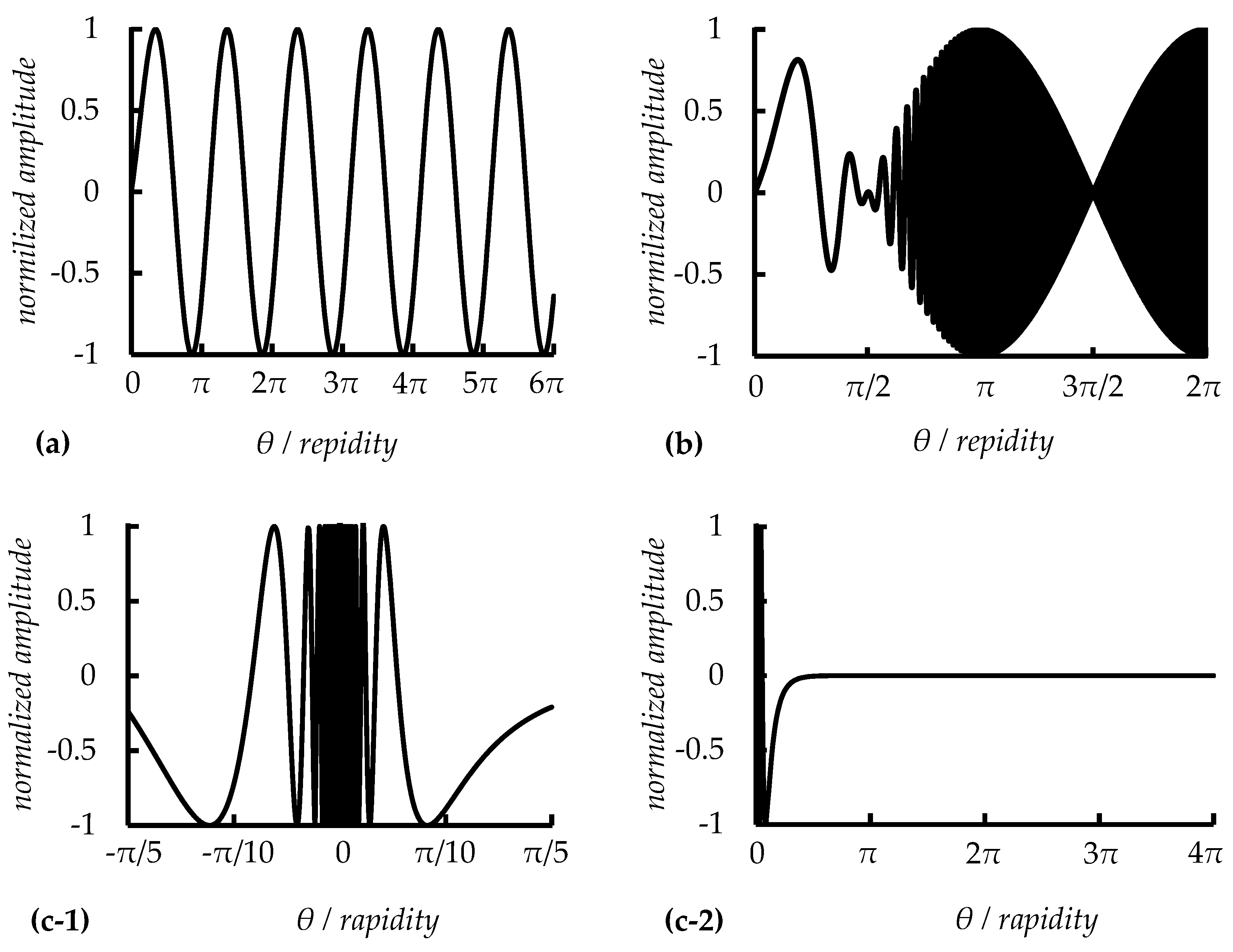
The advantage of using the new Lorentz-invariant form with coupled parameters

ξ_{E}

for plane electromagnetic waves with constant field amplitude as in (44) is that the representation

ξ_{E}^{-} = θ + q_{E}

describes the periodic motion of a charge in the field of a plane monochromatic electromagnetic wave for real and positive

θ

[see Fig. 2(a)]. It is also advantageous to use the new Lorentz-invariant form

ξ_{E}

to describe the dynamics of a particle in a constant uniform field when the oscillation frequency of the particle does not change and

T = 2 π / ω = c o n s t

. If the oscillation frequency of a particle changes according to a harmonic law

ω = ω (ξ_{E})

(see Ref. [27]), then with an increase in

θ

, frequency modulation is observed in the field of a plane wave [see Fig. 2(b)]. Thus, the Lorentz-invariant form

ξ_{E}

is the simplest representation for describing the dynamics of a relativistic particle with coupled parameters.

Using the Lorentz-invariant form

ξ = t - f q

to describe the dynamics of a particle in the field of a plane laser pulse, Fig. 2(c) shows that

ξ

describes a modulated pulse over the interval

θ \in [- 0.2; 0.2]

where the oscillation frequency is considered constant

(ω = c o n s t)

If it is also imagined that the oscillation frequency of a particle changes according to a harmonic law

ω = ω (ξ)

(see Ref. [27]), then in this case the wave oscillation profile does not change and has the same values as for a constant frequency [see Figure 2(c-1) and (c-2)]. Here we see that

ξ

describes the dynamics of a particle in a wave with spatial modulation.

for plane monochromatic wave with

ω = c o n s t

; (b) particle dynamics in frequency-modulated wave for the oscillation phase

ω (ξ_{E}^{-}) ξ_{E}^{-}

; (c) particle dynamics using

ξ

for a wave with both constant frequency (

ω = c o n s t

) and spatial modulation for the oscillation phase

ω (ξ) ξ

Applying the Lorentz transformations for

ξ_{E}

from (74) gives the coordinates

θ^{'} = θ \cosh θ - q_{E} \sinh θ, {q^{'}}_{E} = q_{E} \cosh θ - θ \sinh θ,

(78)

and differentiating (78) with respect to

θ

gives

\frac{d θ^{'}}{d θ} = - {q^{'}}_{E} + \frac{d θ_{s}}{d θ}, \frac{d {q^{'}}_{E}}{d θ} = - θ^{'} .

(79)

Eqs. (3), (5), (7), and (78) give a connection between coordinates in inertial systems K and

K^{'}

in 3+1 dimensions via

θ

, i.e., the general system of equations can be written in the following form:

t^{'} = t \cosh θ - q \sinh θ, q^{'} = q \cosh θ - t \sinh θ, {q^{'}}_{⊥} \equiv θ^{'} = θ \cosh θ - q_{E} \sinh θ, {q^{'}}_{θ} \sim q_{θ},

(80)

where the connection between the angular coordinates

q_{θ}

and

{q^{'}}_{θ}

in inertial systems K and

K^{'}

is also determined via the angular rapidity from (78), i.e.,

{q^{'}}_{θ} = \frac{1}{2} \ln (- \sinh^{2} θ^{'}), q_{θ} = \frac{1}{2} \ln (- \sinh^{2} θ) .

(81)

To the existing Lorentz-invariant coordinate

ξ_{E}

from (74), it is possible to introduce another additional coordinate of the form

ξ_{E ⊥} = θ_{⊥} - f θ,

(82)

and applying the Lorentz transformations for

ξ_{E ⊥}

from (82) gives

{θ^{'}}_{⊥} = θ_{⊥} \cosh θ - θ \sinh θ, {q^{'}}_{⊥} \equiv θ^{'} = θ \cosh θ - θ_{⊥} \sinh θ .

(83)

Differentiating (83) with respect to

θ

gives

\frac{d {θ^{'}}_{⊥}}{d θ} = \frac{d s_{⊥}}{d θ} - θ^{'}, \frac{d θ^{'}}{d θ} = - {θ^{'}}_{⊥},

(84)

and it can be seen that the projection of the motion of a relativistic particle is relative to

{θ^{'}}_{⊥}

and

θ^{'}

chosen along the world line

s_{⊥}

The obtained correct coordinates

θ_{s}

and

s_{⊥}

also give another angular Lorentz-invariant form

ξ_{E θ} = θ_{s} - f s_{⊥},

(85)

where having applied the Lorentz transformation to coordinate (85) yields the following local coordinates in inertial system

K^{'}

{θ^{'}}_{s} = θ_{s} \cosh (θ) - s_{⊥} \sinh (θ), {s^{'}}_{⊥} = s_{⊥} \cosh θ - θ_{s} \sinh θ .

(86)

Differentiating (86) with respect to

θ

gives

\frac{d {θ^{'}}_{s}}{d θ} = - {s^{'}}_{⊥}, \frac{d {s^{'}}_{⊥}}{d θ} = - {θ^{'}}_{s} + \frac{d q}{d θ} .

(87)

The local rapidities

θ^{'}

{θ^{'}}_{s}

{θ^{'}}_{⊥}

and

{s^{'}}_{⊥}

form a Lorentz-invariant form in 3+1 dimensions, where the generalized system of equations for

θ

has the form

θ^{'} = θ \cosh θ - q_{E} \sinh θ, {θ^{'}}_{s} = θ_{s} \cosh θ - s_{⊥} \sinh θ, {θ^{'}}_{⊥} = θ_{⊥} \cosh θ - θ \sinh θ, {s^{'}}_{⊥} = s_{⊥} \cosh θ - θ_{s} \sinh θ .

(88)

Here, the Lorentz-invariant coordinates

ξ_{E}

ξ_{E θ}

, and

ξ_{E ⊥}

are obtained with respect to the Lorentz transformation, and differentiating them gives the derivatives of actions (79), (84), and (87). This result can also be obtained by the method of calculus of variations, similar to Ref. [23], only that here it is necessary to apply the replacements given in (76), where the following correspondences hold:

ξ \to ξ_{E}, ξ_{θ} \to ξ_{E θ}, ξ_{⊥} \to ξ_{E ⊥} .

(89)

From (79), (84), and (87), it is clear that the actions are described by the functions

θ_{s}

s_{⊥}

, and

q

, which are hyperbolic functions that depend on only

θ

12. Conclusion

In this work, the form of local coordinates and local rapidities in 3+1 dimensions was obtained via parametrization with coupled parameters. New Lorentz-invariant coordinates were presented that make it possible to describe the dynamics of a particle in 3+1 dimensions with coupled parameters in terms of hyperbolic functions depending on the rapidity

θ

. This new Lorentz-invariant form is an addition to the Lorentz-invariant form in 1+1 dimensions, which together allow description of the dynamics of a particle in 3+1 dimensions.

From Hamilton’s formalism, a perpendicular rapidity and an angular rapidity were derived; these are not invariants, but in combination with other rapidities they form new Lorentz-invariant coordinates with respect to Lorentz transformations.

Because all parameters are coupled, it was shown that an arbitrary function can be decomposed via rapidity into elementary functions. For those cases when it is not possible to decompose an arbitrary function into elementary ones, a so-called passage to the limit was introduced, which also allows a complex function to be decomposed into elementary functions.

The spectral expansions into elementary functions resulted in the coordinates

ξ_{E}

ξ_{E θ}

, and

ξ_{E ⊥}

, which are invariant under Lorentz transformation, and a comparison and connection between the Lorentz-invariant coordinates

ξ

and

ξ_{E}

was presented. It was shown that for plane waves oscillating according to a harmonic law using the Lorentz-invariant coordinate

ξ

, the coordinate describes the oscillation of a particle over an interval

θ \in [- 0.2; 0.2]

similar to the oscillation of a particle in the field of a short laser pulse. Applying the new Lorentz-invariant form

ξ_{E}

to plane waves oscillating according to the harmonic law, it is clear that the oscillation of a particle in a wave is described by periodic motion on the interval

θ \in [0; + \infty)

Assuming that the presented plane waves have frequency modulation, the frequency of which varies according to the harmonic law

ω = ω (ξ)

and

ω = ω (ξ_{E})

, then for a plane wave described by the Lorentz-invariant form

ξ

, the presence of frequency modulation does not affect the oscillation frequency of the particle, because

ξ

describes the dynamics of the particle with spatial modulation. When applying the frequency modulation

ω = ω (ξ_{E})

to the new Lorentz-invariant form, the wave form clearly has a classical frequency-modulated profile. From the given Lorentz-invariant forms

ξ

and

ξ_{E}

in relation to plane waves, the main conclusion that can be drawn is that (i) the use of

ξ

describes well the dynamics of a particle in short pulses and (ii) the use of the new Lorentz-invariant form

ξ_{E}

describes classical harmonic processes.

In general, it has been shown that the Euler–Hamilton equation describes well the dynamics of a relativistic particle in the field of a plane wave and in the field of a plane laser pulse in 3+1 dimensions, and to describe the motion of a particle in the field of a circularly polarized pulse with left-hand polarization, it is advantageous to use the Euler–Lagrange equations because the resulting equations are compact.

The results of this work will be used in the future to construct a relativistic hydrodynamic model with coupled parameters in 3+1 dimensions.

Author Contributions

Conceptualization, N.S.A.; methodology, N.S.A.; writing—review and editing, N.S.A. and A.P.N.; writing—original draft, N.S.A. and A.P.N.; investigation, G.F.K. and Y.Y.; validation A.P.N. and Y.Y. All authors have read and agreed to the published version of the manuscript.

Funding

This work was partially supported by the Key Research and Development Program of Jiangsu Province of China (Grant No. BE2021013-1), the National Natural Science Foundation of Jiangsu Province of China (Grant No. BK20201438), and in part by the Natural Science Research Project of Jiangsu Provincial Institutions of Higher Education (Grant Nos. 20KJA510002 and 20KJB510010).

Data Availability Statement

Not applicable.

Acknowledgments

The authors would like to thank V.G. Bagrov, V.Ya. Epp, V.A. Isaev, E.N. Tumaev, V.T. Rykov, and A.A. Martynov for their enlightening comments.

Conflicts of Interest

The authors declare no conflict of interest.

References

Friedman, Y.; Scarr, T. Symmetry and Special Relativity. Symmetry 2019, 11, 1235. [Google Scholar] [CrossRef]
Khadka, C.B. Derivation of the Lorentz transformation for determination of space contraction. SPbPU J. Phys & Math 2023, 16, 115–130. [Google Scholar] [CrossRef]
Field, J.H. Space-time exchange invariance: Special relativity as a symmetry principle. Am. J. of Phys 2001, 69(5), 569–575. [Google Scholar] [CrossRef]
Sharp, J.C. Symmetry of the Lorentz boost: the relativity of colocality and Lorentz time contraction. Eur J. of Phys 2016, 37, 055606. [Google Scholar] [CrossRef]
Chao, S.D. Lorentz Transformations from Intrinsic Symmetries. Symmetry 2016, 8, 94. [Google Scholar] [CrossRef]
Minkowski, H. Space and Time: Minkowski’s papers on relativity; Minkowski Institute Press: Montreal, 2012. [Google Scholar]
Popp, B.D. Henri Poincaré: Electrons to Special Relativity; Springer Cham: Bern, 2020. [Google Scholar] [CrossRef]
Robb, A. Optical geometry of motion, a new view of the theory of relativity; Heffner & Sons: Cambridge, 1911. [Google Scholar]
Borel, É. La théorie de la relativité et la cinématique. Comptes rendus de l’Académie des Sciences 1913, 156, 215–218. [Google Scholar]
Varicak, V. Relativity in three dimensional Lobachevsky space; A.F. Kracklauer: NYC, 2007. [Google Scholar]
Karapetoff, V. Special Theory of Relativity in Hyperbolic Functions. Rev. Mod. Phys. 1944, 16, 33–52. [Google Scholar] [CrossRef]
Karapetoff, V. Restricted Theory of Relativity in Terms of Hyperbolic Functions of Rapidities. Am. Math. Monthly 1936, 43(2), 70–82. [Google Scholar] [CrossRef]
Shaw, H. Hyperbolic Functions and Proper Time in Relativity, College Math J. 1995, 26, 312–315. College Math J. 1995, 26, 312–315. [Google Scholar] [CrossRef]
Dray, T. The Geometry of Special Relativity, 2nd ed.; Chapman and Hall/CRC: Boca Raton, Fla, 2021. [Google Scholar]
Ungar, A.A. Analytic Hyperbolic Geometry and Albert Einstein’s Special Theory of Relativity; North Dakota State University: Fargo, ND, 2008. [Google Scholar] [CrossRef]
Landau, L.D. On the multiparticle production in the high-energy collisions. Izv. Akad. Nauk SSSR Ser. Fiz. 1953, 17, 51–64. [Google Scholar]
Khalatnikov, I.M. Some question of the relativistic hydrodynamics. Sov. Phys. JETP 1954, 26, 529. [Google Scholar]
Bjorken, J.D. Highly relativistic nucleus-nucleus collisions: The central rapidity region. Phys. Rev. 1983, D27, 140–151. [Google Scholar] [CrossRef]
Milekhin, G.A. Hydrodynamic theory of multiple production of particles in collisions between fast nucleons and nuclei. Sov. Phys. JETP 1959, 8, 829–837. [Google Scholar]
Lin, D.-H. The 2+1-dimensional special relativity. Symmetry 2022, 14, 2403. [Google Scholar] [CrossRef]
Akintsov, N.S.; Nevecheria, A.P.; Martynov, A.A. The motion of an uncharged relativistic particle: an analysis of its integrable motion integrals dynamics. SPbPU J. Phys & Math 2023, 16, 132–145. [Google Scholar] [CrossRef]
Akintsov, N.S.; Nevecheria, A.P.; Kopytov, G.F.; Yang, Y. Lagrangian and Hamiltonian formalisms for relativistic mechanics with Lorentz-invariant evolution parameters in 1+1 dimensions. Symmetry 2023, 15, 1691. [Google Scholar] [CrossRef]
Akintsov, N.S.; Kopytov, G.F.; Nevecheria, A.P.; Yang, Y. Lorentz-invariant forms of motion of classical relativistic particles in 3+1 dimensions. Izv. Vuzov Fiz 2023, 66, 41–49. [Google Scholar]
Olver, F.W.J.; Lozier, D.W.; Boisvert, R.F.; Clark, C.W. NIST Handbook of Mathematical Functions; Cambridge University Press: Cambridge, 2010. [Google Scholar]
Landau, L.D.; Lifshitz, E.M. The classical theory of fields; Pergamon: Oxford, UK, 1975. [Google Scholar] [CrossRef]
Zhao, J. Multiple zeta functions, multiple polylogarithms and their special values; World Scientific Pub Co Inc: Shanghai, 2016. [Google Scholar]
Akintsov, N.S.; Nevecheria, A.P.; Kopytov, G.F. Modulated laser-induced acceleration of a relativistic charged particle. Indian J. Phys. 2023, 1–15. [Google Scholar] [CrossRef]

Figure 1. This is a figure. Schemes follow the same formatting. How velocities

q / t

(labeled 1) and

n β

(labeled 2) depend on dimensionless field amplitude a.

Figure 1. This is a figure. Schemes follow the same formatting. How velocities

q / t

(labeled 1) and

n β

(labeled 2) depend on dimensionless field amplitude a.

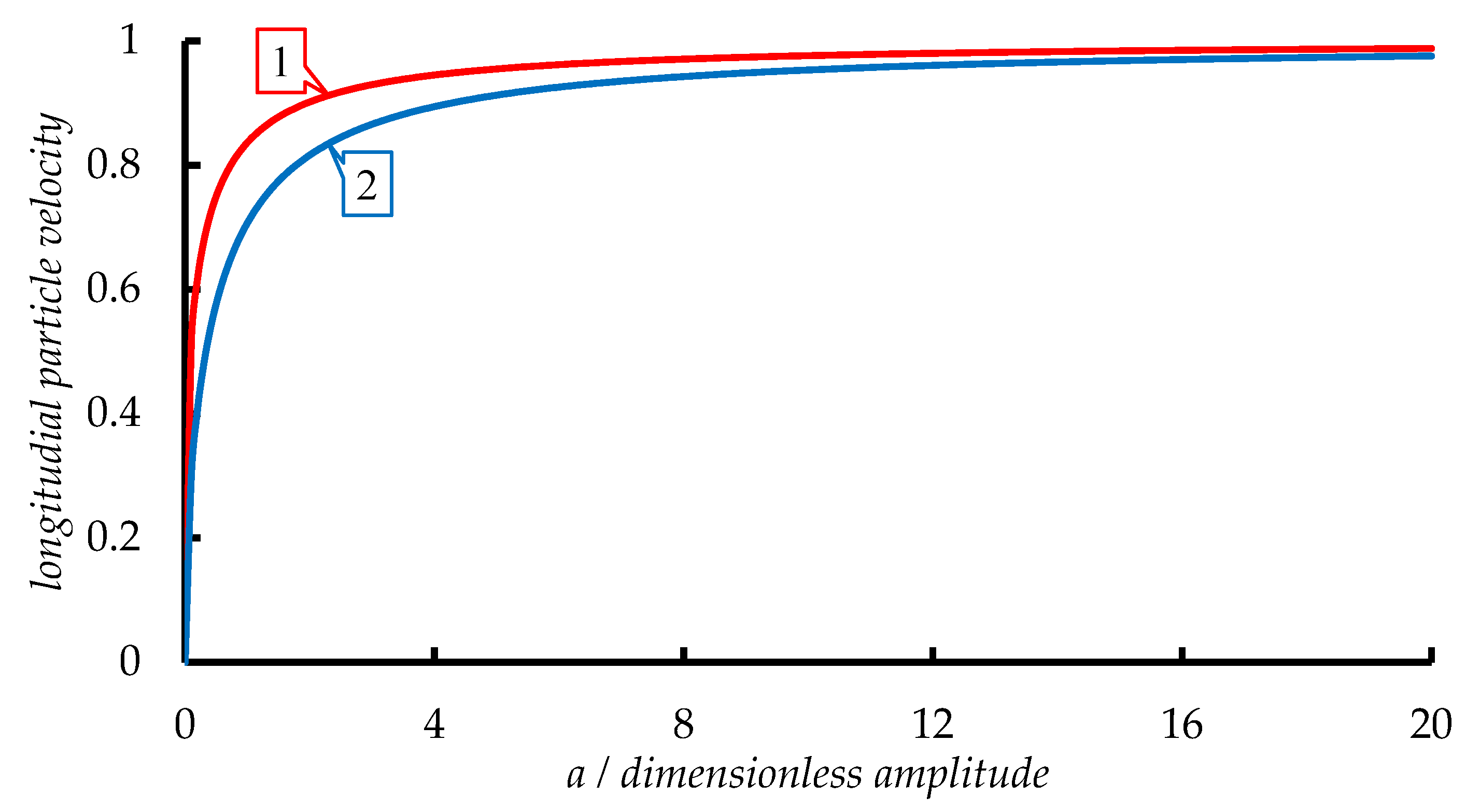
Figure 2. Dependences of particle oscillations in field of plane wave for Lorentz-invariant space–time coordinates, provided that the amplitude of the wave field is normalized to unity: (a) particle dynamics using

ξ_{E}^{-}

ξ_{E}^{-}

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Special Relativity in Terms of Hyperbolic Functions with Coupled Parameters in 3+1 Dimensions

Abstract

1. Introduction

2. Generalization of existing results and problem statements

3. Action of Lorentz-invariant transformation with respect to rapidity θ

in 1+1 dimensions

4. Relationship between perpendicular rapidity and angular rapidity of free relativistic particle

5. Expansion into rapidity spectra for lagrangian, hamiltonian, and momentum of free relativistic particle

6. Euler–Hamilton equations in 3+1 dimensions

7. Decomposition of local coordinates into rapidity spectra

8. Spectral characteristics of relativistic particle in field of circularly polarized electromagnetic wave in 3+1 dimensions

9. Spectral characteristics of relativistic charge in field of plane laser pulse in 3+1 dimensions

10. Dynamics of relativistic particle in field of plane laser pulse with left-handed circular polarization in 3+1 dimensions

11. New Lorentz-invariant transformations in 1+1 and 3+1 dimensions

12. Conclusion

Author Contributions

Funding

Data Availability Statement

Acknowledgments

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe

3. Action of Lorentz-invariant transformation with respect to rapidity $θ$