Prerpints.org logo
Preprint
Article

Concurrent Supra-Postural Auditory-Hand Coordination Task Affects Postural Control: Using Sonification to Explore Environmental Unpredictability in Factors Affecting Fall Risk

Altmetrics

Downloads

91

Views

37

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

11 January 2024

Posted:

11 January 2024

You are already at the latest version

Alerts
Abstract
Clinical screening tests for balance and mobility often fall short of predicting fall risk. Cognitive distractors and unpredictable external stimuli, common in busy natural environments, contrib-ute to this risk, especially in the elderly. Less is known about the effects of upper sensory-motor coordination such as coordinating one’s hand with an external stimulus. We combined move-ment sonification and affordable inertial motion sensors to develop a task for the precise meas-urement and manipulation of full-body interaction with stimuli in the environment. In a double-task design, we studied how a supra-postural activity affected quiet stance. The supra-postural task consisted of rhythmic synchronization with a repetitive auditory stimulus. The stimulus was attentionally demanding because it was being modulated continuously. The participant’s hand movement was sonified in real-time, and their goal was to synchronize their hand move-ment with the stimulus. In the unpredictable condition, the tempo changed at random points in the trial. A separate sensor recorded postural fluctuations. Young healthy adults were compared to elderly participants without known risk of falling. Results supported the hypothesis that su-pra-postural coordination would entrain postural control. The effect was stronger in the elderly, supporting the idea that diminished reserve capacities reduce the ability to isolate postural con-trol from sensory-motor and cognitive activity.
Keywords: 
Subject: Biology and Life Sciences  -   Aging

1. Introduction

Falls occur at an alarming rate in the aging population [1]. A quarter of fallers who are older adults experience an injury [2]. According to the CDC, falls are a major cause of injury and a public health issue, with over 800,000 yearly hospitalizations in the US [3].
Among the environmental stimuli that may interfere with postural control, the effects of cognitive distractors have been confirmed extensively. Far from being an isolated autonomous module, postural control of standing balance has been described as cognitively penetrable [4,5]. Postural sway in older adults becomes more variable in the presence of cognitive double task [6]. In this context, the unpredictability inherent in complex urban environments is particularly salient, with fall risk increasing in outdoor compared to indoor conditions [7]. Urban environments, which can contain uneven surfaces and multiple objects, are associated with falling and fear of falling in older adults. This is consistent with the fact that poor visual acuity is also a risk factor for falls in older adults [8]. Distractors such as other pedestrians passing on one’s sides differentially lock the visual attention of fallers in comparison to non-fallers [9]. The visible layout of outdoor environments, however, is not the only culprit.
Supra-postural tasks involving movement, such as manipulating objects with the hands, have an unavoidable mechanical influence on postural control. Even the slightest, non-load-bearing mechanical coupling with a moving surface using finger touch is enough to re-organize postural control [10,11]. Interestingly, movement in the acoustic environment can influence posture as well. In the laboratory, controlling auditory cues in adults with normal hearing leads to increased postural sway [12]. Sway can couple with audible spatial displacements if the task explicitly demands it [13]. There are also reports of such coupling emerging spontaneously in the presence of repetitive stimuli in the background [14]. In the wild, hearing loss is independently associated with fall risk [15,16] as well as a reduction in gait speed [17]. Impaired hearing leads to poor awareness of moving objects in the spatial environment, perhaps implicitly increasing cognitive load and shared attention [15], p. 20.
It is less known whether older adults are more susceptible to a combination of cognitive-auditory-mechanical interference. Here, we address if postural control is entrained spontaneously by attention-demanding rhythmic auditory-motor synchronization, and compare healthy older adults to young adults. The synchronization task had an easy and a more challenging condition where the auditory stimuli changed tempo unpredictably. We investigated whether low-cost portable sensors were sufficient to detect differences task performance and postural fluctuations, thus widening the potential for practical application of postural tasks for testing of balance control in older adults.

2. Materials and Methods

2.1. Participants

Eleven students (N=11, 8/3 female/male) were recruited in the young adult (YA) group (mean age 23.6, range 20-37) and compensated with a coffee gift card. Eleven members of the community (N=11, 8/3 female/male) were recruited in the older adult (OA) group (mean age 68.7, range 60-73). Only participants who did not report any hearing or mobility issues on initial screening questionnaires were invited to participate. An additional criterion for inclusion was the declared ability to stand and walk for fifteen minutes.

2.2. Apparatus

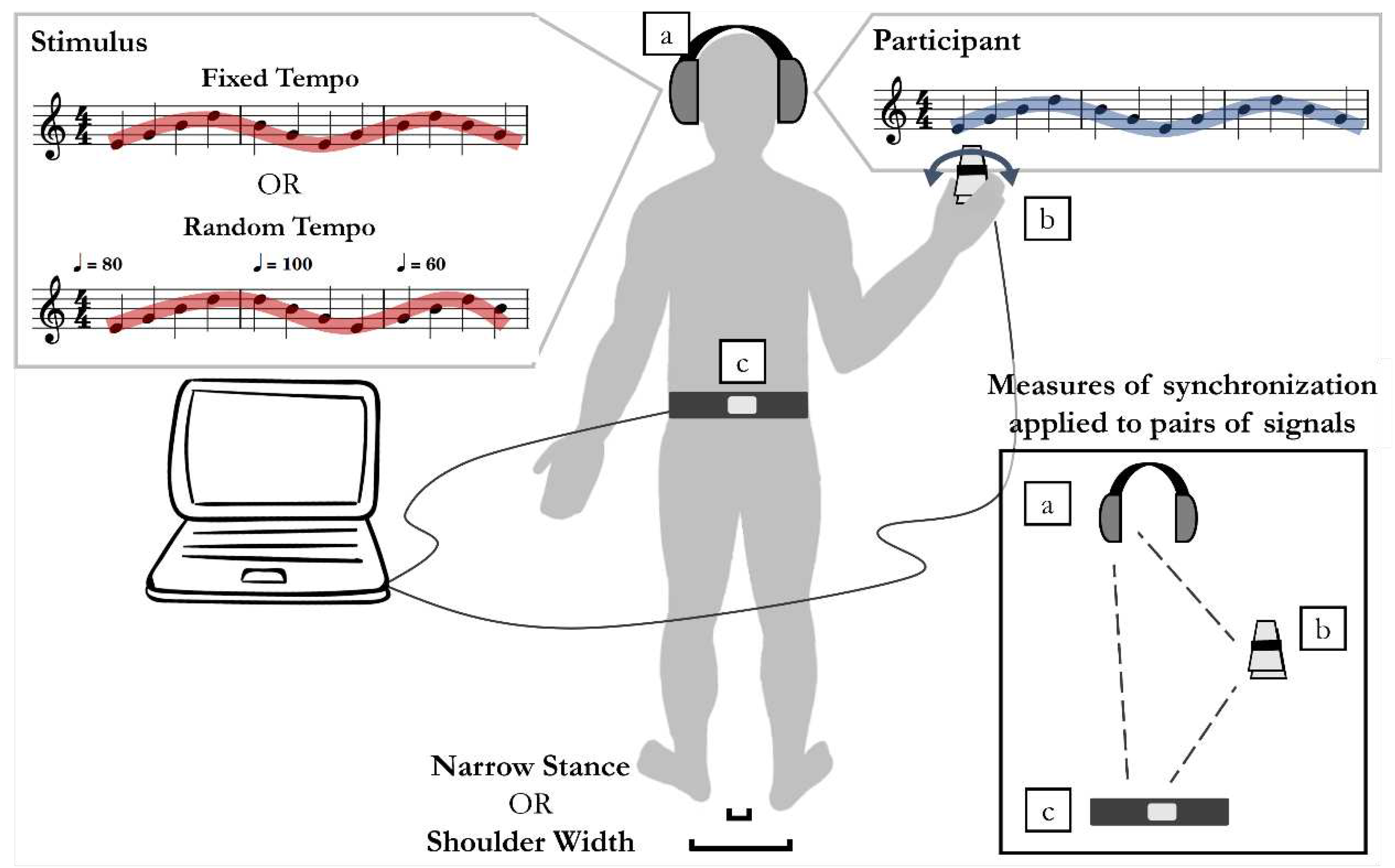
A custom-built hand-held device functioned as a sonified tiltmeter: declination from the vertical controlled the pitch of a continuous tone played in the ipsilateral channel of headphones worn by the participant, see Figure 1. Tilt in the range from -90 (left) to +90 (right) degrees was mapped linearly to the tone fundamental frequency in the range from 261.63 to 349.23 Hz. The device used an encased Arduino UNO board (Arduino LLC, Turin, Italy) and an embedded MPU6050 inertial measurement unit (IMU) with a 3D accelerometer and 3D gyroscope (InvenSense, San Jose, California). This sensor has an on-board digital motion processor for angle and acceleration in real-world coordinates. To sample the postural fluctuations of the participant, a second device identical to the hand-held one (but which did not control a sound) was held in place on the lower back with a soft elastic belt around the torso.
To record the sensor output signals, USB cables connected them to a laptop computer running a real-time GNU/Linux kernel. Custom Python code encoded the sensor tilt signals at a rate between 90 and 100 Hz and used this tilt information signal from the hand-held device to synthesize the pitch of the continuous tone at a 48 kHz sampling rate, see Appendix A. The computer also generated a stimulus tone and the task of the participant was to move the hand-held device so that its sound match that of the stimulus. Both the stimulus and participant-generated tones were played through over-the-ear open-cup headphones. Participants self-selected a comfortable sound level during the practice trials.
The participants stood in front of a desk and held the controller in the air in front and/or to the side of them. The suggested arm and hand posture was similar to holding a key to unlock a door. Participants were asked to find their most comfortable position during practice trials. Participants also self-selected a comfortable grasp of the hand-held controller, either with the thumb and index fingers on its sides or holding it from above and below.
We used hearing and mobility questionnaires for screening whether participants would be invited to participate in the study. PROMIS-Mobility [18] asks participants to select the level of difficulty they experience while performing activities of daily living such as walking, standing up from a chair, and climbing a flight of stairs. A score of 5 (“Without any difficulty”) on all balance-related items was required for participation. The Hearing Handicap Inventory for the Elderly (HHIE-S) asks if respondents fail to understand auditory information in contexts such as talking to family or listening to speech on the radio and in a restaurant [19]. A score of 14 or lower (“Mild-moderate handicap”) was required.

2.3. Task

Participants performed two tasks, a simple postural and a supra-postural task. The simple task was to maintain a quiet standing posture for one minute in either narrow or shoulder-width stance. The supra-postural task involved performing an auditory-motor synchronization task while standing. Participants held and moved the device in their dominant hand to control the pitch of the continuous sound it produced. The goal of the synchronization task was to match the pitch of this sound to the pitch of a target (stimulus) tone (see Figure 1). Both tones were played continuously throughout the trial and were pitch-modulated continuously. The participant’s sound was played in the channel ipsilateral to the hand holding the controller. The target was played in the contralateral channel. Its pitch was modulated in a sinusoidal-like manner in the range between 269 to 339 Hz with a fixed or with an unpredictably changing tempo (see Figure 1). More specifically, the modulation was a symmetric triangle wave. Participants controlled the pitch of the tone produced by their device by changing the declination from the vertical of their sensor, with rotation to their left producing lower pitch and rotation to their right, higher pitch. As the two sounds had identical timbres consisting of a pure tone and two harmonics, ideal synchronization and pitch-matching led to unison between the two channels.

2.4. Design

There were two groups of participants: young adults (YA) and older adults (OA). Stimulus predictability was a within-subject factor with two levels: fixed and random tempo. Stance stability was also a within-subject factor with two levels: shoulder-width and narrow-stance, defined as feet-together.

2.5. Stimuli

The auditory stimulus was a continuous tone with two harmonics. Its fundamental frequency changed from 269 Hz (between C4 and C#4) to 339 Hz (between E4 and F4) following a triangle wave. In the fixed-tempo condition, the period of this oscillation was 909 ms. In the random-tempo condition, the modulation period was taken from a uniform distribution with range [1,4] seconds. This period changed in uniform random intervals in the range [1,5] seconds.

2.6. Procedure

After the participants were seated in a chair in front of an office desk, they heard an explanation of the task, signed an informed consent form, and completed questionnaires on demographic information, history with musical practice and sports, and hearing and motor abilities. All procedures were approved by the ethics board (MREB: #1975). To help their intuition, the task was compared to playing second violin in an orchestra where the first violin could play with an erratic tempo. A pre-recorded video was played where each condition of the task was demonstrated. Participants performed twenty-two trials, one-minute-long each. The first two trials were without the target tone to allow familiarization with the novel musical instrument. The following four trials were considered practice trials. After each practice trial, the experimenter explained a figure on the screen which showed the recorded target and participant trajectories. In the remaining 16 trials, each of the four combinations of the stance and stimulus conditions were repeated four times. Trials were blocked by stimulus condition, and stance condition was randomized within these blocks. The main part of the experiment lasted approximately 40 minutes.

2.7. Measures

2.7.1. Performance

The level of task performance in each trial was quantified by applying bi-variate methods to the two time-series containing the MIDI pitch information from the stimulus and musical instrument device channels. We used two measures: the windowed cross-correlation (C) and the root-mean-squared-error (E) between the two time-series. The former is sensitive to rhythmic synchronization with the target; the latter is sensitive to matching not only the temporal pattern but also the exact pitch. The first ten seconds of the trial were excluded from analysis.
Cross-correlation (C) is the correlation between two processes after they are time-shifted relative to each other by a range of lags from -τ to τ. The time-lag allows C to be sensitive to phase-synchronization. The windowed approach computes the measure successively over subsections of the trial using a running window. We took the absolute cross-correlation values corresponding to the separate windows and then averaged them to obtain a single value for the entire trial. We used non-overlapping windows of length 5 seconds, and a maximum τ of 1000 ms. Each time-series was z-score normalized (zero mean and unit variance).
Root-mean-squared-error (E) is the magnitude of the difference between signals averaged across time points.

2.7.2. Synchronization with Postural Fluctuations

Lower-back Acceleration Magnitude (A). Postural control is typically studied by way of kinematic or ground reaction force data. Here, the postural data contained lower-back accelerations which required pre-processing. We reduced the 3D accelerations to a single time-series by taking the acceleration magnitude across dimensions, A i = ( a X , i 2 + a Y , i 2 + a Z , i 2 ) . 5 , where i was time-sample in the trial [20,21].
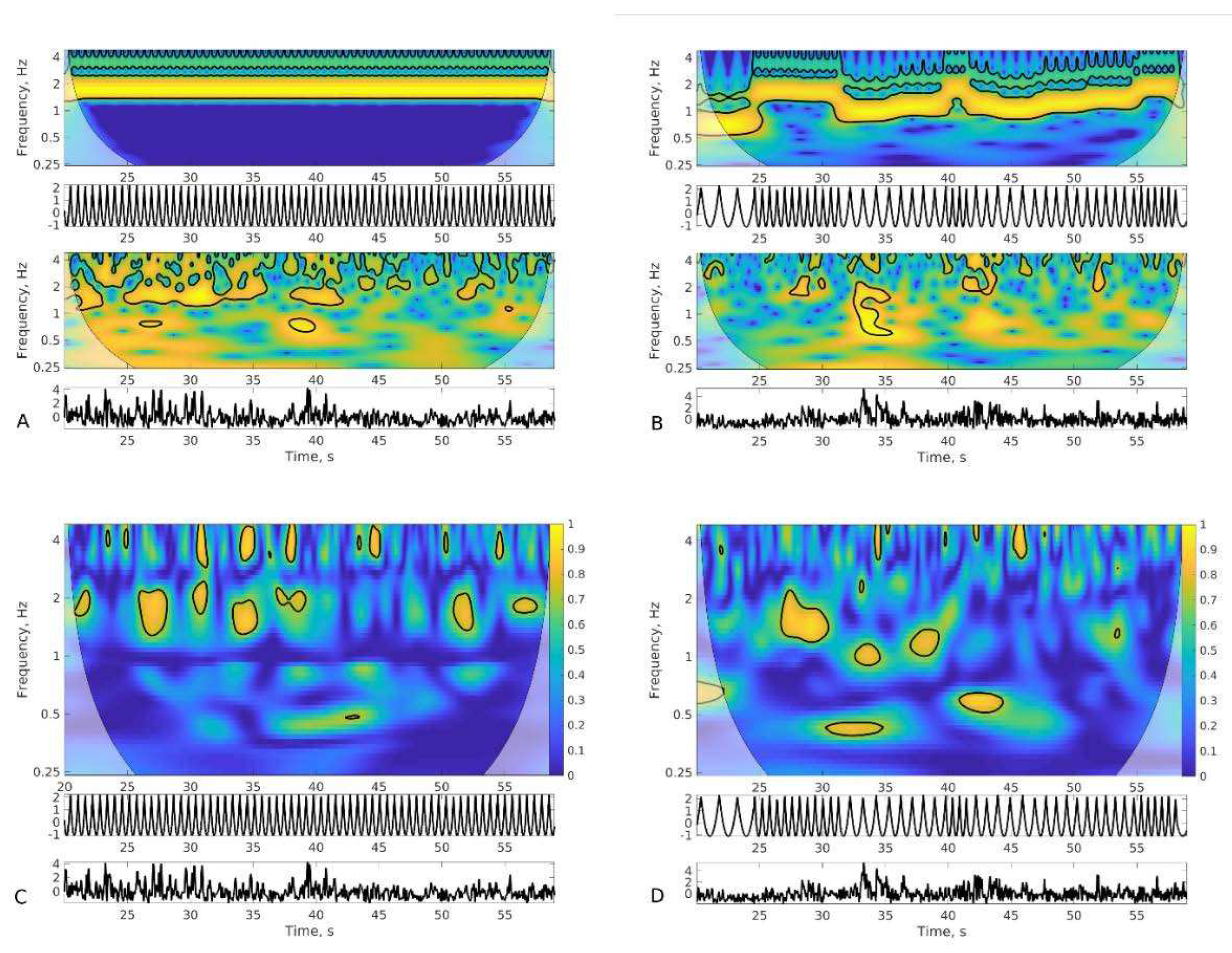
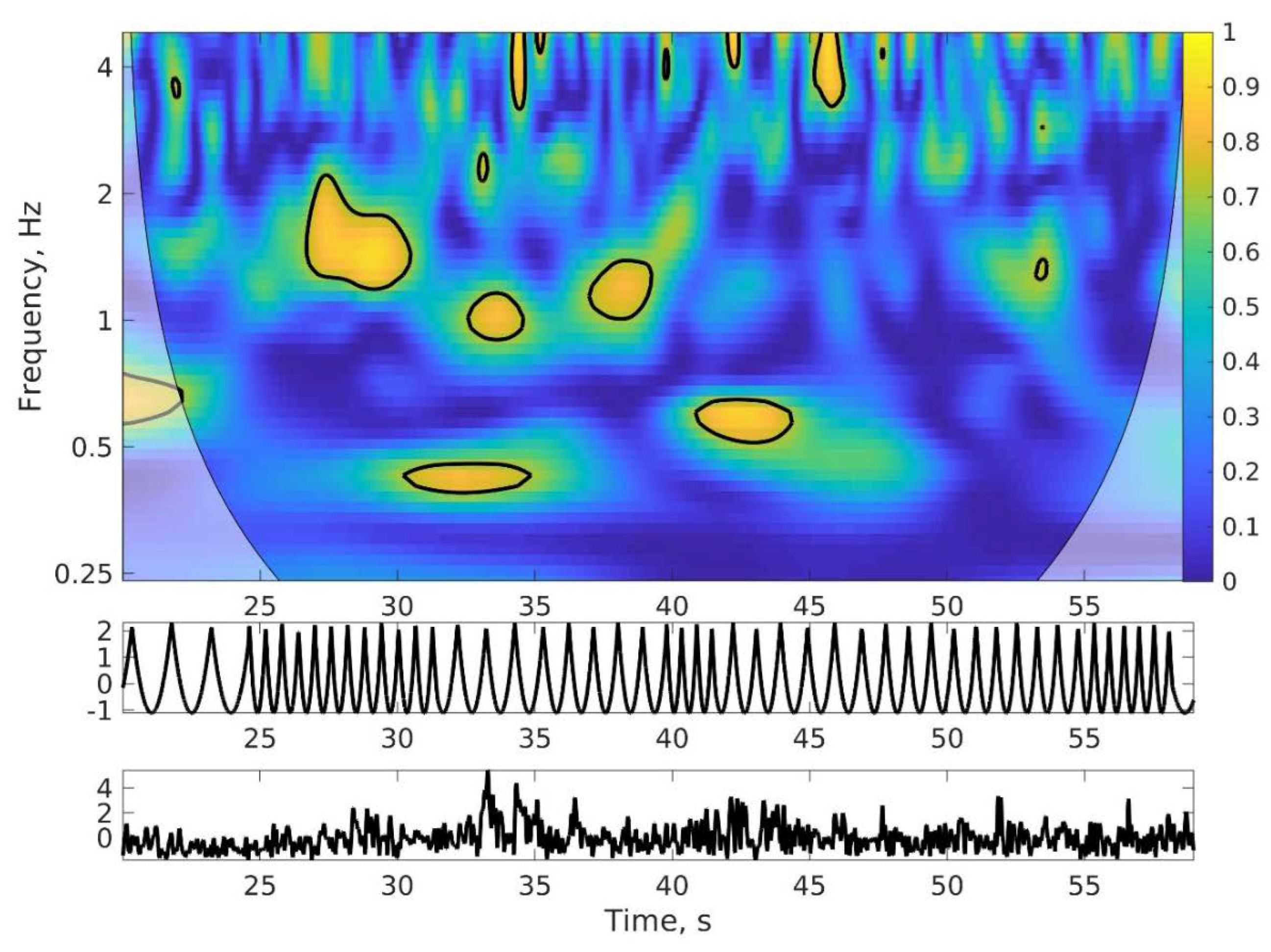
Cross-Wavelet Coherence. To measure coupling among postural and supra-postural effectors, we applied a cross-wavelet synchronization method to the stimulus-lower body and hand-lower body pairs of sensors. It is an extension of the wavelet transform which is a time-frequency representation of an individual signal, see Appendix B. We used the cross-wavelet transform Matlab toolbox [22]. The method is sensitive to the shifting patterns of coordination present in postural tasks [23]. Its main two estimated quantities are common power between two time-series, that is, how much the oscillations in the one match in frequency the oscillations in the other, and coherence, that is, how much they are phase-synchronized, see Figure 2. Here we concentrated on coherence. It is time- and frequency-resolved because it analyzes signals with localization in frequency bands, similar to spectral analysis, and with localization in time. Importantly, the toolbox implements null-hypothesis testing per time-frequency bin to reduce the chance of reporting meaningless values of spurious synchronization. The cross-wavelet synchronization indicates the areas in the time-frequency space with significant phase-synchronization, see Figure 2. To reduce this rich data to a single value per trial, we used the proportion of the time-frequency space where coherence was significant.
We used the same analysis parameters for each trial and sensor pair. The time-series were z-score normalized. We used the Morlet wavelet and limited its scale to the frequency range from .25 to 4 Hz. The number of iterations for computing the surrogate null-hypothesis distribution was set to the default of 300. The magnitude of postural accelerations (A) was band-pass filtered between .5 and 6 Hz. Taking the magnitude of the lower-back acceleration flips negative accelerations in the positive domain. For this reason, the stimulus and hand data were full-wave rectified and squared when analyzing their coupling with acceleration magnitude, meaning that neutral position was zero in the rectified timeseries and movements both to the left and to the right were positive.

2.8. Statistical Analysis

Outcomes from the hearing and mobility questionnaire were compared between groups with a non-parametric Mann-Whitney test. Levels of performance and coupling measures were compared between groups and conditions using ANOVAs. Linear mixed-effects models tested for associations between postural synchronization and performance.

3. Results

3.1. Hearing and Mobility

Comparing the hearing handicap scores in YA (M=3.46, SD=5.07) and OA (M=2.00, SD=4.47) did not show a significant difference (W=80, n1=n2=11, p=.15). When comparing the mobility scores in YA (M=74.90, SD=.30) and OA (M=71.36, SD=5.22), we found that the YA group was significantly higher than OA (W=85, n1=n2=11, p<.05).

3.2. Peformance

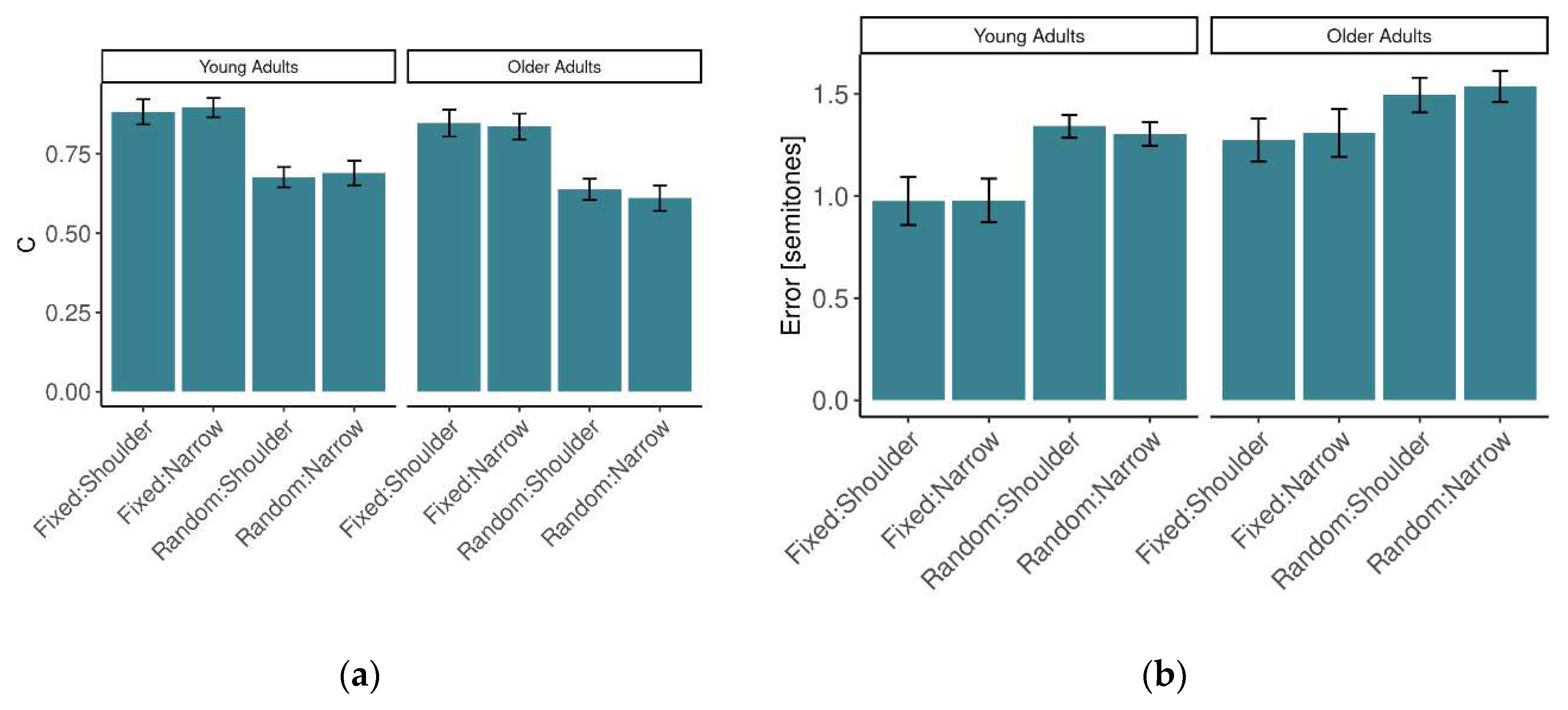
Pitch-matching error exhibited differences between stimulus conditions and groups, see Figure 3A. Pitch-matching error was worse with the random-tempo stimulus (M=1.42, SE=.048) than with the fixed-tempo stimulus (M=1.13, SE=.078) and this was a significant effect [F(1,20)=31.57, p<.001, η2G=.189]. The error was also higher in the OA group (M=1.40, SE=.085) than in the YA group (M=1.15, SE=.085), a significant effect [F(1,20)=4.51, p<.05, η2G=.156]. There was no interaction between age group and stance [F(1,20)=3.32, p=.083]. All other main effects and interactions (stance, age x predictability, predictability x stance, age x predictability x stance) were not significant [all F<1].
As expected, the measure of rhythmic synchronization C in the fixed-tempo condition (M=.865, SE=.027) was higher than in the random-tempo condition (M=.654, SE=.025) and this was a significant effect [F(1,20)=128.63, p<.001, η2G=.445]. There was a significant interaction between age group and stance [F(1,20)=4.90, p=.039, η2G=.005]. Specifically, C tended to be lower in the shoulder-width condition than in the narrow-stance condition in group YA [M(SE)=.780(.035) vs. M(SE)=.793(.034)] but the relationship was reversed for OA where C was higher in shoulder-width than in narrow-stance [M(SE)=.743(.035) vs. M(SE)=.723(.034)], although neither of these two comparisons were significant [p=.224 and p=.075]. The other main effects and interactions were not significant [all F<1].

3.3. Postural Synchronization with the Main Task

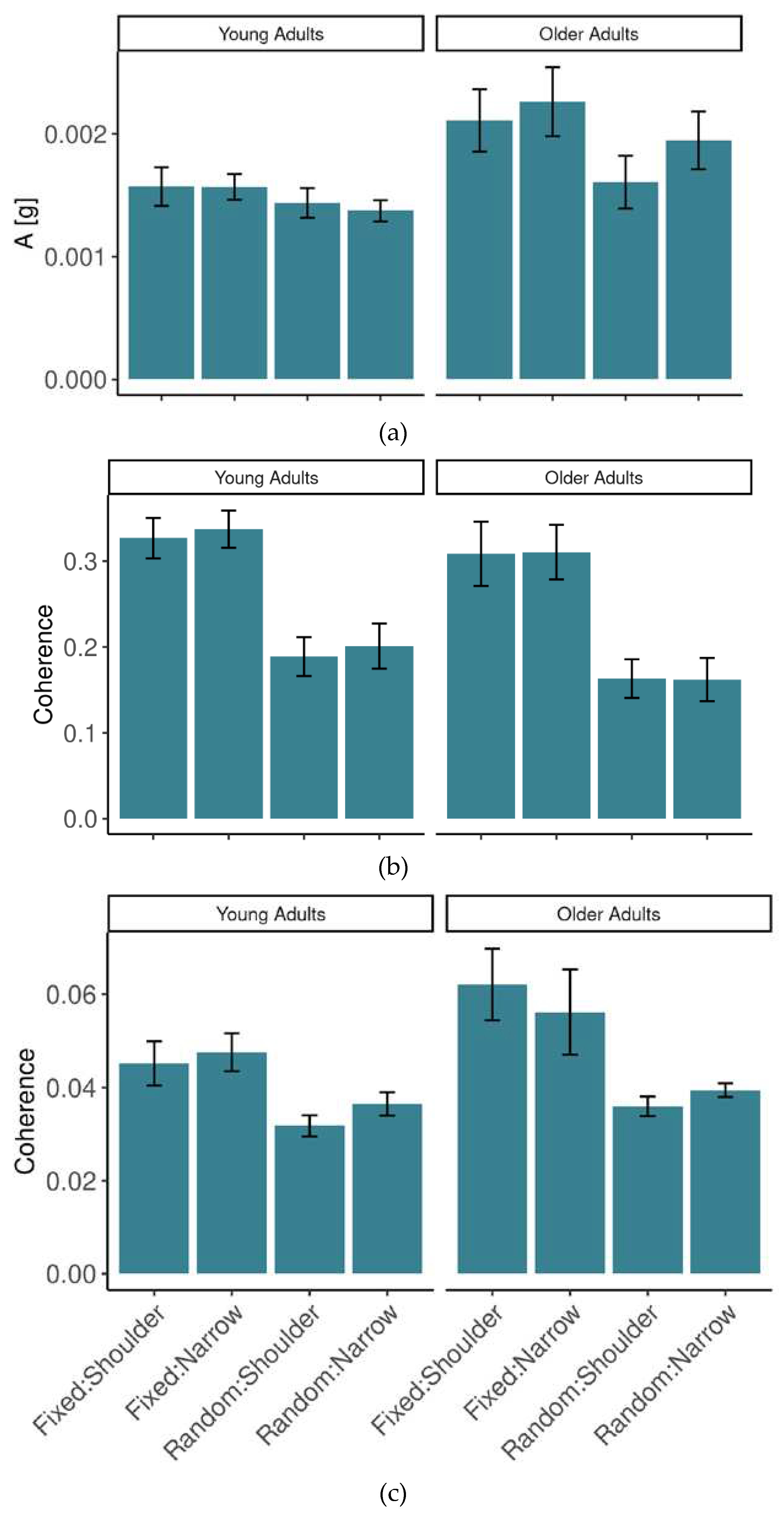
We were interested in how postural control changed in the context of different conditions of the main task. First, we considered the magnitude of lower-back accelerations (see Figure 4A). A was lower in the YA group (M=149*10-5, SE=18*10-5) than in the OA group (M=198*10-5, SE=18*10-5) but the effect was not significant [F(1,20)=3.78, p=.066, η2G=.139]. There was a significant interaction between age group and stance [F(1,20)=5.20, p<.05, η2G=.013]. Specifically, in the narrow-stance condition in OA (M=210*10-5, SE=18*10-5) A was higher than in the shoulder-width condition (M=186*10-5, SE=19*10-5), a significant effect (p<.05), but this comparison in the YA group [M(SE)=147*10-5(18*10-5) vs. M(SE)=150*10-5(19*10-5)] did not exhibit a significant difference (p=.71). Furthermore, A in group OA was higher than in group YA in the narrow-stance condition (p<.05) and not different in the shoulder-width comparison (p=.19). Finally, the main effect of stimulus predictability was significant [F(1,20)=14.29, p<.01, η2G=.051], with A being higher with the fixed-tempo stimulus (M=188*10-5, SE=15*10-5) than with the random-tempo stimulus (M=159*10-5, SE=12*10-5).
The amount of cross-wavelet coherence between postural fluctuations and the target stimulus is summarized in Figure 4B. It appeared to be higher in OA (M=.049, SE=.003) than in YA (M=.040, SE=.003), but the difference was not significant although there was a trend [F(1,20)=3.36, p=.082, η2G=.063]. There was a significant effect of stimulus predictability [F(1,20)=12.62, p<.01, η2G=.222] where there was more coherence with the fixed-tempo stimulus (M=.053, SE=.005) than with the random-tempo stimulus (M=.036, SE=.001). The other main effects and interactions were not significant [all F<1].
The amount of cross-wavelet coherence between postural fluctuations and the hand rotations followed a similar pattern, summarized in Figure 4C. It was higher in OA (M=.059, SE=.003) than in YA (M=.049, SE=.003), a significant effect [F(1,20)=4.62, p<.05, η2G=.088]. There was a main effect of stimulus predictability [F(1,20)=15.36, p<.001, η2G=.176] with more coherence in the fixed-tempo condition (M=.061, SE=.004) than the random-tempo condition (M=.047, SE=.002). There was also an interaction between stimulus predictability and stance [F(1,20)=8.16, p<.05, η2G=.035]. In the shoulder-width stance, the coherence was larger in the fixed-tempo condition (M=.063, SE=.004) than the random-tempo condition (M=.043, SE=.002, p<.001). In contrast, in narrow-stance, coherence in fixed-tempo stimulus trials (M=.060, SE=.005) was not different from random-tempo trials although there was a trend (M=.051, SE=.003, p=.07). The other main effects and interactions were not significant (all F<1).

3.4. Association between Postural Synchronization and Performance

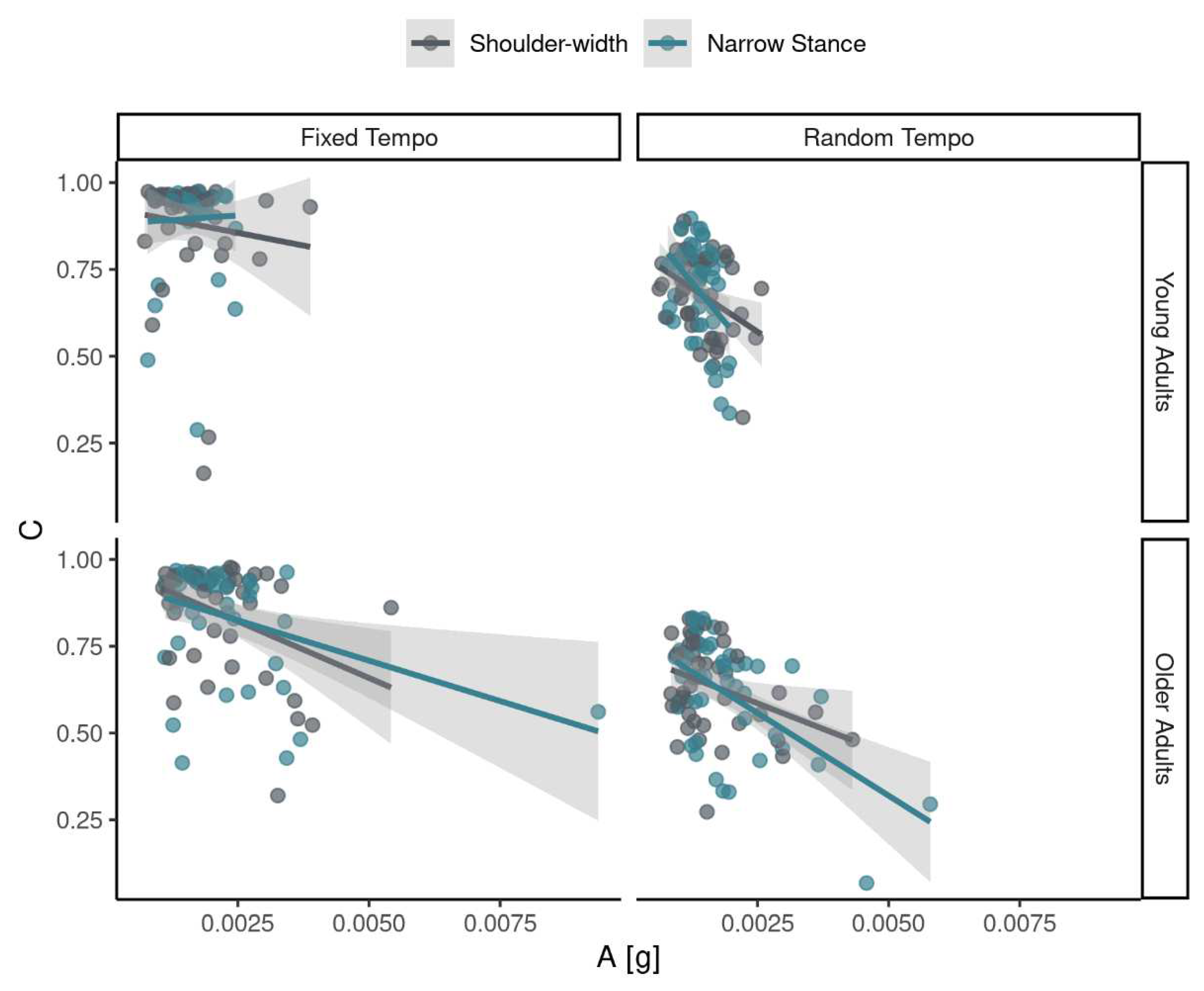
There was a negative association between rhythmic synchronization (C) with the stimulus and the magnitude of postural accelerations (see Figure 5). A linear model showed that the association was not significant in YA (β=21.54, SE=23.74, p=.37) but it was significant in OA (β=-62.15, SE=25.64, p<.05), see Appendix C.

4. Discussion

In both younger and older participants, there was spontaneous coupling between postural sway during quiet stance and supra-postural auditory-motor synchronization on a task requiring hand movements to synchronize with an auditory stimulus. There was also weak evidence that the level of performance in the auditory-motor synchronization task was linked with the amount of postural response. Specifically, higher postural sway was associated with lower hand synchronization with the stimulus. Given that a mechanical linkage exists between the swaying hand and the swaying body, it is not inherently surprising to observe some level of entrainment between the two. While maintaining standing balance, the human body is mechanically unstable because of the narrow base of support, and rotations of the hands can generate momentum which is transferred to the upper body. Interestingly, we found that the effect of spontaneous coupling between posture and the supra-postural task was stronger in older adults. This suggests that this group may be more vulnerable to falling if a distracting upper-body task spontaneously entrains postural control to the extent of inducing destabilizing oscillations. Although the present study did not recruit a high-risk population and did not induce falls, the trend points in that direction.
The overall decrease of physical health and increased multidimensional risk of adverse outcomes in older adults has been described as frailty. Frailty is associated with a risk of falling in circumstances of divided attention [24,25]. To explain why testing of older adults sometimes does not reveal a potential deficit until the participants are exposed to a challenging task and divided attention, the cognitive reserve hypothesis refers to the relative availability of (neural) resources to accommodate habitual and unexpected peak activity [29,30,31]. The reserve hypothesis was formulated primarily to address cognitive phenomena, yet its overall relevance to motor control and sensory-motor performance is striking. In movement science, the redundancy of degrees of freedom is a fundamental problem of theoretical motor control. For example, it is possible to execute the same kinematic trajectory of the hand-held sensor by swaying either the hand, the arm, or the whole upper body, or any combination thereof. This redundancy can be seen as a computationally challenging control problem because the number of variables to be controlled is much higher than the number of dimensions of the task that participants are performing. Yet, when reformulated as a principle of abundance, this can be seen as a possibility for adaptive response to unexpected perturbations [27]. From this perspective, the separate levels of control associated with manual rotations and balance should benefit from orthogonalizing variability associated with the two tasks to spare balance from perturbations [28]. This separation may be more difficult in older adults, as suggested by the present result. Their strategy to perform the challenging task may have been to allow posture to sway along with the hand, even though the task was for standing posture to be still, not free. This response was subtle in the present study, but it would be maladaptive in a busy natural environment where it could diminish the reserve capacities necessary to deal with other unexpected balance perturbations.
The interaction between divided attention and postural control is likely to be mediated not only by motor but also by perceptual constraints. Cognitive activity can increase the amount of postural sway, and evidence indicates that it can be related either to general attentional interference or specific interference with processes for spatial awareness [5]. Consistent with the latter, when supra-postural activity involves sensory-motor coordination, as in the present study, postural sway may be recruited to support stimulus-focused sensing [26].
In sum, we presented multiple reasons why evaluation of balance is needed in situations involving cross-modal, multi-task, and unpredictable elements to detect elevated risk of falling in potentially frail populations where an underlying loss of capacity is suspected. The present work showed how this can be accomplished using portable and affordable apparatus, and a self-explanatory task involving synchronizing hand movements to an auditory stimulus, that in principle can be deployed in a variety of ambulatory settings.

Author Contributions

Conceptualization, D.D. and L.J.T.; methodology, D.D., A.M., and L.J.T.; investigation, D.D., A.M., and L.J.T.; writing, D.D., A.M., and L.J.T., funding acquisition, D.D. and L.J.T.. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by McMaster Institute for Research on Aging (MIRA). D.D. received support from NIH P20GM109090 during preparation of this article.

Institutional Review Board Statement

The study was conducted in accordance with the Declaration of Helsinki, and approved by a McMaster University Ethics Board, MREB #1975.

Informed Consent Statement

Informed consent was obtained from all subjects in the study.

Data Availability Statement

The data that support the findings of this study are available from the corresponding author, D.D., upon reasonable request.

Conflicts of Interest

The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

Appendix A. Sonification Engine

One of the basic challenges in real-time digital sound synthesis is to avoid audible clicks produced by discontinuous shifts in the waveform occurring between packets of the audio buffer. A second problem is to scale the signal amplitude with respect to frequency to achieve equal loudness; inverse scaling of amplitude approximates the equal loudness contour in the range from middle to low pitch [32]. We satisfied both requirements using the so-called canonical-dissipative oscillator [33,34].
x ¨ = − ω 2 x − γ x ˙ . 5 ω 2 x 2 + . 5 x ˙ 2 − β
This oscillator is suitable for synthesizing pure tones because its state variable is a harmonic wave. Its trajectory settles on a parametrically controlled attractor which determines its frequency and amplitude. This means that the system can achieve smooth oscillations and smooth transitions between parametrically controlled frequencies despite the fact that the control parameter arrives discretely from the motion sensor sampled non-synchronously at a much lower rate. Importantly, the amplitude of the oscillator scales inversely with frequency [35]. This automatically solves the problem of determining the amplitude-pitch relation in real-time to achieve reasonable psychophysical properties of the synthesized tone. In complexity, this approach stands between wavetables and nonlinear physical models of musical instruments [36,37]. The dynamical system A1 was Euler-integrated at 48 kHz, the rate of sound synthesis, with parameters β=1000 and γ=1 selected for fast convergence to the attractor controlled by the frequency control parameter ω.
The sensor angle θ x was mapped linearly to the MIDI space of musical notes, n = θ x 90 + 1 2.5 + 60 , and then to frequency in radians, ω = 2 π ( 440 ∗ 2 n − 69 / 12 ) . In short, movement in the range [-90,+90] degrees declination from the vertical was mapped to the MIDI notes range [60, 65] corresponding to [C4,F4]. Two harmonics were added by running parallel oscillators at 2ω and 3ω.

Appendix B. Cross-Wavelet Analysis

Preprints 96098 g0a1
Figure A1. Cross-wavelet analysis of the squared stimulus oscillation data and the lower-back acceleration magnitude. (A, a representative fixed tempo trial; B, a representative random tempo trial). The magnitude of the individual wavelet transform is color-coded along with the time-series as an inset underneath it (first row: stimulus; second row: lower-back). (C, same trial as in A; D, same trial as in B) The cross-wavelet coherence is shown. Coherence is color-coded and the full colorbar given for reference. The values inside the contoured regions are significant. For a single measure of degree of coupling in each trial, we used the proportion of significant area relative to the full time-frequency space.
Figure A1. Cross-wavelet analysis of the squared stimulus oscillation data and the lower-back acceleration magnitude. (A, a representative fixed tempo trial; B, a representative random tempo trial). The magnitude of the individual wavelet transform is color-coded along with the time-series as an inset underneath it (first row: stimulus; second row: lower-back). (C, same trial as in A; D, same trial as in B) The cross-wavelet coherence is shown. Coherence is color-coded and the full colorbar given for reference. The values inside the contoured regions are significant. For a single measure of degree of coupling in each trial, we used the proportion of significant area relative to the full time-frequency space.
Preprints 96098 g0a1

Appendix C. Linear Model Table

Table A1. Association between cross-correlation C as a measure of auditory-motor rhythmic synchronization and magnitude of lower-back accelerations A as a measure of postural control. Steps of the linear mixed-effects model up to the maximal model, Cij=β0+σ0i+β1Aij+β2Oij+β3RTij+β4NSij+β5AijOij+σij. i is individual and j trial. Y is young adults, O older adults. β parameter estimates (standard error) are shown in the upper half of the table. β0 corresponds to C of young adults with fixed-tempo stimulus and shoulder-width stance. Subsequent parameters estimate how C changes as a function of the predictor A and switching the respective age group and condition. The final selected model is in bold. *p<.05, †p<.01, ‡p<.001.
Table A1. Association between cross-correlation C as a measure of auditory-motor rhythmic synchronization and magnitude of lower-back accelerations A as a measure of postural control. Steps of the linear mixed-effects model up to the maximal model, Cij=β0+σ0i+β1Aij+β2Oij+β3RTij+β4NSij+β5AijOij+σij. i is individual and j trial. Y is young adults, O older adults. β parameter estimates (standard error) are shown in the upper half of the table. β0 corresponds to C of young adults with fixed-tempo stimulus and shoulder-width stance. Subsequent parameters estimate how C changes as a function of the predictor A and switching the respective age group and condition. The final selected model is in bold. *p<.05, †p<.01, ‡p<.001.
Model 1 Model 2 Model 3 Model 4 Model 5 Model 6
β0: Y, Fixed tempo, Shoulder-width .760 (.024) ‡ .745 (.034) ‡ .771 (.039) ‡ .943 (.034) ‡ .943 (.035) ‡ .862 (.049) ‡
β1: A 8.325 (13.337) 9.897 (13.418) -31.351 (9.693) † -31.358 (9.735) † 21.544 (23.744)
β2: O -.058 (.048) -.038 (.043) -.038 (.043) .059 (.060)
β3: Random tempo -.221 (.011) ‡ -.221 (.011) ‡ -.218 (.011) ‡
β4: Narrow stance .000 (.011) .002 (.011)
β5: A in O -62.153 (25.639)*
AIC -277.907 -276.264 -275.720 -528.183 -526.183 -529.953
BIC -266.316 -260.810 -256.401 -505.001 -499.137 -499.043
Log-Likelihood 141.953 142.132 142.860 270.091 270.091 272.976
Number of observations 352 352 352 352 352 352
Number of random effects groupings 22 22 22 22 22 22
Variance of individual intercepts σ0i .011 .012 .011 .009 .009 .010
Variance of residual σij .023 .023 .023 .011 .011 .010

References

  1. M. E. Tinetti, M. Speechley, and S. F. Ginter, “Risk Factors for Falls among Elderly Persons Living in the Community,” N. Engl. J. Med., vol. 319, no. 26, pp. 1701–1707, Dec. 1988. [CrossRef]
  2. M. E. Tinetti, J. Doucette, E. Claus, and R. Marottoli, “Risk Factors for Serious Injury During Falls by Older Persons in the Community,” J. Am. Geriatr. Soc., vol. 43, no. 11, pp. 1214–1221, 1995. [CrossRef]
  3. “Facts About Falls | Fall Prevention | Injury Center | CDC.” Accessed: Dec. 11, 2023. [Online]. Available: https://www.cdc.gov/falls/facts.html.
  4. N. Teasdale, C. Bard, J. Larue, and M. Fleury, “On the cognitive penetrability of posture control,” Exp. Aging Res., vol. 19, no. 1, pp. 1–13, Jan. 1993. [CrossRef]
  5. M. Woollacott and A. Shumway-Cook, “Attention and the control of posture and gait: a review of an emerging area of research,” Gait Posture, vol. 16, no. 1, pp. 1–14, Aug. 2002. [CrossRef]
  6. E. V. Fraizer and S. Mitra, “Methodological and interpretive issues in posture-cognition dual-tasking in upright stance,” Gait Posture, vol. 27, no. 2, pp. 271–279, Feb. 2008. [CrossRef]
  7. W. Li, T. H. M. Keegan, B. Sternfeld, S. Sidney, C. P. Quesenberry, and J. L. Kelsey, “Outdoor Falls Among Middle-Aged and Older Adults: A Neglected Public Health Problem,” Am. J. Public Health, vol. 96, no. 7, pp. 1192–1200, Jul. 2006. [CrossRef]
  8. S. R. Lord, “Visual risk factors for falls in older people,” Age Ageing, vol. 35, no. suppl_2, pp. ii42–ii45, Sep. 2006. [CrossRef]
  9. L. A. Zukowski, G. Iyigün, C. A. Giuliani, and P. Plummer, “Effect of the environment on gait and gaze behavior in older adult fallers compared to older adult non-fallers,” PLOS ONE, vol. 15, no. 3, p. e0230479, Mar. 2020. [CrossRef]
  10. J. Jeka, K. Oie, G. Schöner, T. Dijkstra, and E. Henson, “Position and Velocity Coupling of Postural Sway to Somatosensory Drive,” J. Neurophysiol., vol. 79, no. 4, pp. 1661–1674, Apr. 1998. [CrossRef]
  11. J. J. Jeka, G. Schöner, T. Dijkstra, P. Ribeiro, and J. R. Lackner, “Coupling of fingertip somatosensory information to head and body sway,” Exp. Brain Res., vol. 113, no. 3, pp. 475–483, Mar. 1997. [CrossRef]
  12. R. G. Kanegaonkar, K. Amin, and M. Clarke, “The contribution of hearing to normal balance,” J. Laryngol. Otol., vol. 126, no. 10, pp. 984–988, Oct. 2012. [CrossRef]
  13. T. A. Stoffregen, S. Villard, C. G. Kim, K. Ito, and B. G. Bardy, “Coupling of Head and Body Movement With Motion of the Audible Environment,” J. Exp. Psychol. Hum. Percept. Perform., vol. 35, no. 4, 2009. [CrossRef]
  14. A. Coste, R. N. Salesse, M. Gueugnon, L. Marin, and B. G. Bardy, “Standing or swaying to the beat: Discrete auditory rhythms entrain stance and promote postural coordination stability,” Gait Posture, vol. 59, pp. 28–34, Jan. 2018. [CrossRef]
  15. F. R. Lin and L. Ferrucci, “Hearing Loss and Falls Among Older Adults in the United States,” Arch. Intern. Med., vol. 172, no. 4, pp. 369–371, Feb. 2012. [CrossRef]
  16. A. Viljanen et al., “Hearing as a Predictor of Falls and Postural Balance in Older Female Twins,” J. Gerontol. Ser. A, vol. 64A, no. 2, pp. 312–317, Feb. 2009. [CrossRef]
  17. L. Li, E. M. Simonsick, L. Ferrucci, and F. R. Lin, “Hearing loss and gait speed among older adults in the United States,” Gait Posture, vol. 38, no. 1, pp. 25–29, May 2013. [CrossRef]
  18. R. D. Hays et al., “Upper-Extremity and Mobility Subdomains From the Patient-Reported Outcomes Measurement Information System (PROMIS) Adult Physical Functioning Item Bank,” Arch. Phys. Med. Rehabil., vol. 94, no. 11, pp. 2291–2296, Nov. 2013. [CrossRef]
  19. M. Ventry and B. E. Weinstein, “The Hearing Handicap Inventory for the Elderly: a New Tool,” Ear Hear., vol. 3, no. 3, pp. 128–134, 1982.
  20. R. E. Mayagoitia, J. C. Lötters, P. H. Veltink, and H. Hermens, “Standing balance evaluation using a triaxial accelerometer,” Gait Posture, vol. 16, no. 1, pp. 55–59, 2002. [CrossRef]
  21. C. Neville, C. Ludlow, and B. Rieger, “Measuring postural stability with an inertial sensor: Validity and sensitivity,” Med. Devices Evid. Res., vol. 8, pp. 447–455, 2015. [CrossRef]
  22. A. Grinsted, J. C. Moore, and S. Jevrejeva, “Application of the cross wavelet transform and wavelet coherence to geophysical time series,” Nonlinear Process. Geophys., vol. 11, no. 5/6, pp. 561–566, Nov. 2004. [CrossRef]
  23. S. J. Harrison, J. M. Kinsella-Shaw, and D. Dotov, “Effects of footedness and stance asymmetry confirm an inter-leg metastable coordination dynamics of standing posture,” J. Mot. Behav., vol. 53, no. 2, pp. 135–156, 2020. [CrossRef]
  24. O. J. de Vries, G. M. E. E. Peeters, P. Lips, and D. J. H. Deeg, “Does frailty predict increased risk of falls and fractures? A prospective population-based study,” Osteoporos. Int., vol. 24, no. 9, pp. 2397–2403, Sep. 2013. [CrossRef]
  25. Nowak and R. E. Hubbard, “Falls and frailty: lessons from complex systems,” J. R. Soc. Med., vol. 102, no. 3, pp. 98–102, Mar. 2009. [CrossRef]
  26. T. A. Stoffregen, R. J. Pagulayan, B. G. Bardy, and L. J. Hettinger, “Modulating postural control to facilitate visual performance,” Hum. Mov. Sci., vol. 19, no. 2, pp. 203–220, Jul. 2000. [CrossRef]
  27. M. L. Latash, “The bliss (not the problem) of motor abundance (not redundancy),” Exp. Brain Res., vol. 217, no. 1, pp. 1–5, Mar. 2012. [CrossRef]
  28. M. L. Latash, “One more time about motor (and non-motor) synergies,” Exp. Brain Res., vol. 239, no. 10, pp. 2951–2967, Oct. 2021. [CrossRef]
  29. A. M. Brickman et al., “White matter hyperintensities and cognition: Testing the reserve hypothesis,” Neurobiol. Aging, vol. 32, no. 9, pp. 1588–1598, Sep. 2011. [CrossRef]
  30. S. Allen, J. Bruss, and H. Damasio, “The aging brain: The cognitive reserve hypothesis and hominid evolution,” Am. J. Hum. Biol., vol. 17, no. 6, pp. 673–689, 2005. [CrossRef]
  31. R. Katzman et al., “Clinical, pathological, and neurochemical changes in dementia: A subgroup with preserved mental status and numerous neocortical plaques,” Ann. Neurol., vol. 23, no. 2, pp. 138–144, 1988. [CrossRef]
  32. S. Carlile, “Psychoacoustics,” in The Sonification Handbook, Berlin: Logos Publishing House, 2011.
  33. W. Ebeling and I. M. Sokolov, Statistical Thermodynamics and Stochastic Theory of Nonequilibrium Systems. World Scientific, 2005.
  34. H. Haken, “Distribution function for classical and quantum systems far from thermal equilibrium,” Z. Für Phys., vol. 263, no. 4, pp. 267–282, 1973.
  35. D. G. Dotov, S. Kim, and T. D. Frank, “Non-equilibrium thermodynamical description of rhythmic motion patterns of active systems: A canonical-dissipative approach,” Biosystems, vol. 128, pp. 26–36, Feb. 2015. [CrossRef]
  36. S. Cook, P.R., “Sound Synthesis for Auditory Display,” in The Sonification Handbook, Berlin: Logos Publishing House, 2011.
  37. M. Puckette, The Theory and Technique of Electronic Music. World Scientific, 2007. [CrossRef]
Preprints 96098 g001
Figure 1. Auditory-motor synchronization task with quiet standing. The main objective for the participants was to control the continuous tone of their instrument to match the pitch and continuous oscillation of a target tone. (a) The participant’s tone was played through the channel ipsilateral to the dominant hand; the stimulus, through the contralateral channel. (b) Participants controlled the pitch of their instrument by holding a sensor device horizontally and rotating it about an axis roughly aligned with the anterior-posterior axis (in a motion similar to turning a key). (c) An additional sensor attached to a soft elastic belt was held flush against the lower back. A Python program running on a laptop computer sampled the sensors, synthesized the left channel tone (stimulus) and the right channel tone (participant controlled) in real-time, and stored all sensor and stimulus values. The stimulus had two levels of predictability: fixed-tempo and random-tempo. Stance had two conditions of stability: shoulder-width and narrow-stance. Performance variables measured the rhythmic synchronization and pitch-matching between the target tone and the participant’s tone. Additionally, synchronization between postural fluctuations and the stimulus and hand rotations was measured with the cross-wavelet coherence (inset).
Figure 1. Auditory-motor synchronization task with quiet standing. The main objective for the participants was to control the continuous tone of their instrument to match the pitch and continuous oscillation of a target tone. (a) The participant’s tone was played through the channel ipsilateral to the dominant hand; the stimulus, through the contralateral channel. (b) Participants controlled the pitch of their instrument by holding a sensor device horizontally and rotating it about an axis roughly aligned with the anterior-posterior axis (in a motion similar to turning a key). (c) An additional sensor attached to a soft elastic belt was held flush against the lower back. A Python program running on a laptop computer sampled the sensors, synthesized the left channel tone (stimulus) and the right channel tone (participant controlled) in real-time, and stored all sensor and stimulus values. The stimulus had two levels of predictability: fixed-tempo and random-tempo. Stance had two conditions of stability: shoulder-width and narrow-stance. Performance variables measured the rhythmic synchronization and pitch-matching between the target tone and the participant’s tone. Additionally, synchronization between postural fluctuations and the stimulus and hand rotations was measured with the cross-wavelet coherence (inset).
Preprints 96098 g001
Preprints 96098 g002
Figure 2. Coherence of the cross-wavelet transform of the two time-series. Upper inset, squared and normalized stimulus data; lower inset, normalized postural data (total acceleration at the lower-back). Coherence is high for parts of the trial with synchronized movement, coded as a brightness gradient (yellow online). Values exceeding the significance threshold are contoured. The proportion of the area with significant coherence was used as a measure of degree of synchronization in each trial.
Figure 2. Coherence of the cross-wavelet transform of the two time-series. Upper inset, squared and normalized stimulus data; lower inset, normalized postural data (total acceleration at the lower-back). Coherence is high for parts of the trial with synchronized movement, coded as a brightness gradient (yellow online). Values exceeding the significance threshold are contoured. The proportion of the area with significant coherence was used as a measure of degree of synchronization in each trial.
Preprints 96098 g002
Preprints 96098 g003
Figure 3. Performance in the main auditory-motor task and its dependence on group and condition. a). Rhythmic synchronization. b) Pitch-error.
Figure 3. Performance in the main auditory-motor task and its dependence on group and condition. a). Rhythmic synchronization. b) Pitch-error.
Preprints 96098 g003
Preprints 96098 g004
Figure 4. Measures of postural control and synchronization with the main task. a) Lower-back accelerations magnitude. b) Cross-wavelet coherence between the stimulus and lower-back. c) Cross-wavelet coherence between the hand and lower-back.
Figure 4. Measures of postural control and synchronization with the main task. a) Lower-back accelerations magnitude. b) Cross-wavelet coherence between the stimulus and lower-back. c) Cross-wavelet coherence between the hand and lower-back.
Preprints 96098 g004
Preprints 96098 g005
Figure 5. Association between magnitude of lower-back accelerations and cross-correlation, the measure of rhythmic synchronization in the main auditory-motor task. The solid lines are linear fits +/- 95% confidence intervals.
Figure 5. Association between magnitude of lower-back accelerations and cross-correlation, the measure of rhythmic synchronization in the main auditory-motor task. The solid lines are linear fits +/- 95% confidence intervals.
Preprints 96098 g005
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated