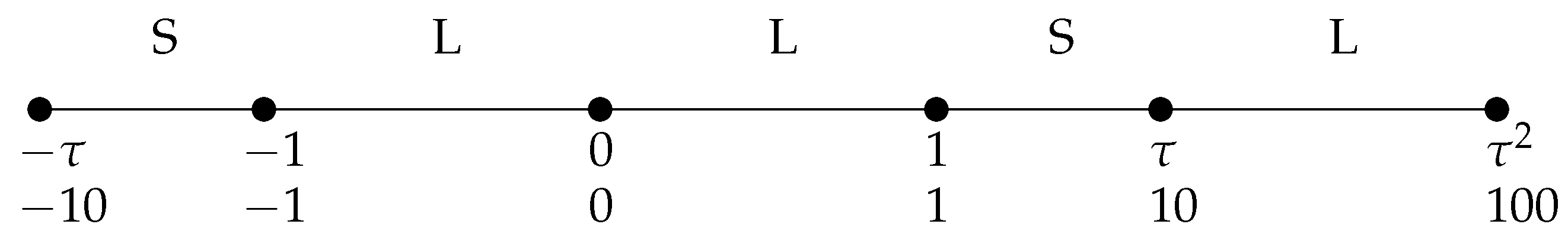The Language of Spheres in Physics

Preprint

Review

The Language of Spheres in Physics

Altmetrics

Downloads

233

Views

160

Comments

A peer-reviewed article of this preprint also exists.

Jean-Pierre Gazeau^*

This version is not peer-reviewed

Submitted:

05 February 2024

Posted:

06 February 2024

You are already at the latest version

Alerts

Abstract

Physical laws manifest themselves through the amalgamation of mathematical symbols, numbers, functions, geometries, and relationships. These intricate combinations unfold within a mathematical model devised to capture and represent the ``objective reality'' of the system under examination. In this symbiotic relationship between physics and mathematics, the language of mathematics becomes a powerful tool for describing and predicting the behavior of the physical world. The language used and the associated concepts are in a perpetual state of evolution, mirroring the ongoing expansion of the phenomena accessible to our scientific understanding. In this contribution, written in honor of Richard Kerner, we delve into fundamental, at times seemingly elementary, elements of the mathematical language inherent to the physical sciences, guided by the overarching principles of symmetry and group theory. Our focus turns to the captivating realm of spheres, those strikingly symmetric entities that manifest prominently within our geometric landscape. By exploring the interplay between mathematical abstraction and the tangible beauty of symmetry, we seek to deepen our understanding of the underlying structures that govern our interpretation of the physical world.

Keywords:

Subject: Physical Sciences - Mathematical Physics

MSC: 58D19; 58J70; 76M60; 52B15

1. Introduction

This contribution serves as a friendly tribute to Richard Kerner, a distinguished figure in the realm of theoretical and mathematical physics, whose methodologies consistently embody a harmonious blend of precision, intuition, and a poetic touch. Kerner’s ability to reveal the concealed facets of diverse phenomena, whether in the domains of general relativity and gauge theory (Kaluza-Klein, e.g., [1]), condensed matter (glasses, e.g., [2]), particle physics (quarks and ternary algebras, e.g., [3]), or noncommutative geometric structures (e.g., [4]), and many others, is an attestation of his profound insights.

In each of his works, Kerner consistently imparts that distinct touch of originality, elevating his contributions beyond the ordinary. His dedication to unraveling the intricacies of the universe is reflected not only in the rigor of his approach but also in the elegance with which he brings to light the hidden dimensions of our physical reality. One of his latest publications, as referenced in [5], stands as a magisterial testament to his multifaceted talents.

This current contribution aligns seamlessly with the theme encapsulated in the title The Languages of Physics of the special issue in honor of Kerner. My focus will be directed towards the mathematical language of physics, emphasizing the inherent limitation in precision when scrutinized from the perspective of a physicist. Such models are transient rather than eternal, subject to the passage of (entropic) time and contingent upon the scale at which they operate. To align with experimental observations and predictions, these models often undergo modifications, sometimes requiring radical transformations. In the dynamic interplay between the modeler and the modeled object, a degree of probability emerges, representing the level of epistemic confidence in the model’s appropriateness [6].

This recognition of inherent uncertainty gives rise to the imperative of introducing some level of coarse-graining into the initial mathematical model, conceived to portray an ontic entity or fact. Take, for example, the inconceivability of irrational numbers in human perception, conceivability being here understood in terms of a measurable physical quantity. Yet physical laws, for several centuries now, have been articulated in terms of real numbers, denoted as

R

, constructed from the abstract concept of limits (such as the limit of Cauchy sequences of rational numbers).

Nevertheless, these profoundly abstract mathematical concepts have evolved to such a degree of familiarity that they now stand as an indispensable foundation for formulating descriptions of our environment. Serving as a robust backdrop, they assist us in imposing structure and establishing a set of physical laws capable of navigating the intricacies of complexity and chaos. In our pursuit of order, we inevitably organize observations through the lens of symmetry.

Beneath the allure of this aesthetic concept lies the intricate framework of mathematics, particularly the concept of a group, with all its potential generalizations, deformations, approximations, and the inherent challenges of incompleteness and partial versions. It is within this mathematical tapestry that we find the tools and principles allowing us to not only conceptualize but also articulate the laws that govern the universe, providing a coherent and profound understanding of our complex reality.

In this contribution, which draws inspiration from a previous review [7] and recent lectures held in both Poland and Brazil, serving as a significant element within the thematic framework of the special issue titled “The Languages of Physics”’, we harness the potency of the concept of symmetry to reexamine the first elements of the sequence of unit spheres, denoted as

S^{n}

, and explore their profound physical implications across various domains of physics. This exploration extends into realms such as atomic, molecular, nuclear, particle, and condensed matter physics, shedding light on the intricate interplay between the mathematical abstraction of spheres and their tangible relevance in understanding the fundamental structures and behaviors that underpin the diverse facets of the physical world. In this regard, I cannot resist quoting the following excerpt from [8], translated from French.

From there comes her fascination for pieces, lids, and other wheels whose circular movement she perpetuates, immersed in a hypnotic contemplation that extracts her from the world and disconnects her from a reality that is too aggressive.

We do not aspire to introduce entirely original content in this paper. Rather, it is conceived as a fusion of fundamental (somewhat very basic) and advanced discussions on the mathematics of symmetry. Rather than striving to introduce entirely novel content, this article is crafted as a synthesis, merging fundamental (yet foundational) discussions with advanced insights into the mathematics of symmetry.

The journey begins with a recapitulation of essential concepts pertaining to groups and semi-groups (Section 2), followed by a freshman level reminder of algebraic and topological aspects of numbers (Section 3). We then show the significant role played by simple or semi-simple Lie groups in elucidating symmetries across classical and quantum physics realms (Section 4).

The core of this presentation centers on a reexamination of the realm of spheres (Section 5), and the ensuing exploration of the associated geometry of Hopf fibrations (Section 6). Furthermore, we unravel the mesmerizing simplifications that the spherical symmetry contributes to explaining the Balmer lines, detailing the spectral line emissions of the hydrogen atom—a proto-quantum formalism dating back to 1885 (Section 7). The paper concludes with a succinct summary in Section 8.

For those seeking a more in-depth understanding, Appendices Appendix A and Appendix B provide additional details on group actions and the Lie algebra formalism.

2. Semi-Groups and Groups

In this section we remind the main definitions concerning semi-groups, groups, and structures built from them. Usually these notions are supposed known, but remind them lies in the self-contained spirit of this contribution.

2.1. Definitions

A semi-group is a set

G = {g \in G}

equipped with an operation that combines any two elements

g_{1} \in G

g_{2} \in G

to form a third element

g_{3} = g_{1} g_{2} \in G

while being associative, i.e.

(g_{1} g_{2}) g_{3} = g_{1} (g_{2} g_{3}) \equiv g_{1} g_{2} g_{3}

A group is a semi-group having an identity element e,

e g = g e = g

and inverse elements,

g^{- 1} g = g g^{- 1} = e

A group or semi-group is abelian if the operation is commutative:

g_{1} g_{2} = g_{2} g_{1}

for all

g_{1}, g_{2} \in G

, e.g., translations in the line or to rotations on the circle or in the plane. Rotations in space are non-commutative.

Groups can be finite (e.g., permutations, point groups of symmetry of molecules), discrete (e.g., space group of symmetry of crystals), continuous (e.g., Euclidean displacements), Lie groups (infinitesimal transformations can be considered as well).

Continuous groups can be compact (parameters of transformation are bounded, e.g., rotations on the sphere) or non compact, e.g., translations in the plane.

Two elements

g_{1}

g_{2}

of a group G are said conjugate if there exists

g \in G

such that

g_{2} = g g_{1} g^{- 1}

. This is an equivalence relation whose equivalence classes are called conjugacy classes (one famous example is the Rubik cube where the essential property for winning is precisely the set of conjugate classes of one permutation group, see Figure 1, and [9] for explanation).

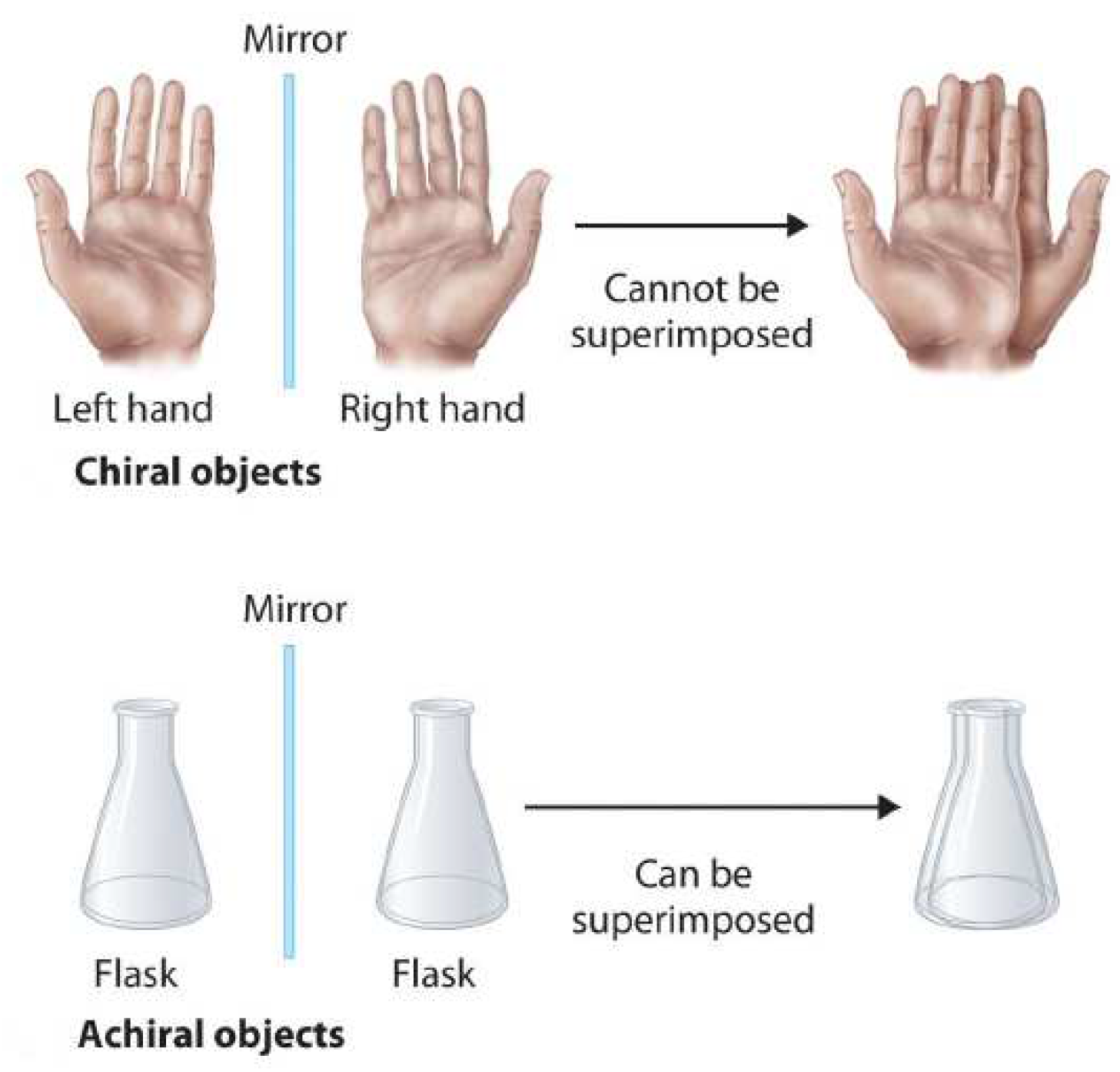
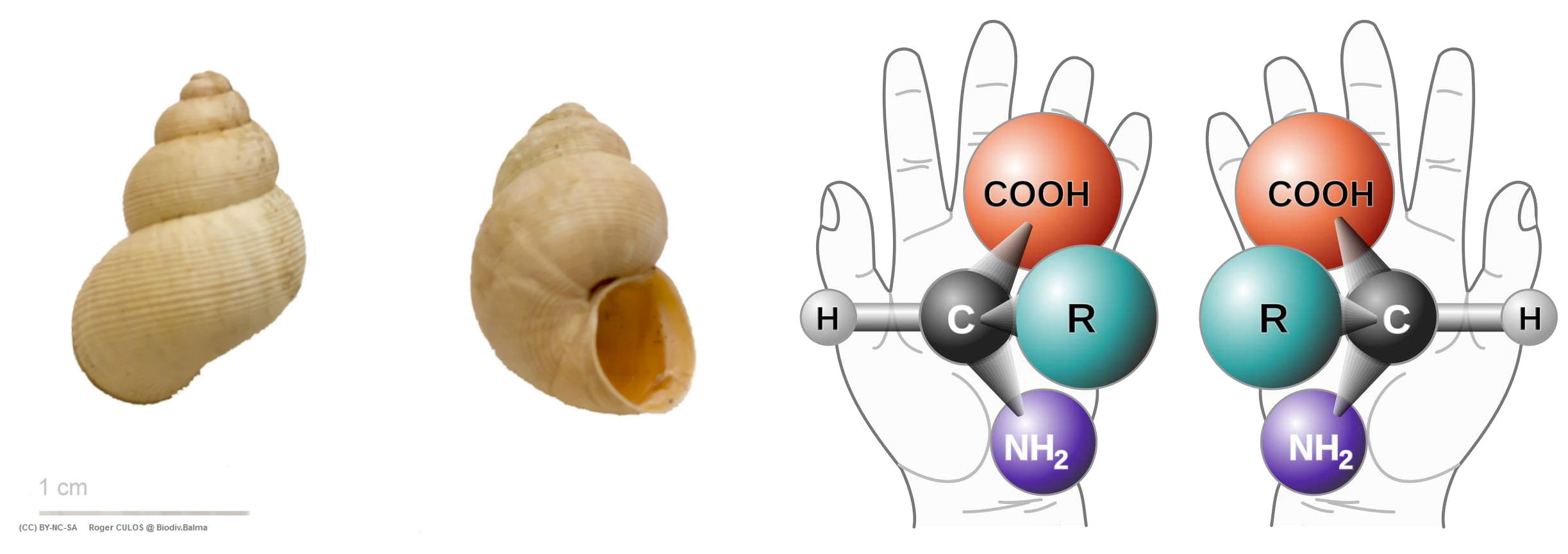
2.2. Example: Chirality

Chirality is the simplest example of a group:

G = {I, P}

, with

I P = P I = P

I^{2} = I = P^{2}

. P is like mirror image. A figure is chiral if it cannot be mapped to its mirror image by rotations and translations alone. Examples are shown in Figure 2 and Figure 3.

A chiral object and its mirror image are said to be enantiomorphs.

An interesting question about mirror is shown in Figure 4: Why does a mirror reverse left to right, but not top to bottom?

Beyond space parity (usually noted P), notable similar instances are observed in the realm of particle physics. These include charge conjugation (C), where the charge of a particle is reversed (

q \leftrightarrow - q

), time reversal (T), involving the reversal of time (

t \leftrightarrow - t

), and the dichotomy between matter and antimatter. Furthermore, the interplay of these individual symmetries gives rise to intriguing combinations such as

P T

C P

, and

C P T

, adding depth and complexity to our understanding of fundamental physical principles.

2.3. Building Groups from Subgroups

A subset H of a group G is a subgroup of G if it contains e and is stable versus group operations:

H H : = {h_{1} h_{2}, h_{1}, h_{2} \in H} \subset H

and

H^{- 1} : = {h^{- 1}, h \in H} \subset H

. Direct product of two groups

G_{1}

and

G_{2}

consists in glueing the two groups together, without interaction:

G = G_{1} \times G_{2}

is simply their Cartesian product, endowed with the group law:

(g_{1}, g_{2}) (g_{1}^{'}, g_{2}^{'}) = (g_{1} g_{1}^{'}, g_{2} g_{2}^{'}), g_{1}, g_{1}^{'} \in G_{1}, g_{2}, g_{2}^{'} \in G_{2} .

Neutral element is

(e_{1}, e_{2})

. With the identifications

g_{1} \sim (g_{1}, e_{2}), g_{2} \sim (e_{1}, g_{2})

, both

G_{1}

and

G_{2}

are invariant subgroups of

G_{1} \times G_{2}

(think to the plane as the product of two lines, or to the torus as the product of two circles).

For semi-direct product of two groups

G_{1}

and

G_{2}

, one suppose given a homomorphism

α

from

G_{2}

into the group

Aut G_{1}

of automorphisms of

G_{1}

. Then one defines the semidirect product

G = G_{1} ⋊ G_{2}

as the Cartesian product, endowed with the group law:

(g_{1}, g_{2}) (g_{1}^{'}, g_{2}^{'}) = (g_{1} α_{g_{2}} (g_{1}^{'}), g_{2} g_{2}^{'})

Neutral element is

(e_{1}, e_{2})

and the inverse of

(g_{1}, g_{2})

is is

{(g_{1}, g_{2})}^{- 1} = ({[α_{g_{2}^{- 1}} (g_{1})]}^{- 1}, g_{2}^{- 1})

(think to the affine group of the line, which combines dilation and translation).

2.4. Group Cosets

Let H be a subgroup of G. One says that

g_{1} \equiv g_{2}

mod H if there exists

h \in H

such that

g_{2} = g_{1} h

. Denoting

\bar{g} = g H

the equivalence class of g mod H, the set of equivalence classes is denoted

G / H

and called the left coset of G by H. Right coset

H ∖ G

is defined in a similar way as the set of equivalence classes

{H g, g \in G}

2.5. Group Actions

Irreducibility linked to symmetry (and invariance) is the mathematical concept of a group, more precisely group of transformations (see Appendix A for more details). Concretely, elements in a group G, like the group of Euclidean displacements in the plane (semi-direct product of rotations and translations), transform into themselves objects in a set X, like the set of triangles, in such a way that we can compose such transformations in an associative way and we can transform back too:

g \in G, x \in X, g \cdot x = y \in X \Leftrightarrow x = g^{- 1} \cdot y, (g g^{'}) \cdot x = g \cdot (g^{'} \cdot x)

3. Numbers and Groups

In this section we implement the group material exposed above through the sequence of numbers, from the most elementary ones to some sophisticated objects like octonions and Cayley algebras.

3.1. Sets $N$ , $Z$ , $Z_{p}$

In preamble, one should remind that Arithmetic with (cardinal) Hindu-Arabic numerals is easy while it is inextricable with (ordinal) Roman numerals (e.g., Figure 5).

The set of natural numbers

N : = {0, 1, 2, 3, \dots}

(note that including 0 is now the common convention among set theorists and logicians, maybe not with artists assents, see Figure 6 and [12]) equipped with addition, is not a group (no inverse), just an abelian semi-group. Equipped with multiplication,

N

is an abelian semi-group as well.

The set of rational integers

Z : = {\dots, - 3, - 2, - 1, 0, 1, 2, 3, \dots} = - N^{*} \cup N

, equipped with addition, is an abelian group. Equipped with multiplication, it is a semi-group.

The set of rational integers modulo p,

p = 2, 3, \dots

Z_{p} = {0, 1, 2, \cdot, p - 1, \mod p}

. Equipped with addition, it is a finite abelian group with p elements. Chirality corresponds to

Z_{2}

3.2. Example: Cubic Relations

Richard Kerner, in a comprehensive series of papers (refer to [3] for a detailed review), posited that cubic (or ternary) relations possess the ability to encapsulate diverse symmetries in relation to the permutation group

S_{3}

or its cyclic subgroup

Z_{3}

Significantly, these insights find applications in the

Z_{3}

-graded generalization of Grassmann algebras, manifesting in their realization within the realm of generalized exterior differential forms. Moreover, they play an important role in the development of gauge theory founded upon this differential calculus and in the ternary generalization of Clifford algebras. These advancements not only unlock new perspectives in mathematical structures but also extend their reach to the realm of physics, providing a framework for describing families of quarks.

3.3. Set $Q$

The set

Q

of rational numbers is defined as the set of equivalence classes of pairs of integers

(p, q)

with

q \neq 0

(p_{1}, q_{1}) \sim (p_{2}, q_{2}) \Leftrightarrow p_{1} q_{2} = p_{2} q_{1}

. The equivalence class of

(p, q)

is denoted

\frac{p}{q}

The set

Q

, together with the addition and multiplication operations shown below, forms a field:

(p_{1}, q_{1}) + (p_{2}, q_{2}) = (p_{1} q_{2} + p_{2} q_{1}, q_{1} q_{2}), (p_{1}, q_{1}) \times (p_{2}, q_{2}) = (p_{1} p_{2}, q_{1} q_{2}) .

Actually

Q

is the prototype of the concept of field: a set on which addition, subtraction, multiplication, and division are defined and behave as the corresponding operations on rational.

3.4. $Q$ Is Not “Complete”

Let us equip the field

Q

with the metrical topology associated with the distance

d (x, y) : = | x - y |

between two rationals x and y. This topology gives a sense to the notion of a Cauchy sequence

{(x_{n})}_{n \in N}

of rationals: one says that

{(x_{n})}_{n \in N}

is Cauchy if for all

ϵ > 0

, there exist

N > 0

such that, for all

m, n \geq N

, one has

| x_{m} - x_{n} | < ϵ, i . e ., \lim_{m, n \to \infty} | x_{m} - x_{n} | = 0 .

(x_{n})

is a convergent rational sequence (that is,

Q ∋ x_{n} \to x \in Q

), then it is a Cauchy sequence. On the other hand not all Cauchy sequences of rationals are convergent in

Q

Our intuitive sense suggests that when a sequence of terms progressively approaches one another, they must be converging towards a specific value. Take, for instance, the sequence

1, 1.4, 1.41, 1.414, \dots

, an approximation for the positive solution to the algebraic equation

x^{2} = 2

, or the sequence

3, 3.1, 3.14, 3.142, 3.1416, 3.14159, \dots

, which approximates the non-algebraic (or transcendant) mythic length of the circumference of the unit circle. Both sequences adhere to the Cauchy criterion, signifying their terms draw near each other, yet they don’t converge to a rational number.

This observation prompts the existence of certain “irrational” numbers, denoted as “

\sqrt{2}

” and “

π

”, towards which these sequences converge. Consequently, to encompass these irrational values, as well as all other numbers that Cauchy sequences seem to approach, one extends the number system beyond rationals [13].

3.5. Unreal “Real” Numbers Complete Real Rationals!

It is this intuition which motivated Cauchy to use such sequences to define the real numbers:

R

is a completion of

Q

. The real numbers are constructed as equivalence classes of Cauchy sequences [14]. Two Cauchy sequences

(x_{n})

and

(y_{n})

of rational numbers are equivalent if

| x_{n} - y_{n} | \to 0

, i.e., if the sequence

(x_{n} - y_{n})

tends to 0. The real numbers

R

are the equivalence classes of Cauchy sequences of rational numbers. That is, each such equivalence class is a real number. Through this construction,

R

inherits the algebraic field structure of

Q

, and is complete for the metric topology: all Cauchy sequences of real numbers are convergent in

R

. In this sense one says that

R

is the closure of

Q

R = \bar{Q}

, i.e.,

R

contains all limit points of

Q

. However there is a big difference: while

Q

is countable, i.e., there exist a one-to-one map

Z \mapsto Q

, the field

R

is uncountable.

3.6. $C$ Is Complete and “Algebraically Closed”

The algebraic equation

x^{2} + 1 = 0

has no solution in

R

. So let us equip the set

R \times R : = {z = (x, y), x, y \in R}

(Cartesian product) with the commutative addition and multiplication operations:

(x_{1}, y_{1}) + (x_{2}, y_{2}) = (x_{1} + x_{2}, y_{1} + y_{2}), (x_{1}, y_{1}) \times (x_{2}, y_{2}) = (x_{1} x_{2} - y_{1} y_{2}, x_{1} y_{2} + x_{2} y_{1}) .

(3.1)

Both operations afford

R \times R

with a commutative field structure,

0 \equiv (0, 0)

and

1 \equiv (1, 0)

being the neutral elements for addition and multiplication respectively. This is the field of complex numbers and is denoted by

C

. One introduces the “imaginary” number

i \equiv (0, 1)

, imaginary because it is the square root of

- 1

[15,16,17]. Indeed, one checks that

i^{2} = - 1

, and so

i

is solution of

z^{2} + 1 = 0

(like the real

\sqrt{2}

is solution of

x^{2} - 2 = 0

). The complex numbers also form the real vector space of dimension two, with

{1, i}

as a standard basis. This justifies the notation

z = x 1 + y i \equiv x + i y

Introducing the mirror symmetry with respect to the real axis,

z = x + i y \mapsto \bar{z} : = x - i y

, one checks that

z \bar{z} = x^{2} + y^{2} \equiv {| z |}^{2}

. Equipped with the topology associated with the distance

| z_{1} - z_{2} |

C

is complete, and, as a vector space, is isomorphic to the Euclidean plane.

Any algebraic equation

a_{n} z^{n} + a_{n} z^{n} + \dots a_{1} z + a_{0} = 0

, with complex coefficients, has n roots in

C

, i.e.,

C

is algebraically closed (fundamental theorem of the algebra).

3.7. Complex Numbers Emerging from Tensor Product of Two Planes

There exists an interesting interpretation of the multiplication law (3.1) in terms of tensor product of two planes. The tensor product stands as a cornerstone, arguably the most distinctive one, in the realm of quantum mechanics. In essence, the Cartesian product, traditionally employed to model two systems independently in classical physics, undergoes a transformative process known as quantization. This metamorphosis results in the emergence of the tensor product of two vector spaces, a fundamental framework indispensable for understanding the intricacies of quantum mechanical systems.

First, we remind that a vector space V over a field

F

, e.g.,

Q

R

, is a set whose elements or vectors, may be added together and multiplied (“scaled”) by elements (“scalars”) in

F

. Two essential properties must be satisfied: the distributivity of scalar multiplication with respect to the vector addition and the distributivity of scalar multiplication with respect to field addition. Then, the tensor product

V \otimes W

of two vector spaces V and W (over the same field) is the vector space over

F

is defined as the vector space over

F

consisting of all bilinear forms from

V \times W

F

. Note that

\dim (V \otimes W) = \dim V \dim W

while

\dim (V \times W) = \dim V + \dim W

Hence the tensor product

R^{2} \otimes R^{2}

of the plane with itself, with basis

(e_{1}, e_{2})

, is the four-dimensional vector space of bilinear forms

\begin{matrix} R^{2} \times R^{2} & ∋ (x = x_{1} e_{1} + x_{2} e_{2}, y = y_{1} e_{1} + y_{2} e_{2}) \mapsto φ (x, y) \\ = \sum_{i, j = 1, 2} x_{i} y_{j} φ_{i j} = (\begin{matrix} x_{1} & x_{2} \end{matrix}) (\begin{matrix} φ_{11} & φ_{12} \\ φ_{21} & φ_{22} \end{matrix}) (\begin{matrix} y_{1} \\ y_{2} \end{matrix}) \equiv^{t} x A_{φ} y, \end{matrix}

where

φ_{i j} = φ (e_{i}, e_{j})

. Any

2 \times 2

real matrix A can decompose as

A = a_{0} 1_{2} + a_{1} σ_{1} + a_{2} τ_{2} + a_{3} σ_{3}

with

σ_{1} = (\begin{matrix} 0 & 1 \\ 1 & 0 \end{matrix}), τ_{2} = (\begin{matrix} 0 & - 1 \\ 1 & 0 \end{matrix}), σ_{3} = (\begin{matrix} 1 & 0 \\ 0 & - 1 \end{matrix}) .

The matrices

σ_{1}, σ_{2} : = - i τ_{2}, σ_{3}

were introduced by Pauli [18]. Hence, we have for the matrix elements of

A_{φ}

a_{0} = \frac{φ_{11} + φ_{11}}{2}, a_{1} = \frac{φ_{21} + φ_{12}}{2}, a_{2} = \frac{φ_{21} - φ_{12}}{2}, a_{3} = \frac{φ_{11} - φ_{11}}{2} .

Due to the algebraic relations

σ_{1} τ_{2} = σ_{3} = - τ_{2} σ_{1}, τ_{2} σ_{3} = σ_{1} = - σ_{3} τ_{2}, σ_{3} σ_{1} = - τ_{2} = - σ_{1} σ_{3},

(3.2)

one can give the decomposition of the matrix

A_{φ}

the bi-complex form:

\begin{matrix} A_{φ} & = a_{0} 1_{2} + a_{2} τ_{2} + σ_{1} (a_{1} 1_{2} + a_{3} τ_{2}) = (\begin{matrix} a_{0} + a_{3} & a_{1} - a_{2} \\ a_{1} + a_{2} & a_{0} - a_{3} \end{matrix}) \end{matrix}

(3.3)

\begin{matrix} \equiv z_{1} + σ_{1} z_{2} = z_{1} +^{t} z_{2} σ_{1} . \end{matrix}

(3.4)

Due to

τ_{2}^{2} = - 1_{2}

, which means that the

\pm τ_{2}

are square roots of

- 1_{2}

, whilst

σ_{1}^{2} = 1_{2} = σ_{3}^{2}

, the expression

z = x 1_{2} + τ_{2} y = (\begin{matrix} x & - y \\ y & x \end{matrix})

(3.5)

is a matrix representation of the complex number

z = x + i y

with the correspondences

1 \mapsto 1

i \mapsto τ_{2}

, and

\bar{z} \mapsto^{t} z

. The multiplication law defined in (3.1) perfectly aligns with the matrix multiplication operation represented as

z_{1} z_{2}

. Now any matrix of the type (3.5) can be factorised as

\begin{matrix} z & = (\begin{matrix} x & - y \\ y & x \end{matrix}) = \sqrt{x^{2} + y^{2}} (\begin{matrix} cos θ & - sin θ \\ sin θ & cos θ \end{matrix}) \\ = \sqrt{x^{2} + y^{2}} exp θ τ_{2}, cos θ = \frac{x}{\sqrt{x^{2} + y^{2}}}, sin θ = \frac{y}{\sqrt{x^{2} + y^{2}}} . \end{matrix}

(3.6)

This is the matrix form of the expression of the complex number

z = r e^{i θ}

in terms of its polar coordinates,

(r, θ)

r \geq 0

θ \in [0, 2 π)

mod

(2 π)

The correspondence

i \leftrightarrow τ_{2}

is not inherently absolute; an alternative choice could be

i \leftrightarrow - τ_{2}

. This ambiguity arises from the existence of two possible orientations when defining trigonometric functions: clockwise and anticlockwise. It is crucial to recognize that this feature should not be disregarded when transitioning from a formalism based on complex numbers to one expressed in terms of real numbers [19].

3.8. 2D Lattices

3.8.1. General

Consider two complex numbers

ω_{1}

ω_{2}

such that

ω_{2} / ω_{1}

is not real. They define the (“Bravais”) lattice in the plane

Λ (ω_{1}, ω_{2}) = {n_{1} ω_{1} + n_{2} ω_{2}, n_{1}, n_{2} \in Z} \equiv Z ω_{1} + Z ω_{2}

with lattice basis (or primitive)

{ω_{1}, ω_{2}}

, and with fundamental parallelogram [or primitive (unit) cell] determined by

(0, ω_{1}, ω_{2})

Λ

is a subgroup of

C

for the addition (∼ translation). Two pairs

(ω_{1}, ω_{2})

(α_{1}, α_{2})

are equivalent if they generate the same lattice, i.e., if there exists

(\begin{matrix} a & b \\ c & d \end{matrix}), a, b, c, d \in Z, a d - b c = \pm 1

, such that

(\begin{matrix} α_{1} \\ α_{2} \end{matrix}) = (\begin{matrix} a & b \\ c & d \end{matrix}) (\begin{matrix} ω_{1} \\ ω_{2} \end{matrix}) .

The set of such matrices form the noncommutative modular group PSL

(2, Z)

(relevant for Weirstrass elliptic functions).

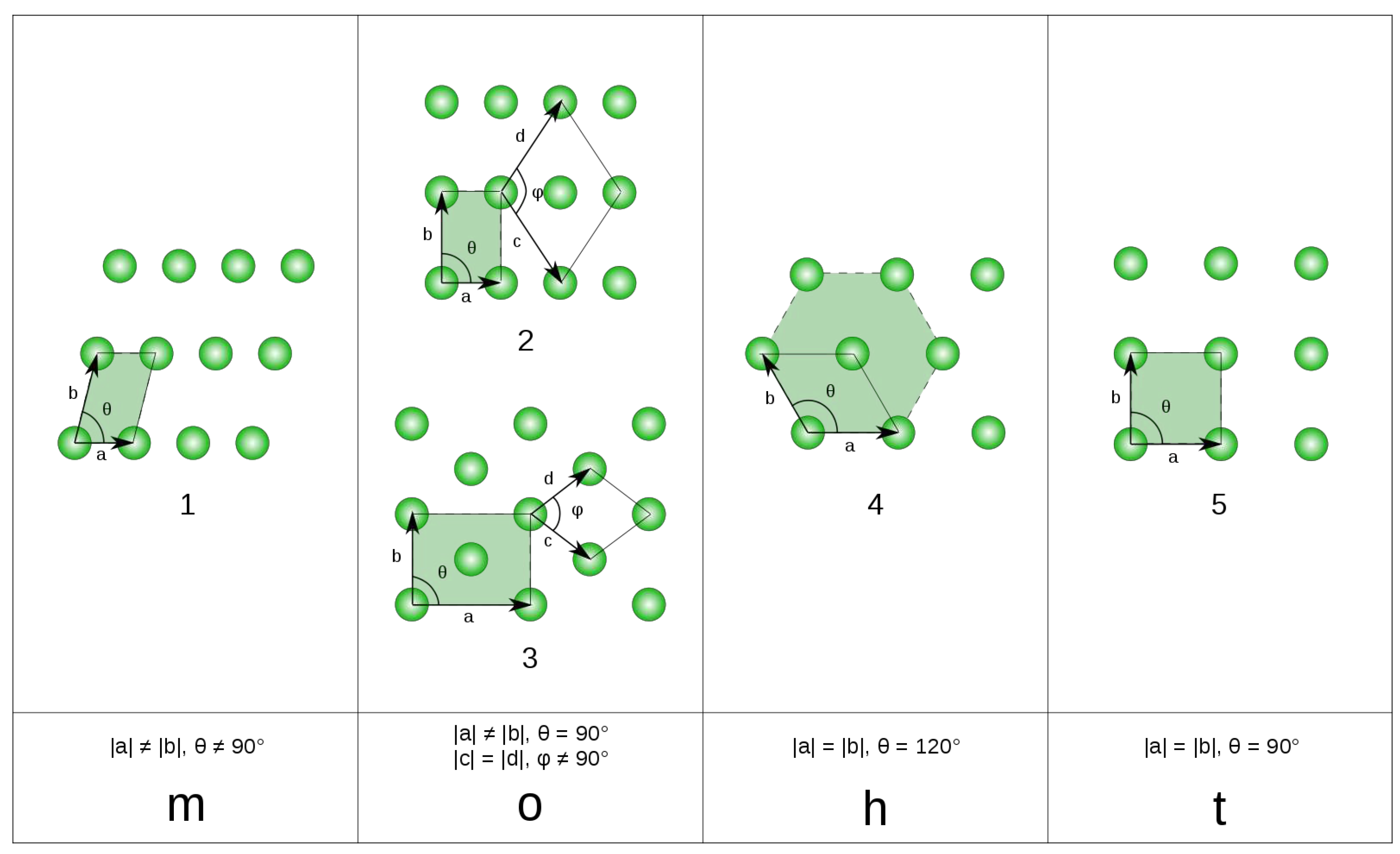
There are 5 possible Bravais lattices in 2-dimensional space: monoclinic (arbitrary

ω_{1}

ω_{2}

), tetragonal or (square

ω_{2} / ω_{1} = e^{\pm i π / 2}

), hexagonal (

ω_{2} / ω_{1} = e^{\pm 2 i π / 3}

), orthorhombic (rectangular

ω_{2} / ω_{1} = ρ e^{\pm i π / 2}

1 \neq ρ > 0

), and orthorhombic centered (rectangular centered). They are shown in Figure 7.

3.8.2. Graphene example

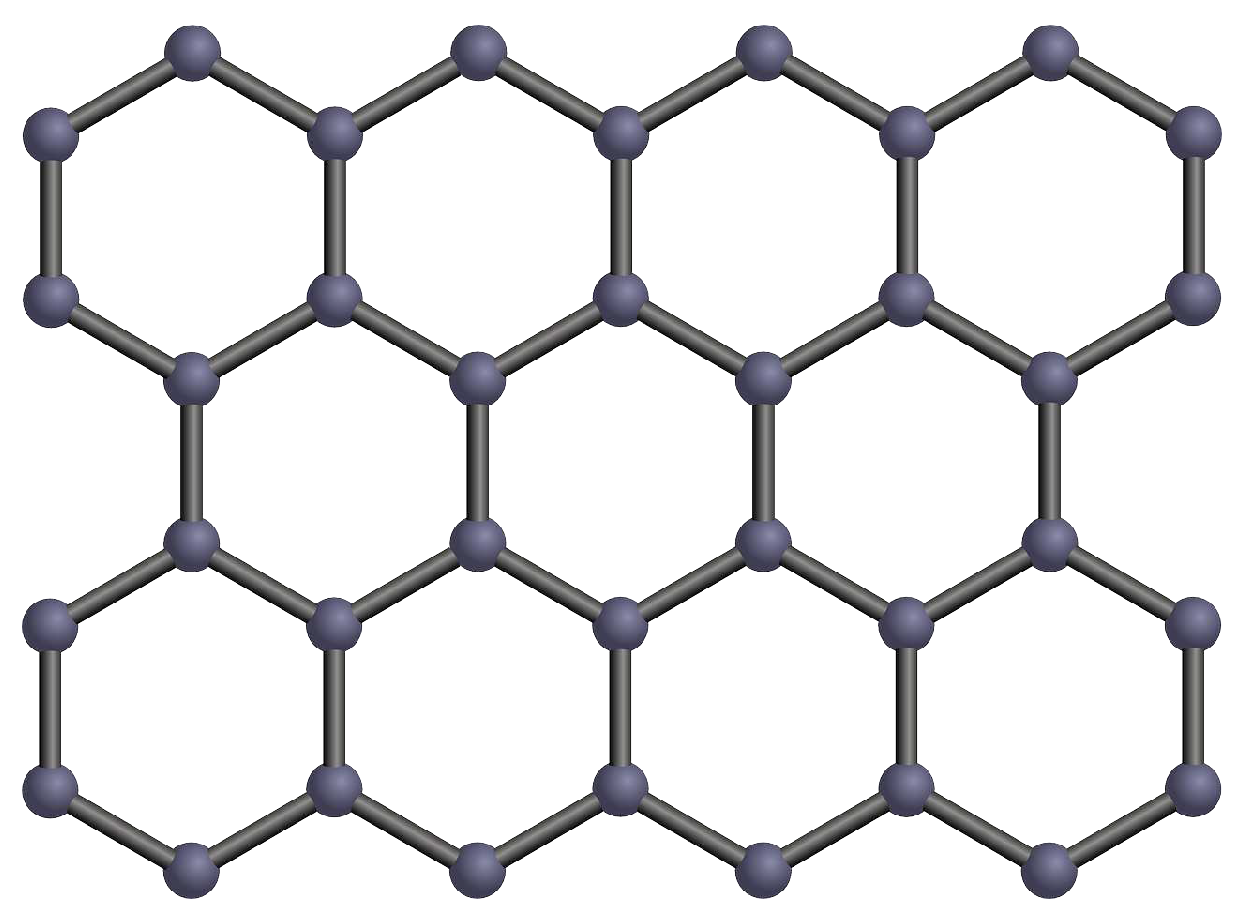
A (two-dimensional) crystal is a periodic array of atoms. For the graphene (hexagonal lattice or honeycomb), Figure 8, the primitive translation vectors are alternatively defined as:

ω_{1} = a (\frac{\sqrt{3}}{2} + \frac{3}{2} i), ω_{2} = a \sqrt{3}, a \approx 1.42 \overset{\circ}{A},

which means that

ω_{2} / ω_{1} = e^{- i π / 3}

4. Symmetry and Group(s)

4.1. Symmetry in Physics

D. Gross, in his enlightening 1995 Physics Today article [20] exploring Wigner’s legacy, aptly observed that

Einstein’s great advance in 1905 was to put symmetry first, to regard the symmetry principle as the primary feature of nature that constrains the allowable dynamical laws.

In contemporary physics, the principles of symmetry hold a paramount status as the most fundamental components of our description of nature. This prominence owes a significant debt to the influential contributions of the Princeton group, comprising notable figures such as Wigner, Bargmann, Weyl, Gödel, von Neumann, ..., from Princeton University and/or the Institute for Advanced Study (IAS). Their collective insights and groundbreaking work have played a pivotal role in elevating the significance of symmetry principles, making them a cornerstone in our understanding of the fundamental laws governing the physical universe.

In this context, it is essential to pay tribute to Emmy Noether, as highlighted in [21]. Albert Einstein hailed Noether as the most “significant” and “creative” female mathematician in history. She formulated a theorem [22] that, with magisterial concision, harmonized two fundamental concepts in physics: symmetry in nature and the universal laws of conservation. Noether’s theorem, now considered as crucial as Einstein’s theory of relativity, forms the bedrock for much of today’s cutting-edge research in physics, including recent breakthroughs such as the observation of the Higgs boson. Despite her pivotal contributions, Noether herself remains largely unknown, not only to the general public but also to a large part of the scientific community.

The foundation of our comprehension regarding the existence of elementary particles is rooted in the relativity principle. This principle posits that physical laws remain invariant under fundamental transformations of inertial frames, specifically translation (implying homogeneity in space-time), rotation (indicating isotropy in space-time), and boosts. Together, these transformations constitute a relativity or kinematic group, known as the Galileo or Poincaré group. Notably, both groups exhibit a structure that can be described as a semi-direct product of subgroups. In addition to these two well-known groups, there are other relativity groups identified and classified by Bacry and Lévy-Leblond in [23]. This group theoretical framework has laid the foundation for quantum field theory, enabling a profound understanding of the nature and existence of elementary particles within the realm of physics [24]. Note that the term “invariant”, strictly denoting the constancy of an observable in a physical system under a particular transformation, is used here in a broader sense of “covariance”. Precisely, “covariance” implies the absence of any alteration in the form of physical laws under a given transformation.

One should add the importance of

•: discrete translational and rotational symmetries in classifying molecules, crystals, quasicrystals,
•: continuous rotational symmetries (together with parity and time reversal) in explaining and classifying atomic spectra,
•: unitary symmetries for describing and classifying nuclear spectra,
•: unitary symmetries for describing strong and weak interactions (gauge fields) and successfully predicting the existence of new elementary particles.

In his 1963 Nobel lecture quoted by D. Gross, Wigner pointed out that progress in physics was partly based on the ability to separate the analysis of a physical phenomenon into two parts:

initial conditions that are arbitrary, complicated, unpredictable, as forming the “phase space" of a physical system in a wide sense, and laws of nature that summarize the regularities which are independent of the initial conditions.
Then, Wigner argued that symmetry or invariance principles provide a structure and coherence to the laws of nature: they summarize the regularities of the laws that are independent of the specific dynamics. Without regularities in the laws of nature we would be unable to discover the laws themselves.

One should also mention what Pierre Curie noticed in 1894 [25] (Neuman-Minnigerode-Curie Principle):

When certain causes produce certain effects, the elements of symmetry of the causes must be found in the effects produced.
When certain effects reveal a certain asymmetry, this asymmetry must be found in the causes which gave rise to it.

Note that the reciprocal of these two assertions is not true. More precisely, the characteristic symmetry of a phenomenon is that symmetry which is best compatible with the existence of the phenomenon. A phenomenon can exist in surroundings which possess its characteristic symmetry or at least one subgroup of its characteristic symmetry. In other words, certain symmetry elements can exist together with certain phenomena but they are not necessary. But it is necessary that certain symmetry elements do not exist (Neuman-Minnigerode-Curie Principle).

4.2. Lie Groups and Lie Algebras

Building upon the foundational principles of symmetries and natural laws, as eloquently discussed by Levy-Leblond [26], we delve deeper into one of their unescapable mathematical frameworks: the theory of Lie groups and algebras [27].

To a Lie group G corresponds its Lie algebra

g ∋ X \mapsto exp X = g \in G

, where the notation exp takes it susual sense when we deal with group of matrices (see Appendix B for more mathematical details). Simple or semi-simple Lie groups (Lie algebras), like (pseudo-)rotation groups or unitary groups or symplectic groups, are ubiquitous in Physics, see Table 1 for the nomenclature.

Following previous works by Killing [28], simple Lie algebras have been classified by Cartan [29] through their one-to-one correspondence to possible (irreducible reduced) root systems in

R^{n}

. See Table 1 for the nomenclature for the most current Lie groups and algebras, and Appendix B.2 and Appendix B.3 for details concerning root systems. There are four classes of classical (irreducible reduced) root systems in

R^{n}

$A_{n}$ associated with unitary groups $SU (n + 1)$ or their complexified $SL (n + 1, C)$ or the real form $SL (n + 1, R)$ .
$B_{n}$ associated with orthogonal (rotation) groups $SO (2 n + 1)$ or their pseudo- rotation counterparts $SO (p, q, p + q = 2 n + 1)$ .
$C_{n}$ associated with symplectic groups $Sp (2 n)$ .
$D_{n}$ associated with orthogonal (rotation) groups $SO (2 n)$ or their pseudo- rotation counterparts $SO (p, q, p + q = 2 n)$ .

Moreover there are five exceptional cases:

G_{2}

F_{4}

E_{6}

E_{7}

E_{8}

4.3. Physics and Low-Dimensional Root Systems

There exist isomorphisms between low-dimensional root systems (see Appendix B). Borrowing its terminology to atomic spectroscopy one can enunciate that the lowest levels in the Cartan classification are occupied by the most familiar or well-known symmetries of our physics discipline:

(i): $A_{1} ≃ B_{1} ≃ C_{1}$ , ( $SO (3) ≃ SU (2) / Z_{2}$ , $SL (2, R) ≃ SU (1, 1) ≃ Sp (2, R) ≃ {SO}_{0} (2, 1) \times Z_{2}$ ): space isotropy, spherical rotator, geometric optical devices, q-bits, Lorentz invariance, infinite well, isospin, kinematic groups of 1 + 1 de Sitter and Anti de Sitter space-times, ...
(ii): $A_{1} \times A_{1}$ ( $SU (2) \times SU (2) ≃ SO (4)$ , $SU (1, 1) \times SU (1, 1) ≃ {SO}_{0} (2, 2))$ : orbital degeneracy of the Coulomb potential or Kepler problem [30], two-dimensional square infinite well (quantum dot), ...
(iii): $A_{2}$ ( $SU (3)$ ): spatial harmonic oscillator, standard model color, q-trits, ...
(iv): $B_{2} ≃ C_{2}$ ( ${SO}_{0} (4, 1) ≃ Sp (2, 2) / Z_{2}$ , ${SO}_{0} (3, 2) ≃ Sp (4) / Z_{2}$ ): kinematic groups of 3+1 de Sitter [31] and Anti de Sitter [32] space-times, dynamical symmetry of the H atom discrete or continuous spectrum [30], ...
(v): $A_{3} ≃ D_{3}$ ( $SO (6) ≃ SU (4) / Z_{2}$ , ${SO}_{0} (4, 2) ≃ SU (2, 2) / Z_{2}$ , ${SO}_{0} (5, 1)$ ): gauge symmetries, conformal group of 3 + 1 de Sitter, Anti de Sitter and Minkowski space-times respectively, and their roles in the interpretation of the dark universe (e.g., see [33], and references therein), dynamical symmetry of the H atom discrete and continuous spectrum, AdS/DS-CFT, ...

5. Playing with Spheres

We now explore the world of unit spheres in light of group theory.

5.1. The Circle and Its Complexified Version

The unit circle is defined in the complex plane as

S^{1} = {e^{i θ}, θ_{0} \leq θ < θ_{0} + 2 π, mod 2 π}

. It is a compact multiplicative commutative group, denoted

U (1)

. One should think to the importance of this group in mathematics (e.g., Fourier series and integral) and in physics (e.g., gauge invariance in electrodynamics).

The complexified unit circle

S_{C}^{1} = {(z_{1}, z_{2}) \in C^{2} ∣ z_{1}^{2} + z_{2}^{2} = 1} = {e^{i z}, z = x + i y \in C}

is also a group. It is the non-compact multiplicative commutative group

\begin{matrix} SO (2, C) = \\ \{(\begin{matrix} cos (x + i y) & - sin (x + i y) \\ sin (x + i y) & cos (x + i y) \end{matrix}) = (\begin{matrix} cos x & - sin x \\ sin x & cos x \end{matrix}) (\begin{matrix} cosh y & - i sinh y \\ i sinh y & cosh i y \end{matrix})\} \\ = \{exp τ_{2} x exp σ_{2} y, x, y \in R\} ≃ U (1) \times R . \end{matrix}

(5.1)

An example is found with the motion of a particle on the unit circle: the corresponding phase space, i.e., the set of pairs (angular position, angular momentum) is the infinite cylinder

\begin{matrix} Cyl & = {(θ, J \propto \dot{θ}), θ \in R mod 2 π, J \in R} \\ \equiv \{e^{i θ} (cosh J + (- 1) sinh J), θ \in R mod 2 π, J \in R\} ≅ S_{C}^{1}, \end{matrix}

whose the matrix form (5.1) is obtained through the maps

i \mapsto τ_{2}

for the first factor and

(- 1) \mapsto σ_{2} = i τ_{2}

for the second factor.

We could as well consider the free motion on the two-dimensional de Sitter space-time [31]. The latter has the topology

S^{1} \times R

. It may be visualized as the one-sheet hyperboloid

{(y^{0}, y^{1}, y^{2}) \in R^{3} ∣ {(y^{0})}^{2} - {(y^{1})}^{2} - {(y^{2})}^{2} = - R^{2}}

The phase space for such a motion is also a one-sheet hyperboloid with the same cylinder topology. In this case both the configuration space and the phase space have SO

_{0} (1, 2) ≃ SU (1, 1) / Z_{2}

as invariance group.

5.2. The Sphere $S^{3}$ through Its Multifaceted Aspects

Our familiar sphere

S^{2}

is “poor": no intrinsic group structure, save the fact that it includes mythological structures, like the five platonic solids (see next subsection). Then let us consider the next one in the sequence: the sphere

S^{3}

. It may be identified with the compact multiplicative non-commutative group

SU (2)

corresponding to

A_{1}

. Think to the importance of this group in mathematics (e.g., harmonic analysis in space) and in physics (angular momentum, spin, q-bit, ...).

5.2.1. Sphere $S^{3}$ and Group SU $(2)$

The relation of

S^{3}

to SU

(2)

is given by:

\begin{matrix} SU (2) ∋ U_{ξ} = (\begin{matrix} α & β \\ - \bar{β} & \tilde{α} \end{matrix}) \equiv (\begin{matrix} ξ_{0} + i ξ_{3} & - ξ_{2} + i ξ_{1} \\ ξ_{2} + i ξ_{1} & ξ_{0} - i ξ_{3} \end{matrix}), ξ_{0}, ξ_{i} \in R, i = 1, 2, 3, \\ det (U_{ξ}) = {| α |}^{2} + {| β |}^{2} = ξ_{0}^{2} + ξ_{1}^{2} + ξ_{2}^{2} + ξ_{3}^{2} = 1, \\ i . e ., ξ \equiv (ξ_{0}, ξ_{1}, ξ_{2}, ξ_{3}) \equiv (ξ_{0}, ξ) \in S^{3} . \end{matrix}

5.2.2. Sphere $S^{3}$ and Rotations in $R^{3}$

Let us explain the relation between

S^{3}

and the proper rotations in space

R^{3}

. Any proper rotation in space is determined by a unit vector

n

defining the rotation axis and a rotation angle

0 \leq θ < 2 π

about

n

in the direct sense.

The action of such a rotation,

R (n, θ)

, on a vector

r

is given by:

\begin{matrix} r^{'} & \overset{def}{=} R (n, θ) • r = r \cdot n n + cos θ n \times (r \times n) + sin θ (n \times r) \\ = [cos θ 1_{3} + (1 - cos θ) n^{t} n + sin θ n \times] r, \\ n \times & : = (\begin{matrix} 0 & - n_{z} & n_{y} \\ n_{z} & 0 & - n_{x} \\ - n_{y} & n_{x} & 0 \end{matrix}) \end{matrix}

The correspondence between elements rotations

R (n, θ)

and the matrix form

U_{ξ} \in SU (2)

ξ = (ξ_{0}, ξ) = (cos \frac{θ}{2}, sin \frac{θ}{2} n)

is understood as :

\begin{matrix} r^{'} = (x_{1}^{'}, x_{2}^{'}, x_{3}^{'}) & = R (n, θ) • r \\ ⇕ \\ (\begin{matrix} i x_{3}^{'} & - x_{2}^{'} + i x_{1}^{'} \\ x_{2}^{'} + i x_{1}^{'} & - i x_{3}^{'} \end{matrix}) & = U_{ξ} (\begin{matrix} i x_{3} & - x_{2} + i x_{1} \\ x_{2} + i x_{1} & - i x_{3} \end{matrix}) U_{ξ}^{†} . \end{matrix}

(5.2)

5.3. Sphere $S^{3}$ and Quaternions (Hamilton, 1843)

Let us equip the set

C \times C = C^{2} : = {q = (u, v), u, v \in C}

with the commutative addition and non-commutative multiplication operations:

(u, v) + (u^{'}, v^{'}) = (u + u^{'}, v + v^{'}), (u, v) (u^{'}, v^{'}) = (u u^{'} - v \bar{v^{'}}, u v^{'} + v \bar{u^{'}}) .

(5.3)

Both operations afford

C^{2}

with a noncommutative field structure,

0 \equiv (0, 0)

and

1 \equiv (1, 0)

being the neutral elements for addition and multiplication respectively. This is the field of quaternions [34,35] (see also [36] and references therein) and is denoted by

H

. One identifies

(u, 0)

with the complex u and one introduces the “quaternionic imaginary”

\hat{j} \equiv (0, 1)

. One checks that

{\hat{j}}^{2} = - 1

and the fundamental commutation rule

u \hat{j} = \hat{j} \bar{u} \forall u \in C, i . e . i \hat{j} = - \hat{j} i .

Hence we have the bicomplex notation for quaternions:

q = (u, v) = u + v \hat{j} = u + \hat{j} \bar{v} .

(5.4)

With the notations

\hat{i} : = (i, 0)

and

\hat{k} : = (0, i) = \hat{i} \hat{j} = - \hat{j} \hat{i}

, one has as well

\hat{i} = \hat{j} \hat{k} = - \hat{k} \hat{j}

, and

\hat{j} = \hat{k} \hat{i} = - \hat{i} \hat{k}

, with

{\hat{i}}^{2} = - 1 {\hat{j}}^{2}

. Quaternions form the real vector space

R^{4}

of dimension 4, with

{1, \hat{i}, \hat{j}, \hat{k}}

as a standard basis. Quaternions with null scalar component, i.e.,

q = (0, q) \equiv q

, are said pure vector quaternions. It results that one can decompose a quaternion in two different forms:

q = (u, v) = q_{0} + q_{1} \hat{i} + q_{2} \hat{j} + q_{3} \hat{k} \equiv (q_{0}, q) (scalar - vector notation),

(5.5)

q = (u, v) = u + v \hat{j} with \{\begin{matrix} u & = & q_{0} + q_{1} \hat{i} \\ v & = & q_{2} + q_{3} \hat{i} \end{matrix} (bicomplex notation) .

(5.6)

With the bicomplex notation, one easily understands the origin of the multiplication law given in (5.3). With the scalar-vector notations, the quaternionic multiplication reads as

q q^{'} = (q_{0} q_{0}^{'} - q \cdot q^{'}, q_{0} q^{'} + q_{0}^{'} q + q \times q^{'}) .

Introducing the mirror symmetry with respect to the 0th axis,

q = (q_{0}, q) \mapsto \bar{q} : = (q_{0}, - q)

, one checks that

q \bar{q} = q_{0}^{2} + q_{1}^{2} + q_{2}^{2} + q_{3}^{2} \equiv {| q |}^{2}

\bar{q q^{'}} = \bar{q^{'}} \bar{q}

(involutive),

| q q^{'} | = | q | | q^{'} |

, and the inverse of

q \neq 0

is given by

q^{- 1} = \bar{q} / | q |

5.4. Quaternions and Space Rotations

Expressed in “polar” coordinates

q = | q | ξ

ξ \in S^{3} \sim SU (2)

, one obtains the matrix realisation of quaternions:

q = (q_{0}, q) \leftrightarrow A_{q} = (\begin{matrix} q_{0} + i q_{3} & i q_{1} - q_{2} \\ i q_{1} + q_{2} & q_{0} - i q_{3} \end{matrix}) .

(5.7)

Hence, the correspondence (5.2) between elements

ξ = (ξ_{0}, ξ) = (cos \frac{θ}{2}, sin \frac{θ}{2} n) \in S^{3}

and rotations

R (n, θ)

in space is now understood in terms of quaternions:

r^{'} = R (n, θ) • r \Leftrightarrow (0, r^{'}) = ξ (0, r) \bar{ξ} .

(5.8)

5.5. Coquaternions (Cockle, 1849) versus Quaternions

It is interesting to compare the matrix realisation of quaternions with the decomposition (3.3) of the (Lie) algebra

M (2, R)

composed of

2 \times 2

real matrices. Forgetting this matrix realisation and considering the matrix basis

(1_{2} \equiv 1, σ_{1}, τ_{2}, σ_{3})

as pure numbers

(1_{2} \leftrightarrow 1, σ_{1} \leftrightarrow ℓ_{1}, τ_{2} \leftrightarrow ℓ_{2}, σ_{3} \leftrightarrow ℓ_{3}),

obeying the same algebraic relations as those given in (3.2), one obtains the noncommutative ring

H_{co}

of numbers

q = (a_{0}, a)

a_{μ} \in R

μ = 0, 1, 2, 3

, named coquaternions [37,38] or split-quaternions. We remind that rings are algebraic structures that generalize fields in the sense that multiplicative inverses need not exist. With this scalar-vector form, the multiplication law for coquaternions reads as

q q^{'} = ((a_{0} a_{0}^{'} + a_{1} a_{1}^{'} - a_{2} a_{2}^{'} + a_{3} a_{3}^{'}, a_{0} a^{'} + a_{0}^{'} a + a \times_{co} a^{'}), a \times_{co} a^{'} : = \{\begin{matrix} a_{2} a_{3}^{'} - a_{2} a_{3}^{'} \\ a_{1} a_{3}^{'} - a_{3} a_{1}^{'} \\ a_{1} a_{2}^{'} - a_{2} a_{1}^{'} \end{matrix}

If instead we start from the bicomplex form (3.4) and adopt the one-to-one correspondence matrix ↔ coquaternion

M (2, R) ∋ A = z_{1} + σ_{1} z_{2} \leftrightarrow q = z_{1} + ℓ_{1} z_{2} \equiv (z_{1}, z_{2}), z_{1} = a_{0} + a_{2} ℓ_{2}, z_{2} = a_{1} + a_{3} ℓ_{2},

then the multiplication law reads

q q^{'} = (z_{1}, z_{2}) (z_{1}^{'}, z_{2}^{'}) = (z_{1} z_{1}^{'} + {\bar{z}}_{2} z_{2}^{'}, {\bar{z}}_{1} z_{2}^{'} + z_{2} z_{1}^{'}),

a formula to be compared with (5.3).

Ring

H_{co}

is equipped with the isotropic quadratic form

N (q) : = a_{0}^{2} - a_{1}^{2} + a_{2}^{2} - a_{3}^{2} = | z_{1} |^{2} - {| z_{2} |}^{2} = q q^{*},

(5.9)

where

q^{*} = (a_{0}, - a)

is the conjugate of q. Each coquaternion q with

N (q) \neq 0

has inverse

q^{- 1} = q^{*} / N (q)

. One checks that

N (q q^{'}) = N (q) N (q^{'})

The multiplicative group of coquaternions with

N (q) = 1

form the unit pseudo-sphere in

R^{4}

H^{3} : = \{ς \in H_{co}, ς ς^{*} = a_{0}^{2} - a_{1}^{2} + a_{2}^{2} - a_{3}^{2} = 1\} .

The topology of

H^{3}

is that of the Cartesian product

S^{1} \times S^{1} \times R \sim T^{2} \times R

. This is inferred from the parametrisation with

(θ, ψ, t)

a_{0} = cosh t cos θ, a_{2} = cosh t sin θ, a_{1} = sinh t cos ψ, a_{3} = sinh t sin ψ .

Like the matrix realisation of

S^{3}

is SU

(2)

, the matrix realisation of

H^{3}

is the group SL

(2, R)

. The symmetry group of the quadratic form (5.9) on

R^{4}

is O

(2, 2)

5.6. Complex Quaternions

The ring of complex quaternions is the tensor product

H \otimes C \equiv H_{C}

. It is just obtained from

H

by extending real scalars to complex ones in (5.5):

H_{C} = \{z = z_{0} + z_{1} \hat{i} + z_{2} \hat{j} + z_{3} \hat{k} \equiv (z_{0}, z), z_{a} \in C, a = 0, 1, 2, 3\} .

Note the biquaternion form of a complex quaternion:

z = p + i q, p, q \in H

(the correct writing should be

z = p \otimes 1 + q \otimes i

), which corresponds to the isomorphism

H_{C} ≅ H \oplus H

. The matrix representation of

H_{C}

is analogous to (5.7):

H_{C} ∋ z = (z_{0}, z) \leftrightarrow A_{z} = (\begin{matrix} z_{0} + i z_{3} & i z_{1} - z_{2} \\ i z_{1} + z_{2} & z_{0} - i z_{3} \end{matrix}) .

This establishes the ring isomorphism

H_{C} ≅ M_{2} (C)

. For more in-depth information, refer to [32] where these objects are efficiently utilized to describe the two-fold covering Sp

(4, R)

of the Anti-de Sitter group SO

_{0} (2, 3)

5.7. The Complexified Sphere $S_{C}^{3}$

The complexified sphere

S_{C}^{3} = {z = (z_{0}, z) \in C^{4} ∣ z_{0}^{2} + z_{1}^{2} + z_{2}^{2} + z_{3}^{2} = 1}

is also a group. It is the (universal) covering

SL (2, C)

of the Lorentz group

{SO}_{0} (3, 1) ≃ SL (2, C) / Z_{2}

. Let us consider the motion of a particle on

S^{3}

. The phase space is the cotangent bundle

T^{*} (S^{3}) = {z = (q, p) \in R^{4} \times R^{4} ≃ H \times H ∣ {| q |}^{2} = 1, q \cdot p = 0} .

This phase space can be identified with the complex sphere

S_{C}^{3}

through the following parametrization of the latter:

z = q cosh | p | + i \frac{p}{| p |} sinh | p | \in H_{C}, | q | = 1, q \cdot p = 0 .

We could as well consider the free motion on the 3 + 1-dimensional de Sitter spacetime. The latter may be viewed as a one-sheeted hyperboloid embedded in a five-dimensional Minkowski space with metric

η_{α β} = diag (1, - 1, - 1, - 1, - 1)

M_{d S} \equiv \{x \in R^{5}; x^{2} = η_{α β} x^{α} x^{β} = - \frac{3}{Λ_{dS}}\}, α, β = 0, 1, 2, 3, 4 .

For the past years it has becoming a realistic model for our space-time because of the observed non zero value of the cosmological constant

Λ

, a model accompanied of concepts like “dark energy" or “quintessence"). The phase space for the motion of a test particle on the de Sitter space-time has also the topology

S^{3} \times R^{3}

or equivalently the complexified

S_{C}^{3} ≃ SL (2, C)

. In this case both configuration space and phase space have

{SO}_{0} (1, 4) ≃ Sp (2, 2) / Z_{2}

as invariance group. More details are found in the volume [31].

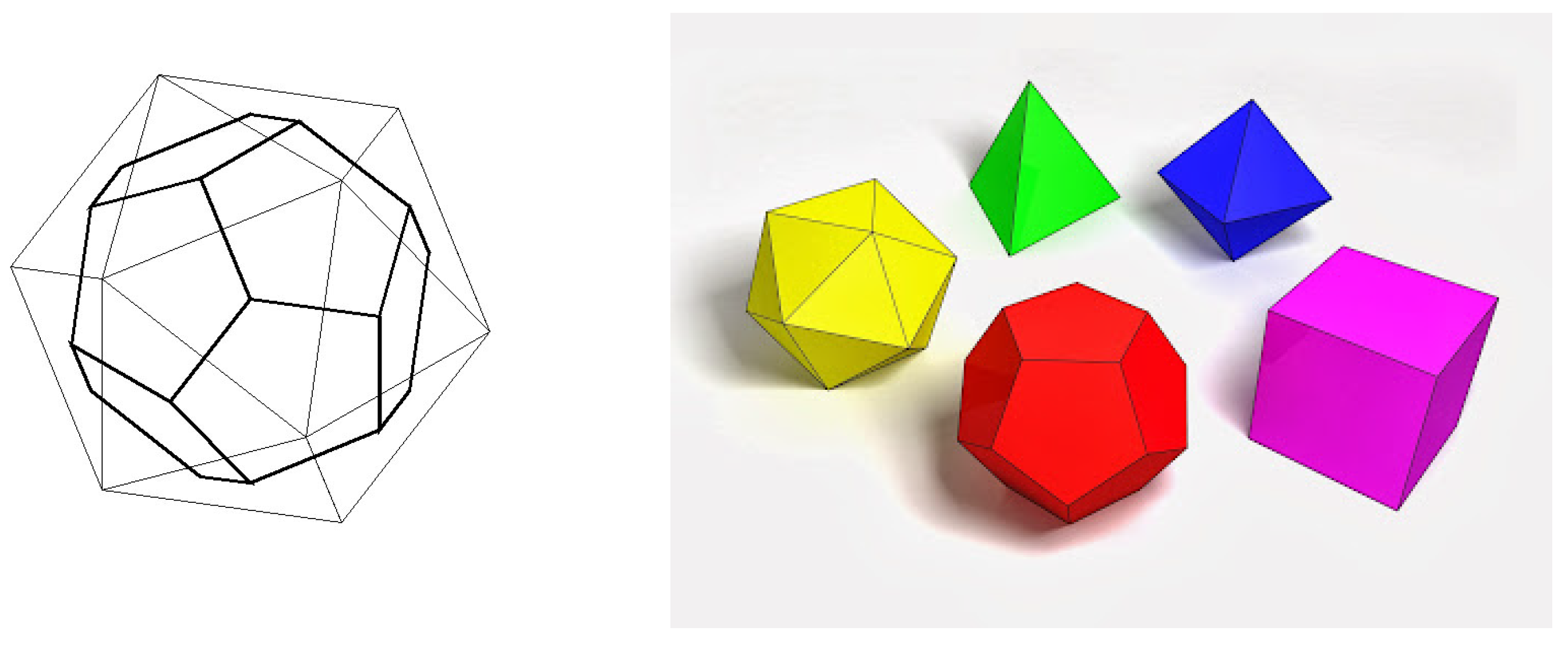
5.8. The Sphere $S^{3}$ , Its Icosians and Its Icosian Ring

The group

SU (2)

has a finite subgroup denoted here by

I

with 120 elements, named icosians by Hamilton. There exists an icosian game invented by Hamilton [39,40]. It is a kind of Eulerian path through the 20 vertices of the dodecahedron, the dual polyhedron of the icosahedron (see Figure 10, and the nice illustration in [41]): a path such that every vertex is visited a single time, no edge is visited twice, and the ending point is the same as the starting point. Winning strategies use the icosian group

I

One has the isomorphism

I / Z_{2} ≃ Y

, where Y is the symmetry group (60 proper rotations) of the icosahedron (or of its dual, the dodecahedron).

Let us consider, together with the quaternionic unity 1, three unit-norm quaternions describing through (5.8) 72

^{\circ}

rotations around three distinct five-fold axes of the icosahedron,

α = \frac{1}{2} (τ, 1, 1 / τ, 0), β = \frac{1}{2} (τ, 0, 1, 1 / τ), γ = \frac{1}{2} (τ, 1 / τ, 0, 1) .

Here,

τ \overset{def}{=} \frac{1 + \sqrt{5}}{2} = 2 cos \frac{π}{5}

is the golden mean, with

- 1 / τ = \frac{1 - \sqrt{5}}{2} = τ - 1

, both being algebraic integers, solutions of the algebraic equation with integer coefficients

x^{2} = x + 1 .

The

Z

-span of

I

is the icosian ring

I

[43] which fills densely

R^{4} ≃ H

. One shows that

I = Z [τ] + Z [τ] α + Z [τ] β + Z [τ] γ,

where

Z [τ] = {m + n τ ∣ m, n \in Z}

is the extension ring of the golden mean.

5.9. The Root System $E_{8}$ and Quasicrystals

Let us now consider the root system

E_{8}

. It is made of 240 vectors in

R^{8}

. The corresponding root lattice

E_{8}

is the

Z

-span of

E_{8}

. Because of the crystallographic properties of

E_{8}

, we have:

E_{8} = \sum_{i = 1}^{8} Z α_{i},

where the

α_{i}

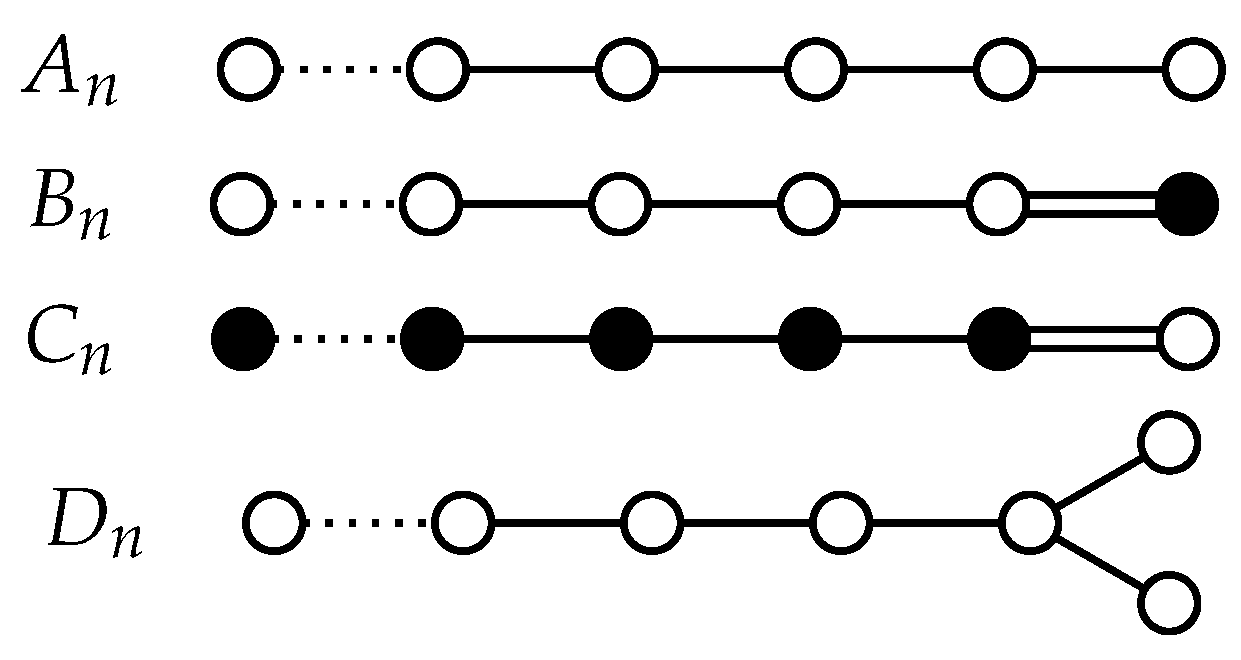
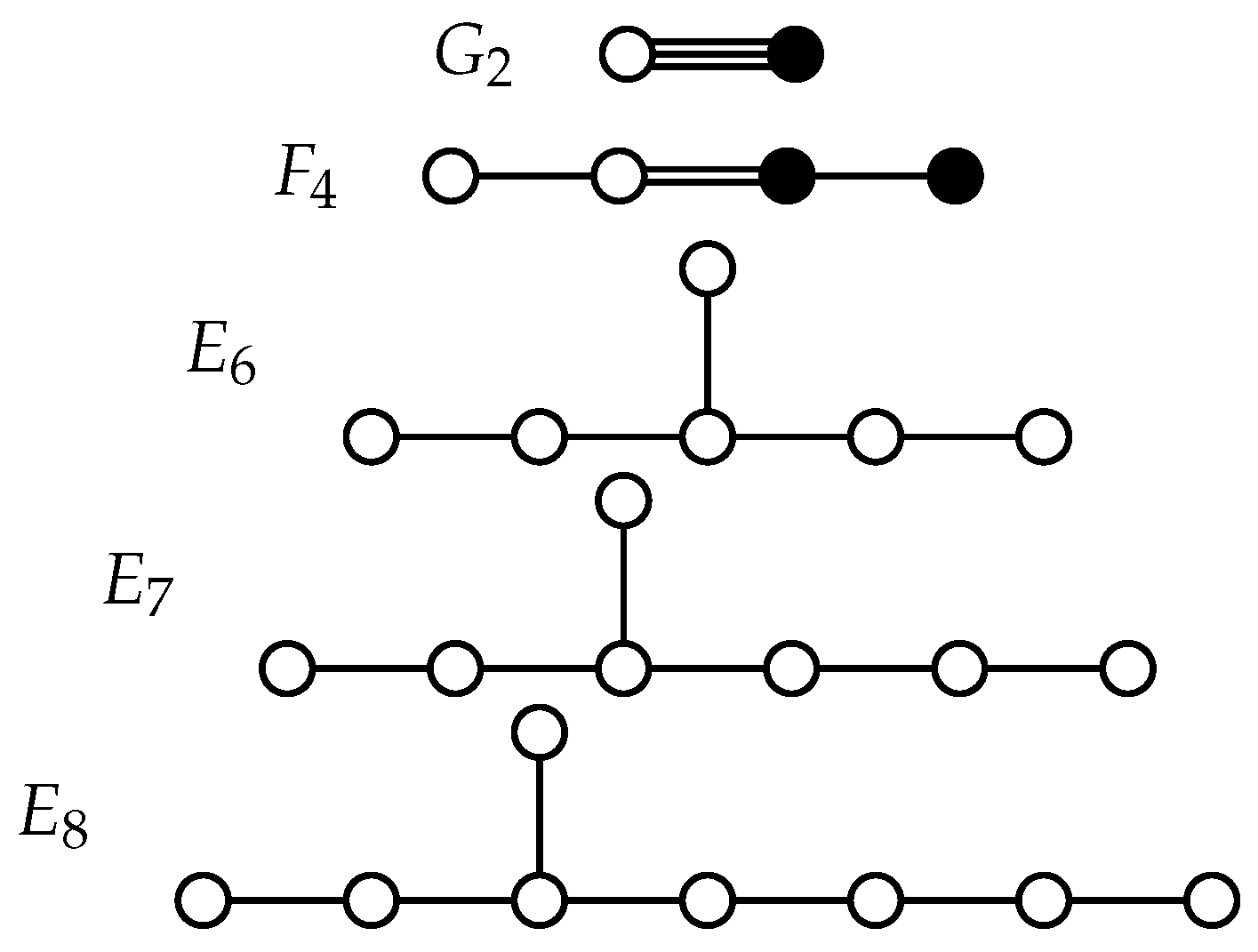
’s are the basis roots of the corresponding Dynkin diagram shown in Figure A2.

Subsequently, by selecting a particular four-dimensional plane within

R^{8}

possessing a distinct “golden mean” orientation and executing the orthogonal projection of the root lattice

E_{8}

onto this hyperplane, the result is the formation of the icosian ring

I

Similar manipulations on the

D_{6}

root lattice projected onto

R^{3}

, on the

A_{4}

root lattice projected onto the plane

R^{2}

, and on the

A_{2}

root lattice projected onto the real line

R

, accompanied by “cuts" based on the choice of appropriate “windows", produce standard models for three-, two- and one-dimensional quasicrystals (e.g., icosahedral quasicrystals, Penrose tilings, Fibonacci chain ...), as is shown in Figure 11, [44].

In Figure 12 is shown an example of observed quasicrystalline surface.

5.10. Algebraic Modelling of Quasicrystals

The identified self-similarity factors, denoted by

β

, within quasicrystals exhibit a distinctive mathematical nature known as quadratic Pisot-Vijayaraghavan (PV) numbers. In essence, these numbers correspond to roots greater than 1 of specific quadratic polynomials. These polynomials possess a leading coefficient of 1 and consist of integer coefficients. Notably, the other root of these polynomials is characterized by an absolute value less than 1.

In the case presented above, the factor is the golden mean

β = τ = \frac{1 + \sqrt{5}}{2}

. The other ones are

β = τ^{2} = \frac{3 + \sqrt{5}}{2}, β = δ = 1 + \sqrt{2}, β = θ = 2 + \sqrt{3} .

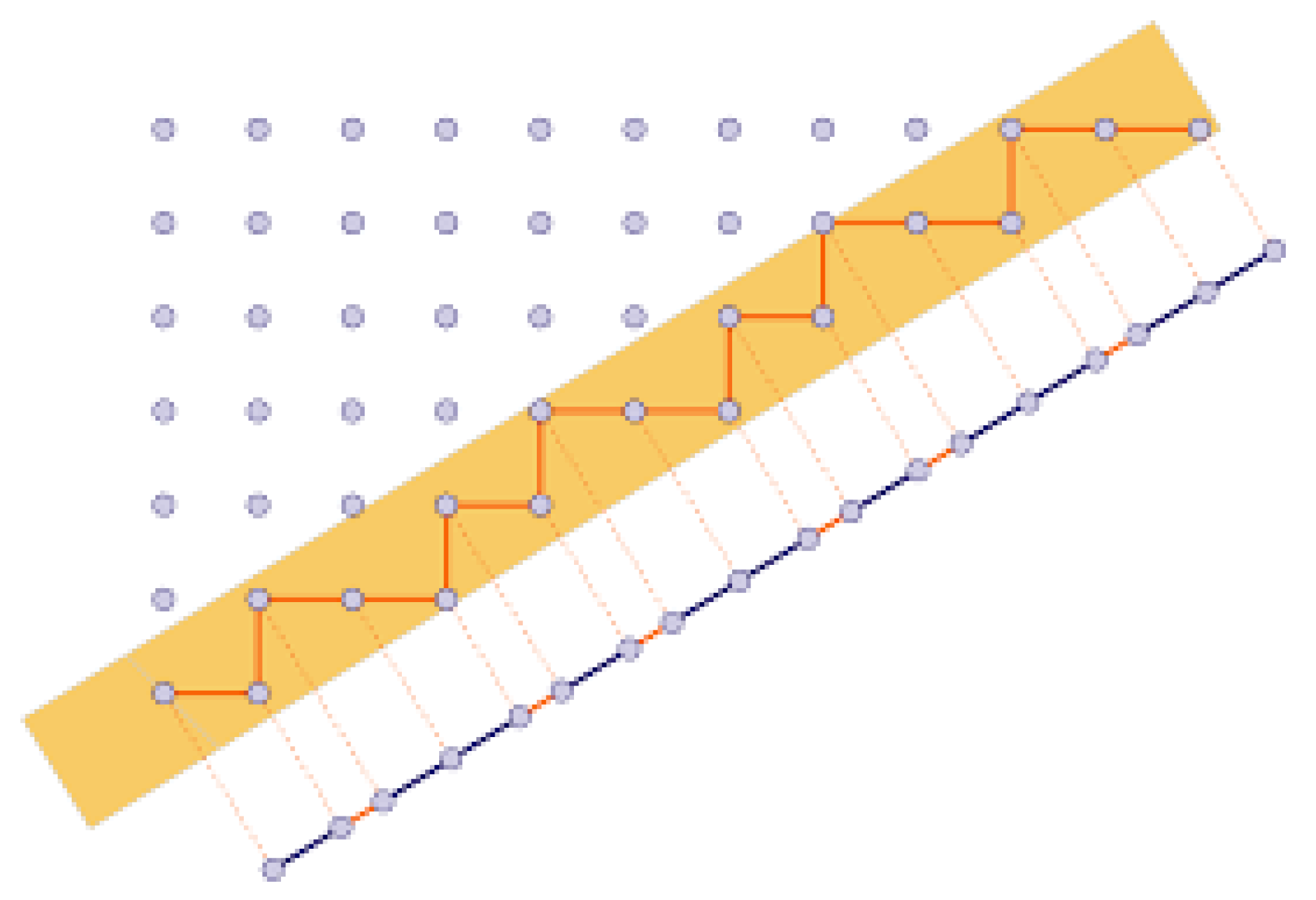
Each value of

β

serves as the defining parameter for a discrete set on the number line, denoted as

Z_{β}

or the set of “beta-integers”, as introduced in [46] (see also [47], and references therein). This set is specifically designed to function analogously to integers within the context of quasicrystalline investigations. A visual representation of this concept is illustrated in Figure 13, depicting the first tau-integers in proximity to the origin.

Beta-lattices are designed to serve as direct substitutes for traditional lattices within the unique framework of quasicrystals. Much like lattices are built upon sets of integers, beta-lattices find their structural basis in beta-integers. This deliberate choice aligns with the goal of seamlessly adapting mathematical structures to the intricate properties of quasicrystals. A typical beta-lattice

Γ

is defined as:

Γ = \sum_{i = 1}^{d} Z_{β} e_{i},

with

(e_{i})

a base of

R^{d}

. Examples are shown in Figure 14 and Figure 15.

5.11. Sphere $S^{7}$ and Octonions (Graves, 1843, Cayley, 1845)

Q, C, H

, the algebra

O

of octonions [48,49] is built by providing the Cartesian product

H \times H = {(p, q), p, q \in H}

with the commutative addition and the non-commutative and non-associative product:

(p, q) + (p^{'}, q^{'}) = (p + p^{'}, q + q^{'}), (p, q) (p^{'}, q^{'}) = (p p^{'} - \bar{q^{'}} q, q^{'} p + q \bar{p^{'}}) .

Let us introduce the 8 octonionic basis numbers:

1 \equiv (1, 0)

(unity) and

\begin{matrix} \hat{i} \equiv (\hat{i}, 0), \hat{j} \equiv (\hat{j}, 0), \hat{k} \equiv (\hat{k}, 0), \end{matrix}

(5.10)

\begin{matrix} \hat{l} \equiv (0, 1), \hat{i} \hat{l} = (0, \hat{i}) \equiv \underset{̲}{\hat{i}}, \hat{j} \hat{l} = (0, \hat{j}) \equiv \underset{̲}{\hat{j}}, \hat{k} \hat{l} = (0, \hat{k}) \equiv \underset{̲}{\hat{k}}, \end{matrix}

(5.11)

with the commutation rules

\hat{i} \hat{l} = (0, \hat{i}) = - \hat{l} \hat{i}, \hat{j} \hat{l} = (0, \hat{j}) = - \hat{l} \hat{j}, \hat{k} \hat{l} = (0, \hat{k}) = - \hat{l} \hat{k} .

(5.12)

We then obtain the biquaternion notation for octonions:

O ∋ x = p + q \hat{l} = p_{0} + p_{1} \hat{i} + p_{2} \hat{j} + p_{3} \hat{k} + q_{0} \hat{l} + q_{1} \underset{̲}{\hat{i}} + q_{2} \underset{̲}{\hat{j}} + q_{3} \underset{̲}{\hat{k}} = p + \hat{l} \bar{q} .

(5.13)

In octonionic calculations we should be aware of the non-associativity of the product, e.g.,

(\hat{j} \hat{k}) \hat{l} = \hat{i} \hat{l}

whilst

\hat{j} (\hat{k} \hat{l}) = - \hat{i} \hat{l}

The octonionic conjugate of the octonion x is defined as

x = (p, q) \mapsto \bar{x} : = (\bar{p}, - q) .

This operation allows to define the Euclidean norm of

x \in O

and its inverse if

x \neq 0

x \bar{x} = \bar{x} x = {| p |}^{2} + {| q |}^{2} \equiv {| x |}^{2}, x^{- 1} = \frac{\bar{x}}{{| x |}^{2}} .

Conjugation is involutive:

\bar{x x^{'}} = \bar{x^{'}} \bar{x}

, and one checks that

| x x^{'} | = | x | | x^{'} |

Like the bicomplex notation (5.4)-(5.6) for quaternions, we also have the quadricomplex notation for octonions:

x = (p, q) = (t, u) + \hat{j} (v, w) where \{\begin{matrix} t = p_{0} + p_{3} \hat{k} & , & u = q_{0} + q_{3} \hat{k} \\ v = p_{2} + p_{1} \hat{k} & , & w = q_{2} - q_{1} \hat{k} \end{matrix} .

(5.14)

The Hurwitz theorem establishes that the real numbers

R

, complex numbers

C

, quaternions

H

, and octonions

O

stand as the exclusive normed division algebras over the real numbers, up to isomorphism. Normed in the sense that the product of any two elements satisfies the norm property:

| x x^{'} | = | x | | x^{'} |

. Moreover, these four algebras represent the sole examples of alternative, finite-dimensional division algebras over the real numbers.

A general rotation in

R^{8}

, i.e., an element among the 28 elements of SO

(8)

, can be written through successive right multiplications:

O ∋ x \mapsto ((((((x η_{1}) η_{2}) η_{3}) η_{4}) η_{5}) η_{6}) η_{7}, η_{i} \in O, | η_{i} | = 1 .

For a recent review on the role of octonions in Nuclear Physics, see [50].

6. Higher Spheres and Hopf Maps and Fibrations

What about

S^{n}, n \geq 4

? There is nothing really special from a strictly group point of view when we deal with higher dimensional spheres. Naturally many interesting topological features exist, like the Hopf fibrations [51,52]:

6.1. Hopf Fibrations

They are the following relations involving spheres the

S^{n}, n = 1, 2, 3, 4, 5, 7, 8, 15

S^{1} ↪ S^{3} \overset{p}{\to} S^{2}, S^{3} ↪ S^{7} \overset{p}{\to} S^{4}, S^{7} ↪ S^{15} \overset{p}{\to} S^{8},

where “↪” stands for embedding, and p is the Hopf map. The first one is displayed in Figure 16.

The Hopf construction, in its broader application, yields circle bundles in the form of

S^{2 n + 1} \overset{p}{\to} C P^{n}

over complex projective space. This construction is essentially a restriction of the topological line bundle over

C P^{n}

to the unit sphere in

C^{n + 1}

Note the elementary example where one considers

S^{1}

embedded in

R^{2}

and factors out by unit real multiplication. One then obtains

R P^{1} = S^{1}

. This results in a fiber bundle

S^{1} \overset{p}{\to} S^{1}

with the circle

S^{0}

as the fiber.

Extending these constructions, one can view

S^{4 n - 1}

within quaternionic n-space (

H^{n}

) and factor out by unit quaternion multiplication (

≃ S^{3}

) to obtain

H P^{n}

. Notably, a bundle

S^{7} \overset{p}{\to} S^{4}

with fiber

S^{3}

emerges from this construction, connecting quaternionic and real projective spaces.

Similarly, leveraging octonions leads to a bundle

S^{15} \overset{p}{\to} S^{8}

with fiber

S^{7}

These constructions are often referred to as Hopf bundles, encompassing the realms of real, quaternionic, and octonionic Hopf bundles. Importantly, Adams’ theorem asserts that these bundles represent the exclusive instances of fiber bundles with spheres as the total space, base space, and fiber.

Hopf fibration surfaces show up in the description of quantum entanglement [53,54]. In particle physics they underly the mathematics of the Dirac monopole. It also appears in general relativity, for instance in the Robinson congruence (see for instance [55]).

6.2. Group Interpretation of the First Hopf Map: $S^{3} \overset{p}{\to} S^{2}$

Let us consider the element

ξ = (ξ_{0}, ξ_{1}, ξ_{2}, ξ_{3})

S^{3} ≅ SU (2)

which brings the north pole of

S^{2}

to the direction

(x, y, z) \in S^{2}

ξ (0, 0, 0, 1) \bar{ξ} = (0, x, y, z), x^{2} + y^{2} + z^{2} = 1 .

This gives the quadratic relations which exemplify the projection p (Hopf’s map) of

S^{3}

onto the base space

S^{2}

S^{3} ∋ \{\begin{matrix} x = & 2 (ξ_{0} ξ_{2} + ξ_{1} ξ_{3}) \\ y = & 2 (ξ_{2} ξ_{3} - ξ_{0} ξ_{1}) \\ z = & ξ_{0}^{2} + ξ_{3}^{2} - ξ_{1}^{2} - ξ_{2}^{2} \end{matrix} .

One easily checks that the Hopf inverse of a point

\in S^{2}

is a circle

S^{1} \subset S^{3}

and that the Hopf inverse of a circle

S^{1} \subset S^{2}

is a torus

S^{1} \times S^{1}

6.3. Group Interpretation of the Second Hopf Map: $S^{7} \overset{p}{\to} S^{4}$

We here consider the special group isomorphism proper to

B_{2} ≅ C_{2}

(see Figure A1):

Spin (5) \equiv SO (5) \times Z_{2} ≃ G = \{g = (\begin{matrix} a & b \\ c & d \end{matrix}), a, b, c, d \in H, g \bar{^{t} g} = 1_{2}\} .

It is understood through the action of the group G on specific

2 \times 2

-quaternionic matrices

g (\begin{matrix} y_{4} & p \\ \bar{p} & - y_{4} \end{matrix}) \bar{^{t} g} = (\begin{matrix} y_{4}^{'} & p^{'} \\ \bar{p^{'}} & - y_{4}^{'} \end{matrix}), p \in H, y_{4} \in R, y_{4}^{2} + {| p |}^{2} = 1 .

Just consider the group element

g = (\begin{matrix} a & b \\ - \bar{b_{α}} & \bar{a} \end{matrix}) \in G

b_{α} = \bar{a} b a / {| a |}^{2}

, which brings the “north pole" of

S^{4}

(y_{4} = 1, p = 0)

, to the point

(y_{4}, p) \in S^{4}

. We have

{| a |}^{2} + {| b |}^{2} = 1

, i.e.,

(a, b) \in S^{7}

. This gives the quadratic relations:

p = - 2 b a, y_{4} = {| a |}^{2} - {| b |}^{2} .

The Hopf inverse of a point

\in S^{4}

is the sphere

S^{3} \subset S^{7}

and the Hopf inverse of a sphere

S^{3} \subset S^{4}

S^{3} \times S^{3} ≃ SO (4)

6.4. Group Interpretation of the Third Hopf Map: $S^{15} \overset{p}{\to} S^{8}$

The octonionic Hopf fibration finds its elegant description through the lens of the automorphism group G2 of the normed algebra of octonions. Actually, one can grasp its essence by considering the group Spin

(9)

(where Spin

(n)

serves as the two-fold covering of SO

(n)

), as explained in [56].

7. Kepler-Coulomb Problem and Spheres

Concluding our exploration of the world of spheres, it is essential to acknowledge the pivotal role played by

S^{1}

and

S^{3}

, and their complexified versions, in understanding the symmetries of a particle’s motion subjected to the Kepler or Coulomb potential. Alongside the harmonic oscillator, it stands as one of the most emblematic examples of integrable systems within the domain of Galilean classical or quantum mechanics. This symmetry elucidates, at the quantum level, the empirical laws discovered by Balmer in 1885 [57] for describing the spectral line emissions of the hydrogen atom. The literature on this topic is extensive (see, for instance, the review [30]), and its content can attain a high level of mathematical sophistication. To provide some insight, we will first examine in detail the one-dimensional case before sketching the main concepts of the realistic three-dimensional model. It is worth noting that providing a comprehensive account of the symmetries inherent in the Kepler-Coulomb problems, both classically and quantum mechanically, would necessitate delving into a much broader scope of material.

7.1. 1-Dimensional Kepler-Coulomb Problem

Consider the energy of a particle of mass m trapped in a well determined on the positive line

q \geq 0

by the attractive Kepler-Coulomb potential:

V (q) = - \frac{k}{q}, k > 0,

and

V (q) = \infty

for

q < 0

. Its energy is given by

E = \frac{p^{2}}{2 m} - \frac{k}{q} .

Regularizing the Kepler problem in the case of negative energy consists in considering the alternative equation:

Θ \overset{def}{=} q (p_{0}^{2} + p^{2}) - 2 m k = 0, q > 0 .

where

p_{0} = \sqrt{- 2 m E}

. Let us see how the Balmer laws [57] come to light from the symmetry

A_{1}

. One considers the three observables defined on the upper half-plane viewed as the phase space

{(q, p) ∣ q > 0, p \in R}

d = q p, γ_{0} = \frac{1}{2} q (p^{2} + p_{0}^{2}), γ_{1} = \frac{1}{2} q (p^{2} - p_{0}^{2}) .

Their Poisson brackets

({f, g} \overset{def}{=} \frac{\partial f}{\partial q} \frac{\partial g}{\partial p} - \frac{\partial f}{\partial p} \frac{\partial g}{\partial q})

obey the commutation relations of the Lie algebra

sl (2, R)

SL (2, R)

{d, γ_{0}} = γ_{1}, {d, γ_{1}} = γ_{0}, {γ_{0}, γ_{1}} = p_{0}^{2} d .

After quantization of these classical observables, say

A \mapsto \hat{A}

, Poisson brackets become commutators, quantum counterparts become (essentially) self-adjoint operators acting in some Hilbert space of quantum states, and a specific unitary irreducible representation of

SL (2, R)

is involved. Precisely, that one for which the generator

\hat{γ_{0}}

has non zero positive integers multiples of

p_{0}

as spectral values. This is due to the fact the inverse operator

{\hat{γ_{0}}}^{- 1}

is compact. We remind that an operator A on a infinite-dimensional Hilbert space

H

is said to be compact if it can be written in the form

A = \sum_{n = 1}^{\infty} λ_{n} 〈 f_{n}, \cdot 〉 e_{n}

where

{e_{n}}

and

{f_{n}}

are orthonormal sets (not necessarily complete) and the

λ_{n}

’s form a sequence of positive numbers with limit zero (they can accumulate only at zero). Since the classical equation

Θ = 2 γ_{0} - 2 m k = 0

becomes

\hat{Θ} = 2 (\hat{γ_{0}} - 2 m k) ψ = 0

, the spectral condition leads directly to the Balmer-like quantization of the energy:

n p_{0} - m k = 0 \Leftrightarrow E = - \frac{m k^{2}}{2 n^{2}} .

7.2. Phase Space of the Regularized 1d-Kepler-Coulomb Problem: The Complexified Circle with Zero Radius

Let us show that the phase space of the regularized 1d-Kepler problem is the complexified circle with zero radius.

Following the Fock method [58,59] for displaying the symmetry of the H-atom, let us introduce the circle variable

ξ = (\frac{p_{0}^{2} - p^{2}}{p_{0}^{2} + p^{2}}, \frac{2 p_{0} p}{p_{0}^{2} + p^{2}}) \in S^{1} .

(Inverse stereographic projection transforming the compactified momentum real line into the unit circle). By imposing that this change of variable be part of a canonical transformation of the phase space, the conjugate variable

π_{ξ}

ξ

reads:

π_{ξ} = (- q p, q \frac{p_{0}^{2} - p^{2}}{2 p_{0}}) = (- d, \frac{γ_{1}}{p_{0}}) .

One easily checks the two constraints:

|π_{ξ}| = \frac{m k}{p_{0}} on the energy shell and ξ \cdot π_{ξ} = 0 .

Therefore, the pair

(ξ, \frac{p_{0}}{m k} π_{ξ})

parametrizes the complex circle in

C^{2}

with null radius:

S_{C}^{1} (0) = {(z_{1}, z_{2}) \in C^{2} ∣ z_{1}^{2} + z_{2}^{2} = 0} .

This is a geometric model for the phase space of the one-dimensional regularized Kepler problem, which can be identified to

T_{0}^{*} S^{1}

(cotangent bundle on

S^{1}

with the zero-section deleted, named Moser manifold or Kepler manifold).

7.3. Phase Space of the Three-Dimensional Regularized Kepler-Coulomb Problem

The above material is easily generalisable to three dimensions. Indeed, the phase space of the three-dimensional regularized Kepler problem is the complexification of

S^{3}

with radius 0.

Following Fock again in dealing with the more realistic 3-dimensional Kepler-Coulomb problem, let us introduce the

S^{3}

variable

ξ = (\frac{p_{0}^{2} - {∥ p ∥}^{2}}{p_{0}^{2} + {∥ p ∥}^{2}}, \frac{2 p_{0} p}{p_{0}^{2} + {∥ p ∥}^{2}}) \in S^{3} .

(Inverse stereographic projection transforming the 3d-compactified momentum space into 3-sphere).

By imposing that this change of variable be part of a canonical transformation of the phase space, the conjugate variable

π_{ξ}

ξ

together with

ξ

parametrizes the complexification of

S^{3}

C^{4}

with null radius. This is the phase space of the three dimensional regularized Kepler problem, which can be identified with

T_{0}^{*} S^{3}

(cotangent bundle on

S^{3}

with the zero-section deleted, Moser manifold or Kepler manifold, as named by Souriau [60]).

The three-dimensional aspect of this structure explains the accidental degeneracy of the discrete spectrum of the hydrogen atom with its SO

(4)

symmetry.

8. Conclusions

This contribution is an invitation to embark on an exploration of the realm governed by numbers, symmetries, and intricate symmetry groups, and, as an appealing illustration, to delve into the profound significance encapsulated within the fundamental aspects of the circle and higher-dimensional spheres. Its aim is to share our appreciation for their value in shaping our mathematical comprehension of the natural world and establishing the foundational principles that underpin the laws of physics.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Data sharing not applicable.

Acknowledgments

The author expresses gratitude both to the Krakow Interdisciplinary Doctoral School under the PROM Project PPI/PRO/2019/1/00016 of the Polish National Agency for Academic Exchange, 9-20 January 2023, and to the Programa de Pós-Graduação which includes both the Master’s and Doctorate programs in Physics, at the Centro Brasileiro de Pesquisas Físicas, Rio de Janeiro, for the invitation to deliver the 2023 course titled Symmetries in Physics in 5 lessons + complements. This article draws inspiration from the aforementioned course, and the author acknowledges the valuable opportunity provided by both invitations. The author is grateful to Danièle Rousselier for providing the opportunity to explore the literary masterpiece crafted by Minh Tran Huy [8].

Conflicts of Interest

The author declares no conflict of interest.

Abbreviations

The following abbreviations are used in this manuscript:

UIR	Unitary irreducible representation

Appendix A. Group Actions

A transformation of a set S is a one-to-one mapping of S onto itself. A group G is realized as a transformation group of a set S if, for each

g \in G

, there exists an associated transformation

s \mapsto g \cdot s

of S, where for any

g_{1}

and

g_{2}

in G and

s \in S

, the property

(g_{1} g_{2}) \cdot s = g_{1} \cdot (g_{2} \cdot s)

holds. The set S is then referred to as a G-space, and a transformation group is deemed transitive on S if, for any

s_{1}

and

s_{2}

in S, there exists a

g \in G

such that

s_{2} = g \cdot s_{1}

. In such a scenario, the set S is termed a homogeneous G-space.

A (linear) representation of a group G is a continuous function

g \mapsto T (g)

that takes values in the group of nonsingular continuous linear transformations of a vector space

V

. This function satisfies the functional equation

T (g_{1} g_{2}) = T (g_{1}) T (g_{2})

and

T (e) = I_{d}

, where e is the identity element of G, and

I_{d}

is the identity operator in

V

. Additionally, it follows that

T (g^{- 1}) = {(T (g))}^{- 1}

, meaning that

T (g)

is a homomorphism of G into the group of nonsingular continuous linear transformations of

V

A representation is deemed unitary if the linear operators

T (g)

are unitary concerning the inner product

〈 \cdot | \cdot 〉

V

. In other words,

〈 T (g) v_{1} | T (g) v_{2} 〉 = 〈 v_{1} | v_{2} 〉

holds for all vectors

v_{1}

and

v_{2}

V

. Furthermore, a representation is irreducible if there is no non-trivial subspace

V_{0} \subset V

such that, for all vectors

v_{0} \in V_{0}

T (g) v_{0}

is in

V_{0}

for all

g \in G

. In simpler terms, there exists no non-trivial subspace

V_{0}

V

that remains invariant under the operators

T (g)

Appendix B. Lie Algebra Material

Appendix B.1. General

Consider a complex Lie algebra

g

, defined as a complex vector space equipped with an antisymmetric bracket

[\cdot, \cdot]

satisfying the Jacobi identity:

[[X, Y], Z] + [[Y, Z], X] + [[Z, X], Y] = 0, \forall X, Y, Z \in g .

(A1)

For any

X, Y \in g

, the adjoint representation is given by

({ad}_{X}) (Y) = [X, Y]

, providing a linear map ad:

g \to End g

, where

End g

represents the endomorphisms of

g

. This is known as the adjoint representation of

g

If the dimension of

g

is finite (dim

g < \infty

), one can define a symmetric bilinear form

B (X, Y)

for

X, Y \in g

as follows:

B (X, Y) = Tr [({ad}_{X}) ({ad}_{Y})], X, Y \in g .

(A2)

Here, B is termed the Killing form of

g

Alternatively, one can choose a basis

X_{j}, j = 1, \dots, n

g

, where

n =

dim

g

. In terms of this basis, the commutation relations are expressed as:

[X_{i}, X_{j}] = \sum_{k = 1}^{n} c_{i j}^{k} X_{k}, i, j = 1, \dots, n,

(A3)

where

c_{i j}^{k}

are the structure constants. It is then evident that

g_{i j} = \sum_{k, m = 1}^{n} c_{i k}^{m} c_{j m}^{k} = B (X_{i}, X_{j})

defines a metric on

g

. This metric is known as the Cartan-Killing metric.

Appendix B.2. Roots and Cartan Classification

The Lie algebra

g

is classified as simple if it lacks any nontrivial ideal. In other words, there is no additive subgroup

I

g

that absorbs the left multiplication by elements of

g

, i.e.,

[I, g] \subset I

. On the other hand, if

g

contains an Abelian ideal, it is referred to as semisimple. A semisimple Lie algebra can be decomposed into a direct sum of simple Lie algebras. Importantly,

g

is semisimple if and only if the Killing form is nondegenerate, as per Cartan’s criterion.

Let

g

be a semisimple Lie algebra. Within

g

, a Cartan subalgebra

h

is chosen, defined as a maximal nilpotent subalgebra. Notably, this subalgebra is maximal Abelian and unique up to conjugation. The dimension ℓ of

h

is referred to as the rank of

g

. A root of

g

with respect to

h

is a linear form on

h

α \in h^{*}

such that there exists a non-zero element X in

g

satisfying

({ad}_{H}) X = α (H) X

for all

H \in h

Then, it is possible to find, as demonstrated by Cartan and Chevalley, a basis

H_{i}, E_{α}

for

g

with the following distinctive properties: the set

{H_{j}, j = 1, \dots, ℓ}

forms a basis for the Cartan subalgebra

h

. Each generator

E_{α}

is associated with a nonzero root

α

. Furthermore, these generators can be organized in such a way that the commutation relations, given by Equation (A3), may be expressed in a specific form. The precise details of this form would depend on the specific properties of the chosen basis:

\begin{matrix} [H_{i}, H_{j}] & = 0, i, j = 1, \dots, ℓ, \end{matrix}

(A4)

\begin{matrix} [H_{i}, E_{α}] & = α (H_{i}) E_{α}, i = 1, \dots, ℓ, \end{matrix}

(A5)

\begin{matrix} [E_{α}, E_{- α}] & = H_{α} \equiv \sum_{i = 1}^{ℓ} α^{i} H_{i} \in h, \end{matrix}

(A6)

\begin{matrix} [E_{α}, E_{β}] & = N_{α β} E_{α + β}, \end{matrix}

(A7)

where

N_{α β} = 0

α + β

is not a root.

The set of roots of

g

is denoted by

Δ

. Notably, the nonzero roots exhibit a specific pairing:

α \in Δ \Leftrightarrow - α \in Δ

, and no other nonzero multiple of a root is itself a root. As a consequence, the set of nonzero roots can be divided into two subsets:

Δ_{+}

, comprising positive roots, and its corresponding counterpart of negative roots, denoted

Δ_{-} = - α,, α \in Δ_{+}

. The set

Δ_{+}

is encapsulated within a simplex (a convex pyramid) in

h^{*}

, where the edges are defined by the so-called simple positive roots. These are positive roots that cannot be expressed as the sum of two other positive roots. This characterization also applies to

Δ_{-}

The examination of root systems provides the foundation for the Cartan classification of simple Lie algebras. This classification encompasses four infinite series, namely

A_{ℓ}, B_{ℓ}, C_{ℓ}, D_{ℓ}

, and five exceptional algebras:

G_{2}, F_{4}, E_{6}, E_{7}, E_{8}

Appendix B.3. Dynkin Diagrams: General

The roots of a complex Lie algebra collectively form a lattice of rank n within the dual space of a Cartan subalgebra

h \subset g

, where n signifies the Lie algebra rank of

g

. Consequently, the root lattice can be viewed as a lattice in

R^{n}

. Each vertex, or node, in the Dynkin diagram corresponds to a Lie algebra simple root, which is a generator of the root lattice. For any pair of nodes

α

and

β

in the Dynkin diagram, an edge is drawn if the simple roots associated with them are not perpendicular. The nature of the edge varies: a single undirected edge is drawn if the angle between them is

2 π / 3

, a directed double edge if the angle is

3 π / 4

, and a directed triple edge is drawn if the angle is

5 π / 6

. It is noteworthy that there are no other possible angles between Lie algebra simple roots. In the case of directed edges, double and triple edges point toward the shorter vector (indicated by a black circle).

Dynkin diagrams are shown in Figure A1, Figure A2, Figure A3, Figure A4.

Appendix B.4. From Top to Bottom, Dynkin Diagrams for A_n, B_n, C_n, D_n

Figure A1. Dynkin diagrams

A_{n}

B_{n}

C_{n}

D_{n}

Figure A1. Dynkin diagrams

A_{n}

B_{n}

C_{n}

D_{n}

Appendix B.5. Dynkin Diagrams G₂, F₄, E₆, E₇, E₈

Figure A2. From top to bottom: Dynkin diagrams for

G_{2}

F_{4}

E_{6}

E_{7}

E_{8}

Figure A2. From top to bottom: Dynkin diagrams for

G_{2}

F_{4}

E_{6}

E_{7}

E_{8}

Appendix B.6. Examples: Roots A₁ × A₁, A₂, B₂

Figure A3. rank-2 root systems

A_{1} \times A_{1}

A_{2}

B_{2}

(from Licence CC BY-SA 3.0 DEED).

Figure A3. rank-2 root systems

A_{1} \times A_{1}

A_{2}

B_{2}

(from Licence CC BY-SA 3.0 DEED).

Appendix B.7. Examples: Roots C₂, D₂, G₂

Figure A4. rank-2 root systems

C_{2}

D_{2}

G_{2}

(from Licence CC BY-SA 3.0 DEED).

Figure A4. rank-2 root systems

C_{2}

D_{2}

G_{2}

(from Licence CC BY-SA 3.0 DEED).

References

Kerner, R. Generalization of the Kaluza-Klein theory for an arbitrary non-abelian gauge group. Ann. Inst. H. Poincaré 1968, 9, 141–150. [Google Scholar]
Kerner, R.; Phillips, J. C. Quantitative principles of silicate glass chemistry. Solid State Com. 2000, 117, 47–51. [Google Scholar] [CrossRef]
Kerner, R. The cubic chessboard. Class. Quantum Grav. 1997, 14, A203. [Google Scholar] [CrossRef]
Dubois-Violette, M.; Kerner, R.; Madore, J. Noncommutative differential geometry of matrix algebras. J. Math. Phys. 1990, 31, 316–322. [Google Scholar] [CrossRef]
Kerner, R. Our Celestial Clockwork From Ancient Origins to Modern Astronomy of the Solar System. World Scientific (2021).
Gazeau, J.-P. From classical to quantum models: The regularising rôle of integrals, symmetry and probabilities. Found. Phys. 2018, 48, 1648–1667. [Google Scholar] [CrossRef]
Gazeau, J.-P. Symmetries in Physics: a journey in (high) spheres. Proceedings of Mario Novello’s 70th Anniversary Symposium, edited by N. Pinto Neto and S. E. Perez Bergliaffa (Editora Livraria da Fisica, Sao Paulo, 2012), pp. 133–149.
Huy, M. T. Un enfant sans histoire. Actes Sud (2022).
Chen, J. Group Theory and the Rubik’s Cube. Available at Rubik.
Taylor, R. Ask Fuzzy: Why does a mirror reverse left to right, but not top to bottom?. Available at Available at Mirror Reverse.
Rooney, A. The Story of Mathematics: From Creating the Pyramids to Exploring Infinity. Arcturus Publishing Limited, 2009.
Chévrier, J. OPAŁKA 1965/1--∞, comme un memento mori à l’ère du digital. Available at Opałka.
Kemp, T. Cauchy’s construction of $R$ . Available at Cauchy.
Rudin, W.: Principles of Mathematical Analysis. Third Edition. International Series in Pure and Applied Mathematics. McGraw-Hill Book Co., New York - Aukland - Düsseldorf, 1976.
Descartes, R. Discours de la méthode. Jan Maire, Leiden, Netherlands, 1637.
Argand, J. R. Essai sur une manière de représenter des quantités imaginaires dans les constructions géométriques, chez Mme Vve Blanc, Paris. 1806; 2nd édition, Gauthier Villars, Paris, 1874; Imaginary Quantities: their geometrical interpretation, translated from the French by Prof. A. S. Hardy, New York, D. Van Nostrand Publisher, 1881.
Nahin, P. An Imaginary Tale: the Story of the Square Root of -1. Princeton: Princeton University Press, (1998).
Pauli, W. Zur Quantenmechanik des magnetischen Elektrons. Zeit. f. Phys. 1927, 43, 601–623. [Google Scholar] [CrossRef]
Renou, M.-O.; Trillo, D.; Weilenmann, M.; Thinh P. Le, T. P.; Tavakoli, A., Gisin, N.; Acín, A.; Navascués, M. Quantum theory based on real numbers can be experimentally falsified. Nature 2021, 600, 625–629. [CrossRef] [PubMed]
Gross, D. J. Symmetry in Physics: Wigner’s Legacy. Physics Today 1995, 12, 46–50. [Google Scholar] [CrossRef]
Angier, N. Emmy Noether, the Most Significant Mathematician You’ve Never Heard Of. Available at Emmy Noether.
Noether, E. Invariante Variationsprobleme. Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen Mathematisch-Physikalische Klasse 1918, 235–257.
Bacry, H.; Lévy-Leblond, J.-M. Possible Kinematics. J. Math. Phys. 1968, 9, 1605. [Google Scholar] [CrossRef]
Streater, R. F.; Wightman, A. S. PCT, spin and statistics, and all that. Princeton Landmarks in Mathematics and Physics, PUP (2001).
Curie, P. Sur la symétrie dans les phénomènes physiques, symétrie d’un champ électrique et d’un champ magnétique. J. Phys. Theor. Appl. 1894, 3, 393–415. [Google Scholar] [CrossRef]
Lévy-Leblond, J.-M. The Pedagogical Role and Epistemological Significance of Group Theory in Quantum Mechanics. Riv. Nuov. Cim. 1974, 4, 99–143. [Google Scholar] [CrossRef]
Lie, S. Theorie der Transformationsgruppen I (in German), Leipzig: B. G. Teubner (1888). Written with the help of Engel, F. Edited and translated from the German and with a foreword by Merker, J. arXiv:1003.3202.
Killing, W. Die Zusammensetzung der stetigen/endlichen Transformationsgruppen. Mathematische Annalen 1888, 31, 252–290; 1889, 33, 1–48; 1889, 34, 57–122; 1890, 35, 423–432; 1890, 36, 161–189; 1890, 36, 239–254. [CrossRef]
Cartan, E. Structure des groupes de transformations finis et continus. Thèse à la Faculté des Sciences de Paris, Nony, Paris (1894).
Maclay, G. J. Dynamical Symmetries of the H Atom, One of the Most Important Tools of Modern Physics: SO(4) to SO(4,2), Background, Theory, and Use in Calculating Radiative Shifts. Symmetry 2020, 12, 1323. [Google Scholar] [CrossRef]
Enayati, M.; Gazeau, J.-P.; Pejhan, H.; Wang, A. The de Sitter (dS) Group and its Representations, An Introduction to Elementary Systems and Modeling the Dark Energy Universe. Synthesis Lectures on Mathematics & Statistics (SLMS), Springer 2022.
Enayati, M.; Gazeau, J.-P.; del Olmo, M. A.; Pejhan, H. Anti-de Sitterian “massive” elementary systems and their Minkowskian and Newtonian limits. arXiv:2307.06690v1 [math-ph].
Cohen-Tannoudji, G; Gazeau, J.-P. Dark matter as a QCD effect in an anti de Sitter geometry: Cosmogonic implications of de Sitter, anti de Sitter and Poincaré symmetries. SciPost Phys. Proc. 2023, 14, 004.
Hamilton, W. R. On quaternions, or on a new system of imaginaries in algebra. Philos. Mag. 1844, 25, 489–495. [Google Scholar]
Girard, P. R. The quaternion group and modern physics. Eur. J. Phys. 1984, 5, 25–32. [Google Scholar] [CrossRef]
Girard, P. R.; Pujol, R.; Clarysse, P.; Delachartre, P. Hyperquaternions and physics. SciPost Phys. Proc. 2023, 14, 030. [Google Scholar] [CrossRef]
Cockle, J. On Systems of Algebra involving more than one Imaginary, Philos. Mag. 1849, 35, 434–435. [Google Scholar]
Brody, D. C.; Graefe, E.-M. On complexified mechanics and coquaternions. J. Phys. A: Math. Gen. 2011, 44, 072001. [Google Scholar] [CrossRef]
Weisstein, E. W. Icosian Game. From MathWorld–A Wolfram Web Resource. Available online: https://mathworld.wolfram.com/IcosianGame.html.
Lucas, E. Récréations Mathématiques, 2nd edition, Librairie scientifique et technique Albert Blanchard, Paris (1992).
Encyclopedia Britannica. Available at Platonic solid.
Coxeter, H. S. M. Regular Polytopes. Methuen. 2nd ed., 1948, Macmillan, 1963. 3rd ed., Dover (1973).
Moody, R. V.; Patera, J. Quasicrystals and icosians. J. Phys. A: Math. Gen. 1993, 26, 2829–2853. [Google Scholar] [CrossRef]
Barache, D.; Champagne, B.; Gazeau, J.-P. Pisot-Cyclotomic Quasilattices and their Symmetry Semi-Groups. Fields Institute Monograph Series 10, Ed. J. Patera, Amer. Math. Soc., pp. 15–66 (1998).
Papadopolos, Z.; Kasner, G.; Ledieu, J.; Cox, E. J.; Richardson, N. V.; Chen, Q.; Diehl, R. D.; Lograsso, T. A.; Ross, A. R.; McGrath, R. Bulk termination of the quasicrystalline fivefold surface of Al₇₀Pd₂₁Mn₉. Phys. Rev. B 2002, 66, 184207–184220. [Google Scholar] [CrossRef]
Gazeau, J. P. Pisot-cyclotomic integers for quasilattices. NATO ASI Series C Mathematical and Physical Sciences-Advanced Study Institute, 489, 175-198 (1997).
Burdík, Č.; Frougny, Ch.; Gazeau, J.-P.; Krejcar, R. Beta-integers as natural counting systems for quasicrystals. J. Phys. A: Math. Gen. 1998, 31, 6449–6472. [Google Scholar] [CrossRef]
Cayley, A. On Jacobi’s elliptic functions, in reply to the Rev. B. Brownwin; and on quaternions. Philos. Mag. 1845, 26, 208–211. [Google Scholar]
Baez, J. C. The Octonions. Bull. Amer. Math. Soc. 2002, 39, 145–205. [Google Scholar] [CrossRef]
Burdík, Č.; Catto, S.; Gürcan, Y.; Khalfan, A.; Nicolescu, B. Characterization of New Algebras Resembling Colour Algebras based on Split-Octonion units in the Classification of Hadronic Symmetries and Supersymmetries. J. Phys.: Conf. Ser. 2023, 2667, 012004. [Google Scholar] [CrossRef]
Hopf, H. Über die Abbildungen der dreidimensionalen Sphäre auf die Kugelfläche. Math. Ann. 1931, 104, 637–665. [Google Scholar] [CrossRef]
Lyons, D. W. An Elementary Introduction to the Hopf Fibration. Mathematics Magazine 2003, 76, 87–98. [Google Scholar] [CrossRef]
Mosseri, R.; Dandoloff, R. Geometry of entangled states, Bloch spheres and Hopf fibrations. J. Phys. A: Math. Gen. 2001, 34, 10243–10253. [Google Scholar] [CrossRef]
Bengtsson, I.; Brännlund, J.; Życzkowski, K. CPⁿ, or, Entanglement Illustrated. Int. J. Mod. Phys. A 2002, 17, 4675–4695. [Google Scholar] [CrossRef]
Dalhuisen, J. W. The Robinson Congruence in Electrodynamics and General Relativity, PhD thesis, U. Leiden, 2014. Available at Robinson Congruence.
Ornea, L.; Parton, M.; Piccinni, P.; Vuletescu, V. Spin(9) geometry of the octonionic Hopf fibration, Transformation Groups 2013, 18, 845–864.
Balmer, J. J. Notiz über die Spectrallinien des Wasserstoffs [Note on the spectral lines of hydrogen]. Annalen der Physik und Chemie. 3rd series 1885, 25, 80–87.
Fock, V. Zur Theorie des Wasserstoffatoms, Zeitschrift für Physik A Hadrons and Nuclei 1935, 98, 145–154.
Onofri, E. Dynamical quantization of the Kepler manifold. J. Math. Phys. 1976, 17, 401–409. [Google Scholar] [CrossRef]
Souriau, J. M. Sur la variété de Kepler. Symp. Math. 1974, 14, 343–360. [Google Scholar]
Dynkin, E. B. The structure of semi-simple algebras. Uspekhi Mat. Nauk, N.S. (in Russian) 1947, 2, 59–127. [Google Scholar]
Baez, J. This Week’s Finds in Mathematical Physics (Week 230). Available at Dynkin diagrams.

Figure 1. Rubik cube.

Figure 2. From https://chem.libretexts.org Licence CC BY-SA 4.0 DEED

Figure 3. Left: from Obs 7352 - Doc 9412 - Credits Roger CULOS - BY-NC-SA; Right from [[File:Chirality with hands.svg|thumb|Chirality with hands]]

Figure 4. Why does a mirror flip the left and right orientation of Ossola, while leaving the top-to-bottom arrangement unaffected? Answer is found at [10].

Figure 5. Andry is acquiring proficiency in the Hindu-Arabic numeral system, encompassing the digits from 0 to 9. See: On the Calculation with Hindu Numerals by al-Kwharizmi (about 825 AD) and On the Use of Indian Numerals by Abu Yusuf Yaqub Ibn Ishdaq al-Kindi (830 AD). Eventually the Hindu-Arabic way of writing numbers and computations replaced the Roman Numerals [11].

Figure 6. OPAŁKA, 1965, série /

1 - \infty

Détail, Acrylic on canvas.

Figure 6. OPAŁKA, 1965, série /

1 - \infty

Détail, Acrylic on canvas.

Figure 7. Five 2D lattice types. From 2d Bravais Licence CC BY-SA 3.0 DEED.

Figure 8. An illustration of atomic organisation of Graphene. From Pixabay: Graphite.

Figure 9. Proper rotation of vector

r

r^{'}

by angle

θ

about unit vector

n

in space

R^{3}

Figure 9. Proper rotation of vector

r

r^{'}

by angle

θ

about unit vector

n

in space

R^{3}

Figure 10. Dodecahedron and its dual, the icosahedron (left). With its twenty triangular faces, twelve vertices and thirty edges, the latter is one of the five Platonic Solids (right). From Don Steward: platonic solids and duals. Among the platonic solids (Theaetetus of Athens, 417- 369 BC; Plato, 428/427–348/347 BC; Euclid, fl. c. 300 BC; Johannes Kepler, 1571-1630), either the dodecahedron or the icosahedron may be seen as the best approximation to the sphere. Remind that a platonic solid is a convex polyhedron with vertices in a sphere

S_{r}^{2}

of radius r. The faces of a platonic solid are congruent regular polygons, with the same number of faces meeting at each vertex. All edges are congruent, as are its vertices and angles. See the celebrated Coxeter treatise [42] to know more about these objects.

S_{r}^{2}

Figure 11. Cut and Project trick is a method to get a quasiperiodic set in

R

from a lattice in

R^{2}

(From Cut&Project Fibonacci CC BY-NC-SA 2.0 Deed).

Figure 11. Cut and Project trick is a method to get a quasiperiodic set in

R

from a lattice in

R^{2}

(From Cut&Project Fibonacci CC BY-NC-SA 2.0 Deed).

Figure 12. Quasicrystalline five-fold surface of

{Al}_{70}

{Pd}_{21}

{Mn}_{9}

, from [45].

Figure 12. Quasicrystalline five-fold surface of

{Al}_{70}

{Pd}_{21}

{Mn}_{9}

, from [45].

Figure 13. First elements of

Z_{τ}

(tau-integers) around the origin and associated tiling.

Figure 13. First elements of

Z_{τ}

(tau-integers) around the origin and associated tiling.

Figure 14.

τ

-lattice

Γ_{2} (τ) : = Z_{τ} + e^{i π / 5} Z_{τ}

R^{2}

Figure 14.

τ

-lattice

Γ_{2} (τ) : = Z_{τ} + e^{i π / 5} Z_{τ}

R^{2}

Figure 15. The mathematical five-fold quasicrystal

Γ_{5} [τ] : = \sum_{n = 0}^{4} e^{i n π / 5} Z_{τ}

R^{2}

Figure 15. The mathematical five-fold quasicrystal

Γ_{5} [τ] : = \sum_{n = 0}^{4} e^{i n π / 5} Z_{τ}

R^{2}

Figure 16. Hopf fibration (from Niles Johnson CC BY 4.0). The described fiber bundle structure, succinctly represented as

S^{1} ↪ S^{3} \overset{p}{\to} S^{2}

, intricately intertwines the components of the fiber space

S^{1}

within the overarching structure of the total space

S^{3}

. The projection, denoted as p and referred to as Hopf’s map, serves as the intermediary, mapping the elements of

S^{3}

onto the base space

S^{2}

. In this visual representation, each fiber of

S^{1}

projects to a circle in three-dimensional space, with one such circle extending to infinity, forming what is termed a “circle through infinity” or effectively a line. The resulting arrangement fills space with a captivating array of tori (products of two circles), each of which is the stereographic projection of the inverse image of a latitude circle on

S^{2}

. The accompanying image on the right, depicting linked keyrings on the right, serves as an illustrative example of one of these tori. Points on

S^{2}

and their corresponding fibers are color-matched, providing a visual insight into the intricate and captivating structure induced by the Hopf fibration.

Figure 16. Hopf fibration (from Niles Johnson CC BY 4.0). The described fiber bundle structure, succinctly represented as

S^{1} ↪ S^{3} \overset{p}{\to} S^{2}

, intricately intertwines the components of the fiber space

S^{1}

within the overarching structure of the total space

S^{3}

. The projection, denoted as p and referred to as Hopf’s map, serves as the intermediary, mapping the elements of

S^{3}

onto the base space

S^{2}

. In this visual representation, each fiber of

S^{1}

S^{2}

. The accompanying image on the right, depicting linked keyrings on the right, serves as an illustrative example of one of these tori. Points on

S^{2}

and their corresponding fibers are color-matched, providing a visual insight into the intricate and captivating structure induced by the Hopf fibration.

Table 1. Nomenclature for the most current Lie groups and algebras. The symbol M

(n, K)

is for the algebra of

n \times n

matrices with coefficients in

K = Z, Q, R, C,

etc. Note that

J = (\begin{matrix} 0_{n} & 1_{n} \\ - 1_{n} & 0_{n} \end{matrix})

and that Sp

(n)

is frequently written as Sp

(2 n)

(M, g)

: Manifold M with metric g,

X (M)

: vector fields on M,

L_{X}

: Lie derivative,

(M, ω)

: Symplectic manifold M with symplectic 2-form

ω

Table 1. Nomenclature for the most current Lie groups and algebras. The symbol M

(n, K)

is for the algebra of

n \times n

matrices with coefficients in

K = Z, Q, R, C,

etc. Note that

J = (\begin{matrix} 0_{n} & 1_{n} \\ - 1_{n} & 0_{n} \end{matrix})

and that Sp

(n)

is frequently written as Sp

(2 n)

(M, g)

: Manifold M with metric g,

X (M)

: vector fields on M,

L_{X}

: Lie derivative,

(M, ω)

: Symplectic manifold M with symplectic 2-form

ω

Lie Group	Lie Algebra
General Linear Group:
$GL (n, K) = {A \in M (n, K), \det A \neq 0}$	$gl (n, K) = {A \in M (n, K)}$
Special Linear Group:
$SL (n, K) = {A \in GL (n, K), \det A = 1}$	$sl (n, K) = {A \in gl (n, K), Tr A = 0}$
Special Orthogonal Group:
$SO (n, K) = {A \in SL (n, K), A^{t} A = 1_{n}}$	$so (n, K) = {A \in sl (n, K), A +^{t} A = 0}$
Special Unitary Group:
$SU (n) = {A \in SL (n, C), A A^{†} = 1_{n}}$	$su (n) = {A \in sl (n, C), A + A^{†} = 0}$
Symplectic Group:
$Sp (n) = {A \in GL (2 n, R), A J^{t} A = J}$	$sp (n) = {A \in gl (2 n, R), A J + J^{t} A = 0}$
Group of Isometries of $(M, g)$ :
$G = {ϕ : M \mapsto M \| ϕ preserves g}$	$g = {X \in X (M) \| L_{X} g = 0}$
Group of Symplectomorphisms of $(M, ω)$ :
$G = {ϕ : M \mapsto M \| ϕ^{*} ω = ω}$	$g = {X \in X (M) \| L_{X} ω = 0}$

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

The Language of Spheres in Physics

Abstract

1. Introduction

2. Semi-Groups and Groups

2.1. Definitions

2.2. Example: Chirality

2.3. Building Groups from Subgroups

2.4. Group Cosets

2.5. Group Actions

3. Numbers and Groups

3.1. Sets N , Z , Z p

3.2. Example: Cubic Relations

3.3. Set Q

3.4. Q Is Not “Complete”

3.5. Unreal “Real” Numbers Complete Real Rationals!

3.6. C Is Complete and “Algebraically Closed”

3.7. Complex Numbers Emerging from Tensor Product of Two Planes

3.8. 2D Lattices

3.8.1. General

3.8.2. Graphene example

4. Symmetry and Group(s)

4.1. Symmetry in Physics

4.2. Lie Groups and Lie Algebras

4.3. Physics and Low-Dimensional Root Systems

5. Playing with Spheres

5.1. The Circle and Its Complexified Version

5.2. The Sphere S 3 through Its Multifaceted Aspects

5.2.1. Sphere S 3 and Group SU ( 2 )

5.2.2. Sphere S 3 and Rotations in R 3

5.3. Sphere S 3 and Quaternions (Hamilton, 1843)

5.4. Quaternions and Space Rotations

5.5. Coquaternions (Cockle, 1849) versus Quaternions

5.6. Complex Quaternions

5.7. The Complexified Sphere S C 3

5.8. The Sphere S 3 , Its Icosians and Its Icosian Ring

5.9. The Root System E 8 and Quasicrystals

5.10. Algebraic Modelling of Quasicrystals

5.11. Sphere S 7 and Octonions (Graves, 1843, Cayley, 1845)

6. Higher Spheres and Hopf Maps and Fibrations

6.1. Hopf Fibrations

6.2. Group Interpretation of the First Hopf Map: S 3 → p S 2

6.3. Group Interpretation of the Second Hopf Map: S 7 → p S 4

6.4. Group Interpretation of the Third Hopf Map: S 15 → p S 8

7. Kepler-Coulomb Problem and Spheres

7.1. 1-Dimensional Kepler-Coulomb Problem

7.2. Phase Space of the Regularized 1d-Kepler-Coulomb Problem: The Complexified Circle with Zero Radius

7.3. Phase Space of the Three-Dimensional Regularized Kepler-Coulomb Problem

8. Conclusions

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Acknowledgments

Conflicts of Interest

Abbreviations

Appendix A. Group Actions

Appendix B. Lie Algebra Material

Appendix B.1. General

Appendix B.2. Roots and Cartan Classification

Appendix B.3. Dynkin Diagrams: General

Appendix B.4. From Top to Bottom, Dynkin Diagrams for An, Bn, Cn, Dn

Appendix B.5. Dynkin Diagrams G2, F4, E6, E7, E8

Appendix B.6. Examples: Roots A1 × A1, A2, B2

Appendix B.7. Examples: Roots C2, D2, G2

References

MDPI Initiatives

Important Links

Subscribe

3.1. Sets $N$ , $Z$ , $Z_{p}$

3.3. Set $Q$

3.4. $Q$ Is Not “Complete”

3.6. $C$ Is Complete and “Algebraically Closed”

5.2. The Sphere $S^{3}$ through Its Multifaceted Aspects

5.2.1. Sphere $S^{3}$ and Group SU $(2)$

5.2.2. Sphere $S^{3}$ and Rotations in $R^{3}$

5.3. Sphere $S^{3}$ and Quaternions (Hamilton, 1843)

5.7. The Complexified Sphere $S_{C}^{3}$

5.8. The Sphere $S^{3}$ , Its Icosians and Its Icosian Ring

5.9. The Root System $E_{8}$ and Quasicrystals

5.11. Sphere $S^{7}$ and Octonions (Graves, 1843, Cayley, 1845)

6.2. Group Interpretation of the First Hopf Map: $S^{3} \overset{p}{\to} S^{2}$

6.3. Group Interpretation of the Second Hopf Map: $S^{7} \overset{p}{\to} S^{4}$

6.4. Group Interpretation of the Third Hopf Map: $S^{15} \overset{p}{\to} S^{8}$

Appendix B.4. From Top to Bottom, Dynkin Diagrams for A_n, B_n, C_n, D_n

Appendix B.5. Dynkin Diagrams G₂, F₄, E₆, E₇, E₈

Appendix B.6. Examples: Roots A₁ × A₁, A₂, B₂

Appendix B.7. Examples: Roots C₂, D₂, G₂