Prerpints.org logo
Preprint
Article

Vertical Center-of-Mass Braking and Motor Performance during Gait Initiation in Young Healthy Adults, Elderly Healthy Adults and Patients with Parkinson’s Disease: A Comparison of Force-Plate and Markerless Motion Capture Systems

Altmetrics

Downloads

99

Views

45

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

12 January 2024

Posted:

12 January 2024

You are already at the latest version

Alerts
Abstract
Background. The markerless motion capture system (MLS) is a new technology that uses deep learning to detect body segments from digital images. This study tested the agreement between the MLS and a force-plate based system (FPS, “gold standard”) to quantify stability control and motor performance (MP) during gait initiation (GI). Methods. Healthy adults (young and elderly) and patients with Parkinson’s disease (PD) performed GI series at spontaneous and maximal velocity on an FPS while being filmed by an MLS. Signals from both systems were used to compute the peak of forward center-of-mass velocity (indicator of MP) and the braking index (BI, indicator of stability control). Results. Descriptive statistics indicated that both systems detected between-groups differences and velocity effects similarly, while a Bland-Altman (BA) plot anal-ysis showed that BI and MP mean biases were virtually zero in all groups and conditions. Bayes factor 01 indicated strong (for BI) and moderate (for MP) evidence that both systems provided equivalent values. However, trial-by-trial analysis of BA plots revealed the possibility of differ-ences > 10% between the two systems. Conclusion. Although non-negligible differences do occur, MLS appears to be as efficient as FPS in detecting PD and velocity condition effects on BI and MP
Keywords: 
Subject: Public Health and Healthcare  -   Other

1. Introduction

Locomotion is a complex task that requires body stabilization and body propulsion simultaneously. Gait initiation, the transient period between a quiet standing posture and steady-state walking [1], is a locomotor task classically used in the literature to investigate the capacity of individuals to meet these two requirements. This capacity can be evaluated using biomechanical indicators.
A biomechanical indicator of body propulsion capacity is the peak velocity of the center of mass along the progression direction [1]. According to the laws of mechanics, this velocity reflects the total amount of propulsive forces applied to the body during the gait initiation process. As an extension, this indicator is used to quantify motor performance of gait initiation.
The braking index, introduced by Do and colleagues [2], is a biomechanical indicator of body stabilization capacity. These authors reported that the vertical velocity of the center of mass reaches a downward-oriented peak at around mid-execution, which had previously been ascribed to center-of-mass fall under the gravity effect. Velocity reverses direction to reach a value close to zero at the time of swing-foot contact, indicating that the fall of the center of mass is actively braked. The central nervous system (CNS) thus prepares for swing-foot contact by reducing the center of mass's vertical velocity in order to create a smooth landing and attenuate the mechanical transmission of the impact of vertical force through the whole body. The braking index reflects this capacity of the CNS to brake the center of mass fall.
These two velocity-based indicators have been used extensively in the literature to quantify the postural disorders that occur in physiological aging [3,4,5] and in various neurological conditions, such as Parkinson’s disease [6], stroke [7], supranuclear palsy [8], etc. To compute these indicators, researchers currently use two systems and related methods: the “Force-Plate” system (FPS) and the “Marker-Based motion capture” system (MBS). In the FPS method, ground reaction forces are recorded with a force-plate to compute the three-dimensional (3D) instantaneous acceleration of the center of mass (according to Newton’s second law). The 3D center-of-mass velocity is then obtained through single integration of this signal. This method has been used widely in both healthy [1,9,10,11,12,13,14,15] and pathological subjects [8,16,17,18,19], and can be considered the “gold standard” to measure the braking index and motor performance of gait initiation. This method offers at least two advantages: i) it requires no body preparation, thus reducing the duration of the experiments, and ii) it requires no approximation of the location of the center of mass of each body segment to compute the whole-body center of mass kinematics, as is the case for the MBS. However, this method has at least three drawbacks: i) it provides no information on body segment kinematics, ii) it requires highly trained operators for data processing, and iii) to record the entire gait initiation process, step length must not exceed the dimensions of the force-plate (which may be an issue when subjects initiate gait at maximal velocity on a single, small force plate).
The MBS typically tracks reflective markers that are attached to the skin (or clothing) using the infrared cameras of a motion capture system to estimate the 3D motion of body segments. A conventional MBS requires thirty-eight markers to compute the whole-body center-of-mass position [20]. In the MBS, this positional signal is then derived to obtain the 3D whole-body center-of-mass velocity. One advantage of the MBS is that it can provide information on both whole-body center of mass and body segment kinematics during gait initiation [11,21]. However, the MBS does have several significant drawbacks. It requires extensive experimental set-up, particularly due to the large number of markers required, which can be a serious issue in experiments involving frail participants who may quickly become tired and/or bored. The MBS also requires a controlled environment [22,23] that may alter participants’ natural movements, due to their awareness of being observed [24]. In addition, the literature stresses that the potential misplacement of markers and the skin motion relative to bones may lead to inaccuracies on whole-body center-of-mass kinematics [25,26,27,28]. Finally, like the FPS, the MBS is expensive, requires time-intensive data processing that can introduce errors [22,23,24,29,30,31], and requires highly trained operators for data processing.
So, there is currently a need to develop more accessible systems that provide researchers and clinicians reliable values of whole-body kinematics to compute the braking index and motor performance of gait initiation.
The Markerless Motion Capture System (MLS) is a recent, innovative technology that has shown potential in overcoming the limitations of FPS and MBS mentioned above. The MLS uses standard video and deep learning-based software instead of infrared cameras to detect body segment landmarks directly from digital images [32,33,34,35,36]. Thus, it eliminates many of the manual processing steps and sources of error inherent to the MBS. Recent studies have investigated the reliability of the MLS in quantifying 3D lower-limb joint kinematics and/or kinetics during various locomotor tasks [35,37,38,39,40]. These studies typically compared data obtained from an MLS vs. an MBS in young healthy adults, with sometimes contrasting results. For example, in Kanko et al. [35], participants performed sessions of over-ground walking trials separated by an average of 8.5 days. 3D pose estimations from an MLS were used to compute lower-limb joint angles. These authors showed that the gait kinematics data provided by this system were as reliable as those from the MBS, as assessed with inter-session variability, inter-trial variability and variability ratio between sessions. Kanko et al. [39] further showed that these two systems provided average distance root mean square (DRMS) between corresponding joint centers less than 2.5 cm for all joints except the hip, which was 3.6 cm. Lower-limb segment angles indicated that the segment pose estimations from both systems were very similar, with DRMS of less than 5.5° for all segment angles except those representing rotations about the long axis of the segment. Ito et al. [37] added that, during walking, squatting and forward hopping, sagittal plane angles were most comparable between the MBS and the MLS at the knee joint followed by the ankle and hip, while frontal and transverse plane angles were not. Song et al. [40] concurrently captured lower-limb kinematics in participants performing eight daily living and exercise movements. These authors found that the estimates from the MLS were very similar to the MBS in the ankle and knee joint angles and moments. There were more differences between the two systems for hip angles and moments, especially during rapid movements such as running. Finally, Tang et al. [38] reported that, during walking on a treadmill, the MLS provided higher values than the MBS for peak hip extension and flexion moments, but, in contrast to Song et al. [40], it also provided higher values for the knee-flexion moment and ankle-plantarflexion moment (along with higher joint powers).
In addition to these disparate results concerning the reliability of the MLS, it is worth noting that these studies systematically used the MBS as the gold standard of the measures. Also, only the kinematics (and/or the kinetics) of lower limb joints in young healthy adults were considered. Therefore, the question of whether the MLS is a reliable technique for computing whole-body center-of-mass kinematics during gait initiation—and associated braking index and motor performance—in both young healthy adults and patients with postural disorders, remains to be clarified.
So, this study tested the agreement between the MLS and the FPS (considered here as the gold standard) to estimate the braking index and motor performance during gait initiation in healthy adults (both young and elderly) and in patients with Parkinson’s disease (PD). This agreement was investigated using the following statistical methods: the Bland-Altman (BA) method (classically used to compare two different measurement techniques [41]), classical descriptive statistics, and the Bayes factor 01. The Bayes factor 01 is a ratio between two competing statistical models represented by their evidence. It is used to quantify support for one model over the other [42]. In this study, it was used to contrast the two following hypotheses: H0 (the “null hypothesis”, i.e., both systems provide the same braking index and motor performance) vs. H1 (the “alternative hypothesis”, i.e., both systems provide different braking index and motor performance). Note that with the Bayes factor 01, evidence can be quantified in favor of or against a null hypothesis, which cannot be done using the p-value provided by classical descriptive statistics.

2. Materials and Methods

Participants

Three groups of participants (n=33) were involved in this experiment: young healthy adults (YH), elderly healthy adults (EH) and patients with Parkinson’s disease (PD) (cf. Table 1 for the anthropometrical features and evaluation scores of the PD patients). The exclusion criteria were as follows: walking with aids, visual, hearing, or orthopedic problems, identified neurological disorders (other than Parkinson’s), dementia, cognitive impairments (i.e., a score < 25 on the Mini Mental State Exam and Montreal Cognitive Assessment), and a medical history of falling. All of the participants gave their written consent after having been informed of the nature and purpose of the experiment, which was approved by local ethics committees from the Université Paris-Saclay. The study complied with the standards established by the Declaration of Helsinki.

Experimental set-up, tasks and conditions

The experiments were conducted in the Biomechanics laboratory of the LADAPT Loiret rehabilitation center (Amilly, France). The physical conditions (room temperature and time of day) were the same for all participants. The participants initially stood barefoot on a force plate with a second force plate positioned in front of it. This system of two force plates in series allowed biomechanical recordings of the entire gait initiation process. Both force plates (0.4 × 0.60 m, AMTI, Watertown, USA) were embedded at the beginning of a six-meter-long walking track (Figure 1). A markerless motion capture system (MLS) equipped with 12 cameras (Qualisys, Göteborg, Sweden) was synchronized with both force plates and recorded the participants’ complete motion on the walking track. The data obtained by the cameras was then transferred to Theia software (Theia3D, Kingston, Canada), which reconstructed body kinematics. The signals from these two systems were used to compute the participants’ whole-body center-of-mass kinematics (cf. “Raw data processing”).
In the initial standing posture, the feet were positioned shoulder-width apart, the arms rested alongside the trunk and the gaze was directed forward to a small target at eye level (2 cm diameter, 6 m away). The locations of the heel and big toe of each foot were marked on the first force plate with strips of adhesive tape and were used as a visual reference on which the participants positioned themselves after each trial under the supervision of the experimenters. From this initial posture, the participants performed series of gait initiation in a “spontaneous velocity condition” (SVC, n=5 trials) and in a “maximal velocity condition” (MVC, n=5 trials).
In both velocity conditions, the participants initiated gait at their own initiative following an auditory signal delivered by the experimenter, and then continued walking straight ahead until they reached the end of the track. One practice trial was conducted in each velocity condition (not recorded) to ensure that the participants clearly understood the instructions and that the material was operational. A 10-second rest time between trials, and a 2-minute rest time between velocity conditions were imposed to avoid the effects of fatigue. Both conditions of velocity were randomized across participants to avoid any rank effects. Visualization of the task and the experimental force-plates set-up can be found in Simonet et al. [13].

Raw data processing

Force-plate system. The FPS recorded the 3D components of the ground reaction force (GRF) and moment vector acting at the surface of each force plate. The instantaneous 3D components of the GRF vector recorded by each force plate were algebraically summed to obtain the 3D components of the “global” GRF vector, i.e., the GRF acting on the whole-body center of mass. The instantaneous acceleration of the center of mass along the anteroposterior and vertical direction were computed from this vector according to Newton’s second law [13]. To obtain the vertical acceleration of the center of mass, the participant’s weight was subtracted from the vertical component of this GRF vector. The instantaneous center-of-mass velocity along the anteroposterior and vertical direction was computed by single numerical integration of the center-of-mass acceleration using the rectangles method and considering the initial center-of-mass velocity as null.
Markerless motion capture system. The MLS recorded the full-body 3D kinematic. The instantaneous center-of-mass (COM) velocity along the vertical direction (z’COM(t)) was computed as follows:
z’COM(t) = [zCOM(t) – zCOM(t-1)]/F
Where zCOM(t), zCOM(t-1): vertical position of the center of mass at time t and at the previous frame (t-1), respectively; F: acquisition frequency.
Similarly, the instantaneous center of mass velocity along the anteroposterior direction (x’COM(t)) was computed as follows:
x’COM(t) = [xCOM(t) – xCOM(t-1)]/F
Where xCOM(t), xCOM(t-1): anteroposterior position of the center of mass at time t and at the previous frame (t-1), respectively; F: acquisition frequency.
The acquisition frequency was 85 Hz for the MLS and 85 Hz for the FPS. Data were filtered with a no-lag low-pass Butterworth order filter with a 15 Hz cut-off frequency. Qualisys Track Manager (QTM) software was used to synchronize the signals from both systems.

Experimental variables

Braking index. The braking index (BI) reflects the CNS’s ability to actively brake the vertical fall of the center of mass under gravity [16,17,18,19]. It is a classical indicator of stability control that is computed as follows:
BI = [Vzmin—VzFC]/Vzmin
Where Vzmin, VzFC: peak of downward center-of-mass vertical velocity, vertical center-of-mass velocity at foot contact, respectively (Figure 2).
Motor Performance. Motor performance corresponds to the peak of the anteroposterior center-of-mass velocity (Figure 2). The braking index and motor performance were computed with the FPS and MLS.

Statistics

To investigate the agreement between the FPS and the MLS, a Bland-Altman (BA) analysis was conducted on a trial-by-trial basis within each group (i.e., PD, young healthy adults and elderly healthy adults) and experimental condition of velocity (i.e., SVC, MVC). The values provided by the FPS were considered as the gold standard against which the values provided by the MLS were compared. BA plots were generated, with the horizontal axis representing the average of the braking index (BI) values (or motor performance) obtained with the FPS and the MLS ([BI-MLS + BI-PFS]/2), and the vertical axis representing the difference between the two methods (BI-PFS minus BI-MLS]). The accuracy of the MLS was estimated with bias, corresponding to the mean difference (d) and the standard deviation of the differences (SD). The normality of the differences was checked using the Shapiro–Wilk test. The reliability of the MLS was estimated with the dispersion of the differences within each plot, as quantified with the 95% limits of agreement. These limits corresponded to d+1.96 SD (upper limit) and d-1.96 SD (lower limit). Absolute and relative values of the biases and agreement limits were reported.
The BA analysis was completed by descriptive statistics, which included means and standard deviations of the braking index, motor performance and corresponding biases. Repeated measures (RM) ANOVAs with the velocity (two levels: SVC vs. MVC) and the system (two levels: MLS vs FPS) as within-subjects factor, and the group (three levels: YH vs. EH vs. PD) as between-subjects factor, were conducted on each variable. Tukey post hoc tests were used when necessary. The alpha level was set at 0.05.
Finally, the Bayes factor 01 was computed for each variable to contrast the following hypotheses: H0 (the null hypothesis, i.e., “both systems provide the same braking index and motor performance”) vs. H1 (the alternative hypothesis, i.e., “both systems provide different braking index and motor performance”). It is generally admitted that if the Bayes factor 01 is above 3, then the null hypothesis is in evidence [43].

3. Results

Description of the biomechanical traces

Visual analysis of the traces reported in Figure 2 shows that the global time courses of the velocity of anteroposterior and vertical center of mass obtained with the FPS and the MLS were very similar. They were also very similar across the three groups (YH, EH, PD) and the two velocity conditions (only the maximal velocity condition is shown in Figure 2). More specifically, the velocity of vertical center of mass reached two successive downward-oriented peaks, the first approximately a few milliseconds before swing-foot off, and the second (larger) before swing-foot contact. The direction of the velocity trace then reversed, showing that the fall of the center of mass was actively braked before foot contact. The anteroposterior center-of-mass velocity increased to reach peak velocity a few milliseconds after swing-foot contact.

Bland-Altman analysis

Braking index. In the spontaneous velocity condition (Figure 3, left), Bland-Altman analysis showed that 95% of the absolute differences between the two systems ranged between -0.06 and 0.12 m/s for the YH group (which corresponded to a range of relative differences of between -7 and 14%), -0.12 and 0.11 m/s for the EH group (-17 and 16%) and -0.13 and 0.12 m/s for the PD group (-28 and 24%). In the maximal velocity condition (Figure 3, right), Bland-Altman analysis showed that 95% of the absolute differences between the two systems ranged between -0.12 and 0.14 m/s for the YH group (-25 and 20%), -0.12 and 0.11 m/s for the EH group (-16 and 14%) and -0.12 and 0.14 m/s for the PD group (-27 and 25%). Therefore, the limits of relative agreement were greater for the PD group than for the two healthy groups. The absolute and relative biases were virtually zero in each velocity condition and group.
Motor performance. In the spontaneous velocity condition (figure 4, left), Bland and Altman analysis showed that 95% of the absolute differences between the two systems ranged between -0.10 and 0.05 m/s for the YH group (which corresponded to a range of relative differences between -9 and 5 %), -0.12 and 0.06 m/s for the EH group (-12 and 6 %) and -0.13 and 0.05 m/s for the PD group (-15 and 6 %). In the maximal velocity condition (figure 4, right), Bland and Altman analysis showed that 95% of the absolute differences between the two systems ranged between -0.12 and 0.07 m/s for the YH group (--8 and 5 %), -0.16 and 0.13 m/s for the EH group (-12 and 9 %) and -0.17 and 0.07 m/s for the PD group (-16 and 7 %). The absolute and relative biases were virtually zero in each velocity condition and group.

Descriptive statistics

Braking index. RM ANOVAs showed that there was a significant main effect of the group (F2,104 = 9.8, p < 0.001), with no significant main effect of the system or the velocity on the braking index. Post hoc testing further showed that the braking index was significantly higher in both the YH and the EH group than in the PD group in both the spontaneous velocity and the maximal velocity condition. It also showed that this between-group difference was detected similarly by both systems (cf. Figure 5 for details on the post hoc tests). There was no significant velocity X group, system X group, system X velocity, or system X velocity X group interaction.
Motor Performance. RM ANOVAs showed that there was no significant main effect of the system, but there was a significant main effect of the group (F2,104 = 51.3, p < 0.001) and the velocity (F1,104 = 250.2, p < 0.001) on motor performance. Post hoc testing further showed that performance decreased significantly between the YH group and the PD group and, as expected, it was higher in the maximal velocity condition than in the spontaneous velocity condition (cf. Figure 6 for details on post hoc testing). There was also a significant group X velocity interaction on this variable (F2,104 = 6.8 p < 0.001). Post hoc testing showed that this interaction could be ascribed to the results that motor performance was not significantly different between the EH group and the PD group in the spontaneous velocity condition, while it was significantly higher in both the YH and the EH group than in the PD group in the maximal velocity condition (Figure 5). There was no significant system X group, system X velocity, or system X velocity X group interaction on this variable. Globally taken, these results show that both systems detected the same between-groups and velocity differences in motor performance. Globally taken, these results show that the two systems detected the same between-groups and velocity differences in motor performance.

Bayes factor01

Braking index. The computation of the Bayes factor 01 (Figure 7) shows that the null hypothesis (H0 = “there is no difference of braking index between both systems”) was 11.18 times as likely as the alternative hypothesis (H1 = “there is a difference of braking index between both systems”), corresponding to “strong evidence”.
Motor performance. The computation of the Bayes factor 01 applied to motor performance (Figure 8) shows that the null hypothesis (H0 = “there is no difference of motor performance between both systems”) was 5.55 times as likely as the alternative hypothesis (H1 = “there is a difference of motor performance between both systems”), corresponding to “moderate evidence”.

4. Discussion

This study tested agreement between the MLS and the FPS (considered as the gold standard) to estimate the braking index and motor performance during gait initiation in healthy adults (both young and elderly) and in PD patients. Agreement was investigated using the BA method and classical descriptive statistics, and was further tested by the Bayes factor 01.
Visual analysis of Figure 2 (mean of five gait initiation trials obtained in a representative participant of each group in the maximal velocity condition) showed that there was a good superimposition of the center-of-mass velocity time-course traces when computed with the MLS and the PFS, thus suggesting the existence of good agreement between the two measurement systems. Similar visual agreement between the time-course traces was also observed in the three groups when gait was initiated at a spontaneous velocity (not shown in Figure 2). The results of the different statistical methods used in this study to compare both measurement systems are in line with these visual observations. Descriptive statistics indicated that there was no significant main effect of the system on either the braking index or on motor performance. In addition, BA analysis showed that the mean biases of both variables were virtually zero in the spontaneous and maximal velocity conditions and for all groups, indicating that the accuracy of the MLS was good. Computation of the Bayes factor 01 further showed that there was strong evidence for the braking index and moderate evidence for motor performance that both systems provided the same values.
However, the results regarding the relative 95% limits of agreement, which reflect the dispersion of the differences between the two systems, attenuate the statement that the MLS may be used in place of the FPS to measure the braking index and motor performance for all groups and velocity conditions. It can be assumed that these relative limits should be lower than an arbitrary upper 10% value (in absolute value) to validate the reliability of the alternative system [e.g., [44] i.e., the MLS in this experiment. Considering the braking index, the results showed that the upper relative limit (in absolute value) reached 14%, 17% and 28% in the YH, EH and PD groups, respectively, when gait was initiated at a spontaneous velocity (app. m/s), and 25%, 16% and 27% in the YH, EH and PD group, respectively, when gait was initiated at maximal velocity (app. m/s). Thus, the 10% threshold was systematically exceeded, especially in the PD group, which calls into question the reliability of the MLS to measure the braking index.
Considering motor performance, the results showed that the upper relative limit reached 9%, 12% and 15% in the YH, EH and PD groups, respectively, when gait was initiated at a spontaneous velocity, and 8%, 12% and 16% in the YH, EH and PD groups, respectively, when gait was initiated at maximal velocity. Therefore, measurement of motor performance by the MLS was reliable for the YH group in both velocity conditions. By contrast, the upper relative limit slightly exceeded the 10% threshold for the EH and PD groups, which calls into question the reliability of the MLS to measure motor performance. The better reliability on motor performance as compared to reliability on the braking index likely arises from the different expressions of these two variables, involving either two measurements (the peak of downward center-of-mass velocity and the vertical center-of-mass velocity at foot contact, for the braking index), or a single measure (the anteroposterior peak of the center of mass for motor performance), and therefore as many biases.
We should emphasize that the descriptive statistics further revealed a main effect of the group on the braking index, with no significant main effect of the system or velocity on this variable. In other words, both systems detected the same group effect, with post hoc tests revealing a higher value in both healthy groups than in the PD group, in both the spontaneous and maximal velocity condition. This altered capacity to brake the center-of-mass fall in PD patients has been repeatedly reported in the literature with FPS [16,17] and is thought to reflect a deficit in postural stability control [21,45,46,47]. Thus, the results of this experiment show that the MLS is as efficient as FPS in revealing this deficit in PD patients. The descriptive statistics also revealed no significant main effect of the system, but a significant main effect of the group and velocity on motor performance. More specifically, both systems similarly detected that motor performance decreased from the YH group to the PD group and increased from the spontaneous to the maximal velocity condition. Both results are consistent with the literature [1,16,17]. Globally taken, these results show that both systems detected the same between-groups difference and velocity effects for the braking index and performance.

5. Conclusions

In conclusion, the results of this study suggest that, although non-negligible differences in the braking index and motor performance do occur between the two systems, the MLS is as efficient as the FPS in detecting an effect of PD and velocity on the braking index and motor performance. These results add to the current literature by showing that the MLS is as reliable as the MBS in computing lower-limb kinematics during various locomotor activities, such as walking, squatting, forward hopping [35,37,38,39,40], etc. These results might be very useful for studies investigating postural control during gait initiation in a research or clinical setting.

References

  1. Brenière, Y.; Cuong Do, M.; Bouisset, S. Are Dynamic Phenomena Prior to Stepping Essential to Walking? J Mot Behav 1987, 19, 62–76. [Google Scholar] [CrossRef] [PubMed]
  2. Do, M.C.; Breniere, Y.; Brenguier, P. A Biomechanical Study of Balance Recovery during the Fall Forward. J Biomech 1982, 15, 933–939. [Google Scholar] [CrossRef] [PubMed]
  3. Chong, R.K.Y.; Chastan, N.; Welter, M.-L.; Do, M.-C. Age-Related Changes in the Center of Mass Velocity Control during Walking. Neurosci Lett 2009, 458, 23–27. [Google Scholar] [CrossRef] [PubMed]
  4. Muir, B.C.; Rietdyk, S.; Haddad, J.M. Gait Initiation: The First Four Steps in Adults Aged 20–25 Years, 65–79 Years, and 80–91 Years. Gait & Posture 2014, 39, 490–494. [Google Scholar] [CrossRef]
  5. Singer, J.C.; Prentice, S.D.; McIlroy, W.E. Age-Related Changes in Mediolateral Dynamic Stability Control during Volitional Stepping. Gait & Posture 2013, 38, 679–683. [Google Scholar] [CrossRef]
  6. Delval, A.; Tard, C.; Defebvre, L. Why We Should Study Gait Initiation in Parkinson’s Disease. Neurophysiologie Clinique/Clinical Neurophysiology 2014, 44, 69–76. [Google Scholar] [CrossRef]
  7. Delafontaine, A.; Vialleron, T.; Hussein, T.; Yiou, E.; Honeine, J.-L.; Colnaghi, S. Anticipatory Postural Adjustments During Gait Initiation in Stroke Patients. Front Neurol 2019, 10, 352. [Google Scholar] [CrossRef]
  8. Welter, M.-L.; Do, M.C.; Chastan, N.; Torny, F.; Bloch, F.; du Montcel, S.T.; Agid, Y. Control of Vertical Components of Gait during Initiation of Walking in Normal Adults and Patients with Progressive Supranuclear Palsy. Gait Posture 2007, 26, 393–399. [Google Scholar] [CrossRef]
  9. Breniere, Y.; Do, M.C. When and How Does Steady State Gait Movement Induced from Upright Posture Begin? J Biomech 1986, 19, 1035–1040. [Google Scholar] [CrossRef] [PubMed]
  10. Gélat, T.; Coudrat, L.; Le Pellec, A. Gait Initiation Is Affected during Emotional Conflict. Neurosci Lett 2011, 497, 64–67. [Google Scholar] [CrossRef]
  11. Honeine, J.-L.; Schieppati, M.; Gagey, O.; Do, M.-C. By Counteracting Gravity, Triceps Surae Sets Both Kinematics and Kinetics of Gait. Physiol Rep 2014, 2, e00229. [Google Scholar] [CrossRef] [PubMed]
  12. Lepers, R.; Brenière, Y.; Maton, B. Changes to the Gait Initiation Programme Following a Running Exercise in Human Subjects. Neurosci Lett 1999, 260, 69–73. [Google Scholar] [CrossRef] [PubMed]
  13. Simonet, A.; Delafontaine, A.; Fourcade, P.; Yiou, E. Postural Organization of Gait Initiation for Biomechanical Analysis Using Force Platform Recordings. J Vis Exp 2022. [Google Scholar] [CrossRef]
  14. Stins, J.F.; Beek, P.J. Organization of Voluntary Stepping in Response to Emotion-Inducing Pictures. Gait Posture 2011, 34, 164–168. [Google Scholar] [CrossRef] [PubMed]
  15. Yiou, E.; Do, M.-C. Effects of Medio-Lateral Postural Perturbation Induced by Voluntary Arm Raising on the Biomechanical Organization of Rapid Step Initiation. Motor Control 2011, 15, 507–524. [Google Scholar] [CrossRef] [PubMed]
  16. Chastan, N.; Do, M.C.; Bonneville, F.; Torny, F.; Bloch, F.; Westby, G.W.M.; Dormont, D.; Agid, Y.; Welter, M.-L. Gait and Balance Disorders in Parkinson’s Disease: Impaired Active Braking of the Fall of Centre of Gravity. Mov Disord 2009, 24, 188–195. [Google Scholar] [CrossRef] [PubMed]
  17. Chastan, N.; Westby, G.W.M.; Yelnik, J.; Bardinet, E.; Do, M.C.; Agid, Y.; Welter, M.L. Effects of Nigral Stimulation on Locomotion and Postural Stability in Patients with Parkinson’s Disease. Brain 2009, 132, 172–184. [Google Scholar] [CrossRef] [PubMed]
  18. Delafontaine, A.; Fourcade, P.; Zemouri, A.; Diakhaté, D.G.; Saiydoun, G.; Yiou, E. In Patients With Parkinson’s Disease in an OFF-Medication State, Does Bilateral Electrostimulation of Tibialis Anterior Improve Anticipatory Postural Adjustments During Gait Initiation? Front Hum Neurosci 2021, 15, 692651. [Google Scholar] [CrossRef]
  19. Vialleron, T.; Delafontaine, A.; Millerioux, I.; Memari, S.; Fourcade, P.; Yiou, E. Acute Effects of Short-Term Stretching of the Triceps Surae on Ankle Mobility and Gait Initiation in Patients with Parkinson’s Disease. Clin Biomech (Bristol, Avon) 2021, 89, 105449. [Google Scholar] [CrossRef]
  20. Jan, S.V.S. Color Atlas of Skeletal Landmark Definitions: Guidelines for Reproducible Manual and Virtual Palpations; Churchill Livingstone/Elsevier, 2007; ISBN 978-0-443-10315-5.
  21. Honeine, J.-L.; Schieppati, M.; Gagey, O.; Do, M.-C. The Functional Role of the Triceps Surae Muscle during Human Locomotion. PLoS One 2013, 8, e52943. [Google Scholar] [CrossRef]
  22. Buckley, C.; Alcock, L.; McArdle, R.; Rehman, R.; Del Din, S.; Mazzà, C.; Yarnall, A.; Rochester, L. The Role of Movement Analysis in Diagnosing and Monitoring Neurodegenerative Conditions: Insights from Gait and Postural Control. Brain Sciences 2019, 9, 34. [Google Scholar] [CrossRef] [PubMed]
  23. Chen, S.; Lach, J.; Lo, B.; Yang, G.-Z. Toward Pervasive Gait Analysis With Wearable Sensors: A Systematic Review. IEEE J. Biomed. Health Inform. 2016, 20, 1521–1537. [Google Scholar] [CrossRef] [PubMed]
  24. Robles-García, V.; Corral-Bergantiños, Y.; Espinosa, N.; Jácome, M.A.; García-Sancho, C.; Cudeiro, J.; Arias, P. Spatiotemporal Gait Patterns During Overt and Covert Evaluation in Patients With Parkinson’s Disease and Healthy Subjects: Is There a Hawthorne Effect? Journal of Applied Biomechanics 2015, 31, 189–194. [Google Scholar] [CrossRef] [PubMed]
  25. Bonci, T.; Camomilla, V.; Dumas, R.; Cappozzo, A. Generation of Realistic Thigh Soft Tissue Artefacts as a Function of Hip and Knee Kinematics. Gait & Posture 2014, 39, S72–S73. [Google Scholar] [CrossRef]
  26. Camomilla, V.; Dumas, R.; Cappozzo, A. Human Movement Analysis: The Soft Tissue Artefact Issue. J Biomech 2017, 62, 1–4. [Google Scholar] [CrossRef] [PubMed]
  27. Cereatti, A.; Bonci, T.; Akbarshahi, M.; Aminian, K.; Barré, A.; Begon, M.; Benoit, D.L.; Charbonnier, C.; Dal Maso, F.; Fantozzi, S.; et al. Standardization Proposal of Soft Tissue Artefact Description for Data Sharing in Human Motion Measurements. J Biomech 2017, 62, 5–13. [Google Scholar] [CrossRef] [PubMed]
  28. Fonseca, M.; Gasparutto, X.; Leboeuf, F.; Dumas, R.; Armand, S. Impact of Knee Marker Misplacement on Gait Kinematics of Children with Cerebral Palsy Using the Conventional Gait Model—A Sensitivity Study. PLoS One 2020, 15, e0232064. [Google Scholar] [CrossRef] [PubMed]
  29. Chiari, L.; Della Croce, U.; Leardini, A.; Cappozzo, A. Human Movement Analysis Using Stereophotogrammetry. Part 2: Instrumental Errors. Gait Posture 2005, 21, 197–211. [Google Scholar] [CrossRef] [PubMed]
  30. Gorton, G.E.; Hebert, D.A.; Gannotti, M.E. Assessment of the Kinematic Variability among 12 Motion Analysis Laboratories. Gait Posture 2009, 29, 398–402. [Google Scholar] [CrossRef]
  31. Whittle, M.W. Clinical Gait Analysis: A Review. Human Movement Science 1996, 15, 369–387. [Google Scholar] [CrossRef]
  32. Colyer, S.L.; Evans, M.; Cosker, D.P.; Salo, A.I.T. A Review of the Evolution of Vision-Based Motion Analysis and the Integration of Advanced Computer Vision Methods Towards Developing a Markerless System. Sports Medicine - Open 2018, 4, 24. [Google Scholar] [CrossRef] [PubMed]
  33. Cronin, N.J. Using Deep Neural Networks for Kinematic Analysis: Challenges and Opportunities. Journal of Biomechanics 2021, 123, 110460. [Google Scholar] [CrossRef] [PubMed]
  34. Drazan, J.F.; Phillips, W.T.; Seethapathi, N.; Hullfish, T.J.; Baxter, J.R. Moving Outside the Lab: Markerless Motion Capture Accurately Quantifies Sagittal Plane Kinematics during the Vertical Jump. J Biomech 2021, 125, 110547. [Google Scholar] [CrossRef]
  35. Kanko, R.M.; Laende, E.; Selbie, W.S.; Deluzio, K.J. Inter-Session Repeatability of Markerless Motion Capture Gait Kinematics. J Biomech 2021, 121, 110422. [Google Scholar] [CrossRef] [PubMed]
  36. Mathis, A.; Mamidanna, P.; Cury, K.M.; Abe, T.; Murthy, V.N.; Mathis, M.W.; Bethge, M. DeepLabCut: Markerless Pose Estimation of User-Defined Body Parts with Deep Learning. Nat Neurosci 2018, 21, 1281–1289. [Google Scholar] [CrossRef] [PubMed]
  37. Ito, N.; Sigurðsson, H.B.; Seymore, K.D.; Arhos, E.K.; Buchanan, T.S.; Snyder-Mackler, L.; Grävare Silbernagel, K. Markerless Motion Capture: What Clinician-Scientists Need to Know Right Now. JSAMS Plus 2022, 1, 100001. [Google Scholar] [CrossRef] [PubMed]
  38. Tang, H.; Pan, J.; Munkasy, B.; Duffy, K.; Li, L. Comparison of Lower Extremity Joint Moment and Power Estimated by Markerless and Marker-Based Systems during Treadmill Running. Bioengineering 2022, 9, 574. [Google Scholar] [CrossRef]
  39. Kanko, R.M.; Laende, E.K.; Davis, E.M.; Selbie, W.S.; Deluzio, K.J. Concurrent Assessment of Gait Kinematics Using Marker-Based and Markerless Motion Capture. J Biomech 2021, 127, 110665. [Google Scholar] [CrossRef]
  40. Song, K.; Hullfish, T.J.; Silva, R.S.; Silbernagel, K.G.; Baxter, J.R. Markerless Motion Capture Estimates of Lower Extremity Kinematics and Kinetics Are Comparable to Marker-Based across 8 Movements. bioRxiv 2023, 2023.02.21.526496. [CrossRef]
  41. Bland, J.M.; Altman, D.G. Statistical Methods for Assessing Agreement between Two Methods of Clinical Measurement. Lancet 1986, 1, 307–310. [Google Scholar] [CrossRef]
  42. Kass, R.E.; Raftery, A.E. Bayes Factors. Journal of the American Statistical Association 1995, 90, 773–795. [Google Scholar] [CrossRef]
  43. Wagenmakers, E.-J. A Practical Solution to the Pervasive Problems Ofp Values. Psychonomic Bulletin & Review 2007, 14, 779–804. [Google Scholar] [CrossRef]
  44. Yiou, E.; Teyssèdre, C.; Artico, R.; Fourcade, P. Comparison of Base of Support Size during Gait Initiation Using Force-Plate and Motion-Capture System: A Bland and Altman Analysis. J Biomech 2016, 49, 4168–4172. [Google Scholar] [CrossRef] [PubMed]
  45. Maillot, P.; Perrot, A.; Hartley, A.; Do, M.-C. The Braking Force in Walking: Age-Related Differences and Improvement in Older Adults with Exergame Training. J Aging Phys Act 2014, 22, 518–526. [Google Scholar] [CrossRef] [PubMed]
  46. Demain, A.; Westby, G.W.M.; Fernandez-Vidal, S.; Karachi, C.; Bonneville, F.; Do, M.C.; Delmaire, C.; Dormont, D.; Bardinet, E.; Agid, Y.; et al. High-Level Gait and Balance Disorders in the Elderly: A Midbrain Disease? J Neurol 2014, 261, 196–206. [Google Scholar] [CrossRef]
  47. Yiou, E.; Caderby, T.; Delafontaine, A.; Fourcade, P.; Honeine, J.-L. Balance Control during Gait Initiation: State-of-the-Art and Research Perspectives. World J Orthop 2017, 8, 815–828. [Google Scholar] [CrossRef]
Preprints 96236 g001
Figure 1. Experimental set-up showing the markerless motion capture system, the force-plate system and the walking track.
Figure 1. Experimental set-up showing the markerless motion capture system, the force-plate system and the walking track.
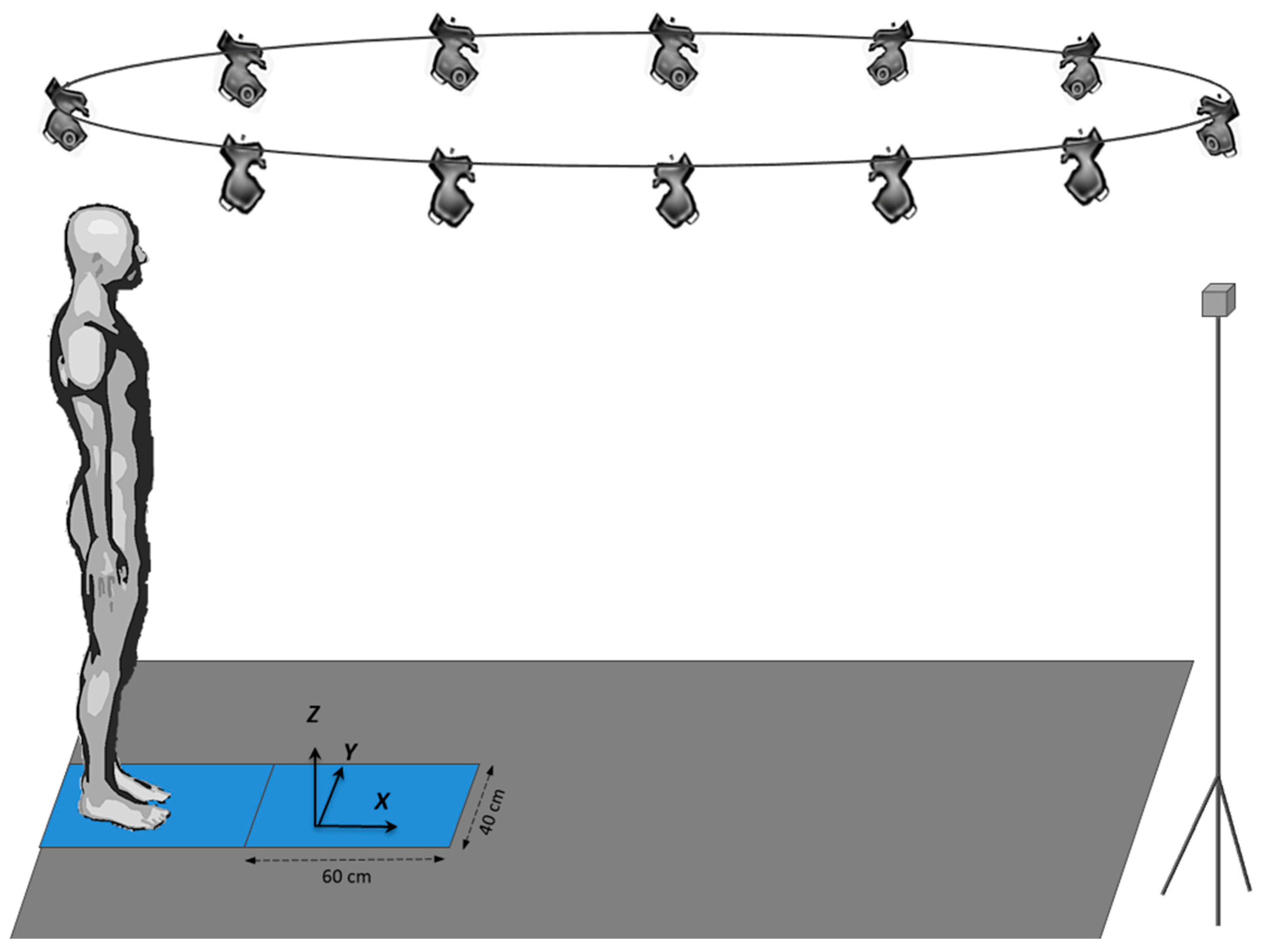
Preprints 96236 g001
Preprints 96236 g002
Figure 2. Typical biomechanical traces of the center-of-mass velocity along the vertical (Vz) and anteroposterior (Vx) directions obtained with the FPS (red trace) and MLS (blue trace) in the three groups. Reported are the mean traces of the five trials obtained in the maximal velocity condition in a representative participant of each group. YH, EH, PD: young healthy adults, elderly healthy adults and PD group, respectively. Velocity (ordinate) is expressed in meters/second. Time (abscissa) is expressed in seconds. Vzmin, VzFC: peak negative velocity and vertical center-of-mass velocity at the time of foot-contact, respectively. MP: motor performance. Note the good agreement between both systems in each plot.
Figure 2. Typical biomechanical traces of the center-of-mass velocity along the vertical (Vz) and anteroposterior (Vx) directions obtained with the FPS (red trace) and MLS (blue trace) in the three groups. Reported are the mean traces of the five trials obtained in the maximal velocity condition in a representative participant of each group. YH, EH, PD: young healthy adults, elderly healthy adults and PD group, respectively. Velocity (ordinate) is expressed in meters/second. Time (abscissa) is expressed in seconds. Vzmin, VzFC: peak negative velocity and vertical center-of-mass velocity at the time of foot-contact, respectively. MP: motor performance. Note the good agreement between both systems in each plot.
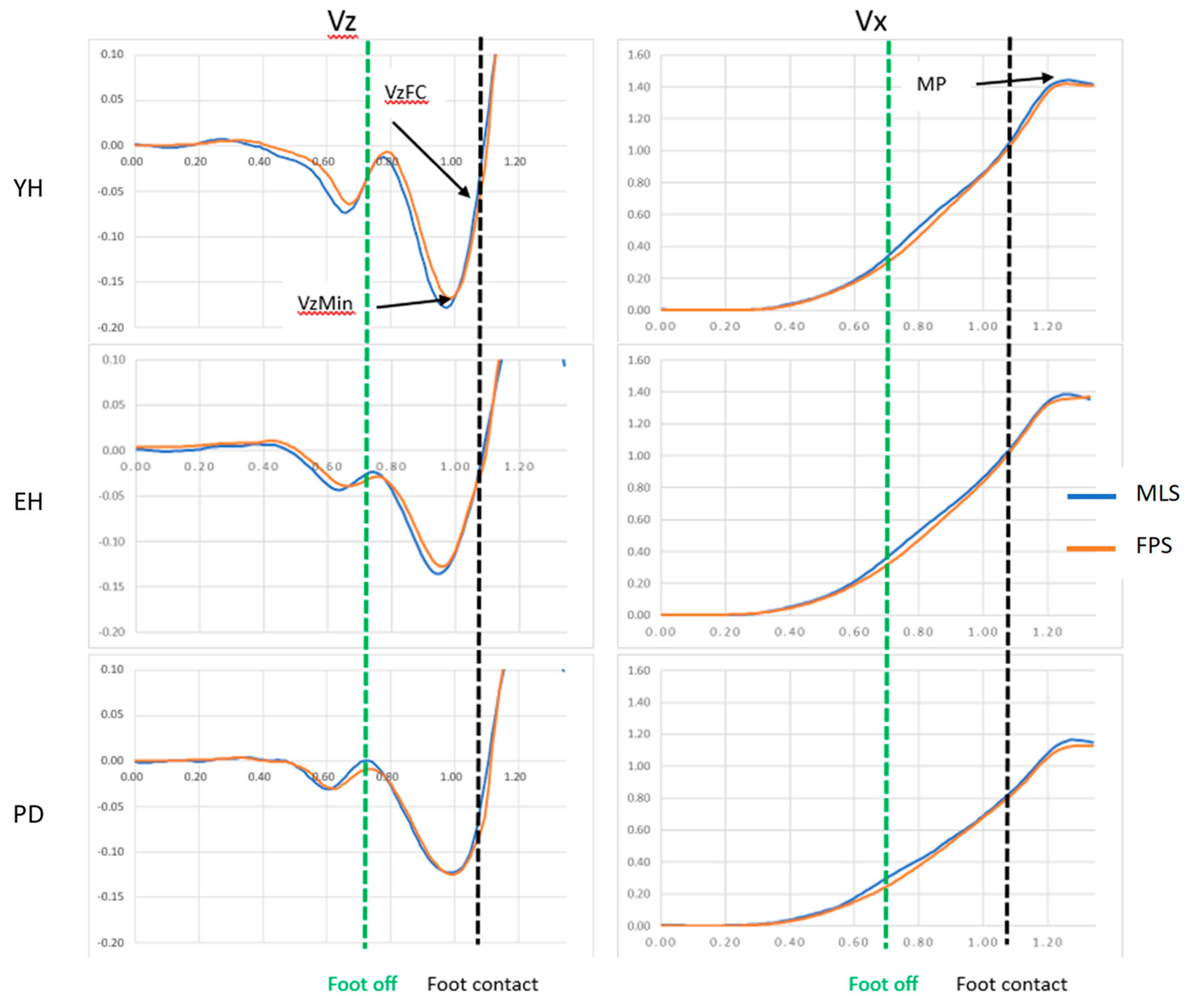
Preprints 96236 g002
Preprints 96236 g003
Figure 3. Bland-Altman plots showing the braking index values obtained with the two measurement systems (mean values, abscissa), against the difference between these two systems (ordinate), for the young healthy (YH), elderly healthy (EH) and PD groups. Each point represents one trial with one participant. Reported are the absolute values obtained in the spontaneous (left) and maximal (right) velocity conditions (SVC, and MVC, respectively). For each plot, the 95% limits of agreement (red dotted lines), standard deviation (green dotted line) and bias (blue full line) are reported.
Figure 3. Bland-Altman plots showing the braking index values obtained with the two measurement systems (mean values, abscissa), against the difference between these two systems (ordinate), for the young healthy (YH), elderly healthy (EH) and PD groups. Each point represents one trial with one participant. Reported are the absolute values obtained in the spontaneous (left) and maximal (right) velocity conditions (SVC, and MVC, respectively). For each plot, the 95% limits of agreement (red dotted lines), standard deviation (green dotted line) and bias (blue full line) are reported.
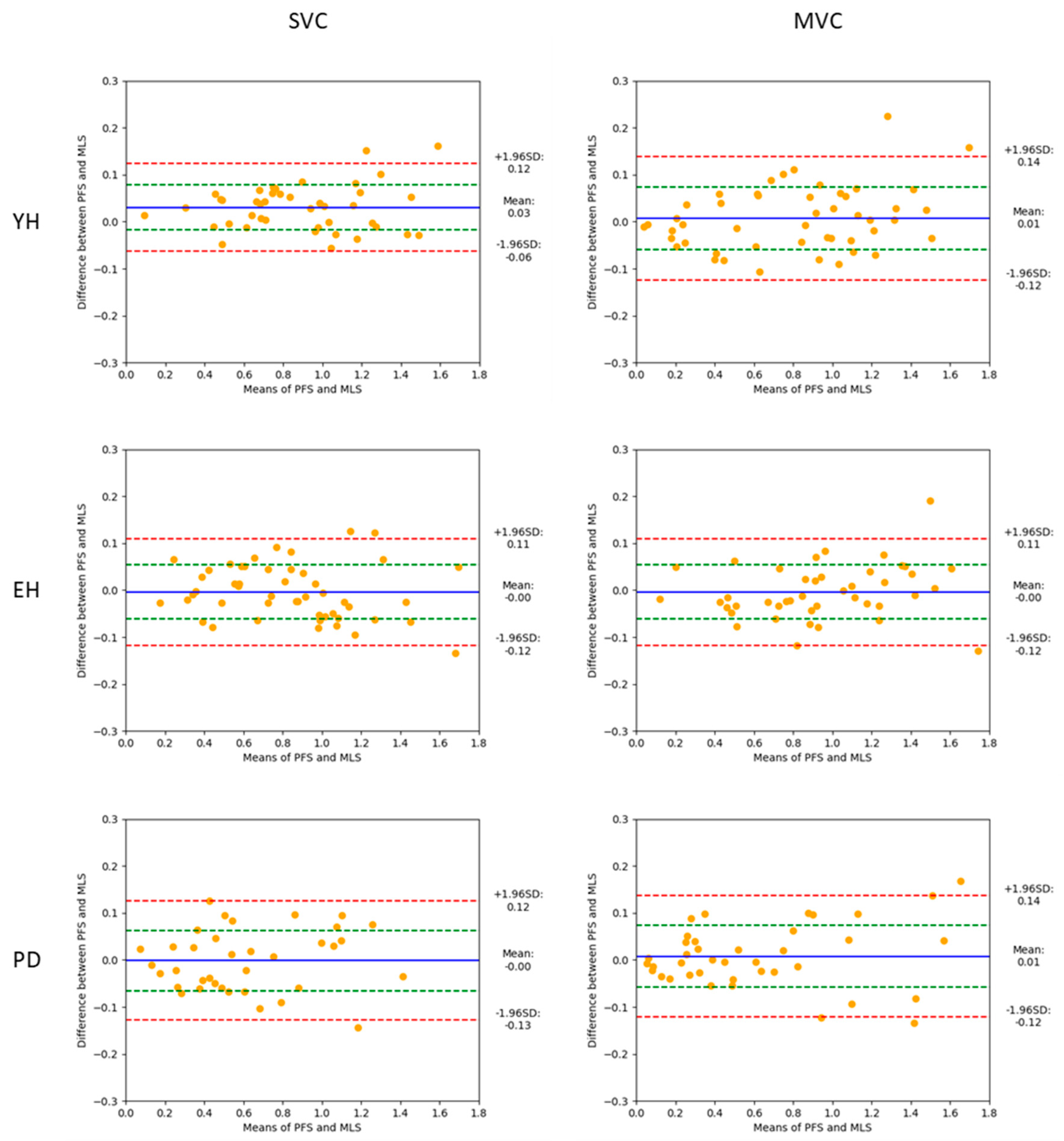
Preprints 96236 g003
Preprints 96236 g004
Figure 4. Bland-Altman plots showing motor performance (peak of anteroposterior center-of-mass velocity) obtained with the two measurement systems (mean values, abscissa), against the difference between these two systems (ordinate), for the young healthy (YH), elderly healthy (EH) and PD groups. Each point represents one trial with one participant. Reported are the absolute values obtained in the spontaneous (left) and maximal (right) velocity conditions. For each plot, the 95% limits of agreement (red dotted lines), standard deviation (green dotted line) and bias (blue full line) are reported.
Figure 4. Bland-Altman plots showing motor performance (peak of anteroposterior center-of-mass velocity) obtained with the two measurement systems (mean values, abscissa), against the difference between these two systems (ordinate), for the young healthy (YH), elderly healthy (EH) and PD groups. Each point represents one trial with one participant. Reported are the absolute values obtained in the spontaneous (left) and maximal (right) velocity conditions. For each plot, the 95% limits of agreement (red dotted lines), standard deviation (green dotted line) and bias (blue full line) are reported.
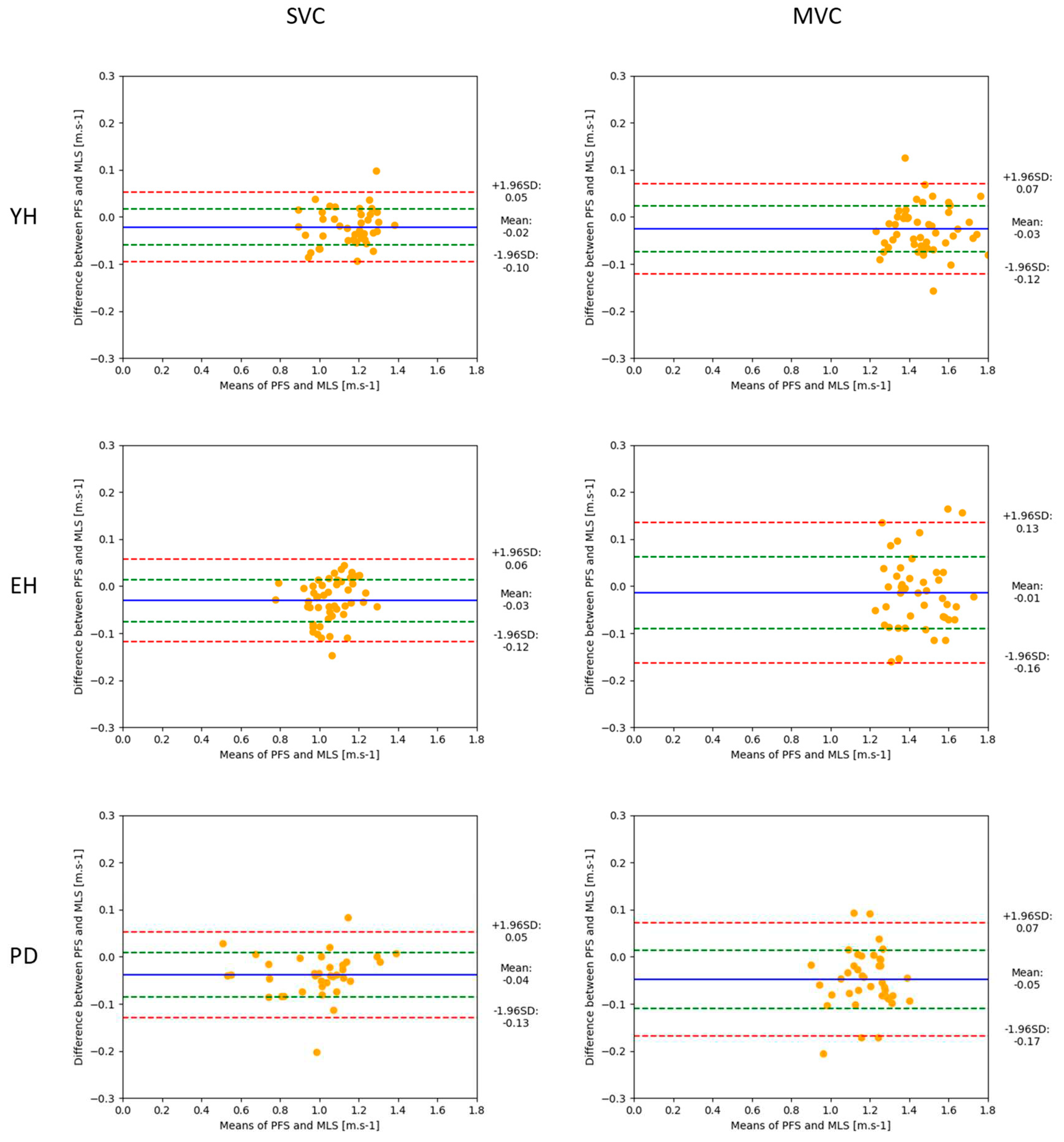
Preprints 96236 g004
Preprints 96236 g005
Figure 5. Descriptive statistics comparing the braking index (BI; left panels) and motor performance (MP; right panels) between the systems, groups and velocity conditions. FPS, MLS: force-plate system and markerless motion system, respectively. SVC, MVC: spontaneous and maximal velocity condition, respectively. YH, EH, PD: young healthy, elderly healthy and PD group, respectively. Reported are mean values (all participants together) ± 1 standard deviation. Upper plots. *, ***: significant difference between the PD group and both the EH and PD group with p < 0.05 and p < 0.001, respectively, as detected by the PFS. °, °°°: significant difference between the PD group and both the EH and PD groups with p < 0.05 and p < 0.001, respectively, as detected by the MLS. Middle plots. ***, +++: significant difference between SVC and MVC, as detected by the PFS and MLS, respectively, with p < 0. 001. Lower plots. ¤, +: significant difference between the PD group and both the EH and the YH groups in SVC and MVC, respectively (with p < 0.05 and p < 0.01). ¤,+,*:, significant difference between the YH group and the EH group in SVC (with p < 0.05), significant difference between the YH group and the PD group in SVC (with p < 0.001), significant difference between the PD group and both the EH and the YH groups in MVC (with p < 0.001). Note the superposition of the traces obtained with the MLS and PFS in both upper panels.
Figure 5. Descriptive statistics comparing the braking index (BI; left panels) and motor performance (MP; right panels) between the systems, groups and velocity conditions. FPS, MLS: force-plate system and markerless motion system, respectively. SVC, MVC: spontaneous and maximal velocity condition, respectively. YH, EH, PD: young healthy, elderly healthy and PD group, respectively. Reported are mean values (all participants together) ± 1 standard deviation. Upper plots. *, ***: significant difference between the PD group and both the EH and PD group with p < 0.05 and p < 0.001, respectively, as detected by the PFS. °, °°°: significant difference between the PD group and both the EH and PD groups with p < 0.05 and p < 0.001, respectively, as detected by the MLS. Middle plots. ***, +++: significant difference between SVC and MVC, as detected by the PFS and MLS, respectively, with p < 0. 001. Lower plots. ¤, +: significant difference between the PD group and both the EH and the YH groups in SVC and MVC, respectively (with p < 0.05 and p < 0.01). ¤,+,*:, significant difference between the YH group and the EH group in SVC (with p < 0.05), significant difference between the YH group and the PD group in SVC (with p < 0.001), significant difference between the PD group and both the EH and the YH groups in MVC (with p < 0.001). Note the superposition of the traces obtained with the MLS and PFS in both upper panels.
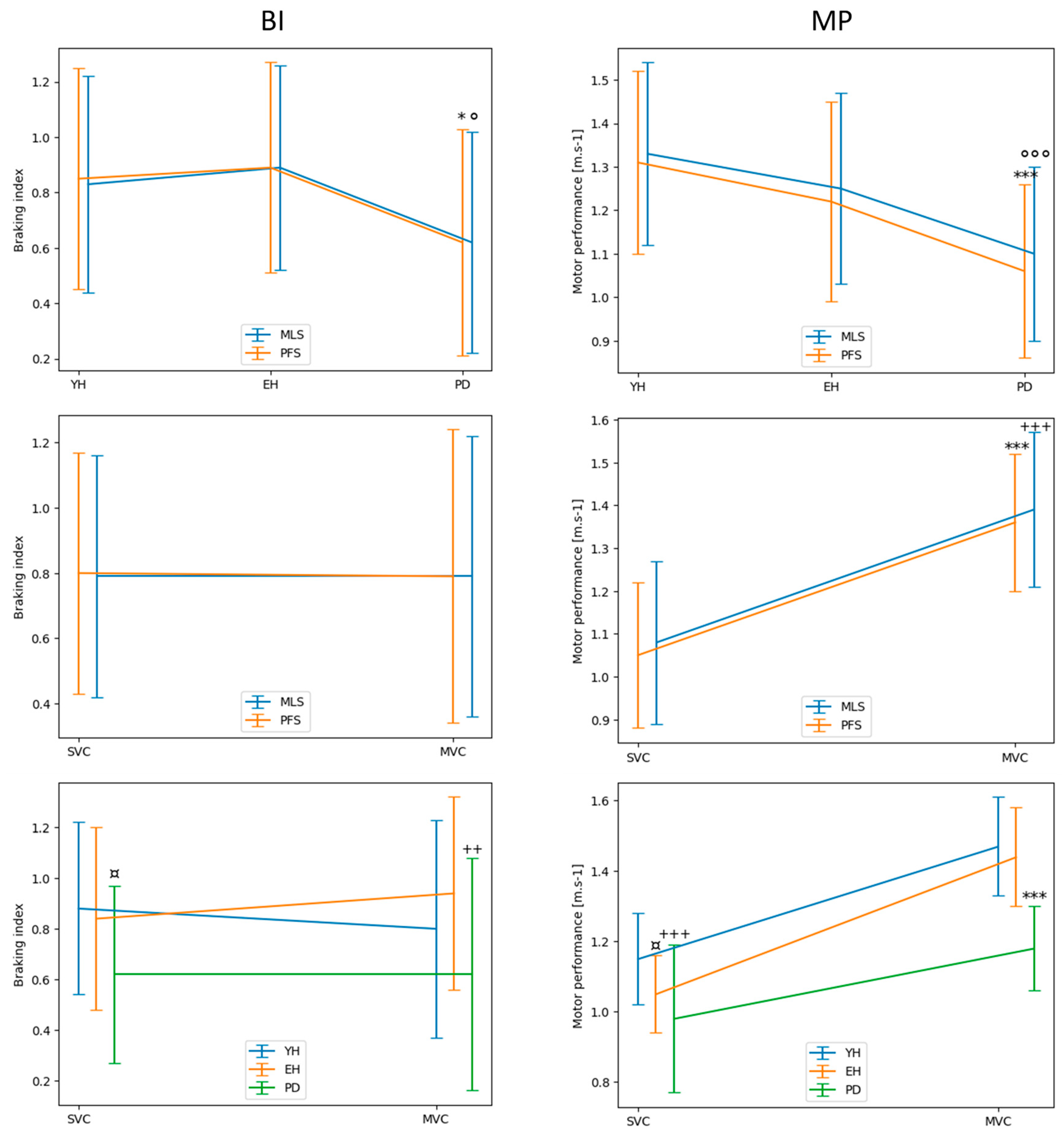
Preprints 96236 g005
Preprints 96236 g006
Figure 6. Between-systems comparison with the Bayes factor 01 applied to the baking index. The plot shows the Cauchy prior width (abscissa) vs. Bayes factor value (ordinate). Reported in the plot are the user value (gray dot), wide value (black dot) and ultrawide value (white dot). H0: null hypothesis (“there is no difference between both systems”); H1: alternative hypothesis (“there is a difference between both systems”).
Figure 6. Between-systems comparison with the Bayes factor 01 applied to the baking index. The plot shows the Cauchy prior width (abscissa) vs. Bayes factor value (ordinate). Reported in the plot are the user value (gray dot), wide value (black dot) and ultrawide value (white dot). H0: null hypothesis (“there is no difference between both systems”); H1: alternative hypothesis (“there is a difference between both systems”).
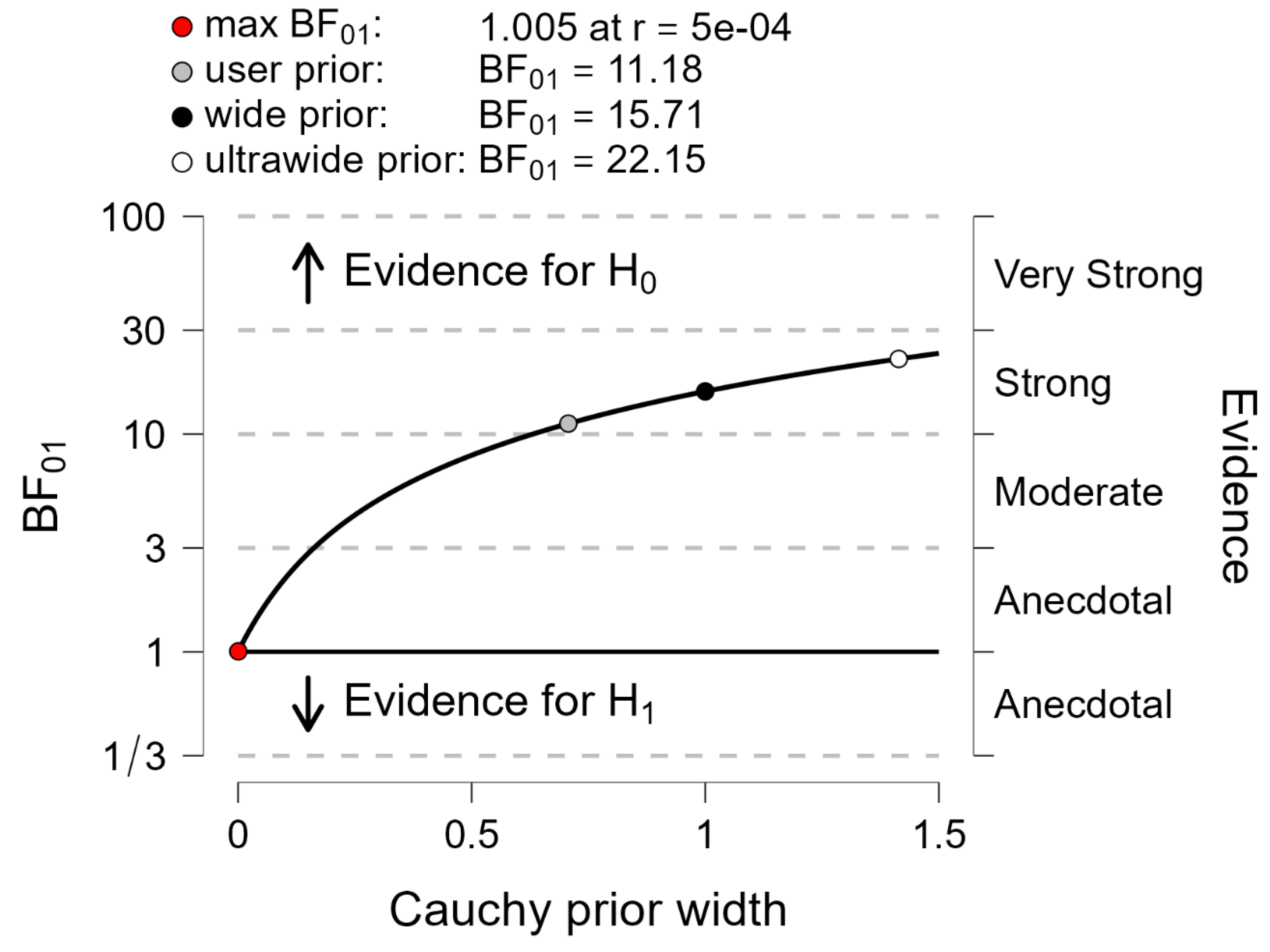
Preprints 96236 g006
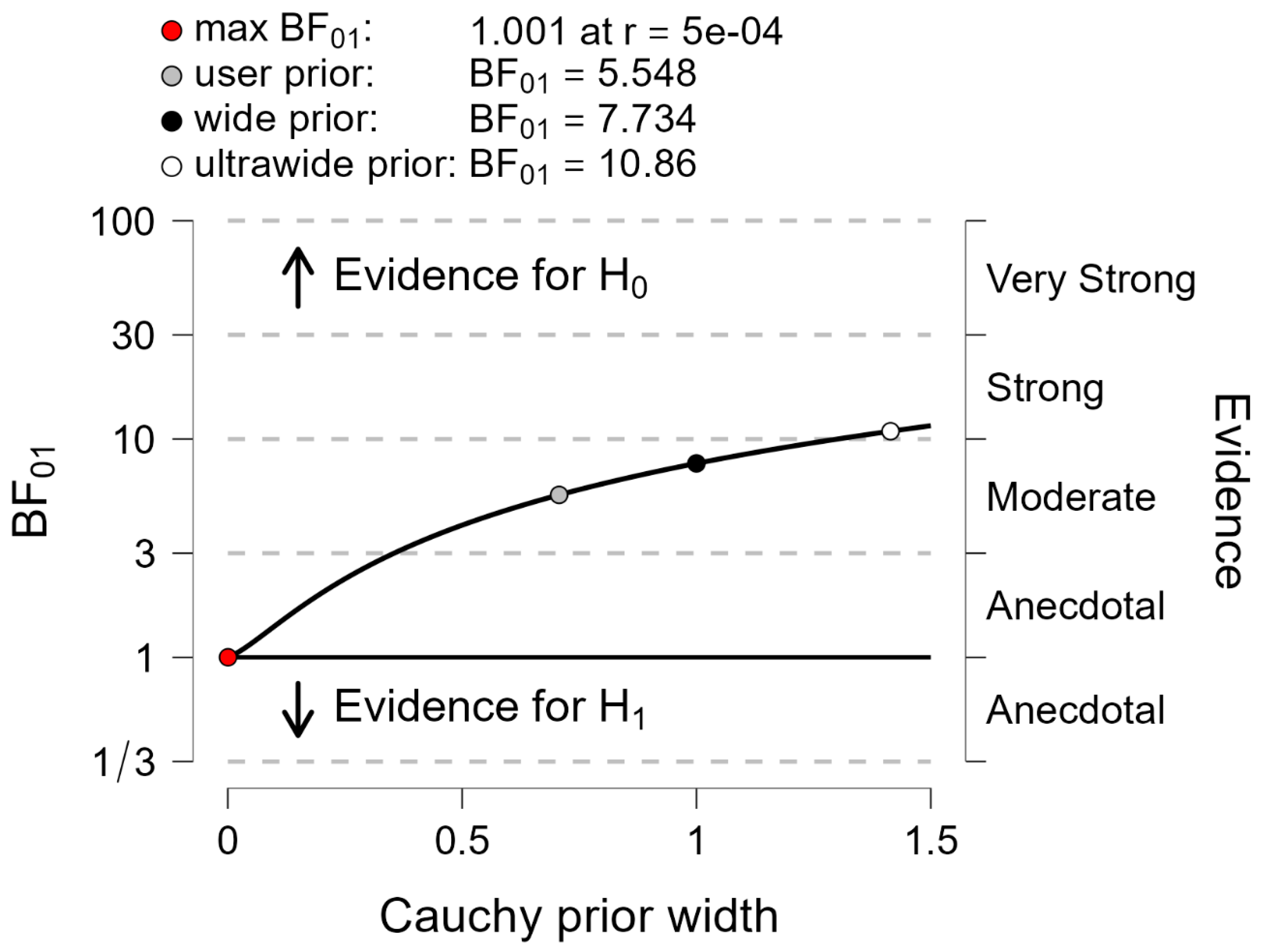
Preprints 96236 g007
Figure 7. Between-systems comparison with the Bayes factor 01 applied to motor performance. Plots show the Cauchy prior width (abscissa) vs. Bayes factor value (ordinate). Reported in the plot are the user value (gray dot), wide value (black dot) and ultrawide value (white dot). H0: null hypothesis (“there is no difference between both systems”); H1: alternative hypothesis (“there is a difference between both systems”).
Figure 7. Between-systems comparison with the Bayes factor 01 applied to motor performance. Plots show the Cauchy prior width (abscissa) vs. Bayes factor value (ordinate). Reported in the plot are the user value (gray dot), wide value (black dot) and ultrawide value (white dot). H0: null hypothesis (“there is no difference between both systems”); H1: alternative hypothesis (“there is a difference between both systems”).
Preprints 96236 g007
Table 1. Participant anthropometrical features and PD evaluation scores. BMI: Body mass index; MoCA: Montreal Cognitive Assessment; MMS: Mini Mental State Exam.
Table 1. Participant anthropometrical features and PD evaluation scores. BMI: Body mass index; MoCA: Montreal Cognitive Assessment; MMS: Mini Mental State Exam.
Variable PD (n = 12) YH (n=10) EH (n=11)
Age (years) 68.4 ± 5.1 24.7 ± 0.7 66.5 ± 3.6
Gender (female/male) 1/10 4/5 8/3
Body mass (kg) 70.5 ± 11.8 70.2 ± 13.5 63.9 ± 10.1
Height (m) 1.70 ± 0.07 1.70 ± 0.12 1.65 ± 0.06
BMI (kg/m2) 24.5 ± 3.6 24.7 ± 0.7 23.4 ± 3.4
Shoe size (EU) 41.3 ± 1.5 40.3 ± 3.7 39.3 ± 1.8
Time of diagnosis (years) 7.4 ± 2.8
H and Y scale (points) 2.0 ± 0.6
UPDRS-III (score) 33.8 ± 11.7
MoCA (score) 25.7 ± 2.3
MMS (score) 27.0 ± 1.7
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated