Preprint
Article
Description of the Electron in the Electromagnetic Field: The Dirac Type Equation and the Equation for the Wave Function in Spinor Coordinate Space
Altmetrics
Downloads
267
Views
464
Comments
0
This version is not peer-reviewed
Submitted:
11 January 2024
Posted:
14 January 2024
Read the latest preprint version here
Alerts
Abstract
Physical processes are usually described using four-dimensional vector quantities - coordinate vector, momentum vector, current vector. But at the fundamental level they are characterized by spinors - coordinate spinors, impulse spinors, spinor wave functions. The propagation of fields and their interaction takes place at the spinor level, and since each spinor uniquely corresponds to a certain vector, the results of physical processes appear before us in vector form. For example, the relativistic Schrödinger equation and the Dirac equation are formulated by means of coordinate vectors, momentum vectors and quantum operators corresponding to them. In the Schrödinger equation the wave function is represented by a single complex quantity, in the Dirac equation a step forward is taken and the wave function is a spinor with complex components, but still coordinates and momentum are vectors. For a closed description of nature using only spinor quantities, it is necessary to have an equation similar to the Dirac equation in which momentum, coordinates and operators are spinors. It is such an equation that is presented in this paper. Using the example of the interaction between an electron and an electromagnetic field, we can see that the spinor equation contains more detailed information about the interaction than the vector equations. This is not new for quantum mechanics, since it describes interactions using complex wave functions, which cannot be observed directly, and only when measured goes to probabilities in the form of squares of the moduli of the wave functions. In the same way spinor quantities are not observable, but they completely determine observable vectors.In Section 2 of the paper, we analyze the quadratic form for an arbitrary four-component complex vector based on Pauli matrices. The form is invariant with respect to Lorentz transformations including any rotations and boosts. The invariance of the form allows us to construct on its basis an equation for a free particle combining the properties of the relativistic wave equation and the Dirac equation. For an electron in the presence of an electromagnetic potential it is shown that taking into account the commutation relations between the momentum and coordinate components allows us to obtain from this equation the known results describing the interactions of the electron spin with the electric and magnetic field. In section 3 of the paper this quadratic form is expressed through momentum spinors, which makes it possible to obtain an equation for the spinor wave function in spinor coordinate space by replacing the momentum spinor components by partial derivative operators on the corresponding coordinate spinor component. At the end of the paper the question on a possibility of second quantization of the electron field in the spinor coordinate space is touch upon.
Keywords:
Subject: Physical Sciences - Particle and Field Physics
1. Introduction
Nowadays, the interest to study applications of the Dirac equation to different situations and to find out the conditions of its generalization is not weakening. In particular, in [1] new versions of an extended Dirac equation and the associated Clifford algebra are presented. In [2] a study of the Schrödinger-Dirac covariant equation in the presence of gravity, where the non-commuting gamma matrices become space-time-dependent, is carried out. In [3] an idea is discussed that the visible properties of the electron, including rest mass and magnetic moment, are determined by a massless charge spinning at light speed within a Compton domain. In [4] some aspects of conformal rescaling in detail are explored and the role of the "quantum" potential is discussed as a natural consequence of non-inertial motion and is not exclusive to the quantum domain. Author establishes the fundamental importance of conformal symmetry, in which rescaling of the rest mass plays a vital role. Thus, the basis for a radically new theory of quantum phenomena based on the process of mass-energy flow is proposed. In [5] author have derived the covariant fourth-order/one-function equivalent of the Dirac equation for the general case of an arbitrary set of γ-matrices.
Supporting these search aspirations, in our work we propose a deeper understanding of the Dirac equation with an emphasis on the direct use of the principles of symmetry and invariance to Lorentz transformations. For the first time we present a formulation of the Dirac and Schrödinger equations in spinor coordinate space.
2. Generalized Dirac type equation
Let us introduce notations, which will be used further on. The speed of light and the reduced Planck constant will be considered as unity.
Pauli matrices
Matrices constructed from Pauli matrices
A vector of matrices
A set of arbitrary complex numbers and a vector of its three components
Let us define a 2×2 matrix of Lorentz transformations given by the set of real rotation angles and boosts
and a similar 4×4 transformation matrix
We also define a 4×4 matrix of Lorentz transformations , where μ and ν take values 0,1,2,3
which can also be written explicitly using the 4×4 matrices of turn generators and boosts
Let's define a 4×4 matrix
In fact, we consider a quaternion with complex coefficients, which we multiply by its conjugate quaternion (due to the complexity of the coefficients, these are biquaternions, but we still use quaternionic conjugation, without complex conjugation).
Let us subject the set of complex numbers to the Lorentz transformation
Let us write a relation whose validity for an arbitrary set of complex numbers can be checked directly
The matrix in the simplest case is diagonal with equal complex elements on the diagonal equal to the square of the length of the vector in the metric of Minkowski space, which we denote . Both and do not change under any rotations and boosts, in physical applications the invariance of is usually used, in particular, for the four-component momentum vector this quantity is called the square of mass.
Since the matrices anticommutate with each other, for a vector whose components commute with each other, we have just the simplest case with a diagonal matrix with on the diagonal. But if the components of vector do not commute, the matrix already has a more complex structure and carries additional physical information compared to . For example, the vector may include the electron momentum vector and the electromagnetic potential vector. The four-component potential vector is a function of the four-dimensional coordinates of Minkowski space. The components of the four-component momentum do not commute with the components of the coordinate vector, respectively, and the coordinate function does not commute with the momentum components, and their commutator is expressed through the partial derivative of this function by the corresponding coordinate. If the components of the vector do not commute, the matrix will no longer be invariant with respect to Lorentz transformations.
Suppose that the complex numbers we consider commute with all matrices, and note that the squares of all matrices are equal to the unit 4×4 matrix I
Taking into account anticommutative properties of matrices and expressions for their pairwise products we obtain
Consider the case when is the sum of the momentum vector and the electromagnetic potential vector, which is a function of coordinates
For now, we'll stick with the Heisenberg approach, that is, we will consider the components of the momentum vector as operators for which there are commutation relations with coordinates or coordinate functions such as . In this approach, the operators do not have to act on any wave function.
Taking into account the commutation relations of the components of the momentum vector and the coordinate vector, the commutator of the momentum component and the coordinate function is expressed through the derivative of this function by the corresponding coordinate, e.g.
As a result, we obtain
where
As a result, we have the expression
Similarly, it can be shown that
The matrix
does not change under Lorentz transformations involving any rotations and boosts.
Taking into account the electron charge we have
Let us summarize our consideration. There is a correlation
where
Let's analyze the obtained equality
Note that the quantity is invariant to the Lorentz transformations irrespective of whether the momentum and field components commute or not. To solve this equation, we have to make additional simplifications. For example, to arrive at an equation similar to the Dirac equation, we must equate with the matrix , where is the square of the mass of a free electron. Then
With this substitution the generalized equation almost coincides with the equation [6], formula (43.25), the difference is that there is a plus sign before, and instead of there is , in which the matrices have the following form
A similar equation is given by Dirac in [7], Para. 76, Equation 24; he does not use the matrices , only the matrices , but the signs of the contributions of the magnetic and electric fields are the same.
Along with the original form
it is possible to consider the form with a different order of the factors. It can be shown that this leads to a change in the sign of the electric field contribution
Since , unlike , is invariant to Lorentz transformations, it would be logical to replace it by . At least both these matrices are diagonal, and in the case of a weak field their diagonal elements are close. Nevertheless, the approach based on the Dirac equation leads to solutions consistent with experiment.
The matrix in the general case has complex elements and is not diagonal, and in the Dirac equations instead of it is substituted the product of the unit matrix by the square of mass , the physical meaning of such a substitution is not obvious. Apparently it is implied that it is the square of the mass of a free electron. But the square of the length of the sum of the lengths of the electron momentum vectors and the electromagnetic potential vector is not equal to the sum of the squares of the lengths of these vectors, that is, it is not equal to the square of the mass of the electron, even if the square of the length of the potential vector were zero. But, for example, in the case of an electrostatic central field, even the square of the length of one potential vector is not equal to zero. Therefore, it is difficult to find a logical justification for using the mass of a free electron in the Dirac equation in the presence of an electromagnetic field. After all, mass is simply the length of a momentum vector, but the concept of a momentum vector, and hence of mass, can be applied only for a free particle. Similarly, energy is the zero component of the momentum vector and the concept of energy can only be strictly defined for a free particle. Due to the noted differences, the solutions of the generalized equation can differ from the solutions arising from the Dirac equation.
In the case when there is a constant magnetic field directed along the z-axis, we can write down
Here . Only when the field is directed along the z-axis, the matrix is diagonal and real because the third Pauli matrix is diagonal and real. And if the field is weak, can be approximated by the matrix. This is probably why it is customary to illustrate the interaction of electron spin with the magnetic field by choosing its direction along the z-axis. In any other direction is not only non-diagonal, but also complex, so that it is difficult to justify the use of .
When the influence of the electromagnetic field was taken into account, no specific characteristics of the electron were used. When deriving a similar result using the Dirac equation, it is assumed that since the electron equation is used, the result is specific to the electron. In our case Pauli matrices and commutation relations are used, apparently these two assumptions or only one of them characterize the properties of the electron, distinguishing it from other particles with non-zero masses.
The proposed equation echoes the Dirac equation, at least from it one can obtain the same formulas for the interaction of spin and electromagnetic field as with the Dirac equation, and in the absence of a field the proposed equation is invariant to the Lorentz transformations. In contrast, to prove the invariance of the Dirac equation even in the absence of a field, the infinitesimal Lorentz transformations are used, but the invariance at finite angles of rotations and boosts is not demonstrated. The proof of invariance of the Dirac equation is based on the claim that a combination of rotations at finite angles can be represented as a combination of infinitesimal rotations. But this is true only for rotations around one axis, and if there are at least two axes, this statement is not true because of non-commutability of Pauli matrices, which are generators of rotations, so that the exponent of the sum is not equal to the product of exponents if the sum includes generators of rotations around different axes.
A test case for any theory is the model of the central electrostatic field used in the description of the hydrogen atom, in which the components of the vector potential are zero
If again we equate the left part with , we obtain
Introducing the notations () we obtain
If we substitute operators acting on the wave function instead of momentum components into the generalized equation, we obtain a generalized analog of the relativistic Schrödinger equation, in which the wave function has four components and changes as a spinor under Lorentz transformations. Using the substitutions
the equation for the four-component wave function before all transformations has the form
and after transformations
Once again, note that the matrix is not diagonal and real.
All the above deductions are also valid when replacing 4×4 matrices by 2×2 matrices , since their commutative and anticommutative properties are the same. The corresponding generalized equation is of the form
where
and the equation for the now two-component wave function looks like
In deriving his equation, Dirac [7, paragraph 74] noted that as long as we are dealing with matrices with two rows and columns, we cannot obtain a representation of more than three anticommuting quantities; to represent four anticommuting quantities, he turned to matrices with four rows and columns. In our case, however, three anticommuting matrices are sufficient, so the wave function can also be two-component. Dirac also explains that the presence of four components results in twice as many solutions, half of which have negative energy. In the case of a two-component wave function, however, no negative energy solutions are obtained. Particles with negative energy in this case also exist, but they are described by the same equation in which the signs of all four matrices or are reversed.
One would seem to expect similar results from other representations of the momentum operator, e.g., [6, formula (24.15)]
under the assumption that this representation can describe a particle with spin one. But this expectation is not justified, since the last three matrices do not anticommutate, and therefore the quadratic form constructed on their basis is not invariant under Lorentz transformations.
Let's see what happens to when we change the sign of the matrices. When changing the sign of we have
swapping the places of the multipliers. The multipliers do not necessarily commute, so is not invariant with respect to the change of sign of , which can be interpreted as a reflection in time. The same picture of invariance absence we have at the sign change of matrices , i.e. at spatial reflection
If we change the signs of all matrices at once, we have
i.e. invariance. The physical interpretation of this case can be given by taking into account the change of signs of the matrices in equation
which can be rewritten as
it can be interpreted as an equation for a particle with negative energy and positive charge, i.e. for the positron. Thus, the generalized equation with matrices describes a particle, and with matrices an antiparticle.
If one consistently adheres to the Heisenberg approach and does not involve the notion of wave function, it is not very clear how to search for solutions of the presented equations. The Schrödinger approach with finding the eigenvalues of the matrix and their corresponding eigenfunctions can help here.
In the left-hand side are the operators acting on the wave function, and in the right-hand side is a constant matrix on which the wave function is simply multiplied. This equality must be satisfied for all values of the four-dimensional coordinates at once. Then is not fixed but can take a set of possible values, finding all these values is the goal of solving the equation.
Thus, we have arrived at an equation containing a matrix which is non-diagonal, complex and in general depends on the coordinates . After the standard procedure of separating the time and space variables, we can go to a stationary equation in which there will be no time dependence, but the dependence the matrix on the coordinates will remain. It is possible to ignore the dependence of on the coordinates and its non-diagonality and simply replace this matrix by a unit matrix with a coefficient in the form of the square of the free electron mass. Then the equation will give solutions coinciding with those of the Dirac equation. But this solution can be considered only approximate and the question remains how far we depart from strict adherence to the principle of invariance with respect to Lorentz transformations and how far we deviate from the hypothetical true solution, which is fully consistent with this principle. To find this solution, we need to approach this equation without simplifying assumptions and look for a set of solutions, each of which represents an eigenvalue matrix of arbitrary form and its corresponding four-component eigenfunction.
When searching for solutions, one can try to use two equations
successively applying the operators with first order derivatives included in them to the eigenfunctions already found, similarly as described in Schrödinger's work [8].
3. Equation for the spinor coordinate space
Let us return to the set of arbitrary complex numbers, for simplicity we will call it a vector
Let us consider in connection with it arbitrary four-component complex spinors
There is a representation of the components of the vector
and there is another way to calculate them
Further we will assume that both spinors are identical, then the vector constructed from them
has real components, and we will assume that this is the electron momentum vector constructed from the complex momentum spinor
Consider the complex quantity
where we introduce one more complex spinor, which in the future we will give the meaning of the complex coordinate spinor
and
Coordinate vector of the four-dimensional Minkowski space
is obtained from the coordinate spinor by the same formulas
The quantity is invariant under the Lorentz transformation simultaneously applied to the momentum and coordinate spinor, which automatically transforms both corresponding vectors as well
This quantity does not change for any combination of turns and boosts
Accordingly, the exponent
characterizes the propagation process of a plane wave in spinor space with phase invariant to Lorentz transformations.
Let us apply the differential operator to the spinor analog of a plane wave
Applying this operator at another definition of the phase gives the same eigenvalue
that is, two different eigenfunctions correspond to this eigenvalue, but in the second case the phase in the exponent is not invariant with respect to the Lorentz transformation, so we will use the first definition.
Since
are complex spinors, which, under the transformation
is affected by the same matrix , then the complex quantity
is invariant under the action on the momentum spinor of the transformation . is an eigenvalue of the differential operator, and the plane wave is the corresponding m eigenfunction, which is a solution of the equation
Here denotes the complex function of complex spinor coordinates.
When substantiating the Schrödinger equation for a plane wave in four-dimensional vector space, an assumption is made (further confirmed in the experiment) about its applicability to an arbitrary wave function. Let us make a similar assumption about the applicability of the reduced spinor equation to an arbitrary function of spinor coordinates, that is, we will consider this equation as universal and valid for all physical processes.
Let us clarify that by the derivative on a complex variable from a complex function we here understand the derivative from an arbitrary stepped complex function using the formula that is valid at least for any integer degrees
In particular, this is true for the exponential function, which is an infinite power series.
It is not by chance that we denote the eigenvalue by the symbol m, because if we form the momentum vector from the momentum spinor included in the expression for the plane wave
then for the square of its length the following equality will be satisfied
That is the square of the modulus m has the sense of the square of the mass of a free particle, which is described by a plane wave in spinor space as well as by a plane wave in vector space. For the momentum spinor of a fermionic type particle having in the rest frame the following form
quantity
is real and not equal to zero, and for the bosonic-type momentum spinor
it is zero
i.e., the boson satisfies the plane wave equation in spinor space with zero eigenvalue.
For the momentum spinor of a fermion-type particle we can consider another form in the rest system
then the mass will be real and negative
This particle with negative mass can be treated as an antiparticle, and in the rest frame its energy is equal to its mass modulo, but it is always positive
To describe the behavior of an electron in the presence of an external electromagnetic field, it is common practice to add the electromagnetic potential vector to its momentum vector. We use the same approach at the spinor level and to each component of the momentum spinor of the electron we add the corresponding component of the electromagnetic potential spinor. For simplicity, the electron charge is equal to unity.
Further we need an expression for the commutation relation between the components of the momentum spinor, to which is added the corresponding component of the electromagnetic potential spinor, which is a function of the spinor coordinates
Let us replace the momenta by differential operators
and find the commutation relation
Thus
Let us apply the proposed equation to analyze the wave function of the electron in a centrally symmetric electric field, this model is used to describe the hydrogen-like atom. For the components of the vector potential of a centrally symmetric electric field it is true that
As a result, it is possible to accept
We are looking for a solution of the spinor equation; we do not consider the electron's spin yet
This equation can be interpreted in another way.
Let us take the invariant expression
And let's do the substitution
We will consider this equation as an equation for determining the eigenvalues of and the corresponding eigenfunctions
Let's introduce the notations
this quantity does not change under rotations and boosts and is some analog of the interval defined for Minkowski space and
this quantity represents time in four-dimensional vector space.
As a result, we have an equation for determining the eigenvalues of m and their corresponding eigenfunctions
Instead of looking for solutions to this equation directly, we can first try substituting already known solutions to the Schrödinger equation for the hydrogen-like atom. If is one of these solutions, we need to find its derivatives over all spinor components
For example
To account for the electron spin, we will further represent the electron wave function as a four-component spinor function of four-component spinor coordinates
where the coefficients are some complex constants.
We will search for the solution of the wave equation considered in the first part of this paper
Let's express the left part through the components of the momentum spinor
Let's distinguish the direct products of vectors in these matrices
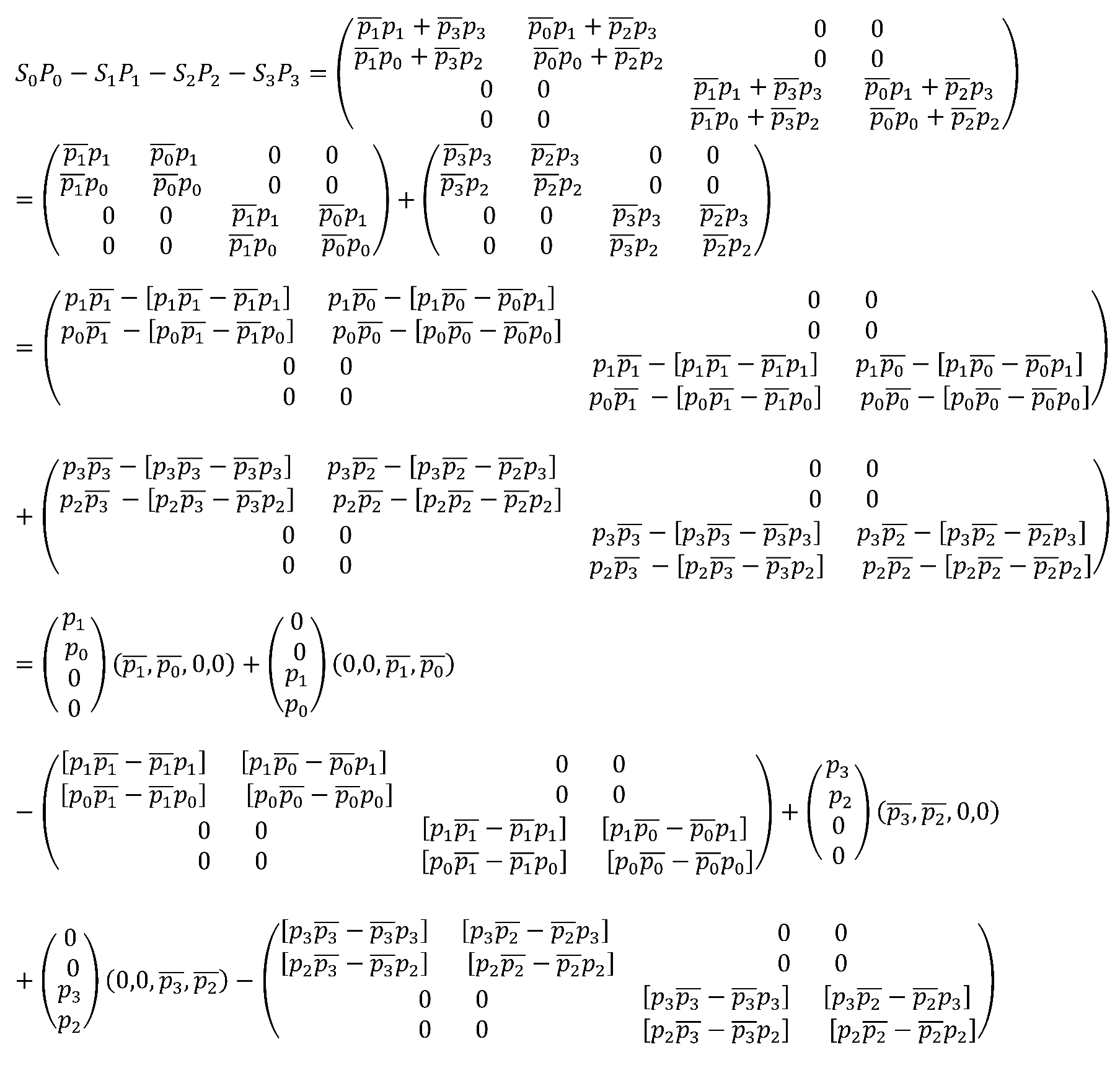
Let's introduce the notations
Let us substitute differential operators instead of spinor components
Then the quantities included in the wave equation
will have the form
Let us consider the case of a free particle and represent the electron field as a four-component spinor function of four-component spinor coordinates
For a free particle, the components of the momentum spinor commute with each other, so all components of the matrix are zero.
Let us use the model of a plane wave in spinor space
Substituting the plane wave solution into the differential equation, we obtain the algebraic equation
Let us take into account the commutativity of the momentum components, besides, let us introduce the notations
for the quantities which are invariant under any rotations and boosts, then we obtain
Additionally, introducing notation for Lorentz invariant quantities
we obtain
We see that in the case of a plane wave in spinor space, the matrix in the left part of the equation is diagonal and remains so at any rotations and boosts, the diagonal element also does not change.
In this case we can consider the matrix in the right part to be diagonal with the same elements on the diagonal , then the equation can be rewritten as an equation for the problem of finding eigenvalues and eigenfunctions
Let us compare our equation with the Dirac equation [6, formula (43.16)]
In the rest frame of reference, the three components of momentum are zero and the equation is simplified
That is, in the rest frame the Dirac equation and the spinor equation analyzed by us look identically and contain a diagonal matrix. The corresponding problem on eigenvalues and eigenvectors of these matrices has degenerate eigenvalues, which correspond to the linear space of eigenfunctions. In this space, one can choose an orthogonal basis of linearly independent functions, and this choice is quite arbitrary. For example, in [9], formula (2.127), solutions in the form of plane waves in the vector space have been proposed for the Dirac equation in the rest frame
and the following spinors are chosen as basis vectors
For transformation to a moving coordinate system in [9], formula (2.133) the following formula is used
Where
The basis spinors form a complete system, that is, any four-component complex spinor can be represented as their linear combination and this arbitrary spinor will be a solution to the problem on eigenvalues and eigenfunctions in a resting coordinate system. The choice of the given particular basis has disadvantages, because if to find a four-dimensional current vector from any of these basis functions
then this current in the rest frame of reference
has non-zero components, and the square of the length of the current vector is zero. It turns out that a resting electron creates a current, which contradicts physical common sense. Since we have freedom of choice of the basis, it is reasonable to choose the spinor of the wave function in the rest frame of reference proportional to the momentum spinor, for example
The proportionality factor is chosen so that in the rest frame the zero component of the current is equal to the charge of, for example, an electron or a positron. If the momentum spinor in the rest frame has the form
then the momentum vector in this rest frame of reference will be
and the current vector
The same momentum vector in the rest frame of reference can be obtained from different spinors, e.g,
after a 30-degree boost along the z-axis we get
After scaling the spinors by the factor , similar relations are true for the current vector. Thus, electrons can have the same momentum and current vector but different spinors, i.e., they are characterized by different spins. As it is supposed, the electron here has two physical degrees of freedom, since in a stationary frame of reference one can choose the components and to be real.
Thus defined spinor wave function for a free particle is invariant to Lorentz transformations, since in this case the mass of electron , its charge and the phase of the plane spinor wave
do not change at rotations and boosts. The matrix on the left side of the equation does not change either, remaining diagonal with on the diagonal.
It is logical to use the same considerations when choosing the basis for the wave function of the photon, whose mass, i.e., the eigenvalues of the wave function equation, are also degenerate and thus equal to zero. In this case, the choice of the proportionality factor between the spinor of the wave function and the momentum spinor is not so obvious, one can, for example, consider the option of
For a fermion, which can be an electron or a positron takes place , so the quantity
which, unlike the mass M in the Dirac equation, is complex in the general case, is also valid for the fermion and can be positive for the electron or negative for the positron. For the momentum spinor of a boson, such as a photon, it is true that , so its mass is zero
The given constructions are not abstract, but describe the physical reality, since the results of the processes occurring in the spinor space are displayed in the Minkowski vector space. In particular, the momentum vector corresponding to the momentum spinor has the following parameters
the square of the length is equal to the square of the mass of the electron or positron
And to the spinor wave function at some point in spinor space corresponds the vector wave function ()
(which for a plane wave coincides with the current vector), taking its value in the corresponding point of physical space with coordinates
The vector wave function can be compared in meaning to the square of the modulus of the conventional scalar wave function, in particular is equal to this square and has the meaning of probability. The conventional scalar wave function itself is closer in meaning to the spinor wave function considered here, they both have complex values, and the four-component wave functions of the electron have in both cases the same meaning.
The arbitrary choice of the basis of the linear space of the eigenvectors of the matrix takes place only for a free particle. In the general case the matrix K is not zero, the wave equation has no solution in the form of plane waves in spinor space and ceases to be invariant with respect to Lorentz transformations, and the eigenvalues become nondegenerate.
We propose to extend the scope of applicability of the presented equation consisting of differential operators in the form of partial derivatives on the components of coordinate spinors with a nonzero matrix K
not only to the case of a plane wave, but to any situation in general. This transition is analogous to the transition from the application of the Schrödinger equation to a plane wave in vector space to its application in a general situation. The legitimacy of such transitions should be confirmed by the results of experiments.
This equation will be called the equation for the spinor wave function defined on the spinor coordinate space. Here the matrix is, generally speaking, neither diagonal nor real, but it does not depend on the coordinates and is determined solely by the parameters of the electromagnetic field. Only in the case of a plane wave it is diagonal and has on the diagonal the square of the mass of the free particle. We can try to simplify the problem and require that the matrix is diagonal with the same elements on the diagonal , then the equation can be rewritten in the form of the equation for the problem of search of eigenvalues and eigenfunctions for any quantum states
This approach is pleasant in the Dirac equation, where the mass is fixed and equated to the mass of a free particle, and at the same time results giving good agreement with experiment are obtained.
We are of the opinion that the spinor equation is more fundamental than the relativistic Schrödinger and Dirac equations, it is not a generalization of them, it is a refinement of them, because it describes nature at the spinor level, and hence is more precise and detailed than the equations for the wave function defined on the vector space.
Let us consider the proposed equation for the special case when the particle is in an external electromagnetic field, which we will also represent by a four-component spinor function at a point of the spinor coordinate space
We will apply to the wave function of the electron the operators corresponding to the components of the momentum spinor, putting for simplicity the electron charge equal to unity
Note that the electromagnetic potential vector can be calculated from the electromagnetic potential spinor by the standard formula
The advantage of the spinor description over the vector description is that instead of summing up the components of the momentum and electromagnetic potential vectors as is usually done
now we sum the spinor components and then the resulting vector is
in addition to the usual momentum and field vectors, contains an additional term
taking real values and describing the mutual influence of the fields of the electron and photon.
After the addition of the electromagnetic field the components of the momentum spinor do not commute, the corresponding commutators are found above
Let's find commutators for other operators
Further we will use these and analogous relations
Let's solve the equation
Since the second factor in the left-hand side of the equation has a simpler structure than the first factor, perhaps as a first step we should find the eigenvalues and eigenfunctions of the equation
and use them when solving the equation as a whole.

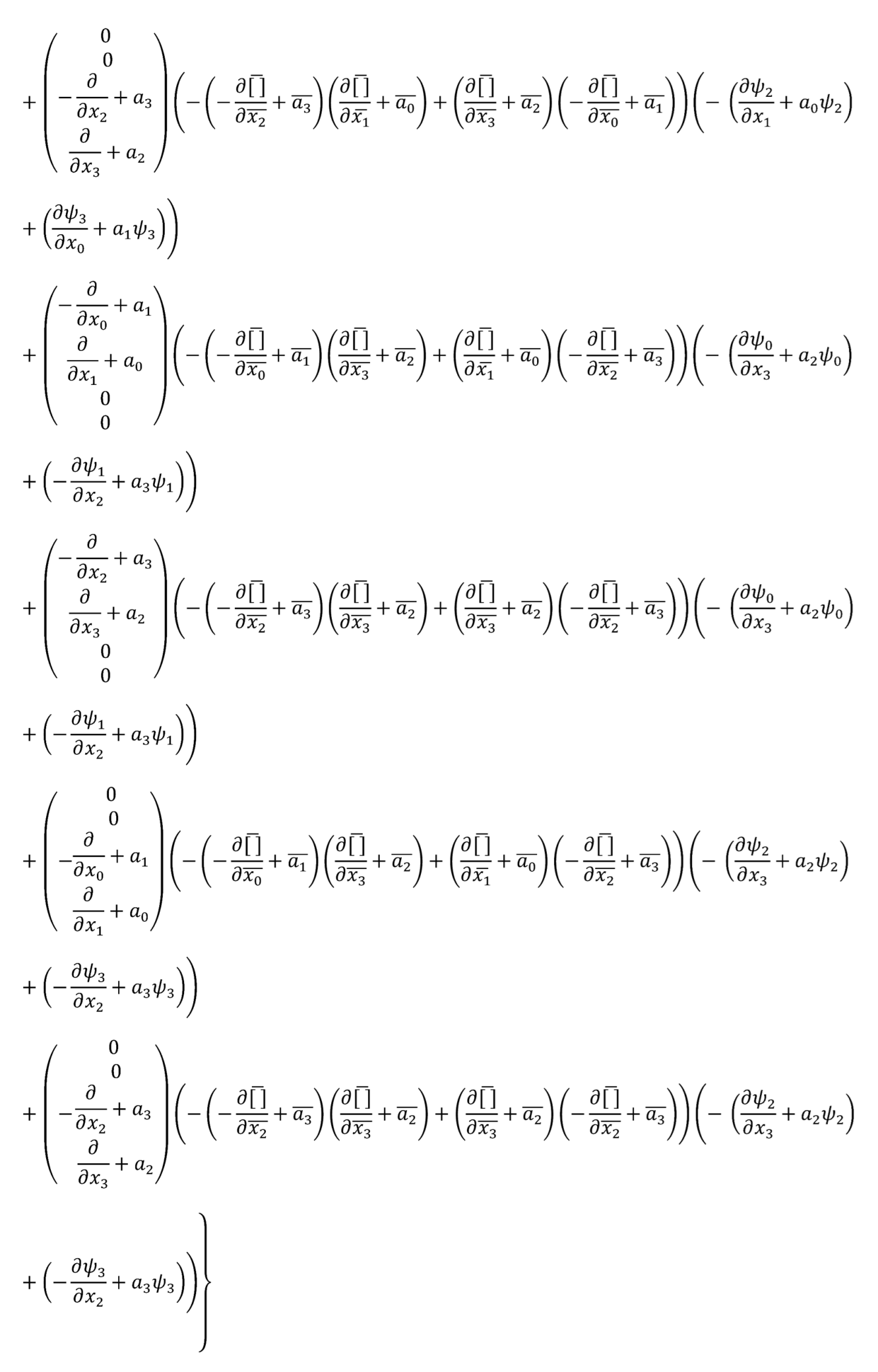

Let's calculate the expressions included in the equation
Let us consider the situation when the electromagnetic potential can be described by a plane wave in spinor space
When the electromagnetic potential is represented by a plane wave, the field created by a charged particle is not taken into account, so this model adequately describes only the situation when the electromagnetic field is strong enough and the influence of the particle charge can be neglected.
It would be interesting in this context to consider for the presented spinor model the case of a centrally symmetric electric field and to find solutions of the spinor wave equation for the hydrogen-like atom, taking into account the presence of spin at the electron. For such a model we can take
As mentioned above, here too we can substitute into the equation the already known exact solutions of the Dirac equation for the hydrogen-like atom by expressing the components of the coordinate vector and derivatives on them through the components of the coordinate spinor and derivatives on them. It is likely that the solution of the Dirac equation would not make the spinor equation an identity; it would be evidence that more arbitrary assumptions are made in the Dirac equation than in the spinor equation, and that the latter claims to be a better description of nature.
We can also consider the case of a constant magnetic field directed along the z-axis
Let's say
We see that the scalar potential grows with time, but does not depend on spatial coordinates, and the vector potential does not depend on time, so that there is no electric field. In this case
If consistently to adhere to the idea of the fundamentality of the spinor space, it is necessary to reformulate the procedure of second quantization of the electron field. According to the known concept, the wave function of the electron field is represented in the form of expansion by plane waves describing a free electron. But we can use plane waves not in vector space, but plane waves in spinor space
In this case, let us assume
We can start the analysis in a stationary frame of reference, for transition to the general case it is necessary to apply the Lorentz transformation to the impulse and coordinate spinors, in this case neither the phase in the exponent nor the mass of the electron changes. In the rest frame, one momentum vector corresponds to four momentum spinors
Signs of the respective masses
say that it's two particles with positive mass and two with negative mass.
The orthogonality relations take place in any reference frame
Let us accept the agreement that spinors p2 and p4 describe the field with zero number of particles in the state with momentum P and masses with different sign. Spinors p1 and p3 describe the field with presence of a particle in a state with momentum P and negative or positive mass, respectively. The transition from one state to another is provided by the annihilation and birth operators
The relations can be directly verified
The action of the operators does not change the sign of the mass of the particle. Here the particle number operator demonstrates that two states are indeed filled and two are empty, since this operator has an eigenvalue in one case of one and in the other case of zero.
The wave function of the electron field at a fixed value of the momentum vector P will be a combination of plane spinor waves with four momentum spinors corresponding to this momentum vector.
A system of particles with different momenta can be described by the direct product of momentum spinors, which includes spinors ,, as well as their versions subjected to an arbitrary Lorentz transformation ,, as co-multipliers
This system can be acted upon by an operator in the form of a direct product of an arbitrary set of annihilation and birth operator matrices or unit matrices for a particle whose state does not change
In this case
The annihilation and birth operators have disadvantage, they do not commute with Lorentz transformations matrix
Let's introduce operators
The product of them commute with the Lorentz transformations matrix and they anticommutate with each other
The product of those operators with the proper order choice transform the state with zero number of particles to the state with presence of a particle and vice versa, and this relation is Lorentz invariant
Double applying this product changes the momentum spinor sign
Conclusion
An alternative approach to analyze relativistic and quantum effects inherent in charged particles in the presence of an electromagnetic field is proposed. Two ways of describing the electron behavior in the electromagnetic field are considered: by means of the vector equation, which is based on the plane wave model for a free electron, and the spinor equation, which is based on the representation of the electron as a plane wave in spinor space. For both equations, which are valid for a free particle, their applicability to an arbitrary physical situation is postulated, in particular to describe the behavior of a particle in the presence of an electromagnetic field. The presented equations are intended to fulfill the same role as the Schrödinger equation and the Dirac equation. At the same time, in our opinion, the spinor equations more accurately describe the details of the interaction between fields and particles.
References
- Marsch, E.; Narita, Y. A New Route to Symmetries through the Extended Dirac Equation. Symmetry 2023, 15, 492. [Google Scholar] [CrossRef]
- Fleury, N.; Hammad, F.; Sadeghi, P. Revisiting the Schrödinger–Dirac Equation. Symmetry 2023, 15, 432. [Google Scholar] [CrossRef]
- Jean Maruani, The Dirac Equation as a Privileged Road to the Understanding of Quantum Matter, Quantum Matter Vol. 4, 3–11, 2015. [CrossRef]
- Hiley, B.; Dennis, G. de Broglie, General Covariance and a Geometric Background to Quantum Mechanics. Symmetry 2024, 16, 67. [Google Scholar] [CrossRef]
- arXiv:1502.02351v9 [quant-ph] 23 Apr 2022.
- Leonard, I. Schiff, Quantum Mechanics, Third edition. McGraw-Hill Book Company, 1959 - 545 p.
- P. A. M. Dirac. The principles of quantum mechanics (International Series of Monographs on Physics), Fourth edition, Oxford Science Publications.
- E. Schrödinger, “A Method of Determining Quantum-Mechanical Eigenvalues and Eigenfunctions”, Proceedings of the Royal Irish Academy, Vol. 46A, 1940, pp. 9-16.
- Lewis, H. Ryder, Quantum Field Theory, University of Kent, Canterbury – 1996 г.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated





