Prerpints.org logo
Preprint
Article

Computation of Real-Fluid Thermophysical Properties Using a Neural Network Approach Implemented in OpenFOAM

Altmetrics

Downloads

133

Views

77

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

12 January 2024

Posted:

14 January 2024

You are already at the latest version

Alerts
Abstract
Machine learning (ML) based on neural network (NN) facilitates data-driven techniques for handling large amounts of data, either obtained through experiments or simulations at multiple spatio-temporal scales, thereby finding the hidden patterns underlying these data and promoting efficient research methods. The main purpose of this paper is to extend the capabilities of a new solver, called realFluidReactingNNFoam, under development at University of Perugia in OpenFOAM with NN algorithm for replacing complex real-fluid thermophysical property evaluations, using the approach of coupling OpenFOAM and Python-trained NN models. Currently, NN models are trained against data generated using the Peng-Robinson equation of state (PR-EoS) assuming mixture frozen temperature. The OpenFOAM solver, where needed, calls the NN models in each grid-cell with appropriate inputs, and the returned results are used and stored in suitable OpenFOAM data structures. Such inference for the thermophysical properties is achieved via the “Neural Network Inference in C made Easy” (NNICE) library, which proved to be very efficient and robust. The overall model is validated considering a liquid-rocket benchmark comprised of liquid-oxygen (LOX) and gaseous-hydrogen (GH2) streams. The model accounts for real-fluid thermodynamics and transport properties, making use of the PR-EoS and the Chung transport models. First, the development of a real-fluid model (RFM) with artificial neural network is described in detail. Then, the numerical results of the transcritical mixing layer (LOX/GH2) benchmark are presented and analyzed in terms of accuracy and computational ef-ficiency. Results of the overall implementation indicate that the combined OpenFOAM and ML approach provides a speed-up factor higher than seven, while preserving the original solver accuracy.
Keywords: 
Subject: Engineering  -   Mechanical Engineering

1. Introduction

This introduction provides an overview of the historical and evolving role of ML in CFD, highlighting its transformative potential across numerous applications. As we delve deeper into the intersection of ML and CFD, we will explore specific methodologies, case studies, and emerging trends that underscore the symbiotic relationship between these two fields, ultimately reshaping our understanding of fluid dynamics and propelling innovation in diverse industries.
Admittedly, much progress has been made the last years to promote understanding of combustion, from computational sides, analyzing hydrogen high-pressure injection and mixing processes [1] including assessment of a model which accounts for real fluid thermodynamics and transport properties, making use of the Peng-Robinson equation of state (PR-EoS) and the Chung transport model [2]. Reitz and co-workers focused on a thermodynamic analysis of the mixture states [3]. The challenges primarily come from real-gas effects, which have significant effects on these processes, introducing non-linearities into the thermodynamic system and resulting in non-physical pressure oscillations that can substantially affect accuracy. Fluid properties in states near a pure component’s critical point are the most difficult to obtain from both experiments and from models such as EoS [4]. The principal experimental difficulty is that the density of a near-critical fluid is so extremely sensitive to variations in pressure and temperature, that maintaining homogeneous and stable conditions takes extreme care [5]. Even gravity influences the measurements. The principal model difficulty is that near-critical property variations do not follow the same mathematics as at conditions well-removed from the critical point [6].
Advanced propulsion and transportation systems, from rocket to diesel engines, often involve high-pressure injection of substances. In liquid-fueled rockets, propellants are introduced in a supercritical or transcritical state, exceeding fluid critical pressure and experiencing temperatures near or below the critical temperature. This deviates from traditional subcritical injection, causing significant changes in fluid properties due to temperature fluctuations. The assumption of negligible molecule volume breaks down, leading to deviations from ideal gas behavior.
Numerous theoretical and experimental studies, such as Puissant et al.'s investigations on shear coaxial injection [7] and Mayer's understanding of LOX/GH2 rocket engine combustion processes [8], have been conducted on high-pressure flows. These studies aim to gain insight into chemical and physical processes, providing a database for improved modeling and validation of simulation codes in combustor design and optimization [9]. Analyzing hydrogen high-pressure injection in the near-nozzle region, investigating the formation process and the structure of the Mach disks and the transition to turbulent jets, is done by Rahantamialisoa et al. [10], and Oschwald et al. [11] present experiments on inert binary injection and mixing processes.
While these works contribute significantly, their constraints in fully capturing information through experiments are acknowledged. Consequently, there is an increasing emphasis on modeling studies focused on transcritical and supercritical flows.
In the near future, the necessity will arise for designing adaptable energy production and propulsion systems that can efficiently utilize a wide range of fuels, including synthetic, bio-derived, fossil fuels, or various combinations thereof. Modeling these fuels, especially when their properties are not initially known, will demand flexible methods that can describe essential operational traits with minimal input data. To achieve this objective, following Koukouvinis et al. [12], we propose the application of machine learning (ML) to provide quantitative predictions under unknown conditions by leveraging existing research, be it from experiments or simulations.
Using tabulation, ML and artificial Neural Networks (NN) models for tackling the complex issue of transcritical sprays, which are relevant to modern compression-ignition engines can assist the speeding up the calculations. Direct simulations can incur significant CPU costs, whereas tabulation may be memory-intensive and challenging to expand as the number of chemical species grows [13,14]. In contrast, NN have emerged as a remarkably efficient technique for classification and response prediction. In high pressure, high temperature conditions, the NN methods are used to predict the thermodynamic properties [12] and the tabulation method offers high-precision calculation results in a wide temperature and pressure range [13,14]. ML techniques are rapidly advancing in this era of big data, and there is high potential in exploring the combination between ML and combustion research and achieving remarkable results. Much of this interest is attributed to the remarkable performance of deep learning architectures, which hierarchically extract informative features from data [15]. In the field of fluid mechanics, NNs are currently being investigated as a complementary tool to Computational Fluid Dynamics (CFD) for accelerating design processes [12]. A recent thorough review discusses a variety of applications in fluid mechanics, involving flow feature extraction, turbulence modelling, optimization and flow control [15]. In addition, an implementation of the NN models in OpenFOAM using PyFOAM tool, which is an in situ data analysis with Python and OpenFOAM is done by R. Maulik et al. [16,17,18].
This work discusses the capabilities of a new solver, called realFluidReactingNNFoam using NN algorithm for replacing complex real-fluid thermophysical properties evaluations, using the approach of coupling OpenFOAM and Python-developed models.

2. Materials and Methods

2.1. CFD Model

The governing equations for a fully conservative, homogeneous, multicomponent, and compressible non-reacting two-phase flow are the conservation equations for mass, momentum, energy, and species which are written below [2,19,20]:
∂ ρ ∂ t + ∇ · ρ U = 0
∂ ρ U ∂ t + ∇ · ρ U U = ∇ · − p I + τ
∂ ( ρ h T ) ∂ t + ∇ · ρ h T U = ∂ p ∂ t + ∇ · U · τ − ∇ · q
∂ ( ρ Y k ) ∂ t + ∇ · ρ Y k U = − ∇ · J k
In the above equations, ρ is the mixture density, U is the mixture velocity vector, p is the pressure shared by all species, τ is the viscous stress tensor of the mixture, Y k is the mass fraction of species k, and J k and q refers to diffusion flux of species k and heat flux, respectively. Also, h T = h + 1 / 2 U 2 is the total enthalpy of the mixture.
Additionally, for the evaluation of thermodynamic fluid properties under supercritical pressure, the PR-EoS is employed:
p v , T = R T v − b m − a m v 2 + 2 b m v − b m 2
where v is molar volume, T is the temperature, b m is the effective molecular volume, a m is the attractive force between molecules (note that the subscript m refers to the mixture) and R is the gas constant. In such approach, local mechanical and thermal equilibrium between the two phases is always enforced. As for transport properties, Chung correlations are used for viscosity and thermal conductivity [21]. Non-linear mixing rules are used to calculate any mixture coefficients appearing inside the PR and Chung models. More details about all the aspects of the RFM thermophysical model can be found in reference [2].
It is important to emphasize that this modeling approach does not account for phase splitting when retrieving the temperature from the mixture enthalpy. Instead, it calculates the so called frozen adiabatic mixing temperature, without considering phase stability and splitting. In other words, phase volume fractions are not considered for the calculation of local temperature, which is an approximation in terms of model accuracy but it does not have any impact for the objective of the present work.
It is also worth stating explicitly that this paper does not focus on the physical accuracy of the numerical results; its sole objective is to evaluate the proposed NN model in contrast to the direct solution based on the cubic EoS for multicomponent systems.

2.2. Artificial Neural Networks (NN) and Multilayer Perceptrons (MLP)

The multilayer perceptron is a widely used NN model for function approximation consisting of multiple layers with each layer containing several neurons [22]. The multilayer perceptron models nonlinear relationships between input and output vectors, utilizing simple nonlinear functions in a feed-forward neural network [23]. The backpropagation algorithm is commonly used for training, adjusting weights based on the local gradient of the error surface. In summary, the network is initialized with weights, processes input vectors to generate output, calculates error signals, and iteratively adjusts weights to minimize errors until an acceptable level is reached [24].
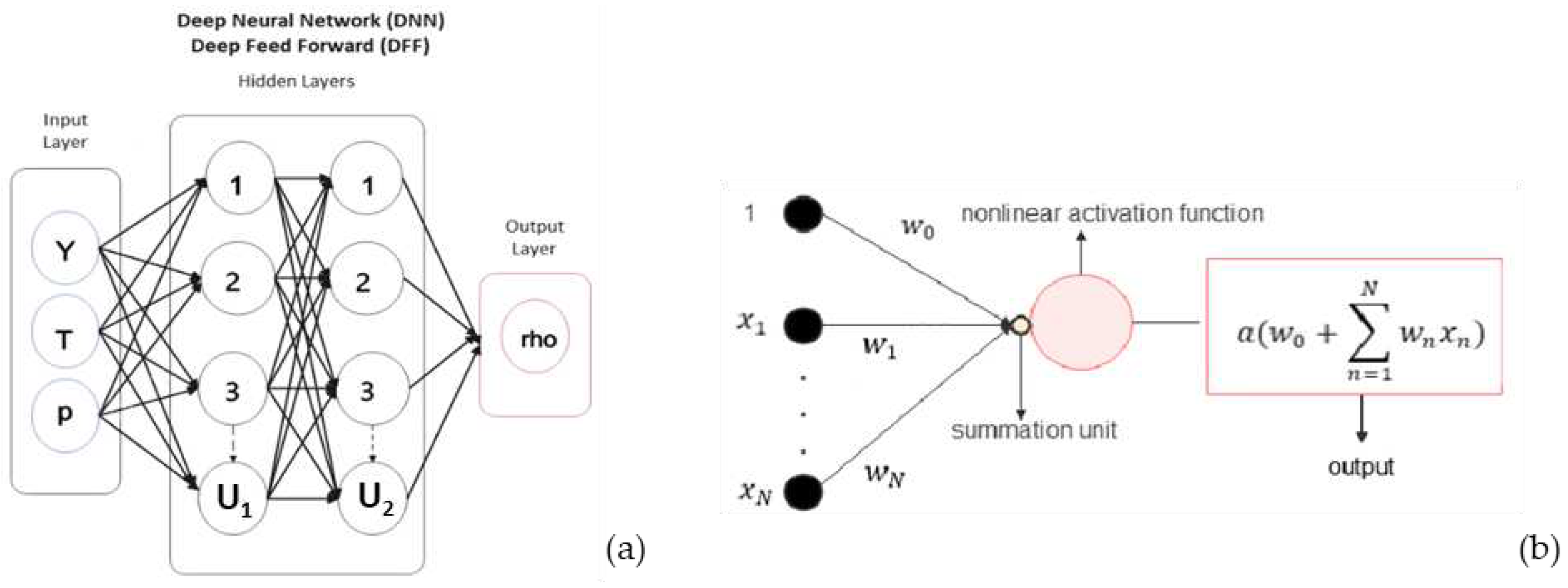
In the present case, the neural network used consists of one input layer including 3 properties (composition, temperature, and pressure), two hidden layers with 100 number of neurons, and one output layer including one parameter, as shown exemplary in Figure 1.a for predicting density. Figure 1.b shows a typical structure of a neuron.
The mathematical representation of a single hidden-layer unit, often referred to as a single layer unit, is straightforward. It involves a linear combination of inputs processed through a nonlinear 'activation' function, typically a simple elementary mathematical function. In general, we will denote such units as follows [25]:
f j 1 x = a v j ( x )
v j x = w j 1 T x = w 0 , j ( 1 ) + ∑ n = 1 N w n , j ( 1 ) x n ,     j = 1 , … , U 1
in which f j 1 is the first layer output, with j the index of each unit in the layer, v j is the linear combination, w j 1 = w 0 , j ( 1 ) , w 1 , j ( 1 ) ,   w 2 , j ( 1 ) , … , w n , j 1 ,   … , w N , j ( 1 ) is the weight vector where w 0 , j ( 1 ) is the bias and w n , j ( 1 ) are the weights from each single input, and x = 1 , x 1 ,   x 2 , … , x n ,   … , x N is the input layer. Then, a v is the nonlinear activation function applied to the value v , which is Rectified Linear Unit (ReLU) activation function in our case. The following equation shows the ReLU activation function:
a v = R e L U v = m a x ( 0 , v )
As expressed by the formula, ReLU acts as a feature detector. To make the concept of extending from a single layer to a multilayer neural network clearer, let us break down the sequence into two key operations: combining inputs linearly and passing the result through a nonlinear activation. This approach is essential for creating single-layer perceptron units [25]. The following equations show the output value for the second layer and the Lth layer respectively. f 2 and f L show the outputs of the second and the Lth layers.
f j 2 x = a w 0 , j ( 2 ) + ∑ i = 1 U 1 w i , j ( 2 ) f i 1 x  
f j L x = a w 0 , j ( L ) + ∑ i = 1 U L − 1 w i , j ( L ) f i L − 1 x  

2.3. Training Database

As training tool, Keras and Tensorflow libraries are used which are open-source libraries that provide a Python interface for NN [26]. To effectively train the network, it requires data featuring properties relevant to the main problem, such as consistent thermophysical properties.
Precision in tuning or optimizing parameters poses a challenge. Hyperparameters, especially the learning rate (α), play a crucial role, impacting computational cost, execution time, and network structure. The learning rate is vital in minimizing the loss function during backpropagation, where it iteratively updates biases and weights in hidden layers. This process, involving multiplying the learning rate by the output error of neurons, continues until an acceptable error is achieved for the specified data in each iteration, influencing prediction accuracy and generalization capability. As it is shown in Table 1, the considered inputs are composition ( Y H 2 ), temperature ( T ), and pressure ( p ) by order, for predicting density ( ρ ), viscosity ( μ ), thermal diffusivity ( α ), enthalpy ( h ) and the compressibility ( ψ ). For predicting temperature ( T ) as output, composition ( Y H 2 ), pressure ( p ) and enthalpy ( h ) are considered as the inputs. The full definitions and units of outputs are shown in Table 2.
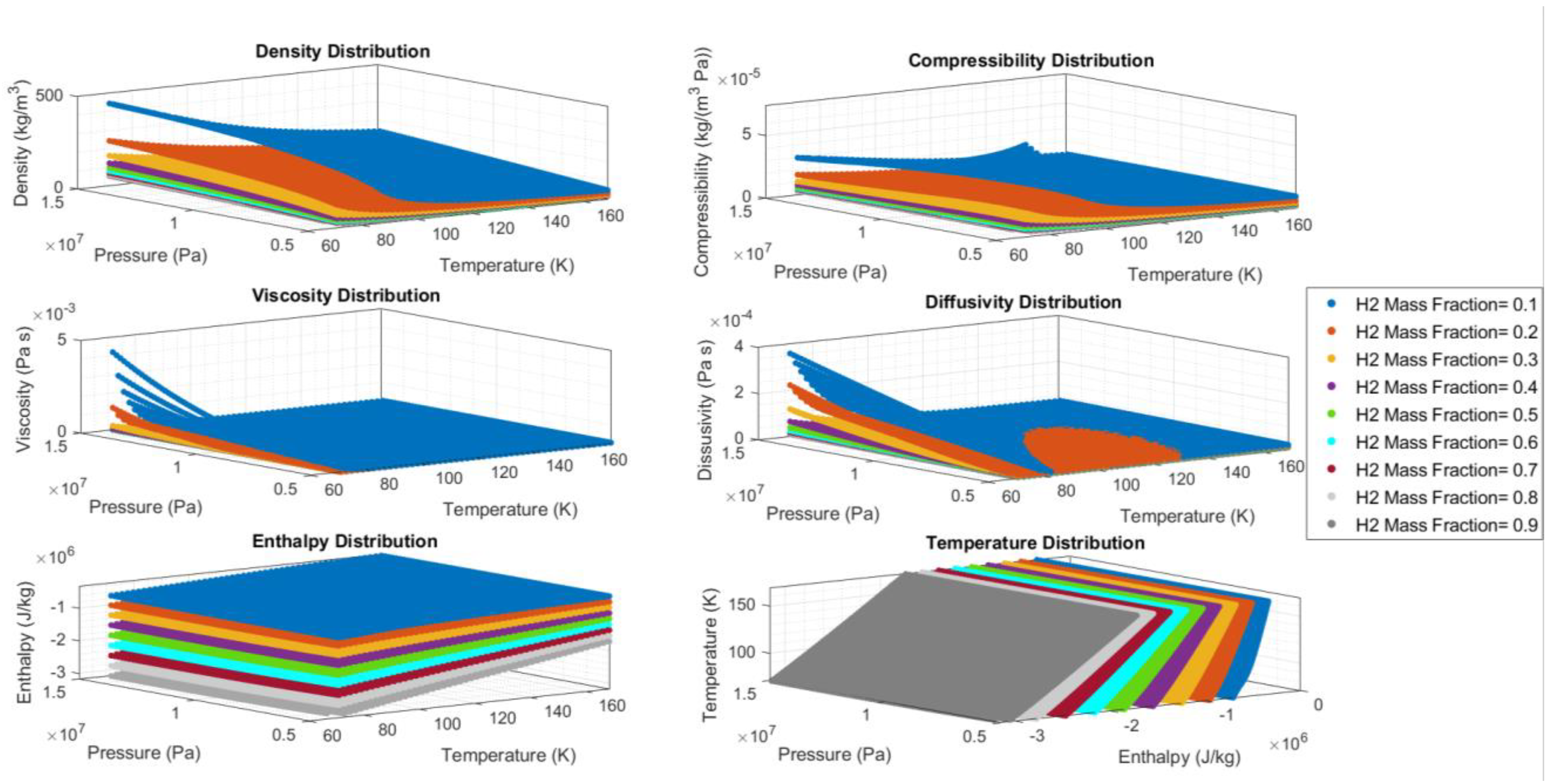
In this specific test case, the properties exhibit highly non-linear distributions. Consequently, various data transformations are experimented to enhance network performance. Figure 2 illustrates that the data distributions for enthalpy and temperature are notably smoother, indicating fewer challenges in training these specific properties.

2.3. Model Training

In the following, all the methods tested to improve the efficiency of the network are elaborated. For all the properties, the min-max scalar is applied for inputs and outputs, to facilitate training. As mentioned before, ReLU is considered as the activation function. The optimizer algorithm is Adam, and the loss metrics is the Mean Squared Error (MSE). The final values of other hyperparameters like hidden layer size, epochs, and batch size is obtained by experience for each output parameter. Table 3 reports the number of epochs, and the loss metrics for each output parameter. Learning rate is 0.0015, the batch size is 256, and the hidden layer size is considered 100×100 for all of the outputs. The influences of choosing different hyperparameters to train the network can be seen in Figure 3 and Figure 4. 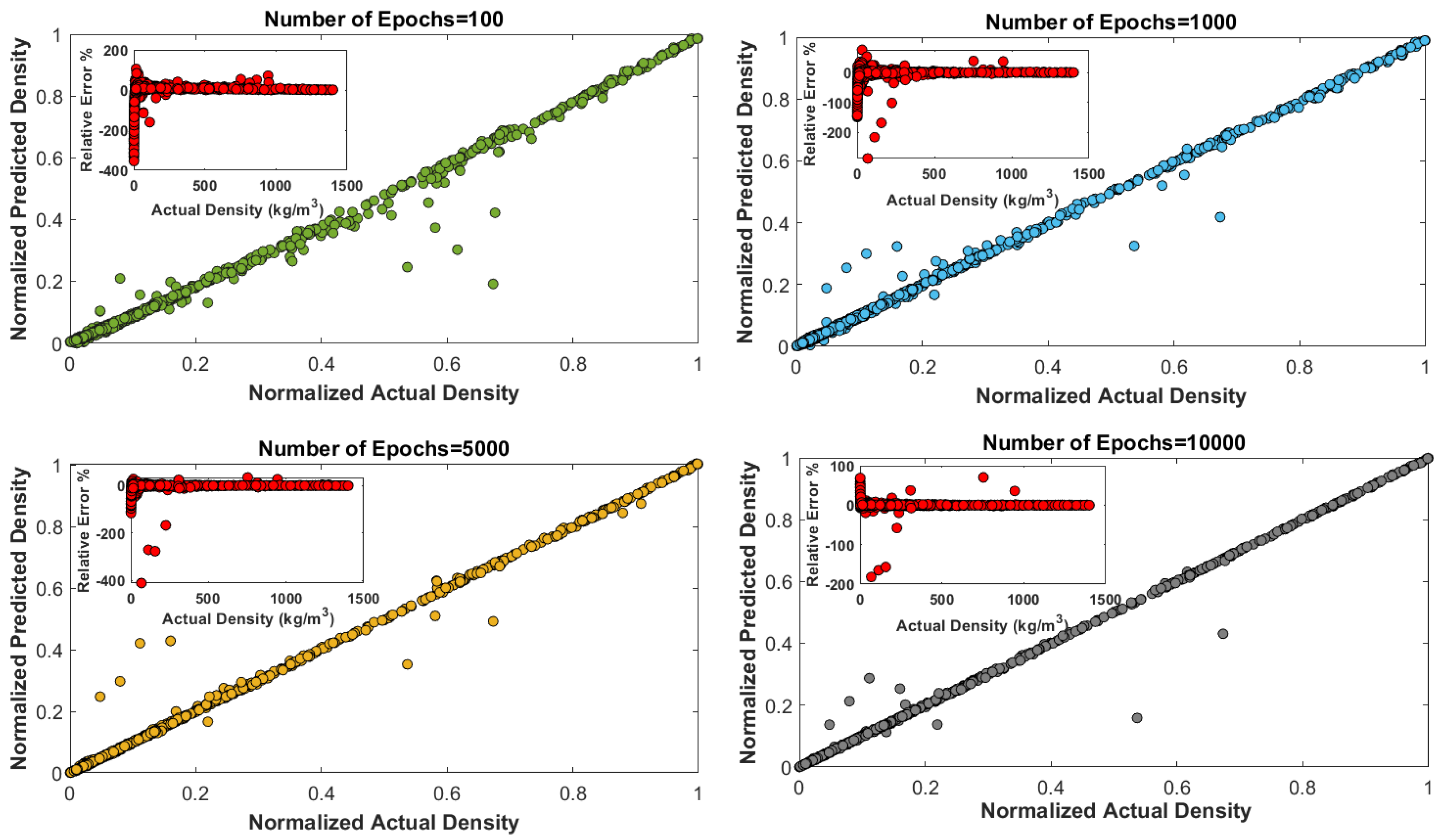As it is shown in Figure 3, by increasing the number of epochs the relative error decreases for the density, but for a greater number of epochs there will be no change, and also it is probable to end up in overfitting. 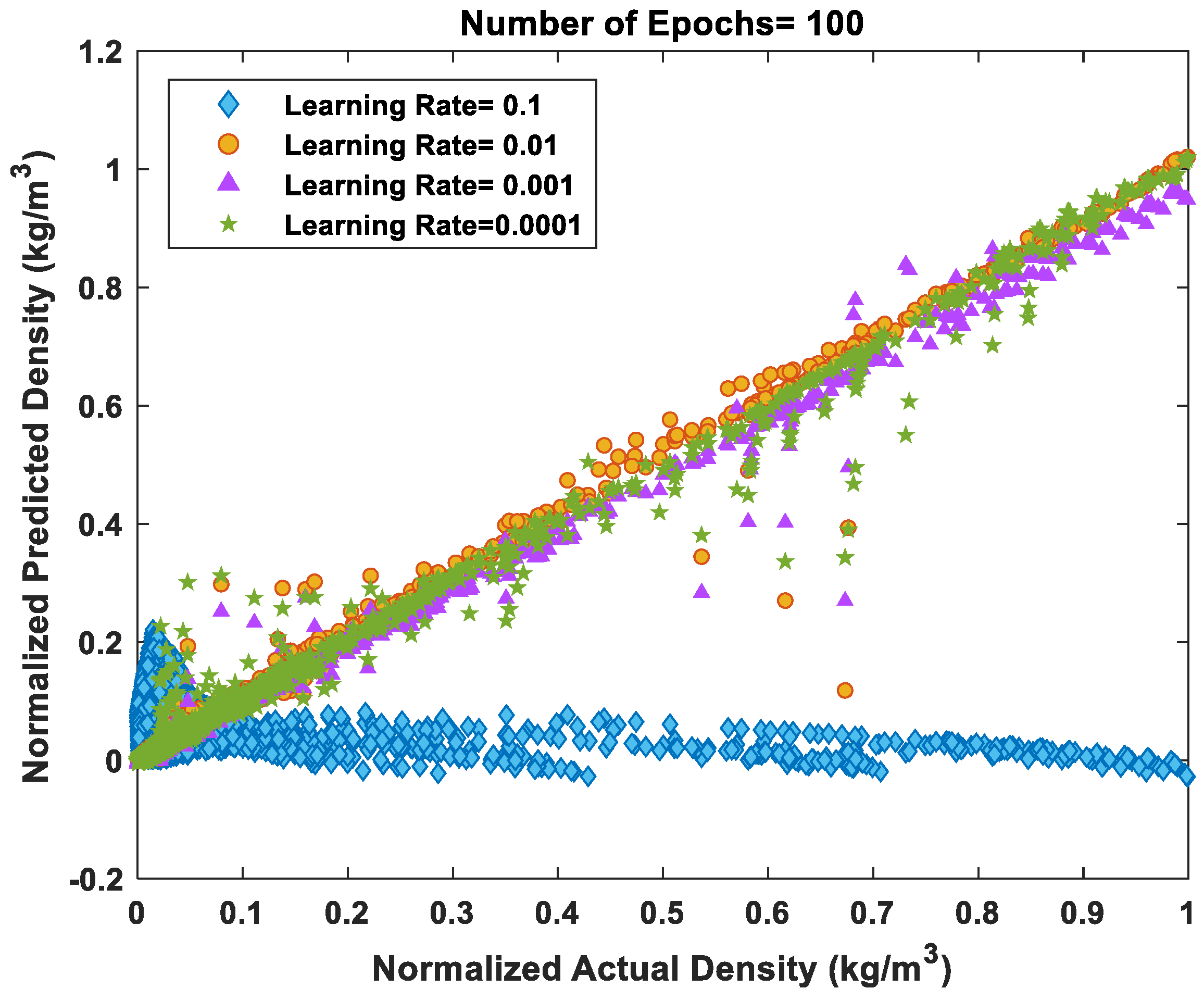Also, the effects of using different learning rates is shown in Figure 4. A good way for choosing the hyperparameters is to use the previous tested ones, or by experience.
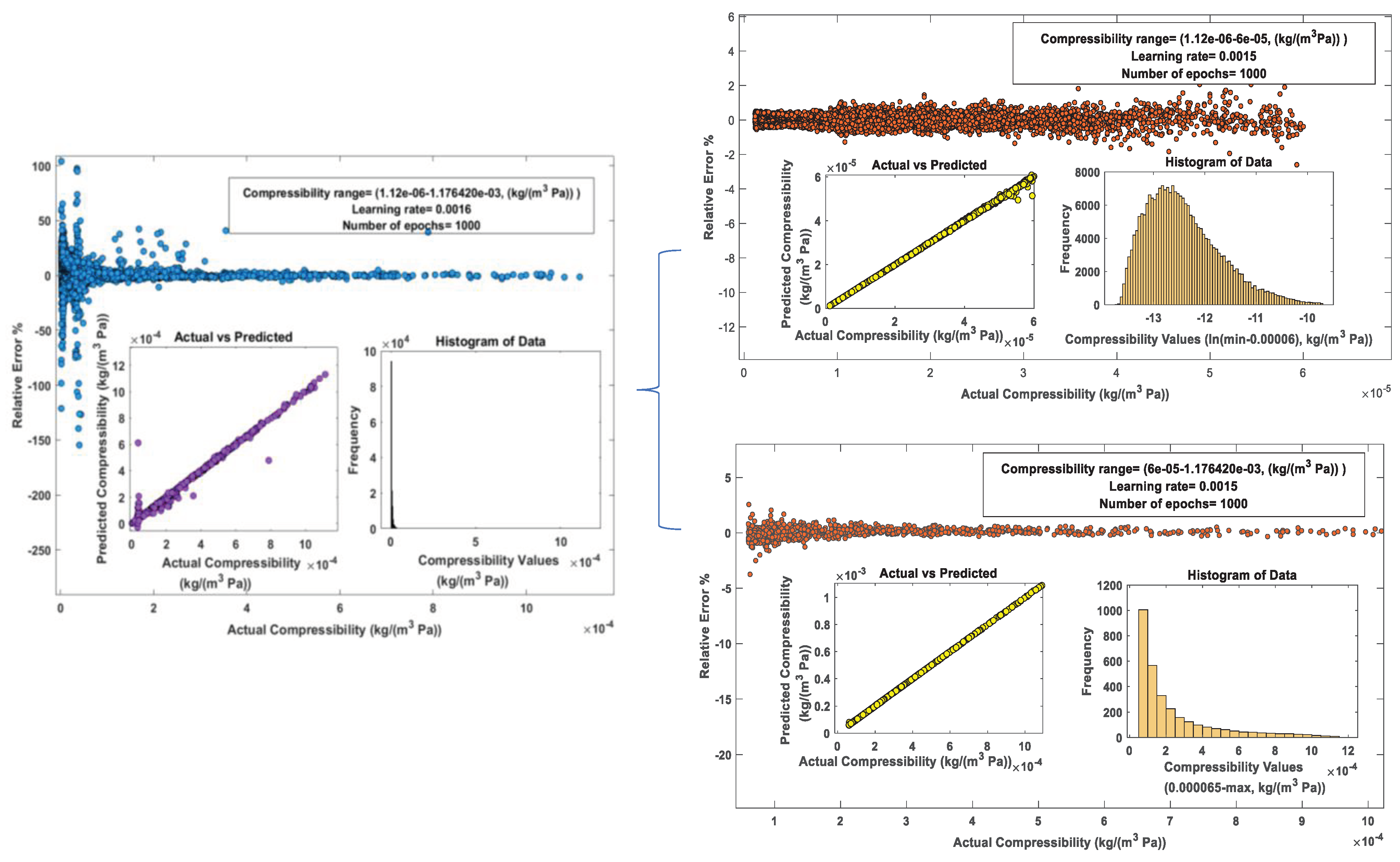
The training algorithm aims to minimize the sum of the square errors [22]. This implies that the training minimizes absolute errors across all MLP outputs, regardless of relative errors. However, upon closer examination, as an example, within the compressibility output value range (1.12e-6 - 1.178e-3 kg/(m3 Pa)), cf. full-range chart in Figure 5, it becomes evident that relative errors are notably high, reaching up to 100 % in certain points. It is crucial to note that these suboptimal outcomes do not necessarily indicate inadequate MLP training. Instead, they underscore the importance of selecting an appropriate indicator of the MLP performance. The substantial relative errors for smaller target outputs could significantly impact the application of MLPs in real simulation [22].
For instance, in our model, temperature serves both as an input and as an output. A substantial relative error in temperature propagates errors in calculating other variables, leading to rapid divergence after a few time steps due to the cumulative effect. To mitigate this, it becomes imperative to diminish the prediction errors of NN for outputs with small magnitudes. One viable approach is to partition the data into ranges and train the network separately for each output within those ranges.
As illustrated in Figure 5, for the compressibility values within the range of 1.12×10-6 -1.178×10-3 kg/(m3 Pa), certain points, despite multiple attempts to optimize performance, exhibit relative errors reaching up to 100 %, as already mentioned, on the small value side. However, the objective is to achieve the least relative error. To address this, the data is split into two ranges: the first encompasses 90 % of the data, and the second covers the remaining 10 %. A log transformation is employed before scaling the data within 0-1, in the first sub-range (1.12×10-6 - 6×10-5 kg/(m3 Pa)). By normalizing the input and output parameters according to their respective characteristics, we can optimize the learning process, resulting in more efficient predictions and improved overall performance [27]. Also, the logarithmic distribution accommodates the specific characteristics and value ranges associated with output parameters, contributing to enhanced model performance and accuracy [27].
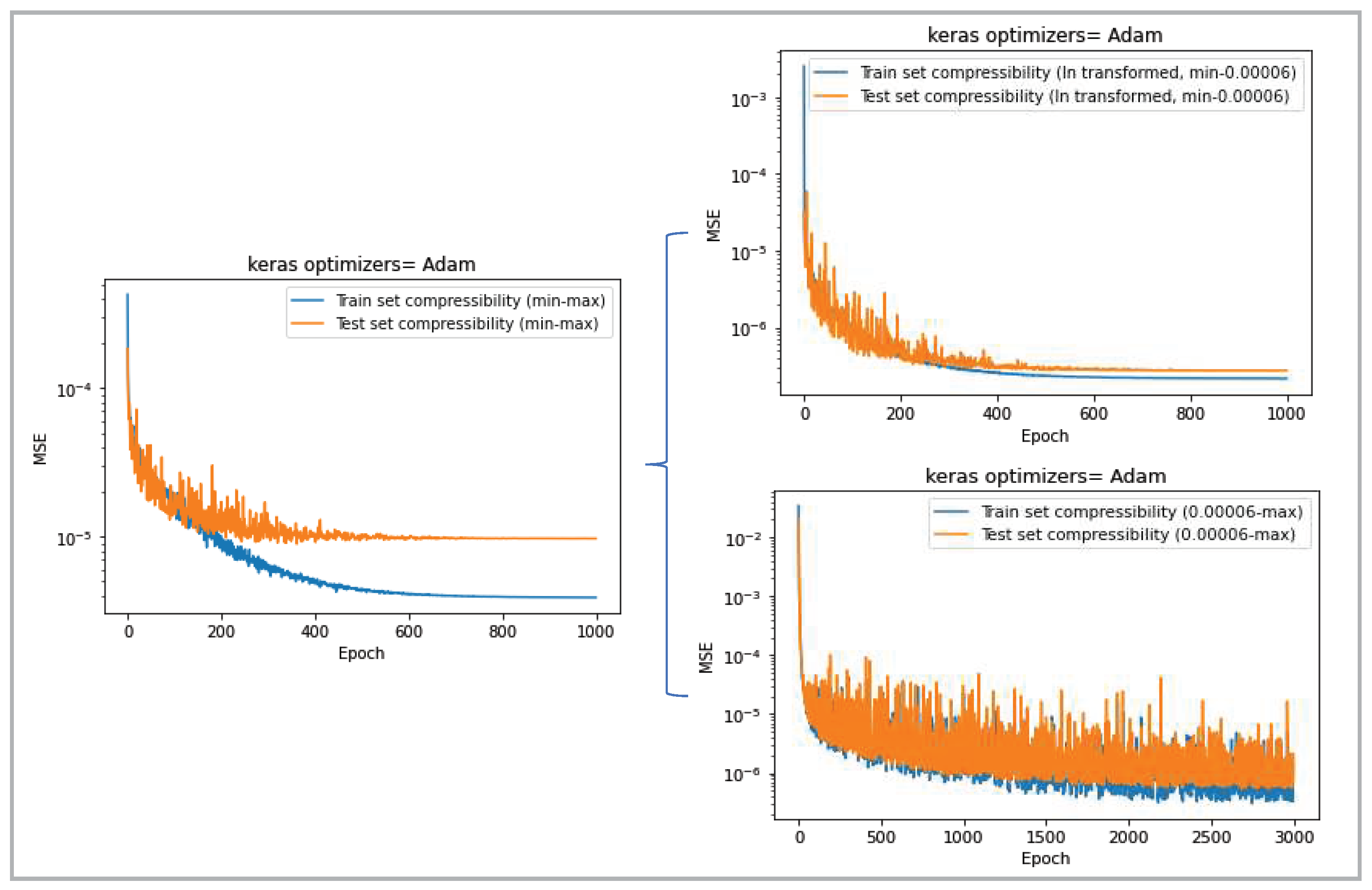
In addition, from the learning curves which are shown in Figure 6, the higher efficiency of this split approach can be seen. Learning curves serve as a frequently employed diagnostic tool for algorithms that iteratively learn from a training dataset. Throughout the training process, the model's performance is assessed on both the training dataset and a separate validation dataset. Plots illustrating the performance measurements are created to display these learning curves. Analyzing the shape and trends within a learning curve can provide insights into the behavior of a machine learning model and potentially offer suggestions for configuration adjustments to enhance learning and performance. The ultimate objective is to achieve a well-fitting model, indicated by a training and validation loss that decreases and stabilizes with minimal disparity between their final loss values. Typically, the model's loss will be lower on the training dataset than on the validation dataset. Consequently, it is expected to observe a gap between the learning curves of training and validation losses like the curve related to the first range of compressibility which is shown in Figure 6, but not too much loss like the curve related to the whole range of compressibility. So, for compressibility after data splitting the curves related to two different ranges show the training development. Learning curves can also be utilized to diagnose characteristics of a dataset, particularly in terms of its representativeness. An unrepresentative dataset implies that it may not accurately capture the statistical characteristics compared to another dataset from the same domain, such as a comparison between a training and a validation dataset. This situation often arises when the dataset's sample size is insufficient relative to another dataset. An example of this behavior is the curve of compressibility in the second range (6×10-5 - 1.17×10-3 kg/(m3 Pa)) in Figure 6, in which the oscillations of the loss show that the training data set is unrepresentative which means that it does not provide enough information for effective learning in comparison to the validation dataset used for evaluation [28,29].
However, this approach poses concerns as there are no predefined criteria for guessing a-priori the range of interest. While the analytical thermophysical library of OpenFOAM could be utilized to get the output value and make the choice, this is a heavy calculation, therefore it cannot be considered as a general method. Another possibility is using information provided by the NN models from a previous timestep, but finding a consistent criterion for subsequent iterations and time steps proves challenging. Another approach would be calling several NN per cell to begin with as it is mentioned in reference [22], in which the training data was clustered in to 400 subdomains, and each subdomain was fitted by an individual MLP. Data clustering using the K-mean method, which is a non-supervised clustering algorithm is done by Xi Chen et al. [29], .Consequently, this method is set aside, and an alternative approach involving the use of a single network for each property is adopted for the present CFD test case. In essence, for the accuracy and stability of the overall solution algorithm it has been experimented that it is easier to have just one network for each property, but with careful selection of the range needed.
As depicted in the Figure 7, the relative error consistently meets less than 1 % for each specified range. This successful outcome is observed across density, compressibility, diffusivity, and viscosity. Here the logarithm transformation is applied, together with an adapted data range close to the needs of the CFD test case (detailed in Section 3). Temperature and enthalpy result in low values of the relative errors without logarithm transformation. An essential lesson learned from experience is the careful selection of input and output ranges, particularly those proximate to the test case where the modules will be implemented. In these modules, various data manipulations such as min-max scaling and log transformation are performed. The interplay of these data treatments hinges on the chosen min-max values. Therefore, the judicious selection of a suitable range for training proves pivotal to the overall performance of the network, in the following implementation step within the OpenFOAM framework.

2.4. Implementation of the NN Models in OpenFOAM

In this study, Machine Learning is used to estimate changes in thermodynamic properties of fluids during the numerical simulation of injection in modern fuel systems and to create surrogate models for two phase flow predictions. To accomplish this, an NN is established for each fluid property and trained using data derived from dedicated codes, such as 0D thermodynamic simulation models. In the realFluidReactingNNFoam solver, evaluations via Python-trained NN models replace direct evaluations via the original thermophysical libraries, for each thermophysical and transport properties. To achieve the implementation of the NN Models in OpenFOAM, the “Neural Network Inference in C made Easy” (NNICE) code is employed for inferences [31] NNICE is a simple C++ library designed to provide neural network inference capabilities without the complexities associated with compiling traditional ML library C++ APIs. Initially developed for seamless integration into 3D CFD codes, this library is utilized in scenarios where calls to neural networks are made in a constrained parallelization environment [31].
Real-fluid thermodynamics and transport are integrated into a solver which utilizes the PIMPLE algorithm. This algorithm is a pressure-based segregated approach that combines elements of both SIMPLE and PISO methods [2]. To tackle severe pressure and velocity oscillations a modified reactingFoam solver in OpenFoam is used, called realFluidReactingFoam, which includes a modification of the pressure equation to include linear formulation of the density and changes in the frequency of updates of enthalpy and species [19]. This solver with direct evaluation of real-fluid properties will be considered as the reference.
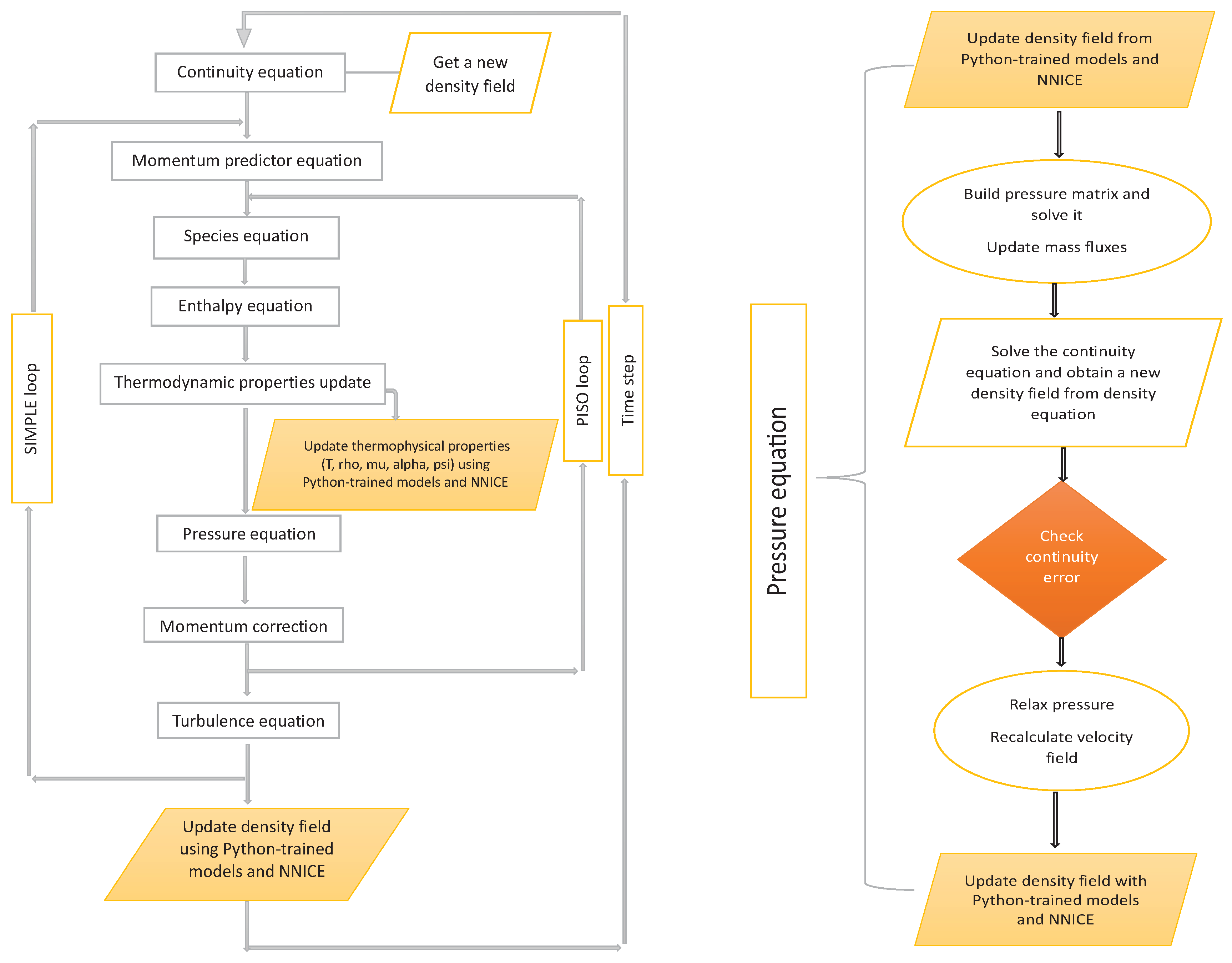
In the following, a description of the overall CFD solution algorithm is provided, focusing on the points where properties need to be evaluated, and therefore when also NN inference replaces direct evaluation.
  • In the initialization stage, Y H 2 , T , p fields are read from dictionaries and values are used to infer each property of the flow through the Python-trained NN models via NNICE.
  • Then, as shown in the flow-chart in Figure 8, at the beginning of a time-step, the continuity equation is first solved, and the PIMPLE iteration begins with the momentum predictor step.
  • With entering the PISO loop the specie and the energy equations are solved. Then the thermodynamic properties, inferred through the Python-trained NN models with NNICE, replace the original thermo.correct() OpenFOAM function call. More in detail, temperature T is first retrieved after the enthalpy equation is solved using Y H 2 , p , h information; then all other properties (density ρ , viscosity μ , thermal diffusivity α , and compressibility ψ ) are updated using most recent values of Y H 2 , T , p .
  • Other inferences are then needed inside each PISO loop. Density is first updated with the corresponding NN model before the pressure equation is solved (details of the pressure equation can be found in Figure 8.b). Afterwards, density is explicitly updated solving the continuity equation, and, after checking the continuity error, the velocity field is updated.
  • The last step with the PISO loop concerns a new recalculation of the density field via its NN model.
  • Outside the PISO loop turbulence equations are solved, but no additional inferences are needed there. In addition, in this paper we do not include a turbulence model and assume a laminar flow, to show the application of the machine learning method in OpenFOAM.

2.5. CFD Case Setup

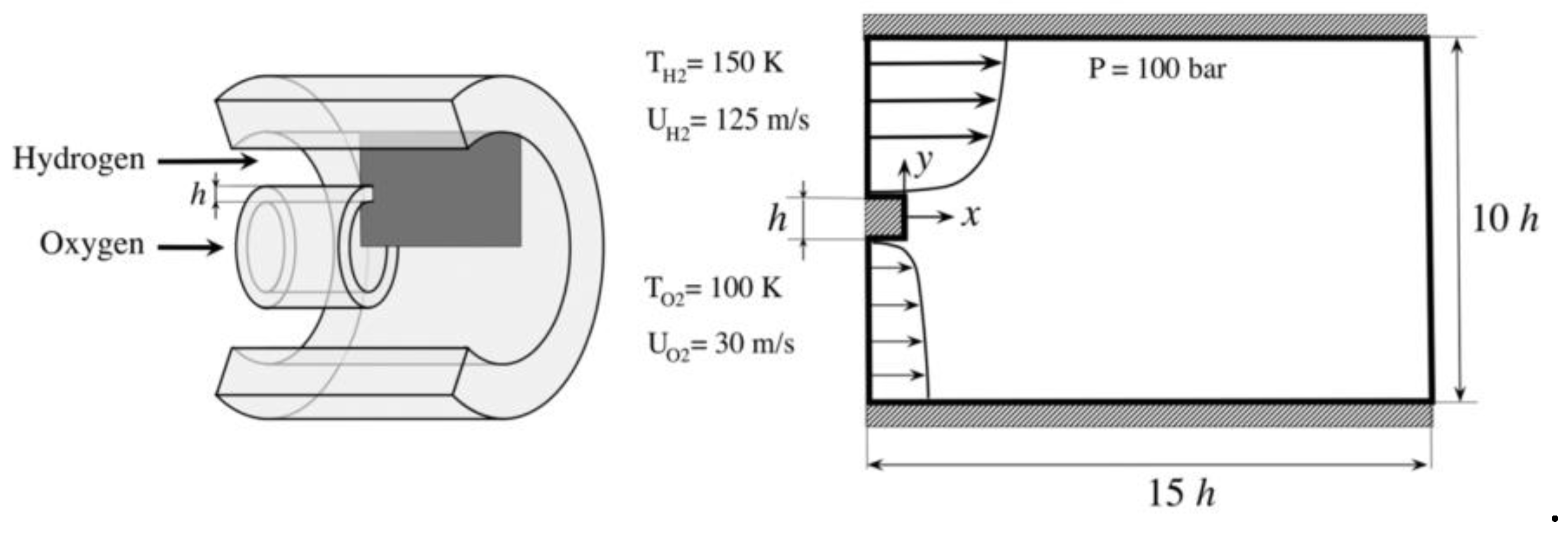
The assessment of the numerical framework is carried out on a cryogenic two-species mixing layer under trans -critical state, which incorporates liquid oxygen (LOX) and gaseous hydrogen (GH2). The case study has already been considered by many researchers, and serves a well-known benchmark test [2,9,32,33,34,35,36,37,38].
Specifically, we analyze a two-dimensional mixing layer with an injector lip that divides streams of liquid oxygen (LOX) and gaseous hydrogen (GH2), both at supercritical pressure. As shown in Figure 9, this setup serves as a general representation of a cryogenic coaxial injector, where a central dense oxygen jet interfaces with high-speed coaxial hydrogen flow, creating conditions to effective control mixing and flame stability in actual rocket engines [37].
The simulation setup involves an injector lip with a height (h) of 0.5 mm, segregating high-speed gaseous hydrogen (GH2) in the surroundings from dense liquid oxygen (LOX) in the center. A two-dimensional layout is considered. The area of interest of the computational domain spans 15h along the axial direction and 10h in the transversal direction. An additional 15h streamwise region serves as sponge layer, designed to mitigate pressure oscillations arising from the outlet. For this study, a relatively coarse mesh is employed with a uniform grid spacing of ∆x/h = ∆y/h = 20. The specified resolution is applied up to 15h in the x-direction and extends to 2.5h on both sides of the lip center in the y-direction. The remaining downstream section (from 15h to 30h) of the domain undergoes stretching in the axial direction with a global expansion ratio of 10 [2]. The boundary conditions and computational domain are based on the description provided in [37], but unlike the original benchmark description, no turbulence modelling is employed. As a matter of fact, the present calculations are not meant for assessing model accuracy, but for proving the effectiveness of the Neural Network approach for fast evaluation of real-fluid properties, therefore direct numerical simulation, not including turbulence model, makes the test case even stronger and more probing.
At the injector lip, we implement an adiabatic no-slip wall condition, while the top and bottom boundaries are treated as adiabatic slip walls. Furthermore, we apply a Dirichlet pressure boundary condition at the outlet [2].
As discussed in reference [2] regarding the time discretization, a first-order Euler scheme is applied, while second-order accurate Gauss limited-linear schemes are employed for both advection and diffusion.

3. Results and Discussion

This paper extensively explains the development of a model that seamlessly combines real-fluid model (RFM) with NN. In terms of surrogate models for approximating thermodynamic functions, NNs demonstrated good performance in predicting properties as a function of pressure, temperature, and mass fraction of a two-component mixture. When used in simulations, since the NN regression requires minimal time during evaluation, the computational cost is small. On the other hand, the only alternatives are either evaluating the complex thermodynamic models through the RFM, which is rather demanding on the fly, or performing interpolations from tables, the latter being the only practical way in complex cases. However, tables have a large storage footprint and become very cumbersome as the interpolation dimensionality increases (interpolating data among pressure, temperature and the mass fractions of multiple components) [12,27]. Therefore, NN seems to be a very attractive option, as the trained network has the size of KBs, which is over a thousand or million times smaller than a table. Further applications where NN can be used, is the development of surrogate models that can be trained using existing, validated data. In the current demonstration case, networks with two hidden layers and 100 neurons each can describe adequately well the properties as a function of pressure, temperature and mass fraction for a LO2/GH2 transcritical mixing layer. It is important to mention that the training for a single vector output network takes about 30-60 minutes (depending on the number of epochs). Its evaluation happens instantaneously much faster than any simulation could produce.
Another noteworthy aspect is the remarkable versatility of ML. The methods discussed here, even when employed in tandem with simulations, exhibit flexibility in terms of input types. ML can effectively handle diverse forms of data presented in suitable formats. It is crucial to emphasize that this work does not assert to have exhaustively explored the full potential of ML. Admittedly, there are numerous avenues for integrating ML, given its expansive range of techniques adaptable to a multitude of problems. It is only very recently that such ML techniques have begun to be explored in the context of multiphase flows [10].
The open-source code OpenFOAM-v2112 is employed to build distinct solvers, whose results and performance are then presented and discussed. Specifically, such CFD model variants are termed as follows.
  • The original CFD model is referred to as realFluidReactingFoam solver. As already explained, it is a real-fluid pressure-based multi-species solver using PR-EoS and Chung models with non-linear mixing rules coded in OpenFOAM [2,10,19,38].
  • The second CFD model is referred to as realFluidReactingNNFoam_1 which adopts a neural network approach (here referred to as NN_1 variant) wherein Python-trained NN models and NNICE inference are used to replace original calculations through the RFM.
  • The third CFD solver is referred to as realFluidReactingNNFoam_2 which is similar to the second model, but incorporates log transformations for density, compressibility, viscosity, and thermal diffusivity to achieve target accuracy criteria (here referred to as NN_2 variant).
  • The last model is referred to as realFluidReactingNNFoam. It is like the previous one, but using the adapted data range, which means that the data range for training is chosen to be as close as possible to the case study needs, to improve networks accuracy (here referred to as NN variant).
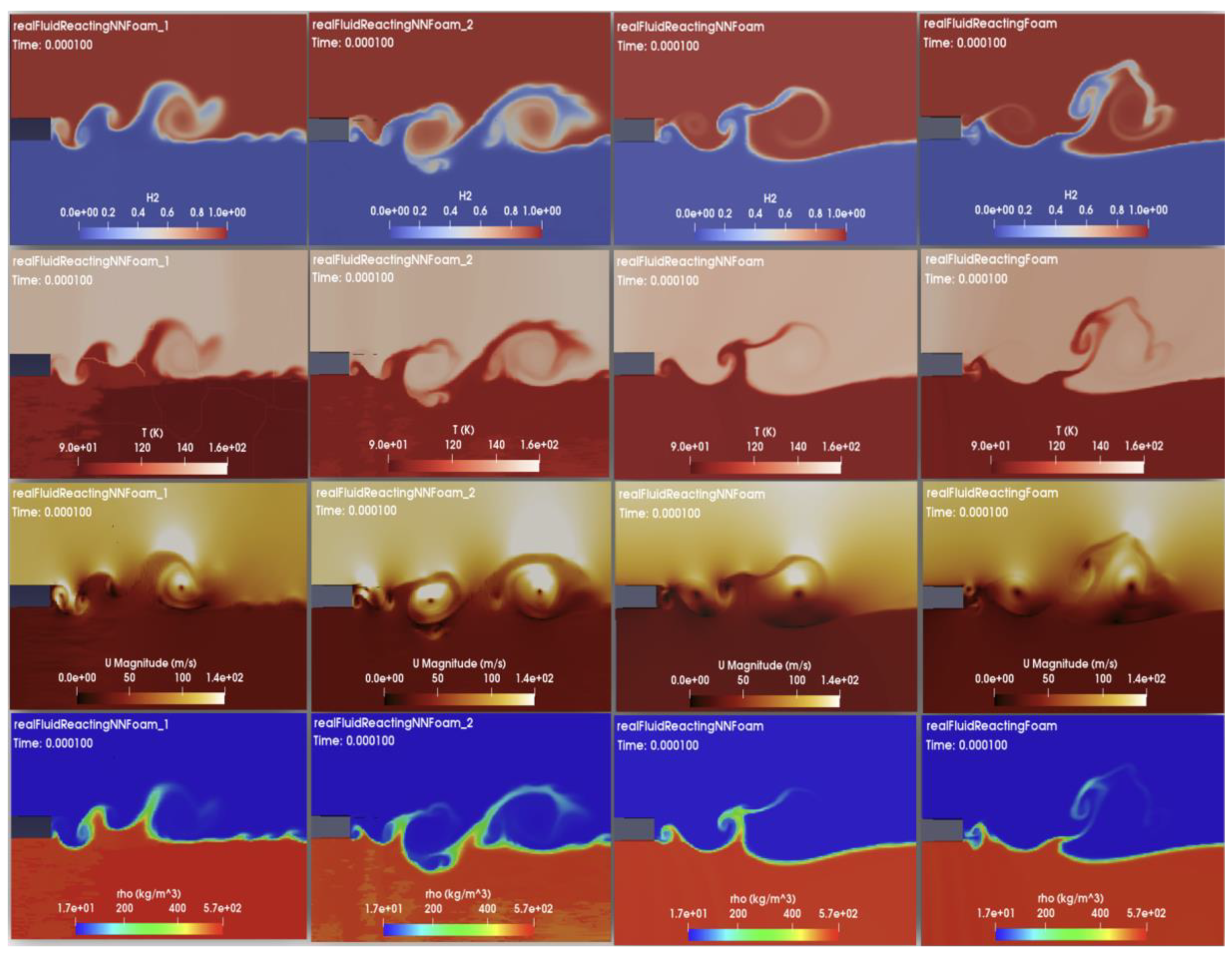
We start by showing in Figure 10 a comparison of the results obtained at 0.1 ms by the codes above listed, namely, the NN variants vs. the original code (realFluidReactingNNFoam_1, realFluidReactingNNFoam_2, realFluidReactingNNFoam, and the reference realFluidReactingFoam). Contours are shown for H2 mass fraction, temperature, velocity, and density, at 0.1 ms. Overall, all fields appear reasonable, and the three ML variants have similar features compared to the original code. Of course, no exact correspondence can be expected, as each simulation produces its own instantaneous results. However, by further scrutinizing these results, it is shown that the first neural network variant (NN_1) starts generating noisy fields for temperature, velocity and density, which are attributed to insufficient ML model accuracy. The second variant (NN_2), with transformed input variables, improves the velocity field quality but does not improve other fields. Conversely, the final neural network variant (NN) preserves clean and smooth fields for all quantities.
The primary objective of this work is to demonstrate the impact of employing NN methods in enhancing real-fluid model simulations by substituting the NN algorithm for the direct RFM model. Considering the final and more accurate solver version, named realFluidReactingNNFoam which as explained uses a tailored dataset for training, results reported in Table 4 show that the code based on neural networks is about 3 times faster on the total execution time, and about 7.5 faster on a time-step basis. This performance is measured considering 0.1 ms of simulated physical time on one compute node with 20 cores, as the test case is not very large in terms of mesh size, to avoid including scalability aspects related to node communication. The tolerances for solving governing equations are kept the same, and in particular 1e-8 is used for the velocity field, which is quite strict. The NN version of the code requires some more iterations per time-step to reach convergence, so despite more iterations are needed in general each one is much faster. Further work can be done on further improving the accuracy of the NN models and optimize the overall code coupling, so that the number of iterations does not increase, to get an even better speed-up, but the current result appears already promising.
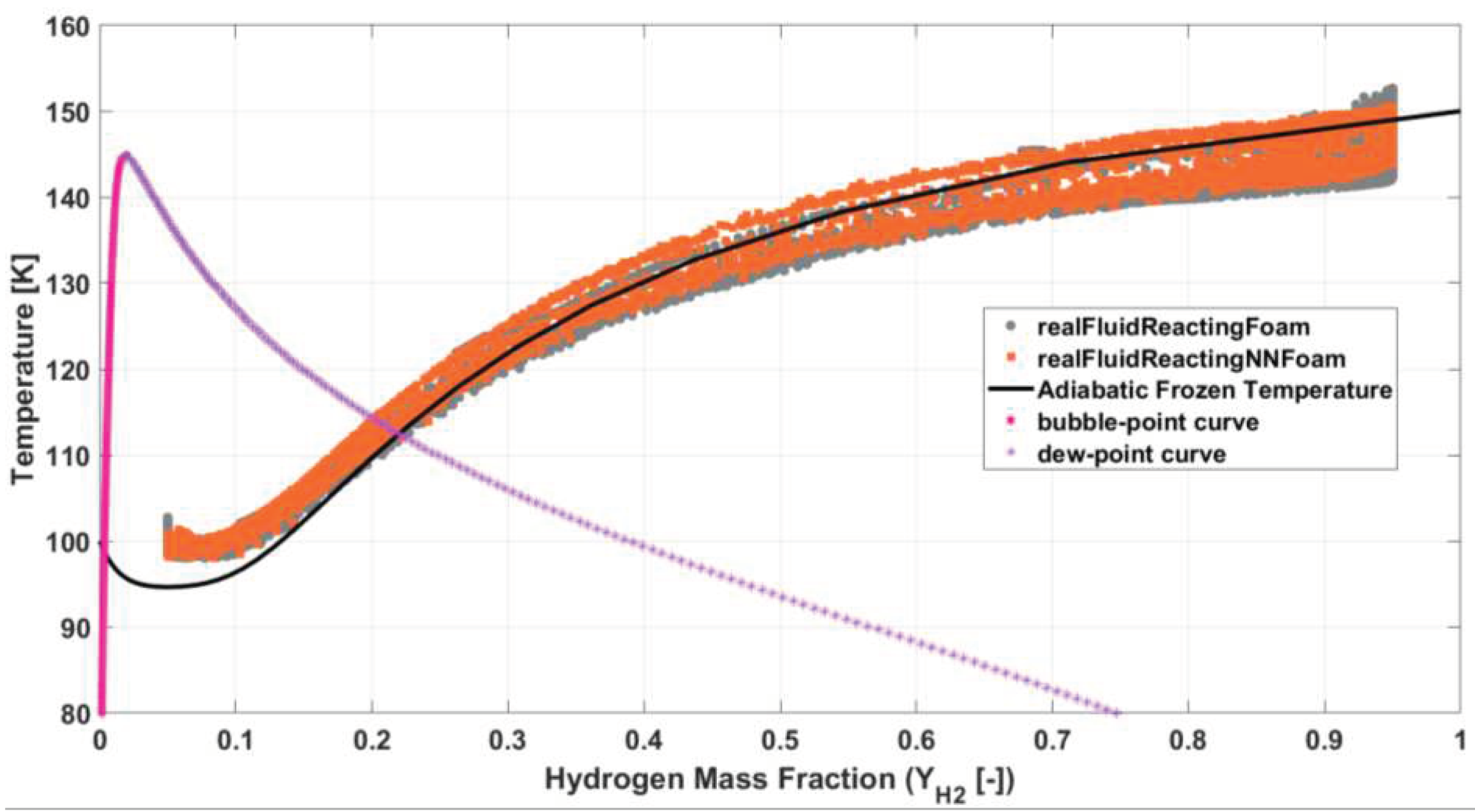
To assess the simulations, result quality, comparisons with those from the original approach proposed in [2,20] are presented. Figure 11 shows a scatter plot of mixture temperature vs. hydrogen mass fractions for an instantaneous field, at 1 ms, which based on the low speed stream velocity (30 m/s) corresponds already to 4 flow through times (FTT) over a distance of 15h (cf. Figure 9). The NN solver reproduces exactly the thermodynamic states of the reference model, without any appreciable discrepancy.
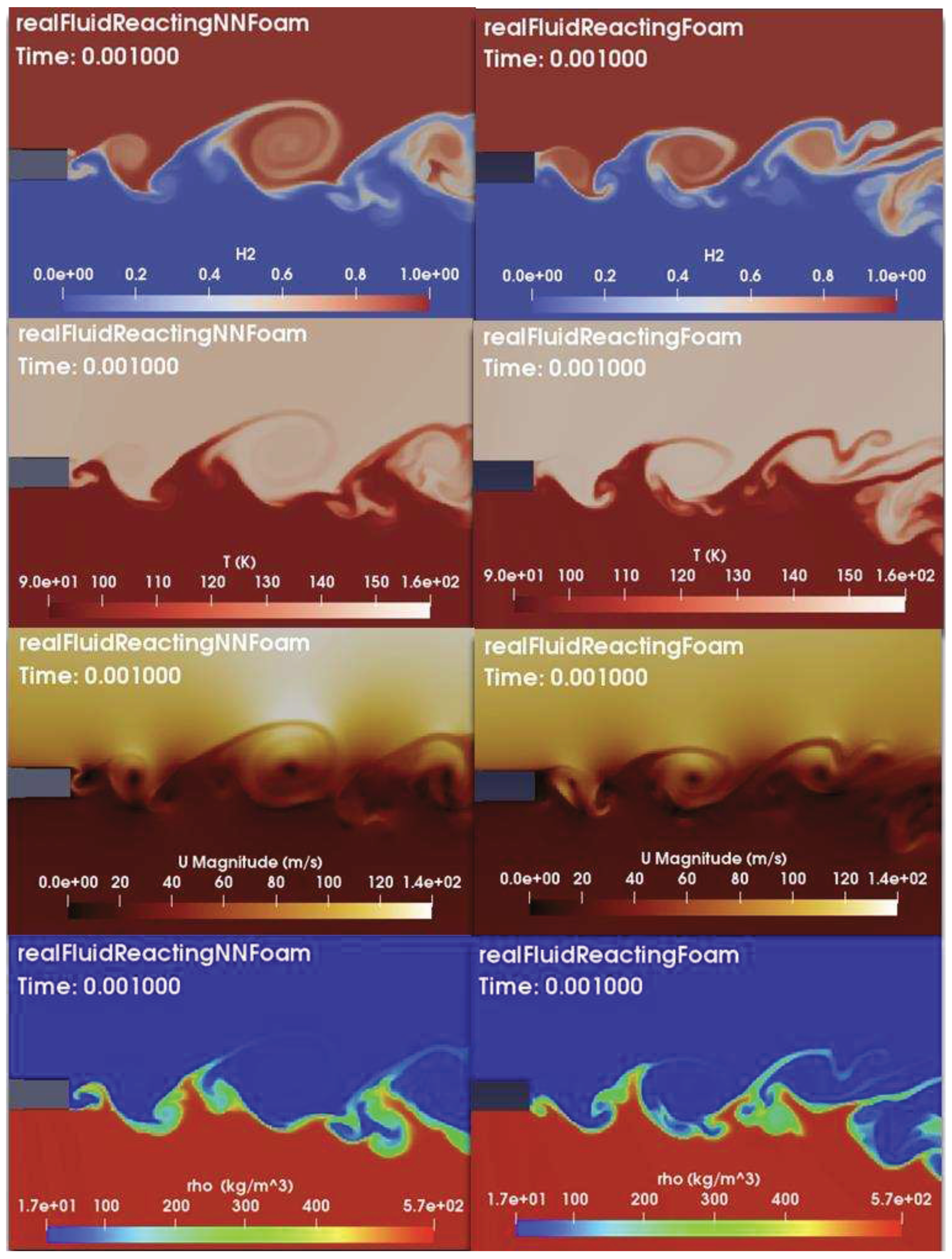
The corresponding instantaneous fields for H2 mass fraction, temperature, velocity, and density at 1 ms are shown in Figure 12, for the NN solver realFluidReactingNNFoam and the original solver realFluidReactingFoam. The current numerical solution effectively captures the three prominent vortical structures in the velocity fields, anticipated within x/h = 10, along with the steep density gradient. Kelvin-Helmholtz mechanisms initiate the formation of the initial eddies in the mixing layer, downstream of the lip, prominently on the hydrogen side. These structures, due to interfacial instabilities, contribute to the development of thicker vortices in the oxygen stream [2]. Results of the NN solver are in good agreement with those obtained by the direct RFM solver. These findings showcase the proficiency of the current numerical NN framework in managing mixing processes involving real-fluid thermodynamic and transport properties, under transcritical conditions under the assumption of frozen temperature [21].
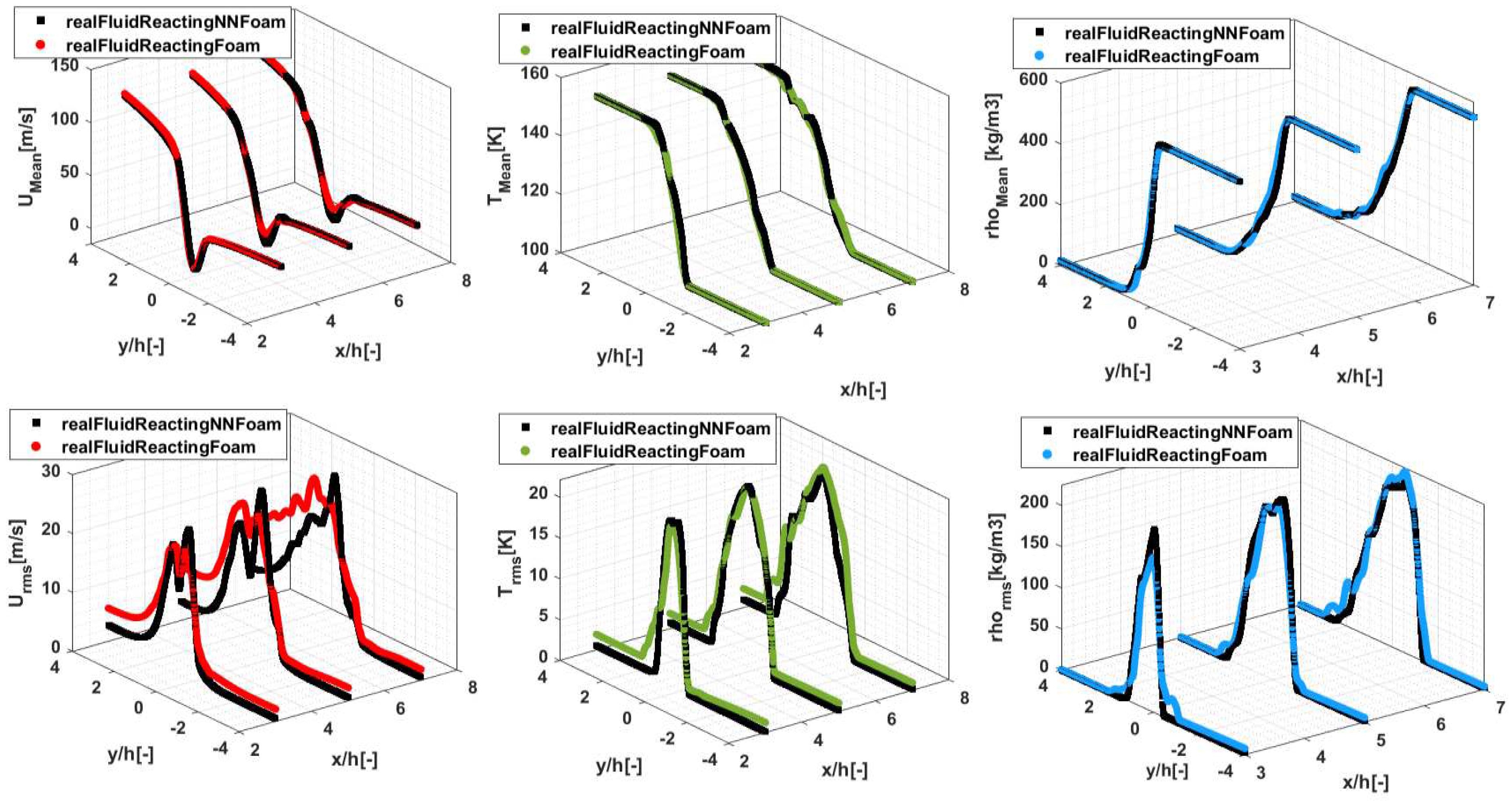
Additionally, as a further assessment, a quantitative comparison of statistics collected over time for axial velocity, temperature, and density are presented in Figure 13. These transversal profiles of mean and fluctuating root-mean-square statistics (rms) are obtained by time-averaging instantaneous fields from 1 to 4 FTTs, and are taken at various axial locations, namely at x/h = 3, 5, and 7. Overall, there is very good agreement with the reference trends provided by the realFluidReactingFoam solver.

5. Conclusions

This paper presents a comprehensive exploration of the integration of NN models within the RFM approach for efficiently simulating complex thermodynamic functions in a CFD code, for non-evaporating binary mixture under transcritical conditions. The study demonstrates the efficiency of NNs as surrogate models, emphasizing their ability to approximate complex thermodynamic properties with very affordable training time compared to traditional dataset derivation and significant savings during CFD runtime. The paper highlights the advantages of using NN models in CFD simulations, where computational costs, though present during evaluation, are notably smaller than the original method using direct evaluation from the equation of state. The versatility of machine learning (ML) is underscored, particularly in handling various data types and distributions. The work acknowledges the vast potential of ML in the context of multiphase flows and suggests numerous avenues for further exploration. The application of the developed NN models in OpenFOAM to simulate a transcritical mixing case reveals the potential of neural networks to replace traditional RFM models, offering faster execution times and very good fit, as evidenced by contour plots and averaged transverse profiles. The comparison of realFluidReactingNNFoam results with the original realFluidreactingFoam indicates that, despite the latter requiring fewer iterations, the NN model outperforms in terms of execution time at the same level of solution accuracy.
In summary, the successful application of NN in conjunction with RFM in simulating real-fluid thermodynamic and transport properties signifies a promising direction for future research in the field of accelerating computational fluid dynamics models. The study opens avenues for exploring the full potential of ML techniques in addressing complex problems related to multiphase flows with more than just two species.

Author Contributions

Conceptualization, N.S., D.A.-K., C.H. and M.B.; methodology, N.S., D.A.-K., G.C., C.H. and M.B.; software, N.S., D.A.-K., F.N.Z.R. and M.B.; validation, N.S.; formal analysis, N.S., D.A.-K., F.N.Z.R. and M.B.; investigation, N.S.; writing—original draft preparation, N.S.; writing—review and editing, C.H. and M.B.; visualization, N.S.; supervision, C.H. and M.B.; project administration, C.H. and M.B.; funding acquisition, M.B. All authors have read and agreed to the published version of the manuscript.

Funding

The first author acknowledges the support from the University of Perugia for the PhD grant and for student mobility EU Erasmus traineeship program, KA1 – Call 2021 – Progetto n. 2021-1-IT02-KA131-HED-000007409.

Data Availability Statement

The data presented in this study are available on request from the corresponding author.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. He Z, Shen Y, Wang C, Zhang Y, Wang Q, Gavaises M. Thermophysical properties of n-dodecane over a wide temperature and pressure range via molecular dynamics simulations with modification methods. J Mol Liq [Internet]. 2023 Feb;371:121102. Available from: https://linkinghub.elsevier.com/retrieve/pii/S0167732222026411.
  2. Rahantamialisoa, F.N., Pandal, A., Ningegowda, B.M., Zembi, J., Sahranavardfard, N., Jasak, H., Im, H.G. and Battistoni, M., 2021, August. Assessment of an open-source pressure-based real fluid model for transcritical jet flows. In International Conference on Liquid Atomization and Spray Systems (ICLASS) (Vol. 1, No. 1).
  3. Qiu L, Reitz RD. An investigation of thermodynamic states during high-pressure fuel injection using equilibrium thermodynamics. International Journ10al of Multiphase Flow. 2015 Jun;72:24–38. [CrossRef]
  4. Kiran E, Sengers JMHL, editors. Supercritical Fluids. Dordrecht: Springer Netherlands; 1994.
  5. Wagner W, Kurzeja N, Pieperbeck B. The thermal behaviour of pure fluid substances in the critical region — experiences from recent pϱT measurements on SF6 with a multi-cell apparatus. Fluid Phase Equilib. 1992 Nov 25;79(C):151–74. [CrossRef]
  6. Poling BE, Prausnitz JM, O’connell JP, York N, San C, Lisbon F, et al. the properties of gases and liquids, Fifth Edition McGRAW-HILL. 2001.
  7. Puissant C, Glogowski MJ. experimental characterization of shear coaxial injectors using liquid/gaseous nitrogen. Atomization and Sprays. 1997;7(5):467–78.
  8. Mayer W, Tamura H. Propellant injection in a liquid oxygen/gaseous hydrogen rocket engine. J Propuls Power. 1996;12(6):1137–47. [CrossRef]
  9. Habiballah M, Orain M, Grisch F, Vingert L, Gicquel P. Experimental studies of high-pressure cryogenic flames on the mascotte facility. Combustion Science and Technology. 2006 Jan 1;178(1–3):101–28. [CrossRef]
  10. Rahantamialisoa, F.N.Z., Zembi, J., Miliozzi, A., Sahranavardfard, N. and Battistoni, M., 2022, December. CFD simulations of under-expanded hydrogen jets under high-pressure injection conditions. In Journal of Physics: Conference Series (Vol. 2385, No. 1, p. 012051). IOP Publishing. [CrossRef]
  11. Oschwald M, Smith JJ, Branam R, Hussong J, Schik A, Chehroudi B, et al. injection of fluids into supercritical environments. Combustion Science and Technology. 2006 Jan;178(1–3):49–100. [CrossRef]
  12. Koukouvinis P, Rodriguez C, Hwang J, Karathanassis I, Gavaises M, Pickett L. Machine Learning and transcritical sprays: A demonstration study of their potential in ECN Spray-A. International Journal of Engine Research. 2022 Sep 1;23(9):1556–72. [CrossRef]
  13. Jafari S, Gaballa H, Habchi C, de Hemptinne JC. Towards understanding the structure of subcritical and transcritical liquid–gas interfaces using a tabulated real fluid modeling approach. Energies (Basel). 2021 Sep 1;14(18). [CrossRef]
  14. Jafari S, Gaballa H, Habchi C, Hemptinne JC De, Mougin P. Exploring the interaction between phase separation and turbulent fluid dynamics in multi-species supercritical jets using a tabulated real-fluid model. Journal of Supercritical Fluids. 2022 May 1;184. [CrossRef]
  15. Brunton SL, Noack BR, Koumoutsakos P. Downloaded from www.annualreviews.org Access provided by 109.114.54.139 on 09/27/23. For personal use only. Annu Rev Fluid Mech 2020 [Internet]. 2019; 52:477–508. . Available from: https://doi.org/10.1146/annurev-fluid-010719-.
  16. Rodriguez S, Cardiff P. A general approach for running Python codes in OpenFOAM using an embedded pybind11 Python interpreter. 2022 Mar 30; Available from: http://arxiv.org/abs/2203.16394.
  17. Maulik R, Fytanidis D, Lusch B, Vishwanath V, Patel S. PythonFOAM: In-situ data analyses with OpenFOAM and Python. 2021 Mar 16; Available from: http://arxiv.org/abs/2103.09389.
  18. Maulik R, Patel SS, Lusch B, Jennings E. Deploying deep learning in OpenFOAM with TensorFlow Machine Learning and Dynamical Systems View project Open Source Code for Spectral Element Discontinuous Galerkin Lattice Boltzmann Method (NEKLBM) View project [Internet]. Available from: https://github.com/argonne-lcf/TensorFlowFoam.
  19. Rahantamialisoa F.N.Z., Madana Gopal J.V., Tretola G., Sahranavardfard N., Vogiatzaki K., Battistoni M., Analyzing single and multicomponent supercritical jets using volume-based and mass-based numerical approaches. Physics of Fluids, Volume 35, Issue 61, Article number 067123, (2023). [CrossRef]
  20. Ningegowda, B.M.; Rahantamialisoa, F.N.Z.; Pandal, A.; Jasak, H.; Im, H.G.; Battistoni, M. Numerical Modeling of Transcritical and Supercritical Fuel Injections Using a Multi-Component Two-Phase Flow Model. Energies 2020, 13, 5676. [CrossRef]
  21. Chung, T. H., Ajlan, M., Lee, L. L., and Starling, K. E., 1988. “Generalized multiparameter correlation for nonpolar and polar fluid transport properties”. Industrial & Engineering Chemistry Research, 27(4), pp. 671–679. [CrossRef]
  22. Ding T, Readshaw T, Rigopoulos S, Jones WP. Machine learning tabulation of thermochemistry in turbulent combustion: An approach based on hybrid flamelet/random data and multiple multilayer perceptrons. Combust Flame. 2021 Sep 1;231. [CrossRef]
  23. Gardner MW, Dorling SR. artificial neural networks (the multilayer perceptron)-a review of applications in the atmospheric sciences. Vol. 32, Atmospheric Environment. 1998. [CrossRef]
  24. Bishop CM. Neural Networks for Pattern Recognition Clarendon Press • Oxford 1995.
  25. Watt, J., Borhani, R. and Katsaggelos, A.K., 2020. Machine learning refined: Foundations, algorithms, and applications. Cambridge University Press.
  26. Abadi, M., Agarwal, A., Barham, P., Brevdo, E., Chen, Z., Citro, C., Corrado, G.S., Davis, A., Dean, J., Devin, M. and Ghemawat, S., 2016. Tensorflow: Large-scale machine learning on heterogeneous distributed systems. arXiv preprint arXiv:1603.04467.
  27. Delhom B, Faney T, Mcginn P, Habchi C, Bohbot J. Development of a multi-species real fluid modelling approach using a machine learning method, ILASS Europe 2023, 32 nd European Conference on Liquid Atomization & Spray Systems.
  28. Anzanello MJ, Fogliatto FS. Learning curve models and applications: Literature review and research directions. Vol. 41, International Journal of Industrial Ergonomics. 2011. p. 573–83. [CrossRef]
  29. Witten, Daniela, and Gareth James. An introduction to statistical learning with applications in R. springer publication, 2013., Goodfellow I, Bengio Y, Courville A. Deep learning. MIT press; 2016 Nov 10.
  30. Chen, X., Mehl, C., Faney, T. and Di Meglio, F., 2023. Clustering-Enhanced Deep Learning Method for Computation of Full Detailed Thermochemical States via Solver-Based Adaptive Sampling. Energy & Fuels, 37(18), pp.14222-14239. [CrossRef]
  31. Aubagnac-Karkar, D., & Mehl, C. (2023). NNICE: Neural Network Inference in C made Easy (Version 1.0.0) [Computer software]. [CrossRef]
  32. Zong N, Yang V. Near-field flow and flame dynamics of LOX/methane shear-coaxial injector under supercritical conditions. Proceedings of the Combustion Institute. 2007 Jan 1;31(2):2309–17. [CrossRef]
  33. Zong N, Yang V. Cryogenic fluid jets and mixing layers in transcritical and supercritical environments. Combustion Science and Technology. 2006 Jan;178(1–3):193–227. [CrossRef]
  34. Oefelein JC. mixing and combustion of cryogenic oxygen-hydrogen shear-coaxial jet flames at supercritical pressure. Combustion Science and Technology. 2006 Jan;178(1–3):229–52. [CrossRef]
  35. Oefelein JC. Thermophysical characteristics of shear-coaxial LOX–H2 flames at supercritical pressure. Proceedings of the Combustion Institute. 2005 Jan 1;30(2):2929–37. [CrossRef]
  36. Oefelein JC, Yang V. Modeling High-Pressure Mixing and Combustion Processes in Liquid Rocket Engines. J Propuls Power. 1998 Sep;14(5):843–57. [CrossRef]
  37. Ruiz AM, Lacaze G, Oefelein JC, Mari R, Cuenot B, Selle L, et al. Numerical benchmark for high-reynolds-number supercritical flows with large density gradients. AIAA Journal. 2016;54(5):1445–60. [CrossRef]
  38. Ningegowda BM, Rahantamialisoa F, Zembi J, Pandal A, Im HG, Battistoni M. Large Eddy Simulations of Supercritical and Transcritical Jet Flows Using Real Fluid Thermophysical Properties. SAE Technical Paper 2020-01-1153, 2020.
Preprints 96233 g001
Figure 1. Schematics of neural network with one input layer, two hidden layers, and one output layer with U1 and U2 number of units, or neurons, a). Typical structure of a neuron showing input weights, bias, and activation function, b).
Figure 1. Schematics of neural network with one input layer, two hidden layers, and one output layer with U1 and U2 number of units, or neurons, a). Typical structure of a neuron showing input weights, bias, and activation function, b).
Preprints 96233 g001
Preprints 96233 g002
Figure 2. Data distribution of outputs consisting of density, compressibility, viscosity, thermal diffusivity, enthalpy, and temperature, for different values of hydrogen mass fraction.
Figure 2. Data distribution of outputs consisting of density, compressibility, viscosity, thermal diffusivity, enthalpy, and temperature, for different values of hydrogen mass fraction.
Preprints 96233 g002
Preprints 96233 g003
Figure 3. Representation of the effects of the higher number of epochs on network performance and the values of the relative error.
Figure 3. Representation of the effects of the higher number of epochs on network performance and the values of the relative error.
Preprints 96233 g003
Preprints 96233 g004
Figure 4. Representation of the effects of the usage of the different learning rates as an important hyperparameter on the network performance.
Figure 4. Representation of the effects of the usage of the different learning rates as an important hyperparameter on the network performance.
Preprints 96233 g004
Preprints 96233 g005
Figure 5. Comparison of the relative error and the data distribution before (left) and after the range splitting (right).
Figure 5. Comparison of the relative error and the data distribution before (left) and after the range splitting (right).
Preprints 96233 g005
Preprints 96233 g006
Figure 6. Mean squared error vs. the number of epochs for the compressibility before (left) and after the range splitting (right).
Figure 6. Mean squared error vs. the number of epochs for the compressibility before (left) and after the range splitting (right).
Preprints 96233 g006
Preprints 96233 g007
Figure 7. Representation of actual vs. predicted values, actual values vs. relative error, and distribution of density, compressibility, thermal diffusivity, viscosity, enthalpy, and temperature (this model is referred to as NN variant, or final version, in Section 3).
Figure 7. Representation of actual vs. predicted values, actual values vs. relative error, and distribution of density, compressibility, thermal diffusivity, viscosity, enthalpy, and temperature (this model is referred to as NN variant, or final version, in Section 3).
Preprints 96233 g007
Preprints 96233 g008
Figure 8. Extended PIMPLE solution flow-chart for the multiphase transport equations with real-fluid properties, a). Pressure equation flow-chart, b).
Figure 8. Extended PIMPLE solution flow-chart for the multiphase transport equations with real-fluid properties, a). Pressure equation flow-chart, b).
Preprints 96233 g008
Preprints 96233 g009
Figure 9. Schematics of the case geometry and boundary conditions, adapted from [37].
Figure 9. Schematics of the case geometry and boundary conditions, adapted from [37].
Preprints 96233 g009
Preprints 96233 g010
Figure 10. Instantaneous fields of H2 mass fraction, temperature, velocity magnitude and density, at 0.1 ms, for realFluidReactingNNFoam_1, realFluidReactingNNFoam_2, realFluidReactingNNFoam, and realFluidReactingFoam solvers.
Figure 10. Instantaneous fields of H2 mass fraction, temperature, velocity magnitude and density, at 0.1 ms, for realFluidReactingNNFoam_1, realFluidReactingNNFoam_2, realFluidReactingNNFoam, and realFluidReactingFoam solvers.
Preprints 96233 g010
Preprints 96233 g011
Figure 11. Scatter plot of instantaneous fields of temperature vs. hydrogen mass fractions, at 1 ms. NN results obtained with realFluidReactingNNFoam solver.
Figure 11. Scatter plot of instantaneous fields of temperature vs. hydrogen mass fractions, at 1 ms. NN results obtained with realFluidReactingNNFoam solver.
Preprints 96233 g011
Preprints 96233 g012
Figure 12. Instantaneous fields of H2 mass fraction, temperature, velocity magnitude and density, at 1 ms, for realFluidReactingNNFoam and realFluidReactingFoam solvers.
Figure 12. Instantaneous fields of H2 mass fraction, temperature, velocity magnitude and density, at 1 ms, for realFluidReactingNNFoam and realFluidReactingFoam solvers.
Preprints 96233 g012
Preprints 96233 g013
Figure 13. Transverse profiles of mean (up) and rms (down) x-velocity, temperature, and density.
Figure 13. Transverse profiles of mean (up) and rms (down) x-velocity, temperature, and density.
Preprints 96233 g013
Table 1. List of inputs used for predicting output values.
Table 1. List of inputs used for predicting output values.
Inputs Outputs
Variable symbol (code name) Definition [units]
Y H 2   ( Y ) Fuel mass fraction [-] all output variables (except T )
T   ( T ) Temperature [K] all variables (except T )
p   ( p ) Pressure [Pa] all variables (except T )
h   ( h e ) Enthalpy [J/kg] T
Table 2. List of output properties with their definitions and the units.
Table 2. List of output properties with their definitions and the units.
Variable
symbol (code name)		 Definition [units]
ρ   ( r h o ) Density [ k g / m 3 ]
μ   ( m u ) Viscosity [ P a   s ]
α   ( a l p h a ) Thermal diffusivity [ P a   s ]
h ( h e ) Specific enthalpy: h = s i e + p / ρ [ J / k g ]
ψ   ( p s i ) Compressibility ψ = 1 / ( Z R T )   [ k g / ( m 3 P a ) ]
T   ( T ) Temperature ( K )
Table 3. Main hyperparameters chosen to train deep networks using Keras library.
Table 3. Main hyperparameters chosen to train deep networks using Keras library.
Output
(applied min-max-scalar)		 Inputs (applied min-max-scalar) Hidden layer size Activation function Solver Learning-rate-init Loss metrics Epochs batch-size
r h o , m u , a l p h a , h e, p s i , Y H 2 ,   T ,   p 100 × 100 ReLU ADAM 0.0015 MSE 1000 256
T Y H 2 ,   p ,   h e 100 × 100 ReLU ADAM 0.0015 MSE 1000 256
Table 4. Summary of realFluidReactingNNFoam speed-up vs. realFluidReactingFoam, measured on 0.1 ms of physical time and one compute node.
Table 4. Summary of realFluidReactingNNFoam speed-up vs. realFluidReactingFoam, measured on 0.1 ms of physical time and one compute node.
Solver Total execution Iteration
Time (s) Speed-up Total number of Iterations Time/Iter
(s/Iter)		 Speed-up
realFluidReactingFoam 511096 1 200550 2.548 1
realFluidReactingNNFoam 179317 2.850 523200 0.343 7.5
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated