Prerpints.org logo
Preprint
Article

Rainfall-Mining Coupling Effects on Slope Failure Mechanism and Evolution Process: A Case Study of Open-Pit to Underground Mining

Altmetrics

Downloads

93

Views

20

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

13 January 2024

Posted:

15 January 2024

You are already at the latest version

Alerts
Abstract
This research examines how rainfall and mining affect the slope damage resulting from the transition from open-pit mining to underground mining. Using unmanned aerial vehicle (UAV), the Huangniu slope of Dexing Copper Mine was fully characterized, and experiments were conducted on rock samples from appropriate sites. First, the mechanical properties of the samples were measured. Then, the parameters of the similarity simulation experiments were derived based on the similarity theory. Subsequently, the rainfall, rock slope, data acquisition and monitoring systems were designed. Finally, the rock mass failure with different slope angles was analyzed, and the deformation and damage patterns under the coupling effect were obtained. The results show that rainfall increases pore water pressure and moisture content. Rainfall and slope-slip water have more impact on the open-pit platform. The pore water pressure values on the upper rock mass rise faster than inside. In the open-pit mining stage, the rock mass shifts slightly to the upper left. In the room mining stage, vertical fractures and goaf sinking occur. The fractures above the mine room form a semi-ellipse. In the pillar mining stage, the overlying rock displacement is evident, and fractures persist. In the continuous pillar mining stage, the overlying rock collapses massively. The 65° slope model is the most damaged, while the 55° slope model is the least damaged. The results also suggest that the UAV guides sample selection.
Keywords: 
Subject: Engineering  -   Mining and Mineral Processing

1. Introduction

Mineral resources play a crucial role in modern industry and infrastructure, yet their extraction presents multifaceted challenges [1]. As open-pit mines become deeper and more concave, some of them switch to underground mining [2]. This transition is very complex because the surrounding rock mass is disturbed by the stress of excavation during open-pit mining, which causes damage and fractures in the rock mass [3,4,5,6]. When underground mining starts, the rock mass is disturbed again [7]. The interaction of the stress fields changes the internal shape of the rock mass, resulting in strong nonlinearity [8,9,10,11]. This dynamic process has attracted many scholars’ attention. Soltani and Osanloo developed a set of models to determine the optimal transition depth between open-pit mining and different underground mining methods [12]. Zhang et al. proposed a cement slurry backfilling technology for the transition stage and found that the backfilling height affected the safety of the roof and the underground column. The vertical displacement was small during the backfilling process [13]. Moreover, Li et al. studied the macroscopic and microscopic characteristics of the surrounding and overlying rock in the transition and found that the mining space size was related to the pressure increase and relief. The pressure relief was more complete near the mining area, and the stress reduction level decreased with the distance [14]. Zhao et al. used micro-seismic monitoring to study the change of stress and volume over time and analyzed the rock failure and damage migration to evaluate the rock mass stability in the transition [15]. Zhu et al. effectively elucidated the toppling failure mechanism of anti-dip layered slopes by conducting physical model tests [16].
Rainfall infiltration and mining unloading are the most common external factors that affect the mining area. They weaken and destroy the stability of the rock mass. Many studies have investigated their effects on the rock mass [17,18,19,20,21,22,23,24,25,26,27,28]. Here, rainfall reduces the connection force between rock particles. It also causes the water wedge effect and dissolution, which damage the rock mass. The free water in the rock mass creates pore water pressure and expansion strengthening, which develop internal fractures in the rock mass. Mining unloading has a more obvious influence on rock mass failure. It changes the structure of the rock mass and induces vibration, which may lead to more microfractures. Li et al. investigated the seepage field evolution of granite residual soil slope under rainfall infiltration. It was observed that the pore water pressure exhibited an increase in response to rainfall infiltration, while the moisture content of the slope displayed a distinct wave-like distribution along its vertical profile [29]. Xiang et al. studied the in-situ unloading damage, core cutting characteristics and mechanical mechanism of deep rock masses in mines. They found that the deep-high-stress rock mass was significantly damaged after in-situ unloading, and the damage time effect increased with depth [28]. Furthermore, Du et al. utilized fiber optic sensing technology to propose a quantitative index of the coupling effect between the mining rock mass and fiber optic, and they quantitatively analyzed and discussed the coupling coefficients of different vertical zones [20].
Most studies on mine stability focus on single factors, and few consider the coupling effects of rainfall and mining in realistic situations [17,18,19,21,22,24,25,26]. Additionally, the experimental methods are usually based on small-scale rock mass samples, and large-scale similarity simulation studies are scarce. Thus, it is important for practical engineering to study rock mass failure and evolution under the rainfall-mining coupling effect. To this end, this research takes the Huangniu slope of Dexing Copper Mine as an example and conducts the following aspects: (1) determining the mechanical properties of the rock samples obtained by remote sensing technology and obtaining the relevant parameters of similarity simulation experiments by the similarity theory; (2) designing the rainfall, physical model, data acquisition and monitoring systems of the similarity experiment; and (3) analyzing the rock mass failure process with different slope angles, obtaining the deformation and damage laws of models with different slope angles under the rainfall-mining coupling effect, and elucidating the damage mechanism and evolution process.

2. Materials and Methods

2.1. Study area

The Huangniu slope of Dexing Copper Mine (Figure 1) is located in Sizhou Town, Dexing City, Jiangxi Province, China. Herein the slope surface is covered with artificial fill, and the lower part is the mined area, which is a rock slope created by human excavation. Herein the cross-section of the study area, which has a height of about 548.5 m and a length of about 400 m. The slope point cloud model indicates that the average dip direction and angle of the slope are 238° and 42°, respectively. The slope surface has several artificial platforms, and the lower part is the mined area. Furthermore, the engineering geological exploration shows that the lithology of the study area is mainly muddy and sandy as well as tuffaceous phyllite. The slope exposes many small faults and fractures (Figure 2), resulting in poor integrity of the rock mass. According to the field investigation, the main failure modes of the slope are wedge failure (Figure 2(a)) and plane failure (Figure 2(b)). Accordingly, the rock mass is prone to instability under engineering disturbances [30,31].
The study area is located in a subtropical monsoon humid climate zone, with even precipitation distribution throughout the year, a long rainy season, a distinct four seasons, a hot and rainy summer, and mild and moist winter. Figure 3 represents the temperature and precipitation changes in the study area. Here, the annual average temperature is 17.7°C, and the highest temperature is 39.6°C, as well as the lowest temperature is 2.4°C. Most of the rainfall is concentrated from March to August, accounting for about 73.7% of the annual precipitation. September to December is the dry season. Therefore, the slope is prone to failure in summer [32,33,34].

2.2. Rock mechanics parameter setting

2.2.1. Specimen preparation

Representative phyllite samples were selected from the field, utilizing unmanned aerial vehicle (UAV) to avoid the broken rock mass area. Subsequently, the samples were processed into standard rock specimens, and a basic cutting of the rock samples was performed using a rock cutter. For the subsequent laboratory tests, the rock samples were cut into cylindrical standard specimens with a diameter of 50 mm and a height of 100 mm and disc-shaped standard specimens with a diameter of 50 mm and a height of 25 mm for the Brazilian splitting test. After rock-cutting, the rock sample specimens were polished using a grinding machine, and fine polishing was performed using diamond sand.

2.2.2. Brazilian splitting test

The Brazilian splitting test was performed on the rock specimens. The sample was placed on the fixed groove, as well as a vertical load was applied in the diameter direction until the specimen was damaged. The load at the time of failure of each specimen was recorded, and then the tensile strength σt (Mpa) of the rock sample was calculated by:
σ t = 2 p t π D h
where, pt is the load at the time of failure of the rock sample, N; D is the diameter of the sample, mm; and L is the height of the sample, mm.

2.2.3. Uniaxial compression test

The uniaxial compression test is performed on the processed rock specimens, and the uniaxial compression strength σd (MPa), elastic modulus E (MPa), as well as Poisson's ratio μ of the rock are calculated by analyzing the stress-strain curve. An electro-hydraulic servo universal testing machine is utilized, and the loading rate was kept at 0.5 mm/min during the experiment. Herein the obtained stress-strain curve is depicted in Figure 4.
According to the data obtained from the uniaxial compression test, the σd, E and μ are calculated by:
σ d = P d S E = σ c ε v μ = ε v ε h
where, Pd is the load at the ultimate failure, N; S is the cross-sectional area of the rock specimen, mm2; σc is the stress at 60% of the ultimate failure, MPa; εv is the axial strain; and εh is the radial strain.

2.2.4. Triaxial compression test

In the real world, the rock is not only subjected to vertical pressure but usually in a multi-directional compression situation. The triaxial compression test can simulate the stress state of the rock sample under three-directional compression [35]. A triaxial compression tester is used to perform the test. By changing the confining pressure (i.e., 5 MPa, 10 MPa, 15 MPa, 20 MPa), the compressive behavior of the rock specimen is measured (Figure 5(a)), as well as the shear strength envelope curve is drawn (Figure 5(b)), thereby obtaining the cohesion C and the internal friction angle Φ of the specimen.

2.2.5. Measured mechanical parameters

The data of the Brazilian splitting test, uniaxial compression test, as well as triaxial compression test were sorted, and the rock mechanics parameters are shown in Table 1.
Because the field sampling avoided the broken rock mass area, the rock samples in the mechanical test were relatively intact. Nevertheless, the actual rock mass of the slope has a lot of fractures due to weathering, unloading and other effects, showing the characteristics of heterogeneity, anisotropy and discontinuity, as well as its mechanical properties are also variable. Considering the properties of the rock mass and the influence of environmental factors, the parameters obtained in the mechanical test cannot fully represent the mechanical characteristics of the natural rock mass. Thus, to better simulate the actual situation, the mechanical parameters obtained by the experiment should be reduced by a certain proportion before they are applied. This research used the most economical and effective empirical analysis method to obtain the parameters. Based on the Hoek-Brown strength criterion [36,37,38,39,40] and field investigation, the data were reduced referring to the research on the selection of the parameters (Table 2).

2.3. Similarity material

The deformation process of slopes cannot be fully replicated in physical models. Only general insights can be derived from reduced-scale physical models that satisfy the similarity theory. The similarity simulation experiment is an important scientific means, and it is the most effective method for some large-scale physical engineering experiments that cannot be realized in nature due to safety, uncontrollability and other reasons. This process uses the similarity characteristics between things to study the natural laws in a limited space. This research used similarity simulation experiments to establish a laboratory model of the slope in the study area.

2.3.1. Similar parameter setting

This experiment is a complex open-pit to underground mining project, so various conditions are needed to ensure the similarity between the model and the prototype [41,42]. In addition to the boundary and initial conditions, the physical model parameters must satisfy the similarity criteria. The subscript p denotes the similarity simulation prototype parameters, and m denotes the similarity simulation model parameters. According to the engineering geological investigation and existing conditions, the similarity coefficients were determined as follows:
Geometry similarity constant   α l = l m l p = 1 : 250
Time similarity constant   α t = t m t p ≈ 1 : 14
Bulk density similarity constant   α r = γ m γ p = 0.625
Stress similarity constant   α σ = σ m σ p = γ m × l m γ p × l p = 2.5 × 10 − 3
Force similarity constant   α p = F m F p = α r α l 3 = 4 × 10 − 8
Strain similarity constant   α ε = 1
Elastic modulus similarity constant   α E = α r α L = 2.5 × 10 − 3
Poisson’s ratio similarity constant   α μ = 1
Internal friction angle similarity constant   α Φ = 1

2.3.2. Similar material proportioning

The selection and proportioning of similar materials are the key to simulating the slope [43,44]. The density of the similar material and the prototype material should be relatively matched to provide a reliable scale for subsequent calculations. It also requires that the physical properties of these two materials are similar, and the mechanical indicators are relatively stable [45]. The material should have a granular bulk, so that it can have a better shape after stacking, air-drying and cementing. This kind of material needs to have a denser structure and a larger friction angle after production, which is closer to the actual rock mass. Economic factors should also be considered under the conditions of practicality. In the process of selecting materials, the model construction should be planned according to the solidification time, and the material scheme that can be recycled, harmless and easy to handle should be preferred. Herein, the mechanical parameters close to the precalculated parameters can be obtained by adjusting the material ratio [46,47].
Through multiple experiments, the scheme with the smallest error from the theoretical value was finally selected. The main materials are sand, lime and gypsum, plus a small amount of mica powder and borax. The design proportioning scheme is shown in Table 3, where coarse sand and fine sand are the main materials, and lime and gypsum can enhance the cohesiveness. Borax plays the role of retardation when making materials, and mica powder can play the role of filling during the air-drying interval when building the model. The amount of water is 1/7 of the total amount, and the borax and mica powder are both 1/90 of the water amount.
The mass Q (kg) of each material can be determined by:
Q = V × ρ × K
where, V is the model volume, m3; ρ is the material density, kg/m3; and K is the material loss coefficient. According to Table 3, the mass of different materials can be determined in Table 4.

2.4. Artificial simulation rainfall test

2.4.1. Test bench design

To meet the requirements of the coupling effect of excavation unloading and heavy rainfall, the experiment was carried out on an artificial simulation rainfall test bench. The bench consists of the base and rainfall test area. The base has a size of 250 cm × 180 cm × 25 cm. Above the base, there is a rainfall test surrounded by double-layer composite tempered glass on three sides. Besides, under the premise of ensuring observability, the glass can constrain the model, meet the boundary conditions and prevent rainwater from leaking out. The rainfall test area has a size of 2.2 m × 1.6 m × 1.8m (Figure 6(a)).

2.4.2. Rainfall system design

To better simulate natural rainfall, a nozzle-type artificial rainfall device was utilized. It can produce uneven raindrop sizes with a certain initial velocity, which is more in line with reality. The rainfall intensity can be controlled by the water pressure regulation device, which has good applicability for this experiment. To ensure sufficient rainfall and uniform spray area, a total of 7 columns of rainfall nozzles were set up, 6 in each column, arranged at equal intervals (Figure 6(a)). The rainfall intensity can be controlled by adjusting the water amount, and the adjustable range is 0~60 liters per hour. The base is equipped with a drainage system (Figure 6(b)).

2.4.3. Rainfall uniformity test

This research used the uniformity coefficient k (%) to judge whether the rainfall system is reliable [48‒50]. The k method is generally to place multiple cylinders evenly in the rainfall area. It needs to perform a period of rainfall, record the precipitation capacity collected in the cylinder and calculate the rainfall uniformity according to:
k = 1 − ∑ i = 1 n L i − L n L
where, n is the number of cylinders; Li​is the value of each cylinder, mm/h; L is the average value of the cylinders, mm/h. In the rainfall uniformity test, 12 labelled cylinders were utilized. All cylinders were placed in a rectangular shape evenly in the rainfall test area. Two groups of rainfall intensities of 20 mm/h and 40 mm/h were selected for the rainfall uniformity test. According to the measured data and Eq. (13), k20 = 96.05% and k40 = 96.92%. Accordingly, it can be judged that the rainfall system can effectively simulate the rainfall in reality and meet the experimental requirements.

2.5. Similarity simulation experiment procedure

2.5.1. Slope model

The slope model was made according to the following steps: (1) put the materials into the mixer and mix them twice according to the material proportioning (Table 4); (2) stack the materials in the mold, stack the wooden boards and place them for about 6 days to make the materials naturally air-dry and harden;(3) bury soil moisture sensors and pore water pressure sensors during the stacking process; and (4) place the model to air-dry naturally for 14 days, remove the wooden boards and use a warm air fan to dry for another 3 days after stacking. Finally, the slope model depicted in Figure 7(a) can be obtained.

2.5.2. Data acquisition

The data acquisition is divided into the sensor and image acquisition systems, which are used to record the internal and surface states of the slope model, respectively. The sensor acquisition system consists of pore water pressure sensors (Figure 7(b)), three -needle soil moisture sensors (Figure 7(c)), data acquisition cards (Figure 7(d)) and direct current stabilized power supplies (Figure 7(e)). A total of 4 pore water pressure sensors and four soil moisture sensors were utilized in this experiment. Moreover, the image acquisition system uses a three-view stereo camera, with a resolution of 1280 × 960 , which has the functions of automatic correction of lens distortion and camera position deviation (Figure 7(f)). It can directly connect with the computer to record data. The data obtained by the camera contains image information and point cloud coordinates. Combining the two can obtain the displacement and damage of the model.
As depicted in Figure 8, the sensors are connected to the data acquisition card, which transfers the internal monitoring data of the model to the computer for recording. The three-view camera can record the whole process of external damage to the model during the experiment. The combination of the two helps us to better analyze and understand the slope model.

2.5.3. Monitoring system

An important task in the physical experiment is to arrange the soil moisture and pore water pressure sensors. The 8 sensor corresponds to 8 monitoring points. As shown in Figure 9, the deepest monitoring point is 70 cm away from the upper plane of the model. The moisture monitoring point h1 and water pressure monitoring point k1 are located 10 cm away from the upper surface of the model. The moisture monitoring point h2 and the water pressure monitoring point k2 are located at the open-pit to underground mining platform, about 10 cm deep. The moisture monitoring points h3, h4 and the water pressure monitoring points, and k3, k4 are arranged about 10 cm away from the goaf. Displacement measurement points are arranged along the direction of the goaf, with 5 displacement measurement lines in total, mainly distributed above the mining area. Each measurement line has 6 measurement points, which are utilized to record the overburden displacement.

2.5.4. Experimental scheme

Before the experiment, it is necessary to check whether the test bench is firm, clean the drainage system and pre-test whether the sensors can work normally. After setting up and adjusting the three-view stereo camera and computer system, the experiment was carried out. As depicted in Figure 10, in the open-pit mining stage, the physical model was open-pit mined, and rainfall was carried out at the same time. The total rainfall duration was 1 hour, and the intensity was 10 mm/h. According to the field investigation, the excavation stopped at the 40 cm open-pit platform, with a slope angle of 45°. After the open-pit mining was completed, it was converted to underground mining. Here, the mining method is the room and pillar method. There was a total of 3 groups, 2 mine rooms in each group, and the mine rooms were set to 10 cm. A mine pillar of 7 cm was left between each mine room, and a continuous mine pillar of 14 cm was left between each group of mine rooms. There were 3 mine pillars and 2 continuous mine pillars in total. A group of mine rooms was excavated each time, and the rainfall was carried out at the same time with an intensity of 20 mm/h. After each group was completed, the rainfall was carried out with the intensity of 40 mm/h for 10 minutes, as well as the experimenters left to facilitate the three-view camera to record the surface morphology of the model.
After the open-pit to underground mine room mining, the mine pillar mining stage was followed. There was a total of 3 reserved mine pillars, and 1 mine pillar was mined each time. The rainfall was carried out at the same time with an intensity of 20 mm/h. After each mining was completed, the rainfall was carried out with an intensity of 40 mm/h for 10 minutes.
When the underground mine room pillar mining was completed, the continuous mine pillar mining was carried out. There was a total of 2 reserved continuous mine pillars, and 1 continuous mine pillar was mined each time. The rainfall was carried out at the same time with an intensity of 20 mm/h. After each mining was completed, the rainfall was carried out with an intensity of 40 mm/h for 10 minutes. After the above steps were completed, a group of experiments was completed, and the slope angles of 55° and 65° were repeated after cleaning.

3. Results and discussion

3.1. Variation characteristics of pore water pressure

According to the experimental scheme, the variation of pore water pressure under different slope angles was obtained, as depicted in Figure 11. The overall law of pore water pressure is that the values of k3 and k4 at the depth are higher than those of k1 on the upper surface and k2 on the open-pit platform. The maximum pore water pressure is k4, with an average of 4.53 kPa, slightly higher than k3 by about 0.55~0.85 kPa. This is because the position of k4 is deeper than k2, which makes the pore water pressure at k4 larger under the same rainfall. Besides, for the two monitoring points above, affected by the water accumulation, k2 on the lower slope is slightly larger than k1 on the upper surface, and the difference between the two values is about 0.18~0.53 kPa. The minimum pore water pressure is k1, with an average of 2.03 kPa.
In the underground mining stage, due to the change in rainfall intensity, the increase rate of pore water pressure increases, with a growth rate of about 0.48%. The pore water pressure before the open-pit mining stage is negative, indicating that it is unsaturated soil and mainly has matrix suction. With the process of rainfall, the values of all monitoring points slowly increase and turn positive and mainly have pressure, as well as the internal particles change from an inward infiltration state to a free seepage state for water molecules [51‒53]. The pore water pressure of each monitoring point change from negative to positive in the later stage of the growth stage and tend to be stable in about 30 minutes. The growth stage of each monitoring point is about 100 minutes, accounting for 60% of the total experimental time.
The pore water pressure of each monitoring point at the beginning of the experiment under three slope angles is different, which is due to the unavoidable error in the production process of different models, resulting in different initial states. However, it can be found that the monitoring points above generally enter the rapid growth stage earlier than the sensors inside, and the growth rate in the open-pit mining stage mainly depends on the negative value size of each place. The smaller value represents the greater suction of the soil, which can produce a faster change rate, but it also tends to a stable growth state after a certain time. In the underground mining stage, to facilitate the construction, the rainfall intensity is constantly changing, which also causes the growth of pore water pressure in the stage to fluctuate constantly, which shows that the change of pore water pressure is sensitive to the rainfall intensity.

3.2. Variation characteristics of moisture content

According to the experimental scheme, the variation of moisture content under different slope angles was obtained, as shown in Figure 12. The basic law of moisture content data recorded at 4 locations under different slope angles is the same. h1 and h2 are located 10 cm below the upper surface and the open-pit platform surface, respectively, and are the first places affected by rainfall. The moisture content of these two places changes earlier than the sensors in the model interior, h3 and h4, and the measured values are larger. The initial values of the surface sensors are lower than those of the internal sensors, which is due to the fact that the materials need to be added with water to make the model during the model stacking process. Even after drying, the rock mass inside the model still stores water, while the exposed surface is drier.
The value of h2 on the open-pit platform is obviously higher than that of h1 after the open-pit mining stage, and the change rate of the value also increases significantly. This is because h2 is located below the open-pit mining slope, which is affected by both rainfall and the accumulated water flowing down from the upper surface. The change rate of h1 in the underground mining stage is 0.43% per minute on average, which is 0.2% higher than that in the open-pit mining stage. After the experiment, the moisture content of h1 and h2 above is higher than that of h3 and h4 inside the model. The maximum moisture content is h2 on the open-pit platform, with an average of 63.67%, which is 22.37% higher than that of h4 inside. Compared with the values of each monitoring point under 3 slope angles, the difference in the moisture content between the platform and upper surface is about 0.46~0.83%. The moisture content inside the 65° slope model is 0.42% lower than that of the 55° slope model and 0.68% lower than that of the 45° slope angle.

3.3. Variation characteristics of rock mass displacement

Before mining, the rock mass is affected by the geological activities and self-weight stress of the surrounding mining operations, as well as the external forces of the environment, rainfall infiltration and other factors, which cause some deformation and damage inside the rock mass and accumulate some energy. As the mining operation changes from open-pit to underground, the stress field of the underground ore body is inevitably damaged, and the most intuitive manifestation of this change is the deformation and movement of the rock mass around the underground mining area. By recording the rock mass displacement under the combined action of heavy rainfall and mining unloading, analyzing its damage characteristics is helpful to summarize the influence of mining under rainfall on the underground mining area under different slope angles.
By analyzing the images and information collected from the similarity simulation experiments, the displacement changes of the models under different slope angles at different stages are statistically analyzed. The measuring lines are divided according to the vertical distance from the mining area, and the measuring lines with vertical distances of 10.1 cm, 20.2 cm, 30.3 cm, 40.4 cm, 50.5 cm, and 60.6 cm are marked as A, B, C, D, E and F, respectively. The point at the slope angle is taken as the starting position in the horizontal direction, and the first measuring point is located above the first mine room, as shown in Figure 13. The value of the horizontal relative displacement of the measuring point is set as negative left and positive right, and the vertical displacement is positive up and negative down. The displacement of the models with different slope angles at different stages was analyzed.
The open-pit mining stage is also the slope-cutting stage. Figure 14 represents the vertical and horizontal displacement of each measuring point under different slope angles. It can be seen that the overall displacement in the open-pit mining stage is not large, and the measuring points near the slope cutting face have slight movement, moving towards the working face (upper left), while the measuring points far away from the working face are hardly affected. By comparing the horizontal and vertical displacement changes of each measuring point, it is found that the most affected measuring line in the open-pit mining stage is F, as well as the maximum horizontal and vertical displacement points are both near the working face of the F measuring line. They are 10.1 cm away from the starting point. Besides, the average horizontal displacement is -0.184 cm, and the vertical displacement is -0.096 cm. As the measuring line goes deeper, the displacement changes in each direction decrease in turn, and the measuring point closer to the interior has less displacement, which can be almost ignored. The maximum horizontal and the maximum displacement points both appear in the 45° slope model, and the 65° slope model changes less. The change value of the 55° model is similar to that of the 45° model. The models with varying slope angles exhibit relative stability during the open-pit mining stage, and there is no significant overall displacement. Comparing the subtle changes, a larger slope angle has a smaller impact on the model.
After the open-pit mining stage, the underground room mining was carried out. In this experiment, a total of 6 rooms were mined, and 2 rooms were grouped together, totaling 3 groups of mine rooms. Figure 15 shows the displacement changes of the first group of mine rooms in this stage. Because the goaf is inclined to the right, the monitoring points moved to the right horizontally after the first room was mined, and the monitoring points far away from the first group moved slightly to the left to balance the internal stress field. The maximum horizontal displacement point is on the A measuring line, which is 10.1 cm away from the starting point. The average horizontal displacement is -0.12 mm, which moves 0.064 mm to the right compared with the open-pit mining stage. After the first group of rooms was mined, the overlying rock above rooms F1 and F2 subsided, and the maximum vertical displacement point was 10.1 cm away from the starting point, with an average vertical displacement of 0.265 m. The measuring points far away from the mining area also have a downward trend, as well as the vertical displacement of each measuring point on the measuring line is inversely proportional to the distance between the measuring line and the mining area. A farther distance indicates less impact. Fine fractures extended from the corners above the room. In the mining of the first group of rooms, the horizontal displacement is not affected by the slope angle, and the maximum horizontal displacement under each slope angle differs by no more than 0.02 mm. The maximum vertical displacement occurs in the 65° slope model, which is -0.288 mm. The vertical displacement of the 55° slope angle is the smallest, which is -0.238 mm.
As the working face advanced, under the influence of mining and rainfall, the phenomenon of overlying rock subsidence and rock-soil collapse occurred in the mining of the second group of mine rooms, and the fractures that had been generated continued to grow, showing signs of penetration and connection. Figure 16 represents the displacement changes of the mine rooms during the underground mining stage (second group). As the second group of rooms were mined, the measuring points above them had a slight tendency to move to the left, and the maximum horizontal displacement point appeared 56.3 cm away from the starting point on the A measuring line, which is above the pillar Z2, with an average maximum horizontal displacement of -0.26 mm. The 45° slope model shows the maximum horizontal displacement. The horizontal displacement of the previous measuring points increased, and persistent fractures appeared at the corner of the mine room. The vertical displacement continued to increase, and the maximum vertical displacement was 17.1 cm away from the starting point on the A measuring line, with an average of -0.82 mm. The horizontal displacement of the measur -ing point which is 36.7 cm away from the starting point changes the most, increasing by 1.39 times compared to the mining of the first group of mine rooms. The measuring points which are 56.3 cm and 75.9 cm away from the starting point began to sink, and the fractures above the second group of mine rooms appeared and gradually combined with the cracks above the first group of mine rooms to form a semi-ellipse. The 65° slope model has the largest vertical displacement, and the 55° model has the smallest vertical displacement, with a difference of 0.22 mm.
The mining operation continued to advance, and the F5 and F6 mine rooms were mined. At this time, the expansion of fractures was more obvious. Since the mine rooms had been completely mined, the support force of the goaf was provided by the pillars and the boundary pillars. Figure 17 shows the displacement changes of the mine rooms during the mining stage (third group). Compared with the first and second groups of mining, the horizontal displacement has a larger change, which indicates that the mining of the third group formed a new stress balance inside the model. The maximum horizontal displacement is 17.1 cm away from the starting point on the A measuring line, with an average of -0.47 mm, which increases by 1.04 times compared with the second group. The measuring points above the mine rooms F5 and F6 moved to the left, and the measuring points farther away from the starting point moved significantly to the left compared with the second group, with an average displacement of -0.24 mm. It can be found that the 65° slope model has the largest horizontal displacement, and the 55° model has the smallest one. Herein the vertical displacement of the model continued to increase, and the displacement points above the mine rooms have the largest increase value. The displacements of the 45°, 55° and 65° models increase by an average of -0.41 mm, -0.34 mm and -0.34 mm, respectively. The maximum displacement measuring points are the two points closest to the starting point, and the measuring lines farther away from the vertical distance of the goaf also have large displacements.
After the room mining stage, the model produced more fractures, and the pillars and boundary pillars were in a critical state. In the pillar mining stage, partial collapse and persistent interlayer fractures occurred in the overlying rock area. At this time, the calculation of horizontal displacement was no longer possible. The vertical displacement of each model under the mining of the 3 groups of pillars is as depicted in Figure 18, Figure 19 and Figure 20.
Since Z1 is located between the mine rooms F1 and F2, it plays a supporting role. After the mining operation, the area above pillar Z1 experienced significant subsidence due to gravitational forces, while the measuring points located further away from the goaf exhibited comparatively smaller displacements, leading to interlayer fractures. The maximum displacement point is on the A measuring line and is 17.1 cm away from the starting point, with an average vertical displacement of -1.772 cm. When the Z2 pillar was mined, only the continuous pillar L1 remained in the area to provide support. It can be found that the measuring points above L1 sank slightly, about -0.11 cm and that the measuring points above Z2 sank significantly. However, the displacement is lower than that above Z1, with an average of -1.643 cm. At the same time, persistent fractures and partial collapse occurred in the overlying rock area. After the Z3 pillar was mined, the measuring points that are 95.5 cm away from the starting point have large displacements, with an average of -1.36 cm. After the continuous pillar L2 was loaded, the measuring points above it sank slightly, about -0.09 cm. Compared with the mining of the Z1 and Z2 pillars, its drop is less, reducing by about 0.13 cm. In the pillar mining stage, it can be found that the 55° model has fewer affected measuring lines, and only the A measuring line has large vertical displacements. The 45° model has large displacement measuring lines A and B, as well as the 65° model has large displacement measuring lines A, B, and C.
After the continuous pillars L1 and L2 were mined, the overlying rock area lost its support completely. Thus, the overlying rock collapsed, and the fractures developed rapidly, forming a semi-elliptical damage area. Here, the vertical displacement of each model under the mining of the continuous pillars L1 and L2 is depicted in Figure 21 and Figure 22. After the continuous pillar L1 was mined, the A and B measuring line areas above L1 of the three slope models all collapsed completely, but the 55° model has a smaller change than the 45° and 65° models on the C measuring line. This indicates that the area affected by the 65° model is larger and that the collapse area of the 55° model is smaller. Therefore, it can be found that after complete excavation, all models have large vertical displacements, and the overlying rock collapses. Compared with the 45° and 55° models, there are large displacement values on the C measuring line of the 65° model. The values of displacement points at distances of 56.3 cm and 75.9 cm from the starting point are lower in the 55° model, indicat -ing that in middle regions, its downward sinking situation is weaker. The values of displacement points at distances far from the goaf are low for all models, indicating that only fractures develop here without large-scale detachment phenomena.

4. Conclusions

This research conducted an indoor slope failure test based on the similarity theory. The selection area of slope rock samples depends on UAV. The mechanical properties of the rock were measured, such as elastic modulus, Poisson’s ratio, tensile strength, cohesion and internal friction angle and used these data to perform a strength reduction calculation and obtain the relevant parameters of the similarity simulation experiment. The rainfall, model, data acquisition and monitoring systems were designed. The rock mass movement in the transition from open-pit mining to underground mining with different slope angles under the rainfall-mining coupling effect was determined. The pore water pressure, moisture content and displacement of each stage were analyzed, and the internal activity law of the rock mass was explored. The following conclusions were obtained:
(1)
The experiment shows how rainfall-mining coupling affects the pore water pressure during the transition from open-pit to underground mining. The pore water pressure is higher in the deep rock mass than on the upper surface and the open-pit platform. Rainfall and slope water increase the pore water pressure on the open-pit platform. In the underground mining stage, the pore water pressure rate rises by 0.48%. The pore water pressure is negative before the open-pit mining stage, indicating unsaturated soil. As the experiment continues, the pore water pressure turns positive, and the internal particles shift from inward penetration to free seepage. The pore water pressure changes from negative to positive in the late growth stage and stabilizes at about 30 minutes. The growth stage lasts about 100 minutes, or 60% of the experiment time. The pore water pressure at the top grows faster than the internal one.
(2)
The moisture content of the upper surface and the open-pit platform changes first and has a larger final value. The surface moisture content value is lower than the internal moisture content of the model. Rainfall and water accumulation from the upper surface make the moisture content of the open-pit platform change significantly after the open-pit mining stage. After the experiment, the moisture content on the upper surface and the platform is higher than that inside the model. The open-pit platform has the maximum moisture content, and the moisture content decreases with depth.
(3)
During the open-pit mining stage, the rock mass displaces to the upper left, and the top area suffers the most damage. Herein, the maximum horizontal and vertical displacement points are both near the upper working face. During the underground mining stage, the model exhibits vertical fractures, and the overall displacement moves slightly to the left. Microfractures propagate at the corner above the mine. The mine room fractures grow and intersect, forming a semi-ellipse. During the pillar mining stage, the overlying rock area displaces significantly, and fractures persist. After continuous pillar mining, the overlying rock collapses extensively. The 45° model displacement changes mainly occur in the A and B measuring lines. The 55° model displacement value in the middle area is low, mainly in the front of the mined area. Furthermore, the 65° model displacement influence area is the largest. There is a large displacement in the A, B and C measuring lines.

Author Contributions

Conceptualization, Q.L., Y.W. and X.L.; methodology, Q.L.; software, Q.L.; validation, Y.W., X.L. and B.G.; formal analysis, Q.L.; investigation, X.L.; resources, X.L.; data curation, B.G.; writing—original draft preparation, Q.L.; writing—review and editing, X.L.; visualization, Y.W.; supervision, B.G.; project administration, X.L.; funding acquisition, X.L. All authors have read and agreed to the published version of the manuscript.

Funding

The research work was funded by the Research Fund of National Natural Science Foundation of China (NSFC) (No. 42277154), Guizhou Province Science and Technology Planning Project (No. Guizhou science and technology cooperation support [2022] common 229), National Natural Science Foundation of Shandong Province of China (NSFC) (No. ZR2022ME188), the State Key Laboratory of Coal Resources and Safe Mining, CUMT (No. SKLCRSM22KF009), and the project of Slope safety control and disaster prevention technology innovation team of "Youth Innovation Talent Introduction and Education Plan" of Shandong Colleges and universities (Grant No. Lu Jiao Ke Han [2021] No. 51).

Data Availability Statement

Most of the data generated during this study are included in the article. For other datasets, please contact the corresponding author with reasonable requests.

Acknowledgments

We would like to express our gratitude to Yulin Xie and Jiawen Wang for their invaluable assistance in determining the material ratio, constructing the physical model, and conducting large-scale similar physical simulation experiments involving excavation and rainfall processes.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Christmann, P. Mineral Resource Governance in the 21st Century and a sustainable European Union. Miner. Econ. 2021, 34, 187–208. [Google Scholar] [CrossRef]
  2. Whittle, D.; Brazil, M.; Grossman, P.A.; Rubinstein, J.H.; Thomas, D.A. Combined optimisation of an open-pit mine outline and the transition depth to underground mining. Eur. J. Oper. Res. 2018, 268, 624–634. [Google Scholar] [CrossRef]
  3. Zhao, J.; Ma, Y.; Lin, B.; Lan, Z.; Shi, W. Geomechanical mode of mining landslides with gently counter-inclined bedding-a case study of Madaling landslide in Guizhou Province. Chinese Journal of Rock Mechanics and Engineering 2016, 35, 2217–2224. [Google Scholar]
  4. Tao, Z.G.; Zhu, C.; He, M.C.; Karakus, M. A physical modeling-based study on the control mechanisms of Negative Poisson's ratio anchor cable on the stratified toppling deformation of anti-inclined slopes. Int. J. Rock Mech. Min. 2021, 138, 104632. [Google Scholar] [CrossRef]
  5. Li, X.; Li, Q.; Wang, Y.; Liu, W.; Hou, D.; Zheng, W.; Zhang, X. Experimental study on instability mechanism and critical intensity of rainfall of high-steep rock slopes under unsaturated conditions. Int. J. Min. Sci. Techno. 2023, 33, 1243–1260. [Google Scholar] [CrossRef]
  6. Zhu, C.; He, M.C.; Karakus, M.; Zhang, X.H.; Tao, Z.G. Numerical simulations of the failure process of anaclinal slope physical model and control mechanism of negative Poisson's ratio cable. B. Eng. Geol. Environ. 2021, 80, 3365–3380. [Google Scholar] [CrossRef]
  7. Lu, W.B.; Yang, J.H.; Yan, P.; Chen, M.; Zhou, C.B.; Luo, Y.; Jin, L. Dynamic response of rock mass induced by the transient release of in-situ stress. Int. J. Rock Mech. Min. 2012, 53, 129–141. [Google Scholar] [CrossRef]
  8. Liu, Y.Q.; Chen, J.P.; Tan, C.; Zhan, J.W.; Song, S.Y.; Xu, W.L.; Yan, J.H.; Zhang, Y.S.; Zhao, M.Y.; Wang, Q. Intelligent scanning for optimal rock discontinuity sets considering multiple parameters based on manifold learning combined with UAV photogrammetry. Eng. Geol. 2022, 309, 106851. [Google Scholar] [CrossRef]
  9. Li, X.; Li, Q.; Hu, Y.; Chen, Q.; Peng, J.; Xie, Y.; Wang, J. Study on Three-Dimensional Dynamic Stability of Open-Pit High Slope under Blasting Vibration. Lithosphere 2022, 2021, 6426550. [Google Scholar] [CrossRef]
  10. Yan, J.H.; Xing, X.S.; Li, X.S.; Zhu, C.; Han, X.D.; Zhao, Y.; Chen, J.P. Forecasting the Landslide Blocking River Process and Cascading Dam Breach Flood Propagation by an Integrated Numerical Approach: A Reservoir Area Case Study. Remote Sens. 2023, 15, 4669. [Google Scholar] [CrossRef]
  11. Liu, W.; Li, Q.H.; Yang, C.H.; Shi, X.L.; Wan, J.F.; Jurado, M.J.; Li, Y.P.; Jiang, D.Y.; Chen, J.; Qiao, W.B.; Zhang, X.; Fan, J.Y.; Peng, T.J.; He, Y.X. The role of underground salt caverns for large-scale energy storage: A review and prospects. Energy Storage Mater. 2023, 63, 103045. [Google Scholar] [CrossRef]
  12. Soltani, K.A.; Osanloo, M. A Set of Classified Integer Programming (IP) Models for Optimum Transition from Open Pit to Underground Mining Methods. Nat. Resour. Res. 2020, 29, 1543–1559. [Google Scholar] [CrossRef]
  13. Zhang, Q.L.; Zhang, B.Y.; Chen, Q.S.; Wang, D.L.; Gao, X. Safety Analysis of Synergetic Operation of Backfilling the Open Pit Using Tailings and Excavating the Ore Deposit Underground. Minerals 2021, 11, 818. [Google Scholar] [CrossRef]
  14. Li, X.; Yang, S.; Wang, Y.M.; Nie, W.; Liu, Z.F. Macro-Micro Response Characteristics of Surrounding Rock and Overlying Strata towards the Transition from Open-Pit to Underground Mining. Geofluids 2021, 2021, 5582218. [Google Scholar] [CrossRef]
  15. Zhao, Y.; Yang, T.H.; Bohnhoff, M.; Zhang, P.H.; Yu, Q.L.; Zhou, J.R.; Liu, F.Y. Study of the Rock Mass Failure Process and Mechanisms During the Transformation from Open-Pit to Underground Mining Based on Microseismic Monitoring. Rock Mech. Rock Eng. 2018, 51, 1473–1493. [Google Scholar] [CrossRef]
  16. Zhu, C.; He, M.C.; Karakus, M.; Cui, X.B.; Tao, Z.G. Investigating Toppling Failure Mechanism of Anti -dip Layered Slope due to Excavation by Physical Modelling. Rock Mech. Rock Eng. 2020, 53, 5029–5050. [Google Scholar] [CrossRef]
  17. Cui, F.; Li, B.; Xiong, C.; Yang, Z.; Peng, J.; Li, J.; Li, H. Dynamic triggering mechanism of the Pusa mining-induced landslide in Nayong County, Guizhou Province, China. Geomat. Nat. Hazards Risk 2022, 13, 123–147. [Google Scholar] [CrossRef]
  18. Deliveris, A.V.; Theocharis, A.I.; Koukouzas, N.C.; Zevgolis, I.E. Numerical Slope Stability Analysis of Deep Excavations Under Rainfall Infiltration. Geotech. Geol. Eng. 2022, 40, 4023–4039. [Google Scholar] [CrossRef]
  19. Doumbouya, L.; Guan, C.S.; Bowa, V.M. Influence of Rainfall Patterns on the Slope Stability of the Lumwana (the Malundwe) Open Pit. Geotech. Geol. Eng. 2020, 38, 1337–1346. [Google Scholar] [CrossRef]
  20. Du, W.; Chai, J.; Zhang, D.; Ouyang, Y.; Liu, Y. Study on Quantitative Characterization of Coupling Effect between Mining-Induced Coal-Rock Mass and Optical Fiber Sensing. Sensors 2022, 22, 5009. [Google Scholar] [CrossRef]
  21. Jhanwar, J.C.; Thote, N.R. Slope Failures in the Opencast Coal Mines of Wardha Valley Coalfield in Central India: A Study. Rock Mech. Rock Eng. 2011, 44, 635–640. [Google Scholar] [CrossRef]
  22. Li, Q.; Song, D.; Yuan, C.; Nie, W. An image recognition method for the deformation area of open-pit rock slopes under variable rainfall. Measurement 2022, 188, 110544. [Google Scholar] [CrossRef]
  23. Liu, W.; Du, J.W.; Li, Q.H.; Shi, X.L.; Chen, J.; Yi, W.K.; He, T.; Li, D.P.; Dong, Y.K.; Jiang, D.Y.; Li, Y. Feasibility analysis on the utilization of TWH-caverns with sediment space for gas storage: A case study of Sanshui salt mine. J. Energy Storage 2024, 75, 109576. [Google Scholar] [CrossRef]
  24. Li, Z.Q.; Xue, Y.G.; Li, S.C.; Zhang, L.W.; Wang, D.; Li, B.; Zhang, W.; Ning, K.; Zhu, J.Y. Deformation features and failure mechanism of steep rock slope under the mining activities and rainfall. J. Mt. Sci. 2017, 14, 31–45. [Google Scholar] [CrossRef]
  25. Ma, G.; Hu, X.; Yin, Y.; Luo, G.; Pan, Y. Failure mechanisms and development of catastrophic rockslides triggered by precipitation and open-pit mining in Emei, Sichuan, China. Landslides 2018, 15, 1401–1414. [Google Scholar] [CrossRef]
  26. Nian, G.Q.; Chen, Z.H.; Zhu, T.Y.; Zhang, L.F.; Zhou, Z. Experimental study on the failure of fractured rock slopes with anti-dip and strong weathering characteristics under rainfall conditions. Landslides 2023, 36, 1–18. [Google Scholar] [CrossRef]
  27. Wang, C.; Min, H.; Zhu, T.; Wang, H.; Qin, W.; Zhang, G. Failure mechanism and stability analysis of the landslide: a case study for open pit iron mine in Xichang, Sichuan, China. Nat. Hazards 2023, 116, 663–691. [Google Scholar] [CrossRef]
  28. Xiang, P.; Ji, H.; Geng, J.; Zhao, Y. Characteristics and Mechanical Mechanism of In Situ Unloading Damage and Core Discing in Deep Rock Mass of Metal Mine. Shock Vib. 2022, 2022, 5147868. [Google Scholar] [CrossRef]
  29. Li, S.; Niu, Y.; Wang, B.; Gao, Y.; Zhu, Y. Influence of Rainfall Infiltration on Stability of Granite Residual Soil High Slope. Math. Probl. Eng. 2022, 2022, 1920403. [Google Scholar] [CrossRef]
  30. Rudy, A.C.A.; Lamoureux, S.F.; Treitz, P.; Collingwood, A. Identifying permafrost slope disturbance using multi-temporal optical satellite images and change detection techniques. Cold Reg. Sci. Technol. 2013, 88, 37–49. [Google Scholar] [CrossRef]
  31. Smith, J.V. Self-stabilization of toppling and hillside creep in layered rocks. Eng. Geol. 2015, 196, 139–149. [Google Scholar] [CrossRef]
  32. Khan, M.S.; Hossain, S.; Ahmed, A.; Faysal, M. Investigation of a shallow slope failure on expansive clay in Texas. Eng. Geol. 2017, 219, 118–129. [Google Scholar] [CrossRef]
  33. Spooner, I.; Batterson, M.; Catto, N.; Liverman, D.; Broster, B.E.; Kearns, K.; Isenor, F.; McAskill, G.W. Slope failure hazard in Canada's Atlantic Provinces: a review. Atl. Geol. 2013, 49, 1–14. [Google Scholar] [CrossRef]
  34. Shin, H. Static and quasi-static slope stability analyses using the limit equilibrium method for mountainous area. Geomech. Eng. 2023, 34, 187–195. [Google Scholar]
  35. Li, X.; Peng, J.; Xie, Y.; Li, Q.; Zhou, T.; Wang, J.; Zheng, W. Influence of High-Temperature Treatment on Strength and Failure Behaviors of a Quartz-Rich Sandstone under True Triaxial Condition. Lithosphere 2022, 2022, 3086647. [Google Scholar] [CrossRef]
  36. Xia, K.; Chen, C.; Liu, X.; Wang, Y.; Liu, X.; Yuan, J. Estimating shear strength of high-level pillars supported with cemented backfilling using the Hoek-Brown strength criterion. J. Rock Mech. Geotech. 2023, 52, 1–16. [Google Scholar] [CrossRef]
  37. Langford, J.C.; Diederichs, M.S. Quantifying uncertainty in Hoek-Brown intact strength envelopes. Int. J. Rock Mech. Min. 2015, 74, 91–102. [Google Scholar] [CrossRef]
  38. Masoumi, H.; Roshan, H.; Hagan, P.C. Size-Dependent Hoek-Brown Failure Criterion. Int. J. Geomech. 2017, 17, 04016048. [Google Scholar] [CrossRef]
  39. Li, X.; Li, Q.; Hou, G.; Zhang, F.; Lu, J. Investigation on the disaster mechanism and dynamic evolution of a dump slope using experimental and numerical methods: Case study, Kunyang phosphate mine, China. Geol. J. 2023, 2023, 1–16. [Google Scholar] [CrossRef]
  40. Hoek, E.; Brown, E. The Hoek-Brown failure criterion and GSI - 2018 edition. J. Rock Mech. Geotech. 2019, 11, 445–463. [Google Scholar] [CrossRef]
  41. Bois, T.; Bouissou, S.; Guglielmi, Y. Influence of major inherited faults zones on gravitational slope deformation: A two-dimensional physical modelling of the La Clapie're area (Southern French Alps). Earth Planet. Sc. Lett. 2008, 272, 709–719. [Google Scholar] [CrossRef]
  42. McFall, B.C.; Mohammed, F.; Fritz, H.M.; Liu, Y.B. Laboratory experiments on three-dimensional deformable granular landslides on planar and conical slopes. Landslides 2018, 15, 1713–1730. [Google Scholar] [CrossRef]
  43. Zhang, B.; Fang, K.; Tang, H.; Sumi, S.; Ding, B. Block-flexure toppling in an anaclinal rock slope based on multi-field monitoring. Eng. Geol. 2023, 327, 107340. [Google Scholar] [CrossRef]
  44. Moo-Young, H.; Myers, T.; Tardy, B.; Ledbetter, R.; Vanadit-Ellis, W.; Kim, T. Centrifuge simulation of the consolidation characteristics of capped marine sediment beds. Eng. Geol. 2003, 70, 249–258. [Google Scholar] [CrossRef]
  45. Wang, H.; Jiang, Z.; Xu, W.; Wang, R.; Xie, W. Physical model test on deformation and failure mechanism of deposit landslide under gradient rainfall. Bull. Eng. Geol. Environ. 2022, 81, 66. [Google Scholar] [CrossRef]
  46. Adhikary, D.P.; Dyskin, A.V.; Jewell, R.J.; Stewart, D.P. A study of the mechanism of flexural toppling failure of rock slopes. Rock Mech. Rock Eng. 1997, 30, 75–93. [Google Scholar] [CrossRef]
  47. Ding, B.; Han, Z.; Zhang, G.; Beng, X.; Yang, Y. Flexural Toppling Mechanism and Stability Analysis of an Anti-dip Rock Slope. Rock Mech. Rock Eng. 2021, 54, 3721–3735. [Google Scholar] [CrossRef]
  48. Aksoy, H.; Unal, N.; Cokgor, S.; Gedikli, A.; Yoon, J.; Koca, K.; Inci, S.; Eris, E. A rainfall simulator for laboratory-scale assessment of rainfall-runoff-sediment transport processes over a two-dimensional flume. Catena 2012, 98, 63–72. [Google Scholar] [CrossRef]
  49. Green, D.; Pattison, I. Christiansen uniformity revisited: Re-thinking uniformity assessment in rainfall simulator studies. Catena 2022, 217, 106424. [Google Scholar] [CrossRef]
  50. Lora, M.; Camporese, M.; Salandin, P. Design and performance of a nozzle-type rainfall simulator for landslide triggering experiments. Catena 2016, 140, 77–89. [Google Scholar] [CrossRef]
  51. Han, Y.; Wang, Q.; Xia, W.; Liu, J.; Wang, J.; Chen, Y.; Shen, J. Experimental study on the hydraulic conductivity of unsaturated dispersive soil with different salinities subjected to freeze-thaw. J. Hydrol. 2020, 583, 124297. [Google Scholar] [CrossRef]
  52. Shen, J.; Wang, Q.; Chen, Y.; Han, Y.; Zhang, X.; Liu, Y. Evolution process of the microstructure of saline soil with different compaction degrees during freeze-thaw cycles. Eng. Geol. 2020, 304, 106699. [Google Scholar] [CrossRef]
  53. Liu, W.; Duan, X.; Li, Q.; Wan, J.; Zhang, X.; Fang, J.; Jiang, D.; Chen, J. Analysis of pressure interval/injection and production frequently on stability of large-scale supercritical CO2 storage in salt caverns. J. Clean. Prod. 2023, 433, 139731. [Google Scholar] [CrossRef]
Preprints 96297 g001
Figure 1. Location of the study area (Google Earth).
Figure 1. Location of the study area (Google Earth).
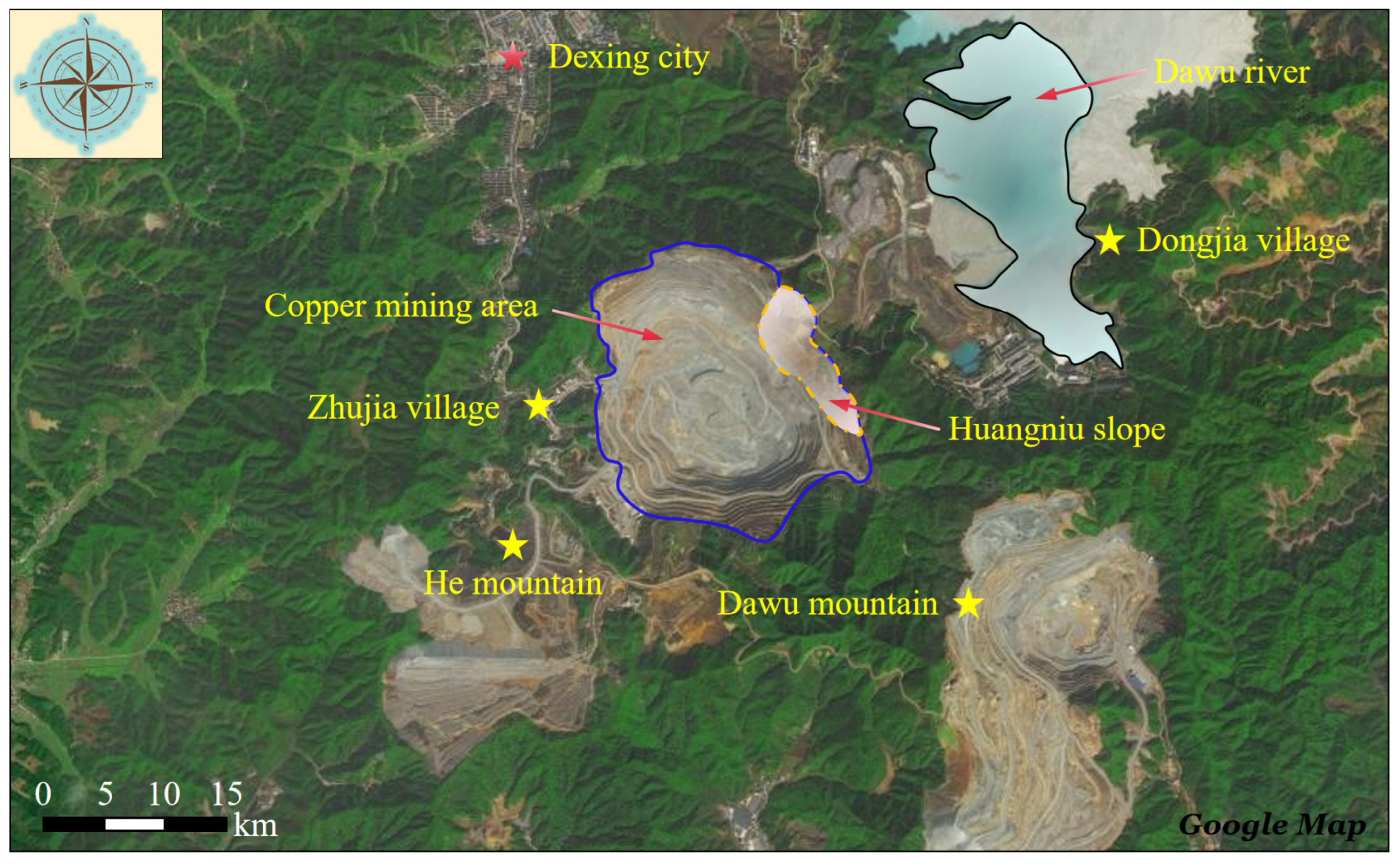
Preprints 96297 g001
Preprints 96297 g002
Figure 2. Failure status of Huangniu rock slope. (a) Wedge failure mode; (b) Plane failure mode.
Figure 2. Failure status of Huangniu rock slope. (a) Wedge failure mode; (b) Plane failure mode.
Preprints 96297 g002
Preprints 96297 g003
Figure 3. Monthly average temperature and precipitation in the study area over the past 20 years.
Figure 3. Monthly average temperature and precipitation in the study area over the past 20 years.
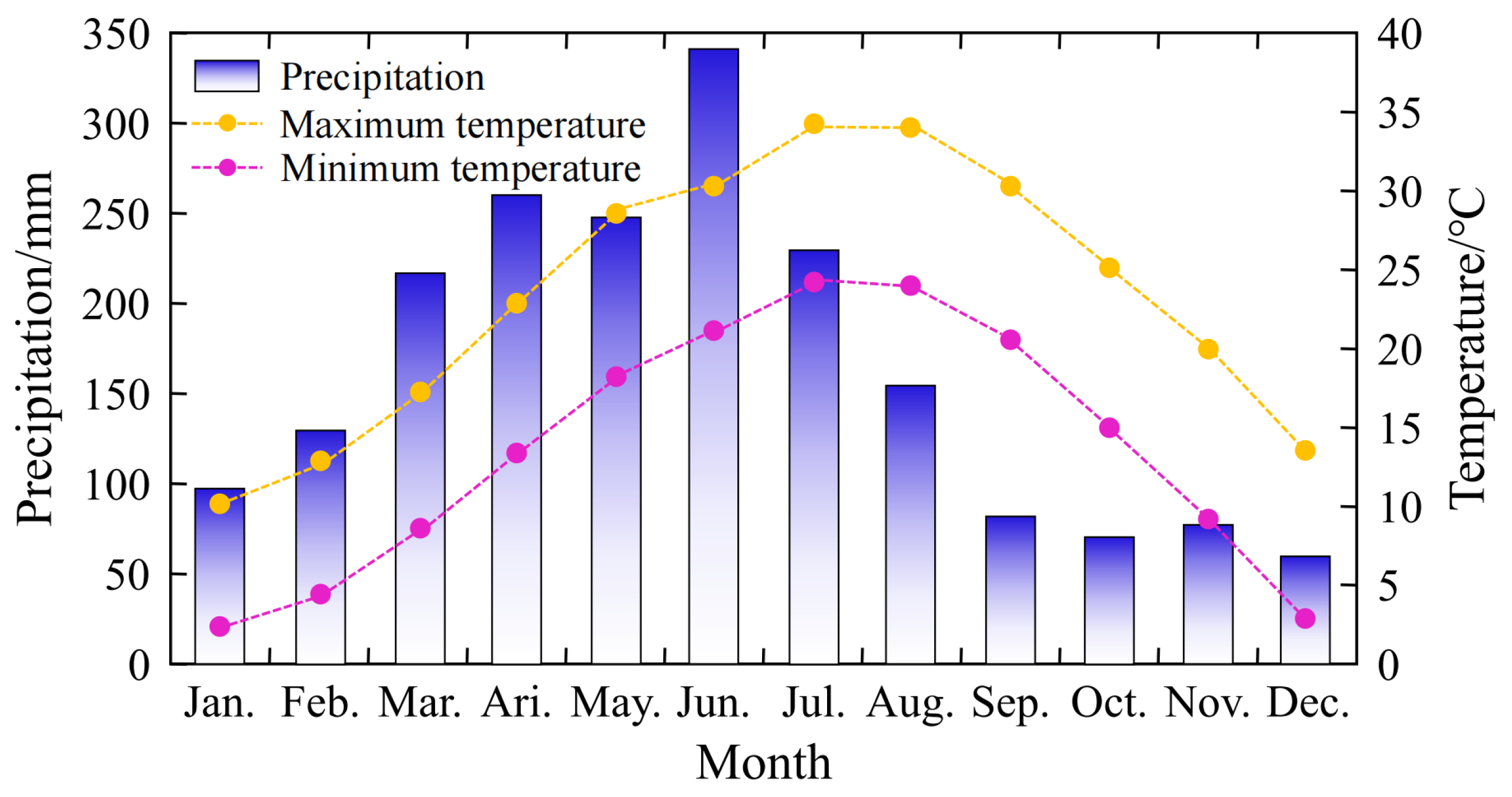
Preprints 96297 g003
Preprints 96297 g004
Figure 4. Figure 4. Uniaxial compression stress-strain curve.
Figure 4. Figure 4. Uniaxial compression stress-strain curve.
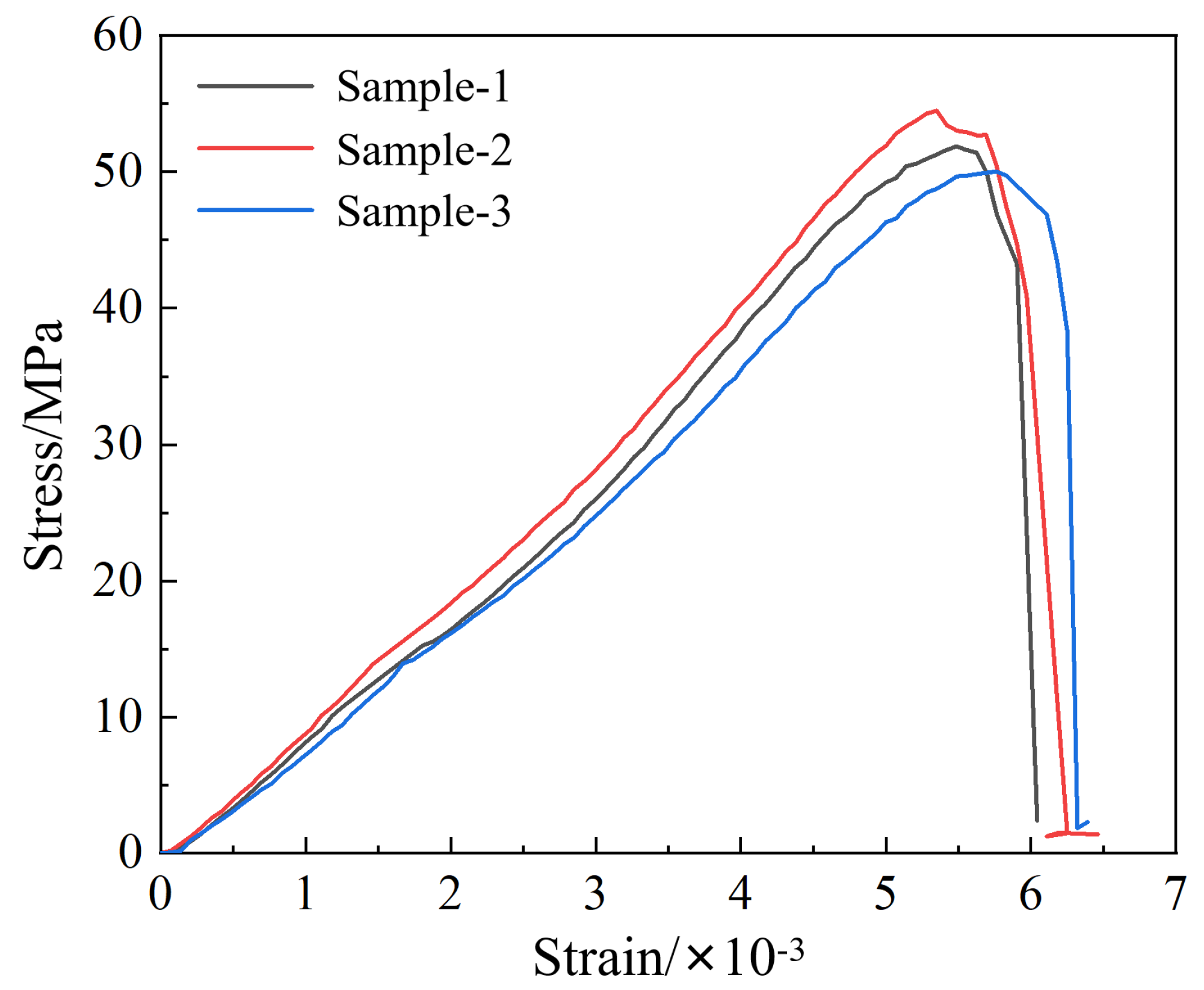
Preprints 96297 g004
Preprints 96297 g005
Figure 5. The test results. (a) Triaxial compression stress-strain curve; (b) Triaxial compression envelope curve.
Figure 5. The test results. (a) Triaxial compression stress-strain curve; (b) Triaxial compression envelope curve.
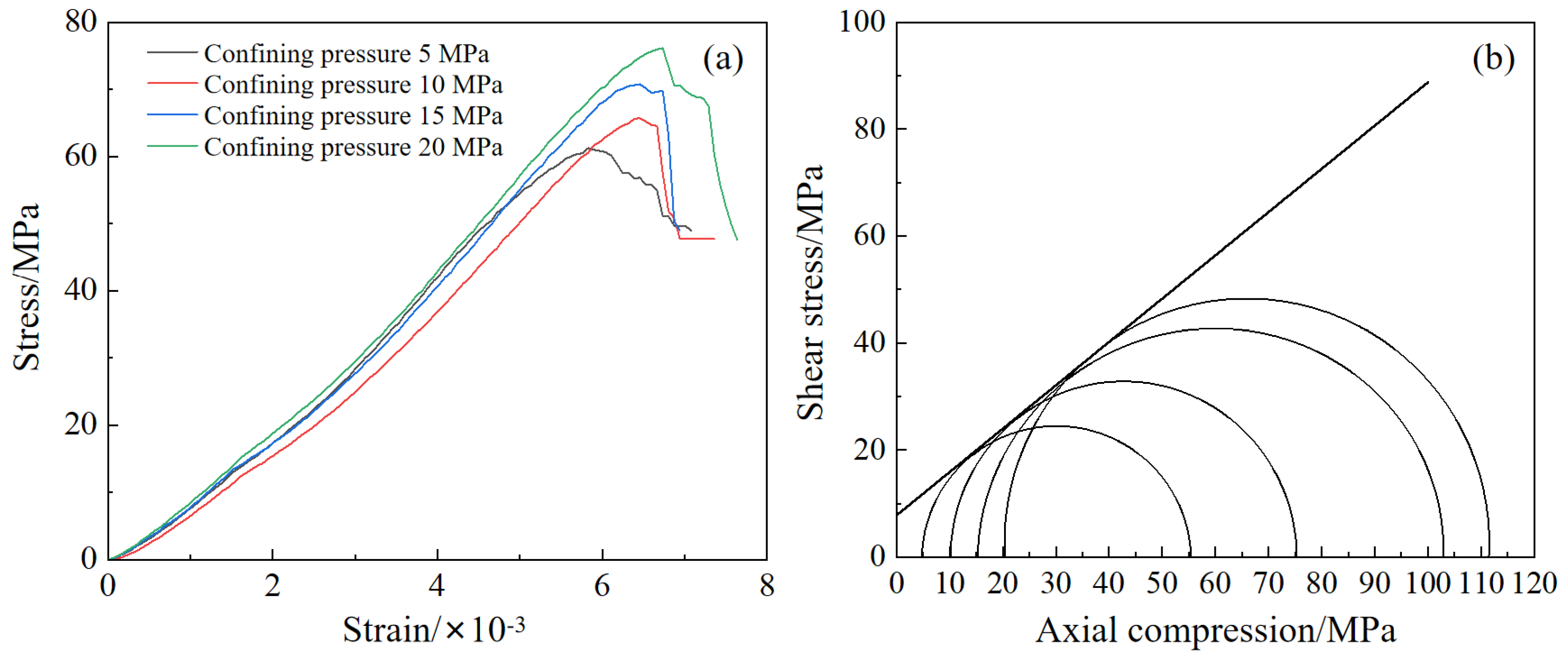
Preprints 96297 g005
Preprints 96297 g006
Figure 6. Similar physical simulation test device. (a) Test bench; (b) Rainfall system.
Figure 6. Similar physical simulation test device. (a) Test bench; (b) Rainfall system.
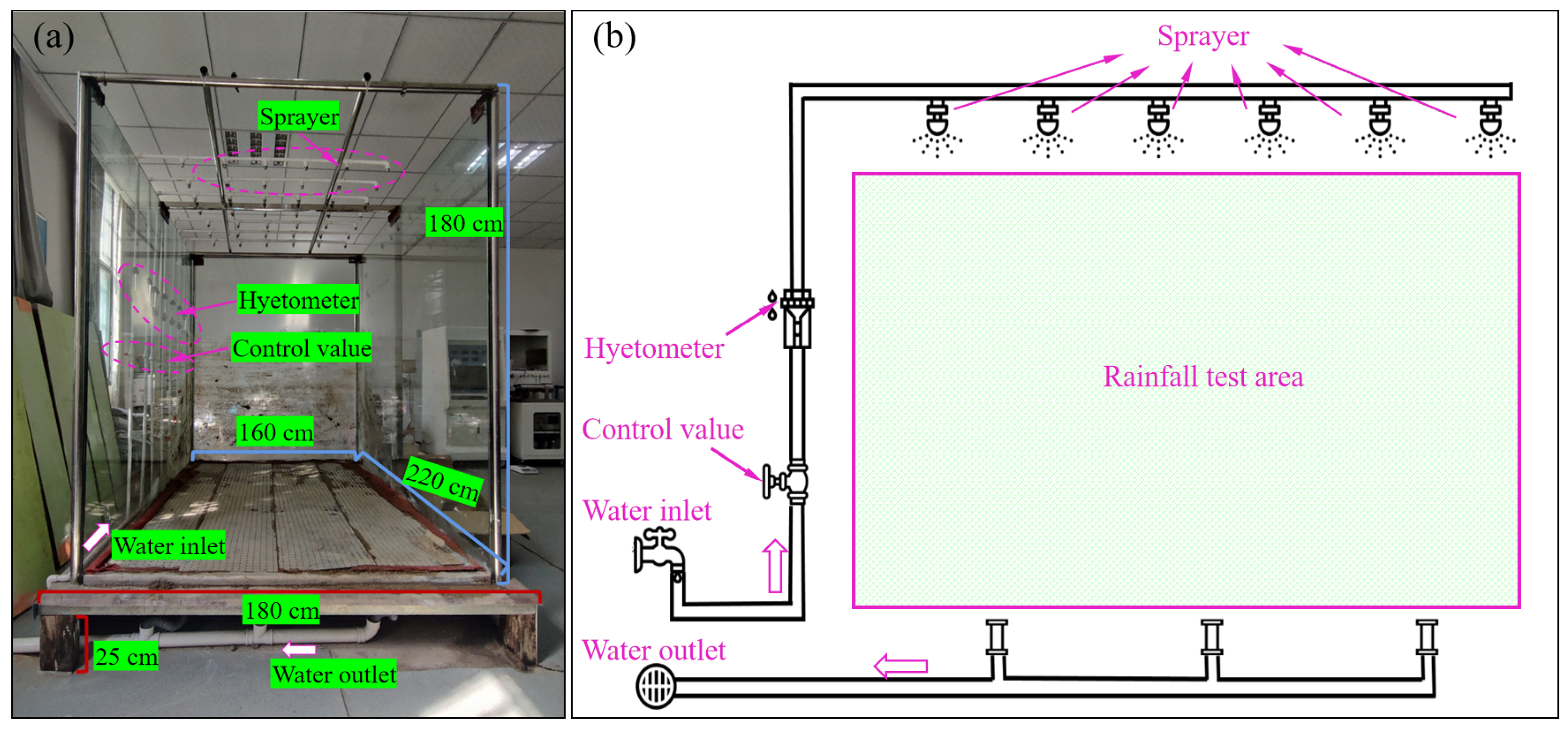
Preprints 96297 g006
Preprints 96297 g007
Figure 7. Similar physical test process. (a) Slope model; (b) Pore water pressure sensor; (c) Soil moisture sensor; (d) Data acquisition card; (e) Direct current stabilized power supply; (f) Three-view stereo camera.
Figure 7. Similar physical test process. (a) Slope model; (b) Pore water pressure sensor; (c) Soil moisture sensor; (d) Data acquisition card; (e) Direct current stabilized power supply; (f) Three-view stereo camera.
Preprints 96297 g007
Preprints 96297 g008
Figure 8. Data acquisition system.
Figure 8. Data acquisition system.
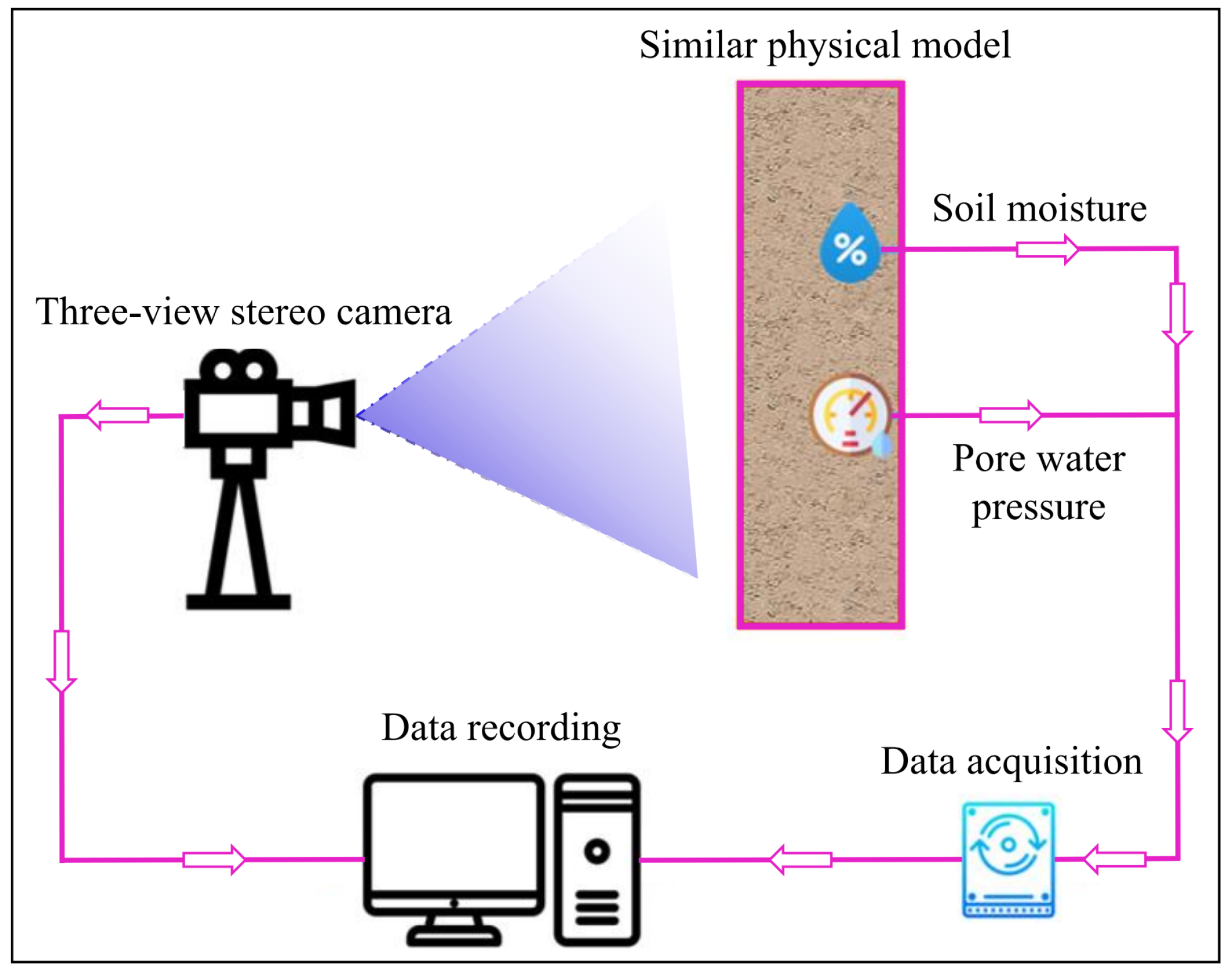
Preprints 96297 g008
Preprints 96297 g009
Figure 9. Figure 9. Layout of monitoring points.
Figure 9. Figure 9. Layout of monitoring points.
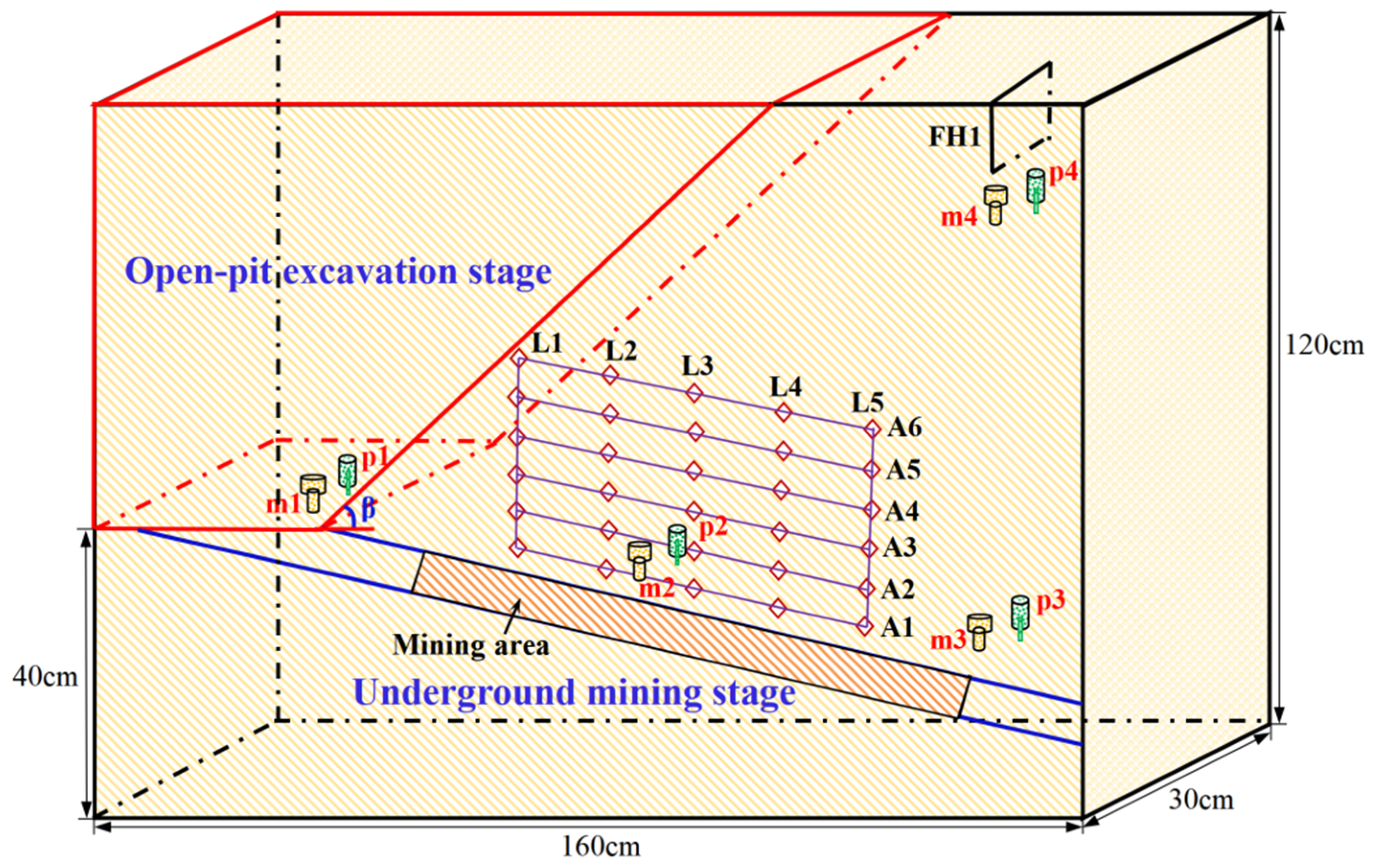
Preprints 96297 g009
Preprints 96297 g010
Figure 10. Figure 10. Experimental scheme.
Figure 10. Figure 10. Experimental scheme.
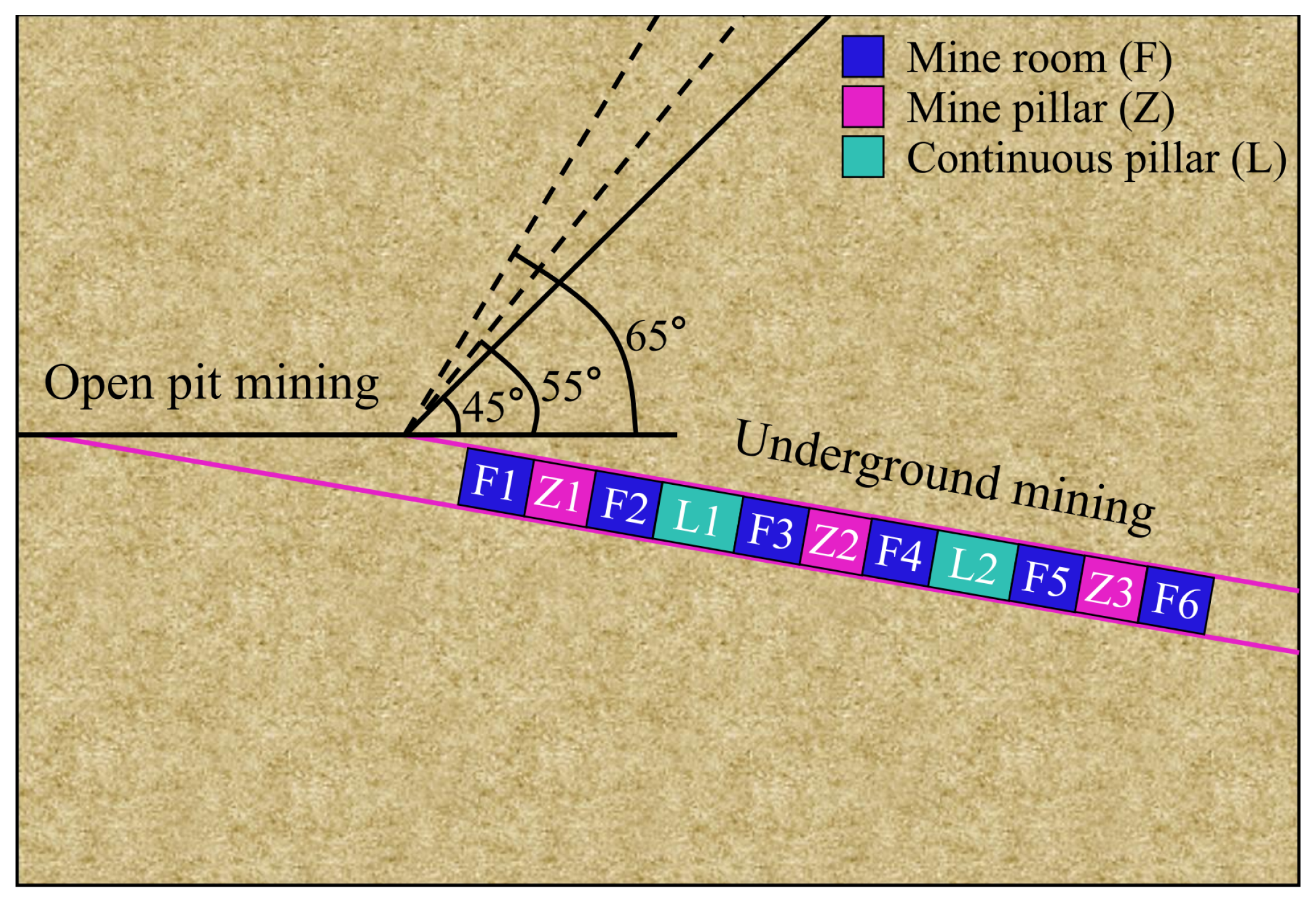
Preprints 96297 g010
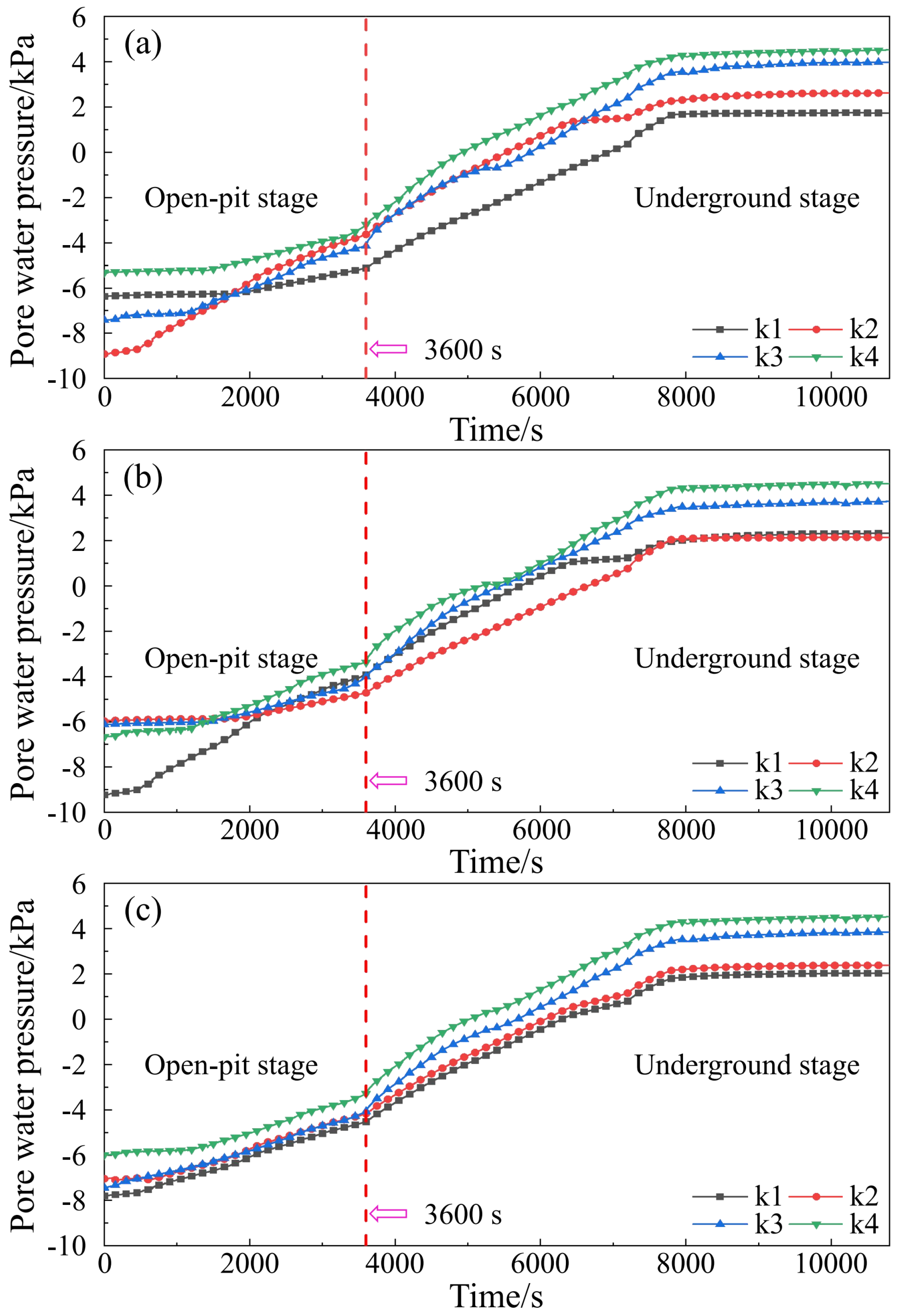
Preprints 96297 g011
Figure 11. Variations in pore water pressure in various slope models. (a) 45° slope; (b) 55° slope; (c) 65° slope.
Figure 11. Variations in pore water pressure in various slope models. (a) 45° slope; (b) 55° slope; (c) 65° slope.
Preprints 96297 g011
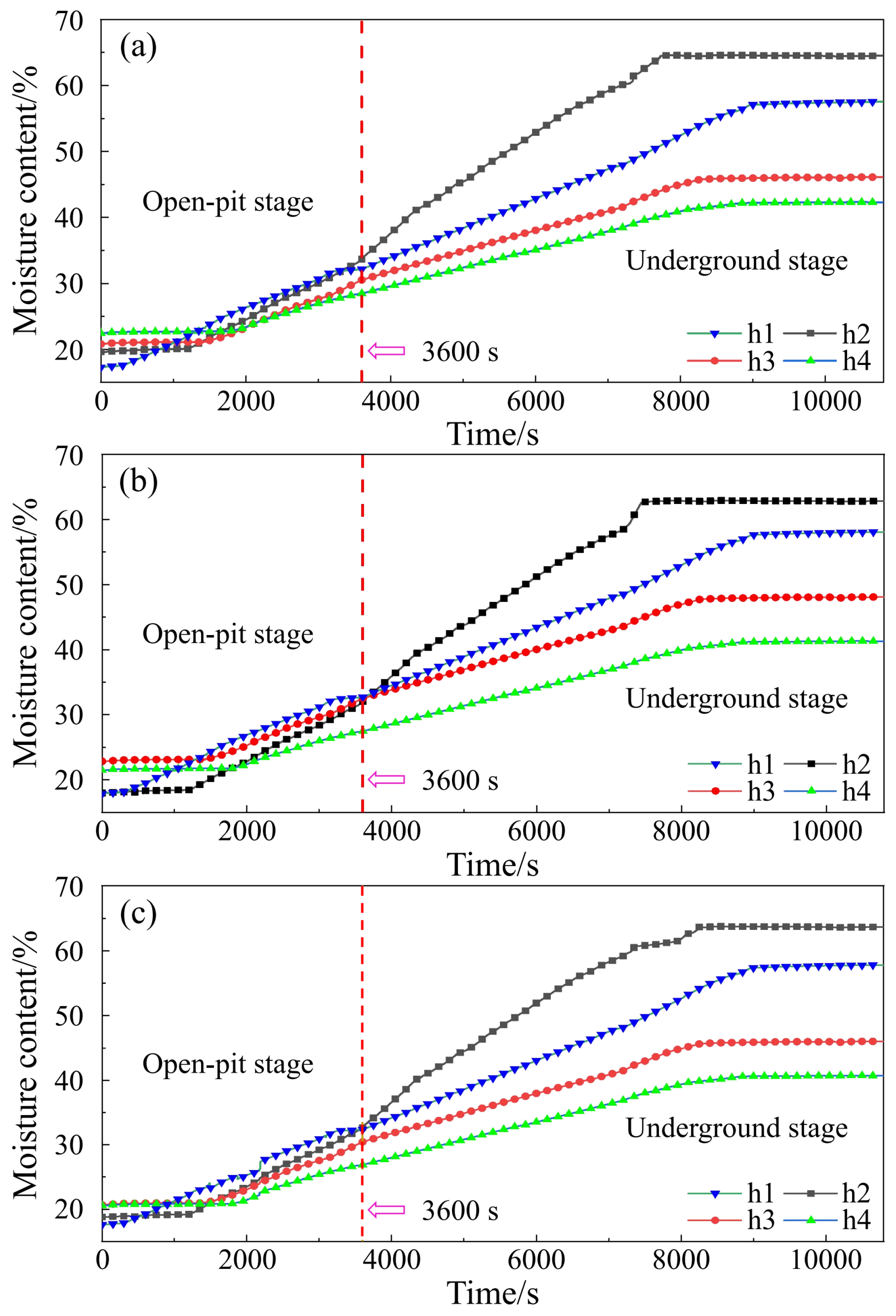
Preprints 96297 g012
Figure 12. Variations in moisture content in various slope models. (a) 45° slope; (b) 55° slope; (c) 65° slope.
Figure 12. Variations in moisture content in various slope models. (a) 45° slope; (b) 55° slope; (c) 65° slope.
Preprints 96297 g012
Preprints 96297 g013
Figure 13. Layout of displacement measuring lines.
Figure 13. Layout of displacement measuring lines.
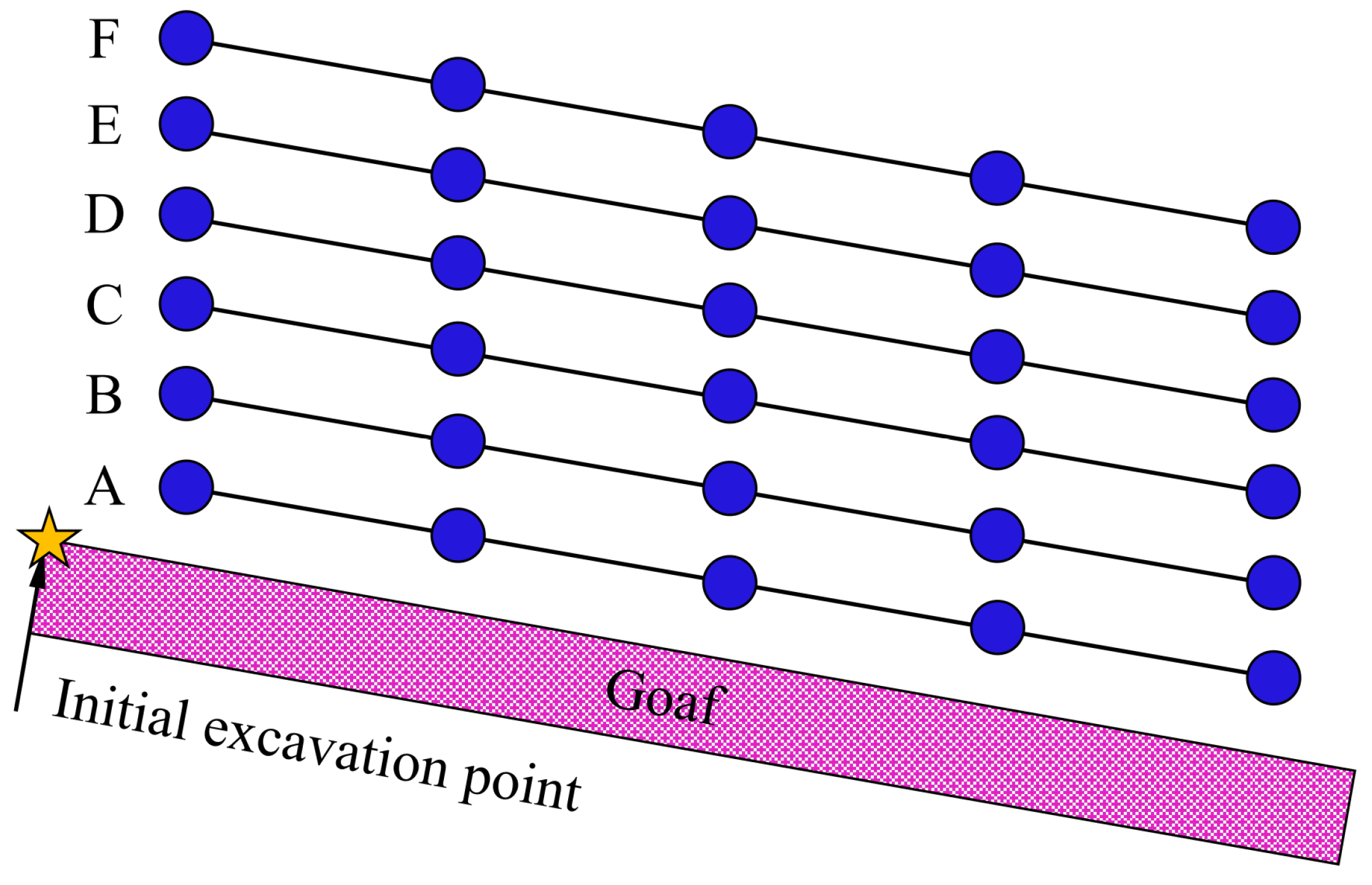
Preprints 96297 g013
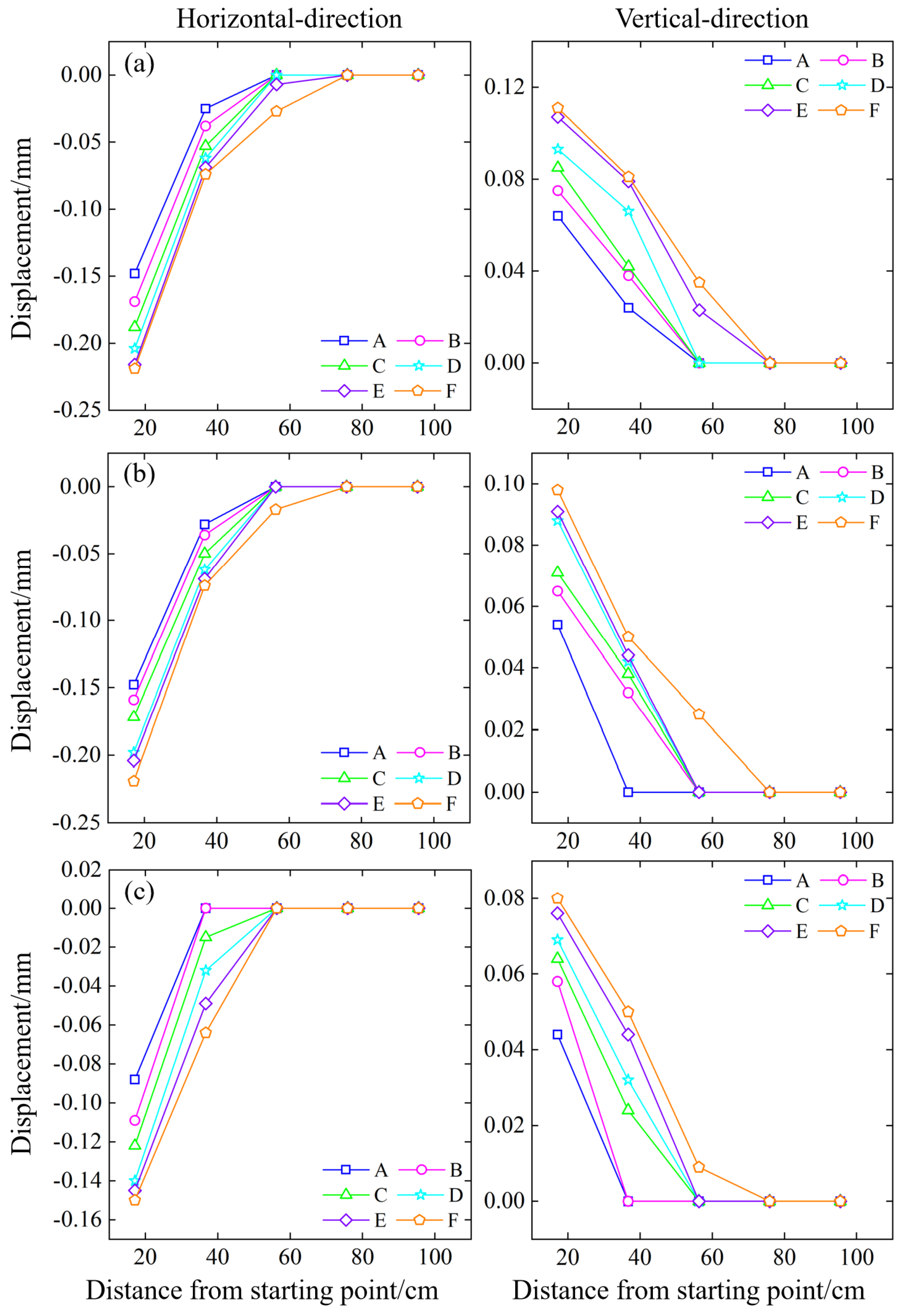
Preprints 96297 g014
Figure 14. Variations in rock mass displacement in the open-pit mining stage; (a) 45° slope model; (b) 55° slope model; (c) 65° slope model.
Figure 14. Variations in rock mass displacement in the open-pit mining stage; (a) 45° slope model; (b) 55° slope model; (c) 65° slope model.
Preprints 96297 g014
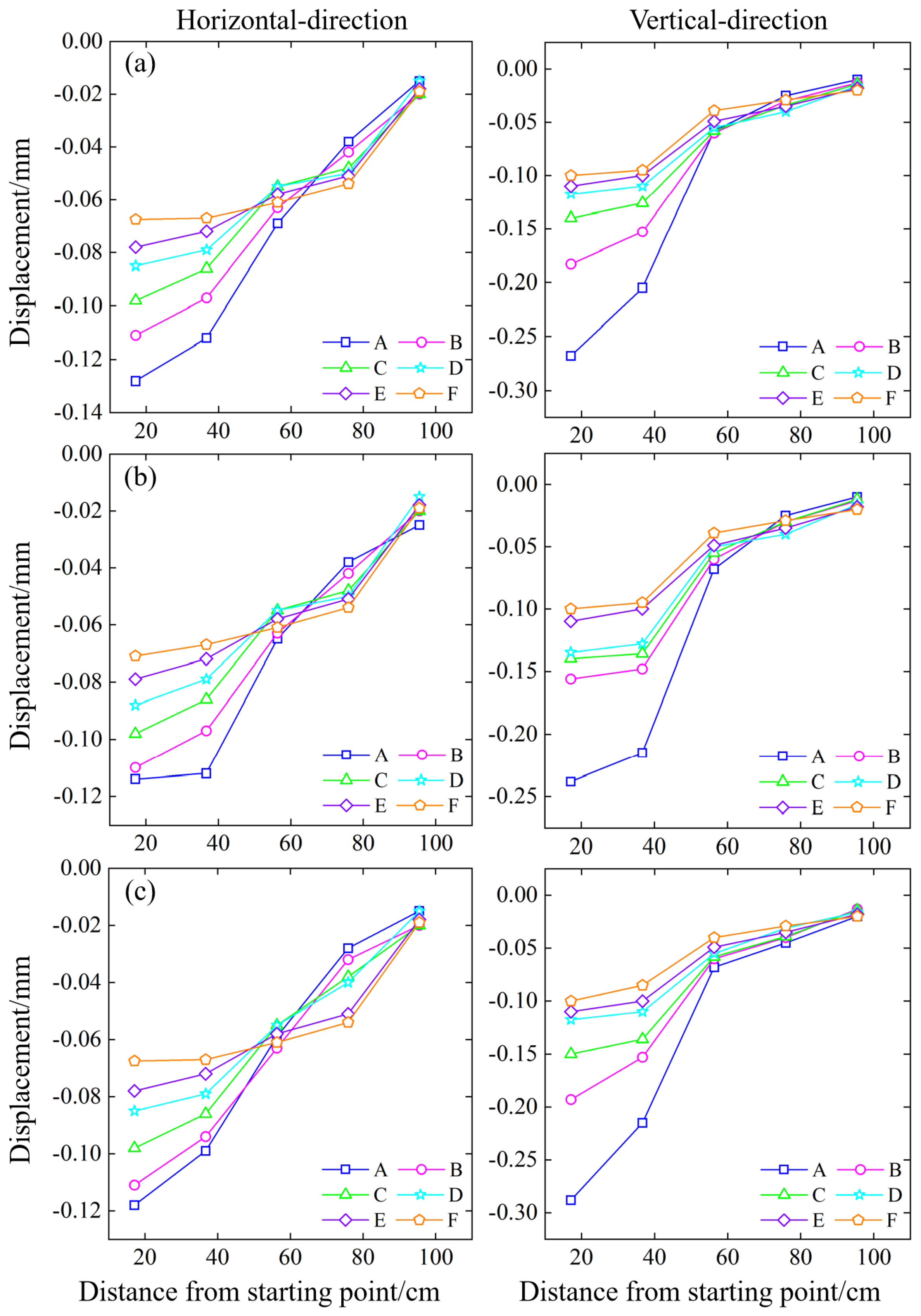
Preprints 96297 g015
Figure 15. Variations in rock mass displacement in the underground room mining stage (first group of mine rooms). (a) 45° slope model; (b) 55° slope model; (c) 65° slope model.
Figure 15. Variations in rock mass displacement in the underground room mining stage (first group of mine rooms). (a) 45° slope model; (b) 55° slope model; (c) 65° slope model.
Preprints 96297 g015
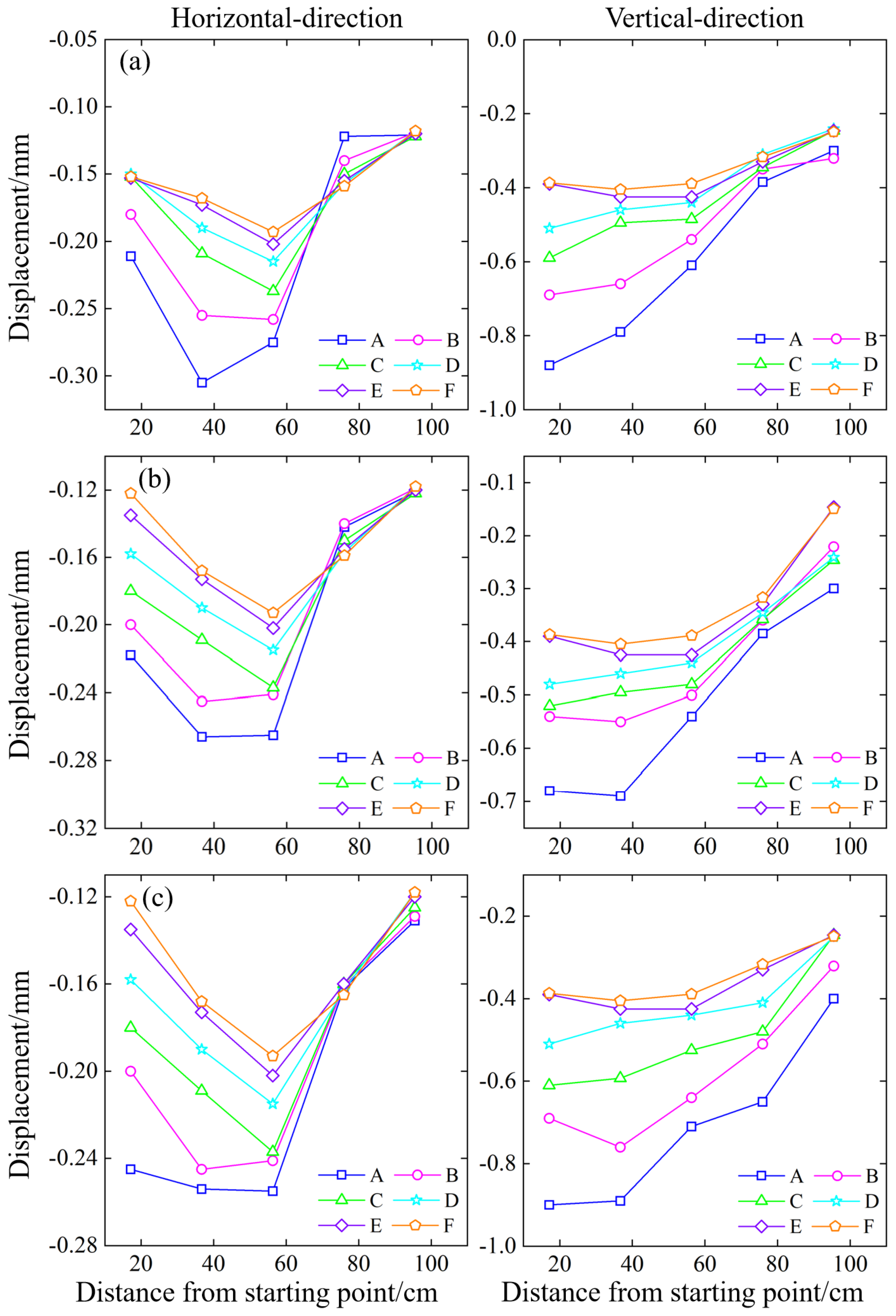
Preprints 96297 g016
Figure 16. Variations in rock mass displacement in the underground room mining stage (second group of mine rooms). (a) 45° slope model; (b) 55° slope model; (c) 65° slope model.
Figure 16. Variations in rock mass displacement in the underground room mining stage (second group of mine rooms). (a) 45° slope model; (b) 55° slope model; (c) 65° slope model.
Preprints 96297 g016
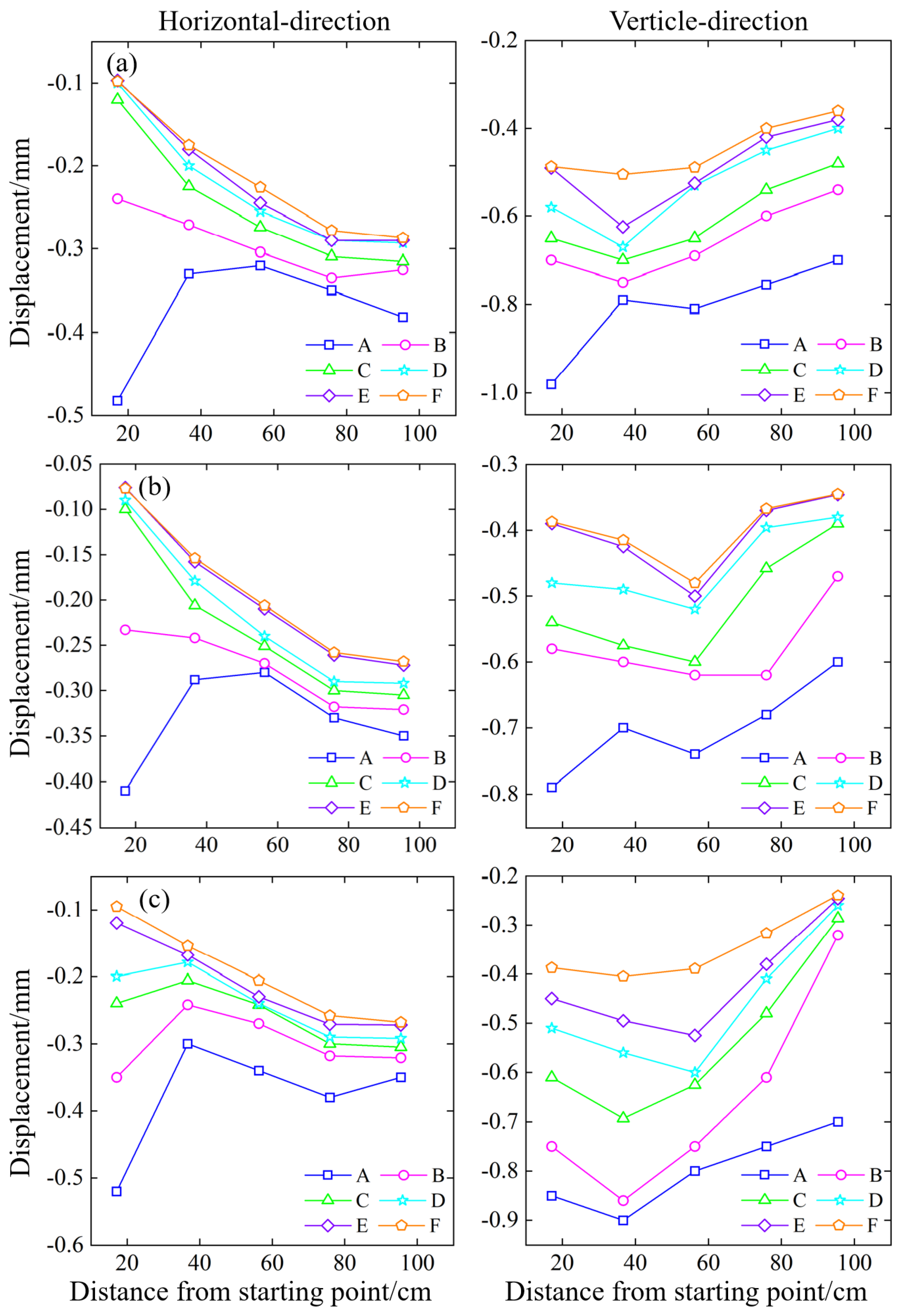
Preprints 96297 g017
Figure 17. Variations in rock mass displacement in the underground room mining stage (third group of mine rooms). (a) 45° slope model; (b) 55° slope model; (c) 65° slope model.
Figure 17. Variations in rock mass displacement in the underground room mining stage (third group of mine rooms). (a) 45° slope model; (b) 55° slope model; (c) 65° slope model.
Preprints 96297 g017
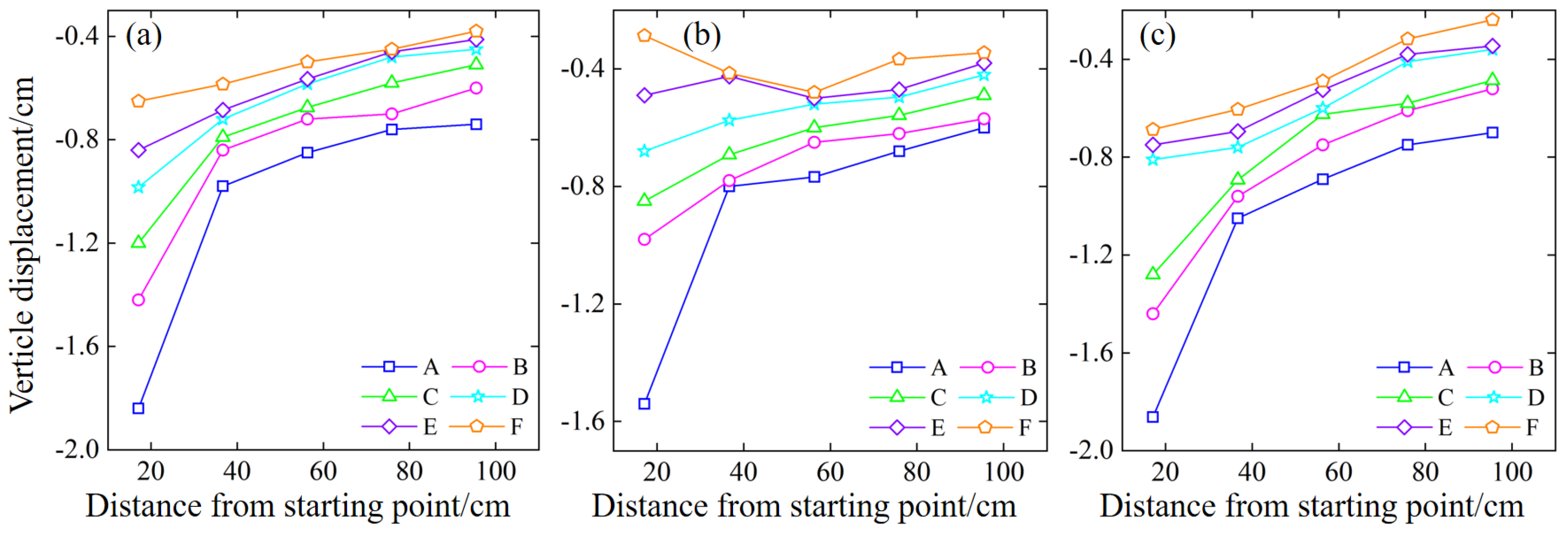
Preprints 96297 g018
Figure 18. Variations in rock mass displacement in the underground pillar mining stage (Z1 pillar). (a) 45° slope model; (b) 55° slope model; (c) 65° slope model.
Figure 18. Variations in rock mass displacement in the underground pillar mining stage (Z1 pillar). (a) 45° slope model; (b) 55° slope model; (c) 65° slope model.
Preprints 96297 g018
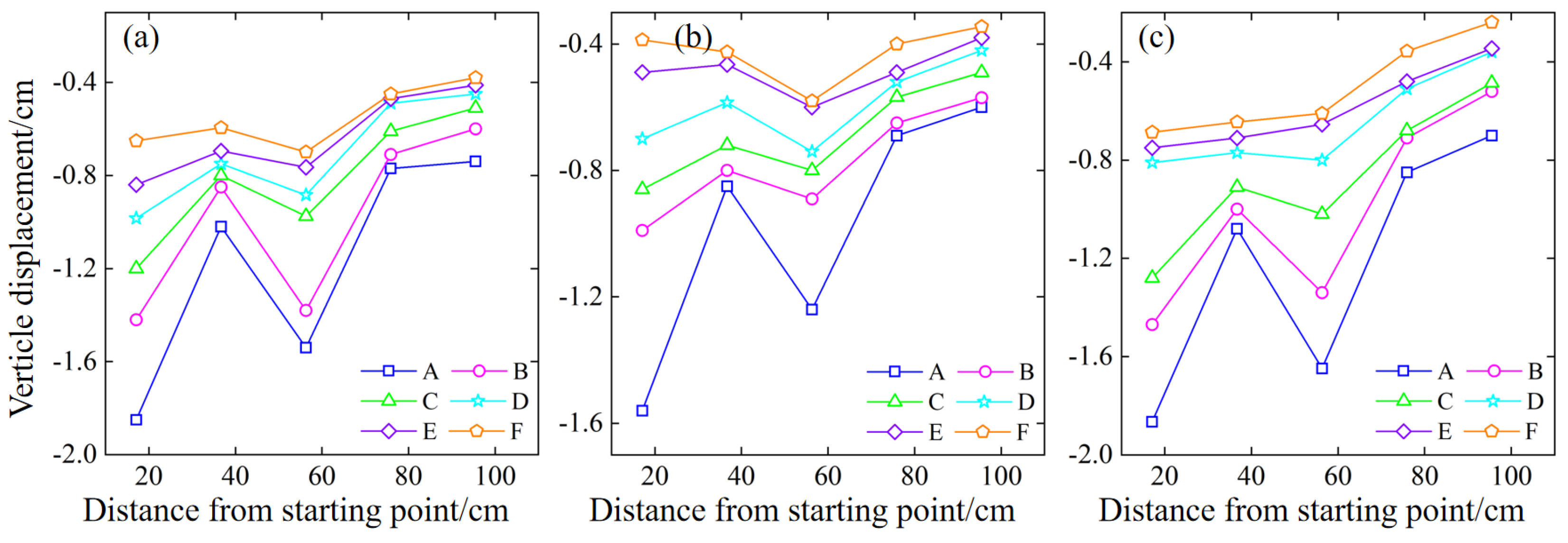
Preprints 96297 g019
Figure 19. Variations in rock mass displacement in the underground pillar mining stage (Z2 pillar). (a) 45° slope model; (b) 55° slope model; (c) 65° slope model.
Figure 19. Variations in rock mass displacement in the underground pillar mining stage (Z2 pillar). (a) 45° slope model; (b) 55° slope model; (c) 65° slope model.
Preprints 96297 g019
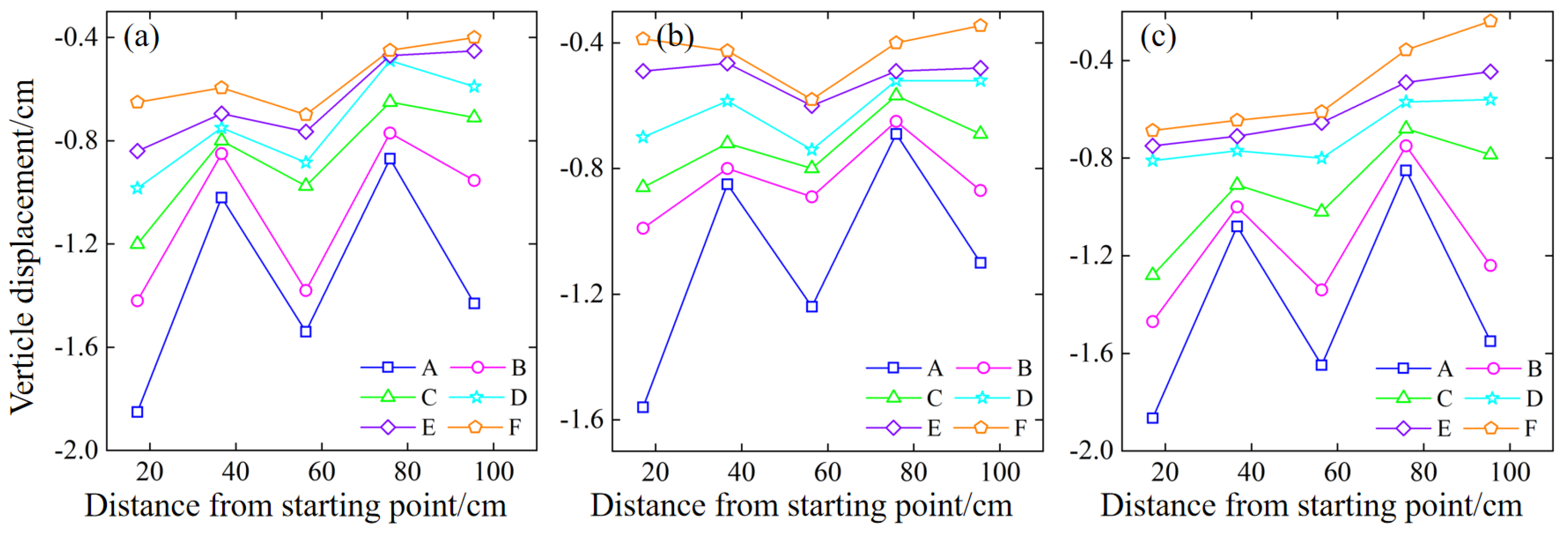
Preprints 96297 g020
Figure 20. Variations in rock mass displacement in the underground pillar mining stage (Z3 pillar). (a) 45° slope model; (b) 55° slope model; (c) 65° slope model.
Figure 20. Variations in rock mass displacement in the underground pillar mining stage (Z3 pillar). (a) 45° slope model; (b) 55° slope model; (c) 65° slope model.
Preprints 96297 g020
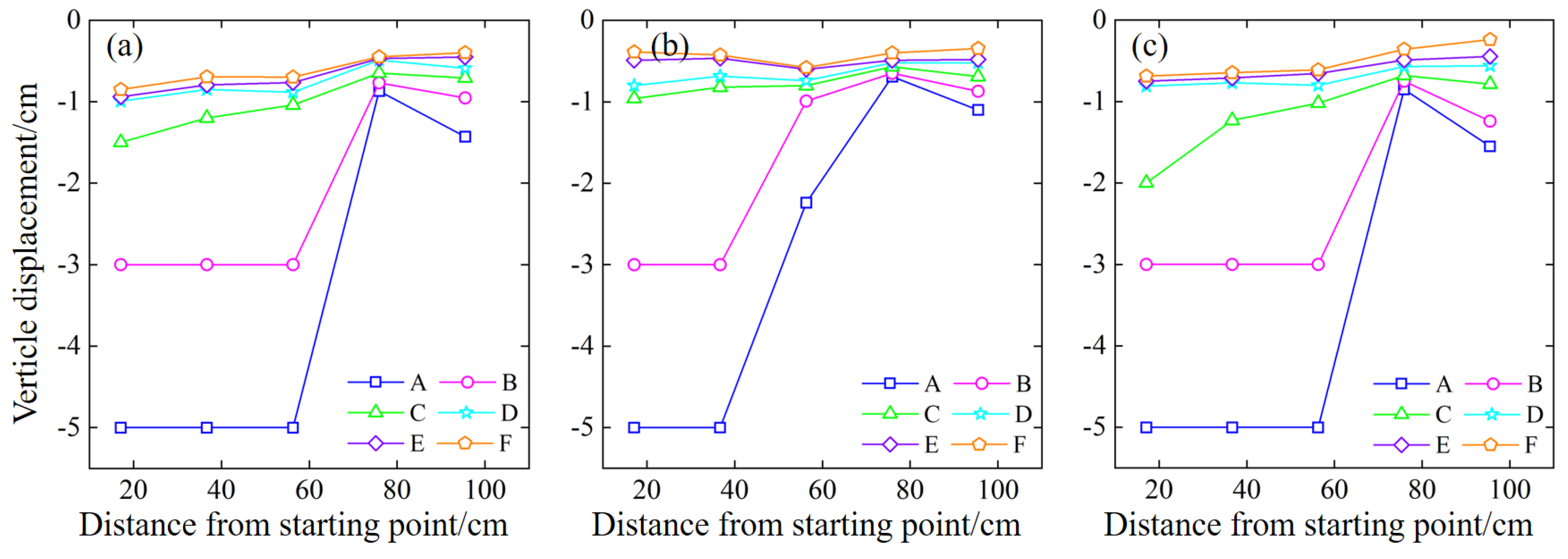
Preprints 96297 g021
Figure 21. Variations in rock mass displacement in the continuous pillar mining stage (L1 pillar). (a) 45° slope model; (b) 55° slope model; (c) 65° slope model.
Figure 21. Variations in rock mass displacement in the continuous pillar mining stage (L1 pillar). (a) 45° slope model; (b) 55° slope model; (c) 65° slope model.
Preprints 96297 g021
Preprints 96297 g022
Figure 22. Variations in rock mass displacement in the continuous pillar mining stage (L2 pillar). (a) 45° slope model; (b) 55° slope model; (c) 65° slope model.
Figure 22. Variations in rock mass displacement in the continuous pillar mining stage (L2 pillar). (a) 45° slope model; (b) 55° slope model; (c) 65° slope model.
Preprints 96297 g022
Table 1. Rock mechanics parameters.
Table 1. Rock mechanics parameters.
σd /MPa σt /MPa E/GPa μ C/MPa Φ/° C of joint surface/MPa Φ of joint surface/°
52.11 4.10 24.20 0.15 7.78 38.38 0.16 28.96
Table 2. Rock mechanics parameters after proportional reduction.
Table 2. Rock mechanics parameters after proportional reduction.
σd /MPa σt /MPa E/GPa μ C/MPa Φ/° C of joint surface/MPa Φ of joint surface/°
26.10 1.03 8.10 0.15 5.20 27.80 0.10 20.99
Table 3. Main material proportioning.
Table 3. Main material proportioning.
Lithology Proportion
Phyllite Coarse sand Fine sand Lime Gypsum
15 10 2 5
Table 4. Different material proportioning.
Table 4. Different material proportioning.
Material Coarse sand/kg Fine sand/kg Lime/kg Gypsum/kg Water/kg Borax/g Mica powder/g
Q 237 158 31.60 79 72.22 0.80 0.80
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated