Preprint

Article

The Models of Primary Particles

Altmetrics

Downloads

209

Views

Comments

Lan Fu^*

This version is not peer-reviewed

Abstract

If we assume that: a. The four fundamental forces of nature are independent waves without rest masses, and their speeds are constant in a vacuum, just like light. b. Light or electromagnetic waves and gravity are comparable in structures. Weak and strong interactions are similar in structures. c. Light and weak interaction have the same speed c_Lwith spin number +1 or –1. d. Gravity and strong interaction have the same speed c_G without spin. e. The primary particles, namely electrons, electron neutrinos, and dark neutrinos in this paper, are made by the above four waves. We can find and describe some fundamental characteristics of the primary particles (e.g., their sizes, energies, and interactions) and introduce new attractive results from them (e.g., the source of the Pauli exclusion principle, the solution to the Einstein-Podolsky-Rosen paradox, and c_G slightly faster than c_L).

Keywords:

Submitted:

19 January 2024

Posted:

19 January 2024

Read the latest preprint version here

Alerts

Abstract

Keywords:

Subject: Physical Sciences - Theoretical Physics

1. Introduction

We know intimately the term "atom" which comes from ancient Greek and means "uncuttable" or translated as "indivisible." In the early 19th century, the scientist John Dalton introduced the modern definition of an atom to characterize chemical elements. It was discovered that Dalton's atoms are not actually indivisible about a century later. An atom consists of three basic types of subatomic particles: electrons, protons, and neutrons, which occupy the tiny space in an atom. Protons and neutrons form the nucleus that contains most of an atom's mass. Electrons are the lightest charged particles in nature and revolve around the nucleus of an atom. An electron is seemingly indivisible yet. Until today, we have not split an electron into two or more smaller particles. We only make the positive and negative electron annihilation. A free neutron is unstable, decaying into a proton, electron, and neutrino. However, a free proton is stable, and is composed of two up quarks and one down quark in the modern Standard Model. Furthermore, whether a quark can be cut into smaller parts or whether the matter is infinitely divisible.

This paper tries to answer the above questions from a different perspective. What will happen when light or electromagnetic, gravity waves and other waves make up the primary particles that constitute the fundamental elements of matter? The assumptions are derived then:

Light or electromagnetic waves, weak interaction, gravity, and strong interaction are independent waves without rest masses. But their structures are different.
Light and gravity can be described by the wave equation with the field strength Ê and speed c.

\nabla^{2} Ê = \frac{1}{c^{2}} \frac{\partial^{2} Ê}{\partial t^{2}}

(1)

c: Weak and strong interaction can be described by the 4-dimensional Laplace equation with field strength Ê' and speed c'.

\nabla^{2} Ê^{'} = - \frac{1}{c'^{2}} \frac{\partial^{2} Ê^{'}}{\partial t^{2}}

(2)

d: According to the unified electro-weak theory, light and weak interaction have the same speed c_L with spin number +1 or –1.
e: Gravity and strong interaction have the same speed c_G without spin, and c_G is constant in a vacuum.
f: The primary particles, which are electrons, electron neutrinos, and dark neutrinos in this paper, are made by the above four types of waves.

2. The Formation of Primary Particles

To suppose that the birth of primary particles may divide into the following two parts:

The light and weak interaction couple together (hereafter referred to as the E-W couple) when they have the same spin number and the second-order partial derivatives of their fields with respect to time $\frac{\partial^{2} Ê}{\partial t^{2}}$ are equal. The gravity and strong interaction couple together too (hereafter referred to as the G-S couple) when the second-order partial derivatives of their fields with respect to time $\frac{\partial^{2} Ê^{'}}{\partial t^{2}}$ are equal. So we have

$c_{L}^{2} \nabla^{2} (Ê_{e} + Ê_{w}) = 0,$

(3)

and

$c_{G}^{2} \nabla^{2} (Ê_{G} + Ê_{S}) = 0 .$

(4)

Where Ê_e, Ê_w, Ê_G, and Ê_S are electric, weak interaction, gravitational, and strong interaction fields.
The E-W couple has no spin. The original spins of the coupled waves convert the electric or weak charge property.
It makes a primary particle when the two coupled waves attract each other and shrink to a tiny sphere. One E-W couple and one G-S couple produce an electron or a positron whose charge property depends on the original spin of the E-W couple. The dark neutrinos are composed of two G-S couples. Two E-W couples with different original spin compress themselves into an electron neutrino. But they cannot attract each other with the same original spin.

Further, we assume that each field around the primary particle is time-independent and spherically symmetrical. Thus, in the spherical coordinate system, we have the uniform Laplace equation for the above equations (3), (4)

c^{2} [\frac{1}{r^{2}} \frac{\partial}{\partial r} (r^{2} \frac{\partial Ê}{\partial r}) + \frac{1}{r^{2} \sin θ} \frac{\partial}{\partial θ} (\sin θ \frac{\partial Ê}{\partial θ}) + \frac{1}{r^{2} \sin^{2} θ} \frac{\partial^{2} Ê}{\partial φ^{2}}] = 0,

(5)

whose general solution is

Ê = \{\begin{array}{l} \frac{1}{c^{2}} \sum_{j = 0}^{+ \infty} \sum_{k = 0}^{j} (A_{j} r^{j} + \frac{B_{j}}{r^{j + 1}}) P_{j}^{k} (\cos θ) e^{- i k φ} \\ \frac{1}{c^{2}} \sum_{j = 0}^{+ \infty} \sum_{k = 0}^{j} (A_{j} r^{j} + \frac{B_{j}}{r^{j + 1}}) P_{j}^{k} (\cos θ) e^{i k φ} \end{array},

(6)

where A_j and B_j are constants,

P_{j}^{k} (\cos θ)

are associated Legendre polynomials, j and k are integers, j = 0, 1, 2, 3, …, k ≤ j, and j is called the degree of associated Legendre polynomials.

3. The Fields and Binding-Energy

We can now derive the electric, gravitational, weak interaction, and strong interaction fields Ê based on equation (6) and existing physical laws and data.

It is reasonable that equation (6) can be transformed into a pair of conjugate solutions.

\begin{matrix} Ê = \frac{1}{c^{2}} (A_{j} r^{j} + \frac{B_{j}}{r^{l + 1}}) \sum_{k = 0}^{j} P_{j}^{k} (\cos θ) e^{- i k φ} \\ Ê^{*} = \frac{1}{c^{2}} (A_{j} r^{j} + \frac{B_{j}}{r^{j + 1}}) \sum_{k = 0}^{j} P_{j}^{k} (\cos θ) e^{i k φ} \end{matrix}

(7)

Clearly, there is

{[{\hat{E}}_{a} + {\hat{E}}_{b}]}^{*} = {\hat{E}}_{a}^{*} + {\hat{E}}_{b}^{*}

(8)

where the subscripts a and b denote electric, gravitational, weak interaction, or strong interaction.

And we let

{({\hat{E}}^{*})}^{*} = \hat{E}

(9)

The field Ê may be split into the macroscopic item

\frac{1}{c^{2}} (A_{j} r^{j} + \frac{B_{j}}{r^{j + 1}})

and the quantum factors

\sum_{k = 0}^{j} P_{j}^{k} (\cos θ) e^{- i k φ}

\sum_{k = 0}^{j} P_{j}^{k} (\cos θ) e^{i k φ}

. The degree of associated Legendre polynomials j rules properties of the field Ê because it is not only an exponent of r in the macroscopic item but also impacts forms of the quantum factors.

Compared equation (7) to Gauss's law of electrostatics and Newton's law of gravity, the electric field Ê_e is

\begin{matrix} {\hat{E}}_{e} = \pm \frac{1}{c_{L}^{2}} \frac{B_{1}}{r^{2}} \sum_{k = 0}^{- 1} P_{1}^{k} (\cos θ) e^{- i k φ} = \pm \frac{\hat{q}}{c_{L}^{2} r^{2}} (\cos θ + \sin θ e^{- i φ}) \\ {\hat{E}}_{e}^{*} = \pm \frac{1}{c_{L}^{2}} \frac{B_{1}}{r^{2}} \sum_{k = 0}^{1} P_{1}^{k} (\cos θ) e^{i k φ} = \pm \frac{\hat{q}}{c_{L}^{2} r^{2}} (\cos θ + \sin θ e^{i φ}) \end{matrix},

(10)

and the gravitational field Ê_G is

\begin{matrix} {\hat{E}}_{G} = - \frac{1}{c_{G}^{2}} \frac{B_{1}}{r^{2}} \sum_{k = 0}^{1} P_{1}^{k} (\cos θ) e^{- i k φ} = - \frac{\hat{m}}{c_{G}^{2} r^{2}} (\cos θ + \sin θ e^{- i φ}) \\ {\hat{E}}_{G}^{*} = - \frac{1}{c_{G}^{2}} \frac{B_{1}}{r^{2}} \sum_{k = 0}^{1} P_{1}^{k} (\cos θ) e^{i k φ} = - \frac{\hat{m}}{c_{G}^{2} r^{2}} (\cos θ + \sin θ e^{i φ}) \end{matrix},

(11)

where '–' means attractive interaction, and '+' means repulsive interaction, as usual in this paper,

\hat{q}

is the mathematical electric charge, and

\hat{m}

is the mathematical mass or the gravitational charge.

Weak interaction has an intensity of a similar magnitude to the electromagnetic force at very short distances (around 10^-18 meters), but this starts to decrease exponentially with increasing distance. Its effective range is about 10^-17 to 10^-16 meters^{[1, 2, 3]}. All of the above can help us to determine weak interaction field Ê_w from equation (7). Ê_w is so supposed to equal to

\begin{matrix} {\hat{E}}_{w} = \{\begin{array}{l} \pm \frac{1}{c_{L}^{2}} \frac{B_{1}}{r^{2}} \sum_{k = 0}^{1} P_{1}^{k} (\cos θ) e^{- i k φ} = \pm \frac{\hat{w}}{c_{L}^{2} r^{2}} (\cos θ + \sin θ e^{- i φ}) r \leq R_{c w} \\ \pm \frac{1}{c_{L}^{2}} \frac{B_{m}}{r^{m + 1}} \sum_{k = 0}^{m} P_{m}^{k} (\cos θ) e^{- i k φ} = \pm \frac{\hat{w} R_{c w}^{m - 1}}{c_{L}^{2} r^{m + 1}} \sum_{k = 0}^{m} P_{m}^{k} (\cos θ) e^{- i k φ} r > R_{c w} \end{array} \\ {\hat{E}}_{w}^{*} = \{\begin{array}{l} \pm \frac{1}{c_{L}^{2}} \frac{B_{1}}{r^{2}} \sum_{k = 0}^{1} P_{1}^{k} (\cos θ) e^{i k φ} = \pm \frac{\hat{w}}{c_{L}^{2} r^{2}} (\cos θ + \sin θ e^{i φ}) r \leq R_{c w} \\ \pm \frac{1}{c_{L}^{2}} \frac{B_{m}}{r^{m + 1}} \sum_{k = 0}^{m} P_{m}^{k} (\cos θ) e^{i k φ} = \pm \frac{\hat{w} R_{c w}^{m - 1}}{c_{L}^{2} r^{m + 1}} \sum_{k = 0}^{m} P_{m}^{k} (\cos θ) e^{i k φ} r > R_{c w} \end{array} \end{matrix}

(12)

where

\hat{w}

is the mathematical weak charge, R_cw is the critical radius of weak interaction, and m is an integer greater than 1.

The strong force is a short-range interaction (around 10^-15 meters) similar to the weak force. But its range is more complex than the weak force. At distances comparable to the diameter of a proton, it is approximately 100 times as strong as the electromagnetic force. At smaller distances, however, it becomes weaker. In particle physics, this effect is known as asymptotic freedom^{[4, 5, 6]}. Moreover, it is supposed that the fields of the four fundamental forces have a unified form in a very tiny range. Hence equation (6) can be translated into the strong interaction field Ê_S

\begin{matrix} {\hat{E}}_{S} = \{\begin{array}{l} - \frac{B_{1}}{c_{G}^{2} r^{2}} \sum_{k = 0}^{1} P_{1}^{k} (\cos θ) e^{- i k φ} = - \frac{\hat{s}}{c_{G}^{2} r^{2}} (\cos θ + \sin θ e^{- i φ}) r \leq R_{c S 1} \\ - \frac{A_{1} r}{c_{G}^{2}} \sum_{k = 0}^{1} P_{1}^{k} (\cos θ) e^{- i k φ} = - \frac{\hat{s} r}{c_{G}^{2} R_{c S 1}^{3}} (\cos θ + \sin θ e^{- i φ}) R_{c S 1} < r \leq R_{c S 2} \\ - \frac{1}{c_{G}^{2}} \frac{B_{n}}{r^{n + 1}} \sum_{k = 0}^{n} P_{n}^{k} (\cos θ) e^{- i k φ} = - \frac{\hat{s} R_{c S 2}^{n + 2}}{c_{G}^{2} R_{c S 1}^{3} r^{n + 1}} \sum_{k = 0}^{n} P_{n}^{k} (\cos θ) e^{- i k φ} r > R_{c S 2} \end{array} \\ {\hat{E}}_{S}^{*} = \{\begin{array}{l} - \frac{B_{1}}{c_{G}^{2} r^{2}} \sum_{k = 0}^{1} P_{1}^{k} (\cos θ) e^{i k φ} = - \frac{\hat{s}}{c_{G}^{2} r^{2}} (\cos θ + \sin θ e^{i φ}) r \leq R_{c S 1} \\ - \frac{A_{1} r}{c_{G}^{2}} \sum_{k = 0}^{1} P_{1}^{k} (\cos θ) e^{i k φ} = - \frac{\hat{s} r}{c_{G}^{2} R_{c S 1}^{3}} (\cos θ + \sin θ e^{i φ}) R_{c S 1} < r \leq R_{c S 2} \\ - \frac{1}{c_{G}^{2}} \frac{B_{n}}{r^{n + 1}} \sum_{k = 0}^{n} P_{n}^{k} (\cos θ) e^{i k φ} = - \frac{\hat{s} R_{c S 2}^{n + 2}}{c_{G}^{2} R_{c S 1}^{3} r^{n + 1}} \sum_{k = 0}^{n} P_{n}^{k} (\cos θ) e^{i k φ} r > R_{c S 2} \end{array} \end{matrix}

(13)

where

\hat{s}

is the mathematical strong charge, R_cS1 and R_cS2 are the 1^st and 2^nd critical radius of the strong interaction, and n is an integer greater than 1.

Further, it is assumed that R_cS1 << R_cw < R_cS2 and m ≠ n.

Now we turn to determine the energy. The energy density of wave equation (1) is given by

{|\hat{E}|}^{2}

, and the equations (1) and (2) are Lorentz invariance. So we hope the equation of energy is Lorentz invariance, too, and let the binding-energy E_a-b of the four fields be

E_{a - b} \propto \frac{1}{t_{2} - t_{1}} \underset{V}{∭} \int_{c t_{1}}^{c t_{2}} |{\hat{E}}_{a} {\hat{E}}_{b}^{*}| d x d y d z d c t

(14)

Note that

{\hat{E}}_{a}

and

{\hat{E}}_{b}^{*}

are independent of time, and there are

\int_{0}^{2 π} e^{i m φ} e^{- i n φ} d φ = 2 π δ_{m n}

(15)

and

\int_{0}^{π} P_{j}^{m} (\cos θ) P_{k}^{m} (\cos θ) s i n θ d θ = \frac{(j + m)!}{(j - m)!} \frac{2}{2 j + 1} δ_{j k} = N_{j}^{m} δ_{j k} .

(16)

When we use light as a measurement medium to determine the energy as usual, we can translate equation (14) into the spherical coordinate system with the optical medium, which is

\begin{array}{l} E_{a - b} & = \frac{1}{(t_{2} - t_{1}) 2 π \sum_{k = 0}^{j} N_{j}^{k}} \int_{R}^{\infty} \int_{0}^{π} \int_{0}^{2 π} \int_{c_{L} t_{1}}^{c_{L} t_{2}} |{\hat{E}}_{a} {\hat{E}}_{b}^{*}| r^{2} \sin θ d r d θ d φ d c_{L} t \\ = \frac{c_{L}^{2}}{2 π \sum_{k = 0}^{j} N_{j}^{k}} \int_{R}^{\infty} \int_{0}^{π} \int_{0}^{2 π} |{\hat{E}}_{a} {\hat{E}}_{b}^{*}| r^{2} \sin θ d r d θ d φ \end{array}

(17)

where R is the radius at which two fields begin to interact with each other.

The general energy expression can be calculated when equation (7) is substituted into equation (17).

\begin{array}{l} E_{a - b} & = \frac{c_{L}^{2}}{2 π \sum_{k = 0}^{j} N_{j}^{k}} \int_{R}^{\infty} \int_{0}^{π} \int_{0}^{2 π} |{\hat{E}}_{a} {\hat{E}}_{b}^{*}| r^{2} \sin θ d r d θ d φ \\ = \frac{c_{L}^{2}}{2 π \sum_{k = 0}^{j} N_{j}^{k}} \int_{R}^{\infty} \int_{0}^{π} \int_{0}^{2 π} [\frac{1}{c_{a}^{2}} |A_{a j} r^{j} + \frac{B_{a j}}{r^{j + 1}}| \sum_{k = 0}^{j} P_{j}^{k} (\cos θ) e^{- i k φ} \\ \times \frac{1}{c_{b}^{2}} |A_{b j} r^{j} + \frac{B_{b j}}{r^{j + 1}}| \sum_{k = 0}^{j} P_{j}^{k} (\cos θ) e^{i k φ}] r^{2} \sin θ d r d θ d φ \\ = \frac{c_{L}^{2}}{2 π \sum_{k = 0}^{j} N_{j}^{k}} \int_{R}^{\infty} \int_{0}^{π} \int_{0}^{2 π} [\frac{1}{c_{b}^{2}} |A_{b j} r^{j} + \frac{B_{b j}}{r^{j + 1}}| \sum_{k = 0}^{j} P_{j}^{k} (\cos θ) e^{- i k φ} \\ \times \frac{1}{c_{a}^{2}} |A_{a j} r^{j} + \frac{B_{a j}}{r^{j + 1}}| \sum_{k = 0}^{j} P_{j}^{k} (\cos θ) e^{i k φ}] r^{2} \sin θ d r d θ d φ \\ = \frac{c_{L}^{2}}{2 π \sum_{k = 0}^{j} N_{j}^{k}} \int_{R}^{\infty} \int_{0}^{π} \int_{0}^{2 π} |{\hat{E}}_{b} {\hat{E}}_{a}^{*}| r^{2} \sin θ d r d θ d φ \\ = E_{b - a} \\ = \frac{c_{L}^{2}}{c_{a}^{2} c_{b}^{2}} \int_{R}^{\infty} |A_{a j} r^{j} + \frac{B_{a j}}{r^{j + 1}}| |A_{b j} r^{j} + \frac{B_{b j}}{r^{j + 1}}| r^{2} d r \end{array}

(18)

Based on equation (18) and associated with equations (10) to (13), we first compute the self-binding-energy of the four fields. The self-binding-energy of the four fields E_e-e, E_G-G, E_w-w, and E_S-S are

E_{e - e} = c_{L}^{2} \int_{r}^{\infty} \frac{{\hat{q}}^{2}}{c_{L}^{4} r^{2}} d r = \frac{{\hat{q}}^{2}}{c_{L}^{2} r},

(19)

E_{G - G} = c_{L}^{2} \int_{r}^{\infty} \frac{{\hat{m}}^{2}}{c_{G}^{4} r^{2}} d r = \frac{c_{L}^{2} {\hat{m}}^{2}}{c_{G}^{4} r},

(20)

E_{w - w} = \{\begin{array}{l} c_{L}^{2} \int_{r}^{R_{c w}} \frac{{\hat{w}}^{2}}{c_{L}^{4} r^{2}} d r + c_{L}^{2} \int_{R_{c w}}^{\infty} \frac{{\hat{w}}^{2} R_{c w}^{2 m - 2}}{c_{L}^{4} r^{2 m}} d r = \frac{{\hat{w}}^{2}}{c_{L}^{2}} [\frac{1}{r} - \frac{2 m - 2}{(2 m - 1) R_{c w}}] r \leq R_{c w} \\ c_{L}^{2} \int_{r}^{\infty} \frac{{\hat{w}}^{2} R_{c w}^{2 m - 2}}{c_{L}^{4} r^{2 m}} d r = \frac{{\hat{w}}^{2} R_{c w}^{2 m - 2}}{c_{L}^{2} (2 m - 1) r^{2 m - 1}} r > R_{c w} \end{array},

(21)

and

E_{S - S} = \{\begin{array}{l} c_{L}^{2} \int_{r}^{R_{c S 1}} \frac{{\hat{s}}^{2}}{c_{G}^{4} r^{2}} d r + c_{L}^{2} \int_{R_{c S 1}}^{R_{c S 2}} \frac{{\hat{s}}^{2} r^{4}}{c_{G}^{4} R_{c S 1}^{6}} d r + c_{L}^{2} \int_{R_{c S 2}}^{\infty} \frac{{\hat{s}}^{2} R_{c S 2}^{2 n + 4}}{c_{G}^{4} R_{c S 1}^{6} r^{2 n}} d r \\ = \frac{c_{L}^{2} {\hat{s}}^{2}}{c_{G}^{4}} [\frac{1}{r} - \frac{6}{5 R_{c S 1}} + \frac{2 (n + 2) R_{c S 2}^{5}}{5 (2 n - 1) R_{c S 1}^{6}}] r \leq R_{c S 1} \\ \begin{array}{l} c_{L}^{2} \int_{r}^{R_{c S 2}} \frac{{\hat{s}}^{2} r^{4}}{c_{G}^{4} R_{c S 1}^{6}} d r + c_{L}^{2} \int_{R_{c S 2}}^{\infty} \frac{{\hat{s}}^{2} R_{c S 2}^{2 n + 4}}{c_{G}^{4} R_{c S 1}^{6} r^{2 n}} d r \\ = \frac{c_{L}^{2} {\hat{s}}^{2}}{c_{G}^{4}} [\frac{1}{5 R_{c S 1}^{6}} (R_{c S 2}^{5} - r^{5}) + \frac{R_{c S 2}^{5}}{(2 n - 1) R_{c S 1}^{6}}] R_{c S 1} < r \leq R_{c S 2} \end{array} \\ c_{L}^{2} \int_{r}^{\infty} \frac{{\hat{s}}^{2} R_{c S 2}^{2 n + 4}}{c_{G}^{4} R_{c S 1}^{6} r^{2 n}} d r = \frac{c_{L}^{2} {\hat{s}}^{2}}{c_{G}^{4}} \times \frac{R_{c S 2}^{2 n + 4}}{(2 n - 1) R_{c S 1}^{6} r^{2 n - 1}} r > R_{c S 2} \end{array} .

(22)

The binding-energy of the four fields, such as E_e-G, E_e-w, E_e-S, etc. are

E_{e - G} = c_{L}^{2} \int_{r}^{\infty} \frac{\hat{q}}{c_{L}^{2} r^{2}} \frac{\hat{m}}{c_{G}^{2} r^{2}} r^{2} d r = \frac{\hat{q} \hat{m}}{c_{G}^{2} r},

(23)

E_{e - w} = \{\begin{array}{l} c_{L}^{2} \int_{r}^{R_{c w}} \frac{\hat{q}}{c_{L}^{2} r^{2}} \frac{\hat{w}}{c_{L}^{4} r^{2}} r^{2} d r + 0 = \frac{\hat{q} \hat{w}}{c_{L}^{2}} (\frac{1}{r} - \frac{1}{R_{c w}}) r \leq R_{c w} \\ 0 r > R_{c w} \end{array},

(24)

E_{e - S} = \{\begin{array}{l} c_{L}^{2} \int_{r}^{R_{c S 1}} \frac{\hat{q}}{c_{L}^{2} r^{2}} \frac{\hat{s}}{c_{G}^{2} r^{2}} r^{2} d r + c_{L}^{2} \int_{R_{c S 1}}^{R_{c S 2}} \frac{\hat{q}}{c_{L}^{2} r^{2}} \frac{\hat{s} r}{c_{G}^{2} R_{c S 1}^{3}} r^{2} d r + 0 = \frac{\hat{q} \hat{s}}{c_{G}^{2}} (\frac{1}{r} - \frac{3}{2 R_{c S 1}} + \frac{R_{c S 2}^{2}}{2 R_{c S 1}^{3}}) r \leq R_{c S 1} \\ c_{L}^{2} \int_{r}^{R_{c S 2}} \frac{\hat{q}}{c_{L}^{2} r^{2}} \frac{\hat{s} r}{c_{G}^{2} R_{c S 1}^{3}} r^{2} d r + 0 = \frac{\hat{q} \hat{s}}{2 c_{G}^{2} R_{c S 1}^{3}} (R_{c S 2}^{2} - r^{2}) R_{c S 1} < r \leq R_{c S 2} \\ 0 r > R_{c S 2} \end{array},

(25)

E_{G - w} = \{\begin{array}{l} c_{L}^{2} \int_{r}^{R_{c w}} \frac{\hat{m}}{c_{G}^{2} r^{2}} \frac{\hat{w}}{c_{L}^{2} r^{2}} r^{2} d r + 0 = \frac{\hat{m} \hat{w}}{c_{G}^{2}} (\frac{1}{r} - \frac{1}{R_{c w}}) r \leq R_{c w} \\ 0 r > R_{c w} \end{array},

(26)

E_{G - S} = \{\begin{array}{l} c_{L}^{2} \int_{r}^{R_{c S 1}} \frac{\hat{m}}{c_{G}^{2} r^{2}} \frac{\hat{s}}{c_{G}^{2} r^{2}} r^{2} d r + c_{L}^{2} \int_{R_{c S 1}}^{R_{c S 2}} \frac{\hat{m}}{c_{G}^{2} r^{2}} \frac{\hat{s} r}{c_{G}^{2} R_{c S 1}^{3}} r^{2} d r + 0 = \frac{c_{L}^{2} \hat{m} \hat{s}}{c_{G}^{4}} (\frac{1}{r} - \frac{3}{2 R_{c S 1}} + \frac{R_{c S 2}^{2}}{2 R_{c S 1}^{3}}) r \leq R_{c S 1} \\ c_{L}^{2} \int_{r}^{R_{c S 2}} \frac{\hat{m}}{c_{G}^{2} r^{2}} \frac{\hat{s} r}{c_{G}^{2} R_{c S 1}^{3}} r^{2} d r + 0 = \frac{c_{L}^{2} \hat{m} \hat{s}}{2 c_{G}^{4} R_{c S 1}^{3}} (R_{c S 2}^{2} - r^{2}) R_{c S 1} < r \leq R_{c S 2} \\ 0 r > R_{c S 2} \end{array},

(27)

and

E_{w - S} = \{\begin{array}{l} c_{L}^{2} \int_{r}^{R_{c S 1}} \frac{\hat{w}}{c_{L}^{2} r^{2}} \frac{\hat{s}}{c_{G}^{2} r^{2}} r^{2} d r + c_{L}^{2} \int_{R_{c S 1}}^{R_{c w}} \frac{\hat{w}}{c_{L}^{2} r^{2}} \frac{\hat{s} r}{c_{G}^{2} R_{c S 1}^{3}} r^{2} d r + 0 = \frac{\hat{w} \hat{s}}{c_{G}^{2}} (\frac{1}{r} - \frac{3}{2 R_{c S 1}} + \frac{R_{c w}^{2}}{2 R_{c S 1}^{3}}) r \leq R_{c S 1} \\ c_{L}^{2} \int_{r}^{R_{c w}} \frac{\hat{w}}{c_{L}^{2} r^{2}} \frac{\hat{s} r}{c_{G}^{2} R_{c S 1}^{3}} r^{2} d r + 0 = \frac{\hat{w} \hat{s}}{2 c_{G}^{2} R_{c S 1}^{3}} (R_{c w}^{2} - r^{2}) R_{c S 1} < r \leq R_{c w} \\ 0 r > R_{c w} \end{array} .

(28)

For the convenience of subsequent calculations, we require the results of our defined energy to be consistent with those of the conventional physical method. Compared equations (19) and (20) to electric and gravitational potential energy formulas, it can easily find that the relations of mathematical electric charge ê and mathematical mass

\hat{m}

to electric charge q and mass m are

\hat{e} = c_{L} \sqrt{k} q

(29)

and

\hat{m} = \frac{c_{G}^{2} \sqrt{G} m}{c_{L}}

(30)

where k is the Coulomb constant, and G is the gravitational constant.

4. The Structures of Primary Particles

A primary particle looks like a tiny spheroidal balloon with two envelopes (Figure 1). Each of them is made by an E-W couple or a G-S couple. The envelopes can characterize as:

The whole biding-energy of the coupled waves concentrates on the envelopes.
The macroscopic items of combined field strengths of the two coupled waves are equal on the envelopes. Outside the envelopes, the coupled waves become two independent static fields. But there are no fields inside the envelopes.
The size of the envelopes, which means the size of a primary particle, too, depends on the critical radius of weak or strong interaction.
The two envelopes have the same inherent frequency ν_in, although this is not mathematically required.
The degree of associated Legendre polynomials j is the same on the two envelopes.
Behaviors of the two envelopes obey the Self-Conjugate Mechanism, which requires that one occupies the surface of $\sum_{k = 0}^{j} P_{j}^{k} (\cos θ) e^{- i k φ}$ and the other must take up $\sum_{k = 0}^{j} P_{j}^{k} (\cos θ) e^{i k φ}$ , or they are conjugate to each other.

Hence, the biding-energy of a primary particle E_pri can be generally described as

\begin{array}{l} E_{p r i} & = \frac{c_{L}^{2}}{2 π \sum_{k = 0}^{j} N_{j}^{k}} \int_{R}^{\infty} \int_{0}^{π} \int_{0}^{2 π} |[{\hat{E}}_{a} + {\hat{E}}_{b}] {[{\hat{E}}_{c} + {\hat{E}}_{d}]}^{*}| r^{2} \sin θ d r d θ d φ \\ = \frac{c_{L}^{2}}{2 π \sum_{k = 0}^{j} N_{j}^{k}} \int_{R}^{\infty} \int_{0}^{π} \int_{0}^{2 π} |{\hat{E}}_{a} {\hat{E}}_{c}^{*} + {\hat{E}}_{a} {\hat{E}}_{d}^{*} + {\hat{E}}_{b} {\hat{E}}_{c}^{*} + {\hat{E}}_{b} {\hat{E}}_{d}^{*}| r^{2} \sin θ d r d θ d φ \\ = E_{a - c} + E_{a - d} + E_{b - c} + E_{b - d} \end{array},

(31)

based on equation (17) E_pri is clearly equivalent to the rest mass.

Evidently, the total energy of a primary particle comprises the biding-energy or the rest mass and the energy in static fields.

4.1. An Electron Neutrino

An electron neutrino is composed of two E-W couples with different original spin. In order to explore its structure, these assumptions should be adopted:

Its radius r_{e_ν} is equal to the critical radius of weak interaction R_cw.
The charges in equations (10) and (12) are equal and minimal for an electron neutrino, which means $ê_{e_ν} = {\hat{w}}_{e_ν}$ when $ê_{e_ν}$ and ${\hat{w}}_{e_ν}$ are the mathematical electric charge and the mathematical weak charge of an electron neutrino.

Integrating equations (10), (12), and the above characters, we have two field equations on envelopes of an electron neutrino Ê_{E, e_ν}

{\hat{E}}_{E, e_ν} \{\begin{array}{l} {[{\hat{E}}_{e} + {\hat{E}}_{w}]}_{r = R_{c w}} = \frac{{\hat{q}}_{e_ν} + {\hat{w}}_{e_ν}}{c_{L}^{2} R_{c w}^{2}} (\cos θ + \sin θ e^{- i φ}) \\ - {[{\hat{E}}_{e} + {\hat{E}}_{w}]}_{r = R_{c w}}^{*} = - \frac{{\hat{q}}_{e_ν} + {\hat{w}}_{e_ν}}{c_{L}^{2} R_{c w}^{2}} (\cos θ + \sin θ e^{i φ}) \end{array}

(32)

where '–' only indicates that two E-W couples are attracted to each other on the envelopes.

Based on equation (31) and associated equations (19), (21), and (24), we can easily compute the biding-energy of an electron neutrino E_{e_ν}.

\begin{array}{l} E_{e_ν} & = {[E_{e - e} + 2 E_{e - w} + E_{w - w}]}_{r = R_{c w}} \\ = {[\frac{{\hat{q}}_{e_ν}^{2}}{c_{L}^{2} r} + \frac{2 {\hat{q}}_{e_ν} {\hat{w}}_{e_ν}}{c_{L}^{2}} (\frac{1}{r} - \frac{1}{R_{c w}}) + \frac{{\hat{w}}_{e_ν}^{2}}{c_{L}^{2} r} (\frac{1}{r} - \frac{2 m - 2}{(2 m - 1) R_{c w}})]}_{r = R_{c w}} \\ = \frac{1}{c_{L}^{2} R_{c w}} ({\hat{q}}_{e_ν}^{2} + \frac{{\hat{w}}_{e_ν}^{2}}{2 m - 1}) = \frac{2 m}{(2 m - 1) R_{c w}} \frac{{\hat{q}}_{e_ν}^{2}}{c_{L}^{2}} = \frac{2 m}{(2 m - 1) R_{c w}} \frac{{\hat{w}}_{e_ν}^{2}}{c_{L}^{2}} \end{array}

(33)

Combining the envelopes' characters b. with equations (10), (12), and (32), the fields around an electron neutrino Ê_{e_ν} can be directly written as

{{\hat{E}}_{e_ν}|}_{r > R_{c w}} \{\begin{array}{l} \begin{array}{l} [{\hat{E}}_{e - e_ν} + {\hat{E}}_{w - e_ν}] = \pm \frac{{\hat{q}}_{e_ν}}{c_{L}^{2} r^{2}} (\cos θ + \sin θ e^{- i φ}) \pm \frac{{\hat{w}}_{e_ν} R_{c w}^{m - 1}}{c_{L}^{2} r^{m + 1}} \sum_{k = 0}^{m} P_{m}^{k} (\cos θ) e^{- i k φ} \\ {[{\hat{E}}_{e - e_ν} + {\hat{E}}_{w - e_ν}]}^{*} = \mp \frac{{\hat{q}}_{e_ν}}{c_{L}^{2} r^{2}} (\cos θ + \sin θ e^{i φ}) \mp \frac{{\hat{w}}_{e_ν} R_{c w}^{m - 1}}{c_{L}^{2} r^{m + 1}} \sum_{k = 0}^{m} P_{m}^{k} (\cos θ) e^{i k φ} \end{array} \end{array} r > R_{c w} .

(34)

4.2. Dark Neutrinos

Two G-S couples make a dark neutrino. However, the strong interaction field has two critical radii, so there are two types of dark neutrinos, and they are named Dark I and Dark II. Similar to Section 4.1, it is assumed that:

The sizes of Dark I and II are equal to the 1^st and 2^nd critical radius of strong interaction.
Dark I and II have the same mathematical mass and mathematical strong charge.
The mathematical mass ${\hat{m}}_{D_ν}$ and the mathematical strong charge ${\hat{s}}_{D_ν}$ are equal, i.e., ${\hat{m}}_{D_ν} = {\hat{s}}_{D_ν}$ . ${\hat{s}}_{D_ν}$ is minimal.

Replicating the process of the previous section, we have the fields of a Dark I on the envelopes Ê_{E, D_νI}

{\hat{E}}_{E, D_ν I} \{\begin{array}{l} {[{\hat{E}}_{G} + {\hat{E}}_{S}]}_{r = R_{c S 1}} = \frac{{\hat{m}}_{D_ν} + {\hat{s}}_{D_ν}}{c_{G}^{2} R_{c S 1}^{2}} (\cos θ + \sin θ e^{- i φ}) \\ - {[{\hat{E}}_{G} + {\hat{E}}_{S}]}_{r = R_{c S 1}}^{*} = - \frac{{\hat{m}}_{D_ν} + {\hat{s}}_{D_ν}}{c_{G}^{2} R_{c S 1}^{2}} (\cos θ + \sin θ e^{i φ}) \end{array},

(35)

where '–' only means that two G-S couples are attracted to each other on the envelopes.

Based on equation (31) and associated equations (20), (22), and (27), we can compute the biding-energy of a Dark I E_{D_νI}

\begin{array}{l} E_{D_ν I} & = {[E_{G - G} + 2 E_{G - S} + E_{S - S}]}_{r = R_{c S 1}} \\ = \frac{c_{L}^{2}}{c_{G}^{4}} {[\frac{{\hat{m}}_{D_ν}^{2}}{r} + {\hat{m}}_{D_ν} {\hat{s}}_{D_ν} (\frac{1}{r} - \frac{3}{2 R_{c S 1}} + \frac{R_{c S 2}^{2}}{2 R_{c S 1}^{3}}) + {\hat{s}}_{D_ν}^{2} (\frac{1}{r} - \frac{6}{5 R_{c S 1}} + \frac{2 (n + 2) R_{c S 2}^{5}}{5 (2 n - 1) R_{c S 1}^{6}})]}_{r = R_{c S 1}} \\ \approx \frac{2 (n + 2) R_{c S 2}^{5}}{5 (2 n - 1) R_{c S 1}^{6}} \frac{c_{L}^{2} {\hat{s}}_{D_ν}^{2}}{c_{G}^{4}} = \frac{2 (n + 2) R_{c S 2}^{5}}{5 (2 n - 1) R_{c S 1}^{6}} \frac{c_{L}^{2} {\hat{m}}_{D_ν}^{2}}{c_{G}^{4}} \end{array}

(36)

To get the fields of a Dark II on the envelopes Ê_{E, D_νII} and the biding-energy of a Dark II E_{D_νII}, we imitate the last process and have

{\hat{E}}_{E, D_ν I I} \{\begin{array}{l} {[{\hat{E}}_{G} + {\hat{E}}_{S}]}_{r = R_{c S 2}} = \frac{1}{c_{G}^{2}} (\frac{{\hat{m}}_{D_ν}}{R_{c S 2}^{2}} + \frac{R_{c S 2}}{R_{c S 1}^{3}} {\hat{s}}_{D_ν}) (\cos θ + \sin θ e^{- i φ}) \\ - {[{\hat{E}}_{G} + {\hat{E}}_{S}]}_{r = R_{c S 2}}^{*} = - \frac{1}{c_{G}^{2}} (\frac{{\hat{m}}_{D_ν}}{R_{c S 2}^{2}} + \frac{R_{c S 2}}{R_{c S 1}^{3}} {\hat{s}}_{D_ν}) (\cos θ + \sin θ e^{i φ}) \end{array},

(37)

and

\begin{array}{l} E_{D_ν I I} & = {[E_{G - G} + 2 E_{G - S} + E_{S - S}]}_{r = R_{c S 2}} \\ = \frac{c_{L}^{2}}{c_{G}^{4}} {[\frac{{\hat{m}}_{D_ν}^{2}}{r} + \frac{{\hat{s}}_{D_ν}^{2}}{5 R_{c S 1}^{6}} (R_{c S 2}^{5} - r^{5}) + \frac{R_{c S 2}^{5} {\hat{s}}_{D_ν}^{2}}{(2 n - 1) R_{c S 1}^{6}}]}_{r = R_{c S 2}} \\ \approx \frac{R_{c S 2}^{5}}{(2 n - 1) R_{c S 1}^{6}} \frac{c_{L}^{2} {\hat{s}}_{D_ν}^{2}}{c_{G}^{4}} = \frac{R_{c S 2}^{5}}{(2 n - 1) R_{c S 1}^{6}} \frac{c_{L}^{2} {\hat{m}}_{D_ν}^{2}}{c_{G}^{4}} \\ \approx \frac{5}{2 (n + 2)} E_{D_ν I} \end{array} .

(38)

Following the computations of the particle external field in the previous section, we can obtain the fields around a Dark I Ê_{D_νI}

{{\hat{E}}_{D_ν I}|}_{r > R_{c S 1}} \{\begin{array}{l} \begin{matrix} [{\hat{E}}_{G - D_ν I} + {\hat{E}}_{S - D_ν I}] = \{\begin{array}{l} {\hat{E}}_{G - D_ν I} - \frac{{\hat{s}}_{D_ν} r}{c_{G}^{2} R_{c S 1}^{3}} (\cos θ + \sin θ e^{- i φ}) R_{c S 1} < r \leq R_{c S 2} \\ {\hat{E}}_{G - D_ν I} - \frac{{\hat{s}}_{D_ν} R_{c S 2}^{n + 2}}{c_{G}^{2} R_{c S 1}^{3} r^{n + 1}} \sum_{k = 0}^{n} P_{n}^{k} (\cos θ) e^{- i k φ} r > R_{c S 2} \\ where {\hat{E}}_{G - D_ν I} = - \frac{{\hat{m}}_{D_ν}}{c_{G}^{2} r^{2}} (\cos θ + \sin θ e^{- i φ}) \end{array} \end{matrix} \\ {[{\hat{E}}_{G - D_ν I} + {\hat{E}}_{S - D_ν I}]}^{*} = \{\begin{array}{l} {\hat{E}}_{G - D_ν I}^{*} - \frac{{\hat{s}}_{D_ν} r}{c_{G}^{2} R_{c S 1}^{3}} (\cos θ + \sin θ e^{i φ}) R_{c S 1} < r \leq R_{c S 2} \\ {\hat{E}}_{G - D_ν I}^{*} - \frac{{\hat{s}}_{D_ν} R_{c S 2}^{n + 2}}{c_{G}^{2} R_{c S 1}^{3} r^{n + 1}} \sum_{k = 0}^{n} P_{n}^{k} (\cos θ) e^{i k φ} r > R_{c S 2} \\ where {\hat{E}}_{G - D_ν I}^{*} = - \frac{{\hat{m}}_{D_ν}}{c_{G}^{2} R_{c S 1}^{2}} (\cos θ + \sin θ e^{i φ}) \end{array} \end{array}

(39)

and the fields around a Dark II Ê_{D_νII}

{{\hat{E}}_{D_ν I I}|}_{r > R_{c S 2}} \{\begin{array}{l} \begin{matrix} [{\hat{E}}_{G - D_ν I I} + {\hat{E}}_{S - D_ν I I}] = - \frac{{\hat{m}}_{D_ν}}{c_{G}^{2} r^{2}} (\cos θ + \sin θ e^{- i φ}) \\ - \frac{{\hat{s}}_{D_ν} R_{c S 2}^{n + 2}}{c_{G}^{2} R_{c S 1}^{3} r^{n + 1}} \sum_{k = 0}^{n} P_{n}^{k} (\cos θ) e^{- i k φ} \\ {[{\hat{E}}_{G - D_ν I I} + {\hat{E}}_{S - D_ν I I}]}^{*} = - \frac{{\hat{m}}_{D_ν}}{c_{G}^{2} R_{c S 1}^{2}} (\cos θ + \sin θ e^{i φ}) \\ - \frac{{\hat{s}}_{D_ν} R_{c S 2}^{n + 2}}{c_{G}^{2} R_{c S 1}^{3} r^{n + 1}} \sum_{k = 0}^{n} P_{n}^{k} (\cos θ) e^{i k φ} \end{matrix} \end{array} r > R_{c S 2} .

(40)

Comparing equations (36) with (38) reveals that, as far as measurements, namely energy, are concerned, there is little difference between Dark I and Dark II. However, their volumes are significant differences in the microscopic domain. There should only be Dark IIs in most cases following the principle of energy minimization.

4.3. An Electron or A Positron

Electrons and positrons have the same structure. We will not distinguish significantly between electrons and positrons during the subsequent descriptions and computations. One E-W couple and one G-S couple attract each other to form an electron or a positron, so its structure is the most complex in primary particles. Following the assumptions about dark neutrinos, it is supposed that:

The radius of an electron r_e equals the critical radius of weak interaction R_cw, although there are three critical radii for weak and strong interactions.
The mathematical electric charge ${\hat{q}}_{e}$ and the mathematical weak charge ${\hat{w}}_{e}$ are equal, i.e., ${\hat{q}}_{e} = {\hat{w}}_{e}$ .
The mathematical strong charge ${\hat{s}}_{e}$ are minimal, which means ${\hat{s}}_{e} = {\hat{s}}_{D_ν}$ .

Referring to the way we did in the previous sections, we can obtain the field of an electron on the envelopes Ê_{E, e} and the biding-energy of an electron E_e.

{\hat{E}}_{E, e} \{\begin{array}{l} {[{\hat{E}}_{e} + {\hat{E}}_{w}]}_{r = R_{c w}} = \frac{{\hat{q}}_{e} + {\hat{w}}_{e}}{c_{L}^{2} R_{c w}^{2}} (\cos θ + \sin θ e^{- i φ}) \\ - {[{\hat{E}}_{G} + {\hat{E}}_{S}]}_{r = R_{c w}}^{*} = - \frac{1}{c_{G}^{2}} (\frac{{\hat{m}}_{e}}{R_{c w}^{2}} + \frac{{\hat{s}}_{e} R_{c w}}{R_{c S 1}^{3}}) (\cos θ + \sin θ e^{i φ}) \\ \frac{{\hat{q}}_{e} + {\hat{w}}_{e}}{c_{L}^{2} R_{c w}^{2}} = \frac{1}{c_{G}^{2}} (\frac{{\hat{m}}_{e}}{R_{c w}^{2}} + \frac{{\hat{s}}_{e} R_{c w}}{R_{c S 1}^{3}}) \end{array},

(41)

and

\begin{array}{l} E_{e} & = {[E_{e - G} + E_{e - S} + E_{G - w} + E_{w - S}]}_{r = R_{c w}} \\ = {[\frac{{\hat{q}}_{e} {\hat{m}}_{e}}{c_{G}^{2} r} + \frac{{\hat{q}}_{e} {\hat{s}}_{e}}{2 c_{G}^{2} R_{c S 1}^{3}} (R_{c S 2}^{2} - r^{2})]}_{r = R_{c w}} \\ = \frac{{\hat{q}}_{e} {\hat{m}}_{e}}{c_{G}^{2} R_{c w}} + \frac{{\hat{q}}_{e} {\hat{s}}_{e}}{2 c_{G}^{2} R_{c S 1}^{3}} (R_{c S 2}^{2} - R_{c w}^{2}) \end{array} .

(42)

According to the previous assumptions R_cS1 << R_cw < R_cS2,

{\hat{q}}_{e} = {\hat{w}}_{e}

, and

{\hat{s}}_{e} = {\hat{s}}_{D_ν}

, we have

\frac{2 {\hat{q}}_{e}}{c_{L}^{2} R_{c w}^{2}} = \frac{2 {\hat{w}}_{e}}{c_{L}^{2} R_{c w}^{2}} \approx \frac{{\hat{s}}_{D_ν} R_{c w}}{c_{G}^{2} R_{c S 1}^{3}}

(43)

and

E_{e} \approx \frac{{\hat{q}}_{e} {\hat{s}}_{D_ν}}{2 c_{G}^{2} R_{c S 1}^{3}} (R_{c S 2}^{2} - R_{c w}^{2}) = \frac{q_{e}^{2}}{c_{L}^{2} R_{c w}} (\frac{R_{c S 2}^{2}}{R_{c w}^{2}} - 1) .

(44)

Now we directly give the result for fields around an electron Ê_e.

{{\hat{E}}_{e}|}_{r > R_{c w}} \{\begin{array}{l} \begin{array}{l} [{\hat{E}}_{e - e} + {\hat{E}}_{w - e}] = \pm \frac{{\hat{q}}_{e}}{c_{L}^{2} r^{2}} (\cos θ + \sin θ e^{- i ϕ}) \pm \frac{{\hat{w}}_{e}}{c_{L}^{2} r^{2}} (\cos θ + \sin θ e^{- i φ}) r > R_{c w} \end{array} \\ {[{\hat{E}}_{G - e} + {\hat{E}}_{S - e}]}^{*} = \{\begin{array}{l} - \frac{{\hat{m}}_{e}}{c_{G}^{2} r^{2}} (\cos θ + \sin θ e^{i ϕ}) - \frac{{\hat{s}}_{e} r}{c_{G}^{2} R_{c S 1}^{3}} (\cos θ + \sin θ e^{i φ}) R_{c w} < r \leq R_{c S 2} \\ - \frac{{\hat{m}}_{e}}{c_{G}^{2} r^{2}} (\cos θ + \sin θ e^{i ϕ}) - \frac{{\hat{s}}_{D_ν} R_{c S 2}^{n + 2}}{c_{G}^{2} R_{c S 1}^{3} r^{n + 1}} \sum_{k = 0}^{n} P_{n}^{k} (\cos θ) e^{i k φ} r > R_{c S 2} \end{array} \end{array}

(45)

Next, the examination of equations (41) and (42) reveals that the 2^nd critical radius of strong interaction R_cS2 should be the geometric characterization parameter of a G-S envelope rather than the 1^st critical radius of strong interaction R_cS1. It is further assumed that R_cw and R_cS2 are proportional to the wavelengths of the E-W and the G-S couple, respectively, i.e.,

R_{c w} = ξ λ_{E - W}

R_{c S 2} = ξ λ_{G - S}

. Thus, we can directly write with the envelopes characters d.

\frac{R_{c S 2}}{R_{c w}} = \frac{λ_{G - S}}{λ_{E - W}} = \frac{c_{G}}{c_{L}},

(46)

which shows that the gravity speed c_G is faster than the light speed c_L when the above equation compares with equation (42).

5. The Interactions Between Two Primary Particles

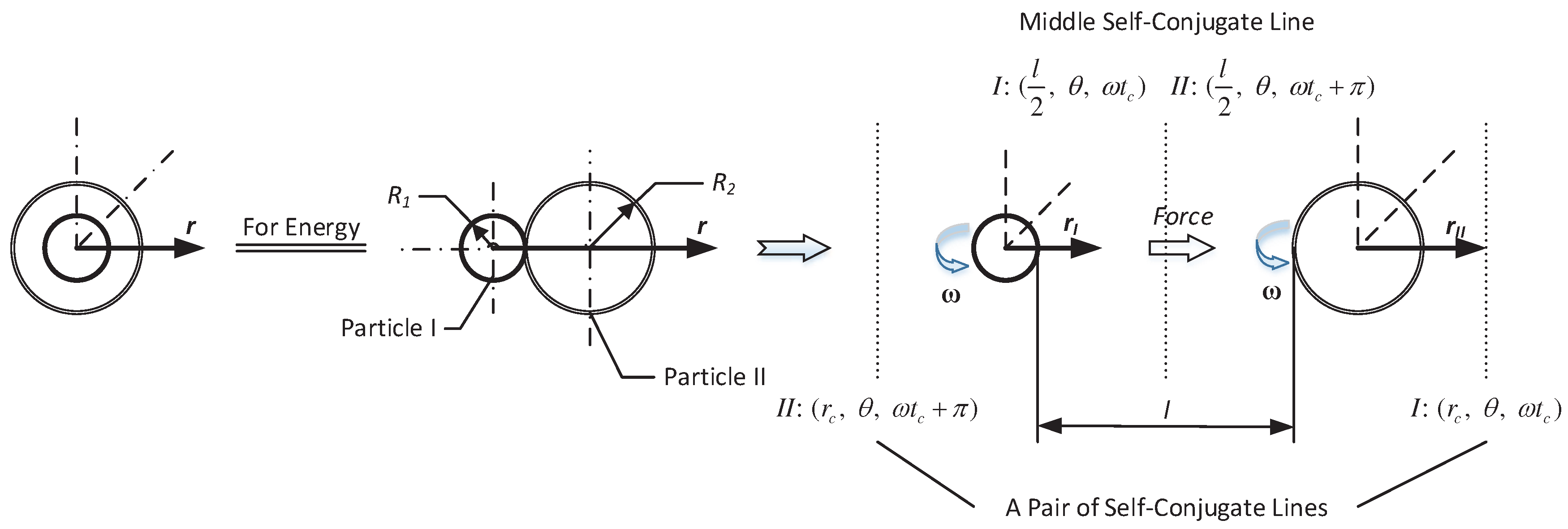
Imagine that two static primary particles are initially rested on each other and then separated by a repulsive force for a distance of l. Particles I and II have the potential and kinetic energy in the separated state (Figure 2). At the initial state, particles I and II are equivalent in that they share a common center of the sphere (Figure 2) because there are no fields in envelopes of primary particles.

Based on the law of conservation of energy, the initial energy of particles I and II is equal to the sum of the potential energy and kinetic energy (including magnetic energy for electrons) after their separation. Therefore, referring to equation (17), the potential energy of the two primary particles

E_{P_{1}^P_{2}}

can be defined as

\begin{array}{l} E_{P_{1}^P_{2}} & = \frac{1}{(t_{2} - t_{1}) 2 π \sum_{k = 0}^{j} N_{j}^{k}} \times \\ (\int_{R_{c}}^{\infty} \int_{0}^{π} \int_{0}^{2 π} \int_{c_{L} t_{1}}^{c_{L} t_{2}} |{\hat{E}}_{P_{1}} {\hat{E}}_{P_{2}}^{*}| r^{2} \sin θ d r d θ d φ d c_{L} t - \int_{R_{c}}^{l} \int_{0}^{π} \int_{0}^{2 π} \int_{c_{L} t_{1}}^{c_{L} t_{2}} |{\hat{E}}_{P_{1}} {\hat{E}}_{P_{2}}^{*}| r^{2} \sin θ d r d θ d φ d c_{L} t) \\ = \frac{1}{(t_{2} - t_{1}) 2 π \sum_{k = 0}^{j} N_{j}^{k}} \int_{l}^{\infty} \int_{0}^{π} \int_{0}^{2 π} \int_{c_{L} t_{1}}^{c_{L} t_{2}} |{\hat{E}}_{P_{1}} {\hat{E}}_{P_{2}}^{*}| r^{2} \sin θ d r d θ d φ d c_{L} t \end{array}

(47)

where

{\hat{E}}_{P_{1}}

and

{\hat{E}}_{P_{2}}

are the external fields of primary particles I and II, l is the distance between the two particles (Figure 2), R_c is the larger of the two particles’ radii, and

\int_{R_{c}}^{l} \int_{0}^{π} \int_{0}^{2 π} \int_{c_{L} t_{1}}^{c_{L} t_{2}} |{\hat{E}}_{P_{1}} {\hat{E}}_{P_{2}}^{*}| r^{2} \sin θ d r d θ d φ d c_{L} t

converts to kinetic energy (including magnetic energy for electrons).

Equation (47) must still hold certainly when two primary particles move in the opposite mode of Figure 2, i.e., two rested on each other particles are attracted at the initial distance l and approach each other until they come together. It is therefore assumed that the Self-Conjugate Mechanism remains between two interacting primary particles. According to existing physics knowledge, the Self-Conjugate Mechanism makes two sets of fields around one particle conjugate to two sets of fields around another depending on the rotation of two particles. In other words, two particles have achieved the Self-Conjugate after they rotate one cycle with angular velocity ω. There are Self-Conjugate lines in pairs that are further presumed at

I : (r_{c}, θ, ω t_{c})

for particle I and

I I : (r_{c}, θ, ω t_{c} + π)

for particle II in their respective spherical coordinate systems, i.e., these lines are in the opposite position while r_I = r_II = r, θ_I = θ_II = θ (Refer to Figure 2). So when we take the r_I-coordinate system of the particle I as a reference (Refer to Figure 2), in equation (47), the item

\int_{R_{c}}^{\infty} \int_{0}^{π} |{\hat{E}}_{P_{1}} (r_{I}) {\hat{E}}_{P_{2}}^{*} (r_{I I})| r_{I}^{2} \sin θ_{I} d r_{I} d θ_{I} = \int_{R_{c}}^{\infty} \int_{0}^{π} |{\hat{E}}_{P_{1}} (r) {\hat{E}}_{P_{2}}^{*} (r)| r^{2} \sin θ d r d θ

, and the item

\int_{0}^{2 π} e^{i m φ_{I}} e^{- i n φ_{I}} d φ_{I}

\int_{0}^{2 π} e^{i m φ_{I}} e^{- i n φ_{I}} d φ_{I} = \{\begin{array}{l} \int_{2 η π}^{2 η π + 2 π} e^{i m (ω t_{c})} e^{- i n (ω t_{c} + π)} d (ω t_{c}) = - 2 π δ_{m n} Same rotation direction of ω \\ \int_{2 η π}^{2 η π + 2 π} e^{i m (ω t_{c})} e^{- i n (- ω t_{c} + π)} d (ω t_{c}) = 0 Opposite rotation direction of ω \end{array},

(48)

where t_c is the time of conjugation of two primary particles, and η = 0, 1, 2, ……, η. Hence, equation (47) still holds, just with a minus sign difference. Here, the minus sign only indicates that energy is gathering in this process, contrary to equation (47). Later, we continue to use equation (47) without distinguishing whether the energy is spreading or gathering in the motion of two primary particles.

Thus we can follow the results from the previous chapters when there is the potential energy between two primary particles, and the distance of l remains constant. There are only two conjugate forms between the two particles because each of the two particles comprises two coupled waves. Hence, equation (47) can be translated into

\begin{array}{l} E_{P_{1}^P_{2}} & = \frac{c_{L}^{2}}{2 π \sum_{k = 0}^{j} N_{j}^{|k|}} \int_{l}^{\infty} \int_{0}^{π} \int_{0}^{2 π} |{\hat{E}}_{P_{1}} {\hat{E}}_{P_{2}}^{*}| r^{2} \sin θ d r d θ d φ = \frac{c_{L}^{2}}{2 π \sum_{k = 0}^{j} N_{j}^{|k|}} \times \\ \int_{l}^{\infty} \int_{0}^{π} \int_{0}^{2 π} |\pm [{\hat{E}}_{a - P_{1}} + {\hat{E}}_{b - P_{1}}] {[{\hat{E}}_{c - P_{2}} + {\hat{E}}_{d - P_{2}}]}^{*} \pm [{\hat{E}}_{w - P_{1}} + {\hat{E}}_{x - P_{1}}] {[{\hat{E}}_{y - P_{2}} + {\hat{E}}_{z - P_{2}}]}^{*}| r^{2} \sin θ d r d θ d φ \\ = {[E_{a - P_{1} - c - P_{2}} + E_{a - P_{1} - d - P_{2}} + E_{b - P_{1} - c - P_{2}} + E_{b - P_{1} - d - P_{2}}]}_{r = l + R_{c}} \\ + {[E_{w - P_{1} - y - P_{2}} + E_{w - P_{1} - z - P_{2}} + E_{x - P_{1} - y - P_{2}} + E_{x - P_{1} - z - P_{2}}]}_{r = l + R_{c}} \end{array}

(49)

where the subscripts a to d, and w to z denote electric, gravitational, weak interaction, or strong interaction.

According to Newtonian mechanics, the work done is the same as the potential energy when primary particles I and II move relative to each other. Reversing the Newtonian mechanics definition of work, i.e.,

F = \nabla W = \nabla E_{P_{1}^P_{2}}

, the force between two primary particles

F_{P_{1}^P_{2}}

is therefore

F_{P_{1}^P_{2}} = \pm \frac{d E_{P_{1}^P_{2}}}{d l} .

(50)

Two Self-Conjugate primary particles have no initial phase difference in zenith and azimuthal angle under the requirements of the assumption of Self-Conjugation lines. From equation (48), they have potential energy or force when they rotate in the same direction, while they have zero potential energy or rest when they do in opposite directions. Therefore, the force mode has two forms, all right-handed or up rotation and all left-handed or down rotation, which shows each primary particle has spin values of

\pm \frac{1}{2}

5.1. Two Particles of the Same Type

Start by computing the interaction between two electron neutrinos. Combining equations (19), (21), and (49), we have the potential energy E_{e_ν^e_ν}

\begin{array}{l} E_{e_ν^e_ν} & = 2 {[E_{e - e_ν - e - e_ν} + 2 E_{e - e_ν - w - e_ν} + E_{w - e_ν - w - e_ν}]}_{r = l + R_{c w}} \\ = 2 [\frac{{\hat{q}}_{e_ν}^{2}}{c_{L}^{2} (l + R_{c w})} + \frac{R_{c w}^{2 m - 2} {\hat{w}}_{e_ν}^{2}}{c_{L}^{2} (2 m - 1) {(l + R_{c w})}^{2 m - 1}}] \\ \approx \frac{2 {\hat{q}}_{e_ν}^{2}}{c_{L}^{2} (l + R_{c w})} = \frac{2 {\hat{w}}_{e_ν}^{2}}{c_{L}^{2} (l + R_{c w})} when l \geq R_{c w} \end{array} .

(51)

Since two equations (34) have attractive and repulsive states under the Self-Conjugate Mechanism, from equation (50), the force of two electron neutrinos F_{e_ν^e_ν} is

\begin{array}{l} F_{e_ν^e_ν} & = \pm 2 [\frac{{\hat{q}}_{e_ν}^{2}}{c_{L}^{2} {(l + R_{c w})}^{2}} + \frac{R_{c w}^{2 m - 2} {\hat{w}}_{e_ν}^{2}}{c_{L}^{2} {(l + R_{c w})}^{2 m - 2}}] \\ \approx \pm \frac{2 {\hat{q}}_{e_ν}^{2}}{c_{L}^{2} {(l + R_{c w})}^{2}} = \pm \frac{2 {\hat{w}}_{e_ν}^{2}}{c_{L}^{2} {(l + R_{c w})}^{2}} when l \geq R_{c w} \end{array},

(52)

where the sign '–' or '+' depends on the Self-Conjugate forms between two electron neutrinos, and the "–" or "+" should be random.

Association equation (49) with equations (20), (22), (27), and (39), we can compute the potential energy between two Dark Is E_{D_νI^D_νI}

\begin{array}{l} E_{D_ν I^D_ν I} & = 2 {[E_{G - D_ν I - G - D_ν I} + 2 E_{G - D_ν I - S - D_ν I} + E_{S - D_ν I - S - D_ν I}]}_{r = l + R_{c S 1}} \\ = \{\begin{cases} \frac{2 c_{L}^{2}}{c_{G}^{4}} [\frac{{\hat{m}}_{D_ν}^{2}}{l + R_{c S 1}} + \frac{{\hat{m}}_{D_ν} {\hat{s}}_{D_ν}}{R_{c S 1}^{3}} (R_{c S 2}^{2} - {(l + R_{c S 1})}^{2}) + \frac{{\hat{s}}_{D_ν}^{2}}{R_{c S 1}^{6}} (\frac{R_{c S 2}^{5} - {(l + R_{c S 1})}^{5}}{5} + \frac{R_{c S 2}^{5}}{2 n - 1})] \\ \approx \frac{2 c_{L}^{2} {\hat{s}}_{D_ν}^{2}}{c_{G}^{4} R_{c S 1}^{6}} [\frac{R_{c S 2}^{5} - {(l + R_{c S 1})}^{5}}{5} + \frac{R_{c S 2}^{5}}{2 n - 1}] \\ = \frac{2 c_{L}^{2} {\hat{m}}_{D_ν}^{2}}{c_{G}^{4} R_{c S 1}^{6}} [\frac{R_{c S 2}^{5} - {(l + R_{c S 1})}^{5}}{5} + \frac{R_{c S 2}^{5}}{2 n - 1}] 0 \leq l \leq R_{c S 2} - R_{c S 1} \\ \frac{2 c_{L}^{2}}{c_{G}^{4}} [\frac{{\hat{m}}_{D_ν}^{2}}{l + R_{c S 1}} + \frac{R_{c S 2}^{2 n + 4}}{(2 n - 1) R_{c S 1}^{6}} \frac{{\hat{s}}_{D_ν}^{2}}{{(l + R_{c S 1})}^{2 n - 1}}] \\ = \frac{2 c_{L}^{2} {\hat{s}}_{D_ν}^{2}}{c_{G}^{4} (l + R_{c S 1})} [1 + \frac{R_{c S 2}^{2 n + 4}}{(2 n - 1) R_{c S 1}^{6} {(l + R_{c S 1})}^{2 n - 2}}] \\ = \frac{2 c_{L}^{2} {\hat{m}}_{D_ν}^{2}}{c_{G}^{4} (l + R_{c S 1})} [1 + \frac{R_{c S 2}^{2 n + 4}}{(2 n - 1) R_{c S 1}^{6} {(l + R_{c S 1})}^{2 n - 2}}] l > R_{c S 2} - R_{c S 1} \end{cases} \end{array},

(53)

and the force between two Dark Is F_{D_νI^D_νI}

F_{D_ν I^D_ν I} = \{\begin{array}{l} \begin{array}{l} - \frac{2 c_{L}^{2}}{c_{G}^{4}} [\frac{{\hat{m}}_{D_ν}^{2}}{{(l + R_{c S 1})}^{2}} + \frac{2 {\hat{m}}_{D_ν} {\hat{s}}_{D_ν}}{R_{c S 1}^{3}} (l + R_{c S 1}) + \frac{{\hat{s}}_{D_ν}^{2}}{R_{c S 1}^{6}} {(l + R_{c S 1})}^{4}] \\ \approx - \frac{2 c_{L}^{2} {\hat{s}}_{D_ν}^{2}}{c_{G}^{4} R_{c S 1}^{6}} {(l + R_{c S 1})}^{4} = - \frac{2 c_{L}^{2} {\hat{m}}_{D_ν}^{2}}{c_{G}^{4} R_{c S 1}^{6}} {(l + R_{c S 1})}^{4} 0 \leq l \leq R_{c S 2} - R_{c S 1} \end{array} \\ \begin{array}{l} - \frac{2 c_{L}^{2}}{c_{G}^{4}} [\frac{{\hat{m}}_{D_ν}^{2}}{{(l + R_{c S 1})}^{2}} + \frac{R_{c S 2}^{2 n + 4}}{R_{c S 1}^{6}} \frac{{\hat{s}}_{D_ν}^{2}}{{(l + R_{c S 1})}^{2 n}}] \\ = - \frac{2 c_{L}^{2} {\hat{s}}_{D_ν}^{2}}{c_{G}^{4} {(l + R_{c S 1})}^{2}} [1 + \frac{R_{c S 2}^{2 n + 4}}{R_{c S 1}^{6} {(l + R_{c S 1})}^{2 n - 2}}] \\ = - \frac{2 c_{L}^{2} {\hat{m}}_{D_ν}^{2}}{c_{G}^{4} {(l + R_{c S 1})}^{2}} [1 + \frac{R_{c S 2}^{2 n + 4}}{R_{c S 1}^{6} {(l + R_{c S 1})}^{2 n - 2}}] l > R_{c S 2} - R_{c S 1} \end{array} \end{array} .

(54)

Duplicating the last process yields the potential energy between two Dark IIs E_{D_νII^D_νII}

\begin{array}{l} E_{D_ν I I^D_ν I I} & = 2 {[E_{G - D_ν I I - G - D_ν I I} + 2 E_{G - D_ν I I - S - D_ν I I} + E_{S - D_ν I I - S - D_ν I I}]}_{r = l + R_{c S 2}} \\ = \frac{2 c_{L}^{2}}{c_{G}^{4}} [\frac{{\hat{m}}_{D_ν}^{2}}{l + R_{c S 2}} + \frac{R_{c S 2}^{2 n + 4}}{(2 n - 1) R_{c S 1}^{6}} \frac{{\hat{s}}_{D_ν}^{2}}{{(l + R_{c S 2})}^{2 n - 1}}] \\ = \frac{2 c_{L}^{2} {\hat{s}}_{D_ν}^{2}}{c_{G}^{4} (l + R_{c S 2})} [1 + \frac{R_{c S 2}^{2 n + 4}}{(2 n - 1) R_{c S 1}^{6} {(l + R_{c S 2})}^{2 n - 2}}] \\ = \frac{2 c_{L}^{2} {\hat{m}}_{D_ν}^{2}}{c_{G}^{4} (l + R_{c S 2})} [1 + \frac{R_{c S 2}^{2 n + 4}}{(2 n - 1) R_{c S 1}^{6} {(l + R_{c S 2})}^{2 n - 2}}] \end{array},

(55)

and the force between two Dark IIs F_{D_νII^D_νII}

\begin{array}{l} F_{D_ν I I^D_ν I I} & = - \frac{2 c_{L}^{2}}{c_{G}^{4}} [\frac{{\hat{m}}_{D_ν}^{2}}{{(l + R_{c S 2})}^{2}} + \frac{R_{c S 2}^{2 n + 4}}{R_{c S 1}^{6}} \frac{{\hat{s}}_{D_ν}^{2}}{{(l + R_{c S 2})}^{2 n}}] \\ = - \frac{2 c_{L}^{2} {\hat{s}}_{D_ν}^{2}}{c_{G}^{4} {(l + R_{c S 2})}^{2}} [1 + \frac{R_{c S 2}^{2 n + 4}}{R_{c S 1}^{6} {(l + R_{c S 2})}^{2 n - 2}}] \\ = - \frac{2 c_{L}^{2} {\hat{m}}_{D_ν}^{2}}{c_{G}^{4} {(l + R_{c S 2})}^{2}} [1 + \frac{R_{c S 2}^{2 n + 4}}{R_{c S 1}^{6} {(l + R_{c S 2})}^{2 n - 2}}] \end{array} .

(56)

The potential energy between two electrons E_e^e has two forms because an electron is composed of one E-W couple and one G-S couple. Same as electron neutrinos, the two forms should be random and rely on the Self-Conjugate forms between two electrons. Combining equations (19) to (28) and (49), we can compute the two forms of the potential energy. One is E_e^eI when the two E-W couples are conjugate, and the two G-S couples are conjugate.

\begin{array}{l} E_{e^e I} & = {[E_{e - e - e - e} + 2 E_{e - e - w - e} + E_{w - e - w - e} + E_{G - e - G - e} + 2 E_{G - e - S - e} + E_{S - e - S - e}]}_{r = l + R_{c w}} \\ = \{\begin{array}{l} \begin{array}{l} \frac{{\hat{q}}_{e}^{2}}{c_{L}^{2} (l + R_{c w})} + \frac{R_{c w}^{2 m - 2} {\hat{w}}_{e}^{2}}{c_{L}^{2} (2 m - 1) {(l + R_{c w})}^{2 m - 1}} + \frac{c_{L}^{2} {\hat{m}}_{e}^{2}}{c_{G}^{4} (l + R_{c w})} + \frac{c_{L}^{2} {\hat{m}}_{e} {\hat{s}}_{e}}{c_{G}^{4} R_{c S 1}^{3}} [R_{c S 2}^{2} - {(l + R_{c w})}^{2}] \\ + \frac{c_{L}^{2} {\hat{s}}_{e}^{2}}{c_{G}^{4}} [\frac{1}{5 R_{c S 1}^{6}} (R_{c S 2}^{5} - {(l + R_{c w})}^{5}) + \frac{R_{c S 2}^{5}}{(2 n - 1) R_{c S 1}^{6}}] 0 \leq l \leq R_{c S 2} - R_{c w} \end{array} \\ \begin{array}{l} \frac{{\hat{q}}_{e}^{2}}{c_{L}^{2} (l + R_{c w})} + \frac{R_{c w}^{2 m - 2} {\hat{w}}_{e}^{2}}{c_{L}^{2} (2 m - 1) {(l + R_{c w})}^{2 m - 1}} + \frac{c_{L}^{2} {\hat{m}}_{e}^{2}}{c_{G}^{4} (l + R_{c w})} \\ + \frac{c_{L}^{2} R_{c S 2}^{2 n + 4}}{c_{G}^{4} (2 n - 1) R_{c S 1}^{6}} \frac{{\hat{s}}_{e}^{2}}{{(l + R_{c w})}^{2 n - 1}} l > R_{c S 2} - R_{c w} \end{array} \end{array} \\ \approx \frac{{\hat{q}}_{e}^{2}}{c_{L}^{2} (l + R_{c w})} + \frac{c_{L}^{2} {\hat{m}}_{e}^{2}}{c_{G}^{4} (l + R_{c w})} when l is large \end{array}

(57)

Another is E_e^eII when the two E-W couples are conjugate to the two G-S couples.

\begin{array}{l} E_{e^e I I} & = 2 {[E_{e - e - G - e} + E_{e - e - S - e} + E_{w - e - G - e} + E_{w - e - S - e}]}_{r = l + R_{c w}} \\ = \{\begin{array}{l} \frac{2 {\hat{q}}_{e} {\hat{m}}_{e}}{c_{G}^{2} (l + R_{c w})} + \frac{{\hat{q}}_{e} {\hat{s}}_{e}}{c_{G}^{2} R_{c S 1}^{3}} [R_{c S 2}^{2} - {(l + R_{c w})}^{2}] 0 \leq l \leq R_{c S 2} - R_{c w} \\ \frac{2 {\hat{q}}_{e} {\hat{m}}_{e}}{c_{G}^{2} (l + R_{c w})} l > R_{c S 2} - R_{c w} \end{array} \end{array}

(58)

Derivation of the last two equations can yield the forces between two electrons in both forms that are

\begin{array}{l} F_{e^e I} & = \{\begin{array}{l} \begin{array}{l} \pm \frac{{\hat{q}}_{e}^{2}}{c_{L}^{2} {(l + R_{c w})}^{2}} \pm \frac{R_{c w}^{2 m - 2} {\hat{w}}_{e}^{2}}{c_{L}^{2} {(l + R_{c w})}^{2 m}} - \frac{c_{L}^{2} {\hat{m}}_{e}^{2}}{c_{G}^{4} {(l + R_{c w})}^{2}} - \frac{2 c_{L}^{2} {\hat{m}}_{e} {\hat{s}}_{e}}{c_{G}^{4} R_{c S 1}^{3}} (l + R_{c w}) \\ - \frac{c_{L}^{2} {\hat{s}}_{e}^{2}}{c_{G}^{4} R_{c S 1}^{6}} {(l + R_{c w})}^{4} 0 \leq l \leq R_{c S 2} - R_{c w} \end{array} \\ \pm \frac{{\hat{q}}_{e}^{2}}{c_{L}^{2} {(l + R_{c w})}^{2}} \pm \frac{R_{c w}^{2 m - 2} {\hat{w}}_{e}^{2}}{c_{L}^{2} {(l + R_{c w})}^{2 m}} - \frac{c_{L}^{2} {\hat{m}}_{e}^{2}}{c_{G}^{4} {(l + R_{c w})}^{2}} - \frac{c_{L}^{2} R_{c S 2}^{2 n + 4}}{c_{G}^{4} R_{c S 1}^{6}} \frac{{\hat{s}}_{e}^{2}}{{(l + R_{c w})}^{2 n}} l > R_{c S 2} - R_{c w} \end{array} \\ \approx \pm \frac{{\hat{q}}_{e}^{2}}{c_{L}^{2} {(l + R_{c w})}^{2}} - \frac{c_{L}^{2} {\hat{m}}_{e}^{2}}{c_{G}^{4} {(l + R_{c w})}^{2}} when l is large \end{array}

(59)

and

F_{e^e I I} = \{\begin{array}{l} - \frac{2 {\hat{q}}_{e} {\hat{m}}_{e}}{c_{G}^{2} {(l + R_{c w})}^{2}} - \frac{2 {\hat{q}}_{e} {\hat{s}}_{e}}{c_{G}^{2} R_{c S 1}^{3}} (l + R_{c w}) 0 \leq l \leq R_{c S 2} - R_{c w} \\ - \frac{2 {\hat{q}}_{e} {\hat{m}}_{e}}{c_{G}^{2} {(l + R_{c w})}^{2}} l > R_{c S 2} - R_{c w} \end{array},

(60)

plus

{\hat{s}}_{e} = {\hat{s}}_{D_ν}

in equations (57) to (60).

Comparing equations (57) and (58), (59) and (60) shows that the potential energy and force between two electrons are very different in the two Self-Conjugate forms, with the smaller one close to zero.

5.2. Two Particles of the Different Type

Similar to the last section, this section still starts by computing the interaction of an electron neutrino with another primary particle. Combining equations (23) to (28), (49), and (50), the potential energy between an electron neutrino and a Dark I E_{e_ν^D_νI} is

\begin{array}{l} E_{e_ν^D_ν I} & = 2 {[E_{e - e_ν - G - D_ν I} + E_{e - e_ν - S - D_ν I} + E_{w - e_ν - G - D_ν I} + E_{w - e_ν - S - D_ν I}]}_{r = l + R_{c w}} \\ = \{\begin{array}{l} \frac{2 {\hat{q}}_{e_ν} {\hat{m}}_{D_ν}}{c_{G}^{2} (l + R_{c w})} + \frac{{\hat{q}}_{e_ν} {\hat{s}}_{D_ν}}{c_{G}^{2} R_{c S 1}^{3}} (R_{c S 2}^{2} - {(l + R_{c w})}^{2}) 0 \leq l \leq R_{c S 2} - R_{c w} \\ \frac{2 {\hat{q}}_{e_ν} {\hat{m}}_{D_ν}}{c_{G}^{2} (l + R_{c w})} l > R_{c S 2} - R_{c w} \end{array} \end{array},

(61)

and the force between an electron neutrino and a Dark I F_{e_ν^D_νI} is

E_{e_ν^D_ν I} = \{\begin{array}{l} - \frac{2 {\hat{q}}_{e_ν} {\hat{m}}_{D_ν}}{c_{G}^{2} {(l + R_{c w})}^{2}} - \frac{2 {\hat{q}}_{e_ν} {\hat{s}}_{D_ν}}{c_{G}^{2} R_{c S 1}^{3}} (l + R_{c w}) 0 \leq l \leq R_{c S 2} - R_{c w} \\ - \frac{2 {\hat{q}}_{e_ν} {\hat{m}}_{D_ν}}{c_{G}^{2} {(l + R_{c w})}^{2}} l > R_{c S 2} - R_{c w} \end{array},

(62)

plus

{\hat{m}}_{D_ν} = {\hat{s}}_{D_ν}

in above two equations.

Repeating the previous processes gives the potential energy between an electron neutrino and a Dark II E_{e_ν^D_νII}

\begin{array}{l} E_{e_ν^D_ν I I} & = 2 {[E_{e - e_ν - G - D_ν I I} + E_{e - e_ν - S - D_ν I I} + E_{w - e_ν - G - D_ν I I} + E_{w - e_ν - S - D_ν I I}]}_{r = l + R_{c S 2}} \\ = \frac{2 {\hat{q}}_{e_ν} {\hat{m}}_{D_ν}}{c_{G}^{2} (l + R_{c S 2})} = \frac{2 {\hat{q}}_{e_ν} {\hat{s}}_{D_ν}}{c_{G}^{2} (l + R_{c S 2})} \end{array},

(63)

the force between an electron neutrino and a Dark I F_{e_ν^D_νII}

F_{e_ν^D_ν I I} = - \frac{2 {\hat{q}}_{e_ν} {\hat{m}}_{D_ν}}{c_{G}^{2} {(l + R_{c S 2})}^{2}} = - \frac{2 {\hat{q}}_{e_ν} {\hat{s}}_{D_ν}}{c_{G}^{2} {(l + R_{c S 2})}^{2}},

(64)

the potential energy between an electron neutrino and an electron E_{e_ν^e}

\begin{array}{l} E_{e_ν^e} & = {[E_{e - e_ν - e - e} + E_{e - e_ν - w - e} + E_{w - e_ν - e - e} + E_{w - e_ν - w - e}]}_{r = l + R_{c w}} \\ + {[E_{e - e_ν - G - e} + E_{e - e_ν - S - e} + E_{w - e_ν - G - e} + E_{w - e_ν - S - e}]}_{r = l + R_{c w}} \\ = \{\begin{array}{l} \begin{array}{l} \frac{{\hat{q}}_{e_ν} {\hat{q}}_{e}}{c_{L}^{2} (l + R_{c w})} + \frac{R_{c w}^{2 m - 2} {\hat{w}}_{e_ν} {\hat{w}}_{e}}{c_{L}^{2} (2 m - 1) {(l + R_{c w})}^{2 m - 1}} + \frac{{\hat{q}}_{e_ν} {\hat{m}}_{e}}{c_{G}^{2} (l + R_{c w})} \\ + \frac{{\hat{q}}_{e_ν} {\hat{s}}_{e}}{2 c_{G}^{2} R_{c S 1}^{3}} (R_{c S 2}^{2} - {(l + R_{c w})}^{2}) 0 \leq l \leq R_{c S 2} - R_{c w} \end{array} \\ \frac{{\hat{q}}_{e_ν} {\hat{q}}_{e}}{c_{L}^{2} (l + R_{c w})} + \frac{R_{c w}^{2 m - 2} {\hat{w}}_{e_ν} {\hat{w}}_{e}}{c_{L}^{2} (2 m - 1) {(l + R_{c w})}^{2 m - 1}} + \frac{{\hat{q}}_{e_ν} {\hat{m}}_{e}}{c_{G}^{2} (l + R_{c w})} l > R_{c S 2} - R_{c w} \end{array} \\ \approx \{\begin{array}{l} \frac{{\hat{q}}_{e_ν} {\hat{q}}_{e}}{c_{L}^{2} (l + R_{c w})} [1 + \frac{R_{c w}^{2 m - 2}}{(2 m - 1) {(l + R_{c w})}^{2 m - 2}}] + \frac{{\hat{q}}_{e_ν} {\hat{s}}_{D_ν}}{2 c_{G}^{2} R_{c S 1}^{3}} (R_{c S 2}^{2} - {(l + R_{c w})}^{2}) 0 \leq l \leq R_{c S 2} - R_{c w} \\ \frac{{\hat{q}}_{e_ν} {\hat{q}}_{e}}{c_{L}^{2} (l + R_{c w})} [1 + \frac{R_{c w}^{2 m - 2}}{(2 m - 1) {(l + R_{c w})}^{2 m - 2}}] l > R_{c S 2} - R_{c w} \end{array} \\ \approx \frac{{\hat{q}}_{e_ν} {\hat{q}}_{e}}{c_{L}^{2} (l + R_{c w})} = \frac{{\hat{w}}_{e_ν} {\hat{w}}_{e}}{c_{L}^{2} (l + R_{c w})} when l \geq R_{c w} \end{array},

(65)

and the force between an electron neutrino and an electro F_{e_ν^e}

\begin{array}{l} F_{e_ν^e} & = \{\begin{array}{l} \pm \frac{{\hat{q}}_{e_ν} {\hat{q}}_{e}}{c_{L}^{2} {(l + R_{c w})}^{2}} \pm \frac{R_{c w}^{2 m - 2} {\hat{w}}_{e_ν} {\hat{w}}_{e}}{c_{L}^{2} {(l + R_{c w})}^{2 m}} - \frac{{\hat{q}}_{e_ν} {\hat{m}}_{e}}{c_{G}^{2} {(l + R_{c w})}^{2}} - \frac{{\hat{q}}_{e_ν} {\hat{s}}_{e}}{c_{G}^{2} R_{c S 1}^{3}} (l + R_{c w}) 0 \leq l \leq R_{c S 2} - R_{c w} \\ \pm \frac{{\hat{q}}_{e_ν} {\hat{q}}_{e}}{c_{L}^{2} {(l + R_{c w})}^{2}} \pm \frac{R_{c w}^{2 m - 2} {\hat{w}}_{e_ν} {\hat{w}}_{e}}{c_{L}^{2} {(l + R_{c w})}^{2 m}} - \frac{{\hat{q}}_{e_ν} {\hat{m}}_{e}}{c_{G}^{2} {(l + R_{c w})}^{2}} l > R_{c S 2} - R_{c w} \end{array} \\ \approx \{\begin{array}{l} \frac{{\hat{q}}_{e_ν} {\hat{q}}_{e}}{c_{L}^{2} {(l + R_{c w})}^{2}} [1 + \frac{R_{c w}^{2 m - 2}}{{(l + R_{c w})}^{2 m - 2}}] + \frac{{\hat{q}}_{e_ν} {\hat{s}}_{D_ν}}{c_{G}^{2} R_{c S 1}^{3}} (l + R_{c w}) 0 \leq l \leq R_{c S 2} - R_{c w} \\ \frac{{\hat{q}}_{e_ν} {\hat{q}}_{e}}{c_{L}^{2} {(l + R_{c w})}^{2}} [1 + \frac{R_{c w}^{2 m - 2}}{{(l + R_{c w})}^{2 m - 2}}] l > R_{c S 2} - R_{c w} \end{array} \\ \approx \pm \frac{{\hat{q}}_{e_ν} {\hat{q}}_{e}}{c_{L}^{2} {(l + R_{c w})}^{2}} = \pm \frac{{\hat{w}}_{e_ν} {\hat{w}}_{e}}{c_{L}^{2} {(l + R_{c w})}^{2}} when l \geq R_{c w} \end{array},

(66)

where

{\hat{q}}_{e_ν} = {\hat{w}}_{e_ν}

{\hat{q}}_{e} = {\hat{w}}_{e}

, and

{\hat{s}}_{e} = {\hat{s}}_{D_ν}

in equations (65) and (66), and the sign '–' or '+' randomizes in equation (66).

It is next computed that the potential energies and forces between the two types of dark neutrinos and between each of them and an electron. Based on equations (20), (22), (27), (49), and (50), the potential energy between a Dark I and a Dark II E_{D_νI^D_νII} is

\begin{array}{l} E_{D_ν I^D_ν I I} & = 2 {[E_{G - D_ν I - G - D_ν I I} + E_{G - D_ν I - S - D_ν I I} + E_{S - D_ν I - G - D_ν I I} + E_{S - D_ν I - S - D_ν I I}]}_{r = l + R_{c S 2}} \\ = 2 [\frac{c_{L}^{2} {\hat{m}}_{D_ν}^{2}}{c_{G}^{4} (l + R_{c S 2})} + \frac{c_{L}^{2} R_{c S 2}^{2 n + 4}}{c_{G}^{4} (2 n - 1) R_{c S 1}^{6}} \frac{{\hat{s}}_{D_ν}^{2}}{{(l + R_{c S 2})}^{2 n - 1}}] \\ = \frac{2 c_{L}^{2} {\hat{s}}_{D_ν}^{2}}{c_{G}^{4} (l + R_{c S 2})} [1 + \frac{R_{c S 2}^{2 n + 4}}{(2 n - 1) R_{c S 1}^{6} {(l + R_{c S 2})}^{2 n - 2}}] \\ = \frac{2 c_{L}^{2} {\hat{m}}_{D_ν}^{2}}{c_{G}^{4} (l + R_{c S 2})} [1 + \frac{R_{c S 2}^{2 n + 4}}{(2 n - 1) R_{c S 1}^{6} {(l + R_{c S 2})}^{2 n - 2}}] \end{array}

(67)

and the force between a Dark I and a Dark II F_{D_νI^D_νII} is

F_{D_ν I^D_ν I I} = - \frac{2 c_{L}^{2} {\hat{s}}_{D_ν}^{2}}{c_{G}^{4} {(l + R_{c S 2})}^{2}} [1 + \frac{R_{c S 2}^{2 n + 4}}{R_{c S 1}^{6} {(l + R_{c S 2})}^{2 n - 2}}] = - \frac{2 c_{L}^{2} {\hat{m}}_{D_ν}^{2}}{c_{G}^{4} {(l + R_{c S 2})}^{2}} [1 + \frac{R_{c S 2}^{2 n + 4}}{R_{c S 1}^{6} {(l + R_{c S 2})}^{2 n - 2}}]

(68)

Based on equations (23) to (28), (43), (49), and (50), the potential energy between a Dark I and an electron E_{D_νI^e} is

\begin{array}{l} E_{D_ν I^e} & = {[E_{G - D_ν I - e - e} + E_{G - D_ν I - w - e} + E_{S - D_ν I - e - e} + E_{S - D_ν I - w - e}]}_{r = l + R_{c w}} \\ = {[E_{G - D_ν I - G - e} + E_{G - D_ν I - S - e} + E_{S - D_ν I - G - e} + E_{S - D_ν I - S - e}]}_{r = l + R_{c w}} \\ = \{\begin{array}{l} \begin{array}{l} \frac{{\hat{q}}_{e} {\hat{m}}_{D_ν}}{c_{G}^{2} (l + R_{c w})} + \frac{{\hat{q}}_{e} {\hat{s}}_{D_ν}}{2 c_{G}^{2} R_{c S 1}^{3}} (R_{c S 2}^{2} - {(l + R_{c w})}^{2}) + \frac{c_{L}^{2} {\hat{m}}_{e} {\hat{m}}_{D_ν}}{c_{G}^{4} (l + R_{c w})} \\ + \frac{c_{L}^{2} {\hat{m}}_{D_ν} {\hat{s}}_{e}}{2 c_{G}^{4} R_{c S 1}^{3}} (R_{c S 2}^{2} - {(l + R_{c w})}^{2}) + \frac{c_{L}^{2} {\hat{m}}_{e} {\hat{s}}_{D_ν}}{2 c_{G}^{4} R_{c S 1}^{3}} (R_{c S 2}^{2} - {(l + R_{c w})}^{2}) \\ + \frac{c_{L}^{2} {\hat{s}}_{D_ν} {\hat{s}}_{e}}{c_{G}^{4}} [\frac{1}{5 R_{c S 1}^{6}} (R_{c S 2}^{5} - {(l + R_{c w})}^{5}) + \frac{R_{c S 2}^{5}}{(2 n - 1) R_{c S 1}^{6}}] 0 \geq l \geq R_{c S 2} - R_{c w} \end{array} \\ \frac{{\hat{q}}_{e} {\hat{m}}_{D_ν}}{c_{G}^{2} (l + R_{c w})} + \frac{c_{L}^{2} {\hat{m}}_{e} {\hat{m}}_{D_ν}}{c_{G}^{4} (l + R_{c w})} + \frac{c_{L}^{2} {\hat{s}}_{D_ν} {\hat{s}}_{e} R_{c S 2}^{2 n + 4}}{c_{G}^{4} (2 n - 1) R_{c S 1}^{6} {(l + R_{c w})}^{2 n - 1}} l > R_{c S 2} - R_{c w} \end{array} \\ \approx \{\begin{array}{l} \begin{array}{l} \frac{c_{L}^{2} {\hat{s}}_{D_ν}^{2}}{c_{G}^{4} R_{c S 1}^{6}} [\frac{R_{c S 2}^{5} - {(l + R_{c w})}^{5}}{5} + \frac{R_{c S 2}^{5}}{2 n - 1}] \\ = \frac{c_{L}^{2} {\hat{m}}_{D_ν}^{2}}{c_{G}^{4} R_{c S 1}^{6}} [\frac{R_{c S 2}^{5} - {(l + R_{c w})}^{5}}{5} + \frac{R_{c S 2}^{5}}{2 n - 1}] 0 \geq l \geq R_{c S 2} - R_{c w} \end{array} \\ \begin{array}{l} \frac{c_{L}^{2} {\hat{s}}_{D_ν}^{2}}{c_{G}^{4} (l + R_{c w})} [\frac{R_{c w}^{3}}{2 R_{c S 1}^{3}} + \frac{R_{c S 2}^{2 n + 4}}{(2 n - 1) R_{c S 1}^{6} {(l + R_{c w})}^{2 n - 2}}] \\ = \frac{c_{L}^{2} {\hat{m}}_{D_ν}^{2}}{c_{G}^{4} (l + R_{c w})} [\frac{R_{c w}^{3}}{2 R_{c S 1}^{3}} + \frac{R_{c S 2}^{2 n + 4}}{(2 n - 1) R_{c S 1}^{6} {(l + R_{c w})}^{2 n - 2}}] l > R_{c S 2} - R_{c w} \end{array} \end{array} \end{array},

(69)

the force between a Dark I and an electron F_{D_νI^e} is

\begin{array}{l} F_{D_ν I^e} & = \{\begin{array}{l} \begin{array}{l} - \frac{{\hat{q}}_{e} {\hat{m}}_{D_ν}}{c_{G}^{2} {(l + R_{c w})}^{2}} - \frac{{\hat{q}}_{e} {\hat{s}}_{D_ν}}{c_{G}^{2} R_{c S 1}^{3}} (l + R_{c w}) - \frac{c_{L}^{2} {\hat{m}}_{e} {\hat{m}}_{D_ν}}{c_{G}^{4} {(l + R_{c w})}^{2}} \\ - \frac{c_{L}^{2} {\hat{m}}_{D_ν} {\hat{s}}_{e}}{c_{G}^{4} R_{c S 1}^{3}} (l + R_{c w}) - \frac{c_{L}^{2} {\hat{m}}_{e} {\hat{s}}_{D_ν}}{c_{G}^{4} R_{c S 1}^{3}} (l + R_{c w}) - \frac{c_{L}^{2} {\hat{s}}_{D_ν} {\hat{s}}_{e}}{c_{G}^{4} R_{c S 1}^{6}} {(l + R_{c w})}^{4} 0 \geq l \geq R_{c S 2} - R_{c w} \end{array} \\ - \frac{{\hat{q}}_{e} {\hat{m}}_{D_ν}}{c_{G}^{2} {(l + R_{c w})}^{2}} - \frac{c_{L}^{2} {\hat{m}}_{e} {\hat{m}}_{D_ν}}{c_{G}^{4} {(l + R_{c w})}^{2}} - \frac{c_{L}^{2} {\hat{s}}_{D_ν} {\hat{s}}_{e} R_{c S 2}^{2 n + 4}}{c_{G}^{4} R_{c S 1}^{6} {(l + R_{c w})}^{2 n}} l > R_{c S 2} - R_{c w} \end{array} \\ \approx \{\begin{array}{l} - \frac{c_{L}^{2} {\hat{s}}_{D_ν}^{2}}{c_{G}^{4} R_{c S 1}^{6}} {(l + R_{c w})}^{4} = \frac{c_{L}^{2} {\hat{m}}_{D_ν}^{2}}{c_{G}^{4} R_{c S 1}^{6}} {(l + R_{c w})}^{4} 0 \geq l \geq R_{c S 2} - R_{c w} \\ \begin{array}{l} - \frac{c_{L}^{2} {\hat{s}}_{D_ν}^{2}}{c_{G}^{4} {(l + R_{c w})}^{2}} [\frac{R_{c w}^{3}}{2 R_{c S 1}^{3}} + \frac{R_{c S 2}^{2 n + 4}}{R_{c S 1}^{6} {(l + R_{c w})}^{2 n - 2}}] \\ = - \frac{c_{L}^{2} {\hat{m}}_{D_ν}^{2}}{c_{G}^{4} {(l + R_{c w})}^{2}} [\frac{R_{c w}^{3}}{2 R_{c S 1}^{3}} + \frac{R_{c S 2}^{2 n + 4}}{R_{c S 1}^{6} {(l + R_{c w})}^{2 n - 2}}] l > R_{c S 2} - R_{c w} \end{array} \end{array} \end{array},

(70)

the potential energy between a Dark II and an electron E_{D_νII^e} is

\begin{array}{l} E_{D_ν I I^e} & = {[E_{G - D_ν I I - e - e} + E_{G - D_ν I I - w - e} + E_{S - D_ν I I - e - e} + E_{S - D_ν I I - w - e}]}_{r = l + R_{c S 2}} \\ = {[E_{G - D_ν I I - G - e} + E_{G - D_ν I I - S - e} + E_{S - D_ν I I - G - e} + E_{S - D_ν I I - S - e}]}_{r = l + R_{c S 2}} \\ = \frac{{\hat{q}}_{e} {\hat{m}}_{D_ν}}{c_{G}^{2} (l + R_{c S 2})} + \frac{c_{L}^{2} {\hat{m}}_{e} {\hat{m}}_{D_ν}}{c_{G}^{4} (l + R_{c S 2})} + \frac{c_{L}^{2} {\hat{s}}_{D_ν} {\hat{s}}_{e} R_{c S 2}^{2 n + 4}}{c_{G}^{4} (2 n - 1) R_{c S 1}^{6} {(l + R_{c S 2})}^{2 n - 1}} \\ \approx \frac{c_{L}^{2} {\hat{s}}_{D_ν}^{2}}{c_{G}^{4} (l + R_{c S 2})} [\frac{R_{c w}^{3}}{2 R_{c S 1}^{3}} + \frac{R_{c S 2}^{2 n + 4}}{(2 n - 1) R_{c S 1}^{6} {(l + R_{c S 2})}^{2 n - 2}}] \\ = \frac{c_{L}^{2} {\hat{m}}_{D_ν}^{2}}{c_{G}^{4} (l + R_{c S 2})} [\frac{R_{c w}^{3}}{2 R_{c S 1}^{3}} + \frac{R_{c S 2}^{2 n + 4}}{(2 n - 1) R_{c S 1}^{6} {(l + R_{c S 2})}^{2 n - 2}}] \end{array},

(71)

and the force between a Dark II and an electron F_{D_νII^e} is

\begin{array}{l} F_{D_ν I I^e} & = - \frac{{\hat{q}}_{e} {\hat{m}}_{D_ν}}{c_{G}^{2} {(l + R_{c S 2})}^{2}} - \frac{c_{L}^{2} {\hat{m}}_{e} {\hat{m}}_{D_ν}}{c_{G}^{4} {(l + R_{c S 2})}^{2}} - \frac{c_{L}^{2} {\hat{s}}_{D_ν} {\hat{s}}_{e} R_{c S 2}^{2 n + 4}}{c_{G}^{4} R_{c S 1}^{6} {(l + R_{c S 2})}^{2 n}} \\ \approx - \frac{c_{L}^{2} {\hat{s}}_{D_ν}^{2}}{c_{G}^{4} {(l + R_{c S 2})}^{2}} [\frac{R_{c w}^{3}}{2 R_{c S 1}^{3}} + \frac{R_{c S 2}^{2 n + 4}}{R_{c S 1}^{6} {(l + R_{c S 2})}^{2 n - 2}}] \\ = - \frac{c_{L}^{2} {\hat{m}}_{D_ν}^{2}}{c_{G}^{4} {(l + R_{c S 2})}^{2}} [\frac{R_{c w}^{3}}{2 R_{c S 1}^{3}} + \frac{R_{c S 2}^{2 n + 4}}{R_{c S 1}^{6} {(l + R_{c S 2})}^{2 n - 2}}] \end{array} .

(72)

6. The Structure Values of Primary Particles

In this chapter, we attempt to import the existing physical data into the computational results of the previous chapters to obtain the structural values of primary particles. Nowadays, we are fully aware of the characteristics of electricity, such as the charge, the potential energy, and the field, at both macro and micro levels. We can be confident that the available measurements reflect the characteristics of the electric charge and no other factors. Thus, comparing equation (45) to Gauss's law of electrostatics and combined equation (29), it can be easily found that the relation of the mathematical electric charge

{\hat{q}}_{e}

of an electron to an electron charge q_e in present physical data.

{\hat{q}}_{e} = c_{L} \sqrt{k} q_{e}

(73)

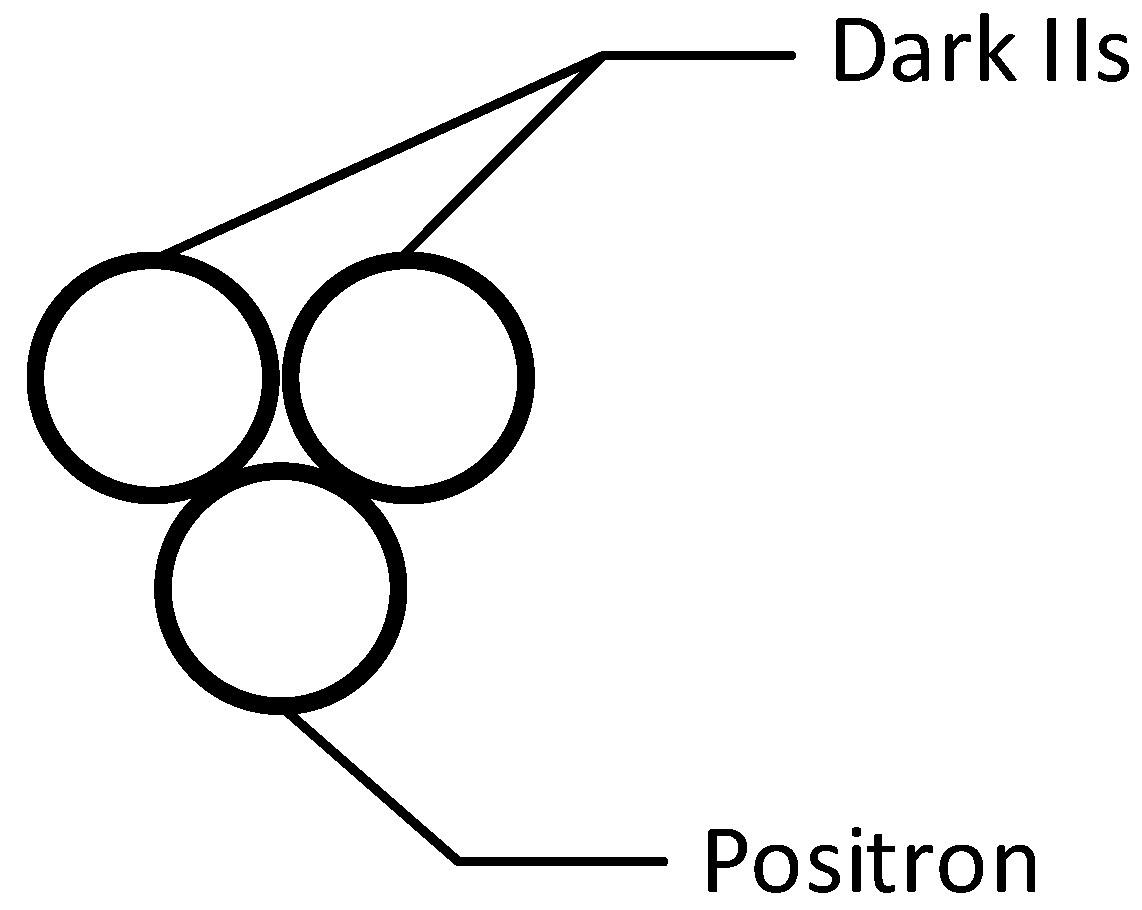
It is somewhat difficult to obtain the charges of gravity and the strong force because gravity is the weakest force in the four fundamental interactions, and the strong force is a short-range interaction. In the models of this paper, although the gravitational and inertial mass are different, it can be hypothesized that Newton's law of gravity is accurate to a large extent because only electron neutrinos in the model do not have gravitational waves and because electron neutrinos have much less biding-energy or rest mass. We focus on protons ---- stable, heavy subatomic particles ---- to explore these charges and start with the components of a proton. A combination of two attractive primary particles is easily separated by external action since there is no third particle to hold it back. However, the aggregation of multiple strongly attracted primary particles can cause the annihilation of these particles. Therefore, a combination of three high biding-energy, mutually attractive primary particles should be an extremely stable particle. Similar to the Quark model[7], it is supposed that a proton is composed of two Dark IIs and one positron instead of two up quarks and one down quark and has the structure of Figure 3 that will not delved into.

From equations (55), (56), (71), and (72), a proton might have the structure of Figure 3, and the mutual distances between the three primary particles are small, i.e.,

l \approx 0

, in a proton. It is further supposed that the kinetic energies of the three primary particles' mutual motion (including magnetic energy) are negligibly small compared to their binding-energies and potential energies. Hence, the energy of a proton E_p equals

\begin{array}{l} E_{p} & = 2 E_{D_ν I I} + E_{e} + {[E_{D_ν I I^D_ν I I} + 2 E_{D_ν I I^e}]}_{l = 0} \\ \approx \frac{2 c_{L}^{2} R_{c S 2}^{5} {\hat{m}}_{D_ν}^{2}}{(2 n - 1) c_{G}^{4} R_{c S 1}^{6}} + E_{e} + \frac{2 c_{L}^{2} {\hat{m}}_{D_ν}^{2}}{c_{G}^{4} (l + R_{c S 2})} {[1 + \frac{R_{c S 2}^{2 n + 4}}{(2 n - 1) R_{c S 1}^{6} {(l + R_{c S 2})}^{2 n - 2}}]}_{l = 0} \\ + 2 \frac{c_{L}^{2} {\hat{m}}_{D_ν}^{2}}{c_{G}^{4} (l + R_{c S 2})} {[\frac{R_{c w}^{3}}{2 R_{c S 1}^{3}} + \frac{R_{c S 2}^{2 n + 4}}{(2 n - 1) R_{c S 1}^{6} {(l + R_{c S 2})}^{2 n - 2}}]}_{l = 0} \\ \approx \frac{6 c_{L}^{2} R_{c S 2}^{5} {\hat{m}}_{D_ν}^{2}}{(2 n - 1) c_{G}^{4} R_{c S 1}^{6}} \approx 6 E_{D_ν I I} \end{array}

(74)

when equations (38), (55), and (71) are subsequently substituted in the above equation, and the energy of an electron E_e is neglected in the above equation because E_p is 1836 times E_e (E_p = 938MeV, E_e = 0.511MeV)^{[7, 8]}. Furthermore,

{\hat{m}}_{D_ν} = \frac{c_{G}^{2} \sqrt{G}}{4 c_{L}} m_{p}

(75)

can be obtained from equations (30) and (40), where m_p is the mass of a proton.

Next, by combing equations (43), (44), and (73) to (75), we have

\{\begin{array}{l} \frac{R_{c w}^{3}}{R_{c S 1}^{3}} = \frac{8 \sqrt{k} q_{e}}{\sqrt{G} m_{p}} \\ \frac{\sqrt{k} q_{e} \sqrt{G} m_{p}}{8} \frac{R_{c S 2}^{2} - R_{c w}^{2}}{R_{c S 1}^{3}} = E_{e} \\ \frac{3 G m_{p}^{2}}{8 (2 n - 1)} \frac{R_{c S 2}^{5}}{R_{c S 1}^{6}} = E_{p} \end{array}

(76)

that we can solve and yield

\begin{array}{l} {[\frac{8 (2 n - 1) E_{p}}{3 G m_{p}^{2}}]}^{\frac{2}{5}} R_{c S 1}^{\frac{2}{5}} - \frac{8 E_{e}}{\sqrt{k} q_{e} \sqrt{G} m_{p}} R_{c S 1} = {[\frac{8 \sqrt{k} q_{e}}{\sqrt{G} m_{p}}]}^{\frac{2}{3}} \\ {[\frac{8 (2 n - 1) \times 938.272 \times 10^{6} \times 1.60218 \times 10^{- 19}}{3 \times 6.67430 \times 10^{- 11} \times {(1.67262 \times 10^{- 27})}^{2}}]}^{\frac{2}{5}} R_{c S 1}^{\frac{2}{5}} \\ - \frac{8 \times 510.999 \times 10^{3} \times 1.60218 \times 10^{- 19}}{\sqrt{8.98755 \times 10^{9}} \times 1.60218 \times 10^{- 19} \times \sqrt{6.67430 \times 10^{- 11}} \times 1.67262 \times 10^{- 27}} R_{c S 1} \\ = {[\frac{8 \sqrt{8.98755 \times 10^{9}} \times 1.60218 \times 10^{- 19}}{\sqrt{6.67430 \times 10^{- 11}} \times 1.67262 \times 10^{- 27}}]}^{\frac{2}{3}} \\ {[(2 n - 1) R_{c S 1}]}^{\frac{2}{5}} - 5.8394 \times 10^{11} R_{c S 1} = 7.9425 \times 10^{- 10} \end{array} .

(77)

Evidently, R_cS1 is very small from the above equation. Hence

\begin{array}{l} {[(2 n - 1) R_{c S 1}]}^{\frac{2}{5}} \approx 7 . 9425 \times 10^{- 10} \\ R_{c S 1} = \frac{1 . 78 \times 10^{- 23}}{2 n - 1} (m) = \frac{1 . 78 \times 10^{- 8}}{2 n - 1} (fm) \end{array} .

(78)

\begin{array}{l} R_{c w} & = {(\frac{8 \sqrt{k} q_{e}}{\sqrt{G} m_{p}})}^{\frac{1}{3}} R_{c S 1} = {(\frac{8 \sqrt{8 . 98755 \times 10^{9}} \times 1 . 6021 8 \times 10^{- 19}}{\sqrt{6 . 67430 \times 10^{- 11}} \times 1.67262 \times 10^{- 27}})}^{\frac{1}{3}} R_{c S 1} \\ = 2 . 0718 \times 10^{6} R_{c S 1} = \frac{3 . 68 \times 10^{- 17}}{2 n - 1} (m) = \frac{3 . 68 \times 10^{- 2}}{2 n - 1} (fm) \end{array} .

(79)

Since in the solution of R_cS1 from equation (76), we actually make

{[\frac{8 (2 n - 1) E_{p}}{3 G m_{p}^{2}}]}^{\frac{2}{5}} R_{c S 1}^{\frac{2}{5}} = {[\frac{8 \sqrt{k} q_{e}}{\sqrt{G} m_{p}}]}^{\frac{2}{3}}

, i.e.,

\frac{8 (2 n - 1) E_{p}}{3 G m_{p}^{2}} R_{c S 1} = {[\frac{8 \sqrt{k} q_{e}}{\sqrt{G} m_{p}}]}^{\frac{5}{3}}

, which can derive

\frac{R_{c S 2}^{5}}{R_{c S 1}^{5}} = {[\frac{8 \sqrt{k} q_{e}}{\sqrt{G} m_{p}}]}^{\frac{5}{3}}

from

\frac{3 G m_{p}^{2}}{8 (2 n - 1)} \frac{R_{c S 2}^{5}}{R_{c S 1}^{6}} = E_{p}

and tell us that R_cS2 and R_cw are almost equal. This computational procedure is not precise enough, so we use

\frac{\sqrt{k} q_{e} \sqrt{G} m_{p}}{8} \frac{R_{c S 2}^{2} - R_{c w}^{2}}{R_{c S 1}^{3}} = E_{e}

in equation (76) to solve R_cS2

\begin{array}{l} R_{c S 2} & = \sqrt{\frac{8 E_{e}}{\sqrt{k} q_{e} \sqrt{G} m_{p}} R_{c S 1}^{3} + R_{c w}^{2}} \approx R_{c w} [1 + \frac{4 E_{e}}{\sqrt{k} q_{e} \sqrt{G} m_{p}} \frac{R_{c S 1}^{2}}{R_{c w}^{2}} R_{c S 1}] \\ = R_{c w} [1 + \frac{4 E_{e}}{\sqrt{k} q_{e} \sqrt{G} m_{p}} {(\frac{\sqrt{G} m_{p}}{8 \sqrt{k} q_{e}})}^{\frac{2}{3}} \frac{3 G m_{p}^{2}}{8 (2 n - 1) E_{p}} {(\frac{8 \sqrt{k} q_{e}}{\sqrt{G} m_{p}})}^{\frac{5}{3}}] \\ = R_{c w} [1 + \frac{1}{2 n - 1} \frac{12 E_{e}}{E_{p}}] = R_{c w} [1 + \frac{1}{2 n - 1} \frac{12 \times 510 . 999 \times 10^{3}}{938 . 272 \times 10^{6}}] \\ = (1 + \frac{6.54 \times 10^{- 3}}{2 n - 1}) R_{c w} \\ = (\frac{3 . 68 \times 10^{- 2}}{2 n - 1}) (1 + \frac{6.54 \times 10^{- 3}}{2 n - 1}) (fm) \end{array} .

(80)

Based on equation (74) the biding-energy of a Dark II E_{D_νII} is

E_{D_ν I I} \approx \frac{E_{p}}{6} = \frac{938 . 272}{6} = 156 (MeV) .

(81)

From equation (38), the biding-energy of a Dark I E_{D_νI} is

\begin{array}{l} E_{D_ν I} & \approx \frac{2 (n + 2)}{5} E_{D_ν I I} = \frac{(n + 2) E_{p}}{15} = (n + 2) \times \frac{938 . 272}{15} \\ = (n + 2) \times 62.6 (MeV) \end{array} .

(82)

However, I have not found a way to calculate the energy of an electron neutrino E_{e_ν}, which also leads to an inability to determine the tiny difference between gravitational and inertial mass, especially when

{\hat{m}}_{e} = \frac{c_{G}^{2} \sqrt{G} m_{e}}{c_{L}}

It can be determined that m > n since R_cS2 ≈ R_cw and the effective range of the weak interaction is smaller than the one of strong interaction. I would suggest further that n = 3 and m = 5 because they seem to fit the current knowledge of strong and weak interactions, and 1, 3, 5 is a tiny, pretty odd series. Of course, exactly how many m, n can only be obtained experimentally.

The gravity speed c_G can easily get from equations (46) and (80)

c_{G} = \frac{R_{c S 2}}{R_{c w}} c_{L} = (1 + \frac{6.54 \times 10^{- 3}}{2 n - 1}) c_{L} .

(83)

In addition, the energy definition equations (14) and (17) reveal that regardless of the light speed c_L or the gravity speed c_G, there is an invariant that is the rest mass m₀. Therefore, we can obtain the relation of momentum and energy between the two measurement media of light and gravitational waves

\frac{1}{c^{2}} (p_{x}^{2} + p_{y}^{2} + p_{z}^{2} - \frac{E^{2}}{c^{2}}) = \frac{1}{{c^{'}}^{2}} ({p^{'}}_{x}^{2} + {p^{'}}_{y}^{2} + {p^{'}}_{z}^{2} - \frac{{E^{'}}^{2}}{{c^{'}}^{2}})

(84)

from the relationship between momentum and energy in Special Relativity

p_{x}^{2} + p_{y}^{2} + p_{z}^{2} - \frac{E^{2}}{c^{2}} = - m_{0}^{2} c^{2}

. Equation (84) directly derives the relation of space-time between the two measurement media

\frac{1}{c^{2}} (d x^{2} + d y^{2} + d z^{2} - c^{2} d t^{2}) = \frac{1}{{c^{'}}^{2}} (d {x^{'}}^{2} + d {y^{'}}^{2} + d {z^{'}}^{2} - c^{2} d {t^{'}}^{2}) .

(85)

So the proper time τ is the same in all reference frames with the two measurement media.

7. Conclusions and Discussions

In this paper, field and energy equations for strong and weak interactions are derived based on a set of fundamental assumptions that are consistent with existing knowledge. With the help of these equations, the structures of the primary particles are established, and the interactions between two primary particles are analyzed. The characteristic parameters of the primary particles (Table 1) are computed from the present physical data.

Moreover, we can derive the matrix

(\begin{matrix} \cos θ & \sin θ e^{- i φ} \\ \sin θ e^{i φ} & - \cos θ \end{matrix})

when we rewrite the quantum factors in equations (32), (35), (37), and (41) as

(\begin{matrix} \cos θ & \sin θ e^{- i φ} \\ \sin θ e^{i φ} & \cos θ \end{matrix})

and multiply it by the Pauli matrix

(\begin{matrix} 1 & 0 \\ 0 & - 1 \end{matrix})

(\begin{matrix} \cos θ & \sin θ e^{- i φ} \\ \sin θ e^{i φ} & - \cos θ \end{matrix})

has well-known results in quantum mechanics with eigenvalues of ±1 and eigenvectors of

(\begin{matrix} \cos \frac{θ}{2} \\ \sin \frac{θ}{2} e^{i φ} \end{matrix})

(\begin{matrix} \sin \frac{θ}{2} e^{- i φ} \\ - \cos \frac{θ}{2} \end{matrix})

, i.e., spin values

\pm \frac{1}{2}

. Thus the conclusions of this paper are compatible with existing physical-mathematical methods.

Furthermore, the interactive analysis reveals that:

The Self-Conjugation condition is that two primary particles have no initial phase difference in zenith and azimuthal angle. Two Self-Conjugation primary particles have potential energy or force when they rotate in the same direction. However, they have zero potential energy or rest when they spin in opposite directions. It is one of the foundations of the Pauli exclusion principle.
Dark Is have the asymptotic freedom characteristic, but following the principle of energy minimization, there should only be Dark IIs in most cases.
The force between two electrons has three values, one large, one small, and one zero.
Whether two electron neutrinos or an electron neutrino and an electron attract or repel each other is randomized. Because of this, electron neutrinos are a weak destabilizer in the nucleus, and even though the binding-energy of electron neutrinos is the smallest, no signs of neutrino destruction have been found so far.
Primary particles behave perfect tiny spheres in terms of energy and interactions, but they also look like uneven minuscule spheres in external fields. Which is the reality of a primary particle? Observation or mathematics? The answer should be that "the Moon is always there, doesn't matter we see it or not", however, the Moon is changed when we see it.

In the interactive analysis, the Self-Conjugate Mechanism plays a significant role in the microscopic domain. Consider the case when external actions cause a combination of two primary particles to rotate from the same to different directions until they are opposite and separated. So the two primary particles have the opposite direction of spin, or in other words, they entangle themselves after the separation. Evidently, the distance of quantum entanglement is finite, not infinite like currently believed, because the strength of fields around primary particles decreases with distance. The transmission speed of quantum entanglement is the speed of light or gravity. Einstein is right in this case.

In addition, the gravity speed c_G is slightly larger than the light speed c_L

(\frac{c_{G}}{c_{L}} = 1 + \frac{6.54 \times 10^{- 3}}{2 n - 1})

, and the rest mass m₀, the proper time τ are the invariants with the two measurement media of light and gravity. Gravity might have similar quantum characteristics, such as

E_{G} = h_{G} ν_{G}

. What are the quantum characteristics of weak and strong interactions?

It can be further hypothesized that a dark matter is formed when the positron in a proton is replaced by one Dark II. Therefore, the energy of a dark matter E_dm is

\begin{array}{l} E_{d m} & = 3 E_{D_ν I I} + 3 {[E_{D_ν I I^D_ν I I}]}_{l = 0} \\ = \frac{3 c_{L}^{2} R_{c S 2}^{5} {\hat{m}}_{D_ν}^{2}}{(2 n - 1) c_{G}^{4} R_{c S 1}^{6}} + \frac{6 c_{L}^{2} {\hat{m}}_{D_ν}^{2}}{c_{G}^{4} (l + R_{c S 2})} {[1 + \frac{R_{c S 2}^{2 n + 4}}{(2 n - 1) R_{c S 1}^{6} {(l + R_{c S 2})}^{2 n - 2}}]}_{l = 0} \\ \approx \frac{9 c_{L}^{2} R_{c S 2}^{5} {\hat{m}}_{D_ν}^{2}}{(2 n - 1) c_{G}^{4} R_{c S 1}^{6}} \approx 9 E_{D_ν I I} = \frac{3}{2} E_{p} \end{array},

(86)

and the mathematical mass of a dark matter

{\hat{m}}_{d m}

{\hat{m}}_{d m} = 6 {\hat{m}}_{D_ν} = \frac{3 c_{G}^{2} \sqrt{G}}{2 c_{L}} m_{p}

(87)

from equations (38) and (55). Equations (86) and (87) remind us again that the difference between gravitational and inertial mass is almost negligible. Certainly, it is also reasonable to assume that a combination of three Dark IIs was annihilated by itself, and there are only free-state Dark IIs as dark matters in our cosmic, since no particle heavier than a proton is as stable as a proton. Or, are we listening to a concerto for solo, triple Dark IIs, and conventional matters in our universe today?

Let us imagine now what will happen when all primary particles in our universe will gather, be crushed, till be destroyed at a point. This consequence should be similar to electron annihilation. There will only be the four fundamental waves with vast high energy in our universe at that moment, namely the scene of the Big Bang.

It is worth noting that this paper cannot answer why positrons and negative protons are so rare in our universe, which means Dark IIs incarcerate only positrons.

References

弱相互作用力. Available online: https://baike.baidu.com/item/%E5%BC%B1%E7%9B%B8%E4%BA%92%E4%BD%9C%E7%94%A8%E5%8A%9B/3960960?fromtitle=%E5%BC%B1%E5%8A%9B&fromid=8723711&fr=aladdin.
weak interaction. https://www.britannica.com/science/weak-force.
Weak interaction. https://en.wikipedia.org/wiki/Weak_interaction.
强相互作用. Available online: https://baike.baidu.com/item/%E5%BC%BA%E7%9B%B8%E4%BA%92%E4%BD%9C%E7%94%A8/830790?fr=ge_ala.
Strong interaction. https://en.wikipedia.org/wiki/Strong_interaction.
strong force. https://www.britannica.com/science/strong-force.
Proton. https://en.wikipedia.org/wiki/Proton.
Fundamental constants of physics. https://physics.nist.gov/cuu/Constants/index.html.

Figure 1. Schematic structures of a primary particle.

Figure 2. Energy conversion between two primary particles.

Figure 3. Schematic structure of a proton.

Table 1. Characteristic Parameters of the Primary Particles.

Particle Name	Biding-Energy^* (MeV)	Elementary Charge (e)	Spin	Radius^* (fm)	Determinants of Radius
Electron	0.511 (Known quantity)	±1	$\pm \frac{1}{2}$	$\frac{3 . 68 \times 10^{- 2}}{2 n - 1}$	Critical radius of weak interaction R_cw
Electron Neutrino	N.A.	0	$\pm \frac{1}{2}$	$\frac{3 . 68 \times 10^{- 2}}{2 n - 1}$	Critical radius of weak interaction R_cw
Dark I	$(n + 2) \times 62.6$	0	$\pm \frac{1}{2}$	$\frac{1 . 78 \times 10^{- 8}}{2 n - 1}$	1^st critical radius of strong interaction R_cS1
Drak II	156	0	$\pm \frac{1}{2}$	$(\frac{3 . 68 \times 10^{- 2}}{2 n - 1}) (1 + \frac{6.54 \times 10^{- 3}}{2 n - 1})$	2^nd critical radius of strong interaction R_cS2

* ----

n = 2, 3, 4, ......

(Undetermined, suggested by 3).

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

The Models of Primary Particles

Abstract

Abstract

1. Introduction

2. The Formation of Primary Particles

3. The Fields and Binding-Energy

4. The Structures of Primary Particles

4.1. An Electron Neutrino

4.2. Dark Neutrinos

4.3. An Electron or A Positron

5. The Interactions Between Two Primary Particles

5.1. Two Particles of the Same Type

5.2. Two Particles of the Different Type

6. The Structure Values of Primary Particles

7. Conclusions and Discussions

References

MDPI Initiatives

Important Links

Subscribe