Prerpints.org logo
Preprint
Article

How Satellite Altimetry Data Can Help Us Understand Sea Level Fluctuations and Classify Water Drainage Areas in the Caspian Sea

Altmetrics

Downloads

138

Views

134

Comments

0

This version is not peer-reviewed

Submitted:

14 January 2024

Posted:

15 January 2024

You are already at the latest version

Alerts
Abstract
This study introduces a technique to uncover concealed patterns in satellite altimetry data, reflecting sea level variations in inland water bodies. We applied the methodology to the Caspian Sea, using altimetry data from four satellite missions over 27 years (1993-2020): TOPEX/Poseidon, Jason1, Jason2, and Jason3. The approach involves two steps: estimating sea level trends and identifying breakpoints that indicate trend shifts; and leveraging time lags between breakpoints at various locations to classify water drainage areas according to their degree of influence on each period. By revealing concealed patterns in the altimetry data, this technique can provide insights to understand the impacts of global warming and local climate changes on sea level fluctuations in the Caspian Sea. We hope that our study can facilitate subsequent interdisciplinary research on the intricate interplay between climate change and hydrological processes in inland water bodies.
Keywords: 
Subject: Environmental and Earth Sciences  -   Remote Sensing

1. Introduction

The Caspian Sea, the world’s largest enclosed water body, covers approximately 371,000 square kilometers and contains around 78,200 cubic kilometers of water (Millero et al. 2008) . Its sea level fluctuated significantly over centuries, ranging from -29 meters to -25 meters relative to the global mean sea level (Ataei et al. 2019; Arpe and Leroy 2007). The Caspian Sea’s isolation from the oceans renders its level sensitive to the balance of river inflow, precipitation, and evaporation loss, and the influence of global warming and local climate changes on the patterns of deriving issues on sea level change (J. L. Chen et al. 2017; Arpe and Leroy 2007; Lahijani et al. 2023). To understand the mechanisms behind the sea-level dynamics in this enclosed water body, one must also consider factors such as tectonic movements, human activities, and sedimentation (Firoozfar et al. 2012; Kaplin and Selivanov 1995; Ollivier et al. 2016).
The utilization of satellite altimetry data, particularly from missions like TOPEX/Poseidon to Sentinel6, plays a crucial role in monitoring inland water bodies that are highly susceptible to climate changes. As highlighted by Asadzadeh Jarihani et al. (2013) and Troitskaya et al. (2012), these data enable us to track sea level fluctuations, which can significantly impact the economy, livelihoods of surrounding communities, and the natural ecosystems in these areas. Given the interconnected nature of Earth's ecosystems, changes in one area can have far-reaching effects. Therefore, it is needed to continuously monitor sea level variations in inland water bodies, understand their causes, and work towards mitigating their impacts (Hofmann et al. 2008). Satellite altimetry observations provide us with invaluable long-term data, allowing us to uncover hidden patterns and gain essential insights into these critical environmental dynamics. This underscores the importance of dedicated efforts to analyze and interpret this data, as it represents our best source of information in this context.
Recent studies utilizing satellite altimetry have significantly advanced our understanding of sea level variations in different environments. For instance, Ghosh et al. (2018) found a positive trend in sea level rise in the Bay of Bengal from 1993 to 2010, attributed to thermal expansion and water mass discharge. Watson (2019) focused on accurately accounting for vertical land motions at tide gauge sites using global navigation satellite systems and evaluated the use of gridded satellite altimetry products for estimating vertical land motions in 20 locations worldwide. Xu et al. (2022) emphasized the importance of monitoring global lake and reservoir water levels using altimetry data, finding methods a significant rise in water levels from 2003 to 2021. Moradi et al. (2019) studied the Caspian Sea's unique water level fluctuations due to changes in temperature and salinity, while Chen et al. (2017) reconstructed long-term Caspian Sea level changes. Additionally, Jain et al. (2012) suggested to determine sea surface height variations in the Arctic Ocean using satellite data, and Amollo (2013) analyzed tide gauge sea level observations in the southwest Indian Ocean and the East coast of Africa, attributing variability to various factors, including longer-term climate phenomena. These studies clearly highlighting the complex interplay of factors influencing sea level fluctuations, including thermal expansion, water mass discharge, climate-driven precipitation and evaporation, and the impact of local and global climate phenomena.
Followings are studies that are outstanding for shedding light on the multifaceted nature of Caspian Sea level changes. Asakereh and Varnaseri (2021) conducted a comprehensive analysis of precipitation patterns along the Iranian coast of the Caspian Sea, revealing higher annual precipitation along the coastline with varying coefficients of variation and month-to-month changes, and identifying spatial patterns and seasonal variations in precipitation. Chen et al. (2017), Azizpour and Ghaffari (2023) and Arpe and Leroy (2007) linked sea level decrease to reduced Volga River discharge, while Jiang and You (2022) emphasized large seasonal variations and a significant drop in sea level. Kitazawa and Yang (2012) focused on water circulation and thermohaline structures, whereas Lavrova and Mityagina (2017) studied the internal waves in non-tidal seas. Furthermore, Chen et al. (2017) and Cazenave et al. (1997) explored long-term changes, with Chen et al. (2023) specifically highlighting a significant decreasing trend and notable acceleration since around 2005 using satellite altimeter data. Lebedev (2018) study using satellite altimetry indicated a shift in sea level in the mid-1970s, while Lebedev and Kostianoy (2008) found oscillations in sea level from related hydrometeorological processes. Masoud et al. 2022 revealed diurnal baroclinic current signals and surface height changes due to sea breeze influence. Lavrova et al. (2019) addressed oil pollution in the Caspian Sea and introduced a Russian Science Foundation Project. Kostianoy et al. (2018) monitored various parameters of the Caspian Sea using satellite data. Amirinia et al. (2017) estimated wind and wave energy potentials in the southern Caspian Sea. Azizpour and Ghaffari (2023) analyzed seasonal and long-term changes in the Caspian Sea level using historical tide gauge data. Kouraev et al. (2011) discussed the significance of interannual sea level changes and satellite altimetry potential for enclosed water bodies.
The study presented here is devoted to the Caspian Sea level changes over the period from 1993 to 2020. To achieve this, we have employed altimetry data, from four satellite missions of TOPEX/Poseidon, Jason1, Jason2, and Jason3. The approach is based on a temporal and spatial latency of sea level trend fluctuations, an overlooked aspect, yet with the potential of providing insights into the impact of drainage basins on the fluctuation patterns of inland water bodies, such as the Caspian Sea. With this introduction, we proceed to the next sections of the paper which are structured as follows: Section 2 provides a comprehensive discussion of the data utilized in this study and the implemented corrections. Section 3 outlines the way that we have generated along-track time series using the satellite altimetry data. The modeling of Caspian Sea level fluctuation trends using an eighth-degree polynomial is elaborated in Sect. 4. Section 5 details the application of the Baarda method, which serves to remove outliers within the sea surface height (SSH) data. Section 6 focuses on the extraction of the information from the modeled trend functions and the development of a filtering procedure designed to identify the influence of drainage basins on the observed Caspian Sea level variations. The numerical computations employed and their application are discussed in Sect. 7. Section 8 comprehensively discusses the achievements and implications of the study. Finally, Sect. 9 presents the conclusion and final discussions. By following this structure, we aim to show how satellite altimetry data can help us to understand sea level fluctuations and classify water drainage areas in the Caspian Sea and other similar inland water bodies.

2. Data preparation

Our computations is based on the 1Hz GDR data, downloaded from AVISO database with the details given in Table 1.
We use the formula below to calculate the corrected SSH observations from the GDR data in Table 1.
Corrected   SSH = Altitude − ( Range + Corrections )
The SSH observations in this study include the following corrections: atmospheric (dry and wet), ionospheric, tide (solid and pole), sea surface topography fluctuations, and sea state bias. We exclude the ocean tide and load corrections, because the Caspian Sea is a closed basin with no tidal variations, and it is too far from the oceans to experience any tidal load effect. We also exclude the inverse barometer correction, because the non-tidal water bodies have periodic signals mainly caused by atmospheric and hydrodynamic effects, and these signals do not influence trend modeling. By excluding the inverse barometer correction, we also avoid possible errors in the SSH observations due to the correction’s imperfection. We will demonstrate that our mathematical model can successfully separate the trend, which is our signal of interest, from the periodic effects.

3. Time series development

We followed these steps to build the time series from the repeated SSH observations within all cycles of the selected satellite altimetry missions. First, we selected the tracks that cover our research area. Then, we used the coordinates of 1Hz observations along the tracks from one cycle as the reference points for our time series development. We identified and interpolated any missing observation points in the selected cycle. Next, we considered a 3km circle around each reference point and searched for SSH observations inside the circle in the subsequent cycles. We added these observations to the time series at the reference point. This way, we included all the SSH values in the GDR files in our time series along the altimetry tracks over the area of interest.

4. Polynomial fit to model the sea level variation trend

To fit the SSH observations, we use a polynomial of degree 8, which we selected by testing different degrees and finding the best one that can capture the sea level trend variations. The Caspian Sea level has several trend fluctuations, and the polynomial of degree 8 can follow them perfectly. Equation (1) shows the polynomial that we use.
S S H t = a 0 + ∑ n = 1 8 a n t n
where, SSH(t) is the observed sea surface height at time t. The coefficients a0, a1, …, a8 of the polynomial function of degree 8 are obtained by fitting the SSH data within each time series using the least squares method. This requires solving the following system of linear equations.
e + l = A x
In Eq. (2), the variables are defined as follows: l represents a vector of length m containing the SSH values within a time series, A is an m by n matrix containing the basis functions evaluated at each observation time, x is a vector of length n containing the unknown coefficients of the basis functions, and e is a vector of length m containing the unknown residuals, as follows
l = S S H ( t 1 ) ⋮ S S H ( t m ) , e = e 1 ⋮ e m   A = 1 ⋮ 1 t ⋮ t t 2 ⋮ t 2 … ⋱ … t 8 ⋮ t 8 , x = a 0 a 1 ⋮ a 8
To find x from l and A, we use the method of least squares adjustment as shown in equations (4), (5) and (6).
x ^ = ( A T Q l − 1 A ) − 1 A T Q l − 1 l
e ^ = A x ^ − l
Q x ^ = ( A T Q l − 1 A ) − 1
Equation (4) gives the least square estimated unknown vector ( x ^ ) by multiplying the inverse of the normal matrix ( A T Q l − 1 A ) − 1 with the transpose of the design matrix ( A T ) and the weighted observation vector ( Q l − 1 l ). Equation (5) gives the estimated residual vector ( e ^ ) by subtracting the observation vector (l) from the product of the design matrix (A) and the least square estimated unknow vector ( x ^ ). Equation (6) gives the estimated covariance matrix of x ^ by taking the inverse of the normal matrix ( A T Q l − 1 A ) − 1 . The observation covariance matrix ( Q l ) and its inverse Q l − 1 are used to weight the observations according to their expected variances. The elements of Q l − 1 show how much each observation influences the solution.

5. Outlier detection and removal

To get the final trend model based on the polynomial of degree 8, we need to remove the outliers from the time series of SSH observations along the altimetry tracks. We apply the Baarda test for outliers, which uses the following statistics (Baarda 1968; Teunissen 2000; Teunissen et al. 2005):
w i = c i T Q l − 1 e ^ c i T Q l − 1 Q e ^ Q l − 1 c i
ci is a vector with one in the ith position and zero elsewhere, and Q e ^ is the covariance matrix of the residuals e ^ calculated as:
Q e ^ = Q l -   A ( A T Q l - 1 A ) - 1 A T
We test the statistics in Eq. (7) based on the following hypotheses (Baarda 1968; Teunissen 2000; Teunissen et al. 2005):
H 0 : w i   ~ N ( 0 , 1 ) H a : w i ~ N ( ∇ w , 1 )
The null hypothesis assumes that the residuals are normal with zero mean and unit variance. The alternative assumes that the residuals have a non-zero mean. The test statistic from Eq. (7) follows a chi-squared distribution under the null hypothesis. If the test statistic is larger than a certain threshold, the null hypothesis is rejected and the residual is marked as an outlier.

6. The significance of the trend models and the information extracted from them

In our study, we have utilized an eighth-degree polynomial to analyze sea level trends along the altimetry tracks of the Caspian Sea. This method effectively eliminates periodic content of the sea surface height (SSH) observations, allowing for a clearer depiction of sea level trend variations at specific time series locations. The models derived from this approach have proven instrumental in identifying trend changing points, a pivotal aspect of our research. These turning points, indicated by local minima and maxima in the fitted polynomials, have enabled us to pinpoint epochs of sea level trend variations in the Caspian Sea. Our examination has revealed four distinct time intervals of trend fluctuations around the years 1995, 2000, 2005, and 2020. We considered a period of ±1.5 year over the years 1995, 2000, 2005, and 2020 and searched for the local extremum points of the eighth degree polynomial at each time series. This way, we found the exact periods of the trend changing points at each location. The trend change in 2020 is noteworthy, as it occurs near the end of our time series. It requires longer time series and validation through future observations. Moreover, the trend changing epochs vary across different locations in each time interval, revealing valuable insights into the sequence and timing differences of drainage basin impacts. This information, if properly extracted, can help us investigate the causes of each trend change period.
In our analysis, despite the various adjustments and removal of outliers, the identified epochs of trend changing points still exhibit a significant level of noise, rendering them unsuitable for direct use in our intended applications. Consequently, it becomes necessary to pinpoint the time series that consistently and systematically convey relevant information, and to base our classification of drainage basin influence solely on the signals derived from these time series during each trend changing time interval. Our numerical findings underscore the necessity of implementing a proper filtering procedure, as without it, the concealed signals within the trend changing epochs remain undetected. Therefore, a key contribution of our study lies in the development of filters designed to identify and extract this hidden information. The forthcoming section is devoted to the details of how these filters are developed and applied.

Filtering procedure of the epoch of turning points

Our filtering procedure begins by examining the derived epoch of trend changes at time series locations for each trend change interval individually. To do this, we first create colormaps of the derived changing epochs at their respective time series, aiming to identify the track with the most consistent epoch variations, which we refer to as the “main-track”. Following this, we pinpoint the cross-overs along main-track that also exhibit the most consistent trend changing epoch values, termed as "main-cross-overs". In this way implicitly we select the track and cross-overs that are having the most accurate SSH observations that is exhibited in the trend modeling and the trend changing epochs that we have extracted from the trend model. The main-track is the longest over the Caspian Sea and is sufficiently distanced from the coasts, allowing for the allocation of time series with more accurate SSH observations. Additionally, the main-cross-overs along this track are situated at a good distance from the coasts. Ultimately, our criterion for selecting main-track and the main-cross-overs is the quality of the derived trend changing epochs, as evidenced by their consistent values in the colormap plot.
At each main-cross-over, we identify neighboring time series within a 30km radius at both crossing tracks. Next, we round the trend changing epoch at these time series to the nearest integer (in years), apply the mode operator to find the time series having the mode value, and calculate the mean of their initial trend changing epoch values before rounding. This mean value is then assigned to the time series at the main-cross-over. Subsequently, we start from one side of the main-track, and group every 11 time series along the track, continuing this grouping to the other end. The last group segment may contain fewer than 11 time-series. We then focus on the group of selected time series containing one of our main-cross-overs. Applying a band pass filter to the trend changing epoch values within this group, we identify the time series whose trend changing epochs fall within a specific band centered on the value of the main-cross-over, with a threshold of ± 0.17 years. In this process, time series with trend changing epochs within this specified interval are retained, while others are eliminated. The mean of these remaining trend changing epochs is calculated and assigned to the time series locations within the group. Additionally, this mean value is used as the center-value for the bandpass filter of the next group of time series on both sides of the main-cross-over, with a threshold of ±0.17 years. This procedure is initiated using all the main-cross-overs as the starting point of the filtering, ensuring that every time series along the main-track receives as many filtered values as the number of main-cross-overs. The distances of all time series along the main-track to the main-cross-overs are then determined and sorted, with the inverse of the sorting rank serving as the weight for the filtered value computed from each main-cross-over. Using these weights, a weighted mean is calculated from the filtered trend changing epoch values for each time series along the main-track, including main-cross-overs, and allocated to the corresponding time series location.
The scheme of grouping every 11 time series is also applied to the tracks which intersect with the main-track. Next, we apply the same filtering process along these intersecting tracks, starting from the corresponding cross-over with its filtered value in the previous procedure. We will explain this custom filtering procedure in more detail in the following numerical computation sections.

7. Numerical computations and results

In order to assess the effectiveness of our trend analysis method, which operates as a form of data mining by identifying patterns within a dataset, we performed numerical computations using the 1Hz GDR data outlined in Table 1. This dataset comprises sea surface height (SSH) measurements over the Caspian Sea, collected from four distinct satellite altimetry missions (TOPEX/Poseidon, Jason1, Jason2, and Jason3) spanning a period of 27 years.

7.1. Time series development

In order to analyze the long-term fluctuations and trends of sea level in the Caspian Sea, we relied on consistent and uninterrupted Sea Surface Height (SSH) measurements obtained from the mentioned satellite missions. Our data processing procedure encompassed several key steps. Firstly, we acquired the relevant data outlined in Table 1 from the AVISO datacenter. Subsequently, we applied the necessary corrections, as detailed in Section 2, to the 1Hz SSH data derived from the GDR files. Following this, we constructed along track time series by leveraging repeated SSH observations within the cycles. This involved two primary actions: (a) selecting the 1Hz GDR observation points of one cycle and establishing the observation points at every 6 km over the Caspian Sea as the coordinates of the time series, and (b) utilizing a 3 km search circle to identify the observations within each circle as the time series elements linked to the center point coordinate of the search circle. We spanned the beginning of the time series of SSH observations on 21st March 1993 and the end on 21st March 2020, with the end of the Jason3 mission. This period provides us with the 27-year dataset for our study.
Using the method of time series development that was explained, we created 675 time series for the Caspian Sea. The length of the data in each time series varies depending on where they are located, as shown in Figure 1. In addition, we did not consider the data from the Garabogaz Gulf in our analysis, as this is a shallow lagoon with high salinity and a distinct sea level variation mechanism that does not pertain to our study. The northern region of the Caspian Sea exhibits a distinct pattern of shorter time series compared to the central and southern regions, as illustrated by Figure 1. The figure also shows that the time series lengths are shorter where the altimetry tracks meet the shorelines. This is because the land affects the satellite measurements by interfering with the signal and lowering the data quality. Therefore, the SSH observations are mostly missing in the GDR files for the points close to the coasts due to the noises. The time series lengths displayed in Fig. 1 have the following descriptive statistics, as shown in Table 2. The minimum and maximum lengths of the time series are 61 and 892, respectively. The average length is 671, with a standard deviation of 224. The most common length is 794, which is the mode of the distribution of the time series lengths.

7.2. Outlier detection and removal using Baarda method

As we mentioned earlier in this paper, we applied the Baarda method to remove outliers from our SSH data. This method evaluates the residuals that are obtained from fitting a trend model to the input data, which is an eighth degree polynomial in this research. The input, are the SSH data from the time series that we constructed for this study. Figure 2 shows some examples of the time series before and after removing outliers using the Baarda method. The Baarda method is an iterative procedure and we only show the SSH observations that passed the final iteration for simplicity. The figure shows that the outliers are more common and larger during the TOPEX/Poseidon era, while they are less frequent and smaller in the SSH data of the later missions. Figure 2 clearly demonstrates the significance of detecting and eliminating the outliers, as they can completely obscure the signal.

8. Spatial analysis of sea level trend changing points from polynomial functions

In this section, our primary objective is to extract spatial information from the turning points of sea level trends and employ it for subsequent analysis. We have successfully computed an eight-degree polynomial that accurately fits the SSH observations at each time series location, passed from Baarda test. We analyzed the results of the trend functions and found four distinct time periods of trend changing points around the years 1995, 2000, 2005, and 2020. As we mentioned earlier, we searched for the local extremum points of the eighth degree polynomial at each time series within a ±1.5 year interval over these years. The spatial distribution of these epochs holds significant in identifying potential causes of sea level variations. The periods shown in Figure 3 are the exact epochs of trend changing points. The identified turning point around the year 2020, as indicated by the trend function, necessitates further validation for several reasons. Firstly, it is not universally observed across all time series. Secondly, it occurs at the outer limit of the altimetry data's time span used in this study. Nonetheless, we have chosen to subject this trend changing point to the same computational analysis, taking into account the aforementioned considerations.
Figure 3 shows that the trend changing epochs have a lot of noise, even after applying corrections, adjustments, and outlier removal. This makes them unsuitable for our applications. We need to find the time series that their trend changing epochs reliably convey information and signals relevant to classify the drainage basin influence for each trend change period. We have designed a filtering procedure for this purpose and we will apply it to derived trend changing epochs and show its performance.
As discussed before, our filtering procedure begins by examining the colormaps of the derived changing epochs at their respective time series, aiming to identify the track with the most consistent epoch variations, which we refer to as the “main-track”. Following this, we pinpoint the cross-overs along main-track that also exhibit the most consistent trend changing epoch values, termed as "main-cross-overs". Figure 4 shows the main-track and main-cross-overs that are selected base on the criterions of having the most accurate SSH observations that is exhibited in the trend modeling and the trend changing epochs that we have extracted from the trend model. Furthermore, as the figure shows the main-track is the longest one over the Caspian Sea and is sufficiently distanced from the coasts, allowing for the allocation of time series with more accurate SSH observations. Additionally, the main-cross-overs along this track are situated at a good distance from the coasts.
Then we select the time series within the radius of 30km around each main-cross-over shown in Fig. 4. Figure 5 shows the changing epochs for these time series in four periods. The changing epochs are consistent within 30 km radius of the main-cross-overs, except for 2020. We explained the reasons for this inconsistency before. We will still apply the same computational procedure to 2020, the suspicious turning epoch period, until the final step.
In the next step, we round the trend changing epochs of the time series displayed within the 30km circles around the main-cross-overs to the nearest integer year. Then, we apply the mode operator to identify the time series with the mode value and calculate the mean of their initial trend changing epoch values. These mean values will be used as the trend changing epoch of main-cross-over points for the following computations. It's important to note that this process aims to enhance the reliability of the trend changing epoch at the main-cross-overs, preparing them to serve as the foundation for subsequent filtering operations.
In our filtering procedure, we initiate by grouping every 11 time series along the main-track, extending this grouping to the opposite end. The final group segment may contain fewer than 11 time series. This process is integral to our filtering method, which commences by filtering the group containing one of the main-cross-over points at a time. Upon identifying a group of time series covering a main-cross-over point, we assess the trend changing epochs' values within this group and apply a band pass filter to identify the time series whose trend changing epochs fall within the band centered on the main-cross-over value, with a threshold of ± 0.17 years, approximately 2 months. With this approach, we can find consistent trend changing epochs within the group, with a maximum deviation of 0.17 years. We keep the time series data with trend changing points within mentioned interval and discard the rest. We calculate the average of these remaining trend changing points and assign it to the locations within the group (the 11 time series). This average value serves as the center for the bandpass filter of the next group of time series on both sides of the main-cross-over, with a threshold of ±0.17 years. This process is repeated up to the last group of 11 time series on both sides of the initial main-cross-over along the main-track. The same filtering procedure is repeated for other main-cross-overs as the starting point, ensuring that each time series along the main track receives three filtered values, each based on one of the main-cross-overs as the starting point. We calculate a weighted mean from the given values by measuring the distance of each time series on the main-track to each of the three main-cross-overs. We rank their values by the distance and use their inverse rating (1 to 3) as the weight of the corresponding filtered value. Using these weights, we derive a weighted mean from the filtered trend changing epoch values for each time series along the main-track, including main-cross-overs. We assign this mean to the corresponding time series.
We use the same grouping scheme for every 11 time series and the intersecting tracks with the main track. We apply the same filtering process along these intersecting tracks, starting from the cross-over point and its filtered value as the center value of the first group covering this point. Figure 6 shows the results of this filtering procedure for four trend changing periods.
After filtering the trend changing epochs, we will present and discuss the findings of the study in the next section.

Interpretation of the trend change epochs

The analysis in the previous sections involved a systematic filtering of trend-changing epochs along altimetry tracks, revealing hidden spatial patterns. Here we begin the discussion by examining plots in the right-hand-side of Figure 2, depicting sea level fluctuations in the Caspian Sea over 27 years. Notably, a decrease in sea level around 1995 followed a period of rise, with another increase around 2000 and a subsequent decrease around 2005. Moreover, there seems to be a partial increase around 2020, which requires further confirmation due to its position at the end of the time series of SSH observations used for this study.
Regarding the tempera-spatial variations of the trend changing epochs, we can refer to Fig. 6, which offers information derived from the filtered plots of trend changing epochs. Examining the two plots on the left-hand-side of Fig. 6, which depict two periods of sea level decrease around 1995 and 2005, we observed that for the period 1995, the first basins to contribute to this decrease were Kura-Sefid Rud followed by Atrak, and the last basin to influence this decrease was Volga, while the effect of the middle part of the Caspian Sea fell between these two limits, potentially caused by the reduction in precipitation pattern at the middle Caspian Sea. For the reduction period in 2005, Kura-Sefid Rud was the first to influence, followed by Atrack and North Alborza basins, and then came the effect of Terek-Reka Kuma and Volga Basins, with the last influence being from the Reka Samure and generally the middle part of the Caspian Sea.
Turning our attention to the period of sea level rise in 2000, Fig. 6 reveals that it commenced with the Atrak basin, followed by the influence of Sefid Rud, and then the influence of the Reka Samure basin, with the last influence being from the Volga basin. In considering the relatively weak signal of sea level increase in 2020, we observed that it originated from the central part of the Caspian Sea, potentially attributed to changes in precipitation patterns. Subsequently, the Atrak exhibited the sea level increase, followed by the Ural basin as the last source of tentative sea level increase observed in 2020.
In conclusion, the findings from Fig. 6 shed light on the dynamic nature of sea level variations in different basins prompting the need to explore the factors that influenced the basins that initiated or followed the sea level trend changes during these periods.

9. Discussion and conclusion

In this study we analyzed satellite altimetry data from four missions over a 27-year period to understand sea level fluctuations in the Caspian Sea and classify water drainage areas. We developed time series of sea surface height (SSH) measurements along the altimetry track. We detected and removed outliers using the Baarda method and computed trend-changing points using eighth-degree polynomial functions. Four distinct periods of trend changes were identified around 1995, 2000, 2005, and 2020. We then applied a filtering procedure to identify the time series with reliable trend-changing epochs and classify the drainage basin influence. We showed that different basins had varying degrees of influence on sea level fluctuations during the different periods. The Kura-Sefid Rud basin had the most influence on sea level decrease in 1995 and 2005, while the Atrak basin had the most influence on sea level increase in 2000 and 2020. We also highlighted the importance of understanding the factors influencing sea level variations in different basins and the potential impact of changes in precipitation patterns.
The Caspian Sea has been the subject of numerous studies over the years, yet previous research has largely overlooked the potential of satellite altimetry data in analyzing the impact of drainage basins on sea level trends. Our study aimed to fill this gap and uncover new opportunities for leveraging this valuable source of satellite data. By harnessing this information, researchers can gain insights into the intricate factors driving long-term changes in the water level of the Caspian Sea and other inland water bodies. This approach, focusing on areas with significant influence on water levels, enhances our understanding of how human activities and climate dynamics affect these crucial water bodies. Moreover, integrating satellite altimetry data with other environmental data can enhance our models for predicting water level changes, aiding in the development of effective solutions. We advocate for extending this research beyond the Caspian Sea to encompass other inland water bodies, thereby broadening our understanding of the Earth's hydrological systems and their responses to human and natural influences. Ultimately, we believe that such studies can offer valuable insights to policymakers and resource managers, guiding them in preserving the planet's vital water resources.

References

  1. Amirinia, Gholamreza, Bahareh Kamranzad, and Somayeh Mafi. 2017. “Wind and Wave Energy Potential in Southern Caspian Sea Using Uncertainty Analysis.” Energy 120 (February): 332–45. [CrossRef]
  2. Amollo, Joseph Odhiambo. 2013. “Aspects of Sea Level Variability in the Southwest Indian Ocean and the East Coast of Africa-(Latitude 0-35 S and from the Coast to 60 E).” Master’s thesis, University of Cape Town.
  3. Arpe, Klaus, and Suzanne A.G. Leroy. 2007. “The Caspian Sea Level Forced by the Atmospheric Circulation, as Observed and Modelled.” Quaternary International 173–174 (SUPPL.): 144–52. [CrossRef]
  4. Asadzadeh Jarihani, Abdollah, John Nikolaus Callow, Kasper Johansen, and Ben Gouweleeuw. 2013. “Evaluation of Multiple Satellite Altimetry Data for Studying Inland Water Bodies and River Floods.” Journal of Hydrology 505 (November): 78–90. [CrossRef]
  5. Asakereh, H., and N. Varnaseri. 2021. “Identifying the Precipitation Regime of the Iranian Coast of Caspian Sea.” Water and Soil 35 (3): 445–59. [CrossRef]
  6. Ataei H, Soheil, Amir Jabari Kh, Amir Mohammad Khakpour, Seyed Ahmad Neshaei, and Dariush Yosefi Kebria. 2019. “Long-Term Caspian Sea Level Variations Based on the ERA-Interim Model and Rivers Discharge.” International Journal of River Basin Management 17 (4): 507–16. [CrossRef]
  7. Azizpour, Jafar, and Peygham Ghaffari. 2023. “Low-Frequency Sea Level Changes in the Caspian Sea: Long-Term and Seasonal Trends.” Climate Dynamics 61 (5–6): 2753–63. [CrossRef]
  8. Cazenave, A., P. Bonnefond, K. Dominh, and P. Schaeffer. 1997. “Caspian Sea Level from Topex-Poseidon Altimetry: Level Now Falling.” Geophysical Research Letters 24 (8): 881–84. [CrossRef]
  9. Chen, J. L., T. Pekker, C. R. Wilson, B. D. Tapley, A. G. Kostianoy, J. F. Cretaux, and E. S. Safarov. 2017. “Long-Term Caspian Sea Level Change.” Geophysical Research Letters 44 (13): 6993–7001. [CrossRef]
  10. Chen, Jianli, Anny Cazenave, Song Yun Wang, and Jin Li. 2023. “Caspian Sea Level Change Observed by Satellite Altimetry.” Remote Sensing 2023, Vol. 15, Page 703 15 (3): 703. [CrossRef]
  11. Firoozfar, Alireza, Edward N. Bromhead, and Alan P. Dykes. 2012. “Caspian Sea Level Change Impacts Regional Seismicity.” Journal of Great Lakes Research 38 (4): 667–72. [CrossRef]
  12. Ghosh, S., S. Hazra, S. Nandy, P. P. Mondal, T. Watham, and S. P.S. Kushwaha. 2018. “Trends of Sea Level in the Bay of Bengal Using Altimetry and Other Complementary Techniques.” Journal of Spatial Science 63 (1): 49–62. [CrossRef]
  13. Hofmann, Hilmar, A E Andreas, Lorke Ae, and Frank Peeters. 2008. “Temporal Scales of Water-Level Fluctuations in Lakes and Their Ecological Implications.” Ecological Effects of Water-Level Fluctuations in Lakes, 85–96. [CrossRef]
  14. Jain, Maulik, O. B. Andersen, L. Stenseng, and L. Ouwehand. 2012. “ Sea Surface Height Determination in the Arctic Ocean from Cryosat2 SAR Data, the Impact of Using Different Empirical Retrackers.” In 20 Years of Progress in Radar Altimetry Symposium, 70. European Space Agency.
  15. Jiang, Wenguan, and Wei You. 2022. “A Combined Denoising Method of Empirical Mode Decomposition and Singular Spectrum Analysis Applied to Jason Altimeter Waveforms: A Case of the Caspian Sea.” Geodesy and Geodynamics 13 (4): 327–42. [CrossRef]
  16. Kaplin, Pavel A., and Andrew O. Selivanov. 1995. “Recent Coastal Evolution of the Caspian Sea as a Natural Model for Coastal Responses to the Possible Acceleration of Global Sea-Level Rise.” Marine Geology 124 (1–4): 161–75. [CrossRef]
  17. Kitazawa, Daisuke, and Jing Yang. 2012. “Numerical Analysis of Water Circulation and Thermohaline Structures in the Caspian Sea.” Journal of Marine Science and Technology (Japan) 17 (2): 168–80. [CrossRef]
  18. Kostianoy, Andrey G., Anna I. Ginzburg, Olga Yu Lavrova, Sergey A. Lebedev, Marina I. Mityagina, Nickolay A. Sheremet, and Dmitry M. Soloviev. 2018. “Comprehensive Satellite Monitoring of Caspian Sea Conditions.” Remote Sensing of the Asian Seas, January, 505–21. [CrossRef]
  19. Kouraev, A. V., J. F. Crétaux, S. A. Lebedev, A. G. Kostianoy, A. I. Ginzburg, N. A. Sheremet, R. Mamedov, et al. 2011. “Satellite Altimetry Applications in the Caspian Sea.” Coastal Altimetry, 331–66. [CrossRef]
  20. Lahijani, H., S. A.G. Leroy, K. Arpe, and J. F. Crétaux. 2023. “Caspian Sea Level Changes during Instrumental Period, Its Impact and Forecast: A Review.” Earth-Science Reviews 241 (June): 104428. [CrossRef]
  21. Lavrova, Olga, and Marina Mityagina. 2017. “Satellite Survey of Internal Waves in the Black and Caspian Seas.” Remote Sensing 2017, Vol. 9, Page 892 9 (9): 892. [CrossRef]
  22. Lavrova, Olga Yu, Marina I. Mityagina, and Andrey G. Kostianoy. 2019. “Online Database ‘See The Sea’ for the Caspian Sea.” Ecologica Montenegrina 25 (Special Issue): 79–90. [CrossRef]
  23. Lebedev, Sergey. 2018. “Climatic Variability of Water Circulation in the Caspian Sea Based on Satellite Altimetry Data.” International Journal of Remote Sensing 39 (13): 4343–59. [CrossRef]
  24. Lebedev, Sergey A., and Andrey G. Kostianoy. 2008. “Integrated Use of Satellite Altimetry in the Investigation of the Meteorological, Hydrological, and Hydrodynamic Regime of the Caspian Sea.” Terrestrial, Atmospheric and Oceanic Sciences 19 (1–2): 71–82. [CrossRef]
  25. Masoud, Mina, Rich Pawlowicz, Mina Masoud, and Rich Pawlowicz. 2022. “Currents Generated by the Sea Breeze in the Southern Caspian Sea.” OcSci 18 (3): 675–92. [CrossRef]
  26. Millero, Frank J., Abzar Mirzaliyev, Javid Safarov, Fen Huang, Mareva Chanson, Astan Shahverdiyev, and Egon Hassel. 2008. “The Equation of State for Caspian Sea Waters.” Aquatic Geochemistry 14 (4): 289–99. [CrossRef]
  27. Moradi, Ayoub, Olivier de Viron, Laurent Metivier, and Saeid Homayouni. 2019. “Construction of Bulk Temperature/Salinity from Surface Temperature and Atlas Profiles for Monitoring Water Volume Variations in the Caspian Sea.” In 4 Th Conference on Contemporary Issues in Computer Information and Sciences.
  28. Ollivier, V., M. Fontugne, B. Lyonnet, and C. Chataigner. 2016. “Base Level Changes, River Avulsions and Holocene Human Settlement Dynamics in the Caspian Sea Area (Middle Kura Valley, South Caucasus).” Quaternary International 395 (February): 79–94. [CrossRef]
  29. Troitskaya, Yu I., G. V. Rybushkina, I. A. Soustova, G. N. Balandina, S. A. Lebedev, A. G. Kostyanoi, A. A. Panyutin, and L. V. Filina. 2012. “Satellite Altimetry of Inland Water Bodies.” Water Resources 39 (2): 184–99. [CrossRef]
  30. Watson, Phil J. 2019. “An Assessment of the Utility of Satellite Altimetry and Tide Gauge Data (ALT-TG) as a Proxy for Estimating Vertical Land Motion.” Journal of Coastal Research 35 (6): 1131–44. [CrossRef]
  31. Xu, Nan, Yue Ma, Zhongwang Wei, Conghong Huang, Guoyuan Li, Huiying Zheng, and Xiao Hua Wang. 2022. “Satellite Observed Recent Rising Water Levels of Global Lakes and Reservoirs.” Environmental Research Letters 17 (7): 074013. [CrossRef]
Preprints 96326 g001
Figure 1. The number of SSH observations in 675 time series from 1Hz GDR data of TOPEX/Poseidon, Jason1, Jason2, and Jason3 missions over the Caspian Sea. The time series are spaced at 6 km intervals. Garabogaz Gulf is not included because it has a different sea level variation mechanism.
Figure 1. The number of SSH observations in 675 time series from 1Hz GDR data of TOPEX/Poseidon, Jason1, Jason2, and Jason3 missions over the Caspian Sea. The time series are spaced at 6 km intervals. Garabogaz Gulf is not included because it has a different sea level variation mechanism.
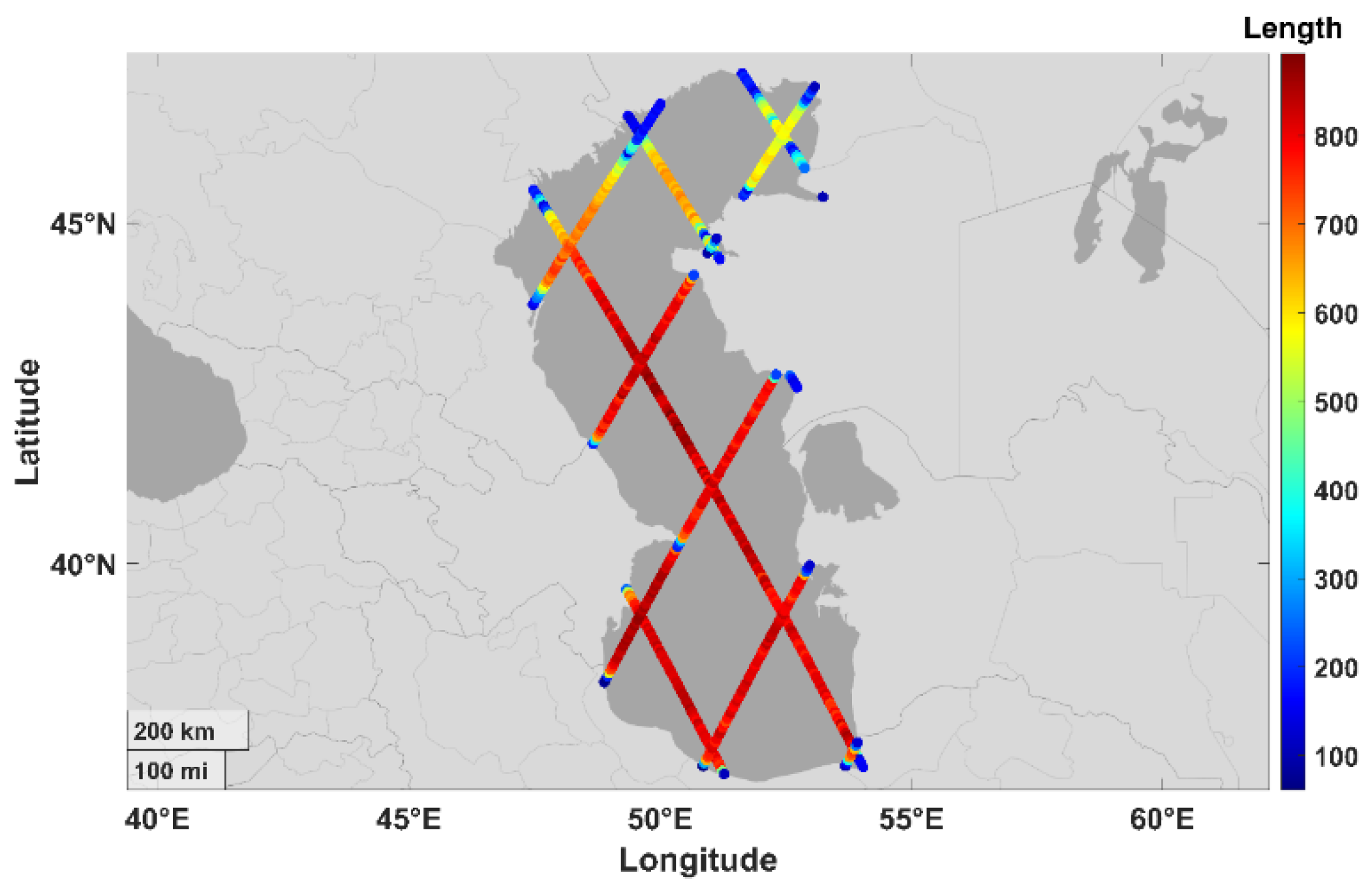
Preprints 96326 g001
Preprints 96326 g002
Figure 2. Time series of SSH data before and after outlier removal by the Baarda method. The first column shows the original SSH data. The second column shows the SSH data with outliers removed and the trend polynomial of degree 8 fitted.
Figure 2. Time series of SSH data before and after outlier removal by the Baarda method. The first column shows the original SSH data. The second column shows the SSH data with outliers removed and the trend polynomial of degree 8 fitted.
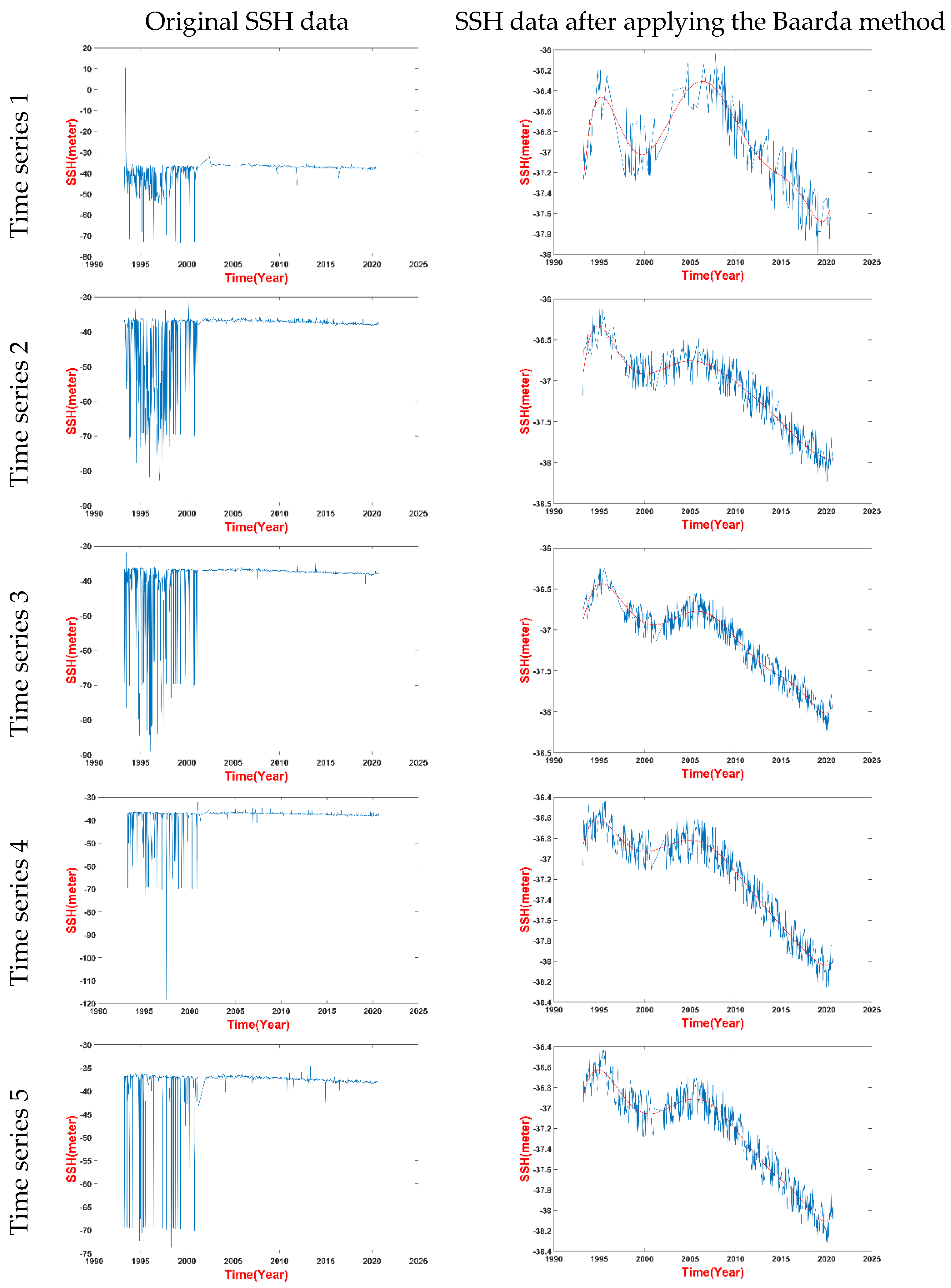
Preprints 96326 g002
Preprints 96326 g003
Figure 3. The epochs of trend changing points for four time periods around 1995, 2000, 2005, and 2020 at the time series locations along the altimetry tracks.
Figure 3. The epochs of trend changing points for four time periods around 1995, 2000, 2005, and 2020 at the time series locations along the altimetry tracks.
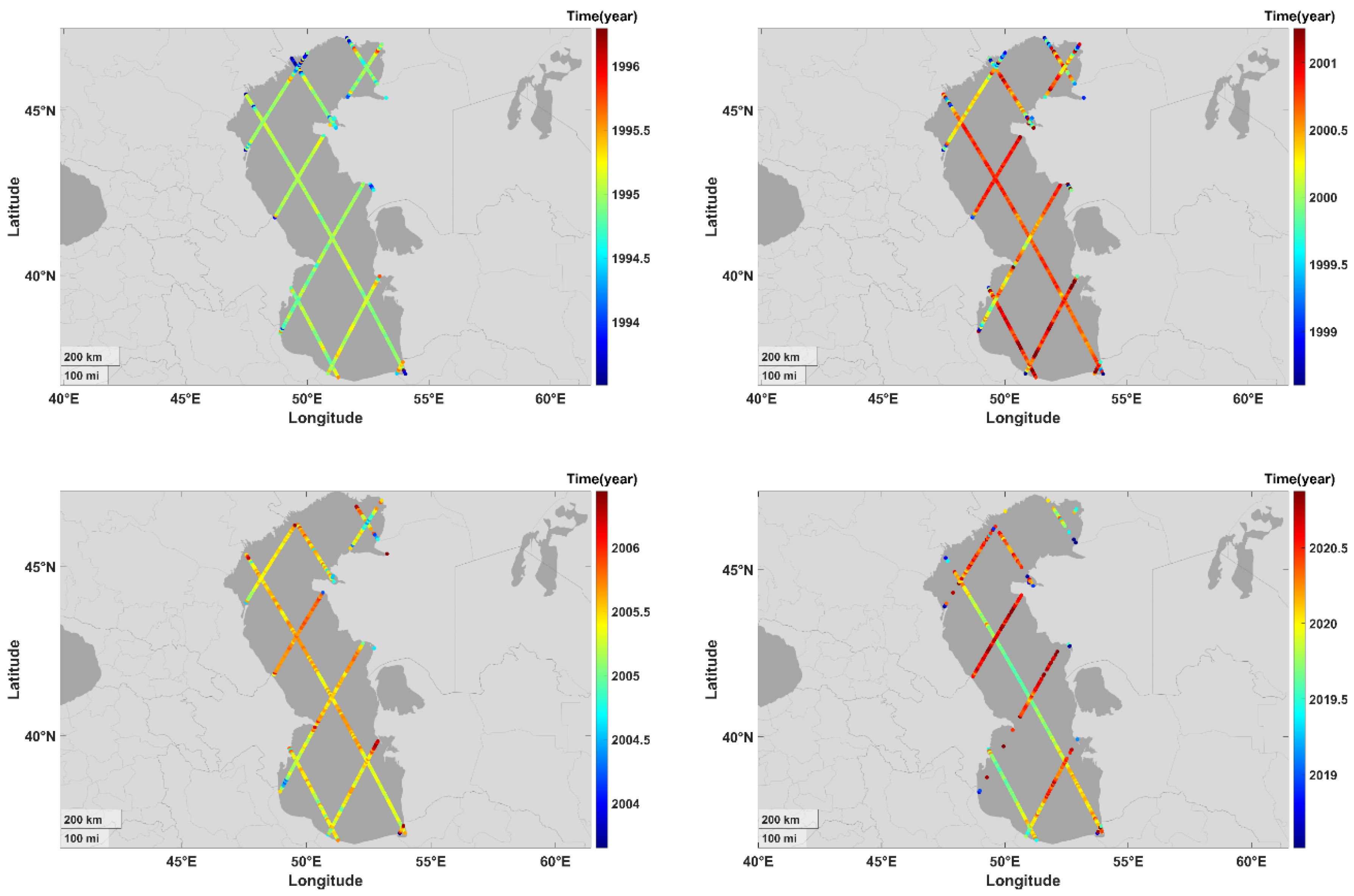
Preprints 96326 g003
Preprints 96326 g004
Figure 4. The main-track and the main-cross-overs used for filtering the trend changing epochs.
Figure 4. The main-track and the main-cross-overs used for filtering the trend changing epochs.
Preprints 96326 g004
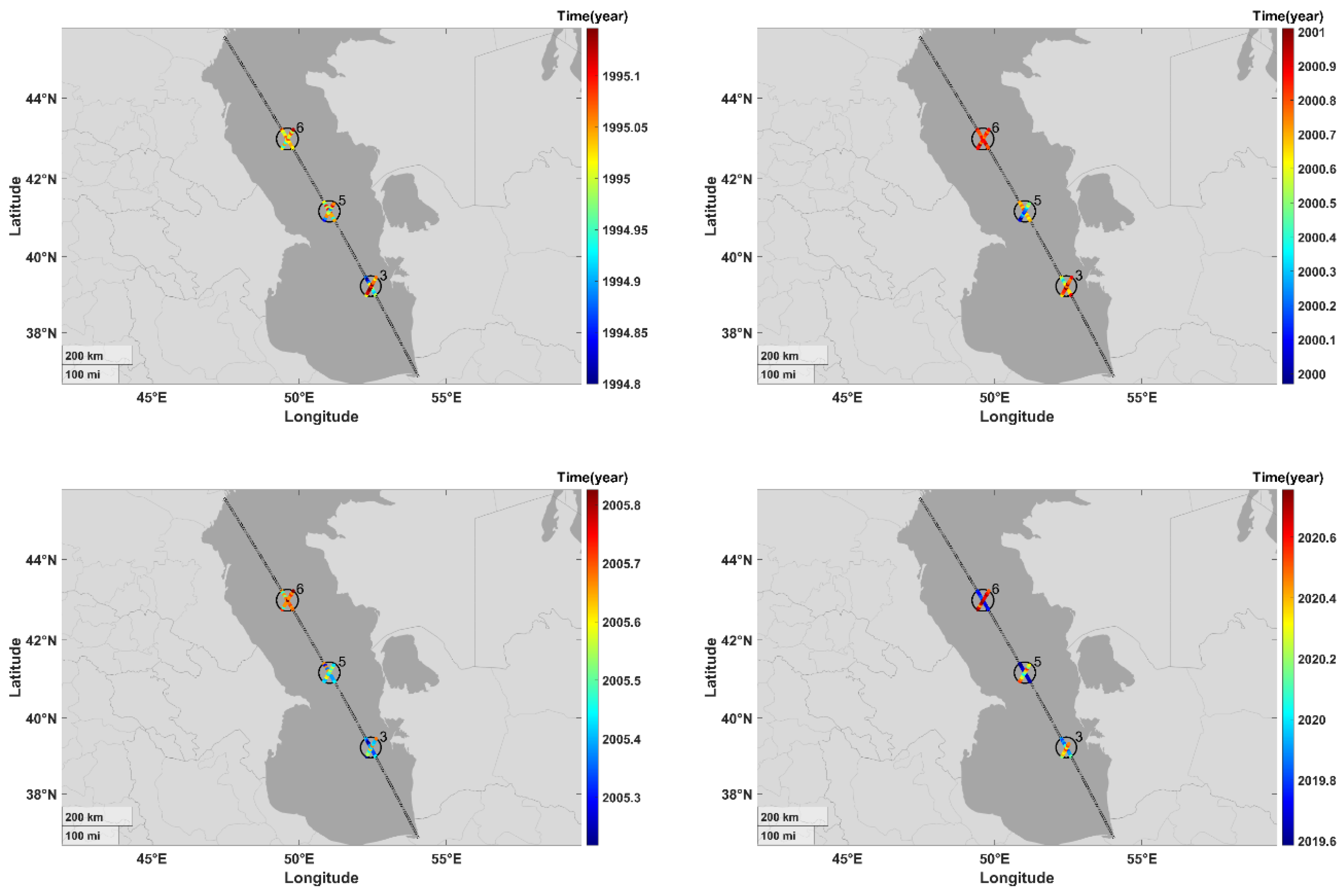
Preprints 96326 g005
Figure 5. The trend changing epochs for four periods at the main-track and main-cross-overs and their neighboring time series within 30 km radius.
Figure 5. The trend changing epochs for four periods at the main-track and main-cross-overs and their neighboring time series within 30 km radius.
Preprints 96326 g005
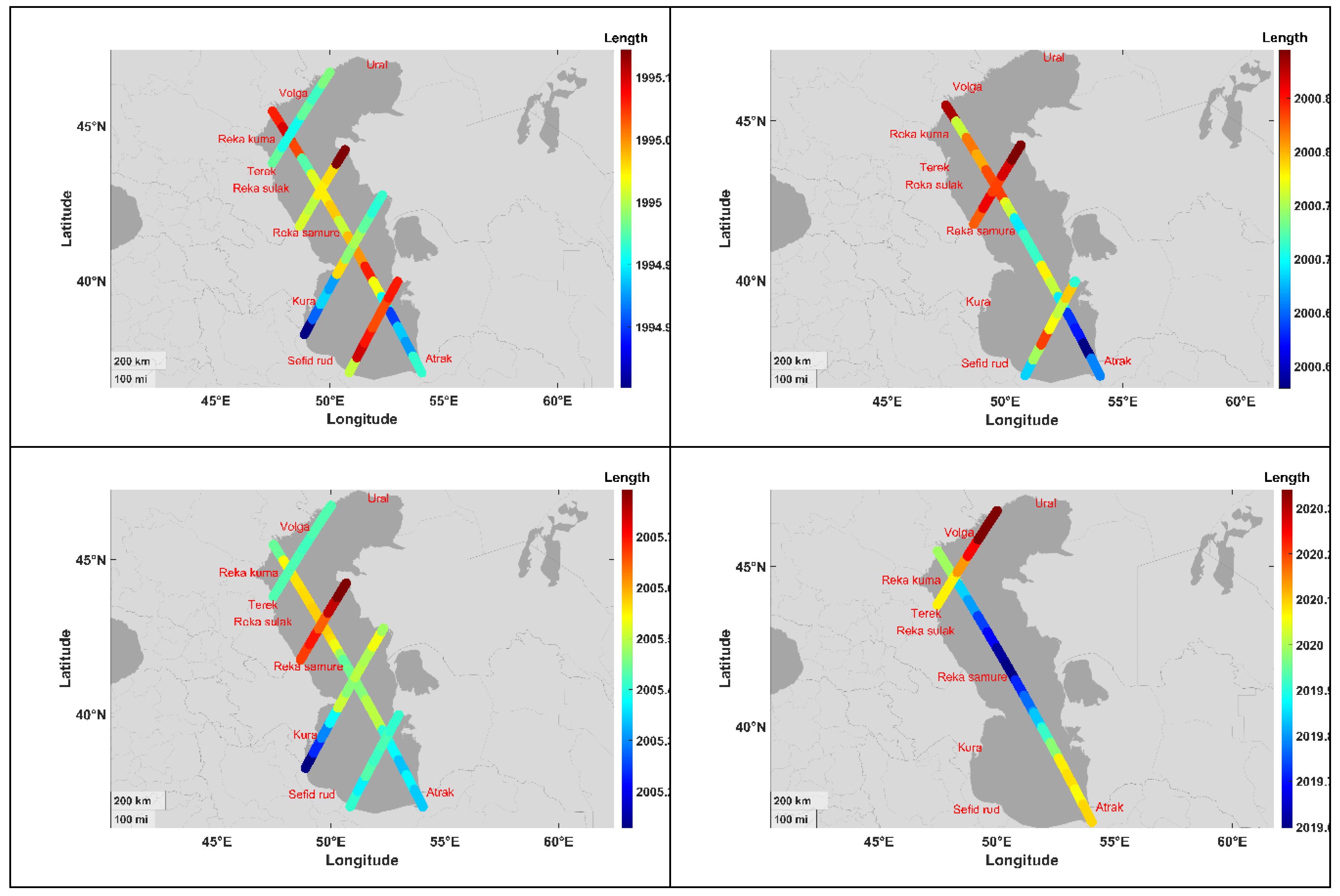
Preprints 96326 g006
Figure 6. The four trend changing epochs of Caspian Sea level fluctuations after the filtering procedure. The name of rivers are also shown as indicators of drainage areas. The tracks that are not shown are those that were filtered out due to inconsistent trend changing epochs.
Figure 6. The four trend changing epochs of Caspian Sea level fluctuations after the filtering procedure. The name of rivers are also shown as indicators of drainage areas. The tracks that are not shown are those that were filtered out due to inconsistent trend changing epochs.
Preprints 96326 g006
Table 1. Satellite altimetry missions, the data versions, durations, and cycles that are used for this study.
Table 1. Satellite altimetry missions, the data versions, durations, and cycles that are used for this study.
Missions Data Formats and Versions Durations Cycles
TOPEX/Poseidon MGDR (Versions C, and D) 1992-2005 1-481
Jason1 GDR (Version e) 2001-2013 1-537
Jason2 GDR (Version d) 2008-2019 1-644
Jason3 GDR (Versions T, and d) 2016-2020 1-170
Table 2. Summary statistics of the number of observations in 675 time series from 1Hz GDR data of TOPEX/Poseidon, Jason1, Jason2, and Jason3 missions over the Caspian Sea. The time series are spaced at 6 km intervals.
Table 2. Summary statistics of the number of observations in 675 time series from 1Hz GDR data of TOPEX/Poseidon, Jason1, Jason2, and Jason3 missions over the Caspian Sea. The time series are spaced at 6 km intervals.
No. of time series Maximum length Minimum length Mean length Mode of lengths STD of lengths
675 892 61 671 794 224
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated