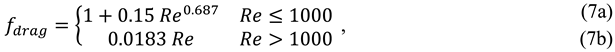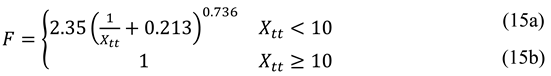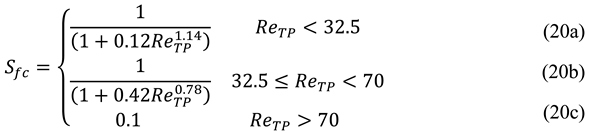Numerical Model of Simultaneous Multi-Regime Boiling Quenching of Metals

This work presents a heat transfer and boiling model that computes the evolution of the temperature field in a representative steel workpiece quenched from 850 or 930°C by immersion in water flowing at average velocities of 0.2 or 0.6 m/s, respectively. Under these conditions, all three boiling regimes were present during cooling: stable vapor film, nucleate boiling, and single-phase convection. The model was based on the numerical solution of the heat conduction equation coupled to the solution of the energy and momentum equations for water. The mixture phase approach was adopted using the Lee model to compute the rates of water evaporation-condensation. Heat flux at the wall was calculated for all regimes using a single semi-mechanistic model. Therefore, evolution of boiling regimes at every position on the wall surface was automatically determined. Predictions were validated using laboratory results, namely: a) Videorecording the upward motion of the wetting front along the workpiece wall surface, and b) cooling curves obtained with embedded thermocouples in the steel probe. Wall heat flux calculations were used to determine the importance of the simultaneous presence of all three boiling regimes on the heat flux distribution. It was found that this simultaneous presence leads to high heat flux variations that should be avoided in production lines.

Keywords:

Subject: Engineering - Metallurgy and Metallurgical Engineering

1. Introduction

Quenching steel workpieces is a heat treatment that includes solubilizing the alloy at temperatures above 800°C, to form austenite phase, followed by fast cooling to form martensite phase. During quenching, fast cooling triggers the solid-state phase transformation. Failure of controlling any, the magnitude, and/or the distribution of cooling rate in the workpiece may result in non-uniform phase transformation and thermal stresses leading to workpiece distortion and/or crack formation. Therefore, a quantitative knowledge of temperature evolution during quenching becomes an essential step to design new quenching systems, diagnose quality-related problems and find solutions to improve productivity.

Convective flow boiling modeling for production lines requires efficient methods to approach complex phenomena, such as turbulent fluid flow and thermal radiation, combined with variable workpiece size and complex geometry. A recent comprehensive review of computational studies on boiling and condensation [1] shows the current knowledge on convective flow boiling modeling. The authors acknowledge that computer modeling of single-phase convection has been tremendously successful for a wide variety of configurations while modeling convective flow boiling had been limited mostly to simple configurations. Nevertheless, in their review, they did not include works regarding the role of heat conduction in a workpiece on the boiling and condensation processes. It is then fair to say that the number/scope of numerical studies on coupled heat conduction with convective flow boiling is considerably more limited than the convective flow boiling modeling reports.

Key studies that are relevant to the present work are summarized in Table 1 and Table 2. Table 1 presents validation methods and remarks on models based on the interpenetrated phases equations. In this approach, vapor and liquid are well mixed in every computational cell. Therefore, the volume fraction of each phase is a continuous function of position. Kopun et al. [2] simulated two routes of immersion quenching process for a cast aluminum step plate with variable thickness sections at different water pool temperatures. Their Eulerian multi-fluid model considered laminar flow and included additional interfacial forces such as lift and wall lubrication, to ensure the drifting of the bubbles just away from the wall, while essentially not affecting the phase distribution away from the wall. The heat flux continuity at the wall was represented by the following equation:

- k_{s} \frac{\partial T}{\partial n} = h_{w} (T_{w} - T_{s a t})

(1)

where k_s is the thermal conductivity of the solid workpiece, n is the normal direction to the wall, and h_w and T_w are the heat transfer coefficient and wall temperature, respectively, and T_sat is the saturation or boiling temperature. In their work, the heat transfer coefficient was estimated for each boiling regime: stable vapor film and transition boiling (the authors call it transition boiling, but it should be nucleation boiling, as explained above). The limit between these regimes is the Leidenfrost temperature, which was computed using empirical correlations implemented in the AVL FIRE® CFD program, used to solve the corresponding differential equations. To improve the results, the authors proposed a variable Leidenfrost temperature, which may depend on the pool temperature, dipping velocity of the heated workpiece, immersion route, geometry of workpiece, and wall surface roughness. Particularly, the authors derived an expression for the Leidenfrost temperature as a function of vertical position along the surface of the workpiece. The rates of vaporization/condensation of water were computed using semi-empirical equations that assume that the heat flux is proportional to the mass flux (between vapor and liquid). The model validation included a comparison between computed and measured cooling curves obtained from sub-superficial thermocouples installed in the workpiece. Sometime later, Zhang et al. [3] presented an application of the previous model for immersion quenching of a cylinder head. Although there was a good agreement between computed and measured cooling curves, their results and conclusions reflect uncertainty on predicting the Leidenfrost temperature. Srinivasan et al. [4] presented a numerical study of immersion quench cooling process of a metallic trapezoidal block using the same Eulerian multi-fluid approach implemented in the AVL-FIRE® software. Their assumptions and the applied empirical and semi-empirical equations were very similar to those used by Kopun et al. [2]. However, two differences should be pointed out. First, the solution method for coupling heat conduction in the solid and convection boiling. The authors used the AVL-Code-Couple-Interface (ACCI) which basically solves first the convection boiling under an isothermal solid wall and then the heat conduction in the solid under a constant heat transfer coefficient. This calculation process is repeated a few iterations to update both wall temperature and heat transfer coefficient, before moving ahead to the next time step. This procedure has the advantage of accepting mutually independent meshes in the solid and fluid. In contrast, Kopun et al. [2] used the Multi-Material Approach (MMAT), which considers both, solid and fluid as a single domain. Therefore, a single whole solution is computed at every time step. A second difference between these works is the Leidenfrost temperature. Srinivasan et al. [4] considered that Leidenfrost temperature did not depend on position on the workpiece surface. Model validation was carried out by comparing computed and measured cooling curves. Another numerical simulation of flow boiling heat transfer was presented by Krause et al. [5]. Their model also belongs to the interpenetrated phases category, however there are some differences with respect to the previously described works. First, they used the mixed model, which solves the continuity and momentum equations for the mixture vapor-liquid, rather than solving these equations individually for each phase. Further, average properties are weighted on volume fractions and phase densities, rather than on exclusively volume fraction. Moreover, the vaporization/condensation rates are computed from a mass source/sink terms in the continuity equation using the bubble crowding model. This model only establishes that the rate of phase transformation is proportional to the super-heating or under-heating of the fluid with respect to the boiling temperature, T_sat. The coefficient of proportionality depends on the local mass transfer coefficient which in turn is a function of the boiling regime, the temperature at the critical heat flux, T_crit, and the Leidenfrost temperature, T_L. Therefore, there is no need for a priori knowledge of nucleation sites density or a vapor-liquid interphase to start boiling from. The authors supported this assumption by recalling that workpiece surfaces are technically rough, and liquids are not pure, resulting in a great number of nucleation/condensation sites. The authors implemented their model in the CFD Fluent 6.3 code to compute iteratively the mass transfer coefficient by assuming a starting value of 1 m/s and minimizing the difference between their computed heat transfer coefficient with the corresponding measured values. Model validation was based on comparing calculations with experimental results for two cases: a steady state case, using an isothermal metallic cylinder immersed in a vertical tube where water was flowing at an average velocity of 0.3 m/s. In this case, validation was based on a qualitative comparison between computed and observed bubble fractions at the half height of the vertical cylinder that was held at 400, 500 and 1000K. The second case was a transient heat transfer during the quenching of the same cylinder. Validation was based on a comparison between computed and experimentally determined heat transfer coefficients. Notice that the mass transfer coefficient, at the vapor-liquid interphase, was determined using this experimental heat transfer coefficient. Stark et al. [6] presented a numerical study of the quenching process using a confined water jet. The liquid velocities at the nozzle were 1 or 3 m/s and the distances from the nozzle to the austenitic steel wall were 50 or 100 mm, respectively. They simulated steady state convection boiling assuming an isothermal wall. The wall temperatures were different values between 300 and 900°C, therefore all the boiling regimes were analyzed. The computed heat transfer coefficients as a function of wall position and temperature were used in a separated calculation to solve the heat conduction equation for the solid plate. Therefore, they decoupled heat conduction in the solid from convection boiling. Regarding convection boiling, it was computed using a mixed model, like Krause et al.’s model, and the interaction between liquid and vapor “bubbles” was defined using the Schiller-Naumann-correlation for momentum exchange and the Ranz-Marshall-correlation for heat transfer. The required bubble diameter for these correlations was a linear function of vapor fraction. Turbulent flow was considered using the k-w-SST (Shear Stress Transport) model. Sinks and sources, included in the conservation equations, expressed the rate of phase change from boiling/condensation. The model was implemented in the CFD-package Ansys Fluent® 13. The authors claimed that their single model approach allows to investigate all occurring boiling phases during the quenching process, avoiding specifying in advance the temperature range where each boiling regime is present. However, the authors did not present a model validation by comparing their numerical results against experimental measurements. Passarella et al. [7] developed another multiphase mixed model to simulate the quenching of a low carbon steel cylinder using mineral oil flowing in a vertical tube at 1 m/s. The momentum equation was solved under turbulent conditions using the k-e model implemented in the Comsol® Multiphysics code.

Interaction between vapor bubbles and liquid was computed using a drift flux mixture model. Liquid heat flux conduction at the wall and wall shear stress were computed using adequate wall functions. Additionally, they assumed that the total heat conduction from the solid was equal to the sum of the heat that increased the liquid temperature plus the heat dedicated to evaporating this fluid. Also, it was considered that vapor temperature was not raised above T_sat to avoid solving the energy equation for this phase. The proportion of heat for each contribution determined the boiling regime that was present. This proportion was controlled by damping functions: one depending on wall temperature, f_T, and another on vapor fraction, f_v. Different empirical and semi-empirical expressions were used for the heat flux under the stable vapor film regime and for the nucleation boiling regime. The authors showed the computed evolution of vapor fraction and solid temperature. The vapor rich layer starts at two zones: the upper area and the lower area of the cylinder surface. Then, it moves towards the mid-height of the cylinder. In spite the authors claiming the correctness of these results, no experimental evidence was shown in the article to support their calculations on the vapor fraction distribution. Nevertheless, the authors obtained computed heat transfer coefficient values the same order of magnitude as previous experimentally determined values. In a recent work, Petrovic and Stevanovic [8] reported a coupled two-fluid flow and wall heat conduction modeling of nucleate pool boiling. Their model is also in the category of Eulerian multi-fluid with interpenetrated phases, solving numerically the mass and momentum differential equations for each phase: liquid and vapor. The energy equation for the liquid was coupled with the heat conduction equation for the solid workpiece. Interaction between liquid and vapor was given by an interfacial drag force per unit volume for momentum transfer, and the rates of evaporation/condensation for mass transfer. The finite volume method [9] was used to solve the conservation differential equations. Differently from the previous works, the total wall heat flux was divided into two contributions: a convective heat flux and a vaporization heat flux. The former represents the heat flowing from the wall to a liquid film while the second one represents the heat flowing to growing bubbles. This approach took several results from previous works regarding the dynamics of bubble growing which required input data like nucleation site density and the wetting contact angle. The authors found that the computed boiling curve strongly depended on these input data. Model validation was carried out using data from steady state experiments, where a heater was used to hold a time-independent temperature distribution in a steel plate immersed in still water. The authors compared the obtained relationship between computed wall heat flux and nucleation site density, with the respective observed relationship reported by other authors. Also, the authors showed comparisons between observed and computed vapor fraction distribution and heat transfer coefficient along the height of the heater. Finally, using transient heat flow results, they compared their computed temperature profiles across a cold spot at the location of a bubble grow with the corresponding measured values reported previously. In this study, wall temperatures were always below 130°C, therefore stable film boiling regime was not present.

Table 2 presents validation methods and remarks of interface-capturing-methods. This approach includes the calculation of the interphase position, therefore volume fraction of each phase in all computational cells is either 0 or 1, depending upon the location of the interphase. This method predicts a more detailed picture of the vapor-liquid distribution than the interpenetrated phases approach does. However, the computational cost is considerably higher. Ramezanzadeh et al. [10] used the Volume-Of-Fluid (VOF) method to compute the temperature evolution in a steel step plate subjected to quenching when immersed in oil flowing at constant velocities of 0.1, 0.2, 0.3, 0.5 or 0.6 m/s. The authors implemented a source term in the continuity equation to create a higher interface resolution between vapor and liquid. The continuous surface force model (CSF) was used to account for the effect of surface tension on the interface shape. The rates of vapor formation and condensation were computed using Lee mass transfer model, since it does not require an initial interface condition, and boiling starts anywhere in the liquid if temperature is higher than the saturation temperature. Validation was carried out in two steps. First, the authors used their model to calculate the one-dimensional Stephan boiling problem, and second, they compared the computed cooling curves against the corresponding measured values as reported by other authors. It is interesting to note that their calculations show the simultaneous presence of different boiling regimes in different zones of the workpiece surface. These numerical results led to an optimal oil velocity of 0.3 m/s to achieve a uniform workpiece temperature during cooling. However, no experimental observations supported this conclusion. Another work based on the VOF method was reported by Moon et al. [11]. The authors reported a numerical study on a vertical water free jet impinging on a superheated stainless-steel plate. Initial steel temperature was 900°C, but they neglected radiation heat transfer and justified this assumption based on an initial fast cooling of the metallic surface. Boiling/condensation rates were calculated from Lee model; therefore, no nucleation site density was required. Fluid flow near the wall was computed using the turbulent k-w SST model. The corresponding wall distance y⁺ was set equal to 10, to properly calculate the turbulent viscosity. The nozzle was 3 mm diameter and was located 100 mm from the plate surface. The circular plate was 100 mm diameter and 60 mm thick. The water left the nozzle at 20°C, at a velocity such that Reynolds number was 15000. The authors compared the measured cooling curves for a location under the stagnation point, with the corresponding model predictions; and they compared the respective boiling curves. The authors computed a radial component of the temperature gradient in the plate that was larger than the axial component of the temperature gradient. This was attributed to the radial distribution of different boiling regimes on the wall, which led to quite different heat fluxes along the metallic surface. Single-phase convection was present at the stagnation point and stable vapor layer prevailed at some distance from the stagnation point. Zhang et al. [12] studied the influence of the wall thickness and thermal diffusivity on dynamics and heat transfer in nucleate pool boiling of a single bubble. They used the Ghost Fluid Method for sharp interface representation. Two Level Set functions were used to capture the liquid-vapor and the liquid-wall interfaces. The computational domain included an axisymmetric solid and a fluid on its upper face. The fluid region was divided into micro and macro regions. The momentum, energy and continuity equations were solved considering laminar flow and constant physical properties. The heat conduction equation was solved for the solid wall, assuming that its lower face was isothermal. The authors found that the bubble growth time decreases with the wall thickness, but the departure bubble diameter increases. A local and periodical expanding-receding low-temperature region was produced inside the wall under the bubble base because of movement of the contact line (vapor-liquid-wall line) due to evaporation of the liquid microlayer. An increase in wall thermal diffusivity lags the movement of the local low-temperature region. The authors did not show any measurements or observations to validate their results. It is evident that this interface-capturing-method offers the capability to compute, from first principles, macroscopic parameters used by multi-fluid interpenetrated models, for example nucleation site density. Ilic et al. [13] presented a review and future prospectus of boiling heat transfer modeling. They pointed out that, besides interpenetrated (macro-scale boiling) and interface-capturing (micro/meso-scale boiling) models, molecular dynamics (nano-scale boiling) methods represent an alternative to improve our understanding of boiling heat transfer mechanisms. These methods are based on computing the trajectories of individual molecules, which move according to the interacting forces. The author’s opinion is that the most important advantage of these methods is that the bubble nucleation site can be detected for different geometrical configurations and wettability conditions of the wall. According to the authors, multi-scale modeling is the future prospectus for an improved predictive methodology of boiling heat transfer phenomena. Multi-scale modeling is a combination of macro-scale, micro/meso-scale and nano-scale models. However, the authors accept that there is no definite answer to the question of how these scales should be coupled to each other.

From the above literature review, it was identified that validation methods are not detailed enough to include information on both solid body and fluid, and generally they consider just one of them, either cooling curves or boiling characteristics. Also, there is no reported model, thoroughly validated, that includes both turbulent flow and thermal radiation, which are very common phenomena during metals quenching. Finally, only the recent work of Moon et al. [11] reports the importance of observing simultaneous multi-regime boiling on the wall heat flux distribution. The present work presents an interpenetrated phases model, that includes turbulent flow and thermal radiation, and was validated using cooling curves and the kinematics of the wetting front along the solid wall. The model was used to determine the wall heat flux components, finding that simultaneous multi-regime boiling is an undesirable condition, from the product quality point of view, since it leads to non-uniform heat flux.

Because of the approach, the model is computationally efficient despite including turbulent flow and thermal radiation calculations. Therefore, this model is suitable for quenching simulations of larger and more complex workpieces.

2. Materials and Methods

The experimental set-up used for this work, was developed previously by one of the authors [14] to study the effect of flat-end and conical-end geometries of cylindrical probes on the hydrodynamic characteristics of the water flowing past axially these probes. The system accounts for facilities to maintain a constant and isothermal water flowrate. The probe was videorecorded from the point of immersion to determine symmetry of wetting and wetting front kinematics. A stable transition between boiling regimes was found. This facilitated the study of the kinematics of the wetting front. In the present work, the conical-end cylindrical probe was chosen. This probe was recommended by the authors who were able to form stable and symmetrical wetting fronts, making it possible to establish the effect of water velocity on heat extraction [15]. For convenience, a summary of the experimental set-up and method is described as follows.

Figure 1 shows a schematic representation of the experimental system that was formed by a closed water loop with automatic control of water temperature and manual control of water flow rate. An instrumented cylindrical probe was heated up in a muffle placed above the quenching zone. Once the preset probe temperature was reached, the specimen was taken out from the furnace and was moved downwards at a manually controlled velocity to be immersed into the ascendant water stream to the quenching position. A high-speed camera recorded events at the probe surface, at a frequency of 125 fps, and at the same time four thermocouples recorded, at an acquisition frequency of 10 Hz, cooling curves at selected positions in the probe.

2.1. Quenching Zone and Probe Geometry

The quenching zone was a segment of vertical tube of Plexiglas with an internal diameter of 44 mm. Water at a constant upward flow rate reaches the open basin and then flows downward to a storing tank for recirculation. The stainless steel (AISI 304) probe had a diameter of 12.7 mm and a length of 68 mm, and was instrumented with four subsurface Inconel-sheathed, 1/16”-dia. (1.6 mm), type K thermocouples, placed as shown in Figure 2a,b.

2.2. Experimental Conditions

Table 3 summarizes the experimental conditions for the present work. Two cases were considered, denoted by V1 and V2 labels. The velocity and temperature of the water flow were stabilized at the values of v_water and T_water, respectively. The probe was removed from the muffle and moved downward at a manually controlled velocity, V_imm. The probe tip touched the water free surface in the open basin just at the time t_imm=0 when the probe temperature was T_imm. The recorded temperatures indicated that after 25 seconds from immersion, the metal reached essentially the water temperature.

*This velocity was controlled manually and estimated from video-recorded images.

3. Mathematical Model

Before presenting the model equations, it is convenient to review the following considerations. The probe was heated up in a muffle until reaching a uniform temperature. Then, this probe was taken out from the muffle and moved down in still air at a manually controlled velocity. During this period, the probe cooled down by natural convection and radiation which led to Newtonian cooling (Bi<0.1). Therefore, the probe temperature was essentially uniform and there was no need to solve the heat conduction equation for the probe. However, after immersion started, at t=0, the sample surface was covered quickly by the flowing water increasing the heat flux at the wall and leading to non-Newtonian cooling (Bi>0.1). Vapor forms on the probe surface leading to a heat transfer coefficient that evolved as a function of the wall temperature and fluid flow conditions. Also, radiation absorption by liquid water and vapor took place. The present analysis of this process was carried out by coupling the solution of the fluid flow equations and the heat conduction equation for the solid probe.

Five phenomena were considered during the quenching process:

1) The fluid dynamics of water, 2) the interfacial heat transfer between solid and fluid, 3) the heat losses from the probe surface by radiation, 4) the interfacial mass transfer between liquid and vapor phases during water boiling and 5) the heat conduction through the solid probe.

The interaction between these phenomena was represented by the numerical solution of the following coupled differential equations.

3.1. Governing Differential Equations

3.1.1. Mixture Model

The mixture model was adopted for this work since the criteria of the Stokes number and the bubble loading are satisfied [16]. The Stokes number (St) is defined as the ratio of the bubble response time to the system response time. Considering a constant bubble diameter of 0.1 mm [17], estimated order of magnitude of Stokes number is 10^-6, which means that the vapor bubbles follow the water streamlines. The bubble loading is defined as the mass density ratio of vapor bubbles to that of the liquid water. Estimated orders of magnitude values considering vapor volume fractions of 0.05 and 0.95 are 10^-5 and 10^-2, respectively. This is a very low loading, so the coupling effect between phases is one-way, which means the water influences bubbles via drag and turbulence, but the bubbles have no effect on the water flow. On the other hand, the Eulerian interpenetrated phases models do not compute explicitly the interphase boundary, as opposed for example to the Level Set or the Volume of Fluid methods, which do track the actual position of the interphase boundary. However, in the mixture model, it is possible to specify an interphase position by setting conventionally a volume fraction value. For example, a vapor-liquid boundary can be defined as those points in space where the volume fraction of vapor is equal to 0.5. Complementary, notice that for pure water, the liquid volume fraction is one, and analogously for pure vapor. Therefore, the considered differential equations also apply for the single-phase regions.

The mixture model solves the continuity, momentum and energy differential equations for the mixture, and the conservation equation for the vapor phase (secondary phase) to compute the rate of evaporation/condensation. These equations are described as follows.

Continuity equation,

\frac{\partial}{\partial t} ρ_{m} + \nabla \cdot (ρ_{m} {\vec{v}}_{m}) = 0,

(2)

where

{\vec{v}}_{m}

is the mass-averaged mixture velocity and it is calculated by the following expression,

{\vec{v}}_{m} = \frac{\sum_{k = 1}^{k = 2} α_{k} ρ_{k} {\vec{v}}_{k}}{ρ_{m}},

(3)

being subindex k equal to 1 for liquid phase and 2 for vapor phase, and

ρ_{m}

is the mixture density, computed from the equation:

ρ_{m} = \sum_{k = 1}^{k = 2} α_{k} ρ_{k},

(4)

where

α_{k}

is the volume fraction of phase k.

Momentum equation,

\frac{\partial (ρ_{m} {\vec{v}}_{m})}{\partial t} + \nabla \cdot (ρ_{m} {\vec{v}}_{m} {\vec{v}}_{m}) = - \nabla p + \nabla \cdot [μ_{m} (\nabla {\vec{v}}_{m} + \nabla {\vec{v}}_{m}^{T})] + ρ_{m} \vec{g} - \nabla \cdot (\sum_{k = 1}^{k = 2} α_{k} ρ_{k} {\vec{v}}_{d r, k} {\vec{v}}_{d r, k}),

(5)

where the present forces are the pressure gradient (

\nabla p

), gravitational force per unit volume of mixture (

ρ_{m} \vec{g}

), viscous forces that depend on dynamic viscosity of mixture

μ_{m}

, computed from the following expression:

μ_{m} = \sum_{k = 1}^{k = 2} α_{k} μ_{k},

(6)

and the momentum transfer due to the relative velocity between phases, so called slip velocity, (

{\vec{v}}_{1,2}

). This relative velocity is computed by using an algebraic slip formulation which assumes that a local equilibrium between phases was reached over a short spatial length scale. Therefore, slip velocity could be expressed as a function of the vapor bubbles acceleration and a drag function. In the present model, this drag function is from Schiller and Naumann [18],

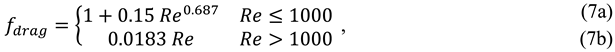
where the Reynolds number, Re, is computed using the slip velocity. On the other hand, the acceleration of bubbles is given by gravity force, therefore the algebraic slip formulation leads to the so-called drift flux model. The drift velocity for phase k, is relative to the mixture velocity and is given by the following equation,

{\vec{v}}_{d r, k} = {\vec{v}}_{k} - {\vec{v}}_{m} .

(8)

Energy equation

Considering incompressible flow and radiation absorption, the energy equation can be written as,

\frac{\partial}{\partial t} \sum_{k} (α_{k} ρ_{k} H_{k}) + \nabla \cdot \sum_{k} (α_{k} {\vec{v}}_{k} (ρ_{k} H_{k} + p)) = \nabla \cdot [k_{e f f} \nabla T] + S_{h},

(9)

where H_k is the sensible enthalpy for phase k, k_eff is the effective thermal conductivity, which is defined by the following equation,

k_{e f f} = \sum_{k = 1}^{k = 2} α_{k} (k_{k} + k_{t}),

(10)

being k_k the material thermal conductivity of phase k, and k_t the turbulent thermal conductivity defined according to the used turbulence model. The heat source, S_h, includes two terms: 1) the latent heat for evaporation/condensation, which was computed from the Lee model combined with the semi-mechanistic boiling model, and 2) the thermal radiation absorption, which was evaluated from the Discrete Ordinates (DO) radiation model. Both models are explained below.

3.1.2. Evaporation/Condensation Model

Calculation of the rate of interphase mass transfer through evaporation-condensation was carried out using the Lee model [19], which is a mechanistic model based in the solution of the vapor conservation equation, written as follows:

\frac{\partial}{\partial t} (α_{2} ρ_{2}) + \nabla \cdot (α_{2} ρ_{2} {\vec{v}}_{m}) = - \nabla \cdot (α_{2} ρ_{2} {\vec{v}}_{d r, 2}) + {\dot{m}}_{12} - {\dot{m}}_{21},

(11)

where

{\dot{m}}_{12}

and

{\dot{m}}_{21}

are the rates of evaporation and condensation, respectively, and are given by the following equations.

\begin{matrix} {\dot{m}}_{12} = c_{e v a p} * α_{1} ρ_{1} \frac{(T_{1} - T_{s a t})}{T_{s a t}}, & F o r T_{1} > T_{s a t} \end{matrix},

(12a)

\begin{matrix} {\dot{m}}_{21} = c_{c o n d} * α_{2} ρ_{2} \frac{(T_{s a t} - T_{2})}{T_{s a t}}, & For T_{2} < T_{s a t} \end{matrix},

(12b)

where c_evap and c_cond are the evaporation and condensation coefficients, respectively, which are interpreted as the inverse of relaxation times which must be fine-tuned to match experimental data for each system; and T₁ and T₂ are the local temperatures for liquid and vapor phases, respectively.

Regarding the wall heat flux, it was computed using the semi-mechanistic boiling model. This approach is particularly useful for low pressure boiling systems, such as metals quenching. The semi-mechanistic model includes heat transfer augmentation at the wall due to boiling, which was computed from empirical correlations developed by Chen [20]. The effective wall heat flux is expressed as the weighted sum of the nucleate boiling heat flux resultant of the micro-convective mechanism associated with bubble nucleation and growth, and the forced convective heat flux associated to the macro-convective mechanism related to the fluid flow. It is assumed that the convective and the boiling contributions could be superimposed but need to be modified by effects of vapor quality and the interaction between mechanisms. Because of that, this model assumes that vapor formed by the evaporation process increases the liquid velocity, and, therefore, the convective heat transfer contribution is augmented relative to that of a single-phase liquid flow. On the other hand, the convection partially suppresses the nucleation of boiling sites, thus, the contribution of nucleate boiling is reduced. These phenomena are represented by the following expression:

q_{w} = F q_{s p} M_{s p} + S q_{n b} M_{n b},

(13)

where F is the forced convective augmentation factor, S is the nucleate boiling suppression factor, M_sp and M_nb are the heat flux multipliers for the single phase and nucleate boiling, respectively. The first term of the right side of this equation represents the single-phase contribution, and the corresponding heat flux, q_sp, was calculated from the basic relationship for heat transfer by convection q_sp = h_spΔT; where the single-phase heat transfer coefficient, h_sp, was obtained from the following equation.

h_{s p} = f h_{1} + (1 - f) h_{2},

(14)

being h₁ and h₂ single-phase heat transfer coefficients for liquid and vapor, respectively, f is the area fraction of wall surface wetted by the liquid, and ΔT is the difference between the wall and boundary cell temperatures (T_w - T_c). The factor F is strictly a fluid flow parameter and is expressed as follows [21]:

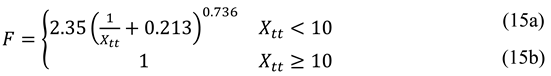
This factor is a function of the Martinelli parameter X_tt, which is used to determine the influence of two-phase presence on convection, and it is calculated from the following expression.

X_{t t} = {(\frac{1 - χ}{χ})}^{0.9} {(\frac{ρ_{2}}{ρ_{1}})}^{0.5} {(\frac{μ_{1}}{μ_{2}})}^{0.5},

(16)

where χ is the local vapor mass fraction (vapor quality).

The second term on the right-hand side of Equation (13) represents the contribution of nucleate boiling mechanism and the respective heat flux, q_nb, was computed using the general equation q_nb=h_nbΔT_sup. The corresponding heat transfer coefficient, h_nb, was calculated using the Foster and Zuber correlation written as follows [22],

h_{n b} = 0.00122 \frac{k_{1}^{0.79} c_{p 1}^{0.45} ρ_{1}^{0.49}}{γ^{0.5} μ_{1}^{0.29} H_{12}^{0.24} ρ_{2}^{0.24}} {(P_{s a t, T w} - P_{s a t, T s a t})}^{0.75} {(T_{w} - T_{s a t})}^{0.24},

(17)

being P_sat,Tw and P_sat,Tsat the saturation pressures corresponding to wall temperature and saturation temperature, respectively; k₁, c_p1, r₁, and μ₁ are the thermal conductivity, specific heat, density, and viscosity of the liquid, respectively, r₂ is the vapor density, H₁₂ is the latent heat of vaporization, and g is the surface tension of water. The superheat, DT_sup, is equal to the difference T_w-T_sat.

The suppression factor, S, is defined according to the following equation:

S = S_{f c} S_{s u b},

(18)

where S_sub accounts for the subcooled effects and it is calculated from the expression proposed by Steiner et al. [23].

S_{s u b} = \frac{T_{w} - T_{s a t}}{T_{w} - T_{r e f}},

(19)

being T_ref a reference temperature. S_fc represents the suppression factor due to forced convection which can be found elsewhere [16] and depends on the two-phase Reynolds number, according to the following expression.

The modified two-phase Reynolds number is defined as follows:

{R e}_{T P} = 10^{- 4} {R e}_{1, r e f} F^{1.25},

(21)

being the reference Reynolds number for liquid calculated as:

{R e}_{1, r e f} = \frac{ρ_{1, T r e f} U_{r e f} L}{μ_{1, T r e f}},

(22)

where,

ρ_{1, T r e f}, μ_{1, T r e f}

are the density and viscosity of liquid, respectively, at the reference temperature.

U_{r e f}

is the reference velocity and L being the characteristic length scale.

3.1.3. Thermal Radiation Model

Vapor and liquid water interact with the thermal radiation from the wall, by absorbing, reflecting, and transmitting the received radiation in different proportions, and emitting their own radiation. Additionally, wall surface properties, such as emittance (ε) and absorptance (ɑ) also play a role to determine the net heat flux from the surface. Nevertheless, most of works on numerical simulation of heat treatment of metals neglect radiation heat flux arguing that the period that surface is at high temperatures is very short. This is misleading since the whole thermal history of the probe and the resulting microstructure and mechanical properties of the probe are dependent on its initial temperature and its initial cooling rate. From the available radiation models, selection of the Discrete Ordinates (DO) method was based on the following advantages: 1) The DO model applies for systems that are optically thin, which is defined by an optical thickness value αL<1, being α the absorption coefficient of the fluid and L is the characteristic length scale of the domain; 2) it allows the solution of radiation at semi-transparent materials, and 3) computational cost is moderate.

The DO model solves the Radiative Transfer Equation (RTE) for a finite number of discrete solid angles,

Ω^{'}

, each associated with a directional vector,

\vec{s}

, fixed in the global cartesian system (x, y, z). The RTE can be expressed as,

\nabla \cdot (I (\vec{r}, \vec{s}) \vec{s}) + (a + σ_{s}) I (\vec{r}, \vec{s}) = a n^{2} \frac{σ T^{4}}{π} + \frac{σ_{s}}{4 π} \int_{0}^{4 π} I (\vec{r}, {\vec{s}}^{'}) ϕ (\vec{s} \cdot {\vec{s}}^{'}) d Ω^{'},

(23)

where

I (\vec{r}, \vec{s})

is the radiation intensity, which depends on position vector,

\vec{r}

, and direction vector,

\vec{s};

ϕ (\vec{s} \cdot {\vec{s}}^{'})

is the phase function which depends on the dot product between the direction vector and the scattering direction vector,

{\vec{s}}^{'};

a, σ_{s}, n

are the absorption coefficient, scattering coefficient, and refractive index of the medium, respectively;

σ = 5.67 x 10^{- 8} W / (m^{2} K^{4})

is the Stefan-Boltzmann constant and

π

=3.141592… Finally,

s

is the path length and T is the absolute temperature. DO method consists in transforming Eq. (23) into a transport equation for radiation intensity, solving for as many transport equations as there are directions

\vec{s}

. The solution method is the same as that used for the fluid flow and energy equations.

DO model allows the specification of an opaque wall adjacent to a fluid or solid zone, however, it is necessary to specify the opacity condition directly at the boundary. Furthermore, the steel surface was considered to reflect diffusely the incoming radiation from the fluid.

3.1.4. Turbulence Model

The turbulence model k-w SST was chosen to compute the interphase turbulence, being k the turbulence kinetic energy and w the specific dissipation rate. This approach is better suited for wall bounded flows than the classical k-e, RMS (Root Mean Square), or LES (Large Eddy Simulation) models which are intended for turbulent core flows, i.e., regions that are far from walls. The k-w semi-empirical model was developed to be applied throughout the boundary layer, provided that the near-wall mesh resolution is sufficient. This standard model has been improved, leading to the k-w Base Line (BSL) and SST versions. Both versions can be used to describe near-wall and far-wall flows present on the same problem. However, the SST model accounts for the transport of the turbulence shear stress in the definition of the turbulent viscosity. Therefore SST – model is more accurate and reliable for a wider class of flows than the standard and the BSL - models. Full set of equations and constants for this model can be found elsewhere [24].

3.1.5. Heat Conduction

The solid probe is the main source of energy in this system. Heat conduction takes place in the axial and radial directions. The heat conduction equation is a particular case of the previous energy equation since there is only solid phase and no velocity. The heat conduction equation can be written as,

\frac{\partial}{\partial t} (ρ_{s} C_{p, s} T) = \nabla \cdot (k_{s} \nabla T),

(24)

where subscript “s” means solid phase.

3.2. Initial, Boundary and Internal Conditions

It is convenient to define several time points that characterize the quenching progress. These points are called “F”, “A”, “B”, “C”, “D” and “E” and are explained below. The initial time, t=0, corresponds to the point when the tip of the conical base of the probe just touched the water free surface in the basin. At this point, the probe starts its immersion into the flowing water, this is point “F”. For modeling purposes, a representation of this process was adopted. It was assumed that at t=0 the whole probe was instantaneously immersed and the steady water up flow velocity was increased by adding the immersion velocity to it and increasing proportionally the turbulent kinetic energy of the water. This velocity increment was applied only to a couple of rows boundary fluid cells which were at distances < 2.8 mm from the wall. The size of boundary cells is 1.4 mm which satisfies the convergence condition to the dimensionless position y⁺ > 30 that grants inclusion of the viscous sublayer and the buffer layer. Notice that quenching modelling starts with the fully immersed probe that still corresponds to point “F” since t=0. The period of duration of this velocity increment was equal to the actual immersion time. After this short period, the probe is at point “A”. Table 4 summarizes the initial conditions for the solved differential equations. The table shows that the initial water velocity field was computed previously in an independent calculation, assuming that the probe is already in its final position inside the vertical tube, and it is at water temperature. Therefore, the continuity, momentum and turbulence equations were solved under steady state and isothermal conditions. The initial pressure and turbulent quantities, k and w, correspond to this previous calculation. Finally, the probe temperature is uniform since the Biot number is smaller than 0.1 during air-cooling when transporting the probe from the muffle to the quenching position.

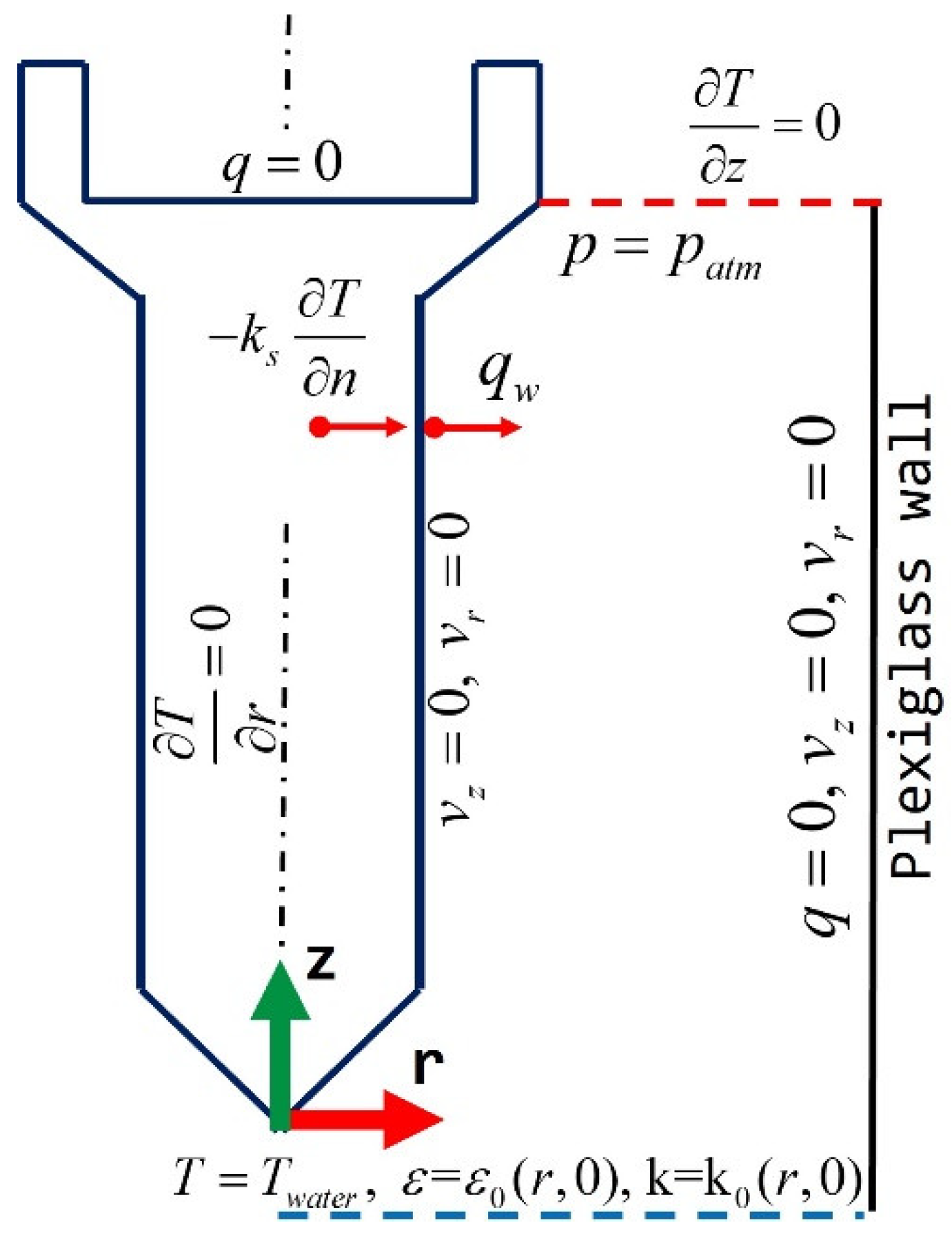
The boundary and internal conditions applied to solve the governing equations are graphically shown in Figure 3. The axisymmetric domain included a water inlet surface, a water outlet surface, a symmetry axis, and the following solid boundaries: a Plexiglas tube wall and a probe top surface; and the internal boundary was the probe lateral surface.

Continuity, momentum, and turbulence equations require the following boundary conditions:

The profiles of inlet velocity and turbulent quantities were previously calculated and correspond to a fully turbulent, developed profile, v(r), since the inlet surface is far enough from the elbow connector located upstream and from the solid probe to avoid any flow distortion. At the outlet, a reference atmospheric pressure, p_atm, was specified. A zero velocity, wetting condition, was specified over the tube surface and on the probe surface, and a near-wall treatment was used to specify turbulent quantities in those wall surfaces.

Energy equation requires to specify an inlet water temperature, an outlet zero temperature derivative in the axial direction, zero heat flux on the Plexiglas wall, zero heat flux on the probe top surface, and a near-wall treatment for turbulent heat flow in the probe wall surface.

The near-wall treatment accounts for the effect of the wall presence on the turbulence. The region that is closer to the wall has tangential velocity fluctuations that are reduced by viscous damping, while the normal velocity fluctuations are reduced by kinematic blocking. Outside of this zone, turbulence is rapidly augmented by generation of turbulent kinetic energy. The limits of the viscous sublayer, the buffer layer, and the fully turbulent region, are represented by the dimensionless distance from the wall, y⁺, which is defined by the following equation.

y^{+} \equiv \frac{ρ u_{τ} y}{μ},

(25)

where the friction velocity, u_t , is defined as

u_{τ} = \sqrt{\frac{τ_{w}}{ρ}},

(26)

being t_w the shear stress on the wall. A value y+ < 30 represents a region that includes the viscous sublayer and the buffer layer. In the present approach, semi-empirical equations, called “wall functions” were used to bridge the variables between the viscous sublayer and the fully turbulent region. Typically, wall functions are used in meshes with y+ > 30. Therefore, the first control volume next to the wall will include the first two regions, viscous and buffer. This avoids the appearance of unbounded errors in computing wall shear stress and heat flux.

3.3. Materials Properties

Water and water-vapor thermophysical properties were obtained from the NIST webpage [25] considering a boiling temperature of 95°C and an atmospheric pressure of 84550 Pa. The properties of these fluids and the properties of solid steel [26] depend on temperature and were fed to the computer code as a lookup table. Density was assumed to be constant, using the values of 7930, 983.2, and 0.507 kg/m³ for the solid metal, water, and water-vapor phases, respectively. The parameters and constants used in the semi-mechanistic boiling model, in the interfacial mass exchange equations, and in the turbulence and radiation models are shown in Table 5. This table also shows additional parameters and constants related to the four models used in the simulation, and not indicated previously. In the case of the Wall Boiling Model, T_bulk, V_bulk, and y* are the reference quantities for temperature, velocity, and reference distance from the wall, respectively, and n is the power law superposition constant. For the Interfacial Mass Transfer Model, D_b is the bubble diameter. For the Turbulence Model, k is the turbulent kinetic energy value. On the other hand, it was recorded that after full immersion of the probe, some incubation period was needed for the wetting front start to move and t_B is the corresponding time, point “B”. Finally, in the Radiation Model e_w is the probe surface emissivity, a_p,water and a_p,vapor are the absorptivity coefficients of liquid and vapor water, respectively, σ_s and C are the scattering and anisotropy coefficients, respectively, and n_w and n_v are the refraction indexes of liquid and vapor water, respectively.

3.4. Solution Method

3.4.1. Meshing

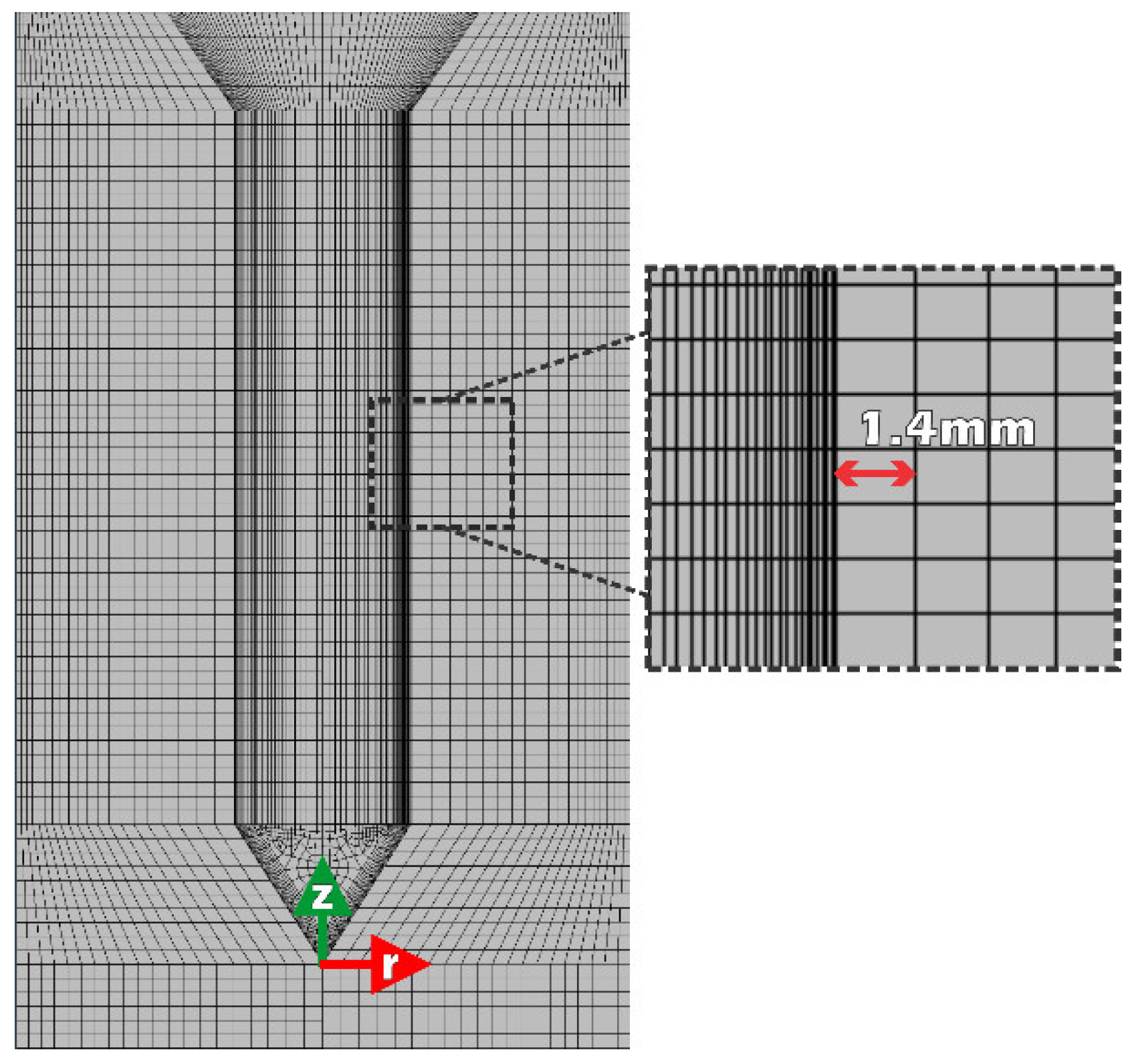
The computational domain is axisymmetric. On the other hand, since an exact and mesh-independent solution can be obtained with a high-quality mesh, extra care was required in the discretization to correctly capture the hydrodynamic behavior in the boundary layer. Because of that, it should be noted that the semi-mechanistic model requires an interfacial discretization based on the y⁺ parameter, defined as the instantaneous fluid film responsible for the thermal diffusion of the heat delivered by the solid. This parameter should remain above a value of 30 or in the worst case equal to or greater than 12 during calculation, this implies that the height of the first element on the solid side must have at least a normal value of 1.4 mm. Attending this criterion, Figure 4 shows a scheme that matches both experimental and discretized domains, the discretized domain consists of 3567 elements, with an average orthogonal quality of 0.98.

3.4.2. Numerical Solution

The mass, momentum and energy conservation equations were solved using the finite volume method [9] implemented in the 2018 ANSYS® Fluent code. Simulations were conducted for the cases shown in Table 3, and included 25 s of quenching process using a time-step of 0.001 s. Convergence was achieved with a residual value of 10^-3 for continuity and momentum equations, while a value of 10^-6 was applied for the energy equation.

4. Results and Discussion

This section presents the validation of the numerical model. It is shown a comparison between the observed evolution of the position of the wetting front and the respective computed motion. Also, the measured cooling curves are compared with the predicted values. Furthermore, it is included calculations of the evolution of wall heat flux distribution during quenching metals. Both, radial and axial heat flux components were computed.

4.1. Wetting Front Position

Figure 5a–d show a sequence of recorded photographs of the cylindrical probe, side “photo”, paired with the corresponding model predictions, side “model”, during immersion quenching of a cylindrical probe from 930°C in water flowing upward at an average velocity of 0.6 m/s. In the “photo” side, the solid sample shows a red color due to thermal radiation, and the wetting front appears as a horizontal gray ring around the probe surface in Figure 5b–d. In the “model” side, the colors indicate the computed water vapor fraction distribution, while the gray tones represent the calculated temperature field in the solid probe. Additionally, the corresponding computed wall heat flux and vapor film thickness profiles along the probe surface are shown on the left side from the probe. Figure 5a corresponds to point “B”, 0.7 s, which is the time to start the wetting front motion, and the computed film thickness profile shows that the vapor blanket is located along the whole wall surface with ~ 3 mm thickness, except in the vertex area and the top conical surface. The later surface shows a decrease in the vapor film thickness as compared with the main surface of the probe. Conversely, the computed wall heat flux reaches its minimum value, ~ 0.3 MW/m², along the main surface of the probe. This is characteristic of the stable vapor film regime. No wetting front appears clearly defined, yet. Figure 5b shows the probe after 3.15 s, that is the time at which the wetting front reaches the base of the inverted cone of the probe, point “C”. The respective photo shows this front as a gray ring which represents the nucleation boiling regime since bubbles are rising from this position. The conical region shows a dark color which indicates a lower temperature, leading to the single-phase convection regime. Above the wetting front position, the stable vapor layer can be observed, and the model predicts its thickness value of ~ 3 mm. Notice that all three regimes are present: stable vapor film, nucleation boiling, and single-phase convection.

Consistently with these observations, the computed heat flux profile shows a peak value whose position nearly matches with the wetting front position but maintains a low value along the cylindrical probe. Notice that at this stage, the stable vapor film covers all the thermocouple surface positions. Figure 5c shows the results after 8.3 s from immersion, which is the time that the wetting front reaches a heigh, z=35.5 mm, which is the height of central thermocouples TC2 and TC4: point “D”. As it is expected, the heat flux has a peak value at this position. Below this position, heat flux decreases under the single-phase convection regime. Above the wetting front, the stable vapor layer prevails. Finally, Figure 5d shows that after 11.9 s from immersion, the wetting front has reached a position z= 52 mm, which is above the thermocouple positions. Most of the probe is under single-phase convection, and a small region is still under the stable vapor layer regime.

A comparison between computed and observed evolution of the wetting front position is shown in Figure 6a,b for cases V1 and V2, respectively. Figure 6a shows that the wetting front moves approximately at a constant velocity, as indicated by the straight line corresponding to the observations. The predicted curve deviates slightly from this behavior but reasonably agrees with the experimental curve. Figure 6b shows again an observed constant velocity of the wetting front. However, the computed curve shows some deviation from the observed one after the wetting front has passed point D. This may be attributed to experimental error. Another interesting feature of these curves is the incubation time, points “B”, required for the wetting point start to move. The higher the water velocity, the shorter the incubation time is, which is a result of an enhanced rate of heat transfer.

The previous results show that the model computes the boiling transitions using a general formulation, i.e., there is no need to apply specific equations or parameters for each boiling regime. The stable vapor film, nucleate boiling and single-phase regimes were reasonably predicted when they occurred simultaneously during quenching a laboratory probe. Therefore, the whole boiling curve is implicitly predicted using this model.

4.2. Cooling and Cooling Rate Curves

Figure 7a,c show comparisons between computed (discontinuous lines) and experimental (continuous lines) cooling curves that were measured with 4 thermocouples embedded in the steel probe for study cases V1 and V2, respectively. Complementary, Figure 7b,d show the corresponding comparisons of the cooling rates, for cases V1 and V2, respectively. Figure 7a shows temperature evolution since the probe was in the furnace, during the transportation period to the quenching position, and during the probe quenching which started at point “F” at t=0, just when the tip of the conical base touched the free surface. Recall that probe is fully immersed into water at point “A”, point “B” is the time at which the wetting front starts to move upward, and point “C” is the time the wetting front reaches the shoulder of the probe. Between point “B” and point “C” the temperature descended according to a straight line and the wetting front moved along the conical base of the probe. During this period “BC”, the wall surface at the z-position of the thermocouples was still in the vapor film regime. This regime is characterized by a low heat flux at the wall which leads to the relatively low slope of the straight line. Figure 7b shows this slope as a cooling rate. During the period “BC” the cooling rate was ~ 25°C/s. This measured initial cooling rate was properly calculated by including radiation heat transfer from the wall. Otherwise, the computed cooling rate was considerably smaller than the measured values. Radiation heat losses are important to predict temperature evolution in the probe when wall temperatures are above the Leidenfrost temperature. For this case, this temperature was ~750°C. The quenching time to reach this temperature was > 6 seconds, which is not negligible when considering that the total quenching time was 20 seconds. Therefore, inclusion of radiation heat transfer in a model is important to properly calculate the temperature evolution of workpieces quenched from an initial high temperature. The figure shows that after point “C” the thermocouples reached in sequence a maximum cooling rate, starting from TC3, then TC2 closely followed by TC4, and finally, TC1, which is the uppermost thermocouple in the probe. At point “D” the wetting front is passing over thermocouples TC2 and TC4, when they reach the maxima cooling rates. This maximum value corresponds to the wetting front associated with the nucleation boiling regime. The figure shows that the computed maxima cooling rates were higher than the corresponding experimental values, although they match each other in the time scale. Despite this difference, it was verified that the area under the curves, measured versus computed, were mutually similar, satisfying the energy conservation principle. It is not clear whether this peaks difference can be attributed to measurement errors or model simplifications, or both. New experiments would be needed to clarify this point.

Figure 7c,d show the respective comparison between computed and measured cooling and cooling rate curves, respectively, when water velocity was 0.2 m/s. Similarly, to the previous case, the temperature histories show a reasonably well agreement between computed and measured curves. Nevertheless, the more sensitive cooling rate curves show that there is a mutual mismatch in the time scale of maxima cooling rates, and additionally the computed maxima values are higher than the measured ones. It is evident that the model predictions are not as accurate as those obtained for the higher water flow velocity. The reason is not clear but the fluid flow considerations in the model may be better suited for fully forced convection. In general terms, prediction of temperature evolution at different locations within the steel probe agrees reasonably well with the corresponding laboratory measurements. Therefore, the model can represent temperature in the solid and boiling regimes in the liquid using first principles, i.e., without introducing empirical equations that are valid within established temperature limits.

4.3. Heat Flux at the Wall

Heat flux at the wall is the combined result of fluid and solid heat transfer phenomena. Commonly, heat flux at the wall is determined from the solution of the Inverse Heat Conduction Problem (IHCP) [27] which uses the cooling curve data. Moreover, the most frequent analysis employs the one-dimensional heat conduction equation. For the present experimental setup, heat flux within the probe is two-dimensional since temperature is function of both, axial and radial positions, as well as time. Since the model predicts this two-dimensional temperature field and the local boiling regime, it is interesting to determine the ratio of wall heat flux components, q_z/q_r, as a function of time, at the thermocouple z-positions.

Figure 8a,b show the computed evolution of the wall heat flux ratio, q_z/q_r, for the studied cases. Figure 8a shows that during the initial quenching, this ratio is << 1, which is a result of no temperature variation in the z-direction at the thermocouples positions. However, once the wetting front reaches these positions, both heat flux components increase. Interestingly, the axial component exceeds, by a factor >5, the radial component of the heat flux. Radial heat flux increases because nucleation boiling regime appears, but axial heat flux increases because different boiling regimes are present in the wall along z-direction. After the wetting front passes over the thermocouples, the wall cools down under the one phase convection regime and the axial heat flux component decreases. The three curves are mutually lagged, consistently with the z-position of the thermocouples in the probe. Figure 8b shows similar curves when water flows at a velocity of 0.2 m/s. However, the heat flux ratio reaches a value of ~10. This is attributed to the lower radial heat flux resulting from the lower water velocity. In contrast, the axial heat flux is maintained high because of the distribution of different boiling regimes along the wall. The main lesson to learn from these results is that quenching under multi-regime boiling convection is undesirable. Wall heat flux changes abruptly with position, and therefore solid-phase transformation along the workpiece should lag behind, specially in a metal layer near the surface. Stresses generated from this lagging may cause deformation or even cracks. Optimal immersion routes should be considered when quenching workpieces [28,29] and they may be related to this multi-regime boiling phenomenon.

On the other hand, modelling residual stresses in quenched workpieces relies on the determination of the heat transfer coefficient (HTC). Medina-Juárez et al. [30] reported a study on the accuracy of a finite element model to predict residual stresses in quenched stainless steel. They solved the mechanical equilibrium equation and the heat conduction equation in the solid using a boundary condition in terms of the HTC. This coefficient was determined independently from thermal analysis, using thermocouples embedded in the solid, and the solution of the IHCP. The authors found that the computed tensile residual stress was overestimated and the compressive residual stress was underestimated by the model. They attributed this result to an effect of plasticity due to twinning in the residual stresses. However, we rise the question, what is the influence of simultaneous multi-regime boiling over an IHCP analysis? Our answer is that the measured temperature is the net result of both, radial and axial heat flux components. Therefore, a one-dimensional inverse heat conduction analysis is not appropriate to determine the wall heat flux for immersion quenching under multi-regime boiling. The vectorial nature of the heat flux requires a two-dimensional IHCP analysis, distributing sub-superficial thermocouples along axial and radial directions.

The characteristics of the computed boiling curves of Figure 8a,b are summarized in Table 6. The first column shows the average values of radial component of the wall heat flux for each boiling regime: Vapor Film (VF), Transition Boiling (TB), Nucleate Boiling (NB), and Single-Phase Convection (SP). Furthermore, the Critical Heat Flux (CHF) is included. Each value was determined by averaging the heat flux within the range of temperature of the corresponding boiling regime. The Leidenfrost temperature, T_L, the temperature at the Critical Heat Flux, T_CHF, and the Nucleate Boiling start temperature, T_NB, are the respective limits and are also included. The computed results are mutually consistent as explained below.

For the case V1, Leidenfrost temperature is 770°C for the lower thermocouple TC3, decreases to 746°C for the higher thermocouple TC2, and is the lowest value for the uppermost thermocouple TC1. This is consistent to the direction of motion of the wetting front. Vapor film lasts for a longer time for the TC1 which contributes to a decrease of its temperature, receiving the wetting front at a lower wall temperature. A similar behavior occurs for the case with a water velocity of 0.2 m/s. However, in this case the Leidenfrost temperatures are lower than the corresponding values for 0.6 m/s. This is consistent with the fact that in order a lower water velocity can break the vapor film, it is required that the wall reaches a lower temperature. Furthermore, as expected, the respective average heat fluxes, q_VF, are also relatively lower than the rest values reported in this table and were obtained by averaging the local wall heat flux in the temperature range, T_L< T < T_s.

In transient boiling experiments, transition and nucleate boiling regimes are generally considered as one and simply called nucleate boiling regime. This is because the narrow zone and short period at which they are present. However, for the sake of completeness, we have separated the transition boiling regime, which is in the temperature range, T_CHF < T < T_L. For the case V1, the table shows that the temperature at the critical heat flux is essentially constant, at 254 ± 3 °C and a constant critical heat flux of 5.8 MW/m². Therefore, the average transition boiling heat flux is also constant (2.1 MW/m²). The results for the case V2 are similar except for the TC3 thermocouple. At this position, T_CHF and q_CHF are higher than the values for thermocouples TC2 and TC1. This is attributed to the combination of a higher wall temperature when the wetting front reaches that position and the low water velocity.

Nucleate boiling regime is in the temperature range, T_NB < T < T_CHF. The table shows that temperature T_NB is essentially constant but is higher for the case V1 as compared with the corresponding values for the V2 case. A similar trend is observed for the average heat flux q_NB. Finally, single phase convection regime occurs for temperatures T<T_NB, and the computed heat flux values are consistent with the expected results.

5. Summary and Conclusions

This work presents a heat transfer and boiling model to understand and predict the thermal evolution of a solid probe under forced convection quenching. The conservation equations of mass, momentum and energy were numerically solved together with the turbulence k-w SST (Shear Stress Transport) and thermal radiation, Discrete Ordinate (DO), differential equations, subjected to proper initial and boundary conditions. The wall heat flux was computed in all three boiling regimes using a single semi-mechanistic equation rather than specific empirical equations to represent each boiling regime. Furthermore, the model is computationally efficient since it solves the interpenetrated phases equations for the vapor-liquid water mixture, avoiding the more computational expensive calculation of the vapor-liquid interphase for every bubble.

An original feature of this work is the validation method for this type of model. Combination of two laboratory measurements was used for validation: 1) the recorded wetting front motion along the surface of a conical-end cylindrical probe and 2) the cooling curves obtained with 4 sub-superficial thermocouples in the probe. The first measurements validate the accuracy of fluid flow and boiling modelling, while the second measurements are aimed to validate heat conduction calculations within the probe.

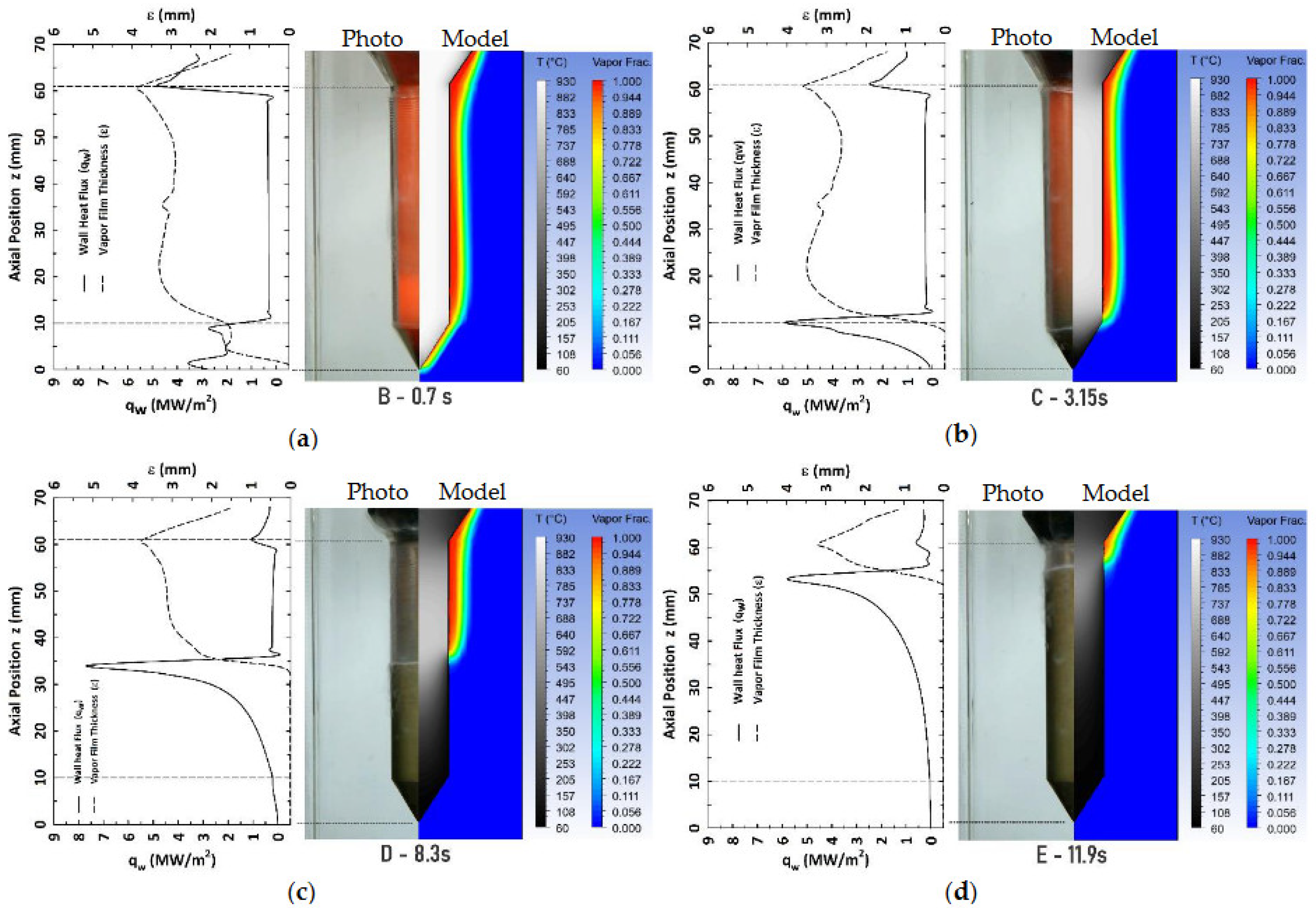
The wetting front motion was accurately represented during its displacement along the vertical wall of the conical-end cylindrical probe. The computed wall heat flux and vapor layer profiles along the probe show the simultaneous presence of the three boiling regimes: stable vapor film, nucleate boiling, and single-phase convection. This is consistent with recorded images which also show the regimes distribution during the quenching process. Model predictions seem to be more accurate for the case with a higher water velocity. This suggests that model assumptions are better suited for full forced convection.

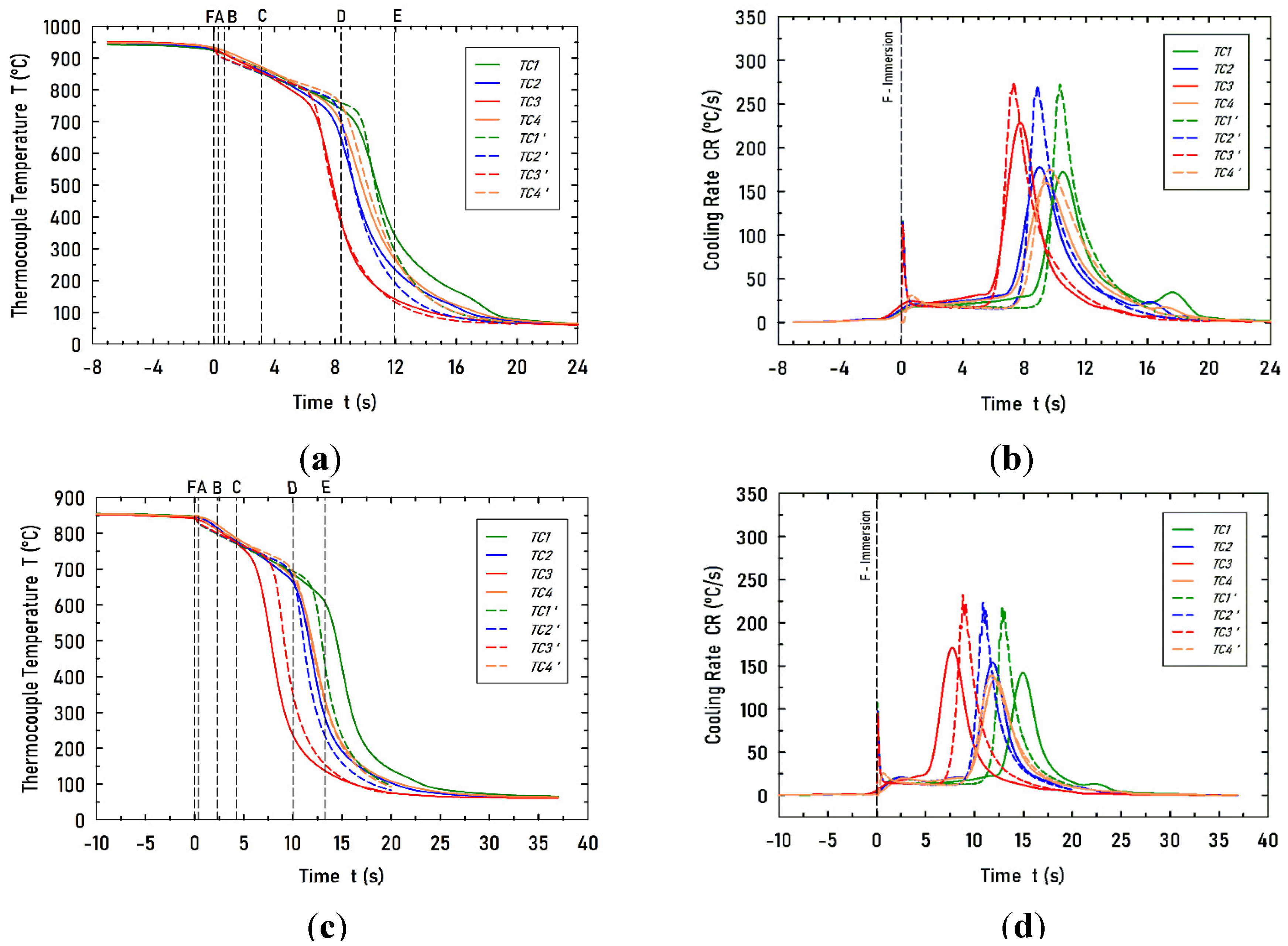
The predicted cooling curves at the four thermocouples positions agree reasonably well with the corresponding measured curves in all boiling regimes: stable vapor film, nucleate boiling, and single-phase convection. A more sensitive comparison between calculations and measurements is the curve of cooling rate versus time. The computed cooling rates also agree with the measured values. The computed temperatures of maximum cooling rates at the thermocouples locations match perfectly with the corresponding measured values for the case V1, water velocity 0.6 m/s and initial probe temperature 930°C. For case V2, which has a lower water velocity, there is no such a perfect match, but a fair agreement. Furthermore, the computed maxima cooling rate values are consistently higher than those measured. It is no clear whether this can be attributed to experimental error or model assumptions.

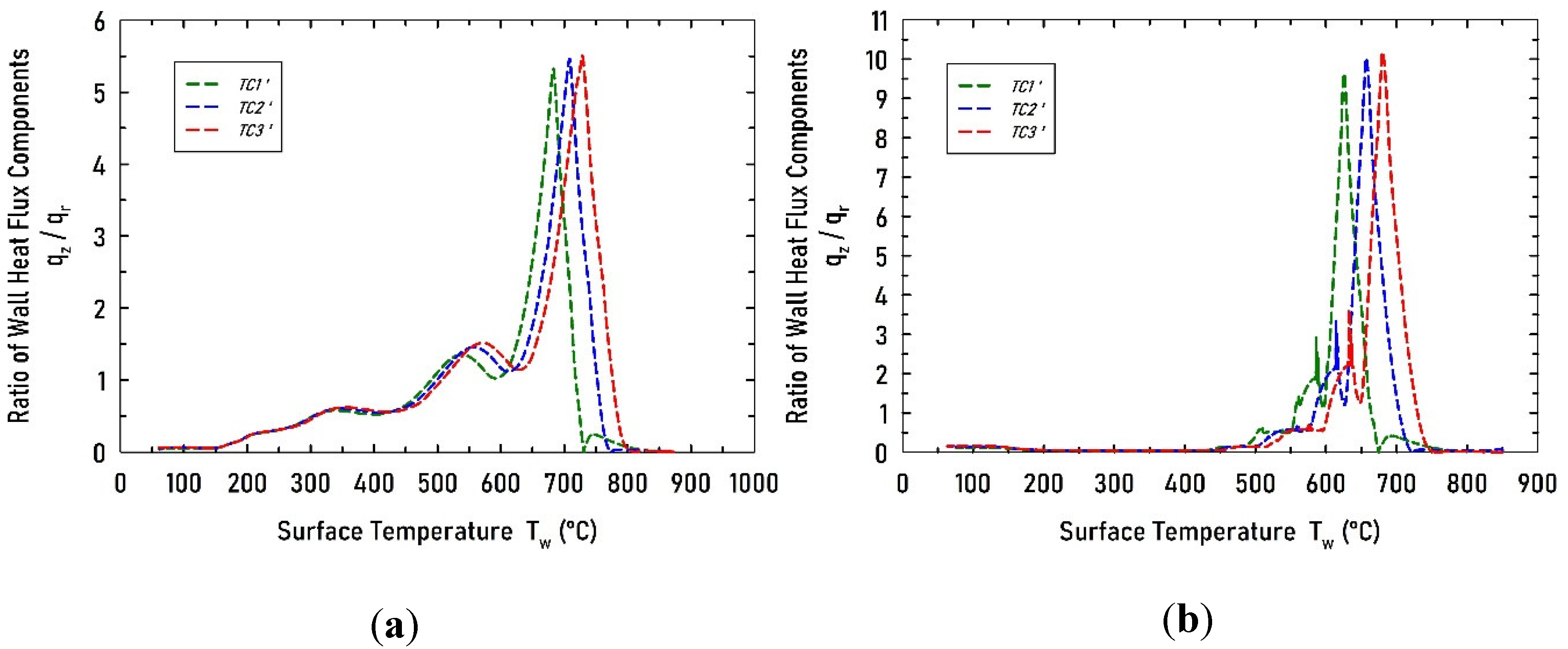
Finally, the model was used to determine the ratio of heat flux components, q_z/q_r, at the wall at the thermocouples z-positions. It was found that the axial component can be up to 5 times larger than the radial component for case V1, and up to 10 times larger than the radial component for case V2. This is a result of having simultaneously all three boiling regimes distributed along the wall. This multi-regime boiling phenomenon is undesirable since leads to non-uniform wall heat flux and potentially poor workpiece quality. Finally, one-dimensional IHCP analysis is not appropriate to determine the wall heat flux when multi-regime boiling is present. Two-dimensional IHCP analysis and using thermocouples embedded along radial and axial directions should be preferred.

Author Contributions

Conceptualization, MAGM is the main author of this paper since the present work is part of his PhD thesis developed under the direction of FAAG; methodology, MAGM, FAAG, BHM; software, MAGM, and the important collaboration of ORR, a knowledgeable and experienced person in the use of ANSYS-Fluent®; validation, MAGM, BHM and ORR; formal analysis, MAGM, FAAG; investigation, MAGM, FAAG, resources, FAAG; data curation, MAGM; writing—original draft preparation, MAGM; writing—review and editing, FAAG; visualization, MAGM; supervision, FAAG; project administration, FAAG; funding acquisition, FAAG. All authors have read and agreed to the published version of the manuscript.

Funding

This project received funding from to CONACYT-SENER-HIDROCARBUROS [grant # 267962]. .

Acknowledgments

The authors are grateful to CONACyT for the scholarship granted to MAGM during his PhD studies at Cinvestav and the assistance of Dr. Roberto Cruces-Reséndez with laboratory work and analysis of the video recordings.

Conflics of Interest: The authors declare no conflict of interest.

References

Kharangate, C.R.; Mudawar, I. Review of Computational Studies on Boiling and Condensation. Int. J. Heat Mass Transf. 2017, 108, 1164–1196. [Google Scholar] [CrossRef]
Kopun, R.; Škerget, L.; Hriberšek, M.; Zhang, D.; Stauder, B.; Greif, D. Numerical Simulation of Immersion Quenching Process for Cast Aluminium Part at Different Pool Temperatures. Appl. Therm. Eng. 2014, 65, 74–84. [Google Scholar] [CrossRef]
Zhang, D.S.; Kopun, R.; Kosir, N.; Edelbauer, W. Advances in the Numerical Investigation of the Immersion Quenching Process. IOP Conf. Ser. Mater. Sci. Eng. 2017, 164, 012004. [Google Scholar] [CrossRef]
Srinivasan, V.; Moon, K.-M.; Greif, D.; Wang, D.M.; Kim, M. Numerical Simulation of Immersion Quench Cooling Process Using an Eulerian Multi-Fluid Approach. Appl. Therm. Eng. 2010, 30, 499–509. [Google Scholar] [CrossRef]
Krause, F.; Schüttenberg, S.; Fritsching, U. Modelling and Simulation of Flow Boiling Heat Transfer. Int. J. Numer. Methods Heat Fluid Flow 2010, 20, 312–331. [Google Scholar] [CrossRef]
Stark, P.; Hinrichs, B.; Hornig, N.; Schuettenberg, S.; Fritsching, U. Simulation of Quenching Process with Liquid Jets.; Chicago, Illinois, USA, 2012.
Passarella, D.N.; L-Cancelos, R.; Vieitez, I.; Varas, F.; Martín, E.B. THERMO-FLUID-DYNAMICS QUENCHING MODEL: EFFECT ON MATERIAL PROPERTIES.; May 2014; pp. 3625–3644.
Petrovic, M.M.; Stevanovic, V.D. Coupled Two-Fluid Flow and Wall Heat Conduction Modeling of Nucleate Pool Boiling. Numer. Heat Transf. Part A Appl. 2021, 80, 63–91. [Google Scholar] [CrossRef]
Patankar, S.V. Numerical Heat Transfer and Fluid Flow; Series in computational methods in mechanics and thermal sciences; CRC Press: Boca Raton, 1978; ISBN 978-0-89116-522-4. [Google Scholar]
Ramezanzadeh, H.; Ramiar, A.; Yousefifard, M. Numerical Investigation into Coolant Liquid Velocity Effect on Forced Convection Quenching Process. Appl. Therm. Eng. 2017, 122, 253–267. [Google Scholar] [CrossRef]
Moon, J.H.; Lee, S.; Lee, J.; Lee, S.H. Numerical Study on Subcooled Water Jet Impingement Cooling on Superheated Surfaces. Case Stud. Therm. Eng. 2022, 32, 101883. [Google Scholar] [CrossRef]
Zhang, L.; Li, Z.-D.; Li, K.; Li, H.-X.; Zhao, J.-F. Influence of Heater Thermal Capacity on Bubble Dynamics and Heat Transfer in Nucleate Pool Boiling. Appl. Therm. Eng. 2015, 88, 118–126. [Google Scholar] [CrossRef]
Ilic, M.; Petrovic, M.; Stevanovic, V. Boiling Heat Transfer Modelling: A Review and Future Prospectus. Therm Sci 2019, 23, 87–107. [Google Scholar] [CrossRef]
Vergara-Hernández, H.J.; Hernández-Morales, B. A Novel Probe Design to Study Wetting Front Kinematics during Forced Convective Quenching. Exp. Therm. Fluid Sci. 2009, 33, 797–807. [Google Scholar] [CrossRef]
Cruces-Reséndez, R.; Hernández-Morales, B.; García, E.I.D. Re-Wetting Behavior and Heat Extraction during Laboratory-Scale Quenching Experiments Using Two Probe Geometries. 2017.
Ch. 14 Multiphase Flows: Mixture Model Available online: http://www.ansys.com (accessed on 14 October 2023).
Matkovič, M.; Končar, B. Bubble Departure Diameter Prediction Uncertainty. Sci. Technol. Nucl. Install. 2012, 2012, 1–7. [Google Scholar] [CrossRef]
Schiller, L.; Naumann, Z. A Drag Coefficient Correlation. VDI Ztg. 1935, 77, 318–320. [Google Scholar]
Lee, W.H. A Pressure Iteration Scheme for Two-Phase Flow Modeling; University of California: Los Alamos, New Mexico, 1979. [Google Scholar]
Chen, J.C. ACS Publications. American Chemical Society July 1 1966, pp. 322–329.
Ch. 14 Multiphase Flows: Semi-Mechanistic Boiling Model Available online: http://www.ansys.com (accessed on 14 October 2023).
Forster, H.K.; Zuber, N. Dynamics of Vapor Bubbles and Boiling Heat Transfer. AIChE J. 1955, 1, 531–535. [Google Scholar] [CrossRef]
Steiner, H.; Kobor, A.; Gebhard, L. A Wall Heat Transfer Model for Subcooled Boiling Flow. Int. J. Heat Mass Transf. 2005, 48, 4161–4173. [Google Scholar] [CrossRef]
Ch. 4 Turbulence: Standard, RNG, and Realizable k-ε Models. Available online: http://www.ansys.com (accessed on 14 October 2023).
Libro Del Web de Química Del NIST, SRD 69. Available online: https://webbook.nist.gov/chemistry/fluid/ (accessed on 7 March 2023).
Pehlke, R.D.; Jeyarajan, A.; Wada, H. Summary of Thermal Properties for Casting Alloys and Mold Materials. NASA STI/Recon Tech. Rep. N 1982, 83, 36293. [Google Scholar]
Beck, J.V.; BLACKWELL, B.; R. ST. CLAIR JR., C. INVERSE HEAT CONDUCTION: ILL-POSED PROBLEMS; 1985;
Lopez-Garcia, R.D.; Garcia-Pastor, F.A.; Castro-Roman, M.J.; Alfaro-Lopez, E.; Acosta-Gonzalez, F.A. Effect of Immersion Routes on the Quenching Distortion of a Long Steel Component Using a Finite Element Model. Trans Indian Inst Met 2016, 69, 1645–1656. [Google Scholar] [CrossRef]
López-García, R.D.; Medina-Juárez, I.; Maldonado-Reyes, A. Effect of Quenching Parameters on Distortion Phenomena in AISI 4340 Steel. Metals 2022, 12, 759. [Google Scholar] [CrossRef]
Medina-Juárez, I.; De Oliveira, J.A.; Moat, R.J.; García-Pastor, F.A. On the Accuracy of Finite Element Models Predicting Residual Stresses in Quenched Stainless Steel. Metals 2019, 9, 1308. [Google Scholar] [CrossRef]

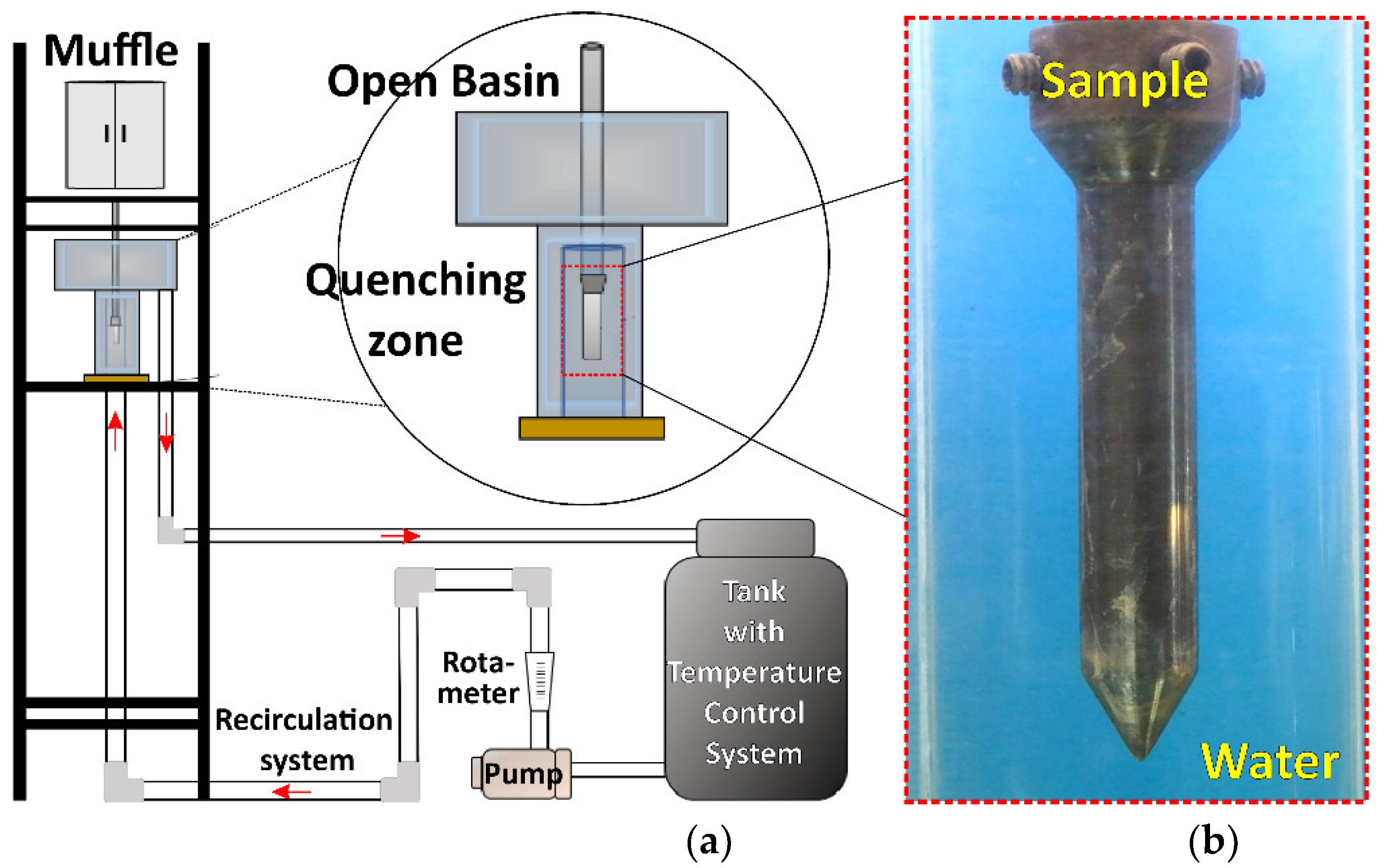
Figure 1. (a) Schematic representation of experimental set-up used to measure the sample thermal history and the wetting front kinematics. (b) Photograph of conical-end cylindrical probe immersed in quenching zone.

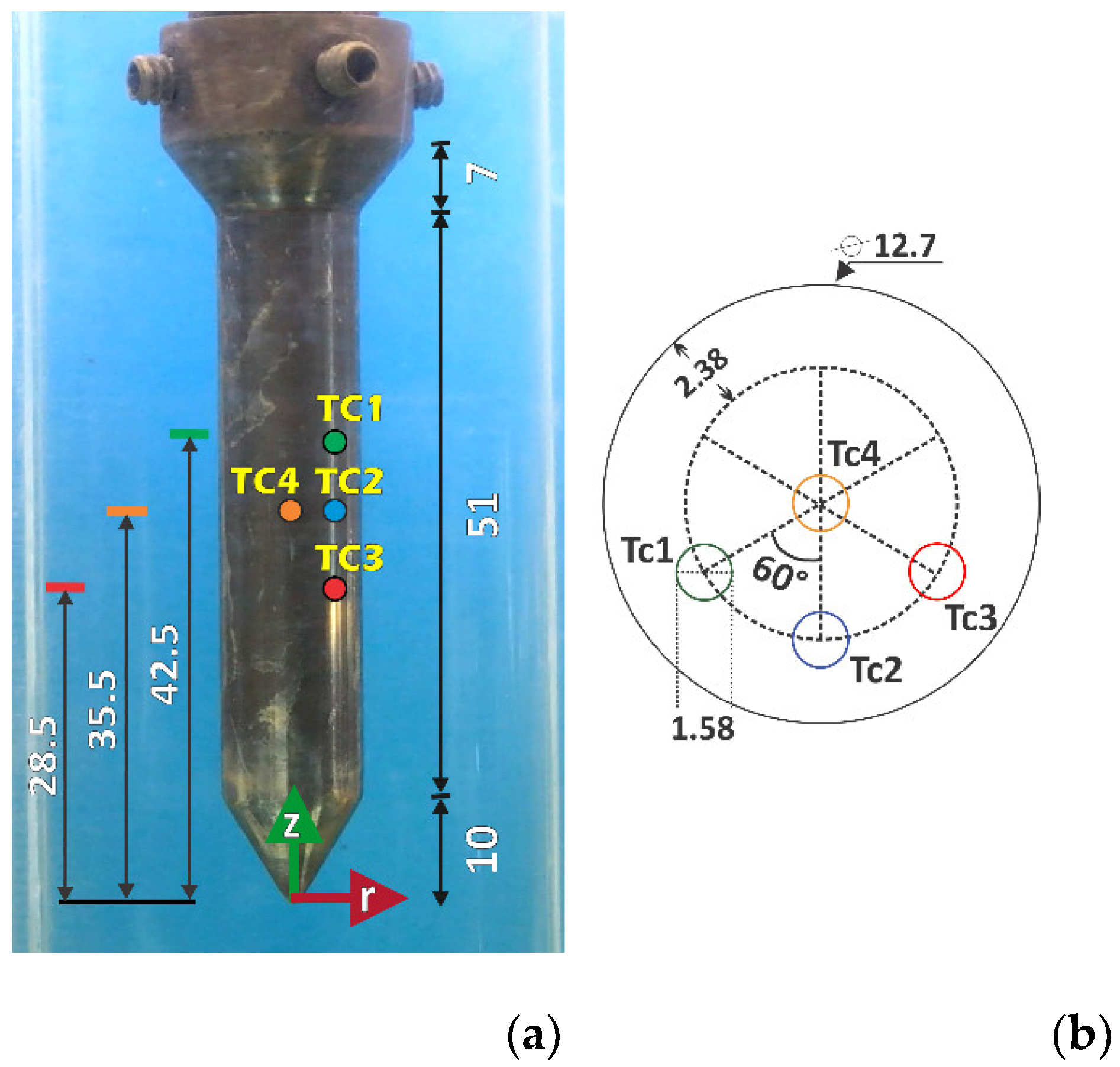
Figure 2. (a) Photograph of probe indicating thermocouple axial positions, z. (b) Top view of a probe, showing thermocouple radial positions, r. Lengths are in mm.

Figure 3. Schematic representation of axisymmetric domain indicating the boundary conditions applied to the numerical solution of the momentum and energy equations.

Figure 4. Discretization of the computational domain, pointing out the first adjacent cell length of 1.4 mm which satisfies the y⁺ parameter requirement.

Figure 5. Sequence of recorded photographs of the cylindrical probe, side “Photo”, paired with the corresponding model predictions, side “Model”, of immersion quenching of a conical-end cylindrical probe from 950°C in water flowing upward at an average velocity of 0.6 m/s, case V1. Each probe is accompanied by its computed profiles of wall heat flux and vapor film thickness along the probe surface. Elapsed time after probe immersion, (a) 0.7, (b) 3.15, (c) 8.3 and (d) 11.9 seconds.

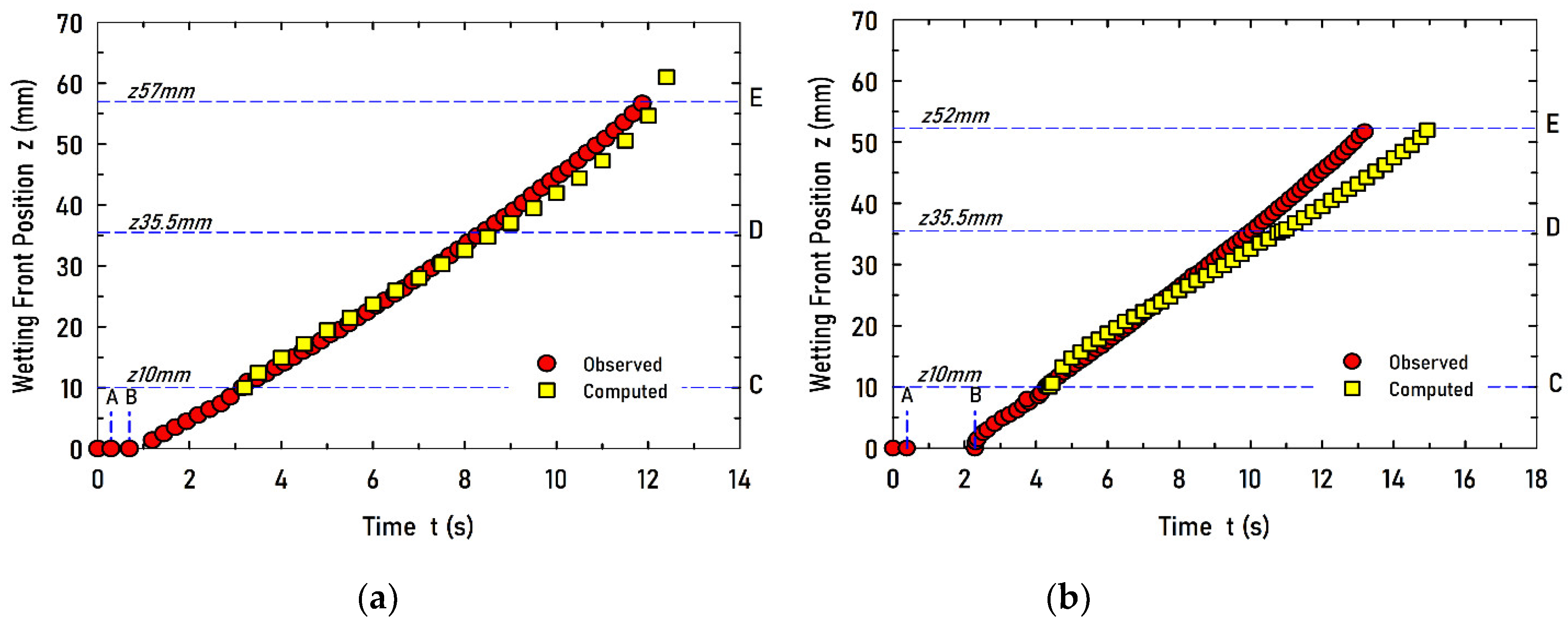
Figure 6. Computed and observed evolution of the wetting front position for study cases (a) V1 and (b) V2.

Figure 7. Computed (discontinuous lines) and experimental (continuous lines) cooling curves and their respective cooling rates. (a) Cooling curves for case V1, and (b) their corresponding cooling rate curves. (c) Cooling curves for case V2, and (d) their corresponding cooling rate curves. .

Figure 8. Computed ratio of wall heat flux components, q_z/q_r, at the positions of the thermocouples for the studies cases: (a) V1 and (b) V2.

Table 1. Interpenetrated phases models, validation methods and remarks.

Author, year	Model validation	Remarks
Srinivasan et al. (2010) [4]	Cooling curves in the solid body	Pool boiling, laminar flow, no radiation. Predetermination of a uniform Leidenfrost temperature to know which boiling regime is present and apply the proper heat transfer coefficient.
Krause et al. (2010) [5]	Qualitative comparison computed and observed bubble fraction on the wall. Heat transfer coefficient as a function of T_w.	Pool or convective flow boiling, laminar flow 10⁴<Re<2x10⁵, no radiation T_w<1000K (727°C). Mass transfer coefficients are computed from experimentally determined heat transfer coefficient during quenching of a workpiece.
Stark et al. (2012) [6]	No validation with experimental results	Steady state convection boiling at wall temperatures in the range from 300 to 900°C. Decoupling heat conduction in the solid by using the computed heat transfer coefficient h(T_w, location) in a separate calculation of solid temperature evolution.
Passarella et al. (2014) [7]	Heat transfer coefficient in the whole temperature range.	Convective flow boiling, turbulent flow, gray medium radiation, solid initial temperature = 850°C. No discussion on the determination of the damping functions.
Petrovic and Stevanovic (2021) [8]	Wall heat flux as a function of nucleation site density	Nucleate pool boiling, laminar flow, no radiation and no stable vapor film regime, T_w<130°C.

Table 2. Interphase-capturing-models, validation methods and remarks.

Author, year	Model validation	Remarks
Ramezanzadeh et al. (2017) [10]	Cooling curves in the workpiece	Volume Of Fluid method. No radiation, T_w < 627°C (900K), laminar flow (Re ≤ 1770). Calculation of simultaneous different boiling regimes on the wall.
Moon et al. (2022) [11]	Cooling curves and boiling curves	Volume Of Fluid method. No radiation, T_w ≤ 900°C. Turbulent flow, Re_nozzle = 15000, k-w SST model. Calculation of simultaneous different boiling regimes on the wall.
Zhang et al. (2015) [12]	No validation with experimental results	Level Set method applied twice: for vapor-liquid interface and for liquid-wall interface. Gosh Fluid Method for a computed sharp interface. No radiation, T_w≤ 106°C. Pool boiling, laminar flow.

Table 3. Summary of experimental conditions.

Case	Immersion temperature $T_{i m m}$ (°C)	Water temperature $T_{w a t e r}$ (°C)	Water average velocity $v_{w a t e r}$ (m/s)	Immersion velocity* $v_{i m m}$ (m/s)
V1	930	60	0.6	0.28
V2	850	60	0.2	0.28

Table 4. Summary of initial conditions for the solved differential equations.

Equation	Initial condition	Comments
Continuity, Eq. (2)	a₁ = 1, a₂ = 0, ${\vec{v}}_{m} = {\vec{v}}_{0} (r, z)$	There is only liquid water, which flows upward at a previously computed steady velocity field.
Momentum, Eq. (5)	p = p₀(r,z)	Previously computed steady pressure field
Energy, Eq. (9)	T = T_water	Measured uniform temperature in water
Turbulence, k-w SST	k = k₀(r,z) w = w₀(r,z)	Previously computed steady turbulent field quantities
Heat conduction, Eq. (24)	T = T_s	Measured temperature in solid probe

Table 5. Summary of the parameters and constants for the models used in the simulation of both study cases V1 and V2.

Study case	Semi-mechanistic Boiling Model		Interfacial Mass Exchange	Turbulence Model	Radiation Model
V1: v_water=0.6 ms^-1, T_s=930°C	y*=250 h_sp(estándar) h_nb (Foster/Zuber)[22] F (Chen)[20] S(Chen-Steiner)[23] n=1	M_sp=5 M_nb=1 h_factor=0.3	C_evap=30 s^-1 C_cond=0.2 s^-1 D_b=10^-4 m	k_c0c1 = 5 m²s^-2	ε_w=0.75 a_p,water=1.678 a_p,vapor=0.25 σ_s=0 C=0 n_w=1.333, n_v=1
V2: v_water=0.2 ms^-1, T_s=850°C		M_sp=4 M_nb=4 h_factor=0.8	C_evap=25 s^-1 C_cond=0.2 s^-1 D_b=10^-4 m	k_c0c1=3 m²s^-2

Table 6. Computed average wall heat flux by regime. The values are computed for wall z-positions of thermocouples TC1, TC2 and TC3, and for cases V1 and V2.

V1: T_s = 930°C, v_z = 0.6 m/s		TC1	TC2	TC3
Vapor Film (VF)
Leidenfrost, T_L (°C)		716	746	770
q_VF (MW/m²)		0.268	0.275	0.297
Transition Boiling (TB)
q_TB (MW/m²)		2.096	2.144	2.149
Critical Heat Flux (CHF)
T_CHF (°C)		251	254	256
q_CHF (MW/m²)		5.746	5.800	5.836
Nucleate Boiling (NB)
T_NB (°C)		141	142	143
q_NB (MW/m²)		3.461	3.524	3.586
Single-Phase Convection (SP)
q_SP (MW/m²)		0.396	0.374	0.344

V2: T_s = 850°C, v_z = 0.2 m/s	TC1		TC2	TC3
Vapor Film (VF)
Leidenfrost, T_L (°C)	639		668	695
q_VF (MW/m²)	0.217		0.226	0.234
Transition Boiling (TB)
q_TB (MW/m²)	0.78		0.872	1.542
Critical Heat Flux (CHF)
T_CHF (°C)	252		251	263
q_CHF (MW/m²)	4.622		4.822	5.797
Nucleate Boiling (NB)
T_NB (°C)	119		120	121
q_NB (MW/m²)	2.247		2.406	2.334
Single-Phase Convection (SP)
q_SP (MW/m²)	0.245		0.229	0.210

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Numerical Model of Simultaneous Multi-Regime Boiling Quenching of Metals

Abstract

1. Introduction

2. Materials and Methods

2.1. Quenching Zone and Probe Geometry

2.2. Experimental Conditions

3. Mathematical Model

3.1. Governing Differential Equations

3.1.1. Mixture Model

3.1.2. Evaporation/Condensation Model

3.1.3. Thermal Radiation Model

3.1.4. Turbulence Model

3.1.5. Heat Conduction

3.2. Initial, Boundary and Internal Conditions

3.3. Materials Properties

3.4. Solution Method

3.4.1. Meshing

3.4.2. Numerical Solution

4. Results and Discussion

4.1. Wetting Front Position

4.2. Cooling and Cooling Rate Curves

4.3. Heat Flux at the Wall

5. Summary and Conclusions

Author Contributions

Funding

Acknowledgments

References

MDPI Initiatives

Important Links

Subscribe