A Control-Oriented Model for Predicting Variations in Membrane Water Content of an Open-Cathode Proton Exchange Membrane Fuel Cell

Preprint

Article

A Control-Oriented Model for Predicting Variations in Membrane Water Content of an Open-Cathode Proton Exchange Membrane Fuel Cell

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

Adwoa Adunyah,Harshal Gawli,

Carrie Michele Hall^*

Adwoa Adunyah,Harshal Gawli,

Carrie Michele Hall^*

This version is not peer-reviewed

Submitted:

12 January 2024

Posted:

15 January 2024

Read the latest preprint version here

Alerts

Abstract

Proton exchange membrane (PEM) fuel cells have emerged as a viable alternative energy production source for stationary and transportation applications. Reliable and sustainable fuel cell operation requires effective water management. Membrane water content can vary along the stack during transients which can lead to losses in fuel cell performance. To control these variations a model that predicts the internal humidity dynamics of the stack is needed. In this study, a control-oriented model for predicting membrane water content variation was developed and implemented in MATLAB/Simulink. A lumped parameter model was initially developed and then further discretized into smaller control volumes to track humidity distribution along the stack. To validate the model’s predictions, the predicted results were compared to computer simulation results from GT-Suite. The root mean square error (RMSE) between the model’s prediction and GT-Suite’s simulation results was found to be within 1.5 membrane water content for all cases, demonstrating the model’s capability to capture the variation of membrane water content along the stack. The developed model will be useful for real-time control of membrane water content variation in PEM fuel cells.

Keywords:

Subject: Engineering - Energy and Fuel Technology

1. Introduction

Due to the negative environmental impacts of fossil fuels, alternatives are being sought and developed particularly in the transportation sector where reliance on petroleum-based fuels is high. While electrification of light-duty vehicles is growing, medium and heavy-duty vehicles can be harder to electrify due to their high energy demands. For medium to heavy-duty vehicles, proton exchange membrane (PEM) fuel cells have received considerable attention. Fuel cells provide an electrification solution for vehicles that alleviates range anxiety due to their refuelling capability. They can also function with a better efficiency than internal combustion engines and produce little to no pollutants on board. Among various fuel cell types, the PEM fuel cell stands out as a popular choice, primarily due to its high-power density and low operating temperature.

There are two types of PEM fuel cells: the closed-cathode and open-cathode varieties. The closed-cathode design is usually equipped with a compressor, a manifold, a dedicated cooling circuit for temperature management and an external humidifier for water management. These auxiliary components in the closed-cathode design induce parasitic loads that impact the stack performance. In contrast, the open-cathode design reduces the system’s complexity by integrating the stack’s air supply and temperature control and consequently water management.

Reliable and sustainable fuel cell operation requires effective water management as the membrane humidity has been shown experimentally to influence the cell performance. (Zeng et al., 2019) investigated the performance of an open cathode PEM fuel cell under variable speed control. They established that strong air flow rate leads to a decrease in cell voltage due to excessive loss in membrane water content. Further (Morner & Klein, 2001) evaluated the dynamic behavior of an air-breathing fuel cell stack experimentally and concluded that the performance of the stack is more dependent on membrane humidity than the stack temperature.

The membrane water content needs to be in the right range to promote ionic conductivity but must not interfere with reactant transport. Due to its dependence on temperature and reactant inlet humidity, control of membrane water content is inherently challenging. Internal cell variations that occur during transients can also lead to losses in fuel cell performance. To guarantee the stack’s performance and continued operation, these variations must be carefully monitored and controlled. As the fuel cell’s internal humidity status cannot be measured, control strategies depend on models to predict the internal humidity dynamics.

There are a number of existing models that aim to predict humidity distribution in a fuel cell stack. For instance, (Zhang & Jiao, 2018) developed a three-dimensional (3D) mathematical model of a PEM fuel cell. The established model can describe the relative humidity distribution of the gases in the anode and cathode channels as well as the membrane water content. (Dutta et al., 2001) established a 3D model using Navier Stoke’s equations with a multi-species mixture. They found that species mass flow direction significantly depends on mass consumption on the membrane electrolyte assembly. To study the water and thermal behaviour of an open-cathode PEM fuel cell, (Sagar et al., 2020) developed a 3D CFD model to predict the spatial distribution of relative humidity, temperature and membrane water content. They concluded that high water content variations in the fuel cell limits the cell performance. The studies provide insight into the fact there are distributions in the fuel cell stack that impact performance and hence need to be controlled. However, these computationally fluid dynamics (CFD)-based models are not suitable for control purposes as they are far too computationally expensive.

A number of control-oriented models have been created over the years. For instance, (Pukrushpan et al., 2004) developed a control-oriented lumped-parameter model for automotive fuel cell systems. The model was proven to be useful for analysis of transient effect of step inputs and analysis of system observability. (Meyer & Yao, 2006) developed a control-oriented model for a self-humidifying fuel cell stack and the model was capable of characterizing the transient response of the fuel cell stack. (X. Chen et al., 2022) developed a physics-based model to control the temperature and humidity of a PEM fuel cell. To study and control water in a fuel cell stack, (X. Chen et al., 2020) developed a dynamic water management model based on the equations developed by (Pukrushpan et al., 2004). (F. Chen et al., 2021) developed a lumped parameter control-oriented model for predicting humidity dynamics for an open-cathode PEM fuel cell. Based on their model, the output performance of an open-cathode PEMFC, taking into account the internal humidity state of the stack, is predicted. All these models adopt the lumped-parameter approach which assumes minimal spatial variations. However, the CFD models reviewed demonstrate that variations exist; therefore, control-oriented models must account for these variations to ensure effective control of the membrane water content in the PEM fuel cell stack.

For predicting humidity spatial variations, (Headley et al., 2016) developed and experimentally validated a control-oriented model that captures variation of relative humidity along the cathode channel but did not explore humidity variation in the anode channel, which can occur due to back diffusion. It is not possible to accurately capture variations in membrane water content with this approach as the membrane water content depends on humidity dynamics in both the cathode and anode channels. In fact, a more conservative approach of determining the membrane water content is to model it as a function of the water activity in the anode alone. (Nguyen & White, 1993) adopted this approach in their work where the membrane water content was taken to be the anode water content to reflect the importance of the anode side water activity as it is often the limiting electrode due to drying conditions. Therefore, for more accurate predictions of variations in membrane water content, a model that predicts both variations of humidity along the cathode and anode channels is needed.

The main contribution of this paper is that it overcomes the limitation of existing control-oriented models for water management by developing a model that predicts humidity variations along both the cathode and anode channels, with the goal of providing more accurate insights into the humidity dynamics in the PEM fuel cell membrane. In this study, a reduced order model that integrates thermal effects to predict spatial variations in membrane water content of a 5kW open-cathode PEM fuel cell stack is presented. First, a lumped parameter model for the stack was developed. This model was then further discretized into smaller control volumes. The model was validated by comparing its predictions to simulation results from GT-Suite and achieved good agreement. The developed model will be useful for real-time control of membrane water content variation in PEM fuel cells.

2. Experimental Setup

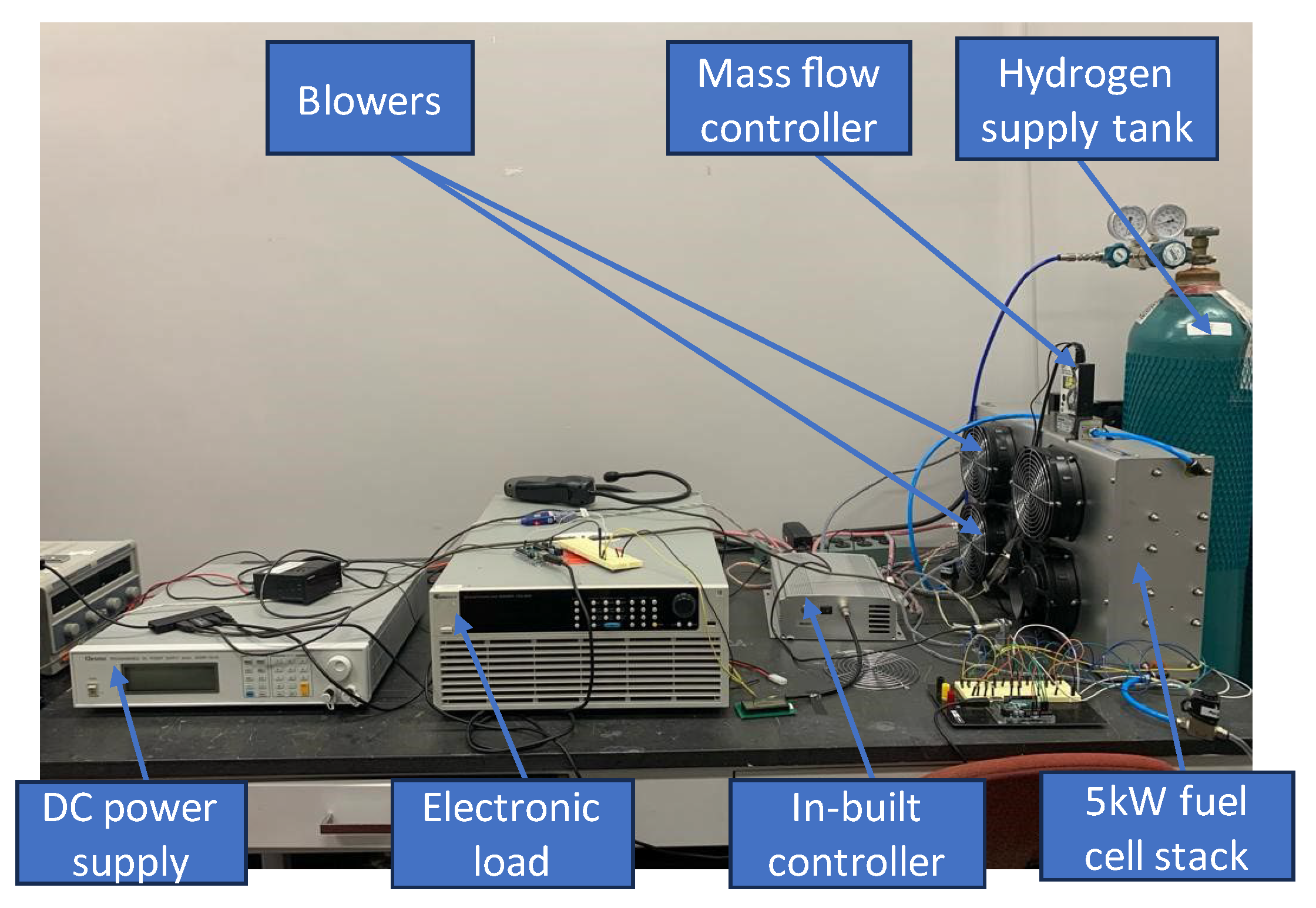
The model is based on the experimental set up shown in Figure 1. The fuel cell stack is a commercially available 5kW open-cathode stack from Horizon. It has 120 cells connected in series. The active area of each cell is 150cm². Air is supplied to the stack by four blowers connected to the casing of the stack. Hydrogen of 99.99% purity is supplied to the stack from a pressurized tank. The stack is equipped with an in-built controller from the manufacturer that monitors and records the current, voltage and stack temperature. A mass flow controller from Aalborg is used to measure the hydrogen inlet pressure and control the supply of hydrogen to the anode. There are also four thermocouples which are attached on the other side of the stack casing (opposite the fans) with the aim of monitoring temperature variation along the stack (Figure 2). Data taken on this experimental setup was used for model validation.

3. Model Development

3.1. Physics-Based Model

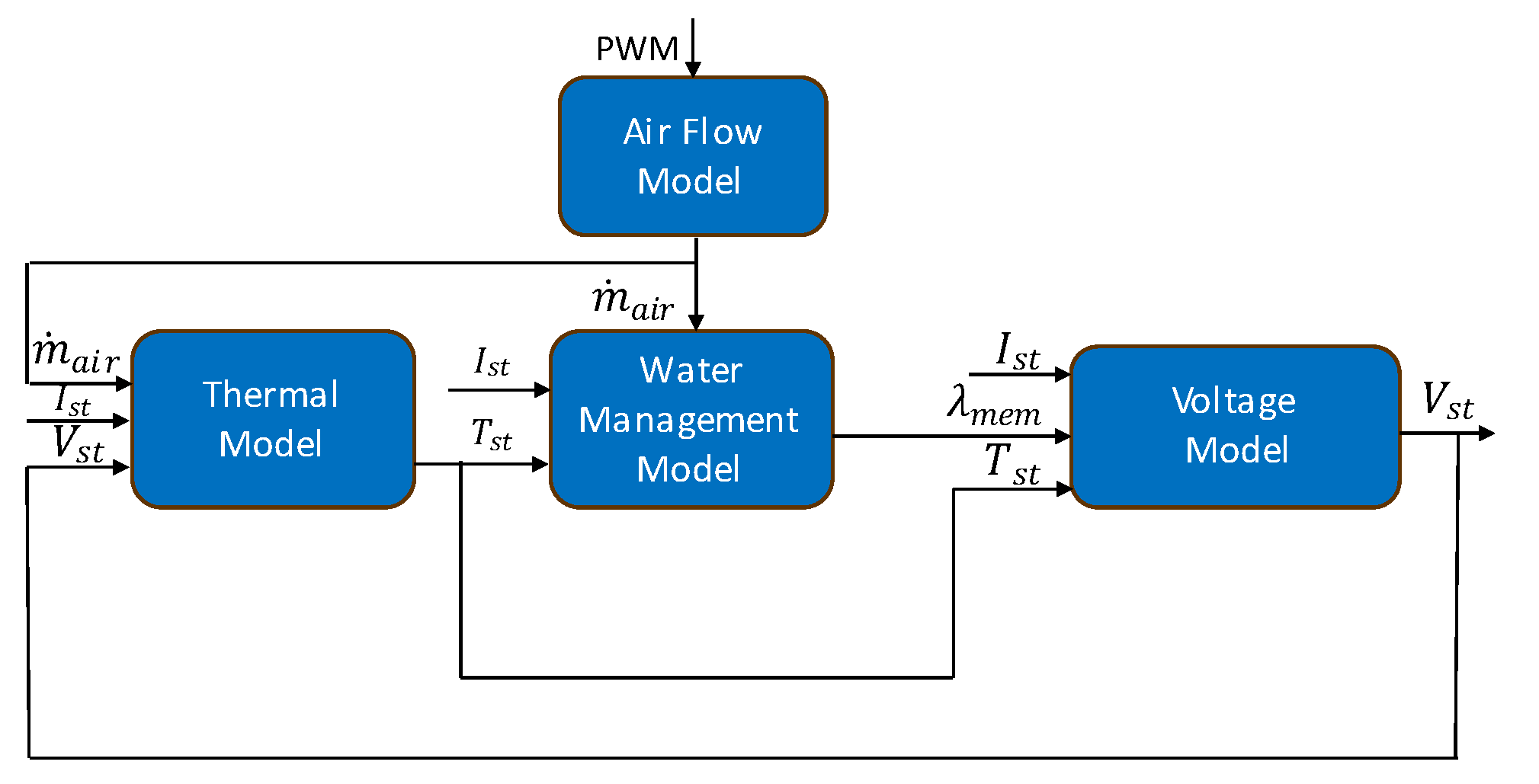
The model is made up of four interconnected sub models. An air flow model computes the mass flow rate of air (

{\dot{m}}_{a i r}

) from the fan’s PWM signal. The air flow rate is then fed into both the thermal and water management models. The thermal model generates the stack temperature

(T_{s t})

,which is used as an input to the water management and stack voltage models. The water management model’s prediction of membrane water content

(λ_{m e m})

then serves as an input to the stack voltage model. Figure 3 depicts the model’s structure.

3.1.1. Stack Voltage Model

The fuel cell reaction is split into the cathodic and anodic half reactions. To facilitate these reactions, air is supplied to the cathode and hydrogen is supplied to the anode. The cathode and the anode are separated by the polymer electrolyte membrane, which is permeable to protons but not electrons, so electrons are transferred via an electrical circuit generating electric current. The electrons then recombine with the protons in the cathode side to generate water. Due to the transfer of electrons, the anodic reaction is referred to as the hydrogen oxidation reaction (HOR) and the cathodic reaction is called the oxygen reduction reaction (ORR) due to the addition of electrons. The electrochemical reactions involved are:

H_{2} \to 2 H^{+} + 2 e (H O R, a n o d e)

2 H^{+} + \frac{1}{2} O_{2} + 2 e \to H_{2} O (O R R, c a t h o d e)

(1)

H_{2} + \frac{1}{2} O_{2} \to H_{2} O (o v e r a l l r e a c t i o n)

The voltage of a single cell is expressed by

V_{c e l l} (V) = V_{o c} - V_{a c t} - V_{o h m i c} - V_{c o n c}

(2)

where

V_{o c}

is the open circuit voltage,

V_{a c t}

is the activation overvoltage,

V_{o h m i c}

is the ohmic overvoltage and

V_{c o n c}

is the concentration overvoltage.

V_{o c}

is the thermodynamic reversible potential or the fuel cell voltage when no load is connected. The reversible fuel cell voltage can be expressed as a function of temperature and pressure as follows (O’hayre et al, 2014):

V_{o c} = E^{o} + \frac{∆ s_{r x n} (T_{s t})}{n F} (T_{s t} - T_{a m b}) - \frac{R T_{s t}}{n F} I n (\frac{1_{}}{P H_{2} * P O_{2}^{0.5}})

(3)

in which

E^{o}

is the non-standard reversible voltage,

∆ s_{r x n}

is the entropy change of the fuel cell reaction,

T_{s t}

is the stack temperature,

T_{a m b}

is the ambient temperature,

R

is the ideal gas constant,

n

is the number of moles of electrons transferred from the anodic reaction,

F

is the Faraday constant,

P H_{2}

is the hydrogen inlet pressure and

P O_{2}

is the oxygen partial pressure.

The activation overvoltage includes losses in voltage that arise due to the kinetic reaction. The activation overvoltage can be determined by

V_{a c t} = \begin{matrix} \frac{R T_{s t}}{a n F} I n (\frac{i}{i_{o}}) \end{matrix}

(4)

where

a

is the charge transfer coefficient,

i

is the cell current density and

i_{o}

is the exchange current density.

The exchange current density can be computed by (F. Chen et al., 2021)

i_{o} = i_{o}^{r e f} {(\frac{P O_{2}}{P_{r e f}})}^{y} e x p [\frac{i}{i_{o}} (- \frac{E_{c}}{R} - \frac{1}{T_{r e f}})]

(5)

where

i_{o}^{r e f}

is the reference exchange current density,

P_{r e f}

is the reference pressure of 1atm,

y

is the pressure coefficient,

T_{r e f}

is the reference temperature of 298K and

E_{c}

is the activation energy for the cathodic reaction. Due to the slower reaction kinetics of the ORR as compared to the HOR, the activation loss in this model is only attributed to the cathodic reaction.

Ohmic overvoltage captures the losses due to ionic and electronic conduction and can be calculated by

V_{o h m i c} = i (R_{i o n i c} + R_{e l e c})

(6)

where

R_{i o n i c}

and

R_{e l e c}

are the ionic resistance and electronic resistance respectively.

R_{i o n i c}

can be computed by (Wang et al., 2014) (Huo & Hall, 2023)

R_{i o n i c} = \frac{181.6 [1 + 0.03 i + 0.062 {(\frac{T_{s t}}{303})}^{2} (i^{2.5})] t_{m e m}}{[λ_{m e m} - 0.634 - 3 i] \exp [4.18 (T_{s t} - \frac{303}{T_{s t}})]}

(7)

in which

t_{m e m}

is the membrane thickness and

λ_{m e m}

is the membrane water content and is determined from the water management model as discussed in Section 3.1.4.

The concentration overvoltage includes losses attributed to mass transport in the fuel cell stack. The concentration overvoltage can be determined by

V_{c o n c} = m e x p (n i)

(8)

where

m

and

n

are empirical coefficients that can be tuned according to experimental polarization data.

The total stack voltage is then computed by

V_{s t} = V_{c e l l} * N_{s t}

(9)

in which

V_{c e l l}

is the voltage of a single cell as computed from Eq. (2) and

N_{s t}

is the total number of cells in the stack.

3.1.2. Air Flow Model

Air is delivered to the cathode channels via fans mounted on the stack casing. The flow to the cathode channel is assumed to be laminar in this model. The cathode air mass flow rate is modeled as

{\dot{m}}_{a i r} (t) = ρ_{a i r} * Q_{a i r} (t)

(10)

where

ρ_{a i r}

is the density of air in kg/m³ at Standard Temperature and Pressure (STP) and

Q_{a i r} (t)

is the volumetric air flow rate in m³/s.

For an arbitrary fan rotational speed,

Q_{a i r} (t)

is determined by (Huo & Hall, 2023)

Q_{a i r} (t) = w (t) \frac{Q_{n o m}}{w_{n o m}}

(11)

in which

w (t)

denotes the arbitrary fan speed in revolutions per minute (rpm),

Q_{n o m}

is the nominal volumetric flow rate of the fan in m³/s and

w_{n o m}

is the nominal fan speed in rpm.

Q_{n o m}

and

w_{n o m}

are determined in a manner as described by (Ishaku et al., 2014). The pressure drop in the cathode channel is calculated as a function of the Reynolds number and friction factor.

Q_{n o m}

is then determined from the intersection of the determined pressure drop on the fan performance curve.

w_{n o m}

is the speed at which the performance curve is expressed in the datasheet. For this study

w_{n o m}

is 6500rpm.

3.1.3. Thermal Model

The thermal dynamics of the stack can be described as follows (Huo & Hall, 2023) (Ishaku et al., 2014)

C_{t} \frac{d T_{s t}}{d t} = P_{t o t a l} (t) - P_{s t} (t) - {\dot{Q}}_{c o o l a n t} (t)

(12)

where

C_{t}

represents the thermal capacitance of the stack,

P_{t o t a l} (t)

is the power from the electrochemical reaction and is computed by

P_{t o t a l} (t) = \frac{N_{s t} * I_{s t} (t) * ∆ h}{2 F}

(13)

in which

∆ h

is the molar enthalpy change of the electrochemical reaction.

P_{s t} (t)

is the total output power from the stack and is determined by

P_{s t} (t) = V_{s t} (t) * I_{s t} (t)

(14)

{\dot{Q}}_{c o o l a n t} (t)

is the heat dissipated from the air to the environment and it is calculated by

{\dot{Q}}_{c o o l a n t} (t) = η_{f a n} * {\dot{m}}_{a i r} (t) * C_{p} (T_{s t} (t) - T_{a m b})

(15)

where

η_{f a n}

is the efficiency of the blower,

{\dot{m}}_{a i r} (t)

is the air mass flow rate as determined from Section 3.1.2,

C_{p}

is the specific heat capacity of air and

T_{a m b}

is the ambient temperature.

3.1.4. Water Management Model

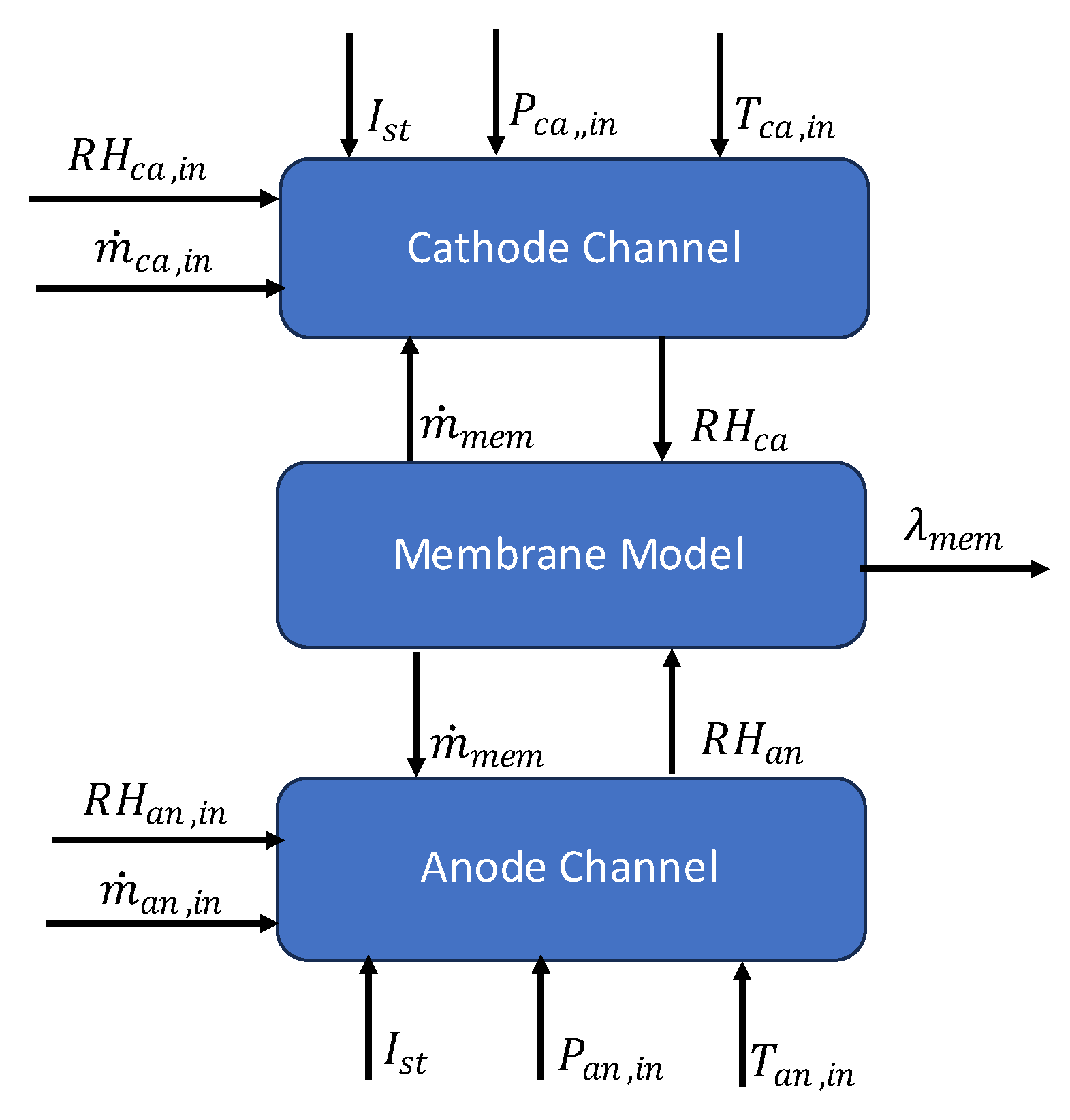
The water management model is divided into three submodels: the cathode channel, the anode channel and the polymer electrolyte membrane. A block diagram of the model is shown in Figure 4.

Cathode Channel

Conservation of mass was utilized to track the mass of species in the cathode channel over time. The conservation of mass of water, oxygen and nitrogen are given by Eqs. (16), (17) and (18), respectively (Pukrushpan et al., 2004). It is assumed that water enters and leaves the channel in vapor form only.

\frac{d m_{H_{2} O c a}}{d t} = {\dot{m}}_{H_{2} {O_{i n}, c a}_{}} + {\dot{m}}_{H_{2} O_{g e n}} - {\dot{m}}_{H_{2} {O_{o u t}, c a}_{}} + {\dot{m}}_{m e m}

(16)

\frac{d m_{O_{2}}}{d t} = {\dot{m}}_{{O_{2, i n}}_{}} - {\dot{m}}_{{O_{2, r e a c t e d}}_{}} - + {\dot{m}}_{{O_{2, o u t}}_{}}

(17)

\frac{d m_{N_{2}}}{d t} = {\dot{m}}_{{N_{2, i n}}_{}} - {\dot{m}}_{{N_{2, o u t}}_{}}

(18)

In these equations,

{\dot{m}}_{H_{2} {O_{i n}, c a}_{}}

{\dot{m}}_{{O_{2, i n}}_{}}

and

{\dot{m}}_{{N_{2, i n}}_{}}

are the mass flow rates of water, oxygen, and nitrogen into the cathode channel, computed by Eqs. (24), (30) and (31), respectively. The mass flow rate of water vapor, oxygen and nitrogen leaving the cathode channel are depicted by

{\dot{m}}_{H_{2} {O_{o u t}, c a}_{}}

{\dot{m}}_{{O_{2}, o u t}_{}}

and

{\dot{m}}_{{N_{2, o u t}}_{}}

and are calculated by Eqs. (33), (43) and (44), respectively. The net flow of water across the membrane,

{\dot{m}}_{m e m}

is determined from the membrane model in Section 3.1.4.3.

The water generated due to the electrochemical reaction is given by

{\dot{m}}_{H 2 O_{g e n}} = \frac{N_{s t} * I_{s t} * {M_{H_{2} O}}_{}}{2 F}

(19)

where

M_{H_{2} O}

is the molar mass of water in kg/mol. The mass flow rate of oxygen that partakes in the electrochemical reaction computed by

{\dot{m}}_{{O_{2, r e a c t e d}}_{}} = \frac{N_{s t} * I_{s t} * {M_{O}}_{2}}{2 F}

(20)

in which

{M_{O}}_{2}

is the molar mass of oxygen in kg/mol.

Anode Channel

Similar to the cathode channel, conservation of mass was utilized to track the mass of water and hydrogen in the anode channel. The anode of the self-humidifying open-cathode PEMFC under consideration is fed with dry hydrogen and it is typically dead-ended except for the occasional purging of water and unused hydrogen by the purge valve. It is assumed in this model that the anode runs exclusively in the dead-ended mode.

The mass balance of water is determined by

\frac{d m_{H 2 O a n}}{d t} = - {\dot{m}}_{m e m}

(21)

The mass balance of hydrogen is given by

\frac{d m_{H_{2}}}{d t} = {\dot{m}}_{{H_{2}}_{i n, a n}_{}} + {\dot{m}}_{{H_{2}}_{o u t, a n}_{}} - {\dot{m}}_{{H_{2}}_{r e a c t e d}}

(22)

The mass rate of hydrogen reacted is determined by

{\dot{m}}_{{H_{2}}_{r e a c t e d}} = \frac{N_{s t} * I_{s t} * {M_{H}}_{2}}{4 F}

(23)

The mass flow rate of water entering the channels is given by

{\dot{m}}_{H_{2} {O_{i n} (.) = y_{H_{2} {O v}_{i n} (.)} * {\dot{m}}_{i n (.)}}_{}}

(24)

where

(.)

represents either the cathode (ca) or anode (an) channel. The term

y_{H_{2} {O v}_{i n}}

is the mass fraction of vapor in the inlet flow and

{\dot{m}}_{i n}

is the inlet flow rate. For the cathode channel,

{\dot{m}}_{i n, c a}

is determined from the air flow rate model in Section 3.1.2 and

{\dot{m}}_{i n, a n}

is a measured input to the model.

The mass fraction of vapor into the channel is computed by (Karnik et al., 2007)

\begin{matrix} y_{H_{2} {O v}_{i n} (.)} = \\ \frac{P_{H_{2} O v_{i n} (.)} * M_{H_{2} O v}}{(P_{H_{2} O v_{i n} (.)} * M_{H_{2} O v}) + (({P_{(.)}}_{i n} - P_{H_{2} O v_{i n} (.)}) * M_{g})} \end{matrix}

(25)

The subscript,

g

represents the gas in the channel. For the cathode, the gas is air, and it is hydrogen for the anode.

The inlet vapor pressure is calculated by

P_{H_{2} O v_{i n} (.)} = R {H_{(.)}}_{i n} * P_{s a t} ({T_{(.)}}_{i n})

(26)

where

R {H_{(.)}}_{i n}

is the channel inlet relative humidity and

P_{s a t} ({T_{(.)}}_{i n})

is the saturation pressure evaluated at the channel inlet temperature.

{P_{(.)}}_{i n}

is the channel inlet pressure and

M_{g}

is the molar mass of gas in the channel. Once the mass flow rate of water in the inlet stream has been determined, the inlet flow rate of the gas is determined by subtracting the water mass flow rate from the total inlet flow rate.

{\dot{m}}_{g_{i n (.)}} = {\dot{m}}_{i n (.) -} {\dot{m}}_{H_{2} O_{i n, (.)}}

(27)

To determine the mass flow rate of each of the nitrogen and oxygen species in the cathode, the mass fraction of each of the gases needs to be computed and this is given by (Pukrushpan et al., 2004)

{x_{O}}_{2} c a_{i n} = \frac{{y_{O}}_{2} c a_{i n} * {M_{O}}_{2}}{({y_{O}}_{2} c a_{i n} * {M_{O}}_{2}) + ((1 - {y_{O}}_{2} c a_{i n}) * {M_{N}}_{2})}

(28)

where

{y_{O}}_{2} c a_{i n}

is the mole fraction of the oxygen in the inlet air which is 0.21.

The mass fraction of nitrogen is then given by

{x_{N}}_{2} c a_{i n} = 1 - {x_{O}}_{2} c a_{i n}

(29)

The mass flow rate of oxygen into the cathode is

{\dot{m}}_{{O_{2}}_{i n . c a}} = {x_{O}}_{2} c a_{i n} * {\dot{m}}_{{a i r}_{i n, c a}}

(30)

and the mass flow rate of nitrogen is

{\dot{m}}_{{N_{2}}_{i n, c a}} = {x_{N}}_{2} c a_{i n} * {\dot{m}}_{{a i r}_{i n, c a}}

(31)

The outlet flow rate is determined from the linearized nozzle equation (Karnik et al., 2007)

{\dot{m}}_{o u t_{(.)}} = {k_{(.)}}_{o u t} (P_{(.)} - P_{d s})

(32)

in which

{k_{(.)}}_{o u t}

is the outlet anode or cathode nozzle constant coefficient,

P_{(.)}

is the anode or cathode channel pressure and

P_{d s}

is the pressure downstream of the stack and for the lumped model this is equal to standard atmospheric pressure.

Knowing the outlet flow rate, the mass flow rate of vapor out can be computed from

{\dot{m}}_{H_{2} O_{o u t} (.)} = y_{H_{2} O v (.)} * {\dot{m}}_{o u t (.)}

(33)

The mass fraction of water vapor is given by

y_{H 2 O v (.)} = \frac{m_{H_{2} O v (.)}}{m_{H_{2} O v (.)} + m_{g} (.)}

(34)

where

m_{H_{2} O v (.)}

and

m_{g} (.)

are the masses of vapor and gas respectively in the cathode or anode channel. The total mass of gas in the cathode channel is obtained by summing the masses of nitrogen and oxygen.

Based on the calculated quantity of water exiting, the amount of gas out of the channels can be computed by

{\dot{m}}_{{g_{o u t, (.)}}_{}} = {\dot{m}}_{o u t_{(.)}} - {\dot{m}}_{H_{2} O_{o u t} (.)}

(35)

To determine the flow rate of the individual species of nitrogen and oxygen out of the cathode, the mass fractions have to be recomputed as oxygen is consumed in the reaction.

The mass fraction of oxygen leaving the cathode is (Pukrushpan et al., 2004)

{x_{O}}_{2} = \frac{{y_{O}}_{2} * {M_{O}}_{2}}{({y_{O}}_{2} * {M_{O}}_{2}) + ((1 - {y_{O}}_{2}) * {M_{N}}_{2})}

(36)

where

{y_{O}}_{2}

is the mole fraction of oxygen in the exit flow rate and it is determined by

{y_{O}}_{2} = \frac{{P_{O}}_{2}}{P a i r_{}}

(37)

Assuming the gases to be ideal, the partial pressures of oxygen and nitrogen in the cathode channel are determined from the ideal gas law as

{P_{O}}_{2} = \frac{m_{O_{2}} * R_{O_{2}} * T_{c a}}{V_{c a}}

(38)

{P_{N}}_{2} = \frac{m_{N_{2}} * R_{N_{2}} * T_{c a}}{V_{c a}}

(39)

where

m_{O_{2} c a}

and

m_{N_{2} c a}

are the masses of oxygen and nitrogen obtained by solving Eqs. (18) and (19) respectively.

R_{O_{2}}

is the gas constant of oxygen and

R_{N_{2}}

is the gas constant of nitrogen.

T_{c a}

is the cathode channel temperature and it is taken to be the same as the stack temperature

(T_{s t})

in this study.

V_{c a}

is the lumped volume of the cathode channel.

Similarly, the partial pressure of hydrogen in the anode channel is calculated by

{P_{H}}_{2} = \frac{m_{H_{2}} * R_{H_{2}} * T_{a n}}{V_{a n}}

(40)

where

m_{H_{2}}

is the mass of hydrogen found in Eq. (22),

R_{H_{2}}

is hydrogen gas constant,

T_{a n}

is the anode temperature, which is equal to

T_{s t}

in this model and

V_{a n}

is the lumped anode channel volume.

The partial pressure of air in the channel is then given by the summation of Eqs. (38) and (39) as

P_{a i r} = {P_{O}}_{2} + {P_{N}}_{2}

(41)

The mass fraction of nitrogen in the exit flow rate is

{x_{N}}_{2} {= 1 -}_{} {x_{O}}_{2}

(42)

Knowing the mass fraction of oxygen and nitrogen in the exit flow rate, the exit mass flow rate of oxygen and nitrogen can then be determined from Eqs. (43) and (44), respectively.

{\dot{m}}_{{O 2_o u t c a}_{}} = {x_{O}}_{2} * {\dot{m}}_{{a i r, o u t}_{}}

(43)

{\dot{m}}_{{N 2_o u t c a}_{}} = {x_{N}}_{2}_{} * {\dot{m}}_{{a i r, o u t}_{}}

(44)

If the mass of water in the channels computed from Eqs. (16) and (21) is greater than the maximum amount of vapor the gas can hold (saturation mass), the extra amount is assumed to condense into liquid form instantaneously.

The saturation mass is computed from

m_{s a t (.)} = \frac{P_{s a t} (T_{s t}) * V (.)}{R_{H 2 O v} * T_{s t}}

(45)

where

V (.)

is the lumped volume of the anode or cathode channel and

P_{s a t} (T_{s t})

is the saturation pressure and can be determined as a function of

T_{s t}

l o g P_{s a t} = - {5.609 * 10}^{- 10} T_{s t}^{4} + 9.8172 * 10^{- 7} T_{s t}^{3} - 6.7687 * 10^{- 4} T_{s t}^{2} + 0.22471 T_{s t} - 28.365

(46)

where

T_{s t}

is in K and the calculated

P_{s a t}

is in kPa.

The relative humidity inside the channels is then calculated by

R H (.) = \frac{P_{H 2 O_{v} (.)}}{P_{s a t} (T_{s t})}

(47)

where

P_{H 2 O_{v} (.)}

Is the partial pressure of water vapor in the channel and is given by

P_{H 2 O_{v} (.)} = \frac{m_{H 2 O_{v} (.)} * R_{H 2 O_{v}} * T_{s t}}{V (.)}

(48)

in which

m_{H 2 O_{v}}

is the minimum of the dynamically computed mass and the saturation mass. For the anode,

m_{H 2 O_{v}}

is the minimum of Eqs. (21) and (45). For the cathode, it is the minimum of Eqs. (16) and (45).

The total anode and cathode channel pressures are then determined by Eqs. (49) and (50) respectively

P_{a n} = {P_{H}}_{2} + P_{H 2 O_{v} a n}

(49)

P_{c a} = P_{a i r} + P_{H 2 O_{v} c a}

(50)

Proton Exchange Membrane

Water is transported across the PEM fuel cell membrane by two main phenomena: electro-osmotic drag (EOD) and back diffusion. As protons move from the anode, they drag water molecules along and this is termed as EOD. This causes a water gradient to form, causing a back diffusion of water from the cathode to the anode.

The net mass flow rate of water across the membrane is given by (Pukrushpan et al., 2002)

{\dot{m}}_{m e m} = M_{H 2 O_{v}} * A_{f c} * N_{s t} * (\frac{n_{d} * i}{F} - D_{w} \frac{(C v_{c a} - C v_{a n})}{t m})

(51)

where

n_{d}

is the electroosmotic drag coefficient,

D_{w}

is the diffusion coefficient,

C v_{c a}

is the concentration of water in the cathode and

C v_{a n}

is the concentration of water in the anode.

The first term,

\frac{n d * i}{F}

represents the molar rate of EOD and the second term,

D_{w} \frac{(C v_{c a} - C v_{a n})}{t m}

represents the molar rate of water vapor by back diffusion.

The electroosmotic drag is determined by (Springer et al., 1991)

n_{d} \frac{2.5 * λ_{m e m}}{22}

(52)

The water concentrations in the cathode and anode are given by Eqs. (53) and (54), respectively,

C v_{c a} = \frac{ρ_{m e m}}{M_{m e m}} * λ_{c a}

(53)

C v_{a n} = \frac{ρ_{m e m}}{M_{m e m}} * λ_{a n}

(54)

where

ρ_{m e m}

and

M_{m e m}

are the membrane dry density and dry equivalent weight, respectively and

λ_{c a}

and

λ_{a n}

are the water content in the cathode and anode channels, respectively. The water content is defined as the number of water molecules per sulfonic acid sites and is determined by the following empirical relation (Springer et al., 1991)

λ_{(.)} = \{\begin{matrix} \begin{matrix} 0.043 + 17.81 R H (.) - 39.85 R H {(.)}^{2} + 36 R H {(.)}^{3}, 0 < R H (.) \leq 1 \\ 14 + 1.4 (R H (.) - 1), 1 < R H (.) \leq 3 \end{matrix} \end{matrix}

(55)

where the subscript (.) represents either the membrane (mem), cathode (ca) or anode (an) and

R H

is the relative humidity.

The relative humidity of the membrane is modeled as the average of the cathode and anode relative humidities.

R H_{m e m} = \frac{({R H}_{c a} + R H_{a n})}{2}

(56)

The diffusion coefficient is expressed by

{D_{w} = D}_{λ} \exp (2416 (\frac{1}{303} - \frac{1}{T_{s t}}))

(57)

in which

D_{λ} = \{\begin{matrix} 10^{- 6}, λ_{m e m} < 2 \\ 10^{- 6} (1 + 2 (λ_{m e m} - 2)), 2 \leq λ_{m e m} \leq 3 \\ 10^{- 6} (3 - 1.67 (λ_{m e m} - 3)), 3 \leq λ_{m e m} \leq 4.5 \\ 1.25 x 10^{- 6}, λ_{m e m} \geq 4.5 \end{matrix}

(58)

Together these submodels allow the water content in the stack to be monitored.

3.2. GT-Suite Model

The fuel cell stack was modeled in GT Suite v2023 using the stack’s specification. The model was calibrated using experimental voltage and temperature data. Throughout the GT modeling process, a steady inlet hydrogen tank pressure was assumed. In addition, the cathode’s input was a scaled version of the air mass flow rate that was determined in Section 3.1.2 which was optimized to provide accurate voltage predictions. The model, like the experimental PEM fuel cell stack, is devoid of a separate cooling channel. A heat transfer multiplier (HTM) is utilized in its place to account for cooling.

4. Model Discretization

4.1. Physics-Based Model

To predict localized effects, the lumped model was divided into four control volumes (CVs), each with 30 cells, and the output of each CV fed into the next in order to capture variations in membrane water content along the fuel cell stack. The choice of the number of CVs was contingent upon experimental data available for model validation. More details on validation of the model are covered in Section 5.2. The governing equations remain unchanged from the lumped model, with slight modifications made to specific equations to account for the subdivision.

In the discretization, a co-flow technique in which the fuel and air both flow in the same direction was employed. The inlet flow to CV1 is the same as the inlet flow to the lumped model. Subsequent CVs however receive their inlet flows from the outlet of the CV immediately preceding it. The outlet flow is determined by using the linearized nozzle equation in (32) which is adjusted as

{\dot{m}}_{{o u t_{(c v i)}}_{}} = {k_{c a}}_{o u t} (P_{c v i} - P_{c v (i + 1)})

(58)

where

P_{c v i}

is the total pressure of the current CV cathode channel and

P_{c v (i + 1)})

is the total pressure of the subsequent CV, which is the downstream pressure. For the last CV,

P_{c v (i + 1)}

is equal to the standard atmospheric pressure.

For the anode, it is assumed that the mass flow controller is able to regulate the flow such that pressure differences in the channel are kept to a minimum. As a result, the flow rate to each CV remains unchanged. To guarantee that there is sufficient flow of oxygen for the fuel cell reaction to occur, the anode channel is assumed to have a low flow resistance. Due to this low resistance, the mass flow controller can regulate the flow without significant pressure variation.

Regarding the stack voltage model, the number of cells was modified to reflect the number of cells in a CV rather than the whole stack. The voltage output for each CV was then determined by

V_{{s t, c v_{i}}_{}} = V_{c e l l} * {N_{c e l l s}}_{c v_{i}}

(59)

where

V_{c e l l}

was computed by Eq. (2) as described in Section 3.1.1 and

{N_{c e l l s}}_{c v_{i}}

is the number of cells in the control volume.

The total stack voltage is then computed by adding the voltages in each CV.

V_{{s t}_{}} = V_{s t, c v 1} + V_{s t, c v 2} + V_{s t, c v 3} + V_{s t, c v 4}

(60)

With regards to discretization of the temperature dynamics model, the efficiency of the fan,

η_{f a n}

in Eq. (15) was optimized at each current input for each CV using Simulink’s parameter estimation feature in the design optimization toolbox to align the model’s prediction with experimental data.

For the water management model, each CV had a distinct thermal subsystem to account for the temperature variations. Also, the anode and cathode channel volumes were divided according to the number of cells in each CV. Another modification to the discretized water management model is that while the anode is fed with dry hydrogen, this was solely the case for CV1. Back diffusion from the cathode channel results in humid hydrogen entering subsequent CVs. This inlet relative humidity is the output relative humidity from the previous CV which is computed by Eq. (47).

4.2. GT-Suite Model

The developed GT-Suite model was discretized by applying the same method used to discretize the lumped physics-based model. The GT-Suite model was discretized using four distinctive fuel cell stacks, one for each control volume. The input for the first stack was the known measured input, much like the physics-based model, and the input for successive stacks was the output of the stack preceding it. Each stack’s thermal and electrical domains were also appropriately linked. The thermocouple readings were used to calibrate each stack of the discretized model. Similar to the lumped model, the HTM was applied to account for cooling and the HTM used for each stack was iteratively optimized to match the temperature to the experimental thermocouple reading.

5. Results and Discussion

5.1. Lumped Model Validation

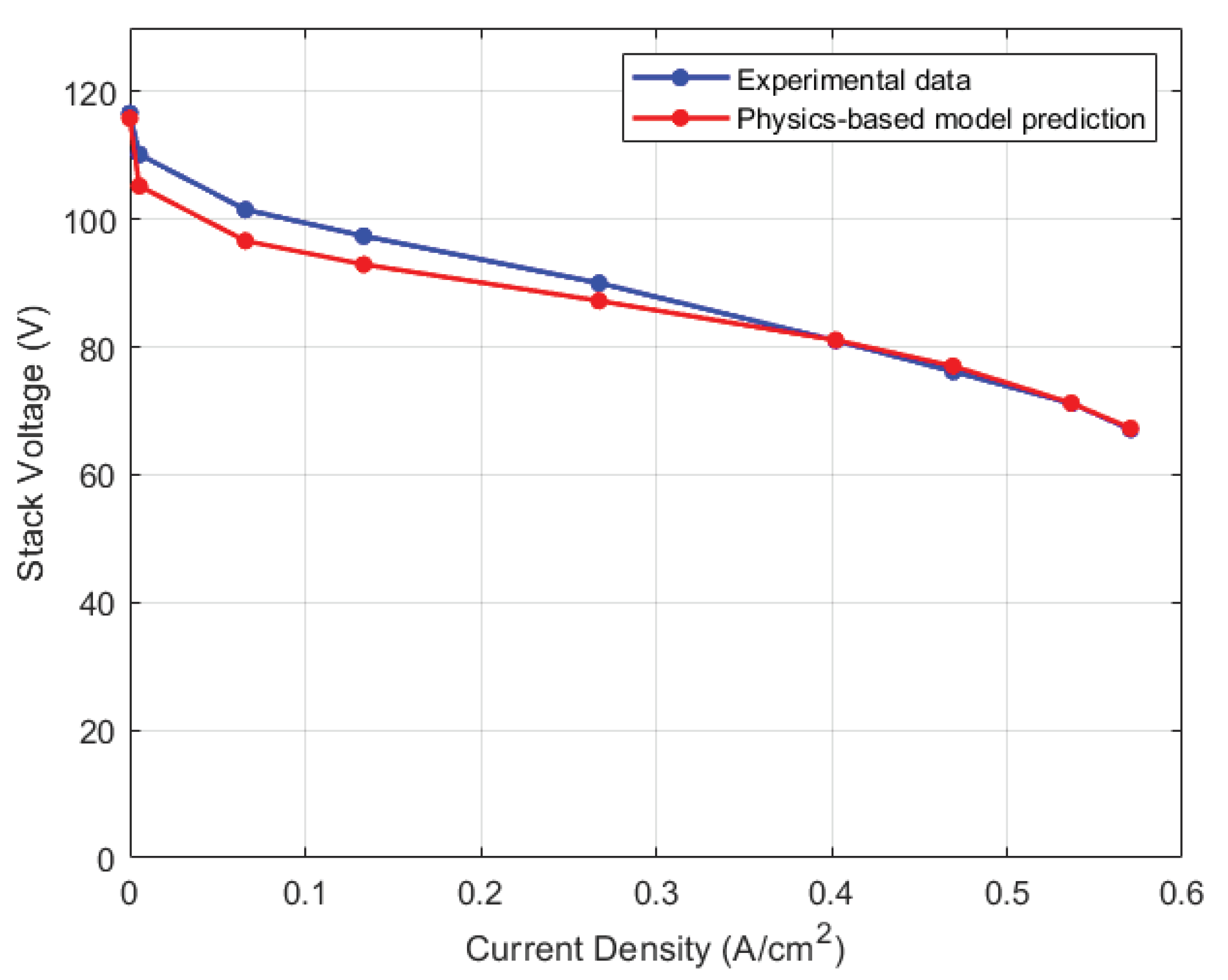
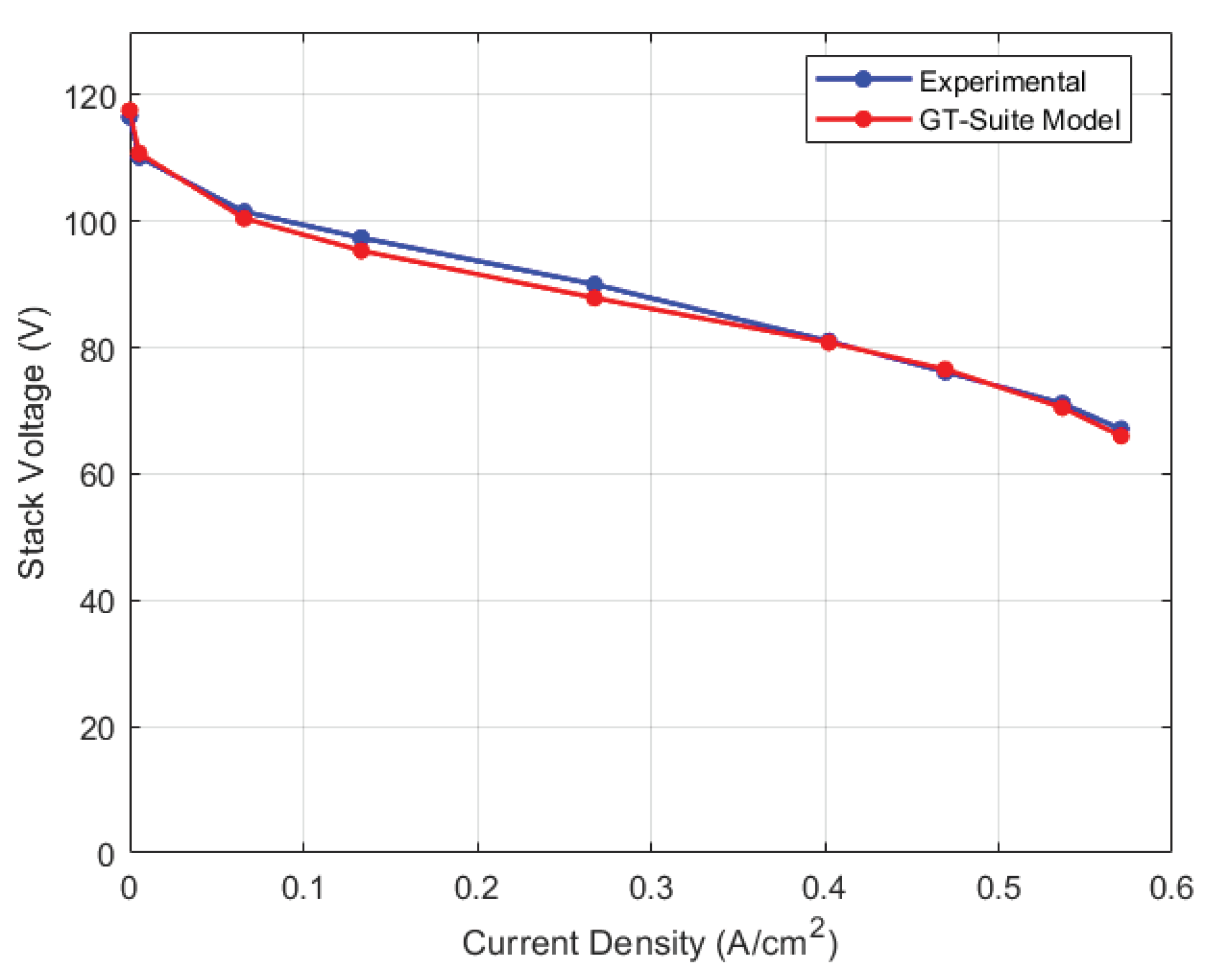
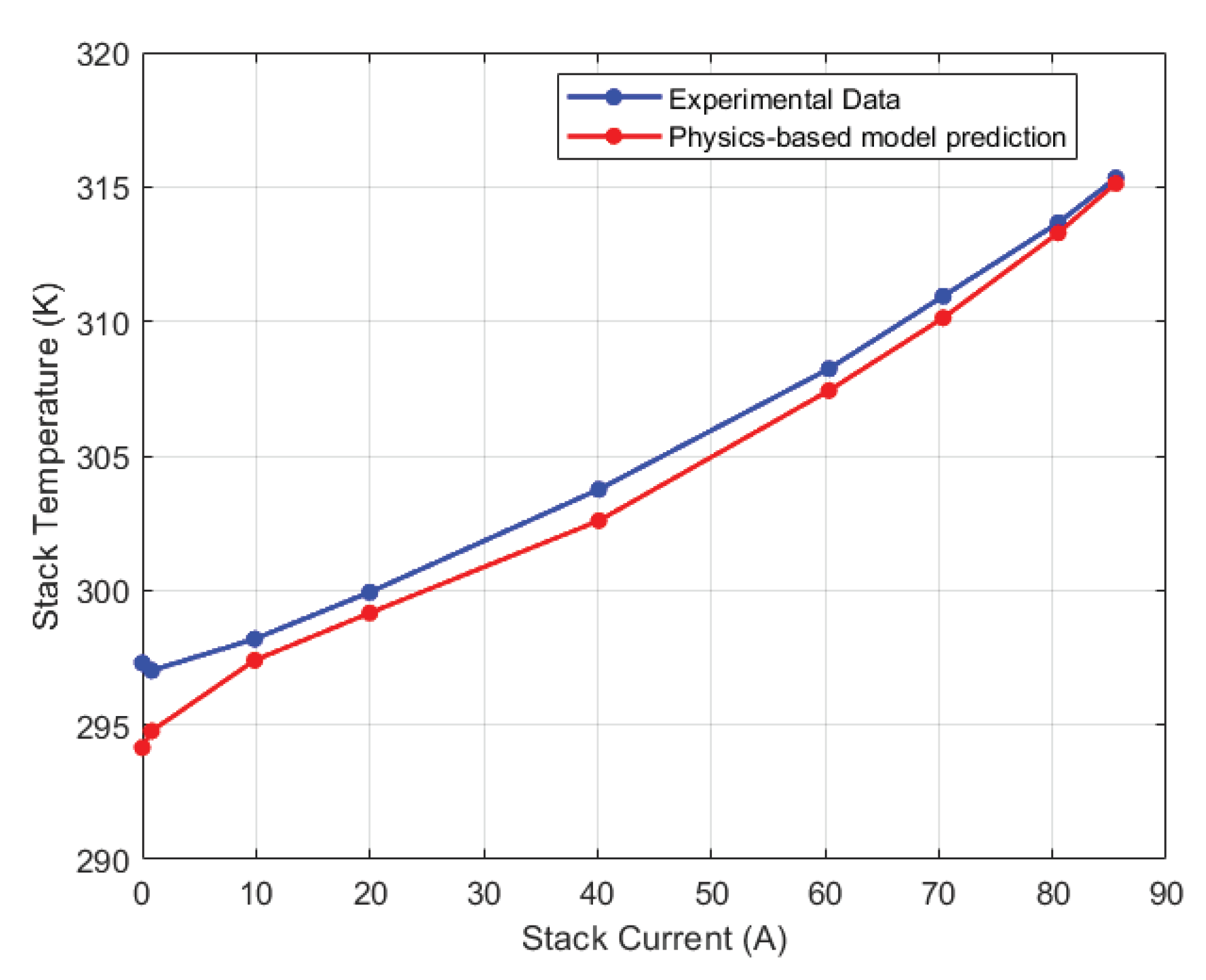
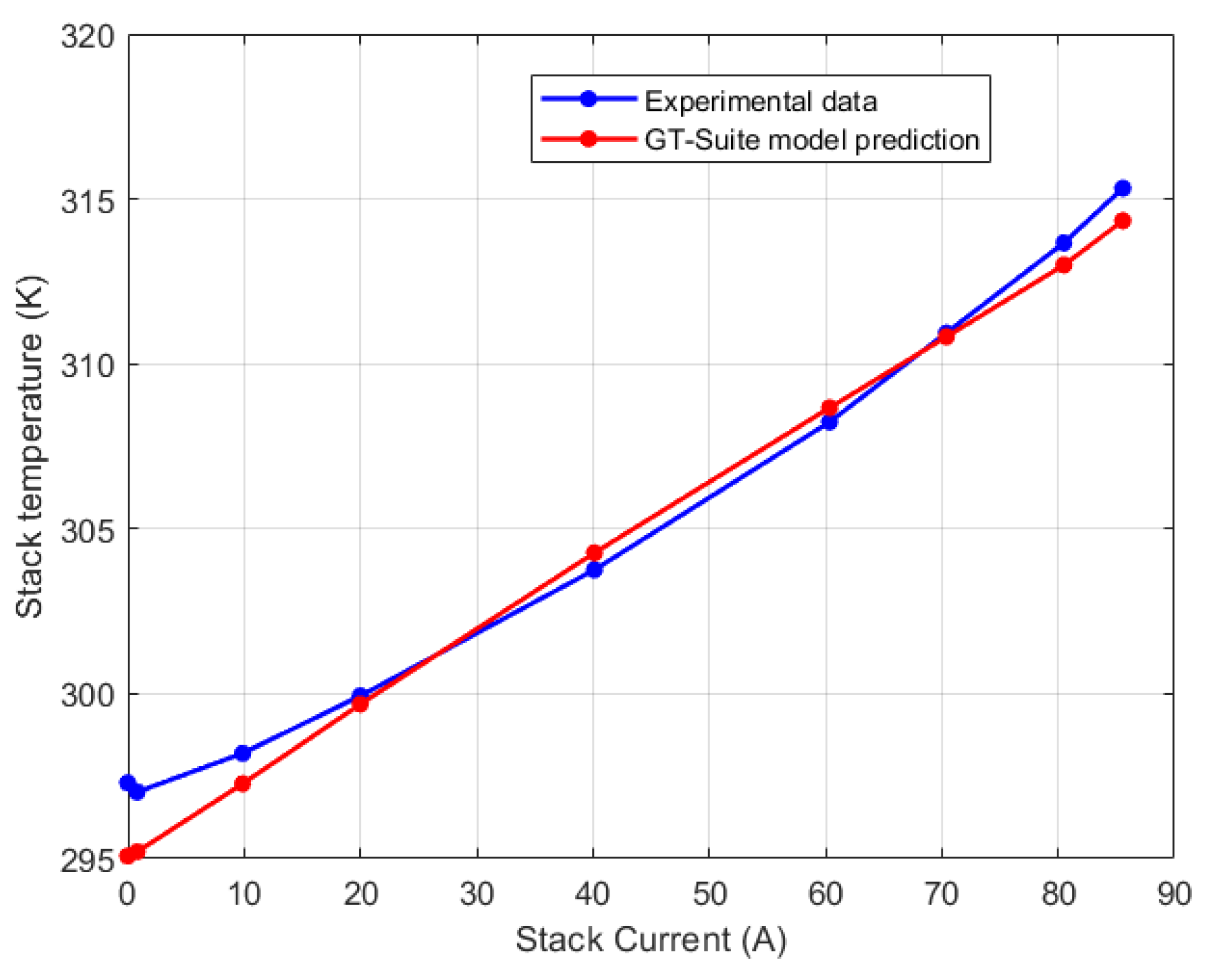
The stack voltage and thermal models were validated using data from the experimental setup as described in Section 2. Figure 5 highlights the steady state calibration result for the physics-based stack voltage model where errors are within 5% of the experimental data.

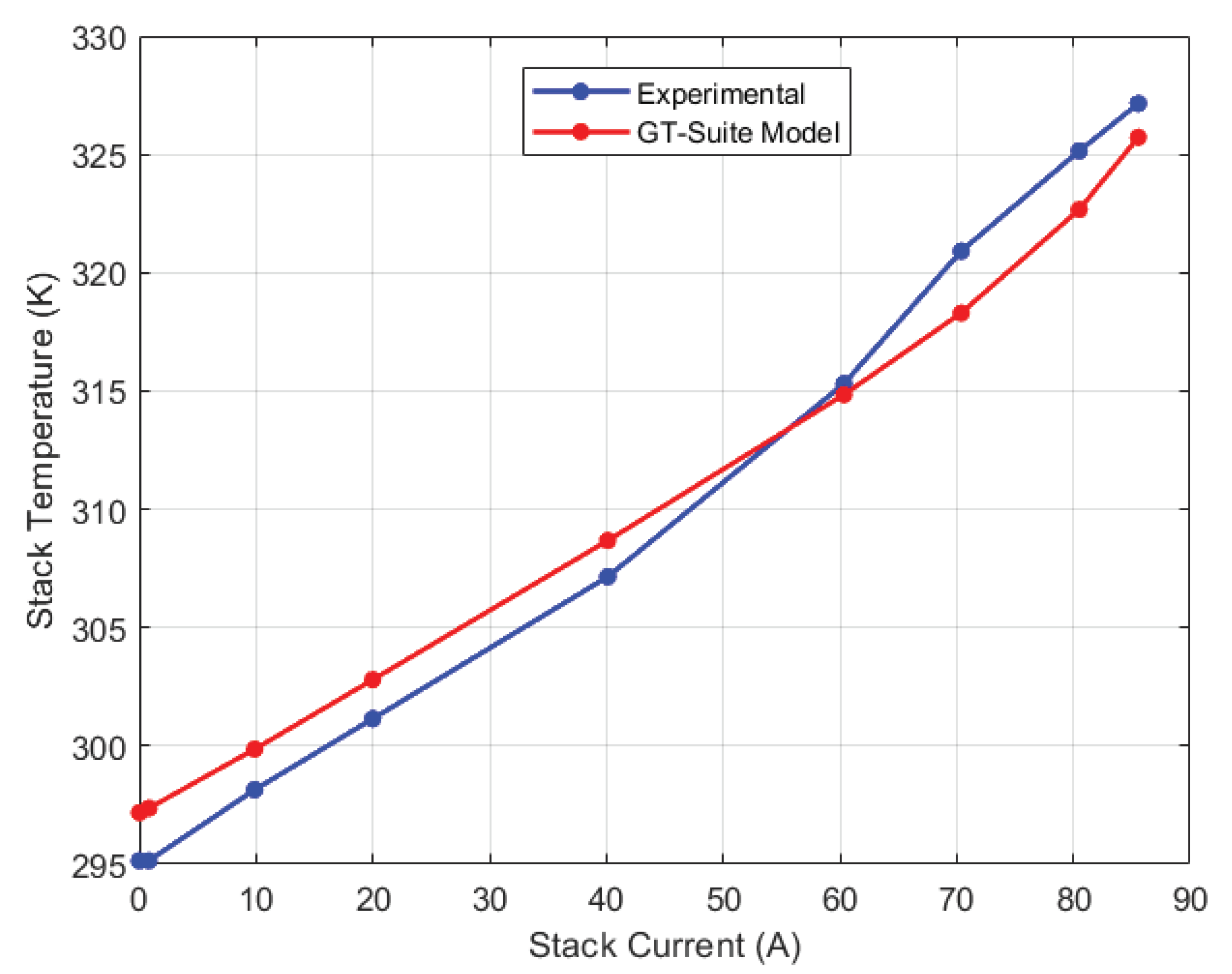
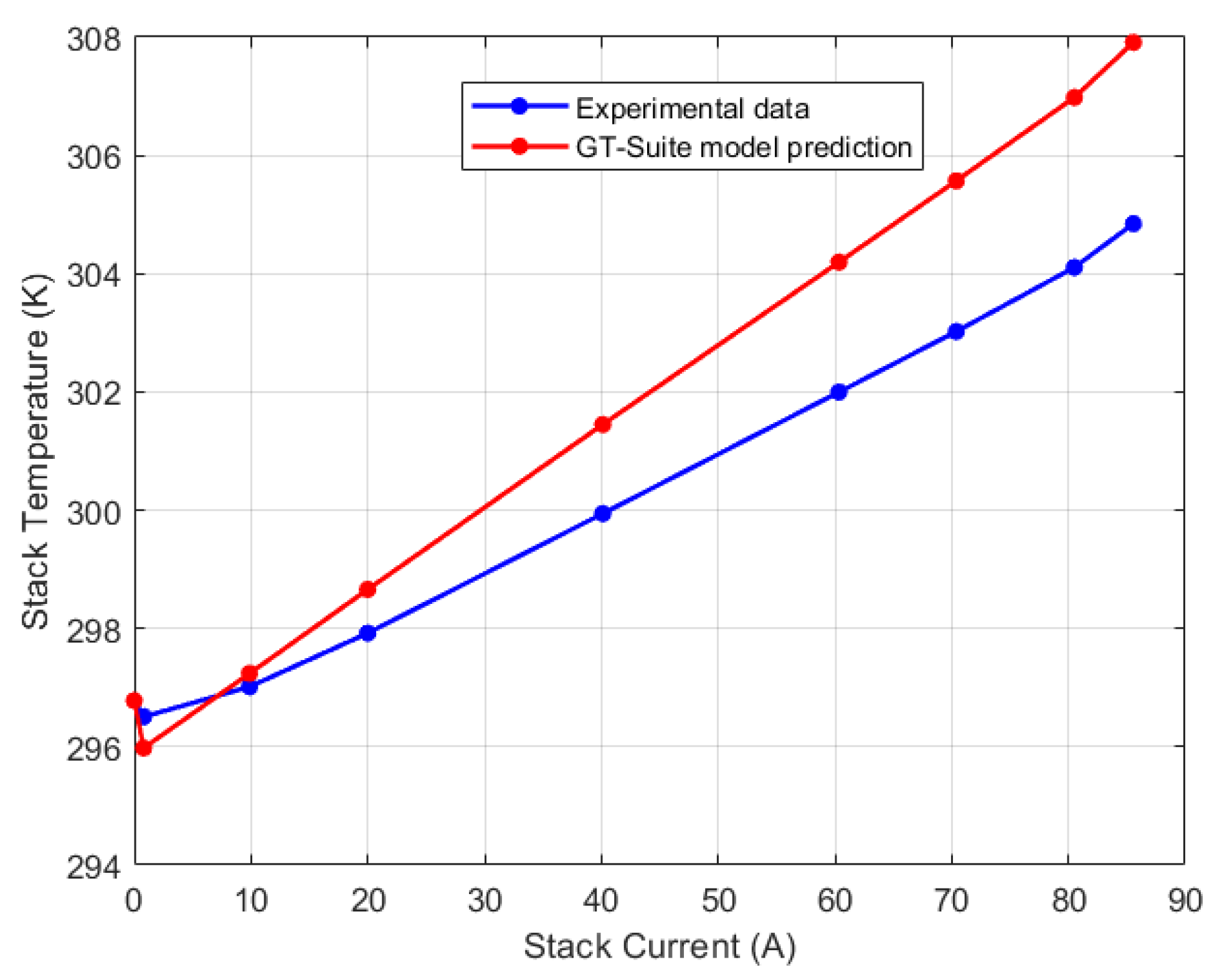
The calibration results for the lumped thermal model are depicted in Figure 6. The fan efficiency was used as a tuning parameter in the thermal model calibration. In Simulink, an optimization search for best efficiency was carried out, and an optimal efficiency of 35.75% was reached. When compared to the experimental data, the maximum steady state error for the thermal model is only 0.4%, highlighting the model’s accuracy in predicting the stack temperature.

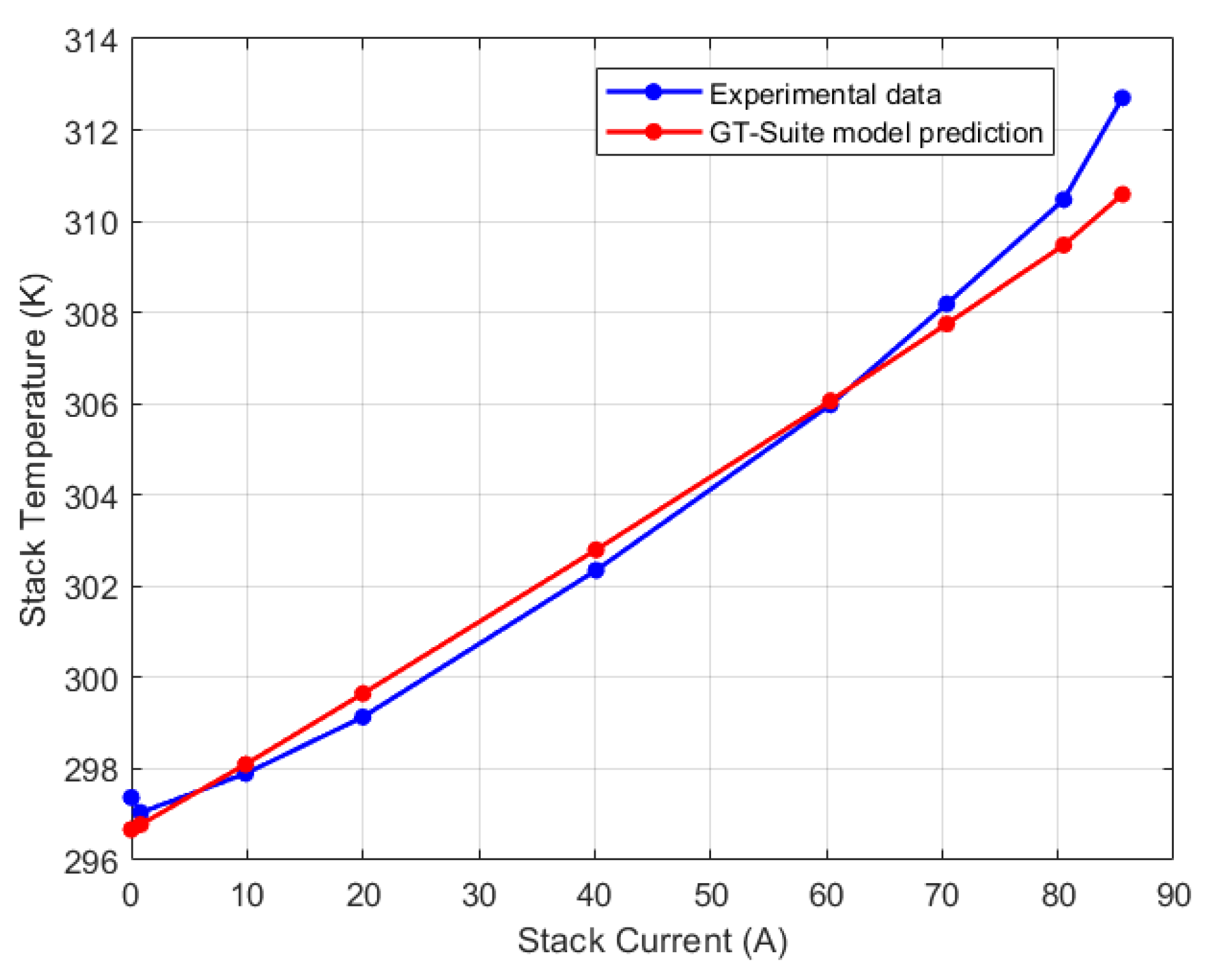
Due to the lack of experimental data to validate the water management model’s prediction, simulation results from GT-Suite model provided a basis for comparison. The GT-Suite model was calibrated using the experimental voltage and temperature data and the results are shown in Figure 7 and Figure 8 respectively, with a maximum relative error of 2.38% for the voltage model and 0.81% for the thermal model.

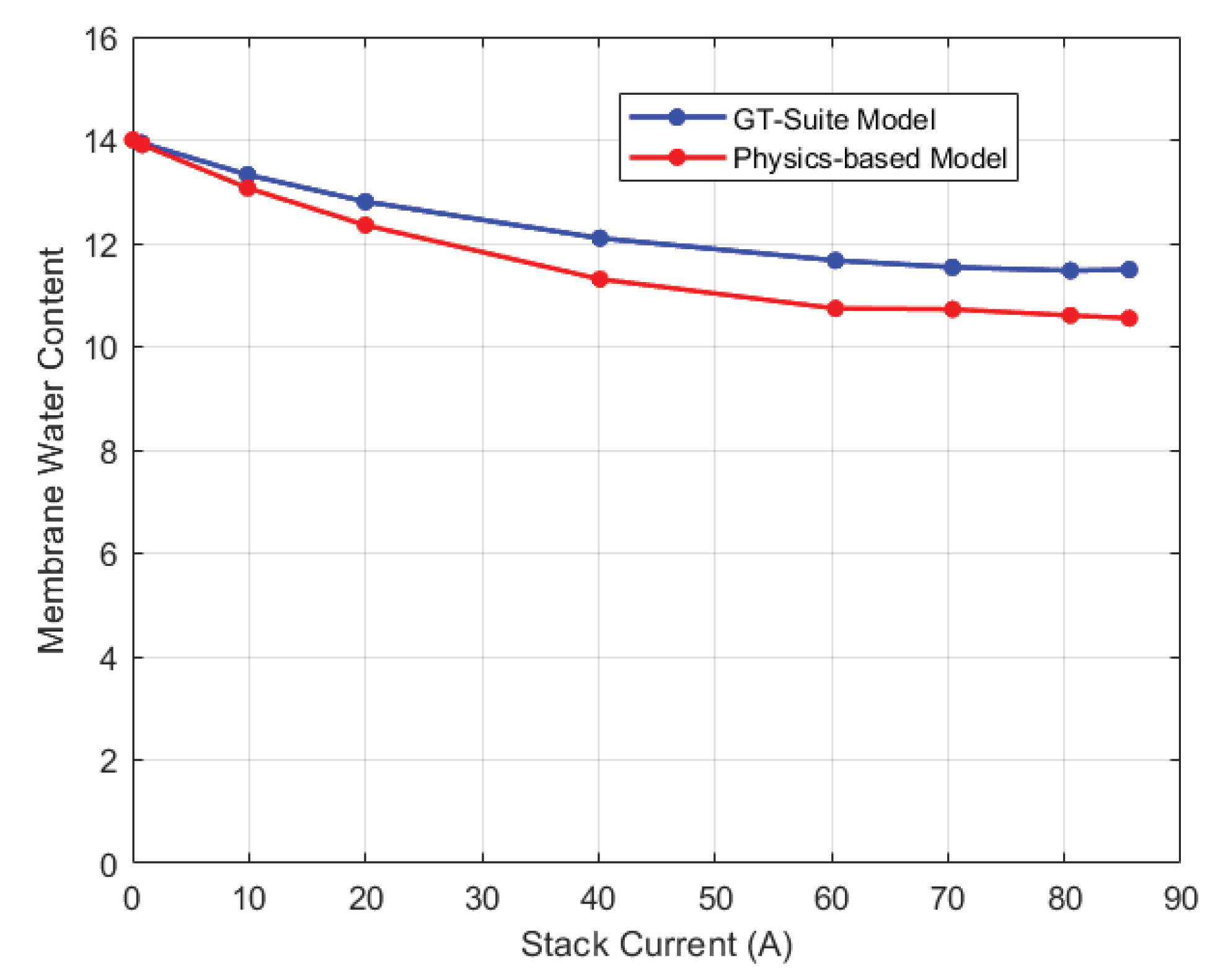
After validating the thermal and voltage predictions of GT-Suite, its membrane water content was used to validate the physics-based water management model. The comparison results are shown in Figure 9. The root mean square error (RMSE) between the predictions was found to be 0.72 membrane water content. Notably, the GT-Suite model predicted higher water content for all current cases than the physics-based model. One plausible explanation for this could be due to the temperature predictions of the GT-Suite model. For current inputs ranging from 0A to 40A, the GT-Suite model overestimates the stack temperature which could lead to an increase in water content. On the contrary, for these same current values, the physics-based model slightly underestimates the stack temperature. The discrepancy in the predictions could be due to variations in the models’ initialization. Even though the GT-Suite model underestimates the water content from 60A to 85A, the water content remains high. This could be due to water saturation as a result of increasing water generation in these high current zones. As a result, despite the modest shift in trend of stack temperature, the water content may remain elevated.

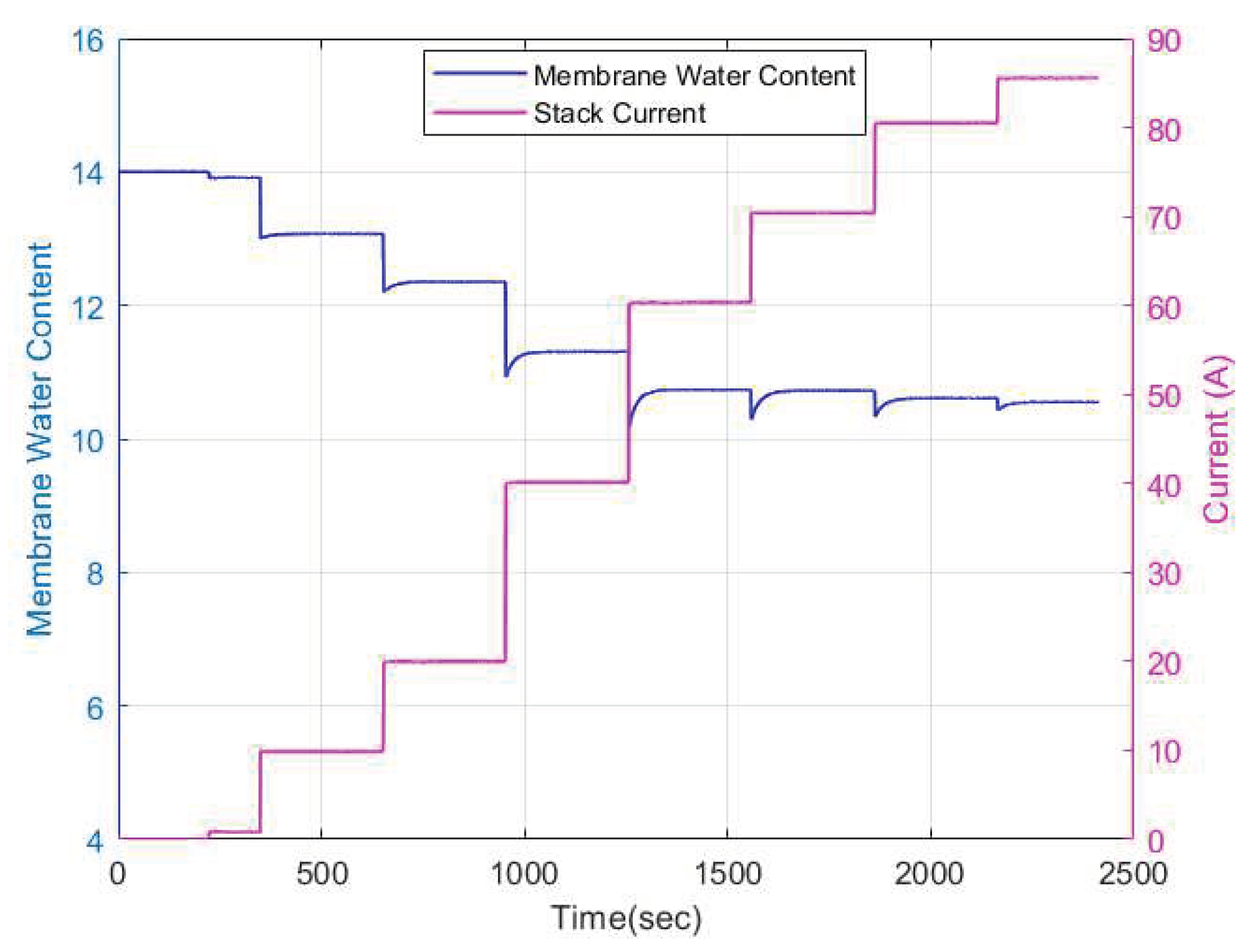
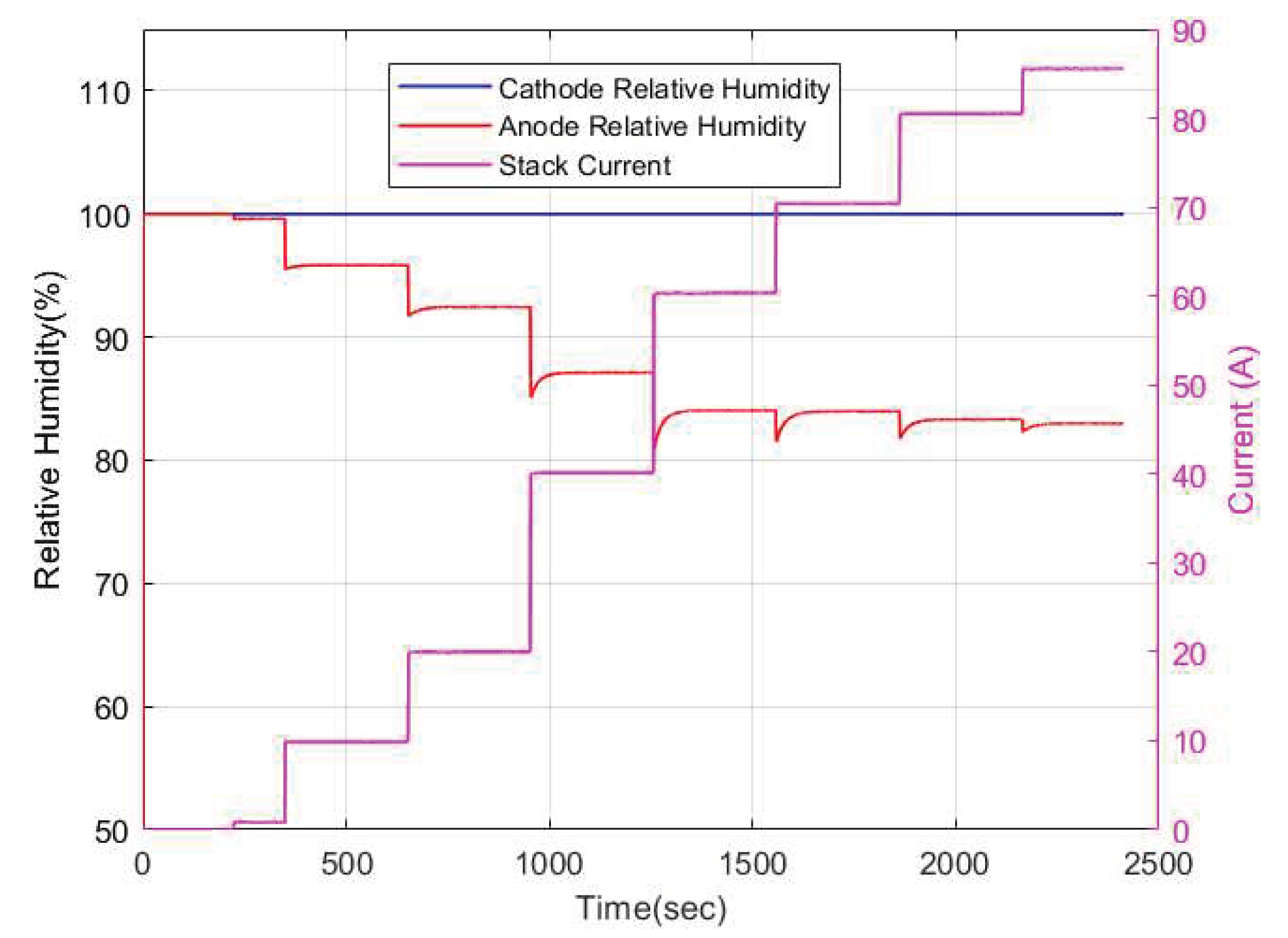
The membrane water content dynamics from the physics-based model is as shown in Figure 10. As can be observed, an increase in current input leads to a decrease in the membrane water content. The dynamics of the membrane water content is influenced by the relative humidity dynamics in the anode and cathode channels as depicted in Figure 11. The cathode relative humidity remains constant at 100% at all current cases due to water generation at the cathode electrode. The relative humidity of the anode channel however decreases with increase in current. This can be due to an increase of electroosmotic drag from the anode to the cathode channel. The parameters used for simulation of the models are shown in Table 1.

5.2. Discretized Model

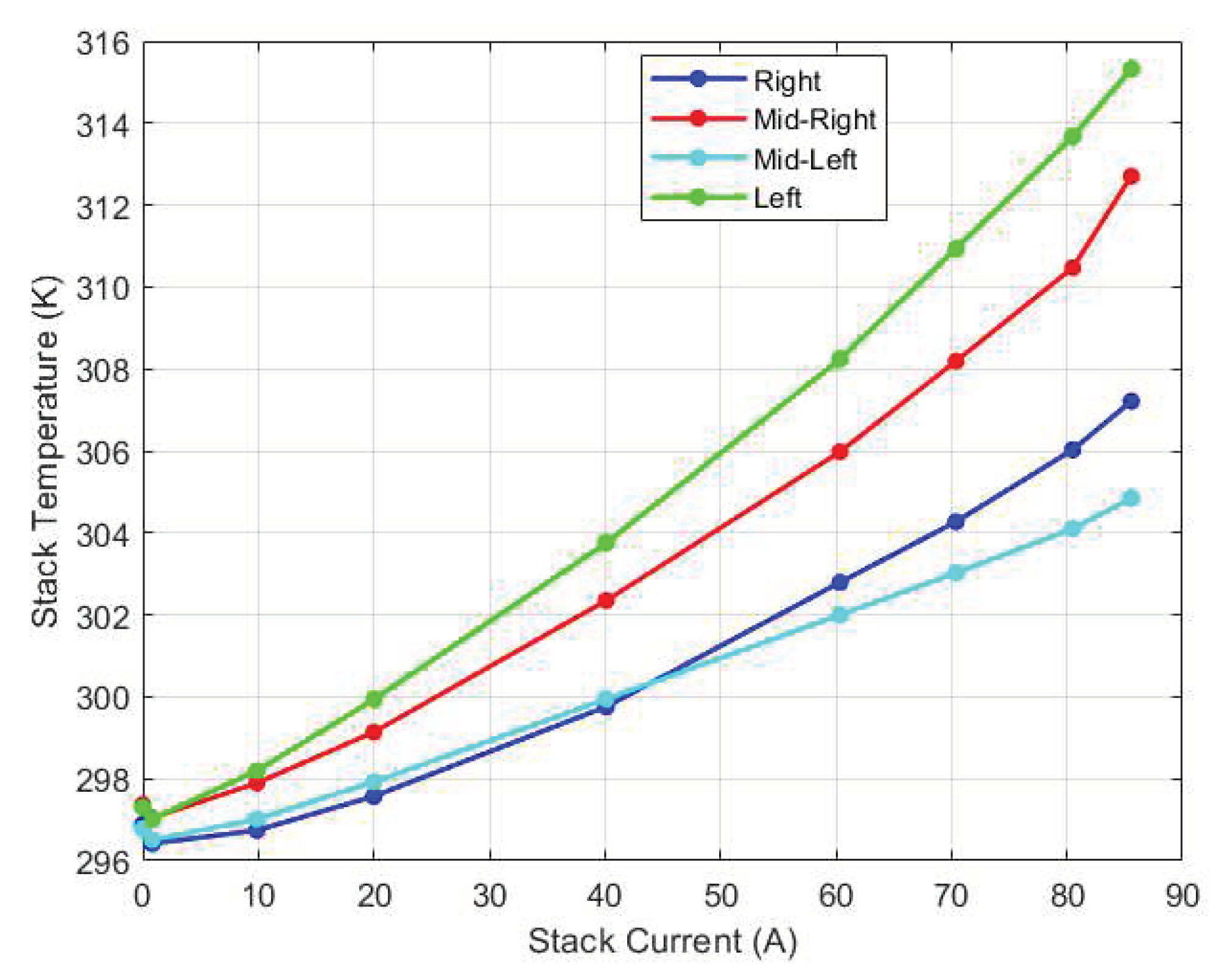
While the lumped model captures the overall stack behavior, variations are present internally. The steady state experimental results of the temperature recorded by the four thermocouples is illustrated in Figure 12. As depicted in the figure, for low current regions (0A-20A), the temperature recorded by the thermocouples is comparable with a variation within 2K. As the current increases, the temperature variation becomes more pronounced due to higher electrochemical reaction kinetics. Particularly at 85A current, there is a maximum temperature variation of 10K recorded. Notably, the left thermocouple (which is farthest from the direction of airflow) recorded the highest temperature for the medium to high current regions. This may be due to reduced cooling efficiency as a result of the location of the thermocouple. Interestingly, the mid-left thermocouple (just before the left thermocouple) recorded the lowest temperature at the higher current region. This suggests that the airflow may be directed in such a manner that it promotes effective cooling in this region.

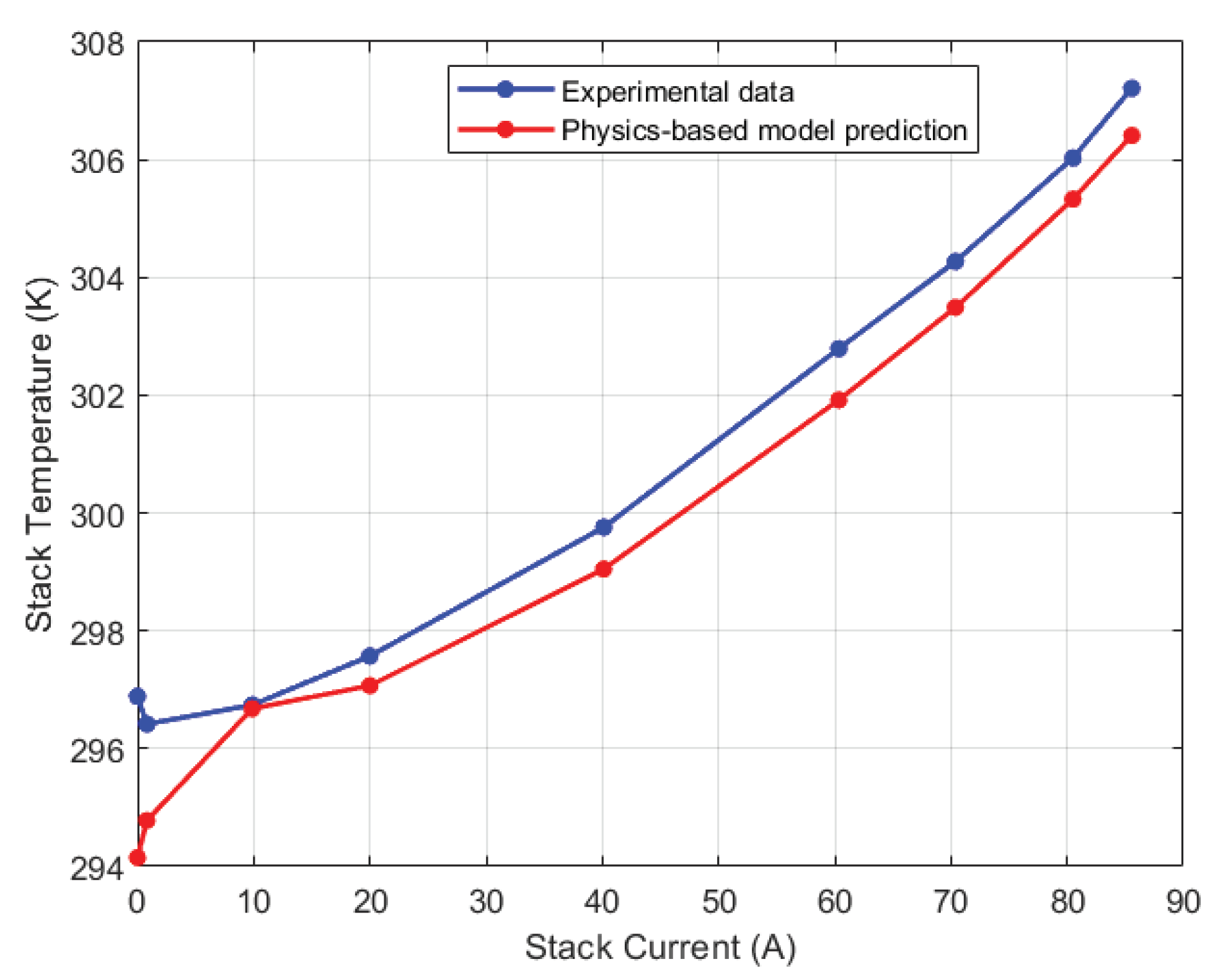
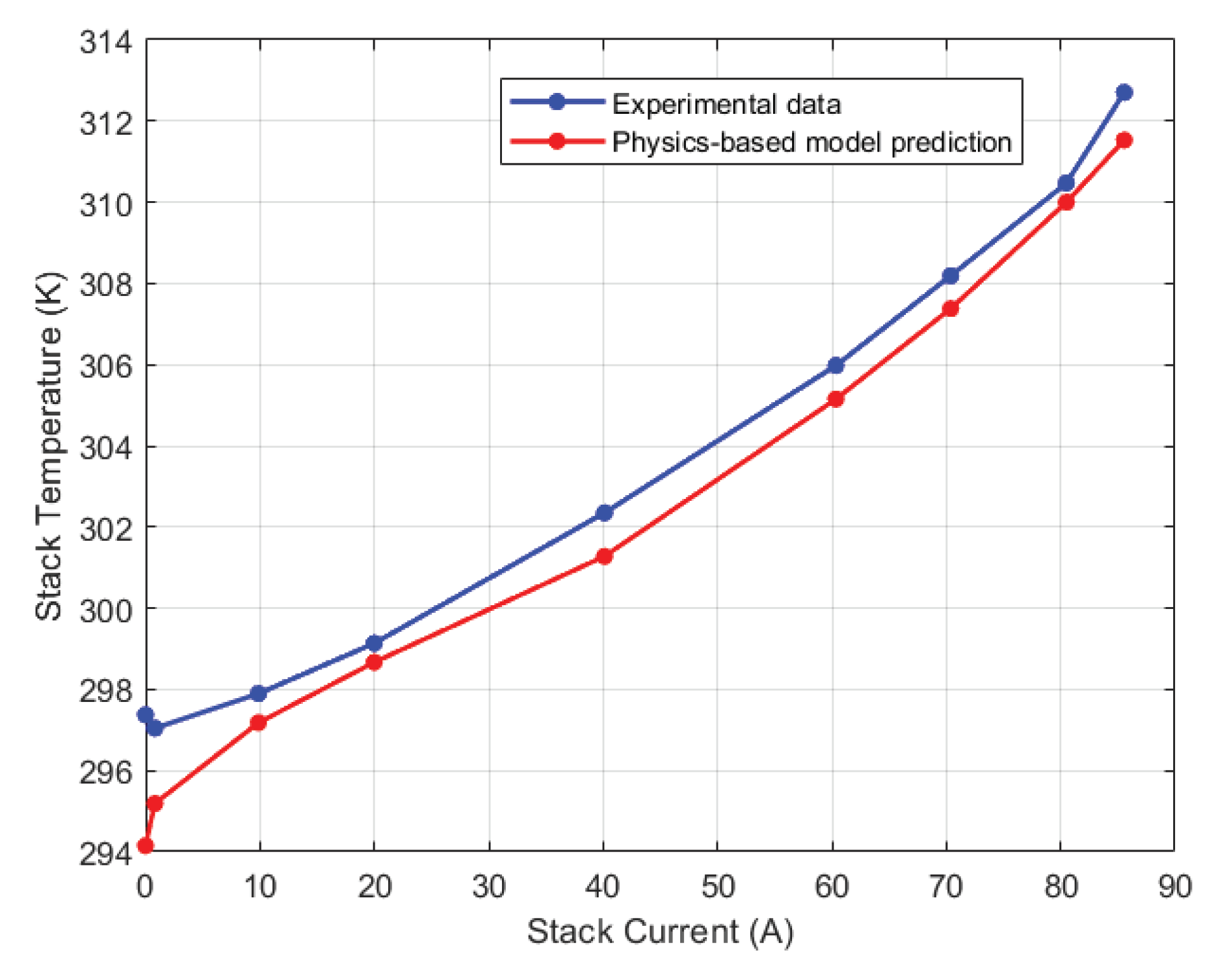
The discretized model was validated using the experimental thermocouple measurements. For the discretized model, the temperature in CV1 corresponds to the right thermocouple reading, in CV2 it is the mid-right, in CV3 it is the mid-left and in CV4 it is the left thermocouple. Figure 13, Figure 14, Figure 15 and Figure 16 display the thermocouple calibration results for each of the four thermocouples. The maximum relative error for each case is shown in Table 2.

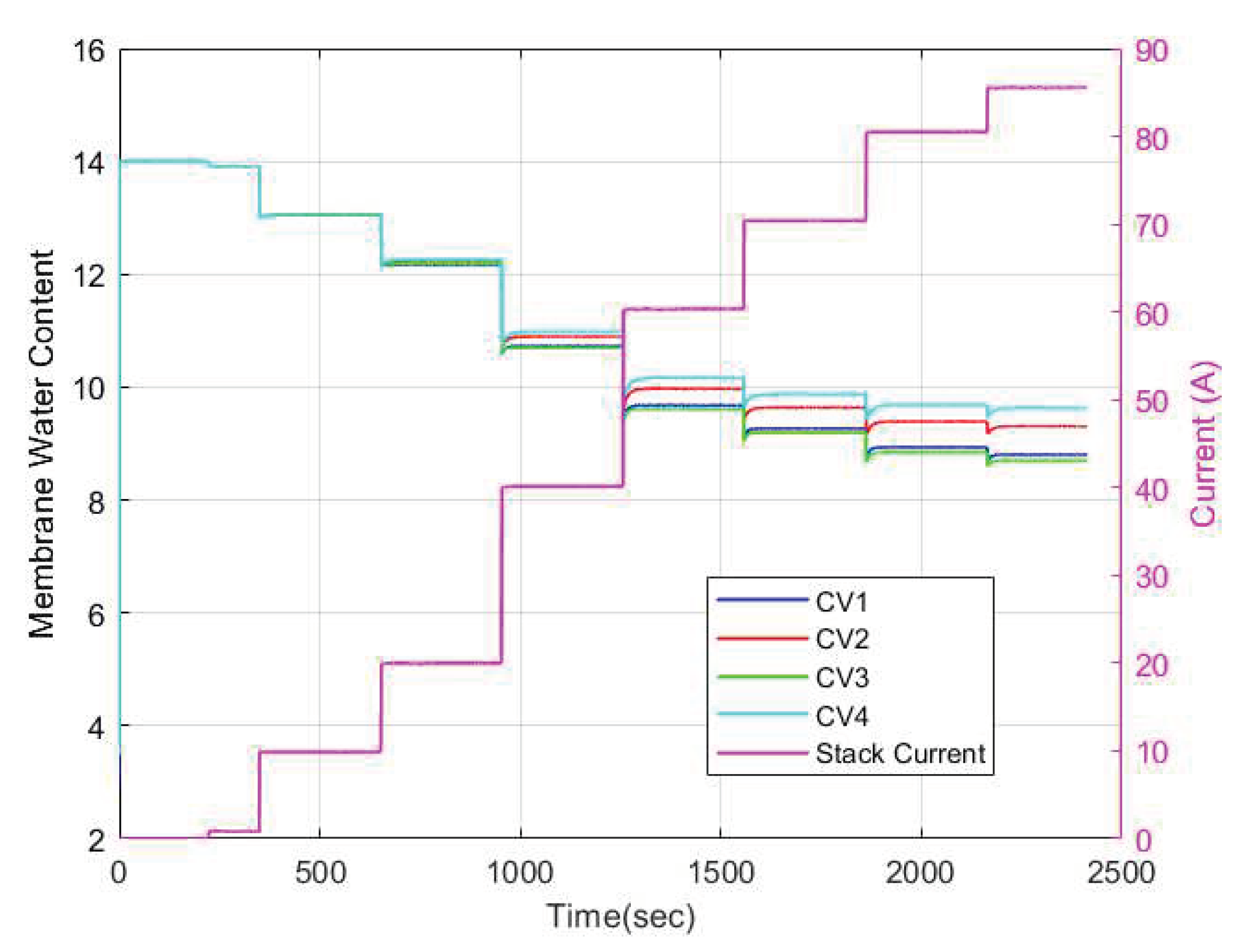
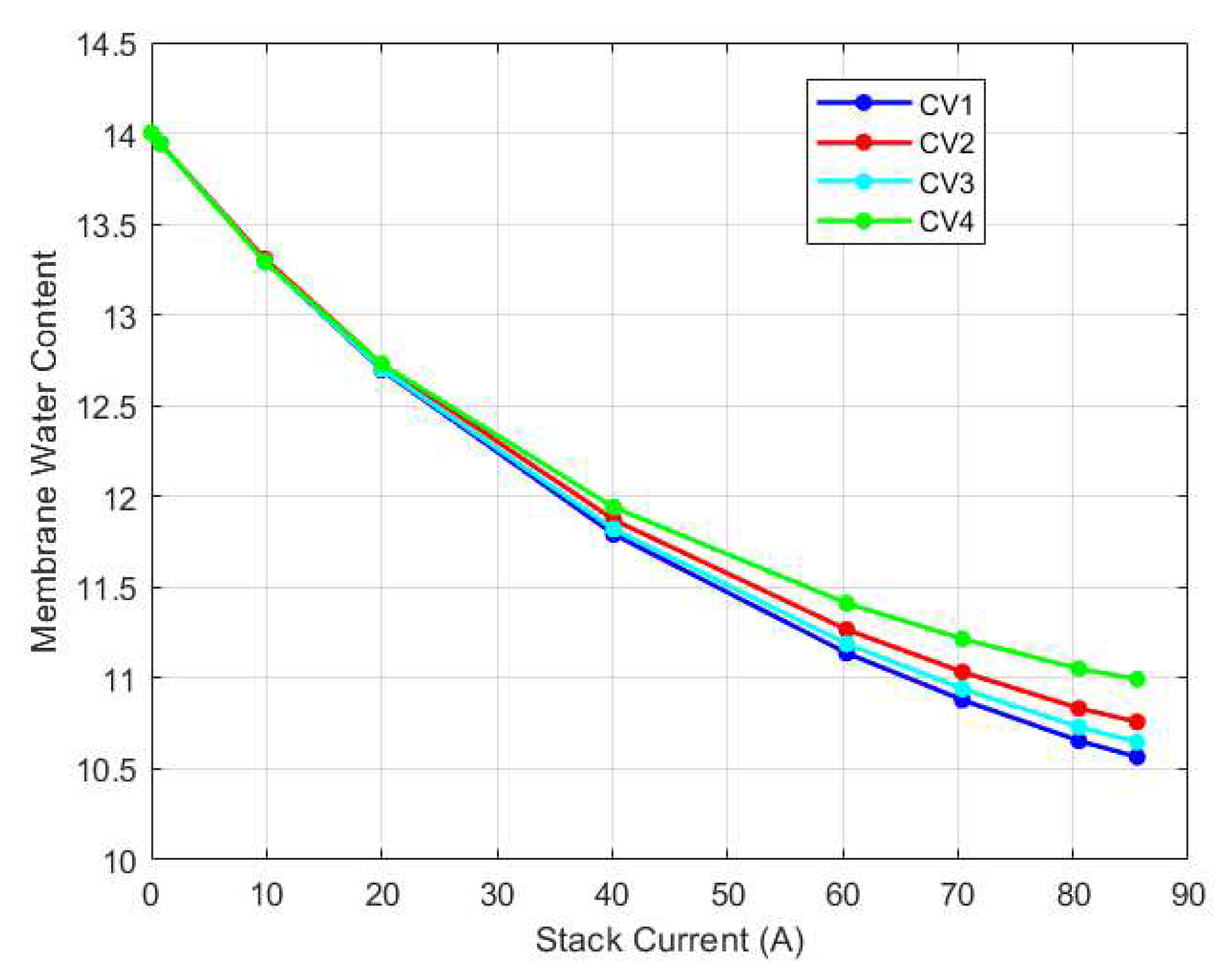
The membrane water content dynamics for each CV is as shown in Figure 17. It is evident that the membrane water content varies along each CV. These variations are most noticeable in the medium to high current regions (40A to 85A) where there is increased water activity. Notably, the trends in the temperature variation results and the variation in membrane water content were the same. The CV with the highest temperature also had the highest water content .

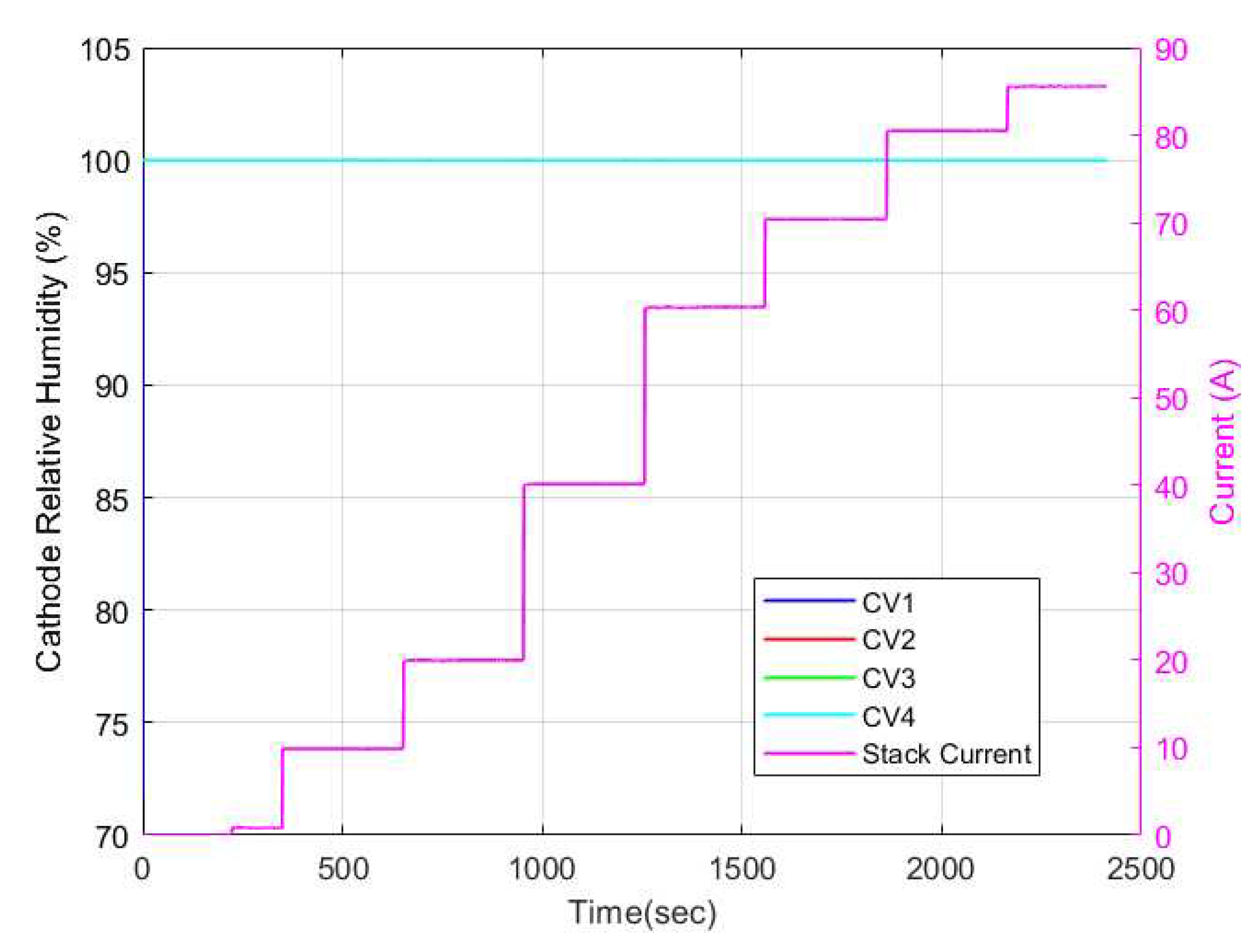
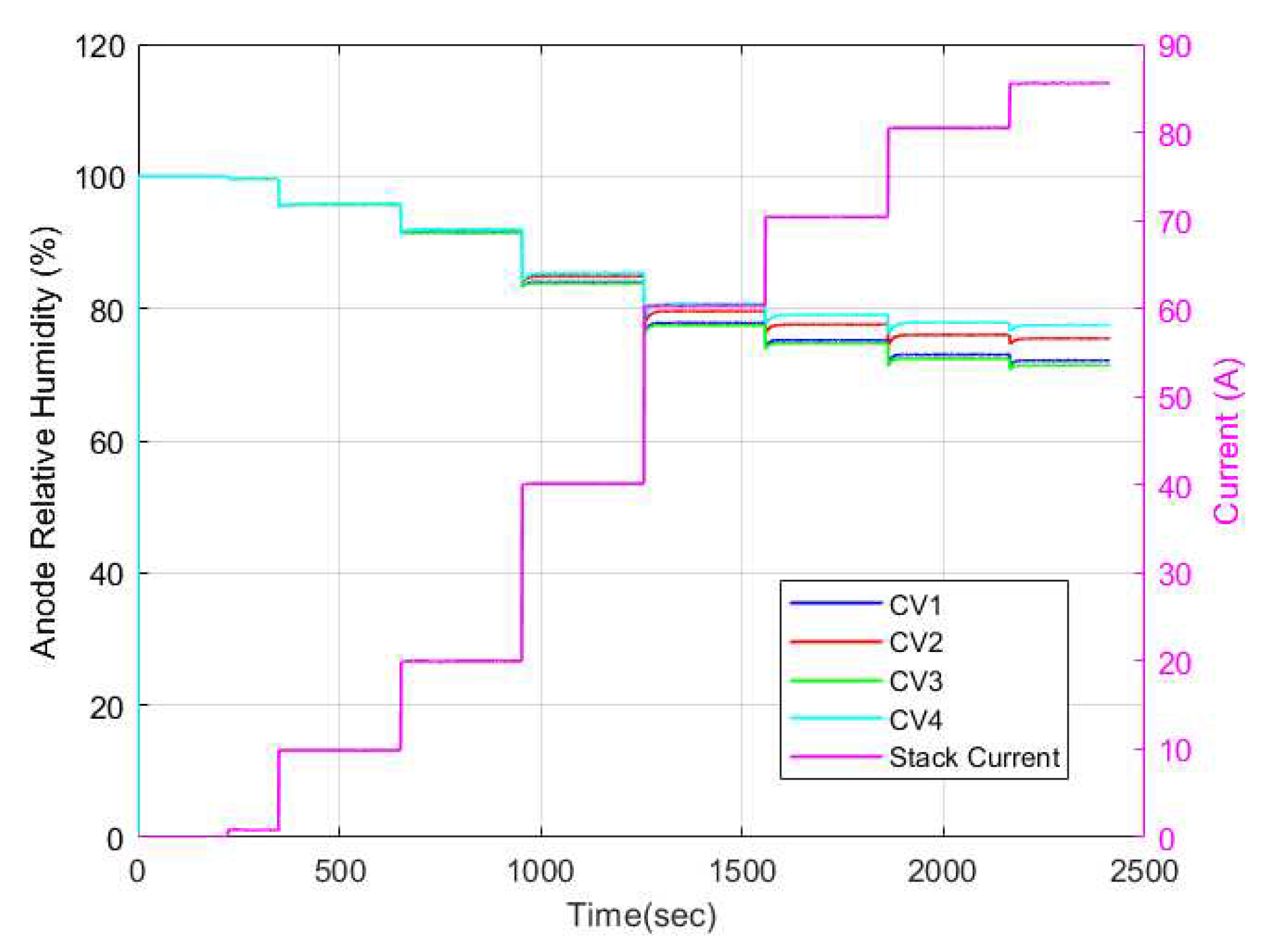
To gain a better understanding of the membrane water activity, the relative humidity dynamics occurring along the cathode and anode channels must be highlighted. The relative humidity dynamics in the anode and cathode channels are shown in Figure 18 and Figure 19 respectively. As can be seen, the cathode channel remained constant at 100% relative humidity for all CVs for all current cases. Conversely, the anode relative humidity varied along each CV. Hence, it is evident then that the observed variation in membrane water content stemmed solely from variations in relative humidity in the anode channel. This explains why some researchers opt to model the membrane water content as a function of simply the anode water content since it is a limiting factor in determining the membrane water content.

To validate the discretized water management model, the model’s steady state predictions were compared to simulation results from the discretized GT-Suite model. Firstly, the GT-Suite model was calibrated and validated using the thermocouple readings and the calibration results are illustrated in Figure 20, Figure 21, Figure 22 and Figure 23. The maximum relative error for each case is shown in Table 2. Following validation of the GT-Suite temperature variations prediction, its membrane water content predictions were used to validate the membrane water content variation of the physics-based model.

The steady state variation of membrane water content in the GT-Suite model is shown in Figure 24. As can be seen, the trend for the physics-based and GT-Suite models are comparable. The variations in membrane water content are much more evident in the medium to high current regions. The highest water content was recorded in the CV with the highest temperature. In the GT-Suite model however, CV3 has a higher membrane water content than CV1 despite having the lowest temperature. Nonetheless the difference in membrane water content between CV1 and CV3 for both the physics-based and GT-Suite model is only about 3%.

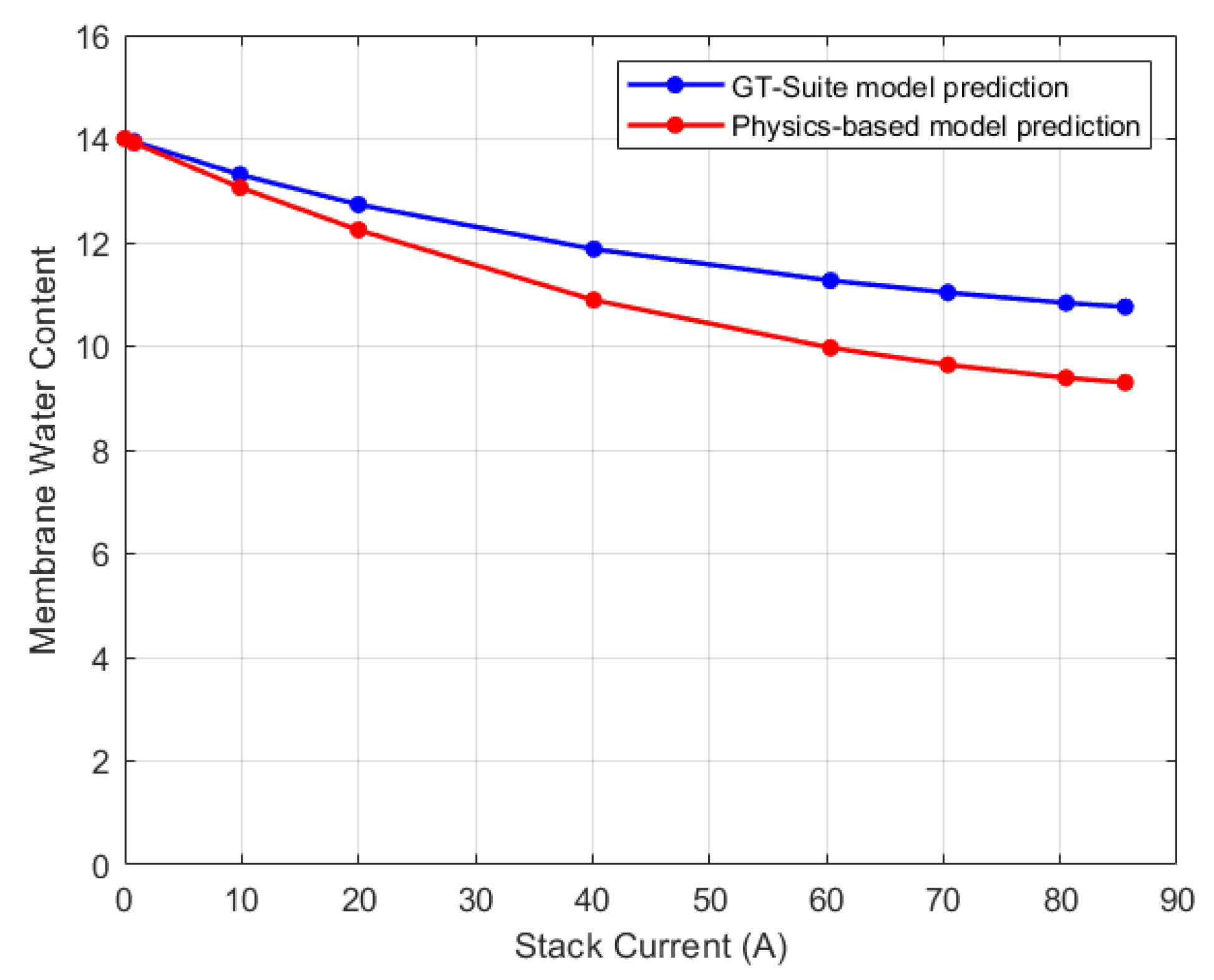
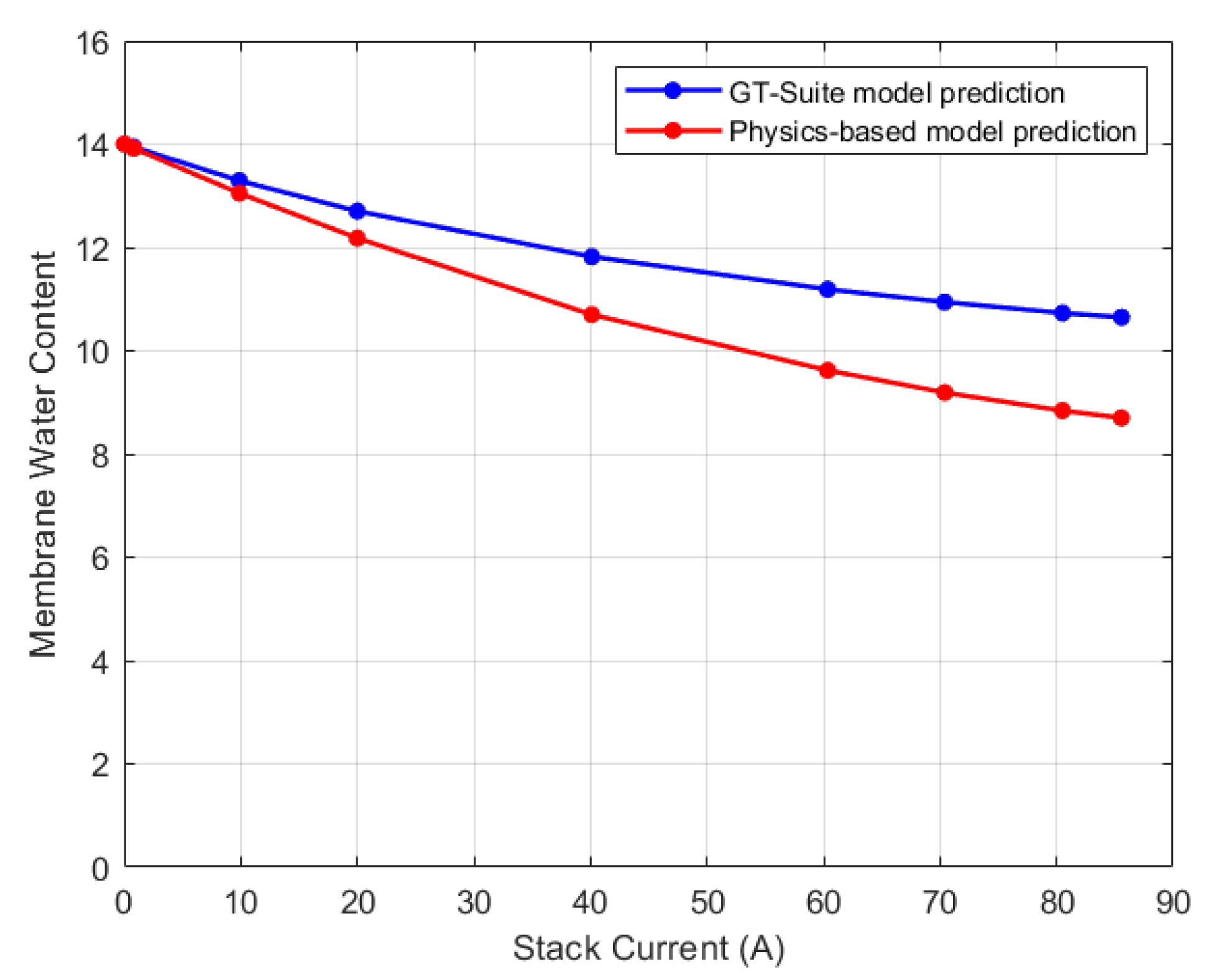
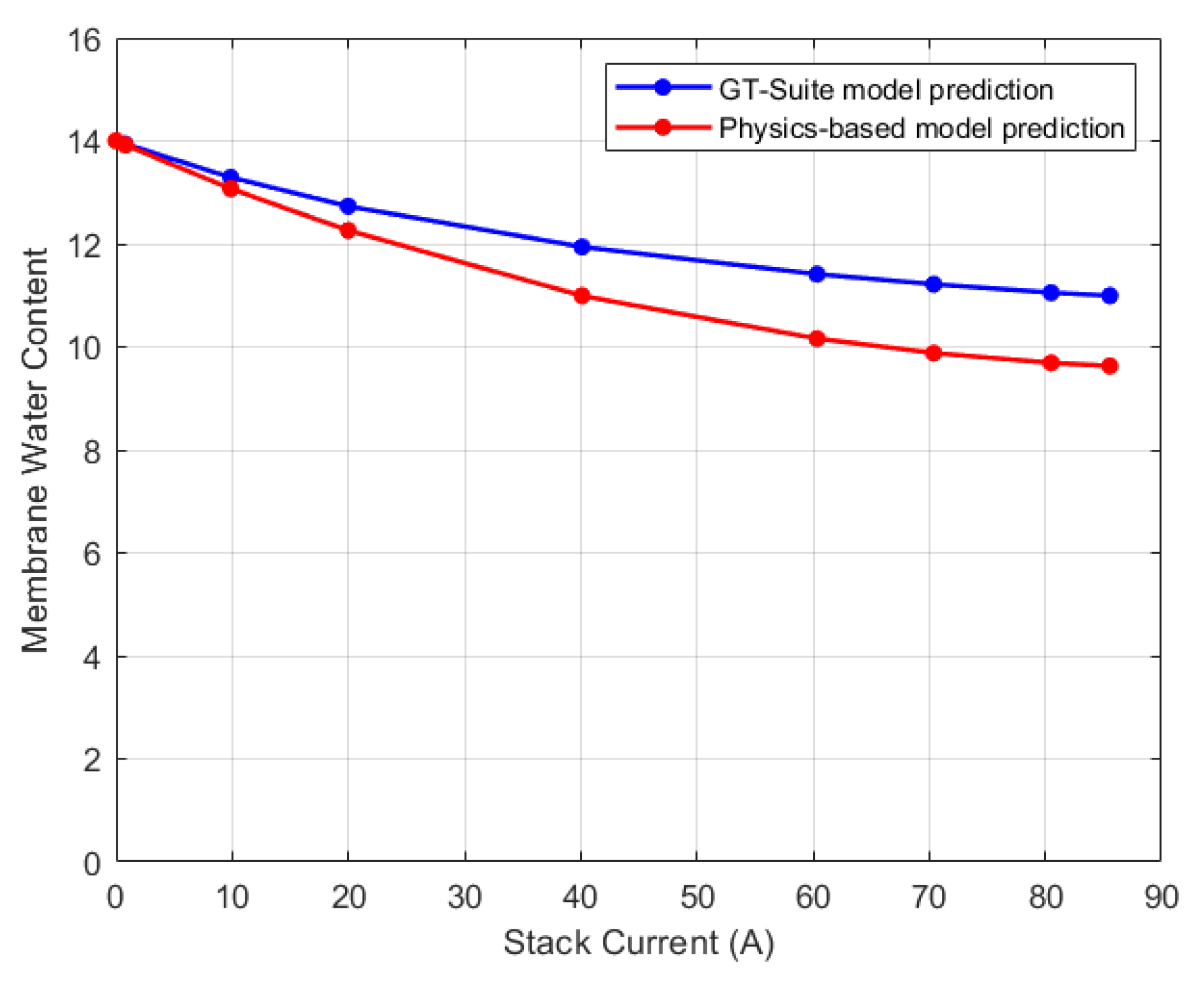
Comparison of the steady state result of the physics-based model to the GT-Suite simulation results for each CV is shown in Figure 25, Figure 26, Figure 27 and Figure 28. For each CV, the trend in membrane water content prediction is the same. Table 3 shows the RMSE values between the models’ predictions. The physics-based model’s ability to predict the distribution of membrane water content in the stack is demonstrated by the RMSE, which was within 1.3 membrane water content for all cases.

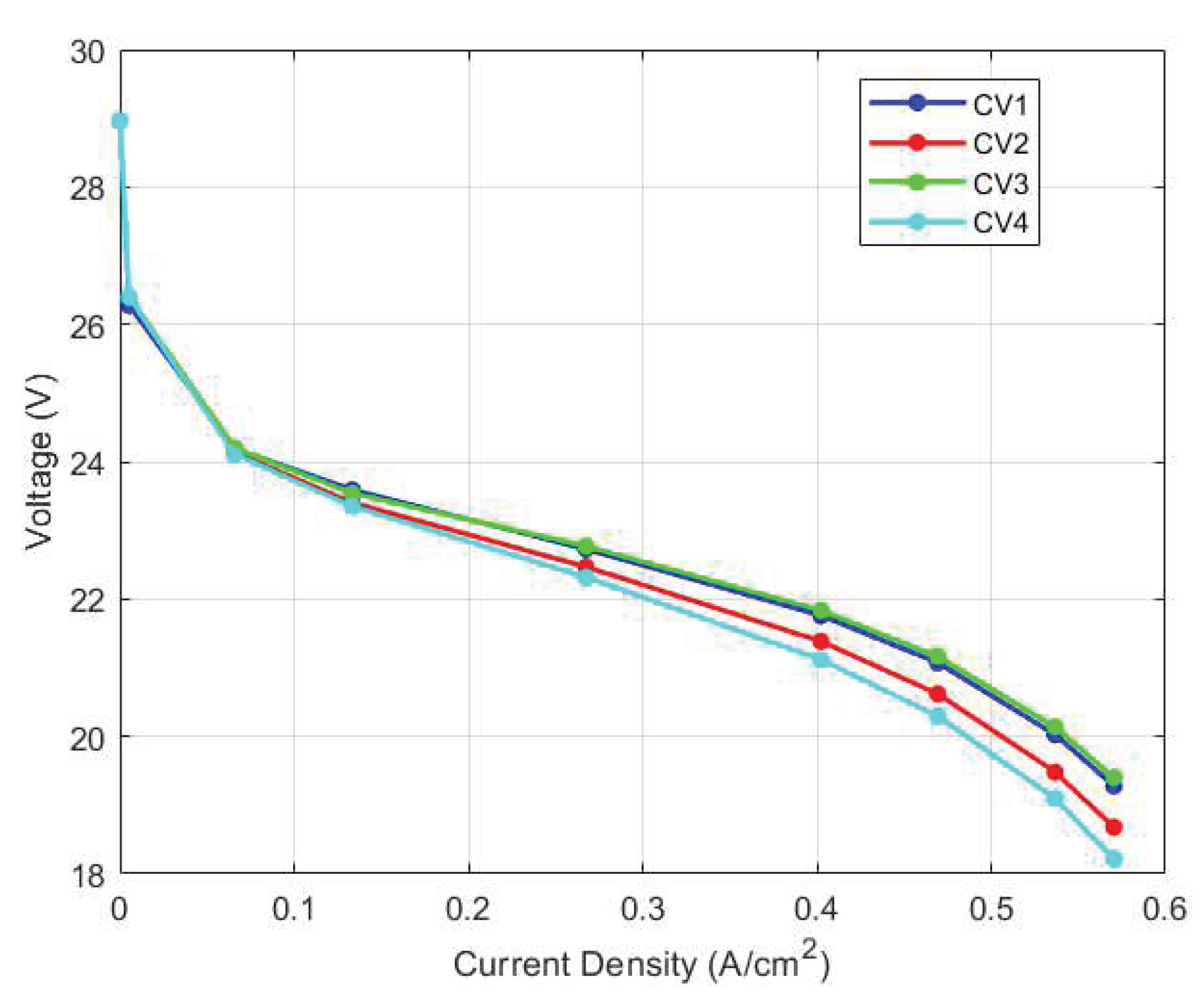
As shown in Figure 29, temperature variation and its ensuing variation in membrane water content resulted in variation in voltage output along the stack. As can be observed, at low current density, the voltage output for each CV is identical but as the current density increases, the voltage output varies more noticeably. Particularly, CV4 recorded the lowest voltage output, while CV3 and CV1 recorded the highest voltage, with CV3 slightly exceeding CV1 in voltage. As determined from the thermal and water management physics-based models, CV3 had the lowest stack temperature and water content followed by CV1 while CV4 recorded the highest stack temperature and the highest water content. One possible explanation for CV3 and CV1’s enhanced performance could be due to the improved cooling system in these regions which resulted in the lower stack temperatures. Better cooling implies higher air flow rate, which increases oxygen availability and in turn, increases performance. It is, however, well documented that lower membrane water content leads to higher ohmic overvoltage in a PEM fuel cell stack. Hence, this improvement in performance only occurs because the increased ohmic resistance is smaller than the increased performance caused by the availability of oxygen.

6. Conclusion and Future Work

A reduced-order control-oriented physics-based model for predicting variation in membrane water content in an open-cathode PEM fuel cell was developed in this study. The water management model was validated by comparing its prediction to GT-Suite simulation results, and RMSE were found to be within 1.3 membrane water content for all cases. The results indicate that the water content of the PEM fuel cell membrane varies along the fuel cell stack. Variations abound, particularly in medium to high current density regions where there is significant water activity. The variations of the membrane water content coupled with the temperature variations leads to variation of the voltage output along the stack. Control of these variations is therefore critical especially during transients. The developed model thereby presents a computationally inexpensive means for prediction and subsequent control of membrane water content variations. Compared to the lumped physics-based model which took ~12 seconds to simulate about 40 minutes of experimental data, the computational time for the 4-CV discretized model was ~80 seconds. Despite the increased computational time, it is still relatively low for control. By contrast, the lumped GT-Suite model took ~240 seconds to compute, which is almost 20 times slower than the lumped physics-based model. The computational time for the discretized GT-Suite model was ~600 seconds, which is about 7.5 times slower than the discretized physics-based model.

Future research will include validating the water management model experimentally to improve the model’s accuracy and reliability by aligning its predictions with real-world observations. In addition, the model will be improved to include liquid water effects to predict flooding conditions particularly in the cathode channel.

Acknowledgments

This material is based on work supported by the National Science Foundation, United States under Grant No. 2135735.

References

Calili-Cankir, F., Ismail, M. S., Berber, M. R., Alrowaili, Z. A., Ingham, D. B., Hughes, K. J., Ma, L., & Pourkashanian, M. (2022). Dynamic models for air-breathing and conventional polymer electrolyte fuel cells: A comparative study. Renewable Energy, 195, 1001–1014. [CrossRef]
Chen, F., Zhang, L., & Jiao, J. (2021). Modelling of humidity dynamics for open-cathode proton exchange membrane fuel cell. World Electric Vehicle Journal, 12(3). [CrossRef]
Chen, X., Xu, J., Fang, Y., Li, W., Ding, Y., Wan, Z., Wang, X., & Tu, Z. (2022). Temperature and humidity management of PEM fuel cell power system using multi-input and multi-output fuzzy method. Applied Thermal Engineering, 203(November 2021), 117865. [CrossRef]
Chen, X., Xu, J., Liu, Q., Chen, Y., Wang, X., Li, W., Ding, Y., & Wan, Z. (2020). Active disturbance rejection control strategy applied to cathode humidity control in PEMFC system. Energy Conversion and Management, 224(September), 113389. [CrossRef]
Di Penta, D., Bencherif, K., Sorine, M., & Zhang, Q. (2006). A reduced fuel cell stack model for control and fault diagnosis. Journal of Fuel Cell Science and Technology, 3(4), 384–388. [CrossRef]
Dutta, S., Shimpalee, S., & Van Zee, J. W. (2001). Numerical prediction of mass-exchange between cathode and anode channels in a PEM fuel cell. International Journal of Heat and Mass Transfer, 44(11), 2029–2042. [CrossRef]
Headley, A., Yu, V., Borduin, R., Chen, D., & Li, W. (2016). Development and Experimental Validation of a Physics-Based PEM Fuel Cell Model for Cathode Humidity Control Design. IEEE/ASME Transactions on Mechatronics, 21(3), 1775–1782. [CrossRef]
Huo, D., & Hall, C. M. (2023). Data-driven prediction of temperature variations in an open cathode proton exchange membrane fuel cell stack using Koopman operator. Energy and AI, 14(May), 100289. [CrossRef]
Ishaku, J., Lotfi, N., Zomorodi, H., & Landers, R. G. (2014). Control-oriented modeling for open-cathode fuel cell systems. Proceedings of the American Control Conference, 268–273. [CrossRef]
Karnik, A. Y., Stefanopoulou, A. G., & Sun, J. (2007). Water equilibria and management using a two-volume model of a polymer electrolyte fuel cell. Journal of Power Sources, 164(2), 590–605. [CrossRef]
Meyer, R. T., & Yao, B. (2006). Modeling and Simulation of a Modern Pem Fuel Cell System. ASME 2006 4th International Conference on Fuel Cell Science, Engineering and Technology, FUELCELL 2006, V, 133–150. [CrossRef]
Nguyen, T. V., & White, R. E. (1993). A Water and Heat Management Model for Proton-Exchange-Membrane Fuel Cells. Journal of The Electrochemical Society, 140(8), 2178–2186. [CrossRef]
O’hayre R., Cha S-W., Colella W., & Prinz, F.B. (2016). Fuel Cell Fundamentals. John Wiley & Sons.
Pathapati, P.R., Xue, X., & Tang, J. (2005). A new dynamic model for predicting transient phenomena in a PEM fuel cell system. Renewable Energy, 30(1), 1-22. [CrossRef]
Pukrushpan, J. T., Peng, H., & Stefanopoulou, A. G. (2004). Control-oriented modeling and analysis for automotive fuel cell systems. Journal of Dynamic Systems, Measurement and Control, Transactions of the ASME, 126(1), 14–25. [CrossRef]
Pukrushpan, J. T., Stefanopoulou, A. G., & Peng, H. (2002). Modeling and control for PEM fuel cell stack system. Proceedings of the American Control Conference, 4, 3117-3122. [CrossRef]
Sagar, A., Chugh, S., Sonkar, K., Sharma, A., & Kjeang, E. (2020). A computational analysis on the operational behaviour of open-cathode polymer electrolyte membrane fuel cells. International Journal of Hydrogen Energy, 45(58), 34125–34138. [CrossRef]
Saleh, I.M.M., Ali,R., & Zhang, H. (2016). Simplified mathematical model of proton exchange membrane fuel cell based on horizon fuel cell stack. Journal of Modern Power Systems and Clean Energy, 4(4), 668-679. [CrossRef]
Springer, T.E., & Zawodzinski, T.A., & Gottesfeld, S. (1991). Polyper electrolyte fuel cell model. Journal of Electrochemical Society,138(8).
Wang, Y., Yu, D., Chen, S., & Kim, Y. (2014). Robust DC / DC converter control for polymer electrolyte membrane fuel cell application. Journal of Power Sources, 261, 292–305. [CrossRef]
Zeng, T., Zhang, C., Huang, Z., Li, M., Chan, S. H., Li, Q., & Wu, X. (2019). Experimental investigation on the mechanism of variable fan speed control in Open cathode PEM fuel cell. International Journal of Hydrogen Energy, 44(43), 24017–24027. [CrossRef]
Zhang, G., & Jiao, K. (2018). Three-dimensional multi-phase simulation of PEMFC at high current density utilizing Eulerian-Eulerian model and two-fluid model. Energy Conversion and Management, 176(June), 409–421. [CrossRef]

Figure 1. Experimental set-up.

Figure 2. Thermocouple layout for fuel cell stack.

Figure 3. Block diagram of physics-based model.

Figure 4. Block diagram of water management model.

Figure 5. Calibration results for stack voltage physics-based model.

Figure 6. Calibration results for lumped thermal physics-based model.

Figure 7. Calibration results for GT-Suite stack voltage model.

Figure 8. Calibration results for GT-Suite lumped thermal model.

Figure 9. Comparison results for membrane water content.

Figure 10. Membrane water content dynamics for lumped physics-based model.

Figure 11. Humidity dynamics in the anode and cathode channels for lumped physics-based model.

Figure 12. Steady state temperature thermocouple data.

Figure 13. Right (CV1) thermocouple steady state calibration results.

Figure 14. Mid-Right (CV2) thermocouple calibration results.

Figure 15. Mid-left (CV3) thermocouple calibration results.

Figure 16. Left (CV4) thermocouple calibration results.

Figure 17. Membrane water content dynamics for discretized physics-based model.

Figure 18. Cathode relative humidity dynamics for discretized physics-based model.

Figure 19. Anode relative humidity dynamics for discretized physics-based model.

Figure 20. Left (CV1) thermocouple GT-Suite calibration results.

Figure 21. Mid-right (CV2) thermocouple GT-Suite calibration results.

Figure 22. Mid-left (CV3) thermocouple GT-Suite calibration results.

Figure 23. Left (CV4) thermocouple GT-Suite calibration results.

Figure 24. Steady state membrane water content variation for GT-Suite model.

Figure 25. Steady state comparison of membrane water content for CV1.

Figure 26. Steady state membrane water content comparison for CV2.

Figure 27. Steady state membrane water content comparison for CV3.

Figure 28. Steady state membrane water content comparison for CV4.

Figure 29. Voltage variation along stack for physics-based model.

Table 1. Parameters used in model simulation.

Symbol	Variable	Value
$A_{f c}$	Active area of fuel cell	150cm²
$N_{s t}$	Number of cells in stack	120
$F_{}$	Faraday constant	96485Coulombs
$t_{m e m}$	Membrane thickness	0.0035cm
$R_{}$	Ideal gas constant	8.314 J/(mol.K)
${R_{H_{2} O}}_{v}_{}$	Water vapor gas constant	461.5 J/(kg.K)
${R_{O}}_{2}$	Oxygen gas constant	259.8 J/(kg.K)
${R_{N}}_{2}$	Nitrogen gas constant	296.9 J/(kg.K)
${R_{H}}_{2}$	Hydrogen gas constant	4124.3 J/(kg.K)
${M_{H_{2} O}}_{v}_{}$	Water vapor molar mass	0.018 kg/mol
${M_{O}}_{2}_{}$	Oxygen molar mass	0.032 kg/mol
${M_{N}}_{2}_{}$	Nitrogen molar mass	0.028 kg/mol
${M_{H}}_{2}_{}$	Hydrogen molar mass	0.002 kg/mol
$n_{}$	No. of electrons transferred	2
$k_{c a, o u t}$	Cathode outlet flow coefficient	2.2e-06 kg/(s.Pa)
$V_{a n}$	Anode volume per cell	2.58e-06m³
$V_{c a}$	Cathode volume per cell	2.59e-05m³
$ρ_{m e m}$	Membrane dry density	0.002 kg/cm³
$M_{m e m}$	Membrane equivalent weight	1.1 kg/mol
$C_{p}$	Specific heat capacity of air	1006 J/(kg.K)
$R_{e l e c}$	Electronic resistance	0.00007W

Table 2. Maximum relative error for discretized thermal model.

Thermocouple/CV	Max. relative error
Thermocouple/CV	Physics-based	GT-Suite
Right/CV1	0.92%	0.95%
Mid-right/CV2	1.08%	0.68%
Mid-left/CV3	0.89%	1.00%
Left/CV4	1.06%	0.75%

Table 3. RMSE results for membrane water content comparison.

Control volume (CV)	RMSE
CV1	1.17
CV2	1.00
CV3	1.27
CV4	0.95

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

A Control-Oriented Model for Predicting Variations in Membrane Water Content of an Open-Cathode Proton Exchange Membrane Fuel Cell

Abstract

1. Introduction

2. Experimental Setup

3. Model Development

3.1. Physics-Based Model

3.1.1. Stack Voltage Model

3.1.2. Air Flow Model

3.1.3. Thermal Model

3.1.4. Water Management Model

Cathode Channel

Anode Channel

Proton Exchange Membrane

3.2. GT-Suite Model

4. Model Discretization

4.1. Physics-Based Model

4.2. GT-Suite Model

5. Results and Discussion

5.1. Lumped Model Validation

5.2. Discretized Model

6. Conclusion and Future Work

Acknowledgments

References

MDPI Initiatives

Important Links

Subscribe