Monitoring Method of VOCs Based on PID in Soil-water-gas Environment

1. Introduction

The introduction should briefly place the study in a broad context and highlight why it is important. It should define the purpose of the work and its significance. The current state of the research field should be carefully reviewed and key publications cited. Please highlight controversial and diverging hypotheses when necessary. Finally, briefly mention the main aim of the work and highlight the principal conclusions. As far as possible, please keep the introduction comprehensible to scientists outside your particular field of research. References should be numbered in order of appearance and indicated by a numeral or numerals in square brackets—e.g., [1] or [2,3], or [4,5,6]. See the end of the document for further details on references.

Benzene compounds, important components of VOCs, are commonly used organic solvents in the organic and coal chemical industries. If emitted into the environment in excess, they can cause symptoms of poisoning in humans [3]. Benzene compounds can also lead to dysfunction in the human nervous system [4]. Prolonged inhalation of benzene compounds can result in abnormal liver function, damage to the hematopoietic organs, and may even lead to symptoms of sepsis, causing abnormalities in human health and potentially triggering disorders such as aplastic anemia. In cases of large-scale vaporization of benzene, individuals may experience acute poisoning, which can lead to fatalities [5].

Efficient and precise VOCs monitoring methods are beneficial for accurately understanding the real-time dynamics of VOC concentrations. This helps enterprises, government agencies, and other departments to promptly implement corresponding measures, preventing harm to human health and the environment caused by VOCs. The Photoionization Detector (PID) is an important method for monitoring Volatile Organic Compounds (VOCs). Utilizing PID for VOC monitoring has characteristics such as high monitoring accuracy, non-destructive monitoring of VOCs, rapid response, long lifespan, and the ability to conduct VOC monitoring at atmospheric pressure [6]. PID typically can achieve monitoring of VOCs at the ppm level, and high-precision PIDs can even achieve monitoring at the ppb level (ppb is one thousandth of ppm). This allows for the detection of extremely low concentrations of volatile organic compounds. PID exhibits high sensitivity and enables non-destructive monitoring of VOCs. The VOCs being measured return to their original state after ionization in the ionization chamber. Due to its non-destructive monitoring characteristics, PID can also collaborate with other VOC monitoring technologies such as mass spectrometry, providing more information about the components and concentrations of the monitored VOCs. The application of PID is extensive, as it can monitor a wide range of volatile organic pollutants and is widely used in the monitoring of VOCs generated in industries such as coal chemical and petrochemical.

Currently, the calibration methods for Photoionization Detectors (PID) used in VOCs monitoring primarily involve determining the concentration of VOCs based on voltage values. This approach is evident in the research of Arnaud Termonia [7], Chung-hwan Je [8], Gianfranco Manes [9], Kentaro Oka [10], Qian [11], Wang J [12], Li [13], Wang Li [14], and others. However, when PID is applied to monitor VOCs in the soil-water-air environment, the signals generated by PID occurs simultaneously complex noise, impacting the numerical values of PID voltage and leading to misjudgments of VOC concentrations. Machine learning methods offer a solution by using multi-dimensional features of the signal instead of relying on a single voltage value for PID calibration. These multi-dimensional features help reduce the impact of noise on PID signals responding to VOC concentrations, thereby improving the robustness of the method [15].

Deep learning methods like artificial neural networks require the collection of a large number of VOCs samples, meaning the preparation of VOCs gas at specific concentrations [13,14,15]. It demands a substantial amount of human resources, materials, and financial investment [11,12,13,14,15]. And the Support Vector Machine (SVM) method, based on small-sample statistical learning theory, addresses this issue by constructing an optimal hyperplane that maximizes the distance between the hyperplane and different sets of samples in the sample or feature space [16]. The objective is to maximize the generalization ability. SVM demonstrates superior generalization ability compared to Deep learning methods such as artificial neural networks. In addition, the solution provided by SVM is the unique globally optimal solution. Therefore, this paper will investigate the method of using SVM regression (SVR) to monitor VOC concentrations in the soil-water-air environment.

2. Relate Work

2.1. Monitoring Method for VOCs based on PID

In 1997, Arnaud Termonia et al. [7] used gas chromatography-mass spectrometry in conjunction with PIDs to construct a VOCs monitoring system for monitoring VOCs in landfill sites. This method enables effective VOCs monitoring but it has issues such as high cost and maintenance difficulties. In 2007, Chung-hwan Je et al. [8] established an online VOCs monitoring system using a set of PID. They focused on the development and application of a multi-channel monitoring system based on PID for measuring, processing, and analyzing the concentration levels of VOCs emitted from a walk-in fume hood in hazardous waste management facilities. This system reduced the noise of PID signals by summing up the data over a time interval. In 2016, Gianfranco Manes et al. [9] addressed the issues of non-linear data, periodic calibration, and replacement distribution associated with PID in long-term monitoring in their VOCs online monitoring system based on PID. The first VOCs online monitoring system was installed in a petrochemical plant in Italy. Since its installation, the system has been continuously operational without human intervention. The successful operation of this system validates the feasibility of regional VOCs monitoring using PID.

In 2015, Qian Kun et al. [11] designed a low-power ZigBee sensor network and a data reception control framework between nodes based on a photoionization detector for monitoring VOCs in indoor environments. Their research focused on the design of a low-power ZigBee sensor network and a data reception control framework for real-time data acquisition and communication of VOCs air pollutant levels, enabling automated indoor VOCs monitoring. In 2019, Healy et al. [17] analyzed the principle and characteristics of VOCs detection using a photoionization detector. They also assessed the advantages and disadvantages of various VOCs detection methods and performed cost analysis. Additionally, they provided a detailed description of the circuit design and software system design for online monitoring systems. In 2020, Wang Jin et al. [12] discussed the issues of low accuracy and high cost associated with produced photoionization detectors in China, which make them difficult to widely deploy and utilize. Then they proposed a method to separate the sensor current detection module from the sensor radio frequency ultraviolet lamp driving module and designed a high-precision photoionization detector. In 2019, Li Hai et al. [13], based on the principles of photoionization technology, conducted theoretical analysis and simulations to determine various parameters of the ionization chamber in the photoionization detector (PID) according to practical conditions.

2.2. Quantitative analysis method for PID signal

Currently, the calibration method for PID used in VOCs monitoring primarily relies on voltage values to determine the current VOCs concentration, as demonstrated in the studies conducted by Arnaud Termonia [7], Chung-hwan Je [8], Gianfranco Manes [9], Kentaro Oka [10], Qian Kun [11], Wang Jin [12], Li Hai [13], Wang Lixin [14], and others. However, when PID is applied to monitor VOCs in real-world soil-water-air environments, the signals generated by PID can be affected by complex noise. This complex noise can impact the numerical value of PID voltage and result in inaccuracies in VOCs concentration estimation. Machine learning methods, on the other hand, can utilize multidimensional features of the PID signal instead of relying solely on voltage values for PID calibration. These multidimensional features help reduce the interference of noise when the PID signal responds to VOCs concentration, thus enhancing the accuracy of VOCs monitoring using PID.

In recent years, the artificial neural network method has been widely applied in various fields. However, artificial neural networks have drawbacks and limitations such as slow convergence speed, slow generalization, and a tendency to get trapped in local optima. Moreover, in practical VOCs engineering processes, artificial neural networks often require a large number of samples for training. In order to achieve precise VOCs concentration, it is necessary to prepare gas at a specific concentration. However, the preparation work is complex and requires a significant amount of manpower and financial resources [10,11,12,13,14,15].

The basic idea of SVM is to construct an optimal hyperplane that maximizes the distance between the hyperplane and the sample sets of different classes in the sample or feature space, aiming to achieve the goal of maximizing generalization ability [15,16]. Unlike traditional artificial neural networks methods, SVM adopts a structural risk minimization criterion, minimizing the generalization error bound to achieve maximum generalization ability [18]. SVM has better generalization ability compared to artificial neural networks methods, and its solution is the unique global optimum. Therefore, in this paper, we apply SVR based on PID signal to monitor VOCs concentration.

3. PID Selection and Problem Statement

3.1. Calibration of PID for various VOCs

Different types of volatile organic compounds (VOCs) exhibit variations in the number of electrons generated and the extent of ionization after being ionized under high-energy ultraviolet light. As a result, the signal generated by the photoionization detector (PID) may reflect varying VOCs concentrations due to differences in their composition, despite the same concentration level. To establish a measurement standard, the PID employs a correction factor (CF) to compute the concentration of the monitored gas in relation to the standard gas [19]. In this study, benzene was used as the calibration gas for the PID, with a predefined calibration factor of 0.53. The CF, as defined by Equation (1), represents the correction factor for a specific component of VOCs gas, where C_b denotes the concentration of the standard benzene gas, R_b signifies the reading of the benzene gas used for calibration, Cm represents the concentration of a particular component of VOCs gas, and Rm denotes the reading of that specific component of VOCs gas.

$$CF=\frac{R_{\mathrm{b}}{C}_{\mathrm{m}}}{C_{\mathrm{b}}{R}_{\mathrm{m}}}$$

(1)

It can be observed that different VOC gases have varying sensitivities in the PID. Certain VOC gases with high calibration coefficients exhibit low sensitivity in the PID, such as isobutanol and cyclohexane. On the other hand, some VOC gases with lower calibration coefficients demonstrate relatively higher sensitivity, such as styrene and chlorobenzene. This leads to varying detection accuracies of different gases by the PID. Hence, in practical VOC monitoring processes, the concentration of the actual monitored VOC gas needs to be multiplied by the corresponding response coefficient (RF) to obtain the respective VOC concentration, which can be determined by formula (2).

CF=ρ*RF

(2)

In which Cc represents the actual concentration of the gas to be measured, and ρ represents the concentration displayed by the PID. Table 1 lists the response coefficients for some VOC gases [12].

For example, if the PID response coefficient for isobutylene is 1, and the PID response coefficient for benzene is 0.5, it implies that when isobutylene generates a response value of 1V, benzene would produce a response value of 2V.

3.2. PID Selection in the Work

The ultraviolet lamp in the PID is a crucial component that directly determines the performance of the photoionization detector. It has significant effects on important functional indicators of the PID, including the detection limits and accuracy of VOC monitoring. Furthermore, the ultraviolet lamp directly influences key performance indicators of the PID, such as power consumption, lifespan, and size [20,21]. To ensure proper transmission, the ultraviolet lamp requires a material with specific lattice constants as the window material to facilitate the transmission of vacuum ultraviolet photons necessary for photoionization detection. Inert gas is filled inside the ultraviolet lamp to extend its lifespan and accelerate the ignition speed, thereby enhancing the output light intensity.

Currently, PIDs utilize ultraviolet lamps with three primary energy levels: 10.6 eV, 9.8 eV, and 8.4 eV [22]. The 10.6 eV ultraviolet lamp demonstrates stable performance during operation. In this research, a 10.6 eV AC-powered ultraviolet lamp was selected for the PID. It emits ultraviolet light with an energy level of 10.6 eV. The window material of this ultraviolet lamp is magnesium fluoride, enabling the detection of VOCs with ionization potentials lower than 10.6 eV, including benzene derivatives, alkenes, esters, and aldehydes.

The PID used in this study has a response time of less than 3 seconds and exhibits varying response values for different VOCs. The detection limit can be obtained by calculating the response coefficient. According to the PID manual, the maximum voltage that the photoionization detector can generate is 2.9V. If the detection limit for isobutylene by the PID is 1ppm-2000ppm, the theoretical detection limit for benzene should be 1ppm-1000ppm. VOCs with varying compositions have different detection limits, Others can be calculated using the response coefficient. The operational temperature range of the PID is -20 to 60 °C.

3.3. Existing Problem in VOCs monitoring with PID

When monitoring VOCs in soil-water-gas systems using PID, it is necessary to volatilize the VOCs from the soil-water environment for measurement. To achieve this, monitoring devices are often equipped with heating devices. However, since VOCs are present in the soil-water medium, volatilization of VOCs is accompanied by a significant amount of water. The presence of this water content increases the humidity in the PID monitoring environment. In an environment with increased humidity, the PID's photocathode surface may exhibit barriers and uneven distribution, resulting in abundant low-frequency noise in the PID signal. This noise can affect the accuracy of the PID voltage readings, thereby leading to misinterpretation of VOCs concentrations.

SVM exhibits superior generalization capability compared to traditional machine learning methods such as Artificial Neural Networks. Moreover, SVM provides a unique global optimum solution. Hence, the research investigates the utilization of SVR for monitoring VOC concentration in soil-water-air environments.

4. Analysis of VOC concentration based on traditional SVR

4.1. SVR

Assuming a given training sample set {(x₁, y₁),……,(x_n, y_n)}，x_i, y_i∈R,considering the use of a linear regression function [16,23].

F(x)=wx+b

(3)

To ensure the flatness of function F(x), it is crucial to find the smallest value of w. Therefore, the generalization of the Euclidean space is minimized. Assuming that all training data points (x_i, y_i) can be approximated by a linear function within an accuracy of ε, the problem of finding the minimum value of w can be formulated as a convex optimization problem.

$$\min \frac{1}{2}\Vert w{\Vert }^2$$

(4)

The constraint condition is as follows.

$$\left\{\begin{array}{l}{y}_i-w\cdot x_i-b\le \epsilon \hfill \\ w\cdot x_i+b-y_i\le \epsilon \hfill \end{array}\right.$$

(5)

In consideration of allowing fitting errors, a relaxation factor is introduced: ${\xi }_i\ge 0$ and ${\xi }_i^{*}\ge 0$.

Similar to maximizing the classification margin in the optimal classification hyperplane, the problem of regression estimation is transformed into the following two equations.

$$\min \frac{1}{2}\Vert w{\Vert }^2+C{\displaystyle \sum _{i=1}^n\left(x_i+x_i^{*}\right)}$$

(6)

The constraint condition is as follows

$$\left\{\begin{array}{c}{y}_i-w\cdot x_i-b\le \epsilon +{\xi }_i\\ w\cdot x_i+b-y_i\le \epsilon +{\xi }_i^{*}\\ {\xi }_i\ge 0\\ {\xi }_i^{*}\ge 0\end{array}\right.i=1,\dots n$$

(7)

The constant C > 0 is used to balance the flatness of the regression function F and the number of sample points with a bias greater than ε. Equations (6) and (7) are derived from the ε-insensitive loss function represented by the following equation (8). The function $|\xi {|}_{\epsilon }$is expressed as follows:

$$|\xi {|}_{\epsilon }:=\left\{\begin{array}{cc}0& \mathrm{if}\left|\xi \right|\le \epsilon \\ \left|\xi \right|-\epsilon & \mathrm{otherwise}\end{array}\right.$$

(8)

When dealing with a limited number of samples, the solution to SVM is commonly approached using the duality theory, which transforms it into a quadratic programming problem. To accomplish this, the Lagrange equation is established.

$$\begin{array}{c}l\left(w,\xi ,{\xi }^{\ast }\right)=\frac{1}{2}(w\cdot w)+C{\displaystyle \sum _{i=1}^n}\left({\xi }_i+{\xi }_i^{\ast }\right)-{\displaystyle \sum _{i=1}^n}{\alpha }_i\left(\epsilon +{\xi }_i+y_i-w,x_i-b\right)-\dots \\ \dots {\displaystyle \sum _{i=1}^n}{\alpha }_i\left(\epsilon +{\xi }_i^{\ast }+y_i-w,x_i-b\right)-{\displaystyle \sum _{i=1}^n}\left({\eta }_i{\xi }_i+{\eta }_i^{\ast }{\xi }_i^{\ast }\right)\end{array}$$

(9)

The partial derivatives of the parameter w, b, ${\xi }_i$, ${\xi }_i^{*}$ should all be equal to zero. Substituting this condition into equation (9) results in the dual optimization problem.

$$\min \frac{1}{2}\sum _{i,j=1}^n\left({\alpha }_i-{\alpha }_i^{\ast }\right)\left({\alpha }_j-{\alpha }_j^{\ast }\right)x_i,x_j+\sum _{i=1}^n{\alpha }_i\left(\epsilon -y_i\right)+\sum _{i=1}^n{\alpha }_i^{\ast }\left(\epsilon +y_i\right)$$

(10)

$$\mathrm{s}.\mathrm{t}\left\{\begin{array}{l}{\displaystyle \sum _{i=1}^n\left({\alpha }_i-{\alpha }_i^{*}\right)}=0\hfill \\ {\alpha }_i,{\alpha }_i^{*}\in [0,C]\hfill \end{array}\right.$$

(11)

For nonlinear regression problems, assuming that the samples X are mapped to a high-dimensional space using a nonlinear function [24], the regression problem is then transformed into minimizing the function under the constraint equations (12).

$$\frac{1}{2}\sum _{i,j=1}^n\left({\alpha }_i-{\alpha }_i^{\ast }\right)\left({\alpha }_j-{\alpha }_j^{\ast }\right)<\varphi \left(x_i\right),\varphi \left(x_j\right)>+\sum _{i=1}^n{\alpha }_i\left(\epsilon -y_i\right)+\sum _{i=1}^n{\alpha }_i^{\ast }\left(\epsilon +y_i\right)$$

(12)

As a result, the following equation is derived: $w={\displaystyle \sum ^{\underset{n}{i}}}\left({\alpha }_i-{\alpha }_i^{*}\right)\varphi \left(x_i\right)$.

Kernel function

In SVR, the kernel function is employed to simplify nonlinear approximation [25]. If the kernel function $k\left(x,x^{\prime }\right)$ satisfying $k\left(x,x^{\prime }\right)=\varphi (x),\varphi (x^{\prime })$, the following equation is formulated.

$$\min \frac{1}{2}\sum _{i,j=1}^n\left({\alpha }_i-{\alpha }_i^{\ast }\right)\left({\alpha }_j-{\alpha }_j^{\ast }\right)k\left(x,x^{\prime }\right)+\sum _{i=1}^n{\alpha }_i\left(\epsilon -y_i\right)+\sum _{i=1}^n{\alpha }_i^{\ast }\left(\epsilon +y_i\right)$$

(13)

A kernel function $k\left(x,x^{\prime }\right)$ is a symmetric positive definite function that must satisfy the Mercer condition:

$${\displaystyle \iint k\left(x,x^{\prime }\right)g(x)g(x\prime )dxdx\prime >0,g\in L2}$$

(14)

The selection and construction of kernel functions were discussed in Ref. [16]. According to it, in the work, the construction of the SVR was performed using the following Gaussian radial basis function (RBF) kernel.

$$k\left(x,x^{\prime }\right)=\exp (-\frac{\left|\right|x-x\prime {\left|\right|}^2}{2{\delta }^2})$$

(15)

4.2. Analysis of VOC concentration based on traditional SVR

Based on the characteristics of SVR in constructing regression models for small-sample data, this work utilizes SVM to build a regression model for VOC concentration data based on PID response.

Initially, a total of 84 sets of VOC concentration data were randomly arranged, with 67 sets used as the training set and 17 sets as the testing set. Each set comprised 6,001 values, where the first 6,000 values represented the PID response to VOC concentration, and the 6,001st value represented the true VOC concentration.

To eliminate the adverse effects caused by anomalous samples, both the training and testing sets were normalized. It is essential to normalize the data for SVM as it ensures feature scaling, preventing elliptical feature distributions that could hinder model training and lead to convergence issues or poor prediction accuracy.

The parameters of SVR were set, and the Gaussian radial basis kernel function was chosen as the core function for SVR. Different values of kernel function parameters and penalty factor C were experimented to observe their impact on the accuracy of SVR. Since no prior knowledge was available, the penalty factor C was initially set to 0.1 and the kernel function parameter was temporarily set to 1. Under these settings, the R² value of the SVR was 0.21. When C was set to 0.2, the R² value decreased to 0.13, and further reduced to 0.015 with C set to 0.3. The model accuracy was not satisfactory. To improve it, C was subsequently set to 1, resulting in an R² value of 0.30. Interestingly, when C was increased to 2, 3, and 5, the R² value remained at 0.30, but it slightly increased to 0.38 with C set to 4. However, no clear mathematical relationship between C and model accuracy was identified. Thus, for SVR, a penalty factor of 4 was provisionally in the work.

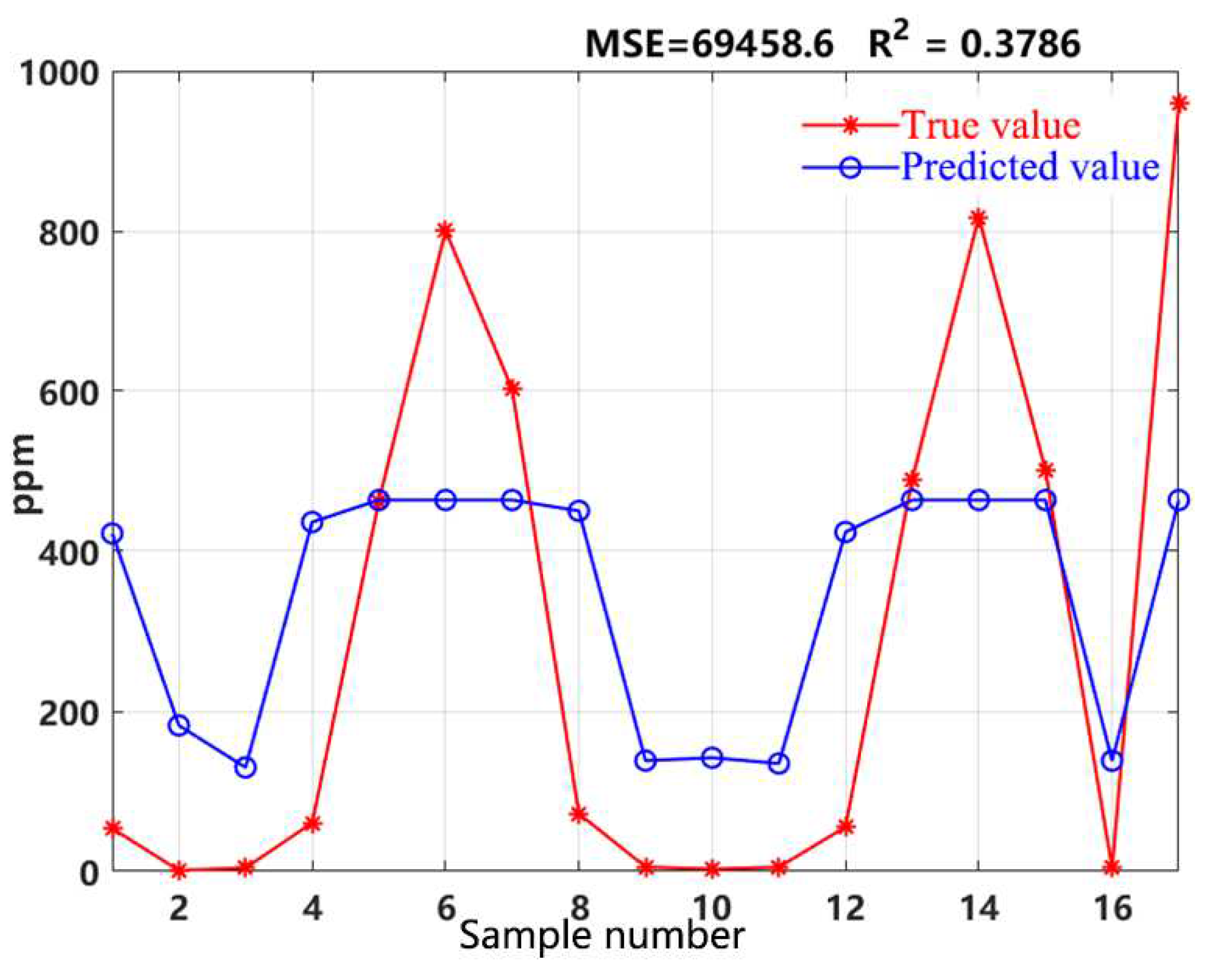
The traditional SVR was ultimately employed to construct a model using a penalty factor of C = 4 and kernel function parameter of β = 0.8 for 84 different concentrations of VOCs. The test set results of this model are shown in Figure 1. The mean squared error (MSE) of this model was 69458.6, and the coefficient of determination (R²) was 0.38. However, there was a significant discrepancy between the predicted VOCs concentrations and the actual VOCs concentrations, indicating a large prediction error.

After repeated comparisons and analysis, the main reasons for the high errors of the model are as follows. Firstly, the uncertainty in determining optimal values for the penalty factor C and kernel function parameters makes it difficult for determination of their optimal values. Secondly, the original training data used in this model contains redundancies, where relevant information is not well-identified while irrelevant information impacts the accuracy of the model construction. Hence, this work will optimize it from the two aspects.

5. Discussion

In the section, the genetic algorithm (GA) is employed to automatically select the values of the penalty factor C and the parameters of the kernel function in SVR. This approach utilizes the expansive search space and global search capability of the genetic algorithm. As a result, an optimized SVR model is built, and the concentration of VOCs is determined through signal generation using PID.

5.1. SVR Based on PCA of PID Signal Features

5.1.1. Subsubsection

Principal Component Analysis (PCA) is an effective and widely applied dimensionality reduction algorithm. It decomposes the principal components into mutually orthogonal directions, thereby effectively eliminating redundant and overlapping information among the original data. Generally, a few significant principal components can cover the majority of information regarding the signal produced by VOCs in PID response. The computational procedure of the PCA algorithm is as follows [16].

• Perform zero-mean normalization on the sample set of dimensionality d and $Oi=(O1,O2,\dots \mathrm{..},On)$

  $$Oi=Oi-\frac{1}{n}{\displaystyle \sum _{i=1}^{n}Oi}$$

  (16)
• Compute the covariance matrix ${\displaystyle \sum }$ of vector O;
• Use the method of singular value decomposition to obtain the eigenvalues and eigenvectors of the covariance matrix ${\displaystyle \sum }$.
• Take the eigenvectors corresponding to the top v eigenvalues to form a new matrix, where v should be smaller than n.
• Obtain a new low-dimensional sample set and calculate the contribution rate of each principal component and the cumulative contribution rate.

The time-domain and frequency-domain features of the PID response signals to VOCs were utilized as the original dataset for PCA to extract the principal components. The contributions of the mean, mean frequency, centroid frequency, root mean square frequency, frequency standard deviation, standard deviation, skewness, kurtosis, and maximum value are 0.4495，0.2439，0.1082，0.0787，0.0557，0.0300，0.0152，0.0080，0.0065, respectively. The cumulative contribution rate of these nine features is 0.9958. Therefore, these nine features are used to replace the original 16 features.

5.1.2. SVR after PCA of PID signal features

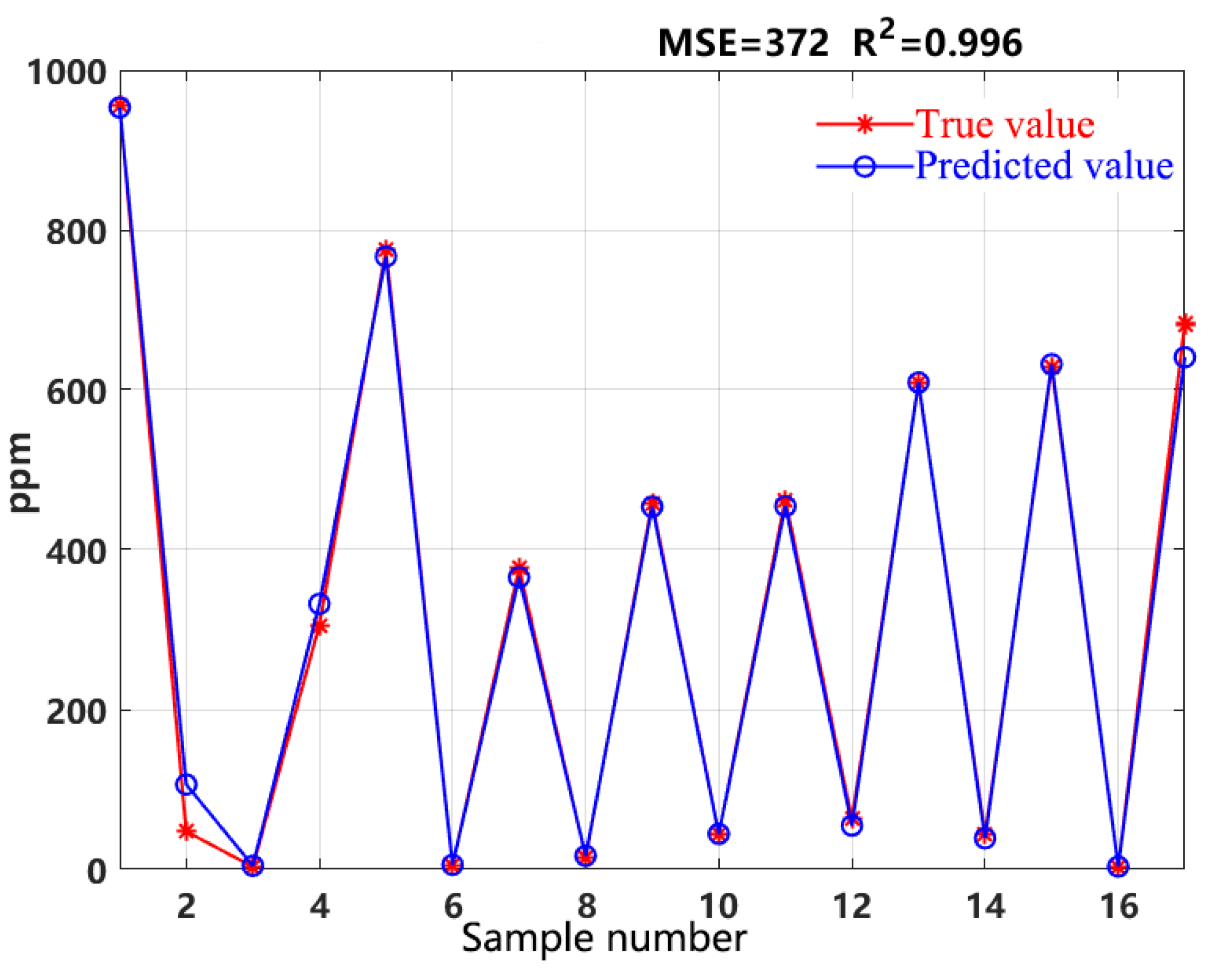
Perform PCA algorithm on the 12 time-domain features and 4 frequency-domain features of 84 different sets of VOCs concentration signals. Use the feature data obtained from principal component analysis of 67 signal sets as the training set, and the feature data obtained from principal component analysis of 17 signal sets as the testing set. Each data set consists of 10 values, where the first 9 values are the PCA-based feature parameters of the PID response signal to VOCs concentration, and the 10th value represents the true concentration of VOCs. Then, the training and testing sets are normalized, and the SVM parameters are set with the Gaussian radial basis kernel function chosen as the kernel function for SVR. Set the parameters of the radial basis kernel function to 0.8 and the penalty factor C in SVR as 4. Finally, the results of the testing set are shown in Figure 2. The model has a mean squared error of 372 and an R² value of 0.996. From the figure 2, it can be seen that the regression performance of the model is improved, but it still has some errors. Based on the analysis, these errors are attributed to suboptimal choices of the penalty factor C and kernel function parameters. To address this issue, the work employs GA algorithm to optimize them.

5.2. Proposed method based on PCA-GA-SVR

5.2.1. SVR after PCA of PID signal features

The genetic algorithm simulates the problem-solving process as a biological evolution, generating the next generation of solutions through operations such as reproduction, crossover, and mutation. It gradually eliminates solutions with low fitness values and increases solutions with high fitness values. After evolving for N generations, it is highly likely to obtain individuals with high fitness values, which represent the optimal results of the objective function [26]. The steps for selecting the optimal kernel function parameters and penalty factor using genetic algorithm are as follows.

• The dataset consisting of 84 group different concentrations of PID response to VOCs was split into an 80% training set and a 20% testing set.
• Normalize the input of the training and testing sets.
• Set the parameters of the genetic algorithm, such as the population size, iteration count, crossover probability, mutation probability, etc. Here, the chromosome dimension is set to 2, where the two numbers in the chromosome represent δ and C.
• Initialize the population by initializing each chromosome and calculating its objective function value.
• Begin iterative loop.
• Selection operator.
• Crossover and mutation operators (simulated binary crossover and polynomial mutation).
• Recalculate the objective function value for the updated chromosomes, where the objective function is the minimum mean squared error.
• Update the optimal objective of the global best chromosome.
• Proceed to the next iteration until the maximum iteration count is reached.
• Export the global best chromosome and C values, and plot the iteration curve.

5.2.2. SVR after PCA of PID signal features

When applying genetic algorithms to problem-solving, there are two encoding methods for chromosomes: binary encoding and floating-point encoding. The floating-point chromosome encoding is suitable for solving problems with a large value range, while the binary encoding is suitable for problems with a smaller value range. Since this paper applies a genetic algorithm to optimize SVM regression and involves processing small-sample data, the binary encoding method is adopted in this paper. Through the study of parameter settings for support vector machine regression in domestic and foreign research, the minimum values for penalty factor and kernel function parameters in this study were determined as 0.001. The maximum value for the penalty factor was set to 100, and the maximum value for the kernel function parameter was set to 10. Genetic algorithm operations are performed based on a population. During iterations, an initial population is provided to the genetic algorithm, and subsequent iterations are performed using this population. The population size was set to 20. Through experiments, it was determined that the convergence of the iteration curve occurs within 50 iterations, hence the iteration limit was set to 50. The population information was defined as a structure, and the population loop was initiated. Chromosomes are formed by encoding, and for each gene of the chromosome, a random number is generated between its maximum and minimum values. This represents the chromosome. The penalty factor is represented by the first number of the chromosome, and the kernel function parameters are represented by the second number of the chromosome.

GA distinguishes individuals based on the evaluation of the fitness function value for each chromosome. In GA, the larger the fitness value of a chromosome, the better the individual it represents. After initialization, the optimal objective and its corresponding chromosome are identified, followed by iterative processes, selection operators, computation of current objective fitness, calculation of the fitness proportion for each chromosome, and generation of nonzero random numbers within the population.

The cumulative fitness proportion is computed by iterating through the population, and when it exceeds the random number, the last accumulated individual is chosen as the selected individual. Select offspring of the same size as the original population, calculate the optimization variable dimension and population number, and then determine the crossover probability. Compare a random number with the crossover probability to decide whether to perform crossover. If crossover is performed, randomly select two different chromosomes. We export the two selected chromosomes and iterate through each dimension of the chromosome. The crossover operator simulates binary crossover and then limits the boundaries of the crossed individuals, replacing values exceeding the maximum with the maximum value and values below the minimum with the minimum value. Copy the resulting individuals back into the population, and then loop through the population. Generate a random number and compare it with the crossover mutation probability. If a mutation occurs, randomly select an individual for mutation preparation. Loop through each gene of the chromosome, perform polynomial mutation on the selected chromosome. Then copy the mutated individuals back into the population. Recalculate the objectives of the offspring from the crossover-mutated individuals to obtain the best and worst objectives. Then compare the current best objective with the global best objective. Replacing the worst with the historical global best increases the probability of the population iterating towards better individuals. Record the average objective and the best objective of the current generation. After the iteration, export C and δ.

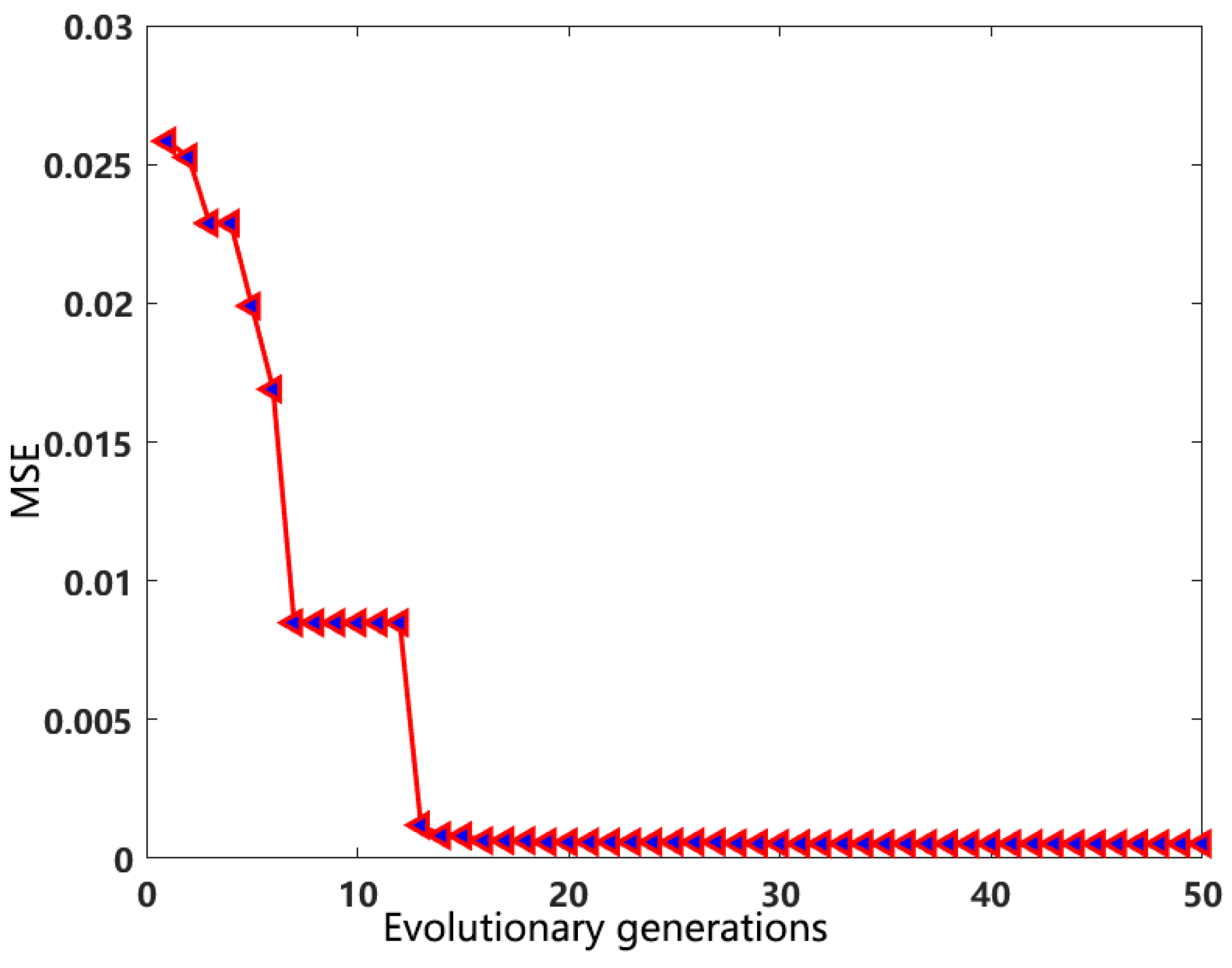
The GA optimizes the iterative curve of SVR parameters, as shown in Figure 3. The iteration curve has converged at 16 iterations, which means that the minimum value of MSE can be obtained after the 16th iteration.

5.2.3. Results

In the genetic algorithm optimized SVM regression method based on PID signal time-domain and frequency-domain with principal component analysis, 84 sets of different PID generate 9 principal component features that reflect the VOCs concentration signal. These 9 features are considered as the characteristics of the signal. Among these, 67 sets of features obtained from the principal component analysis are used as the training set, while 17 sets of features obtained from the principal component analysis are used as the test set. Each set of data consists of 10 values, where the first 9 values represent the principal component analysis parameters of the PID response signal to VOCs concentration, and the 10th value represents the true concentration of VOCs.

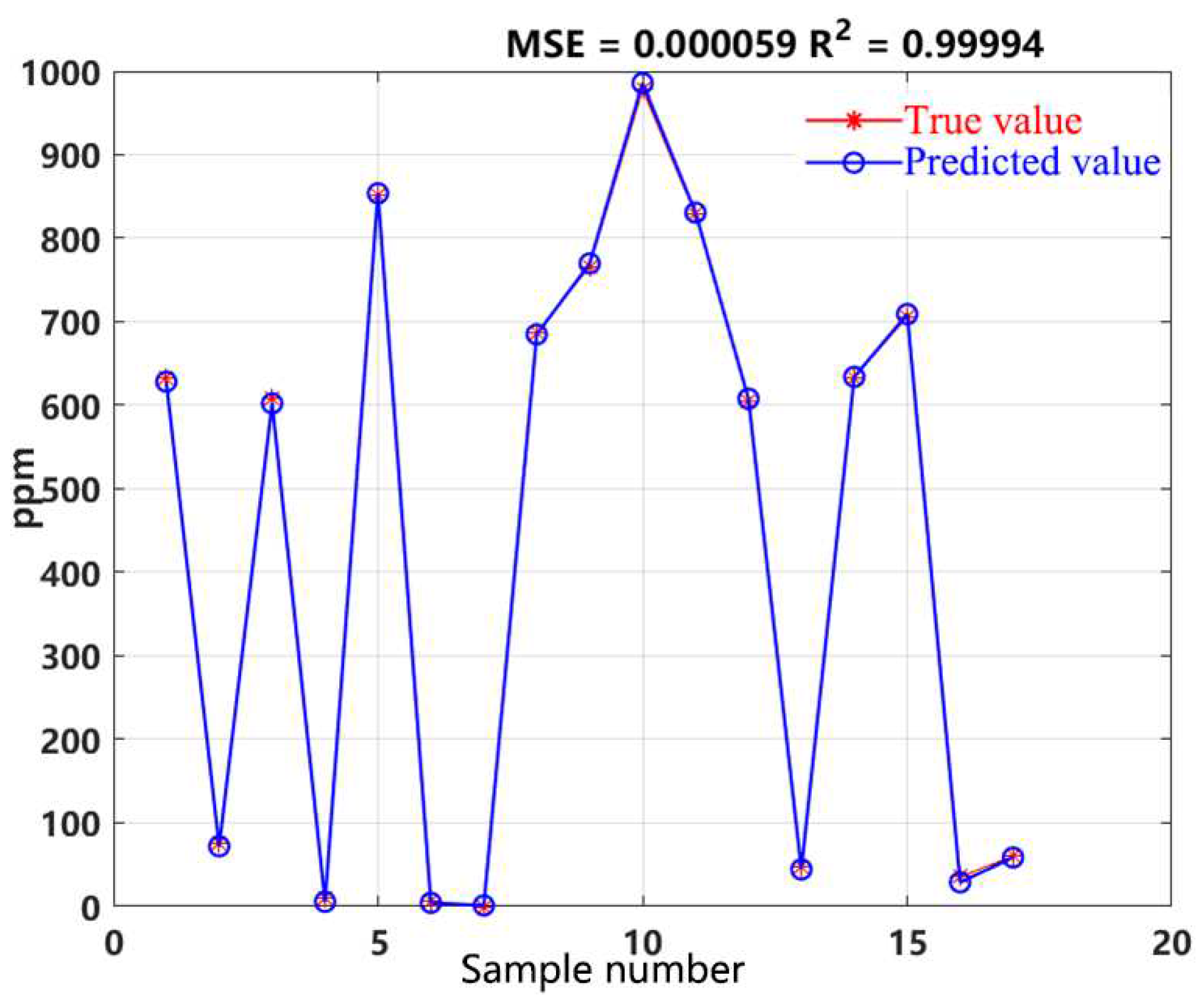
The training set and test set are normalized. Through genetic algorithm, the optimal parameters for the radial basis kernel function are found to be 0.0101, and the optimal penalty factor C is 7.8783. Based on the chosen parameters, the support vector machine regression function is derived as F(x) = w*x + b. The results of the test set are shown in Figure 4. The mean squared error of this model is 0.000059, and the R² value is 0.9999. Compared with the R² values obtained by Wang Jin, which is 99.8%, and Li Hai, which is 98.2%, 98.5%, 96.9%, etc., the proposed research method demonstrated superiority.

5.2.4. Results

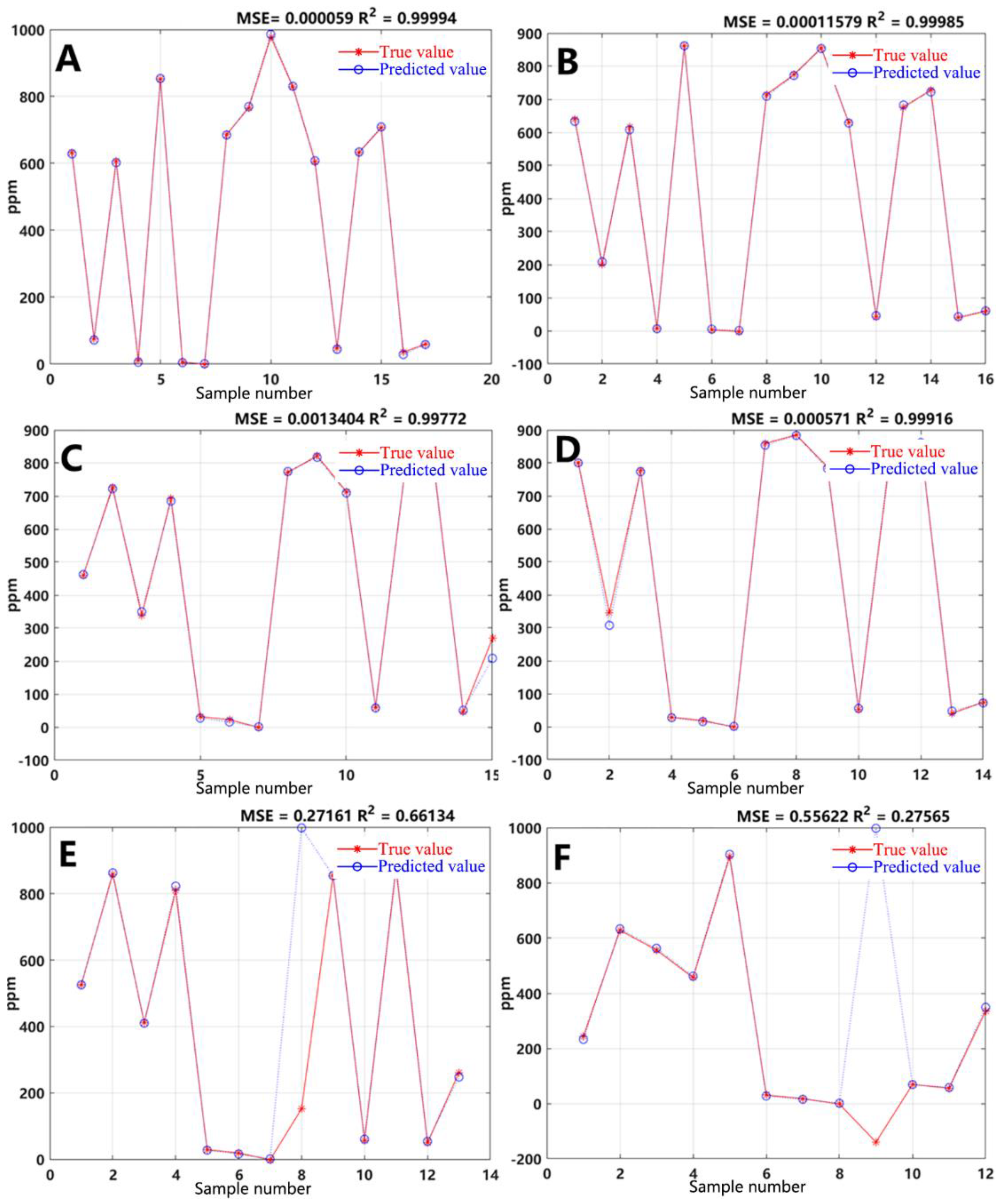
In order to verify the effectiveness of the high-accuracy models for the 84 samples in this study and to determine the minimum sample size required for constructing the PCA-GA-SVM model, the study conducted experiments based on our training data and 17 sets of testing data. By sequentially reducing 4 sets of training data and 1 set of testing data, the study aimed to find the minimum sample size for model establishment. Among them, A represents the original data; B represents the data with a reduction of 4 sets of training data and 1 set of testing data; C represents the data with a reduction of 8 sets of training data and 2 sets of testing data; D represents the data with a reduction of 12 sets of training data and 3 sets of testing data; E represents the data with a reduction of 16 sets of training data and 4 sets of testing data; F represents the data with a reduction of 20 sets of training data and 5 sets of testing data. The accuracy results of the PCA-GA-SVR are shown in Figure 5.

By reducing the number of training sets to 12 and testing sets to 3, the R² of the model can still be maintained above 0.99. However, if the number of training and testing sets is further reduced, the accuracy of the PCA-GA-SVM model will drastically decrease. Therefore, in the calculation of VOCs concentration using the PCA-GA-SVR based on signals generated by PID, it is necessary to ensure that the sample size is greater than 69. In this study, the PID response to VOCs signals consists of 84 groups, thus meeting the requirements for model establishment.

6. Conclusion

This paper addresses the issue of long computation time and low accuracy in SVR caused by redundant data information. It conducts PCA on time-frequency features to reduce the data dimensionality. Furthermore, it solves the difficulty in determining the optimal values for the penalty factor C and kernel function parameters in traditional SVR by utilizing genetic algorithms. This approach effectively improves the generalizability and robustness of the SVR. The mean squared error of signal time-frequency feature extraction - PCA-GA-SVR is 0.000059, with an R² of 0.9999.

Moreover, this paper analyses the impact of the number of experimental samples on the regression accuracy of the signal time-frequency feature extraction-PCA-GA-SVR. The model maintains a high level of accuracy when the number of samples exceeds 69 groups. It also confirms that the 84 sets of data in the study meet the sample requirements for the regression. This demonstrates the effectiveness of the PCA-GA-SVR method for VOCs monitoring in a humid environment and validates the effectiveness and robustness of the proposed method in the paper.