Prerpints.org logo
Preprint
Article

Optimized Localization of Unknown Sensors in WSN-based Smart Agriculture Systems

Altmetrics

Downloads

108

Views

54

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

15 January 2024

Posted:

16 January 2024

You are already at the latest version

Alerts
Abstract
In wireless sensor networks (WSNs) deployed in smart agriculture systems, accurately determining the locations of sensor nodes is crucial for efficient monitoring and control. However, in many cases, the exact positions of certain sensor nodes may be unknown. To address this challenge, this paper presents a novel method for localizing unknown sensor nodes in WSN-based smart agriculture systems using range measurements. The proposed method utilizes the Levenberg-Marquardt optimization algorithm to solve a nonlinear least squares problem and minimize the error in estimating the unknown node locations. By leveraging the known positions of a subset of sensor nodes and the inexact distance measurements between pairs of nodes, the localization problem is transformed into a nonlinear optimization problem. To validate the effectiveness of the approach, extensive simulations and experiments were conducted. The results demonstrate that the proposed method achieves accurate localization of the unknown sensor nodes, effectively enhancing the overall performance of the WSN-based smart agriculture system. Furthermore, the method demonstrates robustness against measurement noise and scalability for large-scale networks. The practical implications of this research extend beyond smart agriculture systems, as the proposed method can be applied to various WSN applications where precise node localization is essential.
Keywords: 
Subject: Engineering  -   Electrical and Electronic Engineering

1. Introduction

Smart agriculture, driven by advancements in technology, holds great promise for optimizing resource utilization and increasing crop productivity. One of the key technologies enabling smart agriculture is wireless sensor networks (WSNs) [1,2]. These networks comprise spatially distributed sensor nodes that collect and transmit data on environmental conditions such as soil moisture, temperature, and humidity. In the context of smart agriculture systems, WSNs play a crucial role in monitoring and controlling these environmental parameters, facilitating efficient water usage and targeted crop management [2]. WSNs offer several advantages in the domain of smart agriculture. Firstly, they enable real-time and continuous monitoring of environmental variables, allowing farmers to make informed decisions regarding agriculture schedules, fertilizer application, and pest management. This data-driven approach enhances precision agriculture practices by enabling tailored interventions at the individual plant level. Secondly, WSNs eliminate the need for manual data collection, reducing labor costs and improving operational efficiency. Additionally, WSNs provide a scalable and cost-effective solution, as they can be deployed over large agricultural areas, covering extensive farmlands [3,4,5].
Accurate localization of sensor nodes within the WSNs is crucial for achieving the desired precision and effectiveness in smart agriculture systems. Node localization refers to the process of determining the physical locations of the sensor nodes in the network. Precise node localization enables spatially aware monitoring and control, allowing for targeted actions based on the specific conditions of different areas within the agricultural field [6,7]. For example, localized data on soil moisture levels can be utilized to implement agriculture strategies that precisely deliver water where and when it is needed, minimizing wastage and optimizing plant growth.
The localization of sensor nodes in WSNs has been a subject of extensive research due to its critical role in various applications, including smart agriculture systems. Traditional localization techniques rely on Global Positioning System (GPS) receivers or manual surveying methods, which may not be feasible or cost-effective for large-scale deployments. Moreover, these methods often assume that the positions of all nodes are known or can be accurately measured. However, in practical scenarios, it is common to have a subset of nodes with known positions while the locations of other nodes remain unknown or imprecisely known [8,9].
The problem of localizing unknown nodes in WSNs has garnered significant attention due to its relevance in various applications [10,11,12,13,14,15,16]. In the context of smart agriculture systems, accurate localization of the unknown nodes allows for complete coverage and spatially aware decision-making. By estimating the coordinates of the unknown nodes based on their range measurements to anchor nodes with known positions, the overall network performance can be improved, resulting in more effective resource allocation and optimized agriculture strategies [17].
In this paper, we address the challenge of localizing unknown sensor nodes in WSN-based smart agriculture systems. We propose a novel approach that can minimize the error in node localization. The range measurements are derived from the estimated distances between pairs of sensor nodes, typically obtained from signal strength measurements. By formulating the problem as a nonlinear least squares optimization task, we propose a novel approach that leverages the Levenberg-Marquardt method to minimize the error in estimating the node locations. Through extensive simulations and experiments, we demonstrate the effectiveness and scalability of the proposed method. The results highlight its potential for practical implementation in real-world smart agriculture applications, ultimately contributing to sustainable resource management and increased crop yields.
The motivation behind this research is twofold. Firstly, accurate localization of all sensor nodes enables fine-grained monitoring and control, facilitating precise water allocation and targeted interventions in smart agriculture systems. Secondly, the localization method presented in this paper can be extended to various applications beyond smart agriculture, where the availability of accurate node positions is essential for efficient operation and decision-making. The key contributions of this work can be summarized as follows:
  • Proposing a novel approach to localize unknown nodes in WSN-based smart agriculture systems using range measurements and the Levenberg-Marquardt method.
  • Demonstrating the effectiveness of the proposed approach through extensive simulations and experiments, showcasing accurate node localization even in the presence of measurement noise.
  • Highlighting the scalability of the proposed approach for large-scale networks, showcasing its potential for practical implementation in real-world scenarios.
  • Discussing the practical implications of the proposed technique, including its relevance to precision agriculture, environmental monitoring, and other resource-constrained network applications.
The detailed abbreviations and definitions used in this paper are listed in Table 1.
The remainder of this paper is organized as follows. Section 2 provides an overview of related work on node localization techniques in WSNs. Section 3 presents the problem formulation and the mathematical framework for localizing unknown nodes using range measurements. In Section 4, the proposed Levenberg-Marquardt optimization approach is described in detail. Section 5 presents the simulation setup and experimental results, followed by a discussion in Section 6. Finally, Section 7 concludes the paper and outlines potential directions for future research.

2. Related Work

In this section, we provide an overview of the existing literature on node localization techniques in WSNs. Localization plays a crucial role in WSNs by enabling spatial awareness and precise monitoring in various applications, including smart agriculture systems. Numerous methods and algorithms have been proposed to address the node localization problem, aiming to achieve accurate and efficient localization results. We categorize the related work into three main approaches: range-based, range-free, and hybrid localization techniques [18,19,20,21,22,23,24,25,26,27].
Range-based localization techniques rely on distance or range measurements between sensor nodes to estimate their positions. These methods often utilize techniques such as Time of Arrival (TOA), Time Difference of Arrival (TDOA), or Received Signal Strength (RSS) to calculate the distances. For instance, the well-known GPS is a range-based localization technique widely used in outdoor environments. However, GPS is not suitable for obstructed environments, making it less practical for smart agriculture systems [18,19,20,21].
Range-free localization techniques, on the other hand, do not rely on distance measurements but instead exploit connectivity information between sensor nodes to estimate their positions. One common range-free approach is the Centroid algorithm, which calculates the centroid of a set of anchor nodes to estimate the position of a target node [22,23]. Another range-free method is the DV-hop algorithm, which utilizes hop-count information and communication range to estimate distances between nodes [24,25]. These range-free techniques are often computationally efficient but may sacrifice localization accuracy compared to range-based methods.
Hybrid localization techniques aim to combine the strengths of both range-based and range-free approaches to achieve more accurate and robust localization results. These methods typically leverage both distance measurements and connectivity information. For instance, the Iterative Triangulation and Trilateration (ITT) algorithm combines triangulation using distance measurements and trilateration using range-free connectivity information [26,27]. By leveraging the complementary nature of these two approaches, hybrid techniques can improve the localization accuracy and overcome limitations of individual methods.
The work in [8] proposes a regularized least squares multi-hops localization algorithm specifically designed for WSNs. The algorithm aims to improve localization accuracy by incorporating both range-based and range-free localization techniques. The authors recognize the limitations of individual localization methods and propose a hybrid approach that combines the advantages of range-based and range-free techniques. They introduce a regularization term to the least squares optimization problem, which helps to mitigate errors and uncertainties in range measurements and connectivity information. By iteratively solving the optimization problem, the algorithm estimates the positions of unknown nodes based on the observed range measurements and connectivity information from neighboring nodes. While the work in [8-9] focuses on addressing the localization challenge in WSNs, our proposed approach complements this work by specifically targeting the localization of unknown sensor nodes in WSN-based smart agriculture systems. Our method leverages range measurements and the Levenberg-Marquardt method to minimize localization errors and enable accurate positioning of the unknown nodes. Through extensive simulations and experiments, we showcase the effectiveness and scalability of our approach, contributing to the body of knowledge in localization techniques for smart agriculture applications.
While various localization techniques have been proposed for WSNs, few studies specifically address the problem of localizing unknown nodes in the context of smart agriculture systems. The localization methods developed for smart agriculture systems often rely on known anchor nodes with GPS receivers or manual surveys. However, in practical scenarios, the locations of some sensor nodes may be unknown or imprecisely known. This presents a unique challenge that requires specialized localization algorithms to estimate the positions of these unknown nodes.
In our work, we propose a novel approach that addresses the challenge of localizing unknown sensor nodes in WSN-based smart agriculture systems. By utilizing range measurements and leveraging the Levenberg-Marquardt method, our approach aims to minimize the error in estimating the node locations. Through extensive simulations and experiments, we demonstrate the effectiveness and scalability of our proposed method, showcasing its potential for practical implementation in real-world smart agriculture applications.
In the following sections, we present the problem formulation and describe the mathematical framework for our proposed localization method. We then provide details on our approach, emphasizing the utilization of the Levenberg-Marquardt method for accurate node localization.

3. Nonlinear Least Squares Problem Formulation

A Smart agriculture System based on WSNs presents a contemporary and forward-thinking approach to achieve efficient and sustainable agriculture practices. This system integrates a network of N sensors strategically positioned within the soil, plants, and environment to monitor and gather crucial data concerning soil moisture, temperature, humidity, rainfall, and other pertinent parameters. Within our WSN, the locations of K sensor nodes are known, while the exact positions of the remaining M = N - K nodes are unknown. Nonetheless, we can overcome this challenge by employing a nonlinear least squares approach to predict the locations of the unknown M nodes. The location of these sensor nodes must be determined from the distances to nearby nodes (for example, estimated from the strength of signals received from those nodes).
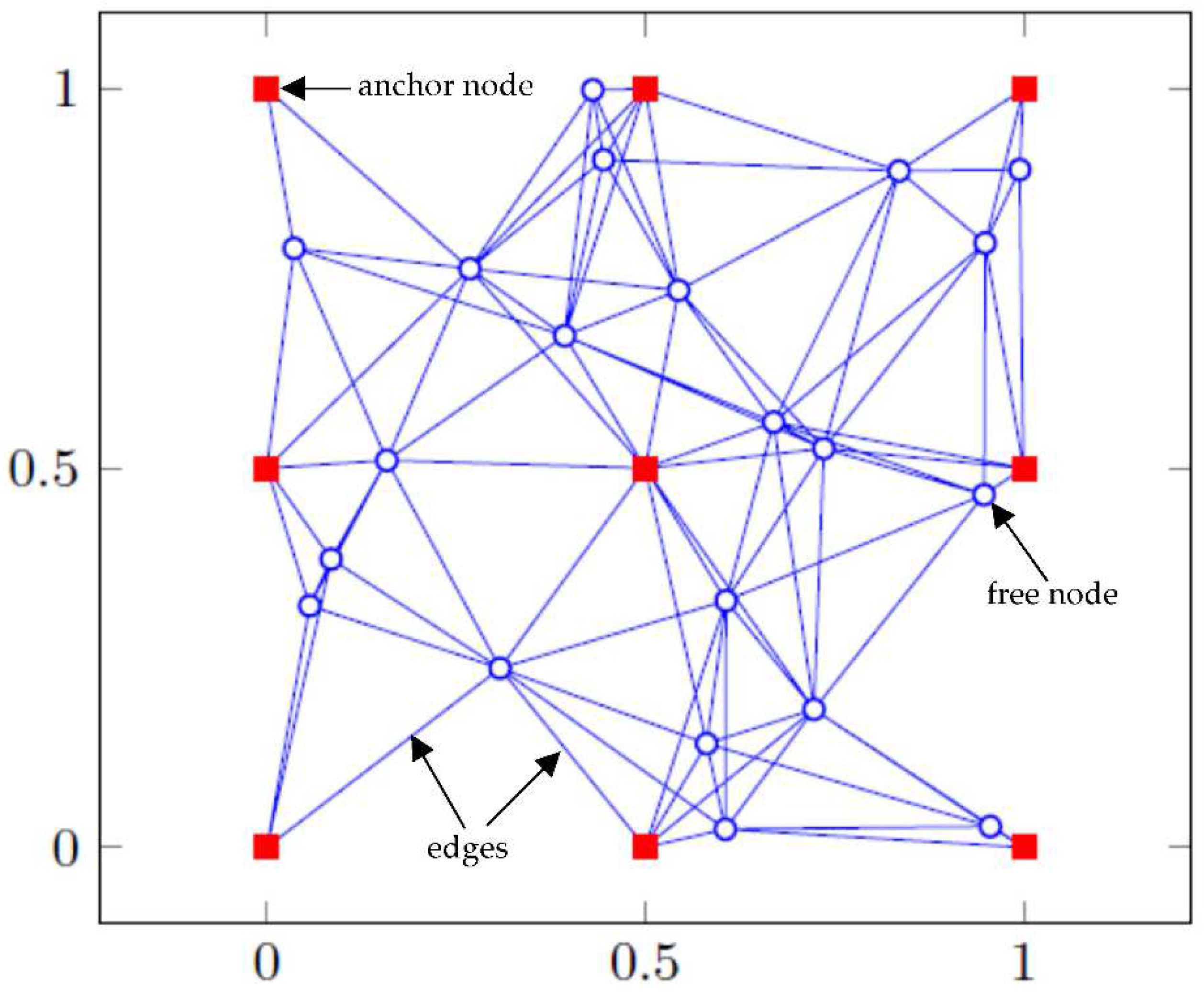
The distance measurements can be represented by an undirected graph as shown in Figure 1. In this figure, the number of vertices in the graph is N. The first M = N - K vertices represent the nodes with unknown position. We refer to these nodes as the free nodes. The last K vertices are the nodes with known position and are the anchor nodes.
The node coordinates are denoted as follows:
p 1 = x 1 , y 1 ,     p 2 = x 2 , y 2 , … ,   p N = x N , y N ,
In Eq. (1), the vectors p1, …, pN-K are the unknowns in the problem where the vectors pN-K+1, …, pN give the positions of the anchor nodes which are known.
The edges in the graph indicate the pairs of nodes for which a distance measurement is available. There are L edges, denoted by (i1, j1), …, (iL, jL). The L distance measurements are given as follows:
d l = ‖ d i l − d j l ‖ + ε l ,   l = 1 ,   2 ,   … ,   L
where εl represents the measurement error. To estimate the location of the free nodes we minimize the error function as follows:
∑ l = 1 L ‖ d i l − d j l ‖ − d l 2 =   ∑ l = 1 L x i l − x j l 2 + y i l − y j l 2 − d l 2
Equation (3) represents a nonlinear least squares problem with variables x1, x2, …, xN-K and y1, y2, …, yN-K. Thus, we can conclude that our cost function f(u(l)) is as follows:
f u l = x i l − x j l 2 + y i l − y j l 2 − d l  
In Eq. (4) we consider the points at the l-th iteration. As a result, utilizing the Levenberg-Marquardt method, we should try to minimize the following:
‖ f u l + D f u l u − u l ‖ 2 + λ l ‖ u − u l ‖ 2
where D represents the Jacobian matrix as explained in the next section and λ is the regularization parameter.
Thus, from our minimizing function in (4) and (5), we can formulate the unknown positions as a nonlinear least squares problem. The solution of this problem is computed as follows:
u ^ = u l − A T A + λ l I − 1 A T f u l ,   A = D f u l
where I represents the identity matrix and (.)T is the matrix transpose.
The algorithm will continue to run until the termination condition is satisfied which is:
∇ g u l = 2 A T f u l   ≤ 10 − 5

4. Levenberg-Marquardt Optimization Approach

A crucial step in executing the Levenberg-Marquardt method involves the computation of the Jacobian matrix. Recall the definition of the Jacobian matrix as follows:
D f z = d f 1 d m 1 z d f 1 d m 2 z d f 2 d m 1 z d f 2 d m 2 z ⋯ ⋯ d f 1 d m n z d f 2 d m n z ⋮ ⋮ ⋱ ⋮ d f n d m 1 z d f n d m 2 z ⋯ d f n d m n z
In the considered WSN, m1, m2, …, mn in (8) refer to x1, x2, …, xN-K and y1, y2, …, yN-K, with function f(z) defined in (4). It is clear that the matrix Df(z) ∈ 𝕀ℝLx2(N−K) , as we have a row for each of the L edges, and we have 2(N - K) variables.
Regarding the actual matrix entries themselves, there are four possible derivatives we could require in each row, with the rest of the entries in that row being 0. The four possible derivative expressions are listed as in Eq. (9):
d f u l d x i l d f u l d x j l d f u l d y i l d f u l d y j l =   x i l − x j l x i l − x j l 2 + y i l − y j l 2 − x i l − x j l x i l − x j l 2 + y i l − y j l 2 y i l − y j l x i l − x j l 2 + y i l − y j l 2 − y i l − y j l x i l − x j l 2 + y i l − y j l 2
However, we can clearly notice that we have four possible conditions as follows: both nodes are anchors, one of the two nodes are anchors (either the first node in the edge or the second node), and neither of the two nodes are anchors. In the following we consider each condition separately.
  • If the i-th edge contains nodes that are both anchors, the Jacobian matrix row is all zeros, since both variables are known (assuming points at the l-th iteration):
    ∇ f i u l T = 0     0     ⋯     0
  • If the i-th edge contains one anchor node, the Jacobian matrix row will contain the derivatives with respect to the unknown node, with the rest of the entries in that row being 0 (assuming points at the l-th iteration), node 2 as anchor:
    ∇ f i u l T = 0      0      ⋯      0      d f u l d x i l      0      ⋯      0 d f u l d y i l      0      ⋯      0
  • Node 1 as anchor:
    ∇ f i u l T = 0      0      ⋯      0      d f u l d x j l      0      ⋯      0      d f u l d y j l      0      ⋯      0
  • Our last of the four conditions occurs if the i-th edge contains no anchor nodes, in which our Jacobian matrix row will contain the derivatives with respect to both of the unknown nodes (i.e. a potential of four non-zero elements in the row), all assuming points at the l-th iteration:
    ∇ f i u l T = 0      0      ⋯      0      d f u l d x j l      0      ⋯      0      d f u l d y j l      0      ⋯      0
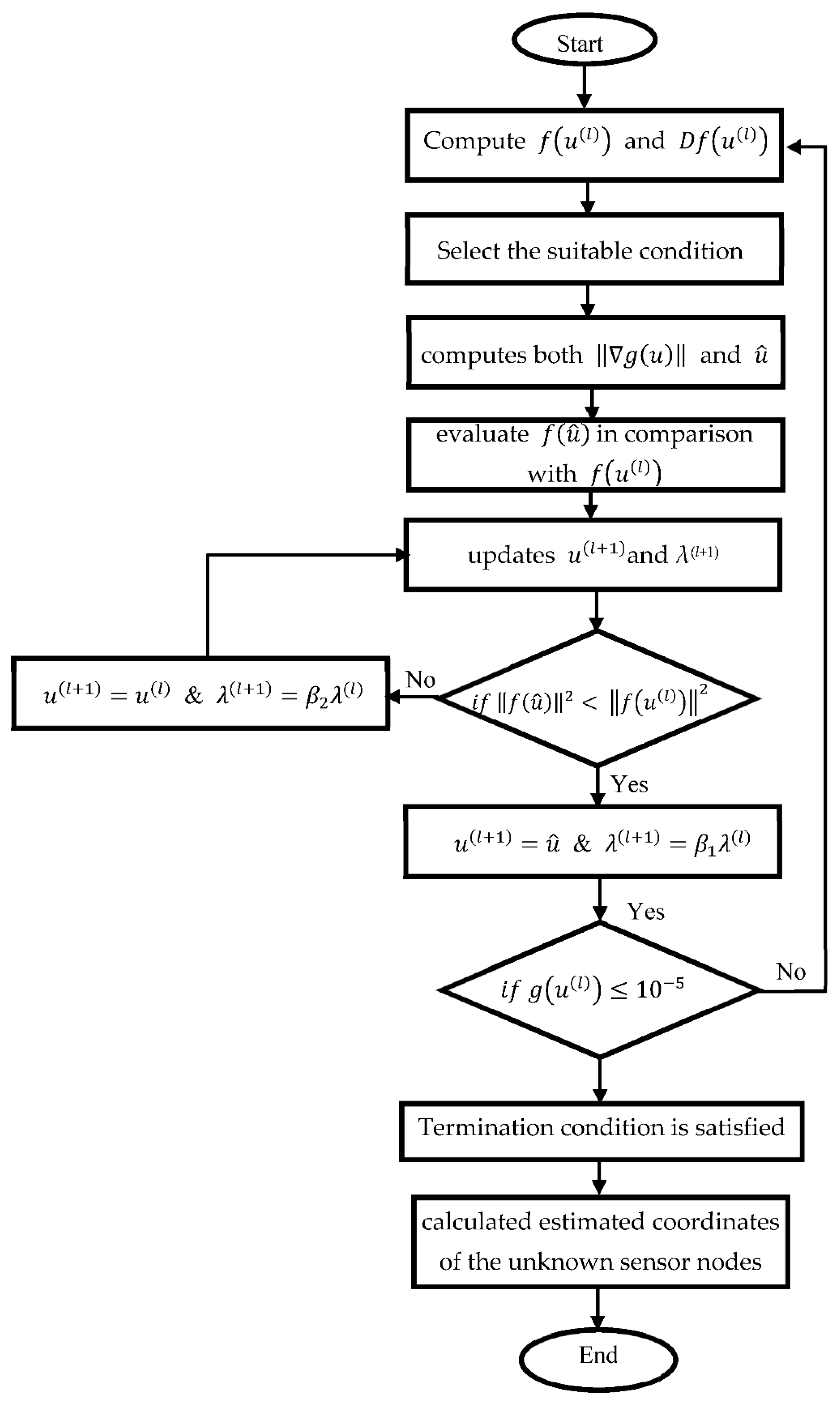
The Levenberg-Marquardt algorithm steps can be summarized as follows:
Step 1: In each iteration of the algorithm, we first compute f u l , and then the Jacobian matrix D f u l   row by row, with each row being evaluated for one of the four conditions described above.
Step 2: Next, within the iteration, the code computes both ∇ g u and u ^ , in order to evaluate f u ^   in comparison with f u l . Depending on this calculation, the algorithm updates u(l+1) and λ(l+1) as follows:
u l + 1 = u ^ ,       i f   f u ^ 2 <   f u l 2 u l ,   o t h e r w i s e                                                    
λ l + 1 = β 1 λ l       i f   f u ^ 2 < f u l 2 β 2 λ l ,     o t h e r w i s e                                                    
Step 3: If ∇ g u l = 2 A T f u l   ≤ 10 − 5 , then the algorithm will terminate out of the loop and return the calculated estimated coordinates of the unknown sensor nodes.
Step 4: If the condition in step 3 not satisfied go to step 1. The following flow chart summarizes the proposed algorithm steps and indicated by Figure 2.

5. Simulation Results and Discussion

In this section, MATLAB programming is used to execute the Levenberg-Marquardt algorithm to predict the estimated coordinates of the unknown sensor nodes in the considered WSN. The algorithm will continue to run until the termination condition, ∇ g u l ≤ 10 − 5 , is satisfied.
The first input argument N is the number of nodes in the network, and it varies according to considered network scale. This includes K = 9 anchor nodes, positioned as in Figure 1. The N - 9 free nodes are placed randomly in a normalized square [0, 1] x [0, 1]. Two nodes are connected by an edge if their distance is less than or equal to normalized R. Figure 1 presents an example with N = 30 and R = 0.4. The first output argument E is an Lx2 array, specifying the L edges. The two entries of row l are il and jl, the nodes connected by edge l. The output argument is an N x 2 array with the coordinates of the N nodes. Typical values of β1 and β2 are β1 = 0.8 and β2 = 2.

5.1. Effect of Network Scale

In this subsection we study the effects of network scale on the performance of proposed approach.
  • Small Scale Network
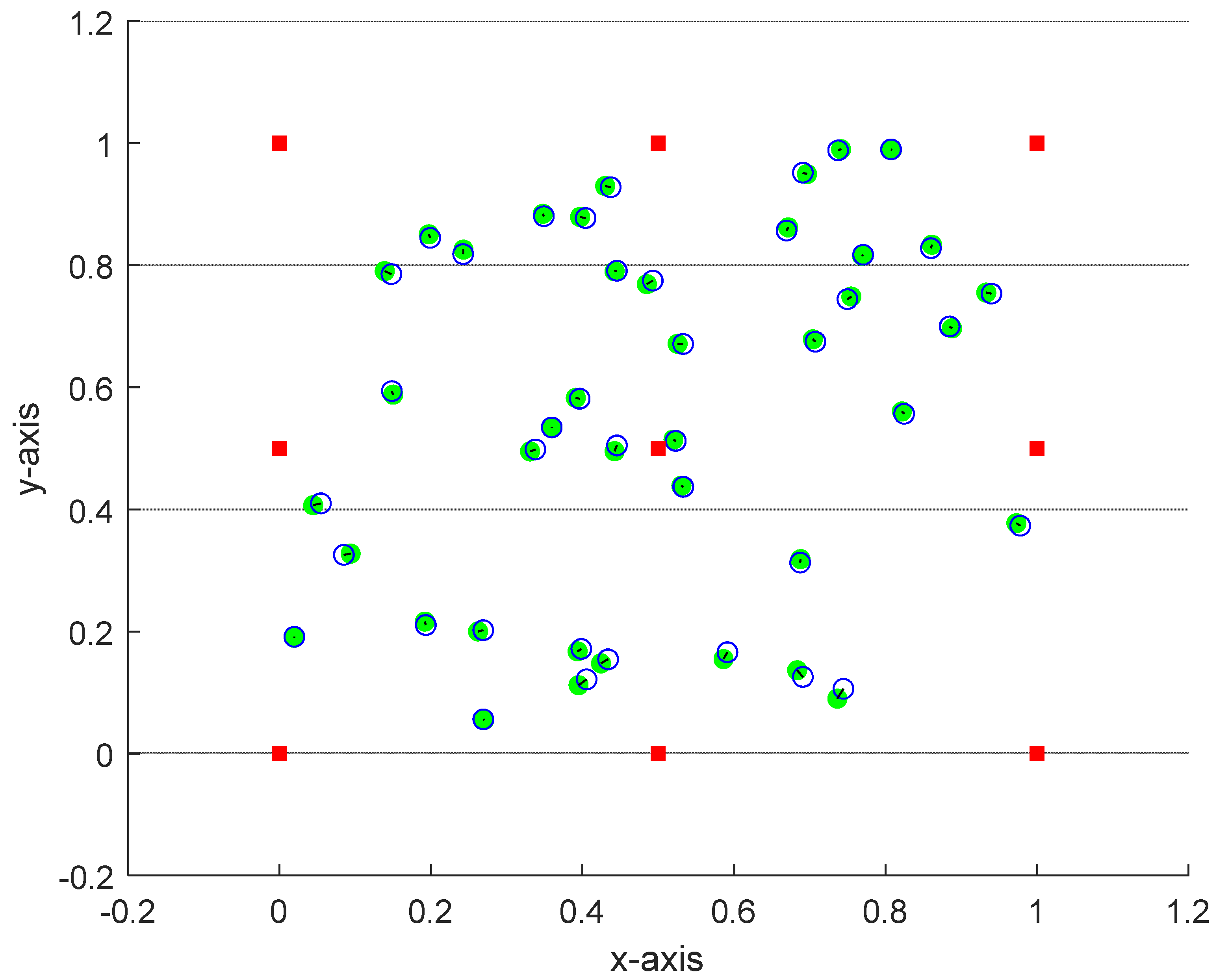
We consider a small-scale network with N = 50 nodes, 9 of them are anchor nodes with known and fixed location as follows: [(0, 0), (0.5, 0), (1, 0), (0, 0.5), (0.5, 0.5), (1, 0.5), (0, 1), (0.5, 1), (1, 1)]. The free nodes (41) are placed randomly in the square [0, 1] x [0, 1]. Figure 3 presents the estimation of the sensor coordinate using the proposed approach. The open circles (blue) are the exact positions while the filled circles (green) are the estimated positions. This figure indicates the accuracy of the proposed approach in estimating the unknown location of the free nodes.
B.
Medium Scale Network
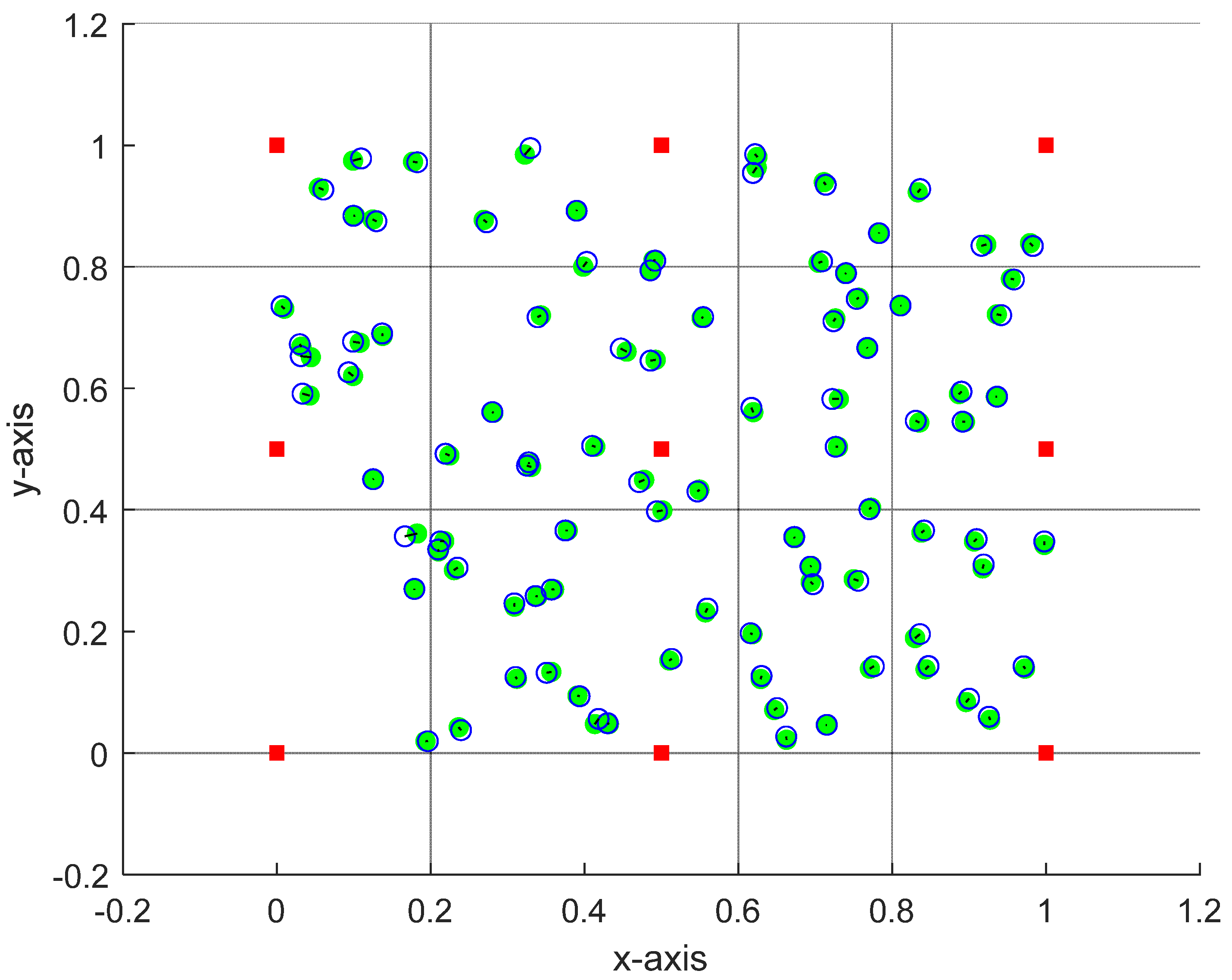
In this part we check the accuracy of the proposed approach when increasing the number of unknown free nodes to 91 nodes, i.e., we consider N =100 nodes. For fair comparison we use 9 anchor nodes at the same location as small-scale case. Figure 4 shows the estimated positions versus the exact positions considering medium scale network. This figure indicates the accuracy of the proposed approach even for large free nodes.
C.
Large Scale Network
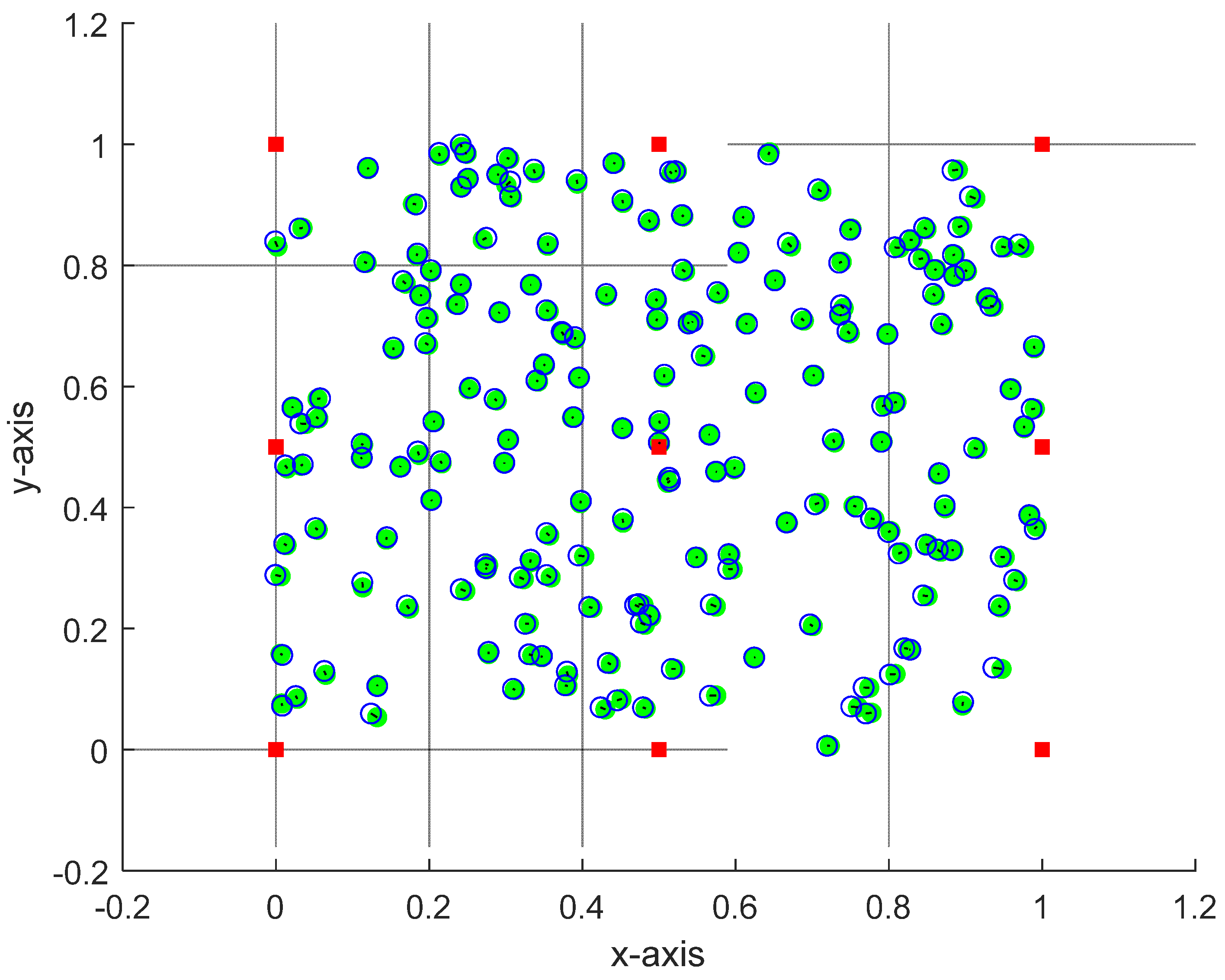
Now we consider large scale network with N = 200 nodes as shown in Figure 5. The obtained result in this figure ensures the ability of the proposed approach to accurately estimate the position of the free nodes even for large scale network.
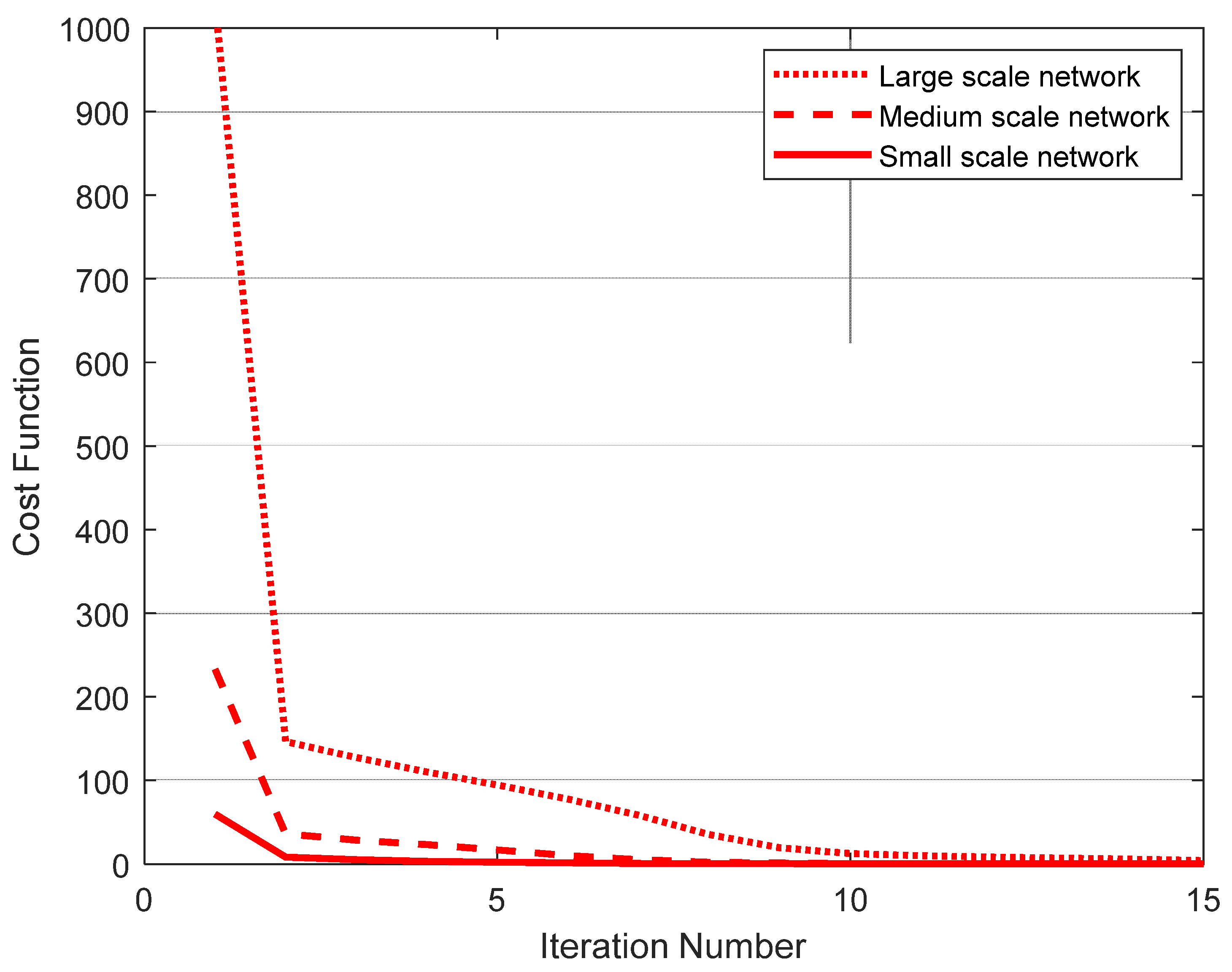
Figure 6 presents the cost function versus number of iterations for the 3 network scenarios. As expected, the large-scale network requires the largest cost function compared to the other networks.

5.2. Effect of Changing the Anchor Nodes Locations

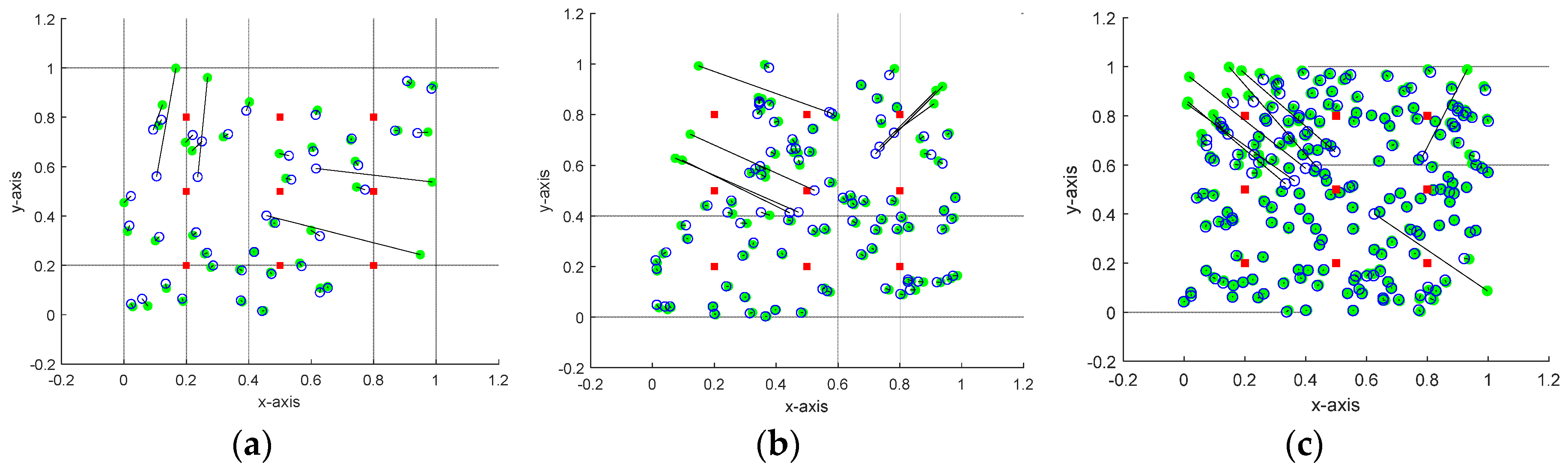
In this subsection we study the effect of changing the position of anchor nodes on the accuracy of position estimation using the proposed approach. The 9 anchor nodes new location is located around network center as follows: [(0.2, 0.2), (0.5, 0.2), (0.8, 0.2), (0.2, 0.5), (0.5, 0.5), (0.8, 0.5), (0.2, 0.8), (0.5, 0.8), (0.8, 0.8)].
Figure 7 presents the least squares estimate of the sensor coordinate using the three network scenarios considered above, i.e., N = 50 (a), 100 (b), and 200 (c). This figure indicates that the accuracy of the proposed approach is affected by changing the anchor node’s location. However, the reduction in estimation accuracy is small which ensures the robustness of the proposed approach. The anchor node’s new location is around the network center therefore, its accuracy become less than that at network boundaries. This figure also shows that as the number of free nodes increase from 50 to 200, the proposed approach estimation accuracy decreases.

5.3. Performance Comparison

In this subsection we compare the performance of the proposed approach with other localization algorithms presented in literature such as improvement of DV-Hop algorithm [8] and SDR+LM algorithm [9]. For fair comparison, we use the average localization error presented in [8] and given as:
A L E = ∑ i = 1 N − K x ^ i − x i 2 + y ^ i − y i 2 N − K
where N-K represents the number of free nodes (unknown position nodes), x i ,   x y i   and   x ^ i , y ^ i are the exact and the estimated locations, respectively of node i.
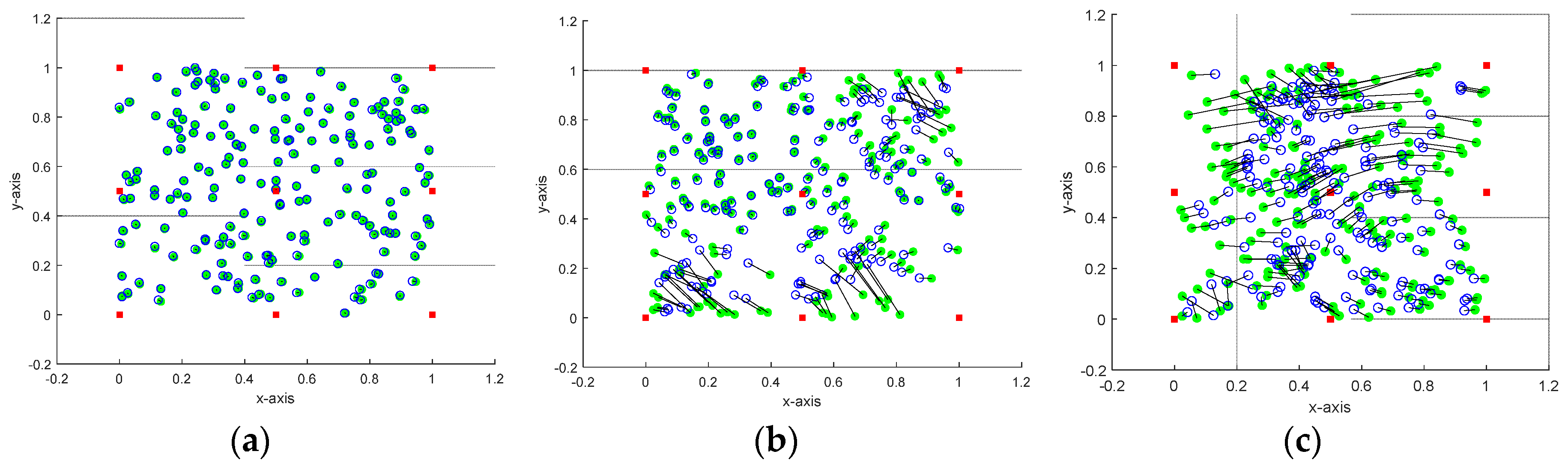
Figure 8 presents a comparison between the proposed approach and the algorithms presented in [8] and [9] using the above-mentioned parameters and the large-scale network case. As explained above, the open circles (blue) are the exact positions while the filled circles (green) are the estimated positions, and the black straight line that connect between the two circle types represents the positioning error. This figure indicates that the proposed approach achieves the lowest localization error when compared to the other algorithms.
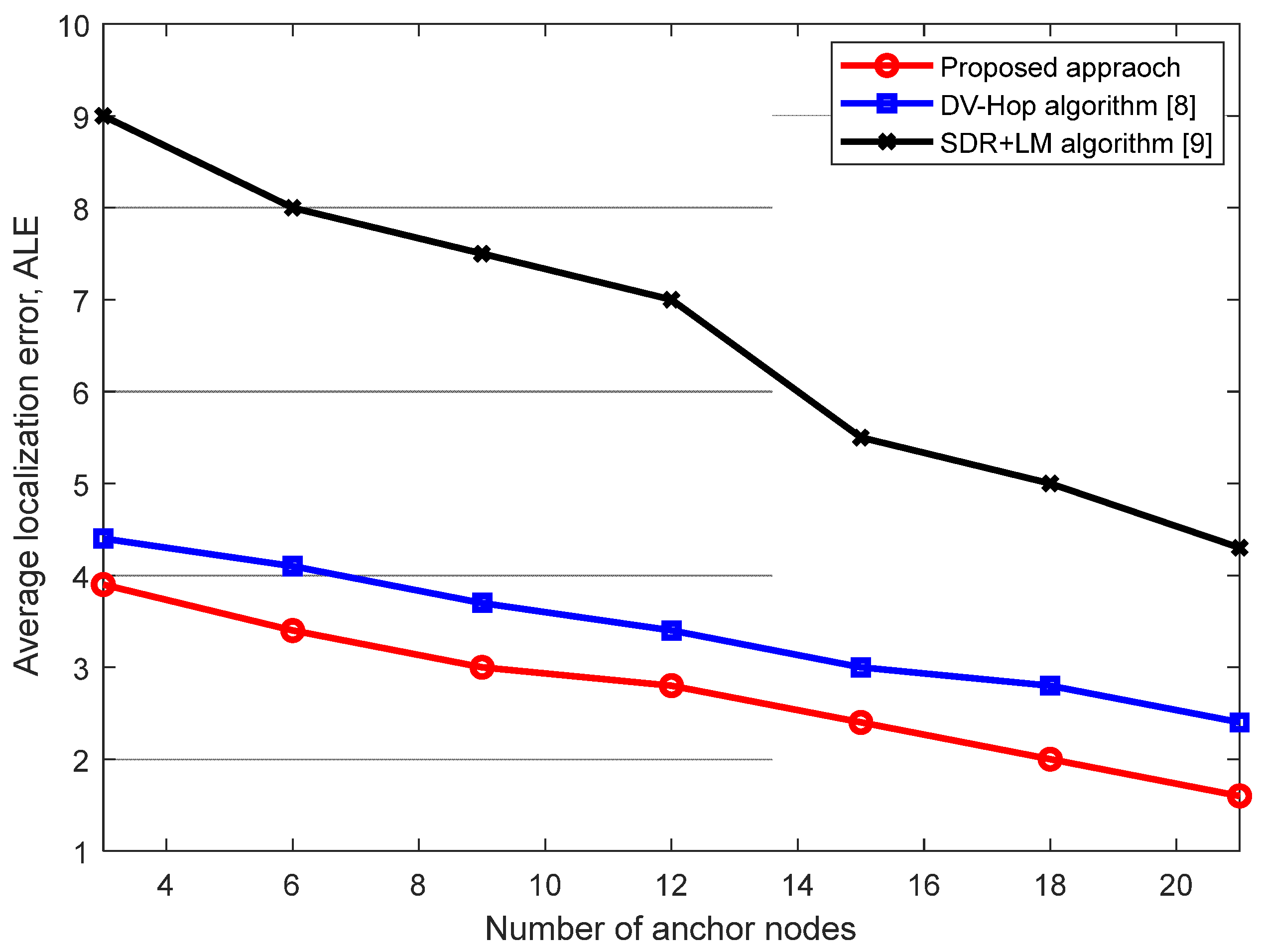
In the following we study the effect of changing the number of anchor nodes on the accuracy of location estimation of the proposed approach. We consider the case of N = 200 nodes and R = 0.4. Figure 9 presents the ALE versus number of anchor nodes for the proposed approach and the cited above localization algorithms [8] and [9].
The depicted figure illustrates a clear trend wherein the ALE diminishes with an increase in the number of anchor nodes. This observation can be attributed to the deliberate augmentation of anchor nodes within the network, while keeping the total number of nodes constant. This augmentation is intended to reduce the hop count between the anchors and unknown nodes. As a result, the estimated distance between an anchor and an unknown node more accurately corresponds to the actual distance, leading to a decrease in the average positioning error. Additionally, the figure demonstrates that the proposed algorithm yields a lower localization error compared to all other algorithms considered in the comparison. At number of anchor nodes of 9, the proposed approach achieves 19% and 58% improvement in estimation accuracy when compared to the cited above localization algorithms [8] and [9].

6. Conclusions

This paper addressed the challenge of localizing unknown sensor nodes in WSN-based smart agriculture systems, highlighting the importance of accurate node localization for efficient monitoring and control. A novel approach was proposed, utilizing range measurements and the Levenberg-Marquardt optimization algorithm to solve a nonlinear least squares problem and minimize the error in estimating the unknown node locations. The obtained results demonstrated the effectiveness and accuracy of the proposed approach in estimating the positions of the unknown sensor nodes. The simulations and experiments conducted for small-scale, medium-scale, and large-scale network scenarios showcased the robustness and scalability of the approach. Even with an increase in the number of unknown nodes, the proposed approach consistently achieved accurate localization. Comparative analysis against other localization algorithms highlighted the superior performance of the proposed approach, with significant improvements in estimation accuracy. Furthermore, the study investigated the impact of changing the position of anchor nodes on the estimation accuracy. While there was a slight reduction in accuracy, the proposed approach remained robust and effective in localizing the unknown nodes, emphasizing its practical viability. The obtained numerical results demonstrate that the proposed approach achieves a significant improvement in estimation accuracy, outperforming the compared localization algorithms by 58%.
Future research includes exploring the influence of environmental factors on localization accuracy, integrating additional sensing modalities for enhanced precision, investigating scalability for larger networks, and developing energy-efficient algorithms to prolong network lifespan.

Funding

This research was funded by Deputyship for Research& Innovation, Ministry of Education in Saudi Arabia, grant number ISP23-56.

Data Availability Statement

No Data Availability Statements are available.

Acknowledgments

The authors extend their appreciation to the Deputyship for Research& Innovation, Ministry of Education in Saudi Arabia for funding this research work through the project number ISP23-56.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. R. Deepa, M. Sankar, R. R, C. Sankari, Venkatasubramanian and R. Kalaivani, "IoT based Energy Efficient using Wireless Sensor Network Application to Smart Agriculture," 2023 International Conference on Intelligent Data Communication Technologies and Internet of Things (IDCIoT), Bengaluru, India, 2023, pp. 90-95. [CrossRef]
  2. Hassan, E.S. Energy-Efficient Resource Allocation Algorithm for CR-WSN-Based Smart Irrigation System under Realistic Scenarios. Agriculture 2023, 13, 1149. [CrossRef]
  3. N. Shanmugasundaram, G. Santhip Kumar, S. Sankaralingam, S. Vishal and N. Kamaleswaran, "Smart Agriculture Using Modern Technologies," 2023 9th International Conference on Advanced Computing and Communication Systems (ICACCS), Coimbatore, India, 2023, pp. 2025-2030. [CrossRef]
  4. Pagano, D. Croce, I. Tinnirello and G. Vitale, "A Survey on LoRa for Smart Agriculture: Current Trends and Future Perspectives," in IEEE Internet of Things Journal, vol. 10, no. 4, pp. 3664-3679, 15 Feb.15, 2023. [CrossRef]
  5. F. K. Shaikh, S. Karim, S. Zeadally and J. Nebhen, "Recent Trends in Internet-of-Things-Enabled Sensor Technologies for Smart Agriculture," in IEEE Internet of Things Journal, vol. 9, no. 23, pp. 23583-23598, 1 Dec.1, 2022. [CrossRef]
  6. Yaping Zhu, Feng Yan, Shengjie Zhao, Song Xing, Lianfeng Shen, “On improving the cooperative localization performance for IoT WSNs,” Ad Hoc Networks, vol. 118, 2021. [CrossRef]
  7. Prabhjot Singh, Parulpreet Singh, Nitin Mittal, Urvinder Singh, Supreet Singh, “An optimum localization approach using hybrid TSNMRA in 2D WSNs,” Computer Networks, vol. 226, 2023. [CrossRef]
  8. H. Liouane, S. Messous, O. Cheikhrouhou, M. Baz and H. Hamam, "Regularized Least Square Multi-Hops Localization Algorithm for Wireless Sensor Networks," in IEEE Access, vol. 9, pp. 136406-136418, 2021. [CrossRef]
  9. D. E. Badawy, V. Larsson, M. Pollefeys and I. Dokmanić, "Localizing Unsynchronized Sensors With Unknown Sources," in IEEE Transactions on Signal Processing, vol. 71, pp. 641-654, 2023. [CrossRef]
  10. X. Zhao, X. Zhang, Z. Sun and P. Wang, "New Wireless Sensor Network Localization Algorithm for Outdoor Adventure," in IEEE Access, vol. 6, pp. 13191-13199, 2018. [CrossRef]
  11. Khan AU, Khan ME, Hasan M, Zakri W, Alhazmi W, Islam T. An Efficient Wireless Sensor Network Based on the ESP-MESH Protocol for Indoor and Outdoor Air Quality Monitoring. Sustainability. 2022; 14(24):16630. [CrossRef]
  12. Alam S, Shuaib M, Ahmad S, Jayakody DNK, Muthanna A, Bharany S, Elgendy IA. Blockchain-Based Solutions Supporting Reliable Healthcare for Fog Computing and Internet of Medical Things (IoMT) Integration. Sustainability. 2022; 14(22):15312. [CrossRef]
  13. Ali Hakami N, Hosni Mahmoud HA, AlArfaj AA. An Intelligent Tracking System for Moving Objects in Dynamic Environments. Actuators. 2022; 11(10):274. [CrossRef]
  14. Alharbi F, Zakariah M, Alshahrani R, Albakri A, Viriyasitavat W, Alghamdi AA. Intelligent Transportation Using Wireless Sensor Networks Blockchain and License Plate Recognition. Sensors. 2023; 23(5):2670. [CrossRef]
  15. Bharany S, Sharma S, Frnda J, Shuaib M, Khalid MI, Hussain S, Iqbal J, Ullah SS. Wildfire Monitoring Based on Energy Efficient Clustering Approach for FANETS. Drones. 2022; 6(8):193. [CrossRef]
  16. Prashar D, Rashid M, Siddiqui ST, Kumar D, Nagpal A, AlGhamdi AS, Alshamrani SS. SDSWSN—A Secure Approach for a Hop-Based Localization Algorithm Using a Digital Signature in the Wireless Sensor Network. Electronics. 2021; 10(24):3074. [CrossRef]
  17. V. Annepu et al., "Review on Unmanned Aerial Vehicle Assisted Sensor Node Localization in Wireless Networks: Soft Computing Approaches," in IEEE Access, vol. 10, pp. 132875-132894, 2022. [CrossRef]
  18. S. Sinha and R. P. M, "Range based improved localization scheme in densely populated wireless sensor network," 2021 6th International Conference on Communication and Electronics Systems (ICCES), Coimbatre, India, 2021, pp. 792-797. [CrossRef]
  19. B. K. Madagouda and R. Sumathi, "Range Based Localization using Least Square Method in WSN," 2022 10th International Conference on Emerging Trends in Engineering and Technology - Signal and Information Processing (ICETET-SIP-22), Nagpur, India, 2022, pp. 1-4. [CrossRef]
  20. M. K. Kumar and V. K. Prasad, "TASLT: Triangular Area Segmentation based Localization Technique for Wireless Sensor Networks using AoA and RSSI Measures – A New Approach," 2021 IEEE 18th International Conference on Mobile Ad Hoc and Smart Systems (MASS), Denver, CO, USA, 2021, pp. 585-590. [CrossRef]
  21. Y. Venkata Lakshmi, P. Singh, M. Abouhawwash, S. Mahajan, A. K. Pandit and A. B. Ahmed, "Improved Chan Algorithm Based Optimum UWB Sensor Node Localization Using Hybrid Particle Swarm Optimization," in IEEE Access, vol. 10, pp. 32546-32565, 2022. [CrossRef]
  22. L. Hai, Z. Yang, Z. Cao and M. Yaug, "An improved weighted centroid localization algorithm based on Zigbee," 2022 5th International Conference on Advanced Electronic Materials, Computers and Software Engineering (AEMCSE), Wuhan, China, 2022, pp. 634-637. [CrossRef]
  23. V. Gupta, A. Gupta and M. Kaur, "Performance Investigation of Centroid Based Localization Algorithm and Comparison of Improvement Achieved in Localization Error using Optimization Techniques in WSN," 2021 2nd International Conference on Computational Methods in Science & Technology (ICCMST), Mohali, India, 2021, pp. 147-151. [CrossRef]
  24. G. Liu, Z. Qian and X. Wang, "An improved DV-Hop localization algorithm based on hop distances correction," in China Communications, vol. 16, no. 6, pp. 200-214, June 2019. [CrossRef]
  25. B. Chen, X. Guo, Y. Huang and M. Yang, "Improved DV-Hop Node location Optimization Algorithm Based on Adaptive Particle Swarm," 2021 2nd International Conference on Artificial Intelligence and Computer Engineering (ICAICE), Hangzhou, China, 2021, pp. 11-17. [CrossRef]
  26. S. Safavi, U. A. Khan, S. Kar and J. M. F. Moura, "Distributed Localization: A Linear Theory," in Proceedings of the IEEE, vol. 106, no. 7, pp. 1204-1223, July 2018. [CrossRef]
  27. Bochem and H. Zhang, "Robustness Enhanced Sensor Assisted Monte Carlo Localization for Wireless Sensor Networks and the Internet of Things," in IEEE Access, vol. 10, pp. 33408-33420, 2022. [CrossRef]
Preprints 96430 g001
Figure 1. Network model example with 9 anchor nodes (squares), 21 free nodes (circles) and 98 edges.
Figure 1. Network model example with 9 anchor nodes (squares), 21 free nodes (circles) and 98 edges.
Preprints 96430 g001
Preprints 96430 g002
Figure 2. Flow chart of the proposed algorithm.
Figure 2. Flow chart of the proposed algorithm.
Preprints 96430 g002
Preprints 96430 g003
Figure 3. Least squares estimate of the sensor coordinate using N = 50.
Figure 3. Least squares estimate of the sensor coordinate using N = 50.
Preprints 96430 g003
Preprints 96430 g004
Figure 4. Least squares estimate of the sensor coordinate using N = 100.
Figure 4. Least squares estimate of the sensor coordinate using N = 100.
Preprints 96430 g004
Preprints 96430 g005
Figure 5. Least squares estimate of the sensor coordinate using N = 200.
Figure 5. Least squares estimate of the sensor coordinate using N = 200.
Preprints 96430 g005
Preprints 96430 g006
Figure 6. Cost function versus number of iterations for 3 network scenarios.
Figure 6. Cost function versus number of iterations for 3 network scenarios.
Preprints 96430 g006
Preprints 96430 g007
Figure 7. Effect of changing the position of anchor nodes on the accuracy of the proposed approach using N = 50, 100, and 200.
Figure 7. Effect of changing the position of anchor nodes on the accuracy of the proposed approach using N = 50, 100, and 200.
Preprints 96430 g007
Preprints 96430 g008
Figure 8. Performance comparison between the proposed approach (a), DV-Hop algorithm [8] (b) and SDR+LM algorithm [9] (c).
Figure 8. Performance comparison between the proposed approach (a), DV-Hop algorithm [8] (b) and SDR+LM algorithm [9] (c).
Preprints 96430 g008
Preprints 96430 g009
Figure 9. ALE versus number of anchor nodes for the proposed approach and the localization algorithms [8] and [9].
Figure 9. ALE versus number of anchor nodes for the proposed approach and the localization algorithms [8] and [9].
Preprints 96430 g009
Table 1. List of abbreviation.
Table 1. List of abbreviation.
Abbreviation Definition
WSNs Wireless Sensor Networks
GPS Global Positioning System
TOA Time of Arrival
TDOA Time Difference of Arrival
RSS Received Signal Strength
ITT Iterative Triangulation and Trilateration
DV-Hop Distance Vector-Hop algorithm
LM Levenberg-Marquardt algorithm
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated