Value-at-Risk Effectiveness: A High-Frequency Data Approach with Semi-heavy Tails

1. Introduction

The launch of Bitcoin in 2009 marked a pivotal moment, propelling cryptocurrencies into the financial limelight. Presently, decentralized exchanges actively trade around 22,932 cryptocurrencies, indicative of the rapid expansion within this emerging market as reported by CoinMarketCap [1]. This surge has not only seized the financial industry’s attention but also underscored the substantial impact of cryptocurrencies. Despite this heightened interest, the complete spectrum of potential applications remains insufficiently explored by researchers.

Cryptocurrencies, characterized by their departure from traditional financial norms, operate in the digital realm, free from central bank oversight, as emphasized by Corbet et al. [2]. Notably, experts such as Weber [3] and Baek et al. [4] assert that Bitcoin aligns more closely with an asset than a conventional currency. A notable statistic reveals that approximately 69.2% of Bitcoin holdings remain inactive, highlighting investors’ preference for holding rather than utilizing them for transactions, Hartmann [5]. This inclination for speculation reinforces Bitcoin’s characterization as an asset primarily intended for speculative purposes rather than functioning as a conventional currency.

Classifying Bitcoin within a specific asset class poses a challenge, with Burniske et al. [6] confirming its emergence as a distinct asset class with unique attributes. This distinctiveness is apparent through its decentralized origin, limited supply structure, and foundational blockchain technology. Micu et al. [7] further emphasize the remarkable growth trajectory of Bitcoin and Ethereum, positioning them as significant financial instruments.

As cryptocurrencies gain popularity, they introduce challenges and opportunities, necessitating exploration by researchers, investors, and policymakers. Traditional research methods struggle to comprehend the intricate and unpredictable behaviors inherent in cryptocurrency markets. To address this, the strategic incorporation of high-frequency data becomes essential, offering unparalleled insights into dynamic digital markets. Therefore, in this paper, we aim to bridge the existing research gap by exploring the complete spectrum of potential applications of cryptocurrencies, particularly focusing on the intricate dynamics of high-frequency trading.

However, the adoption of high-frequency data is not without risks, given the heightened scrutiny of cryptocurrency markets due to volatility, liquidity disparities, and susceptibility to manipulation. The focus on risk measurement leads to the Value-at-Risk (VaR) metric, a prevalent choice in this domain. Researchers, such as Mata et al. [8], have identified the superiority of the Normal Inverse Gaussian (NIG) distribution in VaR estimation over multivariate generalized autoregressive conditional heteroscedastic models.

This paper, therefore, aims to assess the resilience and effectiveness of VaR as a risk assessment tool when applied to the unique dynamics of high-frequency cryptocurrency data. Additionally, we seek to explore the potential of the NIG distribution as a reliable model for estimating VaR, with a particular emphasis on its applicability to high-frequency data.This highlights the NIG distribution’s capability to provide more precise and reliable estimates of downside risk.

Moreover, the NIG distribution assumes a crucial role in examining the influence of socially responsible dimensions on risk dynamics and predictability, as indicated by Viviani et al. [9]. Integrating social responsibility considerations into risk analysis positively impacts risk management and portfolio performance.

Risk management protocols, predominantly focused on daily data, can be extended to intraday data. This study empirically examines one-minute interval price data for Bitcoin and Ethereum from January 1st, 2017, to October 25th, 2022. By employing specialized statistical techniques and constructing a portfolio, the study evaluates its ability to meet established confidence levels. The inclusion of high-frequency data, covering disruptive periods like the global pandemic in 2020, contributes innovative insights to risk evaluation in high-frequency trading.

Through this exploration, we aim to quantitatively evaluate instances where observed risk values surpass estimated values, providing a deeper understanding of the precision and reliability of risk measurement in cryptocurrency markets. Ultimately, our objective is to contribute to the evolving research landscape by shedding light on the practicality and effectiveness of advanced distributional models in accurately modeling and predicting financial risk, especially within the realm of cryptocurrencies like Bitcoin and Ethereum. By explicitly stating the research gap, providing an overview of the methodology, and connecting the introduction to the subsequent literature review, we aim to offer a clearer roadmap for readers and highlight the contributions of our study.

The structure of this document follows a logical progression. Section 2 provides an overview of relevant literature, while Section 3 delves into the specifics of returns and risk measures. Section 4 explains the methods employed and the data collected. Progressing further, Section 5 presents the outcomes and seamlessly transitions to Section 6, where conclusions and discussions converge, ultimately culminating in a coherent ending.

2. Literature Review

Bitcoin, as a pioneering cryptocurrency, wields a profound influence on the intricate realm of digital finance. This review explores pivotal research findings, emphasizing the far-reaching impact of Bitcoin and the crucial role of high-frequency data in modern financial analysis. The investigation’s foundation lies in the use of high-frequency data collected minute by minute for Bitcoin and Ethereum from January 1st, 2017, to October 25th, 2022.

Mahmoudi [10] underscores Bitcoin’s historical eminence, extending beyond intrinsic value, and influencing the valuation of other digital assets. The escalating costs of Bitcoin mining and its inherent supply scarcity initiate upward price trends. This dynamic interplay of factors attracts investors, amplifying demand and culminating in an amplified pricing trajectory. Ma et al. [11] provide insights into temporal price clustering patterns, complementing this discourse.

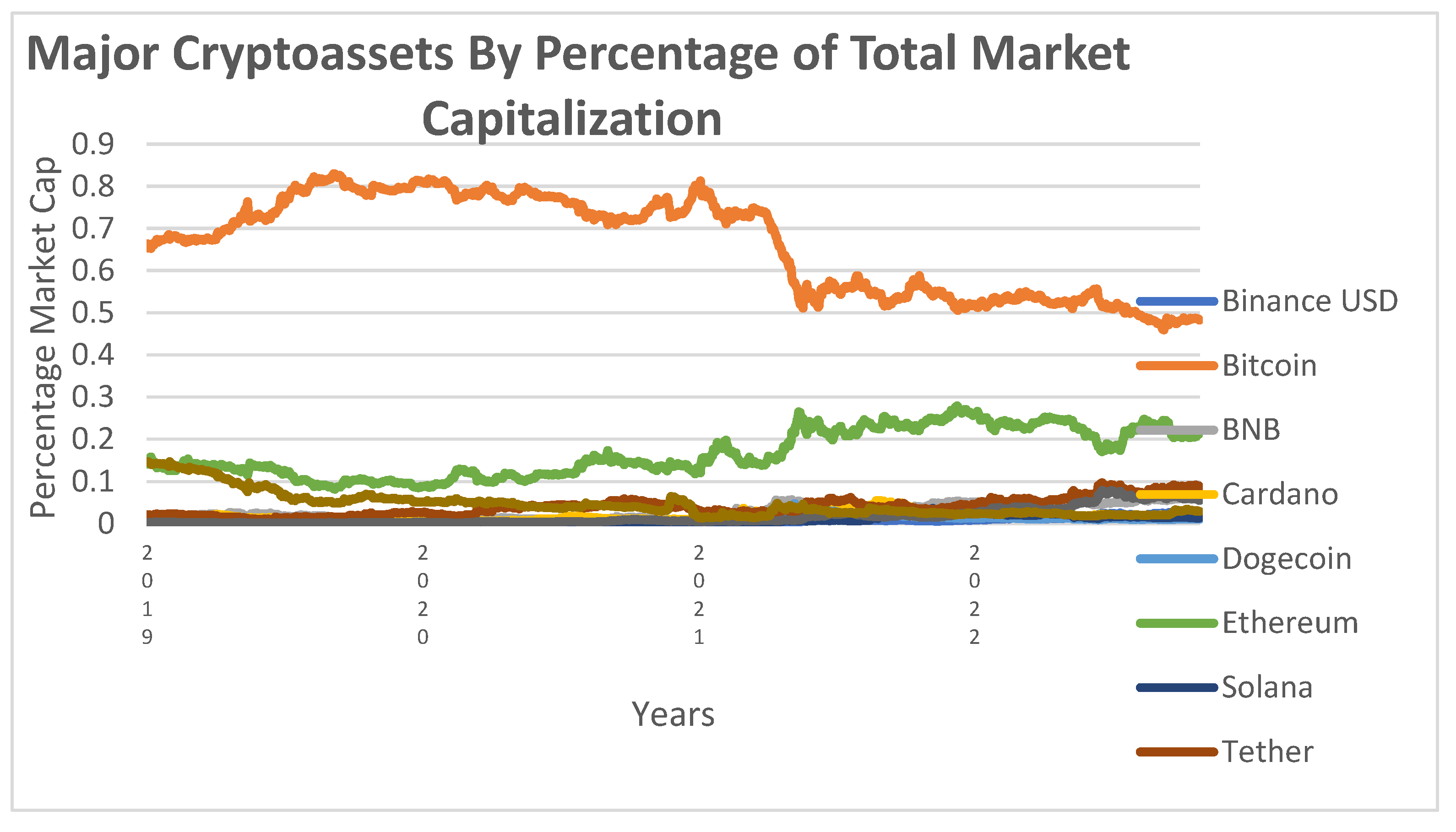
Figure 1 depicts the evolution of market capitalization for major crypto assets, consistently dominated by Bitcoin and Ethereum, affirming Bariviera et al.’s [12] observation that most cryptocurrencies follow Bitcoin’s market patterns. The riskiness of Bitcoin investments is emphasized by Zhang et al. [13], linking it to speculative fervor. Speculator movements during price upswings magnify trading volumes and market attention, leading to price escalations. In a broader economic context, Zhu et al. [14] present empirical evidence of Bitcoin’s susceptibility to economic indicators, while Qarni et al. [15] highlight its role as a hedge against the US dollar and forex-related risks.

Blau [16], Chu et al. [17], and Sahoo [18] discuss Bitcoin’s market volatility vis-à-vis traditional fiat currencies. Kristoufek [19] notes its detachment from governmental backing, preventing direct economic correlations. Troster et al. [20] confirm Bitcoin’s exceptional volatility, exceeding that of traditional assets. This volatility extends to crude oil and gold markets, as evidenced by Gronwald’s [21] empirical findings.

Bouri et al. [22] highlight Bitcoin’s potential as a diversification instrument, while Dyhrberg [23] and Lopez et al. [24] affirm its role as a sanctuary against market vagaries. Fang et al. [25] explore its utility for diversification across global markets, and Mensi et al. [26] validate its hedging advantages when paired with Ethereum.

Pranckevičiūtė [27] underscores volatility modeling in risk assessment, advocating for high-frequency data, echoed by Qi et al. [28]. This approach is further explored by Huang et al. [29], Meng et al. [30], and Huang et al. [31], emphasizing high-frequency data’s efficacy in refining VaR forecasts.

Trucíos et al. [32] shed light on the dichotomy of substantial returns and inherent risk exposure. The upheaval in 2020 witnessed a remarkable ascent in cryptocurrency values, a trend sustained in 2021. Bitcoin and Ethereum consistently assert their dominance, a trend acknowledged by Council [33]. Hambuckers et al. [34] introduce an innovative approach through extreme value regression, offering insights into high-frequency tail risk dynamics.

Schilling et al. [35] delve into the fundamental equilibrium pricing equation, highlighting Bitcoin’s adherence to a martingale pattern. Liu et al. [36] propose factors like momentum and investor attention for predicting Bitcoin’s returns. Sockin et al. [37] introduce cryptocurrency valuation ratios into return prediction models.Guindy [38] emphasizes investor attention in predicting price volatility, echoed by Critien et al. [39] using neural models. Zhang et al. [13] unveil bidirectional links between Bitcoin returns and internet attention.

In risk assessment, VaR emerges as a replacement for conventional measures, as indicated by Christoffersen [40] and Likitratcharoen et al. [41]. Müller et al. [42] and Trucíos et al. [32] emphasize the significance of forecasting risk.

The NIG distribution, effective in modeling stock returns and estimating option prices (Rubenis et al. [43]; Hamza et al. [44]), belongs to the GH family of Lévy processes (Eberlein et al. [45]). It outperforms multivariate models in VaR estimation (Mata et al. [8]) and finds application in various financial contexts, including cryptocurrencies (Sayit [48]).

Subramoney et al. [50] identify heavy tails in cryptocurrency returns, with the NIG distribution excelling in capturing their nature. Ramirez-Garcia [51] showcases its practicality in hedging electricity price volatility. Contreras-Valdez et al. [54] employ the NIG distribution in portfolio selection, affirming its efficacy and versatility.

The NIG distribution’s application in portfolio management, modeling default risk in banks (Jessen et al. [56]), and its role in modeling risk underscore its significance. This study aims to comprehensively analyze high-frequency data and the NIG distribution in estimating VaR for Bitcoin and Ethereum, contributing insights into risk assessment within cryptocurrency markets. Through this exploration, we aim to enhance understanding and provide valuable insights for researchers, investors, and policymakers operating in high-frequency trading within the dynamic cryptocurrency landscape.

This paper’s primary objective is to comprehensively analyze the utilization of high-frequency data and the Normal Inverse Gaussian (NIG) distribution in estimating Value at Risk (VaR) for an evenly weighted portfolio, with a specific focus on Bitcoin and Ethereum.

Our study aims to achieve several key goals. First, we intend to assess the resilience and effectiveness of VaR as a risk assessment tool when applied to the unique dynamics of high-frequency cryptocurrency data. Second, we seek to explore the potential of the NIG distribution as a reliable model for estimating VaR, with a particular emphasis on its applicability to high-frequency data. This exploration will enable us to quantitatively evaluate instances where observed risk values surpass estimated values, providing a deeper understanding of the precision and reliability of risk measurement in cryptocurrency markets. Ultimately, our objective is to contribute to the evolving research landscape by shedding light on the practicality and effectiveness of advanced distributional models in accurately modeling and predicting financial risk, especially within the realm of cryptocurrencies like Bitcoin and Ethereum. Through these objectives, our study aims to provide valuable insights to researchers, investors, and policymakers, facilitating a better comprehension of risk in the context of high-frequency trading, particularly within the fast-paced and ever-changing cryptocurrency markets.

3. Methodology and Data

In this paper, we propose the estimation of a bivariate Normal Inverse Gaussian distribution designed by Barndorff-Nielsen [57]. A univariate version has been applied to the Bitcoin returns in Núñez et al. [58]. In this case, the random variable X has a Normal Inverse Gaussian density, denoted X~NIG(α,β,μ,δ) if:

$$f_{NIG}\left(x;\alpha ,\beta ,\mu ,\delta \right)=\frac{\delta \alpha {exp}^{(\delta \gamma +\beta \left(x-\mu \right))}}{\pi \sqrt{{\delta }^2+{(x-\mu )}^2}}{K}_1\left(\alpha \sqrt{{\delta }^2+{(x-\mu )}^2}\right)$$

(1)

$$K_1\left(\omega \right):=\frac{1}{2}{\int }_0^{\infty }\mathit{exp}\left(-\frac{1}{2}\omega \left(t+t^{-1}\right)\right)dt$$

(2)

The mean, variance, skewness, and kurtosis are shown in Kalemanova et al. [59]:

$$E\left(X\right)=\mu +\delta \frac{\beta }{\gamma }$$

(3)

$$V\left(X\right)=\delta \frac{{\alpha }^2}{{\gamma }^3}$$

(4)

$$S\left(X\right)=3\frac{\beta }{\alpha \sqrt{\delta \gamma }}$$

(5)

$$K\left(X\right)=3+3\left(1+4{\left(\frac{\beta }{\alpha }\right)}^2\right)\frac{1}{\delta \gamma }$$

(6)

A bivariate version of the NIG distribution will be used using Bitcoin and Ethereum rturns. Formally, defined as

$$X=\mu +W\gamma +\sqrt{W}A\overline{Z}$$

(7)

where:

$\overline{Z}~N\left(\overline{0}{I}_k\right)$

$A\in {\mathbb{R}}^{d\times k}$

$\mu ,\gamma \in {\mathbb{R}}^d$

With $W\ge 0$ and $W~GIG(\lambda ,\chi ,\psi )$ is a Generalized Inverse Gaussian variable, which density specification is:

$$f\left(w\right)={\left(\frac{\psi }{\chi }\right)}^{\raisebox{1ex}{$\lambda $}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\frac{w^{\lambda -1}}{2K_{\lambda }\left(\sqrt{\chi \psi }\right)}{e}^{\left\{-\frac{1}{2}\left(\frac{\chi }{w}+\psi w\right)\right\}}$$

(8)

parameters $\chi >0,\psi \ge 0,\lambda <0$ (shape parameters), $\mu$ is the location,$\mathsf{\Sigma }=A{A}^t$ is the dispersion matrix, $\gamma$ stands for the skewness parameter and $K_{\lambda }$ is the modified Bessel function of the third kind.

The expected Value and the Variance of the multivariate distribution of $W\ge 0$ are:

$$E\left[W\right]=\frac{K_{\lambda +1}\left(\sqrt{\chi \psi }\right)}{K_{\lambda }\left(\sqrt{\chi \psi }\right)}\sqrt{\frac{\chi }{\psi }}$$

(9)

And

$$VAR\left[W\right]=\frac{\chi }{\psi }\left(\frac{K_{\lambda +2}\left(\sqrt{\chi \psi }\right)}{K_{\lambda }\left(\sqrt{\chi \psi }\right)}-{\left(\frac{K_{\lambda +1}\left(\sqrt{\chi \psi }\right)}{K_{\lambda }\left(\sqrt{\chi \psi }\right)}\right)}^2\right)$$

(10)

$\lambda =-\frac{1}{2}$ defines the Normal Inverse Gaussian (NIG) distribution.

For the multivariate Generalized Hyperbolic distribution, the expected value and the variance matrix are given by:

$$E\left[X\right]=\mu +E\left[W\right]\gamma$$

(11)

$$VAR\left[X\right]=VAR\left[W\right]\gamma {\gamma }^t+E\left[W\right]\mathsf{\Sigma }$$

(12)

We will use the parametrization $\overline{\alpha }=\sqrt{\chi \psi }$ then for the NIG $\left(\lambda =-\frac{1}{2}\right)$, $\chi =\psi =\overline{\alpha }$, such that $\overline{\alpha }>0$ . With this new definition, calculus becomes even faster from a computational perspectiveWe obtained the data from the Gemini Exchange, which includes intraday information with regular measurements for every minute. To create a homogeneous dataset, we computed the model from 2017 onwards for both cryptocurrencies. The dataset contains minute-by-minute closing prices of Bitcoin and Ethereum, ranging from 00:00 hours on 1st January 2017 to 23:59 hours on 25th October 2022.

Although the dataset was consistent enough to perform most of the models, we encountered some data cleaning requirements. The most recurring issue was atypical information caused by the absence of decimal points. To prevent potential data manipulation skewness, we removed these inconsistencies from the data. The final dataset comprises the statistics presented in Table 1.

The computation of the returns is done minute by minute, descriptive statistics for each year are presented in Table 2.

These statistics clearly reveal non-Gaussian data, with the third and fourth moments deviating significantly from the normal behavior.

Nevertheless, some noteworthy observations can be made: the mean and standard deviation (volatility) derived from minute returns exhibit relatively low volatility themselves. Minute volatility remains within the range of 0.1% for each year analyzed, particularly in the case of Bitcoin. Employing a Multivariate Gaussian adjustment in this scenario would yield nearly identical VaR levels for each year. Allowing for the use of more flexible distributions enables the capture of the more intricate behavior of the returns.

Notably, the year 2018 stands out, with kurtosis values exceeding ten thousand. This data aligns with the bubble observed by the end of that year. However, in 2020 and 2021, during the period of heightened price volatility across all cryptocurrencies, the leptokurtosis of the data was considerably lower than in 2018 for minute information. A similar extreme behavior in statistical moments is also evident in the skewness of the distribution, with the negative level reaching a minimum in 2018 that is not revisited in subsequent years. Ethereum exhibits a similar behavior during the same time periods.

With this information, it becomes evident that there is a need to employ at least semi-heavy-tailed distributions to model this data. As mentioned earlier, the proposed distribution is the Normal Inverse Gaussian (NIG) due to its commendable properties. To perform the multivariate adjustment and evaluate the performance and effectiveness of this distribution, several considerations were considered. Since there is a substantial amount of data, with around 1440 data points for each day, there is enough information to adjust a daily Multivariate NIG distribution. This procedure was conducted on a daily basis using a rolling window approach.

It’s worth noting that on some days, the maximum likelihood algorithm did not converge due to the presence of extreme values that the distribution couldn’t capture. The specific days that were removed are presented in Table 3.

For these days, it is noteworthy that 2020 witnessed the highest concentration of extreme values. The initial periods coincide with the onset of the COVID-19 pandemic, while the subsequent periods are associated with the first and second waves of contagion. This phenomenon offers intriguing potential for further research and analysis.

Once the estimators for each day are calculated, these values are utilized to model the theoretical multivariate distribution for that specific day. Using these estimations, the Value at Risk (VaR) at a 99% confidence level is computed for an equally weighted portfolio. However, relying solely on an in-sample evaluation of the adjustment’s performance is insufficient to draw robust conclusions. To address this limitation, an out-of-sample approach was employed.

The approach involves computing the minute VaR for one day and using it as the benchmark for the following day. If the minute return for the second day exceeds the VaR computed on the first day, it is considered a failure in the estimation. The effectiveness statistic is then calculated as the percentage of minute returns that remained above the VaR. In theory, the level of effectiveness is expected to align with the chosen confidence level.

4. Results

The results align with the year-wise plots and statistics assessing the effectiveness of the Multivariate Normal Inverse Gaussian (NIG) model in capturing return behavior and volatility concerning the Value at Risk (VaR) statistic.

We initiated the analysis by calculating an equally weighted portfolio for each period. It’s essential to note that the portfolio weights were chosen due to the high correlation among the assets, limiting the potential for proper diversification. In the discussion section of this paper, we delve into additional considerations.

In the dynamic world of cryptocurrency, various events of different magnitude have influenced the Value at Risk (VaR), with Bitcoin and Ethereum remaining highly sensitive to changes, not just within financial markets, but also across the spectrum of factors, including fraud and non-financial news. Let’s embark on a journey through the years, starting in 2017, through graphs 2 to 7.

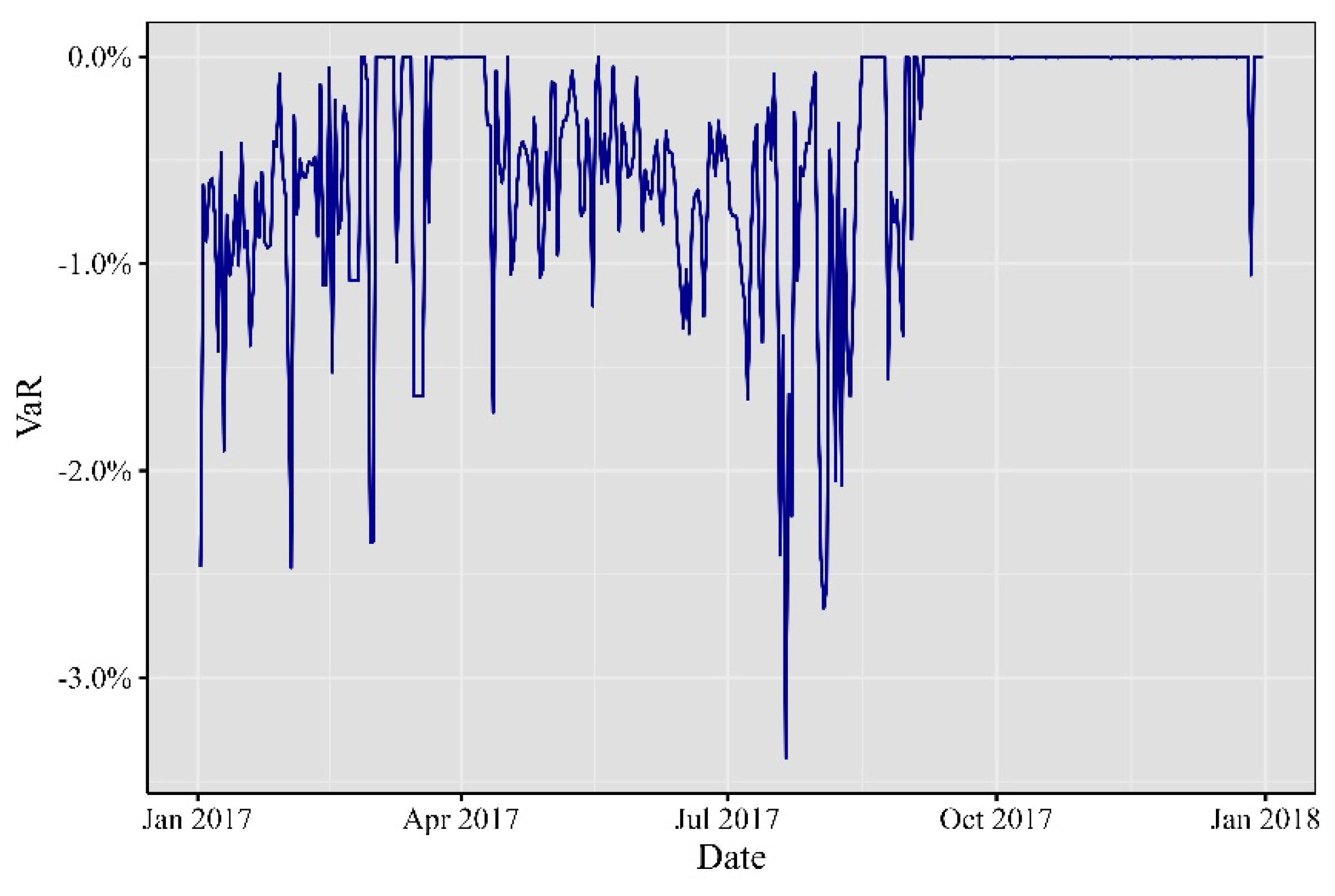
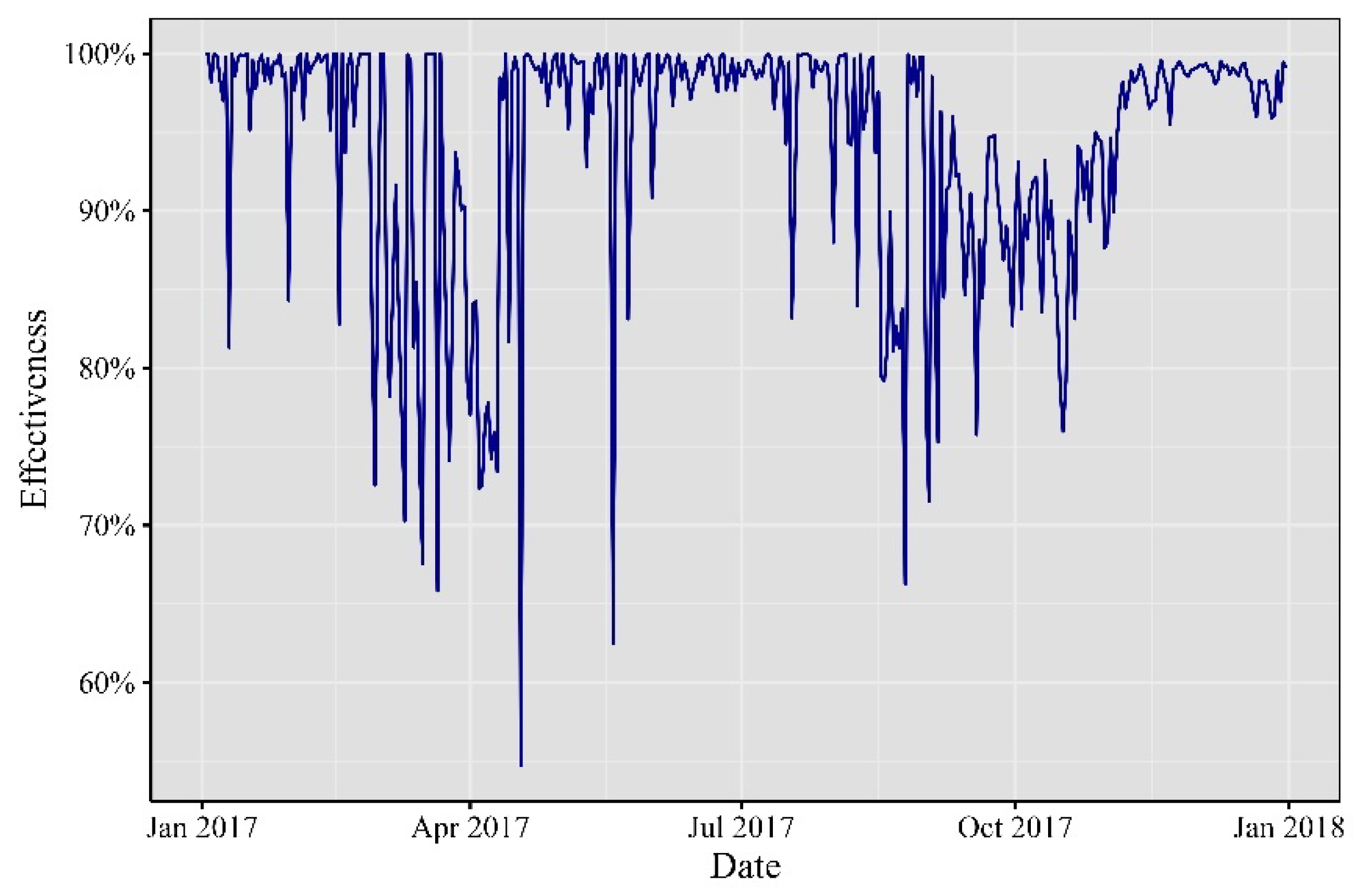
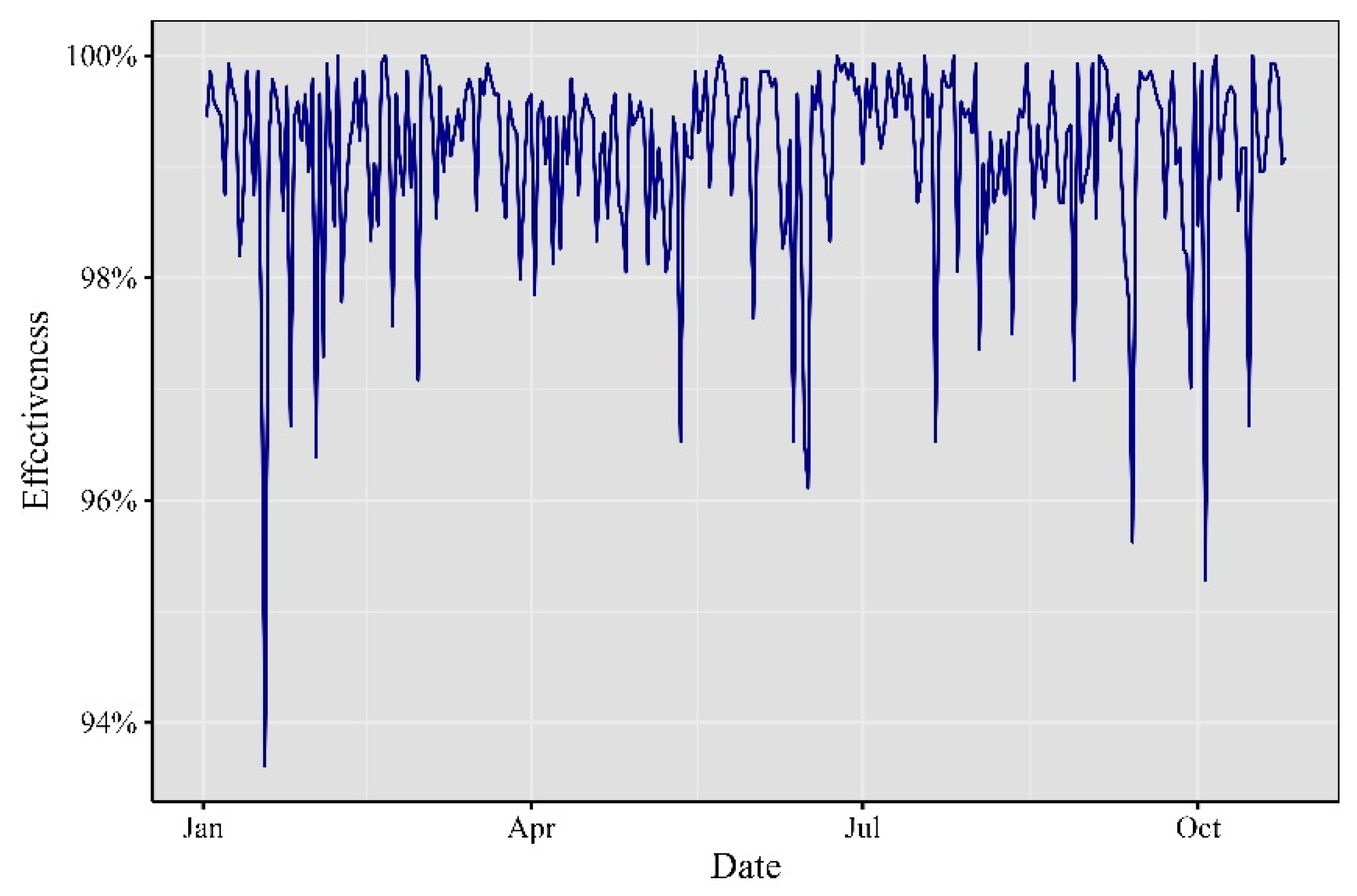
In 2017, the cryptocurrency realm bore witness to a whirlwind of impactful events. Extreme occurrences, market developments, economic announcements, and unforeseen price movements left a significant mark on minute VaR, leading to substantial alterations in its risk profile. Notable troughs were evident throughout the year, stretching from January to October, as depicted in Figure 2. In January 2017, a substantial rally emerged, setting the stage for a trend that persisted until December. In April, an extreme trough primarily stemmed from Japan’s official recognition of Bitcoin as a legal method of payment, catalyzing increased adoption and investment within the country. Then, in June, the cryptocurrency sphere was rocked by the WannaCry ransomware attack, demanding Bitcoin payments, capturing widespread attention, and shedding light on its role in cybercrime. By July, the discovery of a critical vulnerability in the Parity multi-signature wallet led to the freezing of substantial amounts of Ether, sending ripples across the Ethereum community.

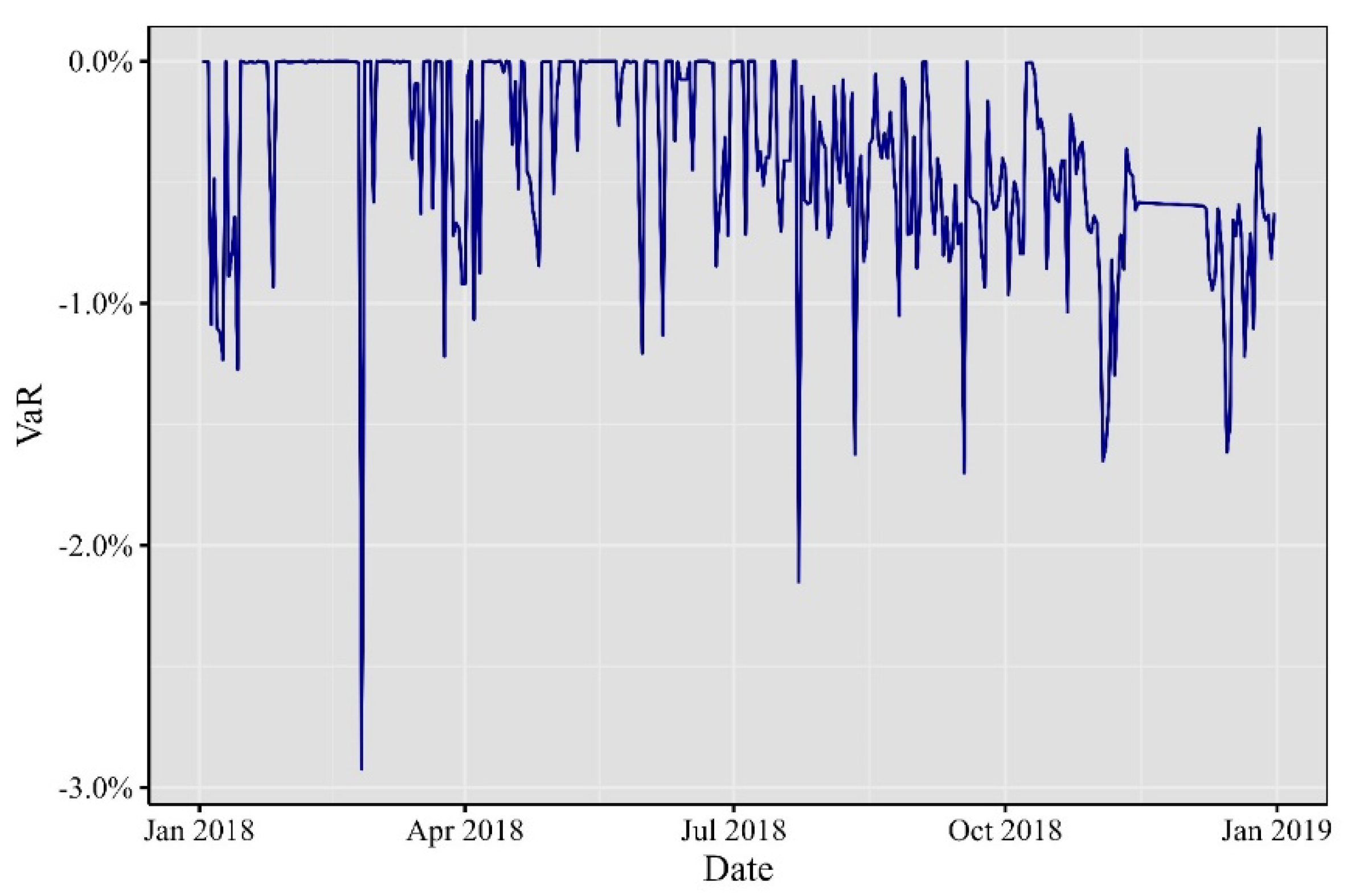
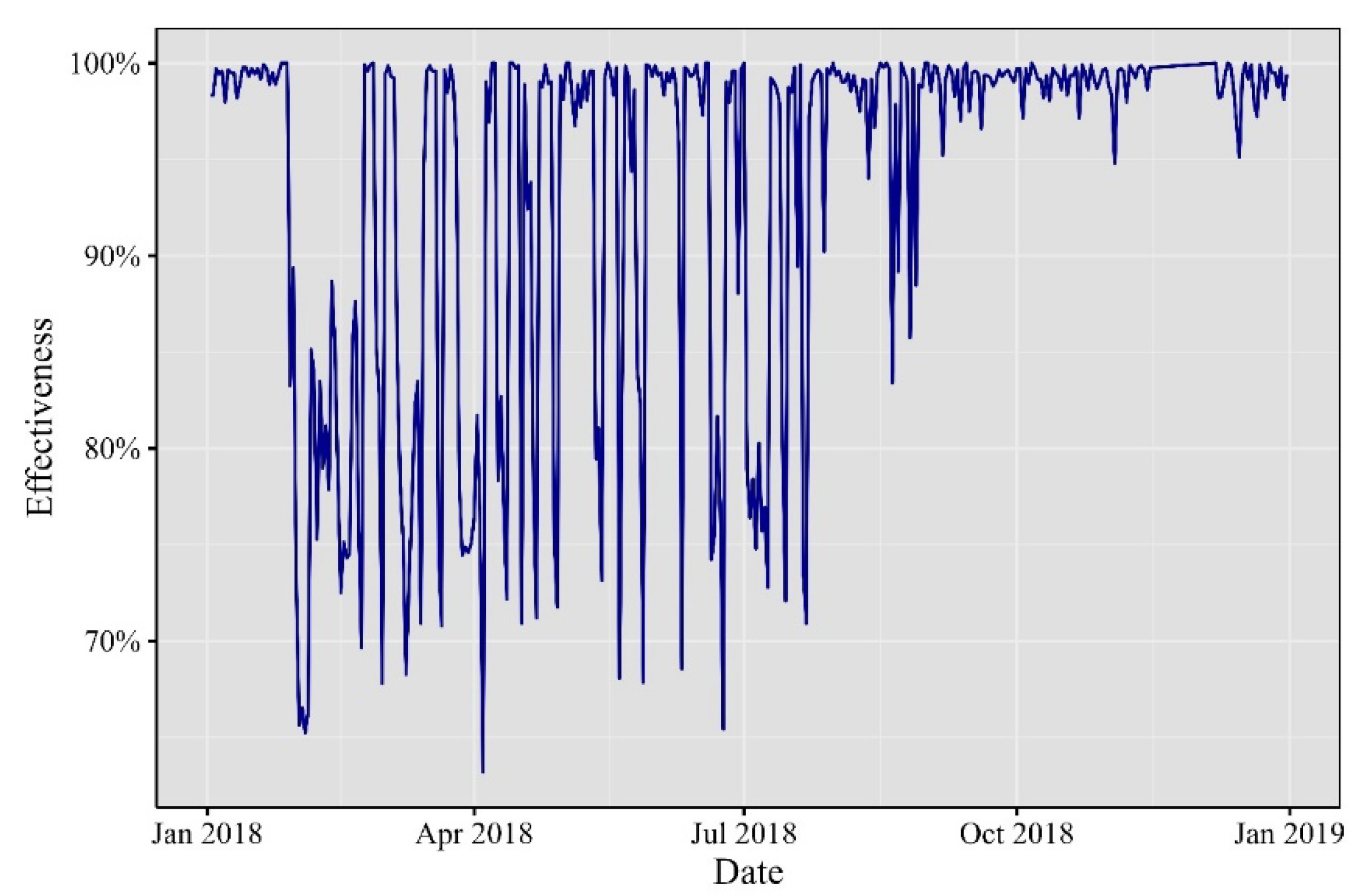
Fast forward to 2018, as depicted in Figure 3, where minute VaR experienced significant fluctuations. January brought forth noteworthy developments; Ethereum soared to an all-time high, surpassing $1,400, buoyed by the surging popularity of initial coin offerings (ICOs) on its platform. Meanwhile, Bitcoin underwent a correction after reaching a record high in late 2017, causing a market-wide downturn. The G20 summit in March became a focal point for discussions on cryptocurrencies and potential regulatory measures, injecting uncertainty and brief price fluctuations into the market. April marked the beginning of Bitcoin’s price stabilization after several months of correction. Ethereum grappled with scalability challenges, with the congestion caused by the blockchain game CryptoKitties taking center stage. In June, regulatory clarity emerged when the U.S. Securities and Exchange Commission (SEC) clarified that Bitcoin was not considered a security. However, August brought the SEC’s rejection of several proposed Bitcoin exchange-traded funds (ETFs), fostering market uncertainty and causing temporary price dips. Finally, by November, Ethereum’s price exhibited a significant decline, aligning with the broader trend in the cryptocurrency market.

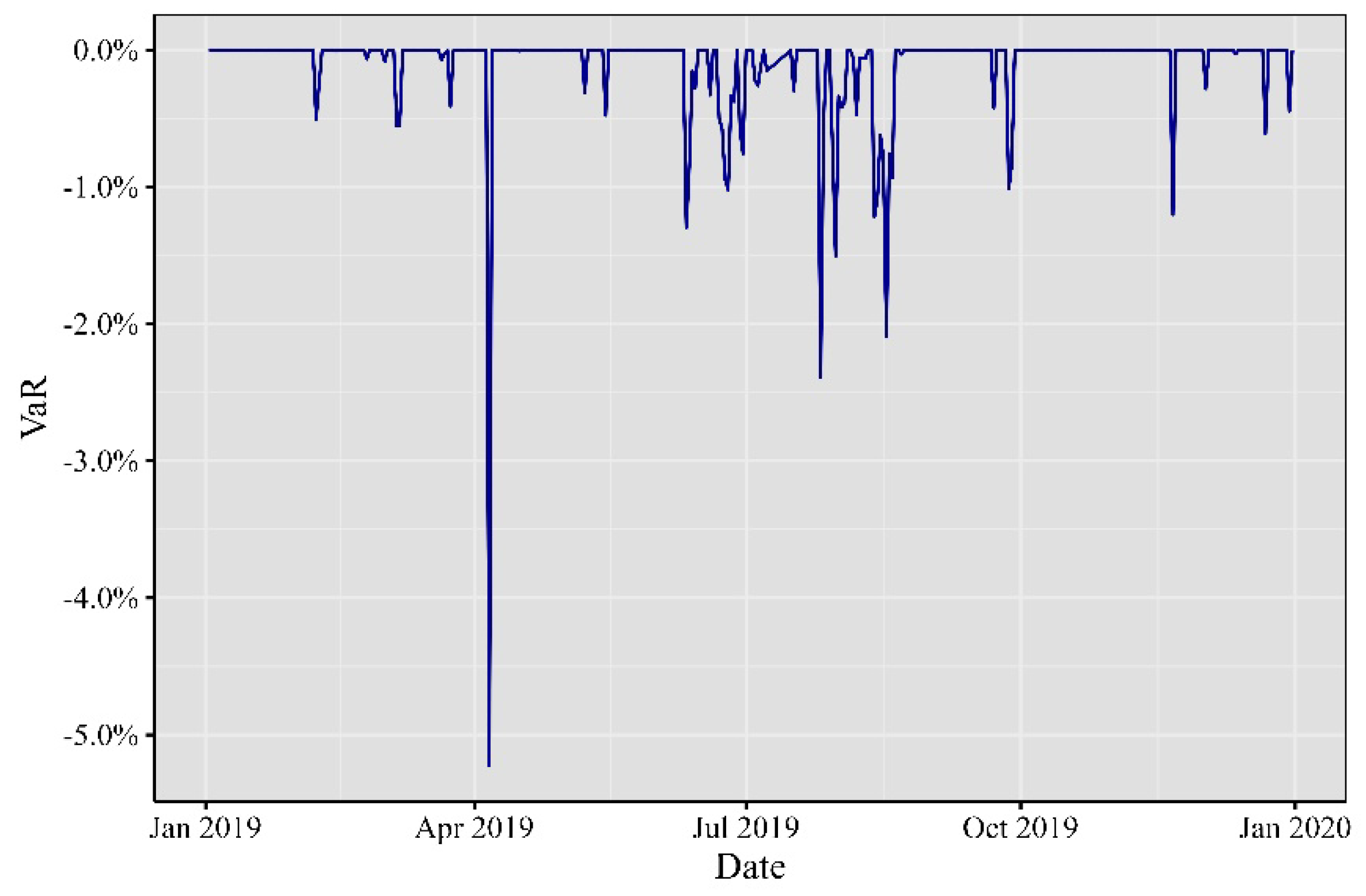
As we journeyed into 2019, depicted in Figure 4, both Bitcoin and Ethereum experienced significant events and developments. Bitcoin commenced the year with anticipation of its halving in May, only to face a price decline in March during the global financial market crash triggered by the COVID-19 pandemic. Ethereum, on the other hand, underwent a hard fork in February and announced Ethereum 2.0 in June, marking its transition to a proof-of-stake consensus mechanism. The decentralized finance (DeFi) sector continued to flourish on the Ethereum network throughout the year.

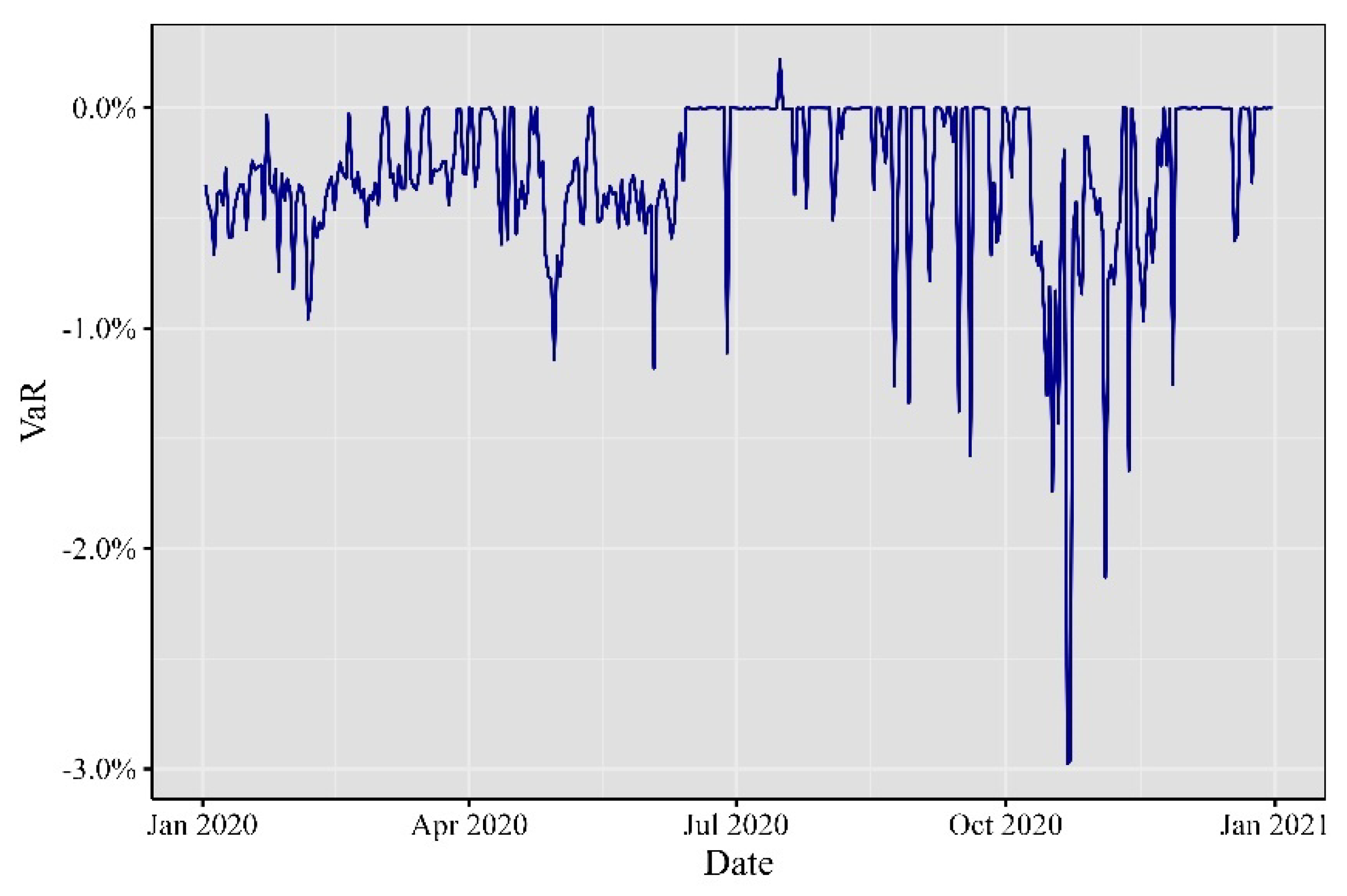
The year 2020, as illustrated in Figure 5, was marked by Bitcoin’s rebound after the 2018 bear market. May brought the long-anticipated Bitcoin halving, impacting its supply dynamics. In June, Facebook’s Libra project announcement triggered discussions on regulation. Ethereum implemented the Beacon Chain testnet as part of the Ethereum 2.0 upgrade in July. August witnessed a surge in institutional interest in Bitcoin, notably with MicroStrategy’s substantial investment.

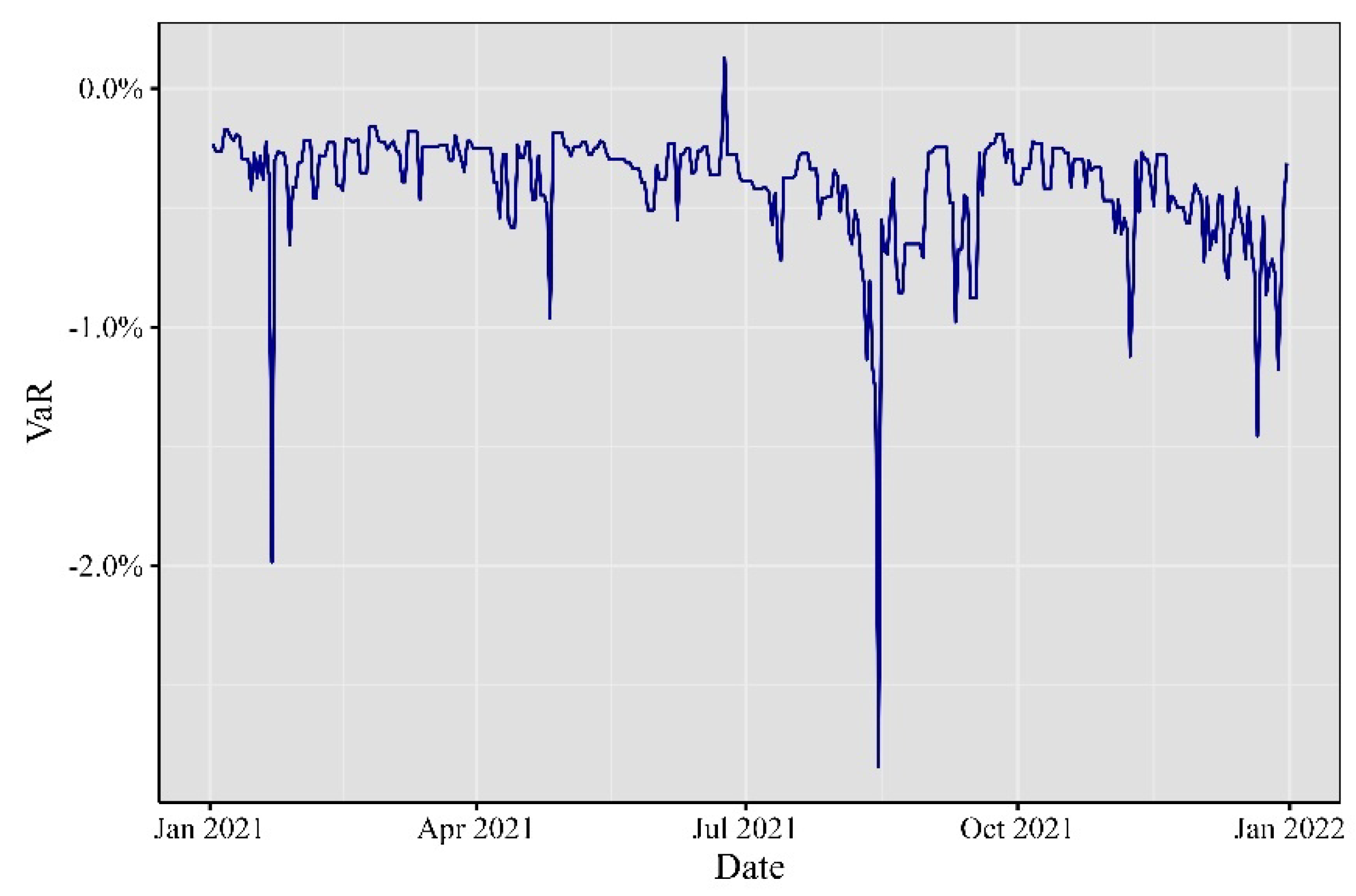
Turning to 2021, as depicted in Figure 6, Bitcoin experienced a remarkable price surge, reaching new all-time highs, driven by institutional investments and positive sentiment. Tesla’s announcement of a significant Bitcoin investment in February further solidified Bitcoin’s mainstream acceptance. Ethereum’s price also soared in February. However, in May, Bitcoin underwent a correction due to environmental and regulatory concerns. In June, El Salvador adopted Bitcoin as legal tender, marking a groundbreaking moment for cryptocurrency adoption. Ethereum introduced key upgrades, including the Berlin hard fork in April, the EIP-1559 upgrade in August, and in November, aiming to enhance its efficiency and address fee-related issues.

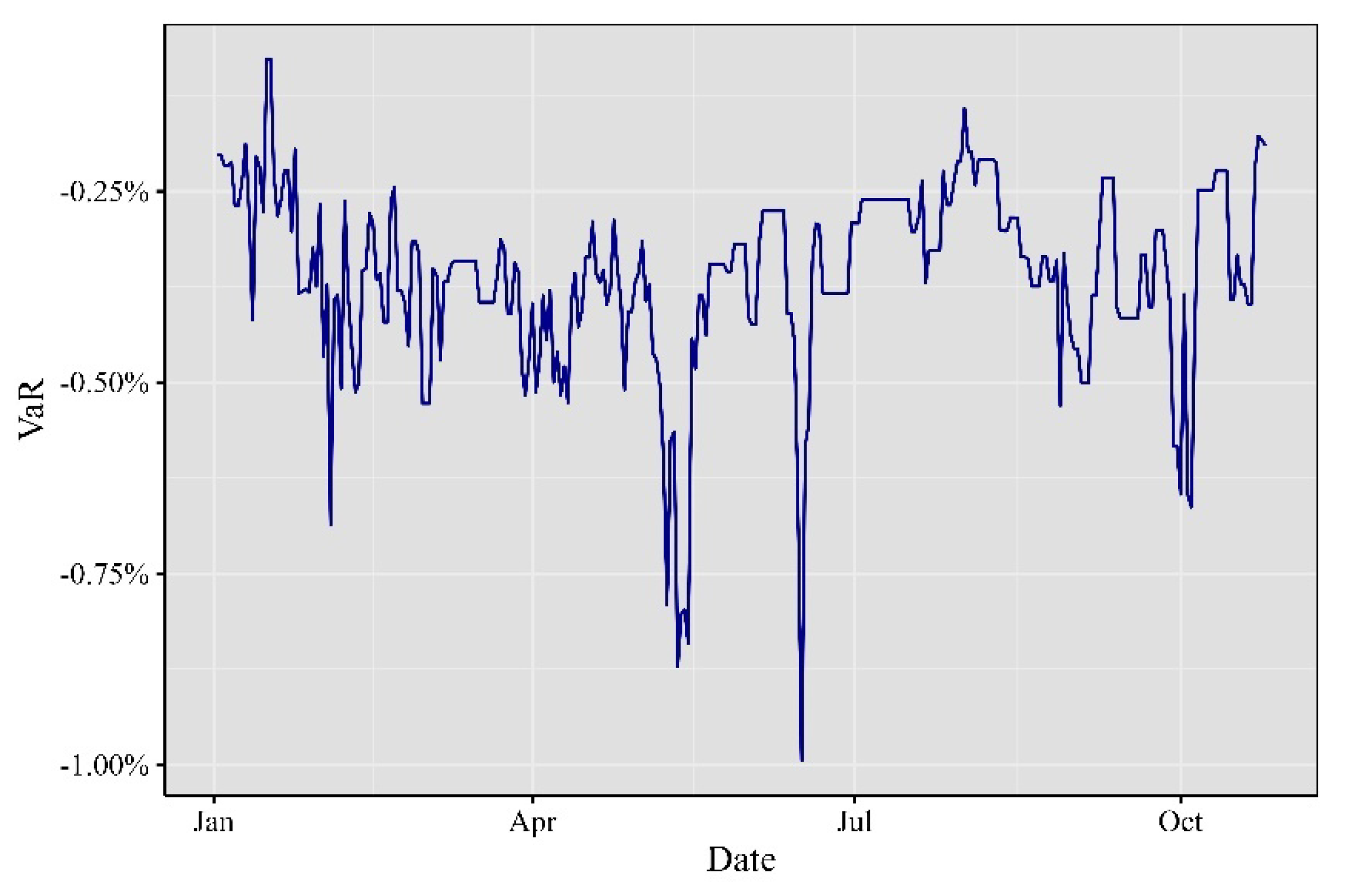
And finally, in 2022, as depicted in Figure 7, the cryptocurrency industry played host to several significant events. February took center stage during the Super Bowl with the "Crypto Bowl," where industry giants like Coinbase, FTX, Crypto.com, and eToro stepped forward to showcase their products to an estimated 200 million viewers. In May, turmoil ensued as Terra’s algorithmic stablecoin TerraUSD (UST) witnessed a wavering U.S. dollar peg, resulting in a substantial value decline. June witnessed a contagion effect as crypto lender Celsius froze operations due to "extreme market conditions," while Voyager issued a notice of default to hedge fund Three Arrows Capital (3AC). Ethereum brightened the year in September with "The Merge" upgrade, making the network significantly more energy-efficient. However, October proved to be a bountiful month for crypto hackers, who managed to abscond with over $718 million from decentralized finance sites in a series of high-profile hacks, underscoring the security challenges inherent in the DeFi sector.

Throughout these years, the cryptocurrency world bore witness to remarkable transformations, from the surge in adoption and institutional investment to regulatory developments and technological upgrades, creating a vibrant and ever-evolving landscape for Bitcoin and Ethereum.

Figure 2. Minute VaR at 99% for 2017.

Figure 2. Minute VaR at 99% for 2017.

Elaborated by the authors. Each observation represents the minute VaR computed day by day.

Figure 3. Minute VaR at 99% for 2018.

Figure 3. Minute VaR at 99% for 2018.

Elaborated by the authors. Each observation represents the minute VaR computed day by day.

Figure 4. Minute VaR at 99% for 2019.

Figure 4. Minute VaR at 99% for 2019.

Elaborated by the authors. Each observation represents the minute VaR computed day by day.

Figure 5. Minute VaR at 99% for 2020.

Figure 5. Minute VaR at 99% for 2020.

Elaborated by the authors. Each observation represents the minute VaR computed day by day.

Figure 6. Minute VaR at 99% for 2021.

Figure 6. Minute VaR at 99% for 2021.

Elaborated by the authors. Each observation represents the minute VaR computed day by day.

Figure 7. Minute VaR at 99% for 2022.

Figure 7. Minute VaR at 99% for 2022.

Elaborated by the authors. Each observation represents the minute VaR computed day by day.

Table 4. VaR Statistics.

Year	VaR Mean	VaR Standard Deviation
2017	-0.0045	0.0059
2018	-0.0034	0.0034
2019	-0.001	0.0039
2020	-0.003	0.0039
2021	-0.004	0.0025
2022	-0.0036	0.0012
Elaborated by the authors. Descriptive statistics of daily VaR computed for each day of the corresponding years

Table 4. VaR Statistics.

Year	VaR Mean	VaR Standard Deviation
2017	-0.0045	0.0059
2018	-0.0034	0.0034
2019	-0.001	0.0039
2020	-0.003	0.0039
2021	-0.004	0.0025
2022	-0.0036	0.0012
Elaborated by the authors. Descriptive statistics of daily VaR computed for each day of the corresponding years

In terms of Value at Risk (VaR) computation, we derived it using the theoretical values of the 1% left tail of the marginal distribution for the portfolio. Several noteworthy phenomena emerged from the analysis. In 2020 and 2021, the one-minute VaR for a given day exhibited positive values, indicating that during these periods, the expected market behavior leaned heavily in favor of the participants. It’s important to note that VaR values might not remain consistent day after day; however, the computation of this statistic revealed its non-stationary nature when applied to intraday data.

Another significant aspect is the evolution of the plots. In 2017, 2018, and 2019, the VaR values displayed relatively stable periods. In contrast, 2021 and 2022 showed a more variable behavior, aligning with expectations for a high-volume and high-volatility asset.

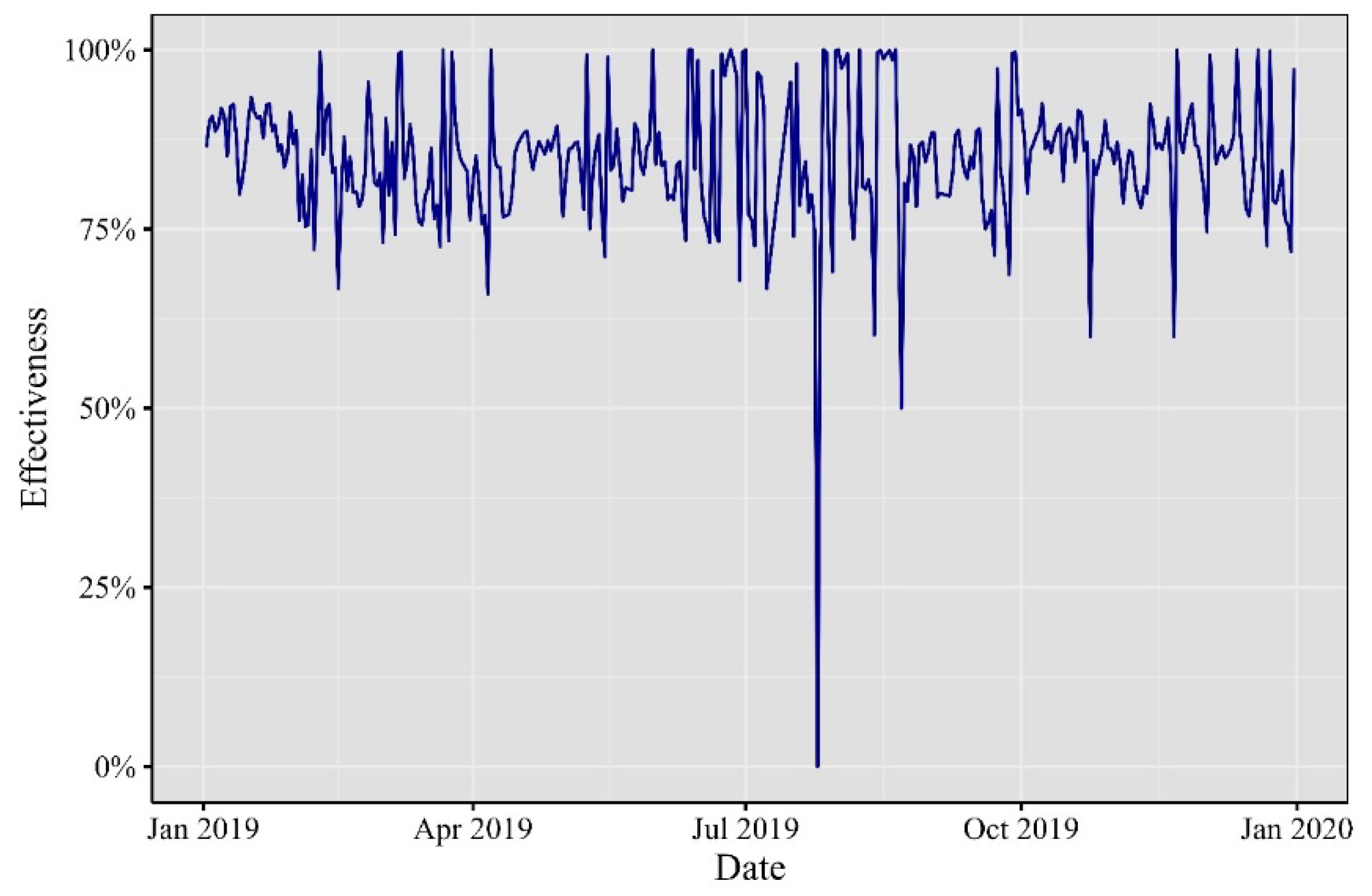
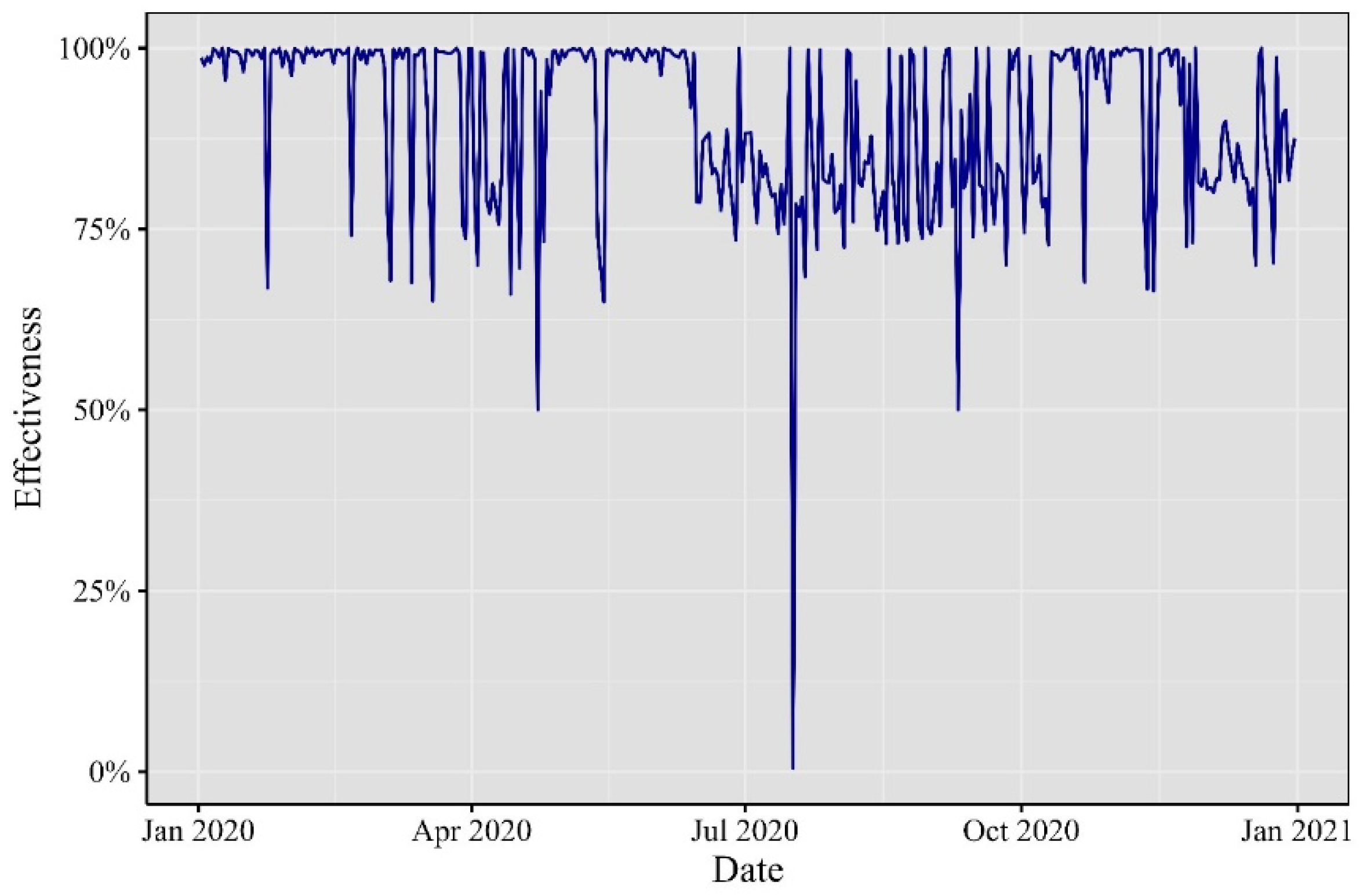
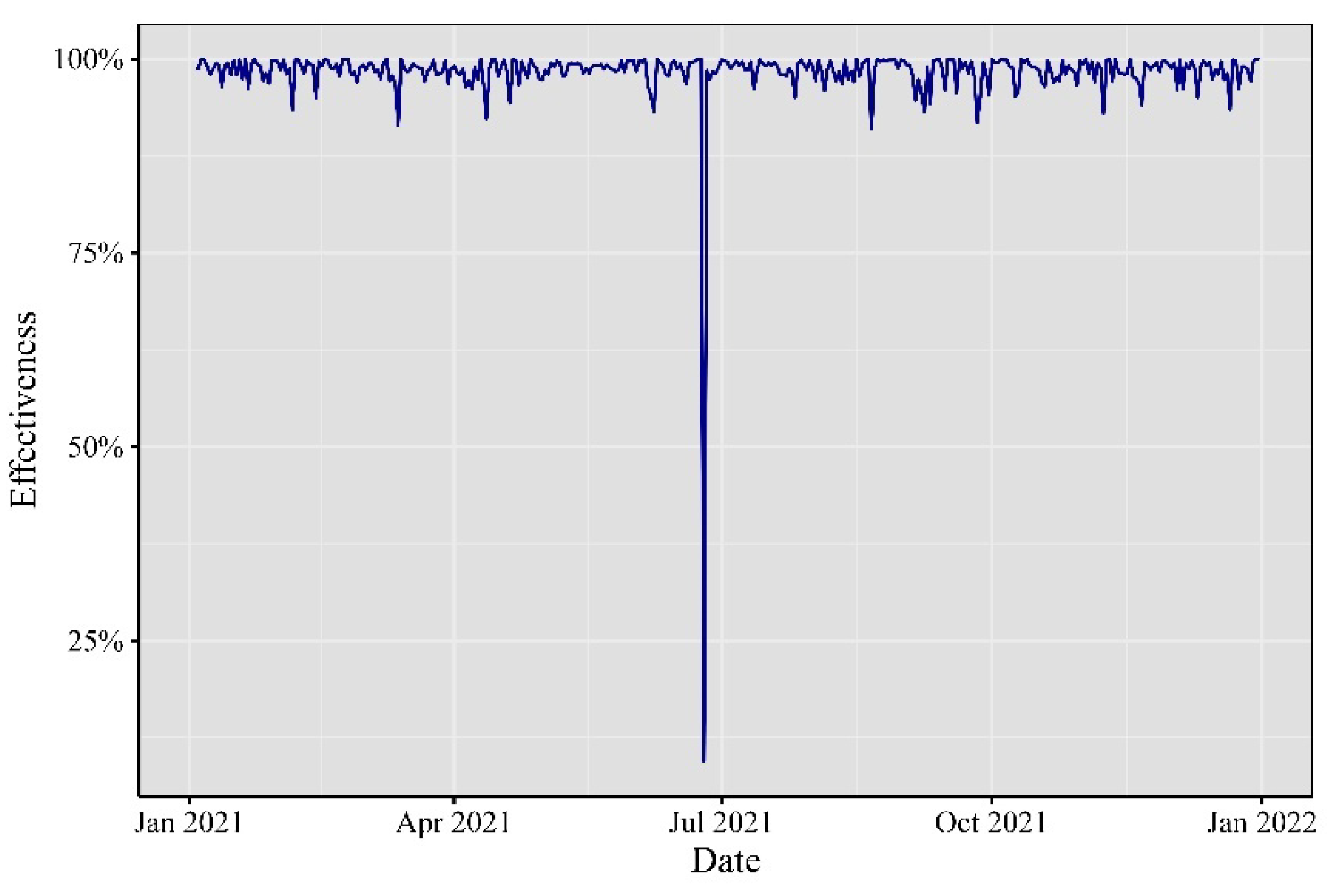
To validate the practical applicability of these computations, a forward testing technique was employed. Using the previous day’s one-minute VaR as a benchmark, we monitored whether the returns fell below this threshold. A return breaching the VaR boundary was considered a failure. This evaluation was conducted for all 1,440 minutes of each day, assessing whether they fell within the VaR limit or not. Finally, we calculated the mean of this Bernoulli distribution as a proxy for the probability of VaR accurately predicting the 99% threshold. Figures 8 through 13 depict the daily effectiveness of this risk measurement.

Figure 8. Effectiveness of the one-minute VaR of in 2017.

Figure 8. Effectiveness of the one-minute VaR of in 2017.

Elaborated by the authors. Percentage of one-minute observations inside the 99% VaR.

Figure 9. Effectiveness of the one-minute VaR in 2018.

Figure 9. Effectiveness of the one-minute VaR in 2018.

Elaborated by the authors. Percentage of one-minute observations inside the 99% VaR.

Figure 10. Effectiveness of the one-minute VaR in 2019.

Figure 10. Effectiveness of the one-minute VaR in 2019.

Elaborated by authors. Percentage of one-minute observations inside the 99% VaR.

Figure 11. Effectiveness of the one-minute VaR in 2020.

Figure 11. Effectiveness of the one-minute VaR in 2020.

Elaborated by authors. Percentage of one-minute observations inside the 99% VaR.

Figure 12. Effectiveness of the one-minute VaR in 2021.

Figure 12. Effectiveness of the one-minute VaR in 2021.

Elaborated by authors. Percentage of one-minute observations inside the 99% VaR.

Figure 13. Effectiveness of the one-minute VaR in 2022.

Figure 13. Effectiveness of the one-minute VaR in 2022.

Elaborated by authors. Percentage of one-minute observations inside the 99% VaR.

Table 5. Effectiveness statistics.

Year	Mean Effectiveness	Min Effectiveness	Max Effectiveness
2017	0.9411	0.5472	1
2018	0.9329	0.6319	1
2019	0.849	0	1
2020	0.9031	0.0048	1
2021	0.9827	0.0945	1
2022	0.9913	0.9361	1
Elaborated by authors. Percentage of returns that lie above the one-minute VaR of one day earlier.

Table 5. Effectiveness statistics.

Year	Mean Effectiveness	Min Effectiveness	Max Effectiveness
2017	0.9411	0.5472	1
2018	0.9329	0.6319	1
2019	0.849	0	1
2020	0.9031	0.0048	1
2021	0.9827	0.0945	1
2022	0.9913	0.9361	1
Elaborated by authors. Percentage of returns that lie above the one-minute VaR of one day earlier.

Across the cryptocurrency landscape from 2017 to 2022, a sequence of impactful events unfolded. Noteworthy rallies, regulatory developments, and technological upgrades marked each year. Interestingly, 2019 exhibited a smaller mean effectiveness, hinting at heightened variability in minute Value at Risk (VaR) values. Despite this, the majority of mean values surpassed 90%, underscoring the enduring impact of these events. In 2021 and 2022, a distinct trend emerges. Theoretical VaR at the 99% confidence level closely aligns with empirical test results, hinting at an evolving behavior in both daily and intraday cryptocurrency data. This observation signifies the dynamic nature of the cryptocurrency market, where events not only influence daily trends but also shape intraday movements.

With an increasing number of financial institutions incorporating high-frequency trading into their investment strategies, models like the one presented here exhibit sufficient power and flexibility to adapt to the volatile nature of these assets.

5. Conclusions

This paper has introduced an intraday risk management procedure, employing one-minute interval data, for the two major cryptocurrencies. By computing VaR on a day-by-day basis, a one-minute 99% confidence level benchmark was established. This benchmark served as a reference point for evaluating the returns on the following day, with success defined as the empirical value remaining within the VaR.

The results demonstrate the effectiveness of the Multivariate Normal Inverse Gaussian (NIG) distribution in capturing the volatile behavior of assets like cryptocurrencies. Intraday data exhibit even more pronounced stylized facts than daily frequency data, making the ability to model them a competitive advantage in risk management. Moreover, from a computational standpoint, implementing these models is relatively cost-effective compared to the Generalized Hyperbolic Distribution.

This study also highlights potential areas for future research. Specifically, it raises questions about the extreme behavior observed on certain dates when the algorithm failed to converge. Exploring heavy-tail distributions and extreme value theory may provide solutions to modeling such episodes and identifying intraday bubble events. The detection of critical dates with extreme behavior is a significant result that warrants further investigation.

Lastly, the successful adjustment of the model for 2021 and 2022 suggests that this approach is promising for diversification techniques. Incorporating diverse assets may be the solution for enhancing the diversification of cryptocurrency portfolios. However, challenges related to data manipulation and standardization could restrict the model’s application. Nevertheless, the evidence from this research supports the consideration of this technique by both practitioners and academics.