Pool boiling heat transfer is recognized as one of the most effective heat transfer methods and has extensive applications in industry. The application of non-azeotropic binary mixtures can not only meet the environmental requirements of modern industrial development, but also improve the coefficient of performance (COP) of many systems. Therefore, studying the boiling heat transfer characteristics of non-azeotropic mixtures is important on improving their potential industrial application. This article selected ethylene glycol/deionized water (EG/DW) at varies concentration as the research working fluids, and conducted experimental research on the pool boiling performance. At the same time, the thermophysical parameters of the mixtures were studied and analyzed. The results showed that the concentration of EG in the mixture had a significant impact on the thermal properties and temperature glide of the mixture, where both affected the heat transfer deterioration. Based on experimental data, six widely used heat transfer coefficient prediction correlations were used for calculation, and two of them were modified. The deviation between the modified correlations and the experimental results remained within 20%.

Keywords:

Subject: Engineering - Energy and Fuel Technology

1. Introduction

Boiling heat transfer, especially phase change boiling heat transfer, is an indispensable way of heat dissipation in industrial technology development. This has been discussed by a significant number of authors in literature [1,2,3]. Due to the development of small heat dissipation devices such as chips, how to obtain more efficient heat transfer performance has become a research hot spot in the field of boiling heat transfer. Heat transfer coefficient(HTC) is at the heart of our understanding of highly efficient boiling heat transfer. The bigger HTC under the same heat flux means the smaller heated surface area it needs.

Previous studies have almost exclusively focused on heat transfer enhancement of pure working fluids. Bang et al.[4] prepared R113 refrigerant with CuO nanoparticles to achieve a maximum 29.7% enhancement in HTC. Xu et al.[5] covered the heated copper rod with foam to enhance the HTC of acetone. The results all showed an increase in HTC even though the foam had different pores per inch. Tang et al.[6] explored porous interconnected microchannels for pool boiling heat transfer enhancement. The HTC of deionized water got significantly increasing. Suriyawong et al.[7] experimentally investigated the heat transfer characteristics of water separated with TiO2. A 15% increase in HTC was obtained compared with the base fluid.

However, the last two decades have seen a growing trend toward utilizing more environment-friendly working fluids[8]. In particular, the energy requirements for reducing carbon emissions are difficult to achieve for traditional pure working fluids. Furthermore, the bad thermal performance of pure refrigerants with low global warming potential(GWP) is arguably an important question to be addressed[9]. To solve this problem, mixed refrigerants have emerged as powerful potential substitutes for traditional working fluids. Not only mixtures can reduce GWP, but also can obtain merits from each component[10]. A significant advantage of multi-component solutions is that the chemical and thermophysical properties of the entire mixture can be intentionally adjusted by selecting the type and arranging the concentration of each component in the mixture. For example, the phase change temperature, physical properties, or ignition point of the mixture can be changed by adjusting the proportion of components in the mixture under constant pressure. Thereby, mixed working fluids can be customized to meet the required operating conditions.

Over time, extensive literature explored on exploring the heat transfer characteristics of binary mixtures. When the two components of a binary mixture have two different saturation boiling temperatures, it is called a non-azeotropic mixture. Non-azeotropic mixtures exhibit a temperature slip characteristic due to uneven temperature rise during boiling caused by differences in boiling points between components. This characteristic can effectively delay or even avoid the phenomenon of burning out of the cooling medium, which has critical applications for the cooling of electronic component equipment that urgently needs a small area and high heat flux dissipation. In addition, effective reduction of irreversible losses in heat exchangers (evaporators and condensers) can be obtained through the use of the temperature slip characteristic of non-azeotropic mixtures during constant pressure phase change. Since the temperature glide means a smaller temperature difference between the inlet and the outlet.

Markmann et al.[11] chose a natural working pair of ammonia/water to optimize a 50kw hybrid absorption-compression heat pump. The simulation results showed a maximum COP of 2.5. Vorster et al.[12] investigated heat pumps with different mixtures, including 34 pure refrigerants as well as 31 non-azeotropic binary mixtures at different concentrations. The conclusions addressed that many non-azeotropic refrigerant mixtures produced higher COP than pure refrigerants. The heat pump system experiments working with non-azeotropic refrigerant mixtures was provided by Zhang et al.[13], too. The results showed that all of the mixtures not only delivered higher COP, but also performed higher discharge temperature and higher heating capacity than pure working fluids.

In spite of all the advantages that mixed refrigerants have in industrial applications, their heat transfer coefficients do exhibit varying degrees of degradation compared to pure refrigerants. Jung et al.[14] carried out the boiling heat transfer experiments of the water-LiBr binary fluids. A decrease in HTC was noticed when the concentration of LiBr increased. FUJITA et al.[15] measured the HTC of a series of binary mixtures, including methanol/water, ethanol/water, methanol/ethanol, ethanol/n-butanol, and methanol/benzene. The boiling heat transfer performance of the mixtures was significantly lower than that of pure components. The author attributed this phenomenon to a large influence of change in the physical properties of mixtures. Jung et al.[16] investigated and compared the HTC of new refrigerant mixtures HFC32/HFC134a, HFC125/HFC134a and HFC32/HFC125 at various compositions. The results showed up to 40% degradation in HTC.

A further question is the factor that contributes to this degradation. The nucleate pool boiling heat transfer characteristics of ethane and isobutane and binary mixtures were investigated by Gong et al.[17] through visualization experiments and a significant reduction in HTC of the mixture was found. The authors declared that the key factor to reducing HTC is the mass transfer resistance between different components. However, the former literature on how the volume concentration of components affects mass transfer resistance is less analyzed. Although studies have been conducted by many authors, this problem is still insufficiently explored. After a review research on nucleate pool boiling of binary mixture, Gupta et al.[18] summarized that the preferential evaporation of the lighter components would influence bubble dynamics of the mixture during boiling. At the same time, the author believed that the vapor-liquid equilibrium between components played an important role in the boiling of binary mixed solutions, and understanding the thermophysical characteristics of the solution could better understand the interactions between solution components.

In order to address the questions outlined above, this article was set out to investigate the degradation in HTC of non-azeotropic mixture during pool boiling. The non-azeotropic mixtures of EG/DW at varies concentration was chosen as experimental working fluids. The boiling curves and the thermophysical properties of mixtures were measured and analyzed. Besides, the experimental data were calculated with six existing heat transfer coefficient prediction correlations, and two of them were further modifications based on the temperature glide characteristic of the non-azeotropic mixture.

2. Experiments

2.1. Experimental apparatus and procedure

An experimental setup was designed to investigate the pool boiling heat transfer performance of non-azeotropic mixtures, as shown in Figure 1. The heat load input system uses a voltage regulator to stabilize the input current while connecting to the voltage regulator, ensuring that the heating temperature increases steadily with the input heat flux density. At the same time, the input values are displayed on the power meter to ensure experimental safety and stability.

The heat load is input to an integrated heating column connected to the bottom of the reaction vessel through 7 heating rods. The heating column is made of red copper, which has characteristics of fast thermal conductivity, high-temperature resistance and uniform heating. Below the heating surface of the copper column, there are three insertion points to place K-type thermocouples for temperature collection, with a spacing of 12mm between each point. At the same time, high-temperature insulation cotton and polytetrafluoroethylene board are wrapped externally to prevent heat loss.

The boiling reaction vessel is a square container made of 5mm thick high borosilicate glass, with an external size of 10×10×10 cm3. The selection of high borosilicate glass is due to its high physical strength and fire resistance, making it more suitable for high-temperature experiments compared to ordinary glass. At the same time, observation ports are left on both sides of the glass container, which not only clearly display the bubble behavior during boiling, but also facilitate the use and adjustment of light sources at any time.

To ensure that the accuracy of the experiment will not be affected by changes in saturation pressure in the reaction vessel during boiling, the glass reflection cover above the vessel is connected to the condenser pipe and the external circulating water pump, and cooling is carried out at all times during the experiment. In addition, the glass reflective cover above the container is also connected to a specially designed high-temperature and corrosion-resistant heating rod for preheating before boiling of the working fluid. A K-type thermocouple is placed 2cm above the heating surface to measure the saturation temperature during boiling.

Except for the observation ports, the rest sides of the vessel are wrapped in high-temperature insulation material. The externally mounted ceramic electrically controlled temperature regulating heater is used as an auxiliary insulation system to ensure stability during boiling inside the container. A digital display recorder was used to connect all K-type thermocouples to collect temperature information, which has built-in software to monitor temperature changes. The recorder also is connected to the computer and uses Matlab software to process temperature data in real-time.

Before the experiment began, the heated copper surface was polished with 600 #, 800 #, and 2000 #sandpaper. Then a polishing machine was used for secondary polishing, followed by careful scrubbing with copper detergent and deionized water. Placing experimental thermocouples and high-temperature mercury thermometers in the thermal oil, and heating the thermal oil to increase the mercury thermometer by 5 ℃ until 200 ℃ each time. At the same time, the temperatures of thermocouples are recorded with the digital display recorder. Then, the temperature data will be liner-fitted by calculate software so that the temperature sensor can be rectified using the least squares method.

Firstly, inject a certain amount of experimental working fluid into the glass container to ensure that it is higher than the preheating rod, and seal the container. Mark the height of the liquid level surface to ensure the repeatability of the experiment, and leave it for 1 hour to check the sealing of the container. Next, turn on the power control system, give an initial power (usually 10w) to heat the working medium, and use a preheating heating rod to preheat the working medium in the container to saturation temperature to remove insoluble gases from the working medium. Wait for the working fluid temperature to approach the saturation boiling temperature, then open the data acquisition system for temperature recording and image recording. Subsequently, turn on the condensing device and auxiliary heating system, gradually increase the power value, and wait for the temperature sensor value to change less than 1℃ within 5 minutes before gradually increasing the heating load until it approaches the critical heat flux density.

2.2. Data reduction

Due to the integrated design of heating rod, the rapid and uniform overall heat transfer characteristic of red copper makes the entire heat transfer process of the heating surface can be regarded as one-dimensional steady-state heat conduction. By combining the real-time temperature values measured by the copper columns with Fourier’s law, the heat transfer coefficient can be calculated as following equation:

h = q / Δ T

(1)

q = λ [(T_{3} - T_{1}) / (ε_{3} - ε_{1}) + (T_{2} - T_{1}) / (ε_{2} - ε_{1}) + (T_{3} - T_{2}) / (ε_{3} - ε_{2})] / 3

(2)

∆ T = T_{w} - T_{s a t}

(3)

In the equation, T_i (i=1,2,3) is the temperature at the corresponding measurement point of thermocouple, and ε is the distance between the corresponding measurement point and the top heating surface. T_w is the temperature of heated surface, which also calculated as one-dimensional steady-state heat conduction:

T_{w} = \sum_{i = 1}^{2} [T_{i} δ - ε_{i} (T_{i + 1} - T_{i})] / 2 δ

(4)

where δ is the distance between two measurement point.

Tsat is the saturate temperature of the liquid, which is measured by the thermocouple above the heated surface. Because the two components of non-azeotropic mixture have different boiling point, the saturate temperature of the mixture is influenced by the fraction of EG. λ Is the thermal conductivity of the heating rod, which is associated with the heated surface temperature:

λ = 4.1631 - 5.904 \times 10^{- 4} \cdot T_{w} + (7.0872 \times 10^{5}) / T_{w}^{3}

(5)

2.3. Uncertainty analysis

Heat flux could be calculated through input heat load as following equation[19]:

q / A = I \cdot V \cdot \cos φ

(6)

cosφ is the error caused by the solenoid effect in the heating part, which can be seen as 1 since the voltage regulator used in this article.

The instrument will be calibrated before each experiment, and each experiment will be repeated 2-3 times. Therefore, random uncertainty brought about by the experimental process could be ignored, the uncertainty was calculated based on the instrument measurement error range provided by the manufacturer’s documents:

{∆ q}^{''} / ∆ q = {[{(∆ I / I)}^{2} + {(∆ V / V)}^{2}]}^{1 / 2}

(7)

∆ T = {({∆ T}^{2} + {∆ T}_{K}^{2})}^{1 / 2}

(8)

T_{K} = 1 / n \sum_{i = 1}^{n} T_{K, i}

(9)

{∆ h}^{''} / ∆ h = {[{(∆ I / I)}^{2} + {(∆ V / V)}^{2} + {(∆ T / T)}^{2}]}^{1 / 2}

(10)

TK is the average measurement value of thermocouples. Based on the measurement data, the parameter range and calculation uncertainty of experiments were listed in Table 1.

In order to verify the reliability of the experimental system, widely studied deionized water was selected for pool boiling experiments, and the experimental results were applied to the Rohsenow[20] equation for comparison:

c_{p} \cdot ∆ T / h_{f g} = C_{s f} {q / μ \cdot h_{f g} {[σ / g \cdot (ρ_{l} - ρ_{v})]}^{1 / 2}}^{0.33} {(c_{p} \cdot μ / λ)}^{n}

(11)

Csf is the empirical constant of heat transfer between solids and fluids, which is 0.013 for water and smooth plane. Comparing the experimental results with the calculated heat flux, as shown in Figure 2, it can be found that the deviations are all within 10%, indicating the reliability of the experimental bench.

3. Results and discussion

3.1. Pool boiling heat transfer performance

The pool boiling performance of EG/DW non-azeotropic mixture was shown in Figure 3. It could be seen from the figure that for the same heat flux, the HTC of mixture decreased with the escalate of EG concentration. What is more, the decrease sharply grown when heat flux increased. When EG weight fraction was 10%, the difference of HTC between DI water and the mixture was near 2 as heat flux was 100kw/m2. Although this difference became higher than 5 when heat flux enhanced to 300kw/m2. When the EG volume fraction increased to 50%, the HTC difference expanded into 20. This heat transfer degradation phenomenon was consistent with previous literature research on the boiling of binary mixtures.

Figure 4 showed that the increasing volume fraction of EG in the mixtures also enlarged the wall superheat temperature. This indicated that if the working fluids want to transmit the same amount of heat, the higher concentration of EG, the higher temperature that the heating surface needed to reach, and the greater input heat load that needed to be consumed. Especially when heat flux was 300.64kW/m2, the mixture with 50% EG needed 20K larger superheat compared to DI water. The temperature glide of mixtures when boiling started were plotted in Figure 5. According to the visualization results, the growing volume fraction of EG also amplified the saturate temperature of mixtures. The delay in the onset temperature of boiling implied that greater input power was required to cause boiling to occur. Similarly, this phenomenon also means that the interactions between the components in the mixture cause significant changes in the properties of the mixture even before boiling occurs.

3.2. Thermophysical properties

In order to investigate the reasons for the decrease in boiling performance, the surface tension and static contact angle of the binary mixtures were measured, as shown in Figure 6. As the concentration of EG increased, the surface tension and contact angle of the mixtures both decreased. The difference lies in that the surface tension continuously reduced with the addition of EG, but the contact angle no longer significantly changed when the EG volume fraction was greater than 50%. The value of contact angle fluctuated until the mixture became pure working fluid EG. The factor that contributes to this situation may be the addition of EG into pure water enriches molecule aggregation on the surface since the polarity of ethylene glycol molecules is strong. The aggregation leads to a negative increase in surface excess at the solid-liquid interface of the mixture, which would reduce the surface tension and enlarge wettability, thereby promoting a decrease in contact angle. As the concentration of EG continues to grow, the decreasing molecular diffusion rate results in the decrease of surface tension decline rate. Subsequently, the scale-down on contact angle of mixtures no longer continues.

According to most previous studies on pool boiling, the decline in surface tension and contact angle usually improves the boiling performance of working fluids. However, the results of the EG/DW pool boiling experiments showed the opposite performance. This indicates that the pool boiling process of a non-azeotropic mixture is different from that of pure working fluids. Two different components and variable concentrations make the boiling process of non-azeotropic mixtures more complex. By querying the ASHRAE2005, some physical parameters of the EG/DW mixture working fluids were obtained, as shown in Figure 7.

It could be seen from the figure that the volume fraction of EG had a significant influence on the thermophysical properties of mixtures. What is more, the thermal conductivity and specific heat capacity both declined with the growth of EG while the viscosity constantly escalated. This may be the factor that contributes to the degradation of boiling performance. The larger wettability between the liquid-solid surface can produce smaller bubbles during boiling, which indicates higher bubble departure frequency. However, the increased viscosity of the mixture may have an impact on the bubble detachment speed. Figure 8 depicted the dynamic contact angle of binary mixtures to exhibited the hysteresis of non-azeotropic mixtures.

Increasing the volume fraction of EG did not significantly affect the advancing angle of the mixtures. So that when the temperature reaches saturation temperature, all mixtures start saturating boiling, and forming bubbles. Moreover, because the forward angle represents the interface three-line movement speed of liquid phase during bubble growth, there is not much difference in the initial bubble growth speed among all mixed working fluids. The receding angle of mixtures decreased continuously with the addition of EG. After reaching its minimum value at a 60% volume fraction, the receding angle showed escalation with the growing EG volume fraction. The receding angle represents the contact surface where the liquid continuously recedes during bubble growth, so its reduction also means a decrease in bubble diameter. However, since the advancing angle remained unchangeable, the reduced receding angle also enlarged the difference between them, as to the hysteresis of the solution. This hysteresis will lead to a greater pinning effect of bubbles during boiling, thereby reducing the bubble departure rate and resulting in a degradation in boiling performance.

3.3. Correlations of heat transfer coefficient

In terms of the nucleate pool boiling models, the most famous and commonly used is the Rohsenow correlation equation, whose expression is shown in equation(11). This theory is based on the boiling theory formula of forced convection heat transfer. The author believes that when saturated boiling occurs, the disturbance of bubbles caused by local forced heat transfer makes the interference of liquid flow velocity negligible, and the oscillation of bubbles becomes the key factor affecting boiling heat transfer performance. The most important parameter in this formula is the empirical constant Csf. By calculating the Prandtl number and Reynolds number and substituting different experimental data, the corresponding Csf for different interfaces and fluids can be obtained. The author was the first to set the value of Csf to a fixed value of 0.013, and experiments have shown that this value can meet the prediction of pool boiling heat transfer coefficients for most boiling fluids using water.

Although the Rohsenow correlation is based on bubble agitation theory, this part is simplified as a fixed empirical constant during calculation, and the convective effect generated by bubble agitation is not the main contribution to heat transfer during pool boiling. Therefore, on this basis, Mikic and Rohsenow reconsidered the impact of bubble dynamics on boiling performance and modified the model with the nuclear bubble diameter parameter[21], as shown in equations (12) to (14).

q = C_{1} \frac{r_{s}^{m}}{\sqrt{π} 2^{m - 1}} {(k ρ c)}_{l}^{1 / 2} {(\frac{h_{f g} ρ_{v}}{T_{s a t} σ})}^{m} \sqrt{f} D_{b}^{2} {∆ T}^{m + 1}

(12)

D_{b} = C_{2} {[\frac{σ g_{0}}{g (ρ_{l} - ρ_{v})}]}^{1 / 2} {J a}^{5 / 4}

(13)

f D_{b} = C_{3} {[\frac{σ g_{0} g (ρ_{l} - ρ_{v})}{ρ_{l}^{2}}]}^{1 / 4}

(14)

C1 is a dimensionless number which can be seen as 1/unit. C2 is an empirical parameter as 1.5×10-4 for water, 4.65×10-4 for other liquids. C3 is an empirical parameter as 0.6. rs is the active cavity radius in the area corresponding to the number of bubble nucleate points. m is an empirical parameter, ranging from 0.5 to 1. Ja is the Jacob number. g0 is the conversion coefficient as 4.17 × 108 lbmft/hr2 lbf.

It can be found that the original M-R correlation not only relies on empirical parameters, but also has a large number of variables and complex forms. Wen and Wang[22] simplified the original M-R formula and modified it with Wang and Dhir’s correlation formula for the number of active nucleation sites[23], which is based on the contact angle between the working fluid and the heating surface. The modified formula was shown in equations(15) to (17):

q = B {[\emptyset (T_{w} - T_{s a t})]}^{m + 1} C (1 - c o s θ) μ_{l} h_{f g} {[\frac{σ}{ρ_{l} - ρ_{v}}]}^{- 1 / 2}

(15)

\emptyset^{m + 1} = (\frac{k^{1 / 2} ρ_{l}^{17 / 8} c_{pl}^{19 / 8} h_{fg}^{m - 23 / 8} ρ_{v}^{m - 15 / 8}}{μ_{l} {(ρ_{l} - ρ_{v})}^{9 / 8} σ^{m - 11 / 8} T_{sat}^{m - 15 / 8}})

(16)

B = C_{2}^{2 / 3} C_{3}^{1 / 2} (\frac{2}{π^{1 / 2} g^{9 / 8}})

(17)

Substituted the physical properties of non-azeotropic mixtures of EG/DW into the Rohsenow correlation and the new M-R correlation for calculation. Figure 9 presented the calculation results comparing with the experimental results.

From the graph, it can be seen that the experimental results deviated significantly from the predicted results of the classical correlations，especially when heat flux increased. The factors that contribute to this situation include:

The empirical constant calculated from using deionized water as the pure working fluid is not applicable to binary mixtures;
The characteristics of non-azeotropic mixture during boiling are much more complex than those of pure components.

The selection of variables in the classical correlations does not include the main factors affecting the boiling heat transfer coefficient of non-azeotropic mixture, that is, the influence of changes in the physical properties of the mixtures caused by EG volume fraction growth on its boiling.

Due to the different performance of binary mixtures and pure refrigerants during boiling, the prediction correlation for their heat transfer coefficient should also reflect the impact of each component on the overall heat transfer performance. Li [24]proposed a simple formula for predicting the ideal heat transfer coefficient of binary mixtures, as shown in equations (18) and (19):

h_{i d} = x h_{1} + y h_{2}

(18)

\frac{h_{i d}}{h_{e x p}} = 1 + K

(19)

Among them, x represents the mole fraction of the volatile phase, while y represents the mole fraction of the non-volatile phase during vapor-liquid phase equilibrium. And the deterioration factor K has been defined, which can more intuitively display the trend of the difference between the ideal heat transfer coefficient and the actual heat transfer coefficient. Substituting experimental values, the calculated heat transfer coefficient was shown in Figure 10.

It could be seen that as the volume fraction of EG increased, the deviation between experimental data and calculated data gradually increased. In addition, this deviation continue to enlarged with the growth of heat flux. The reason for this phenomenon is that although the ideal equation considers the influence of component proportion on the mixture, it ignores the interaction between components caused by concentration differences. Unlike pure working fluids, only the volatile component (DW) in non-azeotropic mixtures evaporates and produces bubbles during boiling. The concentration of liquid phase at the vapor-liquid interface changes constantly, which not only affects mass transfer resistance but also saturation temperature. Besides, the interaction between components will be amplified when the concentration of non volatile components (EG) increases or the heat flux density increases.

Stephan and Körner[25] proposed a formula as equation(20) to (22) for binary mixtures that takes into include the concentration of each pure refrigerant component and the pressure P of the mixture. The heat transfer coefficient is calculated by predicting the wall superheat temperature. Subscripts 1 and 2 represent volatile and non volatile components respectively.

∆ T_{m} / ∆ T_{i} = [1 + B_{0} |x - y| (0.88 + 0.12 \times 10^{- 5} P)]

(20)

∆ T_{i} = ∆ T_{1} (1 - y) + ∆ T_{2} y

(21)

h = q / ∆ T_{m}

(22)

Although this correlation takes into account the effects of component concentration and temperature, the temperature change only comes from the saturated boiling temperature of the pure component, making the final ideal wall superheat completely dependent on the component concentration and ignoring the changes in superheat caused by the interaction between components. In addition, the correlation parameters are simple, especially the empirical parameter B0. The recommended value for B0 is 1.53 when | x-y |<0.635 and 0.1<P<1.0 MPa, which is not suitable for a wide range of binary mixtures. However, the concept of component concentration difference introduced by the formula reflects the mass transfer driving force between binary mixtures during boiling, which is different from pure working fluid boiling and provides a computational approach for subsequent researchers.

On the basis of the Stephan correlation, Ünal[26] refined the formula parameters:

∆ T_{m} / ∆ T_{i} = [1 + {(b}_{1} + b_{2}) (1 + b_{3})] (1 + b_{4})

(23)

b_{1} = (1 - x) l n \frac{1.01 - y}{1.01 - x} + y l n \frac{y}{x} + {| x - y |}^{1.5}

(24)

b_{2} = \{\begin{matrix} 0, y \geq 0.01 \\ ({x / y)}^{0.1} - 1, y < 0.01 \end{matrix}

(25)

b_{3} = 152 {(P / P_{c})}^{3.9}

(26)

b_{4} = 0.92 {| x - y |}^{0.001} {(P / P_{c})}^{0.66}

(27)

In this correlation equation, the empirical parameter K is converted into a series of formulas related to the concentration and pressure of pure working fluid components, so that the correlation equation does not include empirical constants for a certain binary mixture or physical properties, expanding the application range of the correlation equation.

Fujita and Tsutsui[27] considered the temperature differences at the vapor-liquid equilibrium interface caused by instantaneous concentration changes. They introduced the temperature differences between dew point and bubble point temperatures during boiling to modified the prediction correlation for binary mixtures. Fujita believed that during the boiling of binary mixtures, the volatile components in the liquid phase tended to form bubbles easily. Therefore, the molar concentration Xe of the volatile components at the vapot-liquid equilibrium is always lower than the known concentration X1, which resulted in a decrease in temperature difference ∆Tw compared to the corresponding temperature difference ∆Th, as shown in Figure 11.

Therefore, in Fujita’s correlation, the temperature glide at the known molar fraction was used to replace the temperature difference at the vapor-liquid equilibrium:

h / h_{i d} = {1 + \frac{{∆ T}_{b p}}{{∆ T}_{i d}} [1 - e (- \frac{60 q}{ρ_{v} h_{f g} {[σ g (ρ_{l} - ρ_{v}) / ρ_{v}^{2}]}^{1 / 4}})]}^{- 1}

(28)

Gropp and Schlünder[28] also noticed the phenomenon of temperature glide. The difference is that Gropp chose to replace the temperature difference with the difference between the saturation temperatures corresponding to the components:

h / h_{i d} = {1 + \frac{h_{i d}}{q} [(T_{s 2} - T_{s 1}) (x - y) (1 - e (\frac{- B_{1} q}{β_{L} ρ_{l} h_{f g}}))]}^{- 1}

(29)

Where Ts2 is the saturation temperature of non-volatile phase, and Ts1 is the saturation temperature of volatile phase. B1 is an empirical constant, it is usually assumed that the heat flux at the wall is fully converted into the latent heat during vaporization, so B1 is valued as 1. βL is the mass transfer coefficient, and βL is (2~5)×10-4m/s for boiling with Reynolds number between 60 and 1000.

Substituted experimental data into the four prediction correlations mentioned above for calculation, and the results were plotted as shown in Figure 12.

It can be seen that the experimental results did not fit well with several correlations. The Stephan and Ünal correlations took into account the mass transfer resistance caused by concentration , which was suitable to non-azeotropic mixtures. Most of the data also conformed to the optimal accuracy range of the formula itself (22%~38%). However, the calculated heat transfer coefficient was always higher than the experimental value since the value of wall superheat temperature from correlations was smaller than the actual one, resulting in lower accuracy than expected.

The fitness of the Groppe correlation could be maintained within 20% at low heat flux. Nonetheless, as the heat flux grew, the calculated heat transfer coefficient gradually exceeds the experimental results. On the contrary, the Fujita correlation, where the experimental results were consistently higher than the calculated results, can not meet the accuracy requirements either.

Inoue[29] proposed the local temperature and the bulk temperature caused by differences in component concentration during the boiling of binary mixtures. When the solution reaches its boiling point, the concentration and temperature of the solution are in a stable state. At this time, the concentration of volatile components is X1, and the corresponding temperature Tbulk. After the heat flux start to increases, bubbles begin to form on the nucleate point, the liquid phase concentration gradually decreases compared to the initial concentration, and the local temperature gradually increases.

From Figure 13, it can be seen that the difference between the Tbulk and the Tw is the maximum temperature difference during boiling, which is always greater than the temperature difference between the bubble and dew point temperature. Therefore, the heat transfer coefficient obtained from the experiment is always higher than the calculation result of Fujita correlation. When the concentration of volatile component hit the minimum value Xmin, it corresponds to the maximum local temperature. Therefore the concentration of volatile component X2 should be within the range between X1 and Xmin. However, this concentration is unknown. So it is necessary to use the known concentration and its temperature difference between the bubble and dew point temperature to calculate the bubble point temperature rise rate (without unit factor, S<1), and modify the ideal wall temperature difference:

{∆ T}_{i d} = T_{w} - S ∆ T_{E}

(30)

S = 1 - 0.75 e^{(- 0.75 \times 10^{- 5} \cdot q)}

(31)

Where ∆TE is the temperature difference at the dew point corresponding to the initial concentration of volatile components.

Substituted the new method for determining the wall superheat temperature into the prediction correlations of Groppe and Fujita, the results plotted in Figure 14.

It could be seen from the figure that the calculated results of the two correlation equations had a significant change in fitness with the experimental results after modifying. All of the results remained within a deviation range of 20%, which indicated that the modified correlations had better applicability for non-azeotropic mixtures.

4. Conclusions

The aim of the present research was to figure out the factors that influenced on heat transfer performance of EG/DW non-azeotropic mixtures. The boiling experimental results showed deterioration of boiling heat transfer when EG concentration increased. By measuring and analyzing the thermophysical properties, surface tension, static and dynamic contact angles of the mixtures, it was known that an increase in EG concentration can decrease the surface tension of the mixtures, thereby increasing its wettability and reducing its bubble diameter during boiling. However, the viscosity and hysteresis of the mixtures also enlarged with the increase of EG volume fraction, which hindered the growth and departure of bubbles during boiling. It, to some extent, is a major factor in the deterioration of HTC. In addition, due to the temperature slip characteristic of non-azeotropic mixtures, local concentration change would occur at the nucleate point during bubble growth. The results calculated by conventional HTC prediction correlations had a significant deviation from experimental values. Therefore, a new calculation formula for wall superheat temperature was introduced using this temperature characteristic to modify two existing correlations for binary mixtures. The comparison of calculation results showed that the deviation between the new predictive correlation and experimental values was within 20%, making it more suitable for predicting HTC of non-azeotropic mixtures.

Author Contributions

Conceptualization, Chen Xu. and Jie Ren.; methodology, Chen Xu.; software, Chen Xu.; validation, Chen Xu., Jie Ren. and Zuoqin Qian.; formal analysis, Chen Xu.; investigation, Chen Xu.; writing—original draft preparation, Chen Xu.; writing—review and editing, Chen Xu., Jie Ren. and Zuoqin Qian.; funding acquisition, Lumei Zhao. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by Hainan Provincial Natural Science Foundation of China (521MS053).

Conflicts of Interest

The authors declare no conflicts of interest.

Nomenclature

A	heating surface area (m²)
b1,b2,b3,b4	coefficients in Ünal’s correlation
B₀	empirical parameter
B₁	empirical constant
C₁,C₂,C₃	empirical parameter
C_p	specific heat at constant pressure(J·kg^-1·K^-1)
C_sf	empirical constant
D_b	bubble diameter (m)
f	bubble departure frequency
g₀	conversion coefficient (lb_mft/hr² lb_f)
g	gravitational acceleration (m·s^-2)
h	heat transfer coefficient (W·m^-2·K)
h_fg	latent heat of vaporization (kJ·kg^-1)
I	electrical current (A)
Ja	Jacob number
K	deterioration factor
m	empirical parameter
P	pressure (Pa)
P_c	critical pressure of volatile component (Pa)
q	heat flux (kW·m^-2)
r_s	active cavity radius
S	coefficient affected by a heat flux
∆T	superheat temperature (K)
∆T_bp	temperature glide (K)
∆T_E	temperature difference between boiling and dew points (K)
T_bulk	boiling temperature before bubble occurring (K)
T_i	temperature at the corresponding measurement point of thermocouple (K)
T_k	average temperature of three thermocouples (K)
T_local	boiling temperature near nucleate cavity (K)
T_sat	saturate temperature of mixture (K)
T_w	temperature of heated surface (K)
V	electrical voltage (V)
x	mole fraction of the volatile phase
X	mole fraction of the volatile phase during boiling
y	mole fraction of the non-volatile phase
Greek symbols
β_L	mass transfer coefficient (m·s^-1)
δ	the distance between two measurement point (m)
ε	distance between the corresponding measurement point and the top heating surface (m)
θ	static contact angle (°)
λ	thermal conductivity (W·m^-1·K^-1)
μ	dynamic viscosity (mPa·s)
ρ	density (kg·m³)
σ	surface tension (mN·m^-1)
φ	phase difference between voltage and electrical current
Subscripts
sat	saturation
exp	experimental
id	ideal
1	volatile component
2	less volatile component
c	critical
i	serial number of temperature measurement points
l	liquid phase
v	vapor phase

References

M. Song, J. Zhengyong, D. Chaobin, J. Yuyan, S. Jun, and L. Xiaoyan, “Mathematical modeling investigation on flow boiling and high efficiency heat dissipation of two rectangular radial microchannel heat exchangers,” International Journal of Heat and Mass Transfer, vol. 190, p. 122736, Jul. 2022. [CrossRef]
H. Chen et al., “Advance and prospect of power battery thermal management based on phase change and boiling heat transfer,” Journal of Energy Storage, vol. 53, p. 105254, Sep. 2022. [CrossRef]
X. Ma and P. Cheng, “3D simulations of pool boiling above smooth horizontal heated surfaces by a phase-change lattice Boltzmann method,” International Journal of Heat and Mass Transfer, vol. 131, pp. 1095–1108, Mar. 2019. [CrossRef]
H. Peng, G. Ding, W. Jiang, H. Hu, and Y. Gao, “Heat transfer characteristics of refrigerant-based nanofluid flow boiling inside a horizontal smooth tube,” International Journal of Refrigeration, vol. 32, no. 6, pp. 1259–1270, Sep. 2009. [CrossRef]
J. Xu, X. Ji, W. Zhang, and G. Liu, “Pool boiling heat transfer of ultra-light copper foam with open cells,” International Journal of Multiphase Flow, vol. 34, no. 11, pp. 1008–1022, Nov. 2008. [CrossRef]
Y. Tang, J. Zeng, S. Zhang, C. Chen, and J. Chen, “Effect of structural parameters on pool boiling heat transfer for porous interconnected microchannel nets,” International Journal of Heat and Mass Transfer, vol. 93, pp. 906–917, Feb. 2016. [CrossRef]
A. Suriyawong and S. Wongwises, “Nucleate pool boiling heat transfer characteristics of TiO2–water nanofluids at very low concentrations,” Experimental Thermal and Fluid Science, vol. 34, no. 8, pp. 992–999, Nov. 2010. [CrossRef]
H. Lv, H. Ma, Y. Zhao, N. Mao, and T. He, “Numerical simulation of flow boiling heat transfer characteristics of R134a/Ethane binary mixture in horizontal micro-tube,” International Journal of Refrigeration, vol. 146, pp. 126–134, Feb. 2023. [CrossRef]
R. Prabakaran, M. Salman, P. G. Kumar, D. Lee, and S. C. Kim, “Boiling of R290+CF3i mixture inside an offset strip fin plate heat exchanger,” Applied Thermal Engineering, vol. 216, p. 119070, Nov. 2022. [CrossRef]
C. Xu, Z. Qian, and J. Ren, “A Comprehensive Experimental Investigation of Additives to Enhance Pool Boiling Heat Transfer of a Non-Azeotropic Mixture,” Entropy, vol. 24, no. 11, p. 1534, Oct. 2022. [CrossRef]
B. Markmann et al., “Experimental results of an absorption-compression heat pump using the working fluid ammonia/water for heat recovery in industrial processes,” International Journal of Refrigeration, vol. 99, pp. 59–68, Mar. 2019. [CrossRef]
P. P. J. Vorster and J. P. Meyer, “Wet compression versus dry compression in heat pumps working with pure refrigerants or non-azeotropic binary mixtures for dierent heating applications,” International Journal of Refrigeration, 2000.
S. Zhang, H. Wang, and T. Guo, “Experimental investigation of moderately high temperature water source heat pump with non-azeotropic refrigerant mixtures,” Applied Energy, vol. 87, no. 5, pp. 1554–1561, May 2010. [CrossRef]
J.-Y. Jung, E. S. Kim, Y. Nam, and Y. T. Kang, “The study on the critical heat flux and pool boiling heat transfer coefficient of binary nanofluids (H2O/LiBr + Al2O3),” International Journal of Refrigeration, vol. 36, no. 3, pp. 1056–1061, May 2013. [CrossRef]
Y. Fujita and M. Tsutsui, “Heat transfer in nucleate pool boiling of binary mixtures,” International Journal of Heat and Mass Transfer, vol. 37, pp. 291–302, Mar. 1994. [CrossRef]
D. Jung, K. Song, K. Ahn, and J. Kim, “Nucleate boiling heat transfer coefficients of mixtures containing HFC32, HFC125, and HFC134a,” International Journal of Refrigeration, vol. 26, no. 7, pp. 764–771, Nov. 2003. [CrossRef]
M. Gong, Y. Wu, L. Ding, K. Cheng, and J. Wu, “Visualization study on nucleate pool boiling of ethane, isobutane and their binary mixtures,” Experimental Thermal and Fluid Science, vol. 51, pp. 164–173, Nov. 2013. [CrossRef]
P. Gupta, M. Hayat, and R. Srivastava, “A Review on Nucleate Pool Boiling Heat Transfer of Binary Mixtures,” AJW, vol. 16, no. 2, pp. 27–34, Apr. 2019. [CrossRef]
S. A. Alavi Fazel, “A genetic algorithm-based optimization model for pool boiling heat transfer on horizontal rod heaters at isolated bubble regime,” Heat Mass Transfer, vol. 53, no. 9, pp. 2731–2744, Sep. 2017. [CrossRef]
W. M. Rohsenow, “A Method of Correlating Heat-Transfer Data for Surface Boiling of Liquids,” Journal of Fluids Engineering, vol. 74, no. 6, pp. 969–975, Aug. 1952. [CrossRef]
B. B. Mikic and W. M. Rohsenow, “A New Correlation of Pool-Boiling Data Including the Effect of Heating Surface Characteristics,” Journal of Heat Transfer, vol. 91, no. 2, pp. 245–250, May 1969. [CrossRef]
D. S. Wen and B. X. Wang, “Effects of surface wettability on nucleate pool boiling heat transfer for surfactant solutions,” International Journal of Heat and Mass Transfer, vol. 45, no. 8, pp. 1739–1747, Apr. 2002. [CrossRef]
C. H. Wang and V. K. Dhir, “Effect of Surface Wettability on Active Nucleation Site Density During Pool Boiling of Water on a Vertical Surface,” Journal of Heat Transfer, vol. 115, no. 3, pp. 659–669, Aug. 1993. [CrossRef]
J. Li, L. Lin, S. Li, Z. Yang, and Y. Duan, “Experimental study on nucleate pool boiling heat transfer characteristics of R32 + R1234yf binary mixtures,” Applied Thermal Engineering, vol. 205, p. 118047, Mar. 2022. [CrossRef]
K. Stephan and M. Körner, “Berechnung des Wärmeübergangs verdampfender binärer Flüssigkeitsgemische: Berechnung des Wärmeübergangs verdampfender binärer Flüssigkeitsgemische,” Chemie Ingenieur Technik, vol. 41, no. 7, pp. 409–417, Apr. 1969. [CrossRef]
H. C. Ünal, “Prediction of nucleate pool boiling heat transfer coefficients for binary mixtures,” International Journal of Heat and Mass Transfer, vol. 29, no. 4, pp. 637–640, Apr. 1986. [CrossRef]
Y. Fujita and M. Tsutsui, “Heat Transfer in Nucleate Boiling of Binary Mixtures. (Development of a Heat Transfer Correlation).,” JSME Int. J., Ser. B, vol. 40, no. 1, pp. 134–141, 1997. [CrossRef]
U. Gropp and E. U. Schldnder, “The influence of liquid-side mass transfer on heat transfer and selectivity during surface and nucleate boiling of liquid mixtures in a falling film”.
T. Inoue, N. Kawae, and M. Monde, “Characteristics of heat transfer coefficient during nucleate pool boiling of binary mixtures,” Heat and Mass Transfer, vol. 33, no. 4, pp. 337–344, Feb. 1998. [CrossRef]

Figure 1. A scheme of experimental procedure.

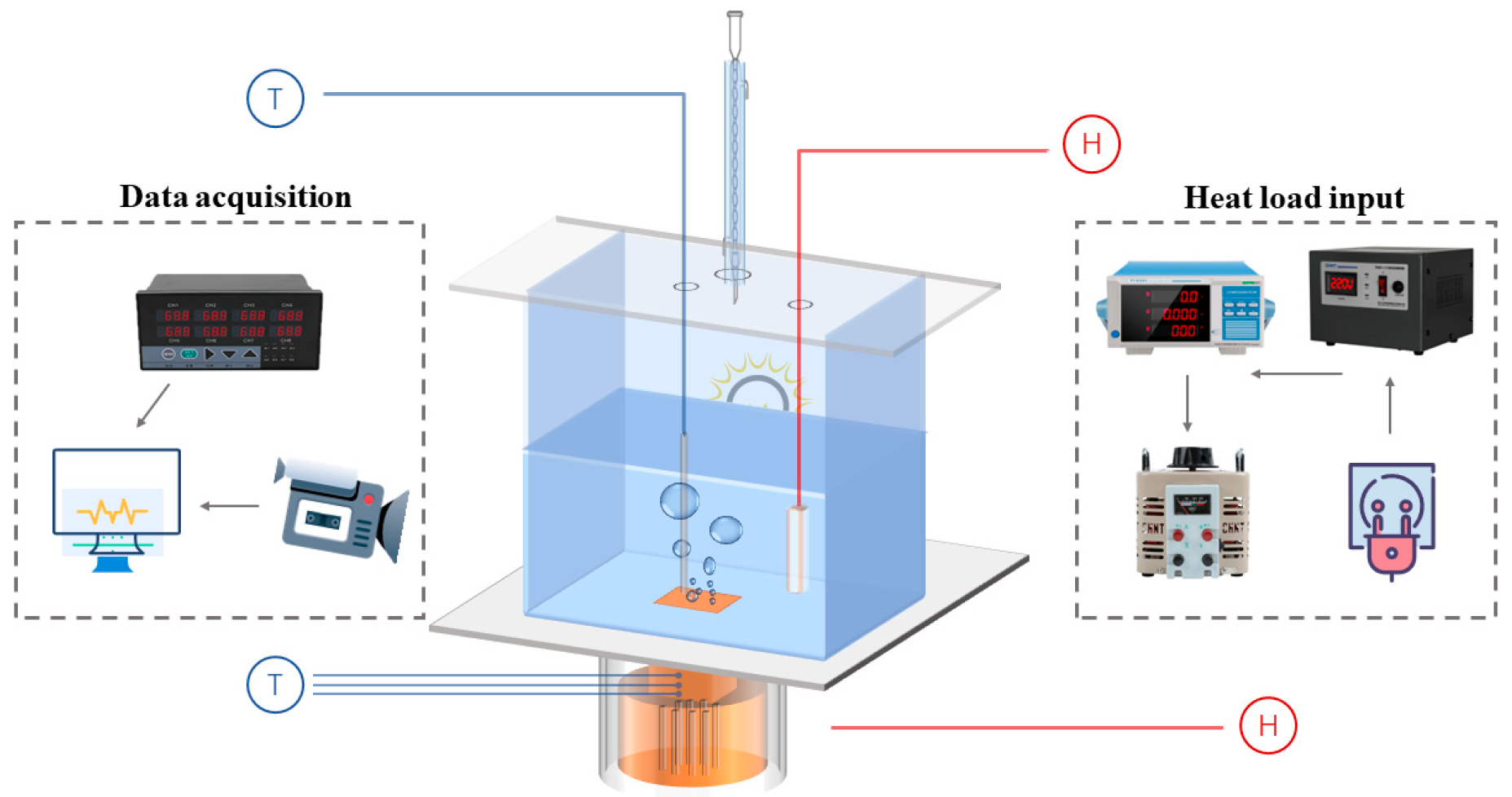
Figure 2. Reliability verification of experimental results.

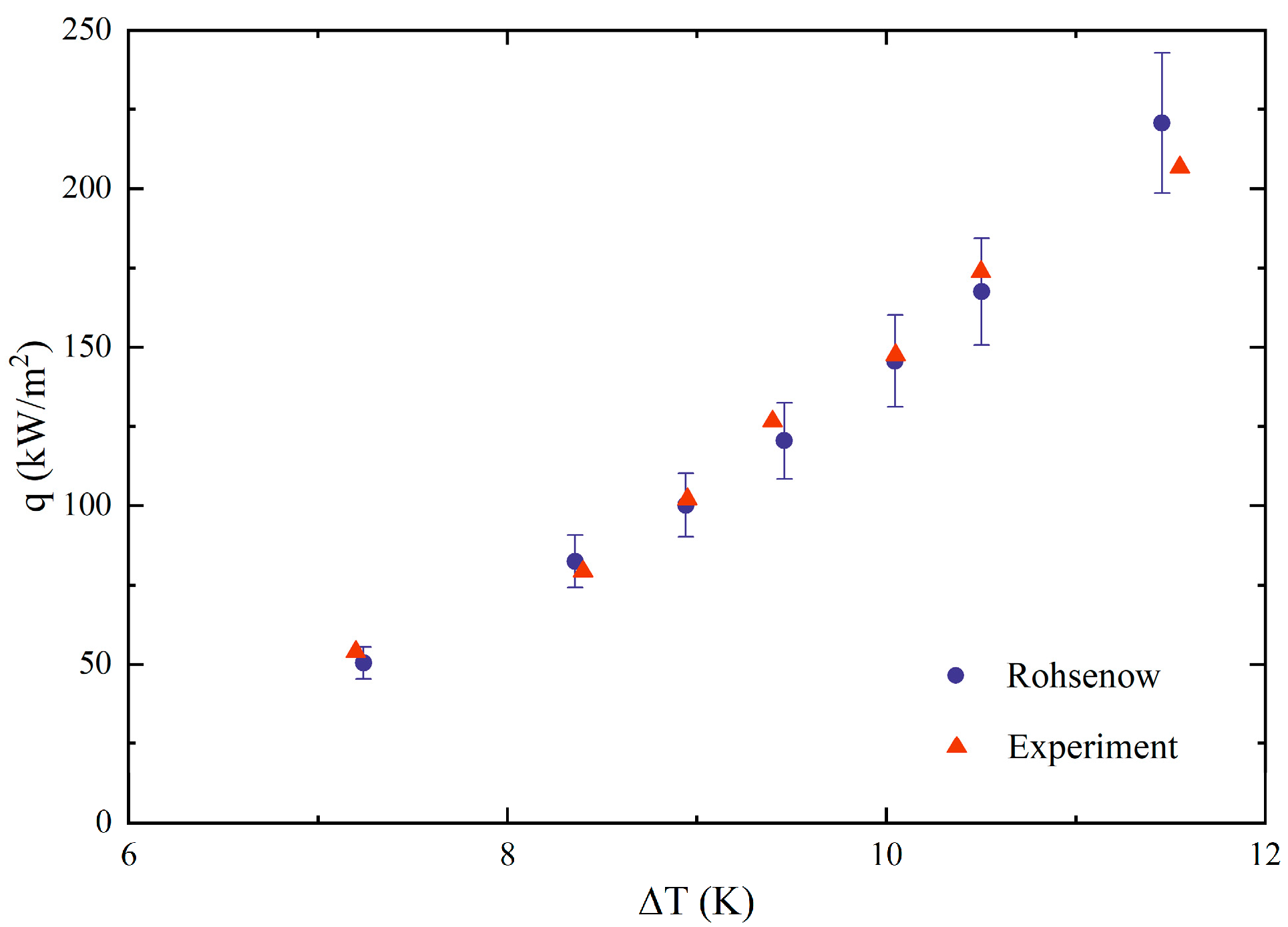
Figure 3. Heat transfer coefficient of mixture.

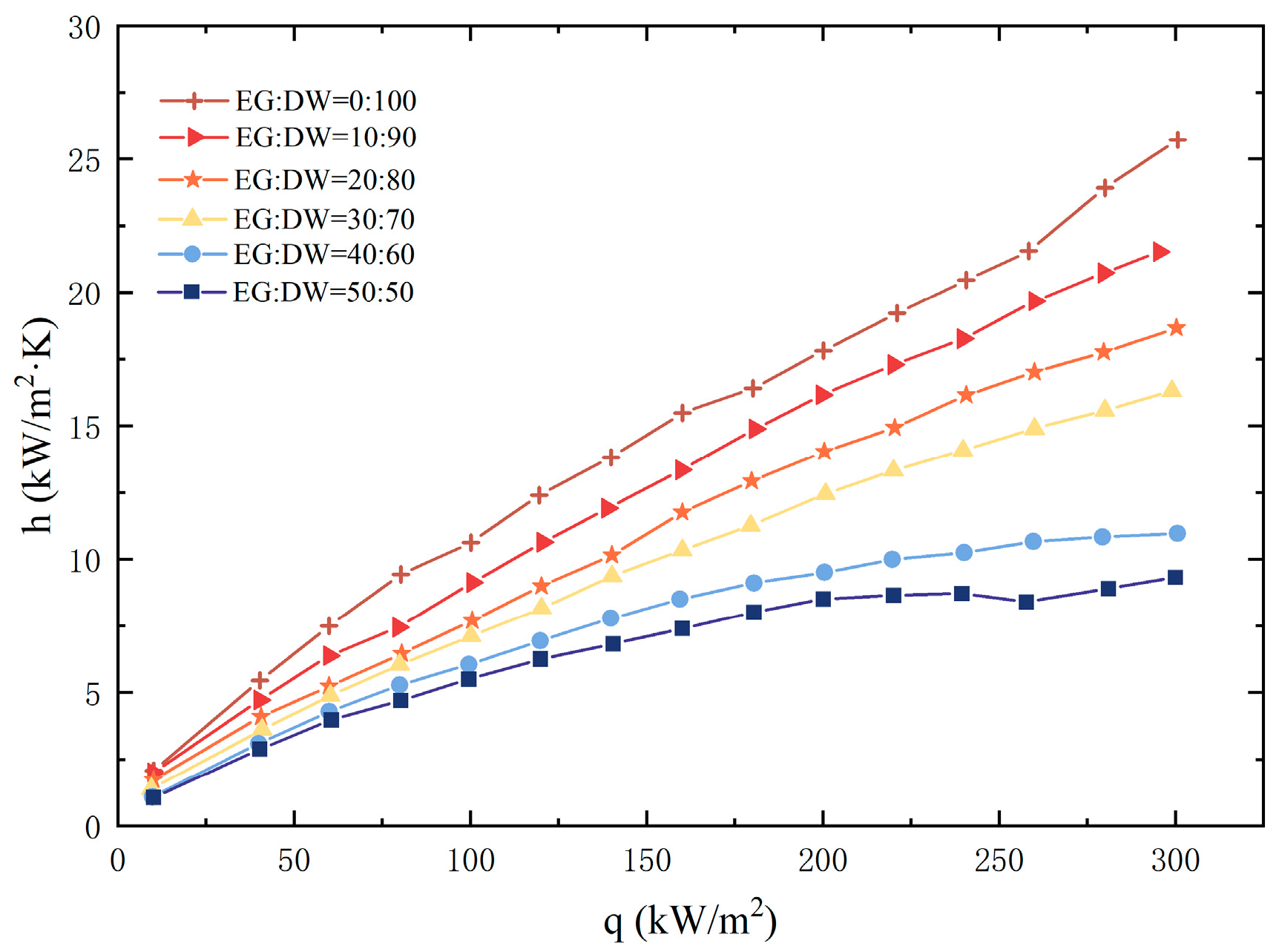
Figure 4. The influences of EG concentration on wall superheat temperature.

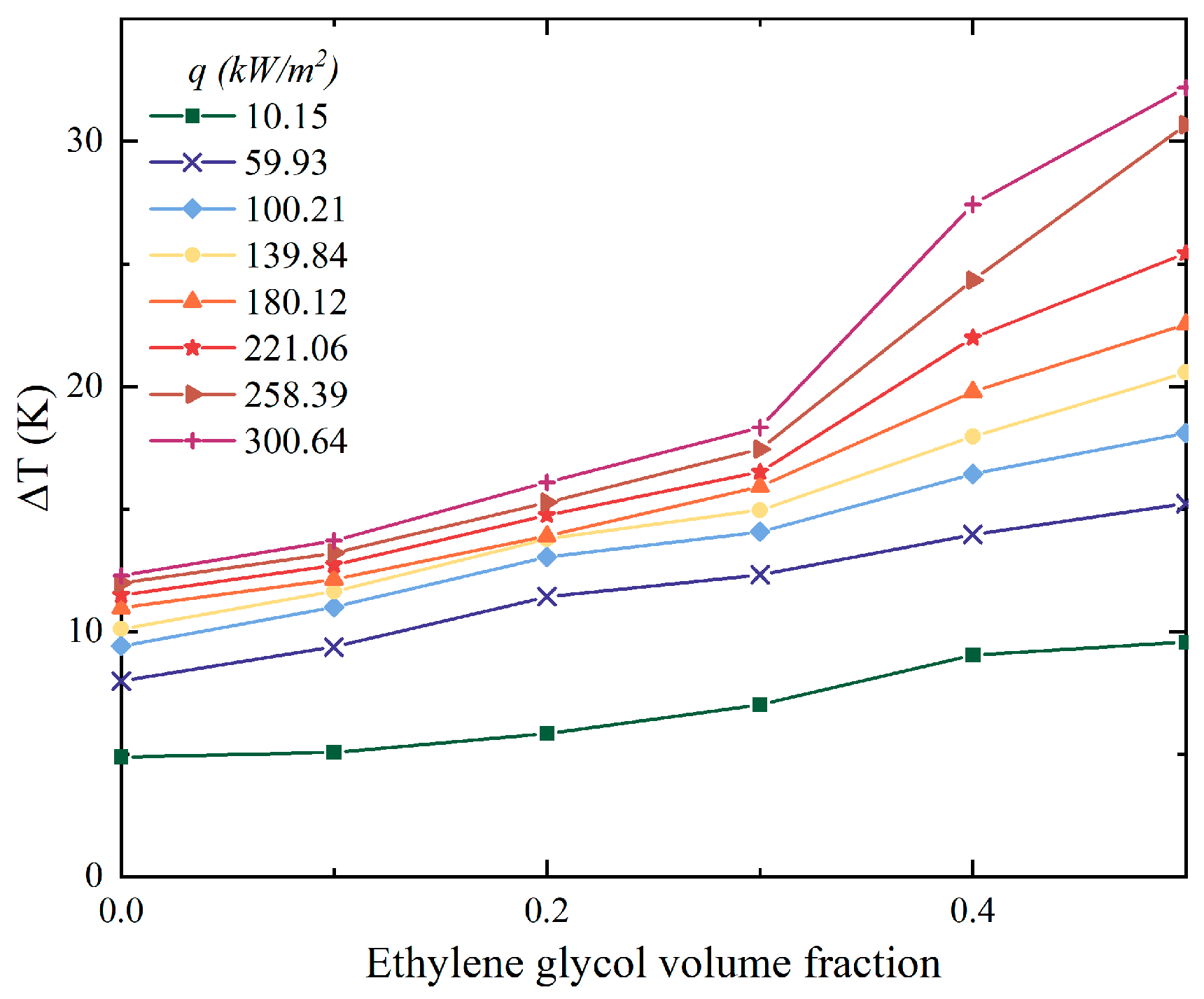
Figure 5. Temperature glide of mixtures.

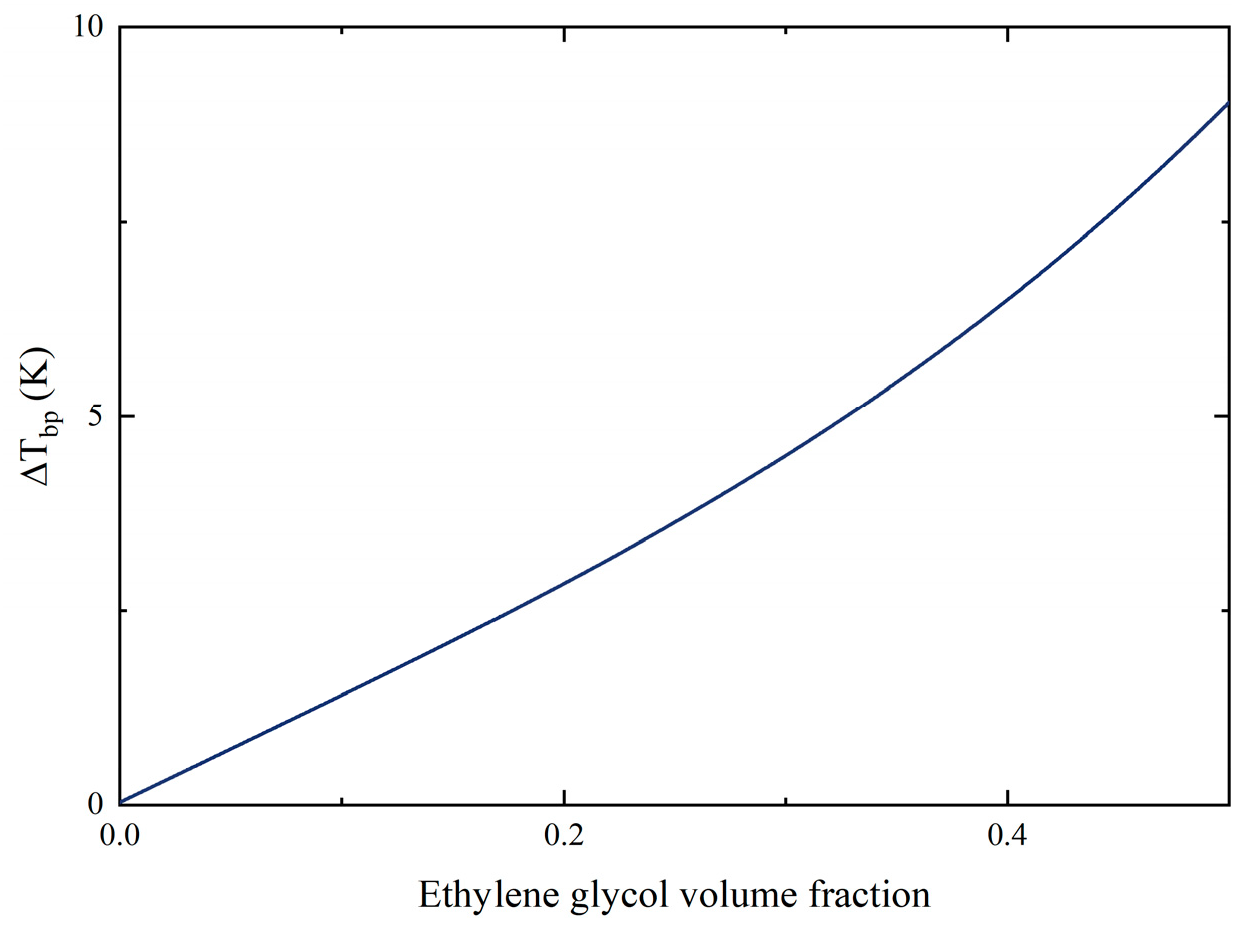
Figure 6. Surface tension and contact angle of mixtures.

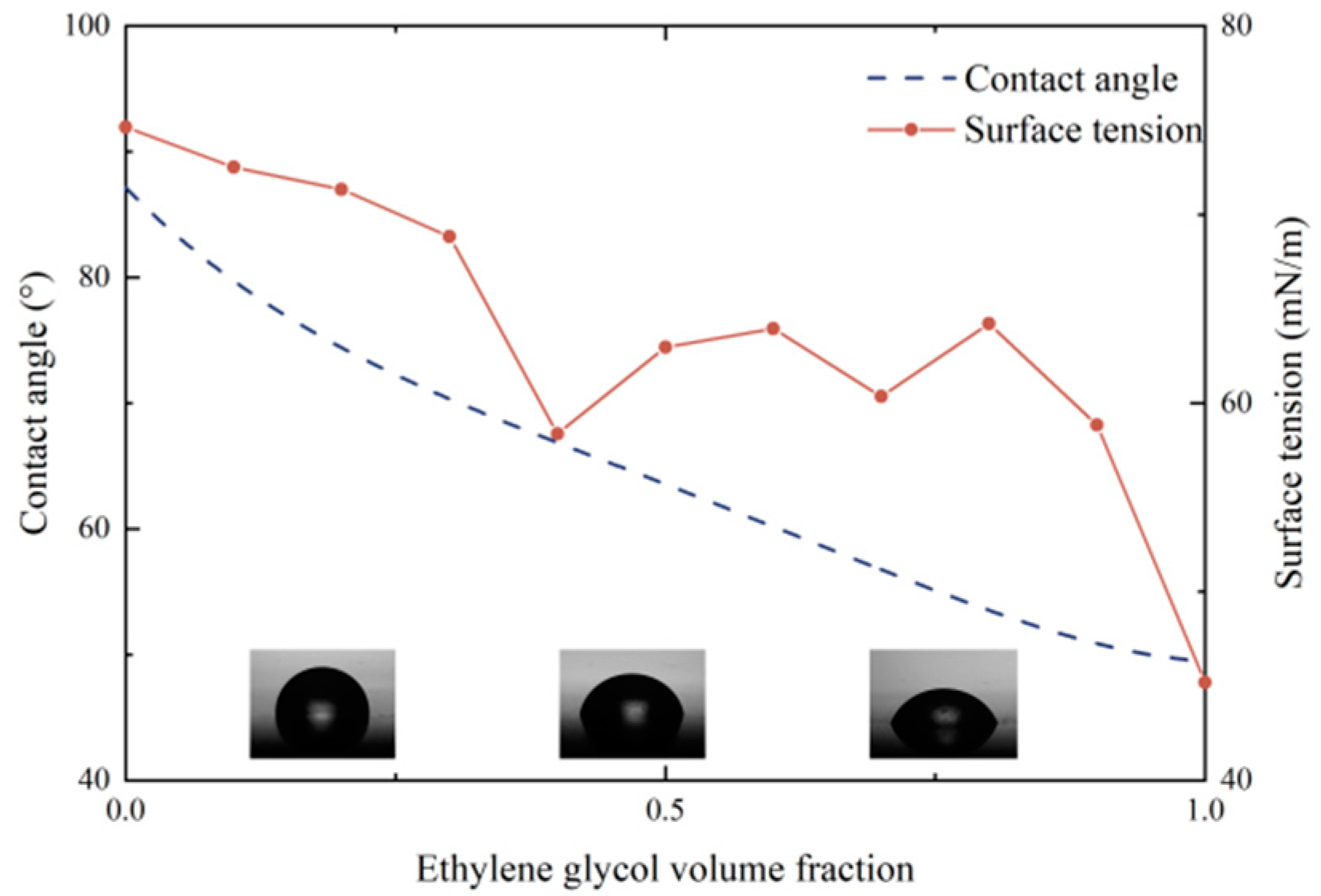
Figure 7. Thermophysical properties of mixtures.

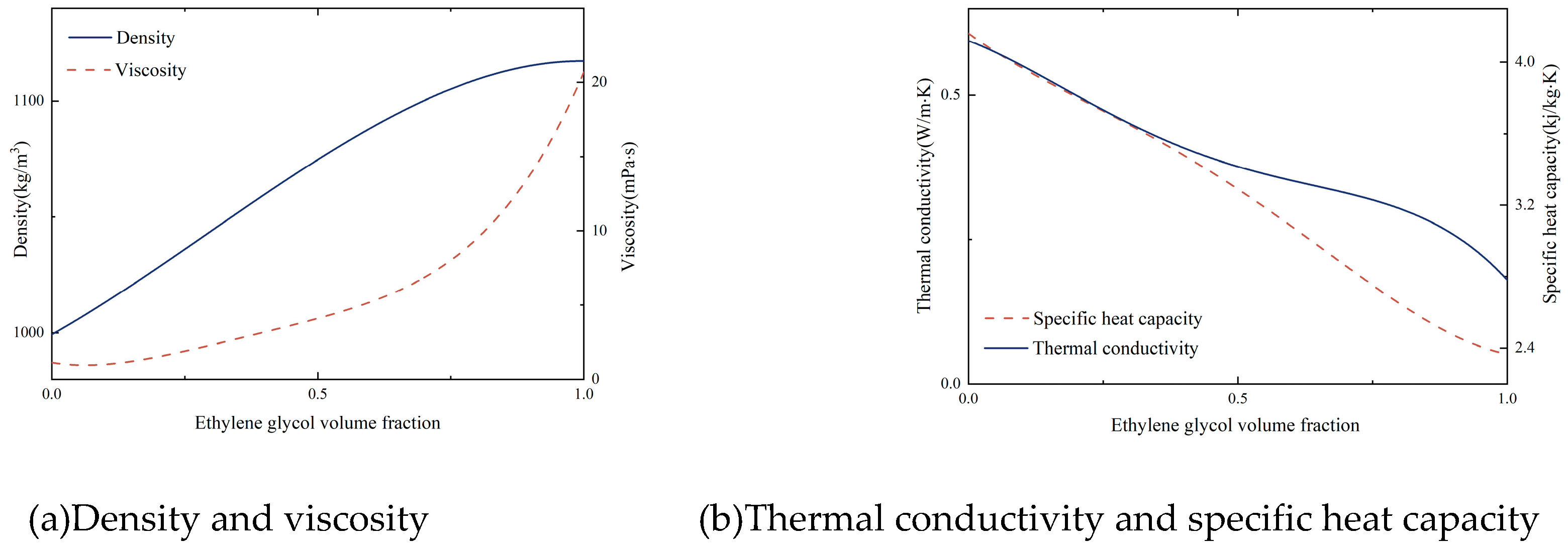
Figure 8. Dynamic contact angle of binary mixtures.

Figure 9. Comparisons of experimental data with predictions by classic correlations.

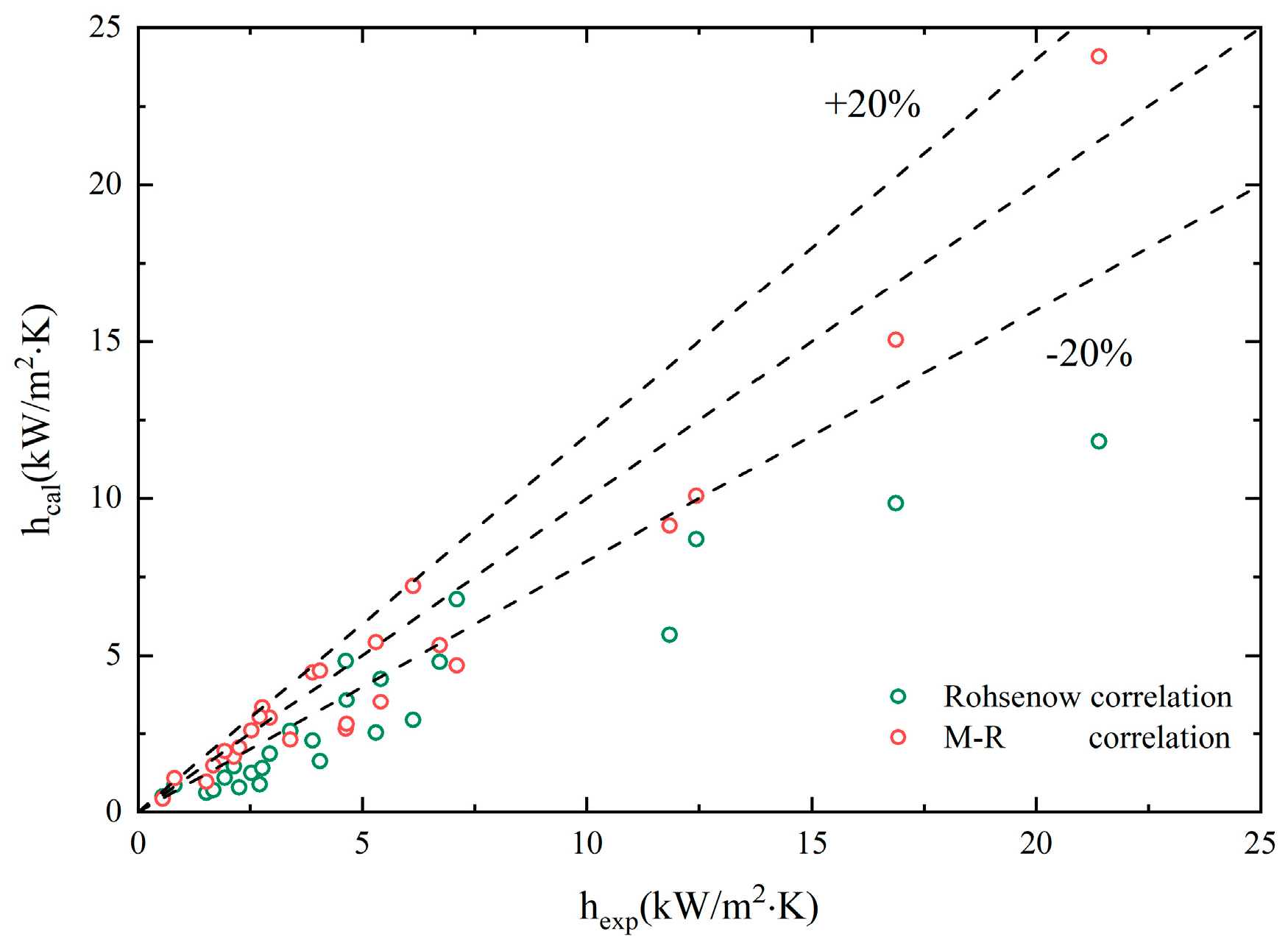
Figure 10. Comparisons of experimental data with predictions by ideal equation.

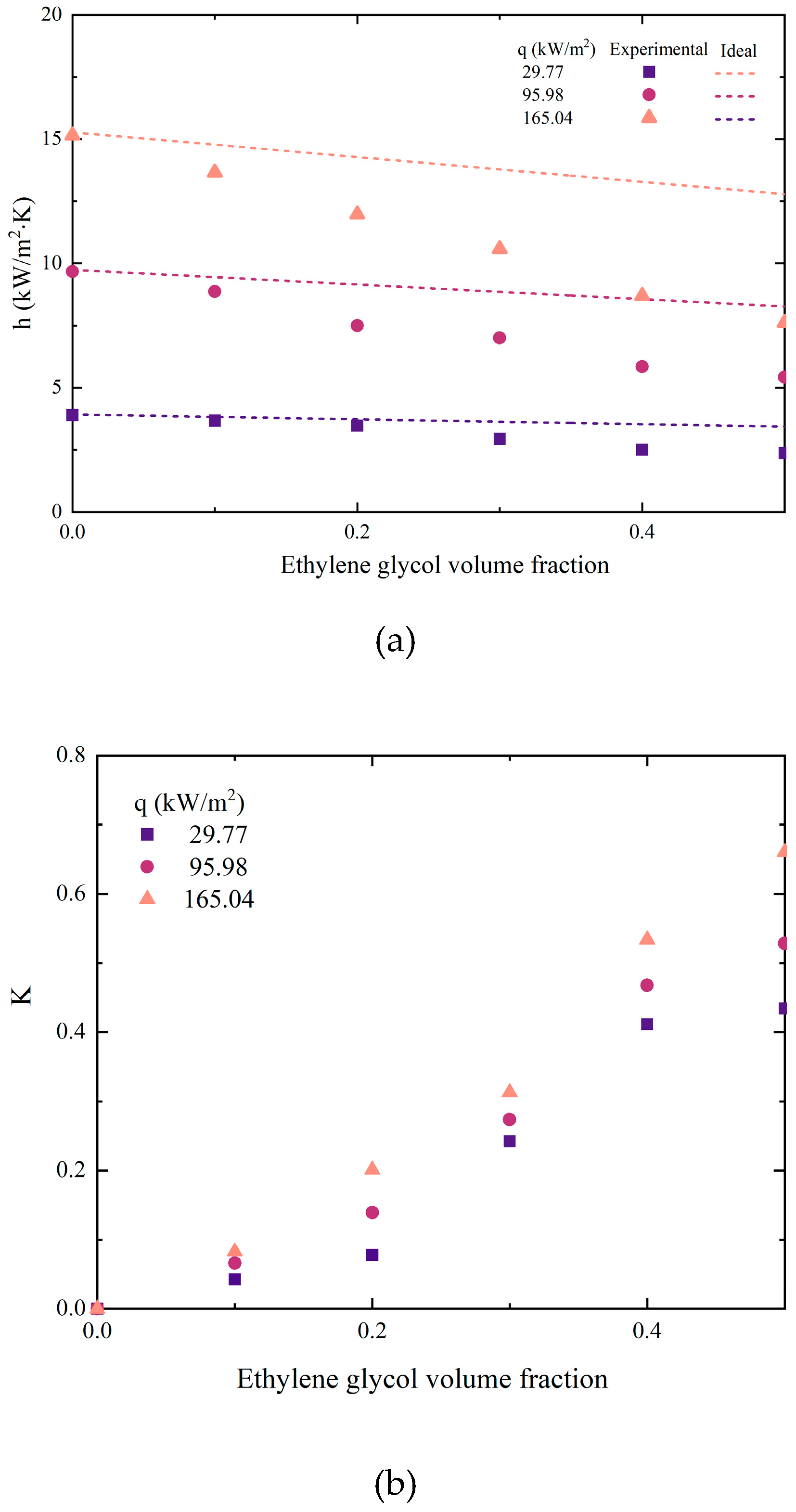
Figure 11. Bubble and dew point temperature curve.

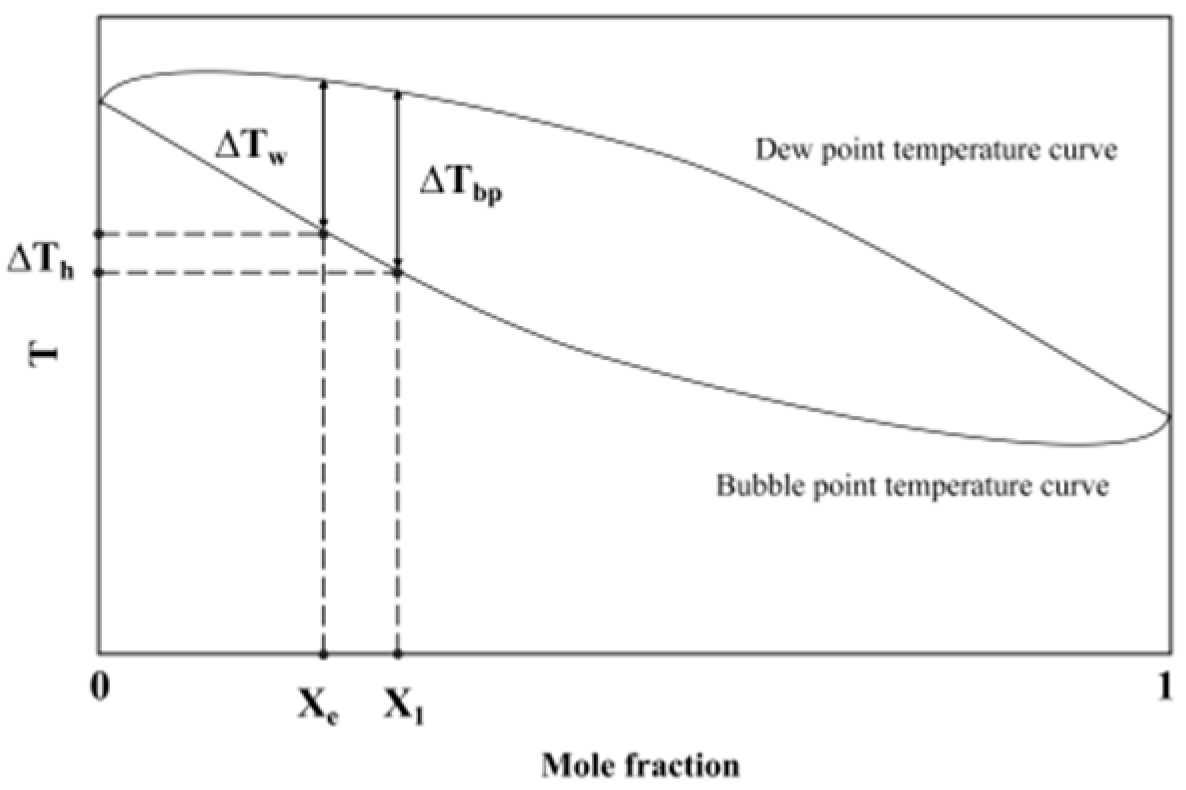
Figure 12. Comparisons of experimental data with predictions by correlations for binary mixtures.

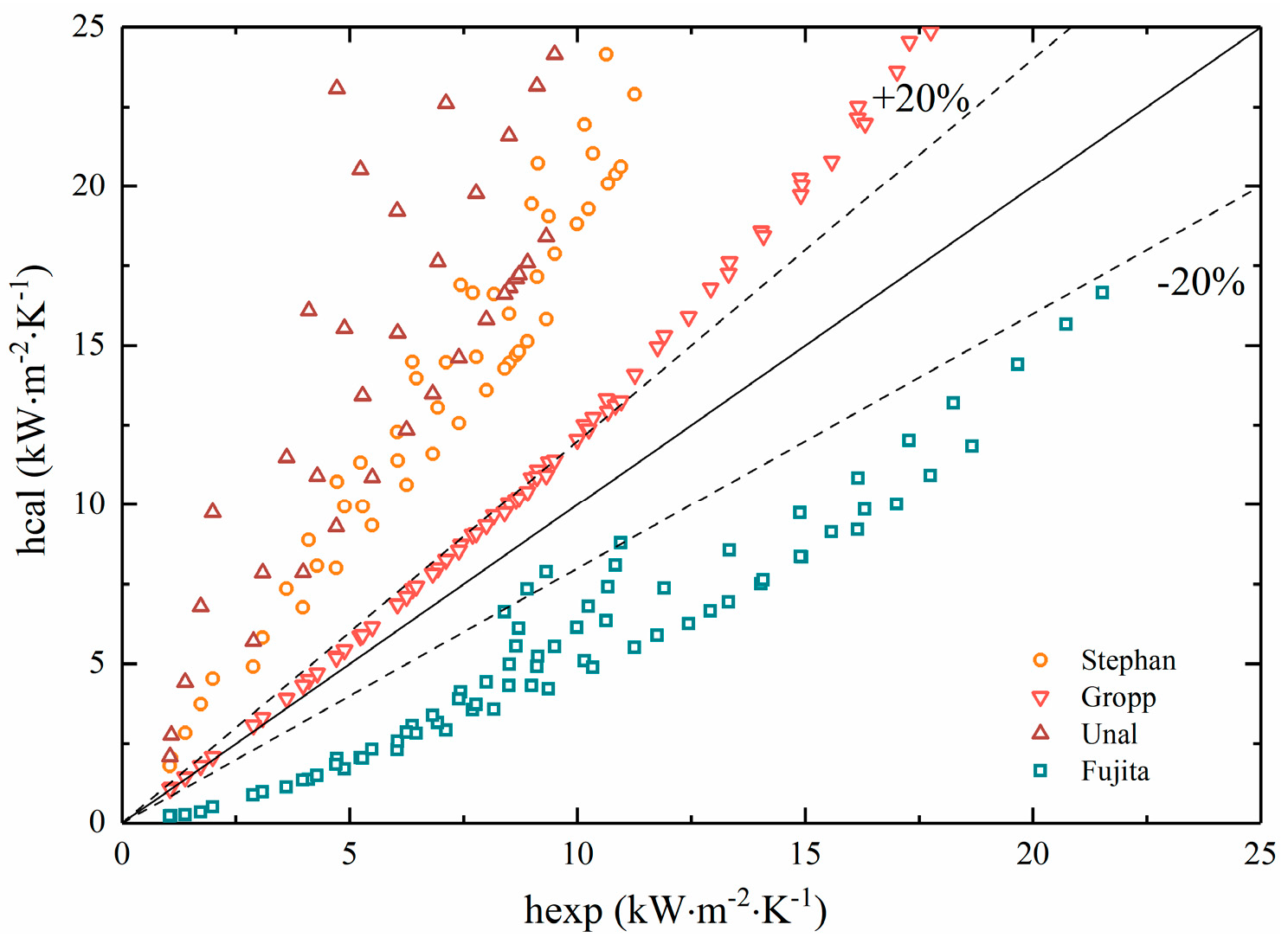
Figure 13. Schematic diagram of vapor-liquid equilibrium for binary mixtures.

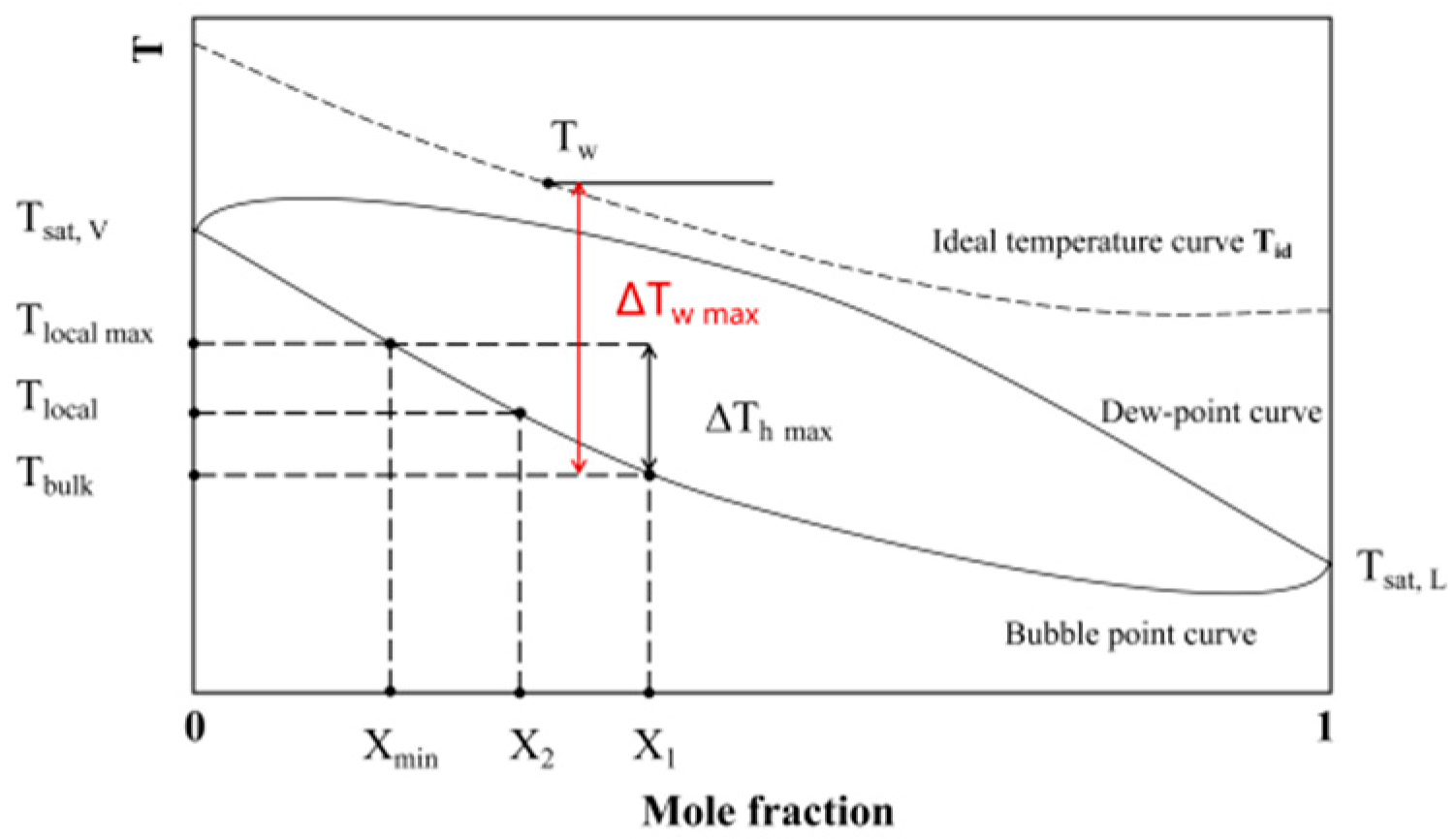
Figure 14. Comparisons of experimental data with modified predictions.

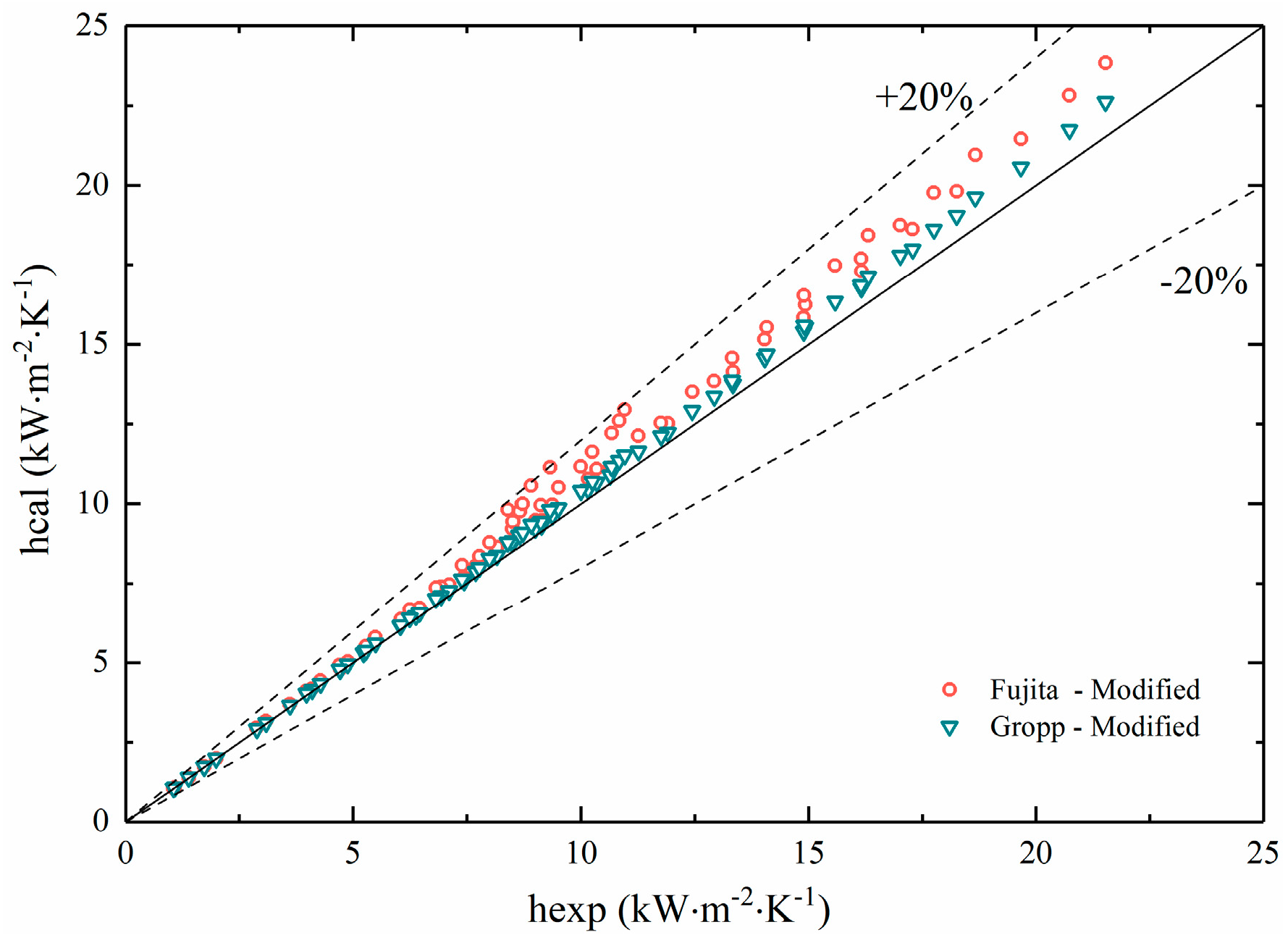
Table 1. Parameter range and calculation uncertainty.

Parameter	Range	Uncertainty
q kW/m²	8~325	1.8%~8.21%
T_w K	373~408	0.1%
T_sat K	373~382	0.1%
h kW/m²·K	0~30	2.01%~8.6%

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Investigation of Heat Transfer Performance in Deionized Water-Ethylene Glycol Binary Mixtures during Nucleate Pool Boiling

Abstract