Deep Deterministic Policy Gradient (DDPG) Agent-Based Sliding Mode Control for Quadrotor Attitudes

Preprint

Article

Deep Deterministic Policy Gradient (DDPG) Agent-Based Sliding Mode Control for Quadrotor Attitudes

Altmetrics

Downloads

125

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

16 January 2024

Posted:

16 January 2024

You are already at the latest version

Alerts

Abstract

A novel reinforcement learning deep deterministic policy gradient agent-based sliding mode control (DDPG-SMC) approach is proposed to suppress the chattering phenomenon in the attitude control for quadrotors, in the presence of external disturbances. First, the attitude dynamics model of the studied quadrotor is derived and the attitude control problem is described by formulas. Second, a sliding mode controller including its sliding mode surface and reaching law is selected for the nonlinear dynamic system, and the stability of the designed SMC system is supported by Lyapunov stability theorem. Third, a reinforcement learning (RL) agent based on deep deterministic policy gradient (DDPG) is trained to adjust the switching control gain adaptively. During the training process, the input signals of agent are the actual and desired attitude angles, and the output action is the time-varying control gain. Finally, the above trained agent is applied to the SMC as a parameter regulator, to implement the adaptive adjustment of the switching control gain related to reaching law, and the simulation results verify the robustness and effectiveness of the proposed DDPG-SMC method.

Keywords:

Subject: Engineering - Aerospace Engineering

1. Introduction

As a kind of unmanned flight platform, quadrotor UAV has the advantages of simple structure, lightweight fuselage and low cost, and is widely used in numerous tasks, such as aerial photography, agricultural plant protection, rescue and relief, remote sensing mapping and reconnaissance [1,2,3,4]. A wide range of application scenarios also put forward strict requirements for its flight control capability, especially the attitude control during the flight of UAV [4,5,6]. However, the lightweight fuselage of quadrotor leads to its poor ability to resist external disturbances, which reduces the accuracy of attitude control.

There have been many researches on attitude control methods of quadrotor. Some linear control methods such as proportional integral derivative (PID) control [7,8,9] and linear quadratic regulator [10] have been widely used in engineering practice, due to their advantages of simple structure and easy implementation. The PID and LQ methods were applied in the attitude angles control for a micro quadrotor, and the control laws were validated by autonomous flight experiments in the presence of external disturbances [11]. A robust PID control methodology was proposed for a quadrotor UAV regulation, which could reduce the power consumption and perform well in the disturbances of parameter uncertainties and aerodynamic interferences [12]. 12 PID coefficients of a quadrotor controller were optimized by 4 classical evolutionary algorithms, respectively, and the simulation results indicated that the coefficients optimized from the differential evolution algorithm (DE) could minimize the energy consumption, compared with other algorithms [7]. While linear or coefficient-optimized linear controllers may be suitable for some of the above scenarios, it is often found that the nonlinear effects of the quadrotor dynamics are non-negligible [13], and that the linear control methodologies are incapable due to the reliance on approximately linearized dynamical models. Various control approaches have been used in the quadrotors considering the nonlinear dynamics model. One of these approaches is nonlinear dynamic inversion (NDI), which can theoretically eliminate the nonlinearities of the control system [14], but this control method is on much dependence of the model accuracies [15]. The incremental nonlinear dynamic inversion (INDI) methodology was used to improve the robustness against the model inaccuracies, which could achieve the stable attitude control even the change in pitch angle was up to [16]. Adaptive control algorithm has also been widely used in quadrotor systems [17,18]. Two adaptive control laws were designed for the attitude stabilization of a quadrotor, to deal with the problem of parametric uncertainty and external disturbance [18]. A robust adaptive control strategy was developed for the attitude tracking of foldable quadrotors, which were modeled as switched systems [19].

Due to the advantages of fast response and strong robustness, the sliding mode control (SMC) methodology has been widely applied in the attitude tracking of quadrotors [20,21]. However, the problem of control input chattering is apparent, as the traditional reaching law designed in SMC. A fuzzy logic system was designed to schedule the control gains of the sign function adaptively, which could effectively suppress the control signal chattering [22].A novel discrete-time sliding mode control (DSMC) reaching law was proposed based on theoretical analysis, which could reduce the chattering significantly [23]. An adaptive fast nonsingular terminal sliding mode (AFNTSM) controller was introduced to achieve the attitude regulation and suppress chattering phenomenon, and the effectiveness of this controller was verified by experiments [24]. A fractional-order sliding mode surface was designed to adjust the parameters of SMC adaptively, in the fault tolerant control for a quadrotor model with mismatched disturbances [25].

The above researches have great reference significance. However, the control signal chattering still needs further improvement and attention, when the SMC method applied in attitude regulation with external disturbances. With the development of artificial intelligence technology, more and more reinforcement learning algorithms have been applied to traditional control methodologies [26,27].Inspired by these studies, a deep deterministic policy gradient (DDPG) [28] agent was introduced to the SMC in this paper. The parameters associated with the sign function can be regulated adaptively by the trained DDPG agent, and the phenomenon of control input chattering can be suppressed in the attitude control, in the presence of external disturbances.

The main contributions of our work are outlined as follows:

(1) A sliding mode controller is designed for attitude control for quadrotor UAV, in the presence of external disturbances.

(2) A reinforcement learning agent based on DDPG is trained to adjust the switching control gain adaptively in the traditional SMC method.

(3) The proposed DDPG-SMC approach can suppress the chattering phenomenon in the attitude control using traditional SMC method.

The remainder of this paper is organized as follows. Section 2 introduces the attitude dynamics modeling for quadrotor UAV. In section 3, the traditional SMC and proposed DDPG-SMC are designed for solving the attitude control problems. In Section 4, the robustness and effectiveness of the proposed control approach are validated through simulation results, followed by key conclusions in Section 5.

2. Attitude Dynamics Modeling for Quadrotor UAV

The quadrotor is considered as a rigid body, which attitude motion can be described by two coordinate frames, an inertial reference frame (frame I)

O_{i} x_{i} y_{i} z_{i}

and a body reference frame (frame B)

O_{b} x_{b} y_{b} z_{b}

, as shown in Figure 1. The attitude motion of the quadrotor can be achieved by the rotation of each propeller. The attitude angles can be described as

η = {[ϕ, θ, ψ]}^{T}

in the frame B, where

ϕ, θ, ψ

are the roll angle (rotation around the x-axis), pitch angle (rotation around the y-axis) and yaw angle (rotation around the z-axis), respectively. The attitude angular velocities are expressed as

ζ = {[p, q, r]}^{T}

, where

p, q, r

are the angular velocities in the roll, pitch and yaw directions, respectively.

According to the relationship between the angular velocities and the attitude rate, the attitude kinematics equation of the quadrotor can be expressed as follows [29]:

\dot{η} = Φ (η) ζ

(1)

where

Φ (η) = [\begin{matrix} 1 & \tan θ \sin ϕ & \tan θ \cos ϕ \\ 0 & \cos ϕ & - \sin ϕ \\ 0 & \sec θ \sin ϕ & \sec θ \cos ϕ \end{matrix}]

(2)

The attitude dynamics equation of the quadrotor can be written as follows [30]:

J \dot{ζ} + ζ \times (J ζ) = τ

(3)

where

J = diag (J_{x}, J_{y}, J_{z})

J_{x}

J_{y}

and

J_{z}

are the moments of inertia along

O_{b} x_{b}

O_{b} y_{b}

and

O_{b} z_{b}

axes, respectively;

τ = {[L, M, N]}^{T}

denotes the control inputs,

L

M

and

N

are the control torques in the roll, pitch and yaw directions, respectively. The control inputs

τ

developed by the four propellers can be defined as follows [31,32]:

τ = [\begin{matrix} L \\ M \\ N \end{matrix}] = [\begin{matrix} l (M_{2} - M_{4}) \\ l (M_{3} - M_{1}) \\ \frac{d}{b} (M_{1} - M_{2} + M_{3} - M_{4}) \end{matrix}]

(4)

where the parameter

b

denotes the lift coefficient, the parameter

d

represents the drag coefficient, the parameter

l

is the length between the quadrotor’s center of mass and the rotation axis of any propeller, and

M_{i} (i = 1, 2, 3, 4)

represents the thrust force provided by the ith propeller.

When the external disturbances are taken into account, the attitude dynamics equation (3) can be rewritten as

J \dot{ζ} = - ζ \times (J ζ) + τ + τ_{d},

(5)

where

τ_{d}

denotes the external disturbances.

3. Control Design for Attitude Control

In view of the attitude control in the presence of external disturbances, a sliding mode controller including its sliding mode surface and reaching law is selected for the quadrotor dynamic system, and the stability of the designed SMC system is supported by Lyapunov stability theorem. Then a reinforcement learning agent based on DDPG is trained and applied to the above SMC method, without affecting the stability of the system.

3.1. SMC Design

In this section, a sliding mode controller is designed for the attitude regulation of the quadrotor. The control objective can be described as: the actual attitude

η = {[ϕ, θ, ψ]}^{T}

need to be regulated to the desired attitude

η_{d} = {[ϕ_{d}, θ_{d}, ψ_{d}]}^{T}

asymptotically, i.e.,

\lim_{t \to \infty} ‖η - η_{d}‖ = 0

In the controller designed process, the sliding mode surface is first selected, then the control law is chosen to compute the control signal, in the end, the stability proof of the designed SMC system is supported by Lyapunov stability theorem. The control scheme of SMC for attitude tracking is depicted in Figure 2.

The specific design of the sliding mode controller can be expressed as follows.

SMC Algorithm

Input:
(1) Desired attitude angles

η_{d}

(2) Actual attitude angles

η

(3) Model parameters of the quadrotor
Output: The control signals for attitude dynamics model
Step 1: Design of the control signal
(a) Define the sliding mode surface s
(b) Select the reaching law

\dot{s}

τ

Step 2: Proof of the stability of closed-loop system
(a) Select a Lyapunov candidate function

V

(b) Calculate the first-order derivative of

V

V

(d) Conclude the convergence of the attitude motion
Step 3: Termination
If the attitude control errors meet the requirements, conduct the algorithm termination and output the control signal

τ

. Otherwise, go to step 1 until the convergence of control errors.

Step 1 (a):

The control error can be defined as

e = η_{d} - η

(6)

Then sliding mode surface can be derived as

s = \dot{e} + ce,

(7)

where

c = diag (c_{1}, c_{2}, c_{3})

, and

c_{1}, c_{2}, c_{3}

are selected positive numbers.

The derivative of s can be expressed as

\dot{s} = \ddot{e} + c \dot{e}

(8)

Substitute Equation (1)-(3), (6) into (8), then we can obtain

\dot{s} = c \dot{e} + \ddot{e} = c \dot{e} + {\ddot{η}}_{d} - \dot{Φ} (η) ζ - Φ (η) J^{- 1} (- ζ \times (J ζ) + τ + τ_{d}),

(9)

where we can define

d = τ_{d}

(10)

Equation (9) can be rewritten as

\dot{s} = c \dot{e} + {\ddot{η}}_{d} - \dot{Φ} (η) ζ - Φ (η) J^{- 1} (- ζ \times (J ζ) + τ + d)

(11)

Assumption 1: The external disturbance

d

is assumed to be bounded and satisfies

‖d‖ \leq D,

(12)

in which

D

is a positive finite variable .

Step 1 (b):

The reaching law of the sliding mode surface can be selected as follows [33]:

\dot{s} = - λ s - k sign (s),

(13)

in which

λ

and

k

are both diagonally positive definite matrices, with

λ = diag (λ_{1}, λ_{2}, λ_{3})

, and

λ_{1}

λ_{2}

λ_{3}

are selected as positive numbers, as same as

k = diag (k_{1}, k_{2}, k_{3})

, and

k_{i}

(

i = 1, 2, 3

) is also a selected positive number, and

sign (\cdot)

represents the sign function.

Step 1 (c):

Based on the calculations of angular velocity

ζ

and transformation matrix

Φ (η)

, as well as the derivation of Equation (9) and (13), the control signal for attitude dynamics model can be designed as follows

τ = ζ \times (J ζ) + J Φ^{- 1} (η) (λ s + k sign (s) + c \dot{e} + {\ddot{η}}_{d} - \dot{Φ} (η) ζ)

(14)

Step 2:

The stability of the closed-loop system is proven as follows.

Theorem 1.

Considering the attitude dynamics system described as Equation (5), with the sliding mode surface selected as Equation (7), if the exponential reaching law is chosen as Equation (13), and the control signals for attitude dynamics model is designed as Equation (14), then the designed SMC system is stable and the actual attitude can converge to the desired attitude in finite time.

Proof of Theorem 1.

We can select a Lyapunov candidate function as

V = \frac{1}{2} s^{T} s

(15)

Based on Equation (11), take the derivative of Equation (15) with respect to time, we can obtain that

\dot{V} = s^{T} \dot{s} = s^{T} \{c \dot{e} + {\ddot{η}}_{d} - \dot{Φ} (η) ζ - Φ (η) J^{- 1} (- ζ \times (J ζ) + τ + d)\}

(16)

Then substitute (14) into (16), we have

\begin{array}{l} \dot{V} = s^{T} \{\begin{array}{l} c \dot{e} + {\ddot{η}}_{d} - \dot{Φ} (η) ζ - Φ (η) J^{- 1} \\ (\begin{array}{l} - ζ \times (J ζ) + ζ \times (J ζ) + J Φ^{- 1} (η) \\ (λ s + k sign (s) + c \dot{e} + {\ddot{η}}_{d} - \dot{Φ} (η) ζ + d) \end{array}) \end{array}\} \\ = s^{T} (- λ s - k sign (s) - d) \\ = - λ s^{T} s - k ‖s‖ - s^{T} d \\ \leq - ‖λ‖ {‖s‖}^{2} - ‖k‖ ‖s‖ - D ‖s‖ \leq 0 \end{array}

(17)

We can assume that the sliding mode surface

s = 0

and obtain the following equation:

\lim_{t \to \infty} s = \lim_{t \to \infty} (e + c \dot{e}) = \lim_{t \to \infty} \{(η_{d} - η) + c ({\dot{η}}_{d} - \dot{η})\}

(18)

Based on the selection of diagonal positive definite matrix

c

, we can obtain the following expression:

\lim_{t \to \infty} ‖η_{d} - η‖ = 0, \lim_{t \to \infty} ‖{\dot{η}}_{d} - \dot{η}‖ = 0,

(19)

Remark 1.

From (19), the designed control law (14) can guarantee the stability of the closed-loop system based on Lyapunov stability theorem. The attitude tracking error will converge to zero asymptotically, if the sliding mode surface is equal to zero. Consequently, the stability prove of the designed SMC system has been completed.

3.2. DDPG-SMC Design

The above derivations have proven that the control error can converge to zero asymptotically in the designed SMC for nonlinear system (5). However, high-frequency chattering of the control signal will appear near the sliding surface, due to the selected reaching law (13) with a sign function, and chattering intensity is determined by the parameter related to the sign function, i.e. control gain

k

Inspired by the combination of reinforcement learning algorithms and traditional control methodologies, a reinforcement learning agent based on DDPG is trained to adjust the switching control gain adaptively. During the training process, the input signals of agent are the actual and desired attitude angles, and the output action is the time-varying control gain. Then the trained agent is applied as a parameter regulator for the designed SMC, and the block diagram of designed DDPG-SMC is shown in Figure 3.

The architecture of the DDPG-based parameter regulator is shown in Figure 4.

DDPG is an algorithm to solve continuous action problem in the framework of Actor-Critic (AC) [34], where the policy network parameters are continuously optimized, so that its output action a can get higher and higher scores in the value network. In the designed DDPG-SMC approach this paper, the DDPG agent need to be trained beforehand. The described system in Figure 3 is served as training environment, and the training data are derived from multiple flight simulations.

The basic principle of DDPG algorithm can be introduced as follows.

DDPG Algorithm

Input: Experience replay buffer

D

, Initial critic networks’ Q-function parameters

θ^{Q}

, actor networks’ policy parameters

θ^{π}

, target networks

Q^{'}

and

π^{'}

.
Initialize the target network parameters:

θ^{Q^{'}} \leftarrow θ^{Q}, θ^{π^{'}} \leftarrow θ^{π}

.
for episode =1 to M do
Initialize stochastic process

N

to add exploration to the action.
Observe initial state

s_{1}

.
for time step =1 to T do
Select action

a_{t} = π (s_{t}| θ^{π}) + N_{t}

.
Perform action

a_{t}

and transfer to next state

s_{t + 1}

, then acquire the reward value

r_{t}

and the termination signal

d_{t}

.
Store the state transition data

(s_{t}, a_{t}, r_{t}, d_{t}, s_{t + 1})

in experience replay buffer

D

.
Calculate the target function:

y (r_{t}, s_{t + 1}, d_{t}) = r_{t} + γ (1 - d_{t}) Q^{'} (s_{t + 1}, π^{'} (s_{t + 1} |θ^{π^{'}}) |θ^{Q^{'}})

Update the critic network by the minimized loss function:

L = \frac{1}{B} \sum_{(s_{t}, a_{t}, r_{t}, d_{t}, s_{t + 1}) \in B} {(y (r_{t}, s_{t + 1}, d_{t}) - Q (s_{t}, a_{t} |θ^{Q}))}^{2}

Update the actor network by policy gradient method:

\nabla_{θ^{π}} J \approx \nabla_{θ^{π}} \frac{1}{|B|} \sum_{s \in B} Q_{θ^{π}} (s, μ_{θ^{Q}} (s))

Update target networks:

θ^{Q^{'}} \leftarrow ρ θ^{Q^{'}} + (1 - ρ) θ^{Q}

θ^{π^{'}} \leftarrow ρ θ^{π^{'}} + (1 - ρ) θ^{π}

end for
end for

The design of DDPG-based parameter regulator consists of two processes: training and validation. In the training process, the flight simulation of the quadrotor is carried out, and all the state and control data of the quadrotor are collected, that is, the accumulation of experience. Then, according to the accumulated experience data, the neural network parameters are optimized and updated with gradient calculation, stochastic gradient descent method and other methods. After multiple episodes of iterative training, the policy in the policy function converged to the optimal one. The validation process is used to validate the feasibility and generalization of the trained agent's optimal policy.

To train the DDPG agent to adjust the switching control gain

k

, the training episodes were set as 200, with the simulation time of each episode being 10 s and the time step being 0.02 s. Initial and desired attitude angles during the training were selected as

η_{0} = {[0.1 rad, 0.2 rad, - 0.1 rad]}^{T}

and

η_{d} = {[0.2 rad, 0.1 rad, 0.1 rad]}^{T}

, respectively. The input signals of the agent were chosen as the actual and desired attitude angles (

η

η_{d}

), and the output action was the time-varying control gain

k

The cumulative reward after each episode of training was recorded and output, and the reward at each step could be calculated using the following equation:

r (t) = - ϖ_{1} t \cdot |η (t) - η_{d} (t)|,

(20)

where

ϖ_{1}

were selected as

[\begin{matrix} 1 & 1 & 1 \end{matrix}]

The training process would be stopped when the average reward of cumulative training was less than -1 or the number of training episodes reached 200. The final training result is shown in Figure 5, it can be seen that the reward value converges to the maximum at the 170th training episodes. It indicates that the agent has completed training, and can be introduced as a parameter regulator in the above sliding mode controller.

In order to verify the generalization of the trained agent's optimal policy, it is necessary to test the control performance for the UAV model under different flight conditions. Specifically, it is necessary to evaluate the improvement of the control performance, through adjusting control parameters adaptively under different flight conditions. The relevant numerical simulation results are shown in Section 4.3.

Remark 2.

By using the designed parameter regulator based on trained DDPG agent, the switching control gain related to reaching law, can be adjusted adaptively according to the attitude control error.

Therefore, the control signal in DDPG-SMC can be represented as

τ = ζ \times (J ζ) + J Φ^{- 1} (η) (λ s + \hat{k} sign (s) + c \dot{e} + {\ddot{η}}_{d} - \dot{Φ} (η) ζ),

(21)

in which

\hat{k}

is the time-varying switching control gain related to reaching law.

4. Simulation Results

The robustness and effectiveness of the proposed control approach can be verified via flight simulation, and the model parameters of the quadrotor are depicted in Table 1.

The basic simulation conditions are described as follows. Initial attitude angles and angular velocities of the quadrotor are set as:

η_{0} = {[0.1 rad, 0.2 rad, - 0.1 rad]}^{T}

and

ζ_{0} = {[0 rad / s, 0 rad / s, 0 rad / s]}^{T}

, respectively. A desired attitude angles are selected as:

η_{d} = {[0 rad, 0.1 rad, 0 rad]}^{T}

. The external disturbances are assumed to act on the system in the form of torques:

τ_{d} = 0.005 \times {[\begin{matrix} \sin (π / 100 t) & \cos (π / 100 t) & \sin (π / 100 t) \end{matrix}]}^{T} N \cdot m

. Three control approaches including SMC, AFGS-SMC proposed in reference [22] and DDPG-SMC designed this paper, are used in the flight simulation, respectively.

4.1. Simulation Results of SMC

The relevant control parameters of sign function in SMC are designed as:

k = diag (0.2, 0.2, 0.2)

and

λ = diag (1.5, 1.5, 1.5)

. The numerical simulation results are depicted in Figure 6.

As shown in Figure 6 (a), the dashed and real lines represent the desired and actual attitude angles, respectively. The convergence time of attitude angles in three directions (roll, pitch and yaw) is 1.8 s, 2.1 s and 1.8 s, respectively, from the initial value to desired value. It indicates that the quadrotor attitude can be regulated into the desired attitude using the SMC algorithm, in the presence of disturbances.

The time histories of angular velocities and control inputs are depicted in Figure 6 (b) and (c), respectively. It can be seen that attitude angular velocities in three directions approach 0 rad/s during time periods of 2.2 s, 2.4 s and 2.2 s, respectively. Then the angular velocities oscillate slightly around 0 rad/s to keep the quadrotor system balanced.

However, the chattering of the control inputs is more severe when the control system is stabilized, and the control input signal in roll direction oscillates in the range from -0.012 N·m to 0.014 N·m, the control input signal in pitch direction oscillates in the range from -0.008 N·m to 0.016 N·m, and the control input signal in yaw direction oscillates in the range from -0.018 N·m to 0.024 N·m. Since the control input signals denote the torques produced by the quadrotor propellers, chattering at high frequencies is absolutely not allowed for the actuators of the quadrotor.

Figure 6 (d) and (e) represent the time evolutions of control gains related to reaching law, and sliding mode surfaces, respectively. It can be seen that sliding mode surfaces are converge to zero asymptotically, and the control gains are constant in entire simulation process, these constant gains result in the chattering phenomenon of control signals.

4.2. Simulation Results of AFGS-SMC

The chattering phenomenon is caused by the high frequency switching around the sliding mode surface, due to the term ksign(s) in the SMC. The adaptive fuzzy gain-scheduling sliding mode control (AFGS-SMC) method in the reference [22] is proposed to suppress the chattering phenomenon. Simulation results of this method are depicted in Figure 7.

As presented in Figure 7 (a), the dashed and real lines represent the desired and actual attitude angles, respectively. The convergence time of attitude angles in three directions (roll, pitch and yaw) is 2.2 s, 2.0 s and 2.2 s, respectively, from the initial value to desired value. It demonstrates that the quadrotor attitude can be regulated into the desired attitude using the AFGS-SMC algorithm, in the presence of disturbances.

The time evolutions of the quadrotor’s angular velocities and control inputs are depicted in Figure 7 (b) and (c), respectively. It can be seen that attitude angular velocities in three directions approach 0 rad/s during time periods of 3.1 s, 2.8 s and 3.1 s, respectively, and the oscillation is much less. Different from the results in SMC, the chattering phenomenon of the control input is significantly reduced.

Figure 7 (d) and (e) represent the time evolutions of control gains related to reaching law, and sliding mode surfaces, respectively. It can be seen that sliding mode surfaces are converge to zero asymptotically, and the control gains are adjusted by the associated fuzzy rules adaptively in AFGS-SMC, which can reduce the chattering phenomenon of control signals.

4.3. Simulation Results of DDPG-SMC

Similar to the above AFGS-SMC method, the control gains

\hat{k} = diag (k_{1}, k_{2}, k_{3})

of DDPG-SMC are time-varying, and they can be scheduled adaptively through the DDPG-based parameter regulator. Simulation results of DDPG-SMC are depicted in Figure 8.

As depicted in Figure 8 (a), the dashed and real lines represent the desired and actual attitude angles, respectively. The convergence time of attitude angles in three directions (roll, pitch and yaw) is 2.0 s, 1.9 s and 2.0 s, respectively, from the initial value to desired value. It demonstrates that the quadrotor attitude can be regulated into the desired attitude using the designed DDPG-SMC algorithm, in the presence of disturbances.

The time evolutions of the quadrotor’s angular velocities and control inputs are presented in Figure 8 (b) and (c), respectively. It can be seen that attitude angular velocities in three directions approach 0 rad/s during time periods of 2.1 s, 2.4 s and 2.6 s, respectively, and the oscillation is much less. Compared with the results in AFGS-SMC, the proposed DDPG-SMC method can reduce the chattering phenomenon significantly, with less convergence time.

Figure 8 (d) and (e) represent the time evolutions of control gains related to reaching law, and sliding mode surfaces, respectively. It can be seen that sliding mode surfaces are converge to zero asymptotically, and the control gains related to reaching law are adjusted adaptively, via trained DDPG agent, which can reduce the chattering phenomenon of control signals.

Remark 3.

1) The traditional SMC, referenced AFGS-SMC and designed DDPG-SMC methods all perform effectively and robustly in attitude control, with the presence of external continuous disturbances. 2) The disadvantage of traditional SMC is that high-frequency chattering phenomenon exists in the control input signals. 3) The control gains related to reaching law in DDPG-SMC, can be adjusted adaptively via the trained reinforcement learning agent, where the chattering phenomenon is reduces effectively.

5. Conclusions

In view of the chattering phenomenon in the traditional SMC for quadrotor attitudes, a novel reinforcement learning-based DDPG-SMC approach is proposed. The attitude dynamics model of the studied quadrotor is derived and the attitude control problem is described by formulas firstly. Then a traditional sliding mode controller is designed for the nonlinear dynamic system, and the stability of the closed-loop system is supported by Lyapunov stability theorem. A reinforcement learning agent based on DDPG is trained to adjust the switching control gain in the traditional SMC adaptively, and this trained agent is applied to SMC as a parameter regulator to design the DDPG-SMC approach. The simulation results indicate that the proposed DDPG-SMC approach has excellent robustness and effectiveness in attitude control for quadrotors. Compared with traditional SMC method, the proposed approach can suppress the chattering phenomenon effectively, in the presence of external disturbances. The research in this paper can provide a method reference for solving the chattering problem of SMC, when the control system is affected by external disturbances.

Author Contributions

Conceptualization, W.H. and Y.Y.; methodology, W.H.; software, W.H.; validation, W.H. and Y.Y.; formal analysis, W.H. and Z.L.; investigation, W.H.; resources, W.H.; data curation, W.H.; writing-original draft preparation, W.H.; writing-review and editing, Y.Y.; visualization, W.H. and Z.L.; supervision, Y.Y.; project administration, Y.Y. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

Grima, S.; Lin, M.; Meng, Z.; Luo, C.; Chen, Y. The application of unmanned aerial vehicle oblique photography technology in online tourism design. Plos One. 2023, 18 (9). [Google Scholar]
Clarke, R. Understanding the drone epidemic. Computer Law & Security Review. 2014, 30 (3), 230–246. [Google Scholar]
Xu, B.; Wang, W.; Falzon, G.; Kwan, P.; Guo, L.; Chen, G.; Tait, A.; Schneider, D. Automated cattle counting using Mask R-CNN in quadcopter vision system. Computers and Electronics in Agriculture. 2020, 171. [Google Scholar] [CrossRef]
Idrissi, M.; Salami, M.; Annaz, F. A review of quadrotor unmanned aerial vehicles: applications, architectural design and control algorithms. Journal of Intelligent & Robotic Systems. 2022, 104 (2). [Google Scholar]
Adiguzel, F.; Mumcu, T. V. Robust discrete-time nonlinear attitude stabilization of a quadrotor UAV subject to time-varying disturbances. Elektronika ir Elektrotechnika. 2021, 27 (4), 4–12. [Google Scholar] [CrossRef]
Shen, J.; Wang, B.; Chen, B. M.; Bu, R.; Jin, B. Review on wind resistance for quadrotor UAVs: modeling and controller design. Unmanned Systems. 2022, 11(01), 5–15. [Google Scholar] [CrossRef]
Gün, A. Attitude control of a quadrotor using PID controller based on differential evolution algorithm. Expert Systems with Applications. 2023, 229. [Google Scholar] [CrossRef]
Zhou, L.; Pljonkin, A.; Singh, P. K. Modeling and PID control of quadrotor UAV based on machine learning. Journal of Intelligent Systems. 2022, 31 (1), 1112–1122. [Google Scholar] [CrossRef]
Khatoon, S.; Nasiruddin, I.; Shahid, M. Design and simulation of a hybrid PD-ANFIS controller for attitude tracking control of a quadrotor UAV. Arabian Journal for Science and Engineering 2017, 42 (12), 5211–5229. [Google Scholar] [CrossRef]
Landry, B.; Deits, R.; Florence, P. R.; Tedrake, R. Aggressive quadrotor flight through cluttered environments using mixed integer programming. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden; 2016. [Google Scholar]
Bouabdallah, S.; Noth, A.; Siegwart, R. PID vs LQ control techniques applied to an indoor micro quadrotor. In Proceedings of the 2004 1EEE/RSJ Internationel Conference On Intelligent Robots and Systems, Sendal, Japan; 2004. [Google Scholar]
Miranda-Colorado, R.; Aguilar, L. T. Robust PID control of quadrotors with power reduction analysis. ISA Transactions. 2020, 98, 47–62. [Google Scholar] [CrossRef]
Wang, Z.; Zhao, J.; Cai, Z.; Wang, Y.; Liu, N. Onboard actuator model-based incremental nonlinear dynamic inversion for quadrotor attitude control: Method and application. Chinese Journal of Aeronautics. 2021, 34 (11), 216–227. [Google Scholar] [CrossRef]
Smeur, E. J. J.; Chu, Q.; de Croon, G. C. H. E. Adaptive incremental nonlinear dynamic inversion for attitude control of micro air vehicles. Journal of Guidance, Control, and Dynamics. 2016, 39 (3), 450–461. [Google Scholar] [CrossRef]
da Costa, R. R.; Chu, Q. P.; Mulder, J. A. Reentry flight controller design using nonlinear dynamic inversion. Journal of Spacecraft and Rockets. 2003, 40(1), 64–71. [Google Scholar] [CrossRef]
Yang, J.; Cai, Z.; Zhao, J.; Wang, Z.; Ding, Y.; Wang, Y. INDI-based aggressive quadrotor flight control with position and attitude constraints. Robotics and Autonomous Systems. 2023, 159. [Google Scholar] [CrossRef]
Wang, B.; Zhang, Y.; Zhang, W. A composite adaptive fault-tolerant attitude control for a quadrotor UAV with multiple uncertainties. Journal of Systems Science and Complexity. 2022, 35 (1), 81–104. [Google Scholar] [CrossRef]
Huang, T.; Li, T.; Chen, C. L. P.; Li, Y. Attitude stabilization for a quadrotor using adaptive control algorithm. IEEE Transactions on Aerospace and Electronic Systems. 2023, 1–14. [Google Scholar] [CrossRef]
Patnaik, K.; Zhang, W. Adaptive attitude control for foldable quadrotors. IEEE Control Systems Letters. 2023, 7, 1291–1296. [Google Scholar] [CrossRef]
Chen, J.; Long, Y.; Li, T.; Huang, T. Attitude tracking control for quadrotor based on time-varying gain extended state observer. Proceedings of the Institution of Mechanical Engineers, Part I: Journal of Systems and Control Engineering. 2022, 237 (4), 585–595. [Google Scholar] [CrossRef]
Zheng, Z.; Su, X.; Jiang, T.; Huang, J. Robust dynamic geofencing attitude control for quadrotor systems. IEEE Transactions on Industrial Electronics. 2023, 70 (2), 1861–1869. [Google Scholar] [CrossRef]
Yang, Y.; Yan, Y. Attitude regulation for unmanned quadrotors using adaptive fuzzy gain-scheduling sliding mode control. Aerospace Science and Technology. 2016, 54, 208–217. [Google Scholar] [CrossRef]
Chen, X.; Li, Y.; Ma, H.; Tang, H.; Xie, Y. A novel variable exponential discrete time sliding mode reaching law. IEEE Transactions on Circuits and Systems II: Express Briefs. 2021, 68 (7), 2518–2522. [Google Scholar] [CrossRef]
Lian, S.; Meng, W.; Lin, Z.; Shao, K.; Zheng, J.; Li, H.; Lu, R. Adaptive attitude control of a quadrotor using fast nonsingular terminal sliding mode. IEEE Transactions on Industrial Electronics. 2022, 69(2), 1597–1607. [Google Scholar] [CrossRef]
Sun, H.; Li, J.; Wang, R.; Yang, K. Attitude control of the quadrotor UAV with mismatched disturbances based on the fractional-order sliding mode and backstepping control subject to actuator faults. Fractal and Fractional. 2023, 7 (3). [Google Scholar] [CrossRef]
Wang, D.; Shen, Y.; Sha, Q. Adaptive DDPG design-based sliding-mode control for autonomous underwater vehicles at different speeds. In Proceedings of the 2019 IEEE Underwater Technology (UT), Kaohsiung, Taiwan; 2019. [Google Scholar]
Nicola, M.; Nicola, C.-I.; Selișteanu, D. Improvement of the control of a grid connected photovoltaic system based on synergetic and sliding mode controllers using a reinforcement learning deep deterministic policy gradient agent. Energies 2022, 15 (7). [Google Scholar] [CrossRef]
Lillicrap, T. P.; Hunt, J. J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. 2015. [Google Scholar]
Mechali, O.; Xu, L.; Huang, Y.; Shi, M.; Xie, X. Observer-based fixed-time continuous nonsingular terminal sliding mode control of quadrotor aircraft under uncertainties and disturbances for robust trajectory tracking: Theory and experiment. Control Engineering Practice. 2021, 111. [Google Scholar] [CrossRef]
Tang, P.; Lin, D.; Zheng, D.; Fan, S.; Ye, J. Observer based finite-time fault tolerant quadrotor attitude control with actuator faults. Aerospace Science and Technology. 2020, 104. [Google Scholar] [CrossRef]
Adiguzel, F.; Mumcu, T. V. Robust discrete-time nonlinear attitude stabilization of a quadrotor UAV subject to time-varying disturbances. Elektronika ir Elektrotechnika. 2021, 27 (4), 4–12. [Google Scholar] [CrossRef]
Lopez-Sanchez, I.; Pérez-Alcocer, R.; Moreno-Valenzuela, J. Trajectory tracking double two-loop adaptive neural network control for a Quadrotor. Journal of the Franklin Institute. 2023, 360 (5), 3770–3799. [Google Scholar] [CrossRef]
Nasiri, A.; Kiong Nguang, S.; Swain, A. Adaptive sliding mode control for a class of MIMO nonlinear systems with uncertainties. Journal of the Franklin Institute. 2014, 351 (4), 2048–2061. [Google Scholar] [CrossRef]
Silver, D.; Lever, G.; Heess, N. Deterministic policy gradient algorithms. In Proceedings of the 31st International Conference on Machine Learning, Beijing, China; 2014. [Google Scholar]

Figure 1. Attitude motion of the quadrotor in coordinate frames.

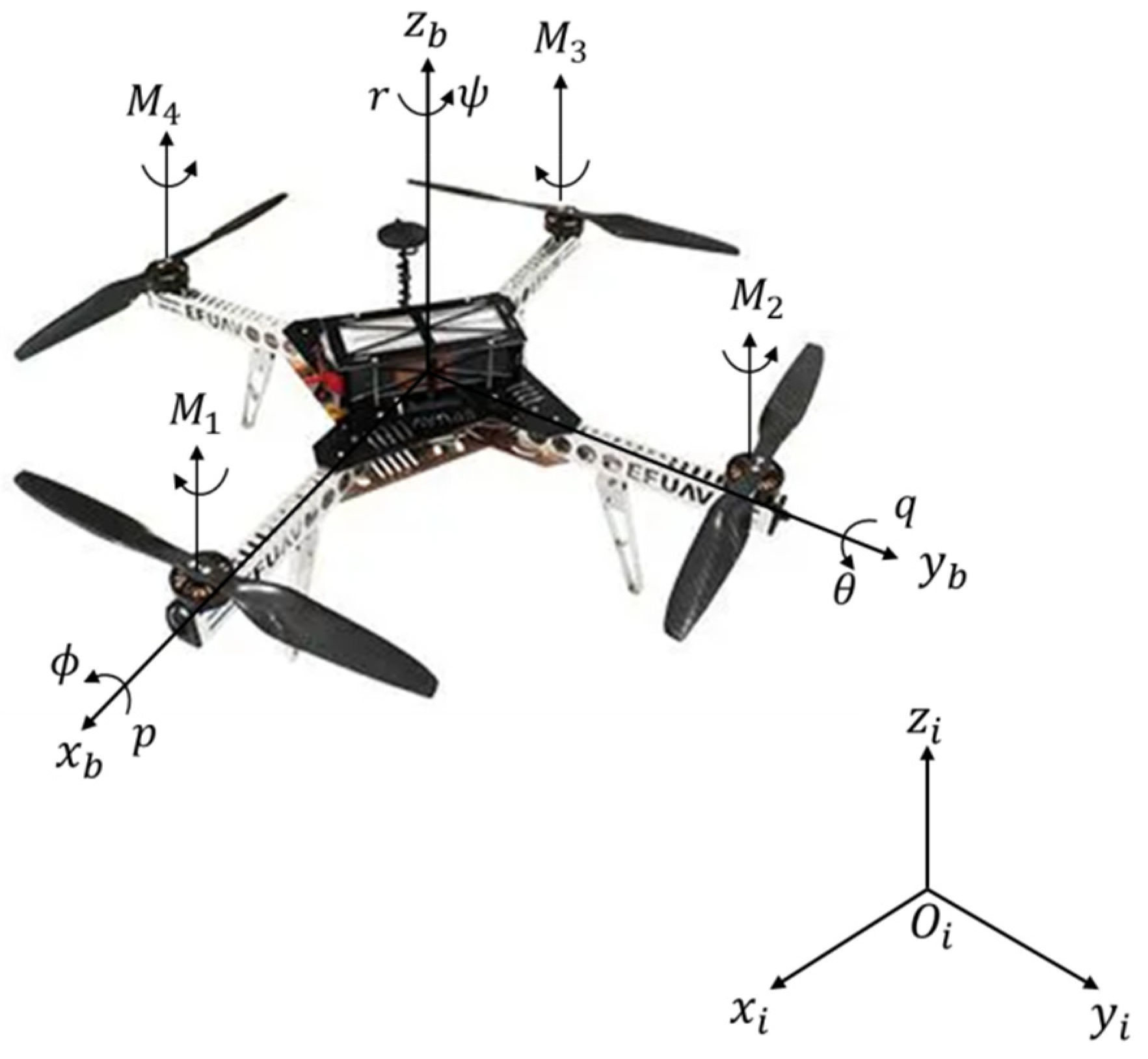
Figure 2. The block diagram of SMC.

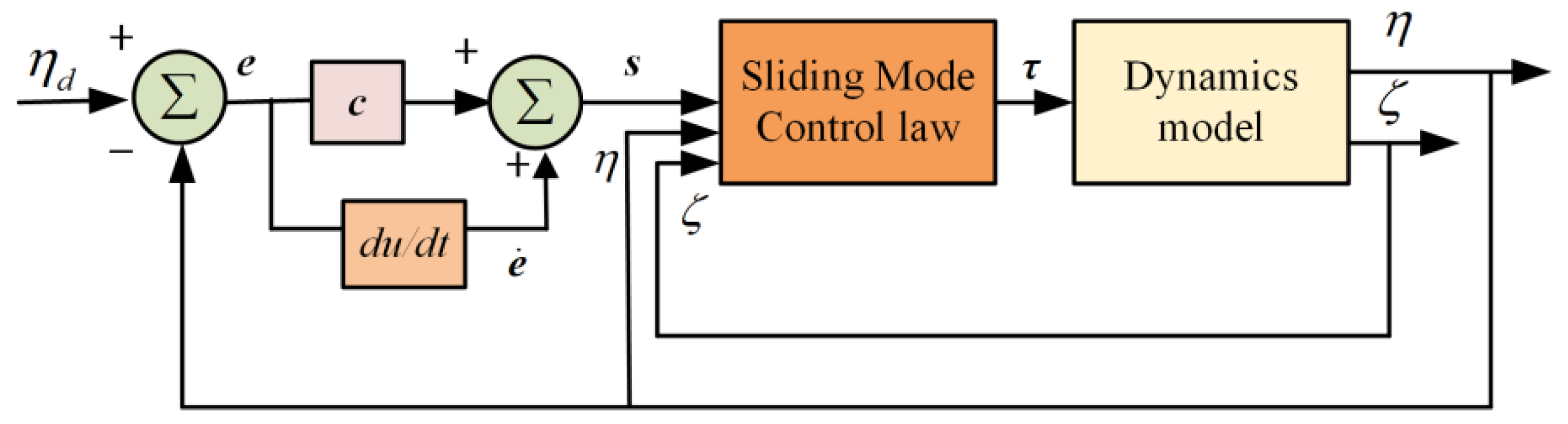
Figure 3. The block diagram of DDPG-SMC.

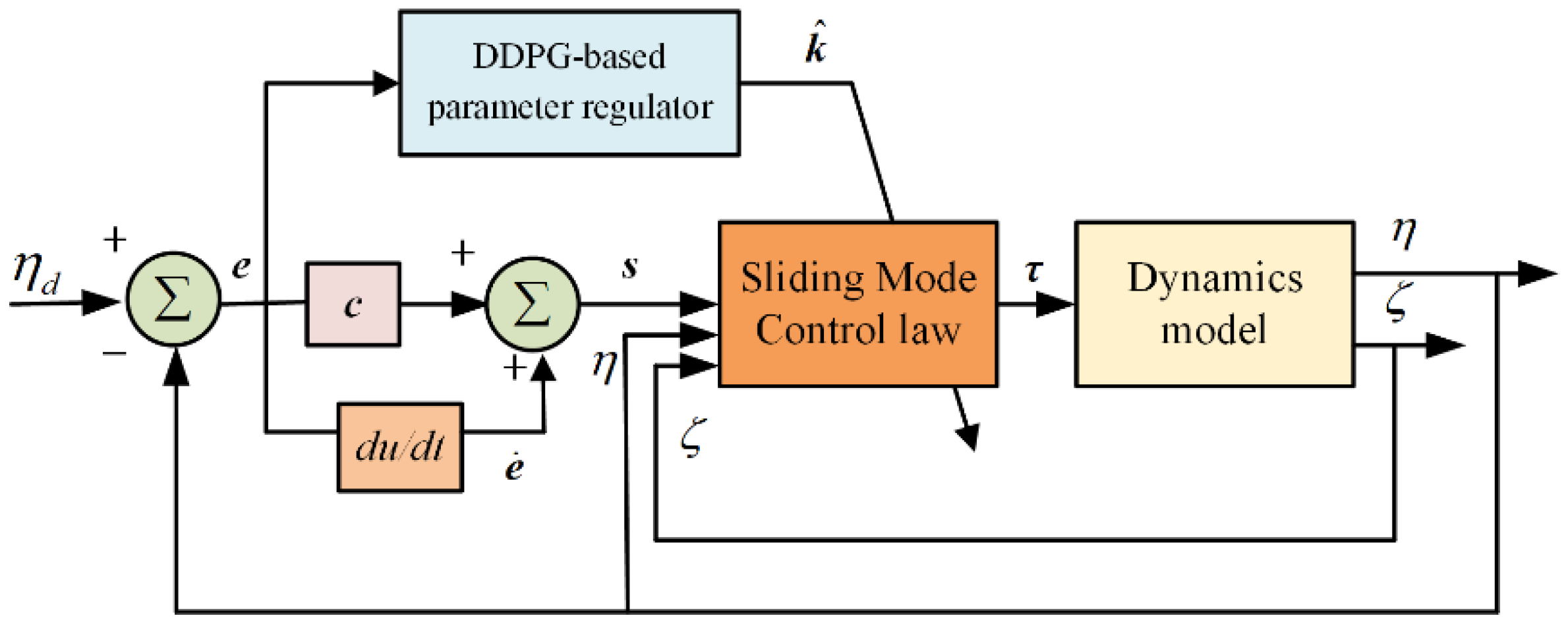
Figure 4. The architecture of the DDPG-based parameter regulator.

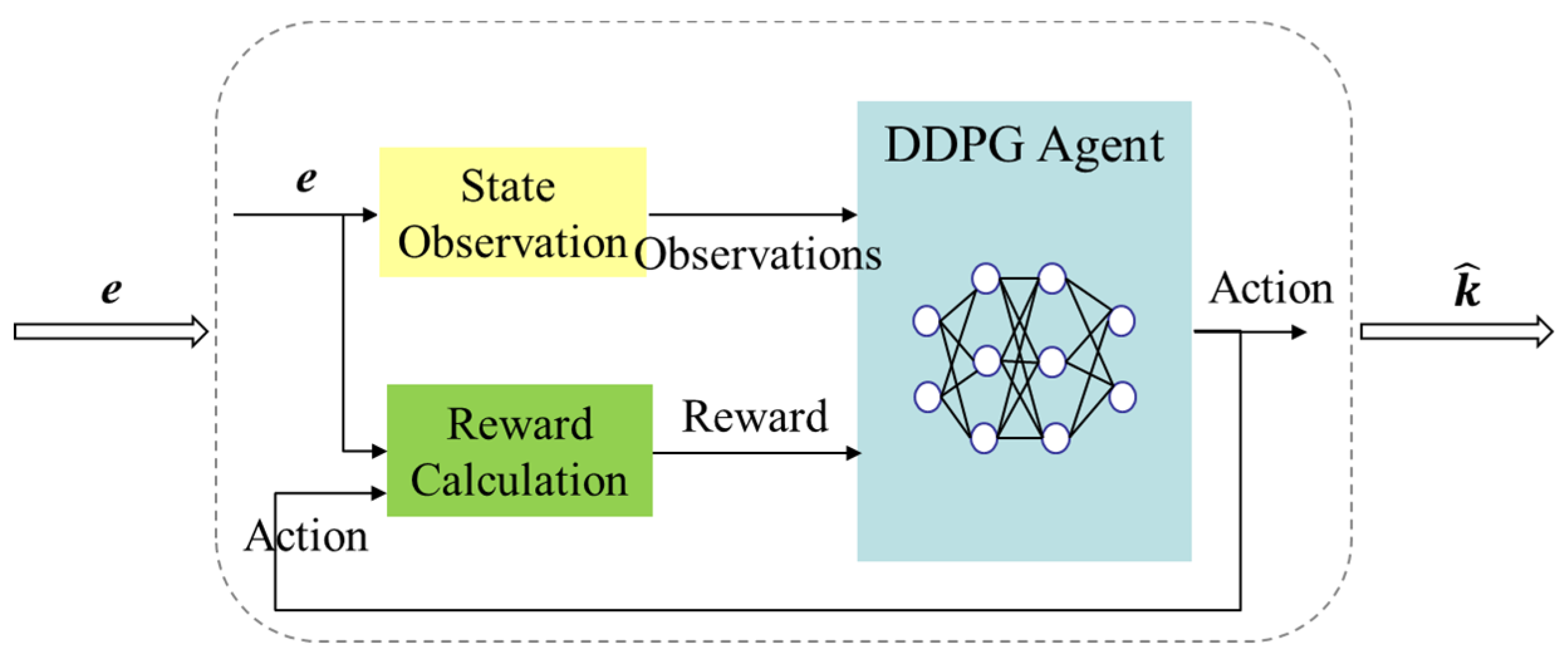
Figure 5. Each episode reward for gain-learning with DDPG agent.

Figure 6. Simulation results of SMC.

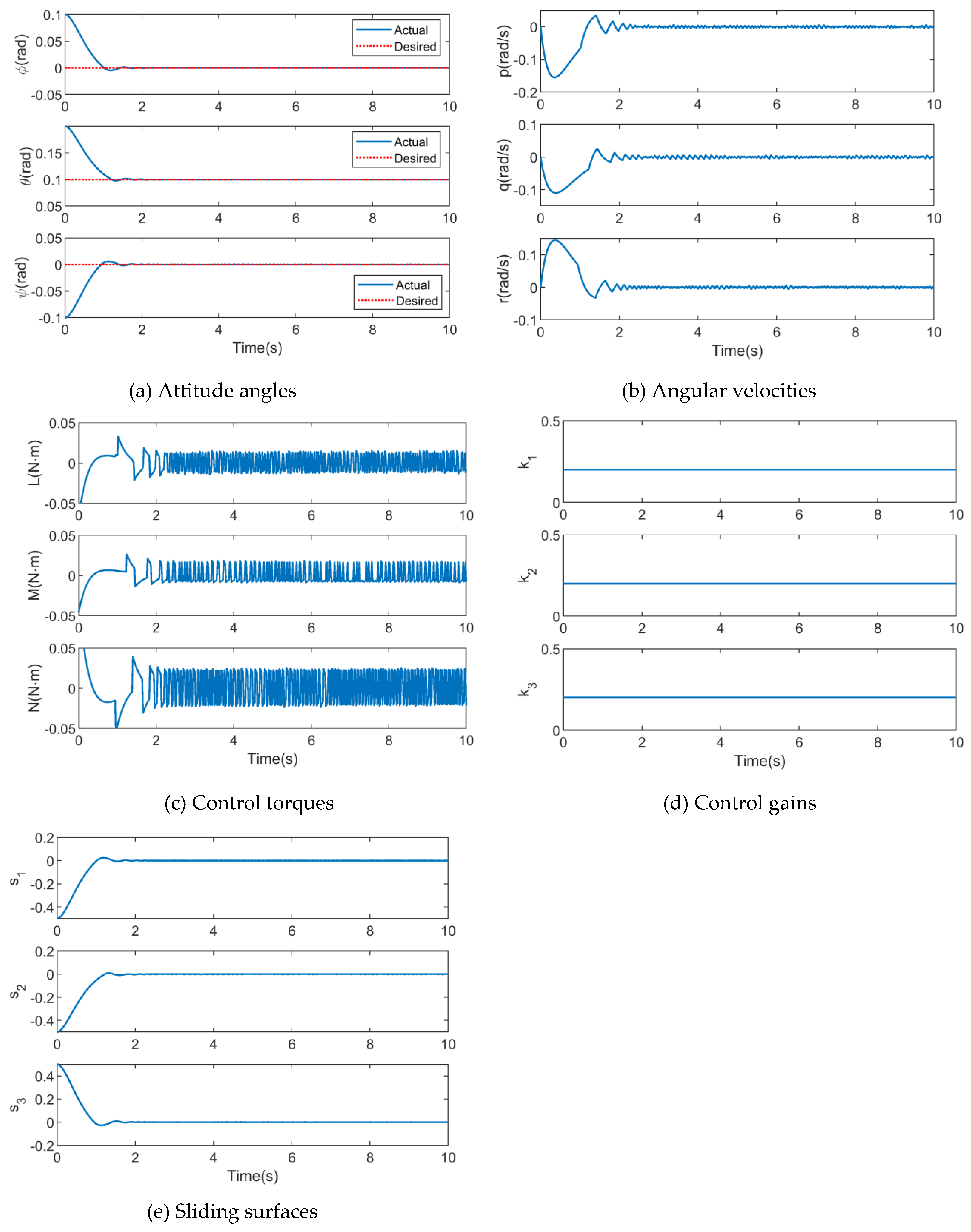
Figure 7. Simulation results of AFGS-SMC.

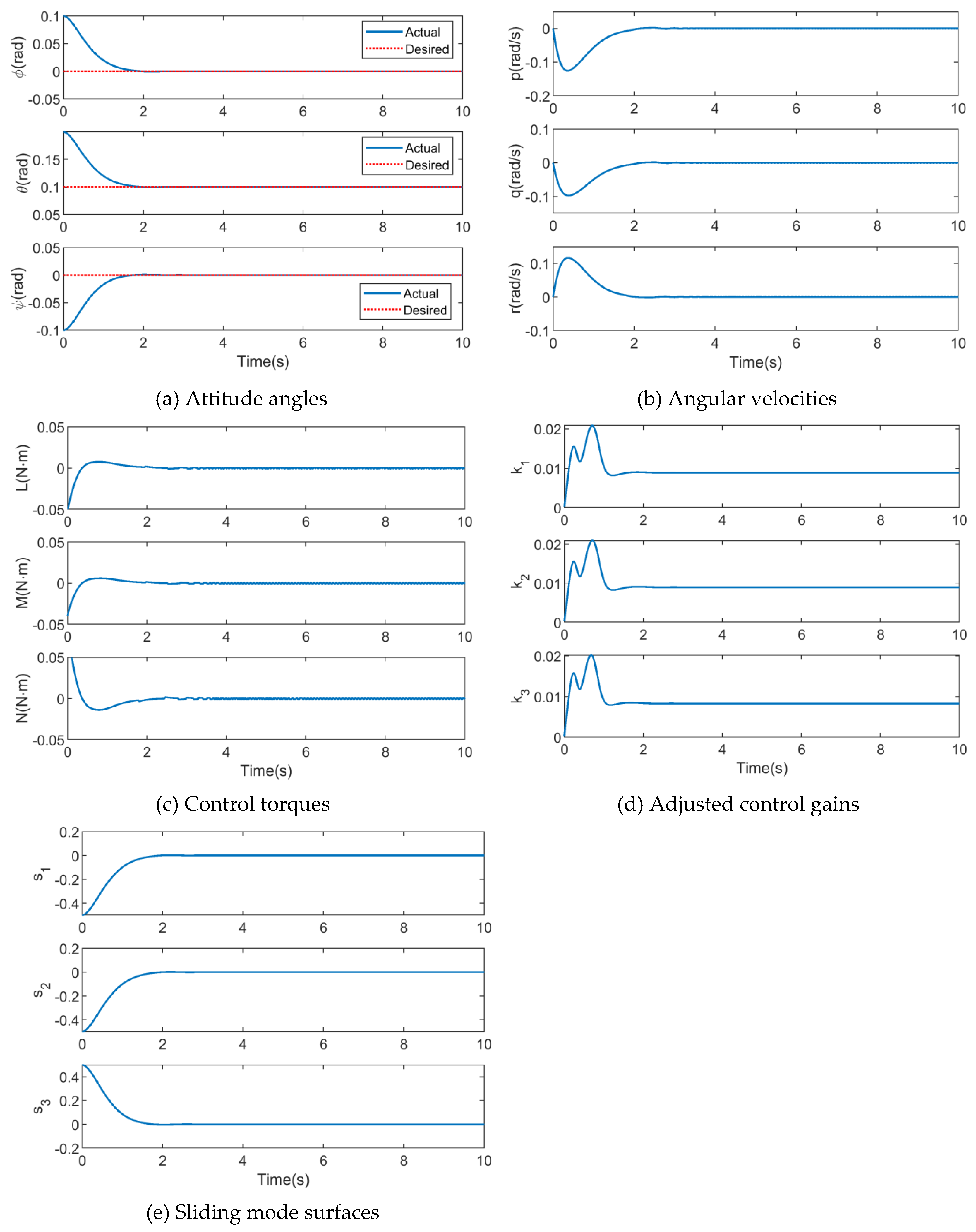
Figure 8. Simulation results of DDPG-SMC.

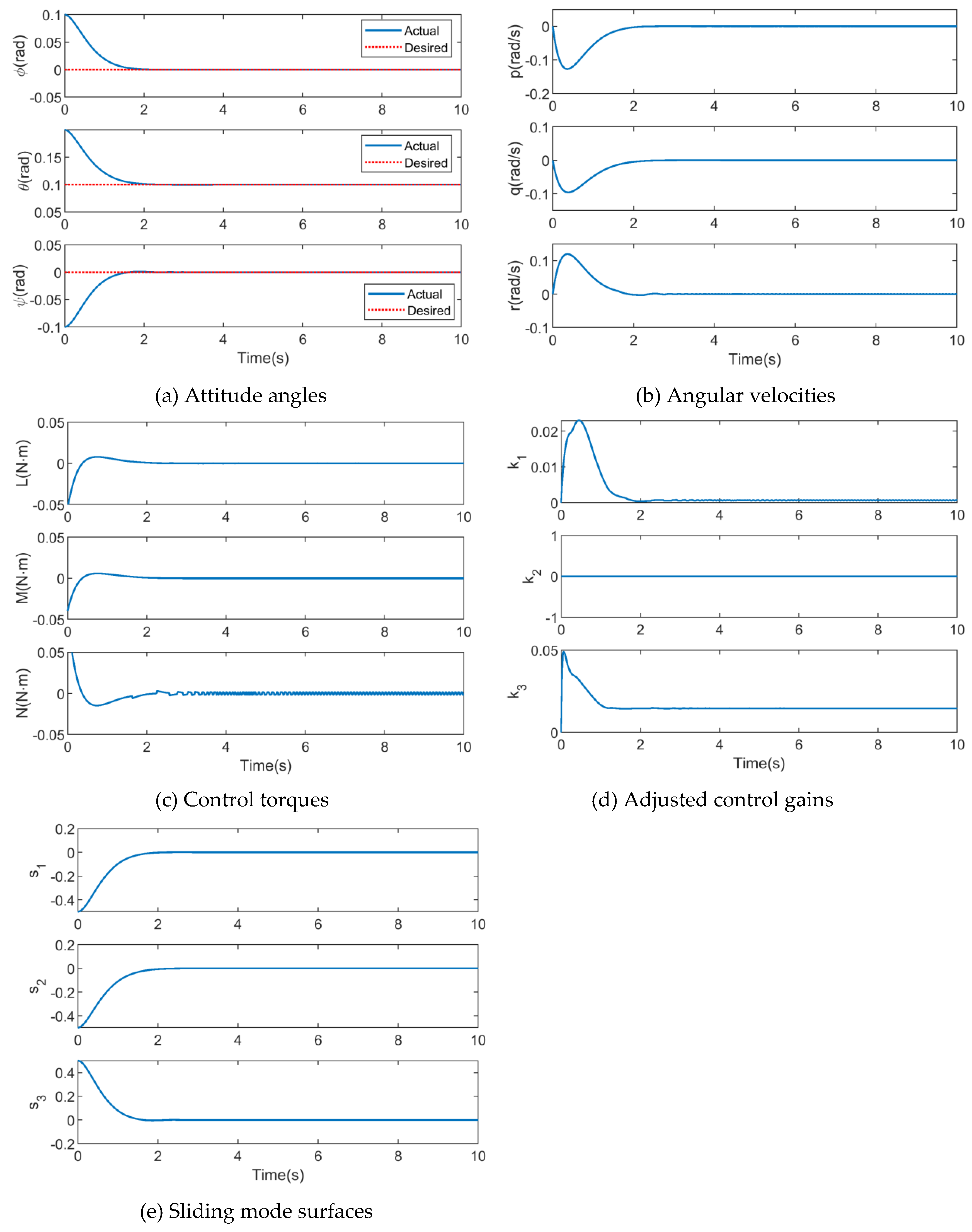
Table 1. Model parameters of the quadrotor.

Parameter	Value
Mass m /kg	3.350
Inertia moment about o_bx_b J_x / (kg·m²)	0.0588
Inertia moment about o_by_b J_y / (kg·m²)	0.0588
Inertia moment about o_bz_b J_z /(kg·m²)	0.1076
Lift factor b	8.159×10^-5
Drag factor d	2.143×10^-6
Distance between the center of mass and the rotation axis of any propeller l /m	0.195

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Deep Deterministic Policy Gradient (DDPG) Agent-Based Sliding Mode Control for Quadrotor Attitudes

Abstract

1. Introduction

2. Attitude Dynamics Modeling for Quadrotor UAV

3. Control Design for Attitude Control

3.1. SMC Design

3.2. DDPG-SMC Design

4. Simulation Results

4.1. Simulation Results of SMC

4.2. Simulation Results of AFGS-SMC

4.3. Simulation Results of DDPG-SMC

5. Conclusions

Author Contributions

Funding

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe