1. Introduction
With the increase in energy demand, it is necessary to make full use of distributed generation units (DGUs) because of their numerous advantages, such as the reduction of both energy losses and greenhouse gas emissions, voltage regulation, maximum load reduction, a greater supply reliability compared with traditional centralized generations and improvements in power quality [
1]. These DGUs are an important part of the electrical microgrid (MG), which is defined as a set of loads, DGUs and Energy Storage Systems (ESSs) with clearly defined electrical boundaries that have the capacity to operate autonomously and independently of the conventional distribution grid, thus ensuring the continuity of the electricity supply with a high level of reliability and to provide effective support for the large electrical grid [
2,
3,
4,
5]. MGs are easily affected by the load, however, mainly if it is unbalanced or nonlinear loads because of the high penetration of DGUs such as a photovoltaic (PV) system and wind power, as well as by the devices based on power electronics, which will significantly affect the power quality of the entire MG and potentially cause the collapse of the MG system itself [
6].
This condition creates voltage issues such as distortion, fluctuations, and variations in a weak grid [
7]. On the other hand, MGs can operate in two operating modes: islanding mode and grid–connected mode. When operating in islanding mode, the probability of disturbances such as distortion or voltage unbalance is high because of the impedance levels of the system. For the MG operating in a mode connected to the electrical grid, the most frequent problems are harmonic distortion and grid unbalances [
8]. These events cause a series of complications, including poor performance of protection relays, the overheating of motors and transformers, as well as failure of capacitors that improve power factor [
9,
10]. Therefore, an important task is to provide a good power quality to supply both basic and commercial end users [
11].
Research on power quality in MGs is not sufficiently addressed in scientific articles since the vast majority of researchers have focused their studies on large electrical grids [
12]. Only a few studies of MGs are available in the literature; for example, in [
13] the authors analyzed the power quality of a hybrid MG composed of a PV system, battery based ESSs and capacitive loads. The study was performed using DSS® software. The result of that study concluded that the total harmonic distortion (THD) values of voltage and current were high when PV system penetration increased in the MG. In [
14], the authors examined the voltage stability limit in a distribution grid based on the IEEE 30-bus grid model for power flow studies. The design of the MG was performed using MATLAB–Simulink® software. The study concluded that voltage stability is robust in bus 30, while voltage stability weakened in bus 26. Power quality problems were analyzed in [
15] in a typical MG by considering different levels of renewable energy penetration (33.3%, 66.6% and 99.9%), as well as different meteorological conditions. The design of the MG was carried out in MATLAB–Simulink®, and it was concluded that power quality problems occur with greater severity as renewable penetration increases. In [
16], the authors analyze the power quality problems of an alternating current (AC) MG composed of a PV system using the PSS–SINCAL® software as a tool for MG modeling. The study determined the power flow variation and voltage at the local bus under solar disturbance conditions where the highest voltage THD index was found at the bus where the nonlinear load was connected. In [
17] the authors examined three power quality problems: voltage imbalances, waveform distortion and voltage THD. Regarding the latter, it was concluded that as solar penetration varies the impact is greater in the nonlinear load than in the linear loads. In addition, it was determined that the voltage THD in non-linear loads was above the IEEE–519 standard limit (greater than 50%). In [
18], the authors examined the performance of an AC–MG, through experimental evaluation, to determine the voltage THD of the MG buses that are within the limit established by IEEE–519. However, the current THD increased as solar generation decreased because of disturbances caused by shading or cloud effect. Finally, it was concluded that the current THD never exceeded the 5% limit permissible by the IEEE–519 standard when solar generation is above 60%.
In summary, most of the research studies available in the literature exhibit particular features determined by the configuration, topology, and the particular components used. Each study addresses challenges such as the dynamics and limited capacity of ESSs, the diversity of DGUs, power converters (PC), and the significant presence of nonlinear phenomena. Some approaches choose to model each DGU, simplifying the model to a linear and time-invariant system, characterized by a constant and a gain factor, without considering the dynamics of the grid. Other studies focus on PC-based DGUs, considering the full dynamic model of the grid instead of the PC, dividing the MG into three elements: PC, power grid, and loads. The design and modeling of the MGs proposed in these studies, however, do not consider the dynamic and steady-state behavior of the DGUs, as well as the imbalance and nonlinearity of the loads and the dynamics of the ESSs. They also do not face the problem of accidental or scheduled disconnection from the electrical grid, nor the minimum or maximum demand to which are subject to in their operation. Therefore, the motivation of this paper focuses on analyzing the most important aspects of the power quality of a 14–bus hybrid MG based on the original IEEE 14–bus distribution system, which operates in a mode connected to the electrical grid while considering the dynamics, the characteristics of the DGUs in steady-state, voltage variations, the nature of the loads, the dynamics of the ESSs, the disconnections of the electrical grids and the maximum demand scenario. Finally, the results obtained are compared and discussed considering the IEEE–519 standard to verify the effectiveness of the proposed model. The most important contributions of this document are listed below.
A fully detailed 14–bus MG system is designed and modeled, which operates in grid-connected mode for power quality studies. In this MG, DGUs, such as solar and wind power, as well as balanced and imbalanced loads that include both linear and nonlinear devices, battery-based ESSs, power transformers and distribution lines, are considered. In addition, some PCs are considered to which open-loop control strategies and other closed-loop control strategies have been implemented. It is worth mentioning that these rectifiers or inverters use pulse width modulation (PWM) techniques of different carrier frequencies.
This study provides information about the conflicts that arise related to the bidirectionality of power flows and the insertion of DGUs such as PV systems and wind power. Note that the proposed MG has a capacity of 4 MW and that 75% of that power is supplied by conventional generation based on a 3–MW diesel generator. Therefore, the most notable conflicts in this study are as follows: voltage variations, variations in the power factor (PF) in each bus of the MG and variations in the voltage and current THD index in each bus of the MG. Therefore, the study and analysis are relevant when compared with the IEEE–519 standard in this document.
Finally, this work is a starting point for the analysis of many current topics regarding MGs, optimization techniques, fault diagnosis, system identification and fault-tolerant control, among others, which will be detailed and expanded in future research.
As follows is how the document is organized.
Section 2 addresses the generalities of MGs, including composition, structure, operation modes, classification and current challenges.
Section 3 describes in detail the design and modeling of the proposed hybrid MG for power quality studies. The hybrid MG model is performed MATLAB–Simulink® software.
Section 4, the results obtained from the hybrid MG operating in the electrical grid-connected mode are analyzed, discussed and compared with the IEEE–519 standard to verify the effectiveness of the proposed model. Finally,
Section 5 summarizes the most important conclusions of the research.
3. Model Description Proposed
This section presents a detailed description of the MG model proposed in this research; see
Figure 6. The model was developed in the specialized software MATLAB–Simulink® that strives to provide a tool for the scientific community to better understand the dynamics of MG, as well as its general performances under different operating conditions.
The MG model is comprised of the three sections:
AC–MG is the orange dotted area that operates at two voltage levels: 220 V and 13.8 kV through distribution lines. This MG is composed of a 725-kW PV system, a 3-MW diesel generator, a 750-kW wind turbine and a battery-based ESS (BESS_1). In addition, it has a variety of linear, non–linear, balanced and unbalanced loads, etc. It is worth mentioning that this MG operates at a frequency of 60 Hz.
DC–MG is the green dotted area where a DC bus comprising BESS_2 is located, as well as 10.5-kW PV system. This MG is connected to the AC–MG through two bidirectional, parallel PCs, which can exchange active and reactive power through the transformers.
Finally, at bus 13, the AC–MG is connected to the electrical grid, which is a Thévenin equivalent of 69 kV, 100 MVA and an X/R ratio of 10.
Below, the components considered in the proposed hybrid MG model in
Figure 6 are described in detail.
3.1. Photovoltaic system (PV)
A PV system is one of the distributed renewable energy resources considered in the MG. This model includes two PVs that operate with a total irradiance of G=1000
and a temperature of 25 °C.
system is connected to bus 6 and has more than 1,750 panels that develop a nominal power of 725 kW, while the
is connected to bus 2 in the DC–MG and has 42 panels, which develop a nominal power of 10.5 kW.
Table 3 shows the main parameters of the PVs, which are used by MATLAB–Simulink® to characterize the performance of the solar panels.
Both PV systems need DC interfaces whit the PC. The system operates with a voltage-controlled step-up DC–DC PC which has a 6,000 capacitor operating at 300 . Additionally, a closed-loop pulse width modulation (PWM) control strategy is used at 5 kHz. The system works with an open-loop sine PWM inverter is used for the system. The modulation index, , is 1 when the voltage drops from 480 to 250 .
3.2. Permant Magnet Synchronous Generator (PMSG) based Wind Turbine
In medium and low voltage MGs, variable speed wind turbines are used: mainly type IV wind turbines, which are also known as permanent magnet synchronous generators (PMSG) [
37]. In this instance, the PCs play an important role by decoupling the electric generator from the grid to which it is interconnected. This model includes a 750-kW PMSG wind turbine at 575 V connected to bus 4.
Table 4 shows the main parameters of the PMSG, used by MATLAB–Simulink® to characterize the performance of the electric generator.
Like PV systems, the wind turbine needs an AC–AC PC (cycloconverter), which adjusts the parameters of the generator to those of the electrical grid. The voltage and frequency of the wind turbine can be controlled using PWM control schemes for the PC and learning systems for the maximum power point tracker (MPPT).
3.3. Battery–based energy storage system (BESS)
The ESS is a fundamental part within the MG since it allows the grid to become more flexible in the event of contingency or in the transition to islanding mode through a battery bank that is used to store and supply energy during the charging process and download. PbA, Ni-Fe, Ni-Cd, Ni–MH and Li–ion batteries are the principal types of battery-based ESSs for MG applications. These last two are the ones used in this study because they offer potential advantages, such as being environmentally friendly, providing a life cycle equi-valent to that of lead-acid batteries and increasing in their capacity (between 25 and 40 %). As for the Li–ion battery, it has the highest energy density but is very expensive [
11].
The operates on the DC bus, which consists of a Li–ion battery with a nominal capacity of 800 Ah and nominal voltage of 120 . On the other hand, is conected to bus 1, which consists of three Ni–MH batteries with a nominal voltage of 650 and an individual nominal capacity of 1.5 Ah. The batteries are connected in parallel to an inverter (cascade topology), which in turn increases the nominal voltage from 650 to 900 . Battery parameters are time varying and depend on the state of charge.
3.4. DC-AC power converters
The system is interconnected to the 13.8 kV AC system through an inverter that reduces the voltage from 480 to 250 . The inverter is modeled using a three-level PWM controlled insolated-gate bipolar transistor (IGBT) bridge. Operating with a closed loop control strategy and a PWM carrier signal of 2 kHz.
Additionally, the is interfaced with the 220 V system with an inverter that increases the nominal voltage from 650 to 900 . This inverter is modeled using a multilevel topology, which, according to the literature, is considered the most efficient and reliable topology because it considers power losses, THD and total efficiency Additionally, it uses an open-loop sinusoidal PWM (SPWM) technique with a carrier frequency of 2.5 kHz. It is worth mentioning that the inverter generates, on the AC inverter side, a modulation index equal to 1.2.
3.5. Power transformers
For this study, eight power transformers are considered. One of them is a substation transformer (T1), with a transformation ratio 69-kV/13.8-kV, ∆-Y, and an equivalent series impedance of 1.5% on its MVA base. This transformer connects the MG distribution system to the 69-kV subtransmission system. T2 and T3 transformers are used to convert from 13.8 kV of industrial or commercial use to 220 V residential use. On the other hand, the PV (T4), wind turbine (T5),
(T6) and diesel generator (T7) are used to interface with the MG inverters.
Table 2 shows the parameters of the transformers.
3.6. Loads
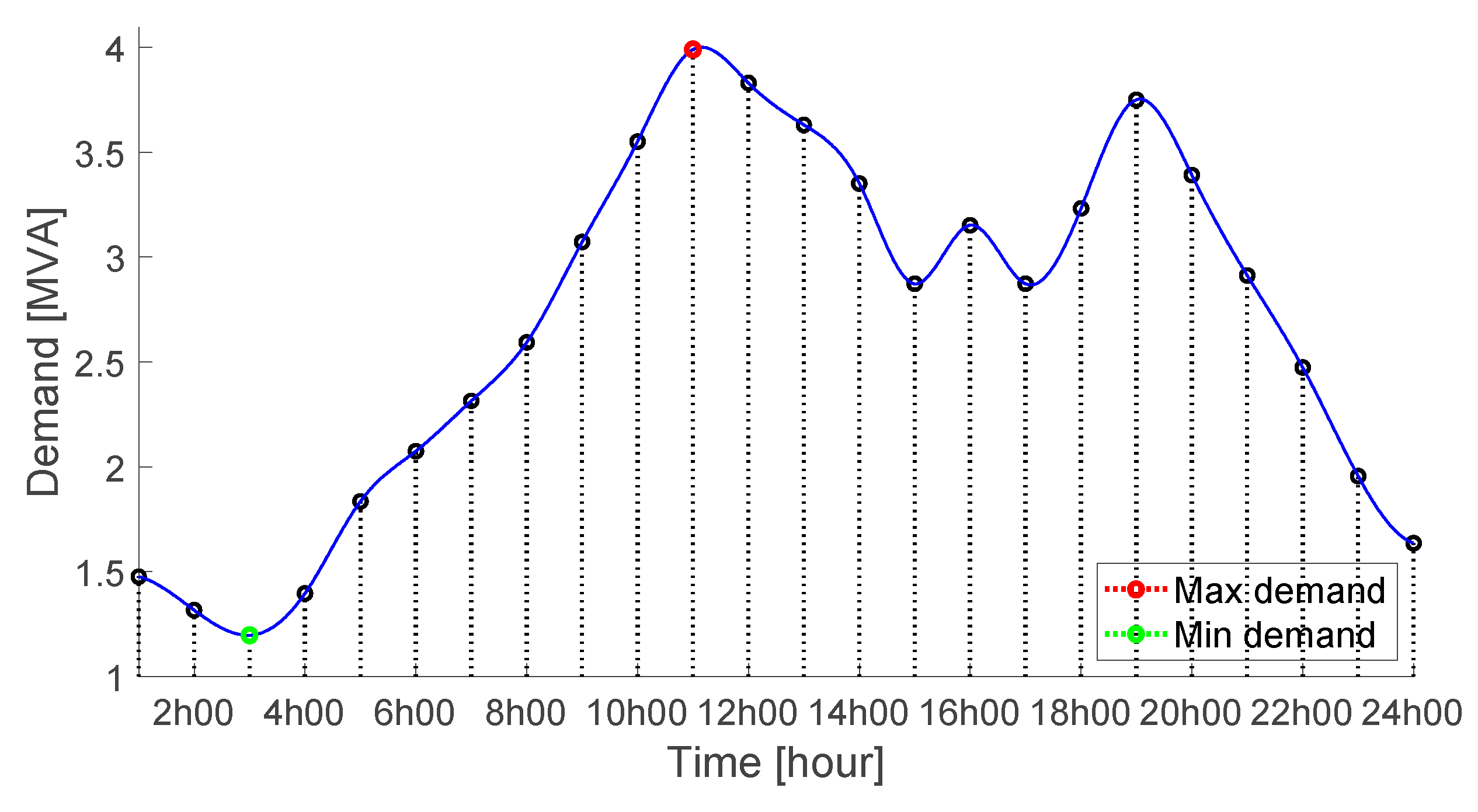
The electrical load is an important element in the design of an EPS since it is considered an unpredictable parameter. In this study, a maximum demand scenario is considered (the highest peak of all powers in a certain period) with different types of loads, as listed in
Table 6, which summarizes the information of the loads connected to the system. It is worth mentioning that balanced and unbalanced linear loads are modeled as constant impedances and that some contain single-phase components that could damage the symmetry of the system voltage and current.
In a distribution system with three-phase currents, the load currents should ideally be equal in magnitude in all three phases of the grid. In the case of an unbalance, however, overloads and heating may occur in power conductors, the activation of protection and the circulation of currents through the electrical grid’s neutral. The percentage of unbalan-ced loads is defined as the percentage value that indicates the maximum deviation of the current in a phase with respect to the average load current. Reducing the value of the unbalance index through different load balancing methods implies reducing losses.
3.6.1. Non-linear loads
In this model, an electric arc furnace located in bus 9 is considered a nonlinear load (see
Figure 6). Electric arc furnaces can result in significant disturbance levels for MG applications. Electric arc furnace consists of a crucible or steel plate body lined with refractory material containing scrap and three graphite electrodes supported by a mobile support, allowing them to be lowered or raised according to the output of the control system. The different phases of electric arc furnaces operation (start-up, smelting and refining) have a different impact in terms of the THD of voltage and current.
Basically, a three-phase electric arc furnace can be represented as a variable resistor.
Table 7 summarizes the electric arc furnace parameters, which is fed directly from the 13.8-kV distribution grid.
3.7. Distribution lines
In this model, two distribution levels are considered: medium and low AC voltage, which are typical values for applications in MGs. A 1/0 bare copper conductor was selected for the 13.8-kV primary grid. The resistance, reactance and impedance of the line are 0.394
, 0.1168
and 0.411
, respectively. A 4/0 copper TW cable was selected for the 220 V secondary grid. The resistance, reactance and impedance of the line are 0.198
, 0.1089
and 0.227
, respectively.
Table 8 shows the line sections used in detail.
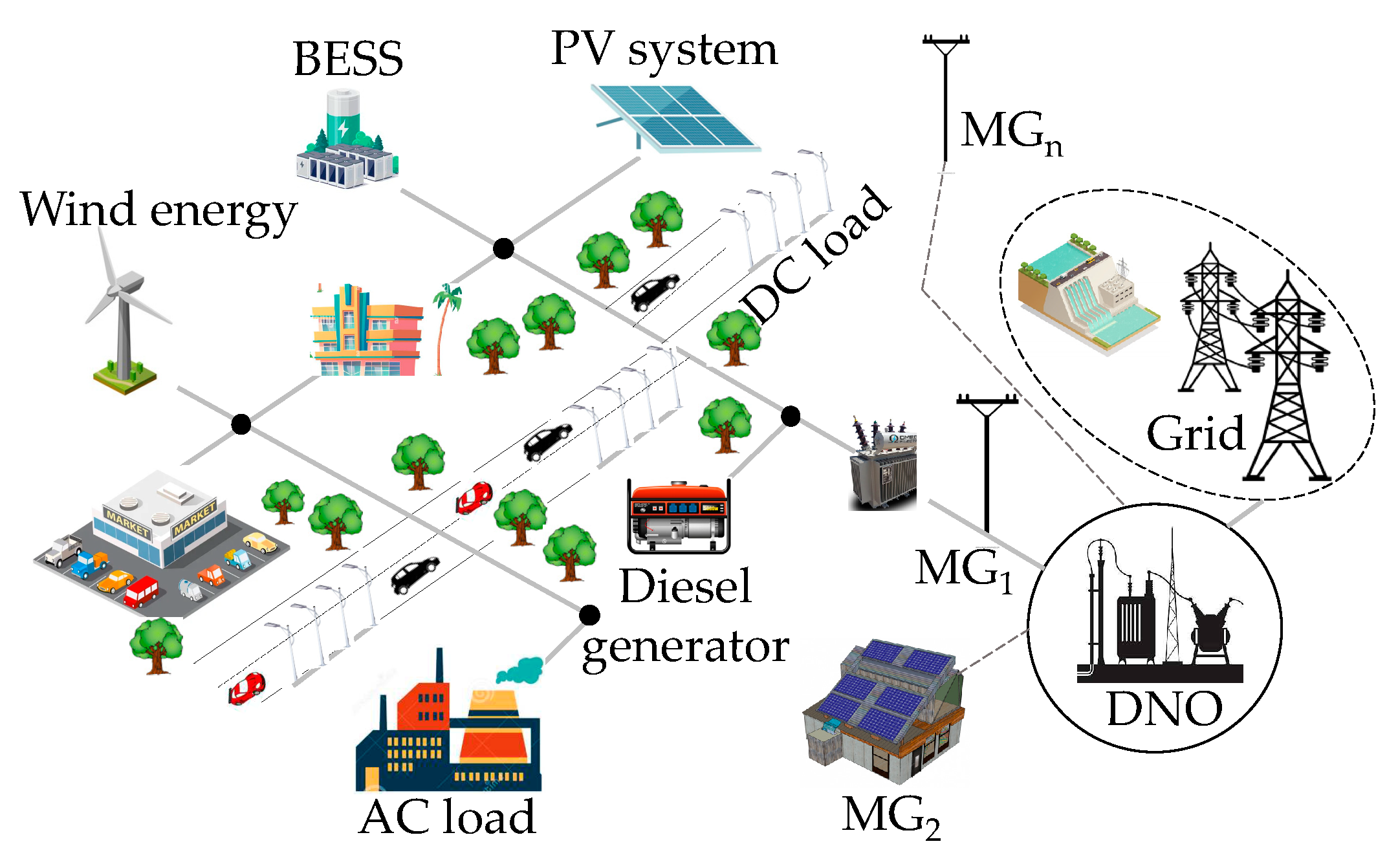
Figure 1.
Typical diagram of an MG.
Figure 1.
Typical diagram of an MG.
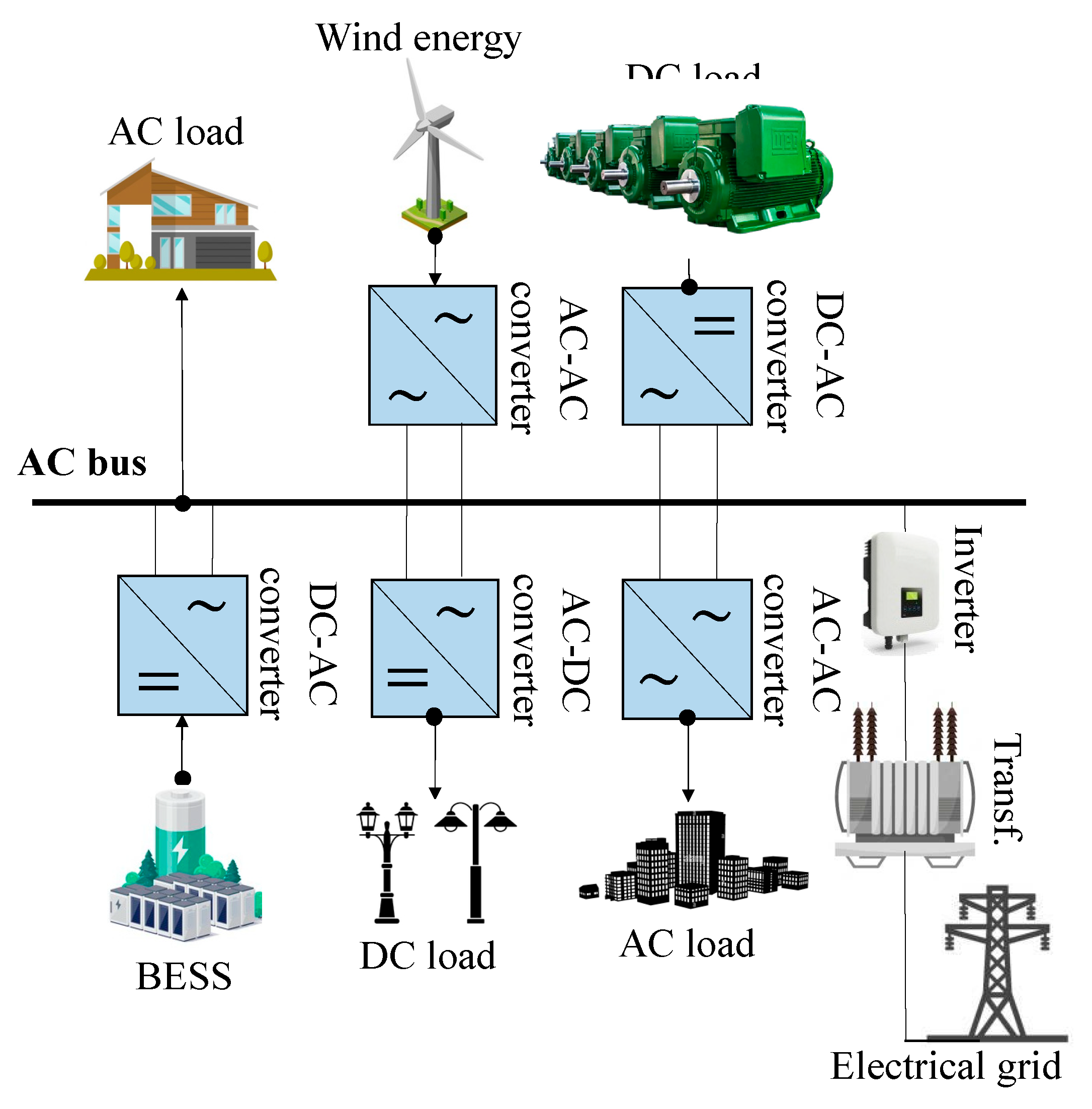
Figure 2.
Typical diagram of an AC–MG.
Figure 2.
Typical diagram of an AC–MG.
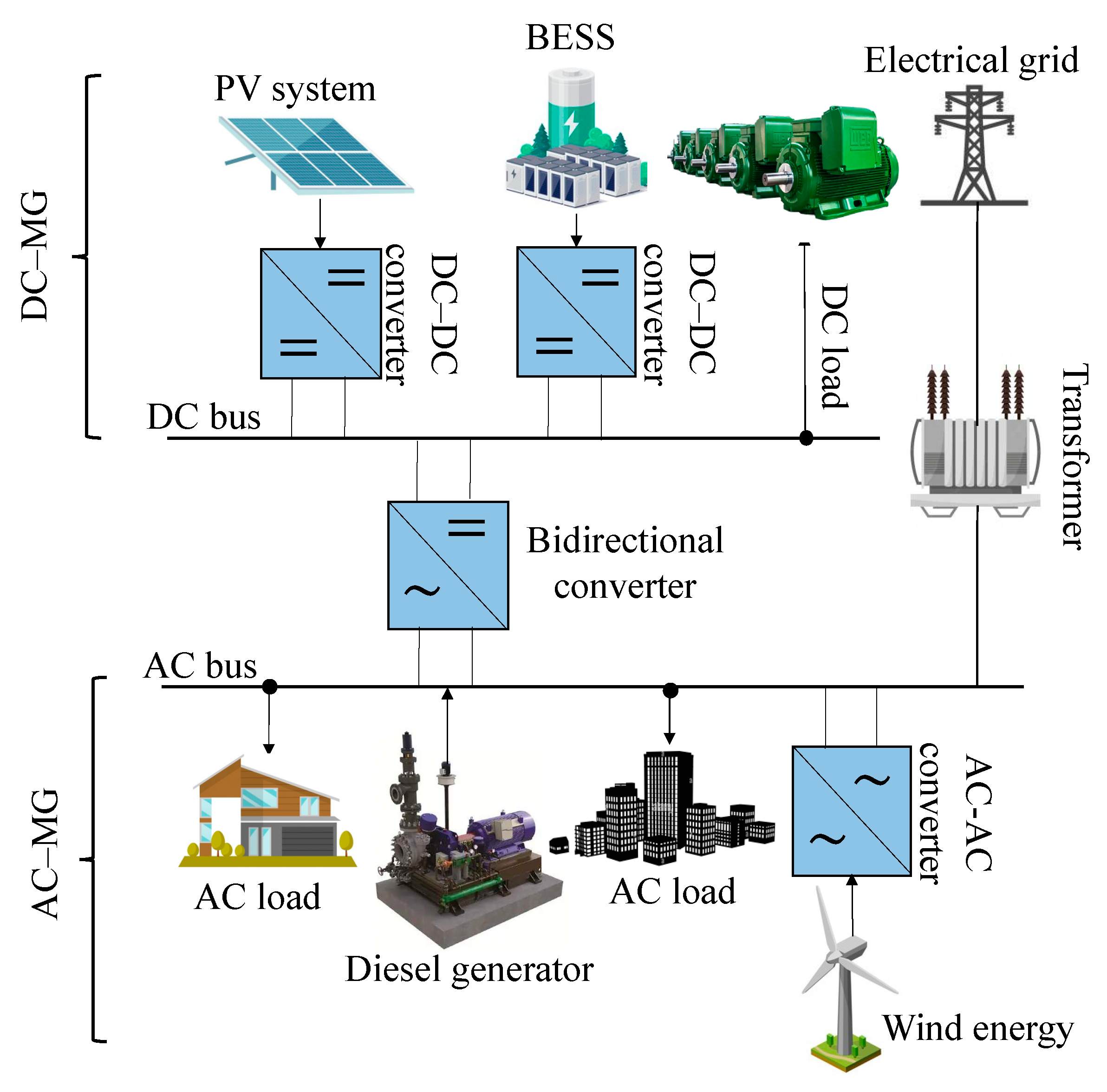
Figure 3.
Typical diagram of an DC–MG.
Figure 3.
Typical diagram of an DC–MG.
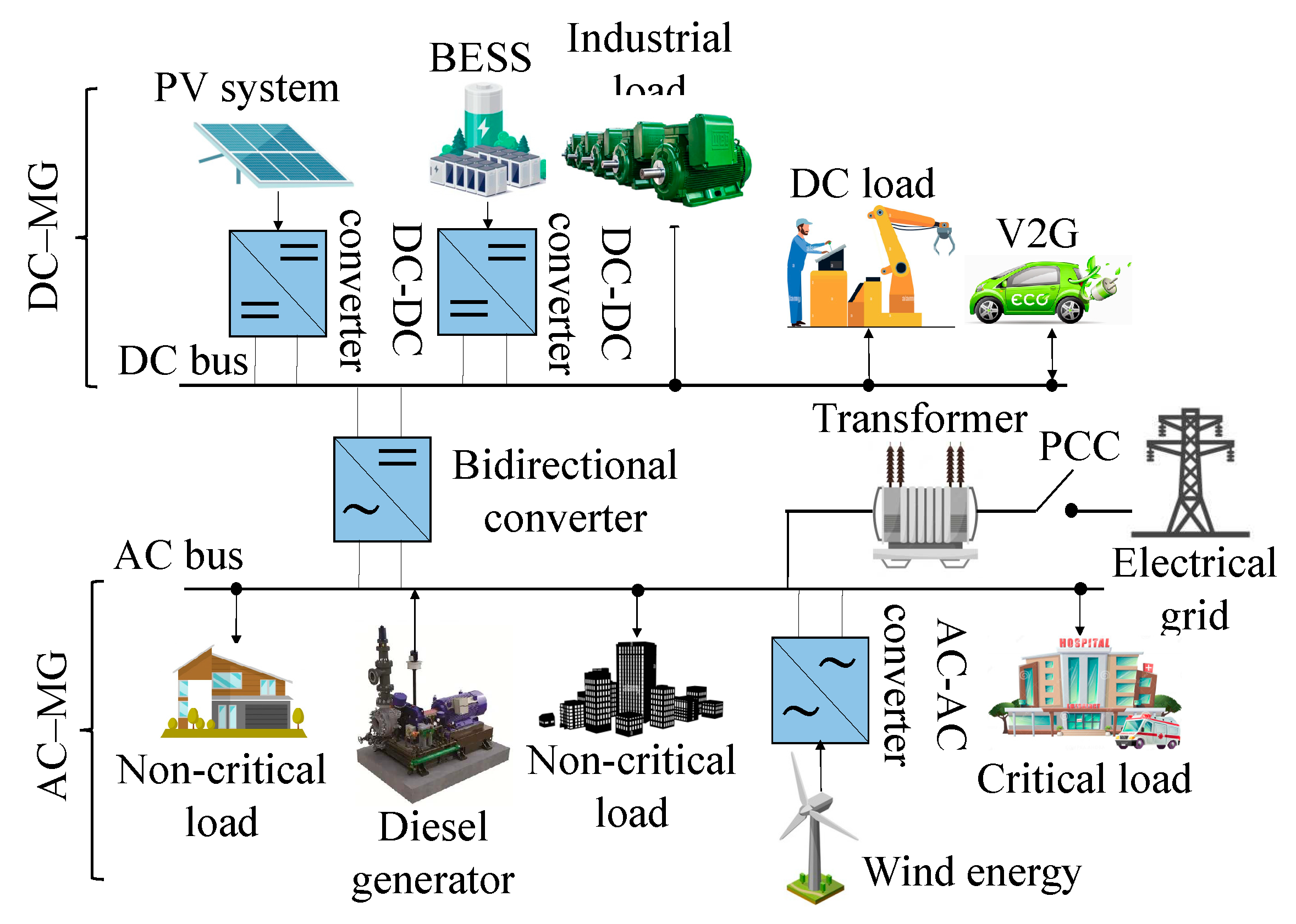
Figure 4.
Typical diagram of an DC–AC or hybrid MG.
Figure 4.
Typical diagram of an DC–AC or hybrid MG.
Figure 5.
Operation modes of a hybrid MG.
Figure 5.
Operation modes of a hybrid MG.
Figure 6.
AC-DC or Hybrid MG modes operation.
Figure 6.
AC-DC or Hybrid MG modes operation.
Figure 7.
Electrical energy demand curve.
Figure 7.
Electrical energy demand curve.
Figure 8.
Voltage profile.
Figure 8.
Voltage profile.
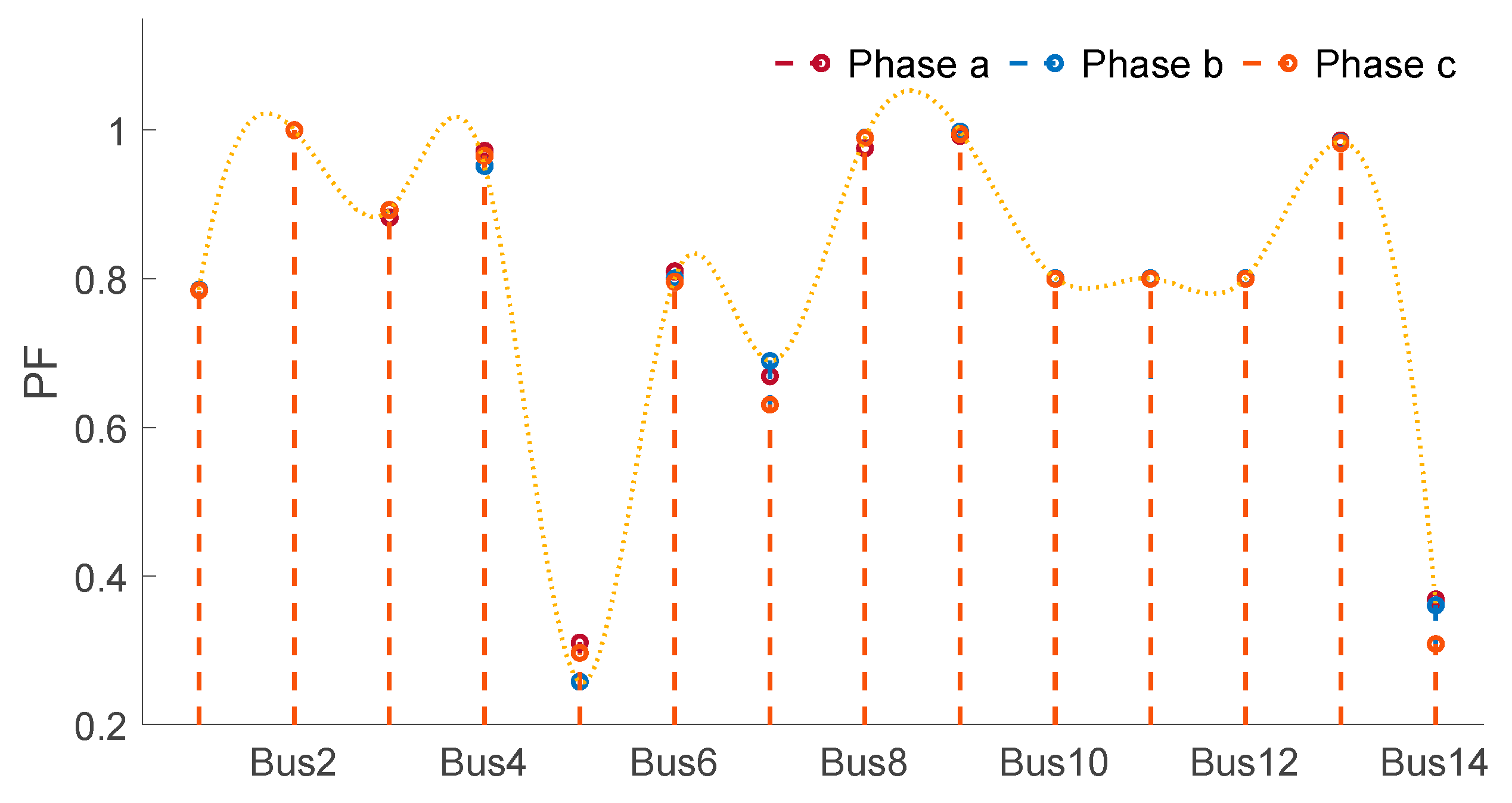
Figure 9.
PF in each of the buses.
Figure 9.
PF in each of the buses.
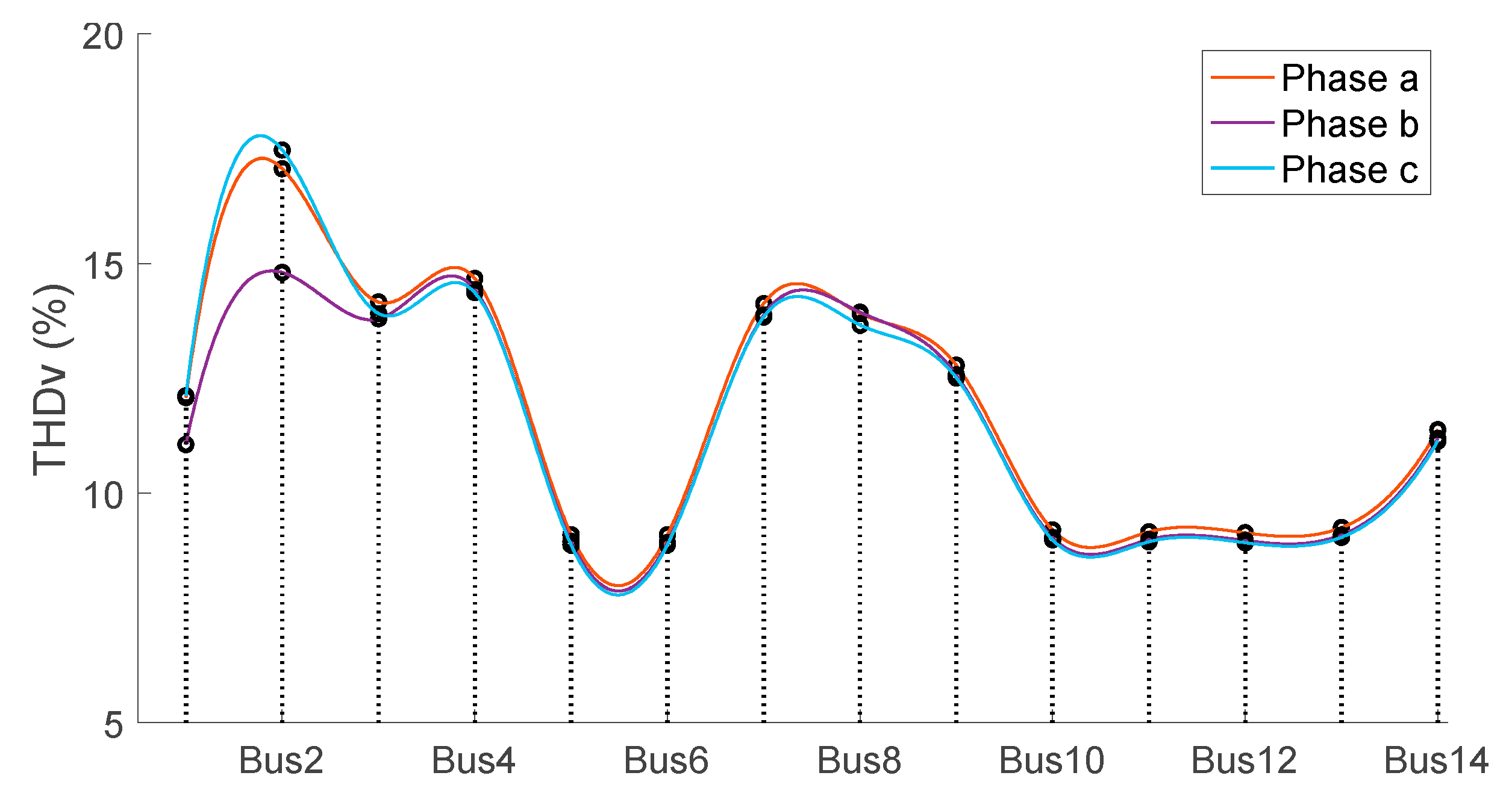
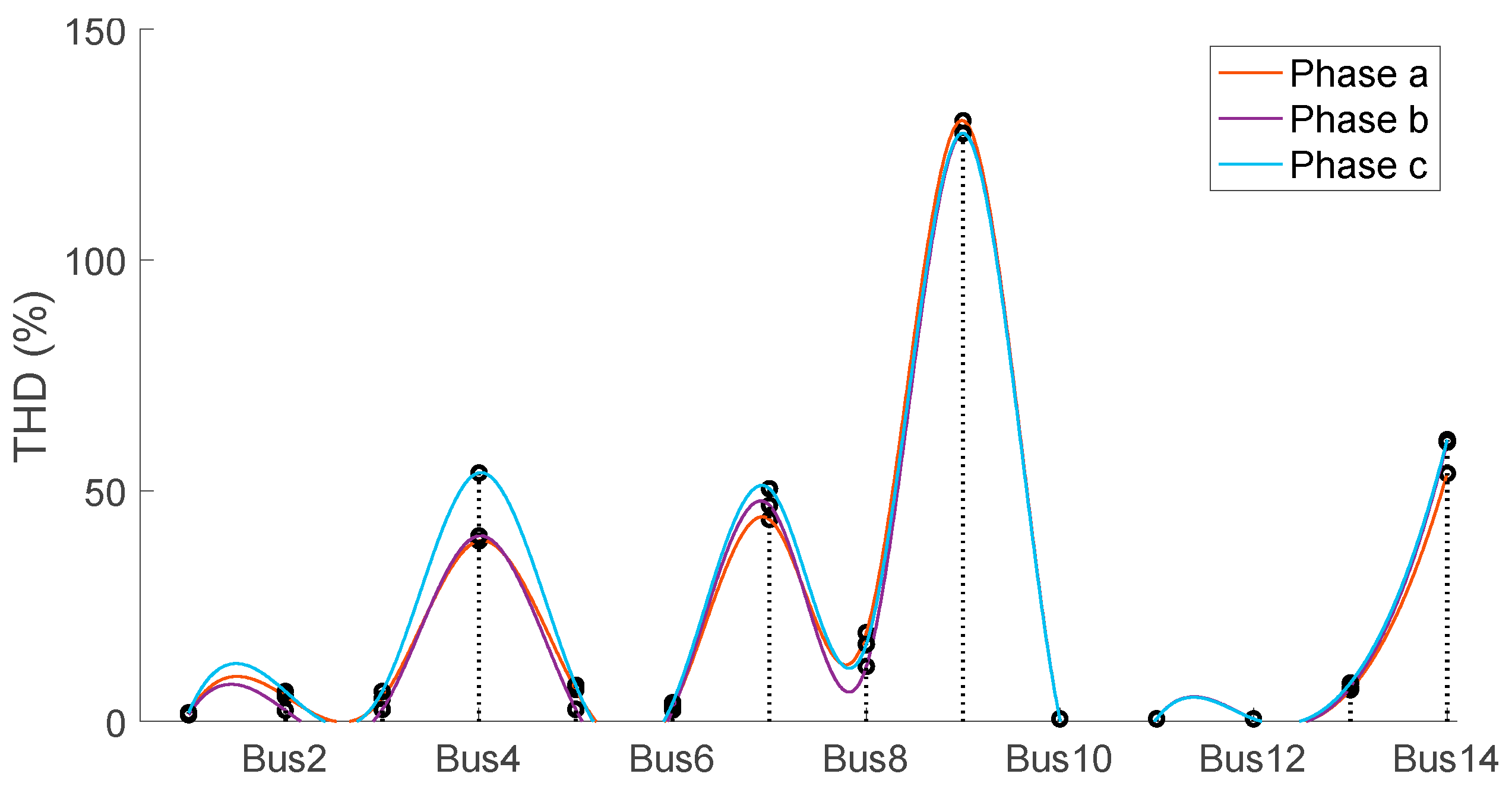
Figure 10.
Voltage THD in each of the buses of the proposed MG.
Figure 10.
Voltage THD in each of the buses of the proposed MG.
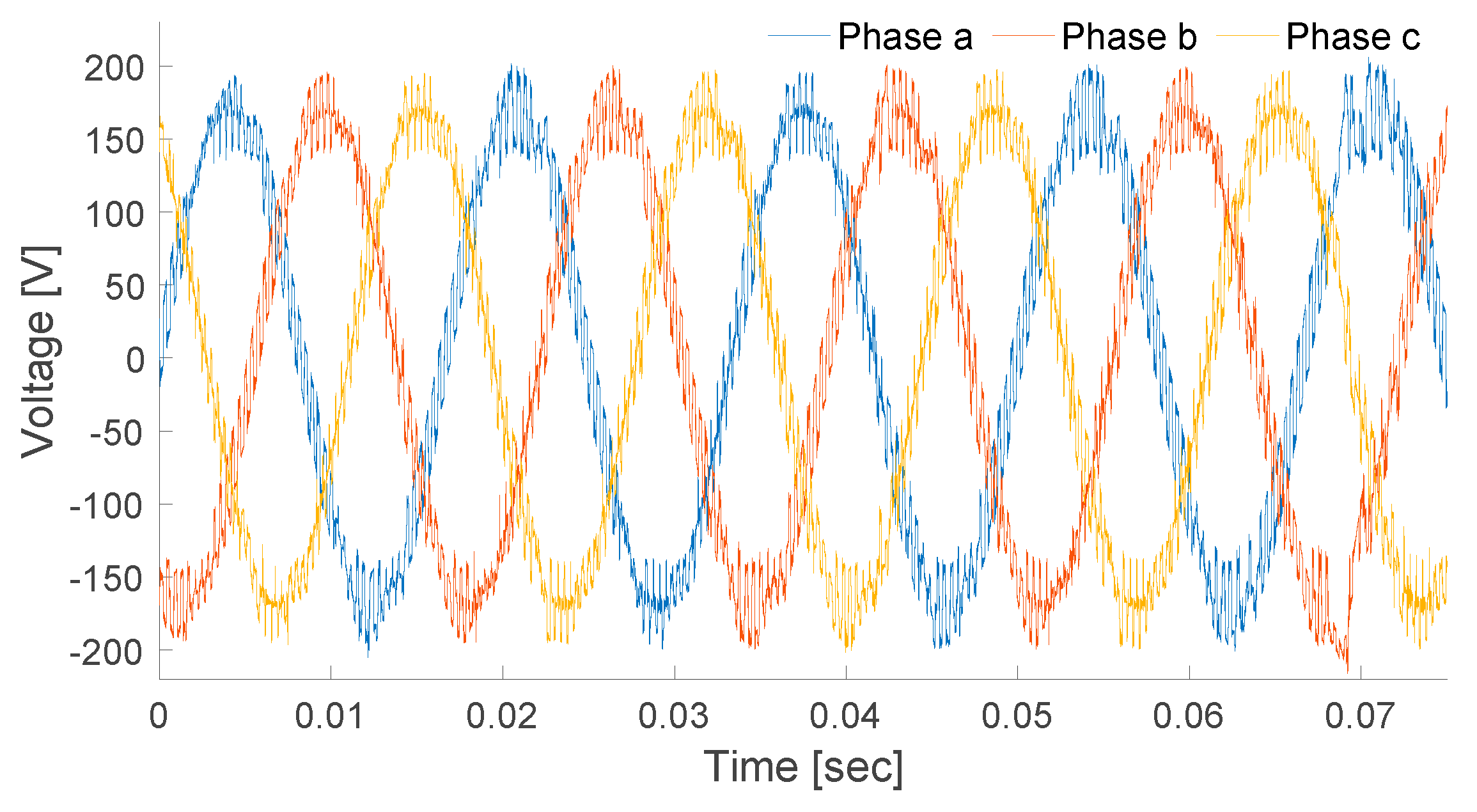
Figure 11.
Three-phase voltage at bus 4.
Figure 11.
Three-phase voltage at bus 4.
Figure 12.
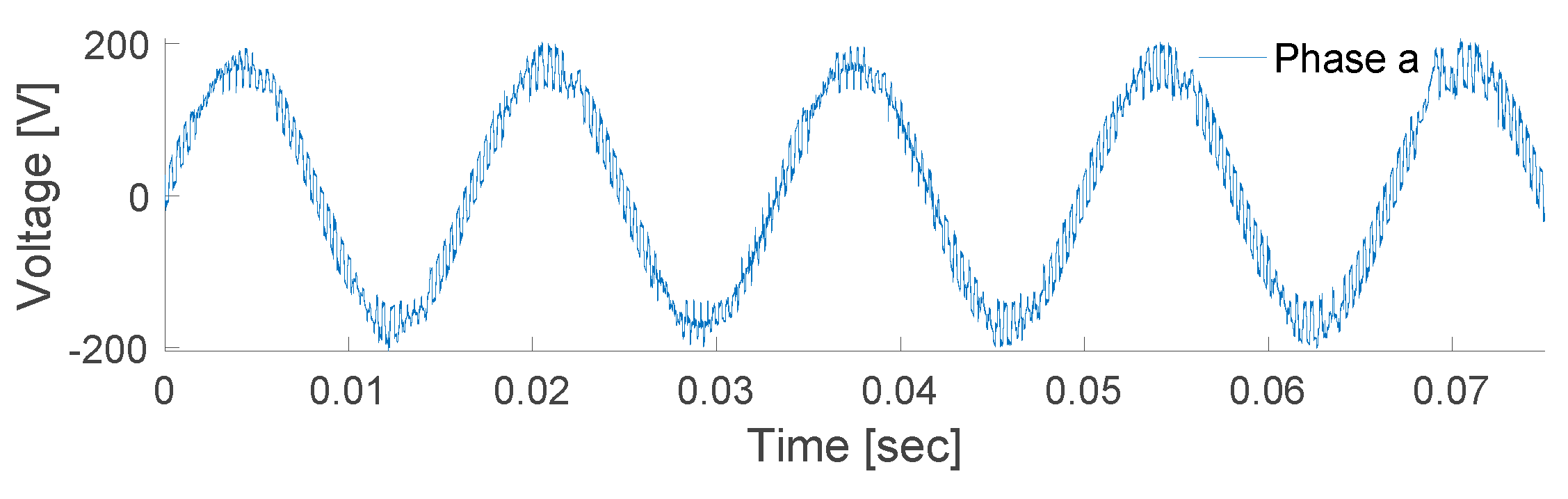
Phase “a” voltage at bus 4.
Figure 12.
Phase “a” voltage at bus 4.
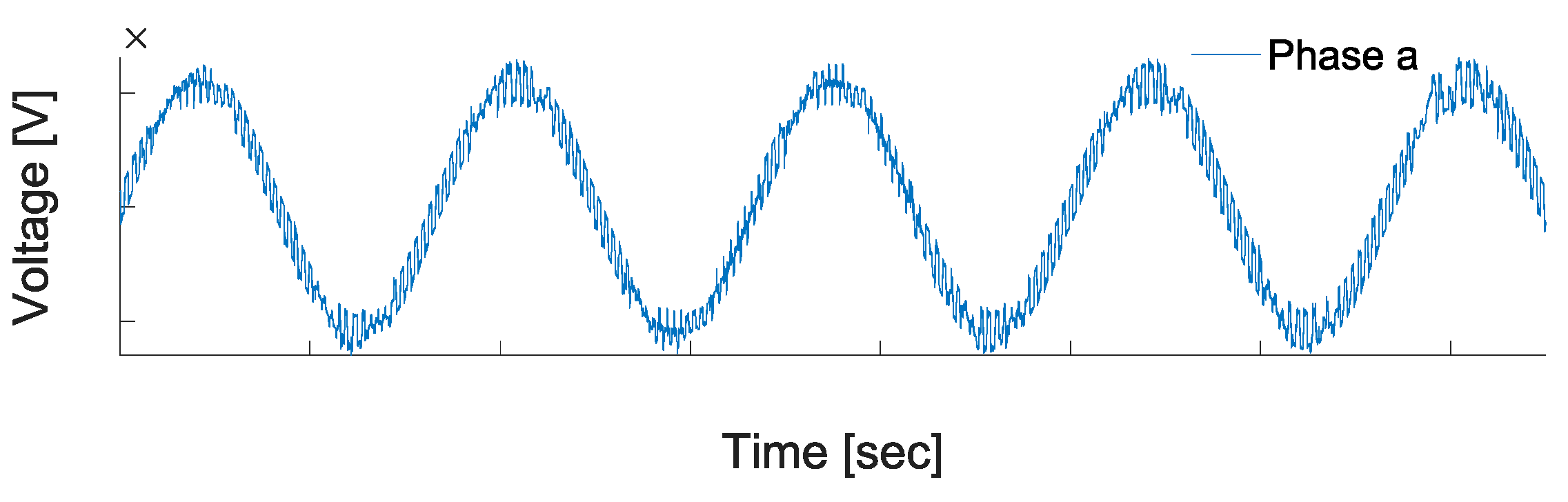
Figure 13.
Phase “a” voltage at bus 7.
Figure 13.
Phase “a” voltage at bus 7.
Figure 14.
Phase “a” voltage at bus 9.
Figure 14.
Phase “a” voltage at bus 9.
Figure 15.
Current THD in each of the buses of the proposed MG.
Figure 15.
Current THD in each of the buses of the proposed MG.
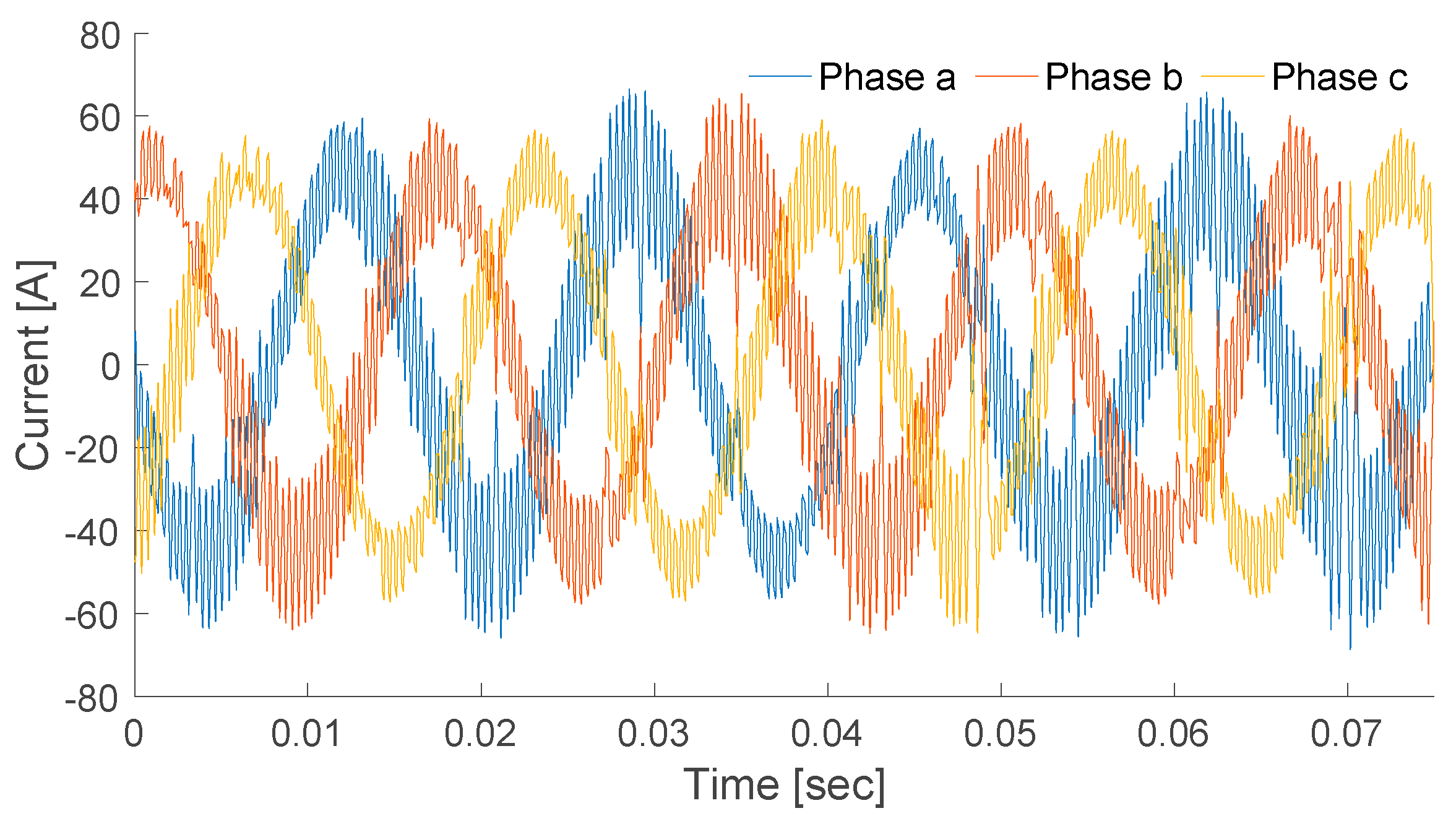
Figure 16.
Three-phase currents at bus 4.
Figure 16.
Three-phase currents at bus 4.
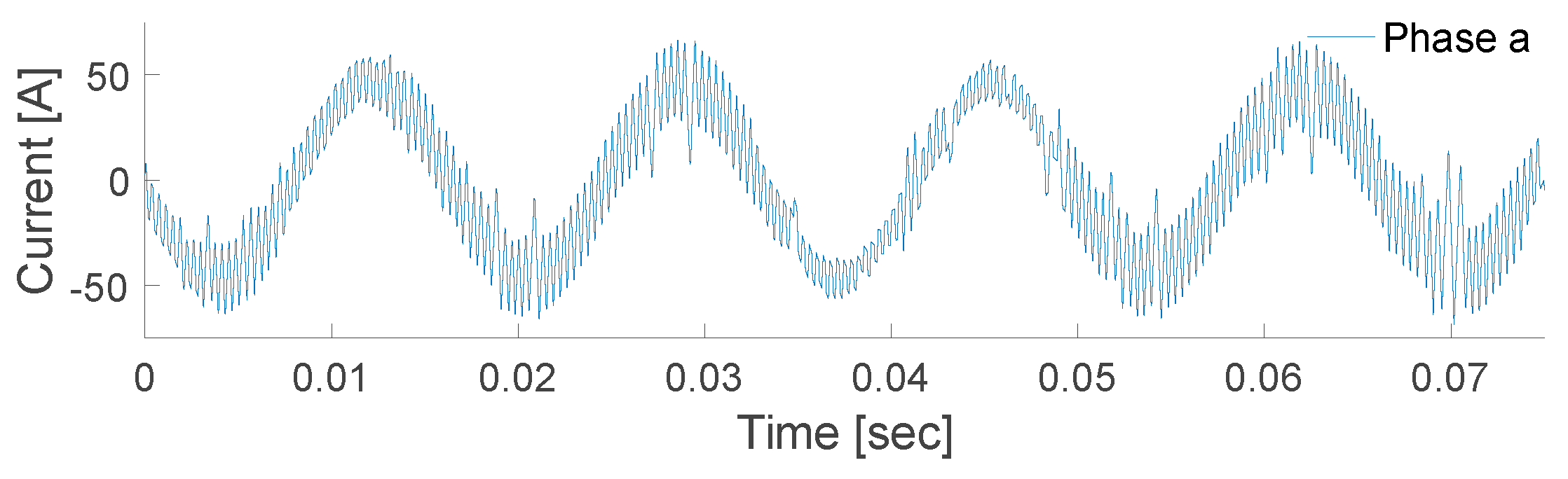
Figure 17.
Current at bus 4.
Figure 17.
Current at bus 4.
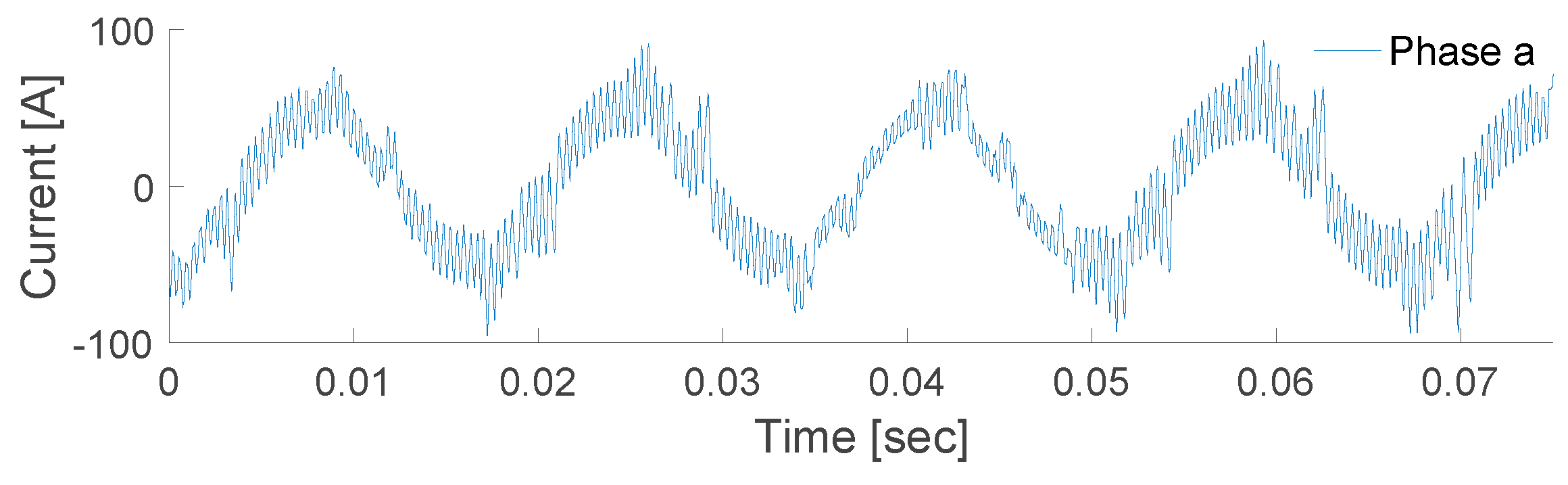
Figure 18.
Current at bus 7.
Figure 18.
Current at bus 7.
Figure 19.
Current at bus 9.
Figure 19.
Current at bus 9.
Table 1.
Synchronization parameters to reconnect the MG to the electrical grid.
Table 1.
Synchronization parameters to reconnect the MG to the electrical grid.
| Power of the DGUs (MVA) |
|
|
|
| 0.0 – 0.5 |
0.3 |
10 |
20 |
|
0.5 – 1.5 |
0.2 |
5 |
15 |
|
1.5 – 10 |
0.1 |
3 |
10 |
Table 2.
Main power quality issues in MGs operating in grid–connected mode.
Table 2.
Main power quality issues in MGs operating in grid–connected mode.
| Power quality issue |
PV |
WT |
Hydro |
Biomass |
Diesel |
| Voltage sags |
|
✓ |
✓ |
✓ |
✓ |
| Voltage swells |
|
✓ |
|
|
✓ |
| Voltage unbalances |
✓ |
|
|
✓ |
|
| THD |
✓ |
✓ |
✓ |
|
|
| Interruptions |
✓ |
✓ |
|
✓ |
|
Table 3.
PVs parameters.
| PV |
|
|
|
|
|
| 1 |
8.6 A |
250 W |
37.4 V |
30.7 V |
8.6 A |
| 2 |
5.7 A |
414.8 W |
85.3 V |
73 V |
6.1 A |
Table 4.
PMSG–based wind turbine parameters.
Table 4.
PMSG–based wind turbine parameters.
| Parameter |
Value |
| Power |
750 kW |
| Torque |
318 kNm |
| Voltage |
575 V |
| Current |
676 A |
| Frequency |
60 Hz |
| Pole Pairs |
26 |
| Speed |
22.5 rpm |
| Stator resistance |
6.5 |
| Rotor resistance |
0.76 |
| Inductance stator |
3.85 mH |
| Rotor inductance |
1.12 mH |
| Flow magnetic |
8.53 Wb
|
| DC Capacitance |
0.16 F |
| DC voltage |
1,220 V |
Table 5.
Transformer parameters.
Table 5.
Transformer parameters.
| Transformer |
(MVA) |
Relationship voltage (kV) (AV/BV) |
(pu) |
(pu) |
| T1 |
100 |
Yg 69/13.8 D1 |
0.015 |
0.015 |
| T2 |
1.5 |
Y 13.8/0.22 Y |
0.03 |
0.03 |
| T3 |
1.5 |
Y 13.8/0.22 Y |
0.03 |
0.03 |
| T4 |
1 |
Yg 13.8/0.25 D1 |
0.0012 |
0.03 |
| T5 |
1 |
Yg 13.8/0.25 D1 |
0.0012 |
0.03 |
| T6 |
0.5 |
D1 0.9/0.22 Y |
0.003 |
0.06 |
| T7 |
3.5 |
Yg 13.8/2.4 D1 |
0.015 |
0.015 |
Table 6.
Parameters of the different types of loads.
Table 6.
Parameters of the different types of loads.
| Bus |
Voltage |
Load type |
kVA |
PF |
% Off |
| 2 |
LV |
Unbalanced |
40 |
0.9 |
13 |
| 3 |
LV |
Unbalanced |
30 |
0.85 |
12.6 |
| 4 |
LV |
Linear |
15 |
0.9 |
– |
| 9 |
MV |
Non-linear |
320 |
1 |
– |
| 10 |
MV |
Linear |
800 |
0.8 |
– |
| 11 |
MV |
Linear |
400 |
0.8 |
– |
| 12 |
MV |
Linear |
800 |
0.8 |
– |
| 14 |
MV |
Linear |
1600 |
0.8 |
– |
| DC |
DC |
DC load |
2 |
1 |
– |
Table 7.
Non–linear load parameters.
Table 7.
Non–linear load parameters.
| Capacitor |
Rated voltage |
Resistance |
|
| 10 F |
18,500 |
1,084 |
30 |
Table 8.
Distribution lines parameters.
Table 8.
Distribution lines parameters.
| Line |
Comes out |
Enters |
|
|
Distance |
| 1 |
LV 1 |
LV 2 |
0.0297 |
0.016335 |
0.15 km |
| 2 |
LV 1 |
LV 5 |
0.0396 |
0.02178 |
0.2 km |
| 3 |
LV 2 |
LV 5 |
0.0297 |
0.016335 |
0.15 km |
| 4 |
LV 2 |
LV 4 |
0.0792 |
0.04356 |
0.4 km |
| 5 |
LV 4 |
LV 5 |
0.0792 |
0.04356 |
0.4 km |
| 6 |
LV 2 |
LV 3 |
0.0792 |
0.04356 |
0.4 km |
| 7 |
LV 3 |
LV 4 |
0.0198 |
0.01089 |
0.1 km |
| 8 |
MV 7 |
MV 9 |
0.788 |
0.2336 |
2 km |
| 9 |
MV 6 |
MV 11 |
2,364 |
0.7008 |
6 km |
| 10 |
MV 6 |
MV 12 |
2,364 |
0.7008 |
6 km |
| 11 |
MV 6 |
MV 13 |
1,182 |
0.3504 |
3 km |
| 12 |
MV 10 |
MV 11 |
2,364 |
0.7008 |
6 km |
| 13 |
MV 13 |
MV 14 |
1,182 |
0.3504 |
3 km |
| 14 |
MV 9 |
MV 14 |
0.788 |
0.2336 |
2 km |
Table 9.
Voltage distortion limits.
Table 9.
Voltage distortion limits.
| Bus voltage at PCC |
Distortion harmonic |
(%) |
| Less than 69 kV |
3.0 |
5.0 |
| 69 kV up to 161 kV |
1.5 |
2.5 |
| Greater than 161 kV |
1.0 |
1.5 |
Table 10.
Maximum limits (%) of odd harmonic current distortion for distribution system (120 V up to 69 kV).
Table 10.
Maximum limits (%) of odd harmonic current distortion for distribution system (120 V up to 69 kV).
|
11 |
17 |
23 |
|
THD |
|
20 |
4.0 |
2.0 |
1.5 |
0.6 |
5 % |
| 2050 |
7.0 |
3.5 |
2.5 |
1.0 |
8 % |
| 50100 |
10.0 |
4.5 |
4.0 |
1.5 |
12 % |
| 1001,000 |
12.0 |
5.5 |
5.0 |
2.0 |
15 % |
|
1,000 |
15.0 |
7.0 |
6.0 |
2.5 |
20 % |
Table 11.
Harmonic currents components at buses 4, 7 and 9.
Table 11.
Harmonic currents components at buses 4, 7 and 9.
| Bus |
Sequence |
Magnitude (%) |
Angle (º) |
Frequency (Hz) |
| 4 |
0 |
10.25 |
148.2 |
180 |
|
5.62 |
152.2 |
300 |
|
2.50 |
65.6 |
420 |
| 0 |
4.86 |
45.3 |
540 |
|
4.18 |
47.3 |
663.2 |
|
8.17 |
24.9 |
780 |
|
6.33 |
64.4 |
840 |
|
7.40 |
97.1 |
1145.2 |
|
7.07 |
37.9 |
1200 |
|
9.66 |
40.1 |
1320.3 |
| 0 |
6.55 |
93.1 |
1440 |
|
4.06 |
250.3 |
1562.9 |
|
3.08 |
110.4 |
1620 |
| 7 |
|
18.54 |
11.1 |
300 |
|
7.49 |
121.6 |
420 |
| 0 |
6.42 |
29.4 |
540 |
|
6.05 |
206.3 |
673.2 |
|
4.94 |
222.9 |
784.6 |
|
3.71 |
255.7 |
840 |
|
3.0 |
125 |
961.3 |
|
6.26 |
245.9 |
1020 |
|
6.44 |
57.6 |
1140 |
| 0 |
2.83 |
27.0 |
1260 |
|
4.18 |
168.1 |
1382.6 |
|
4.94 |
183.0 |
1500 |
| 0 |
4.15 |
246 |
1620 |
| 9 |
|
84.98 |
27.0 |
300 |
|
54.09 |
144.5 |
420 |
| 0 |
19.23 |
77.1 |
540 |
|
38.67 |
191.9 |
693 |
|
6.43 |
85.8 |
781 |
|
7.05 |
163.1 |
856.3 |
|
4.27 |
151.9 |
960 |
|
14.06 |
48.7 |
1022.4 |
|
11.8 |
234.8 |
1320 |
| 0 |
19.57 |
54.0 |
1440 |
|
15.87 |
21.2 |
1579 |
|
9.47 |
237.9 |
1684.5 |