Prerpints.org logo
Preprint
Article

Numerical Simulation Research of Aerodynamic Characteristics during Take-off Phase in Ski Jumping

Altmetrics

Downloads

85

Views

13

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

16 January 2024

Posted:

17 January 2024

You are already at the latest version

Alerts
Abstract
In view of the inability to directly and accurately obtain the athlete's aerodynamic force during take-off phase through wind tunnel test, the athlete's aerodynamic force and surrounding flow field form under different take-off postures are obtained through numerical simulation research, and the effects of different take-off modes on the aerodynamic characteristics during take-off in ski jumping are discussed. The multi-body system composed of the athlete and skis was selected as the research objects. By using partially averaged Navier-Stokes (PANS) turbulence model and 3D numerical simulation of computational fluid dynamics (CFD), the aerodynamic characteristics of the athlete under different take-off postures were predicted. Take-off modes include knee-push-hip (KPH) mode and hip-drive-knee (HDK) mode, and the hip joint angle of HDK mode is significantly greater than KPH mode. First, the aerodynamic force ratio of the athlete’s torso and legs is obviously large. Although the aerodynamic force of arms themselves is not obvious, they have a great impact on the overall aerodynamic characteristics of the athlete, so the posture of arms cannot be ignored. Then, the total drag and moment of HDK mode are significantly higher than that of KPH mode, and the lift-to-drag ratio of HDK mode is significantly lower than that of KPH mode. At first the total lift of HDK mode is higher than that of KPH mode, but in the last attitude the total lift of HDK mode does not rise but fall, and finally the total lift of HDK mode is lower than KPH mode. The aerodynamic characteristics change dramatically during take-off phase, and the aerodynamic characteristics of the two take-off modes are quite different, and these changes and differences are difficult to be observed in real training and competition site. KPH mode has obvious aerodynamic advantage over HDK mode. During the take-off process, the athlete should increasethe force generated by the knee joint extension and appropriately reduce the speed of hip joint extension, and control the using force order of the lower limb joints, and push hip joint extension by knee joint extension, in order to avoid issues such as the hip joint angle is too large, the hip joint extension angle is too fast, the center of gravity is to back and other problems. Studying the aerodynamic characteristics during the take-off phase provides valuable insights for athletes to achieve favorable flight postures after take-off, offering scientific guidance to improve training strategies and enhance competitive performance.
Keywords: 
Subject: Physical Sciences  -   Biophysics

1. Introduction

Ski jumping is an exhilarating winter sports activity where athletes slide down a sloping ramp on specially designed skis. With the help of speed and ground reaction force, they launch themselves into the air and land on a designated slope after a period of flight. The entire technique of ski jumping can be divided into four different phases: inrun, take-off, flight, and landing. These phases involve two major aspects: ballistics and aerodynamics. Ballistics depend on the athlete’s speed and take-off position, while aerodynamics encompasses the aerodynamic characteristics of the anti-body system of the athlete and skis (such as speed, athlete/skis system posture, drag and lift, clothing design, ski length, etc.) [1,2]. Both ballistics and aerodynamics pose specific requirements for ski jumpers, aiming to maximize vertical lift and minimize drag. Aerodynamics plays a crucial role in all the four phases, although current research has predominantly focused on the inrun and flight phases [3,4,5,6,7,8,9]. Computational fluid dynamics (CFD) is an important tool in the study of ski jumping aerodynamics, as it allows for the direct and accurate calculation of the athlete’s aerodynamic forces and moments. CFD can also provide visual or analytical representations of the surrounding flow field. However, current CFD research in ski jumping is primarily focused on the inrun and flight stages [10,11,12,13,14,15]. The main reason for this is that compared to the inrun and flight stages, the take-off stage involves rapid and drastic changes in the athlete’s posture within a very short period. The dynamic complexity of this stage far exceeds that of the inrun and flight stages, making numerical simulation studies of the take-off process more challenging and less cost-effective.
The take-off phase is the transition motion from the in-run posture to the flight posture for the ski jumpers. The take-off motion is considered to be the most important phase for the entire ski jumping performance, because it plays a decisive role on the initial flight conditions [16]. During the take-off phase of ski jumping, the ballistic characteristics become more evident. Although some predictions have been made regarding its aerodynamic properties [17], the aerodynamic effects during take-off phase have not been extensively studied. From an aerodynamic perspective, take-off is crucial because athletes need to strike a balance between maximizing vertical acceleration and minimizing aerodynamic drag. As the athlete extends their body fully exposed to the air during take-off phase, the aerodynamic drag rapidly increases. However, the aerodynamic lift during take-off phase is beneficial as it reduces the load on the athlete, leading to a shorter take-off time and higher power development rate [18]. In actual ski jumping conditions, each jump training session is limited to a few seconds, and the take-off process itself lasts only about 0.3 seconds. However, a significant amount of time is required for preparation, and the number of training jumps per day is limited. Therefore, one effective way to improve the athlete’s subjective perception of aerodynamic forces and training duration is to conduct take-off training in the wind tunnel [19,20,21,22]. Furthermore, based on a series of wind tunnel experiments, Virmavirta et al. (2001) and Zhang et al. (2023) obtained force measurements by using the force measuring balance, which represents the combined effect of take-off force and aerodynamic forces [18,23]. However, direct measurement of transient aerodynamic forces during take-off is still not possible. Additionally, by analyzing the kinematic parameters and take-off patterns of top male ski jumpers in China, Tan et al. (2022) investigated the main factors influencing the flight distance in men’s ski jumping [24]. Cao et al. (2022) found a correlation between the kinematic parameters of athletes during the take-off phase and the jumping distance, emphasizing the importance of powerful leg extension ability while utilizing speed and mastering the timing and direction of take-off [25].
In summary, the research on the aerodynamic characteristics during the take-off phase of ski jumping mainly focuses on wind tunnel training and experimental testing, along with some analysis from a kinematic perspective. However, due to the rapid and significant changes in the athlete’s postures during take-off phase, and limitations in the current level of wind tunnel experimental techniques, it is challenging to achieve consistent and stable reproductions of different take-off postures, and it is unable to accurately test the aerodynamic forces and moments. Nevertheless, wind tunnel training can still be conducted to enhance athletes’ subjective perception of aerodynamic drag and their ability to adapt and adjust. To assist in improving the daily take-off and flight technique training for ski jumpers and accurately obtain the aerodynamic characteristics during the take-off phase, it is necessary to promptly initiate numerical simulation studies on the aerodynamic characteristics of the take-off phase in ski jumping. This will help investigate the influence of athlete posture on the aerodynamic characteristics during take-off phase, ultimately enabling athletes to achieve favorable flight postures after take-off. Considering the difficulties, complexity, and cost-effectiveness of conducting numerical simulations for the dynamic process during take-off, it is proposed to select specific typical postures during take-off for static studies. This study aims to establish a detailed three-dimensional (3D) model and grid model of the athlete/skis system, using the Partially Averaged Navier-Stokes (PANS) turbulence model for CFD numerical simulations. By doing so, the aerodynamic forces acting on the athletes and the flow field around them can be obtained for different take-off postures. The study will explore the impact of different take-off modes on the aerodynamic characteristics of ski jumpers.

2. Methodology

2.1. Research subject

The research focuses on the multi-body system of ski jumpers and the skis. To conduct targeted computational analyses and provide data support directly for national team training, this study conducted body posture scanning and data collection for an elite athlete in the ski jumping national team. By performing 3D scans of the athlete in different postures, a 3D scan model of the athlete’s body during the inrun and take-off phases in ski jumping was obtained. Post-processing of the scanned point cloud data was conducted to obtain a closed 3D model representing the external contour of the athlete’s body, which serves as the original model for CFD research, as shown in Figure 1. In the inrun and take-off phases of ski jumping, important posture parameters for the athlete include the ankle joint angle φ1, knee joint angle φ2, and hip joint angle φ3.

2.2. Research methodology

2.2.1. Simulation model

In this study, the large eddy simulation (LES) technique is employed, which allows for more effective numerical prediction of flow separation around bluff bodies. Previous research has confirmed its efficacy [4,5]. While the standard k-ε PANS model has certain limitations in simulating strong swirling flows and flow over highly curved surfaces, the renormalization group (RNG) k-ε model has shown improvements in predicting such flows [26]. To obtain more accurate results, the RNG k-ε PANS turbulence model is utilized, with its governing equations expressed as follows:
∂ ( ρ k u ) ∂ t + ∂ ( ρ U j k u ) ∂ x j = ∂ ∂ x j [ α k ( μ + μ u σ u ) ∂ k u ∂ x j ] + P k u − ρ ε u
∂ ( ρ ε u ) ∂ t + ∂ ( ρ U j ε u ) ∂ x j = ∂ ∂ x j [ α k ( μ + μ u σ u ) ∂ ε u ∂ x j ] + C ε 1 * P k u ε u k u − C ε 2 * ρ ε u 2 k u
In the equations, Uj represents the resolved velocity field, t denotes time, ρ represents fluid density, μ denotes the dynamic viscosity coefficient, μu represents the turbulent viscosity coefficient, fk represents the unresolved turbulent kinetic energy ratio, fε represents the unresolved turbulent kinetic energy dissipation rate ratio, ku represents the unresolved local time-averaged turbulent kinetic energy, and εu represents the unresolved local time-averaged turbulent kinetic energy dissipation rate.
Where:
f k = k u k
f ε = ε u ε
μ u = ρ C μ k u 2 ε u
σ u = f k 2 f ε
C ε 2 * = C ε 1 * + f k f ε ( C ε 2 − C ε 1 * )
η = ( 2 S i j ⋅ S i j ) 1 / 2 k u ε u f ε f k
S i j = 1 2 ( ∂ U i ∂ x j + ∂ U j ∂ x i )
C ε 1 * = C ε 1 − η ( 1 − η / η 0 ) 1 + δ η 3
The values of the constants in the model are: C μ = 0.0845 , α k = α ε = 1.39 , C ε 1 = 1.42 , C ε 2 = 1.68 , η 0 = 4.377 , δ = 0.012 .
The governing equations are discretized using the finite volume method. The coupling of pressure and velocity is solved using a consistent and coordinated approach based on the semi-implicit algorithm for pressure-linked equations (SIMPLEC). The time discretization is performed using a second-order difference scheme. The turbulent kinetic energy and velocity terms are discretized using a second-order upwind scheme. The time step size is set to 0.0001s.

2.2.2. Validation of Model Independence from the Grid

The original 3D scan model of the research subject was adaptively modified, supplemented, and repaired based on the important parameters of the posture during the take-off phase. This process resulted in a refined 3D solid model of the multi-body system, allowing for the detailed modeling of the athlete’s physical characteristics. Features such as fingers, ears, face, shoulders, and hips can still be clearly distinguished from Figure 1.
The computational domain size for the ski jumper/skis multi-body system is 28m in length, 11m in width, and 14m in height. Considering the presence of flow separation in the wake and the potential influence of the athlete’s body shape on the flow field, the multi-body system’s refined 3D solid model was divided into various regions for grid generation, as shown in Figure 2. These regions include the athlete’s body surface area, the athlete’s front region, the wake region behind the athlete’s head and back, the wake region behind the athlete’s waist and hips, the wake region behind the athlete’s legs, the wake region behind the athlete’s arms, and the region away from the athlete.
To meet the computational requirements of the RNG k-ε PANS model, an appropriate grid refinement strategy was applied around the athlete. The grid partitioning strategy used in this study has been previously validated in previous researches [4,5]. Specifically, for the grid model, four different grid densities were selected for each respective region. These regions were uniformly refined to varying degrees, resulting in grid point numbers ranging from 12.47 million to 23.21 million. The grid independence verification was conducted, and the results are presented in Table 1. The lift-to-drag ratios obtained from the last two grid validations were around 0.708. This shows that the computational domain discretization scheme with 20.03 million grid nodes can accurately predict its aerodynamic characteristics.

2.2.3. Boundary Conditions and Computational Conditions

The boundary conditions were set as follows: 1) The inlet was specified as a velocity inlet, with a chosen inlet velocity of 25 m/s, representing the take-off speed in this study. 2) The outlet was set as a pressure outlet with a pressure value of 101325 Pa, representing atmospheric pressure. 3) The middle cross-section was assigned periodic boundary conditions. 4) The other walls were set as no-slip boundaries. 5) The fluid was assumed to be incompressible air. 6) The environment was subjected to a constant gravitational acceleration of g0= 9.807 m/s².
In this study, two take-off modes were considered: knee-push-hip (KPH) mode and hip-drive-knee (HDK) mode, with the hip joint angle being significantly greater in the HDK mode. The timing for the calculations started from the moment the front of the skis was about to leave the take-off ramp until the skis completely left the ramp, resulting in a total calculation time of approximately 90 ms. Throughout this process, six different postures of the athlete at different time intervals were selected for static computational conditions, as shown in Table 2. The CFD numerical simulations of the aerodynamic characteristics were conducted to analyze under different take-off modes and postures, the forces and moments acting on the athlete were extracted, and the flow field surrounding the athlete was visually shown.

3. Results

3.1. Aerodynamic Forces and Moments

The aerodynamic forces acting on the multi-body system include lift and drag, and most of these forces do not act at the center of mass of the system, resulting in corresponding moments. Table 3 presents the mechanical characteristics of athletes in different postures under the two take-off modes. Figure 3, Figure 4 and Figure 5 depict the variation of these characteristics over time. The forces listed in the results represent the resultant forces acting on various parts of the multi-body system, including the athlete and skis. The pitch moments listed in the results represent the moments relative to the midpoint of the line connecting the athlete’s feet. "+" indicates that the moment causes the system to tilt backward, while "-" indicates that the moment causes the system to tilt forward. The lift-to-drag ratio in the results was calculated by dividing the lift by the drag.
From Figure 3(a) and Table 3, it can be observed that the total drag rapidly increases when the athlete’s body becomes upright. Throughout the entire take-off process, the total drag in the KPH mode always remains significantly lower than in the HDK mode. For the KPH mode, the initial total drag is 40.20 N, and the final total drag is 99.05 N, which is 2.46 times that of the initial value. For the HDK mode, the initial total drag is 50.66 N, and the final total drag is 140.01 N, which is 2.76 times that of the initial value. Although both take-off modes exhibit a similar increasing trend in total drag, the growth rates differ slightly. In the case of the KPH mode, the total drag gradually increases at a nearly constant rate with a slight fluctuation during this phase. For the HDK mode, the total drag initially increases at a similar rate, and then the rise rate significantly increases in the last three postures.
From Figure 3(b) and Table 3, it can be observed that in terms of total lift, the KPH mode initially has lower lift compared to the HDK mode. However, the total lift in the HDK mode steadily increases and reaches its peak at -18 ms, but decreases slightly in the final posture. On the other hand, the total lift in the KPH mode steadily increases at a nearly constant rate. As a result, the final total lift in the KPH mode is higher than in the HDK mode. For the KPH mode, the initial total lift is 31.31 N, and the final total lift is 53.58 N, which is 1.71 times that of the initial value. For the HDK mode, the initial total lift is 35.56 N, the lift peak is 55.54 N, and the final total lift is 51.09 N, with the lift peak being 1.56 times that of the initial value.
From Figure 3(c) and Table 3, it can be observed that the trend of the total pitch moment variation over time is similar to that of the total drag. The moment in the KPH mode steadily increases at a nearly constant rate, while the moment in the HDK mode experiences a significant rise rate increase in the latter half of the take-off. Throughout the entire take-off process, the moment in the KPH mode always remains significantly lower than in the HDK mode. For the KPH mode, the initial moment is 19.69 N·m, and the final moment is 69.05 N·m, which is 3.51 times that of the initial value. For the HDK mode, the initial moment is 28.06 N·m, and the final moment is 98.82 N·m, which is 3.52 times that of the initial value.
From Figure 3(d) and Table 3, it can be observed that the change in the lift-to-drag ratio differs significantly between the two take-off modes, but the KPH mode consistently exhibits a higher lift-to-drag ratio than the HDK mode. For the KPH mode, the lift-to-drag ratio starts at 0.779 and decreases significantly, with some fluctuations around 0.6, and then decreases sharply. On the other hand, the lift-to-drag ratio in the HDK mode steadily decreases at a nearly constant rate. For the KPH mode, the lift-to-drag ratio decreases from 0.779 to 0.541, while for the HDK mode, it decreases from 0.702 to 0.365.
From Figure 4 and Figure 5, it can be observed that for the drag characteristics, the athlete’s torso and legs contribute the majority of the drag, with the torso’s drag slightly lower than that of the legs. Among the remaining parts, the head contributes a significant amount of drag, and the skis’ contribution becomes more pronounced in the later stages when the skis experience a angle of attack, and is almost comparable to that of the head. The arms and hands also contribute to the total drag, but to a lesser extent compared to the torso, legs, and head. For the lift characteristics, the athlete’s torso and legs contribute the majority of the lift, with the torso’s lift generally higher than that of the legs. Among the remaining parts, the head and arms contribute almost the same lift, but the skis’ lift is negative, and its absolute value steadily increases, and then becomes higher than that of the head and arms in the later stages. In terms of the pitch moment characteristics, the athlete’s torso contribute the majority of the moment. Among the remaining parts, the legs and head contribute more moment in turn, and the skis’ moment is negative, and its absolute value is almost comparable to that of the head.

3.2. Flow field morphology

Figure 6 and Figure 7 display the distribution of airflow velocity (i.e., the velocity component along the anterior-posterior direction) on the athlete’s symmetry plane, also known as the sagittal plane. The regions of flow recirculation in the athlete’s wake are highlighted in green or blue. These recirculation regions can be primarily divided into two distinct parts, with one part originating from the athlete’s back and the other part from the athlete’s chest. In certain postures, such as Figures 6(c) and (d), the KPH mode exhibits slightly smaller recirculation regions. Additionally, it can be observed that there is acceleration of airflow behind the head, in certain areas of the back and face, as well as between the athlete’s legs. Conversely, there is deceleration of airflow in the recirculation regions, in front of the athlete (face and chest), behind the neck, and below and behind the knees. The size of the low-velocity regions in the athlete’s wake gradually increases over time, but in the HDK mode, these regions are significantly larger compared to the KPH mode, as shown in Figures 6(e) and (f), and Figures 7(e) and (f). In the HDK mode, these low-velocity regions extend along the back in the last few postures, resulting in more deceleration of flow in front of the body.
Figure 8 illustrates the contour of equal vorticity contours (ω=100s-1) observed from the side and back of the athlete. For the KPH mode, the vortices generated by the arms first separate and then tend to merge while gradually expanding downward. Throughout the entire take-off motion, these two distinct vortices are separated by a narrow vertical space and then generate a descending flow behind the athlete in the latter half of the take-off phase. However, for the HDK mode, these vortices combine with the vortices generated by the torso in the latter half of the take-off phase and transform into disordered vortices.

4. Discussion

4.1. The numerical simulation results’ validity verification

In this study, the aerodynamic forces acting on the initial posture model during take-off phase which is the final posture model during inrun phase were found to be similar to the research results of Virmavirta et al. [18]. They conducted wind tunnel tests on athletes in the inrun phase posture under a wind speed of 27 m/s and measured aerodynamic drag ranging from 39.2 N to 59.7 N and aerodynamic lift ranging from 22.3 N to 50.4 N. In our study, the total drag for the initial posture in the KPH mode was 40.20 N, and in the HDK mode, it was 50.66 N. The total lift for the initial posture in the KPH mode was 31.31 N, and in the HDK mode, it was 35.56 N. The aerodynamic force results obtained in this study fall within the range of variability observed in wind tunnel tests. These results comparison validates the effectiveness of the CFD numerical simulation results and also indicates that even slight differences in the inrun and take-off postures have a significant impact on the aerodynamic characteristics.

4.2. Aerodynamic characteristics of different body parts

From Figure 4 and Figure 5, it can be observed that the mechanical characteristics of different body parts of the athlete show similar variations over time for both take-off modes. Additionally, the mechanical characteristics of the skis have a relatively small impact but should not be ignored. The torso and legs of the athlete are the main contributors to aerodynamic forces, while the arms, head, and skis themselves also contribute, albeit to a lesser extent. In terms of drag characteristics, the torso and legs contribute to the majority of drag, accounting for approximately 80%. For lift characteristics, the torso and legs also contribute to the majority of lift, accounting for approximately 85%. Regarding moment characteristics, the torso contributes to the majority of the moment, accounting for over 57%, and the remaining significant contributors are the legs and head.
In the KPH mode, the double vortex flow generated by the arms creates a downwash vortex behind the athlete, as shown in Figure 8. This downwash vortex increases in circulation around the athlete, resulting in an increased lift effect, leading to a rapid increase in total lift for the same period. In the HDK mode, in the initial take-off posture, the vortex flow from the arms is quite evident, but later on, these vortex flows become disordered (Figure 8, HDK mode, image of -54 ms). It can be inferred that these disordered vortex flows contribute to the increased area of low-speed regions in the wake of the HDK mode (Figure 7(d)), which subsequently leads to a decrease in total lift (Figure 3(b)). The study found that arm position when it is in a low position, particularly in the HDK mode, has a significant influence on the flow. This is because in the HDK mode, the arms are always very close to the athlete’s thighs (Figure 7), generating larger disordered vortex flows during the entire take-off motion. These findings indicate that the vortices generated by the arms have a significant impact on the generation of aerodynamic lift and the flow structure behind the athlete. Although the aerodynamic forces generated by the arms themselves may not be significant, they have a substantial influence on the overall aerodynamic characteristics of the athlete. Meile et al. (2006) suggested considering the arm angle in flight phase postures and found that the aerodynamic lift during the flight phase increases with an increase in shoulder joint abduction angle [15]. Additionally, Keizo, in his CFD study on ski jumping in the inrun and take-off phase, found that the positioning of the athlete’s arms should not be ignored, as elite athletes are able to control the impact of the arms within a smaller range [27].

4.3. Aerodynamic characteristics of different take-off posture

It can be observed that the HDK mode exhibits significantly higher total drag compared to the KPH mode. This is mainly due to the difference in hip joint angles, or we can say the angle of attack of the torso. As shown in Figure 6 and Figure 7, the angle of attack of the torso is noticeably higher in the HDK mode compared to the KPH mode. Figure 7(e) clearly shows a large area of low-speed region behind the athlete in the HDK mode at -18ms. This low-speed region represents a decrease or even stagnation of airflow velocity, and its size is an important factor influencing the pressure drag acting upon the athlete. The separation of airflow behind the athlete is caused by the excessive upright posture of the torso, resulting in the formation of this low-speed region and subsequently increasing the pressure drag acting upon the athlete.
Although the HDK mode initially exhibits higher total lift compared to the KPH mode, in the final take-off posture, the total lift in the HDK mode does not continue to increase but decreases. This results in a reversal of the lift values at the last time stage (Figure 3(b)). It can be considered that the HDK mode experiences a stall phenomenon at the last time stage, where an increase in the angle of attack leads to a decrease in lift coefficient. Virmavirta et al. (2001) suggested that a good take-off helps the athlete achieve a favorable flight posture, specifically a forward-leaning position, during the early flight phase [18]. Additionally, Schmölzer and Müller (2002) proposed that the aerodynamic lift should gradually increase during the early flight phase after the take-off phase [28]. Therefore, when stall occurs in the HDK mode, it can put the athlete’s aerodynamic characteristics in a disadvantageous state during the flight phase.
From Figures 3(a) and (c), it is evident that the moment trends over time are similar to the total drag trend. In this study, the moment refers to the pitch moment, with "+" representing a moment that causes the multi-body system, i.e., the athlete, to tilt backwards, and "-" representing a moment that causes the multi-body system to tilt forwards. Schwameder (2008) suggested that one of the main objectives in the take-off phase is for the athlete to acquire angular momentum for forward rotation[29]. To achieve a favorable flight posture, for the HDK mode the athlete must consume more physical energy to generate more forward rotational angular momentum compared to the KPH mode, as the aerodynamic forces generate a larger pitch moment which causes the athlete to tilt backwards in the HDK mode than in the KPH mode, as shown in Figure 3(c).
From Figure 3(d), it is evident that the lift-to-drag ratio of the KPH mode is consistently higher than that of the HDK mode. From the aerodynamic perspective, this is because the body opening angle in the KPH mode is significantly smaller than in the HDK mode. The KPH mode provides a noticeable aerodynamic advantage for the athlete in the flight phase after take-off phase. During the take-off process, for creating favorable aerodynamic conditions for the early flight phase, the athlete should increase the force generated by the knee joint extension and appropriately reduce the speed of hip joint extension, and control the using force order of the lower limb joints, and push hip joint extension by knee joint extension, in order to avoid issues such as the hip joint angle is too large, the hip joint extension angle is too fast, the center of gravity is too back and other problems, and to avoid the adverse impact of aerodynamic drag on take-off. Cao et al. (2022) demonstrated in their study on Chinese male ski jumpers that athletes should lower their center of gravity as much as possible at the start of the take-off phase to reduce drag, increase knee joint extension force during take-off phase, and simultaneously appropriately reduce hip joint extension speed to avoid adverse effects of aerodynamic drag on the torso during take-off phase [25]. Furthermore, through analyzing the kinematics and take-off patterns of elite Chinese male ski jumpers in the field, it is recommended that athletes should aim to reduce their body’s center of gravity at the beginning of the take-off phase while maximizing the utilization of speed. They should also control the timing and direction of take-off [24].

5. Conclusion

1)
Through numerical simulations using CFD, the aerodynamic characteristics and differences of various postures in the take-off phase in ski jumping have been analyzed. The study focuses on comparing the effects of two take-off modes on aerodynamic characteristics. The aerodynamic characteristics change dramatically during take-off phase, and the aerodynamic characteristics of the two take-off modes are quite different, and these changes and differences are difficult to be observed in real training and competition site.
2)
The aerodynamic forces on the athlete’s torso and legs are significantly larger, while the contribution of the arms may be less pronounced. However, the position of the arms should not be ignored as it can still have a considerable impact on the overall aerodynamic characteristics of the athlete. The KPH mode demonstrates clear aerodynamic advantages. During the take-off process, the athlete should increase the force generated by the knee joint extension and appropriately reduce the speed of hip joint extension, and control the using force order of the lower limb joints, and push hip joint extension by knee joint extension, in order to avoid issues such as the hip joint angle is too large, the hip joint extension angle is too fast, the center of gravity is too back and other problems, and to avoid the adverse impact of aerodynamic drag on take-off. This creates favorable aerodynamic conditions for the early flight phase.
3)
Numerical simulations of the aerodynamics in the take-off phase of ski jumping can accurately capture the aerodynamic characteristics. Numerical simulations combining with repeated training in a wind tunnel to simulate competition scenarios help athletes improve their subjective perception and adaptability to aerodynamic forces during the take-off phase. It also enables athletes to utilize aerodynamic forces to achieve favorable flight postures after take-off phase. This research provides important scientific guidance for athletes to improve their take-off and flight technique training strategies and enhance their competitive performance.

Author Contributions

Formal analysis, Qi HU; Methodology, Qi HU and Weidi TANG; Writing - original draft, Qi HU and Weidi TANG; Writing - review & editing, Qi HU, Weidi TANG and Yu LIU; Funding acquisition, Qi HU and Yu LIU.

Funding

This research was funded by the National Natural Science Foundation of China, grant number 11802068 and 11932013, and the National key research and development plan project of China, grant number 2018YFF0300500.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Acknowledgments

The authors would also like to express their gratitude to Professor Chongli Wang and Professor Qingli Li from Aerodynaiviics Research Institute in China for conducting the 3D scanning of the athletes’ postures and providing the original scanned models of the athletes.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Hu, Q.; Liu, Y. A Review of Wind Tunnel Experimental Research on Aerodynamic Drag Reduction in Winter Sports. China Sport Sci. Tech. 2022, 42, 55–67. [Google Scholar]
  2. Virmavirta, M. Aerodynamics of ski jumping. In The engineering approach to winter sports, 6th ed.; Braghin: NY, USA, 2016; pp. 153–181. [Google Scholar]
  3. Elfmark, O.; Ettema, G. Aerodynamic investigation of the inrun position in Ski jumping. Sports Biomech. 2021, 19, 1. [Google Scholar] [CrossRef]
  4. Hu, Q.; Liu, Y. Effects of Athlete’s Posture on Aerodynamic Characteristics during Flight in Ski Jumping. J. Med. Biomech. 2021, 36, 407–414. [Google Scholar]
  5. Hu, Q.; Liu, Y. Effects of Wind on the Aerodynamic Characteristics during Flight in Ski Jumping. China Sport Sci. 2020, 40, 54–63. [Google Scholar]
  6. Hu, Q.; Liu, Y. Effects of Posture Asymmetry on the Aerodynamic Characteristics during Flight in Ski Jumping. China Sport Sci. 2020, 40, 41–49. [Google Scholar]
  7. Hu, Q.; Chen, Q.; Zhang, W.Y. Effect of the Ski Opening Angle on the Aerodynamic Characteristics during Flight in Ski-Jumping. China Sport Sci. 2018, 38, 42–49. [Google Scholar]
  8. Gardan, N.; Schneider, A.; Polidori, G.; Trenchard, H.; Seigneur, J.M.; Beaumont, F.; Fourchet, F.; Taiar, R. Numerical investigation of the early flight phase in ski-jumping. J. Biomech. 2017, 50, 29–34. [Google Scholar] [CrossRef]
  9. Murakami, M.; Iwase, M.; Seo, K.; Ohgi, Y.; Koyanagi, R. High-speed video image analysis of ski jumping flight posture. Sports Eng. 2014, 17, 217–225. [Google Scholar] [CrossRef]
  10. Tang, W.D.; Suo, X.; Yang, C.H.; Cao, F.R.; Wu, X.; Liu, Y. Computational Fluid Dynamics Simulation and Optimization of In-run Stage in Ski-Jumping. China Sport Sci. 2022, 42, 62–70. [Google Scholar]
  11. Ryu, M.; Cho, L.; Cho, J. Aerodynamic analysis on postures of ski jumpers during flight using computational fluid dynamics. T. Jpn. Soc. Aeronaut. S. 2015, 58, 204–212. [Google Scholar] [CrossRef]
  12. Chen, Z.F. Numerical Study of the Aerodynamical Parameters During the Flying Stage of Ski Jumping. Zhejiang Sport Sci. 2014, 36, 121–124. [Google Scholar]
  13. Lee, K.D.; Park, M.J.; Kim, K.Y. Optimization of ski jumper’s posture considering lift-to-drag ratio and stability. J. Biomech. 2012, 45, 2125–2132. [Google Scholar] [CrossRef]
  14. Nørstrud, H.; ØYE, I.J. On CFD simulation of ski jumping. Computational Fluid Dynamics for Sport Simulation. 2009, 72, 63–82. [Google Scholar]
  15. Meile, W.; Reisenberger, E.; Mayer, M.; Schmolzer, B.; Muller, W.; Brenn, G. Aerodynamics of ski jumping: Experiments and CFD simulations. Exp. Fluids. 2006, 41, 949–964. [Google Scholar] [CrossRef]
  16. Virmavirta, M.; Isolehto, J.; Komi, P.; Schwameder, H.; Pigozzi, F.; Massazza, G. Take-off analysis of the Olympic ski jumping competition (HS-106 m). J. Biomech. 2009, 42, 1095–1101. [Google Scholar] [CrossRef]
  17. Virmavirta, M.; Komi, P.V. Measurements of the take-off forces in ski-jumping Part I and II. Scand. J. Med. Sci. Sports. 1993, 3, 229–243. [Google Scholar] [CrossRef]
  18. Virmavirta, M.; Kivekas, J.; Komi, P.V. Take-off aerodynamics in ski jumping. J. Biomech. 2001, 34, 465–470. [Google Scholar] [CrossRef]
  19. Virmavirta, M. Ski Jumping: Aerodynamics and Kinematics of Take-Off and Flight. In Handbook of Human Motion, 1st ed.; Springer: NY, USA, 2017; pp. 1–21. [Google Scholar]
  20. Virmavirta, M.; Kivekas, J.; Komi, P.V. Ski jumping take-off in a wind tunnel with skis. J. Appl. Biomech. 2011, 27, 375–379. [Google Scholar] [CrossRef]
  21. Muller, W. Performance factors in ski jumping. J. Biomech. 2006, 39, 192–213. [Google Scholar] [CrossRef]
  22. Wang, Z.X.; Li, R.; Guan, Z.H.; Wu, D.Y. Experimental study on the initial attitude during Flight in Ski Jumping. China Sport Sci. 1998, 18, 1–5. [Google Scholar]
  23. Zhang, D.; Zou, X.S.; Liu, Y.; Xu, J.C.; Cao, C.M. Effects of Movement and Postures on Aerodynamic Drag during Ski Jumping In-Run and Take-off Phases in Nordic Combined Athletes. China Sport Sci. Tech. 2023, 59, 3–12. [Google Scholar]
  24. Tan, X.N.; Zhou, Y.; Qu, F.; Huo, B.; Fu, Y.; Jiang, L. Analysis of Take-off Factors Affecting the Flying Distance of Chinese Elite Male Ski Jumpers. China Sport Sci. Tech. 2022, 58, 38–45. [Google Scholar]
  25. Cao, F.R.; Wu, X.; Tang, W.D.; Suo, X.; Yang, C.H.; Liu, Y. A systematic review of research on the biomechanics of take-off and early flight of ski jumping. J. Beijing Univ. Sport. 2022, 45, 35–44. [Google Scholar]
  26. Liu, J.T.; Zuo, Z.G.; Liu, S.H.; Wu, Y.L.; Wang, L.Q. A nonlinear partially-averaged Namer-Stokes model for turbulence flow simulations. J. Drain. Irrig. Mach. Eng. 2015, 33, 572–576. [Google Scholar]
  27. Keizo, Y.; Makoto, T.; Jun, I.; Keiji, O.; Sophie, B. Effect of posture on the aerodynamic characteristics during take-off in ski jumping. J. Biomech. 2016, 49, 3688–3696. [Google Scholar]
  28. Schmolzer, B.; Muller, W. The importance of being light: Aerodynamic forces and weight in ski jumping. J. Biomech. 2002, 36, 1059–1069. [Google Scholar] [CrossRef]
  29. Schwameder, H. Biomechanics research in ski jumping: 1991-2006. Sports Biomech. 2008, 7, 114–136. [Google Scholar] [CrossRef]
Preprints 96506 g001
Figure 1. The original scanning model. φ1, ankle joint angle; φ2, knee joint angle; φ3, hip joint angle.
Figure 1. The original scanning model. φ1, ankle joint angle; φ2, knee joint angle; φ3, hip joint angle.
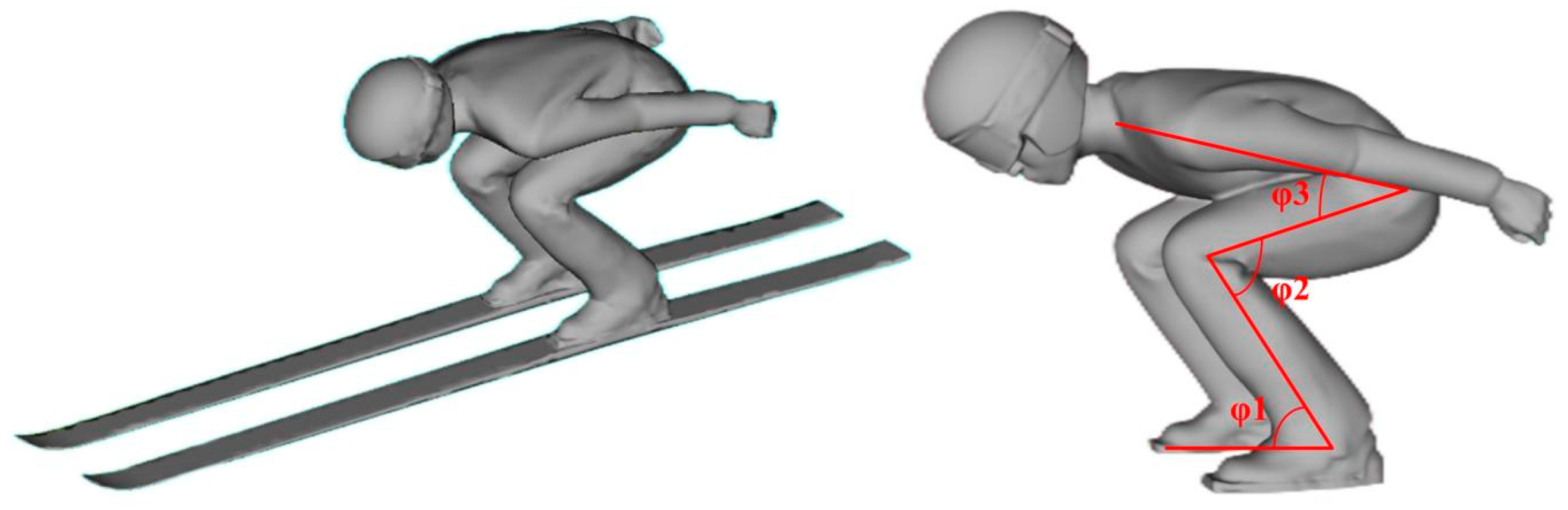
Preprints 96506 g001
Preprints 96506 g002
Figure 2. Grid distribution of the model surface and nearby area.
Figure 2. Grid distribution of the model surface and nearby area.
Preprints 96506 g002
Preprints 96506 g003
Figure 3. Change curves of aerodynamic characteristics of two take-off modes. Time -90ms means the moment that the front of the skis is out of the platform. Time zero means the moment that the end of the skis completely leaves the platform. (a) The temporal changes of total drag, (b) The temporal changes of total lift, (c) The temporal changes of total pitch moment, (d) The temporal changes of lift-to-drag ratio.
Figure 3. Change curves of aerodynamic characteristics of two take-off modes. Time -90ms means the moment that the front of the skis is out of the platform. Time zero means the moment that the end of the skis completely leaves the platform. (a) The temporal changes of total drag, (b) The temporal changes of total lift, (c) The temporal changes of total pitch moment, (d) The temporal changes of lift-to-drag ratio.
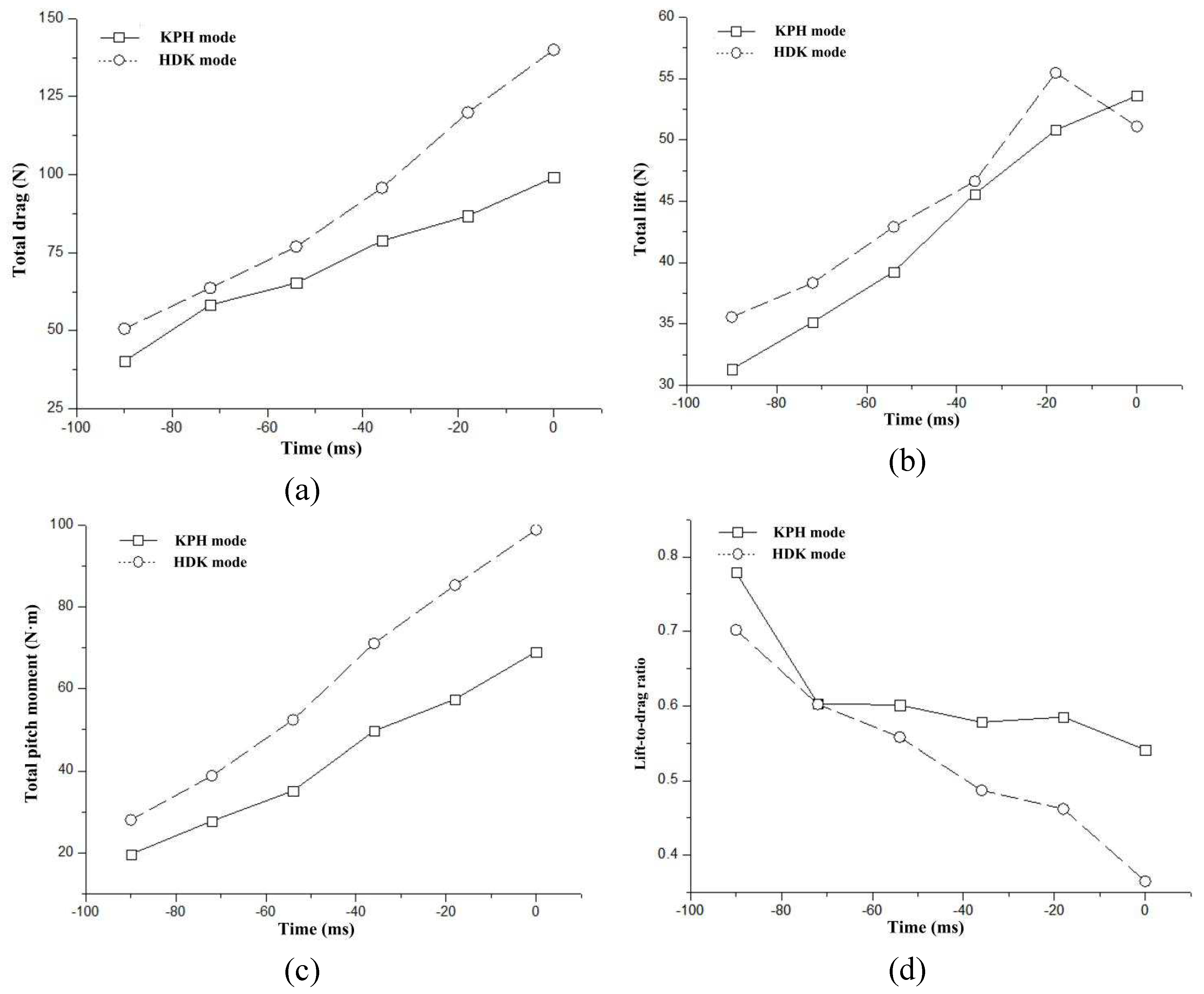
Preprints 96506 g003
Preprints 96506 g004
Figure 4. Change curves of different body parts aerodynamic characteristics in KPH mode. (a) The temporal changes of drag, (b) The temporal changes of lift, (c) The temporal changes of pitch moment.
Figure 4. Change curves of different body parts aerodynamic characteristics in KPH mode. (a) The temporal changes of drag, (b) The temporal changes of lift, (c) The temporal changes of pitch moment.
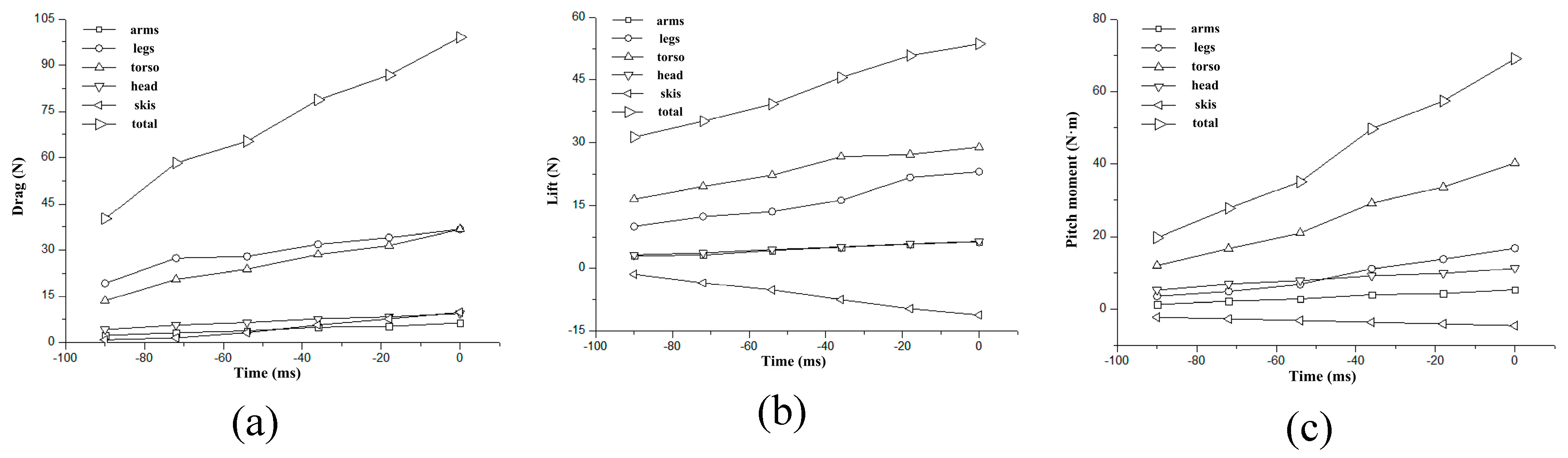
Preprints 96506 g004
Preprints 96506 g005
Figure 5. Change curves of different body parts aerodynamic characteristics in HDK mode. (a) The temporal changes of drag, (b) The temporal changes of lift, (c) The temporal changes of pitch moment.
Figure 5. Change curves of different body parts aerodynamic characteristics in HDK mode. (a) The temporal changes of drag, (b) The temporal changes of lift, (c) The temporal changes of pitch moment.
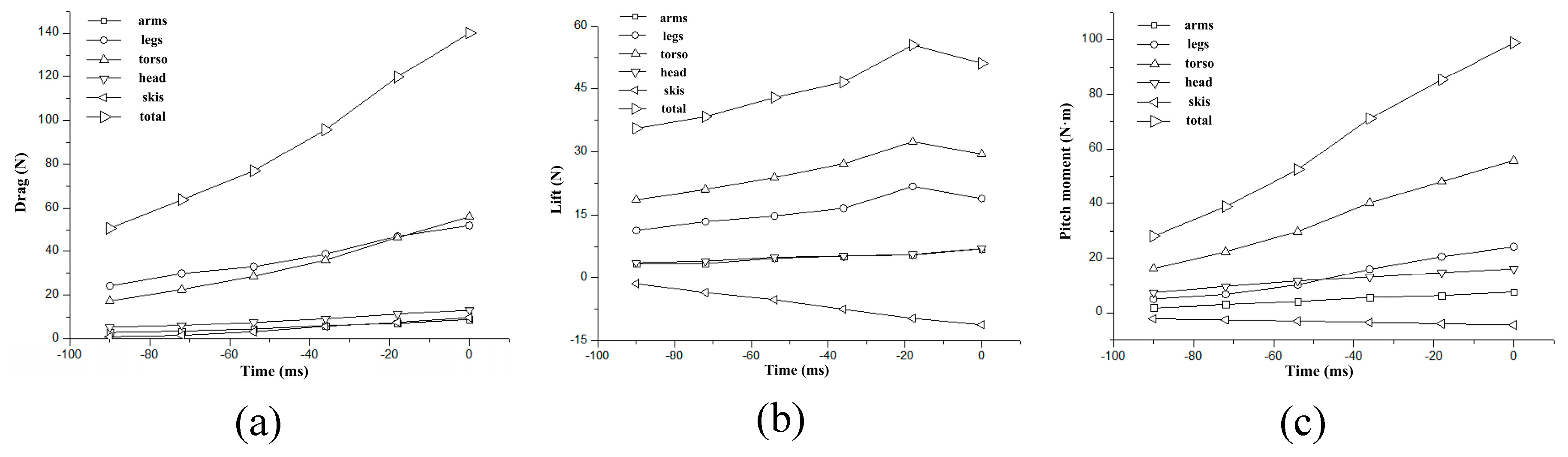
Preprints 96506 g005
Preprints 96506 g006
Figure 6. Airflow visualization of KPH mode. (a)-(f) The distribution of the average velocity u in the sagittal plane.
Figure 6. Airflow visualization of KPH mode. (a)-(f) The distribution of the average velocity u in the sagittal plane.
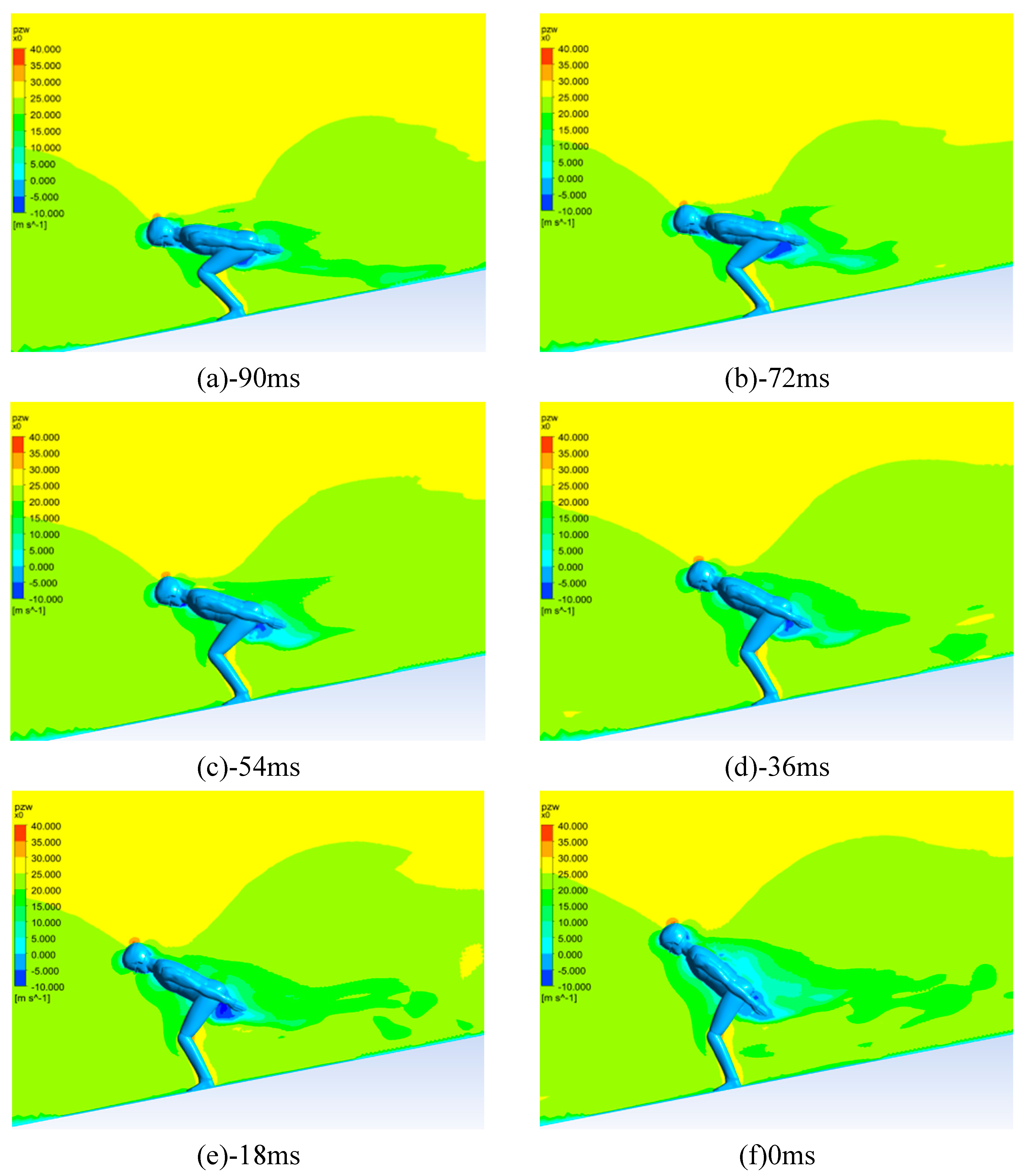
Preprints 96506 g006
Preprints 96506 g007aPreprints 96506 g007b
Figure 7. Airflow visualization of HDK Mode. (a)-(f) The distribution of the average velocity u in the sagittal plane.
Figure 7. Airflow visualization of HDK Mode. (a)-(f) The distribution of the average velocity u in the sagittal plane.
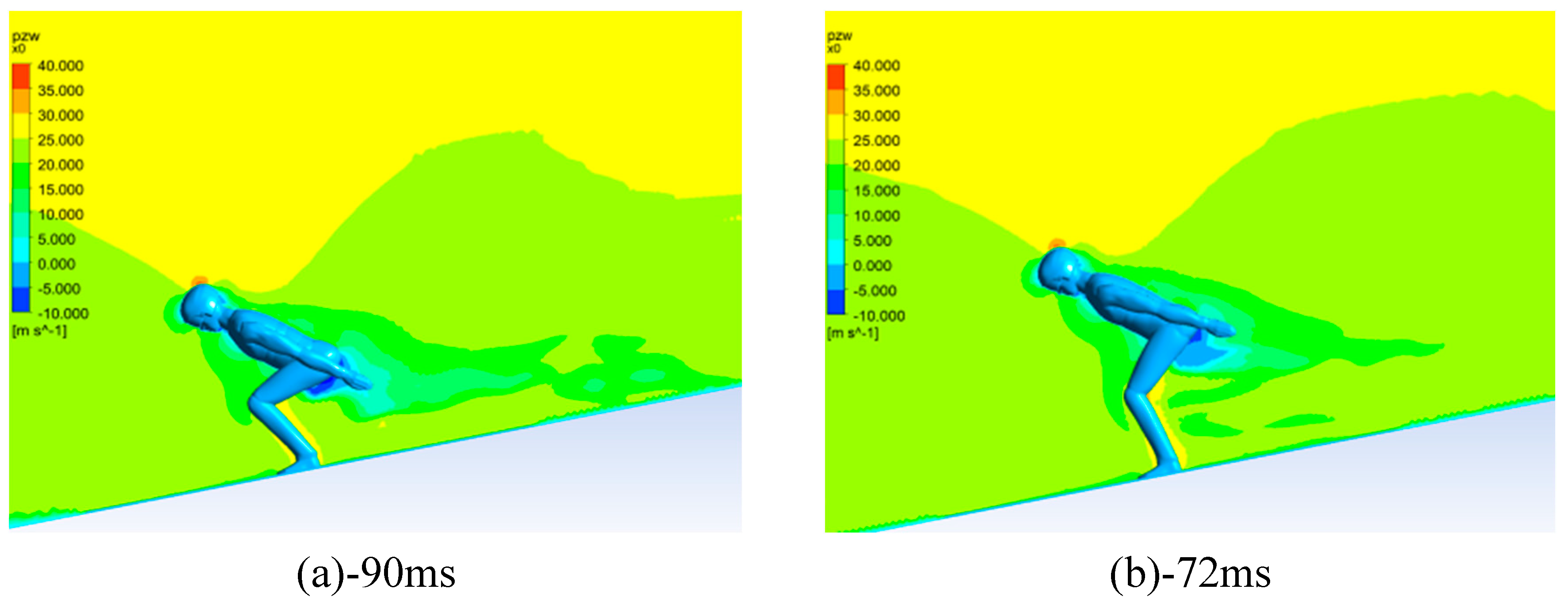
Preprints 96506 g007aPreprints 96506 g007b
Preprints 96506 g008
Figure 8. Comparison of the equal vorticity contours of two take-off modes based on the side and back view. The equal vorticity contours (ω=100s-1) were plotted. The colors indicate the anteroposterior distance from the surface.
Figure 8. Comparison of the equal vorticity contours of two take-off modes based on the side and back view. The equal vorticity contours (ω=100s-1) were plotted. The colors indicate the anteroposterior distance from the surface.
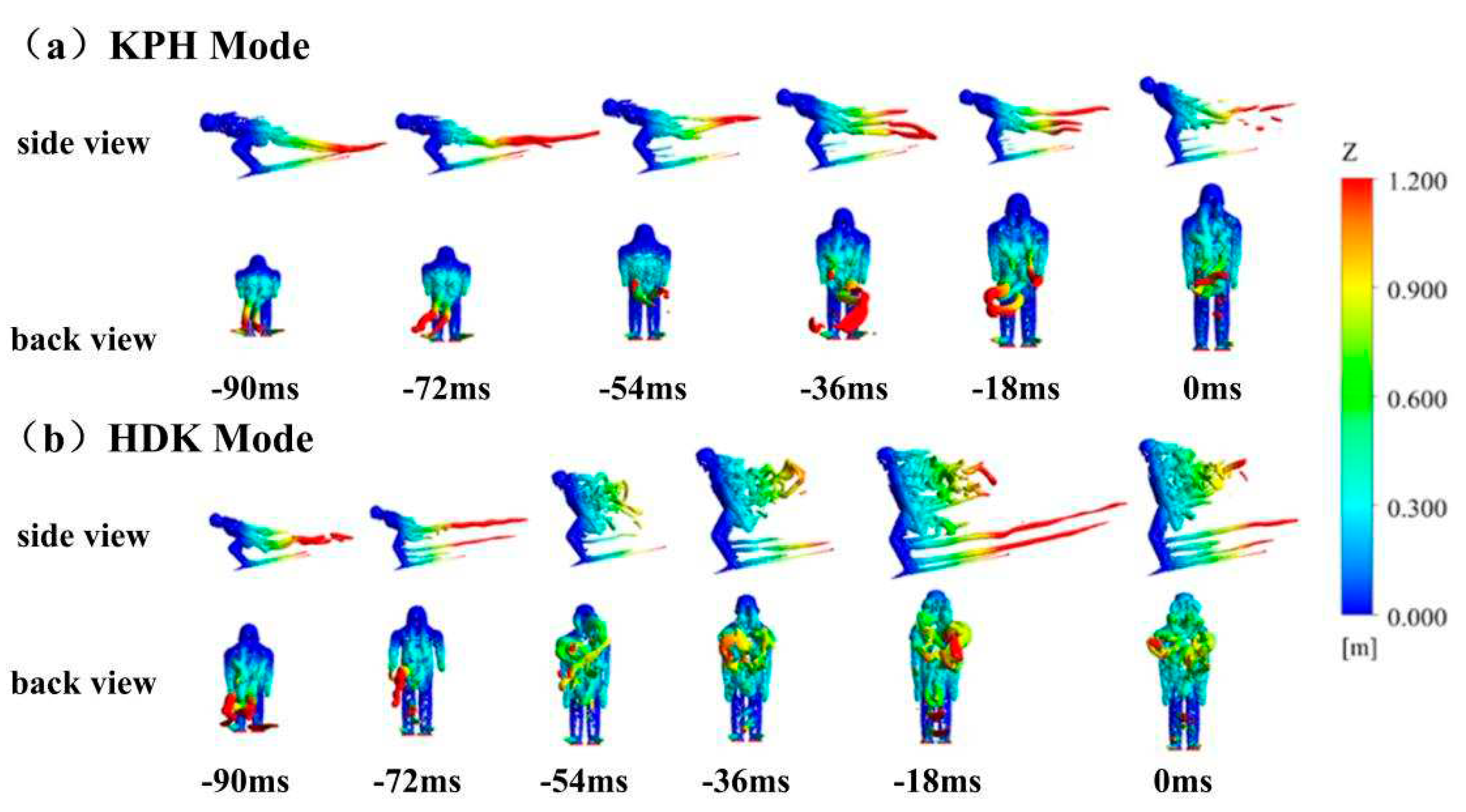
Preprints 96506 g008
Table 1. Results of Grid-independency Test.
Table 1. Results of Grid-independency Test.
Grid partitioning strategy 1 Grid partitioning strategy 2 Grid partitioning strategy 3 Grid partitioning strategy 4
Total grid（million） 12.47 16.26 20.03 23.21
Lift-to-drag 0.749 0.715 0.708 0.708
Table 2. Posture parameters and calculation conditions during take-off phase.
Table 2. Posture parameters and calculation conditions during take-off phase.
Time (ms) φ1(°) φ2(°) φ3(°)
KPH mode HDK mode
-90 60 82 38 55
-72 64 93 47 81
-54 68 105 61 97
-36 72 115 75 109
-18 76 124 81 120
0 80 132 99 130
Table 3. Results of aerodynamic characteristics of two take-off modes.
Table 3. Results of aerodynamic characteristics of two take-off modes.
Time (ms) Total drag (N) Total lift (N) Total pitch moment (N·m) Lift-to-drag ratio
KPH mode HDK mode KPH mode HDK mode KPH mode HDK mode KPH mode HDK mode
-90 40.20 50.66 31.31 35.56 19.69 28.06 0.779 0.702
-72 58.28 63.67 35.15 38.34 27.80 38.84 0.603 0.602
-54 65.27 76.91 39.26 42.91 35.14 52.42 0.601 0.558
-36 78.81 95.78 45.58 46.62 49.69 71.09 0.578 0.487
-18 86.78 119.90 50.79 55.45 57.47 85.31 0.585 0.462
0 99.05 140.01 53.58 51.09 69.05 98.82 0.541 0.365
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated