Preprint
Article
Evaluation of Weather Yield Index Insurance Exposed to Deluge Risk: The Case of Sugarcane in Thailand
Altmetrics
Downloads
107
Views
61
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
17 January 2024
Posted:
17 January 2024
You are already at the latest version
Alerts
Abstract
Insurance serves as a mechanism to effectively manage and transfer revenue-related risks. We conducted a study to explore the potential financial advantages of index insurance, which protects agricultural producers, specifically sugarcane, against excessive rainfall. Creation of the index involved utilizing generalized additive regression models, allowing for consideration of non-linear effects and quantile generalized additive regression to evaluate relationships with lower quantiles, such as low yield events. To quantify the financial benefits for farmers, should they opt for excessive rainfall index insurance, we employed efficiency analysis based on metrics such as Conditional Tail Expectation, Certainty Equivalence of Revenue, and Mean Root Square Loss. The results of the regression model demonstrate its accuracy in predicting sugar cane yields, with a split testing R2 of 0.691. Additionally, our study suggests that this type of insurance could also apply to sugarcane farmers and other crop producers in regions where extreme rainfall threatens the financial sustainability of agricultural production.
Keywords:
Subject: Business, Economics and Management - Finance
1. Introduction
One of the major problems for farmers is their agricultural products being ruined due to natural factors. This issue could be caused by weather conditions since they cannot be controlled. As a result, the government must play a role to help and relieve farmers who face difficulties. Nonetheless, this does not help thoroughly and is not sufficient for the effects because the government has a limited budget and a complex process. Therefore, help and relief for farmers may be delayed. Although farmers currently have some risk management tools, such as setting up a savings cooperative or groups to help each other, these tools are not sufficiently effective to solve the problem. Crop insurance is an alternative way that plays an important role in managing and transferring farmers’ financial risks. It also helps the government to solve the problem of high costs to help farmers.
At present, there are many variants of crop insurances according to the insured purposes and nature of risk (Vroege et al. 2019). Crop insurance protects insured farmers against damage or loss under the terms of the policy that the insured individual has purchased. Climate variability is a major cause of crop loss which affects farmers’ financial condition. This has resulted in the development of insurance products that cover crop damage from weather conditions. Consequently, crop insurance using a weather index is a type of insurance that has been researched and tested for the benefit of farmers and insurance companies.
In 2007, Food and Agriculture reported that Thailand started employing crop insurance utilizing weather indexes insurance (Hnin Ei Win 2016). The most common weather index used as a measure of compensation to insured individuals is the rainfall index, also known as the drought index insurance, because drought and flooding are the main issues for Thai agriculturists. Additionally, when the percentage of the rainfall or drought index follows the insurance policy condition, farmers will be compensated. There are many advantages of weather index insurance, for example the operating costs are relatively low and it is uncomplicated and transparent compared to other types of crop insurance (Conradt et al. 2015; Kath et al. 2018, 2019; Martin et al. 2001; Vedenov and Barnett 2004).
Agricultural in Thailand is a very competitive and diverse subsector, while its exports are highly successful internationally. Various crops effect Thailand’s economy, such as rice, sugarcane, and cassava which account for more than a half of Thailand’s cultivated area. In 2022, Thailand was the world’s fourth largest sugarcane producing country, with production increasing by 8.69% from the previous year (United States Department of Agriculture). Moreover, in 2022 Thailand was ranked the second largest sugar exporter in the world, following Brazil (Office of Agricultural Economics, 2022). Sugarcane was selected as the sample crop for this study because it is crucial to Thailand’s economy and it is sensitive to weather conditions.
In terms of sugarcane production, although Thailand is located in an area with a suitable climate for growing sugarcane, in some years sugarcane production has faced issues with low yields per rai (1 rai = 1,600 square meters) due to weather changes and natural disasters which lower production efficiency. Rainfall is an important variable for sugarcane production because sugarcane yields vary with precipitation levels in different periods of crop growing (Pipitpukdee et al. 2020; Sinnarong et al. 2019, 2022). This means that crop insurance using a rainfall or drought index plays a role and could greatly reduce the risks faced by sugarcane farmers. Therefore, developing a crop insurance system using the rainfall index or the dryness index is important to assist and diversify farmers’ risks. This leads to the tasks of the present study. The first task is to determine how to formulate the crop yield model using a weather index such as rainfall index alongside other climate factors. The second task is to establish an insurance contract by considering the cost-effectiveness of crop insurance.
To complete the first task, sugarcane production including the weather index are used to create statistical models of crop yield. Temperature and rainfall are important factors contributing to climate variability in several studies (Carvalho et al. 2015; Greenland. 2005; Singh et al. 2021; Verón et al. 2015; Mali et al. 2014; Verma et al. 2019, 2021). However, establishing a connection between productivity and climate is a challenging task. The essential conditions are the types of crops and the location of study. The study area in this research is Khon Kaen province which is a significant producer of sugarcane (Office of The Cane and Sugar Board, 2022). Moreover, most sugarcane growing areas are outside the irrigated region. To develop strategies to calculate suitable insurance premiums for farmers, first we utilize statistical models including the generalized additive model (GAM) and quantile generalized additive model (QGAM) in order to obtain an appropriate weather-yield models. The insurance contracts corresponding to the models are then generated to serve the second task of the study. The contracts are accessible to be used by insurance companies and give adequate compensation corresponding to individual farmer’s risk.
The design of weather index insurance and the consideration behind our choice of analysis are detailed in the next section. The subsequent section presents the results of weather-yield modeling. An efficiency analysis of the models is also described in Section 3. Section 4 discusses the efficiency of the model and the implications of the study for climate risk management. Conclusions are then drawn and presented in the final section.
2. Materials and Methods
2.1. Study area and Panel dataset
Sugarcane is a main crop in Thailand’s economy and is ranked first for domestic production by volume when compared with other crops. In this study, Khon Kaen province was selected as a sugarcane cultivation area located in northeastern Thailand, as outlined in Figure 1. This region is one of the most significant places in Thailand for the production of sugarcane which covers a large area, with 651,492 rai of planted sugarcane (Office of The Cane and Sugar Board, 2022). This figure displays reported sugarcane acreage and yield statistics over the past 31 years (1992–2022).
The Office of Agricultural Economics provides annual data on sugarcane yield and farm gate prices at the provincial level from 1992 to 2022 (The Office of Agricultural Economics). Monthly climate data was obtained from the Khon Kaen meteorological station (381201) from January 1992 to December 2022 (Thai Meteorological Department).
2.2. Conceptual framework
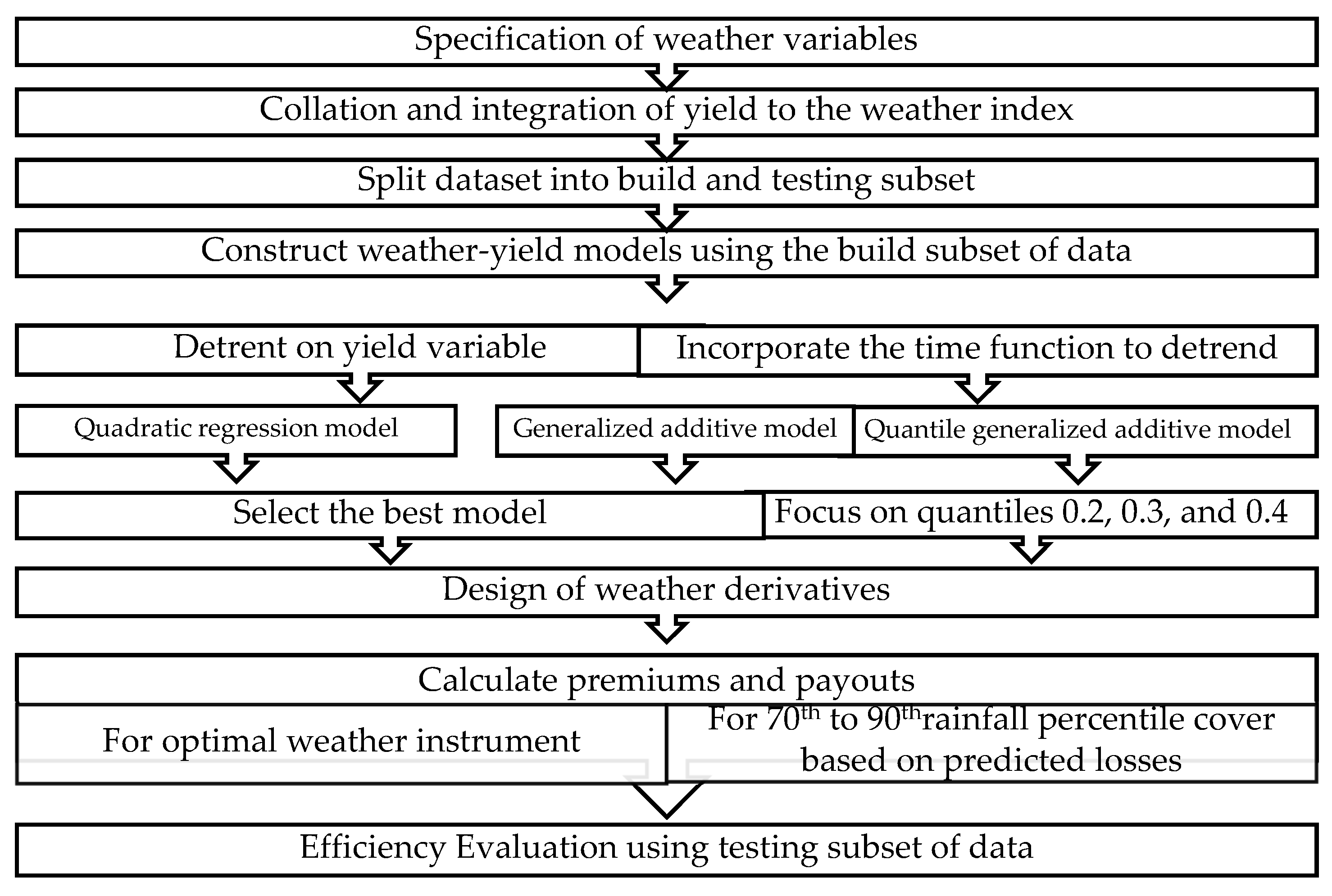
There are many studies of agricultural production or yield modelling that use the weather condition index in combination with other various factors. The reason for creating numerous models is that productions changes between different areas dependent on various factors. A suitable model in one area may not be suitable for others. Thus, the procedures for this study consist of two parts. In the first part, the yield model using the weather index are formulated with various statistical tools according to the selected cultivation area. The appropriate models are adopted in the second part. This part designs and price for weather derivative in order to obtain suitable premiums, corresponding to the yield model. Consequently, the efficiency of the model is measured in scenarios in which farmers are insured or not. The following flowchart outlines the research methodology.
Figure 1.
Schematic of weather index insurance design process and efficiency evaluation.
2.2.1. Step 1: Specification of weather variables
Table 1 pressents a review of the literature on the weather index related to crop yield. Many studies show that the weather index has a significant influence on crop yields.
From Table 1, the maximum temperature and rainfall variables are frequently used in the specification of weather variables. These two variables were therefore selected to create weather-yield models in the study. The model of the relationship between climate variables and crop yields is obtained using a statistical method to estimate the relationship between climate and crop production.
2.2.2. Step 2: Integration of data and data preparation
Climate data in the growing season, i.e., maximum temperature and rainfall were adopted to develop the weather-yield model. Price data is taken from farm gate prices from 1992 to 2022. Details on the variables and calculation methods are in Table 2.
In some casts there is missing data which could have resulted from various factors, such as due to a power cut problem. Data preprocessing was used to deal with this issue. From our historical data, only the rainfall index has missing data. As a result, we employed the work of Kanchai et al. (2022) to handle the problem.
2.2.3. Steps 3-5: Regression model linking yield to climate indices
This study was conducted using data from 1992 to 2022. Data from 1992 to 2017 were used to fit the models, while the remaining data (2018–2022) were used for model validation. Most analytical techniques are carried out with "R" and Mathematica software.
Before constructing the weather-yield model, we considered the effects that time series might have on yield productivity. Detrending the yield is one of the most popular methods for removing the effects of changes in management, technology, and production extent yields over time. One of the techniques for detrending the yield is by adjusting only the yield variable in the model (Vedenov and Barnett 2004; Johari et al. 2022). An alternative approach can be used because the annual impacts do not need to be identical, in which the yield data is implicitly adjusted for trends by incorporating the year as part of the model (Kath et al. 2018, 2019; Verón et al. 2015; Verma et al. 2020). The meteorological factors generally show upward temporal trends.
In our study, the weather-yield model was formulated using different statistic tools, including a quadratic regression model, Generalized Additive Models (GAMs), and Quantile generalized additive model (QGAM). The quadratic regression models are widely used to create yield models, especially where adjusted yield is treated as a variable (Johari et al. 2022). Since several factors influence agricultural yields, removing non-weather influences from agricultural yield data throughout the course of the observation period is the goal of detrending crop output. For example, the factors include geography, governance policies, and technological development.
Alternative approaches in the study are to use GAMs or QGAM. These models were utilized by addressing the function of year into the model. GAMs can be understood as Generalized Linear Models (GLMs) that are estimated while being subjected to smoothing penalties. The primary challenge that arises from this penalization is the requirement to choose the appropriate level of penalization, meaning that the smoothing parameters must be estimated. To analyze and predict productivity in the study, GAMs are utilized corresponding to the following equation:
where is sugarcane yield at time , is smooth function, is the rainfall index at time , is the error term, and stands for year.
QGAM was developed by Fasiolo et al. (2020). This regression model is based on Quantile regression (QR) and GAM. Instead of focusing only on the mean as is the case with GAM, the rainfall index relationship with the lower quantiles of the sugar cane yield distribution is evaluated using the quantile generalized additive model. The equation of QGAM considered in this study is as same as GAM as shown in (1).
It is possible that the model could be overfitted in the model construction step. It is possible to check whether the model is overfitted. For this purpose, the data is divided into a training and a testing subset. After that, the split test technique is employed to check the overfitting. Next, we measure the quality of the fitting model. The adjusted R2 value was used as a criterion (greater than 0.6 in the study) for model selection.
2.2.4. Steps 6 and 7: Design of weather derivatives and premium estimation
To evaluate the efficiency of weather derivatives, a particular contract must be designed. From the litarature in Table 1, the rainfall index is desired as the main factor affecting sugarcane production, especially in excessive rainfall events (Glaz and Lingle, 2012; Gomathi et al., 2015). Thus in the study, an elementary contract in case of excessive rainfall triggered by rainfall index is proposed (adapted from Vedenov and Barnett 2004). This contract pays an optimal indemnity conditional on the realization of an index, as depicted in Figure 3.
where is the rainfall index with percentile levels, denotes maximum indemnity. is a constant, where is the limit of rainfall to pay the maximum insurance claim.
We assume that potential insurance customers will not take any risks at all, so they will be compensated if there is a loss in sugarcane yield the following year. From Figure 3, the contract starts to pay whenever the index raises above a specific rainfall index with percentile levels. The maximum indemnity (equal to ) is paid whenever the index raises above the limit , where 0 < < 1. Therefore, an elementary contract can be identified by fixing three parameters: the rainfall index with percentile levels, limit, and maximum indemnity.
To price an elementary contract, the contract parameters as well as the probability distribution of the essential index must be determined. For weather derivatives, the distribution can be derived based on historical data by using either the parametric or non-parametric approach. If is a probability density function of the index, the expected payoff (equal to pure premium) of the contract can be determined by:
Notice that for any of the rainfall indices with percentile levels and limit parameter , if is the price of a contract with maximum indemnity, then is the premium of a contract with maximum indemnity of baht.
- Selection of contract parameters
The weather-yield model resulting from Step 5 was used to calculate payoffs in insurance contracts. At this point, a rainfall index as a trigger value of the contract must be determined. The rainfall index at strike level can be selected in the sense that the predicted yields were equal to the corresponding long-time yields averages. The remaining parameters, i.e., the limit parameter and the optimal number of ฿1 contracts, were selected in order to minimize an aggregate measure of downside loss. In addition, the parameters and were determined to be solved (adapted from Vedenov and Barnett 2004):
where denotes the farm gate price in the last harvest year (in the training subset, i.e., the year 2017), is the yield at time , is the insurance payout for that strike level of insurance, and is the price of a contract with a maximum indemnity of baht.
Furthermore, we are interested in a rainfall index at different a percentile levels of , exposed to excessive rainfall risk (i.e., 70th, 80th and 90th percentiles of the rainfall index). The payoffs and premium of the contracts corresponding to these percentile levels are illustrated for the purpose of comparison to the strike level. The efficiency of these contracts for excessive rainfall risk were also examined.
2.2.5. Step 8: Efficiency Analysis
Efficiency analysis methods were adapted from Kath et al. (2018). Three methods were used, including conditional tail expectation (CTE), certainty equivalence revenue (CER), and mean root square loss (MRSL), to asses the benefit of the contract. To analyze the impact of the contract on farmer revenue, we compared revenue with and without insurance at level of the rainfall index . We derive the parameters of optimal contracts and measure the in-sample performance (adapted from Vedenov and Barnett 2004). In addition, at different percentile coverage levels for the selected regression model, the revenue without a contract is given by:
and with a contract is:
where denotes revenue at time t without insurance, is the farm gate price, is revenue at time with percentile levels of insurance (here the strike level and the 70th, 80th, 90th percentiles of the excessive rainfall index), is yield at time , is the insurance payout for that level of insurance in that year (predicted from the regression models), and the yearly premium for that percentile levels of insurance and is constant throughout the years in question so it is written as .
Conditional tail expectation (CTE) is a method to assess the effectiveness of insurance to protect against financial risks. The certainty equivalence revenue with percentile levels of insurance () has the following equation:
Next, Certainty equivalence revenue (CER) was used to measure willingness to pay the farmer. Assuming that the risk aversion was taken into account and the constant relative risk aversion was assumed. Therefore,
where is the certainty equivalence revenue with percentile level of insurance.
Finally, Mean root square loss (MRSL) is a value that represents an insurance contract’s ability to mitigate risk. MRSLwith percentile levels of insurance was calculated as
where is the price of agricultural commodity and is the long-term average yield.
3. Results
3.1. Quadratic regression modelling results
The adjusted sugarcane yield is computed based on the estimated sugarcane yield of the last year in the data range. The final year’s sugarcane yield level is anticipated to be the most similar to the output of the next year since the yield increases steadily throughout time. Therefore, the next year’s sugarcane yield may be predicted using the modified sugarcane yield. Since 2022 is the last year for which the sugarcane yield was projected in our instance, the adjusted yield will indicate the quantity of sugarcane output anticipated for 2023 based on 2022. However, data should be gathered up until the current year in order to build a true insurance contract. At that point, the modified sugarcane yield may be useful for the current year. The crop yield data will be detrended by fitting data. A quadratic regression model was then tested to detrend the time trend in crop yield. The results are shown in the following equation:
where is sugarcane yield at and stands for year = 1992, 1993,…, 2022.
This quadratic regression model explained 10.14% of the yield variation. This regression model estimates the intercept of time trend poorly, indicating that it is not a good model to fit the data for sugarcane yield. However, in order to illustrate the relationship between an adjusted sugarcane yield and weather indexes consisting of RI and T.MAX, the Gam was employed to construct a weather-yield model resulting in Equation 11:
From Equation 11, the model with an adjusted R2 value equal to 0.284 is inadequate to use. Therefore, we should neglect this model and it is not necessary to measure the efficiency of the model in Equation 11 in the next step.
3.2. GAM regression modelling results
GAMs can apply to built non-linear models using a spline. By letting time trend interpretation serve as a function into a model, GAM is constucted corresponding to a trained data set. Furthermore, to improve the accuracy of the model, the internal structure of the model was restructured as shown in Equation (12):
3.3. QGAM regression modelling results
QGAM for the response variable sugarcane yield at the time was fit with a smoothing function () for the rainfall index, the maximum temperature, and the year. Moreover, we adjusted the spline in the smooth function for better results as shown in the equation below.
Since we are interested in low-yield event responses to the excessive rainfall index, we concentrate on quantiles 0.4, 0.3, and 0.2. For each tau level (0.2, 0.3, and 0.4) examined with QGAM, the rainfall index was significant at p = 0.1 as shown in Table 4.
3.4. Estimated insurance premiums and revenues
First, the probability density function must be determined which is used in Equation (3) in section Section 2.2.4 to calculate the expected payoff of the contract. The rainfall data indicates that the distribution of this rainfall has a gamma distribution with . Next, the parameters and were settled in Equation (4). The equation introduces the idea that the indemnity amount in the insurance contract depends on the sugarcane yield strike level, which is determined by the weather index. Therefore, we just need to set the strike level of the rainfall index. Since we presume that the prospective insurance customers are completely risk averse, they will profit in the event that the sugarcane yield declines the following year. The average sugarcane yield from our data history should serve as the strike level. Then was calculated. The strike levels including the different percentile of rainfall index for the GAM and QGAM corresponding to Equations (12) and (13), respectively, are shown in Table 5. Consequently, the weather index-based crop insurance is designed as follows in the table below.
From Table 5, the percentile cover and regression method had a significant impact on premium variations. The most costly premiums (9.60079 baht/Rai) came from the QGAM at tau = 0.2 at the 70th percentile cover level, while the least expensive premiums (2.50249 baht/Rai) were estimated from GAM at the 90th percentile level of cover. According to Table 5, the maximum liability was calculated to be the lowest for GAM at 1,204.61 baht/Rai and the highest for QGAM at tau = 0.2 at 1,838.04 baht/Rai. Table 5 shows that premium rates varied from approximately 0.2% to 0.5%. The 90th percentile cover had the lowest premium rates for each model, while the 70th percentile cover had the highest premium rates (Table 5).
In order to illustrate the influence of an insurace contract on a farmer’s revenue, examples of revenue differences for each of the different levels of rainfall in the GAM model that we carried out are shown in Figure 5. Revenues below 0 indicate a year where a premium was paid, but no payout was received. Revenues above 0 indicate a year when the rainfall index triggered a payout.
3.5. Efficiency analysis of weather index
The efficiency of our insurance model is tested according to Equations (7), (8), and (9). The results are shown in Table 6. Based on the CTE, CER, and MRSL efficiency analyses, the excessive rainfall index insurance for sugarcane was found to provide advantages. The most significant potential advantages for farmers were indicated by the 90th percentile cover predicted from the GAM and QGAM (0.2, 0.3, 0.4), which protects them from excessive rainfall.
4. Discussion
4.1. Efficiency of weather index insurance for sugarcane
To develop our crop insurance model, we employed a regression model to assess sugarcane yields using weather condition indices. This involved determining an appropriate insurance premium and evaluating the efficiency of the crop insurance contract. The assessed performance of each insurance model reveals that measuring efficiency using CTE and CER at rainfall percentiles of 70, 80, and 90 as well as at the Strike level yields slightly different results. This is partially because there is little information available on crops and weather. CTE and CER assess whether insurance will increase farmers’ revenue during excessive rainfall. The QGAM model with tau= 0.2 at the 70th percentile demonstrates the highest benefit, whereas the GAM model at the 90th percentile is the least beneficial. However, the risk reduction for farmers in terms of revenue fluctuations or stability may be determined from MRSL. Since MRSL is a farmer’s revenue assessment between those with and those without insurance, MRSL should be considered first. Consequently, the GAM model is at the 90th percentile, indicating the least income variability for farmers. This differs from the findings of Kath et al. (2018), who studied sugarcane insurance under the topic ’Index insurance benefits agricultural producers exposed to excessive rainfall risk.’ Their research showed that measuring efficiency using CTE and CER is most effective at the 95th percentile, the highest percentile. However, the MRSL method performs best at the 70th percentile. These measurements are crucial for evaluating risk and financial impacts in situations characterized by uncertainty and volatility in agricultural data or possible financial events for farmers.
4.2. Implications
At present, natural disasters and excessive drought are the main focus of climate index crop insurance in several studies. Nevertheless, other climate factors could seriously affect farmers’ yields for some crops. Therefore, we raised awareness of the problem of excessive rainfall during the growing season especially for sugarcane. Additionally, this insurance is becoming more important due to increased climate change. It may become an increasingly popular and significant tool for risk management if the government seeks to promote sugarcane insurance, similar to the Thai rice insurance project in which the government helps farmers with insurance costs. The Thai rice insurance project was achieved due to cooperation between the government and the Thai General Insurance Association. Between 2011 to 2022, more than 16,492 million baht of insurance premiums were paid to insurance companies and the total claims accounted for approximately 78% of the premium (Thai General Insurance Association, 2022). This emphasized the role of insurance in managing risk within agricultural economics. For the government to subsidize the cost of farmers’ sugarcane insurance premiums, strike levels may be used to gauge rainfall in order to manage farmer compensation or expand their options. Premiums are then paid based on the QGAM model, which allows for various integrations with coverage increasing or decreasing as required.
5. Conclusions
This study examined the effects of climate change on economic crop production using different regression models and by constructing an insurance model to protect farmer’s revenue from climate change. Determining an association between the weather index and the crop, as well as discovering the point of departure and the level of the weather index that contributes to crop loss, were necessary in order to calculate the pure premium. From the modeling, GAM and QGAM are used to model the yield of sugarcane insurance using the excessive rainfall index for the selected area. The results of this study demonstrate that sugarcane growers’ financial risk decreased with crop insurance. Moreover, the yield model may improve with sufficient weather and yield data. The yield model uses GAM and QGAM, non-linear regressions that can be used for plants sensitive to weather conditions. This yield model concept can therefore be applied to other climate-sensitive crops. This insurance makes it easy to pay indemnity because indemnity is paid for the amount of rain according to the criteria specified in the insurance contract. As a result, the indemnity does not depend on the individual’s actual losses. Moreover, it also reduces the cost of disaster surveys.
Author Contributions
Conceptualization, T.K. and T.P.; methodology, T.K. and T.P.; software, T.K.; validation, T.K., T.P and W.K.; formal analysis, T.K.; investigation, T.K., W.S., T.P. and W.K.; resources, T.K.; data curation, T.K.; writing—original draft preparation, T.K. and T.P.; writing—review and editing, W.S., T.P. and W.K.; visualization, T.K.; supervision, T.P and W.K.; project administration, T.P.; funding acquisition, T.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Fundamental Fund of Khon Kaen University, fiscal year 2022, the National Science, Research and Innovation Fund (NSRF), Thailand.
Data Availability Statement
Publicly available data can be found on the provided website. https://github.com/ThitipongKan/Data-Availability/blob/main/Data%20Availability.rar.
Acknowledgments
The authors would like to express our heartfelt appreciation to Assoc. Prof. Wikanda Phaphan for helpful advice in completing this paper successfully.
Conflicts of Interest
The authors declare no conflict of interest.
References
- (Amnuaylojaroen et al. 2021) Amnuaylojaroen T., Chanvichit P., Janta R., and Surapipith V. 2021. Projection of Rice and Maize Productions in Northern Thailand under Climate Change Scenario RCP8.5. Agriculture 11, 23. [CrossRef]
- (Bucheli et al. 2022) Bucheli J., Dalhaus T., and Finger R. 2022. Temperature effects on crop yields in heat index insurance. Food Policy 107, 102214. [CrossRef]
- (Byrareddy et al. 2023) Byrareddy, V., Kath, J., Kouadio, L., M, S., Vellingiri, G., 2023. Avoiding the Blind Spot: Climate Risks Vary Across Scales in Coffee-Based Agroforestry Systems (preprint).
- (Carvalho et al. 2015) Carvalho A.L. de, Menezes R.S.C., Nóbrega R.S., Pinto A. de S., Ometto J.P.H.B., von Randow C., and Giarolla A. 2015. Impact of climate changes on potential sugarcane yield in Pernambuco, northeastern region of Brazil. Renewable Energy 78, 26–34. [CrossRef]
- (Conradt et al. 2015) Conradt S., Finger R., and Spörri M. 2015. Flexible weather index-based insurance design. Climate Risk Management 10, 106–117. [CrossRef]
- (Fasiolo and Author 2020)Fasiolo M., and Author S. 2020. qgam: Bayesian non-parametric quantile regression modelling in R. [CrossRef]
- (Greenland 2005) Greenland D. 2005. Climate Variability and Sugarcane Yield in Louisiana. Journal of Applied Meteorology 44, 1655–1666. [CrossRef]
- (Glaz and Lingle 2012) Glaz B., and Lingle S.E. 2012. Flood duration and time of flood onset effects on recently planted sugarcane. Agron. J. 104 (3), 575–583. [CrossRef]
- (Gomathi et al. 2015) Gomathi R., Rao P.G., Chandran K., Selvi A. 2015. Adaptive responses of sugarcane to waterlogging stress: an over view. Sugar Tech 17 (4), 325–338. [CrossRef]
- (Hnin Ei Win 2022) Hnin Ei Win. 2016. Crop insurance in Thailand. https://ap.fftc.org.tw/article/1105.
- (Johari et al. 2022) Johari S.N.M., Asdi N.A.H.M., Othman N.S., and Anifruzaidi S.D.Q. 2022. Weather Index Based Microinsurance for Agriculture Industry. IOP Conf. Ser.: Earth Environ. Sci. 1019, 012045. [CrossRef]
- (Kath et al. 2021) Kath J., Mittahalli Byrareddy V., Mushtaq S., Craparo A., andPorcel M. 2021. Temperature and rainfall impacts on robusta coffee bean characteristics. Climate Risk Management 32, 100281.
- (Kath et al. 2018) Kath J., Mushtaq S., Henry R., Adeyinka A., and Stone R. 2018. Index insurance benefits agricultural producers exposed to excessive rainfall risk. Weather and Climate Extremes 22, 1–9. [CrossRef]
- (Kath et al. 2019) Kath J., Mushtaq S., Henry R., Adeyinka A.A., Stone R., Marcussen T., and Kouadio L. 2019. Spatial variability in regional scale drought index insurance viability across Australia’s wheat growing regions. Climate Risk Management 24, 13–29. [CrossRef]
- (Lobell and Burke 2010) Lobell D.B., and Burke M.B. 2010. On the use of statistical models to predict crop yield responses to climate change. Agricultural and Forest Meteorology 150, 1443–1452. [CrossRef]
- (Lobell and Field 2007) Lobell D.B., and Field C.B. 2007. Global scale climate–crop yield relationships and the impacts of recent warming. Environ. Res. Lett. 2, 014002. [CrossRef]
- (Maindonald 2010) Maindonald J. 2010. Smoothing Terms in GAM Models.
- (Mali et al. 2014) Mali S.C., Shrivastava P.K., and Thakare H.S. 2014. Impact of weather changes on sugarcane production 5.
- (Martin et al. 2001) Martin S.W., Barnett B.J., Coble K.H., Martin S.W., Barnett B.J., and Coble K.H. 2001. DEVELOPING AND PRICING PRECIPITATION INSURANCE.
- (Office of Agricultural Economics 2022) Office of Agricultural Economics. 2022. Available online: https://www.oae.go.th/ (accessed 15 July 2022).
- (Office of the Cane and Sugar Board 2022) Office of the Cane and Sugar Board. 2022. Available online: http://www.ocsb.go.th/th/ home/index.php (accessed 15 July 2022).
- (Pignède et al. 2021) Pignède E., Roudier P., Diedhiou A., N’Guessan Bi V.H., Kobea A.T., Konaté D., and Péné C.B. 2021. Sugarcane Yield Forecast in Ivory Coast (West Africa) Based on Weather and Vegetation Index Data. Atmosphere 12, 1459. [CrossRef]
- (Pipitpukdee et al. 2020) Pipitpukdee S., Attavanich W., and Bejranonda S. 2020. Climate Change Impacts on Sugarcane Production in Thailand. Atmosphere 11, 408. [CrossRef]
- (Sattar et al. 2005) Sattar A., Khan S.A., and Kumar M. 2005. Crop Weather Relationship and Cane Yield Prediction of Sugarcane in Bihar 14, 6.
- (Shirsath et al. 2019) Shirsath P., Vyas S., Aggarwal P., and Rao K.N. 2019. Designing weather index insurance of crops for the increased satisfaction of farmers, industry and the government. Climate Risk Management 25, 100189. [CrossRef]
- (Singh et al. 2021) Harpinder Singh, Sudhir Kumar Mishra, Kuldeep Singh, Kulvir Singh R. K. Pal, K. K. Gill, and P. K. Kingra. 2021. Simulating the impact of climate change on sugarcane production in Punjab. J. Agrometeorol. 23, 292–298. [CrossRef]
- (Sinnarong et al. 2019) Sinnarong N., Chen C.-C., McCarl B., and Tran B.-L. 2019. Estimating the potential effects of climate change on rice production in Thailand. Paddy Water Environ 17, 761–769. [CrossRef]
- (Sinnarong et al. 2022) Sinnarong N., Kuson S., Nunthasen W., Puphoung S., and Souvannasouk V. 2022. The potential risks of climate change and weather index insurance scheme for Thailand’s economic crop production. Environmental Challenges 8, 100575. [CrossRef]
- (Sirimanne et al. 2015) Sirimanne S., Srivastava S., Kim S.E., Li H.M.D., Firer A., and Sinha S. 2015. Building Resilience to Droughts; Scaling up Weather Insurance in China, India, and Thailand. International Centre for Integrated Mountain Development (ICIMOD), Kathmandu, Nepal.
- (Tappi et al. 2023) Tappi M., Carucci F., Gatta G., Giuliani M.M., Lamonaca E., and Santeramo F.G. 2023. Temporal and design approaches and yield-weather relationships. Climate Risk Management 40, 100522. [CrossRef]
- (Thai general insurance association 2022) Thai general insurance association. 2022. Available online: https://www.tgia.org. (accessed 10 June 2022).
- (Thai meteorological department 2022) Thai meteorological department. 2022. Available online: https://www.tgia.org. (accessed 10 June 2022).
- (United states department of agriculture 2022) United states department of agriculture. 2022. Available online: https://www.usda.gov/ (accessed 20 July 2022).
- (Vedenov and Barnett 2004) Vedenov D.V., and Barnett B.J. 2004. Efficiency of Weather Derivatives as Primary Crop Insurance Instruments.
- (Verma et al. 2021) Verma A.K., Garg P.K., Hari Prasad K.S., Dadhwal V.K., Dubey S.K., and Kumar, A. 2021. Sugarcane Yield Forecasting Model Based on Weather Parameters. Sugar Tech 23, 158–166. [CrossRef]
- (Verma et al. 2019) Verma R.R., Srivastava T.K., and Singh P. 2019. Climate change impacts on rainfall and temperature in sugarcane growing Upper Gangetic Plains of India. Theor Appl Climatol 135, 279–292. [CrossRef]
- (Verón et al. 2015) Verón S.R., de Abelleyra D., and Lobell D.B. 2015. Impacts of precipitation and temperature on crop yields in the Pampas. Climatic Change 130, 235–245. [CrossRef]
- (Vroege et al. 2019) Vroege W., Dalhaus T., and Finger R. 2019. Index insurances for grasslands – A review for Europe and North-America. Agricultural Systems 168, 101–111. [CrossRef]
- (Wang et al. 2018) Wang J., Vanga S., Saxena R., Orsat V., and Raghavan V. 2018. Effect of Climate Change on the Yield of Cereal Crops: A Review. Climate 6, 41. [CrossRef]
- (Wang et al. 2022) Wang Q., Soksophors Y., Barlis A., Mushtaq S., Phanna K., Swaans C., and Rodulfo D. 2022. Willingness to Pay for Weather-Indexed Insurance: Evidence from Cambodian Rice Farmers. Sustainability 14, 14558. [CrossRef]
- (Wood 2005) Wood S.N. 2005. Generalized Additive Models 497.
- (Xu et al. 2018) Xu Y., Gao C., Li X., Yang T., Sun X., Wang C., and Li D. 2018. The Design of a Drought Weather Index Insurance System for Summer Maize in Anhui Province, China. JRACR 8, 14.
Figure 1.
The Khon Kaen sugarcane region. In the map of Khon Kaen, the green area represents suggested areas for sugarcane cultivation in 2022. The red markers show sugarcane factories.
Figure 1.
The Khon Kaen sugarcane region. In the map of Khon Kaen, the green area represents suggested areas for sugarcane cultivation in 2022. The red markers show sugarcane factories.
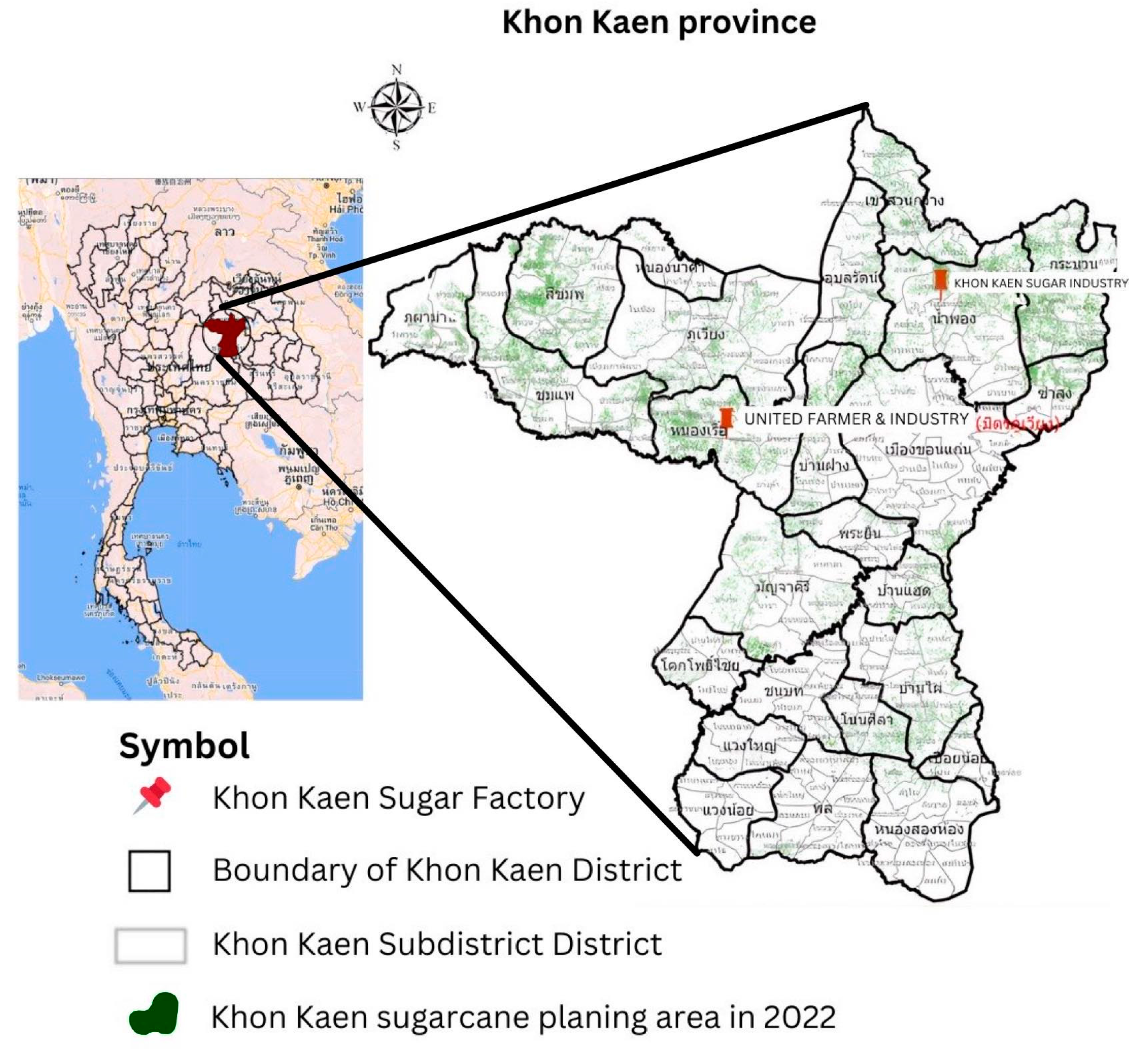
Figure 3.
Payoff design of an element contract.
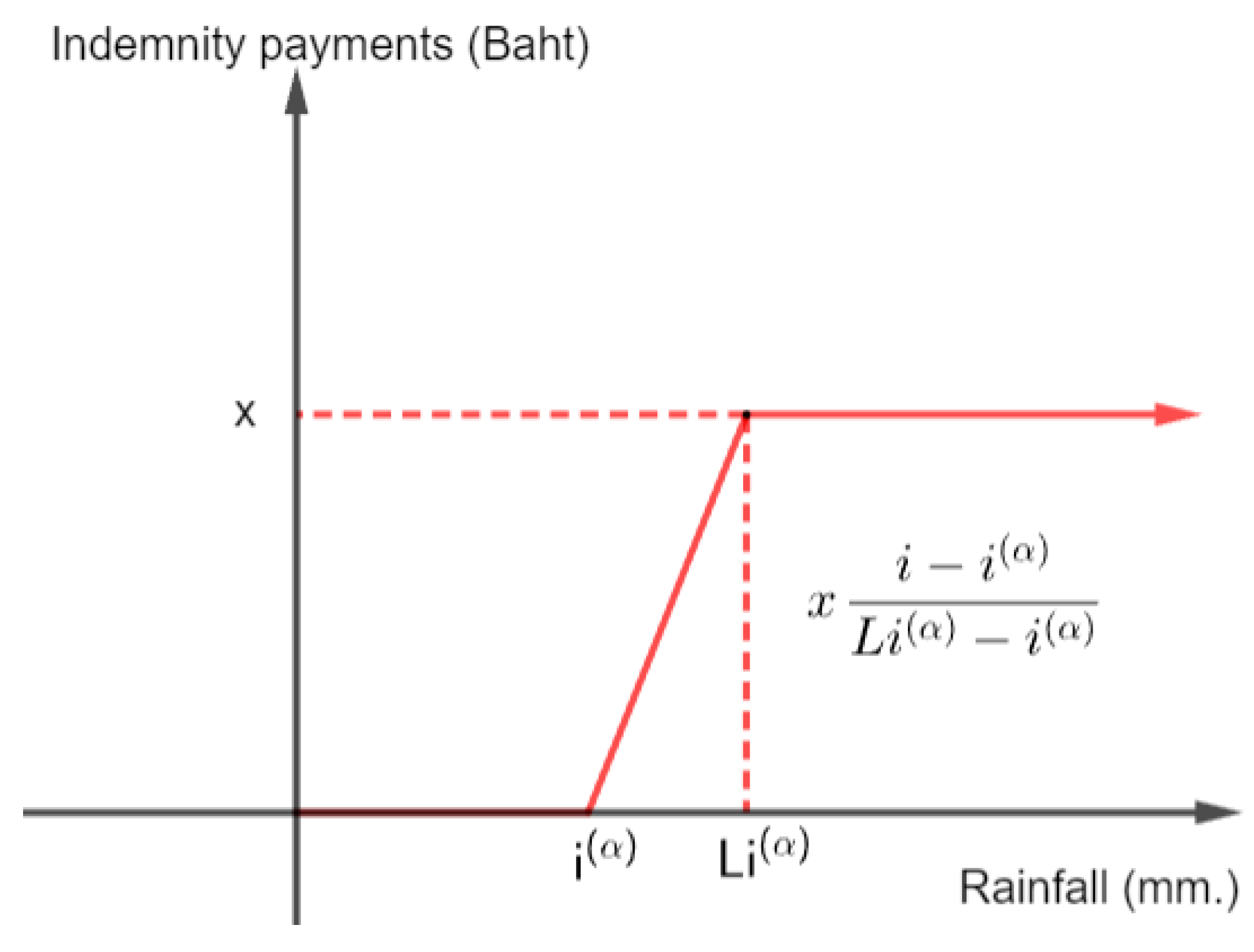
Figure 4.
Predicted yield responses to the rainfall index from the GAM model.
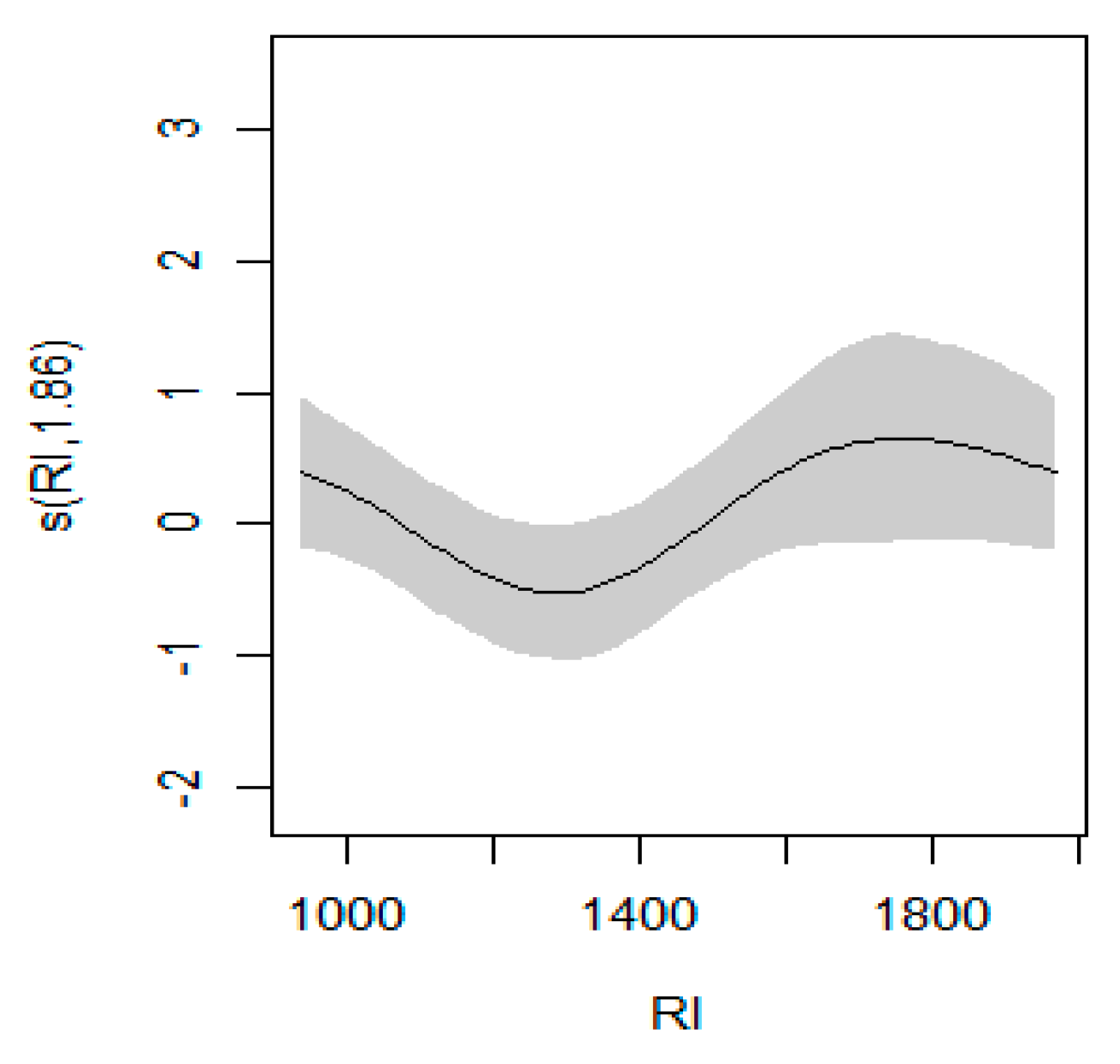
Figure 5.
Examples of difference in revenue.
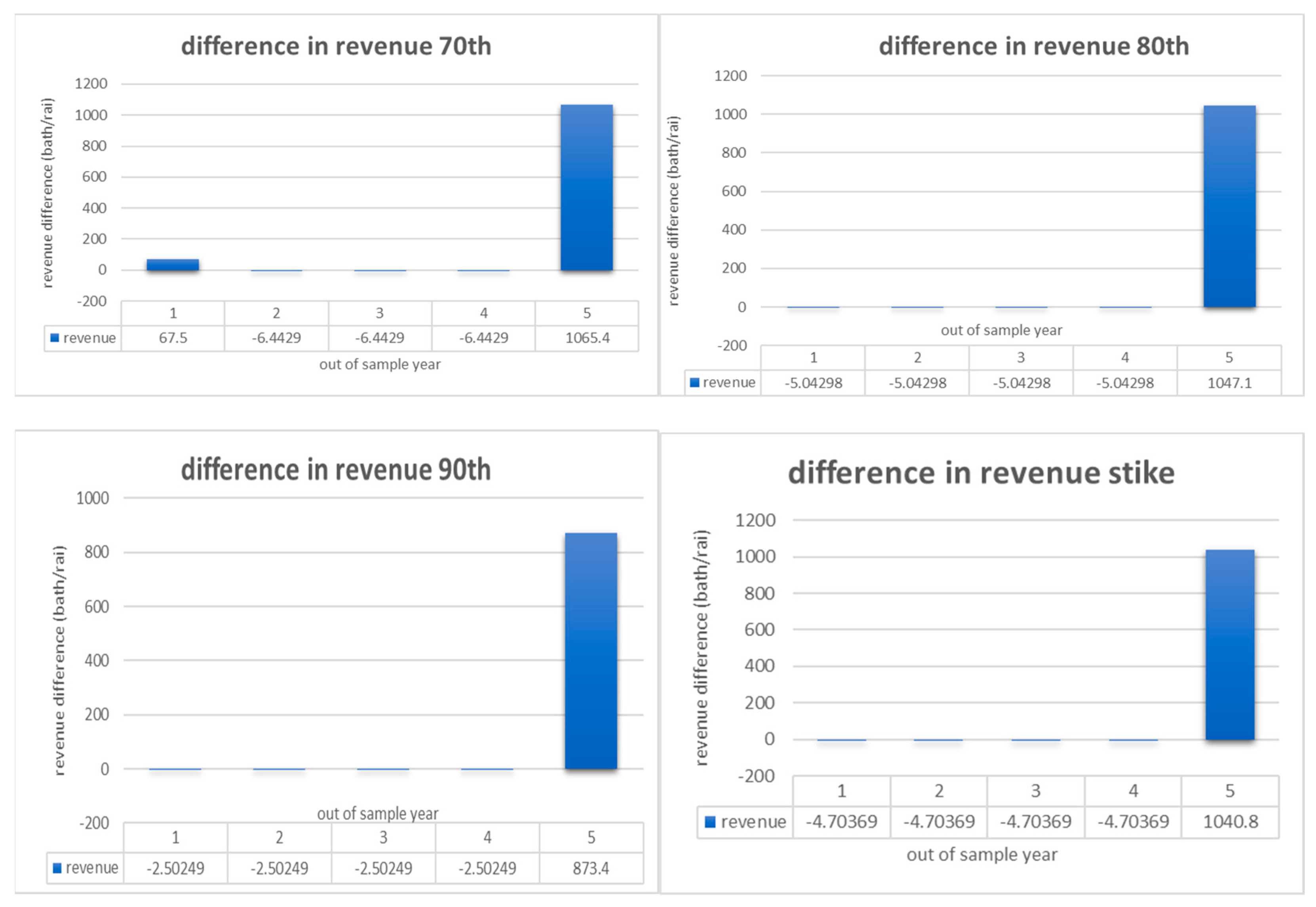
Table 1.
Summary of the literature on climate change variability for crop yield.
| References | RI | T | T.MIN | T.MAX | SR | Other features |
|---|---|---|---|---|---|---|
| Marin et al. 2001 | X | X | CO2 | |||
| Vedenov and Barnett. 2004 | X | X | ||||
| Lobell and Field 2007 | X | X | X | X | ||
| Lobell and Burke 2010 | X | X | ||||
| Verón et al. 2015 | X | X | X | X | ||
| Wang et al. 2018 | X | SH | ||||
| Xu et al. 2018 | X | X | SH | |||
| Shirsath et al. 2019 | X | |||||
| Sinnarong et al. 2019 | X | X | ||||
| Amnuaylojaroen et al. 2021 | X | X | X | |||
| Kath et al. 2021 | X | X | ||||
| Bucheli et al. 2022 | X | |||||
| Byrareddy et al. 2023 | X | X | X | |||
| Tappi et al. 2023 | X | X | X | DTR | ||
| Greenland et al. 2005* | X | X | X | GDDs, FH, Soil water | ||
| Mali et al. 2014* | X | X | X | X | RH.Max, RH.Min | |
| Sattar et al. 2014* | X | X | X | X | X | |
| Carvalho et al. 2015* | X | X | X | X | ||
| Kath et al. 2018* | X | |||||
| Verma et al. 2019* | X | X | X | RH I,RH II | ||
| Pignède et al. 2021* | X | X | X | X | NDVI, PE, MRH | |
| Singh et al. 2021* | X | X | X | X | CDC | |
| Pipitpukdee et al. 2020* | X | X | X | Max.rain, PD,LRP,LW,IA | ||
| Verma et al. 2021* | X | X | X | RH | ||
| Sinnarong et al. 2022* | X | X |
Note: The notation (*) of references represent works involving sugarcane. RI: Annual rainfall (mm); T: Temperature; DTR: average diurnal temperature range; T.MIN: Minimal temperature (); T.MAX: Maximal temperature (); SH: sunshine hours (hour); MRH: Mean relative humidity (%); TR: Temperature range; PE: Potential evapotranspiration; RH I: relative humidity at 8:30 IST; RH II: relative humidity at 14:30 IST; GDDs: Growing degree-days (GDDs) (°C day); FH: Fall (autumn) hurricanes and tropical storms; SR: Solar radiation (%); CDC: Carbon dioxide concentration (ppm); PD: Population density; LRP: Lag received price (USD/ton); LW: Lag wage (USD); IA: % Irrigated area per province area.
Table 2.
Description of the data used in the study.
| Variable | Notation | Details |
|---|---|---|
| Sugarcane yield (tonne/rai) | ||
| Rainfall (mm). | ) | |
| Maximal temperature ) | ) | |
| Year of harvest | t stands for the year of harvest | |
| Price of sugarcane yield per tonne | Farm gate price of the last harvest year |
Table 3.
Sugar cane model with 31 years of harvest as dependent variable results with the approximate significance of smooth terms for predictors.
Table 3.
Sugar cane model with 31 years of harvest as dependent variable results with the approximate significance of smooth terms for predictors.
| Predictor variable | F | p-value |
|---|---|---|
| Year | 9.319 | 0.0007 *** |
| Rainfall index | 1.625 | 0.0444 * |
| Maximum temperature | 0.284 | 0.0976 |
| Adjust R2 | 0.602 | |
| Split testing R2 | 0.691 |
Significant at *** p < 0.001, ** p < 0.01, * p < 0.05, . p < 0.1.
Table 4.
Results of the QGAM model.
| Tau | Predictor variable | p-value |
|---|---|---|
| 0.4 | Year | < 0.0001*** |
| Rainfall index | 0.0535 | |
| Maximum temperature | 0.0740 | |
| 0.3 | Year | < 0.0001 *** |
| Rainfall index | 0.0757 | |
| Maximum temperature | 0.0657 | |
| 0.2 | Year | < 0.0001 *** |
| Rainfall index | 0.0036 ** | |
| Maximum temperature | 0.0960 |
Significant at *** p < 0.001, ** p < 0.01, * p < 0.05, . p < 0.1.
Table 5.
Parameters of optimal weather instruments.
| Model | Levels of the excessive rainfall | Maximum Liability (baht/Rai) |
Premium (baht/Rai) | Premium rate (%) |
|---|---|---|---|---|
| GAM | 1,595.42(strike) | 1216.60 | 4.70369 | 0.38663 |
| 1,492.75(70th) | 1204.61 | 6.44293 | 0.53486 | |
| 1,573(80th) | 1213.06 | 5.04298 | 0.41572 | |
| 1,789.3(90th) | 1239.79 | 2.50249 | 0.20185 | |
|
QGAM Tau = 0.4 |
1,595.42(strike) | 1,704.37 | 6.58927 | 0.38661 |
| 1,492.75(70th) | 1,686.47 | 9.01907 | 0.53479 | |
| 1,573(80th) | 1,700.78 | 7.07056 | 0.41573 | |
| 1,789.3(90th) | 1,726.82 | 3.48553 | 0.20185 | |
|
QGAM Tau = 0.3 |
1,595.42(strike) | 1,733.34 | 6.70155 | 0.38663 |
| 1,492.75(70th) | 1,714.23 | 9.16753 | 0.53479 | |
| 1,573(80th) | 1,729.55 | 7.19016 | 0.41572 | |
| 1,789.3(90th) | 1,756.32 | 3.54507 | 0.20185 | |
|
QGAM Tau = 0.2 |
1,595.42(strike) | 1,814.64 | 7.01588 | 0.38663 |
| 1,492.75(70th) | 1,795.24 | 9.60079 | 0.53479 | |
| 1,573(80th) | 1,811.14 | 7.52931 | 0.41572 | |
| 1,789.3(90th) | 1,838.04 | 3.71002 | 0.20185 |
The premium rate is the ratio of premium to maximum liability.
Table 6.
Efficiency of rainfall index as measured by CTE, CER and MRSL.
| GAM | In sample (1992-2017) | Out of sample (2018-2022) | ||||
|---|---|---|---|---|---|---|
| CTE | CER | MRSL | CTE | CER | MRSL | |
| 70th | 6,918.65 | 8.7275 | 603.900 | 10,497.44 | 9.2389 | 1,410.261 |
| 80th | 6,895.68 | 8.7237 | 607.180 | 10,480.12 |
9.2376 | 1,409.380 |
| 90th | 6,861.85 | 8.7187 | 626.675 | 10,447.41 | 9.2350 | 1,407.782 |
| Strike | 6,891.53 | 8.7230 | 608.646 | 10,479.13 | 9.2375 | 1,409.167 |
|
QGAM (0.2) |
In sample (1992-2017) | Out of sample (2018-2022) | ||||
| CTE | CER | MRSL | CTE | CER | MRSL | |
| 70th | 6,992.90 | 8.7381 | 599.050 | 10,606.64 | 9.2475 | 1,412.251 |
| 80th | 6,958.33 | 8.7325 | 601.313 | 10,581.39 | 9.2455 | 1,410.948 |
| 90th | 6,905.63 | 8.7249 | 626.675 | 10,526.91 | 9.2413 | 1,410.948 |
| Strike | 6,951.80 | 8.7314 | 602.721 | 10,579.09 | 9.2454 | 1,410.948 |
|
QGAM (0.3) |
In sample (1992-2017) | Out of sample (2018-2022) | ||||
| CTE | CER | MRSL | CTE | CER | MRSL | |
| 70th | 6,982.72 | 8.7367 | 599.417 | 10,591.67 | 9.2463 | 1,411.978 |
| 80th | 6,949.79 | 8.7313 | 601.933 | 10,567.57 | 9.2445 | 1,410.734 |
| 90th | 6,899.65 | 8.7241 | 626.675 | 10,515.70 | 9.2404 | 1,410.734 |
| Strike | 6,943.61 | 8.7303 | 603.383 | 10,565.46 | 9.2443 | 1,410.734 |
|
QGAM (0.4) |
In sample (1992-2017) | Out of sample (2018-2022) | ||||
| CTE | CER | MRSL | CTE | CER | MRSL | |
| 70th | 6,979.23 | 8.736 | 599.564 | 10,586.53 | 9.2460 | 1,411.885 |
| 80th | 6,946.77 | 8.731 | 602.165 | 10,562.70 | 9.2441 | 1,410.659 |
| 90th | 6,897.49 | 8.724 | 626.675 | 10,511.66 | 9.2401 | 1,410.659 |
| Strike | 6,940.69 | 8.730 | 603.630 | 10,560.60 | 9.2439 | 1,410.659 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






