Prerpints.org logo
Preprint
Article

Dynamic Right-of-Way Allocation on Bus Priority Lane considering Traffic System Resilience

Altmetrics

Downloads

122

Views

30

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

02 January 2024

Posted:

18 January 2024

You are already at the latest version

Alerts
Abstract
Ensuring bus priority is to improve traffic sustainability at the signalized intersection. To achieve this, the Bus Priority Lane (BPL) is adopted to provide exclusive right-of-way for buses. However, the BPL is underutilization if the frequency of buses is low. To address this issue, many studies focus on improving the BPL’s utilization efficiency by intermittently allowing general vehicles to access it. However, these studies still have some shortcomings: i) bus priority cannot be guaranteed if general vehicles run on the BPL; ii) the traffic system lacks resilience, especially when the traffic demand is unbalanced. This paper proposes a dynamic right-of-way allocation on the BPL considering traffic system resilience. On the one hand, it ensures absolute bus priority by controlling Connected Automated Vehicles (CAVs) to not interfere with buses. On the other hand, it can improve traffic system resilience by allocating right-of-way for CAVs with heavy turning-movement demand. To validate the effectiveness, the proposed control strategy is evaluated against the non-control baseline. Sensitivity analysis is conducted under seven unbalanced traffic demand levels, four congestion levels, and five CAV Penetration Rates. The results show that the proposed control strategy can ensure absolute bus priority and improve traffic efficiency and traffic system resilience.
Keywords: 
Subject: Engineering  -   Transportation Science and Technology

1. Introduction

Congestion at signalized intersections poses significant challenges to urban transportation systems, and ensuring bus priority has emerged as a crucial strategy to mitigate congestion [1,2,3]. One commonly adopted approach is the implementation of a Bus Priority Lane (BPL), which provides exclusive right-of-way for buses, enabling them to bypass general traffic and improve traffic sustainability and efficiency [4,5].
However, an important concern arises when the utilization frequency of buses on the BPL is low, resulting in underutilization of this BPL. Such underutilization not only compromises the effectiveness of the transportation system in reducing congestion but also raises concerns about its overall efficiency and sustainability [6].
In response to this challenge, numerous studies have proposed strategies to improve the utilization efficiency of BPLs. Some of these studies focus on converting BPLs into intermittent BPLs [7,8,9,10]. Such intermittent BPLs allow general vehicles to access the BPL when the utilization frequency of buses is low. By opening up intermittent BPLs for general vehicles, these studies can improve lane occupancy and reduce vehicle delay on the general-purpose lanes [11]. With the advance of Automated Vehicle (AV) technology, AV is emerging to revolutionize the transportation system [12,13,14,15,16,17]. Unfortunately, it is still difficult for AVs at the current stage to cope with complex interactions with surrounding vehicles at the signalized intersection. Hence, other studies focus on providing exclusive right-of-way for AVs by converting BPLs into mixed-use AV/bus lanes [18,19]. Such mixed-use AV/bus lanes not only enhance AV safety but also improve the utilization efficiency of the BPL.
Although these studies can improve the utilization efficiency of the BPL, they still have some shortcomings. Firstly, converting BPLs into intermittent BPLs raises concerns about ensuring bus priority, as the intermittent availability of the BPLs may lead to delays and reduced reliability for bus services [20,21,22]. This is because the transit buses would possibly be disturbed by general vehicles when approaching the signalized intersection. Secondly, the existing studies lack consideration of traffic system resilience [23,24]. Especially when the traffic demand is heavy and unbalanced, the traffic system cannot handle all vehicles and experiences collapse.
To overcome these shortcomings, an innovative control strategy is necessary to ensure bus priority while improving the resilience of the traffic system. This paper proposes a dynamic right-of-way allocation strategy on the bus priority lane, taking into account the concept of traffic system resilience. The proposed control strategy bears the following features:
  • Improve traffic system efficiency at the signalized intersection.
  • Enhance traffic system resilience under various traffic demand patterns.
  • Guarantee absolute bus priority even when traffic is congested.
The remainder of this paper is structured as follows. Section “Problem Statement” describes scenarios and research problems. Section “Logic Structure of the control strategy” illustrates the logic of the proposed control strategy. Section “Mathematical Formulation” presents problem formulation and the associated solution. Section “Evaluation” shows the experiment design and associated results. Section “Conclusion” entails the conclusions from the experiments.

2. Problem statement

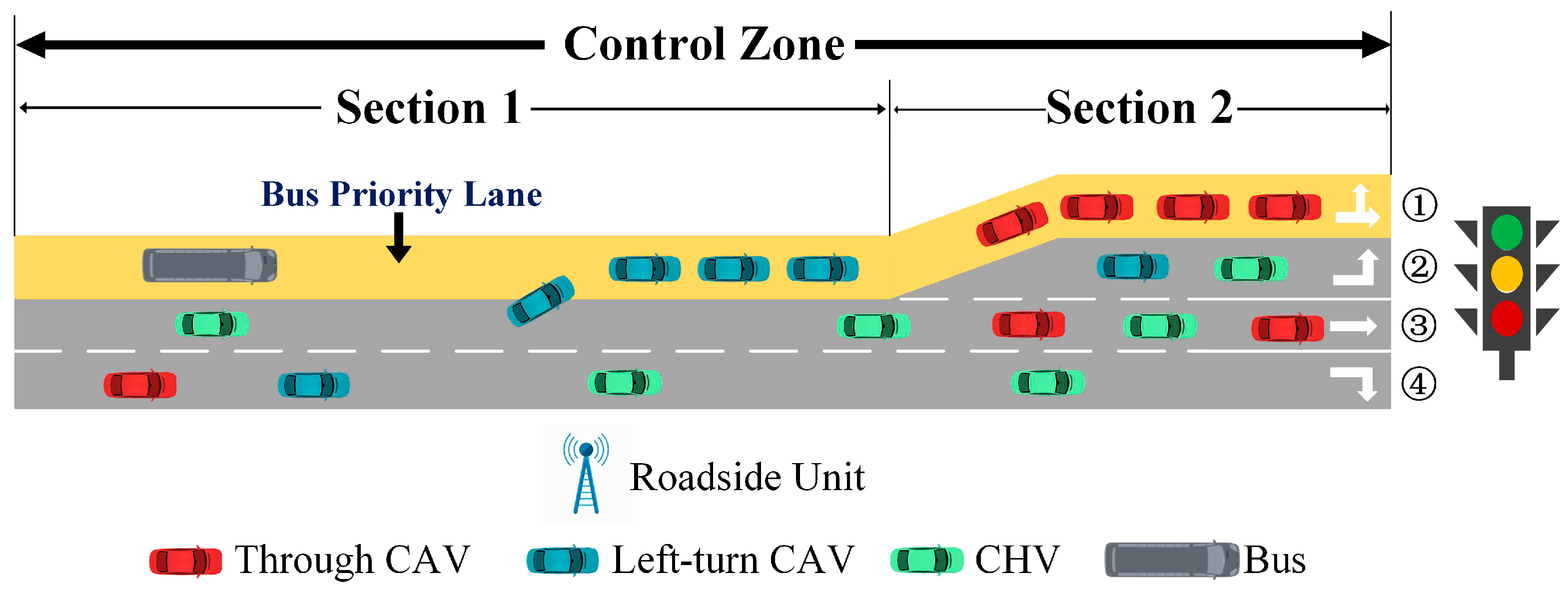
The research scenario is a signalized intersection in a mixed traffic environment. As illustrated in Figure 1, a control zone is divided into two sections: section I and section II. In the section I, there are three lanes. The topmost lane is a Bus Priority Lane (BPL). The other lanes are General Purpose Lanes (GPLs). Section II includes four lanes. One is the BPL and the other lanes are respectively for vehicles with left-turning movement, going-straight movements, and right-turning movement. All vehicles can be divided into general vehicles and buses. The general vehicles include Connected Automated Vehicles (CAVs) and Connected Human-driven Vehicles (CHVs). All vehicles enable communication with other vehicles and the roadside unit via Vehicle-to-Vehicle (V2V) and Vehicle-to-Infrastructure (V2I) in real-time. All general vehicles only run on the GPLs when they come into the control zone. The BPL is designed to ensure absolute bus priority and is open to CAVs with heavy turning-movement demand.

3. Logic structure of the control strategy

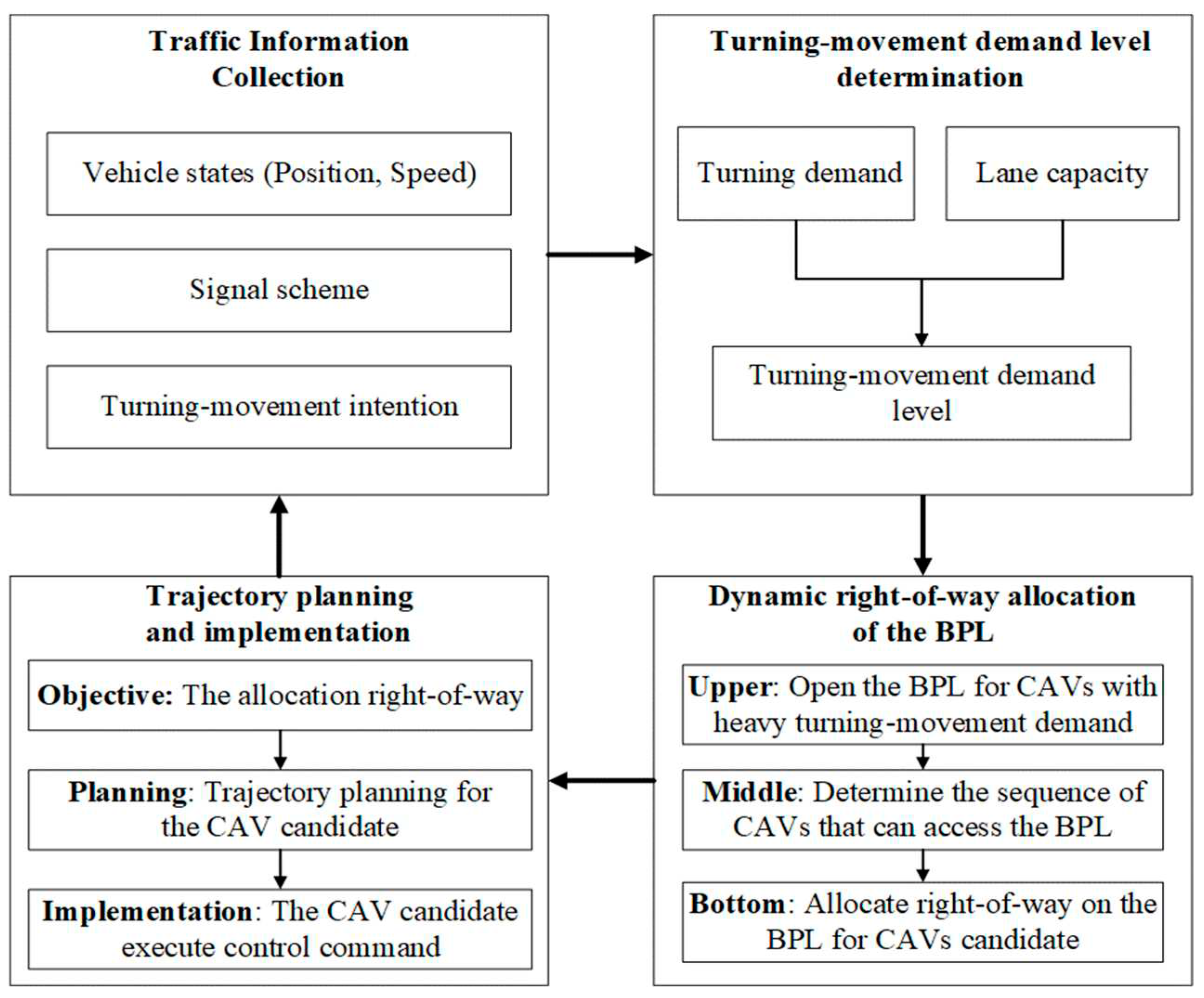
In this section, the logic structure of the proposed control strategy has been illustrated in Figure 2. The proposed control strategy is designed to improve traffic system resilience when the traffic demand is heavy and unbalanced. The strategy can be divided into four components including traffic information collection, turning-movement demand level determination, dynamic right-of-way allocation of the BPL, and trajectory planning and implementation. In each time step, the control logic would be activated. Some detailed information about these four components has been described in the following sections.

3.1. Traffic Information Collection

The traffic information collection is the first component in the logic structure of the proposed control strategy. It is designed to collect traffic information about vehicle states, signal schemes, and turning-movement intentions. All the collected information would be the input of the next component (Turning-movement demand level determination).

3.2. Turning-movement Demand Level Determination

This section introduces the second component of the control logic. This component is a turning-movement demand level determination. It is designed to determine whether the current traffic demand is heavy and unbalanced. When the current signal scheme is fed to this component, this component would calculate the lane capacity for each turning movement. Compared with the current turning demand, this component would determine a demand level for each turning movement. Finally, the turning-movement demand level results would output to the next component.

3.3. Dynamic Right-of-Way Allocation of the BPL

This section introduces the third component of the control logic. This component is called the dynamic right-of-way allocation of the BPL. It is designed to determine whether and how to allocate the right-of-way of the BPL for CAVs. When the turning-movement demand level is high, this component is activated. Firstly, this component determines to open the BPL for turning-movement demand that is heavy and unbalanced. Next, this component would determine the sequence of CAV candidates that can access the BPL. Based on the determined sequence, this component would dynamically allocate the right-of-way of the BPL for CAV candidates. The information about the allocated right-of-way on the BPL would output to the next component.

3.4. Trajectory Planning and Implementation

Trajectory planning and implementation is the fourth component of the control logic. According to the allocated right-of-way, this component would optimize the trajectory plan for CAV candidates to utilize the objective right-of-way on the BPL. Then, the component would convert the trajectory plan into a control command for CAV candidates to implement.

4. Mathematical formulation

4.1. Terminal Time Prediction

The optimized trajectory plan for CAVs accessing the Bus Priority Lane (BPL) consists of trajectory planning for vehicles at each time interval and determining the terminal time when vehicles reach the stop line. However, due to the uncertain behavior of CHVs in mixed traffic, the optimized trajectory plans for CAV candidates need to be updated at each time interval. Consequently, the prediction of the terminal time when vehicles reach the stop line must also be recalculated at each time interval. The calculation of the terminal time prediction is described below.
t n f , d = max ⁡ t n − 1 f + t h , t n f , e                 ∀ n ∈ N
t n f , e = t 0 + L − v m a x 2 − v t n 0 2 2 a m a x v m a x + v m a x − v t 0 n a m a x
t n f = t n f , d t n f , d R + G ∗ R + G + R             ∀ t n f , d ∈ φ G ∀ t n f , d ∈ φ G
where n is the vehicle index in the mixed traffic. N is the vehicle index set in the mixed traffic. t n f , d is the initial time prediction of vehicle n arriving at the stop line. t n − 1 f is the initial time prediction of vehicle n − 1 arriving at the stop line. t n f , e is the earliest time vehicle n arrives at the stop line without considering the preceding vehicles and traffic signal. t 0 is the current time at each time interval for time prediction of the vehicle n arriving at the stop line. L , v m a x and a m a x respectively represent the length of the control zone the maximum speed and acceleration. v t 0 n is the speed of vehicle n at the current time. R and G are the duration of red light and green light. t n f is the terminal time of vehicle n arriving at the stop line.

4.2. CHV Trajectory Prediction

In the mixed traffic, CHVs can run on their own decisions. The implementation of CHVs' trajectory plans is influenced by factors such as the trajectory information of preceding vehicles and traffic signal information. Consequently, it becomes necessary to re-predict CHV trajectories at each time interval to accommodate the mixed traffic conditions. The Intelligent Driver Model (IDM) is a widely accepted model for predicting CHV trajectories. The predicted acceleration for CHVs can be mathematically formulated as follows.
a t p , k = a m a x 1 − v t k v m a x 4 − ∆ x p n , k d ∆ x p n , k 2 ∀ t ∈ T , n ∈ N , k ∈ N k
a t l , k = a m a x 1 − v t k v m a x 4 − ∆ x k d * L − x t k 2 ∀ t ∈ T , k ∈ N k
∆ x n , k d = s 0 + max ⁡ v t k · t h + v t k · ∆ v t p n , k 2 a m a x · a d _ , 0
∆ x n , k d * = s 0 + max ⁡ v t k · t h + v t k 2 2 a m a x · a d _ , 0
t R = t k f R + G · R + G ,       ∀ t c f ∉ ω G , ∀ k ∈ N k
a t k = a o a l             ∀ t ∉ t 0 , ∞ ∩ t R , t R + R ∀ t ∈ t 0 , ∞ ∩ t R , t R + R
where k is the vehicle index of CHVs. N k is the vehicle index set of CHVs. v t k is the speed of vehicle k . x t k is the position of vehicle k . a d _ is the desired deceleration of the vehicle. ∆ v t p n , k is the speed difference between the vehicle k ’s preceding vehicle and the vehicle k . t h is safe time headway. ∆ x p n , k d is the desired minimum distance gap between the vehicle k ’s preceding vehicle and the vehicle k . ∆ x p n , k is the distance gap between the vehicle k ’s preceding vehicle and the vehicle k . ∆ x k d * is the desired minimum distance gap when there is no preceding vehicle. a t p , k is the predicted acceleration of the vehicle k if there is a preceding vehicle. a t l , k is the predicted acceleration of the vehicle k if there is no preceding vehicle. t k f denotes the terminal time of vehicle k arriving at the stop line. a t k is the terminal acceleration of vehicle k .

4.3. Turning-movement Demand Level Calculation

To calculate the turning-movement demand level, the model analyzes the spatiotemporal occupancy of traffic and considers the vehicles' turning-movement demand. To achieve this, we split the traffic flow as follows:
Ω = Ω 1 ∪ Ω 2 ∪ Ω 3
where Ω represents the set of all vehicles on the continuous road, Ω 1 represents the set of all left-turn vehicles on the continuous road, Ω 2 represents the set of all through vehicles on the continuous road, and Ω 3 represents the set of all right-turn vehicles on the continuous road.
D Ω i = Ω i Ω i g r i g q i s
where D Ω i represents the demand intensity of the turning traffic flow, Ω i g represents the set of vehicles with turning i that can pass through the intersection in the most recent signal cycle, r i g represents the effective green signal ratio for the signal controlling the turning movement i , and q i s represents the saturation flow rate for the turning movement. Therefore, the turning movement with the highest demand intensity is:
i * = a r g m a x i D Ω i
If D Ω i * = 0 , it means that all vehicles can pass through the intersection during the current green phase. Hence, the allocated right-of-ways on the BPL are not needed for any vehicles. Otherwise, the allocated right-of-ways are required to be provided for CAVs with heavy turning movement i * .

4.4. Dynamic Allocation of the Right-of-way on the BPL

Right-of-way allocation is the spatial slice that is occupied by the vehicle at time t . The spatial slices for transit buses and CAVs are based on the current traffic conditions. Due to the different lengths of the transit bus and CAVs, the spatial slice determination should be divided into two kinds.
s t c = x x t c − l c ≤ x ≤ x t c + l c     ∀ t ∈ T , c ∈ N c
s t b = x x t b − l b ≤ x ≤ x t b + l b     ∀ t ∈ T , b ∈ N b
where s t c and s t b respectively denote spatial slices of the CAV (vehicle c ) and spatial slices of the transit bus.

4.5. Trajectory Planning for CAVs

4.5.1. Cost Function

The cost function to be minimized consists of three terms, including travel time, fuel consumption, and the efficiency of vehicles passing the signalized intersection. It is formulated as:
J = α ∑ c τ c + β ∑ c ∑ t a t c + μ x t f c − L + v t f c − v m a x
The first term in the cost function is about efficiency. c is the CAV index. The variable in this term is travel time τ c of the vehicle c . The explanation of τ c need to be defined as follows:
τ c = ∑ t ∑ m w m , t c · ∆ t                                   ∀ c ∈ N c
N c is the CAV index set of the mixed traffic. If the vehicle c is in the control zone, the binary decision variable w m , t c must be updated at each time interval. w m , t c is a binary decision variable to denote CAV c on the general-purpose lane or the BPL, Hence, the travel time can be illustrated as Constraint (16).
The second term illustrates the fuel consumption using the acceleration a t c . The last term describes that the vehicles should pass the intersection as fast as possible to improve traffic efficiency. x t f c and v t f c are respectively the position and speed of the vehicle c at the end of the time interval based on the terminal time prediction.

4.5.2. Constraints

1)
Vehicle kinematic constraints
The movement of vehicles has to be subject to kinematic constraints as described below.
v m i n ≤ v t c ≤ v m a x   ∀ t ∈ T , c ∈ N c
a m i n ≤ a t c ≤ a m a x   ∀ t ∈ T , c ∈ N c
v t c = v t − 1 c + a t c ⋅ Δ t   ∀ t ∈ T , c ∈ N c
x t c = x t − 1 c + v t − 1 c · ∆ t + 1 2 a t c ⋅ ∆ t 2       ∀ t ∈ T , c ∈ N c
where v t c is the instantaneous speed of vehicle c at time t , the speed of vehicle c must be limited within the minimum and maximum allowed values ( v m i n , v m a x respectively). Constraint (18) denotes that the acceleration and deceleration of vehicles must be in a feasible range. x t c is the position of vehicle c at time t . Constraints (19) and (20) depict the vehicle dynamics.
2)
Vehicle conflict constraints
To keep safe, the trajectory planning for CAVs should avoid conflict with surrounding vehicles. The following constraints ensure that vehicle trajectories are conflict-free.
x t p c − x t c > s 0 + v t c · t h + 2 ∗ l c             ∀ t ∈ T , c ∈ N c
x t p b − x t b > s 0 + v t b · t h + 2 ∗ l b             ∀ t ∈ T , b ∈ B
x t b − x t f b > s 0 + v t f b · t h + 2 ∗ l c             ∀ t ∈ T , c ∈ N c , b ∈ B
where b is the bus index, B is the bus index set. x t p c is the position of the vehicle c ’s preceding vehicle at time t . x t p b is the position of the bus b ’s preceding vehicle at time t . x t f b is the position of the bus b ’s following vehicle at time t . x t b and v t b respectively denote the position and speed of the bus b at time t .   v t f b is the speed of the bus b ’s following vehicle at time t . l c and l b are the length of one CAV and the length of one bus.
3)
Traffic signal constraints
The optimized vehicle trajectory plans must be subject to the signal phase and timing constraints. The following constraints are imposed:
t o p s + ∑ t ∑ m w m , t c ⋅ Δ t ≥ t o p   e — G + ξ c — 1 · M             ∀ t ∈ T , c ∈ N c
t o p s + ∑ t ∑ m w m , t c ⋅ Δ t ≤ t o p   e + 1 — ξ c · M             ∀ t ∈ T , c ∈ N c
x t o p e c ≥ L + ξ c — 1 · M                   ∀ t ∈ T , c ∈ N c
x t o p e c ≤ L + 1 — ξ c · M                     ∀ t ∈ T , c ∈ N c
where t o p s , and t o p   e are respectively the start time of the optimization horizon and the end time of the optimization horizon. On the other side, another binary variable ξ c has been introduced, and ξ c = 1 if the vehicle c could get through the intersection during the given optimization horizon, otherwise 0. Constraints (24) and (25) ensure vehicles get through the intersection only during the given green time in the optimization horizon. Constraints (26) and (27) ensure vehicles are in the control zone if they cannot get through the signalized intersection in the current optimization horizon.

5. Evaluation

In this section, the proposed control strategy is evaluated through simulation experiments compared with the non-control baseline. The simulation experiments select throughput, delay, and fuel consumption as the measurements of effectiveness. The simulation experiments are conducted under five different congestion levels and five different CAV Penetration Rates. The goal is to fairly confirm the proposed control strategy can improve traffic system resilience while ensuring absolute bus priority.

5.1. Experiment Design

5.1.1. Testbed

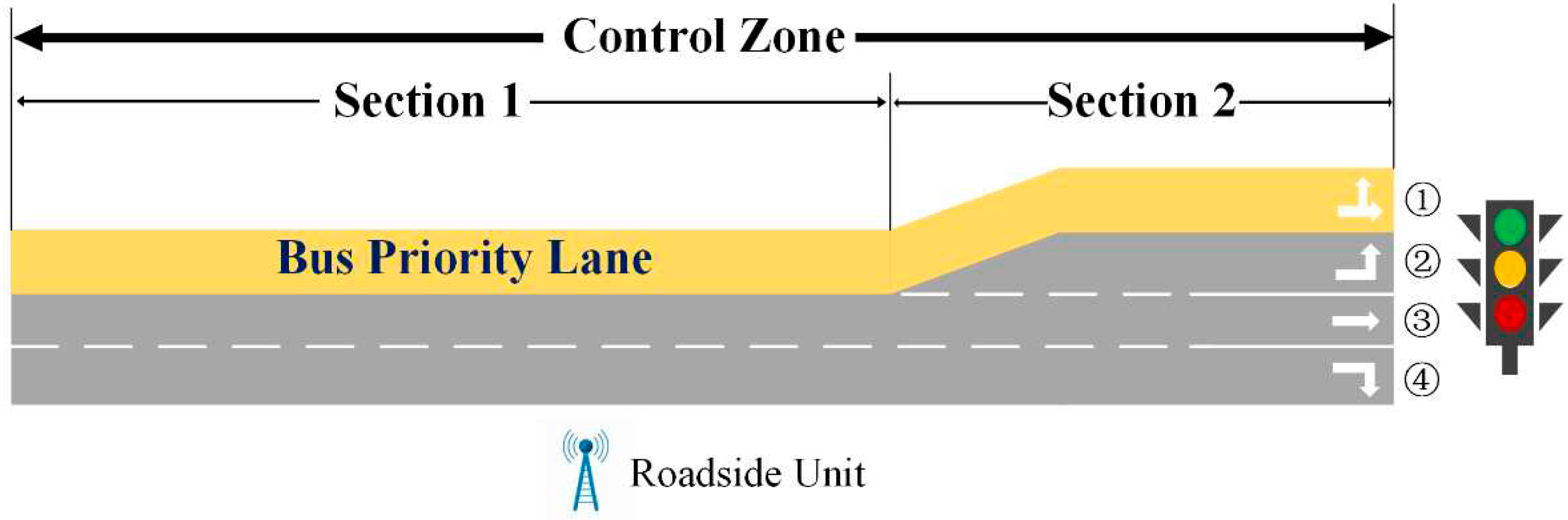
The testbed in the simulation experiment has been illustrated in Figure 3. The testbed is a signalized intersection with a Bus Priority Lane (BPL). The control zone is composed of two sections: section 1 and section 2. The length of section 1 is 350 meters. The length of section 2 is 150 meters. Due to the lane channelization for different turning movements, section 2 contains four lanes. Besides, the roadside unit enabling V2I communication with vehicles is built. All vehicles enable communication via V2V. The simulation platform is based on PTV-VISSIM [25,26].

5.1.2. Scenario

Two scenarios considering absolute bus priority are tested:
  • Non-control baseline: In this scenario, a dedicated bus lane is adopted to separate buses from general vehicles. All vehicles cannot be allowed to run with buses on the same lane. All general vehicles can only run on the General Purpose Lane (GPL).
  • The proposed strategy: In this scenario, the BPL can be open to CAVs when the turning-movement demand is heavy and unbalanced. All CAVs utilize the allocated right-of-way of the BPL without interference with buses.

5.1.3. Measurements of Effectiveness

To validate the effectiveness of the proposed control strategy, three Measurements of Effectiveness (MOE) are selected, including throughput, delay, and traffic system resilience. The definition of the traffic system resilience can be described as follows:
R e s i l i e n c e = D e l a y n − D e l a y o D e l a y n − D e l a y s × 100 %
Where D e l a y n denotes the average vehicle delay in the non-control baseline scenario. D e l a y o represents the average vehicle delay in the proposed control strategy. D e l a y s denotes the average vehicle delay when the congestion level is 1.0 in the non-control baseline.

5.1.4. Sensitivity Analysis

To fairly confirm the validation of the proposed strategy, sensitivity analysis is conducted under seven different unbalanced demand levels, five different congestion levels (0.6, 0.8, 1.0, 1.2, and 1.4), and five different CAV penetration rates (10%, 20%, 30%, 40%, and 50%). Note that, the unbalanced demand level can be described as a different turning-movement demand proportion. For example, proportion 4:4:2 respectively denotes the left-turning demand proportion, go-straight demand proportion, and right-turning proportion. A higher unbalanced demand level means that the difference between the left-turning demand and go-straight demand is larger. Hence, the low unbalanced demand level includes proportions 3:5:2, 4:4:2, and 5:3:2. The high unbalanced demand level contains proportions 1:7:2, 2:6:2, 2:6:2, and 1:7:2.

5.2. Results

The simulation results are shown in this section. The results have validated that the proposed control strategy performs well against the non-control baseline under various turning-movement demand patterns, congestion levels, and CAV Penetration Rates (CPR). The benefit of the proposed control strategy can be observed in traffic efficiency improvement and traffic system resilience improvement. At the same time, the credibility of ensuring absolute bus priority has been confirmed.

5.2.1. Traffic Efficiency Improvement Validation

5.2.1.1 Throughput Comparison Results

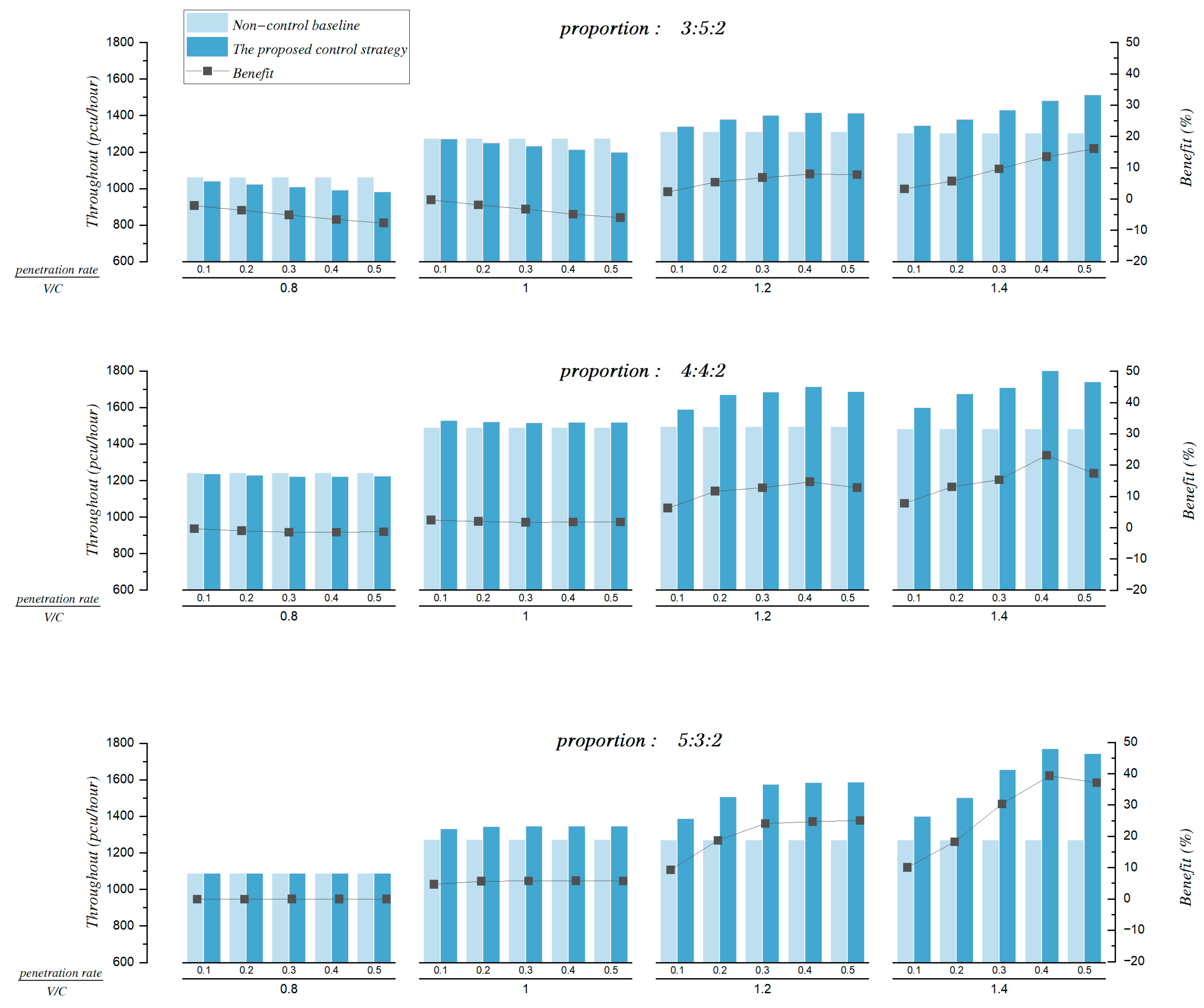
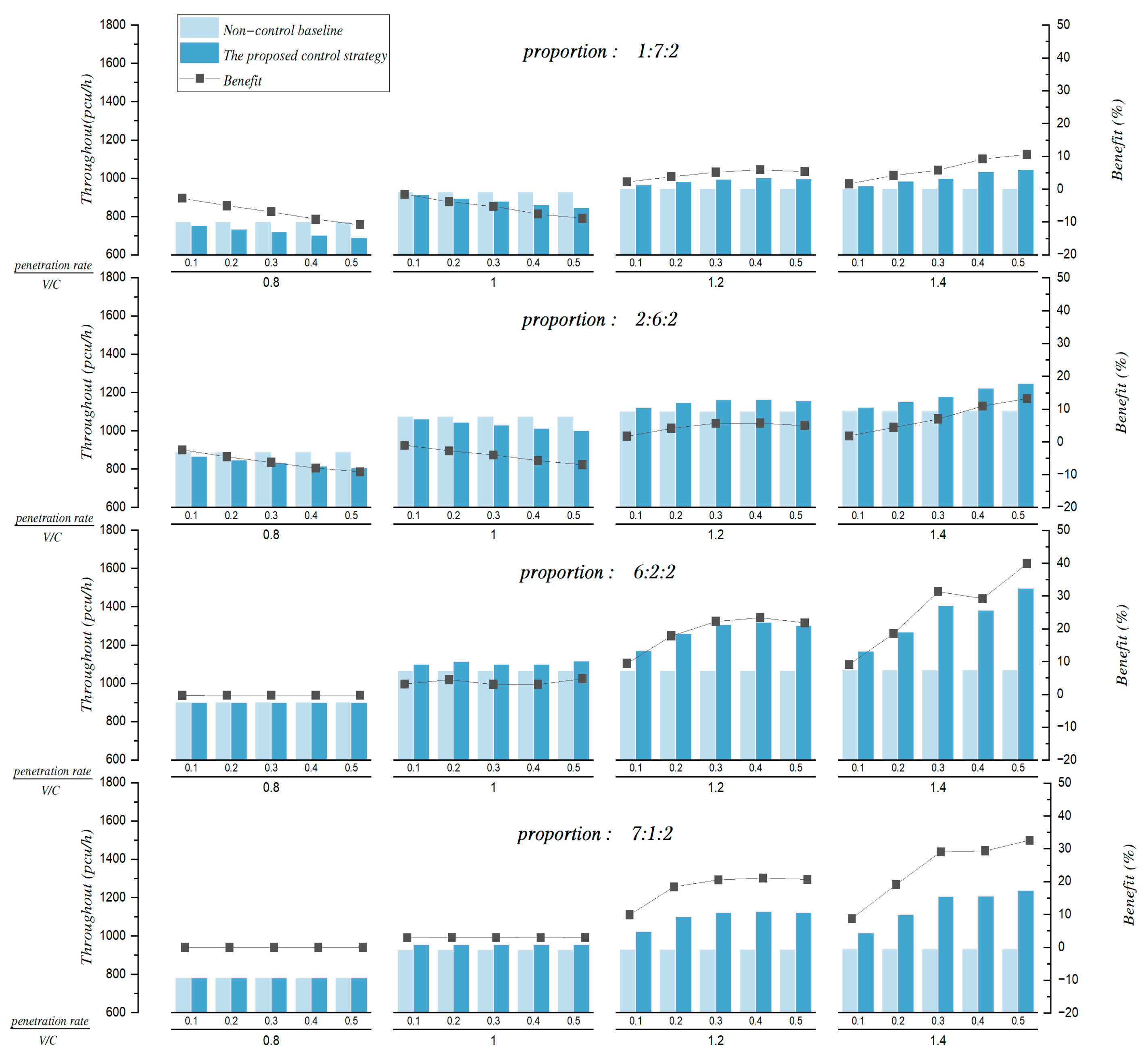
Figure 4 shows the results of the throughput comparison between the non-control baseline and the proposed control strategy under the condition of low unbalanced demand levels (3:5:2, 4:4:2, and 5:3:2). Compared with the non-control baseline, the proposed control strategy has no obvious benefits when the congestion level is less than 1.0. The reason is that the traffic system can easily handle all vehicles when the traffic demand is low. When the congestion level is more than 1.0, it means that the traffic system is in the condition of oversaturated traffic demand. The proposed control strategy has more obvious benefits. This is because the proposed control strategy can improve intersection capacity by controlling CAVs to utilize the right-of-way on the BPL. With the increment of CPRs, the proposed control strategy performs better. The reason is that more CAVs can be controlled to improve traffic efficiency by utilizing the right-of-way on the BPL.
Figure 5 shows the results of the throughput comparison between the non-control baseline and the proposed control strategy under the condition of high unbalanced demand levels (1:7:2, 2:6:2, 6:2:2, and 7:1:2). The proposed strategy still performs well when the congestion level is more than 1.0. With the increment of congestion levels and CPRs, the greater benefits of throughput improvement can be observed. The reason is that the proposed control strategy can improve intersection capacity by allocating the unutilized right-of-way of the BPL for CAVs. To be noted, such allocation can improve the utilization efficiency of road resources. Hence, the proposed control strategy can achieve throughput improvement at the signalized intersection.

5.2.1.2 Delay Comparison Results

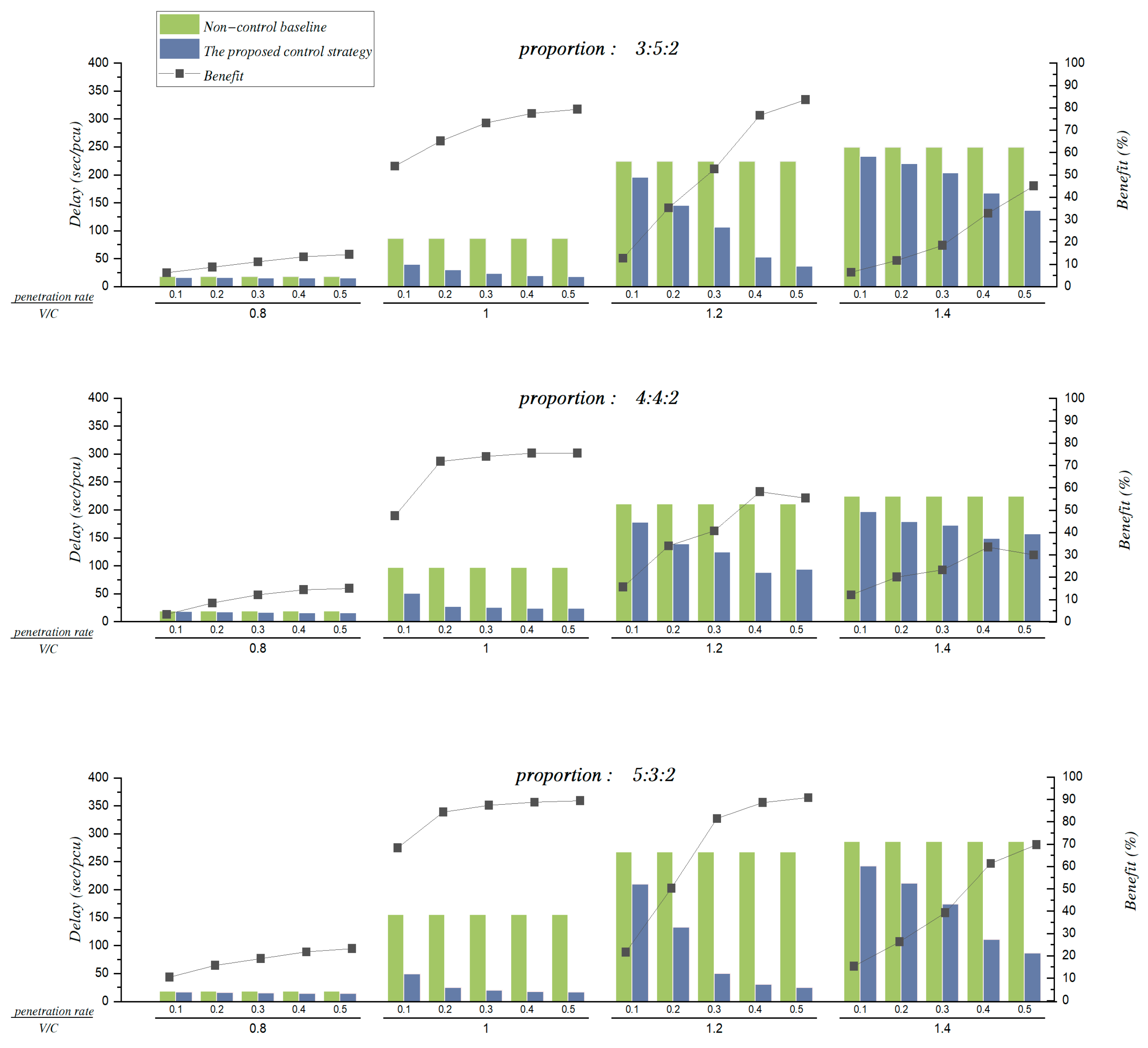
Figure 6 shows the results of the delay comparison between the non-control baseline and the proposed control strategy under the condition of low unbalanced demand levels (3:5:2, 4:4:2, and 5:3:2). Different from the throughput improvement, the proposed control strategy can effectively achieve delay reduction at any congestion levels. With the increment of congestion levels and CPRs, the benefits of delay reduction are more obvious.
The reason is that the proposed control strategy can allocate the right-of-way of the BPL for CAVs to avoid too long a queue on the GPL. When the congestion levels and CPRs are high, the proposed control strategy can reduce traffic delay by controlling more CAVs to utilize the allocated right-of-way on the BPL.
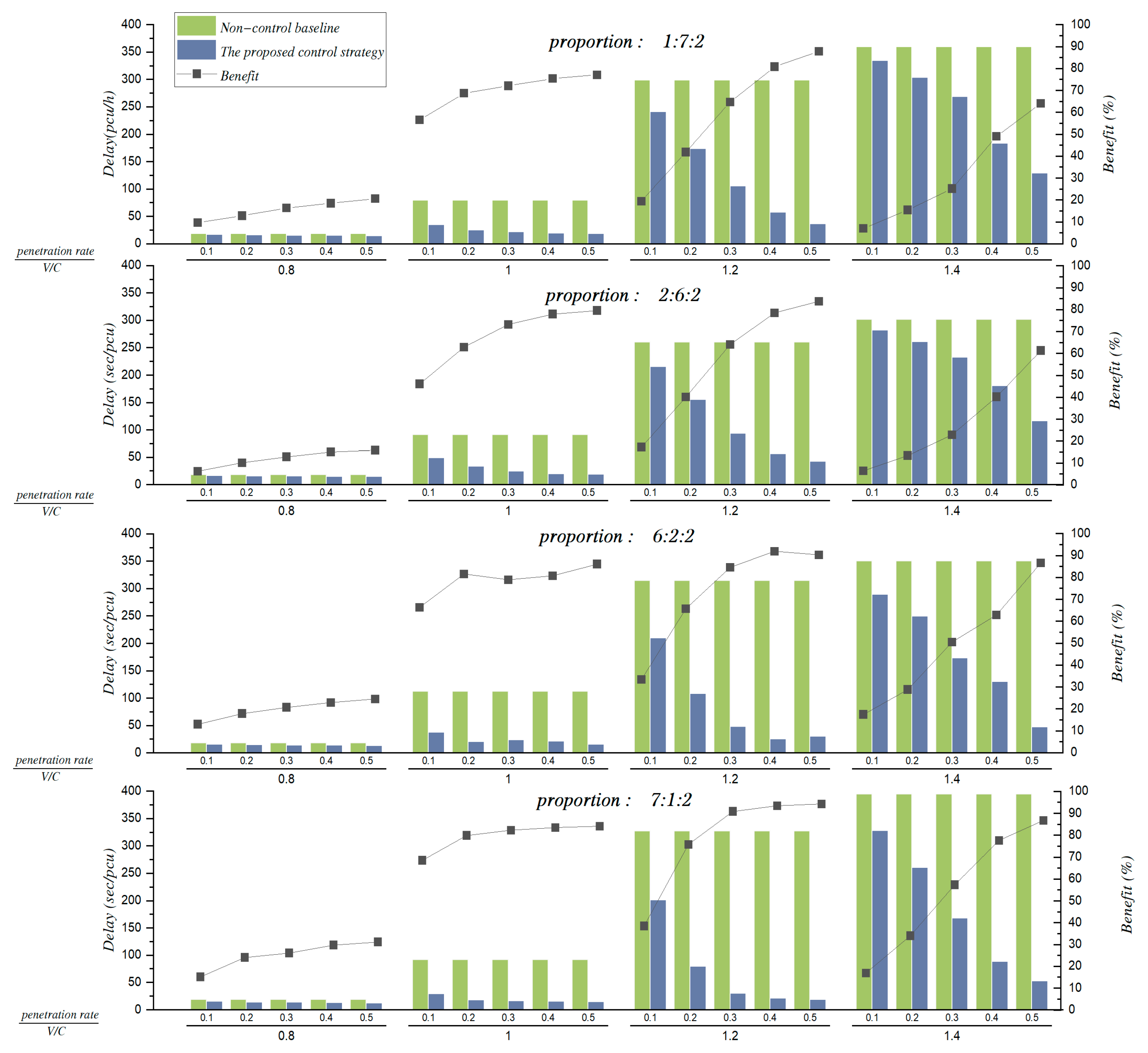
Figure 7 shows the results of the delay comparison between the non-control baseline and the proposed control strategy under the condition of high unbalanced demand levels (1:7:2, 2:6:2, 6:2:2, and 7:1:2). Compared with the low unbalanced demand levels, the proposed control strategy has more benefits of delay reduction. Under the condition of high unbalanced demand levels, heavy turning demand would easily exceed the lane capacity. Due to this, the proposed control strategy would balance traffic demand by controlling more CAVs to utilize the right-of-way of the BPL. Such control can greatly reduce vehicle delay by avoiding too long a queue on the GPL.

5.2.2. Traffic System Resilience Improvement Validation

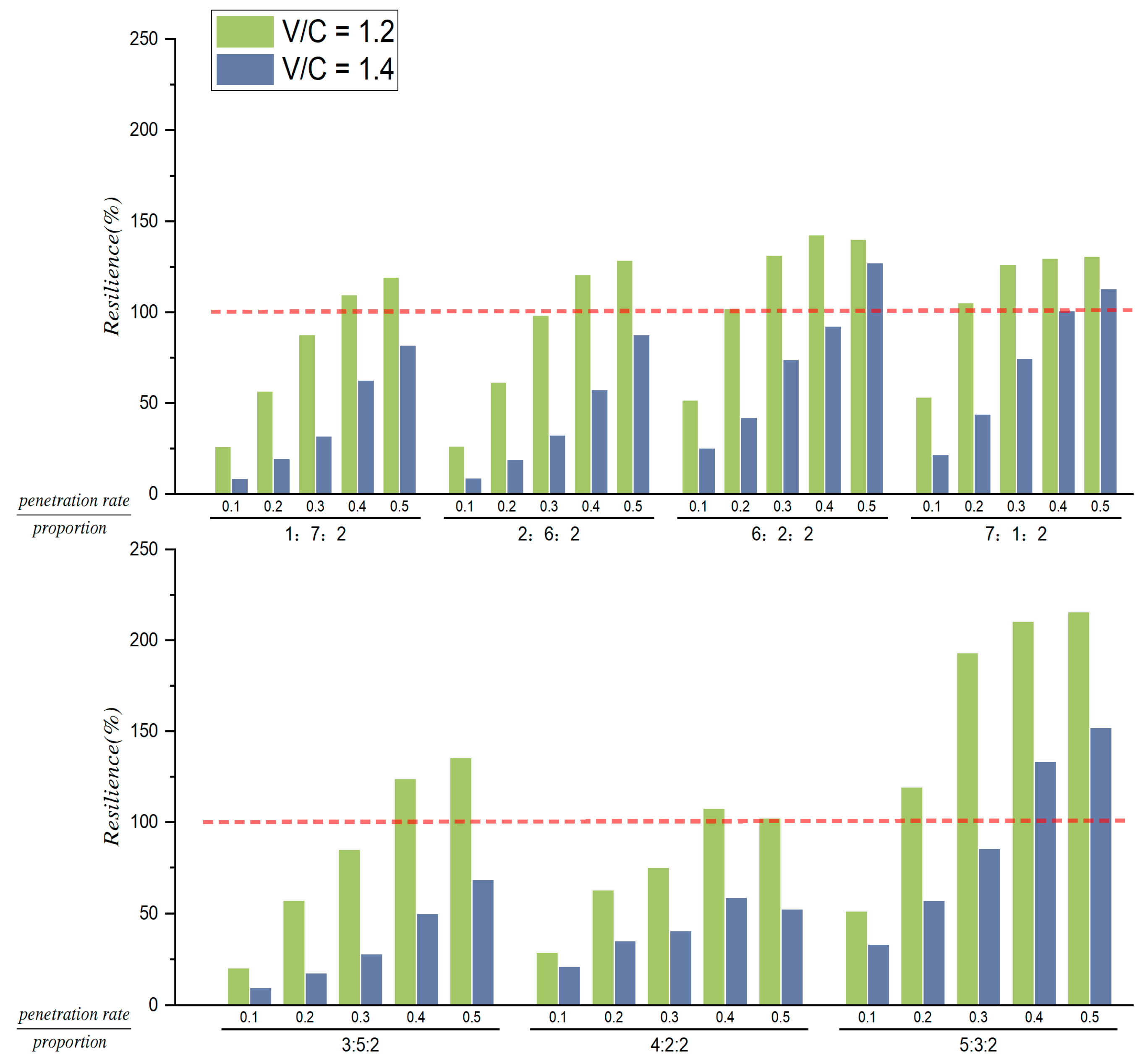
Figure 8 is the result of traffic system resilience comparison under various unbalanced demand levels. The proposed control strategy can improve traffic system resilience when the congestion level is 1.2 and 1.4. The reason for selecting high congestion levels is that the traffic system cannot easily experience system collapse without any control strategies. In Figure 8, the red dotted line denotes the resilience is 100%. To be specific, the proposed control strategy can effectively recover the traffic system from collapse to normal operation if the resilience is more than 1.0. Compared with the high unbalanced demand levels, the benefits of traffic system resilience improvement are more obvious under the conditions of low unbalanced demand levels. With the increment of CPRs, the proposed control strategy can perform better in traffic system resilience improvement.

5.2.3. Bus Priority Validation

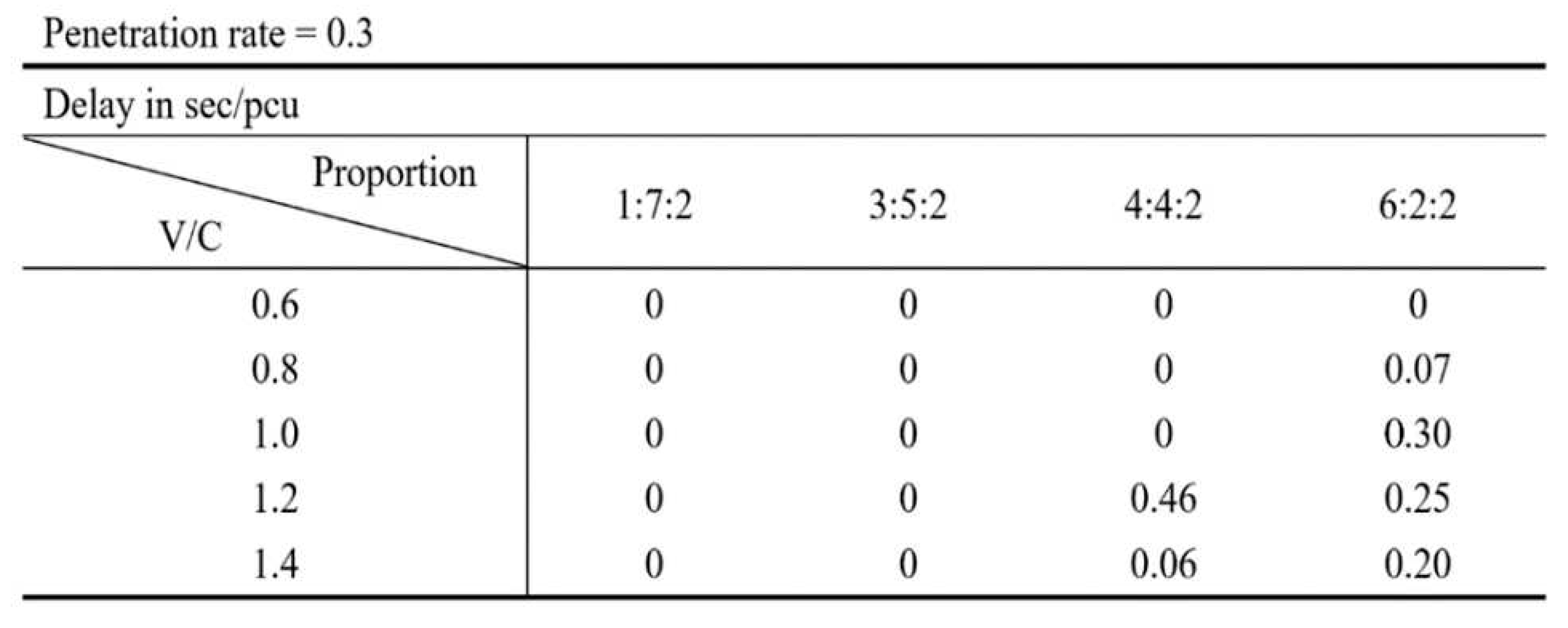
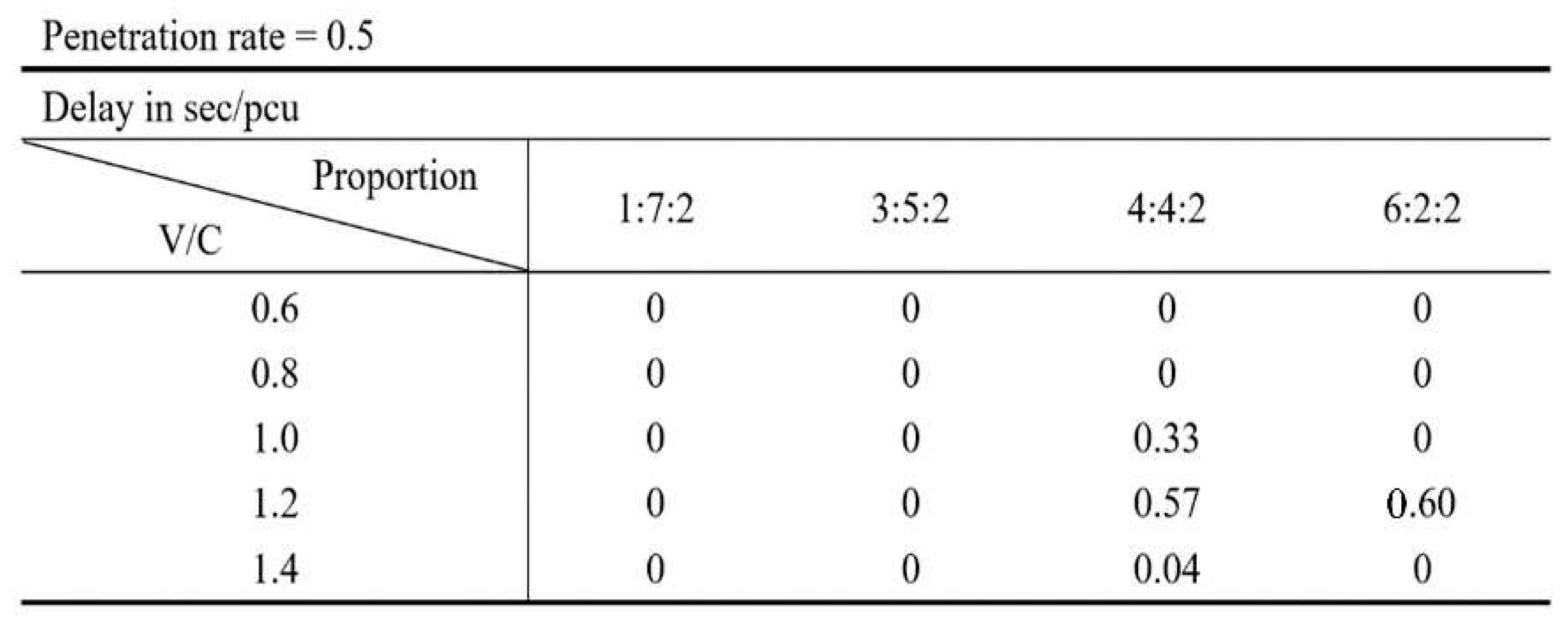
The proposed control strategy can improve traffic efficiency and traffic system resilience while ensuring bus priority. To validate the effectiveness of the capability of ensuring absolute bus priority, some experiments are conducted. As shown in Table 1 and Table 2, the bus delay has been a MOE to evaluate the capability of ensuring absolute bus priority. The results demonstrate that the proposed control strategy can ensure that bus delay is less than 1 second under various congestion levels and unbalanced demand levels. Hence, the proposed control strategy has a credible capability of ensuring absolute bus priority.

6. Conclusion

This paper proposed a control strategy to improve traffic system resilience while ensuring absolute bus priority. The proposed control strategy can achieve traffic demand management by allocating the right-of-way for CAVs with heavy turning demand. To evaluate the proposed control strategy, simulation experiments have been conducted under the low unbalanced traffic demand levels and the high unbalanced traffic demand levels. Sensitivity analysis was performed for congestion levels and CPRs.
Compared with the non-control baseline, the effectiveness of the proposed control strategy is validated in terms of throughput, delay, and traffic system resilience. Some conclusions drawn from the results are as follows:
  • Under various congestion levels, no obvious benefits of throughput improvement exist under the low congestion levels. The proposed control strategy has the benefit of throughput improvement when the congestion level is high (1.2 and 1.4). The throughput improvement benefits can be up to 10%-40%. Different from the throughput improvement, the proposed control strategy can obtain delay reduction benefits at any congestion levels.
  • With the increment of the CPRs, the proposed control strategy can achieve more throughput improvement benefits and delay reduction benefits under high congestion levels. Especially when the congestion level is 1.4, the delay reduction benefits are more obvious.
  • Compared with the non-control baseline, the proposed control strategy outperforms in traffic system resilience under high congestion levels. Especially when the left-turning demand proportion is high, the proposed control strategy can recover the traffic system to handle all vehicles even if the congestion level is 1.4.
  • Absolute bus priority can be guaranteed under various congestion levels and CPRs. The bus delay is less than one second, which means that the bus priority is not interfered with general vehicles accessing the BPL.

Author Contributions

Conceptualization, J.H., and Z.Z.; methodology, J.H., Z.Z., X.S., J.L., and; software, Z.L., and X.S.; validation, Z.Z., Z.L., and J.L.; formal analysis, J.H. and Z.Z.; investigation, J.H.; resources, J.H.; data curation, J.H., and X.S., and Z.Z.; writing—original draft preparation, Z.Z.; writing—review and editing, Z.Z. and J.L.; visualization, X.S., and Z.Z.; supervision, J.H., and J.L.; project administration, J.H., and J.L.; funding acquisition, J.H. and J.L. All authors have read and agreed to the published version of the manuscript.

Funding

This paper is partially supported by National Key R&D Program of China (No. 2022YFE0117100), National Natural Science Foundation of China (Grant No. 52372317), Zhengzhou Major Science and Technology Project (No. 2021KJZX0060-9), Research on Key Technologies for Demolition, Reconstruction, and Reutilization of Pinglu Canal Cross-Line Bridges, and Optimization of Traffic Organization (No. 2023AA14006), Shanghai Automotive Industry Science and Technology Development Foundation (No. 2213), the Fundamental Research Funds for the Central Universities, Tongji Zhongte Chair Professor Foundation (No. 000000375-2018082), and the Science Fund of State Key Laboratory of Advanced Design and Manufacturing Technology for Vehicle (No. 32215011).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data presented in this research are available on request from the corresponding author.

Acknowledgments

This research was supported by PTV VISSIM for the simulation environment.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Zhang, Z.; Lai, J.; Ma, C.; Zhu, J.; Yang, X. In Ensuring Absolute Transit Priority Through Trajectory Based Control of Connected and Automated Traffic, 2021 6th International Conference on Transportation Information and Safety (ICTIS), 2021; IEEE: 2021; pp 1132-1135.
  2. Hu, J.; Park, B. B.; Lee, Y.-J. Transit signal priority accommodating conflicting requests under Connected Vehicles technology. Transportation Research Part C: Emerging Technologies 2016, 69, 173–192. [Google Scholar] [CrossRef]
  3. Zhu, J.; Ma, C.; Yang, X.; Lai, J.; Zhang, Z. In An Asynchronous Cooperative Signal Control Framework in Urban Road Network, 2021 6th International Conference on Transportation Information and Safety (ICTIS), 2021; IEEE: 2021; pp 1105-1111.
  4. He, S.-X.; Dong, J.; Liang, S.-D.; Yuan, P.-C. An approach to improve the operational stability of a bus line by adjusting bus speeds on the dedicated bus lanes. Transportation Research Part C: Emerging Technologies 2019, 107, 54–69. [Google Scholar] [CrossRef]
  5. Petit, A.; Yildirimoglu, M.; Geroliminis, N.; Ouyang, Y. Dedicated bus lane network design under demand diversion and dynamic traffic congestion: An aggregated network and continuous approximation model approach. Transportation Research Part C: Emerging Technologies 2021, 128, 103187. [Google Scholar] [CrossRef]
  6. Ma, Y.; Xie, Y.; Lin, Y. An influence analytical model of dedicated bus lane on network traffic by macroscopic fundamental diagram. Journal of Advanced Transportation 2021, 2021, 1–18. [Google Scholar] [CrossRef]
  7. Eichler, M.; Daganzo, C. F. Bus lanes with intermittent priority: Strategy formulae and an evaluation. Transportation Research Part B: Methodological 2006, 40, (9), 731–744. [Google Scholar] [CrossRef]
  8. Wu, W.; Head, L.; Yan, S.; Ma, W. Development and evaluation of bus lanes with intermittent and dynamic priority in connected vehicle environment. Journal of Intelligent Transportation Systems 2018, 22, 301–310. [Google Scholar] [CrossRef]
  9. Xie, X.; Dong, L.; Feng, L.; Zhang, L.; Li, H. Modelling Method on Dynamic Optimal Setting and Associated Control for Intermittent Bus Lane. Journal of Advanced Transportation 2023, 2023. [Google Scholar] [CrossRef]
  10. Othman, K.; Shalaby, A.; Abdulhai, B. Dynamic Bus Lanes Versus Exclusive Bus Lanes: Comprehensive Comparative Analysis of Urban Corridor Performance. Transportation Research Record 2023, 2677, 341–355. [Google Scholar] [CrossRef]
  11. Fayed, L.; Nilsson, G.; Geroliminis, N. On the utilization of dedicated bus lanes for pooled ride-hailing services. Transportation Research Part B: Methodological 2023, 169, 29–52. [Google Scholar] [CrossRef]
  12. An, L.; Yang, X.; Kim, D.-K.; Hu, J.; Wang, G.; Xu, Z. Speed harmonization for partially connected and automated traffic. IEEE Transactions on Intelligent Transportation Systems 2023. [CrossRef]
  13. Zhang, Y.; Wu, Z.; Zhang, Y.; Shang, Z.; Wang, P.; Zou, Q.; Zhang, X.; Hu, J. Human-lead-platooning cooperative adaptive cruise control. IEEE Transactions on Intelligent Transportation Systems 2022, 23, 18253–18272. [Google Scholar] [CrossRef]
  14. An, L.; Yang, X.; Hu, J. Modeling system dynamics of mixed traffic with partial connected and automated vehicles. IEEE Transactions on Intelligent Transportation Systems 2022, 23, 15755–15764. [Google Scholar] [CrossRef]
  15. Hu, J.; Zhang, Z.; Xiong, L.; Wang, H.; Wu, G. Cut through traffic to catch green light: Eco approach with overtaking capability. Transportation research part C: emerging technologies 2021, 123, 102927. [Google Scholar] [CrossRef]
  16. Wang, H.; Lai, J.; Zhang, X.; Zhou, Y.; Li, S.; Hu, J. Make space to change lane: A cooperative adaptive cruise control lane change controller. Transportation research part C: emerging technologies 2022, 143, 103847. [Google Scholar] [CrossRef]
  17. Ma, C.; Yu, C.; Yang, X. Trajectory planning for connected and automated vehicles at isolated signalized intersections under mixed traffic environment. Transportation research part C: emerging technologies 2021, 130, 103309. [Google Scholar] [CrossRef]
  18. Chen, X.; Lin, X.; He, F.; Li, M. , Modeling and control of automated vehicle access on dedicated bus rapid transit lanes. Transportation Research Part C: Emerging Technologies 2020, 120, 102795. [Google Scholar] [CrossRef]
  19. Zhang, L.; Qian, G.; Song, Z.; Wang, D. Deploying dedicated lanes for connected and autonomous buses in urban transportation networks. Transportmetrica A: Transport Science 2023, 19, 2005181. [Google Scholar] [CrossRef]
  20. Zhu, H. , Numerical study of urban traffic flow with dedicated bus lane and intermittent bus lane. Physica A: Statistical Mechanics and its Applications 2010, 389, 3134–3139. [Google Scholar] [CrossRef]
  21. Zhao, C.; Dong, H.; Wang, K.; Shao, J.; Zhao, C. Setting the Intermittent Bus Approach of Intersections: A Novel Lane Multiplexing-Based Method with an Intersection Signal Coordination Model. Applied Sciences 2023, 13, (18), 10098. [Google Scholar] [CrossRef]
  22. Chiabaut, N.; Xie, X.; Leclercq, L. Road capacity and travel times with bus lanes and intermittent priority activation: analytical investigations. Transportation research record 2012, 2315, 182–190. [Google Scholar] [CrossRef]
  23. Zhang, Z.; Lai, J.; Yang, X. In Dynamic spatial slice optimization for bus priority under the environment of mixed traffic, 2022 IEEE 25th International Conference on Intelligent Transportation Systems (ITSC), 2022; IEEE: 2022; pp 3023-3025.
  24. Wang, G.; Lai, J.; Lian, Z.; Zhang, Z. An Eco-Driving Strategy Considering Phase-Switch-Based Bus Lane Sharing. Sustainability 2023, 15, 7330. [Google Scholar] [CrossRef]
  25. Lai, J.; Hu, J.; Cui, L.; Chen, Z.; Yang, X. A generic simulation platform for cooperative adaptive cruise control under partially connected and automated environment. Transportation Research Part C: Emerging Technologies 2020, 121, 102874. [Google Scholar] [CrossRef]
  26. Hu, J.; Sun, S.; Lai, J.; Wang, S.; Chen, Z.; Liu, T. CACC simulation platform designed for urban scenes. IEEE Transactions on Intelligent Vehicles 2023. [CrossRef]
Preprints 95248 g001
Figure 1. Illustration of research scenario.
Figure 1. Illustration of research scenario.
Preprints 95248 g001
Preprints 95248 g002
Figure 2. Logic structure of the control strategy.
Figure 2. Logic structure of the control strategy.
Preprints 95248 g002
Preprints 95248 g003
Figure 3. Testbed.
Figure 3. Testbed.
Preprints 95248 g003
Preprints 95248 g004
Figure 4. Throughput comparison results under low unbalanced traffic demand levels.
Figure 4. Throughput comparison results under low unbalanced traffic demand levels.
Preprints 95248 g004
Preprints 95248 g005
Figure 5. Throughput comparison results under high unbalanced traffic demand levels.
Figure 5. Throughput comparison results under high unbalanced traffic demand levels.
Preprints 95248 g005
Preprints 95248 g006
Figure 6. Delay comparison results under low unbalanced traffic demand levels.
Figure 6. Delay comparison results under low unbalanced traffic demand levels.
Preprints 95248 g006
Preprints 95248 g007
Figure 7. Delay comparison results under high unbalanced traffic demand levels.
Figure 7. Delay comparison results under high unbalanced traffic demand levels.
Preprints 95248 g007
Preprints 95248 g008
Figure 8. Traffic system resilience comparison results.
Figure 8. Traffic system resilience comparison results.
Preprints 95248 g008
Table 1. Bus delay under various congestion levels and unbalanced demand levels (CPR=0.3).
Table 1. Bus delay under various congestion levels and unbalanced demand levels (CPR=0.3).
Preprints 95248 i001
Table 2. Bus delay under various congestion levels and unbalanced demand levels (CPR=0.5).
Table 2. Bus delay under various congestion levels and unbalanced demand levels (CPR=0.5).
Preprints 95248 i002
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated