Preprint
Article
A Hybrid Machine Learning and Optimization Algorithm for Enhanced User Comfort and Energy Efficiency in Smart Homes
Altmetrics
Downloads
238
Views
210
Comments
0
Submitted:
17 January 2024
Posted:
17 January 2024
You are already at the latest version
Alerts
Abstract
Researchers are always looking to find ways to use energy more efficiently while keeping people comfortable at home. They've tried different methods like fuzzy logic and genetic algorithms to do this. In this paper, we introduce a novel model that combines different techniques like data smoothing, optimization, machine learning, and control algorithms to reach this goal in smart homes. The proposed model is made up of three main parts: smoothing, optimization, and control. The smoothing part uses the Kalman filter to get rid of any unnecessary noise and make sure the data used to predict energy use is clean and smooth. The optimization part uses both genetic with firefly algorithms and artificial neural networks to minimize the gap between the actual environmental conditions and the conditions users find comfortable. It adjusts the comfort settings in real-time using machine learning. The control part uses Mamdani fuzzy logic to make sure energy is delivered in the best way possible to the systems that control temperature, lighting, etc., making the home comfortable and saving energy at the same time. Comparative analyses demonstrate the superiority of the proposed model over existing algorithms, including the Particle Swarm Optimization (PSO) algorithm. Additionally, the paper discusses the importance of adaptive controllers in addressing issues associated with incorrect PID controller selection and highlights the benefits of using the FA-GA in energy optimization and comfort improvement. Overall, the proposed model offers an effective solution for efficient energy consumption optimization and enhanced user comfort in diverse settings through the integration of advanced algorithms and optimization modules.
Keywords:
Subject: Computer Science and Mathematics - Artificial Intelligence and Machine Learning
1. Introduction
Smart homes have gained significant popularity since the late 1990s, offering occupants comfort and energy-efficient solutions [1]. These technologies allow homes to learn from their environment and adjust settings to meet occupants’ preferences while minimizing operational costs. The adoption of smart home technologies not only enhances occupant comfort and energy efficiency but also supports independent living for the elderly, people with dementia, and individuals with intellectual disabilities. Furthermore, smart homes play a crucial role in patient homecare and monitoring [2,3].
The driving forces behind smart homes are communication technology, especially the Internet of Things (IoT), and intelligent algorithms that provide homes with the necessary intelligence. This study focuses on intelligent algorithms that enable smart homes to maximize occupant comfort while minimizing energy consumption. These objectives are interconnected yet contradictory. For instance, thermal comfort is essential for overall comfort, with air conditioning being used in tropical countries to lower indoor temperatures, while heating systems are crucial in temperate climates during winter. However, the usage of heating, ventilation, and air-conditioning (HVAC) systems contributes significantly to energy consumption in buildings [4,5].
To address these contradictory challenges, optimizing the settings of electrical appliances can be employed. Occupant comfort is influenced by various factors, including temperature, indoor air quality (IAQ), and illumination. This study focuses on maximizing the comfort index by considering these parameters, as they have a significant impact on the mental and physical health of occupants [6], ultimately affecting their overall comfort. Maintaining optimal indoor temperature is vital, as extreme temperatures can have adverse effects on occupants’ health. Similarly, ensuring healthy IAQ is essential to prevent sick building syndrome and maintain occupants’ productivity [7]. Additionally, appropriate indoor illumination plays a crucial role in regulating the human circadian clock, positively impacting occupants’ quality of life and well-being [8].
Controlling these parameters is possible through the use of air conditioning systems, air ventilators, and lighting. However, these systems consume substantial amounts of energy. Hence, this study also aims to minimize energy usage by these appliances, achieving energy efficiency in smart homes [9]. In addition to these efforts, the integration of digital twin technology provides a comprehensive approach to optimize user comfort and energy efficiency. A digital twin [10,11] consists of multiple modules, including a physical layout, computer models, data analysis, and communication platforms. These components are coordinated and operate in unison to study, oversee, and enhance the overall performance of the system. Implementing a digital twin necessitates the creation of innovative methods, processes, and software to enable efficient communication and collaboration among the different modules. This paper introduces a detailed model that combines different methods to make sure smart homes are as comfortable as possible while using energy efficiently. The model has three main parts: smoothing, optimization, and control. The smoothing part makes sure the data we use to predict how much energy we’ll use is clear and accurate. The optimization part uses machine learning, a type of artificial intelligence, to change settings in the home to keep it comfortable while using less energy. The control part makes sure that energy is delivered in the most efficient way to make people in the home comfortable.
After comparing our model to others already available, we have determined that our model is more superior. We also found that using flexible control systems and improved methods to optimize energy use are really important in making homes both comfortable and energy efficient.
In the realm of smart home technology [12], the integration of "digital twin" and fuzzy logic controller [13] is becoming increasingly transformative. At its core, a digital twin offers a dynamic digital blueprint of a home’s physical environment, driven by sensor-collected data on key parameters like temperature, air quality, and lighting. This real-time data serves as the foundation upon which the fuzzy logic controller operates [14]. Unlike traditional binary logic systems, a fuzzy logic controller excels in making decisions based on imprecise or "fuzzy" input values, thereby enabling more nuanced adjustments. For instance, if the digital twin detects a slightly elevated room temperature combined with increased humidity, the fuzzy logic controller might determine an optimal thermostat setting that accounts for both comfort and energy efficiency. Similarly, in assessing air quality, the controller could make incremental ventilation adjustments, ensuring a balanced and healthy atmosphere. Moreover, when analyzing lighting conditions, it doesn’t just switch lights on or off but might modulate light intensity based on the time of day, user preferences, and available natural light. In combining the predictive power of a digital twin with the nuanced decision-making of a fuzzy logic controller, smart homes are better equipped to achieve a seamless blend of user comfort and energy conservation.
In conclusion, this study aims to leverage digital twin technology and advanced algorithms to achieve efficient energy consumption optimization and enhanced user comfort in smart homes. By integrating intelligent algorithms, optimization modules, and digital twin capabilities, this research contributes to the advancement of smart home technologies, benefiting occupants, energy efficiency, and overall quality of life. In our work, we have also introduced a model that utilizes smoothing algorithms, optimization algorithms, machine learning algorithms, and control algorithms.
The primary goals of the proposed work are as follows:
- To enhance the comfort level of users in smart homes
- To reduce energy consumption in smart homes with improved comfort
- The Idea of Digital Twin
- To identify optimal user-defined parameters through the utilization of an advanced machine learning algorithm
2. Related Work
Many people and companies are working hard to find ways to use less energy while still keeping homes comfortable. Saving energy is important because it costs a lot, and we want to take care of our planet. There is a need for tools and methods that can help us use energy wisely without making life uncomfortable. One exciting development is the use of advanced technologies and simulations. These tools can be used to test out different ways to save energy and keep comfort levels high. This could be the key to solving the challenge of using less energy while keeping our homes comfortable. These advanced technologies have demonstrated considerable capabilities in smart home and other sectors.
In [15], the evolutionary accretive comfort algorithm (EACA) is introduced. EACA, based on a genetic algorithm (GA), aims to maximize user comfort while adhering to predefined cost constraints. Comfort optimization relies on the usage of appliances, prioritized according to consumer preferences. The proposed EACA can achieve optimal comfort within specified cost limits. It’s important to note that higher comfort levels can be attained by allocating more resources, thus increasing the cost.
In a related study, [16] employs the non-dominated sorting genetic algorithm II (NSGA-II) for optimizing both thermal comfort and energy usage. NSGA-II seeks solutions forming a Pareto front, optimizing both objectives simultaneously. Thermal comfort is evaluated based on Fanger’s predicted mean vote (PMV) and responses obtained from surveys, while energy consumption is quantified using annual gas and electricity consumption data. This technique effectively maintains thermal comfort levels while reducing overall energy consumption. A similar approach is found in [17], where NSGA-II is utilized to minimize energy usage while ensuring thermal comfort. This is achieved by optimizing factors such as humidity, airspeed, temperature, and the percentage of dissatisfied individuals in a given venue.
In [18], a Genetic Algorithm (GA) is employed to determine optimal values for temperature, Indoor Air Quality (IAQ), and illumination that contribute to user comfort. These optimal values, along with environmental data, are then input into a fuzzy controller to minimize the required power consumption. In contrast, [19] treats user comfort maximization and energy usage minimization as a single objective problem by using a weighted penalty function. The parameters considered for determining both comfort and energy usage include indoor temperature, illumination, and IAQ. The results indicate that GA is more effective at reducing energy consumption compared to Particle Swarm Optimization (PSO), while PSO excels in maximizing the comfort index.
Meanwhile, in [20,21], GA is hybridized with the Firefly Algorithm (FA) to optimize temperature, IAQ, and illumination. This combination of algorithms addresses the issue of imbalanced exploration and exploitation in FA, resulting in improved performance compared to the original FA and GA when solving the same problem. Following optimization, the parameters are input into a fuzzy controller to minimize energy consumption. Several other works, such as [22], utilize similar approaches to [18,20,21] but employ different swarm intelligence algorithms. For instance, [23] employs the Artificial Bees Algorithm (ABC) and uses ABC with a knowledge base, while [24] utilizes the original Bat Algorithm (BA). These algorithms are applied to optimize parameters related to user comfort and energy efficiency in a similar manner as described in the aforementioned references.
In [25], a chaotic Bat Algorithm (BA) is employed for fine-tuning the parameters of residential HVAC controllers. This optimization aims to achieve the dual objectives of optimizing energy usage and enhancing thermal comfort. Additionally, the chaotic BA is applied to the task of tuning the coal feed rate in an industrial precalciner temperature control loop, with the goal of optimizing energy usage in this industrial context. [26] focuses on the optimization of illumination comfort levels and power usage for lighting systems. The authors introduce a novel illumination comfort metric called the Illuminance Uniformity Deviation Index (IUDI). They utilize a multi-objective Particle Swarm Optimization (PSO) approach to simultaneously optimize both illumination comfort and power usage. The IUDI considers factors such as illuminance uniformity and daylight contribution factor for indoor illumination when calculating the comfort level, contributing to a more comprehensive optimization of lighting conditions.
In [27], an Internet of Things (IoT) system designed for personalized comfort management is introduced. In their research, they focus on representing comfort using ontologies, drawing from classes derived from the DogOnt ontology [28] and the Semantic Sensor Network (SSN) ontology [29]. A similar approach is employed in [30], where an indoor environmental comfort system utilizes a domain ontology to formalize concepts related to sensors and actuators. While this work does not explicitly model comfort metrics, it does involve the acquisition of contextual data, which is subsequently processed using semantic rules. The topic of air quality is explored in [31], which proposes an ontology that formalizes certain aspects of the ISO 7730:2005 standard. BOnSAI [32], an ontology developed to facilitate the integration of Ambient Intelligence (AmI) in smart buildings, also includes some comfort-related concepts. Although primarily dedicated to describing device functionalities, services, and hardware, BOnSAI encompasses contextual elements representing comfort and users. Similarly, ThinkHome [33] presents a semantic model aimed at encompassing the entire Smart Home (SH) ecosystem, thus incorporating concepts related to comfort.
In [34], a semantic model is introduced for representing thermal comfort within a semantic framework designed for automated modeling of cyber-physical systems. In [35], the authors address the modeling of indoor comfort metrics by reusing reference models, allowing for the customization of comfort in cruise cabins. In this context, the ontology serves as a foundational framework for an IoT system aimed at monitoring and enhancing the cruise experience.
Many people and companies are working hard to find ways to use less energy while still keeping homes comfortable. Saving energy is important because it costs a lot, and we want to take care of our planet. There is a need for tools and methods that can help us use energy wisely without making life uncomfortable. One exciting development is the use of something called a Digital Twin (DT). It’s like a virtual copy of a home that can be used to test out different ways to save energy and keep comfort levels high. This could be the key to solving the challenge of using less energy while keeping our homes comfortable.
The DT has demonstrated considerable capabilities in smart home and other sectors. This section provides a review of relevant studies, concisely outlined in Table I, with detailed discussions in the subsequent subsections.
3. Problem Formulation
Consider the current sensor measurements for temperature, illumination, and air quality represented as . Occupants define their comfort range for each parameter. These ranges are specified by user set points:
where:
The assumption is that the maximum value in the range signifies the most preferred setting, while the minimum represents the least acceptable value. Ideally, if energy costs were negligible, users would prefer settings at their maximum values. However, due to high energy costs, a balance between energy consumption and user comfort becomes necessary. We define the range length for each parameter as , , and .
Assume the energy consumption per unit change in each parameter is given by for temperature, illumination, and air quality, respectively. In an ideal situation without energy constraints, parameters would be set as per user preference. However, practical scenarios require a compromise between energy efficiency and comfort. Table 1 summarizes the notations used in this formulation. Note that this formulation applies to heating scenarios (winter). For cooling scenarios (summer), the equations will be slightly modified.
Optimal parameter values are denoted as , which can lie within the user-specified range. The total energy required for maintaining these optimal settings is given by:
We can also determine the potential minimum and maximum energy consumption:
Our goal is to maximize user comfort and energy savings. This can be abstractly represented as:
where is the gain in user comfort, is the gain in energy savings, and and are the respective weights, satisfying:
User comfort gain is formulated as:
where defines the preference for each parameter. The gain in energy savings is inversely proportional to energy consumption:
Using these formulations, our optimization function becomes:
Constraints are defined as:
4. Proposed Methodology
The proposed model comprises three main modules: the smoothing module, optimization module, and control module. The smoothing module utilizes various algorithms (e.g., Kalman filter [36], alpha-beta filter [37,38,39]) to eliminate sensor data noise and handle missing values. In the optimization module, different algorithms such as the firefly algorithm, and genetic algorithm, are employed. This module also incorporates the comfort index formula, which is fine-tuned using machine learning algorithms to adapt to user-defined factors, thereby enhancing system dynamism and autonomy. The control module applies several control algorithms (e.g., Mamdani FIS [13], Sugeno FIS, PID) to provide the desired energy to actuators through the agent. Figure 1 illustrates a conceptual structure diagram of the proposed model.
The comfort index is inversely related to the error change, which is determined by the environmental parameters and machine learning set parameters. Power consumption is affected by the difference in error, and a smaller error difference leads to a higher comfort index. Consequently, the problem becomes a multifunctional optimization challenge that aims to minimize power consumption while maximizing the comfort index.
After calculating the comfort index, the next step involves controlling the state of other actuators. Fuzzy controllers are employed to determine the error between environmental boundaries and optimized parameters. The regulator’s output tells us how much power is needed to control things in the house like cooling/heating, lighting, and ventilation. This power is then given to those systems based on what the regulator says is needed. The fuzzy controller uses the best values from special methods we use to get the most efficient results, and it also considers the limits of the environment, like temperature, lighting, and air quality, to decide its output. What the fuzzy controller decides depends on the difference between the actual conditions in the environment and the best values we got from our special methods for things like temperature, lighting, and air quality.
The optimization algorithms aim to minimize the difference between the values set by smart home users and the predicted values. This difference would be significant without applying optimization algorithms, requiring higher output values and increased power consumption. By employing optimization techniques, the difference is reduced, leading to more efficient energy usage. In the proposed work, we will utilize the learning to optimization algorithms module, which is further divided into the learning and optimization modules. The learning module employs artificial neural networks (ANN) [10] to make the user-set parameters dynamic within the optimization algorithms module. The primary goal of the optimization technique is to minimize the gap between the user’s preferred parameters and the parameters derived from the surrounding environment.
The optimization module aims to increase the comfort index and reduce power usage. One way to decrease power consumption is by minimizing the gap between user preferences and environmental parameters. Achieving closer alignment between these parameters ultimately leads to lower power consumption. The learning-to-optimization module provides the optimized parameters, while the learning-to-fuzzy logic module takes these optimized parameter values as inputs and determines the energy required for the actuators. The coordinator’s agent receives the output from the fuzzy controller as inputs and adjusts the actuators accordingly.
4.1. Kalman Filter Algorithm
The Kalman Filter is known for its effectiveness and ability to work well without needing a lot of historical data. It uses information from the last known state to make smart predictions about a system’s current state. One key part of this model is the Kalman gain (K), which helps balance the system’s own predictions with data from sensors.
Noise from the environment is a common problem that can make sensor readings less accurate. In this study, we’re looking at a temperature sensor, denoted as that’s affected by this kind of noise. The Kalman filter uses a special model to make an educated guess about the system’s state (like an estimated temperature). It then compares this guess with the actual data from the sensor to come up with a more accurate temperature reading for the next moment in time .
An initial step involves the calculation of the temperature predicted, , derived from the predecessor value estimated through:
Here, represents the predicted temperature internally, while X and Y are the state transition and control matrices, respectively. is the prior temperature reading, and is the control vector.
Uncertainty in this internal prediction is quantified by a covariance factor, updated as:
Where X and are the state transition matrix and its transpose, is the preceding covariance value, and Q denotes the estimated process error.
Subsequent to this, the Kalman gain, K, undergoes an update via:
Here, the observation matrix and its transpose are signified by H and , with R denoting the estimated error measurement.
Assuming the sensor’s reading temperature at time t is , the refined estimated temperature is obtained through:
Conclusively, the covariance is updated for subsequent iterations via:
This explanation highlights how well the Kalman Filter can reduce noise, ensuring accurate measurements. This is especially important in settings where sensor readings can be easily distorted or affected by surrounding conditions.
4.2. Optimization Framework
The optimization framework comprises two main modules: the FA-GA module and the artificial neural network (ANN) segment. Initially, the ANN is trained utilizing historical user data. It accepts smooth parameters and outputs user-defined settings. The FA-GA module then evaluates the discrepancy between the ANN’s output and these smooth parameters. These derived parameters play a pivotal role in the comfort index formula within the FA-GA algorithm, as depicted in the explained diagram.
Referring to the diagram, the database signifies our dataset encompassing three key metrics: air quality, temperature, and illumination. Initially, data acquisition populates this database, capturing values for the aforementioned parameters. This data may arise from sensor readings or other external data sources. Following data collection, it is archived in the database, acting as foundational input for ensuing stages.
The equation for the comfort index is illustrated as:
Within this equation, the factors , and denote user preferences. The comfort index’s span lies between 0 and 1, where 0 signifies no satisfaction, and 1 denotes complete contentment. ANN’s influence on the comfort index formula is encapsulated by , , and settings determined by the ANN. The user preference variables are symbolized as , and , and their cumulative value is unity. The comfort index components
Where , , and represent the error discrepancies between environmental temperature and ANN-set temperature, environmental illumination and ANN-set illumination, and environmental air quality with ANN-set air quality respectively. This formula can be generalized as:
In this generalized equation, the terms capture the deviation between machine learning algorithm-defined parameters and smooth parameters, while signifies the machine learning algorithm’s settings. The components highlight user-defined preferences. Thus, the model’s adaptability is evident, as it can seamlessly incorporate additional parameters in future iterations. Reinforcing the modular nature of the optimization framework, it bifurcates into the FA-GA and ANN modules. Figure shows the complete proposed schematic diagram.
4.2.1. Integration of Firefly Algorithm (FA) and Genetic Algorithm (GA)
In the complex world of energy efficiency, the FA-GA Module stands as a sophisticated model aimed at both reducing energy consumption and enhancing comfort for residents, a dual objective that forms the core of our proposed power management system. The integration of two robust artificial intelligence (AI) algorithms, Firefly Algorithm (FA) and Genetic Algorithm (GA), named FA-GA, is central to addressing this dual-faceted optimization challenge.
The individual applications of FA and GA have their limitations, especially in identifying the optimal parameters for complex problems. The combination of FA and GA, however, accelerates and refines the optimization process, ensuring the identification of the most efficient solution without complications.
FA employs multiple input parameters, including the differences in air quality errors, illumination, and temperature, to create an initial solution in the search space. Each firefly is associated with a unique set of comfort indices, calculated from these parameters. The mathematical foundation of FA is encapsulated in equations (24) to (28), each reflecting a dimension of light intensity and attraction amongst fireflies.
Here, represents the initial light intensity at the source, and the intensity decreases with the square of the distance d from the source.
It explains how light intensity at distance d is influenced by the medium’s absorption coefficient .
This equation establishes the attraction A between fireflies in relation to their light intensity, with being the initial attractiveness at zero distance.
It calculates the Euclidean distance between two fireflies, instrumental in determining their attraction.
Here, the position of each firefly is updated considering the attraction and a random component, with denoting randomization and representing a random number from a Gaussian distribution.
As FA is confined by a specific number of iterations, GA takes over to continue the optimization process. The genes of GA are crafted from the error differences of all parametric values, transforming FA’s fireflies into GA’s chromosomes.
4.2.2. Genetic Algorithm Process
The GA begins with the initial population created by FA and proceeds through a series of steps to refine the solution:
- Compute the comfort user’s fitness function.
- Apply ranked-based selection.
- Execute one-point crossover on selected individuals.
- Generate offsprings post-crossover.
- Initiate mutation procedures.
- Repeat steps 1-5 for a specified number of iterations.
- Select the optimal-sized chromosomes upon reaching the termination criteria.
These optimal chromosomes epitomize the pinnacle of the comfort index value.
GA is renowned for its capacity to explore extensive solution spaces and manage intricate, non-linear problems, attributes that are essential in complex optimization contexts. Its resilience amidst noise and uncertainties and adaptability for bespoke problem requirements underscores its widespread applicative significance.
4.3. Artificial Neural Network
Artificial Neural Networks (ANNs) are computational models that emulate the human brain’s neural structure, functioning as universal function approximators. They typically consist of three primary layers: an input layer, several hidden layers, and an output layer. Each neuron or node within a layer connects to every neuron in the following layer, with the connection strength governed by adjustable parameters known as weight vectors. During training, the network continuously applies an optimization technique, aiming to reduce prediction errors by fine-tuning these parameters, thus enabling precise mapping of new input data to the appropriate output. These networks incorporate non-linear activation functions like Sigmoid, Tanh, or ReLU to reflect data’s non-linear characteristics, allowing ANNs to handle complex functions effectively and generalize well to diverse datasets. In this particular study, the Adaptive Moment Estimation (ADAM) algorithm was employed for optimizing the cost function, with ReLU selected as the activation function. The complete structure of ANN is shown in Figure 3.
Consider a model with H input neurons and N neurons in a hidden layer. The nth neuron in the hidden layer is determined by the weighted sum of the input layer neurons and a bias value. In a three-layer ANN, the values for the hidden layer neuron and output neuron are calculated using the following equations:
where is the input value of the jth neuron in the hidden layer, is the weight between the jth neuron in the hidden layer and the ith neuron in the input layer, is the ith input variable of the input layer, and is the bias term of the jth neuron in the hidden layer. Different activation functions are employed to transform the output of the hidden layer neurons.
where is the output of the jth neuron in the hidden layer, and f is the activation function, such as Sigmoid, Tanh, ReLU, etc.
where is the output neuron, derived by taking the weighted sum of hidden layer neurons () and the bias term of the output neuron. Based on a trial-and-error method, 128 hidden nodes with one hidden layer were employed in the development of ANN models.
4.4. Fuzzy Logic Controller
In the proposed research, a fuzzy controller has been employed to regulate power consumption, a common technique used in various applications. Fuzzy logic, a versatile and effective approach, has garnered significant attention from researchers across different fields. In this study, the Mamdani fuzzy logic method, known for its simplicity and efficacy, has been utilized. The Mamdani fuzzy logic model comprises three core components: fuzzification, rule inference, and defuzzification.
The fuzzification module converts crisp input values into fuzzy inputs by applying input membership functions. The rule inference module generates rules using input and output membership functions, while the defuzzification module employs the centroid method to convert fuzzy outputs into crisp values. Table 1 shows the fuzzzy rules for power optimization, environmental quality and lighting management.
In this investigation, the triangular membership function has been adopted for both input and output membership functions. The mathematical representation of the triangular membership function is provided in Equation (16).
In the realm of fuzzy logic control systems, three distinct controllers have been accurately designed, each designed for a specific application, and ruled by a set of membership functions. These functions play a pivotal role in mapping the input variables to appropriate output responses, enabling the controllers to handle complex, detailed scenarios.The operational process of Mamdani fuzzy logic is depicted in Figure 4. Table 2 shows the temperature fuzzy controller with 14 different combination of fuzzy rules.
The first controller, dedicated to power optimization, operates with the input variable labeled “Var_1” and an output variable known as “RPTemp.” This controller is specifically constructed to manage and optimize power usage efficiently. In its collection, it features fourteen unique membership functions for “Var_1,” each thoroughly labeled from Var_1_1 to Var_1_14. These functions allow the controller to interpret various levels of power requirements or conditions and correspondingly adjust the output, which is also finely segmented into fourteen membership functions, labeled RPTemp_1 through RPTemp_14. The roughness of these functions facilitates a highly detailed approach to power management, ensuring that the controller can respond with great precision to different power-related scenarios.
The second controller is at the controls of lighting management. This controller, encompassing the input variable “Var_2” and the output variable “RPILL,” is designed with a focus on regulating and optimizing lighting conditions. It employs an expanded set of twenty membership functions for “Var_2,” ranging from Var_2_1 to Var_2_20, offering a broad spectrum of input interpretation capabilities.
Similarly, the output variable “RPILL” is equipped with an equally diverse set of twenty membership functions. This expansive range allows the lighting management controller to adjust lighting levels with remarkable accuracy and responsiveness, offering a wide array of lighting conditions and preferences. Table 3 shows the Illumination fuzzy controller with 20 different combination of fuzzy rules.
Lastly, the third controller is centered on environmental quality management. It utilizes “Var_3” as its input variable and “RPAQ” as the output variable. This controller is integral to monitoring and enhancing the quality of the environment. It is equipped with eighteen membership functions for “Var_3,” labeled from Var_3_1 to Var_3_18, which enable it to interpret various environmental factors effectively. The output variable “RPAQ” mirrors this with its own set of eighteen membership functions, from RPAQ_1 to RPAQ_18. The design of these functions allows the controller to make informed decisions about environmental adjustments, striving to maintain or improve the overall environmental quality.
Each of these controllers, with their respective sets of rules and membership functions, exemplifies the versatility and adaptability of fuzzy logic systems. By finely tuning the input and output variables through these functions, the controllers can handle complex, real-world scenarios with a degree of sophistication and accuracy. For a comprehensive understanding of how these controllers operate and interact with their respective variables, a detailed model is presented in Table 1. This table encapsulates the complex web of rules that govern the decision-making processes within these fuzzy logic systems. Table 4 shows the air quality fuzzy controller with 18 different combination of fuzzy rules.
4.5. Coordinator Agent
The Coordinator Agent acts as a critical component in the smart home ecosystem, tasked with processing the outputs from the fuzzy logic controller to regulate environmental conditions. This includes managing the heating or cooling systems, lighting intensity, and CO2 levels to optimize occupant comfort and energy efficiency.
At the outset, the agent assesses two essential metrics: the remaining battery capacity of the home’s energy storage system and the estimated energy consumption based on current usage patterns. Should the projected energy consumption exceed what the stored battery capacity can deliver, the Coordinator Agent dynamically adjusts the power supply to the home’s actuators, engaging in an optimization loop to ensure energy is utilized effectively.
This process is carried out iteratively, sustaining the optimization as long as the energy storage can support the home’s operational demands.
Conversely, if the energy forecast indicates that the battery reserve is inadequate for anticipated needs, the optimization routine is promptly suspended to prevent energy depletion. Figure 6 illustrates a comprehensive structural diagram of the Coordinator Agent’s role and operational logic within the smart home infrastructure. Figure 5 shows the both provide power and required power for coordinator agent.
4.6. Performance Evaluation
Various performance metrics are employed to assess the effectiveness of prediction algorithms. In this proposed study, performance indices such as Mean Absolute Error (MAE), Root Mean Square Error (RMSE), and Mean Absolute Percentage Error (MAPE) are utilized for comparing actual values with predicted values. The distribution of error minimization is quantified through Mean Squared Error (MSE). MAPE assesses the difference as a percentage of the target, while RMSE measures the error between the estimate and the target. The performance metrics, RMSE, MAE, and MAPE, can be expressed through the following equations:
Here, N denotes the total number of values, T represents the target value, and P signifies the estimated value. These performance metrics provide a comprehensive evaluation of the prediction algorithm by quantifying the accuracy and reliability of the predicted values in comparison to the actual values.
5. Experimental Results and Discussion
The proposed model is implemented on an 11th Gen Intel(R) Core(TM) i7-11700KF @ 3.60GHz, utilizing Python 3.12.0. Table 5 provides details of the system configuration for implementation and simulation analysis.
The data utilized in this study is sourced from reference [19], encompassing three factors: temperature, illumination, and air quality. For the temperature fuzzy logic controller, seven input and output rules are specified for input variable and output variable , respectively. Similarly, fifteen input and output rules are defined for the illumination fuzzy logic controller’s input variable and output variable . In the air quality fuzzy logic controller, fifteen input and output rules are specified for input variable and output variable .
In the proposed approach, a Kalman filter is employed to smooth sensor reading data and eliminate outliers from input sensor data. Figure 6 illustrates the actual temperature, sensor reading temperature, and predicted temperature. Likewise, Figure 7 provides a detailed depiction of actual illumination, sensor illumination, and air quality illumination. Figure 8 presents actual air quality, sensed air quality, and predicted air quality values.
Figure 9 illustrates the comfort index levels in scenarios where both optimization techniques are applied and removed. it shows the total comfort with and without optimization. The depicted values are significantly removed from the optimal range, indicating a lower comfort index under typical conditions. On the other hand, the figure also showcases the comfort index levels when the proposed FA-GA optimization approaches are employed. Here, the majority of the values incline towards 1, denoting a higher comfort index. This comparison strongly suggests that the comfort index is considerably improved when the proposed optimization methods are utilized.
Figure 9 presents a comparison of how much electricity is used in two scenarios: one where an optimization scheme is applied and the other where no such scheme is used. The difference is noticeable; when the optimization scheme is in place, there’s a reduction in electricity usage compared to the scenario without it. This optimization scheme is what we are referring to as our proposed approach. It clearly demonstrates that adopting this scheme leads to more efficient energy use. Figure 10 shows the power consumption with and without optimization scheme.
The radar chart depicted in Figure 11 compares two datasets: `Power Consumption with Optimization,’ represented by a green line, and `Power Consumption without Optimization,’ depicted by a red line. The chart features multiple axes extending from a central point, each representing different conditions or categories that are crucial for illustrating variations in power consumption. When the green line is closer to the center, it indicates that optimization has effectively reduced power consumption. In contrast, when the red line is farther from the center, indicating higher power consumption, it suggests that optimization was less effective or did not lead to a reduction in power consumption.
5.1. Analysis of different Models
The comparative analysis conducted in this study critically evaluates a newly developed FA-GA method against existing, well-established methods. This evaluation, detailed in Table 6 and Figure 12, emphasizes both individual energy parameters and the overall consumption.
The results of this analysis clearly demonstrate that the new method offers enhanced efficiency in terms of energy usage compared to other known approaches. if we can see the detail values as defined in Table 6, we observe that the energy consumption for each algorithm is categorized into several key areas: Temperature, Illumination, and Air Quality Power Consumption, in addition to the Total Power Consumption. It’s noteworthy that while the new proposed approach records a slightly higher Temperature Power Consumption (632.5) than GA (440) and PSO (522.63), it shows remarkable efficiency in other areas. Particularly, in Illumination Power Consumption, the proposed method uses only 924.74 units of power, which is significantly lower compared to the 1475.16 and 1531.01 units consumed by GA and PSO, respectively. Similarly, for Air Quality Power Consumption, the new approach also demonstrates superior efficiency, utilizing just 420.65 units compared to GA’s 651.78 and PSO’s 694.54 units.
However, the most remarkable aspect of the analysis is the total energy consumption. The proposed approach has an overall consumption of only 1978.89 units, which is considerably lower than GA’s 2565.94 and PSO’s 2747.18 units. This comprehensive metric is critical as it represents the overall energy footprint of the algorithm. The significant reduction in total energy consumption with the new method, despite its higher usage in temperature adjustment, emphasizes its effectiveness in minimizing the overall energy footprint. This efficiency makes the proposed approach a more favorable option in scenarios where reducing energy consumption is vital.
Table 7 and Figure 13 presents a comparative analysis of power consumption for different environmental parameters with and without the application of optimization techniques. The parameters evaluated include temperature, illumination, and air quality. For each parameter, the power consumption is significantly lower when optimization is applied: 501.5 vs. 1067.1 units for temperature, 703.4 vs. 927.3 units for illumination, and 418.6 vs. 497.2 units for air quality. The total power consumption shows a marked decrease from 2491.7 units without optimization to 1649.97 units with optimization, highlighting the impact and benefit of employing energy-saving measures.
The Table 8 and Figure 14 presents a comprehensive performance evaluation of an optimization algorithm applied to three distinct environmental parameters: Temperature, Illumination, and Air Quality.
The evaluation is based on two key performance measures: Mean Absolute Error (MAE) and Root Mean Square Error (RMSE). For Temperature, the MAE is 2.0389, indicating relatively accurate predictions. Similarly, RMSE measures the algorithm’s predictive accuracy by calculating the root mean square of the prediction errors. For Illumination and Air Quality, the RMSE values are 38.5706 and 41.1463, respectively, suggesting slightly larger prediction errors compared to Temperature.
6. Conclusion
In conclusion, this paper presents a comprehensive and innovative approach to improving energy efficiency while maintaining user comfort in smart homes. The proposed model, consisting of data smoothing, optimization, and control components, leverages advanced techniques such as Kalman filtering, genetic and firefly algorithms, artificial neural networks, and Mamdani fuzzy logic. Through extensive comparative analyses, it is evident that this model outperforms existing algorithms, including the Particle Swarm Optimization (PSO) algorithm, and addresses issues related to incorrect PID controller selection. Furthermore, the integration of the FA-GA algorithm for energy optimization and comfort enhancement highlights the effectiveness of this approach in diverse settings. In essence, this paper offers a promising solution for optimizing energy consumption and elevating user comfort by utilizing cutting-edge algorithms and optimization modules in smart homes. This research covers the way for more sustainable and enjoyable living environments while minimizing energy wastage.
Acknowledgments
This study was partly supported by the Institute of Information & communications Technology Planning & Evaluation (IITP) grant funded by the Korea government (MSIT) (No. RS-2022-00155857, Artificial Intelligence Convergence Innovation Human Resources Development (Chungnam National University)) and “Regional Innovation Strategy (RIS)” through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (MOE) (2021RIS-004).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Choi, H. W., Shin, D. W., Yang, J., Lee, S., Figueiredo, C., Sinopoli, S., ... & Kim, J. M. Smart textile lighting/display system with multifunctional fibre devices for large scale smart home and IoT applications. Nature communications, 2022; 13, 814.
- Bhowmik, T., Mojumder, R., Ghosh, D., & Banerjee, I. (2022, January). IoT based smart home-health monitoring system using dempster-shafer evidence theory for pandemic situation. In Proceedings of the 23rd International Conference on Distributed Computing and Networking (pp. 260-265).
- Dorronzoro-Zubiete, E., Rivera-Romero, O., Giunti, G., & Sevillano, J. L. (2022). Smart home applications for cognitive health of older adults. In Smart Home Technologies and Services for Geriatric Rehabilitation (pp. 123-140). Academic Press.
- Babangida, L., Perumal, T., Mustapha, N., & Yaakob, R. Internet of things (IoT) based activity recognition strategies in smart homes: A review. In IEEE Sensors Journal; 2022; Volume 22, pp. 8327–8336.
- Yildiz, O. F., Yilmaz, M., & Celik, A. Reduction of energy consumption and CO2 emissions of HVAC system in airport terminal buildings. Building and Environment 2022, 208, 108632.
- Bangwal, D., Suyal, J., & Kumar, R. Hotel building design, occupants’ health and performance in response to COVID 19. International journal of hospitality management. 2022, 103, 103212.
- Mahmoud, N. S. A., El Samanoudy, G., & Jung, C. Simulating the natural lighting for a physical and mental Well-being in residential building in Dubai, UAE. 2023, 14, 101810.
- Karimi, H., Adibhesami, M. A., Bazazzadeh, H., & Movafagh, S. Green Buildings: Human-Centered and Energy Efficiency Optimization Strategies. Energies 2023, 16, 3681.
- Alzoubi, A. Machine learning for intelligent energy consumption in smart homes. International Journal of Computations, Information and Manufacturing (IJCIM) 2022, 2.
- Tao, F., Xiao, B., Qi, Q., Cheng, J., & Ji, P. Digital twin modeling. Journal of Manufacturing Systems 2022, 64, 372–389.
- Yu, W., Patros, P., Young, B., Klinac, E., & Walmsley, T. G. Energy digital twin technology for industrial energy management: Classification, challenges and future. Renewable and Sustainable Energy Reviews 2022, 161, 112407.
- Botín-Sanabria, D. M., Mihaita, A. S., Peimbert-García, R. E., Ramírez-Moreno, M. A., Ramírez-Mendoza, R. A., & Lozoya-Santos, J. D. J. Digital twin technology challenges and applications: A comprehensive review. Remote Sensing 2022, 14, 1335.
- Fayaz, M., & Kim, D. Energy consumption optimization and user comfort management in residential buildings using a bat algorithm and fuzzy logic. Energies 2018, 11(1), 161.
- Fayaz, M., Shah, H., Aseere, A. M., Mashwani, W. K., & Shah, A. S. A framework for prediction of household energy consumption using feed forward back propagation neural network. Technologies 2019, 7(2), 30.
- Khan, A., Javaid, N., & Khan, M. I. Time and device based priority induced comfort management in smart home within the consumer budget limitation. Sustainable cities and society 2018, 41, 538–555.
- Ghaderian, M. Ghaderian, M., & Veysi, F. Multi-objective optimization of energy efficiency and thermal comfort in an existing office building using NSGA-II with fitness approximation: A case study. Journal of Building Engineering 2021, 41, 102440. [Google Scholar]
- Taylor, M., Brown, N. C., & Rim, D. Optimizing thermal comfort and energy use for learning environments. Energy and Buildings 2021, 248, 111181.
- Ali, S., & Kim, D. H. Optimized power control methodology using genetic algorithm. Wireless personal communications 2015, 83, 493–505.
- Ullah, I., & Kim, D. An improved optimization function for maximizing user comfort with minimum energy consumption in smart homes. Energies 2017, 10(11), 1818.
- Wahid, F. Wahid, F., Ismail, L. H., Ghazali, R., & Aamir, M. An Efficient Artificial Intelligence Hybrid Approach for Energy Management in Intelligent Buildings. KSII Transactions on Internet & Information Systems 2019, 13. [Google Scholar]
- Selvaraj, R. Selvaraj, R., Kuthadi, V. M., & Baskar, S. Smart building energy management and monitoring system based on artificial intelligence in smart city. Sustainable Energy Technologies and Assessments 2023, 56, 103090. [Google Scholar]
- erma, A., Prakash, S., & Kumar, A. A comparative analysis of data-driven based optimization models for energy-efficient buildings. IETE Journal of Research 2023, 69, 796–812.
- Kaya, E., Gorkemli, B., Akay, B., & Karaboga, D. A review on the studies employing artificial bee colony algorithm to solve combinatorial optimization problems. Engineering Applications of Artificial Intelligence 2022, 115, 105311.
- Shah, A. S., Nasir, H., Fayaz, M., Lajis, A., Ullah, I., & Shah, A. Dynamic user preference parameters selection and energy consumption optimization for smart homes using deep extreme learning machine and bat algorithm. IEEE Access 2020, 8, 204744–204762.
- Divyesh, V. R., Sahu, C., Kirubakaran, V., Radhakrishnan, T. K., & Guruprasath, M. Energy optimization using metaheuristic bat algorithm assisted controller tuning for industrial and residential applications. Transactions of the Institute of Measurement and Control 2018, 40, 2310–2321.
- Wagiman, K. R., Abdullah, M. N., Hassan, M. Y., & Radzi, N. H. M. A new metric for optimal visual comfort and energy efficiency of building lighting system considering daylight using multi-objective particle swarm optimization. Journal of Building Engineering 2021, 43, 10525.
- Gateau, B., Naudet, Y., & Rykowski, J. (2016, October). Ontology-based smart IoT engine for personal comfort management. In 2016 11th International Workshop on Semantic and Social Media Adaptation and Personalization (SMAP) (pp. 35-40). IEEE.
- Bonino, D., & Corno, F. (2008, October). Dogont-ontology modeling for intelligent domotic environments. In International Semantic Web Conference (pp. 790-803). Berlin, Heidelberg: Springer Berlin Heidelberg.
- Compton, M., Barnaghi, P., Bermudez, L., Garcia-Castro, R., Corcho, O., Cox, S., ... & Taylor, K. The SSN ontology of the W3C semantic sensor network incubator group. Journal of Web Semantics 2012, 17, 25–32.
- Tila, F., & Kim, D. H. Semantic IoT System for Indoor Environment Control—A Sparql and SQL based hybrid model. Adv. Sci. Technol. Lett 2015, 120, 678–683.
- Adeleke, J. A., & Moodley, D. (2015, September). An ontology for proactive indoor environmental quality monitoring and control. In Proceedings of the 2015 annual research conference on south African institute of computer scientists and information technologists (pp. 1-10).
- Stavropoulos, T. G., Vrakas, D., Vlachava, D., & Bassiliades, N. (2012, June). BOnSAI: a smart building ontology for ambient intelligence. In Proceedings of the 2nd international conference on web intelligence, mining and semantics (pp. 1-12).
- Reinisch, C., Kofler, M. J., & Kastner, W. (2010, April). ThinkHome: A smart home as digital ecosystem. In 4th IEEE International Conference on Digital Ecosystems and Technologies (pp. 256-261). IEEE.
- Ploennigs, J., Clement, J., Wollschlaeger, B., & Kabitzsch, K. (2016, June). Semantic models for physical processes in CPS at the example of occupant thermal comfort. In 2016 IEEE 25th International Symposium on Industrial Electronics (ISIE) (pp. 1061-1066). IEEE.
- Nolich, M. Nolich, M., Spoladore, D., Carciotti, S., Buqi, R., & Sacco, M. Cabin as a home: a novel comfort optimization framework for IoT equipped smart environments and applications on cruise ships. Sensors, 2019, 19, 1060. [Google Scholar]
- Khan, J., Lee, E., & Kim, K. (2023, July). Optimizing the Performance of Kalman Filter and Alpha-Beta Filter Algorithms through Neural Network. In 2023 9th International Conference on Control, Decision and Information Technologies (CoDIT) (pp. 2187-2192). IEEE.
- Khan, J., Lee, E., & Kim, K. (2022). A higher prediction accuracy–based alpha–beta filter algorithm using the feedforward artificial neural network. CAAI Transactions on Intelligence Technology.
- Khan, J., & Kim, K. (2022, January). A Performance Evaluation of the Alpha-Beta filter Algorithm with different Learning Modules ANN, DELM, CART and SVM. In INTERNATIONAL CONFERENCE ON FUTURE INFORMATION & COMMUNICATION ENGINEERING (Vol. 13, No. 1, pp. 18-21).
- Khan, J., Lee, E., & Kim, K. (2022). A higher prediction accuracy–based alpha–beta filter algorithm using the feedforward artificial neural network. CAAI Transactions on Intelligence Technology.
Figure 1.
Conceptual structure diagram of the proposed model.
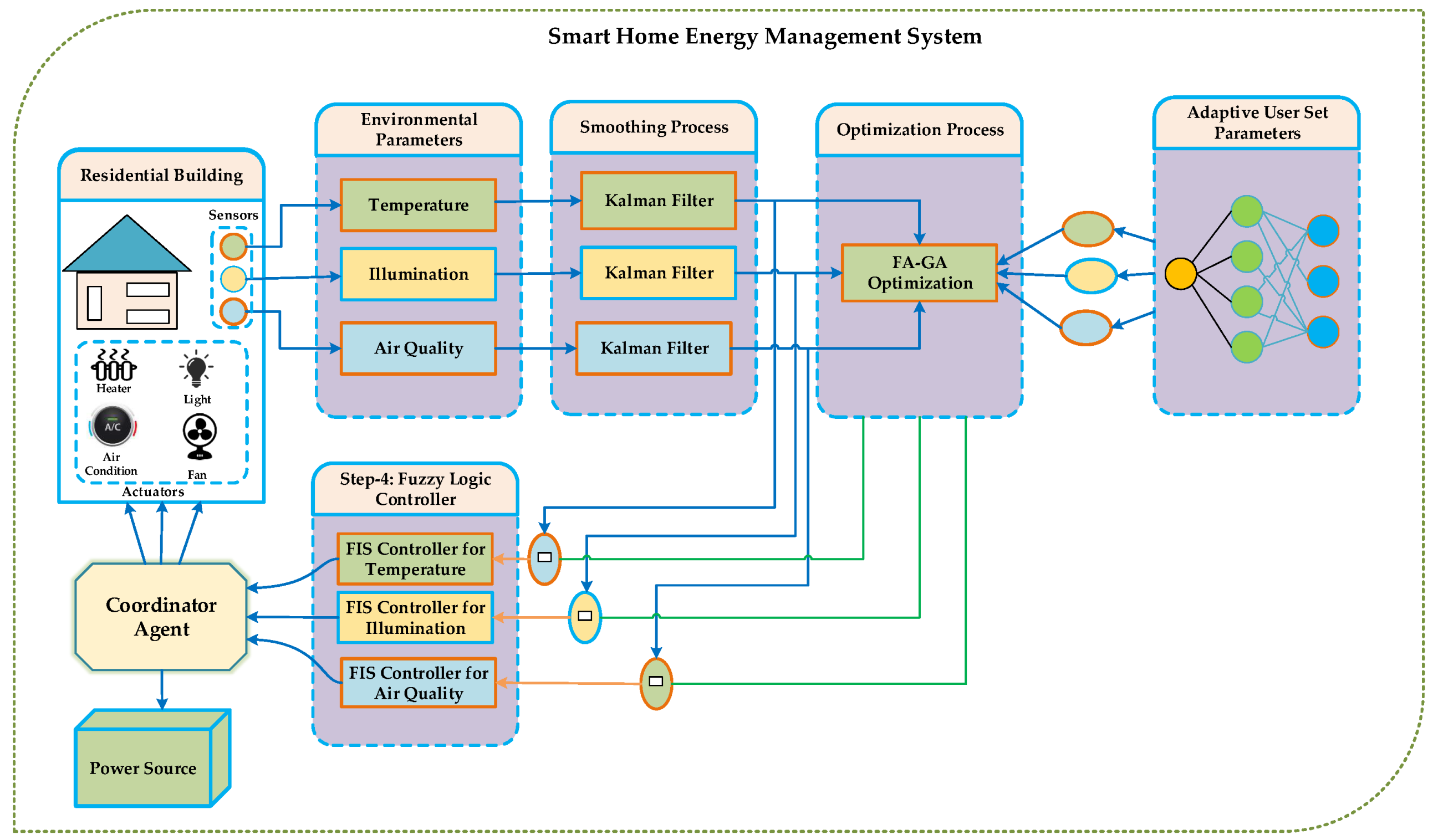
Figure 2.
Detailed proposed schematic diagram.
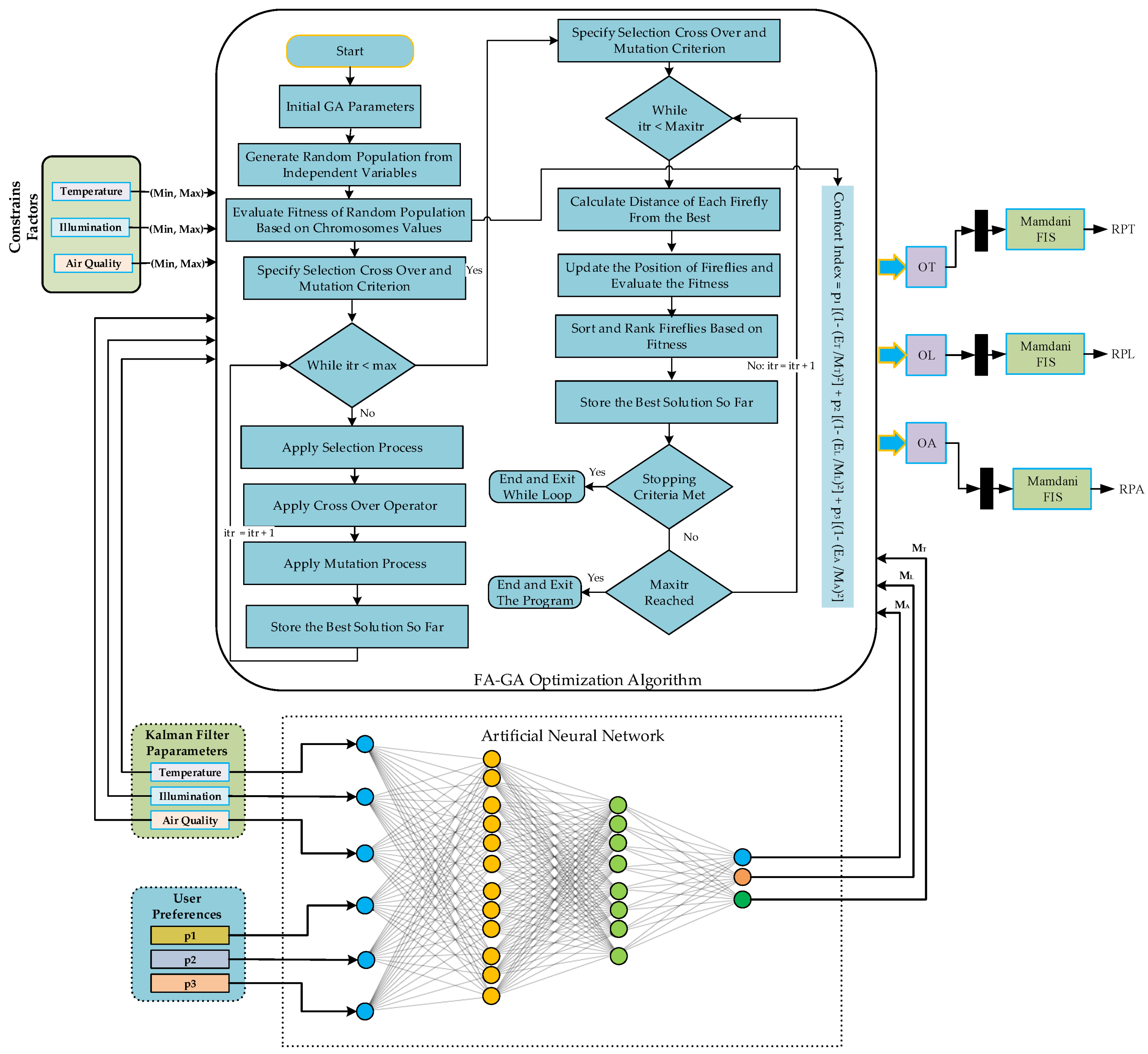
Figure 3.
Complete ANN structure.
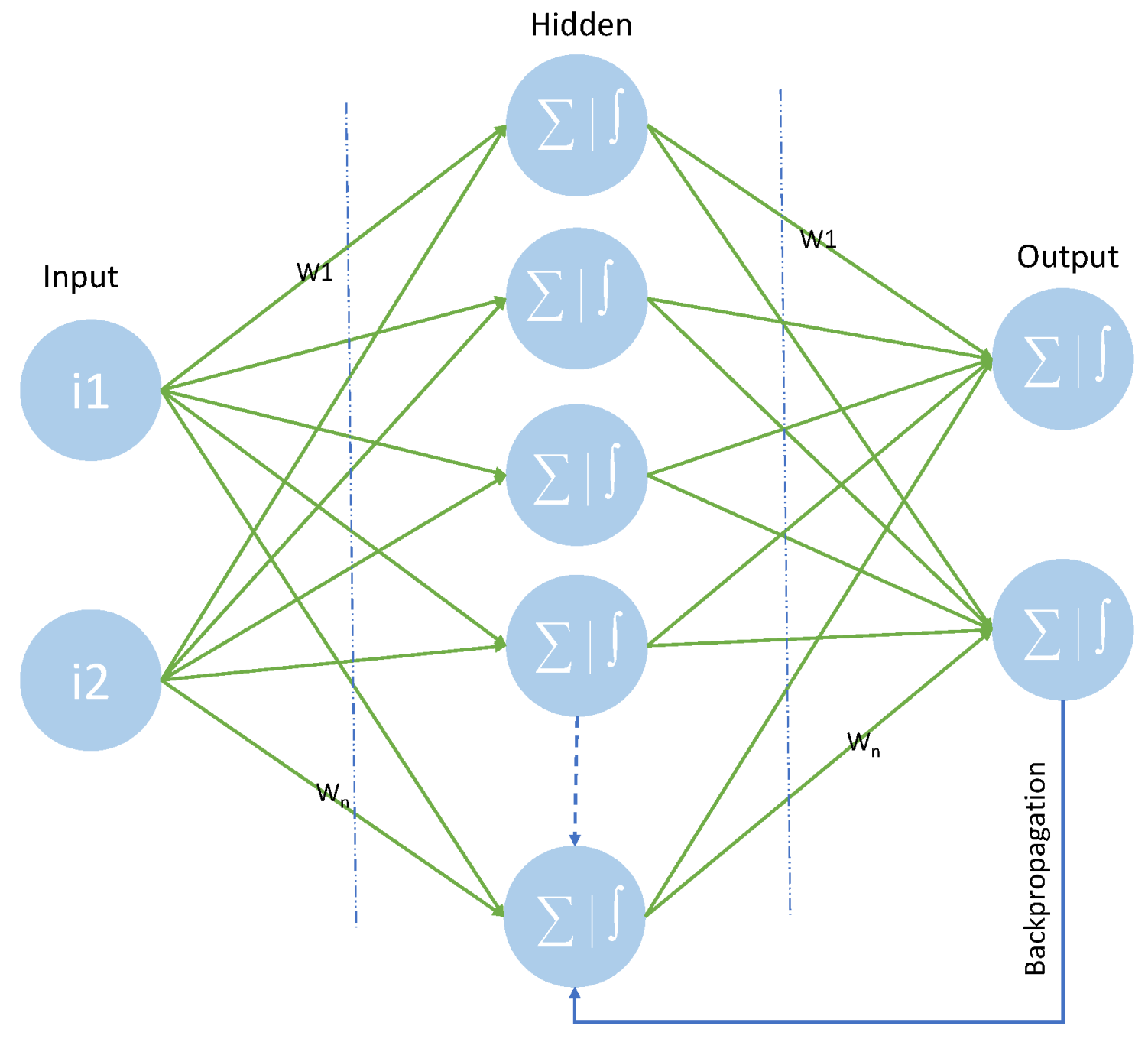
Figure 4.
Operational process of Mamdani fuzzy logic
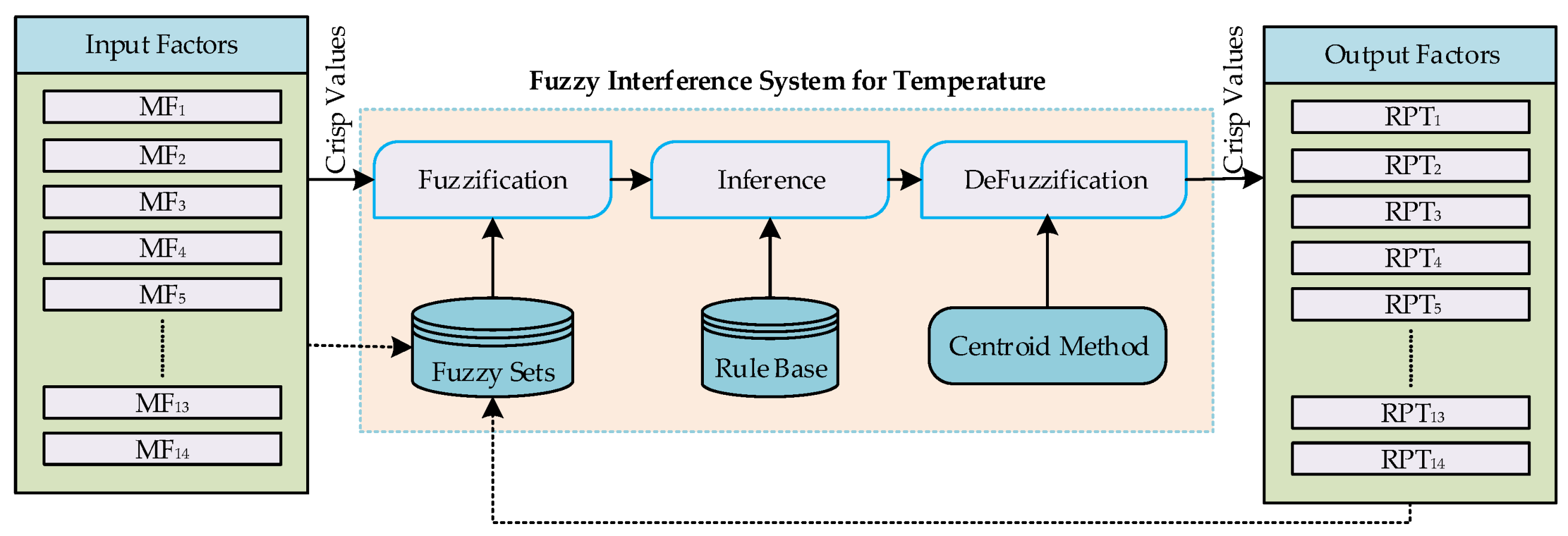
Figure 5.
Provide power and required power for coordinator agent.
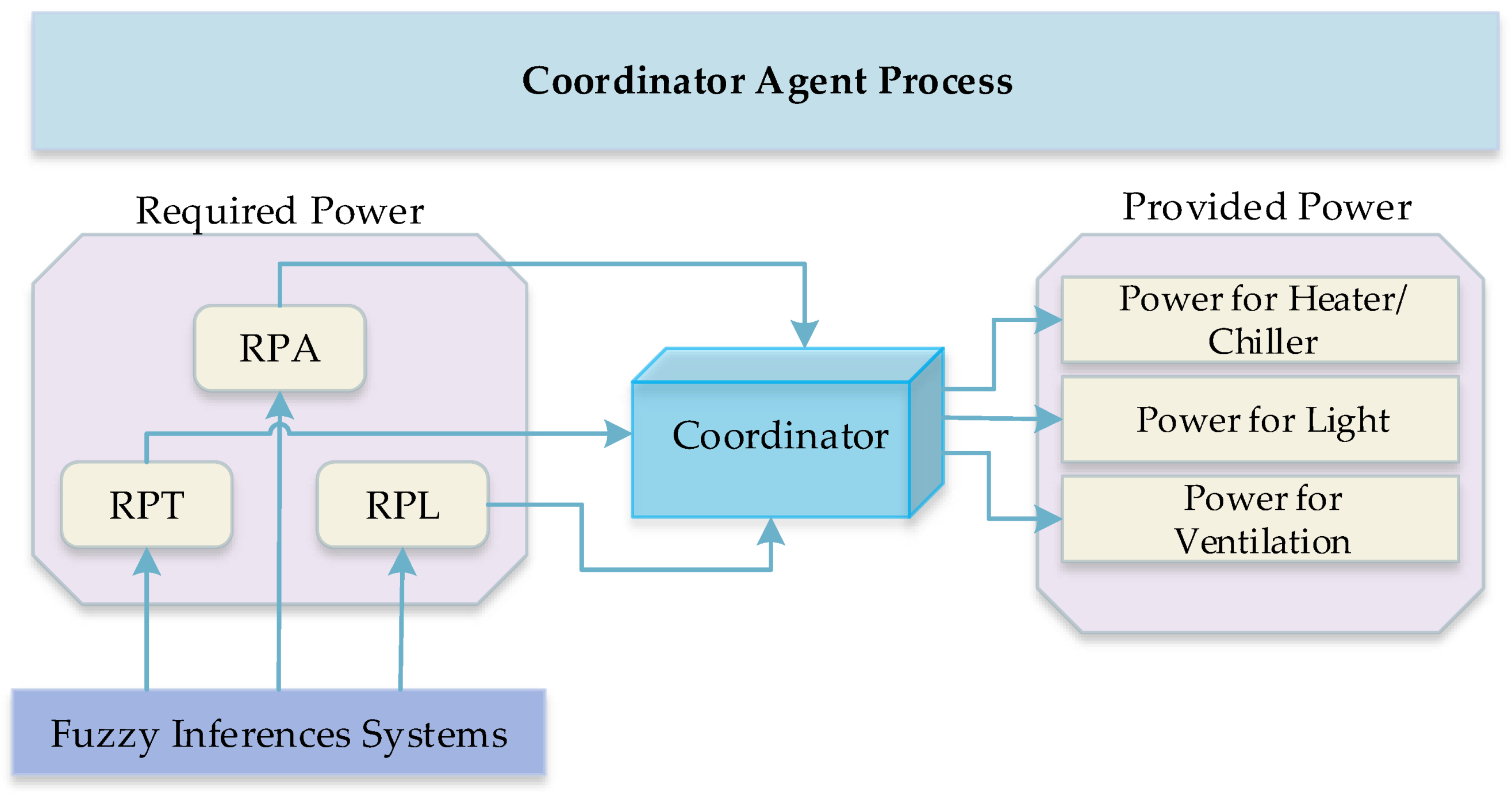
Figure 6.
Actual temperature, sensor reading temperature, and predicted temperature
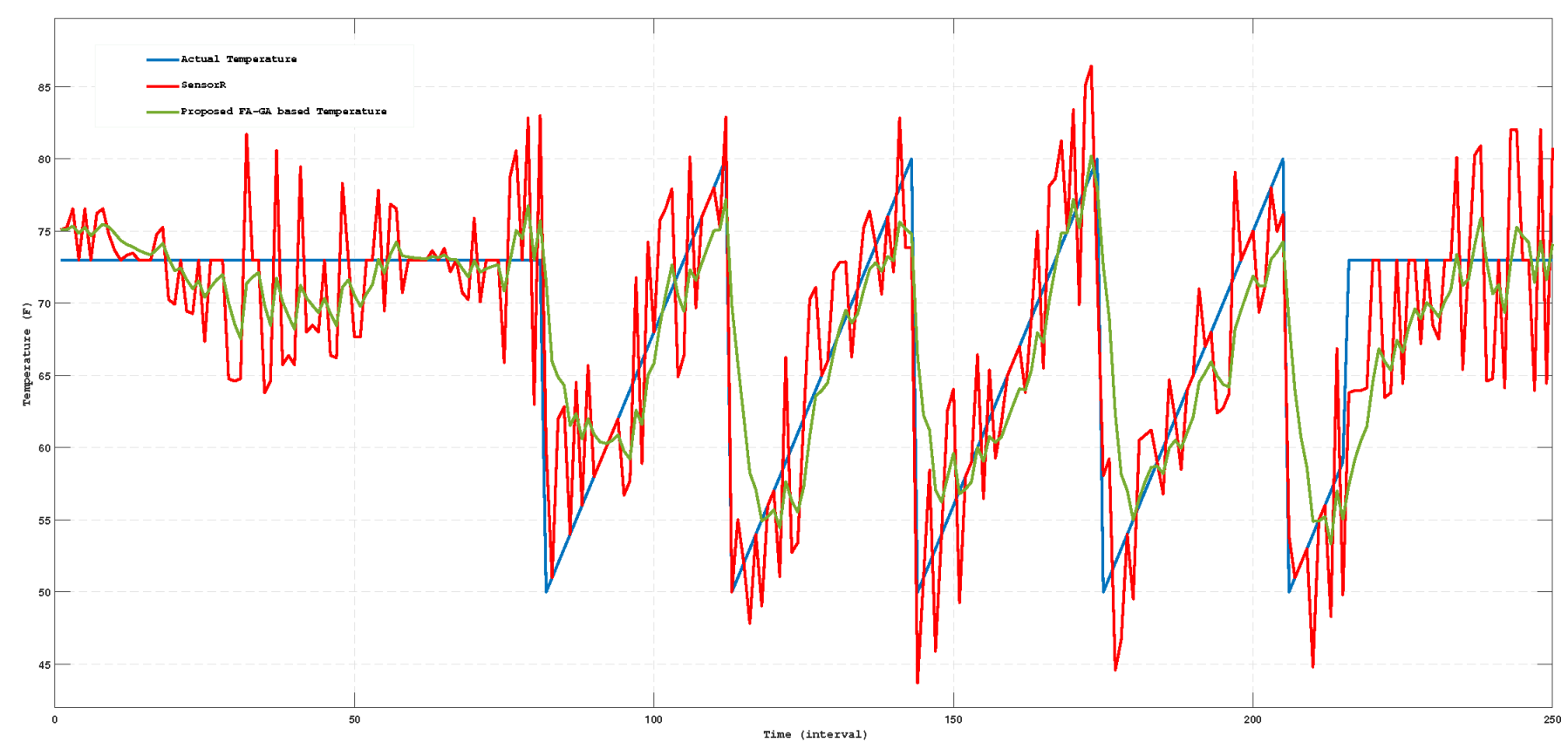
Figure 7.
Actual illumination, sensor illumination, and air quality illumination
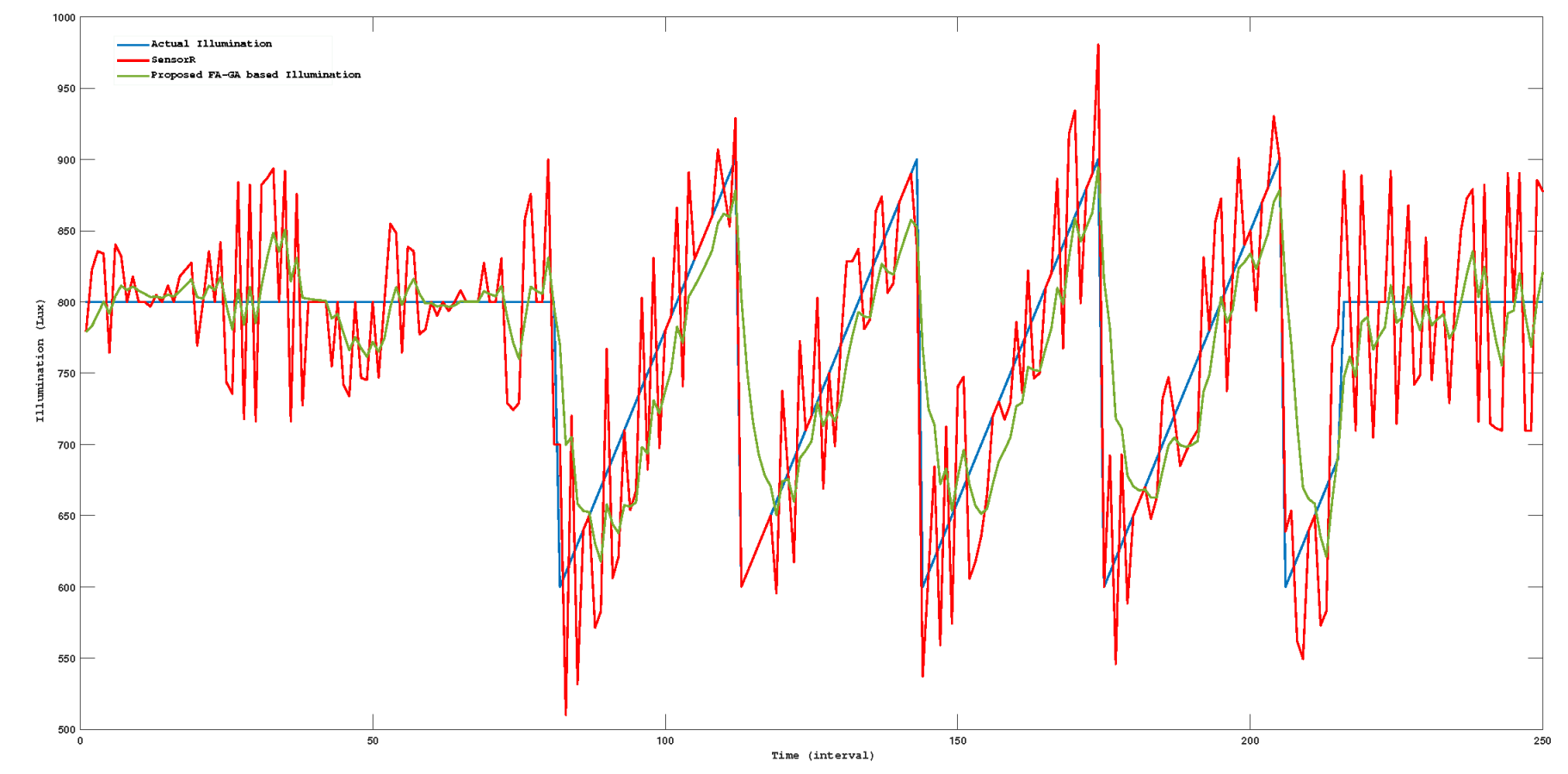
Figure 8.
Actual air quality, sensed air quality, and predicted air quality values
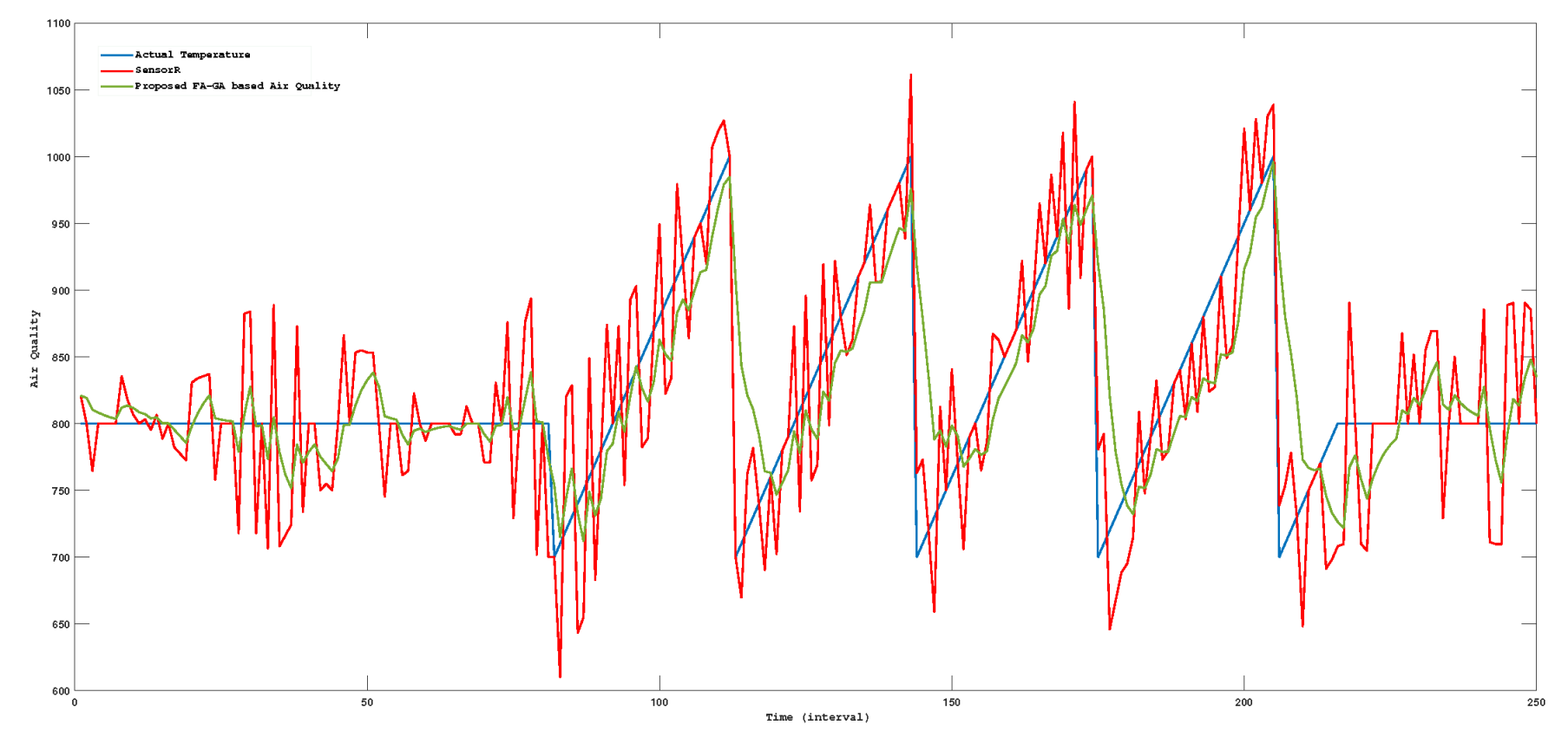
Figure 9.
Total comfort index with and without optimization.
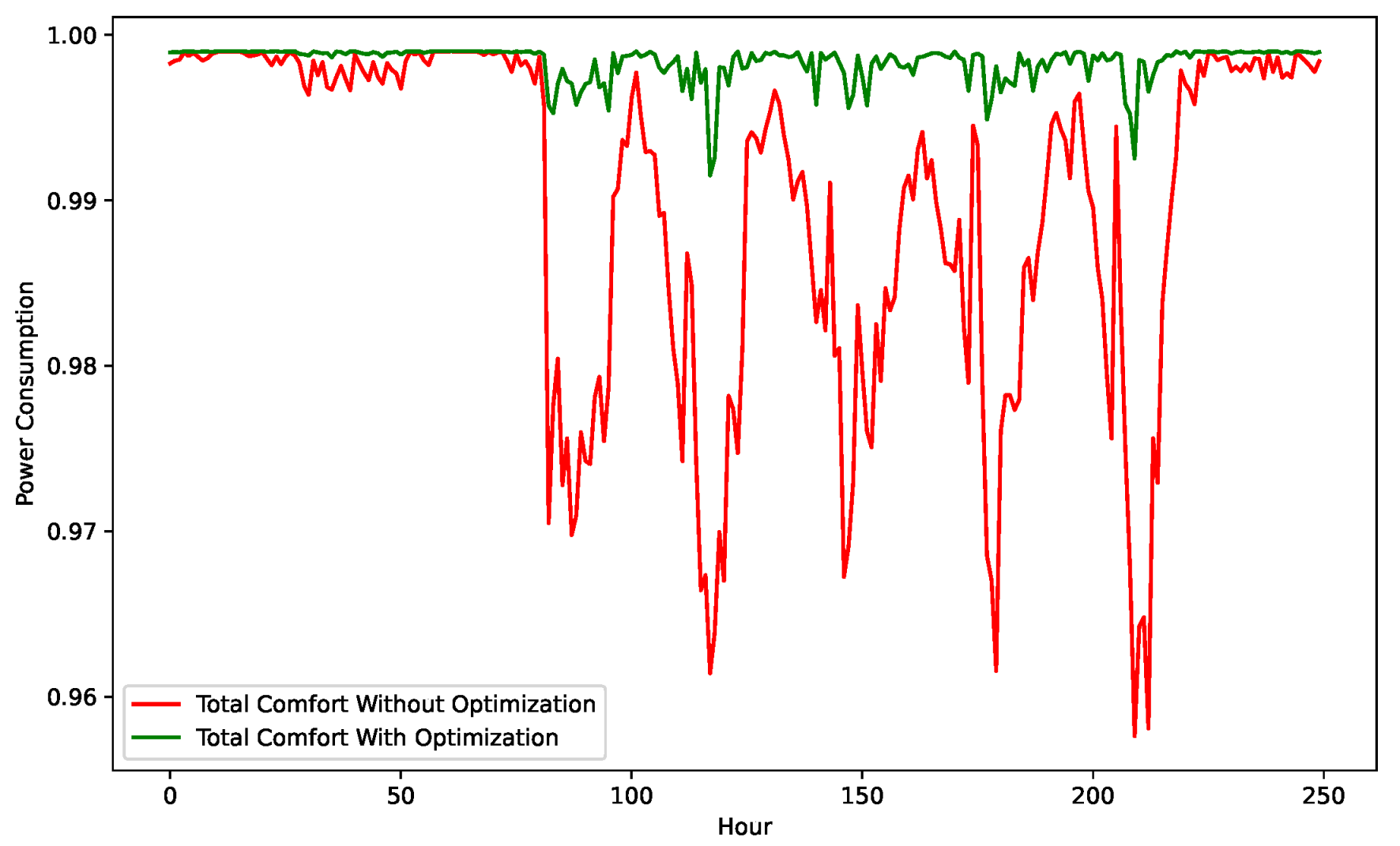
Figure 10.
Total power consumption with and without optimization.
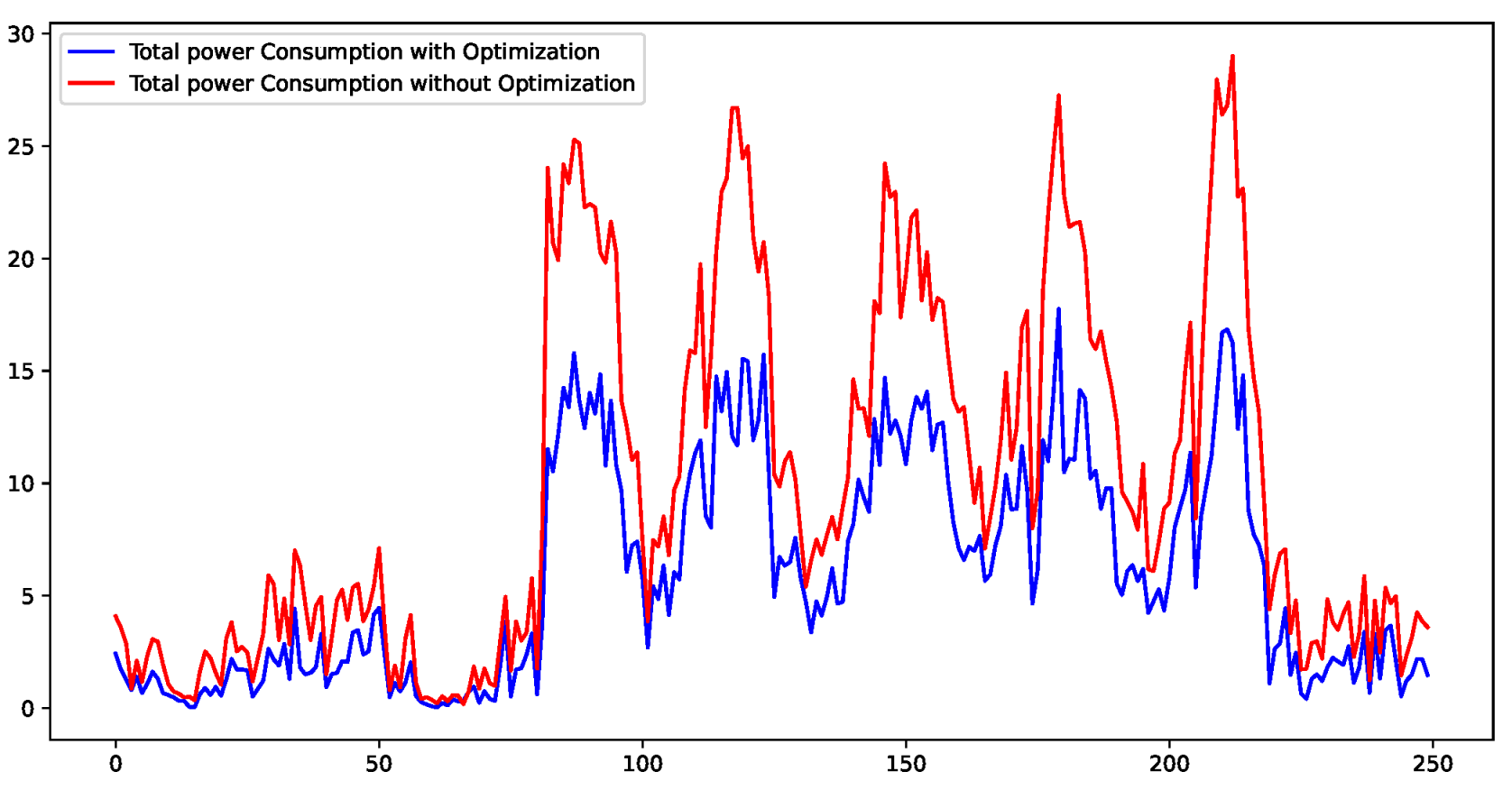
Figure 11.
Total power consumption with and without optimization.
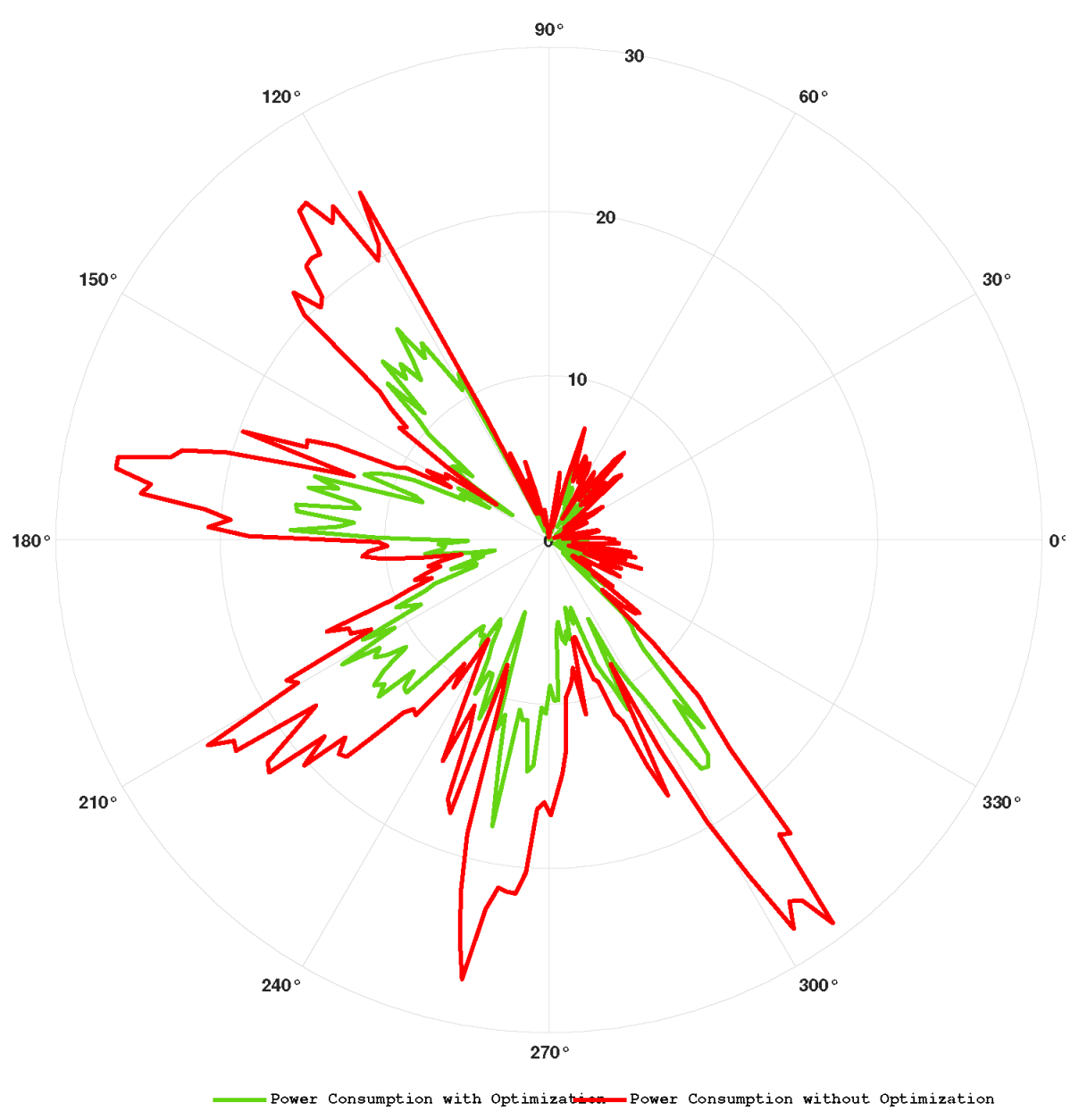
Figure 12.
Comparative analysis of different models.
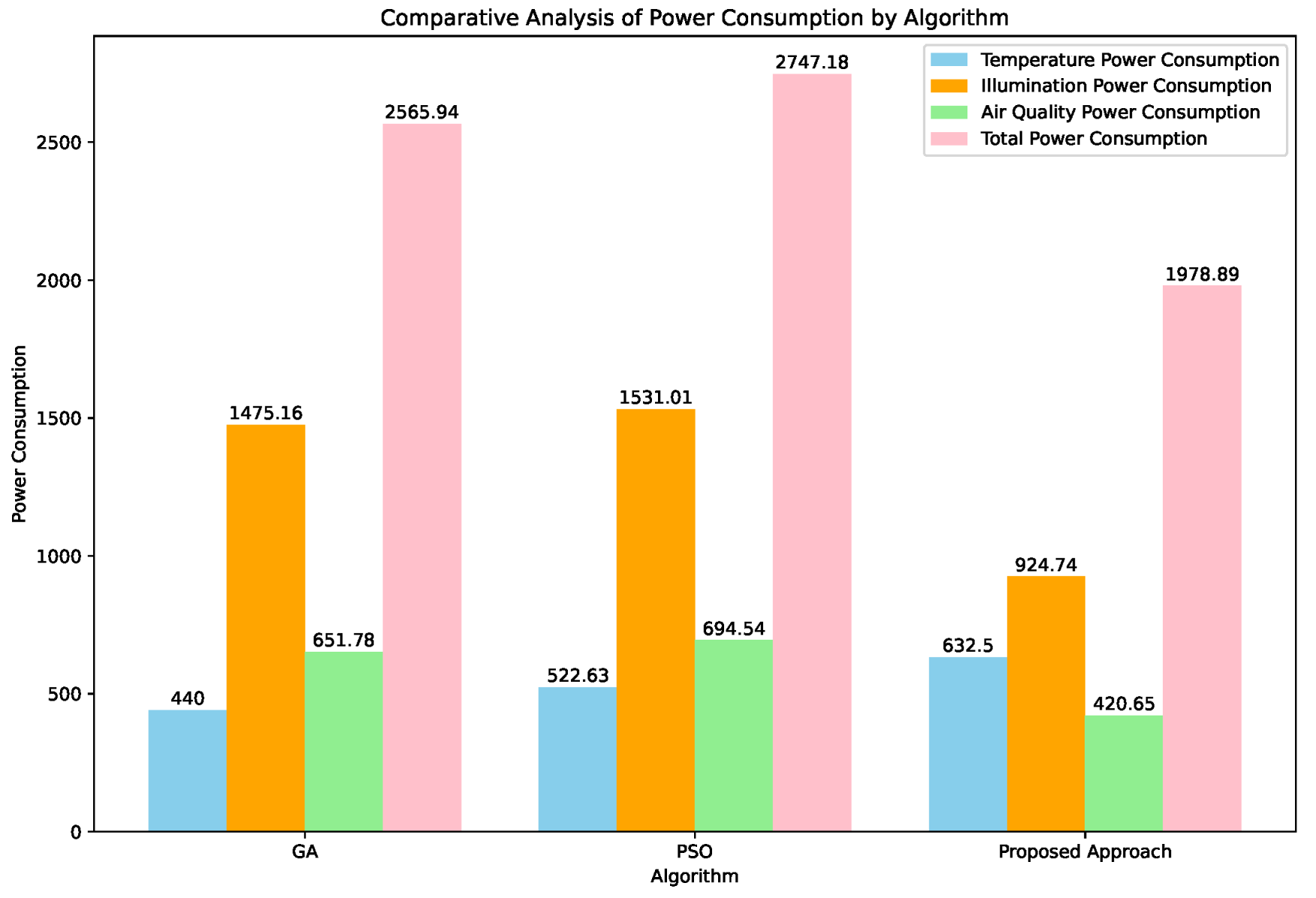
Figure 13.
Fuzzy logic based comparative Analysis of Power Consumption With and Without Optimization.
Figure 13.
Fuzzy logic based comparative Analysis of Power Consumption With and Without Optimization.
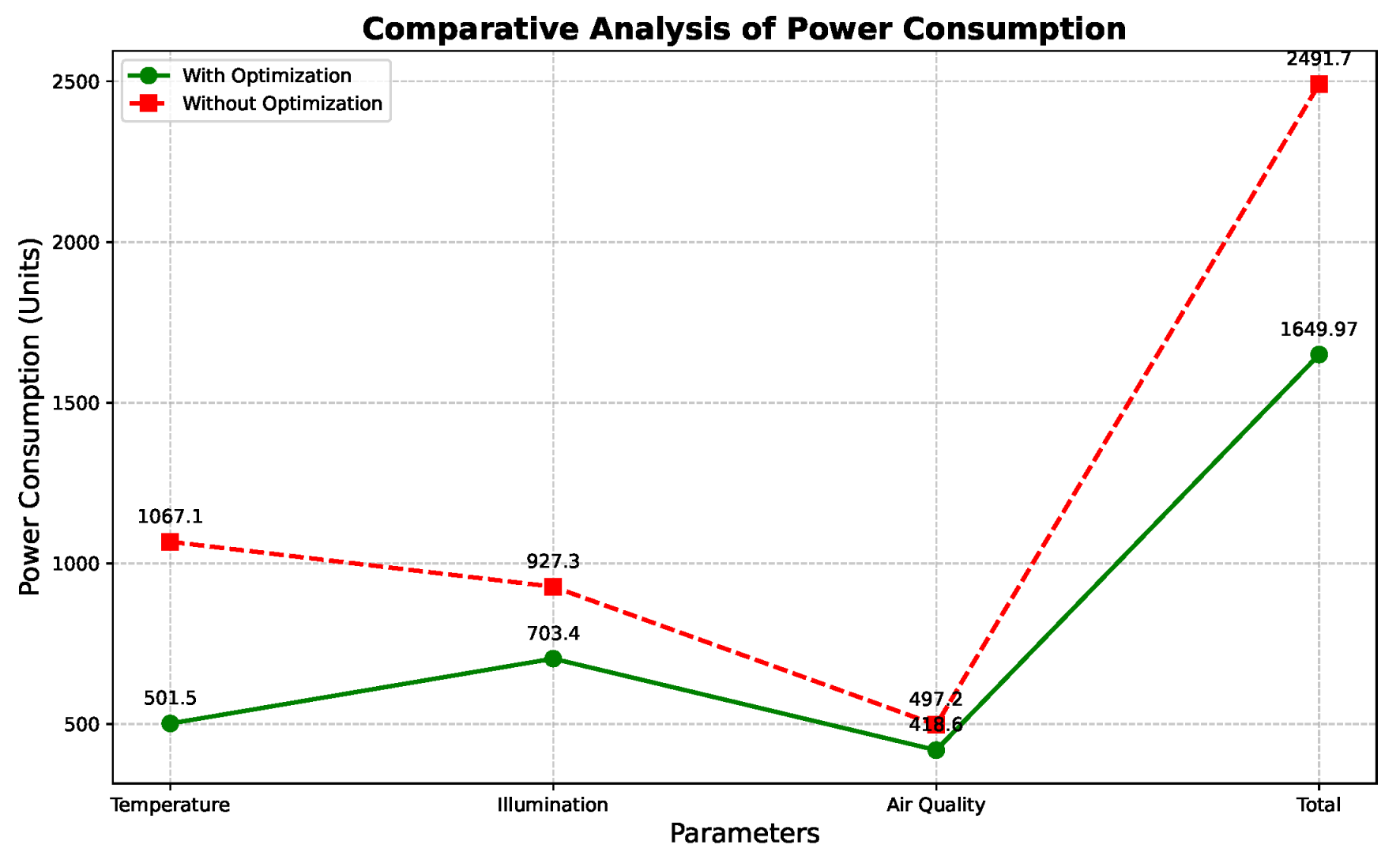
Figure 14.
comparative Analysis with MAE and RMSE.
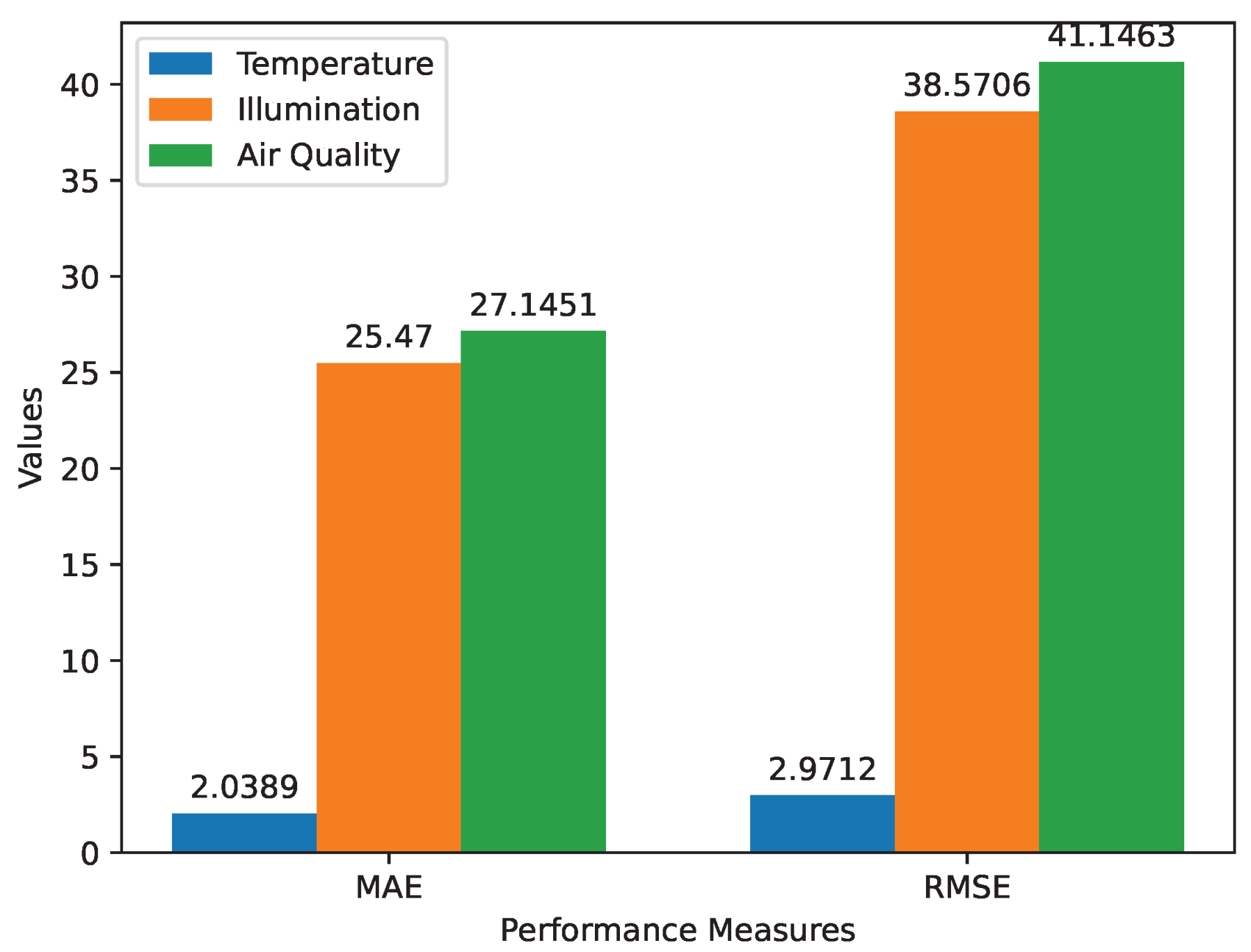
Table 1.
FUZZY RULES FOR POWER OPTIMIZATION, LIGHTING MANAGEMENT, AND ENVIRONMENTAL QUALITY FUZZY CONTROLLERS
Table 1.
FUZZY RULES FOR POWER OPTIMIZATION, LIGHTING MANAGEMENT, AND ENVIRONMENTAL QUALITY FUZZY CONTROLLERS
| Fuzzy Controller 1: | Fuzzy Controller 2: | Fuzzy Controller 3: |
|---|---|---|
| Rules for Power | Rules for Lighting | Rules for Environmental |
| Optimization | Management | Quality |
| Input "Var_1" | Input "Var_2" | Input "Var_3" |
| Output "RPTemp" | Output "RPILL" | Output "RPAQ" |
| Var_1_1 → RPTemp_1 | Var_2_1 → RPILL_1 | Var_3_1 → RPAQ_1 |
| Var_1_2 → RPTemp_2 | Var_2_2 → RPILL_2 | Var_3_2 → RPAQ_2 |
| Var_1_3 → RPTemp_3 | Var_2_3 → RPILL_3 | Var_3_3 → RPAQ_3 |
| Var_1_4 → RPTemp_4 | Var_2_4 → RPILL_4 | Var_3_4 → RPAQ_4 |
| Var_1_5 → RPTemp_5 | Var_2_5 → RPILL_5 | Var_3_5 → RPAQ_5 |
| Var_1_6 → RPTemp_6 | Var_2_6 → RPILL_6 | Var_3_6 → RPAQ_6 |
| Var_1_7 → RPTemp_7 | Var_2_7 → RPILL_7 | Var_3_7 → RPAQ_7 |
| Var_1_8 → RPTemp_8 | Var_2_8 → RPILL_8 | Var_3_8 → RPAQ_8 |
| Var_1_9 → RPTemp_9 | Var_2_9 → RPILL_9 | Var_3_9 → RPAQ_9 |
| Var_1_10 → RPTemp_10 | Var_2_10 → RPILL_10 | Var_3_10 → RPAQ_10 |
| Var_1_11 → RPTemp_11 | Var_2_11 → RPILL_11 | Var_3_11 → RPAQ_11 |
| Var_1_12 → RPTemp_12 | Var_2_12 → RPILL_12 | Var_3_12 → RPAQ_12 |
| Var_1_13 → RPTemp_13 | Var_2_13 → RPILL_13 | Var_3_13 → RPAQ_13 |
| Var_1_14 → RPTemp_14 | Var_2_14 → RPILL_14 | Var_3_14 → RPAQ_14 |
| – | Var_2_15 → RPILL_15 | Var_3_15 → RPAQ_15 |
| – | Var_2_16 → RPILL_16 | Var_3_16 → RPAQ_16 |
| – | Var_2_17 → RPILL_17 | Var_3_17 → RPAQ_17 |
| – | Var_2_18 → RPILL_18 | Var_3_18 → RPAQ_18 |
| – | Var_2_19 → RPILL_19 | – |
| – | Var_2_20 → RPILL_20 | – |
Table 2.
Temperature Fuzzy Controller Fuzzy Rules
| Symbol | Range | Symbol | Range |
|---|---|---|---|
| Var_1_1 | RPTemp_1 | ||
| Var_1_2 | RPTemp_2 | ||
| Var_1_3 | RPTemp_3 | ||
| Var_1_4 | RPTemp_4 | ||
| Var_1_5 | RPTemp_5 | ||
| Var_1_6 | RPTemp_6 | ||
| Var_1_7 | RPTemp_7 | ||
| Var_1_8 | RPTemp_8 | ||
| Var_1_9 | RPTemp_9 | ||
| Var_1_10 | RPTemp_10 | ||
| Var_1_11 | RPTemp_11 | ||
| Var_1_12 | RPTemp_12 | ||
| Var_1_13 | RPTemp_13 | ||
| Var_1_14 | RPTemp_14 |
Table 3.
Illumination Fuzzy Controller Fuzzy Rules
| Symbol | Range | Symbol | Range |
|---|---|---|---|
| Var_2_1 | RPILL_1 | ||
| Var_2_2 | RPILL_2 | ||
| Var_2_3 | RPILL_3 | ||
| Var_2_4 | RPILL_4 | ||
| Var_2_5 | RPILL_5 | ||
| Var_2_6 | RPILL_6 | ||
| Var_2_7 | RPILL_7 | ||
| Var_2_8 | RPILL_8 | ||
| Var_2_9 | RPILL_9 | ||
| Var_2_10 | RPILL_10 | ||
| Var_2_11 | RPILL_11 | ||
| Var_2_12 | RPILL_12 | ||
| Var_2_13 | RPILL_13 | ||
| Var_2_14 | RPILL_14 | ||
| Var_2_15 | RPILL_15 | ||
| Var_2_16 | RPILL_16 | ||
| Var_2_17 | RPILL_17 | ||
| Var_2_18 | RPILL_18 | ||
| Var_2_19 | RPILL_19 | ||
| Var_2_20 | RPILL_20 |
Table 4.
Air Quality Fuzzy Controller Fuzzy Rules
| Symbol | Range | Symbol | Range |
|---|---|---|---|
| Var_3_1 | RPAQ_1 | ||
| Var_3_2 | RPAQ_2 | ||
| Var_3_3 | RPAQ_3 | ||
| Var_3_4 | RPAQ_4 | ||
| Var_3_5 | RPAQ_5 | ||
| Var_3_6 | RPAQ_6 | ||
| Var_3_7 | RPAQ_7 | ||
| Var_3_8 | RPAQ_8 | ||
| Var_3_9 | RPAQ_9 | ||
| Var_3_10 | RPAQ_10 | ||
| Var_3_11 | RPAQ_11 | ||
| Var_3_12 | RPAQ_12 | ||
| Var_3_13 | RPAQ_13 | ||
| Var_3_14 | RPAQ_14 | ||
| Var_3_15 | RPAQ_15 | ||
| Var_3_16 | RPAQ_16 | ||
| Var_3_17 | RPAQ_17 | ||
| Var_3_18 | RPAQ_18 |
Table 5.
Simulation Configuration
| Tool | Specification |
|---|---|
| CPU | Intel(R) Core (TM) i5-3570 |
| @ 3.40 GHz | |
| RAM | 16 GB |
| Graphics | NVIDIA GeForce 9600 GT |
| Operating System | Windows 10 |
| Programming Tool | Matlab 2018a |
Table 6.
Comparative analysis of different models
| Parameters | GA | PSO | Proposed Approach |
|---|---|---|---|
|
Temperature Power Consumption |
440 | 522.63 | 632.5 |
|
Illumination Power Consumption |
1475.16 | 1531.01 | 924.74 |
|
Air Quality Power Consumption |
651.78 | 694.54 | 420.65 |
|
Total Power Consumption |
2565.94 | 2747.18 | 1978.89 |
Table 7.
Fuzzy logic based comparative Analysis of Power Consumption With and Without Optimization
| Parameters | With | Without |
|---|---|---|
| Optimization | Optimization | |
| Temperature | 501.5 | 1067.1 |
| Power Consumption | ||
| Illumination | 703.4 | 927.3 |
| Power Consumption | ||
| Air Quality | 418.6 | 497.2 |
| Power Consumption | ||
| Total | 1649.97 | 2491.7 |
| Power Consumption |
Table 8.
The performance measurement of optimization algorithm for temperature, illumination, and air quality
Table 8.
The performance measurement of optimization algorithm for temperature, illumination, and air quality
| Performance | Temperature | Illumination | Air Quality |
|---|---|---|---|
| Measures | |||
| MAE | 2.0389 | 25.47 | 27.1451 |
| RMSE | 2.9712 | 38.5706 | 41.1463 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated








