Preprint
Article
Corrections to the Reflectance of Graphene by Light Emission
Altmetrics
Downloads
78
Views
37
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
16 January 2024
Posted:
17 January 2024
You are already at the latest version
Alerts
Abstract
Monolayer graphene absorbs 2.3 percent of the incident visible light. This “small” absorption has been used to emphasize the visual transparency of graphene, but it in fact means that multilayer graphene absorbs a sizable fraction of incident light, which causes non-negligible fluorescence. In this paper, we formulate the light emission properties of multilayer graphene composed of tens to hundreds of layers using a transfer matrix method and confirm the method’s validity experimentally. We could quantitatively explain the measured contrasts of multilayer graphene on SiO2/Si substrates and found sizable corrections, which cannot be classified as incoherent light emissions, to the reflectance of visible light. The new component originates from coherent emission caused by absorption at each graphene layer. Multilayer graphene thus functions as a partial coherent light source of various wavelengths, and it may have surface-emitting laser applications.
Keywords:
Subject: Physical Sciences - Optics and Photonics
1. Introduction
The visual detection of graphene on Si substrates involves a complex scientific aspect related to the interference effects of light [1,2,3]. To enhance visibility, it is crucial for the contrast between the reflectances from the substrate and the graphene layer to be sufficiently large. Si substrates with a specific thickness of () are known to provide advantages in this context [4,5]. Specifically, when the optical path length difference of the layer is one-half or three-half the wavelength of the incident light, the contrast reaches its maximum.
The enhanced visibility of graphene is primarily attributed to a substrate-induced enhancement of light absorption. This enhancement is valuable not only for graphene detection but also for exploring notable phenomena. For instance, the reflectance of specific graphene multilayers on SiO2/Si substrates can be reduced to zero for normally incident visible light with a wavelength () approximately equal to . Zero reflectance is achieved through destructive interference caused by and a significant absorption coefficient of graphene [6,7,8]. More importantly, the reflectance of multilayer graphene on SiO2/Si substrates is intricately determined because the significant absorption may result in non-negligible luminescence. This luminescence also functions as a secondary light source, leading to more sophisticated interference effects of light [9,10,11,12,13,14,15].
Since graphene lacks an energy bandgap, unlike semiconductors, it is naturally expected that the impact of light emission on its optical properties is negligible. However, electrons that have absorbed light undergo various relaxation processes towards the ground state, [16,17] generally involving luminescence contributions. For instance, Lui et al. [12] and Suemoto et al. [14] have reported that graphene and graphite emit light under femtosecond laser pulse excitation, respectively. In this paper, we demonstrate that, despite the tiny branching ratio of light emission to absorption, light emission constitutes the primary correction to visible reflectance, thanks to the substantial absorption of graphene. We have found this notable feature for the first time by leveraging both the destructive interference effects of substrates and the coherence of the multilayer structure. Additionally, we can show that light emission significantly contributes to enhancing the visibility of graphene on a substrate.
In this study, we delineate coherent and incoherent corrections to the reflectance of multilayer graphene (on SiO2/Si substrates) caused by the light it emits after absorbing incident light. The coherent corrections are dependent on only two parameters: the branching ratio () of coherent light emission to absorbed light and the phase (+ or −) of the emitted light. Both parameters are assumed to be independent of the number of layers (N) and the wavelength of light. Contrasts (reflectivities) calculated using these phenomenologically determined parameters show reasonable agreement with measured values for various N. Despite the branching ratio, determining the strength of light emitted from a graphene monolayer, being less than one percent, the coherent components become the primary corrections to the reflectance of multilayer graphene. This is due to the coherence increasing the amplitude of reflection through constructive interference. Furthermore, based on the observation that the phase of reflection and transmission coefficients of each layer translates into the amplitude of the emitted light, we hypothesize that the origin of the coherent components is coherent light emission stimulated by the incident light. Meanwhile, the Raman effect is explained as incoherent corrections. These conclusions are independent of the specific values of the two parameters.
Recently, the optical constants of single-layer graphene were measured with high accuracy [18,19]. However, classical electromagnetic models were employed for fitting and interpreting the results. Our approach advances the physical understanding of the measured optical constants of single-layer graphene to a more fundamental level, incorporating principles of quantum electrodynamics that describe the creation of photons (light emission). Moreover, our formulation is versatile and generally applicable to any layered material and superlattice, promising an accurate description of their optical processes.
Multilayer graphene composed of tens to hundreds of layers is an interesting research subject. However, it has not been explored much, partly because the success of the exfoliation method has rapidly shifted the interest of many researchers from infinite layers of graphite to few-layer graphene. The obvious advantage of multilayer graphene is that it can increase the signal strength, [20] whereas the signal strength of few-layer graphene is low and difficult to measure. Besides that, multilayer graphene hosts various intriguing phenomena. For instance, studies have revealed that the optimal number of layers for absorbing infrared radiation is 87 [21]. Additionally, a notable nonlinear optical effect has been attributed to multilayer graphene [22,23,24]. Yang et al., for instance, demonstrated the maximum third-harmonic signal from 24-layer graphene on a quartz substrate [25].
This paper is structured as follows: In Section 2, we present fundamental insights into the reflectance of multilayer graphene on SiO2/Si substrates. By utilizing the Fresnel equation, we can replicate measured contrasts and assert that the optical constants obtained by El-Sayed et al. [19] sufficiently and accurately describe the reflectance. However, it is noteworthy that these optical constants lead to an unexpectedly large effective coupling between light and graphene, a phenomenon inconsistent with existing experiments. Section 4 introduces our formulation of corrections to the reflectance arising from light emissions. Our model effectively describes the reflectance without introducing such inconsistencies. These corrections are categorized into two types: coherent emission, corresponding to stimulated emission with a common phase, and incoherent emission, featuring a random phase identified as the Raman effect. A detailed comparison between calculated and measured contrasts is presented in Section 5. Finally, Section 6 offers a discussion of the findings, and Section 7 provides the conclusions.
2. Reflectance of Graphene Multilayer on Si Substrate
In this section, we demonstrate that the measured reflectance of various graphene multilayers with different thickness aligns well with the Fresnel equation when adopting optical constants (n and k) obtained by El-Sayed et al. [19] through ellipsometric measurements of chemical vapor deposited (CVD) graphene monolayer. The key observation from this section is that electron-light coupling constant, extracted from the established n and k values, deviates significantly from the fine-structure constant . In fact, the difference is beyond the level of small corrections of order of caused by such as a change in the band dispersion at high energy from linear dispersion (commonly known as trigonal warping effects) and Fermi velocity renormalization, [26,27] which have been discussed theoretically thus far. This observation partly motivates the introduction of a new reflectance model developed in the subsequent sections.
2.1. Fresnel Equation
The reflectance of N-layer graphene on SiO2/Si substrate to normally incident light of wavelength can be formulated using the reflection coefficient as (Fresnel equation), where
Here, is the phase acquired by light after it propagates through a distance in SiO2, and is the complex phase acquired when light passes through N-layer graphene of thickness . Multilayer graphene is treated as an effective medium whose unit length is the interlayer spacing d ( nm) and its dielectric constant is given by [19]. and are the refractive indexes of Si and SiO2, respectively. Si is treated as an absorbing substrate having a semi-infinite thickness ( is a complex number) whose dispersion is taken into account, [28] while SiO2 is treated as an absorption-free film [29]. depends sensitively on the two phases, and . When or in Equation (1), corresponds to the reflectance of the substrate without graphene. It can be minimized for a specific by destructive interference; namely, is at a minimum when as [30]. Monolayer graphene is most easily detectable on SiO2/Si substrates when destructive interference occurs, because takes a maximum when (i.e., when because ) [4].
2.2. Comparison of Measured and Calculated Contrasts
Multilayer graphene was prepared by exfoliating highly oriented pyrolytic graphite (HOPG) on the same SiO2/Si substrate. The reflectance of the multilayer graphene was measured with a spectroscopic reflectometer (TohoSpec3100, Toho Technology) using a objective lens. First, we determined that nm from the reflectance of the substrate (Appendix A). This value is used consistently in all the calculations reported in this paper, and it results in that destructive interference occurs for at nm. The thickness of the graphene flakes was determined by atomic force microscopy (Dimension XR, Bruker).
The representative measured spectral contrasts are depicted as black dots (circles) in Figure 1 (The error bars for the data are within each circle). It is important to note that we present contrasts () instead of the reflectivities () to prevent any artificial shifts in the reflectivities (see Appendix A for more details). The general feature of the spectral shapes can be elucidated as follows: for thin samples with fewer than 40 layers, the contrast is subdued due to destructive interference from the substrate, resulting in a concave structure near nm. For thick samples with over 60 layers, is predominantly influenced by contributions from the N-layer graphene and is minimally impacted by the substrate. Consequently, given that , suppressed by destructive interference, is in the denominator of the contrast, a convex structure appears near nm.
The contrasts, calculated using Equation (1), are represented by the red solid curves in Figure 1. A satisfactory fit with no significant deviations is achieved for various multilayer graphene samples, except for and . The observed discrepancy in these thin samples likely arises from differences in the interface between graphene and the substrate compared to that between adjacent graphene layers. This discrepancy is specific to thin samples and becomes negligible at 6 layers. The notable agreement between measured and calculated reflectance for visible light clearly indicates the following two facts. First, multilayer graphene can be treated as a collection of independent single layers, which is plausible since the effect of interlayer stacking does not manifest in the dynamical conductivity within the visible light range. Second, reflectance measurements provide a reliable value of layer number N, averaged within a light spot. This is true even when the thickness of the graphene flakes determined by atomic force microscopy shows positional fluctuations to a certain extent. These facts will be used to validate the underlying assumption of our theoretical model of reflection presented in the subsequent sections.
and vanish at , which has been referred to as zero reflection [5,30]. Zero reflection is useful in knowing the values of basic parameters later (at the end of Section 3). To capture the essential role of graphene in achieving zero reflection, let us consider Equation (1) when . For the numerator to vanish, has to be satisfied. Since is small, this equation can be simplified as , which shows that is an approximate layer number that gives zero reflection. This argument makes it easy to understand that the dominant imaginary part of is essential for zero reflection to occur.
2.3. Effective Coupling Constant
As the difference between the calculated and experimental values of contrasts proves to be sufficiently small for various multilayer graphene samples when utilizing the experimental values in Equation (1), the optical constants [19] are the results that theory should ultimately elucidate. It can be inferred that nearly all the optical information of graphene multilayers is encompassed in the optical constant of monolayer graphene. This inference is partially attributed to the fact that the effect of the stacking order on the reflectance does not manifest in the visible regime. Consequently, we must inquire to what extent the theory of graphene optics can account for the n and k values.
Because of a conical energy-band structure of graphene known as the Dirac cone, the dynamical conductivity is well approximated by for visible light [31]. As a result, (suspended) monolayer graphene absorbs percent () of the incident visible light [32]. A straightforward calculation of the Kubo formula shows that the dynamical conductivity of graphite is given by that of graphene divided by the interlayer spacing d ( nm): [21,33,34]. The reflectance in the visible regime is free from the effects of the stacking order, [35,36,37] Fermi energy position, and temperature at room temperature ranges [38]. Thus, the relative permittivity of graphite for visible light wavelengths is written as
where is the dielectric constant of the interlayer space.
By equating the right-hand side of Equation (2) with , we define an effective coupling constant , which is compared with in Figure 2a. The difference between and is actually larger than the order of 10 percent of which is beyond the level of small corrections of order of considered theoretically so far. Similarly, we define and plot it in Figure 2b. If the interlayer space is a vacuum, an appropriate choice of would be 1. However, is very different from unity because the electronic wave function of the -orbital spreads into the interlayer space, light propagating in it is subjected to the spread of the wave function [39,40]. Fang et al. [39] calculate using a microscopic Poisson equation which has been tested by experiment. [40] The calculated effective dielectric thickness of graphene is found to be 0.22 nm, and the microscopic dielectric permittivity decays from 6.9 in the carbon-atom plane to the vacuum permittivity within approximately 0.1 nm. Though the calculation is for the electric field pointing in the direction perpendicular to the graphene sheet, similar (but slightly smaller) value is expected for the direction parallel to the sheet (let us assume it is here).
3. Corrections to Reflectance by Light Emission
A substantial correction to the dynamical conductivity is deemed impermissible because, if allowed, it would result in an inconsistency with the experimental observation that a (suspended) monolayer graphene absorbs approximately 2.3 percent () of the incident visible light [32]. An accurate theory capable of describing the reflectance does not necessitate corrections to dynamical conductivity but rather requires a mechanism that explains reflectance without altering . The model of light emission from graphene introduced in this section serves as an illustration of such a mechanism. Our model inherently incorporates the crucial concept of wave interference, specifically coherence or incoherence, as the initial phase of light emitted from each graphene layer.
3.1. Basic Idea
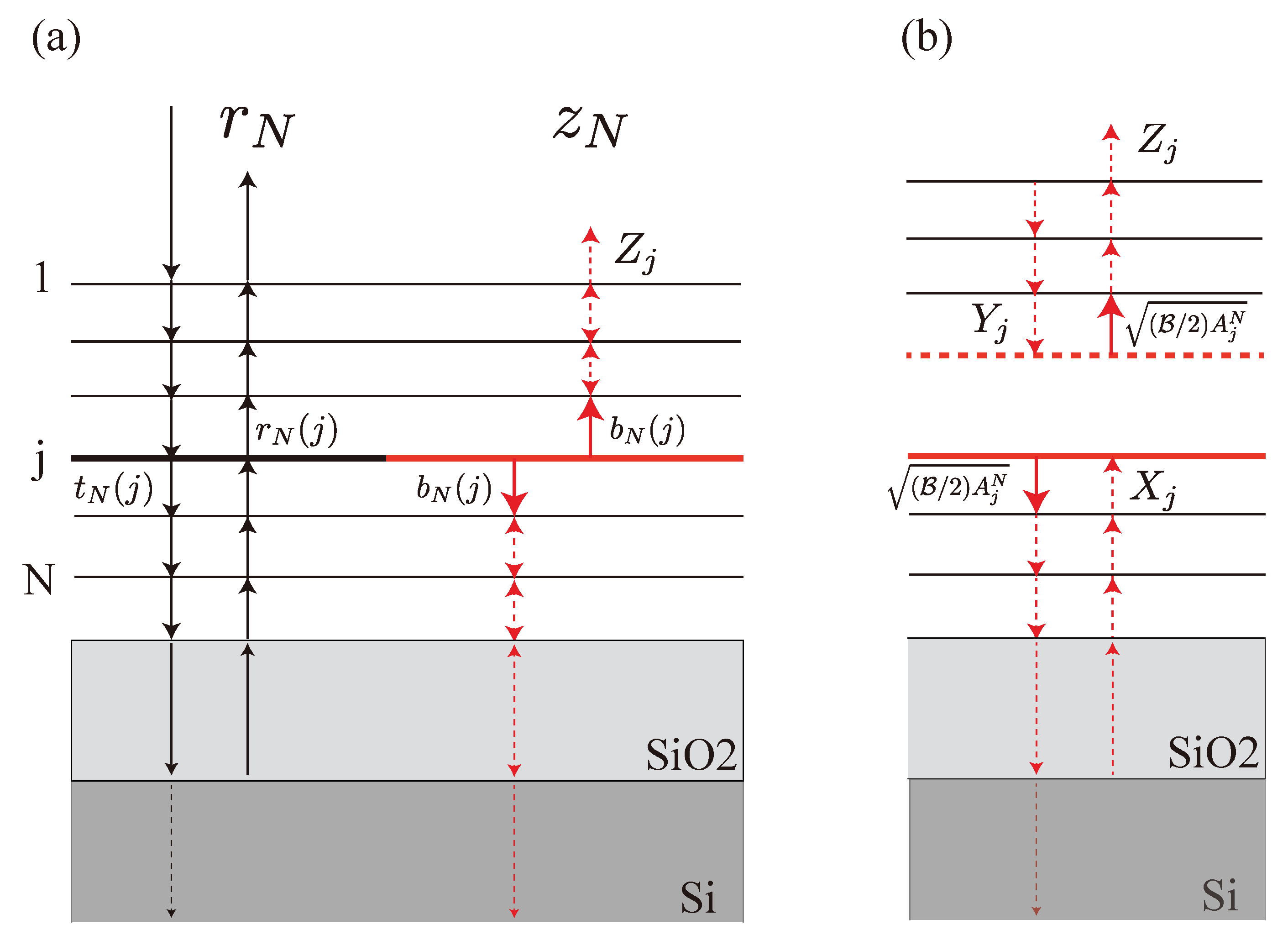
Figure 5a illustrates our model of reflection, where horizontal lines on the substrate represent N-layer graphene, and the vertical lines depict light rays with arrows indicating the directions of light propagation. The light rays on the left side (black in color) of Figure 5a show the primary processes of reflection (excluding contributions from light emission). In this process, incident light from a light source is transmitted and reflected by graphene, while some energy of light being absorbed by each layer. The reflection coefficient, , is calculated from a primary model which is defined in Section 4.2. The light rays on the right side (red in color) correspond to the light emission. Suppose that the jth layer emits light. The emitted light is transmitted and reflected by graphene until the light escapes the system, and it contributes to the reflectance of the system. Thus, there is another “reflection coefficient” when N-layer graphene emits light which is defined in Section 4.3. Let denotes the sum over such amplitudes from all layers. Once we know what and are, then the reflectance is given by .
We use a transfer matrix method to calculate and . [21,34] Transfer matrix method is useful in calculating reflection (up arrow) and transmission (down) coefficients at each layer [ and in Figure 5a] in addition to the electric field () that determines the absorption of the jth layer as . The total absorption of N-layer graphene is . [21]
3.2. Primary model
Basically, primary model means the Fresnel equation of Equation (1) where is given by Equation (2). has a single unknown constant which can be estimated from the following observations. Ultimately, we conclude that .
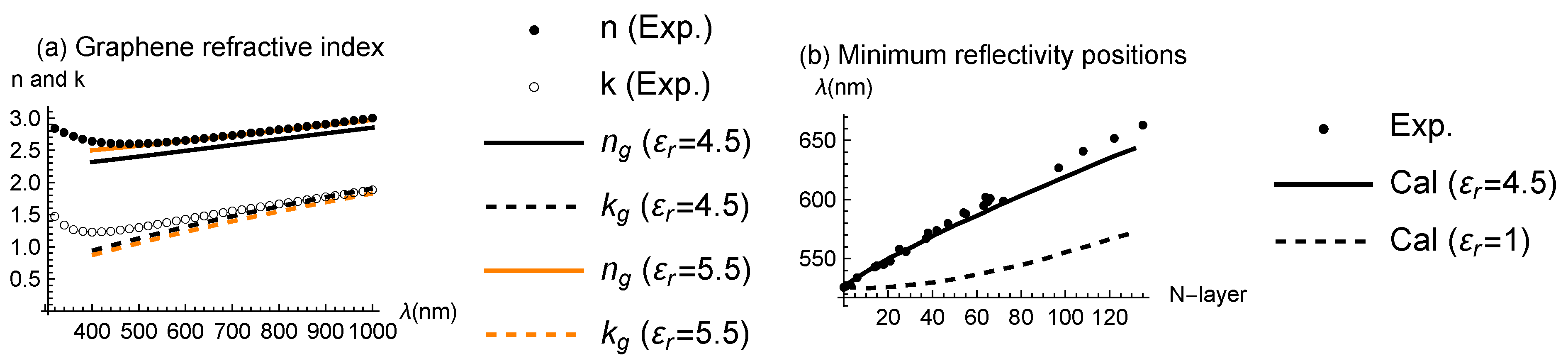
First, there must not be a large discrepancy between and the experimentally determined optical constants [19,41]. Experimental values for n and k [19] are shown as • and ∘ in Figure 6a. The lines depict (bare) optical constants plotted using Equation (2) with the refractive index and absorption coefficient for and 5.5. When , but n has a certain difference from . When , but k has a certain difference from . Because increases with increasing while decreases, there is no value that can reproduce n and k simultaneously. This suggests that there should be such a discrepancy between them which is attributed to the corrections by light emission. Second, has to roughly reproduce the behavior of the reflectance of multilayer graphene. It exhibits a minimum at a certain wavelength, primarily due to destructive interference caused by SiO2. As shown in Figure 6b, the position is red-shifted by increasing N, indicating that even thin graphite samples significantly impact the light interference effect. When , the position changes little, and a sizable artificial shift in wavelength is needed to ensure consistency between theory and experiment, which cannot be explained as a correction. When , a small difference between theory and experiment still remains. However, as we show later, the corrections provide better agreement not only for the wavelengths giving minimum reflectivity but also for the minimum reflectivity values, thus accounting for the difference. Third, roughly reproduces the reflectivity of graphite in the infrared region [42]. Similar values have been used to reproduce the observed reflectivities of graphite and graphene [18,19,41]. We note that the value of is less than the magnitude of the imaginary part of , since visible light has a much longer (400∼800 nm) than d, although is certainly a small quantity. The optical properties of multilayer graphene are thus characterized by the large imaginary part of .
Figure 4.
of the primary model (a) Experimental n and k values are represented by dots, taken from Ref. [19]. The lines depict bare optical constants without corrections. (b) Dots indicate measured wavelengths corresponding to the minimum reflectance. A comparison between the measured and calculated results suggests that is a reasonable value.
Figure 4.
of the primary model (a) Experimental n and k values are represented by dots, taken from Ref. [19]. The lines depict bare optical constants without corrections. (b) Dots indicate measured wavelengths corresponding to the minimum reflectance. A comparison between the measured and calculated results suggests that is a reasonable value.
4. Corrections to Reflectance by Light Emission
A substantial correction to the dynamical conductivity is deemed impermissible because, if allowed, it would result in an inconsistency with the experimental observation that a (suspended) monolayer graphene absorbs approximately 2.3 percent () of the incident visible light [32]. An accurate theory capable of describing the reflectance does not necessitate corrections to dynamical conductivity but rather requires a mechanism that explains reflectance without altering . The model of light emission from graphene introduced in this section serves as an illustration of such a mechanism. Our model inherently incorporates the crucial concept of wave interference, specifically coherence or incoherence, as the initial phase of light emitted from each graphene layer.
4.1. Basic Idea
Figure 5a illustrates our model of reflection, where horizontal lines on the substrate represent N-layer graphene, and the vertical lines depict light rays with arrows indicating the directions of light propagation. The light rays on the left side (black in color) of Figure 5a show the primary processes of reflection (excluding contributions from light emission). In this process, incident light from a light source is transmitted and reflected by graphene, while some energy of light being absorbed by each layer. The reflection coefficient, , is calculated from a primary model which is defined in Section 4.2. The light rays on the right side (red in color) correspond to the light emission. Suppose that the jth layer emits light. The emitted light is transmitted and reflected by graphene until the light escapes the system, and it contributes to the reflectance of the system. Thus, there is another “reflection coefficient” when N-layer graphene emits light which is defined in Section 4.3. Let denotes the sum over such amplitudes from all layers. Once we know what and are, then the reflectance is given by .
Figure 5.
Model description (a) The primary (left side) and secondary (right side) processes involved in the reflection are physically interconnected through light absorption at each graphene layer. (b) The self-consistent calculation of is explained in detail in the text.
Figure 5.
Model description (a) The primary (left side) and secondary (right side) processes involved in the reflection are physically interconnected through light absorption at each graphene layer. (b) The self-consistent calculation of is explained in detail in the text.
We use a transfer matrix method to calculate and [21,34]. Transfer matrix method is useful in calculating reflection (up arrow) and transmission (down) coefficients at each layer [ and in Figure 5a] in addition to the electric field () that determines the absorption of the jth layer as . The total absorption of N-layer graphene is . [21]
4.2. Primary Model
Basically, primary model means the Fresnel equation of Equation (1) where is given by Equation (2). has a single unknown constant which can be estimated from the following observations. Ultimately, we conclude that .
First, there must not be a large discrepancy between and the experimentally determined optical constants [19,41]. Experimental values for n and k [19] are shown as • and ∘ in Figure 4a. The lines depict (bare) optical constants plotted using Equation (2) with the refractive index and absorption coefficient for and 5.5. When , but n has a certain difference from . When , but k has a certain difference from . Because increases with increasing while decreases, there is no value that can reproduce n and k simultaneously. This suggests that there should be such a discrepancy between them which is attributed to the corrections by light emission. Second, has to roughly reproduce the behavior of the reflectance of multilayer graphene. It exhibits a minimum at a certain wavelength, primarily due to destructive interference caused by SiO2. As shown in Figure 4b, the position is red-shifted by increasing N, indicating that even thin graphite samples significantly impact the light interference effect. When , the position changes little, and a sizable artificial shift in wavelength is needed to ensure consistency between theory and experiment, which cannot be explained as a correction. When , a small difference between theory and experiment still remains. However, as we show later, the corrections provide better agreement not only for the wavelengths giving minimum reflectivity but also for the minimum reflectivity values, thus accounting for the difference. Third, roughly reproduces the reflectivity of graphite in the infrared region [42]. Similar values have been used to reproduce the observed reflectivities of graphite and graphene [18,19,41]. We note that the value of is less than the magnitude of the imaginary part of , since visible light has a much longer (400∼800 nm) than d, although is certainly a small quantity. The optical properties of multilayer graphene are thus characterized by the large imaginary part of .
Figure 6.
of the primary model (a) Experimental n and k values are represented by dots, taken from Ref. [19]. The lines depict bare optical constants without corrections. (b) Dots indicate measured wavelengths corresponding to the minimum reflectance. A comparison between the measured and calculated results suggests that is a reasonable value.
Figure 6.
of the primary model (a) Experimental n and k values are represented by dots, taken from Ref. [19]. The lines depict bare optical constants without corrections. (b) Dots indicate measured wavelengths corresponding to the minimum reflectance. A comparison between the measured and calculated results suggests that is a reasonable value.
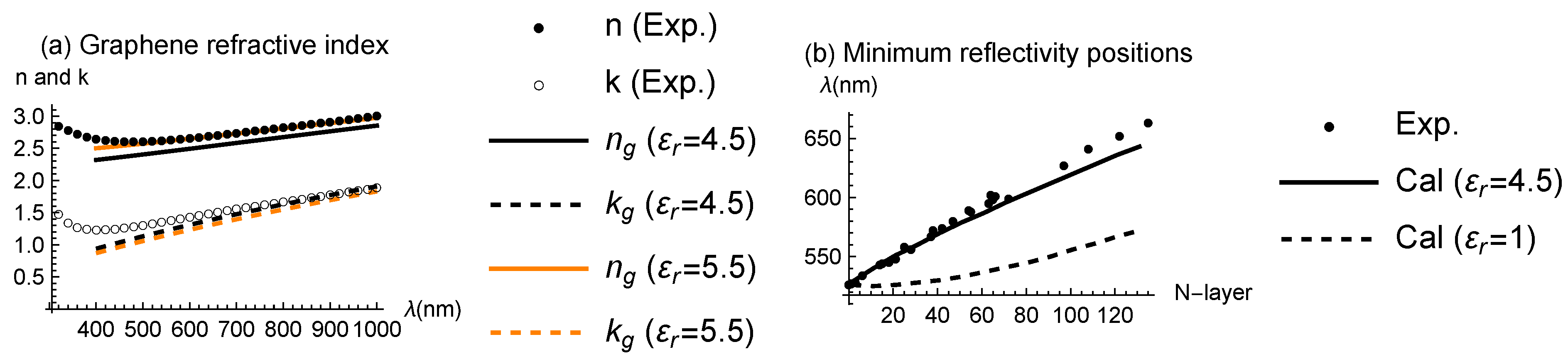
4.3. Model of Light Emission
The corrections to the reflectance are the main subjects of this paper [9,10]. Specifically, we consider corrections where some fraction of the energy absorbed by the jth layer (of N-layer graphene) is transferred to light emitted from that layer [see the right side of Figure 3(a)]. The amplitude of the emitted light is assumed to be the square root of the layer absorption ,34] multiplied by the branching ratio, , i.e., , where means that the light emission is direction-independent along the c-axis. Note that depends not only on j and N but also on and .
To examine how light emitted from the jth layer affects the reflectance, we define two subsystems, as shown in Figure 7b: one is an isolated -layer graphene in the air; the other is -layer graphene on SiO2/Si substrate. Using the transfer matrix method, we can obtain the transmission and reflection coefficients of an isolated -layer graphene in the air [denoted as and ] and the reflection coefficient of -layer graphene on the SiO2/Si substrate [denoted as ] [21,34]. Let the reflection coefficients be and and transmission coefficient be for the combined subsystems [see Figure 7b]. These can be obtained by a self-consistent manner as follows. After calculating , we add it to of the incident light to the -layer graphene (in the air) as and recalculate and . Then, we add a new to of the light incident to the -layer graphene on the SiO2/Si substrate as and recalculate . These computations are repeated until and converge. In this way, we can obtain analytical expressions for the converged , , and for a given :
The “corrected” electric fields at an infinitesimal distance above and below the jth layer become and , respectively. Self-consistency, whereby and , is therefore essential to ensuring that the corrected electric field is continuous at the jth layer, which is a requirement of Maxwell equations. The corrected amplitude of the emitted light is written as
By comparing this with , we see that more accurate value of the amplitude of the emitted light is given by multiplying with as the renormalization constant, and is what in Figure 3(a) represents. Therefore, we redefine as
We can interpret as follows. The transmission coefficient is the direct propagation of the renormalized light emitted from jth layer to the air, and monotonously decreases with increasing j [21]. The effects of scattering and absorption of the emitted light caused by surrounding layers is included by the part in the brace . It tends to suppress the magnitude of , but sometimes enhance. For example, when (i.e., monolayer on a substrate), the part becomes which is larger than unity when is positive.
is the value at zero initial phase, so the transmission coefficient can be given a phase degree of freedom expressing the coherence or incoherence of the light emission from the different layers:
Accordingly, the corrected reflectance is uniquely determined by . The value of depends on these phases [43].
We consider a case in which the phase is given by a coherent phase. The exact derivation of the phase will be shown elsewhere because it is beyond the scope of the present paper. Here, we concisely explain the basic logic leading to the coherent phase in terms of quantum electrodynamics. First, we can define a quantum mechanical state of light () that the primary model describes (see left side of Figure 5). All the information of light is expressed by the coefficients and (). Second, we can also define another quantum state of light () for the emitted light (see right side of Figure 5). All the information of emitted light is expressed by the coefficients . These two states have an overlap caused by jth layer graphene. Thus, if we consider a linear superposition of these states as to form energy eigenstates, the phase must be chosen so that becomes a real number, namely
The factor ± is a global phase () in the sense that it is independent of the value of j. Because the scattered light () and the emitted light () form a two-level state, there are two possible linear superpositions of their energy eigenstates, () or (). The minus sign () is assigned to the lower energy state. From Equations (5) and (8), we obtain .
Including the correction due to coherent light emission leads to
where is the branching ratio of the energy of the emitted coherent photons to that of the absorbed photons. Since coherent photon emission is related to the electron-photon coupling strength of the annihilated photo-excited electron-hole pairs, should be on the order of and insensitive to changes in N.
Next, we apply to the case that in is a random variable. Here, the definition of randomness is that if we take the time average regarding , we have and . We will refer to this case as incoherent corrections, which also include the cases that the global phase takes 0 and if there is a perturbation that can mix the two energy levels. An interference term is now included in as the last term of
but it vanishes when taking the time average and only the first term of the incoherent corrections remains. [44] Inelastic scattering of light such as Raman scattering is usually considered to give rise to incoherent photons. Let be the branching ratio of the energy of the emitted incoherent photons to that of absorbed photons. Since is proportional to [Equation (3)], the incoherent corrections are proportional to . For Raman scattering, the parameter is fundamentally determined by the electron-photon and electron-phonon coupling strengths, and it should not be so sensitive to the change in N. Indeed, the incoherent corrections with a constant follow the measured N dependence of the G band Raman intensity [Section 5.3]. The G band consists of optical phonons at the point, whose lattice vibrations are in-plane.
A generalized reflection formula covering the above two cases (coherent and incoherent corrections) can be written as
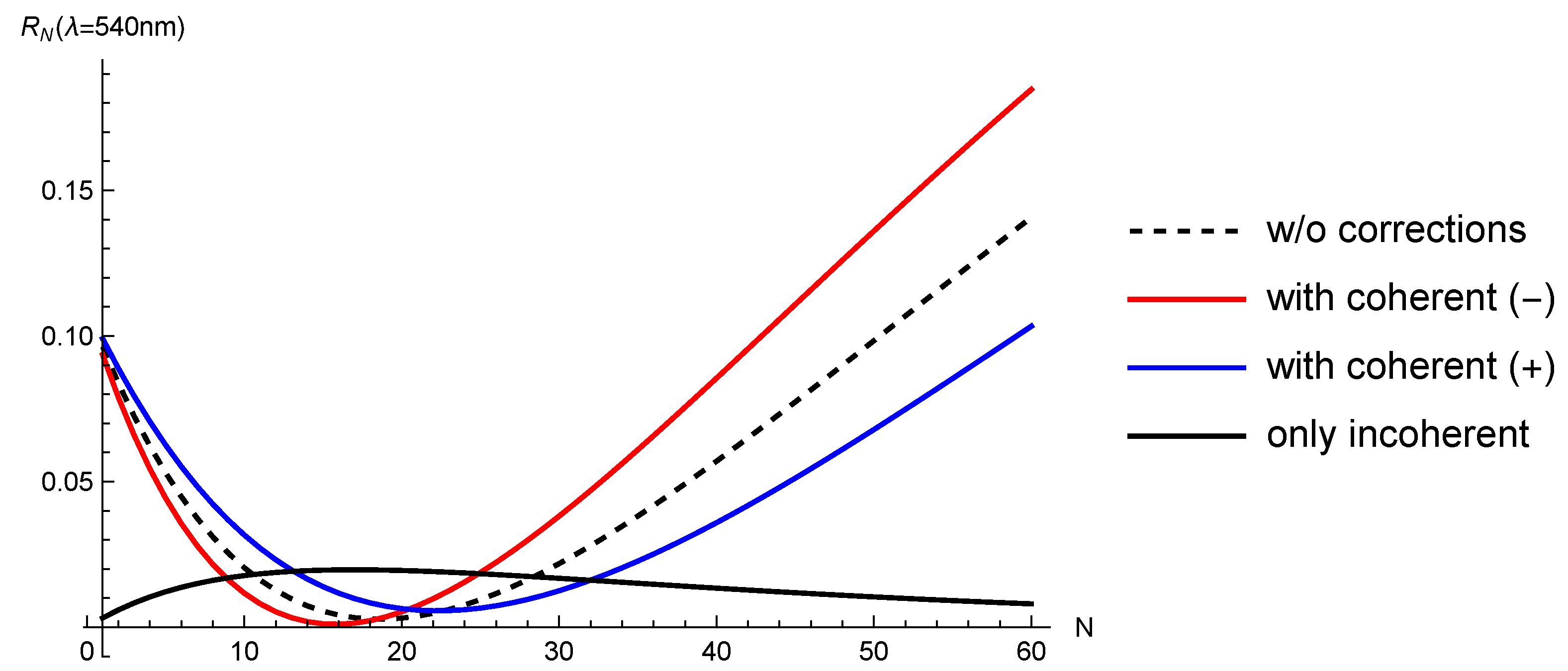
When , reduces to Equation (1) with Equation (2). Figure 7 shows the N dependence of (dashed), (red), (blue), and (black), for a fixed nm. Note that the incoherent corrections always increase the reflectance and preclude zero reflections at , which is in contrast to the coherent corrections. Moreover, the G band Raman intensity is enhanced when zero reflection occurs [10,45,46,47]. This situation is called interference-enhanced Raman scattering, [9] and it is reasonably reproduced by Equation (11). The experimental fact that zero reflection is observed at [see 14 and 15-layer in Figure 1] shows that , is much smaller than 0.1, and (red curve in Figure 7).
Figure 7.
Reflectance of N-layer graphene on SiO2/Si substrate. Dependence of the corrections to [Equation (11)] on N, where nm, , and the global phase is − or +. The incoherent components are enhanced (which is called interference-enhanced Raman scattering) at around 20 layers.
Figure 7.
Reflectance of N-layer graphene on SiO2/Si substrate. Dependence of the corrections to [Equation (11)] on N, where nm, , and the global phase is − or +. The incoherent components are enhanced (which is called interference-enhanced Raman scattering) at around 20 layers.
5. Applications of Model
In this section, we show that the discrepancy between the measured reflectance of multilayer graphene [Figure 1] and the prediction of the model [Equation (11)] is sufficiently small for the present purpose. Our model is, therefore, nearly equivalent to the Fresnel equation with the experimental optical constants (n and k), [19] while our model can describe the interesting aspects of reflection. Using monolayer graphene, we provide a detailed explanation of the mechanism modifying the reflectance without introducing any artificial change in the dynamical conductivity. To showcase the versatility of our model, we also explore Raman scattering as incoherent corrections.
5.1. Comparison of Theory and Experiment
Calculated contrasts are shown in Figure 8 as red solid curves, which include coherent corrections only (i.e., ). Green dashed curves represent the primary model of Equation (1), which does not include any corrections due to light emission. All calculations were performed with , where this value was chosen so that we could obtain good agreement between the calculations and observations for all layers. Note that this value is consistent with zero reflection being observed for .
From the consistency between the calculated and measured contrasts shown in Figure 8 (except and ), we can draw two main conclusions. First, the phase () of the coherent corrections is essential. If we adopt 0 phase (), a serious discrepancy arises, as can be readily imagined from the relative location of the red solid curves with respect to the green dashed ones. Second, the incoherent corrections are rather small. In fact, for most of the layers examined (not shown in Figure 8), the incoherent corrections did not improve the fitting. Our estimated reasonable range of is less than 0.01.
Only for the 226-layer, there is a slight but non-negligible deviation of the red solid curve from the measured contrast. A relatively small difference between the red solid and green dashed curves shows that the strength of is suppressed and that is under some special phase balance by interference for . Thus, a slight shift in might improve the fitting. For example, second order corrections which arise due to a self-consistent calculation of (and ) might be relevant to this.
5.2. Monolayer
Unfortunately, the Fresnel equation is inconsistent with the measured contrast of monolayer graphene (see in Figure 1), probably because reflectance depends on the condition of the interface between graphene and substrates. However, as we have carefully confirmed that almost all the information of the corrections from the emitted light is included in the reflectance of monolayer graphene, we believe that the contrast calculated from the Fresnel equation with the experimental n and k values is the result that we should compare with the model.
In Figure 9a, we present simulated (black dotted) and calculated (green dashed and red solid) spectral contrasts of monolayer graphene on the SiO2/Si substrate. Clearly, the corrections are of physical significance; black dots and red solid curve almost perfectly match. In , becomes a positive number only near as shown in Figure 9c. This is due to the destructive interference caused by SiO2, which also increases the absorption because . This enhanced absorption leads to the main difference between the reflectances from the substrate () and from the graphene on it (), increasing the visibility of graphene. The correction due to light emission is a negative number due to the negative global phase of an energetically stable configuration of light. Thus, the corrections increase . Namely, the increase in the visibility of graphene is mainly due to the substrate-induced enhancement of light absorption and is partly due to light emission.
It is important to note that the primary model can explain the measured contrasts if is more than 20 percent larger than . However, this immediately leads to an inconsistency with the experimental fact that (suspended) monolayer graphene absorbs percent () of the incident visible light [32]. Additionally, the primary model with such corrections to does not reproduce the measured contrasts of many samples with different thickness. Furthermore, the primary model is not applicable to the Raman effect, while our model can include it in a natural way, as shown below.
5.3. Raman Scattering as Incoherent Corrections
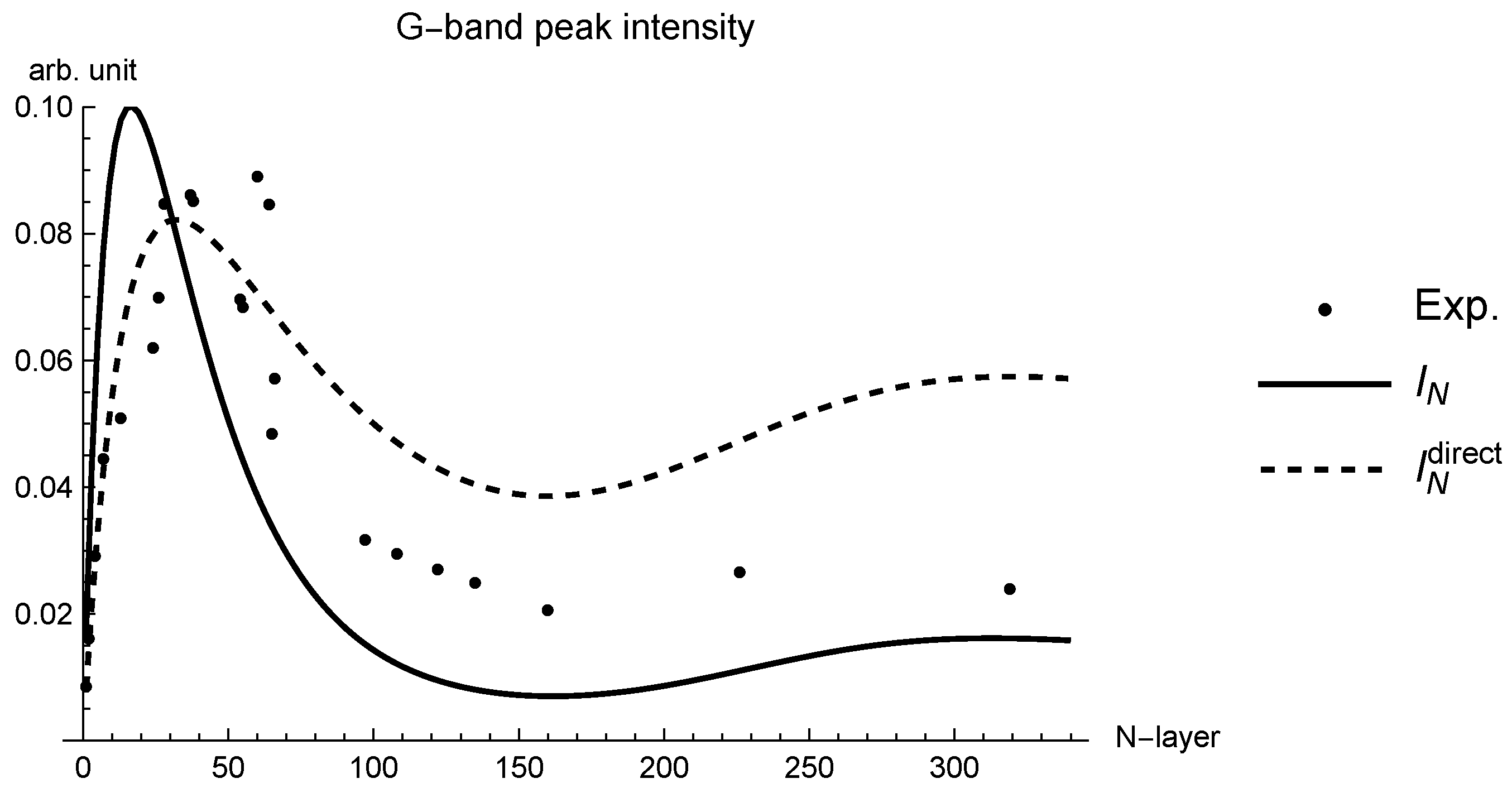
We measured the G band Raman peak intensity as a function of layer number in order to verify the interpretation of Raman scattering being an incoherent light emission [10]. The incoherent correction is defined by the last term of Equation (11) as . is proportional to and does not depend on the value of when scaled. As shown in Figure 10, there is a reasonable similarity between the measured Raman intensity (dots) and calculated incoherent component (dashed curve). Also plotted is an approximation of (dot-dashed curve) defined by
to show the effect of multiple scattering of incoherent light. The approximation overestimates the intensity for thick samples, as readily imagined.
On the other hand, there is a noticeable discrepancy between them for samples with fewer than 30 layers, where there is a dip in the reflectance that is similar to the observation by No et al. [47]. The assumption of a random phase for in Equation (7) is a possible reason for the discrepancy, because random phases can undergo synchronization or entrainment [43]. An intermediate state of the phase that is neither random nor perfectly coherent may account for the behavior.
6. Discussion
There is a possibility that substrates play a decisive role in determining the selection of the two states specified by the global phase (0 and ). To see this, let us consider monolayer graphene suspended in the air. From Equation (1), the reflection and transmission coefficients (without substrates) are and , and the absorption is given by . Light emission modifies the reflection coefficient as follows:
The magnitude of the second term is 0.0028 when which is about 25 percent the magnitude of the first term (0.011). The reflection increases or decreases depending on . When (0), the correction term is negative (positive) in sign; therefore, the light emission increases (decreases) the reflectance. Mathematically speaking, the change in the reflectance is equivalent to a replacement of as . This immediately leads to an inconsistency with the experimental fact that suspended monolayer graphene absorbs percent (, the measured uncertainty is within 5 percent of ) of the incident visible light [32]. This inconsistency is resolved by considering that for graphene suspended in the air the states of and 0 are degenerate and the effect of light emission effectively disappear by interference. This contrasts with monolayer graphene on SiO2/Si substrates for which is selected.
Since coherent and incoherent emissions are two extreme cases (uniform and random) of the phase in Equation (7), a sharp distinction between the coherent and incoherent emissions is not always possible. The proper way to calculate the reflectance is to derive a dynamical model of at a microscopic level, [43,48] and use it to calculate . Especially in the case of monolayer, they are inseparable as
when and have some correlation. Then, the reflectance is always subject to fluctuations created by the last term (through electron-phonon interactions).
Our model postulates that the effect of the emitted light appears as a correction to the reflection (and transmission) coefficient, not as a correction to the dynamical conductivity. Meanwhile, spontaneous emission is generally treated as a loss, and it is often included as a phenomenological relaxation constant in the dynamical conductivity. For example, in Ref. [19], the authors introduce relaxation constants for Drude-Lorentz oscillator model to interpret the measured optical constants. However, an excessively large relaxation constant (or very short lifetime) for the Drude term (0.6 fs) already raises concerns about the naturalness of including such a relaxation parameter [49]. The justification of our postulate needs a theoretical clarification at a more fundamental level of quantum electrodynamics, which is capable of describing photon creation and annihilation, while the excellent agreement between the model and experiments clearly shows that this postulate works well. Our model is also consistent with a theoretical result that the dynamical conductivity is free from such a correction when graphene is undoped (i.e., charge neutrality condition is satisfied) [31]. Moreover, the model explains the N-dependence of the Raman intensity as the incoherent corrections (Section 5.3), besides the contrast, in a unified manner.
7. Conclusions
In summary, we succeeded in explaining the measured visible contrasts of multilayer graphene samples on an SiO2/Si substrate by including coherent light emissions that come from some fraction () of the absorbed photon energy. The coherent corrections are essential for assuring the consistency between theory and experiment, while the incoherent corrections can be neglected for the contrast.
Photo-excited electrons contribute insignificantly to light emission when they are distant from the bottom of the conduction band. Namely, the value of for those electrons would be suppressed. In fact, graphene lacks a bandgap and the branching ratio of coherent light emission to absorbed light is very small (). What we have argued for in this paper is corrections (to the main effect) that have small branching ratios. However, whether light emission from those electrons can be entirely neglected depends on various factors. Graphene serves as an interesting example where corrections are greatly enhanced by its large absorption. The destructive interference effect from the substrate and the multilayer-induced coherence are the means by which it is observable in the reflectance. Similar emission-based corrections could be anticipated for other layered materials without band gaps, and the method developed here may prove useful in accurately understanding their optical properties.
Our formulation of the reflectance using the transfer matrix method has a descriptive ability for layered materials having defects and irregularities. For this reason, and considering the success it has had in describing the reflectance of relatively simple systems (graphene multilayer at visible range), we believe that some future form of this theory may be useful in describing the optical properties of any layered material with or without a band gap.
Author Contributions
Conceptualization, K.S. and T.M.; sample preparation and measurment, M.K., T.Y., T.O. and T.M.; analysis, K.S., K.H. and M.K.; writing—original draft preparation, K.S.; writing—review and editing, K.S.; project administration, K.S. and T.M.; funding acquisition, T.M. All authors have read and agreed to the published version of the manuscript.
Acknowledgments
K. S thanks Y. Sekine, H. Endo, and Y. Taniyasu for raising helpful questions on this subject. Part of this work was supported by “Nanotechnology Platform Japan” of the Ministry of Education, Culture, Sports, Science and Technology (MEXT), Grant Number JPMXP09F21UT0045. The reflectance measurement was conducted in the Takeda Cleanroom with help of the Nanofabrication Platform Center of the School of Engineering, the University of Tokyo, Japan.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Measured Reflectivities
We performed the reflectivity measurements three times on the same sample (run 1, run 2, and run 3). All measurements were consistent in the sense that the measured reflectivities of N-layer graphene on the substrate () divided by that of the SiO2/Si substrate (), that is, the contrast (), were identical. Therefore, we compared with calculations in the main text. However, while of run 2 and run 3 were identical, of run 1 deviated from that of run 2 (run 3), as shown in Figure A1. The same contrast also means that the values of for run 2 and run 3 were identical, while for run 1 deviated from that of run 2 (run 3). The discrepancy between of run 1 and that of run 2 (run 3) was presumably brought about by a change in the focal point along the depth direction when a reference substrate was replaced with the target sample. This could change the incident light intensity and lead to a discrepancy in between run 1 and run 2 (run 3).
Figure A1.
Determination of SiO2 thickness. Measured (black [run 1] and gray [run 2 (run 3)] dots) and calculated (green and blue dashed curves) spectral reflectivities of N-layer graphene on the same SiO2/Si substrate. A white-light source was used, and the reflectivity was measured at room temperature. The horizontal axis is (nm), and the reliable range of our spectrometer is 450 to 800 nm.
Figure A1.
Determination of SiO2 thickness. Measured (black [run 1] and gray [run 2 (run 3)] dots) and calculated (green and blue dashed curves) spectral reflectivities of N-layer graphene on the same SiO2/Si substrate. A white-light source was used, and the reflectivity was measured at room temperature. The horizontal axis is (nm), and the reliable range of our spectrometer is 450 to 800 nm.
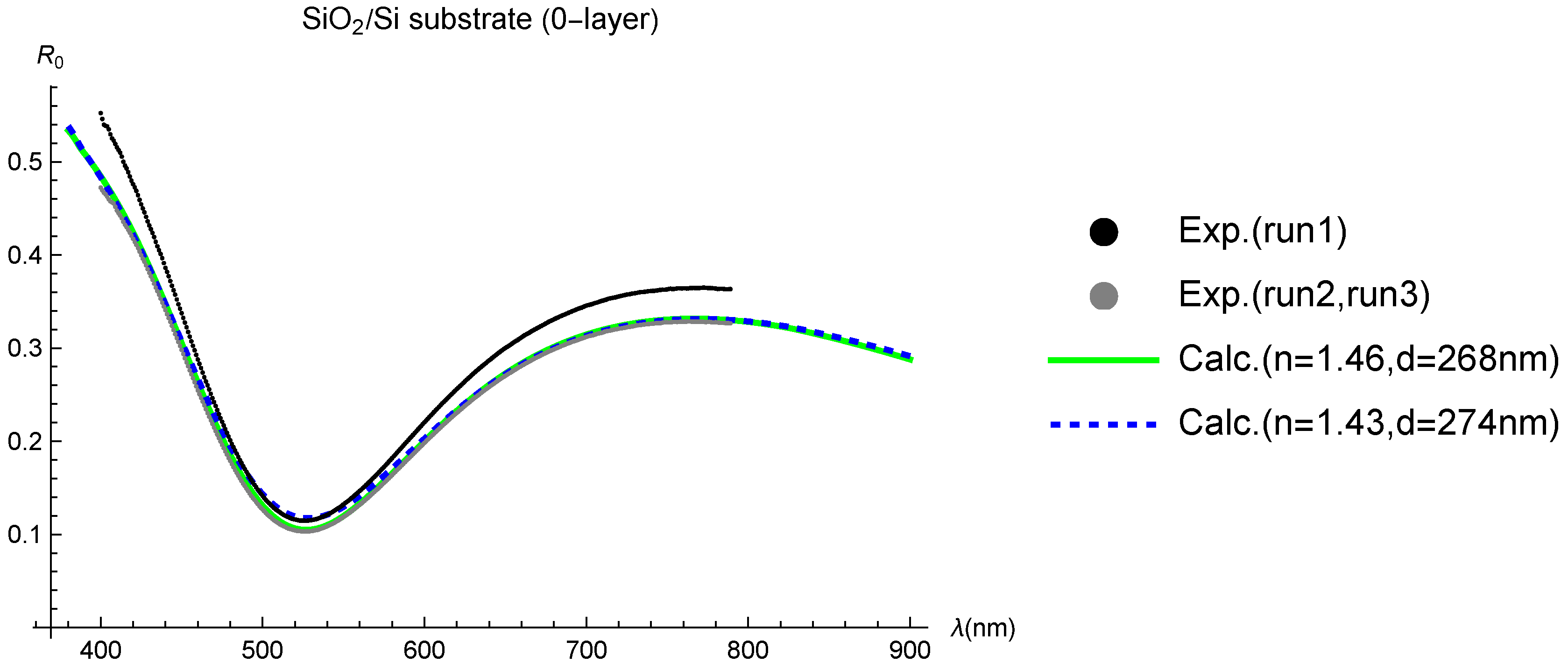
A problem arises when we determine the value of from . Considering that the wavelength giving the reflectivity minimum is the same for the three runs, we can determine nm by assuming that is the standard value (≃1.46) [29]. These parameters reasonably reproduce of run 2 (run 3) [Figure A1]. Meanwhile, 268 nm is inconsistent with another estimation using a reflectometer ( nm), which results in to reproduce the wavelength giving the reflectivity minimum by destructive interference (the same ). When we choose for nm, the corresponding is the (blue) dashed curve, which reproduces of run 1 around the reflectivity minimum (the two curves overlap from 460 to 560 nm) and approaches of run 2 (run 3) away from the reflectivity minimum ( nm and nm). Since is an acceptable value, we need to mindful of the possibility that a true is neither of run 1 nor that of run 2 (run 3). Because we have assumed that the refractive index of Si is the commonly used value, we keep the same standpoint for SiO2. Ultimately, we concluded that nm.
References
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Katsnelson, M.I.; Grigorieva, I.V.; Dubonos, S.V.; Firsov, A.A. Two-dimensional gas of massless Dirac fermions in graphene. Nature 2005, 438, 197–200. [Google Scholar] [CrossRef]
- Zhang, Y.; Tan, Y.W.; Stormer, H.L.; Kim, P. Experimental observation of the quantum Hall effect and Berry’s phase in graphene. Nature 2005, 438, 201–204. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Jiang, D.; Schedin, F.; Booth, T.J.; Khotkevich, V.V.; Morozov, S.V.; Geim, A.K. Two-dimensional atomic crystals. Proceedings of the National Academy of Sciences of the United States of America 2005, 102, 10451–10453. [Google Scholar] [CrossRef] [PubMed]
- Blake, P.; Hill, E.W.; Neto, A.H.C.; Novoselov, K.S.; Jiang, D.; Yang, R.; Booth, T.J.; Geim, A.K. Making graphene visible. Applied Physics Letters 2007, 91, 063124. [Google Scholar] [CrossRef]
- Roddaro, S.; Pingue, P.; Piazza, V.; Pellegrini, V.; Beltram, F. The optical visibility of graphene: Interference colors of ultrathin graphite on SiO2. Nano Letters 2007, 7, 2707–2710. [Google Scholar] [CrossRef] [PubMed]
- Ni, Z.H.; Wang, H.M.; Kasim, J.; Fan, H.M.; Yu, T.; Wu, Y.H.; Feng, Y.P.; Shen, Z.X. Graphene Thickness Determination Using Reflection and Contrast Spectroscopy. Nano Letters 2007, 7, 2758–2763. [Google Scholar] [CrossRef] [PubMed]
- Casiraghi, C.; Hartschuh, A.; Lidorikis, E.; Qian, H.; Harutyunyan, H.; Gokus, T.; S. Novoselov, K.; C. Ferrari, A. Rayleigh Imaging of Graphene and Graphene Layers. Nano Letters 2007, 7, 2711–2717. [Google Scholar] [CrossRef] [PubMed]
- Ghamsari, B.G.; Tosado, J.; Yamamoto, M.; Fuhrer, M.S.; Anlage, S.M. Measuring the Complex Optical Conductivity of Graphene by Fabry-Pérot Reflectance Spectroscopy. Scientific Reports 2016, 6, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Nemanich, R.J.; Tsai, C.C.; Connell, G.A.N. Interference-Enhanced Raman Scattering of Very Thin Titanium and Titanium Oxide Films. Physical Review Letters 1980, 44, 273–276. [Google Scholar] [CrossRef]
- Wang, Y.Y.; Ni, Z.H.; Shen, Z.X.; Wang, H.M.; Wu, Y.H. Interference enhancement of Raman signal of graphene. Applied Physics Letters 2008, 92, 043121. [Google Scholar] [CrossRef]
- Stöhr, R.J.; Kolesov, R.; Pflaum, J.; Wrachtrup, J. Fluorescence of laser-created electron-hole plasma in graphene. Physical Review B 2010, 82, 121408–1006. [Google Scholar] [CrossRef]
- Lui, C.H.; Mak, K.F.; Shan, J.; Heinz, T.F. Ultrafast photoluminescence from graphene. Physical Review Letters 2010, 105, 127404. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.T.; Wu, S.W.; Schuck, P.J.; Salmeron, M.; Shen, Y.R.; Wang, F. Nonlinear broadband photoluminescence of graphene induced by femtosecond laser irradiation. Physical Review B 2010, 82, 081408. [Google Scholar] [CrossRef]
- Suemoto, T.; Sakaki, S.; Nakajima, M.; Ishida, Y.; Shin, S. Access to hole dynamics in graphite by femtosecond luminescence and photoemission spectroscopy. Physical Review B - Condensed Matter and Materials Physics 2013, 87. [Google Scholar] [CrossRef]
- Riaz, A.; Pyatkov, F.; Alam, A.; Dehm, S.; Felten, A.; Chakravadhanula, V.S.; Flavel, B.S.; Kübel, C.; Lemmer, U.; Krupke, R. Light emission, light detection and strain sensing with nanocrystalline graphene. Nanotechnology 2015, 26, 325202. [Google Scholar] [CrossRef] [PubMed]
- Song, J.C.; Tielrooij, K.J.; Koppens, F.H.; Levitov, L.S. Photoexcited carrier dynamics and impact-excitation cascade in graphene. Physical Review B - Condensed Matter and Materials Physics 2013, 87, 155429–1209. [Google Scholar] [CrossRef]
- Massicotte, M.; Soavi, G.; Principi, A.; Tielrooij, K.J. Hot carriers in graphene-fundamentals and applications, 2021. [CrossRef]
- Castriota, M.; Politano, G.G.; Vena, C.; De Santo, M.P.; Desiderio, G.; Davoli, M.; Cazzanelli, E.; Versace, C. Variable Angle Spectroscopic Ellipsometry investigation of CVD-grown monolayer graphene. Applied Surface Science 2019, 467–468. [Google Scholar] [CrossRef]
- El-Sayed, M.A.; Ermolaev, G.A.; Voronin, K.V.; Romanov, R.I.; Tselikov, G.I.; Yakubovsky, D.I.; Doroshina, N.V.; Nemtsov, A.B.; Solovey, V.R.; Voronov, A.A. Optical Constants of Chemical Vapor Deposited Graphene for Photonic Applications. Nanomaterials 2021, 11, 1230. [Google Scholar] [CrossRef] [PubMed]
- Devang, P.; Simone, D.; Naga, A.P.; Kumar, S.; Ralph, K. Enhanced Broadband Photodetection with Geometry and Interface Engineered Nanocrystalline Graphite. In Adv. Sensor Res.; 2023; p. 2300134. [Google Scholar]
- Sasaki, K.; Hitachi, K. Universal layer number in graphite. Communications Physics 2020, 3, 90. [Google Scholar] [CrossRef]
- Hendry, E.; Hale, P.J.; Moger, J.; Savchenko, A.K.; Mikhailov, S.A. Coherent nonlinear optical response of graphene. Physical Review Letters 2010, 105, 097401. [Google Scholar] [CrossRef]
- Sun, Z.; Hasan, T.; Torrisi, F.; Popa, D.; Privitera, G.; Wang, F.; Bonaccorso, F.; Basko, D.M.; Ferrari, A.C. Graphene mode-locked ultrafast laser. ACS Nano 2010, 4, 803–810. [Google Scholar] [CrossRef] [PubMed]
- Mikhailov, S.A. Theory of the nonlinear optical frequency mixing effect in graphene. Physica E: Low-dimensional Systems and Nanostructures 2012, 44, 924–927. [Google Scholar] [CrossRef]
- Yang, H.; Guan, H.; Biekert, N.; Arefe, G.; Chang, D.C.; Sun, Y.; Yeh, P.C.; Liu, X.; Hong, S.Y.; Marion, I.D.; et al. Layer dependence of third-harmonic generation in thick multilayer graphene. Physical Review Materials 2018, 2, 071002. [Google Scholar] [CrossRef]
- Stauber, T.; Peres, N.M.R.; Geim, A.K. Optical conductivity of graphene in the visible region of the spectrum. Physical Review B 2008, 78, 085432. [Google Scholar] [CrossRef]
- Stauber, T.; Parida, P.; Trushin, M.; Ulybyshev, M.V.; Boyda, D.L.; Schliemann, J. Interacting Electrons in Graphene: Fermi Velocity Renormalization and Optical Response. Physical Review Letters 2017, 118. [Google Scholar] [CrossRef] [PubMed]
- Aspnes, D.E.; Studna, A.A. Dielectric functions and optical parameters of Si, Ge, GaP, GaAs, GaSb, InP, InAs, and InSb from 1.5 to 6.0 eV. Physical Review B 1983, 27, 985. [Google Scholar] [CrossRef]
- Malitson, I.H. Interspecimen Comparison of the Refractive Index of Fused Silica*,†. J. Opt. Soc. Am. 1965, 55, 1205–1209. [Google Scholar] [CrossRef]
- Anders, H. Thin Films in Optics; The Focal Press, 1965. [Google Scholar]
- Ando, T.; Zheng, Y.; Suzuura, H. Dynamical Conductivity and Zero-Mode Anomaly in Honeycomb Lattices. Journal of the Physical Society of Japan 2002, 71, 1318–1324. [Google Scholar] [CrossRef]
- Nair, R.R.; Blake, P.; Grigorenko, A.N.; Novoselov, K.S.; Booth, T.J.; Stauber, T.; Peres, N.M.R.; Geim, A.K. Fine Structure Constant Defines Visual Transparency of Graphene. Science 2008, 320, 1308–1308. [Google Scholar] [CrossRef]
- Kuzmenko, A.B.; van Heumen, E.; Carbone, F.; van der Marel, D. Universal Optical Conductance of Graphite. Physical Review Letters 2008, 100, 117401. [Google Scholar] [CrossRef]
- Sasaki, K.i. Layered Dynamical Conductivity for a Transfer Matrix Method ― Application to an N-layer Graphene. Journal of the Physical Society of Japan 2020, 89, 094706. [Google Scholar] [CrossRef]
- Taft, E.A.; Philipp, H.R. Optical Properties of Graphite. Physical Review 1965, 138, A197–A202. [Google Scholar] [CrossRef]
- Ichikawa, Y.H.; Kobayashi, K. Optical properties of graphite in the infrared region. Carbon 1966, 3, 401–406. [Google Scholar] [CrossRef]
- Dresselhaus, M.S.; Dresselhaus, G. Interpretation of infrared modulation spectroscopy data in graphite by the Slonczewski-Weiss- McClure band model. Physical Review B 1976, 13, 4635–4636. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Mostepanenko, V.M.; Petrov, V.M. Impact of chemical potential on the reflectance of graphene in the infrared and microwave domains. Physical Review A 2018, 98, 023809. [Google Scholar] [CrossRef]
- Fang, J.; Vandenberghe, W.G.; Fischetti, M.V. Microscopic dielectric permittivities of graphene nanoribbons and graphene. Physical Review B 2016, 94, 045318. [Google Scholar] [CrossRef]
- Rickhaus, P.; Liu, M.H.; Kurpas, M.; Kurzmann, A.; Lee, Y.; Overweg, H.; Eich, M.; Pisoni, R.; Taniguchi, T.; Watanabe, K.; et al. The electronic thickness of graphene. Science Advances 2020, 6. [Google Scholar] [CrossRef]
- Bruna, M.; Borini, S. Optical constants of graphene layers in the visible range. Applied Physics Letters 2009, 94, 031901. [Google Scholar] [CrossRef]
- Djurišić, A.B.; Li, E.H. Optical properties of graphite. Journal of Applied Physics 1999, 85, 7404–7410. [Google Scholar] [CrossRef]
- Kuramoto, Y. Chemical Oscillations, Waves, and Turbulence. 1984; 19. [Google Scholar] [CrossRef]
- Velson, N.V.; Velson, N.V.; Zobeiri, H.; Wang, X.; Wang, X. Rigorous prediction of Raman intensity from multi-layer films. Optics Express, Vol. 28, Issue 23, pp. 35272–35283 2020, 28, 35272–35283. [Google Scholar] [CrossRef]
- Yoon, D.; Moon, H.; Cheong, H.; Choi, J.S.; Choi, J.A.; Park, B.H. Variations in the Raman Spectrum as a Function of the Number of Graphene Layers. Journal of the Korean Physical Society 2009, 55, 1299–1303. [Google Scholar] [CrossRef]
- Li, X.L.; Qiao, X.F.; Han, W.P.; Lu, Y.; Tan, Q.H.; Liu, X.L.; Tan, P.H. Layer number identification of intrinsic and defective multilayered graphenes up to 100 layers by the Raman mode intensity from substrates. Nanoscale 2015, 7, 8135–8141. [Google Scholar] [CrossRef]
- No, Y.S.; Choi, H.K.; Kim, J.S.; Kim, H.; Yu, Y.J.; Choi, C.G.; Choi, J.S. Layer number identification of CVD-grown multilayer graphene using Si peak analysis. Scientific Reports 2018, 8, 1–9. [Google Scholar] [CrossRef]
- Dicke, R.H. Coherence in Spontaneous Radiation Processes. Physical Review 1954, 93, 99. [Google Scholar] [CrossRef]
- Toqeer, I.; Yaqoob, M.Z.; Ghaffar, A.; Alkanhal, M.A.S.; Khan, Y.; Aladadi, Y.T. Reflectance and transmittance of terahertz waves from graphene embedded into metamaterial structures. Journal of the Optical Society of America A 2021, 38. [Google Scholar] [CrossRef] [PubMed]
Figure 1.
Measured (black circles) and calculated (red solid) spectral contrasts of N-layer graphene on the same SiO2/Si substrate. The measurments were conducted using a white-light source at room temperature. The red solid curves were obtained from Equation (1) with using optical constants obtained by El-Sayed et al. [19] The horizontal axis is (nm), and the reliable range of our spectrometer is 450 to 800 nm.
Figure 1.
Measured (black circles) and calculated (red solid) spectral contrasts of N-layer graphene on the same SiO2/Si substrate. The measurments were conducted using a white-light source at room temperature. The red solid curves were obtained from Equation (1) with using optical constants obtained by El-Sayed et al. [19] The horizontal axis is (nm), and the reliable range of our spectrometer is 450 to 800 nm.
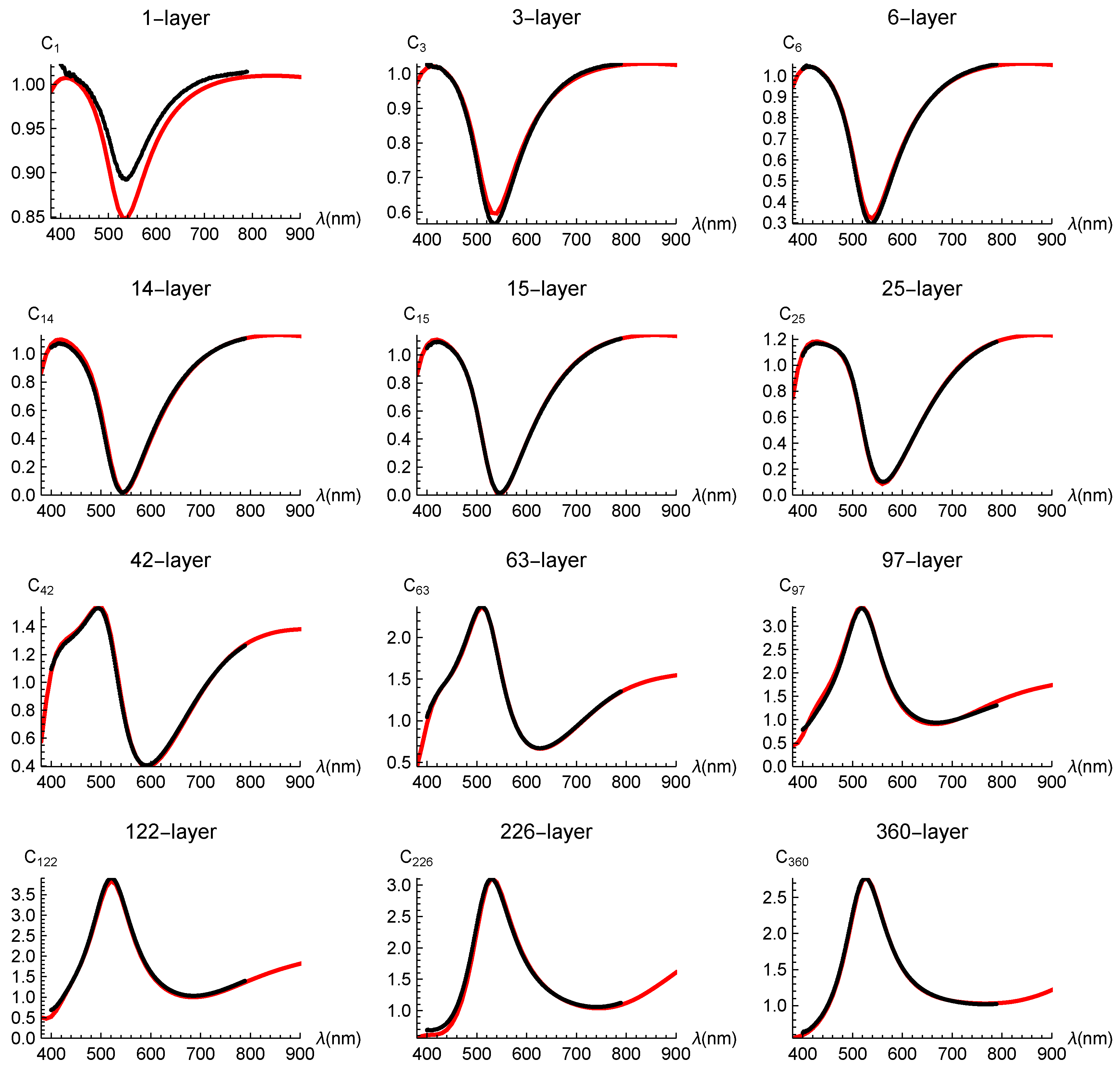
Figure 2.
Effective coupling constants. (a) Plot of calculated with the optical constants obtained by El-Sayed et al. [19]. The horizontal axis is (nm). (b) Plot of .
Figure 2.
Effective coupling constants. (a) Plot of calculated with the optical constants obtained by El-Sayed et al. [19]. The horizontal axis is (nm). (b) Plot of .
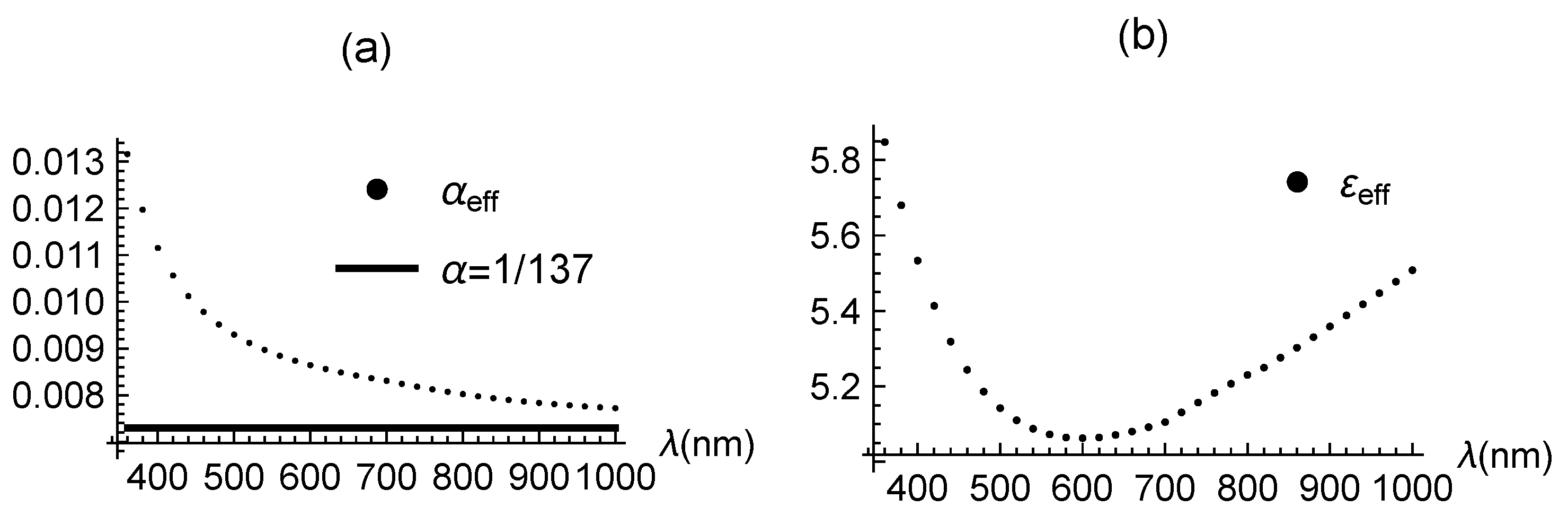
Figure 3.
Model description (a) The primary (left side) and secondary (right side) processes involved in the reflection are physically interconnected through light absorption at each graphene layer. (b) The self-consistent calculation of is explained in detail in the text.
Figure 3.
Model description (a) The primary (left side) and secondary (right side) processes involved in the reflection are physically interconnected through light absorption at each graphene layer. (b) The self-consistent calculation of is explained in detail in the text.
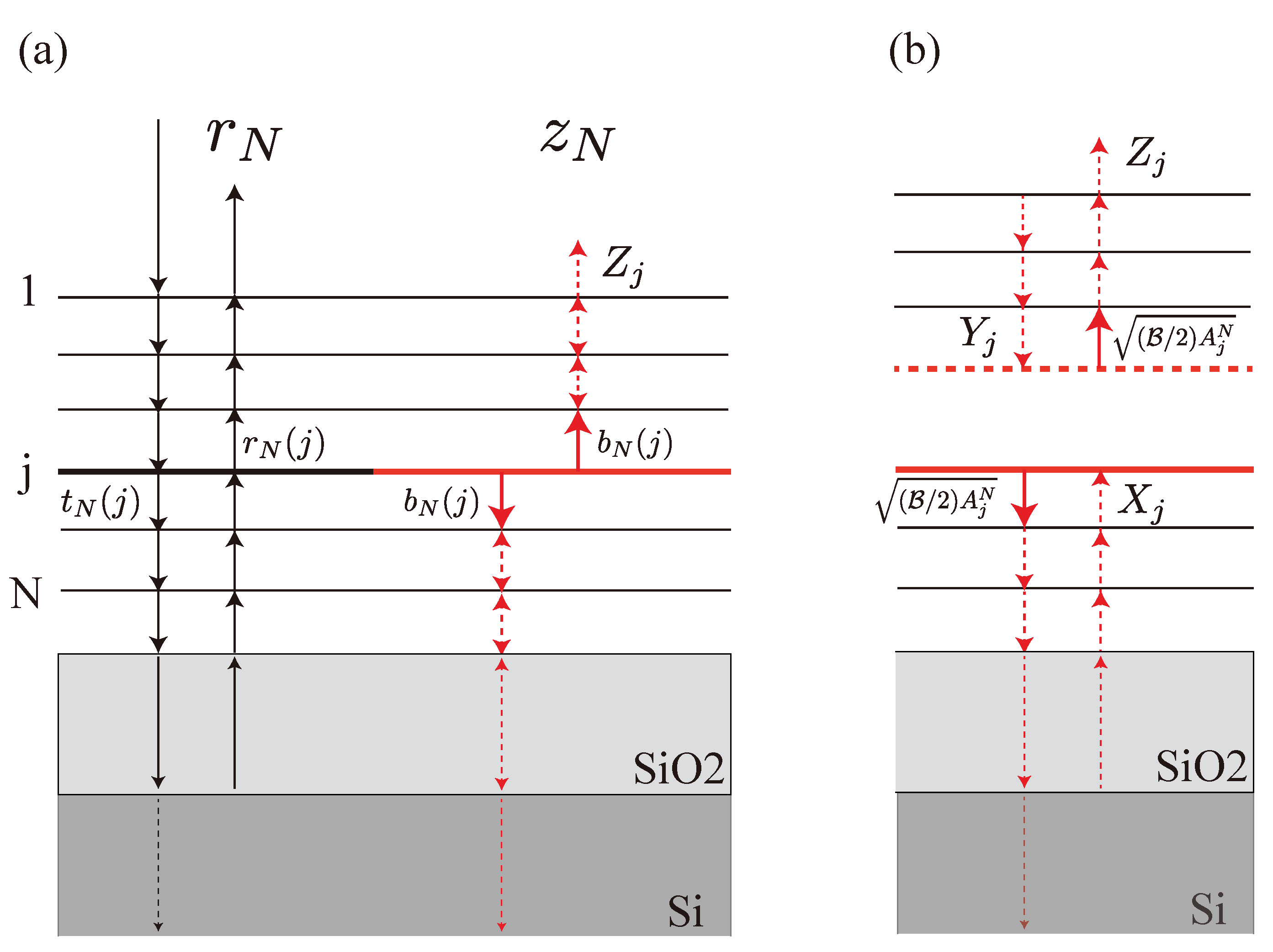
Figure 8.
Measured (black circles) and calculated (green dashed and red solid) spectral contrasts of N-layer graphene on the same SiO2/Si substrate. The green dashed curves represent the primary model [Equation (1) with Equation (2)] which does not include corrections. The red solid curves include coherent corrections. The horizontal axis is (nm), and the reliable range of our spectrometer is 450 to 800 nm.
Figure 8.
Measured (black circles) and calculated (green dashed and red solid) spectral contrasts of N-layer graphene on the same SiO2/Si substrate. The green dashed curves represent the primary model [Equation (1) with Equation (2)] which does not include corrections. The red solid curves include coherent corrections. The horizontal axis is (nm), and the reliable range of our spectrometer is 450 to 800 nm.
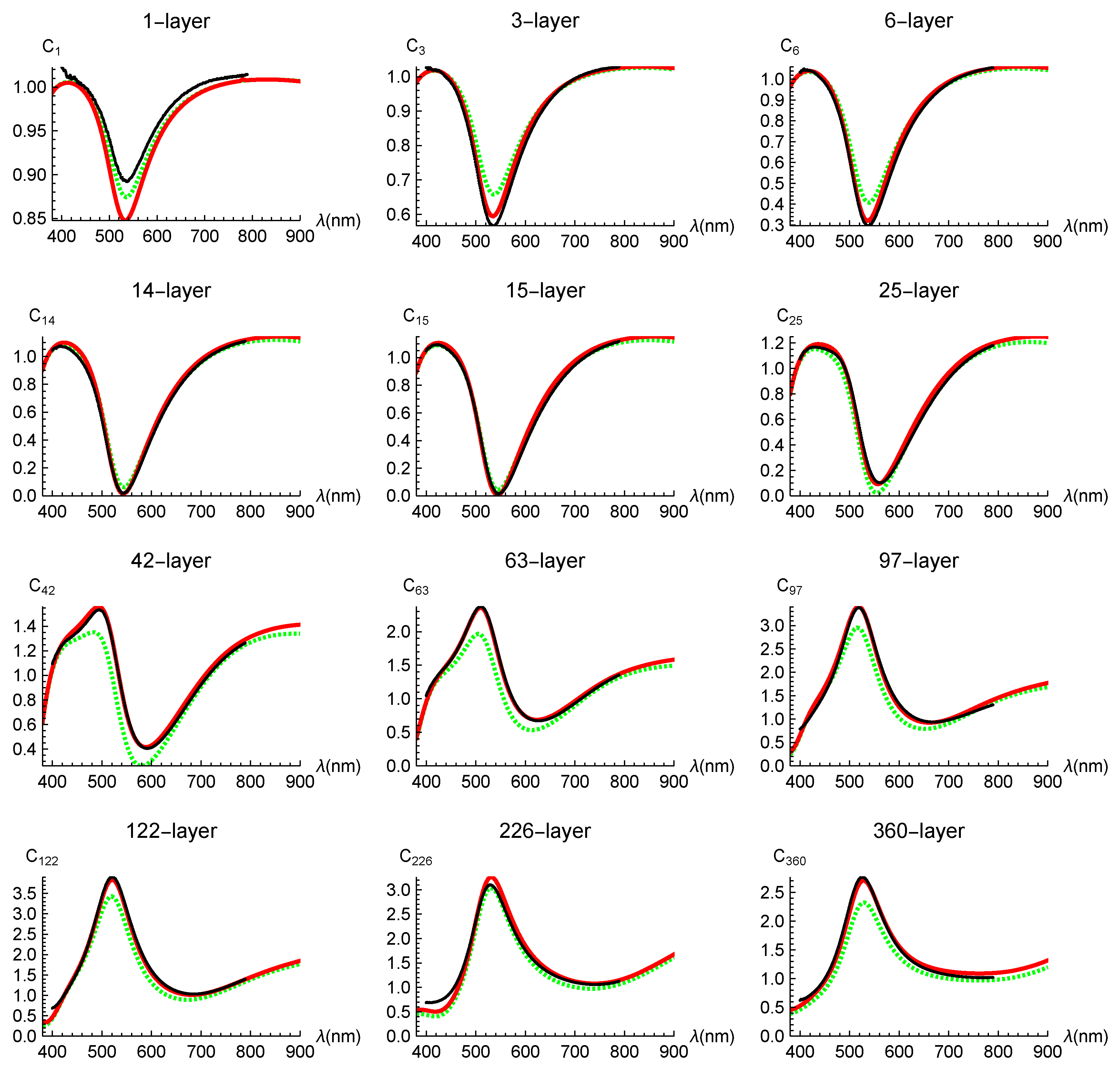
Figure 9.
Contrasts of monolayer graphene on SiO2/Si substrates. (a) One contrast is calculated using Equation (1) with the experimental (black dotted), while the other two curves are obtained using the model with corrections (red solid curve) and without corrections (green dashed curve). The increased visibility of graphene is primarily attributed to substrate-induced enhancement of light absorption and partly to light emission. (b) Layer absorption of monolayer graphene on SiO2/Si substrates . The destructive interference effect of the substrate enhances absorption near , where is a positive number (c).
Figure 9.
Contrasts of monolayer graphene on SiO2/Si substrates. (a) One contrast is calculated using Equation (1) with the experimental (black dotted), while the other two curves are obtained using the model with corrections (red solid curve) and without corrections (green dashed curve). The increased visibility of graphene is primarily attributed to substrate-induced enhancement of light absorption and partly to light emission. (b) Layer absorption of monolayer graphene on SiO2/Si substrates . The destructive interference effect of the substrate enhances absorption near , where is a positive number (c).
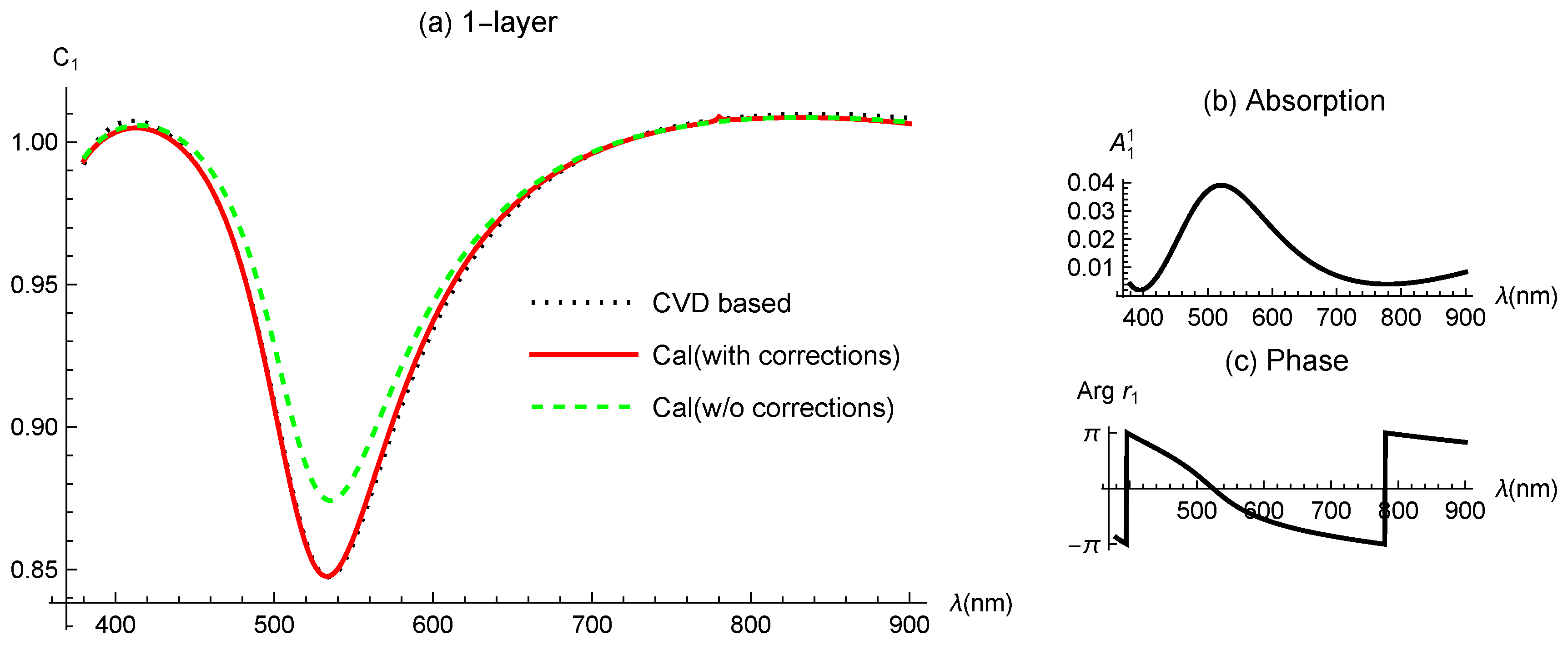
Figure 10.
Raman intensity as incoherent corrections. The dots represent the measured peak intensity of the Raman G band when using a light source with a wavelength of 532 nm. The dashed curve corresponds to the incoherent correction, while the dot-dashed curve is an approximation that ignores multiple scattering.
Figure 10.
Raman intensity as incoherent corrections. The dots represent the measured peak intensity of the Raman G band when using a light source with a wavelength of 532 nm. The dashed curve corresponds to the incoherent correction, while the dot-dashed curve is an approximation that ignores multiple scattering.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated





