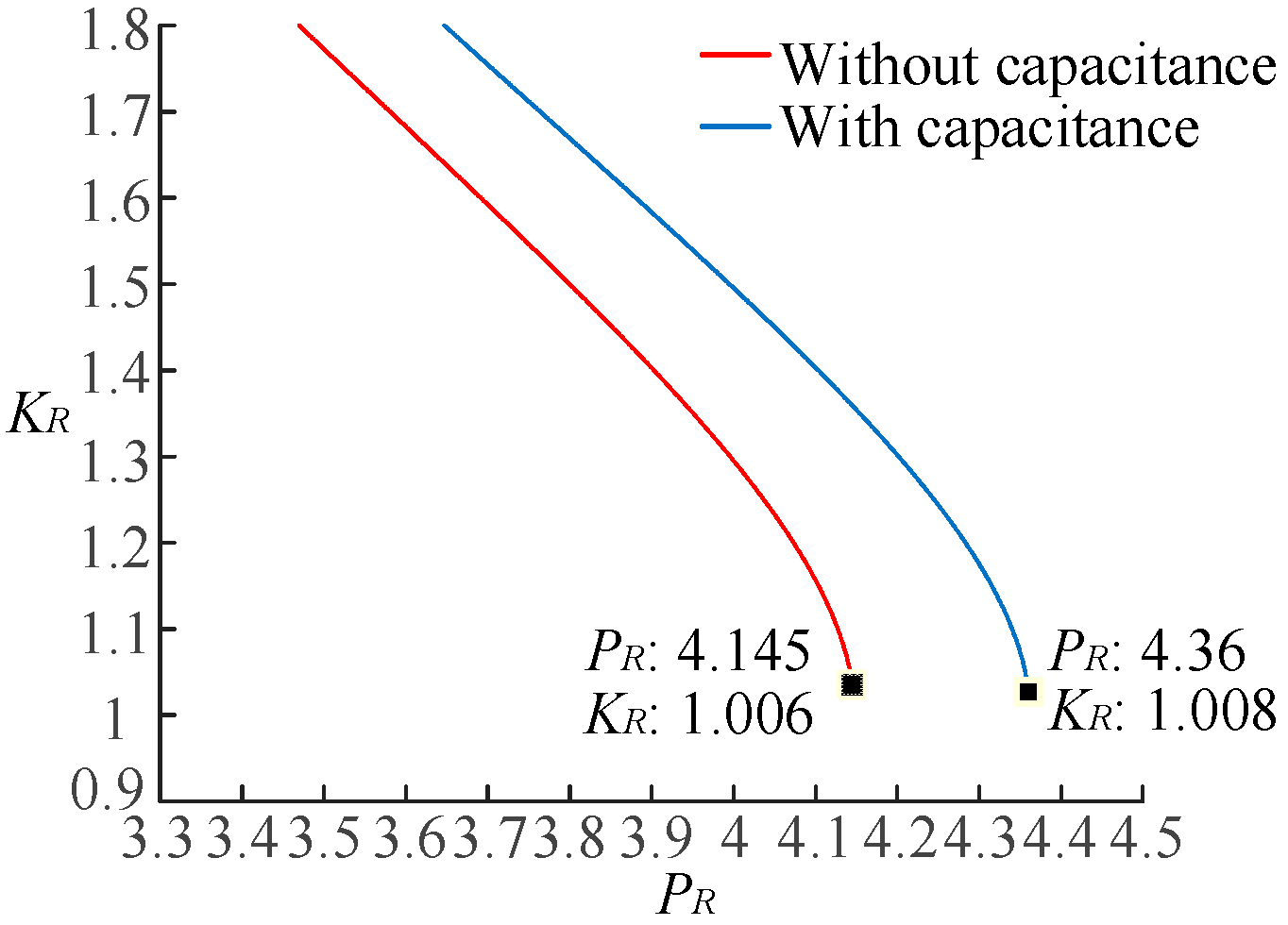Static Voltage Stability Analysis of Renewable Energy Integrated Distribution Power System based on Impedance Model Index

Static voltage stability has become one of the significant risks faced by large-scale renewable energy integration. However, traditional methods for static voltage stability analysis are often overly complex. This paper constructs an equivalent impedance model for renewable energy integrated distribution power systems, proposing a static voltage analysis method for renewable energy integrated distribution power systems based on impedance model index. This method has been verified to be applicable not only to renewable energy single-infeed system but also to multi-infeed system. Furthermore, an analysis is conducted on the influence of the integration capacity, location of renewable energy, and the topology of networks on impedance model index, indicating that a higher impedance model index corresponds to greater static voltage stability margins in the system. Hence, during the planning of renewable energy integration, the plan with the highest impedance model index should be selected. Finally, the accuracy of the analysis methods and conclusions in this paper was validated based on the IEEE 14-node system.

Keywords:

Subject: Engineering - Electrical and Electronic Engineering

1. Introduction

To reduce the proportion of fossil fuel consumption, the vigorous development of renewable energy sources, such as wind and solar power, along with high-capacity energy storage technologies, has become a future trend. The large-scale integration of renewable energy into distribution power systems leads to higher proportion of power electronic devices, lower system inertia, and reduced disturbance resilience in power systems [1]. These characteristics pose new challenges for the stable operation of modern distribution power systems.

In addressing power system stability issues, the joint authoritative working groups of IEEE and CIGRE proposed a definition and classification of traditional power system stability in 2004 [2], which gained widespread recognition in the field of power systems. However, with the integration of various renewable energy sources and a large number of power electronic devices, the stability of traditional power systems has been undergoing continuous changes. In response to this, the working group revised and extended the initial stability definition and classification in 2021 [3]. The updated version retained the concepts of angle stability, frequency stability, and voltage stability while introducing concepts like resonant stability and inverter-driven stability [4]. Thus, whether in traditional or modern power systems,angle stability [5], frequency stability [6], and voltage stability [7] remain core stability concerns. Voltage stability in power systems can be categorized into large disturbance voltage stability and small disturbance voltage stability. Large disturbance voltage stability refers to the voltage stability characteristics considering the dynamic response process of the power system under significant disturbances, often referred to as transient voltage stability. On the other hand, small disturbance voltage stability refers to the voltage stability characteristics under minor disturbances, often known as quasi-steady-state voltage stability or static voltage stability [8].

In recent decades, several major power outages caused by voltage instability have resulted in significant economic losses and widespread negative impacts. For instance, the "8·14" blackout in the United States and Canada in 2003 was triggered by an unexpected grid current reversal, leading to severe load increases in the receiving cities and subsequent voltage instability [9]. Another example is the "9·28" blackout in Australia in 2016, partially caused by the failure of wind turbine units to withstand consecutive low-voltage events, leading to voltage collapse and affecting around 1.7 million customers [10]. Many of these major blackouts were primarily caused by overloaded transmission lines or insufficient reactive power reserve, resulting in protective devices misoperation and uncontrollable cascading effects that exacerbated voltage instability, ultimately leading to large-scale power outages. Therefore, as the interconnection of renewable energy continue to grow, there is a need for further research and exploration of voltage stability in distribution power systems.

This paper establishes an equivalent network model for renewable energy integrated distribution power systems considering the equivalent characteristics of power injection from renewable energy. Subsequently, an impedance model index of renewable energy is proposed for assessing static voltage stability of distribution power systems. Furthermore, considering various network topologies and multi-infeed distribution power systems, a convenient method of calculating impedance model index is proposed. Finally, the selection of network topologies and connection nodes is presented using the impedance model index in different scenarios, verifying the correctness and effectiveness of the conclusions.

2. Introduction to Tradition Static Voltage Stability Analysis Methods

The essence of static voltage stability analysis is to determine whether there is a balance point between the static load model and network algebraic equations as a criterion for voltage collapse [11]. Commonly used methods include: 1) Singular Value Decomposition method [12], 2) Sensitivity Analysis method [13], 3) Continuation Power Flow method [14], 4) Voltage Collapse Point method [15], and 5) Bifurcation Theory method [16], etc.

2.1. Singular Value Decomposition Method

This method decomposes the Jacobian matrix into eigenvalues and eigenvectors, with the smallest eigenvalue representing the degree of singularity of the Jacobian matrix at the current operating point. This singularity indicates the distance between the operating point and the voltage instability point, known as the voltage stability margin, allowing for voltage stability analysis [17]. An improved Singular Value Decomposition method called Modal Analysis is proposed in [18], which uses the left and right eigenvectors (modal vectors) obtained from the Jacobian matrix eigen-decomposition to determine the reactive power-voltage sensitivity at nodes, identifying regions of voltage relative instability.

2.2. Sensitivity Analysis Method

Based on the power flow equations, sensitivity matrices are derived to analyze static voltage stability. Sensitivity coefficients are constructed to represent the relationships between control variables and state variables, where higher values indicate greater system instability. As the power system approaches the critical state of static voltage stability, the corresponding sensitivity tends to infinity, serving as an indicator of voltage proximity to collapse. In [19], voltage-reactive power sensitivity is considered, integrating it with static voltage stability margin to locate voltage weak areas. Addressing the issue of poor linearity near the critical state in complex large-scale power grids, [20] derives an analytical sensitivity relationship between static voltage stability margin and control quantities using Davison equivalent parameter identification, avoiding the need to compute the eigenvectors of the Jacobian matrix near the critical state.

2.3. Continuation Power Flow Method

By iteratively updating and calculating the power flow equations, this method resolves the power flow convergence problem when the power system is close to the critical state, thereby assessing the voltage stability margin. In [21], an extended power flow equation is employed to predict the cosine value changes of angle differences, adaptively adjusting the corresponding step size to quickly and effectively obtain the voltage stability margin. To enhance the engineering applicability of the Continuation Power Flow method for practical large-scale power grids, [22] combines Sensitivity Analysis, Minimum Singular Value method, and Fault-type Continuation Power Flow method through a three-stage progressive approach.

2.4. Voltage Collapse Point Method

By using augmented Jacobian matrix to extend the original power flow equations, the voltage limit points of the system are directly computed, avoiding ill-conditioning issues near the limit points [23]. In [24], the Continuation Power Flow method is first applied to approximate the voltage limit points, then switches to the Voltage Collapse Point method, enabling fast and accurate calculation of voltage stability limit points at the expense of computation time, solving the problem of initial value selection.

2.5. Bifurcation Theory Method

This method analyzes the sudden qualitative changes in voltage stability-related phenomena when certain parameters within the system undergo continuous slow changes and approach critical points. Bifurcation phenomena can be classified as saddle-node bifurcation, Hopf bifurcation, singularity-induced bifurcation, and limit-induced bifurcation, among others [25]. Saddle-node bifurcation falls within the scope of static voltage stability in power systems [26].

As shown in Table I, each of the traditional static voltage stability analysis methods has its unique strengths and limitations. The Singular Value Decomposition (SVD) method is suitable for rapid evaluation of voltage stability in large-scale power systems but relies on eigenvalue decomposition of the Jacobian matrix. The Sensitivity Analysis method identifies regions of voltage relative instability but requires resolving the sensitivity matrix computation and maintenance. The Continuation Power Flow method iteratively solves power flow distribution at critical states but has high computational complexity in iterative calculations. The Voltage Collapse Point method directly calculates system voltage limit points but involves complex augmented Jacobian matrix computations. The Bifurcation Theory method analyzes sudden qualitative changes near critical points but is sensitive to variations in system parameters. Therefore, in practical applications, the appropriate method for static voltage stability analysis of power systems can be chosen based on specific situations and requirements.

Table 1. Summary of advantages, disadvantages, and applicability of traditional static voltage stability analysis methods.

Method	Advantages	Disadvantages	Applicability
Singular Value Decomposition Method	Rapid assessment of voltage stability margin	Computation dependent on eigenvalue decomposition of the Jacobian matrix	Suitable for fast evaluation of voltage stability in large-scale power systems
Sensitivity Analysis Method	Identification of regions of voltage relative instability	Requires solving and maintaining the sensitivity matrix	Used to analyze the impact of control variables on system stability
Continuation Power Flow Method	Iterative calculation of power flow distribution at critical states	High computational complexity in iterative calculations	Applied to compute voltage stability margin near critical states
Voltage Collapse Point Method	Direct computation of system voltage limit points	Increased complexity in augmented Jacobian matrix calculation	Used to determine voltage limit points and stability margins
Bifurcation Theory Method	Analysis of sudden qualitative changes near critical points	Sensitivity to system parameter variations	Utilized to predict stability changes near critical states

3. Static Voltage Stability Analysis Method Based on Impedence Model Index

In order to address the computational complexities posed by conventional analytical approaches, this paper introduces a static voltage stability analysis method based on the impedance model index. This method is applicable to renewable energy connected distribution power systems and generalized network topologies.

3.1. Definition of Impedance Model Index

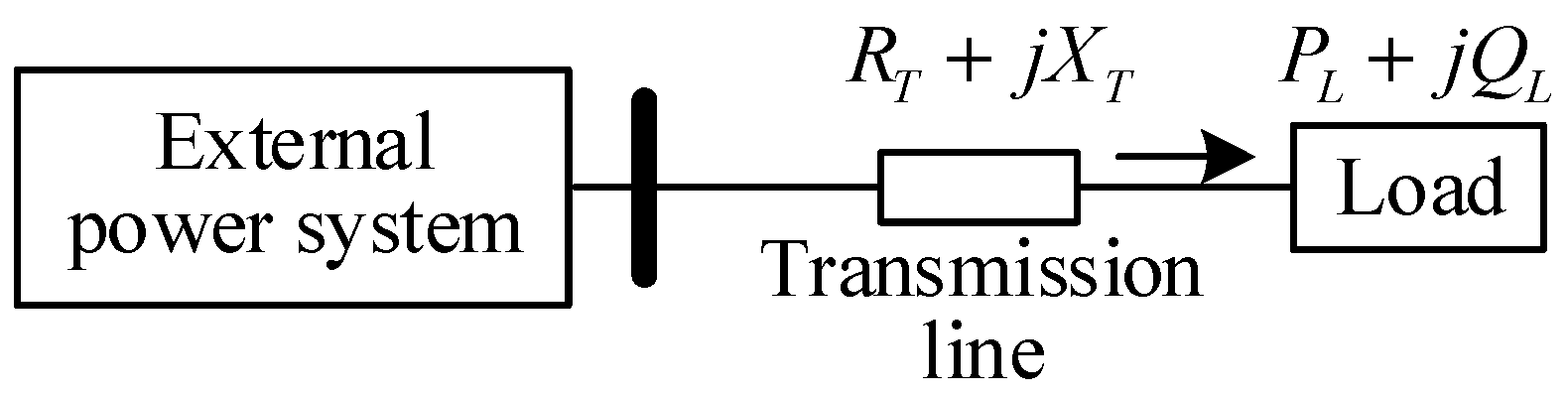
The grid-connected system with a single load is depicted in Figure 1. Where,

Z_{T} = R_{T} + j X_{T}

represents the impedance of the transmission line, and

P_{L} + j Q_{L}

represents the load power. When the load power reaches the critical transmission limit of the system, the system voltage achieves critical stability. However, if the load power surpasses the system's critical transmission limit, it triggers a rapid decline in system voltage, resulting in static voltage instability.

Assuming the equivalent impedance of load is

Z_{L} = R_{L} + j X_{L}

, the impedance model index used to assess system static voltage stability can be defined as follows:

K_{L} = \frac{|Z_{L}|}{|Z_{T}|},

(1)

where, | | represents the magnitude of a vector. According to Equation (1): when

K_{L} > 1

, the system attains static voltage stability; when

K_{L} = 1

, the system achieves critical static voltage stability; and when

K_{L} < 1

, the system undergoes static voltage instability.

3.2. Impedance Model Index for Renewable Energy Single-Infeed Distribution Power Systems

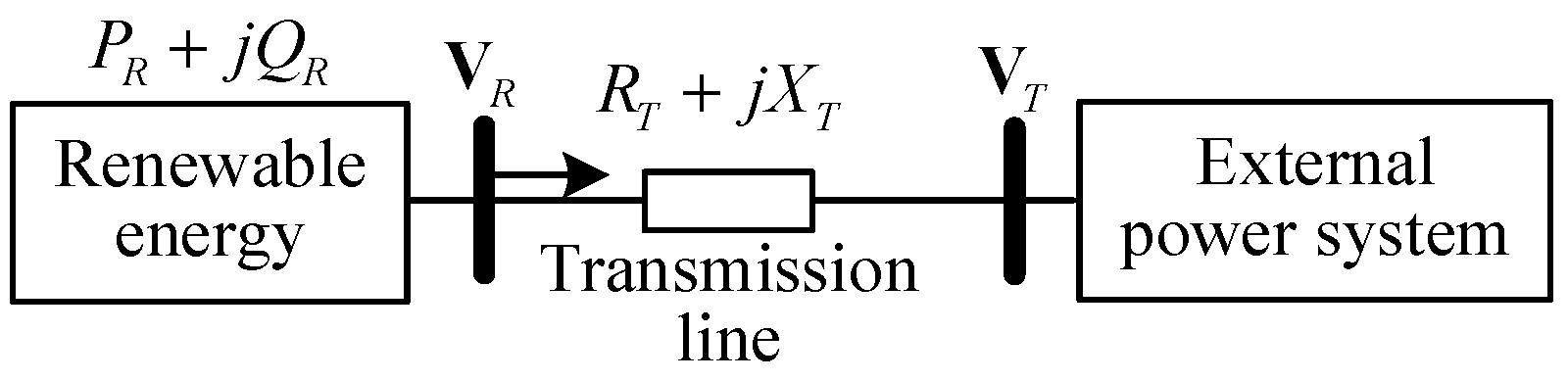
As depicted in Figure 2, it illustrates an distribution power system with a single grid-connected renewable energy, referred as a renewable energy single-infeed distribution power system. Where,

P_{R} + j Q_{R}

represents the output power of the grid-connected renewable energy,

V_{R}

represents the voltage vector at the renewable energy integration node, characterized by its magnitude

V_{R}

and phase angle

θ_{R}

V_{T}

represents for the voltage vector of the external system, with a magnitude

V_{T}

and a phase angle of 0.

From Figure 2, it can be observed that there exists the following relationship between the voltage and power at the renewable energy integration node:

V_{T} = V_{R} - (R_{T} + j X_{T}) \frac{P_{R} + j Q_{R}}{V_{R}}

(2)

Based on Equation (2), the relationship between the terminal voltage and output power at the renewable energy integration node can be derived as follows:

V_{R} = \sqrt{P_{R} R_{T} + Q_{R} X_{T} + \frac{{V_{T}}^{2}}{2} \pm \sqrt{{(P_{R} R_{T} + Q_{R} X_{T} + \frac{{V_{T}}^{2}}{2})}^{2} - Z_{T}^{2} (P_{R}^{2} + Q_{R}^{2})}}

(3)

Based on the voltage and power at the renewable energy integration node, the renewable energy can be equivalently represented at the node by an impedance:

Z_{R} = R_{R} + j X_{R} = \frac{V_{R}^{2}}{- P_{R} + j Q_{R}}

(4)

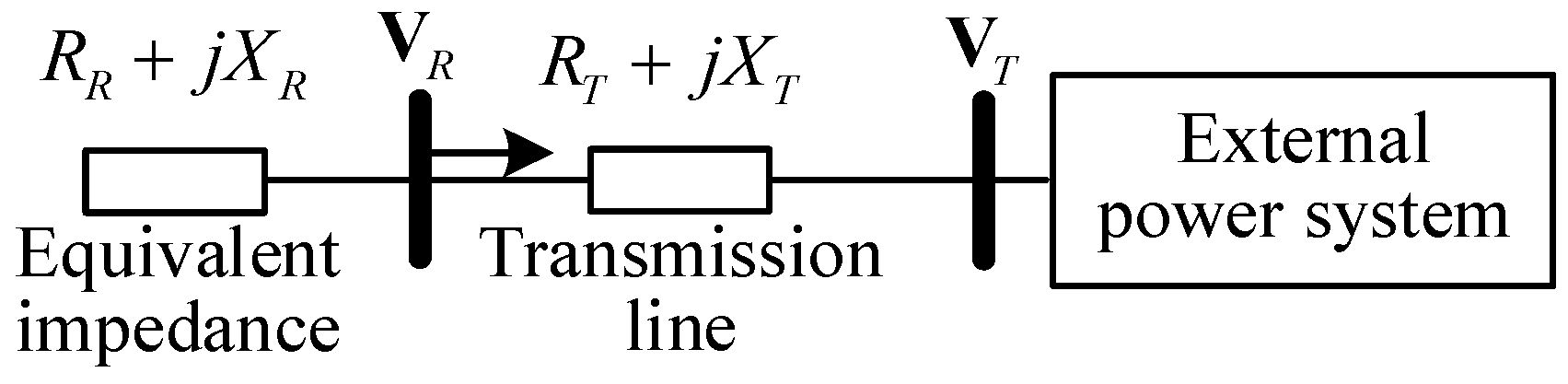
Equation (4) leads to the equivalent system of Figure 2, as illustrated in Figure 3.

Based on Figure 3, the impedance model index for the renewable energy single-infeed distribution power system can be formulated as:

K_{R} = \frac{|Z_{R}|}{|Z_{T}|} = \frac{V_{R}^{2}}{|Z_{T}| \sqrt{P_{R}^{2} + Q_{R}^{2}}}

(5)

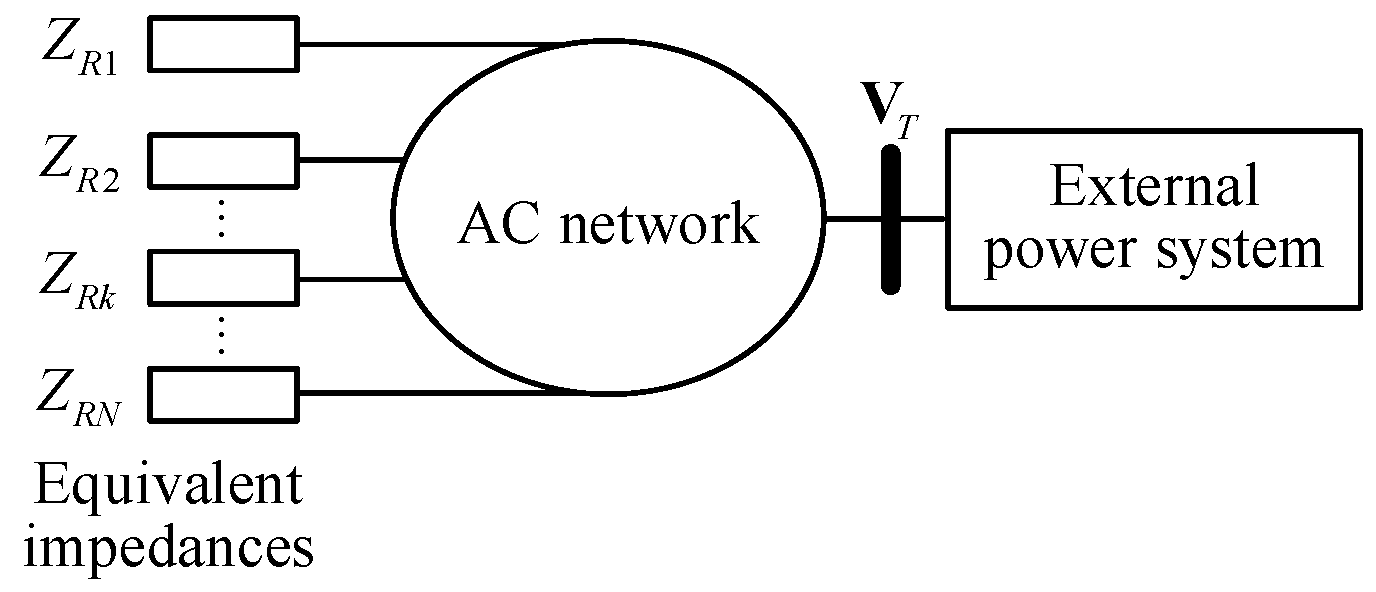
3.3. Impedance Model Index for Renewable Energy Aggregated Distribution Power Systems

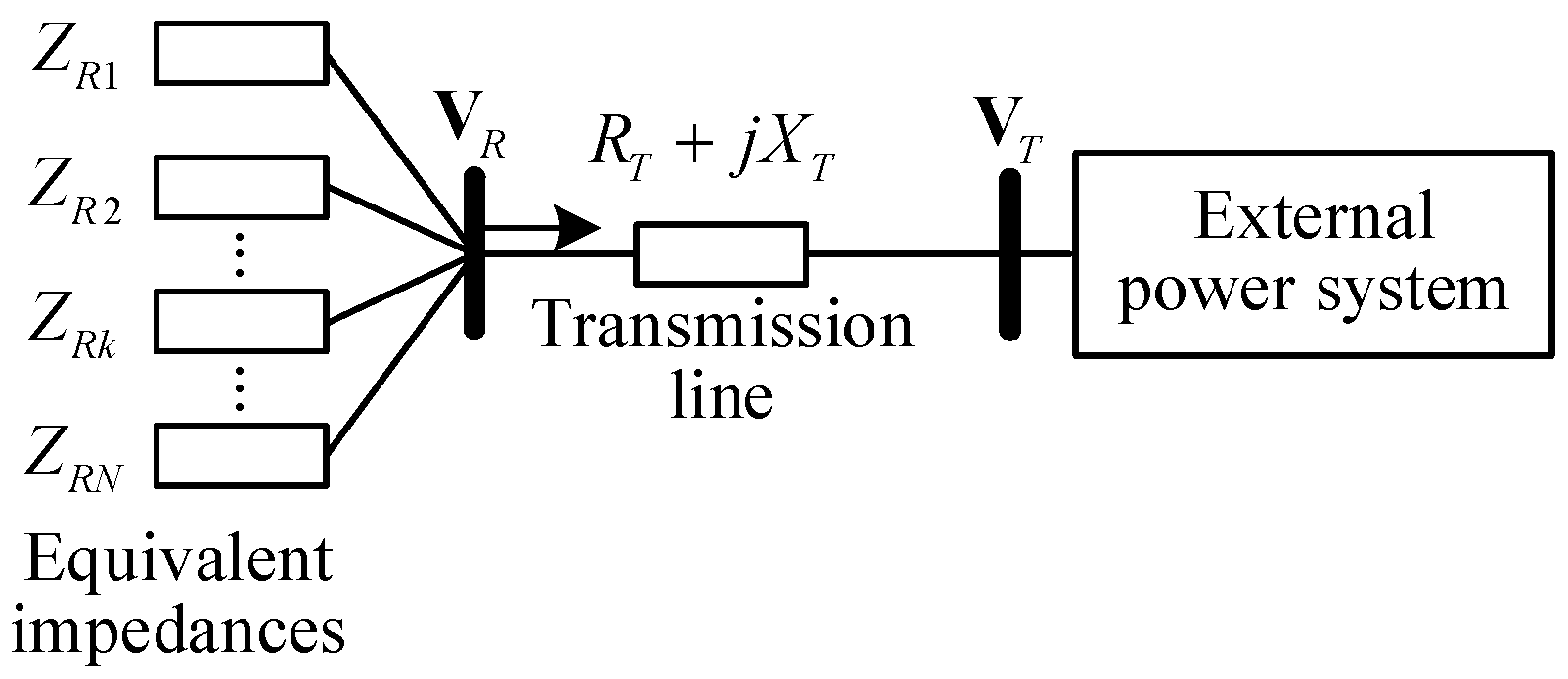
As illustrated in Figure 4, it depicts an aggregated distribution power system comprising N renewable energy sources. In this configuration, N renewable energy sources are connected in parallel to a common node, where the equivalent impedance of the k^th renewable energy source is denoted as

Z_{R k}

, k = 1, 2, 3,…N.

From Figure 4, the total equivalent impedance of the N renewable energy sources is:

|Z_{R s}| = |Z_{R 1} / / \dots Z_{R k} / / \dots / / Z_{R N}|,

(6)

where, // denotes a parallel connection between impedances.

Consequently, when considering N renewable energy sources as a collective entity for calculating the impedance model index of the system, its value is:

K_{R 1} = \frac{|Z_{R s}|}{|Z_{T}|}

(7)

However, when focusing on the kth renewable energy source, the equivalent impedance on the system side changes, as shown in Equation (8):

Z_{T s} = Z_{T} / / Z_{R 1} / / Z_{R 2} / / \dots Z_{R k - 1} / / Z_{R k + 1} / / \dots / / Z_{R N}

(8)

Based on Equation (8), when considering the kth renewable energy source as the subject of study for computing the impedance model index of the system, its value is:

K_{R 2} = \frac{|Z_{R k}|}{|Z_{T s}|}

(9)

Given

|Z_{R k}|

|Z_{R s}|

and

|Z_{T}|

|Z_{T s}|

, it follows that there must exist:

K_{R 2} > K_{R 1}

(10)

Equation (10) illustrates that when a single renewable energy source experiences static voltage instability, multiple renewable energy sources aggregated system will inevitably face static voltage instability, but the reverse is not true. Consequently, static voltage instability in renewable energy aggregated system invariably initiates at the main bus of the aggregated renewable energy sources. Therefore, the impedance model index for renewable energy aggregated system should be computed based on the main bus of the aggregated renewable energy sources.

3.4. Impedance Model Index for Renewable Energy Multi-Infeed Distribution Power Systems

As shown in Figure 5, it represents a multi-infeed system with N renewable energy sources. Where, N renewable energy sources are connected to various nodes of the AC grid. The admittance matrix of the AC grid is:

Y_{N} = [\begin{matrix} Y_{k k} & Y_{k R} \\ Y_{R k} & Y_{R R} \end{matrix}]

(11)

where,

Y_{k k}

represents the self-admittance at the k^th renewable energy source node,

Y_{k R}

and

Y_{R k}

represent the mutual admittance matrices between the k^th renewable energy source node and the remaining N-1 renewable energy source nodes, and

Y_{R R}

represents the self-admittance matrix of the remaining N-1 renewable energy source nodes.

Considering the equivalent impedance of the remaining N-1 renewable energy sources, the equivalent admittance matrix of the AC network is:

Y_{e q} = [\begin{matrix} Y_{k k} & Y_{k R} \\ Y_{R k} & {Y^{'}}_{R R} \end{matrix}],

(12)

where,

where,

{Y^{'}}_{R R}

serves as an intermediate variable for algebraic computation.

By inverting the admittance matrix

Y_{e q}

, the resulting equivalent impedance matrix

Z_{e q}

is obtained after the integration of the remaining N-1 renewable energy sources into the grid.

Z_{e q} = {Y_{e q}}^{- 1} = [\begin{matrix} Z_{k k} & Z_{k R} \\ Z_{R k} & Z_{R R} \end{matrix}]

(13)

In Equation (13),

Z_{k k}

represents the equivalent transmission line impedance corresponding to the k^th renewable energy source.

Based on Equation (13), the impedance model index at the node of the k^th renewable energy source is:

K_{R k} = \frac{|Z_{R k}|}{|Z_{k k}|} = \frac{V_{R k}^{2}}{|Z_{k k}| \sqrt{P_{R k}^{2} + Q_{R k}^{2}}}

(14)

4. Analysis of Factors Affecting Static Voltage Stability

Authors should discuss the results and how they can be interpreted from the perspective of previous studies and of the working hypotheses. The findings and their implications should be discussed in the broadest context possible. Future research directions may also be highlighted.

4.1. Criteria for Static Voltage Stability in Renewable Energy Integrated Distribution Power Systems

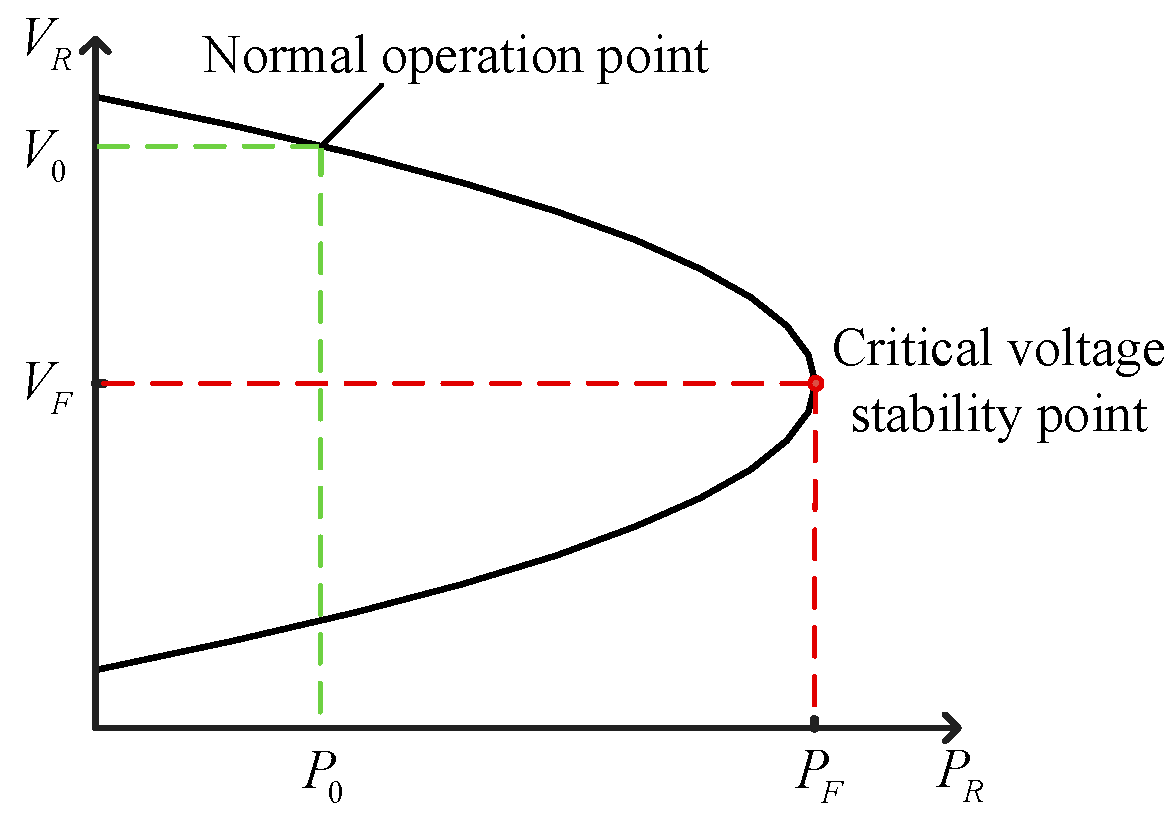
Based on Equation (3), the numerical relationship between power and voltage at the integration node can be plotted, as depicted in Figure 6 [27]. Under normal operation, the voltage at the integration node is

V_{0}

, and the injected power is

P_{0}

.As the injected power increases from

P_{0}

P_{F}

, the node voltage shifts from

V_{0}

V_{F}

. When the injected power surpasses

P_{F}

, the system undergoes static voltage instability.

Static voltage stability of the system can also be determined based on the impedance model index, as shown in Equation (15):

\begin{array}{l} K_{R} > 1, the system is stable \\ K_{R} = 1, the system is critical stable \\ K_{R} < 1, the system is unstable \end{array}

(15)

Based on Equation (15), the permissible range for the impedance model index to maintain system static voltage stability is:

\begin{array}{l} K_{R} = \frac{P_{R} R_{T} + Q_{R} X_{T} + \frac{{V_{T}}^{2}}{2} + \sqrt{{(P_{R} R_{T} + Q_{R} X_{T} + \frac{{V_{T}}^{2}}{2})}^{2} - Z_{T}^{2} (P_{R}^{2} + Q_{R}^{2})}}{|Z_{T}| \sqrt{P_{R}^{2} + Q_{R}^{2}}} \\ \geq \frac{\sqrt{Z_{T}^{2} (P_{R}^{2} + Q_{R}^{2})} + \sqrt{{(P_{R} R_{T} + Q_{R} X_{T} + \frac{{V_{T}}^{2}}{2})}^{2} - Z_{T}^{2} (P_{R}^{2} + Q_{R}^{2})}}{|Z_{T}| \sqrt{P_{R}^{2} + Q_{R}^{2}}} \geq 1 \end{array}

(16)

For a renewable energy multi-infeed system, the criterion for static voltage stability is that for each integration node k, the condition

K_{R k} > 1

must be satisfied.

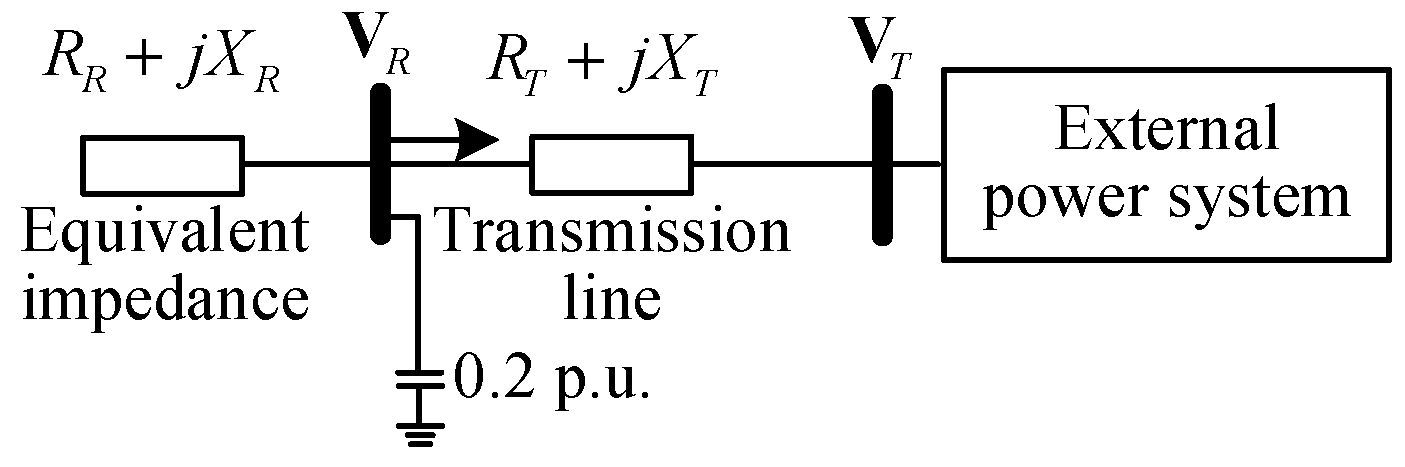
4.2. Impact of Reactive Power Compensation on Impedance Model Index

As illustrated in Figure 7, a shunt compensating capacitor is introduced at the renewable energy source integration node, with a capacitance value of B. The incorporation of the shunt capacitor alters the equivalent impedance of the transmission line from

Z_{T}

Z_{T s}

Z_{T s} = \frac{1}{\frac{1}{R_{T} + j X_{T}} + \frac{1}{- j B}} = \frac{1}{\frac{1}{Z_{T}} + j \frac{1}{B}}

(17)

The parallel connection reduces the equivalent impedance of the transmission line, i.e.,

|Z_{T s}| < |Z_{T}|

. Consequently, the impedance model index at the the renewable energy source integration node will increase, that is:

K_{R} = \frac{|Z_{R}|}{|Z_{T s}|} > \frac{|Z_{R}|}{|Z_{T}|}

(18)

From Equation (18), it is evident that increasing reactive power compensation enhances the impedance model index at the renewable energy source integration node, thereby enhancing the static voltage stability of the system.

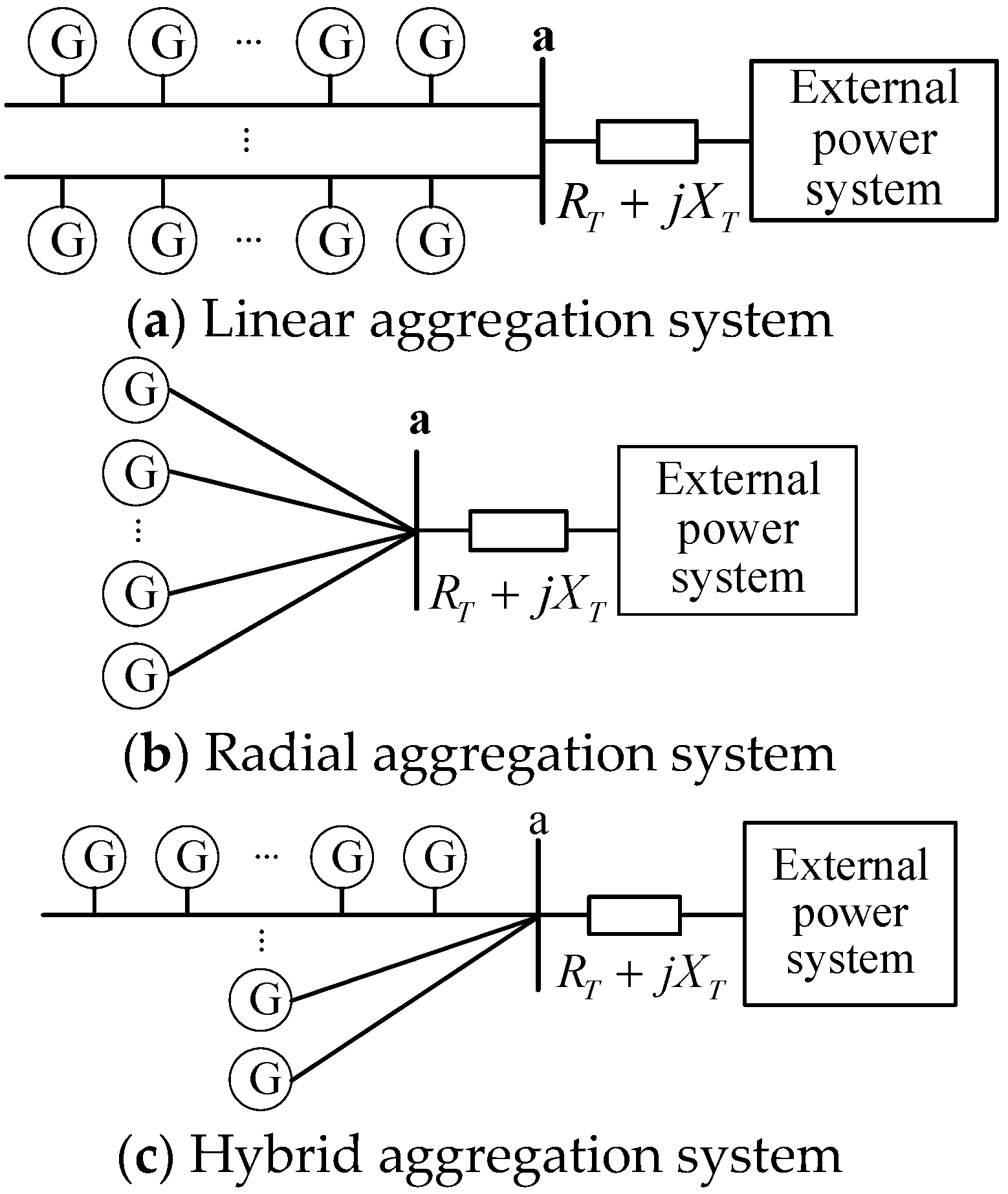
4.3. Influence of Renewable Energy Aggregation Topology on Static Voltage Stability

Figure 8 presents various typical topologies of renewable energy aggregated distribution power systems, including linear, radial, and hybrid configurations. These three network topologies can be collectively represented by the generalized network structure shown in Figure 9.

In Figure 9, the impedance matrix of the generalized network topology can be expressed as:

Z_{N} = X \otimes E_{1},

(19)

where,

\otimes

represents the Kronecker product;

E_{1} = [\begin{matrix} k & - 1 \\ 1 & k \end{matrix}]

, k is the ratio of unit resistance to unit reactance, and

X

denotes the reactance matrix of the renewable energy aggregated system, which can be expressed as:

X = [\begin{matrix} x_{11} + X_{T} & x_{12} + X_{T} & \dots & x_{1 N} + X_{T} \\ x_{21} + X_{T} & x_{22} + X_{T} & \dots & x_{2 N} + X_{T} \\ ⋮ & ⋮ & ⋱ & ⋮ \\ x_{N 1} + X_{T} & x_{N 2} + X_{T} & \dots & x_{N N} + X_{T} \end{matrix}],

(20)

where,

x_{i j}

represents the mutual reactance between the i^th and j^th renewable energy;

X_{T}

signifies the equivalent reactance of the outgoing transmission lines of the renewable energy aggregated system.

Y_{N} = {Z_{N}}^{- 1}

is the admittance matrix of the system, evidently, the eigenvalues of

Y_{N}

and

Z_{N}

are reciprocals of each other. The larger the minimum eigenvalue of matrix

Y_{N}

, the greater the static voltage stability margin of the system. In other words, the smaller the maximum eigenvalue of

Z_{N}

X

, the better the static voltage stability of the system. Assuming the maximum eigenvalue of matrix

X

ρ_{\max}

, then:

ρ_{\max} = \max (P^{- 1} X P),

(21)

where,

P^{- 1}

and

P

represent the left and right eigenvector matrices of matrix

X

. To ensure the best static voltage stability of the system, the choice of aggregation system topology should favor the network topology with the smallest numerical value of

ρ_{\max}

. Next, we will delve into the analysis of the network topology with the smallest numerical value of

ρ_{\max}

under identical line parameters.

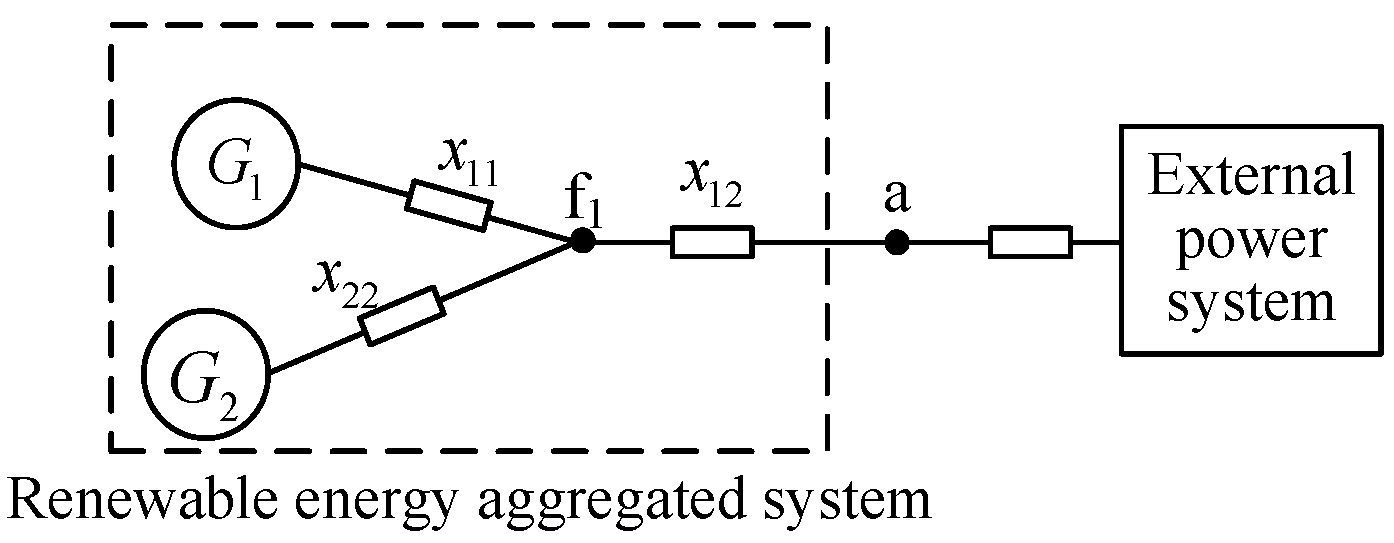
As depicted in Figure 10, the system incorporates two renewable energy devices connected to node a through the AC network. Point f₁ marks the intersection of the internal networks of the two renewable energy sources.

x_{11}

x_{22}

x_{12}

respectively represent the reactance between renewable energy sources G1, G2, and a node f₁.

\begin{array}{l} Z_{N} = X \otimes E_{1} \\ X = [\begin{matrix} x_{11} + x_{12} + X_{T} & x_{12} + X_{T} \\ x_{12} + X_{T} & x_{22} + x_{12} + X_{T} \end{matrix}] \end{array}

(22)

From Equation (22), it is evident that when

ρ_{\max}

takes its minimum value, there exists

x_{12} = 0

, at which point node f1 and node a coincide. Therefore, when two renewable energy sources are directly connected in parallel to the aggregation bus node a, the system exhibits the best static voltage stability.

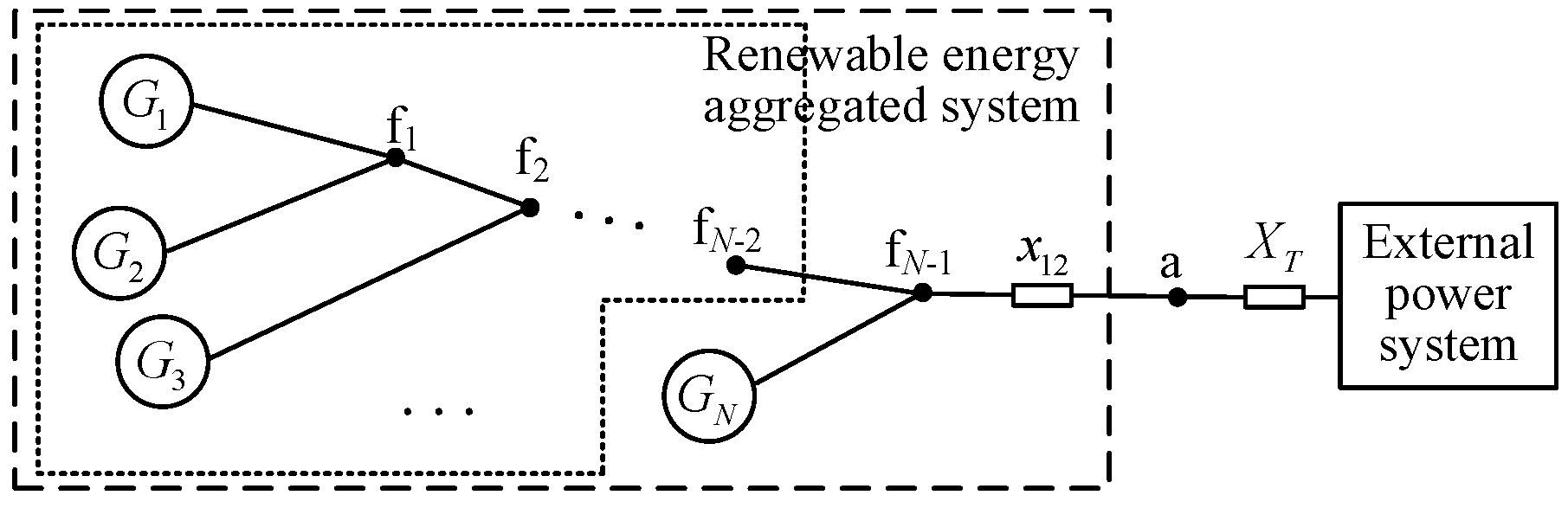
Based on Equation (22), considering the general case of N renewable energy sources, as shown in Figure 11. Using induction, assume that (N-1) renewable energy sources have already aggregated through (N-2) internal nodes to node f_N-2, at which point the network topology formed by these (N-1) renewable energy sources exhibits the best static voltage stability, as depicted by the dashed box in Figure 11. To ensure the best static voltage stability of the system in this scenario, the maximum eigenvalue of the network topology formed by node f_N-2 and the last renewable energy source should be minimized. Consequently, node f_N-1 coincides with node a. Therefore, when all renewable energy sources in the aggregation system are connected in parallel to the aggregation bus, the static voltage stability of the renewable energy aggregated system is optimal. In other words, the radial aggregation system, as shown in Figure 8(b), is the network topology with the best static voltage stability.

5. Case Study Analysis

5.1. Calculation of Impedance Model Index for Renewable Energy Single-Infeed Distribution Power Systems

Figure 12 illustrates a single-infeed renewable energy system with a transmission line impedance of Z_T = 0.012 + j0.132 and a shunt capacitor at the integration point with a reactive compensation capacity of 0.2 p.u. The analysis is conducted by increasing the integration capacity of the renewable energy under two conditions: without capacitor compensation and with capacitor compensation. 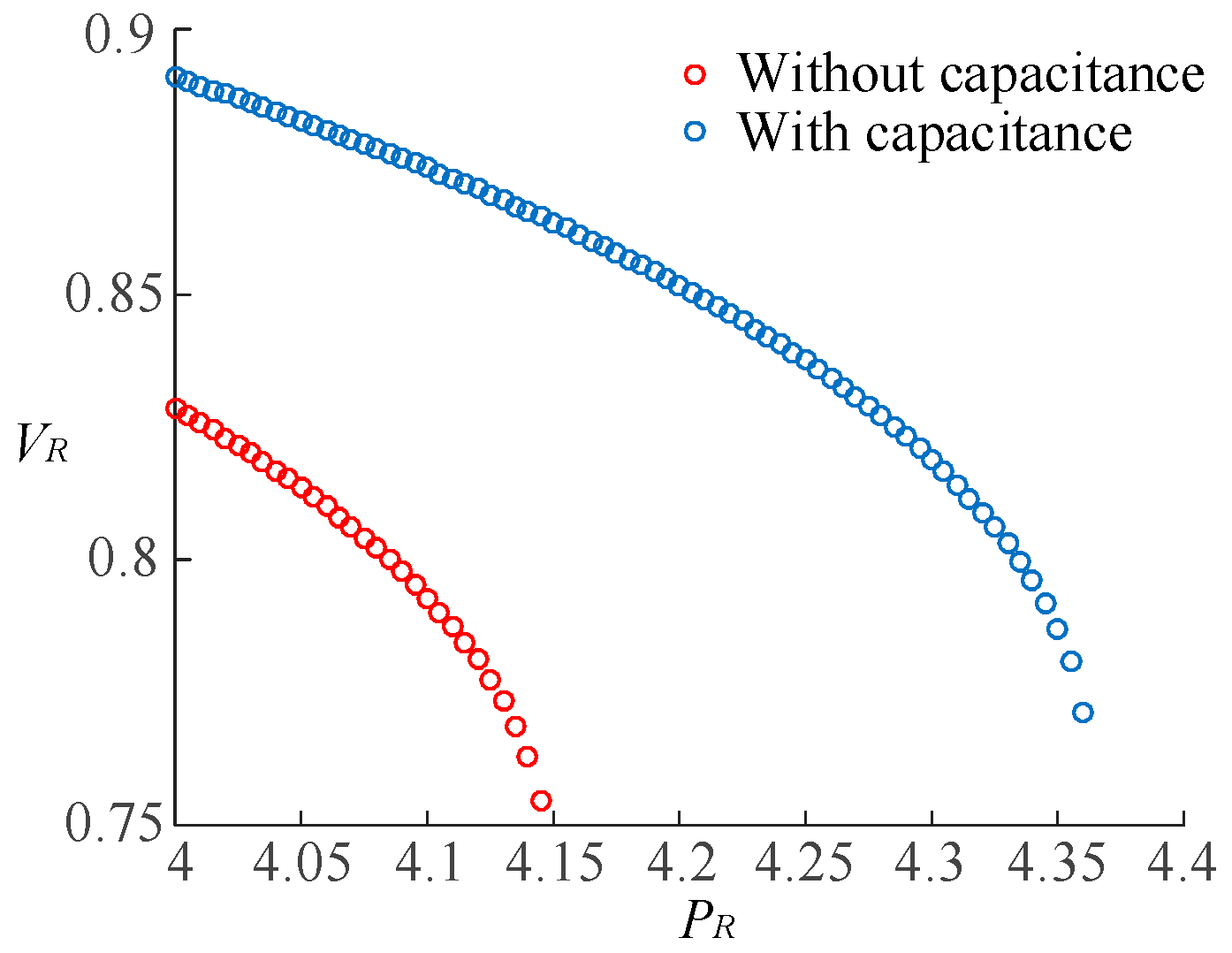The voltage stability at the integration point is evaluated using the continuous power flow method, and the results are shown in Figure 13.

Figure 13 displays the P-V curve at the integration point for the cases with and without capacitor compensation. The analysis reveals that the integration capacity of renewable energy source is approximately 4.15 p.u. without capacitor compensation, beyond which the system experiences static voltage instability. With capacitor compensation, the integration capacity of renewable energy source is approximately 4.36 p.u., and exceeding this value also leads to static voltage instability. These results demonstrate that increasing reactive compensation enhances the integration capacity of renewable energy source. In this scenario, the impedance model index at the integration point for different integration capacities is calculated and shown in Figure 14.

Figure 14 illustrates the variation of the impedance model index at the integration point with increasing integration capacity. When the integration capacity of renewable energy reaches its limit, the system exhibits critical static voltage instability. At this point, the impedance model index is approximately 1.006 without capacitor compensation and approximately 1.008 with capacitor compensation. From Figure 13 and Figure 14, it can be observed that as the renewable energy integration capacity gradually increases and approaches the static voltage stability limit, the impedance model index decreases continuously and converges towards 1. The presence of reactive compensation in the renewable energy integration system results in a higher impedance model index compared to the case without compensation. This conclusion is consistent with the analysis results from the P-V curve, which confirms that the impedance model index accurately reflects the static voltage stability of the system.

5.2. Calculation of Impedance Model Index for Renewable Energy Aggregated Distribution Power Systems

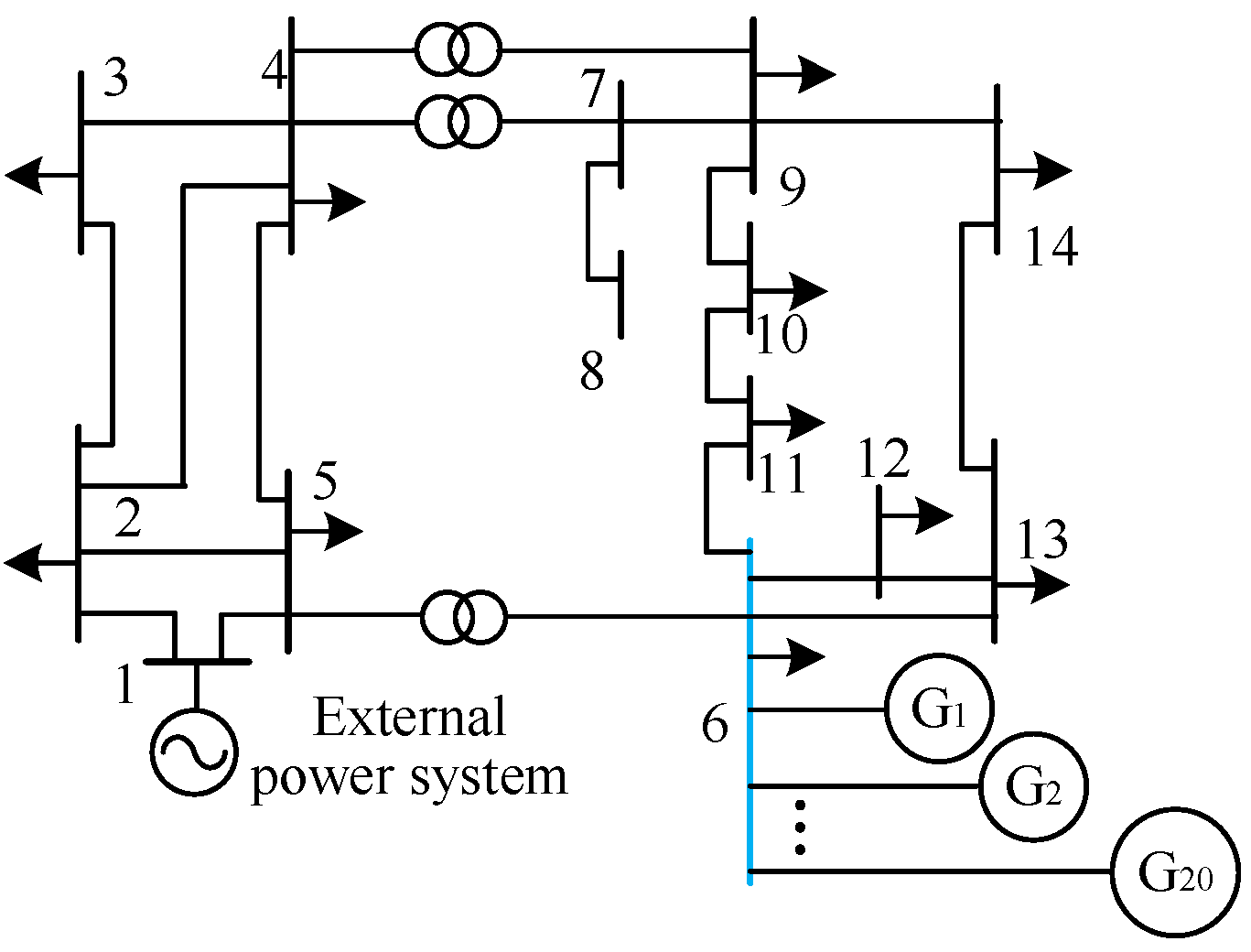
Figure 15 represents a renewable energy aggregated system with 20 renewable energy sources. The system parameters are based on the IEEE 14-bus system, with modifications as follows: the network loads are changed from constant power loads to constant impedance loads, the generators except for node 1 are removed, and 20 renewable energy units are paralleled at node 6. The impedance between each renewable energy unit and the aggregation bus is 0.0002 + j0.03 p.u., while other parameters remain the same as in the original IEEE 14-bus system.

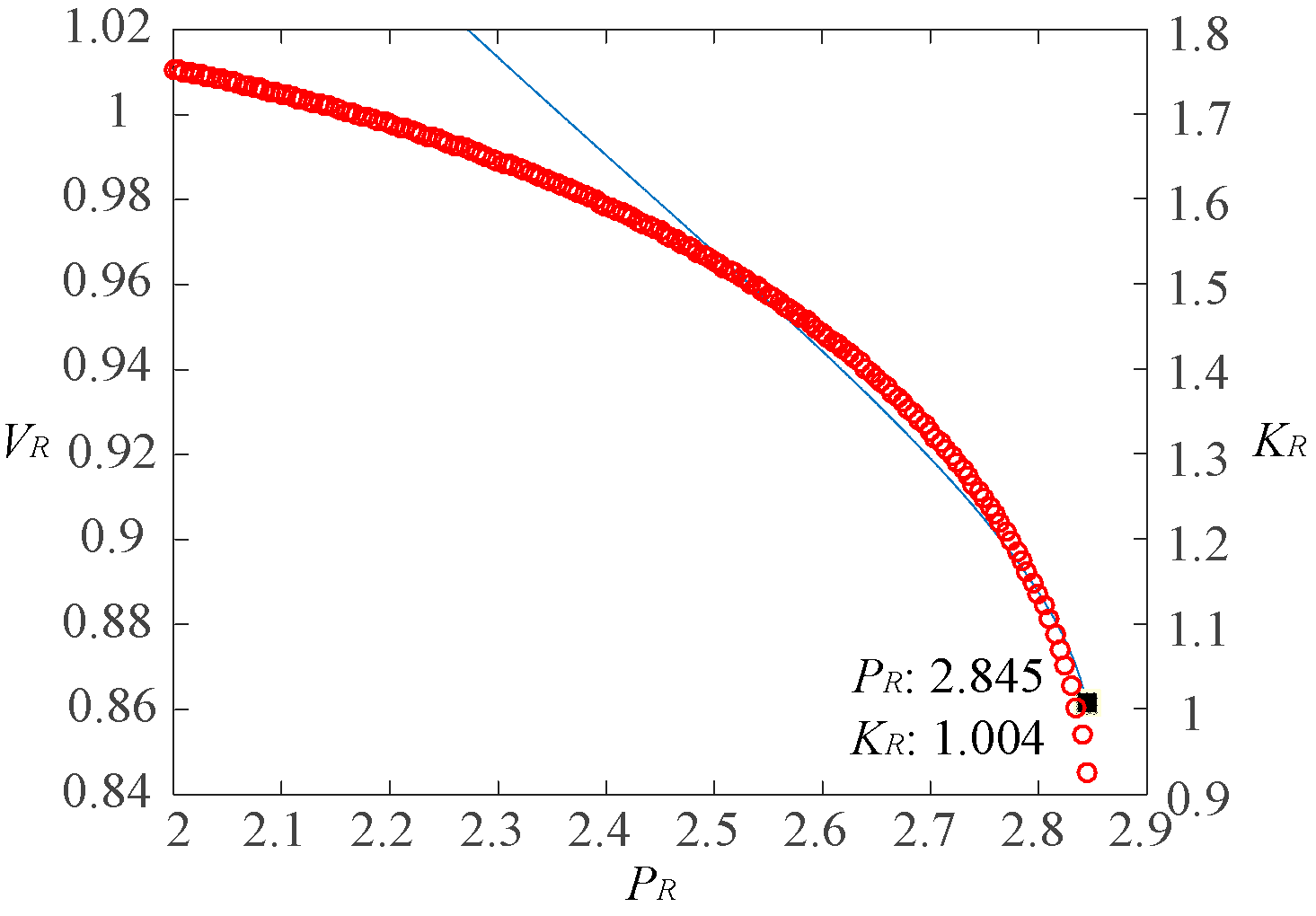
Figure 16 illustrates the P-V curve and impedance model index variation at node 6 (aggregation bus) as the total capacity of the renewable energy units increases. The results are obtained by first calculating the equivalent impedance of the renewable energy units and then using the continuous power flow method to calculate the voltage amplitude at node 6 for increasing power capacities.

The analysis indicates that as the total capacity of the renewable energy units increases, the impedance model index decreases and approaches 1, suggesting that the static voltage stability of the system gradually deteriorates. When the total integration capacity of the renewable energy units reaches 2.85 p.u., the impedance model index is approximately 1.004, indicating that the system is at the critical static voltage instability state. Beyond this value, the system experiences static voltage instability. The analysis results from the P-V curve align with the above analysis, confirming the accuracy of the impedance model index calculation and the reliability of the analysis results.

To further verify that the differences in the integration capacities of individual renewable energy units do not affect the analysis results, the 20 renewable energy units are divided into three groups: 6, 6, and 7 units per group. Each group has different capacities, as shown in the first column of Table 2. The total integration capacity at the aggregation bus (node 6) is calculated for each group, as shown in the second column of Table 2. It is observed that the differences in renewable energy unit capacities have little impact on the total integration capacity at the aggregation bus, which remains approximately 2.8 p.u. When the renewable energy integration capacity reaches its limit, the system experiences static voltage instability, and the impedance model index at the aggregation bus is approximately 1, regardless of the different capacities of the renewable energy units within the aggregation system.

From Table 2, it is evident that regardless of the differences in renewable energy unit capacities, the total integration capacity at the aggregation node remains nearly unchanged at approximately 2.8 p.u. At the critical state when the renewable energy integration capacity reaches its limit, the impedance model index is approximately 1 at the aggregation node. Thus, the impedance model index calculation method proposed in this study effectively reflects the static voltage stability margin of the system. The impedance model index is not influenced by the different capacities of renewable energy units within the aggregation system but is only related to the total integration capacity at the aggregation node.

5.3. Calculation of impedance model index for renewable energy multi-infeed distribution power systems

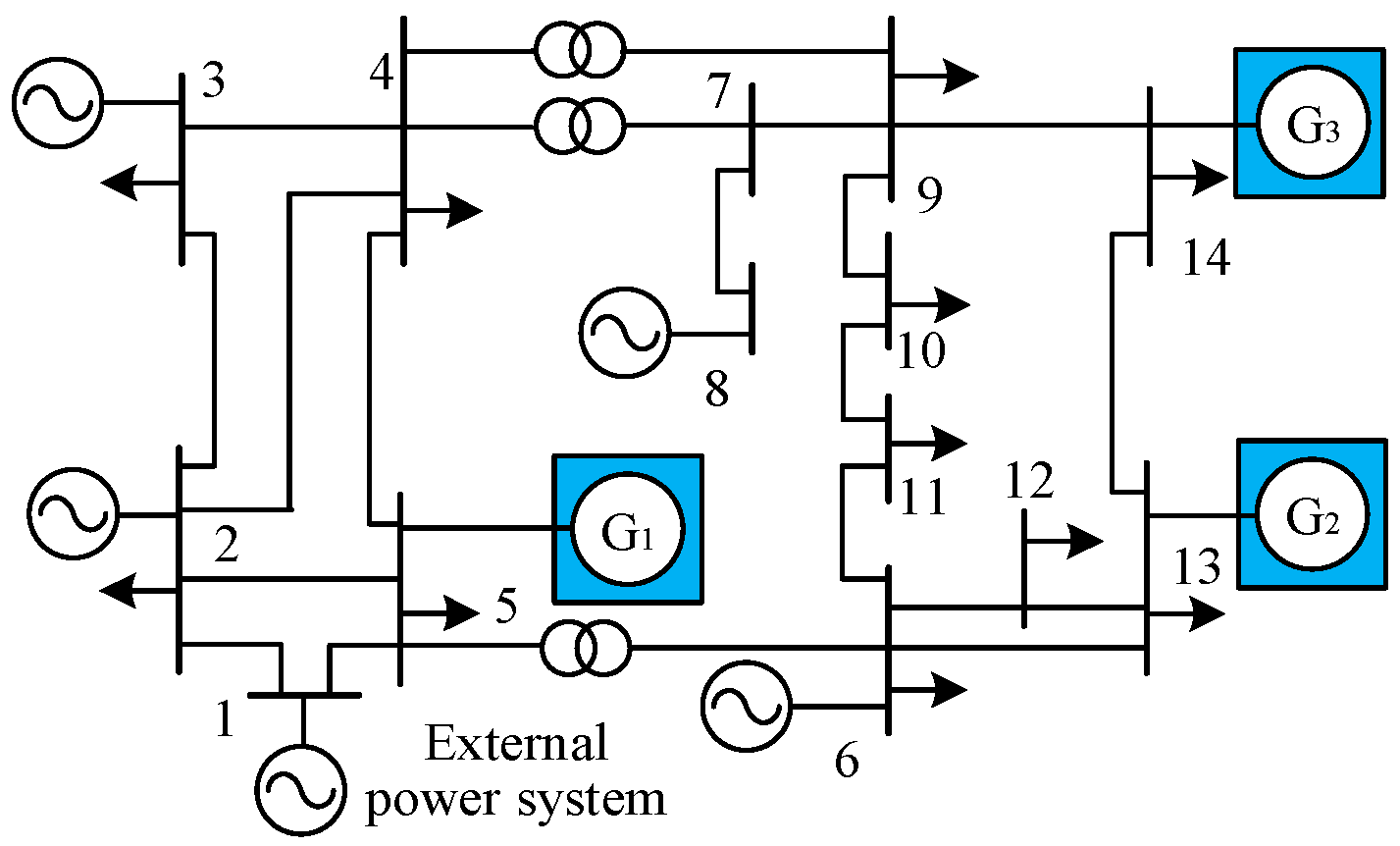
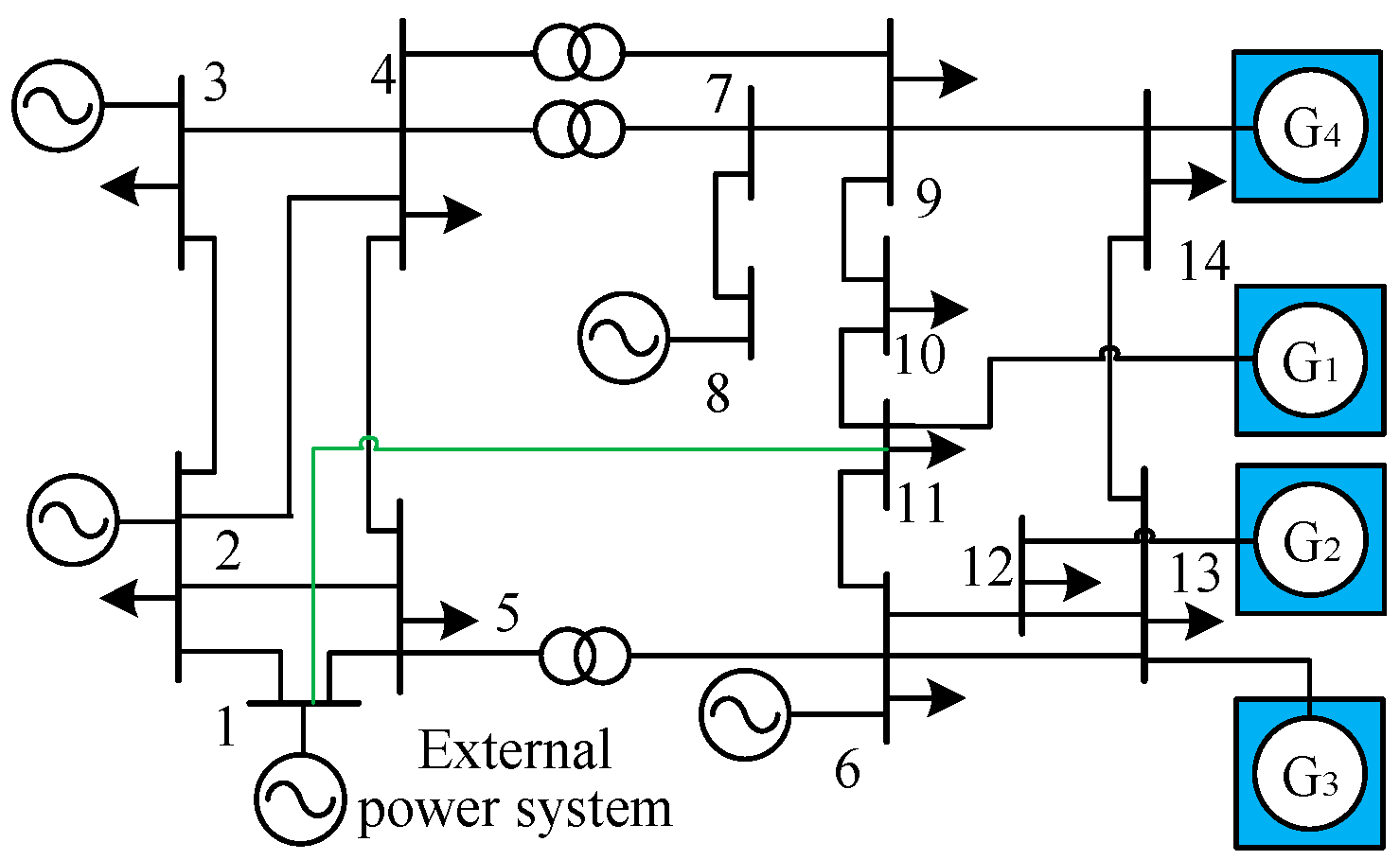
Figure 17 depicts a multi-infeed distribution power system with three renewable energy units, G1, G2, and G3, connected to nodes 5, 13, and 14, respectively, in the IEEE 14-bus system. In this section, three case studies are performed to analyze the impact of each renewable energy unit's maximum integration capacity on the system's static voltage stability, while ensuring the system remains stable.

Case 1: The integration capacities of renewable energy units G2 and G3 are fixed at 1 p.u., and the impact of renewable energy unit G1's integration capacity on the system's static voltage stability is analyzed.

Figure 18 shows the P-V curve and the impedance model index variation at node 5 as the integration capacity of renewable energy unit G1 increases. The calculation starts by determining the equivalent impedances of renewable energy units G2 and G3, which are then used as self-admittances at nodes 13 and 14, respectively. Next, the equivalent impedance of the transmission line between node 5 and node 1 is computed. Finally, the impedance model index at node 5 is calculated for different integration capacities of renewable energy unit G1, as shown by the blue curve in Figure 18. Furthermore, the voltage amplitude at node 5 is calculated using the continuous power flow method as the power capacity of renewable energy unit G1 increases from 8 p.u. to 8.4 p.u., shown by the red curve in Figure 18.

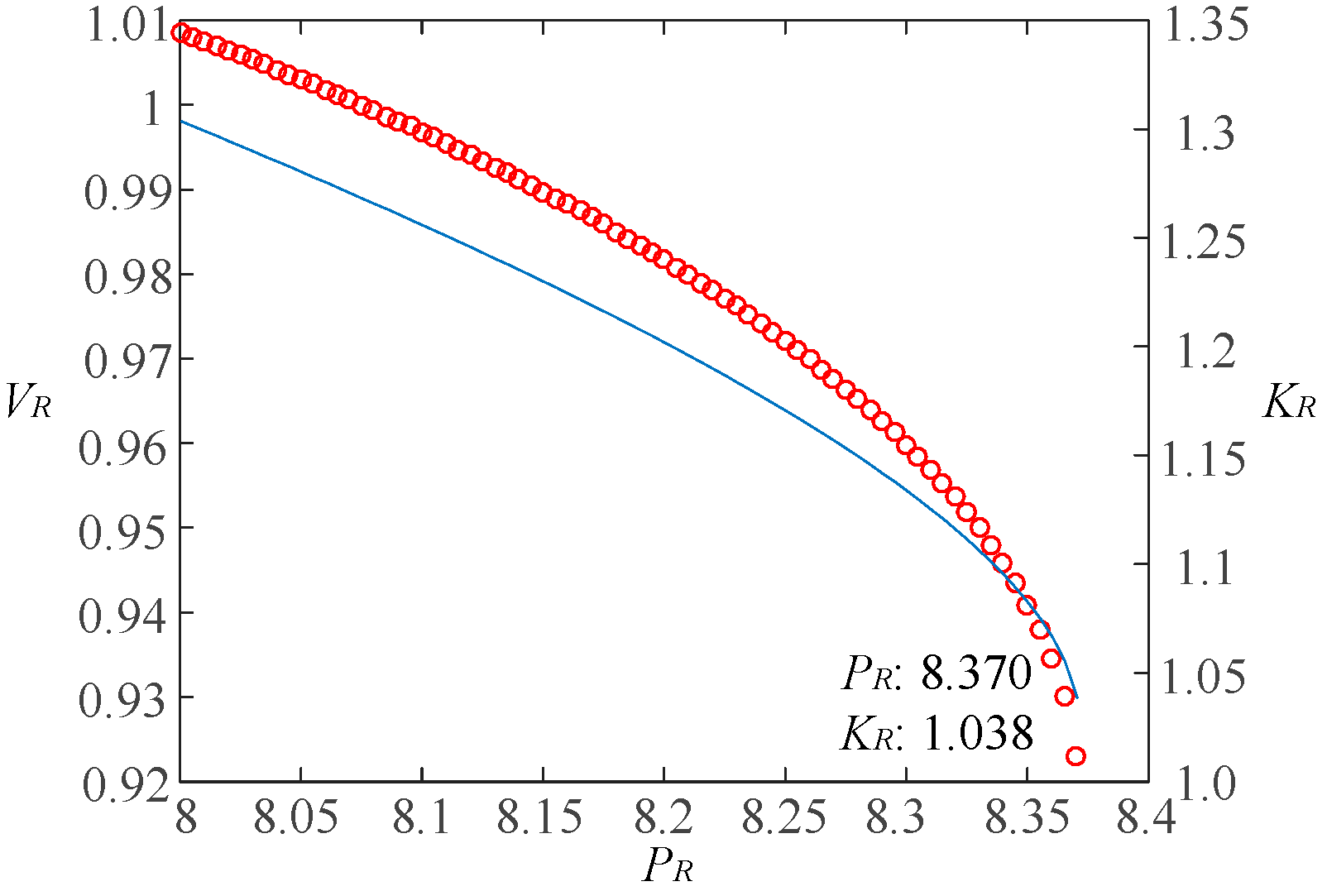
From Figure 18, it is evident that as the integration capacity of renewable energy unit G1 increases, the impedance model index decreases and approaches 1, indicating a gradual decline in the system's static voltage stability. When the total integration capacity of renewable energy unit G1 at node 5 reaches 8.37 p.u., the impedance model index is approximately 1.038, signifying that the system is at the critical static voltage instability state. Beyond this value, the system experiences static voltage instability. The analysis results from the P-V curve are consistent with the above analysis, demonstrating the accuracy of the impedance model index calculation and the reliability of the analysis results.

Case 2: The integration capacities of renewable energy units G1 and G3 are fixed at 1 p.u., and the impact of renewable energy unit G2's integration capacity on the system's static voltage stability is analyzed.

Figure 19 displays the P-V curve and the impedance model index variation at node 13 as the integration capacity of renewable energy unit G2 increases. The calculation process is similar to Case 1, with the equivalent impedances of renewable energy units G1 and G3 used as self-admittances at nodes 5 and 14, respectively. The equivalent impedance of the transmission line between node 13 and node 1 is computed, and then the impedance model index at node 13 is calculated for different integration capacities of renewable energy unit G2, as shown by the blue curve in Figure 19. The voltage amplitude at node 13 is determined using the continuous power flow method as the power capacity of renewable energy unit G2 increases from 2.2 p.u. to 2.45 p.u., shown by the red curve in Figure 19.

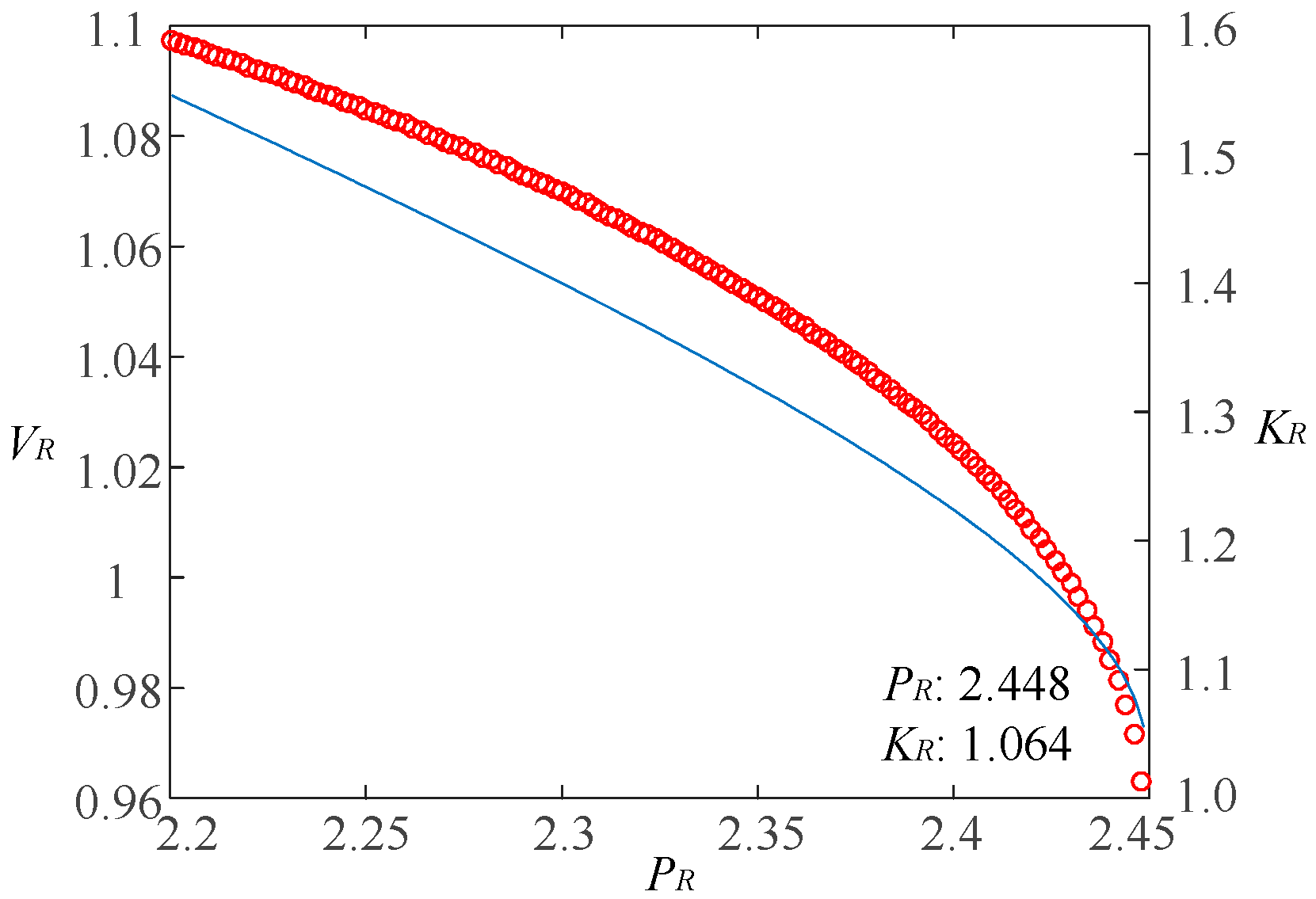
From Figure 19, it is observed that as the integration capacity of renewable energy unit G2 increases, the impedance model index decreases and approaches 1, indicating a decline in the system's static voltage stability. When the total integration capacity of renewable energy unit G2 at node 13 reaches 2.45 p.u., the impedance model index is approximately 1.064, signifying that the system is at the critical static voltage instability state. Beyond this value, the system experiences static voltage instability. The analysis results from the P-V curve align with the above analysis, demonstrating the accuracy of the impedance model index calculation and the reliability of the analysis results.

Case 3: The integration capacities of renewable energy units G1 and G2 are fixed at 1 p.u., and the impact of renewable energy unit G3's integration capacity on the system's static voltage stability is analyzed.

Figure 20 shows the P-V curve and the impedance model index variation at node 14 as the integration capacity of renewable energy unit G3 increases. The calculation procedure is similar to Case 1 and Case 2. The equivalent impedances of renewable energy units G1 and G2 are used as self-admittances at nodes 5 and 13, respectively, and the equivalent impedance of the transmission line between node 14 and node 1 is computed. Then, the impedance model index at node 14 is calculated for different integration capacities of renewable energy unit G3, as shown by the blue curve in Figure 20. The voltage amplitude at node 14 is determined using the continuous power flow method as the power capacity of renewable energy unit G3 increases from 2.0 p.u. to 2.3 p.u., shown by the red curve in Figure 20.

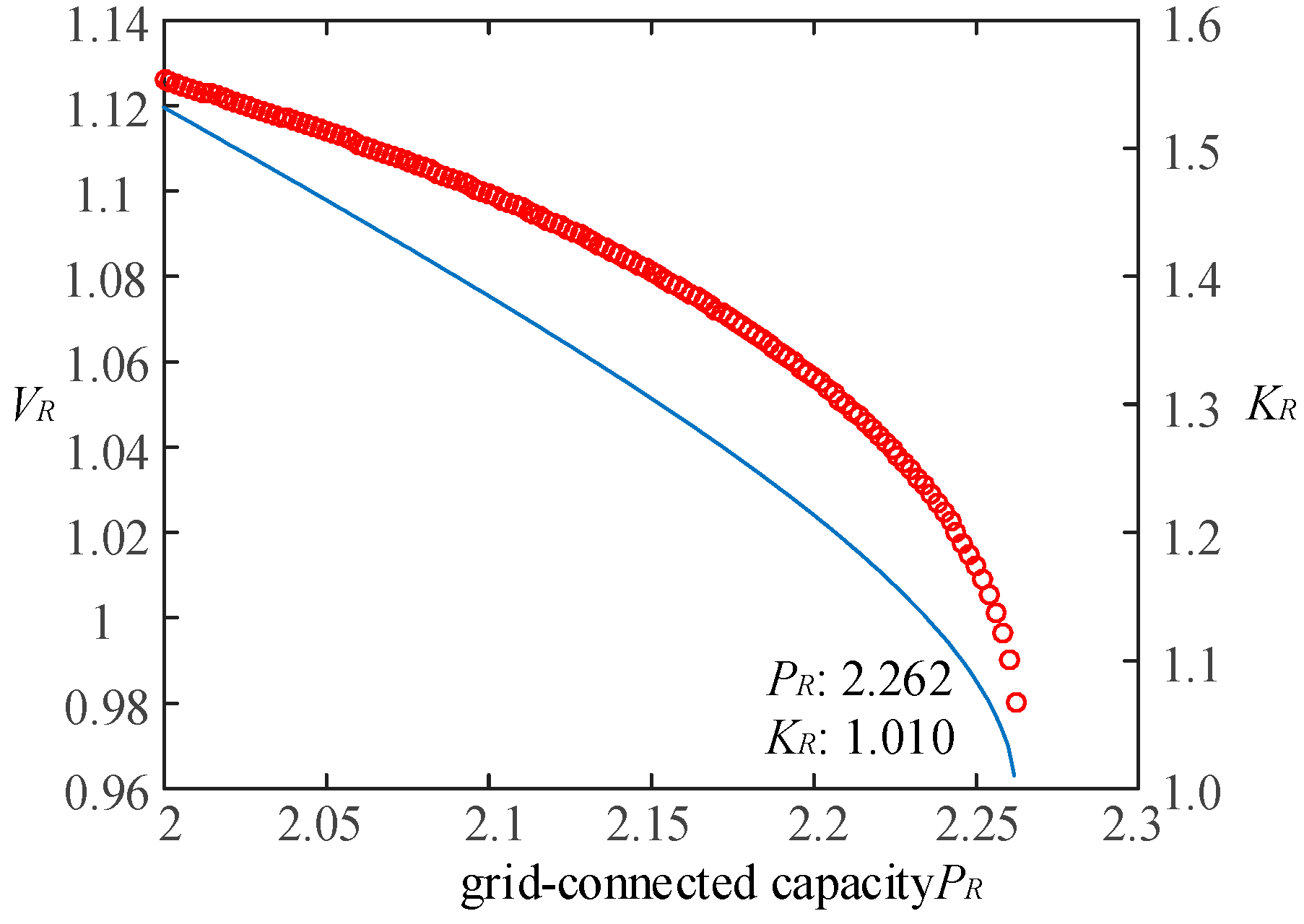
From Figure 20, it is evident that as the integration capacity of renewable energy unit G3 increases, the impedance model index decreases and approaches 1, indicating a decline in the system's static voltage stability. When the total integration capacity of renewable energy unit G3 at node 14 reaches 2.26 p.u., the impedance model index is approximately 1.01, signifying that the system is at the critical static voltage instability state. Beyond this value, the system experiences static voltage instability. The analysis results from the P-V curve are consistent with the above analysis, demonstrating the accuracy of the impedance model index calculation and the reliability of the analysis results.

Based on the above calculation results, it is evident that the impedance model index is also applicable to the renewable energy multi-infeed system. For different integration nodes in the system, the maximum integration capacity of renewable energy units varies, and each node's integration capacity limit can be evaluated by the corresponding limit power at which the impedance model index equals 1. If the integration capacities of renewable energy units are the same, selecting the node with the highest impedance model index as the integration node will result in the best static voltage stability for the system.

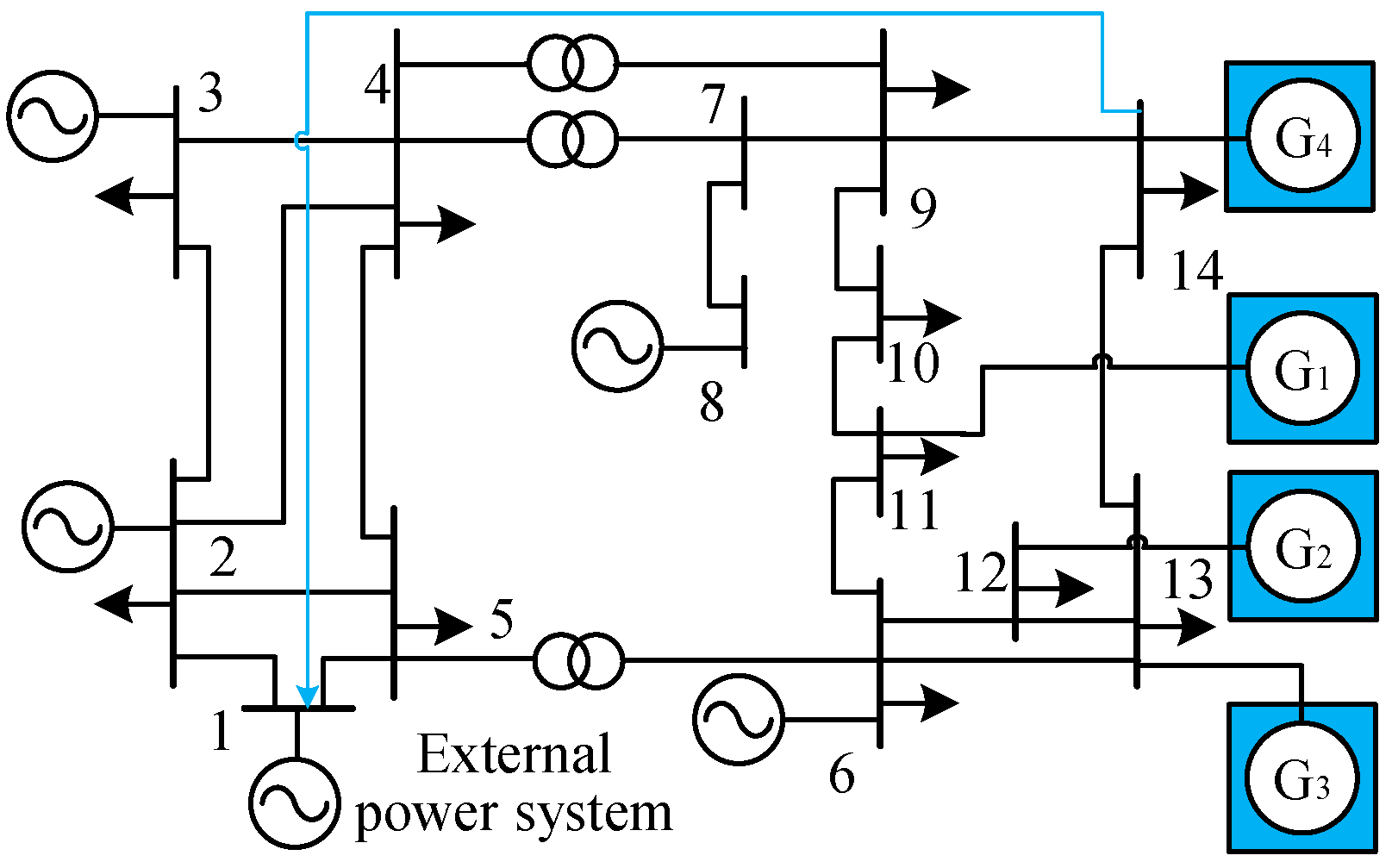
5.4. Impact of Network Topology on Impedance Model Index

Figure 21 illustrates a multi-infeed distribution power system with four renewable energy units, G1, G2, G3, and G4, connected to nodes 11, 12, 13, and 14, respectively, in the IEEE 14-bus system. Each renewable energy unit outputs power at 0.5 p.u. Additionally, an AC branch with an impedance of 0.05+j0.12 is added between node 1 and node 11, as shown by the green line in the figure. The impedance model index calculation results for nodes 11, 12, 13, and 14 are presented in Table 3.

Table 3 demonstrates that adding the AC branch increases the impedance model index at each integration node, indicating that adding AC lines can enhance the system's static voltage stability. The impedance model index at node 11 experiences a significant increase, suggesting that node 11 can accommodate more renewable energy units after the AC line is connected.

Similarly, a DC line is added between node 1 and node 14 in the system, with constant power control, transmitting power at 0.3 p.u. Node 14 serves as the infeed end of the DC line, and node 1 serves as the outfeed end, as shown by the blue line in Figure 22. The impedance model index calculation results for nodes 11, 12, 13, and 14 are shown in Table 4.

Table 4 shows that after adding the DC transmission line, the impedance model index at each integration node increases, indicating that adding DC transmission lines can improve the system's static voltage stability. The impedance model index at node 14 experiences the most significant increase, suggesting that node 14 can accommodate more renewable energy units after the DC transmission line is connected.

Based on the analysis results of these two case studies, it is evident that increasing AC or DC transmission lines can alter the original topology of the transmission network, thereby enhancing the static voltage stability of the renewable energy integration system.

6. Conclusion

In this study, an equivalent impedance model for renewable energy integrated distribution power systems was established. Based on the saddle-node bifurcation theory of static voltage stability, an impedance model index applicable to generalized renewable energy integrated distribution power systems was proposed, and the criterion for static voltage stability of the system based on the impedance model index was derived. Using the proposed analysis method, the impact of the number, location, and network topology of renewable energy integration on the system's static voltage stability was analyzed, providing valuable insights for selecting suitable locations for renewable energy integration and planning renewable energy integration capacities. The specific conclusions are as follows:

1. The impedance model index proposed in this study is not only applicable to renewable energy single-infeed distribution power systems but also suitable for renewable energy multi-infeed distribution power systems. It effectively reflects the static voltage stability margin of the renewable energy integration nodes.

2. The network topology of renewable energy aggregated systems can affect the static voltage stability of the distribution power system. This study demonstrated that the radiation-type network topology for renewable energy offers the best static voltage stability of the distribution power system.

3. The addition of AC and DC lines can increase the impedance model index, thereby improving the system's static voltage stability. When planning the integration of renewable energy, selecting the node with the highest impedance model index can enhance the stability of the distribution power system.

This study provides valuable insights into the static voltage stability of renewable energy integrated distribution power systems, enabling better decision-making in renewable energy planning and operation.

Author Contributions

Conceptualization, Y.W. and Y.C.; methodology, H.B.; software, Z.S.; validation, W.L., and Y.W.; formal analysis, T.L.; investigation, H.B.; resources, Z.H.; data curation, Y.C.; writing—original draft preparation, Y.C.; writing—review and editing, W.L.; visualization, Y.W.; supervision, Z.T.; project administration, Z.S.; funding acquisition, Y.L. All authors have read and agreed to the published version of the manuscript.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors on request.

Acknowledgments

This work was supported by the Science and Technology Support Program of Guizhou Province ([2022] General 012) and the Key Science and Technology Project of China Southern Power Grid Corporation (GZKJXM20220043).

Conflicts of Interest

The authors declare no conflicts of interest.

References

Tielens et al.. The relevance of inertia in power systems[J]. New & Sustainable Energy Reviews, 2016, 55: 999-1009.
P. Kundur et al. Definition and classification of power system stability[J]. IEEE Transactions on Power Systems, 2004, 19(3): 1387-1401.
N. Hatziargyriou et al.. Definition and classification of power system stability – revisited & extended[J]. IEEE Transactions on Power Systems, 2021, 36(4): 3271-3281.
HE Jingbo et al.. New Issues and Classification of Power System Stability With High Shares of News and Power Electronics[J]. Proceedings of the CSEE, 2021,41(2):461-473.
P. Ge et al.. Comprehensive transient stability enhancement control of a VSG considering power angle stability and fault current limitation[J]. CSEE Journal of Power and Energy Systems. [CrossRef]
D. A. Leiva Roca, P. Mercado and G. Suvire, "System Frequency Response Model Considering the Influence of Power System Stabilizers," in IEEE Latin America Transactions, vol. 20, no. 6, pp. 912-920, June 2022. [CrossRef]
S. Ranjan, D. C. Das, A. Latif, N. Sinha, S. M. S. Hussain and T. S. Ustun, "Maiden Voltage Control Analysis of Hybrid Power System With Dynamic Voltage Restorer," in IEEE Access, vol. 9, pp. 60531-60542, 2021. [CrossRef]
Y. Song, D. J. Hill and T. Liu, "Static Voltage Stability Analysis of Distribution Systems Based on Network-Load Admittance Ratio," in IEEE Transactions on Power Systems, vol. 34, no. 3, pp. 2270-2280, May 2019. [CrossRef]
US-Canada Power Outage Task Force. Final report on the August 14th 2003 blackout in the United States and Canada[R/OL]. http://www.ferc.gov/.
Australian Energy Market Operator. Black system South Australia 28 September 2016—third preliminary report[R]. Australia: Australian Energy Market Operator Limited, 2016.
Yusheng Xue, Taishan Xu, Bing Liu and Yaozong Li, "Quantitative assessments for transient voltage security," in IEEE Transactions on Power Systems, vol. 15, no. 3, pp. 1077-1083, Aug. 2000. [CrossRef]
K. Ellithy et al., "Voltage stability evaluation of real power transmission system using singular value decomposition technique," 2008 IEEE 2nd International Power and Energy Conference, Johor Bahru, Malaysia, 2008, pp. 1691-1695. [CrossRef]
K. Alzaareer et al., "Sensitivity Analysis for Voltage Stability Considering Voltage Dependent Characteristics of Loads and DGs," in IEEE Access, vol. 9, pp. 156437-156450, 2021. [CrossRef]
P. S. Nirbhavane, L. Corson, S. M. H. Rizvi and A. K. Srivastava, "TPCPF: Three-Phase Continuation Power Flow Tool for Voltage Stability Assessment of Distribution Networks With Distributed Energy Resources," in IEEE Transactions on Industry Applications, vol. 57, no. 5, pp. 5425-5436, Sept.-Oct. 2021. [CrossRef]
J. Flueck, R. Gonella and J. R. Dondeti, "A new power sensitivity method of ranking branch outage contingencies for voltage collapse," in IEEE Transactions on Power Systems, vol. 17, no. 2, pp. 265-270, May 2002. [CrossRef]
G. Pierrou and X. Wang, "Analytical Study of the Impacts of Stochastic Load Fluctuation on the Dynamic Voltage Stability Margin Using Bifurcation Theory," in IEEE Transactions on Circuits and Systems I: Regular Papers, vol. 67, no. 4, pp. 1286-1295, April 2020. [CrossRef]
J. M. Lim and C. L. DeMarco, "SVD-Based Voltage Stability Assessment From Phasor Measurement Unit Data," in IEEE Transactions on Power Systems, vol. 31, no. 4, pp. 2557-2565, July 2016. [CrossRef]
Gao, G. K. Morison, P. Kundur. Voltage stability evaluation using modal analysis[J]. IEEE Transactions on Power Systems, 1992, 7(4): 1529-1542.
PAN Xueping et al.. Method for evaluating voltage weak area of AC power system at DC receiving end considering sensitivity and static voltage stability margin[J]. Electric Power Automation Equipment,2019,39(3):1-8.
CUI Xinhui et al.. A New Method of Sensitivity Analysis for Static Voltage Stability Online Prevention and Control of Large Power Grids[J]. 2020, 44(1):246-254.
ZHOU Jianfang, HE Yuqing, HE Hongbin, et al. Calculation Method for Continuation Power Flow Based on Line Voltage Stability Index, Proceedings of the CSU-EPSA. 2018(08), pp:140-144.
CHEN Gang, ZHOU Yan, ZHAO Jinquan et al. A Three-Stage Progressive Voltage Stability Contingency Screening and Ranking Method for Large Power Grids, Southern Power System Technology. 2018(01), pp:70-75.
CHEN Chang et al.. Improved point of collapse method for direct calculation of static voltage stability margin[J]. Electric Power Automation Equipment,2020,40(11):150-155.
TANG Xiaobo, GAO Lei. Analysis on Static Voltage Stability Considering Restriction of Branch Power[J]. Power System Technology,2011,35(4):99-102.
Kwatny H, G. Static bifurcati on in electric power networks: loss of steady-state stability and voltage collapse[J]. IEEE Trans on CAS, 1986, 33(10): 981-991.
Chiang H D, Ju meau R J. A more efficient formulation for computation of the maximum l oading in electric power system[J]. IEEE Trans on Power Systems,1995,10(2): 635-646.
Z. A. Kamaruzzaman, A. Mohamed. Impact of grid-connected photovoltaic generator using P-V curve and improved voltage stability index[C]//2014 IEEE International Conference on Power and Energy (PECon). Kuching, Malaysia, 2014: 196-200.

Figure 1. Schematic diagram of grid-connected system with a single load.

Figure 2. Schematic diagram of a renewable energy single-infeed distribution power system.

Figure 3. Schematic diagram of the equivalent structure of a renewable energy single-infeed distribution power system.

Figure 4. A renewable energy aggregated distribution power system.

Figure 5. Multi-infeed distribution power system with N renewable energy sources.

Figure 6. Voltage-active power relationship curve at the integration node in the renewable energy integrated distribution power system.

Figure 7. Schematic diagram of a renewable energy integrated system with reactive power compensation.

Figure 8. Typical network topology of a renewable energy aggregated distribution power systems.

Figure 9. Generalized network topology of renewable energy aggregated distribution power systems.

Figure 10. Structure of distribution power system with two renewable energy sources.

Figure 11. Structure of distribution power system with N renewable energy sources.

Figure 12. Schematic diagram of a single-infeed renewable energy system with reactive power compensation.

Figure 13. P-V curve of the grid-connected node in a single-infeed renewable energy system.

Figure 14. Variation curve of the impedance model index in a single-infeed renewable energy system.

Figure 15. Schematic diagram of a distribution power system with 20 renewable energy sources.

Figure 16. P-V curve and impedance model index variation curve at node 6.

Figure 17. Schematic diagram of a multi-infeed distribution power system.

Figure 18. P-V curve and impedance model index variation curve at node 5.

Figure 19. P-V curve and impedance model index variation curve at node 13.

Figure 20. P-V curve and impedance model index variation curve at node 14.

Figure 21. A renewable energy multi-infeed distribution power system with an additional AC branch.

Figure 22. A renewable energy multi-infeed distribution power system with an additional DC branch.

Table 2. Calculation results of the impedance model index for the renewable energy aggregated system.

Capacities of each group of renewable energy sources	Aggregation bus maximum grid-connected capacity	$Impedance model index K_{R}$
0.115, 0.145, 0.165	2.842	1.008
0.165, 0.130, 0.135	2.841	1.010
0.135, 0.150, 0.140	2.838	1.012

Table 3. Impedance model index as affected by adding AC branch.

	$K_{R 1}$	$K_{R 2}$	$K_{R 3}$	$K_{R 4}$
Before Adding AC Branches	1.5412	1.3155	1.4870	1.2717
After Adding AC Branches	5.0474	1.6547	2.1329	1.6498
Improvement Margin of the Index(%)	227.50	25.78	43.44	29.73

Table 4. Impedance model index as affected by adding DC branch.

	$K_{R 1}$	$K_{R 2}$	$K_{R 3}$	$K_{R 4}$
Before DC Line Connection	1.5412	1.3155	1.4870	1.2717
After DC Line Connection	1.5462	1.3351	1.5062	1.3297
Improvement Margin of the Index(%)	0.32	1.49	1.29	4.56

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Static Voltage Stability Analysis of Renewable Energy Integrated Distribution Power System based on Impedance Model Index

Abstract

1. Introduction

2. Introduction to Tradition Static Voltage Stability Analysis Methods

2.1. Singular Value Decomposition Method

2.2. Sensitivity Analysis Method

2.3. Continuation Power Flow Method

2.4. Voltage Collapse Point Method

2.5. Bifurcation Theory Method

3. Static Voltage Stability Analysis Method Based on Impedence Model Index

3.1. Definition of Impedance Model Index

3.2. Impedance Model Index for Renewable Energy Single-Infeed Distribution Power Systems

3.3. Impedance Model Index for Renewable Energy Aggregated Distribution Power Systems

3.4. Impedance Model Index for Renewable Energy Multi-Infeed Distribution Power Systems

4. Analysis of Factors Affecting Static Voltage Stability

4.1. Criteria for Static Voltage Stability in Renewable Energy Integrated Distribution Power Systems

4.2. Impact of Reactive Power Compensation on Impedance Model Index

4.3. Influence of Renewable Energy Aggregation Topology on Static Voltage Stability

5. Case Study Analysis

5.1. Calculation of Impedance Model Index for Renewable Energy Single-Infeed Distribution Power Systems

5.2. Calculation of Impedance Model Index for Renewable Energy Aggregated Distribution Power Systems

5.3. Calculation of impedance model index for renewable energy multi-infeed distribution power systems

5.4. Impact of Network Topology on Impedance Model Index

6. Conclusion

Author Contributions

Data Availability Statement

Acknowledgments

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe