Prerpints.org logo
Preprint
Article

TLP – NREL 5MW Floating Offshore Wind Turbine Tower Deflection Mitigation Using Optimal-Based Reduced-Stroke Tuned Vibration Absorber

Altmetrics

Downloads

170

Views

96

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

17 January 2024

Posted:

19 January 2024

You are already at the latest version

Alerts
Abstract
The paper presents an implementation and numerical study of the nonlinear optimal-based vibration control solutions for the full-scale TLP – NREL 5MW wind turbine tower-nacelle model with an MR-damper-based 10 ton tuned vibration absorber (TVA) located at the nacelle, under excessive wave/wind polyperiodic excitations yielding continual transient vibration states. The MR damper operates simultaneously with an electromagnetic force actuator (forming a hybrid TVA), or independently (a semiactive TVA). The study includes both actuators’ nonlinearities and dynamics, whereby the former are embedded in the Hamilton-principle-based nonlinear control solutions. As a reference, the structure model with a passive TVA, with a modified ground-hook control law, and without any vibration reduction solutions is used. The TVA was tuned either to the NREL 5MW tower-nacelle 1st bending mode frequency (TVA-TN) or to the TLP surge frequency (TVA-TLP). The optimal control task, redeveloped here with regard to the TVA stroke amplitude minimisation, including the implementation of the protected structure’s acceleration (control case III / III-H) and relative displacement terms as well as nonzero velocity term in the quality index, is stated and solved, yielding optimal-based control propositions for both the MR damper current and the actuator force. On the basis of the obtained results, the TVA-TN solution is by far superior to the TVA-TLP one regarding the tower deflection amplitude / root-mean-square (RMS) and TVA stroke amplitude values. All the regarded TVA-TN solutions provide tower deflection safety factor of ca. 2, while a structure without any vibration reduction solutions or with a TVA tuned to the TLP surge frequency (especially passive and hybrid TVA-TLPs) are at risk of tower structural failure. The obtained TVA stroke amplitudes are reduced with regard to the previously developed approaches. Moreover, these reductions are obtained due to the sole control algorithm enhancement; thus, no additional resources are necessary, while this attainment is accompanied with a reduction in the MR damper force that is necessary for the TVA operation. The protected structure’s acceleration term utilisation produce the TVA stroke amplitude reduction more efficiently than the TVA relative displacement term usage, as in the previously developed approach (the latter being ineffective for the semiactive TVA implementation) which, in turn, efficiently reduces TVA stroke RMS values and the required mean actuator power for the hybrid TVA implementation. Concerning the limited TVA stroke, the most favourable vibration control solutions are the newly introduced semiactive control case III, providing favourable cumulative primary structure deflection indexes at the lowest obtained TVA travel distance, and possibly the hybrid control case III-H, providing even more favourable primary structure deflection qualities and reduced nacelle acceleration levels thanks to the utilisation of the force actuator of the relatively low power (ca. 6 kW); however, side effect of the latter is the increased TVA stroke amplitude as for all hybrid solutions tested (comparing to semiactive solutions). The analysed passive TVA systems along with the modified ground-hook hybrid TVA solution, utilising the assumed absorber mass, can hardly be implemented in the nacelle, especially along the demanding side-side direction, without enforcing end-stop collision bumpers, which result in the efficiency deterioration. The ground-hook control, well proven for the primary structure steady-state deflection minimisation, yielded unsatisfactory results, comparing to the newly implemented solutions. The results of the current study may be used during the design of the full-scale vibration reduction system for the real-world NREL 5MW-class floating, TLP-based, wind turbine structure.
Keywords: 
Subject: Engineering  -   Mechanical Engineering

1. Introduction

Slender structures such as towers, bridges [1], tall buildings [2], wind turbines [3,4,5], plates [6], etc. suffer from mechanical vibrations leading to the increased fatigue and reduced life span. Most of these structures are fitted with dedicated solutions for vibration attenuation and fatigue reduction, such as tuned mass dampers / tuned vibration absorbers (TMDs/TVAs), tuned liquid column dampers, bracing systems, [7,8,9,10] etc. TVAs include an additional mass connected with the protected structure usually by a spring and a damper, and possibly an actuator / inerter connected in parallel. TVAs are widely spread vibration reduction solutions. Depending on the damper and actuator type, passive, semiactive, active, and hybrid TVAs are used. The parameters of the spring, damper or actuator are tuned to the selected mode of the vibration [11]. Passive TVAs cope reasonably with the vibration of a single frequency but cannot adapt to a broader excitation spectrum, structure’s frequency response variations, etc. [4]. Thus, advanced TVA solutions are used, among which TVAs utilising magnetorheological dampers (MR-TVAs) or the additional, small-scale active actuators (hybrid TVAs, H-TVAs, or hybrid MR-TVAs, H-MR-TVAs) gain an increasing interest [12,13,14,15,16,17,18,19,20,21,22,23,24,25,26]. The MR dampers are smart, semiactive actuators exhibiting wide resistance force ranges, millisecond response times and high reliability, but it suffers from a nonzero remanent force and cannot generate active forces (being a semi-active device) [27,28]. The active force actuators of H-TVAs/H-MR-TVAs increase their vibration reduction efficiency; moreover, they provide greater robustness, eco-friendliness, and lower force/power requirements than active TVAs [29,30].
The paper focuses on the vibration control of a tower of a floating offshore wind turbine (FOWT), supported by a tension leg platform (TLP). The FOWT tower vibration arises due to both sea waves-induced platform motion and aerodynamic loads generated by wind, Karman vortices, variable inflow conditions for the blades, etc. Moreover, internal triggers such as unbalance in rotating machinery contribute to structural vibration and fatigue wear of the tower. The development of the offshore wind industry is inevitably linked to the challenge of installation of wind turbines at water depths below the range of 40-70 meters, an area where fixed structures cannot be economically installed and operated. For such depths, several designs have been proposed (spar buoys, barges, semisubmersibles and tension leg platforms), many projects are in the final design stage or in the experimental testing of scaled down prototypes, while there are also many pilot full scale developments. As of 2021, a total of 121.4 MW of floating wind is installed globally, 110.9 MW of them in Europe, and the remaining 10.5 MW in Asia. The offshore wind sector is expanding with a prediction of 18.9 GW likely to be built globally by 2030 [31].
Spars have a simple construction composed of a single vertical cylinder which forms the basis for the installation of the wind turbine tower. Spars are stabilized by ballast weight at the bottom of the cylinder and thus require deep waters. Their conventional mooring arrangement results in a large sea bed footprint. Spars are large structures and require special docking area for building and special equipment turbine installation. Barges and semisubmersible platforms achieve stability through the large metacentric height obtained from the extended water plane area. Their design is a mature technology since they are in use for many years in the oil and gas sector. Barges and semi subs do not require special docks for building and can be towed relatively easily to the installation location. Their mooring arrangement usually follows conventional design resulting in large sea bed footprint. Tension leg platforms usually consist of a submerged hull connected to vertical mooring lines (tendons). The buoyancy of the hull is usually larger that the platform weight, resulting in a buoyancy surplus which loads the tendons with a positive force (pretension). The stability of the platform is maintained by this pretension. The design of the buoyant part of the hull should ensure positive tendon forces in all operating and extreme conditions, since compression in the tendons (which are usually made from steel pipes) results in buckling with catastrophic consequences. TLPs have simple construction which results in a reduced manufacturing cost. Moreover, they can be installed in a wide range of water depths and, due to the vertical arrangement of the tendons, exhibit small seabed footprint. If their hull is similar to semi subs they do not require special equipment-vessel for towing and installation. However, it should noted that TLP mooring system comprises a critical element for the strength of the whole structure and it is usually expensive, as compared against to the conventional mooring arrangements, and. Additionally, TLP concept makes difficult the installation in water areas with large tidal range.
Regarding the type of the support structure, the conventional mooring arrangement of the spars, barges and semisubmersibles permits significant linear and angular motions of the platforms, due to the inherent low stiffness of the catenary type mooring legs. In this respect, the tension leg concept offers the most stable solution, minimising the heave, pitch and roll motions by imposing large pretension mooring forces. In this way, the platform is moving by the wave action mainly in surge and the dynamics of the wind turbine are comparatively less affected. The fatigue damage equivalent loads are lowest for [32]. TLP FOWT concepts combined with wave energy devices of the oscillating water column (OWC) type have been experimentally investigated in [33] and [34]. The surge response of a TLP FOWT combined with OWCs was measured in [33] and forms the basis for the vibration mitigation examined in the current study.
The problem of FOWTs vibration control has been investigated many times within the last decade. The investigations concerned both structural fatigue and strength. National Renewable Energy Laboratory (NREL) is one of the leading parties in this area, providing a systematic background for a broader research (presented below) concerning the offshore version of NREL 5MW wind turbines [35,36]. In [37], a monopile along with a barge, spar buoy, and TLP wind turbine supports were investigated. A set of optimum passive TMDs were developed by creating a limited degree-of-freedom model for each of the offshore wind supports. The TMDs parameters determined by the optimisation were applied to a series of wind turbine FAST SC simulations. A sensitivity analysis of the TMD parameters and a study on the effect of misaligned wind and waves on load reductions were also conducted. The tower fatigue damage reductions of up to 20% were achieved for the various TMD configurations. In [38], the impact of passive and semiactive TMDs applied to both monopile and floating TLP-based FOWTs were evaluated under the fatigue limit state and ultimate limit state. Different control logics based on the ground-hook control policy were implemented, and the frequency responses were investigated. It was shown that the performance of each algorithm varies according to the load conditions. Fully-coupled time domain simulations were conducted through the developed simulation tool integrated into FASTv8 environment. It was shown that a semiactive TMD results in higher load reductions as well as smaller strokes. The ultimate loads at the tower base for the TLP-based structure were reduced by 9% with semiactive TMD. In [39], the nonlinear dynamic behaviour of the NREL 5MW wind turbine structure is evaluated considering different earthquake and wind intensities using a newly developed finite element model. The model is first calibrated and verified using modal and static pushover analysis. From the findings in this research, it is shown that earthquake loads have considerable effects on the design and analysis of wind turbines. Moreover, the NREL 5MW tower failure conditions were established. A study [40] investigates a vibration control strategy for a barge-type FOWT by setting a stroke-limited H-TVA in the nacelle. The LQR controller is designed to reduce vibration and loads of the wind turbine, and weighting coefficients are optimised considering the stroke of the H-TVA and the active control power. The designed controllers are implemented in high fidelity simulations under five typical wind and wave conditions. In [41], the numerical predictions of a TLP wind turbine response are discussed. The numerical model is calibrated vs the physical test measurements. Open-FAST tools are used for hydrodynamic and motion response analyses. The dynamic response of the TLP-based NREL 5MW FOWT model is compared with the physical model response from free-decay, regular and irregular wave tests and discussed in time and frequency domains. This comparison addressed the uncertainties in physical model testing of TLP wind turbines. In [42], a structural vibration control of a FOWT model with barge-type support was investigated. The system was equipped with MR-damper-based TVA located in the nacelle. Tower and barge angular displacement amplitude frequency responses were compared, proving the quality of the adopted optimal-based solutions, and their capability to minimise pitching amplitude of the vibrating structure (yielding improved wind energy extraction) as well as MR damper force and/or stroke amplitude; moreover, all of the actuator dynamics and force constraints were embedded in the control technique. Thus, the solution is optimal or suboptimal for the assumed actuator, respecting its limitations. Larsen et al. [43] investigated the use of a electromagnetic-transducer-based pendulum absorber for damping of tower vibrations in monopile-supported wind turbines. An RCL network was designed as the supplemental shunt for the transducer intrinsic RL properties, resulting in an additional resonance. The optimal system calibration was derived using pole-placement method. The presented frequency and time domain results exhibited slight advantage of the obtained absorber vs the classic dashpot-based pendulum absorber concerning vibration mitigation. In [44], Madsen et al. covered the experimental testing of a TLP-based, pitch-regulated DTU 10 MW wind turbine at 1:60 scale in wind and waves. The responses of the floater to hydrodynamic loading were analysed and compared for two different feedback controllers: a typical onshore one that was tuned by a pole-placement technique, and a floating wind turbine controller. Overall the performance of the onshore controller resulted in larger surge response than the offshore controller, leading to larger front mooring line tensions. This was due to higher blade pitch angle amplitudes, produced by the onshore controller. The shutdown cases of the offshore controller led to larger surge displacement when the shutdown was initialized right before the wave impact as the aerodynamic damping was disabled. The research demonstrated the potential of physical model testing and numerical models validation potential.
Most of the vibration control solutions are based on the bang-bang control (ground-hook, sky-hook, sliding mode, etc.) [45,46], fuzzy logic, or two-stage approaches [1,19,22], which suffer from the inability to generate the force calculated in the first stage by the second stage algorithm due to the actuator limitations, including force and stroke constraints, the inability to produce active forces, etc. The stroke constraints of the real-world vibration reduction system / TVA, is frequently addressed by the use of end-stop collision bumpers or spring-damper buffer systems with stroke-dependent stiffness restoring force [40], which prevent the impact with the protected structure but, at the same time, deteriorate the vibration attenuation quality. Moreover, many first stage algorithms require real-time vibration frequency determination, which is problematic for transient, polyperiodic, multi-mode vibrations, for which these systems switch to the passive mode.
To address the limitations mentioned above, a concept was devised to embed actuators’ constraints into the control problem formulation [25,26,29,30] to avoid efficiency and robustness problems of the calculated control function being imprecisely mapped or beyond the actuator output limits. This involved the use of nonlinear control methods, which may be grouped generally as maximum-principle-based [5,6,47], Lyapunov-function-based [16,46], and linearisation-based methods utilising linear optimal control theory (LQR/LQG/H2/H∞) [7,21,40,48,49]. The main implementation issues regarding these methods are the high computational load of the real-time operation or control quality degradation due to dynamics/disturbances that were unmodelled during offline pre-calculations. Thus, the concept of the maximum-principle-based nonlinear optimal-based vibration control was previously developed [25,26,30], eliminating all of the above computational or control authority problems.
The idea of simultaneous operation of the MR damper and the active force actuator was seldom investigated. Recently, it was literature-reviewed and implemented on a scaled laboratory model of an onshore wind turbine tower-nacelle structure with H-MR-TVA [30]. The developed concurrent MR damper – electric drive quasi-optimal and modified ground-hook control solutions provided significant attenuation of the steady-state monoharmonic vibration with regard to a passive system. The quasi-optimal control solution offered a significant energy efficiency advantage over the modified ground-hook law thanks to its various optimisation fields covered by the quality index; moreover, the MR damper and force actuator constraints were embedded in the optimal control task of the former, so they did not compromise the vibration control quality. No offline calculations nor disturbances assumption was required for proper controller operation. The obtained results may be transferred to a full-scale real-world wind turbine structure thanks to the dynamical similarity [50,51].
Based on these results, the current research addresses the utilisation of the optimal-based, concurrent control algorithm for the TLP – NREL 5MW full-scale FOWT structure under excessive wave/wind conditions (characterised by polyperiodic excitations and continual transient vibration states), along with the design and tuning of the H-MR-TVA located in the nacelle; the optimal control task is enhanced with regard to the TVA stroke amplitude minimisation, including the implementation of the nacelle’s acceleration and relative displacement terms as well as nonzero velocity term in the quality index, yielding the redeveloped optimal-based control propositions for both the MR damper current and the actuator force, being the main contributions of the paper. As a reference, the optimal-based, modified ground-hook law with the sole objective of the primary structure deflection minimisation is used along with the passive TVA system.
The paper is organised as follows. The succeeding section presents a regarded system. Next, the Pontryagin maximum-principle-based nonlinear optimal vibration control problem is stated and solved. Then, the numerical tests conditions, simulation model setup, and control implementation procedure are described. This is followed by the vibration control results and discussion. The paper is summed up with several conclusions.

2. A Regarded System

An NREL 5MW wind turbine (Table 1) tower-nacelle system, supported by a TLP [32] (Table 2) is regarded as a protected structure [35,36]. The NREL 5MW tower-nacelle system’s 1st bending mode corresponds to the dominant modal mass and vibration energy participation, especially for low frequency range associated with wave, wind and rotor excitations. Therefore, the current study takes into account the structure’s 1st bending mode modal parameters, such as: mass m1, stiffness k1 and damping c1 (Table 3). An H-MR-TVA of the absorber mass m2 and spring stiffness k2 embedded in the nacelle is considered (Figure 1), based on the previous research [37]. The movement of both m1 and m2 is assumed to be linear displacement x1 and x2, accordingly (small bending angles assumed), along the common, horizontal axis of an external force F e (representing the resultant load applied to the nacelle i.a. through rotor), and the supporting TLP platform surge motion x 0 (Figure 1). An MR damper and a small-scale electromagnetic actuator [30] of an output force F a are both built-in parallel to the spring k2 in the TVA system. The absorber stiffness k2 (and damping c2 for passive TVA tests) was tuned either to the NREL 5MW tower-nacelle 1st bending mode frequency of 0.30 Hz (hereinafter referred to as TVA-TN) or to the TLP surge frequency of 0.10 Hz (hereinafter referred to as TVA-TLP), using the Den Hartog principle [11] (Table 3). For structural vibration control purposes, the MR damper was used, working in cooperation with the force actuator or independently.
Table 1 and Table 2 present the main particulars of the regarded FOWT structure. The values of the adopted simulation model parameters are given in Tables 3 and 4.
Figure 2 presents bode diagrams of the regarded simulation model without TVA (No TVA legend) and with baseline passive TVA tuned to the NREL 5MW tower-nacelle 1st bending mode (TVA-TN legend). The magnitude of the x1 steady-state resonance vibration due to the passive TVA-TN implementation is reduced by 28.3 dB; however, the efficiency of the passive TVA along with MR-TVA, and H-MR-TVA will be investigated using random sea and wind state excitation patterns, enforcing continual transient vibration states, as described in the Simulation setup section.

3. Control Problem Formulation and Solution

The regarded system dynamics is described in a form of equation (1):
z ˙ t = f z t , u t , t ,   t ∈ t 0 , t 1
where z t is a state vector:
z t = z 1 t z 2 t z 3 t z 4 t T ,
while u t = u 1   t u 2   t T ∈ U ( U = R 2 ) is a piecewise-continuous control vector. A quality function to be minimised is:
G z , u = ∫ t 0 t 1 g z t , u t , t d t .
According to Figure 1, Section 2, let us assume: z 1 = x 1 , z 2 = x ˙ 1 , z 3 = x 2 , z 4 = x ˙ 2 , thus:
f z , u , t =
z 2 t 1 m 1 − k 1 + k 2 z 1 t − c 1 z 2 t + k 2 z 3 t + F m r z , u , t + F a u , t + k 1 x 0 t + c 1 x ˙ 0 t + F e t z 4 t 1 m 2 k 2 z 1 t − k 2 z 3 t − F m r z , u , t − F a u , t
where:
F m r z , u , t = C 1 i m r u , t + C 2 tanh ⁡ ν z 4 t − z 2 t + z 3 t − z 1 t + C 3 i m r u , t + C 4 z 4 t − z 2 t + z 3 t − z 1 t
is the MR damper force as described in [25,42] with parameters tuned to the present application as given in Table 4; i m r u is the MR damper control current, F a u is the actuator force [30], F e t is the nacelle horizontal excitation force, and x 0 t is the TLP surge that is assumed to be independent of the wind turbine tower-nacelle system bending in this research, as the NREL 5.0MW 1st tower bending modal mass is small in relation to the TLP structural mass plus an added mass due to the outgoing waves created by the floater motion [41]. The force produced by the MR damper includes electric current i m r u , t dependent friction force and viscous damping as well as stiffness components with a scaling parameter ν .
The MR damper current limitation to 0 ,   i m a x range ( i m a x > 0 ) and the actuator output nominal force limitation to − F n o m ,   F n o m range were assumed as in [30]:
i m r u , t = i m a x sin 2 ⁡ u 1 t ,
F a u , t = F n o m sin ⁡ u 2 t .
The regarded quality function (8) is:
g z , u , t = g 11 z 1 t − x 0 t 2 + g 12 z 2 t − x ˙ 0 t 2 + g 13 z 1 t − z 3 t 2 + g 14 z 2 t − z 4 t 2 + g 15 z ˙ 2 2 t + g 21 i m r 2 u , t + g 221 F m r 2 z , u , t + g 222 F a 2 u , t + g 23 P a 2 z , u , t
to account for the protected structure relative displacement (i.e., tower deflection) z 1 − x 0 and relative velocity (tower deflection rate) z 2 − x ˙ 0 minimisation, the protected structure (nacelle) acceleration z ˙ 2 = x ¨ 1 minimisation, the TVA stroke z 1 − z 3 and relative velocity z 2 − z 4 minimisation, the MR damper coil current i m r and force F m r minimisation, and the actuator force F a and power P a minimisation, where:
P a z , u , t = F a u , t z 2 t − z 4 t ,
z ˙ 2 t = 1 m 1 − k 1 + k 2 z 1 t − c 1 z 2 t + k 2 z 3 t + F m r z , u , t + F a u , t + k 1 x 0 t + c 1 x ˙ 0 t + F e t .
The newly introduced term g 15 z ˙ 2 2 t implementation, being the original contribution of current research, is intended to minimise the protected structure (i.e., nacelle/rotor with its sensitive instrumentation) acceleration. As the structure acceleration increases with the square of the frequency (for the constant oscillation displacement amplitude), this term is aimed to minimise predominantly higher frequency content of the displacement x 1 (thus minimising the acceleration x ¨ 1 ). At these, higher frequencies, TVA mass vibrates at a close antiphase to the protected structure’s mass – see x1 vs x2 phase diagrams (Figure 2). Thus, the minimisation of the high frequency content of x 1 with the use of appropriate g 15 weight consequently reduces moving away the protected structure and the TVA (due to the close antiphase). This in turn reduces the TVA stroke amplitude and MR damper force amplitude, which will be proven in the Control results section.
Let us consider he Hamiltonian in a form (10):
H ξ , z , u , t = − g z , u , t + ξ T t f z , u , t .
If z * , u * pair is an optimal control process, there exists an adjoint vector function ξ satisfying:
ξ ˙ t = − f z * T z * , u * , t ξ t + g z T z * , u * , t , t ∈ t 0 , t 1
with a transversality condition:
ξ t 1 = 0
so that u * t maximises the Hamiltonian over the set U for almost all t ∈ t 0 , t 1 (see details in [52]). For the regarded system, the adjoint (co-state) vector is:
ξ t = ξ 1 t ξ 2 t ξ 3 t ξ 4 t T ,
whereas:
f z * T z * , u * , t = 0 − 1 m 1 k 1 + k 2 + F ~ m r z * , u * , t 0 1 m 2 k 2 + F ~ m r z * , u * , t 1 − 1 m 1 c 1 + F ~ m r z * , u * , t 0 1 m 2 F ~ m r z * , u * , t 0 1 m 1 k 2 + F ~ m r z * , u * , t 0 − 1 m 2 k 2 + F ~ m r z * , u * , t 0 1 m 1 F ~ m r z * , u * , t 1 − 1 m 2 F ~ m r z * , u * , t  
and:
g z T z * , u * , t =
= 2 g 11 z 1 * t − x 0 t + 2 g 13 z 1 * t − z 3 * t − 2 g 221 F m r ' z * , u * , t − 2 g 15 m 1 z ˙ 2 * t k 1 + k 2 + F ~ m r z * , u * , t 2 g 12 z 2 * t − x ˙ 0 t + 2 g 14 z 2 * t − z 4 * t − 2 g 221 F m r ' z * , u * , t + 2 g 23 F a 2 u * z 2 * t − z 4 * t − 2 g 15 m 1 z ˙ 2 * t c 1 + F ~ m r z * , u * , t − 2 g 13 z 1 * t − z 3 * t + 2 g 221 F m r ' z * , u * , t + 2 g 15 m 1 z ˙ 2 * t k 2 + F ~ m r z * , u * , t − 2 g 14 z 2 * t − z 4 * t + 2 g 221 F m r ' z * , u * , t − 2 g 23 F a 2 u * z 2 * t − z 4 * t + 2 g 15 m 1 z ˙ 2 * t F ~ m r z * , u * , t
with:
F ~ m r z * , u * , t = ν C 1 i m r u * , t + C 2 1 − tanh 2 ⁡ ν z 4 * t + z 3 * t − z 2 * t − z 1 * t + C 3 i m r u * , t + C 4 ,
F m r ' z * , u * , t = F m r z * , u * , t F ~ m r z * , u * , t .
The Hamiltonian therefore takes the form (16):
H ξ , z , u , t =
− g 11 z 1 t − x 0 t 2 − g 12 z 2 t − x ˙ 0 t 2 − g 13 z 1 t − z 3 t 2 − g 14 z 2 t − z 4 t 2 − g 15 z ˙ 2 2 t − g 21 i m r 2 u , t − g 221 F m r 2 z , u , t − g 222 F a 2 u , t − g 23 F a 2 u , t z 2 t − z 4 t 2 + ξ T t f z , u , t .
The Hamiltonian maximisation conditions [52] are:
∂ H ξ , z , u , t ∂ u 1 t =
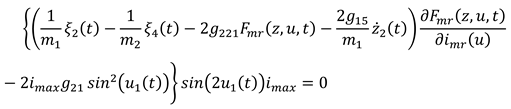Preprints 96670 i001
∂ H ξ , z , u , t ∂ u 2 t =
1 m 1 ξ 2 t − 1 m 2 ξ 4 t − 2 g 15 m 1 z ˙ 2 t − 2 F n o m g 222 + g 23 z 2 t − z 4 t 2 sin ⁡ u 2 t cos ⁡ u 2 t F n o m = 0
with the appropriate sign change conditions, where:
∂ F m r z , u , t ∂ i m r u , t = C 1 tanh ⁡ ν z 4   t + z 3   t − z 2   t − z 1   t + C 3 z 4   t + z 3   t − z 2   t − z 1   t
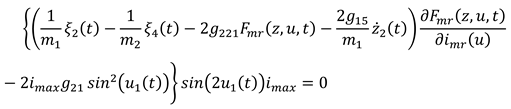
Fixing an attention on 0 , π range of u 1 t , equation (17) results in ( g 21 ≠ 0 ):
sin ⁡ 2 u 1 t = 0
or:
sin 2 ⁡ u 1 t = 1 2 i m a x g 21 1 m 1 ξ 2 t − 1 m 2 ξ 4 t − 2 g 15 m 1 z ˙ 2 t − 2 g 221 F m r z , u , t ∂ F m r z , u , t ∂ i m r u
Analogically to [26]:
i m r * u * , t =
  0 ,   i f   R H S 20 < 0 1 2 g 21 1 m 1 ξ 2 t − 1 m 2 ξ 4 t − 2 g 15 m 1 z ˙ 2 t − 2 g 221 F m r z , u , t ∂ F m r z   , u , t ∂ i m r u , t ,   i f   R H S 20 ∈ [ 0   1 )   i m a x ,   i f   R H S 20 ≥ 1
where R H S 20 is the right-hand side of equation (20).
From condition (18) we obtain ( g 222 ≠ 0 ):
∂ H ξ , z , u , t ∂ u 2 t = 1 2 F n o m g 222 + g 23 z 2 t − z 4 t 2 1 m 1 ξ 2 t − 1 m 2 ξ 4 t − 2 g 15 m 1 z ˙ 2 t − sin ⁡ u 2 t cos ⁡ u 2 t = 0
Fixing an attention on − π , π   range of u 2 t , equation (22) results in proposition (23abc), analogically to [30]:
1)
i f 1 2 F n o m g 222 + g 23 z 2 t − z 4 t 2 1 m 1 ξ 2 t − 1 m 2 ξ 4 t − 2 g 15 m 1 z ˙ 2 t ≤ − 1 ,
2)
t h e n (22) is fulfilled and ∂ H ξ , z , u , t ∂ u 2 t exhibits + / − sign change (Hamiltonian maximisation) for:
u 2 * t = − π 2   only ;   thus :   F a * u * , t = − F n o m .
3)
i f 1 2 F n o m g 222 + g 23 z 2 t − z 4 t 2 1 m 1 ξ 2 t − 1 m 2 ξ 4 t − 2 g 15 m 1 z ˙ 2 t ≥ 1 ,
4)
t h e n (22) is fulfilled and ∂ H ξ , z , u , t ∂ u 2 t exhibits + / − sign change for: u 2 * t = π 2 only; thus:
F a * u * , t = F n o m .
5)
i f 1 2 F n o m g 222 + g 23 z 2 t − z 4 t 2 1 m 1 ξ 2 t − 1 m 2 ξ 4 t − 2 g 15 m 1 z ˙ 2 t ∈ − 1 , 1 ,
6)
t h e n (2) is fulfilled and ∂ H ξ , z , u , t ∂ u 2 t exhibits + / − sign change for:
7)
u 2 * t = a r c s i n 1 2 F n o m g 222 + g 23 z 2 * t − z 4 * t 2 1 m 1 ξ 2 t − 1 m 2 ξ 4 t − 2 g 15 m 1 z ˙ 2 t only; thus:
F a * u * , t = 1 2 g 222 + g 23 z 2 * t − z 4 * t 2 1 m 1 ξ 2 t − 1 m 2 ξ 4 t .

4. Test Conditions

The TLP surge x 0 t realisations used in this research correspond to the response of the platform under the action of an ocean wave spectrum of Bretschneider type. The examined TLP platform is shown in Figure 3 and Figure 4. It forms a floating basis for the installation of a 5MW NREL offshore wind turbine and combines also three wave energy devices, i.e., three vertical cylinders at the vertices of the triangle, which provide the required buoyancy. Each of them is surrounded by a thin skirt, open at its lower end, forming the oscillating water column (OWC) chamber. A central vertical cylinder is also included in the arrangement, for the installation of the wind turbine. All the cylinders of the hull of the platform are structurally connected and supported by cylindrical bracing.
The mooring system of the platform follows the tension leg concept. Three tendons connect the bottom of the corner cylinders to the sea bed foundation, providing also the required pretension for the stabilization of the platform and for station keeping.
The weight groups of the platform and the tendon characteristics are summarised in Table 2. In order to examine the hydrodynamic behaviour of such a system, an extensive set of experiments were conducted on a scaled down model of the platform (scale 1:40), in the wave tank of the Laboratory for Ship and Marine Hydrodynamics of the National Technical University of Athens (NTUA).
The Froude scaling law for dynamic similarity was followed, for the modelling of the wave environment and the seakeeping behaviour of the platform. Experiments were conducted for a wide range of incident waves’ periods and amplitudes, both harmonic and irregular, corresponding to the sea-states the TLP is expected to encounter in the Aegean Sea. Figure 5 depicts the measured surge response amplitude operators, RAOs (i.e., surge motion amplitude due to a harmonic wave of unit amplitude).
For the installation location considered in the Aegean Sea, the most probable severe wave state can be described by a Bretschneider wave spectrum S(ω) (Figure 6) having a significant wave height Hs = 4 m and a peak period Tp = 8.3 s. The corresponding spectrum of the surge response (24) can be found through the combination of the sea wave spectrum and the surge motion RAOs:
S s u r g e ω = S   ω R A O 2 ( ω )
On the basis of the surge spectrum, ten random realizations (numbered 0 through 9) of surge motion were produced by combining the spectral density and random phases for individual motion components.
The external excitation applied on the tower-nacelle structure through the rotor is mainly due to changeable aerodynamic loads. The wind realisations at the height of 90 m above the open sea were generated using the Weibull distribution with a scale parameter of 10 and shape parameter of 2.0, resulting in 8.86 m/s mean wind speed and 4.63 m/s standard deviation. The horizontal nacelle excitation force F e t was then calculated using the rotor thrust data from ‘Steady-state responses as a function of wind speed’ characteristics [35], which is generally consistent with [53].
The most severe vibration response case of uniaxial excitations was assumed. Ten Bredsneider spectrum ocean wave realisations 0÷9 were paired with ten Weibull distribution wind patterns 0÷9, 2500 seconds in length each, 1 ms of time resolution, as described above. Due to a continual thrust asymmetry during all the 360ᵒ rotor angular positions but six ones (i.e., 0ᵒ, 60ᵒ, 120ᵒ, 180ᵒ, 240ᵒ, 300ᵒ), both tower fore-aft and side-side bending mode is excited, whereas TLP horizontal excitation directions (surge/sway) may vary, too. Current analyses are conducted assuming (H-)MR-TVA direction of operation to be the excitations direction. In a practical implementation, two (H-)MR-TVAs operating along mutually perpendicular directions (side-side / fore-aft) may be installed, or a single (H-)MR-TVA operating along side-side direction (fore-aft vibrations attenuated by the rotor aerodynamic damping and collective pitch control of the blades). The assumed here excitations combinations, including their alignment, are not necessarily in the real world conditions. The analyses of the wave/wind misalignment [37] suggest side-side TVA installation necessity due to side-side loads being a large contributor to the overall fatigue. The work [44] indicates that the aerodynamic damping is strongest on the surge motion for unidirectional conditions; thus, a fore-aft TVA may also be essential for wave/wind misalignment.

5. Simulation Setup

The NREL 5MW tower-nacelle 1st bending mode model equipped with passive TVA / MR-TVA / H-MR-TVA located in the nacelle, excited horizontally by the supporting TLP platform surge x 0 and resultant load applied to the nacelle F e , was embedded in MATLAB/Simulink environment, adopting the fixed t s = 1 ms sampling step. A relatively low TVA mass m2 of 10 ton (0.35% of the total structure’s mass) was assumed, yielding 2.33% m2/m1 mass ratio, regarding 1st bending mode mass m1 of 428.8 ton. As discussed earlier [30], an increased TVA mass ratio does not yield a proportional efficiency gain, not to mention the spatial and structural support requirements; however, it contributes to lower TVA sensitivity to detuning [54] and more limited TVA stroke. The selection of 10 ton absorber mass is consistent with [37]. Therefore, the current study discusses the benefits of implementation of an MR damper (and possibly a small-scale force actuator) to address all the regarded efficiency, stroke / space / structural support limitations and detuning issues, using a smaller absorber mass.
In addition to the MR damper’s and actuator’s static non-linearities discussed above (5)(6)(7), their linear dynamics (25)(26) are also included in the current study:
G m r s = F m r a c t s F m r s = 1 0.0051 s + 1 e − 0.0029 s ,
G a s = F a a c t s F a s = 32.6 s 2 + 1.55 e 4 s + 9.66 e 4 s 3 + 140 s 2 + 1.71 e 4 s + 1.06 e 5 e − 0.0060 s ,
where F m r a c t s and F a a c t s are Laplace transforms of actual MR damper and electromagnetic actuator outputs, respectively. However, as the MR damper dynamics (25) may be modelled with a 2nd order inertia, while the electromagnetic actuator time-delayed transfer function (26) [30] may be modelled with a 2nd order oscillatory dynamics with a 1st order inertia, the corresponding optimal control task would be of the 9th order. This would yield a computational load that was real-time tested to be unrealisable. Thus, the dynamics of the MR damper and the electromagnetic actuator are both embedded in the simulation model of the NREL 5MW tower-nacelle system equipped with a TVA, supported by the TLP, and the actual values of F m r a c t / F a a c t are fed as F m r / F a into equations (4)(8)(11)(21)(23abc) (in this way, the modelled MR damper and force actuator responses inertia and delays influence state and co-state variables’ values as well as i m r * and F a * control patterns), but they do not augment optimal problem order. This guarantees simplicity of the real-time implementation, while not impairing the overall system performance (partially due to the frequency spectrum of the regarded vibration problem being low in relation to actuators’ dynamics).
All the structural model parameters as in Table 3 along with the MR damper model parameters (Table 4) were assumed for the simulations. The value of i m a x = 1 A yielding respective F m r ranges and nominal actuator output force F n o m = 7.125 kN were tuned to the current application. As it was previously proven [30], the MR damper responds faster than the electromagnetic actuator, while the actuator may cancel the MR damper undesirable (i.e., of improper sign due to its dissipative nature) force. The resultant maximum MR damper force was ca. 50 kN (excluding the more demanding Mod.GH and Mod.GH-H solutions), whereas the mean actuator power was up to 6.27 kW for TVA-TN hybrid solutions; however, less force/power demanding solutions were investigated as well.

6. Control Implementation

For the vibration control of the FOWT 1st bending mode, the approach described in Section 3 and Section 5 was implemented using the MR damper control formula (21) and the force actuator control formula (23abc). Regarding the considerations presented in [25,26,29,30], the control propositions (21)(23abc) were implemented using the optimisation horizon equal to one integration step [25,30]; as it was proven in [25,26,29], the computationally excessive iteration procedure could be omitted using a relatively short (with regard to system’s time constants) sample step and zero initial conditions for adjoint variables, yielding an optimal-based (suboptimal) control solution that is negligibly different from the optimal one. The control solution incorporates either two simultaneous control outputs: u 1 t (i.e., i m r u , t ) and u 2 t (i.e., F a u , t ) (H-MR-TVA system), or a single control output u 1 t (MR-TVA system).
The weighting factors for the optimal-based control quality index (8) are assumed as follows: g 11 = 10 21 , g 12 = 10 19 , g 14 = 0 , g 21 = 4 , g 222 = 4 ∙ 10 − 12 . The remaining weight values are given for each control case regarded below if are nonzero (the omitted weights are assumed zero all over this section). A significant g 12 value with regard to the previous research [30] is used to address transient states during simulated wave/wind realisations – incorporation of the protected structure velocity significant weight value corresponds to a derivative term of a displacement controller which is known to be efficient during transients. A negligible but nonzero g 222 value was selected to eliminate zero-division errors for z 2 t = z 4 t in (23abc). The detailed weights of the quality function (8) were assumed as follows (control cases I, II, III, I-H, II-H, III-H):
I 
g 11 = 10 21 and g 12 = 10 19 – minimise the tower deflection and deflection rate as a sole objective (being the primary objective for all the control cases) using MR-TVA;
II 
g 13 = 3 · 10 19 (the TVA stroke weight) assumed in addition to control case I weights, MR-TVA used;
III 
g 15 = 10 (the nacelle / tower tip acceleration weight) assumed in addition to control case I weights, MR-TVA used;
I-H 
as for control case I, using H-MR-TVA;
II-H 
as for control case II, using H-MR-TVA;
III-H 
as for control case III, using H-MR-TVA.
As a reference, an optimal-based, modified ground-hook law (Mod.GH using MR-TVA, and Mod.GH-H using H-MR-TVA) with the sole objective of the primary structure deflection minimisation is used [30], along with the passive TVA systems (TVA-TN and TVA-TLP).

7. Control Results

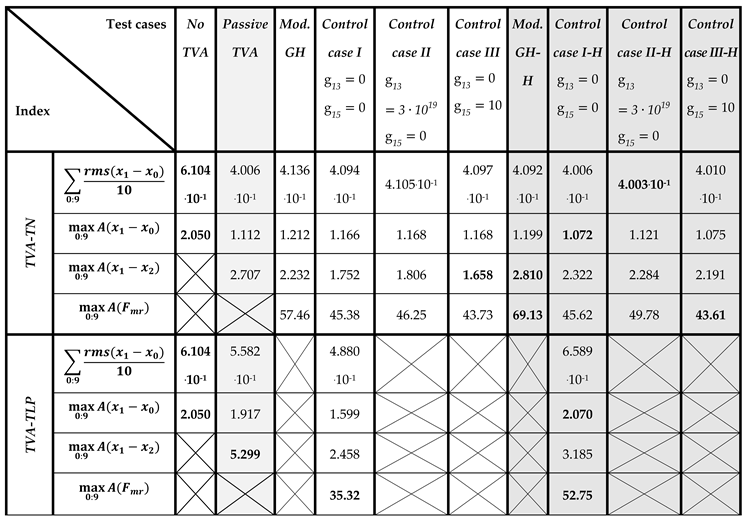
The efficiency of the considered solutions was analysed using the following quality indexes: tower tip relative displacement (i.e., tower deflection) root-mean-square (RMS) r m s ( x 1 − x 0 ) (Figure 7 and Figure 8), tower tip relative displacement (tower deflection) amplitude A ( x 1 − x 0 ) (Figure 9 and Figure 10), TVA stroke amplitude A ( x 1 − x 2 ) (Figure 11 and Figure 12), the MR damper force amplitude (Figure 13 and Figure 14; Mod.GH and Mod.GH-H results excluded due to seriously outlying values – see Table 5), and mean actuator power (Figure 15), along with the time patterns of x 0 , x 1 , x 1 − x 2 , F a , and F m r (Figure 16, Figure 17 and Figure 18) and Table 5 ( A ( • ) states for the amplitude i.e., the maximum deviation from the equilibrium state). The r m s ( x 1 − x 0 ) (equal to standard deviation for zero mean value) value indicates the tower structure operational fatigue, the tower deflection amplitude A ( x 1 − x 0 ) indicates the maximum structural stress, whereas the TVA stroke amplitude A ( x 1 − x 2 ) determines the spatial and structural applicability of the vibration control solution; the required MR damper force F m r , associated with the particular solution, conditions its efficiency. In Table 5, the most favourable results are marked in green bold face, the worst results are marked in red bold face, whereas the runner up solutions are marked in green/red (respectively) regular face.
Figure 7 and Figure 8 present tower tip relative displacement RMSs for a 0÷9 Bredsneider spectrum ocean wave realisations paired with Weibull distribution wind patterns. The TVA was tuned either to the NREL 5MW tower-nacelle first bending mode case (H-MR-TN legend for H-MR-TVA case; MR-TN legend for MR-TVA case), or to the TLP surge frequency case (H-MR-TLP legend for H-MR-TVA case; MR-TLP legend for MR-TVA case). Figure 9 and Figure 10 present tower tip relative displacement amplitudes for the same set of ten ocean wave / wind realisations, for the TVA tuned to the tower-nacelle first bending mode or the TLP surge frequency. Similarly, Figure 11 and Figure 12/Figure 13 and Figure 14 present the TVA stroke amplitudes / MR damper force amplitudes (respectively), whereas Figure 15 presents the mean actuator power values obtained for TVA-TN cases. The regarded control solutions comparison, covering the vibration attenuation results cumulated over all 0÷9 wave/wind realisations, is presented in Table 5, including: mean of RMSs of tower tip relative displacements (tower deflections) 1 10 ∑ 0 : 9 r m s ( x 1 − x 0 ) , tower tip relative displacements (tower deflections) maximum amplitudes max 0 : 9 ⁡ A ( x 1 − x 0 ) , TVA stroke maximum amplitudes max 0 : 9 ⁡ A ( x 1 − x 2 ) , and MR damper force maximum amplitudes max 0 : 9 ⁡ A ( F m r ) .
On the basis of the obtained results, the general conclusion regarding the TVA tuning frequency is consistent with the previous work [42], i.e., the TVA-TN solution is by far superior to the TVA-TLP one regarding tower deflection RMS / amplitude and TVA stroke values. Thus, the TVA-TN case only was selected for more thorough analyses described below. The obtained values of the maximum tower tip relative displacement (tower deflection) amplitude A ( x 1 − x 0 ) indicate that under the assumed extreme wave/wind conditions the regarded TLP – NREL 5MW structure without a TVA (or any other vibration attenuation solution) or with a TVA tuned to the TLP surge frequency (especially passive and hybrid TVA-TLPs) are at risk of tower structural failure, which starts to occur when the tower deflection reaches 2.2 m according to [39] research. All the regarded TVA-TN solutions provide tower structural deflection safety factor of ca. 2 in accordance with [39].
The results shown in Figure 7, Figure 8, Figure 9 and Figure 10 and Table 5 indicate mixed benefits of the force actuator utilisation in the TVA system. Up to a 2.5 % cumulative (i.e., across all ten ocean wave/wind realisations – see Table 5) minimisation of the RMS tower deflection, along with up to an 8.8% tower deflection amplitude minimisation in the TVA-TN case, at the cost of up to 32.5 % increased TVA stroke, is the result of the implementation of this active machinery along with the control circuity and computation resources for the H-MR-TVA system vs the MR-TVA one (BTW, a significant increase in the tower deflection RMSs / amplitudes, TVA strokes, and MR damper force amplitudes may be observed for the active actuator utilisation in the TVA-TLP case). The MR damper is a semiactive, dissipative device, which force F m r attenuates the relative travel of the protected structure and the absorber, whereas the active actuator regularly generates the force F a of the opposite sign, leading to the primary structure deflection and acceleration minimisation through the TVA stroke extension (see Figs. 18 vs Figs 17), as observed for all the regarded H-MR-TVA systems vs MR-TVA systems (Table 5).
According to the assumed here amplitude A ( • ) definition, the TVA effective peak-peak travel distance has to be regarded as 2 A ( x 1 − x 2 ) , i.e., twice the value from Table 5 and Figs. 11–12. Thus, passive TVA solutions with 10 ton absorber mass cannot be implemented along the demanding side-side direction in the nacelle (including the TVA-TN solution with 5.414 m TVA total travel distance), as well as the Mod.GH-H solution, without enforcing end-stop collision bumpers, which limit the TVA stroke, but result in efficiency deterioration with regard to the results presented in Table 5 and Figs. 7–10. Therefore, the promising tower deflection indexes of the passive TVA-TN system are hardly realisable, considering the NREL 5MW nacelle dimensions (Table 1) [37]. The H-MR-TVA travel distance values admissibility must be confirmed prior to implementation, although control case III-H may be regarded as applicable with proper g 15 weight selection (i.e., a possible increase with regard to g 15 = 10 assumed here).
The superiority of the newly developed optimal-based solutions (control case I(-H), II(-H), III(-H)) over the baseline Mod.GH(-H) control law is evident, especially regarding maximum tower deflection amplitude (up to 10.3% reduction) and TVA stroke amplitude (up to 25.7% reduction) values, and the MR damper force amplitudes to even further extend (up to 36.9% reduction). The modified ground-hook approach is devoted to the case when only the protected structure’s relative displacement (tower deflection) has to be minimised. In contrast, the redeveloped control case I(-H), II(-H), and III(-H) use various optimisation fields (i.a., the nacelle relative velocity and acceleration, or the TVA stroke length) embedded in quality function (8), and the MR damper / force actuator constraints embedded in state and co-state equations (4)(11), to produce more favourable results.
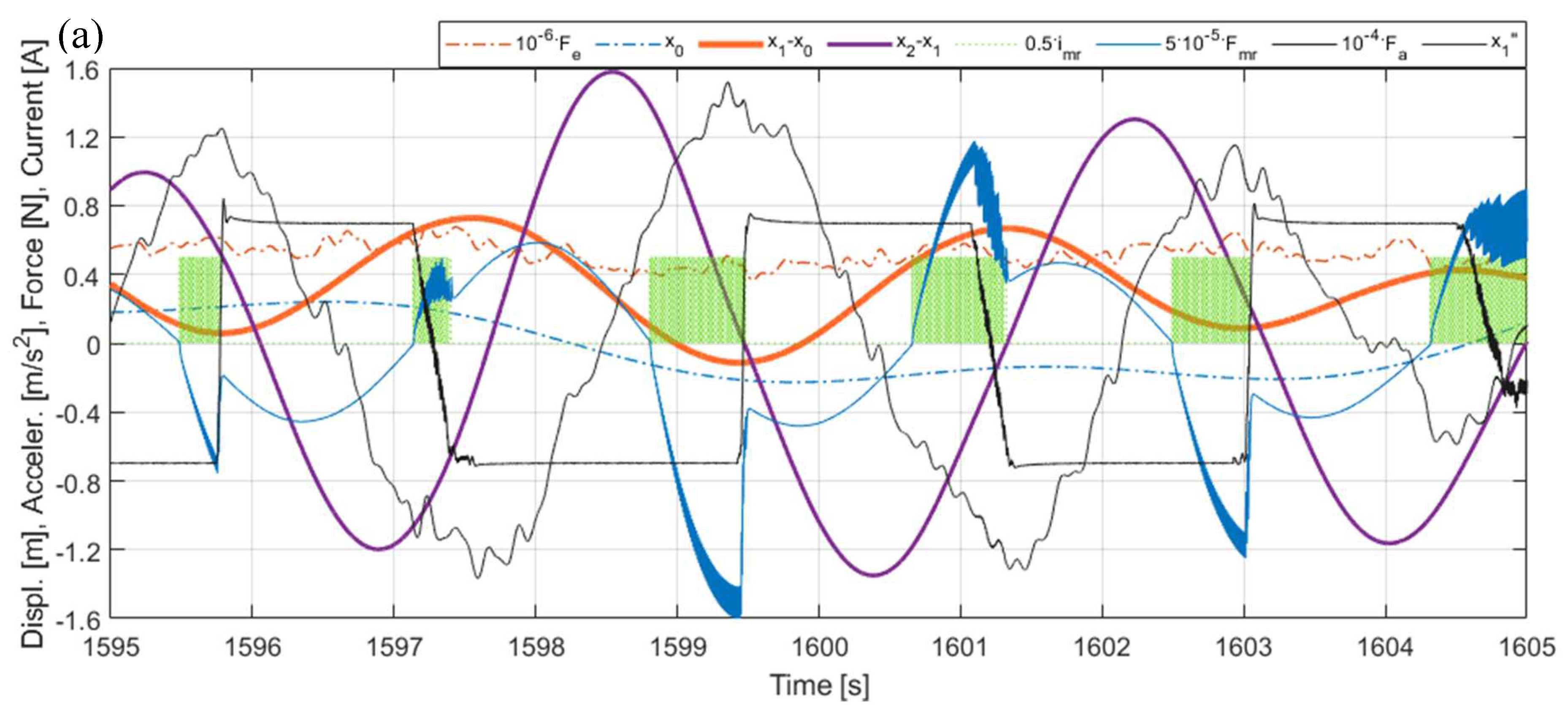
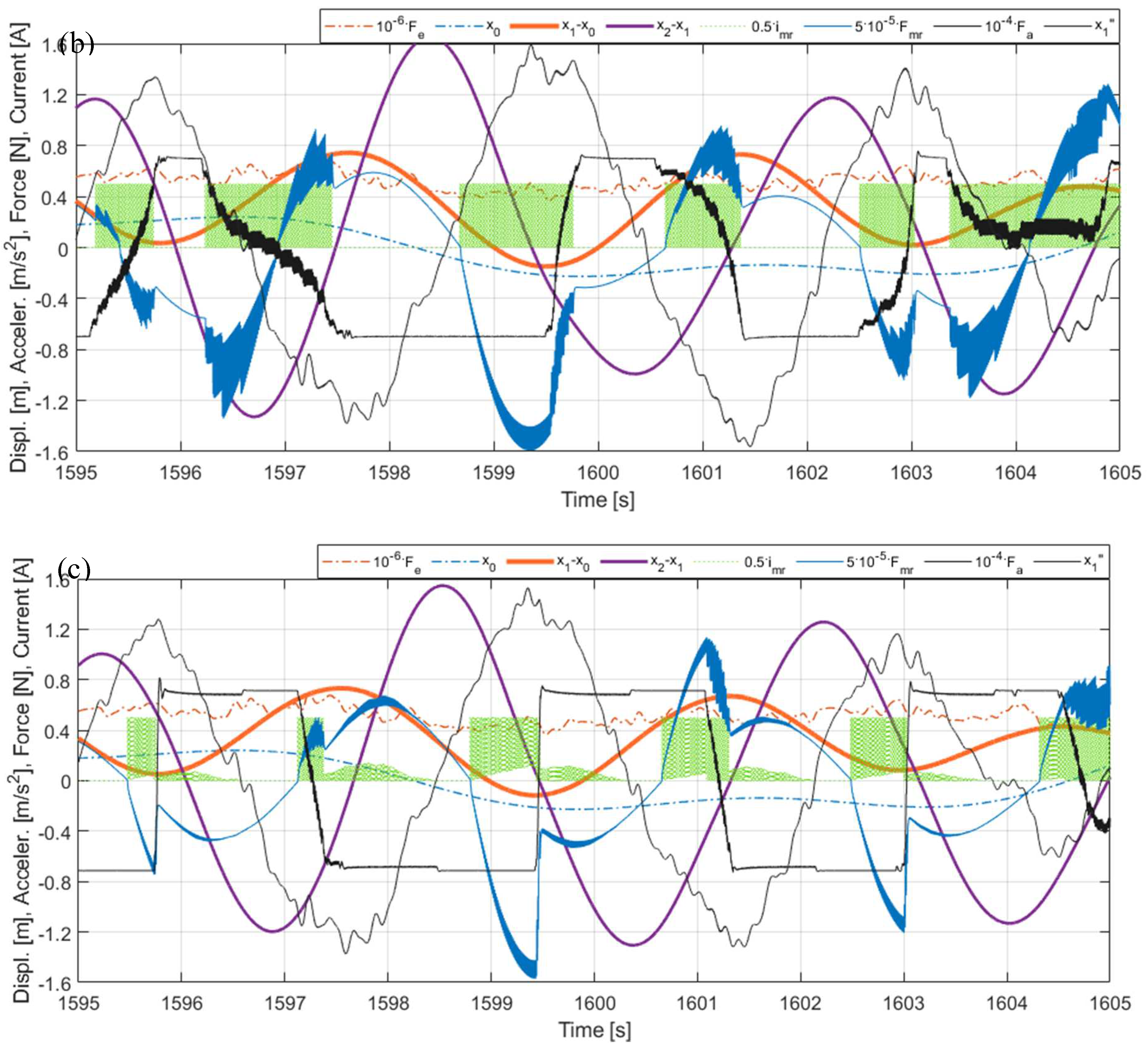
Figure 16, Figure 17 and Figure 18 present selected time characteristics obtained for the exemplary wave/wind realisation no. 7: The excitations (TLP surge x 0 combined with the nacelle horizontal load F e ), the relative displacements of the tower tip (tower deflection x 1 − x 0 ) and the TVA ( x 2 − x 1 ), the nacelle acceleration x ¨ 1 , the force produced by the MR damper F m r (and the electromagnetic actuator F a for the H-MR-TVA system only), and the MR damper electric current i m r , obtained for the TVA tuned to the NREL 5MW tower-nacelle 1st bending mode vs the structure without the TVA (tower deflection for the latter only; mind the signals multipliers in the legends). Figs. 16 (a)(b)(c) present the excitations time patterns and the corresponding tower tip relative displacement and nacelle acceleration responses obtained for the system without the TVA and two (H-)MR-TVA solutions: MR-TN (control case I) and H-MR-TN (control case I-H). Figs. 17 (a) vs (b) vs (c) show comparable time histories, zoomed in along the time axis to illustrate the control action for the MR-TVA system, while Figs. 18 (a) vs (b) vs (c) – for the H-MR-TVA system. As is evident in Figs. 16, both MR-TVA and H-MR-TVA substantially reduce tower deflection as well as nacelle acceleration amplitudes, although the additional force actuator operation of the latter yields preferable protected structure vibration mitigation results. The operation of the MR-TVA system (Figs. 17), control case II vs control case I is characterised by the slightly increased MR damper force modulus mostly during time intervals of high absorber velocity (both x ˙ 2 − x ˙ 1 and x ˙ 2 − x ˙ 0 ) values and the appropriate F m r sign, opposing absorber’s drawing away form the primary structure. On the other hand, the operation of control case III solution vs both control case I and control case II is indicated with nonzero MR damper current during time intervals when force F m r opposes the maximum acceleration x ¨ 1 values. The optimal control task quality function (8) is aimed to minimise H2 norm of the included quantities; thus, the maximum amplitude of the TVA stroke is in fact not reduced for control case II solution vs control case I (Figure 12, Table 5), as for control case III, but the TVA stroke RMS value is actually slightly lower for control case II vs control case I and control case III (0.346 m vs 0.353 m and 0.348 m, respectively, for the regarded exemplary Realisation 7 response, see Figs. 17). The operation of the H-MR-TVA system (Figure 18), control case II-H and control case III-H vs control case I-H, exhibits similar MR damper control i m r conditions as described for the MR-TVA system, although TVA stroke amplitude and RMS values are both reduced for control case II-H and control case III-H with regard to control case I-H thanks to the force actuator active support. When analysing Figs. 18 (a)(b)(c), it is evident that both actuators’ forces are used in cooperation by the vibration control system, e.g., in Figure 18 (c) the F m r modulus increased due to the increased (with regard to Figs. 18 (a)(b)) MR damper current i m r is reflected by decreased F a modulus. Moreover, most F a transients are accompanied by the F m r support, as the MR damper response (25) is faster than the assumed electromagnetic force actuator’s (26). The MR damper force F m r support for the control case II-H solution, as visible in Figure 18 (b), also leads to the mean actuator power reduction (see Figure 15, H-MR-TN g13=3.1019 legend).
The implementation of the protected structure’s acceleration term g 15 z ˙ 2 2 t in the quality index (8) reduces the TVA stroke amplitude A ( x 1 − x 2 ) more effectively than using g 13 z 1 t − z 3 t 2 term and, apart from that, the required MR damper force amplitude is also reduced, as reflected in Figures 12, 14, 17 and 18 and Table 5. It also is worth to mention that g 13 z 1 t − z 3 t 2 term used here for the MR-TVA system (control case II) is ineffective in A ( x 1 − x 2 ) minimisation (see Figure 12 and Figure 17 (b), and Table 5); at the same time, it marginally deteriorates the primary structure response (Figure 8, Figure 10 and Figure 17 (a)(b), Table 5). For the H-MR-TVA, control case II-H yields both less favourable primary structure deflection and less favourable TVA stroke length than control case III-H, i.e., similar mean tower deflection RMS values, but 4.3% higher maximum tower deflection amplitude, and 4.3% higher maximum TVA stroke amplitude over all wave/wind realisations, see Table 5. On the contrary, the g 15 z ˙ 2 2 t term implementation for the MR-TVA (control case III) results in 9.0% and 5.7% maximum TVA stroke amplitude reduction over all wave/wind realisations with regard to control case II and control case I, respectively, while its primary structure response differences with regard to the preferable control case I (Figure 8, Figure 10 and Figure 17, Table 5) are negligible (within 0.2%). The implementation of the g 15 z ˙ 2 2 t term for the H-MR-TVA system (control case III-H) results in 6.0 % maximum TVA stroke amplitude reduction with regard to the baseline control case I-H, while the primary structure response differences are negligible (within 0.3%), as for the MR-TVA system. The TVA travel distance reductions are obtained thanks to the sole control algorithm alteration. Thus, no additional hardware/software resources are necessary, while this pure advantage is accompanied with up to 4.4% reduction in the MR damper force amplitude vs the control case I(-H) solutions.
With regard to the limited TVA stroke, the most favourable vibration control solution is the semiactive MR-TVA control case III implementation, providing favourable cumulative primary structure deflection indexes (over all wave/wind realisations) at the lowest obtained TVA travel distance. A possible alternative is the hybrid H-MR-TVA control case III-H implementation, providing even more favourable cumulative primary structure deflection indexes and reduced nacelle acceleration levels thanks to the utilisation of the force actuator of relatively low mean power (up to 6.15 kW), which side effect is, however, the increased TVA travel distance.

8. Conclusions

The purpose of this research was the implementation and numerical study of the nonlinear optimal-based vibration control solutions for the full-scale TLP – NREL 5MW wind turbine tower-nacelle model with the (H-)MR-TVA vibration reduction system, using the MR damper control, combined with the force actuator operation or independent, under the excessive wave/wind polyperiodic excitations yielding continual transient vibration states.
On the basis of the obtained results, the TVA-TN approach (tuned to the tower-nacelle 1st bending mode) is by far superior to the TVA-TLP one regarding the tower deflection amplitude/RMS and TVA stroke amplitude values. All the regarded TVA-TN solutions provide tower deflection safety factor of ca. 2, while a structure without any vibration reduction solutions or with a TVA tuned to the TLP surge frequency (especially passive and hybrid TVA-TLPs) are at risk of tower structural failure. Thus, TVA-TN solutions are the core of the current research.
The implementation of the protected structure’s acceleration and nonzero relative velocity terms in the quality function (8) results in 23.2% / 21.5% maximum TVA stroke amplitude reduction along with 3.3% / 9.7% maximum tower deflection amplitude reduction for the MR-TVA / H-MR-TVA case vs the baseline, previously developed, modified ground-hook law Mod.GH / Mod.GH-H (respectively) devoted to the single objective of the protected structure deflection minimisation. The sole usage of protected structure’s acceleration term yields ca. 6 % maximum TVA stroke amplitude reduction with regard to the control case I and I-H approaches, while the tower deflection response differences are negligible. The TVA travel distance reductions are obtained thanks to the sole control algorithm enhancement. Thus, no additional resources are necessary, while this pure advantage is accompanied with a reduction in the MR damper force that is necessary for the TVA operation. The protected structure’s acceleration term utilisation produces the TVA stroke amplitude reduction more efficiently than standard TVA relative displacement term usage as in the previously developed approach (the latter being ineffective for the MR-TVA system implementation) which, in turn, efficiently reduces the TVA stroke RMS (H2 norm) values and, apart from that, the required mean actuator power for the H-MR-TVA system implementation.
With regard to the limited TVA stroke, the most favourable vibration control solution is the semiactive MR-TVA control case III implementation, providing favourable cumulative primary structure deflection indexes at the lowest obtained TVA travel distance. A possible alternative may be the hybrid H-MR-TVA control case III-H, providing even more favourable primary structure deflection qualities and reduced nacelle acceleration levels thanks to the utilisation of the force actuator of the relatively low power (ca. 6 kW), which side effect is, however, the increased TVA stroke amplitude. The analysed passive TVA systems (both TVA-TN and TVA-TLP) with relatively small 10 ton absorber mass can hardly be implemented in the nacelle, especially along the demanding side-side direction, without enforcing end-stop collision bumpers, which result in the efficiency deterioration.
The results of the current study may be used in the design process of the full-scale vibration reduction system attached to the real-world NREL 5MW-class floating, TLP-based, wind turbine structure. No offline calculations, MR damper or force actuator force tracking, disturbances or dominant frequency assumption is necessary for proper real-time implementation.

Acknowledgments

This work was supported by AGH University of Science and Technology [research program no. 16.16.130.942].

References

  1. Weber, F.; Maślanka, M. Precise stiffness and damping emulation with MR dampers and its application to semi-active tuned mass dampers of Wolgograd Bridge. Smart Mater. Struct. 2014, 23. [Google Scholar] [CrossRef]
  2. Kavyashree, B.G.; Patil, S.; Rao, V.S. Review on vibration control in tall buildings: from the perspective of devices and applications. Int. J. Dynam. Control 2020. [Google Scholar] [CrossRef]
  3. Caterino, N. Semi-active control of a wind turbine via magnetorheological dampers. J. Sound Vib. 2015, 345, 1–17. [Google Scholar] [CrossRef]
  4. Kirkegaard, P.H.; Nielsen, S.R.K.; Poulsen, B.L.; et al. Semiactive vibration control of a wind turbine tower using an MR damper. In Structural Dynamics - EURODYN. Grundmann, H., Schueller, G.I., Eds.; Swets & Zeitlinger: Lisse, 2002. [Google Scholar]
  5. Kucuk, I.; Yildirim, K.; Sadek, I.; et al. Optimal control of a beam with Kelvin-Voigt damping subject to forced vibrations using a piezoelectric patch actuator. J. Vib. Control 2015, 21, 701–713. [Google Scholar] [CrossRef]
  6. Oates, W.S.; Smith, R.C. Nonlinear Optimal Control Techniques for Vibration Attenuation Using Magnetostrictive Actuators. J. Intell. Mater. Syst. Struct. 2008, 19. [Google Scholar] [CrossRef]
  7. Rotea, M.A.; Lackner, M.A.; Saheba, R. Active Structural Control of Offshore Wind turbines. In 48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Orlando, Florida, 4–7 January.
  8. Tsouroukdissian, A.; Carcangiu, C.E.; Pineda, A.I.; et al. Wind Turbine Tower Load Reduction using Passive and Semiactive Dampers. In European Wind Energy Association Annual Event, Brussels, Belgium, 14-. 17 March.
  9. Spencer, B.F. ; Jr. ; Soong, T.T. New Applications and Development of Active, Semi-Active and Hybrid Control Techniques for Seismic and Non-Seismic Vibration in the USA. In Proceedings of International Post-SMiRT Conference Seminar on Seismic Isolation, Passive Energy Dissipation and Active Control of Vibration of Structures, Cheju, Korea; 1999. [Google Scholar]
  10. Zhang, Z.; Staino, A.; Basu, B.; Nielsen, S.R.K. Performance evaluation of full-scale tuned liquid dampers (TLDs) for vibration control of large wind turbines using real-time hybrid testing. Engineering Structures 2016, 126, 417–431. [Google Scholar] [CrossRef]
  11. Den Hartog, J.P. Mechanical Vibrations, Mineola: Dover Publications, 1985.
  12. Nakamura, Y.; Tanaka, K.; Nakayama, M.; Fujita, T. Hybrid mass dampers using two types of electric servomotors: AC servomotors and linear-induction servomotors. Earthquake Engineering and Structural Dynamics 2001, 30, 1719–1743. [Google Scholar] [CrossRef]
  13. Preumont, A.; Alaluf, D.; Bastaits, R. 2014 Hybrid Mass Damper: A Tutorial Example. In Active and Passive Vibration Control of Structures; Hagedorn, P., Spelsberg-Korspeter, G., Eds.; CISM International Centre for Mechanical Sciences.
  14. Demetriou, D.; Nikitas, N. A Novel Hybrid Semi-Active Mass Damper Configuration for Structural Applications. Appl. Sci. 2016, 6, 397. [Google Scholar] [CrossRef]
  15. Koo, J.H.; Ahmadian, M. Qualitative Analysis of Magneto-Rheological Tuned Vibration Absorbers: Experimental Approach. J. Intell. Mater. Syst. Struct. 2007, 18. [Google Scholar] [CrossRef]
  16. Wang, L.; Liang, Z.; Cai, M.; Zhang, Y.; Yan, J. Adaptive Structural Control of Floating Wind Turbine with Application of MR Damper. Energy Procedia 2019, 158, 254–259. [Google Scholar] [CrossRef]
  17. Martynowicz, P. Szydło Z. In Wind turbine’s tower-nacelle model with magnetorheological tuned vibration absorber: the laboratory test rig. In Proceedings of the 14th International Carpathian Control Conference (ICCC), Rytro, Poland, 2013., 26–29 May.
  18. Martynowicz, P. Development of Laboratory Model of Wind Turbine’s Tower-Nacelle System with Magnetorheological Tuned Vibration Absorber. Solid State Phenom. 2014, 208, 40–51. [Google Scholar] [CrossRef]
  19. Martynowicz, P. Vibration control of wind turbine tower-nacelle model with magnetorheological tuned vibration absorber. J. Vib. Control 2017, 23, 3468–3489. [Google Scholar] [CrossRef]
  20. Martynowicz, P. Study of vibration control using laboratory test rig of wind turbine’s tower-nacelle system with MR damper based tuned vibration absorber. Bulletin of the Polish Academy of Sciences Technical Sciences 2016, 64, 347–359. [Google Scholar] [CrossRef]
  21. Rosół, M.; Martynowicz, P. Implementation of LQG controller for wind turbine tower-nacelle model with MR tuned vibration absorber. J Theor Appl Mech 2016, 54, 1109–1123. [Google Scholar] [CrossRef]
  22. Martynowicz, P. Control of an MR Tuned Vibration Absorber for Wind Turbine Application Utilising the Refined Force Tracking Algorithm. J LOW FREQ NOISE V A 2017, 36, 339–353. [Google Scholar] [CrossRef]
  23. Martynowicz, P.; Rosół, M. Wind Turbine Tower-Nacelle System with MR Tuned Vibration Absorber: Modelling, Test Rig, and Identification. In ICCC 2019: proceedings of the 20th International Carpathian Control Conference, , Kraków-Wieliczka. 26–29 May.
  24. Rosół, M.; Martynowicz, P. Identification of the Wind Turbine Model with MR Damper Based Tuned Vibration Absorber. In ICCC 2019: proceedings of the 20th International Carpathian Control Conference, , Kraków-Wieliczka. 26–29 May.
  25. Martynowicz, P. Nonlinear optimal-based vibration control for systems with MR tuned vibration absorbers. J LOW FREQ NOISE V A 2019, 38, 1607–1628. [Google Scholar] [CrossRef]
  26. Martynowicz, P. Real-time implementation of nonlinear optimal-based vibration control for a wind turbine model. J LOW FREQ NOISE V A 2019, 38, 1635–1650. [Google Scholar] [CrossRef]
  27. Kciuk, S.; Martynowicz, P. Special application magnetorheological valve numerical and experimental analysis. Control engineering in materials processing, Diffusion and Defect Data – Solid State Data, Pt. B, Solid State Phenom. 2011, 177, 102–115. [Google Scholar] [CrossRef]
  28. Laalej, H.; Lang, Z.Q.; Sapinski, B.; Martynowicz, P. MR damper based implementation of nonlinear damping for a pitch plane suspension system. Smart Mater. Struct. 2012, 21. [Google Scholar] [CrossRef]
  29. Martynowicz, P. Nonlinear Optimal-Based Vibration Control of a Wind Turbine Tower Using Hybrid vs. Magnetorheological Tuned Vibration Absorber. Energies 2021, 14, 5145. [Google Scholar] [CrossRef]
  30. Martynowicz, P. Experimental study on the optimal-based vibration control of a wind turbine tower using a small-scale electric drive with MR damper support. Energies 2022, 15, 1–25. [Google Scholar] [CrossRef]
  31. GWEC, 2022. Global Offshore Wind Report, 2022.
  32. Jonkman, J.; Matha, D. A Quantitative Comparison of the Responses of Three Floating Platform Concepts. National Renewable Energy Laboratory, 4672. [Google Scholar]
  33. Katsaounis, G.M.; Polyzos, S.; Mavrakos, S.A. An Experimental Study of the Hydrodynamic Behavior of a TLP Platform for a 5MW Wind Turbine with OWC Devices. Proc. of the VII International Conference on Computational Methods in Marine Engineering MARINE 2017.
  34. Konispoliatis, D.; Katsaounis, G.M.; Manolas, D.; Soukissian, T.; Polyzos, S.; Mazarakos, T.P.; Voutsinas, S.G.; Mavrakos, S.A. REFOS: A Renewable Energy Multi-Purpose Floating Offshore System. Energies 2021, 14. [Google Scholar] [CrossRef]
  35. Jonkman, J.; Butterfield, S.; Musial, W.; Scott, G. Definition of a 5-MW Reference Wind Turbine for Offshore System Development. National Renewable Energy Laboratory, 3806. [Google Scholar]
  36. Bir, G.; Jonkman, J. Modal Dynamics of Large Wind Turbines with Different Support Structures. National Renewable Energy Laboratory, 4304. [Google Scholar]
  37. Stewart, G.; Lackner, M. Offshore Wind Turbine Load Reduction Employing Optimal Passive Tuned Mass Damping Systems. IEEE Trans. Control Syst. Technol. 2013, 21. [Google Scholar] [CrossRef]
  38. Park, S.; Lackner, M.A.; Cross-Whiter, J.; Tsouroukdissian, A.R.; La Cava, W. An investigation of passive and semi-active tuned mass dampers for a tension leg platform floating offshore wind turbine in ULS conditions. In ASME 2016 35th Int. Conf. on Ocean, Offshore and Arctic Engineering 2016.
  39. Asareh, M.A.; Schonberg, W.; Volz, J. Fragility Analysis of a 5-MW NREL Wind Turbine Considering Aero-Elastic and Seismic Interaction Using Finite Element Method. Finite Elements in Analysis and Design 2016, 120, (57–67). [Google Scholar] [CrossRef]
  40. Hu, Y.; He, E. Active structural control of a floating wind turbine with a stroke-limited hybrid mass damper. J. Sound Vib. 2017, 410, 447–472. [Google Scholar] [CrossRef]
  41. Vardaroglu, M.; Gao, Z.; Avossa, A.M.; Ricciardelli, F. Validation of a TLP wind turbine numerical model against model-scale tests under regular and irregular waves. Ocean Engineering 2022, 256, 111491. [Google Scholar] [CrossRef]
  42. Martynowicz, P.; Santos, M. Structural vibration control of NREL 5. In 0 MW FOWT using optimal-based MR tuned vibration absorber. In Proceedings of the 21st IFAC World Congress, Berlin, Germany, 11–17 July 2020. IFAC-PapersOnLine. [Google Scholar]
  43. Larsen, T.G.; Zhang, Z.; Høgsberg, J. Vibration damping of an offshore wind turbine by optimally calibrated pendulum absorber with shunted electromagnetic transducer. Journal of Sound and Vibration 2021. [Google Scholar] [CrossRef]
  44. Madsen, F.J.; Nielsen, T.R.L.; Kim, T.; Bredmose, H.; Pegalajar-Jurado, A.; Mikkelsen, R.F.; Lomholt, A.K.; Borg, M.; Mirzaei, M.; Shin, P. Experimental analysis of the scaled DTU10MW TLP floating wind turbine with different control strategies. Renewable Energy 2020, 155, 330–346. [Google Scholar] [CrossRef]
  45. Shen, Y.J.; Wang, L.; Yang, S.P.; Gao, G.S. Nonlinear dynamical analysis and parameters optimization of four semi-active on-off dynamic vibration absorbers. J. Vib. Control 2013, 19, 143–160. [Google Scholar] [CrossRef]
  46. Hu, Y.; Chen, M.Z.Q.; Li, C. Active structural control for load mitigation of wind turbines via adaptive sliding-mode approach. Journal of the Franklin Institute 2017, 354, 4311–4330. [Google Scholar] [CrossRef]
  47. Bryson, A.E.; Ho, Y.C. Applied Optimal Control, Taylor & Francis, 1975.
  48. Shukla, P.; Ghodki, D.; Manjarekar, N.S.; Singru, P.M. A Study of H infinity and H2 synthesis for Active Vibration Control. IFAC-PapersOnLine, 2405. [Google Scholar]
  49. Itik, M. Optimal control of nonlinear systems with input constraints using linear time varying approximations. Nonlinear analysis: Modelling and Control 2016, 21, 400–412. [Google Scholar] [CrossRef]
  50. Snamina, J.; Martynowicz, P.; Łatas, W. Dynamic similarity of wind turbine’s tower-nacelle system and its scaled model. Solid State Phenom. 2014, 208, 29–39. [Google Scholar] [CrossRef]
  51. Snamina, J.; Martynowicz, P. Prediction of characteristics of wind turbine’s tower-nacelle system from investigation of its scaled model. In 6WCSCM: Sixth World Conference on Structural Control and Monitoring – proceedings of the 6th edition of the World conference of the International Association for Structural Control and Monitoring (IACSM), Barcelona, Spain, 15–17 July.
  52. Ioffe, A.D.; Tihomirov, V.M. Theory of Extremal Problems. Studies in Mathematics and its Applications, 1979.
  53. Länger-Möller, A. Simulation of transient gusts on the NREL 5MW wind turbine using the URANS solver THETA. Wind Energ. Sci. 2018, 3, 461–474. [Google Scholar] [CrossRef]
  54. Maślanka, M. Optimised semi-active tuned mass damper with acceleration and relative motion feedbacks. Mech Syst Signal Process 2019, 130, 707–731. [Google Scholar] [CrossRef]
Preprints 96670 g001
Figure 1. Diagram of a regarded system with an H-MR-TVA.
Figure 1. Diagram of a regarded system with an H-MR-TVA.
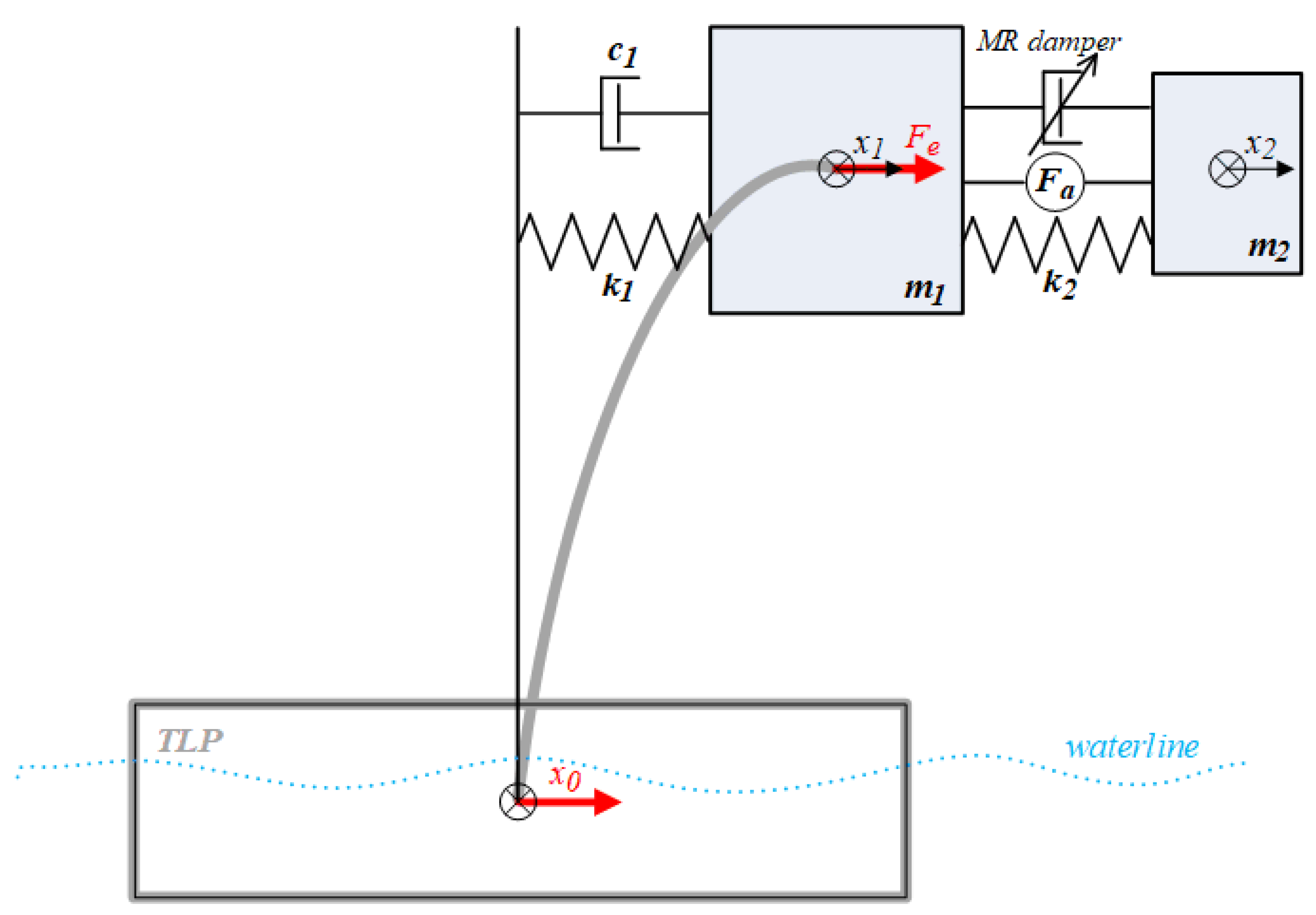
Preprints 96670 g001
Preprints 96670 g002
Figure 2. Bode diagram of a regarded simulation model with and without TVA.
Figure 2. Bode diagram of a regarded simulation model with and without TVA.
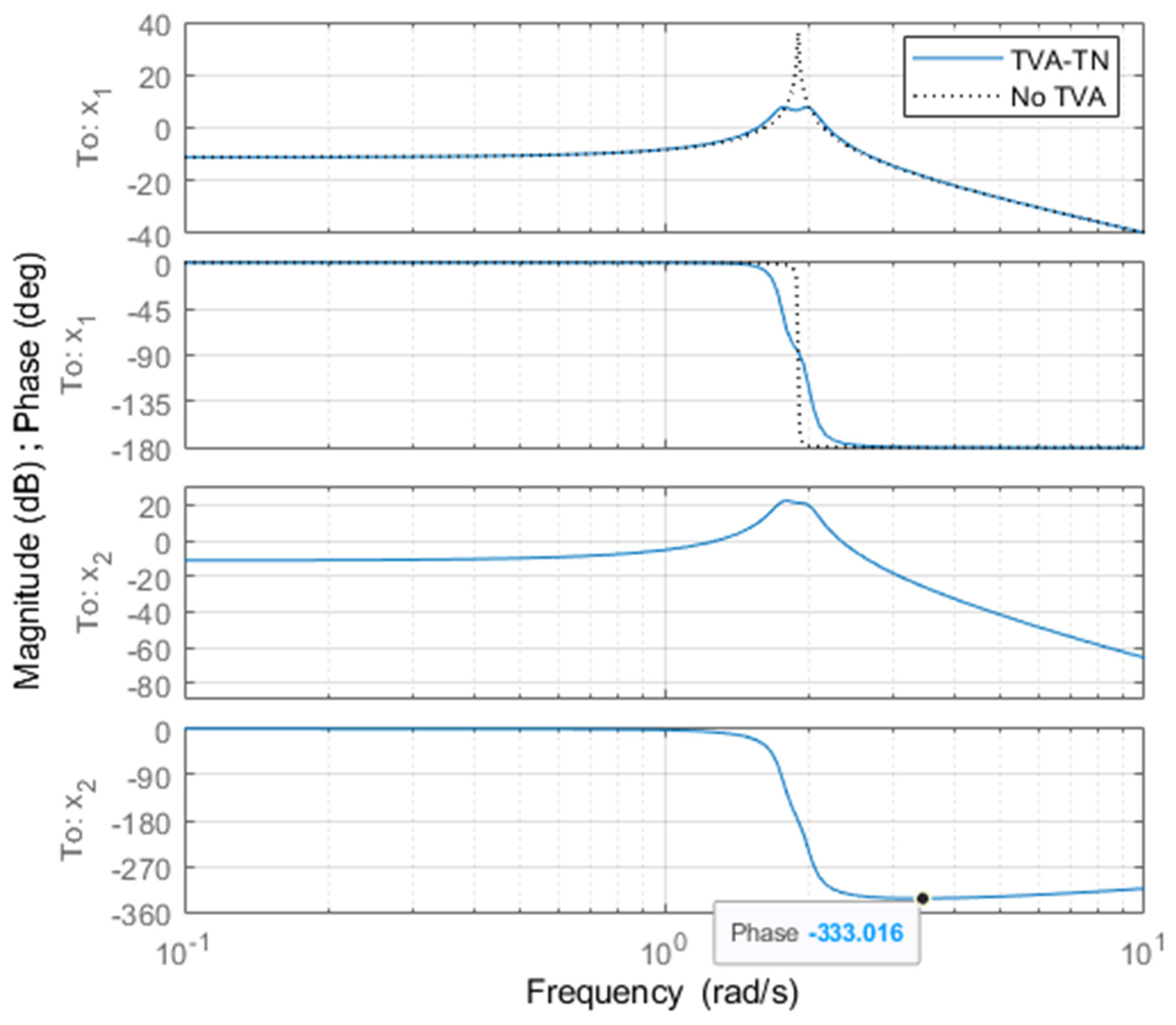
Preprints 96670 g002
Preprints 96670 g003
Figure 3. TLP platform dimensions.
Figure 3. TLP platform dimensions.
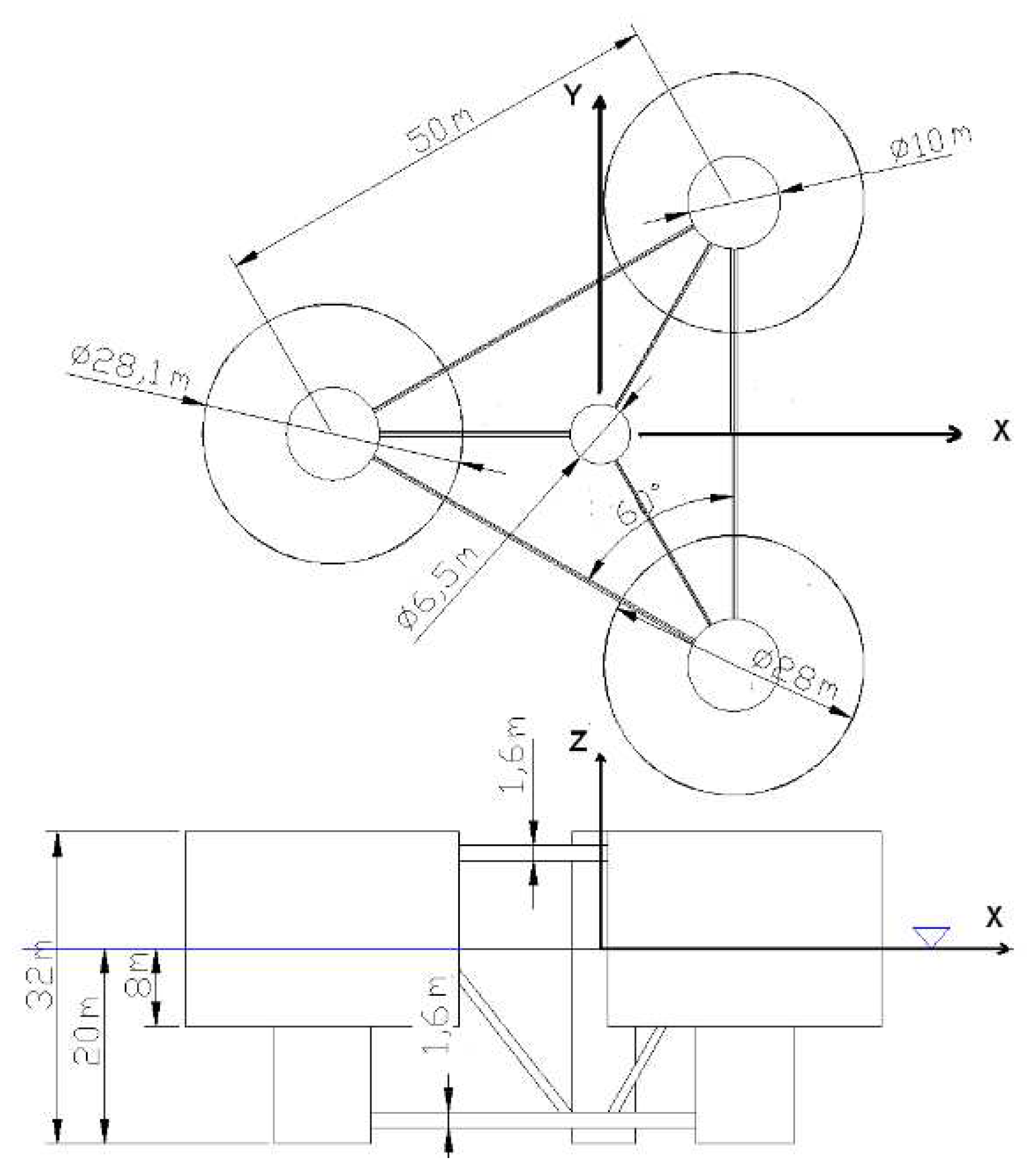
Preprints 96670 g003
Preprints 96670 g004
Figure 4. TLP with NREL 5MW model in the experimental facilities.
Figure 4. TLP with NREL 5MW model in the experimental facilities.
Preprints 96670 g004
Preprints 96670 g005
Figure 5. Surge motion RAOs for the TLP FOWT.
Figure 5. Surge motion RAOs for the TLP FOWT.
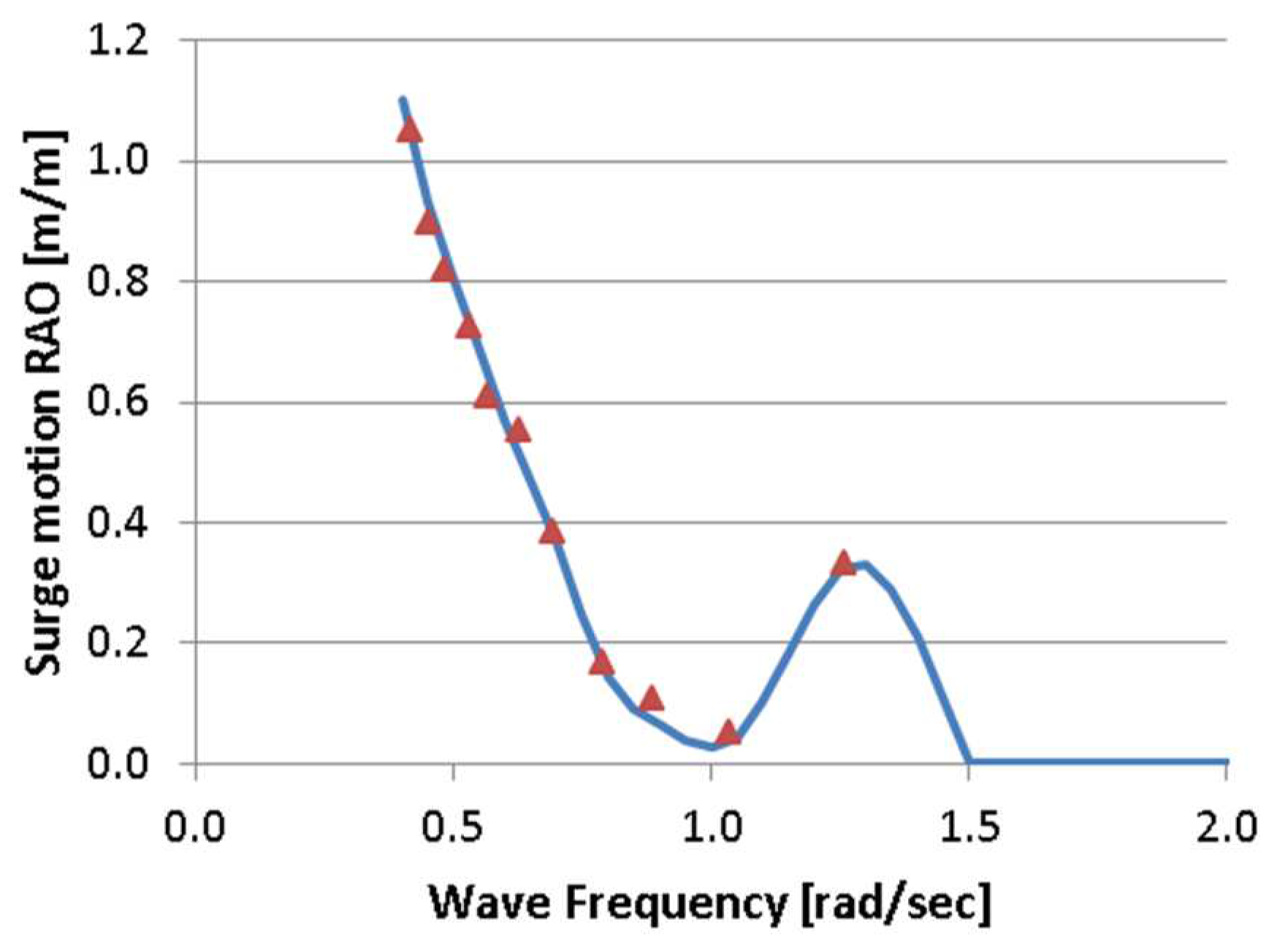
Preprints 96670 g005
Preprints 96670 g006
Figure 6. Wave spectrum considered.
Figure 6. Wave spectrum considered.
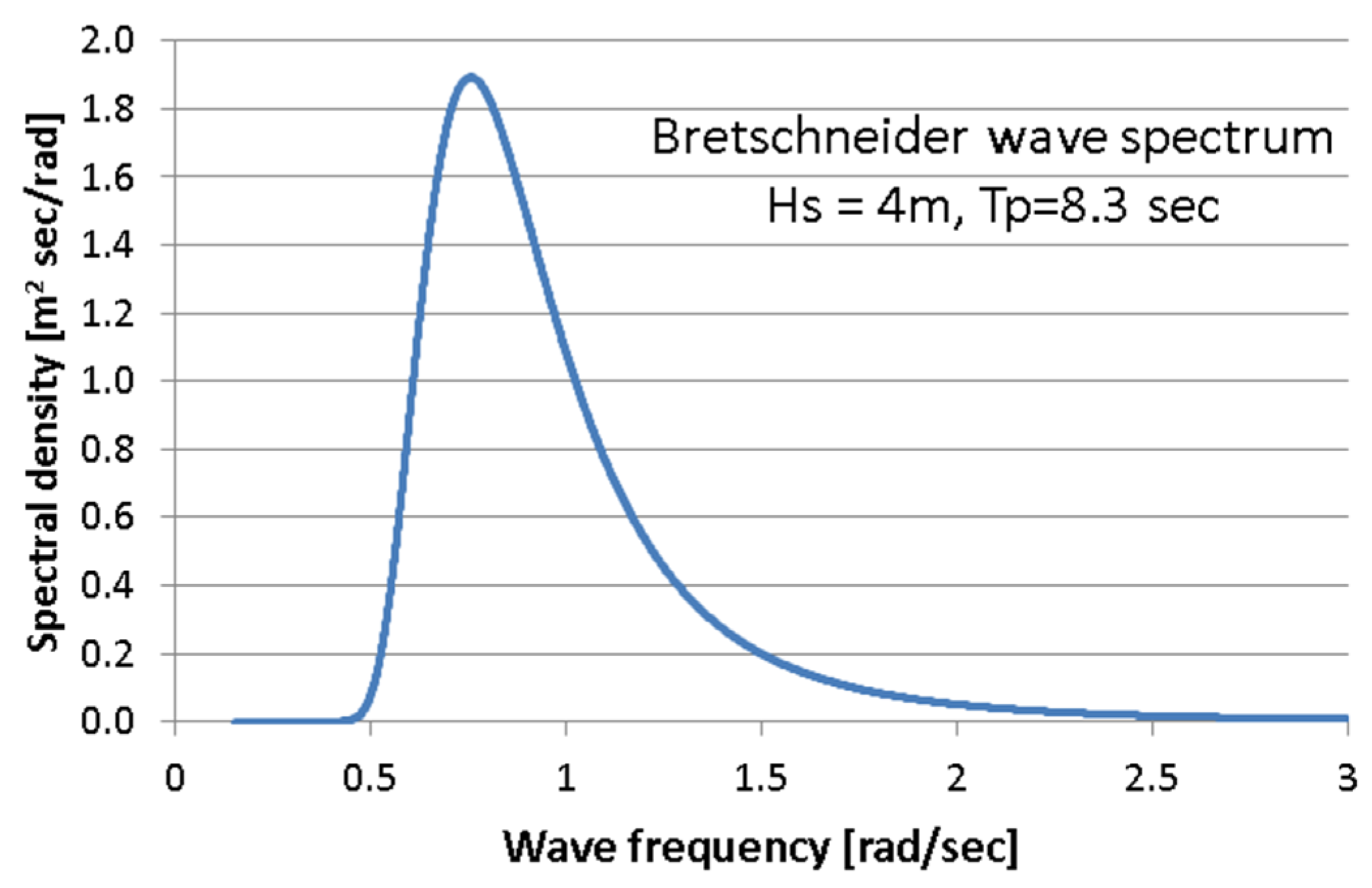
Preprints 96670 g006
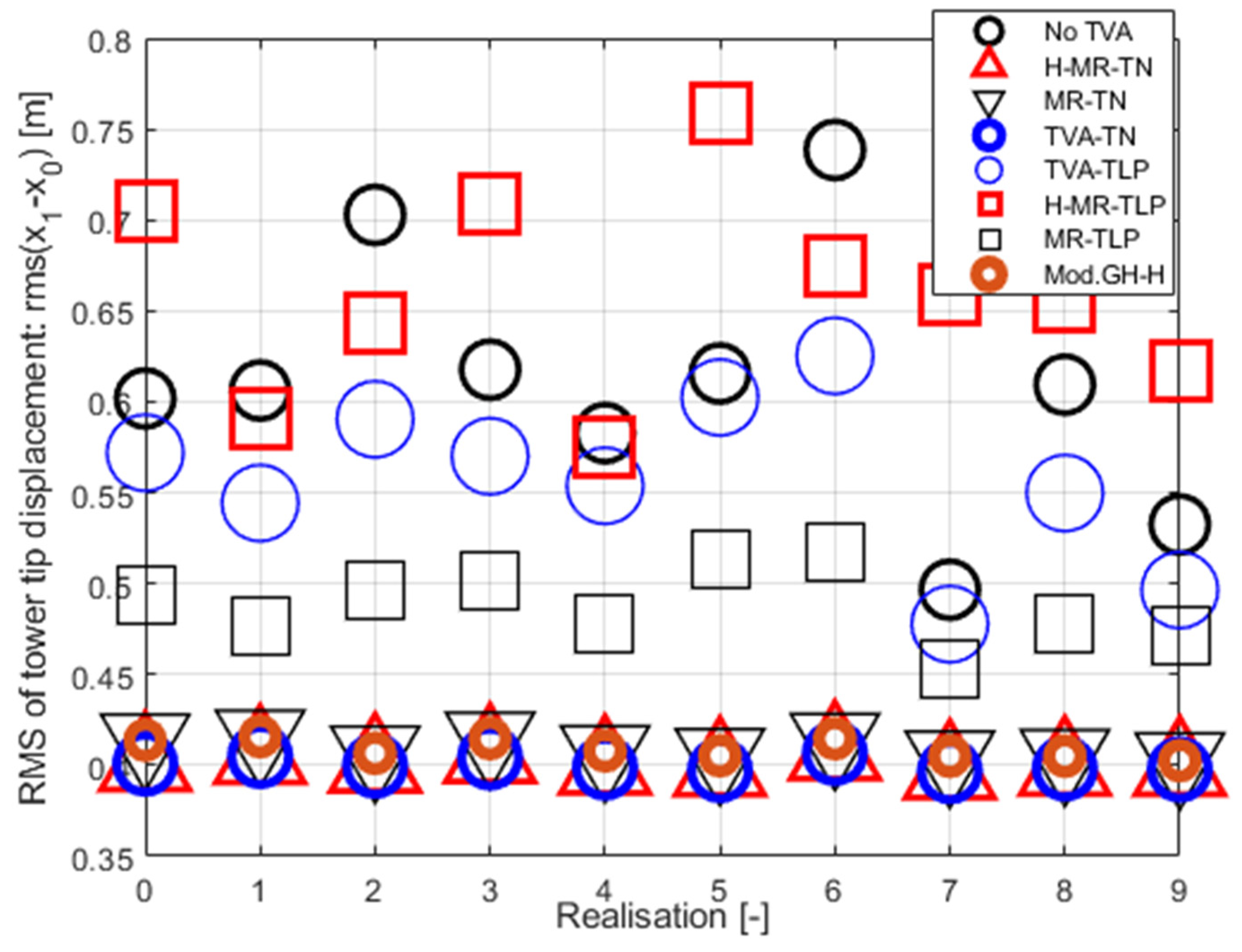
Preprints 96670 g007
Figure 7. RMS of tower tip relative displacement r m s ( x 1 − x 0 ) for g 11 = 10 21 and g 12 = 10 19 Results summary.
Figure 7. RMS of tower tip relative displacement r m s ( x 1 − x 0 ) for g 11 = 10 21 and g 12 = 10 19 Results summary.
Preprints 96670 g007
Preprints 96670 g008
Figure 8. RMS of tower tip relative displacement r m s ( x 1 − x 0 ) for g 11 = 10 21 and g 12 = 10 19 . TVA tuned to the NREL 5MW tower-nacelle 1st bending mode.
Figure 8. RMS of tower tip relative displacement r m s ( x 1 − x 0 ) for g 11 = 10 21 and g 12 = 10 19 . TVA tuned to the NREL 5MW tower-nacelle 1st bending mode.
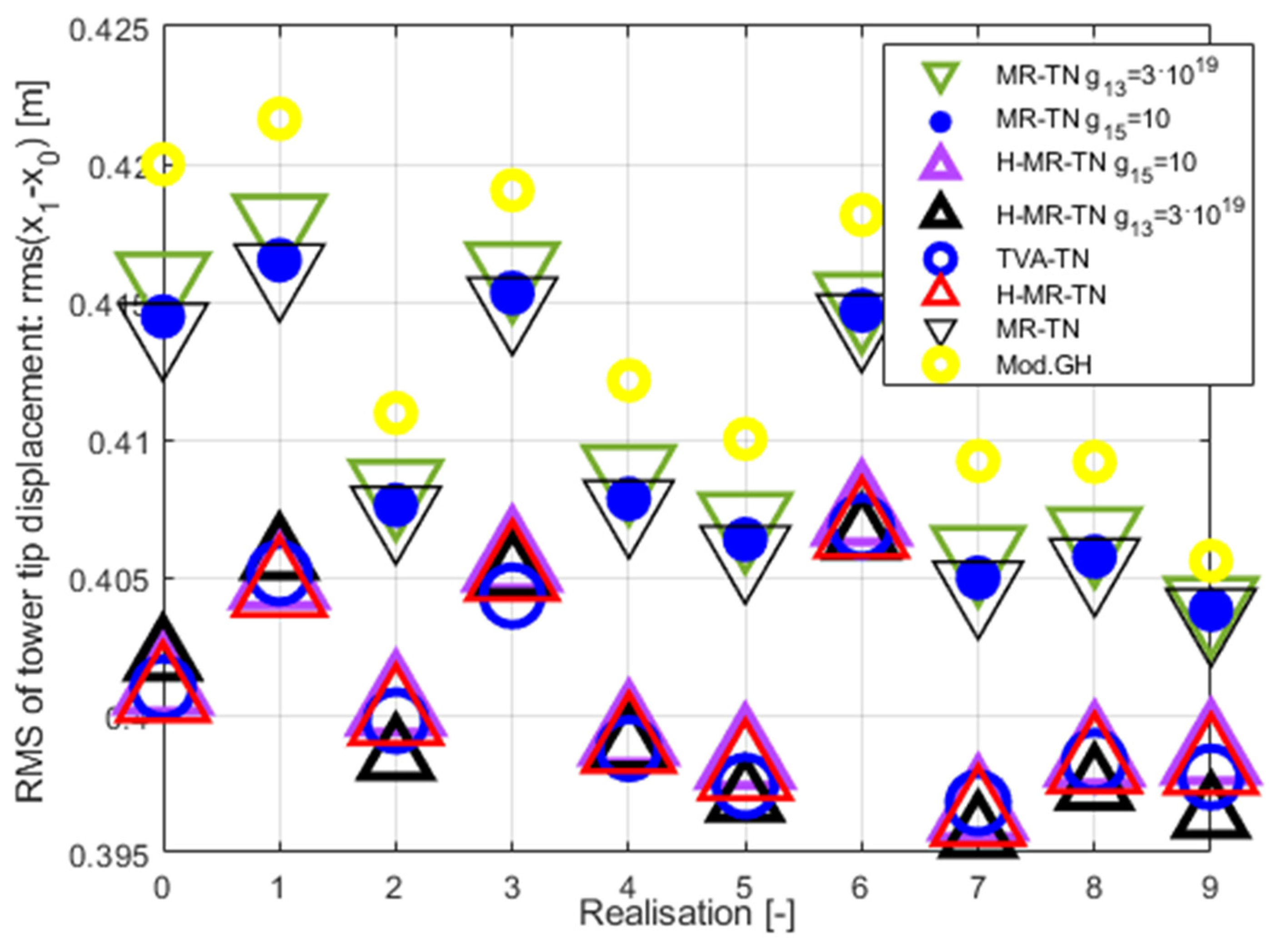
Preprints 96670 g008
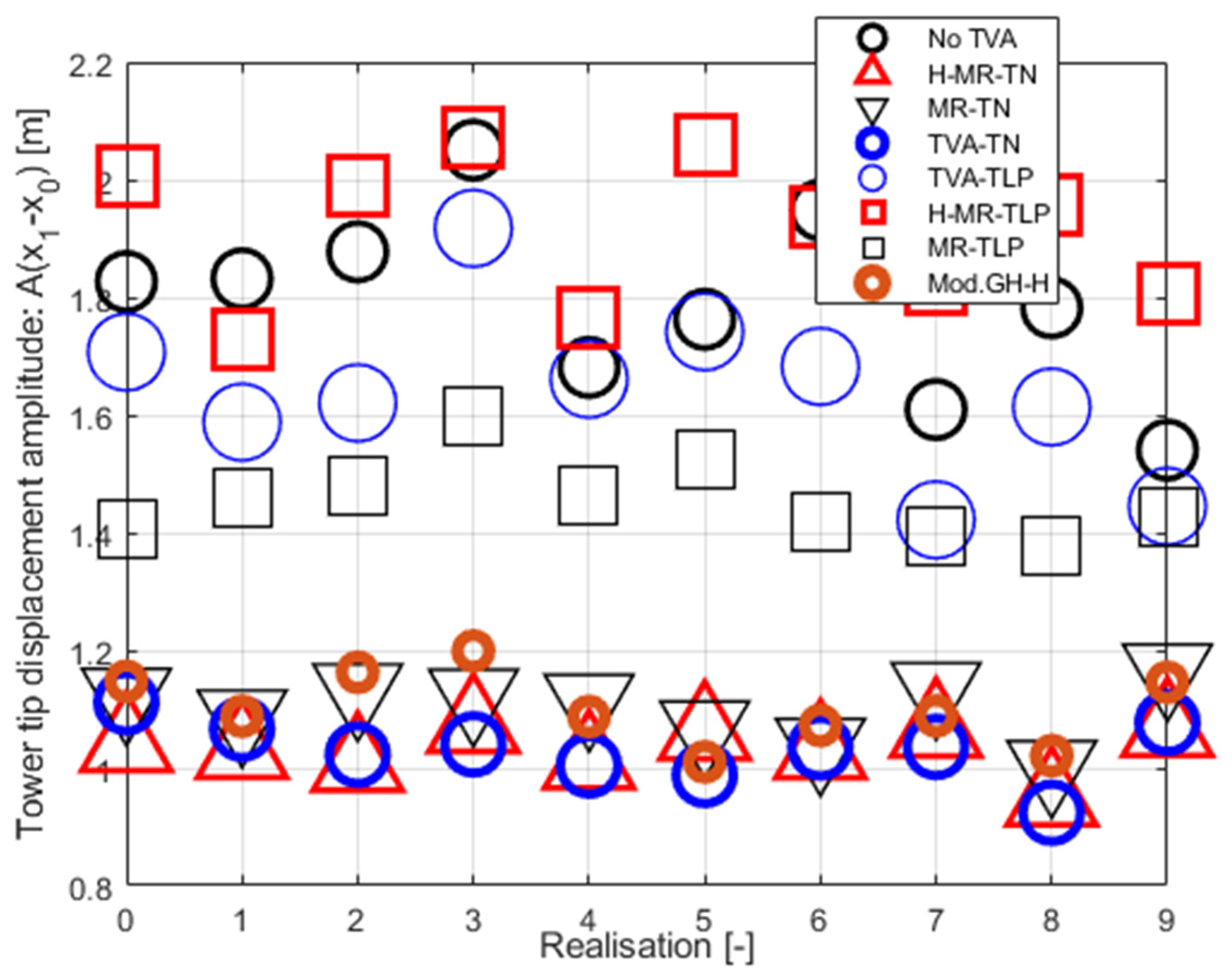
Preprints 96670 g009
Figure 9. Tower tip relative displacement amplitude A ( x 1 − x 0 ) for g 11 = 10 21 and g 12 = 10 19 . Results summary.
Figure 9. Tower tip relative displacement amplitude A ( x 1 − x 0 ) for g 11 = 10 21 and g 12 = 10 19 . Results summary.
Preprints 96670 g009
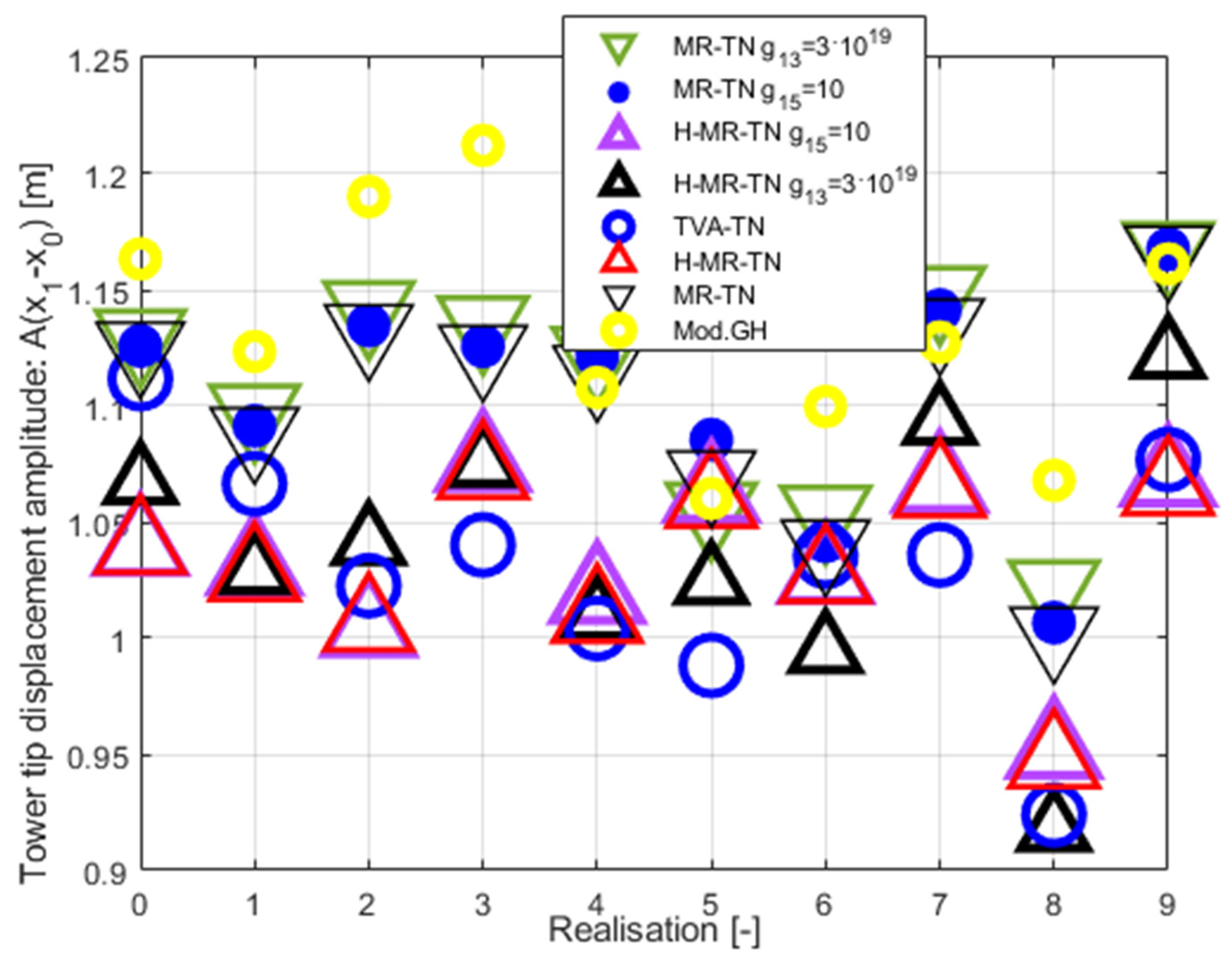
Preprints 96670 g010
Figure 10. Tower tip relative displacement amplitude A ( x 1 − x 0 ) for g 11 = 10 21 and g 12 = 10 19 . TVA tuned to the NREL 5MW tower-nacelle 1st bending mode.
Figure 10. Tower tip relative displacement amplitude A ( x 1 − x 0 ) for g 11 = 10 21 and g 12 = 10 19 . TVA tuned to the NREL 5MW tower-nacelle 1st bending mode.
Preprints 96670 g010
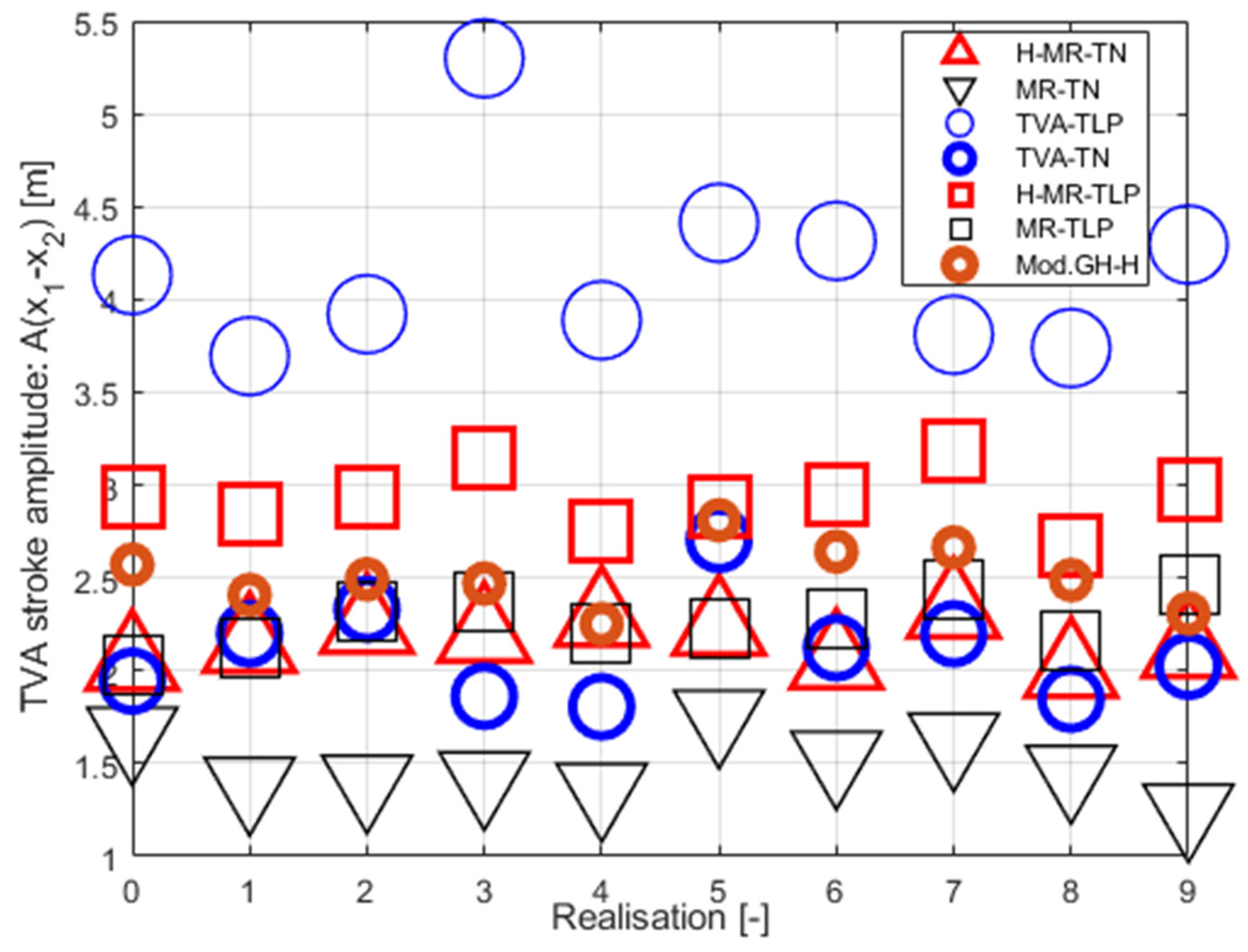
Preprints 96670 g011
Figure 11. TVA stroke amplitude A ( x 1 − x 2 ) for g 11 = 10 21 and g 12 = 10 19 . Results summary.
Figure 11. TVA stroke amplitude A ( x 1 − x 2 ) for g 11 = 10 21 and g 12 = 10 19 . Results summary.
Preprints 96670 g011
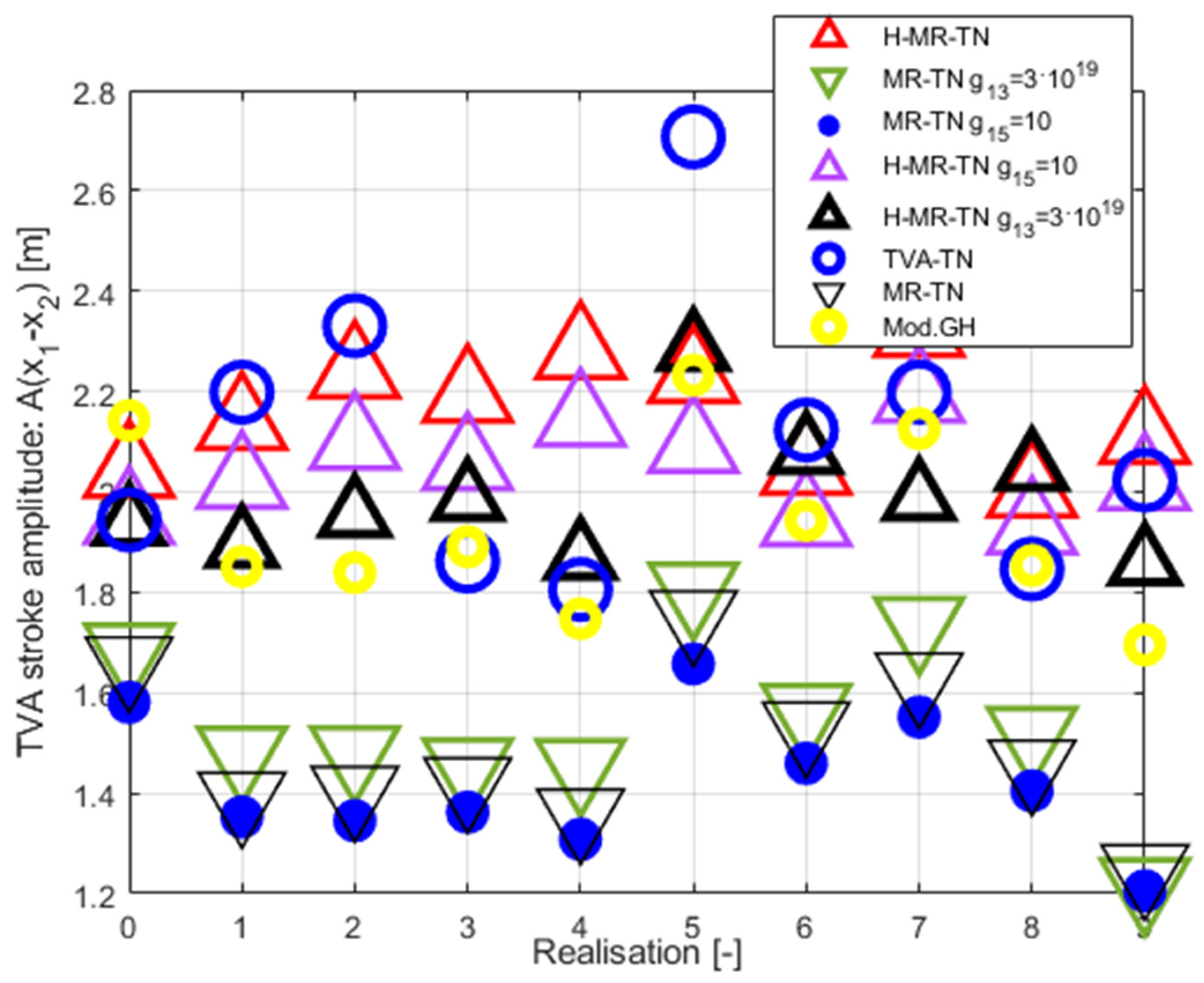
Preprints 96670 g012
Figure 12. TVA stroke amplitude A ( x 1 − x 2 ) for g 11 = 10 21 and g 12 = 10 19 .   TVA tuned to the NREL 5MW tower-nacelle 1st bending mode.
Figure 12. TVA stroke amplitude A ( x 1 − x 2 ) for g 11 = 10 21 and g 12 = 10 19 .   TVA tuned to the NREL 5MW tower-nacelle 1st bending mode.
Preprints 96670 g012
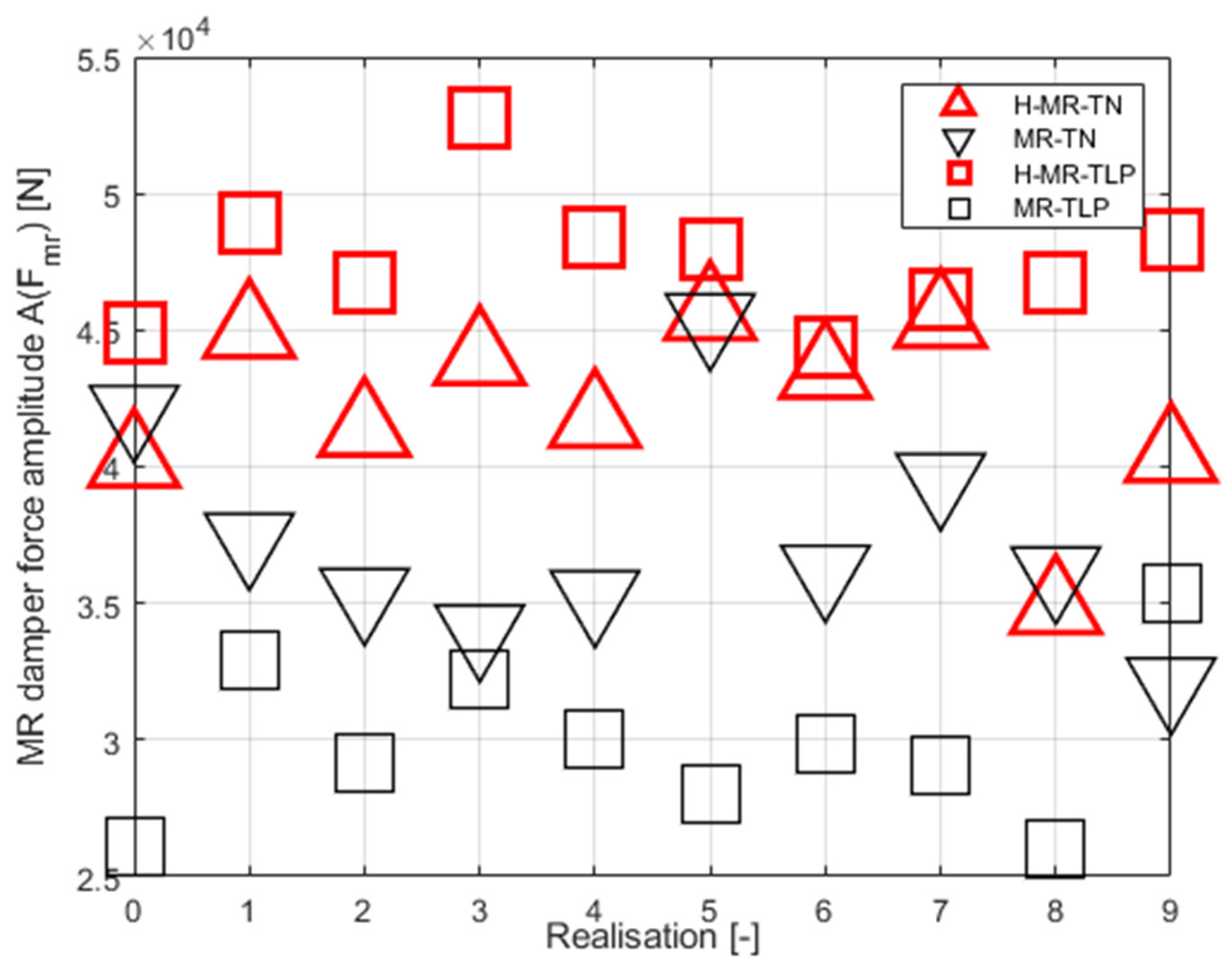
Preprints 96670 g013
Figure 13. MR damper force amplitude A ( F m r ) for g 11 = 10 21 and g 12 = 10 19 . Results summary.
Figure 13. MR damper force amplitude A ( F m r ) for g 11 = 10 21 and g 12 = 10 19 . Results summary.
Preprints 96670 g013
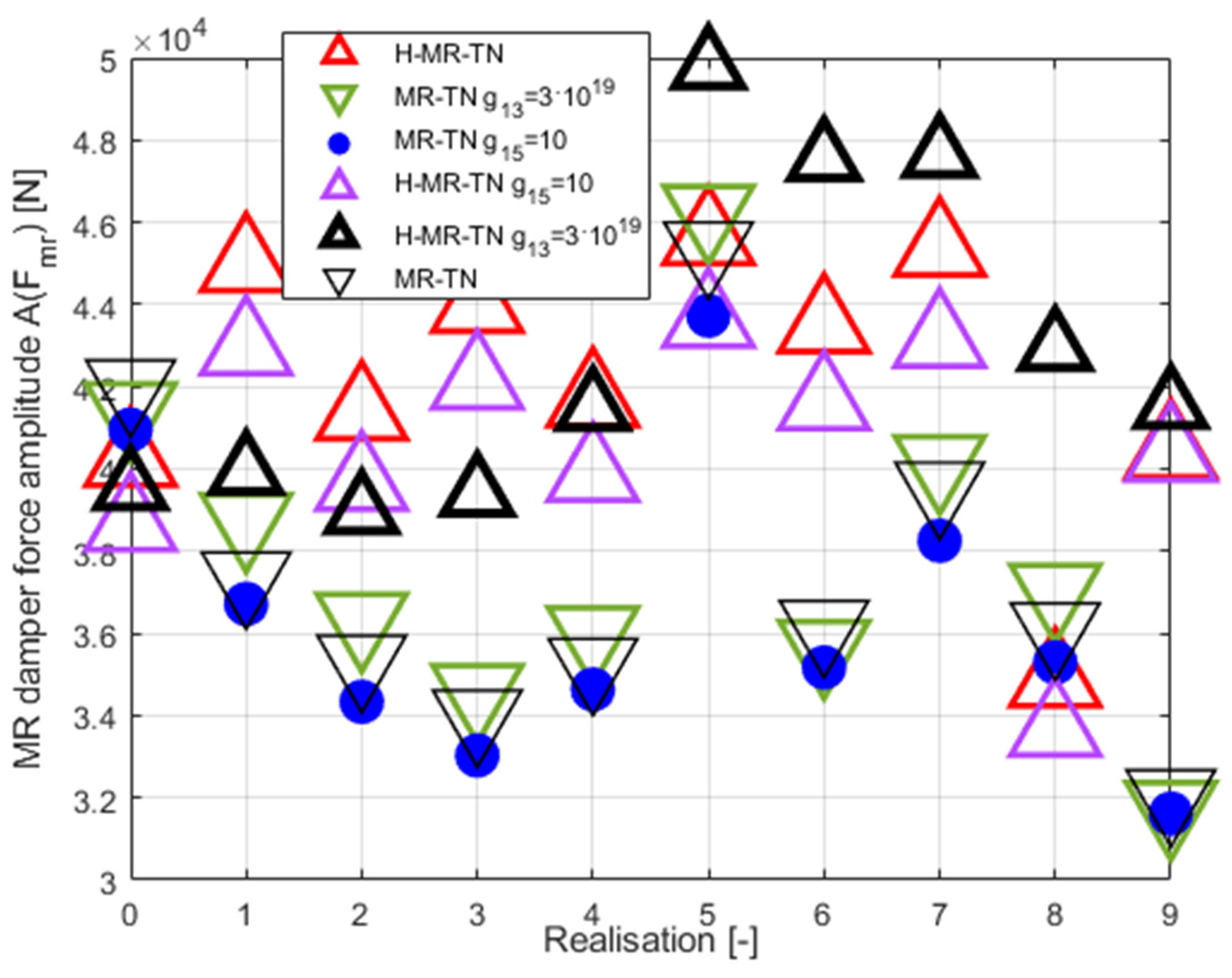
Preprints 96670 g014
Figure 14. MR damper force amplitude A ( F m r ) for g 11 = 10 21 and g 12 = 10 19 . TVA tuned to the NREL 5MW tower-nacelle 1st bending mode.
Figure 14. MR damper force amplitude A ( F m r ) for g 11 = 10 21 and g 12 = 10 19 . TVA tuned to the NREL 5MW tower-nacelle 1st bending mode.
Preprints 96670 g014
Preprints 96670 g015
Figure 15. Mean actuator power P a .
Figure 15. Mean actuator power P a .
Preprints 96670 g015
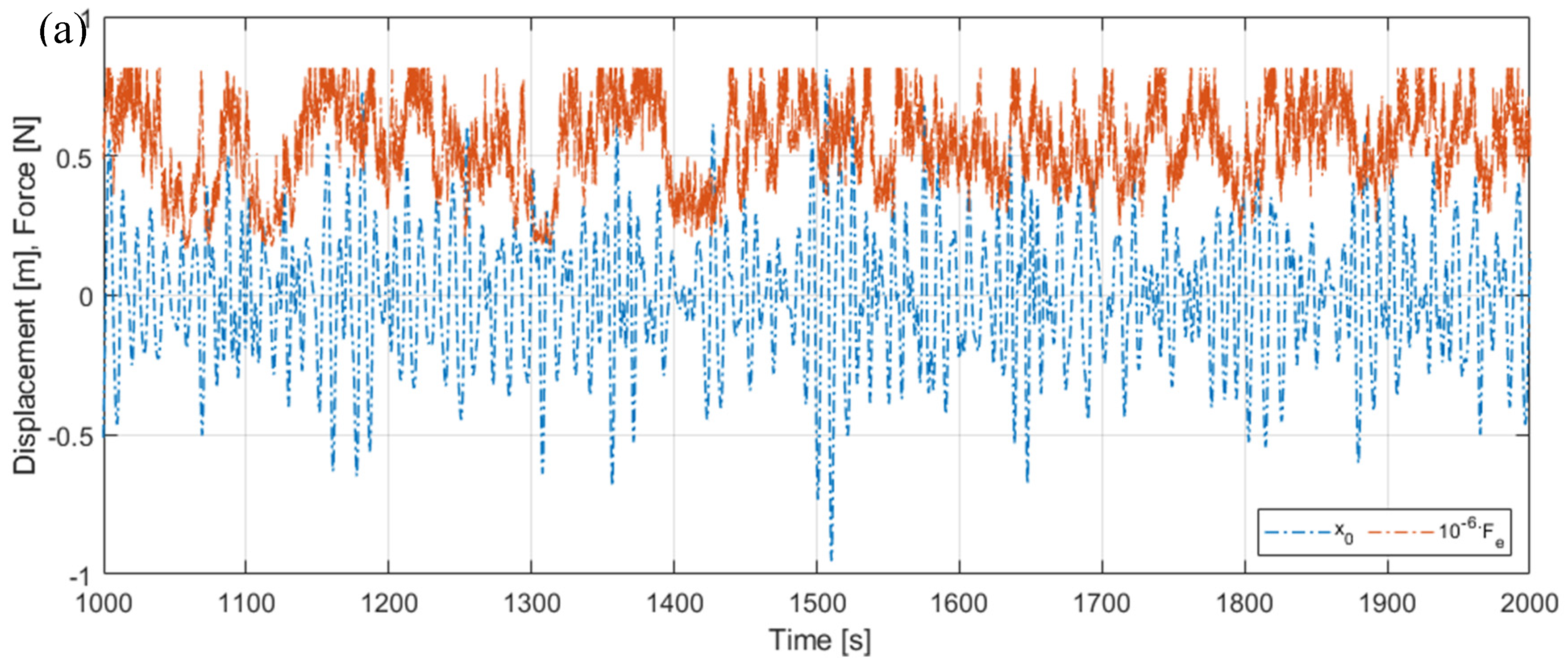
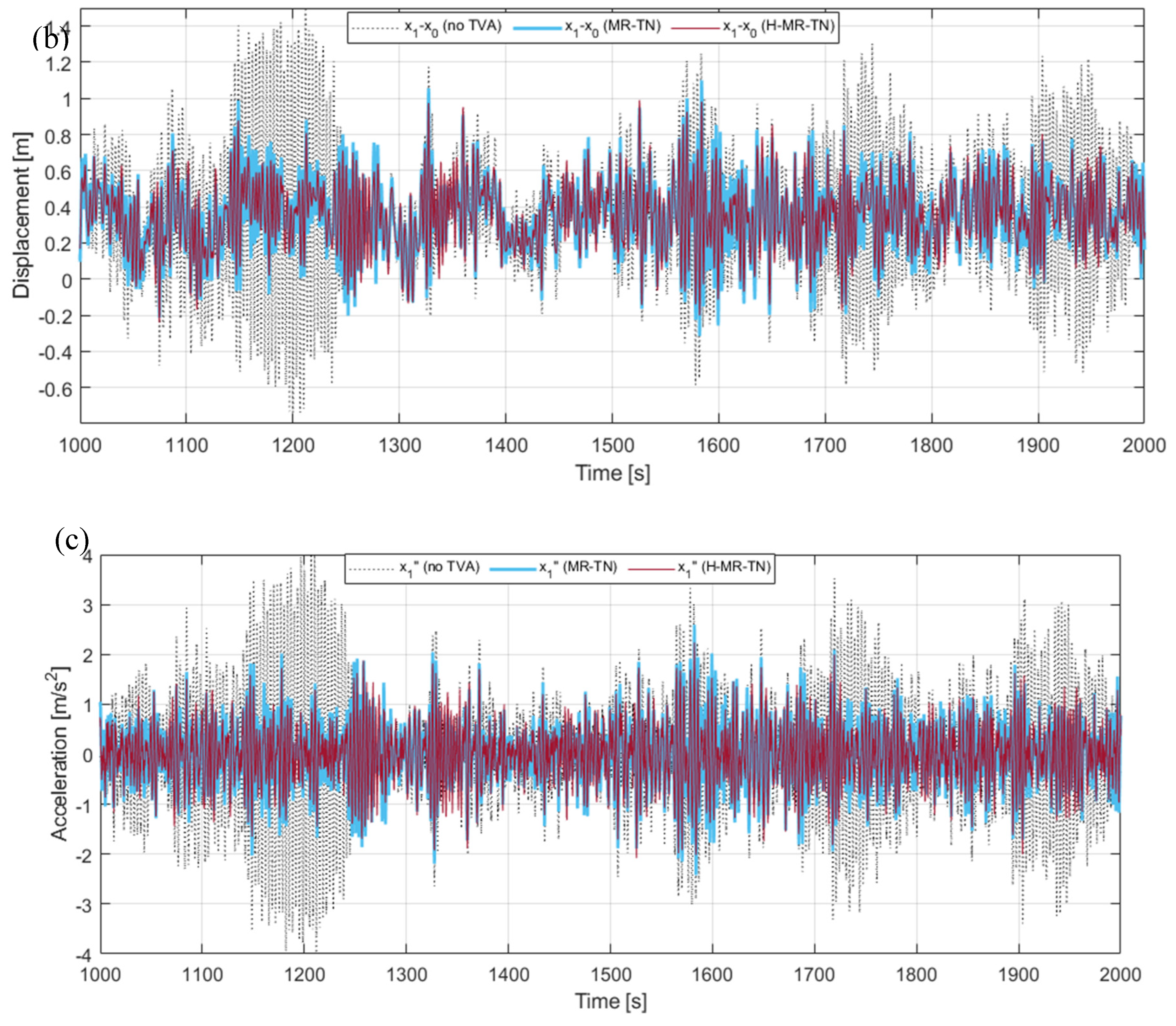
Preprints 96670 g016aPreprints 96670 g016b
Figure 16. Time patterns for exemplary Realisation 7: (a) TLP surge x 0 combined with the nacelle horizontal load F e , (b) tower tip relative displacement (tower deflection), (c) nacelle acceleration.
Figure 16. Time patterns for exemplary Realisation 7: (a) TLP surge x 0 combined with the nacelle horizontal load F e , (b) tower tip relative displacement (tower deflection), (c) nacelle acceleration.
Preprints 96670 g016aPreprints 96670 g016b
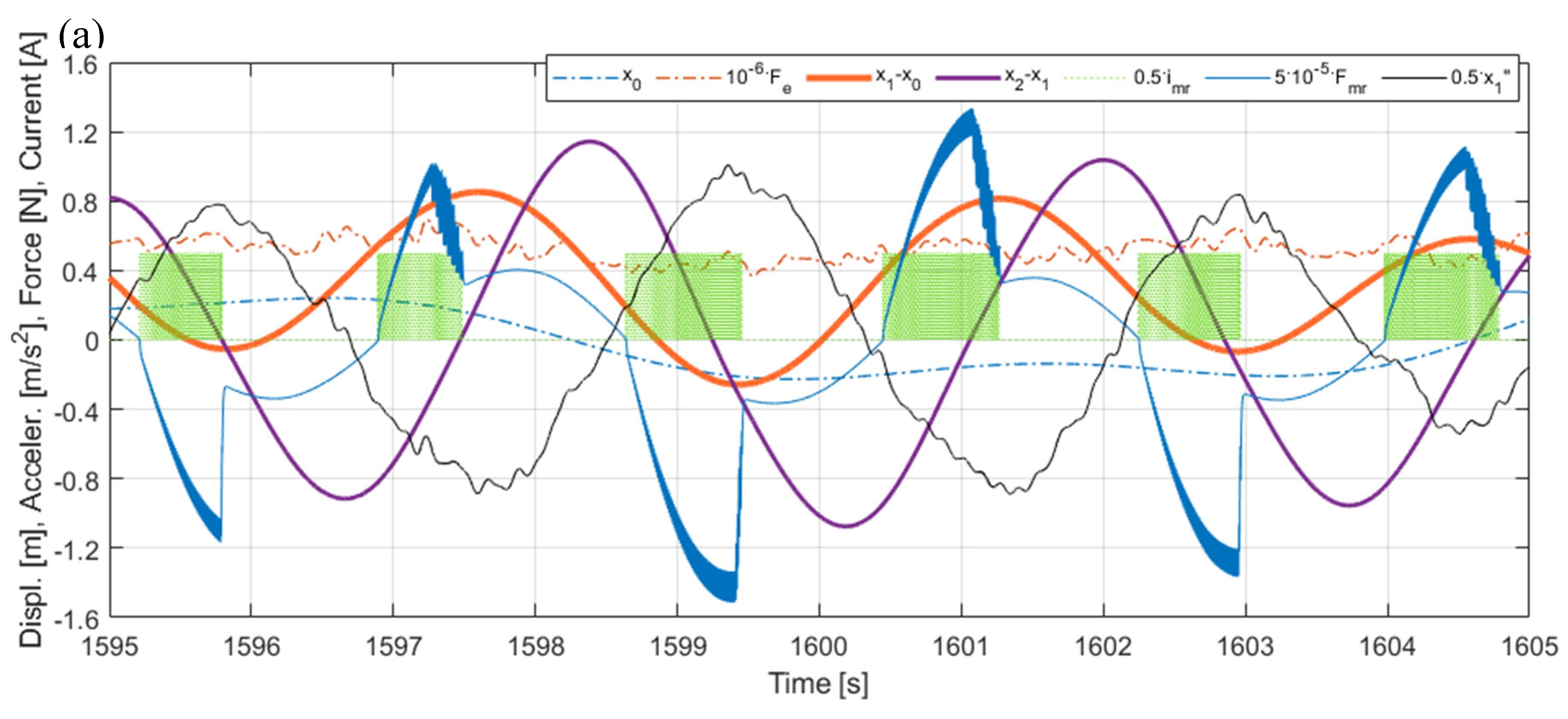
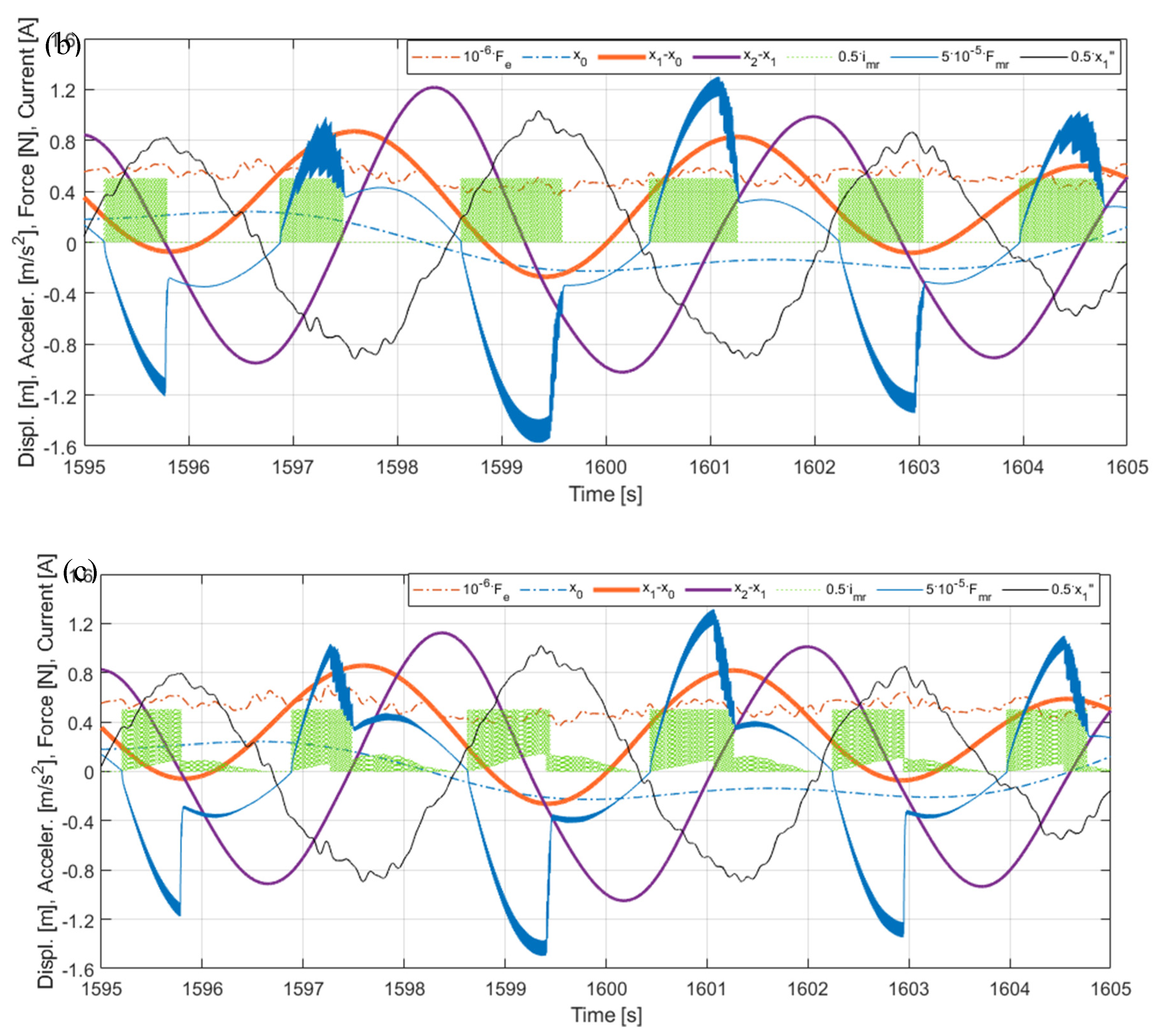
Preprints 96670 g017aPreprints 96670 g017b
Figure 17. Time responses for MR-TVA tuned to the NREL 5MW tower-nacelle 1st bending mode: (a) Control case I, (b) Control case II, (c) Control case III (Realisation 7).
Figure 17. Time responses for MR-TVA tuned to the NREL 5MW tower-nacelle 1st bending mode: (a) Control case I, (b) Control case II, (c) Control case III (Realisation 7).
Preprints 96670 g017aPreprints 96670 g017b
Preprints 96670 g018aPreprints 96670 g018b
Figure 18. Time responses for H-MR-TVA tuned to the NREL 5MW tower-nacelle 1st bending mode: (a) Control case I-H, (b) Control case II-H, (c) Control case III-H (Realisation 7).
Figure 18. Time responses for H-MR-TVA tuned to the NREL 5MW tower-nacelle 1st bending mode: (a) Control case I-H, (b) Control case II-H, (c) Control case III-H (Realisation 7).
Preprints 96670 g018aPreprints 96670 g018b
Table 1. NREL 5MW Baseline Wind Turbine parameters [35,37].
Table 1. NREL 5MW Baseline Wind Turbine parameters [35,37].
Rotor Diameter 126 m
Hub Height 90 m
Wind Speed:
Cut-In, Rated, Cut-Out
3.0, 11.4, 25.0 m/s
Rotor Speed: Cut-In, Rated 6.9, 12.1 rpm
Rotor Mass
Nacelle Mass
Tower Mass		 110.0 t
240.0 t
347.5 t
Nacelle Dimensions 18 × 6 × 6 m
Table 2. TLP platform main particulars [33].
Table 2. TLP platform main particulars [33].
Platform mass 2183 t
Displacement 6086.3 m3
Vertical centre of gravity of the platform (below sea level) 4.05 m
Draft, Freeboard 20, 12 m
Nominal Tendon pretension (each) 10.8 MN
Water depth 120 m
Table 3. TLP – NREL 5MW with TVA-TN/TVA-TLP simulation model parameters.
Table 3. TLP – NREL 5MW with TVA-TN/TVA-TLP simulation model parameters.
NREL 5MW tower-nacelle 1st bending mode model
m1 428.8 t
k1 1.546 MN/m
c1 3.542 kNs/m
TVA tuned to NREL 5MW tower-nacelle 1st bending mode
m2 10.0t (2.33% m1)
k2 34.421 kN/m
c2 3.352 kNs/m
TVA tuned to TLP surge
m2 10.0t (2.33% m1)
k2 3.770 kN/m
c2 1.109 kNs/m
Table 4. MR damper simulation model parameters.
Table 4. MR damper simulation model parameters.
C1 1581
C2 38.25
C3 12240
C4 3570
ν 1300
Table 5. The test cases – cumulative results over realisations 0÷9 (baseline weights: g11 = 1021, g12 = 1019.
Table 5. The test cases – cumulative results over realisations 0÷9 (baseline weights: g11 = 1021, g12 = 1019.
Preprints 96670 i002
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated