Preprint
Article
Unsteady Subsonic/Supersonic Flow Simulations in 3D Unstructured Grids over an Acoustic Cavity
Altmetrics
Downloads
104
Views
27
Comments
0
This version is not peer-reviewed
Submitted:
18 January 2024
Posted:
18 January 2024
You are already at the latest version
Alerts
Abstract
In this study, the unsteady Reynolds-averaged Navier-Stokes (URANS) equations are employed in conjunction with the Menter Shear Stress Transport (SST)-Scale-Adaptive Simulation (SAS) turbulence model in compressible flow, unstructured mesh and complex geometry. Whereas, other scale-resolving approaches in space and time, such as Direct Numerical Simulation (DNS) and Large-Eddy Simulation (LES), supply more comprehensive information about the turbulent energy spectra of the fluctuating component of the flow; however, previously mentioned avenues imply computationally intensive situations, usually performed over structured meshes and relatively simply geometries. In contrast, the SAS approach is designed according to “physically” prescribed length scales of the flow. More precisely, it operates by locally comparing the length scale of the modelled turbulence to the von Karman length scale (which is prescribed according to local fluid velocity derivatives and depends on the grid point distribution in the computational domain). This length scale ratio allows the flow to dynamically adjust the local eddy viscosity in order to better capture the large scale motions (LSM) in unsteady regions of URANS simulations. While SAS may be constrained to model only low flow frequencies or waivenumbers (i.e., LSM), its versatility and computational low-cost make it attractive to obtain a quick first insight of the flow physics; particularly, in those situations dominated by strong flow unsteadiness. The selected numerical application is the well-known M219 three-dimensional rectangular acoustic cavity from the literature at two different freestream Mach numbers, M∞ (0.85 and 1.35) and a length-to-depth ratio of 5:1. Thus, we consider the “deep configuration" in experiments by Henshaw. The SST-SAS model has demonstrated a satisfactory compromise between simplicity, accuracy and flow physics description.
Keywords:
Subject: Engineering - Aerospace Engineering
1. Introduction
Computational fluid dynamics (CFD) has experienced a notable growth in the last few decades. Nowadays, most engineering designs and technical projects rely on computational predictions before making critical design decisions; additionally, CFD may also be employed in order to gain important insight into the flow physics before performing an expensive experiment; particularly, in the aerospace industry as recently reviewed by [1]. In terms of performing turbulent industrial flow simulations over complex geometries, the workhorse has been the consideration of the Reynolds Averaged Navier–Stokes equations (RANS) Araya [2], which are obtained by time averaging the full NS equations. These equations require a model or closure to compute the Reynolds stresses, which arises from the convective terms of the NS equations after applying the time averaging process. Unfortunately, the RANS approach exhibits a deficient performance in massively separated flows or flows with inherently unsteady behavior [3] and in highly accelerated flows [4]. Recently, significant attention has been paid to relatively low-cost, scale-resolving, time-dependent computations of complex flows for industrial applications, e.g. geometries with moving parts, wing flutter, noise prediction, etc. In comparison with the highly computational resources demanded by Direct Numerical or Large Eddy Simulations (i.e. DNS/LES) [5], those approaches can provide the best tradeoff between unsteady simulations and unstructured meshes for industrial applications. Particularly, the unsteady Reynolds-averaged Navier–Stokes (URANS) methodology has became quite popular, due to its success in predicting the most energetic modes or coherent structures. However, URANS has frequently been accused of inaccurately representing the correct spectrum of turbulent scales, even if the numerical grid and the time step would be of sufficient resolution. In this study, the URANS equations for compressible flows are solved in conjunction to the Menter SST turbulence model and the scale-resolving SAS model (Scale Adaptive Simulations) by Menter and Egorov [6,7]. The adaptive simulation concept allows capturing more details of the flow or more turbulent structures. Furthermore, the most significant advantage of the SAS approach over existing RANS/LES methods is that the model is developed independent of the grid spacing. The SAS approach introduced by Menter and Egorov [6,7] is based on the use of the second derivative of the velocity that is highly active on short scales. As a consequence, this corresponds to an improvement over the original DES (detached-eddy simulation) model by Spalart et al.,DES97, which strongly depends on the grid spacing. More recently, a simple modification to the original DES approach (i.e., the delayed DES or DDES) was introduced Spalart et al.,DDES06 to remedy the grid-induced separation problem of the original DES version based on the shear-stress transport formulation (SST) by Menter and Kuntz [13].
To our knowledge, most of the numerical fluid dynamics applications of the SAS turbulence model has been performed in incompressible flows and over structured meshes and relatively simple geometries [21,22,23,24]; whereas, only few studies have focused on unstructured meshes [25,26,27]. With the purpose to fill that research gap, the Menter SST-SAS model is tested in complex geometries via unstructured grids for the subsonic-supersonic flow regime, then validated with experimental data for the M219 acoustic cavity [14]. The FLITE3D flow solver [28] has been applied in the present study, which is based on a finite volume approach with stabilization and discontinuity capturing features.
2. Governing Equations
The unsteady compressible Navier–Stokes equations are expressed, over a 3D domain with closed surface , in the integral form
where is the unit normal vector to . In addition, the unknown vector of conservative variables is expressed as
where is the fluid density, denotes the component of the velocity vector and is the specific total energy and the inviscid and viscous flux vectors are expressed as
respectively. The quantity
is the deviatoric stress tensor, where is the dynamic viscosity. The quantity is the heat flux, where k is the thermal conductivity and T is the absolute temperature. The viscosity varies with temperature according to Sutherlands’s law and the molecular Prandtl number is assumed to be constant and equal to 0.72. In addition, the medium is assumed to be calorically perfect.
3. Solution Procedure
In this section, numerical strategies for unstructured mesh generation and spatial/time discretisation are explained and discussed.
3.1. Hybrid Unstructured Mesh Generation
The computational domain is represented by an unstructured hybrid mesh for viscous problems, [2]. The process of mesh generation begins with the discretization of the domain boundary into a set of triangular or quadrilateral meshes that satisfy a mesh control function specified by the user [29]. Additionally, the distribution of the mesh parameters [30]; such as spacing, stretching and direction of stretching, are described by a background mesh as well as point, line and planar sources. For viscous flows, the boundary layers are generated using the advancing layer method [31] and the rest of the computational domain is filled with tetrahedral elements using a Delaunay incremental Bowyer Watson point insertion [32]. Hybrid unstructured meshes are constructed by merging certain elements of this tetrahedral mesh in the boundary layers.
3.2. Spatial Discretisation
The discretisation of the governing equations can be performed in a number of different ways. A computationally efficient approach is implemented, consisting on a cell vertex finite volume method. This involves the identification of a dual mesh, with the medial dual being constructed as an assembly of triangular facet, , where each facet is formed by connecting edge midpoints, element centroids and face centroids in the basic mesh, in such a way that only one node is contained within each dual mesh cell. Hence, the dual mesh cells form the control volumes for the finite volume process. When hybrid meshes are employed, the method for constructing the median dual has to be modified in order to ensure that no node lies outside its corresponding control volume. To perform the numerical integration of the fluxes, a set of coefficients is calculated for each edge using the dual mesh segment associated with the edge. The values of the internal edge coefficients, , and the boundary edge coefficients, , are defined as follows,
where is the area of facet , is the outward unit normal vector of the facet, is the set of dual mesh faces on the computational boundary touching the edge between nodes I and J and denotes the normal of the facet in the outward direction of the computational domain. The numerical integration of the fluxes over the dual mesh segment associated with an edge is performed by assuming the flux to be constant, and equal to its approximated value at the midpoint of the edge, i.e. a form of mid point quadrature. The calculation of a surface integral for the inviscid flux over the control volume surface for node I is defined as follows,
where denotes the set of nodes connected to node I by an edge and denotes the set of nodes connected to node I by an edge on the computational boundary. Thus, the last term is non-zero only in a boundary node. Similar formula can be implemented for the viscous fluxes. The use of edge based data structure has become widely used due to its efficiency in terms of memory and CPU requirements, compared to the traditional element based data structure, in particular in three–dimensions.
The resulting discretisations are basically central difference in character. Therefore, the addition of a stabilising dissipation is required for practical flow simulations. This is achieved by replacing the physical flux function by a consistent numerical flux function, such as the JST flux function [33] or the HLLC solver [34]. Discontinuity capturing may be accomplished by the use of an additional harmonic term in regions of high pressure gradients, identified using a pressure switch.
3.3. Time Discretization
The FLITE3D flow solver can simulate both unsteady and steady problems. However, in this investigation an unsteady flow analysis is performed. A three-level, second order accurate backward difference scheme is utilized in the present investigation,
Additionally, the relaxation scheme employed at each physical time step consists on a three-stage Runge-Kutta approach with local time stepping. The viscous and artificial dissipation terms are only computed once at every time step in order to reduce the computational requirements of the scheme. More details can be found in [35].
4. Turbulence Modelling in RANS
To obtain the compressible RANS equations, the unsteady equations 1 are averaged in time to smooth the instantaneous turbulent fluctuations in the flow field, while still allowing the capture of the time–dependency in the time scales of interest. In many engineering problems this assumption is valid, but this averaging procedure breaks down if the time scale of the physical phenomena of relevance is similar to that of the turbulence itself. For compressible flows, the density weighted Favre averaging procedure is mostly employed [35]. The Favre averaging procedure applied to equations 1 generates the extra convective term;
which is the Favre averaged Reynolds stress tensor. The most straightforward approach is to associate the unknown Reynolds stresses with the computed mean flow quantities by means of a turbulence model or closure. If the Boussinesq hypothesis is applied, this results in a linear relationship to the mean flow strain tensor through the eddy viscosity [36],
where k is the turbulent kinetic energy. The eddy viscosity depends on the velocity and the length scales of the turbulent eddies, i.e. , where ℓ is the turbulence length scale. In this paper, a two transport equation model is considered in which additional partial differential equations are solved to describe the transport of the eddy viscosity. As a consequence, nonlocal and history effects on are taken into account. Two–equation turbulence models are complete, because transport equations are solved for both turbulent scales, i.e. the velocity and the length scales. In particular, the turbulence model is popular due to its good performance in boundary layer flows subjected to adverse pressure gradients, with eventual separation. The original model [36] exhibits a freestream dependency of , which is generally not present in the model. Menter [37] combined the advantages of both models by means of blending functions, that permit the switching from , close to a wall, to , when approaching the edge of a boundary layer. A further improvement [37] was a modification to the eddy viscosity, based on the idea of the Johnson-King model, which establishes that the transport of the main turbulent shear stresses is crucial in the simulations of strong adverse pressure gradient flows. This new approach was called the Menter shear–stress transport model (SST), which was already implemented in FLITE3D for steady state solutions via the RANS approach [2].
4.1. Scale Adaptive Simulations (SAS) in Unsteady Flows
In this section, a brief description of the SAS equations is shown. The differential equations are presented in the normalized form. A convenient scaling guarantees a unit order of all variables, which decreases round-off errors of calculations. The reader is referred to Appendix B of Sørensen’s thesis [35] for the scaling and the normalized version of momentum and energy equations employed in the present study; however, the normalization symbol ∗ are dropped for simplicity. The corresponding normalized transport equations in the Menter SST model [37] for the turbulent kinetic energy, k, and the specific dissipation rate, , in compressible flows read as follows;
where and are the Strouhal and Reynolds numbers, respectively, represents the time Favre-averaged velocity, and, is the freestream dynamic viscosity. Furthermore, = 0.09, = 3/40, = 2, = 2 and = 5/9, and, = 0.856. is a blending function defined as,
, and,
Thus, the blending function generates values close to one far from the wall ( model) and almost zero values inside the boundary layer ( model). More details can be found in [37]. The main features of the Menter SST model can be summarized as follows: i) the consideration of a cross-diffusion term in the equation, ii) the implementation of a stress limiter for the maximum value of as well as a production limiter to impede the build-up of turbulence in stagnation zones; and, iii) the application of a blending function to compute the corresponding constants of the and models, respectively.
The stress limiter in the Menter SST turbulence model is defined as,
where = 0.31, is the strain rate, and, the normalized function is expressed as,
The production limiter consists on taking the minimum of when solving Equation (10).
The term in eq. 11 is the only modification on the SST model to consider the von Karman length-scale into the turbulence scale equation. Hence, the information provided by the von Karman length-scale, permits the SAS model to dynamically adjust to resolve the large structures in a URANS simulation. This results in a LES-like behavior in unsteady regions of the flow field. In addition, the model yields standard RANS capabilities in stable flow regions. The term reads as follows,
where , , (von Karman constant) and . Furthermore, the corresponding length scales in Equation (16) are,
where (Smagorinsky constant), and is the cubic root of the control volume size. Notice that the term of Equation (16) is always positive, and, basically depends on the ratio between the length scale of the modelled turbulence, L, to the von Karman length scale, . So, where this ratio (i.e., ) is large enough in the computational domain, the term becomes larger, making the turbulence viscosity smaller. Consequently, the large unsteady structures are breaking up into a turbulent spectrum.
4.2. Discretization of the Turbulent Transport Equations
The turbulence model equations involve the solution of partial differential equations, which are discretized in a similar manner as the governing equations. Nevertheless, to avoid instabilities from the convective terms, a first order upwind discretization of this term is used plus an added term to introduce adequate dissipation for stabilization;
where tu stands for turbulence unknowns (, k and ). Furthermore, the volume integrals are calculated using the midpoint rule and the gradients appearing in the model are calculated as follows,
Equation (20) in discrete form reads,
where is the volume of the control volume. Equations (20) and (21) were expressed for the velocity but it can be applied to any flow parameter. The second order diffusion term is calculated using the compact stencil of equation according to eq. (3.38) in [35], where the gradient along the edges are evaluated by means of the compact finite difference scheme.
5. Initial and Boundary Conditions
In all cases, the unsteady solution was started from the steady one. Furthermore, the initial conditions for the first stage (steady solution) were free stream conditions. The boundary conditions for the flow parameters (i.e., velocity, density and total energy) were already discussed in [28]. In this section, focus is given to the corresponding boundary conditions of the turbulence variables. Furthermore, the boundary conditions employed in this investigation are classified as: solid wall, inflow, outflow and symmetry.
5.1. Solid Wall Boundary
In the Menter SST model, the turbulent kinetic energy, k, is assigned a zero value at the wall. The specific dissipation rate, , does not possess a natural boundary condition at the wall. However, based on the asymptotic solution given by Wilcox [36], the following value for is prescribed according to the implemented normalization;
where is the laminar kinematic viscosity at the wall, is a constant (= 3/40), is the local first off-wall point and is the Reynolds number.
5.2. Inflow and Outflow Boundaries
Based on recommendations by [38], the following values for and are adopted in the two-equation turbulence models at these boundaries: and 5, respectively.
5.3. Symmetry Boundary
A symmetry condition is defined as a boundary where the normal velocity component is zero, being the density and total energy normal derivative zero, as well. Furthermore, a symmetry condition can also be compared to an inviscid wall (streamline). Hence, the turbulent eddy viscosity is set to zero at this location in the turbulence models. If the configuration of the problem possesses a symmetry plane, this represents a very convenient way to significantly reduce the computational resources required.
6. Results and Discussion
The Menter SST-SAS turbulence model has been implemented in the FLITE3D flow solver [28]. The results of the classical M219 acoustic cavity are presented in this section, together with a discussion concerning the application of the models.
6.1. M219 Acoustic Cavity
Numerical simulation of flow over a fully 3-D rectangular cavity are presented and discussed in this section. The vortex system and flow patterns inside a rectangular three-dimensional acoustic cavity consist of intricate fluid dynamics structures, highly dictated by the incoming flow regime and geometry dimensions. For the purpose of testing the Menter SST-SAS turbulence model, the cavity configuration is selected as the M219 experimental test case of Henshaw [14] for a deep cavity (4 inches) at two different freestream Mach numbers, (0.85 and 1.35). An schematic of the experimental model as done in [14] is shown in Figure 1. Static pressure was measured at the centerline and off-centerline (i.e., at the rig centerline) of the cavity via Kulite transducers. In the present study, only measured Root Mean Squared (RMS) of static pressure at the cavity centerline (Y = 0) and ceiling was employed for numerical validation (K20 to K29 transducers). Figure 2 depicts the RMS static pressure distribution over the ceiling of the deep empty cavity. It is observed that incoming high subsonic Mach number induces a slightly increasing RMS distribution, with a growing factor of approximately four between the last (K29) and first (K20) Kulite transducer. However, the RMS distribution at Mach 1.35 exhibits a wavy trend with local minima at 0.25 and 0.75, respectively. The geometry dimensions of the M219 cavity in terms of the depth are (length, width, and depth), with a depth D of 4 inches. Since the width and depth of the cavity are the same, this configuration create a fully three-dimensional flow pattern. The Reynolds number spans 9.5 to 21 , based on the cavity depth. The incoming flat-plate boundary layer is turbulent, with the ratio of the upstream boundary layer thickness to the cavity depth, i.e. , approximately ranging from 0.1 to 0.25 for Mach numbers of 0.85 and 1.35, respectively. The unstructured hybrid mesh is composed by approximately 3.37 million tetrahedral elements, 4,472 prisms and 459 pyramids. The previously mentioned element distribution was determined to be deemed appropriate for the goals of this study and cavity representation based on the grid independent study performed. Some views of the computational domains and grid system are displayed in Figure 3. Namely, a side view (plane Y-X) is shown in Figure 3a. An schematic of the grid at the half-plane of the cavity is observed in Figure 4b. Also, an interior cavity view is depicted by Figure 4c. The mesh has 20 viscous layers for efficient boundary layer capturing with the first off-wall point located at . This ensures that first off-wall point locations are within 0.2 to 0.4 wall or plus units, inside the viscous linear layer. The total dimensions of the computational domain are as follows: along the streamwise, wall-normal and spanwise directions, respectively, and in terms of the cavity depth, D. Therefore, the computational domain is tall and wide enough to eliminate any influence from the boundary faces on the flow statistics over the cavity. Moreover, the spanwise side walls are treated as symmetry (periodic) planes, the top boundary is a far-field boundary, and all bottom solid surfaces (including the cavity) are considered as adiabatic non-slip walls. Upstream of the cavity edge, a flat-plate with no-slip condition is prescribed (about 7.5D in length). While a zone with slip condition (and inlet freestream flow parameters) is set up upstream of the flat plate (∼7.5D in length).
The selected normalized time step is or approximately seconds. The time variation of the total drag over the cavity at = 0.85, normalized by the reference surface and freestream dynamic pressure, can be observed in Figure 4. Furthermore, the transient stage took approximately 15 non-dimensional time units from the steady solution, as seen in Figure 4. This transient part was discharged for flow statistics computation. Figure 5 depicts the root mean square (RMS) of pressure fluctuations on the cavity ceiling at 0 (centerline) and both freestream Mach numbers. Approximately 500 flow fields were taken for computing . Notice that in Figure 6, the values of were normalized by the value at the first transducer (i.e., K20) located 1 inch downstream of the front of the cavity in experiments by Henshaw [14]. The comparison of present SST-SAS results at = 0.85 with experimental data by [14] is fairly good. The SAS model has been able to capture the increasing slope of by the cavity end. On the other hand, the performance of the SAS-model at the supersonic regime ( = 1.35) is not as good as in the subsonic case. While the first inflexion point (around = 0.35) is well captured, the second inflexion point in experimental is improperly outlined by the SST-SAS model. This may be attributed to the presence of some important compressibility effect on the cavity flow, which is not taken into account in the SAS approach. The original SAS model was designed and mostly tested in incompressible and low-Mach wall-bounded flow applications [7,8]. Previous work done on turbulent coherent structures by [9,10] via Two-Point Correlations (TPC) and Lagrangian Coherent Structure (LCS) approach has revealed the moderate influence (but not negligible) of compressibility, as the Mach number increases at the supersonic regime level, on the coherent structure dimensions. Specifically, Lagares & Araya [10] stated “coherent structures grow more isotropic proportional to the Mach number, and their inclination angle varies along the streamwise direction". Therefore, it can be inferred that the SAS turbulence model would be greatly enhanced by the addition of a Mach number dependency of the length scale computation of the flow, which is beyond the scope of present manuscript.
Results about the SAS model when switched on and off are shown in Figure 6 and Figure 7 at = 0.85 and 1.35, respectively. The agreement of present URANS results exhibit a moderate better agreement with experiments by [14] when the SAS model is active, particularly by the end of the cavity ceiling. It is hypothesized that the better performance of the SAS model when capturing experimental in that rear cavity corner might be due to the presence of high turbulent kinetic energy, k, and consequently large values of the turbulence length scale, L, according to eq. 17 (as it will be visualized later on). The extra term (see Equation (16)) in the specific dissipation rate equation, , is the sole adjustment to the SST model in equation 11 to account for the von Karman length-scale, , allowing the simulations to dynamically accommodate to resolve the large scale motions (LSM). Notice that the term is directly proportional to the square of the ratio L/.
Furthermore, the corresponding iso-contours of instantaneous turbulence length scales, L, are shown by Figure 8a. The turbulence length scale is proportional to the square root of the turbulent kinetic energy, k, and inversely proportional to the specific dissipation rate, . As seen in the centerline longitudinal plane of the cavity (Figure 8a), the maximum incoming length scale, L, is in the order of 0.01m or , reaching values 0.012m in the back bottom corner. These local large values of L at the rear corner cause: (i) meaningful values for the , and (ii) changes in spatial distribution to better resolve LSM, which could be the physical explanation of better capturing wall pressure fluctuations in Figure 6. Nevertheless, a deeper analysis should be carried out for shedding light on that aspect, which is outside the present manuscript’s scope. It is also clearly seen the formation of the front vortex, characterized by flow recirculation zone (with low values of momentum and turbulent kinetic energy) bounded by large values of L (and turbulent kinetic energy, as well). A rear vortex system (highly energetic) is located by the end of the cavity at the bottom corner and characterized by significant turbulence length scale values. Figure 8b exhibits four cross-sectional planes separated by a distance of approximately with iso-contours of instantaneous turbulence length scales, L. The spatial sequence of the major horseshoe vortex formation can be observed.
In order to describe the different vortical structures observed in the cavity, we should mention the following categories, as described in [15]: open-type cavity flow and closed-type cavity flow, according to the ratio . At subsonic flow regimes, an open-type cavity () is represented by a shear layer that spans the entire cavity opening, and by a large recirculation zone inside the cavity itself [15]. On the other hand, closed-type cavities () are generally pictured by a shear layer generated at the front of the cavity that reattaches on the bottom of the cavity, without the presence of a large recirculation vortex in the centre of the cavity. A transitional regime for rectangular cavities takes place in between. This seems to be the most appropriate category to encase present cavity at . The reasons are supplied hereafter. Also, it is worth highlighting that the cavity is narrow because of ; thus, a completely three-dimensional geometry generates a different set of vortices. Figure 9 shows contours of instantaneous spanwise vorticity. Positive isolines (inward vorticity vector or clockwise spin) are represented by solid curves; whereas, negatives isolines (outward vorticity vector or counterclockwise spin) are represented by dashed curves. It can be seen in Figure 9 that the incoming turbulent boundary penetrates further into the cavity towards the ceiling. That incoming shear layer reattaches on the bottom of cavity, which is confirmed by Figure 10 (contours of instantaneous streamwise velocity normalized by the freestream velocity). Two small recirculation zones with clockwise spins are observed in the front side (12 < < 13) and in the back side (14 < < 15) of the cavity. Particularly, the rear vortex transports fluid from the impinging shear layer on the cavity top downwards and towards the cavity bottom and viceversa, which is consistent with findings by [15]. Those phenomena induce two “curved” and elongated counterclockwise vortices (or “banana-like” vortices) that contributes to the vertical mixing of turbulence inside the cavity. In particular, the vortex duplet located by the end of the cavity at the bottom corner is mainly responsible for turbulent kinetic energy generation, which in turns induces large local values of L, as previously explained. The by [16] is implemented in this study to extract and visualize vortex cores via positive values, which describe regions of the flow where rotation dominates over strain. On the other hand, negative iso-values of represent highly deformed flow regions. Iso-surfaces of the (positive values in red and negative values in blue) are exhibited in Figure 11 at = 0.85. Focusing exclusively on positive (red) iso-surfaces or vortex cores, the most energetic turbulent coherent structures emerge in three clearcut regions: (i) near the front region of the cavity, (ii) along the side cavity edges (see the presence of side vortices), and (iii) in the rear side of the cavity and downstream (vortex shedding). Highly energetic vortical coherent structures can also be observed in the cavity inside. Previously described phenomena related to coherent structure dynamics are consistent with findings and observations by [17]. The streamwise counter-rotating vortex pair described in Figure 8b is accurately captured by positive iso-surfaces of . Interestingly, downstream the cavity, where flow separates, the vortex adopt a horseshoe or hairpin shape (or omega-shaped vortices) as described by [18] with the typical leg, neck and head. These coherent structures are commonly found in turbulent boundary layers, particularly in the log-region, which are mainly responsible for the generation of Reynolds shear stresses and turbulence production [18]. The vortex shedding downstream the cavity resembles the jet in a crossflow situation [19], where horseshoe vortices are continuously created by the interaction of the incoming shear layer with the vertical jet. It is hypothesized that the streamwise counter-rotating vortex pair by the end of the cavity lifts-up low speed fluid, interacting with the incoming shear layer over the cavity and mimicking the crossflow jet problem. Highly strained flow (blue iso-surfaces) can be seen nearby vortex cores, predominantly in the cavity lateral sides and at the rear edge.
Turning to the Mach-1.35 case, it is important to emphasize the acoustic wave system generated when the incoming turbulent flow is supersonic. Figure 12 illustrates idealized time-averaged situations of the incoming supersonic boundary layer facing a rectangular cavity (adapted from [20]). According to Aradag & Knight [20] (and similarly defined by [15] for incoming subsonic flow in rectangular cavities), one can define two major cavity types based on the ratio: open and closed cavity configurations. In the open or “deep" cavity system (i.e., at low values of ), the turbulent free shear layer reattaches on the rear part of the cavity (see top image in Figure 12); therefore, creating a sole recirculation region in the mean flow. On the other hand, in the closed or “shallow" cavity (i.e., at large values of ), the shear layer reattaches on the cavity floor, and the vortex system resembles a combination of a backward and forward facing step. While the flow physics in terms of open and closed cavities is somehow similar for incoming subsonic and supersonic flow; there is no general consensus about the critical values. ratios greater than 13 indicate closed cavity flow, while factors smaller than 10 mean open cavity flow [20]. Furthermore, in Crook et al.,Crook2013 it is reported 8 and 7 as those extreme values previously mentioned. Clearly, one has to visualize the internal vortex system and the flow recirculation zone for better ascertaining if dealing with open or closed cavity flows. Furthermore, the most important aspect to highlight in supersonic cavities is the presence of compression and expansion waves according to the cavity type [20], as depicted by Figure 12. Figure 13 depicts iso-surfaces of positive (vortex cores) and negative (highly deformed or strained flow) values of the by [16] for the supersonic incoming flow, i.e. at = 1.35. The formation of horseshoe, hairpin shape or omega-shaped vortices downstream the cavity is evidently seen, as in the subsonic case of Figure 11. However, the distribution of volumes with either highly rotational (in red) or strained (in blue) flow is clearly different at = 0.85 and 1.35, respectively; which indicates that the vortex systems are rather distinctive in the supersonic case: most of the front side of the cavity is populated by vortex cores (rotational flow); whereas, by the rear cavity side and downstream, various zones coexist either with high level of rotation or deformation in a “twisted" fashion, not observed in the subsonic case. The presence of highly strained flow downstream of the rear cavity could be linked to the significant unsteady expansion, which will be further discussed in this manuscript. In Figure 14, iso-contours of instantaneous spanwise vorticity is shown at = 1.35 and at the centerline plane of the cavity (i.e., at Z = 0). As previously described, inward vorticity vector or clockwise spin is represented by positive solid isolines; while, outward vorticity vector or counterclockwise spin zones are represented by negative dashed curves. At this instant, two large vortical structures with opposite signs or spanwise counter-rotating vortex pair (clockwise and counter-clockwise, respectively) are observed in the cavity center (12 < < 14.5). The incoming turbulent shear layer penetrates further almost to the cavity bottom, and this clockwise spanwise vortex induces the nearby counter-clockwise (by viscous effects and angular momentum conservation). At this point, the previously described instantaneous spanwise vortex pair leads to the generation of high levels of turbulent kinetic energy, wall-normal mixing and strong pressure gradients (with minimum pressure at vortex centers) inside the cavity. Additionally, the instantaneous vortex pair promotes the vortex formation (with opposite sign) in the vicinity of the cavity via viscous effects. It is worth highlighting that for this narrow cavity ( = 5) the turbulent flow generates highly unsteady three-dimensional vortical structures that significantly influences the cavity response. Figure 15 exhibits iso-contours of instantaneous spanwise vorticity at = 1.35 and at an off-centerline plane (i.e., at Z = 0.25D). The strong differences on instantaneous spanwise vorticity distribution at Z = 0.25D with respect to the cavity centerline plane (Z = 0) evidences the non two-dimensionality nature for this cavity configuration. In Figure 16, contours of instantaneous streamwise velocity normalized by the freestream velocity are shown for the supersonic incoming flow case. The incoming turbulent shear layer develops from the front cavity edge, bends down into the first half (10.4 < < 13.4) due to pressure gradients and impinges on the bottom. A clear backflow region is observed (blue) with negative values of the streamwise velocity. The red region just above the cavity edge indicates the presence of moderate instantaneous supersonic expansion or favorable pressure gradient (FPG). In a similar manner, the flow strongly accelerates by the rear edge cavity. That strong supersonic expansion or FPG in the outer region and freestream might be the reason of the presence of extremely strained flow at the trailing edge, represented by iso-surfaces of (in blue) in Figure 13. In addition, the very strong adverse pressure gradient (APG) generated by the rear cavity edge in the near wall region is responsible for the downstream flow separation bubble. Outside of the rectangular cavity, the flow is supersonic, whereas subsonic flow recirculating volumes take place inside [20]. Also, acoustic waves created due to the impingement of the turbulent shear layer at the rear wall of the cavity are able to propagate upstream through the subsonic region of the flow.
7. Conclusions
An evaluation of the Menter SST-SAS turbulence model in URANS of turbulent compressible flows and unstructured mesh is performed for a 3D acoustic cavity. The SAS approach is based on the use of the second derivative of the velocity that is highly active only on short scales. Therefore, this corresponds to an improvement over the original DES (detached-eddy simulation) that strongly depends on the grid spacing. Consequently, the SAS model exhibits simplicity, robustness and moderate mesh dependency, which make it a good candidate for unstructured meshes in complex geometries. The scale adaptive simulation model has been able to predict fairly well the pressure fluctuation distribution over the subsonic and supersonic cavity (M219). However, a definite superiority can not be described when the model was in “on" or “off" mode, at least, based on the present acoustic cavity analysis. The selected problem configuration showed significant numerical challenges: highly 3D flow (deep cavity), sharp corners that induce strong adverse pressure gradient and boundary layer detachment, compressibility effects (presence of compression and expansion waves) and intricate vortex system. Furthermore, the SST-SAS model has exhibited adequate representation of the flow physics.
Author Contributions
Conceptualization, G.A.; methodology, G.A.; software, G.A.; validation, G.A.; formal analysis, G.A.; investigation, G.A.; resources, G.A.; data curation, G.A.; writing—original draft preparation, G.A.; writing—review and editing, G.A.; visualization, G.A.; supervision, G.A.; project administration, G.A.; funding acquisition, G.A. The author has read and agreed to the published version of the manuscript.
Funding
This material is based upon work supported by the National Science Foundation under grant #2314303. This material is based on research sponsored by the Air Force Research Laboratory, under agreement number #FA9550-23-1-0241.
Data Availability Statement
Not applicable.
Conflicts of Interest
The author declares no conflict of interest.
References
- M. Mani and A. J. Dorgan, A Perspective on the State of Aerospace Computational Fluid Dynamics Technology. Annual Review of Fluid Mechanics 2023 55:1, 431-457.
- Araya, G. Turbulence model assessment in compressible flows around complex geometries with unstructured grids. Fluids 2019, 4, 81. [Google Scholar] [CrossRef]
- Paeres, D.; Lagares, C.; Araya, G. Assessment of Turbulence Models over a Curved Hill Flow with Passive Scalar Transport. Energies 2022, 15, 6013. [Google Scholar] [CrossRef]
- Saltar, G. and Araya, G., Reynolds shear stress modeling in turbulent boundary layers subject to very strong favorable pressure gradient. Computers and Fluids, Vol. 202, 104494, 2020.
- Menter, F.R., Kolmogorov, D.K., Garbaruk, A.V., A S. Stabnikov, Direct- and Large Eddy Simulations of Turbulent Flow in CS0 Diffuser on Resolved and Under-resolved Meshes. Flow Turbulence Combustion, 110, 515–546 (2023).
- F.R Menter and Y. Egorov, A scale-adaptive simulation model using two-equation models. AIAA Paper AIAA2055-1095 (2005).
- F.R Menter and Y. Egorov. The Scale-Adaptive Simulation Method for Unsteady Turbulent Flow Predictions. Part 1: Theory and Model Description. Flow Turbulence Combust 85, 113–138 (2010).
- Egorov, Y., Menter, F. R., Lechner, R., & Cokljat, D. The Scale-Adaptive Simulation Method for Unsteady Turbulent Flow Predictions. Part 2: Application to Complex Flows. Flow, Turbulence and Combustion, 85(1), 139–165 (2010).
- Araya, G.; Lagares, C. Implicit subgrid-scale modeling of a Mach-2.5 spatially-developing turbulent boundary layer. Entropy 2022, 24, 555. [Google Scholar] [CrossRef] [PubMed]
- Lagares, C.; Araya, G. A GPU-Accelerated Particle Advection Methodology for 3D Lagrangian Coherent Structures in High-Speed Turbulent Boundary Layers. Energies 2023, 16, 4800. [Google Scholar] [CrossRef]
- P.R. Spalart, W.-H. Jou, M. Strelets and S.R. Allmaras, Comments on the feas1ibility of LES for wings, and on a hybrid RANS/LES approach. In: Proceedings of first AFOSR international conference on DNS/LES, Ruston, Louisiana. Greyden Press, 4-8 Aug. (1997).
- P.R. Spalart, S. Deck, M.L. Shur, K.D. Squires, M. Strelets, A.K. Travin, A new version of detached-eddy simulation, resistant to ambiguous grid densities. Theoretical and Computational Fluid Dynamics 20 (3), 181-195 (2006).
- F.R. Menter and M. Kuntz, Adaptation of eddy-viscosity turbulence models to unsteady separated flow behind vehicles. In: McCallen, R., Browand, F., Ross, J. (eds.) Symposium on the aerodynamics of heavy vehicles: trucks, buses and trains. Springer, Berlin Heidelberg New York (2004).
- Henshaw, M. J., M219 cavity case. In: Verification and validation data for computational unsteady aerodynamics, Tech. Rep. RTO-TR-26, AC/323/(AVT) TP/19, pp. 453-472 (2000).
- Crook, S., Lau, T., & Kelso, R. Three-dimensional flow within shallow, narrow cavities. Journal of Fluid Mechanics, 735, 587-612, (2013).
- Hunt, J. C. R., Wray, A. A., and Moin, P. Eddies, streams, and convergence zones in turbulent flows. In Studying Turbulence Using Numerical Simulation Databases, 2, pages 193–208 (1988).
- Simone Mancini, Alexander Kolb, Ignacio Gonzalez-Martino and Damiano Casalino. Very-Large Eddy Simulations of the M219 Cavity at High-Subsonic and Supersonic Conditions, AIAA 2019-1833. AIAA Scitech 2019 Forum. January 2019. 20 January.
- Adrian RJ, Meinhart CD and Tomkins CD, Vortex organization in the outer region of the turbulent boundary layer. Journal of Fluid Mechanics 422: 1–54 (2000).
- Quiñones, C.; Araya, G. Jet in accelerating turbulent crossflow with passive scalar transport. Energies 2022, 15, 4296. [Google Scholar] [CrossRef]
- Selin Aradag and Doyle Knight. Simulation of Supersonic Flow over a Cavity, AIAA 2005-848. 43rd AIAA Aerospace Sciences Meeting and Exhibit. January 2005. 20 January.
- Parra Rodríguez, J.A.; Abad Romero, M.A.; Huerta Chávez, O.M.; Rangel-López, L.R.; Jiménez-Escalona, J.C.; Diaz Salgado, J. Coherent Structures Analysis of Methanol and Hydrogen Flames Using the Scale-Adaptive Simulation Model. Energies 2023, 16, 7074. [Google Scholar] [CrossRef]
- Kim, S.-J.; Choi, Y.-S.; Cho, Y.; Choi, J.-W.; Hyun, J.-J.; Joo, W.-G.; Kim, J.-H. Effect of Fins on the Internal Flow Characteristics in the Draft Tube of a Francis Turbine Model. Energies 2020, 13, 2806. [Google Scholar] [CrossRef]
- Meana-Fernández, A.; Fernández Oro, J.M.; Argüelles Díaz, K.M.; Velarde-Suárez, S. Turbulence-Model Comparison for Aerodynamic-Performance Prediction of a Typical Vertical-Axis Wind-Turbine Airfoil. Energies 2019, 12, 488. [Google Scholar] [CrossRef]
- Trivedi, C.; Cervantes, M.J.; Gandhi, B.K. Investigation of a High Head Francis Turbine at Runaway Operating Conditions. Energies 2016, 9, 149. [Google Scholar] [CrossRef]
- Wiński, K.; Piechna, A. Comprehensive CFD Aerodynamic Simulation of a Sport Motorcycle. Energies 2022, 15, 5920. [Google Scholar] [CrossRef]
- Hiller, S. and Seitz, P.. Interaction Between a Fluidic Actuator and Main Flow Using SAS Turbulence Modelling, AIAA 2006-3678. 3rd AIAA Flow Control Conference. June 2006.
- Araya, G., Evans, B., Hassan, O., Morgan, K. (2011). Scale Adaptive Simulations over a Supersonic Car. In: Kuzmin, A. (eds) Computational Fluid Dynamics 2010. Springer, Berlin, Heidelberg. [CrossRef]
- K. Morgan, J. Peraire, J. Peiro and O. Hassan, The computation of 3-dimensional flows using unstructured grids, Computer Methods in Applied Mechanics and Engineering, 87 Issue: 2-3 pp 335-352 (1991).
- J. Peiró, J. Peraire and K. Morgan, FELISA system reference manual. Part 1–basic theory. University of Wales, Swansea report C/R/821/94 1994.
- J. Peraire, K. Morgan, and J. Peiró, Unstructured finite element mesh generation and adaptive procedures for CFD. Proceedings No: 464—Applications of Mesh Generation to Complex 3D Configurations, 18.1–18.12. AGARD, Paris, 1990.
- O. Hassan, K. Morgan, E. J. Probert and J. Peraire, Unstructured tetrahedral mesh generation for three-dimensional viscous flows. International Journal for Numerical Methods in Engineering 39:549–567, 1996.
- N.P. Weatherill and O. Hassan, Efficient three–dimensional Delaunay triangulation with automatic boundary point creation and imposed boundary constraints. International Journal for Numerical Methods in Engineering 37:2005–2039, 1994.
- A. Jameson, W. Schmidt and E. Turkel, Numerical simulation of the Euler equations by finite volume methods using Runge–Kutta timestepping schemes. AIAA Paper 81–1259, 1981.
- A. Harten, P. D. Lax, and B. van Leer, On upstreaming differencing and Godunov-type schemes for hyperbolic conservation laws, SIAM Rev., 25, 35 (1983).
- K.A. Sørensen, A multigrid accelerated procedure for the solution of compressible fluid flows on unstructured hybrid meshes. PhD thesis, University of Wales, Swansea, (2002).
- D.C. Wilcox, Turbulence Modeling for CFD, DWC Industries, Inc. La Canada, California (2006).
- F.R. Menter, Review of the shear-stress transport turbulence model experience from an industrial perspective, Int. J. of Computational Fluid Dynamics 23 4 pp 305-316 (2009).
- Spalart, P. R. and Rumsey, C. L., Effective Inflow Conditions for Turbulence Models in Aerodynamic Calculations, AIAA Journal, Vol. 45, No. 10, pp. 2544-2553 (2007).
Figure 1.
Experiment schematic and dimensions (adapted from [14]).
Figure 1.
Experiment schematic and dimensions (adapted from [14]).
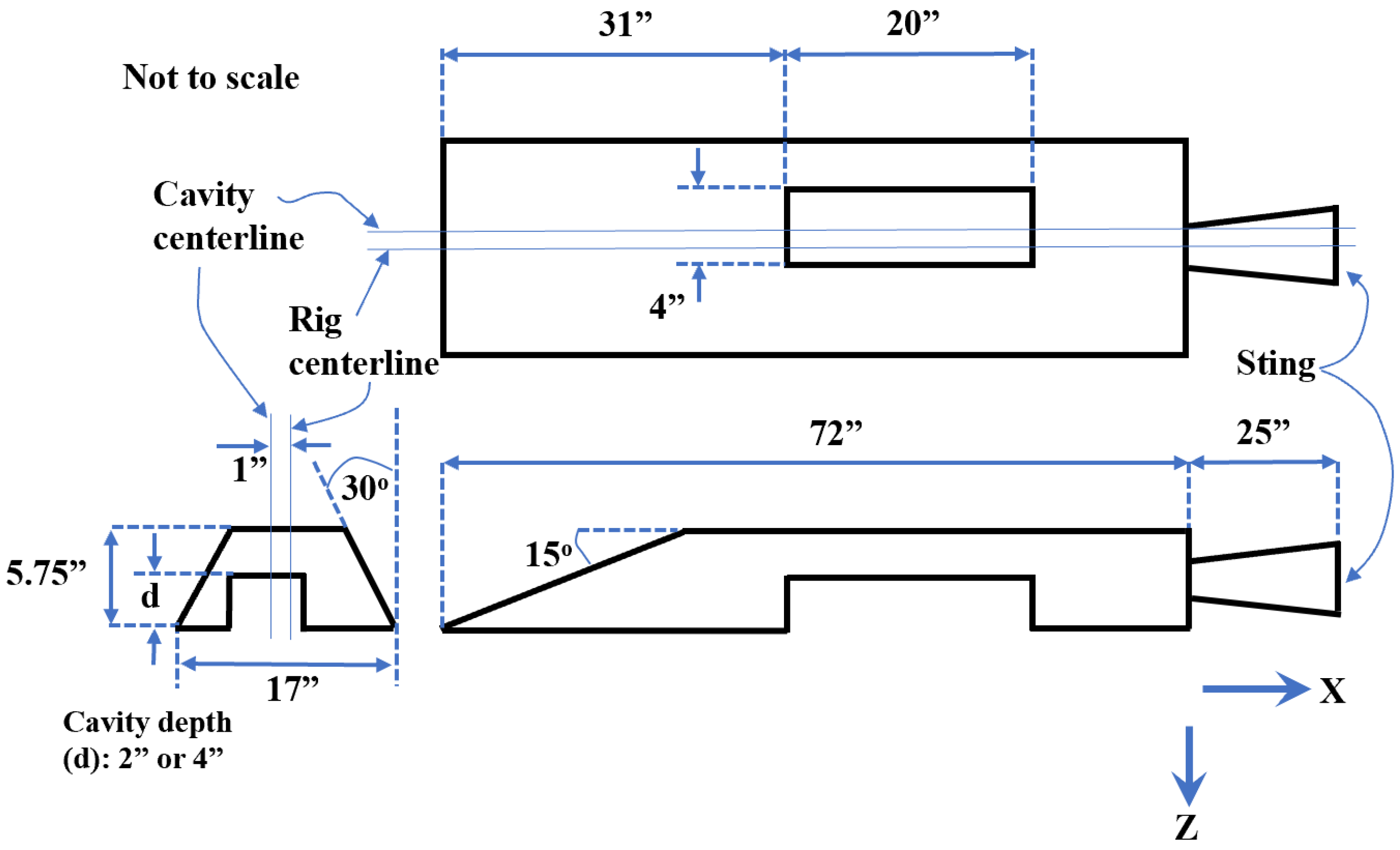
Figure 2.
RMS of pressure fluctuations at the deep cavity ceiling and centerline (Y = 0) from [14].
Figure 2.
RMS of pressure fluctuations at the deep cavity ceiling and centerline (Y = 0) from [14].
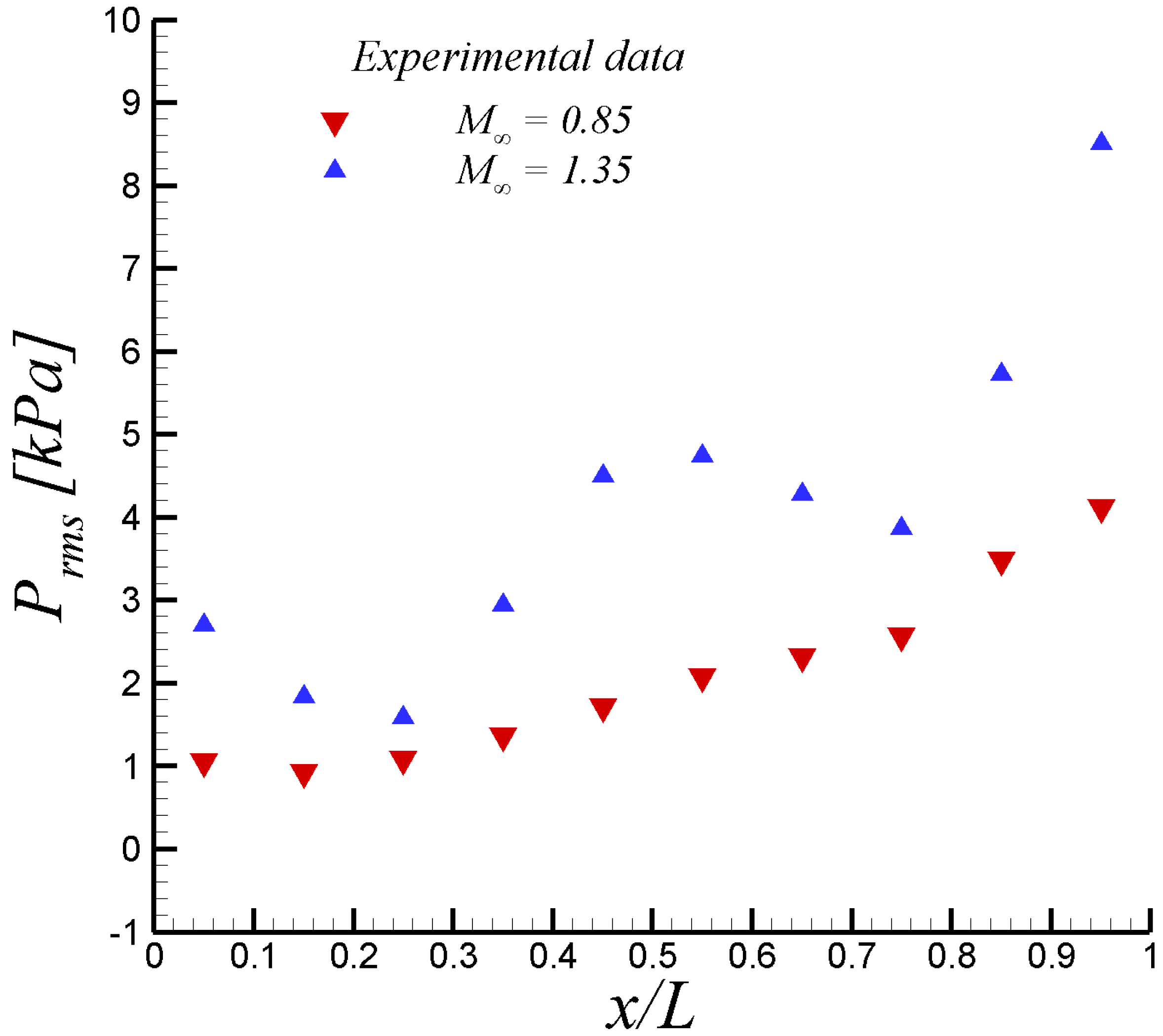
Figure 3.
Several schematics of the computational box and hybrid mesh: (a) lateral view, (b) half plane of the cavity, and (c) interior view.
Figure 3.
Several schematics of the computational box and hybrid mesh: (a) lateral view, (b) half plane of the cavity, and (c) interior view.


Figure 4.
Time variation of the total drag in the acoustic cavity at = 0.85.
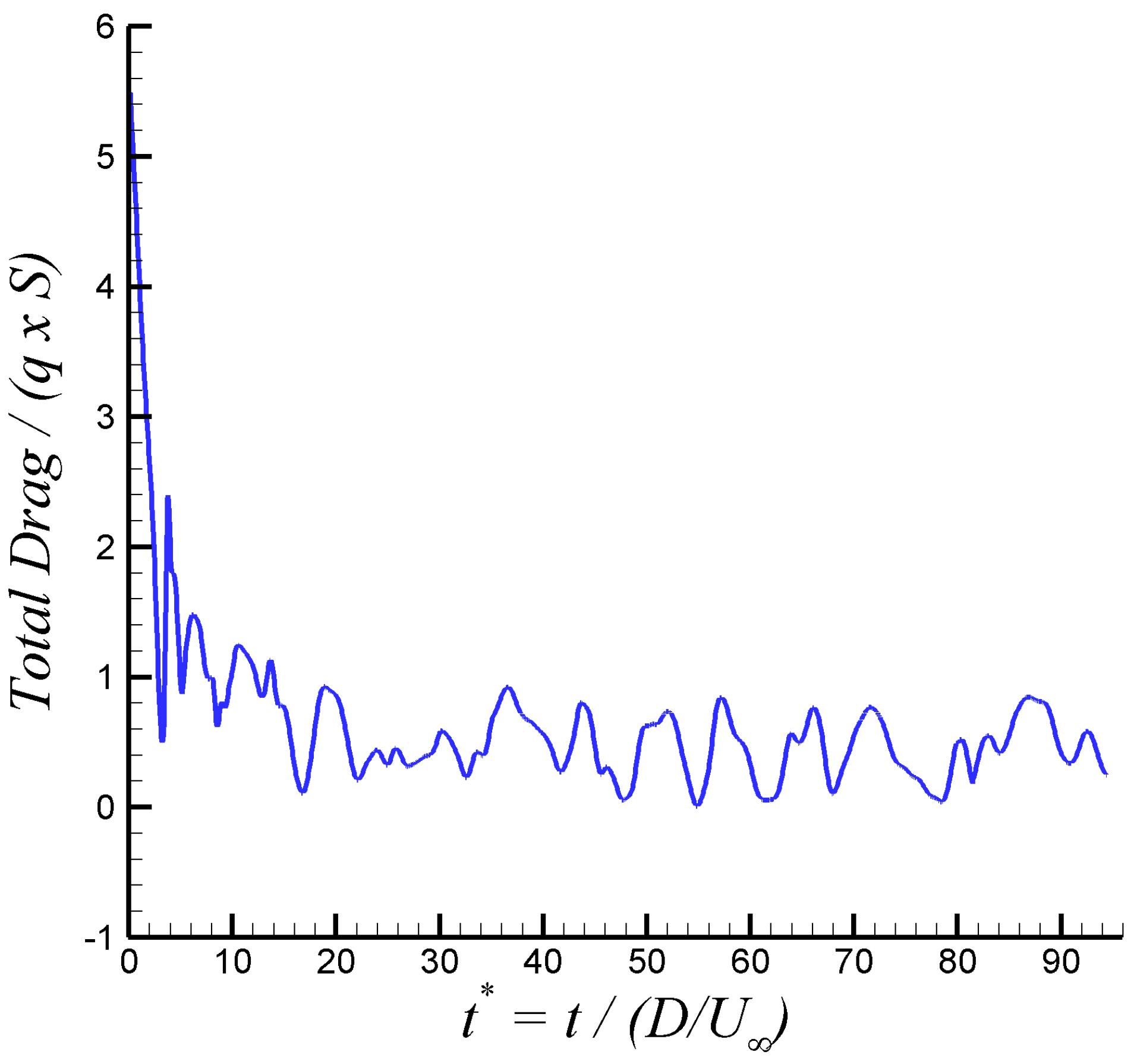
Figure 5.
Root mean square of pressure fluctuations in the acoustic cavity, comparison with experimental values at = 0.85 and 1.35.
Figure 5.
Root mean square of pressure fluctuations in the acoustic cavity, comparison with experimental values at = 0.85 and 1.35.
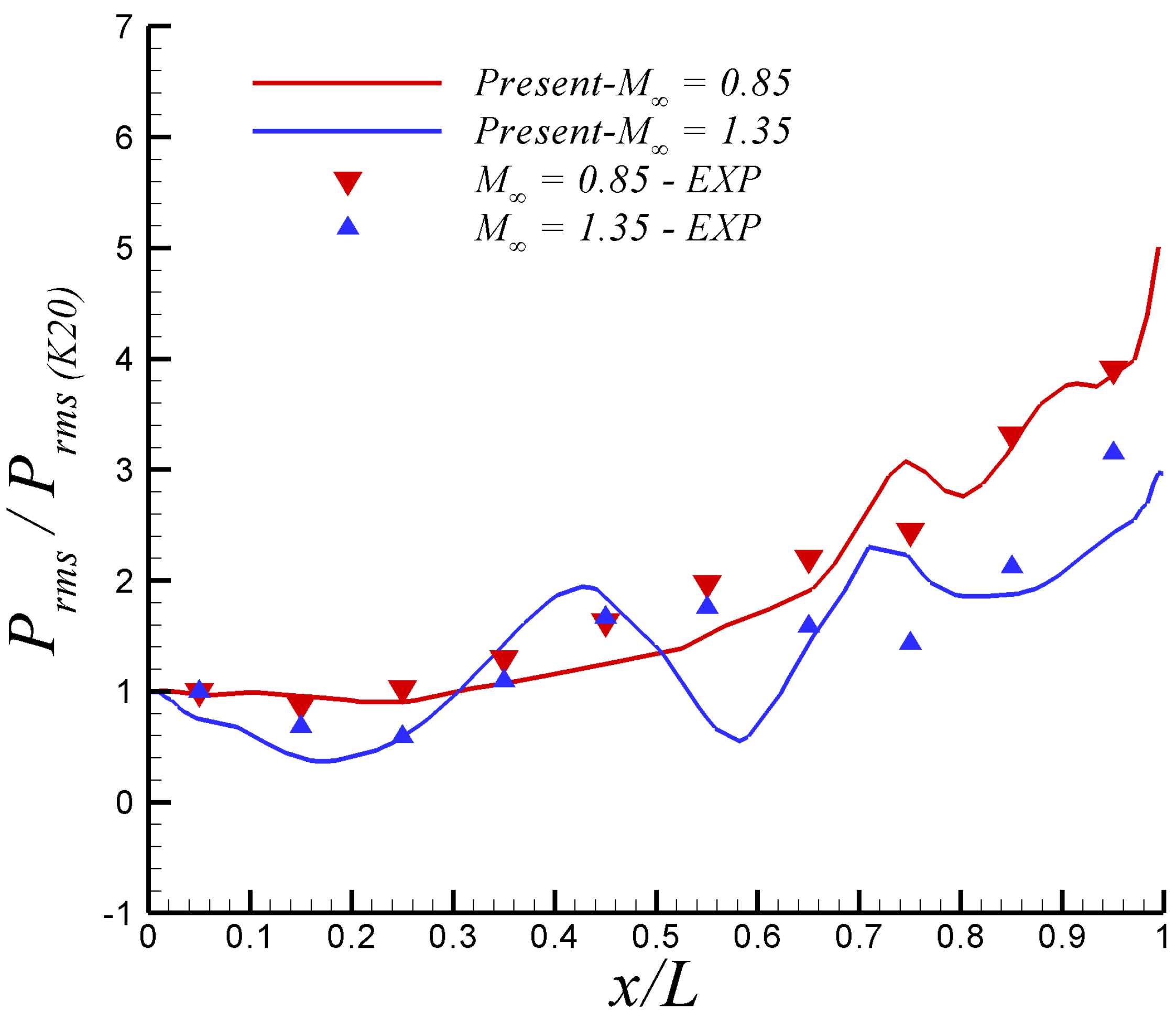
Figure 6.
Root mean square of pressure fluctuations in the acoustic cavity at = 0.85.
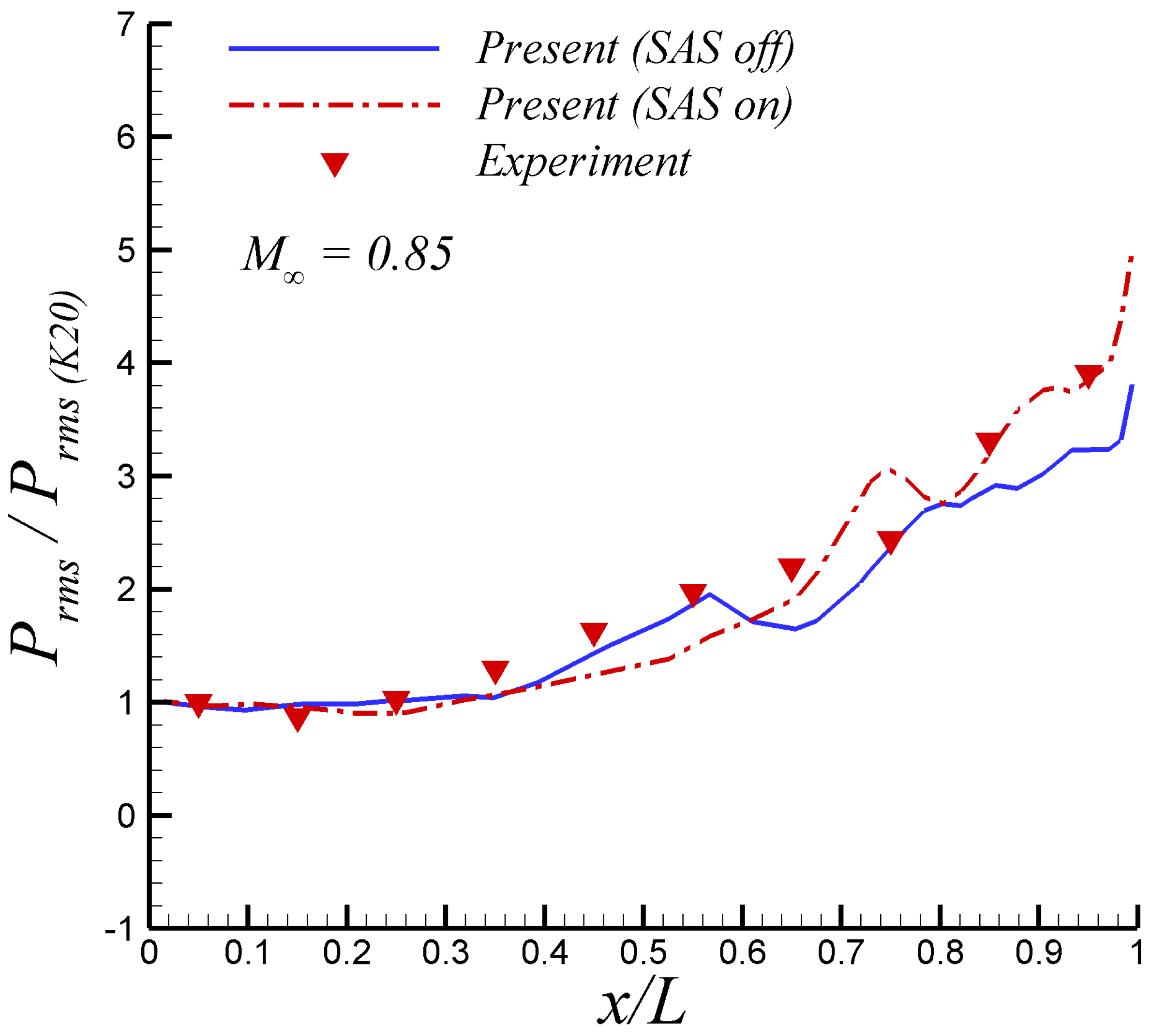
Figure 7.
Root mean square of pressure fluctuations in the acoustic cavity at = 1.35.
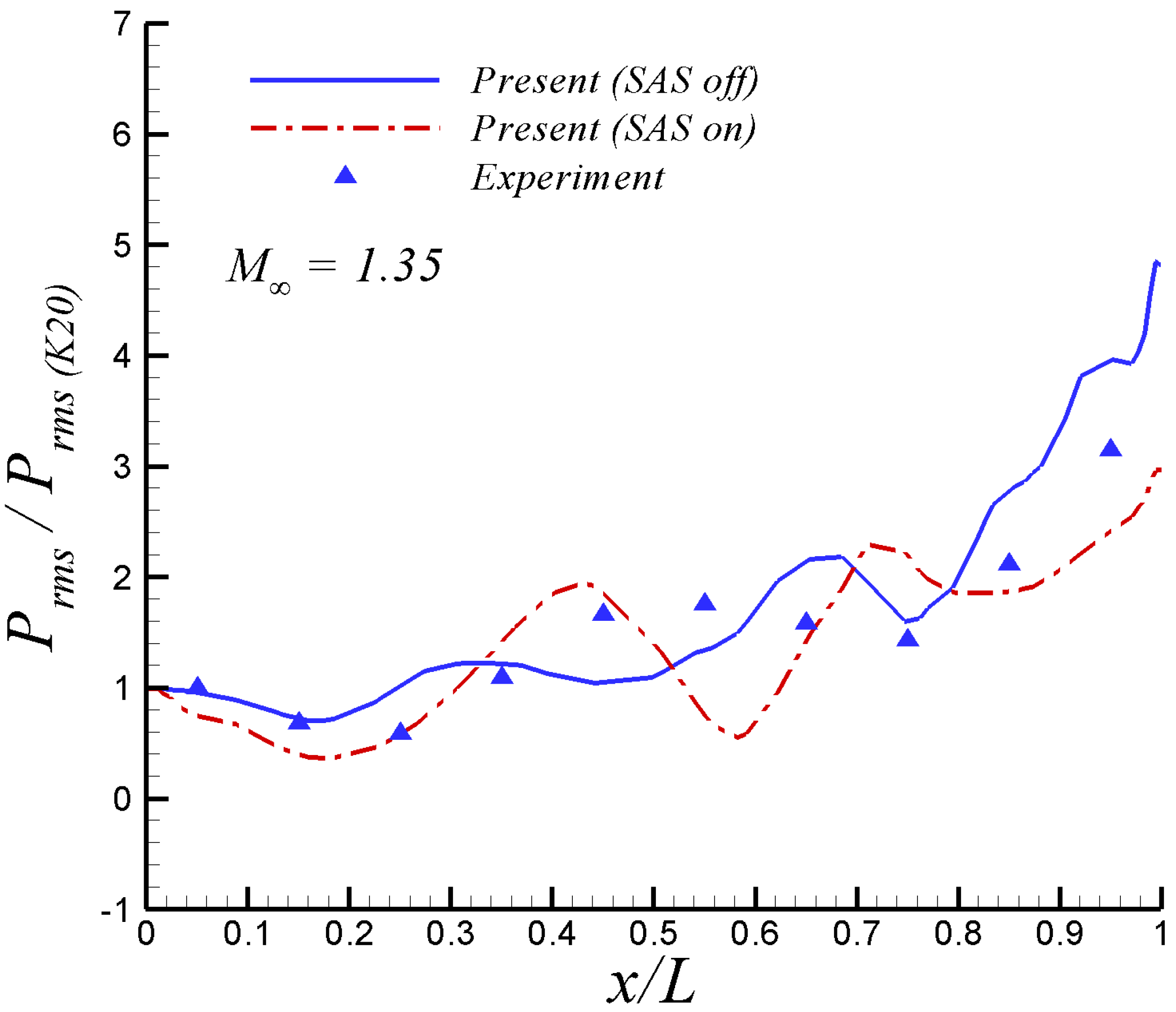
Figure 8.
Contours of the turbulence length-scale over and inside the cavity: (a) longitudinal plane, and, (b) cross-sectional planes at = 0.85.
Figure 8.
Contours of the turbulence length-scale over and inside the cavity: (a) longitudinal plane, and, (b) cross-sectional planes at = 0.85.
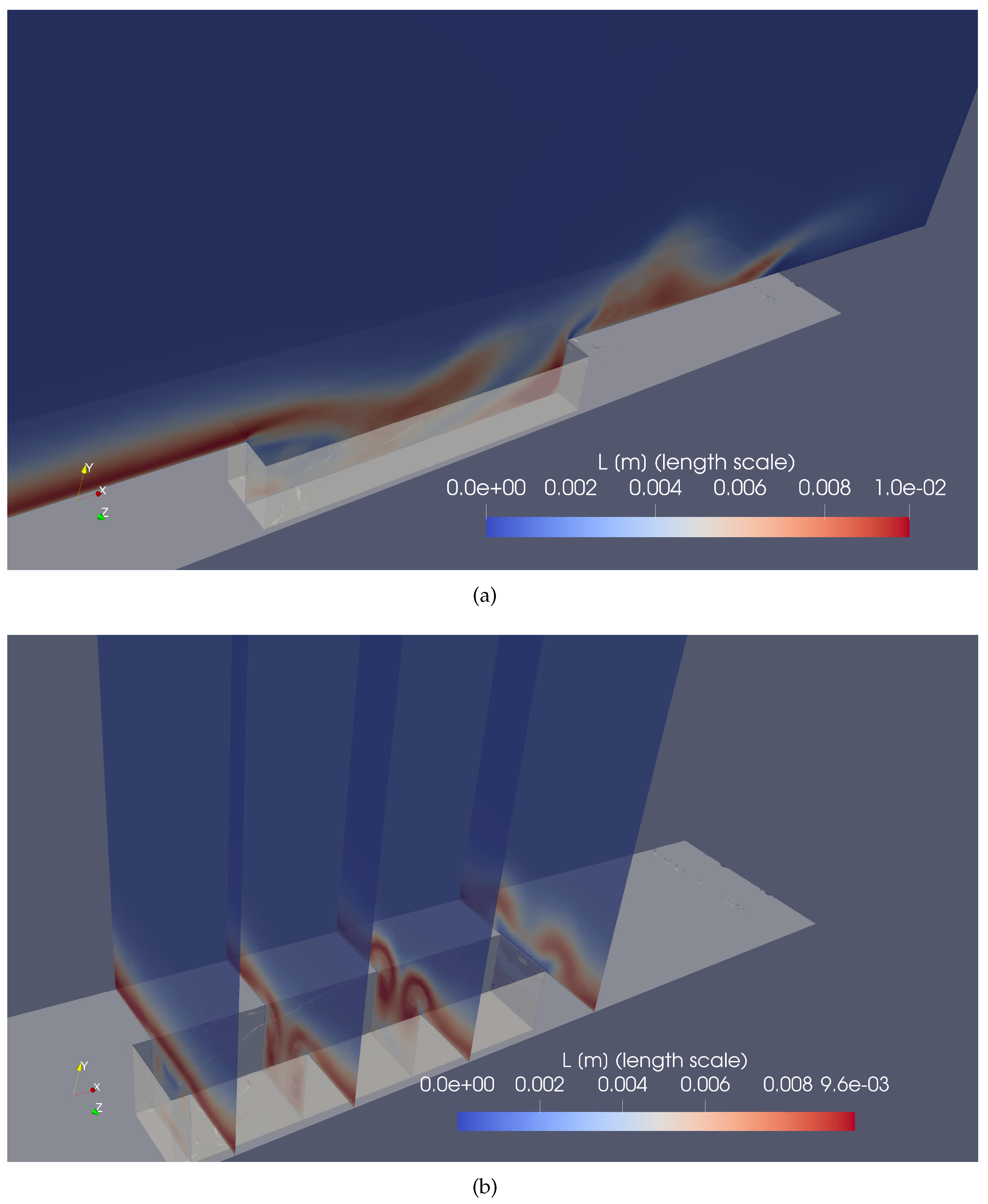
Figure 9.
Iso-contours of instantaneous spanwise vorticity in 1/sec. (flow from left to right) at 0 and = 0.85.
Figure 9.
Iso-contours of instantaneous spanwise vorticity in 1/sec. (flow from left to right) at 0 and = 0.85.
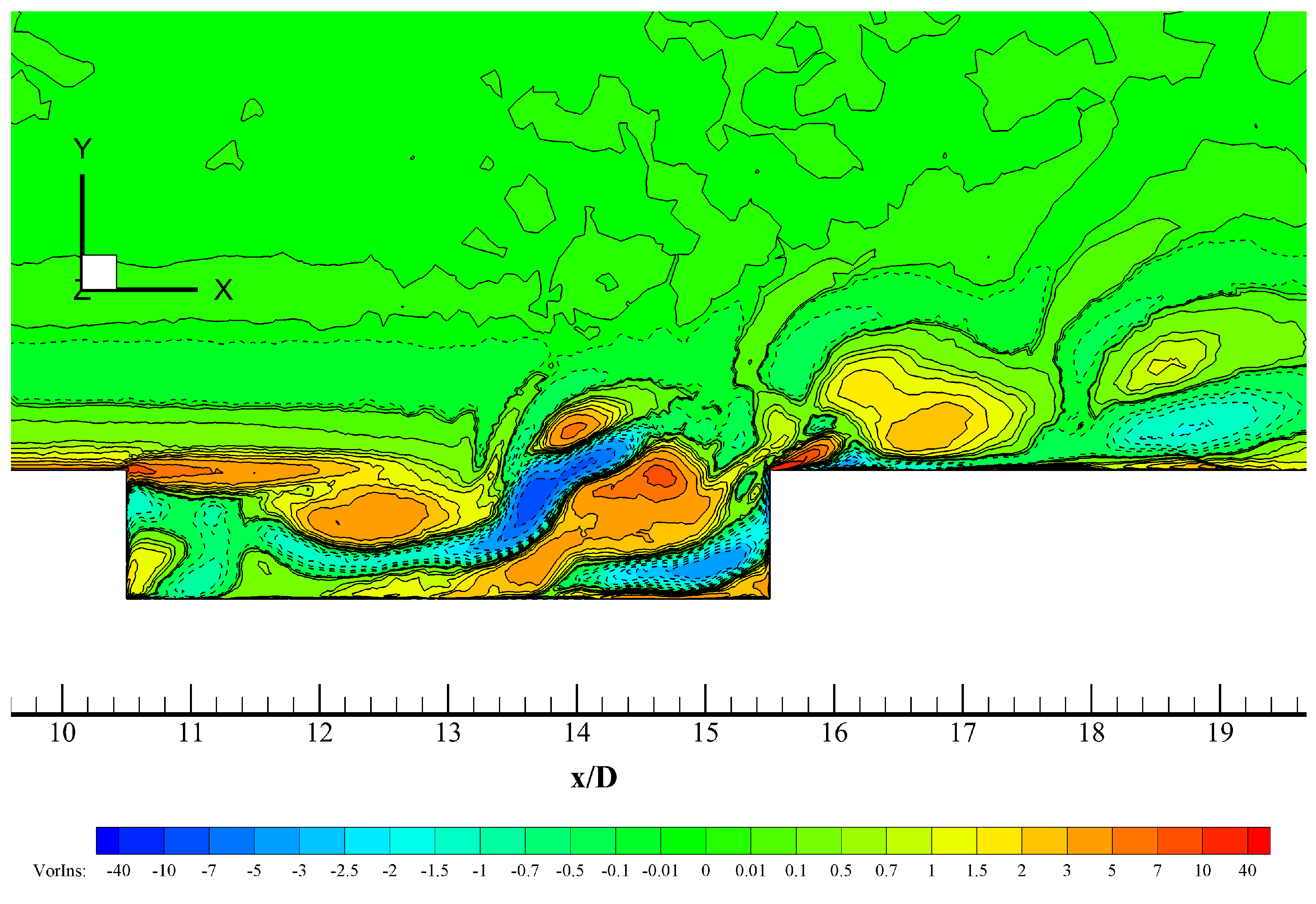
Figure 10.
Iso-contours of instantaneous streamwise velocity normalized by the freestream velocity (flow from left to right) at 0 and = 0.85.
Figure 10.
Iso-contours of instantaneous streamwise velocity normalized by the freestream velocity (flow from left to right) at 0 and = 0.85.
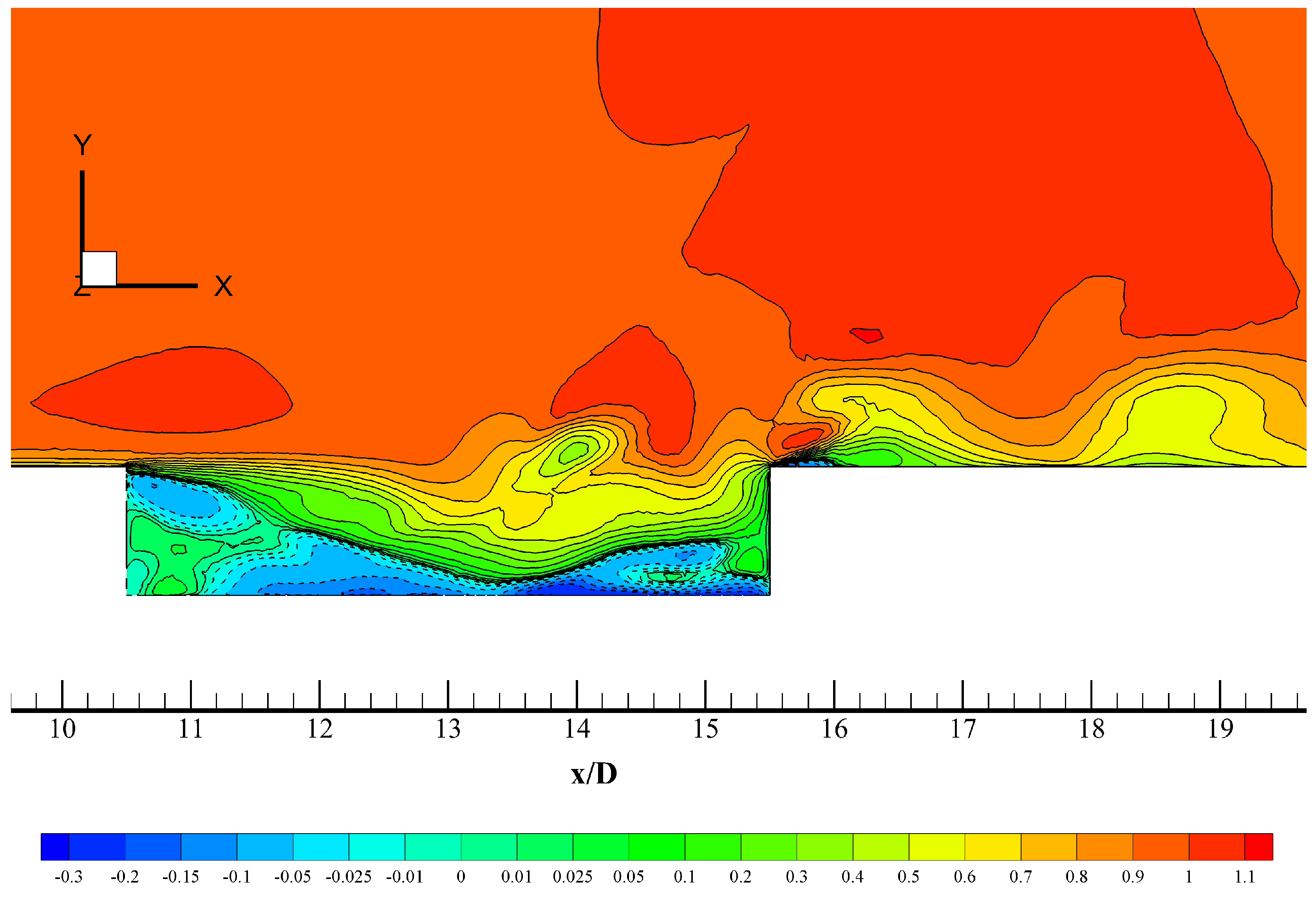
Figure 11.
Iso-surfaces of , positive values in red (vortex cores), negative values in blue (highly deformed flow regions) at = 0.85.
Figure 11.
Iso-surfaces of , positive values in red (vortex cores), negative values in blue (highly deformed flow regions) at = 0.85.
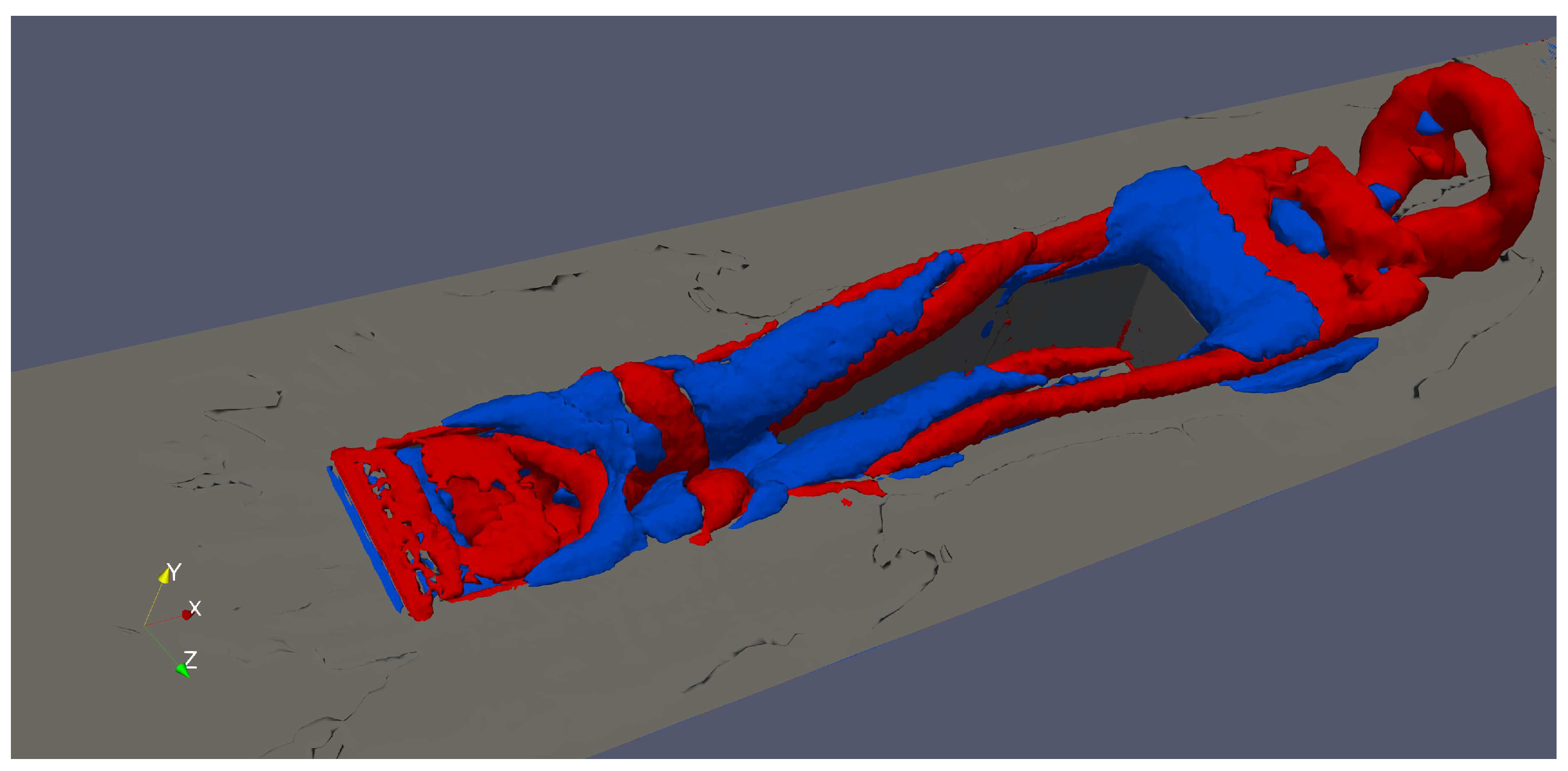
Figure 12.
Types of supersonic cavity flows.
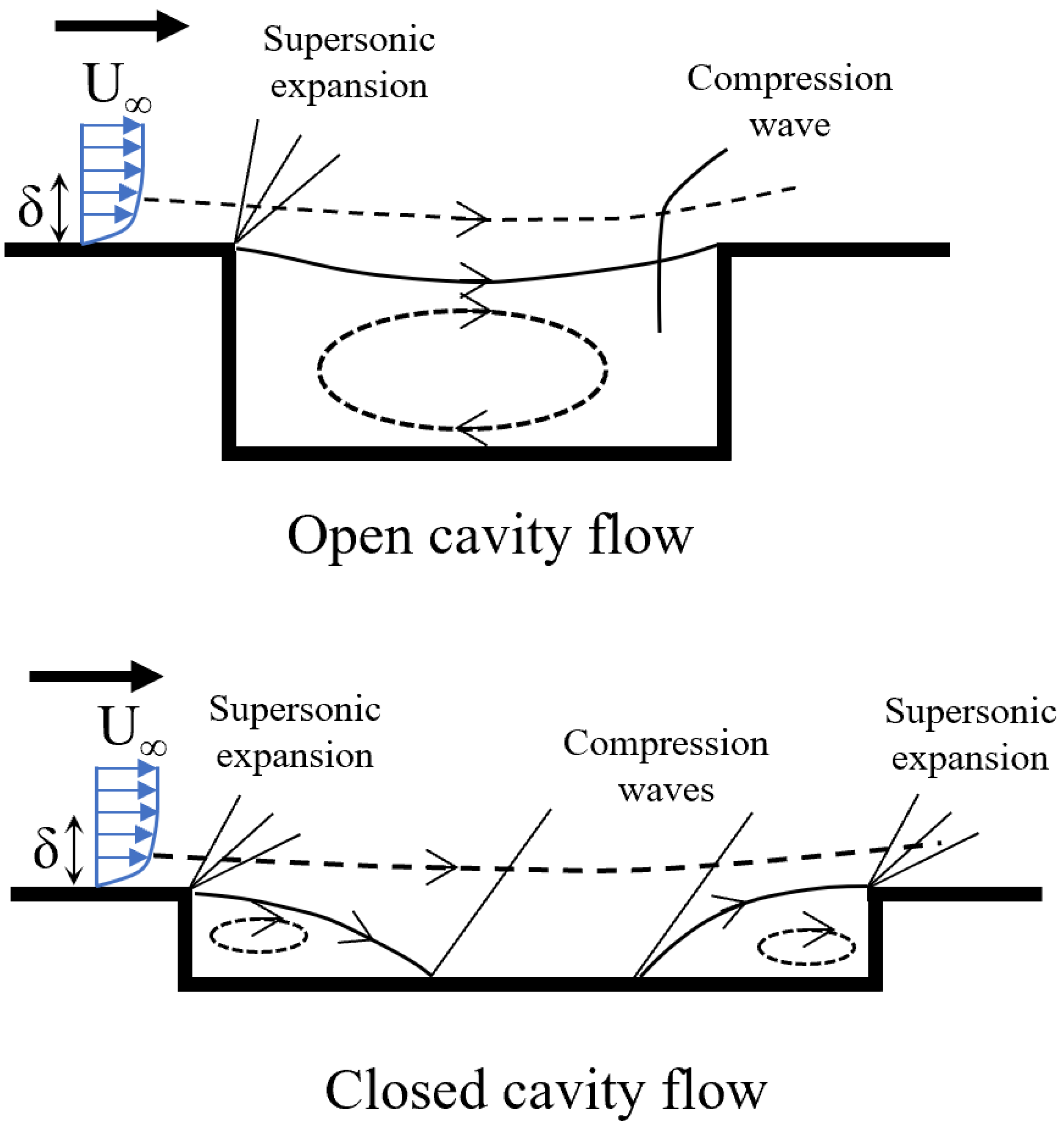
Figure 13.
Iso-surfaces of , positive values in red (vortex cores), negative values in blue (highly deformed flow regions) at = 1.35.
Figure 13.
Iso-surfaces of , positive values in red (vortex cores), negative values in blue (highly deformed flow regions) at = 1.35.
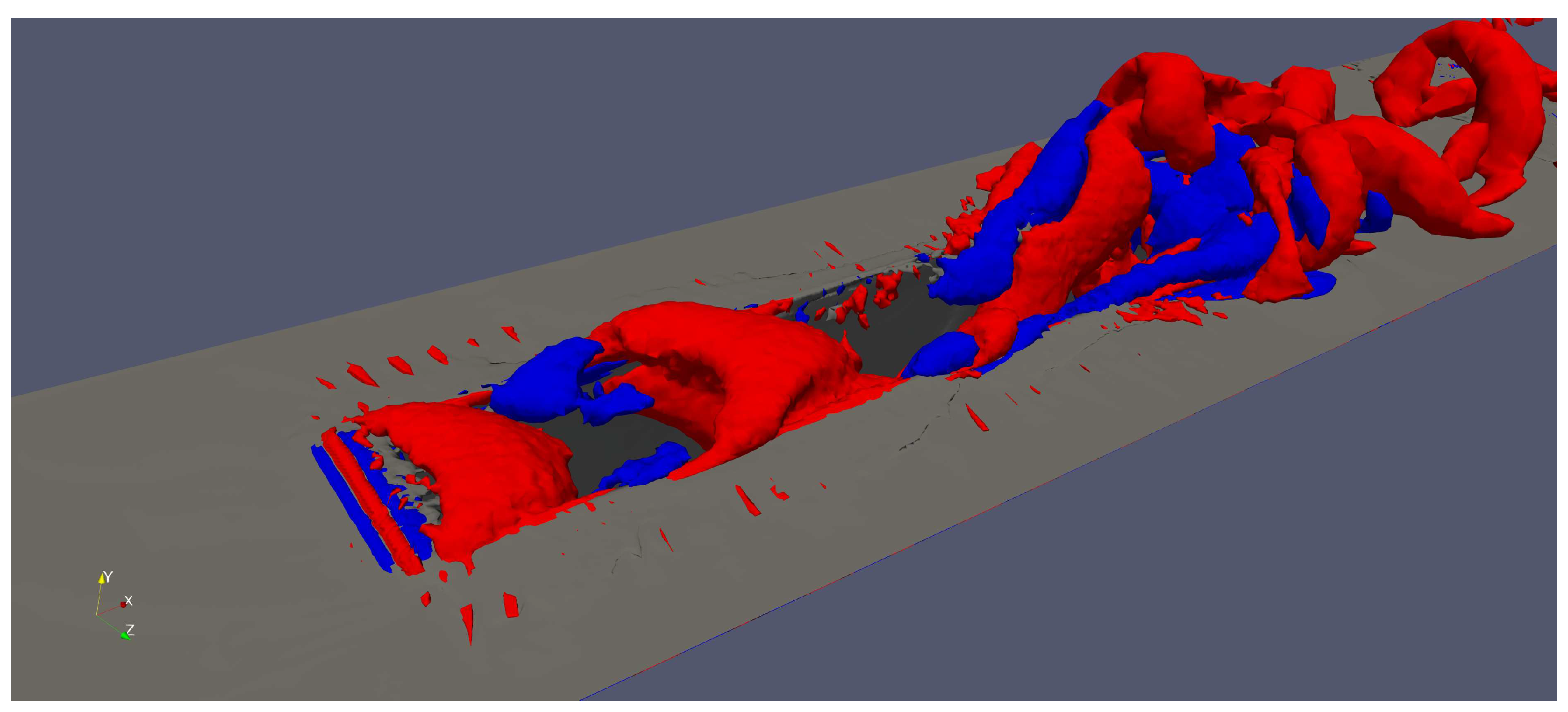
Figure 14.
Iso-contours of instantaneous spanwise vorticity in 1/sec. (flow from left to right) at 0 and = 1.35.
Figure 14.
Iso-contours of instantaneous spanwise vorticity in 1/sec. (flow from left to right) at 0 and = 1.35.
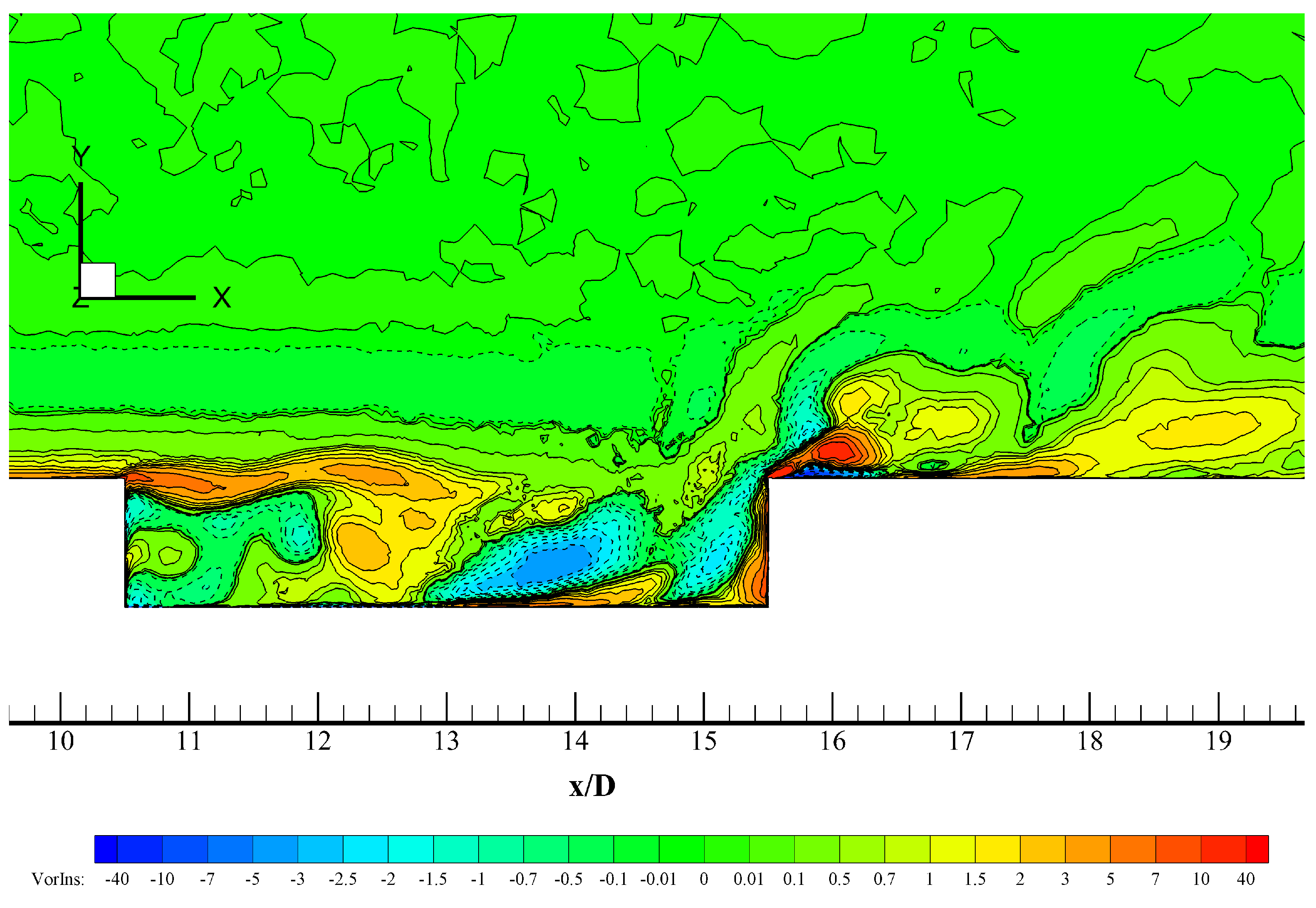
Figure 15.
Iso-contours of instantaneous spanwise vorticity in 1/sec. (flow from left to right) at 0.25D and = 1.35.
Figure 15.
Iso-contours of instantaneous spanwise vorticity in 1/sec. (flow from left to right) at 0.25D and = 1.35.
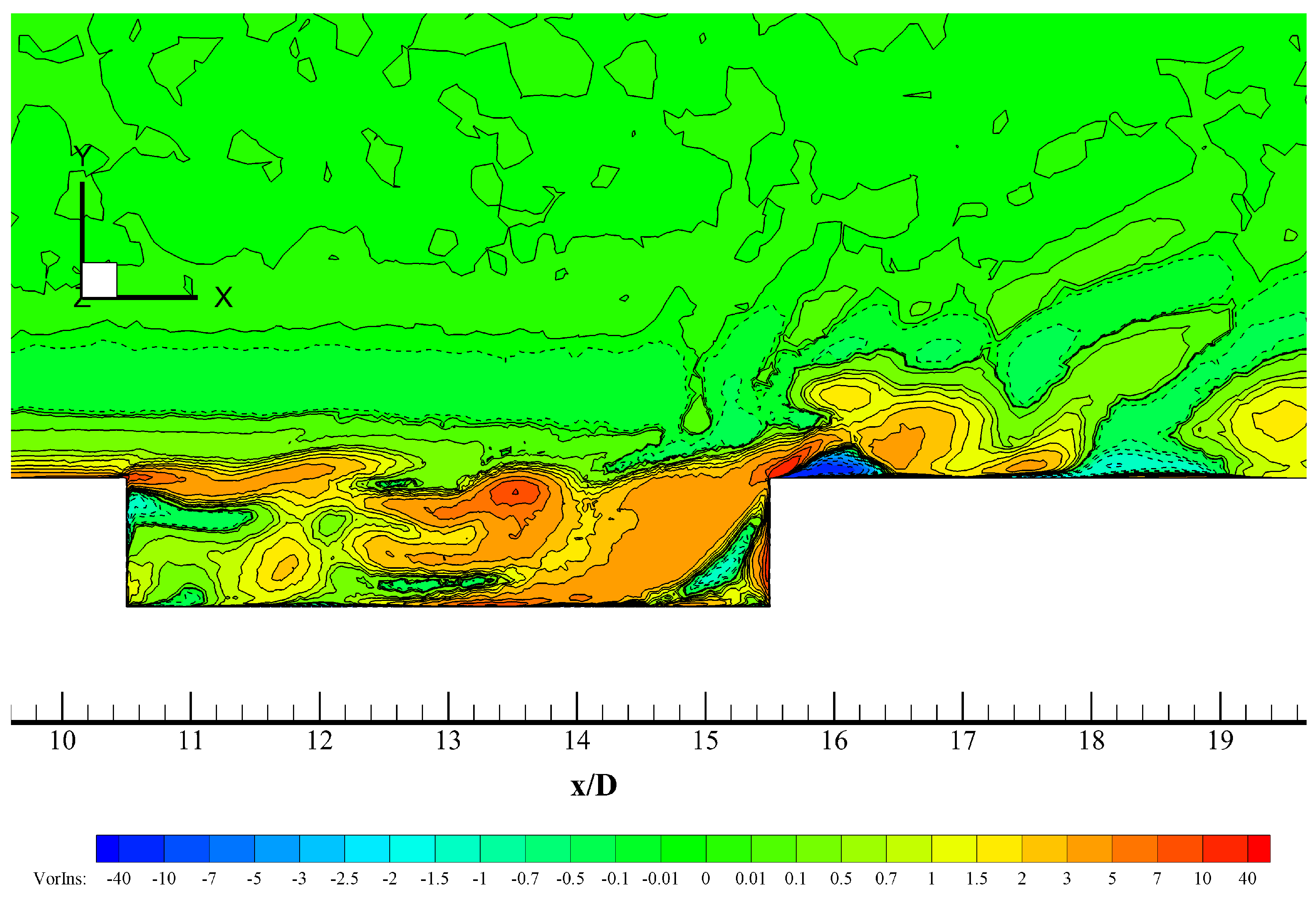
Figure 16.
Iso-contours of instantaneous streamwise velocity normalized by the freestream velocity (flow from left to right) at 0 and = 1.35.
Figure 16.
Iso-contours of instantaneous streamwise velocity normalized by the freestream velocity (flow from left to right) at 0 and = 1.35.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated





