Preprint
Review
In Silico Methods to Assess CNS Penetration of Small Molecules
Altmetrics
Downloads
183
Views
115
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
18 January 2024
Posted:
19 January 2024
You are already at the latest version
Alerts
Abstract
In CNS drug discovery, estimation of brain exposure of lead compounds is critical for their optimization. Compounds need to cross the blood-brain barrier (BBB) to reach the pharmacological targets in the CNS. The BBB is a complex system involving passive and active mechanisms of transport and efflux transporters such as P-glycoproteins (P-gp) and breast cancer resistance protein (BCRP), which play an essential role in CNS penetration of small molecules. Several in vivo, in vitro and in silico methods are available to estimate human brain penetration. Preclinical species are used as in vivo models to understand the unbound brain exposure by deriving the Kp,uu parameter, the brain/plasma ratio of exposure corrected with the plasma and brain free fraction. MDCK-mdr1 (Madin Darby canine kidney cells transfected with the MDR1 gene encoding for the human P-gp) assay is the most commonly used in vitro assay to estimate compound permeability and human efflux. The in silico methods to predict brain exposure, such as CNS MPO, CNS BBB scores and various Machine Learning models, help save costs and speed up compound discovery and optimization at all stages. These methods enable the screening of virtual compounds and building of a CNS penetrable compounds library as well as optimization of lead molecules for CNS penetration. Therefore, it is crucial to understand these methods' reliability and ability to predict CNS penetration. We review the in silico, in vitro and in vivo data and their correlation with each other and assess published in silico approaches to predict the BBB penetrability of compounds.
Keywords:
Subject: Medicine and Pharmacology - Neuroscience and Neurology
1. Introduction
In central nervous system (CNS) drug discovery, estimating brain exposure of lead compounds is critical for their optimization. Compounds need to cross the blood-brain barrier (BBB) to reach the pharmacological targets in the CNS. The BBB is a complex physical barrier that surrounds most of the blood vessels in the brain and prevents the permeation of harmful molecules from circulating blood into the brain (see Figure 1 (a)). The tight junctions of the BBB severely restrict paracellular transport, whereas specialized transporters, pumps, and receptors regulate the transcellular transport of metabolic nutrients and other essential molecules. Small lipophilic molecules can passively diffuse across the lipid bilayer but are often returned to the blood by efflux pumps [1,2]. Due to the impermeability of the CNS, it is a challenge for most molecules to gain access to the brain, although several molecules do transfer from the blood to the brain. Several mechanisms are potentially involved in this process [3]. While passive diffusion is a major mechanism of penetration of drugs into CNS, efflux by several transporters such as P-glycoprotein (P-gp), breast cancer resistance protein (BCRP) and members of the multidrug resistance protein (MRP) family at the BBB limit concentration of drugs in the CNS [4-6]. Influx transporters such as OCT1 and OCT2 surrogate penetration of bulky and charged molecules across BBB (see Figure 1 (b)). P-gp and BCRP are relatively well characterized among these efflux transporters, with considerable overlap among their substrates. P-gp (also known as MDR1 (multidrug resistance protein 1) and ABCB1 (ATP-binding cassette sub-family B member 1)) is widely expressed at BBB. In the last 20 years, with the availability of the P-glycoprotein (P-gp) knockout mouse model, numerous studies conducted in P-gp knockout versus wild-type mice observed significant P-gp efflux of drugs [7]. Thus, the efflux of drugs by P-gp has been regarded as an essential factor determining the drug concentration in the brain. Further, over the past few decades, it has also become clear that reliance on total drug level in the brain is often misleading and that unbound drug concentration is more predictive of target occupancy and, ultimately, in vivo efficacy [8]. These developments led to the use of MDR1-MDCK in vitro assay to estimate the permeability and efflux of lead molecules and in vivo (rat or mouse) models to determine unbound brain exposure of lead molecules.
A reliable in silico method for predicting the brain penetration of lead compounds would provide significant value and acceleration to drug discovery programs, save precious in vivo resources, and prioritize leads for in vivo assessment. The challenges faced in developing such in silico models arise from the complexity of the BBB involving multiple transporters and the influence of multiple pharmacokinetic parameters. Also, the available datasets for training models are small and do not cover the entire drug space. Also, only a subset of compounds in these datasets has both in vitro and in vivo data. Nevertheless, prediction models are being built as they are crucial for assessing the CNS penetrability of compounds in commercial libraries, virtual libraries and molecules generated by AI-enabled de novo design methods. Numerous in silico methods have been developed to predict brain exposure using different classification and/or regression algorithms. The type of experimental data used to build prediction models changed from the simple classification of BBB+ (for penetrating compounds) and BBB- (for non-penetrating compounds) to Kp (logBB, the brain-to-plasma ratio of the total drug concentration) to more recent Kp,uu (the unbound brain-to-unbound plasma concentration ratio). In many publications, the easily accessible and abundant classification data (BBB+ for penetrating and BBB− for non-penetrating compounds), often estimated by the presence or absence of CNS activity, are used. Earlier QSAR and Machine Learning prediction models utilized LogBB (logarithm of the ratio of total steady-state concentration in the brain to that in blood at a given time, also referred to as Kp) and LogPS (logarithm of the permeability surface area product) data. LogBB lacks information regarding the free drug concentration available for transport across the BBB, and LogPS does not incorporate BBB transporter-mediated efflux. These models were extensively reviewed elsewhere [9] and are not discussed in this review as there has been a paradigm shift away from optimizing Kp toward Kp,uu in CNS drug discovery. Free tissue drug concentration, Kp,uu, is considered to be the therapeutically relevant metric for estimating free drug concentration at the receptor site over the time course of its action, not the total drug concentration, Kp, based on the free drug hypothesis [8,10,11]. From a compartmentalized CNS drug distribution model (see Figure 1(b)), steady state Kp,uu can be presented in terms of passive diffusion (), active influx clearance (), active efflux clearance (), brain interstitial fluid bulk flow clearance (), and brain metabolic clearance (). and , become insignificant and can be disregarded for molecules having high permeability and low metabolic clearance. Kp,uu parameter presents efflux and influx permeation across BBB relative to passive diffusion. Passive diffusion, active efflux and active influx correspond to values of unity, below unity and above unity, respectively. Kp,uu can be understood as a measure of lateral efficacy of various efflux and influx transporters independent of the extent of brain or plasma tissue binding (eq 1).
The closer the Kp,uu value is to 1, the less peripheral body burden is required to achieve efficacious free concentration in the brain. Generally, a Kp,uu >0.3 in the rat is considered adequate, although this value depends on the drug’s potency and other ADME properties. Therefore, this review will focus on the models that utilize the preclinical in vivo Kp,uu data and the MDR1-MDCK in vitro data in validation and training sets, as well as the physicochemical properties, different multiparameter scores and the prediction models that distinguish CNS and non-CNS drugs. The applicability and limitations of different in silico methods will also be discussed.
2. Physicochemical Properties of CNS Drugs
Despite significant challenges in designing compounds that cross the BBB, multiple classes of drugs cross BBB as they are known to treat CNS diseases, and many more CNS drugs are in clinical development [12]. The principal medicinal chemistry strategy in drug discovery has been to optimize the physicochemical properties of compounds to maximize CNS penetration.
Since the publication of Lipinski’s rule of 5 in 1997 that defined desirable physicochemical properties (MW < 500 Da, log P < 5, HBD < 5, and HBA < 10) for oral bioavailability of a drug candidate [13], several groups attempted to map the physicochemical space of CNS drugs employing different approaches. Hansch et al. [14] studied a dataset of 201 barbiturates having preclinical in vivo efficacy data and found the in vivo efficacy of the drug to have a parabolic dependency on LogP and suggested LogP = 2 optimal for in vivo activity. The improved chance of CNS penetration was predicted for the following desirability ranges: MW < 450, PSA < 90 Å2 and Log D [1,4] for a dataset of 125 CNS and non-CNS drugs analyzed by Van der Waterbeemd et al. [15]. In a study of 776 CNS and 1590 non-CNS oral drugs that reached at least phase 2 clinical trials, Kelder et al. [16] suggested an upper polar molecular surface area (PSA) limit of < 60-70 Å2 for most CNS drugs. Doan et al. [17] have indicated that physiochemical properties of CNS drugs differ substantially from non-CNS drugs having CNS dataset mean values of cLogP (3.43), cLogD (2.08), HBD (0.67), PSA (40.5 Å2) for a dataset containing 48 CNS and 45 non-CNS drugs. Norinder et al. [18] based on a literature review, have suggested that a molecule having O + N < 5, or cLogP − (O + N) > 0, has an improved chance of CNS penetration. The physiochemical property space suggested by Didziapetris et al. [19] for better CNS penetration while avoiding P-gp efflux liability: MW <400, pKa <8, N+O < 4. Leeson et al. [20] suggested mean values of 310 (MW), 4.32 (O + N), 2.12 (HBA), and 4.7 (RB) for CNS drug molecules based on a review of a dataset of 329 oral drugs marketed during 1983-2002. The recommended attributes of successful CNS drugs suggested by Pajouhesh et al. [12] for a study of a dataset of marketed CNS drugs were MW < 450; H-bonds < 8; pKa 7.5−10.5; HBD < 3; HBA < 7; RB < 8; cLogP < 5; PSA < 60−70 Å2. Based on a medicinal chemistry literature review, Hitchcock et al. [21] recommended physicochemical property ranges for improving BBB penetration: MW < 500, PSA < 90 Å2, cLogD (pH 7.4) [2,5], cLogP [2,5], and HBD < 3.
It was realized that CNS drugs occupy considerably smaller chemical space than oral drugs designed for peripheral targets [22]. Indeed, CNS drugs tend to be smaller with higher lipophilicity and lower polar surface area (PSA) than non-CNS drugs (see Table 1).
In the broadest sense, moderately lipophilic drugs cross the BBB by passive diffusion, and the hydrogen bonding properties of drugs can significantly influence their CNS uptake profiles. Polar molecules are generally poor CNS agents unless they undergo active transport across the CNS. Size, ionization properties, and molecular flexibility are other factors observed to influence the transport of a compound across the BBB. The design of CNS drug candidates with intracellular targets may benefit from increased basicity and/or the number of hydrogen bond donors [23]. However, it should be noted that the “older” CNS drugs modulate ion channels, monoamine GPCR and transporter gene families with common pharmacophoric features of small lipophilic amines [24]. This scenario is rapidly changing as CNS drug discovery efforts have been shifting towards emerging therapeutic areas such as neurodegeneration and neuro-oncology with novel “non-traditional” CNS targets. The compounds targeting these new targets are relatively larger and more polar ligands with wider chemical diversity. It is, therefore, possible that the current understanding of the allowed physicochemical properties space of CNS drugs may expand.
3. BBB Penetration Scoring Schemes for Predicting Brain Penetrance across BBB Primarily by Passive Diffusion
Analyzing the physicochemical properties of CNS (CNS+) and non-CNS (CNS-) drugs led to the formulation of different scoring schemes to design CNS drugs. Recently, multiple algorithms have been proposed to improve RO5 for drug discovery of CNS target space. Wager et al. [25,26] developed an algorithm called the “multiparameter optimization (MPO)” based on a study of 119 CNS drugs and 108 CNS clinical candidates to suggest the optimal range of property space for different physicochemical properties of drug molecules. For each of these calculated properties, a range of values is identified as more favorable (score = 1) or less favorable (score = 0) for a CNS candidate. The algorithm comprises six physiochemical properties with median values for CNS drugs: MW 305.3 Da, PSA 44.8 Å2, HBD = 1, cLogP 2.8, cLogD 1.7, and pKa = 8.4. This scoring method showed that 74% of marketed CNS drugs and Pfizer CNS candidates displayed a high CNS MPO score (MPO desirability score ≥ 4, using a scale of 0-6). However, a follow-up study involving re-examining the MPO score by the authors suggested that MPO score can vary substantially depending on the computational software and method used to calculate physiochemical properties comprising the MPO score (mainly LogD and pKa) [27]. Also, MPO score is congenitally biased toward lipophilicity parameters. MPO score also poses the risk of populating the chemical space with small molecules with very low molecular weights as MPO score does not apply lower limits (e.g., clogP, clogD, MW and pKa) but only apply upper limits to physiochemical properties used. These very low molecular weight small molecules may not bind to certain targets of interest with sufficient binding potency. MPO also does not characterize non-CNS drugs as it is based on CNS drugs (119) and CNS candidates (108); this could potentially make MPO less adequate to capture the physiochemical nature of BBB. A separate study assessing 616 compounds with measured unbound concentrations in the brain confirmed that a higher CNS MPO score correlated with a higher unbound concentration in the brain [22]. A probabilistic MPO scoring function, designated as pMPO, is based on defining the physiochemical properties of a dataset of 299 CNS penetrant and 366 non-CNS penetrant molecules. pMPO physiochemical descriptors, along with their weighing, are as follows: TPSA (0.33), HBD (0.27), MW (0.16), clogD (0.13) and basic pKa (0.12) [28]. Ghose et al. [29] studied a dataset of 317 CNS and 626 non-CNS oral drugs and have proposed property ranges for CNS penetration: TPSA < 76 Å2 (25−60 Å2), 740−970 Å3 volume, N [1,2], linear chains outside of rings <7 [2,4], HBD <3, (0,1), and SAS (460−580) Å2; the ranges given in the parentheses are preferred. They optimized the relative weights of these parameters by comparing the physicochemical property distribution of CNS versus non-CNS oral drugs. Rankovic et al. [30] have mapped the physiochemical properties of a diverse corporate dataset from Eli Lilly based on brain-penetrant and peripherally confined molecules. They developed an algorithm termed MPO_V2, which contained five descriptors. They dropped LogD descriptor from MPO and included double weight for the HBD descriptor (MPO_V2: ∑T0 (clogP, MW, TPSA, pKa, 2 HBD). However, this article was retracted[31]. Recently, Gupta et al. [32] proposed the Blood−Brain Barrier (BBB) Score that is composed of stepwise and polynomial piecewise functions with five physicochemical descriptors: number of aromatic rings, heavy atoms, MWHBN (a descriptor comprising molecular weight, hydrogen bond donor, and hydrogen bond acceptors), topological polar surface area, and pKa. The BBB Score outperformed (AUC = 0.86) the CNS MPO approach (AUC = 0.61).
The ease of calculation of the CNS MPO, CNS MPO_V2, CNS pMPO and CNS BBB scores and their capability to predict BBB penetration of compounds can aid in mapping the property space of large commercial and virtual compound libraries to help lead optimization. CNS MPO and CNS BBB scores are widely utilized for CNS drug discovery programs. Figure 2 and Figure 3 represent 100% stacked bar graphs for low to high CNS MPO, MPO_V2, pMPO and BBB scores for a dataset of CNS and non-CNS drugs. Ideally, a CNS MPO, MPO_V2, and BBB score in the range of (4,6] should correlate to a CNS drug, and a CNS MPO, MPO_V2 and BBB score of (0,4] should correspond to a non-CNS drug. pMPO outputs a score in the range of (0,1], which has been scaled to (0,6] to compare against other scores. However, the CNS BBB score performs better in identifying a higher percentage of CNS compounds than other scores.
In addition to scoring methods, Quantitative Structure-Activity Relationship (QSAR) and Machine Learning (ML) algorithms were successfully applied to predict BBB permeability. The derivation of QSAR and ML models involves calculating molecular descriptors, fitting them to experimental values using a statistical algorithm on a training dataset, and predicting experimental values of the test dataset. ML methods such as s Support Vector Machine (SVM), Decision Tree (DT) and K-Nearest Neighbor (KNN) that combine property-based descriptors with molecular fingerprints of compounds predict the classification of CNS and non-CNS drugs with high accuracy [33]. Chen et al.[34] and Varadharajan et al.[35] employed machine learning algorithms (Random Forest (RF) and Support Vector Machine (SVM)) to develop direct and indirect regression models based on Kp,uu, Kp,brain, Vu,brain and fu,pl using. For 173 compounds in the training set [34], their model used a total of 196 descriptors. Their model predicted Kappa2 descriptor, i.e., the measure of molecular linearity being strongly correlated while poor reliability on lipophilicity of a molecule as predicted by Fridén et al. [36]. Similarly, Saxena et al. [37] published accurate classification models using different ML algorithms using physicochemical properties, Molecular ACCess Systems keys fingerprint (MACCS) [38] and substructure fingerprints. A Deep Learning method was shown to achieve better accuracy than the ML methods on three different datasets [39]. Alsenan et al. [40] published a highly accurate deep-learning model based on a recurrent neural network. Zhang and Ding [41] deployed SVM and Greedy Algorithms to identify key features of CNS Drugs. An excellent review of classification models using different datasets and ML algorithms is published by Saxena et al. [42]. These qualitative classification models are helpful for the quick screening of large compound databases at early-stage drug discovery.
3. Active Transport across BBB (Efflux Transporters, Influx Transporters and Kp,uu)
Kp,uu (the unbound brain-to-unbound plasma concentration ratio) is an important parameter to estimate the unidirectional or bidirectional active transport of drugs across BBB via specified influx and efflux transporters. As discussed in equation 1 above, Kp,uu presents a measure of lateral efficacy of various efflux and influx transporters independent of the extent of brain or plasma tissue binding. Quantitative prediction of Kp,uu by QSAR and ML methods has been challenging [43,44]. The limited size of the training sets of compounds combined with highly variable (fivefold) experimental Kp,uu data is the main reason for the moderate performance of the models. Three experimental techniques are usually employed to estimate experimental Kp,uu: (a) microdialysis, (b) brain homogenate and (c) brain slice method. Each method has advantages and challenges; the variability within experimental results exists even within the same method based on the different experimental set-up, preclinical species and protocol used. A detection probe is implanted into the brain by surgery to estimate the unbound concentration of a molecule in the microdialysis method, which is considered an in vivo gold standard for measuring Kp,uu [45-47]. However, this method poses many technical challenges, including recovery of microdialysis probe while working with lipophilic drugs, high resource and time demanding, involves risk of brain injury and subsequent increase in BBB permeability; additionally, it necessitates use of lots of animals leading to ethical concerns, making it less applicable in the initial phases of drug discovery [48-50]. The brain homogenate method introduced by Kalvass et al. [51] involves dialyzing into a 96-well equilibrium dialysis apparatus a small sample of brain homogenate infused with the molecule. This method is used for high throughput screening of CNS drugs; unbound brain concentration is calculated from total steady-state brain concentration and free fraction [52]. One drawback of this method is that binding properties of brain tissue could be changed during brain homogenization, unfolding new binding sites and resulting in underrepresenting available free fraction [53]. In this review, we have compiled Kp,uu values from Summerfield et al. [54,55] and Culot et al. [56]. In the brain slice method of calculating Kp,uu, animal brain slices (usually rat or mouse) are infused with test molecules incubated at 37°C in either plasma or buffer solution. The test amount of buffer or plasma solution at designed time points is withdrawn. Kp,uu is calculated as a ratio of in vivo total brain to plasma concentration (Kp) and in vitro unbound brain volume of distribution (Vu, brain) and the unbound fraction of drug in plasma (fu, plasma) in the incubated brain slices. The brain slice method has the advantage over other methods as the cell structure in brain tissue is maintained in brain slices, and this method could be developed as a high throughput screening method [53,57,58].
Frieden et al.[36] and Culot et al.[56] have calculated Kp,uu for a dataset of 41 molecules, including substrates of various efflux transporters P-gp, BCRP, multidrug resistance-associated proteins (MRPs)) and influx transporters (organic anion transporters (OATs), organic anion transporting polypeptide (OATPs), and organic cation transporters (OCTs)), making the selection important for BBB penetration study.
Accurate in silico prediction of Kp,uu using various in silico methods has been challenging as limited experimental data for Kp,uu is available in the literature, and only a few in silico models of Kp,uu with moderate accuracy have been reported [23,34-36,59-61]. Poor performance of global models of Kp,uu is understandable as (a) the training datasets do not have good coverage of chemical space, and (b) models need to account for multiple factors that affect brain penetration, e.g., experimental protocols and animal species, as explained above. In some cases, the higher-than-expected accuracy of ML models may be due to model overfitting [62]. Two pioneer Log Kp,uu QSAR models employing the PLS method for a training set of 41 marketed drugs having experimental (brain slice method) Kp,uu range of 300-fold have been developed by Fridén et al. [36]. The first model had 16 molecular descriptors, and the second only had a number of hydrogen bond acceptor descriptor with R2 of 0.45 and 0.43, respectively. The indirect regression model employing Fridén et al. [36] Kp,uu dataset showed reasonable accuracy with an R2 of 0.74 [59]. However, when validated against the dataset given by Summerfield et al. [44], this model resulted in poor performance. Loryan et al. [23] have trained a PLS regression QSAR model on a dataset of 39 Kp,uu values using two molecular descriptors (vsurf_Cw8 and TPSA) having moderate accuracy (R2 = 0.82 and RMSE = 0.31). However, this model’s performance was unsatisfactory when validated against the Fridén et al. [36] dataset. Zhang et al. [61] developed a binary Kp,uu classification model on a dataset containing 677 and 169 molecules in training and test sets, respectively, which showed similar accuracy (R2 ~ 0.75).
Integrating Kp,uu in silico models with the knowledge of molecule interactions in BBB efflux and influx transporters [63], which influence brain permeability, can improve Kp,uu model performance [64]. Of the many influencing factors such as active uptake, brain metabolism, bulk flow, passive permeability, etc., efflux by several membrane transporters, such as P-gp has a dominant role [61,65]. P-gp is widely expressed at BBB. It transports molecules against a concentration gradient utilizing the energy of ATP hydrolysis (See Figure 4).
Dolgikh et al. [60] incorporated the P-gp efflux ratio in direct and indirect regression QSAR models for Kp,uu. The performance of the Kp,uu model improved significantly by adding P-gp efflux data (R2 enhanced from 0.39 to 0.53). For understanding the quantitative correlations between the structure of P-gp and the various molecular descriptors, different computational algorithms accompanying structure and ligand-based approaches [66,67], pharmacophore models [68,69] and machine learning methods [70] have been studied. With the availability of high-throughput P-gp efflux data using MDCK-MDR1 assays, there is an increasing effort to measure the efflux of a large number of compounds experimentally [71]. These data enabled better predictive models for P-gp efflux. Ohashi et al. [72] constructed regression models to predict the value of P-gp-mediated efflux using 2397 data entries with an extensive data set collected under the same experimental conditions. Most compounds in the test set fell within two- and three-fold errors in the random forest regression model. Available literature P-gp transporter efflux data have considerable variability as molecules tested using different protocols, cell lines and biological assays [73]. Broccatelli et al. [74] tested a dataset of 187 compounds in the Borst-derived MDCK-MDR1 cell lines to calculate P-gp Efflux Ratios (ERs). ER presents the ratio of the apparent permeability from the basolateral to the apical direction (excretory) to the apparent permeability from the apical to the basolateral direction (intake) in an overexpressing P-gp cell line. Molecules having ER ≥ 2 are typically considered P-gp substrates [75]. Available P-gp efflux data (measured in MDCK-MDR1 cells) for CNS (CNS+) and non-CNS (CNS-) drugs show that most CNS drugs have P-gp efflux ratio below 10. In cases where brain metabolism and uptake effects are negligible, it has been shown that compounds with higher efflux generally have lower Kp,uu values. (See Figure 5). As CNS distribution of a compound does not depend only on P-gp efflux, a significant percentage of compounds with lower efflux do not distribute into CNS, and a considerable percentage of compounds with higher efflux distribute into CNS. It is important to note that the analysis involves a small number of drugs (128 CNS+ and 39 CNS-) that have MDR1-MDCK efflux data and provide qualitative guidance to utilize efflux data for selecting CNS penetrant compounds.
These efflux transporters modulate the brain exposure of a drug without affecting systemic exposure. It was recognized that passive permeability and P-gp efflux impact the extrusion of drugs from the brain and that in vitro Efflux Ratios (ER) can predict in vivo brain penetration [17,76]. Incorporating in vitro P-gp efflux information into the computational models improved the predictive performance of a QSAR model, as explained above [77]. Recently, Gupta et al. [78] have augmented the previous Kp,uu models by incorporating the Kp,uu model with various efflux (P-gp, BCRP) and influx (Organic Cation Transporters (OCT1, OCT2) and Organic Anion Transporting Polypeptides (OATP2B1). The model is termed the Brain Exposure Efficiency (BEE) Score. The BEE algorithm is devised based on a comprehensive series of QSAR calculations and molecular modeling simulations and implemented as an open-source calculator for predicting the unidirectional or bidirectional active transport of molecules across the BBB via specified transporter proteins. BEE score is also implemented in MOE software as an SVL utility to predict Kp,uu and Cu,b (unbound concentration of the molecule in the brain) as a function of various efflux and influx transporters, experimental methods (i.e., Kp,uu microdialysis, brain homogenate, brain slice). Kp,uu QSAR model based on the brain slice method incorporating efflux and influx transporters data performed better than models based on literature data from microdialysis and brain homogenate methods [78]. More recently, Kosugi et al. [79] reported improvement in the predictivity and coverage of application by machine learning approaches for Kp,uu prediction by incorporating in vitro P-gp and BCRP activities.
In vitro MDR1-MDCK represents a valid assay for predicting human P-gp efflux. It generally correlates well with in vivo Kp,uu of preclinical species, although other transporters (like BCRP) may cause a disconnect. Consistent Kp,uu and P-gp efflux data are available for only a limited number of drugs [55,80-82] and are plotted in Figure 6, showing limited data coverage of the drug space [83].
4. In Silico, In Vitro and In Vivo Correlations
A reliable in silico prediction method for CNS penetration can provide several advantages for discovering small molecule drugs for neurological diseases, but only if prediction results correlate with in vitro and in vivo measurements. Various CNS scoring schemes are fast and easy to apply to screen libraries at the exploratory stage of drug discovery; however, these scores correlate to some extent with in vitro efflux and animal Kp,uu as illustrated by Figure 7 and 8 that plot the relative distribution of CNS and non-CNS drugs based on P-gp efflux ratio and rat Kp,uu corresponding to different CNS scoring schemes (CNS MPO, MPO_V2, pMPO and BBB Score). Ideally, CNS drugs, i.e., the range of scores (4,6], should be more populated with drugs having ER ≤ 3, and non-CNS drugs should be heavily populated in the lower ranges of scores, i.e., (0,4]. It is encouraging to see in Figure 7 that all scoring methods do segregate the drugs with lower ER towards a higher score range (4,6], and the drugs with higher ER towarders lower range (0,3}, but the segregation is not perfect. There is a lot of room for improvement. Figure 8 presents 100% stacked bar graphs for low to high MPO, MPO_V2, pMPO and BBB Scores for the rat Kp,uu dataset. Ideally, any molecule with an MPO, MPO_V2, pMPO and BBB Score in the range of (4,6] should correspond to a CNS drug. Most CNS drugs have Kp,uu in a moderate range (i.e., Kp,uu of (0.1,0.3 ] or < 0.3). Ideally, the in silico scoring schemes plotted in Figure 8 could be interpreted as a probability of a molecule attaining a score between 4 and 6 to have decent Kp,uu. MPO and MPO_V2 predict 33% and 32% of drugs having Kp,uu > 0.3, respectively, in the range (5,6], which is very low compared to the 62% and 68% predicted by the pMPO and BBB Score, respectively. For MPO_V2 and pMPO, drugs in range (3,4] have poor predictability (nearly 50%) in differentiating between high and low Kp,uu exposure. The MPO and BBB Score predict that 69% and 61% of drugs score in the (3,4] range having Kp,uu ≤ 0.1, which is an improvement over the MPO_V2 and pMPO scores.
On the other hand, the efflux ratio correlates well with animal Kp,uu (Figure 9).
Similarly, high rat Kp,uu correlate well with human BBB penetrability. Zhang et al. [61] found the vast majority (>85%) of the CNS drugs show rat Kp,uu over 0.3, which is consistent with our analysis of the available data shown in Figure 10.
Animal Kp,uu measurements are also nontrivial, expensive, and time-consuming. Such measurements are made for compounds at the lead optimization of drug discovery. On the other hand, in vitro measurements are faster, less expensive, and utilized extensively at earlier stages of discovery. In silico methods that rely only on chemical structure information (like the novel Kp,uu prediction method proposed by Watanabe et al. [83]) are highly useful at the Hit identification and Hit expansion stages.
The ultimate purpose of predictive models is to improve the odds of success of drug candidates for CNS diseases. Patel et al. [84] outline a parallel analysis of previously published models for predicting brain penetration that utilizes MDR1-MDCK efflux data as a better predictor of brain penetration. They demonstrate the ability to harness lower species preclinical data to predict human brain availability. Sato et al. [85] described a translational CNS steady-state drug disposition model to predict Kp,uu across rats, monkeys, and humans using only in vitro and physicochemical data. This model can potentially minimize animal use and improve CNS drug discovery.
5. Conclusions
The successful discovery of small-molecule drugs to treat neurological disorders requires CNS penetration of these drugs [86]. The design of CNS penetrable molecules was initially guided by the physicochemical properties of a limited set of known CNS active drugs and drugs that cause side effects in the CNS. The CNS MPO scores and later improvements were useful in simultaneously optimizing multiple properties of molecules for CNS targets. However, these scores do not always correlate well with in vitro (P-gp efflux) and animal in vivo (Kp,uu) data. The Machine Learning and Deep Learning models that classify CNS and non-CNS drugs achieve higher accuracy and are successfully applied to screen vast chemical libraries in the early phase of drug discovery but are found to be less beneficial for lead optimization. The need for higher accuracy in silico models with broader applicability is recognized, but such efforts require much more in vitro and in vivo data. These findings have prompted a generation of in vivo animal Kp,uu data and in vitro efflux data on a large number of compounds covering the available drug-like molecule space. Biogen scientists recently released in vitro efflux data on 3521 compounds [71]. Such expansion of datasets will improve the accuracy and coverage of in silico models. Accurate assessment of a drug molecule’s ability to cross BBB is determined by in vivo measurements. It has been established that Kp,uu data measured in preclinical animal studies predict human brain availability. A threshold of 0.3 for in vivo Kp,uu of mouse and rat are used for estimating good human brain exposure. Moreover, there is a good correlation between animal Kp,uu data and in vitro MDR1-MDCK efflux data, which represents a valid assay for the prediction of human P-gp efflux, although other species-specific transporters may cause a disconnect. A recent publication of the physiologically-based pharmacokinetic (PBPK) model shows that in vitro efflux data can be used to predict the degree of brain penetration across species accurately.
Recent efforts to develop in silico models to predict CNS penetration of small molecules focused on applying machine and deep learning methods using animal Kp,uu and in vitro MDR1-MDCK efflux data has been less successful. Available Kp,uu data is still limited, and in silico models to predict these data with high accuracy have not yet been achieved. In addition to smaller data sets, higher variability of the measured Kp,uu values that are influenced by multiple factors such as pharmacokinetics and transporters appear to limit the accuracy of published models. Better accuracy is achieved for in silico models to predict in vitro efflux data that are measured accurately on larger sets of compounds. These in silico models are deployed to prioritize molecules with higher probability of success to cross BBB.
Author Contributions
Conceptualization, MG and GB; methodology, MG and GB; software, formal analysis and investigation, MG and GB; literature data curation, JF; writing—original draft preparation, writing—review and editing, MG and GB; All authors have read and agreed to the published version of the manuscript.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Acknowledgments
The authors thank Dr. Giuliano Berellini for many helpful discussions and for sharing some of the literature data used in making the figures.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Sweeney, M.D.; Zhao, Z.; Montagne, A.; Nelson, A.R.; Zlokovic, B.V. Blood-Brain Barrier: From Physiology to Disease and Back. Physiological Reviews 2019, 99, 21–78. [Google Scholar] [CrossRef]
- Wong, A.; Ye, M.; Levy, A.; Rothstein, J.; Bergles, D.; Searson, P. The blood-brain barrier: an engineering perspective. Frontiers in Neuroengineering 2013, 6. [Google Scholar] [CrossRef] [PubMed]
- Nau, R.; Sörgel, F.; Eiffert, H. Penetration of Drugs through the Blood-Cerebrospinal Fluid/Blood-Brain Barrier for Treatment of Central Nervous System Infections. Clinical Microbiology Reviews 2010, 23, 858–883. [Google Scholar] [CrossRef] [PubMed]
- Stephens, R.H.; O’Neill, C.A.; Bennett, J.; Humphrey, M.; Henry, B.; Rowland, M.; Warhurst, G. Resolution of P-glycoprotein and non-P-glycoprotein effects on drug permeability using intestinal tissues from mdr1a (−/−) mice. British Journal of Pharmacology 2002, 135, 2038–2046. [Google Scholar] [CrossRef] [PubMed]
- Dickens, D.; Radisch, S.; Pirmohamed, M. Chapter 5 Drug Transporters at the Blood–Brain Barrier. In Drug Transporters: Volume 1: Role and Importance in ADME and Drug Development; The Royal Society of Chemistry, 2016; Vol. 1; pp 151-183.
- Gomez-Zepeda, D.; Taghi, M.; Scherrmann, J.-M.; Decleves, X.; Menet, M.-C. ABC Transporters at the Blood–Brain Interfaces, Their Study Models, and Drug Delivery Implications in Gliomas. Pharmaceutics 2020, 12, 20. [Google Scholar] [CrossRef]
- Löscher, W.; Potschka, H. Blood-brain barrier active efflux transporters: ATP-binding cassette gene family. NeuroRX 2005, 2, 86–98. [Google Scholar] [CrossRef] [PubMed]
- Gupta, A.; Chatelain, P.; Massingham, R.; Jonsson, E.N.; Hammarlund-Udenaes, M. Brain Distribution of Cetirizine Enantiomers: Comparisons of Three Different Tissue to Plasma Partition Coefficients. Drug Metabolism and Disposition, 2006; 34, 318–323. [Google Scholar]
- Radchenko, E.V.; Dyabina, A.S.; Palyulin, V.A. Towards Deep Neural Network Models for the Prediction of the Blood–Brain Barrier Permeability for Diverse Organic Compounds. Molecules 2020, 25, 5901. [Google Scholar] [CrossRef] [PubMed]
- Dubey, R.K.; McAllister, C.B.; Inoue, M.; Wilkinson, G.R. Plasma binding and transport of diazepam across the blood-brain barrier. No evidence for in vivo enhanced dissociation. J Clin Invest 1989, 84, 1155–1159. [Google Scholar] [CrossRef] [PubMed]
- Hammarlund-Udenaes, M.; Fridén, M.; Syvänen, S.; Gupta, A. On the rate and extent of drug delivery to the brain. Pharm Res 2008, 25, 1737–1750. [Google Scholar] [CrossRef]
- Pajouhesh, H.; Lenz, G.R. Medicinal chemical properties of successful central nervous system drugs. NeuroRX 2005, 2, 541–553. [Google Scholar] [CrossRef]
- Lipinski, C.A.; Lombardo, F.; Dominy, B.W.; Feeney, P.J. Experimental and computational approaches to estimate solubility and permeability in drug discovery and development settings. Advanced Drug Delivery Reviews 1997, 23, 3–25. [Google Scholar] [CrossRef]
- Hansch, C.; Steward, A.R.; Anderson, S.M.; Bentley, D.L. Parabolic dependence of drug action upon lipophilic character as revealed by a study of hypnotics. Journal of Medicinal Chemistry 1968, 11, 1–11. [Google Scholar] [CrossRef] [PubMed]
- van de Waterbeemd, H.; Camenisch, G.; Folkers, G.; Chretien, J.R.; Raevsky, O.A. Estimation of Blood-Brain Barrier Crossing of Drugs Using Molecular Size and Shape, and H-Bonding Descriptors. Journal of Drug Targeting 1998, 6, 151–165. [Google Scholar] [CrossRef]
- Kelder, J.; Grootenhuis, P.D.J.; Bayada, D.M.; Delbressine, L.P.C.; Ploemen, J.-P. Polar Molecular Surface as a Dominating Determinant for Oral Absorption and Brain Penetration of Drugs. Pharmaceutical Research 1999, 16, 1514–1519. [Google Scholar] [CrossRef]
- Mahar Doan, K.M.; Humphreys, J.E.; Webster, L.O.; Wring, S.A.; Shampine, L.J.; Serabjit-Singh, C.J.; Adkison, K.K.; Polli, J.W. Passive permeability and P-glycoprotein-mediated efflux differentiate central nervous system (CNS) and non-CNS marketed drugs. J Pharmacol Exp Ther 2002, 303, 1029–1037. [Google Scholar] [CrossRef] [PubMed]
- Norinder, U.; Haeberlein, M. Computational approaches to the prediction of the blood–brain distribution. Advanced Drug Delivery Reviews 2002, 54, 291–313. [Google Scholar] [CrossRef] [PubMed]
- Didziapetris, R.; Japertas, P.; Avdeef, A.; Petrauskas, A. Classification analysis of P-glycoprotein substrate specificity. J Drug Target 2003, 11, 391–406. [Google Scholar] [CrossRef]
- Leeson, P.D.; Davis, A.M. Time-Related Differences in the Physical Property Profiles of Oral Drugs. Journal of Medicinal Chemistry 2004, 47, 6338–6348. [Google Scholar] [CrossRef] [PubMed]
- Hitchcock, S.A.; Pennington, L.D. Structure−Brain Exposure Relationships. Journal of Medicinal Chemistry 2006, 49, 7559–7583. [Google Scholar] [CrossRef]
- Rankovic, Z. CNS Drug Design: Balancing Physicochemical Properties for Optimal Brain Exposure. Journal of Medicinal Chemistry 2015, 58, 2584–2608. [Google Scholar] [CrossRef]
- Loryan, I.; Sinha, V.; Mackie, C.; Van Peer, A.; Drinkenburg, W.H.; Vermeulen, A.; Heald, D.; Hammarlund-Udenaes, M.; Wassvik, C.M. Molecular Properties Determining Unbound Intracellular and Extracellular Brain Exposure of CNS Drug Candidates. Molecular Pharmaceutics 2015, 12, 520–532. [Google Scholar] [CrossRef]
- Freeman, B.B., 3rd; Yang, L.; Rankovic, Z. Practical approaches to evaluating and optimizing brain exposure in early drug discovery. Eur J Med Chem 2019, 182, 111643. [Google Scholar] [CrossRef]
- Wager, T.T.; Chandrasekaran, R.Y.; Hou, X.; Troutman, M.D.; Verhoest, P.R.; Villalobos, A.; Will, Y. Defining desirable central nervous system drug space through the alignment of molecular properties, in vitro ADME, and safety attributes. ACS Chem Neurosci 2010, 1, 420–434. [Google Scholar] [CrossRef] [PubMed]
- Wager, T.T.; Hou, X.; Verhoest, P.R.; Villalobos, A. Moving beyond rules: the development of a central nervous system multiparameter optimization (CNS MPO) approach to enable alignment of druglike properties. ACS Chem Neurosci 2010, 1, 435–449. [Google Scholar] [CrossRef] [PubMed]
- Wager, T.T.; Hou, X.; Verhoest, P.R.; Villalobos, A. Central Nervous System Multiparameter Optimization Desirability: Application in Drug Discovery. ACS Chem Neurosci 2016, 7, 767–775. [Google Scholar] [CrossRef] [PubMed]
- Gunaydin, H. Probabilistic Approach to Generating MPOs and Its Application as a Scoring Function for CNS Drugs. ACS Med Chem Lett 2016, 7, 89–93. [Google Scholar] [CrossRef]
- Ghose, A.K.; Herbertz, T.; Hudkins, R.L.; Dorsey, B.D.; Mallamo, J.P. Knowledge-Based, Central Nervous System (CNS) Lead Selection and Lead Optimization for CNS Drug Discovery. ACS Chemical Neuroscience 2012, 3, 50–68. [Google Scholar] [CrossRef] [PubMed]
- Rankovic, Z. CNS Physicochemical Property Space Shaped by a Diverse Set of Molecules with Experimentally Determined Exposure in the Mouse Brain. J Med Chem 2017, 60, 5943–5954. [Google Scholar] [CrossRef] [PubMed]
- Rankovic, Z. Retraction of “CNS Physicochemical Property Space Shaped by a Diverse Set of Molecules with Experimentally Determined Exposure in the Mouse Brain”. Journal of Medicinal Chemistry 2019, 62, 1699–1699. [Google Scholar] [CrossRef]
- Gupta, M.; Lee, H.J.; Barden, C.J.; Weaver, D.F. The Blood–Brain Barrier (BBB) Score. Journal of Medicinal Chemistry 2019, 62, 9824–9836. [Google Scholar] [CrossRef]
- Yuan, Y.; Zheng, F.; Zhan, C.-G. Improved Prediction of Blood–Brain Barrier Permeability Through Machine Learning with Combined Use of Molecular Property-Based Descriptors and Fingerprints. The AAPS Journal 2018, 20, 54. [Google Scholar] [CrossRef]
- Chen, H.; Winiwarter, S.; Friden, M.; Antonsson, M.; Engkvist, O. In silico prediction of unbound brain-to-plasma concentration ratio using machine learning algorithms. J Mol Graph Model 2011, 29, 985–995. [Google Scholar] [CrossRef] [PubMed]
- Varadharajan, S.; Winiwarter, S.; Carlsson, L.; Engkvist, O.; Anantha, A.; Kogej, T.; Fridén, M.; Stålring, J.; Chen, H. Exploring In Silico Prediction of the Unbound Brain-to-Plasma Drug Concentration Ratio: Model Validation, Renewal, and Interpretation. Journal of Pharmaceutical Sciences 2015, 104, 1197–1206. [Google Scholar] [CrossRef] [PubMed]
- Fridén, M.; Winiwarter, S.; Jerndal, G.; Bengtsson, O.; Wan, H.; Bredberg, U.; Hammarlund-Udenaes, M.; Antonsson, M. Structure−Brain Exposure Relationships in Rat and Human Using a Novel Data Set of Unbound Drug Concentrations in Brain Interstitial and Cerebrospinal Fluids. Journal of Medicinal Chemistry 2009, 52, 6233–6243. [Google Scholar] [CrossRef] [PubMed]
- Saxena, D.; Sharma, A.; Siddiqui, M.H.; Kumar, R. Development of Machine Learning Based Blood-brain Barrier Permeability Prediction Models Using Physicochemical Properties, MACCS and Substructure Fingerprints. Current Bioinformatics 2021, 16, 855–864. [Google Scholar] [CrossRef]
- Durant, J.L.; Leland, B.A.; Henry, D.R.; Nourse, J.G. Reoptimization of MDL keys for use in drug discovery. J Chem Inf Comput Sci 2002, 42, 1273–1280. [Google Scholar] [CrossRef]
- Miao, R.; Xia, L.-Y.; Chen, H.-H.; Huang, H.-H.; Liang, Y. Improved Classification of Blood-Brain-Barrier Drugs Using Deep Learning. Scientific Reports 2019, 9, 8802. [Google Scholar] [CrossRef] [PubMed]
- Alsenan, S.; Al-Turaiki, I.; Hafez, A. A Recurrent Neural Network model to predict blood–brain barrier permeability. Computational Biology and Chemistry 2020, 89, 107377. [Google Scholar] [CrossRef] [PubMed]
- Zhang, R.; Ding, Y. Identification of Key Features of CNS Drugs Based on SVM and Greedy Algorithm. Curr Comput Aided Drug Des 2020, 16, 725–733. [Google Scholar] [CrossRef]
- Saxena, D.; Sharma, A.; Siddiqui, M.H.; Kumar, R. Blood Brain Barrier Permeability Prediction Using Machine Learning Techniques: An Update. Curr Pharm Biotechnol 2019, 20, 1163–1171. [Google Scholar] [CrossRef]
- Morales, F.J.; Montoto, S.S.; Fagiolino, P.; Ruiz, E.M. Current State and Future Perspectives in QSAR Models to Predict Blood- Brain Barrier Penetration in Central Nervous System Drug R&D. Mini-Reviews in Medicinal Chemistry 2017, 17, 247–257. [Google Scholar] [PubMed]
- Liu, H.; Dong, K.; Zhang, W.; Summerfield, S.G.; Terstappen, G.C. Prediction of brain:blood unbound concentration ratios in CNS drug discovery employing in silico and in vitro model systems. Drug Discov Today 2018, 23, 1357–1372. [Google Scholar] [CrossRef] [PubMed]
- UNGERSTEDT, U. Microdialysis—principles and applications for studies in animals and man. Journal of Internal Medicine 1991, 230, 365–373. [Google Scholar] [CrossRef]
- Zapata, A.; Chefer, V.I.; Shippenberg, T.S. Microdialysis in rodents. Current protocols in neuroscience, 2009; Chapter 7, Unit7.2–Unit7.2. [Google Scholar]
- Chefer, V.I.; Thompson, A.C.; Zapata, A.; Shippenberg, T.S. Overview of brain microdialysis. Current protocols in neuroscience, 2009; Chapter 7, Unit7.1–Unit7.1. [Google Scholar]
- de Lange, E.C.M.; de Boer, B.A.G.; Breimer, D.D. Microdialysis for pharmacokinetic analysis of drug transport to the brain. Advanced Drug Delivery Reviews 1999, 36, 211–227. [Google Scholar] [CrossRef]
- Chaurasia, C.S.; Müller, M.; Bashaw, E.D.; Benfeldt, E.; Bolinder, J.; Bullock, R.; Bungay, P.M.; DeLange, E.C.M.; Derendorf, H.; Elmquist, W.F.; Hammarlund-Udenaes, M.; Joukhadar, C.; Kellogg, D.L.; Lunte, C.E.; Nordstrom, C.H.; Rollema, H.; Sawchuk, R.J.; Cheung, B.W.Y.; Shah, V.P.; Stahle, L.; Ungerstedt, U.; Welty, D.F.; Yeo, H. AAPS-FDA Workshop White Paper: Microdialysis Principles, Application and Regulatory Perspectives. Pharmaceutical Research 2007, 24, 1014–1025. [Google Scholar] [CrossRef]
- Read, K.D.; Braggio, S. Assessing brain free fraction in early drug discovery. Expert Opinion on Drug Metabolism & Toxicology 2010, 6, 337–344. [Google Scholar]
- Cory Kalvass, J.; Maurer, T.S. Influence of nonspecific brain and plasma binding on CNS exposure: implications for rational drug discovery. Biopharmaceutics & Drug Disposition 2002, 23, 327–338. [Google Scholar]
- Wan, H.; Rehngren, M.; Giordanetto, F.; Bergström, F.; Tunek, A. High-Throughput Screening of Drug−Brain Tissue Binding and in Silico Prediction for Assessment of Central Nervous System Drug Delivery. Journal of Medicinal Chemistry 2007, 50, 4606–4615. [Google Scholar] [CrossRef]
- Becker, S.; Liu, X. Evaluation of the Utility of Brain Slice Methods to Study Brain Penetration. Drug Metabolism and Disposition 2006, 34, 855–861. [Google Scholar] [CrossRef]
- Summerfield, S.G.; Stevens, A.J.; Cutler, L.; del Carmen Osuna, M.; Hammond, B.; Tang, S.P.; Hersey, A.; Spalding, D.J.; Jeffrey, P. Improving the in vitro prediction of in vivo central nervous system penetration: integrating permeability, P-glycoprotein efflux, and free fractions in blood and brain. J Pharmacol Exp Ther 2006, 316, 1282–1290. [Google Scholar] [CrossRef]
- Summerfield, S.G.; Zhang, Y.; Liu, H. Examining the Uptake of Central Nervous System Drugs and Candidates across the Blood-Brain Barrier. J Pharmacol Exp Ther 2016, 358, 294–305. [Google Scholar] [CrossRef] [PubMed]
- Culot, M.; Fabulas-da Costa, A.; Sevin, E.; Szorath, E.; Martinsson, S.; Renftel, M.; Hongmei, Y.; Cecchelli, R.; Lundquist, S. A simple method for assessing free brain/free plasma ratios using an in vitro model of the blood brain barrier. PloS one 2013, 8, e80634. [Google Scholar] [CrossRef] [PubMed]
- Fridén, M.; Ducrozet, F.; Middleton, B.; Antonsson, M.; Bredberg, U.; Hammarlund-Udenaes, M. Development of a High-Throughput Brain Slice Method for Studying Drug Distribution in the Central Nervous System. Drug Metabolism and Disposition 2009, 37, 1226–1233. [Google Scholar] [CrossRef] [PubMed]
- Fridén, M.; Gupta, A.; Antonsson, M.; Bredberg, U.; Hammarlund-Udenaes, M. In Vitro Methods for Estimating Unbound Drug Concentrations in the Brain Interstitial and Intracellular Fluids. Drug Metabolism and Disposition 2007, 35, 1711–1719. [Google Scholar] [CrossRef] [PubMed]
- Spreafico, M.; Jacobson, M.P. In silico prediction of brain exposure: drug free fraction, unbound brain to plasma concentration ratio and equilibrium half-life. Current topics in medicinal chemistry 2013, 13, 813–820. [Google Scholar] [CrossRef]
- Dolgikh, E.; Watson, I.A.; Desai, P.V.; Sawada, G.A.; Morton, S.; Jones, T.M.; Raub, T.J. QSAR Model of Unbound Brain-to-Plasma Partition Coefficient, Kp,uu,brain: Incorporating P-glycoprotein Efflux as a Variable. J Chem Inf Model 2016, 56, 2225–2233. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.-Y.; Liu, H.; Summerfield, S.G.; Luscombe, C.N.; Sahi, J. Integrating in Silico and in Vitro Approaches To Predict Drug Accessibility to the Central Nervous System. Molecular Pharmaceutics 2016, 13, 1540–1550. [Google Scholar] [CrossRef] [PubMed]
- Lanevskij, K.; Japertas, P.; Didziapetris, R. Improving the prediction of drug disposition in the brain. Expert Opin Drug Metab Toxicol 2013, 9, 473–486. [Google Scholar] [CrossRef] [PubMed]
- The International Transporter, C.; Giacomini, K.M.; Huang, S.-M.; Tweedie, D.J.; Benet, L.Z.; Brouwer, K.L.R.; Chu, X.; Dahlin, A.; Evers, R.; Fischer, V.; Hillgren, K.M.; Hoffmaster, K.A.; Ishikawa, T.; Keppler, D.; Kim, R.B.; Lee, C.A.; Niemi, M.; Polli, J.W.; Sugiyama, Y.; Swaan, P.W.; Ware, J.A.; Wright, S.H.; Wah Yee, S.; Zamek-Gliszczynski, M.J.; Zhang, L. Membrane transporters in drug development. Nature Reviews Drug Discovery 2010, 9, 215. [Google Scholar] [CrossRef]
- Liu, H.; Dong, K.; Zhang, W.; Summerfield, S.G.; Terstappen, G.C. Prediction of brain:blood unbound concentration ratios in CNS drug discovery employing in silico and in vitro model systems. Drug Discovery Today 2018, 23, 1357–1372. [Google Scholar] [CrossRef]
- Garrigues, A.; Escargueil, A.E.; Orlowski, S. The multidrug transporter, P-glycoprotein, actively mediates cholesterol redistribution in the cell membrane. Proceedings of the National Academy of Sciences 2002, 99, 10347–10352. [Google Scholar] [CrossRef] [PubMed]
- Pajeva, I.K.; Globisch, C.; Wiese, M. Combined Pharmacophore Modeling, Docking, and 3D QSAR Studies of ABCB1 and ABCC1 Transporter Inhibitors. ChemMedChem 2009, 4, 1883–1896. [Google Scholar] [CrossRef] [PubMed]
- Gombar, V.K.; Polli, J.W.; Humphreys, J.E.; Wring, S.A.; Serabjit-Singh, C.S. Predicting P-glycoprotein substrates by a quantitative structure–activity relationship model. Journal of Pharmaceutical Sciences 2004, 93, 957–968. [Google Scholar] [CrossRef]
- Penzotti, J.E.; Lamb, M.L.; Evensen, E.; Grootenhuis, P.D.J. A Computational Ensemble Pharmacophore Model for Identifying Substrates of P-Glycoprotein. Journal of Medicinal Chemistry 2002, 45, 1737–1740. [Google Scholar] [CrossRef] [PubMed]
- Pajeva, I.K.; Wiese, M. Pharmacophore Model of Drugs Involved in P-Glycoprotein Multidrug Resistance: Explanation of Structural Variety (Hypothesis). Journal of Medicinal Chemistry 2002, 45, 5671–5686. [Google Scholar] [CrossRef]
- Bikadi, Z.; Hazai, I.; Malik, D.; Jemnitz, K.; Veres, Z.; Hari, P.; Ni, Z.; Loo, T.W.; Clarke, D.M.; Hazai, E.; Mao, Q. Predicting P-Glycoprotein-Mediated Drug Transport Based On Support Vector Machine and Three-Dimensional Crystal Structure of P-glycoprotein. PloS one 2011, 6, e25815. [Google Scholar] [CrossRef] [PubMed]
- Fang, C.; Wang, Y.; Grater, R.; Kapadnis, S.; Black, C.; Trapa, P.; Sciabola, S. Prospective Validation of Machine Learning Algorithms for Absorption, Distribution, Metabolism, and Excretion Prediction: An Industrial Perspective. Journal of Chemical Information and Modeling 2023, 63, 3263–3274. [Google Scholar] [CrossRef]
- Ohashi, R.; Watanabe, R.; Esaki, T.; Taniguchi, T.; Torimoto-Katori, N.; Watanabe, T.; Ogasawara, Y.; Takahashi, T.; Tsukimoto, M.; Mizuguchi, K. Development of Simplified in Vitro P-Glycoprotein Substrate Assay and in Silico Prediction Models To Evaluate Transport Potential of P-Glycoprotein. Mol Pharm 2019, 16, 1851–1863. [Google Scholar] [CrossRef] [PubMed]
- Broccatelli, F.; Larregieu, C.A.; Cruciani, G.; Oprea, T.I.; Benet, L.Z. Improving the prediction of the brain disposition for orally administered drugs using BDDCS. Advanced Drug Delivery Reviews 2012, 64, 95–109. [Google Scholar] [CrossRef]
- Broccatelli, F. QSAR models for P-glycoprotein transport based on a highly consistent data set. J Chem Inf Model 2012, 52, 2462–2470. [Google Scholar] [CrossRef]
- Polli, J.W.; Wring, S.A.; Humphreys, J.E.; Huang, L.; Morgan, J.B.; Webster, L.O.; Serabjit-Singh, C.S. Rational Use of in Vitro P-glycoprotein Assays in Drug Discovery. Journal of Pharmacology and Experimental Therapeutics 2001, 299, 620. [Google Scholar] [PubMed]
- Kikuchi, R.; de Morais, S.M.; Kalvass, J.C. In vitro P-glycoprotein efflux ratio can predict the in vivo brain penetration regardless of biopharmaceutics drug disposition classification system class. Drug Metab Dispos 2013, 41, 2012–2017. [Google Scholar] [CrossRef]
- Dolgikh, E.; Watson, I.A.; Desai, P.V.; Sawada, G.A.; Morton, S.; Jones, T.M.; Raub, T.J. QSAR Model of Unbound Brain-to-Plasma Partition Coefficient, Kp,uu,brain: Incorporating P-glycoprotein Efflux as a Variable. Journal of Chemical Information and Modeling 2016, 56, 2225–2233. [Google Scholar] [CrossRef] [PubMed]
- Gupta, M.; Bogdanowicz, T.; Reed, M.A.; Barden, C.J.; Weaver, D.F. The Brain Exposure Efficiency (BEE) Score. ACS Chemical Neuroscience 2020, 11, 205–224. [Google Scholar] [CrossRef] [PubMed]
- Kosugi, Y.; Mizuno, K.; Santos, C.; Sato, S.; Hosea, N.; Zientek, M. Direct Comparison of the Prediction of the Unbound Brain-to-Plasma Partitioning Utilizing Machine Learning Approach and Mechanistic Neuropharmacokinetic Model. The AAPS Journal 2021, 23, 72. [Google Scholar] [CrossRef]
- Ghose, A.K.; Ott, G.R.; Hudkins, R.L. Technically Extended MultiParameter Optimization (TEMPO): An Advanced Robust Scoring Scheme To Calculate Central Nervous System Druggability and Monitor Lead Optimization. ACS Chemical Neuroscience 2017, 8, 147–154. [Google Scholar] [CrossRef] [PubMed]
- Broccatelli, F. QSAR Models for P-Glycoprotein Transport Based on a Highly Consistent Data Set. Journal of Chemical Information and Modeling 2012, 52, 2462–2470. [Google Scholar] [CrossRef]
- Fridén, M.; Winiwarter, S.; Jerndal, G.; Bengtsson, O.; Wan, H.; Bredberg, U.; Hammarlund-Udenaes, M.; Antonsson, M. Structure-brain exposure relationships in rat and human using a novel data set of unbound drug concentrations in brain interstitial and cerebrospinal fluids. J Med Chem 2009, 52, 6233–6243. [Google Scholar] [CrossRef] [PubMed]
- Watanabe, R.; Esaki, T.; Ohashi, R.; Kuroda, M.; Kawashima, H.; Komura, H.; Natsume-Kitatani, Y.; Mizuguchi, K. Development of an In Silico Prediction Model for P-glycoprotein Efflux Potential in Brain Capillary Endothelial Cells toward the Prediction of Brain Penetration. Journal of Medicinal Chemistry 2021, 64, 2725–2738. [Google Scholar] [CrossRef] [PubMed]
- Patel, N.C.; Feng, B.; Hou, X.; West, M.A.; Trapa, P.E.; Sciabola, S.; Verhoest, P.; Liras, J.L.; Maurer, T.S.; Wager, T.T. Harnessing Preclinical Data as a Predictive Tool for Human Brain Tissue Targeting. ACS Chemical Neuroscience 2021, 12, 1007–1017. [Google Scholar] [CrossRef]
- Sato, S.; Matsumiya, K.; Tohyama, K.; Kosugi, Y. Translational CNS Steady-State Drug Disposition Model in Rats, Monkeys, and Humans for Quantitative Prediction of Brain-to-Plasma and Cerebrospinal Fluid-to-Plasma Unbound Concentration Ratios. Aaps j 2021, 23, 81. [Google Scholar] [CrossRef] [PubMed]
- Gupta, M.; Weaver, D.F. Alzheimer’s: The ABCDE Paradigm. ACS Chemical Neuroscience 2022, 13, 1355–1357. [Google Scholar] [CrossRef] [PubMed]
Figure 1.
(a) The endothelial tight junctions of the BBB (shown in brown) severely restrict paracellular transport, whereas specialized transporters, e.g., P-gp (green diamond) and BCRP (blue oval) (efflux transporters); OCT1 (orange triangle) and OCT2 (yellow hexagon) (influx transporters) regulate the transcellular transport of metabolic nutrients and other essential molecules across BBB. Enclosed in the basal lamina, pericyte cells partially surround these BBB endothelial cells. The complex tight cellular network of BBB is further maintained by astrocytes’ end feet. Astrocytes maintain the cellular link between neurons and microglial cells. The transport across BBB involves concentration gradient-driven passive diffusion and active transport employing various efflux and influx transporters in the endothelial cell membrane. (b) Schematic of plasma and brain compartments presenting different modes of transport across BBB, i.e., passive diffusion and active transport using efflux (e.g., P-gp, BCRP) and influx (e.g., OCT1, OCT2) transporters. Kp,uu represents the unbound brain to unbound plasma drug concentration ratio where Cu,b and Cu,p represent unbound drug concentration in brain and plasma, respectively. Different brain compartments, i.e., Blood BBB, CSF, BCSFB, ISF and ICF, correspond to blood, blood-brain barrier, cerebrospinal fluid, blood-cerebrospinal fluid barrier, interstitial fluid and intracellular fluid, respectively.
Figure 1.
(a) The endothelial tight junctions of the BBB (shown in brown) severely restrict paracellular transport, whereas specialized transporters, e.g., P-gp (green diamond) and BCRP (blue oval) (efflux transporters); OCT1 (orange triangle) and OCT2 (yellow hexagon) (influx transporters) regulate the transcellular transport of metabolic nutrients and other essential molecules across BBB. Enclosed in the basal lamina, pericyte cells partially surround these BBB endothelial cells. The complex tight cellular network of BBB is further maintained by astrocytes’ end feet. Astrocytes maintain the cellular link between neurons and microglial cells. The transport across BBB involves concentration gradient-driven passive diffusion and active transport employing various efflux and influx transporters in the endothelial cell membrane. (b) Schematic of plasma and brain compartments presenting different modes of transport across BBB, i.e., passive diffusion and active transport using efflux (e.g., P-gp, BCRP) and influx (e.g., OCT1, OCT2) transporters. Kp,uu represents the unbound brain to unbound plasma drug concentration ratio where Cu,b and Cu,p represent unbound drug concentration in brain and plasma, respectively. Different brain compartments, i.e., Blood BBB, CSF, BCSFB, ISF and ICF, correspond to blood, blood-brain barrier, cerebrospinal fluid, blood-cerebrospinal fluid barrier, interstitial fluid and intracellular fluid, respectively.
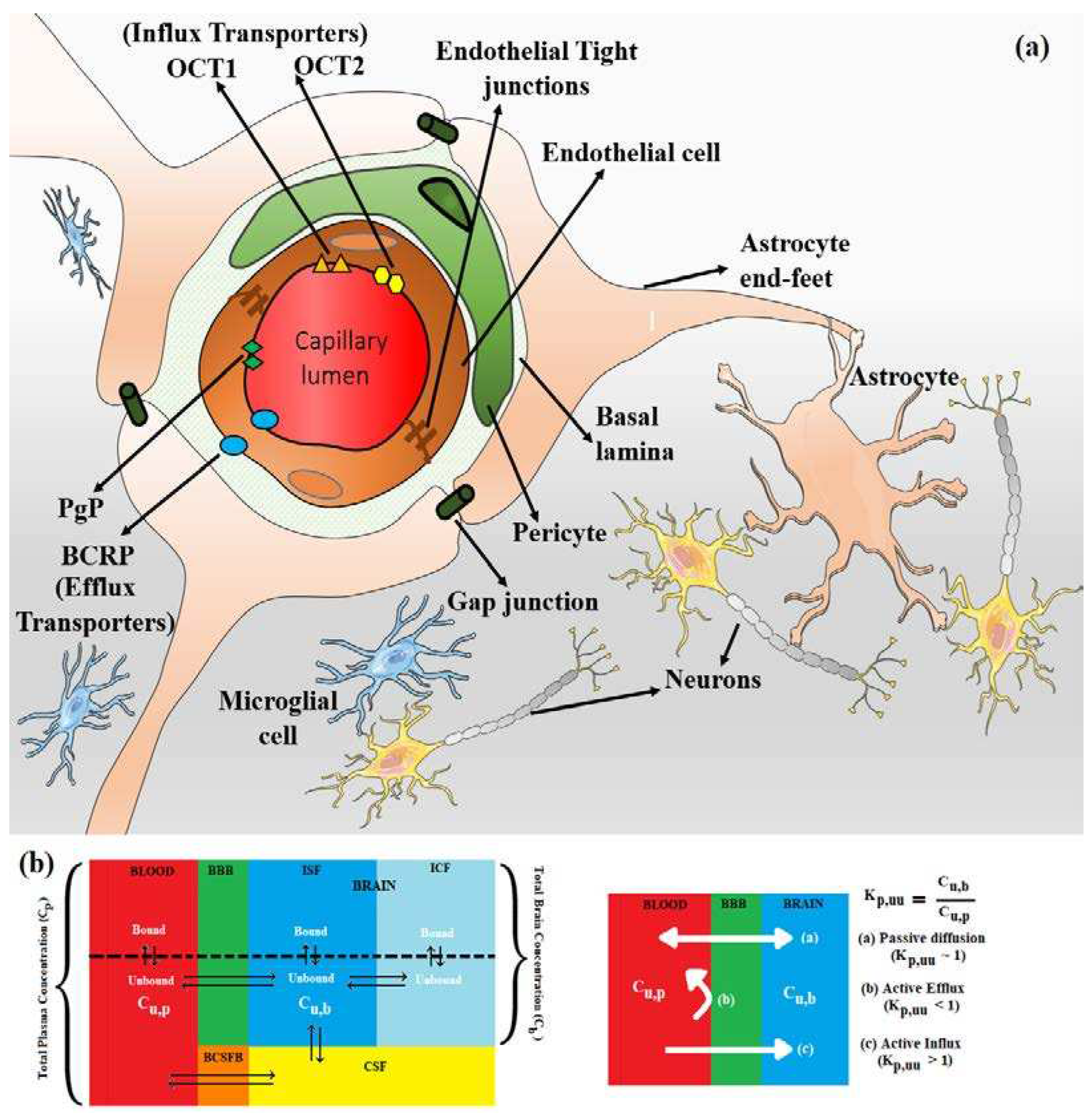
Figure 2.
Relative distribution of CNS class of compounds: CNS+ (green) and non-CNS- (red). The MPO, MPO_V2, pMPO and BBB scores range from 0 to 6 (a score within a range of (4,6] means better CNS penetration). Original pMPO scores range between 0 to 1. To be consistent with MPO scores, we scaled the pMPO scores from 0 to 6.
Figure 2.
Relative distribution of CNS class of compounds: CNS+ (green) and non-CNS- (red). The MPO, MPO_V2, pMPO and BBB scores range from 0 to 6 (a score within a range of (4,6] means better CNS penetration). Original pMPO scores range between 0 to 1. To be consistent with MPO scores, we scaled the pMPO scores from 0 to 6.
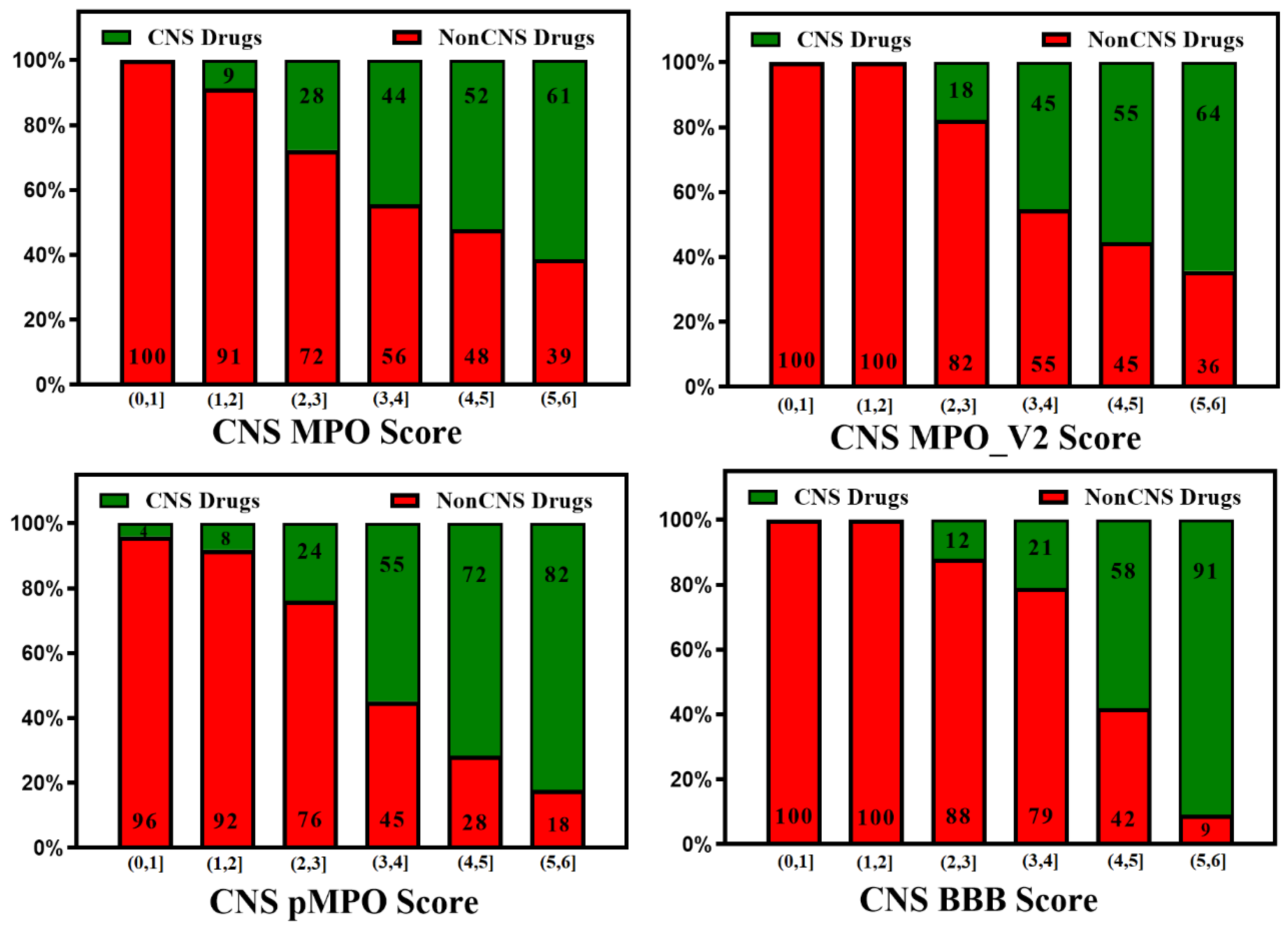
Figure 3.
Relative distribution of CNS class of compounds: CNS+ (green) and non-CNS- (red). The MPO, MPO_V2, pMPO and BBB scores range from 0 to 6 (a score in the range of (4,6] means better CNS penetration). Original pMPO scores range between 0 to 1. To be consistent with MPO scores, we scaled the pMPO scores from 0 to 6. Percentage of CNS drugs and non-CNS drugs correctly identified (for CNS: MPO, MPO_V2, pMPO, BBB Score [4,6]; for non-CNS: MPO, MPO_V2, BBB Scores [0,4)) in their respective CNS and non-CNS database is plotted on 100% stacked bar graph for MPO, MPO_V2, pMPO and BBB Scores.
Figure 3.
Relative distribution of CNS class of compounds: CNS+ (green) and non-CNS- (red). The MPO, MPO_V2, pMPO and BBB scores range from 0 to 6 (a score in the range of (4,6] means better CNS penetration). Original pMPO scores range between 0 to 1. To be consistent with MPO scores, we scaled the pMPO scores from 0 to 6. Percentage of CNS drugs and non-CNS drugs correctly identified (for CNS: MPO, MPO_V2, pMPO, BBB Score [4,6]; for non-CNS: MPO, MPO_V2, BBB Scores [0,4)) in their respective CNS and non-CNS database is plotted on 100% stacked bar graph for MPO, MPO_V2, pMPO and BBB Scores.
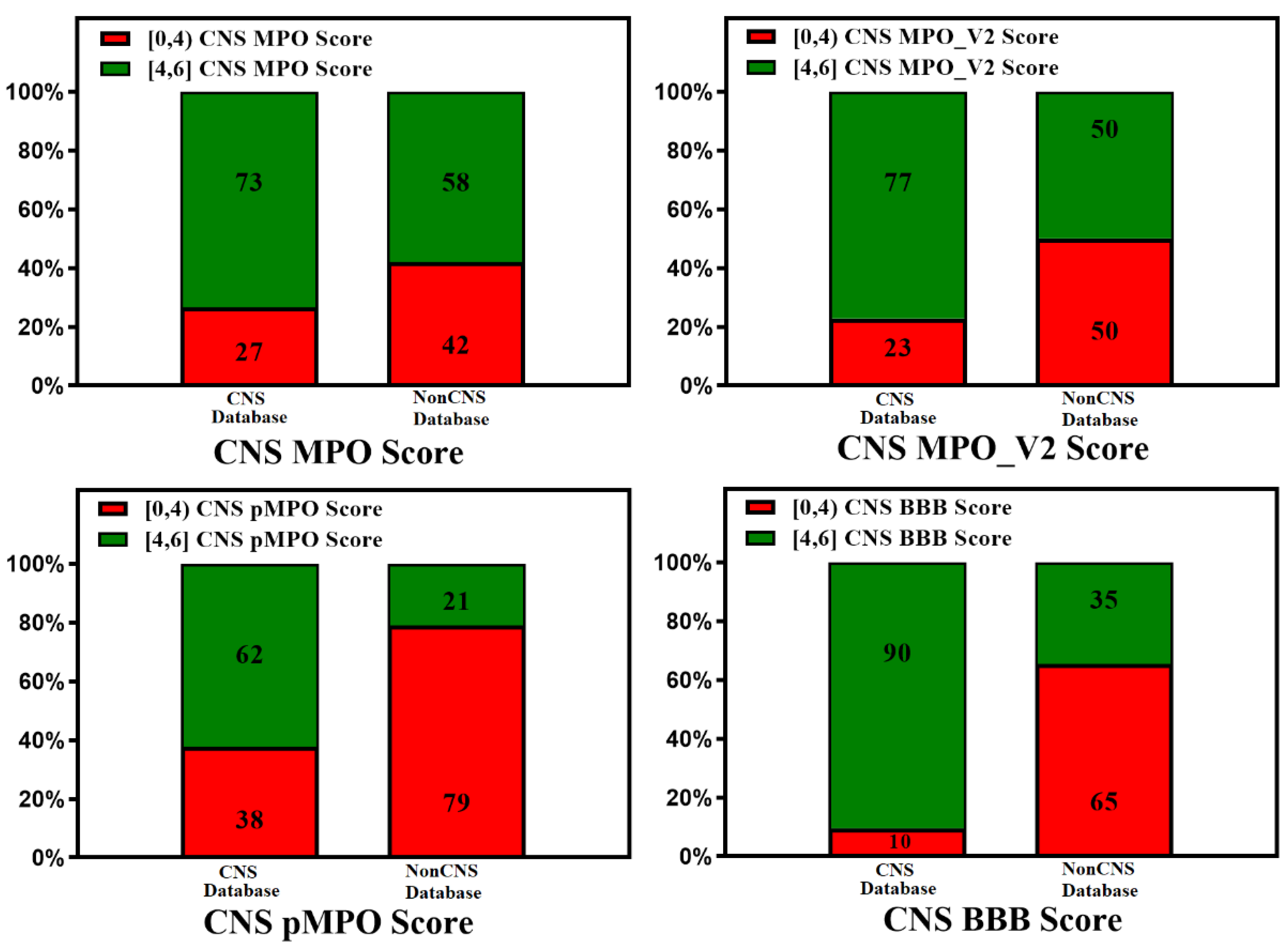
Figure 4.
The schematic diagram of the proposed mechanism of P-gp (MDR1) is represented. Transmembrane (TBDs) and nucleotide (NBDs) binding domains of P-gp are presented in green and red, respectively. The P-gp substrates are shown by black triangles, which cross the BBB membrane by passive diffusion or active transport. The inward-facing, ADP-bound state structure (i) changes conformation, the NBDs dimerize, and the TMDs re-orientate to extracellular space to adopt an outward-facing (ATP-bound state) (ii). The extracellular segment’s transmembrane helices in the outward-facing conformation of P-gp reorient to release the substrate. Upon ATP hydrolysis, the transporter is reoriented to the inward-facing structure, and two phosphate molecules are released.
Figure 4.
The schematic diagram of the proposed mechanism of P-gp (MDR1) is represented. Transmembrane (TBDs) and nucleotide (NBDs) binding domains of P-gp are presented in green and red, respectively. The P-gp substrates are shown by black triangles, which cross the BBB membrane by passive diffusion or active transport. The inward-facing, ADP-bound state structure (i) changes conformation, the NBDs dimerize, and the TMDs re-orientate to extracellular space to adopt an outward-facing (ATP-bound state) (ii). The extracellular segment’s transmembrane helices in the outward-facing conformation of P-gp reorient to release the substrate. Upon ATP hydrolysis, the transporter is reoriented to the inward-facing structure, and two phosphate molecules are released.
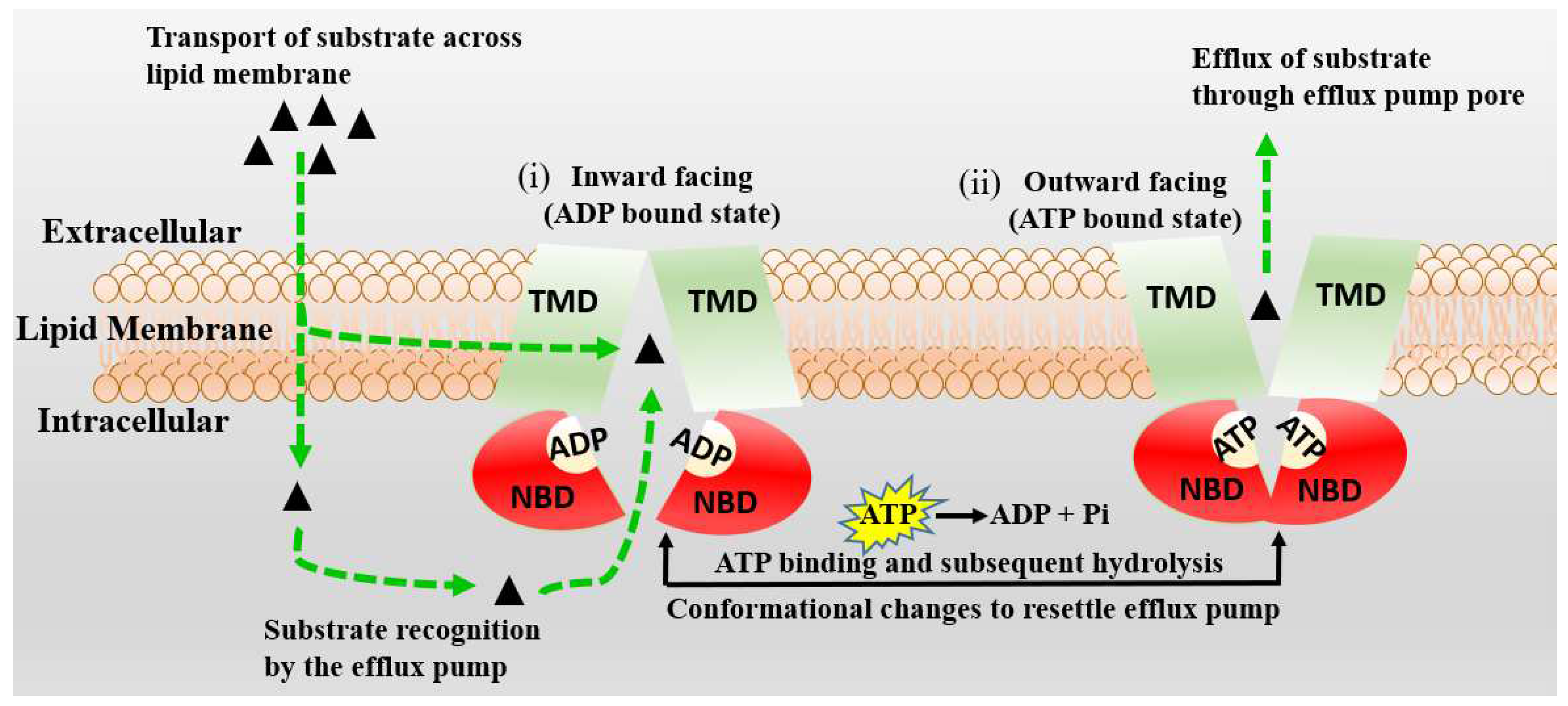
Figure 5.
A plot of the CNS class of compounds CNS+ (green) and CNS- (red) against their measured efflux ratios. CNS+ compounds with good brain exposure have a higher probability of having lower efflux.
Figure 5.
A plot of the CNS class of compounds CNS+ (green) and CNS- (red) against their measured efflux ratios. CNS+ compounds with good brain exposure have a higher probability of having lower efflux.
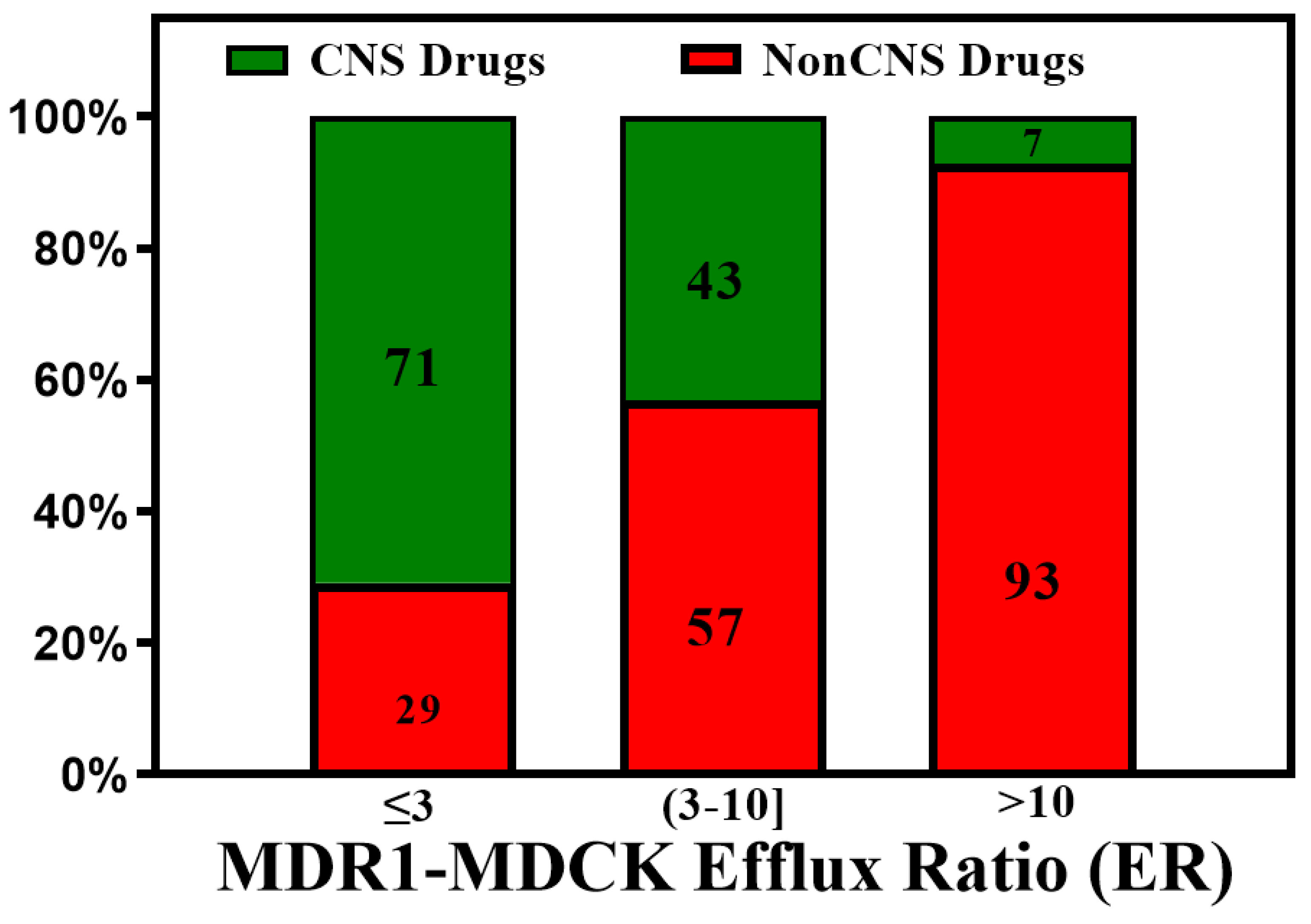
Figure 6.
The bias of available drugs with MDCK (orange) and Kp,uu data (black). The grey and white dots represent CNS+ and CNS- compounds, respectively.
Figure 6.
The bias of available drugs with MDCK (orange) and Kp,uu data (black). The grey and white dots represent CNS+ and CNS- compounds, respectively.
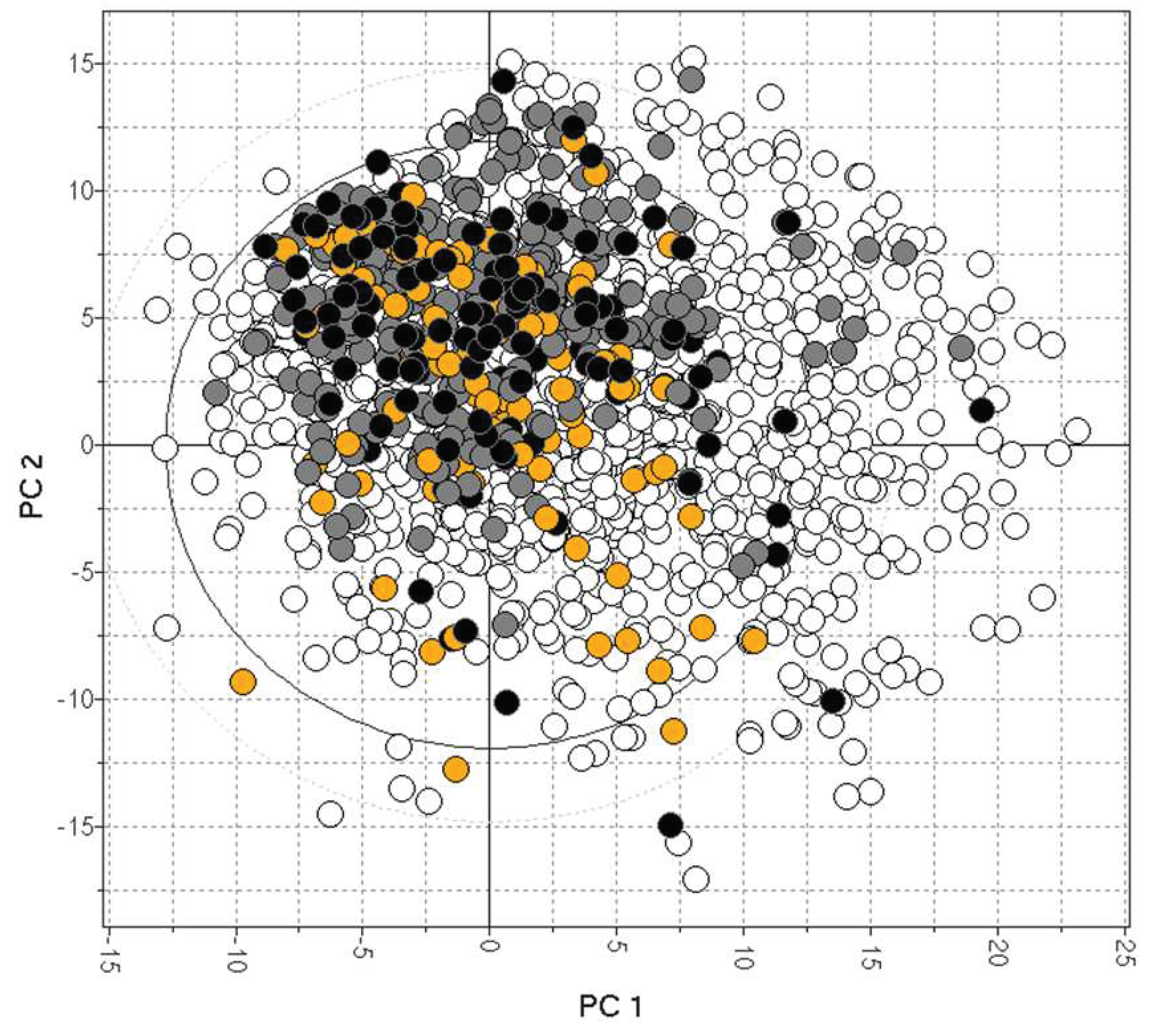
Figure 7.
In silico methods (CNS MPO, MPO_V2, pMPO and BBB Score) segregate low vs. high efflux compounds, but there is much room for improvement.
Figure 7.
In silico methods (CNS MPO, MPO_V2, pMPO and BBB Score) segregate low vs. high efflux compounds, but there is much room for improvement.
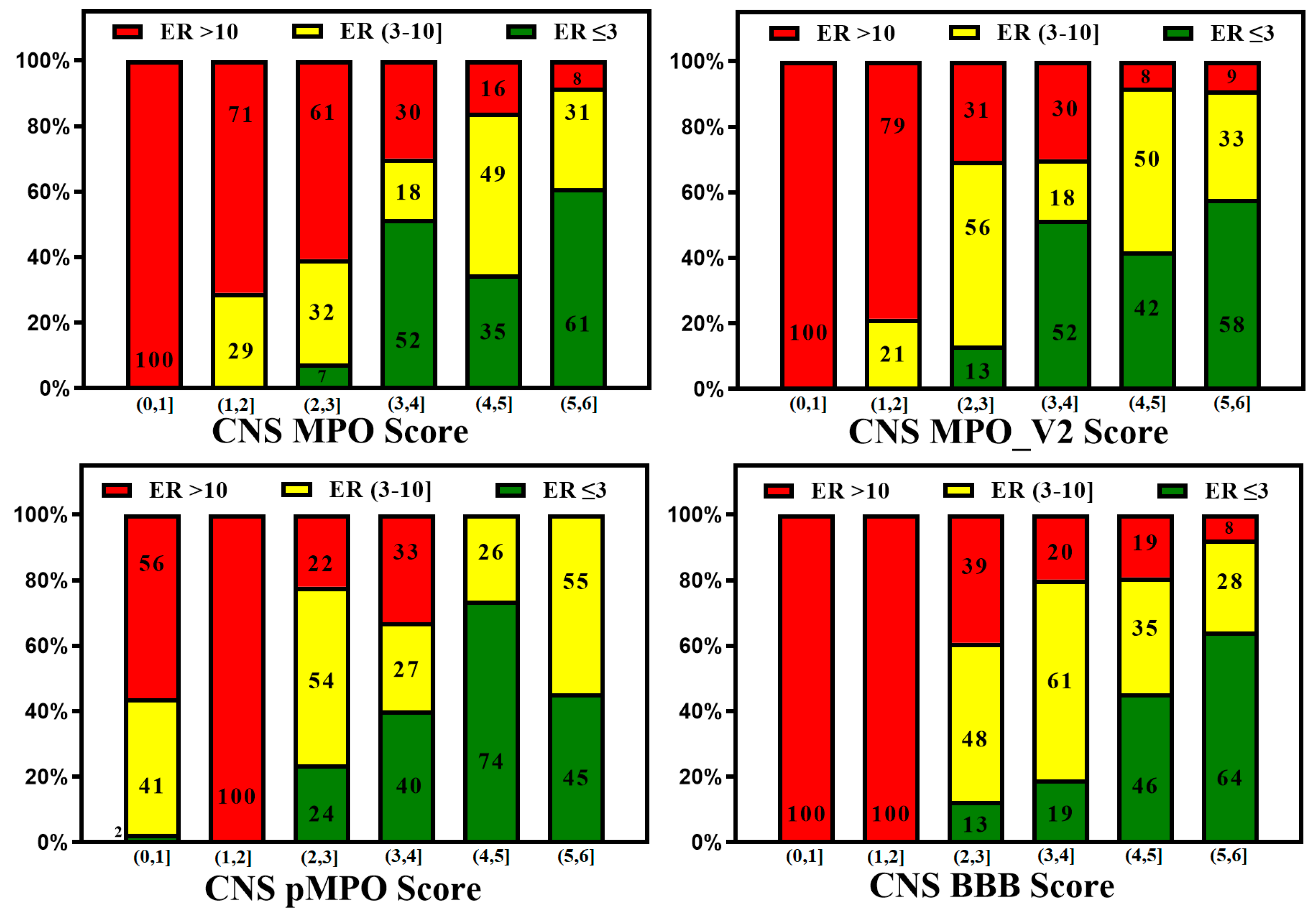
Figure 8.
100% stacked bar graphs for low to high MPO, MPO_V2, pMPO and BBB Scores for rat Kp,uu dataset. Compounds with a higher score tend to show higher unbound brain exposure.
Figure 8.
100% stacked bar graphs for low to high MPO, MPO_V2, pMPO and BBB Scores for rat Kp,uu dataset. Compounds with a higher score tend to show higher unbound brain exposure.
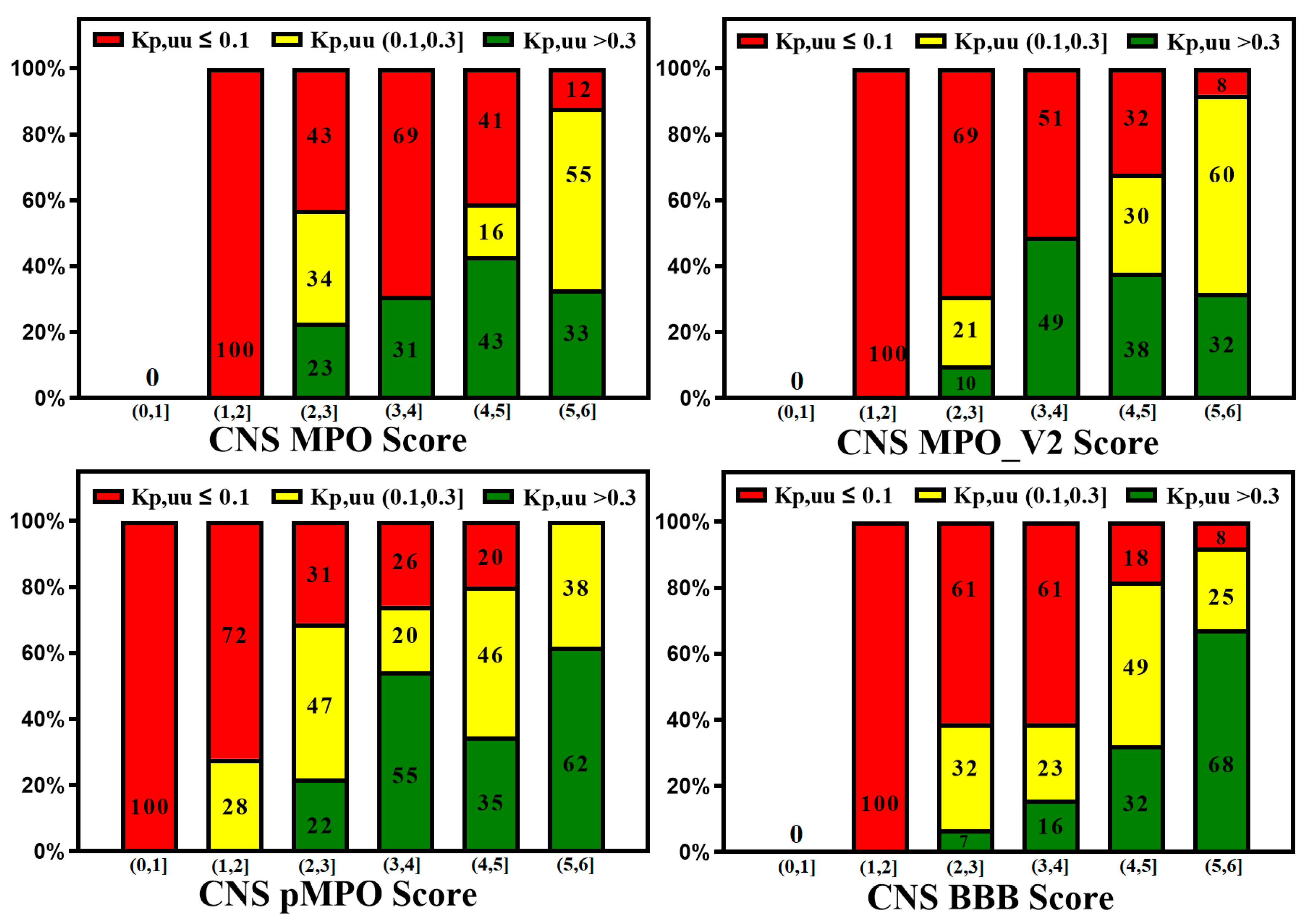
Figure 9.
The MDR1-MDCK in vitro assay predicts good in vivo Kp,uu when ER < 3. However, compounds with medium efflux (3-10) also show moderate in vivo brain exposure.
Figure 9.
The MDR1-MDCK in vitro assay predicts good in vivo Kp,uu when ER < 3. However, compounds with medium efflux (3-10) also show moderate in vivo brain exposure.
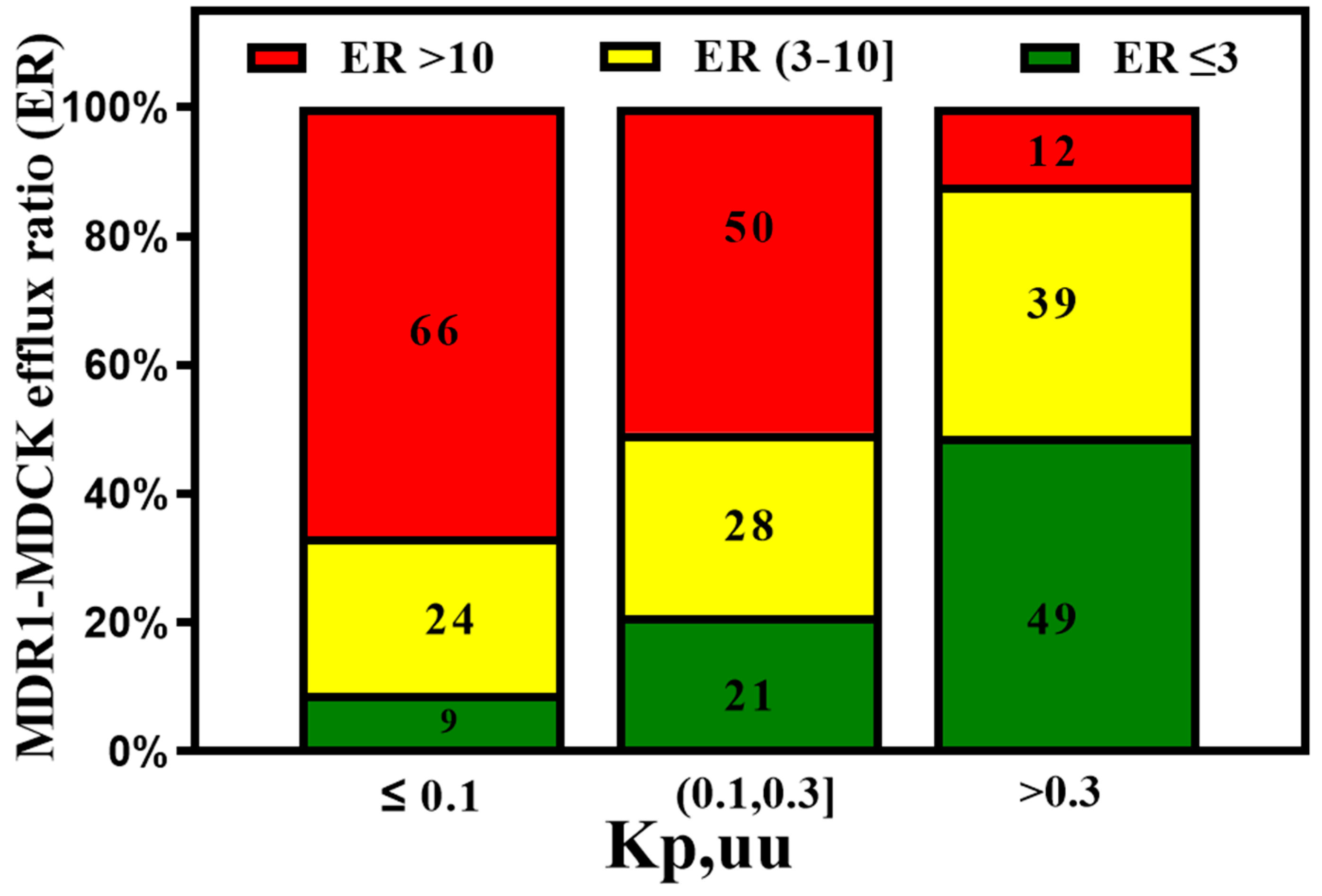
Figure 10.
The Kp,uu of preclinical species is an important parameter for predicting human brain exposure. Most of the CNS drugs show rat Kp,uu over 0.3.
Figure 10.
The Kp,uu of preclinical species is an important parameter for predicting human brain exposure. Most of the CNS drugs show rat Kp,uu over 0.3.
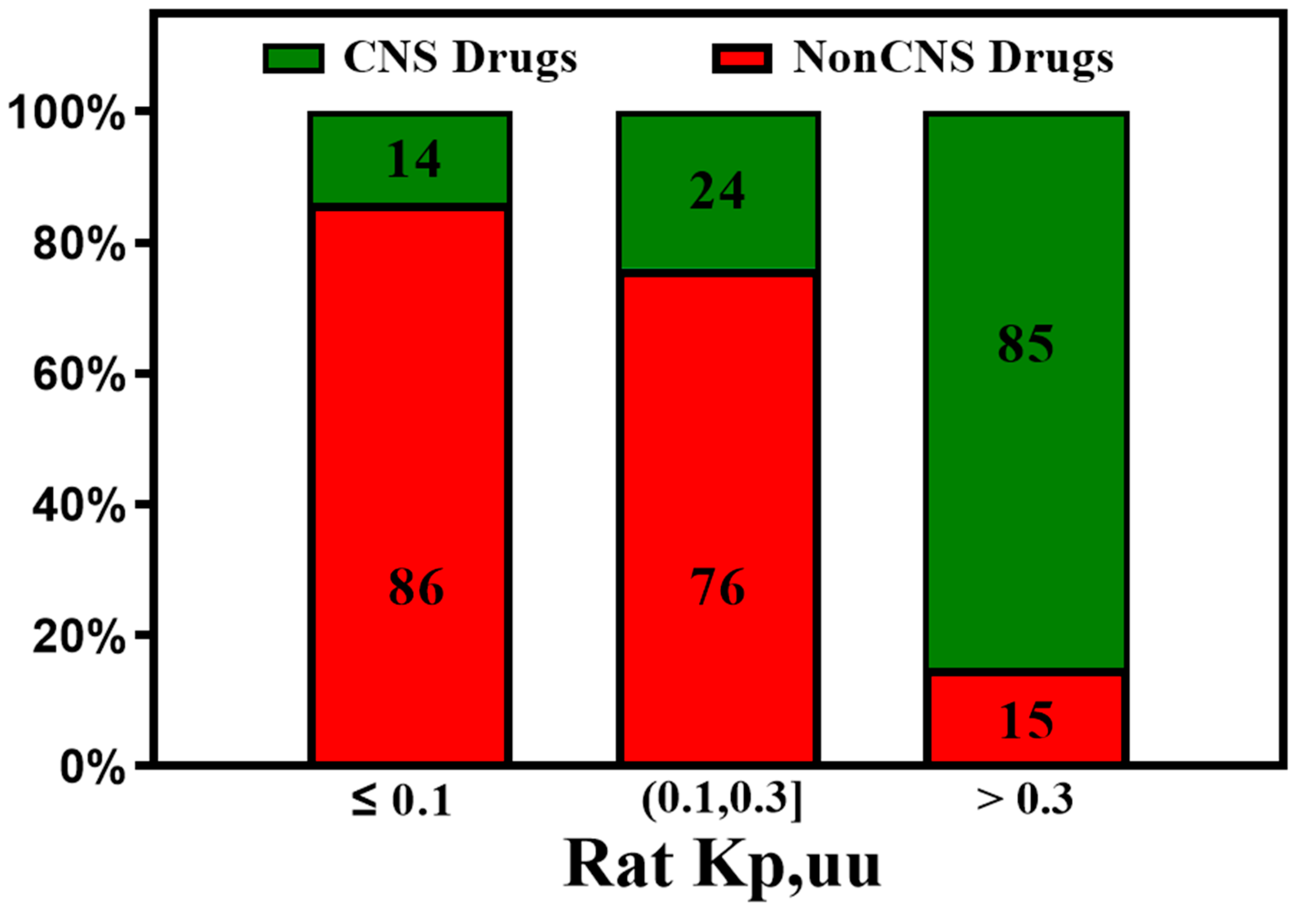
Table 1.
Mean (Range) of Physical Chemical Properties of CNS and Non-CNS Drugs (copied from Pajouhesh et al. [12]).
Table 1.
Mean (Range) of Physical Chemical Properties of CNS and Non-CNS Drugs (copied from Pajouhesh et al. [12]).
| Physical Chemical Properties | CNS | Non-CNS |
|---|---|---|
| Molecular weight | 319 (151–655) | 330 (163–671) |
| ClogP | 3.43* (0.16–6.59) | 2.78* (−2.81–6.09) |
| ClogD | 2.08 (−1.34–6.57) | 1.07 (−2.81–5.53) |
| PSA | 40.5 (4.63–108) | 56.1 (3.25–151) |
| Hydrogen bond donors | 0.85* (0–3) | 1.56* (0–6) |
| Hydrogen bond acceptors | 3.56 (1–10) | 4.51 (1–11) |
| Flexibility (rotatable bonds) | 1.27* (0–5) | 2.18* (0–4) |
| Aromatic rings | 1.92 (0–4) | 1.93 (0–4) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






