Prerpints.org logo
Preprint
Article

Revealing the Impact of Ga/Y Doping on the Thermal and Electrical Behavior in LaMnO3 Ceramics Materials

Altmetrics

Downloads

86

Views

22

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

18 January 2024

Posted:

19 January 2024

You are already at the latest version

Alerts
Abstract
In this work, we report a series of undoped and 1% Ga or Y doped lanthanum manganite compounds which have been synthesized via sol-gel technique. The obtained materials were characterized by X-ray diffraction (XRD), Fourier transform infrared spectroscopy (FT-IR), and scanning electron microscopy (SEM/EDX). The XRD results confirmed a good crystallinity for all the studied samples and a change in the crystal structure of Ga or Y doped lanthanum manganite (Pm-3m space group) is observed compared to pristine sample (R-3c space group). Thermal analysis highlighted a different behavior of the doped samples compared to the undoped sample observed by the different mass loss in the analyzed temperature range. For these materials, it is shown for the first time that the static electrical conductivity, σDC of Ga or Y doped LaMnO3 compounds increases compared to the σDC pristine sample, and the thermal activation energy of the conduction EA,cond increases linearly with the temperature, for all three studied sample.
Keywords: 
Subject: Chemistry and Materials Science  -   Ceramics and Composites

1. Introduction

Manganese oxides, that have perovskite-type structure with the chemical formula AMnO3 (where A = Ca, La, Sr, or Ba) were studied for more than seven decades [1] and Jonker and Van Santen in 1950, were the first to synthesize manganite of mixed valence (La1-xCaxMnO3) [2].
Mixed oxides of manganese and rare earth have been the objects of a investigation in interplaying among orbital, lattice, magnetism and transport properties in various R1-xAxMn1-yByO3 compounds (where R = rare earth; A = divalent cation; B = transition metal). Mn ions in the LaMnO3 system are trivalent and super exchange interaction exists through Mn+3–O–Mn+3 pathways [3]. Lanthanum manganese’s materials presents interesting electric, magnetic and structural properties [4,5,6] and furthermore the doped LaMnO3 have attracted considerable attention due to their improved properties required for different applications domains. These compounds have also been known as suitable cathode materials for fuel cells because of their good electrical conductivity, or chemical stability at high temperature [7].
Many techniques could be applied to synthesize undoped and doped LaMnO3 materials such as: sol-gel, hydrothermal, solid state reaction, the combustion method, or ultrasonically method with immersed sonotrode in the reaction medium [8,9,10,11,12].
By doping, the improving of semiconductors properties is enhanced, while it does not change the host crystal basic characteristics and structure by adding heteroatom’s into a target lattice. For example, in the case of Ga-doped LaMnO3 perovskite materials synthesized by conventional ceramic procedure, the Ga content increase determine a decrease of the transition pressure to the higher symmetry phases [13].
Previous reports on the perovskitic materials doped with various rare earths and transition metals, indicates the the influence of dopants on the materials properties. For example, the electrical conductivity is influenced by both the ionic radius of the dopant and its concentration as shown in [14] where for the studied perovskite materials, the electrical conductivity increases as the ionic radius of the used dopants decrease [14]. In this context, a detailed study carried out in the work herein, is based on the structural, thermal and electrical properties of undoped and Ga or Y doped lanthanum manganite synthesized by sol-gel technique. The dopant influence on the structural properties of LaMnO3 perovskite materials was investigated and for the first time their effect on the electric properties was shown through DC electrical conductivity measurements where Ga or Y ions in the LMO perovskite sample leads to an decrease of the EA,cond. Moreover, the VRH (variable-range-hopping) model of Mott was applied for explained the mechanism of conduction in these samples and comparative the Mott parameters were computed.

2. Materials and Methods

2.1. Materials and reagents

Ga/Y doped LaMnO3 and pure was prepared by sol-gel method [4], followed by heat treatment at low temperature. The chemical reagents used as starting materials are: La(NO3)3•6H2O, Mn(NO3)2•4H2O, Ga(NO3)3•x H2O / Y(NO3)3•6H2O and 2M NaOH solution. All reagents were of analytical grade and used as received without further purification.
For these precursors, the stoichiometric concentrations were initially calculated for each material and then were dissolved in a mixture of distilled water - ethyl alcohol (1:1). Finally, 1% gallium or yttrium dopant was added and the stirring was continued for another 30 minutes at 60 °C, after which the temperature was raised to 140 °C until the gels were obtained. The obtained powders were subjected to thermal treatment at a temperature of 600 °C, for 6h.

2.2. Characterization of materials

The X-ray powder diffraction (XRD) measurements were performed using a PANalytical diffractometer, with Cu-Kα radiations (λ = 0.15406 nm) in a 2θ range from 15° to 80°, with a scan rate of 2°/min in order to confirm the crystal structure of the ceramics.
Thermal behavior was conducted under a dynamic air atmosphere (synthetic air 5.0 Linde Gas with flow 100 mL min−1) to highlight possible thermal-oxidative degradation stability of samples. The measurements were determined using a Diamond TG/DTA PerkinElmer, in the temperature range 25–900 °C, at a heating rate of 10 °C min−1, using open alumina crucibles.
FT-IR studies were performed with a Shimadzu Prestige FT-IR spectrometer, in KBr pellets, in the range 500 - 4000 cm-1. Qualitative analysis of the surface was investigated by scanning electron microscopy, using an Inspect S PANalytical Scanning electron microscopy (SEM/EDX). The real (Z′) and imaginary (Z″) components of the complex impedance of the samples (where i = − 1 ), at a constant frequency, f=1 kHz and different temperatures situated between (28-120) 0C, were performed using a LCR-meter GW-INSTEK LCR-6020 type, in conjunction with an oven, in which a capacitor containing the sample is inserted [15], the experimental setup being similar to ASTM D150-98 [16].

3. Results and discussion

3.1. XRD analysis

The crystal structure analysis through XRD powder diffraction has been performed for all 3 compounds and as observed in Figure 1, the samples present a very good crystallinity as the peaks are sharp and well defined. The perovskite type structure is characteristic for the undoped LaMnO3 sample indexed in the R-3c space group (corresponding to JCPDS card file no. 01-089-0678). This structure has been reported also for other LaMnO3 materials obtained by sol-gel method [17,18]. The 1% Y3+ and Ga3+ doped LaMnO3 structure is inducing changing in the crystal structure as some of the peaks on the observed diffractograms are not splitted compared to the pristine compound (marked with symbols in Figure 1). Therefore, the 1% Ga and Y doped LaMnO3 samples are indexed with Pm-3m space group (JCPDS card file no. 01-075-0440). The refined unit cell parameters extracted for the perovskite samples by using R-3c space group (undoped LaMnO3 sample) and the Pm-3m space group (Ga/Y LaMnO3 samples) are indicated in Table 1.

3.2. Thermal analysis

The thermal analysis performed in the atmosphere of synthetic air in the range 25-900 ℃ revealed a different behavior of the samples, namely in the case of the undoped sample there is a mass loss of 2.13% of the sample mass in the range 25-689 ℃ and then a mass loss of 0.2% in the range 690-820 ℃. Also in this last interval, an exothermic process with an ΔH = -29.48 J ∙ g-1 is observed on the HF curve. In the case of the Ga doped LaMnO3 material, a mass loss of 5.11% of the sample mass is observed in the range of 25-600 ℃ and a mass loss of 2.8% over 600 ℃. This last decomposition process is accompanied by an exothermic process visible on the Heat Flow curve with a ΔH = -22.59 J ∙g-1. The Y doped LaMnO3 shows a higher mass loss than in the undoped and Ga-doped samples. In this case, the mass loss is 7.02% in the range of 25-600 ℃. Over 600 ℃ an exothermic process takes place with a ΔH = -27.15 J ∙g-1 and with a mass loss of 3.01% of the sample mass (Figure 2).

3.3. FT-IR spectroscopy

Figure 3 shows the FT-IR spectra for powder samples of undoped LaMnO3 and doped with Ga3+ or Y3+. The spectra were recorded in the of 400-4000 cm-1 wavenumber ranges. FT-IR spectra for LaMnO3 doped with Ga3+ or Y3+ ions have the same profile compared to the pristine sample and it was found that there are no new bonds for the two dopants transition elements. Thus, the most significant absorption bands are: 600, 850, 980, 1368, 1480 and 3400 cm−1. The absorption bands recorded around at 600 cm-1 for all samples can be attributed to vibrational modes for the bonds Mn-O-Mn bending and Mn-O stretching of the octahedral MeO6 group, associated to the length change of the metal-oxygen bonds, characteristic of perovskite compounds [19].
The two bands located at 1368 and 1480 cm-1 can be attributed to the presence of the CO2 molecule absorbed on the materials surface. The broad low-intensity peak with the maximum around 3400 cm-1 can be attributed for two kinds of OH- groups, such as O-H bonds assigned of the stretching modes of surface adsorbed water and an OH-group corresponding to the lattice connections [20].

3.4. Scanning electron microscopy

Surface morphology obtained by scanning electron microscopy for Ga or Y doped perovskite materials is presented in Figure 4. In order to highlight the shape and size of the particles, the studied materials were analyzed in the low vacuum mode. Thus, from the presented images it can be observed that in both cases the particles have a spherical shape, with dimensions of hundreds of nm, being strongly agglomerated. Furthermore, from the images presented in Figure 4, it can be seen that the nature of the dopant did not influence the shape of the particles.
Moreover, it has to be mentioned that quantitative analysis by EDX demonstrates that the samples are with the expected/determined elemental composition. The stoichiometry of the obtained samples was confirmed by the quantification of the elemental atomic ratio La:Mn:O i.e., 1:1:3. Thus, a homogeneous distribution of the corresponding La, Mn, O, Ga/Y elements in the synthesized samples was observed.

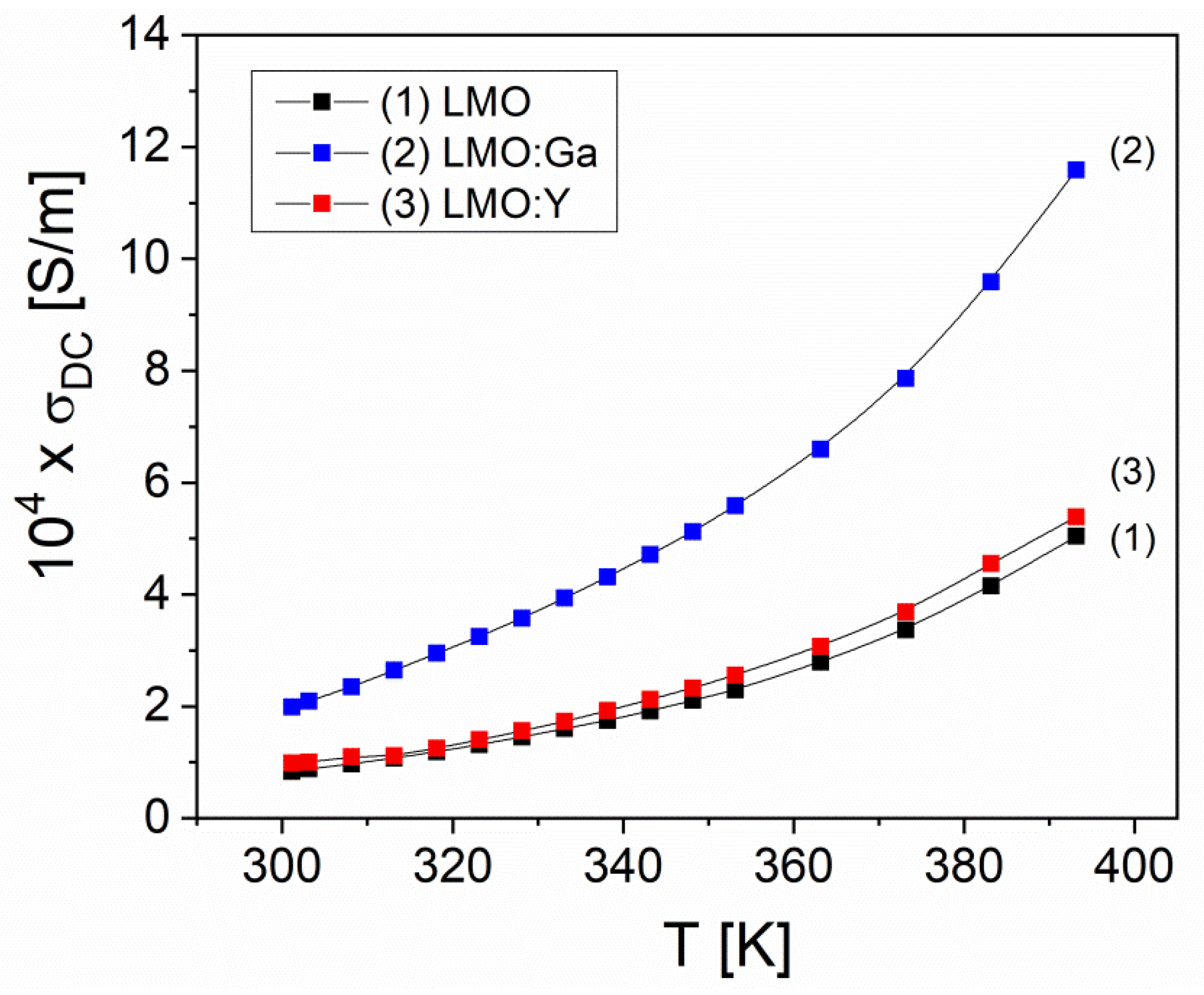
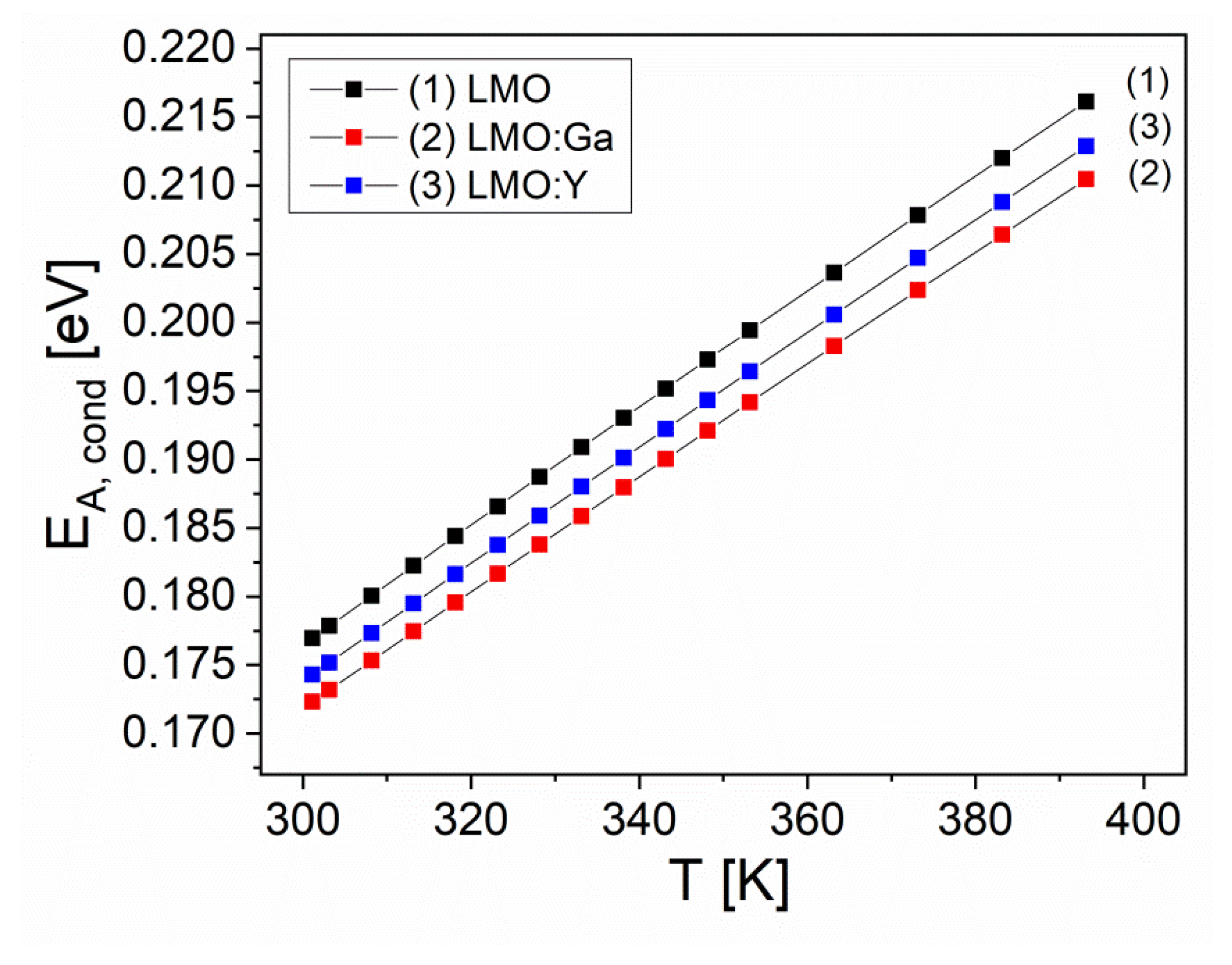
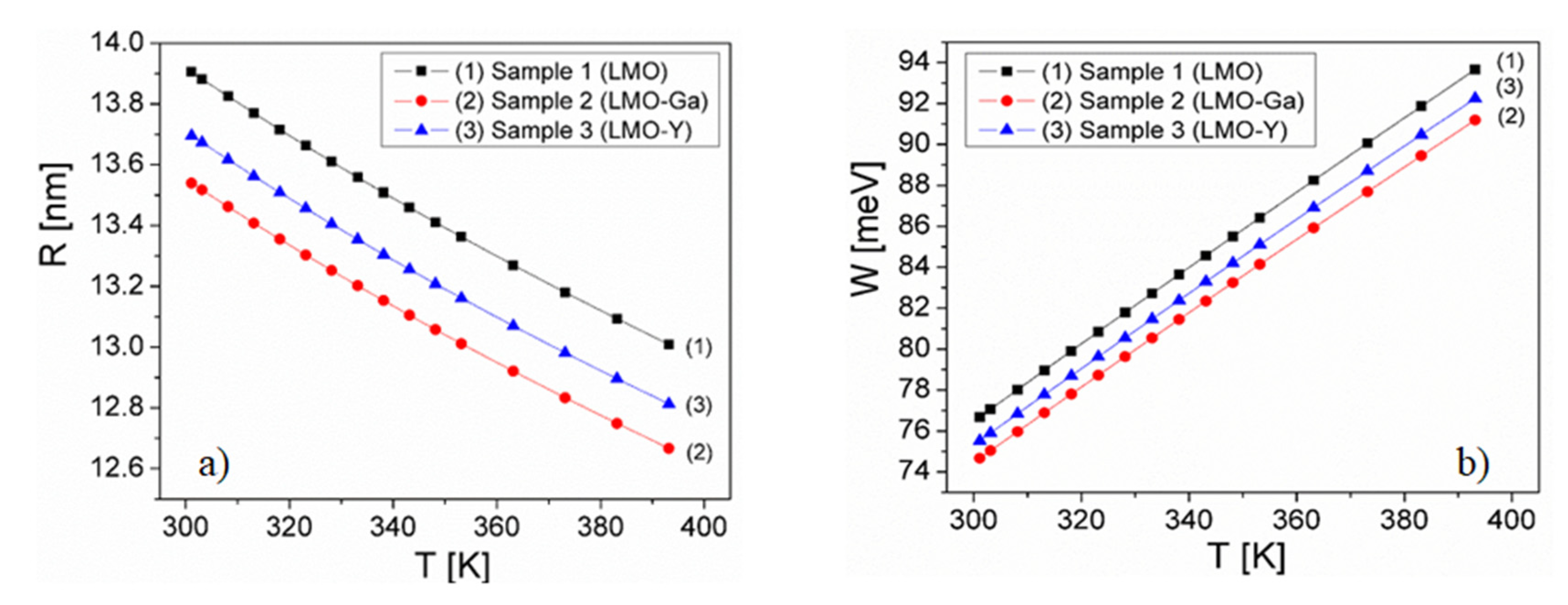
3.5. Electrical properties

Based on the obtained Z ′ and Z ″ values, the electrical conductivity σ, can be computed for each temperature T, with the following equation:
σ = Z ′ | Z * | 2 ⋅ d A
where d and A represent the length and the transversal sectional area of the sample, respectively, and | Z * | = Z ′ 2 + Z ″ 2 is the complex impedance module of the sample. It is known that [21] in the low frequency range, ( f ≤ 1   k H z ) the value σ determined by the relation (1) represents the DC-component of the electrical conductivity, σ D C ( T ) , independent on frequency but dependent on the temperature. Using the values obtained for the static conductivity, σDC, at all the measurement temperatures T and at the frequency f=1 kHz, we plotted the temperature dependence of static conductivity, σDC(T), shown in Figure 5, for all samples.
As can be seen in Figure 5, the static conductivity, σDC(T) increases with the temperature for all samples, indicating that the conduction process is thermally activated in the measurement temperature range (28–120) °C, at low frequency. The electrical conductivity of LMO:Ga and LMO:Y, respectively, is higher than that of LMO sample, which shows that the presence of rare earth ions of Ga3+ or Y3+ type in the LaMnO3 perovskite sample leads to an increase in the electrical conductivity of these samples, comparative with pristine sample (LMO). On the other hand, the substituted Ga3+ ions in the LaMnO3 perovskite crystal lattice behave as an acceptor dopant replacing the Mn3+ ions in the octahedral B-site [22], which leads to the compensation of the charge imbalance by their oxidation. As a result, gallium doping slightly reduces the octahedral distortion and weakens the Jahn-Teller effect by highlighting electronic correlations [23,24], which will determine a higher increase in the electrical conductivity [25] of the LMO system doped with Ga ions, as can be observed in Figure 5. The Yttrium ions replace the lanthanum ions in the tetrahedral A-site of LMO perovskite crystal lattice [26] as a result the Yttrium substitution decreases the average ionic size at La-site, which has an effect the distortion of the MnO6 octahedra. Thus, the Mn3+–O–Mn4+ bond angle deviates from the ideal 180°, which leads to a reduction of the hopping probability of the electron between Mn3+/Mn4+ ions [27], which will determine a smaller increase in the electrical conductivity of the LMO system doped with Y ions, as was obtained experimentally (see Figure 5).
Also, the increase with temperature of the σDC, is due to the increase of drift mobility of the charge carriers from the sample, in accordance with Mott’s model VRH (variable-range-hopping) [28]. Such a behavior with temperature of the conductivity σDC(T), has also been observed for other perovskite materials, such as NaTaO3 undoped [29] or doped with metallic ions (Ag, Fe, Cu) [11,30,31], which shows the fact as the most suitable electrical conduction mechanism in these materials is the VRH mechanism. Consequently, the σDC(T) conductivity based on the VRH model is given by the equation:
σ D C = σ 0 exp [ − B ( T ) 1 / 4 ]
where σ0 is the pre-exponential factor and,
B = 4 E A , c o n d k T 3 / 4
In Eq. (3) k is the Boltzmann constant and EA,cond is the thermal activation energy of electrical conduction [28]. Using Eq. (2) and the σDC(T) conductivity values from Figure 5, we plotted the experimental dependence, lnσDC (T-1/4), which is shown in Figure 6.
By fitting with a straight line of the experimental dependence, ln σDC (T−1∕4) from Figure 6, we have determined the slope B corresponding to each sample. Knowing the slope B, the thermal activation energy of electrical conduction, EA,cond, on the investigated temperature range, was determined with Eq. (3). The temperature dependence of the EA,condn (T), is shown in Figure 7.
As can be observed from Figure 7, EA,cond increases linearly with the temperature, in all the investigated range, from 0.177 eV to 0.218 eV for sample 1 (LMO), from 0.175 eV to 0.213 eV for LMO:Ga sample and from 0.172 eV to 0.210 eV for LMO:Y sample. As a result, the presence of rare earth ions Ga3+ or Y3+ type in the LMO perovskite sample leads to a decrease of the thermal activation energy of electrical conduction, corresponding to these samples (LMO:Ga and LMO:Y), compared to LMO sample, thus determining the increase in conductivity in doped materials, in relation to the electrical conductivity of the undoped sample, as to obtained experimentally (see Figure 5). The mechanism of electrical conduction in the investigated samples can be explained by a hopping process of the charge carriers between the localized states [28,32] on the temperature range, through which σDC(T), with another relationship can be expressed:
σ D C ( T ) = σ 0 exp [ − ( T 0 / T ) 1 / 4 ]
Here, T0 is characteristic temperature coefficient, which represents a measure of the degree of disorder [28], being given by the relation:
T 0 = λ a 3 k N ( E F )
where, λ ≅16.6, is a dimensionless constant [28]; α ≅109 m-1 represents the degree of localization and N(EF) is the density of the localized states at the Fermi level EF [22,33]. From Eqs. (2–5), after some calculations the following relation for the N(EF), result:
N ( E F ) = λ ( a k T ) 3 ( 4 E A , c o n d ) 4
Using the values obtained for EA,cond (T) from Figure 7 and Eq. (6), we computed N(EF) from the temperature range (28-120) °C at a low frequency (f = 1 kHz), for all three samples, obtaining the following values: N(EF)S1=1.158͘˴1018 cm-3˴eV-1, N(EF)S2=1.288͘˴1018 cm-3˴eV-1 and N(EF)S3=1.231˴1018 cm-3˴eV-1. The obtained result shows that the density of states at the Fermi level N(EF), does not depend on the temperature remaining constant on the whole investigated domain, as to shown recently in the papers [34,35], for other oxide materials (Fe-P or Cu-Mn type). Also, it is observed that the value of N(EF) for LMO is lower than the values N(EF), obtained for LMO:Ga and LMO:Y which contain rare earth ions (Ga and Y, respectively), in the investigated temperature range. This result is in agreement with the fact that the thermal activation energy of electrical conduction, EA,cond of doped materials is smaller than EA,cond of LMO sample (see Figure 7). As a result we advance the statement that the decreasing of EA,cond leads to an increase of the density of states at Fermi level N(EF) and to explain this statement, it is necessary to determine two other Mott parameters corresponding to the VRH model: the hopping distance, R and the hopping energy W, with the relations [28,33]:
R = ( 9 8 α k T N ( E F ) ) 1 / 4
W = 3 4 π R 3 N ( E F )
From equation (7), using the values of , we have determined the hopping distance, R, corresponding to the samples, at each temperature within the range (28 – 120) 0C. Knowing the hopping distance R and using equation (8) we have determined the hopping energy W, for studied samples. The temperature dependencies of the Mott parameters R and W, corresponding to the investigate samples, are shown in Figure 8.
From Figure 8, it is observed that by increasing of temperature, the hopping distance R decreases with (Figure 8 a)) and the hopping energy W increases (Figure 8 b)), for all the investigated samples. Also, both R and W for the LMO sample, are higher than for the LMO:Ga and LMO:Y, at all the temperatures. This result is in agreement with our previous statement on the increase of density of states at Fermi level N(EF) of the modified samples which contain rare earth ions (Ga and Y, respectively) due to the decrease of R and W, in these samples compared to R and W of LMO material, thus causing a decrease in the thermal activation energy of conduction EA,cond of Ga or Y doped LaMnO3 relative to EA,cond, of undoped LaMnO3.
Following these promising results observed for the lanthanum manganite compounds it can be assessed that more studies are needed to determine their potential as candidates for energy conversion, metal–air battery or fuel cell electrodes owing to their unique physical and electronic properties.
Taking into account the obtained results namely that the electrical and structural properties of the synthesized Ga or Y doped LaMnO3 ceramics powders can be changed by design and of the temperature variation, demonstrate the potential of these materials can be used in thermo-electric devices and sensors applications.

4. Conclusions

In this paper, we have studied the structural, thermal and electrical properties of undoped and Ga or Y doped lanthanum manganite, synthesized through sol-gel technique, in its R-3c space group (pristine LaMNO3) and Pm-3m space group (1% Y and Ga doped in LaMnO3). The results of the DC electrical conductivity show that in the presence of the Ga or Y ions of in the LMO perovskite material, the static electrical conductivity, σDC of these samples, increases compared to the σDC of the LMO perovskite sample, due increasing of the drift mobility of the charge carriers from the samples, in accordance with Mott’s VRH model. Moreover, the thermal activation energy of the conduction EA,cond, increases linearly with the temperature, for all three samples, but the presence of Ga or Y dopants in the LMO perovskite sample leads to an decrease of the EA,cond, corresponding to these samples (LMO:Ga and LMO:Y), compared to pristine sample (LMO). Based on the VRH model, the following parameters were determined: the density of localized states near the Fermi level N(EF), the hopping distance, R and the hopping energy W, for all samples. The results show that, N(EF) remains constant over the entire temperature range investigated, but the presence of rare earth Ga or Y ions in LMO material, leads to the decrease of N(EF), in these sample in raport with N(EF), from the LMO sample. At the same time, by increasing the temperature, R decreases and W increases for all samples, and at a constant temperature, both R and W decreases, in the presence of Ga or Y ions in LMO material, being in correlation with the decrease of the EA,cond, of doped samples in raport to EA,cond, of the undoped sample.

Author Contributions

Conceptualization, P.V. and P.S. ; methodology, P.V. and P.S.; validation, P.V.,M.P. and P.S.; formal analysis, P.V.,M.P., I.M., C.N.M, G.V., T.V. and P.S.; investigation P.V.,M.P., I.M., C.N.M, G.V., T.V. and P.S.; writing—original draft preparation, P.V.,M.P and P.S.; supervision, P.V.; project administration, P.S. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

The data presented in this study are available on request from the corresponding author.

Acknowledgments

This work was supported by the Experimental Demonstrative Project 683 PED/2022- Executive Unit for Financing Higher Education, Research, Development and Innovation (UEFISCDI).

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. G. Jonker, J. Van Santen, Physica 16, 337(1950).
  2. I. Koriba, B. Lagoun, A. Guibadj, S. Belhadj, A. Ameur, A. Cheriet, Comput. Condens. Matter 29 592 (2021).
  3. S. Punna Rao, K. Suresh Babu, Mater. Chem. Phys. 272 125021(2021).
  4. P. Sfirloaga, M. Poienar, I. Malaescu, A. Lungu, C.V. Mihali, P. Vlazan, Ceram. Int. 44 5823(2018).
  5. P. Sfirloaga, M.Poienar, I. Malaescu, A. Lungu, P.Vlazan, J. Rare Earth 36 499-504(2018).
  6. P. Sfirloaga, G.Vlase, T. Vlase, I. Malaescu, C. N.Marin,P.Vlazan, J. Therm. Anal. Calorim. [CrossRef]
  7. T. H. Tran, T. C. Bach, N. H. Pham, Q. H.Nguyen, C. D. Sai,H. N. Nguyen, V. T. Nguyen, T. T. Nguyen, K. H. Ho,Q. K. Doan, Mat. Sci. Semicon. Proc. 89121 (2019).
  8. A.G. Merzhanov, Int. J. Self-Propag. High. -Temp. Synth. 2 113 (1993).
  9. V.A. Shcherbakov, A.S. Shteinberg, Combust. Sci. Technol. 107 21 (1995).
  10. P. Sfirloaga, M. Poienar, I. Malaescu, A. Lungu, C.V. Mihali, P. Vlazan, Ceram. Int. 44 5823 (2018).
  11. P. Sfirloaga, I. Sebarchievici, B.Taranu, M.Poienar, G. Vlase, T. Vlase, P. Vlazan, J. Alloys Compd.843 155854 (2020).
  12. P. Sfirloaga, C.N. Marinb, I. Malaescu, P. Vlazan, Ceram. Internat. 42 16 18960 (2016).
  13. L. Malavasi, M. Baldini, D. di Castro, A. Nucara, W. Crichton, M. Mezouar, J. Blasco and P. Postorino, J . Mater. Chem. 20 1304 (2010).
  14. S. Hui and A. Petric, J. Electrochem. Soc. 149 J1 (2002).
  15. A. Lungu, I. Malaescu, C. N. Marin, P. Vlazan, P. Sfirloaga, Phys. B: Condens. Matter 462 80 (2015).
  16. ASTMD 150-98 – Standard Test Methods for AC Loss Characteristics and Permittivity (Dielectric Constant) of Solid Electrical Insulation.
  17. E. Hernandez, V. Sagredo and G.E. Delgado, Synthesis and magnetic characterization of LaMnO3 nanoparticles, Rev. Mex. de Fis61 166 (2015).
  18. A.Ansari, N. Ahmad, M. Alam, S. F.Adil, S. M. Ramay,A. Albadri, A. Ahmad, A. M.Al-Enizi, B. F. Alrayes,M. E.Assal and A. A.Alwarthan, Sci. Rep. 9 7747(2019).
  19. S. Daengsakul, C. Mongkolkachit, C. Thomas, I. Thomas, S. Siri,V.Amornkitbamrung, S. Maensiri, J. Optoelectron. Adv. Mat. -Rapid Commun.3 106 (2009).
  20. A.A. Aal, T.R. Hammad, M. Zawrah, I.K.Battisha and A.B. A. Hammad, Acta Phys. Pol. A 126 1318 (2014).
  21. A. K. Jonscher, Universal Relaxation Law, 1st edn. (Chelsea Dielectrics Press, London, 1996) 198–200.
  22. S. Lafuerza, G. Subias, J. Garcıa, S. Di Matteo, J. Blasco, V. Cuartero, C. R. Natoli, J. Phys.: Condens. Matter 23 325601 (8pp) (2011).
  23. M. C. Sanchez et al., Phys. Rev. B 73 094416 (2006).
  24. J. S. Zhou and J. B. Goodenough, Phys. Rev. B 68 144406 (2003).
  25. A. Fondado, J. Mira, J. Rivas, C. Rey, M. P. Breijo, and M. A. Señarı́s-Rodrı́guez, J. Appl. Phys. 87 5612 (2000).
  26. S. Taran, et al., J. Alloys Compd. 644 363–370 (2015).
  27. M. Sangeetha, V. Hari Babu, J. Magn. Magn. Mater. 389 5–9 (2015).
  28. N.F. Mott, E.A. Davis, Electronic Process in Non-Crystalline Materials, 2nd edn. (Clarendon Press, Oxford, 1979) 32–37.
  29. D. Malaescu, I. Grozescu, P. Sfirloaga, P. Vlazan, C. N. Marin, Acta Phys. Pol. A 129133 (2016).
  30. P. Sfirloaga, I. Miron, I. Malaescu, C. N. Marin, C. Ianasi, P. Vlazan, Mat. Sci. Semicon. Proc. 39 721 (2015).
  31. P. Sfirloaga, I.Malaescu, M. Poienar, M. C. Nicolae, D. Malaescu, P. Vlazan, J. Mater. Sci: Mater. Electron.27 11640 (2016).
  32. R.M. Hill, Philos. Mag. 241307 (1971).
  33. E.A. Davis, N.F. Mott, Philos. Mag. 220903 (1970).
  34. S. Brindusoiu, M. Poienar, C. N. Marin, P. Sfirloaga, P. Vlazan, I. Malaescu, J. Mater. Sci. Mater. Electron. 30 15693 (2019).
  35. I. Malaescu, A. Lungu, C.N. Marin, P. Sfirloaga, P. Vlazan, S. Brindusoiu, M. Poienar, Ceram. Int. 411610 (2018).
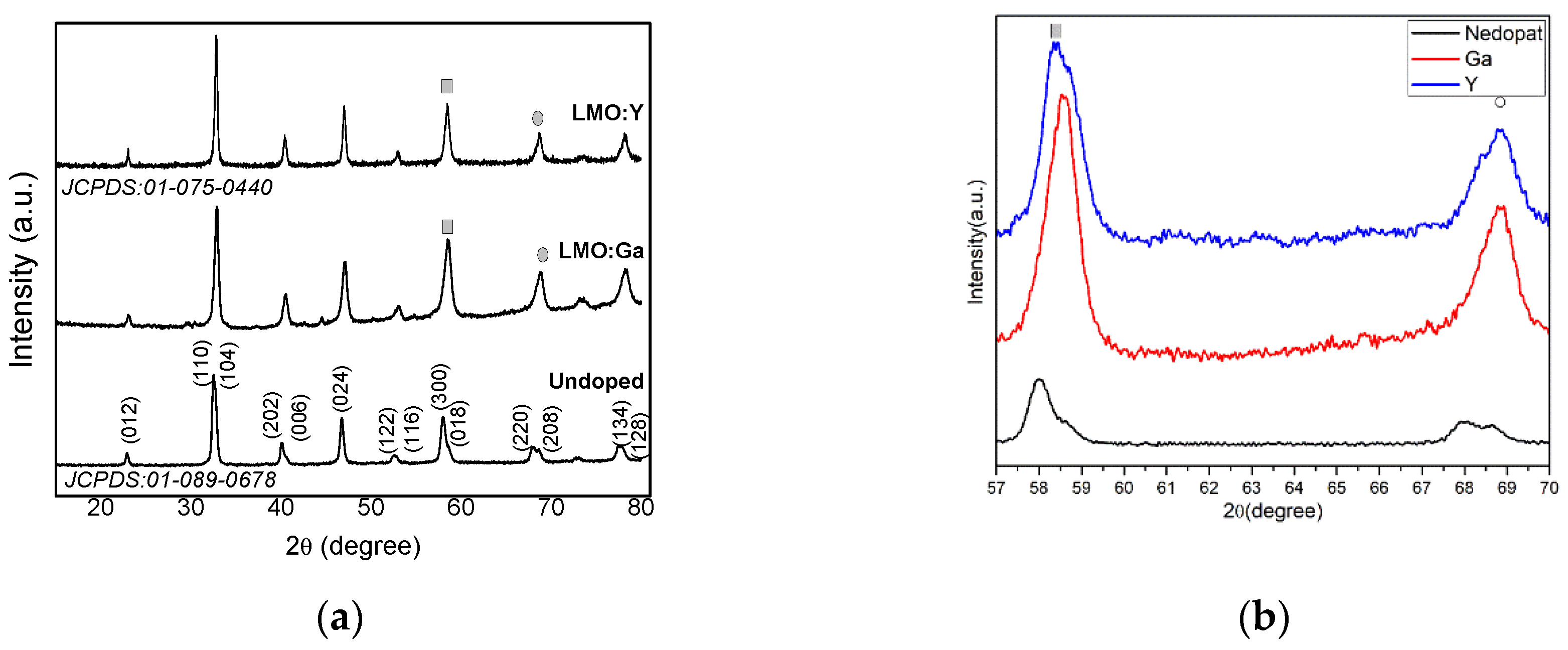
Preprints 96744 g001
Figure 1. (a) X-ray patterns for undoped and Ga or Y doped LaMnO3 materials synthesized by sol-gel technique. The hkl planes for the cubic structure with Pm-3m space group in the case of Ga or Y doped in LMO according to JCPDS card no. 01-4075 -0440 and for R-3c space group in the case of pristine LaMnO3 according to JCPDS:01-089-0678 are marked on the graph; (b) The X-Ray patterns in the 2θ=57-70 ° range.
Figure 1. (a) X-ray patterns for undoped and Ga or Y doped LaMnO3 materials synthesized by sol-gel technique. The hkl planes for the cubic structure with Pm-3m space group in the case of Ga or Y doped in LMO according to JCPDS card no. 01-4075 -0440 and for R-3c space group in the case of pristine LaMnO3 according to JCPDS:01-089-0678 are marked on the graph; (b) The X-Ray patterns in the 2θ=57-70 ° range.
Preprints 96744 g001
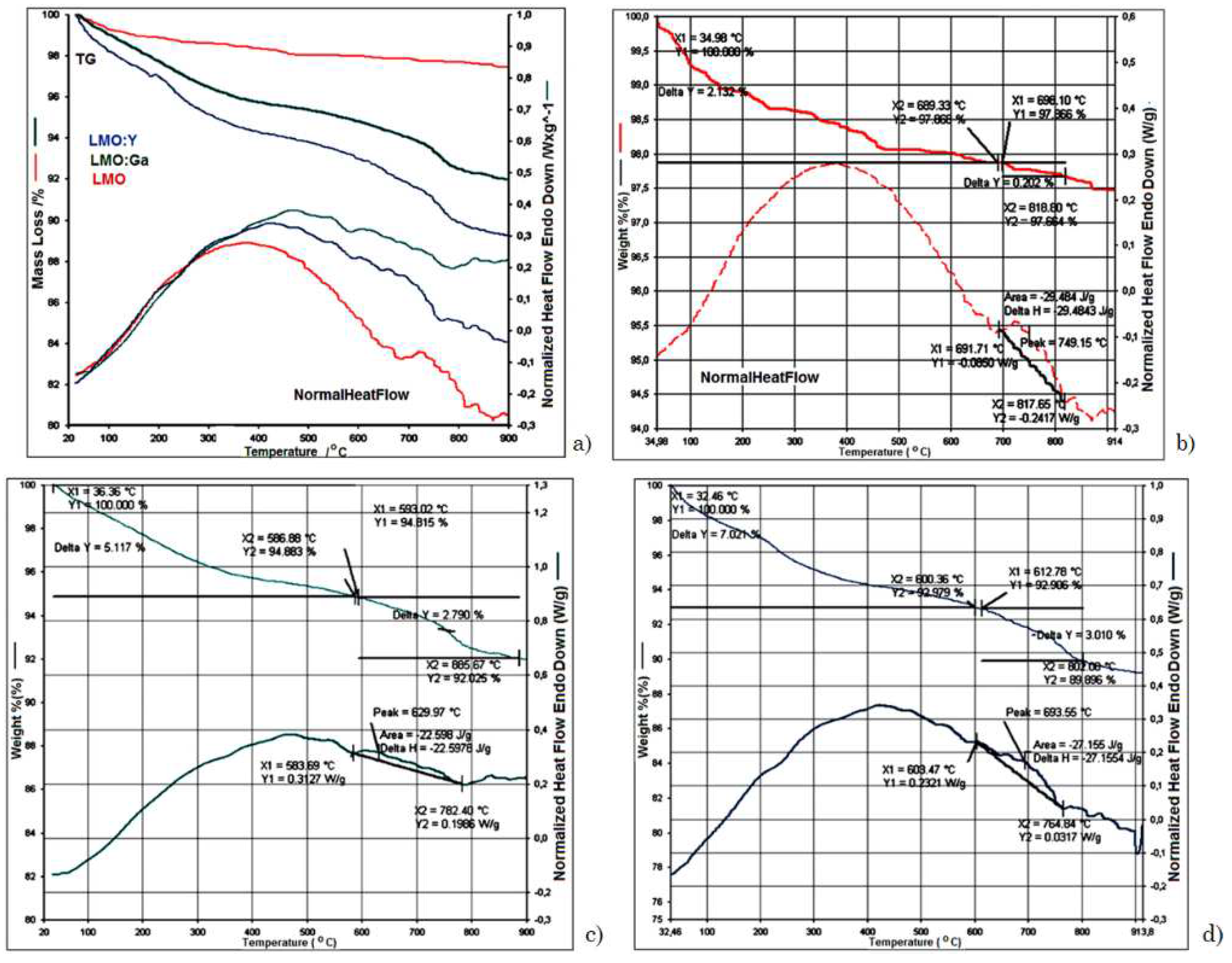
Preprints 96744 g002
Figure 2. TG/DTG curves for undoped and Ga or Y doped LaMnO3 materials.
Figure 2. TG/DTG curves for undoped and Ga or Y doped LaMnO3 materials.
Preprints 96744 g002
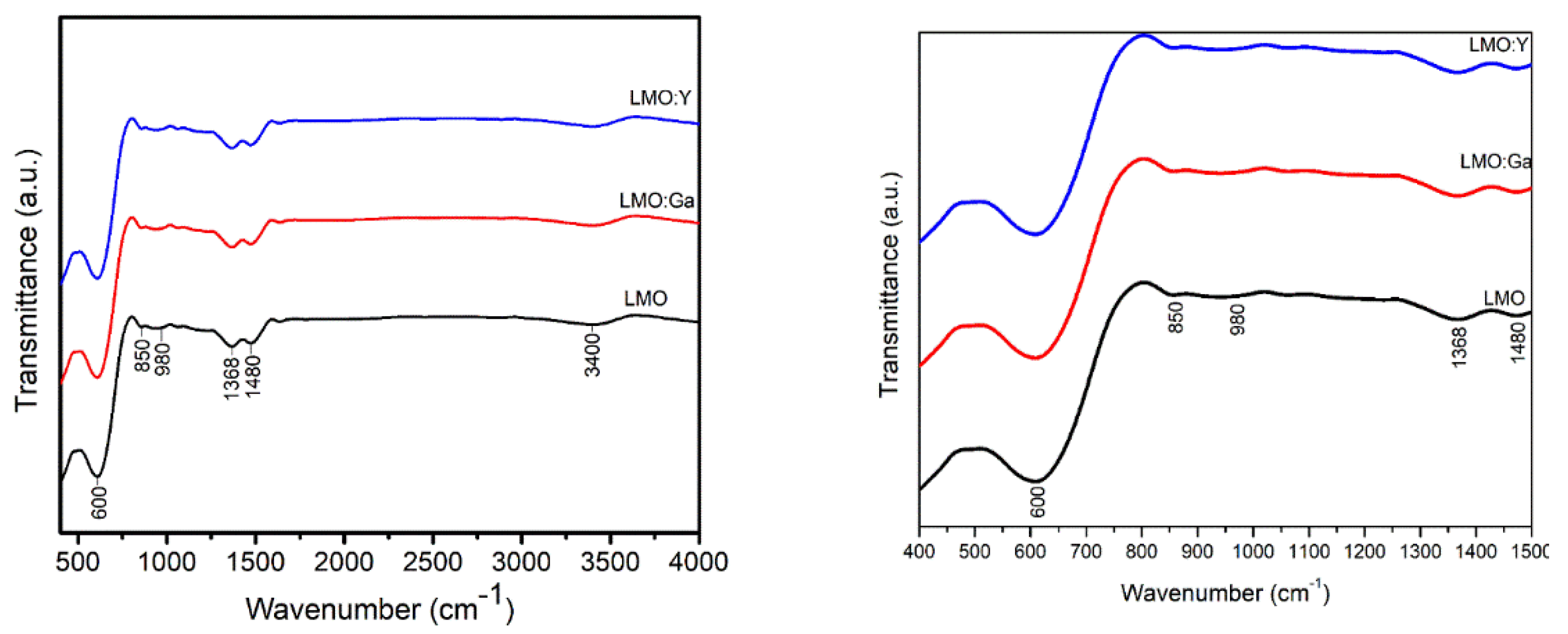
Preprints 96744 g003
Figure 3. (a) FT-IR spectra for undoped and Ga or Y doped LaMnO3 synthesized by sol-gel technique, where the significant absorption bands are marked on the graph. (b) The zoom for the FT-IR spectra in the 400-1500 cm-1 range.
Figure 3. (a) FT-IR spectra for undoped and Ga or Y doped LaMnO3 synthesized by sol-gel technique, where the significant absorption bands are marked on the graph. (b) The zoom for the FT-IR spectra in the 400-1500 cm-1 range.
Preprints 96744 g003
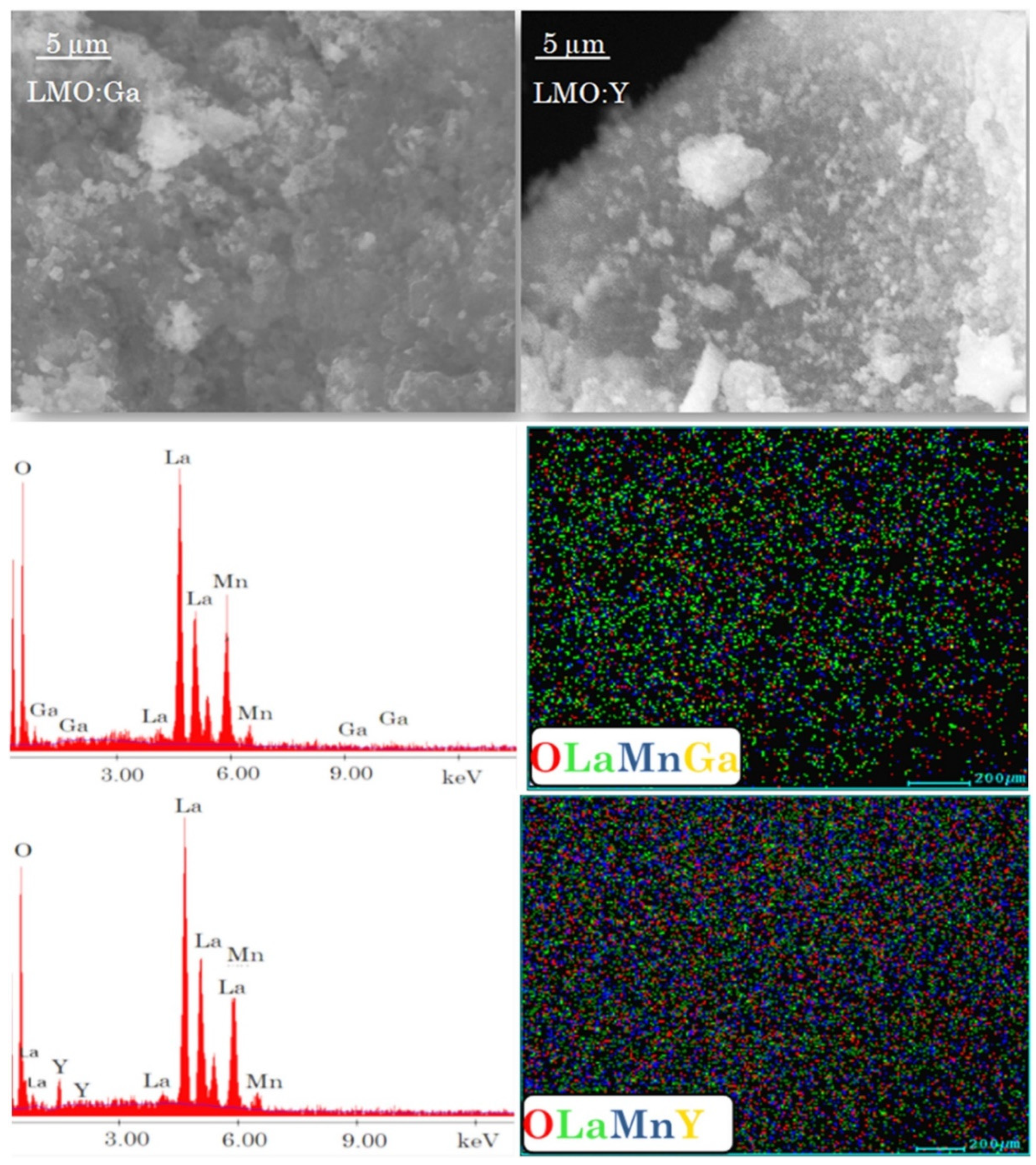
Preprints 96744 g004
Figure 4. SEM images and EDX/ element mapping of LMO:Ga and LMO:Y perovskite materials.
Figure 4. SEM images and EDX/ element mapping of LMO:Ga and LMO:Y perovskite materials.
Preprints 96744 g004
Preprints 96744 g005
Figure 5. Temperature dependence of static conductivity, σDC(T) at the frequency.of 1 kHz for the investigated samples.
Figure 5. Temperature dependence of static conductivity, σDC(T) at the frequency.of 1 kHz for the investigated samples.
Preprints 96744 g005
Preprints 96744 g006
Figure 6. Plot of ln σDC(T−1∕4) for investigated samples at frequency f=1kHz.
Figure 6. Plot of ln σDC(T−1∕4) for investigated samples at frequency f=1kHz.
Preprints 96744 g006
Preprints 96744 g007
Figure 7. The temperature dependence of the thermal activation energy of.the electrical conduction corresponding to all samples.
Figure 7. The temperature dependence of the thermal activation energy of.the electrical conduction corresponding to all samples.
Preprints 96744 g007
Preprints 96744 g008
Figure 8. The temperature dependence of the hopping distance R (a) and of the.hopping energy W (b) corresponding to all samples.
Figure 8. The temperature dependence of the hopping distance R (a) and of the.hopping energy W (b) corresponding to all samples.
Preprints 96744 g008
Table 1. The refined unit cell parameters for undoped LaMnO3 (R-3c space group) and Ga/Y doped LaMnO3 (in Pm-3m space group) samples.
Table 1. The refined unit cell parameters for undoped LaMnO3 (R-3c space group) and Ga/Y doped LaMnO3 (in Pm-3m space group) samples.
Sample Space group Lattice parameter Unit Cell Volume Crystallite size
[Å] [Å3] [nm]
LaMnO3 R-3c a= b= 5.4749(5)
c = 13.327		 345.9341 25.8
LaMnO3ːGa Pm-3m a=b=c=3.8677(7) 57.8584 17.3
LaMnO3ːY Pm-3m a=b=c=3.8687(4) 57.9007 26.8
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated