Prerpints.org logo
Preprint
Article

Multi-Spectral Band-Aware Generation of Satellite Images Across Domains Using Generative Adversarial Networks and Contrastive Learning

Altmetrics

Downloads

112

Views

53

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

18 January 2024

Posted:

19 January 2024

You are already at the latest version

Alerts
Abstract
Generative models have recently gained popularity in Remote Sensing, offering substantial benefits for interpreting and utilizing satellite imagery across diverse applications such as climate monitoring, urban planning, and wildfire detection. These models are particularly adept at addressing the challenges posed by satellite images, which often exhibit domain variability due to seasonal changes, sensor characteristics, and especially variations in spectral bands. Such variability can significantly impact model performance across various tasks. In response to these challenges, our work introduces a novel approach that harnesses the capabilities of Generative Adversarial Networks (GANs), augmented with Contrastive Learning, to generate target domain images that account for multi-spectral band variations effectively. By maximizing mutual information between corresponding patches and leveraging the power of GANs, our model aims to generate realistic-looking images across different multi-spectral domains. We present a comparative analysis of our model against other well-established generative models, demonstrating its efficacy in generating high-quality satellite images while effectively managing domain variations inherent to multi-spectral diversity.
Keywords: 
Subject: Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

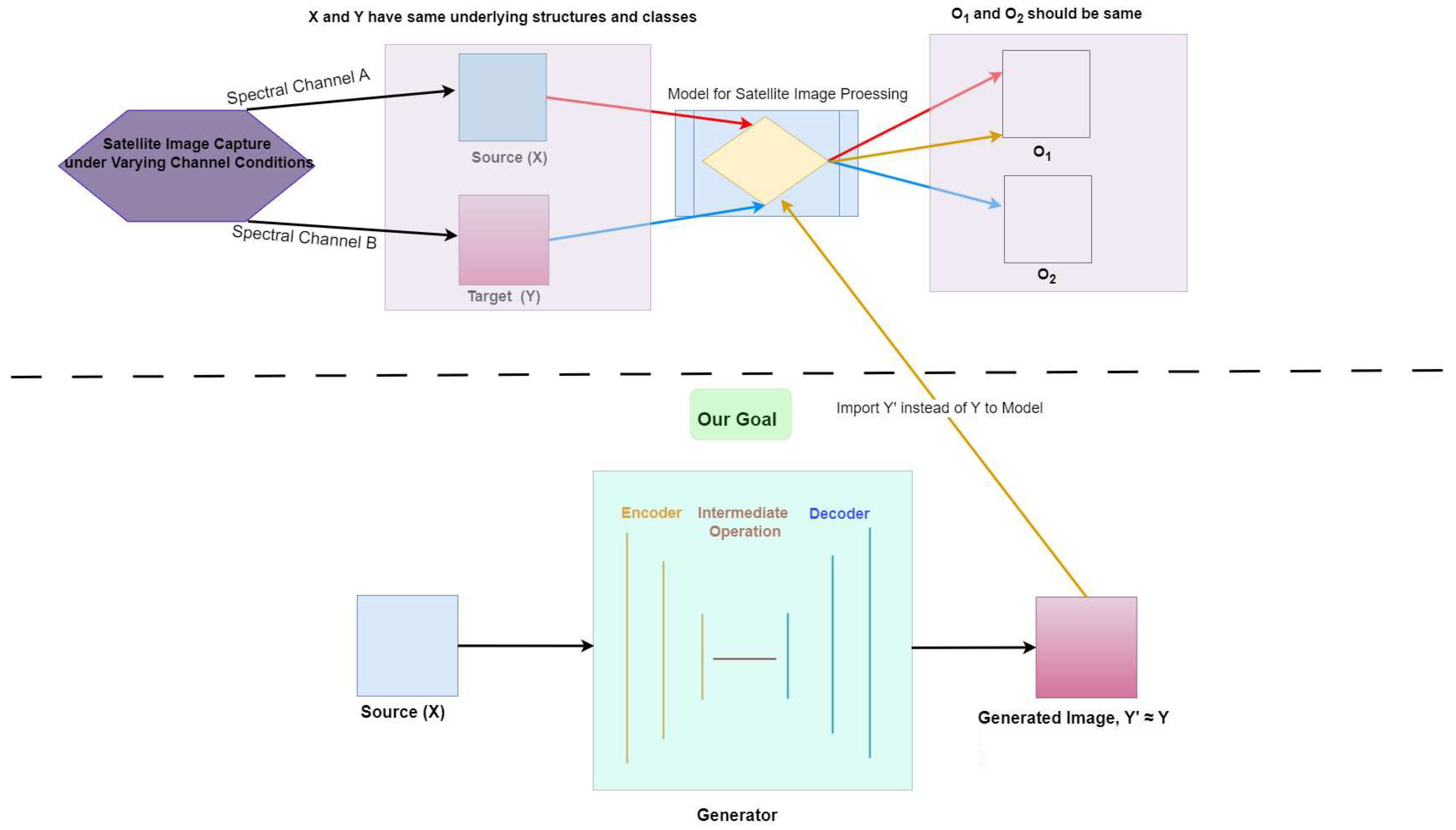
1. Introduction

The field of Remote Sensing is a focal area of research with profound impacts on various aspects of human life, including environmental monitoring, urban planning, and disaster management. Advancements in Remote Sensing technologies, particularly the use of satellite imagery, have transformed our ability to observe and understand the Earth’s geographical features. However, the effectiveness of Remote Sensing applications often depends on the quality and consistency of satellite images, which can vary significantly across different spectral bands and sensors. Satellite images captured under different environmental conditions or with different sensors exhibit inherent feature variations, leading to domain differences [1]. These variations are particularly noticeable across different multi-spectral bands, where each band captures specific wavelength ranges of the electromagnetic spectrum. Such domain variability introduces challenges in applying machine learning models, such as classification and semantic segmentation, which are sensitive to the input data distribution [2]. Deep learning methods, important for the detailed analysis and interpretation of satellite images, are particularly susceptible to performance degradation due to domain variability. For instance, a semantic segmentation model trained on satellite images from one spectral band or sensor configuration may underperform when applied to images from a different spectral band or sensor, even if the underlying geographical features and structures are similar [3]. A similar problem can arise in classification tasks when trained on one set of data and tested on a different set with the same underlying features [4]. This issue is a manifestation of the domain adaptation problem, where the goal is to adapt models to perform well across varying domains [5,6,7,8].
Several ideas have been explored in recent literature to address the domain adaptation challenge [9,10,11]. Notably, many of these works have adapted Generative Adversarial Networks (GANs) to address the domain adaptation issue, showcasing the emergence of GANs as a powerful tool. In the field of Remote Sensing, recent literature, including Benjdira et al. [12] and Zhao et al. [13], has reported the implementation of GANs to generate target domain images from source domain images, effectively bridging the gap between different domains and enhancing model performance on tasks like semantic segmentation. However, while many studies have concentrated on strengthening downstream tasks such as segmentation or classification, the essential initial step of generating high-quality satellite images across multi-spectral bands or color channels has yet to be sufficiently addressed.
Considering this, our present work takes a step back to emphasize the generation aspect that can potentially be extended to domain adaptation as interpreted in Figure 1. We propose a GAN architecture integrated with contrastive learning, specifically designed to generate realistic-looking satellite images across multi-spectral bands, motivated by the work of Han et al. [14]. By focusing on generating high-quality, cross-domain satellite images, our approach addresses the inherent channel variability and lays a foundation for subsequent domain adaptation applications. This enhanced generation capability is expected to significantly improve the performance of various Remote Sensing tasks, including classification and semantic segmentation, by providing more consistent and adaptable input data.

2. Related Work

Domain shift or variation has been an enduring problem in the Remote Sensing domain. Various models have identified and addressed several related issues, yet some aspects of domain variation still require further exploration and solutions. The domain variability problem in satellite images can be traced back to the work of Sharma et al. [15] in 2014. Sharma et al. tackle the challenge of land cover classification in multi-temporal remotely sensed images, mainly focusing on scenarios where labeled data is available only for the source domain. This situation is complicated by variability arising from atmospheric and ground reflectance differences. To address this, they employed an innovative approach using ant colony optimization [16] for cross-domain cluster mapping. The target domain data is over-clustered in their method and then strategically matched to source domain classes using algorithms inspired by ant movement behavior. In the same year, Yilun Liu and Xia Li developed a method to address a similar challenge of insufficient labeled data in land use classification due to domain variability in satellite images [17]. Using the TrCbrBoost model, their approach harnessed old domain data and fuzzy Case-Based Reasoning for effective classifier training in the target domain. This technique demonstrated significant improvement in classification accuracy, highlighting its effectiveness in overcoming the constraints of domain variability. Similarly, Banerjee and Chaudhuri addressed the problem of unsupervised domain adaptation in Remote Sensing [18], focusing on classifying multi-temporal Remote Sensing images with inherent data overlapping and variability in semantic class properties. They introduced a hierarchical subspace learning approach, organizing source domain samples in a binary tree and adapting target domain samples at different tree levels. The method proposed by Banerjee and Chaudhuri demonstrated enhanced cross-domain classification performance for Remote Sensing datasets, effectively managing the challenges of data overlapping and semantic variability [18].
Building on previous advancements in domain adaptation to address domain variability for Remote Sensing, Postadjian et al.’s work addressed large-scale classification challenges in very high-resolution (VHR) satellite images, considering issues such as intra-class variability, diachrony between surveys, and the emergence of new classes not included in predefined labels [19]. Postadjian et al. [19] utilized deep convolutional neural networks (DCNNs) and fine-tuning techniques to adapt to these complexities, effectively handling geographic, temporal, and semantic variations. Following the innovative approaches in domain adaptation to address domain variability, Hofman et al. uniquely applied the CycleGAN [20] network technique to generate target domain images to bridge domain gaps [21]. This approach, leveraging Cycle-Consistent Adversarial Networks, enhances the adaptability of deep convolutional neural networks across varied environmental conditions and sensor bands, facilitating effective domain adaptation in unsupervised adaptation tasks, including digit classification and semantic segmentation of road scenes, effectively overcoming pixel-level and high-level domain shifts.
Building on the momentum in addressing domain variability with generative adversarial networks, Zhang et al.’s work addresses the challenge of adapting neural networks to classify multi-band SAR images [22]. This work by Zhang et al. [22] integrates adversarial learning in their proposed MLADA method to align the features of images from different frequency bands in a shared latent space. This approach effectively bridges the gap between bands, demonstrating how adversarial learning can be strategically used to enhance the adaptability and accuracy of neural networks in multi-band SAR image classification [22]. Similarly, a methodology proposed by Benjdira et al. focuses on improving the semantic segmentation of aerial images through domain adaptation [12]. This work leverages a CycleGAN-inspired adversarial method similar to the work done by Hofman et al. [21] but differentiates by incorporating a U-Net model [23] in the generator to generate target domain images that mimic the source domain, effectively reducing domain shift related to sensor variation and image quality. Their approach demonstrates substantial improvement in segmentation accuracy across different domains, underscoring the potential of GANs to address domain adaptation challenges in aerial imagery segmentation. Along with this, to address a similar kind of domain variability, Tasar et al. introduce an innovative data augmentation approach, SemI2I, that employs generative adversarial networks to transfer the style of test data to training data, utilizing adaptive instance normalization and adversarial losses for style transfer [24]. The approach, highlighted by its ability to generate semantically consistent target domain images, has outperformed existing domain adaptation methods, paving the way for more accurate and robust segmentation models with the generative adversarial mechanism in varied Remote Sensing environments.
Expanding on the work to address domain variability in Remote Sensing, another work by Tasar et al. [25] effectively harnesses the power of GANs to mitigate the multi-spectral band shifts between satellite images from different geographic locations. Through ColorMapGANs, this work adeptly generates training images that are semantically consistent with original images yet spectrally adapted to resemble the test domain, substantially enhancing the segmentation accuracy. This smart use of GANs demonstrates their growing significance in addressing complex domain adaptation challenges in the Remote Sensing field. Consequently, Zhao et al. introduce an advanced method to minimize the pixel-level domain gap in Remote Sensing [13]. The ResiDualGAN framework incorporates a resizing module and residual connections into DualGAN [26] to address scale discrepancies and stabilize the training process effectively. Demonstrating its efficacy, the authors showcase significant improvements in segmentation accuracy on datasets collected from the cities of Potsdam and Vaihingen, open-source Remote Sensing semantic segmentation datasets [27], proving that their approach robustly handles the domain variability and improves cross-domain semantic segmentation with a generative adversarial model. Referring to current literature in Remote Sensing, GANs, and image-to-image translation mechanisms [20,26,28,29] have been promising in solving the domain variation problem. Since the translation of images from the source domain to the target domain is one of the fundamental building blocks in solving the domain variability problem, we present a GAN model inspired by the work of Han et al. [14]. Our model aims to perform better than well-established GAN models by generating realistic satellite images from one multi-spectral band to another. This capability is applicable for image generation and potentially beneficial for domain adaptation tasks.

3. Materials and Methods

This study aims to generate satellite images from one multi-spectral band mode to another, a process that can potentially help in domain adaptation within the field of Remote Sensing. For this purpose, we carefully researched the dataset and selected an open-source dataset available from the ISPRS 2D Open-Source benchmark [27], which has been frequently utilized in recent domain adaptation research in the current literature [12,13]. The dataset contains different multi-spectral bands; for our work, we selected two datasets: the dataset collected from Potsdam city with resolution 5 cm per pixel with RGB (Red, Green, Blue) spectral band, and the dataset collected from Vaihingen city with resolution 9 cm per pixel with IRRG (Near Infrared, Red, Green) spectral band as shown in Figure 2.
We consider two domains of satellite images, S 1 and S 2 , where the underlying features of s 1 ∈ S 1 and s 2 ∈ S 2 vary based on different multi-spectral bands. This scenario is formalized as the input domain S 1 ⊂ R H × W × C 1 and the target domain S 2 ⊂ R H × W × C 2 , where C 1 and C 2 representing the number of channels in each domain, respectively. Given unpaired instances of satellite images, S 1 = { s 1 ∈ S 1 } , S 2 = { s 2 ∈ S 2 } , we aspire to generate satellite images S 2 ′ from S 1 that follow the true distribution formed by real data S 2 . We aim to achieve this generation by constructing two mapping functions, M 1 and M 2 , such that M 1 ( S ) : S 1 → S 2 , and M 2 ( S ) : S 2 → S 1 , where S denotes any satellite images for generalizability. In this study, these two mapping functions, M 1 and M 2 , are demonstrated as two generators, to which there are two corresponding discriminators, D 1 and D 2 .

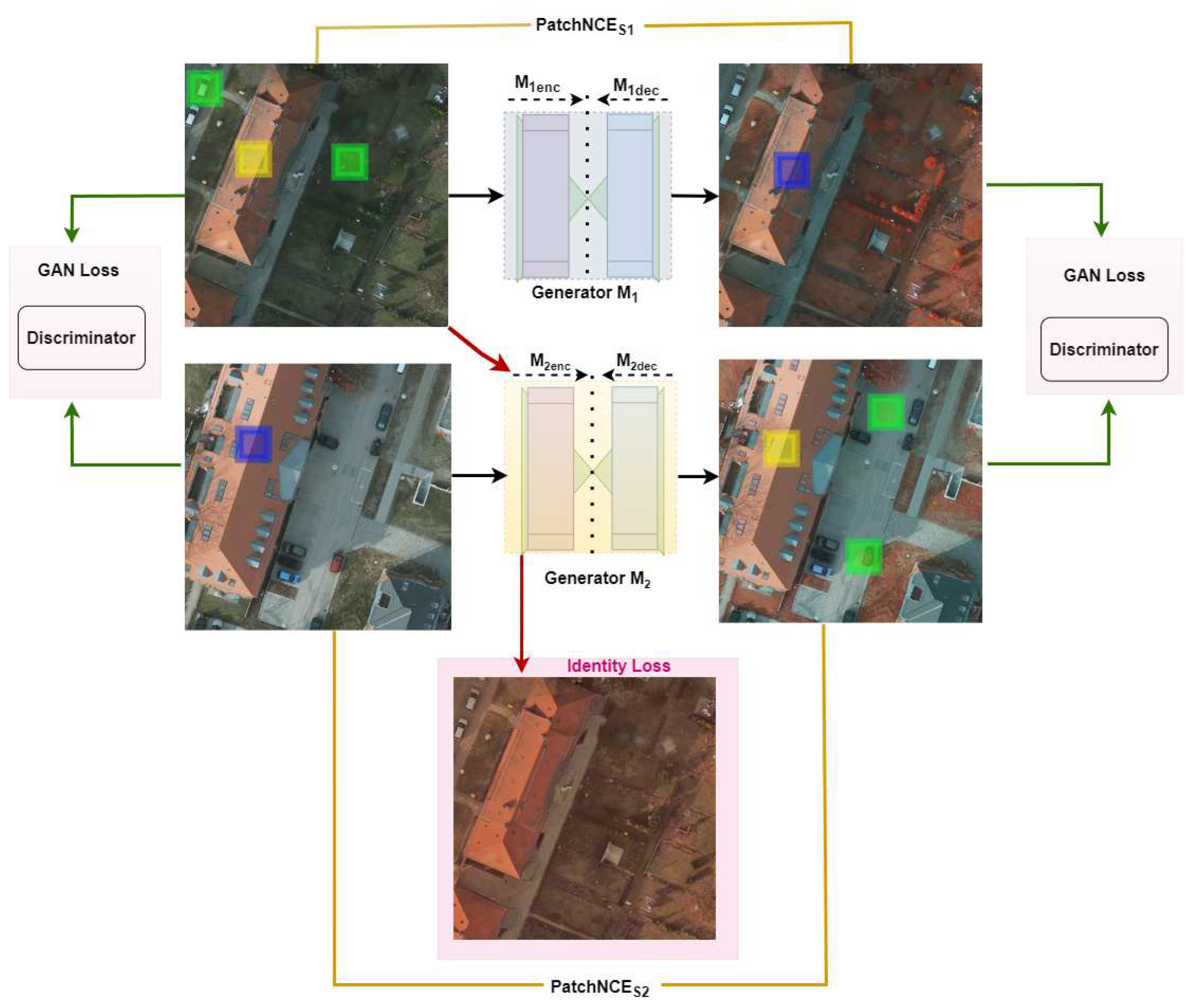
3.1. Efficient Mapping with Generators

In the present work, each generator constitutes an encoder-decoder architecture, drawing inspiration from CUT [28] and DCLGAN [14] to generate designated satellite images. For each mapping and to better utilize the features in satellite images, we extract features from L = 4 encoder layers and propagate them to a two-layer MLP network ( H 1 and H 2 ), as done in SimCLR [30].

ResNet-based Generator

The generators employed in this work are based on a ResNet architecture, which has been proven successful in various generative models [31]. This choice is integral for synthesizing satellite images within our Generative Adversarial Network (GAN) framework. The generator is designed to capture and translate the complex spatial and textural information in satellite images into corresponding images of different multi-spectral band representations. Motivated by [20], each generator constitutes nine residual blocks to help the encoding and decoding processes. These blocks enable the model to handle complex features essential for high-quality satellite images.

Encoder and Decoder Architecture

Building upon the initial framework, where the two mapping functions are represented as generators M 1 and M 2 , to which two corresponding discriminators, D 1 and D 2 , are assigned, we delve deeper into the architecture of these generators. Each generator consists of an encoder and a decoder component. The encoders, M 1 e n c and M 2 e n c , are used to capture and compress the spectral features of the satellite images from their respective domains. This is achieved by extracting features from L = 4 layers of the encoder, as previously mentioned, which are then propagated to a two-layer MLP network to enhance feature utilization and facilitate effective domain translation.
The decoders, M 1 d e c and M 2 d e c , are responsible for reconstructing the image in the new domain while preserving spatial coherence and relevant features. They take the encoded features and, through a series of transformations, generate the output image that corresponds to the target domain. This process ensures that the translated images maintain the target domain’s essential characteristics while reflecting the source domain’s content.
With this procedure, the encoder and decoder collaborate within each generator to facilitate a robust and efficient translation between the multi-spectral bands of satellite images.

3.2. Discriminator Architecture

Discriminators are essential to the adversarial training mechanism within the GAN framework. Our model incorporates two discriminators, D 1 and D 2 , each corresponding to one of the generators, M 1 and M 2 . These discriminators distinguish between authentic satellite images and those synthesized by their respective generators. Their primary role is to provide critical feedback to the generators, encouraging them to produce more accurate and realistic translations of satellite images.
Our architecture employs the PatchGAN [32] discriminator, chosen for its effectiveness in generative tasks. Unlike traditional discriminators that assess the authenticity of an entire image, PatchGAN divides the image into smaller p × p patches and evaluates the realism of each patch individually. The size of each patch, p, is chosen to be less than or equal to the height H of the image, ensuring that each patch is reasonably sized to maintain a balance between training efficiency and feature learning. The scores of all patches assigned by the discriminator are then aggregated to determine the overall authenticity of the image. This approach guides the generator in refining its output and encourages the production of high-quality, realistic textures and patterns at the patch level.
Furthermore, we utilize instance normalization over batch normalization, a decision aligned with best practices in image-to-image translation tasks [20,26,28]. The integration of instance normalization contributes to the stability and performance of the model, particularly in the context of diverse and variable satellite imagery.

3.3. Contrastive Learning in the Present Work

Recently, contrastive learning has significantly advanced unsupervised learning in image processing, often outperforming conventional methods in scenarios with limited data [30,33]. It identifies negative and positive pairs and maximizes the mutual information relevant to the target objective.

Mutual Information Maximization

In our satellite image translation task, we devise an efficient method to maximize the mutual information between corresponding patches of the input and output images across different multi-spectral bands. Specifically, a patch representing a particular land feature in the input image from domain S 1 should be strongly associated with the corresponding element in the generated image in domain S 2 as shown in Figure 3. This approach ensures that relevant geographical and textural information is preserved and accurately represented in the translated images.
In the general procedure of the contrastive learning mechanism, we strategically select an anchor feature, a ∈ R K extracted from s 2 (as shown in Figure 3, highlighted with a blue-colored square), and a corresponding positive feature p ∈ R K extracted from s 1 (as shown in Figure 3, depicted with a yellow-colored square), where K represents the feature space dimensionality. Additionally, we sample a set of negative features { n i } i = 1 N , with each n i ∈ R K , from domain S 1 . These negative features are drawn from different locations within the same image from which the corresponding p was specified (depicted with green-colored squares in Figure 3); mathematically, Area ( n i ) = Area ( s 1 ) - Area (p). All these features are represented as vectors and normalized with L 2 -normalization [34]. Subsequently, we construct an ( N + 1 ) -way classification task. In this task, the model evaluates the similarity between an anchor and various positive or negative elements. We direct the model to adjust the scale of these similarities using a temperature parameter, τ = 0.07, before converting them into probabilities [28]. This temperature scaling fine-tunes the model’s confidence in its predictions, facilitating a more effective learning process through the contrastive mechanism. After establishing this setup for normalization and predictions, we compute the probability that the positive element is more aligned to the anchor than any negative elements. This is obtained using a cross-entropy loss, expressed mathematically as:
L ( a , p , { n i } ) = − log exp ( sim ( a , p ) / τ ) exp ( sim ( a , p ) / τ ) + ∑ i = 1 N exp ( sim ( a , n i ) / τ )
where sim ( a , p ) denotes the cosine similarity between a and p, calculated as a · p ∥ a ∥ ∥ p ∥ [30]. Through this loss equation, we effectively maximize the mutual information between corresponding patches, ensuring that the translation between multi-spectral bands of satellite images retains high fidelity and relevance.

PatchNCE Loss-Mapping of Two Domains of Satellite Images

Utilizing the encoders M 1 e n c and M 2 e n c from the generators M 1 and M 2 , we extract features from the satellite images in domains S 1 and S 2 , respectively. For each domain, features are extracted from selected layers of the respective encoder and then propagated through a two-layer MLP network. This process results in a stack of feature layers { z l } L , where each z l represents the output of the l-th selected layer after processing through the MLP network. Specifically, for an input image s 1 from domain S 1 , the feature stack can be represented as { z l } L = { H 1 l ( M 1 e n c ( l ) ( s 1 ) ) } l = 1 L , where M 1 e n c ( l ) denotes the output of the l-th layer of encoder M 1 e n c , and H 1 l represents the corresponding MLP processing for that layer. Similarly, for domain S 2 , the feature stack is obtained using encoder M 2 e n c and its corresponding MLP layers, which is given by, { z l ′ } L = { H 2 l ( M 2 e n c ( l ) ( s 2 ′ ) ) } l = 1 L , where s 2 ′ is a generated image.
For each layer, we denote the spatial locations as s ∈ { 1 , . . . , S l } , where S l is the number of spatial locations in that layer. We then define an anchor patch and its corresponding positive feature as z l ( s ) ∈ R C l and all other features (the "negatives") as z l ( S ∖ s ) ∈ R ( S l − 1 ) × C l , where C l denotes the number of feature channels in each layer.
By getting insights from CUT [28] and DCLGAN [14], the present work incorporates patch-based PatchNCE loss that aims to match corresponding patches of input and output satellite images across multiple layers. For the mapping M 1 : S 1 → S 2 , the PatchNCE loss is expressed as:
L PatchNCE S 1 ( M 1 , H 1 , H 2 , S 1 ) = E s 1 ∼ S 1 ∑ l = 1 L ∑ s = 1 S l ℓ ( z ^ l ( s ) , z l ( s ) , z l ( S ∖ s ) ) ,
Similarly, for the reverse mapping M 2 : S 2 → S 1 , we utilized similar PatchNCE loss:
L PatchNCE S 2 ( M 2 , H 1 , H 2 , S 2 ) = E s 2 ∼ S 2 ∑ l = 1 L ∑ s = 1 S l ℓ ( z ^ l ( s ) , z l ( s ) , z l ( S ∖ s ) ) ,
Through these formulations, the PatchNCE losses effectively encourage the model to learn translations that maintain the essential characteristics and patterns of the geographic features in satellite images, ensuring that the translated images retain the contextual and spectral integrity necessary for accurate interpretation and analysis.

3.4. Adversarial Loss

The present work utilizes an adversarial loss function to ensure the generation of realistic-looking satellite images from one domain to another based on different multi-spectral bands [35]. The objective is to maintain balanced training of the generator and the discriminator to produce satellite images in the target domain that are indistinguishable from ground truth satellite images. In contrast, the discriminator learns to differentiate between the real and generated satellite images. The training is guided by the adversarial loss function with backpropagation and iterative updates of the layers’ weights in the model. Each generator, M 1 and M 2 , has a corresponding discriminator, D 1 and D 2 , respectively, ensuring a targeted adversarial relationship. The GAN loss for each generator-discriminator pair can be formulated as:
L GAN ( M 1 , D 1 , S 1 , S 2 ) = E s 2 ∼ S 2 [ log D 1 ( s 2 ) ] + E s 1 ∼ S 1 [ log ( 1 − D 1 ( M 1 ( s 1 ) ) ) ]
L GAN ( M 2 , D 2 , S 2 , S 1 ) = E s 1 ∼ S 1 [ log D 2 ( s 1 ) ] + E s 2 ∼ S 2 [ log ( 1 − D 2 ( M 2 ( s 2 ) ) ) ]
In these equations, D 1 ( s 2 ) and D 2 ( s 1 ) represent the discriminator’s decision for a ground truth target satellite image s 2 and s 1 , respectively. M 1 ( s 1 ) and M 2 ( s 2 ) are the images generated from the input satellite images s 1 and s 2 that should hypothetically correspond to s 2 and s 1 respectively. Real satellite images form S 1 and S 2 distributions from each domain. The generators M 1 and M 2 aim to minimize these losses, while the discriminators D 1 and D 2 aim to maximize them [35]. Hence, the given loss function is termed adversarial as the given generator and discriminator compete to get better and produce visually promising satellite images.

3.5. Identity Loss

Identity Loss with Mean Squared Error (MSE) is implemented to preserve the essential characteristics of the input image when it already belongs to the target domain. This approach ensures the generator minimizes alterations when the input image exhibits the target domain’s characteristics. Specifically, in our satellite image translation task, when generator M 1 is trained to convert an image s 1 from domain S 1 to an equivalent image in domain S 2 , it should ideally introduce minimal changes if an image from S 2 is provided as input. This strategy encourages the generator to maintain the identity of the input when it aligns with the target domain.
Mathematically, the identity loss for generator M 1 when an image from S 2 is fed as input using MSE can be expressed as:
L identity - MSE S 2 ( M 1 , S 2 ) = E s 2 ∼ S 2 [ ∥ M 1 ( s 2 ) − s 2 ∥ 2 2 ] ,
where ∥ . ∥ 2 2 denotes the squared L2 norm, representing the sum of the squared differences between the generated image and the input image. A similar identity loss is applied for generator M 2 when an image from S 1 is fed:
L identity - MSE S 1 ( M 2 , S 1 ) = E s 1 ∼ S 1 [ ∥ M 2 ( s 1 ) − s 1 ∥ 2 2 ] .
Total identity loss, combining the contributions from both generators, is given as:
L identity - MSE ( M 1 , M 2 ) = L identity - MSE S 1 ( M 2 , S 1 ) + L identity - MSE S 2 ( M 1 , S 2 ) ,
Although we experimented with identity loss using the L1 norm, i.e., Mean Absolute Error (MAE), we found that the L2 norm provided better results in our model. Therefore, we have chosen to utilize the L2 norm for identity loss. In practice, identity loss aids in stabilizing the training of the generators by ensuring they do not introduce unnecessary changes to images that already possess the desired characteristics of the target domain. This concept, inspired by the work of Zhu et al. [20], is particularly beneficial in maintaining the structural and spectral integrity of satellite images during the translation process.

3.6. Final Objective

Our satellite image generation framework is depicted in Figure 3. In our framework, the objective is to generate images that are not only realistic but also maintain a correspondence between patches in the input and output images. To achieve our goal, we integrate the combination of the GAN loss, PatchNCE loss, and identity loss to have our final loss function, which is given as:
L ( M 1 , M 2 , D 1 , D 2 , H 1 , H 2 ) = λ GAN ( L GAN ( M 2 , D 2 , S 2 , S 1 ) + L GAN ( M 2 , D 1 , S 2 , S 1 ) ) + λ NCE ( L PatchNCE S 1 ( M 1 , H 1 , H 2 , S 1 ) + L PatchNCE S 2 ( M 2 , H 1 , H 2 , S 2 ) ) + λ idt L identity - MSE ( M 1 , M 2 ) ,

4. Results

This section presents two different setups: first, the experimental setup detailing metrics for evaluation and experimental environment; second, the results obtained by comparing our approach with baseline models.

4.1. Evaluation Metrics

The present work utilizes a set of evaluation metrics to measure the quality and accuracy of the generated satellite images. These metrics include the Root Mean Square Error (RMSE), Peak Signal-to-Noise Ratio (PSNR), and the Structural Similarity Index Measure (SSIM).

Root Mean Square Error (RMSE)

It is a widely used measure that quantifies the differences between predicted values by a model and the observed values [36]. It is beneficial in evaluating the accuracy of generated images compared to the original images.

Peak Signal-to-Noise Ratio (PSNR)

PSNR is a metric that measures the quality of reconstruction of lossy compression [37]. It compares the maximum potential power of a signal to the power of the noise affecting it, indicating the visual quality of the generated images.

Structural Similarity Index (SSIM)

SSIM assesses the perceived quality of digital images and videos by evaluating luminance, contrast, and structure changes between a predicted image and the original one. The SSIM index can be computed by the following formula:
S S I M ( a , b ) = 2 a b + C a 2 + b 2 + C .
In this equation, a and b have similarity values within the range of [0,1]. A higher SSIM value indicates better image quality, with a value of 1 signifying perfectly identical images.

4.2. Experimental Environment and Baselines

Experiment Setting

We conducted our experiments in a Python 3.6.8 environment with the PyTorch framework for all the training and testing tasks. The computational workload was executed on a system equipped with dual NVIDIA TITAN RTX GPUs. Each of these GPUs features 24GB of GDDR6 memory with the power of the TU102 architecture. The system operated with CUDA version 12.3 and NVIDIA driver version 545.23.08, ensuring high performance and efficiency for our computational tasks. To maintain uniform training for all the models, we selected 800 images for both the Potsdam and Vaihingen training datasets and 500 images for the testing dataset. We resized all the images to 256*256 dimensions. We train all the models for 100 epochs with a learning rate 0.0001. During the first half of these epochs, we maintained a steady learning rate, whereas, in the latter half, the learning rate decayed linearly to have better convergence. We set the temperature parameter τ = 0.07 . Along with this, we set the loss functions’ parameters: λ GAN = 1 , λ NCE = 1 , and λ idt = 1 .

Baselines

We selected four well-established unsupervised generative adversarial network models and compared them to our model for qualitative and quantitative analysis. These selected four methods are DualGAN[26], CUT[28], CycleGAN [20], and GcGAN [29]. These models were chosen due to their success in image generation tasks and effective utilization to address domain variation problems [12,13,38], which is relevant to the objectives of our study.

4.3. Comparison and Results

Our model’s comparative performance against other generative adversarial network models is detailed in Table 1 and visually illustrated in Figure 4. These results demonstrate the better performance of our model in generating satellite images across multi-spectral bands. Specifically, our model achieved an RMSE of 9.06, PSNR of 20.26, and SSIM of 0.71. In comparison, the CUT model [28] recorded slightly lower metrics with an RMSE of 9.46, PSNR of 18.83, and SSIM of 0.67. It is worth to mention that a lower RMSE value indicates better quality of the generated image [39]. Furthermore, compared to our model and the CUT model, DualGAN [26] achieved marginally lower values for the selected metrics, achieving a PSNR of 17.96, SSIM of 0.64, and RMSE of 9.56. The CycleGAN model scored slighly lower than our model, CUT model, and DualGAN model, with a PSNR of 17.20, SSIM of 0.61, and RMSE of 9.58. Subsequently, the GcGAN model [29] recorded the lowest values among all models, including ours, with a PSNR of 17.19, SSIM of 0.55, and RMSE of 9.80.

5. Discussion

By selecting datasets available from [27], our goal was to generate satellite images with IRRG color composition, similar to those collected from Vaihingen city (example images are shown in Figure 2), by training the model on satellite images with RGB color composition collected from Potsdam city (example images are shown in Figure 4 as Input). These two datasets generally have similar underlying features such as buildings and roads, but the images in the input and target domains do not have one-to-one correspondence as they are taken from two different locations. During this, our training approach yeilded promising results in image generation, as demonstrated in Figure 4.
For the evaluation metrics SSIM, PSNR, and RMSE, it is generally necessary to have the exact generated image corresponding to the input image and the exact ground truth image for the input image. Since the Potsdam and Vaihingen datasets are collected from two different cities, if the input image A is from Potsdam and the target image B is from Vaihingen, the ground truth image should maintain the underlying structure of A but adopt the color composition of B to align with our work of transferring between two different multi-spectral bands. The Potsdam dataset provides corresponding IRRG images for each RGB image, hence during the calculation of SSIM, PSNR, and RMSE, we used the corresponding Potsdam IRRG color composition images (as shown in Figure 5) as ground truth for each corresponding generated image.
Similarly, as observed in Figure 4, the generated images depict color composition similar to the target dataset, i.e., IRRG color composition satellite images from Vaihingen city, as shown in Figure 2, aligning with our primary objective of replicating the target spectral characteristics. Specifically, as seen in Figure 4, our model successfully generated images with more visually distinguishable vehicles, highlighted with blue-colored squares in the first and second rows. The blue squares in the third and fourth rows highlight our model’s success in accurately generating red color compositions where needed, a task at which other models were less successful. Thus, by following the above procedure, we achieved our goal of generating images across different multi-spectral band domains under generalizable conditions.
It is important to note that the present work integrates a GAN model to generate satellite images across different multi-spectral bands. While our current work focuses on image generation, the natural progression is to extend these capabilities to domain adaptation applications in several sub-domains of Remote Sensing. We aim to explore various fields within and beyond Remote Sensing, applying our model to generate images that can then be used with developed models like U-Net for semantic segmentation and other tasks where domain variability is a significant challenge. By continuing to refine and apply our model, we hope to contribute to advancing Remote Sensing techniques and the broader field of image processing.

6. Conclusions

Satellite imagery, characterized by its diverse spectral bands, inherently exhibits domain variability that significantly impacts the performance of various analytical models. In response to this challenge, our work has introduced an approach that leverages the capabilities of Generative Adversarial Networks (GANs) combined with Contrastive Learning. Specifically, the present work incorporates a dual translating strategy: it translates images s 1 ∈ S 1 to s 2 ∈ S 2 and independently translates images from s ’ 2 ∈ S 2 – s 2 to s ’ 1 , where s ’ 1 ∈ S 1 - s 1 . This approach ensures that each translation direction uses original images from the respective domains ( S 1 and S 2 ), rather than relying on previously generated images, maintaining the integrity and quality of the translation process. Our model effectively translates images across multi-spectral bands by integrating adversarial mechanisms between generators and discriminators, maximizing mutual information among important patches, and utilizing identity loss with Mean Squared Error (MSE). The quantitative results, as evidenced by metrics such as SSIM, PSNR, and RMSE, alongside qualitative visualization, demonstrate that our model performs better than well-established methods, including CycleGAN, CUT, DualGAN, and GcGAN. These findings highlight the practicability of our model in generating high-quality satellite images that accurately reflect the desired spectral characteristics highlighting advancement in the Remote Sensing application.

Funding

This material is based in part upon work supported by the National Science Foundation under Grant No. CNS-2018611.

Data Availability Statement

The dataset used in this article is a publicly available dataset that can be obtained from the ISPRS 2D Open-Source benchmark dataset [27]. A few examples of images generated in this study are presented in Figure 4. The complete dataset generated in this research is available upon request from the corresponding author.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Zhao, W.; Lu, H.; Wang, D. Multisensor image fusion and enhancement in spectral total variation domain. IEEE Transactions on Multimedia 2017, 20, 866–879. [Google Scholar] [CrossRef]
  2. Laborte, A.G.; Maunahan, A.A.; Hijmans, R.J. Spectral signature generalization and expansion can improve the accuracy of satellite image classification. PloS one 2010, 5, e10516. [Google Scholar] [CrossRef] [PubMed]
  3. Toldo, M.; Maracani, A.; Michieli, U.; Zanuttigh, P. Unsupervised domain adaptation in semantic segmentation: a review. Technologies 2020, 8, 35. [Google Scholar] [CrossRef]
  4. Lunga, D.; Yang, H.L.; Reith, A.; Weaver, J.; Yuan, J.; Bhaduri, B. Domain-adapted convolutional networks for satellite image classification: A large-scale interactive learning workflow. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing 2018, 11, 962–977. [Google Scholar] [CrossRef]
  5. Farahani, A.; Voghoei, S.; Rasheed, K.; Arabnia, H.R. A brief review of domain adaptation. Advances in data science and information engineering: proceedings from ICDATA 2020 and IKE 2020 2021, pp. 877–894.
  6. Pan, S.J.; Tsang, I.W.; Kwok, J.T.; Yang, Q. Domain adaptation via transfer component analysis. IEEE Transactions on Neural Networks 2010, 22, 199–210. [Google Scholar] [CrossRef]
  7. Ganin, Y.; Lempitsky, V. Unsupervised domain adaptation by backpropagation. International conference on machine learning. PMLR, 2015, pp. 1180–1189.
  8. You, K.; Long, M.; Cao, Z.; Wang, J.; Jordan, M.I. Universal domain adaptation. Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, 2019, pp. 2720–2729.
  9. Bousmalis, K.; Silberman, N.; Dohan, D.; Erhan, D.; Krishnan, D. Unsupervised pixel-level domain adaptation with generative adversarial networks. Proceedings of the IEEE conference on computer vision and pattern recognition, 2017, pp. 3722–3731.
  10. Hong, W.; Wang, Z.; Yang, M.; Yuan, J. Conditional generative adversarial network for structured domain adaptation. Proceedings of the IEEE conference on computer vision and pattern recognition, 2018, pp. 1335–1344.
  11. Rau, A.; Edwards, P.E.; Ahmad, O.F.; Riordan, P.; Janatka, M.; Lovat, L.B.; Stoyanov, D. Implicit domain adaptation with conditional generative adversarial networks for depth prediction in endoscopy. International journal of computer assisted radiology and surgery 2019, 14, 1167–1176. [Google Scholar] [CrossRef] [PubMed]
  12. Benjdira, B.; Bazi, Y.; Koubaa, A.; Ouni, K. Unsupervised domain adaptation using generative adversarial networks for semantic segmentation of aerial images. Remote Sensing 2019, 11, 1369. [Google Scholar] [CrossRef]
  13. Zhao, Y.; Guo, P.; Sun, Z.; Chen, X.; Gao, H. ResiDualGAN: Resize-residual DualGAN for cross-domain remote sensing images semantic segmentation. Remote Sensing 2023, 15, 1428. [Google Scholar] [CrossRef]
  14. Han, J.; Shoeiby, M.; Petersson, L.; Armin, M.A. Dual contrastive learning for unsupervised image-to-image translation. Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, 2021, pp. 746–755.
  15. Sharma, S.; Buddhiraju, K.M.; Banerjee, B. An ant colony optimization based inter-domain cluster mapping for domain adaptation in remote sensing. 2014 IEEE Geoscience and Remote Sensing Symposium, 2014, pp. 2158–2161. [CrossRef]
  16. Dorigo, M.; Birattari, M.; Stutzle, T. Ant colony optimization. IEEE Computational Intelligence Magazine 2006, 1, 28–39. [Google Scholar] [CrossRef]
  17. Liu, Y.; Li, X. Domain adaptation for land use classification: A spatio-temporal knowledge reusing method. ISPRS Journal of Photogrammetry and Remote sensing 2014, 98, 133–144. [Google Scholar] [CrossRef]
  18. Banerjee, B.; Chaudhuri, S. Hierarchical Subspace Learning Based Unsupervised Domain Adaptation for Cross-Domain Classification of Remote Sensing Images. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing 2017, 10, 5099–5109. [Google Scholar] [CrossRef]
  19. Postadjian, T.; Bris, A.L.; Sahbi, H.; Malle, C. Domain Adaptation for Large Scale Classification of Very High Resolution Satellite Images with Deep Convolutional Neural Networks. IGARSS 2018 - 2018 IEEE International Geoscience and Remote Sensing Symposium, 2018, pp. 3623–3626. [CrossRef]
  20. Zhu, J.Y.; Park, T.; Isola, P.; Efros, A.A. Unpaired image-to-image translation using cycle-consistent adversarial networks. Proceedings of the IEEE International Conference on Computer Vision, 2017, pp. 2223–2232.
  21. Hoffman, J.; Tzeng, E.; Park, T.; Zhu, J.Y.; Isola, P.; Saenko, K.; Efros, A.; Darrell, T. Cycada: Cycle-consistent adversarial domain adaptation. International conference on machine learning. Pmlr, 2018, pp. 1989–1998.
  22. Zhang, W.; Zhu, Y.; Fu, Q. Adversarial Deep Domain Adaptation for Multi-Band SAR Images Classification. IEEE Access 2019, 7, 78571–78583. [Google Scholar] [CrossRef]
  23. Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. Medical Image Computing and Computer-Assisted Intervention–MICCAI 2015: 18th International Conference, Munich, Germany, October 5-9, 2015, Proceedings, Part III 18. Springer, 2015, pp. 234–241.
  24. Tasar, O.; Happy, S.; Tarabalka, Y.; Alliez, P. SemI2I: Semantically consistent image-to-image translation for domain adaptation of remote sensing data. IGARSS 2020-2020 IEEE International Geoscience and Remote Sensing Symposium. IEEE, 2020, pp. 1837–1840.
  25. Tasar, O.; Happy, S.; Tarabalka, Y.; Alliez, P. ColorMapGAN: Unsupervised domain adaptation for semantic segmentation using color mapping generative adversarial networks. IEEE Transactions on Geoscience and Remote Sensing 2020, 58, 7178–7193. [Google Scholar] [CrossRef]
  26. Yi, Z.; Zhang, H.; Tan, P.; Gong, M. Dualgan: Unsupervised dual learning for image-to-image translation. Proceedings of the IEEE international conference on computer vision, 2017, pp. 2849–2857.
  27. Rottensteiner, F.; Sohn, G.; Jung, J.; Gerke, M.; Baillard, C.; Bnitez, S.; Breitkopf, U. International society for photogrammetry and remote sensing, 2d semantic labeling contest. Accessed: Oct 2020, 29. [Google Scholar]
  28. Park, T.; Efros, A.A.; Zhang, R.; Zhu, J.Y. Contrastive learning for unpaired image-to-image translation. Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, August 23–28, 2020, Proceedings, Part IX 16. Springer, 2020, pp. 319–345.
  29. Fu, H.; Gong, M.; Wang, C.; Batmanghelich, K.; Zhang, K.; Tao, D. Geometry-consistent generative adversarial networks for one-sided unsupervised domain mapping. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2019, pp. 2427–2436.
  30. Chen, T.; Kornblith, S.; Norouzi, M.; Hinton, G. A simple framework for contrastive learning of visual representations. International conference on machine learning. PMLR, 2020, pp. 1597–1607.
  31. Chen, Y.; Zhao, Y.; Jia, W.; Cao, L.; Liu, X. Adversarial-learning-based image-to-image transformation: A survey. Neurocomputing 2020, 411, 468–486. [Google Scholar] [CrossRef]
  32. Alqahtani, H.; Kavakli-Thorne, M.; Kumar, G. Applications of generative adversarial networks (gans): An updated review. Archives of Computational Methods in Engineering 2021, 28, 525–552. [Google Scholar] [CrossRef]
  33. He, K.; Fan, H.; Wu, Y.; Xie, S.; Girshick, R. Momentum contrast for unsupervised visual representation learning. Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, 2020, pp. 9729–9738.
  34. Miyato, T.; Kataoka, T.; Koyama, M.; Yoshida, Y. Spectral normalization for generative adversarial networks. arXiv preprint arXiv:1802.05957 2018. arXiv:1802.05957 2018.
  35. Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. Advances in neural information processing systems 2014, 27. [Google Scholar]
  36. Chai, T.; Draxler, R.R. Root mean square error (RMSE) or mean absolute error (MAE). Geoscientific model development discussions 2014, 7, 1525–1534. [Google Scholar]
  37. Yuanji, W.; Jianhua, L.; Yi, L.; Yao, F.; Qinzhong, J. Image quality evaluation based on image weighted separating block peak signal to noise ratio. International Conference on Neural Networks and Signal Processing, 2003. Proceedings of the 2003. IEEE, 2003, Vol. 2, pp. 994–997.
  38. Bai, L.; Du, S.; Zhang, X.; Wang, H.; Liu, B.; Ouyang, S. Domain adaptation for remote sensing image semantic segmentation: An integrated approach of contrastive learning and adversarial learning. IEEE Transactions on Geoscience and Remote Sensing 2022, 60, 1–13. [Google Scholar] [CrossRef]
  39. Piñeiro, G.; Perelman, S.; Guerschman, J.P.; Paruelo, J.M. How to evaluate models: observed vs. predicted or predicted vs. observed? Ecological modelling 2008, 216, 316–322. [Google Scholar] [CrossRef]
Preprints 96790 g001
Figure 1. Overview of the Concept and Goal in the Present Work. Our model focuses on generating satellite images, i.e., Y’, given a source image ’X’, across multi-spectral bands. The generation aims to address domain variability that can negatively impact various deep learning models.
Figure 1. Overview of the Concept and Goal in the Present Work. Our model focuses on generating satellite images, i.e., Y’, given a source image ’X’, across multi-spectral bands. The generation aims to address domain variability that can negatively impact various deep learning models.
Preprints 96790 g001
Preprints 96790 g002
Figure 2. Ground truth IRRG images from Vaihingen City’s dataset.
Figure 2. Ground truth IRRG images from Vaihingen City’s dataset.
Preprints 96790 g002
Preprints 96790 g003
Figure 3. Overview of the proposed model’s architecture. Utilizing two generators, M 1 and M 2 , we successfully generate a target image in an unsupervised fashion. Two GAN (adversarial) losses to facilitate the generation of realistic-looking images are depicted with green arrows, and identity loss to prevent unintended translation is depicted with red color lines. The PatchNCE s 1 and PatchNCE s 2 loss functions, as depicted in yellow color lines, maximize the mutual information between corresponding objects (yellow and blue square patches) while minimizing the same against negative samples (green square patches).
Figure 3. Overview of the proposed model’s architecture. Utilizing two generators, M 1 and M 2 , we successfully generate a target image in an unsupervised fashion. Two GAN (adversarial) losses to facilitate the generation of realistic-looking images are depicted with green arrows, and identity loss to prevent unintended translation is depicted with red color lines. The PatchNCE s 1 and PatchNCE s 2 loss functions, as depicted in yellow color lines, maximize the mutual information between corresponding objects (yellow and blue square patches) while minimizing the same against negative samples (green square patches).
Preprints 96790 g003
Preprints 96790 g004
Figure 4. Comparative Results of Satellite Image Generation via Visualization. The blue colored squares drawn in the images generated by our model highlights the area where our model is doing realistic generation based on color and the structure. The difference can be seen mainly in the vehicle depiction and color composition in the images.
Figure 4. Comparative Results of Satellite Image Generation via Visualization. The blue colored squares drawn in the images generated by our model highlights the area where our model is doing realistic generation based on color and the structure. The difference can be seen mainly in the vehicle depiction and color composition in the images.
Preprints 96790 g004
Preprints 96790 g005
Figure 5. Ground truth IRRG images from Potsdam City’s dataset.
Figure 5. Ground truth IRRG images from Potsdam City’s dataset.
Preprints 96790 g005
Table 1. Performance Comparison: Our Model vs. Other GANs
Table 1. Performance Comparison: Our Model vs. Other GANs
Models RMSE SSIM PSNR
Our Model 9.06 0.71 20.26
CUT 9.46 0.67 18.83
DualGAN 9.56 0.64 17.96
CycleGAN 9.58 0.61 17.20
GcGAN 9.80 0.55 17.19
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated